贝叶斯决策的经典例题练习

贝叶斯决策例题(精选.)

例：某工程项目按合同应在三个月内完工，其施工费用与工程完工期有关。

假定天气是影响能否按期完工的决定因素，如果天气好，工程能按时完工，获利5万元；如果天气不好，不能按时完工，施工单位将被罚款1万元；若不施工就要付出窝工费2千元。

根据过去的经验，在计划实施工期天气好的可能性为30%。

为了更好地掌握天气情况，可以申请气象中心进行天气预报，并提供同一时期天气预报资料，但需要支付资料费800元。

从提供的资料中可知，气象中心对好天气预报准确性为80%，对坏天气预报准确性为90%。

问如何进行决策。

解：采用贝叶斯决策方法。

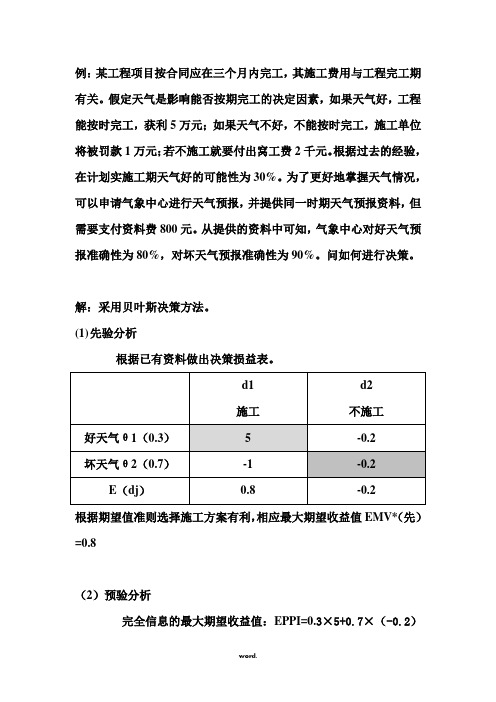
(1)先验分析根据已有资料做出决策损益表。

根据期望值准则选择施工方案有利，相应最大期望收益值EMV*（先）=0.8（2）预验分析完全信息的最大期望收益值：EPPI=0.3×5+0.7×（-0.2）=1.36（万元）完全信息价值： EVPI=EPPI- EMV*（先）=1.36-0.8=0.56（万元）即，完全信息价值大于信息成本，请气象中心进行预报是合算的。

（3）后验分析①补充信息：气象中心将提供预报此时期内两种天气状态x 1(好天气)、x 2(坏天气)将会出现哪一种状态。

从气象中心提供的同期天气资料可得知条件概率：天气好且预报天气也好的概率 P （x 1/θ1）=0.8 天气好而预报天气不好的概率 P （x 2/θ1）=0.2 天气坏而预报天气好的概率 P （x 1/θ2）=0.1 天气坏且预报天气也坏的概率 P （x 2/θ2）=0.9②计算后验概率分布：根据全概率公式和贝叶斯公式，计算后验概率。

预报天气好的概率1111212()()(/)()(/)P x P P x P P x θθθθ=+=0.31预报天气坏的概率2121222()()(/)()(/)P x P P x P P x θθθθ=+=0.69 预报天气好且天气实际也好的概率：111111()(/)(/)()P P x P x P x θθθ⋅==0.3×0.8/0.31=0.77预报天气好而天气坏的概率：212211()(/)(/)()P P x P x P x θθθ⋅==0.7×0.1/0.31=0.23预报天气坏而实际天气好的概率:121122()(/)(/)()P P x P x P x θθθ⋅==0.3×0.2/0.69=0.09预报天气坏且实际天气也坏的概率： 222222()(/)(/)()P P x P x P x θθθ⋅==0.7×0.9/0.69=0.91上述计算可以用表格表示：③ 后验决策：若气象中心预报天气好（x1）,则每个方案的最大期望收益值 E(d1/x1)=0.77×5+0.23×(-1)=3.62 E(d2/x1)=0.77×(-0.2)+0.23×(-0.2)=-0.2选择d1即施工的方案，相应在预报x1时的最大期望收益值E （X1）=3.62若气象中心预报天气不好（x2），各方案的最大期望收益值 E(d1/x2)=0.09×5+0.91×(-1)=-0.46 E(d2/x2)=0.09×(-0.2)+0.91×(-0.2)=-0.2选择d2即不施工的方案，相应在预报x2时的最大期望收益值E （X2）=-0.2④ 计算补充信息的价值：得到天气预报的情况下，后验决策的最大期望收益值：1122*()()()()()EMV P x E x P x E x =⋅+⋅后=0.31×3.62+0.69×（-0.2）=0.9842则补充的信息价值为：EMV*(后)-EMV*(先)=0.9842-0.8=0.1842补充信息价值大于信息费（800元），即这种费用是合算的。

贝叶斯公式例题范文

贝叶斯公式例题范文利用贝叶斯公式，我们可以很容易地计算出一个事件发生的概率，即在给定一些背景信息的情况下，这个事件发生的可能性有多大。

下面我们来看一个实际的例题，以帮助更好地理解贝叶斯公式的应用。

假设地区有很多农场，其中有20%的农场种植了A品种的作物，其他农场种植了其他品种。

现在，我们有一个基因检测方法，可以通过一个人口样本来确定一个人是不是A品种的作物的种植者。

这个基因检测方法的准确率为90%，即当一个人是A品种的作物的种植者时，有90%的概率检测结果是阳性；当一个人不是A品种的作物的种植者时，有90%的概率检测结果是阴性。

现在，我们在随机抽取一个人口样本进行检测，结果显示他是A品种的作物的种植者。

那么，我们应该如何计算他真正是A品种的作物的种植者的概率呢？首先，我们可以根据已知信息计算出一个人是A品种的作物的概率，这就是所谓的先验概率。

根据题目中的信息，已知有20%的农场种植了A品种的作物，那么一个人是A品种的作物的种植者的概率就是20%。

然后，我们可以根据基因检测方法的准确率来计算出当一个人是A品种的作物的种植者时，检测结果为阳性的概率。

根据题目中的信息，基因检测方法的准确率为90%，那么当一个人是A品种的作物的种植者时，检测结果为阳性的概率为90%。

接着，我们可以根据贝叶斯公式计算出一个人检测结果为阳性时，他真正是A品种的作物的种植者的概率。

P(A，B)=P(B，A)*P(A)/P(B)其中P(A，B)表示在事件B发生的条件下事件A发生的概率，也就是待求的真实概率；P(B，A)表示在事件A发生的条件下事件B发生的概率，也就是检测结果为阳性的概率；P(A)表示事件A发生的概率，也就是先验概率；P(B)表示事件B发生的概率，也就是检测结果为阳性的概率。

根据题目中的信息，我们可以将上述参数代入贝叶斯公式进行计算：P(A，B)=0.9*0.2/P(B)接下来，我们需要计算出P(B)，即检测结果为阳性的概率。

贝叶斯公式典型例题

贝叶斯公式典型例题
贝叶斯公式是一种计算条件概率的公式，常用于根据已知条件更新某个事件发生的概率。

下面是一个贝叶斯公式的典型例题：
例：假设有两种类型的围棋棋手，分别是专业棋手和业余棋手。

专业棋手在比赛中获胜的概率为0.9，而业余棋手获胜的概率为0.3。

已知在所有棋手中，专业棋手占70%，业余棋手占30%。

现在有一场比赛，我们只知道其中一位棋手获胜了，那么这位棋手是专业棋手的概率是多少？
解：首先，我们定义以下事件：
•A：棋手是专业的
•B：棋手获胜
根据题意，我们知道：
•P(A) = 0.7（专业棋手占比）
•P(¬A) = 0.3（业余棋手占比）
•P(B|A) = 0.9（专业棋手获胜的概率）
•P(B|¬A) = 0.3（业余棋手获胜的概率）
我们要找的是P(A|B)，即在已知棋手获胜的条件下，棋手是专业的概率。

根据贝叶斯公式，我们有：
P(A|B) = \frac{P(A) \times P(B|A)}{P(A) \times P(B|A) + P(¬A) \times P(B|¬A)}将已知的概率值代入公式中，我们得到：
P(A|B) = \frac{0.7 \times 0.9}{0.7 \times 0.9 + 0.3 \times 0.3} = \frac{0.63}{0.63
+ 0.09} = \frac{0.63}{0.72} = 0.875
所以，在已知棋手获胜的条件下，这位棋手是专业棋手的概率为0.875。

这个例题展示了贝叶斯公式在更新条件概率方面的应用。

通过已知的概率值和贝叶斯公式，我们可以计算出在给定条件下的未知概率。

贝叶斯推理例子

贝叶斯推理例子
1. 嘿，你想想看啊，比如说你去买彩票，你觉得中奖的概率有多大呢？这就可以用贝叶斯推理呀！你先根据以往的开奖情况大概估计一个基础概率，然后每次开奖后根据新的结果来调整你的概率判断，这多有意思啊！
2. 来，咱说个生活中的例子。

你判断今天会不会下雨，你会先根据天气预报和以往的经验来有个初步想法吧，但如果突然天空变得阴沉沉的，你不得赶紧调整你觉得下雨的概率呀，这就是贝叶斯推理在起作用呀，你说是不是？
3. 你知道怎么猜别人手里的牌吗？这也能用贝叶斯推理呢！看他的表情动作，先有个初步判断，然后随着每一轮出牌，不断更新你对他手里牌的估计，哎呀，多带劲啊！
4. 你想想，你找工作的时候，对拿到某个 offer 的概率判断不也是这样嘛！开始根据公司的要求和自己的情况有个想法，然后面试过程中根据各种表现来调整，这可真是贝叶斯推理的活用呀！
5. 就像你猜你喜欢的人对你有没有意思，一开始你有个感觉，然后通过他跟你的每次互动，你不就会调整那个可能性嘛，这就是贝叶斯推理呀，神奇吧！
6. 好比你玩猜数字游戏，你先乱猜一个，然后根据提示不断缩小范围，调整你的猜测，这不就是活脱脱的贝叶斯推理嘛，多好玩呀！
7. 哎呀，你看医生诊断病情也是这样的呀！根据症状先有个初步判断，然后做各种检查，根据检查结果不断改变对病情的推测，贝叶斯推理真的无处不在呢！
8. 再比如你预测一场比赛的结果，先有个大概想法，比赛过程中根据双方的表现来不断调整胜败的概率，这不是贝叶斯推理在帮忙嘛，多有用啊！总之，贝叶斯推理在我们生活中可太常见啦，好多事情都能靠它来让我们的判断更准确呢！。

贝叶斯博弈例子

贝叶斯博弈例子
以下是 8 条关于贝叶斯博弈例子：
1. 你想想在牌桌上呀，就像咱打牌的时候，你先根据对手前面出的牌来判断他手里大概有啥牌，这不就是贝叶斯博弈嘛！比如说你看到对手老是出小牌，那是不是大概率他手里大牌不多呀！
2. 去商场买东西砍价也有点这个感觉呢！你看商家报价，然后根据他的态度和表情猜测他的底线，这也是一种贝叶斯博弈嘞！要是他看起来很犹豫，那是不是代表咱还能往下砍砍价呀！
3. 在求职面试的时候呀，你得根据面试官的提问和反应来调整自己的回答策略，这难道不是贝叶斯博弈吗？好比面试官一直追问某个问题，那就得想着更深入地回答呀！
4. 学生时代考试猜答案也能算呢！当你不确定一个题目的答案时，根据以往对这类题目的了解去猜测，这不是贝叶斯博弈是啥呀！哎呀，要是以前做过类似的，那猜对的几率不就大多啦！
5. 谈恋爱的时候其实也有哦！你通过对方平时的言行举止来判断他的喜好和想法，这算不算是在进行贝叶斯博弈呢？比如说他总提到某个东西，那是不是表示他可能很喜欢呀！
6. 参加比赛的时候呀，观察对手的表现来调整自己的战术，这就是活生生的贝叶斯博弈呀！要是看到对手有个弱点，那不就得抓住机会嘛！
7. 玩游戏抢地盘的时候呢，根据其他玩家的行动来决定自己该怎么行动，不也是贝叶斯博弈嘛！他们都往左边去了，那右边是不是咱的机会就来了呀！
8. 去市场买菜的时候呀，看着菜的品质和价格，还有老板的态度，来决定要不要买，这就是一种贝叶斯博弈嘛！要是老板很热情，菜看着也不错，那咱肯定更愿意买啦！
我觉得贝叶斯博弈在我们生活中可太常见了，很多时候我们都在不知不觉中运用着它呢！。

贝叶斯准则例题

一、贝叶斯准则：例题1：设二元假设检验的观测信号模型为： H 0： x = -1+nH 1： x = 1+n其中n 是均值为0，方差为212nσ=的高斯观测噪声。

若两种假设是等先验概率的，而代价因子为000110111,8,4,2,c c c c ==== 试求贝叶斯（最佳）表达式和平均代价C ：解：因为两种假设是等先验概率的所以 011()()2P H P H ==，这样,贝叶斯准备的似然比函数()x λ为： ① 122110221(1)exp 1122(|)22()exp(4)(|)(1)1exp 112222x p x H x x p x H x πλπ⎛⎫⎡⎤⎪⎢⎥-- ⎪⎢⎥⨯⨯ ⎪⎢⎥⎝⎭⎣⎦==•=⎡⎤⎛⎫⎢⎥+ ⎪-⎢⎥⎪⨯⎢⎥⨯ ⎪⎣⎦⎝⎭ 而似然比检测门限η为：010********(41)()()21()()(82)2P H c c P H c c η--=•=-- =1/2于是贝叶斯判决表达式为11exp(4)2H x H ><，两边取自然对数，并整理的最简判决表达式为10.1733H x H >-<②现在计算判决概率01(|)P H H 和00(|)P H H ,由于本例中检验统计量()l x x =，所以在两个假设下检验统计量的概率密度函数分别为：122012211(1)(|)exp 1122221(1)(|)exp 112222l p l H l p l H ππ⎛⎫⎡⎤⎪⎢⎥+=- ⎪⎢⎥⨯⨯ ⎪⎢⎥⎝⎭⎣⎦⎛⎫⎡⎤⎪⎢⎥-=- ⎪⎢⎥⨯⨯ ⎪⎢⎥⎝⎭⎣⎦这样，0.17330111220.1733(|)(|)1(1)exp 0.0486112222P H H p l H dll dl π--∞--∞=⎛⎫⎡⎤⎪⎢⎥-=-= ⎪⎢⎥⨯⨯ ⎪⎢⎥⎝⎭⎣⎦⎰⎰0.17330001220.1733(|)(|)1(1)exp 0.8790112222P H H p l H dll dl π--∞--∞=⎛⎫⎡⎤⎪⎢⎥+=-= ⎪⎢⎥⨯⨯ ⎪⎢⎥⎝⎭⎣⎦⎰⎰ 最后，利用贝叶斯平均代价表达式,01011110111010100000()()()()(|)()()(|)C P H c P H c P H c c P H H P H c c P H H =++---代入0000110(),(|),(|),P H P H H P H H c 等各数据，计算得： 1.8269C=总结：如果我们把判决表达式中的检测门限-0。

贝叶斯Bayes例题

我们来看一个简单的例子：例：高射炮向敌机发射三发炮弹，每弹击中与否相互独立且每发炮弹击中的概率均为0.3，又知敌机若中一弹，坠毁的概率为0.2，若中两弹，坠毁的概率为0.6，若中三弹，敌机必坠毁。

求敌机坠毁的概率。

解：设事件B=“敌机坠毁”；Ai=“敌机中弹”；i=0,1,2,3 实际上我们从题目知道应该是A0,A1,A2,A3构成完备事件组，但是敌机坠毁只和A1,A2,A3有关，即则我们可用如下公式则贝叶斯准则例题P(B|A) 在A的情况下B发生的概率P（A|B）在B的情况下A发生的概率贝叶斯公式：贝叶斯定理公式：P(A|B)=P(B|A)*P(A)/P(B)如上公式也可变形为：P(B|A)=P(A|B)*P(B)/P(A)1、例如：一座别墅在过去的 20 年里一共发生过 2 次被盗，别墅的主人有一条狗，狗平均每周晚上叫 3 次，在盗贼入侵时狗叫的概率被估计为0.9，问题是：在狗叫的时候发生入侵的概率是多少？我们假设 A 事件为狗在晚上叫，B 为盗贼入侵，则 P(A) = 3 / 7，P(B)=2/(20·365)=2/7300，P(A | B) = 0.9（窃贼入室盗窃狗叫概率），按照公式很容易得出结果：P(B|A)=0.9*(2/7300)*(7/3)=0.000582、另一个例子，现分别有 A，B 两个容器，在容器 A 里分别有 7 个红球和 3 个白球，在容器 B 里有 1 个红球和 9 个白球，现已知从这两个容器里任意抽出了一个球，且是红球，问这个红球是来自容器 A 的概率是多少?假设已经抽出红球为事件 B，从容器 A 里抽出球为事件 A，则有：P(B) = 8 / 20，P(A) = 1 / 2，P(B | A) = 7 / 10（容器A中抽到红球的概率），按照公式，则有：P(A|B)=(7 / 10)*(1 / 2)*(20/8)=7/8。

贝叶斯决策例子

贝叶斯决策练习某石油公司拟在一片估计含油的荒地上钻井。

如果钻井，费用为150万，若出油的概率为0.55，收入为800万元；若无油的概率为0.45，此时的收入为0。

该公司也可以转让开采权，转让费为160万元，但公司可以不担任何风险。

为了避免45％的无油风险，公司考虑通过地震试验来获取更多的信息，地震试验费用需要20万元。

已知有油的情况下，地震试验显示油气好的概率为0.8，显示油气不好的概率为0.2；在无油条件下，地震显示油气好的概率为0.15，而显示油气不好的概率为0.85。

又当试验表明油气好时，出让开采权的费用将增至400万元，试验表明油气不好时，出让开采权费用降至100万元，问该公司应该如何决策，使其期望收益值为最大。

解：该公司面临两个阶段的决策：第一阶段为要不要做地震试验，第二阶段为在做地震试验条件下，当油气显示分别为好与不好时，是采取钻井策略还是出让开采权。

若用A 1表示有油，A 2表示无油；用B 1表示地震试验显示油气好，B 2表示地震试验显示油气不好。

由题意可知：1211211222()0.55 ()0.45(|)0.8 (|)0.2(|)0.15 (|)0.85P A P A P B A P B A P B A P B A ======由贝叶斯公式计算得到：11111111212()(|)0.440.44(|)0.867()(|)()(|)0.440.06750.5075P A P B A P A B P A P B A P A P B A ====++ 同理，有： 2112220.0675(|)0.1330.50750.11(|)0.2230.49250.3825(|)0.7770.4925P A B P A B P A B ======该问题对应的决策树图采用逆序的方法，先计算事件点②③④的期望值：事件点期望值② 800×0.867＋0×0.133＝693.6（万元）③ 800×0.223＋0×0.777＝178.4（万元）④ 800×0.55＋0×0.45＝440（万元）在决策点2，按max[(693.6-150)，400]＝543.6万元，故选择钻井，删除出让开采权策略；在决策点3，按max[(178.4-150)，100]＝100万元，故选择出让开采权，删除钻井策略；在决策点4，按max[(440-150)，160]＝290万元，故选择钻井策略。

贝叶斯分类器例题

贝叶斯分类器例题
1.朴素贝叶斯分类器：一个例子是识别垃圾邮件。

给定一封邮件，可以根据邮件中的关键词和主题来判断该邮件是否为垃圾邮件。

通过朴素贝叶斯分类器，可以将邮件分为垃圾邮件和非垃圾邮件两类。

2.贝叶斯网络分类器：另一个例子是疾病诊断。

给定一个病人的症状和病史，可以根据贝叶斯网络分类器来预测该病人可能患有哪种疾病。

通过计算每个疾病的概率，可以得出最可能的诊断结果。

3.信用卡欺诈识别：在这个例子中，我们使用贝叶斯分类器来识别信用卡欺诈行为。

给定一系列交易数据，包括交易金额、交易地点、交易时间等，我们需要判断这些交易是否为欺诈行为。

通过训练一个贝叶斯分类器，可以学习到正常交易和欺诈交易的特征，并利用这些特征来预测新的交易是否为欺诈行为。

4.情感分析：在这个例子中，我们使用贝叶斯分类器来进行情感分析。

给定一篇文章或一段评论，我们需要判断该文本的情感倾向是积极还是消极。

通过训练一个贝叶斯分类器，可以学习到积极和消极文本的特征，并利用这些特征来预测新的文本的情感倾向。

5.基因分类：在这个例子中，我们使用贝叶斯分类器来进行基因分类。

给定一个基因序列，我们需要将其分类为不同的基因家族或亚家族。

通过训练一个贝叶斯分类器，可以学习到不同基因家族或亚家族的特征，并利用这些特征来预测新的基因序列的家族或亚家族归属。

以上这些例题只是贝叶斯分类器的一些应用示例，实际上贝叶斯分类器的应用非常广泛，它可以应用于任何需要分类的领域，如金融、医疗、社交媒体等。

纯策略贝叶斯纳什均衡例题

纯策略贝叶斯纳什均衡例题引言：纯策略贝叶斯纳什均衡是博弈论中常用的概念之一，它可以用于分析多方参与的决策问题。

本文将通过一个例题来解释纯策略贝叶斯纳什均衡的概念及应用。

例题背景：假设有两家咖啡店，分别是A店和B店。

每天早晨，两家咖啡店都需要决定自己的咖啡价格。

同时，消费者也需要决定去哪家咖啡店购买。

假设消费者根据市场情况作出购买决策。

A店和B店的利润与消费者选择有关。

情景一：A店设置较高的价格，B店设置较低的价格。

这种情况下，消费者更愿意选择购买B店的咖啡。

B店的利润将最大化，而A店的利润将最小化。

情景二：A店和B店都设置较低的价格。

这种情况下，消费者会更加倾向于选择购买A店的咖啡。

A店的利润将最大化，而B店的利润将最小化。

情景三：A店和B店都设置较高的价格。

这种情况下，消费者没有购买的动力，两家咖啡店的利润都会很低。

分析与求解：我们可以将上述情景转化为一个博弈论的模型，其中A店和B店是两个决策者，他们需要根据对方的策略来决定自己的策略。

消费者的选择将影响两家咖啡店的利润。

根据纯策略贝叶斯纳什均衡的概念，我们需要确定每个决策者的策略组合，以获得最优的结果。

在这个例题中，我们需要确定A店和B店的咖啡价格。

假设A店有80%的机会成为消费者的首选，B店有20%的机会。

根据这个信息，我们可以得到以下策略组合：情景一：A店设置高价格，B店设置低价格。

情景二：A店设置低价格，B店设置低价格。

情景三：A店设置高价格，B店设置高价格。

然后我们可以计算每种策略组合下两家咖啡店的利润，并找出使两家咖啡店利润最大化的策略组合。

结论：通过计算，我们可以得到以下结果：情景一：A店设置高价格，B店设置低价格。

这种情况下，A店的利润最大化，B店的利润最小化。

因此，纯策略贝叶斯纳什均衡的结果是，A店设置高价格，B店设置低价格时，两家咖啡店的利润最优化。

扩展思考：本例题中我们假设了A店有80%的机会成为消费者的首选，B店有20%的机会。

贝叶斯纳什均衡例题

贝叶斯纳什均衡例题
贝叶斯纳什均衡 (Bayesian Nash Equilibrium) 是一种非合作的博弈理论。

在贝叶斯纳什均衡中，每个参与者根据其他参与者的策略和历史数据，计算出自己在给定其他参与者的策略下的最大收益，并采取最优策略。

以下是一个贝叶斯纳什均衡的例题。

假设有三个人，分别是 A、B、C，他们玩一个猜拳游戏。

游戏规则如下:
1. A 和 B 随机猜拳，胜负概率均为 50%。

2. 如果 A 和 B 获胜，则 C 获胜的概率为 25%。

3. 如果 A 和 B 失败，则 C 获胜的概率为 75%。

现在问，谁是游戏的胜者，如果 A 和 B 采取随机策略，而 C 采取最优策略。

根据贝叶斯纳什均衡的定义，我们需要计算出每个参与者在给定其他参与者策略下的最优策略。

首先，对于 A 和 B，由于他们是随机的，所以可以采取任何策略，因此他们的最优策略是随机。

其次，对于 C，他需要计算出自己在 A 和 B 随机策略下的最大收益。

根据游戏规则，如果 A 和 B 随机，则 C 的最大收益为 25%。

因此，C 的最优策略是采取赢的概率为 25% 的拳法。

最后，由于 C 已经采取了最优策略，A 和 B 将不得不采取随机策略。

因此，游戏的胜者是 C。

需要注意的是，贝叶斯纳什均衡只适用于非合作的博弈理论。

在合作博弈中，参与者之间的策略选择需要基于信任和相互利益。

贝叶斯决策的例题练习

贝叶斯决策的例题练习公司内部档案编码：[OPPTR-OPPT28-OPPTL98-OPPNN08]一、贝叶斯决策(Bayes decision theory)【例】某企业设计出一种新产品，有两种方案可供选择：—是进行批量生产，二是出售专利。

这种新产品投放市场，估计有3种可能：畅销、中等、滞销，这3种情况发生的可能性依次估计为：，和。

方案在各种情况下的利润及期望利润如下表。

企业可以以1000元的成本委托专业市场调查机构调查该产品销售前景。

若实际市场状况为畅销，则调查结果为畅销、中等和滞销的概率分别为、和；若实际市场状况为中等，则调查结果为畅销、中等和滞销的概率分别为、和；若实际市场状况为滞销，则调查结果为畅销、中等和滞销的概率分别为、和。

问：企业是否委托专业市场调查机构进行调查解：1.验前分析：记方案d1为批量生产，方案d2为出售专利E(d1)=*80+*20+*(-5)=(万元)E(d2)=40*+7*+1*=(万元)记验前分析的最大期望收益为E1，则E1=max{E(d1),E(d2)}=(万元)因此验前分析后的决策为：批量生产E1不作市场调查的期望收益2.预验分析：（1）设调查机构调查的结果畅销、中等、滞销分别用H1、H2、H3表示由全概率公式P(H1)=*+*+*=P(H2)=*+*+*=P(H3)=*+*+*=（2）由贝叶斯公式有P(?1|H1)=*=P(?2|H1)=*=P(?3|H1)=*=P(?1|H2)=*=P(?2|H2)=*=P(?3|H2)=*=P(?1|H3)=*=P(?2|H3)=*=P(?3|H3)=*=（3）用后验分布代替先验分布，计算各方案的期望收益值a)当市场调查结果为畅销时E(d1|H1)=80* P(?1|H1)+20* P(?2|H1)+(-5)* P(?3|H1)=80*+20*+(-5)*=(万元)E(d2|H1)=40* P(?1|H1)+7* P(?2|H1)+1* P(?3|H1)=40*+7*+1*=(万元)因此，当市场调查畅销时，最优方案是d1，即批量生产b)当市场调查结果为中等时E(d1|H2)=80* P(?1|H2)+20* P(?2|H2)+(-5)* P(?3|H2)=(万元)E(d2|H2)=40* P(?1|H2)+7* P(?2|H2)+1* P(?3|H2)=40*+7*+1*=(万元)所以市场调查为中等时，最优方案是：d1，即批量生产c)当市场调查结果为滞销时E(d1|H3)=80* P(?1|H3)+20* P(?2|H3)+(-5)* P(?3|H3)=80*+20*+(-5)*=（万元）E(d2|H3)=40* P(?1|H3)+7* P(?2|H3)+1* P(?3|H3)=40*+7*+1*=（万元）因此市场调查为滞销时，最优方案是：d2，即出售专利（4）通过调查，该企业可获得的收益期望值为E2= E(d1|H1)* P(H1)+ E(d1|H2)* P(H2)+ E(d2|H3)* P(H3)=*+*+*=（万元）通过调查，该企业收益期望值能增加E2-E1=（万元）因此，在调查费用不超过万元的情况下，应进行市场调查3.验后分析（1）本题中调查费用1000<9600,所以应该进行市场调查（2）当市场调查结果为畅销时，选择方案1，即批量生产（3）当市场调查结果为中等时时，选择方案1，即批量生产（4）当市场调查结果为滞销时，选择方案2，即出售专利。

贝叶斯博弈例题及答案

贝叶斯博弈例题及答案贝叶斯博弈是概率论和数理统计中研究决策理论的一个重要方面。

它是游戏理论的一种集合，可以将概率论和统计学与决策理论结合，从而使决策者能够在不确定的环境中作出正确的决策。

贝叶斯博弈的主要术语有：贝叶斯博弈矩阵、贝叶斯博弈策略和贝叶斯博弈操作。

贝叶斯博弈矩阵是一个3行3列的二维数组，分别是玩家A的策略，玩家B的策略和数值。

玩家A与玩家B之间的博弈情况就是通过贝叶斯博弈矩阵来描述的，每一行代表一个玩家，每一列代表另一个玩家，并且每一个单元格都是一个数值，表示该玩家在该情况下所获得的效益程度。

贝叶斯博弈策略是指玩家在贝叶斯博弈中可以采取的不同策略，如:攻击策略，防御策略，逃跑策略等。

贝叶斯博弈操作是指玩家在不同情况下根据自身可获得的信息，以及结合玩家之间的战略，运用贝叶斯博弈策略和贝叶斯博弈矩阵的数据，作出不同的博弈决策，以追求自身最大利益。

下面是一个贝叶斯博弈例题：有两个玩家，A和B，A有两种选择，攻击和逃跑，B有三种选择，攻击，防御和逃跑。

A选择攻击，B选择防御，结果是A得到2点，B得到1点；A选择攻击，B选择逃跑，结果是A得到3点，B得到0点；A选择逃跑，B选择攻击，结果是A得到0点，B得到2点；A选择逃跑，B选择防御，结果是A得到1点，B得到1点。

以上例题的贝叶斯博弈矩阵如下：A 击跑B 击 2 0防御 1 1逃跑 3 0利用贝叶斯博弈矩阵，当双方玩家都想获取最大利益时，A玩家最好选择攻击策略，而B玩家最好选择防御策略。

这样，两个玩家的效益都能达到最大值，A获得2点，B获得1点。

贝叶斯博弈是一种数学模型，它可以让玩家在贝叶斯博弈矩阵的基础上，根据不同的信息量和策略结合，使玩家在不确定的情况下作出最优选择，最终获得最大收益。

贝叶斯博弈可以在生活中得到广泛运用，从商业谈判中到家庭冲突，都可以使用贝叶斯博弈分析，以便更好地分析环境，并做出最优决策。

此外，贝叶斯博弈也可用来分析投资和经济行为，以及社会政治等。

贝叶斯分类例题

贝叶斯分类例题以下是一个贝叶斯分类的例子：假设我们要根据一个人的身高和体重来判断其性别，已知训练集中有一些人的身高、体重以及性别的标签。

我们可以使用贝叶斯分类器来预测新样本的性别。

训练集如下：人1：身高160cm，体重50kg，性别女性人2：身高175cm，体重70kg，性别男性人3：身高168cm，体重55kg，性别女性人4：身高180cm，体重80kg，性别男性现在我们希望根据一个新样本（身高170cm，体重65kg）来预测其性别。

首先，我们需要计算训练集中男性和女性各自的先验概率P(男性)和P(女性)。

训练集中有2个男性和2个女性，所以P(男性) = 2/4 = 0.5，P(女性) = 2/4 = 0.5。

接下来，我们需要计算对于每个特征值的条件概率P(特征值|男性)和P(特征值|女性)。

对于身高特征值170cm，训练集中男性中有1个人的身高大于170cm，所以P(身高 > 170cm|男性) = 1/2 = 0.5，女性中有0个人的身高大于170cm，所以P(身高 > 170cm|女性) = 0/2 = 0。

对于体重特征值65kg，男性中有1个人的体重大于65kg，所以P(体重 > 65kg|男性) = 1/2 = 0.5，女性中有0个人的体重大于65kg，所以P(体重 > 65kg|女性) = 0/2 = 0。

最后，我们可以使用贝叶斯公式来计算新样本为男性和女性的后验概率，然后选择后验概率较大的性别作为预测结果。

贝叶斯决策的经典例题练习

一、贝叶斯决策(Bayes decision theory)【例】某企业设计出一种新产品，有两种方案可供选择：—是进行批量生产，二是出售专利。

这种新产品投放市场，估计有3种可能：畅销、中等、滞销，这3种情况发生的可能性依次估计为：0.2，0.5和0.3。

方案在各种情况下的利润及期望利润如下表。

企业可以以1000元的成本委托专业市场调查机构调查该产品销售前景。

若实际市场状况为畅销，则调查结果为畅销、中等和滞销的概率分别为0.9、0.06和0.04；若实际市场状况为中等，则调查结果为畅销、中等和滞销的概率分别为0.05、0.9和0.05；若实际市场状况为滞销，则调查结果为畅销、中等和滞销的概率分别为0.04、0.06和0.9。

问：企业是否委托专业市场调查机构进行调查？解：1.验前分析：记方案d1为批量生产，方案d2为出售专利E(d1)=0.2*80+0.5*20+0.3*(-5)=24.5(万元)E(d2)=40*0.2+7*0.5+1*0.3=11.8(万元)记验前分析的最大期望收益为E1，则E1=max{E(d1),E(d2)}=24.5(万元)因此验前分析后的决策为：批量生产E1不作市场调查的期望收益2.预验分析：（1）设调查机构调查的结果畅销、中等、滞销分别用H1、H2、H3表示由全概率公式P(H1)=0.9*0.2+0.06*0.5+0.04*0.3=0.232P(H2)=0.05*0.2+0.9*0.5+0.05*0.3=0.475P(H3)=0.04*0.2+0.06*0.5+0.9*0.3=0.308（2）由贝叶斯公式有P(Ɵ1|H1)=0.9*0.2/0.232=0.776P(Ɵ2|H1)=0.06*0.5/0.232=0.129P(Ɵ3|H1)=0.04*0.3/0.232=0.052P(Ɵ1|H2)=0.05*0.2/0.475=0.021P(Ɵ2|H2)=0.9*0.5/0.475=0.947P(Ɵ3|H2)=0.05*0.3/0.475=0.032P(Ɵ1|H3)=0.04*0.2/0.308=0.026P(Ɵ2|H3)=0.06*0.5/0.308=0.097P(Ɵ3|H3)=0.9*0.3/0.308=0.877（3）用后验分布代替先验分布，计算各方案的期望收益值a)当市场调查结果为畅销时E(d1|H1)=80* P(Ɵ1|H1)+20* P(Ɵ2|H1)+(-5)* P(Ɵ3|H1)=80*0.776+20*0.129+(-5)*0.052=64.4(万元)E(d2|H1)=40* P(Ɵ1|H1)+7* P(Ɵ2|H1)+1* P(Ɵ3|H1)=40*0.776+7*0.129+1*0.052=31.995(万元)因此，当市场调查畅销时，最优方案是d1，即批量生产b)当市场调查结果为中等时E(d1|H2)=80* P(Ɵ1|H2)+20* P(Ɵ2|H2)+(-5)* P(Ɵ3|H2)=20.46(万元)E(d2|H2)=40* P(Ɵ1|H2)+7* P(Ɵ2|H2)+1* P(Ɵ3|H2)=40*0.021+7*0.947+1*0.032=7.501(万元)所以市场调查为中等时，最优方案是：d1，即批量生产c)当市场调查结果为滞销时E(d1|H3)=80* P(Ɵ1|H3)+20* P(Ɵ2|H3)+(-5)* P(Ɵ3|H3)=80*0.026+20*0.097+(-5)*0.877=-0.365（万元）E(d2|H3)=40* P(Ɵ1|H3)+7* P(Ɵ2|H3)+1* P(Ɵ3|H3)=40*0.026+7*0.097+1*0.877=2.596（万元）因此市场调查为滞销时，最优方案是：d2，即出售专利（4）通过调查，该企业可获得的收益期望值为E2= E(d1|H1)* P(H1)+ E(d1|H2)* P(H2)+ E(d2|H3)* P(H3)=64.4*0.232+20.46*0.475+2.596*0.308=25.46（万元）通过调查，该企业收益期望值能增加E2-E1=25.46-24.5=0.96（万元）因此，在调查费用不超过0.96万元的情况下，应进行市场调查3.验后分析（1）本题中调查费用1000<9600,所以应该进行市场调查（2）当市场调查结果为畅销时，选择方案1，即批量生产（3）当市场调查结果为中等时时，选择方案1，即批量生产（4）当市场调查结果为滞销时，选择方案2，即出售专利Welcome To Download !!!欢迎您的下载，资料仅供参考！。

模式识别与机器学习：贝叶斯决策与学习习题与答案

一、单选题
1、假设类的观测似然概率是单维高斯分布，且高斯分布的方差已知，则待估计参数就是（）。

A.高斯分布的中位数m
B.高斯分布的均值
C.高斯分布的标准差
D.高斯分布的方差
正确答案：B
二、判断题
4、高斯分布协方差的最大似然估计是无偏估计。

（）
正确答案：√
5、核密度估计不需要存储所有训练样本。

（）
正确答案：×
三、填空题
1、设有三个彩⾊的盒⾊：r（红⾊）、b（蓝⾊）、g（绿⾊）。

盒⾊r⾊有3个苹果，4个橘⾊，3个酸橙；盒⾊b⾊有2个苹果，1个橘⾊，2个酸橙；盒⾊g⾊有3个苹果，3个橘⾊和4个酸橙。

如果盒⾊随机被选中的概率为p(r) = 0.2，p(b) = 0.2，p(g) = 0.6。

选择⾊个⾊果从盒⾊中拿⾊（盒⾊中选择任何⾊果的概率都相同），那么选择苹果的概率是（）。

（用小数表示）
正确答案：0.32
2、接上题，如果我们观察到选择的⾊果实际上是苹果，那么它来⾊
绿⾊盒⾊的概率是（）。

(用小数表示)正确答案：0.5625。

贝叶斯决策例题

解：采用贝叶斯决策方法。

根据期望值准则选择施工方案有利，相应最大期望收益值EMV*（先）=0.8（2）预验分析完全信息的最大期望收益值：EPPI=0.3×5+0.7×（-0.2）=1.36（万元）完全信息价值： EVPI=EPPI- EMV*（先）=1.36-0.8=0.56（万元）即，完全信息价值大于信息成本，请气象中心进行预报是合算的。

（3）后验分析①补充信息：气象中心将提供预报此时期内两种天气状态x 1(好天气)、x 2(坏天气)将会出现哪一种状态。

从气象中心提供的同期天气资料可得知条件概率：天气好且预报天气也好的概率 P （x 1/θ1）=0.8天气好而预报天气不好的概率 P （x 2/θ1）=0.2天气坏而预报天气好的概率 P （x 1/θ2）=0.1天气坏且预报天气也坏的概率 P （x 2/θ2）=0.9②计算后验概率分布：根据全概率公式和贝叶斯公式，计算后验概率。

预报天气好的概率 1111212()()(/)()(/)P x P P x P P x θθθθ=+ =0.31预报天气坏的概率 2121222()()(/)()(/)P x P P x P P x θθθθ=+ =0.69预报天气好且天气实际也好的概率：111111()(/)(/)()P P x P x P x θθθ⋅==0.3×0.8/0.31=0.77 预报天气好而天气坏的概率：212211()(/)(/)()P P x P x P x θθθ⋅==0.7×0.1/0.31=0.23 预报天气坏而实际天气好的概率:121122()(/)(/)()P P x P x P x θθθ⋅==0.3×0.2/0.69=0.09 预报天气坏且实际天气也坏的概率：222222()(/)(/)()P P x P x P x θθθ⋅==0.7×0.9/0.69=0.91。

模式识别第二章贝叶斯决策论习题答案

2
= min p (ω1 x ) , p (ω2 x ) max p (ω1 x ) , p (ω2 x )
= p ω1 x p ω2 x
(
) (
)
所以， p ω1 x p ω2 x 能过给出误差率的下界。 d) 因为：
(
) (
)
pβ ( error ) = ∫ β p (ω1 x ) p ( ω2 x ) p ( x ) dx
α 4
∫
Hale Waihona Puke +∞p ( x ) dx <
显而易见： pα ( error ) < p ( error ) ，因此当 α < 2 时，无法得到误差率的上界。 c) 因为：
p ( error x ) ≥ p ( error x ) − p ( error x ) = p ( error x ) 1 − p ( error x )
i =1 ωi ≠ωmax
∑ P (ω x ) p ( x ) d x
i
c
= ∫ 1 − P (ωmax x ) p ( x ) dx = 1 − ∫ P (ωmax x ) p ( x ) dx
d) 续上式：
(
)
P ( error ) = 1 − ∫ P (ωmax x ) p ( x ) dx ≤ 1− ∫ 1 1 c −1 p ( x ) dx = 1 − = c c c
n t
′ ′ ′ Σ′ = ∑ ( x′ k − μ )( x k − μ )
k =1 n
= ∑ Tt ( x 0 k − μ )( x 0 k − μ ) T
t k =1
n t = Tt ∑ ( x 0 k − μ )( x 0 k − μ ) T k =1 = T t ΣT

(贝叶斯决策例题)

Equation Chapter 1 Section 1例：某工程项目按合同应在三个月内完工，其施工费用与工程完工期有关。

假定天气是影响能否按期完工的决定因素，如果天气好，工程能按时完工，获利5万元；如果天气不好，不能按时完工，施工单位将被罚款1万元；若不施工就要付出窝工费2千元。

根据过去的经验，在计划实施工期天气好的可能性为30%。

为了更好地掌握天气情况，可以申请气象中心进行天气预报，并提供同一时期天气预报资料，但需要支付资料费800元。

从提供的资料中可知，气象中心对好天气预报准确性为80%，对坏天气预报准确性为90%。

问如何进行决策。

解：采用贝叶斯决策方法。

先验分析根据期望值准则选择施工方案有利，相应最大期望收益值EMV*（先）=0.8（2）预验分析完全信息的最大期望收益值：EPPI=0.3×5+0.7×（-0.2）=1.36（万元）完全信息价值： EVPI=EPPI- EMV*（先）=1.36-0.8=0.56（万元）即，完全信息价值大于信息成本，请气象中心进行预报是合算的。

（3）后验分析①补充信息：气象中心将提供预报此时期内两种天气状态x1(好天气)、x2(坏天气)将会出现哪一种状态。

从气象中心提供的同期天气资料可得知条件概率：天气好且预报天气也好的概率 P （x1/θ1）=0.8 天气好而预报天气不好的概率 P （x2/θ1）=0.2 天气坏而预报天气好的概率 P （x1/θ2）=0.1 天气坏且预报天气也坏的概率 P （x2/θ2）=0.9②计算后验概率分布：根据全概率公式和贝叶斯公式，计算后验概率。

预报天气好的概率1111212()()(/)()(/)P x P P x P P x θθθθ=+=0.31预报天气坏的概率2121222()()(/)()(/)P x P P x P P x θθθθ=+=0.69 预报天气好且天气实际也好的概率：111111()(/)(/)()P P x P x P x θθθ⋅==0.3×0.8/0.31=0.77预报天气好而天气坏的概率：212211()(/)(/)()P P x P x P x θθθ⋅==0.7×0.1/0.31=0.23预报天气坏而实际天气好的概率:121122()(/)(/)()P P x P x P x θθθ⋅==0.3×0.2/0.69=0.09预报天气坏且实际天气也坏的概率： 222222()(/)(/)()P P x P x P x θθθ⋅==0.7×0.9/0.69=0.91上述计算可以用表格表示：③ 后验决策：若气象中心预报天气好（x1）,则每个方案的最大期望收益值 E(d1/x1)=0.77×5+0.23×(-1)=3.62 E(d2/x1)=0.77×(-0.2)+0.23×(-0.2)=-0.2选择d1即施工的方案，相应在预报x1若气象中心预报天气不好（x2） E(d1/x2)=0.09×5+0.91×(-1)=-0.46 E(d2/x2)=0.09×(-0.2)+0.91×(-0.2)=-0.2选择d2即不施工的方案，相应在预报x2时的最大期望收益值E （X2）=-0.2④ 计算补充信息的价值：得到天气预报的情况下，后验决策的最大期望收益值：1122*()()()()()EMV P x E x P x E x =⋅+⋅后=0.31×3.62+0.69×（-0.2）=0.9842则补充的信息价值为：EMV*(后)- EMV*(先)=0.9842-0.8=0.1842补充信息价值大于信息费（800元），即这种费用是合算的。

Bayes补充例题及解答

关于Bayes 决策分析的补充例题：1、某公司经营某种商品，可以采取的经营方案有三种：1a （大批量），2a （中批量），3a （小批量）。

市场销售状态有三种：1θ（畅销），2θ（一般），3θ（滞已知市场销售状态概率2.0)(1=θP ，5.0)(2=θP ，3.0)(3=θP 。

该公司市场调研人员拟进行市场预测，其以往市场预测准确概率分布矩阵为：()()()321|||θθθj j j H P H P H P321H H H ⎪⎪⎪⎭⎫⎝⎛90.010.005.008.070.015.002.020.080.0 其中，1H ，2H ，3H 分别表示预测值畅销、一般、滞销。

市场预测费用为5万元。

通过决策分析回答以下问题：（1）如果不进行市场预测，应如何决策？如果有完全信息，计算EVPI ；（一）不进行市场预测时：⎪⎪⎪⎭⎫ ⎝⎛--==⨯69102040506030100)(33ij v V ,2.0)(1=θP ,5.0)(2=θP ,3.0)(3=θP ()173.0)60(5.0302.0100)(3111=⨯-+⨯+⨯==∑=i i i P v a E θ()243.0)20(5.0402.050)(3122=⨯-+⨯+⨯==∑=i i i P v a E θ()3.83.065.092.010)(3133=⨯+⨯+⨯==∑=i i i P v a E θ因此：312a a a ，先验最优方案2a a opt =，即经营中等批量的商品，且期望收益值为：()2421==a E E8.17248.4124)3.065.0402.0100()()()(max )(),(max ),(),(max 31=-=-⨯+⨯+⨯=-=-⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=∑=opt i ij i j opt j j opt a E P v a E a V E a V a V E EVPI θθθθ（2）如果进行市场预测，应如何根据预测结果进行决策；计算EVAI ，并判断是否进行市场预测；（二）如果进行市场预测，并用它修正原先掌握的情况。

贝叶斯决策的经典例题练习

贝叶斯决策例题(精选.)

贝叶斯公式例题范文

贝叶斯公式典型例题

贝叶斯推理例子

贝叶斯博弈例子

贝叶斯准则例题

贝叶斯Bayes例题

贝叶斯决策例子

贝叶斯分类器例题

纯策略贝叶斯纳什均衡例题

贝叶斯纳什均衡例题

贝叶斯决策的例题练习

贝叶斯博弈例题及答案

贝叶斯分类例题

贝叶斯决策的经典例题练习

模式识别与机器学习：贝叶斯决策与学习习题与答案

贝叶斯决策例题

模式识别 第二章 贝叶斯决策论习题答案

(贝叶斯决策例题)

Bayes补充例题及解答

模式识别第二章贝叶斯决策论习题答案