多元线性回归模型的案例讲解
多元线性回归分析范例

多元线性回归分析范例多元线性回归是一种用于预测因变量和多个自变量之间关系的统计分析方法。
它假设因变量与自变量之间存在线性关系,并通过拟合一个多元线性模型来估计因变量的值。
在本文中,我们将使用一个实际的数据集来进行多元线性回归分析的范例。
数据集介绍:我们选取的数据集是一份汽车销售数据,包括了汽车的价格(因变量)和多个与汽车相关的特征(自变量),如车龄、行驶里程、汽车品牌等。
我们的目标是通过这些特征来预测汽车的价格。
数据集包括了100个样本。
数据集的构成如下:车龄(年),行驶里程(万公里),品牌,价格(万元)----------------------------------------5,10,A,153,5,B,207,12,C,10...,...,...,...建立多元线性回归模型:我们首先需要将数据集划分为自变量矩阵X和因变量向量y。
其中,自变量矩阵X包括了车龄、行驶里程和品牌等特征,因变量向量y包括了价格。
在Python中,我们可以使用NumPy和Pandas库来处理和分析数据。
我们可以使用Pandas的DataFrame来存储数据集,并使用NumPy的polyfit函数来拟合多元线性模型。
首先,我们导入所需的库并读取数据集:```pythonimport pandas as pdimport numpy as np#读取数据集data = pd.read_csv('car_sales.csv')```然后,我们将数据集划分为自变量矩阵X和因变量向量y:```python#划分自变量矩阵X和因变量向量yX = data[['车龄', '行驶里程', '品牌']]y = data['价格']```接下来,我们使用polyfit函数来拟合多元线性模型。
我们将自变量矩阵X和因变量向量y作为输入,并指定多项式的次数(线性模型的次数为1):```python#拟合多元线性模型coefficients = np.polyfit(X, y, deg=1)```最后,我们可以使用拟合得到的模型参数来预测新的样本。
多元线性回归模型的案例讲解

多元线性回归模型的案例讲解以下是一个关于房价的案例,用多元线性回归模型来分析房价与其他变量的关系。
假设我们想研究一些城市的房价与以下变量之间的关系:房屋面积、卧室数量、厨房数量和所在区域。
我们从不同的房屋中收集了这些变量的数据,以及对应的房价。
我们希望通过构建多元线性回归模型来预测房价。
首先,我们需要收集数据。
我们找到100个不同房屋的信息,包括房屋的面积、卧室数量、厨房数量和所在区域,以及对应的房价。
接下来,我们需要进行数据处理和探索性分析。
我们可以使用统计软件,如Python的pandas库,对数据进行清洗和处理。
我们可以检查数据的缺失值、异常值和离群点,并对其进行处理。
完成数据处理后,我们可以继续进行变量的选择和模型构建。
在多元线性回归中,我们需要选择合适的自变量,并建立模型。
可以使用统计软件,如Python的statsmodels库,来进行模型的构建。
在本例中,我们使用房屋面积、卧室数量、厨房数量和所在区域作为自变量,房价作为因变量。
我们可以构建如下的多元线性回归模型:房价=β0+β1*面积+β2*卧室数量+β3*厨房数量+β4*所在区域其中,β0、β1、β2、β3和β4是回归模型的系数,表示因变量与自变量之间的关系。
我们需要对模型进行拟合和检验。
使用统计软件,在模型拟合之后,我们可以得到回归模型的系数和统计指标。
常见的指标包括回归系数的显著性、解释方差、调整R方和残差分析等。
根据回归模型的系数,我们可以解释不同自变量对因变量的影响。
例如,如果回归系数β1大于0且显著,说明房屋面积对房价有正向影响。
同理,其他自变量的系数也可以解释其对因变量的影响。
最后,我们可以使用建立的多元线性回归模型进行房价的预测。
通过输入房屋的面积、卧室数量、厨房数量和所在区域等自变量的数值,我们可以预测其对应的房价。
需要注意的是,多元线性回归模型的效果不仅取决于数据的质量,还取决于模型的选择和拟合程度。
因此,在模型选择和拟合过程中,我们需要进行多次实验和优化,以得到较好的模型。
多元线性回归模型案例(DOC)

多元线性回归模型案例分析——中国人口自然增长分析一·研究目的要求中国从1971年开始全面开展了计划生育,使中国总和生育率很快从1970年的5.8降到1980年2.24,接近世代更替水平。
此后,人口自然增长率(即人口的生育率)很大程度上与经济的发展等各方面的因素相联系,与经济生活息息相关,为了研究此后影响中国人口自然增长的主要原因,分析全国人口增长规律,与猜测中国未来的增长趋势,需要建立计量经济学模型。
影响中国人口自然增长率的因素有很多,但据分析主要因素可能有:(1)从宏观经济上看,经济整体增长是人口自然增长的基本源泉;(2)居民消费水平,它的高低可能会间接影响人口增长率。
(3)文化程度,由于教育年限的高低,相应会转变人的传统观念,可能会间接影响人口自然增长率(4)人口分布,非农业与农业人口的比率也会对人口增长率有相应的影响。
二·模型设定为了全面反映中国“人口自然增长率”的全貌,选择人口增长率作为被解释变量,以反映中国人口的增长;选择“国名收入”及“人均GDP”作为经济整体增长的代表;选择“居民消费价格指数增长率”作为居民消费水平的代表。
暂不考虑文化程度及人口分布的影响。
从《中国统计年鉴》收集到以下数据(见表1):表1 中国人口增长率及相关数据设定的线性回归模型为:1222334t t t t t Y X X X u ββββ=++++三、估计参数利用EViews 估计模型的参数,方法是:1、建立工作文件:启动EViews ,点击File\New\Workfile ,在对话框“Workfile Range ”。
在“Workfile frequency ”中选择“Annual ” (年度),并在“Start date ”中输入开始时间“1988”,在“end date ”中输入最后时间“2005”,点击“ok ”,出现“Workfile UNTITLED ”工作框。
其中已有变量:“c ”—截距项 “resid ”—剩余项。
多元线性回归模型案例

多元线性回归模型案例多元线性回归是统计学中常用的一种回归分析方法,它可以用来研究多个自变量与因变量之间的关系。
在实际应用中,多元线性回归模型可以帮助我们理解不同自变量对因变量的影响程度,从而进行预测和决策。
下面,我们将通过一个实际案例来介绍多元线性回归模型的应用。
案例背景:某电商公司希望了解其产品销售额与广告投入、季节因素和竞争对手销售额之间的关系,以便更好地制定营销策略和预测销售额。
数据收集:为了分析这一问题,我们收集了一段时间内的产品销售额、广告投入、季节因素和竞争对手销售额的数据。
这些数据将作为我们多元线性回归模型的输入变量。
模型建立:我们将建立一个多元线性回归模型,以产品销售额作为因变量,广告投入、季节因素和竞争对手销售额作为自变量。
通过对数据进行拟合和参数估计,我们可以得到一个多元线性回归方程,从而揭示不同自变量对产品销售额的影响。
模型分析:通过对模型的分析,我们可以得出以下结论:1. 广告投入对产品销售额有显著影响,广告投入越大,产品销售额越高。
2. 季节因素也对产品销售额有一定影响,不同季节的销售额存在差异。
3. 竞争对手销售额对产品销售额也有一定影响,竞争对手销售额越大,产品销售额越低。
模型预测:基于建立的多元线性回归模型,我们可以进行产品销售额的预测。
通过输入不同的广告投入、季节因素和竞争对手销售额,我们可以预测出相应的产品销售额,从而为公司的营销决策提供参考。
结论:通过以上分析,我们可以得出多元线性回归模型在分析产品销售额与广告投入、季节因素和竞争对手销售额之间关系时的应用。
这种模型不仅可以帮助我们理解不同因素对产品销售额的影响,还可以进行销售额的预测,为公司的决策提供支持。
总结:多元线性回归模型在实际应用中具有重要意义,它可以帮助我们理解复杂的变量关系,并进行有效的预测和决策。
在使用多元线性回归模型时,我们需要注意数据的选择和模型的建立,以确保模型的准确性和可靠性。
通过以上案例,我们对多元线性回归模型的应用有了更深入的理解,希望这对您有所帮助。
多元线性回归分析案例

多元线性回归分析案例1. 引言多元线性回归分析是一种用于探究多个自变量与一个连续型因变量之间关系的统计分析方法。
本文将以一个虚构的案例来介绍多元线性回归分析的应用。
2. 背景假设我们是一家电子产品制造公司,我们想了解哪些因素会对产品销售额产生影响。
为了解决这个问题,我们收集了一些数据,包括产品的价格、广告费用、竞争对手的产品价格和销售额。
3. 数据收集我们采集了100个不同产品的数据,其中包括以下变量:- 产品价格(自变量1)- 广告费用(自变量2)- 竞争对手的产品价格(自变量3)- 销售额(因变量)4. 数据分析为了进行多元线性回归分析,我们首先需要对数据进行预处理。
我们检查了数据的缺失情况和异常值,并进行了相应的处理。
接下来,我们使用多元线性回归模型来分析数据。
模型的方程可以表示为:销售额= β0 + β1 × 产品价格+ β2 × 广告费用+ β3 × 竞争对手的产品价格+ ε其中,β0、β1、β2、β3是回归系数,ε是误差项。
5. 结果解释我们使用统计软件进行回归分析,并得到了以下结果:- 回归系数的估计值:β0 = 1000, β1 = 10, β2 = 20, β3 = -5- 拟合优度:R² = 0.8根据回归系数的估计值,我们可以解释模型的结果:- β0表示当产品价格、广告费用和竞争对手的产品价格都为0时,销售额的估计值为1000。
- β1表示产品价格每增加1单位,销售额平均增加10单位。
- β2表示广告费用每增加1单位,销售额平均增加20单位。
- β3表示竞争对手的产品价格每增加1单位,销售额平均减少5单位。
拟合优度R²的值为0.8,说明模型可以解释销售额的80%变异程度。
这意味着模型对数据的拟合程度较好。
6. 结论根据我们的多元线性回归分析结果,我们可以得出以下结论:- 产品价格、广告费用和竞争对手的产品价格对销售额有显著影响。
(完整word版)多元线性回归模型案例分析

多元线性回归模型案例分析——中国人口自然增长分析一·研究目的要求中国从1971年开始全面开展了计划生育,使中国总和生育率很快从1970年的5.8降到1980年2.24,接近世代更替水平。
此后,人口自然增长率(即人口的生育率)很大程度上与经济的发展等各方面的因素相联系,与经济生活息息相关,为了研究此后影响中国人口自然增长的主要原因,分析全国人口增长规律,与猜测中国未来的增长趋势,需要建立计量经济学模型。
影响中国人口自然增长率的因素有很多,但据分析主要因素可能有:(1)从宏观经济上看,经济整体增长是人口自然增长的基本源泉;(2)居民消费水平,它的高低可能会间接影响人口增长率。
(3)文化程度,由于教育年限的高低,相应会转变人的传统观念,可能会间接影响人口自然增长率(4)人口分布,非农业与农业人口的比率也会对人口增长率有相应的影响。
二·模型设定为了全面反映中国“人口自然增长率”的全貌,选择人口增长率作为被解释变量,以反映中国人口的增长;选择“国名收入”及“人均GDP”作为经济整体增长的代表;选择“居民消费价格指数增长率”作为居民消费水平的代表。
暂不考虑文化程度及人口分布的影响。
从《中国统计年鉴》收集到以下数据(见表1):表1 中国人口增长率及相关数据设定的线性回归模型为:1222334t t t t t Y X X X u ββββ=++++三、估计参数利用EViews 估计模型的参数,方法是:1、建立工作文件:启动EViews ,点击File\New\Workfile ,在对话框“Workfile Range ”。
在“Workfile frequency ”中选择“Annual ” (年度),并在“Start date ”中输入开始时间“1988”,在“end date ”中输入最后时间“2005”,点击“ok ”,出现“Workfile UNTITLED ”工作框。
其中已有变量:“c ”—截距项 “resid ”—剩余项。
多元线性回归分析案例

多元线性回归分析案例多元线性回归分析是统计学中常用的一种分析方法,它可以用来研究多个自变量对因变量的影响,并建立相应的数学模型。
在实际应用中,多元线性回归分析可以帮助我们理解变量之间的关系,预测未来的趋势,以及制定相应的决策。
本文将通过一个实际案例来介绍多元线性回归分析的基本原理和应用方法。
案例背景。
假设我们是一家电子产品制造公司的市场营销团队,我们想要了解产品销量与广告投入、产品定价和市场规模之间的关系。
我们收集了过去一年的数据,包括每个月的产品销量(千台)、广告投入(万元)、产品定价(元/台)和市场规模(亿人)。
数据分析。
首先,我们需要对数据进行描述性统计分析,以了解各变量的分布情况和相关性。
我们计算了产品销量、广告投入、产品定价和市场规模的均值、标准差、最大最小值等统计量,并绘制了相关性矩阵图。
通过分析发现,产品销量与广告投入、产品定价和市场规模之间存在一定的相关性,但具体的关系还需要通过多元线性回归分析来验证。
多元线性回归模型。
我们建立了如下的多元线性回归模型:\[Sales = \beta_0 + \beta_1 \times Advertising + \beta_2 \times Price + \beta_3 \times MarketSize + \varepsilon\]其中,Sales表示产品销量,Advertising表示广告投入,Price表示产品定价,MarketSize表示市场规模,\(\beta_0, \beta_1, \beta_2, \beta_3\)分别为回归系数,\(\varepsilon\)为误差项。
模型验证。
我们利用最小二乘法对模型进行参数估计,并进行了显著性检验和回归诊断。
结果表明,广告投入、产品定价和市场规模对产品销量的影响是显著的,模型的拟合效果较好。
同时,我们还对模型进行了预测能力的验证,结果表明模型对未来产品销量的预测具有一定的准确性。
决策建议。
—多元线性回归分析案例

—多元线性回归分析案例多元线性回归分析是一种广泛使用的统计分析方法,用于研究多个自变量对一个因变量的影响程度。
在实际应用中,多元线性回归可以帮助我们理解变量之间的相互关系,并预测因变量的数值。
下面我们将以一个实际案例来介绍多元线性回归分析的应用。
假设我们是一家电子产品制造商,我们想研究影响手机销量的因素,并尝试通过多元线性回归模型来预测手机的销量。
我们选择了三个自变量作为影响因素:广告投入、价格和市场份额。
我们收集了一段时间内的数据,包括这三个因素以及对应的手机销量。
现在我们将利用这些数据来进行多元线性回归分析。
首先,我们需要将数据进行预处理和清洗。
我们检查数据的完整性和准确性,并去除可能存在的异常值和缺失值。
然后,我们对数据进行描述性统计分析,以了解数据的整体情况和变量之间的关系。
接下来,我们将建立多元线性回归模型。
我们将销量作为因变量,而广告投入、价格和市场份额作为自变量。
通过引入这些自变量,我们可以预测手机销量,并分析它们对销量的影响程度。
为了进行回归分析,我们需要估计模型的系数。
这可以通过最小二乘法来实现,该方法将使得模型的预测结果与实际观测值之间的残差平方和最小化。
接下来,我们将进行统计检验,以确定自变量对因变量的显著影响。
常见的统计指标包括回归系数的显著性水平、t值和p值。
在我们的案例中,假设多元线性回归模型的方程为:销量=β0+β1×广告投入+β2×价格+β3×市场份额+ε。
其中,β0、β1、β2和β3为回归系数,ε为误差项。
完成回归分析后,我们可以进行模型的诊断和评估。
我们可以检查模型的残差是否呈正态分布,以及模型的拟合程度如何。
此外,我们还可以通过交叉验证等方法评估模型的准确性和可靠性。
最后,我们可以利用训练好的多元线性回归模型来进行预测。
通过输入新的广告投入、价格和市场份额的数值,我们可以预测手机的销量,并根据预测结果制定相应的市场策略。
综上所述,多元线性回归分析是一种强大的统计工具,可用于分析多个自变量对一个因变量的影响。
多元线性回归模型案例

多元线性回归模型案例在统计学中,多元线性回归是一种用于研究多个自变量与一个因变量之间关系的方法。
它可以帮助我们了解各个自变量对因变量的影响程度,并预测因变量的取值。
本文将通过一个实际案例来介绍多元线性回归模型的应用。
案例背景:假设我们是一家房地产公司的数据分析师,公司希望通过分析房屋的各项特征来预测房屋的销售价格。
我们收集了一批房屋的数据,包括房屋的面积、卧室数量、浴室数量、地理位置等多个自变量,以及每套房屋的销售价格作为因变量。
数据准备:首先,我们需要对收集到的数据进行清洗和处理。
这包括处理缺失值、异常值,对数据进行标准化等操作,以确保数据的质量和可靠性。
在数据准备阶段,我们还需要将数据分为训练集和测试集,以便后续模型的建立和验证。
模型建立:接下来,我们使用多元线性回归模型来建立房屋销售价格与各项特征之间的关系。
假设我们的模型为:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε。
其中,Y表示房屋销售价格,X1、X2、...、Xn表示房屋的各项特征,β0、β1、β2、...、βn表示模型的系数,ε表示误差项。
模型评估:建立模型后,我们需要对模型进行评估,以验证模型的拟合程度和预测能力。
我们可以使用各项统计指标如R方、均方误差等来评估模型的拟合程度和预测能力,同时也可以通过绘制残差图、QQ图等来检验模型的假设是否成立。
模型优化:在评估模型的过程中,我们可能会发现模型存在欠拟合或过拟合的问题,需要对模型进行优化。
优化的方法包括添加交互项、引入多项式项、进行特征选择等操作,以提高模型的拟合程度和预测能力。
模型应用:最后,我们可以使用优化后的模型来预测新的房屋销售价格。
通过输入房屋的各项特征,模型可以给出相应的销售价格预测值,帮助公司进行房地产市场的决策和规划。
结论:通过本案例,我们了解了多元线性回归模型在房地产数据分析中的应用。
通过建立、评估、优化和应用模型的过程,我们可以更好地理解各项特征对房屋销售价格的影响,并进行有效的预测和决策。
多元线性回归模型的案例讲解

多元线性回归模型的案例讲解案例:房价预测在房地产市场中,了解各种因素对房屋价格的影响是非常重要的。
多元线性回归模型是一种用于预测房屋价格的常用方法。
在这个案例中,我们将使用多个特征来预测房屋的价格,例如卧室数量、浴室数量、房屋面积、地段等。
1.数据收集与预处理为了构建一个准确的多元线性回归模型,我们需要收集足够的数据。
我们可以从多个渠道收集房屋销售数据,例如房地产公司的数据库或者在线平台。
数据集应包括房屋的各种特征,例如卧室数量、浴室数量、房屋面积、地段等,以及每个房屋的实际销售价格。
在数据收集过程中,我们还需要对数据进行预处理。
这包括处理缺失值、异常值和重复值,以及进行特征工程,例如归一化或标准化数值特征,将类别特征转换为二进制变量等。
2.模型构建在数据预处理完成后,我们可以开始构建多元线性回归模型。
多元线性回归模型的基本方程可以表示为:Y=β0+β1X1+β2X2+……+βnXn其中,Y表示房屋价格,X1、X2、……、Xn表示各种特征,β0、β1、β2、……、βn表示回归系数。
在建模过程中,我们需要选择合适的特征来构建模型。
可以通过统计分析或者领域知识来确定哪些特征对房价具有显著影响。
3.模型评估与验证构建多元线性回归模型后,我们需要对模型进行评估和验证。
最常用的评估指标是均方误差(Mean Squared Error)和决定系数(R-squared)。
通过计算预测值与实际值之间的误差平方和来计算均方误差。
决定系数可以衡量模型对观测值的解释程度,取值范围为0到1,越接近1表示模型越好。
4.模型应用完成模型评估与验证后,我们可以将模型应用于新的数据进行房价预测。
通过将新数据的各个特征代入模型方程,可以得到预测的房价。
除了房价预测,多元线性回归模型还可以用于其他房地产市场相关问题的分析,例如预测租金、评估土地价格等。
总结:多元线性回归模型可以在房地产市场的房价预测中发挥重要作用。
它可以利用多个特征来解释房价的变化,并提供准确的价格预测。
多元线性回归模型案例

多元线性回归模型案例多元线性回归模型是一种用于分析多个自变量和一个因变量之间关系的统计方法。
它可以帮助我们理解不同自变量对因变量的影响程度,以及它们之间的相互关系。
在本文中,我们将通过一个实际案例来演示多元线性回归模型的应用。
假设我们想要研究某个地区的房屋价格与房屋面积、房间数量和地理位置之间的关系。
我们收集了一些数据,包括不同房屋的面积、房间数量、地理位置和售价。
我们希望利用这些数据建立一个多元线性回归模型,以预测房屋价格。
首先,我们需要对数据进行预处理。
这包括检查数据是否存在缺失值、异常值或离群点。
如果发现这些问题,我们需要进行相应的处理,例如删除缺失值、调整异常值或使用合适的方法进行离群点处理。
在数据预处理完成后,我们可以开始建立多元线性回归模型。
建立多元线性回归模型的第一步是选择自变量。
在本例中,我们选择房屋面积、房间数量和地理位置作为自变量,售价作为因变量。
接下来,我们需要检验自变量之间是否存在多重共线性。
如果存在多重共线性,我们需要进行相应的处理,例如删除一些自变量或使用主成分分析等方法进行处理。
一旦确定了自变量,我们可以利用最小二乘法来估计回归系数。
最小二乘法是一种常用的估计方法,它可以帮助我们找到使得观测数据和模型预测值之间残差平方和最小的回归系数。
通过最小二乘法,我们可以得到每个自变量的回归系数,从而建立多元线性回归模型。
建立好多元线性回归模型后,我们需要对模型进行检验。
这包括检验模型的拟合优度、残差的正态性和独立性等。
如果模型通过了检验,我们就可以利用该模型进行预测和推断。
例如,我们可以利用模型来预测某个房屋的售价,或者利用模型来推断不同自变量对售价的影响程度。
在实际应用中,多元线性回归模型可以帮助我们理解复杂的数据关系,进行预测和推断。
然而,我们也需要注意模型的局限性和假设条件。
例如,多元线性回归模型假设自变量和因变量之间是线性关系,如果实际情况并非如此,我们需要考虑使用其他模型进行分析。
多元线性回归方法及其应用实例

多元线性回归方法及其应用实例多元线性回归方法(Multiple Linear Regression)是一种广泛应用于统计学和机器学习领域的回归分析方法,用于研究自变量与因变量之间的关系。
与简单线性回归不同,多元线性回归允许同时考虑多个自变量对因变量的影响。
多元线性回归建立了自变量与因变量之间的线性关系模型,通过最小二乘法估计回归系数,从而预测因变量的值。
其数学表达式为:Y=β0+β1X1+β2X2+...+βnXn+ε,其中Y是因变量,Xi是自变量,βi是回归系数,ε是误差项。
1.房价预测:使用多个自变量(如房屋面积、地理位置、房间数量等)来预测房价。
通过建立多元线性回归模型,可以估计出各个自变量对房价的影响权重,从而帮助房产中介或购房者进行房价预测和定价。
2.营销分析:通过分析多个自变量(如广告投入、促销活动、客户特征等)与销售额之间的关系,可以帮助企业制定更有效的营销策略。
多元线性回归可以用于估计各个自变量对销售额的影响程度,并进行优化。
3.股票分析:通过研究多个自变量(如市盈率、市净率、经济指标等)与股票收益率之间的关系,可以辅助投资者进行股票选择和投资决策。
多元线性回归可以用于构建股票收益率的预测模型,并评估不同自变量对收益率的贡献程度。
4.生理学研究:多元线性回归可应用于生理学领域,研究多个自变量(如年龄、性别、体重等)对生理指标(如心率、血压等)的影响。
通过建立回归模型,可以探索不同因素对生理指标的影响,并确定其重要性。
5.经济增长预测:通过多元线性回归,可以将多个自变量(如人均GDP、人口增长率、外商直接投资等)与经济增长率进行建模。
这有助于政府和决策者了解各个因素对经济发展的影响力,从而制定相关政策。
在实际应用中,多元线性回归方法有时也会面临一些挑战,例如共线性(多个自变量之间存在高度相关性)、异方差性(误差项方差不恒定)、自相关(误差项之间存在相关性)等问题。
为解决这些问题,研究人员提出了一些改进和扩展的方法,如岭回归、Lasso回归等。
多元线性回归模型案例

多元线性回归模型案例多元线性回归是统计学中常用的一种回归分析方法,它可以用来研究多个自变量对因变量的影响程度,是一种多元变量之间关系的分析方法。
在实际应用中,多元线性回归模型可以用来预测和解释各种现象,比如销售额、市场份额、股票价格等。
下面我们通过一个实际案例来介绍多元线性回归模型的应用。
假设我们有一个电商平台的数据,其中包括了用户的年龄、性别、购买次数和消费金额等信息。
我们想通过这些信息来建立一个多元线性回归模型,以预测用户的消费金额。
首先,我们收集了一定数量的数据样本,并进行了数据清洗和预处理工作,确保数据的准确性和完整性。
接下来,我们需要建立多元线性回归模型。
在多元线性回归模型中,我们以消费金额作为因变量,而年龄、性别和购买次数作为自变量。
我们假设消费金额与这些自变量之间存在线性关系,然后通过最小二乘法来估计模型参数。
最终得到的多元线性回归模型可以表示为:Y = β0 + β1X1 + β2X2 + β3X3 + ε。
其中,Y代表消费金额,X1、X2、X3分别代表年龄、性别和购买次数,β0、β1、β2、β3是模型的参数,ε是误差项。
通过建立多元线性回归模型,我们可以得到各个自变量对因变量的影响程度,从而进行预测和分析。
比如,我们可以利用模型来预测不同年龄、性别和购买次数的用户的消费金额,以便进行精准营销和产品定位。
另外,我们还可以通过模型来分析各个自变量之间的相关性,从而深入了解用户的消费行为规律。
在实际应用中,多元线性回归模型还可以进行模型检验和优化。
我们可以利用残差分析、方差膨胀因子等方法来检验模型的拟合效果和自变量的共线性问题,从而提高模型的准确性和稳定性。
总的来说,多元线性回归模型是一种强大的分析工具,可以用来研究多个自变量对因变量的影响,进行预测和解释。
在实际应用中,我们可以根据具体的问题和数据特点来选择合适的自变量,建立多元线性回归模型,并进行模型检验和优化,以实现精准分析和预测。
多元线性回归模型的案例讲解
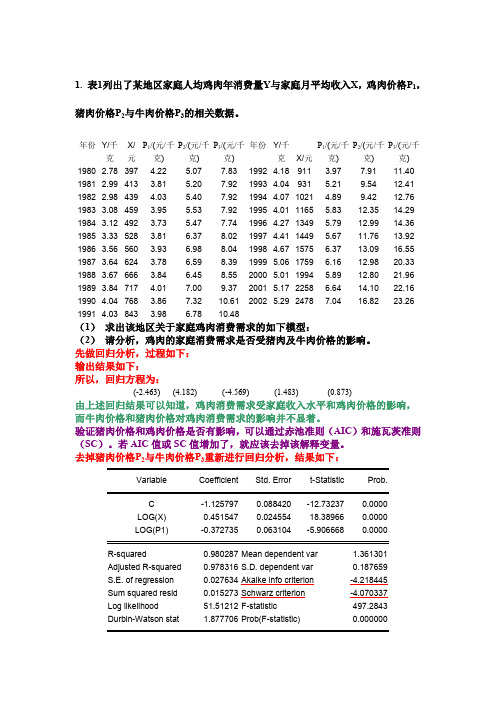
1. 表1列出了某地区家庭人均鸡肉年消费量Y与家庭月平均收入X,鸡肉价格P1,猪肉价格P2与牛肉价格P3的相关数据。
年份Y/千克X/元P1/(元/千克)P2/(元/千克)P3/(元/千克)年份Y/千克X/元P1/(元/千克)P2/(元/千克)P3/(元/千克)1980 2.78 397 4.22 5.07 7.83 1992 4.18 911 3.97 7.91 11.40 1981 2.99 413 3.81 5.20 7.92 1993 4.04 931 5.21 9.54 12.41 1982 2.98 439 4.03 5.40 7.92 1994 4.07 1021 4.89 9.42 12.76 1983 3.08 459 3.95 5.53 7.92 1995 4.01 1165 5.83 12.35 14.29 1984 3.12 492 3.73 5.47 7.74 1996 4.27 1349 5.79 12.99 14.36 1985 3.33 528 3.81 6.37 8.02 1997 4.41 1449 5.67 11.76 13.92 1986 3.56 560 3.93 6.98 8.04 1998 4.67 1575 6.37 13.09 16.55 1987 3.64 624 3.78 6.59 8.39 1999 5.06 1759 6.16 12.98 20.33 1988 3.67 666 3.84 6.45 8.55 2000 5.01 1994 5.89 12.80 21.96 1989 3.84 717 4.01 7.00 9.37 2001 5.17 2258 6.64 14.10 22.16 1990 4.04 768 3.86 7.32 10.61 2002 5.29 2478 7.04 16.82 23.26 1991 4.03 843 3.98 6.78 10.48(1)求出该地区关于家庭鸡肉消费需求的如下模型:(2)请分析,鸡肉的家庭消费需求是否受猪肉及牛肉价格的影响。
多元线性回归模型的案例分析

多元线性回归模型的案例分析在实际生活中,多元线性回归模型可以广泛应用于各个领域。
以下是一个案例分析,以说明多元线性回归模型的应用。
案例:房价预测背景:城市的房地产公司想要推出一款房屋估价服务,帮助人们预测房屋的销售价格。
他们收集了一些相关数据,如房屋的面积、房间的数量、地理位置等因素,并希望通过建立一个多元线性回归模型来实现房价的预测。
步骤:1.数据收集:收集相关数据。
在本案例中,我们收集到了50个样本数据,每个样本包含了房屋的面积、房间的数量和房屋的销售价格。
2.数据预处理:对数据进行预处理,包括缺失值处理、异常值处理等。
在本案例中,我们假设数据已经经过清洗,没有缺失值和异常值。
3.特征选择:选择合适的特征变量。
在本案例中,我们选择房屋的面积和房间的数量作为特征变量,房屋的销售价格作为目标变量。
4.模型建立:建立多元线性回归模型。
根据特征变量和目标变量的关系,建立多元线性回归方程。
在本案例中,假设多元线性回归方程为:房价=β0+β1×面积+β2×房间数量+ε,其中β0、β1和β2分别为回归系数,ε为误差项。
5.模型训练:使用样本数据对模型进行训练。
通过最小二乘法等方法,估计出回归系数的取值。
6.模型评估:评估模型的性能。
通过计算模型的均方误差(MSE)、决定系数(R²)等指标,评估模型的拟合效果和预测能力。
7.模型应用:将模型用于房价的预测。
当有新的房屋数据输入时,通过模型的预测方程,可以得到该房屋的预测销售价格。
通过上述步骤,我们可以建立一个多元线性回归模型,并通过该模型对房价进行预测。
这个模型可以帮助房地产公司提供房价估价服务,也可以帮助购房者了解合理的房价范围。
多元线性回归模型案例

多元线性回归模型案例多元线性回归是一种常见的统计分析方法,用于建立一个因变量与多个自变量之间的关系模型。
该模型可以帮助我们理解自变量对因变量的影响,并用于预测新数据的因变量取值。
本文将介绍一个实际案例,说明如何使用多元线性回归模型进行分析。
假设我们是一家电商公司,想要探究哪些因素会对在线销售额产生影响。
为了实现这一目标,我们收集了一年内的销售数据,并选取了以下变量作为自变量:1.广告费用:对于每个月,我们记录了投入到在线广告的费用。
2.促销活动:我们将每种促销活动的销售额记录成一个二进制变量,代表该促销活动是否进行。
3.季节性:我们记录了每个月的季节性变量,例如,一年中的第一个季度为1,第二个季度为2,以此类推。
同时,我们将每月的销售额作为因变量。
基于这些数据,我们将应用多元线性回归模型来分析这些自变量对销售额的影响。
首先,我们需要进行数据预处理。
这包括处理缺失值,检查异常值,并将分类变量进行独热编码转换。
我们还可以计算自变量之间的相关性,以了解它们是否具有高度相关性。
如果有,我们可能需要进行变量转换或删除一些自变量。
接下来,我们可以使用多元线性回归模型来建立销售额与自变量之间的关系。
模型可以表示如下:销售额=β₀+β₁×广告费用+β₂×促销活动+β₃×季节性+ɛ其中,β₀,β₁,β₂,β₃是回归系数,ɛ是误差项。
我们的目标是估计这些回归系数,以便预测新数据的销售额。
为了估计这些回归系数,我们可以使用最小二乘法。
最小二乘法的核心思想是最小化残差平方和,即模型预测值与实际值之间的差异。
通过最小化这个差异,我们可以找到使模型最拟合数据的回归系数。
在我们的案例中,我们可以使用各种统计软件或编程语言(如R或Python)来实现多元线性回归,并计算回归系数的估计值。
这些软件和语言通常具有内置的回归函数,只需提供数据和自变量就可以进行回归分析。
一旦我们获得了估计的回归系数,我们可以进行模型的解释和推断。
多元线性回归案例分析

多元线性回归案例分析案例背景:我们假设有一家制造业公司,想要研究员工的工作效率与其工作经验、教育水平和工作时间之间的关系。
公司收集了100名员工的数据,并希望通过多元线性回归模型来分析这些变量之间的关系。
数据收集:公司收集了每个员工的工作效率(因变量)、工作经验、教育水平和工作时间(自变量)的数据。
假设工作效率由工作经验、教育水平和工作时间这三个因素决定。
根据所收集的数据,我们可以建立如下的多元线性回归模型:工作效率=β0+β1*工作经验+β2*教育水平+β3*工作时间+ε在这个模型中,β0、β1、β2和β3分别是待估参数,代表截距和自变量的系数;ε是误差项,代表模型中未被解释的因素。
模型参数的估计:通过最小二乘法可以对模型中的参数进行估计。
最小二乘法的目标是让模型的预测值与观测值之间的残差平方和最小化。
模型诊断:在对模型进行参数估计后,我们需要对模型进行诊断,以评估模型的质量和稳定性。
常见的模型诊断方法包括:检查残差的正态分布、残差与自变量的无关性、残差的同方差性等。
模型解释和预测:根据参数估计结果,可以对模型进行解释和预测。
例如,我们可以解释每个自变量与因变量之间的关系,并分析它们的显著性。
我们还可以通过模型进行预测,比如预测一位具有一定工作经验、教育水平和工作时间的员工的工作效率。
结果分析:根据对模型的诊断和解释,我们可以对结果进行分析。
我们可以得出结论,一些自变量对因变量的影响显著,而其他自变量对因变量的影响不显著。
这些结论可以帮助公司更好地理解员工工作效率与工作经验、教育水平和工作时间之间的关系,并采取相应的管理措施来提高工作效率。
总结:通过以上的案例分析,我们可以看到多元线性回归在实际中的应用。
它可以帮助我们理解多个自变量与一个因变量之间的关系,并对因变量进行预测和解释。
通过多元线性回归分析,我们可以更好地了解因素对于结果的作用,并根据分析结果进行决策和管理。
然而,需要注意的是,多元线性回归的结果可能受到多种因素的影响,我们需要综合考虑所有的因素来做出准确的分析和决策。
多元线性回归模型案例

多元线性回归模型案例多元线性回归模型是统计学中常用的一种回归分析方法,它可以用来研究多个自变量对因变量的影响。
在实际应用中,多元线性回归模型可以帮助我们理解和预测各种复杂的现象,比如销售额和广告投入、学生成绩和学习时间等等。
接下来,我们将通过一个实际的案例来详细介绍多元线性回归模型的应用。
案例背景:假设我们是一家电子产品公司的市场营销团队,我们想要了解广告投入、产品定价和促销活动对销售额的影响。
为了实现这个目标,我们收集了一段时间内的销售数据,并且记录了每个月的广告投入、产品定价和促销活动的情况。
现在,我们希望利用这些数据来建立一个多元线性回归模型,从而分析这些因素对销售额的影响。
数据收集:首先,我们需要收集相关的数据。
在这个案例中,我们收集了一段时间内的销售额、广告投入、产品定价和促销活动的数据。
这些数据可以帮助我们建立多元线性回归模型,并且进行相关的分析。
建立模型:接下来,我们将利用收集到的数据来建立多元线性回归模型。
在多元线性回归模型中,我们将销售额作为因变量,而广告投入、产品定价和促销活动作为自变量。
通过建立这个模型,我们可以分析这些因素对销售额的影响,并且进行预测。
模型分析:一旦建立了多元线性回归模型,我们就可以进行相关的分析。
通过分析模型的系数、拟合优度等指标,我们可以了解每个自变量对销售额的影响程度,以及整个模型的拟合情况。
这些分析结果可以帮助我们更好地理解销售额的变化规律,以及各个因素之间的关系。
模型预测:除了分析模型的影响,多元线性回归模型还可以用来进行预测。
通过输入不同的自变量数值,我们可以预测对应的销售额。
这样的预测结果可以帮助我们制定更加合理的市场营销策略,从而提高销售业绩。
模型评估:最后,我们需要对建立的多元线性回归模型进行评估。
通过对模型的残差、预测误差等进行分析,我们可以了解模型的准确性和可靠性。
如果模型的预测效果不理想,我们还可以通过改进模型结构、增加自变量等方式来提高模型的预测能力。
多元线性回归案例

多元线性回归案例多元线性回归是一种统计分析方法,用于研究自变量与因变量之间的关系。
它可以帮助我们理解多个自变量对因变量的影响,并预测因变量的数值。
在本文中,我们将通过一个实际的案例来介绍多元线性回归的应用。
假设我们想要研究一个人的身高与体重之间的关系,同时考虑年龄和性别对这种关系的影响。
我们收集了一组数据,包括个体的身高、体重、年龄和性别。
我们希望利用这些数据建立一个多元线性回归模型,来预测一个人的体重。
首先,我们需要对数据进行分析和处理。
我们可以计算身高、体重、年龄和性别之间的相关系数,来初步了解它们之间的关系。
然后,我们可以利用散点图来观察变量之间的分布情况,以及可能存在的异常值或者离群点。
接下来,我们可以利用多元线性回归模型来建立身高、年龄和性别对体重的预测模型。
在建立模型之前,我们需要进行变量选择,选择那些对体重有显著影响的自变量。
然后,我们可以利用最小二乘法来估计模型的参数,得到回归方程。
在得到回归方程之后,我们可以进行模型的诊断和检验。
我们可以利用残差分析来检验模型的拟合优度,以及模型是否满足多元线性回归的假设。
如果模型不符合要求,我们可以进行适当的变换或者调整,来改善模型的拟合效果。
最后,我们可以利用建立的多元线性回归模型来进行预测。
我们可以输入新的个体数据,来预测其体重,并对预测结果进行评估和验证。
如果模型的预测效果不理想,我们可以考虑进行模型的改进或者调整。
总之,多元线性回归是一种强大的统计分析方法,可以帮助我们理解和预测多个自变量对因变量的影响。
通过本文的案例介绍,相信读者对多元线性回归有了更深入的理解,也能够更好地应用它来解决实际问题。
希望本文能够对读者有所帮助,谢谢阅读!。
多元线性回归的案例

多元线性回归的案例多元线性回归是一种统计方法,用于研究多个自变量对因变量的影响程度和方向。
在实际应用中,多元线性回归可以用于解释自然和社会科学领域中的现象和问题。
以下是一些多元线性回归的案例,以说明其在不同领域中的应用。
1.金融领域:多元线性回归可以用于解释股票市场中股价的涨跌。
自变量可以包括经济指标(如GDP、CPI)、公司财报数据(如销售额、利润)和市场相关信息(如市盈率、市净率)。
通过构建模型,可以分析不同自变量对股价的影响,并预测未来的股价走势。
2.医学研究:多元线性回归可以用于分析医学数据,如研究一种药物对疾病治疗效果的影响。
自变量可以包括药物剂量、患者的年龄、性别等因素。
通过建立模型,可以评估不同因素对治疗效果的影响,并制定合理的治疗方案。
3.教育领域:多元线性回归可以用于研究教育投入和学生考试成绩之间的关系。
自变量可以包括学校的教师数量、教育经费、学生人数等因素。
通过建立模型,可以分析这些因素对学生成绩的影响,并为改善教育质量提供科学依据。
4.市场营销:多元线性回归可以用于分析消费者购买行为。
自变量可以包括产品价格、广告投入和竞争对手的行动等因素。
通过建立模型,可以了解这些因素对消费者决策的影响,制定有效的市场营销策略,提高产品销售量。
5.环境科学:多元线性回归可以用于分析环境污染的原因和影响因素。
自变量可以包括工业排放数量、交通流量、气候条件等因素。
通过建立模型,可以了解不同因素对环境污染的贡献程度,制定合理的环境保护政策。
以上仅是多元线性回归的一些应用案例,实际上,它在各个领域都有广泛的应用。
在使用多元线性回归时,需要注意数据的选择和分析方法的合理性,以准确评估自变量对因变量的影响。
同时,还可以通过模型的调整和检验,不断优化预测效果,提高研究的科学性和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多元线性回归模型的案
例讲解
Revised as of 23 November 2020
1. 表1列出了某地区家庭人均鸡肉年消费量Y与家庭月平均收入X,鸡肉价格P1,猪肉价格P2与牛肉价格P3的相关数据。
年份Y/
千克X/
元
P1/(元/
千克)
P2/(元/
千克)
P3/(元/
千克)
年份Y/
千
克X/元
P1/(元/
千克)
P2/(元/
千克)
P3/(元/
千克)
1980 397 1992 911
1981 413 1993 931
1982 439 1994 1021
1983 459 1995 1165
1984 492 1996 1349
1985 528 1997 1449
1986 560 1998 1575
1987 624 1999 1759
1988 666 2000 1994
1989 717 2001 2258
1990 768 2002 2478
1991 843
(1)求出该地区关于家庭鸡肉消费需求的如下模型:
(2)请分析,鸡肉的家庭消费需求是否受猪肉及牛肉价格的影响。
先做回归分析,过程如下:
输出结果如下:
所以,回归方程为:
由上述回归结果可以知道,鸡肉消费需求受家庭收入水平和鸡肉价格的影响,而牛肉价格和猪肉价格对鸡肉消费需求的影响并不显着。
验证猪肉价格和鸡肉价格是否有影响,可以通过赤池准则(AIC)和施瓦茨准则(SC)。
若AIC值或SC值增加了,就应该去掉该解释变量。
去掉猪肉价格P2与牛肉价格P3重新进行回归分析,结果如下:
Variable Coefficient Std. Error t-Statistic Prob.
C
LOG(X)
LOG(P1)
R-squared
Mean dependent var
Adjusted R-squared . dependent var . of regression
Akaike info criterion Sum squared resid Schwarz criterion Log likelihood
F-statistic
Durbin-Watson stat
Prob(F-statistic)
通过比较可以看出,AIC 值和SC 值都变小了,所以应该去掉猪肉价格P 2与牛肉价格P 3这两个解释变量。
所以该地区猪肉与牛肉价格确实对家庭的鸡肉消费不产生显着影响。
2. 表2列出了中国2012年按行业分的全部制造业国有企业及规模以上制造业非国有企业的工业总产值Y ,资产合计K 及职工人数L 。
序号 工业总产值Y/亿元 资产合计K/亿元 职工人数L/万人
序号 工业总产值Y/亿元 资产合计K/亿元 职工人数L/万人
1 17
2 18
3 19
4 20
5 21
6 22
7 23
8 24
9 25 10 26 11 27 12 28 13 29 14 30 15 31
16
设定模型为:Y AK L e αβμ=
(1) 利用上述资料,进行回归分析;
(2) 回答:中国2000年的制造业总体呈现规模报酬不变状态吗 将模型进行双对数变换如下: 1)进行回归分析:
得到如下回归结果: 于是,样本回归方程为:
从回归结果可以看出,模型的拟合度较好,在显着性水平的条件下,各项系数均通过了t 检验。
从F 检验可以看出,方程对Y 的解释程度较少。
0.7963R =表明,工业总产值对数值的%的变化可以由资产合计对数与职工的对数值
的变化来解释,但仍有%的变化是由其他因素的变化影响的。
从上述回归结果看,ˆˆ0.971α
β+=≈,即资产与劳动的产出弹性之和近似为1,表明中国制造业在2000年基本呈现规模报酬不变的状态。
下面进行Wald 检验对约束关系进行检验。
过程如下: 结果如下:
由对应概率可以知道,不能拒绝原假设,即资产与劳动的产出弹性之和为1,表明中国制造业在2000年呈现规模报酬不变的状态。
一、邹式检验(突变点检验、稳定性检验)
1.突变点检验
1995-2012年中国家用汽车拥有量(t y ,万辆)与城镇居民家庭人均可支配收入(t x ,元),数据见表3。
表3 中国家用汽车拥有量(t y )与城镇居民家庭人均可支配收入(t x )数据
年份 t y (万辆) t
x (元) 年份 t y (万辆) t
x (元) 1995
2004 1996 2005 4283 1997 2006 1998
2007
1999 2008 2000 2009 5854 2001 2010 6280 2002 2011 2003 2012
下图是关于t y 和t x 的散点图:
从上图可以看出,2006年是一个突变点,当城镇居民家庭人均可支配收入突破元之后,城镇居民家庭购买家用汽车的能力大大提高。
现在用邹突变点检验法检验1996年是不是一个突变点。
H 0:两个字样本(1995—2005年,2006—2012年)相对应的模型回归参数相等 H 1:备择假设是两个子样本对应的回归参数不等。
在1995—2012年样本范围内做回归。
在回归结果中作如下步骤: 输入突变点: 得到如下验证结果:
由相伴概率可以知道,拒绝原假设,即两个样本(1995—2005年,2006—2012年)的回归参数不相等。
所以,2006年是突变点。
2.稳定性检验
以表3为例,在用1995—2009年数据建立的模型基础上,检验当把2010—2012年数据加入样本后,模型的回归参数时候出现显着性变化。
因为已经知道2006年为结构突变点,所以设定虚拟变量:019952005
1120062012D -⎧⎨-⎩
对1995—2012年的数据进行回归分析: 做邹氏稳定性检验: 输入要检验的样本点:
得到如下检验结果:
由上述结果可以知道,F 值对应的概率为,所以接受原假设,模型加入2010、2011和2012年的样本值后,回归参数没有发生显着性变化。
二、似然比(LR )检验
有中国国债发行总量(t DEBT ,亿元)模型如下:
其中t GDP 表示国内生产总值(百亿元),t DEF 表示年财政赤字额(亿元),t REPAY 表示年还本付息额(亿元)。
1990—2011年数据见表4。
表4 国债发行总量t DEBT 、t GDP 、财政赤字额t DEF 、年还本付息额(t REPAY )数据
1990 2001 1991 2002 1992 2003 1993 2004 1994 2005 1995 2006 1996 2007 1997 2008
1998 2009 1999 2010 2000 2011 4604
对以上数据进行回归分析: 得到如下输出结果:
对应的回归表达式为:
现在用似然比(LR )统计量检验约束t GDP 对应的回归系数1 等于零是否成立。
过程如下:
输入要检验的变量名: 得到如下输出结果:
输出结果上部是关于约束GDP 系数为零的F 检验和LR 检验。
由于两种检验的相应概率均小于,即拒接原假设,GDP 系数1β不为零,模型中应该保留解释变量GDP 。
输出结果下部是去掉了GDP 变量的约束模型估计结果。
三、Wald 检验(以表4为例进行Wald 检验,对输出结果进行检验。
)
检验过程如下: 输入约束表达式: 得到如下结果:
从输出结果上部可以看出,相应概率非常大,远远大于,表明原假设成立,即约束条件3*(2)(3)c c =成立,2β是1β的3倍。
输出结果的下部给出了约束条件
3*(2)(3)0c c -=的样本值和样本标准差,分别为和。
