中考数学易错题精选-平行四边形练习题及答案
中考数学二轮复习数学平行四边形的专项培优易错试卷练习题含答案

中考数学二轮复习数学平行四边形的专项培优易错试卷练习题含答案一、选择题1.如图,在Rt △ABC 中,∠A=30°,BC=2,点D ,E 分别是直角边BC ,AC 的中点,则DE 的长为( )A .2B .3C .4D .232.将个边长都为1cm 的正方形按如图所示的方法摆放,点分别是正方形对角线的交点,则2019个正方形重叠形成的重叠部分的面积和为( )A .B .C .D .3.如图,在正方形ABCD 中,E ,F 分别为BC ,DC 的中点,P 为对角线AC 上的一个动点,则下列线段的长等于BP EP +最小值的是( )A .AB B .CEC .ACD .AF4.如图,矩形ABCD 中,AB =2,对角线AC 、BD 交于点O ,∠AOD =120°,E 为BD 上任意点,P 为AE 中点,则PO +PB 的最小值为 ( )A 3B .13C 7D .35.如图,四边形ABCD 中,,,,AC a BD b AC BD ==⊥顺次连接四边形ABCD 各边中点,得到四边形1111D C B A ,再顺次连接四边形1111D C B A 各边中点,得到四边形2222A B C D ...如此进行下去,得到四边形.n n n n A B C D 则下列结论正确的个数有( ) ①四边形1111D C B A 是矩形;②四边形4444A B C D 是菱形;③四边形5555A B C D 的周长为4a b +; ④四边形n n n n A B C D 的面积是12n ab +.A .4个B .3个C .2个D .1个 6.如图,E 是边长为2的正方形ABCD 的对角线AC 上一点,且AE AB =,F 为BE 上任意一点,FG AC 于点G ,FH AB ⊥于点H ,则FG FH +的值是( )A .22B .2C .2D .17.将矩形纸片ABCD 按如图所示的方式折叠,AE 、EF 为折痕,∠BAE =30°,AB =3 ,折叠后,点C 落在AD 边上的C 1处,并且点B 落在EC 1边上的B 1处.则BC 的长为( )A .3B .3C .2D .238.如图,四边形ABCD 为平行四边形,D ∠为锐角,BAD ∠的平分线AE 交CD 于点F ,交BC 的延长线于点E ,且AF FE =.若25AB =,ABCD 面积为300,则AF 的长度为( )A .30B .15C .40D .209.如图,在等腰Rt ABC △中,908C AC ∠==°,,F 是AB 边上的中点,点D 、E 分别在AC 、BC 边上运动,且保持AD CE =.连接DE 、DF 、EF .在此运动变化的过程中,下列结论:①DFE △是等腰直角三角形; ②四边形CDFE 不可能为正方形,③DE 长度的最小值为4; ④四边形CDFE 的面积保持不变;⑤△CDE 面积的最大值为8.其中正确的结论是( )A .①②③B .①④⑤C .①③④D .③④⑤10.如图,在平行四边形ABCD 中,AE 平分BAD ∠,交BC 于点E 且AB AE =,延长AB 与DE 的延长线相交于点F ,连接AC 、CF .下列结论:①ABC EAD △≌△;②ABE △是等边三角形;③BF AD =;④BEF ABC S S =△△;⑤CEF ABE S S =△△;其中正确的有( )A .2个B .3个C .4个D .5个二、填空题11.在平行四边形ABCD 中,30,23,2A AD BD ∠=︒==,则平行四边形ABCD 的面积等于_____.12.如图,正方形ABCD 的对角线相交于点O ,对角线长为1cm ,过点O 任作一条直线分别交AD ,BC 于E ,F ,则阴影部分的面积是_____.13.如图,动点E F 、分别在正方形ABCD 的边AD BC 、上,AE CF =,过点C 作CG EF ⊥,垂足为G ,连接BG ,若4AB =,则线段BG 长的最小值为_________.14.如图,直线1l ,2l 分别经过点(1,0)和(4,0)且平行于y 轴.OABC 的顶点A ,C 分别在直线1l 和2l 上,O 是坐标原点,则对角线OB 长的最小值为_________.15.如图,菱形ABCD 的边长是4,60ABC ∠=︒,点E ,F 分别是AB ,BC 边上的动点(不与点A ,B ,C 重合),且BE BF =,若//EG BC ,//FG AB ,EG 与FG 相交于点G ,当ADG 为等腰三角形时,BE 的长为________.16.如图,在Rt △ABC 中,∠BAC =90°,AB =8,AC =6,以BC 为一边作正方形BDEC 设正方形的对称中心为O ,连接AO ,则AO =_____.17.菱形ABCD 的周长为24,∠ABC=60°,以AB 为腰在菱形外作底角为45°的等腰△ABE ,连结AC ,CE ,则△ACE 的面积为___________.18.已知:一组邻边分别为6cm 和10cm 的平行四边形ABCD ,DAB ∠和ABC ∠的平分线分别交CD 所在直线于点E ,F ,则线段EF 的长为________cm .19.如图,正方形ABCD 的边长为4,点E 为AD 的延长线上一点,且DE =DC ,点P 为边AD 上一动点,且PC ⊥PG ,PG =PC ,点F 为EG 的中点.当点P 从D 点运动到A 点时,则CF 的最小值为___________20.如图,在平行四边形ABCD 中,53AB AD ==,,BAD ∠的平分线AE 交CD 于点E ,连接BE ,若BAD BEC ∠=∠,则平行四边形ABCD 的面积为__________.三、解答题21.如图,矩形OBCD 中,OB =5,OD =3,以O 为原点建立平面直角坐标系,点B ,点D 分别在x 轴,y 轴上,点C 在第一象限内,若平面内有一动点P ,且满足S △POB =13S 矩形OBCD ,问:(1)当点P 在矩形的对角线OC 上,求点P 的坐标;(2)当点P 到O ,B 两点的距离之和PO +PB 取最小值时,求点P 的坐标.22.综合与探究(1)如图1,在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF BE =.CE 和CF 之间有怎样的关系.请说明理由.(2)如图2,在正方形ABCD 中,E 是AB 上一点,G 是AD 上一点,如果45GCE ∠=︒,请你利用(1)的结论证明:GE BE CD =+.(3)运用(1)(2)解答中所积累的经验和知识,完成下题:如图3在直角梯形ABCD 中,//()AD BC BC AD >,90B ∠=︒,12AB BC ==,E 是AB 上一点,且45DCE ∠=︒,4BE =,求DE 的长.23.如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH DE⊥交DG的延长线于点H,连接BH.=;(1)求证:GF GC(2)用等式表示线段BH与AE的数量关系,并证明.24.已知:在ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C 重合).以AD为边作正方形ADEF,连接CF.(1)如图1,当点D在线段BC上时,BD与CF的位置关系为__________;CF、BC、CD三条线段之间的数量关系____________________.(2)如图2,当点D在线段BC的延长线上时,其它条件不变,请你写出CF、BC、CD三条线段之间的数量关系并加以证明;(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系.△的形状,并说明理②若连接正方形对角线AE、DF,交点为O,连接OC,探究AOC由.25.如图,矩形ABCD 中,AB=4,AD=3,∠A 的角平分线交边CD 于点E .点P 从点A 出发沿射线AE 以每秒2个单位长度的速度运动,Q 为AP 的中点,过点Q 作QH ⊥AB 于点H ,在射线AE 的下方作平行四边形PQHM (点M 在点H 的右侧),设P 点运动时间为t 秒.(1)直接写出AQH 的面积(用含t 的代数式表示).(2)当点M 落在BC 边上时,求t 的值.(3)在运动过程中,整个图形中形成的三角形是否存在全等三角形?若存在,请写出所有全等三角形,并求出对应的t 的值;若不存在请说明理由(不能添加辅助线).26.如图.正方形ABCD 的边长为4,点E 从点A 出发,以每秒1个单位长度的速度沿射线AD 运动,运动时间为t 秒(t >0),以AE 为一条边,在正方形ABCD 左侧作正方形AEFG ,连接BF .(1)当t =1时,求BF 的长度;(2)在点E 运动的过程中,求D 、F 两点之间距离的最小值;(3)连接AF 、DF ,当△ADF 是等腰三角形时,求t 的值.27.如图,锐角ABC ∆,AB AC =,点D 是边BC 上的一点,以AD 为边作ADE ∆,使AE AD =,EAD BAC ∠=∠.(1)过点E 作//EF DC 交AB 于点F ,连接CF (如图①)①请直接写出EAB ∠与DAC ∠的数量关系;②试判断四边形CDEF 的形状,并证明;(2)若60BAC ∠=,过点C 作//CF DE 交AB 于点F ,连接EF (如图②),那么(1)②中的结论是否任然成立?若成立,请给出证明,若不成立,请说明理由.28.在直角梯形ABCD 中,AB ∥CD ,∠BCD =90°,AB =AD =10cm ,BC =8cm 。
中考数学易错题精选-平行四边形练习题及详细答案

中考数学易错题精选-平行四边形练习题及详细答案一、平行四边形1.四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.(1)如图1,当点E、F在线段AD上时,①求证:∠DAG=∠DCG;②猜想AG与BE的位置关系,并加以证明;(2)如图2,在(1)条件下,连接HO,试说明HO平分∠BHG;(3)当点E、F运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出∠BHO的度数.【答案】(1)①证明见解析;②AG⊥BE.理由见解析;(2)证明见解析;(3)∠BHO=45°.【解析】试题分析:(1)①根据正方形的性质得DA=DC,∠ADB=∠CDB=45°,则可根据“SAS”证明△ADG≌△CDG,所以∠DAG=∠DCG;②根据正方形的性质得AB=DC,∠BAD=∠CDA=90°,根据“SAS”证明△ABE≌△DCF,则∠ABE=∠DCF,由于∠DAG=∠DCG,所以∠DAG=∠ABE,然后利用∠DAG+∠BAG=90°得到∠ABE+∠BAG=90°,于是可判断AG⊥BE;(2)如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,证明△AON≌△BOM,可得四边形OMHN为正方形,因此HO平分∠BHG结论成立;(3)如答图2所示,与(1)同理,可以证明AG⊥BE;过点O作OM⊥BE于点M,ON⊥AG于点N,构造全等三角形△AON≌△BOM,从而证明OMHN为正方形,所以HO 平分∠BHG,即∠BHO=45°.试题解析:(1)①∵四边形ABCD为正方形,∴DA=DC,∠ADB=∠CDB=45°,在△ADG和△CDG中,∴△ADG≌△CDG(SAS),∴∠DAG=∠DCG;②AG⊥BE.理由如下:∵四边形ABCD为正方形,∴AB=DC,∠BAD=∠CDA=90°,在△ABE和△DCF中,∴△ABE≌△DCF(SAS),∴∠ABE=∠DCF,∵∠DAG=∠DCG,∴∠DAG=∠ABE,∵∠DAG+∠BAG=90°,∴∠ABE+∠BAG=90°,∴∠AHB=90°,∴AG⊥BE;(2)由(1)可知AG⊥BE.如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,则四边形OMHN为矩形.∴∠MON=90°,又∵OA⊥OB,∴∠AON=∠BOM.∵∠AON+∠OAN=90°,∠BOM+∠OBM=90°,∴∠OAN=∠OBM.在△AON与△BOM中,∴△AON≌△BOM(AAS).∴OM=ON,∴矩形OMHN为正方形,∴HO平分∠BHG.(3)将图形补充完整,如答图2示,∠BHO=45°.与(1)同理,可以证明AG⊥BE.过点O作OM⊥BE于点M,ON⊥AG于点N,与(2)同理,可以证明△AON≌△BOM,可得OMHN为正方形,所以HO平分∠BHG,∴∠BHO=45°.考点:1、四边形综合题;2、全等三角形的判定与性质;3、正方形的性质2.如图,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.(1)求证:∠APB=∠BPH;(2)当点P在边AD上移动时,求证:△PDH的周长是定值;(3)当BE+CF的长取最小值时,求AP的长.【答案】(1)证明见解析.(2)证明见解析.(3)2.【解析】试题分析:(1)根据翻折变换的性质得出∠PBC=∠BPH,进而利用平行线的性质得出∠APB=∠PBC即可得出答案;(2)首先证明△ABP≌△QBP,进而得出△BCH≌△BQH,即可得出PD+DH+PH=AP+PD+DH+HC=AD+CD=8;(3)过F作FM⊥AB,垂足为M,则FM=BC=AB,证明△EFM≌△BPA,设AP=x,利用折叠的性质和勾股定理的知识用x表示出BE和CF,结合二次函数的性质求出最值.试题解析:(1)解:如图1,∵PE=BE ,∴∠EBP=∠EPB .又∵∠EPH=∠EBC=90°,∴∠EPH-∠EPB=∠EBC-∠EBP .即∠PBC=∠BPH .又∵AD ∥BC ,∴∠APB=∠PBC .∴∠APB=∠BPH .(2)证明:如图2,过B 作BQ ⊥PH ,垂足为Q .由(1)知∠APB=∠BPH ,又∵∠A=∠BQP=90°,BP=BP ,在△ABP 和△QBP 中,{90APB BPHA BQP BP BP∠=∠∠=∠=︒=,∴△ABP ≌△QBP (AAS ),∴AP=QP ,AB=BQ ,又∵AB=BC ,∴BC=BQ .又∠C=∠BQH=90°,BH=BH ,在△BCH 和△BQH 中,{90BC BQC BQH BH BH=∠=∠=︒=,∴△BCH ≌△BQH (SAS ),∴CH=QH .∴△PHD 的周长为:PD+DH+PH=AP+PD+DH+HC=AD+CD=8.∴△PDH 的周长是定值.(3)解:如图3,过F 作FM ⊥AB ,垂足为M ,则FM=BC=AB .又∵EF 为折痕,∴EF ⊥BP .∴∠EFM+∠MEF=∠ABP+∠BEF=90°,∴∠EFM=∠ABP .又∵∠A=∠EMF=90°,在△EFM 和△BPA 中,{EFM ABPEMF A FM AB∠=∠∠=∠=,∴△EFM ≌△BPA (AAS ).∴EM=AP .设AP=x在Rt △APE 中,(4-BE )2+x 2=BE 2.解得BE=2+28x , ∴CF=BE-EM=2+28x -x , ∴BE+CF=24x -x+4=14(x-2)2+3. 当x=2时,BE+CF 取最小值,∴AP=2.考点:几何变换综合题.3.如图,四边形ABCD 中,对角线AC 、BD 相交于点O ,AO =CO ,BO =DO ,且∠ABC +∠ADC =180°.(1)求证:四边形ABCD 是矩形.(2)若∠ADF :∠FDC =3:2,DF ⊥AC ,求∠BDF 的度数.【答案】(1)见解析;(2)18°.【解析】【分析】(1)根据平行四边形的判定得出四边形ABCD是平行四边形,求出∠ABC=90°,根据矩形的判定得出即可;(2)求出∠FDC的度数,根据三角形内角和定理求出∠DCO,根据矩形的性质得出OD=OC,求出∠CDO,即可求出答案.【详解】(1)证明:∵AO=CO,BO=DO∴四边形ABCD是平行四边形,∴∠ABC=∠ADC,∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴四边形ABCD是矩形;(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,∴∠FDC=36°,∵DF⊥AC,∴∠DCO=90°﹣36°=54°,∵四边形ABCD是矩形,∴OC=OD,∴∠ODC=54°∴∠BDF=∠ODC﹣∠FDC=18°.【点睛】本题考查了平行四边形的性质和判定,矩形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:矩形的对角线相等,有一个角是直角的平行四边形是矩形.4.如图,四边形ABCD中,∠BCD=∠D=90°,E是边AB的中点.已知AD=1,AB=2.(1)设BC=x,CD=y,求y关于x的函数关系式,并写出定义域;(2)当∠B=70°时,求∠AEC的度数;(3)当△ACE为直角三角形时,求边BC的长.【答案】(1)()22303y x x x =-++<<;(2)∠AEC =105°;(3)边BC 的长为2117+. 【解析】试题分析:(1)过A 作AH ⊥BC 于H ,得到四边形ADCH 为矩形.在△BAH 中,由勾股定理即可得出结论.(2)取CD 中点T ,连接TE ,则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD ,∠AET =∠B =70°.又AD =AE =1,得到∠AED =∠ADE =∠DET =35°.由ET 垂直平分CD ,得∠CET =∠DET =35°,即可得到结论.(3)分两种情况讨论:①当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 解△ABH 即可得到结论.②当∠CAE =90°时,易知△CDA ∽△BCA ,由相似三角形对应边成比例即可得到结论. 试题解析:解:(1)过A 作AH ⊥BC 于H .由∠D =∠BCD =90°,得四边形ADCH 为矩形. 在△BAH 中,AB =2,∠BHA =90°,AH =y ,HB =1x -,∴22221y x =+-, 则()22303y x x x =-++<<(2)取CD 中点T ,联结TE ,则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD ,∴∠AET =∠B =70°.又AD =AE =1,∴∠AED =∠ADE =∠DET =35°.由ET 垂直平分CD ,得∠CET =∠DET =35°,∴∠AEC =70°+35°=105°.(3)分两种情况讨论:①当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 则在△ABH 中,∠B =60°,∠AHB =90°,AB =2,得BH =1,于是BC =2.②当∠CAE =90°时,易知△CDA ∽△BCA ,又2224AC BC AB x =-- 则22411724AD CA x x AC CB x x -=⇒=⇒=-(舍负) 易知∠ACE <90°,所以边BC 117+ 综上所述:边BC 的长为2117+.点睛:本题是四边形综合题.考查了梯形中位线,相似三角形的判定与性质.解题的关键是掌握梯形中常见的辅助线作法.5.在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.【答案】(1)证明见解析;(2)证明见解析;(3)EF2=2BE2+2DF2.【解析】试题分析:(1)根据旋转的性质可知AF=AG,∠EAF=∠GAE=45°,故可证△AEG≌△AEF;(2)将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由(1)知△AEG≌△AEF,则EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;(3)将△ADF绕着点A顺时针旋转90°,得到△ABG,根据旋转的性质可以得到△ADF≌△ABG,则DF=BG,再证明△AEG≌△AEF,得出EG=EF,由EG=BG+BE,等量代换得到EF=BE+DF.试题解析:(1)∵△ADF绕着点A顺时针旋转90°,得到△ABG,∴AF=AG,∠FAG=90°,∵∠EAF=45°,∴∠GAE=45°,在△AGE与△AFE中,,∴△AGE≌△AFE(SAS);(2)设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.则△ADF≌△ABG,DF=BG.由(1)知△AEG≌△AEF,∴EG=EF.∵∠CEF=45°,∴△BME、△DNF、△CEF均为等腰直角三角形,∴CE=CF ,BE=BM,NF=DF,∴a﹣BE=a﹣DF,∴BE=DF,∴BE=BM=DF=BG,∴∠BMG=45°,∴∠GME=45°+45°=90°,∴EG2=ME2+MG2,∵EG=EF ,MG=BM=DF=NF,∴EF2=ME2+NF2;(3)EF2=2BE2+2DF2.如图所示,延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.由(1)知△AEH≌△AEF,则由勾股定理有(GH+BE)2+BG2=EH2,即(GH+BE)2+(BM﹣GM)2=EH2又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,即2(DF2+BE2)=EF2考点:四边形综合题6.如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.(1)求证:AD=EC;(2)当∠BAC=Rt∠时,求证:四边形ADCE是菱形.【答案】(1)见解析;(2)见解析.【解析】【分析】(1)先证四边形ABDE是平行四边形,再证四边形ADCE是平行四边形即可;(2)由∠BAC=90°,AD是边BC上的中线,得AD=BD=CD,即可证明.【详解】(1)证明:∵AE∥BC,DE∥AB,∴四边形ABDE是平行四边形,∴AE=BD,∵AD是边BC上的中线,∴BD=DC,∴AE=DC,又∵AE∥BC,∴四边形ADCE是平行四边形.(2) 证明:∵∠BAC=90°,AD是边BC上的中线.∴AD=CD∵四边形ADCE是平行四边形,∴四边形ADCE是菱形.【点睛】本题考查了平行四边形的判定、菱形的判定、直角三角形斜边中线定理.根据图形与已知条件灵活应用平行四边形的判定方法是证明的关键.7.图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.(1)在图1中画出等腰直角三角形MON,使点N在格点上,且∠MON=90°;(2)在图2中以格点为顶点画一个正方形ABCD,使正方形ABCD面积等于(1)中等腰直角三角形MON面积的4倍,并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD面积没有剩余(画出一种即可).【答案】(1)作图参见解析;(2)作图参见解析.【解析】试题分析:(1)过点O向线段OM作垂线,此直线与格点的交点为N,连接MN即可;(2)根据勾股定理画出图形即可.试题解析:(1)过点O向线段OM作垂线,此直线与格点的交点为N,连接MN,如图1所示;(2)等腰直角三角形MON面积是5,因此正方形面积是20,如图2所示;于是根据勾股定理画出图3:考点:1.作图﹣应用与设计作图;2.勾股定理.8.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E 是线段AB的中点,连接CE并延长交线段AD于点F.(1)求证:四边形BCFD为平行四边形;(2)若AB=6,求平行四边形ADBC的面积.【答案】(1)见解析;(2)S平行四边形ADBC273【解析】【分析】(1)在Rt△ABC中,E为AB的中点,则CE=12AB,BE=12AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°.又∠D=60°,得∠AFE=∠D=60度.所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD//BC,则四边形BCFD是平行四边形.(2)在Rt△ABC中,求出BC,AC即可解决问题;【详解】解:(1)证明:在△ABC中,∠ACB=90°,∠CAB=30°,∴∠ABC=60°,在等边△ABD中,∠BAD=60°,∴∠BAD=∠ABC=60°,∵E为AB的中点,∴AE=BE,又∵∠AEF=∠BEC,∴△AEF≌△BEC,在△ABC中,∠ACB=90°,E为AB的中点,∴CE=12AB,BE=12AB,∴CE=AE,∴∠EAC=∠ECA=30°,∴∠BCE=∠EBC=60°,又∵△AEF≌△BEC,∴∠AFE=∠BCE=60°,又∵∠D=60°,∴∠AFE=∠D=60°,∴FC∥BD,又∵∠BAD=∠ABC=60°,∴AD∥BC,即FD∥BC,∴四边形BCFD是平行四边形;(2)解:在Rt△ABC中,∵∠BAC=30°,AB=6,∴BC=AF=3,AC=33∴S平行四边形BCFD=3×3393,S△ACF=12×3×3332,S平行四边形ADBC=32.【点睛】本题考查平行四边形的判定和性质、直角三角形斜边中线定理、等边三角形的性质、解直角三角形、勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.9.如图,正方形ABCD的边长为8,E为BC上一定点,BE=6,F为AB上一动点,把△BEF沿EF折叠,点B落在点B′处,当△AFB′恰好为直角三角形时,B′D的长为?【答案】4655或22【解析】【分析】分两种情况分析:如图1,当∠AB′F=90°时,此时A、B′、E三点共线,过点B′作B′M⊥AB,B′N⊥AD,由三角形的面积法则可求得B′M=2.4,再由勾股定理可求得B′N=3.2,在Rt△CB′N中,由勾股定理得,B′D=2222+DN= 3.2 5.6B N'+;如图2,当∠AFB′=90°时,由题意可知此时四边形EBFB′是正方形,AF=2,过点B′作B′N⊥AD,则四边形AFB′N为矩形,在Rt△CB′N中,由勾股定理得,B′D=2222+DN=22B N'+;【详解】如图1,当∠AB′F=90°时,此时A、B′、E三点共线,∵∠B=90°,∴AE=2222AB BE=86++=10,∵B′E=BE=6,∴AB′=4,∵B′F=BF,AF+BF=AB=8,在Rt△AB′F中,∠AB′F=90°,由勾股定理得,AF2=FB′2+AB′2,∴AF=5,BF=3,过点B′作B′M⊥AB,B′N⊥AD,由三角形的面积法则可求得B′M=2.4,再由勾股定理可求得B′N=3.2,∴AN=B′M=2.4,∴DN=AD-AN=8-2.4=5.6,在Rt△CB′N中,由勾股定理得,B′D=2222+DN= 3.2 5.6B N'+ =4655;如图2,当∠AFB′=90°时,由题意可知此时四边形EBFB′是正方形,∴AF=2,过点B′作B′N⊥AD,则四边形AFB′N为矩形,∴AN=B′F=6,B′N=AF=2,∴DN=AD-AN=2,在Rt△CB′N中,由勾股定理得,2222+DN=22B N'+ =22;综上,可得B′D的长为4655或22.【点睛】本题主要考查正方形的性质与判定,矩形有性质判定、勾股定理、折叠的性质等,能正确地画出图形并能分类讨论是解题的关键.10.阅读下列材料:我们定义:若一个四边形的一条对角线把四边形分成两个等腰三角形,则这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如正方形就是和谐四边形.结合阅读材料,完成下列问题:(1)下列哪个四边形一定是和谐四边形.A.平行四边形B.矩形C.菱形D.等腰梯形(2)命题:“和谐四边形一定是轴对称图形”是命题(填“真”或“假”).(3)如图,等腰Rt△ABD中,∠BAD=90°.若点C为平面上一点,AC为凸四边形ABCD 的和谐线,且AB=BC,请求出∠ABC的度数.【答案】(1) C ;(2)∠ABC的度数为60°或90°或150°.【解析】试题分析:(1)根据菱形的性质和和谐四边形定义,直接得出结论.(2)根据和谐四边形定义,分AD=CD,AD=AC,AC=DC讨论即可.(1)根据和谐四边形定义,平行四边形,矩形,等腰梯形的对角线不能把四边形分成两个等腰三角形,菱形的一条对角线能把四边形分成两个等腰三角形够.故选C.(2)∵等腰Rt△ABD中,∠BAD=90°,∴AB=AD.∵AC为凸四边形ABCD的和谐线,且AB=BC,∴分三种情况讨论:若AD=CD,如图1,则凸四边形ABCD是正方形,∠ABC=90°;若AD=AC,如图 2,则AB=AC=BC,△ABC是等边三角形,∠ABC=60°;若AC=DC,如图 3,则可求∠ABC=150°.考点:1.新定义;2.菱形的性质;3.正方形的判定和性质;4.等边三角形的判定和性质;5.分类思想的应用.11.(1)如图1,将矩形ABCD 折叠,使BC 落在对角线BD 上,折痕为BE ,点C 落在点C '处,若42ADB =o ∠,则DBE ∠的度数为______o .(2)小明手中有一张矩形纸片ABCD ,4AB =,9AD =.(画一画)如图2,点E 在这张矩形纸片的边AD 上,将纸片折叠,使AB 落在CE 所在直线上,折痕设为MN (点M ,N 分别在边AD ,BC 上),利用直尺和圆规画出折痕MN (不写作法,保留作图痕迹,并用黑色水笔把线段描清楚);(算一算)如图3,点F 在这张矩形纸片的边BC 上,将纸片折叠,使FB 落在射线FD 上,折痕为GF ,点,A B 分别落在点A ',B '处,若73AG =,求B D '的长.【答案】(1)21;(2)画一画;见解析;算一算:3B D '=【解析】【分析】(1)利用平行线的性质以及翻折不变性即可解决问题;(2)【画一画】,如图2中,延长BA 交CE 的延长线由G ,作∠BGC 的角平分线交AD 于M ,交BC 于N ,直线MN 即为所求;【算一算】首先求出GD=9-72033=,由矩形的性质得出AD∥BC,BC=AD=9,由平行线的性质得出∠DGF=∠BFG,由翻折不变性可知,∠BFG=∠DFG,证出∠DFG=∠DGF,由等腰三角形的判定定理证出DF=DG=203,再由勾股定理求出CF,可得BF,再利用翻折不变性,可知FB′=FB,由此即可解决问题.【详解】(1)如图1所示:∵四边形ABCD是矩形,∴AD∥BC,∴∠ADB=∠DBC=42°,由翻折的性质可知,∠DBE=∠EBC=12∠DBC=21°,故答案为21.(2)【画一画】如图所示:【算一算】如3所示:∵AG=73,AD=9,∴GD=9-72033=,∵四边形ABCD 是矩形,∴AD ∥BC ,BC=AD=9,∴∠DGF=∠BFG ,由翻折不变性可知,∠BFG=∠DFG ,∴∠DFG=∠DGF ,∴DF=DG=203, ∵CD=AB=4,∠C=90°, ∴在Rt △CDF 中,由勾股定理得:CF=22222016433DF CD ⎛⎫-=-= ⎪⎝⎭, ∴BF=BC-CF=9161133-=, 由翻折不变性可知,FB=FB′=113, ∴B′D=DF -FB′=2011333-=. 【点睛】 四边形综合题,考查了矩形的性质、翻折变换的性质、勾股定理、等腰三角形的判定、平行线的性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用翻折不变性解决问题.12.在ABC V 中,ABC 90o ∠=,BD 为AC 边上的中线,过点C 作CE BD ⊥于点E ,过点A 作BD 的平行线,交CE 的延长线于点F ,在AF 的延长线上截取FG BD =,连接BG ,DF .()1求证:BD DF =;()2求证:四边形BDFG 为菱形;()3若AG 5=,CF 7=,求四边形BDFG 的周长.【答案】(1)证明见解析(2)证明见解析(3)8【解析】【分析】()1利用平行线的性质得到90CFA ∠=o ,再利用直角三角形斜边上的中线等于斜边的一半即可得证,()2利用平行四边形的判定定理判定四边形BDFG 为平行四边形,再利用()1得结论即可得证,()3设GF x =,则5AF x =-,利用菱形的性质和勾股定理得到CF 、AF 和AC 之间的关系,解出x 即可.【详解】()1证明:AG //BD Q ,CF BD ⊥,CF AG ∴⊥,又D Q 为AC 的中点,1DF AC 2∴=, 又1BD AC 2=Q , BD DF ∴=,()2证明:BD//GF Q ,BD FG =,∴四边形BDFG 为平行四边形,又BD DF =Q ,∴四边形BDFG 为菱形,()3解:设GF x =,则AF 5x =-,AC 2x =,在Rt AFC V 中,222(2x)(5x)=+-,解得:1x 2=,216x (3=-舍去), GF 2∴=,∴菱形BDFG 的周长为8.【点睛】本题考查了菱形的判定与性质直角三角形斜边上的中线,勾股定理等知识,正确掌握这些定义性质及判定并结合图形作答是解决本题的关键.13.如图1,若分别以△ABC 的AC 、BC 两边为边向外侧作的四边形ACDE 和BCFG 为正方形,则称这两个正方形为外展双叶正方形.(1)发现:如图2,当∠C =90°时,求证:△ABC 与△DCF 的面积相等.(2)引申:如果∠C ≠90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;(3)运用:如图3,分别以△ABC 的三边为边向外侧作的四边形ACDE 、BCFG 和ABMN 为正方形,则称这三个正方形为外展三叶正方形.已知△ABC 中,AC =3,BC =4.当∠C =_____°时,图中阴影部分的面积和有最大值是________.【答案】(1)证明见解析;(2)成立,证明见解析;(3)18.【解析】试题分析:(1)因为AC=DC ,∠ACB=∠DCF=90°,BC=FC ,所以△ABC ≌△DFC ,从而△ABC 与△DFC 的面积相等;(2)延长BC 到点P ,过点A 作AP ⊥BP 于点P ;过点D 作DQ ⊥FC 于点Q .得到四边形ACDE ,BCFG 均为正方形,AC=CD ,BC=CF ,∠ACP=∠DCQ .所以△APC ≌△DQC . 于是AP=DQ .又因为S △ABC =12BC•AP ,S △DFC =12FC•DQ ,所以S △ABC =S △DFC ; (3)根据(2)得图中阴影部分的面积和是△ABC 的面积三倍,若图中阴影部分的面积和有最大值,则三角形ABC 的面积最大,当△ABC 是直角三角形,即∠C 是90度时,阴影部分的面积和最大.所以S 阴影部分面积和=3S △ABC =3×12×3×4=18. (1)证明:在△ABC 与△DFC 中, ∵{AC DCACB DCF BC FC∠∠===,∴△ABC ≌△DFC .∴△ABC 与△DFC 的面积相等;(2)解:成立.理由如下:如图,延长BC 到点P ,过点A 作AP ⊥BP 于点P ;过点D 作DQ ⊥FC 于点Q . ∴∠APC=∠DQC=90°.∵四边形ACDE ,BCFG 均为正方形,∴AC=CD ,BC=CF ,∠ACP+∠PCD=90°,∠DCQ+∠PCD=90°,∴∠ACP=∠DCQ .∴{APC DQCACP DCQ AC CD∠∠∠∠===,△APC ≌△DQC (AAS ),∴AP=DQ .又∵S△ABC=12BC•AP,S△DFC=12FC•DQ,∴S△ABC=S△DFC;(3)解:根据(2)得图中阴影部分的面积和是△ABC的面积三倍,若图中阴影部分的面积和有最大值,则三角形ABC的面积最大,∴当△ABC是直角三角形,即∠C是90度时,阴影部分的面积和最大.∴S阴影部分面积和=3S△ABC=3×12×3×4=18.考点:四边形综合题14.如图,点E是正方形ABCD的边A B上一点,连结CE,过顶点C作CF⊥CE,交AD延长线于F.求证:BE=DF.【答案】证明见解析.【解析】分析:根据正方形的性质,证出BC=CD,∠B=∠CDF,∠BCD=90°,再由垂直的性质得到∠BCE=∠DCF,然后根据“ASA”证明△BCE≌△BCE即可得到BE=DF详解:证明:∵CF⊥CE,∴∠ECF=90°,又∵∠BCG=90°,∴∠BCE+∠ECD =∠DCF+∠ECD∴∠BCE=∠DCF,在△BCE与△DCF中,∵∠BCE=∠DCF,BC=CD,∠CDF=∠EBC,∴△BCE≌△BCE(ASA),∴BE=DF.点睛:本题考查的是正方形的性质,熟知正方形的性质及全等三角形的判定与性质是解答此题的关键.15.正方形ABCD的边长为1,对角线AC与BD相交于点O,点E是AB边上的一个动点(点E不与点A、B重合),CE与BD相交于点F,设线段BE的长度为x.(1)如图1,当AD=2OF时,求出x的值;(2)如图2,把线段CE绕点E顺时针旋转90°,使点C落在点P处,连接AP,设△APE 的面积为S,试求S与x的函数关系式并求出S的最大值.【答案】(1)x=﹣1;(2)S=﹣(x﹣)2+(0<x<1),当x=时,S的值最大,最大值为,.【解析】试题分析:(1)过O作OM∥AB交CE于点M,如图1,由平行线等分线段定理得到CM=ME,根据三角形的中位线定理得到AE=2OM=2OF,得到OM=OF,于是得到BF=BE=x,求得OF=OM=解方程,即可得到结果;(2)过P作PG⊥AB交AB的延长线于G,如图2,根据已知条件得到∠ECB=∠PEG,根据全等三角形的性质得到EB=PG=x,由三角形的面积公式得到S=(1﹣x)•x,根据二次函数的性质即可得到结论.试题解析:(1)过O作OM∥AB交CE于点M,如图1,∵OA=OC,∴CM=ME,∴AE=2OM=2OF,∴OM=OF,∴,∴BF=BE=x,∴OF=OM=,∵AB=1,∴OB=,∴,∴x=﹣1;(2)过P作PG⊥AB交AB的延长线于G,如图2,∵∠CEP=∠EBC=90°,∴∠ECB=∠PEG,∵PE=EC,∠EGP=∠CBE=90°,在△EPG与△CEB中,,∴△EPG≌△CEB,∴EB=PG=x,∴AE=1﹣x,∴S=(1﹣x)•x=﹣x2+x=﹣(x﹣)2+,(0<x<1),∵﹣<0,∴当x=时,S的值最大,最大值为,.考点:四边形综合题。
中考数学平行四边形综合经典题含答案

一、平行四边形真题与模拟题分类汇编(难题易错题)1.四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.(1)如图1,当点E、F在线段AD上时,①求证:∠DAG=∠DCG;②猜想AG与BE的位置关系,并加以证明;(2)如图2,在(1)条件下,连接HO,试说明HO平分∠BHG;(3)当点E、F运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出∠BHO的度数.【答案】(1)①证明见解析;②AG⊥BE.理由见解析;(2)证明见解析;(3)∠BHO=45°.【解析】试题分析:(1)①根据正方形的性质得DA=DC,∠ADB=∠CDB=45°,则可根据“SAS”证明△ADG≌△CDG,所以∠DAG=∠DCG;②根据正方形的性质得AB=DC,∠BAD=∠CDA=90°,根据“SAS”证明△ABE≌△DCF,则∠ABE=∠DCF,由于∠DAG=∠DCG,所以∠DAG=∠ABE,然后利用∠DAG+∠BAG=90°得到∠ABE+∠BAG=90°,于是可判断AG⊥BE;(2)如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,证明△AON≌△BOM,可得四边形OMHN为正方形,因此HO平分∠BHG结论成立;(3)如答图2所示,与(1)同理,可以证明AG⊥BE;过点O作OM⊥BE于点M,ON⊥AG于点N,构造全等三角形△AON≌△BOM,从而证明OMHN为正方形,所以HO 平分∠BHG,即∠BHO=45°.试题解析:(1)①∵四边形ABCD为正方形,∴DA=DC,∠ADB=∠CDB=45°,在△ADG和△CDG中,∴△ADG≌△CDG(SAS),∴∠DAG=∠DCG;②AG⊥BE.理由如下:∵四边形ABCD为正方形,∴AB=DC,∠BAD=∠CDA=90°,在△ABE和△DCF中,∴△ABE≌△DCF(SAS),∴∠ABE=∠DCF,∵∠DAG=∠DCG,∴∠DAG=∠ABE,∵∠DAG+∠BAG=90°,∴∠ABE+∠BAG=90°,∴∠AHB=90°,∴AG⊥BE;(2)由(1)可知AG⊥BE.如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,则四边形OMHN为矩形.∴∠MON=90°,又∵OA⊥OB,∴∠AON=∠BOM.∵∠AON+∠OAN=90°,∠BOM+∠OBM=90°,∴∠OAN=∠OBM.在△AON与△BOM中,∴△AON≌△BOM(AAS).∴OM=ON,∴矩形OMHN为正方形,∴HO平分∠BHG.(3)将图形补充完整,如答图2示,∠BHO=45°.与(1)同理,可以证明AG ⊥BE .过点O 作OM ⊥BE 于点M ,ON ⊥AG 于点N ,与(2)同理,可以证明△AON ≌△BOM ,可得OMHN 为正方形,所以HO 平分∠BHG ,∴∠BHO=45°.考点:1、四边形综合题;2、全等三角形的判定与性质;3、正方形的性质2.问题发现:(1)如图①,点P 为平行四边形ABCD 内一点,请过点P 画一条直线l ,使其同时平分平行四边形ABCD 的面积和周长.问题探究:(2)如图②,在平面直角坐标系xOy 中,矩形OABC 的边OA 、OC 分别在x 轴、y 轴正半轴上,点B 坐标为(8,6).已知点(6,7)P 为矩形外一点,请过点P 画一条同时平分矩形OABC 面积和周长的直线l ,说明理由并求出直线l ,说明理由并求出直线l 被矩形ABCD 截得线段的长度.问题解决:(3)如图③,在平面直角坐标系xOy 中,矩形OABCD 的边OA 、OD 分别在x 轴、y 轴正半轴上,DC x ∥轴,AB y ∥轴,且8OA OD ==,2AB CD ==,点(1052,1052)P --为五边形内一点.请问:是否存在过点P 的直线l ,分别与边OA 与BC 交于点E 、F ,且同时平分五边形OABCD 的面积和周长?若存在,请求出点E 和点F 的坐标:若不存在,请说明理由.【答案】(1)作图见解析;(2)25y x =-,35;(3)(0,0)E ,(5,5)F .【解析】试题分析:(1)连接AC 、BD 交于点O ,作直线PO ,直线PO 将平行四边形ABCD 的面积和周长分别相等的两部分.(2)连接AC ,BD 交于点O ',过O '、P 点的直线将矩形ABCD 的面积和周长分为分别相等的两部分.(3)存在,直线y x =平分五边形OABCD 面积、周长.试题解析:(1)作图如下:(2)∵(6,7)P ,(4,3)O ',∴设:6PO y kx =+',67{43k b k b +=+=,2{5k b ==-, ∴25y x =-,交x 轴于5,02N ⎛⎫ ⎪⎝⎭, 交BC 于11,62M ⎛⎫ ⎪⎝⎭, 2211563522MN ⎛⎫=+-= ⎪⎝⎭.(3)存在,直线y x =平分五边形OABCD 面积、周长.∵(1052,102)P --在直线y x =上,∴连OP 交OA 、BC 于点E 、F ,设:BC y kx b =+,(8,2)(2,8)B C ,82{28k b k +=+=,1{10k b =-=,∴直线:10BC y x =-+,联立10{y x y x =-+=,得55x y =⎧⎨=⎩, ∴(0,0)E ,(5,5)F .3.已知:如图,在平行四边形ABCD 中,O 为对角线BD 的中点,过点O 的直线EF 分别交AD ,BC 于E ,F 两点,连结BE ,DF .(1)求证:△DOE ≌△BOF .(2)当∠DOE 等于多少度时,四边形BFDE 为菱形?请说明理由.【答案】(1)证明见解析;(2)当∠DOE =90°时,四边形BFED 为菱形,理由见解析.【解析】试题分析:(1)利用平行四边形的性质以及全等三角形的判定方法得出△DOE ≌△BOF (ASA );(2)首先利用一组对边平行且相等的四边形是平行四边形得出四边形EBFD 是平行四边形,进而利用垂直平分线的性质得出BE=ED ,即可得出答案.试题解析:(1)∵在▱ABCD 中,O 为对角线BD 的中点,∴BO=DO ,∠EDB=∠FBO ,在△EOD 和△FOB 中,∴△DOE ≌△BOF (ASA );(2)当∠DOE=90°时,四边形BFDE 为菱形,理由:∵△DOE ≌△BOF ,∴OE=OF ,又∵OB=OD ,∴四边形EBFD 是平行四边形, ∵∠EOD=90°,∴EF ⊥BD ,∴四边形BFDE 为菱形.考点:平行四边形的性质;全等三角形的判定与性质;菱形的判定.4.已知矩形纸片OBCD 的边OB 在x 轴上,OD 在y 轴上,点C 在第一象限,且86OB OD ==,.现将纸片折叠,折痕为EF (点E ,F 是折痕与矩形的边的交点),点P 为点D 的对应点,再将纸片还原。
人教备战中考数学培优 易错 难题(含解析)之平行四边形含答案

一、平行四边形真题与模拟题分类汇编(难题易错题)1.在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.(1)如图1,请直接写出线段OE与OF的数量关系;(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由(3)若|CF﹣AE|=2,EF=23,当△POF为等腰三角形时,请直接写出线段OP的长.【答案】(1)OF =OE;(2)OF⊥EK,OF=OE,理由见解析;(3)OP的长为62或23.【解析】【分析】(1)如图1中,延长EO交CF于K,证明△AOE≌△COK,从而可得OE=OK,再根据直角三角形斜边中线等于斜边一半即可得OF=OE;(2)如图2中,延长EO交CF于K,由已知证明△ABE≌△BCF,△AOE≌△COK,继而可证得△EFK是等腰直角三角形,由等腰直角三角形的性质即可得OF⊥EK,OF=OE;(3)分点P在AO上与CO上两种情况分别画图进行解答即可得.【详解】(1)如图1中,延长EO交CF于K,∵AE⊥BE,CF⊥BE,∴AE∥CK,∴∠EAO=∠KCO,∵OA=OC,∠AOE=∠COK,∴△AOE≌△COK,∴OE=OK,∵△EFK是直角三角形,∴OF=12EK=OE;(2)如图2中,延长EO交CF于K,∵∠ABC=∠AEB=∠CFB=90°,∴∠ABE+∠BAE=90°,∠ABE+∠CBF=90°,∴∠BAE=∠CBF,∵AB=BC,∴△ABE≌△BCF,∴BE=CF,AE=BF,∵△AOE≌△COK,∴AE=CK,OE=OK,∴FK=EF,∴△EFK是等腰直角三角形,∴OF⊥EK,OF=OE;(3)如图3中,点P在线段AO上,延长EO交CF于K,作PH⊥OF于H,∵|CF﹣AE|=2,3AE=CK,∴FK=2,在Rt△EFK中,tan∠3∴∠FEK=30°,∠EKF=60°,∴EK=2FK=4,OF=12EK=2,∵△OPF是等腰三角形,观察图形可知,只有OF=FP=2,在Rt△PHF中,PH=12PF=1,3OH=23∴()2212362+-=如图4中,点P 在线段OC 上,当PO=PF 时,∠POF=∠PFO=30°,∴∠BOP=90°,∴OP=33OE=233, 综上所述:OP 的长为62 或233. 【点睛】本题考查了全等三角形的判定与性质、直角三角形斜边中线等于斜边一半、等腰直角三角形的判定与性质、解直角三角形等,综合性较强,正确添加辅助线是解题的关键.2.已知AD 是△ABC 的中线P 是线段AD 上的一点(不与点A 、D 重合),连接PB 、PC ,E 、F 、G 、H 分别是AB 、AC 、PB 、PC 的中点,AD 与EF 交于点M ;(1)如图1,当AB =AC 时,求证:四边形EGHF 是矩形;(2)如图2,当点P 与点M 重合时,在不添加任何辅助线的条件下,写出所有与△BPE 面积相等的三角形(不包括△BPE 本身).【答案】(1)见解析;(2)△APE 、△APF 、△CPF 、△PGH .【解析】【分析】(1)由三角形中位线定理得出EG ∥AP ,EF ∥BC ,EF=12BC ,GH ∥BC ,GH=12BC ,推出EF ∥GH ,EF=GH ,证得四边形EGHF 是平行四边形,证得EF ⊥AP ,推出EF ⊥EG ,即可得出结论;(2)由△APE 与△BPE 的底AE=BE ,又等高,得出S △APE =S △BPE ,由△APE 与△APF 的底EP=FP ,又等高,得出S △APE =S △APF ,由△APF 与△CPF 的底AF=CF ,又等高,得出S △APF =S △CPF ,证得△PGH 底边GH 上的高等于△AEF 底边EF 上高的一半,推出S△PGH=12S△AEF=S△APF,即可得出结果.【详解】(1)证明:∵E、F、G、H分别是AB、AC、PB、PC的中点,∴EG∥AP,EF∥BC,EF=12BC,GH∥BC,GH=12BC,∴EF∥GH,EF=GH,∴四边形EGHF是平行四边形,∵AB=AC,∴AD⊥BC,∴EF⊥AP,∵EG∥AP,∴EF⊥EG,∴平行四边形EGHF是矩形;(2)∵PE是△APB的中线,∴△APE与△BPE的底AE=BE,又等高,∴S△APE=S△BPE,∵AP是△AEF的中线,∴△APE与△APF的底EP=FP,又等高,∴S△APE=S△APF,∴S△APF=S△BPE,∵PF是△APC的中线,∴△APF与△CPF的底AF=CF,又等高,∴S△APF=S△CPF,∴S△CPF=S△BPE,∵EF∥GH∥BC,E、F、G、H分别是AB、AC、PB、PC的中点,∴△AEF底边EF上的高等于△ABC底边BC上高的一半,△PGH底边GH上的高等于△PBC 底边BC上高的一半,∴△PGH底边GH上的高等于△AEF底边EF上高的一半,∵GH=EF,∴S△PGH=12S△AEF=S△APF,综上所述,与△BPE面积相等的三角形为:△APE、△APF、△CPF、△PGH.【点睛】本题考查了矩形的判定与性质、平行四边形的判定、三角形中位线定理、平行线的性质、三角形面积的计算等知识,熟练掌握三角形中位线定理是解决问题的关键.3.如图,现将平行四边形ABCD沿其对角线AC折叠,使点B落在点B′处.AB′与CD交于点E.(1)求证:△AED≌△CEB′;(2)过点E作EF⊥AC交AB于点F,连接CF,判断四边形AECF的形状并给予证明.【答案】(1)见解析(2)见解析【解析】【分析】(1)由题意可得AD=BC=B'C,∠B=∠D=∠B',且∠AED=∠CEB',利用AAS证明全等,则结论可得;(2)由△AED≌△CEB′可得AE=CE,且EF⊥AC,根据等腰三角形的性质可得EF垂直平分AC,∠AEF=∠CEF.即AF=CF,∠CEF=∠AFE=∠AEF,可得AE=AF,则可证四边形AECF是菱形.【详解】证明:(1)∵四边形ABCD是平行四边形∴AD=BC,CD∥AB,∠B=∠D∵平行四边形ABCD沿其对角线AC折叠∴BC=B'C,∠B=∠B'∴∠D=∠B',AD=B'C且∠DEA=∠B'EC∴△ADE≌△B'EC(2)四边形AECF是菱形∵△ADE≌△B'EC∴AE=CE∵AE=CE,EF⊥AC∴EF垂直平分AC,∠AEF=∠CEF∴AF=CF∵CD∥AB∴∠CEF=∠EFA且∠AEF=∠CEF∴∠AEF=∠EFA∴AF=AE∴AF=AE=CE=CF∴四边形AECF是菱形【点睛】本题考查了折叠问题,全等三角形的判定和性质,平行四边形的性质,菱形的判定,熟练掌握这些性质和判定是解决问题的关键.4.如图,已知矩形ABCD中,E是AD上一点,F是AB上的一点,EF⊥EC,且EF=EC.(1)求证:△AEF≌△DCE.(2)若DE=4cm,矩形ABCD的周长为32cm,求AE的长.【答案】(1)证明见解析;(2)6cm.【解析】分析:(1)根据EF⊥CE,求证∠AEF=∠ECD.再利用AAS即可求证△AEF≌△DCE.(2)利用全等三角形的性质,对应边相等,再根据矩形ABCD的周长为32cm,即可求得AE的长.详解:(1)证明:∵EF⊥CE,∴∠FEC=90°,∴∠AEF+∠DEC=90°,而∠ECD+∠DEC=90°,∴∠AEF=∠ECD.在Rt△AEF和Rt△DEC中,∠FAE=∠EDC=90°,∠AEF=∠ECD,EF=EC.∴△AEF≌△DCE.(2)解:∵△AEF≌△DCE.AE=CD.AD=AE+4.∵矩形ABCD的周长为32cm,∴2(AE+AE+4)=32.解得,AE=6(cm).答:AE的长为6cm.点睛:此题主要考查学生对全等三角形的判定与性质和矩形的性质等知识点的理解和掌握,难易程度适中,是一道很典型的题目.5.如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.(1)请判断:FG与CE的关系是___;(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.【答案】(1)FG=CE,FG∥CE;(2)成立;(3)成立.【解析】试题分析:(1)只要证明四边形CDGF是平行四边形即可得出FG=CE,FG∥CE;(2)构造辅助线后证明△HGE≌△CED,利用对应边相等求证四边形GHBF是矩形后,利用等量代换即可求出FG=C,FG∥CE;(3)证明△CBF≌△DCE后,即可证明四边形CEGF是平行四边形.试题解析:解:(1)FG=CE,FG∥CE;(2)过点G作GH⊥CB的延长线于点H.∵EG⊥DE,∴∠GEH+∠DEC=90°.∵∠GEH+∠HGE=90°,∴∠DEC=∠HE.在△HGE与△CED中,∵∠GHE=∠DCE,∠HGE=∠DEC,EG=DE,∴△HGE≌△CED(AAS),∴GH=CE,HE=CD.∵CE=BF,∴GH=BF.∵GH∥BF,∴四边形GHBF是矩形,∴GF=BH,FG∥CH,∴FG∥CE.∵四边形ABCD是正方形,∴CD=BC,∴HE=BC,∴HE+EB=BC+EB,∴BH=EC,∴FG=EC;(3)∵四边形ABCD是正方形,∴BC=CD,∠FBC=∠ECD=90°.在△CBF与△DCE中,∵BF=CE,∠FBC=∠ECD,BC=DC,∴△CBF≌△DCE(SAS),∴∠BCF=∠CDE,CF=DE.∵EG=DE,∴CF=EG.∵DE⊥EG,∴∠DEC+∠CEG=90°.∵∠CDE+∠DEC=90°,∴∠CDE=∠CEG,∴∠BCF=∠CEG,∴CF∥EG,∴四边形CEGF平行四边形,∴FG∥CE,FG=CE.6.如图1,矩形ABCD中,AB=8,AD=6;点E是对角线BD上一动点,连接CE,作EF⊥CE 交AB边于点F,以CE和EF为邻边作矩形CEFG,作其对角线相交于点H.(1)①如图2,当点F与点B重合时,CE=,CG=;②如图3,当点E是BD中点时,CE=,CG=;(2)在图1,连接BG,当矩形CEFG随着点E的运动而变化时,猜想△EBG的形状?并加以证明;(3)在图1,CGCE的值是否会发生改变?若不变,求出它的值;若改变,说明理由;(4)在图1,设DE的长为x,矩形CEFG的面积为S,试求S关于x的函数关系式,并直接写出x 的取值范围.【答案】(1)245,185 ,5,154 ;(2)△EBG 是直角三角形,理由详见解析;(3)34 ;(4)S=34x 2﹣485x+48(0≤x≤325). 【解析】【分析】(1)①利用面积法求出CE ,再利用勾股定理求出EF 即可;②利用直角三角形斜边中线定理求出CE ,再利用相似三角形的性质求出EF 即可;(2)根据直角三角形的判定方法:如果一个三角形一边上的中线等于这条边的一半,则这个三角形是直角三角形即可判断;(3)只要证明△DCE ∽△BCG ,即可解决问题;(4)利用相似多边形的性质构建函数关系式即可;【详解】(1)①如图2中,在Rt △BAD 中,BD=22AD AB +=10, ∵S △BCD =12•CD•BC=12•BD•CE , ∴CE=245.CG=BE=2224186()=55-. ②如图3中,过点E 作MN ⊥AM 交AB 于N ,交CD 于M .∵DE=BE,∴CE=12BD=5,∵△CME∽△ENF,∴CM ENCE EF=,∴CG=EF=154,(2)结论:△EBG是直角三角形.理由:如图1中,连接BH.在Rt△BCF中,∵FH=CH,∴BH=FH=CH,∵四边形EFGC是矩形,∴EH=HG=HF=HC,∴BH=EH=HG,∴△EBG是直角三角形.(3)F如图1中,∵HE=HC=HG=HB=HF,∴C、E、F、B、G五点共圆,∵EF=CG,∴∠CBG=∠EBF,∵CD∥AB,∴∠EBF=∠CDE,∴∠CBG=∠CDE,∵∠DCB=∠ECG=90°,∴∠DCE=∠BCG,∴△DCE∽△BCG,∴6384CG BCCE DC===.(4)由(3)可知:34CG CDCE CB==,∴矩形CEFG∽矩形ABCD,∴2264CEFGABCDS CE CES CD==矩形矩形(),∵CE2=(325-x)2+245)2,S矩形ABCD=48,∴S矩形CEFG=34[(325-x)2+(245)2].∴矩形CEFG的面积S=34x2-485x+48(0≤x≤325).【点睛】本题考查相似三角形综合题、矩形的性质、相似三角形的判定和性质、勾股定理、直角三角形的判定和性质、相似多边形的性质和判定等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造相似三角形或直角三角形解决问题,属于中考压轴题.7.如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG.(1)求证:四边形DEFG为菱形;(2)若CD=8,CF=4,求的值.【答案】(1)证明见试题解析;(2).【解析】试题分析:(1)由折叠的性质,可以得到DG=FG,ED=EF,∠1=∠2,由FG∥CD,可得∠1=∠3,再证明 FG=FE,即可得到四边形DEFG为菱形;(2)在Rt△EFC中,用勾股定理列方程即可CD、CE,从而求出的值.试题解析:(1)由折叠的性质可知:DG=FG,ED=EF,∠1=∠2,∵FG∥CD,∴∠2=∠3,∴FG=FE,∴DG=GF=EF=DE,∴四边形DEFG为菱形;(2)设DE=x,根据折叠的性质,EF=DE=x,EC=8﹣x,在Rt△EFC中,,即,解得:x=5,CE=8﹣x=3,∴=.考点:1.翻折变换(折叠问题);2.勾股定理;3.菱形的判定与性质;4.矩形的性质;5.综合题.8.如图1,若分别以△ABC的AC、BC两边为边向外侧作的四边形ACDE和BCFG为正方形,则称这两个正方形为外展双叶正方形.(1)发现:如图2,当∠C=90°时,求证:△ABC与△DCF的面积相等.(2)引申:如果∠C 90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;(3)运用:如图3,分别以△ABC的三边为边向外侧作的四边形ACDE、BCFG和ABMN为正方形,则称这三个正方形为外展三叶正方形.已知△ABC中,AC=3,BC=4.当∠C=_____°时,图中阴影部分的面积和有最大值是________.【答案】(1)证明见解析;(2)成立,证明见解析;(3)18.【解析】试题分析:(1)因为AC=DC,∠ACB=∠DCF=90°,BC=FC,所以△ABC≌△DFC,从而△ABC与△DFC的面积相等;(2)延长BC到点P,过点A作AP⊥BP于点P;过点D作DQ⊥FC于点Q.得到四边形ACDE,BCFG均为正方形,AC=CD,BC=CF,∠ACP=∠DCQ.所以△APC≌△DQC.于是AP=DQ.又因为S△ABC=12BC•AP,S△DFC=12FC•DQ,所以S△ABC=S△DFC;(3)根据(2)得图中阴影部分的面积和是△ABC的面积三倍,若图中阴影部分的面积和有最大值,则三角形ABC的面积最大,当△ABC是直角三角形,即∠C是90度时,阴影部分的面积和最大.所以S阴影部分面积和=3S△ABC=3×12×3×4=18.(1)证明:在△ABC与△DFC中,∵{AC DCACB DCF BC FC∠∠===,∴△ABC ≌△DFC .∴△ABC 与△DFC 的面积相等;(2)解:成立.理由如下:如图,延长BC 到点P ,过点A 作AP ⊥BP 于点P ;过点D 作DQ ⊥FC 于点Q . ∴∠APC=∠DQC=90°.∵四边形ACDE ,BCFG 均为正方形,∴AC=CD ,BC=CF ,∠ACP+∠PCD=90°,∠DCQ+∠PCD=90°,∴∠ACP=∠DCQ .∴{APC DQCACP DCQ AC CD∠∠∠∠===,△APC ≌△DQC (AAS ),∴AP=DQ .又∵S △ABC =12BC•AP ,S △DFC =12FC•DQ , ∴S △ABC =S △DFC ;(3)解:根据(2)得图中阴影部分的面积和是△ABC 的面积三倍,若图中阴影部分的面积和有最大值,则三角形ABC 的面积最大,∴当△ABC 是直角三角形,即∠C 是90度时,阴影部分的面积和最大.∴S 阴影部分面积和=3S △ABC =3×12×3×4=18. 考点:四边形综合题9.已知边长为1的正方形ABCD 中, P 是对角线AC 上的一个动点(与点A 、C 不重合),过点P 作PE ⊥PB ,PE 交射线DC 于点E ,过点E 作EF ⊥AC ,垂足为点F .(1)当点E 落在线段CD 上时(如图),①求证:PB=PE ;②在点P 的运动过程中,PF 的长度是否发生变化?若不变,试求出这个不变的值,若变化,试说明理由;(2)当点E 落在线段DC 的延长线上时,在备用图上画出符合要求的大致图形,并判断上述(1)中的结论是否仍然成立(只需写出结论,不需要证明);(3)在点P 的运动过程中,△PEC 能否为等腰三角形?如果能,试求出AP 的长,如果不能,试说明理由.【答案】(1)①证明见解析;②点PP 在运动过程中,PF的长度不变,值为2;(2)画图见解析,成立 ;(3)能,1.【解析】 分析:(1)①过点P 作PG ⊥BC 于G ,过点P 作PH ⊥DC 于H ,如图1.要证PB=PE ,只需证到△PGB ≌△PHE 即可;②连接BD ,如图2.易证△BOP ≌△PFE ,则有BO=PF ,只需求出BO 的长即可.(2)根据条件即可画出符合要求的图形,同理可得(1)中的结论仍然成立.(3)可分点E 在线段DC 上和点E 在线段DC 的延长线上两种情况讨论,通过计算就可求出符合要求的AP 的长.详解:(1)①证明:过点P 作PG ⊥BC 于G ,过点P 作PH ⊥DC 于H ,如图1.∵四边形ABCD 是正方形,PG ⊥BC ,PH ⊥DC ,∴∠GPC=∠ACB=∠ACD=∠HPC=45°.∴PG=PH ,∠GPH=∠PGB=∠PHE=90°.∵PE ⊥PB 即∠BPE=90°,∴∠BPG=90°﹣∠GPE=∠EPH .在△PGB 和△PHE 中,PGB PHE PG PHBPG EPH ∠∠⎧⎪⎨⎪∠∠⎩===, ∴△PGB ≌△PHE (ASA ),∴PB=PE .②连接BD ,如图2.∵四边形ABCD 是正方形,∴∠BOP=90°.∵PE ⊥PB 即∠BPE=90°,∴∠PBO=90°﹣∠BPO=∠EPF .∵EF ⊥PC 即∠PFE=90°,∴∠BOP=∠PFE .在△BOP 和△PFE 中,PBO EPF BOP PFE PB PE ∠∠⎧⎪∠∠⎨⎪⎩=== ∴△BOP ≌△PFE (AAS ),∴BO=PF .∵四边形ABCD 是正方形,∴OB=OC ,∠BOC=90°,∴BC=2OB .∵BC=1,∴OB=22, ∴PF=22. ∴点PP 在运动过程中,PF 的长度不变,值为2. (2)当点E 落在线段DC 的延长线上时,符合要求的图形如图3所示.同理可得:PB=PE ,2 (3)①若点E 在线段DC 上,如图1.∵∠BPE=∠BCE=90°,∴∠PBC+∠PEC=180°.∵∠PBC<90°,∴∠PEC>90°.若△PEC为等腰三角形,则EP=EC.∴∠EPC=∠ECP=45°,∴∠PEC=90°,与∠PEC>90°矛盾,∴当点E在线段DC上时,△PEC不可能是等腰三角形.②若点E在线段DC的延长线上,如图4.若△PEC是等腰三角形,∵∠PCE=135°,∴CP=CE,∴∠CPE=∠CEP=22.5°.∴∠APB=180°﹣90°﹣22.5°=67.5°.∵∠PRC=90°+∠PBR=90°+∠CER,∴∠PBR=∠CER=22.5°,∴∠ABP=67.5°,∴∠ABP=∠APB.∴AP=AB=1.∴AP的长为1.点睛:本题主要考查了正方形的性质、等腰三角形的性质、全等三角形的判定与性质、角平分线的性质、勾股定理、四边形的内角和定理、三角形的内角和定理及外角性质等知识,有一定的综合性,而通过添加辅助线证明三角形全等是解决本题的关键.10.倡导研究性学习方式,着力教材研究,习题研究,是学生跳出题海,提高学习能力和创新能力的有效途径.下面是一案例,请同学们认真阅读、研究,完成“类比猜想”的问题.习题如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.解答:∵正方形ABCD中,AB=AD,∠BAD=∠ADC=∠B=90°,∴把△ABE绕点A逆时针旋转90°至△ADE′,点F、D、E′在一条直线上.∴∠E′AF=90°-45°=45°=∠EAF,又∵AE′=AE,AF=AF∴△AE′F≌△AEF(SAS)∴EF=E′F=DE′+DF=BE+DF.类比猜想:(1)请同学们研究:如图(2),在菱形ABCD中,点E、F分别在BC、CD上,当∠BAD=120°,∠EAF=60°时,还有EF=BE+DF吗?请说明理由.(2)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180°,∠EAF=∠BAD时,EF=BE+DF吗?请说明理由.【答案】证明见解析.【解析】试题分析:(1)把△ABE绕点A逆时针旋转120°至△ADE′,如图(2),连结E′F,根据菱形和旋转的性质得到AE=AE′,∠EAF=∠E′AF,利用“SAS”证明△AEF≌△AE′F,得到EF=E′F;由于∠ADE′+∠ADC=120°,则点F、D、E′不共线,所以DE′+DF>EF,即由BE+DF>EF;(2)把△ABE绕点A逆时针旋转∠BAD的度数至△ADE′,如图(3),根据旋转的性质得到AE′=AE,∠EAF=∠E′AF,然后利用“SAS”证明△AEF≌△AE′F,得到EF=E′F,由于∠ADE′+∠ADC=180°,知F、D、E′共线,因此有EF=DE′+DF=BE+DF;根据前面的条件和结论可归纳出结论.试题解析:(1)当∠BAD=120°,∠EAF=60°时,EF=BE+DF不成立,EF<BE+DF.理由如下:∵在菱形ABCD中,∠BAD=120°,∠EAF=60°,∴AB=AD,∠1+∠2=60°,∠B=∠ADC=60°,∴把△ABE绕点A逆时针旋转120°至△ADE′,如图(2),连结E′F,∴∠EAE′=120°,∠1=∠3,AE′=AE,DE′=BE,∠ADE′=∠B=60°,∴∠2+∠3=60°,∴∠EAF=∠E′AF,在△AEF和△AE′F中,∴△AEF≌△AE′F(SAS),∴EF=E′F,∵∠ADE′+∠ADC=120°,即点F、D、E′不共线,∴DE′+DF>EF∴BE+DF>EF;(2)当AB=AD,∠B+∠D=180°,∠EAF=∠BAD时,EF=BE+DF成立.理由如下:如图(3),∵AB=AD,∴把△ABE绕点A逆时针旋转∠BAD的度数至△ADE′,如图(3),∴∠EAE′=∠BAD,∠1=∠3,AE′=AE,DE′=BE,∠ADE′=∠B,∵∠B+∠D=180°,∴∠ADE′+∠D=180°,∴点F、D、E′共线,∵∠EAF=∠BAD,∴∠1+∠2=∠BAD,∴∠2+∠3=∠BAD,∴∠EAF=∠E′AF,在△AEF和△AE′F中,∴△AEF≌△AE′F(SAS),∴EF=E′F,∴EF=DE′+DF=BE+DF;归纳:在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180°,∠EAF=∠BAD时,EF=BE+DF.考点:四边形综合题.。
备战中考数学平行四边形培优易错难题练习(含答案)含详细答案

备战中考数学平行四边形培优易错难题练习(含答案)含详细答案一、平行四边形1.在四边形ABCD中,BD180,对角线AC平分BAD.〔1〕如图1,假设DAB120,且B90,试探究边AD、AB与对角线AC的数量关系并说明理由.2〕如图2,假设将〔1〕中的条件“B90〞去掉,〔1〕中的结论是否成立?请说明理由. 〔3〕如图3,假设DAB 90,探究边AD、AB与对角线AC的数量关系并说明理由.【答案】〔1〕ACAD AB.证明见解析;〔2〕成立;〔3〕ADAB2AC.理由见解析.【解析】11试题分析:〔1〕结论:AC=AD+AB,只要证明AD=AC,AB=AC即可解决问题;22〔2〕〔1〕中的结论成立.以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,只要证明△DAC≌△BEC即可解决问题;3〕结论:AD+AB=2AC.过点C作CE⊥AC交AB的延长线于点E,只要证明△ACE是等腰直角三角形,△DAC≌△BEC即可解决问题;试题解析:解:〔1〕AC=AD+AB.理由如下:如图1中,在四边形ABCD中,∠D+∠B=180°,∠B=90°,∴∠D=90,°∵∠DAB=120,°AC平分∠DAB,∴∠DAC=∠BAC=60,°∵∠B=90,°11∴AB=AC,同理AD=AC.22AC=AD+AB.2〕〔1〕中的结论成立,理由如下:以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,∵∠BAC=60,°∴△AEC为等边三角形,AC=AE=CE,∵∠D+∠ABC=180,°∠DAB=120,°∴∠DCB=60,°∴∠DCA=∠BCE,∵∠D+∠ABC=180,°∠ABC+∠EBC=180,°∴∠D=∠CBE,∵CA=CE,∴△DAC≌△BEC,AD=BE,AC=AD+AB.〔3〕结论:AD+AB=2AC.理由如下:过点C作CE⊥AC交AB的延长线于点E,∵∠D+∠B=180°,∠DAB=90°,DCB=90,°∵∠ACE=90,°∴∠DCA=∠BCE,又∵AC平分∠DAB,∴∠CAB=45,°∴∠E=45.°∴AC=CE.又∵∠D+∠ABC=180°,∠D=∠CBE,∴△CDA≌△CBE,AD=BE,AD+AB=AE.在Rt△ACE中,∠CAB=45°,∴AE AC=2AC=cos45ADAB=2AC.2.如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,那么图中的两个三角形就是互补三角形.〔1〕用尺规将图1中的△ABC分割成两个互补三角形;〔2〕证明图2中的△ABC分割成两个互补三角形;〔3〕如图3,在图2的根底上再以BC为边向外作正方形BCHI.①三个正方形面积分别是17、13、10,在如图4的网格中〔网格中每个小正方形的边长为1〕画出边长为、、的三角形,并计算图3中六边形DEFGHI的面积.②假设△ABC的面积为2,求以EF、DI、HG的长为边的三角形面积.【答案】〔1〕作图见解析〔2〕证明见解析〔3〕①62;②6【解析】试题分析:〔1〕作BC边上的中线AD即可.2〕根据互补三角形的定义证明即可.3〕①画出图形后,利用割补法求面积即可.②平移△CHG到AMF,连接EM,IM,那么AM=CH=BI,只要证明S△EFM=3S△ABC即可.试题解析:〔1〕如图1中,作BC边上的中线AD,△ABD和△ADC是互补三角形.〔2〕如图2中,延长FA到点H,使得AH=AF,连接EH.∵四边形ABDE,四边形ACGF是正方形,AB=AE,AF=AC,∠BAE=∠CAF=90,°∴∠EAF+∠BAC=180,°∴△AEF和△ABC是两个互补三角形.∵∠EAH+∠HAB=∠BAC+∠HAB=90,°∴∠EAH=∠BAC,∵AF=AC,AH=AB,在△AEH和△ABC中,∴△AEH≌△ABC,∴S△AEF=S△AEH=S△ABC.〔3〕①边长为、、的三角形如图4所示.∵S△ABC=3×4﹣2﹣﹣,∴S六边形=17+13+10+4×5.5=62.②如图3中,平移△CHG到AMF,连接EM,IM,那么AM=CH=BI,设∠ABC=x,∵AM∥CH,CH⊥BC,∴AM⊥BC,∴∠EAM=90+90°﹣°x=180﹣°x,∵∠DBI=360﹣°90°﹣90°﹣x=180﹣°x,∴∠EAM=∠DBI,∵AE=BD,∴△AEM≌△DBI,∵在△DBI和△ABC中,DB=AB,BI=BC,∠DBI+∠ABC=180,°∴△DBI和△ABC是互补三角形,∴S△AEM=S△AEF=S△AFM=2,∴S△EFM=3S△ABC=6.考点:1、作图﹣应用与设计,2、三角形面积3.:在菱形ABCD中,E,F是BD上的两点,且AE∥CF.求证:四边形AECF是菱形.【答案】见解析【解析】【分析】由菱形的性质可得AB∥CD,AB=CD,∠ADF=∠CDF,由“SAS〞可证△ADF≌△CDF,可得AF=CF,由△ABE≌△CDF,可得AE=CF,由平行四边形的判定和菱形的判定可得四边形AECF是菱形.【详解】证明:∵四边形ABCD是菱形∴AB∥CD,AB=CD,∠ADF=∠CDF,∵AB=CD,∠ADF=∠CDF,DF=DF∴△ADF≌△CDF〔SAS〕AF=CF,∵AB∥CD,AE∥CF∴∠ABE=∠CDF,∠AEF=∠CFE∴∠AEB=∠CFD,∠ABE=∠CDF,AB=CD∴△ABE≌△CDF〔AAS〕∴AE=CF,且AE∥CF∴四边形AECF是平行四边形又∵AF=CF,∴四边形AECF是菱形【点睛】此题主要考查菱形的判定定理,首先要判定其为平行四边形,这是菱形判定的根本判定. 4.在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°. (1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;(2)假设直线EF与AB,AD的延长线分别交于点222;M,N(如图②),求证:EF=ME+NF(3)将正方形改为长与宽不相等的矩形,假设其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.【答案】〔1〕证明见解析;〔2〕证明见解析;〔3〕EF2=2BE2+2DF2.【解析】试题分析:〔1〕根据旋转的性质可知AF=AG,∠EAF=∠GAE=45°,故可证△AEG≌△AEF;〔2〕将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由〔1〕知△AEG≌△AEF,那么EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;〔3〕将△ADF绕着点A顺时针旋转90°,得到△ABG,根据旋转的性质可以得到ADF≌△ABG,那么DF=BG,再证明△AEG≌△AEF,得出EG=EF,由EG=BG+BE,等量代换得到EF=BE+DF.试题解析:〔1〕∵△ADF绕着点A顺时针旋转90°,得到△ABG,AF=AG,∠FAG=90,°∵∠EAF=45,°∴∠GAE=45,°在△AGE与△AFE中,,∴△AGE≌△AFE〔SAS〕;〔2〕设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.那么△ADF≌△ABG,DF=BG.由〔1〕知△AEG≌△AEF,EG=EF.∵∠CEF=45,°∴△BME、△DNF、△CEF均为等腰直角三角形,CE=CF,BE=BM,NF=DF,a﹣BE=a﹣DF,BE=DF,∴BE=BM=DF=BG,∴∠BMG=45°,∴∠GME=45°+45=90°°,222EG=EF,MG=BM=DF=NF,∴EF2=ME2+NF2;3〕EF2=2BE2+2DF2.如下列图,延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.由〔1〕知△AEH≌△AEF,那么由勾股定理有〔GH+BE〕2+BG2=EH2,即〔GH+BE〕2+〔BM﹣GM〕2=EH2又∴EF=HE,DF=GH=GM,BE=BM,所以有〔GH+BE〕2+〔BE﹣GH〕2=EF2,即2〔DF2+BE2〕=EF2考点:四边形综合题5.Rt△ABD中,边AB=OB=1,∠ABO=90°问题探究:〔1〕以AB为边,在Rt△ABO的右边作正方形 ABC,如图〔1〕,那么点 O与点D的距离为.〔2〕以AB为边,在Rt△ABO的右边作等边三角形ABC,如图〔2〕,求点O与点C的距离.问题解决:〔3〕假设线段DE=1,线段DE的两个端点D,E分别在射线OA、OB上滑动,以DE为边向外作等边三角形DEF,如图〔3〕,那么点O与点F的距离有没有最大值,如果有,求出最大值,如果没有,说明理由.【答案】(1)、5;(2)、62;(3)、321. 22【解析】【分析】试题分析:(1)、如图1中,连接OD,在Rt△ODC中,根据OD=OC2CD2计算即可.(2)、如图2中,作CE⊥OB于E,CF⊥AB于F,连接OC.在Rt△OCE中,根据OC=OE2CE2计算即可.(3)、如图3中,当OF⊥DE时,OF的值最大,设OF交DE 于H,在OH上取一点M,使得OM=DM,连接DM.分别求出MH、OM、FH即可解决问题.【详解】试题解析:(1)、如图1中,连接OD,∵四边形ABCD是正方形,∴AB=BC=CD=AD=1,∠C=90°在Rt△ODC中,∵∠C=90,°OC=2,CD=1,∴OD=OC2CD222125(2)、如图2中,作CE⊥OB于E,CF⊥AB于F,连接OC.1,CF=BE=3,∵∠FBE=∠E=∠CFB=90,°∴四边形BECF是矩形,∴BF=CF=222在Rt△OCE中,OC=OE2CE213122262 =.(3)、如图3中,当OF⊥DE时,OF的值最大,设OF交DE于H,在OH上取一点M,使得OM=DM,连接DM.1FD=FE=DE=1,OF⊥DE,∴DH=HE,OD=OE,∠DOH=∠,°∵OM=DM,2∴∠MOD=∠,°∴∠DMH=∠MDH=45°,∴DH=HM=1,∴DM=OM=2,22∵FH=DF2DH23,∴OF=OM+MH+FH=213=321.22222∴OF的最大值为321.2考点:四边形综合题.6.图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.〔1〕在图1中画出等腰直角三角形MON,使点N在格点上,且∠MON=90°;〔2〕在图2中以格点为顶点画一个正方形ABCD,使正方形ABCD面积等于〔1〕中等腰直角三角形MON面积的4倍,并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD面积没有剩余〔画出一种即可〕.【答案】〔1〕作图参见解析;〔2〕作图参见解析.【解析】试题分析:〔1〕过点O向线段OM作垂线,此直线与格点的交点为N,连接MN即可;〔2〕根据勾股定理画出图形即可.试题解析:〔1〕过点O向线段OM作垂线,此直线与格点的交点为N,连接MN,如图1所示;〔2〕等腰直角三角形MON面积是5,因此正方形面积是20,如图2所示;于是根据勾股定理画出图3:考点:1.作图﹣应用与设计作图; 2.勾股定理.7.菱形ABCD中、∠BAD=120°,点O为射线CA上的动点,作射线OM与直线BC相交于点E,将射线OM绕点O逆时针旋转60°,得到射线ON,射线ON与直线CD相交于点F.〔1〕如图①,点O与点A重合时,点E,F分别在线段BC,CD上,请直接写出CE,CF,CA三条段段之间的数量关系;〔2〕如图②,点O在CA的延长线上,且OA=1AC,E,F分别在线段BC的延长线和线3段CD的延长线上,请写出CE,CF,CA三条线段之间的数量关系,并说明理由;〔3〕点O 在线段AC 上,假设AB =6,BO =2 7,当CF =1时,请直接写出BE 的长.【答案】〔1〕CA=CE+CF .〔2〕CF-CE=4AC .〔3〕BE 的值为3或5或1.( 3 ( 【解析】 ( 【分析】( 1〕如图①中,结论:CA=CE+CF .只要证明△ADF ≌△ACE 〔SAS 〕即可解决问题;2〕结论:CF-CE=4AC .如图②中,如图作OG ∥AD 交CF 于G ,那么△OGC 是等边三角3形.只要证明△FOG ≌△EOC 〔ASA 〕即可解决问题; 〔3〕分四种情形画出图形分别求解即可解决问题 .【详解】〔1〕如图①中,结论:CA=CE+CF .理由:∵四边形ABCD 是菱形,∠BAD=120°AB=AD=DC=BC ,∠BAC=∠DAC=60°∴△ABC ,△ACD 都是等边三角形,∵∠DAC=∠EAF=60,°∴∠DAF=∠CAE ,∵CA=AD ,∠D=∠ACE=60,°∴△ADF≌△ACE〔SAS〕,DF=CE,CE+CF=CF+DF=CD=AC,CA=CE+CF.〔2〕结论:CF-CE=4 AC.3理由:如图②中,如图作OG∥AD交CF于G,那么△OGC是等边三角形.1∵∠GOC=∠FOE=60,°2∴∠FOG=∠EOC,3∵OG=OC,∠OGF=∠ACE=120,°4∴△FOG≌△EOC〔ASA〕,5∴CE=FG,6∵OC=OG,CA=CD,7∴OA=DG,4∴C F-EC=CF-FG=CG=CD+DG=AC+AC=AC,33〕作BH⊥AC于H.∵AB=6,AH=CH=3,BH=33,如图③-1中,当点O在线段AH上,点F在线段CD上,点E在线段BC上时.OB=27,∴OH=OB2BH2=1,OC=3+1=4,由〔1〕可知:CO=CE+CF,OC=4,CF=1,∴CE=3,∴BE=6-3=3.如图③-2中,当点O在线段AH上,点F在线段DC的延长线上,点E在线段BC上时.由〔2〕可知:CE-CF=OC,CE=4+1=5,BE=1.如图③-3中,当点O在线段CH上,点F在线段CD上,点E在线段BC上时.同法可证:OC=CE+CF,∵OC=CH-OH=3-1=2,CF=1,CE=1,BE=6-1=5.如图③-4中,当点O在线段CH上,点F在线段DC的延长线上,点E在线段BC上时.∴∴∴∴∴∴∴∴∴∴∴∴∴∴同法可知:CE-CF=OC,∴CE=2+1=3,∴B E=3,综上所述,满足条件的BE的值为3或5或1.【点睛】此题属于四边形综合题,考查了全等三角形的判定和性质,等边三角形的性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.8.定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形〞.性质:如果两个三角形是“友好三角形〞,那么这两个三角形的面积相等.理解:如图①,在△ABC中,CD是AB边上的中线,那么△ACD和△BCD是“友好三角形〞,并且S△ACD=S△BCD.应用:如图②,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F在BC上,AE=BF,AF与BE交于点O.1〕求证:△AOB和△AOE是“友好三角形〞;2〕连接OD,假设△AOE和△DOE是“友好三角形〞,求四边形CDOF的面积.探究:在△ABC中,∠A=30°,AB=4,点D在线段AB上,连接CD,△ACD和△BCD是“友好三角形〞,将△ACD沿CD所在直线翻折,得到△A′CD,假设△A′CD与△ABC重合局部的面积等于△ABC面积的,请直接写出△ABC的面积.【答案】〔1〕见解析;〔2〕12;探究:2或2.【解析】试题分析:〔1〕利用一组对边平行且相等的四边形是平行四边形,得到四边形ABFE是平行四边形,然后根据平行四边形的性质证得OE=OB,即可证得△AOE和△AOB是友好三角形;〔2〕△AOE和△DOE是“友好三角形〞,即可得到E是AD的中点,那么可以求得△ABE、△ABF的面积,根据S四边形CDOF=S矩形ABCD-2S△ABF即可求解.探究:画出符合条件的两种情况:①求出四边形A′DCB是平行四边形,求出BC和A′D推出∠ACB=90°,根据三角形面积公式求出即可;②求出高CQ,求出△A′DC的面积.即可求出△ABC的面积.试题解析:〔1〕∵四边形ABCD是矩形,∴AD∥BC,AE=BF,∴四边形ABFE是平行四边形,∴OE=OB,∴△AOE和△AOB是友好三角形.〔2〕∵△AOE和△DOE是友好三角形,∴S△AOE=S△DOE,AE=ED=AD=3,∵△AOB与△AOE是友好三角形,∴S△AOB=S△AOE,∵△AOE≌△FOB,∴S△AOE=S△FOB,∴S△AOD=S△ABF,∴S四边形CDOF=S矩形ABCD-2S△ABF=4×6-2×4×3=12.探究:解:分为两种情况:①如图1,∵S△ACD=S△BCD.AD=BD=AB,∵沿CD折叠A和A′重合,AD=A′D=AB=×4=2,∵△A′CD与△ABC重合局部的面积等于△ABC面积的,∴S△DOC=S△ABC=S△BDC=S△ADC=S△A′DC,∴DO=OB,A′O=CO,∴四边形A′DCB是平行四边形,BC=A′D=2,过B作BM⊥AC于M,∵AB=4,∠BAC=30,°∴BM=AB=2=BC,即C和M重合,∴∠ACB=90,°由勾股定理得:AC=,∴△ABC的面积是×BC×AC=×2×2=2;②如图2,∵S△ACD=S△BCD.AD=BD=AB,∵沿CD折叠A和A′重合,AD=A′D=AB=×4=2,∵△A′CD与△ABC重合局部的面积等于△ABC面积的,∴S△DOC=S△ABC=S△BDC=S△ADC=S△A′DC,∴DO=OA′,BO=CO,∴四边形A′BDC是平行四边形,∴A′C=BD=2,过C作CQ⊥A′D于Q,∵A′C=2,∠DA′∠C=BAC=30,°∴CQ=A′C=1,∴S△ABC=2S△ADC=2S△A′DC=2××A′D×CQ=2××2×1=2;即△ABC的面积是2或2.考点:四边形综合题.9.猜想与证明:如图1,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,假设M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.拓展与延伸:〔1〕假设将〞猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,那么DM和ME的关系为.〔2〕如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF 的中点,试证明〔1〕中的结论仍然成立.【答案】猜想: DM=ME,证明见解析;〔 2〕成立,证明见解析.【解析】试题分析:延长EM交AD于点H,根据ABCD和△AMH全等,得到HM=EM,根据Rt△HDE得到CEFG为矩形得到AD∥EF,得到△FME和HM=DE,那么可以得到答案;〔1〕、延长EM交AD于点H,根据ABCD和CEFG为矩形得到AD∥EF,得到△FME和△AMH全等,得到HM=EM,根据Rt△HDE得到HM=DE,那么可以得到答案;〔2〕、连接AE,根据正方形的性质得出∠FCE=45°,∠FCA=45°,根据RT△ADF中AM=MF得出DM=AM=MF,根据RT△AEF中AM=MF得出AM=MF=ME,从而说明DM=ME.试题解析:如图1,延长EM交AD于点H,∵四边形ABCD和CEFG是矩形,∴AD∥EF,∴∠EFM=∠HAM,又∵∠FME=∠AMH,FM=AM,在△FME和△AMH中,∴△FME≌△AMH〔ASA〕∴HM=EM,在RT△HDE中,HM=DE,∴DM=HM=ME,∴DM=ME.〔1〕、如图1,延长EM交AD于点H,∵四边形ABCD和CEFG是矩形,∴AD∥EF,∴∠EFM=∠HAM,又∵∠FME=∠AMH,FM=AM,在△FME和△AMH中,∴△FME≌△AMH〔ASA〕∴HM=EM,在RT△HDE中,HM=EM∴DM=HM=ME,∴DM=ME,〔2〕、如图2,连接AE,∵四边形ABCD和ECGF是正方形,∴∠FCE=45,°∠FCA=45,°∴AE和EC在同一条直线上,在RT△ADF中,AM=MF,∴DM=AM=MF,在RT△AEF中,AM=MF,∴AM=MF=ME,∴DM=ME.考点:〔1〕、三角形全等的性质;〔2〕、矩形的性质.10.问题情境在四边形ABCD中,BA=BC,DC⊥AC,过点D作DE∥AB交BC的延长线于点E,M是边AD的中点,连接特例探究MB,ME.(1)如图(2)如图1,当∠ABC=90°时,写出线段MB2,当∠ABC=120°时,试探究线段与MEMB与的数量关系,位置关系;ME的数量关系,并证明你的结论;拓展延伸(3)如图3,当∠ABC=α时,请直接用含α的式子表示线段MB 与ME之间的数量关系.【答案】(1)MB=ME,MB⊥ME;(2)ME=3MB.证明见解析;(3)ME=MB·tan. 2【解析】【分析】1〕如图1中,连接CM.只要证明△MBE是等腰直角三角形即可;2〕结论:EM=3MB.只要证明△EBM是直角三角形,且∠MEB=30°即可;3〕结论:EM=BM?tan.证明方法类似;2【详解】如图1中,连接CM.∵∠ACD=90,°AM=MD,∴MC=MA=MD,BA=BC,∴BM垂直平分AC,∵∠ABC=90,°BA=BC,1∴∠MBE=∠ABC=45,°∠ACB=∠DCE=45,°2∵AB∥DE,∴∠ABE+∠DEC=180,°∴∠DEC=90,°∴∠DCE=∠CDE=45,°∴EC=ED,∵MC=MD,∴EM垂直平分线段CD,EM平分∠DEC,∴∠MEC=45,°∴△BME是等腰直角三角形,∴BM=ME,BM⊥EM.故答案为BM=ME,BM⊥EM.(2)ME=3MB.证明如下:连接CM,如解图所示.∵DC⊥AC,M是边AD的中点,∴MC=MA=MD.∵BA=BC,∴BM垂直平分AC.∵∠ABC=120,°BA=BC,∴∠MBE=1∠ABC=60°,∠BAC=∠BCA=30°,∠DCE=60°. 2∵AB∥DE,∴∠ABE+∠DEC=180°,∴∠DEC=60°,∴∠DCE=∠DEC=60°,∴△CDE是等边三角形,∴EC=ED.∵MC=MD,∴EM垂直平分CD,EM平分∠DEC,1∴∠MEC=∠DEC=30°,2∴∠MBE+∠MEB=90°,即∠BME=90°.在Rt△BME中,∵∠MEB=30°,∴ME=3MB.(3)如图3中,结论:EM=BM?tan.2理由:同法可证: BM ⊥EM ,BM 平分∠ABC ,所以EM=BM?tan.2【点睛】此题考查四边形综合题、等腰直角三角形的判定和性质、等边三角形的判定和性质、等腰三角形的性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题.11.如图1,矩形 ABCD 中,AB=8,AD=6;点 E 是对角线BD 上一动点,连接CE ,作EF ⊥CE 交AB 边于点F ,以CE和EF 为邻边作矩形CEFG ,作其对角线相交于点 H .〔1〕①如图2,当点F 与点B 重合时,CE= ,CG= ;②如图3,当点E 是BD 中点时,CE= ,CG= ;( 2〕在图1,连接BG ,当矩形CEFG 随着点E 的运动而变化时,猜想△EBG 的形状?并加以证明;3〕在图1,CG的值是否会发生改变?假设不变,求出它的值;假设改变,说明理由;CE4〕在图1,设DE 的长为x ,矩形CEFG 的面积为S ,试求S 关于x 的函数关系式,并直接写出x 的取值范围.【答案】〔1〕24,18 ,5, 15 ;〔2〕△EBG 是直角三角形,理由详见解析;〔3〕55 43 3 248 32〕.;〔4〕S=x ﹣5x+48〔0≤x ≤445【解析】【分析】〔1〕① 利用面积法求出 CE ,再利用勾股定理求出 EF 即可;②利用直角三角形斜边中线定理求出 CE ,再利用相似三角形的性质求出 EF 即可;2〕根据直角三角形的判定方法:如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形即可判断;3〕只要证明△DCE ∽△BCG ,即可解决问题; 4〕利用相似多边形的性质构建函数关系式即可;【详解】〔1〕①如图2中,在Rt△BAD中,BD=AD2AB2=10,11∵S△BCD= ?CD?BC=?BD?CE,22∴CE=24.CG=BE=62(24)2=18.555②如图3中,过点E作MN⊥AM交AB于N,交CD于M.DE=BE,1∴C E=BD=5,2∵△CME∽△ENF,CM EN∴,CE EF15CG=EF=,42〕结论:△EBG是直角三角形.理由:如图1中,连接BH.在Rt△BCF中,∵FH=CH,∴BH=FH=CH,∵四边形EFGC是矩形,∴EH=HG=HF=HC,∴BH=EH=HG,∴△EBG 是直角三角形. 3〕F 如图1中,∵HE=HC=HG=HB=HF , ∴C 、E 、F 、B 、G 五点共圆,∵EF=CG , ∴∠CBG=∠EBF , ∵CD ∥AB , ∴∠EBF=∠CDE , ∴∠CBG=∠CDE , ∵∠DCB=∠ECG=90,° ∴∠DCE=∠BCG , ∴△DCE ∽△BCG ,∴CGBC6 3 . CE DC 8 4〔4〕由〔3〕可知:CGCD3,CE CB 4∴矩形CEFG ∽矩形ABCD ,S矩形CEFG〔CE 2CE 2∴CD 〕,S矩形ABCD64∵CE 2=〔 32 -x 〕2+24〕2,S 矩形ABCD =48,55∴S 矩形CEFG =33222424[〔5-x 〕+〔5〕].3248 32〕.∴矩形CEFG 的面积S=x-x+48〔0≤x ≤455【点睛】此题考查相似三角形综合题、矩形的性质、相似三角形的判定和性质、勾股定理、直角三角形的判定和性质、相似多边形的性质和判定等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造相似三角形或直角三角形解决问题,属于中考压轴题.12.:在矩形ABCD 中,AB =10,BC =12,四边形EFGH 的三个顶点E 、F 、H 分别在矩形ABCD 边AB 、BC 、DA 上,AE =2.〔1〕如图①,当四边形 EFGH 为正方形时,求 △GFC 的面积;2〕如图②,当四边形EFGH为菱形,且BF=a时,求△GFC的面积〔用a表示〕;3〕在〔2〕的条件下,△GFC的面积能否等于2?请说明理由.【答案】〔1〕10;〔2〕12-a;〔3〕不能【解析】解:〔1〕过点G作GM⊥BC于M.在正方形EFGH中,HEF=90°,EH=EF,∴∠AEH+∠BEF=90°.∵∠AEH+∠AHE=90°,∴∠AHE=∠BEF.又∵∠A=∠B=90°,∴△AHE≌△BEF.同理可证△MFG≌△BEF.∴GM=BF=AE=2.∴FC=BC-BF=10.∴.2〕过点G作GM⊥BC交BC的延长线于M,连接HF.∵AD∥BC,∴∠AHF=∠MFH.∵EH∥FG,∴∠EHF=∠GFH.∴∠AHE=∠MFG.又∵∠A=∠GMF=90°,EH=GF,∴△AHE≌△MFG.∴GM=AE=2.∴.〔3〕△GFC的面积不能等于2.说明一:∵假设S△GFC=2,那么12-a=2,∴a=10.此时,在△BEF中,.在△AHE中,,∴AH>AD,即点H已经不在边AD上,故不可能有S=.2△GFC说明二:△GFC的面积不能等于2.∵点H在AD上,∴菱形边EH的最大值为,∴BF的最大值为.又∵函数S△GFC=12-a的值随着a的增大而减小,∴S△GFC的最小值为.又∵,∴△GFC的面积不能等于2.13.如图①,在△ABC中,AB=7,tanA=,∠B=45°.点P从点A出发,沿AB方向以每秒1个单位长度的速度向终点B运动〔不与点 A、B重合〕,过点P作PQ⊥AB.交折线AC-CB于点Q,以PQ为边向右作正方形PQMN,设点P的运动时间为t〔秒〕,正方形PQMN与△ABC重叠局部图形的面积为S〔平方单位〕.1〕直接写出正方形PQMN的边PQ的长〔用含t的代数式表示〕.2〕当点M落在边BC上时,求t的值.3〕求S与t之间的函数关系式.4〕如图②,点P运动的同时,点H从点B出发,沿B-A-B的方向做一次往返运动,在B-A上的速度为每秒2个单位长度,在A-B上的速度为每秒4个单位长度,当点H停止运动时,点P也随之停止,连结MH.设MH将正方形PQMN分成的两局部图形面积分别为S1、S2〔平方单位〕〔0<S1<S2〕,直接写出当S2≥3S1时t的取值范围.【答案】(1)PQ=7-t.(2)t=.(3)当0<t≤时,S=.当<t≤4,.当4<t<7时,.〔4〕或或.【解析】试题分析:〔1〕分两种情况讨论:当点Q在线段AC上时,当点Q在线段BC上时.〔2〕根据AP+PN+NB=AB,列出关于t的方程即可解答;〔3〕当0<t≤时,当<t≤4,当4<t<7时;〔4〕或或.试题解析:〔1〕当点Q在线段AC上时,PQ=tanAAP=t.当点Q在线段BC上时,PQ=7-t.〔2〕当点M落在边BC上时,如图③,由题意得:t+t+t=7,解得:t=.∴当点M落在边BC上时,求t的值为.〔3〕当0<t≤时,如图④,S=当.<t≤4,如图⑤,.当4<t<7时,如图⑥,.〔4〕或或..考点:四边形综合题.14.:如图,四边形ABCD和四边形AECF都是矩形,AE与BC交于点M,CF与AD交于点N.〔1〕求证:△ABM≌△CDN;〔2〕矩形ABCD和矩形AECF满足何种关系时,四边形AMCN是菱形,证明你的结论.【答案】〔1〕证明见解析;〔2〕当AB=AF时,四边形AMCN是菱形.证明见解析;【解析】试题分析:〔1〕由条件可得四边形AMCN是平行四边形,从而可得AM=CN,再由AB=CD,∠B=∠D=90°,利用HL即可证明;2〕假设四边形AMCN为菱形,那么有AM=AN,从可得∠BAM=∠FAN,又∠B=∠F=90°,所以有△ABM≌△AFN,从而得AB=AF,因此当AB=AF时,四边形AMCN是菱形.试题解析:〔1〕∵四边形ABCD是矩形,∴∠B=∠D=90°,AB=CD,AD∥BC.∵四边形AECF是矩形,∴AE∥CF.∴四边形AMCN是平行四边形.∴AM=CN.在Rt△ABM和Rt△CDN中,AB=CD,AM=CN,∴Rt△ABM≌Rt△CDN.〔2〕当AB=AF时,四边形AMCN是菱形.∵四边形ABCD、AECF是矩形,∴∠B=∠BAD=∠EAF=∠F=90°.∴∠BAD-∠NAM=EAF-∠NAM,即∠BAM=∠FAN.又∵AB=AF,∴△ABM≌△AFN.∴AM=AN.由〔1〕知四边形AMCN是平行四边形,∴平行四边形AMCN是菱形.考点:1.矩形的性质;2.三角形全等的判定与性质;3.菱形的判定.15.如图1,在菱形ABCD中,ABC=60°,假设点E在AB的延长线上,EF∥AD,EF=BE,点P是DE的中点,连接FP并延长交AD于点G.〔1〕过D作DH AB,垂足为H,假设DH=,BE=AB,求DG的长;〔2〕连接CP,求证:CP FP;F在〔3〕如图2,在菱形ABCD中,ABC=60°,假设点E在CB的延长线上运动,点AB的延长线上运动,且BE=BF,连接DE,点P为DE的中点,连接FP、CP,那么第〔2〕问的结论成立吗?假设成立,求出的值;假设不成立,请说明理由.【答案】〔1〕1;〔2〕见解析;〔3〕.【解析】试题分析:〔1〕根据菱形得出DA∥BC,CD=CB,∠CDG=∠CBA=60°,那么∠DAH=∠ABC=60,°根据DH⊥AB得出∠DHA=90,°根据Rt△ADH的正弦值得出AD的长度,然后得出BE的长度,然后证明△PDG≌△PEF,得出DG=EF,根据EF∥AD,AD∥BC得出EF∥BC,那么说明△BEF为正三角形,从而得出DG的长度;〔2〕连接CG、CF,根据△PDG≌△PEF得出PG=PF,然后证明△CDG≌△CBF,从而得到CG=CF,根据PG=PF得出垂直;〔3〕过D作EF的平行线,交FP延长于点G,连接CG、CF证△PEF≌△PDG,然后证明△CDG≌△CBF,从而得出∠GCE=120°,根据Rt△CPF求出比值.试题解析:〔1〕解:∵四边形ABCD为菱形∴DA∥BCCD="CB"∠CDG=∠CBA=60°∴∠DAH=∠ABC=60°∵DH⊥AB∴∠DHA=90°在Rt△ADH中sin∠DAH=∴AD=∴BE= AB=×4=1∵EF∥AD∴∠PDG=∠PEB∵P为DE的中点∴PD=PE∵∠DPG=∠EPF∴△PDG≌△PEF∴DG=EF∵EF∥ADAD∥BC∴EF∥BC∴∠FEB=∠CBA=60°∵BE=EF∴△BEF为正三角形∴EF=BE=1∴DG=EF=1、证明:连接CG、CF由〔1〕知△PDG≌△PEF∴PG=PF在△CDG与△CBF中易证:∠CDG=∠CBF=60°CD=CBBF=EF=DG∴△CDG≌△CBF∴CG=CF∵PG=PF∴CP⊥GF〔3〕如图:CP⊥GF仍成立理由如下:过D作EF的平行线,交FP延长于点G连接CG、CF证△PEF≌△PDG∴DG=EF=BF∵DG∥EF∴∠GDP=∠EFP∵DA∥BC∴∠ADP=∠PEC ∴∠GDP-∠ADP=∠EFP-∠PEC∴∠GDA=∠BEF=60∴°∠CDG=∠ADC+∠GDA=120°∵∠CBF=180-°∠EBF=120∴°∠CBF=∠CDG∵CD=BCDG=BF∴△CDG≌△CBF∴CG=CF∠DCG=∠FCE∵PG=PF∴CP⊥PF∠GCP=∠FCP∵∠DCP=180-∠ABC=120∴°∠DCG+∠GCE=120∴°∠FCE+∠GCE=120即°∠GCE=120°∴∠FCP=∠GCE=60在°Rt△CPF中tan∠FCP=tan60=°=考点:三角形全等的证明与性质.。
2020-2021中考数学复习平行四边形专项易错题附答案

2020-2021中考数学复习平行四边形专项易错题附答案一、平行四边形1.问题发现:(1)如图①,点P 为平行四边形ABCD 内一点,请过点P 画一条直线l ,使其同时平分平行四边形ABCD 的面积和周长.问题探究:(2)如图②,在平面直角坐标系xOy 中,矩形OABC 的边OA 、OC 分别在x 轴、y 轴正半轴上,点B 坐标为(8,6).已知点(6,7)P 为矩形外一点,请过点P 画一条同时平分矩形OABC 面积和周长的直线l ,说明理由并求出直线l ,说明理由并求出直线l 被矩形ABCD 截得线段的长度.问题解决:(3)如图③,在平面直角坐标系xOy 中,矩形OABCD 的边OA 、OD 分别在x 轴、y 轴正半轴上,DC x ∥轴,AB y ∥轴,且8OA OD ==,2AB CD ==,点(1052,1052)P --为五边形内一点.请问:是否存在过点P 的直线l ,分别与边OA 与BC 交于点E 、F ,且同时平分五边形OABCD 的面积和周长?若存在,请求出点E 和点F 的坐标:若不存在,请说明理由.【答案】(1)作图见解析;(2)25y x =-,353)(0,0)E ,(5,5)F .【解析】试题分析:(1)连接AC 、BD 交于点O ,作直线PO ,直线PO 将平行四边形ABCD 的面积和周长分别相等的两部分.(2)连接AC ,BD 交于点O ',过O '、P 点的直线将矩形ABCD 的面积和周长分为分别相等的两部分.(3)存在,直线y x =平分五边形OABCD 面积、周长.试题解析:(1)作图如下:(2)∵(6,7)P ,(4,3)O ',∴设:6PO y kx =+',67{43k b k b +=+=,2{5k b ==-, ∴25y x =-,交x 轴于5,02N ⎛⎫ ⎪⎝⎭, 交BC 于11,62M ⎛⎫ ⎪⎝⎭, 2211563522MN ⎛⎫=+-= ⎪⎝⎭.(3)存在,直线y x =平分五边形OABCD 面积、周长.∵(1052,102)P --在直线y x =上,∴连OP 交OA 、BC 于点E 、F ,设:BC y kx b =+,(8,2)(2,8)B C ,82{28k b k +=+=,1{10k b =-=, ∴直线:10BC y x =-+,联立10{y x y x =-+=,得55x y =⎧⎨=⎩, ∴(0,0)E ,(5,5)F .2.如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t 秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(1)求证:AE=DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)当t为何值时,△DEF为直角三角形?请说明理由.【答案】(1)见解析;(2)能,t=10;(3)t=152或12.【解析】【分析】(1)利用t表示出CD以及AE的长,然后在直角△CDF中,利用直角三角形的性质求得DF的长,即可证明;(2)易证四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,据此即可列方程求得t的值;(3)△DEF为直角三角形,分∠EDF=90°和∠DEF=90°两种情况讨论.【详解】解:(1)证明:∵在Rt△ABC中,∠C=90°﹣∠A=30°,∴AB=12AC=12×60=30cm,∵CD=4t,AE=2t,又∵在Rt△CDF中,∠C=30°,∴DF=12CD=2t,∴DF=AE;(2)能,∵DF∥AB,DF=AE,∴四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,即60﹣4t=2t,解得:t=10,∴当t=10时,AEFD是菱形;(3)若△DEF为直角三角形,有两种情况:①如图1,∠EDF=90°,DE∥BC,则AD=2AE,即60﹣4t=2×2t,解得:t=152,②如图2,∠DEF=90°,DE⊥AC,则AE=2AD,即2t2(604t)=-,解得:t=12,综上所述,当t=152或12时,△DEF为直角三角形.3.已知矩形纸片OBCD的边OB在x轴上,OD在y轴上,点C在第一象限,且86OB OD==,.现将纸片折叠,折痕为EF(点E,F是折痕与矩形的边的交点),点P 为点D的对应点,再将纸片还原。
精选中考数学易错题专题复习平行四边形及详细答案
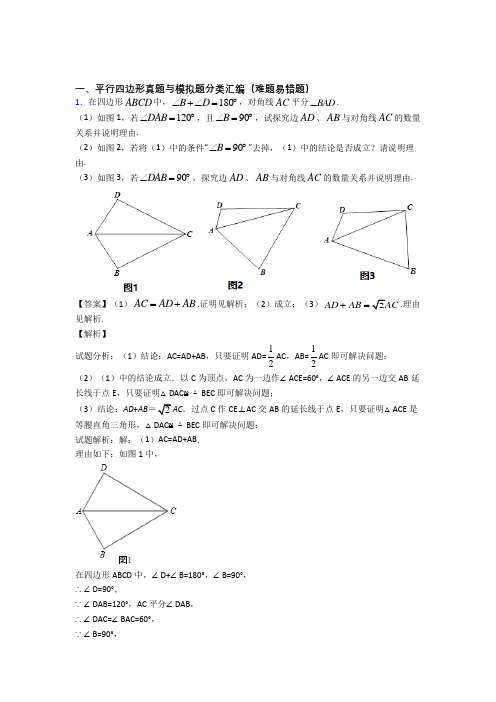
一、平行四边形真题与模拟题分类汇编(难题易错题)1.在四边形ABCD 中,180B D ∠+∠=︒,对角线AC 平分BAD ∠.(1)如图1,若120DAB ∠=︒,且90B ∠=︒,试探究边AD 、AB 与对角线AC 的数量关系并说明理由.(2)如图2,若将(1)中的条件“90B ∠=︒”去掉,(1)中的结论是否成立?请说明理由.(3)如图3,若90DAB ∠=︒,探究边AD 、AB 与对角线AC 的数量关系并说明理由.【答案】(1)AC AD AB =+.证明见解析;(2)成立;(3)2AD AB AC +=.理由见解析.【解析】试题分析:(1)结论:AC=AD+AB ,只要证明AD=12AC ,AB=12AC 即可解决问题; (2)(1)中的结论成立.以C 为顶点,AC 为一边作∠ACE=60°,∠ACE 的另一边交AB 延长线于点E ,只要证明△DAC ≌△BEC 即可解决问题;(3)结论:AD +AB =2AC .过点C 作CE ⊥AC 交AB 的延长线于点E ,只要证明△ACE 是等腰直角三角形,△DAC ≌△BEC 即可解决问题;试题解析:解:(1)AC=AD+AB .理由如下:如图1中,在四边形ABCD 中,∠D+∠B=180°,∠B=90°,∴∠D=90°,∵∠DAB=120°,AC 平分∠DAB ,∴∠DAC=∠BAC=60°,∵∠B=90°,∴AB=12AC,同理AD=12AC.∴AC=AD+AB.(2)(1)中的结论成立,理由如下:以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,∵∠BAC=60°,∴△AEC为等边三角形,∴AC=AE=CE,∵∠D+∠ABC=180°,∠DAB=120°,∴∠DCB=60°,∴∠DCA=∠BCE,∵∠D+∠ABC=180°,∠ABC+∠EBC=180°,∴∠D=∠CBE,∵CA=CE,∴△DAC≌△BEC,∴AD=BE,∴AC=AD+AB.(3)结论:AD+AB=2AC.理由如下:过点C作CE⊥AC交AB的延长线于点E,∵∠D+∠B=180°,∠DAB=90°,∴DCB=90°,∵∠ACE=90°,∴∠DCA=∠BCE,又∵AC平分∠DAB,∴∠CAB=45°,∴∠E=45°.∴AC=CE.又∵∠D+∠ABC=180°,∠D=∠CBE,∴△CDA ≌△CBE ,∴AD=BE ,∴AD+AB=AE .在Rt △ACE 中,∠CAB=45°,∴AE =245AC AC cos ︒= ∴2AD AB AC +=.2.已知:如图,在平行四边形ABCD 中,O 为对角线BD 的中点,过点O 的直线EF 分别交AD ,BC 于E ,F 两点,连结BE ,DF .(1)求证:△DOE ≌△BOF .(2)当∠DOE 等于多少度时,四边形BFDE 为菱形?请说明理由.【答案】(1)证明见解析;(2)当∠DOE =90°时,四边形BFED 为菱形,理由见解析.【解析】试题分析:(1)利用平行四边形的性质以及全等三角形的判定方法得出△DOE ≌△BOF (ASA );(2)首先利用一组对边平行且相等的四边形是平行四边形得出四边形EBFD 是平行四边形,进而利用垂直平分线的性质得出BE=ED ,即可得出答案.试题解析:(1)∵在▱ABCD 中,O 为对角线BD 的中点,∴BO=DO ,∠EDB=∠FBO ,在△EOD 和△FOB 中,∴△DOE ≌△BOF (ASA );(2)当∠DOE=90°时,四边形BFDE 为菱形,理由:∵△DOE ≌△BOF ,∴OE=OF ,又∵OB=OD ,∴四边形EBFD 是平行四边形, ∵∠EOD=90°,∴EF ⊥BD ,∴四边形BFDE 为菱形.考点:平行四边形的性质;全等三角形的判定与性质;菱形的判定.3.如图,四边形ABCD 中,∠BCD =∠D =90°,E 是边AB 的中点.已知AD =1,AB =2.(1)设BC =x ,CD =y ,求y 关于x 的函数关系式,并写出定义域;(2)当∠B =70°时,求∠AEC 的度数;(3)当△ACE 为直角三角形时,求边BC 的长.【答案】(1)()22303y x x x =-++<<;(2)∠AEC =105°;(3)边BC 的长为2或1172. 【解析】试题分析:(1)过A 作AH ⊥BC 于H ,得到四边形ADCH 为矩形.在△BAH 中,由勾股定理即可得出结论.(2)取CD 中点T ,连接TE ,则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD ,∠AET =∠B =70°.又AD =AE =1,得到∠AED =∠ADE =∠DET =35°.由ET 垂直平分CD ,得∠CET =∠DET =35°,即可得到结论.(3)分两种情况讨论:①当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 解△ABH 即可得到结论.②当∠CAE =90°时,易知△CDA ∽△BCA ,由相似三角形对应边成比例即可得到结论. 试题解析:解:(1)过A 作AH ⊥BC 于H .由∠D =∠BCD =90°,得四边形ADCH 为矩形. 在△BAH 中,AB =2,∠BHA =90°,AH =y ,HB =1x -,∴22221y x =+-, 则()22303y x x x =-++<<(2)取CD 中点T ,联结TE ,则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD ,∴∠AET =∠B =70°.又AD =AE =1,∴∠AED =∠ADE =∠DET =35°.由ET 垂直平分CD ,得∠CET =∠DET =35°,∴∠AEC =70°+35°=105°.(3)分两种情况讨论:①当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 则在△ABH 中,∠B =60°,∠AHB =90°,AB =2,得BH =1,于是BC =2.②当∠CAE =90°时,易知△CDA ∽△BCA ,又2224AC BC AB x =-- 则2241174AD CA x x AC CB x -±=⇒=⇒=-(舍负) 易知∠ACE <90°,所以边BC 117+综上所述:边BC的长为2或1172.点睛:本题是四边形综合题.考查了梯形中位线,相似三角形的判定与性质.解题的关键是掌握梯形中常见的辅助线作法.4.已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)请问EG与CG存在怎样的数量关系,并证明你的结论;(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?(请直接写出结果,不必写出理由)【答案】(1)证明见解析(2)证明见解析(3)结论仍然成立【解析】【分析】(1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG=EG.(2)结论仍然成立,连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点;再证明△DAG≌△DCG,得出AG=CG;再证出△DMG≌△FNG,得到MG=NG;再证明△AMG≌△ENG,得出AG=EG;最后证出CG=EG.(3)结论依然成立.【详解】(1)CG=EG.理由如下:∵四边形ABCD是正方形,∴∠DCF=90°.在Rt△FCD中,∵G为DF的中点,∴CG=12FD,同理.在Rt△DEF中,EG=12FD,∴CG=EG.(2)(1)中结论仍然成立,即EG=CG.证法一:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.在△DAG与△DCG中,∵AD=CD,∠ADG=∠CDG,DG=DG,∴△DAG≌△DCG(SAS),∴AG=CG;在△DMG与△FNG中,∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG (ASA),∴MG=NG.∵∠EAM=∠AEN=∠AMN=90°,∴四边形AENM是矩形,在矩形AENM中,AM=EN.在△AMG与△ENG中,∵AM=EN,∠AMG=∠ENG,MG=NG,∴△AMG≌△ENG(SAS),∴AG=EG,∴EG=CG.证法二:延长CG至M,使MG=CG,连接MF,ME,EC.在△DCG与△FMG中,∵FG=DG,∠MGF=∠CGD,MG=CG,∴△DCG≌△FMG,∴MF=CD,∠FMG=∠DCG,∴MF∥CD∥AB,∴EF⊥MF.在Rt△MFE与Rt△CBE中,∵MF=CB,∠MFE=∠EBC=90°,EF=BE,∴△MFE≌△CBE∴∠MEF=∠CEB,∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°,∴△MEC为直角三角形.∵MG=CG,∴EG=12MC,∴EG=CG.(3)(1)中的结论仍然成立.理由如下:过F作CD的平行线并延长CG交于M点,连接EM、EC,过F作FN垂直于AB于N.由于G为FD中点,易证△CDG≌△MFG,得到CD=FM,又因为BE=EF,易证∠EFM=∠EBC,则△EFM≌△EBC,∠FEM=∠BEC,EM=EC∵∠FEC+∠BEC=90°,∴∠FEC+∠FEM=90°,即∠MEC=90°,∴△MEC是等腰直角三角形.∵G为CM中点,∴EG=CG,EG⊥CG【点睛】本题是四边形的综合题.(1)关键是利用直角三角形斜边上的中线等于斜边的一半解答;(2)关键是利用了直角三角形斜边上的中线等于斜边的一半的性质、全等三角形的判定和性质解答.5.如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.(1)证明:BE=CF.(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.【答案】(1)见解析;(2)43;(3)见解析【解析】试题分析:(1)先求证AB=AC,进而求证△ABC、△ACD为等边三角形,得∠4=60°,AC=AB进而求证△ABE≌△ACF,即可求得BE=CF;(2)根据△ABE≌△ACF可得S△ABE=S△ACF,故根据S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC即可解题;(3)当正三角形AEF的边AE与BC垂直时,边AE最短.△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又根据S△CEF=S四边形AECF-S△AEF,则△CEF的面积就会最大.试题解析:(1)证明:连接AC,∵∠1+∠2=60°,∠3+∠2=60°,∴∠1=∠3,∵∠BAD=120°,∴∠ABC=∠ADC=60°∵四边形ABCD是菱形,∴AB=BC=CD=AD,∴△ABC、△ACD为等边三角形∴∠4=60°,AC=AB,∴在△ABE和△ACF中,,∴△ABE≌△ACF.(ASA)∴BE=CF.(2)解:由(1)得△ABE≌△ACF,则S△ABE=S△ACF.故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值.作AH⊥BC于H点,则BH=2,S四边形AECF=S△ABC===;(3)解:由“垂线段最短”可知,当正三角形AEF的边AE与BC垂直时,边AE最短.故△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又S△CEF=S四边形AECF﹣S△AEF,则△CEF的面积就会最大.由(2)得,S△CEF=S四边形AECF﹣S△AEF=﹣=.点睛:本题考查了菱形每一条对角线平分一组对角的性质,考查了全等三角形的证明和全等三角形对应边相等的性质,考查了三角形面积的计算,本题中求证△ABE≌△ACF是解题的关键.6.如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.(1)试猜想AE与GC有怎样的关系(直接写出结论即可);(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和CG.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.(3)在(2)中,若E是BC的中点,且BC=2,则C,F两点间的距离为.【答案】(1) AE=CG,AE⊥GC;(2)成立,证明见解析; (3)2.【解析】【分析】(1)观察图形,AE、CG的位置关系可能是垂直,下面着手证明.由于四边形ABCD、DEFG都是正方形,易证得△ADE≌△CDG,则∠1=∠2,由于∠2、∠3互余,所以∠1、∠3互余,由此可得AE⊥GC.(2)题(1)的结论仍然成立,参照(1)题的解题方法,可证△ADE≌△CDG,得∠5=∠4,由于∠4、∠7互余,而∠5、∠6互余,那么∠6=∠7;由图知∠AEB=∠CEH=90°﹣∠6,即∠7+∠CEH=90°,由此得证.(3)如图3中,作CM⊥DG于G,GN⊥CD于N,CH⊥FG于H,则四边形CMGH是矩形,可得CM=GH,CH=GM.想办法求出CH,HF,再利用勾股定理即可解决问题.【详解】(1)AE=CG,AE⊥GC;证明:延长GC交AE于点H,在正方形ABCD与正方形DEFG中,AD=DC,∠ADE=∠CDG=90°,DE=DG,∴△ADE≌△CDG(SAS),∴AE,CG,∠1=∠2∵∠2+∠3=90°,∴∠1+∠3=90°,∴∠AHG=180°﹣(∠1+∠3)=180°﹣90°=90°,∴AE⊥GC.(2)答:成立;证明:延长AE和GC相交于点H,在正方形ABCD和正方形DEFG中,AD=DC,DE=DG,∠ADC=∠DCB=∠B=∠BAD=∠EDG=90°,∴∠1=∠2=90°﹣∠3;∴△ADE ≌△CDG(SAS),∴AE =CG ,∠5=∠4;又∵∠5+∠6=90°,∠4+∠7=180°﹣∠DCE =180°﹣90°=90°,∴∠6=∠7,又∵∠6+∠AEB =90°,∠AEB =∠CEH ,∴∠CEH+∠7=90°,∴∠EHC =90°,∴AE ⊥GC .(3)如图3中,作CM ⊥DG 于G ,GN ⊥CD 于N ,CH ⊥FG 于H ,则四边形CMGH 是矩形,可得CM =GH ,CH =GM .∵BE =CE =1,AB =CD =2,∴AE =DE =CG ═DG =FG 5∵DE =DG ,∠DCE =∠GND ,∠EDC =∠DGN ,∴△DCE ≌△GND(AAS),∴GCD =2,∵S △DCG =12•CD•NG =12•DG•CM , ∴2×25, ∴CM =GH 45, ∴MG =CH 22CG CM -35, ∴FH =FG ﹣FG 5, ∴CF 22FH CH +22535()()55+2. 2.【点睛】 本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.7.在平面直角坐标系中,O 为原点,点A (﹣6,0)、点C (0,6),若正方形OABC 绕点O 顺时针旋转,得正方形OA′B′C′,记旋转角为α: (1)如图①,当α=45°时,求BC 与A′B′的交点D 的坐标; (2)如图②,当α=60°时,求点B′的坐标;(3)若P 为线段BC′的中点,求AP 长的取值范围(直接写出结果即可).【答案】(1)(62,6)-;(2)(333,333)+;(3)323323AP +. 【解析】 【分析】(1)当α=45°时,延长OA′经过点B ,在Rt △BA′D 中,∠OBC =45°,A′B =626,可求得BD 的长,进而求得CD 的长,即可得出点D 的坐标;(2)过点C′作x 轴垂线MN ,交x 轴于点M ,过点B′作MN 的垂线,垂足为N ,证明△OMC′≌△C′NB′,可得C′N =OM =33,B′N =C′M =3,即可得出点B′的坐标; (3)连接OB ,AC 相交于点K ,则K 是OB 的中点,因为P 为线段BC′的中点,所以PK =12OC′=3,即点P 在以K 为圆心,3为半径的圆上运动,即可得出AP 长的取值范围. 【详解】解:(1)∵A (﹣6,0)、C (0,6),O (0,0), ∴四边形OABC 是边长为6的正方形, 当α=45°时,如图①,延长OA′经过点B ,∵OB =2,OA′=OA =6,∠OBC =45°, ∴A′B =626,∴BD =(626)21262=-, ∴CD =6﹣(1262-=626,∴BC 与A′B′的交点D 的坐标为(662-6);(2)如图②,过点C′作x轴垂线MN,交x轴于点M,过点B′作MN的垂线,垂足为N,∵∠OC′B′=90°,∴∠OC′M=90°﹣∠B′C′N=∠C′B′N,∵OC′=B′C′,∠OMC′=∠C′NB′=90°,∴△OMC′≌△C′NB′(AAS),当α=60°时,∵∠A′OC′=90°,OC′=6,∴∠C′OM=30°,∴C′N=OM=33,B′N=C′M=3,∴点B′的坐标为)-+;333,333(3)如图③,连接OB,AC相交于点K,则K是OB的中点,∵P为线段BC′的中点,∴PK=1OC′=3,2∴P在以K为圆心,3为半径的圆上运动,∵AK=2∴AP最大值为323,AP的最小值为323,AP+.∴AP长的取值范围为323323【点睛】本题考查正方形性质,全等三角形判定与性质,三角形中位线定理.(3)问解题的关键是利用中位线定理得出点P 的轨迹.8.点P 是矩形ABCD 对角线AC 所在直线上的一个动点(点P 不与点A ,C 重合),分别过点A ,C 向直线BP 作垂线,垂足分别为点E ,F ,点O 为AC 的中点.(1)如图1,当点P 与点O 重合时,请你判断OE 与OF 的数量关系;(2)当点P 运动到如图2所示位置时,请你在图2中补全图形并通过证明判断(1)中的结论是否仍然成立;(3)若点P 在射线OA 上运动,恰好使得∠OEF =30°时,猜想此时线段CF ,AE ,OE 之间有怎样的数量关系,直接写出结论不必证明.【答案】(1)OE =OF .理由见解析;(2)补全图形如图所示见解析,OE =OF 仍然成立;(3)CF =OE+AE 或CF =OE ﹣AE . 【解析】 【分析】(1)根据矩形的性质以及垂线,即可判定()AOE COF AAS ∆≅∆,得出OE =OF ; (2)先延长EO 交CF 于点G ,通过判定()AOE COG ASA ∆≅∆,得出OG =OE ,再根据Rt EFG ∆中,12OF EG =,即可得到OE =OF ; (3)根据点P 在射线OA 上运动,需要分两种情况进行讨论:当点P 在线段OA 上时,当点P 在线段OA 延长线上时,分别根据全等三角形的性质以及线段的和差关系进行推导计算即可. 【详解】(1)OE =OF .理由如下: 如图1.∵四边形ABCD 是矩形,∴ OA =OC .∵AE BP ⊥,CF BP ⊥,∴90AEO CFO ∠=∠=︒.∵在AOE ∆和COF ∆中,AEO CFO AOE COF OA OC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AOE COF AAS ∆≅∆,∴ OE =OF ;(2)补全图形如图2,OE =OF 仍然成立.证明如下: 延长EO 交CF 于点G .∵AE BP ⊥,CF BP ⊥,∴ AE //CF ,∴EAO GCO ∠=∠. 又∵点O 为AC 的中点,∴ AO =CO .在AOE ∆和COG ∆中,EAO GCO AO CO AOE COG ∠=∠⎧⎪=⎨⎪∠=⎩,∴()AOE COG ASA ∆≅∆,∴ OG =OE ,∴Rt EFG ∆中,12OF EG =,∴ OE =OF ; (3)CF =OE +AE 或CF =OE -AE .证明如下:①如图2,当点P 在线段OA 上时.∵30OEF ∠=︒,90EFG ∠=︒,∴60OGF ∠=︒,由(2)可得:OF =OG ,∴OGF ∆是等边三角形,∴ FG =OF =OE ,由(2)可得:AOE COG ∆≅∆,∴ CG =AE . 又∵ CF =GF +CG ,∴ CF =OE +AE ;②如图3,当点P 在线段OA 延长线上时.∵30OEF ∠=︒,90EFG ∠=︒,∴60OGF ∠=︒,同理可得:OGF ∆是等边三角形,∴ FG =OF =OE ,同理可得:AOE COG ∆≅∆,∴ CG =AE . 又∵ CF =GF -CG ,∴ CF =OE -AE .【点睛】本题属于四边形综合题,主要考查了矩形的性质、全等三角形的性质和判定以及等边三角形的性质和判定,解决问题的关键是构建全等三角形和证明三角形全等,利用矩形的对角线互相平分得全等的边相等的条件,根据线段的和差关系使问题得以解决.9.如图,AB 为⊙O 的直径,点E 在⊙O 上,过点E 的切线与AB 的延长线交于点D ,连接BE ,过点O 作BE 的平行线,交⊙O 于点F ,交切线于点C ,连接AC (1)求证:AC 是⊙O 的切线;(2)连接EF ,当∠D= °时,四边形FOBE 是菱形.【答案】(1)见解析;(2)30. 【解析】 【分析】(1)由等角的转换证明出OCA OCE ∆∆≌,根据圆的位置关系证得AC 是⊙O 的切线. (2)根据四边形FOBE 是菱形,得到OF=OB=BF=EF ,得证OBE ∆为等边三角形,而得出60BOE ∠=︒,根据三角形内角和即可求出答案. 【详解】(1)证明:∵CD 与⊙O 相切于点E , ∴OE CD ⊥, ∴90CEO ∠=︒,又∵OC BE ,∴COE OEB ∠=∠,∠OBE=∠COA ∵OE=OB ,∴OEB OBE ∠=∠, ∴COE COA ∠=∠, 又∵OC=OC ,OA=OE , ∴OCA OCE SAS ∆∆≌(), ∴90CAO CEO ∠=∠=︒, 又∵AB 为⊙O 的直径, ∴AC 为⊙O 的切线;(2)解:∵四边形FOBE 是菱形, ∴OF=OB=BF=EF , ∴OE=OB=BE ,∴OBE ∆为等边三角形, ∴60BOE ∠=︒, 而OE CD ⊥, ∴30D ∠=︒. 故答案为30. 【点睛】本题主要考查与圆有关的位置关系和圆中的计算问题,熟练掌握圆的性质是本题的解题关键.10.(本题14分)小明在学习平行线相关知识时总结了如下结论:端点分别在两条平行线上的所有线段中,垂直于平行线的线段最短.小明应用这个结论进行了下列探索活动和问题解决.问题1:如图1,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AC边上的一动点,以PB,PA为边构造□APBQ,求对角线PQ的最小值及PQ最小时的值.(1)在解决这个问题时,小明构造出了如图2的辅助线,则PQ的最小值为,当PQ最小时= _____ __;(2)小明对问题1做了简单的变式思考.如图3,P为AB边上的一动点,延长PA到点E,使AE=nPA(n为大于0的常数).以PE,PC为边作□PCQE,试求对角线PQ长的最小值,并求PQ最小时的值;问题2:在四边形ABCD中,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.(1)如图4,若为上任意一点,以,为边作□.试求对角线长的最小值和PQ最小时的值.(2)若为上任意一点,延长到,使,再以,为边作□.请直接写出对角线长的最小值和PQ最小时的值.【答案】问题1:(1)3,;(2)PQ=,=.问题2:(1)=4,.(2)PQ的最小值为..【解析】试题分析:问题1:(1)首先根据条件可证四边形PCBQ是矩形,然后根据条件“四边形APBQ是平行四边形可得AP=QB=PC,从而可求的值.(2)由题可知:当QP⊥AC 时,PQ最小.过点C作CD⊥AB于点D.此时四边形CDPQ为矩形,PQ=CD,在Rt△ABC中,∠C=90°,AC=4,BC=3,利用面积可求出CD=,然后可求出AD=,由AE=nPA可得PE=,而PE=CQ=PD=AD-AP=,所以AP=.所以=.问题2:(1)设对角线与相交于点.Rt≌Rt.所以AD=HC,QH=AP.由题可知:当QP⊥AB时,PQ最小,此时=CH=4,根据条件可证四边形BPQH为矩形,从而QH=BP=AP.所以.(2)根据题意画出图形,当AB 时,的长最小,PQ的最小值为..试题解析:问题1:(1)3,;(2)过点C作CD⊥AB于点D.由题意可知当PQ⊥AB时,PQ最短.所以此时四边形CDPQ为矩形.PQ=CD,DP=CQ=PE.因为∠BCA=90°,AC=4,BC=3,所以AB=5.所以CD=.所以PQ=.在Rt△ACD中AC=4,CD=,所以AD=.因为AE=nPA,所以PE==CQ=PD=AD-AP=.所以AP=.所以=.问题2:(1)如图2,设对角线与相交于点.所以G是DC的中点,作QH BC,交BC的延长线于H,因为AD//BC,所以.所以.又,所以Rt≌Rt.所以AD=HC,QH=AP.由图知,当AB时,的长最小,即=CH=4.易得四边形BPQH为矩形,所以QH=BP=AP.所以.(若学生有能力从梯形中位线角度考虑,若正确即可评分.但讲评时不作要求)(2)PQ的最小值为..考点:1.直角三角形的性质;2.全等三角形的判定与性质;3.平行四边形的性质;4矩形的判定与性质.。
中考数学易错题专题复习-平行四边形练习题附答案

一、平行四边形真题与模拟题分类汇编(难题易错题)1.问题发现:(1)如图①,点P 为平行四边形ABCD 内一点,请过点P 画一条直线l ,使其同时平分平行四边形ABCD 的面积和周长.问题探究:(2)如图②,在平面直角坐标系xOy 中,矩形OABC 的边OA 、OC 分别在x 轴、y 轴正半轴上,点B 坐标为(8,6).已知点(6,7)P 为矩形外一点,请过点P 画一条同时平分矩形OABC 面积和周长的直线l ,说明理由并求出直线l ,说明理由并求出直线l 被矩形ABCD 截得线段的长度.问题解决:(3)如图③,在平面直角坐标系xOy 中,矩形OABCD 的边OA 、OD 分别在x 轴、y 轴正半轴上,DC x ∥轴,AB y ∥轴,且8OA OD ==,2AB CD ==,点(1052,1052)P --为五边形内一点.请问:是否存在过点P 的直线l ,分别与边OA 与BC 交于点E 、F ,且同时平分五边形OABCD 的面积和周长?若存在,请求出点E 和点F 的坐标:若不存在,请说明理由.【答案】(1)作图见解析;(2)25y x =-,353)(0,0)E ,(5,5)F .【解析】试题分析:(1)连接AC 、BD 交于点O ,作直线PO ,直线PO 将平行四边形ABCD 的面积和周长分别相等的两部分.(2)连接AC ,BD 交于点O ',过O '、P 点的直线将矩形ABCD 的面积和周长分为分别相等的两部分.(3)存在,直线y x =平分五边形OABCD 面积、周长.试题解析:(1)作图如下:(2)∵(6,7)P ,(4,3)O ',∴设:6PO y kx =+',67{43k b k b +=+=,2{5k b ==-, ∴25y x =-,交x 轴于5,02N ⎛⎫ ⎪⎝⎭, 交BC 于11,62M ⎛⎫ ⎪⎝⎭, 2211563522MN ⎛⎫=+-= ⎪⎝⎭.(3)存在,直线y x =平分五边形OABCD 面积、周长.∵(1052,102)P --在直线y x =上,∴连OP 交OA 、BC 于点E 、F ,设:BC y kx b =+,(8,2)(2,8)B C ,82{28k b k +=+=,1{10k b =-=, ∴直线:10BC y x =-+,联立10{y x y x =-+=,得55x y =⎧⎨=⎩, ∴(0,0)E ,(5,5)F .2.操作:如图,边长为2的正方形ABCD,点P在射线BC上,将△ABP沿AP向右翻折,得到△AEP,DE所在直线与AP所在直线交于点F.探究:(1)如图1,当点P在线段BC上时,①若∠BAP=30°,求∠AFE的度数;②若点E 恰为线段DF的中点时,请通过运算说明点P会在线段BC的什么位置?并求出此时∠AFD 的度数.归纳:(2)若点P是线段BC上任意一点时(不与B,C重合),∠AFD的度数是否会发生变化?试证明你的结论;猜想:(3)如图2,若点P在BC边的延长线上时,∠AFD的度数是否会发生变化?试在图中画出图形,并直接写出结论.【答案】(1)①45°;②BC的中点,45°;(2)不会发生变化,证明参见解析;(3)不会发生变化,作图参见解析.【解析】试题分析:(1)当点P在线段BC上时,①由折叠得到一对角相等,再利用正方形性质求出∠DAE度数,在三角形AFD中,利用内角和定理求出所求角度数即可;②由E为DF中点,得到P为BC中点,如图1,连接BE交AF于点O,作EG∥AD,得EG∥BC,得到AF 垂直平分BE,进而得到三角形BOP与三角形EOG全等,利用全等三角形对应边相等得到BP=EG=1,得到P为BC中点,进而求出所求角度数即可;(2)若点P是线段BC上任意一点时(不与B,C重合),∠AFD的度数不会发生变化,作AG⊥DF于点G,如图1(a)所示,利用折叠的性质及三线合一性质,根据等式的性质求出∠1+∠2的度数,即为∠FAG度数,即可求出∠F度数;(3)作出相应图形,如图2所示,若点P在BC边的延长线上时,∠AFD的度数不会发生变化,理由为:作AG⊥DE于G,得∠DAG=∠EAG,设∠DAG=∠EAG=α,根据∠FAE为∠BAE一半求出所求角度数即可.试题解析:(1)①当点P在线段BC上时,∵∠EAP=∠BAP=30°,∴∠DAE=90°﹣30°×2=30°,在△ADE中,AD=AE,∠DAE=30°,∴∠ADE=∠AED=(180°﹣30°)÷2=75°,在△AFD中,∠FAD=30°+30°=60°,∠ADF=75°,∴∠AFE=180°﹣60°﹣75°=45°;②点E为DF 的中点时,P也为BC的中点,理由如下:如图1,连接BE交AF于点O,作EG∥AD,得EG∥BC,∵EG∥AD,DE=EF,∴EG=AD=1,∵AB=AE,∴点A在线段BE的垂直平分线上,同理可得点P在线段BE的垂直平分线上,∴AF垂直平分线段BE,∴OB=OE,∵GE∥BP,∴∠OBP=∠OEG,∠OPB=∠OGE,∴△BOP≌△EOG,∴BP=EG=1,即P为BC的中点,∴∠DAF=90°﹣∠BAF,∠ADF=45°+∠BAF,∴∠AFD=180°﹣∠DAF﹣∠ADF=45°;(2)∠AFD的度数不会发生变化,作AG⊥DF于点G,如图1(a)所示,在△ADE中,AD=AE,AG⊥DE,∵AG平分∠DAE,即∠2=∠DAG,且∠1=∠BAP,∴∠1+∠2=×90°=45°,即∠FAG=45°,则∠AFD=90°﹣45°=45°;(3)如图2所示,∠AFE的大小不会发生变化,∠AFE=45°,作AG⊥DE于G,得∠DAG=∠EAG,设∠DAG=∠EAG=α,∴∠BAE=90°+2α,∴∠FAE=∠BAE=45°+α,∴∠FAG=∠FAE﹣∠EAG=45°,在Rt△AFG中,∠AFE=90°﹣45°=45°.考点:1.正方形的性质;2.折叠性质;3.全等三角形的判定与性质.3.已知矩形纸片OBCD的边OB在x轴上,OD在y轴上,点C在第一象限,且,.现将纸片折叠,折痕为EF(点E,F是折痕与矩形的边的交点),点P ==86OB OD为点D的对应点,再将纸片还原。
2020-2021中考数学易错题精选-平行四边形练习题及答案解析

2020-2021中考数学易错题精选-平行四边形练习题及答案解析一、平行四边形1.在平面直角坐标系中,四边形AOBC 是矩形,点O (0,0),点A (5,0),点B (0,3).以点A 为中心,顺时针旋转矩形AOBC ,得到矩形ADEF ,点O ,B ,C 的对应点分别为D ,E ,F .(1)如图①,当点D 落在BC 边上时,求点D 的坐标;(2)如图②,当点D 落在线段BE 上时,AD 与BC 交于点H .①求证△ADB ≌△AOB ;②求点H 的坐标.(3)记K 为矩形AOBC 对角线的交点,S 为△KDE 的面积,求S 的取值范围(直接写出结果即可).【答案】(1)D (1,3);(2)①详见解析;②H (175,3);(3)303344-≤S ≤303344+. 【解析】【分析】(1)如图①,在Rt △ACD 中求出CD 即可解决问题;(2)①根据HL 证明即可;②,设AH=BH=m ,则HC=BC-BH=5-m ,在Rt △AHC 中,根据AH 2=HC 2+AC 2,构建方程求出m 即可解决问题;(3)如图③中,当点D 在线段BK 上时,△DEK 的面积最小,当点D 在BA 的延长线上时,△D′E′K 的面积最大,求出面积的最小值以及最大值即可解决问题;【详解】(1)如图①中,∵A (5,0),B (0,3),∴OA=5,OB=3,∵四边形AOBC是矩形,∴AC=OB=3,OA=BC=5,∠OBC=∠C=90°,∵矩形ADEF是由矩形AOBC旋转得到,∴AD=AO=5,在Rt△ADC中,CD=22AD AC-=4,∴BD=BC-CD=1,∴D(1,3).(2)①如图②中,由四边形ADEF是矩形,得到∠ADE=90°,∵点D在线段BE上,∴∠ADB=90°,由(1)可知,AD=AO,又AB=AB,∠AOB=90°,∴Rt△ADB≌Rt△AOB(HL).②如图②中,由△ADB≌△AOB,得到∠BAD=∠BAO,又在矩形AOBC中,OA∥BC,∴∠CBA=∠OAB,∴∠BAD=∠CBA,∴BH=AH,设AH=BH=m,则HC=BC-BH=5-m,在Rt△AHC中,∵AH2=HC2+AC2,∴m2=32+(5-m)2,∴m=175,∴BH=175,∴H(175,3).(3)如图③中,当点D在线段BK上时,△DEK的面积最小,最小值=12•DE•DK=12×3×(34)30334-当点D 在BA 的延长线上时,△D ′E ′K 的面积最大,最大面积=12×D ′E ′×KD ′=12×3×(5+342)=303344+. 综上所述,303344-≤S ≤303344+. 【点睛】 本题考查四边形综合题、矩形的性质、勾股定理、全等三角形的判定和性质、旋转变换等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会利用参数构建方程解决问题.2.如图,四边形ABCD 中,∠BCD =∠D =90°,E 是边AB 的中点.已知AD =1,AB =2. (1)设BC =x ,CD =y ,求y 关于x 的函数关系式,并写出定义域;(2)当∠B =70°时,求∠AEC 的度数;(3)当△ACE 为直角三角形时,求边BC 的长.【答案】(1)()22303y x x x =-++<<;(2)∠AEC =105°;(3)边BC 的长为2117+. 【解析】试题分析:(1)过A 作AH ⊥BC 于H ,得到四边形ADCH 为矩形.在△BAH 中,由勾股定理即可得出结论.(2)取CD 中点T ,连接TE ,则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD ,∠AET =∠B =70°.又AD =AE =1,得到∠AED =∠ADE =∠DET =35°.由ET 垂直平分CD ,得∠CET =∠DET =35°,即可得到结论.(3)分两种情况讨论:①当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 解△ABH 即可得到结论.②当∠CAE =90°时,易知△CDA ∽△BCA ,由相似三角形对应边成比例即可得到结论. 试题解析:解:(1)过A 作AH ⊥BC 于H .由∠D =∠BCD =90°,得四边形ADCH 为矩形. 在△BAH 中,AB =2,∠BHA =90°,AH =y ,HB =1x -,∴22221y x =+-,则()22303y x x x =-++<<(2)取CD 中点T ,联结TE ,则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD ,∴∠AET =∠B =70°.又AD =AE =1,∴∠AED =∠ADE =∠DET =35°.由ET 垂直平分CD ,得∠CET =∠DET =35°,∴∠AEC =70°+35°=105°.(3)分两种情况讨论:①当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 则在△ABH 中,∠B =60°,∠AHB =90°,AB =2,得BH =1,于是BC =2.②当∠CAE =90°时,易知△CDA ∽△BCA ,又2224AC BC AB x =-=-,则2241174AD CA x x AC CB x -±=⇒=⇒=-(舍负) 易知∠ACE <90°,所以边BC 的长为117+. 综上所述:边BC 的长为2或1172+.点睛:本题是四边形综合题.考查了梯形中位线,相似三角形的判定与性质.解题的关键是掌握梯形中常见的辅助线作法.3.如图,在平行四边形ABCD 中,AD ⊥DB ,垂足为点D ,将平行四边形ABCD 折叠,使点B 落在点D 的位置,点C 落在点G 的位置,折痕为EF ,EF 交对角线BD 于点P . (1)连结CG ,请判断四边形DBCG 的形状,并说明理由;(2)若AE =BD ,求∠EDF 的度数.【答案】(1)四边形BCGD是矩形,理由详见解析;(2)∠EDF=120°.【解析】【分析】(1)根据平行四边形的性质和折叠性质以及矩形的判定解答即可;(2)根据折叠的性质以及直角三角形的性质和等边三角形的判定与性质解答即可.【详解】解:(1)四边形BCGD是矩形,理由如下,∵四边形ABCD是平行四边形,∴BC∥AD,即BC∥DG,由折叠可知,BC=DG,∴四边形BCGD是平行四边形,∵AD⊥BD,∴∠CBD=90°,∴四边形BCGD是矩形;(2)由折叠可知:EF垂直平分BD,∴BD⊥EF,DP=BP,∵AD⊥BD,∴EF∥AD∥BC,∴AE PD1==BE BP∴AE=BE,∴DE是Rt△ADB斜边上的中线,∴DE=AE=BE,∵AE=BD,∴DE=BD=BE,∴△DBE是等边三角形,∴∠EDB=∠DBE=60°,∵AB∥DC,∴∠DBC=∠DBE=60°,∴∠EDF=120°.【点睛】本题考查了平行四边形的性质,折叠性质,等边三角形的性质和判定,主要考查学生运用定理进行推理和计算的能力,题目综合性比较强,有一定的难度4.如图所示,矩形ABCD中,点E在CB的延长线上,使CE=AC,连接AE,点F是AE的中点,连接BF、DF,求证:BF⊥DF.【答案】见解析.【解析】【分析】延长BF,交DA的延长线于点M,连接BD,进而求证△AFM≌△EFB,得AM=BE,FB=FM,即可求得BC+BE=AD+AM,进而求得BD=BM,根据等腰三角形三线合一的性质即可求证BF⊥DF.【详解】延长BF,交DA的延长线于点M,连接BD.∵四边形ABCD是矩形,∴MD∥BC,∴∠AMF=∠EBF,∠E=∠MAF,又FA=FE,∴△AFM≌△EFB,∴AM=BE,FB=FM.∵矩形ABCD中,∴AC=BD,AD=BC,∴BC+BE=AD+AM,即CE=MD.∵CE=AC,∴AC=CE= BD =DM.∵FB=FM,∴BF⊥DF.【点睛】本题考查了矩形的性质,全等三角形的判定和对应边相等的性质,等腰三角形三线合一的性质,本题中求证DB=DM是解题的关键.5.现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,点B落在四边形AECD内,记为点B′,过E作EF垂直B′C,交B′C于F.(1)求AE、EF的位置关系;(2)求线段B′C的长,并求△B′EC的面积.【答案】(1)见解析;(2)S△B′EC=108 25.【解析】【分析】(1)由折线法及点E是BC的中点,可证得△B'EC是等腰三角形,再有条件证明∠AEF=90°即可得到AE⊥EF;(2)连接BB′,通过折叠,可知∠EBB′=∠EB′B,由E是BC的中点,可得EB′=EC,∠ECB′=∠EB′C,从而可证△BB′C为直角三角形,在Rt△AOB和Rt△BOE中,可将OB,BB′的长求出,在Rt△BB′C中,根据勾股定理可将B′C的值求出.【详解】(1)由折线法及点E是BC的中点,∴EB=EB′=EC,∠AEB=∠AEB′,∴△B'EC是等腰三角形,又∵EF⊥B′C∴EF为∠B'EC的角平分线,即∠B′EF=∠FEC,∴∠AEF=180°﹣(∠AEB+∠CEF)=90°,即∠AEF=90°,即AE⊥EF;(2)连接BB'交AE于点O,由折线法及点E是BC的中点,∴EB=EB′=EC,∴∠EBB′=∠EB′B,∠ECB′=∠EB′C;又∵△BB'C三内角之和为180°,∴∠BB'C=90°;∵点B′是点B关于直线AE的对称点,∴AE垂直平分BB′;在Rt△AOB和Rt△BOE中,BO2=AB2﹣AO2=BE2﹣(AE﹣AO)2将AB=4cm,BE=3cm,AE=5cm,∴AO=165cm,∴BO22AB AO125cm,∴BB ′=2BO =245cm , ∴在Rt △BB 'C 中,B ′C =22BC BB '-=518cm , 由题意可知四边形OEFB ′是矩形,∴EF =OB ′=125, ∴S △B ′EC =*111812108225525B C EF '⨯=⨯⨯=.【点睛】考查图形的折叠变化及三角形的内角和定理勾股定理的和矩形的性质综合运用.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.6.如图1,在正方形ABCD 中,AD=6,点P 是对角线BD 上任意一点,连接PA ,PC 过点P 作PE ⊥PC 交直线AB 于E .(1) 求证:PC=PE;(2) 延长AP 交直线CD 于点F.①如图2,若点F 是CD 的中点,求△APE 的面积;②若ΔAPE 的面积是21625,则DF 的长为 (3) 如图3,点E 在边AB 上,连接EC 交BD 于点M,作点E 关于BD 的对称点Q ,连接PQ ,MQ ,过点P 作PN ∥CD 交EC 于点N ,连接QN ,若PQ=5,MN=723,则△MNQ 的面积是【答案】(1)略;(2)①8,②4或9;(3)56【解析】【分析】 (1)利用正方形每个角都是90°,对角线平分对角的性质,三角形外角等于和它不相邻的两个内角的和,等角对等边等性质容易得证;(2)作出△ADP 和△DFP 的高,由面积法容易求出这个高的值.从而得到△PAE 的底和高,并求出面积.第2小问思路一样,通过面积法列出方程求解即可;(3)根据已经条件证出△MNQ 是直角三角形,计算直角边乘积的一半可得其面积.【详解】(1) 证明:∵点P 在对角线BD 上,∴△ADP ≌△CDP ,∴AP=CP , ∠DAP =∠DCP ,∵PE ⊥PC ,∴∠EPC=∠EPB+∠BPC=90°,∵∠PEA=∠EBP+∠EPB=45°+90°-∠BPC=135°-∠BPC,∵∠PAE=90°-∠DAP =90°-∠DCP ,∠DCP=∠BPC-∠PDC=∠BPC-45°,∴∠PAE=90°-(∠BPC-45°)= 135°-∠BPC,∴∠PEA=∠PAE,∴PC=PE;(2)①如图2,过点P 分别作PH ⊥AD,PG ⊥CD,垂足分别为H 、G.延长GP 交AB 于点M.∵四边形ABCD 是正方形,P 在对角线上,∴四边形HPGD 是正方形,∴PH=PG,PM ⊥AB,设PH=PG=a,∵F 是CD 中点,AD =6,则FD=3,ADF S n =9,∵ADF S n =ADP DFP S S +n n =1122AD PH DF PG ⨯+⨯, ∴1163922a a ⨯+⨯=,解得a=2, ∴AM=HP=2,MP=MG-PG=6-2=4,又∵PA=PE,∴AM=EM,AE=4,∵APE S n =1144822EAMP ⨯=⨯⨯=, ②设HP =b,由①可得AE=2b,MP=6-b, ∴APE S n =()121626225b b ⨯⨯-=, 解得b=2.4 3.6或,∵ADF S n =ADP DFP S S +n n =1122AD PH DF PG ⨯+⨯, ∴11166222b DF b DF ⨯⨯+⨯=⨯, ∴当b=2.4时,DF=4;当b =3.6时,DF =9, 即DF 的长为4或9;(3)如图,∵E 、Q 关于BP 对称,PN ∥CD, ∴∠1=∠2,∠2+∠3=∠BDC=45°, ∴∠1+∠4=45°,∴∠3=∠4,易证△PEM ≌△PQM, △PNQ ≌△PNC, ∴∠5=∠6, ∠7=∠8 ,EM=QM,NQ=NC, ∴∠6+∠7=90°,∴△MNQ 是直角三角形,设EM=a,NC=b 列方程组222252372 3a b a b ⎧+=⎪⎪⎨⎛⎪+= ⎪⎝⎭⎩, 可得12ab=56,∴MNQ 56S V =, 【点睛】 本题是四边形综合题目,考查了正方形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质等知识;本题综合性强,有一定难度,熟练掌握正方形的性质,证明三角形全等是解决问题的关键.要注意运用数形结合思想.7.△ABC 为等边三角形,AF AB =.BCD BDC AEC ∠=∠=∠.(1)求证:四边形ABDF 是菱形.(2)若BD 是ABC ∠的角平分线,连接AD ,找出图中所有的等腰三角形.【答案】(1)证明见解析;(2)图中等腰三角形有△ABC ,△BDC ,△ABD ,△ADF ,△ADC ,△ADE .【解析】【分析】(1)先求证BD ∥AF ,证明四边形ABDF 是平行四边形,再利用有一组邻边相等的平行四边形是菱形即可证明;(2)先利用BD 平分∠ABC ,得到BD 垂直平分线段AC ,进而证明△DAC 是等腰三角形,根据BD ⊥AC,AF ⊥AC ,找到角度之间的关系,证明△DAE 是等腰三角形,进而得到BC =BD =BA =AF =DF ,即可解题,见详解.【详解】(1)如图1中,∵∠BCD =∠BDC ,∴BC =BD ,∵△ABC 是等边三角形,∴AB =BC ,∵AB =AF ,∴BD =AF ,∵∠BDC =∠AEC ,∴BD ∥AF ,∴四边形ABDF 是平行四边形,∵AB =AF ,∴四边形ABDF 是菱形.(2)解:如图2中,∵BA =BC ,BD 平分∠ABC ,∴BD 垂直平分线段AC ,∴DA=DC,∴△DAC是等腰三角形,∵AF∥BD,BD⊥AC∴AF⊥AC,∴∠EAC=90°,∵∠DAC=∠DCA,∠DAC+∠DAE=90°,∠DCA+∠AEC=90°,∴∠DAE=∠DEA,∴DA=DE,∴△DAE是等腰三角形,∵BC=BD=BA=AF=DF,∴△BCD,△ABD,△ADF都是等腰三角形,综上所述,图中等腰三角形有△ABC,△BDC,△ABD,△ADF,△ADC,△ADE.【点睛】本题考查菱形的判定,等边三角形的性质,等腰三角形的判定等知识,属于中考常考题型,熟练掌握等腰三角形的性质是解题的关键.8.如图,现将平行四边形ABCD沿其对角线AC折叠,使点B落在点B′处.AB′与CD交于点E.(1)求证:△AED≌△CEB′;(2)过点E作EF⊥AC交AB于点F,连接CF,判断四边形AECF的形状并给予证明.【答案】(1)见解析(2)见解析【解析】【分析】(1)由题意可得AD=BC=B'C,∠B=∠D=∠B',且∠AED=∠CEB',利用AAS证明全等,则结论可得;(2)由△AED≌△CEB′可得AE=CE,且EF⊥AC,根据等腰三角形的性质可得EF垂直平分AC,∠AEF=∠CEF.即AF=CF,∠CEF=∠AFE=∠AEF,可得AE=AF,则可证四边形AECF是菱形.【详解】证明:(1)∵四边形ABCD是平行四边形∴AD=BC,CD∥AB,∠B=∠D∵平行四边形ABCD沿其对角线AC折叠∴BC=B'C,∠B=∠B'∴∠D=∠B',AD=B'C且∠DEA=∠B'EC∴△ADE≌△B'EC(2)四边形AECF是菱形∵△ADE≌△B'EC∴AE=CE∵AE=CE,EF⊥AC∴EF垂直平分AC,∠AEF=∠CEF∴AF=CF∵CD∥AB∴∠CEF=∠EFA且∠AEF=∠CEF∴∠AEF=∠EFA∴AF=AE∴AF=AE=CE=CF∴四边形AECF是菱形【点睛】本题考查了折叠问题,全等三角形的判定和性质,平行四边形的性质,菱形的判定,熟练掌握这些性质和判定是解决问题的关键.9.猜想与证明:如图1,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.拓展与延伸:(1)若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为.(2)如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF 的中点,试证明(1)中的结论仍然成立.【答案】猜想:DM=ME,证明见解析;(2)成立,证明见解析.【解析】试题分析:延长EM交AD于点H,根据ABCD和CEFG为矩形得到AD∥EF,得到△FME和△AMH全等,得到HM=EM,根据Rt△HDE得到HM=DE,则可以得到答案;(1)、延长EM交AD于点H,根据ABCD和CEFG为矩形得到AD∥EF,得到△FME和△AMH全等,得到HM=EM,根据Rt△HDE得到HM=DE,则可以得到答案;(2)、连接AE,根据正方形的性质得出∠FCE=45°,∠FCA=45°,根据RT△ADF中AM=MF得出DM=AM=MF,根据RT△AEF中AM=MF得出AM=MF=ME,从而说明DM=ME.试题解析:如图1,延长EM交AD于点H,∵四边形ABCD和CEFG是矩形,∴AD∥EF,∴∠EFM=∠HAM,又∵∠FME=∠AMH,FM=AM,在△FME和△AMH中,∴△FME≌△AMH(ASA)∴HM=EM,在RT△HDE中,HM=DE,∴DM=HM=ME,∴DM=ME.(1)、如图1,延长EM交AD于点H,∵四边形ABCD和CEFG是矩形,∴AD∥EF,∴∠EFM=∠HAM,又∵∠FME=∠AMH,FM=AM,在△FME和△AMH中,∴△FME≌△AMH(ASA)∴HM=EM,在RT△HDE中,HM=EM∴DM=HM=ME,∴DM=ME,(2)、如图2,连接AE,∵四边形ABCD和ECGF是正方形,∴∠FCE=45°,∠FCA=45°,∴AE和EC在同一条直线上,在RT△ADF中,AM=MF,∴DM=AM=MF,在RT△AEF中,AM=MF,∴AM=MF=ME,∴DM=ME.考点:(1)、三角形全等的性质;(2)、矩形的性质.10.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.【答案】(1)AG2=GE2+GF2(2)【解析】试题分析:(1)结论:AG2=GE2+GF2.只要证明GA=GC,四边形EGFC是矩形,推出GE=CF,在Rt△GFC中,利用勾股定理即可证明;(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.易证AM=BM=2x,MN=x,在Rt△ABN中,根据AB2=AN2+BN2,可得1=x2+(2x+x)2,解得x=,推出BN=,再根据BG=BN÷cos30°即可解决问题.试题解析:(1)结论:AG2=GE2+GF2.理由:连接CG.∵四边形ABCD是正方形,∴A、C关于对角线BD对称,∵点G在BD上,∴GA=GC,∵GE⊥DC于点E,GF⊥BC于点F,∴∠GEC=∠ECF=∠CFG=90°,∴四边形EGFC是矩形,∴CF=GE,在Rt△GFC中,∵CG2=GF2+CF2,∴AG2=GF2+GE2.(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.∵∠AGF=105°,∠FBG=∠FGB=∠ABG=45°,∴∠AGB=60°,∠GBN=30°,∠ABM=∠MAB=15°,∴∠AMN=30°,∴AM=BM=2x,MN=x,在Rt△ABN中,∵AB2=AN2+BN2,∴1=x2+(2x+x)2,解得x=,∴BN=,∴BG=BN÷cos30°=.考点:1、正方形的性质,2、矩形的判定和性质,3、勾股定理,4、直角三角形30度的性质11.在矩形纸片ABCD中,AB=6,BC=8,现将纸片折叠,使点D与点B重合,折痕为EF,连接DF.(1)说明△BEF是等腰三角形;(2)求折痕EF的长.【答案】(1)见解析;(2).【解析】【分析】(1)根据折叠得出∠DEF=∠BEF,根据矩形的性质得出AD∥BC,求出∠DEF=∠BFE,求出∠BEF=∠BFE即可;(2)过E作EM⊥BC于M,则四边形ABME是矩形,根据矩形的性质得出EM=AB=6,AE=BM,根据折叠得出DE=BE,根据勾股定理求出DE、在Rt△EMF中,由勾股定理求出即可.【详解】(1)∵现将纸片折叠,使点D与点B重合,折痕为EF,∴∠DEF=∠BEF.∵四边形ABCD是矩形,∴AD∥BC,∴∠DEF=∠BFE,∴∠BEF=∠BFE,∴BE=BF,即△BEF 是等腰三角形;(2)过E作EM⊥BC于M,则四边形ABME是矩形,所以EM=AB=6,AE=BM.∵现将纸片折叠,使点D与点B重合,折痕为EF,∴DE=BE,DO=BO,BD⊥EF.∵四边形ABCD是矩形,BC=8,∴AD=BC=8,∠BAD=90°.在Rt△ABE中,AE2+AB2=BE2,即(8﹣BE)2+62=BE2,解得:BE==DE=BF,AE=8﹣DE=8﹣==BM,∴FM=﹣=.在Rt△EMF中,由勾股定理得:EF==.故答案为:.【点睛】本题考查了折叠的性质和矩形性质、勾股定理等知识点,能熟记折叠的性质是解答此题的关键.12.如图,抛物线交x轴的正半轴于点A,点B(,a)在抛物线上,点C是抛物线对称轴上的一点,连接AB、BC,以AB、BC为邻边作□ABCD,记点C纵坐标为n,(1)求a的值及点A的坐标;(2)当点D恰好落在抛物线上时,求n的值;(3)记CD与抛物线的交点为E,连接AE,BE,当△AEB的面积为7时,n=___________.(直接写出答案)【答案】(1), A(3,0);(2)【解析】试题解析:(1)把点B的坐标代入抛物线的解析式中,即可求出a的值,令y=0即可求出点A的坐标.(2)求出点D的坐标即可求解;(3)运用△AEB的面积为7,列式计算即可得解.试题解析:(1)当时,由,得(舍去),(1分)∴A(3,0)(2)过D作DG⊥轴于G,BH⊥轴于H.∵CD∥AB,CD=AB∴,∴,∴(3)13.小明在矩形纸片上画正三角形,他的做法是:①对折矩形纸片ABCD(AB>BC),使AB 与DC重合,得到折痕EF,把纸片展平;②沿折痕BG折叠纸片,使点C落在EF上的点P 处,再折出PB、PC,最后用笔画出△PBC(图1).(1)求证:图1中的PBC是正三角形:(2)如图2,小明在矩形纸片HIJK上又画了一个正三角形IMN,其中IJ=6cm,且HM=JN.①求证:IH=IJ②请求出NJ的长;(3)小明发现:在矩形纸片中,若一边长为6cm,当另一边的长度a变化时,在矩形纸片上总能画出最大的正三角形,但位置会有所不同.请根据小明的发现,画出不同情形的示意图(作图工具不限,能说明问题即可),并直接写出对应的a的取值范围.【答案】(1)证明见解析;(2)①证明见解析;②12-63(3)33<a<43,a>43【解析】分析:(1)由折叠的性质和垂直平分线的性质得出PB=PC,PB=CB,得出PB=PC=CB即可;(2)①利用“HL”证Rt△IHM≌Rt△IJN即可得;②IJ上取一点Q,使QI=QN,由Rt△IHM≌Rt△IJN知∠HIM=∠JIN=15°,继而可得∠NQJ=30°,设NJ=x,则IQ=QN=2x、QJ=3x,根据IJ=IQ+QJ求出x即可得;(3)由等边三角形的性质、直角三角形的性质、勾股定理进行计算,画出图形即可.(1)证明:∵①对折矩形纸片ABCD(AB>BC),使AB与DC重合,得到折痕EF∴PB=PC∵沿折痕BG折叠纸片,使点C落在EF上的点P处∴PB=BC∴PB=PC=BC∴△PBC是正三角形:(2)证明:①如图∵矩形AHIJ∴∠H=∠J=90°∵△MNJ是等边三角形∴MI=NI在Rt △MHI 和Rt △JNI 中MI NI MH NJ=⎧⎨=⎩ ∴Rt △MHI ≌Rt △JNI (HL )∴HI=IJ②在线段IJ 上取点Q ,使IQ=NQ∵Rt △IHM ≌Rt △IJN ,∴∠HIM=∠JIN ,∵∠HIJ=90°、∠MIN=60°,∴∠HIM=∠JIN=15°,由QI=QN 知∠JIN=∠QNI=15°,∴∠NQJ=30°,设NJ=x ,则IQ=QN=2x ,QJ=22=3QN NJ -x ,∵IJ=6cm ,∴2x+3x=6,∴x=12-63,即NJ=12-63(cm ).(3)分三种情况:①如图:设等边三角形的边长为b ,则0<b≤6,则tan60°3=2ab ,∴3b , ∴0<b≤32=33 ②如图当DF与DC重合时,DF=DE=6,∴a=sin60°×DE=632=33,当DE与DA重合时,a=6643 sin6032==︒,∴33<a<43;③如图∵△DEF是等边三角形∴∠FDC=30°∴DF=643 cos303==︒∴a>43点睛:本题是四边形的综合题目,考查了折叠的性质、等边三角形的判定与性质、旋转的性质、直角三角形的性质、正方形的性质、全等三角形的判定与性质等知识;本题综合性强,难度较大.14.如图,P是边长为1的正方形ABCD对角线BD上一动点(P与B、D不重合),∠APE=90°,且点E在BC边上,AE交BD于点F.(1)求证:①△PAB≌△PCB;②PE=PC;(2)在点P的运动过程中,的值是否改变?若不变,求出它的值;若改变,请说明理由;(3)设DP=x,当x为何值时,AE∥PC,并判断此时四边形PAFC的形状.【答案】(1)见解析;(2);(3)x=﹣1;四边形PAFC是菱形.【解析】试题分析:(1)根据四边形ABCD是正方形,得出AB=BC,∠ABP=∠CBP°,再根据PB=PB,即可证出△PAB≌△PCB,②根据∠PAB+∠PEB=180°,∠PEC+∠PEB=180°,得出∠PEC=∠PCB,从而证出PE=PC;(2)根据PA=PC,PE=PC,得出PA=PE,再根据∠APE=90°,得出∠PAE=∠PEA=45°,即可求出;(3)先求出∠CPE=∠PEA=45°,从而得出∠PCE,再求出∠BPC即可得出∠BPC=∠PCE,从而证出BP=BC=1,x=﹣1,再根据AE∥PC,得出∠AFP=∠BPC=67.5°,由△PAB≌△PCB 得出∠BPA=∠BPC=67.5°,PA=PC,从而证出AF=AP=PC,得出答案.试题解析:(1)①∵四边形ABCD是正方形,∴AB=BC,∠ABP=∠CBP=∠ABC=45°.∵PB=PB,∴△PAB≌△PCB (SAS).②由△PAB≌△PCB可知,∠PAB=∠PCB.∵∠ABE=∠APE=90°,∴∠PAB+∠PEB=180°,又∵∠PEC+∠PEB=180°,∴∠PEC=∠PAB=∠PCB,∴PE=PC.(2)在点P的运动过程中,的值不改变.由△PAB≌△PCB可知,PA=PC.∵PE=PC,∴PA=PE,又∵∠APE=90°,∴△PAE是等腰直角三角形,∠PAE=∠PEA=45°,∴=.(3)∵AE∥PC,∴∠CPE=∠PEA=45°,∴在△PEC中,∠PCE=∠PEC=(180°﹣45°)=67.5°.在△PBC中,∠BPC=(180°﹣∠CBP﹣∠PCE)=(180°﹣45°﹣67.5°)=67.5°.∴∠BPC=∠PCE=67.5°,∴BP=BC=1,∴x=BD﹣BP=﹣1.∵AE∥PC,∴∠AFP=∠BPC=67.5°,由△PAB≌△PCB可知,∠BPA=∠BPC=67.5°,PA=PC,∴∠AFP=∠BPA,∴AF=AP=PC,∴四边形PAFC是菱形.考点:四边形综合题.15.(本题满分10分)如图1,已知矩形纸片ABCD中,AB=6cm,若将该纸片沿着过点B的直线折叠(折痕为BM),点A恰好落在CD边的中点P处.(1)求矩形ABCD的边AD的长.(2)若P为CD边上的一个动点,折叠纸片,使得A与P重合,折痕为MN,其中M在边AD上,N在边BC上,如图2所示.设DP=x cm,DM=y cm,试求y与x的函数关系式,并指出自变量x的取值范围.(3)①当折痕MN的端点N在AB上时,求当△PCN为等腰三角形时x的值;②当折痕MN的端点M在CD上时,设折叠后重叠部分的面积为S,试求S与x之间的函数关系式【答案】(1)AD=3;(2)y=-其中,0<x<3;(3)x=;(4)S=.【解析】试题分析:(1)根据折叠图形的性质和勾股定理求出AD的长度;(2)根据折叠图形的性质以及Rt△MPD的勾股定理求出函数关系式;(3)过点N作NQ⊥CD,根据Rt△NPQ 的勾股定理进行求解;(4)根据Rt△ADM的勾股定理求出MP与x的函数关系式,然后得出函数关系式.试题解析:(1)根据折叠可得BP=AB=6cm CP=3cm 根据Rt△PBC的勾股定理可得:AD=3.(2)由折叠可知AM=MP,在Rt△MPD中,∴∴y=-其中,0<x<3.(3)当点N在AB上,x≥3,∴PC≤3,而PN≥3,NC≥3.∴△PCN为等腰三角形,只可能NC=NP.过N点作NQ⊥CD,垂足为Q,在Rt△NPQ中,∴解得x=.(4)当点M在CD上时,N在AB上,可得四边形ANPM为菱形.设MP=y,在Rt△ADM中,,即∴ y=.∴ S=考点:函数的性质、勾股定理.。
中考数学复习平行四边形专项易错题含答案解析

一、平行四边形真题与模拟题分类汇编(难题易错题)1.操作:如图,边长为2的正方形ABCD,点P在射线BC上,将△ABP沿AP向右翻折,得到△AEP,DE所在直线与AP所在直线交于点F.探究:(1)如图1,当点P在线段BC上时,①若∠BAP=30°,求∠AFE的度数;②若点E 恰为线段DF的中点时,请通过运算说明点P会在线段BC的什么位置?并求出此时∠AFD 的度数.归纳:(2)若点P是线段BC上任意一点时(不与B,C重合),∠AFD的度数是否会发生变化?试证明你的结论;猜想:(3)如图2,若点P在BC边的延长线上时,∠AFD的度数是否会发生变化?试在图中画出图形,并直接写出结论.【答案】(1)①45°;②BC的中点,45°;(2)不会发生变化,证明参见解析;(3)不会发生变化,作图参见解析.【解析】试题分析:(1)当点P在线段BC上时,①由折叠得到一对角相等,再利用正方形性质求出∠DAE度数,在三角形AFD中,利用内角和定理求出所求角度数即可;②由E为DF中点,得到P为BC中点,如图1,连接BE交AF于点O,作EG∥AD,得EG∥BC,得到AF 垂直平分BE,进而得到三角形BOP与三角形EOG全等,利用全等三角形对应边相等得到BP=EG=1,得到P为BC中点,进而求出所求角度数即可;(2)若点P是线段BC上任意一点时(不与B,C重合),∠AFD的度数不会发生变化,作AG⊥DF于点G,如图1(a)所示,利用折叠的性质及三线合一性质,根据等式的性质求出∠1+∠2的度数,即为∠FAG度数,即可求出∠F度数;(3)作出相应图形,如图2所示,若点P在BC边的延长线上时,∠AFD的度数不会发生变化,理由为:作AG⊥DE于G,得∠DAG=∠EAG,设∠DAG=∠EAG=α,根据∠FAE为∠BAE一半求出所求角度数即可.试题解析:(1)①当点P在线段BC上时,∵∠EAP=∠BAP=30°,∴∠DAE=90°﹣30°×2=30°,在△ADE中,AD=AE,∠DAE=30°,∴∠ADE=∠AED=(180°﹣30°)÷2=75°,在△AFD中,∠FAD=30°+30°=60°,∠ADF=75°,∴∠AFE=180°﹣60°﹣75°=45°;②点E为DF 的中点时,P也为BC的中点,理由如下:如图1,连接BE交AF于点O,作EG∥AD,得EG∥BC,∵EG∥AD,DE=EF,∴EG=AD=1,∵AB=AE,∴点A在线段BE的垂直平分线上,同理可得点P在线段BE的垂直平分线上,∴AF垂直平分线段BE,∴OB=OE,∵GE∥BP,∴∠OBP=∠OEG,∠OPB=∠OGE,∴△BOP≌△EOG,∴BP=EG=1,即P为BC的中点,∴∠DAF=90°﹣∠BAF,∠ADF=45°+∠BAF,∴∠AFD=180°﹣∠DAF﹣∠ADF=45°;(2)∠AFD的度数不会发生变化,作AG⊥DF于点G,如图1(a)所示,在△ADE中,AD=AE,AG⊥DE,∵AG平分∠DAE,即∠2=∠DAG,且∠1=∠BAP,∴∠1+∠2=×90°=45°,即∠FAG=45°,则∠AFD=90°﹣45°=45°;(3)如图2所示,∠AFE的大小不会发生变化,∠AFE=45°,作AG⊥DE于G,得∠DAG=∠EAG,设∠DAG=∠EAG=α,∴∠BAE=90°+2α,∴∠FAE=∠BAE=45°+α,∴∠FAG=∠FAE﹣∠EAG=45°,在Rt△AFG中,∠AFE=90°﹣45°=45°.考点:1.正方形的性质;2.折叠性质;3.全等三角形的判定与性质.2.如图(1)在正方形ABCD中,点E是CD边上一动点,连接AE,作BF⊥AE,垂足为G 交AD于F(1)求证:AF=DE;(2)连接DG,若DG平分∠EGF,如图(2),求证:点E是CD中点;(3)在(2)的条件下,连接CG,如图(3),求证:CG=CD.【答案】(1)见解析;(2)见解析;(3)CG=CD,见解析.【解析】【分析】(1)证明△BAF≌△ADE(ASA)即可解决问题.(2)过点D作DM⊥GF,DN⊥GE,垂足分别为点M,N.想办法证明AF=DF,即可解决问题.(3)延长AE,BC交于点P,由(2)知DE=CD,利用直角三角形斜边中线的性质,只要证明BC=CP即可.【详解】(1)证明:如图1中,在正方形ABCD中,AB=AD,∠BAD=∠D=90o,∴∠2+∠3=90°又∵BF⊥AE,∴∠AGB=90°∴∠1+∠2=90°,∴∠1=∠3在△BAF与△ADE中,∠1=∠3 BA=AD ∠BAF=∠D,∴△BAF≌△ADE(ASA)∴AF=DE.(2)证明:过点D作DM⊥GF,DN⊥GE,垂足分别为点M,N.由(1)得∠1=∠3,∠BGA=∠AND=90°,AB=AD ∴△BAG≌△ADN(AAS)∴AG=DN,又DG平分∠EGF,DM⊥GF,DN⊥GE,∴DM=DN,∴DM=AG,又∠AFG=∠DFM,∠AGF=∠DMF∴△AFG≌△DFM(AAS),∴AF=DF=DE=12AD=12CD,即点E是CD的中点.(3)延长AE,BC交于点P,由(2)知DE=CD,∠ADE=∠ECP=90°,∠DEA=∠CEP,∴△ADE≌△PCE(ASA)∴AE=PE,又CE∥AB,∴BC=PC,在Rt△BGP中,∵BC=PC,∴CG=12BP=BC,∴CG=CD.【点睛】本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,角平分线的性质定理,直角三角形斜边中线的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.3.如图,在平行四边形ABCD中,AD⊥DB,垂足为点D,将平行四边形ABCD折叠,使点B落在点D的位置,点C落在点G的位置,折痕为EF,EF交对角线BD于点P.(1)连结CG,请判断四边形DBCG的形状,并说明理由;(2)若AE=BD,求∠EDF的度数.【答案】(1)四边形BCGD是矩形,理由详见解析;(2)∠EDF=120°.【解析】【分析】(1)根据平行四边形的性质和折叠性质以及矩形的判定解答即可;(2)根据折叠的性质以及直角三角形的性质和等边三角形的判定与性质解答即可.【详解】解:(1)四边形BCGD是矩形,理由如下,∵四边形ABCD是平行四边形,∴BC∥AD,即BC∥DG,由折叠可知,BC=DG,∴四边形BCGD是平行四边形,∵AD⊥BD,∴∠CBD=90°,∴四边形BCGD是矩形;(2)由折叠可知:EF垂直平分BD,∴BD⊥EF,DP=BP,∵AD⊥BD,∴EF∥AD∥BC,∴AE PD1==BE BP∴AE=BE,∴DE是Rt△ADB斜边上的中线,∴DE=AE=BE,∵AE=BD,∴DE=BD=BE,∴△DBE是等边三角形,∴∠EDB=∠DBE=60°,∵AB∥DC,∴∠DBC=∠DBE=60°,∴∠EDF=120°.【点睛】本题考查了平行四边形的性质,折叠性质,等边三角形的性质和判定,主要考查学生运用定理进行推理和计算的能力,题目综合性比较强,有一定的难度4.如图1,矩形ABCD中,AB=8,AD=6;点E是对角线BD上一动点,连接CE,作EF⊥CE 交AB边于点F,以CE和EF为邻边作矩形CEFG,作其对角线相交于点H.(1)①如图2,当点F与点B重合时,CE=,CG=;②如图3,当点E是BD中点时,CE=,CG=;(2)在图1,连接BG,当矩形CEFG随着点E的运动而变化时,猜想△EBG的形状?并加以证明;(3)在图1,CGCE的值是否会发生改变?若不变,求出它的值;若改变,说明理由;(4)在图1,设DE的长为x,矩形CEFG的面积为S,试求S关于x的函数关系式,并直接写出x的取值范围.【答案】(1)245,185,5,154;(2)△EBG是直角三角形,理由详见解析;(3)3 4;(4)S=34x2﹣485x+48(0≤x≤325).【解析】【分析】(1)①利用面积法求出CE,再利用勾股定理求出EF即可;②利用直角三角形斜边中线定理求出CE,再利用相似三角形的性质求出EF即可;(2)根据直角三角形的判定方法:如果一个三角形一边上的中线等于这条边的一半,则这个三角形是直角三角形即可判断;(3)只要证明△DCE∽△BCG,即可解决问题;(4)利用相似多边形的性质构建函数关系式即可;【详解】(1)①如图2中,在Rt △BAD 中,BD=22AD AB +=10, ∵S △BCD =12•CD•BC=12•BD•CE , ∴CE=245.CG=BE=2224186()=55-. ②如图3中,过点E 作MN ⊥AM 交AB 于N ,交CD 于M .∵DE=BE ,∴CE=12BD=5, ∵△CME ∽△ENF ,∴CM EN CE EF=, ∴CG=EF=154, (2)结论:△EBG 是直角三角形.理由:如图1中,连接BH .在Rt △BCF 中,∵FH=CH ,∴BH=FH=CH ,∵四边形EFGC 是矩形,∴EH=HG=HF=HC ,∴BH=EH=HG ,∴△EBG 是直角三角形.(3)F 如图1中,∵HE=HC=HG=HB=HF ,∴C 、E 、F 、B 、G 五点共圆,∵EF=CG ,∴∠CBG=∠EBF ,∵CD ∥AB ,∴∠EBF=∠CDE ,∴∠CBG=∠CDE ,∵∠DCB=∠ECG=90°,∴∠DCE=∠BCG ,∴△DCE ∽△BCG , ∴6384CG BC CE DC ===. (4)由(3)可知: 34CG CD CE CB ==, ∴矩形CEFG ∽矩形ABCD , ∴2264CEFG ABCD S CE CE S CD ==矩形矩形(), ∵CE 2=(325-x )2+245)2,S 矩形ABCD =48, ∴S 矩形CEFG =34[(325-x )2+(245)2]. ∴矩形CEFG 的面积S=34x 2-485x+48(0≤x≤325). 【点睛】 本题考查相似三角形综合题、矩形的性质、相似三角形的判定和性质、勾股定理、直角三角形的判定和性质、相似多边形的性质和判定等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造相似三角形或直角三角形解决问题,属于中考压轴题.5.如图,在矩形ABCD 中,点E 在边CD 上,将该矩形沿AE 折叠,使点D 落在边BC 上的点F 处,过点F 作FG ∥CD ,交AE 于点G ,连接DG .(1)求证:四边形DEFG为菱形;(2)若CD=8,CF=4,求的值.【答案】(1)证明见试题解析;(2).【解析】试题分析:(1)由折叠的性质,可以得到DG=FG,ED=EF,∠1=∠2,由FG∥CD,可得∠1=∠3,再证明 FG=FE,即可得到四边形DEFG为菱形;(2)在Rt△EFC中,用勾股定理列方程即可CD、CE,从而求出的值.试题解析:(1)由折叠的性质可知:DG=FG,ED=EF,∠1=∠2,∵FG∥CD,∴∠2=∠3,∴FG=FE,∴DG=GF=EF=DE,∴四边形DEFG为菱形;(2)设DE=x,根据折叠的性质,EF=DE=x,EC=8﹣x,在Rt△EFC中,,即,解得:x=5,CE=8﹣x=3,∴=.考点:1.翻折变换(折叠问题);2.勾股定理;3.菱形的判定与性质;4.矩形的性质;5.综合题.6.小明在矩形纸片上画正三角形,他的做法是:①对折矩形纸片ABCD(AB>BC),使AB与DC重合,得到折痕EF,把纸片展平;②沿折痕BG折叠纸片,使点C落在EF上的点P 处,再折出PB、PC,最后用笔画出△PBC(图1).(1)求证:图1中的PBC 是正三角形: (2)如图2,小明在矩形纸片HIJK 上又画了一个正三角形IMN ,其中IJ=6cm ,且HM=JN .①求证:IH=IJ②请求出NJ 的长; (3)小明发现:在矩形纸片中,若一边长为6cm ,当另一边的长度a 变化时,在矩形纸片上总能画出最大的正三角形,但位置会有所不同.请根据小明的发现,画出不同情形的示意图(作图工具不限,能说明问题即可),并直接写出对应的a 的取值范围.【答案】(1)证明见解析;(2)①证明见解析;②12-63(3)33<a <43,a >43【解析】分析:(1)由折叠的性质和垂直平分线的性质得出PB=PC ,PB=CB ,得出PB=PC=CB 即可;(2)①利用“HL”证Rt △IHM ≌Rt △IJN 即可得;②IJ 上取一点Q ,使QI=QN ,由Rt △IHM ≌Rt △IJN 知∠HIM=∠JIN=15°,继而可得∠NQJ=30°,设NJ=x ,则IQ=QN=2x 、QJ=3x ,根据IJ=IQ+QJ 求出x 即可得;(3)由等边三角形的性质、直角三角形的性质、勾股定理进行计算,画出图形即可. (1)证明:∵①对折矩形纸片ABCD(AB>BC),使AB 与DC 重合,得到折痕EF∴PB=PC∵沿折痕BG 折叠纸片,使点C 落在EF 上的点P 处∴PB=BC∴PB=PC=BC∴△PBC 是正三角形:(2)证明:①如图∵矩形AHIJ∴∠H=∠J=90°∵△MNJ 是等边三角形∴MI=NI在Rt △MHI 和Rt △JNI 中MI NI MH NJ =⎧⎨=⎩∴Rt △MHI ≌Rt △JNI (HL )∴HI=IJ②在线段IJ上取点Q,使IQ=NQ∵Rt△IHM≌Rt△IJN,∴∠HIM=∠JIN,∵∠HIJ=90°、∠MIN=60°,∴∠HIM=∠JIN=15°,由QI=QN知∠JIN=∠QNI=15°,∴∠NQJ=30°,设NJ=x,则IQ=QN=2x,QJ=22=3QN NJx,∵IJ=6cm,∴2x+3x=6,∴x=12-63,即NJ=12-63(cm).(3)分三种情况:①如图:设等边三角形的边长为b,则0<b≤6,则tan60°=3=2ab,∴a=3b,∴0<b≤63=33;②如图当DF与DC重合时,DF=DE=6,∴a=sin60°×DE=632=33,当DE与DA重合时,a=6643 sin6032==︒,∴33<a<43;③如图∵△DEF是等边三角形∴∠FDC=30°∴DF=643 cos303==︒∴a>43点睛:本题是四边形的综合题目,考查了折叠的性质、等边三角形的判定与性质、旋转的性质、直角三角形的性质、正方形的性质、全等三角形的判定与性质等知识;本题综合性强,难度较大.7.如图1,在长方形纸片ABCD中,AB=mAD,其中m⩾1,将它沿EF折叠(点E. F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设AMnAD=,其中0<n⩽1.(1)如图2,当n=1(即M点与D点重合),求证:四边形BEDF为菱形;(2)如图3,当12n =(M 为AD 的中点),m 的值发生变化时,求证:EP=AE+DP ; (3)如图1,当m=2(即AB=2AD),n 的值发生变化时,BE CFAM-的值是否发生变化?说明理由.【答案】(1)证明见解析;(2)证明见解析;(3)值不变,理由见解析. 【解析】试题分析:(1)由条件可知,当n=1(即M 点与D 点重合),m=2时,AB=2AD ,设AD=a ,则AB=2a ,由矩形的性质可以得出△ADE ≌△NDF ,就可以得出AE=NF ,DE=DF ,在Rt △AED 中,由勾股定理就可以表示出AE 的值,再求出BE 的值就可以得出结论. (2)延长PM 交EA 延长线于G ,由条件可以得出△PDM ≌△GAM ,△EMP ≌△EMG 由全等三角形的性质就可以得出结论.(3)如图1,连接BM 交EF 于点Q ,过点F 作FK ⊥AB 于点K ,交BM 于点O ,通过证明△ABM ∽△KFE ,就可以得出EK KF AM AB =,即BE BK BCAM AB-=,由AB=2AD=2BC ,BK=CF 就可以得出BE CFAM -的值是12为定值. (1)∵四边形ABCD 是矩形,∴AB=CD ,AD=BC ,∠A=∠B=∠C=∠D=90°. ∵AB=mAD ,且n=2,∴AB=2AD .∵∠ADE+∠EDF=90°,∠EDF+∠NDF=90°,∴∠ADE=∠NDF . 在△ADE 和△NDF 中,∠A =∠N ,AD =ND ,∠ADE =∠NDF , ∴△ADE ≌△NDF (ASA ).∴AE=NF ,DE=DF . ∵FN=FC ,∴AE=FC .∵AB=CD ,∴AB-AE="CD-CF." ∴BE="DF." ∴BE=DE .Rt △AED 中,由勾股定理,得222AE DE AD =-,即2222AE AD AE AD ()=--,∴AE=34AD. ∴BE=2AD-34AD=54.∴554334ADBE AE AD ==. (2)如图3,延长PM 交EA 延长线于G ,∴∠GAM=90°. ∵M 为AD 的中点,∴AM=DM .∵四边形ABCD 是矩形,∴AB=CD ,AD=BC ,∠A=∠B=∠C=∠D=90°,AB ∥CD. ∴∠GAM=∠PDM .在△GAM 和△PDM 中,∠GAM =∠PDM ,AM =DM ,∠AMG =∠DMP , ∴△GAM ≌△PDM (ASA ).∴MG=MP .在△EMP 和△EMG 中,PM =GM ,∠PME =∠GME ,ME =ME ,∴△EMP ≌△EMG (SAS ).∴EG=EP . ∴AG+AE=EP .∴PD+AE=EP ,即EP=AE+DP .(3)12BE CF AM -=,值不变,理由如下: 如图1,连接BM 交EF 于点Q ,过点F 作FK ⊥AB 于点K ,交BM 于点O , ∵EM=EB ,∠MEF=∠BEF ,∴EF ⊥MB ,即∠FQO=90°. ∵四边形FKBC 是矩形,∴KF=BC ,FC=KB. ∵∠FKB=90°,∴∠KBO+∠KOB=90°.∵∠QOF+∠QFO=90°,∠QOF=∠KOB ,∴∠KBO=∠OFQ. ∵∠A=∠EKF=90°,∴△ABM ∽△KFE. ∴EK KF AM AB =即BE BK BC AM AB-=. ∵AB=2AD=2BC ,BK=CF ,∴12BE CF AM -=. ∴BE CFAM-的值不变.考点:1.折叠问题;2.矩形的性质;3.全等三角形的判定和性质;4.勾股定理;5.相似三角形的判定和性质.8.如图,在菱形ABCD 中,AB=6,∠ABC=60°,AH ⊥BC 于点H .动点E 从点B 出发,沿线段BC 向点C 以每秒2个单位长度的速度运动.过点E 作EF ⊥AB ,垂足为点F .点E 出发后,以EF为边向上作等边三角形EFG,设点E的运动时间为t秒,△EFG和△AHC的重合部分面积为S.(1)CE= (含t的代数式表示).(2)求点G落在线段AC上时t的值.(3)当S>0时,求S与t之间的函数关系式.(4)点P在点E出发的同时从点A出发沿A-H-A以每秒2个单位长度的速度作往复运动,当点E停止运动时,点P随之停止运动,直接写出点P在△EFG内部时t的取值范围.【答案】(1)6-2t;(2)t=2;(3)当<t≤2时,S=t2+t-3;当2<t≤3时,S=-t2+t-;(4)<t<.【解析】试题分析:(1)由菱形的性质得出BC=AB=6得出CE=BC-BE=6-2t即可;(2)由菱形的性质和已知条件得出△ABC是等边三角形,得出∠ACB=60°,由等边三角形的性质和三角函数得出∠GEF=60°,GE=EF=BE•sin60°=t,证出∠GEC=90°,由三角函数求出CE==t,由BE+CE=BC得出方程,解方程即可;(3)分两种情况:①当<t≤2时,S=△EFG的面积-△NFN的面积,即可得出结果;②当2<t≤3时,由①的结果容易得出结论;(4)由题意得出t=时,点P与H重合,E与H重合,得出点P在△EFG内部时,t的不等式,解不等式即可.试题解析:(1)根据题意得:BE=2t,∵四边形ABCD是菱形,∴BC=AB=6,∴CE=BC-BE=6-2t;(2)点G落在线段AC上时,如图1所示:∵四边形ABCD是菱形,∴AB=BC,∵∠ABC=60°,∴△ABC是等边三角形,∴∠ACB=60°,∵△EFG是等边三角形,∴∠GEF=60°,GE=EF=BE•sin60°=t,∵EF⊥AB,∴∠BEF=90°-60°=30°,∴∠GEB=90°,∴∠GEC=90°,∴CE==t,∵BE+CE=BC,∴2t+t=6,解得:t=2;(3)分两种情况:①当<t≤2时,如图2所示:S=△EFG的面积-△NFN的面积=××(t)2-××(-+2)2=t2+t-3,即S=t2+t-3;当2<t≤3时,如图3所示:S=t2+t-3-(3t-6)2,即S=-t2+t-;(4)∵AH=AB•sin60°=6×=3,3÷2=,3÷2=,∴t=时,点P与H重合,E与H重合,∴点P在△EFG内部时,-<(t-)×2<t-(2t-3)+(2t-3),解得:<t<;即点P在△EFG内部时t的取值范围为:<t<.考点:四边形综合题.9.(本题14分)小明在学习平行线相关知识时总结了如下结论:端点分别在两条平行线上的所有线段中,垂直于平行线的线段最短.小明应用这个结论进行了下列探索活动和问题解决.问题1:如图1,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AC边上的一动点,以PB,PA为边构造□APBQ,求对角线PQ的最小值及PQ最小时的值.(1)在解决这个问题时,小明构造出了如图2的辅助线,则PQ的最小值为,当PQ最小时= _____ __;(2)小明对问题1做了简单的变式思考.如图3,P为AB边上的一动点,延长PA到点E,使AE=nPA(n为大于0的常数).以PE,PC为边作□PCQE,试求对角线PQ长的最小值,并求PQ最小时的值;问题2:在四边形ABCD中,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.(1)如图4,若为上任意一点,以,为边作□.试求对角线长的最小值和PQ最小时的值.(2)若为上任意一点,延长到,使,再以,为边作□.请直接写出对角线长的最小值和PQ最小时的值.【答案】问题1:(1)3,;(2)PQ=,=.问题2:(1)=4,.(2)PQ的最小值为..【解析】试题分析:问题1:(1)首先根据条件可证四边形PCBQ是矩形,然后根据条件“四边形APBQ是平行四边形可得AP=QB=PC,从而可求的值.(2)由题可知:当QP⊥AC 时,PQ最小.过点C作CD⊥AB于点D.此时四边形CDPQ为矩形,PQ=CD,在Rt△ABC中,∠C=90°,AC=4,BC=3,利用面积可求出CD=,然后可求出AD=,由AE=nPA可得PE=,而PE=CQ=PD=AD-AP=,所以AP=.所以=.问题2:(1)设对角线与相交于点.Rt≌Rt.所以AD=HC,QH=AP.由题可知:当QP⊥AB时,PQ最小,此时=CH=4,根据条件可证四边形BPQH为矩形,从而QH=BP=AP.所以.(2)根据题意画出图形,当AB 时,的长最小,PQ的最小值为..试题解析:问题1:(1)3,;(2)过点C作CD⊥AB于点D.由题意可知当PQ⊥AB时,PQ最短.所以此时四边形CDPQ为矩形.PQ=CD,DP=CQ=PE.因为∠BCA=90°,AC=4,BC=3,所以AB=5.所以CD=.所以PQ=.在Rt△ACD中AC=4,CD=,所以AD=.因为AE=nPA,所以PE==CQ=PD=AD-AP=.所以AP=.所以=.问题2:(1)如图2,设对角线与相交于点.所以G是DC的中点,作QH BC,交BC的延长线于H,因为AD//BC,所以.所以.又,所以Rt≌Rt.所以AD=HC,QH=AP.由图知,当AB时,的长最小,即=CH=4.易得四边形BPQH为矩形,所以QH=BP=AP.所以.(若学生有能力从梯形中位线角度考虑,若正确即可评分.但讲评时不作要求)(2)PQ的最小值为..考点:1.直角三角形的性质;2.全等三角形的判定与性质;3.平行四边形的性质;4矩形的判定与性质.10.如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(3,3).将正方形ABCO 绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.(1)求证:△AOG≌△ADG;(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;(3)当∠1=∠2时,求直线PE的解析式;(4)在(3)的条件下,直线PE上是否存在点M,使以M、A、G为顶点的三角形是等腰三角形?若存在,请直接写出M点坐标;若不存在,请说明理由.【答案】(1)见解析(2)∠PAG =45°,PG=OG+BP.理由见解析(3)y=x﹣3.(4)、.【解析】试题分析:(1)由AO=AD,AG=AG,根据斜边和一条直角边对应相等的两个直角三角形全等,判断出△AOG≌△ADG即可.(2)首先根据三角形全等的判定方法,判断出△ADP≌△ABP,再结合△AOG≌△ADG,可得∠DAP=∠BAP,∠1=∠DAG;然后根据∠1+∠DAG+∠DAP+∠BAP=90°,求出∠PAG的度数;最后判断出线段OG、PG、BP之间的数量关系即可.(3)首先根据△AOG≌△ADG,判断出∠AGO=∠AGD;然后根据∠1+∠AGO=90°,∠2+∠PGC=90°,判断出当∠1=∠2时,∠AGO=∠AGD=∠PGC,而∠AGO+∠AGD+∠PGC=180°,求出∠1=∠2=30°;最后确定出P、G两点坐标,即可判断出直线PE的解析式.(4)根据题意,分两种情况:①当点M在x轴的负半轴上时;②当点M在EP的延长线上时;根据以M、A、G为顶点的三角形是等腰三角形,求出M点坐标是多少即可.试题解析:(1)在Rt△AOG和Rt△ADG中,(HL)∴△AOG≌△ADG.(2)在Rt△ADP和Rt△ABP中,∴△ADP≌△ABP,则∠DAP=∠BAP;∵△AOG≌△ADG,∴∠1=∠DAG;又∵∠1+∠DAG+∠DAP+∠BAP=90°,∴2∠DAG+2∠DAP=90°,∴∠DAG+∠DAP=45°,∵∠PAG=∠DAG+∠DAP,∴∠PAG=45°;∵△AOG≌△ADG,∴DG=OG,∵△ADP≌△ABP,∴DP=BP,∴PG=DG+DP=OG+BP.(3)解:∵△AOG≌△ADG,∴∠AGO=∠AGD,又∵∠1+∠AGO=90°,∠2+∠PGC=90°,∠1=∠2,∴∠AGO=∠PGC,又∵∠AGO=∠AGD,∴∠AGO=∠AGD=∠PGC,又∵∠AGO+∠AGD+∠PGC=180°,∴∠AGO=∠AGD=∠PGC=180°÷3=60°,∴∠1=∠2=90°﹣60°=30°;在Rt△AOG中,∵AO=3,∴OG=AOtan30°=3×=,∴G点坐标为(,0),CG=3﹣,在Rt△PCG中,PC===3(﹣1),∴P点坐标为:(3,3﹣3 ),设直线PE的解析式为:y=kx+b,则,解得:,∴直线PE的解析式为y=x﹣3.(4)①如图1,当点M在x轴的负半轴上时,,∵AG=MG,点A坐标为(0,3),∴点M坐标为(0,﹣3).②如图2,当点M在EP的延长线上时,,由(3),可得∠AGO=∠PGC=60°,∴EP与AB的交点M,满足AG=MG,∵A点的横坐标是0,G点横坐标为,∴M的横坐标是2,纵坐标是3,∴点M坐标为(2,3).综上,可得点M坐标为(0,﹣3)或(2,3).考点:几何变换综合题.。
中考数学平行四边形-经典压轴题附答案

一、平行四边形真题与模拟题分类汇编(难题易错题)1.如图1,正方形ABCD的一边AB在直尺一边所在直线MN上,点O是对角线AC、BD 的交点,过点O作OE⊥MN于点E.(1)如图1,线段AB与OE之间的数量关系为.(请直接填结论)(2)保证点A始终在直线MN上,正方形ABCD绕点A旋转θ(0<θ<90°),过点 B作BF⊥MN于点F.①如图2,当点O、B两点均在直线MN右侧时,试猜想线段AF、BF与OE之间存在怎样的数量关系?请说明理由.②如图3,当点O、B两点分别在直线MN两侧时,此时①中结论是否依然成立呢?若成立,请直接写出结论;若不成立,请写出变化后的结论并证明.③当正方形ABCD绕点A旋转到如图4的位置时,线段AF、BF与OE之间的数量关系为.(请直接填结论)【答案】(1)AB=2OE;(2)①AF+BF=2OE,证明见解析;②AF﹣BF=2OE 证明见解析;③BF ﹣AF=2OE,【解析】试题分析:(1)利用直角三角形斜边的中线等于斜边的一半即可得出结论;(2)①过点B作BH⊥OE于H,可得四边形BHEF是矩形,根据矩形的对边相等可得EF=BH,BF=HE,根据正方形的对角线相等且互相垂直平分可得OA=OB,∠AOB=90°,再根据同角的余角相等求出∠AOE=∠OBH,然后利用“角角边”证明△AOE和△OBH全等,根据全等三角形对应边相等可得OH=AE,OE=BH,再根据AF-EF=AE,整理即可得证;②过点B作BH⊥OE交OE的延长线于H,可得四边形BHEF是矩形,根据矩形的对边相等可得EF=BH,BF=HE,根据正方形的对角线相等且互相垂直平分可得OA=OB,∠AOB=90°,再根据同角的余角相等求出∠AOE=∠OBH,然后利用“角角边”证明△AOE和△OBH全等,根据全等三角形对应边相等可得OH=AE,OE=BH,再根据AF-EF=AE,整理即可得证;③同②的方法可证.试题解析:(1)∵AC,BD是正方形的对角线,∴OA=OC=OB,∠BAD=∠ABC=90°,∵OE⊥AB,∴OE=12 AB,∴AB=2OE,(2)①AF+BF=2OE证明:如图2,过点B作BH⊥OE于点H∴∠BHE=∠BHO=90°∵OE⊥MN,BF⊥MN∴∠BFE=∠OEF=90°∴四边形EFBH为矩形∴BF=EH,EF=BH∵四边形ABCD为正方形∴OA=OB,∠AOB=90°∴∠AOE+∠HOB=∠OBH+∠HOB=90°∴∠AOE=∠OBH∴△AEO≌△OHB(AAS)∴AE=OH,OE=BH∴AF+BF=AE+EF+BF=OH+BH+EH=OE+OE=2OE.②AF﹣BF=2OE证明:如图3,延长OE,过点B作BH⊥OE于点H ∴∠EHB=90°∵OE⊥MN,BF⊥MN∴∠AEO=∠HEF=∠BFE=90°∴四边形HBFE为矩形∴BF=HE,EF=BH∵四边形ABCD是正方形∴OA=OB,∠AOB=90°∴∠AOE+∠BOH=∠OBH+∠BOH∴∠AOE=∠OBH∴△AOE≌△OBH(AAS)∴AE=OH,OE=BH,∴AF﹣BF=AE+EF﹣HE=OH﹣HE+OE=OE+OE=2OE③BF﹣AF=2OE,如图4,作OG⊥BF于G,则四边形EFGO是矩形,∴EF=GO,GF=EO,∠GOE=90°,∴∠AOE+∠AOG=90°.在正方形ABCD中,OA=OB,∠AOB=90°,∴∠AOG+∠BOG=90°,∴∠AOE=∠BOG.∵OG⊥BF,OE⊥AE,∴∠AEO=∠BGO=90°.∴△AOE≌△BOG(AAS),∴OE=OG,AE=BG,∵AE﹣EF=AF,EF=OG=OE,AE=BG=AF+EF=OE+AF,∴BF﹣AF=BG+GF﹣(AE﹣EF)=AE+OE﹣AE+EF=OE+OE=2OE,∴BF﹣AF=2OE.2.如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C 关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.(1)求∠FDP的度数;(2)连接BP,请用等式表示AP、BP、DP三条线段之间的数量关系,并证明;(3)连接AC,若正方形的边长为2,请直接写出△ACC′的面积最大值.【答案】(1)45°;(2)BP+DP=2AP,证明详见解析;(3)2﹣1.【解析】【分析】(1)证明∠CDE=∠C'DE和∠ADF=∠C'DF,可得∠FDP'=12∠ADC=45°;(2)作辅助线,构建全等三角形,证明△BAP≌△DAP'(SAS),得BP=DP',从而得△PAP'是等腰直角三角形,可得结论;(3)先作高线C'G,确定△ACC′的面积中底边AC为定值2,根据高的大小确定面积的大小,当C'在BD上时,C'G最大,其△ACC′的面积最大,并求此时的面积.【详解】(1)由对称得:CD=C'D,∠CDE=∠C'DE,在正方形ABCD中,AD=CD,∠ADC=90°,∴AD=C'D,∵F是AC'的中点,∴DF⊥AC',∠ADF=∠C'DF,∴∠FDP=∠FDC'+∠EDC'=12∠ADC=45°;(2)结论:BP+DP=2AP,理由是:如图,作AP'⊥AP交PD的延长线于P',∴∠PAP'=90°,在正方形ABCD中,DA=BA,∠BAD=90°,∴∠DAP'=∠BAP,由(1)可知:∠FDP =45°∵∠DFP =90°∴∠APD =45°,∴∠P '=45°,∴AP =AP ',在△BAP 和△DAP '中,∵BA DA BAP DAP AP AP '=⎧⎪∠=∠⎨='⎪⎩,∴△BAP ≌△DAP '(SAS ),∴BP =DP ',∴DP +BP =PP '=2AP ;(3)如图,过C '作C 'G ⊥AC 于G ,则S △AC 'C =12AC •C 'G ,Rt △ABC 中,AB =BC 2,∴AC 22(2)(2)2+=,即AC 为定值,当C 'G 最大值,△AC 'C 的面积最大,连接BD ,交AC 于O ,当C '在BD 上时,C 'G 最大,此时G 与O 重合,∵CD =C 'D 2OD =12AC =1, ∴C 'G 2﹣1,∴S △AC 'C =112(21)2122AC C G '•=⨯=. 【点睛】本题考查四边形综合题、正方形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.3.如图,四边形ABCD 中,对角线AC 、BD 相交于点O ,AO =CO ,BO =DO ,且∠ABC +∠ADC =180°.(1)求证:四边形ABCD 是矩形.(2)若∠ADF :∠FDC =3:2,DF ⊥AC ,求∠BDF 的度数.【答案】(1)见解析;(2)18°.【解析】【分析】(1)根据平行四边形的判定得出四边形ABCD是平行四边形,求出∠ABC=90°,根据矩形的判定得出即可;(2)求出∠FDC的度数,根据三角形内角和定理求出∠DCO,根据矩形的性质得出OD=OC,求出∠CDO,即可求出答案.【详解】(1)证明:∵AO=CO,BO=DO∴四边形ABCD是平行四边形,∴∠ABC=∠ADC,∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴四边形ABCD是矩形;(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,∴∠FDC=36°,∵DF⊥AC,∴∠DCO=90°﹣36°=54°,∵四边形ABCD是矩形,∴OC=OD,∴∠ODC=54°∴∠BDF=∠ODC﹣∠FDC=18°.【点睛】本题考查了平行四边形的性质和判定,矩形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:矩形的对角线相等,有一个角是直角的平行四边形是矩形.4.在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.【答案】(1)证明见解析;(2)证明见解析;(3)EF2=2BE2+2DF2.【解析】试题分析:(1)根据旋转的性质可知AF=AG,∠EAF=∠GAE=45°,故可证△AEG≌△AEF;(2)将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由(1)知△AEG≌△AEF,则EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;(3)将△ADF绕着点A顺时针旋转90°,得到△ABG,根据旋转的性质可以得到△ADF≌△ABG,则DF=BG,再证明△AEG≌△AEF,得出EG=EF,由EG=BG+BE,等量代换得到EF=BE+DF.试题解析:(1)∵△ADF绕着点A顺时针旋转90°,得到△ABG,∴AF=AG,∠FAG=90°,∵∠EAF=45°,∴∠GAE=45°,在△AGE与△AFE中,,∴△AGE≌△AFE(SAS);(2)设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.则△ADF≌△ABG,DF=BG.由(1)知△AEG≌△AEF,∴EG=EF.∵∠CEF=45°,∴△BME、△DNF、△CEF均为等腰直角三角形,∴CE=CF,BE=BM,NF=DF,∴a﹣BE=a﹣DF,∴BE=DF,∴BE=BM=DF=BG,∴∠BMG=45°,∴∠GME=45°+45°=90°,∴EG2=ME2+MG2,∵EG=EF,MG=BM=DF=NF,∴EF2=ME2+NF2;(3)EF2=2BE2+2DF2.如图所示,延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.由(1)知△AEH≌△AEF,则由勾股定理有(GH+BE)2+BG2=EH2,即(GH+BE)2+(BM﹣GM)2=EH2又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,即2(DF2+BE2)=EF2考点:四边形综合题5.(问题情境)在△ABC中,AB=AC,点P为BC所在直线上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.当P在BC边上时(如图1),求证:PD+PE=CF.证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.(不要证明)(变式探究)(1)当点P在CB延长线上时,其余条件不变(如图3),试探索PD、PE、CF之间的数量关系并说明理由;请运用上述解答中所积累的经验和方法完成下列两题:(结论运用)(2)如图4,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD =16,CF=6,求PG+PH的值.(迁移拓展)(3)在直角坐标系中,直线l1:y=-43x+8与直线l2:y=﹣2x+8相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为2.求点P的坐标.【答案】【变式探究】证明见解析【结论运用】8【迁移拓展】(﹣1,6),(1,10)【解析】【变式探究】连接AP,同理利用△ABP与△ACP面积之差等于△ABC的面积可以证得;【结论运用】过点E作EQ⊥BC,垂足为Q,根据勾股定理和矩形的性质解答即可;【迁移拓展】分两种情况,利用结论,求得点P到x轴的距离,再利用待定系数法可求出P的坐标.【详解】变式探究:连接AP,如图3:∵PD⊥AB,PE⊥AC,CF⊥AB,且S△ABC=S△ACP﹣S△ABP,∴12AB•CF=12AC•PE﹣12AB•PD.∵AB=AC,∴CF=PD﹣PE;结论运用:过点E作EQ⊥BC,垂足为Q,如图④,∵四边形ABCD是长方形,∴AD=BC,∠C=∠ADC=90°.∵AD=16,CF=6,∴BF=BC﹣CF=AD﹣CF=5,由折叠可得:DF=BF,∠BEF=∠DEF.∴DF=5.∵∠C=90°,∴DC2222106DF CF-=-8.∵EQ⊥BC,∠C=∠ADC=90°,∴∠EQC=90°=∠C=∠ADC.∴四边形EQCD是长方形.∴EQ=DC=4.∵AD∥BC,∴∠DEF=∠EFB.∵∠BEF=∠DEF,∴∠BEF=∠EFB.∴BE=BF,由问题情境中的结论可得:PG+PH=EQ.∴PG+PH=8.∴PG+PH的值为8;迁移拓展:如图,由题意得:A (0,8),B (6,0),C (﹣4,0)∴AB 2268+10,BC =10.∴AB =BC ,(1)由结论得:P 1D 1+P 1E 1=OA =8∵P 1D 1=1=2,∴P 1E 1=6 即点P 1的纵坐标为6又点P 1在直线l 2上,∴y =2x+8=6,∴x =﹣1,即点P 1的坐标为(﹣1,6);(2)由结论得:P 2E 2﹣P 2D 2=OA =8∵P 2D 2=2,∴P 2E 2=10 即点P 1的纵坐标为10又点P 1在直线l 2上,∴y =2x+8=10,∴x =1,即点P 1的坐标为(1,10)【点睛】本题考查了矩形的性质与判定、等腰三角形的性质与判定及勾股定理等知识点,利用面积法列出等式是解决问题的关键.6.△ABC 为等边三角形,AF AB =.BCD BDC AEC ∠=∠=∠.(1)求证:四边形ABDF 是菱形.(2)若BD 是ABC ∠的角平分线,连接AD ,找出图中所有的等腰三角形.【答案】(1)证明见解析;(2)图中等腰三角形有△ABC,△BDC,△ABD,△ADF,△ADC,△ADE.【解析】【分析】(1)先求证BD∥AF,证明四边形ABDF是平行四边形,再利用有一组邻边相等的平行四边形是菱形即可证明;(2)先利用BD平分∠ABC,得到BD垂直平分线段AC,进而证明△DAC是等腰三角形,根据BD⊥AC,AF⊥AC,找到角度之间的关系,证明△DAE是等腰三角形,进而得到BC=BD=BA=AF=DF,即可解题,见详解.【详解】(1)如图1中,∵∠BCD=∠BDC,∴BC=BD,∵△ABC是等边三角形,∴AB=BC,∵AB=AF,∴BD=AF,∵∠BDC=∠AEC,∴BD∥AF,∴四边形ABDF是平行四边形,∵AB=AF,∴四边形ABDF是菱形.(2)解:如图2中,∵BA=BC,BD平分∠ABC,∴BD垂直平分线段AC,∴DA=DC,∴△DAC是等腰三角形,∵AF∥BD,BD⊥AC∴AF⊥AC,∴∠EAC=90°,∵∠DAC=∠DCA,∠DAC+∠DAE=90°,∠DCA+∠AEC=90°,∴∠DAE=∠DEA,∴DA=DE,∴△DAE是等腰三角形,∵BC=BD=BA=AF=DF,∴△BCD ,△ABD ,△ADF 都是等腰三角形,综上所述,图中等腰三角形有△ABC ,△BDC ,△ABD ,△ADF ,△ADC ,△ADE .【点睛】本题考查菱形的判定,等边三角形的性质,等腰三角形的判定等知识,属于中考常考题型,熟练掌握等腰三角形的性质是解题的关键.7.在平面直角坐标系中,O 为原点,点A (﹣6,0)、点C (0,6),若正方形OABC 绕点O 顺时针旋转,得正方形OA′B′C′,记旋转角为α:(1)如图①,当α=45°时,求BC 与A′B′的交点D 的坐标;(2)如图②,当α=60°时,求点B′的坐标;(3)若P 为线段BC′的中点,求AP 长的取值范围(直接写出结果即可).【答案】(1)(62,6)-;(2)(333,333)+;(3)323323AP +.【解析】【分析】(1)当α=45°时,延长OA′经过点B ,在Rt △BA′D 中,∠OBC =45°,A′B =626,可求得BD 的长,进而求得CD 的长,即可得出点D 的坐标;(2)过点C′作x 轴垂线MN ,交x 轴于点M ,过点B′作MN 的垂线,垂足为N ,证明△OMC′≌△C′NB′,可得C′N =OM =33,B′N =C′M =3,即可得出点B′的坐标;(3)连接OB ,AC 相交于点K ,则K 是OB 的中点,因为P 为线段BC′的中点,所以PK =12OC′=3,即点P 在以K 为圆心,3为半径的圆上运动,即可得出AP 长的取值范围. 【详解】解:(1)∵A(﹣6,0)、C(0,6),O(0,0),∴四边形OABC是边长为6的正方形,当α=45°时,如图①,延长OA′经过点B,∵OB=62,OA′=OA=6,∠OBC=45°,∴A′B=626-,∴BD=(626=-,-)×21262∴CD=6﹣(1262-)=626-,∴BC与A′B′的交点D的坐标为(662-,6);(2)如图②,过点C′作x轴垂线MN,交x轴于点M,过点B′作MN的垂线,垂足为N,∵∠OC′B′=90°,∴∠OC′M=90°﹣∠B′C′N=∠C′B′N,∵OC′=B′C′,∠OMC′=∠C′NB′=90°,∴△OMC′≌△C′NB′(AAS),当α=60°时,∵∠A′OC′=90°,OC′=6,∴∠C′OM=30°,∴C′N=OM=33,B′N=C′M=3,∴点B′的坐标为()-+;333,333(3)如图③,连接OB,AC相交于点K,则K是OB的中点,∵P 为线段BC′的中点,∴PK =12OC′=3, ∴P 在以K 为圆心,3为半径的圆上运动,∵AK =32,∴AP 最大值为323+,AP 的最小值为323-,∴AP 长的取值范围为323323AP -+.【点睛】本题考查正方形性质,全等三角形判定与性质,三角形中位线定理.(3)问解题的关键是利用中位线定理得出点P 的轨迹.8.如图,在正方形ABCD 中,点E 在CD 上,AF ⊥AE 交CB 的延长线于F .求证:AE=AF .【答案】见解析【解析】【分析】根据同角的余角相等证得∠BAF=∠DAE ,再利用正方形的性质可得AB=AD ,∠ABF=∠ADE=90°,根据ASA 判定△ABF ≌△ADE ,根据全等三角形的性质即可证得AF=AE .【详解】∵AF ⊥AE ,∴∠BAF+∠BAE=90°,又∵∠DAE+∠BAE=90°,∴∠BAF=∠DAE ,∵四边形ABCD 是正方形,∴AB=AD ,∠ABF=∠ADE=90°,在△ABF 和△ADE 中,,∴△ABF≌△ADE(ASA),∴AF=AE.【点睛】本题主要考查了正方形的性质、全等三角形的判定和性质等知识点,证明△ABF≌△ADE是解决本题的关键.9.正方形ABCD的边长为1,对角线AC与BD相交于点O,点E是AB边上的一个动点(点E不与点A、B重合),CE与BD相交于点F,设线段BE的长度为x.(1)如图1,当AD=2OF时,求出x的值;(2)如图2,把线段CE绕点E顺时针旋转90°,使点C落在点P处,连接AP,设△APE的面积为S,试求S与x的函数关系式并求出S的最大值.【答案】(1)x=﹣1;(2)S=﹣(x﹣)2+(0<x<1),当x=时,S的值最大,最大值为,.【解析】试题分析:(1)过O作OM∥AB交CE于点M,如图1,由平行线等分线段定理得到CM=ME,根据三角形的中位线定理得到AE=2OM=2OF,得到OM=OF,于是得到BF=BE=x,求得OF=OM=解方程,即可得到结果;(2)过P作PG⊥AB交AB的延长线于G,如图2,根据已知条件得到∠ECB=∠PEG,根据全等三角形的性质得到EB=PG=x,由三角形的面积公式得到S=(1﹣x)•x,根据二次函数的性质即可得到结论.试题解析:(1)过O作OM∥AB交CE于点M,如图1,∵OA=OC,∴CM=ME,∴AE=2OM=2OF,∴OM=OF,∴,∴BF=BE=x,∴OF=OM=,∵AB=1,∴OB=,∴,∴x=﹣1;(2)过P作PG⊥AB交AB的延长线于G,如图2,∵∠CEP=∠EBC=90°,∴∠ECB=∠PEG,∵PE=EC,∠EGP=∠CBE=90°,在△EPG与△CEB中,,∴△EPG≌△CEB,∴EB=PG=x,∴AE=1﹣x,∴S=(1﹣x)•x=﹣x2+x=﹣(x﹣)2+,(0<x<1),∵﹣<0,∴当x=时,S的值最大,最大值为,.考点:四边形综合题10.如图①,在△ABC中,AB=7,tanA=,∠B=45°.点P从点A出发,沿AB方向以每秒1个单位长度的速度向终点B运动(不与点A、B重合),过点P作PQ⊥AB.交折线AC-CB于点Q,以PQ为边向右作正方形PQMN,设点P的运动时间为t(秒),正方形PQMN 与△ABC重叠部分图形的面积为S(平方单位).(1)直接写出正方形PQMN的边PQ的长(用含t的代数式表示).(2)当点M落在边BC上时,求t的值.(3)求S与t之间的函数关系式.(4)如图②,点P运动的同时,点H从点B出发,沿B-A-B的方向做一次往返运动,在B-A上的速度为每秒2个单位长度,在A-B上的速度为每秒4个单位长度,当点H停止运动时,点P也随之停止,连结MH.设MH将正方形PQMN分成的两部分图形面积分别为S1、S2(平方单位)(0<S1<S2),直接写出当S2≥3S1时t的取值范围.【答案】(1) PQ=7-t.(2) t=.(3) 当0<t≤时,S=.当<t≤4,.当4<t<7时,.(4)或或.【解析】试题分析:(1)分两种情况讨论:当点Q在线段AC上时,当点Q在线段BC上时.(2)根据AP+PN+NB=AB,列出关于t的方程即可解答;(3)当0<t≤时,当<t≤4,当4<t<7时;(4)或或.试题解析:(1)当点Q在线段AC上时,PQ=tanAAP=t.当点Q在线段BC上时,PQ=7-t.(2)当点M落在边BC上时,如图③,由题意得:t+t+t=7,解得:t=.∴当点M落在边BC上时,求t的值为.(3)当0<t≤时,如图④,S=.当<t≤4,如图⑤,.当4<t<7时,如图⑥,.(4)或或..考点:四边形综合题.。
人教中考数学复习平行四边形专项易错题含答案

一、平行四边形真题与模拟题分类汇编(难题易错题)1.如图,矩形ABCD 中,AB =6,BC =4,过对角线BD 中点O 的直线分别交AB ,CD 边于点E ,F .(1)求证:四边形BEDF 是平行四边形;(2)当四边形BEDF 是菱形时,求EF 的长.【答案】(1)证明见解析;(2)133. 【解析】 分析:(1)根据平行四边形ABCD 的性质,判定△BOE ≌△DOF (ASA ),得出四边形BEDF 的对角线互相平分,进而得出结论;(2)在Rt △ADE 中,由勾股定理得出方程,解方程求出BE ,由勾股定理求出BD ,得出OB ,再由勾股定理求出EO ,即可得出EF 的长.详解:(1)证明:∵四边形ABCD 是矩形,O 是BD 的中点,∴∠A=90°,AD=BC=4,AB ∥DC ,OB=OD ,∴∠OBE=∠ODF ,在△BOE 和△DOF 中,OBE ODF OB ODBOE DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BOE ≌△DOF (ASA ),∴EO=FO ,∴四边形BEDF 是平行四边形;(2)当四边形BEDF 是菱形时,BD ⊥EF ,设BE=x ,则 DE=x ,AE=6-x ,在Rt △ADE 中,DE 2=AD 2+AE 2,∴x 2=42+(6-x )2,解得:x=133, ∵22AD AB +13 ∴OB=1213 ∵BD ⊥EF ,∴EO=22BE OB=2133,∴EF=2EO=4133.点睛:本题主要考查了矩形的性质,菱形的性质、勾股定理、全等三角形的判定与性质,熟练掌握矩形的性质和勾股定理,证明三角形全等是解决问的关键2.如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.(1)证明:BE=CF.(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.【答案】(1)见解析;(2)33)见解析【解析】试题分析:(1)先求证AB=AC,进而求证△ABC、△ACD为等边三角形,得∠4=60°,AC=AB进而求证△ABE≌△ACF,即可求得BE=CF;(2)根据△ABE≌△ACF可得S△ABE=S△ACF,故根据S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC即可解题;(3)当正三角形AEF的边AE与BC垂直时,边AE最短.△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又根据S△CEF=S四边形AECF-S△AEF,则△CEF的面积就会最大.试题解析:(1)证明:连接AC,∵∠1+∠2=60°,∠3+∠2=60°,∴∠1=∠3,∵∠BAD=120°,∴∠ABC=∠ADC=60°∵四边形ABCD是菱形,∴AB=BC=CD=AD,∴△ABC、△ACD为等边三角形∴∠4=60°,AC=AB,∴在△ABE和△ACF中,,∴△ABE≌△ACF.(ASA)∴BE=CF.(2)解:由(1)得△ABE≌△ACF,则S△ABE=S△ACF.故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值.作AH⊥BC于H点,则BH=2,S四边形AECF=S△ABC===;(3)解:由“垂线段最短”可知,当正三角形AEF的边AE与BC垂直时,边AE最短.故△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又S△CEF=S四边形AECF﹣S△AEF,则△CEF的面积就会最大.由(2)得,S△CEF=S四边形AECF﹣S△AEF=﹣=.点睛:本题考查了菱形每一条对角线平分一组对角的性质,考查了全等三角形的证明和全等三角形对应边相等的性质,考查了三角形面积的计算,本题中求证△ABE≌△ACF是解题的关键.3.如图,在平行四边形ABCD中,AD⊥DB,垂足为点D,将平行四边形ABCD折叠,使点B落在点D的位置,点C落在点G的位置,折痕为EF,EF交对角线BD于点P.(1)连结CG,请判断四边形DBCG的形状,并说明理由;(2)若AE=BD,求∠EDF的度数.【答案】(1)四边形BCGD是矩形,理由详见解析;(2)∠EDF=120°.【解析】【分析】(1)根据平行四边形的性质和折叠性质以及矩形的判定解答即可;(2)根据折叠的性质以及直角三角形的性质和等边三角形的判定与性质解答即可.【详解】解:(1)四边形BCGD是矩形,理由如下,∵四边形ABCD是平行四边形,∴BC∥AD,即BC∥DG,由折叠可知,BC=DG,∴四边形BCGD是平行四边形,∵AD⊥BD,∴∠CBD=90°,∴四边形BCGD是矩形;(2)由折叠可知:EF垂直平分BD,∴BD⊥EF,DP=BP,∵AD⊥BD,∴EF∥AD∥BC,∴AE PD1==BE BP∴AE=BE,∴DE是Rt△ADB斜边上的中线,∴DE=AE=BE,∵AE=BD,∴DE=BD=BE,∴△DBE是等边三角形,∴∠EDB=∠DBE=60°,∵AB∥DC,∴∠DBC=∠DBE=60°,∴∠EDF=120°.【点睛】本题考查了平行四边形的性质,折叠性质,等边三角形的性质和判定,主要考查学生运用定理进行推理和计算的能力,题目综合性比较强,有一定的难度4.如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.(1)试猜想AE与GC有怎样的关系(直接写出结论即可);(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和CG.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.(3)在(2)中,若E是BC的中点,且BC=2,则C,F两点间的距离为.【答案】(1) AE=CG,AE⊥GC;(2)成立,证明见解析;2.【解析】【分析】(1)观察图形,AE、CG的位置关系可能是垂直,下面着手证明.由于四边形ABCD、DEFG都是正方形,易证得△ADE≌△CDG,则∠1=∠2,由于∠2、∠3互余,所以∠1、∠3互余,由此可得AE⊥GC.(2)题(1)的结论仍然成立,参照(1)题的解题方法,可证△ADE≌△CDG,得∠5=∠4,由于∠4、∠7互余,而∠5、∠6互余,那么∠6=∠7;由图知∠AEB=∠CEH=90°﹣∠6,即∠7+∠CEH=90°,由此得证.(3)如图3中,作CM⊥DG于G,GN⊥CD于N,CH⊥FG于H,则四边形CMGH是矩形,可得CM=GH,CH=GM.想办法求出CH,HF,再利用勾股定理即可解决问题.【详解】(1)AE=CG,AE⊥GC;证明:延长GC交AE于点H,在正方形ABCD与正方形DEFG中,AD=DC,∠ADE=∠CDG=90°,DE=DG,∴△ADE≌△CDG(SAS),∴AE,CG,∠1=∠2∵∠2+∠3=90°,∴∠1+∠3=90°,∴∠AHG=180°﹣(∠1+∠3)=180°﹣90°=90°,∴AE⊥GC.(2)答:成立;证明:延长AE和GC相交于点H,在正方形ABCD和正方形DEFG中,AD=DC,DE=DG,∠ADC=∠DCB=∠B=∠BAD=∠EDG=90°,∴∠1=∠2=90°﹣∠3;∴△ADE≌△CDG(SAS),∴AE=CG,∠5=∠4;又∵∠5+∠6=90°,∠4+∠7=180°﹣∠DCE=180°﹣90°=90°,∴∠6=∠7,又∵∠6+∠AEB=90°,∠AEB=∠CEH,∴∠CEH+∠7=90°,∴∠EHC=90°,∴AE⊥GC.(3)如图3中,作CM⊥DG于G,GN⊥CD于N,CH⊥FG于H,则四边形CMGH是矩形,可得CM=GH,CH=GM.∵BE =CE =1,AB =CD =2,∴AE =DE =CG ═DG =FG 5∵DE =DG ,∠DCE =∠GND ,∠EDC =∠DGN ,∴△DCE ≌△GND(AAS),∴GCD =2,∵S △DCG =12•CD•NG =12•DG•CM , ∴2×25, ∴CM =GH 45, ∴MG =CH 22CG CM -355, ∴FH =FG ﹣FG 5, ∴CF 22FH CH +22535()()55+2. 2.【点睛】 本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.5.(1)(问题发现)如图1,在Rt △ABC 中,AB =AC =2,∠BAC =90°,点D 为BC 的中点,以CD 为一边作正方形CDEF ,点E 恰好与点A 重合,则线段BE 与AF 的数量关系为(2)(拓展研究)在(1)的条件下,如果正方形CDEF 绕点C 旋转,连接BE ,CE ,AF ,线段BE 与AF 的数量关系有无变化?请仅就图2的情形给出证明;(3)(问题发现)当正方形CDEF 旋转到B ,E ,F 三点共线时候,直接写出线段AF 的长.【答案】(1)2AF ;(2)无变化;(3)AF 313.【解析】试题分析:(1)先利用等腰直角三角形的性质得出2 ,再得出BE=AB=2,即可得出结论;(2)先利用三角函数得出22CA CB =,同理得出22CF CE =,夹角相等即可得出△ACF ∽△BCE ,进而得出结论;(3)分两种情况计算,当点E 在线段BF 上时,如图2,先利用勾股定理求出2,6,即可得出62,借助(2)得出的结论,当点E 在线段BF 的延长线上,同前一种情况一样即可得出结论.试题解析:(1)在Rt △ABC 中,AB=AC=2,根据勾股定理得,22,点D 为BC 的中点,∴AD=122, ∵四边形CDEF 是正方形,∴2,∵BE=AB=2,∴2AF ,故答案为2AF ;(2)无变化;如图2,在Rt △ABC 中,AB=AC=2,∴∠ABC=∠ACB=45°,∴sin ∠ABC=2CA CB = 在正方形CDEF 中,∠FEC=12∠FED=45°, 在Rt △CEF 中,sin ∠FEC=2CF CE = ∴CF CA CE CB=, ∵∠FCE=∠ACB=45°,∴∠FCE ﹣∠ACE=∠ACB ﹣∠ACE ,∴∠FCA=∠ECB ,∴△ACF ∽△BCE ,∴BE CB AF CA=2∴2AF , ∴线段BE 与AF 的数量关系无变化;(3)当点E 在线段AF 上时,如图2,由(1)知,CF=EF=CD=2,在Rt△BCF中,CF=2,BC=22,根据勾股定理得,BF=6,∴BE=BF﹣EF=6﹣2,由(2)知,BE=2AF,∴AF=3﹣1,当点E在线段BF的延长线上时,如图3,在Rt△ABC中,AB=AC=2,∴∠ABC=∠ACB=45°,∴sin∠ABC=2 CACB=,在正方形CDEF中,∠FEC=12∠FED=45°,在Rt△CEF中,sin∠FEC=2CFCE=,∴CF CACE CB=,∵∠FCE=∠ACB=45°,∴∠FCB+∠ACB=∠FCB+∠FCE,∴∠FCA=∠ECB,∴△ACF∽△BCE,∴BE CBAF CA= =2,∴BE=2AF,由(1)知,CF=EF=CD=2,在Rt△BCF中,CF=2,BC=22,根据勾股定理得,BF=6,∴BE=BF+EF=6+2,由(2)知,BE=2AF,∴AF=3+1.即:当正方形CDEF旋转到B,E,F三点共线时候,线段AF的长为3﹣1或3+1.6.如图,已知矩形ABCD中,E是AD上一点,F是AB上的一点,EF⊥EC,且EF=EC.(1)求证:△AEF≌△DCE.(2)若DE=4cm,矩形ABCD的周长为32cm,求AE的长.【答案】(1)证明见解析;(2)6cm.【解析】分析:(1)根据EF⊥CE,求证∠AEF=∠ECD.再利用AAS即可求证△AEF≌△DCE.(2)利用全等三角形的性质,对应边相等,再根据矩形ABCD的周长为32cm,即可求得AE的长.详解:(1)证明:∵EF⊥CE,∴∠FEC=90°,∴∠AEF+∠DEC=90°,而∠ECD+∠DEC=90°,∴∠AEF=∠ECD.在Rt△AEF和Rt△DEC中,∠FAE=∠EDC=90°,∠AEF=∠ECD,EF=EC.∴△AEF≌△DCE.(2)解:∵△AEF≌△DCE.AE=CD.AD=AE+4.∵矩形ABCD的周长为32cm,∴2(AE+AE+4)=32.解得,AE=6(cm).答:AE的长为6cm.点睛:此题主要考查学生对全等三角形的判定与性质和矩形的性质等知识点的理解和掌握,难易程度适中,是一道很典型的题目.7.猜想与证明:如图1,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.拓展与延伸:(1)若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为.(2)如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF 的中点,试证明(1)中的结论仍然成立.【答案】猜想:DM=ME,证明见解析;(2)成立,证明见解析.【解析】试题分析:延长EM交AD于点H,根据ABCD和CEFG为矩形得到AD∥EF,得到△FME和△AMH全等,得到HM=EM,根据Rt△HDE得到HM=DE,则可以得到答案;(1)、延长EM交AD于点H,根据ABCD和CEFG为矩形得到AD∥EF,得到△FME和△AMH全等,得到HM=EM,根据Rt△HDE得到HM=DE,则可以得到答案;(2)、连接AE,根据正方形的性质得出∠FCE=45°,∠FCA=45°,根据RT△ADF中AM=MF得出DM=AM=MF,根据RT△AEF中AM=MF得出AM=MF=ME,从而说明DM=ME.试题解析:如图1,延长EM交AD于点H,∵四边形ABCD和CEFG是矩形,∴AD∥EF,∴∠EFM=∠HAM,又∵∠FME=∠AMH,FM=AM,在△FME和△AMH中,∴△FME≌△AMH(ASA)∴HM=EM,在RT△HDE中,HM=DE,∴DM=HM=ME,∴DM=ME.(1)、如图1,延长EM交AD于点H,∵四边形ABCD和CEFG是矩形,∴AD∥EF,∴∠EFM=∠HAM,又∵∠FME=∠AMH,FM=AM,在△FME和△AMH中,∴△FME≌△AMH(ASA)∴HM=EM,在RT△HDE中,HM=EM∴DM=HM=ME,∴DM=ME,(2)、如图2,连接AE,∵四边形ABCD和ECGF是正方形,∴∠FCE=45°,∠FCA=45°,∴AE和EC在同一条直线上,在RT△ADF中,AM=MF,∴DM=AM=MF,在RT△AEF中,AM=MF,∴AM=MF=ME,∴DM=ME.考点:(1)、三角形全等的性质;(2)、矩形的性质.8.问题探究(1)如图①,已知正方形ABCD的边长为4.点M和N分别是边BC、CD上两点,且BM =CN,连接AM和BN,交于点P.猜想AM与BN的位置关系,并证明你的结论.(2)如图②,已知正方形ABCD的边长为4.点M和N分别从点B、C同时出发,以相同的速度沿BC、CD方向向终点C和D运动.连接AM和BN,交于点P,求△APB周长的最大值;问题解决(3)如图③,AC为边长为23的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA向终点C和A运动.连接AM和BN,交于点P.求△APB周长的最大值.【答案】(1)AM⊥BN,证明见解析;(2)△APB周长的最大值4+42;(3)△PAB的周长最大值=23+4.【解析】试题分析:根据全等三角形的判定SAS证明△ABM≌△BCN,即可证得AM⊥BN;(2)如图②,以AB为斜边向外作等腰直角△AEB,∠AEB=90°,作EF⊥PA于E,作EG⊥PB于G,连接EP,证明PA+PB=2EF,求出EF的最大值即可;(3)如图③,延长DA到K,使得AK=AB,则△ABK是等边三角形,连接PK,取PH=PB,证明PA+PB=PK,求出PK的最大值即可.试题解析:(1)结论:AM⊥BN.理由:如图①中,∵四边形ABCD是正方形,∴AB=BC,∠ABM=∠BCN=90°,∵BM=CN,∴△ABM≌△BCN,∴∠BAM=∠CBN,∵∠CBN+∠ABN=90°,∴∠ABN+∠BAM=90°,∴∠APB=90°,∴AM⊥BN.(2)如图②中,以AB为斜边向外作等腰直角三角形△AEB,∠AEB=90°,作EF⊥PA于E,作EG⊥PB于G,连接EP.∵∠EFP=∠FPG=∠G=90°,∴四边形EFPG是矩形,∴∠FEG=∠AEB=90°,∴∠AEF=∠BEG,∵EA=EB,∠EFA=∠G=90°,∴△AEF≌△BEG,∴EF=EG,AF=BG,∴四边形EFPG是正方形,∴PA+PB=PF+AF+PG﹣BG=2PF=2EF,∵EF≤AE,∴EF的最大值=AE=2,∴△APB周长的最大值=4+4.(3)如图③中,延长DA到K,使得AK=AB,则△ABK是等边三角形,连接PK,取PH=PB.∵AB=BC,∠ABM=∠BCN,BM=CN,∴△ABM≌△BCN,∴∠BAM=∠CBN,∴∠A PN=∠BAM+∠ABP=∠CBN+∠ABN=60°,∴∠APB=120°,∵∠AKB=60°,∴∠AKB+∠APB=180°,∴A、K、B、P四点共圆,∴∠BPH=∠KAB=60°,∵PH=PB,∴△PBH是等边三角形,∴∠KBA=∠HBP,BH=BP,∴∠KBH=∠ABP,∵BK=BA,∴△KBH≌△ABP,∴HK=AP,∴PA+PB=KH+PH=PK,∴PK的值最大时,△APB的周长最大,∴当PK是△ABK外接圆的直径时,PK的值最大,最大值为4,∴△PAB的周长最大值=2+4.9.如图,在正方形ABCD中,点E在CD上,AF⊥AE交CB的延长线于F.求证:AE=AF.【答案】见解析【解析】【分析】根据同角的余角相等证得∠BAF=∠DAE,再利用正方形的性质可得AB=AD,∠ABF=∠ADE=90°,根据ASA判定△ABF≌△ADE,根据全等三角形的性质即可证得AF=AE.【详解】∵AF⊥AE,∴∠BAF+∠BAE=90°,又∵∠DAE+∠BAE=90°,∴∠BAF=∠DAE,∵四边形ABCD是正方形,∴AB=AD,∠ABF=∠ADE=90°,在△ABF和△ADE中,,∴△ABF≌△ADE(ASA),∴AF=AE.【点睛】本题主要考查了正方形的性质、全等三角形的判定和性质等知识点,证明△ABF≌△ADE是解决本题的关键.10.如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(3,3).将正方形ABCO 绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.(1)求证:△AOG≌△ADG;(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;(3)当∠1=∠2时,求直线PE的解析式;(4)在(3)的条件下,直线PE上是否存在点M,使以M、A、G为顶点的三角形是等腰三角形?若存在,请直接写出M点坐标;若不存在,请说明理由.【答案】(1)见解析(2)∠PAG =45°,PG=OG+BP.理由见解析(3)y=x﹣3.(4)、.【解析】试题分析:(1)由AO=AD,AG=AG,根据斜边和一条直角边对应相等的两个直角三角形全等,判断出△AOG≌△ADG即可.(2)首先根据三角形全等的判定方法,判断出△ADP≌△ABP,再结合△AOG≌△ADG,可得∠DAP=∠BAP,∠1=∠DAG;然后根据∠1+∠DAG+∠DAP+∠BAP=90°,求出∠PAG的度数;最后判断出线段OG、PG、BP之间的数量关系即可.(3)首先根据△AOG≌△ADG,判断出∠AGO=∠AGD;然后根据∠1+∠AGO=90°,∠2+∠PGC=90°,判断出当∠1=∠2时,∠AGO=∠AGD=∠PGC,而∠AGO+∠AGD+∠PGC=180°,求出∠1=∠2=30°;最后确定出P、G两点坐标,即可判断出直线PE的解析式.(4)根据题意,分两种情况:①当点M在x轴的负半轴上时;②当点M在EP的延长线上时;根据以M、A、G为顶点的三角形是等腰三角形,求出M点坐标是多少即可.试题解析:(1)在Rt△AOG和Rt△ADG中,(HL)∴△AOG≌△ADG.(2)在Rt△ADP和Rt△ABP中,∴△ADP≌△ABP,则∠DAP=∠BAP;∵△AOG≌△ADG,∴∠1=∠DAG;又∵∠1+∠DAG+∠DAP+∠BAP=90°,∴2∠DAG+2∠DAP=90°,∴∠DAG+∠DAP=45°,∵∠PAG=∠DAG+∠DAP,∴∠PAG=45°;∵△AOG≌△ADG,∴DG=OG,∵△ADP≌△ABP,∴DP=BP,∴PG=DG+DP=OG+BP.(3)解:∵△AOG≌△ADG,∴∠AGO=∠AGD,又∵∠1+∠AGO=90°,∠2+∠PGC=90°,∠1=∠2,∴∠AGO=∠PGC,又∵∠AGO=∠AGD,∴∠AGO=∠AGD=∠PGC,又∵∠AGO+∠AGD+∠PGC=180°,∴∠AGO=∠AGD=∠PGC=180°÷3=60°,∴∠1=∠2=90°﹣60°=30°;在Rt△AOG中,∵AO=3,∴OG=AOtan30°=3×=,∴G点坐标为(,0),CG=3﹣,在Rt△PCG中,PC===3(﹣1),∴P点坐标为:(3,3﹣3 ),设直线PE的解析式为:y=kx+b,则,解得:,∴直线PE的解析式为y=x﹣3.(4)①如图1,当点M在x轴的负半轴上时,,∵AG=MG,点A坐标为(0,3),∴点M坐标为(0,﹣3).②如图2,当点M在EP的延长线上时,,由(3),可得∠AGO=∠PGC=60°,∴EP与AB的交点M,满足AG=MG,∵A点的横坐标是0,G点横坐标为,∴M的横坐标是2,纵坐标是3,∴点M坐标为(2,3).综上,可得点M坐标为(0,﹣3)或(2,3).考点:几何变换综合题.。
中考数学数学平行四边形的专项培优易错试卷练习题含答案

中考数学数学平行四边形的专项培优易错试卷练习题含答案一、选择题1.如图,在正方形ABCD 中,CE =MN ,∠MCE =35°,那么∠ANM 等于( )A .45°B .50°C .55°D .60°2.如图所示,等边三角形ABC 沿射线BC 向右平移到DCE ∆的位置,连接AD 、BD ,则下列结论:(1)AD BC =(2)BD 与AC 互相平分(3)四边形ACED 是菱形(4)BD DE ⊥,其中正确的个数是( )A .1B .2C .3D .43.如图,正方形ABCD 中,AB =4,E 为CD 上一动点,连接AE 交BD 于F ,过F 作FH ⊥AE 于F ,过H 作HG ⊥BD 于 G .则下列结论:①AF =FH ;②∠HAE =45°;③BD =2FG ;④△CEH 的周长为 8.其中正确的个数是( )A .1个B .2个C .3个D .4个4.如图,将一个矩形纸片ABCD 折叠,使点B 与点D 重合,若3,9,AB BC ==则折痕EF 的长度为( )A .3B .23C .10D .31025.如图,E 是边长为2的正方形ABCD 的对角线AC 上一点,且AE AB =,F 为BE 上任意一点,FG AC 于点G ,FH AB ⊥于点H ,则FG FH +的值是( )A .22B .2C .2D .16.线段AB 上有一动点C (不与A ,B 重合),分别以AC ,BC 为边向上作等边△ACM 和等边△BCN ,点D 是MN 的中点,连结AD ,BD ,在点C 的运动过程中,有下列结论:①△ABD 可能为直角三角形;②△ABD 可能为等腰三角形;③△CMN 可能为等边三角形;④若AB=6,则AD+BD 的最小值为37. 其中正确的是( )A .②③B .①②③④C .①③④D .②③④7.已知四边形ABCD 中,对角线BD 被AC 平分,那么再加上下述中的条件( ) 可以得到结论: “四边形ABCD 是平行四边形”.A .AB =CD B .∠BAD=∠BCDC .∠ABC=∠ADCD .AC= BD8.如图,正方形ABCD 的边长为1,以对角线AC 为边作第二个正方形ACEF ,再以对角线AE 为边作第三个正方形AEGH ,依此下去,第n 个正方形的面积为( )A .2n ﹣1B .2n ﹣1C .2)nD .2n9.如图,在菱形ABCD 中,5AB cm =,120ADC =∠︒,点E 、F 同时由A 、C 两点出发,分别沿AB 、CB 方向向点B 匀速移动(到点B 为止),点E 的速度为1/cm s ,点F 的速度为2/cm s ,经过t 秒DEF ∆为等边三角形,则t 的值为( )A .34B .43C .32D .5310.如图,BD 为平行四边形ABCD 的对角线,45DBC ∠=︒,DE BC ⊥于E ,BF CD ⊥于F ,DE 、BF 相交于H ,直线BF 交线段AD 的延长线于G ,下面结论:①2BD BE =;②A BHE =∠∠;③AB BH =;④BHD BDG ∠=∠其中正确的个数是( )A .1B .2C .3D .4二、填空题11.如图,在矩形ABCD 中,4AB =,2AD =,E 为边CD 的中点,点P 在线段AB 上运动,F 是CP 的中点,则CEF ∆的周长的最小值是____________.12.如图,正方形ABCD 的对角线相交于点O ,对角线长为1cm ,过点O 任作一条直线分别交AD ,BC 于E ,F ,则阴影部分的面积是_____.13.已知:点B 是线段AC 上一点,分别以AB ,BC 为边在AC 的同侧作等边ABD △和等边BCE ,点M ,N 分别是AD ,CE 的中点,连接MN .若AC=6,设BC=2,则线段MN 的长是__________.14.如图,在Rt △ABC 中,∠BAC=90°,AB=5,AC=12,P 为边BC 上一动点(P 不与B 、C 重合),PE ⊥AB 于E ,PF ⊥AC 于F ,M 为EF 中点,则AM 的取值范围是__.15.如图,在平行四边形ABCD ,AD =2AB ,F 是AD 的中点,作CE ⊥AB ,垂足E 在线段AB 上,连接EF 、CF ,则下列结论:①∠BCD =2∠DCF ;②EF =CF ;③S △CDF =S △CEF ;④∠DFE =3∠AEF ,-定成立的是_________.(把所有正确结论的序号都填在横线上)16.如图,在矩形ABCD 中,16AB =,18BC =,点E 在边AB 上,点F 是边BC 上不与点B 、C 重合的一个动点,把EBF △沿EF 折叠,点B 落在点B '处.若3AE =,当CDB '是以DB '为腰的等腰三角形时,线段DB '的长为__________.17.在平面直角坐标系xOy 中,点A 、B 分别在x 轴、y 轴的正半轴上运动,点M 为线段AB 的中点.点D 、E 分别在x 轴、y 轴的负半轴上运动,且DE =AB =10.以DE 为边在第三象限内作正方形DGFE ,则线段MG 长度的最大值为_____.18.如图,在ABC 中,D 是AB 上任意一点,E 是BC 的中点,过C 作//CF AB ,交DE 的延长线于F ,连BF ,CD ,若30FDB ∠=︒,45ABC ∠=︒,22BC =,则DF =_________.19.如图,矩形纸片ABCD ,AB =5,BC =3,点P 在BC 边上,将△CDP 沿DP 折叠,点C 落在点E 处,PE ,DE 分别交AB 于点O ,F ,且OP =OF ,则AF 的值为______.20.如图,在四边形ABCD 中, //,5,18,AD BC AD BC E ==是BC 的中点.点P 以每秒1个单位长度的速度从点A 出发,沿AD 向点D 运动;点Q 同时以每秒3个单位长度的速度从点C 出发,沿CB 向点B 运动.点P 停止运动时,点Q 也随之停止运动,当运动时间为t 秒时,以点,,,P Q E D 为顶点的四边形是平行四边形,则t 的值等于_______.三、解答题21.如图正方形ABCD ,DE 与HG 相交于点O (O 不与D 、E 重合).(1)如图(1),当90GOD ∠=︒,①求证:DE GH =; ②求证:2GD EH DE +>;(2)如图(2),当45GOD ∠=︒,边长4AB =,25HG =,求DE 的长.22.如图,在正方形ABCD 中,点M 是BC 边上任意一点,请你仅用无刻度的直尺,用连线的方法,分别在图(1)、图(2)中按要求作图(保留作图痕迹,不写作法).(1)在如图(1)的AB 边上求作一点N ,连接CN ,使CN AM =;(2)在如图(2)的AD 边上求作一点Q ,连接CQ ,使CQ AM .23.社团活动课上,数学兴趣小组的同学探索了这样的一个问题:如图1,90MON ∠=,点A 为边OM 上一定点,点B 为边ON 上一动点,以AB 为一边在∠MON 的内部作正方形ABCD ,过点C 作CF OM ⊥,垂足为点F (在点O 、A 之间),交BD 与点E ,试探究AEF ∆的周长与OA 的长度之间的等量关系该兴趣小组进行了如下探索:(动手操作,归纳发现)(1)通过测量图1、2、3中线段AE 、AF 、EF 和OA 的长,他们猜想AEF ∆的周长是OA 长的_____倍.请你完善这个猜想(推理探索,尝试证明)为了探索这个猜想是否成立,他们作了如下思考,请你完成后续探索过程:(2)如图4,过点C 作CG ON ⊥,垂足为点G则90CGB ∠=90GCB CBG ∴∠+∠= 又四边形ABCD 正方形,AB BC =,90ABC ∠=则90CBG ABO ∠+∠=GCB ABO ∴∠=∠在CBE ∆与ABE ∆中,(类比探究,拓展延伸)(3)如图5,当点F 在线段OA 的延长线上时,直接写出线段AE 、EF 、AF 与OA 长度之间的等量关系为 .24.共顶点的正方形ABCD 与正方形AEFG 中,AB =13,AE 2.(1)如图1,求证:DG =BE ;(2)如图2,连结BF ,以BF 、BC 为一组邻边作平行四边形BCHF .①连结BH ,BG ,求BH BG的值; ②当四边形BCHF 为菱形时,直接写出BH 的长.25.猜想与证明:如图①摆放矩形纸片ABCD 与矩形纸片ECGF ,使B ,C ,G 三点在一条直线上,CE 在边CD 上.连结AF ,若M 为AF 的中点,连结DM ,ME ,试猜想DM 与ME 的数量关系,并证明你的结论.拓展与延伸:(1)若将“猜想与证明”中的纸片换成正方形纸片ABCD 与正方形纸片ECGF ,其他条件不变,则DM 和ME 的关系为__________________;(2)如图②摆放正方形纸片ABCD 与正方形纸片ECGF ,使点F 在边CD 上,点M 仍为AF 的中点,试证明(1)中的结论仍然成立.[提示:直角三角形斜边上的中线等于斜边的一半]① ②26.如图,在正方形ABCD 中,点E 是BC 边所在直线上一动点(不与点B 、C 重合),过点B 作BF ⊥DE ,交射线DE 于点F ,连接CF .(1)如图,当点E 在线段BC 上时,∠BDF=α.①按要求补全图形;②∠EBF =______________(用含α的式子表示);③判断线段 BF ,CF ,DF 之间的数量关系,并证明.(2)当点E 在直线BC 上时,直接写出线段BF ,CF ,DF 之间的数量关系,不需证明.27.感知:如图①,在正方形ABCD 中,E 是AB 一点,F 是AD 延长线上一点,且DF BE =,求证:CE CF =;拓展:在图①中,若G 在AD ,且45GCE ∠︒=,则GE BE GD +=成立吗?为什么? 运用:如图②在四边形ABCD 中,()//AD BC BC AD >,90A B ∠∠︒==,16AB BC ==,E 是AB 上一点,且45DCE ∠︒=,4BE =,求DE 的长.28.如图,已知平面直角坐标系中,1,0A 、()0,2C ,现将线段CA 绕A 点顺时针旋转90︒得到点B ,连接AB .(1)求出直线BC 的解析式;(2)若动点M 从点C 出发,沿线段CB 10,过M 作//MN AB 交y 轴于N ,连接AN .设运动时间为t 分钟,当四边形ABMN 为平行四边形时,求t 的值.(3)P 为直线BC 上一点,在坐标平面内是否存在一点Q ,使得以O 、B 、P 、Q 为顶点的四边形为菱形,若存在,求出此时Q 的坐标;若不存在,请说明理由.29.在四边形ABCD 中,对角线AC 、BD 相交于点O ,过点O 的直线EF ,GH 分别交边AB 、CD ,AD 、BC 于点E 、F 、G 、H .(1)观察发现:如图①,若四边形ABCD 是正方形,且EF ⊥GH ,易知S △BOE =S △AOG ,又因为S △AOB =14S 四边形ABCD ,所以S 四边形AEOG = S 正方形ABCD ; (2)类比探究:如图②,若四边形ABCD 是矩形,且S 四边形AEOG =14S 矩形ABCD ,若AB =a ,AD =b ,BE =m ,求AG 的长(用含a 、b 、m 的代数式表示); (3)拓展迁移:如图③,若四边形ABCD 是平行四边形,且S 四边形AEOG =14S ▱ABCD ,若AB =3,AD =5,BE =1,则AG = .30.在边长为5的正方形ABCD中,点E在边CD所在直线上,连接BE,以BE为边,在BE的下方作正方形BEFG,并连接AG.(1)如图1,当点E与点D重合时,AG=;(2)如图2,当点E在线段CD上时,DE=2,求AG的长;(3)若AG=517,请直接写出此时DE的长.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】过B作BF∥MN交AD于F,则∠AFB=∠ANM,根据正方形的性质得出∠A=∠EBC=90°,AB=BC,AD∥BC,推出四边形BFNM是平行四边形,得出BF=MN=CE,证Rt△ABF≌Rt△BCE,推出∠AFB=∠ECB即可.【详解】解:过B 作BF ∥MN 交AD 于F ,则∠AFB =∠ANM ,∵四边形ABCD 是正方形,∴∠A =∠EBC =90°,AB =BC ,AD ∥BC ,∴FN ∥BM ,BF ∥MN ,∴四边形BFNM 是平行四边形,∴BF =MN ,∵CE =MN ,∴CE =BF ,在Rt △ABF 和Rt △BCE 中BF CE AB BC =⎧⎨=⎩∴Rt △ABF ≌Rt △BCE (HL ),∴∠ABF =∠MCE =35°,∴∠ANM =∠AFB =55°,故选:C .【点睛】本题考查了直角三角形全等的判定即性质,还涉及正方形的性质以及平行四边形的判定与性质,构造全等三角形是解题关键.2.D解析:D【分析】先求出∠ACD=60°,继而可判断△ACD 是等边三角形,从而可判断①是正确的;根据①的结论,可判断四边形ABCD 是平行四边形,从而可判断②是正确的;再结合①的结论,可判断③正确;根据菱形的对角线互相垂直可得AC ⊥BD ,再根据平移后对应线段互相平行可得∠BDE=∠COD=90°,进而判断④正确.【详解】解:如图:∵△ABC ,△DCE 是等边三角形∴∠ACB=∠DCE=60°,AC=CD∴∠ACD=180°-∠ACB-∠DCE=60°∴△ACD 是等边三角形∴AD=AC=BC ,故①正确;由①可得AD=BC∵AB=CD∴四边形ABCD是平行四边形,∴BD、AC互相平分,故②正确;由①可得AD=AC=CE=DE故四边形ACED是菱形,即③正确∵四边形ABCD是平行四边形,BA=BC∴.四边形ABCD是菱形∴AC⊥BD,AC//DE∴∠BDE=∠COD=90°∴BD⊥DE,故④正确综上可得①②③④正确,共4个.故选:D【点睛】此题主要考查了菱形的判定与性质,以及平移的性质,关键是掌握菱形四边相等,对角线互相垂直.3.D解析:D【分析】①作辅助线,延长HF交AD于点L,连接CF,通过证明△ADF≌△CDF,可得:AF=CF,故需证明FC=FH,可证:AF=FH;②由FH⊥AE,AF=FH,可得:∠HAE=45°;③作辅助线,连接AC交BD于点O,证BD=2FG,只需证OA=GF即可,根据△AOF≌△FGH,可证OA=GF,故可证BD=2FG;④作辅助线,延长AD至点M,使AD=DM,过点C作CI∥HL,则IL=HC,可证AL=HE,再根据△MEC≌△MIC,可证:CE=IM,故△CEH的周长为边AM的长.【详解】①连接FC,延长HF交AD于点L,∵BD为正方形ABCD的对角线,∴∠ADB=∠CDF=45°.∵AD=CD,DF=DF,∴△ADF≌△CDF.∴FC=AF,∠ECF=∠DAF.∵∠ALH+∠LAF=90°,∴∠LHC+∠DAF=90°.∵∠ECF=∠DAF,∴∠FHC=∠FCH,∴FH=FC.∴FH=AF.②∵FH⊥AE,FH=AF,∴∠HAE=45°.③连接AC交BD于点O,可知:BD=2OA,∵∠AFO+∠GFH=∠GHF+∠GFH,∴∠AFO=∠GHF.∵AF=HF,∠AOF=∠FGH=90°,∴△AOF≌△FGH.∴OA=GF.∵BD=2OA,∴BD=2FG.④连接EM,延长AD至点M,使AD=DM,过点C作CI∥HL,则:LI=HC,∵HL⊥AE,CI∥HL,∴AE⊥CI,∴∠DIC+∠EAD=90°,∵∠EAD+∠AED=90°,∴∠DIC=∠AED,∵ED⊥AM,AD=DM,∴EA=EM,∴∠AED=∠MED,∴∠DIC=∠DEM,∴∠CIM=∠CEM,∵CM=MC ,∠ECM=∠CMI=45°,∴△MEC ≌△CIM ,可得:CE=IM ,同理,可得:AL=HE ,∴HE+HC+EC=AL+LI+IM=AM=8.∴△CEH 的周长为8,为定值.故①②③④结论都正确.故选D .【点睛】解答本题要充分利用正方形的特殊性质,在解题过程中要多次利用三角形全等.4.C解析:C【分析】设AE x =,根据勾股定理得到AE ,进而得出BE 的长,再证明5BF BE ==,根据EG AB =,求出GF 的长,最后在运用勾股定理即可得到EF .【详解】解:过E 作EG BC ⊥于G ,设AE x =,则9DE BE x ==-,在Rt ABE △中,222AB AE BE +=,2223(9)x x ∴+=-解得4x =,4AE ∴=,945BE DE ∴==-=,DEF BFE ∠=∠,DEF BEF ∠=∠,BFE BEF ∴∠=∠,5BF BE ∴==,1GF ∴=,Rt EFG ∴中,22223110EF EG GF =+=+=即EF 10,故选:C .【点睛】本题主要考查了折叠问题,矩形的性质以及勾股定理的运用,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.解题时注意方程思想的运用.5.B解析:B 【分析】过点E作EM⊥AB,连接AF,先求出EM,由S△ABE=12AB•EM=12AE•GF+12AB•FH,可得FG+FH=EM,则FG+FH的值可求.【详解】解:如图,过点E作EM⊥AB,连接AF,∵四边形ABCD是正方形,∴∠ACB=45°,∴△AEM是等腰直角三角形,∵AB=AE=2,∴222224 AM EM EM AE+===∴EM2,∵S△ABE=S△AEF+S△ABF,∴S△ABE=12AB•EM=12AE•GF+12AB•FH,∴2;故选:B.【点睛】本题考查了正方形的性质,等腰直角三角形的性质,运用面积法得出线段的和差关系是解题的关键.6.D解析:D【分析】根据题意并结合图形,我们可以得出当C为AB的中点时,可判断所给结论正确与否.【详解】解:当C为AB中点时,有图如下,∵ACM 与BCN 为等边三角形,∵C 为AB 中点,∴AM=AC=MC=NC=BC=NB,MD=ND ,∵MCN 60∠=︒∴CMN CNM 60∠∠==︒∴CMN 为等边三角形,③正确;∵AMD BND 120∠∠==︒∴AMD BND ≅∴AD=BD,△ABD 此时为等腰三角形,②正确;当C 为AB 中点时,AD+BD 值最小,∵D 为MN 的中点,∴CD 为MN 的垂直平分线, ∴1MD 4AB =,∵AB=6, ∴22333CD 322⎛⎫=-= ⎪⎝⎭∴223337AD 32⎛⎫=+= ⎪ ⎪⎝⎭∵AD=BD ∴AD+BD=37若△ABD 可能为直角三角形,则ADB 90∠=︒,∴CD 为AB 的垂直平分线∴ADC 45∠=︒∴AC=CD,与所求结论不符,①错误.故选:D .【点睛】本题考查的知识点是等边三角形的性质以及全等三角形的判定定理及性质,弄清题意,画出当C 为AB 中点时的图形是解题的关键. 7.B解析:B【分析】设BD与AC交于O点,已知条件为BO=DO,∠AOB=∠COD,结合选项条件应证出能判断平行四边形的条件,或举出反例证明不成立.【详解】解:A、BO=DO,∠AOB=∠COD, AB=CD不能证出四边形ABCD是平行四边形, 反例如图,故本选项错误;B、如图,在直线AC上任取一点C´,使OA=OC´,∵BO=DO,∴四边形ABC´D是平行四边形,∴AD∥BC´,AB∥C´D,∴∠BC´A=∠C´AD, ∠AC´D=∠BAC´,∴∠BC´A+∠AC´D=∠C´AD+∠BAC´,即∠BC´D=∠BAD,∵∠BAD=∠BCD∴∠BC´D=∠BCD,∴点C与点C´重合,∴四边形ABCD是平行四边形.故本选项正确;C、当BO=DO,∠ABC=∠ADC不能证出四边形ABCD是平行四边形, 反例如图,故本选项错误;D、当BO=DO,AC=BD, 不能证出四边形ABCD是平行四边形, 反例如图,故本选项错误.故选:B.【点睛】本题考查平行四边形的判定,根据已知条件证出判定平行四边形的条件及举出反例图形是解答此题的关键.8.B解析:B【解析】【分析】先求出第一个正方形面积、第二个正方形面积、第三个正方形面积,…探究规律后,即可解决问题.【详解】第一个正方形的面积为1=20,第二个正方形的面积为(2)2=2=21,第三个正方形的边长为22,…第n个正方形的面积为2n﹣1,故选B.【点睛】本题考查了规律型:图形的变化类,正方形的性质,根据前后正方形边长之间的关系找到S n的规律是解题的关键.9.D解析:D【分析】连接BD,证出△ADE≌△BDF,得到AE=BF,再利用AE=t,CF=2t,则BF=BC-CF=5-2t求出时间t的值.【详解】解:连接BD,∵四边形ABCD是菱形,∠ADC=120°,∴AB=AD,∠ADB=12∠ADC=60°,∴△ABD是等边三角形,∴AD=BD,又∵△DEF是等边三角形,∴∠EDF=∠DEF=60°,又∵∠ADB=60°,∴∠ADE=∠BDF,在△ADE和△BDF中,AD BDA DBCADE BDF=⎧⎪∠=∠⎨⎪∠=∠⎩∴△ADE≌△BDF(ASA),∴AE=BF,∵AE=t,CF=2t,∴BF=BC−CF=5−2t,∴t=5−2t∴t=53,故选:D.【点睛】本题考查全等三角形,等边三角形,菱形等知识,熟练掌握全等三角形的判定与性质,等边三角形的判定与性质,菱形的性质为解题关键.10.B解析:B【分析】通过判断△BDE为等腰直角三角形,根据等腰直角三角形的性质和勾股定理可对①进行判断;根据等角的余角相等得到∠BHE=∠C,再根据平行四边形的性质得到∠A=∠C,则∠A=∠BHE,于是可对②进行判断;证明△BEH≌△DEC,得到BH=CD,接着由平行四边形的性质得AB=CD,则AB=BH,可对③进行判断;因为∠BHD=90°+∠EBH,∠BDG=90°+∠BDE,由∠BDE>∠EBH,推出∠BDG>∠BHD,可判断④.【详解】解:∵∠DBC=45°,DE⊥BC,∴△BDE为等腰直角三角形,,BE DE BD∴====,所以①错误;∵BF⊥CD,∴∠C+∠CBF=90°,而∠BHE+∠CBF=90°,∴∠BHE=∠C,∵四边形ABCD为平行四边形,∴∠A=∠C,∴∠A=∠BHE,所以②正确;在△BEH 和△DEC 中BHE C HEB CED BE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BEH ≌△DEC ,∴BH=CD ,∵四边形ABCD 为平行四边形,∴AB=CD ,∴AB=BH ,所以③正确;∵∠BHD=90°+∠EBH ,∠BDG=90°+∠BDE ,∵∠BDE=∠DBE >∠EBH ,∴∠BDG >∠BHD ,所以④错误;故选:B .【点睛】本题考查平行四边形的性质,全等三角形的性质和判定,等腰直角三角形的判定和性质,三角形外角的性质.熟练掌握平行四边形的性质并能灵活运用是解题关键,本题中主要用到平行四边形对边相等,对角相等.二、填空题11.2【分析】由题意根据三角形的中位线的性质得到EF=12PD ,得到C △CEF =CE+CF+EF=CE+12(CP+PD )=12(CD+PC+PD )=12C △CDP ,当△CDP 的周长最小时,△CEF 的周长最小;即PC+PD 的值最小时,△CEF 的周长最小;并作D 关于AB 的对称点D ′,连接CD ′交AB 于P ,进而分析即可得到结论.【详解】解:∵E 为CD 中点,F 为CP 中点,∴EF=12PD , ∴C △CEF =CE+CF+EF=CE+12(CP+PD )=12(CD+PC+PD )=12C △CDP ∴当△CDP 的周长最小时,△CEF 的周长最小;即PC+PD 的值最小时,△CEF 的周长最小;如图,作D 关于AB 的对称点T ,连接CT ,则PD=PT ,∵AD=AT=BC=2,CD=4,∠CDT=90°, ∴22224442CT CD DT =+=+=,∵△CDP 的周长=CD+DP+PC=CD+PT+PC ,∵PT+PC ≥CT ,∴PT+PC ≥42,∴PT+PC 的最小值为42,∴△PDC 的最小值为4+42,∴C △CEF =12C △CDP =222+. 故答案为:222+.【点睛】本题考查轴对称-最短距离问题以及三角形的周长的计算等知识,解题的关键是学会利用轴对称解决最值问题.12.218cm 【分析】根据正方形的性质可以证明△AEO ≌CFO ,就可以得出S △AEO =S △CFO ,就可以求出△AOD 面积等于正方形面积的14,根据正方形的面积就可以求出结论. 【详解】解:如图:∵正方形ABCD 的对角线相交于点O ,∴△AEO 与△CFO 关于O 点成中心对称,∴△AEO ≌CFO ,∴S △AEO =S △CFO ,∴S △AOD =S △DEO +S △CFO ,∵对角线长为1cm ,∴S 正方形ABCD =1112⨯⨯=12cm 2, ∴S △AOD =18cm 2, ∴阴影部分的面积为18cm 2. 故答案为:18cm 2. 【点睛】 本题考查了正方形的性质的运用,全等三角形的判定及性质的运用正方形的面积及三角形的面积公式的运用,在解答时证明△AEO ≌CFO 是关键.13【分析】如图(见解析),先根据等边三角形的性质、平行四边形的判定与性质可得//,4ME AB ME AB ==,再根据平行线的性质可得60FEM C ∠=∠=︒,然后利用直角三角形的性质、勾股定理可得2,EF MF ==,从而可得3FN =,最后在Rt FMN 中,利用勾股定理即可得.【详解】如图,连接ME ,过点M 作MF CE ⊥,交CE 延长线于点F ,ABD △和BCE 都是等边三角形,2BC =,60,2,A CBE C BE CE AD A C B B ∴∠=∠=∠=︒====,//AD BE ∴,6AC =,624AD AB ∴==-=,点M ,N 分别是AD ,CE 的中点,112,122AM AD EN CE ∴====, AM BE ∴=,∴四边形ABEM 是平行四边形,//,4ME AB ME AB ∴==, 60FEM C ∴∠=∠=︒,在Rt EFM △中,906030EMF ∠=︒-︒=︒,12,2EF ME MF ∴==== 123FN EN EF ∴=+=+=,则在Rt FMN 中,MN ===故答案为:21.【点睛】本题考查了等边三角形的性质、勾股定理、平行四边形的判定与性质、直角三角形的性质等知识点,通过作辅助线,构造直角三角形和平行四边形是解题关键.14.3013≤AM<6 【分析】 由勾股定理得BC=13从而得到点A 到BC 的距离, M 为EF 中点,所以AM=12EF ,继而求得AM 的范围.【详解】因为∠BAC=90°,AB=5,AC=12,所以由勾股定理得BC=13,则点A 到BC 的距离为AC 512BC 13AB ⨯⨯==6013, 所以AM 的最小值为6013÷2=3013, 因为M 为EF 中点,所以AM=12EF , 当E 越接近A ,F 越接近C 时,EF 越大,所以EF <AC ,则AM <6,所以3013≤AM<6, 故答案为3013≤AM<6. 15.①②④【分析】①根据平行四边形的性质和等腰三角形的性质即可判断;②延长EF ,交CD 延长线于点M ,首先根据平行四边形的性质证明AEFDFM ≅△△,得出,FE MF AEFM =∠=∠,进而得出90ECD AEC ∠=∠=︒,从而利用直角三角形斜边中线的性质即可判断;③由FE MF =,得出EFC CFMS S =,从而可判断正误;④设FEC x ∠= ,利用三角形内角和定理分别表示出∠DFE 和∠AEF ,从而判断正误.【详解】①∵点F 是AD 的中点,∴AF FD = .∵在平行四边形ABCD 中,AD =2AB ,//,AD BC AF FD CD ∴==,,DFC FCB DFC DCF ∴∠=∠∠=∠ ,FCB DCF ∴∠=∠,∴∠BCD =2∠DCF ,故①正确;②延长EF ,交CD 延长线于点M ,∵四边形ABCD 是平行四边形,//AB CD ∴,A MDF ∴∠=∠,∵点F 是AD 的中点,∴AF FD = .在AEF 和DFM 中,A FDM AF DFAFE DFM ∠=∠⎧⎪=⎨⎪∠=∠⎩()AEF DFM ASA ∴≅△△,FE MF AEF M ∴=∠=∠.CE AB ⊥ ,90AEC ∴∠=︒,90ECD AEC ∴∠=∠=︒,12CF EM EF ∴==,故②正确; ③∵FE MF =,∴EFC CFM S S = .CFM CDF MDF S S S =+△△△CDF EFC S S ∴<△△,故③错误;④设FEC x ∠= ,则FCE x ∠=,90DCF DFC x ∴∠=∠=︒- ,1802EFC x ∴∠=︒-,9018022703∴∠=︒-+︒-=︒-.EFD x x x∠=︒-,90AEF x∴∠=∠,故④正确;DFE AEF3综上所述,正确的有①②④,故答案为:①②④.【点睛】本题主要考查平行四边形的性质,全等三角形的判定及性质,三角形内角和定理,掌握这些性质和定理是解题的关键.16.16或10【分析】等腰三角形一般分情况讨论:(1)当DB'=DC=16;(2)当B'D=B'C时,作辅助线,构建平行四边形AGHD和直角三角形EGB',计算EG和B'G的长,根据勾股定理可得B'D的长;【详解】∵四边形ABCD是矩形,∴DC=AB=16,AD=BC=18.分两种情况讨论:(1)如图2,当DB'=DC=16时,即△CDB'是以DB'为腰的等腰三角形(2)如图3,当B'D=B'C时,过点B'作GH∥AD,分别交AB与CD于点G、H.∵四边形ABCD是矩形,∴AB∥CD,∠A=90°又GH∥AD,∴四边形AGHD是平行四边形,又∠A=90°,∴四边形AGHD是矩形,∴AG=DH,∠GHD=90°,即B'H⊥CD,又B'D=B'C,∴DH=HC=183CD=,AG=DH=8,∵AE=3,∴BE=EB'=AB-AE=16-3=13,EG=AG-AE=8-3=5,在Rt△EGB'中,由勾股定理得:GB′=2213512,∴B'H=GH×GB'=18-12=6,在Rt△B'HD中,由勾股定理得:B′D=226810+=综上,DB'的长为16或10.故答案为: 16或10【点睛】本题是四边形的综合题,考查了矩形的性质,勾股定理,等腰三角形一般需要分类讨论.17.10+55【分析】取DE的中点N,连结ON、NG、OM.根据勾股定理可得55NG=.在点M与G之间总有MG≤MO+ON+NG(如图1),M、O、N、G四点共线,此时等号成立(如图2).可得线段MG的最大值.【详解】如图1,取DE的中点N,连结ON、NG、OM.∵∠AOB=90°,∴OM=12AB=5.同理ON=5.∵正方形DGFE,N为DE中点,DE=10,∴222210555NG DN DG++===.在点M与G之间总有MG≤MO+ON+NG(如图1),如图2,由于∠DNG的大小为定值,只要∠DON=12∠DNG,且M、N关于点O中心对称时,M、O、N、G四点共线,此时等号成立,∴线段MG取最大值10+55.故答案为:10+55.【点睛】此题考查了直角三角形的性质,勾股定理,四点共线的最值问题,得出M、O、N、G四点共线,则线段MG长度的最大是解题关键.18.4【分析】证明CF∥DB,CF=DB,可得四边形CDBF是平行四边形,作EM⊥DB于点M,解直角三角形即可.【详解】解:∵CF∥AB,∴∠ECF=∠EBD.∵E是BC中点,∴CE=BE.∵∠CEF=∠BED,∴△CEF≌△BED(ASA).∴CF=BD.∴四边形CDBF是平行四边形.作EM⊥DB于点M,∵四边形CDBF是平行四边形,22BC=∴BE=122BC=,DF=2DE,在Rt△EMB中,EM2+BM2=BE2且EM=BM ∴EM=1,在Rt△EMD中,∵∠EDM=30°,∴DE=2EM=2,∴DF=2DE=4.故答案为:4.【点睛】本题考查平行四边形的判定和性质、全等三角形的判定和性质、勾股定理、直角三角形30度角性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题, 19.207【分析】根据折叠的性质可得出DC=DE 、CP=EP ,由“AAS”可证△OEF ≌△OBP ,可得出OE=OB 、EF=BP ,设EF=x ,则BP=x 、DF=5-x 、BF=PC=3-x ,进而可得出AF=2+x ,在Rt △DAF 中,利用勾股定理可求出x 的值,即可得AF 的长.【详解】解:∵将△CDP 沿DP 折叠,点C 落在点E 处,∴DC =DE =5,CP =EP .在△OEF 和△OBP 中,90EOF BOP B E OP OF ∠=∠⎧⎪∠=∠=⎨⎪=⎩, ∴△OEF ≌△OBP (AAS ),∴OE =OB ,EF =BP .设EF =x ,则BP =x ,DF =DE -EF =5-x ,又∵BF =OB +OF =OE +OP =PE =PC ,PC =BC -BP =3-x ,∴AF =AB -BF =2+x .在Rt △DAF 中,AF 2+AD 2=DF 2,∴(2+x )2+32=(5-x )2,∴x =67∴AF =2+67=207故答案为:207 【点睛】本题考查了翻折变换,矩形的性质,全等三角形的判定与性质以及勾股定理的应用,解题时常常设要求的线段长为x ,然后根据折叠和轴对称的性质用含x 的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.20.2或3.5【分析】分别从当Q 运动到E 和B 之间、当Q 运动到E 和C 之间去分析求解即可求得答案.如图,∵E 是BC 的中点,∴BE=CE= 12BC=9, ①当Q 运动到E 和B 之间,则得:3t ﹣9=5﹣t ,解得:t=3.5;②当Q 运动到E 和C 之间,则得:9﹣3t=5﹣t ,解得:t=2,∴当运动时间t 为2秒或3.5秒时,以点P ,Q ,E ,D 为顶点的四边形是平行四边形.【点睛】“点睛”此题考查了梯形的性质以及平行四边形的判定与性质.解题时注意掌握辅助线的作法,注意掌握数形结合思想、分类讨论思想与方程思想的应用.三、解答题21.(1)①证明见解析;②证明见解析;(2)410DE =. 【分析】(1)过点D 作//DM GH 交BC 延长线于点M ,连接EH ,①由正方形的性质可得//AD BC ,AD CD =,90A ADC DCM ∠=∠=∠=︒,即可证明四边形DGHM 是平行四边形,可得DM=GH ,由90GOD ∠=︒可得∠EDM=90°,根据直角三角形两锐角互余的性质可得12∠=∠,利用ASA 可证明△ADE≌△CDM,可得DE=DM ,即可证明DE=GH ;②由①得DM=DE ,根据勾股定理可得2,利用三角形三边关系即可得结论; (2)过点D 作DN//GH 交BC 于点N ,作ADM CDN ∠=∠,DM 交BA 延长线于点M ,可证明四边形GHND 为平行四边形,可得DN HG =,GD HN =,根据勾股定理可求出CN 的长,利用AAS 可证明ADM CDN ∆∆≌,可得AM NC =,DM DN =,根据平行线的性质∠EDN=45°,根据角的和差故选可得∠MDE=∠EDN ,利用SAS 可证明MDE NDE ∆∆≌,即可证明AE CN EN +=,设AE x =,利用勾股定理可求出x 的值,进而利用勾股定理求出DE 的值即可得答案.(1)如图(1),过点D 作//DM GH 交BC 延长线于点M ,连接EH ,EM , ①∵四边形ABCD 为正方形,∴//AD BC ,AD CD =,90A ADC DCM ∠=∠=∠=︒∴四边形DGHM 为平行四边形,∴DM=GH ,GD HM =,∵90GOD ∠=︒,∴90EDM EOH ∠=∠=︒,∴290EDC ∠+∠=︒,∵90ADC ∠=︒,∴190EDC ∠+∠=︒,∴12∠=∠,在ADE ∆和CDM ∆中12A DCM AD DC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴ADE CDM ∆∆≌,∴DE DM =,∴DE GH =.②在DEM ∆中,∠EDM=90°,∴222DE DM EM +=,∵DE DM =,∴222DE EM =, ∴2EM DE =,在EHM ∆中,HM EH EM +>,∵GD HM =, ∴2GD EH GH +≥.(2)如图(2),过点D 作DN//GH 交BC 于点N ,则四边形GHND 为平行四边形, ∴DN HG =,GD HN =,∵90C ∠=︒,4CD AB ==,25HG DN ==∴222CN DN DC=-=,∴422BN BC CN =-=-=,作ADM CDN ∠=∠,DM 交BA 延长线于点M ,在ADM ∆和CDN ∆中90C MAD CDN ADM DC AD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴ADM CDN ∆∆≌,∴AM NC =,DM DN =,∵45GOD EOH ∠=∠=︒,∴45EDN ∠=︒,∴45ADE CDN ∠+∠=︒,∴45ADE ADN MDE ∠+∠=︒=∠,在MDE ∆和NDE ∆中MD ND MDE EDN DE DE =⎧⎪∠=∠⎨⎪=⎩,∴MDE NDE ∆∆≌,∴EM EN =,即AE AM AE CN EN +=+=,设AE x =,则BE=4-x ,在Rt BEN ∆中,2222(2)x x +=+,解得:43x =, ∴22224410433DE AD AE ⎛⎫=+=+= ⎪⎝⎭.【点睛】本题考查正方形的性质、平行四边形的判定与性质、全等三角形的判定与性质、三角形的三边关系及勾股定理,熟练掌握相关性质及判定定理,并正确作出辅助线是解题关键.22.(1)见解析;(2)见解析.【分析】(1)连接BD,BD与AM交于点O,连接CO并延长交于AB,则CO与AB的交点为点N.可先证明△AOD≌△COD,再证明△MOB≌NOB,从而可得NB=MB;(2)连接MO并延长与AE交于点Q,连接QC,则CQ∥AM.理由如下:由正方形的性质以及平行线等分线段可证QO=MO,从而可知四边形AQCM为平行四边形,从而可得CQ∥AM.【详解】解:(1)如图(1),连接BD,BD与AM交于点O,连接CO并延长交于AB,则CO与AB的交点为点N,则CN 为所作.理由:在△AOD与△COD中,∵AD CDADO CDO OD OD⎧⎪∠∠⎨⎪⎩===,∴△AOD≌△COD(SAS),∴∠OAD=∠OCD,∴∠BAM=∠BCN.在△ABM与△CBN中,∵BAM BCN AB CBABM CBN ∠∠⎧⎪⎨⎪∠∠⎩===,∴△ABM≌△CBN(ASA),∴CN=AM.(2)如图2连接AC、BD交与O点,连接MO并延长与AE交于点Q,连接QC,则CQ为所求的线段.在正方形ABCD中,OA=OB=OC=OD,AD∥BC,∴QO =MO∴四边形AQCM 为平行四边形,∴QC ∥AM【点睛】本题考查了作图-基本作图,解决此题的关键是利用正方形的性质求解.23.(1)2;(2)证明见解析过程;(3)AE+EF-AF=2OA .【分析】(1)通过测量可得;(2)过点C 作CG ⊥ON ,垂足为点G ,由AAS 可证△ABO ≌△BCG ,可得BG=AO ,BO=CG ,由SAS 可证△ABE ≌△CBE ,可得AE=CE ,由线段的和差关系可得结论; (3)过点C 作CG ⊥ON ,垂足为点G ,由AAS 可证△ABO ≌△BCG ,可得BG=AO ,BO=CG ,由SAS 可证△ABE ≌△CBE ,可得AE=CE ,可得结论.【详解】解:(1)△AEF 的周长是OA 长的2倍,故答案为:2;(2)如图4,过点C 作CG ⊥ON ,垂足为点G ,则∠CGB=90°,∴∠GCB+∠CBG=90°,又∵四边形ABCD 是正方形,∴AB=BC ,∠ABC=90°,∠DBC=∠DBA=45°,则∠CBG+∠ABO=90°,∴∠GCB=∠ABO ,在△BCG 与△ABO 中,GCB ABO GCB AOB BC AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCG ≌△ABO (AAS ),∴BG=AO ,CG=BO ,∵∠AOB=90°=∠CGB=∠CFO ,∴四边形CGOF 是矩形,∴CF=GO ,CG=OF=OB ,在△ABE 和△CBE 中,BE BE ABE CBE AB BC =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△CBE (SAS ),∴AE=CE ,∴△AEF 的周长=AE+EF+AF=CE+EF+AF=CF+AF=GO+AF=BG+BO+AF=2AO ;(3)如图5,过点C 作CG ⊥ON 于点G ,则∠CGB=90°,∴∠GCB+∠CBG=90°,又∵四边形ABCD 是正方形,∴AB=BC ,∠ABC=90°,∠DBC=∠DBA=45°,则∠CBG+∠ABO=90°,∴∠GCB=∠ABO ,在△BCG 与△ABO 中GCB ABO GCB AOB BC AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCG ≌△ABO (AAS ),∴BG=AO ,BO=CG ,∵∠AOB=90°=∠CGB=∠CFO ,∴四边形CGOF 是矩形,∴CF=GO ,CG=OF=OB ,在△ABE 和△CBE 中,BE BE ABE CBE AB BC =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△CBE (SAS ),∴AE=CE ,∴AE+EF-AF=EF+CE-AF=NB+BO-(OF-AO )=OA+OB-(OB-OA )=2OA .【点睛】本题是四边形综合题,考查了全等三角形的判定和性质,正方形的性质,矩形的判定和性质,添加恰当的辅助线构造全等三角形是本题的关键.24.(1)证明见解析;(2)①2BH BG=;②BH 的长为172或72. 【分析】(1)证()DAG BAE SAS △≌△,即可得出结论;(2)①连接GH ,延长HF 交AB 于N ,设AB 与EF 的交点为M ,证()GAB GFH SAS △≌△,得GH GB =,GHF GBA ∠=∠,证GHB ∆为等腰直角三角形,即得结论;②分两种情况,证出点B 、E 、G 在一条直线上,求出210AF EG AE ===,则5OA OG OE ===,由勾股定理求出12OB =,求出BG ,即可得出答案.【详解】(1)∵四边形ABCD 和四边形AEFG 是正方形,∴AD =AB =CB ,AG =AE ,∠DAB =∠GCE =90°,∴∠DAB ﹣∠GAF =∠GCE ﹣∠GAF ,即∠DAG =∠BAE ,在△DAG 和△BAE 中,AD AE DAG BAE AG AE =⎧⎪∠=∠⎨⎪=⎩,∴△DAG ≌△BAE (SAS),∴DG =BE ;(2)①连接GH ,延长HF 交AB 于N ,设AB 与EF 的交点为M ,如图2所示:∵四边形BCHF 是平行四边形,∴HF //BC ,HF =BC =AB .∵BC ⊥AB ,∴HF ⊥AB ,。
中考数学二轮 平行四边形 专项培优 易错 难题及答案

中考数学二轮平行四边形专项培优易错难题及答案一、平行四边形1.如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.(1)①猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系,不必证明;②将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度α,得到如图2情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并证明你的判断.(2)将原题中正方形改为矩形(如图3、4),且AB=a,BC=b,CE=ka,CG=kb (a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图4为例简要说明理由.(3)在第(2)题图4中,连接DG、BE,且a=3,b=2,k=12,求BE2+DG2的值.【答案】(1)①BG⊥DE,BG=DE;②BG⊥DE,证明见解析;(2)BG⊥DE,证明见解析;(3)16.25.【解析】分析:(1)①根据正方形的性质,显然三角形BCG顺时针旋转90°即可得到三角形DCE,从而判断两条直线之间的关系;②结合正方形的性质,根据SAS仍然能够判定△BCG≌△DCE,从而证明结论;(2)根据两条对应边的比相等,且夹角相等可以判定上述两个三角形相似,从而可以得到(1)中的位置关系仍然成立;(3)连接BE、DG.根据勾股定理即可把BE2+DG2转换为两个矩形的长、宽平方和.详解:(1)①BG⊥DE,BG=DE;②∵四边形ABCD和四边形CEFG是正方形,∴BC=DC,CG=CE,∠BCD=∠ECG=90°,∴∠BCG=∠DCE,∴△BCG≌△DCE,∴BG=DE,∠CBG=∠CDE,又∵∠CBG+∠BHC=90°,∴∠CDE+∠DHG=90°,∴BG⊥DE.(2)∵AB=a,BC=b,CE=ka,CG=kb,∴BC CG b==,DC CE a又∵∠BCG=∠DCE,∴△BCG∽△DCE,∴∠CBG=∠CDE,又∵∠CBG+∠BHC=90°,∴∠CDE+∠DHG=90°,∴BG⊥DE.(3)连接BE、DG.根据题意,得AB=3,BC=2,CE=1.5,CG=1,∵BG⊥DE,∠BCD=∠ECG=90°∴BE2+DG2=BO2+OE2+DO2+OG2=BC2+CD2+CE2+CG2=9+4+2.25+1=16.25.点睛:此题综合运用了全等三角形的判定和性质、相似三角形的判定和性质以及勾股定理.2.(1)、动手操作:如图①:将矩形纸片ABCD折叠,使点D与点B重合,点C落在点处,折痕为EF,若∠ABE=20°,那么的度数为 .(2)、观察发现:小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图②);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图③).小明认为△AEF是等腰三角形,你同意吗?请说明理由.(3)、实践与运用:将矩形纸片ABCD按如下步骤操作:将纸片对折得折痕EF,折痕与AD边交于点E,与BC 边交于点F;将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠,使点A、点D都与点F 重合,展开纸片,此时恰好有MP=MN=PQ(如图④),求∠MNF的大小.【答案】(1)125°;(2)同意;(3)60°【解析】试题分析:(1)根据直角三角形的两个锐角互余求得∠AEB=70°,根据折叠重合的角相等,得∠BEF=∠DEF=55°,根据平行线的性质得到∠EFC=125°,再根据折叠的性质得到∠EFC′=∠EFC=125°;(2)根据第一次折叠,得∠BAD=∠CAD;根据第二次折叠,得EF垂直平分AD,根据等角的余角相等,得∠AEG=∠AFG,则△AEF是等腰三角形;(3)由题意得出:∠NMF=∠AMN=∠MNF,MF=NF,由对称性可知,MF=PF,进而得出△MNF≌△MPF,得出3∠MNF=180°求出即可.试题解析:(1)、∵在直角三角形ABE中,∠ABE=20°,∴∠AEB=70°,∴∠BED=110°,根据折叠重合的角相等,得∠BEF=∠DEF=55°.∵AD∥BC,∴∠EFC=125°,再根据折叠的性质得到∠EFC′=∠EFC=125°.;(2)、同意,如图,设AD与EF交于点G由折叠知,AD平分∠BAC,所以∠BAD=∠CAD.由折叠知,∠AGE=∠DGE=90°,所以∠AGE=∠AGF=90°,所以∠AEF=∠AFE.所以AE=AF,即△AEF为等腰三角形.(3)、由题意得出:∠NMF=∠AMN=∠MNF,∴MF=NF,由折叠可知,MF=PF,∴NF=PF,而由题意得出:MP=MN,又∵MF=MF,∴△MNF≌△MPF,∴∠PMF=∠NMF,而∠PMF+∠NMF+∠MNF=180°,即3∠MNF=180°,∴∠MNF=60°.考点:1.折叠的性质;2.等边三角形的性质;3.全等三角形的判定和性质;4.等腰三角形的判定3.已知,在矩形ABCD中,AB=a,BC=b,动点M从点A出发沿边AD向点D运动.(1)如图1,当b=2a,点M运动到边AD的中点时,请证明∠BMC=90°;(2)如图2,当b>2a时,点M在运动的过程中,是否存在∠BMC=90°,若存在,请给与证明;若不存在,请说明理由;(3)如图3,当b<2a时,(2)中的结论是否仍然成立?请说明理由.【答案】(1)见解析;(2)存在,理由见解析;(3)不成立.理由如下见解析.【解析】试题分析:(1)由b=2a,点M是AD的中点,可得AB=AM=MD=DC=a,又由四边形ABCD 是矩形,即可求得∠AMB=∠DMC=45°,则可求得∠BMC=90°;(2)由∠BMC=90°,易证得△ABM∽△DMC,设AM=x,根据相似三角形的对应边成比例,即可得方程:x2﹣bx+a2=0,由b>2a,a>0,b>0,即可判定△>0,即可确定方程有两个不相等的实数根,且两根均大于零,符合题意;(3)由(2),当b<2a,a>0,b>0,判定方程x2﹣bx+a2=0的根的情况,即可求得答案.试题解析:(1)∵b=2a,点M是AD的中点,∴AB=AM=MD=DC=a,又∵在矩形ABCD中,∠A=∠D=90°,∴∠AMB=∠DMC=45°,∴∠BMC=90°.(2)存在,理由:若∠BMC=90°,则∠AMB+∠DMC=90°,又∵∠AMB+∠ABM=90°,∴∠ABM=∠DMC,又∵∠A=∠D=90°,∴△ABM∽△DMC,∴AM ABCD DM=,设AM=x,则x aa b x =-,整理得:x2﹣bx+a2=0,∵b>2a,a>0,b>0,∴△=b2﹣4a2>0,∴方程有两个不相等的实数根,且两根均大于零,符合题意,∴当b>2a时,存在∠BMC=90°,(3)不成立.理由:若∠BMC=90°,由(2)可知x2﹣bx+a2=0,∵b<2a,a>0,b>0,∴△=b2﹣4a2<0,∴方程没有实数根,∴当b<2a时,不存在∠BMC=90°,即(2)中的结论不成立.考点:1、相似三角形的判定与性质;2、根的判别式;3、矩形的性质4.如图,△ABC是等边三角形,AB=6cm,D为边AB中点.动点P、Q在边AB上同时从点D出发,点P沿D→A以1cm/s的速度向终点A运动.点Q沿D→B→D以2cm/s的速度运动,回到点D停止.以PQ为边在AB上方作等边三角形PQN.将△PQN绕QN的中点旋转180°得到△MNQ.设四边形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<3).(1)当点N落在边BC上时,求t的值.(2)当点N到点A、B的距离相等时,求t的值.(3)当点Q沿D→B运动时,求S与t之间的函数表达式.(4)设四边形PQMN的边MN、MQ与边BC的交点分别是E、F,直接写出四边形PEMF 与四边形PQMN的面积比为2:3时t的值.【答案】(1)(2)2(3)S=S菱形PQMN=2S△PNQ=t2;(4)t=1或【解析】试题分析:(1)由题意知:当点N落在边BC上时,点Q与点B重合,此时DQ=3;(2)当点N到点A、B的距离相等时,点N在边AB的中线上,此时PD=DQ;(3)当0≤t≤时,四边形PQMN与△ABC重叠部分图形为四边形PQMN;当≤t≤时,四边形PQMN与△ABC重叠部分图形为五边形PQFEN.(4)MN、MQ与边BC的有交点时,此时<t<,列出四边形PEMF与四边形PQMN的面积表达式后,即可求出t的值.试题解析:(1)∵△PQN与△ABC都是等边三角形,∴当点N落在边BC上时,点Q与点B重合.∴DQ=3∴2t=3.∴t=;(2)∵当点N到点A、B的距离相等时,点N在边AB的中线上,∴PD=DQ,当0<t<时,此时,PD=t,DQ=2t∴t=2t∴t=0(不合题意,舍去),当≤t<3时,此时,PD=t,DQ=6﹣2t∴t=6﹣2t,解得t=2;综上所述,当点N到点A、B的距离相等时,t=2;(3)由题意知:此时,PD=t,DQ=2t当点M在BC边上时,∴MN=BQ∵PQ=MN=3t,BQ=3﹣2t∴3t=3﹣2t∴解得t=如图①,当0≤t≤时,S△PNQ=PQ2=t2;∴S=S菱形PQMN=2S△PNQ=t2,如图②,当≤t≤时,设MN、MQ与边BC的交点分别是E、F,∵MN=PQ=3t,NE=BQ=3﹣2t,∴ME=MN﹣NE=PQ﹣BQ=5t﹣3,∵△EMF是等边三角形,∴S△EMF=ME2=(5t﹣3)2.;(4)MN、MQ与边BC的交点分别是E、F,此时<t<,t=1或.考点:几何变换综合题5.如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD 的延长线于点F,连接CF.(1)求证:四边形BCFD是菱形;(2)若AD=1,BC=2,求BF的长.【答案】(1)证明见解析(2)3【解析】(1)∵AF∥BC,∴∠DCB=∠CDF,∠FBC=∠BFD,∵点E为CD的中点,∴DE=EC,在△BCE与△FDE中,FBC BFDDCB CDFDE EC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCE≌△FDE,∴DF=BC,又∵DF∥BC,∴四边形BCDF为平行四边形,∵BD=BC,∴四边形BCFD是菱形;(2)∵四边形BCFD是菱形,∴BD=DF=BC=2,在Rt△BAD中,AB223BD AD-,∵AF=AD+DF=1+2=3,在Rt△BAF中,BF22AB AF+3.6.(问题情境)在△ABC中,AB=AC,点P为BC所在直线上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.当P在BC边上时(如图1),求证:PD+PE=CF.证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.(不要证明)(变式探究)(1)当点P在CB延长线上时,其余条件不变(如图3),试探索PD、PE、CF之间的数量关系并说明理由;请运用上述解答中所积累的经验和方法完成下列两题:(结论运用)(2)如图4,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD =16,CF=6,求PG+PH的值.(迁移拓展)(3)在直角坐标系中,直线l1:y=-43x+8与直线l2:y=﹣2x+8相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为2.求点P的坐标.【答案】【变式探究】证明见解析【结论运用】8【迁移拓展】(﹣1,6),(1,10)【解析】【变式探究】连接AP,同理利用△ABP与△ACP面积之差等于△ABC的面积可以证得;【结论运用】过点E作EQ⊥BC,垂足为Q,根据勾股定理和矩形的性质解答即可;【迁移拓展】分两种情况,利用结论,求得点P到x轴的距离,再利用待定系数法可求出P的坐标.【详解】变式探究:连接AP,如图3:∵PD⊥AB,PE⊥AC,CF⊥AB,且S△ABC=S△ACP﹣S△ABP,∴12AB•CF=12AC•PE﹣12AB•PD.∵AB=AC,∴CF=PD﹣PE;结论运用:过点E作EQ⊥BC,垂足为Q,如图④,∵四边形ABCD是长方形,∴AD=BC,∠C=∠ADC=90°.∵AD=16,CF=6,∴BF=BC﹣CF=AD﹣CF=5,由折叠可得:DF=BF,∠BEF=∠DEF.∴DF=5.∵∠C=90°,∴DC2222-=-8.DF CF106∵EQ⊥BC,∠C=∠ADC=90°,∴∠EQC=90°=∠C=∠ADC.∴四边形EQCD是长方形.∴EQ=DC=4.∵AD∥BC,∴∠DEF=∠EFB.∵∠BEF=∠DEF,∴∠BEF=∠EFB.∴BE=BF,由问题情境中的结论可得:PG+PH=EQ.∴PG+PH=8.∴PG+PH的值为8;迁移拓展:如图,由题意得:A(0,8),B(6,0),C(﹣4,0)∴AB226810,BC=10.∴AB=BC,(1)由结论得:P1D1+P1E1=OA=8∵P1D1=1=2,∴P1E1=6 即点P1的纵坐标为6又点P1在直线l2上,∴y=2x+8=6,∴x=﹣1,即点P1的坐标为(﹣1,6);(2)由结论得:P2E2﹣P2D2=OA=8∵P2D2=2,∴P2E2=10 即点P1的纵坐标为10又点P1在直线l2上,∴y=2x+8=10,∴x=1,即点P1的坐标为(1,10)【点睛】本题考查了矩形的性质与判定、等腰三角形的性质与判定及勾股定理等知识点,利用面积法列出等式是解决问题的关键.7.正方形ABCD,点E在边BC上,点F在对角线AC上,连AE.(1)如图1,连EF,若EF⊥AC,4AF=3AC,AB=4,求△AEF的周长;(2)如图2,若AF=AB,过点F作FG⊥AC交CD于G,点H在线段FG上(不与端点重合),连AH.若∠EAH=45°,求证:EC=2.+;(2)证明见解析【答案】(1)2542【解析】【分析】(1)由正方形性质得出AB=BC=CD=AD=4,∠B=∠D=90°,∠ACB=∠ACD=∠BAC=∠ACD=45°,得出AC=2AB=42,求出AF=32,CF=AC﹣AF=2,求出△CEF 是等腰直角三角形,得出EF=CF=2,CE=2CF=2,在Rt△AEF中,由勾股定理求出AE,即可得出△AEF的周长;(2)延长GF交BC于M,连接AG,则△CGM和△CFG是等腰直角三角形,得出CM=CG,CG=2CF,证出BM=DG,证明Rt△AFG≌Rt△ADG得出FG=DG,BM=FG,再证明△ABE≌△AFH,得出BE=FH,即可得出结论.【详解】(1)∵四边形ABCD是正方形,∴AB=BC=CD=AD=4,∠B=∠D=90°,∠ACB=∠ACD=∠BAC=∠ACD=45°,∴AC=2AB=42,∵4AF=3AC=122,∴AF=32,∴CF=AC﹣AF=2,∵EF⊥AC,∴△CEF是等腰直角三角形,∴EF=CF=2,CE=2CF=2,在Rt△AEF中,由勾股定理得:AE=2225+=,AF EF++=+;∴△AEF的周长=AE+EF+AF=252322542(2)证明:延长GF交BC于M,连接AG,如图2所示:则△CGM和△CFG是等腰直角三角形,∴CM=CG,CG2,∴BM =DG ,∵AF =AB ,∴AF =AD ,在Rt △AFG 和Rt △ADG 中,AG AG AF AD =⎧⎨=⎩, ∴Rt △AFG ≌Rt △ADG (HL ),∴FG =DG ,∴BM =FG ,∵∠BAC =∠EAH =45°,∴∠BAE =∠FAH ,∵FG ⊥AC ,∴∠AFH =90°,在△ABE 和△AFH 中,90B AFH AB AFBAE FAH ︒⎧∠=∠=⎪=⎨⎪∠=∠⎩, ∴△ABE ≌△AFH (ASA ),∴BE =FH ,∵BM =BE +EM ,FG =FH +HG ,∴EM =HG ,∵EC =EM +CM ,CM =CG =2CF ,∴EC =HG +2FC .【点睛】本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理等知识;熟练掌握等腰直角三角形的判定与性质,证明三角形全等是解题的关键.8.在ABC V 中,AD BC ⊥于点D ,点E 为AC 边的中点,过点A 作//AF BC ,交DE 的延长线于点F ,连接CF .()1如图1,求证:四边形ADCF 是矩形;()2如图2,当AB AC =时,取AB 的中点G ,连接DG 、EG ,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形ADCF ).【答案】(1) 证明见解析;(2)四边形ABDF 、四边形AGEF 、四边形GBDE 、四边形AGDE 、四边形GDCE 都是平行四边形.【解析】【分析】(1)由△AEF ≌△CED ,推出EF=DE ,又AE=EC ,推出四边形ADCF 是平行四边形,只要证明∠ADC=90°,即可推出四边形ADCF 是矩形.(2)四边形ABDF 、四边形AGEF 、四边形GBDE 、四边形AGDE 、四边形GDCE 都是平行四边形.【详解】()1证明:∵//AF BC ,∴AFE EDC ∠=∠,∵E 是AC 中点,∴AE EC =,在AEF V 和CED V 中,AFE CDE AEF CED AE EC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴AEF CED ≅V V ,∴EF DE =,∵AE EC =,∴四边形ADCF 是平行四边形,∵AD BC ⊥,∴90ADC ∠=o ,∴四边形ADCF 是矩形.()2∵线段DG 、线段GE 、线段DE 都是ABC V 的中位线,又//AF BC , ∴//AB DE ,//DG AC ,//EG BC ,∴四边形ABDF 、四边形AGEF 、四边形GBDE 、四边形AGDE 、四边形GDCE 都是平行四边形.【点睛】考查平行四边形的判定、矩形的判定、三角形的中位线定理、全等三角形的判定和性质等知识,正确寻找全等三角形解决问题是解题的关键.9.如图,在正方形ABCD 中,对角线AC 与BD 交于点O ,在Rt △PFE 中,∠EPF=90°,点E 、F 分别在边AD 、AB 上.(1)如图1,若点P 与点O 重合:①求证:AF=DE ;②若正方形的边长为,当∠DOE=15°时,求线段EF 的长;(2)如图2,若Rt △PFE 的顶点P 在线段OB 上移动(不与点O 、B 重合),当BD=3BP 时,证明:PE=2PF .【答案】(1)①证明见解析,②22;(2)证明见解析.【解析】【分析】(1)①根据正方形的性质和旋转的性质即可证得:△AOF ≌△DOE 根据全等三角形的性质证明; ②作OG ⊥AB 于G ,根据余弦的概念求出OF 的长,根据勾股定理求值即可;(2)首先过点P 作HP ⊥BD 交AB 于点H ,根据相似三角形的判定和性质求出PE 与PF 的数量关系.【详解】(1)①证明:∵四边形ABCD 是正方形,∴OA=OD ,∠OAF=∠ODE=45°,∠AOD=90°,∴∠AOE+∠DOE=90°,∵∠EPF=90°,∴∠AOF+∠AOE=90°,∴∠DOE=∠AOF ,在△AOF 和△DOE 中,OAF ODE OA ODAOF DOE ===∠∠⎧⎪⎨⎪∠∠⎩, ∴△AOF ≌△DOE ,∴AF=DE ;②解:过点O 作OG ⊥AB 于G ,∵正方形的边长为3∴OG=123∵∠DOE=15°,△AOF ≌△DOE ,∴∠AOF=15°,∴∠FOG=45°-15°=30°,∴OF=OG cos DOG∠=2, ∴EF=22=22OF OE +;(2)证明:如图2,过点P 作HP ⊥BD 交AB 于点H ,则△HPB 为等腰直角三角形,∠HPD=90°,∴HP=BP ,∵BD=3BP , ∴PD=2BP ,∴PD=2HP ,又∵∠HPF+∠HPE=90°,∠DPE+∠HPE=90°,∴∠HPF=∠DPE ,又∵∠BHP=∠EDP=45°,∴△PHF ∽△PDE ,∴12PF PH PE PD ==, ∴PE=2PF .【点睛】 此题属于四边形的综合题.考查了正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质以及勾股定理.注意准确作出辅助线是解此题的关键.10.定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等.理解:如图①,在△ABC 中,CD 是AB 边上的中线,那么△ACD 和△BCD 是“友好三角形”,并且S △ACD =S △BCD .应用:如图②,在矩形ABCD 中,AB=4,BC=6,点E 在AD 上,点F 在BC 上,AE=BF ,AF 与BE 交于点O .(1)求证:△AOB 和△AOE 是“友好三角形”;(2)连接OD ,若△AOE 和△DOE 是“友好三角形”,求四边形CDOF 的面积.探究:在△ABC 中,∠A=30°,AB=4,点D 在线段AB 上,连接CD ,△ACD 和△BCD 是“友好三角形”,将△ACD沿CD所在直线翻折,得到△A′CD,若△A′CD与△ABC重合部分的面积等于△ABC面积的,请直接写出△ABC的面积.【答案】(1)见解析;(2)12;探究:2或2.【解析】试题分析:(1)利用一组对边平行且相等的四边形是平行四边形,得到四边形ABFE是平行四边形,然后根据平行四边形的性质证得OE=OB,即可证得△AOE和△AOB是友好三角形;(2)△AOE和△DOE是“友好三角形”,即可得到E是AD的中点,则可以求得△ABE、△ABF的面积,根据S四边形CDOF=S矩形ABCD-2S△ABF即可求解.探究:画出符合条件的两种情况:①求出四边形A′DCB是平行四边形,求出BC和A′D推出∠ACB=90°,根据三角形面积公式求出即可;②求出高CQ,求出△A′DC的面积.即可求出△ABC的面积.试题解析:(1)∵四边形ABCD是矩形,∴AD∥BC,∵AE=BF,∴四边形ABFE是平行四边形,∴OE=OB,∴△AOE和△AOB是友好三角形.(2)∵△AOE和△DOE是友好三角形,∴S△AOE=S△DOE,AE=ED=AD=3,∵△AOB与△AOE是友好三角形,∴S△AOB=S△AOE,∵△AOE≌△FOB,∴S△AOE=S△FOB,∴S△AOD=S△ABF,∴S四边形CDOF=S矩形ABCD-2S△ABF=4×6-2××4×3=12.探究:解:分为两种情况:①如图1,∵S△ACD=S△BCD.∴AD=BD=AB,∵沿CD折叠A和A′重合,∴AD=A′D=AB=×4=2,∵△A′CD与△ABC重合部分的面积等于△ABC面积的,∴S△DOC=S△ABC=S△BDC=S△ADC=S△A′DC,∴DO=OB,A′O=CO,∴四边形A′DCB是平行四边形,∴BC=A′D=2,过B作BM⊥AC于M,∵AB=4,∠BAC=30°,∴BM=AB=2=BC,即C和M重合,∴∠ACB=90°,由勾股定理得:AC=,∴△ABC的面积是×BC×AC=×2×2=2;②如图2,∵S△ACD=S△BCD.∴AD=BD=AB,∵沿CD折叠A和A′重合,∴AD=A′D=AB=×4=2,∵△A′CD与△ABC重合部分的面积等于△ABC面积的,∴S△DOC=S△ABC=S△BDC=S△ADC=S△A′DC,∴DO=OA′,BO=CO,∴四边形A′BDC是平行四边形,∴A′C=BD=2,过C作CQ⊥A′D于Q,∵A′C=2,∠DA′C=∠BAC=30°,∴CQ=A′C=1,∴S△ABC=2S△ADC=2S△A′DC=2××A′D×CQ=2××2×1=2;即△ABC的面积是2或2.考点:四边形综合题.11.如图,已知矩形ABCD中,E是AD上一点,F是AB上的一点,EF⊥EC,且EF=EC.(1)求证:△AEF≌△DCE.(2)若DE=4cm,矩形ABCD的周长为32cm,求AE的长.【答案】(1)证明见解析;(2)6cm.【解析】分析:(1)根据EF⊥CE,求证∠AEF=∠ECD.再利用AAS即可求证△AEF≌△DCE.(2)利用全等三角形的性质,对应边相等,再根据矩形ABCD的周长为32cm,即可求得AE的长.详解:(1)证明:∵EF⊥CE,∴∠FEC=90°,∴∠AEF+∠DEC=90°,而∠ECD+∠DEC=90°,∴∠AEF=∠ECD.在Rt△AEF和Rt△DEC中,∠FAE=∠EDC=90°,∠AEF=∠ECD,EF=EC.∴△AEF≌△DCE.(2)解:∵△AEF≌△DCE.AE=CD.AD=AE+4.∵矩形ABCD的周长为32cm,∴2(AE+AE+4)=32.解得,AE=6(cm).答:AE的长为6cm.点睛:此题主要考查学生对全等三角形的判定与性质和矩形的性质等知识点的理解和掌握,难易程度适中,是一道很典型的题目.12.如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.(1)请判断:FG与CE的关系是___;(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.【答案】(1)FG=CE,FG∥CE;(2)成立;(3)成立.【解析】试题分析:(1)只要证明四边形CDGF是平行四边形即可得出FG=CE,FG∥CE;(2)构造辅助线后证明△HGE≌△CED,利用对应边相等求证四边形GHBF是矩形后,利用等量代换即可求出FG=C,FG∥CE;(3)证明△CBF≌△DCE后,即可证明四边形CEGF是平行四边形.试题解析:解:(1)FG=CE,FG∥CE;(2)过点G作GH⊥CB的延长线于点H.∵EG⊥DE,∴∠GEH+∠DEC=90°.∵∠GEH+∠HGE=90°,∴∠DEC=∠HE.在△HGE与△CED中,∵∠GHE=∠DCE,∠HGE=∠DEC,EG=DE,∴△HGE≌△CED(AAS),∴GH=CE,HE=CD.∵CE=BF,∴GH=BF.∵GH∥BF,∴四边形GHBF是矩形,∴GF=BH,FG∥CH,∴FG∥CE.∵四边形ABCD是正方形,∴CD=BC,∴HE=BC,∴HE+EB=BC+EB,∴BH=EC,∴FG=EC;(3)∵四边形ABCD是正方形,∴BC=CD,∠FBC=∠ECD=90°.在△CBF与△DCE中,∵BF=CE,∠FBC=∠ECD,BC=DC,∴△CBF≌△DCE(SAS),∴∠BCF=∠CDE,CF=DE.∵EG=DE,∴CF=EG.∵DE⊥EG,∴∠DEC+∠CEG=90°.∵∠CDE+∠DEC=90°,∴∠CDE=∠CEG,∴∠BCF=∠CEG,∴CF∥EG,∴四边形CEGF平行四边形,∴FG∥CE,FG=CE.13.如图,在平面直角坐标系xOy中,四边形OABC的顶点A在x轴的正半轴上,OA=4,OC=2,点D、E、F、G分别为边OA、AB、BC、CO的中点,连结DE、EF、FG、GD.(1)若点C在y轴的正半轴上,当点B的坐标为(2,4)时,判断四边形DEFG的形状,并说明理由.(2)若点C在第二象限运动,且四边形DEFG为菱形时,求点四边形OABC对角线OB长度的取值范围.(3)若在点C的运动过程中,四边形DEFG始终为正方形,当点C从X轴负半轴经过Y轴正半轴,运动至X轴正半轴时,直接写出点B的运动路径长.【答案】(1)正方形(2)256OB <<(3)2π【解析】分析:(1)连接OB ,AC ,说明OB ⊥AC ,OB=AC ,可得四边形DEFG 是正方形.(2)由四边形DEFG 是菱形,可得OB=AC ,当点C 在y 轴上时,AC=25,当点C 在x 轴上时,AC=6, 故可得结论;(3)根据题意计算弧长即可.详解:(1)正方形,如图1,证明连接OB ,AC ,说明OB ⊥AC ,OB=AC ,可得四边形DEFG 是正方形.(2)256OB <<如图2,由四边形DEFG 是菱形,可得OB=AC ,当点C 在y 轴上时,AC=25,当点C 在x 轴上时,AC=6, ∴256OB << ;(3)2π.如图3,当四边形DEFG 是正方形时,OB ⊥AC ,且OB=AC ,构造△OBE ≌△ACO ,可得B 点在以E (0,4)为圆心,2为半径的圆上运动.所以当C 点从x 轴负半轴到正半轴运动时,B 点的运动路径为2π .图1 图2 图3点睛:本题主要考查了正方形的判定,菱形的性质以及弧长的计算.灵活运用正方形的判定定理和菱形的性质运用是解题的关键.14.在正方形ABCD 中,动点E ,F 分别从D ,C 两点同时出发,以相同的速度在直线DC ,CB 上移动.(1)如图①,当点E 自D 向C ,点F 自C 向B 移动时,连接AE 和DF 交于点P ,请你写出AE 与DF 的位置关系,并说明理由;(2)如图②,当E ,F 分别移动到边DC ,CB 的延长线上时,连接AE 和DF ,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不须证明)(3)如图③,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?请说明理由;(4)如图④,当E,F分别在边DC,CB上移动时,连接AE和DF交于点P,由于点E,F 的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP 的最小值.【答案】(1)AE=DF,AE⊥DF;(2)是;(3)成立,理由见解析;(4)CP=QC﹣QP=.【解析】试题分析:(1)AE=DF,AE⊥DF.先证得△ADE≌△DCF.由全等三角形的性质得AE=DF,∠DAE=∠CDF,再由等角的余角相等可得AE⊥DF;(2)是.四边形ABCD是正方形,所以AD=DC,∠ADE=∠DCF=90°,DE=CF,所以△ADE≌△DCF,于是AE=DF,∠DAE=∠CDF,因为∠CDF+∠ADF=90°,∠DAE+∠ADF=90°,所以AE⊥DF;(3)成立.由(1)同理可证AE=DF,∠DAE=∠CDF,延长FD交AE于点G,再由等角的余角相等可得AE⊥DF;(4)由于点P在运动中保持∠APD=90°,所以点P的路径是一段以AD为直径的弧,设AD 的中点为Q,连接QC交弧于点P,此时CP的长度最小,再由勾股定理可得QC的长,再求CP即可.试题解析:(1)AE=DF,AE⊥DF.理由:∵四边形ABCD是正方形,∴AD=DC,∠ADC=∠C=90°.在△ADE和△DCF中,,∴△ADE≌△DCF(SAS).∴AE=DF,∠DAE=∠CDF,由于∠CDF+∠ADF=90°,∴∠DAE+∠ADF=90°.∴AE⊥DF;(2)是;(3)成立.理由:由(1)同理可证AE=DF,∠DAE=∠CDF延长FD交AE于点G,则∠CDF+∠ADG=90°,∴∠ADG+∠DAE=90°.∴AE⊥DF;(4)如图:由于点P在运动中保持∠APD=90°,∴点P的路径是一段以AD为直径的弧,设AD的中点为Q,连接QC交弧于点P,此时CP的长度最小,在Rt△QDC中,QC=,∴CP=QC﹣QP=.考点:四边形的综合知识.15.已知:如图,四边形ABCD和四边形AECF都是矩形,AE与BC交于点M,CF与AD交于点N.(1)求证:△ABM≌△CDN;(2)矩形ABCD和矩形AECF满足何种关系时,四边形 AMCN是菱形,证明你的结论.【答案】(1)证明见解析;(2)当AB=AF时,四边形AMCN是菱形.证明见解析;【解析】试题分析:(1)由已知条件可得四边形AMCN是平行四边形,从而可得AM=CN,再由AB=CD,∠B=∠D=90°,利用HL即可证明;(2)若四边形AMCN为菱形,则有AM=AN,从已知可得∠BAM=∠FAN,又∠B=∠F=90°,所以有△ABM≌△AFN,从而得AB=AF,因此当AB=AF时,四边形AMCN是菱形.试题解析:(1)∵四边形ABCD是矩形,∴∠B=∠D=90°,AB=CD,AD∥BC.∵四边形AECF是矩形,∴AE∥CF.∴四边形AMCN是平行四边形.∴AM=CN.在Rt△ABM和Rt△CDN中,AB=CD,AM=CN,∴Rt△ABM≌Rt△CDN.(2)当AB=AF时,四边形AMCN是菱形.∵四边形ABCD、AECF是矩形,∴∠B=∠BAD=∠EAF=∠F=90°.∴∠BAD-∠NAM=∠EAF-∠NAM,即∠BAM=∠FAN.又∵AB=AF,∴△ABM≌△AFN.∴AM=AN.由(1)知四边形AMCN是平行四边形,∴平行四边形AMCN是菱形.考点:1.矩形的性质;2.三角形全等的判定与性质;3.菱形的判定.。
人教备战中考数学压轴题之平行四边形(备战中考题型整理,突破提升)附详细答案

一、平行四边形真题与模拟题分类汇编(难题易错题)1.如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C 关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.(1)求∠FDP的度数;(2)连接BP,请用等式表示AP、BP、DP三条线段之间的数量关系,并证明;(3)连接AC,若正方形的边长为2,请直接写出△ACC′的面积最大值.【答案】(1)45°;(2)BP+DP2AP,证明详见解析;(32﹣1.【解析】【分析】(1)证明∠CDE=∠C'DE和∠ADF=∠C'DF,可得∠FDP'=12∠ADC=45°;(2)作辅助线,构建全等三角形,证明△BAP≌△DAP'(SAS),得BP=DP',从而得△PAP'是等腰直角三角形,可得结论;(3)先作高线C'G,确定△ACC′的面积中底边AC为定值2,根据高的大小确定面积的大小,当C'在BD上时,C'G最大,其△ACC′的面积最大,并求此时的面积.【详解】(1)由对称得:CD=C'D,∠CDE=∠C'DE,在正方形ABCD中,AD=CD,∠ADC=90°,∴AD=C'D,∵F是AC'的中点,∴DF⊥AC',∠ADF=∠C'DF,∴∠FDP=∠FDC'+∠EDC'=12∠ADC=45°;(2)结论:BP+DP2AP,理由是:如图,作AP'⊥AP交PD的延长线于P',∴∠PAP'=90°,在正方形ABCD中,DA=BA,∠BAD=90°,∴∠DAP'=∠BAP,由(1)可知:∠FDP=45°∵∠DFP=90°∴∠APD=45°,∴∠P'=45°,∴AP=AP',在△BAP和△DAP'中,∵BA DABAP DAP AP AP'=⎧⎪∠=∠⎨='⎪⎩,∴△BAP≌△DAP'(SAS),∴BP=DP',∴DP+BP=PP'=2AP;(3)如图,过C'作C'G⊥AC于G,则S△AC'C=12AC•C'G,Rt△ABC中,AB=BC2,∴AC22(2)(2)2+=,即AC为定值,当C'G最大值,△AC'C的面积最大,连接BD,交AC于O,当C'在BD上时,C'G最大,此时G与O重合,∵CD =C 'D =2,OD =12AC =1, ∴C 'G =2﹣1,∴S △AC 'C =112(21)2122AC C G '•=⨯-=-. 【点睛】 本题考查四边形综合题、正方形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.2.如图,四边形ABCD 中,∠BCD =∠D =90°,E 是边AB 的中点.已知AD =1,AB =2. (1)设BC =x ,CD =y ,求y 关于x 的函数关系式,并写出定义域;(2)当∠B =70°时,求∠AEC 的度数;(3)当△ACE 为直角三角形时,求边BC 的长.【答案】(1)()22303y x x x =-++<<;(2)∠AEC =105°;(3)边BC 的长为2117+. 【解析】试题分析:(1)过A 作AH ⊥BC 于H ,得到四边形ADCH 为矩形.在△BAH 中,由勾股定理即可得出结论.(2)取CD 中点T ,连接TE ,则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD ,∠AET =∠B =70°.又AD =AE =1,得到∠AED =∠ADE =∠DET =35°.由ET 垂直平分CD ,得∠CET =∠DET =35°,即可得到结论.(3)分两种情况讨论:①当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 解△ABH 即可得到结论.②当∠CAE =90°时,易知△CDA ∽△BCA ,由相似三角形对应边成比例即可得到结论. 试题解析:解:(1)过A 作AH ⊥BC 于H .由∠D =∠BCD =90°,得四边形ADCH 为矩形. 在△BAH 中,AB =2,∠BHA =90°,AH =y ,HB =1x -,∴22221y x =+-,则()22303y x x x =-++<<(2)取CD 中点T ,联结TE ,则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD ,∴∠AET =∠B =70°.又AD=AE=1,∴∠AED=∠ADE=∠DET=35°.由ET垂直平分CD,得∠CET=∠DET=35°,∴∠AEC=70°+35°=105°.(3)分两种情况讨论:①当∠AEC=90°时,易知△CBE≌△CAE≌△CAD,得∠BCE=30°,则在△ABH中,∠B=60°,∠AHB=90°,AB=2,得BH=1,于是BC=2.②当∠CAE=90°时,易知△CDA∽△BCA,又2224AC BC AB x=-=-,则2241174AD CA xxAC CB x-±=⇒=⇒=-(舍负)易知∠ACE<90°,所以边BC的长为117+.综上所述:边BC的长为2或1172+.点睛:本题是四边形综合题.考查了梯形中位线,相似三角形的判定与性质.解题的关键是掌握梯形中常见的辅助线作法.3.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E 是线段AB的中点,连接CE并延长交线段AD于点F.(1)求证:四边形BCFD为平行四边形;(2)若AB=6,求平行四边形ADBC的面积.【答案】(1)见解析;(2)S平行四边形ADBC273【解析】【分析】(1)在Rt△ABC中,E为AB的中点,则CE=12AB,BE=12AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°.又∠D=60°,得∠AFE=∠D=60度.所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD//BC,则四边形BCFD是平行四边形.(2)在Rt△ABC中,求出BC,AC即可解决问题;【详解】解:(1)证明:在△ABC中,∠ACB=90°,∠CAB=30°,∴∠ABC=60°,在等边△ABD中,∠BAD=60°,∴∠BAD=∠ABC=60°,∵E为AB的中点,∴AE=BE,又∵∠AEF=∠BEC,∴△AEF≌△BEC,在△ABC中,∠ACB=90°,E为AB的中点,∴CE=12AB,BE=12AB,∴CE=AE,∴∠EAC=∠ECA=30°,∴∠BCE=∠EBC=60°,又∵△AEF≌△BEC,∴∠AFE=∠BCE=60°,又∵∠D=60°,∴∠AFE=∠D=60°,∴FC∥BD,又∵∠BAD=∠ABC=60°,∴AD∥BC,即FD∥BC,∴四边形BCFD是平行四边形;(2)解:在Rt△ABC中,∵∠BAC=30°,AB=6,∴BC=AF=3,AC=33,∴S平行四边形BCFD=3×33=93,S△ACF=12×3×33=93,S平行四边形ADBC=2732.【点睛】本题考查平行四边形的判定和性质、直角三角形斜边中线定理、等边三角形的性质、解直角三角形、勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.4.如图,在平行四边形ABCD中,AD⊥DB,垂足为点D,将平行四边形ABCD折叠,使点B落在点D的位置,点C落在点G的位置,折痕为EF,EF交对角线BD于点P.(1)连结CG,请判断四边形DBCG的形状,并说明理由;(2)若AE=BD,求∠EDF的度数.【答案】(1)四边形BCGD是矩形,理由详见解析;(2)∠EDF=120°.【解析】【分析】(1)根据平行四边形的性质和折叠性质以及矩形的判定解答即可;(2)根据折叠的性质以及直角三角形的性质和等边三角形的判定与性质解答即可.【详解】解:(1)四边形BCGD是矩形,理由如下,∵四边形ABCD是平行四边形,∴BC∥AD,即BC∥DG,由折叠可知,BC=DG,∴四边形BCGD是平行四边形,∵AD⊥BD,∴∠CBD=90°,∴四边形BCGD是矩形;(2)由折叠可知:EF垂直平分BD,∴BD⊥EF,DP=BP,∵AD⊥BD,∴EF∥AD∥BC,∴AE PD1==BE BP∴AE=BE,∴DE是Rt△ADB斜边上的中线,∴DE=AE=BE,∵AE=BD,∴DE=BD=BE,∴△DBE是等边三角形,∴∠EDB=∠DBE=60°,∵AB∥DC,∴∠DBC=∠DBE=60°,∴∠EDF=120°.【点睛】本题考查了平行四边形的性质,折叠性质,等边三角形的性质和判定,主要考查学生运用定理进行推理和计算的能力,题目综合性比较强,有一定的难度5.菱形ABCD中、∠BAD=120°,点O为射线CA上的动点,作射线OM与直线BC相交于点E,将射线OM绕点O逆时针旋转60°,得到射线ON,射线ON与直线CD相交于点F.(1)如图①,点O与点A重合时,点E,F分别在线段BC,CD上,请直接写出CE,CF,CA三条段段之间的数量关系;(2)如图②,点O在CA的延长线上,且OA=13AC,E,F分别在线段BC的延长线和线段CD的延长线上,请写出CE,CF,CA三条线段之间的数量关系,并说明理由;(3)点O在线段AC上,若AB=6,BO=27,当CF=1时,请直接写出BE的长.【答案】(1)CA=CE+CF.(2)CF-CE=43AC.(3)BE的值为3或5或1.【解析】【分析】(1)如图①中,结论:CA=CE+CF.只要证明△ADF≌△ACE(SAS)即可解决问题;(2)结论:CF-CE=43AC.如图②中,如图作OG∥AD交CF于G,则△OGC是等边三角形.只要证明△FOG≌△EOC(ASA)即可解决问题;(3)分四种情形画出图形分别求解即可解决问题.【详解】(1)如图①中,结论:CA=CE+CF.理由:∵四边形ABCD是菱形,∠BAD=120°∴AB=AD=DC=BC,∠BAC=∠DAC=60°∴△ABC,△ACD都是等边三角形,∵∠DAC=∠EAF=60°,∴∠DAF=∠CAE,∵CA=AD,∠D=∠ACE=60°,∴△ADF≌△ACE(SAS),∴DF=CE,∴CE+CF=CF+DF=CD=AC,(2)结论:CF-CE=43 AC.理由:如图②中,如图作OG∥AD交CF于G,则△OGC是等边三角形.∵∠GOC=∠FOE=60°,∴∠FOG=∠EOC,∵OG=OC,∠OGF=∠ACE=120°,∴△FOG≌△EOC(ASA),∴CE=FG,∵OC=OG,CA=CD,∴OA=DG,∴CF-EC=CF-FG=CG=CD+DG=AC+13AC=43AC,(3)作BH⊥AC于H.∵AB=6,AH=CH=3,∴BH=33,如图③-1中,当点O在线段AH上,点F在线段CD上,点E在线段BC上时.∵7,∴22OB BH=1,∴OC=3+1=4,由(1)可知:CO=CE+CF,∴CE=3,∴BE=6-3=3.如图③-2中,当点O在线段AH上,点F在线段DC的延长线上,点E在线段BC上时.由(2)可知:CE-CF=OC,∴CE=4+1=5,∴BE=1.如图③-3中,当点O在线段CH上,点F在线段CD上,点E在线段BC上时.同法可证:OC=CE+CF,∵OC=CH-OH=3-1=2,CF=1,∴CE=1,∴BE=6-1=5.如图③-4中,当点O在线段CH上,点F在线段DC的延长线上,点E在线段BC上时.同法可知:CE-CF=OC,∴CE=2+1=3,∴BE=3,综上所述,满足条件的BE的值为3或5或1.【点睛】本题属于四边形综合题,考查了全等三角形的判定和性质,等边三角形的性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.6.如图1,在正方形ABCD中,AD=6,点P是对角线BD上任意一点,连接PA,PC过点P 作PE⊥PC交直线AB于E.(1)求证:PC=PE;(2)延长AP交直线CD于点F.①如图2,若点F是CD的中点,求△APE的面积;②若ΔAPE的面积是21625,则DF的长为(3)如图3,点E在边AB上,连接EC交BD于点M,作点E关于BD的对称点Q,连接PQ,MQ,过点P作PN∥CD交EC于点N,连接QN,若PQ=5,MN=723,则△MNQ的面积是【答案】(1)略;(2)①8,②4或9;(3)5 6【解析】【分析】(1)利用正方形每个角都是90°,对角线平分对角的性质,三角形外角等于和它不相邻的两个内角的和,等角对等边等性质容易得证;(2)作出△ADP和△DFP的高,由面积法容易求出这个高的值.从而得到△PAE的底和高,并求出面积.第2小问思路一样,通过面积法列出方程求解即可;(3)根据已经条件证出△MNQ是直角三角形,计算直角边乘积的一半可得其面积.【详解】(1) 证明:∵点P在对角线BD上,∴△ADP ≌△CDP ,∴AP=CP , ∠DAP =∠DCP ,∵PE ⊥PC ,∴∠EPC=∠EPB+∠BPC=90°,∵∠PEA=∠EBP+∠EPB=45°+90°-∠BPC=135°-∠BPC,∵∠PAE=90°-∠DAP =90°-∠DCP ,∠DCP=∠BPC-∠PDC=∠BPC-45°,∴∠PAE=90°-(∠BPC-45°)= 135°-∠BPC,∴∠PEA=∠PAE,∴PC=PE;(2)①如图2,过点P 分别作PH ⊥AD,PG ⊥CD,垂足分别为H 、G.延长GP 交AB 于点M.∵四边形ABCD 是正方形,P 在对角线上,∴四边形HPGD 是正方形,∴PH=PG,PM ⊥AB,设PH=PG=a,∵F 是CD 中点,AD =6,则FD=3,ADF S=9, ∵ADF S=ADP DFP S S +=1122AD PH DF PG ⨯+⨯, ∴1163922a a ⨯+⨯=,解得a=2, ∴AM=HP=2,MP=MG-PG=6-2=4,又∵PA=PE,∴AM=EM,AE=4,∵APE S =1144822EA MP ⨯=⨯⨯=, ②设HP =b,由①可得AE=2b,MP=6-b,∴APE S =()121626225b b ⨯⨯-=, 解得b=2.4 3.6或,∵ADF S =ADP DFP S S +=1122AD PH DF PG ⨯+⨯, ∴11166222b DF b DF ⨯⨯+⨯=⨯,∴当b=2.4时,DF=4;当b =3.6时,DF =9,即DF 的长为4或9;(3)如图,∵E 、Q 关于BP 对称,PN ∥CD,∴∠1=∠2,∠2+∠3=∠BDC=45°,∴∠1+∠4=45°,∴∠3=∠4,易证△PEM ≌△PQM, △PNQ ≌△PNC,∴∠5=∠6, ∠7=∠8 ,EM=QM,NQ=NC,∴∠6+∠7=90°,∴△MNQ 是直角三角形,设EM=a,NC=b 列方程组222252372 a b a b ⎧+=⎪⎪⎨⎛⎪+= ⎪⎝⎭⎩, 可得12ab=56, ∴MNQ 56S =, 【点睛】本题是四边形综合题目,考查了正方形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质等知识;本题综合性强,有一定难度,熟练掌握正方形的性质,证明三角形全等是解决问题的关键.要注意运用数形结合思想.7.如图,在正方形ABCD 中,点G 在对角线BD 上(不与点B ,D 重合),GE ⊥DC 于点E ,GF ⊥BC 于点F ,连结AG .(1)写出线段AG ,GE ,GF 长度之间的数量关系,并说明理由;(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.【答案】(1)AG2=GE2+GF2(2)【解析】试题分析:(1)结论:AG2=GE2+GF2.只要证明GA=GC,四边形EGFC是矩形,推出GE=CF,在Rt△GFC中,利用勾股定理即可证明;(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.易证AM=BM=2x,MN=x,在Rt△ABN中,根据AB2=AN2+BN2,可得1=x2+(2x+x)2,解得x=,推出BN=,再根据BG=BN÷cos30°即可解决问题.试题解析:(1)结论:AG2=GE2+GF2.理由:连接CG.∵四边形ABCD是正方形,∴A、C关于对角线BD对称,∵点G在BD上,∴GA=GC,∵GE⊥DC于点E,GF⊥BC于点F,∴∠GEC=∠ECF=∠CFG=90°,∴四边形EGFC是矩形,∴CF=GE,在Rt△GFC中,∵CG2=GF2+CF2,∴AG2=GF2+GE2.(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.∵∠AGF=105°,∠FBG=∠FGB=∠ABG=45°,∴∠AGB=60°,∠GBN=30°,∠ABM=∠MAB=15°,∴∠AMN=30°,∴AM=BM=2x,MN=x,在Rt△ABN中,∵AB2=AN2+BN2,∴1=x2+(2x+x)2,解得x=,∴BN=,∴BG=BN÷cos30°=.考点:1、正方形的性质,2、矩形的判定和性质,3、勾股定理,4、直角三角形30度的性质8.(问题发现)(1)如图(1)四边形ABCD中,若AB=AD,CB=CD,则线段BD,AC的位置关系为;(拓展探究)(2)如图(2)在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;(解决问题)(3)如图(3)在正方形ABCD中,AB=2,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.【答案】(1)AC垂直平分BD;(2)四边形FMAN是矩形,理由见解析;(3)16+8或16﹣8【解析】【分析】(1)依据点A在线段BD的垂直平分线上,点C在线段BD的垂直平分线上,即可得出AC 垂直平分BD;(2)根据Rt△ABC中,点F为斜边BC的中点,可得AF=CF=BF,再根据等腰三角形ABD 和等腰三角形ACE,即可得到AD=DB,AE=CE,进而得出∠AMF=∠MAN=∠ANF=90°,即可判定四边形AMFN是矩形;(3)分两种情况:①以点A为旋转中心将正方形ABCD逆时针旋转60°,②以点A为旋转中心将正方形ABCD顺时针旋转60°,分别依据旋转的性质以及勾股定理,即可得到结论.【详解】(1)∵AB=AD,CB=CD,∴点A在线段BD的垂直平分线上,点C在线段BD的垂直平分线上,∴AC垂直平分BD,故答案为:AC垂直平分BD;(2)四边形FMAN是矩形.理由:如图2,连接AF,∵Rt△ABC中,点F为斜边BC的中点,∴AF=CF=BF,又∵等腰三角形ABD和等腰三角形ACE,∴AD=DB,AE=CE,∴由(1)可得,DF⊥AB,EF⊥AC,又∵∠BAC=90°,∴∠AMF=∠MAN=∠ANF=90°,∴四边形AMFN是矩形;(3)BD′的平方为16+8或16﹣8.分两种情况:①以点A为旋转中心将正方形ABCD逆时针旋转60°,如图所示:过D'作D'E⊥AB,交BA的延长线于E,由旋转可得,∠DAD'=60°,∴∠EAD'=30°,∵AB=2=AD',∴D'E=AD'=,AE=,∴BE=2+,∴Rt△BD'E中,BD'2=D'E2+BE2=()2+(2+)2=16+8②以点A为旋转中心将正方形ABCD顺时针旋转60°,如图所示:过B作BF⊥AD'于F,旋转可得,∠DAD'=60°,∴∠BAD'=30°,∵AB=2=AD',∴BF=AB=,AF=,∴D'F=2﹣,∴Rt△BD'F中,BD'2=BF2+D'F2=()2+(2-)2=16﹣8综上所述,BD′平方的长度为16+8或16﹣8.【点睛】本题属于四边形综合题,主要考查了正方形的性质,矩形的判定,旋转的性质,线段垂直平分线的性质以及勾股定理的综合运用,解决问题的关键是作辅助线构造直角三角形,依据勾股定理进行计算求解.解题时注意:有三个角是直角的四边形是矩形.9.如图1,若分别以△ABC的AC、BC两边为边向外侧作的四边形ACDE和BCFG为正方形,则称这两个正方形为外展双叶正方形.(1)发现:如图2,当∠C=90°时,求证:△ABC与△DCF的面积相等.(2)引申:如果∠C 90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;(3)运用:如图3,分别以△ABC的三边为边向外侧作的四边形ACDE、BCFG和ABMN为正方形,则称这三个正方形为外展三叶正方形.已知△ABC中,AC=3,BC=4.当∠C=_____°时,图中阴影部分的面积和有最大值是________.【答案】(1)证明见解析;(2)成立,证明见解析;(3)18.【解析】试题分析:(1)因为AC=DC ,∠ACB=∠DCF=90°,BC=FC ,所以△ABC ≌△DFC ,从而△ABC 与△DFC 的面积相等;(2)延长BC 到点P ,过点A 作AP ⊥BP 于点P ;过点D 作DQ ⊥FC 于点Q .得到四边形ACDE ,BCFG 均为正方形,AC=CD ,BC=CF ,∠ACP=∠DCQ .所以△APC ≌△DQC . 于是AP=DQ .又因为S △ABC =12BC•AP ,S △DFC =12FC•DQ ,所以S △ABC =S △DFC ; (3)根据(2)得图中阴影部分的面积和是△ABC 的面积三倍,若图中阴影部分的面积和有最大值,则三角形ABC 的面积最大,当△ABC 是直角三角形,即∠C 是90度时,阴影部分的面积和最大.所以S 阴影部分面积和=3S △ABC =3×12×3×4=18. (1)证明:在△ABC 与△DFC 中, ∵{AC DCACB DCF BC FC∠∠===,∴△ABC ≌△DFC .∴△ABC 与△DFC 的面积相等;(2)解:成立.理由如下:如图,延长BC 到点P ,过点A 作AP ⊥BP 于点P ;过点D 作DQ ⊥FC 于点Q . ∴∠APC=∠DQC=90°.∵四边形ACDE ,BCFG 均为正方形,∴AC=CD ,BC=CF ,∠ACP+∠PCD=90°,∠DCQ+∠PCD=90°,∴∠ACP=∠DCQ .∴{APC DQCACP DCQ AC CD∠∠∠∠===,△APC ≌△DQC (AAS ),∴AP=DQ .又∵S△ABC=12BC•AP,S△DFC=12FC•DQ,∴S△ABC=S△DFC;(3)解:根据(2)得图中阴影部分的面积和是△ABC的面积三倍,若图中阴影部分的面积和有最大值,则三角形ABC的面积最大,∴当△ABC是直角三角形,即∠C是90度时,阴影部分的面积和最大.∴S阴影部分面积和=3S△ABC=3×12×3×4=18.考点:四边形综合题10.如图1,在菱形ABCD中,ABC=60°,若点E在AB的延长线上,EF∥AD,EF=BE,点P是DE的中点,连接FP并延长交AD于点G.(1)过D作DH AB,垂足为H,若DH=,BE=AB,求DG的长;(2)连接CP,求证:CP FP;(3)如图2,在菱形ABCD中,ABC=60°,若点E在CB的延长线上运动,点F在AB的延长线上运动,且BE=BF,连接DE,点P为DE的中点,连接FP、CP,那么第(2)问的结论成立吗?若成立,求出的值;若不成立,请说明理由.【答案】(1)1;(2)见解析;(3).【解析】试题分析:(1)根据菱形得出DA∥BC,CD=CB,∠CDG=∠CBA=60°,则∠DAH=∠ABC=60°,根据DH⊥AB得出∠DHA=90°,根据Rt△ADH的正弦值得出AD的长度,然后得出BE的长度,然后证明△PDG≌△PEF,得出DG=EF,根据EF∥AD,AD∥BC 得出EF∥BC,则说明△BEF为正三角形,从而得出DG的长度;(2)连接CG、CF,根据△PDG≌△PEF得出PG=PF,然后证明△CDG≌△CBF,从而得到CG=CF,根据PG=PF得出垂直;(3)过D作EF的平行线,交FP延长于点G,连接CG、CF证△PEF≌△PDG,然后证明△CDG≌△CBF,从而得出∠GCE=120°,根据Rt△CPF求出比值.试题解析:(1)解:∵四边形ABCD为菱形∴DA∥BC CD="CB" ∠CDG=∠CBA=60°∴∠DAH=∠ABC=60°∵DH⊥AB ∴∠DHA=90°在Rt△ADH中 sin∠DAH=∴AD=∴BE=AB=×4=1 ∵EF∥AD ∴∠PDG=∠PEB ∵P为DE的中点∴PD=PE∵∠DPG=∠EPF ∴△PDG≌△PEF ∴DG=EF ∵EF∥AD AD∥BC ∴EF∥BC∴∠FEB=∠CBA=60°∵BE=EF ∴△BEF为正三角形∴EF=BE=1 ∴DG=EF=1、证明:连接CG、CF由(1)知△PDG≌△PEF ∴PG=PF在△CDG与△CBF中易证:∠CDG=∠CBF=60° CD=CB BF=EF=DG ∴△CDG≌△CBF∴CG=CF ∵PG=PF ∴CP⊥GF(3)如图:CP⊥GF仍成立理由如下:过D作EF的平行线,交FP延长于点G连接CG、CF证△PEF≌△PDG ∴DG=EF=BF ∵DG∥EF ∴∠GDP=∠EFP ∵DA∥BC∴∠ADP=∠PEC∴∠GDP-∠ADP=∠EFP-∠PEC ∴∠GDA=∠BEF=60°∴∠CDG=∠ADC+∠GDA=120°∵∠CBF=180°-∠EBF=120°∴∠CBF=∠CDG ∵CD=BC DG=BF ∴△CDG≌△CBF∴CG=CF ∠DCG=∠FCE ∵PG=PF ∴CP⊥PF ∠GCP=∠FCP∵∠DCP=180-∠ABC=120°∴∠DCG+∠GCE=120°∴∠FCE+∠GCE=120°即∠GCE=120°∴∠FCP=∠GCE=60°在Rt△CPF中 tan∠FCP=tan60°==考点:三角形全等的证明与性质.。
重庆中考数学易错题专题训练-平行四边形练习题
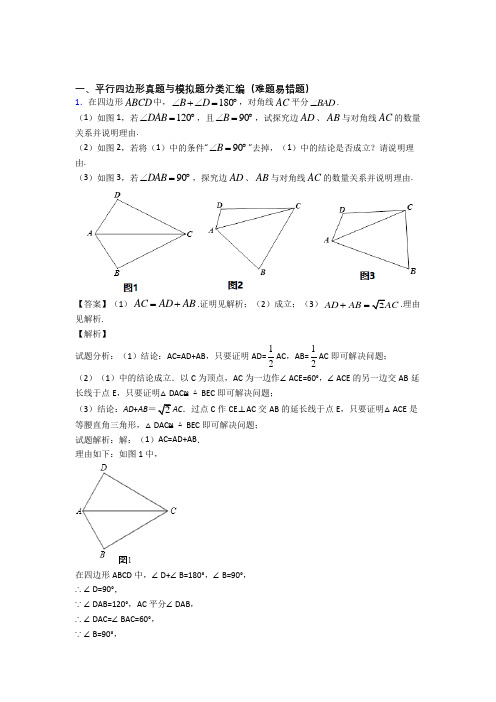
一、平行四边形真题与模拟题分类汇编(难题易错题)1.在四边形ABCD 中,180B D ∠+∠=︒,对角线AC 平分BAD ∠.(1)如图1,若120DAB ∠=︒,且90B ∠=︒,试探究边AD 、AB 与对角线AC 的数量关系并说明理由.(2)如图2,若将(1)中的条件“90B ∠=︒”去掉,(1)中的结论是否成立?请说明理由.(3)如图3,若90DAB ∠=︒,探究边AD 、AB 与对角线AC 的数量关系并说明理由.【答案】(1)AC AD AB =+.证明见解析;(2)成立;(3)2AD AB AC +=.理由见解析.【解析】试题分析:(1)结论:AC=AD+AB ,只要证明AD=12AC ,AB=12AC 即可解决问题; (2)(1)中的结论成立.以C 为顶点,AC 为一边作∠ACE=60°,∠ACE 的另一边交AB 延长线于点E ,只要证明△DAC ≌△BEC 即可解决问题;(3)结论:AD +AB =2AC .过点C 作CE ⊥AC 交AB 的延长线于点E ,只要证明△ACE 是等腰直角三角形,△DAC ≌△BEC 即可解决问题;试题解析:解:(1)AC=AD+AB .理由如下:如图1中,在四边形ABCD 中,∠D+∠B=180°,∠B=90°,∴∠D=90°,∵∠DAB=120°,AC 平分∠DAB ,∴∠DAC=∠BAC=60°,∵∠B=90°,∴AB=12AC,同理AD=12AC.∴AC=AD+AB.(2)(1)中的结论成立,理由如下:以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,∵∠BAC=60°,∴△AEC为等边三角形,∴AC=AE=CE,∵∠D+∠ABC=180°,∠DAB=120°,∴∠DCB=60°,∴∠DCA=∠BCE,∵∠D+∠ABC=180°,∠ABC+∠EBC=180°,∴∠D=∠CBE,∵CA=CE,∴△DAC≌△BEC,∴AD=BE,∴AC=AD+AB.(3)结论:AD+AB=2AC.理由如下:过点C作CE⊥AC交AB的延长线于点E,∵∠D+∠B=180°,∠DAB=90°,∴DCB=90°,∵∠ACE=90°,∴∠DCA=∠BCE,又∵AC平分∠DAB,∴∠CAB=45°,∴∠E=45°.∴AC=CE.又∵∠D+∠ABC=180°,∠D=∠CBE,∴△CDA ≌△CBE ,∴AD=BE ,∴AD+AB=AE .在Rt △ACE 中,∠CAB=45°,∴AE =245AC AC cos ︒= ∴2AD AB AC +=.2.如图,将矩形纸片ABCD 沿对角线AC 折叠,使点B 落到到B′的位置,AB′与CD 交于点E.(1)求证:△AED ≌△CEB′ (2)若AB = 8,DE = 3,点P 为线段AC 上任意一点,PG ⊥AE 于G ,PH ⊥BC 于H.求PG + PH 的值. 【答案】(1)证明见解析;(2). 【解析】 【分析】(1)由折叠的性质知,,,,则由得到; (2)由,可得,又由,即可求得的长,然后在中,利用勾股定理即可求得的长,再过点作于,由角平分线的性质,可得,易证得四边形是矩形,继而可求得答案.【详解】(1)四边形为矩形,,, 又,; (2),,,, 在中,, 过点作于,,,,,,,、、共线,,四边形是矩形,,.【点睛】此题考查了折叠的性质、矩形的性质、角平分线的性质、等腰三角形的判定与性质以及勾股定理等知识.此题难度较大,注意掌握折叠前后图形的对应关系,注意掌握辅助线的作法,注意数形结合思想的应用.3.如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD 的延长线于点F,连接CF.(1)求证:四边形BCFD是菱形;(2)若AD=1,BC=2,求BF的长.【答案】(1)证明见解析(2)3【解析】(1)∵AF∥BC,∴∠DCB=∠CDF,∠FBC=∠BFD,∵点E为CD的中点,∴DE=EC,在△BCE与△FDE中,FBC BFDDCB CDFDE EC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCE≌△FDE,∴DF=BC,又∵DF∥BC,∴四边形BCDF为平行四边形,∵BD=BC,∴四边形BCFD是菱形;(2)∵四边形BCFD是菱形,∴BD=DF=BC=2,在Rt△BAD中,AB223BD AD-,∵AF=AD+DF=1+2=3,在Rt△BAF中,BF22AB AF+3.4.如图,四边形ABCD中,∠BCD=∠D=90°,E是边AB的中点.已知AD=1,AB=2.(1)设BC =x ,CD =y ,求y 关于x 的函数关系式,并写出定义域;(2)当∠B =70°时,求∠AEC 的度数;(3)当△ACE 为直角三角形时,求边BC 的长.【答案】(1)()22303y x x x =-++<<;(2)∠AEC =105°;(3)边BC 的长为2或1172. 【解析】试题分析:(1)过A 作AH ⊥BC 于H ,得到四边形ADCH 为矩形.在△BAH 中,由勾股定理即可得出结论.(2)取CD 中点T ,连接TE ,则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD ,∠AET =∠B =70°.又AD =AE =1,得到∠AED =∠ADE =∠DET =35°.由ET 垂直平分CD ,得∠CET =∠DET =35°,即可得到结论.(3)分两种情况讨论:①当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 解△ABH 即可得到结论.②当∠CAE =90°时,易知△CDA ∽△BCA ,由相似三角形对应边成比例即可得到结论. 试题解析:解:(1)过A 作AH ⊥BC 于H .由∠D =∠BCD =90°,得四边形ADCH 为矩形. 在△BAH 中,AB =2,∠BHA =90°,AH =y ,HB =1x -,∴22221y x =+-, 则()22303y x x x =-++<<(2)取CD 中点T ,联结TE ,则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD ,∴∠AET =∠B =70°.又AD =AE =1,∴∠AED =∠ADE =∠DET =35°.由ET 垂直平分CD ,得∠CET =∠DET =35°,∴∠AEC =70°+35°=105°.(3)分两种情况讨论:①当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 则在△ABH 中,∠B =60°,∠AHB =90°,AB =2,得BH =1,于是BC =2.②当∠CAE =90°时,易知△CDA ∽△BCA ,又2224AC BC AB x =-- 则2241174AD CA x x AC CB x -±=⇒=⇒=-(舍负) 易知∠ACE <90°,所以边BC 117+综上所述:边BC的长为2或1172.点睛:本题是四边形综合题.考查了梯形中位线,相似三角形的判定与性质.解题的关键是掌握梯形中常见的辅助线作法.5.如图所示,矩形ABCD中,点E在CB的延长线上,使CE=AC,连接AE,点F是AE的中点,连接BF、DF,求证:BF⊥DF.【答案】见解析.【解析】【分析】延长BF,交DA的延长线于点M,连接BD,进而求证△AFM≌△EFB,得AM=BE,FB=FM,即可求得BC+BE=AD+AM,进而求得BD=BM,根据等腰三角形三线合一的性质即可求证BF⊥DF.【详解】延长BF,交DA的延长线于点M,连接BD.∵四边形ABCD是矩形,∴MD∥BC,∴∠AMF=∠EBF,∠E=∠MAF,又FA=FE,∴△AFM≌△EFB,∴AM=BE,FB=FM.∵矩形ABCD中,∴AC=BD,AD=BC,∴BC+BE=AD+AM,即CE=MD.∵CE=AC,∴AC=CE= BD =DM.∵FB=FM,∴BF⊥DF.【点睛】本题考查了矩形的性质,全等三角形的判定和对应边相等的性质,等腰三角形三线合一的性质,本题中求证DB=DM是解题的关键.6.正方形ABCD,点E在边BC上,点F在对角线AC上,连AE.(1)如图1,连EF,若EF⊥AC,4AF=3AC,AB=4,求△AEF的周长;(2)如图2,若AF=AB,过点F作FG⊥AC交CD于G,点H在线段FG上(不与端点重合),连AH.若∠EAH=45°,求证:EC=HG+2FC.【答案】(1)25422)证明见解析【解析】【分析】(1)由正方形性质得出AB=BC=CD=AD=4,∠B=∠D=90°,∠ACB=∠ACD=∠BAC=∠ACD=45°,得出AC2AB=2,求出AF=2,CF=AC﹣AF2,求出△CEF 是等腰直角三角形,得出EF=CF2,CE2CF=2,在Rt△AEF中,由勾股定理求出AE,即可得出△AEF的周长;(2)延长GF交BC于M,连接AG,则△CGM和△CFG是等腰直角三角形,得出CM=CG,CG2CF,证出BM=DG,证明Rt△AFG≌Rt△ADG得出FG=DG,BM=FG,再证明△ABE≌△AFH,得出BE=FH,即可得出结论.【详解】(1)∵四边形ABCD是正方形,∴AB=BC=CD=AD=4,∠B=∠D=90°,∠ACB=∠ACD=∠BAC=∠ACD=45°,∴AC2AB=2,∵4AF=3AC=2,∴AF=2∴CF=AC﹣AF2∵EF⊥AC,∴△CEF是等腰直角三角形,∴EF=CF2CE2CF=2,在Rt△AEF中,由勾股定理得:AE2225+=AF EF=∴△AEF的周长=AE+EF+AF=252322542(2)证明:延长GF交BC于M,连接AG,如图2所示:则△CGM 和△CFG 是等腰直角三角形,∴CM =CG ,CG 2,∴BM =DG ,∵AF =AB ,∴AF =AD ,在Rt △AFG 和Rt △ADG 中,AG AG AF AD =⎧⎨=⎩, ∴Rt △AFG ≌Rt △ADG (HL ),∴FG =DG ,∴BM =FG ,∵∠BAC =∠EAH =45°,∴∠BAE =∠FAH ,∵FG ⊥AC ,∴∠AFH =90°,在△ABE 和△AFH 中,90B AFH AB AFBAE FAH ︒⎧∠=∠=⎪=⎨⎪∠=∠⎩, ∴△ABE ≌△AFH (ASA ),∴BE =FH ,∵BM =BE +EM ,FG =FH +HG ,∴EM =HG ,∵EC =EM +CM ,CM =CG 2CF ,∴EC =HG 2.【点睛】本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理等知识;熟练掌握等腰直角三角形的判定与性质,证明三角形全等是解题的关键.7.如图1,矩形ABCD 中,AB=8,AD=6;点E 是对角线BD 上一动点,连接CE ,作EF ⊥CE 交AB 边于点F ,以CE 和EF 为邻边作矩形CEFG ,作其对角线相交于点H .(1)①如图2,当点F 与点B 重合时,CE= ,CG= ;②如图3,当点E 是BD 中点时,CE= ,CG= ;(2)在图1,连接BG ,当矩形CEFG 随着点E 的运动而变化时,猜想△EBG 的形状?并加以证明;(3)在图1,CG CE 的值是否会发生改变?若不变,求出它的值;若改变,说明理由; (4)在图1,设DE 的长为x ,矩形CEFG 的面积为S ,试求S 关于x 的函数关系式,并直接写出x 的取值范围.【答案】(1)245,185,5,154 ;(2)△EBG 是直角三角形,理由详见解析;(3)34 ;(4)S=34x 2﹣485x+48(0≤x≤325). 【解析】【分析】(1)①利用面积法求出CE ,再利用勾股定理求出EF 即可;②利用直角三角形斜边中线定理求出CE ,再利用相似三角形的性质求出EF 即可;(2)根据直角三角形的判定方法:如果一个三角形一边上的中线等于这条边的一半,则这个三角形是直角三角形即可判断;(3)只要证明△DCE ∽△BCG ,即可解决问题;(4)利用相似多边形的性质构建函数关系式即可;【详解】(1)①如图2中,在Rt △BAD 中,22AD AB +, ∵S △BCD =12•CD•BC=12•BD•CE , ∴CE=245.2224186()55-. ②如图3中,过点E 作MN ⊥AM 交AB 于N ,交CD 于M .∵DE=BE ,∴CE=12BD=5, ∵△CME ∽△ENF ,∴CM EN CE EF=, ∴CG=EF=154, (2)结论:△EBG 是直角三角形. 理由:如图1中,连接BH .在Rt △BCF 中,∵FH=CH ,∴BH=FH=CH ,∵四边形EFGC 是矩形,∴EH=HG=HF=HC ,∴BH=EH=HG ,∴△EBG 是直角三角形.(3)F 如图1中,∵HE=HC=HG=HB=HF , ∴C 、E 、F 、B 、G 五点共圆, ∵EF=CG ,∴∠CBG=∠EBF , ∵CD ∥AB ,∴∠EBF=∠CDE ,∴∠CBG=∠CDE ,∵∠DCB=∠ECG=90°,∴∠DCE=∠BCG ,∴△DCE ∽△BCG ,∴6384CG BC CE DC ===.(4)由(3)可知: 34CG CD CE CB ==, ∴矩形CEFG ∽矩形ABCD , ∴2264CEFG ABCD S CE CE S CD ==矩形矩形(), ∵CE 2=(325-x )2+245)2,S 矩形ABCD =48, ∴S 矩形CEFG =34[(325-x )2+(245)2]. ∴矩形CEFG 的面积S=34x 2-485x+48(0≤x≤325). 【点睛】 本题考查相似三角形综合题、矩形的性质、相似三角形的判定和性质、勾股定理、直角三角形的判定和性质、相似多边形的性质和判定等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造相似三角形或直角三角形解决问题,属于中考压轴题.8.数学活动课上,老师给出如下问题:如图,将等腰直角三角形纸片沿斜边上的高AC 剪开,得到等腰直角三角形△ABC 与△EFD ,将△EFD 的直角顶点在直线BC 上平移,在平移的过程中,直线AC 与直线DE 交于点Q ,让同学们探究线段BQ 与AD 的数量关系和位置关系.请你阅读下面交流信息,解决所提出的问题.展示交流:小敏:满足条件的图形如图甲所示图形,延长BQ 与AD 交于点H .我们可以证明△BCQ ≌△ACD ,从而易得BQ=AD ,BQ ⊥AD .小慧:根据图甲,当点F 在线段BC 上时,我们可以验证小慧的说法是正确的.但当点F 在线段CB 的延长线上(如图乙)或线段CB 的反向延长线上(如图丙)时,我对小慧说法的正确性表示怀疑.(1)请你帮助小慧进行分析,小敏的结论在图乙、图丙中是否成立?请说明理由. (选择图乙或图丙的一种情况说明即可).(2)小慧思考问题的方式中,蕴含的数学思想是 .拓展延伸:根据你上面选择的图形,分别取AB、BD、DQ、AQ的中点M、N、P、T.则四边形MNPT 是什么样的特殊四边形?请说明理由.【答案】成立;分类讨论思想;正方形.【解析】试题分析:利用等腰直角三角形的性质结合全等三角形的判定与性质得出BQ=AD,BQ⊥AD;利用已知条件分类得出,体现数学中的分类讨论思想,拓展延伸:利用三角形中位线定理结合正方形的判定方法,首先得出四边形MNPT是平行四边形进而得出它是菱形,再求出一个内角是90°,即可得出答案.试题解析:(1)、成立,理由:如图乙:由题意可得:∠FDE=∠QDC=∠ABC=∠BAC=45°,则DC=QC,AC=BC,在△ADC和△BQC中∵,∴△ADC≌△BQC(SAS),∴AD=BQ,∠DAC=∠QBC,延长AD交BQ于点F,则∠ADC=∠BDF,∴∠BFD=∠ACD=90°,∴AD⊥BQ;(2)、小慧思考问题的方式中,蕴含的数学思想是:分类讨论思想;拓展延伸:四边形MNPT是正方形,理由:∵取AB、BD、DQ、AQ的中点M、N、P、T,∴MN AD,TP AD,∴MN TP,∴四边形MNPT是平行四边形,∵NP BQ,BQ=AD,∴NP=MN,∴平行四边形MNPT 是菱形,又∵AD⊥BQ,NP∥BQ,MN∥AD,∴∠MNP=90°,∴四边形MNPT是正方形.考点:几何变换综合题9.倡导研究性学习方式,着力教材研究,习题研究,是学生跳出题海,提高学习能力和创新能力的有效途径.下面是一案例,请同学们认真阅读、研究,完成“类比猜想”的问题.习题如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.解答:∵正方形ABCD中,AB=AD,∠BAD=∠ADC=∠B=90°,∴把△ABE绕点A逆时针旋转90°至△ADE′,点F、D、E′在一条直线上.∴∠E′AF=90°-45°=45°=∠EAF,又∵AE′=AE,AF=AF∴△AE′F≌△AEF(SAS)∴EF=E′F=DE′+DF=BE+DF.类比猜想:(1)请同学们研究:如图(2),在菱形ABCD中,点E、F分别在BC、CD上,当∠BAD=120°,∠EAF=60°时,还有EF=BE+DF吗?请说明理由.(2)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180°,∠EAF=∠BAD时,EF=BE+DF吗?请说明理由.【答案】证明见解析.【解析】试题分析:(1)把△ABE绕点A逆时针旋转120°至△ADE′,如图(2),连结E′F,根据菱形和旋转的性质得到AE=AE′,∠EAF=∠E′AF,利用“SAS”证明△AEF≌△AE′F,得到EF=E′F;由于∠ADE′+∠ADC=120°,则点F、D、E′不共线,所以DE′+DF>EF,即由BE+DF>EF;(2)把△ABE绕点A逆时针旋转∠BAD的度数至△ADE′,如图(3),根据旋转的性质得到AE′=AE,∠EAF=∠E′AF,然后利用“SAS”证明△AEF≌△AE′F,得到EF=E′F,由于∠ADE′+∠ADC=180°,知F、D、E′共线,因此有EF=DE′+DF=BE+DF;根据前面的条件和结论可归纳出结论.试题解析:(1)当∠BAD=120°,∠EAF=60°时,EF=BE+DF不成立,EF<BE+DF.理由如下:∵在菱形ABCD中,∠BAD=120°,∠EAF=60°,∴AB=AD,∠1+∠2=60°,∠B=∠ADC=60°,∴把△ABE绕点A逆时针旋转120°至△ADE′,如图(2),连结E′F,∴∠EAE′=120°,∠1=∠3,AE′=AE,DE′=BE,∠ADE′=∠B=60°,∴∠2+∠3=60°,∴∠EAF=∠E′AF,在△AEF和△AE′F中,∴△AEF≌△AE′F(SAS),∴EF=E′F,∵∠ADE′+∠ADC=120°,即点F、D、E′不共线,∴DE′+DF>EF∴BE+DF>EF;(2)当AB=AD,∠B+∠D=180°,∠EAF=∠BAD时,EF=BE+DF成立.理由如下:如图(3),∵AB=AD,∴把△ABE绕点A逆时针旋转∠BAD的度数至△ADE′,如图(3),∴∠EAE′=∠BAD,∠1=∠3,AE′=AE,DE′=BE,∠ADE′=∠B,∵∠B+∠D=180°,∴∠ADE′+∠D=180°,∴点F、D、E′共线,∵∠EAF=∠BAD,∴∠1+∠2=∠BAD,∴∠2+∠3=∠BAD,∴∠EAF=∠E′AF,在△AEF和△AE′F中,∴△AEF≌△AE′F(SAS),∴EF=E′F,∴EF=DE′+DF=BE+DF;归纳:在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180°,∠EAF=∠BAD时,EF=BE+DF.考点:四边形综合题.10.(本题满分10分)如图1,已知矩形纸片ABCD中,AB=6cm,若将该纸片沿着过点B的直线折叠(折痕为BM),点A恰好落在CD边的中点P处.(1)求矩形ABCD的边AD的长.(2)若P为CD边上的一个动点,折叠纸片,使得A与P重合,折痕为MN,其中M在边AD上,N在边BC上,如图2所示.设DP=x cm,DM=y cm,试求y与x的函数关系式,并指出自变量x的取值范围.(3)①当折痕MN的端点N在AB上时,求当△PCN为等腰三角形时x的值;②当折痕MN的端点M在CD上时,设折叠后重叠部分的面积为S,试求S与x之间的函数关系式【答案】(1)AD=3;(2)y=-其中,0<x<3;(3)x=;(4)S=.【解析】试题分析:(1)根据折叠图形的性质和勾股定理求出AD的长度;(2)根据折叠图形的性质以及Rt△MPD的勾股定理求出函数关系式;(3)过点N作NQ⊥CD,根据Rt△NPQ 的勾股定理进行求解;(4)根据Rt△ADM的勾股定理求出MP与x的函数关系式,然后得出函数关系式.试题解析:(1)根据折叠可得BP=AB=6cm CP=3cm 根据Rt△PBC的勾股定理可得:AD=3.(2)由折叠可知AM=MP,在Rt△MPD中,∴∴y=-其中,0<x<3.(3)当点N在AB上,x≥3,∴PC≤3,而PN≥3,NC≥3.∴△PCN为等腰三角形,只可能NC=NP.过N点作NQ⊥CD,垂足为Q,在Rt△NPQ中,∴解得x=.(4)当点M在CD上时,N在AB上,可得四边形ANPM为菱形.设MP=y,在Rt△ADM中,,即∴ y=.∴ S=考点:函数的性质、勾股定理.。
中考数学压轴题之平行四边形(中考题型整理,突破提升)含答案解析

考点:1.正方形的性质;2.全等三角形的判定与性质;3.三角形中位线定理;4.旋转的性 质.
3.如图,△ ABC 中,AD 是边 BC 上的中线,过点 A 作 AE∥ BC,过点 D 作 DE∥ AB,DE 与 AC、AE 分别交于点 O、点 E,连接 EC. (1)求证:AD=EC;
(2)当∠ BAC=Rt∠ 时,求证:四边形 ADCE 是菱形.
【答案】(1)见解析; (2)见解析. 【解析】 【分析】 (1)先证四边形 ABDE 是平行四边形,再证四边形 ADCE 是平行四边形即可; (2)由∠ BAC=90°,AD 是边 BC 上的中线,得 AD=BD=CD,即可证明. 【详解】 (1)证明:∵ AE∥ BC,DE∥ AB , ∴ 四边形 ABDE 是平行四边形, ∴ AE=BD, ∵ AD 是边 BC 上的中线, ∴ BD=DC, ∴ AE=DC, 又∵ AE∥ BC, ∴ 四边形 ADCE 是平行四边形. (2) 证明:∵ ∠ BAC=90°,AD 是边 BC 上的中线. ∴ AD=CD ∵ 四边形 ADCE 是平行四边形, ∴ 四边形 ADCE 是菱形. 【点睛】 本题考查了平行四边形的判定、菱形的判定、直角三角形斜边中线定理.根据图形与已知条 件灵活应用平行四边形的判定方法是证明的关键.
中考数学培优 易错 难题(含解析)之平行四边形附答案

中考数学培优易错难题(含解析)之平行四边形附答案一、平行四边形1.四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.(1)如图1,当点E、F在线段AD上时,①求证:∠DAG=∠DCG;②猜想AG与BE的位置关系,并加以证明;(2)如图2,在(1)条件下,连接HO,试说明HO平分∠BHG;(3)当点E、F运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出∠BHO的度数.【答案】(1)①证明见解析;②AG⊥BE.理由见解析;(2)证明见解析;(3)∠BHO=45°.【解析】试题分析:(1)①根据正方形的性质得DA=DC,∠ADB=∠CDB=45°,则可根据“SAS”证明△ADG≌△CDG,所以∠DAG=∠DCG;②根据正方形的性质得AB=DC,∠BAD=∠CDA=90°,根据“SAS”证明△ABE≌△DCF,则∠ABE=∠DCF,由于∠DAG=∠DCG,所以∠DAG=∠ABE,然后利用∠DAG+∠BAG=90°得到∠ABE+∠BAG=90°,于是可判断AG⊥BE;(2)如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,证明△AON≌△BOM,可得四边形OMHN为正方形,因此HO平分∠BHG结论成立;(3)如答图2所示,与(1)同理,可以证明AG⊥BE;过点O作OM⊥BE于点M,ON⊥AG于点N,构造全等三角形△AON≌△BOM,从而证明OMHN为正方形,所以HO 平分∠BHG,即∠BHO=45°.试题解析:(1)①∵四边形ABCD为正方形,∴DA=DC,∠ADB=∠CDB=45°,在△ADG和△CDG中,∴△ADG≌△CDG(SAS),∴∠DAG=∠DCG;②AG⊥BE.理由如下:∵四边形ABCD为正方形,∴AB=DC,∠BAD=∠CDA=90°,在△ABE和△DCF中,∴△ABE≌△DCF(SAS),∴∠ABE=∠DCF,∵∠DAG=∠DCG,∴∠DAG=∠ABE,∵∠DAG+∠BAG=90°,∴∠ABE+∠BAG=90°,∴∠AHB=90°,∴AG⊥BE;(2)由(1)可知AG⊥BE.如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,则四边形OMHN为矩形.∴∠MON=90°,又∵OA⊥OB,∴∠AON=∠BOM.∵∠AON+∠OAN=90°,∠BOM+∠OBM=90°,∴∠OAN=∠OBM.在△AON与△BOM中,∴△AON≌△BOM(AAS).∴OM=ON,∴矩形OMHN为正方形,∴HO平分∠BHG.(3)将图形补充完整,如答图2示,∠BHO=45°.与(1)同理,可以证明AG ⊥BE .过点O 作OM ⊥BE 于点M ,ON ⊥AG 于点N ,与(2)同理,可以证明△AON ≌△BOM ,可得OMHN 为正方形,所以HO 平分∠BHG ,∴∠BHO=45°.考点:1、四边形综合题;2、全等三角形的判定与性质;3、正方形的性质2.在四边形ABCD 中,180B D ∠+∠=︒,对角线AC 平分BAD ∠.(1)如图1,若120DAB ∠=︒,且90B ∠=︒,试探究边AD 、AB 与对角线AC 的数量关系并说明理由.(2)如图2,若将(1)中的条件“90B ∠=︒”去掉,(1)中的结论是否成立?请说明理由.(3)如图3,若90DAB ∠=︒,探究边AD 、AB 与对角线AC 的数量关系并说明理由.【答案】(1)AC AD AB =+.证明见解析;(2)成立;(3)2AD AB +=.理由见解析.【解析】试题分析:(1)结论:AC=AD+AB ,只要证明AD=12AC ,AB=12AC 即可解决问题; (2)(1)中的结论成立.以C 为顶点,AC 为一边作∠ACE=60°,∠ACE 的另一边交AB 延长线于点E ,只要证明△DAC ≌△BEC 即可解决问题;(3)结论:AD +AB 2AC .过点C 作CE ⊥AC 交AB 的延长线于点E ,只要证明△ACE 是等腰直角三角形,△DAC ≌△BEC 即可解决问题;试题解析:解:(1)AC=AD+AB .理由如下:如图1中,在四边形ABCD中,∠D+∠B=180°,∠B=90°,∴∠D=90°,∵∠DAB=120°,AC平分∠DAB,∴∠DAC=∠BAC=60°,∵∠B=90°,∴AB=12AC,同理AD=12AC.∴AC=AD+AB.(2)(1)中的结论成立,理由如下:以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,∵∠BAC=60°,∴△AEC为等边三角形,∴AC=AE=CE,∵∠D+∠ABC=180°,∠DAB=120°,∴∠DCB=60°,∴∠DCA=∠BCE,∵∠D+∠ABC=180°,∠ABC+∠EBC=180°,∴∠D=∠CBE,∵CA=CE,∴△DAC≌△BEC,∴AD=BE,∴AC=AD+AB.(3)结论:AD+AB2AC.理由如下:过点C作CE⊥AC交AB的延长线于点E,∵∠D+∠B=180°,∠DAB=90°,∴DCB=90°,∵∠ACE=90°,∴∠DCA=∠BCE ,又∵AC 平分∠DAB ,∴∠CAB=45°,∴∠E=45°.∴AC=CE .又∵∠D+∠ABC=180°,∠D=∠CBE ,∴△CDA ≌△CBE ,∴AD=BE ,∴AD+AB=AE .在Rt △ACE 中,∠CAB=45°,∴AE =245AC AC cos ︒= ∴2AD AB AC +=.3.如图,平面直角坐标系中,四边形OABC 为矩形,点A ,B 的坐标分别为(4,0),(4,3),动点M ,N 分别从O ,B 同时出发.以每秒1个单位的速度运动.其中,点M 沿OA 向终点A 运动,点N 沿BC 向终点C 运动.过点M 作MP ⊥OA ,交AC 于P ,连接NP ,已知动点运动了x 秒.(1)P 点的坐标为多少(用含x 的代数式表示);(2)试求△NPC 面积S 的表达式,并求出面积S 的最大值及相应的x 值;(3)当x 为何值时,△NPC 是一个等腰三角形?简要说明理由.【答案】(1)P 点坐标为(x ,3﹣x ).(2)S的最大值为,此时x=2.(3)x=,或x=,或x=.【解析】试题分析:(1)求P点的坐标,也就是求OM和PM的长,已知了OM的长为x,关键是求出PM的长,方法不唯一,①可通过PM∥OC得出的对应成比例线段来求;②也可延长MP交BC于Q,先在直角三角形CPQ中根据CQ的长和∠ACB的正切值求出PQ的长,然后根据PM=AB﹣PQ来求出PM的长.得出OM和PM的长,即可求出P点的坐标.(2)可按(1)②中的方法经求出PQ的长,而CN的长可根据CN=BC﹣BN来求得,因此根据三角形的面积计算公式即可得出S,x的函数关系式.(3)本题要分类讨论:①当CP=CN时,可在直角三角形CPQ中,用CQ的长即x和∠ABC的余弦值求出CP的表达式,然后联立CN的表达式即可求出x的值;②当CP=PN时,那么CQ=QN,先在直角三角形CPQ中求出CQ的长,然后根据QN=CN﹣CQ求出QN的表达式,根据题设的等量条件即可得出x的值.③当CN=PN时,先求出QP和QN的长,然后在直角三角形PNQ中,用勾股定理求出PN 的长,联立CN的表达式即可求出x的值.试题解析:(1)过点P作PQ⊥BC于点Q,有题意可得:PQ∥AB,∴△CQP∽△CBA,∴∴解得:QP=x,∴PM=3﹣x,由题意可知,C(0,3),M(x,0),N(4﹣x,3),P点坐标为(x,3﹣x).(2)设△NPC的面积为S,在△NPC中,NC=4﹣x,NC边上的高为,其中,0≤x≤4.∴S=(4﹣x)×x=(﹣x2+4x)=﹣(x﹣2)2+.∴S的最大值为,此时x=2.(3)延长MP交CB于Q,则有PQ⊥BC.①若NP=CP,∵PQ⊥BC,∴NQ=CQ=x.∴3x=4,∴x=.②若CP=CN,则CN=4﹣x,PQ=x,CP=x,4﹣x=x,∴x=;③若CN=NP,则CN=4﹣x.∵PQ=x,NQ=4﹣2x,∵在Rt△PNQ中,PN2=NQ2+PQ2,∴(4﹣x)2=(4﹣2x)2+(x)2,∴x=.综上所述,x=,或x=,或x=.考点:二次函数综合题.4.如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C 关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.(1)求∠FDP的度数;(2)连接BP,请用等式表示AP、BP、DP三条线段之间的数量关系,并证明;(3)连接AC2,请直接写出△ACC′的面积最大值.【答案】(1)45°;(2)BP+DP=2AP,证明详见解析;(3)2﹣1.【解析】【分析】(1)证明∠CDE=∠C'DE和∠ADF=∠C'DF,可得∠FDP'=12∠ADC=45°;(2)作辅助线,构建全等三角形,证明△BAP≌△DAP'(SAS),得BP=DP',从而得△PAP'是等腰直角三角形,可得结论;(3)先作高线C'G,确定△ACC′的面积中底边AC为定值2,根据高的大小确定面积的大小,当C'在BD上时,C'G最大,其△ACC′的面积最大,并求此时的面积.【详解】(1)由对称得:CD=C'D,∠CDE=∠C'DE,在正方形ABCD中,AD=CD,∠ADC=90°,∴AD=C'D,∵F是AC'的中点,∴DF⊥AC',∠ADF=∠C'DF,∴∠FDP=∠FDC'+∠EDC'=12∠ADC=45°;(2)结论:BP+DP=2AP,理由是:如图,作AP'⊥AP交PD的延长线于P',∴∠PAP'=90°,在正方形ABCD中,DA=BA,∠BAD=90°,∴∠DAP'=∠BAP,由(1)可知:∠FDP=45°∵∠DFP =90°∴∠APD =45°,∴∠P '=45°,∴AP =AP ',在△BAP 和△DAP '中,∵BA DA BAP DAP AP AP '=⎧⎪∠=∠⎨='⎪⎩,∴△BAP ≌△DAP '(SAS ),∴BP =DP ',∴DP +BP =PP '=2AP ;(3)如图,过C '作C 'G ⊥AC 于G ,则S △AC 'C =12AC •C 'G ,Rt △ABC 中,AB =BC 2,∴AC 22(2)(2)2+=,即AC 为定值,当C 'G 最大值,△AC 'C 的面积最大,连接BD ,交AC 于O ,当C '在BD 上时,C 'G 最大,此时G 与O 重合,∵CD =C 'D 2OD =12AC =1, ∴C 'G 2﹣1,∴S △AC 'C =112(21)2122AC C G '•=⨯=. 【点睛】本题考查四边形综合题、正方形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.5.如图,四边形ABCD 中,AD ∥BC ,∠A=90°,BD=BC ,点E 为CD 的中点,射线BE 交AD 的延长线于点F ,连接CF .(1)求证:四边形BCFD 是菱形;(2)若AD=1,BC=2,求BF 的长.【答案】(1)证明见解析(2)23【解析】(1)∵AF∥BC,∴∠DCB=∠CDF,∠FBC=∠BFD,∵点E为CD的中点,∴DE=EC,在△BCE与△FDE中,FBC BFDDCB CDFDE EC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCE≌△FDE,∴DF=BC,又∵DF∥BC,∴四边形BCDF为平行四边形,∵BD=BC,∴四边形BCFD是菱形;(2)∵四边形BCFD是菱形,∴BD=DF=BC=2,在Rt△BAD中,AB=223BD AD-=,∵AF=AD+DF=1+2=3,在Rt△BAF中,BF=22AB AF+=23.6.如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t 秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(1)求证:AE=DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)当t为何值时,△DEF为直角三角形?请说明理由.【答案】(1)见解析;(2)能,t=10;(3)t=152或12.【解析】【分析】(1)利用t表示出CD以及AE的长,然后在直角△CDF中,利用直角三角形的性质求得DF的长,即可证明;(2)易证四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,据此即可列方程求得t的值;(3)△DEF为直角三角形,分∠EDF=90°和∠DEF=90°两种情况讨论.【详解】解:(1)证明:∵在Rt△ABC中,∠C=90°﹣∠A=30°,∴AB=12AC=12×60=30cm,∵CD=4t,AE=2t,又∵在Rt△CDF中,∠C=30°,∴DF=12CD=2t,∴DF=AE;(2)能,∵DF∥AB,DF=AE,∴四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,即60﹣4t=2t,解得:t=10,∴当t=10时,AEFD是菱形;(3)若△DEF为直角三角形,有两种情况:①如图1,∠EDF=90°,DE∥BC,则AD=2AE,即60﹣4t=2×2t,解得:t=152,②如图2,∠DEF=90°,DE⊥AC,则AE=2AD,即2t2(604t)=-,解得:t=12,综上所述,当t=152或12时,△DEF为直角三角形.7.如图所示,矩形ABCD中,点E在CB的延长线上,使CE=AC,连接AE,点F是AE的中点,连接BF、DF,求证:BF⊥DF.【答案】见解析.【解析】【分析】延长BF,交DA的延长线于点M,连接BD,进而求证△AFM≌△EFB,得AM=BE,FB=FM,即可求得BC+BE=AD+AM,进而求得BD=BM,根据等腰三角形三线合一的性质即可求证BF⊥DF.【详解】延长BF,交DA的延长线于点M,连接BD.∵四边形ABCD是矩形,∴MD∥BC,∴∠AMF=∠EBF,∠E=∠MAF,又FA=FE,∴△AFM≌△EFB,∴AM=BE,FB=FM.∵矩形ABCD中,∴AC=BD,AD=BC,∴BC+BE=AD+AM,即CE=MD.∵CE=AC,∴AC=CE= BD =DM.∵FB=FM,∴BF⊥DF.【点睛】本题考查了矩形的性质,全等三角形的判定和对应边相等的性质,等腰三角形三线合一的性质,本题中求证DB=DM是解题的关键.8.菱形ABCD中、∠BAD=120°,点O为射线CA上的动点,作射线OM与直线BC相交于点E,将射线OM绕点O逆时针旋转60°,得到射线ON,射线ON与直线CD相交于点F.(1)如图①,点O与点A重合时,点E,F分别在线段BC,CD上,请直接写出CE,CF,CA三条段段之间的数量关系;(2)如图②,点O在CA的延长线上,且OA=13AC,E,F分别在线段BC的延长线和线段CD的延长线上,请写出CE,CF,CA三条线段之间的数量关系,并说明理由;(3)点O在线段AC上,若AB=6,BO=7CF=1时,请直接写出BE的长.【答案】(1)CA=CE+CF.(2)CF-CE=43AC.(3)BE的值为3或5或1.【解析】【分析】(1)如图①中,结论:CA=CE+CF.只要证明△ADF≌△ACE(SAS)即可解决问题;(2)结论:CF-CE=43AC.如图②中,如图作OG∥AD交CF于G,则△OGC是等边三角形.只要证明△FOG≌△EOC(ASA)即可解决问题;(3)分四种情形画出图形分别求解即可解决问题.【详解】(1)如图①中,结论:CA=CE+CF.理由:∵四边形ABCD是菱形,∠BAD=120°∴AB=AD=DC=BC,∠BAC=∠DAC=60°∴△ABC,△ACD都是等边三角形,∵∠DAC=∠EAF=60°,∴∠DAF=∠CAE,∵CA=AD,∠D=∠ACE=60°,∴△ADF≌△ACE(SAS),∴DF=CE,∴CE+CF=CF+DF=CD=AC,∴CA=CE+CF.(2)结论:CF-CE=43 AC.理由:如图②中,如图作OG∥AD交CF于G,则△OGC是等边三角形.∵∠GOC=∠FOE=60°,∴∠FOG=∠EOC,∵OG=OC,∠OGF=∠ACE=120°,∴△FOG≌△EOC(ASA),∴CE=FG,∵OC=OG,CA=CD,∴OA=DG,∴CF-EC=CF-FG=CG=CD+DG=AC+13AC=43AC,(3)作BH⊥AC于H.∵AB=6,AH=CH=3,∴BH=33,如图③-1中,当点O在线段AH上,点F在线段CD上,点E在线段BC上时.∵7,∴22OB BH=1,∴OC=3+1=4,由(1)可知:CO=CE+CF,∵OC=4,CF=1,∴CE=3,∴BE=6-3=3.如图③-2中,当点O在线段AH上,点F在线段DC的延长线上,点E在线段BC上时.由(2)可知:CE-CF=OC,∴CE=4+1=5,∴BE=1.如图③-3中,当点O在线段CH上,点F在线段CD上,点E在线段BC上时.同法可证:OC=CE+CF,∵OC=CH-OH=3-1=2,CF=1,∴CE=1,∴BE=6-1=5.如图③-4中,当点O在线段CH上,点F在线段DC的延长线上,点E在线段BC上时.同法可知:CE-CF=OC,∴CE=2+1=3,∴BE=3,综上所述,满足条件的BE的值为3或5或1.【点睛】本题属于四边形综合题,考查了全等三角形的判定和性质,等边三角形的性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.9.在平面直角坐标系中,O 为原点,点A (﹣6,0)、点C (0,6),若正方形OABC 绕点O 顺时针旋转,得正方形OA′B′C′,记旋转角为α:(1)如图①,当α=45°时,求BC 与A′B′的交点D 的坐标;(2)如图②,当α=60°时,求点B′的坐标;(3)若P 为线段BC′的中点,求AP 长的取值范围(直接写出结果即可).【答案】(1)(62,6)-;(2)(333,333)+;(3)323323AP 剟.【解析】【分析】(1)当α=45°时,延长OA′经过点B ,在Rt △BA′D 中,∠OBC =45°,A′B =626,可求得BD 的长,进而求得CD 的长,即可得出点D 的坐标;(2)过点C′作x 轴垂线MN ,交x 轴于点M ,过点B′作MN 的垂线,垂足为N ,证明△OMC′≌△C′NB′,可得C′N =OM =33,B′N =C′M =3,即可得出点B′的坐标;(3)连接OB ,AC 相交于点K ,则K 是OB 的中点,因为P 为线段BC′的中点,所以PK =12OC′=3,即点P 在以K 为圆心,3为半径的圆上运动,即可得出AP 长的取值范围. 【详解】解:(1)∵A (﹣6,0)、C (0,6),O (0,0),∴四边形OABC 是边长为6的正方形,当α=45°时,如图①,延长OA′经过点B ,∵OB =2,OA′=OA =6,∠OBC =45°,∴A′B =626,∴BD =(626)21262=-,∴CD =6﹣(1262-=626,∴BC 与A′B′的交点D 的坐标为(662-,6);(2)如图②,过点C′作x 轴垂线MN ,交x 轴于点M ,过点B′作MN 的垂线,垂足为N , ∵∠OC′B′=90°,∴∠OC′M =90°﹣∠B′C′N =∠C′B′N ,∵OC′=B′C′,∠OMC′=∠C′NB′=90°,∴△OMC′≌△C′NB′(AAS ),当α=60°时,∵∠A′OC′=90°,OC′=6,∴∠C′OM =30°,∴C′N =OM =33,B′N =C′M =3,∴点B′的坐标为)333,333-+;(3)如图③,连接OB ,AC 相交于点K ,则K 是OB 的中点,∵P 为线段BC′的中点,∴PK =12OC′=3, ∴P 在以K 为圆心,3为半径的圆上运动,∵AK =2∴AP 最大值为323,AP 的最小值为323,∴AP 长的取值范围为323323AP +剟.【点睛】本题考查正方形性质,全等三角形判定与性质,三角形中位线定理.(3)问解题的关键是利用中位线定理得出点P 的轨迹.10.在ABC V 中,ABC 90o ∠=,BD 为AC 边上的中线,过点C 作CE BD ⊥于点E ,过点A 作BD 的平行线,交CE 的延长线于点F ,在AF 的延长线上截取FG BD =,连接BG ,DF .()1求证:BD DF =;()2求证:四边形BDFG 为菱形;()3若AG 5=,CF 7=,求四边形BDFG 的周长.【答案】(1)证明见解析(2)证明见解析(3)8【解析】【分析】()1利用平行线的性质得到90CFA ∠=o ,再利用直角三角形斜边上的中线等于斜边的一半即可得证,()2利用平行四边形的判定定理判定四边形BDFG 为平行四边形,再利用()1得结论即可得证,()3设GF x =,则5AF x =-,利用菱形的性质和勾股定理得到CF 、AF 和AC 之间的关系,解出x 即可.【详解】()1证明:AG //BD Q ,CF BD ⊥,CF AG ∴⊥,又D Q 为AC 的中点,1DF AC 2∴=, 又1BD AC 2=Q , BD DF ∴=, ()2证明:BD//GF Q ,BD FG =,∴四边形BDFG 为平行四边形,又BD DF =Q ,∴四边形BDFG 为菱形,()3解:设GF x =,则AF 5x =-,AC 2x =,在Rt AFC V 中,222(2x)(7)(5x)=+-,解得:1x 2=,216x (3=-舍去), GF 2∴=,∴菱形BDFG 的周长为8.【点睛】本题考查了菱形的判定与性质直角三角形斜边上的中线,勾股定理等知识,正确掌握这些定义性质及判定并结合图形作答是解决本题的关键.11.小明在矩形纸片上画正三角形,他的做法是:①对折矩形纸片ABCD(AB>BC),使AB 与DC 重合,得到折痕EF ,把纸片展平;②沿折痕BG 折叠纸片,使点C 落在EF 上的点P 处,再折出PB 、PC ,最后用笔画出△PBC(图1).(1)求证:图1中的PBC 是正三角形: (2)如图2,小明在矩形纸片HIJK 上又画了一个正三角形IMN ,其中IJ=6cm ,且HM=JN .①求证:IH=IJ②请求出NJ 的长; (3)小明发现:在矩形纸片中,若一边长为6cm ,当另一边的长度a 变化时,在矩形纸片上总能画出最大的正三角形,但位置会有所不同.请根据小明的发现,画出不同情形的示意图(作图工具不限,能说明问题即可),并直接写出对应的a 的取值范围.【答案】(1)证明见解析;(2)①证明见解析;②1233)3<a <3,a >43【解析】分析:(1)由折叠的性质和垂直平分线的性质得出PB=PC ,PB=CB ,得出PB=PC=CB 即可;(2)①利用“HL”证Rt △IHM ≌Rt △IJN 即可得;②IJ 上取一点Q ,使QI=QN ,由Rt △IHM ≌Rt △IJN 知∠HIM=∠JIN=15°,继而可得∠NQJ=30°,设NJ=x ,则IQ=QN=2x 、QJ=3x ,根据IJ=IQ+QJ 求出x 即可得;(3)由等边三角形的性质、直角三角形的性质、勾股定理进行计算,画出图形即可. (1)证明:∵①对折矩形纸片ABCD(AB>BC),使AB 与DC 重合,得到折痕EF ∴PB=PC∵沿折痕BG 折叠纸片,使点C 落在EF 上的点P 处∴PB=BC∴PB=PC=BC∴△PBC 是正三角形:(2)证明:①如图∵矩形AHIJ∴∠H=∠J=90°∵△MNJ 是等边三角形∴MI=NI在Rt △MHI 和Rt △JNI 中MI NI MH NJ=⎧⎨=⎩ ∴Rt △MHI ≌Rt △JNI (HL )∴HI=IJ②在线段IJ 上取点Q ,使IQ=NQ∵Rt △IHM ≌Rt △IJN ,∴∠HIM=∠JIN ,∵∠HIJ=90°、∠MIN=60°,∴∠HIM=∠JIN=15°,由QI=QN知∠JIN=∠QNI=15°,∴∠NQJ=30°,设NJ=x,则IQ=QN=2x,QJ=22=3QN NJ-x,∵IJ=6cm,∴2x+3x=6,∴x=12-63,即NJ=12-63(cm).(3)分三种情况:①如图:设等边三角形的边长为b,则0<b≤6,则tan60°=3=2ab,∴a=3b,∴0<b≤63=33;②如图当DF与DC重合时,DF=DE=6,∴a=sin60°6333当DE与DA重合时,a=63sin6032==︒∴33a<3③如图∵△DEF是等边三角形∴∠FDC=30°∴DF=643cos303==︒∴a>43点睛:本题是四边形的综合题目,考查了折叠的性质、等边三角形的判定与性质、旋转的性质、直角三角形的性质、正方形的性质、全等三角形的判定与性质等知识;本题综合性强,难度较大.12.如图,点E是正方形ABCD的边A B上一点,连结CE,过顶点C作CF⊥CE,交AD延长线于F.求证:BE=DF.【答案】证明见解析.【解析】分析:根据正方形的性质,证出BC=CD,∠B=∠CDF,∠BCD=90°,再由垂直的性质得到∠BCE=∠DCF,然后根据“ASA”证明△BCE≌△BCE即可得到BE=DF详解:证明:∵CF⊥CE,∴∠ECF=90°,又∵∠BCG=90°,∴∠BCE+∠ECD =∠DCF+∠ECD∴∠BCE=∠DCF,在△BCE与△DCF中,∵∠BCE=∠DCF,BC=CD,∠CDF=∠EBC,∴△BCE≌△BCE(ASA),∴BE=DF.点睛:本题考查的是正方形的性质,熟知正方形的性质及全等三角形的判定与性质是解答此题的关键.13.在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.(1)如图①,当点E自D向C,点F自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的位置关系,并说明理由;(2)如图②,当E,F分别移动到边DC,CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不须证明)(3)如图③,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?请说明理由;(4)如图④,当E,F分别在边DC,CB上移动时,连接AE和DF交于点P,由于点E,F 的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP 的最小值.【答案】(1)AE=DF,AE⊥DF;(2)是;(3)成立,理由见解析;(4)CP=QC﹣QP=.【解析】试题分析:(1)AE=DF,AE⊥DF.先证得△ADE≌△DCF.由全等三角形的性质得AE=DF,∠DAE=∠CDF,再由等角的余角相等可得AE⊥DF;(2)是.四边形ABCD是正方形,所以AD=DC,∠ADE=∠DCF=90°,DE=CF,所以△ADE≌△DCF,于是AE=DF,∠DAE=∠CDF,因为∠CDF+∠ADF=90°,∠DAE+∠ADF=90°,所以AE⊥DF;(3)成立.由(1)同理可证AE=DF,∠DAE=∠CDF,延长FD交AE于点G,再由等角的余角相等可得AE⊥DF;(4)由于点P在运动中保持∠APD=90°,所以点P的路径是一段以AD为直径的弧,设AD 的中点为Q,连接QC交弧于点P,此时CP的长度最小,再由勾股定理可得QC的长,再求CP即可.试题解析:(1)AE=DF,AE⊥DF.理由:∵四边形ABCD是正方形,∴AD=DC,∠ADC=∠C=90°.在△ADE和△DCF中,,∴△ADE≌△DCF(SAS).∴AE=DF,∠DAE=∠CDF,由于∠CDF+∠ADF=90°,∴∠DAE+∠ADF=90°.∴AE⊥DF;(2)是;(3)成立.理由:由(1)同理可证AE=DF,∠DAE=∠CDF延长FD交AE于点G,则∠CDF+∠ADG=90°,∴∠ADG+∠DAE=90°.∴AE⊥DF;(4)如图:由于点P在运动中保持∠APD=90°,∴点P的路径是一段以AD为直径的弧,设AD的中点为Q,连接QC交弧于点P,此时CP的长度最小,在Rt△QDC中,QC=,∴CP=QC﹣QP=.考点:四边形的综合知识.14.正方形ABCD的边长为1,对角线AC与BD相交于点O,点E是AB边上的一个动点(点E不与点A、B重合),CE与BD相交于点F,设线段BE的长度为x.(1)如图1,当AD=2OF时,求出x的值;(2)如图2,把线段CE绕点E顺时针旋转90°,使点C落在点P处,连接AP,设△APE 的面积为S,试求S与x的函数关系式并求出S的最大值.【答案】(1)x=﹣1;(2)S=﹣(x﹣)2+(0<x<1),当x=时,S的值最大,最大值为,.【解析】试题分析:(1)过O作OM∥AB交CE于点M,如图1,由平行线等分线段定理得到CM=ME,根据三角形的中位线定理得到AE=2OM=2OF,得到OM=OF,于是得到BF=BE=x,求得OF=OM=解方程,即可得到结果;(2)过P作PG⊥AB交AB的延长线于G,如图2,根据已知条件得到∠ECB=∠PEG,根据全等三角形的性质得到EB=PG=x,由三角形的面积公式得到S=(1﹣x)•x,根据二次函数的性质即可得到结论.试题解析:(1)过O作OM∥AB交CE于点M,如图1,∵OA=OC,∴CM=ME,∴AE=2OM=2OF,∴OM=OF,∴,∴BF=BE=x,∴OF=OM=,∵AB=1,∴OB=,∴,∴x=﹣1;(2)过P作PG⊥AB交AB的延长线于G,如图2,∵∠CEP=∠EBC=90°,∴∠ECB=∠PEG,∵PE=EC,∠EGP=∠CBE=90°,在△EPG与△CEB中,,∴△EPG≌△CEB,∴EB=PG=x,∴AE=1﹣x,∴S=(1﹣x)•x=﹣x2+x=﹣(x﹣)2+,(0<x<1),∵﹣<0,∴当x=时,S的值最大,最大值为,.考点:四边形综合题15.倡导研究性学习方式,着力教材研究,习题研究,是学生跳出题海,提高学习能力和创新能力的有效途径.下面是一案例,请同学们认真阅读、研究,完成“类比猜想”的问题.习题如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.解答:∵正方形ABCD中,AB=AD,∠BAD=∠ADC=∠B=90°,∴把△ABE绕点A逆时针旋转90°至△ADE′,点F、D、E′在一条直线上.∴∠E′AF=90°-45°=45°=∠EAF,又∵AE′=AE,AF=AF∴△AE′F≌△AEF(SAS)∴EF=E′F=DE′+DF=BE+DF.类比猜想:(1)请同学们研究:如图(2),在菱形ABCD中,点E、F分别在BC、CD上,当∠BAD=120°,∠EAF=60°时,还有EF=BE+DF吗?请说明理由.(2)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180°,∠EAF=∠BAD时,EF=BE+DF吗?请说明理由.【答案】证明见解析.【解析】试题分析:(1)把△ABE绕点A逆时针旋转120°至△ADE′,如图(2),连结E′F,根据菱形和旋转的性质得到AE=AE′,∠EAF=∠E′AF,利用“SAS”证明△AEF≌△AE′F,得到EF=E′F;由于∠ADE′+∠ADC=120°,则点F、D、E′不共线,所以DE′+DF>EF,即由BE+DF>EF;(2)把△ABE绕点A逆时针旋转∠BAD的度数至△ADE′,如图(3),根据旋转的性质得到AE′=AE,∠EAF=∠E′AF,然后利用“SAS”证明△AEF≌△AE′F,得到EF=E′F,由于∠ADE′+∠ADC=180°,知F、D、E′共线,因此有EF=DE′+DF=BE+DF;根据前面的条件和结论可归纳出结论.试题解析:(1)当∠BAD=120°,∠EAF=60°时,EF=BE+DF不成立,EF<BE+DF.理由如下:∵在菱形ABCD中,∠BAD=120°,∠EAF=60°,∴AB=AD,∠1+∠2=60°,∠B=∠ADC=60°,∴把△ABE绕点A逆时针旋转120°至△ADE′,如图(2),连结E′F,∴∠EAE′=120°,∠1=∠3,AE′=AE,DE′=BE,∠ADE′=∠B=60°,∴∠2+∠3=60°,∴∠EAF=∠E′AF,在△AEF和△AE′F中,∴△AEF≌△AE′F(SAS),∴EF=E′F,∵∠ADE′+∠ADC=120°,即点F、D、E′不共线,∴DE′+DF>EF∴BE+DF>EF;(2)当AB=AD,∠B+∠D=180°,∠EAF=∠BAD时,EF=BE+DF成立.理由如下:如图(3),∵AB=AD,∴把△ABE绕点A逆时针旋转∠BAD的度数至△ADE′,如图(3),∴∠EAE′=∠BAD,∠1=∠3,AE′=AE,DE′=BE,∠ADE′=∠B,∵∠B+∠D=180°,∴∠ADE′+∠D=180°,∴点F、D、E′共线,∵∠EAF=∠BAD,∴∠1+∠2=∠BAD,∴∠2+∠3=∠BAD,∴∠EAF=∠E′AF,在△AEF和△AE′F中,∴△AEF≌△AE′F(SAS),∴EF=E′F,∴EF=DE′+DF=BE+DF;归纳:在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180°,∠EAF=∠BAD时,EF=BE+DF.考点:四边形综合题.。
中考数学 易错压轴选择题精选:平行四边形选择题(含答案)50

中考数学 易错压轴选择题精选:平行四边形选择题(含答案)50一、易错压轴选择题精选:平行四边形选择题1.如图,在正方形ABCD 中,AB =4,E 是CD 的中点,将BCE 沿BE 翻折至BFE ,连接DF ,则DF 的长度是( )A .55B .255C .355D .4552.如图,BD 为平行四边形ABCD 的对角线,45DBC ∠=︒,DE BC ⊥于E ,BF CD ⊥于F ,DE 、BF 相交于H ,直线BF 交线段AD 的延长线于G ,下面结论:①2BD BE =;②A BHE =∠∠;③AB BH =;④BHD BDG ∠=∠其中正确的个数是( )A .1B .2C .3D .43.如图所示,四边形ABCD 是边长为1的正方形,E 为BC 边的中点,沿AP 折叠使D 点落在AE 上的点H 处,连接PH 并延长交BC 于点F ,则EF 的长为( )A 525-B 55-C .353D .144.如图,矩形ABCD 的面积为20cm 2,对角线相交于点O .以AB 、AO 为邻边画平行四边形AOC 1B ,对角线相交于点O ;以AB 、AO 为邻边画平行四边形AO 1C 2B ,对角线相交于点O 2 :……以此类推,则平行四边形AO 4C 5B 的面积为( )A .58cm 2B .54cm 2C .516cm 2D . 5 32cm 2 5.如图,一个四边形花坛ABCD ,被两条线段MN , EF 分成四个部分,分别种上红、黄、紫、白四种花卉,种植面积依次是S 1、S 2、S 3、S 4,若MN ∥AB ∥DC ,EF ∥DA ∥CB ,则有( )A .S 1= S 4B .S 1 + S 4 = S 2 + S 3C .S 1 + S 3 = S 2 + S 4D .S 1·S 4 = S 2·S 36.如图,在菱形ABCD 中,AB=AC=1,点E 、F 分别为边AB 、BC 上的点,且AE=BF ,连接CE 、AF 交于点H ,连接DH 交AC 于点O ,则下列结论:①△ABF ≌△CAE ;②∠FHC=∠B ;③△ADO ≌△ACH ;④=3ABCD S 菱形;其中正确的结论个数是( )A .1个B .2个C .3个D .4个7.如图,正方形ABCD 中,AB =6,点E 在边CD 上,且CD =3DE .将△ADE 沿AE 对折至△AFE ,延长EF 交边BC 于点G ,连结AG 、CF .下列结论:①△ABG ≌△AFG ;②BG =GC ;③AG ∥CF ;④S △FGC =185.其中正确结论的个数是( )A .1B .2C .3D .48.如图,在正方形ABCD 中,点E ,F 分别在BC ,CD 上,AE AF =,AC 与EF 相交于点G .下列结论:①AC 垂直平分EF ;②BE DF EF +=;③当15DAF ∠=︒时,AEF 为等边三角形;④当60EAF ∠=︒时,AEB AEF ∠=∠.其中正确的结论是( )A .①③B .②④C .①③④D .②③④9.如图,矩形ABCD 的对角线AC 、BD 交于点O ,点P 在边AD 上从点A 到点D 运动,过点P 作PE ⊥AC 于点E ,作PF ⊥BD 于点F ,已知AB=3,AD=4,随着点P 的运动,关于PE+PF 的值,下面说法正确的是( )A .先增大,后减小B .先减小,后增大C .始终等于2.4D .始终等于310.如图,正方形ABCD 中,延长CB 至E 使2CB EB =,以EB 为边作正方形EFGB ,延长FG 交DC 于M ,连接AM ,AF ,H 为AD 的中点,连接FH 分别与AB ,AM 交于点,N K .则下列说法:①ANH GNF △≌△;②DAM NFG ∠=∠;③2FN NK =;④:2:7AFN DMKH S S =△四边形.其中正确的有( )A .4个B .3个C .2个D .1个11.如图,正方形ABCD 中,在AD 的延长线上取点E ,F ,使DE =AD ,DF =BD ,连接BF 分别交CD ,CE 于H ,G 下列结论:①EC≠2HG ;②∠GDH =∠GHD ;③图中有8个等腰三角形;④CDG DHF S S △△=.其中正确的结论有( )个A .1B .2C .3D .412.如图,在Rt ABC 中,90ACB ∠=︒,分别以AB ,AC ,BC 为边,在AB 的同侧作正方形ABHI ,ACFG ,BCED .若图中两块阴影部分的面积分别记为1S ,2S ,则对1S ,2S 的大小判断正确的是( )A .12S S >B .12S SC .12S S <D .无法确定13.如图,在矩形ABCD 中,AB =8,BC =4.将矩形沿AC 折叠,CD ′与AB 交于点F ,则AF :BF 的值为( )A .2B .53C .54D .3 14.如图,ABCD 中,点E 是AD 上一点,BE ⊥AB ,△ABE 沿BE 对折得到△BEG ,过点D 作DF ∥EG 交BC 于点F ,△DFC 沿DF 对折,点C 恰好与点G 重合,则AB AD的值为( )A .12B 3C 2D .3215.如图,在ABC 中,AB =AC =6,∠B =45°,D 是BC 上一个动点,连接AD ,以AD 为边向右侧作等腰ADE ,其中AD =AE ,∠ADE =45°,连接CE .在点D 从点B 向点C 运动过程中,CDE △周长的最小值是( )A .62B .626+C .92D .926+16.如图,四边形ABCD 中,AD ∥BC ,∠ABC+∠DCB=90°,且BC=2AD ,以AB 、BC 、DC 为边向外作正方形,其面积分别为1S 、2S 、3S ,若1S =3,3S =8,则2S 的值为( )A .22B .24C .44D .4817.如图,点P ,Q 分别是菱形ABCD 的边AD ,BC 上的两个动点,若线段PQ 长的最大值为85 ,最小值为8,则菱形ABCD 的边长为( )A .4 6B .10C .12D .1618.如图,90MON ∠=︒,矩形ABCD 在MON ∠的内部,顶点A ,B 分别在射线OM ,ON 上,4AB =,2BC =,则点D 到点O 的最大距离是( )A .22B .222C .252D 22+19.矩形纸片ABCD 中,AB =5,AD =4,将纸片折叠,使点B 落在边CD 上的点B '处,折痕为AE .延长B E '交AB 的延长线于点M ,折痕AE 上有点P ,下列结论中:①M DAB '∠∠=;②PB PB '=;③AE =552;④MB CD '=;⑤若B P CD '⊥,则EB B P ''=.正确的有( )个A .2B .3C .4D .520.如图,在菱形ABCD 中,若E 为对角线AC 上一点,且CE CD =,连接DE ,若5,8AB AC ==,则DE AD=( )A .104B .105C .35D .4521.如图,ABCD 的对角线,AC BD 交于点,O DE 平分ADC ∠交BC 于点,60,E BCD ∠=︒2,AD AB =连接OE .下列结论:ABCD S AB BD =⋅①;DB ②平分ADE ∠;AB DE =③;CDE BOC S S =④,其中正确的有( )A .1个B .2个C .3个D .4个22.如图,ABCD 的对角线AC 、BD 相较于点O ,AE 平分∠BAD 交BC 于点E ,∠ADC =60°,AB =12BC ,连接OE ,下列结论:①∠CAD =30°;②·ABCD A S AB C =;③OA =OB ;④OE =14B C .其中成立的个数是( )A .1B .2C .3D .423.如图,正方形ABCD 的边长为1,以对角线AC 为边作第二个正方形ACEF ,再以对角线AE为边作第三个正方形AEGH,依此下去,第n个正方形的面积为()A.(2)n﹣1B.2n﹣1C.(2)n D.2n24.如图,已知△ABC的面积为12,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为()A.2 B.3 C.4 D.525.如图,已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(10,0),点B(0,6),点P为BC边上的动点,将△OBP沿OP折叠得到△OPD,连接CD、AD.则下列结论中:①当∠BOP=45°时,四边形OBPD为正方形;②当∠BOP=30°时,△OAD的面积为15;③当P在运动过程中,CD的最小值为234﹣6;④当OD⊥AD时,BP=2.其中结论正确的有()A.1个B.2个C.3个D.4个26.如图,在ABC中,AB=5,AC=12,BC=13,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为()A.6013B.3013C.2413D.121327.如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:①OH ∥BF ,②GH=14BC ,③BF=2OD ,④∠CHF=45°.正确结论的个数为( )A .4个B .3个C .2个D .1个28.已知,如图,在菱形ABCD 中.(1)分别以C ,D 为圆心,大于12CD 长为半径作弧,两弧分别交于点E ,F ;(2)作直线EF ,且直线EF 恰好经过点A ,且与边CD 交于点M ;(3)连接BM .根据以上作图过程及所作图形,判断下列结论中错误..的是( )A .∠ABC =60°B .如果AB =2,那么BM =4C .BC =2CMD .2ABM ADM S S =△△29.如图,在□ABCD 中,AD=2AB ,F 是AD 的中点,作CE ⊥AB ,垂足E 在线段AB 上(E 不与A 、B 重合),连接EF 、CF ,则下列结论中一定成立的是 ( )①∠DCF=12∠BCD ;②EF=CF ;③2BEC CEF S S ∆∆<;④∠DFE=4∠AEF A .①②③④B .①②③C .①②D .①②④ 30.如图,在边长为6的正方形ABCD 中,E 是边CD 的中点,将ADE 沿AE 对折至AFE ,延长交BC 于点G ,连接AG.则BG 的长( )A .1B .2C 3D .3【参考答案】***试卷处理标记,请不要删除一、易错压轴选择题精选:平行四边形选择题1.D【分析】由勾股定理可求BE的长,由折叠的性质可得CE=EF=2,BE⊥CF,FH=CH,由面积法可求CH=455,由勾股定理可求EH的长,由三角形中位线定理可求DF=2EH=455.【详解】解:如图,连接CF,交BE于H,∵在正方形ABCD中,AB=4,E是CD的中点,∴BC=CD=4,CE=DE=2,∠BCD=90°,∴BE2216425BC CE+=+=∵将△BCE沿BE翻折至△BFE,∴CE=EF=2,BE⊥CF,FH=CH,∵S△BCE=12×BE×CH=12×BC×CE,∴CH=55,∴22165 455CE CH-=-=,∵CE=DE,FH=CH,∴DF=2EH=55,故选:D.【点睛】本题考查了翻折变换,正方形的性质,全等三角形的判定与性质,掌握折叠的性质是本题的关键.2.B【分析】通过判断△BDE为等腰直角三角形,根据等腰直角三角形的性质和勾股定理可对①进行判断;根据等角的余角相等得到∠BHE=∠C,再根据平行四边形的性质得到∠A=∠C,则∠A=∠BHE ,于是可对②进行判断;证明△BEH ≌△DEC ,得到BH=CD ,接着由平行四边形的性质得AB=CD ,则AB=BH ,可对③进行判断;因为∠BHD=90°+∠EBH ,∠BDG=90°+∠BDE ,由∠BDE >∠EBH ,推出∠BDG >∠BHD ,可判断④.【详解】解:∵∠DBC=45°,DE ⊥BC ,∴△BDE 为等腰直角三角形,,BE DE BD ∴====,所以①错误;∵BF ⊥CD ,∴∠C+∠CBF=90°,而∠BHE+∠CBF=90°,∴∠BHE=∠C ,∵四边形ABCD 为平行四边形,∴∠A=∠C ,∴∠A=∠BHE ,所以②正确;在△BEH 和△DEC 中BHE C HEB CED BE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BEH ≌△DEC ,∴BH=CD ,∵四边形ABCD 为平行四边形,∴AB=CD ,∴AB=BH ,所以③正确;∵∠BHD=90°+∠EBH ,∠BDG=90°+∠BDE ,∵∠BDE=∠DBE >∠EBH ,∴∠BDG >∠BHD ,所以④错误;故选:B .【点睛】本题考查平行四边形的性质,全等三角形的性质和判定,等腰直角三角形的判定和性质,三角形外角的性质.熟练掌握平行四边形的性质并能灵活运用是解题关键,本题中主要用到平行四边形对边相等,对角相等.3.A【分析】首先证明Rt △AFB ≌Rt △AFH ,推出BF=FH ,设EF=x ,则BF=FH=12x -,在Rt △FEH 中,根据222,EF EH FH =+构建方程即可解决问题;【详解】解:连接AF .∵四边形ABCD 是正方形, ∴AD=BC=1,∠B=90°,∵BE=EC=12, ∴225AB BE += 由翻折不变性可知:AD=AH=AB=1,∴51-, ∵∠B=∠AHF=90°,AF=AF ,AH=AB ,∴Rt △AFB ≌Rt △AFH ,∴BF=FH ,设EF=x ,则BF=FH=12x -, 在Rt △FEH 中,∵222,EF EH FH =+ ∴22215()1),22x x =-+- ∴5252x -= 故选:A .【点睛】本题考查翻折变换、正方形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是准确寻找全等三角形解决问题,学会利用参数构建方程解决问题,4.A【分析】设矩形ABCD 的面积为S=20cm 2,由O 为矩形ABCD 的对角线的交点,可得平行四边形AOC 1B 底边AB 上的高等于BC 的12,依此类推可得下一个图形的面积是上一个图形的面积的12,然后求解即可. 【详解】 设矩形ABCD 的面积为S=20cm 2,∵O 为矩形ABCD 的对角线的交点,∴平行四边形AOC 1B 底边AB 上的高等于BC 的12, ∴平行四边形AOC 1B 的面积=12S , ∵平行四边形AOC 1B 的对角线交于点O 1,∴平行四边形AO 1C 2B 的边AB 上的高等于平行四边形AOC 1B 底边AB 上的高的12, ∴平行四边形AO 1C 2B 的面积=12×12S=22S , ……依此类推,平行四边形AO 4C 5B 的面积=52S =5202=58(cm 2), 故选:A .【点睛】本题考查了矩形的对角线互相平分,平行四边形的对角线互相平分的性质,得到下一个图形的面积是上一个图形的面积的12是解题的关键. 5.D【分析】由于在四边形中,MN ∥AB ∥DC ,EF ∥DA ∥CB ,因此MN 、EF 把一个平行四边形分割成四个小平行四边形.可设MN 到DC 的距离为h 1,MN 到AB 的距离为h 2,根据AB=CD ,DE=AF ,EC=FB 及平行四边形的面积公式即可得出答案.【详解】解:∵MN ∥AB ∥DC ,EF ∥DA ∥CB ,∴四边形ABCD ,四边形ADEF ,四边形BCEF ,红、紫、黄、白四边形都为平行四边形, ∴AB=CD ,DE=AF ,EC=BF .设MN 到DC 的距离为h 1,MN 到AB 的距离为h 2,则S 1=DE •h 1,S 2=AF •h 2,S 3=EC •h 1,S 4=FB •h 2,因为DE ,h 1,FB ,h 2的关系不确定,所以S 1与S 4的关系无法确定,故A 错误; S 1+S 4=DE •h 1+FB •h 2=AF •h 1+FB •h 2,S 2+S 3=AF •h 2+EC •h 1=AF •h 2+FB •h 1,故B 错误; S 1+S 3=CD •h 1,S 2+S 4=AB •h 2,又AB=CD ,而h 1不一定与h 2相等,故C 错误;S 1·S 4=DE •h1•FB •h 2=AF •h 1•FB •h 2,S 2·S 3=AF •h 2•EC •h 1=AF •h 2•FB •h 1,所以S 1·S 4=S 2·S 3, 故D 正确;故选:D .【点睛】本题考查平行四边形的判定与性质,注意掌握平行四边形的面积等于平行四边形的边长与该边上的高的积.即S=a •h .其中a 可以是平行四边形的任何一边,h 必须是a 边与其对边的距离,即对应的高.6.B【分析】根据菱形的性质,利用SAS 证明即可判断①;根据△ABF ≌△CAE 得到∠BAF=∠ACE ,再利用外角的性质以及菱形内角度数即可判断②;通过说明∠CAH≠∠DAO ,判断△ADO ≌△ACH 不成立,可判断③;再利用菱形边长即可求出菱形面积,可判断④.【详解】解:∵在菱形ABCD 中,AB=AC=1,∴△ABC 为等边三角形,∴∠B=∠CAE=60°,又∵AE=BF ,∴△ABF ≌△CAE (SAS ),故①正确;∴∠BAF=∠ACE ,∴∠FHC=∠ACE+∠HAC=∠BAF+∠HAC=60°,故②正确;∵∠B=∠CAE=60°,则在△ADO 和△ACH 中,∠OAD=60°=∠CAB ,∴∠CAH≠60°,即∠CAH≠∠DAO ,∴△ADO ≌△ACH 不成立,故③错误;∵AB=AC=1,过点A 作AG ⊥BC ,垂足为G ,∴∠BAG=30°,BG=12, ∴AG=22AB BG -=32, ∴菱形ABCD 的面积为:BC AG ⨯=312⨯=32,故④错误; 故正确的结论有2个,故选B.【点睛】本题考查了全等三角形判定和性质,菱形的性质和面积,等边三角形的判定和性质,外角的性质,解题的关键是利用菱形的性质证明全等.7.D【分析】由正方形和折叠的性质得出AF =AB ,∠B =∠AFG =90°,由HL 即可证明Rt △ABG ≌Rt △AFG ,得出①正确;设BG =x ,则CG =BC−BG =6−x ,GE =GF +EF =BG +DE =x +2,由勾股定理求出x =3,得出②正确;由等腰三角形的性质和外角关系得出∠AGB =∠FCG ,证出平行线,得出③正确; 根据三角形的特点及面积公式求出△FGC 的面积=185,得出④正确. 【详解】∵四边形ABCD 是正方形,∴AB =AD =DC =6,∠B =D =90°,∵CD =3DE ,∴DE =2,∵△ADE 沿AE 折叠得到△AFE ,∴DE =EF =2,AD =AF ,∠D =∠AFE =∠AFG =90°,∴AF =AB ,∵在Rt △ABG 和Rt △AFG 中, AG AG AB AF =⎧⎨=⎩, ∴Rt △ABG ≌Rt △AFG (HL ),∴①正确;∵Rt △ABG ≌Rt △AFG ,∴BG =FG ,∠AGB =∠AGF ,设BG =x ,则CG =BC−BG =6−x ,GE =GF +EF =BG +DE =x +2,在Rt △ECG 中,由勾股定理得:CG 2+CE 2=EG 2,∵CG =6−x ,CE =4,EG =x +2∴(6−x )2+42=(x +2)2解得:x =3,∴BG =GF =CG =3,∴②正确;∵CG =GF ,∴∠CFG =∠FCG ,∵∠BGF =∠CFG +∠FCG ,又∵∠BGF =∠AGB +∠AGF ,∴∠CFG +∠FCG =∠AGB +∠AGF ,∵∠AGB =∠AGF ,∠CFG =∠FCG ,∴∠AGB =∠FCG ,∴AG ∥CF ,∴③正确;∵△CFG 和△CEG 中,分别把FG 和GE 看作底边,则这两个三角形的高相同. ∴35CFG CEG S FG S GE ==, ∵S △GCE =12×3×4=6, ∴S △CFG =35×6=185, ∴④正确;正确的结论有4个,故选:D .【点睛】本题考查了正方形性质、折叠性质、全等三角形的性质和判定、等腰三角形的性质和判定、平行线的判定等知识点的运用;主要考查学生综合运用性质进行推理论证与计算的能力,有一定难度.8.A【分析】①通过条件可以得出△ABE ≌△ADF ,从而得出∠BAE=∠DAF ,BE=DF ,由正方形的性质就可以得出EC=FC ,就可以得出AC 垂直平分EF ,②设BC=x ,CE=y ,由勾股定理就可以得出EF 与x 、y 的关系,表示出BE 与EF ,即可判断BE+DF 与EF 关系不确定;③当∠DAF=15°时,可计算出∠EAF=60°,即可判断△EAF 为等边三角形,④当∠EAF=60°时,可证明△AEF 是等边三角形,从而可得∠AEF=60°,而△CEF 是等腰直角三角形,得∠CEF=45°,从而可求出∠AEB=75°,进而可得结论.【详解】解:①四边形ABCD 是正方形,∴AB ═AD ,∠B=∠D=90°.在Rt △ABE 和Rt △ADF 中,AE AF AB AD ⎧⎨⎩==, ∴Rt △ABE ≌Rt △ADF (HL ),∴BE=DF∵BC=CD ,∴BC-BE=CD-DF ,即CE=CF ,∵AE=AF ,∴AC 垂直平分EF .(故①正确).②设BC=a ,CE=y ,∴BE+DF=2(a-y )EF=y ,∴BE+DF 与EF关系不确定,只有当y=()a 时成立,(故②错误).③当∠DAF=15°时,∵Rt △ABE ≌Rt △ADF ,∴∠DAF=∠BAE=15°,∴∠EAF=90°-2×15°=60°,又∵AE=AF∴△AEF 为等边三角形.(故③正确).④当∠EAF=60°时,由①知AE=AF ,∴△AEF 是等边三角形,∴∠AEF=60°,又△CEF 为等腰直角三角形,∴∠CEF=45°∴∠AEB=180°-∠AEF-∠CEF=75°,∴∠AEB≠∠AEF ,故④错误.综上所述,正确的有①③,故选:A .【点睛】本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,等边三角形的性质的运用,三角形的面积公式的运用,解答本题时运用勾股定理的性质解题时关键.9.C【分析】在矩形ABCD 中,由矩形边长,可得矩形面积是12,进而得134AOD ABCD S S ==矩形,由矩形对角线相等且互相平分得AO OC =,OB OD =,AC BD =,利用勾股定理可解得5AC =,则52OA OD ==,111()3222AOD AOP DOP S S S OA PE OD PF OA PE PF =+=+=+==,即可求出PE+PF 的值.【详解】解:连接PO ,如下图:∵在矩形ABCD 中,AB=3,AD=4,∴12ABCD S AB BC ==矩形,AO OC =,OB OD =,AC BD =,5AC , ∴1112344AOD ABCD S S ==⨯=矩形, 52OA OD ==, 11115()()322222AOD AOP DOP S S S OA PE OD PF OA PE PF PE PF =+=+=+=⨯+=,∴12 2.45PE PF +==; 故选C .【点睛】本题主要考查了矩形的性质,利用等积法间接求三角形的高线长及用勾股定理求直角三角形的斜边;利用面积法求解,是本题的解题突破点.10.A【分析】根据正方形的性质,以及中点的性质可得△FGN ≌△HAN ,即证①;利用角度之间的等量关系的转换可以判断②;根据△AKH ∽△MKF ,进而利用相似三角形的性质即可判断③;设AN=12AG=x ,则AH=2x ,FM=6x ,根据△AKH ∽△MKF 得出2163AH x MF x ==,再利用三角形的面积公式求出△AFN 的面积,再利用DHKM ADM AKH S SS =-即可求出四边形DHKM的面积,作比即可判断④.【详解】 ∵四边形EFGB 是正方形,CE=2EB ,四边形ABCD 是正方形∴G 为AB 中点,∠FGN=∠HAN=90°,AD=AB即FG=AG=GB=12AB 又H 是AD 的中点AH=12AD ∴FG=HA又∠FNG=∠HNA∴△FGN ≌△HAN ,故①正确;∵∠DAM+∠GAM=90°又∠NFG+∠FNG=90°即∠FNG=∠GAM∵∠FNG+∠NFG+90°=180°∠AMD+∠DAM+90°=180°∠FNG=∠GAM=∠AMD∴DAM NFG ∠=∠,故②正确;由图可得:MF=FG+MG=3EB△AKH ∽△MKF ∴13KH AH KF MF == ∴KF=3KH又∵NH=NF 且FH=KF+KH=4KH=NH+NF∴NH=NF=2KH∴KH=KN∴FN=2NK ,故③正确;∵AN=GN 且AN+GN=AG∴可设AN=12AG=x ,则AH=2x ,FM=6x 由题意可得:△AKH ∽△MKF 且相似比为:2163AH x MF x == ∴△AKH 以AH 为底边的高为:11242x x ⨯= ∴212AFN S AN FG x =⨯⨯= 112225DHKM ADM AKH S S S AD DM AH x =-=⨯⨯-⨯⨯ 211172422222x x x x x =⨯⨯-⨯⨯= ∴2:7AFN DHKM S S =,故④正确; 故答案选择A .【点睛】本题考查了矩形、全等三角形的判定与性质以及相似三角形的判定与性质,难度较大,需要熟练掌握相关基础知识.11.B【分析】关键结合图形证明△CHG ≌△EGD ,即可逐项判断求解【详解】解:∵DF=BD ,∴∠DFB=∠DBF ,∵AD ∥BC ,DE=BC ,∴四边形DBCE 是平行四边形,∠DFB=∠GBC ,∴∠DEC=∠DBC=45°,∴∠DEC=2∠EFB ,∴∠EFB=22.5°,∠CGB=∠CBG=22.5°,∴CG=BC=DE ,∵DE=DC ,∴∠DEG=∠DCE ,∵∠GHC=∠CDF+∠DFB=90°+22.5°=112.5°,∠DGE=180°-(∠BGD+∠EGF ),=180°-(∠BGD+∠BGC ),=180°-(180°-∠DCG )÷2,=180°-(180°-45°)÷2,=112.5°,∴∠GHC=∠DGE ,∴△CHG ≌△EGD ,∴∠EDG=∠CGB=∠CBF ,∴∠GDH=90°-∠EDG ,∠GHD=∠BHC=90°-∠CGB ,∴∠GDH=∠GHD故②正确;∴∠GDH=∠GHD又∠EFB=22.5°,∴∠DHG=∠GDH=67.5°∴∠GDF=90°-∠GDH=22.5°=∠EFB,∴DG=GF,∴HG=DG=GF∴HF=2HG,显然CE≠HF=2HG,故①正确;∵△CHG ≌△EGD ,∴CHG EGD S S ∆∆=∴CHG DHG EGD DHG S S S S ∆∆∆∆+=+,即CDG DHGE S S △四边形=而=EFG DHGE DHF S S S ∆+四边形△,故CDG DHF S S ≠△△故④不正确;结合前面条件易知等腰三角形有△ABD ,△CDB ,△BDF ,△CDE ,△BCG ,△DGH ,△EGF ,△CDG ,△DGF 共9个,∴③错误;故正确的有①②,有2个,故选:B【点睛】本题主要考查对三角形的内角和定理,全等三角形的判定和性质,等腰三角形的性质和判定,正方形的性质,等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.12.B【分析】连接EH,过点H作HK⊥BF于点K,令AE与BH交于点J,HL与BF交于点L,根据已知条件易证△BHK≌△ABC,继而由全等三角形的性质得S△BHK=S△ABC,BC=HK,∠ABC=∠BHK,再由全等三角形的判定可得△BCJ≌△HKL,进而可得S1=S△BHK=S△ABC,由正方形的性质和全等三角形的判定可知△ABC≌△AIG,继而可得S△ABC=S△AIG=S2,等量代换即可求解.【详解】解:连接EH,过点H作HK⊥BF于点K,令AE与BH交于点J,HL与BF交于点L,由题意可知:四边形BCED是正方形,四边形ACFG是正方形,四边形ABHI是正方形,∠ACB=90°∴∠CEH=∠ECK=90° ,CE=BC∵∠BKH=90°,∴四边形CEHK是矩形,∴ CE=HK又∠HBK+∠ABC=90°, ∠BAC+∠ABC=90°∴∠HBK=∠BAC∴△BHK≌△ABC(AAS)∴S△BHK=S△ABC,BC=HK,∠ABC=∠BHK,∵∠ABC+∠CBJ=90°,∠BHK+∠KHL=90°∴∠CBJ=∠KHL∴△BCJ≌△HKL(ASA)∴S△BCJ=S△HKL,∴S1=S△BHK=S△ABC,∵四边形ACFG是正方形,四边形ABHI是正方形,∴AB=AI,AC=AG,∠G=∠ACB=90°∴△ABC≌△AIG(SAS)∴S△ABC=S△AIG=S2,即S1=S2故选:B【点睛】本题主要考查正方形的性质,全等三角形的判定及其性质,解题的关键是熟练掌握正方形的性质及全等三角形的判定方法.13.B【分析】由折叠的性质可得∠DCA =∠ACF ,由平行线的性质可得∠DCA =∠CAB =∠ACF ,可得FA =FC ,设BF =x ,在Rt △BCF 中,根据CF 2=BC 2+BF 2,可得方程(8﹣x )2=x 2+42,可求BF =3,AF =5,即可求解.【详解】解:设BF =x ,∵将矩形沿AC 折叠,∴∠DCA =∠ACF ,∵四边形ABCD 是矩形,∴CD ∥AB ,∴∠DCA =∠CAB =∠ACF ,∴FA =FC =8﹣x ,在Rt △BCF 中,∵CF 2=BC 2+BF 2,∴(8﹣x )2=x 2+42,∴x =3,∴BF =3,∴AF =5,∴AF :BF 的值为53, 故选:B .【点睛】本题考查矩形的性质、翻折变换、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.14.B【分析】根据平行线的性质和轴对称的性质,利用SAS 证明BEG DEG ≅,进而得到ADG 90∠=︒,设AB=x ,则AG=2x ,CD=x ,2243x x x -,即可求解.【详解】解:在ABCD 中∵DF ∥EG∴∠DEG=∠DFB∵△ABE 沿BE 对折得到△BEG∴∠DEG =2∠A∵∠DFB =∠C +∠CDF∠A=∠C∴∠CDF=∠A∵△DFC 沿DF 对折∴∠BGE=∠DGEBG=DGEG=EG∴BEG DEG ≅∵BE⊥AB∴ADG 90∠=︒设AB=x ,则AG=2x ,CD=x ,=∴3AB AD == 故选:B .【点睛】此题主要考查平行线的性质、轴对称的性质、全等三角形的判断和性质、勾股定理,熟练运用平行线的性质和轴对称的性质证明BEG DEG ≅是解题关键.15.B【分析】 如图(见解析),先根据等腰直角三角形的判定与性质可得90,BAC DAE BC DE ∠=∠=︒==,再根据三角形全等的判定定理与性质可得BD CE =,从而可得CDE △周长为BC +,然后根据垂线段最短可求出AD 的最小值,由此即可得.【详解】在ABC 中,6,45AB AC B ==∠=︒,ABC ∴是等腰直角三角形,90,BAC BC ∠=︒==在ADE 中,,45AD AE ADE =∠=︒,ADE ∴是等腰直角三角形,90,DAE DE ∠=︒==,90BAD CAD CAE CAD ∴∠+∠=∠+∠=︒,BAD CAE ∴∠=∠,在ABD △和ACE △中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,()ABD ACE SAS ∴≅,BD CE ∴=,CDE ∴周长为622CD CE DE CD BD DE BC DE AD ++=++=+=+, 则当AD 取得最小值时,CDE △的周长最小,由垂线段最短可知,当AD BC ⊥时,AD 取得最小值,AD ∴是BC 边上的中线(等腰三角形的三线合一),1322AD BC ∴==(直角三角形斜边上的中线等于斜边的一半), CDE ∴周长的最小值为62232626+⨯=+,故选:B .【点睛】本题考查了等腰直角三角形的判定与性质、直角三角形斜边上的中线、三角形全等的判定定理与性质、垂线段最短等知识点,正确找出两个全等三角形是解题关键.16.C【分析】根据已知条件得到AB 3CD =2,过A 作AE ∥CD 交BC 于E ,则∠AEB =∠DCB ,根据平行四边形的性质得到CE =AD ,AE =CD =2BAE =90°,根据勾股定理得到BE 22AB AE +,于是得到结论.【详解】∵S 1=3,S 3=8∴AB 3,CD =2过A 作AE ∥CD 交BC 于E则∠AEB =∠DCB∵AD ∥BC∴四边形AECD 是平行四边形∴CE =AD ,AE =CD =22 ∵∠ABC +∠DCB =90°∴∠AEB +∠ABC =90°∴∠BAE =90°∴BE =3811+=∵BC =2AD∴BC =2BE =211∴S 2=()221144=故选:C .【点睛】本题考查平行四边形的判定和性质,勾股定理,能正确作辅助线构造直角三角形是解决此题的关键.17.B【分析】当点P 和点A 重合时,当点C 和点Q 重合时,PQ 的值最大,当PQ ⊥BC 时,PQ 的值最小,利用这两组数据,在Rt△ABQ 中,可求得答案.【详解】当点P 和点A 重合时,当点C 和点Q 重合时,PQ 的值最大,85PQ =当PQ ⊥BC 时,PQ 的值最小,∴PQ=8,∠Q=90°,在Rt △ACQ 中, ()2285816.CQ =-=在Rt △ABQ 中,设AB=BC=x ,则BQ=16-x ,∴AQ 2+BQ 2=AB 2即82+(16-x )2=x 2解之:x=10.故答案为:B .【点睛】本题考查菱形的性质和勾股定理的运用,解题关键是根据菱形的性质,判断出PQ 最大和最小的情况.18.B【分析】取DC 的中点E ,连接OE 、DE 、OD ,根据三角形的任意两边之和大于第三边可知当O 、E 、D 三点共线时,点D 到点O 的距离最大,再根据勾股定理求出DE 的长,根据直角三角形斜边上的中线等于斜边的一半求出OE 的长,两者相加即可得解.【详解】取AB 中点E ,连接OE 、DE 、OD ,90MON ∠=︒,122OE AB ∴==. 在Rt DAE ∆中,利用勾股定理可得22DE =.在ODE ∆中,根据三角形三边关系可知DE OE OD +>,∴当O 、E 、D 三点共线时,OD 最大为222OE DE +=+.故选B .【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半得到性质,三角形的三边关系,矩形的性质,勾股定理,根据三角形的三边关系判断出点O 、E 、D 三点共线时,点D 到点O 的距离最大是解题的关键.19.C【分析】①由翻折知∠ABE=∠AB'E=90º,再证∠M=∠CB'E=∠B'AD 即可;②借助轴对称可知;③利用计算,勾股定理求B′D ,构造方程,求EB ,在构造勾股定理求55;④由相似CB':BM=CE:BE,BM=103,在计算B'M>5;⑤证△BEG≌△B′PG得BE=B′P,再证菱形即可.【详解】①由折叠性质知∠ABE=∠AB'E=90º,∴∠CB'E+∠AB'D=90º∵∠D=90º∴∠B'AD+∠AB'D=90º∴∠CB'E=∠B'AD,∵CD∥MB,∴∠M=∠CB'E=∠B'AD;②点P在对称轴上,则B'P=BP;③由翻折,AB=AB'=5,AD=4,由勾股定理DB'=3,∴CB'=5-3=2,设BE=x=B'E,CE=4-x,在Rt△B′CE中,∠C=90º,由勾股定理(4-x)2+22=x2,解得x=52,∴CE=4-52=32,在Rt△ABE中,∠ABE=90º,AE=22555+5=22⎛⎫⎪⎝⎭;④由BM∥CB′∴△ECB′∽△EBM,∴CB':BM=CE:BE,∴2:BM=32:52, ∴BM=103, 则B'M=221020+4=33⎛⎫ ⎪⎝⎭>5=CD ; ⑤连接BB′,由对称性可知,BG=B′G ,EP ⊥BB′,BE ∥B′P ,∴△BEG ≌△B′PG ,∴BE=B′P ,∴四边形BPB′E 为平行四边形,又BE=EB′,所以四边形BPB′E 是菱形,所以PB′=B'E .故选择:C .【点睛】此题考查了矩形的性质、图形的翻折变换以及相似三角形的性质等知识的应用,此题的关键是能够发现△BEG ≌△B′PG .20.B【分析】连接BD ,与AC 相交于点O ,则AC ⊥BD ,142AO AC ==,由5AD AB ==,根据勾股定理求出DO ,求出EO ,由勾股定理求出DE ,即可得到答案.【详解】解:连接BD ,与AC 相交于点O ,则AC ⊥BD ,在菱形ABCD 中,142AO AC ==, ∵5AD AB CD ===,在Rt △AOD 中,由勾股定理,得:3DO ==,∵=5CE CD =,8AC =,∴853AE =-=,∴431OE =-=,在Rt △ODE 中,由勾股定理,得DE ==∴DE AD = 故选:B.【点睛】本题考查了菱形的性质,勾股定理,以及线段的和差关系,解题的关键是正确作出辅助线,利用勾股定理求出DE 的长度.21.D【分析】求得∠ADB =90°,即AD ⊥BD ,即可得到S ▱ABCD =AD•BD ;依据∠CDE =60°,∠BDE =30°,可得∠CDB =∠BDE ,进而得出DB 平分∠CDE ;依据Rt △BCD 中,斜边上的中线DE =斜边BC 的一半,即可得到AD =BC =2DE ,进而得到AB =DE ;依据OE 是中位线,即可得到OE ∥CD ,因为两平行线间的距离相等,进而得到S △CDE =S △OCD ,再根据OC 是△BCD 的中线,可得S △BOC =S △COD ,即可得到S △CDE =S △BOC .【详解】∵∠BCD =60°,四边形ABCD 是平行四边形,∴∠ADC =180°-∠BCD =120°,BC//AD ,BC =AD ,∵DE 平分∠ADC ,∴∠CDE =∠CED =60°=∠BCD ,∴△CDE 是等边三角形,∴CE =CD = AD = BC ,∴E 是BC 的中点,∴DE =BE ,∴∠BDE = ∠CED =30°,∴∠CDB =90°,即CD ⊥BD ,∴S ▱ABCD =CD•BD =AB•BD ,故①正确;∵∠CDE =60°,∠BDE =30°,∴∠ADB =30°=∠BDE ,∴DB 平分∠CDE ,故②正确;∵△CDE 是等边三角形,∴DE =CD =AB ,故③正确;∵O 是BD 的中点,E 是BC 的中点,∴OE 是△CBD 的中位线,∴OE ∥CD ,∴S △OCD =S △CDE ,∵OC 是△BCD 的中线,∴S △BOC =S △COD ,∴S △CDE =S △BOC ,故④正确,故选D .【点睛】本题考查了平行四边形的性质、等边三角形的判定与性质、三角形中位线、平行线间的距离相等、直角三角形斜边上的中线等于斜边的一半等,综合性较强,熟练掌握和灵活运用相关性质与定理是解题的关键.22.C【分析】①先根据平行四边形的性质可得120,60,BAD ABC OA OC ∠=︒∠=︒=,再根据角平分线的定义可得60=︒∠BAE ,然后根据等边三角形的判定与性质可得AB AE BE ==,60AEB ∠=︒,又根据等腰三角形的性质、三角形的外角性质可得30ACE CAE ∠=∠=︒,最后根据角的和差即可得;②由①已推得90BAC ∠=︒,再根据2ABCD ABC S S =即可得;③在Rt AOB 中,根据直角边小于斜边即可得;④在ABC 中,利用三角形中位线定理可得12OE AB =,再根据12AB BC =即可得. 【详解】 四边形ABCD 是平行四边形,60ADC ∠=︒,120,60,BAD ABC OA OC ∴∠=︒∠=︒=,AE ∵平分BAD ∠,1602BAE BAD ∴∠=∠=︒, ABE ∴是等边三角形,,60AB AE BE AEB ∴==∠=︒, 12AB BC =, AB AE BE CE ∴===,ACE CAE ∴∠=∠,60AEB ACE CAE ∠=∠+∠=︒,30ACE CAE ∴∠=∠=︒,90,30BAC BAE CAE CAD BAD BAC ∴∠=∠+∠=︒∠=∠-∠=︒,则结论①成立, AB AC ∴⊥,122··2ABCD ABC AB AC AB AC S S ==⨯=∴,则结论②成立, 在Rt AOB 中,OA 是直角边,OB 是斜边,OA OB ∴<,则结论③不成立,,OA OC BE CE ==,OE ∴是ABC 的中位线, 11112224OE AB BC BC ∴==⨯=,则结论④成立, 综上,结论成立的个数是3个,故选:C .【点睛】本题考查了平行四边形的性质、三角形中位线定理、等边三角形的判定与性质等知识点,熟练掌握并灵活运用各判定定理与性质是解题关键.23.B【解析】【分析】先求出第一个正方形面积、第二个正方形面积、第三个正方形面积,…探究规律后,即可解决问题.【详解】第一个正方形的面积为1=20,第二个正方形的面积为(2)2=2=21,第三个正方形的边长为22,…第n 个正方形的面积为2n ﹣1,故选B .【点睛】本题考查了规律型:图形的变化类,正方形的性质,根据前后正方形边长之间的关系找到S n 的规律是解题的关键.24.C【分析】想办法证明S 阴=S △ADE +S △DEC =S △AEC ,再由EF ∥AC ,可得S △AEC =S △ACF 解决问题.【详解】连接AF 、EC .∵BC =4CF ,S △ABC =12,∴S △ACF =13×12=4, ∵四边形CDEF 是平行四边形,∴DE ∥CF ,EF ∥AC ,∴S △DEB =S △DEC ,∴S 阴=S △ADE +S △DEC =S △AEC ,∵EF ∥AC ,∴S △AEC =S △ACF =4,∴S 阴=4.故选C .【点睛】本题考查平行四边形的性质、三角形的面积、等高模型等知识,解题的关键是熟练掌握等高模型解决问题,学会用转化的思想思考问题,属于中考常考题型.25.D【分析】①由矩形的性质得到90OBC ∠=︒,根据折叠的性质得到OB OD =,90PDO OBP ,BOP DOP ∠=∠,推出四边形OBPD 是矩形,根据正方形的判定定理即可得到四边形OBPD 为正方形;故①正确;②过D 作DH OA ⊥于H ,得到10OA =,6OB =,根据直角三角形的性质得到132DH OD ,根据三角形的面积公式得到OAD ∆的面积为113101522OA DH ,故②正确; ③连接OC ,于是得到OD CD OC ,即当OD CD OC +=时,CD 取最小值,根据勾股定理得到CD 的最小值为6;故③正确;④根据已知条件推出P ,D ,A 三点共线,根据平行线的性质得到OPBPOA ,等量代换得到OPAPOA ,求得10AP OA ,根据勾股定理得到1082BP BC CP ,故④正确.【详解】解:①四边形OACB 是矩形,90OBC ∴∠=︒,将OBP ∆沿OP 折叠得到OPD ∆, OB OD ∴=,90PDO OBP ,BOP DOP ∠=∠,45BOP ,45DOP BOP ,90BOD =∴∠︒,90BOD OBP ODP , ∴四边形OBPD 是矩形,OB OD =,∴四边形OBPD 为正方形;故①正确;②过D 作DH OA ⊥于H ,点(10,0)A ,点(0,6)B ,10OA ∴=,6OB =,6OD OB,30BOP DOP , 30DOA , 132DH OD , OAD ∴∆的面积为113101522OA DH ,故②正确; ③连接OC ,则OD CD OC ,即当OD CD OC +=时,CD 取最小值,6ACOB ,10OA =, 2222106234OC OA AC ,2346CD OC OD ,即CD 的最小值为2346;故③正确;④⊥OD AD ,90ADO ∴∠=︒, 90ODP OBP ,180ADP ,P ∴,D ,A 三点共线,//OA CB ,OPBPOA , OPBOPD , OPAPOA , 10AP OA ,6AC =, 221068CP , 1082BP BC CP ,故④正确;故选:D .【点睛】本题考查了正方形的判定和性质,矩形的判定和性质,折叠的性质,勾股定理,三角形的面积的计算,正确的识别图形是解题的关键.26.B【分析】。
中考数学复习平行四边形专项易错题含详细答案

中考数学复习平行四边形专项易错题含详细答案一、平行四边形1.(1)、动手操作:如图①:将矩形纸片ABCD折叠,使点D与点B重合,点C落在点处,折痕为EF,若∠ABE=20°,那么的度数为 .(2)、观察发现:小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图②);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图③).小明认为△AEF是等腰三角形,你同意吗?请说明理由.(3)、实践与运用:将矩形纸片ABCD按如下步骤操作:将纸片对折得折痕EF,折痕与AD边交于点E,与BC 边交于点F;将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠,使点A、点D都与点F 重合,展开纸片,此时恰好有MP=MN=PQ(如图④),求∠MNF的大小.【答案】(1)125°;(2)同意;(3)60°【解析】试题分析:(1)根据直角三角形的两个锐角互余求得∠AEB=70°,根据折叠重合的角相等,得∠BEF=∠DEF=55°,根据平行线的性质得到∠EFC=125°,再根据折叠的性质得到∠EFC′=∠EFC=125°;(2)根据第一次折叠,得∠BAD=∠CAD;根据第二次折叠,得EF垂直平分AD,根据等角的余角相等,得∠AEG=∠AFG,则△AEF是等腰三角形;(3)由题意得出:∠NMF=∠AMN=∠MNF,MF=NF,由对称性可知,MF=PF,进而得出△MNF≌△MPF,得出3∠MNF=180°求出即可.试题解析:(1)、∵在直角三角形ABE中,∠ABE=20°,∴∠AEB=70°,∴∠BED=110°,根据折叠重合的角相等,得∠BEF=∠DEF=55°.∵AD∥BC,∴∠EFC=125°,再根据折叠的性质得到∠EFC′=∠EFC=125°.;(2)、同意,如图,设AD与EF交于点G由折叠知,AD平分∠BAC,所以∠BAD=∠CAD.由折叠知,∠AGE=∠DGE=90°,所以∠AGE=∠AGF=90°,所以∠AEF=∠AFE.所以AE=AF,即△AEF为等腰三角形.(3)、由题意得出:∠NMF=∠AMN=∠MNF,∴MF=NF,由折叠可知,MF=PF,∴NF=PF,而由题意得出:MP=MN,又∵MF=MF,∴△MNF≌△MPF,∴∠PMF=∠NMF,而∠PMF+∠NMF+∠MNF=180°,即3∠MNF=180°,∴∠MNF=60°.考点:1.折叠的性质;2.等边三角形的性质;3.全等三角形的判定和性质;4.等腰三角形的判定2.如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t 秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(1)求证:AE=DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)当t为何值时,△DEF为直角三角形?请说明理由.【答案】(1)见解析;(2)能,t=10;(3)t=152或12.【解析】【分析】(1)利用t表示出CD以及AE的长,然后在直角△CDF中,利用直角三角形的性质求得DF的长,即可证明;(2)易证四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,据此即可列方程求得t的值;(3)△DEF为直角三角形,分∠EDF=90°和∠DEF=90°两种情况讨论.【详解】解:(1)证明:∵在Rt△ABC中,∠C=90°﹣∠A=30°,∴AB=12AC=12×60=30cm,∵CD=4t,AE=2t,又∵在Rt△CDF中,∠C=30°,∴DF=12CD=2t,∴DF=AE;(2)能,∵DF∥AB,DF=AE,∴四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,即60﹣4t=2t,解得:t=10,∴当t=10时,AEFD是菱形;(3)若△DEF为直角三角形,有两种情况:①如图1,∠EDF=90°,DE∥BC,则AD=2AE,即60﹣4t=2×2t,解得:t=152,②如图2,∠DEF=90°,DE⊥AC,则AE=2AD,即2t2(604t)=-,解得:t=12,综上所述,当t=152或12时,△DEF为直角三角形.3.在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.【答案】(1)证明见解析;(2)证明见解析;(3)EF2=2BE2+2DF2.【解析】试题分析:(1)根据旋转的性质可知AF=AG,∠EAF=∠GAE=45°,故可证△AEG≌△AEF;(2)将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由(1)知△AEG≌△AEF,则EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;(3)将△ADF绕着点A顺时针旋转90°,得到△ABG,根据旋转的性质可以得到△ADF≌△ABG,则DF=BG,再证明△AEG≌△AEF,得出EG=EF,由EG=BG+BE,等量代换得到EF=BE+DF.试题解析:(1)∵△ADF绕着点A顺时针旋转90°,得到△ABG,∴AF=AG,∠FAG=90°,∵∠EAF=45°,∴∠GAE=45°,在△AGE与△AFE中,,∴△AGE≌△AFE(SAS);(2)设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.则△ADF≌△ABG,DF=BG.由(1)知△AEG≌△AEF,∴EG=EF.∵∠CEF=45°,∴△BME、△DNF、△CEF均为等腰直角三角形,∴CE=CF ,BE=BM,NF=DF,∴a﹣BE=a﹣DF,∴BE=DF,∴BE=BM=DF=BG,∴∠BMG=45°,∴∠GME=45°+45°=90°,∴EG2=ME2+MG2,∵EG=EF ,MG=BM=DF=NF,∴EF2=ME2+NF2;(3)EF2=2BE2+2DF2.如图所示,延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.由(1)知△AEH≌△AEF,则由勾股定理有(GH+BE)2+BG2=EH2,即(GH+BE)2+(BM﹣GM)2=EH2又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,即2(DF2+BE2)=EF2考点:四边形综合题4.已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)请问EG与CG存在怎样的数量关系,并证明你的结论;(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?(请直接写出结果,不必写出理由)【答案】(1)证明见解析(2)证明见解析(3)结论仍然成立【解析】【分析】(1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG=EG.(2)结论仍然成立,连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点;再证明△DAG≌△DCG,得出AG=CG;再证出△DMG≌△FNG,得到MG=NG;再证明△AMG≌△ENG,得出AG=EG;最后证出CG=EG.(3)结论依然成立.【详解】(1)CG=EG.理由如下:∵四边形ABCD是正方形,∴∠DCF=90°.在Rt△FCD中,∵G为DF的中点,∴CG=12FD,同理.在Rt△DEF中,EG=12FD,∴CG=EG.(2)(1)中结论仍然成立,即EG=CG.证法一:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.在△DAG与△DCG中,∵AD=CD,∠ADG=∠CDG,DG=DG,∴△DAG≌△DCG(SAS),∴AG=CG;在△DMG与△FNG中,∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG (ASA),∴MG=NG.∵∠EAM=∠AEN=∠AMN=90°,∴四边形AENM是矩形,在矩形AENM中,AM=EN.在△AMG与△ENG中,∵AM=EN,∠AMG=∠ENG,MG=NG,∴△AMG≌△ENG(SAS),∴AG=EG,∴EG=CG.证法二:延长CG至M,使MG=CG,连接MF,ME,EC.在△DCG与△FMG中,∵FG=DG,∠MGF=∠CGD,MG=CG,∴△DCG≌△FMG,∴MF=CD,∠FMG=∠DCG,∴MF∥CD∥AB,∴EF⊥MF.在Rt△MFE与Rt△CBE中,∵MF=CB,∠MFE=∠EBC=90°,EF=BE,∴△MFE≌△CBE∴∠MEF=∠CEB,∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°,∴△MEC为直角三角形.∵MG=CG,∴EG=1MC,∴EG=CG.2(3)(1)中的结论仍然成立.理由如下:过F作CD的平行线并延长CG交于M点,连接EM、EC,过F作FN垂直于AB于N.由于G为FD中点,易证△CDG≌△MFG,得到CD=FM,又因为BE=EF,易证∠EFM=∠EBC,则△EFM≌△EBC,∠FEM=∠BEC,EM=EC∵∠FEC+∠BEC=90°,∴∠FEC+∠FEM=90°,即∠MEC=90°,∴△MEC是等腰直角三角形.∵G为CM中点,∴EG=CG,EG⊥CG【点睛】本题是四边形的综合题.(1)关键是利用直角三角形斜边上的中线等于斜边的一半解答;(2)关键是利用了直角三角形斜边上的中线等于斜边的一半的性质、全等三角形的判定和性质解答.5.已知AD是△ABC的中线P是线段AD上的一点(不与点A、D重合),连接PB、PC,E、F、G、H分别是AB、AC、PB、PC的中点,AD与EF交于点M;(1)如图1,当AB=AC时,求证:四边形EGHF是矩形;(2)如图2,当点P与点M重合时,在不添加任何辅助线的条件下,写出所有与△BPE面积相等的三角形(不包括△BPE本身).【答案】(1)见解析;(2)△APE、△APF、△CPF、△PGH.【解析】【分析】(1)由三角形中位线定理得出EG∥AP,EF∥BC,EF=12BC,GH∥BC,GH=12BC,推出EF∥GH,EF=GH,证得四边形EGHF是平行四边形,证得EF⊥AP,推出EF⊥EG,即可得出结论;(2)由△APE与△BPE的底AE=BE,又等高,得出S△APE=S△BPE,由△APE与△APF的底EP=FP,又等高,得出S△APE=S△APF,由△APF与△CPF的底AF=CF,又等高,得出S△APF=S△CPF,证得△PGH底边GH上的高等于△AEF底边EF上高的一半,推出S△PGH=12S△AEF=S△APF,即可得出结果.【详解】(1)证明:∵E、F、G、H分别是AB、AC、PB、PC的中点,∴EG∥AP,EF∥BC,EF=12BC,GH∥BC,GH=12BC,∴EF∥GH,EF=GH,∴四边形EGHF是平行四边形,∵AB=AC,∴AD⊥BC,∴EF⊥AP,∵EG∥AP,∴EF⊥EG,∴平行四边形EGHF是矩形;(2)∵PE是△APB的中线,∴△APE与△BPE的底AE=BE,又等高,∴S△APE=S△BPE,∵AP是△AEF的中线,∴△APE与△APF的底EP=FP,又等高,∴S△APE=S△APF,∴S △APF =S △BPE ,∵PF 是△APC 的中线,∴△APF 与△CPF 的底AF =CF ,又等高,∴S △APF =S △CPF ,∴S △CPF =S △BPE ,∵EF ∥GH ∥BC ,E 、F 、G 、H 分别是AB 、AC 、PB 、PC 的中点,∴△AEF 底边EF 上的高等于△ABC 底边BC 上高的一半,△PGH 底边GH 上的高等于△PBC 底边BC 上高的一半,∴△PGH 底边GH 上的高等于△AEF 底边EF 上高的一半,∵GH =EF ,∴S △PGH =12S △AEF =S △APF , 综上所述,与△BPE 面积相等的三角形为:△APE 、△APF 、△CPF 、△PGH .【点睛】本题考查了矩形的判定与性质、平行四边形的判定、三角形中位线定理、平行线的性质、三角形面积的计算等知识,熟练掌握三角形中位线定理是解决问题的关键.6.(1)如图1,将矩形ABCD 折叠,使BC 落在对角线BD 上,折痕为BE ,点C 落在点C '处,若42ADB =o ∠,则DBE ∠的度数为______o .(2)小明手中有一张矩形纸片ABCD ,4AB =,9AD =.(画一画)如图2,点E 在这张矩形纸片的边AD 上,将纸片折叠,使AB 落在CE 所在直线上,折痕设为MN (点M ,N 分别在边AD ,BC 上),利用直尺和圆规画出折痕MN (不写作法,保留作图痕迹,并用黑色水笔把线段描清楚);(算一算)如图3,点F 在这张矩形纸片的边BC 上,将纸片折叠,使FB 落在射线FD 上,折痕为GF ,点,A B 分别落在点A ',B '处,若73AG =,求B D '的长.【答案】(1)21;(2)画一画;见解析;算一算:3B D'=【解析】【分析】(1)利用平行线的性质以及翻折不变性即可解决问题;(2)【画一画】,如图2中,延长BA交CE的延长线由G,作∠BGC的角平分线交AD于M,交BC于N,直线MN即为所求;【算一算】首先求出GD=9-72033=,由矩形的性质得出AD∥BC,BC=AD=9,由平行线的性质得出∠DGF=∠BFG,由翻折不变性可知,∠BFG=∠DFG,证出∠DFG=∠DGF,由等腰三角形的判定定理证出DF=DG=203,再由勾股定理求出CF,可得BF,再利用翻折不变性,可知FB′=FB,由此即可解决问题.【详解】(1)如图1所示:∵四边形ABCD是矩形,∴AD∥BC,∴∠ADB=∠DBC=42°,由翻折的性质可知,∠DBE=∠EBC=12∠DBC=21°,故答案为21.(2)【画一画】如图所示:【算一算】如3所示:∵AG=73,AD=9,∴GD=9-72033=,∵四边形ABCD是矩形,∴AD∥BC,BC=AD=9,∴∠DGF=∠BFG,由翻折不变性可知,∠BFG=∠DFG,∴∠DFG=∠DGF,∴DF=DG=203,∵CD=AB=4,∠C=90°,∴在Rt△CDF中,由勾股定理得:22222016433 DF CD⎛⎫-=-=⎪⎝⎭,∴BF=BC-CF=9161133-=,由翻折不变性可知,FB=FB′=11 3,∴B′D=DF-FB′=2011333-=.【点睛】四边形综合题,考查了矩形的性质、翻折变换的性质、勾股定理、等腰三角形的判定、平行线的性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用翻折不变性解决问题.7.如图,在正方形ABCD中,对角线AC与BD交于点O,在Rt△PFE中,∠EPF=90°,点E、F分别在边AD、AB上.(1)如图1,若点P与点O重合:①求证:AF=DE;②若正方形的边长为3,当∠DOE=15°时,求线段EF的长;(2)如图2,若Rt△PFE的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP 时,证明:PE=2PF.【答案】(1)①证明见解析,②22;(2)证明见解析. 【解析】 【分析】(1)①根据正方形的性质和旋转的性质即可证得:△AOF ≌△DOE 根据全等三角形的性质证明;②作OG ⊥AB 于G ,根据余弦的概念求出OF 的长,根据勾股定理求值即可;(2)首先过点P 作HP ⊥BD 交AB 于点H ,根据相似三角形的判定和性质求出PE 与PF 的数量关系. 【详解】(1)①证明:∵四边形ABCD 是正方形, ∴OA=OD ,∠OAF=∠ODE=45°,∠AOD=90°, ∴∠AOE+∠DOE=90°, ∵∠EPF=90°, ∴∠AOF+∠AOE=90°, ∴∠DOE=∠AOF , 在△AOF 和△DOE 中,OAF ODE OA ODAOF DOE ===∠∠⎧⎪⎨⎪∠∠⎩, ∴△AOF ≌△DOE , ∴AF=DE ;②解:过点O 作OG ⊥AB 于G ,∵正方形的边长为3 ∴OG=123∵∠DOE=15°,△AOF ≌△DOE , ∴∠AOF=15°, ∴∠FOG=45°-15°=30°, ∴OF=OGcos DOG∠=2,∴EF=22=22OF OE +;(2)证明:如图2,过点P 作HP ⊥BD 交AB 于点H ,则△HPB 为等腰直角三角形,∠HPD=90°, ∴HP=BP , ∵BD=3BP , ∴PD=2BP , ∴PD=2HP ,又∵∠HPF+∠HPE=90°,∠DPE+∠HPE=90°, ∴∠HPF=∠DPE , 又∵∠BHP=∠EDP=45°, ∴△PHF ∽△PDE ,∴12PF PH PE PD ==, ∴PE=2PF . 【点睛】此题属于四边形的综合题.考查了正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质以及勾股定理.注意准确作出辅助线是解此题的关键.8.如图1,在正方形ABCD 中,AD=6,点P 是对角线BD 上任意一点,连接PA ,PC 过点P 作PE ⊥PC 交直线AB 于E . (1) 求证:PC=PE;(2) 延长AP 交直线CD 于点F.①如图2,若点F 是CD 的中点,求△APE 的面积; ②若ΔAPE 的面积是21625,则DF 的长为 (3) 如图3,点E 在边AB 上,连接EC 交BD 于点M,作点E 关于BD 的对称点Q ,连接PQ,MQ,过点P作PN∥CD交EC于点N,连接QN,若PQ=5,MN=723,则△MNQ的面积是【答案】(1)略;(2)①8,②4或9;(3)5 6【解析】【分析】(1)利用正方形每个角都是90°,对角线平分对角的性质,三角形外角等于和它不相邻的两个内角的和,等角对等边等性质容易得证;(2)作出△ADP和△DFP的高,由面积法容易求出这个高的值.从而得到△PAE的底和高,并求出面积.第2小问思路一样,通过面积法列出方程求解即可;(3)根据已经条件证出△MNQ是直角三角形,计算直角边乘积的一半可得其面积.【详解】(1) 证明:∵点P在对角线BD上,∴△ADP≌△CDP,∴AP=CP, ∠DAP =∠DCP,∵PE⊥PC,∴∠EPC=∠EPB+∠BPC=90°,∵∠PEA=∠EBP+∠EPB=45°+90°-∠BPC=135°-∠BPC,∵∠PAE=90°-∠DAP=90°-∠DCP,∠DCP=∠BPC-∠PDC=∠BPC-45°,∴∠PAE=90°-(∠BPC-45°)= 135°-∠BPC,∴∠PEA=∠PAE,∴PC=PE;(2)①如图2,过点P分别作PH⊥AD,PG⊥CD,垂足分别为H、G.延长GP交AB于点M.∵四边形ABCD 是正方形,P 在对角线上, ∴四边形HPGD 是正方形, ∴PH=PG,PM ⊥AB, 设PH=PG=a,∵F 是CD 中点,AD =6,则FD=3,ADF S n =9, ∵ADF S n =ADP DFP S S +n n =1122AD PH DF PG ⨯+⨯, ∴1163922a a ⨯+⨯=,解得a=2, ∴AM=HP=2,MP=MG-PG=6-2=4, 又∵PA=PE, ∴AM=EM,AE=4,∵APE S n =1144822EA MP ⨯=⨯⨯=,②设HP =b,由①可得AE=2b,MP=6-b,∴APE S n =()121626225b b ⨯⨯-=, 解得b=2.4 3.6或,∵ADF S n =ADP DFP S S +n n =1122AD PH DF PG ⨯+⨯, ∴11166222b DF b DF ⨯⨯+⨯=⨯, ∴当b=2.4时,DF=4;当b =3.6时,DF =9, 即DF 的长为4或9; (3)如图,∵E 、Q 关于BP 对称,PN ∥CD, ∴∠1=∠2,∠2+∠3=∠BDC=45°, ∴∠1+∠4=45°, ∴∠3=∠4,易证△PEM ≌△PQM, △PNQ ≌△PNC, ∴∠5=∠6, ∠7=∠8 ,EM=QM,NQ=NC, ∴∠6+∠7=90°, ∴△MNQ 是直角三角形, 设EM=a,NC=b 列方程组222252372 3a b a b ⎧+=⎪⎪⎨⎛⎪+= ⎪⎝⎭⎩, 可得12ab=56, ∴MNQ 56S V =, 【点睛】本题是四边形综合题目,考查了正方形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质等知识;本题综合性强,有一定难度,熟练掌握正方形的性质,证明三角形全等是解决问题的关键.要注意运用数形结合思想.9.在矩形纸片ABCD 中,AB=6,BC=8,现将纸片折叠,使点D 与点B 重合,折痕为EF ,连接DF .(1)说明△BEF 是等腰三角形; (2)求折痕EF 的长.【答案】(1)见解析;(2).【解析】【分析】(1)根据折叠得出∠DEF=∠BEF,根据矩形的性质得出AD∥BC,求出∠DEF=∠BFE,求出∠BEF=∠BFE即可;(2)过E作EM⊥BC于M,则四边形ABME是矩形,根据矩形的性质得出EM=AB=6,AE=BM,根据折叠得出DE=BE,根据勾股定理求出DE、在Rt△EMF中,由勾股定理求出即可.【详解】(1)∵现将纸片折叠,使点D与点B重合,折痕为EF,∴∠DEF=∠BEF.∵四边形ABCD是矩形,∴AD∥BC,∴∠DEF=∠BFE,∴∠BEF=∠BFE,∴BE=BF,即△BEF 是等腰三角形;(2)过E作EM⊥BC于M,则四边形ABME是矩形,所以EM=AB=6,AE=BM.∵现将纸片折叠,使点D与点B重合,折痕为EF,∴DE=BE,DO=BO,BD⊥EF.∵四边形ABCD是矩形,BC=8,∴AD=BC=8,∠BAD=90°.在Rt△ABE中,AE2+AB2=BE2,即(8﹣BE)2+62=BE2,解得:BE==DE=BF,AE=8﹣DE=8﹣==BM,∴FM=﹣=.在Rt△EMF中,由勾股定理得:EF==.故答案为:.【点睛】本题考查了折叠的性质和矩形性质、勾股定理等知识点,能熟记折叠的性质是解答此题的关键.10.如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG.(1)求证:四边形DEFG为菱形;(2)若CD=8,CF=4,求的值.【答案】(1)证明见试题解析;(2).【解析】试题分析:(1)由折叠的性质,可以得到DG=FG,ED=EF,∠1=∠2,由FG∥CD,可得∠1=∠3,再证明 FG=FE,即可得到四边形DEFG为菱形;(2)在Rt△EFC中,用勾股定理列方程即可CD、CE,从而求出的值.试题解析:(1)由折叠的性质可知:DG=FG,ED=EF,∠1=∠2,∵FG∥CD,∴∠2=∠3,∴FG=FE,∴DG=GF=EF=DE,∴四边形DEFG为菱形;(2)设DE=x,根据折叠的性质,EF=DE=x,EC=8﹣x,在Rt△EFC中,,即,解得:x=5,CE=8﹣x=3,∴=.考点:1.翻折变换(折叠问题);2.勾股定理;3.菱形的判定与性质;4.矩形的性质;5.综合题.11.如图1,在长方形纸片ABCD中,AB=mAD,其中m⩾1,将它沿EF折叠(点E. F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设AMnAD,其中0<n⩽1.(1)如图2,当n=1(即M 点与D 点重合),求证:四边形BEDF 为菱形; (2)如图3,当12n =(M 为AD 的中点),m 的值发生变化时,求证:EP=AE+DP ; (3)如图1,当m=2(即AB=2AD),n 的值发生变化时,BE CFAM-的值是否发生变化?说明理由.【答案】(1)证明见解析;(2)证明见解析;(3)值不变,理由见解析. 【解析】试题分析:(1)由条件可知,当n=1(即M 点与D 点重合),m=2时,AB=2AD ,设AD=a ,则AB=2a ,由矩形的性质可以得出△ADE ≌△NDF ,就可以得出AE=NF ,DE=DF ,在Rt △AED 中,由勾股定理就可以表示出AE 的值,再求出BE 的值就可以得出结论. (2)延长PM 交EA 延长线于G ,由条件可以得出△PDM ≌△GAM ,△EMP ≌△EMG 由全等三角形的性质就可以得出结论.(3)如图1,连接BM 交EF 于点Q ,过点F 作FK ⊥AB 于点K ,交BM 于点O ,通过证明△ABM ∽△KFE ,就可以得出EK KF AM AB =,即BE BK BCAM AB-=,由AB=2AD=2BC ,BK=CF 就可以得出BE CFAM -的值是12为定值. (1)∵四边形ABCD 是矩形,∴AB=CD ,AD=BC ,∠A=∠B=∠C=∠D=90°. ∵AB=mAD ,且n=2,∴AB=2AD .∵∠ADE+∠EDF=90°,∠EDF+∠NDF=90°,∴∠ADE=∠NDF . 在△ADE 和△NDF 中,∠A =∠N ,AD =ND ,∠ADE =∠NDF , ∴△ADE ≌△NDF (ASA ).∴AE=NF ,DE=DF . ∵FN=FC ,∴AE=FC .∵AB=CD ,∴AB-AE="CD-CF." ∴BE="DF." ∴BE=DE .Rt △AED 中,由勾股定理,得222AE DE AD =-,即2222AE AD AE AD ()=--,∴AE=34AD. ∴BE=2AD-34AD=54.∴554334ADBE AE AD ==. (2)如图3,延长PM 交EA 延长线于G ,∴∠GAM=90°. ∵M 为AD 的中点,∴AM=DM .∵四边形ABCD 是矩形,∴AB=CD ,AD=BC ,∠A=∠B=∠C=∠D=90°,AB ∥CD. ∴∠GAM=∠PDM .在△GAM 和△PDM 中,∠GAM =∠PDM ,AM =DM ,∠AMG =∠DMP , ∴△GAM ≌△PDM (ASA ).∴MG=MP .在△EMP 和△EMG 中,PM =GM ,∠PME =∠GME ,ME =ME , ∴△EMP ≌△EMG (SAS ).∴EG=EP . ∴AG+AE=EP .∴PD+AE=EP ,即EP=AE+DP .(3)12BE CF AM -=,值不变,理由如下: 如图1,连接BM 交EF 于点Q ,过点F 作FK ⊥AB 于点K ,交BM 于点O , ∵EM=EB ,∠MEF=∠BEF ,∴EF ⊥MB ,即∠FQO=90°. ∵四边形FKBC 是矩形,∴KF=BC ,FC=KB. ∵∠FKB=90°,∴∠KBO+∠KOB=90°.∵∠QOF+∠QFO=90°,∠QOF=∠KOB ,∴∠KBO=∠OFQ. ∵∠A=∠EKF=90°,∴△ABM ∽△KFE. ∴EK KF AM AB =即BE BK BC AM AB-=. ∵AB=2AD=2BC ,BK=CF ,∴12BE CF AM -=. ∴BE CFAM-的值不变.考点:1.折叠问题;2.矩形的性质;3.全等三角形的判定和性质;4.勾股定理;5.相似三角形的判定和性质.12.如图,在平面直角坐标系xOy 中,四边形OABC 的顶点A 在x 轴的正半轴上,OA=4,OC=2,点D 、E 、F 、G 分别为边OA 、AB 、BC 、CO 的中点,连结DE 、EF 、FG 、GD .(1)若点C 在y 轴的正半轴上,当点B 的坐标为(2,4)时,判断四边形DEFG 的形状,并说明理由.(2)若点C 在第二象限运动,且四边形DEFG 为菱形时,求点四边形OABC 对角线OB 长度的取值范围.(3)若在点C 的运动过程中,四边形DEFG 始终为正方形,当点C 从X 轴负半轴经过Y 轴正半轴,运动至X 轴正半轴时,直接写出点B 的运动路径长.【答案】(1)正方形(2)256OB <<(3)2π【解析】分析:(1)连接OB ,AC ,说明OB ⊥AC ,OB=AC ,可得四边形DEFG 是正方形.(2)由四边形DEFG 是菱形,可得OB=AC ,当点C 在y 轴上时,AC=25C 在x 轴上时,AC=6, 故可得结论;(3)根据题意计算弧长即可.详解:(1)正方形,如图1,证明连接OB ,AC ,说明OB ⊥AC ,OB=AC ,可得四边形DEFG 是正方形.(2)256OB <如图2,由四边形DEFG 是菱形,可得OB=AC ,当点C 在y 轴上时,AC=25C 在x 轴上时,AC=6, ∴256OB < ;(3)2π.如图3,当四边形DEFG是正方形时,OB⊥AC,且OB=AC,构造△OBE≌△ACO,可得B点在以E(0,4)为圆心,2为半径的圆上运动.所以当C点从x轴负半轴到正半轴运动时,B点的运动路径为2 .图1 图2 图3点睛:本题主要考查了正方形的判定,菱形的性质以及弧长的计算.灵活运用正方形的判定定理和菱形的性质运用是解题的关键.13.如图,P是边长为1的正方形ABCD对角线BD上一动点(P与B、D不重合),∠APE=90°,且点E在BC边上,AE交BD于点F.(1)求证:①△PAB≌△PCB;②PE=PC;(2)在点P的运动过程中,的值是否改变?若不变,求出它的值;若改变,请说明理由;(3)设DP=x,当x为何值时,AE∥PC,并判断此时四边形PAFC的形状.【答案】(1)见解析;(2);(3)x=﹣1;四边形PAFC是菱形.【解析】试题分析:(1)根据四边形ABCD是正方形,得出AB=BC,∠ABP=∠CBP°,再根据PB=PB,即可证出△PAB≌△PCB,②根据∠PAB+∠PEB=180°,∠PEC+∠PEB=180°,得出∠PEC=∠PCB,从而证出PE=PC;(2)根据PA=PC,PE=PC,得出PA=PE,再根据∠APE=90°,得出∠PAE=∠PEA=45°,即可求出;(3)先求出∠CPE=∠PEA=45°,从而得出∠PCE,再求出∠BPC即可得出∠BPC=∠PCE,从而证出BP=BC=1,x=﹣1,再根据AE∥PC,得出∠AFP=∠BPC=67.5°,由△PAB≌△PCB 得出∠BPA=∠BPC=67.5°,PA=PC,从而证出AF=AP=PC,得出答案.试题解析:(1)①∵四边形ABCD是正方形,∴AB=BC,∠ABP=∠CBP=∠ABC=45°.∵PB=PB,∴△PAB≌△PCB (SAS).②由△PAB≌△PCB可知,∠PAB=∠PCB.∵∠ABE=∠APE=90°,∴∠PAB+∠PEB=180°,又∵∠PEC+∠PEB=180°,∴∠PEC=∠PAB=∠PCB,∴PE=PC.(2)在点P的运动过程中,的值不改变.由△PAB≌△PCB可知,PA=PC.∵PE=PC,∴PA=PE,又∵∠APE=90°,∴△PAE是等腰直角三角形,∠PAE=∠PEA=45°,∴=.(3)∵AE∥PC,∴∠CPE=∠PEA=45°,∴在△PEC中,∠PCE=∠PEC=(180°﹣45°)=67.5°.在△PBC中,∠BPC=(180°﹣∠CBP﹣∠PCE)=(180°﹣45°﹣67.5°)=67.5°.∴∠BPC=∠PCE=67.5°,∴BP=BC=1,∴x=BD﹣BP=﹣1.∵AE∥PC,∴∠AFP=∠BPC=67.5°,由△PAB≌△PCB可知,∠BPA=∠BPC=67.5°,PA=PC,∴∠AFP=∠BPA,∴AF=AP=PC,∴四边形PAFC是菱形.考点:四边形综合题.14.已知点O是△ABC内任意一点,连接OA并延长到E,使得AE=OA,以OB,OC为邻边作▱OBFC,连接OF与BC交于点H,再连接EF.(1)如图1,若△ABC为等边三角形,求证:①EF⊥BC;②EF=BC;(2)如图2,若△ABC为等腰直角三角形(BC为斜边),猜想(1)中的两个结论是否成立?若成立,直接写出结论即可;若不成立,请你直接写出你的猜想结果;(3)如图3,若△ABC是等腰三角形,且AB=AC=kBC,请你直接写出EF与BC之间的数量关系.【答案】(1)见解析;(2)EF⊥BC仍然成立;(3)EF=BC【解析】试题分析:(1)由平行四边形的性质得到BH=HC=BC,OH=HF,再由等边三角形的性质得到AB=BC,AH⊥BC,根据勾股定理得到AH=BC,即可;(2)由平行四边形的性质得到BH=HC=BC,OH=HF,再由等腰直角三角形的性质得到AB=BC,AH⊥BC,根据勾股定理得到AH=BC,即可;(3)由平行四边形的性质得到BH=HC=BC,OH=HF,再由等腰三角形的性质和AB=AC=kBC得到AB=BC,AH⊥BC,根据勾股定理得到AH=BC,即可.试题解析:(1)连接AH,如图1,∵四边形OBFC是平行四边形,∴BH=HC=BC,OH=HF,∵△ABC是等边三角形,∴AB=BC,AH⊥BC,在Rt△ABH中,AH2=AB2﹣BH2,∴AH==BC,∵OA=AE,OH=HF,∴AH是△OEF的中位线,∴AH=EF,AH∥EF,∴EF⊥BC,BC=EF,∴EF⊥BC,EF=BC;(2)EF⊥BC仍然成立,EF=BC,如图2,∵四边形OBFC是平行四边形,∴BH=HC=BC,OH=HF,∵△ABC是等腰三角形,∴AB=BC,AH⊥BC,在Rt△ABH中,AH2=AB2﹣BH2=(BH)2﹣BH2=BH2,∴AH=BH=BC,∵OA=AE,OH=HF,∴AH是△OEF的中位线,∴AH=EF,AH∥EF,∴EF⊥BC,BC=EF,∴EF⊥BC,EF=BC;(3)如图3,∵四边形OBFC是平行四边形,∴BH=HC=BC,OH=HF,∵△ABC是等腰三角形,∴AB=kBC,AH⊥BC,在Rt△ABH中,AH2=AB2﹣BH2=(kBC)2﹣(BC)2=(k2-)BC2,∴AH=BH=BC,∵OA=AE,OH=HF,∴AH是△OEF的中位线,∴AH=EF,AH∥EF,∴EF⊥BC,BC=EF,∴EF=BC.考点:四边形综合题.15.已知:如图,四边形ABCD和四边形AECF都是矩形,AE与BC交于点M,CF与AD交于点N.(1)求证:△ABM≌△CDN;(2)矩形ABCD和矩形AECF满足何种关系时,四边形 AMCN是菱形,证明你的结论.【答案】(1)证明见解析;(2)当AB=AF时,四边形AMCN是菱形.证明见解析;【解析】试题分析:(1)由已知条件可得四边形AMCN是平行四边形,从而可得AM=CN,再由AB=CD,∠B=∠D=90°,利用HL即可证明;(2)若四边形AMCN为菱形,则有AM=AN,从已知可得∠BAM=∠FAN,又∠B=∠F=90°,所以有△ABM≌△AFN,从而得AB=AF,因此当AB=AF时,四边形AMCN是菱形.试题解析:(1)∵四边形ABCD是矩形,∴∠B=∠D=90°,AB=CD,AD∥BC.∵四边形AECF是矩形,∴AE∥CF.∴四边形AMCN是平行四边形.∴AM=CN.在Rt△ABM和Rt△CDN中,AB=CD,AM=CN,∴Rt△ABM≌Rt△CDN.(2)当AB=AF时,四边形AMCN是菱形.∵四边形ABCD、AECF是矩形,∴∠B=∠BAD=∠EAF=∠F=90°.∴∠BAD-∠NAM=∠EAF-∠NAM,即∠BAM=∠FAN.又∵AB=AF,∴△ABM≌△AFN.∴AM=AN.由(1)知四边形AMCN是平行四边形,∴平行四边形AMCN是菱形.考点:1.矩形的性质;2.三角形全等的判定与性质;3.菱形的判定.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∴ △ BCH≌ △ BQH(SAS),
∴ CH=QH. ∴ △ PHD 的周长为:PD+DH+PH=AP+PD+DH+HC=AD+CD=8. ∴ △ PDH 的周长是定值. (3)解:如图 3,过 F 作 FM⊥AB,垂足为 M,则 FM=BC=AB.
又∵ EF 为折痕, ∴ EF⊥BP.
∴ ∠ EFM+∠ MEF=∠ ABP+∠ BEF=90°,
∴ ∠ EFM=∠ ABP.
又∵ ∠ A=∠ EMF=90°, 在△ EFM 和△ BPA 中,
EFM ABP
{EMF A ,
FM AB
∴ △ EFM≌ △ BPA(AAS). ∴ EM=AP.
设 AP=x
∵ PE=BE, ∴ ∠ EBP=∠ EPB. 又∵ ∠ EPH=∠ EBC=90°, ∴ ∠ EPH-∠ EPB=∠ EBC-∠ EBP. 即∠ PBC=∠ BPH. 又∵ AD∥ BC, ∴ ∠ APB=∠ PBC. ∴ ∠ APB=∠ BPH. (2)证明:如图 2,过 B 作 BQ⊥PH,垂足为 Q.
∴ ∠ ADN=∠ AGE, ∴ DN∥ GF, 在 Rt△ GDF 中,M 是 FG 的中点,
∴ DM= 1 FG=GM,∠ GDM=∠ AGE, 2
∴ ∠ GDM=∠ DAN, ∴ DM∥ AE, ∴ 四边形 DMEN 是平行四边形,
∴ EM=DN= 1 AC, 2
∵ AC=AB=5,
∴ EM= 5 . 2
【详解】
解:(1)证明:在△ ABC 中,∠ ACB=90°,∠ CAB=30°,∴ ∠ ABC=60°,在等边△ ABD 中, ∠ BAD=60°,∴ ∠ BAD=∠ ABC=60°,∵ E 为 AB 的中点,∴ AE=BE,又∵ ∠ AEF=∠ BEC,
∴ △ AEF≌ △ BEC,在△ ABC 中,∠ ACB=90°,E 为 AB 的中点,∴ CE= 1 AB,BE= 1 AB,
(2)解:在 Rt△ ABC 中,∵ ∠ BAC=30°,AB=6,∴ BC=AF=3,AC= 3 3 ,∴ S 平行四边形
BCFD=3× 3
3=9
3
,S△
ACF=
1 2
×3× 3
3 = 9 3 ,S = 平行四边形 ADBC 27 3 .
2
2
【点睛】
本题考查平行四边形的判定和性质、直角三角形斜边中线定理、等边三角形的性质、解直
(1)求证:四边形 BCFD 为平行四边形;(2)若 AB=6,求平行四边形 ADBC 的面积.
【答案】(1)见解析;(2)S 平行四边形 ADBC= 27 3 . 2
【解析】 【分析】
(1)在 Rt△ ABC 中,E 为 AB 的中点,则 CE= 1 AB,BE= 1 AB,得到∠ BCE=∠ EBC=60°.由
∵ AC=BC,AD⊥BC, ∴ BD=CD, ∴ AG 是 BC 的垂直平分线, ∴ GC=GB, ∴ ∠ GBF=∠ BCG, ∵ BG=BF, ∴ GC=BE, ∵ CE=EF, ∴ ∠ CEF=180°﹣2∠ F, ∵ BG=BF, ∴ ∠ GBF=180°﹣2∠ F, ∴ ∠ GBF=∠ CEF, ∴ ∠ CEF=∠ BCG, ∵ ∠ BCE=∠ CEF+∠ F,∠ BCE=∠ BCG+∠ GCE, ∴ ∠ GCE=∠ F, 在△ BEF 和△ GCE 中,
1 如图1,求证:四边形 ADCF 是矩形; 2 如图 2 ,当 AB AC 时,取 AB 的中点 G ,连接 DG 、 EG ,在不添加任何辅助线
PH 的值.
【答案】(1)证明见解析;(2) . 【解析】
【分析】
(1)由折叠的性质知,
,
,
,则由
得到
;
(2)由
,可得
,又由
,即可求得 的长,然后在
中,利用勾股定理即可求得 的长,再过点 作
于 ,由角平分线的性
质,可得 【详解】
,易证得四边形
是矩形,继而可求得答案.
(1) 四边形
为矩形,
,
,
又
,
;
【点睛】 本题是三角形的综合题,主要考查了全等三角形的判定与性质,直角三角形斜边中线的性 质,等腰三角形的性质和判定,平行四边形的性质和判定等知识,解题的关键是作辅助 线,并熟练掌握全等三角形的判定方法,特别是第三问,辅助线的作法是关键.
6.在 ABC 中, AD BC 于点 D ,点 E 为 AC 边的中点,过点 A 作 AF / / BC ,交 DE 的延长线于点 F ,连接 CF .
(2)
,
,
,
,
在
中,
,
过点 作
于,
,
,
,
,
,
,
、 、 共线,
,
四边形
是矩形,
,
. 【点睛】 此题考查了折叠的性质、矩形的性质、角平分线的性质、等腰三角形的判定与性质以及勾 股定理等知识.此题难度较大,注意掌握折叠前后图形的对应关系,注意掌握辅助线的作
法,注意数形结合思想的应用.
4.如图,在△ ABC 中,∠ ACB=90°,∠ CAB=30°,以线段 AB 为边向外作等边△ ABD,点 E 是线段 AB 的中点,连接 CE 并延长交线段 AD 于点 F.
CE EF GCE F , CG BF
∴ △ BEF≌ △ GEC(SAS), ∴ BE=EG; (3)如图 3,连接 DM,取 AC 的中点 N,连接 DN,
由(1)得 AE=EG, ∴ ∠ GAE=∠ AGE, 在 R DAN=∠ ADN, 2
由(1)知∠ APB=∠ BPH, 又∵ ∠ A=∠ BQP=90°,BP=BP, 在△ ABP 和△ QBP 中,
APB BPH {A BQP 90 , BP BP
∴ △ ABP≌ △ QBP(AAS), ∴ AP=QP,AB=BQ, 又∵ AB=BC, ∴ BC=BQ. 又∠ C=∠ BQH=90°,BH=BH, 在△ BCH 和△ BQH 中,
2
2
∴ CE=AE,∴ ∠ EAC=∠ ECA=30°,∴ ∠ BCE=∠ EBC=60°,又∵ △ AEF≌ △ BEC,
∴ ∠ AFE=∠ BCE=60°,又∵ ∠ D=60°,∴ ∠ AFE=∠ D=60°,∴ FC∥ BD,又
∵ ∠ BAD=∠ ABC=60°,∴ AD∥ BC,即 FD∥ BC,∴ 四边形 BCFD 是平行四边形;
【答案】(1)证明见解析(2)证明见解析(3) 5 2
【解析】 【分析】 (1)根据平行线的性质和等腰三角形的三线合一的性质得:∠ CAD=∠ G,可得 AE=EG; (2)作辅助线,证明△ BEF≌ △ GEC(SAS),可得结论; (3)如图 3,作辅助线,构建平行线,证明四边形 DMEN 是平行四边形,得 EM=DN=
2
2
△ AEF≌ △ BEC,得∠ AFE=∠ BCE=60°.又∠ D=60°,得∠ AFE
=∠ D=60 度.所以 FC∥ BD,又因为∠ BAD=∠ ABC=60°,所以 AD∥ BC,即 FD//BC,则四边形
BCFD 是平行四边形.
(2)在 Rt△ ABC 中,求出 BC,AC 即可解决问题;
1 AC,计算可得结论. 2
【详解】 证明:(1)如图 1,过 E 作 EH⊥CF 于 H,
∵ AD⊥BC, ∴ EH∥ AD, ∴ ∠ CEH=∠ CAD,∠ HEF=∠ G, ∵ CE=EF, ∴ ∠ CEH=∠ HEF, ∴ ∠ CAD=∠ G, ∴ AE=EG; (2)如图 2,连接 GC,
CD DM
设 AM=x,则 x a , a bx
整理得:x2﹣bx+a2=0, ∵ b>2a,a>0,b>0, ∴ △ =b2﹣4a2>0, ∴ 方程有两个不相等的实数根,且两根均大于零,符合题意, ∴ 当 b>2a 时,存在∠ BMC=90°, (3)不成立. 理由:若∠ BMC=90°, 由(2)可知 x2﹣bx+a2=0, ∵ b<2a,a>0,b>0, ∴ △ =b2﹣4a2<0, ∴ 方程没有实数根, ∴ 当 b<2a 时,不存在∠ BMC=90°,即(2)中的结论不成立. 考点:1、相似三角形的判定与性质;2、根的判别式;3、矩形的性质
角三角形、勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考
题型.
5.如图 1,在△ ABC 中,AB=AC,AD⊥BC 于 D,分别延长 AC 至 E,BC 至 F,且 CE=EF,
延长 FE 交 AD 的延长线于 G. (1)求证:AE=EG; (2)如图 2,分别连接 BG,BE,若 BG=BF,求证:BE=EG; (3)如图 3,取 GF 的中点 M,若 AB=5,求 EM 的长.
2.如图,现有一张边长为 4 的正方形纸片 ABCD,点 P 为正方形 AD 边上的一点(不与点 A、点 D 重合),将正方形纸片折叠,使点 B 落在 P 处,点 C 落在 G 处,PG 交 DC 于 H, 折痕为 EF,连接 BP、BH.
(1)求证:∠ APB=∠ BPH; (2)当点 P 在边 AD 上移动时,求证:△ PDH 的周长是定值; (3)当 BE+CF 的长取最小值时,求 AP 的长. 【答案】(1)证明见解析.(2)证明见解析.(3)2. 【解析】 试题分析:(1)根据翻折变换的性质得出∠ PBC=∠ BPH,进而利用平行线的性质得出 ∠ APB=∠ PBC 即可得出答案; (2)首先证明△ ABP≌ △ QBP,进而得出△ BCH≌ △ BQH,即可得出 PD+DH+PH=AP+PD+DH+HC=AD+CD=8; (3)过 F 作 FM⊥AB,垂足为 M,则 FM=BC=AB,证明△ EFM≌ △ BPA,设 AP=x,利用折 叠的性质和勾股定理的知识用 x 表示出 BE 和 CF,结合二次函数的性质求出最值. 试题解析:(1)解:如图 1,
