高一数学暑假作业(含解析)
高一数学暑假作业练习(含解析)

高一数学暑假作业练习(含解析)2021高一数学暑假作业练习下面查字典数学网为大家整理了高一数学暑假作业练习,希望大家在空余时间停止温习练习和学习,供参考。
大家暑期快乐哦。
一、选择题1.某工厂第三年的产量比第一年的产量增长44%,假定每年的平均增长率相反(设为x),那么以下结论中正确的选项是()A.x22%B.x22%C.x=22%D.x的大小由第一年产量确定[答案] B[解析] 由题意设第一年产量为a,那么第三年产量为a(1+44%)=a(1+x)2,x=0.2.应选B.2.(2021~2021学年度湖北黄冈中学高一月考)某种细菌在培育进程中,每15 min分裂一次(由1个分裂成2个),那么这种细菌由1个繁衍成212个需经过()A.12 hB.4 hC.3 hD.2 h[答案] C[解析] 细菌的个数y与分裂次数x的函数关系为y=2x,令2x=212,解得x=12,又每15 min分裂一次,所以共需1512=180 min,即3 h.3.(2021~2021学年度安徽阜阳一中高一月考)某山区为增强环境维护,绿色植被的面积每年都比上一年增长10.4%,那么,经过x年,绿色植被面积可以增长为原来的y倍,那么函数y=f(x)的图象大致为()[答案] D[解析] 此题考察指数函数的解析式与图象.设山区第一年绿色植被面积为a,那么y==(1+10.4%)x,应选D.4.光线每经过一块玻璃板,光线的强度就失掉10%,要使经过玻璃板的光线的强度削弱到原来强度的以下,那么至少需求堆叠玻璃板数为()A.8块B.9块C.10块D.11块[答案] D[解析] 设至少需求堆叠玻璃板数为n,由题意,得(1-10%)n,解得n11.5.某工厂消费两种本钱不同的产品,由于市场销售发作变化,A产品延续两次降价20%,B产品延续两次降价20%,结果都以23.04元出售,此时厂家同时出售A、B产品各1件,盈亏状况是()A.不亏不赚B.亏5.92元C.赚5.92元D.赚28.96元[答案] B[解析] 设A产品的原价为a元,B产品的原价为b元,那么a(1+20%)2=23.04,求得a=16;b(1-20%)2=23.04,求得b=36.那么a+b=52元,而23.042=46.08元.故亏52-46.08=5.92(元).应选B.6.某企业的产品本钱前两年平均每年递增20%,经过改良技术,后两年的产品本钱平均每年递减20%,那么该企业的产品本钱如今与原来相比()A.不增不减B.约增8%C.约增5%D.约减8%[答案] D[解析] 设原来本钱为a,那么如今的本钱为a(1+20%)2(1-20%)2=0.9216a,比原来约减8%.二、填空题7.某商品的市场需求量y1(万件)、市场供应量y2(万件)与市场价钱x(元/件)区分近似地满足关系:y1=-x+70,y2=2x-20.y1=y2时的市场价钱称为市场平衡价钱,那么市场平衡价钱为________元/件.[答案] 30[解析] 由题意,知y1=y2,-x+70=2x-20,x=30.8.某池塘中野生水葫芦的面积与时间的函数关系图象如下图.假定其函数关系为指数函数,并给出以下说法:此指数函数的底数为2;在第5个月时,野生水葫芦的面积就会超越30m2;野生水葫芦从4m2蔓延到12m2只需1.5个月;设野生水葫芦蔓延至2m2、3m2、6m2所需的时间区分为t1、t2、t3,那么有t1+t2=t3;野生水葫芦在第1到第3个月之间蔓延的平均速度等于在第2到第4个月之间蔓延的平均速度.其中,正确的选项是________.(填序号).[答案][解析] 关系为指数函数,可设y=ax(a0且a1).由图可知2=a1.a=2,即底数为2,说法正确;25=3230,说法正确;指数函数添减速度越来越快,说法不正确;t1=1,t2=log23,t3=log26,t1+t2=t3.说法正确;指数函数添减速度越来越快,说法不正确.故正确的有.三、解答题9.(2021~2021学年度山东实验中学高一期末测试)某乡镇目先人均一年占有粮食360kg,假设该乡镇人口平均每年增长1.2%,粮食总产量平均每年增长4%,那么x年先人均一年占有ykg粮食,求函数y关于x的解析式.[解析] 设该乡镇目先人口量为M,那么该乡镇目前一年的粮食总产量为360M.经过1年后,该乡镇粮食总产量为360M(1+4%),人口总量为M(1+1.2%),那么人均占有粮食为;经过2年后,人均占有粮食为;经过x年后,人均占有粮食为y==360()x=360()x.即所求函数解析式为y=360()x.一、选择题1.据报道,全球变暖使北冰洋夏季冰雪掩盖面积在最近50年内增加了5%,假设按此速度,设2021年的夏季冰雪掩盖面积为m,从2021年起,经过x年后,北冰洋夏季冰雪掩盖面积y与x的函数关系式是 ()A.y=0.95m B.y=(1-0.05)m C.y=0.9550-xm D.y=(1-0.0550-x)m[答案] A[解析] 设每年增加的百分比为a,由在50年内增加5%,得(1-a)50=1-5%=95%,即a=1-(95%)..所以,经过x年后,y与x的函数关系式为y=m(1-a)x=m(95%)=(0.95) m.2.某地为了抑制一种有害昆虫的繁衍,引入了一种以该昆虫为食物的特殊植物.该植物繁衍数量y(只)与引入时间x(年)的关系为y=alog2(x+1),假定该植物在引入一年后的数量为100,那么到第7年它们的数量为()A.300B.400C.600D.700[答案] A[解析] 将x=1,y=100代入y=alog2(x+1)中,得100=alog2(1+1),解得a=100,那么y=100log2(x+1),所以当x=7时,y=100log2(7+1)=300,应选A.3.某种型号的手机自投放市场以来,经过两次降价,单价由原来的2021元降到1280元,那么这种手机平均每次降价的百分率是()A.10%B.15%C.18%D.20%[答案] D[解析] 设平均每次降价的百分率为x,那么2021(1-x)2=1280,所以x=20%,应选D.读懂题意正确树立函数模型,求解可得.4.(2021~2021学年度广东广雅中学高一月考)抽气机每次可抽出容器内空气的60%,要使容器内的空气少于原来的0.1%,那么至少要抽(参考数据:lg20.3010)()A.6次B.7次C.8次D.9次[答案] C[解析] 此题考察对数函数的运用.设至少抽x次可使容器内的空气少于原来的0.1%,那么(1-60%)x0.1%,即0.4x0.001,xlg0.4-3,x7.5,应选C.二、填空题5.如图,由桶1向桶2输水,末尾时,桶1有a L水,t min 后,剩余水y L满足函数关系y=ae-nt,那么桶2的水就是y=a-ae-nt.假定经过5 min,桶1和桶2的水相等,那么再过________min,桶1中的水只要L.[答案] 10[解析] 由题意可得,经过5 min时,ae-5n=,n= ln2,那么,所以t=15,从而再经过10min后,桶1中的水只要L 6.一种产品的本钱原来是a元,在今后m年内,方案使本钱平均每年比上一年降低p%,那么本钱y随经过的年数x变化的函数关系为________.[答案] y=a(1-p%)x(xN*,且xm)[解析] 本钱经过x年降低到y元,那么y=a(1-p%)x(xN*,且xm).三、解答题7.地震的震级R与地震释放的能量E的关系为R=(lg E-11.4).据报道中国青海玉树2021年4月14日发作地震的震级为7.1级.而2021年3月11日,日本发作9.0级地震,那么9.0级地震释放的能量是7.1级地震的多少倍(准确到1)?[解析] 9.0级地震所释放的能量为E1,7.1级地震所释放的能量为E2,由9.0=(lg E1-11.4),得lg E1=9.0+11.4=24.9.同理可得lg E2=7.1+11.4=22.05,从而lg E1-lgE2=24.9-22.05=2.85,故lg E1-lg E2=lg=2.85,那么=102.85708,即9.0级地震释放的能量是7.1级地震的708倍.8.关于5年可成材的树木,在此时期的年生长率为18%,以后的年生长率为10%.树木成材后,即可出售,然后重新栽树木;也可以让其继续生长.问:哪一种方案可取得较大的木材量(注:只需思索10年的情形)?[解析] 设新树苗的木材量为Q,那么10年后有两种结果:延续生长10年,木材量N=Q(1+18%)5(1+10%)5;生长5年后重新栽树木,木材量M=2Q(1+18%)5.那么=.(1+10%)51.611,即MN.因此,生长5年后重新栽树木可取得较大的木材量.9.某集体运营者把末尾六个月试销A,B两种商品的逐月投资与所获纯利润列成下表:投资A商品金额(万元) 1 2 3 4 5 6 获纯利润(万元) 0.65 1.39 1.85 2 1.84 1.40 投资B商品金额(万元) 1 2 3 4 5 6 获纯利润(万元) 0.25 0.49 0.76 1 1.26 1.51 该运营者预备下月投入12万元运营这两种产品,但不知投入A,B两种商品各多少万元才合算.请你协助确定一个资金投入方案,使得该运营者能取得最大利润,并按你的方案求出该运营者下月可取得的最大纯利润(结果保管两位有效数字). [解析] 以投资额为横坐标,纯利润为纵坐标,在平面直角坐标系中画出散点图,如下图:观察散点图可以看出:A种商品的所获纯利润y与投资额x 之间的变化规律可以用二次函数模型停止模拟,如下图:取(4,2)为最高点,那么y=a(x-4)2+2.把点(1,0.65)代入,得0.65=a(1-4)2+2,解得a=-0.15.所以y=-0.15(x-4)2+2.B种商品所获纯利润y与投资额x之间的变化规律是线性的,可用一次函数模型模拟,如下图:设y=kx+b,取点(1,0.25)和(4,1)代入,得,解得.所以y=0.25x.即前6个月所获纯利润y关于月投资A种商品的金额x的函数关系式是y=-0.15(x-4)2+2;前6个月所获纯利润y关于月投资B种商品的金额x的函数关系式是y=0.25x.设下月投入A,B两种商品的资金区分为xA,xB(万元),总利润为W(万元),那么,所以W=-0.15(xA-)2+0.15()2+2.6,当xA=3.2(万元)时,W取最大值,约为4.1万元.此时xB8.8(万元).即该运营者下月把12万元中的3.2万元投资A种商品,8.8万元投资B种商品,可取得最大利润约为4.1万元.以上就是高一数学暑假作业练习,希望能协助到大家。
2020高一数学暑期作业本(人教必修1、2、4、5共40套含参考答案)

【文库独家】高一数学暑期作业本(人教必修1、2、4、5)1.函数(1)1.如果M={x|x+1>0},则 ( ) A 、φ∈MB 、0ÌMC 、{0}∈MD 、{0}⊆M2.若集合}4,3,2,1{}3,2,1{P = ,则满足条件的集合P 的个数为 ( ) A 、6B 、7C 、8D 、13.已知集合A={y|y=-x 2+3,x ∈R},B={y|y=-x+3,x ∈R},则A ∩B=( ) A 、{(0,3),(1,2)} B 、{0,1} C 、{3,2} D 、{y|y ≤3} 4.用列举法表示集合:M m m Z m Z =+∈∈{|,}101= 。
5.设全集{}(,),U x y x y R =∈,集合2(,)12y M x y x ⎧+⎫==⎨⎬-⎩⎭,{}(,)4N x y y x =≠-, 那么()()U U C M C N 等于________________。
6.若-3∈{a-3,2a-1,a 2-4},求实数a7.已知集合P={x|x 2+x-6=0},Q={x|ax+1=0}满足Q ⊂P,求a 的一切值。
8.已知集合A={x|-2≤x ≤5},B={x|m+1≤x ≤2m-1} (1)若B ⊆A ,求实数m 的取值范围。
(2)当x ∈Z 时,求A 的非空真子集个数。
(3)x ∈R 时,没有元素x 使x ∈A 与x ∈B 同时成立,求实数m 的取值范围。
2.函数(2)1.函数()y f x =的图象与直线1x =的公共点数目是( )A .1B .0C .0或1D .1或22.已知集合{}{}421,2,3,,4,7,,3A k B a a a ==+,且*,,a N x A y B ∈∈∈,使B 中元素31y x =+和A 中的元素x 对应,则,a k 的值分别为( )A .2,3B .3,4C .3,5D .2,53.已知)0(1)]([,21)(22≠-=-=x x x x g f x x g ,那么)21(f 等于( ) A .15 B .1 C .3 D .304.若函数234y x x =--的定义域为[0,]m ,值域为25[4]4--,,则m 的取值范围是( )A .(]4,0B .3[]2,4 C .3[3]2, D .3[2+∞,) 5.设()f x 是奇函数,且在(0,)+∞内是增函数,又(3)0f -=,则()0x f x ⋅<的解集是( ) A .{}|303x x x -<<>或 B .{}|303x x x <-<<或 C .{}|33x x x <->或 D .{}|3003x x x -<<<<或6.设函数()f x 与()g x 的定义域是x R ∈且1x ≠±,()f x 是偶函数, ()g x 是奇函数,且1()()1f xg x x +=-,求()f x 和()g x 的解析式.7.已知22()444f x x ax a a =-+--在区间[]0,1内有一最大值5-,求a 的值.8.已知函数()f x 定义域是),0(+∞,且()()()f xy f x f y =+,1()12f =,对于0x y <<,都有()()f x f y >, (1)求(1)f ; (2)解不等式2)3()(-≥-+-x f x f 。
暑假作业高一数学含详解
α
的值.
tan α π cos α
3.已知
0,
4
,
4
,
0
,
cos
4
3 5
,
cos
β
π 4
5 13
.
(1)求 sin 2 的值;
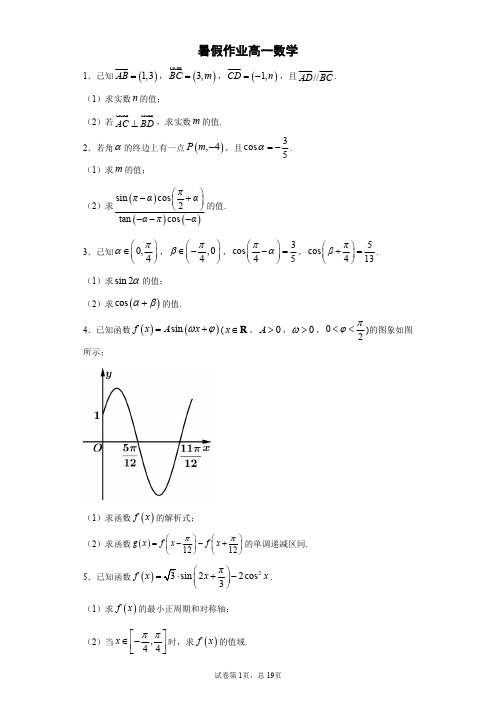
(2)求 cos 的值. 4.已知函数 f x Asin x ( x R , A 0 , 0 , 0 )的图象如图
2
(2)将函数 f x 的图象先向左平移 个单位,再把图象上各点的横坐标伸长为原来 6
的
2
倍,得到函数
h
x
的图象.若对任意的
x
0,
2
,不等式
p
h
x
1
h
x
2
1
h
2x
成立,求实数
p
的取值范围.
44.在 ABC 中,角 A , B , C 对应的边分别是 a , b , c .已知
cos 2A 3cos B C 1.
41.已知向量 a 与 b 的夹角为
60°,
a
3,
b
ur 2,m
r rr r r 2a 3b , n 3a kb .
(1)若 m n ,求实数 k 的值
ur r (2)是否存在实数 k ,使得 m//n ,说明理由.
42.如图是函数
f
(x) sin(x )(
0,
) 一个周期内的图象,已知点
g x
f
xk
在区间
6
, 13 12
上有三个零点,求实数 k
的取值范围.
32.已知函数 f x 是定义域为 R 的奇函数,且当 x 0 时,
高一数学暑期作业本(人教必修1、2、4、5共40套含参考答案)

高一数学暑期作业本(人教必修1、2、4、5)1.函数(1)1.如果M={x|x+1>0},则 ( ) A 、φ∈MB 、0ÌMC 、{0}∈MD 、{0}⊆M2.若集合}4,3,2,1{}3,2,1{P = ,则满足条件的集合P 的个数为 ( ) A 、6B 、7C 、8D 、13.已知集合A={y|y=-x 2+3,x ∈R},B={y|y=-x+3,x ∈R},则A ∩B=( ) A 、{(0,3),(1,2)} B 、{0,1} C 、{3,2} D 、{y|y ≤3} 4.用列举法表示集合:M m m Z m Z =+∈∈{|,}101= 。
5.设全集{}(,),U x y x y R =∈,集合2(,)12y M x y x ⎧+⎫==⎨⎬-⎩⎭,{}(,)4N x y y x =≠-, 那么()()U U C M C N 等于________________。
6.若-3∈{a-3,2a-1,a 2-4},求实数a7.已知集合P={x|x 2+x-6=0},Q={x|ax+1=0}满足Q ⊂P,求a 的一切值。
8.已知集合A={x|-2≤x ≤5},B={x|m+1≤x ≤2m-1} (1)若B ⊆A ,求实数m 的取值范围。
(2)当x ∈Z 时,求A 的非空真子集个数。
(3)x ∈R 时,没有元素x 使x ∈A 与x ∈B 同时成立,求实数m 的取值范围。
2.函数(2)1.函数()y f x =的图象与直线1x =的公共点数目是( )A .1B .0C .0或1D .1或22.已知集合{}{}421,2,3,,4,7,,3A k B a a a ==+,且*,,a N x A y B ∈∈∈,使B 中元素31y x =+和A 中的元素x 对应,则,a k 的值分别为( )A .2,3B .3,4C .3,5D .2,53.已知)0(1)]([,21)(22≠-=-=x xx x g f x x g ,那么)21(f 等于( ) A .15 B .1 C .3 D .304.若函数234y x x =--的定义域为[0,]m ,值域为25[4]4--,,则m 的取值范围是( )A .(]4,0B .3[]2,4 C .3[3]2, D .3[2+∞,) 5.设()f x 是奇函数,且在(0,)+∞内是增函数,又(3)0f -=,则()0x f x ⋅<的解集是( ) A .{}|303x x x -<<>或 B .{}|303x x x <-<<或 C .{}|33x x x <->或 D .{}|3003x x x -<<<<或6.设函数()f x 与()g x 的定义域是x R ∈且1x ≠±,()f x 是偶函数, ()g x 是奇函数,且1()()1f xg x x +=-,求()f x 和()g x 的解析式.7.已知22()444f x x ax a a =-+--在区间[]0,1内有一最大值5-,求a 的值.8.已知函数()f x 定义域是),0(+∞,且()()()f xy f x f y =+,1()12f =,对于0x y <<,都有()()f x f y >, (1)求(1)f ; (2)解不等式2)3()(-≥-+-x f x f 。
【高一】湖北高一数学暑假作业答案

【高一】湖北高一数学暑假作业答案暑假作业(一)I多项选择题:DCA二.填空题:4.5.6.4.解决方案:同样,a,B和C形成一个等比序列,,由余弦定理,得。
,即。
5.解:,。
6.解:由正弦定理及,得,即,而。
.再说一次,我必须这么做。
,即(当且仅当时“=”成立)。
,即δABC的最大面积为。
所以请填写。
三.解答题:7.解答:(I)from,to,from,to所以.(二)根据正弦定理,面积.8.解:(I)根据余弦定理和已知条件得出,因为,所以,得.联立方程组解得,.(二)从问题的意义,也就是正弦定理,联立方程组解得,.所以的面积.9.解决方案:∵ 新浪+cosa=cos(a-45°)=,∵ cos(a-45°)=。
0 °a=105°.∴tana=tan(45°+60°)=.sina=sin105°=sin(45°+60°)=sin45°cos60°+cos45°sin60°=。
s△abc=ac·absina=×二×三×=解法二:∵sina+cosa=①,∴(sina+cosa)2=.∴2sinacosa=-.∵0°① - ②, cosa=。
∴tana=(与下面的解决方案相同)10.解:(1)依题意,,由正弦定理及(2)按(将负值四舍五入)从而由余弦定理,得替换数值以获得解决方案:暑假作业(二)I多项选择题:bdb3.解:在△abc中,∵a,b,c成等差数列,∴2b=a+c.又由于∠b=30°,∴s△abc=acsinb=ac·sin30°=。
∴ac=6。
∴b2=a2+c2-2ac·cosb=(a+c)2-2ac-2ac·cosb=4b2-2×6-2×6·cos30°。
高一数学暑假作业精选(附解析)

高一数学暑假作业精选(附解析)C.03,x0+11,即x00,无解;当x02时,log2x03,x023,即x08,x08.4.函数f(x)=ax+loga(2x+1)(a0且a1)在[0,2]上的最大值与最小值之和为a2,则a的值为()A. B.5 C. D.4[答案] A[解析] 当a1时,ax随x的增大而增大,loga(2x+1)随x的增大而增大,函数f(x)在[0,2]上为增函数,f(x)max=a2+loga5,f(x)min=1,a2+loga5+1=a2,loga5+1=0,loga5=-1,a=(不合题意舍去).当0f(x)max=1,f(x)min=a2+loga5,1+a2+loga5=a2,loga5=-1,a=.二、填空题5.(2019~2019学年度江西南昌市联考)定义在R上的偶函数f(x)在[0,+)上单调递减,且f()=0,则满足f(x)0的集合为____________.[答案] (0,)(2,+)[解析] 本题主要考查函数的奇偶性、单调性的应用和对数不等式的解法.因为定义在R上的偶函数f(x)在[0,+)上单调递减,所以在(-,0]上单调递增.又f()=0,所以f(-)=0,由f(x)0可得x-,或x,解得x(0,)(2,+).6.(2019福建文,15)函数f(x)=的零点个数是________.[答案] 2[解析] 当x2,令x2-2=0,得x=-;当x0时,令2x-6+lnx=0,即lnx=6-2x,在同一坐标系中,画出函数y=6-2x与y=lnx的图象如图所示.由图象可知,当x0时,函数y=6-2x与y=lnx的图象只有一个交点,即函数f(x)有一个零点.综上可知,函数f(x)有2个零点.三、解答题7.已知函数f(x)=lg(4-x2).(1)求函数f(x)的定义域;(2)判断函数f(x)的奇偶性,并证明.[解析] (1)要使函数f(x)有意义,应满足4-x20,x24,-20,且a1)的图象关于原点对称.(1)求m的值;(2)判断函数f(x)在(1,+)上的单调性.[解析] (1)f(x)=loga(a0,且a1)的图象关于原点对称,f(x)为奇函数.f(-x)=-f(x).loga=-loga=loga,1-m2x2=1-x2,m2=1,m=1或m=-1.当m=1时,不满足题意,舍去,故m=-1.(2)f(x)=loga=loga.设x1,x2(1,+),且x10,x1x2-x1+x2-1x1x2-x2+x1-1,又x1,x2(1,+),(x1+1)(x2-1)=x1x2-x1+x2-10,(x2+1)(x1-1)=x1x2-x2+x1-10,1.当01时,loga0,即f(x1)f(x2),故函数f(x)在(1,+)上是减函数.综上可知,当a1时, f(x)在(1,+)上为减函数;当0f(1)=-2,即x1时, f(x)的值域是(-2,+).当x1时, f(x)=logx是减函数,所以f(x)f(1)=0,即x1, f(x)的值域是(-,0].于是函数f(x)的值域是(-,0](-2,+)=R.(2)若函数f(x)是(-,+)上的减函数,则下列三个条件同时成立:当x1时, f(x)=x2-(4a+1)x-8a+4是减函数,于是1,则a当x1时, f(x)=logax是减函数,则0以上就是高一数学暑假作业精选,希望能帮助到大家。
高一数学暑假作业及答案

2021年高一数学暑假作业及答案2021年高一数学暑假作业及答案【】复习的重点一是要掌握所有的知识点,二就是要大量的做题,查字典数学网的编辑就为各位考生带来了2021年高一数学暑假作业及答案一、选择题1.T1=,T2=,T3=,那么以下关系式正确的选项是()A.T1,即T2bdB.dcaC. dbaD.bda【解析】由幂函数的图象及性质可知a0,b1,0ca.应选D. 【答案】 D3.设{-1,1,,3},那么使函数y=x的定义域为R且为奇函数的所有的值为()A.1,3B.-1,1C.-1,3D.-1,1,3【解析】 y=x-1=的定义域不是R;y=x=的定义域不是R;y=x 与y=x3的定义域都是R,且它们都是奇函数.应选A.【答案】 A4.幂函数y=f(x)的图象经过点,那么f(4)的值为()A.16B.2C. D.【解析】设f (x)=x,那么2==2-,所以=-,f(x)=x-,f(4)=4-=.应选C.【答案】 C二、填空题5.n{-2,-1,0,1,2,3},假设nn,那么n=________. 【解析】∵--,且nn,y=xn在(-,0)上为减函数.又n{-2,-1,0,1,2,3},n=-1或n=2.【答案】 -1或26.设f(x)=(m-1)xm2-2,假如f(x)是正比例函数,那么m=________,假如f(x)是反比例函数,那么m=________,假如f(x)是幂函数,那么m=________.【解析】 f(x)=(m-1)xm2-2,假设f(x)是正比例函数,那么m=假设f(x)是反比例函数,那么即m=-1;假设f(x)是幂函数,那么m-1=1,m=2.【答案】-1 2三、解答题7.f(x)=,(1)判断f(x)在(0,+)上的单调性并证明;(2)当x[1,+)时,求f(x)的最大值.【解析】函数f(x)在(0,+)上是减函数.证明如下:任取x1、x2(0,+),且x10,x2-x10,x12x220.f(x1)-f(x2)0,即f(x1)f(x2).函数f(x)在(0,+)上是减函数.(2)由(1)知,f(x)的单调减区间为(0,+),函数f(x)在[1,+)上是减函数,函数f(x)在[1,+)上的最大值为f(1)=2.8.幂函数y=xp-3(pN*)的图象关于y轴对称,且在(0,+)上是减函数,求满足(a-1)(3+2a)的a的取值范围. 【解析】∵函数y=xp-3在(0,+)上是减函数,p-30,即p3,又∵pN*,p=1,或p=2.∵函数y=xp-3的图象关于y轴对称,p-3是偶数,取p=1,即y=x-2,(a-1)(3+2a)∵函数y=x在(-,+)上是增函数,由(a-1)(3+2a),得a-13+2a,即a-4.所求a的取值范围是(-4,+).以上就是查字典数学网高中频道为您整理的2021年高一数学暑假作业及答案,欢送大家进入高考频道理解2021年最新的信息,帮助同学们学业有成!。
高一数学暑期作业本(必修25含参考答案)

高一数学暑期作业本(必修25含参考答案)高一数学暑期作业本(必修2、5含参考答案)高一暑期数学作业(必修2和5)1.解三角形(1)abc1。
在里面△ ABC,如果==,则为△ ABC是()abccoscoscos222a.等腰三角形b.等边三角形c.直角三角形d.等腰直角三角形2.在△abc中,若a=60°,b=16,且此三角形的面积s=2203,则a的值是()a、 2400b.25c、 55d.493.在△ ABC,如果acosa=bcosb,那么△ ABC是()a.等腰三角形b.直角三角形c、等腰直角三角形D.等腰三角形或直角三角形4英寸△ ABC,a=120°,B=30°,a=8,然后是C=15.在△abc中,已知a=32,cosc=,s△abc=43,则b=.36.在△ ABC,D在边缘BC,BD=2,DC=1,∠ B=60度,∠ ADC=150O,找到AC的长及△abc的面积.7.在△ ABC,已知角度a、B和C的对边分别为a、B和C,且bcosb+ccosc=acosa,试判断△abc的形状.-1-2.解三角形(2)1.设m、m+1和m+2为钝角三角形的三条边长,则实数m的取值范围为()a.0<m<3b.1<m<3c.3<m<4d.4<m<62.在△ ABC,如果是新浪∶ 辛布∶ sinc=3∶ 5.∶ 7,三角形的最大内角等于()a.75°b.120°c.135°d.150°3、sabc中,若c=a2?b2?ab,则角c的度数是()c、60°或120°d.45°a?b?c4、在△abc中,a=60°,b=1,面积为3,则=.新浪?辛布?Sinc5。
在里面△ ABC,已知a,B和C形成一个等差序列,边B=2,然后是外切圆的半径r=136、在△abc中,tana?,tanb?.45(I)找出角度c的大小;(ⅱ)若△abc最大边的边长为17,求最小边的边长.7.如图所示,海中有一个小岛,3.8海里内有暗礁。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019 年高一数学暑假作业(含解析) 2019 年高一数学暑假作业为您介绍了试题及答案,希望你喜欢。
一选择题(本大题共小题,每小题5 分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知,则是的( )
A. 充分但不必要条件
B. 必要但不充分条件
C. 充要条件
D. 既不充分也不必要条件
2. 在区间上为增函数的是: ( )
A. B. C. D.
3. 抛物线y=的顶点在第三象限,试确定m的取值范围是()
A.m-1 或m
B.m0 或m
C.-1
4. 等差数列{}的公差不为零,首项=1,是和的等比中项,则数列的前10 项之和是
A. 90
B. 100
C. 145
D. 190 5. 若厶ABC的三边长为a,b,c,且则f(x)的图象()
(A) 在x 轴的上方(B) 在x 轴的下方
(C) 与x 轴相切(D) 与x 轴交于两点
6. 已知向量a = (2,1) , ab = 10,| a + b | =,贝,b |
(A) (B) (C)5 (D)25
7. 设集合( )
A. B.
C. D.
8. 如图,该程序运行后输出的结果为( )
A.1
B.10
C.19
D.28 本大题共小题,每小题5 分,9. 设
A={x|x2+x-6=0} , B={x|mx+ 仁0},且AB=A 贝U m的取值范围
是.
10. 抛物线y=-b+3 的对称轴是___,顶点是___。
11. 若是一个等比数列的连续三项,贝的值为.
12. 在厶ABC中,若,则____ 。
本大题共小题,每小题分,
13. 设函数的最小正周期为.
(I )求的最小正周期
(n)若函数的图像是由的图像向右平移个单位长度得到,求的单调增区间.
14. 一个有穷等比数列的首项为,项数为偶数,如果其奇数项的和为,偶数项的和为,求此数列的公比和项数。
15. 求关于x的方程ax+仁-x2+2x+2a(a0且a1)的实数解的个数.
16. 解不等式(1)(2)
1.B
2.D
3.D
4. B解析:设公差为,则.v0,解得=2, =100
5. A
6. 解析:本题考查平面向量数量积运算和性质,由知(a+b)2=a2+b2+2ab=50 ,得|b|=5 选C。
7. B解析:
8. C
9.
10. y 轴(0,3)
11. -4
12. 解析:
则
13. 解析: 依题意得,故的最小正周期为.
(n)依题意得:
由
解得
故的单调增区间为:
14. 解析:设此数列的公比为,项数为,则
项数为
15.2 个
16. 解析:(1) 得,
(2)
2019 年高一数学暑假作业就为大家介绍到这里,
希望对你有所帮助。
