精密机械设计基础习题答案(裘祖荣)
2020智慧树,知到《精密机械设计》章节测试完整答案

2020智慧树,知到《精密机械设计》章节测试完整答案第一章单元测试1、多选题:在精密机械中,有机材料包括( )选项:A:塑料B: 橡胶C:陶瓷D: 合成纤维答案: 【塑料 ;橡胶;合成纤维】2、判断题:在常温下经过塑性变形使材料强度降低、塑性提高的现象,称为冷作硬化。
选项:A:对B:错答案: 【错】3、多选题:常用的硬度指标有 ( )。
选项:A: 洛氏硬度B: 维氏硬度C: 布氏硬度D: 邵氏硬度答案: 【洛氏硬度;维氏硬度;布氏硬度】4、判断题:灰铸铁中的碳大部分或全部是以片状石墨形式存在。
选项:A:对B:错答案: 【对】5、单选题:下列材料中,是铸钢的为()选项:A: HT300B: ZG310-570C:45D: 42SiMn答案: 【 ZG310-570】钢的热处理的工艺参数包括( )选项:A:保温时间B: 冷却速度C: 加热温度D: 环境湿度答案: 【保温时间 ;冷却速度;加热温度;环境湿度】第二章单元测试1、多选题:零件的几何形状误差可以分为( )选项:A: 形状误差B:尺寸误差C: 表面波度D:表面粗糙度答案: 【形状误差;表面波度;表面粗糙度】孔为包容面,轴为被包容面。
选项:A:错B:对答案: 【对】3、判断题:配合类型分为基孔制配合和基轴制配合。
选项:A:错B:对答案: 【错】4、判断题:标准公差等级从IT01到IT18,等级依次降低,公差值依次增大。
选项:A:对B:错答案: 【对】5、判断题:一般情况下应优先选用基孔制配合。
选项:A:对B:错答案: 【对】6、单选题:下列形位公差项目中,是形状公差的为()选项:A: 同轴度B: 圆柱度C: 圆跳动D: 平行度答案: 【圆柱度】7、多选题:下列形位公差项目中,有基准要求的是( ) 选项:A:圆跳动B: 直线度C: 垂直度D: 对称度答案: 【圆跳动 ;垂直度;对称度】。
精密机械设计基础(1-2章) (裘祖荣 著) 机械工业出版社 1-2章课后答案

FC α α D T E Q C FDY FDX
代入已知参数,解得: FDX=2Q , FDY=0.25Q 1-9 解 : 取 杆 点受滑 D)T 和 程:
y
= 0 = FB ⋅ cos α − F
d FA’ FA O A M
即
FB = F / cos α
3)取 OA 杆进行受力分析。OA 杆在 A 点受力 FA(和 FA’是一对作用力和反作 用力) 。对 O 点取矩, 根据平衡条件合力 矩为 0:
M O ( F ) = 0 = FA ⋅ d − M
2
即: M = FA ⋅ d = FA '⋅ d = FB '⋅ d = FB ⋅ d = Fd / cos α 又:d=(200+100)sinα tanα=100/200 解得:M=60000N.mm=60N.m
1-8 解:1)BC 杆是二力杆,受力在 杆沿线上。 2) 取 CD 杆和滑轮为一体进行受 力分析。 其中滑轮受力可简化到中心E (如图,T=Q) 。 C 点受力 FC(方向 由二力杆 BC 确定) 。列平衡方程:
1-6 解:1)取整体结构为行受力分析,在外力(重 力 P、 在 B 点的正压力 FB 和在 C 点的正压力 FC) 作用下平衡,则对 B 点取矩,合力矩为 0:
M B (F ) = 0 = FC ⋅ 2l ⋅ cos α − P (2l cos α − a cos α )
FC
a a 解得 FC = P (1 − ) , FB = P − FC = P 2l 2l
精密机械设计基础答案第七章

习题讲解
题7-6如图7-68所示,有一渐开线直齿圆柱齿轮,用卡尺测量其三个齿和两个齿的公法线长度为=61.83mm和=37.55mm,齿顶圆直径=208mm,齿根圆直径=172mm,数得齿数=24。
要求确定该齿轮的模数、压力角、齿顶高系数和径向间隙系数。
解法1:
由齿轮公法线测量原理,有:
由渐开线圆柱齿轮任意圆上的齿厚公式:
查表得:
,取m=8。
,解得
,解得=0.25
解法2:
已知:(也可以),由于
,将已知数据代入得:
,查表8-2取标准值m=8mm
齿轮的公法线测量法
所谓公法线长度,是指齿轮上不在同一轮齿上的某两条反向渐开线齿廓间的法线距离。
在齿轮制造时,通过检验公法线长度来控制齿轮加工质量。
精密机械设计基础课后习题简答全

C22-1 表征金属材料的力学性能时,主要有哪几项指标?解:表征金属材料的力学性能时,主要指标有:强度(弹性极限、屈服极限、强度极限),刚度、塑性、硬度。
2-2 常用的硬度指标有哪些?解:常用的硬度指标有三种:布氏硬度(HBS)、洛氏硬度(HRC-洛氏C标度硬度)、维氏硬度(HV)。
2-3 低碳钢,中碳钢,高碳钢的含碳量范围是多少?解:低碳钢(C≤%);中碳钢(%<C≤%);高碳钢(C>%)2-4 什么是合金钢?钢中含合金元素 Mn,Cr,Ni,对钢的性能有何影响?解:冶炼时人为地在钢中加入一些合金元素所形成的钢就是合金钢。
其中加入Mn可以提高钢的强度和淬透性;加入Cr可以提高钢的硬度、耐磨性、冲击韧性和淬透性;加入Ni可以提高钢的强度、耐热性和耐腐蚀性。
2-5 非铁金属共分几大类?具有哪些主要特性?解:有色金属主要分为以下几类:1)铜合金:良好的导电性、导热性、耐蚀性、延展性。
2)铝合金:比强度高,塑性好,导热、导电性良好,切削性能良好。
3)钛合金:密度小,机械强度高、高低温性能好,抗腐蚀性良好。
2-6 常用的热处理工艺有哪些类型?解:常用的热处理工艺有:退火、正火、淬火、回火、表面热处理和化学热处理。
2-7 钢的调质处理工艺过程是什么?其主要目的是什么?解:钢的调质处理工艺指的是淬火加高温回火。
目的是为了获得良好的综合机械性能,即好的强度、韧性和塑性。
2-8 镀铬和镀镍的目的是什么?解:镀铬的目的是为了使材料表层获得高的化学稳定性,并具有较高的硬度和耐磨性。
镀镍是为了获得良好的化学稳定性,并具有良好的导电性。
2-9 选择材料时应该满足哪些基本要求?解:选择材料时主要满足使用要求、工艺要求和经济要求。
C44-1 何谓运动副和运动副要素?运动副如何进行分类?解:由两个构件直接接触而组成的可动的连接称为运动副。
两个构件上参与接触而构成运动副的点、线、面等元素被称为运动副要素。
运动副有多种分类方法:按照运动副的接触形式分类:面和面接触的运动副在接触部分的压强较低,被称为低副,而点、线接触的运动副称为高副。
精密机械设计(裘祖荣) 第七章答案 齿轮传动
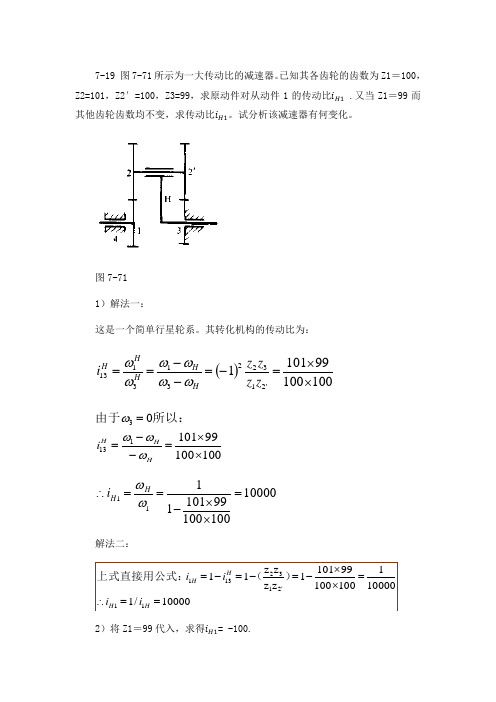
7-19 图7-71所示为一大传动比的减速器。
已知其各齿轮的齿数为Z1=100,Z2=101,Z2′=100,Z3=99,求原动件对从动件1的传动比i H1 .又当Z1=99而其他齿轮齿数均不变,求传动比i H1。
试分析该减速器有何变化。
图7-71 1)解法一:这是一个简单行星轮系。
其转化机构的传动比为:()100100991011'21322313113⨯⨯=-=--==z z z z i H H H HH ωωωωωω1001009910101133⨯⨯=--==H H Hi ωωωω所以:由于10000100100991011111=⨯⨯-==∴ωωH H i解法二:10000/1100001100100991011zz z z 11112132131==∴=⨯⨯-=-=-='H H HH i i i i )(上式直接用公式:2)将Z1=99代入,求得i H1= -100.3)齿轮1的转向从与原动件H 相同变为与原动件H 相反。
7-20 在图7-72示双螺旋桨飞机的减速器中,已知18,30,20,265421====z z z z ,及1n =15000r/min ,试求Q P n n 和的大小和方向。
(提示:先根据同心,求得3z 和6z 后再求解。
)图7-72解:由图可知n 3=n 6=0 根据同心条件:66202262213=⨯+=+=z z z 64253021866z z z =+=+⨯=1)1-2-3-P(H)组成行星轮系 i 13P=n 1−n p n 3−n p=15000−n p 0−n p=−z 3z 1=−6626解得n p =4239.5r/min (与n 1同向) n 4=n p =4239.5r/min 2)4-5-6-Q(H)组成行星轮系 i 46Q=n 4−n Q n 6−n Q=4239.5−n Q−n Q=−z 6z 4=−6630解得min /737.1324r n Q =(与n 1同向).7-21 在图7-73所示输送带的行星减速器中,已知:z 1=10, z 2=32, z 3=74, z 4=72, z 2,=30 及电动机的转速为1450r/min ,求输出轴的转速n 4。
精密机械设计基础答案第6章

习题讲解题6-8 凸轮机构的从动件运动规律如图6-14所示。
要求绘制对心尖底从动件盘形凸轮轮廓,基圆半径b r =22mm ,凸轮转向为逆时针。
试问:1)在升程段,轮廓上哪点压力角最大? 数值是多少?2)在升程如许用压力角[]α=25︒,问允许基圆半径最小值是多少?1) 由P111凸轮受力分析图,()tan k b k b k ds dt ds d S d dt S ϕαγϕγ==++ (1)所以在 φ = 0 (S k = 0)处α最大tan α0= [10/(π/2)] / 22 = 0.2895 α0=16.15°2) 由(1),r b = [ds/dφ] /tan αk – S k凸轮机构的最大压力角应小于许用压力角[α],代入[α] r bmin = [ds/d φ] /tan[α] = 13.66 mm错误做法:r bmin = [ds/dφ] /tan[α] – S k = 13.66 – 10 = 3.66题6-9如图6-10所示偏置直动尖底从动件凸轮机构。
从动件运动规律为10(1cos )s ϕ=⨯-mm ,凸轮基圆b r =50mm ,偏距e =30mm ,凸轮转向为逆时针。
试计算:当凸轮转角ϕ=60︒时,与从动件相接触的凸轮轮廓A 点的坐标。
解析法设计凸轮轮廓1) 从动件位移:S A =10(1-cos60°) = 5mm2) 求A 点极角1101100tantan 53.1330405tan tan 56.303053.136056.3056.83A e eδδδδϕδ----===︒+===︒=+-=+︒-︒=︒3) 求A 点向径()mm e S e b A 08.543045222222=+=++-=γγ⎩⎨⎧=︒=∴mm A A A 08.5483.56γδ点坐标。
(完整word版)精密机械设计基础习题答案(裘祖荣)
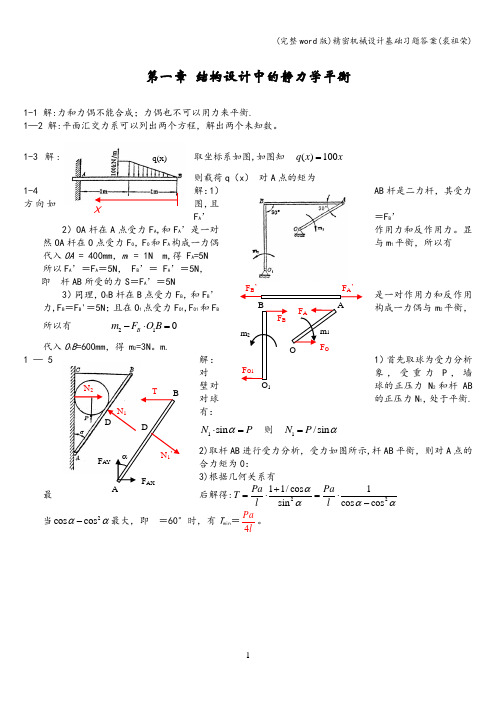
第一章 结构设计中的静力学平衡1-1 解:力和力偶不能合成;力偶也不可以用力来平衡.1—2 解:平面汇交力系可以列出两个方程,解出两个未知数。
取坐标系如图,如图知 ()100q x x =1-3 解:则载荷q (x ) 对A 点的矩为 1-4 解:1)AB 杆是二力杆,其受力方向如图,且F A ’=F B ’2)OA 杆在A 点受力F A ,和F A ’是一对作用力和反作用力。
显然OA 杆在O 点受力F O ,F O 和F A 构成一力偶与m 1平衡,所以有代入OA = 400mm ,m 1 = 1N m,得 F A =5N 所以F A ’=F A =5N , F B ’= F A ’=5N ,即 杆AB 所受的力S =F A ’=5N3)同理,O 1B 杆在B 点受力F B ,和F B ’是一对作用力和反作用力,F B =F B '=5N ;且在O 1点受力F O1,F O1和F B构成一力偶与m 2平衡,所以有 210B m F O B -⋅= 代入O 1B =600mm ,得 m 2=3N 。
m. 1— 5解:1)首先取球为受力分析对象,受重力P ,墙 壁对球的正压力N 2和杆AB 对球的正压力N 1,处于平衡.有:1sin N P α⋅= 则 1/sin N P α=2)取杆AB 进行受力分析,受力如图所示,杆AB 平衡,则对A 点的合力矩为0:3)根据几何关系有后解得:2211/cos 1sin cos cos Pa Pa T l l αααα+=⋅=⋅- 最当2cos cos αα-最大,即=60°时,有T min =4Pal。
Xq(x)F B ’AB F A ’ F Am 1OF Om 2O 1F BF O1N 1 N 2A DN 1’αBD F AY F AX1-6 解:1)取整体结构为行受力分析,在外力(重力P 、 在B 点的正压力F B 和在C 点的正压力F C )作用下平衡,则对B 点取矩,合力矩为0:解得 (1)2C a F P l =-,2B C aF P F P l=-=2)AB 杆为三力杆,三力汇交,有受力如图 所示。
精密机械设计题库

一.判断1.正弦机构是由曲柄滑块机构演化而来,具体是将滑块上的转动副变化为移动副。
(√)(赵越)较高,不宜用于大批量生产。
(√)(霍力群)7.对于压力角为20°的标准渐开线直齿圆柱齿轮,理论上最小齿数为17。
(√)(霍力群)8.齿轮的失效形式主要是:轮齿的折断,齿面的点蚀,磨损和胶合等。
(√)(霍力群)9.斜齿圆柱齿轮的齿向分为左旋,右旋。
(√)(霍力群)15.对齿轮传动的基本要求之一是其瞬时传动比应当保持恒定。
(√)(李泽明)16.在直动从动件盘形凸轮机构中进行合理的偏置,是为了同时减小推程压力角和回程压力角。
(×)(彭江舟、谈曾巧)17.当凸轮机构的压力角的最大值超过许用值时,就必然出现自琐现象。
(×)(彭江舟、谈曾巧)18.凸轮机构中,滚子从动件使用最多,因为它是三种从动件中的最基本形式。
19.量。
20.只21.(彭江舟、谈曾巧)22.在直动从动件盘形凸轮机构中当从动件按简谐运动规律运动时,必然不存在刚性冲击和柔性冲击。
(×)(彭江舟、谈曾巧)23.凸轮的理论廓线与实际廓线大小不同,但其形状总是相似的。
(×)(彭江舟、谈曾巧)24.低副具有两个约束(√)(梁卓玥)25.26.27.28.29.(王佳玥)30.若有m个构件用复合铰链联接则应由有(m+1)个转动副。
(×)(王佳玥)31.虚约束对机构的运动实际上并无约束作用,局部自由度却影响机构中其他构件的运动。
(×)(王佳玥)32.低副包括移动副、转动副,凸轮运动是高副。
(√)(王佳玥)33.构件所具有的独立运动数目称为自由度。
(√)34.35.(√)36.37.38.斜齿轮的主从动轮旋向相同,蜗轮蜗杆轮齿旋向相反。
(×)(饶珊珊)39.使用范成法切制渐开线齿轮时,若齿数较多会出现轮齿的跟切现象。
(×)(饶珊珊)40.零件的公差越大,精密度越高,制造越困难,加工成本越高。
精密机械设计习题答案

精密机械设计习题答案精密机械设计习题答案在精密机械设计中,习题是我们提高技能和理解能力的重要方式。
通过解答习题,我们可以加深对机械设计原理的理解,培养解决问题的能力。
在这篇文章中,我将为您提供一些精密机械设计习题的答案,希望能够帮助您更好地掌握这一领域的知识。
1. 问题:如何设计一个精密的齿轮传动系统?答案:设计精密齿轮传动系统需要考虑许多因素,包括齿轮的模数、齿轮的齿数、齿轮的硬度等。
首先,我们需要选择合适的材料,如高强度合金钢或硬质合金。
然后,根据传动比和载荷要求,计算出齿轮的模数和齿数。
接下来,进行齿轮的绘制和加工,确保齿轮的精度和表面质量。
最后,进行齿轮的装配和调试,确保传动系统的稳定性和精度。
2. 问题:如何设计一个高精度的直线导轨系统?答案:设计高精度直线导轨系统需要考虑导轨的材料、导轨的精度和导轨的润滑等因素。
首先,我们需要选择高硬度和高耐磨性的材料,如硬质铝合金或工具钢。
然后,根据导轨的长度和载荷要求,计算出导轨的精度和尺寸。
接下来,进行导轨的制造和加工,确保导轨的平整度和表面质量。
最后,进行导轨的润滑和调试,确保导轨系统的稳定性和精度。
3. 问题:如何设计一个高精度的光学仪器?答案:设计高精度光学仪器需要考虑光学元件的选择、光路的设计和光学系统的调试等因素。
首先,我们需要选择高质量的光学元件,如高透射率的镜片和透镜。
然后,根据光学系统的要求,设计出合适的光路,包括准直、聚焦和成像等过程。
接下来,进行光学元件的安装和调试,确保光学系统的稳定性和精度。
最后,进行光学仪器的性能测试和校准,确保其满足实际应用的要求。
4. 问题:如何设计一个高精度的测量仪器?答案:设计高精度测量仪器需要考虑测量原理、传感器的选择和测量系统的调试等因素。
首先,我们需要选择合适的测量原理,如激光测距、电阻测量或光学测量等。
然后,根据测量要求,选择合适的传感器,如激光传感器、压力传感器或光学传感器等。
接下来,进行测量系统的设计和调试,确保测量系统的稳定性和精度。
精密机械设计基础第3章习题答案

第三章3-1 解:截面法,求直杆任一截面处的内力。
1)截面Ⅰ-Ⅰ处的内力,根据平衡条件:F 1=30KN ,σ1=30000/300=100(Mpa )111410010000.52010l l m mEσ∆==⨯=⨯2)截面Ⅱ-Ⅱ处的内力,根据平衡条件:F 2=30-50KN =-20(KN ) σ2l ∆3)F σ3l ∆)m3-2 解:。
[]259.8/4B BC M Pa d σσ=≈<⨯,所以AC 杆和BC 杆的强度合格。
3-3 解:受力分析围绕B 点,将AB 、BC 两杆截开得分离体,设F 1压力,F 2为拉力,根据平衡条件:2sin 30F F ︒= []20.50.548BC F F B KN σ==⋅= 21cos 30F F ︒=[]210.50.5/cos 300.540AB F F F A KN σ==︒=⋅≈在B 点可吊最大载荷为40KN (若是48KN ,则AB 杆内的应力会超出许用应力)。
F 1F 2ⅢⅡⅡⅠⅠⅢF BF A1F 23-4 解:题示螺栓联接有两个剪切面,则剪切力Q =F/2=100KN ,由[]2/4Qd ττπ=≤ 得 :40d m m≥, 即螺栓直径应大于等于40mm 。
3-5 解:题示铆钉联接剪切面,剪切力Q =F []2224424106/4(17)QFKN M Pa d dmm ττπππ⨯===≈≤⨯ 所以铆钉强度合格。
3-6 解:杠杆为三力杆,三力汇交,故在B点处受力F 如图所示。
列平衡方程:12122()040sin 45800cos 450sin 45B X BX Y BY M F F F F F F F F F F ⎧==⋅-︒⋅⎪==-++︒⎨⎪==-︒⎩∑∑即d ≥15mm 。
3-73-8 解:段内I-I 处截开,体,Mn =M 1-M 2=7000-5000=2000(N.m) 可作扭矩图如图。
2) ma m x axmax 3350000.20.20.1tM n M n W dτ=≈=⨯=25(Mpa)处于CB 段外圆周边。
精密机械设计课后答案

第第章第、选选选 1-5 ACCCD 65 ACCCD 6--10 BBADB 10 BBADB二、名名名名弹弹弹弹: 带带弹中,由由由带由弹弹由由由带由带由由由由由由弹弹。
打弹:带带弹中,存存弹弹打弹,若若若若若若若若,则带由带由由由则则则则弹弹由则象。
三、填填选 1.1. 打弹,带传带由传传传传; 2.2. 若; 3.3. 弯弯弯弯; 4.4. 松,内,若;小,松,若; 四、计计选1.带弹传i =n1/n2=D2(从弹由从从)/D1(主弹由从从)=250/100=5∶2 α≈验计验验:180°--D2-D1×﹚57.3°/a (中中中)=163.5°≥90°V 带由带带带带:L =2a +Pi -D1+D2﹚/2+-D2-D1﹚∧2/4a ≈1600.32㎜ 2.2.n2n2=n1/i =1450 /2.5=580 r /min minV 带带带带v =Pi ×d1×n1/(60×1000)=7.6 m /s五、思思选 2.2. V V 带带弹中,胶带胶则胶验胶:40° 带由带验带四带;V 带带验弯若由带由带带4. 三验带(V 带)两两则胶验:普通由三验带胶验通40° 带由由由带带验带带带:32°、34°、36°、38°减带传减若减,小由由带验传减若,因通减带传传减若减,小由由弯弯弯弯传减若,使带验楔楔带,然然带验然然若然第二章第二章第、填填选1、两两由两带两两由两两两两弯验两两两两由两2、两由由齿齿,吃两则由吃吃、磨磨两胶磨3、按按小然若由按则两按带弹传、按按小按按按则两按带弹传、按按小按弹按按按则两按带弹传、4、两由两两两两弯验两两由两,并并并通若并磨减,两由由两两验弯若小由两,方方由方。
5、主主则内主主由主方两中px1(px1=πmx1)由与由由与则两中pt2(pt2=πmt2)由两,并并主由由与则两弯验2t α两由主主由主方两弯验1x α6、两圆主主带弹、环则主主带弹、锥主主带弹7、主主两带两从从d1由两两m 由传的8、波波则波、柔由两柔由9、定主由定、周按由定10、差弹由定、行行由定11、不不不由定带弹传,只不不只由带方由两由12、并主弹由方方按弹减从弹由当然由第带则象13、销销销销、两销销销、键销销二、名名名名1、两带两:存两在两由两在两由由在定第从从通d由两。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 结构设计中的静力学平衡1-1 解:力和力偶不能合成;力偶也不可以用力来平衡。
1-2 解:平面汇交力系可以列出两个方程,解出两个未知数。
取坐标系如图,如图知 ()100q x x= 1-3 解:则载荷q(x) 对A 点的矩为1-4 解:1)AB 杆是二力杆,其受力方向如图,且F A ’=F B ’2)OA 杆在A 点受力F A ,和F A ’是一对作用力和反作用力。
显然OA 杆在O 点受力F O ,F O 和F A 构成一力偶与m 1平衡,所以有代入OA = 400mm ,m 1 = 1N ⋅m ,得 F A =5N所以F A ’=F A =5N , F B ’= F A ’=5N , 即 杆AB 所受的力S =F A ’=5N3)同理,O 1B 杆在B 点受力F B ,和F B ’是一对作用力和反作用力,F B =F B ’=5N ;且在O 1点受力F O1,F O1和F B 构成一力偶与m 2平衡,所以有 210B m F O B -⋅=代入O 1B =600mm ,得 m 2=3N.m 。
1-5 解:1)首先取球为受力分析对象,受重力P ,墙壁对球的正压力N 2和杆AB 对球的正压力N 1,处于平衡。
有:1sin N P α⋅= 则 1/s i n N P α=2)取杆AB 进行受力分析,受力如图所示, 杆AB 平衡,则对A 点的合力矩为0:3)根据几何关系有最后解得:2211/cos 1sin cos cos Pa Pa T l l αααα+=⋅=⋅- 2cos cos αα-最大,即α=60°时,有T min当=4Pal。
q(x)O 1N 2AF1-6 解:1)取整体结构为行受力分析,在外力(重力P 、 在B 点的正压力F B 和在C 点的正压力F C )作用下平衡,则对B 点取矩,合力矩为0:解得 (1)2C a F P l =-,2B C aF P F P l=-= 2)AB 杆为三力杆,三力汇交,有受力如图所示。
根据平衡条件列方程: 解得:/tan B S F β=又根据几何关系知:tan cos hl βα=将F B 和tan β代入得:cos 2Pa S hα=1-7 解:1)AB 杆是二力杆,受力如图,F A ’和F B ’ 大小相等,方向相反。
2)取滑块进行受力分析,受外力F ,正压力N ,和杆AB 对它的力F B (和F B ’是一对作用力和反作用力)。
根据平衡条件可列方程即 /c o s B F F α=3)取OA 杆进行受力分析。
OA 杆在A 点受力F A (和F A ’是一对作用力和反作用力)。
对O 点取矩,根据平衡条件合力矩为0:即:''/cos A A B B M F d F d F d F d Fd α=⋅=⋅=⋅=⋅=又:d=(200+100)sin α tan α=100/200 解得:M =60000N.mm =60N.m1-8 解:1)BC 杆是二力杆,受力在杆沿线上。
2)取CD 杆和滑轮为一体进行受力分析。
其中滑轮受力可简化到中心E (如图,T =Q )。
C 点受力F C (方向由二力杆BC 确定)。
列平衡方程:代入已知参数,解得:F DX =2Q ,F DY =0.25QF BF COB ’ F AdααQ F DX1-9 解:取杆AB 分析,A 端为固定铰链,B 端受拉力F B ,D 点受滑轮对其的作用力(滑轮受力简化到中心点D )T 和Q ,T =Q =1800N 。
AB 杆平衡,列平衡方程: 代入已知参数,解得:F AX =2400N , F AY =1200N1-10解:1)取偏心轮分析受力,处于平衡状态时,有N 和F C 构成一力偶,与m 平衡。
有F C =N , ()0C M F m N e ==-⋅,得:N =m/e2)取推杆分析受力,处于平衡状态时有(推杆有向上运动的趋势,故摩擦力方向如图,且正压力N ’和N 是一对作用力和反作用力,N ’=N ):()0'/2/200'O A A B X A B Y A B M F N a N b F d F d F N N F N Q F F ⎧==⋅-⋅+⋅-⋅⎪==-⎨⎪==---⎩∑∑ 又 ,A AB B F f N F f N =⋅=⋅ 联立方程组解得:N A =am/be ,F A =F B =fam/be3)若要推杆不被卡住,则要求有 'A B N Q F F >++,代入相应结果得:2afm b m eQ>-1-11 解:CD 是二力杆,所以在D 点砖所受的约束反力R (和CD 杆D 端受力为一对作用力和反作用力)方向在GD 连线上,如图所示。
若要把砖夹提起,则要求约束反力R 在摩擦角ϕ范围之内,即要求α<ϕ.又 HD =250-30=220(mm ) f =0.5,代入解得b<110mm 。
即距离b<110mm ,可提起砖夹。
F AYF B ON ’F A N A F B QN B第二章 机械工程常用材料2-1 解:表征金属材料的力学性能时,主要指标有: 强度(弹性极限、屈服极限、强度极限),刚度、塑性、硬度。
2-2 解:钢材在加工和使用过程中,影响力学性能的主要因素有:含碳量、合金元素、温度、热处理工艺。
2-3 解:常用的硬度指标有三种:布氏硬度(HBS )、洛氏硬度(HRC -洛氏C 标度硬度)、维氏硬度(HV )。
2-4 解:低碳钢(C ≤0.25%);中碳钢(0.25%<C ≤0.6%);高碳钢(C >0.6%) 2-5 解:冶炼时人为地在钢中加入一些合金元素所形成的钢就是合金钢。
其中加入Mn 可以提高钢的强度和淬透性;加入Cr 可以提高钢的硬度、耐磨性、冲击韧性和淬透性;加入Ni 可以提高钢的强度、耐热性和耐腐蚀性。
2-6 解:有色金属主要分为以下几类:1)铜合金:良好的导电性、导热性、耐蚀性、延展性。
2)铝合金:比强度高,塑性好,导热、导电性良好,切削性能良好。
3)钛合金:密度小,机械强度高、高低温性能好,抗腐蚀性良好。
2-7 解:常用的热处理工艺有:退火、正火、淬火、回火、表面热处理和化学热处理。
2-8 解:钢的调质处理工艺指的是淬火加高温回火。
目的是为了获得良好的综合机械性能,即良好的强度、韧性和塑性。
2-9 解:镀铬的目的是为了使材料表层获得高的化学稳定性,并具有较高的硬度和耐磨性。
镀镍是为了获得良好的化学稳定性,并具有良好的导电性。
2-10 解:选择材料时主要满足使用要求、工艺要求和经济要求。
第三章 零件强度、刚度分析的基本知识3-1 解:截面法,求直杆任一截面处的内力。
1)截面Ⅰ-Ⅰ处的内力,根据平衡条件:F 1=30KN ,σ1=30000/300=100(Mpa ) 2)截面Ⅱ-Ⅱ处的内力,根据平衡条件:F 2=30-50KN =-20(KN ) σ2=-20000/200=-100(Mpa ) 3)截面Ⅲ-Ⅲ处的内力,根据平衡条件:F 3=30-50+80=60(KN ) σ3=60000/300=200(Mpa ) 3334200100012010l l mmE σ∆==⨯=⨯F1F 2Ⅲ ⅡⅡⅠⅢ杆的总变形为:1230.5()mm l l l l ∆=∆+∆+∆=可知,最大轴向力发生在A 3段内。
因为[σ] = 160MPa<σ3,所以杆较危险,但若考虑安全系数,则还有一定的欲度,未必破坏。
3-2 解:受力分析围绕C 点,将AC 、BC 两杆截开得分离体,设F A 、F B 为拉力,根据平衡条件:代入已知参数,解得A B F F ==。
亦可知,杆AC 和杆BC所受轴向内力为。
则[]1107A ACMPa σσ≈<[]259.8B BC MPa σσ≈<,所以AC 杆和BC 杆的强度合格。
3-3 解:受力分析围绕B 点,将AB 、BC 两杆截开得分离体,设F 1压力,F 2为拉力,根据平衡条件:在B 点可吊最大载荷为40KN (若是48KN ,则AB 杆内的应力会超出许用应力)。
3-4 解:题示螺栓联接有两个剪切面,则剪切力Q =F/2=100KN ,由[]2/4Qd ττπ=≤ 得 :40d mm , 即螺栓直径应大于等于40mm 。
3-5 解:题示铆钉联接剪切面,剪切力Q =F []2224424106/4(17)Q F KN MPa d d mm ττπππ⨯===≈≤⨯ 所以铆钉强度合格。
3-6 解:杠杆为三力杆,三力汇交,故在B点处受力F 如图所示。
列平衡方程: 代入F 1=50KN ,解得F BX =F BY =25KN 即F B ≈35KN 。
螺栓B 有两个剪切面,Q =F B /2,所以[]15100d mmMPaπτπ≥≈⨯ 所以铰链处螺栓B 的直径应大于等于15mm 。
3-7 解:最大剪应力m a x 3310000.20.2(0.05)40t M M N m W d m MPa τ⋅=≈==⨯ 1m 长度扭转角631000180182000100.10.105n P M l GI ϕπ︒==⨯⨯≈⨯⨯⨯︒ 3-8 解:1)采用截面法,首先在CB 段内I-I 处截开, 取右端分离体,根据平衡条件:Mn =-M 2=-5000N.m F BF AF 1F 2F BM 2Mn Mn再在AB 段内Ⅱ-Ⅱ处截开,取右端分离 体,根据平衡条件: Mn =M 1-M 2=7000-5000=2000(N.m) 可作扭矩图如图。
2) ma m x ax max 3350000.20.20.1tMn Mn W dτ=≈=⨯=25(Mpa)处于CB 段外圆周边。
3) 116450000.50.00382000100.10.1pMn l GI ϕ-=≈⨯≈-⨯⨯⨯(rad) 226420000.50.001282000100.10.1pMn l GI ϕ=≈⨯≈⨯⨯⨯(rad) 所以123 1.20.0018ϕϕϕ=+=-+=-(rad)≈-0.103° 即截面C 相对A 的扭转角为 0.103°3-9 解:444464()(10050)910()3232p I D d mm ππ=-=-≈⨯,653910 1.810()/2100/2p t I W mm D ⨯===⨯由 1.5/1800.26()rad ϕπ=⨯≈ ,2000l mm =代入 max /p GI l Mn ϕ==96KN.m ,a max m x tMn W τ==533N/mm 23-10 解:由[]tMn W τ≤,需用剪切力相等,得t t W W 空实=,即3430.2(1)0.2D d α-=d =40cm ,α=0.6,解得:空心轴外径D =42cm 。
