高斯烟羽模式公式

LNG低温储罐泄漏事故危险性分析综述(全文)

第三届中国LNG 论坛论文编号：1260304LNG 低温储罐泄漏扩散危险性分析方法综述张文冬张永信路江华（中国石化青岛液化天然气有限责任公司，山东青岛，266400）摘要:液化天然气（LNG ）低温储罐泄漏可能导致喷射火、闪火、沸腾液体扩展蒸气爆炸和蒸气云爆炸等事故，国内外学者在LNG 泄漏扩散的危险性分析方面取得了一定的理论和实验研究成果。

文章从数值模拟和实地物理模拟两个方面，总结了近年来国内外学者LNG 泄漏事故危险性分析尤其是泄漏扩散方面的成果。

数值模拟方面，介绍了基于不同原理泄漏扩散的数值计算模型，如三维传递模型、高斯模型、经验模型、BM 模型、一维积分模型、浅层模型等的建立及其在LNG 泄漏扩散中的应用，并总结了目前广泛应用于定量风险评估的计算机软件。

物理模拟试验以风洞试验为主，本文归纳了国内外LNG 泄漏试验的研究成果，作为数值模型的验证和进一步补充。

通过对比分析不同的分析研究方法在LNG 储罐泄漏事故中的应用，为进一步研究提供参考，以便更加合理地进行LNG 接收站安全设计。

关键词：LNG 储罐；泄漏；扩散；数值模拟；试验随着社会经济的发展，液化天然气（LNG ）作为一种清洁能源越来越受到人们的普遍关注，其在储存过程中的安全性也备受关注。

液化天然气储罐一旦发生泄漏，将可能导致喷射火、闪火、沸腾液体扩展蒸气爆炸和蒸气云爆炸等事故，会对周围的环境、人员、设备等造成极大危害。

国内外此类事故常有发生，如美国俄亥俄州发生的天然气泄漏事故造成128人死亡和难以计数的财产损失。

许多国家对LNG 的相关设施制定了严格的安全标准，如美国联邦规范将LNG 设备的安全归于管网安全。

国内外学者对于LNG 泄漏扩散危险性分析的理论和试验研究工作已开展多年，并且得到了很多具有实际指导意义的成果。

1.LNG泄漏模型LNG 储罐的泄漏形式包括气相泄漏、液相泄漏和两相流泄漏，不同的泄漏模式对应有不同的泄漏模型。

由于LNG 储罐主要发生液相泄漏和两相流泄漏，这里只介绍这两种泄漏模式的预测模型。

高斯烟羽模型课件

温度和湿度
温度和湿度影响大气稳定度和湍流强度，进而影响污染物的扩散。这些数据可以通过气象观测站获取。
排放参数的估算方法
源强
源强表示污染物的排放速率。根据工厂或设施的工艺流程、设备运行状况等因素进行估算。
排放高度
排放高度决定了烟羽在垂直方向上的扩散范围。根据工厂或设施的建筑高度、排放设备的位置等因素进行估算。
案例一：城市空气质量预测
总结词：动态模拟
详细描述：高斯烟羽模型能够模拟城市空气质量的动态变化过程，揭示不同气象条件和地形地貌对空气质量的影响。
案例一：城市空气质量预测
总结词
可视化展示
详细描述
通过可视化技术，高斯烟羽模型能够将预测结果以直观的方式呈现出来，便于分析和理解。
案例二：工业区污染物扩散模拟
特点
高斯烟羽模型适用于污染物在大气中扩散的情况，特别是对于低空污染物的扩散，如工厂排放、汽车尾气等。该模型能够考虑气象条件、地形等因素对污染物扩散的影响，提供较为准确的预测结果。
模型的应用领域
环境评估
高斯烟羽模型广泛应用于环境评估领域，用于评估工厂、交通工具等污染源对周围环境的影响，为环境管理和污染控制提供依据。
z
垂直距离，表示烟羽扩散的垂直方向上的距离。
公式的应用场景
高斯烟羽模型适用于描述烟羽在大气中的扩散情况，特别是
在稳定气象条件下。
该模型广泛应用于环境科学、大气污染控制等领域，用于预测烟羽的扩散范围、浓度分布等。
通过高斯烟羽模型，可以评估烟羽对周围环境和居民的影响，
为制定相应的污染控制措施提供科学依据。
03
高斯烟羽模型的参数估算
扩散参数的估算方法
扩散系数

高斯烟羽模型

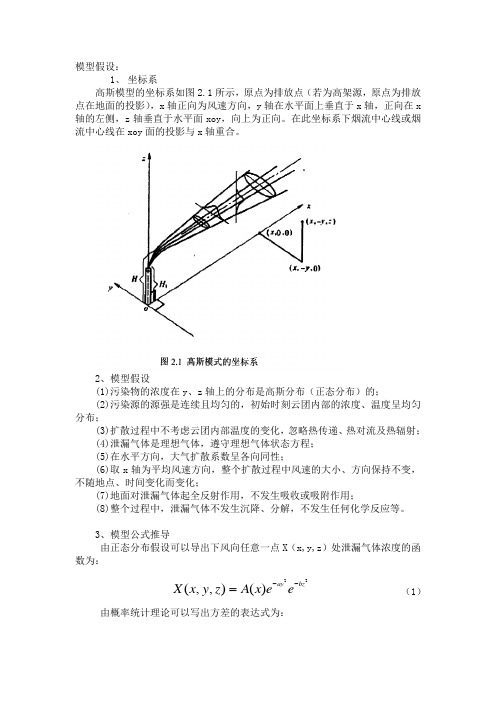
模型假设：1、坐标系高斯模型的坐标系如图2.1所示，原点为排放点（若为高架源，原点为排放点在地面的投影），x 轴正向为风速方向，y 轴在水平面上垂直于x 轴，正向在x 轴的左侧，z 轴垂直于水平面xoy ，向上为正向。

在此坐标系下烟流中心线或烟流中心线在xoy 面的投影与x 轴重合。

2、模型假设(1)污染物的浓度在y 、z 轴上的分布是高斯分布（正态分布）的；(2)污染源的源强是连续且均匀的，初始时刻云团内部的浓度、温度呈均匀分布；(3)扩散过程中不考虑云团内部温度的变化，忽略热传递、热对流及热辐射； (4)泄漏气体是理想气体，遵守理想气体状态方程； (5)在水平方向，大气扩散系数呈各向同性；(6)取x 轴为平均风速方向，整个扩散过程中风速的大小、方向保持不变，不随地点、时间变化而变化；(7)地面对泄漏气体起全反射作用，不发生吸收或吸附作用；(8)整个过程中，泄漏气体不发生沉降、分解，不发生任何化学反应等。

3、模型公式推导由正态分布假设可以导出下风向任意一点X （x,y,z ）处泄漏气体浓度的函数为：22(,,)()aybzX x y z A x ee--= （1）由概率统计理论可以写出方差的表达式为：22022y z y XdyXdyz Xdz Xdzσσ∞∞∞∞==⎧⎪⎪⎪⎨⎪⎪⎪⎩⎰⎰⎰⎰（2）由假设可以写出源强的积分公式：⎰⎰∞∞-∞∞-=uXdydz Q （3）式中：y σ、z σ为泄漏气体在y 、z 方向分布的标准差，单位为 m ；X （x,y,z ）为任一点处泄漏气体的浓度，单位为 kg/m 3；u 为平均风速，单位为 m/s ；Q 为源强（即泄漏速度），单位为 kg/s ；将（1）式代入（2）式，积分可得：221212y za b σσ==⎧⎪⎪⎨⎪⎪⎩ （4）将（1）式和（4）式代入（3）式，积分可得：zy u Qx A σσπ2=）（（5）再将（4）式和（5）式代入（1）式，可得：⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-=222222exp 2,,z y z y zy u Qz y x X σσσσπ）（（6）上式为无界空间连续点源扩散的高斯模型公式，然而在实际中，由于地面的存在，烟羽的扩散是有界的。

高斯模型

2.1 高斯模型燃气泄漏后会在泄漏源附近形成气团，气团在大气中的扩散计算通常采用高斯模型。

高斯模型的基本形式是在如下的假设条件下推导出来的[1、9]：假定燃气在扩散的过程中没有沉降、化合、分解及地面吸收的发生；燃气连续均匀地排放；扩散空间的风速、大气稳定度都均匀、稳定；在水平和垂直方向上都服从正态分布。

泄漏燃气相对密度小于或接近1的连续泄漏采用高斯烟羽模型。

以泄漏点为原点，风向方向为x轴的空间坐标系中的某一点(x，y，z)处的质量浓度计算公式如下[9]：平均风速＞1m/s时：平均风速=0.5～1m/s时：平均风速＜0.5m/s时，假设气团围绕泄漏点浓度均匀分布，则距离泄漏点r处的燃气质量浓度为：式中ρd(x，y，z)——扩散燃气在点(x，y，z)处的质量浓度，kg/m3x、y、z——x、y、z方向上距泄漏点的距离，mua——平均风速，m/sδx 、δy、δz——x、y、z方向的扩散系数，mh——泄漏点高度，mρd(r)——距离泄漏点r处的燃气质量浓度，kg/m3r——空间内任意一点到泄漏点的距离，ma、b——扩散系数，mt——静风持续时间，s，取3600的整数倍扩散系数可查HJ/T 2.2—93《环境影响评价技术导则大气环境》得到。

2.2 重气扩散模型液化石油气密度比空气密度大，属于重气。

该类气体泄漏时在重力的作用下会下沉，这时使用高斯模型计算的结果会使泄漏燃气扩散速度偏大，泄漏源附近的浓度偏小。

为了解决这个问题，可以引入最早由Van Ulden提出，并由Manju Mohan等发展的箱式模型[1]。

箱式模型分为两个阶段：泄漏后的重气扩散阶段和重气效应消失后的被动气体扩散阶段。

重气泄漏后首先是重气扩散阶段。

在这个阶段，重气云团由于重力作用逐渐下沉并不断卷吸周围的空气，在卷吸空气的同时，气云受热，最终当重气云团与空气的密度差＜0.001kg/m3时，可认为气云转变成中性状态。

随着重气的继续扩散，气云所受的重力不再是影响扩散的主要因素，而大气湍流扩散逐渐占主要地位，这时便是被动气体扩散阶段，可以应用高斯模型计算泄漏燃气的扩散。

高斯烟羽模式
高斯烟羽模式是计算释入大气中的气载污染物下风向浓度的应用最广的方法。

此模式假定烟羽中污染物浓度在水平方向和垂直方向都遵循高斯分布。

对于在恒定气象条件（指风向、风速、大气稳定度不随时间而改变）高架点源的连续排放，在考虑了烟羽在地面的全反射后，下风向任一点的污染物浓度C （x ，y ，z ）由下式给出：
][2),,(2z 22z 2y 22)(2)(2σσσｚｙσπσσHe z He z y e e e u z y x C +----+=
式中 C （x ，y ，z ）—— 下风某点（x ，y ，z ）处的空气中污染物浓度，g/m 3。

x —— 下风向距离，m ；
y —— 横截风向距离，m ；
Q —— 气载污染物源强，即释放率，g/s ；
U —— 排放高度处的平均风速，m/s ；
He —— 有效排放高度；m 。

σy ，σz —— 水平方向和垂直方向扩散参数，m ，它们是下风距离x 急大气稳
定度的函数：
下风地面处（z = 0）的污染物浓度则为：
y 2z 222z y σσσσπy H e e u Q C --=。

基于FICK定律和高斯烟羽模型的放射性气体扩散研究

基于FICK定律和高斯烟羽模型的放射性气体扩散研究放射性气体扩散是核能安全领域的重要研究课题之一，研究其扩散规律有助于评估周围环境的辐射水平，制定相应的应对措施。

本文将基于FICK定律和高斯烟羽模型，对放射性气体扩散进行研究。

FICK定律是描述气体、液体或固体中物质扩散的基本定律。

根据FICK定律，物质的扩散速率正比于物质浓度梯度的变化率，与物质的分子扩散系数成正比。

对于放射性气体的扩散，可以用FICK定律表示为：J=-D*(∂C/∂x)其中，J为扩散通量，D为扩散系数，C为浓度，x为扩散距离。

高斯烟羽模型则是用于预测大气中污染物传输的经典模型。

根据该模型，气体扩散呈现高斯分布，其浓度随距离的增加呈指数衰减。

具体来说，高斯烟羽模型可以表示为：C(x, y, z) = (Q/(2πσu)) * exp(-(x-x0)^2/(2σx^2) - (y-y0)^2/(2σy^2) - (z-z0)^2/(2σz^2))其中，C为扩散浓度，Q为释放速率，(x0,y0,z0)为源的位置，σx、σy和σz分别为扩散系数。

基于上述理论，针对放射性气体扩散研究，可以首先确定材料的扩散系数。

放射性气体通常是从核电站、核工厂等活动中释放出来的，因此首先要进行放射性气体浓度的测量，以便计算扩散系数，然后可以利用FICK定律进行扩散速率的估算。

然后，可以利用高斯烟羽模型进一步研究放射性气体的扩散规律。

首先需要确定放射性气体的释放速率和源位置，然后利用高斯烟羽模型计算不同点的浓度。

通过浓度的计算，可以得到放射性气体在空间中的分布情况，以及随着距离的增加浓度的衰减情况。

最后，将根据模型计算出的数据与实际测量数据进行对比，以验证所建模型的准确性和可靠性。

如果模型与实测数据吻合良好，则可以通过该模型来预测放射性气体的扩散情况，为相关工程和环境保护提供科学依据。

总之，基于FICK定律和高斯烟羽模型的放射性气体扩散研究可以提供对该气体扩散规律的理论解释和预测，并为核能安全领域的决策制定提供科学依据。

云团扩散模型

1 云团扩散模型根据物质泄漏后所形成的气云的物理性质的不同，可以将描述气云扩散的模型分为非重气云模型和重气云模型两种[5-13]。

非重气云模型高斯模型是一种常用的非重气扩散模型，高斯烟羽(Plume model)模型又称高架点连续点源扩散模型，适用于连续源的扩散，即连续源或泄放时间大于或等于扩散时间的扩散。

高斯烟团(Puff model)模型适用于短时间泄漏的扩散，即泄放时间相对于扩散时间比较短的情形，如突发性泄放等。

若假设气体云内空间上的分布为高斯分布，则地面地处风向的烟团浓度分布算式为式中，c(x，y，H)——点(x，y，H)处浓度值，mg/m3；Q——源强，即单位时问的排放量，mg/s；u——环境平均风速，m/s；σx，σy，σz——扩散参数；H——源高(烟团高度)，m；x——下方向到泄漏原点的距离，m；y，z——侧风方向、垂直向上方向离泄漏原点的距离，m。

高斯模式的实际应用效果很大程度上依赖于如何给定模式中的一些参数，尤其要注意源强、扩散参数等的确定。

源强与污染物的物理化学属性、扩散方式、释放点的地理环境等有关。

扩散参数表征大气边界层内湍流扩散的强弱，是高斯模式的一项重要数据。

高斯扩散模式所描述的扩散过程(实质上也包含了在实际应用中对高斯模式的一些限制)主要有：1)下垫面平坦、开阔、性质均匀，平均流场稳定，不考虑风场的切变。

2)扩散过程中，污染物本身是被动、保守的，即污染物和空气无相对运动，且扩散过程中污染物无损失、无转化，污染物在地面被反射。

3)扩散在同一温度层结中发生，平均风速大于 m/s。

4)适用范围一般小于10～20 km。

重气云模型由于重气本身的特殊性，在重气扩散领域也有大量基于不同理论的模型。

鉴于重气扩散与中性或浮性气体扩散有着明显的区别，目前国内外已开发大量的不同复杂程度的重气扩散模型，如箱模型、相似模型、LTA－HGDM模型、CFD模型等。

箱(BOX)模型箱模型是指假定浓度、温度和其他场，在任何下风横截面处为矩形分布等简单形状，这里的矩形分布是指在某些空间范围内场是均匀的，而在其他地方为零。

基于高斯烟羽模型的放射性气体扩散的预估模型

基于核电站泄漏放射性气体扩散的预估模型摘要由于核泄漏导致放射性气体扩散对经济和人身造成巨大损失的报道在国内外屡见不鲜，本文中日本福岛核泄漏事件更加使我们认识到对放射性气体扩散进行合理性的预估从而为以后类似于此的突发性事件作积极有效的补救措施的重要性。

对于问题一我们运用了点源烟羽扩散模型，用抛物型二阶偏微分方程解出理想状态下的不同时刻、不同地点的浓度表达式：222432 (,,,)(4)x y zktQC x y z t ektπ++-=。

此模型是建立在以泄漏点为圆心的一个无界球形区域内的。

为了使模型更符合实际情况，能够被应用于现实生活中，我们在泄漏源有效高度的确定和考虑地面反射与吸收作用下对此模型进行了修正，最终得到问题一浓度的确定公式(14)(,,,)C x y z t的表达式。

对于问题二，我们采用高位连续点源烟羽扩散模式，其扩散服从正态分布，并根据概率论的相关知识通过数学公式推导，得到理想状态下的高斯模型，由泄漏源有效高度，地面反射等因素的影响对其进行修正，又由于重力干沉积，雨洗湿沉积以及核衰变等因素对源强的影响，对高斯烟羽模型再次进行修正，最终得到泄漏源周边浓度变化情况即公式(32)，在风速为k m/s的条件下浓度为(,,,)C x y z H。

对于问题三，我们在第二问建立的模型的基础上，引入时间变量rt和t，和扩散速度变量s，在风速和扩散速度的共同影响下，可分别求出上风向和下风向浓度预估模型即公式(40)和(41)。

对于问题四，本文参阅整理大量气象、地理、新闻资料，选择我国东海岸典型地域---山东半岛和美国西海岸典型地域---加利福尼亚州作为研究对象，综合考虑对应海域平均风速及风向、地理距离、海水对放射性物质扩散的部分反射系数等因素，并通过计算机模拟，预测出放射性核物质将经过6天到达我国东海岸，且131I浓度预测值为：0.1053mBq m-⋅,，经过6.8天到达美国西海岸，且氙-133浓度的预测值几乎为零，与实际情况比较吻合。

高斯烟羽模型

高斯烟羽模型 Prepared on 22 November 2020模型假设：1、坐标系高斯模型的坐标系如图所示，原点为排放点（若为高架源，原点为排放点在地面的投影），x轴正向为风速方向，y轴在水平面上垂直于x轴，正向在x轴的左侧，z 轴垂直于水平面xoy，向上为正向。

在此坐标系下烟流中心线或烟流中心线在xoy面的投影与x轴重合。

2、模型假设(1)污染物的浓度在y、z轴上的分布是高斯分布（正态分布）的；(2)污染源的源强是连续且均匀的，初始时刻云团内部的浓度、温度呈均匀分布；(3)扩散过程中不考虑云团内部温度的变化，忽略热传递、热对流及热辐射；(4)泄漏气体是理想气体，遵守理想气体状态方程；(5)在水平方向，大气扩散系数呈各向同性；(6)取x轴为平均风速方向，整个扩散过程中风速的大小、方向保持不变，不随地点、时间变化而变化；(7)地面对泄漏气体起全反射作用，不发生吸收或吸附作用；(8)整个过程中，泄漏气体不发生沉降、分解，不发生任何化学反应等。

3、模型公式推导由正态分布假设可以导出下风向任意一点X（x,y,z）处泄漏气体浓度的函数为：22)(),,(bz ay eex A z y x X --=（1）由概率统计理论可以写出方差的表达式为：⎪⎪⎪⎩⎪⎪⎪⎨⎧==⎰⎰⎰⎰∞∞∞∞22022XdzXdz z XdyXdyy z y σσ （2）由假设可以写出源强的积分公式：⎰⎰∞∞-∞∞-=uXdydz Q （3）式中：y σ、z σ为泄漏气体在y 、z 方向分布的标准差，单位为 m ；X （x,y,z ）为任一点处泄漏气体的浓度，单位为 kg/m 3；u 为平均风速，单位为 m/s ；Q 为源强（即泄漏速度），单位为 kg/s ；将（1）式代入（2）式，积分可得：⎪⎪⎩⎪⎪⎨⎧==222121z y b a σσ （4）将（1）式和（4）式代入（3）式，积分可得：zy u Qx A σσπ2=）（（5）再将（4）式和（5）式代入（1）式，可得：⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-=222222exp 2,,z yz y zy u Qz y x X σσσσπ）（（6）上式为无界空间连续点源扩散的高斯模型公式，然而在实际中，由于地面的存在，烟羽的扩散是有界的。

高斯烟雨扩散模型在空气中PM2.5实际问题的应用

高斯烟雨扩散模型在空气中PM2.5实际问题的应用董赫;翟哲;李夺;李伟凯【摘要】通过建立高斯烟雨扩散模型并采用多元线性回归等数学方法，进一步探索产生雾霾的主要因素PM2.5的形成、扩散过程以及与风速之间的关系。

以武汉市和西安市2013年AQI监测数据为基础，得到空气中PM2.5与其他污染物之间的相关性。

预测了西安市某一区域PM2.5浓度骤增并持续数小时的情况下，污染严重和相对安全的区域。

为研究空气中PM2.5成因、监测和治理提供了一定的理论依据。

%Through establishing gauss misty rain diffusion model and adopting mathematical methods of multiple linear regression,the relations of the formation and diffusion process of PM2.5 with wind speed were explored further. Basing on AQI monitoring data of Wuhan City and Xi’an City in 2013,the correlation between PM2.5 and other pollutants was obtained,and the seriously polluted and relatively secure area were predicted under the circumstances of the sharp increase in PM2.5 content for several hours in certain region of Xi’an. The articl e could provide certain theoretical basis to research the cause,monitoring and governance of PM2.5 in air.【期刊名称】《黑龙江八一农垦大学学报》【年(卷),期】2014(000)003【总页数】6页(P69-73,118)【关键词】PM2.5;多元线性回归;高斯烟雨扩散模型【作者】董赫;翟哲;李夺;李伟凯【作者单位】黑龙江八一农垦大学信息技术学院，大庆 163319;黑龙江八一农垦大学信息技术学院，大庆 163319;黑龙江八一农垦大学工程学院;黑龙江八一农垦大学信息技术学院，大庆 163319【正文语种】中文【中图分类】X502随着国民经济飞速发展和城市化进程的日益加快，我国已有1/4的国土面积相继出现因大气细粒子污染增多而导致的雾霾天气，影响近6亿人的工作和生活。

高斯模型

高斯模型介绍高斯模式是一种应用较为广泛的气体扩散模型，适用于均一的大气条件，以及地面开阔平坦的地区、点源的扩散模式。

排放大量污染物的烟囱、放散管、通风口等，虽然其大小不一，但是只要不是讨论例如烟囱底部很近距离的污染问题，均可视其为点源。

本附录A 介绍高斯模型坐标系、模型假设及模型公式等内容。

F.1坐标系高斯模型的坐标系如图A-1所示，原点为排放点(若为高架源，原点为排放点在地面的投影)，x 轴正向为风速力一向，y 轴在水平面上垂直于x 轴，正向在x 轴左侧，z 轴垂直于水平面xoy ，向上为正向。

在此坐标下烟流中心线或烟流中心线在xoy 面的投影与x 轴重合。

图A-1 高斯模型坐标系F.2 模型假设高斯模型有如下假设条件：（1）污染物的浓度在y 、z 轴上的分布是高斯分布(正态分布)的；（2）污染源的源强是连续且均匀的，初始时刻云团内部的浓度、温度呈均匀分布；（3）扩散过程中不考虑云团内部温度的变化，忽略热传递、热对流及热辐射；（4）泄漏气体是理想气体，遵守理想气体状态方程；（5）在水平方向，大气扩散系数呈各向同性；（6）取x 轴为平均风速方向，整个扩散过程中风速的大小、方向保持不变，不随地点、时间变化而变化；（7）地面对泄漏气体起全反射作用，不发生吸收或吸附作用；（8）整个过程中，泄漏气体不发生沉降、分解，不发生任何化学反应等。

F.3 模型公式距地面一定高度连续点源烟羽扩散模式的高斯修正模型为：()()()()⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-+⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=22222221exp 21exp 21exp 2,,,z z y z y H z H z y k x Q H z y x C σασσσσπ（A-1）式（A-1）中：C (x,y,z,H)——表示横向x、纵向y、地面上方z处气体浓度，kg/m3；Q(x)——表示源强(即源释放速率)，kg/s；k——表示平均风速，m/s；σy——表示水平扩散参数，m;σz——表示垂直扩散参数，m；H——表示泄漏源有效高度，m；y——表示横向距离，m；z——表示纵向距离，m。

高斯扩散模型几何意义

高斯扩散模型几何意义的研究摘要：高斯模型是大气预测的基本模型，我们平时用的eiaproa2008也是基于高斯模型的，只不过是同时加入了一些地形、气象的修正。

本发明通过分析高斯扩散模型的几何意义，了解高架点源排放烟气的扩散特点，根据研究结果观察不同烟羽形状对应的大气稳定度，并结合观察所得的大气稳定度，预测分析污染物经高架点源排放后在评价范围内的浓度。

关键词：高斯模型正态分布影响预测几何意义1.高斯扩散模型简介c（x、y、z）=式中：c(x,y,z)—表示坐标为x，y，z处污染物浓度；he—烟囱的有效高度，m；q—烟囱排放源强（污染物单位时间排放量，mg/s）；σy—垂直于主导风向的横向扩散参数，m；σz—铅直扩散参数，m；u—排气筒高度处的风速，m/s。

高斯模式的四点假设为：（1）假定大气流动是稳定的、有主导方向的；（2）假定污染物在大气中只有物理运动、没有化学和生物变化；（3）假定在所要预测的范围内没有其他同类污染源和汇，也就是说源强是连续均匀的；（4）在有主导风的情况下，主导风对污染物的输送应远远大于湍流运动引起的污染物在主导风向上的扩散，即在x方向只考虑迁移，不考虑扩散。

2.正态函数的特点及几何意义简介①正态分布密度函数：，（σ＞0，-∞＜x＜∞）其中π是圆周率；e是自然对数的底；x是随机变量的取值；μ为正态分布的均值；σ是正态分布的标准差。

正态分布一般记为。

②正态分布的图像是由μ和σ决定。

当μ=0，σ分别为0.5、1、2时的正态函数图像见图1；当μ=1，σ分别为0.5、1、2时的正态函数图像见图2；由图1及图2可见，正态函数的图像依赖于两个变量: σ和μ,其中σ确定了函数图像的扁平情况；μ确定了函数图像偏离y轴的距离，当μ=0时函数f（x）关于y轴对称。

图1当μ=0，σ分别为0.5、1、2时的正态函数图图2当μ=1，σ分别为0.5、1、2时的正态函数图3．烟羽扩散过程的分解与高斯模型的拆分由几何知识可知，点动成线，线动成面，面动成体。

AE大气扩散模型算法

不满足均匀、定常条件，因此高斯模式应用于下垫面均匀平坦、气流稳定的小尺度扩散问题更为有效。
3高斯计算公式
对于在恒定气象条件（指风向、风速、大气稳定度不随时间而变）下的高架点源的连续排放，在考虑了烟羽在地面的全反射后，下风向任一点的污染物浓度C(x,y,z)可由下式计算：
C(x,
y, z)
Q
1 相关菜单的添加
在空间分析主菜单中添加如下图所示菜单项。
2 大气污染扩散分析窗口的设计
设计一个大气污染扩散分析窗口。
这些Label的 AutoSize属性设置为： False BorderStyle 属性设置为： Fixed3D
一些主要控件的属性设置如下：
控件编号
1 2 3 4 5 6 7 8 9 10 11 12
diffusedParameter50[2].Qz = 0.996;
diffusedParameter50[3].Py = 0.640;
y Py X qy 、 z Pz X qz 是下风距离X及大气稳定度的函数，而下风方向的距离X是一变量，它是风速和时间的函数。高架电源烟气扩散是三维扩散过程，x方向上风速较大，以对流扩散为主，y方向和z方向则以弥散扩散为主。本实例编程只是实现了二维扩散模型。即只是实现了xy 方向上的扩散模拟。
1>大气稳定度的确定
Pasquill根据五类地面风速、三类日间的日射和两类夜间云量把扩散天气分为6类，即强不稳定、不稳定、弱不稳定、中性、较稳定和稳定。分别用英文字母A、B、C、D、 E和F表示。
在国标“制订地方大气污染排放标准的技术原则和方法” （GB3840-83）与“环境影响评价技术原则”(HJ/T2.1-93) 中，建议采用下属修订的帕斯奎尔稳定度分类方法。首先由云量与太阳高度角按表1查出太阳辐射等级数，再由太阳辐射等级数与地面风速按表2查找稳定度等级。

高斯烟羽扩散模型再研究

高斯烟羽扩散模型再研究孙志宽【摘要】高斯烟羽扩散模型自二十世纪50年代提出后,一直在空气污染扩散研究及大气环境质量预测领域广泛使用,我国及美国、欧盟将其列为环境影响评价中大气环境预测的基本模型.不少国内外学者发现,该模型与实际监测有一定的误差.作者通过认真研究,对模型的两个重要参数U和△H的选取和计算方法提出质疑,并通过严密的数学推导,得到严谨数学表达式,进而提出新的高斯烟羽扩散模型.通过边界层污染气象观测、烟羽对比观测和对比计算证明,修正后的高斯烟羽扩散模型更接近实际.【期刊名称】《环境与可持续发展》【年(卷),期】2013(038)005【总页数】3页(P107-109)【关键词】高斯模型;平均风速;抬升高度【作者】孙志宽【作者单位】神华国能集团(神东电力)集团公司,北京10033【正文语种】中文【中图分类】X211 引言在大气环境质量预测及空气污染等问题中，用数学模型模拟并预测大气污染物输送与扩散是一种常用且有效的手段。

对连续的气态污染源在有风时对周围空气质量的影响预测，无论是我国目前现行的《境影响评价技术导则-大气环境》(HJ 2.2-2008)［1］，还是美国EPA推荐的AERMOD模型［2］，其基本形式都是高斯烟流扩散模型，其数学表达式为:式中，C(x，y，z)为污染源下方向任一点(x，y，z)处的污染物浓度，mg/m3;Q为源强，mg/m;U为水平输送速度，m;σy和σz分别为横向扩散参数和垂直扩散参数，m;h为混合层高度，m;k为反射次数;He为烟囱有效高度，m，其值为烟囱几何高度(Hs)与烟气抬升高度(△H)之和，即:通常所需预测的是地面浓度，在无界情况下，其表达式为:有不少国内外学者发现，上式计算结果与实测值有较大的偏差［2，5］，Herman 和 Mccaffrey 的实验研究［4］和我国原水电部及南京大学在徐州所做的烟流抬升和扩散试验的结果［6］都表明:一是高斯模型预报的峰值浓度几乎全部低于实测值，预报与实测的误差以D类稳定度最大，A类最小。

基于MATLAB仿真模拟炼油厂尾气燃烧模型的优化

基于MATLAB仿真模拟炼油厂尾气燃烧模型的优化宋伟华;朱斌;吴治荣【摘要】基于数学物理思想和热传导理论,对炼油厂尾气燃烧模型进行优化.假设为连续性火源,利用粒子经典的扩散方程,得到了炼油厂的火势蔓延函数N(r,t)及在t 时刻距离井曹底部r处的烟雾扩散密度随时间的变化规律.最后,假定烟雾扩散是以烟团为基本状态的方式进行,并对烟雾扩散进行了必要的简化,从而建立了高斯扩散模型,并利用MATLAB软件进行仿真模拟,得到了烟雾在近地面扩散的浓度随时间的分布函数图.【期刊名称】《陇东学院学报》【年(卷),期】2019(030)005【总页数】4页(P31-34)【关键词】炼油厂尾气;热传导理论;扩散方程;扩散浓度;仿真【作者】宋伟华;朱斌;吴治荣【作者单位】长庆油田分公司第十二采油厂,甘肃庆阳 745000;长庆油田分公司第十二采油厂,甘肃庆阳 745000;陇东学院电气工程学院,甘肃庆阳 745000【正文语种】中文【中图分类】X51;P49如今，石油作为人类最重要的化石原料之一，在给人类带来巨大利用价值的同时其燃烧产物也给环境带来了严重的污染，尤其是炼油厂尾气的燃烧处理显得尤为重要[1]。

过去几年，时有石油化工厂发生爆炸、火灾等发生，不但对人身安全造成严重危害，而且也带来巨大的财产损失。

据调查，火灾中造成人员死亡的主要原因是浓烟导致呼吸困难、窒息死亡。

因此研究石油化工厂爆炸、火灾中烟雾扩散规律，了解烟雾分布情况，科学合理地设计出炼油厂尾气燃烧的模型，对解救受困人员、受困人员自救和安全灭火等工作均具有重要的指导意义。

国内许多专家一直在致力于燃烧尾气、火灾烟雾扩散等方面的研究，提出了基于数学原理的物理模型、基于粒子群的扩散模型及基于复杂环境的烟雾扩散模型[2-10]。

尽管这些模型对尾气燃烧、烟雾扩散进行了理论层面的描述，但不能用于实际火灾的救援过程。

为了更好地解释尾气燃烧、烟雾扩散规律，辅助灾难救援，本文在对炼油厂燃烧尾气火源进行连续性假设的基础上，将炼油厂尾气燃烧火焰简化成由一定数量的粒子组成，利用粒子经典的扩散方程[11-17]，对其进行求解，得到火焰场的火势蔓延函数N(r,t)及在t时刻距离井曹底部r处的烟雾扩散密度随时间的变化规律。

高斯烟羽模型

X ( x, y, z ) = A( x)e
− ay
2
e
− bz
2
• （1） • 由概率统计理论可以写出方差的表达式为： y Xdy σ = ∫ • （2） Xdy
∞ 2 2 y 0
σ ∫∞源自02 z=
∫
∞
0
z 2 Xdz
∞
∫
0
Xdz
• 由假设可以写出源强的积分公式： ∞ ∞ • （3） Q = ∫ ∫ uXdydz −∞ −∞
• 将（1）式和（4）式代入（3）式，积分可得： Q • （5） A（x） =
2πuσ yσ z
• 再将（4）式和（5）式代入（1）式，可得：
y2 z2 X（x, y, z） = exp− 2 + 2σ 2πuσ y σ z 2σ z2 y Q
• 为泄漏后是时间，单位为s；H为泄漏源有效高度，单位为m；y为横向距离，单位为 m；z为垂直方向距离，单位为m。 • 如：式中，令z=0，即可得到地面气体浓度计算公式： • 1 y H2 (11) Q
X（ , y,0, H） x =
2 exp − （） exp 2 πuσ yσz 2 σ y 2σz
• (6)取x轴为平均风速方向，整个扩散过程中风速的大小、方向保持不变，不随地点、时间变化而变化； • (7)地面对泄漏气体起全反射作用，不发生吸收或吸附作用； • (8)整个过程中，泄漏气体不发生沉降、分解，不发生任何化学反应等。 • 3、模型公式推导 • 由正态分布假设可以导出下风向任意一点X （x,y,z）处泄漏气体浓度的函数为：
• 式中：、为泄漏气体在y、z方向分布的标准差，单位为 m；X（x,y,z）为任一点处泄漏气体的浓度，单位为 kg/m；u为平均风速，单位为 m/s；Q为源强（即泄漏速度），单位为 kg/s； • 将（1）式代入（2）式，积分可得：

结合Fluent的液氨泄漏扩散模拟及中毒定量评估

结合Fluent的液氨泄漏扩散模拟及中毒定量评估江南;陈玉明【摘要】Apply the Fluent numerical simulation software to calculate and analyze the liquid ammonia leakage diffusion concentration field and diffusion rule,compare it with theoretical calculation results based on Gaussian plume model to verify the reliability of bine the numerical simulation results and exposure duration to conduct the quantitative evaluation on the personnel mortality percentage under the conditions of stationary state and evacuation state.The results show that the acute poisoning qualitative e-valuation method combined with Fluent numerical simulation can intuitional,dynamic and reliable reflect the leakage diffusion scope and influence and it has very good application prospect.%运用Fluent数值模拟软件计算分析液氨泄漏扩散浓度场及扩散规律，并与基于高斯烟羽模型的理论计算结果相对比，验证其结果的可靠性。

结合数值模拟结果和暴露时间，对人员在静止状态及疏散状态下的死亡百分率进行定量评估。

高斯烟羽模式公式

LNG低温储罐泄漏事故危险性分析综述(全文)

高斯烟羽模型课件

高斯烟羽模型

高斯模型