2015中考二次函数的综合题及应用-答案
中考数学模拟题汇总《二次函数的综合》专项练习(附答案解析)

中考数学模拟题汇总《二次函数的综合》专项练习(附答案解析)一、综合题1.某商店销售一种销售成本为40元/件的商品,销售一段时间后发现,每天的销量y(件)与当天的销售单价x(元/件)满足一次函数关系,并且当x=20时,y=1000,当x=25时,y=950.(1)求出y与x的函数关系式;(2)求出商店销售该商品每天获得的最大利润;(3)如果该商店要使每天的销售利润不低于13750元,且每天的总成本不超过20000元,那么销售单价应控制在什么范围内?,0),在第一象限内与直线y=x 2.如(图1),已知经过原点的抛物线y=ax2+bx与x轴交于另一点A( 32交于点B(2,t)(1)求抛物线的解析式;(2)在直线OB下方的抛物线上有一点C,点C到直线OB的距离为√2,求点C的坐标;(3)如(图2),若点M在抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC ∽△MOB?若存在,求出点P坐标;若不存在,请说明理由.3.如图,二次函数y=ax2-6ax+4a+3的图像与y轴交于点A,点B是x轴上一点,其坐标为(1,0),连接AB,tan∠ABO=2.(1)则点A的坐标为,a= ;(2)过点A作AB的垂线与该二次函数的图象交于另一点C,求点C的坐标;(3)连接BC,过点A作直线l交线段BC于点P,设点B、点C到l的距离分别为d1、d2,求d1+d2的最大值.4.如图正方形ABCD,点P,Q,R,S分别在AB,BC,CD,DA上,且BQ=2AP,CR=3AP,DS=4AP(1)若正方形边长为4,则当AP为何值时,四边形PQRS的面积为正方形面积的一半(2)若正方形边长为a(a为常数),则当AP为何值时,四边形PQRS的面积最小,并求出最小面积. 5.如图1,在Rt△ABC中,∠ABC=90°,∠C=30°,BC=12,D是BC的中点经过A,B,D的O交AC于E 点.(1)求AE的长.(2)当点P从点A匀速运动到点E时,点Q恰好从点C匀速运动点B.记AP=x,BQ=y.①求y关于x的表达式.②连结PQ,当△PQC的面积最大时,求x的值.(3)如图2,连结BE,BP,延长BP交⊙O于点F,连结FE.当EF与△BDE中的某一边相等时,求四边形BDEF 的面积.6.如图,抛物线y =﹣13x 2+13x +4交x 轴于A ,B 两点(点B 在A 的右边),与y 轴交于点C ,连接AC ,BC.点P 是第一象限内抛物线上的一个动点,点P 的横坐标为m ,过点P 作PM ⊥x 轴,垂足为点M ,PM 交BC 于点Q.(1)求A 、B 两点坐标;(2)过点P 作PN 上BC ,垂足为点N ,请用含m 的代数式表示线段PN 的长,并求出当m 为何值时PN 有最大值,最大值是多少?(3)试探究点P 在运动过程中,是否存在这样的点Q ,使得以A ,C ,Q 为顶点的三角形是等腰三角形.若存在,请求出此时点Q 的坐标,若不存在,请说明理由.7.如图,已知二次函数L 1:y=ax 2-2ax+a+3(a >0)和二次函数L 2:y=-a (x+1)2+1(a >0)图象的顶点分别为M ,N ,与y 轴分别交于点E ,F .(1)函数y=ax 2-2ax+a+3(a >0)的最小值为 ,当二次函数L 1,L 2的y 值同时随着x 的增大而减小时,x 的取值范围是(2)当EF=MN 时,求a 的值,并判断四边形ENFM 的形状(直接写出,不必证明).(3)若二次函数L 2的图象与x 轴的右交点为A (m ,0),当△AMN 为等腰三角形时,求方程-a (x+1)2+1=0的解.8.在平面直角坐标系中,抛物线y =−x 2+bx +c (b ,c 为常数)的图象与x 轴交于点A(1,0),B 两点,与y轴交于点C,当x=−3时,函数有最大值.2(1)抛物线的解析式;(2)点M在y轴上,使得∠MBC=15°,求点M的坐标;(3)若点P(x1,m)与点Q(x2,m)在抛物线上,且x1<x2,PQ=n,求证:x22−2x2=x12−4n+3.9.如图,已知抛物线y=x2﹣(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴交于D、E两点.(1)求m的值.(2)求A、B两点的坐标.(3)点P(a,b)(﹣3<a<1)是抛物线上一点,当△PAB的面积是△ABC面积的2倍时,求a,b的值.10.若y是x的函数,h为常数(ℎ>0),若对于该函数图象上的任意两点(x1,y1)、(x2,y2),当a≤x1≤b,a≤x2≤b(其中a、b为常数,a<b)时,总有|y1−y2|≤ℎ,就称此函数在a≤x≤b时为有界函数,其中满足条件的所有常数h的最小值,称为该函数在a≤x≤b时的界高.(1)函数:①y=2x,②y=1,③y=x2在−1≤x≤1时为有界函数的是:(填序号);x(2)若一次函数y=kx+2(k≠0),当a≤x≤b时为有界函数,且在此范围内的界高为b−a,请求出此一次函数解析式;(3)已知函数y=x2−2ax+5(a>1),当1≤x≤a+1时为有界函数,且此范围内的界高不大于4,求实数a的取值范围.11.已知函数y=(n+1)x m+mx+1−n(m,n为实数).(1)当m,n取何值时,函数是二次函数.(2)若它是一个二次函数,假设n>−1,那么:①它一定经过哪个点?请说明理由.②若取该函数上横坐标满足x=2k(k为整数)的所有点,组成新函数y1.当x≥12时,y1随x的增大而增大,且x=12时是函数最小值,求n满足的取值范围.12.如图1,已知在平面直角坐标系xOy中,抛物线y=-x2-2x+c(c>0)的图象与x轴交于A,B两点,与y 轴交于点C.抛物线的顶点为E,若点B的坐标是(1,0),点D是该抛物线在第二象限图象上的一个动点。
中考数学总复习《二次函数与一次函数的综合应用》练习题及答案
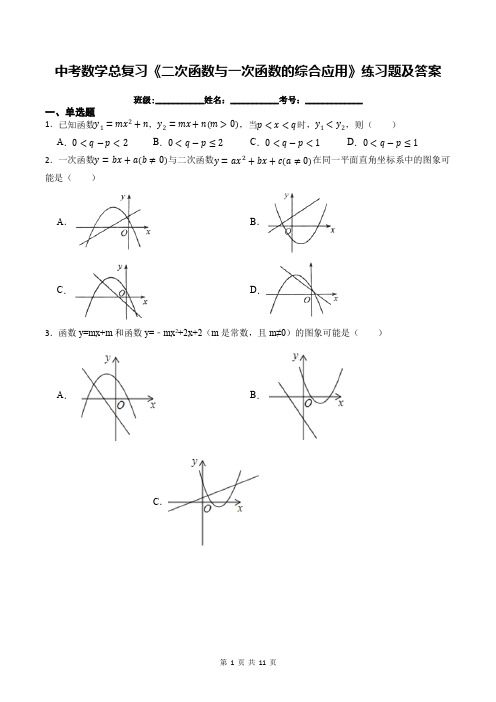
中考数学总复习《二次函数与一次函数的综合应用》练习题及答案班级:___________姓名:___________考号:_____________一、单选题1.已知函数y1=mx2+n,y2=mx+n(m>0),当p<x<q时,y1<y2,则()A.0<q−p<2B.0<q−p≤2C.0<q−p<1D.0<q−p≤12.一次函数y=bx+a(b≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是()A.B.C.D.3.函数y=mx+m和函数y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是()A.B.C.D.4.小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时如下结论:①这个函数图象的顶点始终在直线y=-x+1上;②存在一个m的值,使得函数图象的顶点与x轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2其中错误结论的序号是()A.①B.②C.③D.④5.将二次函数y=x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为()A.﹣734或﹣12B.﹣734或2C.﹣12或2D.﹣694或﹣126.如图,函数y1=|x2﹣m|的图象如图,坐标系中一次函数y2=x+b的图象记为y2,则以下说法中:①当m=1,且y1与y2恰好有三个交点时b有唯一值为1;②当m=4,且y1与y2只有两个交点时,b>174或﹣2<b<2;③当m=﹣b时,y1与y2一定有交点:④当m=b时,y1与y2至少有2个交点,且其中一个为(0,m).正确的有()A.1个B.2个C.3个D.4个7.直线y=ax﹣6与抛物线y=x2﹣4x+3只有一个交点,则a的值为()A.a=2B.a=10C.a=2或a=﹣10D.a=2或a=108.已知一次函数y1=2x−2,二次函数y2=x2,对于x的同一个值,这两个函数所对应的函数值分别为y1和y2,则下列表述正确的是()A.y1>y2B.y1<y2C.y1=y2D.y1,y2的大小关系不确定9.已知一次函数y1=kx+m(k≠0)和二次函数y2=ax2+bx+c(a≠0)部分自变量和对应的函数值如表:x…-10245…y1…01356…y2…0-1059…21A.-1<x<2B.4<x<5C.x<-1或x>5D.x<-1或x>410.对于每个x,函数y是y1=-x+6,y2=-2x2+4x+6这两个函数的较小值,则函数y的最大值是()A.3B.4C.5D.611.如图是王阿姨晚饭后步行的路程s(单位:m)与时间t(单位:min)的函数图象,其中曲线段AB是以B为顶点的抛物线一部分.下列说法不正确的是()A.25min~50min,王阿姨步行的路程为800mB.线段CD的函数解析式为s=32t+400(25≤t≤50)C.5min~20min,王阿姨步行速度由慢到快D.曲线段AB的函数解析式为s=-3(t-20)2+1200(5≤t≤20)12.如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y= 12x2+bx+c的顶点,则抛物线y= 12x2+bx+c与直线y=1交点的个数是()A.0个或1个B.0个或2个C.1个或2个D.0个、1个或2个二、填空题13.抛物线y=2x2+x+a与直线y=−x+3没有交点,则a的取值范围是.14.如图,已知抛物线y1=−2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1,y2,若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2,例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0,下列判断:①当x<0时,y1>y2;②当x<0时,x值越大,M值越小;③使得M大于2的x值不存在;④使得M=1的x值是−12或√22.其中正确的是.15.如图,已知直线y=﹣34x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣12x2+2x+5的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣34x+3于点Q,则当PQ=BQ时,a的值是.16.已知一次函数y1=kx+m(k≠0)和二次函数y2=ax2+bx+c(a≠0)部分自变量和对应的函数值如表:x…﹣10245…y1…01356…y2…0﹣1059…21的取值范围是.17.如图,在平面直角坐标系中,O为坐标原点,点C为y轴正半轴上的一个动点,过点C的直线与二次函数y=x2的图象交于A、B两点,且CB=3AC,P为CB的中点,设点P的坐标为P(x,y)(x>0),写出y关于x的函数表达式为:.18.直线y=x+2与抛物线y=x2的交点坐标是.三、综合题19.随着互联网的普及,某手机厂商采用先网络预定,然后根据订单量生产手机的方式销售,2015年该厂商将推出一款新手机,根据相关统计数据预测,定价为2200元,日预订量为20000台,若定价每减少100元,则日预订量增加10000台.(1)设定价减少x元,预订量为y台,写出y与x的函数关系式;(2)若每台手机的成本是1200元,求所获的利润w(元)与x(元)的函数关系式,并说明当定价为多少时所获利润最大;(3)若手机加工成每天最多加工50000台,且每批手机会有5%的故障率,通过计算说明每天最多接受的预订量为多少?按最大量接受预订时,每台售价多少元?20.在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.(1)试求抛物线的解析式;(2)记抛物线顶点为D,求△BCD的面积;(3)若直线y=﹣12x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.21.如图,已知抛物线 y =−12x 2+bx +c 经过A (2,0)、B (0,-6)两点,其对称轴与轴交于点C(1)求该抛物线和直线BC 的解析式;(2)设抛物线与直线BC 相交于点D ,连结AB 、AD ,求△ABD 的面积.22.某企业研发了一种新产品,已知这种产品的成本为30元/件,且年销售量 y (万件)与售价 x (元/件)的函数关系式为 y ={−2x +140,(40≤x <60)−x +80.(60≤x ≤70)(1)当售价为60元/件时,年销售量为 万件;(2)当售价为多少时,销售该产品的年利润最大?最大利润是多少? (3)若销售该产品的年利润不少于750万元,直接写出 x 的取值范围.23.抛物线y =ax 2与直线y =2x -3交于点A(1,b).(1)求a ,b 的值;(2)求抛物线y =ax 2与直线y =-2的两个交点B ,C 的坐标(B 点在C 点右侧); (3)求△OBC 的面积.24.如图,平面直角坐标系中,抛物线 y =ax 2+bx +c 经过 A(−1,0) , B(3,0) 两点,与 y 轴交于点 C(0,−3) ,点 D 是抛物线的顶点.(1)求抛物线的解析式;(2)设P(m,n)为对称轴上一点,若∠PCD为钝角,求n的取值范围.参考答案1.【答案】D 2.【答案】C 3.【答案】D 4.【答案】C 5.【答案】A 6.【答案】B 7.【答案】C 8.【答案】B 9.【答案】D 10.【答案】D 11.【答案】C 12.【答案】D 13.【答案】a >3.5 14.【答案】③④15.【答案】﹣1,4,4+2 √5 ,4﹣2 √5 16.【答案】x <﹣1或x >4 17.【答案】y =83x 218.【答案】(-1,1)和(2,4)19.【答案】(1)解:根据题意:y =20000+ x 100 ×10000=100x+20000(2)解:设所获的利润w (元) 则W =(2200﹣1200﹣x )(100x+20000) =﹣100(x ﹣400)2+36000000;所以当降价400元,即定价为2200﹣400=1800元时,所获利润最大 (3)解:根据题意每天最多接受50000(1﹣0.05)=47500台 此时47500=100x+20000 解得:x =275.所以最大量接受预订时,每台定价2200﹣275=1925元.20.【答案】(1)解:由题意 {4a −2b +2=64b +2b +2=2 解得 {a =12b =−1∴抛物线解析式为y= 12x 2﹣x+2.(2)解:∵y= 12 x 2﹣x+2= 12 (x ﹣1)2+ 32.∴顶点坐标(1,3 2)∵直线BC为y=﹣x+4,∴对称轴与BC的交点H(1,3)∴S△BDC=S△BDH+S△DHC= 12×32•3+ 12×32•1=3.(3)解:由{y=−12x+by=12x2−x+2消去y得到x2﹣x+4﹣2b=0当△=0时,直线与抛物线相切,1﹣4(4﹣2b)=0∴b= 15 8当直线y=﹣12x+b经过点C时,b=3当直线y=﹣12x+b经过点B时,b=5∵直线y=﹣12x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点∴158<b≤3.21.【答案】(1)解:将A(2,0)、B(0,-6)代入y=−12x2+bx+c中可得{−12×22+2b+c=0c=−6解得:b=4;c=-6∴该抛物线的解析式为y=−12x2+4x−6∴抛物线对称轴为x=−42×(−12)=4∴C(4,0)设直线BC的解析式为y=kx+b(k≠0)将B(0,-6),C(4,0)代入得解得:k=32,b=−6∴直线BC 的解析式为 y =32x −6(2)解:连立方程组可得 {y =32x −6y =−12x 2+4x −6解得 {x =5y =32∴D(5, 32)∴△ABD 的面积为 12×2×(23+6)=15222.【答案】(1)20(2)解:设销售该产品的年利润为 W 万元当 40≤x <60 时, W =(x −30)(−2x +140)=−2(x −50)2+800 . ∵-2<0 ∴当 x =50 时 当 60≤x ≤70 时 ∵−1<0 ∴当 x =60 时 ∵800>600 ∴当 x =50 时∴当售价为50元/件时,年销售利润最大,最大为800万元. (3)解: 45≤x ≤55 理由如下:由题意得(x −30)(−2x +140)≥750解得 45≤x ≤5523.【答案】(1)解:∵点 A(1,b) 在直线 y =2x −3 上∴b =−1∴点 A 坐标 (1,−1)把点 A(1,−1) 代入 y =ax 2 得到 a =−1∴a =b =−1.(2)解:由 {y =−x 2y =−2 解得 {x =√2y =−2 或 {x =−√2y =−2 ∴点 C 坐标 (−√2,−2), 点 B 坐标 (√2,−2). (3)解: S △BOC =12×2√2×2=2√2.24.【答案】(1)解:由已知,设 y =a(x +1)(x −3)把C(0,−3)代入,得−3a=−3∴y=(x+1)(x−3)即y=x2−2x−3.(2)解:由y=x2−2x−3,得y=(x−1)2−4∴顶点D(1,−4).过点D作DH⊥y轴于点H,连结BC交对称轴于点E,连结DC.∵B(3,0),C(0,−3)∴OB=OC=3∴∠BCO=∠DCH=45°∴∠DCE=90°设BC函数表达式为y=kx+b把B(3,0),C(0,−3)两点代入y=kx+b得{k=1b=−3即BC函数表达式为y=x−3∵点E在对称轴上∴点E横坐标为1,代入y=x−3得E(1,−2)由∠PCD为钝角,则点P在点E上方即n>−2.第11页共11页。
2015年中考真题初中数学---二次函数
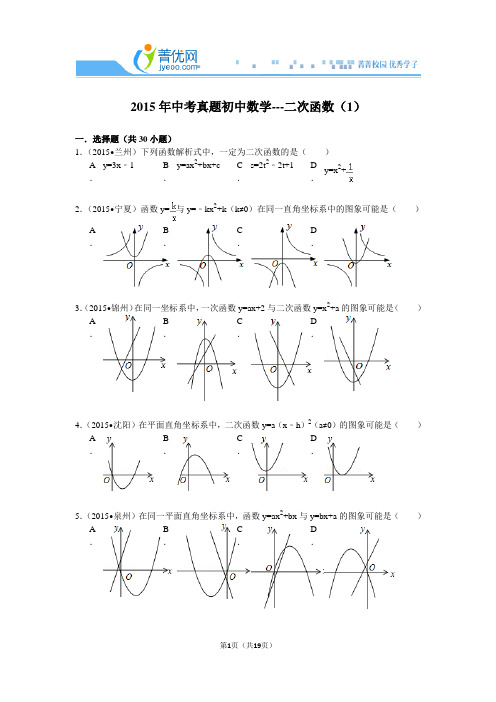
2015年中考真题初中数学---二次函数(1)一.选择题(共30小题)1.(2015•兰州)下列函数解析式中,一定为二次函数的是()A .y=3x﹣1 B.y=ax2+bx+c C.s=2t2﹣2t+1 D.y=x2+2.(2015•宁夏)函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是()A .B.C.D.3.(2015•锦州)在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是()A .B.C.D.4.(2015•沈阳)在平面直角坐标系中,二次函数y=a(x﹣h)2(a≠0)的图象可能是()A .B.C.D.5.(2015•泉州)在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是()A .B.C.D.6.(2015•安徽)如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b﹣1)x+c的图象可能是()A .B.C.D.7.(2015•咸宁)如图是二次函数y=ax2+bx+c的图象,下列结论:①二次三项式ax2+bx+c的最大值为4;②4a+2b+c<0;③一元二次方程ax2+bx+c=1的两根之和为﹣1;④使y≤3成立的x的取值范围是x≥0.其中正确的个数有()A .1个B.2个C.3个D.4个8.(2015•衢州)下列四个函数图象中,当x>0时,y随x的增大而减小的是()A .B.C.D.9.(2015•湖北)二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系中的图象可能是()A .B.C.D.10.(2015•泰安)某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:x …﹣2 ﹣1 0 1 2 …y …﹣11 ﹣2 1 ﹣2 ﹣5 …由于粗心,他算错了其中一个y值,则这个错误的数值是()A .﹣11 B.﹣2 C.1 D.﹣511.(2015•泰安)在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是()A .B.C.D.12.(2015•梅州)对于二次函数y=﹣x2+2x.有下列四个结论:①它的对称轴是直线x=1;②设y1=﹣x12+2x1,y2=﹣x22+2x2,则当x2>x1时,有y2>y1;③它的图象与x轴的两个交点是(0,0)和(2,0);④当0<x<2时,y>0.其中正确的结论的个数为()A .1 B.2 C.3 D.413.(2015•兰州)在下列二次函数中,其图象对称轴为x=﹣2的是()A .y=(x+2)2B.y=2x2﹣2 C.y=﹣2x2﹣2 D.y=2(x﹣2)214.(2015•益阳)若抛物线y=(x﹣m)2+(m+1)的顶点在第一象限,则m的取值范围为()A m>1B m>0C m>﹣1 D﹣1<m<0....15.(2015•黔南州)二次函数y=x2﹣2x﹣3的图象如图所示,下列说法中错误的是()A .函数图象与y 轴的交点坐标是(0,﹣3)B .顶点坐标是(1,﹣3)C .函数图象与x 轴的交点坐标是(3,0)、(﹣1,0)D .当x<0时,y 随x的增大而减小16.(2015•甘孜州)二次函数y=x2+4x﹣5的图象的对称轴为()A .x=4 B.x=﹣4 C.x=2 D.x=﹣217.(2015•常州)已知二次函数y=x2+(m﹣1)x+1,当x>1时,y随x的增大而增大,而m的取值范围是()A .m=﹣1 B.m=3 C.m≤﹣1 D.m≥﹣118.(2015•玉林)如图,反比例函数y=的图象经过二次函数y=ax2+bx图象的顶点(﹣,m)(m>0),则有()A .a=b+2k B.a=b﹣2k C.k<b<0 D.a<k<019.(2015•台州)设二次函数y=(x﹣3)2﹣4图象的对称轴为直线l,若点M在直线l上,则点M的坐标可能是()A .(1,0)B.(3,0)C.(﹣3,0)D.(0,﹣4)20.(2015•福州)已知一个函数图象经过(1,﹣4),(2,﹣2)两点,在自变量x的某个取值范围内,都有函数值y随x的增大而减小,则符合上述条件的函数可能是()A .正比例函数B.一次函数C.反比例函数D.二次函数21.(2015•日照)如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A (1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,其中正确的是()A .①②③B.①③④C.①③⑤D.②④⑤22.(2015•毕节市)二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是()A .a<0 B.b>0 C.b2﹣4ac>0 D.a+b+c<023.(2015•深圳)二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法正确的个数是()①a>0;②b>0;③c<0;④b2﹣4ac>0.A .1 B.2 C.3 D.424.(2015•恩施州)如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c>0;④若点B(﹣,y1)、C(﹣,y2)为函数图象上的两点,则y1<y2,其中正确结论是()A .②④B.①④C.①③D.②③25.(2015•兰州)二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则()A .ac+1=b B.ab+1=c C.bc+1=a D.以上都不是26.(2015•孝感)如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y 轴交于点C,且OA=OC.则下列结论:①abc<0;②>0;③ac﹣b+1=0;④OA•OB=﹣.其中正确结论的个数是()A .4 B.3 C.2 D.127.(2015•南宁)如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=﹣1,下列结论中:•①ab>0, ②a+b+c>0, ③当﹣2<x<0时,y<0.正确的个数是()A .0个B.1个C.2个D.3个28.(2015•遂宁)二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2﹣4ac>0;④a+b+c<0;⑤4a﹣2b+c<0,其中正确的个数是()A .2 B.3 C.4 D.529.(2015•广安)如图,抛物线y=ax2+bx+c(c≠0)过点(﹣1,0)和点(0,﹣3),且顶点在第四象限,设P=a+b+c,则P的取值范围是()A .﹣3<P<﹣1 B.﹣6<P<0 C.﹣3<P<0 D.﹣6<P<﹣330.(2015•凉山州)二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0②当﹣1≤x≤3时,y<0③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2④9a+3b+c=0其中正确的是()A .①②④B.①④C.①②③D.③④2015年中考真题初中数学---二次函数(2)一.选择题(共30小题)1.(2015•湘潭)如图,观察二次函数y=ax2+bx+c的图象,下列结论:①a+b+c>0,②2a+b>0,③b2﹣4ac>0,④ac>0.其中正确的是()A .①②B.①④C.②③D.③④2.(2015•枣庄)如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是()A .①②④B.③④C.①③④D.①②3.(2015•烟台)如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是()A.b2>4abB .ax2+bx+c≥﹣6C .若点(﹣2,m),(﹣5,n)在抛物线上,则m>nD .关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣14.(2015•巴中)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=﹣1,下列结论:①abc<0;②2a+b=0;③a﹣b+c>0;④4a﹣2b+c<0其中正确的是()A .①②B.只有①C.③④D.①④5.(2015•潜江)二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论有()A .1个B.2个C.3个D.4个6.(2015•齐齐哈尔)抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a ﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2,则y1≤y2,其中正确结论的个数是()A .1个B.2个C.3个D.4个7.(2015•乐山)已知二次函数y=ax2+bx+c的图象如图所示,记m=|a﹣b+c|+|2a+b+c|,n=|a+b+c|+|2a﹣b﹣c|.则下列选项正确的是()A .m<n B.m>nC .m=n D.m、n的大小关系不能确定8.(2015•潍坊)已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是()A .1 B.2 C.3 D.49.(2015•黔东南州)如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;其中正确的结论有()A .1个B.2个C.3个D.4个10.(2015•包头)如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:①当x>3时,y<0;②3a+b<0;③﹣1≤a≤﹣;④4ac﹣b2>8a;其中正确的结论是()A .①③④B.①②③C.①②④D.①②③④11.(2015•茂名)在平面直角坐标系中,下列函数的图象经过原点的是()A .y=B.y=﹣2x﹣3 C.y=2x2+1 D.y=5x12.(2015•天水)二次函数y=ax2+bx﹣1(a≠0)的图象经过点(1,1),则a+b+1的值是()A .﹣3 B.﹣1 C.2 D.313.(2015•大庆)已知二次函数y=a(x﹣2)2+c,当x=x1时,函数值为y1;当x=x2时,函数值为y2,若|x1﹣2|>|x2﹣2|,则下列表达式正确的是()A .y1+y2>0 B.y1﹣y2>0 C.a(y1﹣y2)>D.a(y1+y2)>014.(2015•义乌市)如果一种变换是将抛物线向右平移2个单位或向上平移1个单位,我们把这种变换称为抛物线的简单变换.已知抛物线经过两次简单变换后的一条抛物线是y=x2+1,则原抛物线的解析式不可能的是()A .y=x2﹣1 B.y=x2+6x+5 C.y=x2+4x+4 D.y=x2+8x+1715.(2015•临沂)要将抛物线y=x2+2x+3平移后得到抛物线y=x2,下列平移方法正确的是()A .向左平移1个单位,再向上平移2个单位B .向左平移1个单位,再向下平移2个单位C向右平移1个.单位,再向上平移2个单位D .向右平移1个单位,再向下平移2个单位16.(2015•成都)将抛物线y=x2向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数表达式为()A .y=(x+2)2﹣3B.y=(x+2)2+3 C.y=(x﹣2)2+3 D.y=(x﹣2)2﹣317.(2015•荆州)将抛物线y=x2﹣2x+3向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为()A .y=(x﹣1)2+4 B.y=(x﹣4)2+4 C.y=(x+2)2+6 D.y=(x﹣4)2+618.(2015•河池)将抛物线y=x2向右平移2个单位,再向上平移3个单位后,抛物线的解析式为()A .y=(x+2)2+3 B.y=(x﹣2)2+3 C.y=(x+2)2﹣3D.y=(x﹣2)2﹣319.(2015•牡丹江)抛物线y=3x2+2x﹣1向上平移4个单位长度后的函数解析式为()A .y=3x2+2x﹣5 B.y=3x2+2x﹣4 C.y=3x2+2x+3 D.y=3x2+2x+420.(2015•攀枝花)将抛物线y=﹣2x2+1向右平移1个单位长度,再向上平移1个单位长度所得的抛物线解析式为()A .y=﹣2(x+1)2B.y=﹣2(x+1)2+2C.y=﹣2(x﹣1)2+2D.y=﹣2(x﹣1)2+121.(2015•乐山)二次函数y=﹣x2+2x+4的最大值为()A .3 B.4 C.5 D.622.(2014•舟山)当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为()A .﹣B.或C.2或D.2或或23.(2014•淄博)如图,二次函数y=x2+bx+c的图象过点B(0,﹣2).它与反比例函数y=﹣的图象交于点A(m,4),则这个二次函数的解析式为()A .y=x2﹣x﹣2 B.y=x2﹣x+2 C.y=x2+x﹣2 D.y=x2+x+224.(2014•成都)将二次函数y=x2﹣2x+3化为y=(x﹣h)2+k的形式,结果为()A .y=(x+1)2+4 B.y=(x+1)2+2 C.y=(x﹣1)2+4 D.y=(x﹣1)2+225.(2015•柳州)如图,二次函数y=ax2+bx+c的图象与x轴相交于(﹣2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是()A .x<﹣2 B.﹣2<x<4 C.x>0 D.x>426.(2015•陕西)下列关于二次函数y=ax2﹣2ax+1(a>1)的图象与x轴交点的判断,正确的是()A.没有交点B .只有一个交点,且它位于y轴右侧C .有两个交点,且它们均位于y轴左侧D .有两个交点,且它们均位于y轴右侧27.(2015•宁波)二次函数y=a(x﹣4)2﹣4(a≠0)的图象在2<x<3这一段位于x轴的下方,在6<x<7这一段位于x轴的上方,则a的值为()A .1 B.﹣1 C.2 D.﹣228.(2015•兰州)二次函数y=x2+x+c的图象与x轴的两个交点A(x1,0),B(x2,0),且x1<x2,点P(m,n)是图象上一点,那么下列判断正确的是()A .当n<0时,m<0B.当n>0时,m>x2C .当n<0时,x1<m<x2D.当n>0时,m<x129.(2015•天津)已知抛物线y=﹣x2+x+6与x轴交于点A,点B,与y轴交于点C.若D为AB的中点,则CD的长为()A .B.C.D.30.(2015•苏州)若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为()A .x1=0,x2=4 B.x1=1,x2=5 C.x1=1,x2=﹣5 D.x1=﹣1,x2=5 2015年中考真题初中数学---二次函数(3)一.选择题(共10小题)1.(2015•济南)如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是()A .﹣2<m <B.﹣3<m <﹣C.﹣3<m<﹣2 D.﹣3<m <﹣2.(2015•杭州)设二次函数y1=a(x﹣x1)(x﹣x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e (d≠0)的图象交于点(x1,0),若函数y=y1+y2的图象与x轴仅有一个交点,则()A a(x1﹣x2)=dB a(x2﹣x1)=dC a(x1﹣x2)2=dD a(x1+x2)2=d....3.(2015•达州)若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0)、(x2,0),且x1<x2,图象上有一点M(x0,y0),在x轴下方,则下列判断正确的是()A .a(x0﹣x1)(x0﹣x2)<0B.a>0C .b2﹣4ac≥0 D.x1<x0<x24.(2015•贵港)如图,已知二次函数y1=x2﹣x的图象与正比例函数y2=x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是()A .0<x<2 B.0<x<3 C.2<x<3 D.x<0或x>35.(2015•泸州)若二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为x=﹣1,则使函数值y>0成立的x的取值范围是()A .x<﹣4或x>2B.﹣4≤x≤2 C.x≤﹣4或x≥2 D.﹣4<x<26.(2015•六盘水)如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD的最大面积是()A .60m2B.63m2C.64m2D.66m27.(2015•铜仁市)河北省赵县的赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为y=﹣x2,当水面离桥拱顶的高度DO是4m时,这时水面宽度AB为()A .﹣20m B.10m C.20m D.﹣10m8.(2015•金华)图2是图1中拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可近似看成抛物线y=﹣(x﹣80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为()A .16米B.米C.16米D.米9.(2015•潍坊)如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是()A .cm2B.cm2C.cm2D.cm210.(2015•嘉兴)如图,抛物线y=﹣x2+2x+m+1交x轴与点A(a,0)和B(b,0),交y 轴于点C,抛物线的顶点为D,下列四个命题:①当x>0时,y>0;②若a=﹣1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6.其中真命题的序号是()A .①B.②C.③D.④2015年中考真题初中数学---二次函数(1)参考答案一.选择题(共30小题)1.C 2.B 3.C 4.D 5.C 6.A 7.B 8.B 9.C 10.D 11.D 12.C 13.A 14.B 15.B 16.D 17.D 18.D 19.B20.D 21.C 22.D 23.B 24.B 25.A 26.B 27.D 28.B29.B 30.B2015年中考真题初中数学---二次函数(2)参考答案一.选择题(共30小题)1.C 2.A 3.C 4.D 5.B 6.C 7.A 8.B 9.C 10.B 11.D 12.D 13.C 14.B 15.A 16.A 17.B 18.B 19.C20.C 21.C 22.C 23.A 24.D 25.B 26.D 27.A 28.C29.D 30.D2015年中考真题初中数学---二次函数(3)参考答案一.选择题(共10小题)1.D 2.B 3.A 4.C 5.D 6.C 7.C 8.B 9.C 10.C。
二次函数综合应用题(有答案)中考题必练经典(学有余力的看)

函数综合应用题题目分析及题目对学生的要求1. 求解析式:要求能够根据题意建立相应坐标系,将实际问题转化成数学问题。
需要注意的是:(1) 不能忘记写自变量的取值范围(需要用的前提下)(2) 在考虑自变量的取值范围时要结合它所代表的实际意义。
2. 求最值:实际生活中的最值能够指导人们进行决策,这一问要求能够熟练地对二次三项式进行配方,利用解析式探讨实际问题中的最值问题。
(一般式化为定点式)最值的求法:(1) 一次函数和反比例函数中求最值是根据函数在自变量取值范围内的增减性来确定的。
(2) 二次函数求最值是将解析式配方后,结合自变量取值范围来确定的。
3. 求范围,要求学生利用解析式求实际问题中的范围问题,主要是将函数与不等式结合起来。
推荐思路:画出不等式左右两边的图象,结合函数图象求出x 的取值范围。
备选思路一:先将不等号看做等号,求出x 的取值,再结合图象考虑将等号还原为不等号后x 的取值范围;备选思路二:通过分类讨论或者其它方法,直接解出这个不等式。
这一问里需要注意的是在注意:最后下结论时一定要结合它的实际意义和前面所求得的自变量取值范围进行判断。
一、求利润的最值1. (本题满分10分) 某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满。
当每个房间每天的房价每增加10元时,就会有一个房间空闲。
宾馆需对游客居住的每个房间每天支出20元的各种费用。
根据规定,每个房间每天的房价不得高于340元。
设每个房间的房价每天增加x 元(x 为10的正整数倍)。
(1) 设一天订住的房间数为y ,直接写出y 与x 的函数关系式及自变量x 的取值范围;(2) 设宾馆一天的利润为w 元,求w 与x 的函数关系式;(3) 一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?解:(1) y=50-101x (0≤x ≤160,且x 是10的整数倍)。
(2) W=(50-101x)(180+x -20)= -101x 2+34x +8000; (3) W= -101x 2+34x +8000= -101(x -170)2+10890, 当x<170时,W 随x 增大而增大,但0≤x ≤160,∴当x=160时,W 最大=10880,当x=160时,y=50-101x=34。
备战中考数学压轴题专题二次函数的经典综合题附详细答案

一、二次函数真题与模拟题分类汇编(难题易错题)1.(6分)(2015•牡丹江)如图,抛物线y=x2+bx+c经过点A(﹣1,0),B(3,0).请解答下列问题:(1)求抛物线的解析式;(2)点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE中点,连接FH,求线段FH的长.注:抛物线y=ax2+bx+c(a≠0)的对称轴是x=﹣.【答案】(1)y=-2x-3;(2).【解析】试题分析:(1)把A,B两点坐标代入,求待定系数b,c,进而确定抛物线的解析式;(2)连接BE,点F是AE中点,H是AB中点,则FH为三角形ABE的中位线,求出BE的长,FH就知道了,先由抛物线解析式求出点E坐标,根据勾股定理可求BE,再根据三角形中位线定理求线段HF的长.试题解析:(1)∵抛物线y=x2+bx+c经过点A(﹣1,0),B(3,0),∴把A,B两点坐标代入得:,解得:,∴抛物线的解析式是:y=-2x-3;(2)∵点E(2,m)在抛物线上,∴把E点坐标代入抛物线解析式y=-2x-3得:m=4﹣4﹣3=﹣3,∴E(2,﹣3),∴BE==.∵点F是AE中点,点H是抛物线的对称轴与x轴交点,即H为AB的中点,∴FH是三角形ABE的中位线,∴FH=BE=×=.∴线段FH的长.考点:1.待定系数法求抛物线的解析式;2.勾股定理;3.三角形中位线定理.2.如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为P(2,9),与x轴交于点A,B,与y轴交于点C(0,5).(Ⅰ)求二次函数的解析式及点A,B的坐标;(Ⅱ)设点Q在第一象限的抛物线上,若其关于原点的对称点Q′也在抛物线上,求点Q的坐标;(Ⅲ)若点M在抛物线上,点N在抛物线的对称轴上,使得以A,C,M,N为顶点的四边形是平行四边形,且AC为其一边,求点M,N的坐标.【答案】(1)y=﹣x2+4x+5,A(﹣1,0),B(5,0);(2)Q553)M (1,8),N(2,13)或M′(3,8),N′(2,3).【解析】【分析】(1)设顶点式,再代入C点坐标即可求解解析式,再令y=0可求解A和B点坐标;(2)设点Q(m,﹣m2+4m+5),则其关于原点的对称点Q′(﹣m,m2﹣4m﹣5),再将Q′坐标代入抛物线解析式即可求解m的值,同时注意题干条件“Q在第一象限的抛物线上”;(3)利用平移AC的思路,作MK⊥对称轴x=2于K,使MK=OC,分M点在对称轴左边和右边两种情况分类讨论即可.【详解】(Ⅰ)设二次函数的解析式为y=a(x﹣2)2+9,把C(0,5)代入得到a=﹣1,∴y=﹣(x﹣2)2+9,即y=﹣x2+4x+5,令y=0,得到:x2﹣4x﹣5=0,解得x=﹣1或5,∴A(﹣1,0),B(5,0).(Ⅱ)设点Q(m,﹣m2+4m+5),则Q′(﹣m,m2﹣4m﹣5).把点Q′坐标代入y=﹣x2+4x+5,得到:m2﹣4m﹣5=﹣m2﹣4m+5,∴55∴Q55(Ⅲ)如图,作MK⊥对称轴x=2于K.①当MK=OA ,NK=OC=5时,四边形ACNM 是平行四边形. ∵此时点M 的横坐标为1, ∴y=8,∴M (1,8),N (2,13),②当M′K=OA=1,KN′=OC=5时,四边形ACM′N′是平行四边形, 此时M′的横坐标为3,可得M′(3,8),N′(2,3). 【点睛】本题主要考查了二次函数的应用,第3问中理解通过平移AC 可应用“一组对边平行且相等”得到平行四边形.3.如图,过()A 1,0、()B 3,0作x 轴的垂线,分别交直线y 4x =-于C 、D 两点.抛物线2y ax bx c =++经过O 、C 、D 三点.()1求抛物线的表达式;()2点M 为直线OD 上的一个动点,过M 作x 轴的垂线交抛物线于点N ,问是否存在这样的点M ,使得以A 、C 、M 、N 为顶点的四边形为平行四边形?若存在,求此时点M 的横坐标;若不存在,请说明理由;()3若AOC 沿CD 方向平移(点C 在线段CD 上,且不与点D 重合),在平移的过程中AOC 与OBD 重叠部分的面积记为S ,试求S 的最大值.【答案】(1)2413y x x 33=-+;(2)32或32+或32-;(3)13. 【解析】 【分析】(1)利用待定系数法求出抛物线的解析式;(2)由题意,可知MN ∥AC ,因为以A 、C 、M 、N 为顶点的四边形为平行四边形,则有MN =AC =3.设点M 的横坐标为x ,则求出MN =|43x 2﹣4x |;解方程|43x 2﹣4x |=3,求出x 的值,即点M 横坐标的值;(3)设水平方向的平移距离为t (0≤t <2),利用平移性质求出S 的表达式:S 16=-(t ﹣1)213+;当t =1时,s 有最大值为13. 【详解】(1)由题意,可得C (1,3),D (3,1).∵抛物线过原点,∴设抛物线的解析式为:y =ax 2+bx ,∴3931a b a b +=⎧⎨+=⎩,解得43133a b ⎧=-⎪⎪⎨⎪=⎪⎩,∴抛物线的表达式为:y 43=-x 2133+x . (2)存在.设直线OD 解析式为y =kx ,将D (3,1)代入,求得k 13=,∴直线OD 解析式为y 13=x . 设点M 的横坐标为x ,则M (x ,13x ),N (x ,43-x 2133+x ),∴MN =|y M ﹣y N |=|13x ﹣(43-x 2133+x )|=|43x 2﹣4x |. 由题意,可知MN ∥AC ,因为以A 、C 、M 、N 为顶点的四边形为平行四边形,则有MN =AC =3,∴|43x 2﹣4x |=3. 若43x 2﹣4x =3,整理得:4x 2﹣12x ﹣9=0,解得:x =或x = 若43x 2﹣4x =﹣3,整理得:4x 2﹣12x +9=0,解得:x 32=,∴存在满足条件的点M ,点M 的横坐标为:32. (3)∵C (1,3),D (3,1),∴易得直线OC 的解析式为y =3x ,直线OD 的解析式为y 13=x . 如解答图所示,设平移中的三角形为△A 'O 'C ',点C '在线段CD 上. 设O 'C '与x 轴交于点E ,与直线OD 交于点P ; 设A 'C '与x 轴交于点F ,与直线OD 交于点Q .设水平方向的平移距离为t (0≤t <2),则图中AF =t ,F (1+t ,0),Q (1+t ,1133+t ),C '(1+t ,3﹣t ).设直线O 'C '的解析式为y =3x +b ,将C '(1+t ,3﹣t )代入得:b =﹣4t ,∴直线O 'C '的解析式为y =3x ﹣4t ,∴E (43t ,0). 联立y =3x ﹣4t 与y 13=x ,解得:x 32=t ,∴P (32t ,12t ). 过点P 作PG ⊥x 轴于点G ,则PG 12=t ,∴S =S △OFQ ﹣S △OEP 12=OF •FQ 12-OE •PG 12=(1+t )(1133+t )12-•43t •12t 16=-(t ﹣1)213+当t =1时,S 有最大值为13,∴S 的最大值为13.【点睛】本题是二次函数压轴题,综合考查了二次函数的图象与性质、待定系数法、函数图象上点的坐标特征、平行四边形、平移变换、图形面积计算等知识点,有一定的难度.第(2)问中,解题的关键是根据平行四边形定义,得到MN =AC =3,由此列出方程求解;第(3)问中,解题的关键是求出S 的表达式,注意图形面积的计算方法.4.如图,直线y =-12x-3与x 轴,y 轴分别交于点A ,C ,经过点A ,C 的抛物线y =ax 2+bx﹣3与x 轴的另一个交点为点B(2,0),点D 是抛物线上一点,过点D 作DE ⊥x 轴于点E ,连接AD ,DC .设点D 的横坐标为m . (1)求抛物线的解析式;(2)当点D 在第三象限,设△DAC 的面积为S ,求S 与m 的函数关系式,并求出S 的最大值及此时点D 的坐标;(3)连接BC ,若∠EAD =∠OBC ,请直接写出此时点D 的坐标.【答案】(1)y =14x 2+x ﹣3;(2)S △ADC =﹣34(m+3)2+274;△ADC 的面积最大值为274;此时D(﹣3,﹣154);(3)满足条件的点D 坐标为(﹣4,﹣3)或(8,21). 【解析】 【分析】(1)求出A 坐标,再用待定系数法求解析式;(2)设DE 与AC 的交点为点F.设点D 的坐标为:(m ,14m 2+m ﹣3),则点F 的坐标为:(m ,﹣12m ﹣3),根据S △ADC =S △ADF +S △DFC 求出解析式,再求最值;(3)①当点D 与点C 关于对称轴对称时,D(﹣4,﹣3),根据对称性此时∠EAD =∠ABC .②作点D(﹣4,﹣3)关于x 轴的对称点D′(﹣4,3),直线AD′的解析式为y =32x+9,解方程组求出函数图像交点坐标. 【详解】解:(1)在y =﹣12x ﹣3中,当y =0时,x =﹣6, 即点A 的坐标为:(﹣6,0),将A(﹣6,0),B(2,0)代入y =ax 2+bx ﹣3得:366304230a b a b --=⎧⎨+-=⎩, 解得:141a b ⎧=⎪⎨⎪=⎩,∴抛物线的解析式为:y =14x 2+x ﹣3; (2)设点D 的坐标为:(m ,14m 2+m ﹣3),则点F 的坐标为:(m ,﹣12m ﹣3), 设DE 与AC 的交点为点F.∴DF =﹣12m ﹣3﹣(14m 2+m ﹣3)=﹣14m 2﹣32m , ∴S △ADC =S △ADF +S △DFC=12DF•AE+12•DF•OE =12DF•OA =12×(﹣14m 2﹣32m)×6 =﹣34m 2﹣92m =﹣34(m+3)2+274,∵a =﹣34<0, ∴抛物线开口向下,∴当m =﹣3时,S △ADC 存在最大值274, 又∵当m =﹣3时,14m 2+m ﹣3=﹣154,∴存在点D(﹣3,﹣154),使得△ADC 的面积最大,最大值为274; (3)①当点D 与点C 关于对称轴对称时,D(﹣4,﹣3),根据对称性此时∠EAD =∠ABC . ②作点D(﹣4,﹣3)关于x 轴的对称点D′(﹣4,3), 直线AD′的解析式为y =32x+9, 由2392134y x y x x ⎧=+⎪⎪⎨⎪=+-⎪⎩,解得60x y =-⎧⎨=⎩或821x y =⎧⎨=⎩,此时直线AD′与抛物线交于D(8,21),满足条件, 综上所述,满足条件的点D 坐标为(﹣4,﹣3)或(8,21)【点睛】本题属于二次函数综合题,考查了待定系数法,一次函数的应用,二次函数的性质等知识,解题的关键是学会构建二次函数解决最值问题,学会构建一次函数解决实际问题,属于中考压轴题..5.如图:在平面直角坐标系中,直线l:y=13x﹣43与x轴交于点A,经过点A的抛物线y=ax2﹣3x+c的对称轴是x=32.(1)求抛物线的解析式;(2)平移直线l经过原点O,得到直线m,点P是直线m上任意一点,PB⊥x轴于点B,PC⊥y轴于点C,若点E在线段OB上,点F在线段OC的延长线上,连接PE,PF,且PE=3PF.求证:PE⊥PF;(3)若(2)中的点P坐标为(6,2),点E是x轴上的点,点F是y轴上的点,当PE⊥PF时,抛物线上是否存在点Q,使四边形PEQF是矩形?如果存在,请求出点Q的坐标,如果不存在,请说明理由.【答案】(1)抛物线的解析式为y=x2﹣3x﹣4;(2)证明见解析;(3)点Q的坐标为(﹣2,6)或(2,﹣6).【解析】【分析】(1)先求得点A 的坐标,然后依据抛物线过点A ,对称轴是x=32列出关于a 、c 的方程组求解即可;(2)设P (3a ,a ),则PC=3a ,PB=a ,然后再证明∠FPC=∠EPB ,最后通过等量代换进行证明即可;(3)设E (a ,0),然后用含a 的式子表示BE 的长,从而可得到CF 的长,于是可得到点F 的坐标,然后依据中点坐标公式可得到22x x x x Q P F E ++=,22y y y yQ P F E ++=,从而可求得点Q 的坐标(用含a 的式子表示),最后,将点Q 的坐标代入抛物线的解析式求得a 的值即可. 【详解】 (1)当y=0时,14033x -=,解得x=4,即A (4,0),抛物线过点A ,对称轴是x=32,得161203322a c a -+=⎧⎪-⎨-=⎪⎩,解得14a c =⎧⎨=-⎩,抛物线的解析式为y=x 2﹣3x ﹣4;(2)∵平移直线l 经过原点O ,得到直线m ,∴直线m 的解析式为y=13x . ∵点P 是直线1上任意一点,∴设P (3a ,a ),则PC=3a ,PB=a . 又∵PE=3PF , ∴PC PBPF PE=. ∴∠FPC=∠EPB . ∵∠CPE+∠EPB=90°, ∴∠FPC+∠CPE=90°, ∴FP ⊥PE .(3)如图所示,点E 在点B 的左侧时,设E (a ,0),则BE=6﹣a .∵CF=3BE=18﹣3a , ∴OF=20﹣3a . ∴F (0,20﹣3a ). ∵PEQF 为矩形,∴22x x x x Q P F E ++=,22y y y yQ P F E ++=, ∴Q x +6=0+a ,Q y +2=20﹣3a+0, ∴Q x =a ﹣6,Q y =18﹣3a .将点Q 的坐标代入抛物线的解析式得:18﹣3a=(a ﹣6)2﹣3(a ﹣6)﹣4,解得:a=4或a=8(舍去). ∴Q (﹣2,6).如下图所示:当点E 在点B 的右侧时,设E (a ,0),则BE=a ﹣6.∵CF=3BE=3a ﹣18, ∴OF=3a ﹣20. ∴F (0,20﹣3a ). ∵PEQF 为矩形,∴22x x x x Q P F E ++=,22y y y yQ P F E ++=, ∴Q x +6=0+a ,Q y +2=20﹣3a+0, ∴Q x =a ﹣6,Q y =18﹣3a .将点Q 的坐标代入抛物线的解析式得:18﹣3a=(a ﹣6)2﹣3(a ﹣6)﹣4,解得:a=8或a=4(舍去). ∴Q (2,﹣6).综上所述,点Q 的坐标为(﹣2,6)或(2,﹣6). 【点睛】本题主要考查的是二次函数的综合应用,解答本题主要应用了矩形的性质、待定系数法求二次函数的解析式、中点坐标公式,用含a 的式子表示点Q 的坐标是解题的关键.6.在平面直角坐标系中,抛物线223y x x =--+与x 轴交于A ,B 两点(A 在B 的左侧),与y 轴交于点C ,顶点为D .(1)请直接写出点A ,C ,D 的坐标;(2)如图(1),在x 轴上找一点E ,使得△CDE 的周长最小,求点E 的坐标; (3)如图(2),F 为直线AC 上的动点,在抛物线上是否存在点P ,使得△AFP 为等腰直角三角形?若存在,求出点P 的坐标,若不存在,请说明理由.【答案】(1)A (﹣3,0),C (0,3),D (﹣1,4);(2)E (37-,0);(3)P (2,﹣5)或(1,0). 【解析】试题分析:(1)令抛物线解析式中y=0,解关于x 的一元二次方程即可得出点A 、B 的坐标,再令抛物线解析式中x=0求出y 值即可得出点C 坐标,利用配方法将抛物线解析式配方即可找出顶点D 的坐标;(2)作点C 关于x 轴对称的点C′,连接C′D 交x 轴于点E ,此时△CDE 的周长最小,由点C 的坐标可找出点C′的坐标,根据点C′、D 的坐标利用待定系数法即可求出直线C′D 的解析式,令其y=0求出x 值,即可得出点E 的坐标;(3)根据点A 、C 的坐标利用待定系数法求出直线AC 的解析式,假设存在,设点F (m ,m+3),分∠PAF=90°、∠AFP=90°和∠APF=90°三种情况考虑.根据等腰直角三角形的性质结合点A 、F 点的坐标找出点P 的坐标,将其代入抛物线解析式中即可得出关于m 的一元二次方程,解方程求出m 值,再代入点P 坐标中即可得出结论.试题解析:(1)当223y x x =--+中y=0时,有2230x x --+=,解得:1x =﹣3,2x =1,∵A 在B 的左侧,∴A (﹣3,0),B (1,0).当223y x x =--+中x=0时,则y=3,∴C (0,3). ∵223y x x =--+=2(1)4x -++,∴顶点D (﹣1,4).(2)作点C 关于x 轴对称的点C′,连接C′D 交x 轴于点E ,此时△CDE 的周长最小,如图1所示.∵C (0,3),∴C′(0,﹣3).设直线C′D 的解析式为y=kx+b ,则有:3{4b k b =--+=,解得:7{3k b =-=-,∴直线C′D 的解析式为y=﹣7x ﹣3,当y=﹣7x ﹣3中y=0时,x=37-,∴当△CDE 的周长最小,点E 的坐标为(37-,0). (3)设直线AC 的解析式为y=ax+c ,则有:3{30c a c =-+=,解得:1{3a c ==,∴直线AC 的解析式为y=x+3.假设存在,设点F (m ,m+3),△AFP 为等腰直角三角形分三种情况(如图2所示): ①当∠PAF=90°时,P (m ,﹣m ﹣3),∵点P 在抛物线223y x x =--+上,∴2323m m m --=--+,解得:m 1=﹣3(舍去),m 2=2,此时点P 的坐标为(2,﹣5);②当∠AFP=90°时,P (2m+3,0)∵点P 在抛物线223y x x =--+上,∴20(23)2(23)3m m =-+-++,解得:m 3=﹣3(舍去),m 4=﹣1,此时点P 的坐标为(1,0);③当∠APF=90°时,P (m ,0),∵点P 在抛物线223y x x =--+上,∴2023m m =--+,解得:m 5=﹣3(舍去),m 6=1,此时点P 的坐标为(1,0). 综上可知:在抛物线上存在点P ,使得△AFP 为等腰直角三角形,点P 的坐标为(2,﹣5)或(1,0).考点:二次函数综合题;最值问题;存在型;分类讨论;综合题.7.如图1,已知抛物线y=﹣x 2+bx+c 与x 轴交于A (﹣1,0),B (3,0)两点,与y 轴交于C 点,点P 是抛物线上在第一象限内的一个动点,且点P 的横坐标为t . (1)求抛物线的表达式;(2)设抛物线的对称轴为l ,l 与x 轴的交点为D .在直线l 上是否存在点M ,使得四边形CDPM 是平行四边形?若存在,求出点M 的坐标;若不存在,请说明理由.(3)如图2,连接BC,PB,PC,设△PBC的面积为S.①求S关于t的函数表达式;②求P点到直线BC的距离的最大值,并求出此时点P的坐标.【答案】(1)y=﹣x2+2x+3.(2)当t=2时,点M的坐标为(1,6);当t≠2时,不存在,理由见解析;(3)y=﹣x+3;P点到直线BC的距离的最大值为28,此时点P的坐标为(32,154).【解析】【分析】(1)由点A、B的坐标,利用待定系数法即可求出抛物线的表达式;(2)连接PC,交抛物线对称轴l于点E,由点A、B的坐标可得出对称轴l为直线x=1,分t=2和t≠2两种情况考虑:当t=2时,由抛物线的对称性可得出此时存在点M,使得四边形CDPM是平行四边形,再根据点C的坐标利用平行四边形的性质可求出点P、M的坐标;当t≠2时,不存在,利用平行四边形对角线互相平分结合CE≠PE可得出此时不存在符合题意的点M;(3)①过点P作PF∥y轴,交BC于点F,由点B、C的坐标利用待定系数法可求出直线BC的解析式,根据点P的坐标可得出点F的坐标,进而可得出PF的长度,再由三角形的面积公式即可求出S关于t的函数表达式;②利用二次函数的性质找出S的最大值,利用勾股定理可求出线段BC的长度,利用面积法可求出P点到直线BC的距离的最大值,再找出此时点P的坐标即可得出结论.【详解】(1)将A(﹣1,0)、B(3,0)代入y=﹣x2+bx+c,得10930b cb c-++=⎧⎨-++=⎩,解得:23bc=⎧⎨=⎩,∴抛物线的表达式为y=﹣x2+2x+3;(2)在图1中,连接PC,交抛物线对称轴l于点E,∵抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,∴抛物线的对称轴为直线x=1,当t=2时,点C、P关于直线l对称,此时存在点M,使得四边形CDPM是平行四边形,∵抛物线的表达式为y=﹣x2+2x+3,∴点C的坐标为(0,3),点P的坐标为(2,3),∴点M的坐标为(1,6);当t≠2时,不存在,理由如下:若四边形CDPM是平行四边形,则CE=PE,∵点C的横坐标为0,点E的横坐标为0,∴点P的横坐标t=1×2﹣0=2,又∵t≠2,∴不存在;(3)①在图2中,过点P作PF∥y轴,交BC于点F.设直线BC的解析式为y=mx+n(m≠0),将B(3,0)、C(0,3)代入y=mx+n,得303m nn+=⎧⎨=⎩,解得:13mn=-⎧⎨=⎩,∴直线BC的解析式为y=﹣x+3,∵点P的坐标为(t,﹣t2+2t+3),∴点F的坐标为(t,﹣t+3),∴PF=﹣t2+2t+3﹣(﹣t+3)=﹣t2+3t,∴S=12PF•OB=﹣32t2+92t=﹣32(t﹣32)2+278;②∵﹣32<0,∴当t=32时,S取最大值,最大值为278.∵点B的坐标为(3,0),点C的坐标为(0,3),∴线段BC=2232OB OC+=,∴P点到直线BC的距离的最大值为27292832⨯=,此时点P的坐标为(32,154).【点睛】本题考查了待定系数法求一次(二次)函数解析式、平行四边形的判定与性质、三角形的面积、一次(二次)函数图象上点的坐标特征以及二次函数的性质,解题的关键是:(1)由点的坐标,利用待定系数法求出抛物线表达式;(2)分t=2和t≠2两种情况考虑;(3)①利用三角形的面积公式找出S 关于t 的函数表达式;②利用二次函数的性质结合面积法求出P 点到直线BC 的距离的最大值.8.已知函数()()22,1,222x nx n x n y n nx x x n ⎧-++≥⎪=⎨-++<⎪⎩(n 为常数) (1)当5n =,①点()4,P b 在此函数图象上,求b 的值; ②求此函数的最大值.(2)已知线段AB 的两个端点坐标分别为()()2,24,2A B 、,当此函数的图象与线段AB 只有一个交点时,直接写出n 的取值范围.(3)当此函数图象上有4个点到x 轴的距离等于4,求n 的取值范围.【答案】(1)①92b =②458;(2)1845n <≤,823n ≤<时,图象与线段AB 只有一个交点;(3)函数图象上有4个点到x 轴的距离等于4时,8n >或3142n ≤<. 【解析】 【分析】(1)①将()4,P b 代入2155222y x x =-++;②当5x ≥时,当5x =时有最大值为5;当5x <时,当52x =时有最大值为458;故函数的最大值为458; (2)将点()4,2代入2y x nx n =-++中,得到185n =,所以1845n <≤时,图象与线段AB 只有一个交点;将点()2,2)代入2y x nx n =-++和21222n n y x x =-++中,得到82,3n n ==, 所以823n ≤<时图象与线段AB 只有一个交点; (3)当xn =时,42n >,得到8n >;当2n x =时,1482n +≤,得到312n ≥,当x n=时,22y n n n n =-++=,4n <. 【详解】解:(1)当5n =时,()()225551555222x x x y x x x ⎧-++≥⎪=⎨-++<⎪⎩, ①将()4,P b 代入2155222y x x =-++, ∴92b =; ②当5x ≥时,当5x =时有最大值为5; 当5x <时,当52x =时有最大值为458; ∴函数的最大值为458; (2)将点()4,2代入2y x nx n =-++中,∴185n =, ∴1845n <≤时,图象与线段AB 只有一个交点; 将点()2,2代入2y x nx n =-++中, ∴2n =, 将点()2,2代入21222n ny x x =-++中, ∴83n =, ∴823n ≤<时图象与线段AB 只有一个交点; 综上所述:1845n <≤,823n ≤<时,图象与线段AB 只有一个交点; (3)当xn =时,22112222n n y n n =-++=,42n>,∴8n >; 当2n x =时,182n y =+, 1482n +≤,∴312n ≥, 当xn =时,22y n n n n =-++=,4n <;∴函数图象上有4个点到x轴的距离等于4时,8n>或3142n≤<.【点睛】考核知识点:二次函数综合.数形结合分析问题是关键.9.如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA=12.(1)求抛物线的解析式;(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA面积的最大值;(3)在(2)中四边形BMCA面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q 的坐标;若不存在,请说明理由.【答案】(1)y=12x2+32x﹣2;(2)9;(3)点Q的坐标为(﹣2,4)或(﹣2,﹣1).【解析】(1)如答图1所示,利用已知条件求出点B的坐标,然后用待定系数法求出抛物线的解析式.(2)如答图1所示,首先求出四边形BMCA面积的表达式,然后利用二次函数的性质求出其最大值.(3)如答图2所示,首先求出直线AC与直线x=2的交点F的坐标,从而确定了Rt△AGF 的各个边长;然后证明Rt△AGF∽Rt△QEF,利用相似线段比例关系列出方程,求出点Q的坐标.考点:二次函数综合题,曲线上点的坐标与方程的关系,锐角三角函数定义,由实际问题列函数关系式,二次函数最值,勾股定理,相似三角形的判定和性质,圆的切线性质.10.已知二次函数y=﹣316x 2+bx+c 的图象经过A (0,3),B (﹣4,﹣92)两点. (1)求b ,c 的值. (2)二次函数y=﹣316x 2+bx+c 的图象与x 轴是否有公共点,求公共点的坐标;若没有,请说明情况.【答案】(1)983b c ⎧=⎪⎨⎪=⎩;(2)公共点的坐标是(﹣2,0)或(8,0).【解析】【分析】(1)把点A 、B 的坐标分别代入函数解析式求得b 、c 的值;(2)利用根的判别式进行判断该函数图象是否与x 轴有交点,由题意得到方程﹣239168x x ++3=0,通过解该方程求得x 的值即为抛物线与x 轴交点横坐标. 【详解】(1)把A (0,3),B (﹣4,﹣92)分别代入y=﹣316x 2+bx+c ,得339164162c b c =⎧⎪⎨-⨯-+=-⎪⎩,解得983b c ⎧=⎪⎨⎪=⎩;(2)由(1)可得,该抛物线解析式为:y=﹣316x 2+98x+3, △=(98)2﹣4×(﹣316)×3=22564>0, 所以二次函数y=﹣316x 2+bx+c 的图象与x 轴有公共点, ∵﹣316x 2+98x+3=0的解为:x 1=﹣2,x 2=8, ∴公共点的坐标是(﹣2,0)或(8,0).【点睛】本题考查了抛物线与x 轴的交点,二次函数图象上点的坐标特征.注意抛物线解析式与一元二次方程间的转化关系.。
初三中考数学专题复习:二次函数综合题(相似三角形问题)含答案

中考数学专题复习:二次函数综合题(相似三角形问题)1.如图①,二次函数y =﹣x 2+bx +c 的图象与x 轴交于点A (﹣1,0)、B (3,0),与y 轴交于点C ,连接BC ,点P 是抛物线上一动点.(1)求二次函数的表达式.(2)当点P 不与点A 、B 重合时,作直线AP ,交直线BC 于点Q ,若①ABQ 的面积是①BPQ 面积的4倍,求点P 的横坐标.(3)如图①,当点P 在第一象限时,连接AP ,交线段BC 于点M ,以AM 为斜边向①ABM 外作等腰直角三角形AMN ,连接BN ,①ABN 的面积是否变化?如果不变,请求出①ABN 的面积;如果变化,请说明理由.2.如图,二次函数2314y x bx =++的图像经过点()8,3A ,交x 轴于点B ,C (点B 在点C 的左侧),与y 轴交于点D .(1)填空:b = ______;(2)点P 是第一象限内抛物线上一点,直线PO 交直线CD 于点Q ,过点P 作x 轴的垂线交直线CD 于点T ,若PQ QT =,求点P 的坐标;(3)在x 轴的正半轴上找一点E ,过点E 作AE 的垂线EF 交y 轴于F ,若AEF 与EFO △相似,求OE 的长.3.如图,已知抛物线2y ax bx c =++与x 轴相交于点()1,0A -,()3,0B ,与y 轴的交点()0,6C .(1)求抛物线的解析式;(2)点(),P m n 在平面直角坐标系第一象限内的抛物线上运动,设PBC 的面积为S ,求S 关于m 的函数表达式(指出自变量m 的取值范围)和S 的最大值;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M 、点N 使得①CMN =90°,且∆CMN 与OBC ∆相似,如果存在,请求出点M 和点N 的坐标.4.如图,抛物线L 1:y =ax 2﹣2x +c (a ≠0)与x 轴交于A 、B (3,0)两点,与y 轴交于点C (0,﹣3),抛物线的顶点为D .抛物线L 2与L 1关于x 轴对称.(1)求抛物线L 1与L 2的函数表达式;(2)已知点E 是抛物线L 2的顶点,点M 是抛物线L 2上的动点,且位于其对称轴的右侧,过M 向其对称轴作垂线交对称轴于P ,是否存在这样的点M ,使得以P 、M 、E 为顶点的三角形与△BCD 相似,若存在请求出点M 的坐标,若不存在,请说明理由.5.如图,在平面直角坐标系中,已知直线4y x =+与x 轴、y 轴分别相交于点A 和点C ,抛物线21y x kx k =++-的图象经过点A 和点C ,与x 轴的另一个交点是点B .(1)求出此抛物线的解析式; (2)求出点B 的坐标;(3)若在y 轴的负半轴上存在点D .能使得以A ,C ,D 为顶点的三角形与①ABC 相似,请求出点D 的坐标.6.如图1,已知抛物线23y ax bx =++经过点()1,5D ,且交x 轴于A ,B 两点,交y 轴于点C ,已知点()1,0A -,(),P m n 是抛物线在第一象限内的一个动点,PQ BC ⊥于点Q .(1)求抛物线的解析式;(2)当PQ =m 的值;(3)是否存在点P ,使BPQ 与BOC 相似?若存在,请求出P 点的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系中,直线y =12x +2与x 轴交于点A ,与y 轴交于点C .抛物线y =ax 2+bx +c的对称轴是x=-32且经过A、C两点,与x轴的另一交点为点B.(1)求二次函数y=ax2+bx+c的表达式;(2)点P为线段AB上的动点,求AP+2PC的最小值;(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A,M,N为顶点的三角形与①ABC 相似?若存在,求出点M的坐标;若不存在,请说明理由.8.如图,抛物线y=−x2+bx+c与x轴相交于A(−1,0),B(3,0)两点,与y轴交于点C,顶点为点D,抛物线的对称轴与BC相交于点E,与x轴相交于点F.(1)求抛物线的函数关系式;(2)连结DA,求sin A的值;(3)若点H线段BC上,BOC与BFH△相似,请直接写出点H的坐标.9.如图,抛物线y=1-2x2+bx+c与x轴交于点A(﹣2,0)和点B(8,0),与y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.(1)求抛物线的表达式;(2)点P 是第一象限内抛物线上的动点,连接PB ,PC ,当S △PBC =720S △ABC 时,求点P 的坐标; (3)点N 是对称轴l 右侧抛物线上的动点,在射线ED 上是否存在点M ,使得以点M ,N ,E 为顶点的三角形与①OBC 相似?若存在,求点M 的坐标;若不存在,请说明理由.10.如图,抛物线23y ax bx =++与x 轴交于1,0A 、()3,0B -两点,与y 轴交于点C ,设抛物线的顶点为D .(1)求该抛物线的表达式与顶点D 的坐标; (2)试判断BCD △的形状,并说明理由;(3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形与BCD △相似?若存在,请求出点P 的坐标;若不存在,请说明理由.11.如图,抛物线y =ax 2﹣2ax ﹣3a (a ≠0)与x 轴交于点A ,B .与y 轴交于点C .连接AC ,BC .已知ABC 的面积为2.(1)求抛物线的解析式;(2)平行于x 轴的直线与抛物线从左到右依次交于P ,Q 两点.过P ,Q 向x 轴作垂线,垂足分别为G ,H .若四边形PGHQ 为正方形,求正方形的边长;(3)抛物线上是否存在一点N ,使得①BCN =①CAB ﹣①CBA ,若存在,请求出满足条件N 点的横坐标,若不存在请说明理由.12.如图,二次函数2y x bx c =-++的图像与x 轴交于点A (-1,0),B (2,0),与y 轴相交于点C .(1)求这个二次函数的解析式;(2)若点M 在此抛物线上,且在y 轴的右侧.①M 与y 轴相切,过点M 作MD ①y 轴,垂足为点D .以C ,D ,M 为顶点的三角形与①AOC 相似,求点M 的坐标及①M 的半径长.13.如图,在平面直角坐标系中,抛物线2()0y ax bx c ac =++≠与x 轴交于点A 和点B (点A 在点B 的左侧),与y 轴交于点C .若线段OA OB OC 、、的长满足2OC OA OB =⋅,则这样的抛物线称为“黄金”抛物线.如图,抛物线22(0)y ax bx a =++≠为“黄金”抛物线,其与x 轴交点为A ,B (其中B 在A 的右侧),与y 轴交于点C .且4OA OB =(1)求抛物线的解析式;(2)若P 为AC 上方抛物线上的动点,过点P 作PD AC ⊥,垂足为D . ①求PD 的最大值;①连接PC ,当PCD 与ACO △相似时,求点P 的坐标.14.如图,在平面直角坐标系xOy 中,已知抛物线2y x bx c =++与x 轴交于点A 、B 两点,其中1,0A ,与y 轴交于点()0,3C .(1)求抛物线解析式;(2)如图1,过点B 作x 轴垂线,在该垂线上取点P ,使得①PBC 与①ABC 相似,请求出点P 坐标;(3)如图2,在线段OB 上取一点M ,连接CM ,请求出12CM BM +最小值.15.如图,抛物线y =ax 2+k (a >0,k <0)与x 轴交于A ,B 两点(点B 在点A 的右侧),其顶点为C ,点P 为线段OC 上一点,且PC =14OC .过点P 作DE ①AB ,分别交抛物线于D ,E 两点(点E 在点D 的右侧),连接OD ,DC .(1)直接写出A ,B ,C 三点的坐标;(用含a ,k 的式子表示) (2)猜想线段DE 与AB 之间的数量关系,并证明你的猜想;(3)若①ODC =90°,k =﹣4,求a 的值.16.如图,抛物线223y x bx c =++与x 轴交于A ,B 两点,与y 轴交于C 点,连接AC ,已知B (﹣1,0),且抛物线经过点D (2,﹣2).(1)求抛物线的表达式;(2)若点E 是抛物线上第四象限内的一点,且2ABES=,求点E 的坐标;(3)若点P 是y 轴上一点,以P ,A ,C 三点为顶点的三角形是等腰三角形,求P 点的坐标.17.如图,在直角坐标系xOy 中,抛物线y =ax 2+bx +2(a ≠0)与x 轴交于点A (﹣1,0)和B (4,0),与y 轴交于点C ,点P 是抛物线上的动点(不与点A ,B ,C 重合).(1)求抛物线的解析式;(2)当点P 在第一象限时,设①ACP 的面积为S 1,①ABP 的面积为S 2,当S 1=S 2时,求点P 的坐标; (3)过点O 作直线l ①BC ,点Q 是直线l 上的动点,当BQ ①PQ ,且①BPQ =①CAB 时,请直接写出点P 的坐标.18.如图,在平面直角坐标系xOy中,直线y=﹣x+3与两坐标轴交于A、B两点,抛物线y=x2+bx+c 过点A和点B,并与x轴交于另一点C,顶点为D.点E在对称轴右侧的抛物线上.(1)求抛物线的函数表达式和顶点D的坐标;(2)若点F在抛物线的对称轴上,且EF①x轴,若以点D,E,F为顶点的三角形与①ABD相似,求出此时点E的坐标;(3)若点P为坐标平面内一动点,满足tan①APB=3,请直接写出①P AB面积最大时点P的坐标及该三角形面积的最大值.19.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A、B,与y轴交于点C,且OC=2OB=6OA=6,点P是第一象限内抛物线上的动点.(1)求抛物线的解析式;(2)连接BC与OP,交于点D,当S△PCD:S△ODC的值最大时,求点P的坐标;(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N.使①CMN=90°,且①CMN与①BOC 相似,若存在,请求出点M、点N的坐标.20.如图,抛物线y=x2+bx+12(b<0)与x轴交于A,B两点(A点在B点左侧),且OB=3OA.(1)请直接写出b=,A点的坐标是,B点的坐标是;(2)如图(1),D点从原点出发,向y轴正方向运动,速度为2个单位长度/秒,直线BD交抛物线于点E,若BE=5DE,求D点运动时间;(3)如图(2),F点是抛物线顶点,过点F作x轴平行线MN,点C是对称轴右侧的抛物线上的一定点,P 点在直线MN上运动.若恰好存在3个P点使得①P AC为直角三角形,请求出C点坐标,并直接写出P点的坐标.答案1.(1)y =﹣x 2+2x +3.(2)P 352或 (3)①ABN 的面积不变,为4.2.(1)2-(2)5⎛ ⎝⎭或5⎛ ⎝⎭(3)4或493.(1)2246y x x =-++(2)S 关于m 的函数表达式为239(03)S m m m =-+<<,S 的最大值是274 (3)存在,M (1,8),N (0,172)或M (74,558),N (0,838)或M (94,398),N (0,38)或M (3,0),N (0,﹣32)4.(1)抛物线L 1:223y x x =--,抛物线L 2:2y x 2x 3=-++;(2)435(,)39M 或(4,5)M -.5.(1)254y x x =++(2)点B 的坐标为(-1,0)(3)点D 的坐标是(0,-203) 6.(1)215322y x x =-++ (2)1或5(3)存在;P (53,529)7.(1)抛物线表达式为:213222y x x =--+;(2)AP +2PC 的最小值是4;(3)存在M(0,2)或(-3,2)或(2,-3)或(5,-18),使得以点A 、M 、N 为顶点的三角形与ABC 相似.8.(1)y =-x 2+2x +3(3)点H 的坐标为(1,2)或(2,1)9.(1)21382y x x =++ (2)P 1(1,10.5),P 2(7,4.5)(3)存在,(3,8)或(3,5或(3,11)30.(1)y =﹣x 2﹣2x +3,(﹣1,4);(2)直角三角形,理由见解析;(3)存在,(0,0)或(0,﹣13)或(-9,0)11.(1)y =﹣13x 2+23x +1(2)﹣6﹣(3)存在,5或11712.(1)22y x x =-++; (2)M 的坐标为(12,94),(32, 54 ),(3,-4),①M 的半径长为12或32或313.(1)213222y x x =--+(2)①PD ①P 坐标为(3,2)-或325()28,-14.(1)243y x x =-+(2)P 点坐标为()3,9或()3,215.(1)点A 、B 、C 的坐标分别为(、、(0,k ) (2)DE =12AB(3)a =1316.(1)224233y x x =--(2)E ,-1)(3)P 点的坐标(0,2)或(02)或(0,﹣2或(0,54)17.(1)213222y x x =-++ (2)点P 的坐标为(103,139)(3)点P 的坐标为(32,﹣2)或(32,﹣2)或(173,﹣509)18.(1)y =x 2﹣4x +3,(2,﹣1)(2)(5,8)或(73,89-)(3)①P AB ,此时P )19.(1)y =﹣2x 2+4x +6 (2)点P 的坐标为(32,152) (3)存在,M 、N 的坐标分别为(3,0)、(0,﹣32)或(94,398)、(0,38)或(1,8)、(0,172)或(74,558)、(0,838)20.(1)﹣8,(2,0),(6,0)(2)3秒或212秒 (3)C 点坐标为(143,﹣329),P 点的坐标为(103,﹣4)或(﹣103,﹣4)或(11027,﹣4)。
中考数学:函数的图象与实际应用综合问题真题+模拟(原卷版北京专用)

中考数学函数的图象与实际应用综合问题【方法归纳】利用二次函数解决实际问题,要建立数学模型,即把实际问题转化为二次函数问题,利用题中存在的公式、内含的规律等相等关系,建立函数关系式,再利用函数的图象及性质去研究问题.在研究实际问题时要注意自变量的取值范围应具有实际意义.利用二次函数解决实际问题的一般步骤是:(1)建立适当的平面直角坐标系;(2)把实际问题中的一些数据与点的坐标联系起来;(3)用待定系数法求出抛物线的关系式;(4)利用二次函数的图象及其性质去分析问题、解决问题.常见的问题:求最大(小)值(如求最大利润、最大面积、最小周长等)、涵洞、桥梁、抛物体、抛物线的模型问题等.解决这些实际问题关键是找等量关系,把实际问题转化为函数问题,列出相关的函数关系式.【典例剖析】【例1】(2022·北京·中考真题)单板滑雪大跳台是北京冬奥会比赛项目之一,举办场地为首钢滑雪大跳台,运动员起跳后的飞行路线可以看作是抛物线的一部分,建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=a(x−ℎ)2+k(a<0).某运动员进行了两次训练.(1)第一次训练时,该运动员的水平距离x与竖直高度y的几组数据如下:根据上述数据,直接写出该运动员竖直高度的最大值,并求出满足的函数关系y=a(x−ℎ)2+k(a<0);(2)第二次训练时,该运动员的竖直高度y与水平距离x近似满足函数关系y=−0.04(x−9)2+23.24.记该运动员第一次训练的着陆点的水平距离为d1,第二次训练的着陆点的水平距离为d2,则d1______d2(填“>”“=”或“<”).【真题再现】1.(2015·北京·中考真题)有这样一个问题:探究函数y=12x2+1x的图象与性质.小东根据学习函数的经验,对函数y=12x2+1x的图象与性质进行了探究.下面是小东的探究过程,请补充完整:(1)函数y=12x2+1x的自变量x的取值范围是____;(2)下表是y与x的几组对应值.求m的值:(3)如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象:(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,32),结合函数的图象,写出该函数的其它性质(一条即可):_________.2.(2016·北京·中考真题)已知y是x的函数,自变量x的取值范围是x >0,下表是y与x的几组对应值.小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.下面是小腾的探究过程,请补充完整:(1)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(2)根据画出的函数图象,写出:①x=4对应的函数值y约为________;②该函数的一条性质:__________________.3.(2017·北京·中考真题)如图,P是弧AB所对弦AB上一动点,过点P作PM⊥AB交AB于点M,连接MB,过点P作PN⊥MB于点N.已知AB =6cm,设A 、P两点间的距离为xcm,P、N两点间的距离为ycm.(当点P与点A或点B重合时,y的值为0)小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:(说明:补全表格时相关数值保留一位小数)(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.(3)结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为____________cm.⌢与弦AB所围成的图形的内部的一定点,P是弦AB上4.(2018·北京·中考真题)如图,Q是AB⌢于点C,连接AC.已知AB=6cm,设A,P两点间的距离为x cm,一动点,连接PQ并延长交ABP,C两点间的距离为y1cm,A,C两点间的距离为y2cm.小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值;y1),(x,y2),并画出函数y1,y2的图象;(3)结合函数图象,解决问题:当△APC为等腰三角形时,AP的长度约为____cm.【模拟精练】一、解答题1.(2022·北京朝阳·二模)某公园在垂直于湖面的立柱上安装了一个多孔喷头,从喷头每个孔喷出的水柱形状都相同,可以看作是抛物线的一部分,当喷头向四周同时喷水时,形成一个环状喷泉,安装后,通过测量其中一条水柱,获得如下数据,在距立柱水平距离为d米的地点,水柱距离湖面的高度为h米,请解决以下问题:(1)在网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接;(2)结合表中所给数据或所画图象,直接写出这条水柱最高点距离湖面的高度;(3)求所画图象对应的函数表达式;(4)从安全的角度考虑,需要在这个喷泉外围设立一圈正方形护栏,这个喷泉的任何一条水柱在湖面上的落点到护栏的距离不能小于1米,请通过计算说明公园至少需要准备多少米的护栏(不考虑接头等其他因素).2.(2022·北京四中模拟预测)跳台滑雪是冬季奥运会的比赛项目.如图,运动员通过助滑道后在点A处腾空,在空中沿抛物线飞行,直至落在着陆坡BC上的点P处.腾空点A到地面OB的距离OA为70 m,坡高OC为60 m,着陆坡BC的坡度(即tan α)为3:4,以O 为原点,OB所在直线为x轴,OA所在直线为y轴,建立如图所示的平面直角坐标系.已知这段抛物线经过点(4,75),(8,78).(1)求这段抛物线表示的二次函数表达式;(2)在空中飞行过程中,求运动员到坡面BC竖直方向上的最大距离;(3)落点P与坡顶C之间的距离为m.3.(2022·北京北京·二模)某公园内人工喷泉有一个竖直的喷水枪,喷出的水流路径可以看作是抛物线的一部分.记喷出的水流距喷水枪的水平距离为x m,距地面的竖直高度为y m,获得数据如下:小景根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小景的探究过程,请补充完整:(1)在平面直角坐标系xOy中,描出以表中各对对应值为坐标的点,并画出该函数的图象;(2)水流的最高点距喷水枪的水平距离为________m;(3)结合函数图象,解决问题:公园准备在距喷水枪水平距离为3.5m处加装一个石柱,使该喷水枪喷出的水流刚好落在石柱顶端,则石柱的高度约为_____m.4.(2022·北京市广渠门中学模拟预测)某景观公园计划在圆形水池内修建一个小型喷泉,水柱从池中心且垂直于水面的水枪喷出,水柱喷出后落于水面的形状是抛物线.现测量出如下数据,在距水枪水平距离为d米的地点,水柱距离水面的高度为h米.请解决以下问题:(1)请结合表中所给数据,直接写出水柱最高点距离水面的高度为______米.(2)在网格中建立适当的平面直角坐标系,描出表中已知各对对应值为坐标的点,并用平滑的曲线画出该函数的图象.(3)求表格中m的值.(4)以节水为原则,为体现公园喷泉景观的美观性,在不改变水柱形状的基础上,修建工人打算将水枪的高度上升0.4米.若圆形喷水池的半径为3米,提升水枪高度后水柱是否会喷到水池外面?请说明理由.(其中√10≈3.2)5.(2022·北京·二模)某社区文化广场修建了一个人工喷泉,人工喷泉有一个竖直的喷水枪AB,喷水口为A,喷水口A距地面2m,喷出水流的轨迹是抛物线.水流最高点P到喷水枪AB所在直线的距离为1m,水流落地点C距离喷水枪底部B的距离为3m.请解决以下问题:(1)如图,以B为原点,BC所在的直线为x轴,AB所在的直线为y轴,建立平面直角坐标系,则点A的坐标是______,点C的坐标是______,水流轨迹抛物线的对称轴是______.(2)求出水柱最高点P到地面的距离.(3)在线段BC上到喷水枪AB所在直线的距离为2m处放置一物体,为避免物体被水流淋到,物体的高度应小于多少米?请说明理由.6.(2022·北京门头沟·二模)如图,杂技团进行杂技表演,演员要从跷跷板右端A处弹跳后恰好落在人梯的顶端B处,其身体(看成一点)的路径是一条抛物线.现测量出如下的数据,设演员身体距起跳点A水平距离为d米时,距地面的高度为h米.请你解决以下问题:(1)在下边网格中建立适当平面直角坐标系,根据已知数据描点,并用平滑曲线连接;(2)结合表中所给的数据或所画的图象,直接写出演员身体距离地面的最大高度;(3)求起跳点A距离地面的高度;(4)在一次表演中,已知人梯到起跳点A的水平距离是3米,人梯的高度是3.40米.问此次表演是否成功?如果成功,说明理由;如果不成功,说明应怎样调节人梯到起跳点A的水平距离才能成功?7.(2022·北京顺义·二模)如图是某抛物线形拱桥的截面图.某数学小组对这座拱桥很感兴趣,他们利用测量工具测出水面AB的宽为8米.设AB上的点E到点A的距离AE=x米,点E到拱桥顶面的垂直距离EF=y米.通过取点、测量,数学小组的同学得到了x与y的几组值,如下表:(1)拱桥顶面离水面AB的最大高度为______米;(2)请你帮助该数学小组建立平面直角坐标系,描出上表中各对对应值为坐标的点,并用平滑的曲线连接;(3)测量后的某一天,由于降雨原因,水面比测量时上升1米.现有一游船(截面为矩形)宽度为4米,船顶到水面的高度为2米.要求游船从拱桥下面通过时,船顶到拱桥顶面的距离应大于0.5米.结合所画图象,请判断该游船是否能安全通过:______(填写“能”或“不能”).8.(2022·北京市十一学校模拟预测)某运动馆使用发球机进行辅助训练,假设发球机每次发球的运动路线是抛物线,且形状固定不变的,在球运行时,球与发球机的水平距离为x(米),与地面的高度为y(米),经多次测试后,得到如下数据:(1)在网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接;(2)球经发球机发出后,最高点离地面________米,并求出y与x的函数解析式;(3)当球拍触球时,球离地面的高度为5米.4①求此时发球机与球的水平距离;米,为确保球拍在原高度还能接到球,球拍的接球位置应前进多②现将发球机向下平移了1516少米?9.(2022·北京昌平·二模)如图,在一次学校组织的社会实践活动中,小龙看到农田上安装了很多灌溉喷枪,喷枪喷出的水流轨迹是抛物线,他发现这种喷枪射程是可调节的,且喷射的水流越高射程越远,于是他从该农田的技术部门得到了这种喷枪的一个数据表,水流的最高点与喷枪的水平距离记为x,水流的最高点到地面的距离记为y.y与x的几组对应值如下表:(1)该喷枪的出水口到地面的距离为________m;(2)在平面直角坐标系xOy中,描出表中各组数值所对应的点,并画出y与x的函数图像;(3)结合(2)中的图像,估算当水流的最高点与喷枪的水平距离为8m时,水流的最高点到地面的距离为________m(精确到1m).根据估算结果,计算此时水流的射程约为________m(精确到1m)10.(2022·北京海淀·二模)由于惯性的作用,行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”.某公司设计了一款新型汽车,现在对它的刹车性能(车速不超过150 km/h)进行测试,测得数据如下表:(1)以车速v为横坐标,刹车距离s为纵坐标,在坐标系中描出表中各组数值所对应的点,并用平滑曲线连接这些点;(2)由图表中的信息可知:①该型汽车车速越大,刹车距离越(填“大”或“小”);②若该型汽车某次测试的刹车距离为40 m,估计该车的速度约为km/h;(3)若该路段实际行车的最高限速为120 km/h,要求该型汽车的安全车距要大于最高限速时刹车距离的3倍,则安全车距应超过m.11.(2022·北京东城·一模)某公园内人工湖上有一座拱桥(横截面如图所示),跨度AB为4米.在距点A水平距离为d米的地点,拱桥距离水面的高度为h米.小红根据学习函数的经验,对d和h之间的关系进行了探究.下面是小红的探究过程,请补充完整:(1)经过测量,得出了d和h的几组对应值,如下表.在d和h这两个变量中,________是自变量,________是这个变量的函数;(2)在下面的平面直角坐标系xOy中,画出(1)中所确定的函数的图象;(3)结合表格数据和函数图象,解决问题:①桥墩露出水面的高度AE为_______米;②公园欲开设游船项目,现有长为3.5米,宽为1.5米,露出水面高度为2米的游船.为安全起见,公园要在水面上的C,D两处设置警戒线,并且CE=DF,要求游船能从C,D两点之间安全通过,则C处距桥墩的距离CE至少为_______米.(精确到0.1米)12.(2022·北京市十一学校二模)如图,排球运动场的场地长18m,球网高度2.24m,球网在场地中央,距离球场左、右边界均为9m.一名球员在场地左侧边界练习发球,排球的飞行路线可以看作是对称轴垂直于水平面的抛物线的一部分.在球运行时,将球与场地左边界的水平距离记为x(米),与地面的高度记为y(米),经多次测试后,得到如下数据:(1)在网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接;(2)击球点的高度为______米,排球飞行过程中可达到的最大高度为______米;(3)求出y与x的函数解析式;(4)判断排球能否过球网,并说明理由.13.(2022·北京大兴·一模)某景观公园内人工湖里有一组喷泉,水柱从垂直于湖面的喷水枪喷出,水柱落于湖面的路径形状是一条曲线.现有一个垂直于湖面的喷水枪,在距喷水枪水平距离为x米处,水柱距离湖面高度为y米.经测量得到如下数据:请解决以下问题:(1)如下图,在平面直角坐标系xOy描出了上表中y与x各对对应值为坐标的点.请根据描出的点,画出这条曲线;(2)结合所画曲线回答:①水柱的最高点距离湖面约______米;②水柱在湖面上的落点距喷水枪的水平距离约为______米;(3)若一条游船宽3米,顶棚到湖面的高度2米,为了保证游客有良好的观光体验,游船需从喷泉水柱下通过,如果不计其他因素,根据图象判断______(填“能”或“不能”)避免游船被喷泉喷到.14.(2022·北京丰台·一模)某公园在人工湖里安装一个喷泉,在湖心处竖直安装一根水管,在水管的顶端安一个喷水头,水柱从喷水头喷出到落于湖面的路径形状可以看作是抛物线的一部分.若记水柱上某一位置与水管的水平距离为d米,与湖面的垂直高度为h米.下面的表中记录了d与h的五组数据:根据上述信息,解决以下问题:(1)在下面网格(图1)中建立适当的平面直角坐标系,并根据表中所给数据画出表示h与d 函数关系的图象;(2)若水柱最高点距离湖面的高度为m米,则m=;(3)能从水柱下方通过.如图2所示,为避免游船被喷泉淋到,要求游船从水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于0.5米.已知游船顶棚宽度为3米,顶棚到湖面的高度为2米,那么公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到多少米才能符合要求?请通过计算说明理由(结果保留一位小数).15.(2022·北京一七一中一模)某运动馆使用发球机进行辅助训练,假设发球机每次发球的运动路线是抛物线,且形状固定不变的,在球运行时,球与发球机的水平距离为x(米),与地面的高度为y(米),经多次测试后,得到如下数据:(1)在网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接;(2)球经发球机发出后,最高点离地面__________米,并求出y与x的函数解析式;(3)当球拍触球时,球离地面的高度为5米.8①求此时发球机与球的水平距离;米,为确保球拍在原高度还能接到球,球拍的接球位置应后退多②现将发球机向上平移了58少米?16.(2022·北京市燕山教研中心一模)某景观公园内人工湖里有一组小型喷泉,水柱从垂直于湖面的水枪喷出,水柱落于湖面的路径形状是抛物线.现测量出如下数据,在湖面上距水枪水平距离为d米的位置,水柱距离湖面高度为h米.请解决以下问题:(1)以水枪与湖面交点为原点,原点与水柱落地处所在直线为x轴,水枪所在直线为y轴,在下边网格中建立平面直角坐标系,根据已知数据描点,并用平滑的曲线连接.(2)请结合表中所给数据或所画图象,写出水柱最高点的坐标.(3)湖面上距水枪水平距离为3.5米时,水柱距离湖面的高度m=____________米.(4)现公园想通过喷泉设立新的游玩项目,准备通过调节水枪高度,使得公园湖中的游船能从喷泉下方通过.游船左右两边缘最宽处有一个长方体形状的遮阳棚,若游船宽(指船的最大宽度)为2米,从水面到棚顶的高度为2.1米,要求是游船从喷泉水柱中间通过时,为避免游船被喷泉淋到,顶棚到水柱的垂直距离均不小于0.5米.请问公园该如何调节水枪高度以符合要求?请通过计算说明理由.17.(2022·北京·东直门中学模拟预测)某景观公园内人工湖里有一组喷泉,水柱从垂直于湖面的水枪喷出,水柱落于湖面的路径形状是抛物线.现测量出如下数据,在距水枪水平距离为d米的地点,水柱距离湖面高度为h米.请解决以下问题:(1)在下边网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接;(2)请结合表中所给数据或所画图象,估出喷泉的落水点距水枪的水平距离约为米(精确到0.1);(3)公园增设了新的游玩项目,购置了宽度4米,顶棚到水面高度为4.2米的平顶游船,游船从喷泉正下方通过,别有一番趣味,请通过计算说明游船是否有被喷泉淋到的危险.18.(2022·北京门头沟·一模)某景观公园内人工湖里有一组喷泉,水柱从垂直于湖面的水枪喷出,水柱落于湖面的路径形状是一条抛物线.现测量出如下数据,在距水枪水平距离为d米的地点,水柱距离湖面高度为ℎ米.(1)在下边网格中建立适当平面直角坐标系,根据已知数据描点,并用平滑曲线连接.(2)结合表中所给数据或所画的图象,直接写出水柱最高点距离湖面的高度;(3)求水柱在湖面上的落点距水枪的水平距离是多少?(4)现公园想通过喷泉设立一个新的游玩项目.准备通过调节水枪高度使得公园的平顶游船能从喷泉最高点的正下方通过(两次水柱喷出水嘴的初速度相同),如果游船宽度为3米,顶棚到水面的高度为2米,为了避免游船被淋到,顶棚到水柱的垂直距离不小于0.8米.问应如何调节水枪的高度才能符合要求?请通过计算说明理由.19.(2022·北京房山·一模)如图,一个单向隧道的断面,隧道顶是一条抛物线的一部分,经测量,隧道顶的跨度为4米,最高处到地面的距离为4米,两侧墙高均为3米,距左侧墙壁1米和3米时,隧道高度均为3.75米.设距左侧墙壁水平距离为x米的地点,隧道高度为y米.请解决以下问题:(1)在网格中建立适当的平面直角坐标系,根据题中数据描点,并用平滑的曲线连接;(2)请结合所画图象,写出抛物线的对称轴;(3)今有宽为2.4米的卡车在隧道中间行驶,如果卡车载物后的高度为3.2米,要求卡车从隧道中间通过时,为保证安全,要求卡车载物后最高点到隧道顶面对应的点的距离均不小于0.6米,结合所画图象,试判断该卡车能否通过隧道.20.(2022·北京通州·一模)如图1是某条公路的一个单向隧道的横断面.经测量,两侧墙AD和与路面AB垂直,隧道内侧宽AB=4米.为了确保隧道的安全通行,工程人员在路面AB上取点E,测量点E到墙面AD的距离和到隧道顶面的距离EF.设AE=x米,EF=y米.通过取点、测量,工程人员得到了x与y的几组值,如下表:(1)隧道顶面到路面AB的最大高度为______米;(2)请你帮助工程人员建立平面直角坐标系,描出上表中各对对应值为坐标的点,画出可以表示隧道顶面的图象.(3)今有宽为2.4米,高为3米的货车准备在隧道中间通过(如图2).根据隧道通行标准,其车厢最高点到隧道顶面的距离应大于0.5米.结合所画图象,请判断该货车是否安全通过:______(填写“是”或“否”).21.(2022·北京朝阳·一模)某公园在人工湖里建造一道喷泉拱门,工人在垂直于湖面的立柱上安装喷头,从喷头喷出的水柱的形状可以看作是抛物线的一部分.安装后,通过测量获得如下数据,喷头高出湖面3米,在距立柱水平距离为d米的地点,水柱距离湖面高度为h 米.请解决以下问题:(1)在网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接;(2)结合表中所给数据或所画图象,直接写出水柱最高点距离湖面的高度;(3)求h关于d的函数表达式;(4)公园希望游船能从喷泉拱门下穿过,已知游船的宽度约为2米,游船的平顶棚到湖面的高度约为1米,从安全的角度考虑,要求游船到立柱的水平距离不小于1米,顶棚到水柱的竖直距离也不小于1米,工人想只通过调整喷头距离湖面的高度(不考虑其他因素)就能满足上述要求,请通过计算说明应如何调整.22.(2022·北京西城·一模)要修建一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,记喷出的水与池中心的水平距离为x m,距地面的高度为y m.测量得到如下数值:小腾根据学习函数的经验,发现y是x的函数,并对y随x的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:(1)在平面直角坐标系xOy中,描出表中各组数值所对应的点(x,y),并画出函数的图象;(2)结合函数图象,出水口距地面的高度为_______m,水达到最高点时与池中心的水平距离约为_______m(结果保留小数点后两位);(3)为了使水柱落地点与池中心的距离不超过3.2m,如果只调整水管的高度,其他条件不变,结合函数图象,估计出水口至少需要_______(填“升高”或“降低”)_______m(结果保留小数点后两位).23.(2022·北京东城·二模)小强用竹篱笆围一个面积为9平方米的矩形小花园,他考虑至少4需要几米长的竹篱笆(不考虑接缝),根据学习函数的经验,他做了如下的探究,请你完善他的思考过程.(1)建立函数模型:设矩形小花园的一边长为x米,则矩形小花园的另一边长为__________米(用含x的代数式表示);若总篱笆长为y米,请写出总篱笆长y(米)关于边长x(米)的函数关系式__________;(2)列表:根据函数的表达式,得到了x与y的几组对应值,如下表:表中a=________,b=________;(3)描点、画出函数图象:,b)补充完整,并根据描出的如图,在平面直角坐标系xOy中,将表中未描出的点(2,a),(92点画出该函数的图象;。
中考数学总复习《二次函数的实际应用与几何问题》练习题及答案

中考数学总复习《二次函数的实际应用与几何问题》练习题及答案班级:___________姓名:___________考号:_____________一、单选题1.如图,⊙O的半径为2,C1是函数y=12x2的图象,C2是函数y=-12x2的图象,则图中阴影部分的面积为()A.πB.2πC.3πD.4π2.如图,已知抛物线y=mx2﹣6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l⊙x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2√3,则MN的长为()A.2√6B.4√2C.5D.63.如图,已知⊙ABC的顶点坐标分别为A(0,2)、B(1,0)、C(2,1),若二次函数y=x2+bx+1的图象与阴影部分(含边界)一定有公共点,则实数b的取值范围是()A.b≤﹣2B.b<﹣2C.b≥﹣2D.b>﹣24.如图,在⊙ABC中,⊙C=90°,AC=BC=3cm.动点P从点A出发,以√2cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC →CB方向运动到点B.设⊙APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是()A.B.C.D.5.长方形的周长为24cm,其中一边为x(其中x>0),面积为ycm2,则这样的长方形中y与x的关系可以写为()A.y=x2B.y=(12﹣x2)C.y=(12﹣x)•x D.y=2(12﹣x)6.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留2m宽的门。
已知计划中的建筑材料可建围墙(不包括门)的总长度为50m。
设饲养室长为x(m),占地面积为y(m²),则y关于x的函数表达式是()A.y=-x²+50x B.y= −12x²+24xC.y= −12x2+25x D.y= −12x2+26x7.如图,四边形ABCD中,AB=AD,CE⊙BD,CE= 12BD.若⊙ABD的周长为20cm,则⊙BCD的面积S(cm2)与AB的长x(cm)之间的函数关系式可以是()2−10x+100B.S=2x2−40x+200A.S=14xC.S=x2−20x+100D.S=x2+20x+1008.如图,四边形ABCD的两条对角线互相垂直,AC+BD=12,则四边形ABCD的面积最大值是()A.12B.18C.24D.369.如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若⊙ABC与⊙ABD的面积比为1:4,则k值为()A.1B.12C.43D.4510.半径是3的圆,如果半径增加2x,那么面积S和x之间的函数关系式是()A.S=2π(x+3)2B.S=9π+xC.S=4πx2+12x+9D.S=4πx2+12πx+9π11.设抛物线y=ax2+bx+c(ab≠0)的顶点为M ,与y轴交于N点,连接直线MN,直线MN与坐标轴所围三角形的面积记为S.下面哪个选项的抛物线满足S=1 () A.y=−3(x−1)2+1B.y=2(x−0.5)(x+1.5)C.y=13x 2−43x+1D.y=(a2+1)x2−4x+2(a为任意常数)12.已知坐标平面上有两个二次函数y=a(x+1)(x−7),y=b(x+1)(x−15)的图形,其中a、b为整数.判断将二次函数y=b(x+1)(x−15)的图形依下列哪一种方式平移后,会使得此两图形的对称轴重叠().A.向左平移4单位B.向右平移4单位C.向左平移8单位D.向右平移8单位二、填空题13.如图,点A(0,1),平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=14x2(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE⊙AC,交y2于点E,则DE =.14.用一根长为24cm的绳子围成一个矩形,则围成矩形的最大面积是cm2.15.如图,在平面直角坐标系中,菱形OABC的边长为2,⊙AOC=60°,点D为AB边上的一点,经过O,A,D三点的抛物线与x轴的正半轴交于点E,连结AE交BC于点F,当DF⊙AB时,CE的长为。
中考数学复习专题训练 二次函数的综合应用(含解析)
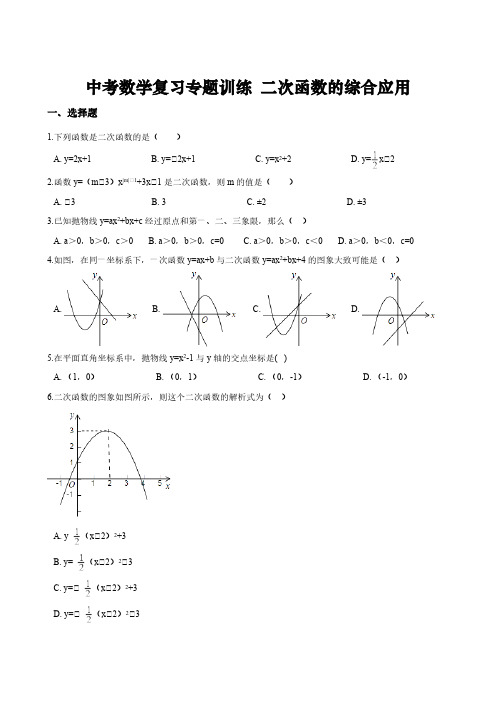
中考数学复习专题训练二次函数的综合应用一、选择题1.下列函数是二次函数的是( )A. y=2x+1B. y=﹣2x+1C. y=x2+2D. y=x﹣22.函数y=(m﹣3)x|m|﹣1+3x﹣1是二次函数,则m的值是( )A. ﹣3B. 3C. ±2D. ±33.已知抛物线y=ax2+bx+c经过原点和第一、二、三象限,那么()A. a>0,b>0,c>0B. a>0,b>0,c=0C. a>0,b>0,c<0D. a>0,b<0,c=04.如图,在同一坐标系下,一次函数y=ax+b与二次函数y=ax2+bx+4的图象大致可能是()A. B. C. D.5.在平面直角坐标系中,抛物线y=x2-1与y轴的交点坐标是( )A. (1,0)B. (0,1)C. (0,-1)D. (-1,0)6.二次函数的图象如图所示,则这个二次函数的解析式为()A. y (x﹣2)2+3B. y= (x﹣2)2﹣3C. y=﹣(x﹣2)2+3D. y=﹣(x﹣2)2﹣37.如图,已知二次函数y1= x2﹣x的图象与正比例函数y2= x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是()A. 0<x<2B. 0<x<3C. 2<x<3D. x<0或x>38. 设二次函数y1=a(x﹣x1)(x﹣x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1,0),若函数y=y1+y2的图象与x轴仅有一个交点,则()A. a(x1﹣x2)=dB. a(x2﹣x1)=dC. a(x1﹣x2)2=dD. a(x1+x2)2=d9.二次函数y=x2﹣8x+15的图象与x轴相交于M,N两点,点P在该函数的图象上运动,能使△PMN的面积等于的点P共有( )A. 1个B. 2个C. 3个D. 4个10.已知二次函数y=3x2+c与正比例函数y=4x的图象只有一个交点,则c的值为()A. B. C. 3 D. 411.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )A. -B. 或-C. 2或-D. 2或或-12.现有A、B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A 立方体朝上的数字为x小明掷B立方体朝上的数字为y来确定点P(x,y),那么它们各掷一次所确定的点P落在已知抛物线y=﹣x2+4x上的概率为()A. B. C. D.二、填空题13.若函数y=(m+2)是二次函数,则m=________14.抛物线y= (x﹣4)2+3与y轴交点的坐标为________.15.已知抛物线的顶点坐标为(1,﹣1),且经过原点(0,0),则该抛物线的解析式为________.16.二次函数y=x2+4x+5中,当x=________时,y有最小值.17.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表x﹣1013y﹣1353下列结论:①ac<0;②当x>1时,y的值随x值的增大而减小.③当x=2时,y=5;④3是方程ax2+(b﹣1)x+c=0的一个根;其中正确的有________.(填正确结论的序号)18.已知抛物线y=ax2+bx+c(a>0)的对称轴为直线,且经过点(-3,y1),(4,y2),试比较y1和y2的大小:y1________y2(填“>”,“<”或“=”).19.如图是二次函数和一次函数y2=kx+t的图象,当y1≥y2时,x的取值范围是________.20.如图,二次函数的图象经过点,对称轴为直线,下列5个结论:①;②;③;④;⑤,其中正确的结论为________ .(注:只填写正确结论的序号)三、解答题21.已知抛物线y= x2﹣2x的顶点是A,与x轴相交于点B、C两点(点B在点C的左侧).(1)求A、B、C的坐标;(2)直接写出当y<0时x的取值范围.22.在平面直角坐标系中,抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.(1)求点A的坐标;(2)当S△ABC=15时,求该抛物线的表达式;(3)在(2)的条件下,经过点C的直线与抛物线的另一个交点为D.该抛物线在直线上方的部分与线段CD组成一个新函数的图象。
2015二次函数中考真题卷高难度专项练习及答案

组卷二次函数难题1-30一、选择题(共12小题)1.(2011•包头)已知二次函数y=ax2+bx+c同时满足下列条件:对称轴是x=1;最值是15;二次函数的图象与x轴有两个交点,其横坐标的平方和为15﹣a,则b的值是()A.4或﹣30 B.﹣30 C.4D.6或﹣20 2.(2011•玉溪)如图,函数y=﹣x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=﹣1,在下列结论中,错误的是()A.顶点坐标为(﹣1,4)B.函数的解析式为y=﹣x2﹣2x+3C.当x<0时,y随x的增大而增大D.抛物线与x轴的另一个交点是(﹣3,0)3.(2010•钦州)已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①ac>0;②a﹣b+c<0;③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.其中错误的结论有()A.②③B.②④C.①③D.①④4.(2010•柳州)抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:x …﹣2 ﹣1 0 1 2 …y …0 4 6 6 4 …从上表可知,下列说法正确的个数是()①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);③抛物线的对称轴是x=1;④在对称轴左侧y随x增大而增大.A.1B.2C.3D.45.(2010•自贡)y=x2+(1﹣a)x+1是关于x的二次函数,当x的取值范围是1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是()A.a≤﹣5 B.a≥5 C.a=3 D.a≥36.(2010•十堰)方程x2+2x﹣1=0的根可看出是函数y=x+2与y=的图象交点的横坐标,用此方法可推断方程x3+x ﹣1=0的实根x所在范围为()A.﹣B.C.D.17.(2010•西宁)下列哪一个函数,其图象与x轴有两个交点()A.B.C.D.8.(2010•台州)如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x﹣m)2+n的顶点在线段AB上运动(抛物线随顶点一起平移),与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标最大值为()A.﹣3 B.1C.5D.89.(2010•东营)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx﹣ac 与反比例函数在同一坐标系内的图象大致为()A.B.C.D.10.(2010•广安)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②b<a+c;③2a+b=0;④a+b>m(am+b)(m≠1的实数).其中正确的结论有()A.1个B.2个C.3个D.4个11.(2010•丽水)如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD 的面积为y,则y与x之间的函数关系式是()A.y=B.y=C.y=D.y=12.(2011•兰州)如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是()A.B.C.D.二、填空题(共12小题)(除非特别说明,请填准确值)13.(2009•黄石)若抛物线y=ax2+bx+3与y=﹣x2+3x+2的两交点关于原点对称,则a、b 分别为_________、_________.14.(2010•成都)如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s 的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过_________秒,四边形APQC的面积最小.15.(2009•金华)如图,在第一象限内作射线OC,与x轴的夹角为30°,在射线OC上取一点A,过点A作AH⊥x 轴于点H.在抛物线y=x2(x>0)上取点P,在y轴上取点Q,使得以P,O,Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是_________.16.(2009•江津区)锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0),当x=_________,公共部分面积y最大,y最大值=_________.17.(2008•庆阳)兰州市“安居工程”新建成的一批楼房都是8层高,房子的价格y(元/平方米)随楼层数x(楼)的变化而变化(x=1,2,3,4,5,6,7,8);已知点(x,y)都在一个二次函数的图象上(如图所示),则6楼房子的价格为_________元/平方米.18.(2009•浙江)如图,抛物线y=ax2+bx+c与x轴的一个交点A在点(﹣2,0)和(﹣1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则:(1)abc_________0(填“>”或“<”);(2)a的取值范围是_________.19.(2009•包头)已知二次函数y=ax2+bx+c的图象与x轴交于点(﹣2,0)、(x1,0),且1<x1<2,与y轴的正半轴的交点在(0,2)的下方.下列结论:①4a﹣2b+c=0;②a<b<0;③2a+c>0;④2a﹣b+1>0.其中正确结论的个数是_________个.20.(2010•兰州)如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为_________米.21.(2008•黄石)若实数a,b满足a+b2=1,则2a2+7b2的最小值是_________.22.(2009•包头)将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是_________cm2.23.(2008•长春)将抛物线y=ax2+bx+c(a≠0)向下平移3个单位,再向左平移4个单位得到抛物线y=﹣2x2﹣4x+5,则原抛物线的顶点坐标是_________.24.(2009•兰州)二次函数y=x2的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2008在y轴的正半轴上,B1,B2,B3,…,B2008在二次函数y=x2第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2007B2008A2008都为等边三角形,请计算△A0B1A1的边长=_________;△A1B2A2的边长=_________;△A2007B2008A2008的边长=_________.三、解答题(共6小题)(选答题,不自动判卷)25.(2013•徐州)如图,二次函数y=x2+bx﹣的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.(1)请直接写出点D的坐标:_________;(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.26.(2013•雅安)如图,已知抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.(1)求该抛物线的解析式;(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;(3)如图(2),若E是线段AD上的一个动点(E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.①求S与m的函数关系式;②S是否存在最大值?若存在,求出最大值及此时点E的坐标;若不存在,请说明理由.27.(2013•烟台)如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,二次函数y=ax2+bx+c的图象经过点A,B,与x轴分别交于点E,F,且点E的坐标为(﹣,0),以0C为直径作半圆,圆心为D.(1)求二次函数的解析式;(2)求证:直线BE是⊙D的切线;(3)若直线BE与抛物线的对称轴交点为P,M是线段CB上的一个动点(点M与点B,C不重合),过点M作MN∥BE交x轴与点N,连结PM,PN,设CM的长为t,△PMN的面积为S,求S与t的函数关系式,并写出自变量t的取值范围.S是否存在着最大值?若存在,求出最大值;若不存在,请说明理由.28.(2013•新疆)如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).(1)求抛物线的解析式;(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由;(3)若点E是(1)中抛物线上的一个动点,且位于直线AC的下方,试求△ACE的最大面积及E点的坐标.29.(2013•宜宾)如图,抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B.(1)求抛物线的解析式;(2)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线BC对称的点的坐标;(3)在(2)的条件下,连接BD,点P为抛物线上一点,且∠DBP=45°,求点P的坐标.30.(2013•宜宾)某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.(1)求y与x的函数关系式并直接写出自变量x的取值范围;(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?【章节训练】第2章二次函数-3参考答案与试题解析一、选择题(共12小题)组卷二次函数难题61-90 难度 5 级1.(2011•包头)已知二次函数y=ax2+bx+c同时满足下列条件:对称轴是x=1;最值是15;二次函数的图象与x轴有两个交点,其横坐标的平方和为15﹣a,则b的值是()A.4或﹣30 B.﹣30 C.4D.6或﹣20抛物线与x轴的交点;二次函数的性质;二次函数的最值.专题:压轴题;函数思想.分析:由在x=1时取得最大值15,可设解析式为:y=a(x﹣1)2+15,只需求出a即可,又与x轴交点横坐标的平方和为15﹣a,可求出a,所以可求出解析式得到b的值.解答:解:解法一:∵x轴上点的纵坐标是0,∴由题可设抛物线与x轴的交点为(1﹣t,0),(1+t,0),其中t>0,∵两个交点的横坐标的平方和等于15﹣a即:(1﹣t)2+(1+t)2=15﹣a,可得t=,由顶点为(1,15),可设解析式为:y=a(x﹣1)2+15,将(1﹣,0)代入可得a=﹣2或a=15(不合题意,舍去)∴y=﹣2(x﹣1)2+15=﹣2x2+4x+13,∴b=4;解法二:∵对称轴是x=1,最值是15,∴设y=ax2+bx+c=a(x﹣1)2+15,∴y=ax2﹣2ax+15+a,设方程ax2﹣2ax+15+a=0的两个根是x1,x2,则x1+x2=﹣=2,x1•x2=,∵二次函数的图象与x轴有两个交点,其横坐标的平方和为15﹣a,(x1)2+(x2)2=(x1+x2)2﹣2x1x2=15﹣a,∴22﹣=15﹣a,a2﹣13a﹣30=0,a1=15(不合题意,舍去),a2=﹣2,∴y=﹣2(x﹣1)2+15=﹣2x2+4x+13;∴b=4.故选C.点评:本题考查了二次函数的最值及待定系数法求解析式,难度一般,关键算出a的值.组卷二次函数难题61-90 难度 4 级2.(2011•玉溪)如图,函数y=﹣x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=﹣1,在下列结论中,错误的是()A.顶点坐标为(﹣1,4)B.函数的解析式为y=﹣x2﹣2x+3C.当x<0时,y随x的增大而增大D.抛物线与x轴的另一个交点是(﹣3,0)考点:抛物线与x轴的交点;二次函数的性质.专题:计算题;压轴题.分析:由于y=﹣x2+bx+c的图象与x轴、y轴的交点分别为A(1,0),B(0,3),将交点代入解析式求出函数表达式,即可作出正确判断.解答:解:将A(1,0),B(0,3)分别代入解析式得,,解得,,则函数解析式为y=﹣x2﹣2x+3;将x=﹣1代入解析式可得其顶点坐标为(﹣1,4);当y=0时可得,﹣x2﹣2x+3=0;解得,x1=﹣3,x2=1.可见,抛物线与x轴的另一个交点是(﹣3,0);由图可知,当x<﹣1时,y随x的增大而增大.可见,C答案错误.故选C.点评:本题考查了抛物线与x轴的交点及二次函数的性质,利用待定系数法求出函数解析式是解题的关键,同时要注意数形结合.组卷二次函数难题61-90 难度 4 级3.(2010•钦州)已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①ac>0;②a﹣b+c<0;③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.其中错误的结论有()A.②③B.②④C.①③D.①④考点:二次函数图象与系数的关系.专题:压轴题.分析:①由二次函数y=ax2+bx+c(a≠0)的图象开口方向知道a<0,与y轴交点知道c>0,由此即可确定ac的符号;②由于当x=﹣1时,y=a﹣b+c,而根据图象知道当x=﹣1时y<0,由此即可判定a﹣b+c的符号;③根据图象知道当x<﹣1时抛物线在x轴的下方,由此即可判定此结论是否正确;④根据图象与x轴交点的情况即可判定是否正确.解答:解:①∵二次函数y=ax2+bx+c(a≠0)的图象开口向下,∴a<0,∵与y轴交点在x轴上方,∴c>0,∴ac<0;②∵当x=﹣1时,y=a﹣b+c,而根据图象知道当x=﹣1时y<0,∴a﹣b+c<0;③根据图象知道当x<﹣1时抛物线在x轴的下方,∴当x<﹣1,y<0;④从图象可知抛物线与x轴的交点的横坐标都大于﹣1,∴方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.故错误的有①③.故选C.点评:此题主要考查了利用图象求出a,b,c的范围,以及特殊值的代入能得到特殊的式子,如:当x=1时,y>0,a+b+c>0;x=﹣1时,y<0,a﹣b+c<0.组卷二次函数难题61-90 难度4.5级4.(2010•柳州)抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:x …﹣2 ﹣1 0 1 2 …y …0 4 6 6 4 …从上表可知,下列说法正确的个数是()①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);③抛物线的对称轴是x=1;④在对称轴左侧y随x增大而增大.A.1B.2C.3D.4考点:抛物线与x轴的交点.专题:压轴题;图表型.分析:从表中知道当x=﹣2时,y=0,当x=0时,y=6,由此可以得到抛物线与x轴的一个交点坐标和抛物线与y 轴的交点坐标,从表中还知道当x=﹣1和x=2时,y=4,由此可以得到抛物线的对称轴方程,同时也可以得到在对称轴左侧y随x增大而增大.解答:解:从表中知道:当x=﹣2时,y=0,当x=0时,y=6,∴抛物线与x轴的一个交点为(﹣2,0),抛物线与y轴的交点为(0,6),从表中还知道:当x=﹣1和x=2时,y=4,∴抛物线的对称轴方程为x=(﹣1+2)=0.5,同时也可以得到在对称轴左侧y随x增大而增大.所以①②④正确.故选C.点评:此题主要考查了抛物线与坐标轴的交点坐标与自变量和的函数值的对应关系,也考查了利用自变量和对应的函数值确定抛物线的对称轴和增减性.组卷二次函数难题61-90 难度4.5 级5.(2010•自贡)y=x2+(1﹣a)x+1是关于x的二次函数,当x的取值范围是1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是()A.a≤﹣5 B.a≥5 C.a=3 D.a≥3考点:二次函数的最值.专题:压轴题.分析:由于二次函数的顶点坐标不能确定,故应分对称轴不在[1,3]和对称轴在[1,3]内两种情况进行解答.解答:解:第一种情况:当二次函数的对称轴不在1≤x≤3内时,此时,对称轴一定在1≤x≤3的右边,函数方能在这个区域取得最大值,x=>3,即a>7,第二种情况:当对称轴在1≤x≤3内时,对称轴一定是在区间1≤x≤3的中点的右边,因为如果在中点的左边的话,就是在x=3的地方取得最大值,即:x=≥,即a≥5(此处若a取5的话,函数就在1和3的地方都取得最大值)综合上所述a≥5.故选B.点评:本题考查了二次函数的最值确定与自变量x的取值范围的关系,难度较大.组卷二次函数难题61-90 难度 4 级6.(2010•十堰)方程x2+2x﹣1=0的根可看出是函数y=x+2与y=的图象交点的横坐标,用此方法可推断方程x3+x ﹣1=0的实根x所在范围为()A.﹣B.C.D.1考点:二次函数的图象;反比例函数的图象.专题:压轴题.分析:首先根据题意推断方程x3+x﹣1=0的实根是函数y=x2+1与y=的图象交点的横坐标,再根据四个选项中x 的取值代入两函数解析式,找出抛物线的图象在反比例函数上方和反比例函数的图象在抛物线的上方两个点即可判定推断方程x3+x﹣1=0的实根x所在范围.解答:解:依题意得方程x3+x﹣1=0的实根是函数y=x2+1与y=的图象交点的横坐标,这两个函数的图象如图所示,∴它们的交点在第一象限,当x=1时,y=x2+1=2,y==1,此时抛物线的图象在反比例函数上方;当x=时,y=x2+1=1,y==2,此时反比例函数的图象在抛物线的上方;∴方程x3+x﹣1=0的实根x 所在范围为<x<1.故选C.点评:此题考查了学生从图象中读取信息的数形结合能力.解决此类识图题,同学们要注意分析其中的“关键点”,还要善于分析各图象的变化趋势.组卷二次函数难题61-90 难度 4 级7.(2010•西宁)下列哪一个函数,其图象与x轴有两个交点()A.B.C.D.考点:抛物线与x轴的交点.专题:计算题.分析:由题意得,令y=0,看是否解出x值,对A,B,C,D,一一验证从而得出答案.解答:解:A、令y=0得,,移项得,,方程无实根;B、令y=0得,,移项得,,方程无实根;C、令y=0得,,移项得,,方程无实根;D、令y=0得,,移项得,,方程有两个实根.故选D.点评:此题考查二次函数的性质及与一元二次方程根的关系.(利用开口方向和顶点坐标也可解答)组卷二次函数难题61-90 难度 4.5 级8.(2010•台州)如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x﹣m)2+n的顶点在线段AB上运动(抛物线随顶点一起平移),与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标最大值为()A.﹣3 B.1C.5D.8考点:二次函数综合题.专题:压轴题;动点型.分析:当C点横坐标最小时,抛物线顶点必为A(1,4),根据此时抛物线的对称轴,可判断出CD间的距离;当D点横坐标最大时,抛物线顶点为B(4,4),再根据此时抛物线的对称轴及CD的长,可判断出D点横坐标最大值.解答:解:当点C横坐标为﹣3时,抛物线顶点为A(1,4),对称轴为x=1,此时D点横坐标为5,则CD=8;当抛物线顶点为B(4,4)时,抛物线对称轴为x=4,且CD=8,故C(0,0),D(8,0);由于此时D点横坐标最大,故点D的横坐标最大值为8;故选D.点评:能够正确地判断出点C横坐标最小、点D横坐标最大时抛物线的顶点坐标是解答此题的关键.组卷二次函数难题61-90 难度 4.5级9.(2010•东营)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx﹣ac 与反比例函数在同一坐标系内的图象大致为()A.B.C.D.考点:二次函数的图象;一次函数的图象;反比例函数的图象.专题:压轴题.分析:先根据二次函数y=ax2+bx+c的图象判断出a、b、c、a﹣b+c的符号,再用排除法对四个答案进行逐一检验.解答:解:由二次函数y=ax2+bx+c的图象开口向上可知,a>0,因为图象与y轴的交点在y轴的负半轴,所以c<0,根据函数图象的对称轴x=﹣>0,可知b<0,∵a>0,b<0,c<0,ac<0,∴一次函数y=bx﹣ac的图象过一、二、四象限,故可排除A、C;由函数图象可知,当x=﹣1时,y>0,即y=a﹣b+c>0,∴反比例函数的图象在一、三象限,可排除D选项,故选B.点评:此题比较复杂,综合考查了二次函数、一次函数及反比例函数图象的特点,锻炼了学生数形结合解题的思想方法.组卷二次函数难题61-90 难度4.5 级10.(2010•广安)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②b<a+c;③2a+b=0;④a+b>m(am+b)(m≠1的实数).其中正确的结论有()A.1个B.2个C.3个D.4个考点:二次函数图象与系数的关系.专题:压轴题.分析:①由抛物线开口向下a<0,抛物线和y轴的正半轴相交,c>0,﹣=1>0,b>0,②令x=﹣1,时y<0,即a﹣b+c<0,③﹣=1,即2a+b=0,④把x=m代入函数解析式中表示出对应的函数值,把x=1代入解析式得到对应的解析式,根据图形可知x=1时函数值最大,所以x=1对应的函数值大于x=m对应的函数值,化简得到不等式成立,故④正确.解答:解:①根据图象,a<0,b>0,c>0,故①错误;②令x=﹣1,时y<0,即a﹣b+c<0,故②错误;③∵﹣=1,∴2a+b=0,故③正确;④x=m对应的函数值为y=am2+bm+c,x=1对应的函数值为y=a+b+c,又x=1时函数取得最大值,∴a+b+c>am2+bm+c,即a+b>am2+bm=m(am+b),故④正确.故选B.点评:主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.组卷二次函数难题61-90 难度 5 级11.(2010•丽水)如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD 的面积为y,则y与x之间的函数关系式是()A.y=B.y=C.y=D.y=考点:根据实际问题列二次函数关系式.专题:压轴题.分析:四边形ABCD图形不规则,根据已知条件,将△ABC绕A点逆时针旋转90°到△ADE的位置,求四边形ABCD的面积问题转化为求梯形ACDE的面积问题;根据全等三角形线段之间的关系,结合勾股定理,把梯形上底DE,下底AC,高DF分别用含x的式子表示,可表示四边形ABCD的面积.解答:解:作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,∵∠BAD=∠CAE=90°,即∠BAC+∠CAD=∠CAD+∠DAE∴∠BAC=∠DAE又∵AB=AD,∠ACB=∠E=90°∴△ABC≌△ADE(AAS)∴BC=DE,AC=AE,设BC=a,则DE=a,DF=AE=AC=4BC=4a,CF=AC﹣AF=AC﹣DE=3a,在Rt△CDF中,由勾股定理得,CF2+DF2=CD2,即(3a)2+(4a)2=x2,解得:a=,∴y=S四边形ABCD=S梯形ACDE =×(DE+AC)×DF=×(a+4a)×4a=10a2=x2.故选C.点评:本题运用了旋转法,将求不规则四边形面积问题转化为求梯形的面积,充分运用了全等三角形,勾股定理在解题中的作用.组卷二次函数难题61-90 难度4.5级12.(2011•兰州)如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是()A.B.C.D.考点:二次函数的应用;全等三角形的判定与性质;勾股定理.专题:压轴题.分析:根据条件可知△AEH≌△BFE≌△CGF≌△DHG,设AE为x,则AH=1﹣x,根据勾股定理EH2=AE2+AH2=x2+(1﹣x)2,进而可求出函数解析式,求出答案.解答:解:∵根据正方形的四边相等,四个角都是直角,且AE=BF=CG=DH,∴可证△AEH≌△BFE≌△CGF≌△DHG.设AE为x,则AH=1﹣x,根据勾股定理,得EH2=AE2+AH2=x2+(1﹣x)2即s=x2+(1﹣x)2.s=2x2﹣2x+1,∴所求函数是一个开口向上,对称轴是直线x=.∴自变量的取值范围是大于0小于1.故选B.点评:本题需根据自变量的取值范围,并且可以考虑求出函数的解析式来解决.二、填空题(共12小题)(除非特别说明,请填准确值)组卷二次函数难题61-90 难度5 级13.(2009•黄石)若抛物线y=ax2+bx+3与y=﹣x2+3x+2的两交点关于原点对称,则a、b 分别为、3.考点:二次函数图象与几何变换;关于原点对称的点的坐标.专题:压轴题.分析:有交点,可让两个抛物线组成方程组.解答:解:由题意可得,两个函数有交点,则y相等,则有ax2+bx+3=﹣x2+3x+2,得:(a+1)x2+(b﹣3)x+1=0.∵两交点关于原点对称,那么两个横坐标的值互为相反数;两个纵坐标的值也互为相反数.则两根之和为:﹣=0,两根之积为<0,解得b=3,a<﹣1.设两个交点坐标为(x1,y1),(x2,y2).这两个根都适合第二个函数解析式,那么y1+y2=﹣(x12+x 22)+3 (x 1+x2)+4=0,∵x1+x2=0,∴y1+y2=﹣(x1+x2)2+2x1x2+4=0,解得x1x 2=﹣2,代入两根之积得=﹣2,解得a=﹣,故a=﹣,b=3.另法:(若交点关于原点对称,那么在y=﹣x2+3x+2中,必定自身存在关于原点对称的两个点,设这两个点横坐标分别为k和﹣k,直接在y=﹣x2+3x+2代入k,然后相加两个式子﹣k2+3k+2=0与﹣k2﹣3k+2=0,可得出k为±,从而直接得到两个点,再待定系数法,将两点代入y=ax2+bx+3,直接可以得出a,b的值.点评:本题用到的知识点为:两个函数有交点,那么应让这两个函数图象组成方程组,而后根据根与系数的关系求解.组卷二次函数难题61-90 难度 4.5 级14.(2010•成都)如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s 的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B 同时出发,那么经过3秒,四边形APQC的面积最小.考点:二次函数的应用.专题:计算题.分析:根据等量关系“四边形APQC的面积=三角形ABC的面积﹣三角形PBQ的面积”列出函数关系求最小值.解答:解:设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Smm2,则有:S=S△ABC﹣S△PBQ==4t2﹣24t+144=4(t﹣3)2+108.∵4>0∴当t=3s时,S取得最小值.点评:本题考查了函数关系式的求法以及最值的求法.组卷二次函数难题61-90 难度 5 级15.(2009•金华)如图,在第一象限内作射线OC,与x轴的夹角为30°,在射线OC上取一点A,过点A作AH⊥x 轴于点H.在抛物线y=x2(x>0)上取点P,在y轴上取点Q,使得以P,O,Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是(3,),(,),(2,2),(,).考点:二次函数综合题.专题:压轴题.分析:在△AOH中,因为∠AOH=30°,所以A的纵坐标是横坐标的倍,若设A的坐标为(t,t),则Q、P 点坐标均可求出,然后根据全等三角形的判定,对应求解即可.解答:解:由题可得A的横坐标是纵坐标的倍,故设A的坐标为(t,t);则Q的坐标为(0,2t)或(0,t);可求得P点对应的坐标,解可得t的值有4个,为,,2,;故点A的坐标是(3,)、(,)、(2,2)、(,).点评:本题考查二次函数的有关性质,涉及图象与点的坐标的求法.组卷二次函数难题61-90 难度 4 级16.(2009•江津区)锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0),当x=3,公共部分面积y最大,y最大值=6.考点:二次函数的应用.专题:压轴题;动点型.分析:公共部分分为三种情形:在三角形内;刚好一边在BC上,此时为正方形;正方形有一部分在三角形外,此时为矩形.显然在内部时的面积比刚好在边上时要小,所以需比较后两种情形时的面积大小.为正方形时可求出面积的值,为矩形时需求面积表达式再求最大值.解答:解:公共部分分为三种情形:在三角形内;刚好一边在BC上,此时为正方形;正方形有一部分在三角形外,此时为矩形.显然在内部时的面积比刚好在边上时要小,所以需比较后两种情形时的面积大小.(1)求公共部分是正方形时的面积,作AD⊥BC于D点,交MN于E点,∵BC=6,S△ABC=12,∴AD=4,∵MN∥BC,∴即,解得x=2.4,此时面积y=2.42=5.76.(2)当公共部分是矩形时如图所示:设DE=a,根据得=,所以a=4﹣x,公共部分的面积y=x(4﹣x)=﹣x2+4x,∵﹣<0,∴y有最大值,当x=﹣=3时,y最大值==6.综上所述,当x=3时,公共部分的面积y最大,最大值为6.点评:此题需分类讨论,综合比较后得结论.组卷二次函数难题61-90 难度4 级17.(2008•庆阳)兰州市“安居工程”新建成的一批楼房都是8层高,房子的价格y(元/平方米)随楼层数x(楼)的变化而变化(x=1,2,3,4,5,6,7,8);已知点(x,y)都在一个二次函数的图象上(如图所示),则6楼房子的价格为2080元/平方米.考点:二次函数的应用.专题:操作型;函数思想.分析:从图象中找出顶点坐标、对称轴,利用对称性即可解答.解答:解:由图象可知(4,2200)是抛物线的顶点,∵x=4是对称轴,∴点(2,2080)关于直线x=4的对称点是(6,2080).∴6楼房子的价格为2080元.点评:要求熟悉二次函数的对称性,并准确的找到所求的点与那个已知点是对称点,此题的关键是能找到顶点是(4,2200).组卷二次函数难题61-90 难度 5 级18.(2009•浙江)如图,抛物线y=ax2+bx+c与x轴的一个交点A在点(﹣2,0)和(﹣1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则:(1)abc<0(填“>”或“<”);(2)a的取值范围是≤a≤.考点:二次函数综合题.专题:压轴题;动点型.分析:(1)观察图形发现,由抛物线的开口向下得到a<0,顶点坐标在第一象限得到b>0,抛物线与y轴的交点在y轴的上方推出c>0,由此即可判定abc的符号;(2)顶点C是矩形DEFG上(包括边界和内部)的一个动点,当顶点C与D点重合,可以知道顶点坐标为(1,3)且抛物线过(﹣1,0),则它与x轴的另一个交点为(3,0),由此可求出a;当顶点C与F点重合,顶点坐标为(3,2)且抛物线过(﹣2,0),则它与x轴的另一个交点为(8,0),由此也可求a,然后由此可判断a的取值范围.解答:解:(1)观察图形发现,抛物线的开口向下,∴a<0,∵顶点坐标在第一象限,∴﹣>0,∴b>0,而抛物线与y轴的交点在y轴的上方,∴c>0,∴abc <0;(2)顶点C是矩形DEFG上(包括边界和内部)的一个动点,当顶点C与D点重合,顶点坐标为(1,3),则抛物线解析式y=a(x﹣1)2+3,由,解得﹣≤a≤﹣;当顶点C与F点重合,顶点坐标为(3,2),则抛物线解析式y=a(x﹣3)2+2,由,解得﹣≤a≤﹣;∵顶点可以在矩形内部,∴﹣≤a≤﹣.点评:本题主要考查了抛物线的解析式y=ax2+bx+c中a、b、c对抛物线的影响,在对于抛物线的顶点在所给图形内进行运动的判定,充分利用了利用形数结合的方法,展开讨论,加以解决.组卷二次函数难题61-90 难度 5.5 级。
中考必练二次函数综合应用题(带答案)

中考必练二次函数综合应用题(带答案)二次函数应用题1.某果农在销瓯柑时,经市场调査发现:瓯柑若售价为5元/千克,日销售量为34千克,若售价每提高1元/千克,日销售量就减少2千克.现设瓯柑售价为x元/千克(x≥5且为正整数).(1)若某日销售量为24千克,求该日瓯柑的单价;(2)若政府将销售价格定为不超过15元/千克.设每日销售额为w元,求w关于x的函数表达式,并求w的最大值和最小值;(3)市政府每日给果农补贴a元后(a为正整数),果农发现最大日收入(日收入=销售额+政府补贴)还是不超过350元,并且只有5种不同的单价使日收入不少于340元,请直按写出所有符合题意的a的值.2.某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查,在一段时间内,销售单价是40元,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.x>),请你分别用x的代数式来表示销售(1)不妨设该种品牌玩具的销售单价为x元(40量y件和销售该品牌玩具获得利润ω元.(2)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?3.某地草莓已经到了收获季节,已知草莓的成本价为10元/千克,投入市场销售后,发现该草莓销售不会亏本,且每天销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.(1)求y与x的函数关系式,并写出x的取值范围.(2)若产量足够,当该品种的草莓定价为多少时,每天销售获得的利润最大?最大利润是多少?4.某服装厂批发应季T恤衫,其单价y(元)与一次批发数量x(件)(x为正整数....)之间的关系满足图中折线的函数关系.(1)求y 与x 的函数关系式;(2)若每件T 恤衫的成本价是60元,当100400x <≤时,求服装厂所获利润w (元)与x (件)之间的函数关系式,并求一次批发多少件时所获利润最大,最大利润是多少? 5.问题提出(1)如图①,在矩形ABCD 中,4AB =,6BC =,点F 是AB 的中点,点E 在BC 上,2BE EC =,连接FE 并延长交DC 的延长线于点G ,求CG 的长;问题解决(2)如图②,某生态农庄有一块形状为平行四边形ABCD 的土地,其中4km AB =,6km BC =,60B ∠=︒.管理者想规划出一个形状为EMP 的区域建成亲子采摘中心,根据设计要求,点E 是AD 的中点,点P 、M 分别在BC 、AB 上,PM AB ⊥.设BP 的长为(km)x ,EMP 的面积为y 2(km ).①求y 与x 之间的函数关系式;②为容纳更多的游客,要求EMP 的面积尽可能的大,请求出EMP 面积的最大值,并求出此时BP 的长.6.某公司分别在A ,B 两城生产同种产品,共100件.A 城生产产品的成本y (万元)与产品数量x (件)之间具有函数关系220100y x x =++,B 城生产产品的每件成本为60万元.(1)当A 城生产多少件产品时,A ,B 两城生产这批产品成本的和最小,最小值是多少?(2)从A 城把该产品运往C ,D 两地的费用分别为1万元/件和3万元/件;从B 城把该产品运往C ,D 两地的费用分别为1万元/件和2万元/件.C 地需要90件,D 地需要10件,在(1)的条件下,怎样调运可使A ,B 两城运费的和最小?7.安徽省在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y (万元)与年产量x (万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为W万元.(毛利润=销售额-生产费用)(1)请直接写出y与x以及z与x之间的函数关系式;(写出自变量x的取值范围)(2)求W与x之间的函数关系式;(写出自变量x的取值范围):并求年产量多少万件时,所获毛利润最大(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润8.某商场销售一款服装,经市场调查发现,每月的销售量y(件)与销售单价x(元/件)之间的函数关系如表格所示.同时,商场每出售1件服装,还要扣除各种费用150元.销售单价x(元/件)260240220销售量y(件)637791(1)求y与x之间的函数关系式;(2)当销售单价为多少元时,商场每月能够获得最大利润?最大利润是多少?(3)4月底,商场还有本款服装库存580件.若按(2)中获得最大月利润的方式进行销售,到12月底商场能否销售完这批服装?请说明理由.9.某商店购进一批成本为每件30元的商品,销售单价为40元时,每天销售量为80件,经调查发现,销售单价每上涨1元,每天销售量减少2件.设该商品每天的销售量y (件)与销售单价x(元).(1)求该商品每天的销售量y与销售单价x之间的函数关系式;(2)求当销售单价定为多少元时,才能使销售该商品每天获得的利润最大?最大利润是多少元?(3)若商店按单价不低于成本价且不高于50元销售,则销售单价定为多少,才能使销售该商品每天获得的利润最大?最大利润是多少?(4)若商店要使销售该商品每天获得的利润不低于800元,试利用函数图象确定销售单价最多为多少元?10.某商场将进价为30元的台灯以40元售出,平均每月能售出600个.调查发现,售价在40元至70元范围内,这种台灯的售价每上涨1元,其销售量就减少10个.为了实现每月获得最大的销售利润,这种台灯的售价应定为多少?最大利润为多少元?【参考答案】二次函数应用题1.(1)10元/千克(2)2244w x x =-+(515x ≤≤,且x 为正整数)最大值是242元,最小值为170元(3)106 107 108【解析】【分析】(1)根据售价每提高1元/千克,日销售量就减少2千克,且某日销售量为24千克,列方程可解答;(2)根据题意,利用销售额等于销售量乘以销售单价,列出函数关系式,根据二次函数的性质及配方法可求得答案;(3)由题意得:2340244350x x a ≤-++≤,由二次函数的对称性可知x 的取值为9,10,11,12,13,从而计算可得a 值.(1)解:根据题意得342524x --=(), 解得10x =.答:该日瓯柑的单价是10元/千克;(2)解:根据题意得222342524422212112121124]2[w x x x x x x x =--=-+=--+-=--+()()(),由题意得515x ≤≤,且x 为正整数,∵20-< ,∴11x =时,w 有最大值是242元,∵11-5=6,15-11=4,抛物线开口向下,∴5x =时,w 有最小值是22511242170--+=()元;则w 关于x 的函数表达式为:23425244[]w x x x x =--=-+()(515x ≤≤,且x 为正整数);(3)解:由题意得2340244350x x a ≤-++≤,∵只有5种不同的单价使日收入不少于340元,5为奇数,∴由二次函数的对称性可知,x 的取值为9,10,11,12,13当9x =或13时,2244234x x -+=;当10x =或12时,2244240x x -+=,当11x =时,2244242x x -+=.∵补贴后不超过350元,234+106=340,242+108=350,∴当106a =或107或108时符合题意.答:所有符合题意的a 值为:106,107,108.【点睛】本题主要考查二次函数的应用.得到每天可售出的千克数是解决本题的突破点;本题需注意x 的取值应为整数.解题的关键是熟练掌握待定系数法求函数解析式、根据销售额的相等关系列出函数解析式及二次函数的性质.2.(1)y=1000−10x ,w =−10x 2+1300x −30000;(2)商场销售该品牌玩具获得的最大利润为8640元.【解析】【分析】(1)由销售单价每涨1元,就会少售出10件玩具,得y =600−(x −40)×10=1000−10x ,利润w =(1000−10x )(x −30)=−10x 2+1300x −30000;(2)首先求出x 的取值范围,然后把w =−10x 2+1300x −30000转化成y =−10(x −65)2+12250,结合x 的取值范围,求出最大利润.(1)解:由题意得:销售量y=600−(x −40)×10=1000−10x ,销售玩具获得利润w =(1000−10x )(x −30)=−10x 2+1300x −30000;(2)解:根据题意得10001054045x x -≥⎧⎨≥⎩, 解之得:45≤x ≤46,w =−10x 2+1300x −30000=−10(x −65)2+12250,∵a =−10<0,对称轴是直线x =65,∴当45≤x ≤46时,w 随x 增大而增大.∴当x =46时,w 最大值=8640(元).答:商场销售该品牌玩具获得的最大利润为8640元.【点睛】本题主要考查了二次函数的应用的知识点,解答本题的关键熟练掌握二次函数的性质以及二次函数最大值的求解,此题难度不大.3.(1)10300y x =-+,1030x ≤≤;(2)当该品种的草莓定价为20元时,每天销售获得的利润最大,为1000元.【解析】【分析】(1)由图象可知每天销售量y (千克)与销售单价x (元/千克)之间是一次函数的关系,设y kx b =+,将(10,200),(15,150)代入解析式求解即可;(2)设利润为w 元,求得w 与x 的关系式,然后利用二次函数的性质求解即可.(1)解:由图象可知每天销售量y (千克)与销售单价x (元/千克)之间是一次函数的关系, 设y kx b =+,将(10,200),(15,150)代入解析式,可得1020015150k b k b +=⎧⎨+=⎩,解得10300k b =-⎧⎨=⎩ 即10300y x =-+,由题意可得,10x ≥,103000x -+≥,解得1030x ≤≤即10300y x =-+,1030x ≤≤,(2)解:设利润为w 元,则2(10)(10300)104003000w x x x x =--+=-+-,∵100-<,开口向下,对称轴为20x,1030x ≤≤ ∴当20x时,w 有最大值,为1000元,【点睛】此题考查了一次函数与二次函数的应用,解题的关键是掌握二次函数的性质,理解题意,找到题中的等量关系,正确列出函数关系式.4.(1)100(0100)1110(100400)1070(400)y x y y x x y x =≤≤⎧⎪⎪==-+<≤⎨⎪=>⎪⎩ (2)一次批发250件时,获得的最大利润为6250元【解析】【分析】(1)利用待定系数法结合图象求出解析式;(2)根据件数乘以单件的利润列得函数关系式,根据二次根式的性质解答.(1)解:当0≤x ≤100时,y =100;当100<x ≤400时,设y 与x 的函数关系式为y =kx +b ,则10010040070k b k b +=⎧⎨+=⎩,解得110110k b ⎧=-⎪⎨⎪=⎩, ∴111010y x =-+; 当x >400时,y =70; 综上,100(0100)1110(100400)1070(400)y x y y x x y x =≤≤⎧⎪⎪==-+<≤⎨⎪=>⎪⎩ (2)11106010w x x ⎛⎫=-+- ⎪⎝⎭=215010x x -+=()21250625010x --+ 当x =250时,w 有最大值,即一次批发250件时,最大利润为6250元.【点睛】此题考查了求函数解析式,二次函数的最值问题,正确理解函数图象求出函数解析式是解题的关键.5.(1)1CG =(2)①2311388y x x =-+;②EMP 面积的最大值为21213km 32,此时BP 的长为11km 2 【解析】【分析】(1)证明FEB GEC △∽△,依据相似三角形的性质进行求解即可;(2)①分点P 在点H 左侧和右侧两种情况讨论求解即可;②由二次函数的性质可得解.(1)在矩形ABCD 中,90ABC BCD BCG ∠=∠=∠=︒,∵FEB GEC ∠=∠,∴FEB GEC △∽△,∴BF BE CG CE =, ∵4AB =,6BC =,点F 是AB 的中点,2BE EC =,∴2BF =,4BE =,2CE =,∴242CG =, ∴1CG =.(2)①过点E 作EH //AB 交BC 于点H ,交射线MP 于点G ,易得四边形ABHE 是平行四边形, ∴4EH AB ==.∵EH //AB ,PM AB ⊥,∴60PHG B ∠=∠=︒,EG PM ⊥,即EG 是PME △边MP 上的高.∵点E 是AD 的中点,∴3BH AE ==.如图1-1,当点P 在点H 左侧时,3PH x =-,∴1322x HG PH -==, ∴311422x x EG EH HG --=+=+=. 如图1-2,当点P 在点H 右侧时,3PH x =-,∴1322x HG PH -==, ∴311422x x EG EH HG --=-=-=, ∴PME △的边MP 上的高112x EG -=. 在Rt MBP 中,3sin 60x MP BP =⋅︒=∴2113113113222x x y MP EG x -=⋅==. ②)222311333111213112y x x x x ⎫==-=-⎪⎝⎭ ∴当112x =时,1213y =最大 ∴EMP 21213,此时BP 的长为11km 2. 【点睛】 本题是一道相似形的综合题,考查了全等三角形的判定及性质,相似三角形的判定及性质,三角函数值的运用.在解答时添加辅助线构建全等形和相似形是关键.6.(1)A 城生产20件,最小值是5700万元;(2)从A 城把该产品运往C 地的产品数量为20件,则从A 城把该产品运往D 地的产品数量为0件;从B 城把该产品运往C 地的产品数量为70件,则从B 城把该产品运往D 地的产品数量为10件时,可使A ,B 两城运费的和最小.【解析】【分析】(1)设A ,B 两城生产这批产品的总成本的和为W (万元),则W 等于A 城生产产品的总成本加上B 城生产产品的总成本,由此可列出W 关于x 的二次函数,将其写成顶点式,根据二次函数的性质可得答案;(2)设从A 城把该产品运往C 地的产品数量为n 件,分别用含n 的式子表示出从A 城把该产品运往D 地的产品数量、从B 城把该产品运往C 地的产品数量及从B 城把该产品运往D 地的产品数量,再列不等式组求得n 的取值范围,然后用含n 的式子表示出A ,B 两城总运费之和P ,根据一次函数的性质可得答案.(1)解:设A ,B 两城生产这批产品的总成本的和为W (万元),则22010060(100)W x x x =+++-2406100x x =-+2(20)5700x =-+,∴当20x时,W 取得最小值,最小值为5700万元, ∴城生产20件,A ,B 两城生产这批产品成本的和最小,最小值是5700万元;(2) 设从A 城把该产品运往C 地的产品数量为n 件,则从A 城把该产品运往D 地的产品数量为(20)n -件,从B 城把该产品运往C 地的产品数量为(90)n -件,则从B 城把该产品运往D 地的产品数量为(1020)n -+件,运费的和为P (万元),由题意得:20010200n n -⎧⎨-+⎩, 解得1020n ,3(20)(90)2(1020)P n n n n =+-+-+-+60390220n n n n =+-+-+-2130n n =-+130n =-+,根据一次函数的性质可得:P 随n 增大而减小,∴当20n =时,P 取得最小值,最小值为110,∴从A 城把该产品运往C 地的产品数量为20件,则从A 城把该产品运往D 地的产品数量为0件;从B 城把该产品运往C 地的产品数量为70件,则从B 城把该产品运往D 地的产品数量为10件时,可使A 、B 两城运费的和最小.【点睛】本题考查了二次函数和一次函数在实际问题中的应用,解题的关键是理清题中的数量关系并熟练掌握一次函数和二次函数的性质.7.(1)21(0100)10y x x =≤≤,130(0100)10z x x =-+≤≤; (2)21(75)1125(0100)5W x x =--+≤≤,年产量75万件时,所获毛利润最大; (3)今年最多可获得1080万元的毛利润【解析】【分析】(1)利用待定系数法可求出y 与x 以及z 与x 之间的函数关系式;(2)根据(1)的表达式及毛利润=销售额-生产费用,可得出w 与x 之间的函数关系式; (3)首先求出x 的取值范围,再利用二次函数增减性得出答案即可.(1)解:设y 与x 之间的函数关系式为2y ax =,21000100a =⨯,得110a =, 即y 与x 之间的函数关系式为21(0100)10y x x =≤≤; 设z 与x 的函数关系式为z kx b =+,3010020b k b =⎧⎨+=⎩,得1,1030k b ⎧=-⎪⎨⎪=⎩ 即z 与x 的函数关系式为130(0100)10z x x =-+≤≤; (2)解:由题意可得, 2211130(75)112510105W zx y x x x x ⎛⎫=-=-+-=--+ ⎪⎝⎭, 即W 与x 之间的函数关系式为21(75)1125(0100)5W x x =--+≤≤, ∵21(75)11255W x =--+, ∴当75x =时,W 取得最大值,此时1125W =,即年产量75万件时,所获毛利润最大;(3)解:∵今年投入生产的费用不会超过360万元,∴360y ≤,令y =360,得2136010x =, 解得:x =±60(负值舍去),由图象可知,当0<y ≤360时,0<x ≤60, ∵21(75)11255W x =--+, ∴当60x =时,W 取得最大值,此时1080W =,即今年最多可获得1080万元的毛利润.【点睛】本题考查了二次函数的应用及一次函数的应用,解题的关键是利用待定系数法求函数解析式,注意培养自己利用数学知识解决实际问题的能力,难度一般.8.(1)724510y x =-+ (2)当售价为250元时,商场每月所获利润最大,最大利润为7000元(3)不能,理由见解析【解析】【分析】(1)根据表格数据判断为一次函数,设y kx b =+,用待定系数法求出解析时; (2)利润=单件利润⨯销售数量,化简为二次函数的顶点式,根据函数性质判断; (3)计算按(2)中获得最大月利润的方式进行销售时的数量,与580比较.(1)解:由表格可知,此函数为一次函数,故设y kx b =+;则有24077{22091k b k b +=+=, 解得710245k b ⎧=-⎪⎨⎪=⎩, 724510y x ∴=-+; (2)设销售利润为w 元,由题意得:7(150)(245)10w x x =--+ 273503675010x x =-+- 27(250)700010x =--+ 7010a =-<, w ∴有最大值,∴当250x =时,w 取最大值,7000w =最大,答:当售价为250元时,商场每月所获利润最大,最大利润为7000元;(3)当250x =时,70y =(件),70(124)560580⨯-=<,∴12月底不能销售完这批服装.【点睛】本题考查一次函数和二次函数的实际应用,解题关键用待定系数法求出一次函数解析式,注意二次函数最值讨论时,一般整理成顶点式,再通过看a 值确定最大值或最小值. 9.(1)y =-2x +160(2)定价为55元时,每天的销售利润有最大值为1250(3)销售单价定为50元时,该超市每天的利润最大,最大利润1200元(4)70元【解析】【分析】(1)根据题意可得y 与x 的关系式;(2)由题意得w =(x -30)(-2x +160)=-2(x -55)2+1250,即可求解;(3)根据二次函数的关系式和单价的取值范围可得最大利润;(4)由题意可得:(x -30)(-2x +160)=800,再根据函数的图象可得答案.(1)依题意得,y =80-2(x -40)=-2x +160;(2)由题意得:2(30)(2160)2(55)1250w x x x =--+=--+,20-<,∴当55x =时,w 有最大值,此时,1250w =,(3)20-<,故当55x <时,w 随x 的增大而增大,而3050x ≤≤,∴当50x =时,w 有最大值,此时,1200w =,故销售单价定为50元时,该超市每天的利润最大,最大利润1200元;(4)由题意得:(30)(2160)800x x --+≥,解得:4070x ≤≤,∴销售单价最多为70元.【点睛】此题主要考查了二次函数的应用,正确利用销量×每件的利润=w 得出函数关系式是解题关键.10.这种台灯的售价应定为65元时,最大利润为12250元.【解析】【分析】设这种台灯应涨价x 元,那么就少卖出10x 个,根据“总利润=每个台灯的利润×销售量”列出函数解析式,最后运用二次函数求最值即可.【详解】解:设售价为x 元,根据题意得:()()()2306001040106512250W x x x =---=--+⎡⎤⎣⎦,∴当x =65时,12250y =最大,答:这种台灯的售价应定为65元时,最大利润为12250元.【点睛】本题主要考查二次函数的应用,根据“总利润=每个台灯的利润×销售量”列出函数解析式是解答本题的关键.。
中考压轴题中的二次函数(三)带答案和详细解析30道解答题.docx

中考压轴题中的二次函数⑶一.解答题(共3()小题)1.(2015*雅安校级一模)己知:如图,抛物线y= - x'+bx+c与x轴,y轴分别相交于点A (-1, 0),B (0, 3)两点,其顶点为D.(1)求该抛物线的解析式;(2)若该抛物线与x轴的另一个交点为E.求四边形ABDE的面积;(3)AAOB与ABDE是否和似?如果相似,请予以证明;如果不相似,请说明理由.2.(2()15・余姚市模拟)如果抛物线©的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C]上,那么,我们称抛物线C|与C2关联.(1)已知抛物线①y=x2+2x - 1,判断下列抛物线②y=- X2+2X+1; ®y=x2+2x+l与已知抛物线①是否关联,并说明理由.(2)抛物线C】:y=| (x+1) —2,动点P的坐标为(t, 2),将抛物线绕点P (t, 2)旋转180。
得到抛物线C2,若抛物线Ci与C2关联,求抛物线C2的解析式.(3)A为抛物线Ci: y=g(x+l)2-2的顶点,B为与抛物线0关联的抛物线顶点,是否8存在以AB为斜边的等腰直角AABC,使其直角顶点C在y轴上?若存在,求出C点的坐标;若不存在,请说明理由.3.(2015*临淄区校级模拟)设抛物线y=ax2+bx・2与x轴交于两个不同的点A (・1, 0)、B (m, 0),与y轴交于点C.且ZACB=90度.(1)求m的值;(2)求抛物线的解析式,并验证点D (1, -3)是否在抛物线上:(3)已知过点A的直线y=x+l交抛物线于另一点E.问:在x轴上是否存在点P,使以点P、B、D为顶点的三角形与AAEB相似?若存在,请求出所有符合耍求的点P的坐标;若4.(2015*营口模拟)如图,二次函数尸-丄,+bx+c的图象经过点A (4, 0), B (・4,-4),且与y轴交于点C.(1)试求此二次函数的解析式;(2)试证明:ZBAO=ZCAO(H屮O是原点);(3)若P是线段AB±的一个动点(不与A、B重合),过P作y轴的平行线,分别交此二次函数图彖及x轴于Q、H两点,试问:是否存在这样的点P,便PH=2QH?若存在,请求出点P的坐标;若不存在,请说明理由.5.(2()15・杭州模拟)己知经过原点的抛物线y=・2X2+4X(如图所示)与x的另一交点为A 现将它向右平移m (m>0)位,所得抛物线与x轴交于C、D点,与原抛物线交于点P (1)求点P的坐标(可用含m式子表示);(2)设APCD的面积为s,求s关于m关系式;(3)过点P作x轴的平行线交原抛物线于点E,交平移后的抛物线于点F.请问是否存在m,使以点E、0、A、F为顶点的四边形为平行四边形?若存在,求出m的值;若不存在,6.(2()15・温州模拟)如图,已知抛物线y=ax2+bx+c经过A (0, 4), B (4, 0), C (・1, 0)三点.过点A作垂直于y轴的直线1.在抛物线上有一动点P,过点P作直线PQ平行于y轴交直线1于点Q ・连接AP.(1)求抛物线y=ax2+bx+c的解析式;(2)是否存在点P,使得以A、P、Q三点构成的三角形与AAOC相似?如果存在,请求出点P的坐标;若不存在,请说明理由;(3)当点P位于抛物线y=ax2+bx+c的对称轴的右狈9.若将AAPQ沿AP对折,点Q的对7.(2015*來凤县二模)如图1,在平面直角坐标系xOy屮,直线1: y=-|x+K与x轴、y轴分别交于点A和点B (0,・1),抛物线尸吉,+bx+c经过点B,且与直线1的另一个交点乙(2) 点D 在抛物线上,且点D 的横坐标为t (0<t<4).。
中考数学专题:二次函数综合题带答案

二次函数综合题类型一线段、周长、面积问题1.如图,直线y=-x+分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+经过A,B两点.(1)求A、B两点的坐标;(2)求抛物线的解析式;(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.2.如图1,在平面直角坐标系中,直线y=﹣5x+5与x轴,y轴分别交于A,C两点,抛物线y=x2+bx+c经过A,C两点,与x轴的另一交点为B.(1)求抛物线解析式及B点坐标;(2)若点M为x轴下方抛物线上一动点,连接MA、MB、BC,当点M运动到某一位置时四边形AMBC面积最大,求此时点M的坐标及四边形AMBC的面积;(3)如图2,若P点是半径为2的⊙B上一动点,连接PC、PA,当点P运动到某一位置时,PC+PA的值最小,请求出这个最小值,并说明理由.3.已知抛物线y=ax2+bx-4经过点A(2,0)、B(-4,0),与y轴交于点C.(1)求这条抛物线的解析式;(2)如图1,点P是第三象限内抛物线上的一个动点,当四边形ABPC的面积最大时,求点P的坐标;(3)如图2,线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,在直线DE上是否存在一点G,使△CMG的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.4.如图,抛物线y=ax2-3ax-4a的图象经过点C(0,2),交x轴于点A、B(点A在点B左侧),连接BC,直线y=kx+1(k>0)与y轴交于点D,与BC上方的抛物线交于点E,与BC交于点F.(1)求抛物线的解析式及点A、B的坐标;(2)是否存在最大值?若存在,请求出其最大值及此时点E的坐标;若不存在,请说明理由.类型二存在性问题5.如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,-2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=-1.(1)求抛物线的函数表达式;(2)若点P在第二象限内,且PE=OD,求△PBE的面积.(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM是以BD为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.6.如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0).抛物线y=-x2+bx+c经过A、B两点.(1)求抛物线的解析式;(2)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=DE.①求点P的坐标;②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.7.在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.(1)若抛物线经过点C、A、A′,求此抛物线的解析式;(2)在(1)的情况下,点M是第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;(3)在(1)的情况下,若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.7.如图,二次函数y═ax2+bx+4的图象与x轴交于点A(-1,0),B(4,0),与y轴交于点C,抛物线的顶点为D,其对称轴与线段BC交于点E,垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F,动直线l在抛物线的对称轴的右侧(不含对称轴)沿x轴正方向移动到B点.(1)求出二次函数y=ax2+bx+4和BC所在直线的表达式;(2)在动直线l移动的过程中,试求使四边形DEFP为平行四边形的点P的坐标;(3)连接CP,CD,在动直线l移动的过程中,抛物线上是否存在点P,使得以点P,C,F为顶点的三角形与△DCE相似?如果存在,求出点P的坐标;如果不存在,请说明理由.类型三角相等问题8.如图,已知点A(-1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.(1)求抛物线解析式;(2)在直线BC上方的抛物线上求一点P,使△PBC面积为1;(3)在x轴下方且在抛物线对称轴上,是否存在一点Q,使∠BQC=∠BAC?若存在,求出Q点坐标;若不存在,说明理由.9.如图,抛物线y=ax2+bx+c经过A(-1,0),B(4,0),C(0,3)三点,D为直线BC上方抛物线上一动点,DE⊥BC于E.(1)求抛物线的函数表达式;(2)如图1,求线段DE长度的最大值;(3)如图2,设AB的中点为F,连接CD,CF,是否存在点D,使得△CDE中有一个角与∠CFO相等?若存在,求点D的横坐标;若不存在,请说明理由.答案和解析1.【答案】解:(1)∵直线y=-x+分别与x轴、y轴交于B、C两点,∴B(3,0),C(0,),∴OB=3,OC=,∴tan∠BCO==,∴∠BCO=60°,∵∠ACB=90°,∴∠ACO=30°,∴=tan30°=,即=,解得AO=1,∴A(-1,0);(2)∵抛物线y=ax2+bx+经过A,B两点,∴,解得,∴抛物线解析式为y=-x2+x+;(3)∵MD∥y轴,MH⊥BC,∴∠MDH=∠BCO=60°,则∠DMH=30°,∴DH=DM,MH=DM,∴△DMH的周长=DM+DH+MH=DM+DM+DM=DM,∴当DM有最大值时,其周长有最大值,∵点M是直线BC上方抛物线上的一点,∴可设M(t,-t2+t+),则D(t,-t+),∴DM=-t2+t+-(-t+)=-t2+t=-(t-)2+,∴当t=时,DM有最大值,最大值为,此时DM=×=,即△DMH周长的最大值为.【解析】(1)由直线解析式可求得B、C坐标,在Rt△BOC中由三角函数定义可求得∠OCB=60°,则在Rt△AOC中可得∠ACO=30°,利用三角函数的定义可求得OA,则可求得A点坐标;(2)由A、B两点坐标,利用待定系数法可求得抛物线解析式;(3)由平行线的性质可知∠MDH=∠BCO=60°,在Rt△DMH中利用三角函数的定义可得到DH、MH与DM的关系,可设出M点的坐标,则可表示出DM的长,从而可表示出△DMH 的周长,利用二次函数的性质可求得其最大值.本题为二次函数的综合应用,涉及待定系数法、三角函数的定义、二次函数的性质、方程思想等知识.在(1)中注意函数图象与坐标的交点的求法,在(2)中注意待定系数法的应用,在(3)中找到DH、MH与DM的关系是解题的关键.本题考查知识点较多,综合性较强,难度适中.2.【答案】解:(1)直线y=-5x+5,x=0时,y=5∴C(0,5)y=-5x+5=0时,解得:x=1∴A(1,0)∵抛物线y=x2+bx+c经过A,C两点,∴解得:,∴抛物线解析式为y=x2-6x+5;当y=x2-6x+5=0时,解得:x1=1,x2=5∴B(5,0);(2)如图1,过点M作MH⊥x轴于点H,∵A(1,0),B(5,0),C(0,5)∴AB=5-1=4,OC=5∴S△ABC=AB•OC=×4×5=10∵点M为x轴下方抛物线上的点∴设M(m,m2-6m+5)(1<m<5)∴MH=|m2-6m+5|=-m2+6m-5∴S△ABM=AB•MH=×4(-m2+6m-5)=-2m2+12m-10=-2(m-3)2+8∴S四边形AMBC=S△ABC+S△ABM=10+[-2(m-3)2+8]=-2(m-3)2+18∴当m=3,即M(3,-4)时,四边形AMBC面积最大,最大面积等于18;(3)如图2,在x轴上取点D(4,0),连接PD、CD,∴BD=5-4=1∵AB=4,BP=2∴∵∠PBD=∠ABP∴△PBD∽△ABP∴∴PD=AP∴PC+PA=PC+PD∴当点C、P、D在同一直线上时,PC+PA=PC+PD=CD最小∵CD=∴PC+PA的最小值为.【解析】本题考查了二次函数的图象与性质,求二次函数最大值,解一次方程(组)和一元二次方程,相似三角形的判定和性质,两点之间线段最短.求线段与线段的几分之几的和的最小值,一般将“线段的几分之几”进行转换,变成能用“两点之间线段最短”的图形来求最小值.(1)由直线y=-5x+5求点A、C坐标,用待定系数法求抛物线解析式,进而求得点B坐标.(2)从x轴把四边形AMBC分成△ABC与△ABM;由点A、B、C坐标求△ABC面积;设点M横坐标为m,过点M作x轴的垂线段MH,则能用m表示MH的长,进而求△ABM的面积,得到△ABM面积与m的二次函数关系式,配方即求得m为何值时取得最大值,进而求点M坐标和四边形AMBC的面积最大值.(3)作点D坐标为(4,0),可得BD=1,进而有,再加上公共角∠PBD=∠ABP,根据两边对应成比例且夹角相等可证△PBD∽△ABP,得等于相似比,进而得PD=AP,所以当C、P、D在同一直线上时,PC+PA=PC+PD=CD最小.用两点间距离公式即求得CD的长.3.【答案】解:(1)∵抛物线y=ax+bx-4经过点A(2,0),B(-4,0),∴,解得,∴抛物线解析式为y=x2+x-4;(2)如图1,连接OP,设点P(x,),其中-4<x<0,四边形ABPC的面积为S,由题意得C(0,-4),∴S=S△AOC+S△OCP+S△OBP=+,=4-2x-x2-2x+8,=-x2-4x+12,=-(x+2)2+16.∵-1<0,开口向下,S有最大值,∴当x=-2时,四边形ABPC的面积最大,此时,y=-4,即P(-2,-4).因此当四边形ABPC的面积最大时,点P的坐标为(-2,-4).(3),∴顶点M(-1,-).如图2,连接AM交直线DE于点G,此时,△CMG的周长最小.设直线AM的解析式为y=kx+b,且过点A(2,0),M(-1,-),∴,∴直线AM的解析式为y=-3.在Rt△AOC中,=2.∵D为AC的中点,∴,∵△ADE∽△AOC,∴,∴,∴AE=5,∴OE=AE-AO=5-2=3,∴E(-3,0),由图可知D(1,-2)设直线DE的函数解析式为y=mx+n,∴,解得:,∴直线DE的解析式为y=--.∴,解得:,∴G().【解析】(1)把点A、B的坐标代入抛物线解析式,利用待定系数法求函二次数解析式解答;(2)连接OP,由S=S△AOC+S△OCP+S△OBP,可得出关于P点横坐标的表达式,然后利用二次函数的最值问题求出点P的坐标;(3)连接AM交直线DE于点G,此时,△CMG的周长最小.求出直线AM的解析式,再由△ADE∽△AOC,求出点E的坐标,求出直线DE的解析式,则由AM、DE两直线的交点可求得G点坐标.本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,待定系数法求一次函数解析式,三角形的面积,相似三角形的判定与性质,勾股定理,二次函数的最值问题.理解坐标与图形性质;会运用数形结合思想解决数学问题.4.【答案】解:(1)把C(0,2)代入y=ax2-3ax-4a得:-4a=2.解得a=-.则该抛物线解析式为y=-x2+x+2.由于y=-x2+x+2=-(x+1)(x-4).故A(-1,0),B(4,0);(2)存在,理由如下:由题意知,点E位于y轴右侧,作EG∥y轴,交BC于点G,∴CD∥EG,∴=.∵直线y=kx+1(k>0)与y轴交于点D,则D(0,1).∴CD=2-1=1.∴=EG.设BC所在直线的解析式为y=mx+n(m≠0).将B(4,0),C(0,2)代入,得.解得.∴直线BC的解析式是y=-x+2.设E(t,-t2+t+2),则G(t,-t+2),其中<t<4.∴EG=(-t2+t+2)-(-t+2)=-(t-2)2+2.∴=-(t-2)2+2.∵<0,∴当t=2时,存在最大值,最大值为2,此时点E的坐标是(2,3).【解析】(1)将点C的坐标代入函数解析式求得a值即可;将所求得的抛物线解析式转化为两点式,易得点A、B的坐标;(2)由题意知,点E位于y轴右侧,作EG∥y轴,交BC于点G,根据平行线截线段成比例将求的最大值转化为求的最大值,所以利用一次函数图象上点的坐标特征、二次函数图象上点的坐标特征,两点间的距离公式以及配方法解题即可.本题考查了二次函数综合题型,需要综合运用一次函数的性质,一次函数图象上点的坐标特征,二次函数图象上点的坐标特征,二次函数最值的求法,待定系数法确定函数关系式以及平行线截线段成比例等知识点,综合性较强,难度不是很大.5.【答案】解:(1)点A的坐标是(2,0),抛物线的对称轴是直线x=-1,则点B(-4,0),则函数的表达式为:y=a(x-2)(x+4)=a(x2+2x-8),即:-8a=-2,解得:a=,故抛物线的表达式为:y=x2+x-2;(2)将点B、C的坐标代入一次函数表达式:y=mx+n并解得:直线BC的表达式为:y=-x-2,则tan∠ABC=,则sin∠ABC=,设点D(x,0),则点P(x,x2+x-2),点E(x,x-2),∵PE=OD,∴PE=(x2+x-2+x+2)=(-x),解得:x=0或-5(舍去x=0),即点D(-5,0)S△PBE=×PE×BD=(x2+x-2+x+2)(-4-x)=;(3)由题意得:△BDM是以BD为腰的等腰三角形,只存在:BD=BM的情况,BD=1=BM,则y M=-BM sin∠ABC=-1×=-,则x M=,故点M(,-).【解析】(1)点A(2,0)、点B(-4,0),则函数的表达式为:y=a(x-2)(x+4)=a (x2+2x-8),即可求解;(2)PE=OD,则PE=(x2+x-2-x+2)=(-x),求得:点D(-5,0),利用S△PBE= PE×BD=(x2+x-2-x+2)(-4-x),即可求解;(3)BD=1=BM,则y M=-BM sin∠ABC=-1×=-,即可求解.主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.6.【答案】解:(1)∵B(1,0),∴OB=1,∵OC=2OB=2,∴C(-2,0),Rt△ABC中,tan∠ABC=2,∴,∴,∴AC=6,∴A(-2,6),把A(-2,6)和B(1,0)代入y=-x2+bx+c得:,解得:,∴抛物线的解析式为:y=-x2-3x+4;(2)①∵A(-2,6),B(1,0),易得AB的解析式为:y=-2x+2,设P(x,-x2-3x+4),则E(x,-2x+2),∵PE=DE,∴-x2-3x+4-(-2x+2)=(-2x+2),x=1(舍)或-1,∴P(-1,6);②∵M在直线PD上,且P(-1,6),设M(-1,y),∴AM2=(-1+2)2+(y-6)2=1+(y-6)2,BM2=(1+1)2+y2=4+y2,AB2=(1+2)2+62=45,分三种情况:i)当∠AMB=90°时,有AM2+BM2=AB2,∴1+(y-6)2+4+y2=45,解得:y=3,∴M(-1,3+)或(-1,3-);ii)当∠ABM=90°时,有AB2+BM2=AM2,∴45+4+y2=1+(y-6)2,y=-1,∴M(-1,-1),iii)当∠BAM=90°时,有AM2+AB2=BM2,∴1+(y-6)2+45=4+y2,y=,∴M(-1,);综上所述,点M的坐标为:∴M(-1,3+)或(-1,3-)或(-1,-1)或(-1,).【解析】(1)先根据已知求点A的坐标,利用待定系数法求二次函数的解析式;(2)①先得AB的解析式为:y=-2x+2,根据PD⊥x轴,设P(x,-x2-3x+4),则E(x,-2x+2),根据PE=DE,列方程可得P的坐标;②先设点M的坐标,根据两点距离公式可得AB,AM,BM的长,分三种情况:△ABM为直角三角形时,分别以A、B、M为直角顶点时,利用勾股定理列方程可得点M的坐标.此题是二次函数的综合题,考查了待定系数法求二次函数的解析式,铅直高度和勾股定理的运用,直角三角形的判定等知识.此题难度适中,解题的关键是注意方程思想与分类讨论思想的应用.7.【答案】解:(1)∵平行四边形ABOC绕点O顺时针旋转90°,得到平行四边形A′B′OC′,且点A的坐标是(0,4),∴点A′的坐标为:(4,0),∵点A、C的坐标分别是(0,4)、(-1,0),抛物线经过点C、A、A′,设抛物线的解析式为:y=ax2+bx+c,∴,解得:,∴此抛物线的解析式为:y=-x2+3x+4;(2)如图1,连接AA′,设直线AA′的解析式为:y=kx+m,∴,解得:,∴直线AA′的解析式为:y=-x+4,设点M的坐标为:(x,-x2+3x+4),则S△AMA′=×4×[-x2+3x+4-(-x+4)]=-2x2+8x=-2(x-2)2+8,∴当x=2时,△AMA′的面积最大,最大值S△AMA′=8,∴M的坐标为:(2,6);(3)设点P的坐标为(x,-x2+3x+4),当P,N,B,Q构成平行四边形时,∵平行四边形ABOC中,点A、C的坐标分别是(0,4)、(-1,0),∴点B的坐标为(1,4),∵点Q坐标为(1,0),P为抛物线上一动点,N为x轴上的一动点,①当BQ为边时,PN∥BQ,PN=BQ,∵BQ=4,∴-x2+3x+4=±4,当-x2+3x+4=4时,解得:x1=0,x2=3,∴P1(0,4),P2(3,4);当-x2+3x+4=-4时,解得:x3=,x4=,∴P3(,-4),P4(,-4);②当BQ为对角线时,BP∥QN,BP=QN,此时P与P1,P2重合;综上可得:点P的坐标为:P1(0,4),P2(3,4),P3(,-4),P4(,-4);如图2,当这个平行四边形为矩形时,点N的坐标为:(0,0)或(3,0).【解析】此题属于二次函数的综合题,考查了待定系数法求函数解析式的知识、平行四边形的性质以及三角形面积问题.掌握分类讨论思想的应用是解此题的关键.(1)由平行四边形ABOC绕点O顺时针旋转90°,得到平行四边形A′B′OC′,且点A 的坐标是(0,4),可求得点A′的坐标,然后利用待定系数法即可求得经过点C、A、A′的抛物线的解析式;(2)首先连接AA′,设直线AA′的解析式为:y=kx+m,利用待定系数法即可求得直线AA′的解析式,再设点M的坐标为:(x,-x2+3x+4),继而可得△AMA′的面积,继而求得答案;(3)分别从BQ为边与BQ为对角线去分析求解,即可求得答案.结合平行四边形的情况分析即可得到矩形的情况.8.【答案】解:(1)将点A(-1,0),B(4,0),代入y═ax2+bx+4,得:,解得:,∴二次函数的表达式为:y=-x2+3x+4,当x=0时,y=4,∴C(0,4),设BC所在直线的表达式为:y=mx+n,将C(0,4)、B(4,0)代入y=mx+n,得:,解得:,∴BC所在直线的表达式为:y=-x+4;(2)∵DE⊥x轴,PF⊥x轴,∴DE∥PF,只要DE=PF,四边形DEFP即为平行四边形,∵y=-x2+3x+4=-(x-)2+,∴点D的坐标为:(,),将x=代入y=-x+4,即y=-+4=,∴点E的坐标为:(,),∴DE=-=,设点P的横坐标为t,则P的坐标为:(t,-t2+3t+4),F的坐标为:(t,-t+4),∴PF=-t2+3t+4-(-t+4)=-t2+4t,由DE=PF得:-t2+4t=,解得:t1=(不合题意舍去),t2=,当t=时,-t2+3t+4=-()2+3×+4=,∴点P的坐标为(,);(3)存在,理由如下:如图2所示:由(2)得:PF∥DE,∴∠CED=∠CFP,又∵∠PCF与∠DCE有共同的顶点C,且∠PCF在∠DCE的内部,∴∠PCF≠∠DCE,∴只有∠PCF=∠CDE时,△PCF∽△CDE,∴=,∵C(0,4)、E(,),∴CE==,由(2)得:DE=,PF=-t2+4t,F的坐标为:(t,-t+4),∴CF==t,∴=,∵t≠0,∴(-t+4)=3,解得:t=,当t=时,-t2+3t+4=-()2+3×+4=,∴点P的坐标为:(,).【解析】(1)由题意得出方程组,求出二次函数的解析式为y=-x2+3x+4,则C(0,4),由待定系数法求出BC所在直线的表达式即可(2)证DE∥PF,只要DE=PF,四边形DEFP即为平行四边形,由二次函数解析式求出点D的坐标,由直线BC的解析式求出点E的坐标,则DE=,设点P的横坐标为t,则P的坐标为:(t,-t2+3t+4),F的坐标为:(t,-t+4),由DE=PF得出方程,解方程进而得出答案;(3)由平行线的性质得出∠CED=∠CFP,当∠PCF=∠CDE时,△PCF∽△CDE,则=,得出方程,解方程即可.本题是二次函数综合题目,考查了待定系数法求二次函数和一次函数的解析式、二次函数的性质、平行四边形的判定与性质、平行线的性质、相似三角形的判定与性质、勾股定理等知识;本题综合性强,熟练掌握待定系数法求函数解析式,熟记二次函数的性质是解题的关键.9.【答案】解:(1)设抛物线的解析式为y=a(x+1)(x-3),将C(0,1)代入得-3a=1,解得:a=-,∴抛物线的解析式为y=-x2+x+1.(2)过点P作PD⊥x,交BC与点D.设直线BC的解析式为y=kx+b,则,解得:k=-,∴直线BC的解析式为y=-x+1.设点P(x,-x2+x+1),则D(x,-x+1)∴PD=(-x2+x+1)-(-x+1)=-x2+x,∴S△PBC=OB•DP=×3×(-x2+x)=-x2+x.又∵S△PBC=1,∴-x2+x=1,整理得:x2-3x+2=0,解得:x=1或x=2,∴点P的坐标为(1,)或(2,1).(3)存在.如图:∵A(-1,0),C(0,1),∴OC=OA=1∴∠BAC=45°.∵∠BQC=∠BAC=45°,∴点Q为△ABC外接圆与抛物线对称轴在x轴下方的交点.设△ABC外接圆圆心为M,则∠CMB=90°.设⊙M的半径为x,则Rt△CMB中,由勾股定理可知CM2+BM2=BC2,即2x2=10,解得:x=(负值已舍去),∵AC的垂直平分线的为直线y=-x,AB的垂直平分线为直线x=1,∴点M为直线y=-x与x=1的交点,即M(1,-1),∴Q的坐标为(1,-1-).【解析】本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、三角形的外心的性质,求得点M的坐标以及⊙M的半径的长度是解题的关键.(1)设抛物线的解析式为y=a(x+1)(x-3),将C(0,1)代入求得a的值即可;(2)过点P作PD⊥x,交BC与点D,先求得直线BC的解析式为y=-x+1,设点P(x,-x2+x+1),则D(x,-x+1),然后可得到PD与x之间的关系式,接下来,依据△PBC的面积为1列方程求解即可;(3)首先依据点A和点C的坐标可得到∠BQC=∠BAC=45°,设△ABC外接圆圆心为M,则∠CMB=90°,设⊙M的半径为x,则Rt△CMB中,依据勾股定理可求得⊙M的半径,然后依据外心的性质可得到点M为直线y=-x与x=1的交点,从而可求得点M的坐标,然后由点M的坐标以及⊙M的半径可得到点Q的坐标.10.【答案】解:(1)由题意,得,解得,抛物线的函数表达式为y=-x2+x+3;(2)设直线BC的解析是为y=kx+b,,解得∴y=-x+3,设D(a,-a2+a+3),(0<a<4),过点D作DM⊥x轴交BC于M点,如图1,M(a,-a+3),DM=(-a2+a+3)-(-a+3)=-a2+3a,∵∠DME=∠OCB,∠DEM=∠BOC,∴△DEM∽△BOC,∴=,∵OB=4,OC=3,∴BC=5,∴DE=DM∴DE=-a2+a=-((a-2)2+,当a=2时,DE取最大值,最大值是,(3)假设存在这样的点D,△CDE使得中有一个角与∠CFO相等,∵点F为AB的中点,∴OF=,tan∠CFO==2,过点B作BG⊥BC,交CD的延长线于G点,过点G作GH⊥x轴,垂足为H,如图2,①若∠DCE=∠CFO,∴tan∠DCE==2,∴BG=10,∵△GBH∽BCO,∴==,∴GH=8,BH=6,∴G(10,8),设直线CG的解析式为y=kx+b,∴,解得∴直线CG的解析式为y=x+3,∴,解得x=,或x=0(舍).②若∠CDE=∠CFO,同理可得BG=,GH=2,BH=,∴G(,2),同理可得,直线CG的解析是为y=-x+3,∴,解得x=或x=0(舍),综上所述,存在点D,使得△CDE中有一个角与∠CFO相等,点D的横坐标为或.【解析】(1)根据待定系数法,可得函数解析式;(2)根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得DM,根据相似三角形的判定与性质,可得DE的长,根据二次函数的性质,可得答案;(3)根据正切函数,可得∠CFO,根据相似三角形的性质,可得GH,BH,根据待定系数法,可得CG的解析式,根据解方程组,可得答案.本题考查了二次函数综合题,解(1)的关键是待定系数法,解(2)的关键是利用相似三角形的性质得出DE的长,又利用了二次函数的性质;解(3)的关键是利用相似三角形的性质得出G点的坐标,由;利用了待定系数法求函数解析式,解方程组的横坐标.。
中考数学总复习《二次函数与一次函数的综合应用》练习题附带答案
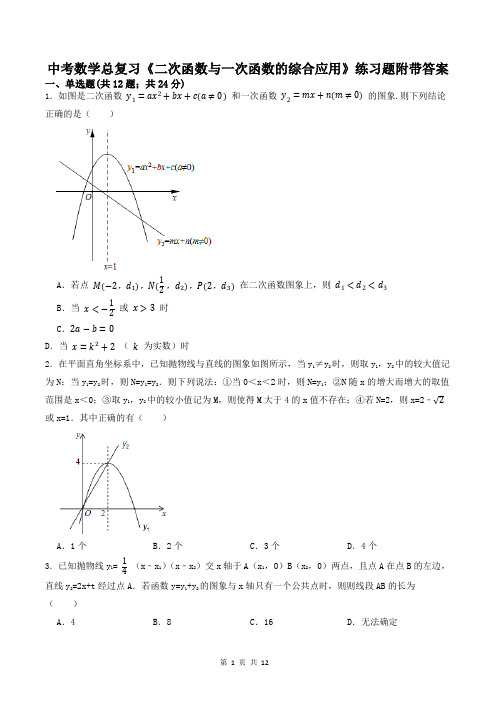
中考数学总复习《二次函数与一次函数的综合应用》练习题附带答案一、单选题(共12题;共24分)1.如图是二次函数 y 1=ax 2+bx +c(a ≠0) 和一次函数 y 2=mx +n(m ≠0) 的图象.则下列结论正确的是( )A .若点 M(−2,d 1),N(12,d 2),P(2,d 3) 在二次函数图象上,则 d 1<d 2<d 3B .当 x <−12或 x >3 时C .2a −b =0D .当 x =k 2+2 ( k 为实数)时2.在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y 1≠y 2时,则取y 1,y 2中的较大值记为N ;当y 1=y 2时,则N=y 1=y 2.则下列说法:①当0<x <2时,则N=y 1;②N 随x 的增大而增大的取值范围是x <0;③取y 1,y 2中的较小值记为M ,则使得M 大于4的x 值不存在;④若N=2,则x=2﹣√2或x=1.其中正确的有( )A .1个B .2个C .3个D .4个3.已知抛物线y 1= 14(x ﹣x 1)(x ﹣x 2)交x 轴于A (x 1,0)B (x 2,0)两点,且点A 在点B 的左边,直线y 2=2x+t 经过点A .若函数y=y 1+y 2的图象与x 轴只有一个公共点时,则则线段AB 的长为( ) A .4B .8C .16D .无法确定4.如图,抛物线y =ax 2+bx +c 和直线y =kx +b 都经过点(﹣1,0),抛物线的对称轴为x =1,那么下列说法正确的是( )A .ac >0B .b 2﹣4ac <0C .k =2a +cD .x =4是ax 2+(b ﹣k )x +c <b 的解5.直线y=ax ﹣6与抛物线y=x 2﹣4x+3只有一个交点,则a 的值为( )A .a=2B .a=10C .a=2或a=﹣10D .a=2或a=106.如图是函数y =x 2+bx+c 与y =x 的图象,有下列结论:(1)b 2﹣4c >0;(2)b+c+1=0;(3)方程x 2+(b ﹣1)x+c =0的解为x 1=1,x 2=3;(4)当1<x <3时,则x 2+(b ﹣1)x+c <0.其中正确结论的个数为( ) A .1B .2C .3D .47.在直角坐标系中,直线y=x+2和抛物线y=x 2-x+1的若干组函数值如下表所示:x … 1 1.5 2 2.5 3 … y=x+2 … 3 3.5 4 4.5 6 … y=x 2-x+1…11.7534.7513…A .1<x<1.5B .1.5<Xx2C .2<x<2.5D .2.5<x<38.割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法:随着圆内接正多边形边数的增加,它的周长和面积越来越接近圆周长和圆面积,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽就是大胆地应用了以直代曲、无限趋近的思想方法求出了圆周率.请你也用这个方法求出二次函数 y=14(x −4)2的图象与两坐标轴所围成的图形最接近的面积是( )A .5B .225C .4D .17﹣4π9.如图,“心”形是由抛物线 y =−x 2+6和它绕着原点O ,顺时针旋转60°的图形经过取舍而成的,其中顶点C 的对应点为D ,点A ,B 是两条抛物线的两个交点,直线AB 为“心”形对称轴,点E ,F ,G 是抛物线与坐标轴的交点,则AB=( )A .6√3B .8C .10D .10√310.已知一次函数y=ax+c 与二次函数y=ax 2+bx+c ,它们在同一坐标系内的大致图象是( )A .B .C .D .11.如图,抛物线y =﹣x 2+4x ﹣3与x 轴交于点A 、B ,把抛物线在x 轴及其上方的部分记作C 1,将C 1向右平移得到C 2,C 2与x 轴交于B 、D 两点.若直线y =kx ﹣k 与C 1、C 2共有3个不同的交点,则k 的最大值是( )A .12B .2 √5 ﹣6C .6+4 √2D .6﹣4 √212.在平面直角坐标系中,已知点 A(−1,4) , B(2,1) 直线 AB 与 x 轴和 y 轴分别交于点 M ,N 若抛物线 y =x 2−bx +2 与直线 AB 有两个不同的交点,其中一个交点在线段 AN 上(包含 A , N 两个端点),另一个交点在线段 BM 上(包含 B , M 两个端点),则 b 的取值范围是( )A.1≤b≤52B.b≤1或b≥52C.52≤b≤113D.b≤52或b≥113二、填空题(共6题;共6分)13.如图,抛物线y=ax2﹣2与y轴交于点A,过点A与x轴平行的直线交抛物线y=﹣12 x2于点B,C,则S△BOC= .14.在平面直角坐标系xOy中,函数y1=x(x<m)的图象与函数y2=x2(x≥m)的图象组成图形G.对于任意实数n,过点P(0,n)且与x轴平行的直线总与图形G有公共点,写出一个满足条件的实数m的值为(写出一个即可).15.如图,抛物线y=ax2+bx+1的顶点在直线y=kx+1上,对称轴为直线x=1,以下四个结论:①ab<0;②b<13;③a=−k;④当0<x<1其中正确的是.(填序号)16.如图,抛物线y=x2﹣2x+k与x轴交于A、B两点,与y轴交于点C(0,﹣3).若抛物线y=x2﹣2x+k上有点Q,使△BCQ是以BC为直角边的直角三角形,则点Q的坐标为.17.已知抛物线p :y=ax 2+bx+c 的顶点为C ,与x 轴相交于A 、B 两点(点A 在点B 左侧),点C 关于x轴的对称点为C ′,我们称以A 为顶点且过点C ′,对称轴与y 轴平行的抛物线为抛物线p 的“梦之星”抛物线,直线AC ′为抛物线p 的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x 2+2x+1和y=2x+2,则这条抛物线的解析式为 .18.如图,抛物线y=13x 2﹣4√33x+3与x 轴交于A ,B 两点,与y 轴交于点C ,点M 的坐标为(2√3,1).以M 为圆心,2为半径作⊙M .则下列说法正确的是 (填序号). ①tan ∠OAC=√3; ②直线AC 是⊙M 的切线; ③⊙M 过抛物线的顶点; ④点C 到⊙M 的最远距离为6;⑤连接MC ,MA ,则△AOC 与△AMC 关于直线AC 对称.三、综合题(共6题;共73分)19.在平面直角坐标系中,已知A ,B 是抛物线y=ax 2(a >0)上两个不同的点,其中A 在第二象限,B 在第一象限.(1)如图1所示,当直线AB 与x 轴平行,∠AOB=90°,且AB=2时,则求此抛物线的解析式和A ,B 两点的横坐标的乘积;(2)如图2所示,在(1)所求得的抛物线上,当直线AB 与x 轴不平行,∠AOB 仍为90°时,则求证:A、B两点横坐标的乘积是一个定值;(3)在(2)的条件下,如果直线AB与x轴、y轴分别交于点P、D,且点B的横坐标为1 2.那么在x轴上是否存在一点Q,使△QDP为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.20.某公司成功开发出一种产品,正式投产后,生产成本为5元/件.公司按订单生产该产品(销售量=产量),年销售量y(万件)与售价x(元/件)之间满足如图1所示的函数关系,公司规定产品售价不超过15元/件,受产能限制,年销售量不超过30万件;为了提高该产品竞争力,投入研发费用P 万元(P万元计入成本),P与x之间的函数关系式如图2所示,当10≤x≤15时可看成抛物线P= 14x2−4x+m.(1)求y与x之间的函数关系式.(2)求这种产品年利润W(万元)与售价x(元/件)满足的函数关系式.(3)当售价x为多少元时,则年利润W最大,并求出这个最大值.21.如图,抛物线y=ax2+32 x+c(a≠0)与x轴交于点A,B两点,其中A(-1,0),与y轴交于点C(0,2).(1)求抛物线的表达式及点B坐标;(2)点E是线段BC上的任意一点(点E与B、C不重合),过点E作平行于y轴的直线交抛物线于点F,交x轴于点G.①设点E的横坐标为m,用含有m的代数式表示线段EF的长;②线段EF长的最大值是.22.已经二次函数y=ax2+bx+1 .(1)如图,其图象与x轴交于点A(−1,0)和点B,与y轴交于点C,对称轴为直线x=1 .①求二次函数解析式;②F为线段BC上一点,过F分别作x轴,y轴垂线,垂足分别为E、F,当四边形OEFG为正方形时,则求点F坐标;(2)其图象上仅有一个点的横坐标、纵坐标互为相反数,且二次函数y=ax2+bx+1函数值存在负数,求b的取值范围.23.定义符号min{a,b}的含义为:当a≥b时,则min{a,b}=b;当a<b时,则min{a,b}=a.如:min{1,﹣2}=﹣2,min{﹣1,2}=﹣1.(1)求min{x2﹣1,﹣2};(2)已知min{x2﹣2x+k,﹣3}=﹣3,求实数k的取值范围;(3)已知当﹣2≤x≤3时,则min{x2﹣2x﹣15,m(x+1)}=x2﹣2x﹣15.直接写出实数m的取值范围.24.某企业研发了一种新产品,已知这种产品的成本为30元/件,且年销售量y(万件)与售价x(元/件)的函数关系式为y={−2x+140,(40≤x<60)−x+80.(60≤x≤70)(1)当售价为60元/件时,则年销售量为万件;(2)当售价为多少时,则销售该产品的年利润最大?最大利润是多少?(3)若销售该产品的年利润不少于750万元,直接写出x的取值范围.参考答案1.【答案】D 2.【答案】B 3.【答案】B 4.【答案】D 5.【答案】C 6.【答案】B 7.【答案】C 8.【答案】A 9.【答案】A 10.【答案】C 11.【答案】C 12.【答案】C 13.【答案】414.【答案】1(答案不唯一) 15.【答案】①③④16.【答案】(1,﹣4)和(﹣2,5) 17.【答案】y=x 2﹣2x ﹣3 18.【答案】①②③④ 19.【答案】(1)解:如图1作BE ⊥x 轴∴△AOB 是等腰直角三角形 ∴BE=OE= 12AB=1∴A (﹣1,1),B (1,1)∴A ,B 两点的横坐标的乘积为﹣1×1=﹣1∵抛物线y=ax 2(a >0)过A ,B ∴a=1 ∴抛物线y=x 2 (2)解:如图2作BN ⊥x 轴,作AM ⊥x 轴 ∴∠AOB=AMO=∠BNO=90° ∴∠MAO=∠BON ∴△AMO ∽△ONB ∴AM ON =OM BN ∴AM ×BN=OM ×ON设A (x 1,y 1),B (x 2,y 2)在抛物线上 ∴AM=y 1=x 12,BN=y 2=x 22,OM=﹣x 1,ON=x 2 ∴x 12×x 22=﹣x 1×x 2 ∴x 1×x 2=﹣1∴A ,B 两点横坐标的乘积是一个定值;(3)解:由(2)得,A ,B 两点横坐标的乘积是一个定值为﹣1,∵点B 的横坐标为 12,∴点A 的横坐标为﹣2,∵A ,B 在抛物线上,∴A (﹣2,4),B ( 12 , 14 ),∴直线AB 解析式为y=﹣ 32x+1,∴P ( 23 ,0),D (0,1)设Q (n ,0),∴DP 2= 139 ,PQ 2=(n ﹣ 23)2,DQ 2=n 2+1∵△QDP 为等腰三角形∴①DP=PQ ,∴DP 2=PQ 2,∴139 =(n ﹣ 23 )2,∴n= 2±√133 ,∴Q 1( 2+√133 ,0),Q 2( 2−√133 ,0)②DP=DQ ,∴DP 2=DQ 2,∴139 =n 2+1,∴n= 23 (舍)或n=﹣ 23 ,Q 3(﹣ 23 ,0)③PQ=DQ ,∴PQ 2=DQ 2,∴(n ﹣ 23 )2=n 2+1∴n=﹣ 512 ,∴Q4(﹣ 512 ,0),∴存在点Q 坐标为Q 1( 2+√133 ,0),Q 2(2−√133 ,0),Q 3(﹣ 23 ,0),Q4(﹣ 512 ,0)20.【答案】(1)解:设y 与x 的函数关系式为:y=kx+b将点(5,30),(15,10)代入可得:{30=5k +b 10=15k +b解得:{b =40k =−2∴y 与x 的函数关系式为:y=-2x+40(5≤x ≤15); (2)解:当5≤x ≤10时,则根据图像可得:P=60 ∴W=(x-5)y-P=(x-5)(-2x+40)-60=-2x 2+50x-260;当10≤x ≤15时,则P =14x 2−4x +m由图可得经过点(10,60),将其代入可得:60=14×102−4×10+m 解得:m=75∴P =14x 2−4x +75;∴W=(x-5)y-P=(x-5)(-2x+40)-(14x 2−4x +75)=−94x 2+54x −275;综上:W ={−2x 2+50x −260(5≤x ≤10)−94x 2+54x −275(10≤x ≤15);(3)解:由(2)可得:当5≤x ≤10时W=-2x 2+50x-260=-2(x −252)2+1052∴x =252不在5≤x <10,由于开口向下在5≤x <10内随x 增大而增大 在x=10时,则取得最大值为W=40; 当10≤x ≤15时W=−94x 2+54x −275对称轴为x=−b2a=12 由于函数开口向下 ∴当x=12时,则W=49∴当x=12时,则W 取得最大值为49;综上可得:当售价为12元时,则年利润最大,最大为49万元.21.【答案】(1)解:将A(-1,0)、 C(0,2)代入y =ax 2+ 32x +c (a ≠0)得:a =- 12, c =2y =- 12 x 2+ 32x +2 当y =0时,则x 1=-1,x 2=4,故B(4,0)(2)解:设直线BC 的函数表达式为y =kx +b ,将B(4,0)、 C(0,2)代入 得:y =- x +2,EF =FG -GE =- m 2+ m +2-(- m +2) =- m 2+2m ;2 22.【答案】(1)解:①由题: {a −b +1=0−b 2a =1 解得 {a =−13b =23∴ 二次函数解析式为: y =−13x 2+23x +1 ; ②设BC 解析式为: y =kx +b 对称轴为直线 x =1 .∵ 图象与x 轴交于点 A(−1,0) 和点B ,对称轴为直线 x =1 .∴ 点 B(3,0)将 B(3,0) , C(0,1) 代入得: {3k +b =0b =1解得: {a =−13b =1∴BC 解析式为: y =−13x +1 设点 F(m,−13m +1) ∵ 四边形 OEFG 是正方形∴EF =GF∴m =−13m +1解得 m =34∴F(34,34) (2)解:二次函数的图象其有且只有一个点横、纵坐标之和互为相反数∴−x =ax 2+bx +1 有两相等实根,即 ax 2+(b +1)x +1=0 有两相等实根 ∴{a ≠0(b +1)2−4a =0解得: a =(b+1)24>0 ,且 b ≠−1 ∵y =ax 2+bx +1 存在负值∴b 2−4a =b 2−(b +1)2>0 ,解得 b <−12综上: b <−12且 b ≠−123.【答案】(1)解:∵x2≥0∴x2﹣1≥﹣1∴x2﹣1>﹣2.∴min{x2﹣1,﹣2}=﹣2(2)解:∵x2﹣2x+k=(x﹣1)2+k﹣1∴(x﹣1)2+k﹣1≥k﹣1.∵min{x2﹣2x+k,﹣3}=﹣3∴k﹣1≥﹣3.∴k≥﹣2(3)解:对于y=x2﹣2x﹣15,当x=﹣2时,则y=﹣7当x=3时,则y=﹣12由题意可知抛物线y=x2﹣2x﹣15与直线y=m(x+1)的交点坐标为(﹣2,﹣7),(3,﹣12)所以m的范围是:﹣3≤m≤7.24.【答案】(1)20(2)解:设销售该产品的年利润为W万元当40≤x<60时W=(x−30)(−2x+140)=−2(x−50)2+800 .∵-2<0∴当x=50时W最大=800当60≤x≤70时W=(x−30)(−x+80)=−(x−55)2+625∵−1<0∴当x=60时W最大=600∵800>600∴当x=50时W最大=800∴当售价为50元/件时,则年销售利润最大,最大为800万元.(3)解:45≤x≤55理由如下:由题意得(x−30)(−2x+140)≥750解得45≤x≤55。
二次函数难题综合(附答案)

庞圣洁(二次函数难题)一.选择题(共22小题)1.(2015•陕西模拟)已知二次函数y=ax2+bx+c(a>0)经过点M(﹣1,2)和点N(1,﹣2),交x轴于A,B两点,交y轴于C.则:①b=﹣2;②该二次函数图象与y轴交于负半轴;③存在这样一个a,使得M、A、C三点在同一条直线上;④若a=1,则OA•OB=OC2.以上说法正确的有()A.①②③④B.②③④ C.①②④ D.①②③2.(2013•泰安模拟)如图,抛物线y=x2﹣x﹣与直线y=x﹣2交于A、B两点(点A在点B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点B.若使点P运动的总路径最短,则点P运动的总路径的长为()A. B. C.D.3.(2015•潍坊模拟)若函数y=的自变量x的取值范围是全体实数,则c的取值范围是()A.c<1 B.c=1 C.c>1 D.c≤14.(2015•天桥区一模)如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是﹣2,点B的横坐标是3,则以下结论:①抛物线y=ax2(a≠0)的图象的顶点一定是原点;②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;③AB的长度可以等于5;④△OAB有可能成为等边三角形;⑤当﹣3<x<2时,ax2+kx<b,其中正确的结论是()A.①②④ B.①②⑤ C.②③④ D.③④⑤5.(2013•遵义)二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b﹣c,N=4a﹣2b+c,P=2a﹣b.则M,N,P中,值小于0的数有()A.3个B.2个C.1个D.0个6.(2015•杭州模拟)关于x的方程2x2+ax+b=0有两个不相等的实数根,且较小的根为2,则下列结论:①2a+b<0;②ab<0;③关于x的方程2x2+ax+b+2=0有两个不相等的实数根;④抛物线y=2x2+ax+b﹣2的顶点在第四象限.其中正确的结论有()A.1个B.2个C.3个D.4个7.(2015•无锡校级三模)已知抛物线y=﹣x2+1的顶点为P,点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,连结PA、PD,PD交AB于点E,△PAD与△PEA相似吗?()A.始终不相似B.始终相似C.只有AB=AD时相似D.无法确定8.(2015•杭州模拟)下列关于函数y=(m2﹣1)x2﹣(3m﹣1)x+2的图象与坐标轴的公共点情况:①当m≠3时,有三个公共点;②m=3时,只有两个公共点;③若只有两个公共点,则m=3;④若有三个公共点,则m≠3.其中描述正确的有()个.A.一个 B.两个 C.三个 D.四个9.(2011•黄石)设一元二次方程(x﹣1)(x﹣2)=m(m>0)的两实根分别为α,β,且α<β,则α,β满足()A.1<α<β<2 B.1<α<2<βC.α<1<β<2 D.α<1且β>210.(2013•盐城模拟)如图,分别过点P i(i,0)(i=1、2、…、n)作x轴的垂线,交的图象于点A i,交直线于点B i.则的值为()A.B.2 C.D.11.(2008•西湖区校级模拟)已知二次函数y=ax2﹣2ax+1(a<0)图象上三点A(﹣1,y1),B(2,y2)C(4,y3),则y1、y2、y3的大小关系为()A.y1<y2<y3B.y2<y1<y3C.y1<y3<y2D.y3<y1<y212.(2008•乐山)已知二次函数y=ax2+bx+c的图象如图所示,令M=|4a﹣2b+c|+|a+b+c|﹣|2a+b|+|2a﹣b|,则()A.M>0 B.M<0C.M=0 D.M的符号不能确定13.(2007•包头)已知二次函数y=ax2+2x+c(a≠0)有最大值,且ac=4,则二次函数的顶点在()A.第一象限 B.第二象限 C.第三象限 D.第四象限14.(2012•蚌埠自主招生)二次函数y=ax2+bx+c的图象如图所示,Q(n,2)是图象上的一点,且AQ⊥BQ,则a的值为()A.﹣B.﹣C.﹣1 D.﹣215.(2010•秀洲区一模)已知点A(x1,y1),B(x2,y2)均在抛物线y=ax2+2ax+4(0<a <3)上,若x1<x2,x1+x2=1﹣a,则()A.y1>y2B.y1<y2C.y1=y2D.y1与y2大小不能确定16.(2013•天河区一模)如图,二次函数y1=ax2+bx+c与一次函数y2=kx+b的交点A,B的坐标分别为(1,﹣3),(6,1),当y1>y2时,x的取值范围是()A.1<x<6 B.x<1或x>6 C.﹣3<x<1 D.x<﹣3或x>117.已知关于x的二次函数y=ax2+2ax+7a﹣3在﹣2≤x≤5上的函数值始终是正的,则a的取值范围()A.a>B.a<0或a> C.D.18.(2012•荣县校级二模)已知直线经过点A(0,2),B(2,0),点C在抛物线y=x2的图象上,则使得S△ABC=2的点有()个.A.4 B.3 C.2 D.119.(2012•下城区校级模拟)关于二次函数y=2x2﹣mx+m﹣2,以下结论:①抛物线交x轴有交点;②不论m取何值,抛物线总经过点(1,0);③若m>6,抛物线交x轴于A、B两点,则AB>1;④抛物线的顶点在y=﹣2(x﹣1)2图象上.其中正确的序号是()A.①②③④B.①②③ C.①②④ D.②③④20.(2002•湖州)已知抛物线y=x2+bx+c(c<0)经过点(c,0),以该抛物线与坐标轴的三个交点为顶点的三角形面积为S,则S可表示为()A.|2+b||b+1| B.c(1﹣c)C.(b+1)2D.21.(2005•茂名)下列四个函数:①y=kx(k为常数,k>0)②y=kx+b(k,b为常数,k>0)③y=(k为常数,k>0,x>0)④y=ax2(a为常数,a>0)其中,函数y的值随着x值得增大而减少的是()A.①B.②C.③D.④22.(2013•碑林区校级一模)已知函数y=﹣(x﹣m)(x﹣n)+3,并且a,b是方程(x﹣m)(x﹣n)=3的两个根,则实数m,n,a,b的大小关系可能是()A.m<a<b<n B.m<a<n<b C.a<m<b<n D.a<m<n<b二.解答题(共8小题)23.(2014•本溪)如图,直线y=x﹣4与x轴、y轴分别交于A、B两点,抛物线y=x2+bx+c经过A、B两点,与x轴的另一个交点为C,连接BC.(1)求抛物线的解析式及点C的坐标;(2)点M在抛物线上,连接MB,当∠MBA+∠CBO=45°时,求点M的坐标;(3)点P从点C出发,沿线段CA由C向A运动,同时点Q从点B出发,沿线段BC由B 向C运动,P、Q的运动速度都是每秒1个单位长度,当Q点到达C点时,P、Q同时停止运动,试问在坐标平面内是否存在点D,使P、Q运动过程中的某一时刻,以C、D、P、Q 为顶点的四边形为菱形?若存在,直接写出点D的坐标;若不存在,说明理由.24.(2014•黔南州)如图,在平面直角坐标系中,顶点为(4,﹣1)的抛物线交y轴于A 点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3).(1)求此抛物线的解析式;(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明;(3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积.25.(2014•遵义)如图,二次函数y=x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.(1)求该二次函数的解析式及点C的坐标;(2)当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E,使得以A,E,Q为顶点的三角形为等腰三角形?若存在,请求出E点坐标;若不存在,请说明理由.(3)当P,Q运动到t秒时,△APQ沿PQ翻折,点A恰好落在抛物线上D点处,请判定此时四边形APDQ的形状,并求出D点坐标.26.(2014•兰州)如图,抛物线y=﹣x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).(1)求抛物线的表达式;(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.27.(2014•义乌市)如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x 轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.(1)求该抛物线的函数解析式;(2)已知直线l的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l于点H,连结OP,试求△OPH的面积;②当m=﹣3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.28.(2015•黄冈模拟)已知:如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.(1)求抛物线的函数表达式;(2)设P(x,y)(0<x<6)是抛物线上的动点,过点P作PQ∥y轴交直线BC于点Q.①当x取何值时,线段PQ的长度取得最大值,其最大值是多少?②是否存在这样的点P,使△OAQ为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.29.(2014•武汉)如图,已知直线AB:y=kx+2k+4与抛物线y=x2交于A,B两点.(1)直线AB总经过一个定点C,请直接出点C坐标;(2)当k=﹣时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;(3)若在抛物线上存在定点D使∠ADB=90°,求点D到直线AB的最大距离.30.(2014•六盘水)如图,二次函数y=x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).(1)求二次函数的解析式.(2)求函数图象的顶点坐标及D点的坐标.(3)该二次函数的对称轴交x轴于C点.连接BC,并延长BC交抛物线于E点,连接BD,DE,求△BDE的面积.(4)抛物线上有一个动点P,与A,D两点构成△ADP,是否存在S△ADP=S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.庞圣洁(二次函数难题)参考答案与试题解析一.选择题(共22小题)1.(2015•陕西模拟)已知二次函数y=ax2+bx+c(a>0)经过点M(﹣1,2)和点N(1,﹣2),交x轴于A,B两点,交y轴于C.则:①b=﹣2;②该二次函数图象与y轴交于负半轴;③存在这样一个a,使得M、A、C三点在同一条直线上;④若a=1,则OA•OB=OC2.以上说法正确的有()A.①②③④B.②③④ C.①②④ D.①②③【考点】二次函数综合题.【专题】压轴题;数形结合.【分析】①二次函数y=ax2+bx+c(a>0)经过点M(﹣1,2)和点N(1,﹣2),因而将M、N两点坐标代入即可消去a、c解得b值.②根据图象的特点及与直线MN比较,可知当﹣1<x<1时,二次函数图象在直线MN的下方.③同②理.④当y=0时利用根与系数的关系,可得到OA•OB的值,当x=0时,可得到OC的值.通过c建立等量关系求证.【解答】解:①∵二次函数y=ax2+bx+c(a>0)经过点M(﹣1,2)和点N(1,﹣2),∴,解得b=﹣2.故该选项正确.②方法一:∵二次函数y=ax2+bx+c,a>0∴该二次函数图象开口向上∵点M(﹣1,2)和点N(1,﹣2),∴直线MN的解析式为y﹣2=,即y=﹣2x,根据抛物线的图象的特点必然是当﹣1<x<1时,二次函数图象在y=﹣2x的下方,∴该二次函数图象与y轴交于负半轴;方法二:由①可得b=﹣2,a+c=0,即c=﹣a<0,所以二次函数图象与y轴交于负半轴.故该选项正确.③根据抛物线图象的特点,M、A、C三点不可能在同一条直线上.故该选项错误.④当a=1时,c=﹣1,∴该抛物线的解析式为y=x2﹣2x﹣1当y=0时,0=x2﹣2x+c,利用根与系数的关系可得x1•x2=c,即OA•OB=|c|,当x=0时,y=c,即OC=|c|=1=OC2,∴若a=1,则OA•OB=OC2,故该选项正确.总上所述①②④正确.故选C.【点评】本题是二次函数的综合题型,其中涉及到的知识点有抛物线的图象性质及特点、一元二次方程根与系数的关系、直线解析式的确定.2.(2013•泰安模拟)如图,抛物线y=x2﹣x﹣与直线y=x﹣2交于A、B两点(点A在点B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点B.若使点P运动的总路径最短,则点P运动的总路径的长为()A. B. C.D.【考点】二次函数综合题.【专题】压轴题.【分析】首先根据题意求得点A与B的坐标,求得抛物线的对称轴,然后作点A关于抛物线的对称轴x=的对称点A′,作点B关于x轴的对称点B′,连接A′B′,则直线A′B′与直线x=的交点是E,与x轴的交点是F,而且易得A′B′即是所求的长度.【解答】解:如图∵抛物线y=x2﹣x﹣与直线y=x﹣2交于A、B两点,∴x2﹣x﹣=x﹣2,解得:x=1或x=,当x=1时,y=x﹣2=﹣1,当x=时,y=x﹣2=﹣,∴点A的坐标为(,﹣),点B的坐标为(1,﹣1),∵抛物线对称轴方程为:x=﹣=作点A关于抛物线的对称轴x=的对称点A′,作点B关于x轴的对称点B′,连接A′B′,则直线A′B′与对称轴(直线x=)的交点是E,与x轴的交点是F,∴BF=B′F,AE=A′E,∴点P运动的最短总路径是AE+EF+FB=A′E+EF+FB′=A′B′,延长BB′,AA′相交于C,∴A′C=++(1﹣)=1,B′C=1+=,∴A′B′==.∴点P运动的总路径的长为.故选A.【点评】此题考查了二次函数与一次函数的综合应用.注意找到点P运动的最短路径是解此题的关键,还要注意数形结合与方程思想的应用.3.(2015•潍坊模拟)若函数y=的自变量x的取值范围是全体实数,则c的取值范围是()A.c<1 B.c=1 C.c>1 D.c≤1【考点】二次函数的性质;分式有意义的条件;函数自变量的取值范围.【专题】计算题;压轴题.【分析】先根据分式的意义,分母不等于0,得出x2﹣2x+c≠0,再根据二次函数y=ax2+bx+c (a≠0)的图象性质,可知当二次项系数a>0,△<0时,有y>0,此时自变量x的取值范围是全体实数.【解答】解:由题意,得△=(﹣2)2﹣4c<0,解得c>1.故选C.【点评】本题考查了函数自变量取值范围的求法.要使得本题函数式子有意义,必须满足分母不等于0.难点在于分母是关于自变量x的二次函数,要使自变量x的取值范围是全体实数,必须满足△<0.4.(2015•天桥区一模)如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是﹣2,点B的横坐标是3,则以下结论:①抛物线y=ax2(a≠0)的图象的顶点一定是原点;②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;③AB的长度可以等于5;④△OAB有可能成为等边三角形;⑤当﹣3<x<2时,ax2+kx<b,其中正确的结论是()A.①②④ B.①②⑤ C.②③④ D.③④⑤【考点】二次函数综合题.【专题】综合题;压轴题.【分析】①由顶点坐标公式判断即可;②根据图象得到一次函数y=kx+b为增函数,抛物线当x大于0时为增函数,本选项正确;③AB长不可能为5,由A、B的横坐标求出AB为5时,直线AB与x轴平行,即k=0,与已知矛盾;④三角形OAB不可能为等边三角形,因为OA与OB不可能相等;⑤直线y=﹣kx+b与y=kx+b关于y轴对称,作出对称后的图象,故y=﹣kx+b与抛物线交点横坐标分别为﹣3与2,找出一次函数图象在抛物线上方时x的范围判断即可.【解答】解:①抛物线y=ax2,利用顶点坐标公式得:顶点坐标为(0,0),本选项正确;②根据图象得:直线y=kx+b(k≠0)为增函数;抛物线y=ax2(a≠0)当x>0时为增函数,则x>0时,直线与抛物线函数值都随着x的增大而增大,本选项正确;③由A、B横坐标分别为﹣2,3,若AB=5,可得出直线AB与x轴平行,即k=0,与已知k≠0矛盾,故AB不可能为5,本选项错误;④若OA=OB,得到直线AB与x轴平行,即k=0,与已知k≠0矛盾,∴OA≠OB,即△AOB不可能为等边三角形,本选项错误;⑤直线y=﹣kx+b与y=kx+b关于y轴对称,如图所示:可得出直线y=﹣kx+b与抛物线交点C、D横坐标分别为﹣3,2,由图象可得:当﹣3<x<2时,ax2<﹣kx+b,即ax2+kx<b,则正确的结论有①②⑤.故选B.【点评】此题考查了二次函数综合题,涉及的知识有:抛物线顶点坐标公式,一次函数与二次函数的增减性,关于y轴对称点的性质,利用了数形结合的思想,熟练对称性质及数形结合思想是判断命题⑤的关键.5.(2013•遵义)二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b﹣c,N=4a﹣2b+c,P=2a﹣b.则M,N,P中,值小于0的数有()A.3个B.2个C.1个D.0个【考点】二次函数图象与系数的关系.【专题】计算题;压轴题.【分析】根据图象得到x=﹣2时对应的函数值小于0,得到N=4a﹣2b+c的值小于0,根据对称轴在直线x=﹣1右边,利用对称轴公式列出不等式,根据开口向下得到a小于0,变形即可对于P作出判断,根据a,b,c的符号判断得出a+b﹣c的符号.【解答】解:∵图象开口向下,∴a<0,∵对称轴在y轴左侧,∴a,b同号,∴a<0,b<0,∵图象经过y轴正半轴,∴c>0,∴M=a+b﹣c<0当x=﹣2时,y=4a﹣2b+c<0,∴N=4a﹣2b+c<0,∵﹣>﹣1,∴<1,∵a<0,∴b>2a,∴2a﹣b<0,∴P=2a﹣b<0,则M,N,P中,值小于0的数有M,N,P.故选:A.【点评】此题主要考查了二次函数图象与系数的关系,根据图象判断出对称轴以及a,b,c 的符号是解题关键.6.(2015•杭州模拟)关于x的方程2x2+ax+b=0有两个不相等的实数根,且较小的根为2,则下列结论:①2a+b<0;②ab<0;③关于x的方程2x2+ax+b+2=0有两个不相等的实数根;④抛物线y=2x2+ax+b﹣2的顶点在第四象限.其中正确的结论有()A.1个B.2个C.3个D.4个【考点】二次函数图象与系数的关系.【专题】压轴题.【分析】把方程的根x=2代入计算即可求出2a+b=﹣8,判定①正确;利用根与系数的关系求出a<﹣8,b>8,从而判定②正确;根据二次函数y=2x2+ax+b与x轴有两个交点,且顶点坐标在第四象限,向上平移2个单位,与x轴不一定有交点,判定③错误,向下平移2个单位,顶点一定在第四象限,判定④正确.【解答】解:∵x=2是方程2x2+ax+b=0的根,∴2×4+2a+b=0,∴2a+b=﹣8<0,故①正确;∵x=2是方程2x2+ax+b=0的两个根中较小的根,∴﹣>2+2,>2×2,∴a<﹣8,b>8,∴ab<0,故②正确;∵方程2x2+ax+b=0有两个不相等的实数根,且较小的根为2,∴二次函数y=2x2+ax+b与x轴有两个交点,且对称轴在直线x=2的右边,∴二次函数y=2x2+ax+b顶点坐标在第四象限,向上平移2个单位得到二次函数y=2x2+ax+b+2,与x轴不一定有交点,∴关于x的方程2x2+ax+b+2=0有两个不相等的实数根错误,故③错误;向下平移2个单位得到二次函数y=2x2+ax+b﹣2,顶点坐标一定在第四象限,故④正确;综上所述,正确的结论有①②④共3个.故选C.【点评】本题考查了二次函数图象与系数的关系,主要利用了一元二次方程的根的定义,根与系数的关系,二次函数图象与几何变换,③④两题考虑用二次函数的平移求解是解题的关键.7.(2015•无锡校级三模)已知抛物线y=﹣x2+1的顶点为P,点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,连结PA、PD,PD交AB于点E,△PAD与△PEA相似吗?()A.始终不相似B.始终相似C.只有AB=AD时相似D.无法确定【考点】二次函数综合题.【专题】压轴题.【分析】先求出点P的坐标,从而得到OP的长,再设点A的横坐标为m,表示出AD,再表示出OD、OF、PF、AF,然后根据△PEF和△PDO相似,根据相似三角形对应边成比例列式求出EF,然后利用勾股定理表示出PA2、PE、PD,从而得到=,再根据两边对应成比例且夹角相等,两三角形相似解答.【解答】解:令x=0,则y=1,∴OP=1,设点A的横坐标为m,则AD=﹣m2+1,∵AB⊥y轴,AD⊥x轴,∴AF=OD=m,OF=﹣m2+1,PF=1﹣(﹣m2+1)=m2,在Rt△PAF中,PA2=PF2+AF2=(m2)2+m2=m4+m2,在Rt△POD中,PD===,由AB∥x轴得,△PEF∽△PDO,∴=,即=,解得,PE=m2,∴PA2=PD•PE=m4+m2,∴=,∵∠APE=∠DPA,∴△PAD∽△PEA,即,△PAD与△PEA始终相似.故选B.【点评】本题是二次函数综合题,主要考查了二次函数图象上点的坐标特征,相似三角形的判定与性质,勾股定理的应用,表示出两个三角形的公共角的夹边成比例是解题的关键.8.(2015•杭州模拟)下列关于函数y=(m2﹣1)x2﹣(3m﹣1)x+2的图象与坐标轴的公共点情况:①当m≠3时,有三个公共点;②m=3时,只有两个公共点;③若只有两个公共点,则m=3;④若有三个公共点,则m≠3.其中描述正确的有()个.A.一个 B.两个 C.三个 D.四个【考点】抛物线与x轴的交点.【专题】压轴题.【分析】令y=0,可得出(m2﹣1)x2﹣(3m﹣1)x+2=0,得出判别式的表达式,然后根据m的取值进行判断,另外要注意m的取值决定函数是一次函数还是二次函数,不要忘了考虑一次函数的情况.【解答】解:令y=0,可得出(m2﹣1)x2﹣(3m﹣1)x+2=0,△=(3m﹣1)2﹣8(m2﹣1)=(m﹣3)2,①当m≠3,m=±1时,函数是一次函数,与坐标轴有两个交点,故错误;②当m=3时,△=0,与x轴有一个公共点,与y轴有一个公共点,总共两个,故正确;③若只有两个公共点,m=3或m=±1,故错误;④若有三个公共点,则m≠3且m≠±1,故正确;综上可得只有②④正确,共2个.故选B.【点评】此题考查了抛物线与x轴交点的知识,同学们容易忽略m=±1时,函数是一次函数的情况,这是我们要注意的地方.9.(2011•黄石)设一元二次方程(x﹣1)(x﹣2)=m(m>0)的两实根分别为α,β,且α<β,则α,β满足()A.1<α<β<2 B.1<α<2<βC.α<1<β<2 D.α<1且β>2【考点】抛物线与x轴的交点;根与系数的关系.【专题】压轴题;数形结合.【分析】先令m=0求出函数y=(x﹣1)(x﹣2)的图象与x轴的交点,画出函数图象,利用数形结合即可求出α,β的取值范围.【解答】解:令m=0,则函数y=(x﹣1)(x﹣2)的图象与x轴的交点分别为(1,0),(2,0),故此函数的图象为:∵m>0,∴原顶点沿抛物线对称轴向下移动,两个根沿对称轴向两边逐步增大,∴α<1,β>2.故选D.【点评】本题考查的是抛物线与x轴的交点,能根据x轴上点的坐标特点求出函数y=(x ﹣1)(x﹣2)与x轴的交点,画出函数图象,利用数形结合解答是解答此题的关键.10.(2013•盐城模拟)如图,分别过点P i(i,0)(i=1、2、…、n)作x轴的垂线,交的图象于点A i,交直线于点B i.则的值为()A.B.2 C.D.【考点】二次函数综合题.【专题】压轴题;规律型.【分析】根据A i的纵坐标与B i纵坐标的绝对值之和为A i B i的长,分别表示出所求式子的各项,拆项后抵消即可得到结果.【解答】解:根据题意得:A i B i=x2﹣(﹣x)=x(x+1),∴==2(﹣),∴++…+=2(1﹣+﹣+…+﹣)=.故选A【点评】此题考查了二次函数综合题,属于规律型试题,找出题中的规律是解本题的关键.11.(2008•西湖区校级模拟)已知二次函数y=ax2﹣2ax+1(a<0)图象上三点A(﹣1,y1),B(2,y2)C(4,y3),则y1、y2、y3的大小关系为()A.y1<y2<y3B.y2<y1<y3C.y1<y3<y2D.y3<y1<y2【考点】二次函数图象上点的坐标特征.【专题】压轴题;推理填空题.【分析】求出抛物线的对称轴,求出A关于对称轴的对称点的坐标,根据抛物线的开口方向和增减性,即可求出答案.【解答】解:y=ax2﹣2ax+1(a<0),对称轴是直线x=﹣=1,即二次函数的开口向下,对称轴是直线x=1,即在对称轴的右侧y随x的增大而减小,A点关于直线x=1的对称点是D(3,y1),∵2<3<4,∴y2>y1>y3,故选D.【点评】本题考查了学生对二次函数图象上点的坐标特征的理解和运用,主要考查学生的观察能力和分析能力,本题比较典型,但是一道比较容易出错的题目.12.(2008•乐山)已知二次函数y=ax2+bx+c的图象如图所示,令M=|4a﹣2b+c|+|a+b+c|﹣|2a+b|+|2a﹣b|,则()A.M>0 B.M<0C.M=0 D.M的符号不能确定【考点】二次函数图象与系数的关系.【专题】压轴题.【分析】根据图象特征,首先判断出M中的各代数式的符号,然后去绝对值.【解答】解:因为开口向下,故a<0;当x=﹣2时,y>0,则4a﹣2b+c>0;当x=1时,y<0,则a+b+c<0;因为对称轴为x=<0,又a<0,则b<0,故2a+b<0;又因为对称轴x=﹣>﹣1,则b>2a∴2a﹣b<0;∴M=4a﹣2b+c﹣a﹣b﹣c+2a+b+b﹣2a=3a﹣b,因为2a﹣b<0,a<0,∴3a﹣b<0,即M<0,故选B.【点评】考查二次函数y=ax2+bx+c系数符号的确定.13.(2007•包头)已知二次函数y=ax2+2x+c(a≠0)有最大值,且ac=4,则二次函数的顶点在()A.第一象限 B.第二象限 C.第三象限 D.第四象限【考点】二次函数的性质.【专题】压轴题.【分析】已知二次函数y=ax2+2x+c(a≠0)有最大值,即抛物线的开口向下,因而a<0.求抛物线的顶点坐标利用公式法:y=ax2+bx+c的顶点坐标为(,),对称轴是x=;代入就可以求出顶点坐标,从而确定顶点所在象限.【解答】解:顶点横坐标x==,纵坐标y==;∵二次函数有最大值,即抛物线的开口向下,a<0,∴,,即:横坐标x>0,纵坐标y<0,顶点在第四象限.故选D.【点评】考查求抛物线的顶点坐标、对称轴及最值的方法:14.(2012•蚌埠自主招生)二次函数y=ax2+bx+c的图象如图所示,Q(n,2)是图象上的一点,且AQ⊥BQ,则a的值为()A.﹣B.﹣C.﹣1 D.﹣2【考点】抛物线与x轴的交点;勾股定理.【专题】压轴题.【分析】由勾股定理,及根与系数的关系可得.【解答】解:设ax2+bx+c=0的两根分别为x1与x2.依题意有AQ2+BQ2=AB2.(x1﹣n)2+4+(x2﹣n)2+4=(x1﹣x2)2,化简得:n2﹣n(x1+x2)+4+x1x2=0.有n2+n+4+=0,∴an2+bn+c=﹣4a.∵(n,2)是图象上的一点,∴an2+bn+c=2,∴﹣4a=2,∴a=﹣.故选B.【点评】此题考查了二次函数的性质和图象,解题的关键是注意数形结合思想.15.(2010•秀洲区一模)已知点A(x1,y1),B(x2,y2)均在抛物线y=ax2+2ax+4(0<a <3)上,若x1<x2,x1+x2=1﹣a,则()A.y1>y2B.y1<y2C.y1=y2D.y1与y2大小不能确定【考点】二次函数图象上点的坐标特征.【专题】压轴题.【分析】将点A(x1,y1),B(x2,y2)分别代入y=ax2+2ax+4(0<a<3)中得y1=ax12+2ax1+4﹣﹣﹣﹣①;y2=ax22+2ax2+4﹣﹣﹣﹣②;利用作差法求出y2﹣y1>0,即可得到y1>y2.【解答】解:将点A(x1,y1),B(x2,y2)分别代入y=ax2+2ax+4(0<a<3)中,得:y1=ax12+2ax1+4﹣﹣﹣﹣①,y2=ax22+2ax2+4﹣﹣﹣﹣②,②﹣①得:y2﹣y1=(x2﹣x1)[a(3﹣a)],因为x1<x2,3﹣a>0,则y2﹣y1>0,即y1<y2.故选B.【点评】本题难度较大,要充分利用数据特点,进行计算.16.(2013•天河区一模)如图,二次函数y1=ax2+bx+c与一次函数y2=kx+b的交点A,B的坐标分别为(1,﹣3),(6,1),当y1>y2时,x的取值范围是()A.1<x<6 B.x<1或x>6 C.﹣3<x<1 D.x<﹣3或x>1【考点】二次函数的图象;一次函数的图象.【专题】压轴题;数形结合.【分析】根据函数图象,找出抛物线在直线上方的部分的自变量x的取值范围即可.【解答】解:由图可知,当x<1或x>6时,抛物线在直线的上方,所以,当y1>y2时,x的取值范围是x<1或x>6.故选B.【点评】本题考查了二次函数的图象,利用数形结合的思想解答即可,比较简单.17.已知关于x的二次函数y=ax2+2ax+7a﹣3在﹣2≤x≤5上的函数值始终是正的,则a的取值范围()A.a>B.a<0或a> C.D.【考点】二次函数的性质.【专题】压轴题.【分析】按照a>0和a<0两种情况讨论:当a>0时,图象开口向上,只要顶点纵坐标为正即可;当a<0时,抛物线对称轴为x=﹣1,根据对称性,只要x=5时,y>0即可.【解答】解:当a>0时,图象开口向上,顶点纵坐标为=6a﹣3,当6a﹣3>0,即a>时,y>0;当a<0时,抛物线对称轴为x=﹣1,根据对称性,只要x=5时,y>0即可,此时y=25a+10a+7a ﹣3>0,解得a>,不符合题意,舍去.故选A.【点评】本题考查了二次函数开口方向,顶点坐标,对称轴在实际问题中的运用,还考查了分类讨论的数学思想.18.(2012•荣县校级二模)已知直线经过点A(0,2),B(2,0),点C在抛物线y=x2的图象上,则使得S△ABC=2的点有()个.A.4 B.3 C.2 D.1【考点】二次函数的性质.【专题】计算题;压轴题.【分析】解:通过计算发现,当O与C重合时,S△ABC=2,据此推断出以AB为底边的三角形的高,从图上找到点C1、C2,再作CC3∥AB,使得C3与C到AB的距离相等,若求出C的坐标,则存在C3点,使得以AB为底的三角形面积为2.【解答】解:∵S△ABC=×2×2=2,可见,当O与C重合时,S△ABC=2,作CD⊥AB,∵AO=BO=2,可见,△ACB为等腰直角三角形,CD=2×cos45°=2×=.由图易得,到AB距离为的点有C、C1、C2,作CC3∥AB,则CC3的解析式为y=﹣x,将y=﹣x和y=x2组成方程组得,,解得,,,则C3坐标为(﹣1,1),可见,有四个点,使得S△ABC=2.故选A.【点评】本题考查了二次函数的性质,知道平行线间的距离相等以及知道同底等高的三角形面积相等是解题的关键.19.(2012•下城区校级模拟)关于二次函数y=2x2﹣mx+m﹣2,以下结论:①抛物线交x轴有交点;②不论m取何值,抛物线总经过点(1,0);③若m>6,抛物线交x轴于A、B两点,则AB>1;④抛物线的顶点在y=﹣2(x﹣1)2图象上.其中正确的序号是()A.①②③④B.①②③ C.①②④ D.②③④【考点】抛物线与x轴的交点;二次函数的性质.【专题】计算题;压轴题.【分析】由二次函数的解析式,找出二次项系数a,一次项系数b及常数项c,将a,b及c 的值代入b2﹣4ac,利用完全平方公式化简后,根据完全平方式恒大于等于0,可得出b2﹣4ac大于等于0,进而确定出该抛物线与x轴有交点,故①正确;将x=1代入抛物线解析式,求出y=0,可得出此抛物线恒过(1,0),故②正确;令抛物线解析式中y=0,得到关于x 的一元二次方程,设方程的两个解分别为x1,x2,利用根与系数的关系表示出x1+x2,x1x2,AB的长可以用|x1﹣x2|表示,利用二次根式的化简根式=|a|变形后,再利用完全平方公式化简,将表示出的x1+x2及x1x2代入,化简后根据m大于6,可得出AB的长大于1,故③正确;利用顶点坐标公式表示出抛物线的顶点坐标,代入y=﹣2(x﹣1)2中经验,可得出抛物线的顶点在y=﹣2(x﹣1)2图象上,故④正确,综上,得到正确的序号.【解答】解:二次函数y=2x2﹣mx+m﹣2,∵a=2,b=﹣m,c=m﹣2,∴b2﹣4ac=(﹣m)2﹣8(m﹣2)=(m﹣4)2≥0,则抛物线与x轴有交点,故①正确;∵当x=1时,y=2﹣m+m﹣2=0,∴不论m取何值,抛物线总经过点(1,0),故②正确;设A的坐标为(x1,0),B(x2,0),令y=0,得到2x2﹣mx+m﹣2=0,∴x1+x2=,x1x2=,∴AB=|x1﹣x2|===||,当m>6时,可得m﹣4>2,即>1,∴AB>1,故③正确;∵抛物线的顶点坐标为(,),∴将x=代入得:y=﹣2(﹣1)2=﹣2(﹣+1)=,∴抛物线的顶点坐标在y=﹣2(x﹣1)2图象上,故④正确,综上,正确的序号有①②③④.故选A【点评】此题考查了抛物线与x轴的交点,以及二次函数的性质,涉及的知识有:抛物线与x轴交点的判断方法,根与系数的关系,顶点坐标公式,以及判断一个点是否在抛物线上,熟练掌握二次函数的性质是解本题的关键.20.(2002•湖州)已知抛物线y=x2+bx+c(c<0)经过点(c,0),以该抛物线与坐标轴的三个交点为顶点的三角形面积为S,则S可表示为()A.|2+b||b+1| B.c(1﹣c)C.(b+1)2D.【考点】抛物线与x轴的交点.【专题】压轴题.【分析】把点(c,0)代入抛物线中,可得b、c的关系式,再设抛物线与x轴的交点分别为x1、x2,则x1、x2满足x2+bx+c=0,根据根的判别式结合两点间的距离公式可求|x1﹣x2|,那么就可得到以该抛物线与坐标轴的三个交点为顶点的三角形面积.【解答】解:∵抛物线y=x2+bx+c(c<0)经过点(c,0),∴c2+bc+c=0;∴c(c+b+1)=0;∵c<0,∴c=﹣b﹣1;设x1,x2是一元二次方程x2+bx+c=0的两根,∴x1+x2=﹣b,x1•x2=c=﹣b﹣1,∴抛物线与x轴的交点间的距离为|x1﹣x2|=====|2+b|,∴S可表示为|2+b||b+1|.故选A.【点评】此题考查了点与函数的关系,还考查了二次函数与一元二次方程的关系,要注意根与系数的关系;此题考查了学生的分析能力,属于难度较大的题目.。
中考数学总复习《二次函数综合题》专项提升练习题(附答案)
中考数学总复习《二次函数综合题》专项提升练习题(附答案)学校:___________班级:___________姓名:___________考号:___________类型一 线段问题1. 如图,抛物线y =14 x 2+bx +c 过点A (4,0),B (-4,4),与y 轴交于点C ,连接AB .(1)求抛物线的表达式;(2)若E 是线段AB 上的一个动点(不与点A ,B 重合),过点E 作y 轴的平行线,分别交抛物线,x 轴于F ,D 两点,若DE =2DF ,请求出点E 的坐标.第1题图2. 平面直角坐标系中已知抛物线y =ax 2+83 x +c (a ≠0)与x 轴交于点A (1,0)和点B ,与y轴交于点C (0,-4).(1)求这条抛物线的函数解析式;(2)P 是抛物线上一动点(不与点A ,B ,C 重合),作 PD ⊥x 轴,垂足为D ,连接PC . ①如图,若点P 在第三象限,且tan ∠CPD =2,求点P 的坐标;②直线PD 交直线BC 于点E ,当点E 关于直线PC 的对称点E ′落在y 轴上时,请直接写出四边形 PECE ′的周长.第2题图 备用图类型二 面积问题1. 如图,抛物线y =ax 2+bx +5(a ≠0)交x 轴于A (-1,0),B (5,0)两点,交y 轴于点C ,连接AC ,BC ,点G 为线段BC 上方的抛物线上一点,过点G 作GH ∥AC 交BC 于点H . (1)求抛物线的解析式;(2)连接AG ,AH ,BG ,设h =S △AGB -S △AHB ,点G 的横坐标为t ,求h 关于t 的函数解析式,并求出h 的最大值.第1题图2. 在平面直角坐标系中点O 是坐标原点,抛物线y =ax 2+bx (a ≠0)经过点A (3,3),对称轴为直线x =2. (1)求a ,b 的值;(2)已知点B ,C 在抛物线上,点B 的横坐标为t ,点C 的横坐标为t +1.过点B 作x 轴的垂线交直线OA 于点D ,过点C 作x 轴的垂线交直线OA 于点E . (ⅰ)当0<t <2时,求△OBD 与△ACE 的面积之和;(ⅱ)在抛物线对称轴右侧,是否存在点B ,使得以B ,C ,D ,E 为顶点的四边形的面积为32 ?若存在,请求出点B 的横坐标t 的值;若不存在,请说明理由.类型三存在性问题典例精析例如图,在平面直角坐标系xOy中抛物线y=-x2+2x+3与x轴交于点A(-1,0),B(3,0),与y轴交于点C,连接BC,点D为抛物线的顶点.(1)若点M为抛物线对称轴上一点,是否存在点M,使得△BCM为等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由;例题图①【思路点拨】判断等腰三角形存在性问题,一般要进行分类讨论.①BC为腰时:分别以点B,C为圆心,BC长为半径画圆,与直线x=1的交点即为所求作的点;②BC为底时:作线段BC的垂直平分线,与直线x=1的交点即为所求作的点.(2)在抛物线上是否存在一点N,使得△BCN是以BC为直角边的直角三角形?若存在,求出点N的坐标;若不存在,请说明理由;例题图②【思路点拨】判断直角三角形存在性问题,一般要进行分类讨论.①BC 为直角边时:分别过点B ,C 作BC 的垂线,与抛物线的交点即为所求作的N 点; ②BC 为斜边,点N 为直角顶点时:以BC 的中点为圆心,12 BC 的长为半径作圆,所作的圆与抛物线的交点即为所求作的N 点.(3)若点Q 为第一象限内抛物线上一点,过点Q 作QG ⊥x 轴,垂足为G ,连接AC ,OQ .是否存在点Q ,使得△QGO ∽△AOC ?若存在,求出点Q 的坐标;若不存在,请说明理由; 【思路点拨】判断相似三角形存在性问题,通常利用相似三角形的性质,列出线段比例关系,求解即可.例题图③(4)若点E 在抛物线上,点F 在x 轴上,是否存在点E ,使得以D ,C ,E ,F 为顶点的四边形是平行四边形?若存在,求出点E 的坐标;若不存在,请说明理由; 【思路点拨】判断平行四边形存在性问题,一般要进行分类讨论. ①当DE ,FC 是平行四边形对角线时; ②当DF ,EC 是平行四边形对角线时; ③当DC ,EF 是平行四边形对角线时.再利用平行四边形对角线的性质结合中点坐标公式求点坐标即可.例题图④(5)若点H是x轴上一点,点K是平面任意一点,是否存在点H,使得以点A,C,H,K为顶点的四边形是矩形?若存在,求出点H的坐标;若不存在,请说明理由;【思路点拨】判断矩形存在性问题,一般要进行分类讨论.①当AC为矩形的边时,∠ACH=90°;②当AC为矩形的对角线时,∠AHC=90°.再利用勾股定理求解即可.例题图⑤(6)若点S是第一象限抛物线上一点,过点S作ST⊥BC于点T,连接AC,CS,是否存在点S使得△CST中有一个角与∠CAO相等,若存在,求出S点坐标;若不存在,请说明理由.【思路点拨】判断角度存在性问题,一般要进行分类讨论.①若∠SCT=∠CAO;②若∠CST=∠CAO.再构造直角三角形,利用三角函数求解即可.例题图⑥对接中考1. 如图,抛物线y=x2+bx+c过点A(-1,0),点B(5,0),交y轴于点C.(1)求b,c的值;(2)点P(x0,y0)(0<x0<5)是抛物线上的动点.①当x0取何值时,△PBC的面积最大?并求出△PBC面积的最大值;②过点P作PE⊥x轴,交BC于点E,再过点P作PF∥x轴,交抛物线于点F,连接EF,问:是否存在点P,使△PEF为等腰直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.第1题图2. 如图,将一块自制的直角三角板放置在平面直角坐标系中顶点为坐标原点,A(0,-3),B(6,0),将此三角板绕原点O顺时针旋转90°,得到△A′B′O,抛物线L经过点A′,B′,B.(1)求抛物线L的解析式;(2)点Q为平面内一点,在直线AB上是否存在点P,使得以点A,B′,P,Q为顶点的四边形是菱形?若存在,求出点P的坐标;若不存在,请说明理由.第2题图拓展类型二次函数性质综合题1. 在二次函数y=x2-2tx+3(t>0)中(1)若它的图象过点(2,1),则t的值为多少?(2)当0≤x≤3时,y的最小值为-2,求出t的值;(3)如果A(m-2,a),B(4,b),C(m,a)都在这个二次函数的图象上,且a<b<3,求m的取值范围.2. 已知抛物线y=ax2+bx+3(a,b均为常数,且a≠0)的对称轴为直线x=2.(1)求抛物线顶点M的坐标和b的值(用含a的代数式表示);(2)已知点A(x1,y1),B(x2,y2)都在此抛物线上,且x1<2<x2,x1+x2<4,若a>0,试比较y1与y2的大小,并说明理由;(3)若自变量x的值满足-1≤x≤1,与其对应的函数的最大值为18,请直接写出b的值.3. 在平面直角坐标系中抛物线y=ax2-4ax+c(a<0)与x轴交于A(1,0),B两点,与y轴交于点C.(1)若OC=2OB,求抛物线的解析式;(2)若抛物线的最大值为6,求a 的值;(3)若点P (x 0,m ),Q (52,n )在抛物线上,且m <n ,求x 0的取值范围.参考答案类型一 线段问题1. 解:(1)∵抛物线y =14 x 2+bx +c 过点A (4,0),B (-4,4)∴将A (4,0),B (-4,4)分别代入y =14x 2+bx +c 中得⎩⎪⎨⎪⎧4+4b +c =04-4b +c =4 解得⎩⎪⎨⎪⎧b =-12c =-2∴抛物线的表达式为y =14 x 2-12x -2;(2)由点A (4,0),B (-4,4)可得直线AB 的表达式为y =-12 x +2设点E (x ,-12 x +2),其中-4<x <4,则F (x ,14 x 2-12 x -2)∴DE =2-12 x ,DF =|14 x 2-12 x -2|分两种情况讨论:①当点F 在x 轴上方时,即2-12 x =2×(14 x 2-12 x -2)解得x 1=-3,x 2=4(舍去) 将x =-3代入y =-12 x +2中得y =72∴E (-3,72);②当点F 在x 轴下方时,即2-12 x =2×(-14 x 2+12 x +2)解得x 1=-1,x 2=4(舍去)将x =-1代入y =-12 x +2得y =52 ,∴E (-1,52);综上所述,当DE =2DF 时,点E 的坐标为(-3,72 )或(-1,52).2. 解:(1)∵抛物线y =ax 2+83 x +c (a ≠0)与x 轴交于点A (1,0),与y 轴交于点C (0,-4)∴⎩⎪⎨⎪⎧a +83+c =0c =-4 ,解得⎩⎪⎨⎪⎧a =43c =-4∴抛物线的函数解析式为y =43 x 2+83x -4;(2)①如解图①,过点C 作CE ⊥PD 于点E第2题解图①则∠PEC =∠CED =90° ∵C (0,-4) ∴OC =4∵PD ⊥x 轴,垂足为D ∴∠PDO =90°,∠DOC =90° ∴四边形DOCE 是矩形 ∴DE =OC =4 设P (x ,43 x 2+83 x -4)∴CE =-x∴PE =PD -DE =-(43 x 2+83 x -4)-4=-43 x 2-83 x∵tan ∠CPD =CEPE =2∴-x -43x 2-83x =2解得x 1=-138 ,x 2=0(不合题意,舍去)当x =-138 时,43 x 2+83 x -4=-7716∴P (-138 ,-7716);②四边形PECE ′的周长为353 或853.【解法提示】设P (m ,43 m 2+83 m -4),对于y =43 x 2+83 x -4,当y =0时,43 x 2+83 x -4=0,解得x 1=1,x 2=-3,∴B (-3,0),∴OB =3,在Rt △BOC 中由勾股定理得BC =OB 2+OC 2 =5.当点P 在第三象限时,如解图②,过点E 作EF ⊥y 轴于点F第2题解图②则四边形DEFO 是矩形,∴EF =DO =-m ,∵点E 与点E ′关于PC 对称,∴∠ECP =∠E ′CP ,CE =CE ′,PE =PE ′,∵PE ∥y 轴,∴∠EPC =∠PCE ′,∴∠EPC =∠ECP ,∴PE =CE ,∴PE =CE =CE ′=PE ′,∴四边形PECE ′是菱形,∵EF ∥OA ,∴△CEF ∽△CBO ,∴CE CB =EFBO,∴CE 5 =-m 3 ,∴CE =-53m ,设直线BC 的解析式为y =kx +b (k ≠0),把B (-3,0),C (0,-4)代入得,⎩⎪⎨⎪⎧-3k +b =0b =-4 ,解得⎩⎪⎨⎪⎧k =-43b =-4,∴直线BC 的解析式为y =-43 x -4,∴E (m ,-43 m -4),∴PE =-43 m 2-4m ,∵PE =CE ,∴-43 m 2-4m =-53 m ,解得m 1=-74 ,m 2=0(舍去),∴CE =-53 ×(-74 )=3512 ,∴四边形PECE ′的周长为4CE =4×3512 =353;当点P 在第二象限时,如解图③第2题解图③同理可得43 m 2+4m =-53 m ,解得m 1=-174 ,m 2=0(舍去),∴CE =-53 ×(-174 )=8512 ,∴四边形PECE ′的周长为4CE =4×8512 =853 ;综上所述,四边形PECE ′的周长为353 或853.类型二 面积问题1. 解:(1)∵抛物线y =ax 2+bx +5(a ≠0)交x 轴于A (-1,0),B (5,0)两点∴⎩⎪⎨⎪⎧a -b +5=025a +5b +5=0 ,解得⎩⎪⎨⎪⎧a =-1b =4 ∴抛物线的解析式为y =-x 2+4x +5;(2)如解图,过点G 作GD ∥y 轴交BC 于点D ,连接CG ∵当x =0时,y =-x 2+4x +5=5 ∴C (0,5) ∵GH ∥AC ∴S △AGH =S △CGH∴h =S △AGB -S △AHB =S △AGH +S △BGH =S △CGH +S △BGH =S △BGC . 设直线BC 的解析式为y =kx +b 1(k ≠0) 将B (5,0),C (0,5)代入y =kx +b 1中∴⎩⎪⎨⎪⎧5k +b 1=0b 1=5 ,解得⎩⎪⎨⎪⎧k =-1b 1=5 ∴直线BC 的解析式为y =-x +5∵点G 的横坐标为t (0<t <5),∴G (t ,-t 2+4t +5),D (t ,-t +5) ∴GD =-t 2+4t +5-(-t +5)=-t 2+5t ∴h =S △BGC =S △CGD +S △BGD =12 GD ·t +12 GD ·(5-t ) =-52 (t -52 )2+1258∵-52<0,0<t <5∴当t =52 时,h 取最大值,最大值为1258.第1题解图2. 解:(1)由题意得⎩⎪⎨⎪⎧-b 2a =2,9a +3b =3,解得⎩⎪⎨⎪⎧a =-1,b =4;(2)(i)如解图①,延长BD 与x 轴交于点M ,延长CE 与x 轴交于点N ,过点A 作AF ⊥CE 于点F ,连接OB ,AC第2题解图①由(1)知抛物线的解析式为y =-x 2+4x ,易知直线OA 的解析式为y =x ∵点B ,C 在抛物线上,点B 横坐标为t ,点C 的横坐标为t +1 ∴B (t ,-t 2+4t ),C (t +1,-(t +1)2+4(t +1)),D (t ,t ),E (t +1,t +1) ∴OM =t ,BD =-t 2+3t ,CE =-(t +1)2+3(t +1),AF =-t +2 ∵0<t <2 ∴1<t +1<3∴S △OBD +S △ACE =12 OM ·BD +12 CE ·AF =12 t ·(-t 2+3t )+12 [-(t +1)2+3(t +1)]·(-t +2)=2;(ii)存在.如解图②,当点B 在点D 上方,即2<t <3时,过点D 作DQ ⊥EC 于点Q ,连接BE ,CD第2题解图②∵BD ∥EC∴四边形DBEC 为梯形此时,BD =-t 2+3t ,CE =-(t +1)2+3(t +1) ∵DQ =1∴S 四边形DBEC =12 (BD +EC )·DQ =12 [-t 2+3t -(t +1)2+3(t +1)]·1=t -1当S 四边形DBEC =32 时,可得t -1=32 ,解得t =52;当点D 在点B 上方,即t >3时,如解图③,过点D 作DQ ⊥EC 于点Q ,连接BC第2题解图③此时BD =t 2-3t ,CE =(t +1)2-3(t +1)∴S 四边形DBCE =12 (BD +EC )·DQ =12 [t 2-3t +(t +1)2-3(t -1)]·1=t 2-2t -1令t 2-2t -1=32 ,解得t 1=142 +1<3,t 2=-142 +1<3,均舍去;综上所述,t 的值为52.类型三 存在性问题典例精析例 解:(1)存在 设点M (1,m )由题意得BC =32 ,BM =4+m 2 ,CM =1+(m -3)2①当BC 为腰时 a .若BC =BM ,如解图①例题解图①即32=4+m2解得m=±14则M1(1,14),M2(1,-14);b.若BC=CM,如解图②即32=1+(m-3)2,解得m=3±17,则M3(1,3+17),M4(1,3-17);②当BC为底边时,则CM=BM,如解图②,即1+(m-3)2=4+m2解得m=1,则M5(1,1);∴综上所述,满足条件的点M的坐标为(1,14)或(1,-14)或(1,3+17)或(1,3-17)或(1,1);例题解图②(2)存在设点N(x,-x2+2x+3).①当点C为直角顶点时,如解图③,则∠N1CB=90°,过点N1作N1H⊥y轴于点H∵△BOC是等腰直角三角形∴∠BCO=45°∴∠N1CH=180°-90°-45°=45°∴△N1CH是等腰直角三角形∴N1H=HC,即x=-x2+2x+3-3解得x1=0(舍去),x2=1∴N1(1,4);例题解图③②当点B 为直角顶点时,如解图③,则∠CBN 2=90°,过点N 2作N 2G ⊥y 轴,过点B 作BG ⊥x 轴交N 2G 于点G∴同理可得∠BN 2G =45°,△BN 2G 是等腰直角三角形 ∴N 2G =BG ,即3-x =-(-x 2+2x +3) 解得x 1=-2,x 2=3(舍去) ∴N 2(-2,-5).综上所述,满足条件的点N 的坐标为 (1,4)或(-2,-5); (3)存在∵点Q 在第一象限内抛物线上 ∴设Q (m ,-m 2+2m +3),0<m <3 ∵QG ⊥x 轴∴G (m ,0),OG =m ,QG =-m 2+2m +3 ∵△AOC ∽△QGO ∴AO QG =CO OG ,即1-m 2+2m +3 =3m解得m 1=5+1336 或m 2=5-1336 (舍去)此时点Q 的坐标为(5+1336 ,5+13318 );(4)存在设E (m ,-m 2+2m +3),F (n ,0),易得抛物线顶点D 的坐标为(1,4),点C 的坐标为(0,3)①如解图④,当DE ,FC 是平行四边形对角线时 ∵平行四边形对角线互相平分 ∴DE ,FC 的中点重合∴⎩⎪⎨⎪⎧1+m =n +04-m 2+2m +3=0+3 解得m =1+5 或m =1-5∴E 1(1+5 ,-1)或E 2(1-5 ,-1);例题解图④②如解图⑤,当DF ,EC 是平行四边形对角线时,同理DF ,EC 的中点重合∴⎩⎪⎨⎪⎧1+n =m +04+0=-m 2+2m +3+3 解得m =1+3 或m =1-3 ∴E 3(1+3 ,1)或E 4(1-3 ,1);例题解图⑤③当DC ,EF 是平行四边形对角线时,DC ,EF 的中点重合∴⎩⎪⎨⎪⎧1+0=m +n 4+3=-m 2+2m +3+0方程组无实数解.综上所述,满足条件的点E 的坐标为(1+5 ,-1)或(1-5 ,-1)或(1+3 ,1)或(1-3 ,1); (5)存在如解图⑥,由题意知,A (-1,0),C (0,3),设点H 的坐标为(p ,0) ∴AH 2=(p +1)2,CH 2=p 2+32,AC 2=12+32=10 当AC 为矩形的边时,∠ACH =90° ∴AH 2=CH 2+AC 2即(p +1)2=p 2+32+10,解得p =9 ∴点H 的坐标为(9,0);当AC 为矩形的对角线时,∠AHC =90° ∴此时点H 与原点重合,点H 的坐标为(0,0). 综上所述,满足条件的点H 的坐标为(9,0)或(0,0);例题解图⑥(6)存在如解图⑦,过点S 作SZ ⊥x 轴于点Z ,交BC 于点X ∵A (-1,0),B (3,0),C (0,3)∴OA =1,OC =OB =3,易得直线BC 的函数解析式为y =-x +3 ∴∠OBC =∠OCB =45° ∵SZ ⊥x 轴∴∠BXZ =∠SXT =45° ∵ST ⊥BC ∴XT =ST设S (m ,-m 2+2m +3),且0<m <3,则X (m ,-m +3) ∴CX =m 2+(-m +3-3)2 =2 m ,SX =-m 2+3m ∴ST =TX =22 SX =-22 m 2+322m ∴CT =CX -TX =2 m -(-22 m 2+322 m )=22 m 2-22m ①若∠SCT =∠CAO∴tan ∠SCT =tan ∠CAO =OCOA =3∵tan ∠SCT =STCT =3∴ST =3CT ∴-22 m 2+322 m =3×(22 m 2-22m )解得m =32 或m =0(舍去)∴点S 的坐标为(32 ,154 );②若∠CST =∠CAO 则tan ∠CST =tan ∠CAO =3 ∵tan ∠CST =CTST =3∴3ST =CT ∴3×(-22 m 2+322 m )=22 m 2-22m 解得m =52 或m =0(舍去)∴点S 的坐标为(52 ,74);综上所述,存在点S ,使得△CST 中有一个角与∠CAO 相等,点S 的坐标为(32 ,154 )或(52 ,74).例题解图⑦对接中考1. 解:(1)由题意可知,抛物线y =x 2+bx +c 过点A (-1,0),点B (5,0)∴⎩⎪⎨⎪⎧1-b +c =025+5b +c =0 ,解得⎩⎪⎨⎪⎧b =-4c =-5; (2)①如解图,过点P 作y 轴的平行线交BC 于点D ∴S △PBC =S △CPD +S △PDB由(1)可知,c =-5,故点C 的坐标为(0,-5) 易知BC 的表达式为y =x -5∵点P 的坐标为(x 0,y 0)(0<x 0<5),点P 在抛物线上 ∴y 0=x 20 -4x 0-5设点D 的坐标为(x 0,x 0-5)∴|PD |=x 0-5-x 20 +4x 0+5=-x 20 +5x 0∴S △PBC =12 ×|PD |×5=12 ×(-x 20 +5x 0)×5 =-52 (x 0-52 )2+1258∴当x 0=52 时,△PBC 面积最大,最大值为1258;第1题解图②存在.由题意可知,∠EPF =90°,△PEF 为等腰直角三角形 ∴PE =PF∵PE ⊥x 轴,PF ∥x 轴,且点E 在线段BC 上,点F 在抛物线上 由(2)可知PE =-x 20 +5x 0 易知PF =|4-2x 0|∴|PF |=|PE |,即|4-2x 0|=|-x 20 +5x 0|解得x 0=4或x 0=7-332 或x 0=-1(舍去)或x 0=7+332 (舍去)当x 0=4时,解得y =-5当x 0=7-332 时,解得y 0=3-3332∴综上所述,当△PEF 为等腰直角三角形时,点P 的坐标为(4,-5)或(7-332 ,3-332 ).2. 解:(1)由题意得A ′(-3,0),B ′(0,-6),B (6,0)已知抛物线L 经过点A ′,B ′,B ,设抛物线L 的解析式为y =a (x +3)(x -6)(a ≠0) 将点B ′(0,-6)代入抛物线解析式中得-6=a (0+3)(0-6),解得a =13∴抛物线L 的解析式为y =13 (x +3)(x -6)=13 x 2-x -6;(2)存在.∵A (0,-3),B ′(0,-6) ∴AB ′=3设直线AB 的解析式为y =kx +b (k ≠0) 将A (0,-3),B (6,0)代入直线AB 的解析式得⎩⎪⎨⎪⎧b =-36k +b =0 ,解得⎩⎪⎨⎪⎧b =-3k =12∴直线AB 的解析式为y =12 x -3∵点P 在直线AB 上∴设点P (m ,12m -3),分情况讨论:①当以AB ′为边且AP 2=AB ′2时,即m 2+(12 m )2=9解得m 1=655 ,m 2=-655∴点P 的坐标为(655 ,355 -3)或(-655 ,-355 -3);②当以AB ′为边且B ′P 2=AB ′2时,即m 2+(12 m +3)2=9解得m 1=0(舍去),m 2=-125∴P (-125 ,-215 );③当以AB ′为对角线时 ∵AB ′=3∴AB ′的中点坐标为(0,-92 )由菱形的性质可得y P =-92即12 m -3=-92 ,解得m =-3 ∴P (-3,-92);综上所述,点P 的坐标为(655 ,355 -3)或(-655 ,-355 -3)或(-125 ,-215 )或(-3,-92). 拓展类型 二次函数性质综合题1. 解:(1)把点(2,1)代入y =x 2-2tx +3中 得4-4t +3=1解得t =32; (2)∵抛物线对称轴为直线x =t①若0<t ≤3∵a =1>0∴当x =t 时,函数y 取得最小值∵y 的最小值为-2∴t 2-2t 2+3=-2解得t =±5 .∵0<t ≤3∴t =5 ;②若t >3,∵a =1>0∴当0≤x ≤3时,y 随x 的增大而减小∴当x =3时,函数y 取得最小值∵y 的最小值为-2∴9-6t +3=-2解得t =73(不符合题意,舍去). 综上所述,t 的值为5 ;(3)∵A (m -2,a ),C (m ,a )关于对称轴直线x =t 对称∴m -2+m 2=t ,即m -1=t ,且点A 在对称轴左侧,点C 在对称轴右侧. 在y =x 2-2tx +3中令x =0,则y =3∴抛物线与y 轴交点为(0,3)∴此交点关于对称轴直线x =t 的对称点为(2m -2,3).∵a <3,b <3且t >0∴4<2m -2,解得m >3.当点A ,B 都在对称轴左边时∵a <b∴4<m -2,解得m >6∴m >6;当点A ,B 分别在对称轴两侧时∴B 到对称轴的距离大于A 到对称轴的距离∴4-(m -1)>m -1-(m -2),解得m <4∴3<m <4.综上所述,m 的取值范围为3<m <4或m >6.2. 解:(1)由题意得,-b 2a=2 解得b =-4a∴4ac -b 24a =12a -(-4a )24a=3-4a ∴抛物线顶点M 的坐标为(2,3-4a );(2)y 2<y 1,理由如下:由题可知,抛物线的对称轴为直线x =2∴A (x 1,y 1)关于直线x =2的对称点为(4-x 1,y 1)∵x 1<2<x 2,x 1+x 2<4∴2<x 2<4-x 1∵a >0∴抛物线开口向上∴在对称轴右侧y 随x 的增大而增大∴y 2<y 1;(3)b 的值为-12或20.【解法提示】由(1)知,b =-4a ,∴抛物线的解析式为y =ax 2-4ax +3,当a >0时,抛物线开口向上,此时在对称轴左侧,y 随x 的增大而减小,∴当x =-1时,函数值y 最大,最大值为a +4a +3,∴a +4a +3=18,解得a =3,∴b =-4a =-12;当a <0时,抛物线开口向下,此时在对称轴左侧,y 随x 的增大而增大,∴当x =1时,函数值y 最大,最大值为a -4a +3,∴a -4a +3=18,解得a =-5,∴b =-4a =20.综上所述,b 的值为-12或20.3. 解:(1)∵抛物线的对称轴为直线x =--4a 2a=2,抛物线与x 轴的交点为A (1,0),B ∴B (3,0)∴OB =3.∵OC =2OB∴OC =6.∴抛物线开口向下∴C (0,-6).把A (1,0),C (0,-6)代入y =ax 2-4ax +c 中得⎩⎪⎨⎪⎧a -4a +c =0,c =-6, 解得⎩⎪⎨⎪⎧a =-2,c =-6, ∴抛物线的解析式为y =-2x 2+8x -6;(2)由解析式可知抛物线的最大值为4ac -(-4a )24a =4ac -16a 24a=c -4a . ∵抛物线的最大值为6∴c -4a =6.∵抛物线过点A (1,0)∴a -4a +c =0,即c -4a =-a∴-a =6,即a =-6;(3)已知抛物线的对称轴为直线x =2,a <0∴(52 ,n )与(32,n )关于对称轴对称 当点P 在对称轴的左侧(含顶点)时,y 随x 的增大而增大,由m <n ,得x 0<32; 当点P 在对称轴的右侧时,y 随x 的增大而减小,由m <n ,得x 0>52. 综上所述,x 0的取值范围为x 0<32 或x 0>52.。
2015年中考数学试题及答案(解析版)

中考数学试卷一.选择题(本大题共8小题,每小题3分,满分24分。
在每小题给出的四个选项中,只有一个是符合题目要求的,请将正确选项填在括号内。
)1.(2013宜宾)下列各数中,最小的数是()A.2 B.﹣3 C.﹣D.0考点:有理数大小比较.分析:根据正数都大于0,负数都小于0,正数大于一切负数,两个负数绝对值大的反而小,进行比较即可.解答:解:∵﹣3<﹣<0<2,∴最小的数是﹣3;故选B.点评:此题考查了有理数的大小比较,要熟练掌握任意两个有理数比较大小的方法:正数都大于0,负数都小于0,正数大于一切负数,两个负数绝对值大的反而小.2.(2013宜宾)据宜宾市旅游局公布的数据,今年“五一”小长假期间,全市实现旅游总收入330000000元.将330000000用科学记数法表示为()A.3.3×108B.3.3×109C.3.3×107D.0.33×1010考点:科学记数法—表示较大的数.专题:计算题.分析:找出所求数字的位数,减去1得到10的指数,表示成科学记数法即可.解答:解:330000000用科学记数法表示为3.3×108.故选A.点评:此题考查了科学记数法﹣表示较大的数,科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a的值以及n的值.3.(2013宜宾)下列水平放置的四个几何体中,主视图与其它三个不相同的是()A. B. C.D.考点:简单几何体的三视图.分析:分别找到四个几何体从正面看所得到的图形比较即可.解答:解:A.主视图为长方形;B.主视图为长方形;C.主视图为长方形;D.主视图为三角形.则主视图与其它三个不相同的是D.故选D.点评:本题考查了三视图的知识,主视图是从物体的正面看得到的视图.4.(2013宜宾)要判断小强同学的数学考试成绩是否稳定,那么需要知道他最近几次数学考试成绩的()A.方差 B.众数 C.平均数D.中位数考点:方差;统计量的选择.分析:根据方差的意义作出判断即可.解答:解:要判断小强同学的数学考试成绩是否稳定,只需要知道他最近几次数学考试成绩的方差即可.故选A.点评:本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.5.(2013宜宾)若关于x的一元二次方程x2+2x+k=0有两个不相等的实数根,则k的取值范围是()A.k<1 B.k>1 C.k=1 D.k≥0考点:根的判别式.分析:判断上述方程的根的情况,只要看根的判别式△=b2﹣4ac的值的符号就可以了.解答:解:∵关于x的一元二次方程x2+2x+k=0有两个不相等的实数根,a=1,b=2,c=k,∴△=b2﹣4ac=22﹣4×1×k>0,∴k<1,故选:A.点评:此题主要考查了根的判别式,一元二次方程根的情况与判别式△的关系:(1)△>0⇔方程有两个不相等的实数根;(2)△=0⇔方程有两个相等的实数根;(3)△<0⇔方程没有实数根.6.(2013宜宾)矩形具有而菱形不具有的性质是()A.两组对边分别平行 B.对角线相等C.对角线互相平分D.两组对角分别相等考点:矩形的性质;菱形的性质.分析:根据矩形与菱形的性质对各选项分析判断后利用排除法求解.解答:解:A.矩形与菱形的两组对边都分别平行,故本选项错误;B.矩形的对角线相等,菱形的对角线不相等,故本选项正确;C.矩形与菱形的对角线都互相平分,故本选项错误;D.矩形与菱形的两组对角都分别相等,故本选项错误.故选B.点评:本题考查了矩形的性质,菱形的性质,熟记两图形的性质是解题的关键.7.(2013宜宾)某棵果树前x年的总产量y与x之间的关系如图所示,从目前记录的结果看,前x年的年平均产量最高,则x的值为()A.3 B.5 C.7 D.9考点:算术平均数.分析:由已知中图象表示某棵果树前x年的总产量y与n之间的关系,可分析出平均产量的几何意义为原点与该点边线的斜率,结合图象可得答案.解答:解:若果树前x年的总产量y与n在图中对应P(x,y)点则前x年的年平均产量即为直线OP的斜率,由图易得当x=7时,直线OP的斜率最大,即前7年的年平均产量最高,x=7.故选C.点评:本题以函数的图象与图象变化为载体考查了斜率的几何意义,其中正确分析出平均产量的几何意义是解答本题的关键.8.(2013宜宾)对于实数a、b,定义一种运算“⊗”为:a⊗b=a2+ab﹣2,有下列命题:①1⊗3=2;②方程x⊗1=0的根为:x1=﹣2,x2=1;③不等式组的解集为:﹣1<x<4;④点(,)在函数y=x⊗(﹣1)的图象上.其中正确的是()A.①②③④B.①③C.①②③D.③④考点:二次函数图象上点的坐标特征;有理数的混合运算;解一元二次方程-因式分解法;解一元一次不等式组;命题与定理.专题:新定义.分析:根据新定义得到1⊗3=12+1×3﹣2=2,则可对①进行判断;根据新定义由x⊗1=0得到x2+x﹣2=0,然后解方程可对②进行判断;根据新定义得,解得﹣1<x<4,可对③进行判断;根据新定义得y=x⊗(﹣1)=x2﹣x﹣2,然后把x=代入计算得到对应的函数值,则可对④进行判断.解答:解:1⊗3=12+1×3﹣2=2,所以①正确;∵x⊗1=0,∴x2+x﹣2=0,∴x1=﹣2,x2=1,所以②正确;∵(﹣2)⊗x﹣4=4﹣2x﹣2﹣4=﹣2x﹣2,1⊗x﹣3=1+x﹣2﹣3=x﹣4,∴,解得﹣1<x<4,所以③正确;∵y=x⊗(﹣1)=x2﹣x﹣2,∴当x=时,y=﹣﹣2=﹣,所以④错误.故选C.点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足二次函数的解析式.也考查了阅读理解能力、解一元二次方程以及解一元一次不等式组.二.填空题(本大题共8小题,每小题3分,满分24分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015湖南中考复习
二次函数的综合题及应用
考点一:确定二次函数关系式
例1 (1)如图,已知二次函数y=x 2
+bx+c 过点A (1,0),C (0,-3) (1)求此二次函数的解析式;
(2)在抛物线上存在一点P 使△ABP 的面积为10,请直接写出点P 的坐标.
思路分析:(1)利用待定系数法把A (1,0),C (0,-3)代入)二次函数y=x 2
+bx+c 中,即可算出b 、c
的值,进而得到函数解析式是y=x 2
+2x-3;
(2)首先求出A 、B 两点坐标,再算出AB 的长,再设P (m ,n ),根据△ABP 的面积为10可以计算出n 的值,然后再利用二次函数解析式计算出m 的值即可得到P 点坐标.
解:(1)∵二次函数y=x 2
+bx+c 过点A (1,0),C (0,-3),
∴103b c c ++=⎧⎨=⎩,解得23
b c =⎧⎨=⎩,∴二次函数的解析式为y=x 2+2x-3; (2)∵当y=0时,x 2
+2x-3=0, 解得:x 1=-3,x 2=1;
∴A (1,0),B (-3,0), ∴AB=4,
设P (m ,n ),
∵△ABP 的面积为10, ∴
1
2
AB•|n|=10, 解得:n=±5,
当n=5时,m 2
+2m-3=5, 解得:m=-4或2,
∴P (-4,5)(2,5);
当n=-5时,m 2
+2m-3=-5, 方程无解,
故P (-4,5)(2,5);
点评:此题主要考查了待定系数法求二次函数解析式,以及求点的坐标,关键是掌握凡是函数图象经过的点必能满足解析式.
(2)在直角坐标平面中,O 为坐标原点,二次函数2
y x bx c =++的图象与x 轴的负半轴相交于点C ,如图3-3,点C 的坐标为(0,-3),且BO =CO (1) 求这个二次函数的解析式;
(2) 设这个二次函数的图象的顶点为M ,求AM 的长.
【考点要求】本题考查二次函数解析式的确定。
【思路点拨】由题目条件,可用待定系数法求解析式
(1)(0,3),|3|3,3C OC c -=-=∴=-Q ,
OC BO =Q 又,
,
9330,630,2b b b +-=+==-。
223y x x ∴=--。
(
2
)
21,(1)1234,(1,0),(1,4)22
b f A M a --
=-==--=---, 222425AM ∴=+=
【答案】(1)223y x x =--;(2)25AM =。
点二:二次函数与x 轴的交点问题
例2 (1)已知二次函数y=x 2
-3x+m (m 为常数)的图象与x 轴的一个交点为(1,0),则关于x 的一元
二次方程x 2
-3x+m=0的两实数根是( ) A .x 1=1,x 2=-1 B .x 1=1,x 2=2 C .x 1=1,x 2=0 D .x 1=1,x 2=3
点评:本题考查了抛物线与x 轴的交点.解答该题时,也可以利用代入法求得m 的值,然后来求关于x 的
一元二次方程x 2
-3x+m=0的两实数根. 对应训练
(2)二次函数y=2x 2
+mx+8的图象如图所示,则m 的值是( ) A .-8 B .8 C .±8 D .6
(3)若二次函数y=ax 2
+bx+c (a≠0)的图象与x 轴有两个交点,坐标分别为(x 1,0),(x 2,0),且x 1<x 2,图象上有一点M (x 0,y 0)在x 轴下方,则下列判断正确的是( )
A .a >0
B .b 2
-4ac≥0 C .x 1<x 0<x 2 D .a (x 0-x 1)(x 0-x 2)<0
考点三:二次函数的实际应用
例3 (1)为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y (千克)与销售价x (元/千克)有如下关系:y=-2x+80.设这种产品每天的销售利润为w 元. (1)求w 与x 之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
y
C
B A -6
-4-2
8
642
-6-4
-264
2
O
图3-3
(3)某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体形.其中,抽屉底面周长为180cm,高为20cm.请通过计算说明,当底面的宽x为何值时,抽屉的体积y最大?最大为多少?(材质及其厚度等暂忽略不计).
4.解:已知抽屉底面宽为x cm,则底面长为180÷2-x=(90-x)cm.
由题意得:y=x(90-x)×20=-20(x2-90x)=-20(x-45)2+40500
当x=45时,y有最大值,最大值为40500.
答:当抽屉底面宽为45cm时,抽屉的体积最大,最大体积为40500cm3.
考点四:二次函数综合性题目
例4 如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
例4.解:(1)∵C(0,1),OD=OC,∴D点坐标为(1,0).设直线CD的解析式为y=kx+b(k≠0),
将C(0,1),D(1,0)代入得:
1
b
k b
=
⎧
⎨
+=
⎩
,解得:b=1,k=-1,∴直线CD的解析式为:y=-x+1.
(2)设抛物线的解析式为y=a(x-2)2+3,将C(0,1)代入得:1=a×(-2)2+3,
解得a=-1
2
.∴y=-
1
2
(x-2)2+3=-
1
2
x2+2x+1.
(3)证明:由题意可知,∠ECD=45°,
∵OC=OD,且OC⊥OD,∴△OCD为等腰直角三角形,∠ODC=45°,∴∠ECD=∠ODC,∴CE∥x轴,则点C、E关于对称轴(直线x=2)对称,∴点E的坐标为(4,1).
如答图①所示,设对称轴(直线x=2)与CE交于点F,则F(2,1),
∴ME=CM=QM=2,∴△QME与△QMC均为等腰直角三角形,∴∠QEC=∠QCE=45°.
又∵△OCD为等腰直角三角形,∴∠ODC=∠OCD=45°,∴∠QEC=∠QCE=∠ODC=∠OCD=45°,∴△CEQ∽△CDO.
(4)存在.
如答图②所示,作点C 关于直线QE 的对称点C′,作点C 关于x 轴的对称点C″,连接C′C″,交OD 于点F ,交QE 于点P ,则△PCF 即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF 的周长等于线段C′C″的长度. (证明如下:不妨在线段OD 上取异于点F 的任一点F′,在线段QE 上取异于点P 的任一点P′,连接F′C″,F′P′,P′C′.
由轴对称的性质可知,△P′CF′的周长=F′C″+F′P′+P′C′; 而F′C″+F′P′+P′C′是点C′,C″之间的折线段,
由两点之间线段最短可知:F′C″+F′P′+P′C′>C′C″, 即△P′CF′的周长大于△PCE 的周长.) 如答图③所示,连接C′E,
∵C ,C′关于直线QE 对称,△QCE 为等腰直角三角形, ∴△QC′E 为等腰直角三角形, ∴△CEC′为等腰直角三角形, ∴点C′的坐标为(4,5);
∵C ,C″关于x 轴对称,∴点C″的坐标为(-1,0). 过点C′作C′N⊥y 轴于点N ,则NC′=4,NC″=4+1+1=6, 在Rt △C′NC″中,由勾股定理得:
C′C″=222246213NC NC '''+=+=.
综上所述,在P 点和F 点移动过程中,△PCF 的周长存在最小值,最小值为213.。
