第七章:CPLEX在公交乘务排班问题中的应用
线性规划求解在客户服务中心排班问题中的应用

线性规划求解在客户服务中心排班问题中的应用赵红艳(山东英才职业技术学院,山东济南250104)摘要:线性规划被广泛地应用于工业、交通、国防、经济、管理等领域,已成为现代科学管理的重要手段和管理决策的有效方法,在管理中的有代表性的应用案例有资源分配问题、员工的排班问题、运输问题、投资问题和成本效益平衡问题等。
Exce的普及性和易学性也会让读者感到利用计算机求解线性规划十分容易。
本文给出运用规划求解,解决客户服务中心每个班次的上班人数,使在满足客户服务的情况下,达到成本最低。
关键词:线性规划;规划求解;客户中心;排班中图分类号:TP311文献标识码:A文章编号:1009-3044(2008)06-11143-05TheApplicationofSettlementbyLinearProgrammingintheStuffShiftArrangementofConsumerServiceCenterZHAOHong-yan(ShandongYingcaiVocationalTechnologyCollege,Jinan250104,China)Abstract:Linearprogramminghasbeenappliedinindustry,communications,economy,andmanagementwidely,andithasbecomeanimportantandefficientmeansofmodernscientificmanagement.Thebalancesofresourceallocation,thestuffshiftarrangement,theinvest-mentandcostaretherepresentativeappliedcasesinmanagement.Excelispopularandeasytolearn,whichmakesthelinearprogramset-tledbycomputereasyforpeople.Settlementbyprogrammingisexplainedinthisarticle,whichisusedtogivethemostreasonablenumberofpeopleineachshiftintheconsumerservicecenter,inpurposeofusingthelowestcosttomeettheconsumer'sneed.Keywords:linearprogramming;thesettlementofprogramming;consumerservicecenter;stuffshiftarrangement1引言线性规划是运筹学的一个分支,它的应用已愈来愈深入到社会生产和经济活动的各个领域。
关于公交排班方案的模型建立及研究

关于公交排班方案的模型建立及研究思绪如泉涌,关于公交排班方案的模型建立及研究,就从这里开始吧。
一、问题背景城市公交作为市民出行的重要交通工具,其运营效率和服务质量直接关系到市民的出行体验。
然而,在现有的公交系统中,排班问题一直是一个棘手的难题。
如何合理安排公交车辆的运行时间、路线和班次,使得车辆运行效率最大化,同时满足市民的出行需求,成为了我们研究的核心问题。
二、模型建立1.基本假设在建立模型之前,我们需要对公交系统进行一些基本假设:(1)公交车辆在运行过程中,不考虑交通拥堵、故障等因素;(2)公交车辆在站点停靠时间固定;(3)市民出行需求相对稳定;(4)公交车辆运行速度恒定。
2.模型参数(1)车辆数:N(2)线路数:M(3)站点数:S(4)运行周期:T(5)班次间隔:D(6)市民出行需求:Q3.模型构建(1)目标函数我们的目标是在满足市民出行需求的前提下,最小化公交车辆的运行成本。
运行成本包括车辆折旧、燃料消耗、人工成本等。
因此,我们可以将目标函数定义为:f(排班方案)=车辆折旧成本+燃料消耗成本+人工成本(2)约束条件①车辆运行时间约束:车辆在运行周期内,必须完成至少一次往返;②线路运行时间约束:车辆在运行周期内,必须完成所有线路的运行;③站点停靠时间约束:车辆在站点停靠时间不能超过规定时间;④市民出行需求约束:车辆在运行周期内,必须满足市民的出行需求。
三、模型求解1.算法选择针对公交排班问题,我们可以选择遗传算法、蚁群算法、粒子群算法等智能优化算法进行求解。
这里,我们选择遗传算法进行求解。
2.求解步骤(1)初始化种群:根据车辆数、线路数和站点数,一定规模的初始种群;(2)适应度评价:计算每个排班方案的适应度,适应度越高的排班方案,其运行成本越低;(3)选择操作:根据适应度评价结果,选择优秀个体进行交叉和变异;(4)交叉操作:将优秀个体进行交叉,新的排班方案;(5)变异操作:对新的排班方案进行变异,增加种群的多样性;(6)适应度更新:计算新排班方案的适应度;(7)终止条件:判断是否达到终止条件,如达到,则输出最优排班方案;否则,返回步骤(3)继续迭代。
运筹学在公共交通管理中的应用

运筹学在公共交通管理中的应用运筹学是一门研究在有限的资源条件下进行优化决策的学科。
它利用数学、统计学和计算机科学等方法来解决各种管理问题,其中包括公共交通管理。
公共交通管理是指对公共交通系统进行有效规划、组织和运营,以提供高效、安全、便捷的服务。
运筹学在公共交通管理中的应用可以帮助提高交通系统的运行效率,减少能源消耗,改善城市交通状况。
本文将介绍几种常见的运筹学方法在公共交通管理中的应用。
一、线路规划与优化公共交通线路规划是指确定适合乘客出行需求的线路,使得线路覆盖范围广、换乘次数少、运行时间短等。
运筹学方法可以通过建立数学模型来优化线路规划。
首先,需要根据乘客分布和需求进行数据收集和分析,确定潜在的线路候选集合。
然后,可以利用网络优化、图论等方法来计算出最优线路,使得每个节点都能被尽可能多的线路覆盖,同时尽量减少线路交叉和冗余。
二、车辆调度与运营车辆调度与运营是指合理安排车辆的出发时间、路径以及车辆之间的间隔,以最大限度地满足乘客需求和减少系统拥堵。
运筹学方法可以通过建立数学模型来优化车辆调度与运营方案。
例如,可以利用线性规划模型来确定每个车辆的出发时间和运行路径,使得乘客的等待时间和行程时间最小化,同时保证车辆之间的间隔合理。
三、乘客流量预测与优化乘客流量预测是指根据历史数据和其他相关因素,对未来一段时间内的乘客流量进行预测。
运筹学方法可以通过建立时间序列模型或者机器学习模型来进行乘客流量预测。
预测的结果可以用于优化公共交通系统的运营策略,如增加或减少车辆数量,调整车辆的发车频率,以满足不同时间段的乘客出行需求。
四、动态路径选择与导航动态路径选择与导航是指根据实时交通状况,为乘客提供最佳的出行路径和导航建议。
运筹学方法可以通过建立交通仿真模型来模拟不同路径的交通状况,并根据实时数据进行更新。
基于这些模型和数据,可以选择最佳的路径,为用户提供准确的导航建议,避免拥堵和浪费时间。
五、资源分配与调度资源分配与调度是指将有限的资源,如车辆、车站、人力等,合理分配和调度,以最大程度地提高交通系统的效率。
排队论在公共交通调度中的应用

排队论在公共交通调度中的应用随着城市化进程的不断加快,公共交通系统的重要性日益凸显。
公共交通调度是保障城市交通有序运行的关键环节,而排队论作为一种重要的数学工具,为公共交通调度提供了有效的解决方案。
本文将探讨排队论在公共交通调度中的应用,并分析其在提高运输效率、优化资源配置、减少拥堵等方面所取得的成效。
首先,排队论可以帮助提高公共交通系统的运输效率。
在高峰时段,人们集中出行导致车站拥堵、车辆满载等问题频发。
通过排队论模型可以分析乘客到达车站和乘车时间之间的关系,并据此优化发车间隔和乘客上下车时间。
例如,在地铁站点设置自助售票机和自动闸机,可以减少人工售票和验票所需时间,加快乘客进出站速度;通过合理设置发车间隔和增加运力,在高峰时段保证足够多列地铁列车供人们选择。
其次,排队论可以优化资源配置,在有限资源下提供更多服务。
城市中有限数量的公交车辆需要满足大量乘客的出行需求,如何合理配置车辆成为调度的关键问题。
排队论可以通过模拟乘客到达和乘车的过程,预测不同时间段和不同线路的客流量。
根据预测结果,可以调整车辆运行路线和数量,以满足不同线路上的需求。
例如,在繁忙的商业区增加公交车数量,以应对高峰时段的客流压力;在低峰时段缩减运力,以减少资源浪费。
此外,排队论还可以减少拥堵现象。
城市交通拥堵是公共交通系统面临的重要问题之一。
排队论模型可以通过分析乘客到达时间、上下车时间和运输能力之间的关系,在高峰时段合理安排发车间隔和增加运力。
例如,在高峰时段增加地铁列车数量,并根据实际情况调整发车间隔;在繁忙路段设置优先通行公交道,并对公交优先信号进行优化控制。
此外,排队论还可以提供决策支持工具,在应急情况下提供快速响应方案。
例如,在突发事件或自然灾害发生时,排队论可以通过模拟乘客流动和车辆调度过程,分析不同应急方案的可行性和效果,为决策者提供科学依据。
通过排队论模型,可以预测不同方案下的乘客等待时间、车辆调度时间等关键指标,并据此选择最优方案。
遗传算法在公交车辆智能排班系统中的应用研究的开题报告

遗传算法在公交车辆智能排班系统中的应用研究的开题报告一、研究背景公交车是城市公共交通的重要组成部分,公交车司机的排班管理直接影响到公交运输的安全、准时性和效率。
传统的排班方法往往是人工制定,缺乏科学可靠的数据支持和分析,容易出现排班不合理、车队错车、误点和低效等问题,引起乘客和公司的不满和投诉。
因此,如何利用现代信息技术和智能算法对公交车司机的排班进行优化和自动化,实现公交运输的智能化和高效化,是当前公交运输企业和研究者亟待探索的课题。
遗传算法是一种模拟自然进化生物优化问题解决方法,其模拟的是生物进化的过程。
在实际应用中,遗传算法具有搜索范围广、优化效果好、不受约束条件限制、并行性强等优点,适合于解决复杂的调度问题,包括公交车司机排班问题。
二、研究目的与意义本研究旨在运用遗传算法优化公交车司机排班问题,实现公交运输的智能化管理,提高运输效率和服务质量,同时减少成本和能源消耗,具有以下意义:1.提高公交运输服务的水平和满意度。
2.优化排班方案,降低司机的疲劳程度,提高工作效率和安全性。
3.减少人工处理的难度和复杂性,提高调度效率和准确性。
4.降低总成本和能源消耗,提高社会资源的利用效率。
三、研究内容与方法1.研究内容(1)公交车司机排班问题的基本原理和算法设计。
(2)遗传算法的工作原理和优化构架设计。
(3)公交车司机排班问题的建模、参数设置和实现方法。
(4)基于MATLAB编程工具的遗传算法程序设计和实验分析。
2.研究方法(1)文献调研。
对国内外相关研究文献进行搜集、筛选和分析,了解公交车司机排班问题及当前解决方案的研究进展和存在的问题。
(2)模型设计。
对公交车司机排班问题进行建模,并针对遗传算法的优化特点进行相应的参数设置和实现。
(3)程序编程。
采用MATLAB编程工具进行遗传算法的程序设计和实验分析,验证其优化效果和可行性。
(4)实验分析。
对程序实现的结果进行统计和分析,比较不同算法模型的优劣,优化公交车司机排班的方案。
基于集对分析的随机需求接驳公交调度模型

基于集对分析的随机需求接驳公交调度模型SUN Bo;YANG Chunfeng;WEI Ming;CHEN Hao【摘要】针对需求点的出行客流服从正态分布,基于集对分析理论,利用二元联系数刻画随机客流的确定和不确定部分,将其转化为带联系数的确定性数学模型,研究一类随机需求接驳公交调度模型,将乘客从需求点运输至轨道站点,追求总里程最少.同时,该模型集成了这些乘客的最大容忍在车时间对调度结果的影响.利用Cplex求解模型的精确解,结合实际算例,给出了不同车辆数的最优调度方案,比较了有无乘客在车时间限制的2种方案差异,并分析了客流的不确定程度对调度结果的影响.实验表明,随着客流的不确定程度逐渐增加引起需求点的上车人数变多,受车辆的额定载客量限制,这致使车辆偏好访问较远距离但不超过其额定载客量的需求点,因而总行驶里程也变大;考虑乘客的最大在车时间限制,这引导车辆提供\"直达\"服务,因而会增加总行使里程,但是满足了乘客的个性化出行需求.【期刊名称】《交通信息与安全》【年(卷),期】2018(036)006【总页数】5页(P130-134)【关键词】城市交通;需求响应型接驳公交;随机客流出行;正态分布;集对分析;Cplex 【作者】SUN Bo;YANG Chunfeng;WEI Ming;CHEN Hao【作者单位】【正文语种】中文【中图分类】U1210 引言若要发挥轨道交通在城市客运交通系统的主干道作用,必须将客运交通的主体客流吸引到轨道交通上来,接驳公交是满足市民出行“最后一公里”需求的一种重要补充公共交通方式。
目前,其运营管理模式多数与地面常规公交相似,以客流需求时空分布为基础,按固定线路、固定时间运营将乘客疏散至轨道站点,存在问题包括没法提供“门到门”服务、实现居民的零等待、按需求发车等。
借助互联网技术,需求响应型接驳公交(demand-responsive feeder transit services,DRFTS)是一种以满足乘客需求为导向的非固定线路灵活公交,可以弥补传统接驳公交的缺陷,吸引了国内外学者的广泛关注[1-5]。
对于公交排班问题的研究

题目 对于公交排班问题的研究摘 要本文针对公交排班问题,建立多元非线性规划模型和改进遗传算法,旨在为公交排班困难的问题提供有效建议。
针对问题一,求徐州2路公交车在早高峰时段运行所需要的最小公交车数量。
发车间隔决定公交车数量,以等车费用、乘客辆、乘车折损费用等为约束条件,建立关于发车间隔的多元非线性规划模型:1611,=()ik ij m i k m nT mink maxc v b δδ==ϒ+∑∑∑∑等 通过0-1规划,得出两个方案:方案一2辆单班车16辆双班车和方案二3辆单班车15辆双班车。
针对问题二,计算徐州市2路公交车完成一天的运行所需要的最少车辆,并完成发车表格。
以问题一求解早高峰运行车辆为例,对全天各个时段运行车辆进行求解,得出最少公交车数量。
以单班车一天不超过五个班次为约束条件,建立非刚性目标规划模型:'123()5p d d p d p d -+++-=使用发车间隔对发车表格进行填写。
进行单班车规划,确定单班车数为2辆,双班车数为18辆,总车数为20辆,发车表格详见附录I 。
针对问题三,求徐州市2路公交车完成一天运行所需要的最少车辆并完成发车表格。
根据单班车的工作性质,建立多元约束模型:41i i iT x y αβδ=+≥∑用Matlab 对单班车数量求解,使用3辆单班车,17辆双班车,总车辆数为20辆,根据发车间隔填表,详见附录II 。
针对问题四,计算完成一整天的运行所需要最少的公交车数量并完成发车表格。
改进遗传算法,应用双种群设计,将算法过程分为两步。
解出单班车数量为3辆,双班车数量为17辆,总车辆数为22辆,根据实际因素和发车间隔填表,详见附录III 。
关键词 多元非线性规划 0-1规划 非刚性目标规划模型 修正遗传算法一、问题背景与重述1.1问题背景随着徐州城市经济的快速发展和人民生活水平的不断提高,城市道路的不断增多容易引起突发客流短时间聚集和消散,对城市公共交通的运营提出了严峻的挑战。
数学建模辅导3--线性规划的应用

2
3
100
60
25
35
10
解:设 xij 表示第 i 种(i=1(甲)、i=2(乙)、i=3(丙))产品中 原料 j 的含量。(注意:正确定义决策变量。) 这样我们建立数学模型时,要考虑: 对于甲: x11,x12,x13;产品甲的产量为 x11 + x12+ x13 对于乙: x21,x22,x23;产品乙的产量为 x21+x22+ x23 对于丙: x31,x32,x33;产品丙的产量为 x31+x32 + x33 对于原料1: x11,x21,x31;原料1的需求量为 x11+x21 + x31 对于原料2: x12,x22,x32;原料2的需求量为 x12+x22 + x32 对于原料3: x13,x23,x33;原料3的需求量为 x13+x23 + x33 目标函数: 利润最大,利润 = 收入-原料支出 约束条件: 规格要求 4 个 供应量限制 3 个
11
利润 =总收入-总成本 =甲乙丙三种产品的销售单价*产品数量-甲乙丙使用的原料单价*原料数量 目标函数 max z=50(x11+x12+x13)+35(x21+x22+x23)+25(x31+x32+x33) -65(x11+x21+x31)-25(x12+x22+x32)-35(x13+x23+x33) = -15x11+25x12+15x13-30x21+10x22-40x31-10x33
minZ x 1 x 2 x 3 x 4 x 5 x 6 x1 x 6 x1 x 2 x2 x3 x3 x4 s .t x4 x5 x5 x6 x j 0 且为整数 60 70 60 50 20 30 j 1, 2 , , 6 .
公交车排班模型

公交车排班模型中的线性规划求解问题摘要本文研究的是在满足各时段(早高峰、日间平峰、晚高峰,晚平峰四个时段)时间,公交车以一定间隔连续发车的条件下,排班的最优问题。
根据各小题的约束条件,用运筹学中的线性规划知识建立模型,再利用Lingo求解,分别算出所需公交车总数以及单班车、双班车各需求量,制定排班的优化方案。
对于题目条件,我们有三个设想,其一,根据现实生活经验可知,公交车发车间隔相对固定,方便市民安排计划候车出行;其二,从简化模型的角度考虑,每辆车的司机固定,即司机间不允许换车开车;其三,单班车一天不超过5个班次,即认定为所有单班车一天总班次相加不超过5班。
对于题目一,从各班次发车间隔相等这一假定条件出发,要使在早高峰时段运行的车辆数最少,只需发车间隔尽可能大,于是我们取早的最大发车间隔5分钟来安排发车,由于该题无对单班车数量的其他要求,我们假定单班车在早高峰时段安排2辆,同时考虑到车辆要完成一个班次的运行后才可进行下一班次,建立相关模型,用Lingo编程求解得早高峰时段总共运行24个班次,所需的最少公交车数为16辆。
对于问题二,在已有模型的基础上,综合考虑全天的工作安排,发车间隔仍取每个阶段的最大发车间隔,同样的,考虑到单班车只在高峰期运行,在早高峰运行2到3个班次,在晚高峰运行2到3个班次,且每天运行不超过五个班次,,根据资源利用的最大化原则,我们知道单班车数不能超过3辆,这里我们仍假设单班车数为2辆,根据题目要求,我们要使每辆公交车的工作时间和上下午司机的工作时间尽可能均匀,且要使车辆的利用率得到最大,根据以上条件建立公交车排班模型,用Lingo编程求解得全天总共运行120个班次,所需的最少公交车数为16辆。
具体公交车排班计划表见表2—1。
对于问题三,该题约束了单班车数量不少于3辆,由问题二的分析既得单班车数量为3辆,改变问题二模型中的相关参数,用Lingo编程求解得全天总共运行120个班次,所需的最少公交车数为16辆。
cplex 指数函数

cplex 指数函数CPLEX定义了指数函数(exponential function)作为一种优化问题中的数学函数。
指数函数是一个以常数e为底数的幂函数,常用来表示增长率恒定的情况。
在优化中,指数函数通常用来描述约束或目标函数中的非线性关系。
在CPLEX中,指数函数可以通过非线性约束或目标函数来表示。
对于约束而言,指数函数常用来约束某个变量的取值不能超过一个指数函数的上界,或者限制变量之间的指数函数关系。
对于目标函数而言,指数函数常用来表示非线性的目标函数,即待优化的函数。
指数函数在优化问题中的应用广泛,一些常见的应用包括:1. 生产规模与利润关系的建模:指数函数可以用来描述生产规模与单位利润之间的关系,从而帮助企业找到最佳的生产规模。
2. 资源分配问题:指数函数可以用来描述资源分配与生产产出之间的关系,帮助企业决定如何分配资源以达到最大化产出。
3. 网络流量优化:指数函数可以用来描述网络中流量与带宽之间的关系,帮助决策者优化网络资源的分配。
4. 金融风险管理:指数函数可以用来描述投资收益与风险之间的关系,帮助投资者选择最佳的投资组合。
然而,由于指数函数的非线性特性,使得包含指数函数的优化问题具有一定的难度。
在求解这类问题时,CPLEX采用了一些先进的数值优化算法,如非线性规划方法、内点法等,来找到最优解或近似最优解。
这些算法结合了牛顿法、拟牛顿法等经典数学理论,在效率和精度方面取得了很大的进展。
CPLEX提供了一套友好的API,使得用户可以很方便地在优化模型中使用指数函数。
用户只需在模型中定义指数函数的约束或目标函数,并设置合适的参数和界限,然后将模型交给CPLEX进行求解即可。
总之,指数函数在优化问题中的应用非常广泛,在CPLEX中得到了良好的支持。
使用CPLEX的指数函数来建模和求解优化问题,可以帮助决策者更好地理解和优化现实世界中的复杂问题。
关于公交排班方案的模型建立及研究

关于公交司机排班方案的数学模型建立及研究摘要一、问题重述目前,随着南昌市经济进一步的发展,道路变得越来越多,公交线路也随之越来越多。
但相应的问题也相应的问题也层出不穷,例如:有的线路司机不足、有的线路司机每天需要开车的时间太长以至于给交通造成安全隐患、还有的线路经常堵车打乱了线路的运行计划等等。
为此建立公交排班问题的数学模型,并依据数学模型给出各种问题的优化方案就具有重要的现实意义。
本题就是基于公交排班安排的问题。
问题1:根据公交车运行线路及五月份具体情况,求当月总班次的最小值。
一般,公交公司按月给司机排班。
而为了使得公司的运行成本最低则必须综合分析公交线路的运行状况、公交车发班的频率,并且这两个因素又随着五月份每天不同的状况(工作日、节假日)进行变化。
因此必须先分析五月份工作日以及节假日不同时段公交车运行的情况,找出其内在的规律。
以公交线路的发班的间隔、车辆在线路中的运行情况、车辆的运行时间的可控性为参量建立数学模型。
问题2:根据对于司机工作情况的具体规定,建立模型求解五月份该线路的司机排班方案。
公交公司对于司机排班的规定主要有:(1)司机每天上班时间不超过8小时;(2)司机连续开车不得超过4小时;(3)每名司机至少每月完成120班次。
五月份有20个工作日,11个节假日。
因此为了对司机进行五月份的排班就必须解决以下问题:(1)让排班符合公交公司给出的条件;(2)各个条件之间的关系,满足条件应该遵守的顺序;(3)公交司机排班必须要合理,并且参与排班的人数为最小。
问题3:假如规定每个司机每周连续工作五天,休息两天。
求出每周需要司机的人数以及排班方案。
公交司机每周连续工作五天,休息两天。
需要优化司机的人数,这就是在问题二的司机日工作时间规定的基础上增加了司机周工作时间的控制条件。
对本问进行解答主要就是要理清司机日工作时间的与周工作时间的关系,以排班司机人数最少的前提下对司机进行排班。
二、问题分析问题1:根据公交车运行线路及五月份具体情况,求当月总班次的最小值。
CPLEX中文教程(第七章)

(一)公交乘务排班优化问题概述
公交乘务排班问题属活动资源的优化利用问题。一般是根 据给定的乘务任务、乘务规则等条件,考虑一定的优化目 标,对乘务员(组)的出乘时间、地点,担当的乘务任务、时 刻,退乘时间、地点等做出具体安排,以确保一定周期内 的所有乘务任务被执行。
第七章:IBM ILOG CPLEX在公交乘务排班优化问题中的应用
例1. 下面是某条线路的基本情况: 1、该线路的开收班时间: 冬令(12月~3月):6:20~18:10,夏令(4月~11月):6:15~18:20 2、该线路的司机人数:15人 3、该线路排班间隔: 平时:8~10分钟/班; 上下班高峰(6:00~8:30,11:30~13:30,16:30~18:00):4~8分钟/班 节假日:5~10分钟/班 4、该线路的运行时间: 正常:80~85分钟/班 高峰:100~120分钟/班 规定:(1)司机每天上班时间不超过8小时;(2)司机连续开车不得超 过4小时;(3)每名司机至少每月完成120班次。 问题一:针对五月份的节假日和非节假日,分别求出每日最少班次总数; 问题二:阐述你对上述规定的理解,并根据你的理解建立适当的数学模型, 合理地设计五月份该线路的司机排班方案。
第七章:IBM ILOG CPLEX在公交乘务排班优化问题中的应用 公交乘务排班问题的基本元素和各元素的基本属性如下: 1)公交线路:具有出发站、出发时刻、到达站、到达时刻、 中途停站等基本属性; 2)乘务员类型(组):包括司机、售票员等属性; 3)乘务规则:包括间休时间、工作时间、休息时间、乘务周 期、月工时等乘务值乘规则。 4)目标函数:乘务成本最小、需要的乘务员数量最少等。 5)约束条件:乘务员的工作时间必须满足乘务规则;每个线路、 每个班次都必须有乘务员值乘;乘务员劳动负衡均衡等约束 条件。
基于遗传算法的公交智能排班方法的研究

基于遗传算法的公交智能排班方法的研究陈远【摘要】研究公交车智能排班问题,建立数学模型,兼顾乘客出行效率和公交企业运营效益,给出利用遗传算法解决此问题的方法.重点阐述了智能排班的目标函数、适应度函数和遗传算子的设计.编制程序进行仿真实验,结果证明利用遗传算法解决公交智能排班问题,可以优化车辆调度,能在交通高峰和平峰期不均匀排班,符合公众和企业的利益,并提高了交通运行效率.【期刊名称】《智能计算机与应用》【年(卷),期】2012(002)005【总页数】3页(P75-77)【关键词】智能排班;遗传算法;公共交通【作者】陈远【作者单位】苏州经贸职业技术学院机电系,江苏苏州215009【正文语种】中文【中图分类】TP18在城市交通系统中,公交车辆的运行效率在城市顺畅交通方面一直发挥着主力型的重要作用。
公交运营的核心是通过科学、合理的排班调度,确定快捷、最佳的行车时刻表。
公交排班是公交企业管理的基础,是疏导城市客流、提供优质服务的关键。
行车时刻表的设计结果直接影响乘客的出行效率,并直接关系企业的经营效益。
因此,在城市公交网络中,运用科学的方法对车辆加以高效的排班调度是至关重要的。
遗传算法是建立在自然选择原理和自然遗传机制上的迭代式自适应概率性搜索算法[1]。
算法过程是,从一个种群开始,利用选择、交叉、变异等遗传算子使种群实现不断进化,最后达到全局最优解或近似最优解。
根据遗传算法的特点可以推知,该算法非常适合于建立数学模型,以利于得到公交排班优化方案。
1 公交排班的模型设计公交车运行时刻表的制定依据,是基于每条线路的乘客出行规律和客流量,来最终确定首/末班车的运营时间和发车密度的。
发车密度越大,乘客等待时间就越短,但是公交公司的运营成本就会相应增加。
运行时刻表的编排原则是,应当在能满足大部分乘客出行要求的前提下,尽量减少过多的班次投入,做到同时兼顾乘客和公交公司的双方利益,实现效益上的共赢。
本项目选用苏州公共交通公司的38路公交车线路作为智能排班的研究对象,这趟车从苏州火车站开出,途经市区商业中心,多个住宅小区和大型工厂,具有一定的典型性。
带时间窗的多车场公交乘务排班优化

带时间窗的多车场公交乘务排班优化陈明明;牛惠民【摘要】考虑多车场因素下的城市公交乘务排班问题,允许车辆空驶策略增加了排班结果的灵活性;引入乘务时间窗的概念,充分考虑了乘务人员的基本利益。
以最小化乘务组的车场驶入/驶出成本、停留等待成本和空驶成本为目标函数,建立了带时间窗的多车场公交乘务排班优化模型及禁忌搜索算法。
最后通过算例计算得到多车场下公交线路的最优乘务排班方案。
结果表明该方法在处理带有时间窗的多车场公交乘务组跨线排班问题具有良好的应用效果。
%The crew scheduling problem with multiple depots is considered in this paper.Adding the deadheading strategy can make the scheduling plan more flexible and introducing the concept of time window can satisfy the benefits of crew members.An optimization model with the mini-mum cost of pull-in/pull-out time,waiting time and deadheading as the objective function for bus crew scheduling with multiple depots under time window condition is formulated.The tabu search algorithm was used to solve the proposed model.Finally,the optimal crew scheduling program with multiple depots operated on several bus lines are calculated by one real example.The results show the method has a better effect on dealing with the bus crew scheduling problem with multi-ple depots under time window condition.【期刊名称】《兰州交通大学学报》【年(卷),期】2015(000)004【总页数】7页(P100-106)【关键词】乘务排班;时间窗;多车场;禁忌搜索算法【作者】陈明明;牛惠民【作者单位】兰州交通大学交通运输学院,甘肃兰州 730070;兰州交通大学交通运输学院,甘肃兰州 730070【正文语种】中文【中图分类】U491随着城市交通拥堵问题的不断凸显以及公交优先策略的不断推进,如何提升公交调度管理水平,尤其是公交乘务排班质量,已成为衡量一个城市服务水平的重要标志,也是当前公交调度理论研究的热点之一.近年来,很多国内外学者针对公交乘务排班问题进行了大量的研究[1-4].Smith等提出了一种基于集覆盖问题的乘务排班模型,其中被覆盖的元素为工作时间段[5].Clement等根据贪婪算法将班次划分成工作时间段,并使用遗传算法求解乘务人员排班问题[6].沈吟东等提出了带时间窗的多邻域结构和禁忌搜索算法[7].以上研究主要探讨了带有时间窗的单车场公交乘务排班问题,并未考虑多车场因素下的公交乘务排班问题.在城市公交调度实践中,由于公交车辆和乘务人员均按线路划分并固定配属,且每条线路在高峰时期均配有额外的车辆和人员,这种传统的单车场公交乘务排班模式,很难实现跨线调度问题,难以实现资源有效地利用 .多车场公交乘务排班问题,有助于整合不同车场的车辆和乘务组资源,在一定区域范围内将多个车场的车辆和乘务组人员相协调,高效地完成多条公交线路的班次任务. 钟石泉等分析了多车场车辆调度中能力、时间窗、多车型等约束的处理方法[8],但没有分析乘务组排班问题对多车场公交调度的影响.Boschetti等利用集分割方法同时解决了多车场的车辆调度和单车场的乘务排班问题[9];陈明明等以班次时间接续、乘务组劳动强度、车场能力等为约束条件,建立了多车场乘务排班问题的数学模型,但模型中未考虑乘务组时间窗的因素[10].鉴于乘务人员对班次时间有诸多要求,在保证完成班次任务的前提下,尽可能考虑乘务人员的时间需求,有必要深入研究带时间窗的公交乘务排班问题.基于此,本文将班次、乘务组、时间窗和多车场相结合,提出相应的乘务排班优化模型,并设计禁忌搜索算法求解模型,最后利用实例说明算法的有效性.1.1 模型假设1)所有公交线路的日班次数量及班次的起始站点及到发时刻均已确定.班次以起始站点的发车时刻的时间数列升序排列.2)乘务人员的签到和签退车场为同一车场,且人员和车辆固定,中途不更换车辆.以图1为例,乘务组1从车场1出发执行一系列班次,最后返回车场1,其所执行任务为有效任务;乘务组2从车场2出发执行一系列班次,返回车场1,其所执行任务为无效任务.3)乘务人员对工作时间均有不同要求,需满足时间窗约束.图2为乘务组时间窗约束示意图.乘务组1的时间窗为[6∶00,9∶00],在车场1的签到和签退时刻分别为6∶00和8∶55,满足时间窗约束,其所执行的班次为有效任务;乘务组2的时间窗为[6∶20,9∶20],在车场2的签到时刻为6∶00,不满足时间窗约束,其所执行的班次为无效任务.1.2 符号及参数设某城市公交车场数量为M;车场m中乘务组k对工作时间有特殊要求,对应的时间窗为[em,k,lm,k];其中,em,k为最早开始服务时间,lm,k为最迟结束服务时间;公交时刻表规定的一天班次数量为N;i为班次任务标记;di与ai分别为班次i在起始站的开始时刻及终点站的结束时刻.定义ti,j为车辆从节点i到节点j的空驶时间.由于车辆的空驶类型包括车场与班次起讫点之间(驶入、驶出车场)的空驶以及班次起讫点之间(跨线运行)的空驶,则节点i、j均可代表车场或班次的起讫点.当节点表示班次的起讫点时,其序号可与班次序号一致;当节点表示车场时,为避免与班次序号相混淆,车场序号可采用与班次总数N进行叠加处理的方法,即车场m的序号用N+m来表示.例如tN+2,4表示车辆从车场2到班次4起始站(驶出车场)的空驶时间;t1,4为车辆从班次1的终点站到班次4的起始站之间(跨线运行)的空驶时间;t5,N+2表示乘务组执行完班次5后返回车场2(驶入车场)的空驶时间.为0-1决策变量,若班次i由车场为m的乘务组k执行,其值为1,否则为0;为0-1变量,若车场为m的乘务组k执行班次任务i后,下一个执行任务为班次j,其值为1,否则为0.1.3 目标函数乘务组的成本包括班次运营时间成本、驶入/驶出车场时间成本、班次间空驶时间成本和停留等待时间成本,如图3所示.排班的优化目标是最小化乘务总成本.由于每个班次的运营时间固定,任意一种排班方案均包括所有的班次,因此班次运营成本在目标函数中可不予以考虑.驶入/驶出车场成本大小依赖于乘务组所执行的第一个班次和最后一个班次任务.对于车场m的第k个乘务组,其驶入/驶出车场的时间成本计算如下:式中|;|;ωd为乘务组的单位空驶成本.对于车场m的第k个乘务组,班次间的总空驶成本可由班次间空驶时间与单位空驶成本的乘积进行计算,即:式中:δi,j为0-1变量,若班次i与j间存在空驶现象,取值为1;否则为0.计算如下:式中:Start(i)表示班次i的起始站;End(i)表示班次i的终点站.停留等待时间是指乘务组执行下一班次的开始时刻与上一班次结束时刻的时间差.若班次间有空驶,应减去空驶时间.则对于车场m的第k个乘务组,停留等待总成本可表示为其中:ωw为乘务组的单位停留等待成本.基于以上分析,该数学模型的目标函数为1.4 约束条件模型的约束条件表述如下:约束(6)表示对于任意一个班次,由唯一车场的乘务组执行.约束(7)表示对于两个接续班次,必须保证由同一乘务组执行,其中表示车场m的乘务组k执行完班次i 的接续班次序号,可由式(8)计算.约束(9)为班次时间接续约束,表示乘务组执行的后一班次的开始时刻和其相邻前一班次的结束时刻相差应大于最小停留时间.对于有空驶现象的连续班次,必须考虑空驶约束.公式(10)和(11)为时间窗约束,分别表示乘务组k所执行的任意班次的在起始站的开始时刻应大于等于其最早开始服务时间,在终点站的结束时刻应小于等于其最晚结束服务时间.禁忌搜索算法通过模拟人类智能的记忆机制,通过引入灵活的存储结构和禁忌策略限制搜索过程陷入局部最优来避免迂回搜索,同时引入藐视准则来赦免一些被禁忌的优良状态,保证搜索过程的多样化和有效性,达到全局最优.本文所构建的模型是一个复杂的0-1规划问题,可用禁忌搜索算法进行求解.2.1 解的表示形式问题的解可采用二维数组形式表示,其中行表示乘务组,列表示乘务组所对应的车场(第一列元素的值)和执行班次(其余列元素的值)其余列元素的值.假定5个乘务组执行18个班次,问题解的表示形式如图4所示.解码是依据二位数组中数值对问题解进行操作.以图4中数据为例,第1组乘务组的驶入/驶出车场为1,执行的班次链为1-4-8-12,则变量=1.其余乘务组的解码方法同理可得,如图5所示.2.2 初始解的生成Step1:初始化,令车场m的第k个乘务组所完成的班次集合λm,k=Ø,∀m,k.令车场m的最大乘务组序号sm=max{v|,∀m.置,∀m,k,i.Step2:确定执行班次i的乘务组所对应的车场序号m.m={m'|且{∃k,di≥em',k,ai≤lm',k}}.Step3:确定执行班次i的乘务组编号k和最大班次序号i'.令αl=max{j|j∈λm,l}}.若sm>0,则k={l'||di≥em,t,ai≤lm,l}},i'=αk,转Step4;否则转Step5.Step4:班次时间接续检验,若di-ai'-δi',i×ti',i≥T0,则转Step6;否则转Step5. Step5:令sm←sm+1,k←sm,转Step6.Step6:令,转Step7.Step7:若i>N,算法终止,输出结果;否则转Step2.2.3 邻域结构邻域结构采用班次交换与插入策略.班次交换策略,即分别从两个乘务组所执行的班次中选一个进行对换.例如将乘务组: 2-3-6-14的班次6和乘务组: 2-7-11-13-17的班次11进行交换,可得到新解:乘务组: 2-3-11-14和乘务组: 2-6-7-13-17,如图6所示.班次插入策略,即从一个乘务组执行的班次中选择一个班次按升序顺序插入到另一乘务组的执行班次中.例如将乘务组2-7-11-13-17中的班次11插入到乘务组: 2-3-6-14中,可得新解:乘务组2-7-13-17和乘务组2-3-6-11-14,如图7所示.交换或插入策略的乘务班次链中的班次需满足时间接续和时间窗约束,否则不进行该操作.2.4 禁忌表、禁忌长度、藐视准则及终止条件禁忌表中数据是交换和插入的节点;禁忌长度取固定长度;藐视准则选取基于目标评价值的规则,即若出现一个解的目标值优于最佳候选解,可特赦;若最优值在给定的步数内没有变化,算法终止.2.5 解的评价在评价中既要计算目标函数值,又要考虑约束条件.由于初始解已满足时间接续和时间窗约束,且在邻域搜索过程中生成的新解也都满足该约束,故解的评价采用的适应值函数为3 算例研究考虑有4条公交线路L1、L2、L3、L4,3个公交首末站A、B、C,和2个公交车场,如图8所示.L1、L2分别为A、B区间的上行和下行线路;L3、L4分别为B、C区间的上行和下行线路;乘务组可从任一车场出发执行一系列班次,最后返回到出发车场.所有公交线路一天共337个班次,每个班次对应的线路序号及在首站的出发时刻已知,原始数据参照文献[10]中的表1.车辆在线路L1、L2的运行时间均为25min,线路L3、L4的运行时间均为30min.两个节点间的空驶时间如表1所示.每个乘务组时间窗的开始和结束时刻如表2所示.从表2可以看出,车场1和车场2一天能安排的最大乘务组数量分别为16和19,每个乘务组的开始时刻和结束时刻均不相同,其中车场1乘务组平均运营时间要大于车场2乘务组的运营时间.乘务组的单位空驶成本和单位停留等待成本分别为2元/min和0.4元/min.乘务组班次间的最小停留时间为3min.禁忌搜索算法的参数设置为:禁忌长度为6,最大迭代次数为800.应用VC++编程得到最优解如表3所示.最优解总成本6 393元,其中驶入/驶出车场成本1 480元,班次间空驶成本704元,停留等待成本4 209元.从表3可以看出,乘务组所执行的班次任务完全满足时间窗约束,此外,允许乘务组选择起始车场执行公交任务,减少了乘务组驶入/驶出车场成本.由乘务排班优化方案以及每个班次的所属线路,可以得到乘务空驶班次结果,如表4所示.由讫点B空驶到起点A(B→A)的班次序列共有14个,且主要集中在班次序号1-200之间,这主要是因为在该区间内线路L1的班次任务71个,线路L2的班次56个.为了减少线路L1的乘务组和车辆数量需求,可以允许部分车辆执行完线路L1的班次任务后从站点B空驶到站点A,继续完成线路L1的其它班次任务.讫点A空驶到起点B(A→B)的班次序列共有13个,且主要集中在班次序号200~337之间,这是因为在该区间内线路L1的班次任务39个,线路L2的班次52个.为完成线路L2的班次任务需求,可以允许部分车辆执行完线路L2的班次任务后从站点A空驶到站点B,继续完成线路L2的其它班次任务.B→C与C→A的班次空驶序列相对较少,各有2个.这主要是由于线路L3和L4的班次任务的时间分布较为均衡的缘故.因此,允许乘务组和公交车辆在线路间进行空驶,可以有效地解决班次任务存在时间不均衡的问题.针对城市多条公交线路的乘务排班问题,本文考虑了多车场和车辆空驶的因素;针对乘务组人员对工作时间的特殊要求,本文引入了时间窗的概念,以最小化乘务组的驶入/驶出成本、空驶成本、停留等待成本为目标函数,考虑了班次时间接续约束,建立了公交乘务排班优化模型,并设计了相应的禁忌搜索算法.最后,利用四条公交线路一天的班次信息,计算了最佳乘务排班方案,结果表明,可以有效解决带有时间窗的公交乘务排班任务,从而为公交管理部门提供辅助决策.本文的研究仅限于公交班次运营时间固定的情况下,实际运行中公交班次受信号控制、交通拥挤、驾驶员心理等因素的影响,公交班次运营时间是动态变化的.因此,考虑带有随机扰动条件下公交乘务排班问题将是下一步研究的主要方向.【相关文献】[1] Wren puter scheduling of public transport: urban passenger vehicle and crew scheduling[M].North-Holland Publishing Co.,1981.[2] Ceder A.Public transit planning and operation,theory,modelling andpractice[M].Butterworth-Heinemann,2007.[3] Mingozzi A,Boschtti M A,Ricciardelli S,et al.A set partitioning approach to the crew scheduling problem[J].Operations Research,1999,47(6):873-888.[4] Shen Y.,Peng K.,Chen K.,et al.Evolutionary crew scheduling with adaptive chromosomes[J].Transportation Research Part B,2013,56:174-185.[5] Smith B M,Wren A.A bus crew scheduling system using a set coveringformulation[J].Transportation Research Part A General,1988,22(88):97-108.[6] Clement R,Wren A.Greedy Genetic Algorithms,Optimizing Mutations and Bus Driver Scheduling[J].Lecture Notes in Economics & Mathematical Systems,1995,430:213-235. [7] 沈吟东,倪郁东.含时间窗的司售员调度模型及多邻域结构设计[J].华中科技大学学报:自然科学版,2008,(12):31-34.[8] 钟石泉,贺国光.多车场有时间窗的多车型车辆调度及其禁忌算法研究[J].运筹学学报,2005(4): 67-73.[9] Boschetti M A,Mingozzi A,Ricciardelli S.An Exact Algorithm for the Simplified Multiple Depot Crew Scheduling Problem[J].Annals of Operations Research,2004,127(1-4):177-201(25).[10] 陈明明,牛惠民.多车场公交乘务排班问题优化[J].交通运输系统工程与信息,2013,13(5):159-166.。
公交车排班问题数学建模

公交车排班问题数学建模
公交车排班问题可以用数学建模来解决。
以下是建模步骤:
1. 确定时间段和班次:首先,需要确定公交车公司的营业时间段以及规划的班次数目。
2. 收集数据:收集历史乘客流量、不同时间段的平均载客量、行车路线、拐点等数据,以这些数据为基础进行排班计划。
3. 建立模型:根据收集到的数据建立排班数学模型,如线性规划模型或整数规划模型。
4. 优化计算:通过计算机模拟或数学优化软件,寻找最优排班方案。
5. 调整和验证:根据实际情况对模型进行调整和验证,不断优化排班计划。
需要注意的是,公交车排班问题还涉及车辆维护、司机轮换等因素,需要考虑多种因素进行综合优化。
因此,在建模过程中需要综合考虑各种变量和约束条件。
cplex语法

cplex语法CPLEX是一个用于求解复杂优化问题的软件工具。
它提供了一种高效的数学建模语言,可以描述和求解各种线性规划、整数规划、混合整数规划等数学模型。
本文将介绍CPLEX语法的一些基本知识和使用方法。
CPLEX语法主要由三个部分组成:参数设置、模型定义和求解过程。
首先,我们需要设置一些参数来指定求解器的行为。
例如,我们可以设置求解时间限制、容忍度等。
这些参数可以根据实际情况进行调整,以获得更好的求解效果。
接下来,我们需要定义数学模型。
在CPLEX中,可以使用变量、约束和目标函数来描述数学模型。
变量可以是连续型、整数型或二进制型,约束可以是等式或不等式,目标函数可以是最大化或最小化。
通过定义这些元素,我们可以构建一个数学模型,用于描述实际问题。
在模型定义完成后,我们可以使用CPLEX求解器来求解模型。
CPLEX 提供了多种求解算法,可以根据问题的性质选择合适的算法。
求解过程包括建立模型、设置参数、调用求解器进行求解和获取求解结果等步骤。
在求解过程中,CPLEX会尝试找到一个满足约束条件的最优解,或者证明问题无解。
除了基本的数学建模和求解功能,CPLEX还提供了一些高级功能,如约束编程、分布式求解和灵敏度分析等。
约束编程可以用于求解一些特殊类型的问题,如资源分配和调度问题。
分布式求解可以通过将求解任务分配给多台计算机来加速求解过程。
灵敏度分析可以用来评估模型对参数变化的敏感性,帮助我们理解问题的特性。
CPLEX语法具有良好的可读性和可扩展性。
它支持多种数学运算和逻辑运算,可以灵活地描述各种复杂问题。
此外,CPLEX还提供了丰富的文档和示例代码,帮助用户快速上手和解决实际问题。
CPLEX语法是一种强大的数学建模语言,可以帮助我们解决各种复杂优化问题。
通过合理地使用CPLEX语法,我们可以高效地建立数学模型,并利用CPLEX求解器来求解模型,从而得到最优解或近似最优解。
无论是在学术研究还是实际应用中,CPLEX都是一个非常有用的工具。
基于机器学习的特大城市公交车辆调度优化

基于机器学习的特大城市公交车辆调度优化随着城市人口的不断增长和人们生活水平的提高,特大城市的公交系统面临着巨大的挑战。
公交车辆的调度和优化对于提高公共交通效率、减少拥堵、改善市民出行体验至关重要。
传统的公交车辆调度方法往往依赖于人工经验和规则,无法适应特大城市复杂多变的交通环境。
基于机器学习的特大城市公交车辆调度优化成为了解决这一难题的新思路。
机器学习是人工智能领域的重要分支,通过训练计算机系统从历史数据中学习规律和模式,探讨如何根据这些规律和模式进行预测和决策。
将机器学习应用于特大城市公交车辆调度优化,可以有效解决公交车辆调度过程中面临的挑战。
首先,基于机器学习的公交车辆调度优化能够更精准地预测乘客流量。
通过分析历史数据、天气情况、节假日等相关因素,机器学习模型可以预测某个时间段某个地点的乘客人数。
基于这些预测数据,调度系统可以合理安排公交车辆的发车间隔和车辆数量,提高运输效率,缓解客流压力。
其次,机器学习可以提供实时的交通状况信息,优化公交车辆的路线选择和调度安排。
传统的车辆调度方法依赖于人工的观察和判断,容易受到主观因素的影响。
而机器学习模型可以通过实时的交通数据,如交通流量、道路拥堵情况等,判断不同路段的通行情况,选择最佳的路线和发车时间,避免拥堵,提高车辆运行效率。
此外,基于机器学习的公交车辆调度优化还能够提供智能化的客流预测和公交线路规划。
通过分析历史数据和人口分布等因素,机器学习模型可以预测不同线路的客流热点和高峰时段。
调度系统可以根据这些预测结果,合理安排运力资源,优化线路规划,提高公交车辆的满载率和运输效率。
除了以上的优势,基于机器学习的公交车辆调度优化还可以实现自动化调度。
传统的公交车辆调度工作需要进行大量的人工计算和决策,工作量繁重且容易出错。
而机器学习模型可以通过学习大量历史数据和自我优化的过程,实现自动调度和优化,减少人为干预的需求,提高运输效率和服务质量。
然而,基于机器学习的特大城市公交车辆调度优化也存在一些挑战。
第八章:CPLEX在ITS中应用

1.Dijkstra算法 它是用于解决非负权网络中寻找一个指定点到其他 点的最短路的最好方法。 基本思想是:采用标号法 2.PDM算法 能够解决有负权的网络 3.逐次逼近法 4.Floyd算法
4
优化数学模型的建立
分析
1.已知是什么? 2.目标是什么? 3.约束有哪些? 4.决策变量应该如何选择?结合决策变量如何ຫໍສະໝຸດ 数学语言表示目标函数和约束条件?
11
模型文件(2): int C[arcs]=...; //弧长或权重
dvar boolean x[arcs];//以每条弧的选择与否为决策变量 minimize sum(a in arcs) C[a]*x[a];//起始点 subject to{ sum(a in st_arcs)x[a]==1; forall(j in md_nod) sum(<k,j>in arcs:k!=j)x[<k,j>]-sum(<j,k>in arcs:k!=j)x[<j,k>]==0; //中间点的流入量与流出量相等 sum(a in en_arcs)x[a]==1;}
12
数据文件:
nodes={A B C D E F G H I}; md_nod={B C D E F G H}; st_nod={A}; en_nod={I}; arcs={<A,B>,<A,C>,<A,D>,<B,E>,<B,F>,<C,E>,<C,F>,<D,E>,<D,F>,<E,G>,<E, H>,<F,G>,<F,H>,<G,I>,<H,I>}; st_arcs={<A,B>,<A,C>,<A,D>}; en_arcs={<G,I>,<H,I>}; C=[6,3,3,6,5,8,6,7,4,6,7,8,9,5,6];
第五章:CPLEX在车流组织优化中的应用

CPLEX在车流组织优化中的应用
例:下图表示5个支点方向的直达车流, 表示 从某站开行直达列车的集结车小时, 表示车流 在某站改编时所消耗的车小时。问在不考虑各 个站改编能力的情况下,如何编制一个单组列 车编组计划,使得总消耗的车小时最小?
A4 A3 A2 A1 A0
T集 t节
600 N40=60 N41=250 N42=180
如果不开行(3, 0)这支列流,则
这里之所以用“≥”号,是因为 或 中包含 ,当 时,上式取“=”号,否则取“>” 号。综合这两种情况,得约束方程: (6) 同理,对于 和 ,有 (7) (8)
第3组 考虑远程车流压缩到站与较短车流合并的 情况 由图可知,只有当列流(4, 1)(4, 2)(3, 1) 至少有一支开行时,才有远程车流压缩到站的可 能。 当列流(4, 1)开行, ,这时 可以和 合并,即压缩到站在 改编,有 ,也可 以不和 合并,则 ,因此, ,即 (9)
一、车流组织问题的概述 车流组织包括:车流径路和列车编组计划。 列车编组计划确定技术站开出什么样的列 车,才能在满足铁路运输能力的条件下, 以总的车流输送时间最小完成车流输送任 务。
一、车流组织问题的概述
方向上各技术站所产生的车流应以不同的 组合方式编入适当的列车而将其送往各自 的目的地,这些车流的每一种组合方式为 一个编组计划方案。满足划为单独编组到 达站基本条件的车流在一定条件下与其他 车流合并编组可能会得到更多的车小时节 省。列车编组计划方案一方面要保证有尽 可能大的经济效果,使方案车小时消耗总 额最小或节省最大;另一方面,方案的选 择还必须考虑实际执行的可能性。
第07章 交通方式分担
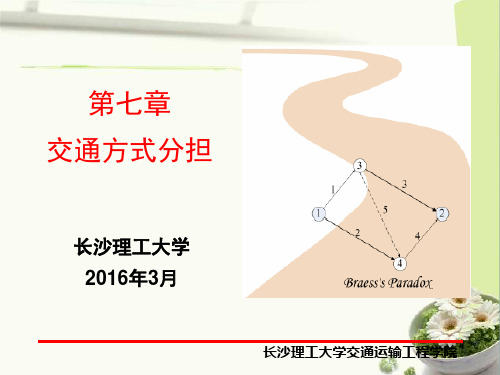
IV 类:
V 类:
长沙理工大学交通运输工程学院 A-MS
6.2 影响方式选择的因素
出行主体(出行者)的特性
职业、年龄、性别
是否拥有或是否可以利用小汽车 是否拥有驾驶执照 家庭结构(年轻夫妇?、夫妇加小孩?、退休人员?、 单身?、家庭人口构成、年龄构成、性别构成等) 收入 其他方面的因素
交通方式划分的阶段 交通方式划分依据其在四阶段模型中所处阶段位置的不同,有如 下的5种分类。
方式划分阶段可以单独解决,也可以与某个子问题中的任何一个 结合起来共同解决。
MS
G
I 类:
D
D MS D D-MS D D MS
A
A A A A
G-MS G G G G
II 类:
III 类:
非集计模型(Disaggregate Model):以个人为单位出发研究
用户对交通方式的选择,并构造模型来确定各交通方式的选 择概率,然后再将每个人的方式选择结果集计起来,进而预
测各方式分担量的模型。该模型始于20世纪60年代,70年代
之后应用于实际。常见的有多元Logit模型(MNL)、多元 Probit(MVN)模型,模型较于复杂。
(trip interchange model)两大类。
出行末端模型:将各个交通小区的发生交通量(集中交通量) 在交通分布计算之前就分配到各方式上。 地区间模型:先计算各交通小区间的分布量,然后再推算方 式分担量。
长沙理工大学交通运输工程学院
6.3.2 方式分担的预测模型 出行末端模型 (Trip End Model)
长沙理工大学交通运输工程学院
OD交通量 个人属性 小汽车用户 固定阶层 交通方式 选择可能者 方式分担率 公共交通用 户固定阶层
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、运行配置与求解 在所在OPL项目下面新建一个运行配置文件,命名为“配置2”, 将以上代码的mod文件添加进这个运行配置中,再右键,立即 运行则可以对这个问题进行求解。 求解后的结果如下: // solution (optimal) with objective 17 x = [0 1 0 0 5 0 0 0 0 0 0 0 0 0 0 0 0 0 11] 该结果给出了一天需要的最少司机人数为17人,同时给出了一 个可行的排班方案,即17位司机中,有1位采用第2种排班情况, 有5位采用第5种排班情况,有11位采用第19种排班情况。 问题的引申: 得到的排班方案能够保证需要的司机人数最少,但是并不能保 证排班方案最优。因此,在确保司机人数为17人的基础上,可 以继续优化排班方案。
6:15
8:30
11:30
13:30
16:30
18:00 18:20
5月非节假日时段划分
则例1中五月份非节假日排班的数学模型可以是:
ti mi Qi t m m Q i i i i s.t. 8 mi 10 4 mi 8 i 1, 2,3, 4,5, 6 i 1, 2,3, 4,5, 6 i 2, 4, 6 i 1,3,5
例: 下面是某条线路的基本情况:
1、该线路的首末班车时间 冬令(12月~3月):6:20~18:10,夏令(4月~11月): 6:15~18:20 2、该线路发车间隔 平时高峰期(6:00~8:30, 11:30~13:30, 6:30~18:00) : 4~8分钟/班, 平时非高峰期:8~10分钟/班; 节假日:5~10分钟/班 3、该线路的运行时间 非高峰期:80~85分钟/班;高峰期:100~120分钟/ 班
二、公交乘务排班优化问题的数学模型及 其在CPLEX中的建模与求解
问题一 (首先考虑非节假日的最少班次问题) 1、数学模型的建立(1) 根据高峰期分布,将5 月非节假日一天的工作时间分为6个时段(如下图 所示),第i( i =1,2,3,4,5,6)个时段的时 长用Qi表示,发车间隔用mi表示,该时段内发车 班次数用ti表示。取合适的mi使得ti的总和最少。
minimize sum(o in Times) t[o]; subject to { (t["T1"]-1)*m["T1"]<=Q["T1"]; Q["T1"]<=t["T1"]*m["T1"]; t["T1"]*m["T1"]+(t["T2"]-1)*m["T2"]<=Q["T1"]+Q["T2"]; Q["T1"]+Q["T2"]<=t["T1"]*m["T1"]+t["T2"]*m["T2"]; t["T1"]*m["T1"]+t["T2"]*m["T2"]+(t["T3"]1)*m["T3"]<=Q["T1"]+Q["T2"]+Q["T3"]; Q["T1"]+Q["T2"]+Q["T3"]<=t["T1"]*m["T1"]+t["T2"]*m["T2"]+t["T3"]*m["T3 "]; t["T1"]*m["T1"]+t["T2"]*m["T2"]+t["T3"]*m["T3"]+(t["T4"]1)*m["T4"]<=Q["T1"]+Q["T2"]+Q["T3"]+Q["T4"];
目标函数是为了寻求一天内的发车班次最少; 约束条件1和2是为了确保每个时段的发车时间不少于 该时段的时长,; 约束条件3和4是各个时段发车间隔范围的约束。
(2)用Q表示节假日一天的工作时长,发车间隔用 m表示,则例1中节假日最少班次的数学公式为:
2、模型的实例编码语言 如果只建立一个mod文件的话,假如命名为 “paiban1.mod”,例1中非节假日排班模型的 OPL建模语言可以是: {string} Times ={"T1", "T2", "T3", "T4", "T5", "T6"}; float Q[Times] = [135, 180, 120, 180, 90, 20]; float m[Times] = [8, 10, 8, 10, 8, 10]; dvar int+ t[Times] in 0..50;
j 1 j 1
S
S
仅有以下19种情况,即S=19:
xj代表被安排为第j种情况的司机数。 构建数学模型如下:
a
j 1
s
s
j
xj
44
b
j 1
j
x j 38
x j 0 且为整数 j 1,2,, s
2、模型的实例编码语言(1) 如果只建立一个mod文件的话,假如命名为“paiban2.mod”,此模型的OPL建模语言可以是: {string} Categories ={"C1", "C2", "C3", "C4", "C5", "C6", "C7", "C8", "C9", "C10", "C11", "C12", "C13", "C14", "C15", "C16", "C17", "C18", "C19"}; int a[Categories] = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4]; int b[Categories] = [1, 2, 3, 4, 5, 0, 1, 2, 3, 4, 0, 1, 2, 3, 0, 1, 2, 0, 1]; dvar int+ x[Categories] in 0..50; minimize sum(o in Categories) x[o]; subject to { sum( o in Categories ) a[o]*x[o] == 44; sum( o in Categories ) b[o]*x[o] == 38; }
3、运行配置与求解 在所在OPL项目下面新建一个运行配置文件,命名 为“配置1”,将以上代码的mod文件添加进这个运 行配置中,再右键,立即运行则可以对这个问题进 行求解。 求解后的结果如下: // solution (optimal) with objective 82 t = [17 18 15 18 12 2] 据此,得到该线路非节假日的最少班次排班如下:
CPLEX在公交乘务排班问题中的应用源自一、公交乘务排班问题的概述
公交乘务排班问题属活动资源的优化利 用问题。一般是根据给定的乘务任务、乘务 规则等条件,考虑一定的优化目标,对乘务 员(组)的出乘时间、地点,担当的乘务任务、 时刻,退乘时间、地点等做出具体安排,以 确保一定周期内的所有乘务任务被执行。
Q["T1"]+Q["T2"]+Q["T3"]+Q["T4"]<=t["T1"]*m["T1"]+t["T2"]*m["T2"]+t["T3"]* m["T3"]+t["T4"]*m["T4"]; t["T1"]*m["T1"]+t["T2"]*m["T2"]+t["T3"]*m["T3"]+t["T4"]*m["T4"]+(t["T5"]1)*m["T5"]<=Q["T1"]+Q["T2"]+Q["T3"]+Q["T4"]+Q["T5"]; Q["T1"]+Q["T2"]+Q["T3"]+Q["T4"]+Q["T5"]<=t["T1"]*m["T1"]+t["T2"]*m["T2"]+ t["T3"]*m["T3"]+t["T4"]*m["T4"]+t["T5"]*m["T5"]; t["T1"]*m["T1"]+t["T2"]*m["T2"]+t["T3"]*m["T3"]+t["T4"]*m["T4"]+t["T5"]*m[ "T5"]+(t["T6"]1)*m["T6"]<=Q["T1"]+Q["T2"]+Q["T3"]+Q["T4"]+Q["T5"]+Q["T6"]; Q["T1"]+Q["T2"]+Q["T3"]+Q["T4"]+Q["T5"]+Q["T6"]<=t["T1"]*m["T1"]+t["T2"]* m["T2"]+t["T3"]*m["T3"]+t["T4"]*m["T4"]+t["T5"]*m["T5"]+t["T6"]*m["T6"]; } execute DISPLAY { writeln("t = ",t); }
