高中数学第一章导数及其应用微积分基本定理学案人教复习

合集下载

高中数学第一章导数及其应用 1.6 微积分基本定理导学案新人教A版选修2-2(2021年整理)

1。

6微积分基本定理【学习目标】1．理解定积分的概念和定积分的性质，理解微积分基本原理；2．掌握微积分基本定理，并会求简单的定积分；3．能够运用基本初等函数的求导公式和导数的四则运算法则从反方向上求出，满足的函数。

【学习重难点】重点：定积分的概念和定积分的性质难点：微积分基本定理,并会求简单的定积分。

【问题导学】预习教材P 51～ P 54，找出疑惑之处. 微积分基本定理(牛顿—莱布尼茨公式）（1）条件：函数在区间上连续，并且。

(2）结论: .(3）符号表示：= .（4）作用：建立了与间的密切联系,并提供了计算定积分的有效方法. 【合作探究】探究任务一:利用微积分基本定理求定积分问题1：计算下列定积分: (1） ;（2） ;（3) ; (4）；(5) ; （6）;(7) ；（8）。

答案：,,， ,，2，，.规律总结:用微积分基本定理求定积分时，求被积函数的原函数是关键，需要注意一下两点(1）熟练掌握基本函数的导数及导数的运算法则，学会逆运算；（2）当被积函数较为复杂，不容易找到原函数时,可适当变形后再求解。

特别地，需要弄清积分变量，精确定位积分区间,分清积分上限与积分下限.探究任务二：求分段函数的定积分问题2:已知计算。

答案：()()Fx f x '=()F x ()f x [],a b ()b af x dx =⎰()baf x dx =⎰321(4)x x d x--⎰251(1)x dx-⎰21(2)t dx +⎰211(1)dx x x +⎰12x dx⎰22(co s 2)x x d xππ-+⎰0332edx x +⎰222sin xdxππ-⎰203162t +4ln31ln 232ln2e +2π42,02(),cos ,2x x f x x x ππππ⎧-≤≤⎪⎪=⎨⎪<≤⎪⎩0()f x dxπ⎰2112π--变式:计算定积分.答案：5规律总结：若被积函数是分段函数，利用定积分的性质3，根据函数的定义域,将积分区间分解为相应的几部分,带入相应的解析式求解。

人教版高中数学第一章1.6微积分基本定理

的研究方向；分析小说，一般都是从人物、环境、情节三个要素入手；写记叙文，则要从时间、地点、人物和事情发生的起因、经过、结果六个方面进
行叙述。这些都是语文学习中的一些具体方法。其他的科目也有适用的学习方法，如解数学题时，会用到反正法；换元法；待定系数法；配方法；消元
法；因式分解法等，掌握各个科目的方法是大家应该学习的核心所在。
归纳升华 (1)利用微积分基本定理求定积分，关键是求使 F′(x) ＝f(x)的 F(x)，其求法是反方向运用求导公式． (2)当被积函数是积的形式时，应先化和差的形式，再利用定积分的性质化简，最后再用微积分基本定理求定积分的值．
(3)对于多项式函数的原函数，应注意 xn(n≠－1)的原 xn＋1
函数为，它的应用很广泛． n＋1
[变式训练] 下列积分值为 2 的是( )
A.∫50(2x－4)dx C.∫311xdx
B.∫0π cos xdx D.∫0π sin xdx
解析：∫50(2x－4)dx＝(x2－4x)|50＝5，∫0π cos xdx＝sin
x|π0 ＝0，∫311xdx＝ln x|31＝ln 3，∫π0 sin xdx＝－cos x|0π ＝2.
x 的原函数为
F(x)
π
＝12x－12sin x，所以 sin2 x2dx＝12x－12sin x|20＝π4－12＝
π－2 4. π－2 答案： 4
5．曲线 y＝2x2 与直线 x＝1，x＝2 及 y＝0 所围成的平面图形的面积为________．
解析：依题意，所求面积为 S＝∫212x2dx＝23x3|21＝136－ 23＝134. 答案：134
＝sin 1－23. 答案：sin 1－23
类型 3 微积分基本定理的综合应用(互动探究)

高中数学第1章导数及其应用1-6微积分基本定理学案理新人教A版选修2-2【2019-2020学年度】

教学资料范本
高中数学第1章导数及其应用16微积分基本定理学案理新人教A版选修2-2【2019-2020学年度】
编辑：__________________ 时间：__________________
1/4
1.6微积分基本定理
一、知识目标 ⒈通过实例，直观了解微积分基本定理的含义，会用牛顿-
莱布尼兹公式求简单的积 ⒉通过探究变速直线运动物体的速度与位移的关系，直观了解微积分基本定
上的
，并且
。那么
为了方便起见，还常用
表示
，即
=
上述微积分基本定理也叫做牛顿—莱布尼兹公式，四、例题精析
例1．计算下列定积分：（1）
；
（2）
例2．计算下列定积分：
。
由计算结果你能发现什么结论？试利用曲边梯形的面积表示所发现的结论。 3/4
变式应用．汽车以每小时32公里速度行驶，到某处需要减速停车。设汽车以等减速度 =1.8米/秒2刹车，问从开始刹车到停车，汽车走的距离为
（1）物体在时间间隔
内经过的路程可用速度函数v(t)表示为
；
（2）物体在时间间隔
内经过的路程可用位置函数S(t)的增量表示为
即：
=
，而
【猜想】：对于一般函数，设
，是否也有
？
2/4
若上式成立，我们就找到了用
的原函数（即满足
）的数值差
来计算在
上的定积分的方法。
【新知】：微积分基本定理：
一般地，如果函数是
4/4
五．巩固练习： 1.设
3 A.4
，则 4 B.5
等于(
)
5 C.6
D．不存在
2. |x|dx等于(
)

高中数学第一章导数及其应用 1.5 定积分的概念 1.6 微积分基本定理要点讲解素材新人教A版选修22

定积分和微积分要点讲解一、定积分的概念教材上从求曲边梯形的面积和变速运动的路程出发引入了定积分的概念：如果函数()f x 在区间[],a b 上是连续的，用分点011i i n a x x x x x b -=<<<<<<=将区间[],a b 等分成n 个小区间，在每个小区间[]1,i i x x -上任取一点i ξ（1,2,,i n =），作和式()()11nni i i i b af x f nξξ==-∆=∑∑，当n →∞时，上述和式无限接近某个常数，这个常数叫做函数()f x 在区间[],a b 上的定积分，记作()baf x dx ⎰，即()()1li m nbi an i b af x dx f n ξ→∞=-=∑⎰．对这个概念我们应从如下几个方面进行理解１．对区间[],a b 分割的绝对任意性：在定义中我们将区间[],a b 进行等分是为了计算上的方便，实际上对区间[],a b 的分割是任意的，这时只要这些区间中长度最大的区间的长度趋向于零即可．２．在每个小区间[]1,i i x x -上取点的绝对任意性：在教材上的两个例题是为了计算的方便将点取小区间[]1,i i x x -的端点，实际上我们可以在区间[]1,i i x x -上任意取点，如取中点等．３．当n →∞时，和式()()11nni i i i b af x f nξξ==-∆=∑∑无限接近某个常数的唯一确定性．它不依赖于对区间[],a b 的分割方法，也不依赖于在每个小区间[]1,i i x x -上取点的方式．即()baf x dx ⎰是一个客观上存在的仅仅依赖于积分上下限和被积函数的唯一确定的常数．同时它也与积分变量无关，即()()b baaf x dx f t dt =⎰⎰．４．数学思想上的划时代意义．产生定积分概念的＂以直代曲＂＂以匀速代变速＂和＂无限逼近＂的数学思想，使人类在认识数学世界的观念上有了重大突破，在数学的发展史上具有重大意义．我们要仔细理解体会这种思想，可以说这才是我们在高中阶段学习定积分的真正目的．例如在求曲边梯形的面积的课本例１中，我们把区间[]0,1等分成n 个小区间，在每个小区间上＂以直代曲＂就将曲边问题转化为直边问题，随着n 的增大这些小区间的宽度越来越小，这时在每个小区间上直边形的面积已经和曲边形的面积非常接近，我们就可以以这些小直边形的面积之和近似代替曲边形的面积，而当n →∞时这些小直边形就几乎变成了线段，这时小直边形的面积几乎就等于小曲边形的面积，这无穷个几乎变成了线段的直边形的面积之和就是所求的曲边形的面积了．我们常说＂线动成面＂，对课本例１，我们也可以这样形象的理解：就将小直边形的宽度变成零，使其成为线段，这时小直边形和小曲边形的就完全重合了，而将这些线段从0到1运动就形成了()2f x x =，1x =， x 轴所围成的曲边形，将这些线段的＂面积＂积累起来就是所求的曲边形的面积．二、微积分基本定理的应用作变速直线运动的物体如果其运动方程是()S t ，那么该物体在时间区间[],a b 内通过的路程是()()S b S a -，另一方面由导数的物理意义，该物体在任意时刻的瞬时速度为()()'S t s t =，我们把该物体运动的时间区间[],a b 无限细分，在每个小时间段上，将其速度看作匀速，就能求出该物体在每个小时间段上通过的路程，将这无限个小时间段上的路程加起来，就是该物体在时间区间[],a b 上通过的路程，由定积分的定义可知，这个数值是()bas t dt ⎰．由此可知()()()()'b baaS t dt s t dt S b S a ==-⎰⎰．一般地有如下结论：如果()f x 是[],a b 上的连续函数，并且有()()F x f x '=，则()()()baf x dx F b F a =-⎰．这就是微积分基本定理，是微积分学最为辉煌的定理，是数学发展史的一个重要里程碑，利用这个定理可以很方便的计算定积分，其关键是找到一个函数使其导数等于被积函数，下面举例说明它在计算定积分上的应用．例１计算定积分()1xx ee dx --⎰分析：()'x x e e =，()'x x e e --=-，故()'x x x x e e e e --+=-．解：()()11'112xxxx xx eedx eedx ee e e---⎡⎤-=+=+=+-⎣⎦⎰⎰．点评：关键是找()F x ，使()'x xF x e e -=-，可以通过求导运算求探求．例２计算定积分220cos sin 22x x dx π⎛⎫- ⎪⎝⎭⎰．分析：被积函数比较复杂，我们可以先化简，再探求．由于222cos sin cos 2cos sin sin 1sin 222222x x x x x x x ⎛⎫-=-+=- ⎪⎝⎭，而'1x =，()cos 'sin x x =-，故()2cos '1sin cos sin 22x x x x x ⎛⎫+=-=- ⎪⎝⎭．解：()()[]2'2222000cos sin 1sin cos cos 2212x x dx x dx x x dx x x πππππ⎛⎫-=-=+=+ ⎪⎝⎭=-⎰⎰⎰点评：被积函数较为复杂时要先化简在求解．掌握如下的定积分计算公式对解题是有帮助的．①111bm m ab x dx xa m +=+⎰（,1m Q m ∈≠-），②1ln bab dx x a x =⎰，③b x x a b e dx e a =⎰，④ln x n xm n a a dx ma =⎰，⑤cos sin bab xdx xa=⎰，⑥()sin cos babxdx x a=-⎰．例如例３计算定积分()1223x x dx -⎰．分析：先展开再利用上面的定积分公式．解：()1223xx dx -⎰=()104269xxxdx -⋅+⎰=146920ln 4ln 6ln 9x x x ⎛⎫-⋅+ ⎪⎝⎭ 3108ln 4ln 6ln 9=-+．点评：根据定积分公式结合定积分的运算性质是计算定积分的根本．从上面不难看出利用微积分基本定理计算定积分比用定义计算要方便的多，在实际解题中要注意对被积函数的化简展开以及有意识的利用定积分的三条运算性质，以起到化难为易的作用．三、定积分的三条性质根据定积分的定义不难得到定积分的三条性质性质1．常数因子可提到积分号前，即：()()bbaakf x dx k f x dx =⎰⎰（k 为常数）；性质2．代数和的积分等于积分的代数和：即：()()()()bb bx aa a f x g x dx f x d g x dx ±=±⎡⎤⎣⎦⎰⎰⎰；性质3．（定积分的可加性）如果积分区间[],a b 被点c 分成两个小区间[],a c 与[],c b ，则：()()()bc daacf x dx f x dx f x dx =+⎰⎰⎰。

高中数学第一章导数及其应用 1.5.3 定积分的概念1 新人教A版选修2-2

i＝1
ni 3·1n＝n14i＝n1i3＝n14n
n＋ 2
2＝141＋n2＋n12，
∴01x3dx＝nli→m∞ 141＋n2＋n12＝14.
(此处用到了求和公式 13＋23＋…＋n3＝(1＋2＋…＋n)2 ＝n(n2＋1)2) 因此01x3dx＝41.
规律总结
用定义法求积分的步骤
(1)分割：将积分区间[a，b]n 等分．
i＝1
当 n→∞时，上述和式无限接近某个常数，这个常数叫做
函数 f(x)在区间[a，b]上的___定__积__分_____，记作f(x)dx＝___ln_i→m_∞_i＝_1_[ __n__f_(ξ_i_)]___.
a
这里，a与b分别叫做__积__分__下__限____与___积__分__上__限___，区间 [a，b]叫做__积__分__区__间____，函数f(x)叫做__被__积__函__数____，x 叫做__积__分__变__量____，f(x)dx叫做__被__积__式______． 2．定积分的几何意义如果在区间[a，b]上函数 f(x)连续且恒有_____f(_x_)_≥_0___，那么定积分bf(x)dx 表示由___直__线__x_＝__a_，__x_＝__b_(_a_≠_b_)___，
(2)近似代替：取点 ξi∈[xi－1，xi]，可取 ξi＝xi－1 或者 ξi＝xi.
n
(3)求和：
i＝1
b－n af(ξi)．(4)求极限：abf(x)dx＝nli→m∞i＝n1
b－n af(ξi)．
跟踪练习 1 (1)定积分af(x)dx 的大小( A ) b
A．与 f(x)和积分区间有关，与 ξi 的取法无关 B．与 f(x)有关，与区间及 ξi 的取法无关 C．与 f(x)及 ξi 的取法有关，与区间无关 D．与 f(x)、积分区间和 ξi 的取法都有关

高中数学第1章导数及其应用1.6微积分基本定理学案新人教A版选修2_2

1.6 微积分基本定理1．微积分基本定理[提示] 不唯一，如F 1(x )＝x ＋1，F 2(x )＝x ＋5，…等其导数为1，故F (x )不唯一． 2．定积分和曲边梯形面积的关系设曲边梯形在x 轴上方的面积为S 上，x 轴下方的面积为S 下．则 (1)当曲边梯形在x 轴上方时，如图①，则⎠⎛a b f (x )d x ＝S 上．(2)当曲边梯形在x 轴下方时，如图②，则⎠⎛ab f (x )d x ＝－S 下．(3)当曲边梯形在x 轴上方、x 轴下方均存在时，如图③，则⎠⎛ab f (x )d x ＝S 上－S 下，若S 上＝S 下，则⎠⎛ab f (x )d x ＝0.图① 图② 图③1．若a ＝⎠⎛01(x －2)d x ，则被积函数的原函数为( )A ．f (x )＝x －2B ．f (x )＝x －2＋CC ．f (x )＝12x 2－2x ＋CD ．f (x )＝x 2－2x[答案] C2．⎠⎜⎛0π2cos x d x ＝________. 1 [⎠⎜⎛0π2cos x d x ＝sin x ⎪⎪⎪⎪π2＝sin π2－sin 0＝1.]3．如图所示，定积分⎠⎛a b f (x )d x 的值用阴影面积S 1，S 2，S 3表示为⎠⎛ab f (x )d x ＝________.S 1－S 2＋S 3 [根据定积分的几何意义知⎠⎛ab f (x )d x ＝S 1－S 2＋S 3.](1)⎠⎛01(2x ＋e x)d x ；(2)⎠⎛12⎝ ⎛⎭⎪⎫1x－3cos x d x ； (3)⎠⎜⎛0π2⎝ ⎛⎭⎪⎫sin x 2－cos x 22d x ；(4)⎠⎛03(x －3)(x －4)d x .[解] (1)⎠⎛01(2x ＋e x )d x ＝(x 2＋e x)⎪⎪⎪10＝(1＋e 1)－(0＋e 0)＝e.(2)⎠⎛12⎝ ⎛⎭⎪⎫1x－3cos x d x ＝(ln x －3sin x )⎪⎪⎪21＝(ln 2－3sin 2)－(ln 1－3sin 1) ＝ln 2－3sin 2＋3sin 1.(3)∵⎝⎛⎭⎪⎫sin x 2－cos x 22＝1－2sin x 2cos x2＝1－sin x ， ∴⎠⎜⎛0π2⎝ ⎛⎭⎪⎫sin x 2－cos x 22d x ＝⎠⎜⎛π2(1－sin x )d x ＝(x ＋cos x )⎪⎪⎪⎪π2＝⎝⎛⎭⎪⎫π2＋cos π2－(0＋cos 0)＝π2－1.(4)∵(x －3)(x －4)＝x 2－7x ＋12， ∴⎠⎛03(x －3)(x －4)d x＝⎠⎛03(x 2－7x ＋12)d x＝⎝ ⎛⎭⎪⎫13x 3－72x 2＋12x ⎪⎪⎪3＝9－632＋36＝272.(1)当被积函数为两个函数的乘积或乘方形式时一般要转化为和的形式，便于求得函数F (x ).(2)由微积分基本定理求定积分的步骤,第一步：求被积函数f (x )的一个原函数F (x )；第二步：计算函数的增量F (b )－F (a ).1．计算下列定积分． (1)⎠⎛12⎝⎛⎭⎪⎫x －x 2＋1x d x ；(2)∫π20⎝ ⎛⎭⎪⎫cos 2 x 2－sin 2 x 2d x ；(3)⎠⎛49x (1＋x )d x .[解] (1)⎠⎛12⎝⎛⎭⎪⎫x －x 2＋1x d x ＝⎝ ⎛⎭⎪⎫x 2－x 33＋ln x ⎪⎪⎪21＝⎝ ⎛⎭⎪⎫4－83＋ln 2－⎝ ⎛⎭⎪⎫1－13＝ln 2＋23.(2)⎠⎜⎛0π2⎝ ⎛⎭⎪⎫cos 2 x 2－sin 2 x 2d x ＝⎠⎜⎛π2cos x d x ＝sin x ⎪⎪⎪⎪π2＝1.(3)⎠⎛49x (1＋x )d x ＝⎠⎛49(x ＋x )d x ＝⎝ ⎛⎭⎪⎫23x 32＋x 22⎪⎪⎪94＝⎝ ⎛⎭⎪⎫23×27＋812－⎝ ⎛⎭⎪⎫23×8＋162＝⎝ ⎛⎭⎪⎫18＋812－163－8 ＝2716.(1)f (x )＝⎩⎪⎨⎪⎧sin x ，0≤x <π2，1，π2≤x ≤2，x －1，2<x ≤4，求⎠⎛04f (x )d x ；(2)⎠⎛02|x 2－1|d x .思路探究：(1)按f (x )的分段标准，分成⎣⎢⎡⎭⎪⎫0，π2，⎣⎢⎡⎦⎥⎤π2，2，(2,4]三段求定积分，再求和．(2)先去掉绝对值号，化成分段函数，再分段求定积分．[解] (1)⎠⎛04f (x )d x ＝⎠⎜⎛π2sin x d x ＋⎠⎜⎛π221d x ＋⎠⎛24(x －1)d x ＝(－cos x )⎪⎪⎪⎪π20＋x ⎪⎪⎪⎪2π2＋⎝ ⎛⎭⎪⎫12x 2－x ⎪⎪⎪42＝1＋⎝⎛⎭⎪⎫2－π2＋(4－0)＝7－π2.(2)⎠⎛02|x 2－1|d x ＝⎠⎛01(1－x 2)d x ＋⎠⎛12(x 2－1)d x＝⎝ ⎛⎭⎪⎫x －13x 3⎪⎪⎪1＋⎝ ⎛⎭⎪⎫13x 3－x ⎪⎪⎪21＝2.1．本例(2)中被积函数f (x )含有绝对值号，可先求函数f (x )的零点，结合积分区间，分段求解．2．分段函数在区间[a ，b ]上的定积分可分成n 段定积分和的形式，分段的标准可按照函数的分段标准进行．3．带绝对值号的解析式，可先化为分段函数，然后求解．2．(1)f (x )＝⎩⎪⎨⎪⎧1＋2x ，0≤x ≤1，x 2，1＜x ≤2，求⎠⎛02f (x )d x .(2)求⎠⎛-22|x 2－x |d x 的值．[解] (1)⎠⎛02f (x )d x ＝⎠⎛01(1＋2x )d x ＋⎠⎛12x 2d x＝(x ＋x 2)⎪⎪⎪ 1＋13x 3⎪⎪⎪21＝2＋73＝133.(2)∵|x 2－x |＝⎩⎪⎨⎪⎧x 2－x ，－2≤x ＜0，x －x 2，0≤x ≤1，x 2－x ，1＜x ≤2，∴⎠⎛-22|x 2－x |d x＝⎠⎛-20(x 2－x )d x ＋⎠⎛01(x －x 2)d x ＋⎠⎛12(x 2－x )d x＝⎝ ⎛⎭⎪⎫13x 3－12x 2⎪⎪⎪－2＋⎝ ⎛⎭⎪⎫12x 2－13x 3⎪⎪⎪10＋⎝ ⎛⎭⎪⎫13x 3－12x 2⎪⎪⎪21＝143＋16＋56＝173.1．求f (a )＝⎠⎛01(2ax 2－a 2x )d x 的表达式．[提示] f (a )＝⎠⎛01(2ax 2－a 2x )d x ＝⎝ ⎛⎭⎪⎫23ax 3－12a 2x 2⎪⎪⎪10＝23a －12a 2.2．试求f (a )取得最大时a 的值．[提示] f (a )＝23a －12a 2＝－12⎝ ⎛⎭⎪⎫a 2－43a ＋49＋29＝－12⎝ ⎛⎭⎪⎫a －232＋29，∴当a ＝23时，f (a )的最大值为29.【例3】 (1)已知t ＞0，f (x )＝2x －1，若⎠⎛0t f (x )d x ＝6，则t ＝________.(2)已知2≤⎠⎛12(kx ＋1)d x ≤4，则实数k 的取值范围为________.[解] (1)⎠⎛0t f (x )d x ＝⎠⎛0t (2x －1)d x ＝t 2－t ＝6，解得t ＝3或－2，∵t ＞0，∴t ＝3. (2)⎠⎛12(kx ＋1)d x ＝⎝ ⎛⎭⎪⎫12kx 2＋x ⎪⎪⎪21＝32k ＋1. 由2≤32k ＋1≤4，得23≤k ≤2.利用定积分求参数应注意的问题利用定积分求参数时，注意方程思想的应用．一般地，首先要弄清楚积分变量和被积函数．当被积函数中含有参数时，必须分清常数和变量，再进行计算，其次要注意积分下限小于积分上限．1．求定积分的一些常用技巧(1)对被积函数，要先化简，再求积分．(2)若被积函数是分段函数，依据定积分“对区间的可加性”，分段积分再求和． (3)对于含有绝对值符号的被积函数，要去掉绝对值符号才能积分．2．由于定积分的值可取正值，也可取负值，还可以取0，而面积是正值，因此不要把面积理解为被积函数对应图形在某几个区间上的定积分之和，而是在x 轴下方的图形面积要取定积分的相反数．1．下列值等于1的是( )A.⎠⎛01x d x B.⎠⎛01(x ＋1)d x C.⎠⎛011d x D.⎠⎛0112d x C [选项A ，因为⎝ ⎛⎭⎪⎫x 22′＝x ，所以⎠⎛01x d x ＝x 22| 10＝12；选项B ，因为⎝ ⎛⎭⎪⎫x 22＋x ′＝x ＋1，所以⎠⎛01(x ＋1)d x ＝⎝ ⎛⎭⎪⎫x 22＋x | 10＝32；选项C ，因为x ′＝1，所以⎠⎛011d x ＝x | 10＝1；选项D ，因为⎝ ⎛⎭⎪⎫12x ′＝12，所以⎠⎛0112d x ＝12x | 10＝12.]2．若⎠⎛1a ⎝⎛⎭⎪⎫2x ＋1x d x ＝3＋ln 2，则a 的值是( )A ．5B ．4C ．3D ．2D [⎠⎛1a ⎝⎛⎭⎪⎫2x ＋1x d x ＝()x 2＋ln x | a 1＝a 2＋ln a －1，∴a 2－1＝3，且ln a ＝ln 2，故a ＝2.]3.⎠⎛02⎝⎛⎭⎪⎫x 2－23x d x ＝________.43 [⎠⎛02⎝ ⎛⎭⎪⎫x 2－23x d x ＝⎠⎛02x 2d x －⎠⎛0223x d x＝x 33| 2－x 23| 20＝83－43＝43.] 4．设函数f (x )＝⎩⎪⎨⎪⎧x 2＋1，0≤x ＜1，3－x ，1≤x ≤2，则⎠⎛02f (x )d x ＝________.176 [⎠⎛02f (x )d x ＝⎠⎛01(x 2＋1)d x ＋⎠⎛12(3－x )d x ＝⎝ ⎛⎭⎪⎫x 33＋x | 10＋⎝ ⎛⎭⎪⎫3x －x 22| 21＝176.]5．已知f (x )是二次函数，其图象过点(1,0)，且f ′(0)＝2，⎠⎛01f (x )d x ＝0，求f (x )的解析式．[解] 设f (x )＝ax 2＋bx ＋c (a ≠0)， ∴a ＋b ＋c ＝0. ∵f ′(x )＝2ax ＋b ， ① ∴f ′(0)＝b ＝2.②⎠⎛01f (x )d x ＝⎠⎛01(ax 2＋bx ＋c )d x ＝⎝ ⎛⎭⎪⎫13ax 3＋12bx 2＋c x | 10＝13a ＋12b ＋c ＝0.③由①②③得⎩⎪⎨⎪⎧a ＝－32，b ＝2，c ＝－12，∴f (x )＝－32x 2＋2x －12.。

高中数学第一章导数及其应用1.6第1课时微积分基本定理学案新人教A版选修

高中数学第一章导数及其应用1.6第1课时微积分基本定理学案新人教A版选修1、6第一课时微积分基本定理一、课前准备1、课时目标1、了解导数与定积分的关系以及微积分基本定理的含义；2、能够运用微积分基本定理计算简单的定积分；3、能解决简单的含参数积分问题。

2、基础预探1、如果f(x)是区间[a，b]上的________，并且F′(x)＝________，那么f(x)dx＝________、这个结论叫做微积分基本定理，又叫做________、2、微积分基本定理的符号表示f(x)dx＝F(x)|＝ ________、3、常见求定积分的公式（1）；（2）（c为常数）；（3）；（4）；（5）；（6）；（7）。

二、学习引领1、微积分基本定理需注意的问题(1)在微积分基本定理中，F′(x)＝f(x)，且f(x)在[a，b]上连续可积，则F(x)称为f(x)的一个原函数、(2)微积分基本定理沟通了定积分与导数的关系，揭示了被积函数与原函数之间的逆运算关系，为定积分的计算提供了一个简单有效的方法转化为计算其原函数在积分区间上的增量、(3)用微积分基本定理求定积分的关键是找到满足F′(x)＝f(x)的原函数F(x)，即找被积函数的原函数，利用求导运算与求原函数运算互为逆运算，运用基本函数求导公式和四则运算法则从反方向上求出F(x)、(4)根据导数知识，连续函数f(x)的原函数F(x)不唯一，这是由于[F(x)＋C]′＝f(x)，所以F(x)＋C也是函数f(x)的原函数，其中C为常数、求定积分可以选取任意一个原函数，由于f(x)dx＝[F(x)＋C]|＝[F(b)＋C]－[F(a)＋C]＝F(b)－F(a)，显然常数C对定积分的求解没有影响、2、计算简单定积分的步骤①把被积函数变为幂函数、正弦函数、余弦函数、指数函数与常数的和或差；②利用定积分的性质把所求的定积分化为若干个定积分的和与差；③分别用求导公式找到F(x)，使得F (x)=f(x);④利用牛顿莱布尼兹公式2、F(b)－F(a)3、三、典例导析例1 变式训练解: (1)∵(x5)′＝5x4，∴5x4dx＝x5|＝105－25＝99968、(2)(1＋x＋x2)dx＝dx＋xdx＋x2dx＝x|＋x2|＋x3|＝(3－1)＋(32－12)＋(33－13)＝、(3)、(4－2x)(4－x2)dx＝(16－8x－4x2＋2x3)dx＝＝32－16－＋8＝、(4)|sinx|dx＝（-sinx）dx=cosx、=1、例2 变式训练解析：由于，例3 变式训练解析：(1)0≤a≤1时，f(a)＝|x2－a2|dx＝(a2－x2)dx＋(x2－a2)dx＝(a2x－x3)＋(－a2x)＝a3－a3－0＋0＋－a2－＋a3＝a3－a2＋。

高中数学第一章导数及其应用1.4.2微积分基本定理学案新人教B版选修2_2

1.4.2 微积分基本定理1．理解并掌握微积分基本定理．(重点、易混点)2．能用微积分基本定理求定积分．(难点)3．能用定积分解决有关的问题．[基础·初探]教材整理微积分基本定理阅读教材P40～P41，完成下列问题．1．F′(x)从a到b的积分等于F(x)在两端点的取值之__________.2．如果F′(x)＝f(x)，且f(x)在[a，b]上可积，则b f(x)d x＝____________________.⎠⎛a其中F(x)叫做f(x)的一个__________．由于[F(x)＋c]′＝f(x)，F(x)＋c也是f(x)的原函数，其中c为常数．一般地，原函数在[a，b]上的改变量F(b)－F(a)简记作F(x)|b a.因此，微积分基本定理可以写成形式：____________________.b f(x)d x＝F(x)|b a＝F(b)－F(a)【答案】 1.差 2.F(b)－F(a) 原函数⎠⎛a1．判断(正确的打“√”，错误的打“×”)(1)微积分基本定理中，被积函数f(x)是原函数F(x)的导数．( )(2)应用微积分基本定理求定积分的值时，为了计算方便通常取原函数的常数项为0.( )(3)应用微积分基本定理求定积分的值时，被积函数在积分区间上必须是连续函数．( )【答案】(1)√(2)√(3)√1(x－2)d x，则被积函数的原函数为( )2．若a＝⎠⎛A ．f (x )＝x －2B ．f (x )＝x －2＋C C ．f (x )＝12x 2－2x ＋CD ．f (x )＝x 2－2x【解析】由微积分基本定理知，f ′(x )＝x －2，∵⎝ ⎛⎭⎪⎫12x 2－2x ＋C ′＝x －2，∴选C. 【答案】 C[质疑·手记]预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流：疑问1：解惑：疑问2：解惑：疑问3：解惑：[小组合作型](1)定积分⎠⎛0(2＋e )d 的值为( )A ．e ＋2B ．e ＋1C ．eD ．e －1(2)求下列定积分．①⎠⎛12(x 2＋2x ＋3)d x ；②⎠⎜⎛0π2 sin 2x2d x .【自主解答】 (1)⎠⎛01(2x ＋e x)d x ＝(x 2＋e x ) | 10＝(12＋e)－(02＋e 0)＝1＋e －1＝e.【答案】 C(2)①⎠⎛12(x 2＋2x ＋3)d x＝⎠⎛12x 2d x ＋⎠⎛122x d x ＋⎠⎛123d x＝x 33| 21＋x 2| 21＋3x | 21＝253.②sin 2x 2＝1－cos x 2，而⎝ ⎛⎭⎪⎫12x －12sin x ′＝12－12cos x ＝sin 2x 2，∴⎠⎜⎛0π2 sin 2x2d x＝⎝ ⎛⎭⎪⎫12x －12sin x ⎪⎪⎪⎪π20＝π4－12＝π－24.求简单的定积分关键注意两点1．掌握基本函数的导数以及导数的运算法则，正确求解被积函数的原函数，当原函数不易求时，可将被积函数适当变形后再求解．2．精确定位积分区间，分清积分下限与积分上限．[再练一题]1．(1)若⎠⎛01(kx ＋1)d x ＝2，则k 的值为( )A ．1B ．2C ．3D ．4(2)⎠⎛12x －1x2d x ＝________. 【导学号：05410032】【解析】 (1)⎠⎛01(kx ＋1)d x ＝⎝ ⎛⎭⎪⎫12kx 2＋x | 10＝12k ＋1＝2，∴k ＝2.(2)⎠⎛12x －1x 2d x ＝⎠⎛12⎝ ⎛⎭⎪⎫1x －1x 2d x＝⎝ ⎛⎭⎪⎫ln x ＋1x | 21＝⎝⎛⎭⎪⎫ln 2＋12－(ln 1＋1)＝ln 2－12.【答案】 (1)B (2)ln 2－12(1)f (x )＝⎩⎪⎨⎪⎧sin x ，0≤x <π2，1，π2≤x ≤2，x －1，2<x ≤4，求⎠⎛04f (x )d x ；(2)⎠⎛02|x 2－1|d x .【精彩点拨】 (1)按f (x )的分段标准，分成⎣⎢⎡⎭⎪⎫0，π2，⎣⎢⎡⎦⎥⎤π2，2，(2,4]三段求定积分，再求和．(2)先去掉绝对值号，化成分段函数，再分段求定积分．【自主解答】 (1)⎠⎛04f (x )d x ＝⎠⎜⎛0π2sin x d x ＋⎠⎜⎛π221d x ⎠⎛24(x －1)d x ＝ (－cos x )⎪⎪⎪⎪ π20＋x ⎪⎪⎪⎪0 π2＋⎝ ⎛⎭⎪⎫12x 2－x | 41 ＝1＋⎝⎛⎭⎪⎫2－π2＋(4－0)＝7－π2. (2)⎠⎛02|x 2－1|d x ＝⎠⎛01(1－x 2)d x ＋⎠⎛12(x 2－1)d x＝⎝ ⎛⎭⎪⎫x －13x 3| 10＋⎝ ⎛⎭⎪⎫13x 3－x | 21＝2.1．本例(2)中被积函数f (x )含有绝对值号，可先求函数f (x )的零点，结合积分区间，分段求解．2．分段函数在区间[a ，b ]上的定积分可分成n 段定积分和的形式，分段的标准可按照函数的分段标准进行．3．带绝对值号的解析式，可先化为分段函数，然后求解．[再练一题]2．计算定积分：⎠⎛-33 (|2x ＋3|＋|3－2x |)d x .【解】设f (x )＝|2x ＋3|＋|3－2x |，x ∈[－3,3]，则f (x )＝⎩⎪⎨⎪⎧－4x ，－3≤x <－32，6，－32≤x ≤32，4x ，32<x ≤3.所以⎠⎛-33(|2x ＋3|＋|3－2x |)d x＝⎠⎜⎛-3－32 (－4x )d x ＋⎠⎜⎜⎛－323232－326 d x ＋⎠⎜⎛3234x d x＝－2x 2⎪⎪⎪⎪－32－3＋6x⎪⎪⎪⎪32－32＋2x 2⎪⎪⎪⎪332＝－2×⎝ ⎛⎭⎪⎫94－9＋6×⎝ ⎛⎭⎪⎫32＋32＋2×⎝ ⎛⎭⎪⎫9－94 ＝45.[探究共研型]探究1 满足【提示】不唯一，它们相差一个常数，但不影响定积分的值．探究2 如何求对称区间上的定积分？【提示】在求对称区间上的定积分时，应首先考虑函数性质和积分的性质，使解决问题的方法尽可能简便．已知f (x )是一次函数，其图象过点(1,4)，且⎠⎛01f (x )d x ＝1，求f (x )的解析式．【精彩点拨】设出函数解析式，由题中条件建立两方程，联立求解．【自主解答】设f (x )＝kx ＋b (k ≠0)，因为函数的图象过点(1,4)，所以k ＋b ＝4.①又⎠⎛01f (x )d x ＝⎠⎛01(kx ＋b )d x ＝⎝ ⎛⎭⎪⎫k 2x 2＋bx ⎪⎪⎪1＝k 2＋b ，所以k2＋b ＝1.②由①②得k ＝6，b ＝－2，所以f (x )＝6x －2.1．含有参数的定积分可以与方程、函数或不等式综合起来考查，利用微积分基本定理计算定积分是解决此类综合问题的前提．2．计算含有参数的定积分，必须分清积分变量与被积函数f (x )、积分上限与积分下限、积分区间与函数F (x )等概念．[再练一题]3．上例中，若把“已知f (x )是一次函数”改为“已知f (x )＝ax 2＋bx (a ≠0)”，其余条件不变，求f (x )的解析式．【解】 ∵函数的图象过点(1,4)，∴a ＋b ＝4，①又⎠⎛01f(x )d x ＝⎠⎛01(ax 2＋bx )d x ＝⎝ ⎛⎭⎪⎫a 3x 3＋b 2x 2⎪⎪⎪10＝a 3＋b2，∴a 3＋b2＝1，② 由①②得a ＝6，b ＝－2，所以f (x )＝6x 2－2x .[构建·体系]1．下列值等于1的是( ) A.⎠⎛01x d xB.⎠⎛01(x ＋1)d xC.⎠⎛011d xD.⎠⎛0112d x 【解析】选项A ，因为⎝ ⎛⎭⎪⎫x 22′＝x ，所以⎠⎛01x d x ＝x 22⎪⎪⎪10＝12；选项B ，因为 ⎝ ⎛⎭⎪⎫x 22＋x ′＝x ＋1，所以⎠⎛01(x ＋1)d x ＝⎝ ⎛⎭⎪⎫x 22＋x ⎪⎪⎪10＝32；选项C ，因为x ′＝1，所以⎠⎛011d x ＝x ⎪⎪⎪1＝1；选项D ，因为⎝ ⎛⎭⎪⎫12x ′＝12，所以⎠⎛0112d x ＝12x ⎪⎪⎪1＝12. 【答案】 C2．⎠⎜⎜⎛-π2π2 (sin x ＋cos x )d x 的值是( ) A ．0 B.π4C ．2D ．4【解析】 ⎠⎜⎜⎛-π2π2 (sin x ＋cos x )d x ＝⎠⎜⎜⎛-π2π2sin x d x ＋⎠⎜⎜⎛-π2π2cos x d x ＝(－cos x )⎪⎪⎪⎪π2-π2π2－π2＋sin⎪⎪⎪⎪π2-π2＝2.【答案】 C3．计算⎠⎛01x 2d x ＝________. 【导学号：05410033】【解析】由于⎝ ⎛⎭⎪⎫13x 3′＝x 2，所以⎠⎛01x 2d x ＝13x 3⎪⎪⎪10＝13. 【答案】 134.⎠⎛49x(1＋x)d x 等于________．【解析】 ⎠⎛49x(1＋x)d x ＝⎠⎛49(x ＋x)d x ＝⎝ ⎛⎭⎪⎫23x 32＋12x 2⎪⎪⎪94＝⎝ ⎛⎭⎪⎫23×932＋12×92－⎝ ⎛⎭⎪⎫23×432＋12×42＝4516.【答案】 45165．已知f (x )＝ax ＋b ，且⎠⎛-11f 2(x )d x ＝1，求f (a )的取值范围．【解】由f (x )＝ax ＋b ，⎠⎛-11f 2(x )d x ＝1，得2a 2＋6b 2＝3,2a 2＝3－6b 2≥0，所以－22≤b ≤22，所以f (a )＝a 2＋b ＝－3b 2＋b ＋32＝－3⎝ ⎛⎭⎪⎫b －162＋1912，所以－22≤f (a )≤1912.我还有这些不足：(1) (2) 我的课下提升方案：(1) (2)。

高中数学《第一章导数及其应用》复习学案新人教A版

第一章导数及其应用（复习）学习目标提高学生综合、灵活运用导数的知识解决有关函数问题的能力.学习过程一、课前准备108109，找出疑惑之处）复习1：已知点P 和点Q 是曲线223y x x =--上的两点，且点P 的横坐标是1，点Q 的横坐标是4，求：（1）割线的P Q 斜率；（2）点P 处的切线方程.复习2：求下列函数的导数：（1）2tan y x x =；（2）ln x y e x =.二、新课导学学习探究探究任务一：本章知识结构问题：本章学过哪些知识点?新知：试试：一杯80℃的热红茶置于20℃的房间里，它的温度会逐渐下降，温度T （单位：℃）与时间t （单位：min ）间的关系，由函数()T f t =给出.请问：（1）()f t '的符号是什么？为什么？（2）(3)4f '=-的实际意义是什么？若(3)65f =℃，你能画出函数在点3t =时图象的大致形状吗？反思：1、导数的概念是：2、导数的几何意义是：3、导数的物理意义是：典型例题例1 已知函数2()()f x x x c=-在2x=处有极大值，求c的值.变式：已知函数22(),[1,)x x af x xx++=∈+∞,若()0f x>恒成立,试求实数a的取值范围.小结：例2 如图：过点(1,1)P作直线AB，分别与x轴的正半轴，y轴的正半轴交于,A B两点，当直线AB在什么位置时，ABC∆的面积最小，最小面积是多少？变式：用总长14.8m的钢条制作一个长方体容器的框架，如果所制容器底面一边的长比另一边的长多0.5m，那么高为多少时容器的容积最大？最大容积是多少？动手试试练1. 如图，直线l和圆C，当l从l开始在平面上绕O点按逆时针方向匀速转动（转动角度不超过90°）时，它扫过的圆内阴影部分的面积S是时间t的函数，这个函数的图象大致是（）.练2. 某旅行社在暑假期间推出如下组团办法：达到100人的团体，每人收费1000元.如果团体的人数超过100人，那么每超过1人，每人平均收费降低5元，但团体人数不能超过180人.如何组团，可使旅行社的收费最多？三、总结提升学习小结运用导数的知识解决有关函数问题的方法步骤.知识拓展导数是研究函数的有力工具，也是解决函数最（极）值问题，从而是解决优化问题的一种通法.虽然用配方法求二次函数极值的方法很漂亮，但它只是特殊情况下的特殊解法，并不能解决三次函数等一般函数的极值问题，利用导数，我们可以求出满足方程()0f x '=的点，然后根据此点附近两侧导数的符号求出极值.这同时体现了导数这个工具的力量.学习评价当堂检测（时量：5分钟满分：10分）计分：1. 已知函数()y f x =在区间(,)a b 内可导，且0(,)x a b ∈，则000()()lim h f x h f x h h→+-- 的值为（） A ．0()f x ' B ．02()f x ' C ．02()f x '- D ．02. 32()32f x ax x =++，若(1)4f '-=，则a 的值为（）A ．19/3 B.16/3 C.13/3 D. 10/33. 设28ln y x x =-，则此函数在区间1(0,)4和1(,1)2内分别为（） A.单调递增，单调递减 B.单调递增，单调递增C.单调递减，单调递增D.单调递减，单调递减4. 曲线32y x x =+- 在点0P 处的切线平行于直线41y x =-，则点0P 的坐标是5. 函数y=x+2cosx 在区间[0，21]上的最大值是课后作业1. 已知某养殖场每年的固定成本是20000元，每年最大规模的养殖量是400头牛，.每养1头牛，成本增加100元.如果收入函数是21()4002R q q q =-+（q 是猪的数量），每年多少头牛可使总利润最大？总利润是多少？（可使用计算器）。

人教版数学高二第一章 1.6微积分基本定理

1.6 微积分基本定理数学选修2－21.6 微积分基本定理[核心必知]1．预习教材，问题导入根据以下提纲，预习教材P 51～P 54的内容，回答下列问题．(1)观察教材P 51图1.6－1，一个做变速直线运动的物体的运动规律是y ＝y (t )，并且y (t )有连续的导数，设这个物体在时间段[a ，b ]内的位移为S .①由导数的概念可知，它在任意时刻t 的速度v (t )与y (t )之间有什么关系？提示：v (t )＝y ′(t )．②如何利用y ＝y (t )表示物体在t ∈[a ，b ]上的位移S? 提示：S ＝y (b )－y (a )．③若v (t )表示物体在任意时刻t 的速度，如何用v (t )求物体在t ∈[a ，b ]上的位移S? 提示：S ＝⎠⎛a bv (t )d t .④由①②③能否得出结论S ＝⎠⎛a bv (t )d t ＝⎠⎛a by ′(t )d t ＝y (b )－y (a )成立？提示：能．(2)计算定积分⎠⎛0πS i n x d x ，∫2ππS i n x d x ，∫2π0S i n x d x ，由计算结论你能发现什么规律？提示：⎠⎛0πS i n x d x ＝2，∫2ππS i n x d x ＝－2，∫2π0 S i n x d x ＝0. 即定积分的值可正，可负，还可能为0.(3)根据⎠⎛0πS i n x d x ，∫2ππS i n x d x 和∫2π0S i n x d x 值的特点以及曲边梯形的面积，你能得出定积分与曲边梯形的面积有什么关系吗？(参阅教材P 54图1.6－3，图1.6－4，图1.6－5)．提示：当曲边梯形在x 轴上方时，定积分的值取正值；当曲边梯形在x 轴下方时，定积分的值取负值；当位于x 轴上方的曲边梯形面积等于位于x 轴下方的曲边梯形面积时，定积分的值为0.2．归纳总结，核心必记 (1)微积分基本定理内容如果f (x )是区间[a ，b ]上的连续函数，并且F ′(x )＝f (x )，那么⎠⎛a bf (x )d x ＝F (b )－F (a )．符号⎠⎛a bf (x )d x ＝F (x )|b a ＝F (b )－F (a ). 设曲边梯形在x 轴上方的面积为S 上，x 轴下方的面积为S 下．则 ①当曲边梯形在x 轴上方时，如图(1)，则⎠⎛a bf (x )d x ＝S 上． ②当曲边梯形在x 轴下方时，如图(2)，则⎠⎛a b f (x )d x ＝－S 下．③当曲边梯形在x 轴上方、x 轴下方均存在时，如图(3)，则⎠⎛a bf (x )d x ＝S 上－S 下，若S 上＝S 下，则⎠⎛a bf (x )d x ＝0.[问题思考](1)满足F ′(x )＝f (x )的函数F (x )唯一吗？提示：不唯一，它们相差一个常数，但不影响定积分的值．(2)如果⎠⎛a bf (x )d x ＝⎠⎛a bg (x )d x ，那么是否一定有f (x )＝g (x )？请举例说明．提示：不一定，例如：当f (x )＝2x ，g (x )＝3x 2时，⎠⎛012xdx ＝⎠⎛013x 2dx ，但f(x )≠g(x )．(3)如图，如何用阴影面积S 1，S 2，S 3表示定积分⎠⎛a bf(x )dx 的值？提示：⎠⎛a bf(x )dx ＝S 1－S 2＋S 3.(4)你认为⎠⎛a bf(x )dx ，⎠⎛a b|f(x )|dx 和||⎠⎛a bf (x )d x 有什么不同？提示：①⎠⎛a b f(x )dx 表示的是由x 轴，函数f(x )的图象及直线x ＝a ，x ＝b(a<b)所围图形面积的代数和(即x 轴上方的面积减去x 轴下方的面积)；②||f (x )是非负的，所以⎠⎛a b|f(x )|dx 表示在区间[a ，b]上所有以||f (x )的图象为曲边的曲边梯形的面积和；③||⎠⎛a bf (x )d x 则是⎠⎛a bf(x )dx 的绝对值．三者的值一般情况下是不同的，但对于f(x )≥0，x ∈[a ，b]，三者的值是相同的．[课前反思](1)微积分基本定理的内容是什么？ (2)定积分与曲边梯形的面积有什么关系？知识点1求简单函数的定积分[思考1] 如何利用微积分基本定理求函数f(x )在[a ，b]上的定积分⎠⎛a bf(x )dx ?名师指津：用微积分基本定理求定积分的步骤： (1)求f(x )的一个原函数F(x )； (2)计算F(b)－F(a)．[思考2] 我们知道，已知函数f(x )，则满足F ′(x )＝f(x )的函数y ＝F(x )不唯一，那么⎠⎛abf(x )dx 的值唯一吗？名师指津：由于⎠⎛a bf(x )dx ＝F(b)－F(a)，且f(x )的原函数间相差一个常数，在计算时，不影响F(b)－F(a)的值，故⎠⎛a b f(x )dx 是唯一的．讲一讲1．(链接教材P 53－例1)计算下列定积分． (1)⎠⎛01(x 3－2x )dx ； (2)∫π20(x ＋coS x )dx ；(3)∫π20Sin 2x 2dx ; (4)⎠⎛121x (x ＋1)dx .[尝试解答] (1)∵⎝⎛⎭⎫14x 4－x 2′＝x 3－2x ， ∴⎠⎛01(x 3－2x )dx ＝⎝⎛⎭⎫14x 4－x 2|10＝－34. (2)∵⎝⎛⎭⎫12x 2＋sin x ′＝x ＋coS x ， ∴∫π20(x ＋coS x )dx ＝⎝⎛⎭⎫12x 2＋sin x |π20＝π28＋1. (3)Sin 2x 2＝1－cos x 2，而⎝⎛⎭⎫12x －12sin x ′＝12－12coS x ， ∴∫π20Sin 2x 2dx ＝∫π20⎝⎛⎭⎫12－12cos x dx ＝⎝⎛⎭⎫12x －12sin x |π20＝π4－12＝π－24. (4)∵f(x )＝1x (x ＋1)＝1x －1x ＋1，且[ln x －ln(x ＋1)]′＝1x －1x ＋1，∴⎠⎛121x (x ＋1)dx ＝⎠⎛12⎝⎛⎭⎫1x －1x ＋1dx＝[ln x －ln(x ＋1)]21＝ln 43.类题·通法用微积分基本定理求定积分，实质上是导数的逆运算，即求导数等于被积函数的一个函数，求解时需要注意以下两点：(1)熟练掌握基本函数的导数及导数的运算法则，学会逆运算；(2)当被积函数较为复杂，不容易找到原函数时，可适当变形后再求解．特别地，需要弄清楚积分变量，精确定位积分区间，分清积分上限与积分下限．练一练1．计算下列定积分．(1)⎠⎛1－2(1－t 3)d t ；(2)⎠⎛0－π(coS x ＋e x )dx ；(3)⎠⎛49x(1＋x)dx ；(4)⎠⎛0e33x ＋2dx ；(5)∫π2－π2coS 2xdx .解：(1)∵⎝⎛⎭⎫t －14t 4′＝1－t 3， ∴⎠⎛1－2(1－t 3)d t ＝⎝⎛⎭⎫t －14t 41－2＝⎝⎛⎭⎫1－14－⎣⎡⎦⎤－2－14(－2)4＝274. (2)∵(Sin x ＋e x )′＝coS x ＋e x ， ∴⎠⎛0－π(coS x ＋e x )dx ＝(Sin x ＋e x )0－π＝(0＋1)－(0＋e －π)＝1－e －π. (3)原式＝⎠⎛49(x ＋x )dx＝⎠⎛49x 12dx ＋⎠⎛49xdx . ∵⎝⎛⎭⎫23x 32′＝x 12，⎝⎛⎭⎫12x 2′＝x ， ∴⎠⎛49x 12dx ＋⎠⎛49xdx＝23x 3294＋12x 294＝2716. (4)∵[ln(3x ＋2)]′＝33x ＋2，∴⎠⎛0e33x ＋2dx ＝ln(3x ＋2)e 0＝ln(3e ＋2)－ln(3×0＋2)＝ln 3e ＋22.(5)原式＝∫π2－π2coS 2xdx ＝∫π2－π21＋cos 2x2dx∵⎝⎛⎭⎫x 2＋sin 2x 4′＝1＋cos 2x 2，∴∫π2－π2coS 2xdx ＝⎝⎛⎭⎫12x ＋14sin 2x |π2－π2 ＝π4＋14Sin π－⎝⎛⎭⎫－π4＋14sin (－π) ＝π2.知识点2求分段函数的定积分[思考] ⎠⎛ab f(x )dx 、⎠⎛ac f(x )dx 、⎠⎛cb f(x )dx (其中a<c<b)之间有什么关系？名师指津：⎠⎛a b f(x )dx ＝⎠⎛a c f(x )dx ＋⎠⎛cb f(x )dx (其中a<c<b)．讲一讲2．求函数f(x )＝⎩⎪⎨⎪⎧x 3，x ∈[0，1]，x ，x ∈[1，2]，2x ，x ∈[2，3]在区间[0,3]上的积分．[尝试解答] 由积分性质，得：⎠⎛03f(x )dx ＝⎠⎛01f(x )dx ＋⎠⎛12f(x )dx ＋⎠⎛23f(x )dx＝⎠⎛01x 3dx ＋⎠⎛12x dx ＋⎠⎛232x dx＝⎠⎛01x 3dx ＋⎠⎛12x 12dx ＋⎠⎛232x dx ＝x 4410＋23x 3221＋2x ln 232＝14＋432－23＋8ln 2－4ln 2 ＝－512＋432＋4ln 2.类题·通法分段函数定积分的求法求分段函数的定积分时，可利用积分性质将其表示为几段定积分和的形式，若函数解析式中含有绝对值，应根据绝对值的意义找到分界点，去掉绝对值符号，化为分段函数后再求积分．练一练2．计算定积分⎠⎛0－4|x ＋3|dx . 解：因为f(x )＝|x ＋3|＝⎩⎪⎨⎪⎧－x －3，x<－3，x ＋3，x ≥－3，所以⎠⎛－40|x ＋3|dx＝⎠⎜⎛－4－3(－x －3)dx ＋⎠⎛－30(x ＋3)dx＝⎝⎛⎭⎫－12x 2－3x |－3－4＋⎝⎛⎭⎫12x 2＋3x |0－3＝5.知识点3根据定积分求参数讲一讲3．设函数f(x )＝a x 2＋c(a ≠0)，若⎠⎛01f(x )dx ＝f(x 0)，0≤x 0≤1，求x 0的值．[思路点拨] 分别求出⎠⎛01f(x )dx 和f(x 0)的值，然后利用二者相等建立关于x 0的方程求解．[尝试解答] 因为f(x )＝a x 2＋c(a ≠0)，且⎝⎛⎭⎫a 3x 3＋cx ′＝a x 2＋c ，所以⎠⎛01f(x )dx ＝∫10(a x 2＋c)dx ＝⎝⎛⎭⎫a 3x 3＋cx |10＝a 3＋c ＝a x 20＋c ，解得x 0＝33或x 0＝－33(舍去)．即x 0的值为33.类题·通法利用定积分求参数应注意的问题利用定积分求参数时，注意方程思想的应用．一般地，首先要弄清楚积分变量和被积函数．当被积函数中含有参数时，必须分清常数和变量，再进行计算，其次要注意积分下限小于积分上限．练一练3．设f(x )＝a x ＋b ，且⎠⎛1－1[f(x )]2dx ＝1，求f(a)的取值范围．解：由⎠⎛1－1[f(x )]2dx ＝1可得，⎠⎛1－1(a x ＋b)2dx ＝⎠⎛1－1(a 2x 2＋2ab x ＋b 2)dx ＝⎝⎛⎭⎫a 23x 3＋abx 2＋b 2x |1－1＝1，即2a 2＋6b 2＝3，则b 2＝3－2a 26≤36＝12，即－22≤b ≤22. 于是f(a)＝a 2＋b ＝－3b 2＋b ＋32＝－3⎝⎛⎭⎫b －162＋1912，所以－22≤f(a)≤1912.即f(a)的取值范围为⎣⎡⎦⎤－22，1912. [课堂归纳·感悟提升]1．本节课的重点是利用微积分基本定理求定积分，难点是根据定积分求参数． 2．本节课要重点掌握的规律方法(1)利用微积分基本定理求定积分，见讲1和讲2； (2)根据定积分求参数的值(或取值范围)，见讲3.3．正确确定原函数是利用微积分基本定理求定积分的关键，也是本节课的易错点．课下能力提升(十)[学业水平达标练]题组1 求简单函数的定积分 1.⎠⎛02(x －1)d x 等于( )A ．－1B ．1C ．0D ．2解析：选C ⎠⎛02(x －1)d x ＝⎝⎛⎭⎫12x 2－x |20＝12×22－2＝0.2.⎠⎛01(e x ＋2x )dx 等于( )A ．1B ．e －1C ．eD ．e ＋1解析：选C ⎠⎛01(e x ＋2x )dx ＝(e x ＋x 2)10＝(e 1＋1)－e 0＝e .3．∫π2－π2(1＋coS x )dx ＝( )A ．πB ．2C ．π－2D ．π＋2解析：选D ∵(x ＋Sin x )′＝1＋coS x ， ∴∫π2－π2(1＋coS x )dx ＝(x ＋Sin x )π2－π2＝π＋2.4．计算定积分∫1－1(x 2＋Sin x )dx ＝________.解析：∫1－1(x 2＋Sin x )dx ＝⎝⎛⎭⎫x 33－cos x |1－1＝23. 答案：23题组2 求分段函数的定积分5．设f(x )＝⎩⎪⎨⎪⎧x 2，0≤x ≤1，2－x ，1<x ≤2，则⎠⎛02f(x )d x 等于( )A.34B.45C.56D ．不存在解析：选C ⎠⎛02f(x )dx ＝⎠⎛01x 2dx ＋⎠⎛12(2－x )dx ＝13x 310＋⎝⎛⎭⎫2x －12x 221＝13＋4－2－2＋12＝56. 6．计算下列定积分： (1)⎠⎛25|x －3|dx ；(2)若f(x )＝⎩⎪⎨⎪⎧x 2，x ≤0，cos x －1，x>0，求∫π2－1f(x )dx .解：(1)∵|x －3|＝⎩⎪⎨⎪⎧3－x ，x ∈[2，3)，x －3，x ∈[3，5]，∴⎠⎛25|x －3|dx ＝⎠⎛23|x －3|dx ＋⎠⎛35|x －3|dx＝⎠⎛23(3－x )dx ＋⎠⎛35(x －3)dx＝⎝⎛⎭⎫3x －12x 232＋⎝⎛⎭⎫12x 2－3x 53 ＝⎝⎛⎭⎫9－12×9－6＋2＋⎝⎛⎭⎫252－15－92＋9＝52.(2)由已知∫π2－1f(x )dx ＝⎠⎛0－1x 2dx ＋∫π20(coS x －1)dx ＝13x 30－1＋(Sin x －x )π20 ＝13＋⎝⎛⎭⎫1－π2＝43－π2. 题组3 根据定积分求参数7．若∫a 1⎝⎛⎭⎫2x ＋1x dx ＝3＋ln 2，则a 的值是( )A ．6B ．4C ．3D ．2解析：选D ∫a 1⎝⎛⎭⎫2x ＋1x dx ＝(x 2＋ln x )|a 1 ＝(a 2＋ln a)－(1＋ln 1)＝(a 2－1)＋ln a ＝3＋ln 2.∴⎩⎪⎨⎪⎧ a 2－1＝3，a>1，a ＝2，∴a ＝2.8．设f(x )＝⎩⎪⎨⎪⎧ lg x ，x ＞0，x ＋⎠⎛0a 3t 2d t ，x ≤0，若f(f(1))＝1，则a ＝________. 解析：显然f(1)＝lg 1＝0，f(0)＝0＋⎠⎛0a 3t 2d t ＝t 3a 0＝a 3，得a 3＝1，a ＝1. 答案：19．已知2≤⎠⎛12(k x ＋1)dx ≤4，则实数k 的取值范围为________．解析：⎠⎛12(k x ＋1)dx ＝⎝⎛⎭⎫12kx 2＋x 21＝(2k ＋2)－12k ＋1＝32k ＋1，所以2≤32k ＋1≤4，解得23≤k ≤2.答案：⎣⎡⎦⎤23，210．已知f(x )是二次函数，其图象过点(1,0)，且f ′(0)＝2，⎠⎛01f(x )dx ＝0，求f(x )的解析式．解：设f(x )＝a x 2＋b x ＋c(a ≠0)，∴a ＋b ＋c ＝0.∵f ′(x )＝2a x ＋b ，①∴f ′(0)＝b ＝2.②⎠⎛01f(x )dx ＝⎠⎛01(a x 2＋b x ＋c)dx ＝⎝⎛⎭⎫13ax 3＋12bx 2＋cx |10＝13a ＋12b ＋c ＝0.③ 由①②③得⎩⎪⎨⎪⎧ a ＝－32，b ＝2，c ＝－12，∴f(x )＝－32x 2＋2x －12. [能力提升综合练] 1．已知⎠⎛02f(x )dx ＝3，则⎠⎛02[f(x )＋6]dx ＝( ) A ．9 B ．12 C ．15 D ．18解析：选C ⎠⎛02[f(x )＋6]dx ＝⎠⎛02f(x )dx ＋⎠⎛026dx ＝3＋6x 20＝3＋12＝15. 2．若函数f(x )＝x m ＋nx 的导函数是f ′(x )＝2x ＋1，则⎠⎛12f (－x )d x ＝( )A .56B .12C .23D .16 解析：选A ∵f(x )＝x m ＋nx 的导函数是f ′(x )＝2x ＋1，∴f(x )＝x 2＋x ，∴⎠⎛12f(－x )dx ＝⎠⎛12(x 2－x )dx ＝⎝⎛⎭⎫13x 3－12x 221＝56.3．若y ＝⎠⎛0x (Sin t ＋coS t·Sin t)d t ，则y 的最大值是( ) A ．1 B ．2 C ．－1 D ．0解析：选B y ＝⎠⎛0x (Sin t ＋coS t·Sin t)d t ＝⎠⎛0x Sin t d t ＋⎠⎛0x sin 2t 2d t ＝－coS t x 0－14coS 2t x 0＝－coS x ＋1－14(coS 2x －1)＝－14coS 2x －coSx ＋54＝－12coS 2x －coS x ＋32＝－12(coS x ＋1)2＋2≤2. 4．若f(x )＝x 2＋2⎠⎛01f(x )dx ，则⎠⎛01f(x )dx 等于( ) A ．－1 B ．－13 C .13D ．1解析：选B 因为⎠⎛01f(x )dx 是常数，所以f ′(x )＝2x ，所以可设f(x )＝x 2＋c(c 为常数)，所以c ＝2⎠⎛01f(x )dx ＝2⎠⎛01(x 2＋c)dx ＝2⎝⎛⎭⎫13x 3＋cx |10，解得c ＝－23，⎠⎛01f(x )dx ＝⎠⎛01(x 2＋c)dx ＝⎠⎛01⎝⎛⎭⎫x 2－23dx ＝⎝⎛⎭⎫13x 3－23x 10＝－13. 5.⎠⎛02(4－2x )(4－3x 2)dx ＝________. 解析：⎠⎛02(4－2x )(4－3x 2)dx ＝⎠⎛02(16－12x 2－8x ＋6x 3)dx ＝⎝⎛⎭⎫16x －4x 3－4x 2＋32x 420＝8. 答案：86．若f(x )＝⎩⎪⎨⎪⎧x 2，x ≤0，sin x －1，x>0，则⎠⎛1－1f(x )dx ＝________. 解析：⎠⎛1－1f(x )dx ＝⎠⎛0－1x 2dx ＋⎠⎛01(Sin x －1)dx ＝13x 30－1＋(－coS x －x )10＝13－coS 1. 答案：13－coS 1 7．计算下列定积分．(1)⎠⎛3－3(|2x ＋3|＋|3－2x |)dx ；(2)⎠⎛14⎝⎛⎭⎫2x －1x dx . 解：(1)∵|2x ＋3|＋|3－2x |＝⎩⎪⎨⎪⎧ －4x ，x ≤－32，6，－32＜x ＜32，4x ，x ≥32.∴⎠⎛3－3(|2x ＋3|＋|3－2x |)dx ＝∫－32－3(－4x )dx ＋∫32－326dx ＋⎠⎛3324xdx ＝－2x 2－32－3＋6x 32－32＋2x 2332＝(－2)×⎝⎛⎭⎫－322－(－2)×(－3)2＋6×32－6×⎝⎛⎭⎫－32＋2×32－2×⎝⎛⎭⎫322＝45.(2)⎠⎛14⎝⎛⎭⎫2x －1x dx ＝⎠⎛142x dx －⎠⎛141xdx ＝2x ln 241－2x 41＝⎝⎛⎭⎫16ln 2－2ln 2－(24－2)＝14ln 2－2. 8．已知f(x )＝⎠⎛x －a (12t ＋4a)d t ，F(a)＝⎠⎛01[f(x )＋3a 2]dx ，求函数F(a)的最小值．解：∵f(x )＝⎠⎛x －a (12t ＋4a)d t ＝(6t 2＋4at)x －a ＝6x 2＋4a x －(6a 2－4a 2)＝6x 2＋4a x －2a 2， ∴F(a)＝⎠⎛01[f(x )＋3a 2]dx ＝⎠⎛01(6x 2＋4a x ＋a 2)dx ＝(2x 3＋2a x 2＋a 2x )10＝a 2＋2a ＋2＝(a ＋1)2＋1≥1，∴当a ＝－1时，F(a)最小值＝1.。

高中数学第一章导数及其应用 1.6 微积分基本定理(1)教学设计理新人教A版选修2-2

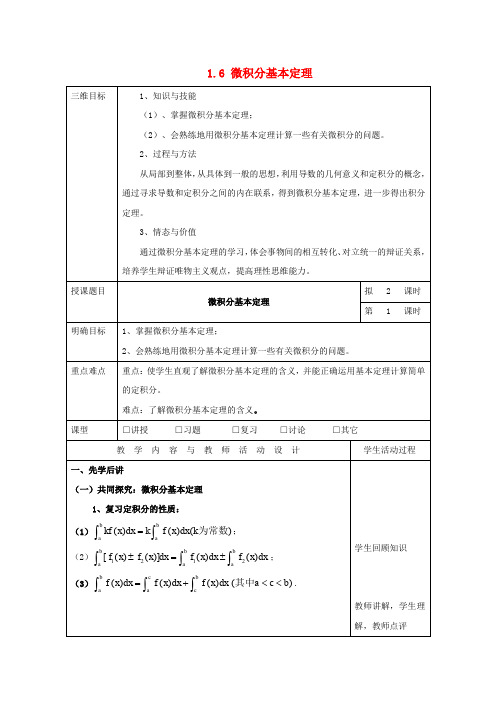
（2）
3
(2x
1
1 x2
)dx
。
注：引导学生发现
例 2．计算下列定积分：
定积分的正负与面

2
2
0 sin xdx, sin xdx, 0 sin xdx 。
积的关系。
由计算结果你能发现什么结论？试利用曲边梯形的面积表示所发现
的结论。
解：因为 ( cos x)' sin x ，
通过微积分基本定理的学习，体会事物间的相互转化、对立统一的辩证关系，
培养学生辩证唯物主义观点，提高理性思维能力。
授课题目
微积分基本定理
拟 2 课时第 1 课时
明确目标 1、掌握微积分基本定理；
2、会熟练地用微积分基本定理计算一些有关微积分的问题。
重点难点重点：使学生直观了解微积分基本定理的含义，并能正确运用基本定理计算简单
的定积分。
难点：了解微积分基本定理的含义。
课型
□讲授
□习题
□复习 □讨论
□其它
教学内容与教师活动设计
学生活动过程
一、先学后讲
（一）共同探究：微积分基本定理
1、复习定积分的性质：
（1）
b
kf (x)dx k
b f (x)dx(k为常数) ；
a
a
b
b
b
（2） a [ f1(x) f2 (x)]dx a f1(x)dx a f2 (x)dx ；
（3）
b
f (x)dx
c
f (x)dx
b f (x)dx (其中a c b) .
a
a
c
学生回顾知识教师讲解，学生理

高中数学选修2-2(人教B版)第一章导数及其应用1.4知识点总结含同步练习题及答案

x x [n, 2n] 上的 n 个矩形的面积之和小于曲边梯形的面积，
1 1 1 25 ． + +⋯+ < n+1 n+2 2n 36
即
2n 1 1 1 1 n + +⋯+ <∫ dx = ln x| 2 n = ln 2n − ln n = ln 2， n+1 n+2 2n x n
因为ln 2 ≈ 0.6931 ， 25 ≈ 0.6944 ，所以ln 2 < 25 ．所以
3 1
π 2 dx；（3）∫ 0 2 (sin x − cos x)dx． x
∫
(1 + x + x2 ) = ∫
3 1
1 2 3 1 x | 1 + x3 | 3 1 2 3 1 1 = (3 − 1) + (3 2 − 1 2 ) + (3 3 − 1 3 ) 2 3 44 = . 3 = x| 3 1 +
∑ f (ξi )Δx = ∑
i =1 i =1 n n
b−a f (ξi )， n
当 n → ∞ 时，上述和式无限接近某个常数，这个常数叫做函数 f (x) 在区间 [a, b] 上的定积分（definite integral），记作 ∫ ab f (x)dx，即
∫
b a
f (x)dx = lim ∑
∫
b a
f (x)dx = F (x)| b a = F (b) − F (a).
例题：利用定积分定义计算：（1）∫ 1 (1 + x)dx；（2）∫ 0 xdx．解：（1）因为 f (x) = 1 + x 在区间 [1, 2] 上连续，将区间 [1, 2] 分成 n 等份，则每个区间的

高中数学第1章导数及其应用1.4.2微积分基本定理学案新人教B版选修2_2

1.4.2 微积分基本定理1．理解微积分基本定理的含义．2．会用定理求定积分．微积分基本定理(1)F′(x)从a到b的积分等于F(x)在两端点的取值之____．(2)微积分基本定理．如果F′(x)＝f(x)，且其中F(x)叫做f(x))，F(x)＋c也是f(x)的原函数，其中c为常数．一般地，原函数在[a，b]上的改变量F(b)－F(a)简记作F(x)|ba.因此，微积分基本定理可以写成形式：________________________________.(1)微积分基本定理揭示了导数和定积分之间的内在联系，同时也提供了计算定积分的一种有效方法．但当运用公式不能直接求积分时，需考虑用定积分的几何意义来解决．(2)利用微积分基本定理求定积分ba⎰f(x)d x的关键是找出使F′(x)＝f(x)的函数F(x)．通常，我们可以运用基本初等函数的求导公式和导数的四则运算法则从反方向求出F(x)．(3)求导运算与求原函数运算互为逆运算．【做一做1－1】下列各式中，正确的是( )．A．ba⎰F′(x)d x＝F′(b)－F′(a)B．ba⎰F′(x)d x＝F′(a)－F′(b)C．ba⎰F′(x)d x＝F(b)－F(a)D．ba⎰F′(x)d x＝F(a)－F(b)【做一做1－2】计算5⎰(2x－4)d x＝________.求定积分有哪些常用技巧？剖析：(1)对被积函数，要先化简，再求积分．(2)对被积函数是分段函数的定积分，依据定积分“对区间的可加性”，分段积分再求和．(3)对于含有绝对值符号的被积函数，要去掉绝对值符号才能积分．题型一利用微积分基本定理求函数的定积分【例题1】求下列定积分：(1)12--⎰(2＋x2)2d x；(2)41⎰x ＋1xd x ； (3)ππ3⎰cos(x －π6)d x .分析：将被积函数适当变形，确定原函数，再运用微积分基本定理求解．反思：(1)求ba⎰f (x )d x 一般分为两步：①求f (x )的原函数F (x )，②计算F (b )－F (a )的值即为所求．(2)求复杂函数定积分要依据定积分的性质．①有限个函数代数和(差)的积分，等于各个函数积分的代数和(差)，即ba⎰[f 1(x )±f 2(x )±…±f n (x )]d x＝ba⎰f 1(x )d x ±ba⎰f 2(x )d x ±…±ba⎰f n (x )d x .②常数因子可提到积分符号外面，即ba⎰kf (x )d x ＝kba⎰f (x )d x .③当积分上限与下限交换时，积分值一定要反号，即ba⎰f (x )d x ＝－ab⎰f (x )d x .④定积分对区间的可加性，若c ∈[a ，b ]，则有ba⎰f (x )d x ＝ca⎰f (x )d x ＋bc⎰f (x )d x .题型二几类特殊被积函数的定积分【例题2】求下列定积分： (1)32-⎰16＋6x －x 2d x ；(2)若f (x )＝20cos 10,x x x x ⎧≤⎨⎩，，－，＞求11-⎰f (x )d x ；(3)π2⎰1－sin2x d x .分析：由于被积函数不是基本初等函数，因此需要先变换被积函数，再求定积分．反思：(1)对于直接用微积分基本定理不易求解的题目，转化为用定积分的几何意义来求解，不仅简捷可行，而且充分体现了初等数学与高等数学间的关系，因而充分把握定积分的几何意义，也是学好本节内容的关键．(2)对于被积函数是分段函数的定积分，通常是依据定积分“对区间的可加性”，先分段积分再求和．要注意各段定积分的上、下限的取值．(3)对于较复杂的被积函数，要先化简，再求定积分．若是计算ba⎰|f (x )|d x ，需要去掉绝对值符号，这时要讨论f (x )的正负，转化为分段函数求原积分．题型三利用定积分求平面图形的面积【例题3】下图中，阴影部分的面积是( )．A ．16B ．18C ．20D ．22 反思：求平面图形的面积的一般步骤是：(1)画图，并将图形分割成若干曲边梯形；(2)对每个曲边梯形确定其存在的范围，从而确定积分上、下限； (3)确定被积函数；(4)求出各曲边梯形的面积的和，即各积分的绝对值之和．1π2π2-⎰(sin x ＋cos x )d x 的值是( )．A ．0B ．π4C ．2D ．42曲线y ＝cos x ⎝⎛⎭⎪⎫0≤x ≤32π与坐标轴所围成的图形的面积是( )． A ．2 B ．3 C ．52D ．43如图，阴影部分的面积是( )．A ．2 3B ．2－ 3C ．323D ．3534计算e 1⎰1xd x ＝________.5已知函数f (x )＝3x 2＋2x ＋1，若11-⎰f (x )d x ＝2f (a )成立，则a ＝________.答案：基础知识·梳理(1)差 (2)F (b )－F (a ) 原函数 ⎠⎛a bf (x )d x ＝F (x )|ba ＝F (b )－F (a )【做一做1－1】C【做一做1－2】5 ∵(x 2－4x )′＝2x －4，∴⎠⎛05(2x －4)d x ＝(x 2－4x )|50＝(52－4×5)－0＝5. 典型例题·领悟【例题1】解：(1)∵(x 2＋2)2＝x 4＋4x 2＋4，又⎝ ⎛⎭⎪⎫15x 5＋43x 3＋4x ′＝x 4＋4x 2＋4，∴⎠⎛－2－1(2＋x 2)2d x ＝⎠⎛－2－1(x 4＋4x 2＋4)d x ＝⎝ ⎛⎭⎪⎫15x 5＋43x 3＋4x |－1－2＝29315. (2)∵x ＋1x ＝x ＋1x ＝1122x x -+，又3122223x x ⎛⎫+ ⎪⎝⎭′＝1122x x -+，∴⎠⎛14x ＋1x d x ＝⎠⎛14(1122x x -+)d x ＝3122223x x ⎛⎫+ ⎪⎝⎭|41＝23×324＋2×124－⎝ ⎛⎭⎪⎫23×1＋2×1＝203.(3)∵cos(x －π6)＝32cos x ＋12sin x ，∴ππ3⎰cos(x －π6)d x ＝ππ3⎰⎝ ⎛⎭⎪⎫32cos x ＋12sin x d x ＝32ππ3⎰cos x d x ＋12ππ3⎰sin x d x ＝32sin x ππ3－12cos x ππ3＝－32sin π3－12⎝ ⎛⎭⎪⎫cos π－cos π3＝－34＋14＋12＝0.【例题2】解：(1)设y ＝16＋6x －x 2，即(x －3)2＋y 2＝25(y ≥0)， ∵32-⎰16＋6x －x 2d x 表示圆(x －3)2＋y 2＝25的面积的14，∴32-⎰16＋6x －x 2d x ＝25π4.(2)11-⎰f (x )d x ＝1-⎰x 2d x ＋⎠⎛01(cos x －1)d x＝13x 301-＋(sin x －x )|10＝－23＋sin 1.(3)π20⎰1－sin 2x d x ＝π2⎰x －cos x2d x＝π2⎰|sin x －cos x |d x ＝π4⎰|sin x －cos x |d x ＋π2π4⎰|sin x －cos x |d x＝π4⎰(cos x －sin x )d x ＋π2π4⎰(sin x －cos x )d x＝(sin x ＋cos x )π40－(cos x ＋sin x )π2π4＝2(2－1)．【例题3】B 由题意，阴影部分的面积S ＝42-⎰⎝ ⎛⎭⎪⎫y ＋4－y 22d y ＝⎝ ⎛⎭⎪⎫y 22＋4y －y 36|4－2＝⎝ ⎛⎭⎪⎫422＋4×4－436－⎣⎢⎡⎦⎥⎤－22＋－－－36＝18 随堂练习·巩固1．C 原式＝(－cos x ＋sin x )π2π2-＝2.2．B 结合y ＝cos x ⎝ ⎛⎭⎪⎫0≤x ≤32π的图象可知，面积S ＝π20⎰cos x d x －3π2π2⎰cos x d x＝sin x π20－sin x3π2π2＝1＋2＝3.3．C S ＝13-⎰(3－x 2－2x )d x＝⎝ ⎛⎭⎪⎫3x －13x 3－x 213-＝323. 4．1 ⎠⎛1e1x d x ＝ln x |e1＝ln e －ln 1＝1－0＝1. 5．－1或1311-⎰(3x 2＋2x ＋1)d x ＝(x 3＋x 2＋x )|1－1＝4.∴2(3a 2＋2a ＋1)＝4，即3a 2＋2a －1＝0，∴a ＝－1或a ＝13.。

2018_2019学年高中数学第一章导数及其应用1.6微积分基本定理学案新人教A版

1．6 微积分基本定理1.了解微积分基本定理的含义．2.掌握微积分基本定理的数学表达式．3.会利用微积分基本定理求函数的定积分．微积分基本定理从微积分基本定理可以看出，求定积分的关键是寻找原函数，如此就建立了积分与微分的联系．中学阶段的定积分寻找原函数都是关注基本初等函数的导函数的原函数．值得注意的是由于f (x )＝F ′(x )＝[F (x )＋c ]′，c 为常数，因此原函数有无穷个，但是由于⎠⎛ab f (x )d x＝[F (x )＋c ]|ba ＝[F (b )＋c ]－[F (a )＋c ]＝F (b )－F (a )，所以我们一般选取最简单的原函数，不用加任意常数．判断正误(正确的打“√”，错误的打“×”) (1)若F ′(x )＝f (x )，则F (x )唯一．( )(2)微积分基本定理中，被积函数f (x )是原函数F (x )的导数．( )(3)应用微积分基本定理求定积分的值时，被积函数在积分区间上必须是连续函数．( )答案：(1)× (2)√ (3)√⎠⎛241xd x 等于( )A ．－2ln 2B ．2ln 2C ．－ln 2D ．ln 2解析：选D.⎠⎛241xd x ＝ln x |42＝ln 4－ln 2＝ln 2.⎠⎛01(e x＋2x )d x 等于( )A ．1B ．e －1C ．eD ．e ＋1解析：选C.⎠⎛01(e x ＋2x )d x ＝(e x ＋x 2)|10＝(e ＋1)－1＝e.⎠⎛0πsin x d x ＝________．解析：⎠⎛0πsin x d x ＝－cos x |π0＝(－cos π)－(－cos 0)＝2.答案：2探究点1 求简单函数的定积分求下列定积分． (1)⎠⎛01x nd x ；(2)⎠⎛02π(cos x －sin x )d x ；(3)⎠⎛12⎝⎛⎭⎪⎫e x －1x d x . 【解】 (1)⎠⎛01x nd x＝1n ＋1x n ＋1|10 ＝1n ＋1×1n ＋1－1n ＋1×0n ＋1＝1n ＋1. (2)⎠⎛02π(cos x －sin x )d x＝(sin x ＋cos x )⎪⎪⎪2π＝(sin 2π＋cos 2π)－(sin 0＋cos 0) ＝0.(3)⎠⎛12⎝⎛⎭⎪⎫e x －1x d x ＝(e x －ln x )|21＝(e 2－ln 2)－(e 1－ln 1) ＝e 2－e －ln 2.(1)用微积分基本定理求定积分的步骤①求f (x )的一个原函数F (x )； ②计算F (b )－F (a )． (2)注意事项①有时需先化简被积函数，再求积分；②f (x )的原函数有无穷多个，如F (x )＋c ，计算时，一般只写一个最简单的，不再加任意常数c.1.⎠⎛12⎝⎛⎭⎪⎫1x ＋1x2d x ＝________．解析：⎠⎛12⎝ ⎛⎭⎪⎫1x ＋1x 2d x＝⎝ ⎛⎭⎪⎫ln x －1x |21＝⎝ ⎛⎭⎪⎫ln 2－12－(ln 1－1)＝ln 2＋12. 答案：ln 2＋122．求下列定积分．(1) ⎠⎜⎜⎛0π2sin 2 x 2d x ；(2)⎠⎛23(2－x 2)(3－x )d x ；(3)⎠⎛49x (1＋x )d x .解：(1)sin 2x 2＝1－cos x2，而⎝ ⎛⎭⎪⎫12x －12sin x ′＝12－12cos x ，所以⎠⎜⎜⎛0π2sin 2 x 2d x ＝⎠⎜⎜⎛0π2⎝ ⎛⎭⎪⎫12－12cos x d x ＝⎝ ⎛⎭⎪⎫12x －12sin x ⎪⎪⎪⎪π20＝π4－12＝π－24.(2)原式＝⎠⎛23(6－2x －3x 2＋x 3)d x＝⎝⎛⎭⎪⎫6x －x 2－x 3＋14x 4|32 ＝⎝ ⎛⎭⎪⎫6×3－32－33＋14×34－⎝ ⎛⎭⎪⎫6×2－22－23＋14×24＝－74. (3)⎠⎛49x (1＋x )d x ＝⎠⎛49(x ＋x )d x＝⎝ ⎛⎭⎪⎫23x x ＋12x 2|94＝⎝ ⎛⎭⎪⎫23×9×3＋12×92－⎝ ⎛⎭⎪⎫23×4×2＋12×42＝4516.探究点2 求分段函数的定积分(1)若f (x )＝⎩⎪⎨⎪⎧x 2，x ≤0，cos x －1，x ＞0，求⎠⎜⎜⎛-1π2f (x )d x ； (2)计算定积分⎠⎛12|3－2x |d x .【解】 (1) ⎠⎜⎜⎛-1π2f (x )d x ＝⎠⎛－10x 2d x ＋⎠⎜⎜⎛-1π2 (cos x －1)d x ，又因为⎝ ⎛⎭⎪⎫13x 3′＝x 2，(sin x －x )′＝cos x －1，所以原式＝13x 3|0－1＋(sin x －x ) ⎪⎪⎪⎪π20＝⎝ ⎛⎭⎪⎫0＋13＋⎝⎛⎭⎪⎫sin π2－π2－(sin 0－0)＝43－π2. (2)⎠⎛12|3－2x |d x ＝⎠⎜⎛132 (3－2x )d x ＋⎠⎜⎛322 (2x －3)d x ＝(3x －x 2) ⎪⎪⎪⎪321＋(x 2－3x ) ⎪⎪⎪⎪232＝12.分段函数的定积分的求法(1)利用定积分的性质(3)，转化为各区间上定积分的和计算．(2)当被积函数含有绝对值时，常常去掉绝对值号，转化为分段函数的定积分再计算．1.⎠⎛－11e |x |d x ＝________．解析：⎠⎛－11e |x |d x＝⎠⎛－10e －xd x ＋⎠⎛01e xd x＝－e －x |0－1＋e x |1＝－e 0＋e 1＋e 1－e 0＝2e －2. 答案：2e －22．已知f (x )＝⎩⎪⎨⎪⎧2x ＋e x，0≤x ≤1，x －1x，1＜x ≤2，求⎠⎛02f (x )d x .解：⎠⎛02f (x )d x ＝⎠⎛01(2x ＋e x)d x ＋⎠⎛12⎝⎛⎭⎪⎫x －1x d x＝(x 2＋e x )|10＋⎝ ⎛⎭⎪⎫12x 2－ln x |21＝(1＋e)－(0＋e 0)＋⎝ ⎛⎭⎪⎫12×22－ln 2－⎝ ⎛⎭⎪⎫12×1－ln 1＝e ＋32－ln 2.探究点3 利用定积分求参数(1)若⎠⎛0k (2x －3x 2)d x ＝0(k >0)，则k 等于________．(2)已知x ∈(0，1]，f (x )＝⎠⎛01(1－2x ＋2t )d t ，则f (x )的值域是________．【解析】 (1)⎠⎛0k (2x －3x 2)d x ＝(x 2－x 3)|k 0＝k 2－k 3＝0，所以k ＝0(舍)或k ＝1.(2)⎠⎛01(1－2x ＋2t )d t ＝[(1－2x )t ＋t 2]⎪⎪⎪10＝2－2x ，即f (x )＝－2x ＋2，因为x ∈(0，1]，所以f (1)≤f (x )<f (0)，即0≤f (x )<2，所以函数f (x )的值域是[0，2)．【答案】 (1)1 (2)[0，2)本例(2)中已知条件改为f (t )＝⎠⎛01(1－2x ＋2t )d x ，则f (t )＝________.解析：f (t )＝⎠⎛01(1－2x ＋2t )d x＝[(1＋2t )x －x 2]⎪⎪⎪1＝2t .答案：2t含参数问题的求解方法利用定积分求参数时，注意方程思想的应用．一般地，首先要弄清楚积分变量和被积函数．当被积函数中含有参数时，必须分清参数和变量，再进行计算．另外，需注意积分下限不大于积分上限．1.已知⎠⎛01(x 2＋mx )d x ＝0，则实数m 的值为( )A ．－13B ．－23C ．－1D ．－2解析：选B.根据题意有⎠⎛01(x 2＋mx )d x ＝⎝ ⎛⎭⎪⎫13x 3＋12mx 2|10＝13＋12m ＝0，解得m ＝－23.2．若函数f (x )＝ax 2＋bx ＋c (a ≠0)且f (1)＝4，f ′(1)＝1，⎠⎛01f (x )d x ＝316，求函数f (x )的解析式．解：由题意知f (1)＝a ＋b ＋c ＝4，①f ′(1)＝2a ＋b ＝1，②又由⎠⎛01f (x )d x ＝⎠⎛01(ax 2＋bx ＋c )d x ＝316知a 3＋b 2＋c ＝316.③①②③联立，解得a ＝－1，b ＝3，c ＝2，所以函数f (x )的解析式为f (x )＝－x 2＋3x ＋2.1．下列各式的值等于1的是( ) A.⎠⎛01x d xB.⎠⎛01(x ＋1)d xC.⎠⎛011d xD.⎠⎛0112d x 解析：选C.选项A ，因为⎝ ⎛⎭⎪⎫x 22′＝x ，所以⎠⎛01x d x ＝⎪⎪⎪x 2210＝12；选项B ，因为⎝ ⎛⎭⎪⎫x 22＋x ′＝x ＋1，所以⎠⎛01(x ＋1)d x ＝⎪⎪⎪⎝ ⎛⎭⎪⎫x 22＋x 10＝32；选项C ，因为x ′＝1，所以⎠⎛011d x ＝x |10＝1；选项D ，因为⎝ ⎛⎭⎪⎫12x ′＝12，所以⎠⎛0112d x ＝12x |10＝12.故选C.2．已知f (x )＝⎩⎪⎨⎪⎧x 2，－1≤x ≤0，x 3，0<x ≤1，则⎠⎛－11f (x )d x 的值为( )A.13B.14C.112D.712解析：选D.⎠⎛－11f (x )d x ＝⎠⎛－10f (x )d x ＋⎠⎛01f (x )d x ＝⎠⎛－10x 2d x ＋⎠⎛01x 3d x ＝13x 3|0－1＋14x 4|10＝0－13×(－1)3＋14＝712. 3．若⎠⎛1a ⎝⎛⎭⎪⎫2x ＋1x d x ＝3＋ln 2，则a 的值是________．解析：⎠⎛1a ⎝⎛⎭⎪⎫2x ＋1x d x ＝(x 2＋ln x )|a 1＝(a 2＋ln a )－(1＋ln 1)＝(a 2－1)＋ln a ＝3＋ln 2.所以⎩⎪⎨⎪⎧a 2－1＝3，a >0，a ＝2，所以a ＝2. 答案：24．⎠⎜⎜⎛0π3⎝⎛⎭⎪⎫1－2sin 2θ2d θ的值为________．解析：因为1－2sin2θ2＝cos θ，所以⎠⎜⎜⎛0π3⎝ ⎛⎭⎪⎫1－2sin 2θ2d θ＝⎠⎜⎜⎛0π3cos θd θ＝sin θ⎪⎪⎪⎪π30＝32. 答案：32[A 基础达标]1．定积分⎠⎛01(x －x 2)d x ＝( )A ．0 B. 13 C ．－13D ．1解析：选B.⎠⎛01(x －x 2)d x ＝⎝ ⎛⎭⎪⎫23x 32－13x 3|10＝13.2.⎠⎛12（x ＋1）2xd x 等于( )A ．3 B. 72＋ln 2 C. 52＋ln 2 D. 92解析：选B.⎠⎛12（x ＋1）2xd x ＝⎠⎛12x 2＋2x ＋1x d x＝⎠⎛12⎝⎛⎭⎪⎫x ＋2＋1x d x ＝⎝ ⎛⎭⎪⎫12x 2＋2x ＋ln x |21＝⎝ ⎛⎭⎪⎫12×22＋2×2＋ln 2－⎝ ⎛⎭⎪⎫12×12＋2×1＋ln 1＝72＋ln 2.故选B. 3．已知f (x )＝2－|x |，则⎠⎛－12f (x )d x ＝( )A ．3B ．4 C. 72D. 92解析：选C.因为f (x )＝2－|x |＝⎩⎪⎨⎪⎧2＋x ，x ≤0，2－x ，x >0，所以⎠⎛－12f (x )d x ＝⎠⎛－10(2＋x )d x ＋⎠⎛02(2－x )d x ＝⎝ ⎛⎭⎪⎫2x ＋x 22|0－1＋⎝ ⎛⎭⎪⎫2x －x 22|20＝32＋2＝72.4．已知函数f (a )＝⎠⎛0a sin x d x ，则f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫π2等于( )A ．1B ．1－cos 1C ．0D ．cos 1－1解析：选B .f ⎝ ⎛⎭⎪⎫π2＝⎠⎜⎜⎛0π2sin x d x ＝－cos x ⎪⎪⎪⎪π20＝1，f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫π2＝f (1)＝⎠⎛01sin x d x ＝－cos x |10＝1－cos 1.5．若⎠⎛12(x －a )d x ＝⎠⎜⎛03π4cos 2x d x ，则a ＝( )A ．－1B ．1C ．2D ．4解析：选C.⎠⎛12(x －a )d x ＝⎝ ⎛⎭⎪⎫12x 2－ax |21＝32－a ，⎠⎜⎛03π4cos 2x d x ＝12sin 2x ⎪⎪⎪⎪3π40＝－12，所以32－a ＝－12，解得a ＝2，故选C. 6．计算⎠⎛－11(x 2＋sin x )d x ＝________．解析：⎠⎛－11(x 2＋sin x )d x ＝⎝ ⎛⎭⎪⎫x 33－cos x |1－1＝23.答案：237．已知2≤⎠⎛12(kx ＋1)d x ≤4，则实数k 的取值范围为________．解析：⎠⎛12(kx ＋1)d x ＝⎝ ⎛⎭⎪⎫12kx 2＋x |21＝(2k ＋2)－⎝ ⎛⎭⎪⎫12k ＋1＝32k ＋1，所以2≤32k ＋1≤4，解得23≤k ≤2. 答案：⎣⎢⎡⎦⎥⎤23，2 8．设f (x )＝kx ＋b ，若⎠⎛01f (x )d x ＝2，⎠⎛12f (x )d x ＝3.则f (x )的解析式为________．解析：由⎠⎛01(kx ＋b )d x ＝2，得⎝ ⎛⎭⎪⎫12kx 2＋bx ⎪⎪⎪1＝2，即12k ＋b ＝2，① 由⎠⎛12(kx ＋b )d x ＝3，得⎝ ⎛⎭⎪⎫12kx 2＋bx ⎪⎪⎪21＝3，即(2k ＋2b )－⎝ ⎛⎭⎪⎫12k ＋b ＝3.所以32k ＋b ＝3，②由①②联立解得，k ＝1，b ＝32，所以f (x )＝x ＋32.答案：f (x )＝x ＋329．若f (x )是一次函数，且⎠⎛01f (x )d x ＝5，⎠⎛01xf (x )d x ＝176.求⎠⎛12f （x ）x d x 的值．解：设f (x )＝kx ＋b ，k ≠0，则⎠⎛01(kx ＋b )d x ＝⎝ ⎛⎭⎪⎫k 2x 2＋bx |10＝k2＋b ＝5，①⎠⎛01xf (x )d x ＝⎠⎛01(kx 2＋bx )d x＝⎝ ⎛⎭⎪⎫kx 33＋bx 22|10＝k 3＋b 2＝176，②联立①②可得⎩⎪⎨⎪⎧k ＝4，b ＝3.所以f (x )＝4x ＋3. 则⎠⎛12f （x ）x d x ＝⎠⎛124x ＋3x d x＝⎠⎛12⎝ ⎛⎭⎪⎫4＋3x d x ＝(4x ＋3ln x )|21 ＝(8＋3ln 2)－(4＋3ln 1)＝4＋3ln 2.10．计算⎠⎛－33(|2x ＋3|＋|3－2x |)d x . 解：设y ＝|2x ＋3|＋|3－2x |＝⎩⎪⎨⎪⎧－4x ⎝ ⎛⎭⎪⎫x ≤－32，6⎝ ⎛⎭⎪⎫－32<x <32，4x ⎝ ⎛⎭⎪⎫x ≥32，则⎠⎛－33(|2x ＋3|＋|3－2x |)d x＝⎠⎜⎛-332 (－4x )d x ＋⎠⎜⎜⎛－32326d x ＋⎠⎜⎛3234x d x＝－2×⎝ ⎛⎭⎪⎫－322－(－2)×(－3)2＋6×32－6×⎝ ⎛⎭⎪⎫－32＋2×32－2×⎝ ⎛⎭⎪⎫322＝45. [B 能力提升]11．已知f (a )＝⎠⎛01(2ax 2－a 2x )d x ，则函数f (a )的最大值为( ) A. 19B. 29 C ．－19 D ．－29解析：选B.f (a )＝⎠⎛01(2ax 2－a 2x )d x ＝⎝ ⎛⎭⎪⎫23ax 3－12a 2x 2|10 ＝－12a 2＋23a ，由二次函数的性质，可得f (a )max ＝－12×⎝ ⎛⎭⎪⎫232＋⎝ ⎛⎭⎪⎫232＝29. 12．设f (x )＝⎩⎪⎨⎪⎧ln x ，x >0x ＋⎠⎛0a 3t 2d t ，x ≤0，若f (f (1))＝8，则实数a ＝________．解析：显然f (1)＝ln 1＝0，f (0)＝0＋⎠⎛0a 3t 2d t ＝t 3|a 0＝a 3，得a 3＝8，即a ＝2.答案：213．已知⎠⎛－11(x 3＋ax ＋3a －b )d x ＝2a ＋6且f (t )＝⎠⎛0t (x 3＋ax ＋3a －b )d x 为偶函数，求a ，b .解：因为f (x )＝x 3＋ax 是奇函数，所以⎠⎛－11(x 3＋ax )d x ＝0，所以⎠⎛－11(x 3＋ax ＋3a －b )d x＝⎠⎛－11(x 3＋ax )d x ＋⎠⎛－11(3a －b )d x ＝0＋(3a －b )[1－(－1)]＝6a －2b ，所以6a －2b ＝2a ＋6，即2a －b ＝3.①又f (t )＝⎠⎛0t (x 3＋ax ＋3a －b )d x ＝⎣⎢⎡⎦⎥⎤x 44＋ax 22＋（3a －b ）x |t 0＝t 44＋at 22＋(3a －b )t 为偶函数，所以3a －b ＝0.②由①②得a ＝－3，b ＝－9.14．(选做题)已知f ′(x )是f (x )在(0，＋∞)上的导函数，满足xf ′(x )＋2f (x )＝1x 2，且⎠⎛12[x 2f (x )－ln x ]d x ＝1. (1)求f (x )的解析式；(2)当x >0时，证明不等式2ln x ≤e x 2－2.解：(1)由xf ′(x )＋2f (x )＝1x 2得 x 2f ′(x )＋2xf (x )＝1x，即[x 2f (x )]′＝1x，所以x 2f (x )＝ln x ＋c (c 为常数)，即x 2f (x )－ln x ＝c .又⎠⎛12[x 2f (x )－ln x ]d x ＝1，即⎠⎛12c d x ＝1，所以cx |21＝1，即2c －c ＝1，所以c ＝1.所以x 2f (x )＝ln x ＋1，所以f (x )＝ln x ＋1x 2. (2)证明：由第一问知f (x )＝ln x ＋1x 2(x >0)，所以f ′(x )＝1x ×x 2－2x （ln x ＋1）x 4 ＝－2ln x －1x ，当f ′(x )＝0时，x ＝e －12， f ′(x )>0时，0<x <e －12， f ′(x )<0时，x >e －12，所以f (x )在(0，e －12)上单调递增，在(e －12，＋∞)上单调递减．所以f (x )max ＝f (e －12)＝e 2，所以f (x )＝ln x ＋1x ≤e 2，即2ln x ≤e x 2－2.。

全国通用版版高中数学第一章导数及其应用1.6微积分基本定理学案新人教A版选修2_2

§1.6 微积分基本定理学习目标 1.直观了解并掌握微积分基本定理的含义.2.会利用微积分基本定理求函数的积分．知识点一微积分基本定理(牛顿—莱布尼茨公式)思考已知函数f (x )＝2x ＋1，F (x )＝x 2＋x ，则ʃ10(2x ＋1)d x 与F (1)－F (0)有什么关系？答案由定积分的几何意义知，ʃ10(2x ＋1)d x ＝12×(1＋3)×1＝2，F (1)－F (0)＝2，故ʃ10(2x ＋1)d x ＝F (1)－F (0)．梳理 (1)微积分基本定理①条件：f (x )是区间[a ，b ]上的连续函数，并且F ′(x )＝f (x )； ②结论：ʃba f (x )d x ＝F (b )－F (a )；③符号表示：ʃba f (x )d x ＝F (x )|ba ＝F (b )－F (a )． (2)常见的原函数与被积函数关系 ①ʃba c d x ＝cx |b a (c 为常数)． ②ʃb a x nd x ＝⎪⎪⎪1n ＋1x n ＋1ba (n ≠－1)． ③ʃb a sin x d x ＝－cos x |ba . ④ʃba cos x d x ＝sin x |ba .⑤ʃb a 1xd x ＝ln x |ba (b >a >0)． ⑥ʃb a e x d x ＝e x |ba . ⑦ʃb aa xd x ＝⎪⎪⎪a x ln a ba (a >0且a ≠1)． ⑧ʃb ax d x ＝⎪⎪⎪2332x ba (b >a >0)．知识点二定积分和曲边梯形面积的关系思考定积分与曲边梯形的面积一定相等吗？答案当被积函数f (x )≥0恒成立时，定积分与曲边梯形的面积相等，若被积函数f (x )≥0不恒成立，则不相等．梳理设曲边梯形在x 轴上方的面积为S 上，在x 轴下方的面积为S 下，则(1)当曲边梯形在x 轴上方时，如图①，则ʃba f (x )d x ＝S 上． (2)当曲边梯形在x 轴下方时，如图②，则ʃba f (x )d x ＝－S 下．(3)当曲边梯形在x 轴上方，x 轴下方均存在时，如图③，则ʃba f (x )d x ＝S 上－S 下．特别地，若S 上＝S 下，则ʃba f (x )d x ＝0.1．若F ′(x )＝f (x )，则F (x )唯一．( × )2．微积分基本定理中，被积函数f (x )是原函数F (x )的导数．( √ )3．应用微积分基本定理求定积分的值时，被积函数在积分区间上必须是连续函数．( √ )类型一求定积分命题角度1 求简单函数的定积分例1 计算下列定积分． (1)ʃ10(2x ＋e x)d x ；(2)ʃ21⎝ ⎛⎭⎪⎫1x－3cos x d x ；(3)π220(sincos )d ;22x xx -⎰(4)ʃ30(x －3)(x －4)d x .考点利用微积分基本定理求定积分题点利用微积分基本定理求定积分解 (1)ʃ10(2x ＋e x )d x ＝(x 2＋e x )|10 ＝(1＋e 1)－(0＋e 0)＝e.(2)ʃ21⎝ ⎛⎭⎪⎫1x－3cos x d x＝(ln x －3sin x )|21＝(ln 2－3sin 2)－(ln 1－3sin 1) ＝ln 2－3sin 2＋3sin 1. (3)∵⎝⎛⎭⎪⎫sin x2－cos x 22＝1－2sin x 2cos x2＝1－sin x ，∴ππ22200(sin cos )d (1-sin )d 22x x x x x -=⎰⎰π20(cos )|x x =＋＝⎝⎛⎭⎪⎫π2＋cos π2－(0＋cos 0)＝π2－1.(4)∵(x －3)(x －4)＝x 2－7x ＋12， ∴ʃ30(x －3)(x －4)d x ＝ʃ30(x 2－7x ＋12)d x ＝⎪⎪⎪⎝ ⎛⎭⎪⎫13x 3－72x 2＋12x 30＝⎝ ⎛⎭⎪⎫13×33－72×32＋12×3－0＝272. 反思与感悟 (1)当被积函数为两个函数的乘积或乘方形式时一般要转化为和的形式，便于求得原函数F (x )．(2)由微积分基本定理求定积分的步骤第一步：求被积函数f (x )的一个原函数F (x )；第二步：计算函数的增量F (b )－F (a )．跟踪训练1 计算下列定积分． (1)ʃ21⎝ ⎛⎭⎪⎫x －x 2＋1x d x ；(2)π222(cos sin )d 22x xx -⎰； (3)ʃ94x (1＋x )d x . 考点利用微积分基本定理求定积分题点利用微积分基本定理求定积分解 (1)ʃ21⎝ ⎛⎭⎪⎫x －x 2＋1x d x ＝⎪⎪⎪⎝ ⎛⎭⎪⎫12x 2－13x 3＋ln x 21＝⎝ ⎛⎭⎪⎫12×22－13×23＋ln 2－⎝ ⎛⎭⎪⎫12－13＋ln 1 ＝ln 2－56.(2)π222(cos sin )d 22x xx -⎰π20cos d x x =⎰＝sin x π20|＝1. (3)ʃ94x (1＋x )d x ＝ʃ94(x ＋x )d x ＝⎪⎪⎪⎝ ⎛⎭⎪⎫2332x ＋12x 294＝⎝ ⎛⎭⎪⎫23×329＋12×92－⎝ ⎛⎭⎪⎫23×324＋12×42＝2716.命题角度2 求分段函数的定积分例2 (1)若f (x )＝⎩⎪⎨⎪⎧x 2，x ≤0，cos x －1，x >0，求π21()d ;f x x -⎰(2)计算定积分ʃ21|3－2x |d x . 考点分段函数的定积分题点分段函数的定积分解 (1)π21()d f x x -⎰＝ʃ0－1x 2d x ＋π2(cos 1)d ,x x -⎰又因为⎝ ⎛⎭⎪⎫13x 3′＝x 2，(sin x －x )′＝cos x －1，所以原式＝⎪⎪⎪13x 30－1＋(sin x －x )π20| ＝⎝ ⎛⎭⎪⎫0＋13＋⎝⎛⎭⎪⎫sin π2－π2－(sin 0－0)＝43－π2. (2)ʃ21|3－2x |d x322312(32)d (23)d x x x x =-+-⎰⎰＝(3x －x 2)321|＋(x 2－3x )232|＝12.反思与感悟分段函数定积分的求法(1)利用定积分的性质，转化为各区间上定积分的和计算．(2)当被积函数含有绝对值时，常常去掉绝对值号，转化为分段函数的定积分再计算．跟踪训练2 (1)ʃ1－1e |x |d x ＝________. 考点分段函数的定积分题点分段函数的定积分答案 2e －2 解析 ʃ1－1e |x |d x ＝ʃ0－1e －xd x ＋ʃ10e xd x ＝－e －x |0－1＋e x |10 ＝－e 0＋e 1＋e 1－e 0＝2e －2.(2)已知f (x )＝⎩⎪⎨⎪⎧2x ＋e x，0≤x ≤1，x －1x ，1<x ≤2，求ʃ20f (x )d x .考点分段函数的定积分题点分段函数的定积分解 ʃ20f (x )d x＝ʃ10(2x ＋e x )d x ＋ʃ21⎝ ⎛⎭⎪⎫x －1x d x＝(x 2＋e x )|10＋⎪⎪⎪⎝ ⎛⎭⎪⎫12x 2－ln x 21 ＝(1＋e)－(0＋e 0)＋⎝ ⎛⎭⎪⎫12×22－ln 2－⎝ ⎛⎭⎪⎫12×1－ln 1＝e ＋32－ln 2.类型二利用定积分求参数例3 (1)已知t >0，f (x )＝2x －1，若ʃt0f (x )d x ＝6，则t ＝________. (2)已知2≤ʃ21(kx ＋1)d x ≤4，则实数k 的取值范围为________．考点微积分基本定理的应用题点利用微积分基本定理求参数答案 (1)3 (2)⎣⎢⎡⎦⎥⎤23，2解析 (1)ʃt 0f (x )d x ＝ʃt 0(2x －1)d x ＝t 2－t ＝6，解得t ＝3或－2，∵t >0，∴t ＝3. (2)ʃ21(kx ＋1)d x ＝⎪⎪⎪⎝ ⎛⎭⎪⎫12kx 2＋x 21＝32k ＋1.由2≤32k ＋1≤4，得23≤k ≤2.引申探究1．若将例3(1)中的条件改为ʃt0f (x )d x ＝f ⎝ ⎛⎭⎪⎫t 2，求t .解由ʃt0f (x )d x ＝ʃt0(2x －1)d x ＝t 2－t ，又f ⎝ ⎛⎭⎪⎫t 2＝t －1，∴t 2－t ＝t －1，得t ＝1.2．若将例3(1)中的条件改为ʃt0f (x )d x ＝F (t )，求F (t )的最小值．解 F (t )＝ʃt 0f (x )d x ＝t 2－t ＝⎝ ⎛⎭⎪⎫t －122－14(t >0)，当t ＝12时，F (t )min ＝－14.反思与感悟 (1)含有参数的定积分可以与方程、函数或不等式综合起来考查，先利用微积分基本定理计算定积分是解决此类综合问题的前提．(2)计算含有参数的定积分，必须分清积分变量与被积函数f (x )、积分上限与积分下限、积分区间与函数F (x )等概念．跟踪训练3 (1)已知x ∈(0,1]，f (x )＝ʃ10(1－2x ＋2t )d t ，则f (x )的值域是________． (2)设函数f (x )＝ax 2＋c (a ≠0)．若ʃ10f (x )d x ＝f (x 0)，0≤x 0≤1，则x 0的值为________．考点微积分基本定理的应用题点利用微积分基本定理求参数答案 (1)[0,2) (2)33解析 (1)f (x )＝ʃ10(1－2x ＋2t )d t ＝(t －2xt ＋t 2)|10＝－2x ＋2(x ∈(0,1])． ∴f (x )的值域为[0,2)． (2)∵ʃ10f (x )d x ＝ʃ10(ax 2＋c )d x ＝⎪⎪⎪⎝ ⎛⎭⎪⎫13ax 3＋cx 10＝a 3＋c .又f (x 0)＝ax 20＋c ，∴a 3＝ax 20，即x 0＝33或－33. ∵0≤x 0≤1，∴x 0＝33.1．若ʃa 1⎝ ⎛⎭⎪⎫2x ＋1x d x ＝3＋ln 2，则a 的值是( )A ．5B ．4C ．3D ．2 考点微积分基本定理的应用题点利用微积分基本定理求参数答案 D解析 ʃa 1⎝ ⎛⎭⎪⎫2x ＋1x d x ＝ʃa 12x d x ＋ʃa 11xd x＝x 2|a 1＋ln x |a1＝a 2－1＋ln a ＝3＋ln 2，解得a ＝2. 2．π23(12sin )d 2θθ-⎰等于( )A ．－32 B ．－12 C.12 D.32考点利用微积分基本定理求定积分题点利用微积分基本定理求定积分答案 D 解析π23(12sin )d 2θθ-⎰π3=cos d θθ⎰＝sin θπ30|＝32. 3．设f (x )＝⎩⎪⎨⎪⎧x 2，0≤x ≤1，2－x ，1<x ≤2，则ʃ20f (x )d x 等于( )A.34B.45 C.56D ．不存在考点分段函数的定积分题点分段函数的定积分答案 C解析 ʃ20f (x )d x ＝ʃ10x 2d x ＋ʃ21(2－x )d x ＝⎪⎪⎪13x 310＋⎪⎪⎪⎝ ⎛⎭⎪⎫2x －12x 221＝56.4．已知函数f (x )＝x n＋mx 的导函数f ′(x )＝2x ＋2，则ʃ31f (－x )d x ＝________.考点微积分基本定理的应用题点微积分基本定理的综合应用答案 23解析 ∵f (x )＝x n＋mx 的导函数f ′(x )＝2x ＋2， ∴nxn －1＋m ＝2x ＋2，解得n ＝2，m ＝2，∴f (x )＝x 2＋2x ，则f (－x )＝x 2－2x ， ∴ʃ31f (－x )d x ＝ʃ31(x 2－2x )d x ＝⎪⎪⎪⎝ ⎛⎭⎪⎫13x 3－x 231＝9－9－13＋1＝23.5．已知f (x )＝⎩⎪⎨⎪⎧4x －2π，0≤x ≤π2，cos x ，π2<x ≤π，计算：ʃπ0f (x )d x .解 ʃπf (x )d x ππ2π02()d ()d f x x f x x =+⎰⎰ππ2π02=(4-2π)d cos d ,x x x x +⎰⎰取F 1(x )＝2x 2－2πx ，则F 1′(x )＝4x －2π；取F 2(x )＝sin x ，则F 2′(x )＝cos x . 所以ππ2π02(4-2π)d cos d x x x x +⎰⎰＝(2x 2－2πx )π20|＋sin x ππ2|＝－12π2－1，即ʃπ0f (x )d x ＝－12π2－1.1．求定积分的一些常用技巧(1)对被积函数，要先化简，再求积分．(2)若被积函数是分段函数，依据定积分“对区间的可加性”，分段积分再求和． (3)对于含有绝对值符号的被积函数，要去掉绝对值符号才能积分．2．由于定积分的值可取正值，也可取负值，还可以取0，而面积是正值，因此不要把面积理解为被积函数对应图形在某几个区间上的定积分之和，而是在x 轴下方的图形面积要取定积分的相反数.一、选择题1．ʃ21⎝⎛⎭⎪⎫e x＋1x d x 等于( )A ．e 2－ln 2B ．e 2－e －ln 2 C ．e 2＋e ＋ln 2D ．e 2－e ＋ln 2考点利用微积分基本定理求定积分题点利用微积分基本定理求定积分答案 D解析 ʃ21⎝ ⎛⎭⎪⎫e x ＋1x ＝(e x ＋ln x )|21＝(e 2＋ln 2)－(e ＋ln 1)＝e 2－e ＋ln 2. 2．若π2(sin cos )d x a x x -⎰＝2，则实数a 等于( )A ．－1B ．1C ．－ 3D. 3考点微积分基本定理的应用题点利用微积分基本定理求参数答案 A 解析π2(sin cos )d x a x x -⎰＝(－cos x －a sin x )π20| ＝0－a －(－1－0)＝1－a ＝2， ∴a ＝－1，故选A.3．若S 1＝ʃ21x 2d x ，S 2＝ʃ211xd x ，S 3＝ʃ21e xd x ，则S 1，S 2，S 3的大小关系为( )A ．S 1<S 2<S 3B ．S 2<S 1<S 3C ．S 2<S 3<S 1D ．S 3<S 2<S 1考点利用微积分基本定理求定积分题点利用微积分基本定理求定积分答案 B解析因为S 1＝ʃ21x 2d x ＝⎪⎪⎪13x 321＝13×23－13＝73， S 2＝ʃ211x d x ＝ln x |21＝ln 2，S 3＝ʃ21e x d x ＝e x |21＝e 2－e ＝e(e －1)．又ln 2<ln e ＝1，且73<2.5<e(e －1)，所以ln 2<73<e(e －1)，即S 2<S 1<S 3.4．ʃ30|x 2－4|d x 等于( ) A.213 B.223 C.233D.253考点分段函数的定积分题点分段函数的定积分答案 C解析 ∵|x 2－4|＝⎩⎪⎨⎪⎧x 2－4，2≤x ≤3，4－x 2，0≤x ≤2，∴ʃ30|x 2－4|d x ＝ʃ32(x 2－4)d x ＋ʃ20(4－x 2)d x ＝⎪⎪⎪⎝ ⎛⎭⎪⎫13x 3－4x 32＋⎪⎪⎪⎝ ⎛⎭⎪⎫4x －13x 320＝⎣⎢⎡⎦⎥⎤(9－12)－⎝ ⎛⎭⎪⎫83－8＋⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫8－83－0＝－3－83＋8＋8－83＝233.5．若函数f (x )，g (x )满足ʃ1－1f (x )g (x )d x ＝0，则称f (x )，g (x )为区间[－1,1]上的一组正交函数．给出三组函数： ①f (x )＝sin 12x ，g (x )＝cos 12x ；②f (x )＝x ＋1，g (x )＝x －1； ③f (x )＝x ，g (x )＝x 2.其中为区间[－1,1]上的正交函数的组数为( ) A ．0 B ．1 C ．2 D ．3 考点微积分基本定理的应用题点微积分基本定理的综合应用答案 C解析对于①，ʃ1－1sin 12x cos 12x d x ＝ʃ1－112sin x d x ＝0，所以①是区间[－1,1]上的一组正交函数；对于②，ʃ1－1(x ＋1)(x －1)d x ＝ʃ1－1(x 2－1)d x ≠0，所以②不是区间[－1,1]上的一组正交函数；对于③，ʃ1－1x ·x 2d x ＝ʃ1－1x 3d x ＝0，所以③是区间[－1,1]上的一组正交函数．6．若f (x )＝x 2＋2ʃ10f (x )d x ，则ʃ10f (x )d x 等于( )A ．－13B ．－1C.13 D ．1考点利用微积分基本定理求定积分题点利用微积分基本定理求定积分答案 A解析 ∵f (x )＝x 2＋2ʃ10f (x )d x ，∴ʃ10f (x )d x ＝ ⎪⎪⎪⎝ ⎛⎭⎪⎫13x 3＋2x ʃ10f (x )d x 1＝13＋2ʃ10f (x )d x ，∴ʃ10f (x )d x ＝－13.二、填空题7．设f (x )＝⎩⎪⎨⎪⎧ x 2，x ≤0，cos x －1，x >0，则ʃ1－1f (x )d x ＝________. 考点分段函数的定积分题点分段函数的定积分答案 sin 1－23解析 ʃ1－1f (x )d x ＝ʃ0－1x 2d x ＋ʃ10(cos x －1)d x＝ ⎪⎪⎪13x 30－1＋(sin x －x )|1＝⎣⎢⎡⎦⎥⎤13×03－13×(－1)3＋[(sin 1－1)－(sin 0－0)]＝sin 1－23. 8．已知f (x )＝3x 2＋2x ＋1，若ʃ1－1f (x )d x ＝2f (a )成立，则a ＝________.考点微积分基本定理的应用题点利用微积分基本定理求参数答案－1或13解析 ʃ1－1f (x )d x ＝(x 3＋x 2＋x )|1－1＝4，2f (a )＝6a 2＋4a ＋2，由题意得6a 2＋4a ＋2＝4，解得a ＝－1或13. 9.从如图所示的长方形区域内任取一个点M (x ，y )，则点M 取自阴影部分的概率为________．考点微积分基本定理的应用题点微积分基本定理的综合应用答案 13解析长方形的面积为S 1＝3，S 阴＝ʃ103x 2d x ＝x 3|10＝1，则P ＝S 阴S 1＝13. 10．设f (x )＝⎩⎪⎨⎪⎧ lg x ，x >0，x ＋ʃa 03t 2d t ，x ≤0，若f (f (1))＝1，则a ＝____________.考点微积分基本定理的应用题点利用微积分基本定理求参数答案 1解析因为x ＝1>0，所以f (1)＝lg 1＝0.又当x ≤0时，f (x )＝x ＋ʃa 03t 2d t ＝x ＋t 3|a 0＝x ＋a 3，所以f (0)＝a 3.因为f (f (1))＝1，所以a 3＝1，解得a ＝1.11．设f (x )是一次函数，且ʃ10f (x )d x ＝5，ʃ10xf (x )d x ＝176，则f (x )的解析式为________．考点微积分基本定理的应用题点利用微积分基本定理求参数答案 f (x )＝4x ＋3解析 ∵f (x )是一次函数，∴设f (x )＝ax ＋b (a ≠0)，∴ʃ10f (x )d x ＝ʃ10(ax ＋b )d x ＝ʃ10ax d x ＋ʃ10b d x＝12a ＋b ＝5，ʃ10xf (x )d x ＝ʃ10x (ax ＋b )d x＝ʃ10(ax 2)d x ＋ʃ10bx d x ＝13a ＋12b ＝176.∴⎩⎪⎨⎪⎧ 12a ＋b ＝5，13a ＋12b ＝176，解得⎩⎪⎨⎪⎧ a ＝4，b ＝3.∴f (x )＝4x ＋3.12．已知α∈⎣⎢⎡⎦⎥⎤0，π2，则当ʃα0(cos x －sin x )d x 取最大值时，α＝________.考点微积分基本定理的应用题点微积分基本定理的综合应用答案 π4解析 ʃα0(cos x －sin x )d x ＝(sin x ＋cos x )|α＝sin α＋cos α－1＝2sin ⎝ ⎛⎭⎪⎫α＋π4－1.∵α∈⎣⎢⎡⎦⎥⎤0，π2，则α＋π4∈⎣⎢⎡⎦⎥⎤π4，34π，当α＋π4＝π2，即α＝π4时，2sin ⎝ ⎛⎭⎪⎫α＋π4－1取得最大值．三、解答题13．已知f (x )＝ʃx －a (12t ＋4a )d t ，F (a )＝ʃ10[f (x )＋3a 2]d x ，求函数F (a )的最小值．考点微积分基本定理的应用题点微积分基本定理的综合应用解因为f (x )＝ʃx －a (12t ＋4a )d t ＝(6t 2＋4at )|x－a＝6x 2＋4ax －(6a 2－4a 2)＝6x 2＋4ax －2a 2，F (a )＝ʃ10[f (x )＋3a 2]d x ＝ʃ10(6x 2＋4ax ＋a 2)d x＝(2x 3＋2ax 2＋a 2x )|1＝a 2＋2a ＋2＝(a ＋1)2＋1≥1.所以当a ＝－1时，F (a )取到最小值为1.四、探究与拓展 14．已知函数f (x )＝⎩⎨⎧ (x ＋1)2，－1≤x ≤0，1－x 2，0<x ≤1，则ʃ1－1f (x )d x 等于( ) A.3π－812 B.4＋3π12 C.4＋π4 D.－4＋3π12考点分段函数的定积分题点分段函数的定积分答案 B解析 ʃ1－1f (x )d x ＝ʃ0－1(x ＋1)2d x ＋ʃ101－x 2d x ， ʃ0－1(x ＋1)2d x ＝⎪⎪⎪13(x ＋1)30－1＝13， ʃ101－x 2d x 以原点为圆心，以1为半径的圆的面积的四分之一，故ʃ101－x 2d x ＝π4，故ʃ1－1f (x )d x ＝13＋π4＝4＋3π12. 15．已知f ′(x )是f (x )在(0，＋∞)上的导数，满足xf ′(x )＋2f (x )＝1x2，且ʃ21[x 2f (x )－ln x ]d x ＝1.(1)求f (x )的解析式；(2)当x >0时，证明不等式2ln x ≤e x 2－2.考点微积分基本定理的应用题点微积分基本定理的综合应用(1)解由xf ′(x )＋2f (x )＝1x2，得 x 2f ′(x )＋2xf (x )＝1x，即[x 2f (x )]′＝1x，所以x 2f (x )＝ln x ＋c (c 为常数)，即x 2f (x )－ln x ＝c .又ʃ21[x 2f (x )－ln x ]d x ＝1，即ʃ21c d x ＝1，所以cx |21＝1，所以2c －c ＝1，所以c ＝1.所以x 2f (x )＝ln x ＋1，所以f (x )＝ln x ＋1x 2.(2)证明由(1)知f (x )＝ln x ＋1x 2(x >0)，所以f ′(x )＝1x ×x 2－2x (ln x ＋1)x 4＝－2ln x －1x 3，当f ′(x )＝0时，x ＝12e -，f ′(x )>0时，0<x <12e -， f ′(x )<0时，x >12e -，所以f (x )在(0，12e -)上单调递增，在(12e -，＋∞)上单调递减．所以f (x )max ＝ 12(e )f -＝e 2，所以f (x )＝ln x ＋1x 2≤e 2，即2ln x ≤e x 2－2.。