2016年上数学建模与数学实验选修课作业题目

2016校数学建模竞赛题目A

福州大学第十二届数学建模竞赛题目
请先仔细阅读“论文格式规范”
A题高等院校排课系统的设计
长期以来，高等院校每个学期的排课在整个教务工作中是一项繁重琐碎的工作，基本上靠手工操作，既花费大量的时间和精力，又可能使得排课结果在时间段上不能充分满足教师的个性化需求，且存在许多不尽合理之处，比如教室利用上不够均衡，有的教室使用频率很高，有的教室使用频率却太低。

排课问题早在1975年就被S.Even等证明是一个NP-完全问题，说明排课问题可以通过建立数学模型找到问题的近似最优解。

从公开正式发表的文献来看，目前针对排课的建模主要有涉及遗传算法、图论法、模拟退火算法、蚁群算法以及基于优先级的排课算法等多种方法。

这些方法针对性均太强，且各有优缺点。

某校数学系把学生分成数学实验班与数学普通班两类，具体又分成数学与应用数学、信息与计算科学两个不同专业。

不同班级开设的课程不完全相同，但同一学期中若是由同一教师开设的相同课程都是合班上课的。

下面的表3和表4列出2014—2015学年下学期整个系要开的所有课程。

请你们通过建立数学模型，设计出一种适用于该系的通用排课系统。

给出用你们的模型计算出的排课结果，要求列出每个班的课表（具体应体现各时间段对应的课程、教师和教室编号）。

说明：以下时间段为全校2013级公共课安排时间：08、12、13、16、20，不得占用。

以下时间段为全校2014级公共课安排时间：03、05、06、11、13、18，不得占用。

教务人员在安排教室时，教室一般事先会被分块，数学系的课程只能被安排在10间教室内，具体见表2：
表2 数学系排课教室
表3 数学实验班编号数据。

2016年数学建模考试试卷综述

湖南某学院数学与计算科学学院2016年《线性规划与数学建模》考查试题考查要求：1. 以下共有10题，任选一题撰写建模论文，题目自拟，可以一人单独完成，也可以2人一组（2人合作的需在第一页说明每个人在完成论文中的分工，成绩由论文质量与分工任务确定）。

论文要求格式规范，表述清楚，结构完整。

2. 纸质文档+电子文档，纸质文档的第一页必须写好姓名、学号、所选题名。

成绩评定以纸质文档为依据，电子文档主要验证作业的真实性（没交电子文档将扣分）。

3. 纸质文档（A4纸打印）于6月27日17：00前以班级为单位上交到实A102，规定时间内缺交答卷（纸质文档）者以缺考论处。

电子文档以班级为单位打包发送至邮箱79752148@，文档名称：班级+2个人的姓名.doc，例如：623班+张三,李四.doc。

注意：如有雷同两份答卷同时计0分，如查实为抄袭网上已有论文计0分。

考查试题：一、深洞的估算假如你站在洞口且身上仅带着一只具有跑秒功能的计算器，你出于好奇心想用扔下一块石头听回声的方法来估计洞的深度，假定你捡到一块质量是1kg的石头，并准确的测定出听到回声的时间T=5S，就下面给定情况，分析这一问题，给出相应的数学模型，并估计洞深。

1．不计空气阻力；2．受空气阻力，并假定空气阻力与石块下落速度成正比，比例系数k1=0.05；3．受空气阻力，并假定空气阻力与石块下落速度的平方成正比，比例系数k2=0.0025；4．在上述三种情况下，如果再考虑回声传回来所需要的时间。

二、最佳工资预发方案一般公司给职员发放薪金，通常按每月等额发放。

某公司即将改进薪金发放方案，允许任职5年以上的职员向公司财务部门申请工资每月可变额度发放，每月工资发放额度不超过年收入20%，前半年收入不超过年收入的80%, 剩余部分则作为年终奖在年底一次性发放. 职员们想通过调整每月的预发金额以及年终一次性发放金额，使得一年内个人的总收益最高.针对以下各种情况.1. 请你查阅国家个人所得税税率表，为薪金年收入分别为8万元、12万元、18万元的职员们设计个人薪金领取方案，合理避税，使得一年的税后收入最高.2. 该公司部分职员每月可以将80%收入用于一些投资理财项目，如某些收益宝（百赚、余额宝等）、开放式基金、银行存款、债券、股票等, 请为他们设计个人薪金领取方案，使其年总收益最高。

数学建模与数学实验习题答案

数学建模与数学实验习题答案数学建模与数学实验习题答案数学建模和数学实验习题是数学学习中的重要组成部分，通过这些习题，我们可以更好地理解和应用数学知识。

本文将介绍数学建模和数学实验习题的一些答案和解题方法，帮助读者更好地掌握数学学习。

一、数学建模数学建模是将数学方法和技巧应用于实际问题的过程。

在数学建模中，我们需要将实际问题抽象为数学模型，并通过数学方法进行求解和分析。

下面是一个简单的数学建模问题和其解题过程。

问题：某工厂生产产品A和产品B，每天的产量分别为x和y。

产品A的生产成本为10x+20y，产品B的生产成本为15x+10y。

如果工厂每天的总成本不超过5000元，且产品A的产量必须大于产品B的产量，求工厂一天最多能生产多少个产品。

解题过程：首先，我们需要建立数学模型来描述这个问题。

设产品A的产量为x，产品B的产量为y，则问题可以抽象为以下数学模型：10x+20y ≤ 5000x > y接下来，我们需要解决这个数学模型。

首先，我们可以通过图像法来解决这个问题。

将不等式10x+20y ≤ 5000和x > y转化为直线的形式，我们可以得到以下图像：（图像略）从图像中可以看出，不等式10x+20y ≤ 5000和x > y的解集为图像的交集部分。

通过观察图像，我们可以发现交集部分的最大值为x=250，y=125。

因此，工厂一天最多能生产250个产品A和125个产品B。

除了图像法，我们还可以通过代数法来解决这个问题。

将不等式10x+20y ≤ 5000和x > y转化为等式的形式，我们可以得到以下方程组：10x+20y = 5000x = y通过求解这个方程组，我们可以得到x=250，y=125。

因此，工厂一天最多能生产250个产品A和125个产品B。

二、数学实验习题数学实验习题是通过实际操作和实验来学习数学知识和技巧的一种方式。

下面是一个关于概率的数学实验习题和其答案。

习题：一枚硬币抛掷10次，求出现正面的次数为偶数的概率。

数学建模与数学实验课后习题答案

P594•学校共1002名学生，237人住在A 宿舍，333人住在B 宿舍，432 人住在C 宿舍。

学生要组织一个10人的委员会，使用Q 值法分配各宿舍的委员数。

解:设P 表示人数，N 表示要分配的总席位数。

i 表示各个宿舍（分别取 A,B,C ）， p i 表示i 宿舍现有住宿人数， n i 表示i 宿舍分配到的委员席位。

首先，我们先按比例分配委员席位。

23710 A 宿舍为:n A ==2.365 1002 333"0 B 宿舍为：n B =3.323 1002 432X0 C 宿舍为：n C =4.3111002现已分完9人，剩1人用Q 值法分配。

经比较可得，最后一席位应分给 A 宿舍。

所以，总的席位分配应为： A 宿舍3个席位，B 宿舍3个席位，C 宿舍4个席位。

QA23722 3= 9361.5 Q B33323 4 = 9240.7 Q C4322 4 5=9331.2商人们怎样安全过河傻麴删舫紬削＜ I 11山名畝臥蹄峨颂禮训鋤嫌邂韻靖甘讹岸讎鞍輯毗匍趾曲展縣確牡GH 錚俩軸飙奸比臥鋪謎 smm 彌鯉械即第紘麵觎岸締熾 x^M 曲颁M 删牘HX …佛讪卜过樹蘇卜允棘髒合岡仇卅毘冋如;冋冋1卯;砰=口於广歎煙船上觸人敦% V O J U;xMmm朗“…他1曲策D 咿川| thPl,2卜允隸策集合刼為和啊母紳轉多步贱就匚叫=1入“山使曲并按腿翻律由汩3』和騒側），模型求解 -穷举法〜编程上机 ■图解法S={(x ?jOI x=o, j-0,1,2,3;X =3? J =0,1,2,3； X =»*=1,2}J规格化方法，易于推广考虑4名商人各带一随从的情况状态$=（xy¥）~ 16个格点允许状态〜U ）个。

点 , 允许决策〜移动1或2格； k 奇）左下移；&偶，右上移. 右，…，必I 给出安全渡河方案评注和思考［廿rfn片,rfl12 3xmm賤縣臓由上题可求：4个商人，4个随从安全过河的方案。

《数学建模与数学实验》(第三版)6.5习题作业2

1.根据物理定律K K K R I V =,R I P 2=,建立如下模型：（1）：目标函数为：∑==412k k k R IP 约束条件⎪⎪⎩⎪⎪⎨⎧===++=≤≤8,6,41023213214I I I I I I I I R I k k k 1)直接计算求解183214=++=I I I I()K K k K K K K R I I R I P ∑∑====41412min min=K k K V I∑=41min现在K V 一定，要想求P 的最小值，只需K I 最小即可。

又因为K I 已知，代入数据即可求解。

即218282624min 44332211⨯+⨯+⨯+⨯=+++=V I V I V I V I P2）有K I 已知及K V 的取值范围，可得K R 的取值范围。

min =I1^2*R1+I2^2*R2+I3^2*R3+I4^2*R4;I1=4;I2=6;I3=8;I4=18;R1>=1/2;R2>=1/3;R3>=1/4;R4>=1/9;R1<=5/2;R2<=5/3;R3<=5/4;R4<=5/9;EndGlobal optimal solution found.Objective value: 72.00000Total solver iterations: 0Variable Value Reduced Cost I1 4.000000 0.000000 R1 0.5000000 0.000000 I2 6.000000 0.000000 R2 0.3333333 0.000000 I3 8.000000 0.000000 R3 0.2500000 0.000000 I4 18.00000 0.000000 R4 0.1111111 0.000000Row Slack or Surplus Dual Price 1 72.00000 -1.000000 2 0.000000 -4.000122 3 0.000000 -4.000081 4 0.000000 -4.000061 5 0.000000 -4.000027 6 0.000000 -16.00000 7 0.000000 -36.00000 8 0.000000 -64.00000 9 0.000000 -324.0000 10 2.000000 0.000000 11 1.333333 0.000000 12 1.000000 0.000000 13 0.4444444 0.000000（2）：目标函数：∑==412k k k R I P 约束条件为：⎪⎪⎩⎪⎪⎨⎧≤≤===≤≤++=628,6,4263213214k kk kI V V V V R V I I II1)183214=++=I I I I()K K k K KK K R I I R I P ∑∑====41412min min=K k K V I ∑=41min)min(44332211V I V I V I V I P +++=要使P 最小，取4V =0，则)min(332211V I V I V I P ++=现在K V 一定，要想求P 的最小值，只需K I 最小即可。

2016数学建模d题

2016数学建模d题摘要：一、数学建模简介1.数学建模的定义2.数学建模的重要性3.数学建模的应用领域二、2016 数学建模D 题背景及内容1.题目背景2.题目内容3.题目难度及挑战三、解题思路及方法1.问题分析2.解题思路3.常用数学建模方法四、2016 数学建模D 题案例分析1.案例一2.案例二3.案例三五、总结与反思1.2016 数学建模D 题的启示2.数学建模能力的培养3.对未来数学建模比赛的展望正文：数学建模是一种运用数学方法解决实际问题的过程，它涉及到多个学科领域，如统计学、计算机科学、经济学等。

数学建模在现代社会具有很高的实用价值，可以帮助我们更好地理解世界、预测未来和优化决策。

在我国，数学建模竞赛是一项重要的赛事，吸引了大量的高校学生参与。

2016 年的数学建模D 题以“飞行器航迹优化问题”为背景，要求参赛者针对给定的飞行器、目标和航路约束条件，设计出一种飞行器航迹优化算法。

该题目具有一定的难度和挑战性，需要参赛者具备较强的数学功底和实际问题解决能力。

在解题过程中，首先要对题目进行深入分析，明确问题的关键信息和隐含条件。

然后根据问题特点，选择合适的解题思路和方法。

常用的数学建模方法有：线性规划、动态规划、遗传算法、模拟退火算法等。

为了更好地理解2016 数学建模D 题，我们可以通过以下三个案例进行分析：案例一：采用线性规划方法求解飞行器航迹优化问题。

通过建立线性目标函数和约束条件，求解最优航迹。

该方法简单易行，但对于复杂问题可能无法得到全局最优解。

案例二：利用动态规划方法解决飞行器航迹优化问题。

通过将问题拆分为子问题，并采用动态规划的思想，逐步求解子问题，最终得到全局最优解。

该方法在时间复杂度上具有优势，但在空间复杂度上可能较高。

案例三：采用遗传算法求解飞行器航迹优化问题。

通过模拟自然界的生物进化过程，对飞行器航迹进行迭代优化。

遗传算法具有全局搜索能力，能够较快地找到最优解，但可能受初始种群和参数设置的影响。

数学建模选修课作业

⑹Editor/Debugger M文件编辑调试器可以用来处理复杂的问题。
二﹑MATLAB解决线性代数问题
⑴①矩阵A的逆矩阵-0.1250 -0.1250 0.4000 -0.0500
0.1250 0.1250 0.2000 -0.1500
1.7500 0.7500 -1.0000 0.5000
1.5000 0.5000 -1.2000 0.4000
3.利用三维曲面绘图命令绘制3个三维曲面的图形
(1)绘制平面z=x+y的图形
程序:x=0:1:2;
y=0:1:2;
[x,y]=meshgrid(x,y)%生成xy平面上网格坐标矩阵
z=x+y;
axis([0,2,0,2,0,4])
mesh(x,y,z)%做三维曲面命令
(2)绘制螺旋抛物面z=x2+y2的图形
ans secx*tanx
(4)求导exyz,
程序：syms u x y z;
u=exp(x*y*z);
diff(diff(u,(x),y),z)
ans xexyz+x2zyexyz
(5)求导e2xy,
程序：syms u x y
u=exp(2*x*y)
diff(diff(u,(2x),y),z)
ans 2xexyz+x2zyexyz
-0.1616 - 1.4968i
1.0452
-1.0554
⑷利用MATLAB矩阵访问命令对下面的矩阵做初等行变换使其成为一个上三角矩阵
1 -2 2 -1 1
0 -4 8 0 2
0 0 -2 3 3
0 0 0 -6 4
三﹑MATLAB绘图绘制下面的曲线
1.在区间0≤x≤2中绘制cosx的图形

数学建模作业

克 8 元，原料占用资金不得超过 30000 元，已知生产单位产品所需工时，原料消
耗，产品单价，A，B 两道工序有效工时如表 1-19 所示，要求安排最优的生产计
划，使该厂利润最大？
表 1-19
Ⅰ
Ⅱ
工序有效工时
A 工序（工时）
2000
B 工序（工时）
1500
原料（千克）
1
2
单价（元/件）
20
28
解：该问题的目标是使得利润最大，设产品Ⅰ和产品Ⅱ的生产数量分别为
乙的售价为元/千克，加工费甲为元/千克，乙为元/千克。已知天然饲料 A，B，
C 中蛋白质、矿物质、维生素的含量，A，B，C 的单价及每周的限用量如表 1-22
所示。问该厂应如何安排生产，才能使利润收入为最大？
表 1-22
天然饲料蛋白质(%) 矿物质(%) 维生素(%) 单价每周限制用量
(元/千克)
其运行结果如下：
7.在同一平面的两个窗口中分别画出心形线和马鞍面，要求： (1)在图形上加格栅、图例和标注； (2)定制坐标； (3)以不同的角度观察马鞍面。解：编写以下程序：
subplot(2,2,1); ezplot('2*(2*cos(t)-cos(2*t))','2*(2*sin(t)-sin(2*t))'); title('心形线'); view(-45,45); subplot(2,2,2); [X,Y]=meshgrid(-2::2); Z=X.^2-Y.^2; surf(X,Y,Z); colormap('default'); grid on;view(40,0); title('以(40,0)视角观看马鞍面'); subplot(2,2,3);surf(X,Y,Z); colormap('default'); grid on;view(-60,10);

数学建模与数学实验课程设计题目与参考答案

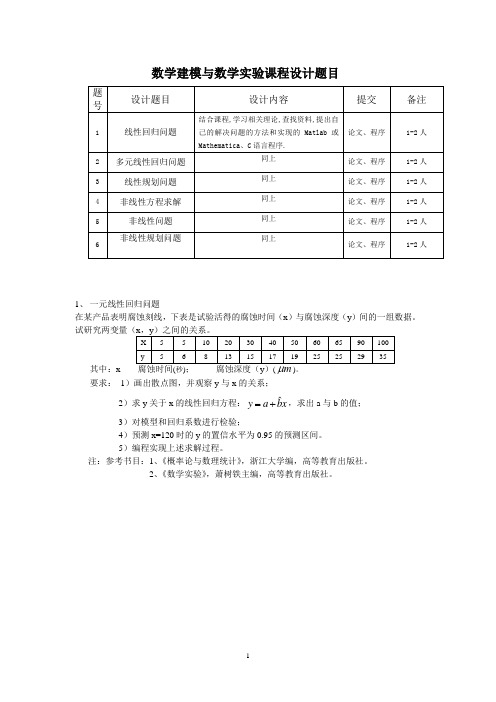
数学建模与数学实验课程设计题目1、一元线性回归问题在某产品表明腐蚀刻线，下表是试验活得的腐蚀时间（x）与腐蚀深度（y）间的一组数据。

试研究两变量（x，y）之间的关系。

其中：(秒)()。

要求：1）画出散点图，并观察y与x的关系；=+，求出a与b的值；2）求y关于x的线性回归方程：y a bx3）对模型和回归系数进行检验；4）预测x=120时的y的置信水平为0.95的预测区间。

5）编程实现上述求解过程。

注：参考书目：1、《概率论与数理统计》，浙江大学编，高等教育出版社。

2、《数学实验》，萧树铁主编，高等教育出版社。

2、多元线性回归问题根据下述某猪场25头育肥猪4个胴体性状的数据资料，试进行瘦肉量y 对眼肌面积（x1）画出散点图y 与x1，y 与x2，y 与x3并观察y 与x1，x2， x3的关系；2）求y 关于x1，x2， x3的线性回归方程：0112233y a a x a x a x =+++-----（1），求出0123,,,a a a a 的值；3）对上述回归模型和回归系数进行检验；4）再分别求y 关于单个变量x1，x2, x3的线性回归方程：10111y a a x =+----（2），20222y a a x =+-----（3）,30333y a a x =+--- --（4）求出ij a 的值；分别求y 关于两个变量x1，x2, x3的线性回归方程：10111122y a a x a x =++----(2’)，20211222y a a x a x =++---（3’）,30311322y a a x a x =++ --- --（4’）求出系数ij a 的值；并说明这六个回归方程对原来问题求解的优劣。

5）编程实现上述求解过程。

注：参考书目：1、《概率论与数理统计》，浙江大学编，高等教育出版社。

2、《数学实验》，萧树铁主编，高等教育出版社。

3、优化理论中的线性规划问题---生产安排。

2016数学建模作业

说明：本电子版题目与教材原题不符者以教材为准，教材上没有的做了会适当加分。

教材上有而本电子版题目没有原题的，请同学们自行录入原题。

所有基本题目解答过程均须不少于姜启源先生《数学模型第三版习题参考解答》之答案长度！第1章数学模型引论1.1 在稳定的椅子问题中，如设椅子的四脚连线呈长方形，结论如何？（稳定的椅子问题见姜启源《数学模型》第6页）（小型题目模版）解：模型分析（黑体五号字）：……宋体五号字模型假设与符号说明（黑体五号字）：……宋体五号字模型建立：……宋体五号字模型求解：……宋体五号字程序源代码（如果需要编程）：……宋体五号字程序运行结果（如果有图形或数据）：……宋体五号字模型讨论：……宋体五号字1.2 在商人们安全过河问题中，若商人和随从各四人，怎样才能安全过河呢？一般地，有n 名商人带n 名随从过河，船每次能渡k 人过河，试讨论商人们能安全过河时，n 与k 应满足什么关系。

（商人们安全过河问题见姜启源《数学模型》第7页）1.3 人、狗、鸡、米均要过河，船需要人划，另外至多还能载一物，而当人不在时，狗要吃鸡，鸡要吃米。

问人、狗、鸡、米怎样过河？1.4 有3对阿拉伯夫妻过河，船至多载两人，条件是根据阿拉伯法典，任一女子不能在其丈夫不在的情况下与其他的男子在一起。

问怎样过河？1.5 如果银行存款年利率为5.5%，问如果要求到2010年本利积累为100000元，那么在1990年应在银行存入多少元？而到2000年的本利积累为多少元？1.6 某城市的Logistic 模型为2610251251N N dt dN ⨯-=，如果不考虑该市的流动人口的影响以及非正常死亡。

设该市1990年人口总数为8000000人，试求该市在未来的人口总数。

当∞→t 时发生什么情况。

1.7 假设人口增长服从这样规律：时刻t 的人口为)(t x ，最大允许人口为m x ，t 到t t ∆+时间内人口数量与)(t x x m -成正比。

数学建模案例_选修课问题

数学建模案例_选修课问题某学校对某年级开设9门选修课，这些选修课之间可能存在学习先后顺序。

学校要求毕业前至少选两门数学课、三门运筹学课和两门计算机课。

在符合学校要求的条件下，考虑以下问题：（1）为了选修课程门数最少，应学习哪些课程？（2）选修课程少，且学分尽量多，应学习哪些课程？选修课程和限制条件如下：问题(1)分析：目标：最少的选课门数决策: 对是否选修某门课做出决策，选或不选.符号说明：对应9个0-1变量，设为i x ，选修第i 门课则取值为1，不选则取值为0.建立数学模型：目标函数明确为∑=91i i x min描述约束（翻译—建模）至少选两门数学课⇔254321≥++++x x x x x至少选三门运筹学课程⇔398653≥++++x x x x x至少选两门计算机课⇔29764≥+++x x x x最优化方法3的先修课程是微积分1⇔13x x ≤最优化方法3的先修课程是线性代数23x x ≤数据结构4的先修课程是计算机编程7⇔74x x ≤应用统计5的先修课程是微积分1，线性代数2；⇔1525,x x x x ≤≤ 计算机模拟6的先修课程是计算机编程7；⇔76x x ≤预测理论8的先修课程是应用统计5；⇔58x x ≤数学实验9的先修课程是微积分1和线性代数2；⇔1929,x x x x ≤≤第一问的数学模型：∑=91min i i x254321≥++++x x x x x398653≥++++x x x x x29764≥+++x x x x13x x ≤，23x x ≤，74x x ≤ 1525,x x x x ≤≤ 76x x ≤58x x ≤ 1929,x x x x ≤≤}1,0{∈i x使用lingo求解：model:sets:kecheng/1..9/:c,x; !c代表学分属性，x代表选或不选决策; endsetsdata:c=5 4 4 3 4 3 2 2 3;enddatamin=@sum(kecheng(i):x(i));x(1)+x(2)+x(3)+x(4)+x(5)>=2;x(3)+x(5)+x(6)+x(8)+x(9)>=3;x(4)+x(6)+x(7)+x(9)>=2;x(3)<=x(1);x(3)<=x(2);x(4)<=x(7);x(5)<=x(1);x(5)<=x(2);x(6)<=x(7);x(8)<=x(5);x(9)<=x(1);x(9)<=x(2);@for(kecheng(i):@bin(x(i)));zongfen=@sum(kecheng(i):c(i)*x(i));!zongfen代表此策略下总学分;end结果解释：满足所有选课限制条件的选课门数最少为6门（但不一定唯一），分别是第1，2，3，6，7，9门课；此时总学分21分。

2016年数学建模大作业题

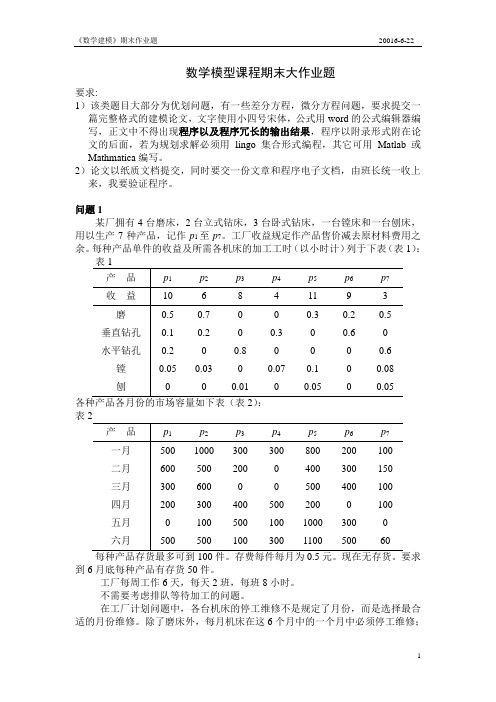
数学模型课程期末大作业题要求:1）该类题目大部分为优划问题，有一些差分方程，微分方程问题，要求提交一篇完整格式的建模论文，文字使用小四号宋体，公式用word的公式编辑器编写，正文中不得出现程序以及程序冗长的输出结果，程序以附录形式附在论文的后面，若为规划求解必须用lingo集合形式编程，其它可用Matlab或Mathmatica编写。

2）论文以纸质文档提交，同时要交一份文章和程序电子文档，由班长统一收上来，我要验证程序。

问题1某厂拥有4台磨床，2台立式钻床，3台卧式钻床，一台镗床和一台刨床，用以生产7种产品，记作p1至p7。

工厂收益规定作产品售价减去原材料费用之余。

每种产品单件的收益及所需各机床的加工工时（以小时计）列于下表（表1）：表到6月底每种产品有存货50件。

工厂每周工作6天，每天2班，每班8小时。

不需要考虑排队等待加工的问题。

在工厂计划问题中，各台机床的停工维修不是规定了月份，而是选择最合适的月份维修。

除了磨床外，每月机床在这6个月中的一个月中必须停工维修；6个月中4台磨床只有2台需要维修。

扩展工厂计划模型，以使可作上述灵活安排维修时间的决策。

停工时间的这种灵活性价值若何？注意，可假设每月仅有24个工作日。

问题2：在某给定区域内均匀分布若干个几何形状相同的小区域（小区域为边长a的正三角形）。

在每个区域中心安排一个寻呼台，管理部门将拿出一贯频域区间由于安排这些寻呼台，这个频域区间被规则地分成若干频域区间，分别被依次标号为：1、2、3、……，每一个寻呼台被分配给一个具有标号的频率小区间，只要不相互干扰，标号相同的频域小区间可以被分配多个寻呼台使用，为了避免干扰，在安排过程中，应满足以下要求：1）、距离为2a以内的两个寻呼台的编号至少必须相差2，在4a以内的寻呼台编号不能相同；2）、除1）以外并考虑三角形区域在三个方向任意延伸的情况；3）、除条件1），2）外，但要求距离在2a以内的寻呼台编号至少相差R，此时能够得到什么结果？请你在上述各种情况条件下建立数学模型，确立需要的频域区间的最小长度，即要求给出各种不同分配方案中所使用的最大编号达到最小。

数学建模与数学实验课程设计题目与参考答案

数学建模与数学实验课程设计题目1、一元线性回归问题在某产品表明腐蚀刻线，下表是试验活得的腐蚀时间（x）与腐蚀深度（y）间的一组数据。

试研究两变量（x，y）之间的关系。

其中：(秒)()。

要求：1）画出散点图，并观察y与x的关系；=+，求出a与b的值；2）求y关于x的线性回归方程：y a bx3）对模型和回归系数进行检验；4）预测x=120时的y的置信水平为0.95的预测区间。

5）编程实现上述求解过程。

注：参考书目：1、《概率论与数理统计》，浙江大学编，高等教育出版社。

2、《数学实验》，萧树铁主编，高等教育出版社。

2、多元线性回归问题根据下述某猪场25头育肥猪4个胴体性状的数据资料，试进行瘦肉量y 对眼肌面积（x1）画出散点图y 与x1，y 与x2，y 与x3并观察y 与x1，x2， x3的关系；2）求y 关于x1，x2， x3的线性回归方程：0112233y a a x a x a x =+++-----（1），求出0123,,,a a a a 的值；3）对上述回归模型和回归系数进行检验；4）再分别求y 关于单个变量x1，x2, x3的线性回归方程：10111y a a x =+----（2），20222y a a x =+-----（3）,30333y a a x =+--- --（4）求出ij a 的值；分别求y 关于两个变量x1，x2, x3的线性回归方程：10111122y a a x a x =++----(2’)，20211222y a a x a x =++---（3’）,30311322y a a x a x =++ --- --（4’）求出系数ij a 的值；并说明这六个回归方程对原来问题求解的优劣。

5）编程实现上述求解过程。

注：参考书目：1、《概率论与数理统计》，浙江大学编，高等教育出版社。

2、《数学实验》，萧树铁主编，高等教育出版社。

3、优化理论中的线性规划问题---生产安排。

《数学建模与数学实验》(第三版)6.5习题作业

1.电路问题一电路由三个电阻123R R R 、、并联，再与电阻4R 串联而成，记k R 上电流为k I ，电压为k V ，在下列情况下确定k R 使电路总功率最小(1,2,3,4)k =： 1）1234,6,8,2k I I I ===≤V ≤10; 2）1234,6,8,2k V V V I ===≤≤6;1）解：根据建立2;P I R U IR ==数学模型为：W=min 421k k k I R =∑123412346..82(1,...,4)kI I s t I I I I Ik I ⎧⎪=⎪=⎪⎪=⎨⎪=++⎪⎪=⎪⎩k k 10≤R ≤I用Lingo 求解：min =I1^2*R1+I1^2*R1+I2^2*R2 结果：+I3^2*R3+I4^2*R4;I1=4;I2=6;I3=8; I4=18; R1>1/2; R2>1/3; R3>1/4; R4>1/9; end2）解：根据建立2;P I R U IR ==数学模型为：W=min 421k k k I R =∑ 4123112233R =4/I ;..R =6/I ;R =8/I ;2I I I I s t I =++⎧⎪⎪⎪⎨⎪⎪⎪⎩k ≤≤6(k =1,...,4);用Lingo 求解：min =I1^2*R1+I2^2*R2+I3^2*R3 结果：+I4^2*R4;I4=I1+I2+I3;I1<6; I2<6;I3<6;I4<6; 《数学建模与数学实验》（第三版）6.5习题作业专业班级姓名学号12340.50000.33330.25000.1111R R R R =⎧⎪=⎪⎨=⎪⎪=⎩ , 1234 4.00006.00008.000018.0000I I I I =⎧⎪=⎪⎨=⎪⎪=⎩ 80P = 112233440.5835976E+08 0.6854038E-07 0.1586609E+08 0.3781429E-06 1.3333 6.000000 0.4752196E+27 6.000000R I R I R I R I ==⎧⎧⎪⎪==⎪⎪⎨⎨==⎪⎪⎪⎪==⎩⎩0.1710790E+29P =R1=4/I1; R2=6/I2; R3=8/I3; end3.（设计最优化问题）要设计和发射一个带有X 射线望远镜和其他科学仪器的气球。

数学建模试题(带答案)

数学建模试题（带答案）第一章4.在1.3节“椅子能在不平的地面上放稳吗”的假设条件中，将四脚的连线呈正方形改为长方形，其余不变。

试构造模型并求解。

答：相邻两椅脚与地面距离之和分别定义为)()(a g a f 和。

f 和g 都是连续函数。

椅子在任何位置至少有三只脚着地，所以对于任意的a ，)()(a g a f 和中至少有一个不为零。

不妨设0)0(,0)0(g >=f 。

当椅子旋转90°后，对角线互换，0π/2)(,0)π/2(>=g f 。

这样，改变椅子的位置使四只脚同时着地。

就归结为证明如下的数学命题：已知a a g a f 是和)()(的连续函数，对任意0)π/2()0(,0)()(,===⋅f g a g a f a 且，0)π/2(,0)0(>>g f 。

证明存在0a ，使0)()(00==a g a f证：令0)π/2(0)0(),()()(<>-=h h a g a f a h 和则，由g f 和的连续性知h 也是连续函数。

根据连续函数的基本性质，必存在0a （0＜0a ＜π/2）使0)(0=a h ，即0)()(00==a g a f 因为0)()(00=•a g a f ，所以0)()(00==a g a f8第二章7.10.用已知尺寸的矩形板材加工半径一定的圆盘，给出几种简便有效的排列方法，使加工出尽可能多的圆盘。

第三章5.根据最优定价模型考虑成本随着销售量的增加而减少，则设kx q x q -=0)( (1)k 是产量增加一个单位时成本的降低，销售量x 与价格p 呈线性关系0,,>-=b a bp a x (2) 收入等于销售量乘以价格p :px x f =)( (3) 利润)()()(x q x f x r -= (4) 将（1）（2）（3）代入（4）求出ka q kbp pa bp x r --++-=02)(当k q b a ,,,0给定后容易求出使利润达到最大的定价*p 为bakb ka q p 2220*+--=6.根据最优定价模型 px x f =)( x 是销售量 p 是价格，成本q 随着时间增长，ββ,0t q q +=为增长率，0q 为边际成本（单位成本）。

2016华为杯数学建模题目

2016华为杯数学建模题目在2016年的华为杯数学建模竞赛中，参赛者们需面对一道关于数学建模的题目。

这个题目的要求是基于给定的问题，运用数学模型和方法，利用计算机技术进行仿真和数据处理，进行问题的分析和解决。

本文将深入探讨这道数学建模题目，并提供一种解决方法。

1. 题目背景在这个部分，我们将介绍题目的背景和相关信息。

根据2016年华为杯数学建模题目，我们假设题目是关于交通流量模拟的问题。

为了简化问题，我们假设一个城市有多个交叉路口，每个路口都有不同的交通流量。

2. 问题的分析在这个部分，我们将对问题进行仔细的分析。

首先，我们需要明确问题的具体要求和约束条件。

例如，题目要求我们通过数学模型和方法来模拟交通流量，并找到最佳的交通信号控制方式来优化路口的交通状况。

3. 模型的建立在这个部分，我们将建立数学模型来解决问题。

首先，我们可以通过实地调研和数据收集来获取相关的交通流量数据。

然后，我们可以使用统计学方法和数据分析技术来分析这些数据，并建立交通流量模型。

最后，我们可以运用优化算法和模拟技术来寻找最佳的交通信号控制方式。

4. 模型的仿真和优化在这个部分，我们将进行模型的仿真和优化。

我们可以使用计算机软件来进行仿真实验，模拟不同交通信号控制方式下的交通流量情况，并通过对比和分析来找到最佳的控制方式。

同时，我们也可以利用优化算法来对模型进行优化，以达到最优的交通流量状况。

5. 结果分析与讨论在这个部分，我们将对模型的结果进行分析和讨论。

我们将探讨最佳交通信号控制方式对交通流量的影响，以及可能的改进和优化方法。

我们还可以对模型进行灵敏度分析，以探索模型中各个参数的影响和敏感度。

6. 结论在这个部分，我们将总结我们的研究结果，并提出进一步的研究方向和建议。

我们可以总结我们找到的最佳交通信号控制方式，并讨论其在实际应用中的可行性和可持续性。

我们还可以提出改进和优化模型的建议，以提高交通流量模拟的准确性和精度。

2016数学建模大作业

三人一组，所有问题中选做三题(问题一、二中任选一题，问题三、四题任选一题，问题五必做，要用Mathematica或Matlab编程计算。

作业要用电子格式文件（doc、pdf格式），每题作业要由题目、模型描述、计算或推导、具体程序命令、结果讨论，程序附在大作业里，上传FTP上（账户：sxjmstu，密码：sxjm123，具体文件夹：上传文件夹）。

如果两人组成一组要求同三人一组，一人一组必做问题五，其它问题一、二、三、四选做一题。

第一个问题：2.2双层玻璃窗的功效要求：1、模型描述（可参考课件）；2、选两组具体k1和k2比值，具体参数求出（用Mathematica 数学软件，要有具体程序、结果和图表）；3、结果分析和适当讨论，最终形成一篇小文章。

第二个问题：3.2 生猪的出售时机要求：1、模型描述（可参考课件）；2、选择具体两组参数，求出相应结果（用Mathematica数学软件，要有具体程序、结果和图表）；3、结果分析和适当讨论，最终形成一篇小文章。

第三个问题：3.1 存贮模型中的允许缺货的存贮模型要求：1、最优值推导，可以手算也可用Mathematica 数学软件；2、原始费用函数，详细推导过程以及具体结果何时有最大值，最大值是什么等。

第四个问题：3.4消费者的选择模型为当效用函数u (x 1,x 2)为如下形式时分析何时达到最优？要求：1、最优值推导，手算或用Mathematica 数学软件；2、详细推导过程以及何时有最大值，最大值是什么等。

第五个问题：用层次分析法解决如下问题：毕业时面临三个选择：就业、考研、自主创业，请自行选择有关准则，用层次分析法做出决策。

23.(,,0u a b =+>121122max (,)s.t.u x x p x p x y+=。

2016版数学建模B作业全部

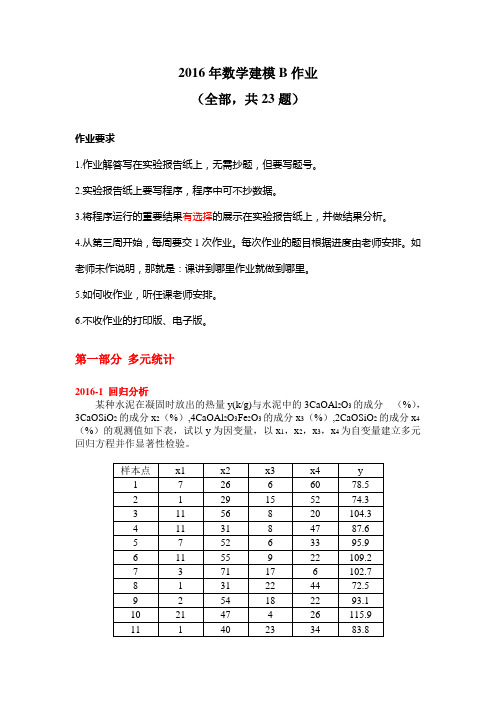
2016年数学建模B作业（全部，共23题）作业要求1.作业解答写在实验报告纸上，无需抄题，但要写题号。

2.实验报告纸上要写程序，程序中可不抄数据。

3.将程序运行的重要结果有选择的展示在实验报告纸上，并做结果分析。

4.从第三周开始，每周要交1次作业。

每次作业的题目根据进度由老师安排。

如老师未作说明，那就是：课讲到哪里作业就做到哪里。

5.如何收作业，听任课老师安排。

6.不收作业的打印版、电子版。

第一部分多元统计2016-1 回归分析某种水泥在凝固时放出的热量y(k/g)与水泥中的3CaOAl2O3的成分（%），3CaOSiO2的成分x2（%）,4CaOAl2O3Fe2O3的成分x3（%）,2CaOSiO2的成分x4（%）的观测值如下表，试以y为因变量，以x1，x2，x3，x4为自变量建立多元回归方程并作显著性检验。

样本点x1 x2 x3 x4 y1 7 26 6 60 78.52 1 29 15 52 74.33 11 56 8 20 104.34 11 31 8 47 87.65 7 526 33 95.96 11 55 9 22 109.27 3 71 17 6 102.78 1 31 22 44 72.59 2 54 18 22 93.110 21 47 4 26 115.911 1 40 23 34 83.812 11 66 9 12 113.313 10 68 8 12 109.42016-2 聚类分析DNA是由A，T，C，G这4种碱基按一定顺序排成的序列，长短不一，其中碱基含量的百分比不同通常能揭示该序列的一些规律，试根据下表所给出的20条DNA序列的碱基含量百分比对其20条DNA序列进行分类。

（注，计算式下面的数据需要转置）1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20A 33 30 30 47 26 39 39 31 23 20 39 36 28 33 32 40 39 32 24 22 T 15 17 7 32 12 14 21 21 17 15 55 55 57 55 71 51 29 55 62 62 C 19 18 24 12 26 14 11 18 23 30 5 3 11 9 0 9 27 13 16 19 G 44 46 50 20 47 44 40 41 48 45 11 16 14 13 7 10 15 10 8 72016-3 判别分析观测3名健康人和4名心肌梗塞病人心电图的3项指标x1，x2，x3所得观测值如下表，试判别心电图3项指标为（400.72，49.46，2.25）的人属于两类中的哪一类，并指出哪个指标在判别分析中占有最重要的地位。