第九届希望杯-四年级-第1试试卷及解析
希望杯四年级试题及答案

希望杯四年级试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是正确的?A. 2+3=5B. 3+4=7C. 5+5=10D. 4+5=9答案:C2. 哪个图形是正方形?A. □B. ○C. △D. ▢答案:A3. 以下哪个单词拼写正确?A. colerB. colerfulC. colerfullD. colorful答案:D4. 下列哪个是正确的分数?A. 1/2B. 2/1C. 3/1D. 4/2答案:A5. 哪个数字是最小的?A. 3B. 2C. 1D. 0答案:D6. 下列哪个选项是正确的?A. 4-2=1B. 5-3=2C. 6-4=3D. 7-5=4答案:B7. 哪个是正确的乘法?A. 2×3=6B. 3×4=10C. 4×5=15D. 5×6=30答案:A8. 哪个是正确的除法?A. 8÷2=3B. 9÷3=2C. 10÷4=2D. 12÷6=1答案:B9. 下列哪个是正确的时间?A. 12:00 PMB. 12:00 AMC. 6:00 PMD. 6:00 AM答案:A10. 哪个是正确的月份?A. 一月B. 二月C. 三月D. 四月答案:B二、填空题(每题4分,共20分)1. 一个长方形的长是6厘米,宽是4厘米,它的面积是______平方厘米。
答案:242. 一个数的3倍是9,这个数是______。
答案:33. 一个数加上5等于10,这个数是______。
答案:54. 一个数减去2等于3,这个数是______。
答案:55. 一个数乘以2等于8,这个数是______。
答案:4三、解答题(每题5分,共20分)1. 一个苹果比一个梨重200克,如果一个苹果重500克,那么一个梨重多少克?答案:一个梨重300克。
2. 小明有10个苹果,他给了小红3个,然后又买了5个,小明现在有多少个苹果?答案:小明现在有12个苹果。
四年级希望杯奥数试卷【含答案】

四年级希望杯奥数试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪个数字是偶数?A. 3B. 4C. 5D. 62. 一个正方形的四条边长相等,那么它的周长是?A. 边长的两倍B. 边长的三倍C. 边长的四倍D. 边长的五倍3. 下列哪个数字是质数?A. 12B. 13C. 15D. 184. 一个长方形的长是10厘米,宽是5厘米,那么它的面积是?A. 50平方厘米B. 60平方厘米C. 70平方厘米D. 80平方厘米5. 下列哪个数字是最大的两位数?A. 90B. 91C. 92D. 93二、判断题(每题1分,共5分)1. 1+1=3 ()2. 9乘以9等于81 ()3. 2加2等于4 ()4. 10减去5等于7 ()5. 8除以2等于4 ()三、填空题(每题1分,共5分)1. 5加5等于______。
2. 20减去10等于______。
3. 6乘以6等于______。
4. 49除以7等于______。
5. 100减去25等于______。
四、简答题(每题2分,共10分)1. 请写出5个两位数。
2. 请写出5个三位数。
3. 请写出5个两位数的和。
4. 请写出5个两位数的差。
5. 请写出5个两位数的积。
五、应用题(每题2分,共10分)1. 小明有10个苹果,他吃掉了3个,还剩下几个苹果?2. 小红有20个糖果,她给了小华5个糖果,还剩下几个糖果?3. 一个长方形的长是8厘米,宽是4厘米,求这个长方形的面积。
4. 一个正方形的边长是6厘米,求这个正方形的周长。
5. 两个数的和是15,其中一个数是7,另一个数是多少?六、分析题(每题5分,共10分)1. 请用两种方法计算24加36的和。
2. 请用两种方法计算56减去28的差。
七、实践操作题(每题5分,共10分)1. 请用纸和剪刀剪出一个正方形,边长为10厘米,然后计算这个正方形的面积。
2. 请用纸和剪刀剪出一个长方形,长为12厘米,宽为8厘米,然后计算这个长方形的周长。
全国四年级希望杯数学竞赛全部试题与答案

全国四年级希望杯数学竞赛全部试题与答案一、竞赛介绍“希望杯”是全国小学生奥数竞赛之一,自1996年创办以来,已经成为小学生数学竞赛中最有影响力的赛事之一。
本次比赛是面向四年级的“希望杯”数学竞赛,包含两个考试科目:数学(含应用题)和口算。
这个文档将介绍全部试题和答案。
二、数学试题试题一下列哪一个数是偶数?A. 1B. 3C. 5D. 2答案D. 2试题二根据下列算式,1 + 2 + 3 + 4 + 5 + 6 = ?A. 15B. 18C. 20D. 21答案D. 21试题三张三一周的零花钱是12元,他每天都要花1元,那么他一周之后还剩下多少钱?A. 5元B. 6元C. 7元D. 8元B. 6元试题四计算:(1 + 2 - 3)× 5A. 0B. 5C. 10D. 15答案B. 5试题五根据下列数字,找到其中的三个连续数字使它们的和最大。
{3, 6, 8, 2, 7, 1, 9, 0}A. 3, 6, 8B. 8, 2, 7C. 1, 9, 0D. 6, 8, 2答案B. 8, 2, 7三、口算试题试题一计算:1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10答案55试题二计算:9 × 5答案45计算:16 ÷ 4答案4试题四计算:47 - 23答案24试题五计算:200 ÷ 8答案25四、以上是全国四年级希望杯数学竞赛的全部试题和答案。
经过这次竞赛的练习,寻找方法和答案的过程不仅能够锻炼孩子们的思维能力和逻辑思维能力,同时也是对他们平时所学知识的一种回顾和检验。
希望这份文档能够对您有所帮助。
小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)

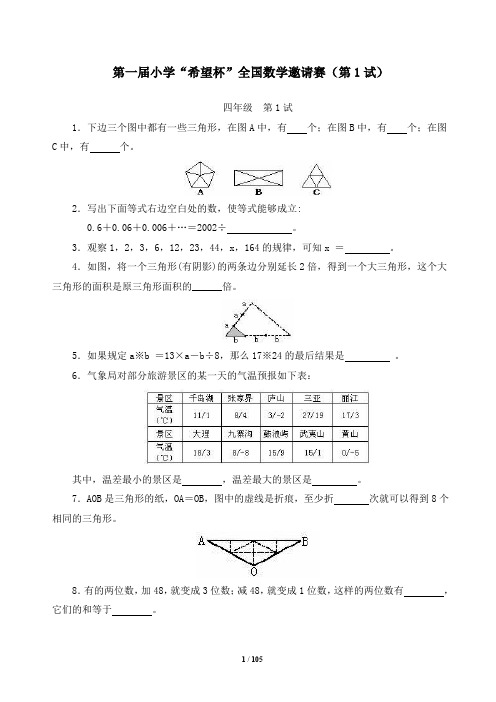
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
四年级希望杯奥数试卷【含答案】

四年级希望杯奥数试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪个数字是偶数?A. 3B. 4C. 5D. 62. 一个正方形的四条边长相等,那么它的周长是?A. 边长的两倍B. 边长的三倍C. 边长的四倍D. 边长的五倍3. 下列哪个数字是质数?A. 12B. 17C. 20D. 214. 1千克等于多少克?A. 100克B. 1000克C. 10,000克D. 1,000,000克5. 下列哪个图形是平行四边形?A. 正方形B. 长方形C. 三角形D. 圆形二、判断题(每题1分,共5分)1. 1+1=3 ()2. 长方形和正方形的周长都是边长的四倍。
()3. 9乘以9等于81。
()4. 0是最小的自然数。
()5. 圆的周长等于直径的两倍。
()三、填空题(每题1分,共5分)1. 一个正方形的边长是5厘米,那么它的面积是____平方厘米。
2. 1千克等于____克。
3. 2乘以2等于____。
4. 下列数字中,____是最大的偶数。
5. 下列图形中,____是唯一有曲线边的图形。
四、简答题(每题2分,共10分)1. 解释什么是质数。
2. 什么是平行四边形?3. 解释什么是周长。
4. 什么是面积?5. 什么是自然数?五、应用题(每题2分,共10分)1. 一个长方形的长是10厘米,宽是5厘米,求它的周长和面积。
2. 一个正方形的边长是6厘米,求它的周长和面积。
3. 一个圆形的半径是4厘米,求它的周长和面积。
4. 一个数字加上它的两倍等于15,求这个数字。
5. 一个数字减去5等于10,求这个数字。
六、分析题(每题5分,共10分)1. 小明有10个苹果,他吃了一半,然后又吃了一个,他还剩几个苹果?2. 一个长方形的长是8厘米,宽是4厘米,求它的对角线长度。
七、实践操作题(每题5分,共10分)1. 画一个边长为5厘米的正方形,并标出它的周长和面积。
2. 画一个半径为3厘米的圆形,并标出它的周长和面积。
小学四年级希望杯数学竞赛第一届至十一历届全部试题与答案(最新最全)

第一届小学“希望杯”全国数学邀请赛四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在a=20032003×2002和b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
15.长方形被分成了4个小长方形,图4中的数字是它们每个的面积,阴影部分的面积是。
小学四年级希望杯数学竞赛第一届至十一届全部试题与答案

第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
【通用】小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
【推荐】小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)

第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
第九届小学“希望杯”全国数学邀请赛试卷(四年级第1试)

2011年第九届小学“希望杯”全国数学邀请赛试卷(四年级第1试)一、解答题(共20小题,满分114分)1.(6分)计算:(7777+8888)÷5﹣(888﹣777)×3=.2.(6分)计算:1+11+21+…+1991+2001+2011=.3.(6分)在小于30的质数中,加3以后是4的倍数的是.4.(6分)小于100的最大的自然数与大于300的最小的自然数的和,是不大于200的最大的自然数的倍.5.既是6的倍数又是8的倍数的所有两位数的和是.6.(6分)四年级一班第2小组共12人,其中5人会打乒乓球,8人会下象棋,3人既会打乒乓球又会下象棋,那么这个小组中既不会打乒乓球又不会下象棋的有人.7.(6分)按照左侧四个图中数的规律,在第五个图中填上适当的数:8.(6分)已知9个数的乘积是800,将其中一个数改为4,这9个数的乘积是200,若再将另外一个数改为30,则这9个数的乘积变为1200,则这两个被改动的数以外的7个数的乘积是.9.(6分)如图,△ABC的面积为36,点D在AB上,BD=2AD,点E在DC 上,DE=2EC,则△BEC的面积是.10.(6分)今年,李林和他爸爸的年龄的和是50岁,4年后,他爸爸的年龄比他的年龄的3倍小2岁,则李林的爸爸比他大岁.11.(6分)某次考试,A、B、C、D、E五人的平均分是90分.若A、B、C 的平均分是86分,B、D、E的平均分是95分,则B的得分是分.12.(6分)如图,已知直线AB和CD交于点O,若∠AOC=20°,∠EOD=60°,则∠AOE=,∠BOC=.13.(6分)如图,四边形ABCD与CEFG是边长相等的正方形,且B、C、G 在一条直线上,则图中共有个正方形,个等腰直角三角形.14.(6分)一个水桶里有水,若将水加到原来的4倍,桶和水共重16千克;若将水加到原来的6倍,桶和水共重22千克.则桶内原有水千克,桶重千克.15.(6分)某个两位数的个位数字和十位数字的和是12,个位数和十位数字交换后所得两位数比原数小36,则原数是.16.(6分)王强步行去公园,回来时坐车,往返用了一个半小时,如果他来回都步行,则需要2个半小时,那么,他来回都坐车,则需分钟.17.(6分)图中“C”形图形的周长是厘米.18.(6分)如图,从1,2,3,4,5,6中选出5个数填在图中空格内,使填好的格内的数右边的比左边的大,下边的比上边的大,则共有种不同的填法.19.(6分)三个连续自然数中最小的数是9的倍数,中间的数是8的倍数,最大的数是7的倍数,则这三个数的和最小是.20.(6分)甲、乙、丙、丁、戊五人猜测全班个人学科总成绩的前五名:甲:“第一名是D,第五名是E.”乙:“第二名是A,第四名是C.”丙:“第三名是D,第四名是A”,丁:“第一名是C,第三名是B.”戊:“第二名是C,第四名是B.”若每个人都是只猜对一个人的名次,且每个名次只有一个人猜对,则第一、二、三、四、五名分别是.2011年第九届小学“希望杯”全国数学邀请赛试卷(四年级第1试)参考答案与试题解析一、解答题(共20小题,满分114分)1.(6分)计算:(7777+8888)÷5﹣(888﹣777)×3=3000 .【分析】把7777+8888与888﹣777,拆成两个数的乘积,再根据乘法分配律进行计算即可.【解答】解:(1111×7+1111×8)÷5﹣(111×8﹣111×7)×3,=1111×(7+8)÷5﹣111×(8﹣7)×3,=1111×(15÷5)﹣111×1×3,=1111×3﹣111×3,=(1111﹣111)×3,=1000×3,=3000.故答案为:3000.【点评】本题主要考查乘法分配律的灵活运用,根据数字特点找出巧算的方法进行计算即可.2.(6分)计算:1+11+21+…+1991+2001+2011=203212 .【分析】通过观察,相邻两个数的差是10,这是一个等差数列,可以用高斯求和公式进行简算.这一数列共有(2011﹣1)÷10+1=202个数,然后运用公式计算即可.【解答】解:1+11+21+…+1991+2001+2011,=(1+2011)×[(2011﹣1)÷10+1]÷2,=2012×202÷2,=203212.故答案为:203212.【点评】此题的关键是先探索出这是一个等差数列,运用“项数=(末项﹣首项)÷公差+1”算出项数.3.(6分)在小于30的质数中,加3以后是4的倍数的是5,13,17,29 .【分析】根据质数的意义,一个自然数,如果只有1和它本身两个因数,这样的数叫做质数.30以内的质数有:2,3,5,7,11,13,17,19,23,29;4的倍数特征是个位上的数是偶数;由此解答.【解答】解:5+3=8;13+3=16;17+3=20;29+3=32;8,16,20,32都是4的倍数;故答案为:5,13,17,29.【点评】此题的解答主要明确质数的意义,掌握30以内的10个质数,和4的倍数的特征.4.(6分)小于100的最大的自然数与大于300的最小的自然数的和,是不大于200的最大的自然数的 2 倍.【分析】此题要找出小于100的最大自然数是99,大于300的最小自然数是301,不大于200(即小于或等于200)的最大自然数是200,由此本题可以看做是:“99和301的和是200的多少倍?”.【解答】解:(99+301)÷200,=400÷200,=2;答:是不大于200的最大的自然数的2倍.故答案为:2.【点评】解决此题的关键是,根据题干先得出“小于100的最大的自然数”是99、“大于300的最小的自然数”是301,“不大于200的最大的自然数”是200.5.既是6的倍数又是8的倍数的所有两位数的和是240 .【分析】既是6的倍数,又是8的倍数,先分解质因数,6分为2×3,8分为2×2×2,再找出最小公倍数,两位数的公倍数只有四个数:24,48,72,96,相加即得答案240.【解答】解:根据分析,先分解质因数6=2×3,8=2×2×2,则两者的最小公倍数即为24,符合条件的所有两位数公倍数为:24,48,72,96;所有这些两位数之和:24+48+72+96=240,故答案为:240.【点评】本题考查了公倍数和数的整除运算知识,本题突破点是:找出两者之间的最小公倍数.6.(6分)四年级一班第2小组共12人,其中5人会打乒乓球,8人会下象棋,3人既会打乒乓球又会下象棋,那么这个小组中既不会打乒乓球又不会下象棋的有 2 人.【分析】只要从总人数12人中,把会打乒乓球和会下象棋的人数减掉,剩下的就是这个小组中既不会打乒乓球又不会下象棋的人数;此题可以画图分析:5+8=13人,这里重复加了一次既会打乒乓球有会下象棋的3人,所以会打乒乓球和会下象棋的人数为13﹣3=10人,则剩下的12=2人就是这个小组中既不会打乒乓球又不会下象棋的人数.【解答】解:12﹣(5+8﹣3)=2(人),答:这个小组中既不会打乒乓球又不会下象棋的有 2人.故答案为:2.【点评】此题考查了利用容斥原理解决实际问题的灵活应用.7.(6分)按照左侧四个图中数的规律,在第五个图中填上适当的数:【分析】(1)根据题干,图中1的位置变化规律是:按顺时针方向依次移动一个格;(2)数字排列规律是:分别按1、3、5、2、4、6的顺序排列的,而且第奇数幅是按顺时针排列,第偶数幅是按逆时针排列;第五幅图是第奇数幅,所以按顺时针排列.【解答】解:根据题干分析可得:(1)图中1的位置变化规律是:按顺时针方向依次移动一个格;所以先确定1的位置如下图所示;(2)第五幅图是第奇数幅,所以按顺时针排列,所以可以在图中添上正确的数字如下图所示:【点评】根据题干得出1的位置变化规律和图中数字1、3、5、2、4、6的排列特点是解决此题的关键.8.(6分)已知9个数的乘积是800,将其中一个数改为4,这9个数的乘积是200,若再将另外一个数改为30,则这9个数的乘积变为1200,则这两个被改动的数以外的7个数的乘积是10 .【分析】只要求出被改动的两个数是多少,即能求出这两个被改动的数以外的7个数的乘积是多少.已知9个数的乘积是800,将其中一个数改为4,这9个数的乘积是200,积缩小了800÷200=4(倍),则这个被改动的数也被缩小了4倍,则被改动的这个数为:4×4=16;同理,1200÷200=6,积扩大了6倍,第二个被改动的数也被扩大了6倍,其原来应为:30÷6=5,所以则这两个被改动的数以外的7个数的乘积是:800÷(16×5)=10.【解答】解:第一个数原来为:(800÷200)×4=16;第二个数原来为:30÷(1200÷200)=5;则两个被改动的数以外的7个数的乘积是:800÷(16×5)=10.故答案为:10.【点评】在乘法算式,其中一个因数扩大(或缩小)多少倍,积也相应的扩大(或缩小)多少倍.9.(6分)如图,△ABC的面积为36,点D在AB上,BD=2AD,点E在DC 上,DE=2EC,则△BEC的面积是8 .【分析】(1)△ABC的面积是36,BD=2AD,根据高一定时,三角形的面积与底成正比的性质即可得出:△ABC的面积:△BDC的面积=3:2,所以:△BDC的面积是:36×2÷3=24;(2)△BDC的面积是36×2÷3=24,DE=2EC,根据高一定时,三角形的面积与底成正比的性质即可得出:△BEC的面积:△BDC的面积=1:3,所以△BEC的面积是24÷3=8.【解答】解:因为BD=2AD,根据高一定时,三角形的面积与底成正比的性质即可得出:△ABC的面积:△BDC的面积=3:2,故△BDC的面积是36×2÷3=24;因为DE=2EC,同理可得:△BEC的面积:△BDC的面积=1:3,故△BEC的面积是24÷3=8.答:△BEC的面积是8.故答案为:8.【点评】此题反复考查了高一定时,三角形的面积与底成正比的性质的灵活应用.10.(6分)今年,李林和他爸爸的年龄的和是50岁,4年后,他爸爸的年龄比他的年龄的3倍小2岁,则李林的爸爸比他大28 岁.【分析】4年后,李林和他爸爸的年龄之和是50+4×2=58岁,设李林4年后的年龄为x岁,则爸爸的年龄是3x﹣2岁,根据他们的年龄之和是58岁列出方程即可解决问题.【解答】解:设李林4年后的年龄为x岁,则爸爸的年龄是3x﹣2岁,根据题意可得方程:x+3x﹣2=50+4×2,4x=60,x=15,3×15﹣2=43(岁),43﹣15=28(岁),答:李林的爸爸比他大28岁.故答案为:28.【点评】此题也可以这样分析,4年后,李林和爸爸的年龄之和就是58岁,把李林的年龄看做1份,那么爸爸的年龄就是3份少2岁,由此可以求出1份即李林的年龄为:(58+2)÷4=15(岁),由此可得爸爸58﹣15=43岁,则爸爸比李林大28岁.11.(6分)某次考试,A、B、C、D、E五人的平均分是90分.若A、B、C 的平均分是86分,B、D、E的平均分是95分,则B的得分是93 分.【分析】根据“平均数×数量=总数”分别计算出A、B、C三个数的和与B、D、E三个数的和与这五个数的和,进而用“A、B、C三个数的和+B、D、E三个数的和﹣五个数的和”进行解答即可.【解答】解:(86×3+95×3)﹣(90×5),=543﹣450,=93(分);故答案为:93.【点评】解答此题的关键:根据平均数和数量、总量之间的关系进行分析解答.12.(6分)如图,已知直线AB和CD交于点O,若∠AOC=20°,∠EOD=60°,则∠AOE=100°,∠BOC=160°.【分析】由图可知,∠AOC=20°、∠EOD=60°与∠AOE相加等于180°,由此即可求得∠AOE的度数;∠BOC与∠AOC=20°互为补角,根据补角的定义即可解答.【解答】解:∠AOE=180°﹣∠AOC﹣∠EOD=180°﹣20°﹣60°=100°.∠BOC=180°﹣∠AOC=180°﹣20°=160°.故答案为:100°;160°.【点评】本题主要考查角的度量与补角的定义,根据几个角的和差关系进行计算是解题关键.13.(6分)如图,四边形ABCD与CEFG是边长相等的正方形,且B、C、G 在一条直线上,则图中共有 3 个正方形,22 个等腰直角三角形.【分析】根据图形可知,正方形有:ABCD、CEFG、BEGD三个;在正方形ABCD、CEFG和BEGD中,单一三角形是10个,有两个小三角形组成的是8个;由3个三角形组成的等腰直角三角形是4个;由此解答.【解答】解:图中共有正方形3个;等腰直角三角形有:10+8+4=22(个);故答案为:3;22【点评】此题主要考查通过分类、观察、思考探寻事物规律的能力.14.(6分)一个水桶里有水,若将水加到原来的4倍,桶和水共重16千克;若将水加到原来的6倍,桶和水共重22千克.则桶内原有水 3 千克,桶重 4 千克.【分析】根据题意知道,桶的重量不变,(22﹣16)千克的水就是水原来的(6﹣4)倍,由此即可求出原来的水的千克数,那桶的重量即可求出.【解答】解:桶内原有水:(22﹣16)÷(6﹣4),=6÷2,=3(千克),桶重:16﹣4×3,=16﹣12,=4(千克);答:桶内原有水3千克,桶重4千克.故答案为:3,4.【点评】解答此题的关键是,根据题意,找出对应的数和对应的倍数,由此列式解答即可.15.(6分)某个两位数的个位数字和十位数字的和是12,个位数和十位数字交换后所得两位数比原数小36,则原数是84 .【分析】设个位数字是x,则十位数字是12﹣x,所以可得:原来两位数是10(12﹣x)+x,交换位置后的新两位数是10x+12﹣x;根据新数比原数小36,列出方程即可解决问题.【解答】解:设个位数字是x,则十位数字是12﹣x,那么原来两位数是10(12﹣x)+x,交换位置后的新两位数是10x+12﹣x;根据题意可得方程:10(12﹣x)+x﹣(10x+12﹣x)=36,18x=72,x=4;12﹣4=8,答:原数是84.故答案为:84.【点评】此题设出个位数字和十位数字,从而得出原两位数和新两位数是解决本题的关键.16.(6分)王强步行去公园,回来时坐车,往返用了一个半小时,如果他来回都步行,则需要2个半小时,那么,他来回都坐车,则需30 分钟.【分析】来回都步行,需要2个半小时说明王强步行单程用:2.5÷2=1.25(小时),又因为步行去公园,回来时坐车,往返用了一个半小时,则坐车单程用:1.5﹣1.25=0.25(小时),则来回都坐车用时:0.25×2=0.5(小时).【解答】解:(1.5﹣2.5÷2)×2,=0.25×2,=0.5(小时);0.5小时=30分钟.故答案为:30.【点评】完成本题的关健是:在求出步行单程所用时间的基础上,求出坐车单程所用时间.17.(6分)图中“C”形图形的周长是32 厘米.【分析】如图,将内部的2厘米边平移到外面红色线段处,这样这个图形的周长就是这个边长为6厘米的正方形的边长与内部横着的两条长为6﹣2=4厘米的线段的长度之和,由此利用正方形周长公式代入数据即可解决问题.【解答】解:根据题干分析可得:6×4+(6﹣2)×2,=24+8,=32(厘米),答:这个图形的周长是32厘米.故答案为:32.【点评】借助平移的性质将图形中的某些线段移动到规则图形的边上,使求这个不规则图形的周长转化成求规则图形的周长是解决此类题目的主要解题思路.18.(6分)如图,从1,2,3,4,5,6中选出5个数填在图中空格内,使填好的格内的数右边的比左边的大,下边的比上边的大,则共有30 种不同的填法.【分析】此题根据乘法原理进行解答,从6个数中选出5个进行填空,共有6×5种.【解答】解:从6个数中选出5个进行填空,共有:6×5=30(种);故答案为:30.【点评】此题运用了乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,…,做第n步有m n种不同的方法,那么完成这件事共有N=m1×m2×m3×…×m n种不同的方法.19.(6分)三个连续自然数中最小的数是9的倍数,中间的数是8的倍数,最大的数是7的倍数,则这三个数的和最小是1488 .【分析】据题意可知,这是三个相连的自然数,又7、8、9也是相连的自然数,因此先找到7、8、9的最小公倍数:7×8×9=504,则减9是9的倍数,减8是8的倍数,减7是7的倍数,得到495、496、497是符合要求的.【解答】解:7、8、9的最小公倍数为:7×8×9=504;504﹣7=497,504﹣8=496,504﹣9=495;495+496+497=1488.故填:1488.【点评】任何三个连续自然数(零除外)的最小公倍分别减(或加)这三个数得到的三个连续的自然数分别是这三数的倍数.20.(6分)甲、乙、丙、丁、戊五人猜测全班个人学科总成绩的前五名:甲:“第一名是D,第五名是E.”乙:“第二名是A,第四名是C.”丙:“第三名是D,第四名是A”,丁:“第一名是C,第三名是B.”戊:“第二名是C,第四名是B.”若每个人都是只猜对一个人的名次,且每个名次只有一个人猜对,则第一、二、三、四、五名分别是CADBE .【分析】本题可用假设法分两步进行推理:第一步:假设甲说的前半句是真的,那么D是第1名,那么此时丙说的前半句错,后半句对.则A是第4名.同理乙的后半句对,C是第4名.矛盾.由此可知甲的后半句对.第二步:已知E是第5名,D不是第1名.和第一名有关的话只剩下丁说的,设C是第1名.则戊:“第2名是c,第4名是B”.可知前错后对,B 是第4名.且有乙:“第二名是A,第四名是c”.可知,A是第2名.D是第3名.【解答】解:第一步:假设甲说的前半句是真的,那么D是第1名,那么此时丙说的前半句错,后半句对.则A是第4名.同理乙的后半句对,C是第4名.矛盾.由此可知甲的后半句对.即第五名是E;第二步:已知E是第5名,D不是第1名.和第一名有关的话只剩下丁说的,设C是第1名.则戊:“第2名是c,第4名是B”.可知前错后对,B是第4名.且有乙:“第二名是A,第四名是c”.可知,A是第2名.D是第3名.综上可知,第一、二、三、四、五名分别是CADBE.【点评】完成此类题目思路要清晰,根据所给条件中的逻辑关系细心推理,从而得出结论.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/4/22 16:49:14;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800。
小学四年级希望杯历年数学竞赛试题与答案1-13届

第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
第九届小学“希望杯”全国数学邀请赛四年级第1试+答案

第九届小学“希望杯”全国数学邀请赛四年级 第1试2011年3月13日 上午8:30至10:00 得分____________亲爱的小朋友,欢迎你参加第九届小学”希望杯”全国数学邀请赛!你将进入一个新颖、有趣、有挑战性的数学天地,将会留下一个难忘的经历……以下每题6分,共120分。
1. 计算:(7777+8888)÷5—(888—777)×3= . 2. 计算:1+11+21+…+1991+2001+2011= .3. 在小于30的质数中,加3以后是4的倍数的是 .4. 小于100的最大的自然数与大于300的最小的自然数的和,是不大于200的最大的自然数的 倍. 5. 既是6的倍数又是8的倍数的所有两位数的和是 .6. 四年级一班2个小组共12人,其中5人会打乒乓球,8人会下象棋,3人既会打乒乓球又会下象棋,那么这两个小组中既不会打乒乓球又不会下象棋的有 人. 7. 按照左侧四个图中数的规律,在第五个图中填上适当的数:6135241642534253161642538. 已知9个数的乘积是800,将其中一个数改为4,这9个数的乘积是200,若再将另外一个数改为30,则这9个数的乘积变为1200.则这两个被改动的数以外的7个数的乘积是 .9. 如图1,△ABC 的面积为36,点D 在AB 上,BD=2AD ,点E 在DC 上,DE=2EC ,则△BEC 的面积是 .EDCBAO60︒20︒ED C BAFB图1 图2 图310.今年,李林和他爸爸的年龄的和是50岁,4年后,他爸爸的年龄比他的年龄的3倍小2岁,则李林的爸爸比他大 岁.11.某次考试,A 、B 、C 、D 、E 五人的平均分是90分.若A 、B 、C 的平均分是86分,B 、D 、E 的平均分是95分,则B 的得分是 .12.如图2,已知直线AB 和CD 交于点O ,若∠AOC=20°,∠EOD=60°,则∠AOE= °,∠BOC= °.13.如图3,四边形ABCD 与CEFG 是边长相等的正方形,且B 、C 、G 在一条直线上,则图中共有 个正方形, 个等腰直角三角形.14.一个水桶里有水,若将水加到原来的4倍,桶和水共重16千克;若将水加到原来的6倍,桶和水共重22千克.则桶内原有水 千克,桶重 千克.15.某个两位数的个位数字和十位数字的和是12,个位数字和十位数字交换后所得两位数比原数小36,则原数是 .16.王强步行去公园,回来时坐车,往返用了一个半小时,如果他来回都步行,则需要2个半小时,那么他来回都坐车,则需 分钟.17.图4中“C ”形图形的周长是 厘米.图418.如图5,从1,2,3,4,5,6,中选出5个数填在图中的空格内,使填好的格内的数右边的比左边的大,下边的比上边的大,则共有 种不同的填法.图519.三个连续自然数中最小的数是9的倍数,中间的数是8的倍数,最大的数是7的倍数,则这三个数的和最小是 .20.甲、乙、丙、丁、戊五人猜测全班个人学科总成绩的前五名:甲:“第一名是D ,第五名是E .” 乙:“第二名是A ,第四名是C .” 丙:“第三名是D ,第四名是A .” 丁:“第一名是C ,第三名是B .” 戊:“第二名是C ,第四名是B .”若每个人都只猜对一个人的名次,且每个名次只有一个人猜对,则第一、二、三、四、五名分别是 .7第九届小学“希望杯”全国数学邀请赛答案四年级第1试1.30002.3.5,13,17,294. 25.2406. 27.8.109.810.2811.9312.100;16013.3;2214.3;415.8416.3017.3218.3019.148820.C、A、D、B、E。
希望杯数学竞赛第一届至十三历届四年级全部试题与答案打

教育精品资料目录1.第一届小学“希望杯”全国数学邀请赛(第1试) (2)2. 第一届小学“希望杯”全国数学邀请赛(第2试) (5)3. 第二届小学“希望杯”全国数学邀请赛(第1试) (7)4. 第二届小学“希望杯”全国数学邀请赛(第2试) (10)5. 第三届小学“希望杯”全国数学邀请赛(第1试) (12)6. 第三届小学“希望杯”全国数学邀请赛(第2试) (15)7. 第四届小学“希望杯”全国数学邀请赛(第1试) (17)8. 第四届小学“希望杯”全国数学邀请赛(第2试) (20)9. 第五届小学“希望杯”全国数学邀请赛(第1试) (22)10. 第五届小学“希望杯”全国数学邀请赛(第2试) (24)11. 第六届小学“希望杯”全国数学邀请赛(第1试) (26)12. 第六届小学“希望杯”全国数学邀请赛(第2试) (28)13. 第七届小学“希望杯”全国数学邀请赛(第1试) (30)14. 第七届小学“希望杯”全国数学邀请赛(第2试) (34)15. 第八届小学“希望杯”全国数学邀请赛(第1试) (37)16. 第八届小学“希望杯”全国数学邀请赛(第2试) (39)17. 第九届小学“希望杯”全国数学邀请赛(第1试) (41)18. 第九届小学“希望杯”全国数学邀请赛(第2试) (43)19. 第十届小学“希望杯”全国数学邀请赛(第1试) (45)20. 第十届小学“希望杯”全国数学邀请赛(第2试) (47)21.第一届---第八届“希望杯”全国数学邀请赛参考答案 (53)第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C 中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九届小学“希望杯”全国数学邀请赛四年级第Ⅰ试
姓名__________ 以下每题6分,共120分.
1.计算:(7777+8888)÷5-(888-777)×3=___________________.
2.计算:1+11+22+…+1991+2001+2011=__________________.
3.在小于30的质数中,加3以后是4的倍数的是______________________.
4.小于100的最大的自然数与大于300的最小的自然数的和,是不大于200的最大的自然数
的__________________倍.
5.既是6的倍数又是8的倍数的所有两位数的和是___________________.
6.四年级一班第2小组共12人,其中5人会打乒乓球,8人会下象棋,3人既会打乒乓球又会
下象棋,那么这个小组中既不会打乒乓球又不会下象棋的有__________人.
7.按照左侧四个图中数的规律,在第五个图中填上适当的数:
8.已知9个数的乘积
是800,将其中一个数改为4,这9个数的乘积是200,若再将另外一个
数改为30,则这9个数的乘积变为1200,则这两个被改动的数以外的7
个数的乘积是_______________.
9.如图1,ABC
∆的面积为36,点D在AB上,BD=2AD,点E在DC
上,DE=2EC,则BEC
∆的面积是____________________.
10.今年,李林和他爸爸的年龄的和是50岁,4年后,他爸爸的年龄比他的年龄的3倍小2岁,
则李林的爸爸比他大______________岁.
11.某此考试,A、B、C、D、E五人的平均分是90分.若A、B、C的平均分是86分,B、D、E的
平均分是95分,则B的得分是______________分.
12.如图2,已知直线AB和CD交于点O,若
=
∠EOD,则
60
=
∠AOC,
20
__________
,
AOE.
=
∠BOC
__________=
∠
13.如图3,四边形ABCD与CEFG是边长相等的正方形,且B、C、G在一条
直线上,则图中共有______________个正方形,______________个等腰
直角三角形.。
