平面初中几何竞赛题
初中数学竞赛平面几何讲座---巧添辅助-- 妙解竞赛题

初中数学巧添辅助-- 妙解竞赛题在某些数学竞赛问题中,巧妙添置辅助圆常可以沟通直线形和圆的内在联系,通过圆的有关性质找到解题途径.下面举例说明添置辅助圆解初中数学竞赛题的若干思路.1 挖掘隐含的辅助圆解题有些问题的题设或图形本身隐含着“点共圆”,此时若能把握问题提供的信息,恰当补出辅助圆,并合理挖掘图形隐含的性质,就会使题设和结论的逻辑关系明朗化.1.1 作出三角形的外接圆例1如图1,在△ABC中,AB=AC,D是底边BC上一点,E是线段AD上一点且∠BED=2∠CED=∠A.求证:BD=2CD.ABGC DFE 图1例 2 凸四边形ABCD 中,∠ABC =60°,∠BAD =∠BCD =90°, AB =2,CD =1,对角线AC 、BD 交于点O ,如图2.则sin ∠AOB =____.例3 已知:如图3,AB =BC =CA =AD ,AH ⊥CD 于H ,CP ⊥BC ,CP 交AH 于P . 求证:△ABC 的面积S =43AP ·BD .A图3BP QD HC ABCDPO图22 构造相关的辅助圆解题有些问题貌似与圆无关,但问题的题设或结论或图形提供了某些与圆的性质相似的信息,此时可大胆联想构造出与题目相关的辅助圆,将原问题转化为与圆有关的问题加以解决. 2.1 联想圆的定义构造辅助圆例4 如图4,四边形ABCD 中,AB ∥CD ,AD =DC =DB =p ,BC =q .求对角线AC 的长.2.2 联想直径的性质构造辅助圆例5 已知抛物线y =-x 2+2x +8与x 轴交于B 、C 两点,点D 平分BC .若在x 轴上侧的A 点为抛物线上的动点,且∠BAC 为锐角,则AD 的取值范围是____.A EDCB图4图5例6 AD 是Rt △ABC 斜边BC 上的高,∠B 的平行线交AD 于M ,交AC 于N . 求证:AB 2-AN 2=BM ·BN .例7 如图7,ABCD 是⊙O 的内接四边形,延长AB 和DC 相交于E ,延长AB 和DC 相交于E ,延长AD 和BC 相交于F ,EP 和FQ 分别切⊙O 于P 、Q .求证:EP 2+FQ 2=EF 2.EANCD B FM 12345图6例8 如图8,△ABC 与△A 'B 'C '的三边分别为a 、b 、c 与a '、b '、c ',且∠B =∠B ',∠A +∠A '=180°.试证:aa '=bb '+cc '.同步练习题1. 作一个辅助圆证明:△ABC 中,若AD 平分∠A ,则AC AB =DCBD.2. 已知凸五边形ABCDE 中,∠BAE =3a ,BC =CD =DE ,∠BCD =∠CDE =180°-2a . 求证:∠BAC =∠CAD =∠DAE .3. 在△ABC 中AB =BC ,∠ABC =20°,在AB 边上取一点M ,使BM =AC .求∠AMC 的度数.(1)(2)图8ABCA'B'C'cb a'c'b'3. 如图10,AC 是ABCD 较长的对角线,过C 作CF ⊥AF ,CE ⊥AE .求证:AB ·AE +AD ·AF =AC 2.4. 如图11.已知⊙O 1和⊙O 2相交于A 、B ,直线CD 过A 交⊙O 1和⊙O 2于C 、D ,且AC =AD ,EC 、ED 分别切两圆于C 、D . 求证:AC 2=AB ·AE .6.已知E 是△ABC 的外接圆之劣弧BC 的中点. 求证:AB ·AC =AE 2-BE 2.7. 若正五边形ABCDE 的边长为a ,对角线长为b ,试证:a b -ba=1.F DAB EC图10C图11初中数学巧添辅助-- 妙解竞赛题答案在某些数学竞赛问题中,巧妙添置辅助圆常可以沟通直线形和圆的内在联系,通过圆的有关性质找到解题途径.下面举例说明添置辅助圆解初中数学竞赛题的若干思路.1 挖掘隐含的辅助圆解题有些问题的题设或图形本身隐含着“点共圆”,此时若能把握问题提供的信息,恰当补出辅助圆,并合理挖掘图形隐含的性质,就会使题设和结论的逻辑关系明朗化. 1.1 作出三角形的外接圆例1 如图1,在△ABC 中,AB =AC ,D 是底边BC 上一点,E 是线段AD 上一点且∠BED =2∠CED = ∠A .求证:BD =2CD .分析:关键是寻求∠BED =2∠CED 与结论的联系. 容易想到作∠BED 的平分线,但因BE ≠ED ,故不能 直接证出BD =2CD .若延长AD 交△ABC 的外接圆 于F ,则可得EB =EF ,从而获取.证明:如图1,延长AD 与△ABC 的外接圆相交于点F ,连结CF 与BF ,则∠BFA =∠BCA =∠ABC =∠AFC ,即∠BFD =∠CFD .故BF :CF =BD :DC .又∠BEF =∠BAC ,∠BFE =∠BCA ,从而∠FBE =∠ABC =∠ACB =∠BFE . 故EB =EF .作∠BEF 的平分线交BF 于G ,则BG =GF . 因∠GEF =21∠BEF =∠CEF ,∠GFE =∠CFE ,故△FEG ≌△FEC .从而GF =FC . 于是,BF =2CF .故BD =2CD . 1.2 利用四点共圆例2 凸四边形ABCD 中,∠ABC =60°,∠BAD = ∠BCD =90°,AB =2,CD =1,对角线AC 、BD 交于点O ,如图2. 则sin ∠AOB =____.ABGCD FE图1ABCDPO 图2分析:由∠BAD =∠BCD =90°可知A 、B 、C 、D四点共圆,欲求sin ∠AOB ,联想到托勒密定理,只须求出BC 、AD 即可.解:因∠BAD =∠BCD =90°,故A 、B 、C 、D 四点共圆.延长BA 、CD 交于P ,则∠ADP =∠ABC =60°.设AD =x ,有AP =3x ,DP =2x .由割线定理得(2+3x )3x =2x (1+2x ).解得AD =x =23-2,BC =21BP =4-3. 由托勒密定理有BD ·CA =(4-3)(23-2)+2×1=103-12.又S ABCD =S △ABD +S △BCD =233. 故sin ∠AOB =263615 . 例3 已知:如图3,AB =BC =CA =AD ,AH ⊥CD 于H ,CP ⊥BC ,CP 交AH 于P .求证: △ABC 的面积S =43AP ·BD . 分析:因S △ABC =43BC 2=43AC ·BC ,只 须证AC ·BC =AP ·BD ,转化为证△APC ∽△BCD .这由A 、B 、C 、Q 四点共圆易证(Q 为BD 与AH 交点).证明:记BD 与AH 交于点Q ,则由AC =AD ,AH ⊥CD 得∠ACQ =∠ADQ . 又AB =AD ,故∠ADQ =∠ABQ .从而,∠ABQ =∠ACQ .可知A 、B 、C 、Q 四点共圆. ∵∠APC =90°+∠PCH =∠BCD ,∠CBQ =∠CAQ , ∴△APC ∽△BCD . ∴AC ·BC =AP ·BD . 于是,S =43AC ·BC =43AP ·BD . A图3BPQDHC2 构造相关的辅助圆解题有些问题貌似与圆无关,但问题的题设或结论或图形提供了某些与圆的性质相似的信息,此时可大胆联想构造出与题目相关的辅助圆,将原问题转化为与圆有关的问题加以解决. 2.1 联想圆的定义构造辅助圆例4 如图4,四边形ABCD 中,AB ∥CD ,AD =DC =DB =p ,BC =q .求对角线AC 的长.分析:由“AD =DC =DB =p ”可知A 、B 、C 在 半径为p 的⊙D 上.利用圆的性质即可找到AC 与 p 、q 的关系.解:延长CD 交半径为p 的⊙D 于E 点,连结AE . 显然A 、B 、C 在⊙D 上. ∵AB ∥CD ,∴BC =AE . 从而,BC =AE =q .在△ACE 中,∠CAE =90°,CE =2p ,AE =q ,故 AC =22AE CE -=224q p -. 2.2 联想直径的性质构造辅助圆例5 已知抛物线y =-x 2+2x +8与x 轴交于B 、C 两点,点D 平分BC .若在x 轴上侧的A 点为抛物线上的动点,且∠BAC 为锐角,则AD 的取值范围是____.分析:由“∠BAC 为锐角”可知点A 在以定线段BC 为直径的圆外,又点A 在x 轴上侧,从而可确定动点A 的范围,进而确定AD 的取值范围. 解:如图5,所给抛物线的顶点为A 0(1,9), 对称轴为x =1,与x 轴交于两点B (-2,0)、 C (4,0).分别以BC 、DA 为直径作⊙D 、⊙E ,则两圆与抛物线均交于两点P (1-22,1)、A EDCB图4图5Q (1+22,1).可知,点A 在不含端点的抛物线PA 0Q 内时,∠BAC <90°.且有3=DP =DQ <AD ≤DA 0=9,即AD 的取值范围是3<AD ≤9. 2.3 联想圆幂定理构造辅助圆例6 AD 是Rt △ABC 斜边BC 上的高,∠B 的平行线交AD 于M ,交AC 于N .求证:AB 2-AN 2=BM ·BN .分析:因AB 2-AN 2=(AB +AN )(AB -AN )=BM ·BN ,而由题设易知AM =AN ,联想割线定理,构造辅助圆即可证得结论. 证明:如图6,∵∠2+∠3=∠4+∠5=90°, 又∠3=∠4,∠1=∠5, ∴∠1=∠2.从而,AM =AN . 以AM 长为半径作⊙A ,交AB 于F ,交 BA 的延长线于E .则AE =AF =AN . 由割线定理有 BM ·BN =BF ·BE =(AB +AE )(AB -AF ) =(AB +AN )(AB -AN ) =AB 2-AN 2, 即 AB 2-AN 2=BM ·BN .例7 如图7,ABCD 是⊙O 的内接四边形,延长AB 和DC 相交于E ,延长AB 和DC 相交于E ,延长AD 和BC 相交于F ,EP 和FQ 分别切⊙O 于P 、Q .求证:EP 2+FQ 2=EF 2. 分析:因EP 和FQ 是⊙O 的切线,由结论联想到切割线定理,构造辅助圆使EP 、FQ 向EF 转化.证明:如图7,作△BCE 的外接圆交EF 于G ,连 结CG .因∠FDC =∠ABC =∠CGE ,故F 、D 、C 、G 四点共圆.EA N D BFM 12345图6由切割线定理,有 EF 2=(EG +GF )·EF =EG ·EF +GF ·EF =EC ·ED +FC ·FB=EC ·ED +FC ·FB =EP 2+FQ 2,即 EP 2+FQ 2=EF 2.2.4 联想托勒密定理构造辅助圆 例8 如图8,△ABC 与△A 'B ' C '的三边分别为a 、b 、c 与a '、 b '、c ',且∠B =∠B ',∠A +∠A '=180°.试证:aa '=bb '+cc '. 分析:因∠B =∠B ',∠A +∠A '=180°,由结论联想到托勒密定理,构造圆内接四边形加以证明.证明:作△ABC 的外接圆,过C 作CD ∥AB 交圆于D ,连结AD 和BD ,如图9所示. ∵∠A +∠A '=180°=∠A +∠D , ∠BCD =∠B =∠B ',∴∠A '=∠D ,∠B '=∠BCD .∴△A 'B 'C '∽△DCB .有DC B A ''=CB C B ''=DBC A '',即 DC c '=a a '=DB b '.故DC =''a ac ,DB =''a ab .又AB ∥DC ,可知BD =AC =b ,BC =AD =a . 从而,由托勒密定理,得 AD ·BC =AB ·DC +AC ·BD , 即 a 2=c ·''a ac +b ·''a ab . 故aa '=bb '+cc '.练习题(1)(2)图8ABCA'B'C'ca b a'c'b'A BCDa b b c图91. 作一个辅助圆证明:△ABC 中,若AD 平分∠A ,则AC AB =DCBD. (提示:不妨设AB ≥AC ,作△ADC 的外接圆交AB 于E ,证△ABC ∽△DBE ,从而AC AB =DEBD=DCBD.) 2. 已知凸五边形ABCDE 中,∠BAE =3a ,BC =CD =DE ,∠BCD =∠CDE =180°-2a .求证:∠BAC =∠CAD =∠DAE .(提示:由已知证明∠BCE =∠BDE =180°-3a ,从而A 、B 、C 、D 、E 共圆,得∠BAC =∠CAD =∠DAE .)3. 在△ABC 中AB =BC ,∠ABC =20°,在AB 边上取一点M ,使BM =AC .求∠AMC 的度数. (提示:以BC 为边在△ABC 外作正△KBC ,连结KM ,证B 、M 、C 共圆,从而∠BCM =21∠BKM =10°,得∠AMC =30°.) 4.如图10,AC 是ABCD 较长的对角线,过C 作CF ⊥AF ,CE ⊥AE .求证:AB ·AE +AD ·AF =AC 2. (提示:分别以BC 和CD 为直径作圆交AC 于点 G 、H .则CG =AH ,由割线定理可证得结论.) 5. 如图11.已知⊙O 1和⊙O 2相交于A 、B ,直线CD 过A 交⊙O 1和⊙O 2于C 、D ,且AC =AD ,EC 、ED 分别切两圆于C 、D .求证:AC 2=AB ·AE . (提示:作△BCD 的外接圆⊙O 3,延长BA 交⊙O 3 于F ,证E 在⊙O 3上,得△ACE ≌△ADF ,从而AE =AF ,由相交弦定理即得结论.)6.已知E 是△ABC 的外接圆之劣弧BC 的中点. 求证:AB ·AC =AE 2-BE 2.(提示:以BE 为半径作辅助圆⊙E ,交AE 及其延长线于N 、M ,由△ANC ∽△ABM 证AB ·AC =AN ·AM .)7. 若正五边形ABCDE 的边长为a ,对角线长为b ,试证:a b -ba=1. (提示:证b 2=a 2+ab ,联想托勒密定理作出五边形的外接圆即可证得.)FDAEC图10图11。
人教版九年级数学竞赛专题:平面几何的定值问题(含答案)

(第 3 题图)
(第 4 题图)
4.如图,正△ABO 的高等于⊙O 的半径,⊙O 在 AB 上滚动,切点为 T,⊙O 交 AO,BO 于 M,N,则 弧 MTN( )
A.在 0°到 30°变化
B.在 30°到 60°变化
C.保持 30°不变
D.保持 60°不变
5.如图,AB 是⊙O 的直径,且 AB=10,弦 MN 的长为 8.若 MN 的两端在圆上滑动时,始终与 AB 相交, 记点 A,B 到 MN 的距离分别为 h1,h2,则∣h1-h2∣等于( )
A
C
(P) O
D
B
①
D
A
C P O
B D ①
D
C
PB O
D ①
O
C A
P
①
B
O
C
P
A (B)
①
O
(D)C
A(B)
P ①
(2)已知⊙O 的半径为一定值 r,若点 P 是不在⊙O 上的一个定点,请你过点 P 任作一直线交⊙O 于 不重合的两点 E,F. PE·PF 的值是否为定值?为什么?由此你发现了什么结论?请你把这一结论用文 字叙述出来.
(第 7 题图)
(第 8 题图)
8.如图,设 H 是等腰三角形 ABC 两条高的交点,在底边 BC 保持不变的情况下让顶点 A 至底边 BC 的 距离变小,这时乘积 S△ABC·S△HBC 的值变小、变大,还是不变?证明你的结论.
9.如图,在平面直角坐标系 xOy 中,抛物线 y 1 x 2 4 x 10 与 x 轴的交点为点 A,与 y 轴的交点 18 9
人教版九年级数学竞赛专题:平面几何的定值问题(含答案)
【例 1】 如图,已知 P 为正方形 ABCD 的外接圆的劣弧A⌒D上任意一点.求证: PA PC 为定值. PB
人教版 初三数学竞赛专题:平面几何的定值问题(包含答案)
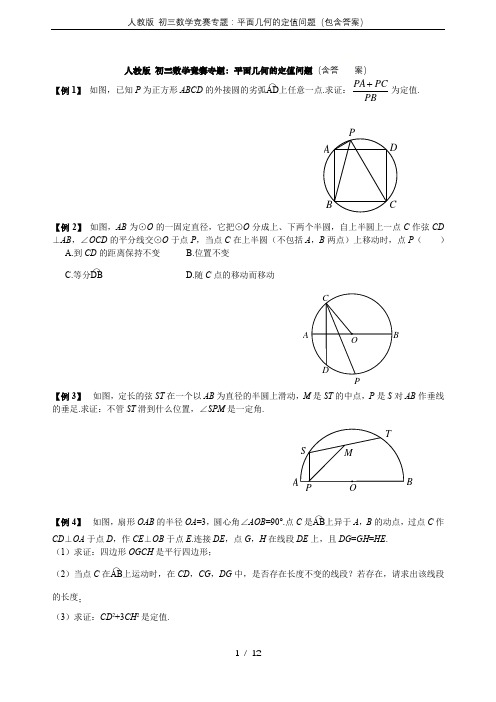
人教版 初三数学竞赛专题:平面几何的定值问题(含答案)【例1】 如图,已知P 为正方形ABCD 的外接圆的劣弧AD⌒上任意一点.求证:PA PC PB为定值.【例2】 如图,AB 为⊙O 的一固定直径,它把⊙O 分成上、下两个半圆,自上半圆上一点C 作弦CD ⊥AB ,∠OCD 的平分线交⊙O 于点P ,当点C 在上半圆(不包括A ,B 两点)上移动时,点P ( ) A.到CD 的距离保持不变 B.位置不变C.等分DB⌒ D.随C 点的移动而移动【例3】 如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂线的垂足.求证:不管ST 滑到什么位置,∠SPM 是一定角.【例4】 如图,扇形OAB 的半径OA =3,圆心角∠AOB =90°.点C 是AB⌒上异于A ,B 的动点,过点C 作CD ⊥OA 于点D ,作CE ⊥OB 于点E .连接DE ,点G ,H 在线段DE 上,且DG =GH =HE .(1)求证:四边形OGCH 是平行四边形;(2)当点C 在AB ⌒上运动时,在CD ,CG ,DG 中,是否存在长度不变的线段?若存在,请求出该线段的长度;(3)求证:CD 2+3CH 2是定值.P AB CDAPB【例5】 如图1,在平面直角坐标系xOy 中,点M 在x 轴的正半轴上,⊙M 交x 轴于A ,B 两点,交y 轴于C ,D 两点,且C 为弧AE 的中点,AE 交y 轴于G 点.若点A 的坐标为(-2,0),AE =8. (1)求点C 的坐标;(2)连接MG ,BC ,求证:MG ∥BC ;(3)如图2,过点D 作⊙M 的切线,交x 轴于点P .动点F 在⊙M 的圆周上运动时,PFOF的比值是否发生变化?若不变,求出比值;若变化,说明变化规律.(图1)(图2)【例6】 如图,已知等边△ABC 内接于半径为1的圆O ,P 是⊙O 上的任意一点.求证:P A 2+PB 2+PC 2为定值.【能力训练】1.如图,点A ,B 是双曲线xy 3上的两点,分别经过A ,B 两点向x 轴,y 轴作垂线段.若S 阴影=1,则BOACE HG D A=+21S S _______.(第1题图) (第3题图) (第4题图)2.从等边三角形内一点向三边作垂线段,已知这三条垂线段的长分别为1,3,5,则这个等边三角形的面积是__________.3.如图,OA ,OB 是⊙O 任意两条半径,过B 作BE ⊥OA 于E ,又作OP ⊥AB 于P ,则定值OP 2+EP 2为_________.4.如图,在菱形ABCD 中,∠ABC =120°,F 是DC 的中点,AF 的延长线交BC 的延长线于点E ,则直线BF 与直线DE 所夹的锐角的度数为( )A.30°B.40°C.50°D.60°5.如图,在⊙O 中,P 是直径AB 上一动点,在AB 同侧作A A '⊥AB ,AB B B ⊥',且A A '=AP ,B B '=BP .连接B A '',当点P 从点A 移动到点B 时,B A ''的中点的位置( ) A .在平分AB 的某直线上移动 B.在垂直AB 的某直线上移动 C.在弧AMB 上移动 D.保持固定不移动(第5题图) (第6题图) 6.如图,A ,B 是函数xky =图象上的两点,点C ,D ,E ,F 分别在坐标轴上,且分别与点A ,B ,O 构成正方形和长方形.若正方形OCAD 的面积为6,则长方形OEBF 的面积是( ) A.3 B.6 C.9 D.127.(1)经过⊙O 内或⊙O 外一点P 作两条直线交⊙O 于A ,B 和C ,D 四点,得到如图①~⑥所表示的六种不同情况.在六种不同情况下,P A ,PB ,PC ,PD 四条线段之间在数量上满足的关系式可以用同一个式子表示出来.请你首先写出这个式子,然后只就如图②所示的圆内两条弦相交的一般情况给出它的证明.A ABCDEFAB'(2)已知⊙O 的半径为一定值r ,若点P 是不在⊙O 上的一个定点,请你过点P 任作一直线交⊙O 于不重合的两点E ,F . PE ·PF 的值是否为定值?为什么?由此你发现了什么结论?请你把这一结论用文字叙述出来.8.在平面直角坐标系中,边长为2的正方形OABC 的两顶点A ,C 分别在y 轴,x 轴的正半轴上,点O 在原点,现将正方形OABC 绕O 点顺时针旋转,当A 点第一次落在直线x y =上时停止旋转.旋转过程中,AB 边交直线x y =于点M ,BC 边交x 轴于点N .(1)求OA 在旋转过程中所扫过的面积;(2)旋转过程中,当MN 与AC 平行时,求正方形OABC 旋转度数;(3)设△MBN 的周长为P ,在正方形OABC 旋转的过程中,P 值是否有变化?请证明你的结论.⑥⑤④③②①P(B )A PB9.如图,AB 是半圆的直径,AC ⊥AB ,AC =AB .在半圆上任取一点D ,作DE ⊥CD ,交直线AB 于点E ,BF ⊥AB ,交线段AD 的延长线于点F .(1)设弧AD 是x °的弧,若要点E 在线段BA 的延长线上,则x 的取值范围是_______.(2)不论点D 取在半圆的什么位置,图中除AB =AC 外,还有两条线段一定相等.指出这两条相等的线段,并予证明.(第9题图) (第10题图)(第11题图)10.如图,内接于⊙O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ,设⊙O 的半径为R .求证: (1)2222DK CK BK AK +++是定值; (2)2222DA CD BC AB +++是定值.11.如图,设P 是正方形ABCD 外接圆劣弧弧AB 上的一点,求证:DPCP BPAP ++的值为定值.1.等腰△ABC 的底边BC 为定长2,H 为△ABC 的垂心.当顶点A 在保持△ABC 为等腰三角形的情况下 改变位置时,面积S △ABC ·S △HBC 的值保持不变,则S △ABC ·S △HBC =________.2.已知A ,B ,C ,D ,E 是反比例函数xy 16=(x >0)图象上五个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是__________(用含π的代数式表示).P D CB A A折叠,使点A ,B 落在六边形ABCDEF 的内部,记∠C +∠D + )A. ∠1+∠2=900°-2α B. ∠1+∠2=1080°-2α C. ∠1+∠2=720°-α D. ∠1+∠2=360°-21α(第3题图) (第4题图)4.如图,正△ABO 的高等于⊙O 的半径,⊙O 在AB 上滚动,切点为T ,⊙O 交AO ,BO 于M ,N ,则弧MTN ( )A.在0°到30°变化B.在30°到60°变化C.保持30°不变D.保持60°不变5.如图,AB 是⊙O 的直径,且AB =10,弦MN 的长为8.若MN 的两端在圆上滑动时,始终与AB 相交,记点A ,B 到MN 的距离分别为h 1,h 2,则∣h 1-h 2∣等于( )A.5B.6C.7D.8(第5题图) 12GF EDCHBAB6.如图,已知△ABC 为直角三角形,∠ACB =90°,AC =BC ,点A ,C 在x 轴上,点B 坐标为(3,m )(m >0),线段AB 与y 轴相交于点D ,以P (1,0)为顶点的抛物线过点B ,D . (1)求点A 的坐标(用m 表示) (2)求抛物线的解析式;(3)设点Q 为抛物线上点P 至点B 之间的一动点,连接PQ 并延长交BC 于点E ,连接BQ 并延长交AC 于点F .试证明:FC (AC +EC )为定值.7.如图,已知等边△ABC 内接于圆,在劣弧AB 上取异于A ,B 的点M .设直线AC 与BM 相交于K ,直线CB 与AM 相交于点N .证明线段AK 和BN 的乘积与M 点的选择无关.(第7题图) (第8题图)8.如图,设H 是等腰三角形ABC 两条高的交点,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积S △ABC ·S △HBC 的值变小、变大,还是不变?证明你的结论.9.如图,在平面直角坐标系xOy 中,抛物线10941812--=x x y 与x 轴的交点为点A ,与y 轴的交点为点B .过点B 作x 轴的平行线BC ,交抛物线于点C ,连接AC .现有两动点P ,Q 分别从O ,C 两点同时出发,点P 以每秒4个单位的速度沿OA 向终点A 移动,点Q 以每秒1个单位的速度沿CB 向点B 移动.点P 停止运动时,点Q 也同时停止运动.线段OC ,PQ 相交于点D ,过点D 作DE ∥OA ,交CA 于E ,射线QE 交x 轴于点F .设动点P ,Q 移动的时间为t (单位:秒). (1)求A ,B ,C 三点的坐标和抛物线的顶点坐标;(2)当t 为何值时,四边形PQCA 为平行四边形?请写出计算过程; (3)当290<<t 时,△PQF 的面积是否总是定值?若是,求出此值;若不是,请说明理由; (4)当t 为何值时,△PQF 为等腰三角形,请写出解答过程.NKMB AC HCBA(第9题图) (第10题图) 10.已知抛物线C 1:12121+-=x x y ,点F (1,1). (1)求抛物线C 1的顶点坐标;(2)若抛物线C 1与y 轴的交点为A ,连接AF ,并延长交抛物线C 1于点B ,求证:211=+BFAF . (3)抛物线C 1上任意一点P (x P ,y P )(0<x P <1),连接PF ,并延长交抛物线C 1于点 Q (x Q ,y Q ),试判断211=+QFPF 是否成立?请说明理由.11.已知A ,B 是平面上的两个顶点,C 是位于AB 一侧的一个动点,分别以AC ,BC 为边在△ABC 外作正方形ACDE 和正方形BCFG .求证:不论C 在直线AB 同一侧的任何位置,EG 的中点P 的位置不变. 参考答案例 1 延长PC 至E ,使CE =AP ,连结BE ,则△BCE ≌△BAP ,及△PBE 为等腰直角三角形,故PA PC CE PC PEPB PB PB++=== 例2 B 提示:连结AC ,BC ,可以证明P 为APB 的中点. 例3 ∵SP ⊥OP ,OM ⊥ST ,∴S ,M ,O ,P 四点共圆,于是∠SPM =∠SOM =12∠SOT 为定角. 例4 (1)连结OC 交DE 于M ,则OM =CM , EM =DM ,而DG = HE ,则HM =GM 故四边形OGCH 是平行四边形. (2)DG 不变.DE =OC =OA =3 .DG =13DE =13×3=1. (3)设CD =x ,延长OG 交CD 于N ,则CN =DN =12 x ,229CE x =- , 2214DN x = .∴22394ON x =-,而ON =32CH ,∴22143CH x =-.故CD 2+3CH 2=x 2+3(4-13x 2)=x 2+12-x 2为定值. 例5 ⑴C (0,4) ⑵先求得AM =CM =5,连接MC 交AE 于N ,由△AO G ∽△ANM ,得OG AO MN AN =,O G =32,38OG OM OC OB ==,又∠BOC =∠G OM ,∴△G OM ∽△COB ,∠G MO =∠CBO ,得M G ∥BC .⑶连结DM ,则DM ⊥PD ,DO ⊥PM ,DO 2=OM •OP ,OP =163.动点F 在⊙M 的圆周上运动时,从特殊位置探求OFPF的值.当F 与点A 重合时,2316523OF AO PF AP ===-;当点F 与点B 重合时,8316583OF OB PF PB ===+;当点F 不与点A ,B 重合时,连接OF 、PF 、MF ,∴DM 2=MO •MP ,∴FM 2=MO •MP ,即FM MPOM FM=,又∠OMP =∠FMP ,∴△MFO ∽△MPF ,35OF MO PF MF ==,故OF PF 的比值不变,比值为35. 例6 ∠BPC =120°,在△BPC 中,由余弦定理得BC 2=PB 2+PC 2-2PB •PC =BC 2,又由上托勒密定理得BC •P A +PC •AB ,而AB =BC =AC ,∴P A =PB +PC ,从而P A 2+ PB 2+ PC 2= (PB +PC )2+ PB 2+ PC 2=2 (PB 2+PC 2+PB •PC )=2BC 2=2×()23=6.故P A 2+PB 2+PC 2为定值.A 级 1.4提示:∵S 1+S 阴= S 2+S 阴=xy =3,∴S 1+S 2=2xy -2S 阴=6-2=4.2.273 提示:1+3+5=9是等边三角形的高. 3.r 2提示:先考查OB 与OA 垂直的情形.4.D 提示:延长BF 交DE 于点M ,连接BD ,则△BCD 为等边三角形,BF 平分∠CBD .∵F 为CD 中点,且AD ∥CE ,∴△ADF 与△ECF 关于点F 中心对称.∴CE =AD =CD ,∴∠CEM=30°,∠DMF=60°,5.D 提示:A′B′的中点均在⊙O 的上半圆的中点处. 6.B 提示:S 正方形OCAD =OD •OC =A A x y k ==6,∴S OEBF =OE •OF =x B •y B k ==6. 7.⑴略⑵当点P在⊙O 内时,过P 作直径CD ,则PE •PF =PD •PC =r 2-OP 2为定值;当点P 在⊙O 外时,PE •PF 为定值22OP r -.结论:过不在圆上的一个定点任作一条直线与圆相交,则这点到直线与圆相交点的两条线段长的积为定值. 8.⑴2π⑵22.5° ⑶P 值无变化.理由如下:如图,延长BA 交y 轴于E 点,可证明△OAE ≌△OCN ,得OE =ON ,AE =CN ,又∠MOE =∠MON =45°,OM =ON ,∴△OME ≌△OMN ,得MN =ME =AM +AE =AM +CN .∴P =MN +BN +BM =AM +CM +CN +BN +BM =AB +AC =4.9.⑴0<x <90 ⑵BE =BF 提示:连接BD ,可证明△BDF ∽△ADB ,△BDE ∽△ADC . 10.⑴作OP ⊥BD 于P ,OQ ⊥AC 于Q ,连接AO ,则AO 2=()()221122BK DK CK AK ⎡⎤⎡⎤-++⎢⎥⎢⎥⎣⎦⎣⎦,又AK •CK =BK •DK ,得AK 2+BK 2+CK 2+DK 2=4R 2为定值. ⑵作直径DE ,连接AE ,BE ,CE ,AB 2+CD 2=4R 2,AD 2+BC 2=4R 2,故AB 2+BC 2+CD 2+DA 2=8K 2为定值. 11.设正方形的边长为a ,根据托勒密定理,对于四边形APBC 和四边形APBD ,有CP •a =AP •a +BP •2a ,DP •a =BP •a +AP •2a ,两式相加并整理得(CP +DP )a =(AP +BP )(a +2a ),从而21AP BPCP DP+=-+为定值.B 级1.1 提示:不妨设∠A 为锐角,AD ,BE ,CF 为△ABC 的三条高,H 为垂心,由AB =AC 知∠HBD =∠HCD =∠HAE ,∠HDC =∠CDA =90°,故R t △CHD ∽R t △ACD .∴AD DC DC HD =,即AD •HD =DC 2=14BC 2=1.∴S △ABC •S △HBC =2111224BC AD BC HD BC ⎛⎫⎛⎫⋅⋅⋅= ⎪ ⎪⎝⎭⎝⎭=1.当∠A ≥90°时,结论成立.2.13π-26 提示:∵A ,B ,C ,DE 是反比例函数y =16x(x >0)图象上五个整数点,由图象可知,这些点的横坐标分别为1,2,4,8,16.∴五个正方形的边长分别为1,3,4,2,1.∴这五人橄榄形的面积总和是2221111112211122222444424242πππ⎡⎤⎛⎫⎛⎫⎛⎫⨯-⨯⨯+⨯-⨯⨯+⨯-⨯⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=5π-10+8π-16=13π-26. 3.B 提示:如图,设F A 的延长线与CB 的延长线交于点P ,G A ′的延长线与HB ′的延长线交于点P ′.由对称性可知∠1=2∠APP ′,∠2=2∠BPP ′.∴∠1+∠2=2∠APB .∵∠APB =540°-α,∴∠1+∠2=1080°-2α. 4.D 5.B 提示:如图,设AB 与MN 交于点C ,过点O 作OD ⊥MN 于D ,连接FO 并延长交EB 于G .由垂径定理,得OD =2254-=3.由△AFO ≌△B G O ,得AF =B G ,即h 1=B G .由AF ⊥MN ,BE ⊥MN ,得△FOD ∽△F G E .∴12OD FO GE FG ==.∴E G =2OD =6,∴12h h AF BE -=-=E G =6. 6.⑴A (3-m ,0) ⑵y =x 2-2x +1 ⑶过点Q 作QM ⊥AC 于M ,过点Q 作QN ⊥BC 于N ,设Q 点的坐标为(x ,x 2-2x +1),则QM =CN =(x -1)2,MC =QN=3-x .∵QM ∥CE ,∴PQM ∽△PEC .∴QM PMEC PC=,即()2112x x EC--=,得EC =2(x -1).∵QN ∥CF ,∴△BQN ∽△BFC .∴QN BN FC BC =,即()24134x x FC ---=,得FC =41x +.又AC =4,∴FC (AC +EC )=()44211x x +-⎡⎤⎣⎦+=8为定值. 7.提示:易证△ABK ∽△BNA ,故AK •BN =AB 2为定值,即AK 与BN 的乘积与M 点的选择无关. 8.提示:S △ABC •S △HBC =116BC 4,由于BC 是不变的,所以当点A 至BC 的距离变小时,乘积S △ABC •S △HBC 保持不变. 9.⑴A (18,0),B (0,-10),顶点坐标为(4,-989)⑵若四边形PQCA 为平行四边形,由于QC ∥P A ,故只要QC =P A 185. ⑶即可,而P A =18-4t ,CQ =t ,故18-4t =t ,得t =设点P 运动t s ,则OP =4t ,CQ =t ,0<t <4.5.说明P在线段OA 上,且不与点O ,A 重合.由于QC ∥OP 知△QDC ∽△PDO ,故144QD QC t DP OP t ===.同理QC ∥AF ,故14QC CE AF EA ==,即14t AF =,∴AF =4t =OP .∴PF =P A +AF =P A +OP =18.又点Q 到直线PF 的距离d =10,∴S △PQF =12•PF •d =12×18×10=90.于是S △PQF 的面积总为定值90. ⑷由前面知道,P (4t ,0),F (18+4t ,0),Q (8-t ,-10),0≤t ≤4.5.构造直角三角形后易得PQ 2=(4t -8+t )2+102=,FQ 2=(18+4t -8+t )2+102=(5t +10)2+100.①若FP =FQ ,即182=(5t +10)2+100,故25(t +2)2=224,(t +2)2=24425.∵2≤t +2≤6.5,∴t +2=244414255=.∴t = 4145-2. ②若QP =QF ,即(5t -8)2+100=(5t +10)2+100,即(5t -8)2=(5t +10)2,无0≤t ≤4.5的t 满足. ③若PQ =PF ,即(5t -8)2+100=182,∴(5t -8)2=224.由于224≈15,又0≤5t ≤22.5,∴-8≤5t -8≤14.5,14.52=22984124⎛⎫= ⎪⎝⎭<224.故没有t (0≤t ≤4.5)满足此方程.综上所述,当t =4145-2时,△PQ R 为等腰三角形. 10.⑴C 1的顶点坐标为(1,12). ⑵略 ⑶作PM ⊥AB 于M ,作QN ⊥AB 交AB 延长线于N ,∴PM =1-y P ,FM =1-x P .在R t △PMF 中,PF 2=(1-y P )2+(1-x P )2=1-2y P +y P 2+1-2x P +x P 2,又∵点P 在抛物线上,∴y P =12x P 2-x P +1,∴PF 2=1-x P 2+2x P -2+y P 2+1-2x P +x P 2=y P 2,∴PF =y P ,同理,QF =y Q ,易证△PMF ∽△QNF ,则PM QN PF QF =,∴11Q P y y PF QF --=,即11PF QF PF QF --=,∴11PF QF+=2. 11.先从特殊情况出发.当△ABC 是等腰直角三角形时,点P 与点C 重合,此时点P 的位置在AB 的中垂线上,且到AB的距离为12AB ,如图①所示.下面就一般情况来证明上面的结论(结论②所示).过C ,E ,G 分别作直线AB 的垂线CH ,EM ,G N ,垂足分别是H ,M ,N .容易证明△AEM ≌△ACH ,△B G N ≌△BCH .从而有AM =CH =BN ,EM =AH ,G N =BH .这样,线段AB 的中点O 也是线段MN 的中点,连接OP ,则OP 是梯形EMN G 的中位线,从而OP ⊥AB ,OP =12(EM +G N )= 12(AH +BH )=12AB .∴无论点C 在AB 同一侧的位置如何,E G 中点P 的位置不变.。
初中数学竞赛专题复习 第二篇 平面几何 第10章 四边形试题(无答案) 新人教版

第10章 四边形§10.1 平行四边形与梯形10.1.1★如图(a),在四边形ABCD 中,AC 、BD 是对角线,已知ABC △是等边三角形,30ADC ∠=︒,3AD =,5BD =,求边CD 的长.DABC DAB CE(a)(b)解析 如图(b),以CD 为边向四边形ABCD 外作等边CDE △,连结AE .由于AC BC =,CD CE =, BCD BCA ACD ∠=∠+∠DCE ACD =∠+∠ACE ∠. 所以BCD △≌ACE △,从而BD AE =.又因为30ADC ∠=︒,5BD =,3AD =,于是90ADE ∠=︒,从而在Rt ADE △中,4DE =.所以4CD =.10.1.2★在ABCD 中,2AB AD =,F 为AB 中点,CE AD ⊥D 交AD (或延长线)于E .求证:3BFE AEF ∠=∠.解析 如图,取CD 中点G ,连结FG 、CF .A FBE DGC易知四边形ADGF 与FGCB 均为菱形,FG 垂直平分CE ,于是EFG ∠CFG CFB =∠=∠,于是33BFE EFG AEF ∠=∠∠=∠.10.1.3★AD 、BE 、CF 是ABC △的三条中线,FG BE ∥,EG AB ∥,四边形ADCG 是平行四边形. 解析 如图,连结EF ,则EF 是中位线.AGFEB D C由条件知EG BF ∥,故EG AF ∥,于是AG EF CD ∥∥,故结论成立. 10.1.4★延长矩形ABCD 的边CB 到E ,使CE CA =,F 是AE 的中点,求证:BF FD ⊥.解析 如图,取BD 中点G ,连结FG ,则()11112222FG AD BE CE CA BD =+===,于是BF FD ⊥. ADBCADFGEBC题10.1.4题10.1.510.1.5★菱形ABCD中,2BD AC -=120BAD ∠=︒,求菱形的面积. 解析 如图,易知ABC △与ACD △均为正三角形.设菱形边长为x ,则由120BAD ∠=︒,得BD ,AC x =,所以)12x =x =此菱形面积为212BD AC ⋅=. 10.1.6★在梯形ABCD 中,AD BC ∥,中位线MN 分别交AB 、CD 、AC 、BD 于M 、N 、P 、Q ,若延长AQ 、DP 的交点正好位于BC 上,求BCAD. ADMQPNB RC解析 设AQ 、DP 延长后交于R ,且R 在BC 上,则由中位线知2AD PQ =,2AD PN =,2BC QN =,故2BCAD=. 10.1.7★★四边形ABCD 中,135ABC ∠=︒,120BCD ∠=︒,AB =5BC =6CD =,求AD . 解析 如图所示,作AF BC ⊥,DE BC ⊥分别交BC 所在直线于F 、E ,作FG AD ∥交DE 于G ,则AFB △为等腰直角三角形,90AFB ∠=︒,AB =故FB A F =;90DEC ∠=︒,60DCE ∠=︒,6CD =,故3CE =,DE =.F BCEADG所以EF FB BC CE =++538+=,GE DE DG DE AF =-=-==从而AD FG ==10.1.8★★★已知ABC △中,90A ∠=︒,D 是BC 上一点,D 关于AB 、AC 的对称点分别为F 、E ,若BE CF =,12AD BC =.解析 如图,连结AF 、AE 、BF 、CE .FAEBDC由对称,有22180FAD EAD BAD CAD ∠+∠=∠+∠=︒,故F 、A 、E 共线.又180BFE FEC ADB ADC ∠+∠=∠+∠=︒,故FB ∥EC ,而BE CF =,所以梯ECBF 为等腰梯形.又AF AD AE ==,于是1122AD EF BC ==.10.1.9★★将梯形的各个顶点均作关于不包含该顶点的对角线的对称点,证明:如果所得到的四个像点也形成四边形,则必为一个梯形.B'C'ADBCA'D'O解析 如图,AD BC ∥,A 、B 、C 、D 关于对应对角线的对称点分别为A ′、B ′、C ′、D ′. 设AC 、BD 交于O ,连结A ′O 、B ′O 、C ′O 、D ′O .则A ∠′OB =AOB COD C ∠=∠=∠′OD ,故A ′、O 、C ′共线,且A O AO C O CO '=',同理B ′、O 、D ′共线,B O D O ''BO DO =,所以由1BO CODO AO=≠得1B O C OD O A O''=≠''. 故如A ′、B ′、C ′、D ′不位于同一直线上,则A ′D ′∥B ′C ′,即A ′B ′C ′D ′成梯形.10.1.10★已知:直角梯形ABCD ,AD BC ∥,AB BC ⊥,AB BC =,E 是AB 上一点,AE AD =,75CEB ∠=︒,求ECD ∠.A DE BC解析 如图,连结AC ,则由AB BC =,AB BC ⊥,得45BAC DAC ∠=︒=∠. 又AE AD =,故AEC △≌ADC ,EC CD =.又180754560DEC ∠=︒-︒-︒=︒,故DEC △为正三角形,于是60ECD ∠=︒.10.1.11★★在四边形ABCD 中,60A ∠=︒,90B D ∠=∠=︒,2AB =,1CD =,求BC 、AD 和BD 的长.ACED解析 如图,延长AD 、BC 至E ,则60DCE ∠=︒,22CE CD ==.又60A ∠=︒,故BE =2BC =,又4AE =,CE,故4AD =.至于求BD ,有多种方法,如勾股定理或余弦定理,也可用A 、B 、C 、D 四点共圆的性质:AC,sin 60BD AC =⋅︒=§10.2 正方形10.2.1★在正方形ABCD 中,E 为BC 的中点,F 为CD 上的点,且AF BC CF =+.求证:2BAF BAE ∠=∠.ADBECFP解析 如图,延长AE 、DC ,设交于P ,则B E C E =得CP AB BC ==,FP FC CP FC BC AF =+++=.于是BAE P FAP ∠=∠=∠,即2BAF BAE ∠=∠.10.2.2★正方形边长等于1,通过它的中心引一条直线,求正方形的四个顶点到这条直线的距离平方和的取值范围.AMDONBCl解析 如图,设O 是正方形ABCD 的中心,l 通过O ,AM 、DN 分别与l 垂直于M 、N . 由于90MAO AOM DON ∠=︒-∠=∠,AO OD =,故AMO △≌OND △,2222212AM DN AM MO AO +=+==.对B 、C 的垂线也有类似结论,因此所求距离的平方和是常数1.10.2.3★正方形ABCD 的对角线交于O ,BAC ∠的平分线交BD 于G ,交BC 于F ,求证:2CFOG =. 解析 如图,作OE FC ∥,交AF 于E ,OE 为ACF △中位线,2CF EO =. 问题变为证明EO GO =.因为么4545GEO OAF FAF OGE ∠=︒+∠=∠+︒=∠,于是结论成立.ADE OG BFC10.2.4★设M 、N 分别为正方形ABCD 的边AD 、CD 的中点,且CM 与BN 交于P ,求证:PA AB =. 解析 如图,由MD CN =知BNC △≌CMD △,故90PBC PCB NCM PCB ∠+∠=∠+∠=︒,故C M B N ⊥.延长CM 、BA ,设交于Q ,则QA CD AD ==,A 为直角三角形QPB 斜边BQ 之中点,于是AP AB =.QADMBCN P题10.2.410.2.5★已知两个正方形ABCD 、AKLM (顶点均按照顺时针方向排列),求证:这两个正方形的中心和BM 、DK 的中点组成一个正方形.题10.2.5MAQBP CDRSLK解析 如图,设DB 、BM 、MK 、KD 的中点分别为P 、Q 、R 、S .由于DA AB =,AK AM =,90DAM BAM BAK ∠=︒+∠=∠,于是DAM △≌BAK △,由此得KB 与DM 垂直且相等.由于12SR DM PQ ∥∥,12SP KB RQ ∥∥,故四边形PQRS 为正方形.10.2.6★★M 是正方形ABCD 内一点,若2222AB MA MB -=,90CMB ∠=︒,求MCD ∠.解析 如图,作MN AB ⊥于N ,则22222,2,AB AN BN AM BM AN BN AB ⎧-=-=⎪⎨⎪+=⎩ADBLCMN解得34AN AB =,14BN AB =. 不妨设3AN =,3BN =,MN x =,则 ()22229(4)DM AN AD MN x =+-=+-, ()2222()14CM BN CM MN x =+-=+-,由条件90CMD ∠=︒,知222DM CM CD +=,即()2102416x +-=,解得4x = 又作ML BC ⊥于L,于是4LC x =-1ML NB ==,故60MCD LMC ∠=∠=︒.10.2.7★O 是正方形ABCD 的两对角线的交点,P 是BD 上异于O 的任一点,PE AD ⊥于E ,PF AB⊥于F ,G 是EO 的延长线和BC 的交点,求OFG ∠.CGB OPFDEA解析 如图,易知AF EP ED ==,AO DO =,45FAO EDO ∠=︒=∠,于是AFO △≌DEO △≌BGO △,于是OF OG =,90AOB FOG ∠=︒-∠,故OFG △为等腰直角三角形,45OFG ∠=︒.10.2.8★★K 是正方形ABCD 的边AB 的中点,点L 分对角线AC 的比为:3AL LC =,证明:90KLD ∠=︒.解析 连结BL ,由正方形关于AC 对称,知BL DL =. 又作LJ AB ⊥于J ,由3AL LC =,易知1142JB AB KB ==,故J 为KB 中点,JL 垂直平分KB ,于是LK LB =,LKB LBK ADL ∠=∠=∠,或180AKL ADL ∠+∠=︒,故90KLD ∠=︒.A EDFPOB GC10.2.9★已知ABC △,向外作正方形ABEF 和ACGH .直线AK 垂直BC 于K ,反向延长交FH 于M ,求证:M 是FH 的中点.解析 如图,作FQ 、HP 分别与直线KA 垂直,垂足为Q 、P .P HMFQ AEBKC G易见,90QFA QAF BAK ∠=︒-∠=∠,又90FQA AKB ∠=︒=∠,FA AB =,故有AQF △≌BKA △,FQ AK =,同理PH AK =,于是FQ PH =,FM MH =.10.2.10★已知:正方形ABCD 中,E 、F 分别在BC 、CD 上,AG EF ⊥于G .若45EAF ∠=︒,求证:AG AB =.反之,若AG AB =,则45EAF ∠=︒.解析 如图,延长CB 至H ,使BH DF =,连结AH ,则AHB △≌AFD △,90HAF BAD ∠=∠=︒,904545HAE EAF ∠=︒-︒=︒=∠,又AH AF =,AE AE =,故AHE △≌AFE △,AB 、AG 为其对应 边上的高,于是AG AB =.A D F GH B E C反之,若AG AB =,则Rt ABE △≌Rt AGE △,EAG BAE ∠=∠,同理,FAG DAF ∠=∠,于是1452EAF BAD ∠=∠=︒.10.2.11★★在梯形ABCD 中,AD BC ∥(BC >AD ),90D ∠=︒,12BC CD ==,E 在边CD 上,45ABE ∠=︒,若10AE =,求CE 的长.解析 延长DA 至M ,使BM BE ⊥过B 作BG AM ⊥,G 为垂足.易知四边形BCDG 为正方形,所以BC BG =.又CBE GBM ∠=∠,Rt BEC △≌Rt BMG △,故BM BE =. 又45ABE ABM ∠=∠=︒,故ABE △≌ABM △,10AM AE ==. 设CE x =,则10AG x =-,()12102AD x x =--=+,12DE x =-.在Rt ADE △中,222AE AD DE =+,故()()22100212x x =++-,即210240x x -+=,解之,得14x =,26x =.故CE 的长为4或6.DEC BAGM10.2.12★★在正方形ABCD 的边BC 上任取一点M ,过C 作CQ DM ⊥于Q ,且延长交AB 于N ,设正方形对角线的交点为O ,连结OM 、ON ,求证:OM ON ⊥.解析 如图,易知MDC NCB ∠=∠,故DMC △≌CNB △,故NB MC =,又45NBO OCM ∠=︒=∠,BO CO =,于是ONB △≌OMC △,90NOM BOC ∠=∠=︒.\ADBCMQON10.2.13★★四边形ABCD 是正方形,四边形ACEF 是菱形,E 、F 、B 在一直线上.求证:AE 、AF 三等分CAB ∠.解析 如图,作BM 、FN 与AC 垂直,垂足为M 、N ,于是由AB BF ∥知1122FN BM AC AF ===,于是30FAC ∠=︒.又45CAB ∠=︒,于是15BAF ∠=︒,15FAE CAE ∠=∠=︒,AE 、AF 三等分CAB ∠. ADBCMNFE。
数学初中竞赛大题训练:几何专题(包含答案)

数学初中竞赛大题训练:几何专题1.阅读理解:如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”.证明“四点共圆”判定定理有:1、若线段同侧两点到线段两端点连线夹角相等,那么这两点和线段两端点四点共圆;2、若平面上四点连成的四边形对角互补,那么这四点共圆.例:如图1,若∠ADB=∠ACB,则A,B,C,D四点共圆;或若∠ADC+∠ABC=180°,则A,B,C,D四点共圆.(1)如图1,已知∠ADB=∠ACB=60°,∠BAD=65°,则∠ACD=55°;(2)如图2,若D为等腰Rt△ABC的边BC上一点,且DE⊥AD,BE⊥AB,AD=2,求AE 的长;(3)如图3,正方形ABCD的边长为4,等边△EFG内接于此正方形,且E,F,G分别在边AB,AD,BC上,若AE=3,求EF的长.解:(1)∵∠ADB=∠ACB=60°,∴A,B,C,D四点共圆,∴∠ACD=∠ABD=180°﹣∠ADB﹣∠BAD=180°﹣60°﹣65°=55°,故答案为:55°;(2)在线段CA取一点F,使得CF=CD,如图2所示:∵∠C=90°,CF=CD,AC=CB,∴AF=DB,∠CFD=∠CDF=45°,∴∠AFD=135°,∵BE⊥AB,∠ABC=45°,∴∠ABE=90°,∠DBE=135°,∴∠AFD=∠DBE,∵AD⊥DE,∴∠ADE=90°,∵∠FAD+∠ADC=90°,∠ADC+∠BDE=90°,∴∠FAD=∠BDE,在△ADF和△DEB中,,∴△ADF≌△DEB(ASA),∴AD=DE,∵∠ADE=90°,∴△ADE是等腰直角三角形,∴AE=AD=2;(3)作EK⊥FG于K,则K是FG的中点,连接AK,BK,如图3所示:∴∠EKG=∠EBG=∠EKF=∠EAF=90°,∴E、K、G、B和E、K、F、A分别四点共圆,∴∠KBE=∠EGK=60°,∠EAK=∠EFK=60°,∴△ABK是等边三角形,∴AB=AK=KB=4,作KM⊥AB,则M为AB的中点,∴KM=AK•sin60°=2,∵AE=3,AM=AB=2,∴ME=3﹣2=1,∴EK===,∴EF===.2.问题再现:如图1:△ABC 中,AF 为BC 边上的中线,则S △ABF =S △ACP =S △ABC由这个结论解答下列问题:问题解决:问题1:如图2,△ABC 中,CD 为AB 边上的中线,BE 为AC 边上的中线,则S △BOC =S 四边形ADOE .分析:△ABC 中,CD 为AB 边上的中线,则S △BCD =S △ABC ,BE 为AC 边上的中线,则S △ABE =S △ABC∴S △BCD =S △ABE∴S △BCD ﹣S △BOD =S △ABE ﹣S △BOD又∵S △BOC =S △BCD ﹣S △BOD ,S 四边形ADOE =S △ABE ﹣S △BOD即S △BOC =S 四边形ADOE问题2:如图3,△ABC 中,CD 为AB 边上的中线,BE 为AC 边上的中线,AF 为BC 边上的中线.(1)S △BOD =S △COE 吗?请说明理由.(2)请直接写出△BOD 的面积与△ABC 的面积之间的数量关系:S △BOD =S △ABC .问题拓广:(1)如图4,E 、F 分别为四边形ABCD 的边AD 、BC 的中点,请直接写出阴影部分的面积与四边形ABCD 的面积之间的数量关系:S 阴= S 四边形ABCD . (2)如图5,E 、F 、G 、H 分别为四边形ABCD 的边AD 、BC 、AB 、CD 的中点,请直接写出阴影部分的面积与四边形ABCD 的面积之间的数量关系:S 阴= S 四边形ABCD .(3)如图6,E 、F 、G 、H 分别为四边形ABCD 的边AD 、BC 、AB 、CD 的中点,若S △AME =1、S △BNG =1.5、S △CQF =2、S △DPH =2.5,则S 阴= 7 .解:问题2:S △BOD =S △COE 成立,理由:∵△ABC 中,CD 为AB 边上的中线,∴S △BCD =S △ABC ,∵BE 为AC 边上的中线,∴S △CBE =S △ABC∴S △BCD =S △CBE∵S △BCD =S △BOD +S △BOC ,S △CBE =S △COE +S △BOC∴S △BOD =S △COE(2)由(1)有S △BOD =S △COE ,同(1)方法得,S △BOD =S △AOD ,S △COE =S △AOE ,S △BOF =S △COF ,∴S △BOD =S △COE =S △AOE =S △AOD ,∵点O 是三角形三条中线的交点,∴OA =2OF ,∴S △AOC =2S △COF =S △AOE +S △COE =2S △COE ,∴S △COF =S △COE ,∴S △BOD =S △COE =S △AOE =S △AOD =S △BOF =S △COF ,∴S △BOD =S △ABC ,故答案为问题拓广:(1)如图4:连接BD,由问题再现:S△BDE =S△ABD,S△BDF =S△BCD,∴S阴影=S四边形ABCD,故答案为,(2)如图5:连接BD,由问题解决:S△BMD =S△ABD,S△BDN=S△BCD,∴S阴影=S四边形ABCD,故答案为;(3)如图6,设四边形的空白区域分别为a,b,c,d,∵S△AME =1、S△BNG=1.5、S△CQF=2、S△DPH=2.5,由(1)得出:a+1+2.5=a+3.5=S△ACD①,c+1.5+2=c+3.5=S△ACB②,b +1+1.5=b +2.5=S △ABD ③,d +2+2.5=d +4.5=S △BCD ④,①+②+③+④得,a +3.5+c +3.5+b +2.5+d +4.5=a +b +c +d +14=S 四边形ABCD ⑤而S 四边形ABCD =a +b +c +d +7+S 阴影⑥∴S 阴影=7,故答案为7.3.如图,在△ABC 中,AB >AC ,内切圆⊙I 与边BC 切于点D ,AD 与⊙I 的另一个交点为E ,⊙I 的切线EP 与BC 的延长线交于点P ,CF ∥PE 且与AD 交于点F ,直线BF 与⊙I 交于点M 、N ,M 在线段BF 上,线段PM 与⊙I 交于另一点Q .证明:∠ENP =∠ENQ .证明:如图,设⊙I 与AC 、AB 分别切于点S 、T ,连接ST 、AI 、IT ,设ST 与AI 交于点G .则IE ⊥PE ,ID ⊥PD ,故I 、E 、P 、D 四点共圆,∵AS 2=AE •AD =AG •AI ,∵∠EAG =∠DAI ,∴△AEG ∽△AID ,∴∠AGE=∠AID,∴E,G,D,I四点共圆,∴I、G、E、P、D五点共圆,∴∠IGP=∠IEP=90°,即IG⊥PG,∴P、S、T三点共线,对直线PST截△ABC,由梅涅劳斯定理知,∵AS=AT,CS=CD,BT=BD,∴,设BN的延长线与PE交于点H,对直线BFH截△PDE,由梅涅劳斯定理知,∵CF∥BE,∴,∴,∴PH=HE,∴PH2=HE2=HM•HN,∴,∴△PHN∽△MHP,∴∠HPN=∠HMP=∠NEQ,∵∠PEN=∠EQN,∴∠ENP=∠ENQ.4.如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足,直线ED交外接圆于点M.求证:∠AMH=90°.证明:作高BP,CQ.连结MB、MC、MP、MQ、PQ.===•①=•=•②由①②得:=,又∵∠MBA=∠MCA,∴△MBQ∽△MCP,∴点M、A、P、Q四点共圆,即点M、A、P、Q、H五点共圆,又AH为直径,∴∠AMH=90°.5.如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD 和AC交于点N.求证:OH⊥MN.证明:∵A 、C 、D 、F 四点共圆,∴∠BDF =∠BAC又∵∠OBC =(180°﹣∠BOC )=90°﹣∠BAC ,∴OB ⊥DF .∵CF ⊥MA ,∴MC 2﹣MH 2=AC 2﹣AH 2(①)∵BE ⊥NA ,∴NB 2﹣NH 2=AB 2﹣AH 2 (②)∵DA ⊥BC ,∴BD 2﹣CD 2=BA 2﹣AC 2 (③)∵OB ⊥DF ,∴BN 2﹣BD 2=ON 2﹣OD 2 (④)∵OC ⊥DE ,∴CM 2﹣CD 2=OM 2﹣OD 2,①﹣②+③+④﹣⑤,得NH 2﹣MH 2=ON 2﹣OM 2 MO 2﹣MH 2=NO 2﹣NH 2∴OH ⊥MN .6.在图1到图4中,已知△ABC 的面积为m .(1)如图1,延长△ABC 的边BC 到点D 使CD =BC ,连接DA ,若△ACD 的面积为S 1,则S 1= m .(用含m 的式子表示)(2)如图2,延长△ABC 的边BC 到点D ,延长边CA 到点E ,使CD =BC ,AE =CA ,连接DE .若△DEC 的面积为S 2,则S 2= 2m .(用含a 的代数式表示)(3)如图3,在图2的基础上延长AB 到点F ,使BF =AB ,连接FD 于E ,得到△DEF ,若阴影部分的面积为S 3,则S 3= 6m .(用含a 的代数式表示)(4)可以发现将△ABC 各边均顺次延长一倍,连接所得端点,得到△DEF ,如图3,此时,我们称△ABC 向外扩展了一次.可以发现扩展一次后得到的△DEF 的面积是原来△ABC 面积的 7 倍.(5)应用上面的结论解答下面问题:去年在面积为15平方面的△ABC 空地上栽种了各种花卉,今年准备扩大种植规模,把△ABC 内外进行两次扩展,第一次由△ABC 扩展成△DEF ,第二次由△DEF 扩展成△MGH ,如图4,求这两次扩展的区域(即阴影部分)面积共为多少平方米?解:(1)∵CD =BC ,∴△ABC 和△ACD 的面积相等(等底同高),故得出结论S 1=m .(2)连接AD ,,∵AE =CA ,∴△DEC 的面积S 2为△ACD 的面积S 1的2倍,故得出结论S 2=2m .(3)结合(1)(2)得出阴影部分的面积为△DEC 面积的3倍, 故得出结论则S 3=6m .(4)S △DEF =S 阴影+S △ABC=S 3+S △ABC=6m +m=7m=7S △ABC故得出结论扩展一次后得到的△DEF 的面积是原来△ABC 面积的7倍.(5)根据(4)结论可得两次扩展的区域(即阴影部分)面积共为(7×7﹣1)×15=720(平方米),答:求这两次扩展的区域(即阴影部分)面积共为720平方米. 7.(1)如图①,AD 是△ABC 的中线,△ABD 与△ACD 的面积有怎样的数量关系?为什么?(2)若三角形的面积记为S ,例如:△ABC 的面积记为S △ABC ,如图②,已知S △ABC =1,△ABC 的中线AD 、CE 相交于点O ,求四边形BDOE 的面积.小华利用(1)的结论,解决了上述问题,解法如下:连接BO ,设S △BEO =x ,S △BDO =y ,由(1)结论可得:S,S △BCO =2S △BDO =2y ,S △BAO =2S △BEO =2x . 则有,即.所以.请仿照上面的方法,解决下列问题: ①如图③,已知S △ABC =1,D 、E 是BC 边上的三等分点,F 、G 是AB 边上的三等分点,AD 、CF 交于点O ,求四边形BDOF 的面积.②如图④,已知S △ABC =1,D 、E 、F 是BC 边上的四等分点,G 、H 、I 是AB 边上的四等分点,AD 、CG 交于点O ,则四边形BDOG 的面积为 .解:(1)S △ABD =S △ACD .∵AD 是△ABC 的中线,∴BD =CD ,又∵△ABD 与△ACD 高相等,∴S △ABD =S △ACD .(2)①如图3,连接BO ,设S △BFO =x ,S △BDO =y ,S △BCF =S △ABD =S △ABC =S △BCO =3S △BDO =3y ,S △BAO =3S △BFO =3x .则有,即,所以x +y =,即四边形BDOF 的面积为;②如图,连接BO ,设S △BDO =x ,S △BGO =y ,S△BCG =S△ABD=S△ABC=,S△BCO =4S△BDO=4x,S△BAO =4S△BGO=4y.则有,即,所以x+y=,即四边形BDOG的面积为,故答案为:.8.我们初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差公式、完全平方公式.【提出问题】如何用表示几何图形面积的方法推证:13+23=32?【解决问题】A表示1个1×1的正方形,即:1×1×1=13B表示1个2×2的正方形,C与D恰好可以拼成1个2×2的正方形,因此:B、C、D就可以表示2个2×2的正方形,即:2×2×2=23而A、B、C、D恰好可以拼成一个(1+2)×(1+2)的大正方形.由此可得:13+23=32【递进探究】请仿用上面的表示几何图形面积的方法探究:13+23+33=62.要求:自己构造图形并写出详细的解题过程.【推广探究】请用上面的表示几何图形面积的方法探究:13+23+33+…+n3=.(参考公式:)注意:只需填空并画出图形即可,不必写出解题过程.【提炼运用】如图,下列几何体是由棱长为1的小立方体按一定规律在地面上摆成的,如图(1)中,共有1个小立方体,其中1个看的见,0个看不见;如图(2)中,共有8个小立方体,其中7个看的见,1个看不见;如图(3)中,共有27个小立方体,其中19个看的见,8个看不见;求:从第(1)个图到第(101)个图中,一切看不见的棱长为1的小立方体的总个数.解:【递进探究】如图,A表示一个1×1的正方形,即:1×1×1=13,B、C、D表示2个2×2的正方形,即:2×2×2=23,E、F、G表示3个3×3的正方形,即:3×3×3=33,而A、B、C、D、E、F、G恰好可以拼成一个大正方形,边长为:1+2+3=6,,∵S A+S B+S C+S D+S E+S F+S G=S大正方形∴13+23+33=62;【推广探究】由上面表示几何图形的面积探究知,13+23+33+…+n3=(1+2+3+…+n)2,又∵1+2+3+…+n=,∴13+23+33+…+n3=()2=.【提炼运用】图(1)中,共有1个小立方体,其中1个看的见,0=(1﹣1)3个看不见;如图(2)中,共有8个小立方体,其中7个看的见,1=(2﹣1)3个看不见;如图(3)中,共有27个小立方体,其中19个看的见,8=(3﹣1)3个看不见;…,从第(1)个图到第(101)个图中,一切看不见的棱长为1的小立方体的总个数为:(1﹣1)3+(2﹣1)3+(3﹣1)3+…+(101﹣1)3=03+13+23+…+1003=50502=25502500.故一切看不见的棱长为1的小立方体的总个数为25502500.故答案为:62;.9.问题引入:如图,在△ABC中,D是BC上一点,AE=AD,求:尝试探究:过点A作BC的垂线,垂足为F,过点E作BC的垂线,垂足为G,如图所示,有=,=,.类比延伸:若E为AD上的任一点,如图所示,试猜S四边形ABEC 与S△ABC的比是图中哪条线段的比,并加以证明.拓展应用:如图,E为△ABC内一点,射线AE于BC于点D,射线BE交AC于点F,射线CE交AB于点G,求的值.解:问题引入:∵在△ABC中,D是BC上一点,AE=AD,∴,,∴==;尝试探究:∵AE=AD,∴=,∵AF⊥BC,EG⊥BC,∴AF∥EG,∴△EDG∽△ADB,∴=;∵===,∴=1﹣=;故答案为:,,;类比延伸:=,∵E为AD上的一点,∴=,=,∴==;拓展应用:∵==,同理:=,=,∴==2.10.如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过点C、D作边BC、AD 的垂线,设两条垂线的交点为P,过点P作PQ⊥AB于Q,求证:∠PQC=∠PQD.证明:连接AP、BP,取AP的中点E,取BP的中点F,连接DE、ME、QE、CF、QF、MF,如图.∵E为AP的中点,F为BP的中点,M为AB的中点,∴EM∥BP,EM=BP,MF∥AP,MF=AP.∵E为AP的中点,F为BP的中点,∠ADP=∠BCP=90°,∴DE=AE=EP=AP,FC=PF=BF=BP,∴DE=MF,EM=FC.在△DEM和△MFC中,,∴△DEM≌△MFC(SSS),∴∠DEM=∠MFC.∵EM∥BP,MF∥AP,∴四边形PEMF是平行四边形,∴∠PEM=∠PFM.又∵∠DEM=∠MFC,∴∠DEP=∠CFP.∵DE=AE,FC=BF,∴∠DAE=∠ADE=∠DEP,∠FBC=∠FCB=∠CFP,∴∠DAE=∠FBC,即∠DAP=∠PBC.∵∠ADP=∠AQP=90°,E为AP中点,∴ED=EA=EQ=EP=AP,∴D、A、Q、P四点共圆,∴∠PQD=∠DAP.同理可得:∠PQC=∠PBC,∴∠PQD=∠PQC.11.如图:D是以AB为直径的圆O上任意一点,且不与点A、B重合,点C是弧BD的中点,作CE∥AB,交AD或其延长线于E,连接BE交AC与G,AE=CE,过C作CM⊥AD交AD延长线于点M,MC与⊙O相切,CE=7,CD=6,求EG的长.解:连接OC,如图.∵MC与⊙O相切,∴OC⊥MC.∵CM⊥AD,∴OC∥AM.∵CE∥AB,∴四边形AOCE是平行四边形,∴OA=CE=7,∴AB=14.∵点C是弧BD的中点,∴BC=CD=6.∵AB是⊙O的直径,∴∠ACB=90°,∴AC===4.∵CE∥AB,∴△CGE∽△AGB,∴===,∴AG=AC=.在Rt△ACB中,cos∠BAC===.∵点C是弧BD的中点,∴∠BAC=∠CAD,即∠BAC=∠EAG,∴cos∠EAG=.在△EAG中,cos∠EAG=.∴=.∵AG=,AE=CE=7,∴=.整理得:GE2=.∵GE>0,∴GE=.∴EG的长为.12.如图,圆内接四边形ABCD的边AB、DC的延长线交于E,AD、BC延长线交于F,EF中点为G,AG与圆交于K.求证:C、E、F、K四点共圆.证明:延长AG到H,使得GH=AG,连接EH、FH、CK,如图所示.∵GH=AG,EG=FG,∴四边形AEHF是平行四边形,∴∠EAG=∠GHF,∠GAF=∠GHE.∵A、B、C、K四点共圆,∴∠KCF=∠EAG,∴∠KCF=∠GHF,∴K、C、H、F四点共圆.∵K、C、A、D四点共圆,∴∠KCD=∠KAF,∴∠KCD=∠GHE,∴K、C、E、H四点共圆,∴K、C、E、H、F五点共圆,∴C、E、F、K四点共圆.13.在半圆O中,AB为直径,一直线交半圆周于C、D,交AB延长线于M(MB<MA,AC<MD),设K是△AOC与△DOB的外接圆除点O外的另一个交点,求证:∠MKO=90°.证明:连接CK,BK,BC,如图所示.∵AB是⊙O直径,∴∠ACB=90°,∴∠OAC+∠ABC=90°.∵A、B、C、D四点共圆,∴∠BDC=∠BAC.∵A、O、C、K四点共圆,∴∠CKO=∠OAC.∵D、O、B、K四点共圆,∴∠BKO=∠BDO.∴∠BKC=∠BKO﹣∠CKO=∠BDO﹣∠OAC.∵OB=OD,∴∠ABD=∠BDO.∴∠BMC=∠ABD﹣∠BDC=∠BDO﹣∠BAC=∠BKC.∴B、C、K、M四点共圆.∴∠ABC=∠MKC.∴∠MKO=∠MKC+∠CKO=∠ABC+∠OAC=90°.14.已知,在△ABC中,AC>AB,BC边的垂直平分线与∠BAC的外角∠PAC的平分线相交于E,与BC相交点D,DE与AC相交于点F.(1)如图1,当∠ABC=3∠ACB时,求证:AB=AE;(2)如图2,当∠BAC=90°,∠ABC=2∠ACB,过点D作AC的垂线,垂足为点H,并延是点D关于直线AC的对长DH交射线AE于点M,过点E作BP的垂线,垂足为点G,点D1称点,试探究AG和MD之间的数量关系,并证明你的结论.1解:(1)证明:连接BF,如图1.设∠A CB=x,则∠ABC=3x,∵FD垂直平分BC,∴FB=FC,∴∠FBC=∠FCB=x,∴∠ABF=∠AFB=2x,∴AB=AF,∠PAC=4x.∵AE平分∠PAC,∴∠EAC=2x.∵∠AFE=∠DFC=90°﹣x,∴∠AEF=180°﹣∠EAF﹣∠AFE=180°﹣2x﹣(90°﹣x)=90°﹣x,∴∠AEF=∠AFE,∴AE=AF,∴AB=AE..(2)AG=MD1证明:作EN⊥AC于N,取EC中点O,、NM、MC、MO、NO、EB、EC,如图2.连接AD1∵AE平分∠PAC,EN⊥AC,EG⊥AP,∴EG=EN,∠EGA=∠ENA=90°.∵∠BAC=90°,∴∠EGA=∠ENA=∠BAC=90°,∴四边形EGAN是矩形.∵EG=EN,∴矩形EGAN是正方形,∴AG=AN,∠EAN=45°,∠GEN=90°.∵ED垂直平分BC,∴EB=EC.在Rt△BEG和Rt△CEN中,,∴Rt△BEG≌Rt△CEN(HL),∴∠GBE=∠NCE,∠GEB=∠NEC,∴∠GEN=∠BEC=90°∵EB=EC,∴∠ECB=∠EBC=45°.∵∠BAC=90°,∠ABC=2∠ACB,∴∠ABC=60°,∠ACB=30°,∴∠ABE=∠ACE=15°.∵∠BAC=90°,点D为BC中点,∴AD=CD,∴∠DAC=∠DCA=30°.∵点D与点D关于AC对称,1AC=∠DAC=30°,∴∠D1=45°﹣30°=15°.∴∠MAD1∵DA=DC,DM⊥AC,∴DM垂直平分AC,∴MA=MC,∴∠CMH=∠AMH=90°﹣45°=45°,∴∠AMC=90°,∴∠ENC=∠AMC=90°.∵点O为EC中点,∴ON=OM=OE=OC=EC,∴E、N、C、M四点共圆,∴∠EMN=∠ECN=15°,∴∠MAD=∠EMN=15°,1中,在△AMN和△MAD1,,∴△AMN≌△MAD1,∴AN=MD1.∴AG=MD115.在平面直角坐标系中,已知A(2,2),AB⊥y轴于B,AC⊥x轴于C.(1)如图1,E为线段OB上一点,连接AE,过A作AF⊥AE交x轴于F,连EF,ED平分∠OEF交OA于D,过D作DG⊥EF于G,求DG+EF的值;(2)如图2,D为x轴上一点,AC=CD,E为线段OB上一动点,连接DA、CE、F是线段CE的中点,若BF⊥FK交AD于K,请问∠KBF的大小是否变化?若不变,求其值;若改变,求其变化范围.解:(1)∵AB⊥y轴于B,AC⊥x轴于C,∴∠ABO=∠ACO=90°.∵∠BOC=90°,∴四边形ABOC是正方形,∴AB=AC=BO=CO=2,OA平分∠BOC,∠BAC=90°.∵AF⊥AE,∴∠EAF=90°,∴∠BAC=∠EAF,∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,即∠BAE=∠CAF.在△ABE和△ACF中,,∴△ABE≌△ACF(ASA),∴AE=AF,BE=CF.设BE=CF=t,OE=2﹣t,OF=2+t.∵ED平分∠OEF,∴点D是△OEF的内心.如图1,作DM⊥OB于M,作DH⊥OF于H,且DG⊥EF于G,∴DG=DM=DH,∴四边形MOHD是正方形,∴MO=HO=DM=DG.设DG=MO=x,∴x=,∴x=,∴EF=4﹣2x,∴WF=2﹣x.∴DG+EF=x+2﹣x=2.即DG+EF的值为2;(2)∠KBF的大小不变,∠KBF=45°如图2,延长BF交AC于G,连接KG,作KM⊥AB于M,KN⊥AC于N,∵四边形ABOC是正方形,∴O B∥AC.∴∠EBF=∠CGF,∠BEF=∠GCF.∵F是CE的中点,∴EF=CF.在△BEF和△GCF中,,∴△BEF≌△GCF(AAS),∴BF=GF.∵BF⊥FK,∴∠BFK=∠GFK=90°.在△BFK和△GFK中,,∴△BFK≌△GFK(SAS)∴BK=GK.∵AC=CD,∠ACD=90°,∴△ACD是等腰直角三角形,∴∠CAD=45°.∵KN⊥AC,∴∠ANK=90°,∴∠AKN=45°,∴AN=KN.∵KM⊥AB,∴四边形AMKN是正方形,∴KM=KN.∠M=∠GNK=90°AM∥KN.在Rt△BKM和Rt△GKN中,,∴Rt△BKM≌Rt△GKN(HL),∴∠MBK=∠NGK.∠GKN=∠BKM.∵AM∥KN,∴∠BKN=∠MBK.∵∠BKM+∠BKN=90°,∴∠GKN+∠BKN=90°,即∠BKG=90°.∵BK=GK,∴△BKG是等腰直角三角形.∴∠KBF=45°,∴∠KBF的大小不变,∠KBF=45°.16.如图,已知⊙O1与⊙O2相交于A,B两点,直线MN⊥AB于A,且分别与⊙O1,⊙O2交于M、N,P为线段MN的中点,又∠AO1Q1=∠AO2Q2,求证:PQ1=PQ2.解:连接MQ1、BQ1、BQ2、NQ2,过点P作PH⊥Q1B于H,如图所示.则由圆内接四边形的性质可得:∠Q1MA+∠ABQ1=180°,∠ABQ2+∠ANQ2=180°,∠MAB=∠BQ2N.由圆周角定理可得:∠ABQ 1=∠AO 1Q 1,∠ANQ 2=∠AO 2Q 2. ∵∠AO 1Q 1=∠AO 2Q 2,∴∠ABQ 1=∠ANQ 2,∴∠ABQ 2+∠ABQ 1=∠ABQ 2+∠ANQ 2=180°, ∴Q 1、B 、Q 2三点共线.由圆内接四边形的性质可得:∠ABQ 1=∠ANQ 2, ∴∠Q 1MA +∠ANQ 2=∠Q 1MA +∠ABQ 1=180°, ∴MQ 1∥NQ 2.∵AB ⊥MN ,∴∠MAB =90°,∴∠Q 1Q 2N =∠MAB =90°.∵PH ⊥Q 1B ,即∠Q 1HP =90°,∴∠Q 1HP =∠Q 1Q 2N ,∴PH ∥NQ 2,∴MQ 1∥PH ∥NQ 2.∵P 为线段MN 的中点,∴H 为线段Q 1Q 2的中点,∴PH 垂直平分Q 1Q 2,∴PQ 1=PQ 2.。
初中数学竞赛第二十三讲平面几何的定值与最值问题(含解答)

第二十三讲平面几何的定值与最值问题【趣题引路】传说从前有一个虔诚的信徒,他是集市上的一个小贩.••每天他都要从家所在的点A出发,到集市点B,但是,到集市之前他必须先拐弯到圆形古堡朝拜阿波罗神像.古堡是座圣城,阿波罗像供奉在古堡的圆心点O,•而周围上的点都是供信徒朝拜的顶礼地点如图1.这个信徒想,我怎样选择朝拜点,才能使从家到朝拜点,•然后再到集市的路程最短呢?(1) (2)解析在圆周上选一点P,过P作⊙O的切线MN,使得∠APK=∠BPK,即α=β.那么朝圣者沿A→P→B的路线去走,距离最短.证明如图2,在圆周上除P点外再任选一点P′.连结BP•′与切线MN•交于R,AR+BR>AP+BP.∵RP′+AP′>AR.∴AP′+BP′=AP′+RP′+RB>AR+BP>AP+BP.不过,用尺规作图法求点P的位置至今没有解决.•“古堡朝圣问题”属于数学上“最短路线问题”,解决它的方法是采用“等角原理”.【知识延伸】平面几何中的定值问题,是指变动的图形中某些几何元素的几何量保持不变,或几何元素间的某些几何性质或位置关系不变的一类问题.•所谓几何定值问题就是要求出这个定值.在解决这类问题的过程中,可以直接通过计算来求出定值;也可以先考虑某一个特殊情形下的该相关值,然后证明当相应几何元素变化时,此值保持不变.例1如果△ABC的外接圆半径R一定,求证: abcS是定值.(S表示△ABC的面积)解析 由三角形面积S=12absinC 和正弦定理sin c C =2R,∴c=2RsinC. ∴abc S =2sin c C =4sin sin R CC=4R 是定值. 点评通过正弦定理和三角形面积公式经过变形,计算出结果是4R,即为定值.平面几何中不仅有等量关系,还有不等关系,例如在变动一些几何元素时,•某一相关的值保持不大于(或不小于)某个定值,如果这个定值在某个情形下可以取得,•这就是一个几何极值.确定几何极值的问题称为几何极值问题,解决这些问题总要证明相关的几何不等式,并指明不等式成为等式的情形(或者至少证明不等式可以成为等式).例2如图,已知⊙O 的半径为⊙O 上一点,过A 作一半径为r=3的⊙O ′,问OO ′何时最长?最长值是多少?OO ′何时最短?最短值是多少?解析 当O ′落在OA 的连线段上(即⊙A 与线段OA 的交点B 时)OO ′最短,且最短长度为当O ′落在OA 的延长线上(即⊙O 与OA 的延长线交点C 时)OO ′最长,且最长的长度为点评⊙O ′是一个动圆,满足条件的⊙O ′有无数个,但由于⊙O ′过A 点,所以⊙O ′的圆心O ′在以A 为圆心半径为3的⊙A 上.【好题妙解】佳题新题品味例1 如图,已知P 为定角O 的角平分线上的定点,过O、P•两点任作一圆与角的两边分别交于A 、B 两点.求证:OA+OB 是定值.证明 连结AP 、BP,由于它们为有相同圆周角的弦,AP=PB,不妨记为r.•另记x 1=OA,x 2=OB.对△POA 应用余弦定理,得x 12+OP 2-2OP ·cos ∠AOP ·x 1=r 2.故x 1为方程x 2-2OP ·cos 12∠AOB ·x+(O P 2-r 2)=0的根,同理x 2亦为其根. 因此x 1,x 2为此方程的两根,由韦达定理,得x 1+x 2=2OP(12∠AOB)是定值.点评当x 1=x 2时,x 1+x 2为此定值,事实上此时OP 一定是直径.例2 如图,在矩形ABCD 中,AB=8,BC=9,⊙O 与外切,且⊙O 与AB 、BC•相切.⊙O ′与AD 、CD 相切,设⊙O 的半径为x,⊙O 与⊙O ′的面积的和为S,求S•的最大值和最小值. 解析 设⊙O ′的半径为y,过O 与O ′分别作CD 与BC 的垂线OH,O ′F,•垂足分别为H,F,OH 、O ′F 交于点E,则有:O ′E=8-(x+y),OE=9-(x+y) 由勾股定理可得:(x+y)2=[8-(x+y)]2+[9-(x+y)]2. 整理,得(x+y-29)(x+y-5)=0,由题意知1≤x ≤4,∴x+y=5,y=-x+5,∴S=πx+πy=π(2x-10x+25),=2π[(x-52)2+254], 故当x=52时,S min =252π;当x=4时,S=17π.点评先由已知求出⊙O ′的半径也⊙O 的半径x 之间的关系,然后再根据面积公式写出S 与x 之间的关系,这个关系就是一个函数关系,再通过函数的性质得解.中考真题欣赏例 (南京市中考题)如图,⊙O 1与⊙O 2内切于点P,切⊙O 2•的直径BE 于点C,连结PC 并延长交⊙O 2于点⊙O 1,⊙O 2的半径分别为r 、R,且R ≥2r.•求证:PC ·AC 解析 若放大⊙O 1,使⊙O 1切⊙O 2的直径于点O 2(如图显然此时有PC ·AC=PO 2·AO 2=2r ·R(定值). 再证明如图的情况:连结C O 1,PO 2,• 则PO 2•必过点O 1,•且O 1C ⊥BE,得CO 2, 从而.所以PC ·AC=EC ·BC=2Rr,故PC ·AC 是定值. 点评解答几何定值问题时,可先在符合题目条件的前提下用运动的观点,从特殊位置入手,找出相应定值,然后可借助特殊位置为桥梁,完成一般情况的证明.竞赛样题展示例1 (第十五届江苏省初中数学竞赛题)如图,正方形ABCD 的边长为1,•点P 为边BC 上任意一点(可与点B 或点C 重合),分别过点B 、C 、D 作射线AP 的垂线,•垂足分别为点B ′、C ′、D ′.求BB ′+CC ′+DD ′的最大值和最小值.解析 ∵S △DPC = S △APC =12AP ·CC ′, 得S 四边形BCDA = S △ABP + S △ADP + S △DPC=12AP(BB ′+DD ′+CC ′), 于是BB ′+CC ′+DD ′=2AP.又1≤APBB ′+CC ′+DD•′≤2,∴BB ′+CC ′+DD最大值为2.点评本题涉及垂线可考虑用面积法来求. 例2 (2000年“新世纪杯”广西竞赛题)已知△ABC 内接于⊙O,D 是BC•或其延长线上一点,AE 是△ABC 外接圆的一条弦,若∠BAE=∠CAD.求证:AD.AE 为定值.证明 如图 (1),当点D 是BC 上任意一点且∠BAE=∠CAD 时,连结BE, 则∠E=∠C,∠BAE=∠CAD, ∴△ABE ∽△ADC. ∴AB AEAD AC=,即AD ·AE=AB ·AC 为定值. 如图 (2),当点D 在BC 的延长线上时,∠BAE=∠CAD.此时,∠ACD=∠AEB. ∴△AEB ∽△ACD,∴AB AEAD AC=即AD·AE=AB·AC为定值.综上所述,当点D在BC边上或其延长线上时,只要∠CAD=∠BAE,总有AD·AE为定值. 点评先探求定值,当AD⊥BC,AE为圆的直径时,满足∠BAE=∠CAD这一条件,•不难发现△ACD ∽△AEB,所以AD·AE=AB·AC,因为已知AB,AC均为定值.•再就一般情况分点D•在BC上,点D在BC的延长线上两种情况分别证明.全能训练A级1.已知MN是⊙O的切线,AB是⊙O的直径.求证:点A、B与MN的距离的和为定值.2.已知:⊙O与⊙O1外切于C,P是⊙O上任一点,PT与⊙O1相切于点T.求证:PC:PT是定值.3.⊙O1与⊙O2相交于P、Q两点,过P作任一直线交⊙O1于点E,交⊙O2于点F.求证:∠EQF 为定值.4.以O为圆心,1为半径的圆内有一定点A,过A引互相垂直的弦PQ,RS.求PQ+RS的最大值和最小值.5.如图,已知△ABC的周长为2p,在AB、AC上分别取点M和N,使MN•∥BC,•且MN与△ABC的内切圆相切.求:MN的最值.AM NBA 级(答案)1.定长为圆的直径;2.利用特殊位置探求定值(当PC 构成直径时)(R,r 是两圆的半径). 3.因∠E,∠F 为定角(大小固定)易得∠EQF 为定值.4.如图,设OA=a(定值),过O 作OB ⊥PQ,OC ⊥RS,B 、C 为垂足, 设OB=x,OC=y,0≤x ≤a,(0≤y ≤a),且x 2+y 2=a 2.所以所以∴(PQ+RS)2=4(2-a 2+而x 2y 2=x 2(a 2-x 2)=-(x 2-22a )2+44a . 当x 2=22a 时,(x 2y 2)最大值=44a .此时当x 2=0或x 2=a 2时,(x 2y 2)最小值=0,此时(PQ+RS )最小值=2(). 5.设BC=a,BC 边上的高为h,内切圆半径为r. ∵△AMN ∽△ABC,2MN h r BC h -=,MN=a(1-2rh),• 由S △ABC =rp,∴r=2ABC S ahp p∆=, ∴MN=a(1-a p )=p ·a p (1-a p )≤p 2(1)2aa p p⎡⎤+-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=4p ,当且仅当a p =1-ap,即a=2p 时,取等号,∴MN 的最大值为4p .B级1.如图1,已知正方形ABCD的边长为3,点E在BC上,且BE=2,点P在BD上,则PE+PC的最小值为( )E D CAB PSQA B PM(1) (2) (3)2.用四条线段a=14,b=13,c=9,d=7.作为四条边构成一个梯形,•则在所构成的梯形中,中位线长的最大值是__________.3.如图2,⊙O、B两点在⊙O上,切线AQ和BQ相交于Q,P是AB•延长线上任一点,QS⊥OP于S,则OP·OS=_______.4.已知,如图3,线段AB上有任一点M,分别以AM,BM为边长作正方形AMFE•、•MBCD.正方形AMFE、MBCD的外接圆⊙O、⊙O′交于M、N两点,则直线MN的情况是( •)A.定直线B.经过定点C.一定不过定点D.以上都有可能5.如图,已知⊙O的半径为R,以⊙O上一点A为圆心,以r为半径作⊙A,•又PQ与⊙A 相切,切点为D,且交⊙O于P、Q.求证:AP·AQ为定值.6.如图,⊙O 1与⊙O 2相交于A 、B 两点,经过点B•的一直线和两圆分别相交于点C 和D,设此两圆的半径为R 1,R 2.求证:AC:AD=R 1:R 2.B 级(答案)1.B.∵A 、C 关于BD 对称,连结AE 交BD 于P,此时PE+PC=AE 最短.2.11.5 (1)当上底为7,下底分别为14,13,9时,中位线长分别为10.5,10,8; (2)当上底为9和13时,均构不成梯形.3.连结OQ 交AB 于M,则OQ ⊥AB.连结OA,则OA ⊥AQ. ∵∠QMP=∠QSP=90°,∴S,P,•Q,M 四点共圆,故OS ·OP=OM ·OQ. 又∵OM ·OQ=OA 2=2,∴OS ·OP=2.4.B.由图可知直线MN 可看作⊙O 和⊙O ′的割线, 当M 在点A 时,直线MN 变为⊙O•′的切线, 当M 在点B 时,直线MN 变为⊙O 的切线.这两种情况是以AB•为直角边的等腰直角三角形的两直角边所在的直线,交点是第三个顶点M.M 是AB 的中点时,MN 是AB•的垂直平分线,也过第三个顶点,所以选B. 5.如图,作⊙O 的直径AB,连结AD. ∵PQ 切⊙A 于D,∴AD ⊥PQ, ∴AP ·AQ=AD ·AB.•而AD=r,AB=2R,∴AP ·AQ=2Rr 为定值.6.作AN ⊥CD,垂足为点N,连结AB,有AC.AB=AN.2R1,① AB ·AD=AN ·2R 2 .② ①÷②,得12R AC AD R,∴AC:A D=R 1:R 2.。
数学竞赛平面几何题目

一、选择题
1.在一个直角三角形中,如果一个锐角是另一个锐角的两倍,那么这两个锐角分别是多少
度?
A.30°, 60°(答案)
B.45°, 45°
C.20°, 70°
D.15°, 75°
2.一个正方形的对角线长为d,其边长为a,则a与d的关系是?
A. a = d/2
B. a = d/√2(答案)
C. a = d√2
D. a = 2d
3.在一个等腰三角形中,顶角为40°,则底角为多少度?
A.70°(答案)
B.60°
C.50°
D.80°
4.一个圆的半径为r,则其面积为?
A.πr
B.2πr
C.πr2(答案)
D.2πr2
5.在一个平行四边形中,如果一组邻角互补,则这个平行四边形一定是?
A.矩形(答案)
B.菱形
C.正方形
D.梯形
6.一个正六边形的内角和为多少度?
A.180°
B.360°
C.540°
D.720°(答案)
7.在一个圆中,如果一条弦等于半径,那么这条弦所对的圆心角为多少度?
A.30°
B.60°(答案)
C.90°
D.120°
8.一个梯形的上底为a,下底为b,高为h,则其面积为?
A.(a+b)h
B.(a+b)h/2(答案)
C.ah
D.bh。
初中数学竞赛专题复习 第二篇 平面几何 第18章 整数几何试题 新人教版

第18章 整数几何18.1.1★已知ABC △的两条高长分别是5、15,第三条高的长数,求这条高之长的所有可能值.解析 由面积知,三条高的倒数可组成三角形三边,这是它们的全部条件. 设第三条高为h ,则111,155111.515h h⎧+>⎪⎪⎨⎪+>⎪⎩ 解得151545h <<,h 可取4、5、6、7这四个值. 18.1.2★已知ABC △的三边长分别为3AB n x =+,2BC n x =+,CA n x =+,且BC 边上的高AD 的长为n ,其中n 为正整数,且01x <≤,问:满足上述条件的三角形有几个? 解析 注意AB 为ABC △之最长边,故90B ∠<︒,设BD y =,CD z =,则0y >,而z 可正可负.AB D C由2y z n x +=+,及()()()22223242y z n x n x n x x -=+-+=+⋅,得4y z x -=,32ny x =+,由勾股定理,知()222332n x n n x ⎛⎫++=+ ⎪⎝⎭,展开得12n x =,由01x <≤及n 为正整数,知1n =,2,…,12,这样的三角形有12个.18.1.3★已知一个直角三角形的三条边均为正整数,其中一条直角边不超过20,其外接圆半径与内切圆半径之比为52∶,求此三角形周长的最大值.解析设该直角三角形直角边长为a 、b ,斜边为c ,则外接圆半径2cR =,内切圆半径2a b cr +-=,不妨设20a ≤. 由条件知52c a b c =+-,557a b c +=,平方,得()()222225249a b ab a b ++=+,即()2212250a b ab +-=,()()34430a b a b --=,于是3a k =,4b k =,5c k =,或4a k =,3b k =,5c k =,周长为12k ,k 为正整数.k 的最大值为6,此时各边为18、24、30,周长最大值为72.18.1.4★ABC △为不等边三角形,60A ∠=︒,7BC =,其他两边长均为整数,求ABC △的面积.A BCx y60°解析设AB x =,AC y =,则由余弦定理,有2249x y xy +-=.由条件x y ≠,不妨设x y <,则AB 为ABC △之最小边,x 只能取值1、2、3、4、5、6,分别代入,发现当3x =或5时,8y =,其余情形均无整数解.于是1sin 602ABC S xy =︒=△. 18.1.5★★一点P 与半径为15的圆的圆心距离是9,求经过P 且长为整数的弦的条数. 解析 如图,O e 半径为15,9OP =,过P 的弦ST 长为整数,APB 为直径,6AP =,24PB =,则144SP TP PA PB ⋅=⋅=,因此24ST SP TP =+≥.又30ST AB =≤,故这样的弦共有()302412212-+⨯-=条,其中与AB 垂直的弦及AB 各一条,其余的弦每种长度有两条(关于AB 对称).18.1.6★★在直角三角形ABC 中,各边长都是整数,90C ∠=︒,CD 为边AB 上的高,D 为垂足,且3BD p =(p 奇素数),求ACAB的值(用p 表示). C解析由2BC BD AB =⋅知2BD BC ,故设2BC p t =(t 为正整数),则2BA pt =,又由勾股定理,知22442AC p t p t =-,故tp AC .设AC kpt =,代入得()()222p t k t k t k =-=+-,易知只能有2t k p +=,1t k -=,解得212p t +=,212p k -=,于是2211AC p AB p -=+. 18.1.7★★设正三角形ABC ,M 、N 分别在AB 、AC 上,MN BC ∥,两端延长MN ,交ABC △外接圆于P 、Q ,若PM 、MN 、AB 长均为正整数,求AB 的最小值. 解析 如图, 易知NQ PM =也是整数.设AM x =,BM y =,PM NQ z ==,则MN x =,于是由相交弦定理,得()xy z x z =+,2z x y z=-.APQM NB C设y ks =,z kt =,(),k y z =,s t >,(),1s t =,则2kt x s t=-,由于()2,1s t t -=,故s t k -,要使2t AB x y k ks s t=+=+-达到最小,k 得取s t -,于是()2AB t s t s =+-.由于s t >,2s ≥,1t ≥,知()223t s t s t s +-+≥≥.当1AM =,2BM =时AB 取到最小值3,此时1PM =.18.1.8★★已知凸四边形ABCD 的四边长是两两不相等的整数,对边乘积之和等于四边形面积的两倍,且22250AD BC +=,求该四边形面积、对角线长度.解析 不妨设AB α=,BC b =,CD c =,DA d =,AC 与BD 交于O ,则sin 2ABCD AC BD AOB S ac bd AC BD ⋅⋅∠==+⋅≥,于是由托勒密定理,知A 、B 、C 、D 必共圆,且满足AC BD ⊥.又由已知条件,22250b d +=,22250a c +=.经搜索知250表为平方和只有两组:22515+和22913+.由对称性,不妨设5a =,13b =,15c =,9d =,则19622ABCD ac bdS AC BD +=⋅==.由余弦定理,因cos cos 0BAD BCD ∠+∠=,得222222591315045195BD BD +-+-+=,得BD =AC18.1.9★★是否存在一个三边长恰是三个连续正整数,且其中一个内角等于另一个内角2倍的ABC △?证明你的结论. 解析 存在满足条件的三角形.当ABC △的三边长分别为6a =,4b =,5c =时,2A B ∠=∠.如图,当2A B ∠=∠时,延长BA 至点D ,使AD AC b ==.连结CD ,ACD △为等腰三角形.CD A因为BAC ∠为ACD △的一个外角,所以2BAC D ∠=∠.由已知,2BAC B ∠=∠,所以B D ∠=∠.所以CBD △为等腰三角形.又D ∠为ACD △与CBD △的一个公共角,有~ACD CBD △△,于是AD CD CD BD =,即b aa b c=+,所以()2a b b c =+.而()26445=⨯+,所以此三角形满足题设条件,故存在满足条件的三角形. 评注满足条件的三角形是唯一的.若2A B ∠=∠,可得()2a b b c =+.有如下三种情形:(ⅰ)当a c b >>时,设1a n =+,c n =,1b n =-(n 为大于1的正整数),代入()2a b bc =+,得()()()21121n n n +=--,解得5n =,有6a =,4b =,5c =;(ⅱ)当c a b >>时,设1c n =+,c n =,1b n =-(n 为大于1的正整数),代入()2a b bc =+,得()212n n n =-⋅.解得2n =,有2a =,1b =,3c =,此时不能构成三角形;(ⅲ)当a b c >>时,设1a n =+,b n =,1c n =-(n 为大于1的正整数),代入()2a b b c =+,得()()2121n n n +=-,即2310n n --=,此方程无整数解.所以,三边长恰为三个连续的正整数,且其中一个内角等于另一个内角的2倍的三角形存在,而且只有三边长分别为4、5、6构成的三角形满足条件.18.1.10★★三边长为连续整数、周长不大于100、且面积是有理数的三角形共有多少个? 解析 设三角形三边依次为1n -、n 、1n +,则333n ≤≤,()131122p n n n n =-+++=,S △==于是()234n -是平方数,令()()22343n k -=,得2243n k -=,则32n ≤,224102034033n k -==≤,18k ≤.又k 不可能是奇数,否则()222343n k k =+≡,得2243n k -=,则32n ≤,224102034033n k -==≤,18k ≤.又k 不可能是奇数,否则()22343mod 4n k =+≡,将2k =,4,6,8,10,12,14,16,18代入,发现仅当2k =,8时满足要求.因此这样的三角形共有两个,三边长依次为3、4、5与13、14、15.18.1.11★★某直角三角形边长均为整数,一直角边比斜边小1575,求其周长的最小值. 解析 设直角三角形直角边长a 、b ,斜边为1575a +,则 ()2221575a b a +=+,()2157521575b a =+.由于221575357=⨯⨯,设105b k =,则2721575k a =+,设7a s =,则22225k s =+,于是k 的最小值为17,此时32s =,224a =,1785b =,1799c =.此时的最小周长为3808. 18.1.12★★已知ABC △,AD 是角平分线,14AB =,24AC =,AD 也是整数,求AD 所有可取的值.AEB DC解析 如图,作DE AB ∥,E 在AC 上,则易知AE ED =. 又ED CD AC AB BC AB AC==+,故 22AB ACAD AE DE ED AB AC⋅<+==+33617.6819==…, 故17AD ≤.又当17AD ≤时,不难通过AED △构造出ABC △,故AD 所有可取的值为1,2, (17)18.1.13★面积为c 的正方形DEFG 内接于面积为1的正三角形ABC ,其中a 、b 、c 是整数,且b 不能被任何质娄的平方整除,求a cb-的值.ADGB E F C解析设正方形DEFG 的边长为x ,正三角形ABC 的边长为m ,则2m ,由ADG ABC △∽△,可得xx m -=.解得()3x m =.于是()222348x m ==.由题意得28a =,3b =,48c =,所以203a cb -=-. 17.1.14★★如图,AD 是ABC △的高,四边形PQRS 是ABC △的内接正方形,若BC ab =(即两位数),SRc =,ADd =,且a 、b 、c 、d 恰为从小到大的4个连续正整数,求ABC S △的所有可能值.AS RP D Q解析易知11SR AR CR SR BC AC AC AD ==-=-,于是有110c c a b d +=+,或11111132a a a +=+++,移项,得()()1111123a a a =+++,或2650a a -+=,解得1a =或5.于是有两解: 12,3,4;BC SR AD =⎧⎪=⎨⎪=⎩56,7,8.BC SR AD =⎧⎪=⎨⎪=⎩易知这两组数据都符合要求,故24ABC S =△或224.18.1.15★★已知ABC △中,B ∠是锐角.从顶点A 向BC 边或其延长线作垂线,垂足为D ;从顶点C 向AB 边或其延长线作垂线,垂足为E .当2BD BC 和2BEAB均为正整数时,ABC △是什么三角形?并证明你的结论. 解析设2BD m BC =,2BEn AB=,m 、n 均为正整数,则 244cos 4BD BE mn B AB BC=⋅⋅=<, 所以,1mn =,2,3. (1)当1mn =时,1cos 2B =,60B ∠=︒,此时1m n ==.所以AD 垂直平分BC ,CE 垂直平分AB ,于是ABC △是等边三角形.(2)当2mn =时,cos B =45B ∠=︒,此时1m =,2n =,或2m =1n =,所以点E 与点A 重合,或点D 与点C 重合.故90BAC ∠=︒,或90BCA ∠=︒,于是ABC △是等腰直角三角形.(3)3mn =时,cos B =,30B ∠=︒,此时1m =,3n =,或3m =,1n =.于是AD 垂直平分BC ,或CE 垂直平分AB .故30ACB ∠=︒,或30BAC ∠=︒,于是ABC △是顶角为120︒的等腰三角形.18.1.6★★某直角三角形两直角边长均为整数,周长是面积的整数倍(就数字上讲),问问这样的直角三角形有多少个?解析 设直角边分别为a 、b ,则斜边c =,由条件知它是有理数,故必定是整数.设2ka b ab +=,k 为正整数,于是k =.由于a b +1、2或4,记作k '.由a b k +-'=()2220ab k a b k -'++'=,()()22a k b k k -'-'=',1k '=时无解;2k '=时,有()()222a b --=,{a ,b }={3,4};4k '=时,()()448a b --=,{a ,b }={5,12}或{6,8},所以这样的直角三角形共有3个.18.1.17★★在等腰ABC △中,已知AB AC kBC ==,这里k 为大于1的自然数,点D 、E 依次在AB 、AC 上,且DB BC CE ==,CD 与BE 相交于O ,求使OCBC为有理数的最小自然数k .ADEBCO解析如图,连结DE ,则DE BC ∥,11DE AD AB BC BC AB AB k -===-,1k DE BC k-=. 由于四边形DBCE 为等腰梯形,则由托勒密定理(或过D 、E 作BC 垂线亦可),2222121k k CD CD BE DE BC DB CE BC BC BCk k --=⋅=⋅+⋅=+=,又21CO BC kCD DE BC k ==+-,于是CO BC =k 与21k -互质,由题设知其必须均为平方数,1k >,25k =适合,这是满足要求的最小自然数.18.1.18★★★对于某些正整数n 来说,只有一组解xyz n =(不计顺序),这里,x 、y 、z是正整数且可构成三角形的三边长,这样的()100n ≤共有多少个? 解析显然,当n p =(素数)时无解;当2n p =或1时只有一组解(1,p ,p )或(1,1,1);当n pq =(p 、q 为不同素数)时无解;当4n p =(p 为大于3的素数)时也无解.剩下的数为8,12,16,18,24,27,30,32,36,40,42,45,48,50,54,56,60,63,64,66,70,72,75,78,80,81,84,88,90,96,98,99,100. 易验证,无解的n 有:30,42,54,56,63,66,70,78,88,99;唯一解的n 有:8,12,16,18,24,27,32,40,45,48,50,75,80,81,84,90,96,98;不止一组解的n 有:36,60,64,72,100.注意:判定无解的主要依据是,abc n =,c ab >时无解,困为1c ab a b ++≥≥. 因此,有解的n 共有23个.18.1.19★★面积为整数的直角三角形周长为正整数k ,求k 的最小值,并求此时这个直角三角形的两条直角边的可取值(如不止一组解,只需举了一组即可).解析设该直角三角形的直角三角形周长分别为a 、b ,则112ab ≥,a b +≥2,2k a b =+,故5k ≥.下令5k =,2ab =,如有解,则可.()5a b -+,平方得()222225102a b a b a b ab +=-++++.取2ab =,得29,102.a b ab ⎧+=⎪⎨⎪=⎩因此a 、b 为方程21029200x x -+=的根,解得a 、bk 的最小值是5.18.1.20★★若ABC △的三边长a 、b 、c 均为整数,且140abc =,求ABC △内切圆半径. 解析 不妨设a b c ≤≤,于是7c ≥.又14011c a b ab c<++=+≤,故140c c ≤,得10c ≤.于是c 只可能为7或10. 7c =时,20ab =,只可能4a =,5b =,()182p a b c =++=,内切圆半径r =. 10c =时,14ab =,没有满足要求的解.18.1.21★★证明:若a 、b 、c 是一组勾股数()222a b c +=,则存在正整数k 、u 、v 、u v >,(),1u v =使得()22c k u v =+,而()22a k u v =-,2b kuv =;或2a kuv =,()22b k u v =-.解析222a b c +=,设(a ,b ,c )k =,则1a ka =,1b kb =,1c kc =,222111a b c +=.易知1a 、1b 、1c 两两互质;1a 与1b 不可能同偶,否则12a ,1b ,1c ;1a 与1b 也不会同奇,否则()212mod 4c =,矛盾.于是1a 与1b 必一奇一偶,不妨设1a 奇而1b 偶,于是1c 为奇数.从而()()211111a c b c b =+-,11c b +与11c b -必互质,否则有一奇素数11|p c b +,11c b -,得|2p c ,12b ,故|p (1c ,1b ),与(1c ,1b )=1矛盾. 于是可设2111c b u +=,2111c b v -=,(1u ,1v )=1,且1u 、1v 均为奇数,解得221111122u v u v c +-⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭,11111222u v u v b +-=⋅⋅,221111122u v u v a +-⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭,令112u v u +=,112u v v -=,即得结论. 18.1.22★★★如图,F 、E 在ABC △的边AB 、AC 上,FE 的延长线与BC 的延长线交于D ,求证:AF 、BF 、CB 、CD 、AE 、EC 、FE 、ED 的长度不可能是1~8的排列. 解析 如果1EF =,则1AE AF EF -<=,得AE AF =,矛盾,故1EF ≠,同理AF 、AE 、ED 、CD 、EC 都不等于1.AFE GDCB因此1只可能等于FB 或BC 之长,不失对称性,设1BF =,则1FD BD BF -<=,FD BD =,作CG AB ∥,G 在ED 上,四边形FBCG 乃一等腰梯形,于是EG FG EF BC EF =-=-为正整数.又1EG EC CG BF -<<=,故EG EC =,但BFD ∠为等腰三角形DFB 的底角,90BFD <︒∠,18090EGC BFD =︒->︒∠∠,为EGC △的最大内角,EC EG >,矛盾,因此结论证毕.18.1.23★★★已知梯形ABCD 中,AD BC <,E 、F 分别在AB 、CD 上,EF AD BC ∥∥,ED BF ∥,如果AD 、EF 、BC 均为正整数,称该梯形为“整数梯形”.现对于正整数n ,有正整数x x <′<y ′<y ,x y x +=′+y ′=n ,且x 、y 为一“整数梯形”的上、下底, x ′、y ′为另一“整数梯形”的上、下底,求n 的最小值.解析 如图,由AED EFD △∽△,DEF FBC △∽△,得AD AE DF EFEF BE FC BC===,得EF =,于是问题变为求最小的n ,使xy 与x ′y ′均为平方数.A DEFB Cxy 、x ′y ′不可能都为4,故至少有一组≥9,显然另一组也不可能为4,于是xy ,x ′y ′≥9.如果xy 或x ′y ′25≥,则10n =≥.若xy 或x ′y ′=9或16,则19n =+或2810+=.于是n 的最小值为10,1x =,x ′=2,y ′=8,y =9.18.1.24★★★求证:存在无穷多个每边及对角线长均为不同整数的、两两不相似的凸四边形.ABDPC解析 如图,作圆内接四边形ABCD ,AC 与BD 垂直于P ,设a 为一整数,2a >,4AP a =,24BP a =-,241DP a =-,则24AB a =+,241AD a=+,,由此知()()224414aa CP a--=,而由ABP DCP △∽△,BPC APD △∽△知,()224414a BC a a -=+,()224144a CD a a -=+.同时乘以系数4a ,得()244AB a a =+,()2441AD a a =+,()()22441BC a a =-+,()()22414CD a a =-+,4244AC a a =-+,()2201BD a a =-.易知上述6个多项式无二者恒等,于是任两者相等只能得有限个a ,但正整数有无限个,因此有无限个a ,使6个多项式两两不等,又当a →+∞时,0BDAC→,因此有无限个这样的凸四边形两两不相似. 18.1.25★★★已知PA 、PB 为圆的切线,割线过P ,与圆交于M 、N ,与AB 交于S ,若PA 、PM 、MS 、SN 均为正整数,求PA 的最小值. PMABSN解析 如图,易知有PM PNMS SN=(调和点列). 设PM a =,MS b =,SN c =,则()b a b c ac ++=,()b c b c a b+=-,从而PA == 设a ks =,b kt =,k =(a ,b ),则(s ,t )=1,s t >,s tc kts t+=-,PA =易见(s t +,s t -)=1,则s 、t 一奇一偶.于是由(()t s t +,s t -)=1,得|s t k -,且由PA 为整数知2s t x +=,2s t y -=,x 、y 为奇数.因为|s t k -,于是k 的最小值为s t -,()c t s t =+,PA sxy ==,当s =1,2,3,4时,t 无解(即PA 不是整数),故5s ≥,又3x ≥,1y ≥,于是PA ≥15,当a =5,b =4,c =36时取到15PA =.若(s t +,s t -)=2,此时s 、t 同奇,k 的最小值为2s t-,此时()2t s t c +=,PA =22s t x +=,22s t y -=,当1s =,3时,无t 使PA 为整数,于是5s ≥,又x y >,所以1y ≥,2x ≥,5210PA sxy =⨯=≥.当5a =,3b =,12c =时取到PA =10. 综上,PA 的最小值是10.18.1.26★★★一圆内接四边形的四边长及对角线长都是整数,求这类四边形中周长最小者. 解析 显然长与宽为4、3的矩形满足要求,其周长=14.若等腰梯形上、下底分别为3、4,腰为2,则由托勒密定理,对角线长为4,满足要求,此时周长为11.故最小周长≤11. 显然对圆内接凸四边形ABCD ,无边长为1.否则若设1AB =,—1AD BD AB <=,得AD BD =,同理AC CB =,于是C 、D 均在AB 中垂线上,构不成凸四边形.因此最小周长≥2×4=8.四边均为2,得正方形,对角线为2,另一边为3,得等腰梯形,10.当周长为10时,显然至少有两边为2.若是2、2、2、4能为2、2、3、3故最小周长为11.18.1.27★★★在Rt ABC △中,90BCA =︒∠,CD 是高,已知ABC △的三边长都是整数,且311BD =,求BCD △与ACD △的周长之比.CB D解析 设ABC △的三边长分别为a 、b 、c .由题设知 2BC BD BA =⋅,故2311a c =.于是设211a l =,得211l c =由勾股定理得11b ==2211l -是 完全平方数,设为()20t t >,则22211l t -=,()()211l t l t -+=.由于0l t l t <-<+,所以21,11.l t l t -=⎧⎨+=⎩解得61,60.l t =⎧⎨=⎩于是21161a =⨯,116160b =⨯⨯. 因为BCD CAD △∽△,所以它们的周长比等于它们的相似比,即1160a b =.18.1.28★★★已知锐角三角形ABC 中,AD 是高,矩形SPQR 的面积是ABC △的1/3,其顶点S 、P 在BC 上,Q 、R 分别在AC 、AB 上,且BC 、AD 及矩形SPQR 的周长均为有理数,求AB ACBC+的最小值. 解析 如图,设ABC △的三边长依次为a 、b 、c ,AD h =,PQ x =,RS y =,则16xy ah =,及1x y AQ CQ a h AC AC+=+=.由条件,知a 、h 、x y +均为有理数. AR QB S D P C由16x aa x+=,得x a =y h =)2a h x y a h ++=-,因此只能有a h =.若过A 作BC 的平行线l ,再作C 关于l 的对称点C ',则AB AC AB AC +=+′≥BC ′=,于是AB ACBC+,仅当AB AC =时取到. 18.1.29★★★★整数边三角形ABC 中,90BAC =︒∠,AD 是斜边上的高,BD 也是整数.若对同一个BD 能长度,有两个不全等的直角整数边三角形ABC 满足要求,求BD 的最小值. 解析 不妨设ABC △的三边长为a 、b 、c ,AD h =,BD d =,首先bch a=为有理数,又222h c d =-为整数,因此h 也是整数.又CD 为整数,故2h d也是整数.又ABD CBA △∽△,故h b d c=. AB D C因此,只需正整数h 、c 、d 满足222h c d =-及2|d h ,这样的整数边三角形就存在.因为此时hcb d=是有理数,而222b h CD =+为整数,从而b 为整数.易知由2|d h 可得2|d c . 设21d d σ=,σ、1d 为正整数,且σ无平方因子,于是由2|h σ及2c 知|h σ,c .设1h h σ=,1c c σ=,代入得422111d c h =-,又由2|d h ,2c 得2211|d h σ,21c σ,今对1d 的任一素因子p ,其在1d 的指数()1s d 不会比1h 的指数高,否则()()111s d s h +≥,()()22112s d s h +≥,而()s σ最多为1,于是()()2211s d s h σ>,这是不可能的.于是11|d h ,同理11|d c .又令112h d h =,112c d c =,代入422111d c h =-得222122d c h =-. 于是对1d 有两组不同的2c 、2h 满足222122d c h =-.经计算18d ≥,故64d ≥.当64d =时,确实有满足要求的两组解:80AB =,60AC =,100BC =,和136AB =,255AC =,289BC =.故BD 的最小值是64.18.1.30★★★★试找一不等边三角形ABC ,使BC 及BC 边上的中线、角平分线、高的长度都是整数,BC 可以是多少(此时的中线、角平分线、高的长度分别为多少)?若要求BC 不是整数,但2BC 是整数,则BC 可为多少(此时中线、角平分线、高的长度分别为多少)? 解析 首先处理BC 为整数的问题,我们选择的是直角三角形ABC ,对应边为a 、b 、c ,中线AM ,角平分线AD ,高AH ,2aAM =,bc AH a =,又ABC ABD ACD S S S =+△△△,得)bc b c AD +,故AD ,于是a 为偶数2k ,b ,c =,mnAH k =而2mn AD m n =+,2222m n k +=,这个方程有解1m =,7n =,5k =,得75AH =,5AM =,74AD =.乘以一个系数20,即得直角三角形ABC ,它的斜边为200,斜边上的中线为100,角平分线为35,高为28. 下面处理BC 为无理数、2BC 为整数的情形,如图,延长AD ,与MP 交于P ,此处MP BC ⊥.易知A 、B 、P 、C 共圆(P 是ABC △外接圆弧»BC之中点). 今从基本勾股数出发构造.取12AH =,13AD =,15AM =,则5DH =,9MH =,4MD =,485MD MP AH HD =⋅=,45255PD AD ==. ABMD HCP易知BPD APB △∽△,于是25211760845525BP PD PA =⋅=⨯=,()22222608448302444425255BC BM PB MP ⎛⎫==-=-= ⎪⎝⎭. 再乘以系数5,得所求三角形的高60AH =,角平分线65AD =,中线75AM =,边BC =是无理数,但15120BC =.18.1.31★★作圆外切凸五边形ABCDE ,现知该五边形每边长均为整数,1AB =,又圆与BC 切于K ,求BK .解析 如图,设CD 、DE 、EA 、AB 分别与圆切于P 、Q 、R 、S .则RE DP ED +=为整数,于是由题设,AR CP +亦为整数,而AR CP AS KC +=+.于是22BK BS BK BS ==+为整数,由于1BS AB <=,故22BS <,221BK BS ==,12BK =. A S RB EQ K CPD。
平面几何名定理、名题与竞赛题

平面几何名定理、名题与竞赛题江苏省常州高级中学 顾九华平面几何在其漫长的发展过程中,得出了大量的定理,积累了大量的题目,其中很多题目都是大数学家的大手笔,这些题目本身就是典范,这些题目的解决方法则更是我们学习平面几何的圭臬.通过学习这些题目,大家可以体会到数学的美.而且这些题目往往也是数学竞赛命题的背景题,在很多竞赛题中都可以找到他们的身影.本讲及下讲拟介绍几个平几名题及其应用.定理1 (Ptolemy 定理)圆内接四边形对角线之积等于两组对边乘积之和;(逆命题成立) 分析 如图,即证AC ·BD =AB ·CD +AD ·BC .可设法把 AC ·BD 拆成两部分,如把AC 写成AE +EC ,这样,AC ·BD 就拆成了两部分:AE ·BD 及EC ·BD ,于是只要证明AE ·BD =AD ·BC 及EC ·BD =AB ·CD 即可.证明 在AC 上取点E ,使∠ADE =∠BDC , 由∠DAE =∠DBC ,得⊿AED ∽⊿BCD .∴ AE ∶BC =AD ∶BD ,即AE ·BD =AD ·BC . ⑴ 又∠ADB =∠EDC ,∠ABD =∠ECD ,得⊿ABD ∽⊿ECD . ∴ AB ∶ED =BD ∶CD ,即EC ·BD =AB ·CD . ⑵ ⑴+⑵,得 AC ·BD =AB ·CD +AD ·BC .说明 本定理的证明给证明ab =cd +ef 的问题提供了一个典范.用类似的证法,可以得到Ptolemy 定理的推广(广义Ptolemy 定理):对于一般的四边形ABCD ,有AB ·CD +AD ·BC ≥AC ·BD .当且仅当ABCD 是圆内接四边形时等号成立.例1 (1987年第二十一届全苏)设A 1A 2A 3…A 7是圆内接正七边形,求证: 1A 1A 2=1A 1A 3+1A 1A 4. 证明 连A 1A 5,A 3A 5,并设A 1A 2=a ,A 1A 3=b ,A 1A 4=c . 本题即证1a =1b +1c.在圆内接四边形A 1A 3A 4A 5中,有A 3A 4=A 4A 5=a ,A 1A 3=A 3A 5=b ,A 1A 4=A 1A 5=c .于是有ab +ac =bc ,同除以abc ,即得1a =1b +1c,故证. 例2.(美国纽约,1975)证明:从圆周上一点到圆内接正方形的四个顶点的距离不可能都是有理数. 分析:假定其中几个是有理数,证明至少一个是无理数.证明:设⊙O 的直径为2R ,不妨设P 在⌒AD 上,则∠APB =45︒,设∠PBA =α,则∠P AB =135︒-α.若P A =2R sin α及PC =2R sin(90︒-α)=2R cos α为有理数, 则 PB =2R sin ∠P AB =2R sin(135︒-α)=2R (22cos α+22sin α)=2R (sin α+cos α)即为无理数. 或用Ptolemy 定理:PB·AC=P A·BC+PC·AB .⇒2PB=P A+PC .故P A 、PB 、PC 不能同时为有理数.例3.⑴ 求证:锐角三角形的外接圆半径与内切圆半径的和等于外心到各边距离的和. ⑵ 若∆ABC 为直角三角形或钝角三角形,上面的结论成立吗?证明:如图,∆ABC 内接于⊙O ,设⊙O 的半径=R ,∆ABC 的边长分别为a ,b ,c .三边的中点分别为X 、Y 、Z .由A 、X 、O 、Z 四点共圆,据Ptolemy 定理,有A BC DE 16例1OA ·XZ=OX ·AZ +OZ ·AX ,⇒R ·12a=OX ·12b +OZ ·12c .即R ·a=OX ·b +OZ ·c , ①同理,R ·b=OX ·a +OY ·c , ② R ·c=OY ·b +OZ ·a , ③三式相加,得R (a +b +c )=OX (a +b )+OY (b +c )+OZ (c +a ). ④但 r (a +b +c )=OX ·a +OY ·b +OZ ·c .(都等于三角形面积的2倍) ⑤ ④式与⑤式两边分别相加,得R (a +b +c )+r (a +b +c )= OX (a +b )+OY (b +c )+OZ (c +a )+OX ·c +OY ·a +OZ ·b .故, R +r=OX +OY +OZ .⑵ 当∆ABC 为直角三角形(∠C 为直角),则O 在边AB 上,OX=0,上述结论仍成立. 当∆ABC 为钝角三角形 (∠C 为直角或钝角)时,则有 R +r=-OX +OY +OZ . 证明同上.定理2 设P 、Q 、A 、B 为任意四点,则P A 2-PB 2=QA 2-QB 2⇔PQ ⊥AB . 证明 先证P A 2-PB 2=QA 2-QB 2⇒PQ ⊥AB .作PH ⊥AB 于H ,则 P A 2-PB 2=( PH 2+AH 2)-(PH 2+BH 2)=AH 2-BH 2=(AH +BH )(AH -BH )=AB (AB -2BH ). 同理,作QH ’⊥AB 于H ’,则 QA 2-QB 2=AB (AB -2AH’)∴H =H ’,即点H 与点H ’重合.PQ ⊥AB ⇒P A 2-PB 2=QA 2-QB 2显然成立.说明 本题在证明两线垂直时具有强大的作用.点到圆的幂:设P 为⊙O 所在平面上任意一点,PO =d ,⊙O 的半径为r ,则d 2-r 2就是点P 对于⊙O 的幂.过P 任作一直线与⊙O 交于点A 、B ,则P A·PB = |d 2-r 2|.“到两圆等幂的点的轨迹是与此二圆的连心线垂直的一条直线,如果此二圆相交,则该轨迹是此二圆的公共弦所在直线”这个结论.这条直线称为两圆的“根轴”.三个圆两两的根轴如果不互相平行,则它们交于一点,这一点称为三圆的“根心”.三个圆的根心对于三个圆等幂.当三个圆两两相交时,三条公共弦(就是两两的根轴)所在直线交于一点.例5.以O 为圆心的圆通过⊿ABC 的两个顶点A 、C ,且与AB 、BC 两边分别相交于K 、N 两点,⊿ABC 和⊿KBN 的两外接圆交于B 、M 两点.证明:∠OMB 为直角.(1985年第26届国际数学竞赛)分析 对于与圆有关的问题,常可利用圆幂定理,若能找到BM 上一点,使该点与点B对于圆O 等幂即可. 证明:由BM 、KN 、AC 三线共点P ,知PM ·PB =PN ·PK =PO 2-r 2. ⑴ 由∠PMN =∠BKN =∠CAN ,得P 、M 、N 、C 共圆,故 BM ·BP =BN ·BC =BO 2-r 2. ⑵ ⑴-⑵得, PM ·PB -BM ·BP = PO 2 - BO 2, 即 (PM -BM )(PM +BM )= PO 2 - BO 2,就是PM 2 -BM 2= PO 2 - BO 2,于是OM ⊥PB .定理3 (Ceva 定理)设X 、Y 、Z 分别为△ABC 的边BC 、CA 、AB 上的一点,则AX 、BY 、CZ 所在直线交于一点的充要条件是A BC PXYZA B PQHH'分析 此三个比值都可以表达为三角形面积的比,从而可用面积来证明. 证明:设S ⊿APB =S 1,S ⊿BPC =S 2,S ⊿CPA =S 3. 则AZ ZB =S 3S 2,BX XC =S 1S 3,CY YA =S 2S 1, 三式相乘,即得证.说明 用同一法可证其逆正确.本题也可过点A 作MN ∥BC 延长BY 、CZ 与MN 分别交于M 、N ,再用比例来证明,例6.以△ABC 的三边为边向形外作正方形ABDE 、BCFG 、ACHK ,设L 、M 、N 分别为DE 、FG 、HK 的中点.求证:AM 、BN 、CL 交于一点.分析 设AM 、BN 、CL 分别交BC 、CA 、AB 于P 、Q 、R .利用面积比设法证明BP PC ·CQ QA ·ARRB=1. 证明 设AM 、BN 、CL 分别交BC 、CA 、AB 于P 、Q 、R .易知,∠CBM =∠BCM =∠QCN =∠QAN =∠LAR =∠LBR =θ. BP PC =S ∆ABM S ∆ACM =AB ·BM sin(B +θ)AC ·CM sin(A +θ)=AB sin(B +θ)AC sin(C +θ). CQ QA =BC sin(C +θ)AB sin(A +θ),AR RB =AC sin(A +θ)BC sin(B +θ), 三式相乘即得BP PC ·CQ QA ·ARRB=1,由Ceva 定理的逆定理知AM 、BN 、CL 交于一点.例7.如图,在△ABC 中,∠ABC 和∠ACB 均是锐角,D 是BC 边上的内点,且AD 平分∠BAC ,过点D 分别向两条直线AB 、AC 作垂线DP 、DQ ,其垂足是P 、Q ,两条直线CP 与BQ 相交与点K .求证:AK ⊥BC ;证明:⑴ 作高AH . 则由∆BDP ∽∆BAH ,⇒BH PB =BA BD ,由∆CDQ ∽∆CAH ,⇒CQ HC =DC CA .由AD 平分∠BAC ,⇒DC BD =ACAB ,由DP ⊥AB ,DQ ⊥AC ,⇒AP=AQ .∴AP PB ·BH HC ·CQ QA =AP QA ·BH PB ·CQ HC =BA BD ·DC CA =DC BD ·BACA=1,据Ceva 定理,AH 、BQ 、CP 交于一点,故AH 过CP 、BQ 的交点K ,∴ AK 与AH 重合,即AK ⊥BC .例8.在四边形ABCD 中,对角线AC 平分∠BAD ,在CD 上取一点E ,BE 与AC 相交于F ,延长DF 交BC 于G .求证:∠GAC =∠EAC .(1999年全国高中数学联赛)分析 由于BE 、CA 、DG 交于一点,故可对此图形用Ceva 定理,再构造全等三角形证明两角相等.证明 连结BD 交AC 于H ,对⊿BCD 用Ceva 定理,可得CG GB ·BH HD ·DEEC =1.因为AH 是∠BAD 的角平分线,由角平分线定理,可得BH HD =ABAD,故ABC DEFGH IJHK Q PDCBARQPN MLKHGFC EDBA过点C 作AB 的平行线交AG 延长线于I ,过点C 作AD 的平行线交AE 的延长线于J , 则CG GB =CI AB ,DE EC =ADCJ,所以, CI AB ·AB AD ·ADCJ=1. 从而,CI =CJ .又因CI ∥AB ,CJ ∥AD ,故∠ACI =π-∠BAC =π-∠DAC =∠ACJ , 因此,⊿ACI ≌⊿ACJ ,从而∠IAC =∠JAC ,即∠GAC =∠EAC .定理4 (Menelaus 定理)设X 、Y 、Z 分别在△ABC 的BC 、CA 、AB 所在直线上,则X 、Y 、Z 共线的充要条件是AZ ZB ·BX XC ·CYYA=1. 证明:作CM ∥BA ,交XY 于N , 则AZ CN =CY YA ,CN ZB =XC BX. 于是AZ ZB ·BX XC ·CY YA =AZ CN ·CN ZB ·BX XC ·CYYA=1.本定理也可用面积来证明:如图,连AX ,BY , 记S ∆AYB =S 1,S ∆BYC =S 2,S ∆CYX =S 3,S ∆XYA =S 4.则 AZ ZB =S 4S 2+S 3;BX XC =S 2+S 3S 3;CY YA =S 3S 4,三式相乘即得证. 说明 用同一法可证其逆正确.Ceva 定理与Menelaus 定理是一对“对偶定理”.例9.(南斯拉夫,1983)在矩形ABCD 的外接圆弧AB 上取一个不同于顶点A 、B 的点M ,点P 、Q 、R 、S 是M 分别在直线AD 、AB 、BC 与CD 上的投影.证明,直线PQ 和RS 是互相垂直的,并且它们与矩形的某条对角线交于同一点.证明:设PR 与圆的另一交点为L .则→PQ ·→RS =(→PM +→P A )·(→RM +→MS )=→PM ·→RM +→PM ·→MS +→P A ·→RM +→P A ·→MS =-→PM ·→PL +→P A ·→PD =0.故PQ ⊥RS .设PQ 交对角线BD 于T ,则由Menelaus 定理,(PQ 交∆ABD )得DP P A ·AQ QB ·BT TD =1;即BT TD =P A DP ·QBAQ; 设RS 交对角线BD 于N ,由Menelaus 定理,(RS 交∆BCD )得BN ND ·DS SC ·CR RB =1;即BN ND =SC DS ·RBCR; 显然,P A DP =RB CR ,QB AQ =SC DS .于是BT TD =BNND,故T 与N 重合.得证.例10.(评委会,土耳其,1995)设∆ABC 的内切圆分别切三边BC 、CA 、AB 于D 、E 、F ,X 是∆ABC内的一点,∆XBC 的内切圆也在点D 处与BC 相切,并与CX 、XB 分别切于点Y 、Z ,证明,EFZY 是圆内接四边形.分析:圆幂定理的逆定理与Menelaus 定理.ZY XC BANZ Y XCBAS 1S 2 S 3S 4 题11T,NSRQPM A BCDL证明:延长FE 、BC 交于Q .AF FB ·BD DC ·CE EA =1,XZ ZB ·BD DC ·CY YA =1,⇒AF FB ·CE EA =XZ ZB ·CY YA . 由Menelaus 定理,有AF FB · BQ QC · CEEA=1. 于是得XZ ZB ·BQ QC ·CYYA=1.即Z 、Y 、Q 三点共线.但由切割线定理知,QE ·QF =QD 2=QY ·QZ .故由圆幂定理的逆定理知E 、F 、Z 、Y 四点共圆.即EFZY 是圆内接四边形.定理5 (蝴蝶定理)AB 是⊙O 的弦,M 是其中点,弦CD 、EF 经过点M ,CF 、DE 交AB 于P 、Q ,求证:MP =QM .分析 圆是关于直径对称的,当作出点F 关于OM 的对称点F'后,只要设法证明⊿FMP≌⊿F'MQ 即可.证明:作点F 关于OM 的对称点F ’,连FF ’,F’M ,F’Q ,F’D .则 MF =MF ’,∠4=∠FMP =∠6.圆内接四边形F ’FED 中,∠5+∠6=180︒,从而∠4+∠5=180︒, 于是M 、F ’、D 、Q 四点共圆,∴ ∠2=∠3,但∠3=∠1,从而∠1=∠2, 于是⊿MFP ≌⊿MF ’Q .∴ MP =MQ .说明 本定理有很多种证明方法,而且有多种推广.例11.在筝形ABCD 中,AB =AD ,BC =CD ,经AC 、BD 交点O 作二直线分别交AD 、BC 、AB 、CD 于点E 、F 、G 、H ,GF 、EH 分别交BD 于点I 、J ,求证:IO =OJ .(1990年冬令营选拔赛题)分析 通常的解法是建立以O 为原点的直角坐标系,用解析几何方法来解,下面提供的解法则利用了面积计算.证明:如图,由S ⊿AOB =S ⊿AOG +S ⊿GOB 得 12(at 1cos α+bt 1sin α)=12ab . ∴ t 1=ab a cos α+b sin α.即1t 1=cos αb +sin αa ;同理得,1t 2=cos βb +sin βc ;1t 3=cos αb +sin αc ;1t 4=cos βb +sin βa .再由S ⊿GOF =S ⊿GOI +S ⊿IOF ,又可得sin(α+β)IO =sin αt 2+sin βt 1;同理,得sin(α+β)OJ =sin αt 4+sin βt 3.∴ IO =OJ ⇔(1t 4-1t 2)sin α=(1t 1-1t 3)sin β.以1t 4、1t 2的值代入左边得,(1t 4-1t 2)sin α=(1a -1c)sin αsin β,同样得右边.可证. 定理6 张角定理:从一点出发三条线段长分别为a 、b 、t 、(t 在a 、b 之间),则sin(α+β)t =sin αb +sin βa. 例12.(评委会,爱尔兰,1990)设l 是经过点C 且平行于∆ABC 的边AB 的直线,∠A 的平分线交BC 于D ,交l 于E ,∠B 的平分线交AC 于F ,交l 于G ,已知,GF =DE ,证明:AC =BC .A BCDEFGHOI J αβab ct t t t 1234A BC D E F MF'123456O PQ 例12QP I Z Y X F EABC D abtβα分析:设∠A =2α,∠B =2β,即证α=β. 证明:设α>β,则BC >AC , 利用张角定理可得,sin A t a =sin αc +sin αb ,⇒2cos αt a =1c +1b ,⇒t a =2bc cos αb+c. 再作高CH ,则AE =CH csc α=b sin2αcsc α=2b cos α.⇒DE=AE -t a =2b cos α-2bc cos αb+c =2b 2cos αb+c .同理,GF =2a 2cos βa+c .由α>β,a >b ,知cos β<cos α.1+c a <1+c b ,⇒ GF=2a 2cos βa+c=2a cos β1+c a >2b cos α1+c b=2b 2cos αb+c =DE .矛盾.又证:设BC >AC ,即a>b ,故α>β,由张角定理得,sin A t a =sin αc +sin αb ,⇒2cos αt a =1c +1b. 同理2cos βt b =1c +1a,由于a >b ,故cos αt a >cos βt b ,⇒t b t a >cos β cos α >1,即t b >t a .就是BF>AD . ⑴∴ BG =BF +FG >AD +DE=AE .即是BG >AE . ∴GF BF = CF AF ⇒GF =BG ·CF AF+FC =BG 1+AF CF =BG 1+AB BC >AE 1+AB AC =AE 1+BD DC =AE ·DCBC=DE .矛盾.故BC =AC . 或BF GF =AF CF =AB CB <AB CA =BD DC =ADDE,注意到GF=DE ,故BF <AD .与⑴矛盾.故证. 定理7 (Simson line ) P 是ΔABC 的外接圆⊙O 上的任意一点,PX ⊥AB ,PY ⊥BC ,PZ ⊥CA ,垂足为X 、Y 、Z ,求证: X 、Y 、Z 三点共线.分析 如果连ZX 、ZY ,能证得∠1=∠3,则由∠AZB =180︒得∠YZX =180︒,即可证此三点共线. 证明 ∠PXB =∠PZB =90︒⇒P 、Z 、X 、B 四点共圆⇒∠1=∠2.∠PZA =∠PYA =90︒⇒P 、Z 、A 、Y 四点共圆⇒∠3=∠4.但∠2+∠5=90︒,∠4+∠6=90︒,而由P 、A 、C 、B 四点共圆, 得∠5=∠6.故∠2=∠4,从而∠1=∠3.故X 、Y 、Z 共线. 说明 本题的证法也是证三点共线的重要方法.本题的逆命题成立,该逆命题的证明曾是江苏省高中数学竞赛的试题.例13.设H 为ΔABC 的垂心,P 为ΔABC 的外接圆上一点,则从点P 引出的三角形的西姆松线平分PH .分析:考虑能否用中位线性质证明本题:找到一条平行于Simson 线的线段,从PX ∥AH 入手.连PE ,得∠1=∠2,但∠2=∠3,再由四点共圆得∠3=∠4,于是得∠6=∠7.可证平行.证明 连AH 并延长交⊙O 于点E ,则DE =DH ,连PE 交BC 于点F ,交XY 于点K ,连FH 、PB . ∵ PX ∥AE ,∴ ∠1=∠2,又∠2=∠3, ∵ P 、Z 、X 、B 四点共圆, ∴∠3=∠4,∴ ∠1=∠4. ∴ K 为PF 中点.∵ DE =DH ,BD ⊥EH ,∴ ∠2=∠5.AB C P X YZ 123456AB C X YZP KD HE M 12345F 672α2βαβαβFEDC BA G∴ FH ∥XY . ∴ XY 平分PH .又证:延长高CF ,交圆于N ,则F 是HN 的中点,若K 为PH 中点,则应有FK ∥PN .再证明K 在ZX 上.即证明∠KZF=∠XZB . 设过P 作三边的垂线交BC 、CA 、AB 于点X 、Y 、Z .连KZ 、KF 、ZX ,延长CF 交⊙O 于点N ,连PN . 由PZ ⊥AB ,CF ⊥AB ,K 为PH 中点知,KZ =KF . ∴ ∠KZF =∠KFZ . 易证HF =FN ,故KF ∥PN .∴ ∠PNC =∠KFH . 但∠PNC +∠PBC =180︒,∴ ∠KFZ +∠ZFH +∠PBC =180︒. 即∠KFZ +∠PBC =90︒.又PX ⊥BC ,PZ ⊥BZ ⇒P 、Z 、X 、B 共圆. ∴ ∠XZB =∠XPB ,而∠XPB +∠PBC =90︒.∴ ∠KZF =∠KFZ =∠XZB .∴ ZK 与ZX 共线.即点K 在⊿ABC 的与点P 对应的Simson line 上.)定理8(Euler line )三角形的外心、重心、垂心三点共线,且外心与重心的距离等于重心与垂心距离的一半.分析 若定理成立,则由AG =2GM ,知应有AH =2OM ,故应从证明AH =2OM入手.证明:如图,作直径BK ,取BC 中点M ,连OM 、CK 、AK ,则∠KCB =∠KAB =90︒,从而KC ∥AH ,KA ∥CH ,⇒□CKAH ,⇒AH =CK =2MO .由OM ∥AH ,且AH =2OM ,设中线AM 与OH 交于点G ,则⊿GOM ∽⊿GHA ,故得MG ∶GA =1∶2,从而G 为⊿ABC 的重心.且GH =2GO .说明 若延长AD 交外接圆于N ,则有DH =DN .这一结论也常有用.例14.设A 1A 2A 3A 4为⊙O 的内接四边形,H 1、H 2、H 3、H 4依次为⊿A 2A 3A 4、⊿A 3A 4A 1、⊿A 4A 1A 2、⊿A 1A 2A 3的垂心.求证:H 1、H 2、H 3、H 4四点在同一个圆上,并定出该圆的圆心位置.(1992年全国高中数学联赛)分析 H 1、H 2都是同一圆的两个内接三角形的垂心,且这两个三角形有公共的底边.故可利用上题证明中的AH =2OM 来证明. 证明 连A 2H 1,A 1H 2,取A 3A 4的中点M ,连OM ,由上证知A 2H 1∥OM ,A 2H 1=2OM ,A 1H 2∥OM , A 1H 2=2OM ,从而H 1H 2A 1A 2是平行四边形,故H 1H 2∥A 1A 2 ,H 1H 2=A 1A 2. 同理可知,H 2H 3∥A 2A 3,H 2H 3=A 2A 3; H 3H 4∥A 3A 4,H 3H 4=A 3A 4; H 4H 1∥A 4A 1,H 4H 1=A 4A 1. 故 四边形A 1A 2A 3A 4≌四边形H 1H 2H 3H 4. 由四边形A 1A 2A 3A 4有外接圆知,四边形H 1H 2H 3H 4也有外接圆.取H 3H 4∥的中点M 1,作M 1O 1⊥H 3H 4,且M 1O 1=MO ,则点O 1即为四边形H 1H 2H 3H 4的外接圆圆心.又证:以O 为坐标原点,⊙O 的半径为长度单位建立直角坐标系,设OA 1、OA 2、OA 3、OA 4与OX 正方向所成的角分别为α、β、γ、δ,则点A 1、A 2、A 3、A 4的坐标依次是(cos α,sin α)、(cos β,sin β)、(cos γ,sin γ)、(cos δ,sin δ).显然,⊿A 2A 3A 4、⊿A 3A 4A 1、⊿A 4A 1A 2、⊿A 1A 2A 3的外心都是点O ,而它们的重心依次是:(13(cos β+cos γ+cos δ),13(sin β+sin γ+sin δ))、(13(cos γ+cos δ+cos α),13(sin α+sin δ+sin γ))、 (13(cos δ+cos α+cos β),13(sin δ+sin α+sin β))、(13(cos α+cos β+cos γ),13(sin α+sin β+sin γ)). ABC MD O HG FKA A A A H H H H OM12341234M O 11从而,⊿A 2A 3A 4、⊿A 3A 4A 1、⊿A 4A 1A 2、⊿A 1A 2A 3的垂心依次是H 1(cos β+cos γ+cos δ, sin β+sin γ+sin δ)、H 2 (cos γ+cos δ+cos α,sin α+sin δ+sin γ)、 H 3 (cos δ+cos α+cos β,sin δ+sin α+sin β)、H 4 (cos α+cos β+cos γ,sin α+sin β+sin γ).而H 1、H 2、H 3、H 4点与点O 1(cos α+cos β+cos γ+cos δ,sin α+sin β+sin γ+sin δ)的距离都等于1,即H 1、H 2、H 3、H 4四点在以O 1为圆心,1为半径的圆上.证毕.定理9 (Nine point round )三角形的三条高的垂足、三条边的中点以及三个顶点与垂心连线的中点,共计九点共圆.分析 要证九个点共圆,可先过其中三点作一圆,再证其余的点在此圆上.为此可考虑在三种点中各选一点作圆,再在其余三类共六个点中每类取一个点证明其在圆上,即可证明.证明:取BC 的中点M ,高AD 的垂足D ,AH 中点P ,过此三点作圆,该圆的直径即为MP .由中位线定理知,MN ∥AB ,NP ∥CH ,但CH ⊥AB ,故∠PNM =90︒,于是,点N 在⊙MDP 上,同理,AB 中点在⊙MDP 上. 再由QM ∥CH ,QP ∥AB ,又得∠PQM =90︒,故点Q 在⊙MDP 上,同理,CH 中点在⊙MDP 上.由FP 为Rt .⊿AFH 的斜边中线,故∠PFH =∠PHF =∠CHD ,又FM 为Rt .⊿BCF 的斜边中线,得∠MFC =∠MCF ,但∠CHD +∠DCH =90︒,故∠PFM =90︒.又得点F 在⊙MDP 上,同理,高BH 的垂足在⊙MDP 上.即证.说明 证明多点共圆的通法,就是先过三点作圆,再证明其余的点在此圆上. 九点圆的圆心在三角形的Euler 线上.九点圆的直径等于三角形外接圆的半径.由OM ∥AP ,OM =AP ,知PM 与OH 互相平分,即九点圆圆心在OH 上.且九点圆直径MP =OA =⊿ABC 的外接圆半径.定理10(三角形的内心的一个重要性质)设I 、I a 分别为⊿ABC 的内心及∠A 内的旁心,而∠A 平分线与⊿ABC 的外接圆交于点P ,则PB =PC =PI =PI a .例15.设ABCD 为圆内接四边形,ΔABC 、ΔABD 、ΔACD 、ΔBCD 的内心依次为I 1、I 2、I 3、I 4,则I 1I 2I 3I 4为矩形.(1986年国家冬令营选拔赛题)分析 只须证明该四边形的一个角为直角即可.为此可计算∠1、∠2、∠XI 2Y .证明 如图,BI 2延长线与⊙O 的交点X 为⌒AD 中点.且XI 2=XI 3=XA =XD , 于是∠1=12(180︒-∠X )=90︒-14⌒BC ,同理,∠2=90︒-14⌒CD .∠XI 2Y =12(⌒XY +⌒BD )= 14(⌒AB +⌒AD )+12(⌒BC +⌒CD ), 故∠1+∠2+∠XI 2Y =90︒+90︒+14(⌒AB +⌒BC +⌒CD +⌒DA )=270︒.从而∠I 1I 2I 3=90︒.同理可证其余.说明 亦可证XZ ⊥YU ,又XZ 平分∠I 2XI 3及XI 2=XI 3⇒I 2I 3⊥XZ ,从而I 2I 3∥YU ,于是得证.定理11 (Euler 定理)设三角形的外接圆半径为R ,内切圆半径为r ,外心与内心的距离为d ,则d 2=R 2-2Rr .(1992年江苏省数学竞赛)分析 改写此式,得:d 2-R 2=2Rr ,左边为圆幂定理的表达式,故可改为过I 的任一直线与圆交得两段的积,右边则为⊙O 的直径与内切圆半径的积,故应添出此二者,并构造相似三角形来证明.F HD MC BA PQ N10.22ABCD I I I I 123412XYZU证明:如图,O 、I 分别为⊿ABC 的外心与内心.连AI 并延长交⊙O 于点D ,由AI 平分∠BAC ,故D 为弧BC 的中点.连DO 并延长交⊙O 于E ,则DE为与BC 垂直的⊙O 的直径.由圆幂定理知,R 2-d 2=(R +d )(R -d )=IA ·ID .(作直线OI 与⊙O 交于两点,即可用证明)但DB =DI (可连BI ,证明∠DBI =∠DIB 得),故只要证2Rr =IA ·DB ,即证2R ∶DB =IA ∶r 即可.而这个比例式可由⊿AFI ∽⊿EBD 证得.故得R 2-d 2=2Rr ,即证.例16.(1989IMO)锐角∆ABC 的内角平分线分别交外接圆于点A 1、B 1、C 1,直线AA 1与∠ABC 的外角平分线相交于点A 0,类似的定义B 0,C 0,证明:⑴ S A 0B 0C 0=2S A 1CB 1AC 1B ;⑵ S A 0B 0C 0≥4S ABC .分析:⑴利用A 1I=A 1A 0,把三角形A 0B 0C 0拆成以I 为公共顶点的六个小三角形,分别与六边形A 1CB 1AC 1B 中的某一部分的2倍相等. ⑵ 若连OA 、OB 、OC 把六边形A 1CB 1AC 1B 分成三个四边形,再计算其面积和,最后归结为证明R ≥2r .也可以这样想:由⑴知即证S A 1CB 1AC 1B ≥2 S ABC ,而IA 1、IB 1、IC 1把六边开分成三个筝形,于是六边形的面积等于∆A 1B 1C 1面积的2倍.故只要证明S A 1B 1C 1≥S ABC .证明:⑴ 设∆ABC 的内心为I ,则A 1A 0=A 1I ,则S A 0BI =2S A 1BI ;同理可得其余6个等式.相加⑴即得证. ⑵ 连OA 、OB 、OC 把六边形A 1CB 1AC 1B 分成三个四边形,由OC 1⊥AB ,OA 1⊥BC ,OB 1⊥CA ,得∴ S A 1CB 1AC 1B =S OAC 1B + S OB 1A 1C + S OCB 1A =12AB ·R +12BC ·R +12CA ·R =Rp .但由Euler 定理,R 2-2Rr =R (R -2r )=d 2≥0,知R ≥2r ,故Rp ≥2rp =2S ∆ABC .故得证.⑵ 证明:记A =2α,B =2β,C =2γ.0<α,β,γ<π2.则S ABC =2R 2sin2αsin2βsin2γ,S A 1B 1C 1=2R 2sin(α+β)sin(β+γ)sin(γ+α).又sin(α+β)=sin αcos β+cos αsin β≥2sin αcos β cos αsin β =sin2αsin2β ,同理,sin(β+γ)≥sin2βsin2γ ,sin(γ+α)≥sin2γsin2α ,于是S A 1B 1C 1≥S ABC 得证.又证:连OA 、OB 、OC 把六边形A 1CB 1AC 1B 分成三个四边形, 由OC 1⊥AB ,OA 1⊥BC ,OB 1⊥CA ,得∴ S A 1CB 1AC 1B =S OAC 1B + S OB 1A 1C + S OCB 1A =12AB ·R +12BC ·R +12CA ·R =Rp .但由Euler 定理,R 2-2Rr =R (R -2r )=d 2≥0,知R ≥2r ,故Rp ≥2rp =2S ∆ABC .故得证.又证:α+β+γ=π,故sin(α+β)=cos γ,sin(β+γ)=cos α,sin(γ+α)=cos β. 于是,sin(α+β)sin(β+γ)sin(γ+α)=cos αcos βcos γ,故sin(α+β)sin(β+γ)sin(γ+α)≥sin2αsin2βsin2γ,⇔ cos αcos βcos γ≥8sin αsin βsin γcos αcos βcos γ,由0<α、β、γ<π2,故cos αcos βcos γ≥8sin αsin βsin γcos αcos βcos γ,⇔sin αsin βsin γ≤18.而最后一式可证.定理12 (Fermat point )分别以ΔABC 的三边AB ,BC ,CA 为边向形外作正三角形ABD ,BCE ,CAH ,则此三个三角形的外接圆交于一点.此点即为三角形的Fermat point .AB C D O IE F例C 0分析 证三圆共点,可先取二圆的交点,再证第三圆过此点.证明:如图,设⊙ABD 与⊙ACH 交于(异于点A 的)点F ,则由A 、F 、B 、D共圆得∠AFB =120︒,同理∠AFC =120︒,于是∠BFC =120︒,故得B 、E 、C 、F 四点共圆.即证. 由此得以下推论:1︒ A 、F 、E 三点共线;因∠BFE =∠BCE =60︒,故∠AFB +∠BFE =180︒,于是A 、F 、E 三点共线.同理,C 、F 、D 三点共线;B 、F 、H 三点共线. 2︒ AE 、BH 、CD 三线共点. 3︒ AE =BH =CD =F A +FB +FC .由于,F 在正三角形BCE 的外接圆的弧BC 上,故由Ptolemy 定理,有FE =FB +FC .于是AE =AF +FB +FC .同理可证BH =CD =F A +FB +FC .也可用下法证明:在FE 上取点N ,使FN =FB ,连BN ,由⊿FBN 为正三角形,可证得⊿BNE ≌⊿BFC .于是得,NE =FC .故AE =F A +FN +NE =F A +FB +FC .例17.(Steiner 问题)在三个角都小于120°的ΔABC 所在平面上求一点P ,使P A +PB +PC 取得最小值. 证明:设P 为平面上任意一点,作等边三角形PBM (如图)连ME , 则由BP =BM ,BC =BE ,∠PBC =∠MBE =60︒-∠MBC . 得⊿BPC ≌⊿BME ,于是ME =PC ,故得折线APME =P A +PB +PC ≥AE =F A +FB +FC . 即三角形的Fermat point 就是所求的点.说明:本题也可用Ptolemy 的推广来证明:由PB ·CE +PC ·BE ≥PE ·BC ,可得,PB +PC ≥PE .于是P A +PB +PC ≥P A +PE ≥AE .定理13 到三角形三顶点距离之和最小的点——费马点. 例18.凸六边形ABCDEF ,AB =BC =CD ,DE =EF =F A ,∠BCD =∠EF A =60︒,G、H在形内, 且∠AGB =∠DHE =120︒.求证:AG +GB +GH +DH +HE ≥CF .证明 连BD 、AE 、BE ,作点G 、H 关于BE 的对称点G '、H ',连BG '、DG '、G 'H '、AH '、EH '。
全国各地初中(九年级)数学竞赛《几何》真题大全 (附答案)

全国各地初中(九年级)数学竞赛专题大全竞赛专题7 几何一、单选题 1.(2021·全国·九年级竞赛)某种产品由甲、乙、丙三种元件构成,如图为生产效率最高,在表示工人分配的扇形图中,生产甲、乙、丙元件的工人数量所对应的扇形圆心角的大小依次是( ).A .120,180,60︒︒︒B .108,144,108︒︒︒C .90,180,90︒︒︒D .72,216,720︒︒︒2.(2021·全国·九年级竞赛)如图所示,一次函数y kx b =+的图象过点(1,4)P 且与x 轴和y 轴的正半轴交于AB 、两点,点O 为坐标原点,当AOB 的面积最小时,k ,b 的值为( )A .4k =-,8b =B .4k =-,4b =C .2k =-,4b =D .2k =-,2b =3.(2021·全国·九年级竞赛)如图,已知DEF 的边长分别为3,2,正六边形网格由24个边长为2的正三角形组成,以这些正三角形的顶点画ABC ,使得ABC DEF ∽△△,相似比为ABk DE=,那么k 的不同值共有( )个.A .1B .2C .3D .4二、填空题4.(2021·全国·九年级竞赛)如图所示,正方形ABCD 的边长为10cm ,点E 在边CB 的延长线上且10cm EB =,点P 在边CD 上运动,EP 与AB 的交点为F .设cm DP x =,EFB △与四边形AFPD 的面积和为2cm y ,那么y 与x 之间的函数关系式是________.5.(2021·全国·九年级竞赛)把两个半径为5及一个半径为8的圆形纸片放在桌面上,使它们两两外切.若要用一个大圆形纸片把这三个圆形纸片完全盖住,则这个大圆形纸片的最小半径等于________. 6.(2021·全国·九年级竞赛)由一次函数2,2y x y x =+=-+和x 轴围成的三角形与圆心在(1,1)、半径为1的圆构成的图形覆盖的面积等于______.7.(2021·全国·九年级竞赛)某广场地面铺满了边长为36cm 的正六边形地砖,现向上抛掷半径为3cm 的圆碟,圆碟落地后与地面不相交的概率大约是_________. 三、解答题8.(2021·全国·九年级竞赛)平面上7个点,它们之间可以连一些线段,使7个点中任意三点必存在两点有线段相连.问最少要连几条线段?证明你的结论.9.(2021·全国·九年级竞赛)在直径为5的圆内放入10个点,证明其中必有两点的距离小于2.10.(2021·全国·九年级竞赛)设1M 是凸五边形12345A A A A A ,将1M 沿1i A A 方向平移,使1A 移到i A 得到凸五边形(2,3,4,5)i M i =.证明:12345,,,,M M M M M 中至少有两个图形,它们有公共内点.11.(2021·全国·九年级竞赛)在圆周上任取21个点,证明:以这些点为端点的弧中至少存在100条不超过120︒的弧.12.(2021·全国·九年级竞赛)两人A 和B 相约在12点与下午1点之间在某地会面,先到的人要等候另一人20分钟,过时就可以离开.如果每人可在指定的一小时内任何时刻到达,并且两人到达的时刻是彼此独立的(即一人到达的时刻与另一人到达的时刻没有影响),试计算两人能会面的概率.13.(2021·全国·九年级竞赛)平面上给出n个不全共线的点,求证:存在一条直线l,它恰通过其中两个点.14.(2021·全国·九年级竞赛)已知A,B,C,D为平面上两两距离不超过1的任意4点,今欲作一圆覆盖这4点(即A,B,C,D在圆内或圆周上)问圆的半径最小该是多少?试证明之.15.(2021·全国·九年级竞赛)任意凸四边形ABCD中总存在一条对角线和一条边,以它们为直径的两个圆可以覆盖这个四边形.16.(2021·全国·九年级竞赛)设甲是边长为1的正三角形纸片,乙是边长为1的正方形纸片,丙是边长为1的正五边形纸片,丁是边长为1的正六边形纸片.证明:(1)不能用甲、乙、丙合起来盖住一个半径为1的圆;(2)能用甲、乙、丙、丁合起来盖住一个半径为1的圆.17.(2021·全国·九年级竞赛)在一个半径等于6的圆内任意放入六个半径等于1的小圆.证明:其中总还有一块空位置,可以完整地放入一个半径为1的小圆.18.(2021·全国·九年级竞赛)将4张圆形纸片放在桌面上,使得其题中任何3张圆形纸片都有公共点,那么这4张圆形纸片是否一定有公共点?证明你的结论.19.(2021·全国·九年级竞赛)平面上给定了若干个圆,它们覆盖的面积为1.证明:从中可选出若干个两两不重叠的圆,使它们覆盖的面积不小于19.20.(2021·全国·九年级竞赛)证明:一个边长为5的正方形可以被3个边长为4的正方形所覆盖.21.(2021·全国·九年级竞赛)如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液,现将此容器倾斜一定角度α(图②),且倾斜时底面的一条棱始终在桌面上(图①,②均为容器的纵截面).(1)当30α=︒时,通过计算说明此溶液是否会溢出;(2)现需要倒出不少于33000cm的溶液,当α等于60︒时,能实现要求吗?通过计算说明理由.22.(2021·全国·九年级竞赛)甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头停泊,它们在一昼夜内到达的时间是等可能的,如果甲的停泊时间是1小时,乙的停泊时间是2小时,求它们中任何一艘都不需要等候码头空出的概率(精确到0.001).23.(2021·全国·九年级竞赛)把长为a 的线段任意分成3条线段,求这3条线段能够构成一个三角形的3条边的概率.24.(2022·福建·九年级竞赛)如图,四边形ABCD 是平行四边形,∠DAC =45°,以线段AC 为直径的圆与AB 和AD 的延长线分别交于点E 和F ,过点B 作AC 的垂线,垂足为H .求证:E ,H ,F 三点共线.竞赛专题7 几何答案解析一、单选题 1.(2021·全国·九年级竞赛)某种产品由甲、乙、丙三种元件构成,如图为生产效率最高,在表示工人分配的扇形图中,生产甲、乙、丙元件的工人数量所对应的扇形圆心角的大小依次是( ).A .120,180,60︒︒︒B .108,144,108︒︒︒C .90,180,90︒︒︒D .72,216,720︒︒︒【答案】B 【详解】解 设分配生产甲、乙、丙3种元件的人数分别为x 人,y 人,z 人,于是每小时生产甲、乙、丙三种元件的个数分别为50,30,20x y z .为了提高效率应使生产出来的元件全部组成成品而没有剩余.设共可组成k 件成品,则503020504020x y z k ===,即4,,3x k y k z k ===,从而4::1::13:4:33x y z ==.设在扇形图中生产甲、乙、丙三种元件的圆心角分别为,,αβγ,则3336036036010834310x x y z α=⨯︒=⨯︒=⨯︒=︒++++,4436036036014434310y x y z β=⨯︒=⨯︒=⨯︒=︒++++,3336036036010834310z x y z γ=⨯︒=⨯︒=⨯︒=︒++++.故应选B .2.(2021·全国·九年级竞赛)如图所示,一次函数y kx b =+的图象过点(1,4)P 且与x 轴和y 轴的正半轴交于A B 、两点,点O 为坐标原点,当AOB 的面积最小时,k ,b 的值为( )A .4k =-,8b =B .4k =-,4b =C .2k =-,4b =D .2k =-,2b =【答案】A 【详解】解 因函数y kx b =+的图象过点(1,4)P ,所以4,4k b b k =+=-,于是(4)y kx k =+-. 令0y =得4,0k A k -⎛⎫⎪⎝⎭. 令0x =得(0,4)B k -.连OP ,得 114122OABOAP OPBSSSOA OB =+=⨯⨯+⨯⨯ 14141(4)22k k k -=⨯⨯+⨯⨯- 11642k k ⎛⎫=-+ ⎪⎝⎭.显然0k <.令k u =-,则0u >,于是116116442822OABSu u u u⎛⎫=++≥+⨯⨯= ⎪⎝⎭.等号成立当且仅当16(0)u u u=>,即4u =,这时4,48k b k =-=-=. 故选A .注:OAB 的面积也可用114(4)22OABk SOA OB k k-=⨯⨯=⨯⨯-算出. 3.(2021·全国·九年级竞赛)如图,已知DEF 的边长分别为3,2,正六边形网格由24个边长为2的正三角形组成,以这些正三角形的顶点画ABC ,使得ABC DEF ∽△△,相似比为ABk DE=,那么k 的不同值共有( )个.A .1B .2C .3D .4【答案】C 【详解】作图知与DEF 相似的三角形,而相似比不同的三角形只有如图所示的三种,故选C .二、填空题4.(2021·全国·九年级竞赛)如图所示,正方形ABCD 的边长为10cm ,点E 在边CB 的延长线上且10cm EB =,点P 在边CD 上运动,EP 与AB 的交点为F .设cm DP x =,EFB △与四边形AFPD 的面积和为2cm y ,那么y 与x 之间的函数关系式是________.【答案】550(010)y x x =+<< 【详解】解 由DP x =得10PC x =-. 又12BF BE PC EC ==,即11(10),10(10)22BF x AF BF x =-=-=+, 所以EFBAFPD y SS =+四边形11()22BE BF AF DP AD =⨯⨯++⨯ 111110(10)(10)102222x x x ⎡⎤=⨯⨯-+++⨯⎢⎥⎣⎦550(010)x x =+<<. 故应填550(010)y x x =+<<.5.(2021·全国·九年级竞赛)把两个半径为5及一个半径为8的圆形纸片放在桌面上,使它们两两外切.若要用一个大圆形纸片把这三个圆形纸片完全盖住,则这个大圆形纸片的最小半径等于________. 【答案】1133.【详解】如图,设1O 的半径为8,2O ,3O 的半径为5,切点为A .由对称性,能盖住这3个圆的最小圆形纸片的中心O 在对称轴1O A 上,且与已知三个圆内切.若设这个圆形纸片的半径为r ,则在12Rt O O A 中22221122(85)512O A OO O A =-=+-=,在2Rt OO A 中,25OO r =-,1112(8)OA O A OO r =-=--,25O A =,于是,由22222OO O A OA =+得222(5)5(128)r r -=+-+,由此解出4011333r ==,即所求圆形纸片的最小半径等于1133.6.(2021·全国·九年级竞赛)由一次函数2,2y x y x =+=-+和x 轴围成的三角形与圆心在(1,1)、半径为1的圆构成的图形覆盖的面积等于______. 【答案】42π+【详解】如图,所覆盖面积2 114214222ABCS S S ππ=+=⨯⨯+⋅=+半圆.故答案为:42π+.7.(2021·全国·九年级竞赛)某广场地面铺满了边长为36cm 的正六边形地砖,现向上抛掷半径为3cm 的圆碟,圆碟落地后与地面不相交的概率大约是_________. 【答案】49【详解】解 要使圆碟与地砖的边缘不相交的条件是落地后圆碟的中心到正六边形地砖ABCDEF 的任何一边的距离不小于圆的半径63cm ,也就是圆碟的中心必落在与地砖ABCDEF 同中心且边与地砖边彼此平行、距离为63111111A B C D E F 内(图6-1).作OG AB ⊥于G ,交11A B 于1G 且163cm GG =,所以33336183OG AB ====1118363123OG OG GG =-==而113OG =,所以1132433OA ===,故11124A B OA ==. 设正六边形ABCDEF 和111111A B C D E F 的面积分别为S 和1S ,则所求概率为22211122224243639S A B p S AB =====.故应填49. 三、解答题8.(2021·全国·九年级竞赛)平面上7个点,它们之间可以连一些线段,使7个点中任意三点必存在两点有线段相连.问最少要连几条线段?证明你的结论.【答案】9条,见解析 【详解】解法一:设最少要连n 条线段,如图4-3中7个点之间共连有9条线段,其中任意三点间必有两点连有线段,故9n ≤.另一方面,我们证明9n ≥,下面分4种情形讨论: (1)若7点中存在一点1A 不与其他6点237,,,A A A 连线,则依题意1A ,i A ,j A (27)i j ≤<≤中必有2点连线,于是只可能i A 与j A 连有线,即237,,,A A A 这6点中任意两点连有线,图中一共连了65152⨯=条线. (2)若7点中存在一点1A 只连出一条线段,设1A 仅与2A 连有线而与其余5点3A ,4A ,5A ,6A ,7A ,没有连线,则同(1)可知3A ,4A ,5A ,6A ,7A 这5点中任意两点连有线,至少连有54102⨯=条线.(3)若每点出发至少连出2条线,且有一点恰连出2条线.设该点为1A ,它连出的两条线为12A A ,13A A ,则不与1A 相连的4个点每两点连有线,要连4362⨯=条线,而2A 连出的线段至少2条,除21A A 外,至少还有一条,所以此时至少要连6219++=条线. (4)若每点至少连出3条线,则至少要连73102⨯>条线. 综上所述,最少要连9条线段.解法二:设7点中从1A 出发所连的线段最少,只有k 条,设它们是121311,,,k A A A A A A +,其余6k -个点126,,,k B B B -都与1A 没有连线,于是对任意2点i B ,j B (16)i j k ≤<≤-,由已知条件知1A ,i B ,j B 中必有2点连有线,而1A 与i B ,1A 与j B 没有连线,故只可能i B 与j B 连有线,即16,,k B B -中每点与其余5k -点连有线,于是从各点连出的线段数的总和不少于(1)(6)(5)k k k k ++--221030k k =-+.但上述计数中每条线段计算了2次,故图中所连线段至少为()21210302k k -+=22551522k ⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭22151522⎛⎫⎛⎫≥+- ⎪ ⎪⎝⎭⎝⎭1569=-=,即至少要连9条线段. 另一方面,如图4-3中,7点中连有9条线段时满足题设条件. 综上所述,最少要连9条线段.9.(2021·全国·九年级竞赛)在直径为5的圆内放入10个点,证明其中必有两点的距离小于2. 【答案】见解析 【详解】分析 把圆等分为9个扇形显然不行(虽然必有一扇形内至少有2点,但不保证它们的距离小于2),因此,我们先作一个与已知圆同心的小圆(其直径必须小于2,但不能太小),然后将余下的圆环部分8等分. 证明 设O 是已知圆心,如图,以O 为圆心作半径为0.9的圆,再将余下的圆环8等分,于是将已知圆面分成了9个部分,由抽屉原理知其中必有一部分内至少有已知10点中的101129-⎡⎤+=⎢⎥⎣⎦点,M N ,若,M N 在小圆内,则220.9 1.82MN OC ≤=⨯=<. 若,M N 同在一个扇面形内,则由余弦定理,有222cos45MN AC OC OA OC OA ≤+-⋅︒0.81 6.2520.9 2.50.7 3.912+-⨯⨯⨯<.从例2可以看出,分割图形制造“抽屉”时,可能不是将图形等分为几部分,而是要求分割的每一部分图形都具有所需要的性质(例2中每一部分图形内任意两点的距离都小于2),读者应用这种方法解题时,应该注意到这一点.10.(2021·全国·九年级竞赛)设1M 是凸五边形12345A A A A A ,将1M 沿1i A A 方向平移,使1A 移到i A 得到凸五边形(2,3,4,5)i M i =.证明:12345,,,,M M M M M 中至少有两个图形,它们有公共内点.【答案】见解析 【详解】证明 如图,以1A 为位似中心,以2:1为相似比作1M 的位似图形M ,则M 仍为凸五边形且1M 在M 内.下面我们证明2345,,,M M M M 都在M 内,例如先证4M 在M 内.设P 是4M 内任意一点,它是1M 内的点Q 经过平移得到的,于是14QP A A ∥,故14A A PQ 为平行四边形,又R 是14A A PQ 的两条对角线的交点,因Q 和4A 属于1M ,且1M 是凸五边形,故R 属于M ,而111,:2:1A R RP A P A R ==,故P 属于M .又P 是M ,内任意一点,所以4M 包含在M 之内,同理235,,M M M 都包含在M 内,设12345,,,,M M M M M 及M 的面积分别为12345,,,,S S S S S 及S ,则2123451152S S S S S S S S ++++=>⋅=.于是,由图形重叠原理知,12345,,,,M M M M M 中至少有两个图形,它们有公共内点.11.(2021·全国·九年级竞赛)在圆周上任取21个点,证明:以这些点为端点的弧中至少存在100条不超过120︒的弧.【答案】见解析 【详解】证明:我们称不超过120︒的弧为好弧.不妨设以1A 为端点的好弧最少,并且设它只有1n -条,它们是12131,,,n A A A A A A ,从而以231,,,n A A A -为端点的好弧都至少有1n -条,故以这n 个点为端点的好弧至少有1(1)2n n ⋅-条,除这n 个点外,其余21n -个点记为1221,,,n n A A A ++,从中任取两点,(121)i j A A n i j +≤<≤.因1i j A A A ,至少有一个内角不超过60︒,故11,,i j i j A A A A A A 中至少有一条弧不超过260120⨯︒=︒,根据1A 的取法,这条弧不能是1i A A 和1j A A ,而只能是j i A A ,即j i A A 是好弧.可见以1221,,,n n A A A ++中任意两点,(121)i j A A n i j +≤<≤为端点的弧都为好弧.这样的好弧有1(21)(20)2n n ⋅--条.综上所述知好弧至少有2211213991399(1)(21)(20)100222424y n n n n n ⎛⎫⎛⎫=⋅-+⋅--=-+≥+= ⎪ ⎪⎝⎭⎝⎭条.当10n =或11时,y 取到最小值100,于是结论成立.12.(2021·全国·九年级竞赛)两人A 和B 相约在12点与下午1点之间在某地会面,先到的人要等候另一人20分钟,过时就可以离开.如果每人可在指定的一小时内任何时刻到达,并且两人到达的时刻是彼此独立的(即一人到达的时刻与另一人到达的时刻没有影响),试计算两人能会面的概率. 【答案】59 【详解】解 我们用,x y 分别表示,A B 到达的时刻,而两人能会面的充分必要条件为20x y -≤,其中060,060x y ≤≤≤≤.我们用平面直角坐标系中的点(),x y 表示,A B 到达的时刻(从中午12点以后算起,以分为单位),于是所有可能结果是一个边长为60的正方形OABC .代表能够会面的点都落在图中画有阴影线的区域H 内(图6-2),于是21260240402H ADE OABC S S S =-⨯=-⨯⨯⨯正方形 226040=-,故两人能会面的概率为22226040251()6039HOABC S p S -===-=正方形. 答:两人能会面的概率等于59. 13.(2021·全国·九年级竞赛)平面上给出n 个不全共线的点,求证:存在一条直线l ,它恰通过其中两个点.【答案】见解析【详解】证明:平面上只有有限点,过每两点作一直线只有有限点直线,每条直线与不在这条直线上的点(由已知条件知这样的点必存在)配成对,则这样的点只有有限个,每个点线对中都有该点到直线的距离,记这些距离最小的点对为(,)P l ,则l 为所求.实际上,设l 上有不少于3个给定的已知点,则过P 作PA l ⊥于A (如图),则在l 上A 的某一侧(包括A )必有2个已知点,设为,M N (M 可能与A 重合,连PN ,并M 作MQ PN ⊥于Q ,过A 作AR PN ⊥于R ,则MQ AR AP d ≤<=,这与AP d =最小矛盾,于是结论得证.注 本题是英国著名数学家希尔维斯特(J.J. Sylvester)在其逝世前不久提出的一个有趣的问题.这个貌似简单的问题,当时困扰过不少的数学家,并且这状况持续350年之久,直到1933年,伽莱(T. Callai)给出了一个非常复杂的证明.不久以后,凯里(L. M. Kelly) 才给出上述很简单的证明,其证法的关键就是利用极端原理.14.(2021·全国·九年级竞赛)已知A ,B ,C ,D 为平面上两两距离不超过1的任意4点,今欲作一圆覆盖这4点(即A ,B ,C ,D 在圆内或圆周上)问圆的半径最小该是多少?试证明之. 3 【详解】注意最不利的情形点A 、B 、C 、D 中有3点构成边长等于1的正三角形,覆盖此三角形的圆的半径不小33 (1)A 、B 、C 、D 共线,这时4点在一条长度不超过1的线段内,结论显然成立;(2)A 、B 、C 、D 中有3点(例如A 、B 、C )构成一个三角形,第4点D 在此三角形内,不妨设60C ∠≥︒,以AB 为弦作圆O ,使AB 所对的弓形弧(含C 的一侧)为60︒,则此圆O 覆盖A 、B 、C 、D 4点.作此圆直径2AE R =,则22222(2)1R R AE BE AB -=-=≤,即3R ≤,故A 、B 、C 、D 4点被一个半径不大3 (3)A 、B 、C 、D 是一个凸四边形的4个顶点,则A C ∠+∠,B D ∠+∠中必有一个不小于180︒,不妨设180B D ∠+∠≥︒,同(2)可证ABC 的外接圆半径3≤180B D ∠+∠≥︒知D 点也在这个圆内或圆周上,故A 、B 、C 、D 3 315.(2021·全国·九年级竞赛)任意凸四边形ABCD 中总存在一条对角线和一条边,以它们为直径的两个圆可以覆盖这个四边形.【答案】见解析【详解】四边形的4个内角中至少有一个90≥︒,不妨设90A ∠≥︒,以对角BD 为直径的圆O 必覆盖ABD △.若90C ∠≥︒,圆O 覆盖四边形ABCD 结论成立,若90C ∠>︒,则C 在圆外,圆O 与CD 、CB 中至少一条线段相交,不妨设圆O 与CD 交于E ,于点分别以BD 、BC 为直径的两个圆覆盖四边形ABCD .16.(2021·全国·九年级竞赛)设甲是边长为1的正三角形纸片,乙是边长为1的正方形纸片,丙是边长为1的正五边形纸片,丁是边长为1的正六边形纸片.证明:(1)不能用甲、乙、丙合起来盖住一个半径为1的圆;(2)能用甲、乙、丙、丁合起来盖住一个半径为1的圆.【答案】(1)见解析;(2)见解析【详解】(1)因为对于半径为1的圆,边长为1的正三角形至多盖住60︒的弧,边长为1的正方形至多盖住90︒的弧,边长为1的正五边形至多盖住120︒的弧(因边长为1的正五边形对角线的长<边长为1的正六边形对角线的长3=,而6090120360︒+︒+︒<︒,所以甲、乙、丙合起来不得盖住半径为1的圆.(2)如图所示,用甲、乙、丙、丁合起来可盖住半径为1的圆.17.(2021·全国·九年级竞赛)在一个半径等于6的圆内任意放入六个半径等于1的小圆.证明:其中总还有一块空位置,可以完整地放入一个半径为1的小圆.【答案】见解析【详解】分析 与证明设半径为6的大圆O 内任意放入6个半径为1的小圆,则小圆圆心都在以O 为中心,615-=为半径的圆内.如果大圆内无论怎样再放入一个半径为1的小圆7O ,都要与6个小圆中某个(16)i O i ≤≤重叠,那么7112i O O ≤+≤,即半径为5的圆将被6个半径为2的圆所覆盖.由图形重叠原理知6个小圆的总面积将不小于半径为5的圆的面积.但实际上226224255ππππ⋅=<=⋅,得到矛盾,于是命题得证.注:本例的证题关键是将外圆缩小,而将里圆扩大,这是解决嵌入问题的一种技巧,即收缩与膨胀技巧或裁边与镶边技巧.18.(2021·全国·九年级竞赛)将4张圆形纸片放在桌面上,使得其题中任何3张圆形纸片都有公共点,那么这4张圆形纸片是否一定有公共点?证明你的结论.【答案】见解析.【解析】【分析】【详解】设4张圆形纸片是(1,2,3,4)k O k ,其中1O ,2O ,3O 有公共点1A ,1O ,2O ,4O 有公共点2A ,1O ,3O ,4O 有公共点3A ,2O ,3O ,4O 公共点4A .(1)若1A ,2A ,3A ,4A 共线(如图顺序),因为1A ,3A 都是圆形纸片1O 与3O 的公共点,故线段13A A 在圆形纸片1O 与2O 的公共部分内,又24A A 都是圆形纸片2O 与4O 的公共点,故线段24A A 在圆形纸片2O 与4O 的公共部分内,所以线段23A A 上任意一点都是这4张圆形纸片的公共点.(2)若1A ,2A ,3A ,4A 中有一点在以其余3点为顶点的三角形的边界上或内部(如图).因为1A ,2A ,3A 都在1O 内,故123A A A △被圆形纸片1O 所覆盖,从而4A 在圆形纸片1O 内,而4A 是圆形纸片2O ,3O ,4O 的公共点,所以4A 是这张圆形纸片的公共点.(3)若1A ,2A ,3A ,4A 是一个凸四边形的4个顶点(如图),同上可知线段13A A 在圆形纸片1O 与3O 的公共部分内,线段24A A 在圆形纸片2O 与4O 的公共部分内,所以13A A 与24A A 的交点是这4张圆形纸片的公共点.总之,这4张圆形纸片一定有公共点.19.(2021·全国·九年级竞赛)平面上给定了若干个圆,它们覆盖的面积为1.证明:从中可选出若干个两两不重叠的圆,使它们覆盖的面积不小于19. 【答案】见解析.【解析】【分析】【详解】从给定圆中选出半径最大的圆1O ,其半径为1r ,面积为1S ,则与圆1O 有重叠的圆连同圆1O 一起覆盖的面积()211139M r S π≤=,即1119S M ≥.然后去掉与圆1O 重叠的圆,再从剩下的圆(圆1O 除外)选出半径最大的圆2O ,其半径为2r ,并将与圆2O 有重叠的圆去掉.这样经过有限步可得有限个两两不重叠的圆1O ,2O ,…k O ,它们覆盖的面积为()12121199k k S S S M M M ++⋅⋅⋅+≥++⋅⋅⋅+=. 20.(2021·全国·九年级竞赛)证明:一个边长为5的正方形可以被3个边长为4的正方形所覆盖.【答案】见解析.【解析】【分析】【详解】设正方形ABCD 的边长为5,先放置一个边长为4的正方形CEFG ,其中C 为原正方形ABCD 的一个顶点,E 在边CD 上,F 在正方形ABCD 内,G 在边CB 上.连AF ,再放置第二个边长为4的正方形111AB C D ,其中A 是原正方形的一个顶点,且使D 在射线11D C 上(如图),由勾股定理有:2211D D AD AD =-2211543D C =-=<.故D 在线段11D C 内,且1111431C D D C D D =-=-=.设11B C 与CD 交于H ,则1541DE CD CE DC DH =-=-==<,故E 在线段DH 内,从而E 被正方形111AB C D 覆盖.又11145B AD B AC FAD ∠>∠=︒=∠,即AF 在1B AD 内,且1224AF DE AB ==,故F 也被正方形111AB C D 覆盖,这就证明了梯形AFED 可以被一个边长为4的正方形111AB C D 所覆盖.同理,梯形AFGB 也可以被一个边长为4的正方形222AB C D 所覆盖,于是正方形ABCD 可被3个边长为4的正方形所覆盖. 21.(2021·全国·九年级竞赛)如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm 的正方形,高为30cm ,内有20cm 深的溶液,现将此容器倾斜一定角度α(图②),且倾斜时底面的一条棱始终在桌面上(图①,②均为容器的纵截面).(1)当30α=︒时,通过计算说明此溶液是否会溢出;(2)现需要倒出不少于33000cm 的溶液,当α等于60︒时,能实现要求吗?通过计算说明理由.【答案】(1)不会溢出,理由见解析;(2)不能实现要求,见解析.【解析】【分析】【详解】(1)当30α=︒时,如图a ,过C 作//CF BP 交AD 所在直线于F .在Rt CDF △中,20330,20cm,30cm FCD CD DF ∠=︒==<,所以点F 在线段AD 上,20330AF =此时容器内能容纳的溶液量为()3 ()203320203030201040003cm 2ABCF AF BC AB S ⎛⎫⎛+⋅=⋅=⋅⋅= ⎪ ⎪ ⎝⎭⎝⎭梯形.而容器中原有溶液量为()32020208000cm ⨯⨯=.因为3400038000⎛> ⎝⎭,所以当30α=︒时溶液不会溢出. (2)如图b ,当60α=︒时,过C 作//CF BP 交AB 所在直线于F .在Rt CBF △中,30cm 30BC BCF =∠=︒,,10320cm BF =<,所以点F 在线段AB 上,故溶液纵截面为Rt BFC △.因211503cm 2BFC S BC BF =⨯⨯=,容器内溶液量为315032030003cm =,倒出的溶液量为3(80003)3000cm -<,所以不能实现要求. 22.(2021·全国·九年级竞赛)甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头停泊,它们在一昼夜内到达的时间是等可能的,如果甲的停泊时间是1小时,乙的停泊时间是2小时,求它们中任何一艘都不需要等候码头空出的概率(精确到0.001).【答案】0.879.【解析】【分析】【详解】设自当天零时算起,甲、乙两船到达码头的时刻分别是x 和y ,则必须024,024x y ≤≤≤≤.我们视(),x y 为平面直角坐标系内的点,于是点(),x y 落在一个面积为224S =的正方形OABC 的内部或边界上(如下图).如果轮船不需要等候码头空出,那么当船甲先到时,船乙应迟来1个小时以上,即1y x -≥,即1y x ≥+;当船乙先到时,船甲应迟来2个小时以上,即2x y -≥,即2y x ≤-,即点(),x y 应在直线1y x =+的上方且在直线2y x =-的下方,也就是点(),x y 应在如图所示的两个三角形ADE 和CFG △中某一个的内部或边界上,故所求概率ADE CFGABCD S S p S +=四边形.而24123,24222CG CF AD AE ==-===-=,所以211222223231103220.879241152p ⨯⨯+⨯⨯===. 答:两船中任何一艘都不需要等候码头空出的概率为0.879.23.(2021·全国·九年级竞赛)把长为a 的线段任意分成3条线段,求这3条线段能够构成一个三角形的3条边的概率.【答案】14【解析】【分析】【详解】解 设其中两条线段的长为,x y ,则第3条线段的长为()a x y -+,于是,x y 的取值范围是0,0,0,0,0()0.x a x a y a y a a x y a x y a ⎧<<<<⎧⎪⎪<<⇔<<⎨⎨⎪⎪<-+<<+<⎩⎩ ① 要使3条线段构成一个三角形的3条边,其充要条件是其中任意一条线段的长度小于其余两条线段的长度之和.这等价于每条线段的长度都小于2a ,即 0,0,220,0,220().22a a x x a a y y a a a x y x y a ⎧⎧<<<<⎪⎪⎪⎪⎪⎪<<⇔<<⎨⎨⎪⎪⎪⎪<-+<<+<⎪⎪⎩⎩ ②将(),x y 视为平面直角坐标系的坐标,则满足条件①的点(),x y 在以()()()0,0,,0,0,O A a B a 为顶点的OAB 内.而满足条件②的点(),x y 在以(,),(0,),,0()2222a a a a C D E 为顶点的CDE △内,故所求概率为11222142CDE OAB a a CD DE Sp S a a OA OB ⨯⨯⨯====⨯⨯⨯.答:3条线段能构成一个三角形的三边的概率为14. 24.(2022·福建·九年级竞赛)如图,四边形ABCD 是平行四边形,∠DAC =45°,以线段AC 为直径的圆与AB 和AD 的延长线分别交于点E 和F ,过点B 作AC 的垂线,垂足为H .求证:E ,H ,F 三点共线.【答案】见解析【解析】【分析】如图:证明P ,A ,B ,C 四点共圆.可得CBE APC ∠=∠.①,证明C ,E ,B ,H 四点共圆,可得CHE CBE ∠=∠.②,证明C ,H ,F ,P 四点共圆,可得180APC CHF ∠=︒-∠.③,由①②③代换可得180CHE CHF ∠+∠=︒.可得结论;【详解】如图,延长BH 与直线AD 相交于点P ,连接CP .因为45DAC ∠=︒,BP AC ⊥,所以45BPA ∠=︒.又45BCADAC∠=∠=︒,所以BPA BCA ∠=∠,于是P ,A ,B ,C 四点共圆.所以CBE APC ∠=∠.①连接CE ,由AC 为圆直径,得90CEA CHB ∠=︒=∠,所以C ,E ,B ,H 四点共圆,于是CHE CBE ∠=∠.②连接CF ,由AC 为圆直径,得90CFP CHP ∠=︒=∠,所以C ,H ,F ,P 四点共圆,于是180APC CHF ∠=︒-∠.③由②,①,③,得180CHE CBE APC CHF ∠=∠=∠=︒-∠,所以180CHE CHF ∠+∠=︒.所以E ,H ,F 三点共线.【点睛】本题考查了圆内接罩边形的判断及性质,难度较大,解题的关键是构造圆内接四边形.。
初中平面几何竞赛题

初中平面几何竞赛题题目一:已知在△ABC 中,AB = AC,D 是BC 中点,E 是AD 上一点,求证:BE = CE。
解析:因为AB = AC,D 是BC 中点,根据等腰三角形三线合一性质,AD 垂直平分BC。
所以BE = CE(垂直平分线上的点到线段两端距离相等)。
题目二:在矩形ABCD 中,E、F 分别是AB、CD 上的点,且AE = CF,求证:四边形AECF 是平行四边形。
解析:因为四边形ABCD 是矩形,所以AB△CD,AB = CD。
又因为AE = CF,所以BE = DF。
且BE△DF,所以四边形BEDF 是平行四边形,所以BF△DE。
又因为AB△CD,AE = CF,所以四边形AECF 是平行四边形。
题目三:已知在圆O 中,弦AB 与弦CD 相交于点E,且△AEC = 45°,AE = 3,CE = 5,求圆O 的半径。
解析:连接OA、OC,过O 作OF△AB 于F,OG△CD 于G。
则AF = FB,CG = GD。
因为△AEC = 45°,所以△FEG = 45°,则OF = OG。
设圆O 的半径为r,在Rt△AOF 和Rt△COG 中,根据勾股定理可得:AF² + OF² = r²,CG² + OG² = r²。
又因为AF = (AE + EF)/2,CG = (CE - EG)/2,且EF = EG = OF = OG。
设OF = OG = x,则可得方程组:[(3 + x)/2]² + x² = r²,[(5 - x)/2]² + x² = r²。
解方程组可得r 的值。
题目四:在△ABC 中,△BAC = 90°,AD 是BC 边上的高,E 是BC 中点,求证:AE² = DE² + BD²。
【同一法】用同一法证平面几何竞赛题

∠B FD = 90°. 故 DG ⊥B E. 于是 ,
BG2 - GE2 = BD2 - DE2 = BD2 - DF2 = B F2 .
因此 ,结论成立.
2004 年第 2 期
例 5 设 ⊙O1 和 ⊙O2 外切于 W ,且它
们都与 ⊙O 内切 ,作 ⊙O1 和 ⊙O2 的一条外
公切线交 ⊙O 于点 A 、B ,作 ⊙O1 和 ⊙O2 的
B2 B3 = BB3 - BB2
=
AB
+
BB 1 2
-
AB 1
-
AB + BD 2
AD
=
AD +
DB 1 2
-
AB1 .
10
中等数学
同理 , C2 C3
=
AD +
DC1 2
-
AC1 .
由 AB1 DC1 有 内 切 圆 知 DB1 - AB1 =
DC1 - AC1 ,于是 , B2 B3 = C2 C3 .
点 , CC1 、BB1 相
交于 D. 证明 :当
且仅当 △ABD 和
△ACD 的内切圆
外切时 , 四边形
AB1 DC1 有 内 切
圆.
图2
(1999 ,保加利亚数学奥林匹克) 证明 : 当四边形 AB1 DC1 有内切圆 ⊙I 时 ,设 ⊙I 分别切 BB1 、CC1 于点 B3 、C3 , 设 △ABD的内切圆 ⊙I1 切 BB1 于点 B2 , △ACD 的内切圆 ⊙I2 切 CC1 于点 C2 . 则
圆 ⊙I′1 . 则由前面的证明可知 ⊙I′1 与 ⊙I2 外
切于 AD 上一点. 再由 ⊙I′1 与 ⊙I1 的圆心同
【九年级数学几何培优竞赛专题】专题1 巧构圆,妙解题【含答案】

第一章 圆专题1巧构圆,妙解题知识解读在处理平面几何中的许多问题时,常常需要借助圆的性质,问题才能解决.而有时候我们需要的圆并不存在,这就需要我们能利用已知的条件,借助图形的特点把实际存在的圆找出来,从而运用圆中的性质来解决问题,往往有事半功倍的效果,使问题获得巧解或简解,这是我们解题必须要掌握的技巧. 作辅助圆的常用依据有以下几种:①圆的定义:若几个点到某个固定点的距离相等,则这几个点在同一个圆上; ②有公共斜边的两个直角三角形的顶点在同一个圆上;③对角互补的四边形四个顶点在同一个圆上,简记为:对角互补,四点共圆;④若两个三角形有一条公共边,这条边所对的角相等,并且在公共边的同侧,则这两个三角形有公共的外接圆,简记为:同旁张等角,四点共圆.培优学案典例示范例1将线段AB 绕点A 逆时针旋转60°得到线段AC ,继续旋转(0120)αα<<得到线段AD ,连接CD . (1)连接BD .①如图1-1-1①,若α=80°,则∠BDC 的度数为;②在第二次旋转过程中,请探究∠BDC 的大小是否改变?若不变,求出∠BDC 的度数;若改变,请说明理由;(2)如图1-1-1②,以AB 为斜边作Rt △ABE ,使得∠B =∠ACD ,连接CE ,DE .若∠CED =90°,求α的值.图1-1-1②①EDCBADBA【提示】(1)①∠BDC =∠ADC -∠ADB ,利用“等边对等角及三角形内角和为180°”可求出∠BDC 为30°; ②由题意知,AB =AC =AD ,则点B ,C ,D 在以A 为圆心,AB 为半径的圆上,利用“一条弧所对的圆周角等于它所对的圆心角的一半”可快速求出∠BDC 仍然为30°;(2)过点A 作AM ⊥CD 于点M ,连接EM ,证明“点A ,C ,D 在以M 为圆心,MC 为半径的圆上”.跟踪训练如图1-1-2,菱形ABCD 中,∠B =60°,点E 在边BC 上,点F 在边CD 上.若∠EAF =60°,求证:△AEF 是等边三角形.角相等”获证.图1-1-2BFEDC A例2 (1)如图1-1-3①,正方形ABCD 中,点E 是BC 边上的任意一点,∠AEF =90°,且EF 交正方形外角平分线CF 于点F .求证:AE =EF ;(2)若把(1)中的条件“点E 是BC 边上的任意一点”,改为“点E 是BC 边延长线上的一点”,其余条件不变,如图1-1-3②,那么结论AE =EF 是否还成立?若成立,请证明;若不成立,请说明理由.①②图1-1-3A B E CFDFDCEBA【提示】连接AC ,AF ,显然∠ACF =∠AEF =90°,所以A ,E ,C ,F 四点在以AF 为直径的圆上. (1)如图1-1-4①,当点E 在BC 边上,则∠AFE =∠ACE =45°,于是△AEF 是等腰直角三角形,AE =EF 获证;(2)如图1-1-4②,当点E 在BC 边的延长线上,则∠F AE =∠FCE =45°,于是△AEF 是等腰直角三角形,AE=EF 获证.F图1-1-4②①【拓展】本题将“正方形”改为“正三角形”,“∠AEF =90°”相应改为“∠AEF =60°”,仍然可以运用构造“辅助圆”的思路.还可进一步拓展为“正n 边形”,360180AEF =-∠,仍然可延续这种思路,读者可自己完成.跟踪训练已知,将一副三角板(Rt △ABC 和Rt △DEF )如图1-1-5①摆放,点E ,A ,D ,B 在一条直线上,且D 是AB的中点.将Rt △DEF 绕点D 顺时针方向旋转角(090)αα<<,在旋转过程中,直线DE ,AC 相交于点M ,直线DF ,BC 相交于点N ,分别过点M ,N 作直线AB 的垂线,垂足为G ,H . (1)如图1-1-5②,当α=30°时,求证:AG =DH ; (2)如图1-1-5③,当α=60°时,(1)中的结论是否成立?请写出你的结论,并说明理由; (3)当090α<<时,(1)中的结论是否成立?请写出你的结论,并根据图1-1-5④说明理由.③④图1-1-5②①HGEAF D C (N )BFE DCBA【提示】本题除了常规解法外,还可考虑构造“辅助圆”.例3 已知,在△ABC 中,AB =AC ,过A 点的直线a 从与边AC 重合的位置开始绕点A 按顺时针方向旋转角θ,直线a 交BC 边于点P (点P 不与点B ,点C 重合),△BMN 的边MN 始终在直线a 上(点M 在点N 的上方),且BM =BN ,连接CN . (1)当∠BAC =∠MBN =90°时.①如图1-1-6①,当θ=45时,∠ANC 的度数为 ; ②如图1-1-6②,当45θ≠时,①中的结论是否发生变化?说明理由;(2)如图1-1-6③,当∠BAC =∠MBN ≠90°时,请直接写出∠ANC 与∠BAC 之间的数量关系,不必证明.③②C【提示】由于在旋转过程中不变的关系是:∠BAC =∠MBN ,AB =AC ,BM =BN ,易知∠ABC =∠ACB =∠BMN =∠BNM .由∠ACB =∠BNM 可知A ,B ,N ,C 四个点在同一个圆上(如图1-1-7),则∠ANC =∠ABC =1902BAC -∠,这样思考,所有问题都会迎刃而解.跟踪训练在△ABC 中,BA =BC ,∠BAC =α,M 是AC 的中点,P 是线段BM 上的动点,将线段P A 绕点P 顺时针旋转2α得到线段PQ . (1)若α=60°且点P 与点M 重合(如图1-1-8①),线段CQ 的延长线交射线BM 于点D ,请补全图形,并写出∠CDB 的度数;(2)在图1-1-8②中,点P 不与点B ,M 重合,线段CQ 的延长线与射线BM 交于点D ,猜想∠CDB 的大小(用含α的代数式表示),并加以证明;(3)对于适当大小的α,当点P 在线段BM 上运动到某一位置(不与点B ,M 重合)时,能使得线段CQ 的延长线与射线BM 交于点D ,且PQ =QD ,请直接写出α的范围.①图1-1-8②DP BACMQQM (P )CB A例4如图1-1-9,点A与点B的坐标分别是(1,0),(5,0),点P是该直角坐标系内的一个动点.(1)使∠APB=30°的点P有个;(2)若点P在y轴上,且∠APB=30°,求满足条件的点P的坐标;(3)当点P在y轴上移动时,∠APB是否有最大值?若有,求点P的坐标,并说明此时∠APB最大的理由;若没有,也请说明理由.图1-1-9【提示】(1)已知点A、点B是定点,要使∠APB=30°,只需点P在过点A、点B的圆上,且弧AB所对的圆心角为60°即可,显然符合条件的点P有无数个.(2)结合(1)中的分析可知:当点P在y轴的正半轴上时,点P是(1)中的圆与y轴的交点,借助于垂径定理、等边三角形的性质、勾股定理等知识即可求出符合条件的点P的坐标;当点P在y轴的负半轴上时,同理可求出符合条件的点P的坐标.(3)由三角形外角的性质可证得:在同圆或等圆中,同弧所对的圆周角大于同弧所对的圆外角.要∠APB最大,只需构造过点A、点B且与y轴相切的圆,切点就是使得∠APB最大的点P,然后结合切线的性质、三角形外角的性质、矩形的判定与性质、勾股定理等知识即可解决问题.跟踪训练已知,如图1-1-10①,,∠MON=60°,点A,B为射线OM,ON上的动点(点A,B不与点O重合),且AB=43,在∠MON的内部,△AOB的外部有一点P,且AP=BP,∠APB=120°.(1)求AP的长;(2)求证:点P在∠MON的平分线上.(3)如图1-1-10②,点C,D,E,F分别是四边形AOBP的边AO,OB,BP,P A的中点,连接CD,DE,EF,FC,OP.若四边形CDEF的周长用t表示,请直接写出t的取值范围.图1-1-10例5已知,在矩形ABCD中,AB=a,BC=b,动点M从点A出发沿边AD向点D运动.(1)如图1,当b=2a,点M运动到边AD的中点时,请证明∠BMC=90°;(2)如图2,当b>2a时,点M在运动的过程中,是否存在∠BMC=90°,若存在,请给与证明;若不存在,请说明理由;(3)如图3,当b<2a时,(2)中的结论是否仍然成立?请说明理由.、① ②③图1-1-11【提示】本题除了建立方程模型,将问题转化为方程是否有解的判断外,还可以通过构造辅助圆,将问题转化为直线与圆的位置关系来讨论.跟踪训练1.如图1-1-12,直线y=﹣x+3与x,y轴分别交于点A,B,与反比例函数的图象交于点P(2,1).(1)求该反比例函数的关系式;(2)设PC⊥y轴于点C,点A关于y轴的对称点为A′;①求△A′BC的周长和sin∠BA′C的值;②对大于1的常数m,求x轴上的点M的坐标,使得sin∠BMC1m .图1-1-12【提示】(1)①由直线y=-x+3写出OA=3,OB=3;由等腰直角三角形的边长关系,可得AB2;由PC⊥y轴,可得QC=1,BC=2;由对称知A'B=AB2,OA'=0A=3,然后用勾股定理求出A'C的长,也就可以求出△A'BC的周长;(2)②如果选用上一题的思路求∠BMC的正弦值,会陷入计算的麻烦,这里采用转化的思想,找到外接圆的半径,另外还应分类讨论。
初中数学竞赛专题复习第二篇平面几何第11章比例与相似试题1新人教版

第11章 比例与相似§11.1比例线段11.1.1★在ABC △中,角平分线AD 与BC 交于D ,AB c =,BC a =,CA b =,求BD 、CD 之长度(用a 、b 、f 表示). 解析 如图,易知有BD CD a +=,BD AB c CD AC b ==,故ac BD b c =+,abCD b c=+. AB D C11.1.2★已知:等腰梯形ABCD 中,M 、N 分别是腰AB 、CD 的中点,BD BC =,BD CA ⊥且交于E ,求证:CE MN =.解析 如图,不妨设1BE CE ==,则BC BD AC ==,1AE ED =,故2AD =,()112MN AD BC CE =+==. ADEMN BC11.1.3★在ABC △中,2AC AB =,A ∠的平分线交BC 于D ,过D 分别作AB 、AC 的平行线交AC 、AB 于F 、E ,FE 和CB 的延长线交于G ,求证:EF EG =. 解析 如图,由ED AC ∥,及AD 平分BAC ∠,知12GE BE BE BD AB GF DF AE CD AC =====,故2GF GE =,因此EF EG =.AEFGBDC11.1.4★设D 为ABC △的边BC 的中点,过D 作一直线,交AB 、AC 或其延长线于E 、F ,又过A 作AG BC ∥,交FE 的延长线于G ,则EG FD GF DE ⋅=⋅.G AE BDCF解析 由平行知GE AG AG GFDE BD CD DF===. 于是由第一式与最后一式,转化为乘法,即可得结论. 11.1.5★已知O 是平行四边形ABCD 内的任意一点,过点O 作EF AB ∥,分别交AD 、BC 于E 、F ,又过O 作GH BC ∥,分别交AB 、CD 于G 、H ;连结BE ,交GH 于P ;连结DG ,交EF 于Q .如果OP OQ =,求证:平行四边形ABCD 是菱形. 解析 如图,易知OP EO GA BF EF AB ==,OQ GO AEDH GH AD==. 由于AE BF =,GA DH =,故OP AB GA BF AE DH OQ AD ⋅=⋅=⋅=⋅,于是AB AD =,四边形ABCD 是菱形.A E DQGH POB F C11.1.6★ABC △中,AB AC >.AD 是BAC ∠的角平分线.G 是BC 的中点,过G 作直线平行于AD 交AB 、AC 或延长线于E 和F .求证:2AB ACBE CF +==. 解析 如图,易知G 比D 靠近B ,E 在AB 上,而F 在CA 延长线上.易知12BG BC =,而AB BC BD AB AC ⋅=+,故2BE BG AB ACAB BD AB+==,同理,CF 也是此值. F AEB G D C评注 不用比例线段的方法是:延长EG 一倍至P ,则CP BE =,再证AEF △和FCP △均为等腰三角形.11.1.7★凸四边形ABCD 中,ADC ∠,90BCD ∠>︒,BE 平行于AD 交AC 延长线于点E ,AF 平行于BC 交BD 延长线于点F ,连结E 、F ,证明:EF CD ∥. 解析 如图,设AC 、BD 交于O ,则由平行线性质,知FO AO BO CO =,AOFO BO CO=⋅,同理,BO EO AO DO =⋅,故FO DOEO CO=,故EF CD ∥. AF DOB CE11.1.8★★如图,在ABC △中.AB AC =,BP 、BQ 为B ∠的三等分角线,交A ∠的平分线AD 于P 、Q ,连结CQ 并延长交AB 于R ,求证:PR QB ∥.ARP Q BDC解析 易知ABC △关于AD 对称.又设QBC QCB θ∠=∠=,则2ABQ RQB θ∠==∠,故RQ RB =,于是由角平分线之性质,知AR AR AC AB APBR RQ CQ BQ PQ====,于是PR QB ∥. 11.1.9★★梯形ABCD 中,AD BC ∥(AD BC <),AC 和BD 交于M ,过M 作EF AD ∥,交AB 、CD 于E 、F ,EC 和FB 交于N ,过N 作GH AD ∥,交AB 、CD 于G 、H .求证:1212AD BC EF GH+=+.A DE MF GNHBC解析 11EM AM DM BM EM BC AC DB DB AD ===-=-,故111EM AD BC =+,同理111FM AD BC =+,故11112EF AD BC ⎛⎫=+ ⎪⎝⎭,同理11112GH EF BC ⎛⎫=+ ⎪⎝⎭,两式相加并整理即得结论.11.1.10★设a 、b 、c 分别是ABC △的三边的长,且a a bb a b c+=++,求它的内角A ∠、B ∠. 解析 由条件,得22a ab ac ab b -+=+,即()2b a a c =+,所以b a ca b+=. 如图,延长CB 至D ,使BD AB =,于是CD a c =+.因此在ABC △与DAC △,AC DCBC AC=,且C ∠为公共角,所以ABC △∽DAC △,BAC D ∠=∠.而BAD D ∠=∠,故22ABC D BAD D BAC ∠=∠+∠=∠=∠.CABbca D11.1.11★设凸四边形ABCD ,对角线交于E ,过E 作直线与BC 平行,交AB 、CD 及DA 延长线于G 、H 、F .若1GE =,2EH =,求EF .DA FGEHBC K解析 延长DF 与CB 延长线交于K ,则有FG GE KB FEBC EH==. 设EF x =,则1FG x =-,代人上式,便得12xx -=.故2EF x ==. 11.1.12★★AP 为等腰三角形ABC 底边BC 上的高,CD 为ACB ∠的平分线,作DE BC ⊥于E ,又作DF DC ⊥与直线BC 交于F ,求证:4CFPE =. 解析 如图,设AB AC m ==,BC n =,则由角平分线性质知PE AD ACBP AB AC BC==+, 故()2mnPE m n =+.又取FC 中点G ,连结DG ,1902F C ∠=︒-∠,DG FG =,故1902FDG C ∠=︒-∠,DGF C ∠=∠,故DG AC ∥,从而DG BD BC AC AB AC BC ==+,故mnDG m n=+.于是224FC FG DG PE ===.ADF B EG P C11.1.13★★足球场四周有四盏很高的灯,在长方形的四角,且一样高,求某一运动员任何时刻的四个影子长之间的关系.跳起来呢?解析 设运动员P 在矩形球场ABCD 内,如图(a),过P 作MPN BC ∥,M 在AB 上,N 在CD 上,则22222222AP BP AM BM DN CN PD PC -=-=-=-,或2222AP CP BP DP +=+.A MBCND P图(a)又设灯高为H ,运动员身高为h ,点A 处的灯造成的影子长为PA ′,如图(b),则A P h AA H'=',得A P h PA H h '=-,同理B PC PD P hPB PC PD H h'''===-,故四个影子的关系是2222A P C P B P D P '+'='+'.图(b)图(c)A'hHAP A'AA''P lh H跳起来时,不妨设脚底离地l ,此时点A 处的灯造成的影子长度为A ′A ″,如图(c),则h l A P PA H h l +'=--,lA P PA H l"=-,于是A A A P A P '"='-"h l l PA H h l H l +⎛⎫=- ⎪---⎝⎭()()Hh PA H h l H l =---, 同理B B C C D D PB PC PD '"'"'"==()()Hh H h l H l =---,所以A ′2A "+2C C '"=22B B D D '"+'"仍旧成立.11.1.14★★求日高公式.解析 如图所示,设太阳高度为RD x =,杆AB =A ′B =h 直立在地上,影子的长度分别为BC a =,B ′C ′b =,两杆距离为d .所谓日高公式就是用a 、b 、d 、h 表示x ,这里假定大地为平面,且AB 、A ′B ′与R 在同一平面上.RxDB'A A'hhCB易知CB AB CD RD =,代入得a h a BD x =+,故1x BD a h ⎛⎫=- ⎪⎝⎭;同理,B ′1x D b h ⎛⎫=- ⎪⎝⎭.由BD B -′D B =B ′d =,代入得()1x a b d h ⎛⎫--= ⎪⎝⎭,由此解得1d x h a b ⎛⎫=+⎪-⎝⎭. 11.1.15★★设梯形ABCD ,E 、F 分别在AB 、CD 上,且AD EF BC ∥∥,若3AD =,7BC =,5AB =,6CD =,梯形AEFD 和梯形EBCF 的周长相等,求EF .解析 如图,作平行四边形DABH ,H 在BC 上,则5DH AB ==,4CH =.设DH 与EF 交于G .A DEG FB HC易知梯形AEFD 的周长为DGF △的周长加上6,梯形EBCF 的周长为梯形FGHC 的周长加6,故DGF △的周长=梯形GHCF 的周长,也即DG DF DHC +=△周长的一半即152. 又56DG DH DF CD ==,故6154511211DF =⨯=.453046611DF GF CH CD =⋅=⨯=,306331111EF =+=.11.1.16★★如图,已知ABC △中,AD 、CE 交于F ,BF 、ED 交于G ,过G 作GMN BC ∥,交CE 于M ,交AC 于N ,求证:GM MN =.AEP BDCG K MNF解析 设AD 与GM 交于K ,AB 与直线NG 交于P ,则KN CD KMPK BD GK==. 于是1PK PG CD GM MN KN KM KM KM PG PG GM GK GK BD PG ⎛⎫=-=-=⋅=⋅=⋅=⎪⎝⎭. 11.1.17★四边形ABCD 为正方形,E 、F 在BC 延长线上,CE CD =,CF CA =,H 、G 分别是CD 、DE 与AF 的交点.求证:CHG △为等腰三角形. 解析 如图,不妨设正方形边长为1,则CF ,1CE =,1EF .ADH JBCEFG作GJ CF ∥,交CD 于J.则JG DG AD CE DE AD EF ==+于是12HG JG HF CF ===,即G 为直角三角形斜边HF 之中点,于是GH GC =. 11.1.18★★在ABC △中,4AB =,2BC =,3CA =,P 是ABC △内一点,D 、E 、F 分别在AB 、BC 、CA 上,且PD BC ∥,PE AC ∥,PF AB ∥.若PD PE PF ==,求PD . 解析 如图,延长CP 交AB 于C ′(同理定义A ′、B ′,图中未画出),设PD PE PF x ===,则2x C P CC '=',同理,4x B P BB '=',3x PA AA '=',由于1PA PB PC AA BB CC '''++=''',故1234x x x ++=,1213x =. AC'FPDE B C11.1.19★ABC △内有一点O ,AO 的延长线交边BC 于点A ′,BO 的延长线交边AC 于点B ′,CO 的延长线交边AB 于点C ′.若AO BO CO k OA OB OC ++=''',求AO BO COOA OB OC ⋅⋅'⋅'⋅'的值(用k 表示). 解析 如图,设AO x OA =',BO y OB =',CO z OC =',则x y z k ++=,而1OA OB OCAA BB CC ''++=''',即1111111x y z++=+++,展开得 ()32x y z xy yz zx ++++++()1x y z xy yz zx xyz =+++++++,故22xyz x y z k =+++=+.AC'B'B A'CO11.1.20★已知ABC △的三边长分别为a 、b 、c ,三角形中有一点P ,过P 作三边的平行线,长度均为x ,试用a 、b 、c 来表示x .解析 设AP 延长后与BC 交于A ′(同理定义B ′与C ′),则1x AP PA a AA AA '==-'',同理1x PB b BB '=-', 1x PC b CC '=-',三式相加,得11132PA PB PC x a b c AA BB CC '''⎛⎫⎛⎫++=-++= ⎪ ⎪'''⎝⎭⎝⎭,所以2abcx ab bc ca=++.ABCPA'评注 P 存在的条件是x a <,b ,c ,代人得:1a 、1b 、1c可组成三角形三边之长. 11.1.21★已知D 、E 、F 分别是锐角三角形ABC 的三边BC 、CA 、AB 上的点,且AD 、BE 、CF 相交于点P ,6AP BP CP ===.设PD x =,PE y =,PF z =,28xy yz zx ++=,求xyz 的大小.解析 由熟知结论1PD PE PFAD BE CF++=,得1666x y z x y z ++=+++,因此(6)(6)(6)(6)(6)(6)x x z y x z z x y ++++++++=(6)(6)(6)x y z +++,即 1083()xyz xy yz zx =-++=24.11.1.22★如图,正方形ABCD 边长为1,Q 为BC 延长线上一点,QA 与CD 、BD 分别交于点P 、E ,QO (点O 是AC 与BD 交点)与CD 交于点F ,若EF AC ∥,求AP 的长.ADEPFOCBQ解析 连结DQ ,则由EF AC ∥,得EQ EF EF DEQA AO CO DO===,于是DQ AC ∥,CQ AD =,P 为CD 中点,所以AP =. 11.1.23★★如图,已知EF BC <,G 、D 分别在EF 、BC 上,则下面任两条可推出第三条:(1)BE 、DG 、CF 共点;(2)EF BC ∥;(3)EG BDFG CD=. AA'E'EGF F'B DC解析 (1),(2)⇒(3):EF BC ∥,则EG AG GF BD AD CD ==,故EG BDGF CD=. (2),(3)⇒(1):EG BD FG CD =⇒1EG FG EFBD CD BC==<,故可设BE 、DG 延长后交于A ,DG 、CF 延长后交于AG EG GF AD BD CD ===A G A D '',AG A GGD GD'=,A 与A '重合. (1),(3)⇒(2):若EF 与BC 不平行,作E 'GF 'BC ∥,E '在AB 上,F '在AC 上,则有E G BD EG F G CD FG'==',得EE 'FF ∥',即AB AC ∥,矛盾. 11.1.24★ABC △中,AK 为A ∠的平分线,在BA 、CA 上取BD CE =,G 、F 分别为DE 、BC 的中点,则GF AK ∥.解析 如图,连结BE ,设BE 中点为M ,连结CM 、FM ,则12GM BD =∥12CE MF ∥,所以GM FM =,且GMF GME EMF ABE ∠=∠+∠=∠+180180BEC BAC ︒-∠=︒-∠. 取AC 上的点S ,使KS AB ∥,则等腰GMF △∽等腰AKS △,且对应边KS GM ∥,AS MF ∥,故第三边也平行,即GF AK ∥.AE SGD MBFKC11.1.25★★★已知:ABC 中,90A ∠=︒,D 为BC 上一点,且非BC 中点,211AD BD CD=+,P 为AD 中点,求证:2BDA BAD ∠=∠,PD 平分BPC ∠.解析 如图,作BR AD ∥,与CA 延长线交于R ,延长CP 交BR 于Q ,则由AP PD =,AD RB ∥,有RQ BQ =.又90RAB ∠=︒,故AQ BQ =.由条件,知111BCPD BD CD BD CD++=⋅,于是PD CD PD BD BC BQ ==,BD BQ AQ ==,四边形AQBD 乃等腰梯形(若四边形AQBD 是菱形,则C ∠=QAR R DAC ∠=∠=∠,D 为BC 中点,与题设矛盾),12BAD QBA QAD ∠=∠=∠12BDA =∠.又P 为AD 中点,显然(比如由全等)有BPD APQ DPC ∠=∠=∠.RQBDCAP11.1.26★★★已知M 、N 分别为矩形ABCD 的边AD 、BC 的中点,CD 延长线上有一点P ,PM 延长后与AC 交于Q .求证.NM 平分PNQ ∠.解析 如图,设AC 与MN 交于O ,则MO NO =,过O 作OR MN ⊥,交QN 于R ,则MR NR =.AMDPROB N C又OR BC ∥,MO PC ∥,故QM QO QRMP OC RN==,于是MR PN ∥,由于OR 将MN 垂直平分,于是RNO RMO PNM ∠=∠=∠. 11.1.27★★在ABC △中,3A B ∠=∠,求证:2a b b c a b -⎛⎫= ⎪+⎝⎭,a 、b 、c 为ABC △的对应边长.解析 如图,延长CA 至D ,使223D BAC ABC ∠=∠=∠,于是DBA ABC ∠=∠,故CD BC =,AD a b =-.ABD △中,2D DBA ∠=∠,则2()AB AD AD BD =+.又由角平分线性质BD AD BC AC =,得()a a b BD b-=,22a b AD BD b -+=,代人前式,得222()()a b a b c b --=,即得结论.DACB评注 ABC △中,22()A B BC AC AC AB ∠=∠⇔=+,证明如下:延长CA 至D ,使AD AB =,于是2()D ABC BC AC AC AD ∠=∠⇔=+或()AC AC AB +.11.1.28★★已知AB CD ∥,E 、F 分别是AB 、CD 上任两点,DE 、FB 延长后交于M ,AF 、EC 延长后交于N ,求证:若AB CD ≠,则AD 、BC 、MN 共点;若AB CD =,则AD BC MN ∥∥.解析 如图,设AE a =,BE b =,CF c =,DF d =,延长AB 、DC 分别与MN 交于P 、Q ,设BP x =,CQ y =.由AP FQ ∥知a cb x y =+,同理d bc y x=+,即ay bc cx =+,dx bc by =+,于是ay cc dx by -=-,a b c d x y ++=,或AB CDBP CQ=.若AB CD =,则BP CQ =,又BP CQ ∥,做AD BC PQ ∥∥;AB CD ≠,由AB ∥CD ,得AD 、BC 、MN 共点(见题11.1.23).ADE FB C MPQN11.1.29★★正三角形ABC ,D 、E 、F 是BC 、CA 、AB 的中点,P 、Q 、R 分别在EF 、FD 、DE 上,A 、P 、Q 共线,B 、Q 、R 共线,C 、R 、P 共线,求FPPE. 解析 如图,不妨设ABC △边长为2,PF x =,QD y =,ER z =,则1PE x =-,1FQ y =-,1DR z =-.AE PQRBDCF由PE ER CD RD =,得11z x z -=-,同理11y z y -=-,11x y x -=-,于是121xy x -=-,121y x yx -=-,13111111212x x x z x x--=-=-=---,x y z ===.所以1x -=1FPx PE x ===- 11.1.30★★任给锐角ABC △,问在BC 、CA 、AB 上是否各存在一点D 、E 、F ,使FD BC ⊥,DE AC ⊥,EF AB ⊥?解析 这样的DEF △是存在的.作法如下:在BC 上任取一点D ′,作D ′E ′AC ⊥于E ′,分别过D ′、E ′作BC 、AB 的垂直线交于点F ′.A RF SB D'D CEE'F'若F ′恰在AB 上,则D ′、E ′、F ′,即为满足条件的三点D 、E 、F ;若,F ′不在AB 上,设C 、F ′,所在直线与AB 交点为F (因为ABC △是锐角三角形,所以交点必在AB 上),过F 分别作BC 、AB 的垂线交BC 、AC 于D 、E ,则FD BC ⊥,EF AB ⊥,连结DE ,易知CD CF CECD CF CE ==''',得DE ∥D ′E ′,由作法D ′E ′AC ⊥,所以DE AC ⊥,D 、E 、F 满足条件.11.1.31★★★已知凸四边形内有一点P ,APB ∠、BPC ∠、CPD ∠、DPA ∠的平分线分别交AB 、BC 、CD 、DA 于K 、L 、M 、N ,求证:四边形KLMN 为平行四边形的充要条件是P 为AC 、BD 的中垂线的交点.解析 若P 为AC 、BD 的中垂线之交点,则AP CP =,BP DP =,于是AK AP AP ANBK BP DP ND===,于是KN BD ∥,同理ML ∥BD ,又同理MN AC KL ∥∥,故四边形KLMN 为平行四边形.D反之,若四边形KLMN 为平行四边形,由于AN DM AP AK BLND MC CP KB LC⋅==⋅,故由梅氏定理,若MN 、KL 不与AC 平行,它们将与AC 交于同一点,这与NM KL ∥矛盾,因此NM AC ∥,AP CP =,同理BP DP =,故P 在AC 、BD 的中垂线上. 11.1.32★★★已知梯形ABCD 中,AD ∥BC ,E 、F 分别在AB 、CD 上,求证:若ED BF ∥,则AF CE ∥.又此时若ED 、AF 交于M ,CE 、BF 交于N ,问三直线AB 、MN 、CD 共点的条件.解析 如图(a),不妨议BA 、CD 延长后交于P ,于是有PQ PD BP PC =,PE PDPB PF=.PA D M EFN BC图(a)于是PA PC PB PD PE PF ⋅=⋅=⋅,由此可得PA PFPE PC=,故AF CE ∥. 因为四边形MENF 为平行四边形,MN 过EF 的中点,若P 、M 、N 共线,则由塞瓦定理,有AD EF ∥BC ∥.下面刻画E 或F 的位置,如图(b),设BD 与EF 交于Q ,AEk EB=,则由ED BF ∥,DF DQ EQ k FC BQ FQ ===,而111EQ AD K =++,1QF k BC k =+,故1ADk k BC =⋅,此即AEBE= ADEFQBC图(b)11.1.33★★如图,已知ABC △中,AD 、BE 、CF 交于G ,FH AD ∥,FH 延长后与ED 的延长线交于K ,求证:FH HK =.AFEMG N BH DJ CK解析 作EJ AD ∥,EJ 与CF 交于N ,FK 与BE 交于M ,则由平行,知FH AD EJFM AG EN==,故FH FM FG HD HKEJ EN GN DJ EJ====,于是FH HK =.11.1.34★★★已知ABC △,AD 、BE 、CF 是角平分线,M 、N 在BC 上,且FM AD EN ∥∥,求证:AD 平分MAN ∠.AF EPI TSBMDN C解析1 设ABC △内心为I ,FM 与BE 交于S ,EN 与CF 交于T ,连结EF ,交AD 于P .由角平分线及平行性质,有FM AD EN FS AI ET ==,故有FM FS SI FP AFEN ET IE PE AE====,又11802AFM BAC ∠=︒-∠∠AEN =∠,故AFM △∽AEN △,于是FAM EAN ∠=∠,于是AD 平分MAN ∠.解析2 由角平分线性质,知AE AB EC BC =,AF AC BF BC =,于是AE AB CE AF AC BF =⋅.又易见FM BFAD AB=,EN CE AD AC =,故EN CE AB FM BF AC ⋅=⋅,于是AE ENAF FM =,以下同解析1. 评注 注意解析1更好些,因为只要求AD 平分BAC ∠.不要求I 是内心,本题结论也成立.于是本题的逆命题是,由AD 平分MAN ∠得出AD 平分BAC ∠,而不能证明I 是内心.这个逆命题也是正确的,读诗者不妨一试.11.1.35★★P 为XOY ∠内一点,A 、B 在OX 上,C 、D 在OY 上,线段AD 、BC 交于P .若1111OA OD OB OC+=+,则OP 平分XOY ∠,反之亦然. 解析 如图,作平行四边形PQOR ,Q 、R 分别在OX 、OY 上.设QP OR a ==,OQ PR b ==. 此时易得1a b a b OD OA OC OB +=-+,因此1111a b a b b b OD OD OA OC OC OB --⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭,于是a b a bOD OC --=.但OD OC >,故a b =.所以平行四边形PQOR 是菱形,OP 为XOY ∠之平分线.XYBA Q POR C反之,可设所作平行四边形PQOR 为菱形.设菱形边长为n ,则1a PR RD aOA OA OD OD===-,即得111OA OD a +=.同理,111OB OC a+=,于是命题得证.11.1.36★★已知ABC △,三边分别为a 、b 、c ,AD 是角平分线.求AD 之长(用a 、b ,c 表示)解析 如图,延长AD 至E ,使E B ∠=∠,于是A 、B 、E 、C 共圆,又ABD △∽AEC △,故AB AC ⋅=()AD AE AD AD DE ⋅=+=22AD AD DE AD BD CD +⋅=+⋅.ABDCE设AB c =,AC b =,则ac BD b c =+,abCD b c=+,故AD ===. 11.1.37★★在ABC △中,AD 、AE 三等分BAC ∠,且BD =2,DE =3,EC =6,求AB 的长. 解析 如图,设AB x =,AD y =,则由角平分线性质知32AE x =,2AC y =. AB D E由于2AB AE AD BD DE ⋅-=⋅,即22362x y -=,同理2292184y x -=,消去y ,得AB x ==11.1.38★★★已知平行四边形ABCD ,点E 是点B 在AD 上的垂足,点F 在CD 上,90AFB ∠=︒,EG AB ∥,点G 在BF 上,点H 是AF 与BE 的交点,又DH 延长后与CB 的延长线交于点I ,求证:FI GH ⊥.解析 如图,作IK HF ⊥.对OKF △与HFG △来说,KF FG ⊥,IK HF ⊥,而90HFG IKF ∠=︒=∠,如果能证明两三角形(顺向)相似,那么第三组对应边OF 与HG 就垂直了,于是只需证明KF IK FG HF =或KF FGIK HF=.事实上设AF 、BC 延长后交于点J ,且设J θ∠=∠,则易知cos KF BO θ=,sin KI IJ θ=,于是cot cot cot KF BI DE FGIK IJ AD FBθθθ===,又HB BJ ⊥,故HBF θ∠=,于是tan FB HF θ=,代人上式,即得KF FGKI HF=. θθθCJ IB G KF HAE D§11.2相似三角形11.2.1★已知,B 是AC 中点,D 、E 在AC 的同侧,且ADB EBC ∠=∠,DAB BCE ∠=∠,证明:BDE ADB ∠=∠.解析 如图,易知DBE DBC EBC A ADB EBC A ∠=∠-∠=∠+∠-∠=∠. 又ABD △∽BDE △,故BD AD ADBE BC AB==,于是ADB △∽BDE △,故BDE ADB ∠=∠. DEA B C11.2.2★已知αβ+=α′+β′<180︒,sin sin αβ=sin sin αβ'',则αα=′,ββ='. 解析 如图,作ABC △与A △′B ′C ′,使B α∠=,B ∠′α=′,C β∠=,C ∠′β=',则由条件A A ∠=∠′,且sin sin sin sin AB A B AC A C ββαα'''===''',故ABC △∽A △′B ′C ′,从而B B ∠=∠′,C C ∠=∠′.此即αα=′,ββ=′.AB C A'B'C'评注 这个结果用途极广.11.2.3★线段BE 分ABC △为两个相似的三角形,求ABC △的各内角. 解析 如图,不妨设BCE △∽ABE △,BCE △比较“大”.BA EC由于BEA ∠>EBC ∠及C ∠,故只能有BEA CEB ∠=∠,于是BE AC ⊥.ABE CBE ∠=∠不可能(否则ABE △≌BCE △),故ABE C ∠=∠,CBE A ∠=∠,90ABC ∠=︒,BCAB=ABC △三内角为:30︒、60︒、90︒. 11.2.4★★设ABC △中,D 在BC 在上,且22BD AD BC AC =,求证:ABD △∽CBA △. AEB D C解析 过D 作DE AC ∥,E 是AB 是一点.于是BD EDBC AC=,代入条件并整理,即得ED ADAD AC=. 又EDA DAC ∠=∠,于是EDA ∠∽DAC △,于是BAD C ∠=∠,故ABD △∽CBA △.。
初中数学竞赛专题复习第二篇平面几何第9章三角形试题 新人教版

第9章三角形§9.1全等三角形9.1.1★已知等腰直角三角形ABC ,BC 是斜边.B ∠的角平分线交AC 于D ,过C 作CE 与BD 垂直 且交BD 延长线于E ,求证.2BD CE =.解析如图,延长CE 、BA ,设交于F .则FBE ACF ∠=∠,AB AC =,得ABD ACF △△≌,CF BD =. 又BE CF ⊥,BE 平分FBC ∠,故BE 平分CF ,E 为CF 中点,所以2CE FC BD ==.9.1.2★在ABC △中,已知60A ∠=︒,E 、F 、G 分别为AB 、AC 、BC 的中点,P 、Q 为ABC △形外两点,使PE AB ⊥,2AB PE =,QF AC ⊥,2ACQF =,若1GP =,求PQ 的长. F AE DBC解析如图,连结EG 、FG ,则EG AC ∥,FG AB ∥,故150PEG QFG ∠=︒=∠.又12QF AC EG ==,12PE AB FG==,故PEG GFQ △△≌,所以PG GQ =,30EGP FGQ FQG FGQ ∠+∠=∠+∠=︒,又60EGF ∠=︒,所以90PGQ ∠=︒,于是PQ ==ACG QPEF9.1.3★在梯形ABCD 的底边AD 上有一点E ,若ABE △、BCE △、CDE △的周长相等,求BCAD. 解析作平行四边形ECBA ',则A BE CEB '△△≌,若A '与A 不重合,则A '在EA (或延长线)上,但由三角形不等式易知,A '在EA 上时,ABE △的周长>A BE '△的周长;A '在EA 延长线上时,ABE △的周长A BE '<△周长,均与题设矛盾,故A 与A '重合,AE BC ∥,同理ED BC ∥,12BC AD =.B CEDAA'9.1.4★★ABC △内,60BAC ∠=︒,40ACB ∠=︒,P 、Q 分别在边BC 、CA 上,并且AP 、BQ 分别是BAC ∠、ABC ∠的角平分线.求证.BQ AQ AB BP +=+. 解析延长AB 到D ,使BD BP =,连结DP .易知80ABC ∠=︒,所以40QBC ACB ∠=︒=∠,AC AQ QC AQ QB =+=+.ABCDQP因1402BDP BPD ABC ACB ∠=∠=∠=︒=∠,所以ADP ACP △△≌,AC AD AB BD AB BP ==+=+. 于是BQ AQ AB BP +=+.9.1.5★★设等腰直角三角形ABC 中,D 是腰AC 的中点,E 在斜边BC 上,并且AE BD ⊥.求证. BDA EDC ∠=∠.解析如图,作BAD ∠的平分线AF ,F 在BD 上.ABCEFD由于45BAF ACE ∠=︒=∠,AB AC =,ABF CAE ∠=∠,故ABF CAE △△≌,故EC AF =. 又45C FAD ∠=∠=︒,AD CD =,于是AFD CED △△≌,于是ADB EDC ∠=∠.9.1.6★★设ABE △、ACF △都是等腰直角三角形,AE 、AF 是各自的斜边,G 是EF 的中点,求证.GBC △也是等腰直角三角形.解析如图,作AQ 、GP 、EM 、FN 分别垂直于直线BC ,垂足为Q 、P 、M 、N .AE FGMBQ PC由90EBM ABQ BAQ ∠=︒-∠=∠,AB BE =,EMB BQA △△≌,故有EM BQ =,BM AQ =.同理FN QC =,CN AQ =,所以BM CN =, EM FN BQ QC BC +=+=. 又EG GF =得BP CP =,且()1122GP EM FN BC =+=,故GP BP CP ==.又由GP BC ⊥,故 结论成立.9.1.7★★已知AB AC ⊥,AB AC =,D 、E 在BC 上(D 靠近B ),求证.222DE BD CE =+的充要条件是45DAE ∠=︒.ABEFC解析如图,作FC BC ⊥,且FC BD =,则45ACF B ∠=︒=∠,又AB AC =,故ABD ACF △△≌,AD AF =,且490D F BAC ∠=∠=︒.若45DAE ∠=︒,则45EAF ∠=︒,因AD AF =,得ADE AFE △△≌,则222222DE EF EC FC EC BD ==+=+.反之,若222DE EC BD =+,由222EF EC FC =+得EF DE =.又AD AF =,故ADE AEF △△≌,又90DAF ∠=︒,于是45DAE ∠=︒.9.1.8★★两三角形全等且关于一直线对称,求证.可以将其中一个划分成3块,每一块通过平移、 旋转后拼成另一个三角形.解析如图,设ABC △与A B C '''△关于l 对称,分别找到各自的内心I 、I ',分别向三边作垂线ID 、IE 、 IF 与I D ''、I E ''、I F '',于是6个四边形AFIE ……均为轴对称的筝形,且四边形AFIE ≌四边形A E J F '''',所以两者可通过平移、旋转后重合;同理,另外两对筝形也可通过平移、旋转后重合.AECDF BA'B'C'D'F'E'l l'l9.1.9★★★已知.两个等底等高的锐角三角形,可以将每个三角形分别分成四个三角形,分别涂上红色、蓝色、黄色和绿色,使得同色三角形全等.解析如图,设BC B C ''=,A 至BC 距离等于A '至B C ''距离,取各自的中位线FE 、F E '',则FE FE '=.由ABC △、A B C '''△均为锐角三角形,可在BC 、B C ''上各取一点D 、D ',使图中标相同数字的角相等,于是AEF D E F '''△△≌,DEF A E F '''△△≌,FBD FD B ''△△≌,EDC E C D '''△△≌. 评注还有一种旋转而不是对称的构造法.A BC DEF A'B'D'C'E'F'123451465264152432519.1.10★已知ABC △与A B C '''△中,A A '∠=∠,BC B C ''=,ABC A B C S S '''=△△,ABC △与A B C '''△是否一定全等?A B CA'解析如图,让B 与B '重合,C 与C '重合,A 、A '在BC 同侧,若A 与A '重合,则ABC A B C '''△△≌;否则由条件知四边形ABCA '为梯形和圆内接四边形,于是它是一个等腰梯形,于是ABC A CB '∠=∠,AB A C '=,ABC A C B '''△△≌.综上,可知ABC △与A B C '''△全等. 评注本题也可以运用三角形面积公式、余弦定理结合韦达定理来证明.9.1.11★★如图所示,已知ABC △、CED △均为正三角形,M 、N 、L 分别为BD 、AC 和CE 的中点,求证.MNL △为正三角形.ABEDM TS CN L解析如图,设BC 、CD 中点分别为S 、T ,连结NS 、SM 、MT 、TL .则四边形CSMT 为平行四 边形,设BCD θ∠=,则60180240NSM LTM θθ∠=︒+︒-=︒-=∠,360120240NCL θθ∠=︒-︒-=︒-,又NC SN SC MT ===,LC LT CT SM ===,故CNL SNM TML △△△≌≌, NL NM ML ==,于是MNL △为正三角形.评注注意有时S 在MN 另一侧,此时120NSM LTM NCL θ∠=∠=∠=︒+,不影响最终结论.9.1.12★★★ABC △中,90A ∠=︒,AB c =.6AC =,BC a =,M 是BC 中点,P 、Q 分别在AB 、AC 上(可落在端点),满足MP MQ ⊥,求22BP CQ +的最小值(用a 、b 、c 表示).解析如图,延长QM 至N ,使QM MN =,连结PN 、BN 、PQ 、AM 由于M 是BC 、NQ 的中点,故BN CQ =,BN AC ∥,BN BP ⊥,又PM 垂直平分NQ ,故222222BP CQ BP BN PN PQ +=+==.取PQ 中点K (图中未画出),则2a PQ AK MK AM =+=≥,于是22BP CQ +的最小值为24a ,取到等号仅当PQ AM =即四边形APMQ 为矩形时.NMP CBQA9.1.13★★★已知P 为ABC △内一点,PAC PBC ∠=∠,由P 作BC 、CA 的垂线,垂足分别是L 、M .C ABDEFMP L设D 为AB 中点,求证.DM DL =.解析如图所示,取AP 中点E ,BP 中点F ,连ME 、ED 、DF 、FL .显然四边形DEPF 是平行四边形,所以EP DF =,FP DE =.DEP DFP ∠=∠.又由PM AC ⊥,所以EM EA EP DF ===,2PEM PAC ∠=∠;同理FL DE =,2PFL PBC ∠=∠.由PAC PBC ∠=∠,所以DEM DEP PEM DFP PFL DFL ∠=∠+∠=∠+∠=∠,从而DFM LFD △△≌,所以DM DL =.9.1.14★★在ABC △中,已知60CAB ∠=︒,D 、E 分别是边AB 、AC 上的点,且60AED ∠=︒,ED DB CE +=,2CDB CDE ∠=∠,求DCB ∠的度数. 解析如图,延长AB 到F ,使BF ED =,连CF 、EF .CEA DB F因为60EAB AED ∠=∠=︒,所以60FDA ∠=︒,120EDB CED ∠=∠=︒, AD AE ED BF ===.CE ED DB DB BF DF =+=+=.于是,AC AF =,60ACF AFC ∠=∠=︒. 又因为120EDB ∠=︒,2CDB CDE ∠=∠, 所以40CDE ∠=︒,80CDB ∠=︒,18020ECD CED EDC ∠=︒-∠-∠=︒.在CDA △和CBF △中,CA CF =,60CAD CFB ∠=∠=︒,AD BF =,所以CDA CBF △△≌,故 20FCB ACD ∠=∠=︒.于是,6020DCB CDE FCB ∠=︒-∠-∠=︒.9.1.15★★在ABC △中,B ∠、C ∠为锐角,M 、N 、D 分别为边AB 、AC 、BC 上的点,满足AM AN =,BD DC =,且BDM CDN ∠=∠.求证.AB AC =.解析若DM DN >,则在DM 上取一点E ,使DN DE =.连结BE 并延长交AC 于F ,连结EN .在BED △与CND △中,BD DC =,BDE CDN ∠=∠,DE DN =,故BDE CDN △△≌.于是有EBD NCD ∠=∠,BE NC =,所以FB FC =.又易知EN BC ∥,因此ENF ACB ∠=∠. 但另一方面,由DM DN >,知ABC FBC ACB ∠>∠=∠,所以AFM NE BDC1(180)2ANM BAC ∠=︒-∠()12ABC ACB =∠+∠ ()12ACB ACB ACB >∠+∠=∠. 从而ENF MNA ACB ∠>∠>∠.矛盾,故假设DM DN >不成立. 若DM DN <,同法可证此假设不成立.综上所述DM DN =,于是由BDM CDN △△≌ 知DBM DCN ∠=∠,从而AB AC =.9.1.16★★如图,ABC △为边长是1的等边三角形,BDC △为顶角()BDC ∠是120︒的等腰三角形,以D 为顶点作一个60︒角,角的两边分别交AB 、AC 于M 、N ,连结MN ,形成一个AMN △. 求AMN △的周长.AM NBC DE解析延长AC 到E ,使CE BM =,连结DE .易知在BMD △与CED △中有BD DC =,90MBD ECD ∠=∠=︒,BM CE =,从而MBD ECD △△≌.所以MD DE =,MDB EDC ∠=∠. 于是在DMN △与DEN △中有DN DN =,MD DE =,60MDN MDB CDN EDC CDN EDN ∠=︒=∠+∠=∠+∠=∠.从而MDN EDN △△≌,故NE MN =. 所以AM MN AN AM NE AN AM NC CE AN AM MB NC AN ++=++=+++=+++= 2AB AC +=.9.1.17★★★ABC △为等腰直角三角形,90C ∠=︒,点M 、N 分别为边AC 和BC 的中点,点D 在射线BM 上,且2BD BM =,点E 在射线NA 上,且2NE NA =,求证.BD DE ⊥. 解析取AD 中点F ,连EF .EADF MBNC在BMC △与DMA △中,AM MC =,12BM BD MD ==,BMC DMA ∠=∠,故AMD CMB △△≌.于是有ADM CBM ∠=∠,AD BC =,AD BC ∥.同样易知BMC ANC △△≌,于是有CBM CAN ∠=∠.在ANC △与EAF △中,12NA NE AE ==,1122AF AD BC NC ===,由AD BC ∥知EAF ANC ∠=∠,所以FAF ANC △△≌.于是有AEF NAC ∠=∠,90EFA ACN EFD ∠=∠=︒=∠.从而在EAF △与EDF △中有AF FD =,EF EF =,故FAF EDF △△≌.于是有EDF EAF ∠=∠, FED FEA ∠=∠.总之,90EDF MDA EDF NAC EDF AEF EDF FED ∠+∠=∠+∠=∠+∠=∠+∠=︒,即 BD DE ⊥.9.1.18★★★已知ABCD ,延长DC 至P ,使DP AD =,连结PA 与BC 交于Q ,O 为PQC △的外心,则B 、O 、C 、D 共圆.ADBC O PQ解析如图连好辅助线,由于DPA BAP PAD CQP ∠=∠=∠=∠,故CQ CP =,设OCP OCQ OQC θ∠=∠=∠=,则180BQO DCO θ∠=︒-=∠,又BQ AB CD ==,QO CO =,故BQO DCO △△≌,于是QOB COD ∠=∠,于是2BOD QOC QPC BCD ∠=∠=∠=∠,因此B 、O 、C 、D 共圆.9.1.19★★★已知ABC △和A B C '''△,A A '∠=∠,且BC B C ''=,D 和D '分别是BC 、B C ''的中点,AD A D ''=,问两个三角形是否必定全等?解析如图,作出ABC △外心O (A B C '''△及相应的O '、D '图中未画出). 若O 在BC 上,则90A A '∠=︒=∠,此时ABC △与A B C '''△未必全等. 若O 不与D 重合,则2sin 2sin BC B C AO A O A A ''''===', cos cos OD BO A AO A == cos A O A O D '''''==,AD A D ''=.当A 、O 、D 共线,则AD BC ⊥,A D B C ''''⊥,所以ABD A B D '''△△≌,ACD A C D '''△△≌,从而 ABC A B C '''△△≌.当A 、O 、D 不共线,则AOD A O D '''△△≌,ODA O D A '''∠=∠,于是'ADC A D C ''∠=∠(或A D B '''∠),于是由三角形全等可得AC A C ''=(或A B ''),AB A B ''=(或A C ''),故有ABC A B C '''△△≌(或A CB '''△). 评注此题亦可用中线长公式证明.9.1.20★★如果两个三角形满足“ASS ”,它们不一定全等,此时称它们是相近的,现在有一三角形1△,作2△与之“相近”,……一般有1n +△与n △相近,问是否存在一个k ,使1△与k △相做且不全等? 解析这是不可能的.因为由正弦定理,1△与2△有等大的外接圆(它们有一对内角相等或互补),从而 推出1△与x k △有等大的外接圆,它们不可能只相似不全等.9.1.21★★★是否存在两个全等的三角形△与'△,△可划分为两个三角形1△与2△,'△可划分成两个三角形1'△与2'△,使12△△≌,2△与2'△却不全等?解析这样的两个三角形是存在的,如图(a)、(b),设不等边三角形ABC A B C '''△△≌,其中22''BC AB AC A B A C B C ''''=⋅=⋅=,不妨设AC A C ''=是各自的最长边,则AB 、A B ''为各自的最短边.在AC 、B C ''上分别找D 、D ',使CD AB =,BA D C ''∠=∠,则由于2BC AB AC CD AC =⋅=⋅,故ABC BDC △∽△,所以'BDC ABC A B C ''∠=∠=∠,又因为C B A D '''∠=∠,CD A B ''=,因此BDC D B A '''△△≌,而ABD △显然不与A C D '''△全等.(若90B B '∠=∠=︒,还可避免相似.) ABCDA'B'D'图(a)图(b)9.1.22★★★已知ABC △中,60A ∠=︒,I 是ABC △内心,AI 的垂直平分线分别交AB 、AC 于M 、N ,E 、F 在BC 上,BE EF FC ==,求证.ME NF ∥.解析如图,连结MI 、BI 、CI 、NI .易诮AMN △与IMN △为全等之正三角形,120BIC ∠=︒, 180MIB NIC ∠+∠=︒.ANMTB E F CIS两端延长MN 至S 与T ,使SM MN NT ==,则60SMB AMN BMI ∠=∠=∠=︒,于是SMB IMB △△≌,同理NTC NIC △△≌,因此180S T MIB NIC ∠+∠=∠+∠=︒,SB TC ∥.而M 、N 将ST 三等分,E 、F 将BC 三等分,于是由平行线分线段成比例,知ME NF ∥(SB ∥). 评注读者可以考虑.如果ME NF ∥是否有60BAC ∠=︒.9.1.23★★★已知锐角三角形ABC ,60BAC ∠=︒,AB AC >,ABC △的垂心和外心分别为M 和O ,OM 分别与AB 、AC 交于X 、Y ,证明.AXY △的周长为AB AC +,OM AB AC =-.解析如图,连结AO 、BO 、CO 、AM .由AB AC >可知O 在AB 一侧,M 在AC 一侧.因120BOC ∠=︒,故AO =,而tan BC AM BAC ==∠于是AO AM =,AOM AMO ∠=∠. 又90OAB C YAM ∠=︒-∠=∠,故AXY AYX ∠=∠,AXY △为正三角形.又60XOB YOC YOC OCY ∠+∠=︒=∠+∠,故XOB YCO ∠=∠,120BXO CYO ∠=︒=∠,又BO CO =,故XBO YOC △△≌,XY XO YO BX YC =+=+.于是AX XY YA AB AC ++=+.又XO MY YC ==,做()()112233OM XY YC AB AC AC AB AC AB AC ⎡⎤=-=+--+=-⎢⎥⎣⎦.§9.2特殊三角形9.2.1★在直角三角形ABC 中,BC 是斜边,5AC =,D 是BC 中点,E 是AC 上一点,2DE AE ==,求AB .BADEC解析如图,连结AD .设AD CD x ==,因2DE =,2AE =,3CE =,则 22223x -=⨯,x =AB ==9.2.2★已知ABC △中,14AB =,16BC =,28CA =,P 为B 在A ∠平分线上的射影,M 为BC 中 点,求PM .解析延长BP 交AC 于Q .由BAP QAP ∠=∠.AP BQ ⊥知BP QP =,AB AQ =.又BM CM =,故()()11128147222PM CQ AC AQ =-=⨯-=∥.ABCQ P M9.2.3★等腰三角形ABC 中,AB AC =,D 为直线BC 上一点,则22AB AD BD CD -=⋅(D 在BC 上),22AD AB BD CD -=⋅(D 在BC 外). 解析如图,设D 在BC 上且较靠近B .作AE BC ⊥于E ,则E 为BC 中点,于是AB D E C()()BD CD BE DE CE DE ⋅=-⋅+2222BE DE AB AD =-=-.当D 在BC 外时的结论同理可证.评注这是斯图沃特定理在等腰三角形的特殊情形,具有十分广泛的用途(例如题9.2.1),亦可用相 交弦定理证明.9.2.4★★已知锐角三角形ABC 中,AD 、CE 是高,H 为垂心,AD BC =,F 是BC 的中点,求证.12FH DH BC +=.AEBFDCH解析如图,连结EF ,则12EF CF BC ==.于是2222FH EF EH CH EF AH HD EF =-⋅=-⋅=- 222AH HD HD HD EF HD AD ⋅-+=-⋅+22222HD EF HD BC HD EF HD =-⋅+=-⋅ ()22EF HD EF HD +=-.由于EF FH HD >>,故12FH EF DH BC DH =-=-. 9.2.5★已知斜边为AC 的直角三角形ABC 中,B 在AC 上的投影为H .若以AB 、BC 、BH 为三边可以构成一个直角三角形,求AHCH的所有可能值. BHAC解析显然由AB 、BC 、BH 构成的直角三角形中,BH 不是斜边,且AB BC ≠.若AB BC >,则AB 为斜边.设AB c =,BC a =,BH h =,则由ABC △的面积知h ac ,又h =,故4422c a a c -=.易知2222AH AB c kCH BC a ===,则由前式知21k k -=,得k =,故AH CH =同理,若AB BC <,可得AH CH =.所以AHCH9.2.6★★已知ABC △中,AD 为高,D 在BC 上, 以下哪些条件能判定AB AC =. (1)AB CD AC BD +=+. (2)AB CD AC BD ⋅=⋅;(3)1111AB CD AC BD+=+. AB D C解析设BD x =,CD y =,AD h =,则AB ,AC先看条件y x =.若x y =,则AB AC =;否则不妨设x y >,则22x y -==.x y =+,于是0h =,矛盾. 故AB AC =.再看见条件(2).=22222222h y x y h x x y +=+,于是x y =,故AB AC =. 最后条件(3).11y x =+.于是22x y xy -=.若x y ≠,则()xy x y =+,仍有0h =,矛盾,故AB AC =.所以三个条件都能判定AB AC =.9.2.7★已知P 是等腰直角三角形ABC 的斜边BC 上任意一点,求222BP CP AP +.解析如图,作AD BC ⊥于D .AB D CP不妨设1AD BD CD ===.P 在CD 上,PD a =,则1BP BD PD a =+=+,1CP CD PD a =-=-,于是()()222221122BP CP a a a +=++-=+.又22221AP AD PD a =+=+.故2222BP CP AP +=.评注请读者考虑,若对BC 上任一点P ,有222BP CP AP+为定值,是否可认为ABC △为等腰直角三角形. 9.2.8★★在ABC △中,19AB =,17BC =,18CA =,P 是ABC △内一点,过点P 向ABC △的 三边BC 、CA 、AB 分别垂线PD 、PE 、PF ,垂足分别为D 、E 、F ,且27BD CE AF ++=,求BD BF + 的长.解析如图,由于2222220BD CD CE AE AF BF -+-+-=,于是AFEPBDC()()222222(17)18190BD BD CE CE AF AF --+--+--=,此即171819487BD CE AF ++=.而181818486BD CE AF ++=,故1AF BD -=.所以118BD BF BD AB AF AB +=+-=-=. 9.2.9★★已知ABC △中,AB AC =,AE 是BC 的中垂线,AE BC =,3BDC BAC ∠=∠, 求ADDE.AF DBEC解析如图,不妨设1BE CE ==,则2AE =,AB =.作ABD ∠的平分线BF ,由于3BDE BAE ABD BAE ∠=∠=∠+∠,故ABF DBF BAE ∠=∠=∠.因此AF BF =,ABD BFD △∽△, AB AD BD BF BD DF ==,从而2BD DF DA =⋅,DB ADDF AB DB⋅=+,所以()2DA BD BD AB =⋅+. 设DE x=,则221BD x =+,2DA x=-,因此()2221x x -=+,()223455x x -=+,2112440x x -+=,211x =(2x =舍).于是2011AD =,10AD DE =. 9.2.10★★正三角形ABC 内有一点P ,P 关于AB 、AC 的对称点分别为Q 、R ,作平行四边形QPRS ,求证.AS BC ∥.A SMRQBCP解析如图,设QS 与AB 交于M ,连结MP ,则60Q ∠=︒,AB 垂直平分PQ ,QM PM =,MPQ △ 为正三角形,MP PQ SR ==,于是四边形MPRS 为等腰梯形,PR 的中垂线即MS 的中垂线. 于是60SAC MAC C ∠=∠==∠,AS BC ∥.9.2.11★★AB 与O 相切于点B ,AC 与O 相交于C 、D ,若45C ∠=︒,60BDA ∠=︒,CD =求AB .BC D AK T解析如图,由题意可得45ABD ∠=︒,作BK AC ⊥于K ,则BK CK=,又CK CD DK =+=,故32BK =,BD =再作AT BD ⊥于T ,设BT AT x ==,则DT =,x =x =于是6AB ==.9.2.12★已知大小相等的等边ABC △与等边PQR △有三组边分别平行,一个指向上方,一个指向 下方,相交部分是一个六边形,则这个六边形的主对角线共点.A D KR QEHBFGCP解析如图,设两个三角形的边的交点依次为D 、E 、F 、G 、H 、K .设ABC △、PQR △的高为h ,则正ADK △的高h =(RQ 与BC 的距离)=正FPG △的高,于是DK FG ∥,DG 、KF 互相平分,同理DG 、EH 互相平分,于是DG 、EH 、KF 的中点为同一点,结论成立.9.2.13★★★★求证.过正三角形ABC 的中心O 任作一条直线l ,则A 、B 、C 三点至l 的距离平方和为常数.AlB'A'OC'B QC P解析如图,不妨设l 与AB 、AC 相交,且与BC 延长线交于P (平行容易计算).由中位线及重心性质,知BB CC AA '''+=.故222222()B B C C A A B B C C B B C C '''''''++=++⋅.连结OB 、OC ,作OQ BC ⊥,易知B BP QOP C CP ''△∽△∽△,故C C CP OQ OP '=,B B BPOQ OP'=. 对于等腰三角形OBC ,有22OP OC CP BP -=⋅.因此()()222222222223OQ OQ B B C C B B C C CP BP CP BP BC CP BP OP OP ''''++⋅=++⋅=+⋅= ()222222333OQ BC OP OC OQ OP+-=(定值),这里用到了BC =. 于是A 、B 、C 三点至l 的距离平方和为22162OQ BC =,结论得证.§9.3三角形中的巧合点9.3.1★已知.H 是ABC △内一点,AH 、BH 、CH 延长后分别交对边于D 、E 、F ,若AH HD BH HE CH HF ⋅=⋅=⋅,则H 是ABC △的垂心,解析如图,由条件知AHE BHD △∽△,故AEH BDH ∠=∠,同理,AFH CDH ∠=∠,故180AFH AEH ∠+∠=︒.A FEHBDC又FBH ECH △∽△,故BFH CEH ∠=∠,这样可得90AFH AEH ∠=∠=︒,故H 为ABC △之垂 心.9.3.2★★求证.到三角形三顶点的距离平方和最小的点是三角形的重心.解析设ABC △中,AD 、BE 、CF 是中线,G 是重心,M 是任一点.由斯图沃特定理,并考虑到 结论成立. 123DG GA AD =∶∶∶∶,得2222122339MG AM DM AD =+-22212233AM DM GD =+-.① 又由中线长公式,有 ()22221124MD BM CM BC =+-, ()22221124GD BG CG BC =+-. 代入式①,得()()222222230MG MA MB MC GA GB GC =++-++≥.结论成立. 9.3.3★★★已知,H 是锐角ABC △的垂心,D 是BC 中点,过H 作DH 的垂线,交AB 、AC 于M 、N ,求证.H 是MN 中点.AQ NMHBD PC解析设ABC △两条高为AP 、CQ .又不妨设D 在BP 上.由于HAM DCH ∠=∠,90AHM DHP HDC ∠=︒-∠=∠,故AMH CHD △∽△,于是MH AH HD CD =,同理NH AHHD BD=, 又CD BD =,故MH NH =.9.3.4★★★ABC △的边BC 、CA 、AB 上分别有点D 、E 、F ,且BD CE AFDC EA FB==,求证.ABC △的重心与DEF △的重心是同一点.解析在AB 上取一点M ,使MD AC ∥,则MD BD CEAC BC AC==,所以MD CE =,四边形MDCE 为平行四边形,设MC 与DE 交于N ,又设BC 的中点为,P 连结PN 、AP 、FN ,AP 与FN 交于G ,于是由 BM BD CE AF AB BC AC AB ===,得RM AF =,于是1122PN BM AF ∥∥,于是12PG GN PN GA FG AF ===,所以G 为ABC △与DEF △之重心.AFMG EBDPCN9.3.5★★★已知ABC △,60A ∠=︒,G 是ABC △重心,120BGC ∠=︒,求证.ABC △是正三角形. 解析设ABC △三条中线分别为AD 、BE 、CF .连EF 为中位线.于是由条件知A 、F 、G 、E 共圆,故GBD FEG BAD ∠=∠=∠,于是2BD GD DA =⋅.由于12BD BC =,13GD AD =,代入,得AD =. 在ABC △外作等腰BCP △,使BP CP =,120BPC ∠=︒,连结DP ,DP BC ⊥.由圆心角与圆周角的关系,211333GP BP AD AD AD GD PD ====+=+,故G 、D 、P 三点共线,故AD BC ⊥,于是AB AC =,又60RAC ∠=︒,故ABC △为正三角形.AFEBD CPG9.3.6★★★已知D 是BC 上一点,ABD △、ECD △、BCF △都是正三角形,A 、E 在BC 同侧,F 在另一侧,求证.以这三个正三角形的中心为顶点的三角形是正三角形,且它的中心在BC 上.又问此题如何推广?A BCEFR R'DQ'P'Q解析如图,设P 、Q 、R 分别为BCF △、DCE △和ABD △的中心,则由题11.2.25知PQR △为正三角形.过P 、Q 、R 分别作BC 的垂线PP '、QQ '、RR ',则RR QQ PP BD CD BC ⎛'''=== ⎝⎭,又BD CD BC +=, 故RR QQ PP '''+=.又设RQ 中点为S (图中未画出),SS BC '⊥于S ',则SS PP ''∥,且()1122SS RR QQ PP ''''=+=.设SP 与BC 交于G ,则12SG SS GP PP '==',所以G 为PQR 的中点. 评注此题不难推广,只需AB DE CF ∥∥,AD CE BF ∥∥,此时ABD DC FCB △∽△∽△, P 、Q 、R 为各自对应的重心,则必有PQR △之重心位于BC 上. 9.3.7★★★ABC △内有一点P ,连结AP 、BP 、CP 并延长,分别与对边相交,把ABC △分成六个小三角形,若这六个小三角形中有三个面积相等,则点P 是否必为ABC △之重心? 解析如图,设AD 、BE 、CF 交于P .由对称性,可分四种情况讨论.AFEPBDC(1)BPD CDP BPF S S S ==△△△.于是BD CD =,2CPPF=,由梅氏定理(或添平行线),得AF BF =,P 为中心.(2)BPD CDP APF S S S ==△△△.此时FD AC ∥,故D 、F 分别为BC 、AB 中点,P 为重心.(3)BPD BPF APE S S S ==△△△.此时有DE AB ∥,由塞瓦定理,AF BF =,于是APF BPF S S =△△,回到情形(1).(4)APF BPD CPE S S S ==△△△,见题15.1.58.综上所知,答案是肯定的.9.3.8★★★设有一个三角形三角之比为124∶∶,作两较大角的平分线,分别交对边于M 、N .求证.这个三角形的重心在MN 上.解析如图(a),设A ∠为最小角,作中线AD ,交MN 于G ,于是只要证明2AG GD =.分别作EB AD CF ∥∥,E 、F 在直线MN 上,则2GD EB CF =+,故问题变成1EB FCAG AG+=,或 1BC BC CM BN CF BEAB AC AM AN AG AG+=+=+=. 不妨设A θ∠=,2C θ∠=,4B θ∠=,7180θ=︒,在AC 上找一点P ,使ABP θ∠=,又作PQ BC ∥,Q 在AB 上,则各角大小如图(b)所示.于是BC BP AP BQ ===,故 11BC AP CP BQ BCAC AC AC AB AB==-=1-=-. ABCD E FNMGA QP B C2θ3θ2θ3θ3θθθ图(a)图(b)9.3.9★★★不等边锐角ABC △中,H 、G 分别是其垂心和重心,求证.若112HABHACHBCS S S +=△△△,AG HG ⊥.ABDECGH解析设ABC △的一条中线与高分别为AD 、AE ,则欲证结论等价于AG AD AH AE ⋅=⋅.熟知cot AH BC A =⋅,23AG AD =.于是结论变为22cot cos 3AD BC AE A AB AC A =⋅⋅=⋅⋅. 设AB c =,BC a =,CA b =,则由中线长及余弦定理,知欲证式左端()2221226b c a =+-, 右端2222b c a +-=,整理,得2222b c a +=,于是剩下的任务是证明这个等价条件.1cos 2BHC S BH BC C =⋅⋅⋅△1cot cos 2AC BC B C =⋅⋅⋅⋅ cot cot ABC S B C =⋅⋅△,同理有另两式,于是条件变为cot cot 2cot C B A +=,由正弦及余弦定理,知上式即cos cos ab C ac B +=2cos bc A ,或()()22222222262()ac a c b b c a +-++-=+-,化简即得2222b c a +=.9.3.10★★已知凸四边形ABCD 中,2BAC BDC ∠=∠,2CAD CBD ∠=∠,A 是否一定为BCD △之外心?ABDC解析当BCD △固定.由题设BAC ∠、CAD ∠固定,于是BAC △、ACD △外接圆固定,它们的交点 C 、A '固定,又若A 为BCD △外心时,确为BAC △的外接圆和ACD △的外接圆之异于C 的交点,因此A A '=,结论成立.9.3.11★★★已知锐角ABC △的外接圆与内切圆的半径分别为R 、r ,O 是外心,O 至三边距离之和为L ,试用R 、r 表示L .解析易知()cos cos cos L R A B C =++.设ABC △三边分别为a 、b 、c ,由于cos cos a B b A c +=等,则()()cos cos cos a b c A B C ++⋅++=cos cos cos a b c a A b B c C +++++,于是 cos cos cos 1A B C ++-cos cos cos a A b B c Ca b c++=++.①又1cos 2BOC Ra A S =△等,可得()()11cos cos cos 22ABC R a A b B c C S r a b c ++==++△,故式①的右端r R =. 于是L R r =+. 9.3.12★★★★.已知ABC △,D 、E 分别在AC 、AB 上,BD 、CE 交于F ,ED BC ∥,求证.AEF △、ADF △、EFB △、DFC △的外心四点共圆.AED BCOKO 1O 2解析如图,设BEF △、DFC △的外心分别为1O 、2O ,O 为EFD △的外心,于是1OO 垂直平分EF .2OO 垂直平分DF .设EFB DFC θ∠=∠=,则由垂径定理知11sin 2OO BD θ=,21sin 2OO CE θ=,于是12OO BD FD OO CE EF ==. 易知AF 过ED 中点(由塞瓦定理或面积比),作KD EF ∥,K 在AF 上,则KD EF =,又 12180KDF EFD O OO ∠=︒-∠=∠,故12O OO FDK △∽△.又设AEF △,ADF △的外心分别为3O 、4O (图中未画出),于是3O 、4O 分别在直线1O O 与2O O 上, 且34O O AF ⊥,于是4312OO O KFD OO O ∠=∠=∠,于是1O 、2O 、3O 、4O 四点共圆.9.3.13★★★已知.ABC △中,AB AC =,D 是AB 中点,F 为ADC △重心,O 为ABC △外心,求证.FO CD ⊥.解析1如图,延长DF 交AC 于E ,则AE CE =,2DF EF =.连结AO 并延长,分别交CD 、BC 于G 、H ,则G 为ABC △重心,BH CH =,2233DF DE BH ==,易见2323BHDO BH DF AD AH AG AH ===. ADEF OGB H C又OD AB ⊥,90ODF ADE DAG ∠=︒-∠=∠,ODF DAG △∽△,对应边垂直,所以FO CD ⊥. 解析2O 为ABC △外心,故22222CO DO AO DO AD -=-=; 而由中线公式,CF =DF 于是22222CF DF AD CO DO -==-,于是FO CD ⊥.9.3.14★★★设I 和O 分别是ABC △的内心和外心,求证.90AIO ∠︒≤的充分必要条件是2BC AB AC +≤.解析延长AI 与外接圆交于点D ,连结BD 、CD 、OD ,则 90AIO ∠︒≤ AI ID ⇔≥.2ADDI⇔≤D由内心性质知,DI DB DC ==,结合托勒密定理得 AD BC AB CD AC BD ⋅=⋅+⋅ AB DI AC DI =⋅+⋅, 所以AD AB ACDI BC+=, 所以902AB ACAIO BC+∠︒⇔≤≤, 故90AIO ∠︒≤的充要条件是2BC AB AC +≤.评注本题的关键是先把90AIO ∠︒≤转换为AI ID ≥,然后再用托勒密定理.托勒密定理是.圆内接四边形的对角线的乘积等于对边乘积的和.9.3.15★★★设O 是ABC △的外接圆,G 是三角形重心,延长AG 、BG 、CG ,分别交O 于D 、E 、F ,则3AG BG CGGD GE GF++=. AF ERQGBP DC解析设BC 、CA 、AB 的中点分别为P 、Q 、R ,则由中线长公式及相交弦定理,有(此处ABC △三边分别设为a 、b 、c ) AG AG AGBP CPGD GP PD GP AP==⋅++22223133APAP BP CP AP BP CP AP AP ==⋅+⋅+ 2222222222222122211132244b c a b c a a b c b c a a +-+-==+++-+. 同理,有22222222BG c a b GE a b c +-=++ , 22222222CG a b c GF a b c +-=++. 三式相加,即得结论.9.3.16★★I 在ABC △内,AI 平分BAC ∠,1902BIC A ∠=︒+∠,求证.I 是ABC △内心.解析如图,作EIF AI ⊥,E 在AB 上,F 在AC 上,则AE AF =,LE IF =,AEF BCI1902BEI IFC A BIC ∠=∠=︒+∠=∠.又1902EBI EIB A EIB FIC ∠+∠=︒-∠=∠+∠,故EBI FIC ∠=∠,于是EBI FIC △∽△,BI BE BEIC IF EI==.而BEI BIC ∠=∠,故BEI BIC △∽△,ABI IBC ∠=∠,所以I 为ABC △内心.9.3.17★★已知.ABC △中,2BC AB AC =+,D 是内心,DE 与BC 垂直于E ,求2DE BE CE⋅的值.解析设ABC △三边长分别为a 、b 、c ,则2a b c =+. 易知若设DE r =,()12p a b c =++,则BE p b =-,CE p c =-.r =于是2133DE P a b c a a BE CE p a b c a -+-====⋅++. 9.3.18★★设ABC △中,AB 最长,在其上分别找两点M 、N ,使AN AC =,BM BC =,又设I 为ABC △内心,求MIN ∠(用A ∠、B ∠、C ∠及其组合表示). 解析如图,连结CM 、CN 、CI 、AI .CABM NI易知ACI ANI △△≌,CI NI =,同理CI MI =,I 为CMN △的外心,因此 MCN ACN BCM C ∠=∠+∠-∠11909022A B C =︒-∠+︒-∠-∠1902C =︒-∠,2180MIN MCN C ∠=∠=︒-∠.9.3.19★★★★ABC △的边BC 上有一点D ,ABD △与ACD △的内心与B 、C 四点共圆,求证. AD BD ABAD CD AC+=+. AMNE FBDCPI 1I 2解析如图,设ABD △与ACD △的内心分别为1I 与2I .连结1AI 、2AI 、1BI 、2CI 、12I I ,两端延长12I I ,分别交AB 、AC 于E 、F ,则由条件知()1112AEF ABI EI B ABC ACB ∠=∠+∠=∠+∠,同理AFE ∠也是此值,于是AE AF =. 又设12I I 与AD 交于P ,则由角平分线性质知1212EI FI AE AF I P AP AP I P ===,故由梅氏定理(直线AB 截1PDI △及直线AC 截2PDI △),得1212I D I DI M I N=(此处M 、N 分别为1DI 、2DI 延长后与AB 、AC 之交点),又由角平分线性质,知11I D AD BD I M AB +=,22I D AD CDI N AC+=于是结论成立. 9.3.20★★★已知ABC △中,AB AC =,O 、I 分别为其外心与内心,D 在AC 上,DI AB ∥,求证.OD CI ⊥.解析如图,不妨设O 在ABC △内,且在I “之上”(O 在形外、I 之下类似处理),连结AOI 、OC ,则IOC BAC IDC ∠=∠=∠,故O 、I 、C 、D 共圆,于是ODC ICD OIK ICD ∠+∠=∠+∠.这里K 为DO 、CI 直线之交点.AD O KIBC由于AOI BC ⊥,故9090OIK ICD BCI ICD ∠+∠=︒-∠+∠=︒,于是90DKC ∠=︒.9.3.21★★设G 为ABC △的重心,已知GA =GB =2GC =,求ABC △的面积.解析1由题意可画出图(a),令D 为AB 中点,GE AB ⊥,垂足为点E ,因G 为重心,可知112GD GC ==.由勾股定理可知222222222GE GB EB GE GA EA GE GD DE ⎧=-⎪=-⎨⎪=-⎩①②③,C ABD E G22322(a)令AD BD c ==.由①与②可得(()(()2222c DE c DE -+=--,化简后可得1c DE ⨯=,即1DE c =,代入③得2211GE c=-,再代入①式可得 22118c c c ⎛⎫1-=-- ⎪⎝⎭, 解方程可得3c =,GE =,故 ABC △的面积=6GBD ⨯△的面积1632=⨯⨯= 解析2由题意可画出图(b),令D 为AB 中点,在GD 的延长线上取E 点使得GD DE =,因此GBD △ 之面积为AEG △之面积的一半.此时因AB 与GE互相平分,可知四边形AEBG 为平行四边形,也因此可知AE GB ==,即AEG △的三边长为2、,故可知AEG △为直角三角形,故GBD △的面积为11222⨯⨯=,所以ABC △的面积6GBD =⨯△的面积=(b)22232GD BAC 22E 119.3.22★★★已知120AFB BFC CFA ∠=∠=∠=︒,P 为异于F 的任一点,求证. PA PB PC FA FB FC ++>++.解析如图,在ABC △外作正三角形ABD ,由于ABC ∠,120BAC ∠<︒,故四边形DBCA 的内角均小于180︒,是凸四边形.ADF F'PP'BC对于ABC △中任一异于F 的点P ,将ABP △、ABF △均以点A 为中心顺时针旋转60︒,至ADP '△ 和ADF '△,则AFF △与APP '△均为正三角形.由全等知AP BP CP PP DP CP CD DF F F FC AF BF CF ''''++=++>=++=++,这是因为DP PC '是一条折线,而120DF A AFC '∠=∠=︒,60AFF AF F ''∠=∠=︒,D 、F '、F 、C 四点共线且仅对于F 满足四点共线.评注当ABC △内角均小于120︒时,满足条件的点F 称为ABC △的费马点(当ABC △有内角比如120A ∠︒≥时,到A 、B 、C 距离之和最小的点正是点A ).。
人教版 初三数学竞赛专题:平面几何的定值问题(包含答案)

人教版 初三数学竞赛专题:平面几何的定值问题(含答案)【例1】 如图,已知P 为正方形ABCD 的外接圆的劣弧AD⌒上任意一点.求证:PA PC PB为定值.【例2】 如图,AB 为⊙O 的一固定直径,它把⊙O 分成上、下两个半圆,自上半圆上一点C 作弦CD ⊥AB ,∠OCD 的平分线交⊙O 于点P ,当点C 在上半圆(不包括A ,B 两点)上移动时,点P ( ) A.到CD 的距离保持不变 B.位置不变C.等分DB⌒ D.随C 点的移动而移动【例3】 如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂线的垂足.求证:不管ST 滑到什么位置,∠SPM 是一定角.【例4】 如图,扇形OAB 的半径OA =3,圆心角∠AOB =90°.点C 是AB⌒上异于A ,B 的动点,过点C 作CD ⊥OA 于点D ,作CE ⊥OB 于点E .连接DE ,点G ,H 在线段DE 上,且DG =GH =HE .(1)求证:四边形OGCH 是平行四边形;(2)当点C 在AB ⌒上运动时,在CD ,CG ,DG 中,是否存在长度不变的线段?若存在,请求出该线段的长度;(3)求证:CD 2+3CH 2是定值.P AB CDAPB【例5】 如图1,在平面直角坐标系xOy 中,点M 在x 轴的正半轴上,⊙M 交x 轴于A ,B 两点,交y 轴于C ,D 两点,且C 为弧AE 的中点,AE 交y 轴于G 点.若点A 的坐标为(-2,0),AE =8. (1)求点C 的坐标;(2)连接MG ,BC ,求证:MG ∥BC ;(3)如图2,过点D 作⊙M 的切线,交x 轴于点P .动点F 在⊙M 的圆周上运动时,PFOF的比值是否发生变化?若不变,求出比值;若变化,说明变化规律.(图1)(图2)【例6】 如图,已知等边△ABC 内接于半径为1的圆O ,P 是⊙O 上的任意一点.求证:P A 2+PB 2+PC 2为定值.【能力训练】1.如图,点A ,B 是双曲线xy 3上的两点,分别经过A ,B 两点向x 轴,y 轴作垂线段.若S 阴影=1,则BOACE HG D A=+21S S _______.(第1题图) (第3题图) (第4题图)2.从等边三角形内一点向三边作垂线段,已知这三条垂线段的长分别为1,3,5,则这个等边三角形的面积是__________.3.如图,OA ,OB 是⊙O 任意两条半径,过B 作BE ⊥OA 于E ,又作OP ⊥AB 于P ,则定值OP 2+EP 2为_________.4.如图,在菱形ABCD 中,∠ABC =120°,F 是DC 的中点,AF 的延长线交BC 的延长线于点E ,则直线BF 与直线DE 所夹的锐角的度数为( )A.30°B.40°C.50°D.60°5.如图,在⊙O 中,P 是直径AB 上一动点,在AB 同侧作A A '⊥AB ,AB B B ⊥',且A A '=AP ,B B '=BP .连接B A '',当点P 从点A 移动到点B 时,B A ''的中点的位置( ) A .在平分AB 的某直线上移动 B.在垂直AB 的某直线上移动 C.在弧AMB 上移动 D.保持固定不移动(第5题图) (第6题图) 6.如图,A ,B 是函数xky =图象上的两点,点C ,D ,E ,F 分别在坐标轴上,且分别与点A ,B ,O 构成正方形和长方形.若正方形OCAD 的面积为6,则长方形OEBF 的面积是( ) A.3 B.6 C.9 D.127.(1)经过⊙O 内或⊙O 外一点P 作两条直线交⊙O 于A ,B 和C ,D 四点,得到如图①~⑥所表示的六种不同情况.在六种不同情况下,P A ,PB ,PC ,PD 四条线段之间在数量上满足的关系式可以用同一个式子表示出来.请你首先写出这个式子,然后只就如图②所示的圆内两条弦相交的一般情况给出它的证明.A ABCDEFAB'(2)已知⊙O 的半径为一定值r ,若点P 是不在⊙O 上的一个定点,请你过点P 任作一直线交⊙O 于不重合的两点E ,F . PE ·PF 的值是否为定值?为什么?由此你发现了什么结论?请你把这一结论用文字叙述出来.8.在平面直角坐标系中,边长为2的正方形OABC 的两顶点A ,C 分别在y 轴,x 轴的正半轴上,点O 在原点,现将正方形OABC 绕O 点顺时针旋转,当A 点第一次落在直线x y =上时停止旋转.旋转过程中,AB 边交直线x y =于点M ,BC 边交x 轴于点N .(1)求OA 在旋转过程中所扫过的面积;(2)旋转过程中,当MN 与AC 平行时,求正方形OABC 旋转度数;(3)设△MBN 的周长为P ,在正方形OABC 旋转的过程中,P 值是否有变化?请证明你的结论.⑥⑤④③②①P(B )A PB9.如图,AB 是半圆的直径,AC ⊥AB ,AC =AB .在半圆上任取一点D ,作DE ⊥CD ,交直线AB 于点E ,BF ⊥AB ,交线段AD 的延长线于点F .(1)设弧AD 是x °的弧,若要点E 在线段BA 的延长线上,则x 的取值范围是_______.(2)不论点D 取在半圆的什么位置,图中除AB =AC 外,还有两条线段一定相等.指出这两条相等的线段,并予证明.(第9题图) (第10题图)(第11题图)10.如图,内接于⊙O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ,设⊙O 的半径为R .求证: (1)2222DK CK BK AK +++是定值; (2)2222DA CD BC AB +++是定值.11.如图,设P 是正方形ABCD 外接圆劣弧弧AB 上的一点,求证:DPCP BPAP ++的值为定值.1.等腰△ABC 的底边BC 为定长2,H 为△ABC 的垂心.当顶点A 在保持△ABC 为等腰三角形的情况下 改变位置时,面积S △ABC ·S △HBC 的值保持不变,则S △ABC ·S △HBC =________.2.已知A ,B ,C ,D ,E 是反比例函数xy 16=(x >0)图象上五个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是__________(用含π的代数式表示).P D CB A A折叠,使点A ,B 落在六边形ABCDEF 的内部,记∠C +∠D + )A. ∠1+∠2=900°-2α B. ∠1+∠2=1080°-2α C. ∠1+∠2=720°-α D. ∠1+∠2=360°-21α(第3题图) (第4题图)4.如图,正△ABO 的高等于⊙O 的半径,⊙O 在AB 上滚动,切点为T ,⊙O 交AO ,BO 于M ,N ,则弧MTN ( )A.在0°到30°变化B.在30°到60°变化C.保持30°不变D.保持60°不变5.如图,AB 是⊙O 的直径,且AB =10,弦MN 的长为8.若MN 的两端在圆上滑动时,始终与AB 相交,记点A ,B 到MN 的距离分别为h 1,h 2,则∣h 1-h 2∣等于( )A.5B.6C.7D.8(第5题图) 12GF EDCHBAB6.如图,已知△ABC 为直角三角形,∠ACB =90°,AC =BC ,点A ,C 在x 轴上,点B 坐标为(3,m )(m >0),线段AB 与y 轴相交于点D ,以P (1,0)为顶点的抛物线过点B ,D . (1)求点A 的坐标(用m 表示) (2)求抛物线的解析式;(3)设点Q 为抛物线上点P 至点B 之间的一动点,连接PQ 并延长交BC 于点E ,连接BQ 并延长交AC 于点F .试证明:FC (AC +EC )为定值.7.如图,已知等边△ABC 内接于圆,在劣弧AB 上取异于A ,B 的点M .设直线AC 与BM 相交于K ,直线CB 与AM 相交于点N .证明线段AK 和BN 的乘积与M 点的选择无关.(第7题图) (第8题图)8.如图,设H 是等腰三角形ABC 两条高的交点,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积S △ABC ·S △HBC 的值变小、变大,还是不变?证明你的结论.9.如图,在平面直角坐标系xOy 中,抛物线10941812--=x x y 与x 轴的交点为点A ,与y 轴的交点为点B .过点B 作x 轴的平行线BC ,交抛物线于点C ,连接AC .现有两动点P ,Q 分别从O ,C 两点同时出发,点P 以每秒4个单位的速度沿OA 向终点A 移动,点Q 以每秒1个单位的速度沿CB 向点B 移动.点P 停止运动时,点Q 也同时停止运动.线段OC ,PQ 相交于点D ,过点D 作DE ∥OA ,交CA 于E ,射线QE 交x 轴于点F .设动点P ,Q 移动的时间为t (单位:秒). (1)求A ,B ,C 三点的坐标和抛物线的顶点坐标;(2)当t 为何值时,四边形PQCA 为平行四边形?请写出计算过程; (3)当290<<t 时,△PQF 的面积是否总是定值?若是,求出此值;若不是,请说明理由; (4)当t 为何值时,△PQF 为等腰三角形,请写出解答过程.NKMB AC HCBA(第9题图) (第10题图) 10.已知抛物线C 1:12121+-=x x y ,点F (1,1). (1)求抛物线C 1的顶点坐标;(2)若抛物线C 1与y 轴的交点为A ,连接AF ,并延长交抛物线C 1于点B ,求证:211=+BFAF . (3)抛物线C 1上任意一点P (x P ,y P )(0<x P <1),连接PF ,并延长交抛物线C 1于点 Q (x Q ,y Q ),试判断211=+QFPF 是否成立?请说明理由.11.已知A ,B 是平面上的两个顶点,C 是位于AB 一侧的一个动点,分别以AC ,BC 为边在△ABC 外作正方形ACDE 和正方形BCFG .求证:不论C 在直线AB 同一侧的任何位置,EG 的中点P 的位置不变. 参考答案例 1 延长PC 至E ,使CE =AP ,连结BE ,则△BCE ≌△BAP ,及△PBE 为等腰直角三角形,故PA PC CE PC PEPB PB PB++=== 例2 B 提示:连结AC ,BC ,可以证明P 为APB 的中点. 例3 ∵SP ⊥OP ,OM ⊥ST ,∴S ,M ,O ,P 四点共圆,于是∠SPM =∠SOM =12∠SOT 为定角. 例4 (1)连结OC 交DE 于M ,则OM =CM , EM =DM ,而DG = HE ,则HM =GM 故四边形OGCH 是平行四边形. (2)DG 不变.DE =OC =OA =3 .DG =13DE =13×3=1. (3)设CD =x ,延长OG 交CD 于N ,则CN =DN =12 x ,229CE x =- , 2214DN x = .∴22394ON x =-,而ON =32CH ,∴22143CH x =-.故CD 2+3CH 2=x 2+3(4-13x 2)=x 2+12-x 2为定值. 例5 ⑴C (0,4) ⑵先求得AM =CM =5,连接MC 交AE 于N ,由△AO G ∽△ANM ,得OG AO MN AN =,O G =32,38OG OM OC OB ==,又∠BOC =∠G OM ,∴△G OM ∽△COB ,∠G MO =∠CBO ,得M G ∥BC .⑶连结DM ,则DM ⊥PD ,DO ⊥PM ,DO 2=OM •OP ,OP =163.动点F 在⊙M 的圆周上运动时,从特殊位置探求OFPF的值.当F 与点A 重合时,2316523OF AO PF AP ===-;当点F 与点B 重合时,8316583OF OB PF PB ===+;当点F 不与点A ,B 重合时,连接OF 、PF 、MF ,∴DM 2=MO •MP ,∴FM 2=MO •MP ,即FM MPOM FM=,又∠OMP =∠FMP ,∴△MFO ∽△MPF ,35OF MO PF MF ==,故OF PF 的比值不变,比值为35. 例6 ∠BPC =120°,在△BPC 中,由余弦定理得BC 2=PB 2+PC 2-2PB •PC =BC 2,又由上托勒密定理得BC •P A +PC •AB ,而AB =BC =AC ,∴P A =PB +PC ,从而P A 2+ PB 2+ PC 2= (PB +PC )2+ PB 2+ PC 2=2 (PB 2+PC 2+PB •PC )=2BC 2=2×()23=6.故P A 2+PB 2+PC 2为定值.A 级 1.4提示:∵S 1+S 阴= S 2+S 阴=xy =3,∴S 1+S 2=2xy -2S 阴=6-2=4.2.273 提示:1+3+5=9是等边三角形的高. 3.r 2提示:先考查OB 与OA 垂直的情形.4.D 提示:延长BF 交DE 于点M ,连接BD ,则△BCD 为等边三角形,BF 平分∠CBD .∵F 为CD 中点,且AD ∥CE ,∴△ADF 与△ECF 关于点F 中心对称.∴CE =AD =CD ,∴∠CEM=30°,∠DMF=60°,5.D 提示:A′B′的中点均在⊙O 的上半圆的中点处. 6.B 提示:S 正方形OCAD =OD •OC =A A x y k ==6,∴S OEBF =OE •OF =x B •y B k ==6. 7.⑴略⑵当点P在⊙O 内时,过P 作直径CD ,则PE •PF =PD •PC =r 2-OP 2为定值;当点P 在⊙O 外时,PE •PF 为定值22OP r -.结论:过不在圆上的一个定点任作一条直线与圆相交,则这点到直线与圆相交点的两条线段长的积为定值. 8.⑴2π⑵22.5° ⑶P 值无变化.理由如下:如图,延长BA 交y 轴于E 点,可证明△OAE ≌△OCN ,得OE =ON ,AE =CN ,又∠MOE =∠MON =45°,OM =ON ,∴△OME ≌△OMN ,得MN =ME =AM +AE =AM +CN .∴P =MN +BN +BM =AM +CM +CN +BN +BM =AB +AC =4.9.⑴0<x <90 ⑵BE =BF 提示:连接BD ,可证明△BDF ∽△ADB ,△BDE ∽△ADC . 10.⑴作OP ⊥BD 于P ,OQ ⊥AC 于Q ,连接AO ,则AO 2=()()221122BK DK CK AK ⎡⎤⎡⎤-++⎢⎥⎢⎥⎣⎦⎣⎦,又AK •CK =BK •DK ,得AK 2+BK 2+CK 2+DK 2=4R 2为定值. ⑵作直径DE ,连接AE ,BE ,CE ,AB 2+CD 2=4R 2,AD 2+BC 2=4R 2,故AB 2+BC 2+CD 2+DA 2=8K 2为定值. 11.设正方形的边长为a ,根据托勒密定理,对于四边形APBC 和四边形APBD ,有CP •a =AP •a +BP •2a ,DP •a =BP •a +AP •2a ,两式相加并整理得(CP +DP )a =(AP +BP )(a +2a ),从而21AP BPCP DP+=-+为定值.B 级1.1 提示:不妨设∠A 为锐角,AD ,BE ,CF 为△ABC 的三条高,H 为垂心,由AB =AC 知∠HBD =∠HCD =∠HAE ,∠HDC =∠CDA =90°,故R t △CHD ∽R t △ACD .∴AD DC DC HD =,即AD •HD =DC 2=14BC 2=1.∴S △ABC •S △HBC =2111224BC AD BC HD BC ⎛⎫⎛⎫⋅⋅⋅= ⎪ ⎪⎝⎭⎝⎭=1.当∠A ≥90°时,结论成立.2.13π-26 提示:∵A ,B ,C ,DE 是反比例函数y =16x(x >0)图象上五个整数点,由图象可知,这些点的横坐标分别为1,2,4,8,16.∴五个正方形的边长分别为1,3,4,2,1.∴这五人橄榄形的面积总和是2221111112211122222444424242πππ⎡⎤⎛⎫⎛⎫⎛⎫⨯-⨯⨯+⨯-⨯⨯+⨯-⨯⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=5π-10+8π-16=13π-26. 3.B 提示:如图,设F A 的延长线与CB 的延长线交于点P ,G A ′的延长线与HB ′的延长线交于点P ′.由对称性可知∠1=2∠APP ′,∠2=2∠BPP ′.∴∠1+∠2=2∠APB .∵∠APB =540°-α,∴∠1+∠2=1080°-2α. 4.D 5.B 提示:如图,设AB 与MN 交于点C ,过点O 作OD ⊥MN 于D ,连接FO 并延长交EB 于G .由垂径定理,得OD =2254-=3.由△AFO ≌△B G O ,得AF =B G ,即h 1=B G .由AF ⊥MN ,BE ⊥MN ,得△FOD ∽△F G E .∴12OD FO GE FG ==.∴E G =2OD =6,∴12h h AF BE -=-=E G =6. 6.⑴A (3-m ,0) ⑵y =x 2-2x +1 ⑶过点Q 作QM ⊥AC 于M ,过点Q 作QN ⊥BC 于N ,设Q 点的坐标为(x ,x 2-2x +1),则QM =CN =(x -1)2,MC =QN=3-x .∵QM ∥CE ,∴PQM ∽△PEC .∴QM PMEC PC=,即()2112x x EC--=,得EC =2(x -1).∵QN ∥CF ,∴△BQN ∽△BFC .∴QN BN FC BC =,即()24134x x FC ---=,得FC =41x +.又AC =4,∴FC (AC +EC )=()44211x x +-⎡⎤⎣⎦+=8为定值. 7.提示:易证△ABK ∽△BNA ,故AK •BN =AB 2为定值,即AK 与BN 的乘积与M 点的选择无关. 8.提示:S △ABC •S △HBC =116BC 4,由于BC 是不变的,所以当点A 至BC 的距离变小时,乘积S △ABC •S △HBC 保持不变. 9.⑴A (18,0),B (0,-10),顶点坐标为(4,-989)⑵若四边形PQCA 为平行四边形,由于QC ∥P A ,故只要QC =P A 185. ⑶即可,而P A =18-4t ,CQ =t ,故18-4t =t ,得t =设点P 运动t s ,则OP =4t ,CQ =t ,0<t <4.5.说明P在线段OA 上,且不与点O ,A 重合.由于QC ∥OP 知△QDC ∽△PDO ,故144QD QC t DP OP t ===.同理QC ∥AF ,故14QC CE AF EA ==,即14t AF =,∴AF =4t =OP .∴PF =P A +AF =P A +OP =18.又点Q 到直线PF 的距离d =10,∴S △PQF =12•PF •d =12×18×10=90.于是S △PQF 的面积总为定值90. ⑷由前面知道,P (4t ,0),F (18+4t ,0),Q (8-t ,-10),0≤t ≤4.5.构造直角三角形后易得PQ 2=(4t -8+t )2+102=,FQ 2=(18+4t -8+t )2+102=(5t +10)2+100.①若FP =FQ ,即182=(5t +10)2+100,故25(t +2)2=224,(t +2)2=24425.∵2≤t +2≤6.5,∴t +2=244414255=.∴t = 4145-2. ②若QP =QF ,即(5t -8)2+100=(5t +10)2+100,即(5t -8)2=(5t +10)2,无0≤t ≤4.5的t 满足. ③若PQ =PF ,即(5t -8)2+100=182,∴(5t -8)2=224.由于224≈15,又0≤5t ≤22.5,∴-8≤5t -8≤14.5,14.52=22984124⎛⎫= ⎪⎝⎭<224.故没有t (0≤t ≤4.5)满足此方程.综上所述,当t =4145-2时,△PQ R 为等腰三角形. 10.⑴C 1的顶点坐标为(1,12). ⑵略 ⑶作PM ⊥AB 于M ,作QN ⊥AB 交AB 延长线于N ,∴PM =1-y P ,FM =1-x P .在R t △PMF 中,PF 2=(1-y P )2+(1-x P )2=1-2y P +y P 2+1-2x P +x P 2,又∵点P 在抛物线上,∴y P =12x P 2-x P +1,∴PF 2=1-x P 2+2x P -2+y P 2+1-2x P +x P 2=y P 2,∴PF =y P ,同理,QF =y Q ,易证△PMF ∽△QNF ,则PM QN PF QF =,∴11Q P y y PF QF --=,即11PF QF PF QF --=,∴11PF QF+=2. 11.先从特殊情况出发.当△ABC 是等腰直角三角形时,点P 与点C 重合,此时点P 的位置在AB 的中垂线上,且到AB的距离为12AB ,如图①所示.下面就一般情况来证明上面的结论(结论②所示).过C ,E ,G 分别作直线AB 的垂线CH ,EM ,G N ,垂足分别是H ,M ,N .容易证明△AEM ≌△ACH ,△B G N ≌△BCH .从而有AM =CH =BN ,EM =AH ,G N =BH .这样,线段AB 的中点O 也是线段MN 的中点,连接OP ,则OP 是梯形EMN G 的中位线,从而OP ⊥AB ,OP =12(EM +G N )= 12(AH +BH )=12AB .∴无论点C 在AB 同一侧的位置如何,E G 中点P 的位置不变.。
九年级数学中考典型及竞赛训练专题25 平面几何的最值问题2(附答案解析)

第2题图 第3题图 第4题图 第5题图
3.如图⊙O的半径为2,⊙O内的一点P到圆心的距离为1,过点P的弦与劣弧 组成一个弓形,则此弓形面积的最小值为.
4.如图,△ABC的面积为1,点D,G,E和F分别在边AB,AC,BC上,BD<DA,DG∥BC,DE∥AC,GF∥AB,则梯形DEFG面积的最大可能值为.(上海市竞赛试题)
所以,应选择路线2.
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1分米,高AB为5分米”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:l12=AC2=25+π2;
路线2:l22=(AB+BC)2=49.∵l12l22,∴l1<l2(填“>”或“<”),所以应选择路线1
8.(1)连结ME,过N作NF⊥AB于F,可证明Rt△EB A≌Rt△MNF,得MF=AE=x.∵ME2=AE2+AM2,故MB2=x2+AM2,即(2-AM)2=x2+AM2,AM=1- x2,∴S= ×AD= ×2=AM+AM+MF=2AM+AE=2(1- x2)+x=- x2+x+2.
(2)S=- (x2-2x+1)+ =- (x-1)2+ .故当AE=x=1时,四边形ADNM的面积最大,此时最大值为 .
(1)当MN为何值时,点P恰好落在BC上?
(2)设MN=x,△MNP与等腰△ABC重叠部分的面积为y,试写出y与x的函数关系式,当x为何值时,y的值最大,最大值是多少?(宁夏省中考试题)
B级
1.已知凸四边形ABCD中,AB+AC+CD= 16,且S四边彤ABCD=32,那么当AC=,BD=时,四边形ABCD面积最大,最大值是.(“华杯赛”试题)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学竞赛中的平面几何(学生班级用) 满涛 20XX 年7月
亲爱的同学们,欢迎你们参加江苏省初中生数学夏令营。
数学学习是艰苦的,也是美
妙有趣的,几何问题特别能够体现数学的美妙。
竞赛中的几何又比我们平时学习的几何要高
一个层次,但又能体现她的美丽。
单墫教授曾经在我本科学习的时候提及了一本小书——《平
面几何中的小花》,从那时起,我喜欢上几何……
对于要参加江苏省初中生数学竞赛的你们,我从近两年的竞赛真题讲起,从分析竞赛
真题到触类旁通,归纳出:
◆ 如何复习全面的几何知识
◆ 如何掌握解决几何问题的一般方法
◆ 几何问题需要的能力
◆ 与几何问题相关的其他问题
▲ 面积问题
1、(20届省竞赛)如图,△ABC 中,AD 、BE 相交于点O ,BD :CD =3 :2,
AE :CE = 2 :1.那么S ⊿BOC :S ⊿AOC :S ⊿AOB 为
(A )2 :3 :4 (B )2 :3:5 (C )3 :4:5 (D )3 :4 :6
从本题推想到三角形的面积,和求面积的比例方法。
(中线相交、中线的比,面积问题系列)
同样,20XX 年第19届的一道问题
2、如图,正方形ABCD 面积为144cm 2,P 为BC 边上的任意一点,E 为AP 的中点,F 为
PD 上的一点,且DF =2FP ,则△PEF 的面积是_____________ cm 2.
还有几道关于三角形的问题
3、(20届省竞赛)下面有三个判断:
(1)存在这样的三角形,它有两条角平分线互相垂直.
A B C D P E F
(2)存在这样的三角形,它的三条高的比是1 :2 :3.
(3)存在这样的三角形,其一边上的中线不小于其他两边和的一半.
其中正确的判断有 ( )
(A )0个 (B )1个 (C )2个 (D )3个
4、下列4个判断:
(1) 有两边及其中一边上的高对应相等的两个三角形全等;
(2) 有两边及第三边上的高对应相等的两个三角形全等;
(3) 三角形6个边、角元素中,有5个元素分别相等的两个三角形全等;
(4) 一边及其他两边上的高对应相等的两个三角形全等。
上述判断是否正确?若正确,说明理由;若不正确,请举出反例。
▲ 面积与最优化有关的问题
5、(20届省竞赛)平行四边形ABCD 中,AB = 6,BC = 4,∠ABC = 60°.要用一块矩形铝
板切割出这样的平行四边形并使废料最少,则矩形的面积最小为 .
6、将长为156 cm 的铁丝剪成两段,每段都围成一个边长为整数(cm )的正方形,则这两个正
方形面积和的最小值是 cm 2.
7、如果△ABC 的两边长分别为a 、b ,那么△ABC 的面积不可能等于 ( )
(A ) 14 (a 2 + b 2) (B ) 12 (a 2 + b 2 ) (C ) 18 (a + b )2 (D ) 14
ab 由这一题目联想到20XX 年初二的一道试题
8、凸四边形ABCD 中,AB+AC+CD=16,问:对角线AC,BD 为何值时,四边形ABCD 面积最
大?面积最大值是多少?
同样是给几个联加号,应该同样考虑不等式
9、四面体DABC 的体积为61,且满足,32
,45=++︒=∠AC BC AD ACB 则=CD 。
10、长边与短边之比为2:1的长方形为“标准长方形”。
约定用短边分别为a 1、a 2、a 3、a 4、
a 5(其中a 1<a 2<a 3<a 4<a 5的5个不同“标准长方形”拼成的大长方形记为(a 1、a 2、a 3、a 4、
a 5),如图,短边长分别为1,2,2.5,4.5,7的“标准长方形”拼成的大长方形记为(1,2,
2.5,4.5,7),解答下列问题:
(1)写出长方形(1,2,5,a 4,a 5)中a 4和a 5可取的值及相应的面积不同的长方形(用
上述长方形的记法表示出来),并画出其中两个符合要求的长方形示意图。
(2)所有这些长方形(1,2,5,a 4,a 5)的面积的最大值是多少?
▲ 与角度有关的问题
11、如图,AB 为⊙O 的直径,诸角p 、q 、r 、s 之间的关系 (1) p = 2q ;(2) q = r ;(3) p + s =
180° 中,正确的是 ( )
(A ) 只有(1)和(2) (B ) 只有(1)和(3) (C ) 只有(2)和(3) (D ) (1)、(2)和(3)
12、如图,DC ∥AB ,∠BAF =∠BCD ,AE ⊥DE ,∠D = 130°,则∠B = .
13、在凸四边形ABCD 中,AB=BC=BD ,∠ABC =700,则∠ADC 等于 ( )
(A)1450 (B)1500 (C)1550 (D)1600
14、如图,△ABC 为等边三角形,且BM=CN ,AM 与BN 相交于点P ,则∠APN ( )
(A)等于700 (B)等于600 (C)等于500 (D)大小不确定
▲ 几何计数问题
15、设一个三角形的三边长为正整数,,a n b ,其中b n a ≤≤。
则对于给定的边长n ,所有
这样的三角形的个数是
(A )n (B )1n + (C )2n n + (D )1(1)2
n n + 16、空间6个点(任意三点不共线)两两连线,用红、蓝两色染这些线段,其中A 点连出
的线段都是红色的,以这6个点为顶点的三角形中,三边同色的三角形至少有 ( )
(A )3个 (B )4个 (C )5个 (D )6个
17、在一张3×3的方格纸上(如图),用铅笔涂其中的5个方格,要求每横行和每竖列被涂方
格的个数都是奇数。
如果两种涂法经过旋转后相同,则认为它们是相同类型的涂法,
否则是
不同类型的涂法。
例如图1和图2是相同类型的涂法。
回答最多有多少种不同类型的涂法?说明理由。
引申到4×
4的方格。
18、两条直线相交所成的锐角或直
角称为两条直线的“夹角”. 现平
面上有W 条直线,它们两两相交,
并且“夹角”只能是 15°、30°、
45
°、60°、75°、90°、105°、
120°、135°、150°、165°之一,
问:
(1) W 的最大值是多少?
(2) 当W 取最大值时,问所有的“交角”的和是多少?
19、右图中,在圆周上有十个等分
点,每隔两个等分点用一条线段连
接两个等分点,共十条线段,它们
彼此相交,构成各种几何图形。
请
回答:图中共有多少个三边形?
图中共有多少个四边形?(包括凹
四边形)
▲ 其他 20、如图,在五边形ABCDE 中,M 、N 分别是AB 、AE 的中点,四边形AMPN ,△CPM ,△CPD ,△DPN 的面积分别为9、6、9、6。
求五边形ABCDE 的面积。
E。
