第一章概念答案
新概念物理教程热学答案第一章温度

新概念物理教程热学答案第一章温度1-1在什么温度下,下列一对温标给出相同的读数:(1)华氏温标和摄氏温标;(2)华氏温标和热力学温标;(3)摄氏温标和热力学温标?解:(1)当时,即可由时,解得故在(2)又当时则即解得:故在(3)若则有时,显而易见此方程无解,因此不存在的情况。
1-2定容气体温度计的测温泡浸在水的三相点槽内时,其中气体的压强为50mmHg。
(1)用温度计测量300K的温度时,气体的压强是多少?(2)当气体的压强为68mmHg时,待测温度是多少?解:对于定容气体温度计可知:(2)1-3用定容气体温度计测得冰点的理想气体温度为273.15K,试求温度计内的气体在冰点时的压强与水的三相点时压强之比的极限值。
解:根据已知冰点。
1-4用定容气体温度计测量某种物质的沸点。
原来测温泡在水的三相点时,其中气体的压强;当测温泡浸入待测物质中时,测得的压强值为减为200mmHg时,重新测得,当从,当再抽出一些测温泡中抽出一些气体,使气体使减为100mmHg时,测得.试确定待测沸点的理想气体温度.解:根据从理想气体温标的定义:时,T约为400.5K亦即沸点为400.5K.依以上两次所测数据,作T-P图看趋势得出题1-4图1-5铂电阻温度计的测量泡浸在水的三相点槽内时,铂电阻的阻值为90.35欧姆。
当温度计的测温泡与待测物体接触时,铂电阻的阻值为90.28欧姆。
试求待测物体的温度,假设温度与铂电阻的阻值成正比,并规定水的三相点为273.16K。
解:依题给条件可得则故,1-6在历史上,对摄氏温标是这样规定的:假设测温属性某随温度t 做线性变化即,并规定冰点为设解:和,汽化点为分别表示在冰点和汽化点时某的值,试求上式中的常数a和b。
由题给条件可知由(2)-(1)得将(3)代入(1)式得1-7水银温度计浸在冰水中时,水银柱的长度为4.0cm;温度计浸在沸水中时,水银柱的长度为24.0cm。
(1)在室温时,水银柱的长度为多少?(2)温度计浸在某种沸腾的化学溶液中时,水银柱的长度为25.4cm,试求溶液的温度。
应用数理统计吴翊李永乐第一章数理统计的基本概念课后习题答案

第一章 数理统计的基本概念课后习题参考答案1.1 设对总体X 得到一个容量为10的子样值:4.5,2.0,1.0,1.5,3.4,4.5,6.5,5.0,3.5,4.0,试分别计算子样均值X -和子样方差2S 的值。
解:12,n X X X 为总体X 的样本,根据 121()n XX X X n=+++ 求得X=3.59;根据2211()ni i S X X n ==-∑ 求得2S =2.5929。
1.2 设总体X 的分布函数为()x F ,密度函数为()x f ,n X X X ,,,21 为X 的子样,求最大顺序统计量()n X 及最小顺序统计量()1X 的分布函数及密度函数。
解:将总体X 中的样本按照从小到大的顺序排列成()()()n X X X ≤≤≤ 21 1.3 设总体X 服从正态分布N(12,4),今抽取容量为5的子样521,,,X X X ,试问:(1)子样的平均值X 大于13的概率为多少?(2)子样的极小值(最小顺序统计量)小于10的概率为多少? (3) 子样的极大值(最大顺序统计量)大于15的概率为多少? 解:(1)()()1314.08686.0112.1n /-X 15/41213n /-X P -113X P -113X P =-=⎪⎪⎭⎫ ⎝⎛≤-=⎪⎪⎭⎫⎝⎛-≤=≤=>σμσμP(2) ()()()5785.08412.011-X P -121210-X P -110P -110P 551i 51i 51min =-=⎪⎭⎫ ⎝⎛≤=⎪⎭⎫ ⎝⎛->=>=<∏∏∏===i i i i X X σμσμ(3) ()()()2923.093315.015.1-X P -121215-X P -115P -115P 551i 51i 51max =-=⎪⎭⎫ ⎝⎛≤=⎪⎭⎫⎝⎛->=≤=>∏∏∏===i i i i X X σμσμ1.4 试证:(1)22211()()()n niii i x a x x n x a ==-=-+-∑∑ 对任一实数a 成立。
工程热力学思考题答案,第一章

第一章基本概念与定义1。
闭口系与外界无物质交换,系统内质量保持恒定,那么系统内质量保持恒定的热力系一定是闭口系统吗? 答:不一定.稳定流动开口系统内质量也可以保持恒定.2.有人认为,开口系统中系统与外界有物质交换,而物质又与能量不可分割,所以开口系统不可能是绝热系。
对不对,为什么?答:这种说法是不对的。
工质在越过边界时,其热力学能也越过了边界。
但热力学能不是热量,只要系统和外界没有热量地交换就是绝热系。
3.平衡状态与稳定状态有何区别和联系,平衡状态与均匀状态有何区别和联系?答:只有在没有外界影响的条件下,工质的状态不随时间变化,这种状态称之为平衡状态。
稳定状态只要其工质的状态不随时间变化,就称之为稳定状态,不考虑是否在外界的影响下,这是他们的本质区别.平衡状态并非稳定状态之必要条件.物系内部各处的性质均匀一致的状态为均匀状态。
平衡状态不一定为均匀状态,均匀并非系统处于平衡状态之必要条件。
4。
倘使容器中气体的压力没有改变,试问安装在该容器上的压力表的读数会改变吗?绝对压力计算公式b e p p p =+()e p p >,b e p p p =-()e p p <中,当地大气压是否必定是环境大气压?答:压力表的读数可能会改变,根据压力仪表所处的环境压力的改变而改变.当地大气压不一定是环境大气压。
环境大气压是指压力仪表所处的环境的压力。
5.温度计测温的基本原理是什么?答:选作温度计的感应元件的物体应具备某种物理性质随物体的冷热程度不同有显著的变化。
有两个系统分别和第三个系统处于热平衡,则两个系统彼此必然处于热平衡。
6.经验温标的缺点是什么?为什么?答:任何一种经验温标不能作为度量温度的标准.由于经验温标依赖于测温物质的性质,当选用不同测温物质的温度计、采用不同的物理量作为温度的标志来测量温度时,除选定为基准点的温度,其他温度的测定值可能有微小的差异。
7。
促使系统状态变化的原因是什么?举例说明答:系统内部各部分之间的传热和位移或系统与外界之间的热量的交换与功的交换都是促使系统状态变。
护理学导论 第一章护理学的发展及基本概念习题及答案

一、名词解释1.护理学2.独立性护理功能3.专业性护理工作二、填空题1.按照护理专业的划分,护士应用自己的专业知识及能力分析及解决护理问题,称为护理工作。
2.南丁格尔两本最著名的护理经典著作为及。
三、判断题1.文艺复兴时期是西方护理界最黑暗的时期。
2.西方学者卡渤认为,护理学的知识中应包含个人知识。
3.护理专业的自主性体现为护士能自行决定所有的护理措施及护理行为。
4.南丁格尔的办学宗旨是将护理学作为一门科学的职业,采用新的教育体制及方法来培养护士。
5.解放以前,中国没有高等护理专业教育。
6.中国现代护理的发展在最初阶段主要受西方护理界的影响。
四、选择题【A型题】1.护理艺术、技能及行为方面的知识称为A.个人知识B.美学知识C.行为知识D.伦理学知识E.科学知识2.护理人员应用自己的专业知识及技能决定护理措施及护理服务,属于A独立性护理功能B.合作性护理功能C.技术性护理功能D.依赖性护理功能E.艺术性护理功能3.下列哪一项不属于护理专业特征A.为人类服务为目的B.有完善的教育体制C.有系统而坚实的专业理论基础D.有良好的科研体系E.有专业自主性4.自1964年以来,中国护理界群众性团体称为A.中国护士会B.中华护士学会C.中华护理学会D.中国护理学会E.中华护士会5.5月12日国际护士节命名根据是A.南丁格尔的生日B.南丁格尔所建立的第一所护士学校的日期C.南丁格尔逝世的日期D.南丁格尔受国际护士会奖励的日期E.南丁格尔受英国政府奖励的日期6.下列哪一项不属于以健康为中心阶段的护理特点:A.护理模式转变B.护理理论指导护理实践C.服务场所从医院扩展到了社区、家庭及各种机构D.护理的服务对象为所有年龄段的健康人及病人E.护理从属于医疗【B型题】(1~5题共用备选答案)A.护理学是研究帮助健康人或患病的人保持或恢复健康,预防疾病或者平静死亡的科学。
B.护理学是研究如何判断和处理人类对已经存在或潜在健康问题反应的科学。
人教版八上物理第一章基础概念填空(附答案)

人教版物理八年级上第一章机械运动(基础概念填空)一、长度的单位国际单位:__________。
常用单位:千米( ) ______(dm) 微米()_______(nm)。
1μm=__________m,1nm=__________m二、长度的测量1、测量工具:______________、______________、______________、______________等。
2、刻度尺的起始刻度称为:______________。
3、两条相邻刻度线之间的距离称为:______________。
4、测量范围又称为______________。
5、刻度尺要与被测物体________,________紧贴被测物体,________与被测物体一端对齐。
6、视线正对刻度尺的刻度线,不能________。
7、记录的测量结果要有________值、________值和________。
三、时间的测量1、__________能方便地用手启动和停止,常在实验室中用来测量时间。
2、在国际单位制中,时间的单位是______,常用的单位还有______和______等。
3、停表有两个表盘,大表盘:s/圈,分度值:小表盘:min/圈,分度值:四、误差与错误1、受测量工具等因素的影响,测量值和真实值之间________(选填“总有”或“没有”)误差,误差只能尽量,不能。
2、减小误差的方法:(1);(2);(3)。
五、运动的描述1、物理学中,把物体位置的变化叫,简称。
2、如果一个物体相对于参照物发生了变化,就说它是的;如果没有发生变化,就说它是的。
3、一般选择或相对于地面的物体作为参照物。
六、运动的快慢1、路程与时间之比叫。
2、1m/s= km/h。
3、物体沿着且不变的运动,称为匀速直线运动。
4、匀速直线运动的s-t图像是过的直线。
5、匀速直线运动的v-t图像是平行于轴的直线。
6、在相等的时间内通过的路长不相等,这种运动称为。
数据挖掘概念与技术习题答案-第1章

数据挖掘概念与技术(原书第3版)第一章课后习题及解答1.9习题1.1什么是数据挖掘?在你的回答中,强调以下问题:(a)它是又一种广告宣传吗?(b)它是一种从数据库、统计学、机器学习和模式识别发展而来的技术的简单转换或应用吗?(c)我们提出了一种观点,说数据挖掘是数据库技术进化的结果。
你认为数据挖掘也是机器学习研究进化的结果吗?你能基于该学科的发展历史提出这一观点吗?针对统计学和模式识别领域,做相同的事。
(d)当把数据挖掘看做知识发现过程时,描述数据挖掘所涉及的步骤。
答:狭义的数据挖掘是知识发现过程中的一个步骤,广义的数据挖掘通常用来表示整个知识发现过程,我们一般采用广义的观点:数据挖掘是从大量数据中挖掘有趣模式和知识的过程。
数据源包括数据库、数据仓库、WEB、其他信息存储库或动态地流入系统的数据。
a.它不是一种广告宣传,它基于实际的需求,提供从数据中发现知识的工具。
b。
数据挖掘不是从数据库、统计学、机器学习和模式识别发展而来的技术的简单转换或应用,它可以看做是信息技术的自然进化,是一些相关学科和应用领域的交汇点.c。
数据挖掘是数据库技术进化的结果,也是机器学习、统计学和模式识别领域技术进化的结果。
机器学习是一个快速成长的学科,这一领域中的监督学习、无监督学习、半监督学习和主动学习问题,与数据挖掘高度相关,数据挖掘和机器学习有许多相似之处,对于分类和聚类任务,机器学习研究通常关注模型的准确率。
除准确率之外,数据挖掘研究非常强调挖掘方法在大型数据集上的有效性和可伸缩性,以及处理复杂数据类型的方法,开发新的非传统的方法.统计学研究数据的收集、分析、解释和表示。
数据挖掘和统计学具有天然联系。
(1)统计模型是一组数学函数,它们利用随机变量及其概率分布刻画目标类对象的行为,可以是数据挖掘的结果,也可以是数据挖掘任务的基础。
(2)统计学研究开发一些使用数据和统计模型进行预测和预报的工具,描述统计可以帮助理解数据;推理统计学用某种方式对数据建模,可以解释观测中的随机性和确定性,并用来提取关于所考察的过程中或总体的结论.(3)统计假设检验使用实验数据进行统计判决,可以用来验证数据挖掘结果。
(完整版)代数学引论(聂灵沼_丁石孙版)第一章习题答案

第一章代数基本概念1.如果群G中,对任意元素a,b有(ab)2=a2b2,则G为交换群.证明:对任意a,bG,由结合律我们可得到(ab)2=a(ba)b, a2b2=a(ab)b再由已知条件以及消去律得到ba=ab,由此可见群G为交换群.2.如果群G中,每个元素a都适合a2=e, 则G为交换群.证明: [方法1]对任意a,bG,ba=bae=ba(ab)2=ba(ab)(ab)=ba2b(ab)=beb(ab)=b2(ab)=e(ab)=ab因此G为交换群.[方法2]对任意a,bG,a2b2=e=(ab)2,由上一题的结论可知G为交换群.3.设G是一非空的有限集合,其中定义了一个乘法ab,适合条件:(1)a(bc)=(ab)c;(2)由ab=ac推出a=c;(3)由ac=bc推出a=b;证明G在该乘法下成一群.证明:[方法1]设G={a1,a2,…,a n},k是1,2,…,n中某一个数字,由(2)可知若ij(I,j=1,2,…,n),有a k a i a k a j------------<1>a i a k a j a k------------<2>再由乘法的封闭性可知G={a1,a2,…,a n}={a k a1, a k a2,…, a k a n}------------<3>G={a1,a2,…,a n}={a1a k, a2a k,…, a n a k}------------<4>由<1>和<3>知对任意a t G, 存在a m G,使得a k a m=a t.由<2>和<4>知对任意a t G, 存在a s G,使得a s a k=a t.由下一题的结论可知G在该乘法下成一群.下面用另一种方法证明,这种方法看起来有些长但思路比较清楚。
[方法2]为了证明G在给定的乘法运算下成一群,只要证明G内存在幺元(单位元),并且证明G内每一个元素都可逆即可.为了叙述方便可设G={a1,a2,…,a n}.(Ⅰ) 证明G内存在幺元.<1> 存在a t G,使得a1a t=a1.(这一点的证明并不难,这里不给证明);<2> 证明a1a t= a t a1;因为a1(a t a1)a t=(a1a t) (a1a t)=(a1)2a1(a1a t)a t=(a1a1)a t=a1(a1a t)= (a1)2,故此a1(a t a1)a t= a1(a1a t)a t.由条件(1),(2)可得到a1a t= a t a1.<3> 证明a t就是G的幺元;对任意a k G,a1(a t a k) =(a1a t)a k=a1a k由条件(2)可知a t a k=a k.类似可证a k a t=a k.因此a t就是G的幺元.(Ⅱ) 证明G内任意元素都可逆;上面我们已经证明G内存在幺元,可以记幺元为e,为了方便可用a,b,c,…等符号记G 内元素.下面证明任意aG,存在bG,使得ab=ba=e.<1> 对任意aG,存在bG,使得ab=e;(这一点很容易证明这里略过.)<2> 证明ba=ab=e;因为a(ab)b=aeb=ab=ea(ba)b=(ab)(ab)=ee=e再由条件(2),(3)知ba=ab.因此G内任意元素都可逆.由(Ⅰ),(Ⅱ)及条件(1)可知G在该乘法下成一群.4.设G是非空集合并在G内定义一个乘法ab.证明:如果乘法满足结合律,并且对于任一对元素a,bG,下列方程ax=b和ya=b分别在G内恒有解,则G在该乘法下成一群.证明:取一元aG,因xa=a在G内有解, 记一个解为e a ,下面证明e a为G内的左幺元. 对任意bG, ax=b在G内有解, 记一个解为c,那么有ac=b ,所以e a b= e a(ac)= (e a a)c=ac=b,因此e a为G内的左幺元.再者对任意dG, xd=e a在G内有解,即G内任意元素对e a存在左逆元, 又因乘法满足结合律,故此G在该乘法下成一群.[总结]群有几种等价的定义:(1)幺半群的每一个元素都可逆,则称该半群为群.(2)设G是一个非空集合,G内定义一个代数运算,该运算满足结合律, 并且G内包含幺元, G内任意元素都有逆元,则称G为该运算下的群.(3)设G是一个非空集合,G内定义一个代数运算,该运算满足结合律, 并且G内包含左幺元, G内任意元素对左幺元都有左逆元,则称G为该运算下的群.(4)设G是一个非空集合,G内定义一个代数运算,该运算满足结合律, 并且对于任一对元素a,bG,下列方程ax=b和ya=b分别在G内恒有解,则称G为该运算下的群.值得注意的是如果一个有限半群满足左右消去律, 则该半群一定是群.5.在S3中找出两个元素x,y,适合(xy)2x2y2.[思路] 在一个群G中,x,yG, xy=yx (xy)2x2y2(这一点很容易证明).因此只要找到S3中两个不可交换的元素即可. 我们应该在相交的轮换中间考虑找到这样的元素.解: 取x=, y=那么(xy)2= x2y2.[注意]我们可以通过mathematica软件编写S n的群表,输出程序如下:Pr[a_,b_,n_]:=(*两个置换的乘积*)(Table[a[[b[[i]]]],{I,1,n}]);Se[n_]:=(*{1,2,…,n}的所有可能的排列做成一个表格*)(Permutations[Table[i,{I,1,n}]]);Stable[n_]:=(*生成S n群表*)(a=Se[n];Table[pr[a[[i]],a[[j]],n],{I,1,n},{j,1,n}])当n=3时群表如下:[说明]:表示置换, 剩下的类似.为了让更清楚,我们分别用e,a,b,c,d,f表示,,,,那么群表如下:6.对于n>2,作一阶为2n的非交换群.7.设G是一群, a,bG,如果a-1ba=b r,其中r为一正整数,证明a-i ba i=.证明:我们采用数学归纳法证明.当k=1时, a-1ba=b r=, 结论成立;假设当k=n时结论成立, 即a-n ba n=成立, 下面证明当k=n+1时结论也成立.我们注意到a-1b k a== b kr,因此a-(n+1)ba n+1= a-1 (a-n ba n)a=a-1a==,可见k=n+1时结论也成立.由归纳原理可知结论得证.8.证明:群G为一交换群当且仅当映射是一同构映射.证明:(Ⅰ)首先证明当群G为一个交换群时映射是一同构映射.由逆元的唯一性及可知映射为一一对应,又因为,并且群G为一个交换群,可得.因此有.综上可知群G为一个交换群时映射是一同构映射.(Ⅱ)接着证明当映射是一同构映射,则群G为一个交换群.若映射是一同构映射,则对任意有,另一方面,由逆元的性质可知.因此对任意有,即映射是一同构映射,则群G为一个交换群.9.设S为群G的一个非空子集合,在G中定义一个关系a~b当且仅当ab-1S.证明这是一个等价关系的充分必要条件为S是一个子群.证明:首先证明若~是等价关系,则S是G的一个子群.对任意aG,有a~a,故此aa-1=eS;对任意a,bS,由(ab)b-1=aS,可知ab~b,又be-1=bS,故b~e,由传递性可知ab~e,即(ab)e-1=abS.再者因ae-1=aS, 故a~e,由对称性可知e~a,即ea-1=a-1S.可见S是G的一个子群.接着证明当S是G的一个子群,下面证明~是一个等价关系.对任意aG, 有aa-1=eS,故此a~a(自反性);若a~b,则ab-1S,因为S为G的子群,故(ab-1)-1=ba-1S,因此b~a(对称性);若a~b,b~c,那么ab-1S,bc-1S,故ab-1 bc-1=ac-1S,因此a~c(传递性).综上可知~是一个等价关系.10.设n为一个正整数, nZ为正整数加群Z的一个子群,证明nZ与Z同构.证明:我们容易证明为Z到nZ的同构映射,故此nZ与Z同构.11.证明:在S4中,子集合B={e,(1 2)(3 4),(1 3)(2 4),(1 4)(2 3)}是子群,证明B与U4不同构.证明:为其本身),因此B为S4的子群. 这个群(以及与其同构的群)称为Klein(C.L.Klein,1849-1925)四元群.假设B与U4同构,并设f为B到U4的同构映射, 则存在B中一元x使得f(x)=i(i为虚数单位),那么f(x2)= f2(x)=i2=-1另一方面, f(x2)=f(e)=1(注意x2=e),产生矛盾.所以假设不成立, 即B与U4不同构. [讨论] B与U4都是4元交换群,但是后者是循环群, 前者不是, 这是这两个群的本质区别.12.证明:如果在一阶为2n的群中有一n阶子群,它一定是正规子群.证明:[方法1]设H是2n阶群G的n阶子群, 那么对任意aH, 有HaH=,并且aHG,HG,又注意到aH和H中都有n个元素, 故此HaH=G.同理可证对任意aH, 有HHa=, HHa=G,因此对任意aH,有aH=Ha.对任意aH, 显然aHH, HaH又因aH,Ha及H中都有n个元素,故aH=Ha=H.综上可知对任意aG,有aH=Ha,因此H是G的正规子群.[方法2]设H是2n阶群G的n阶子群,那么任取aH, hH, 显然有aha-1H.对给定的xH, 有HxH=, HxH=G.这是因为若假设yHxH, 则存在hH,使得y=xh,即x=yh-1H产生矛盾,因此HxH=;另一方面, xHG,HG, 又注意到xH和H中都有n个元素, 故此HxH=G.那么任取aH,由上面的分析可知axH, 从而可令a=xh1这里h1H.假设存在hH, 使得aha-1H,则必有aha-1xH,从而可令aha-1=xh2这里h2H.那么xh1ha-1=xh2,即a= h2h1hH,产生矛盾.因此,任取aH, hH, 有aha-1H.综上可知对任取aG, hH, 有aha-1H,因此H为G的一个正规子群.13.设群G的阶为一偶数,证明G中必有一元素ae适合a2=e.证明:设bG,且阶数大于2,那么b≠b-1,而b-1的阶数与b的阶数相等.换句话说G中阶数大于2的元素成对出现,幺元e的阶数为1,注意到G的阶数为宜偶数,故此必存在一个2阶元,(切确的说阶数为2的元素有奇数个).[讨论][1] 设G是一2n阶交换群,n为奇数则G中只有一个2阶元.为什么?提示:采用反证法,并注意用Lagrange定理.[2] 群G中,任取aG,有a n=e,那么G一定是有限群吗?如果不是请举出反例,若是有限群,阶数和n有什么关系?14.令A=, B=证明:集合{B,B2,…,B n,AB,AB2,…,AB n}在矩阵的乘法下构成一群, 而这个群与群D n同构. 证明:下面证明G={B,B2,…,B n,AB,AB2,…,AB n}在矩阵的乘法下构成一群.(Ⅰ)首先证明对乘法运算封闭. 下面进行分类讨论:(1)B i B j=B i+j,注意到B n=故此B i B j=B r G这里i+j=kn+r,kZ,0<rn.(2)A B i B j=B r G这里i+j=kn+r,kZ,0<rn.(3)容易证明BAB=A=AB n,BA=B i AB(s+1)n=AB n-t G,这里i=sn+t,kZ,0<tn.那么B i(AB j)=( B i A)B j=(AB n-t)B j G(4)(AB i)(AB j)=A(B i AB j)=A((AB n-t)B j)=A2(B n-t B j)= B n-t B j)G由(1),(2),(3),(4)知G对乘法运算封闭.(Ⅱ)因集合G对矩阵乘法封闭,再由矩阵乘法的性质可知,结合律肯定成立.(Ⅲ)显然B n=A2=E为幺元.(Ⅳ)对B i(i=1,2,…,n),有B i B n-i=E;对AB i(i=1,2,…,n),有(AB i)(B n-i A)=E,因此G内任何一元都可逆.由(Ⅰ),(Ⅱ),(Ⅲ),(Ⅳ)可知G在矩阵乘法下构成一群.最后证明G与D n同构.令f:G→D nf(B i)=T i, f(AB i)=ST i(i=1,2,…,n),可以证明f就是G到D n的同构映射,这里不予证明了.15.设i是一个正整数, 群G中任意元素a,b都适合(ab)k=a k b k, k=I,i+1,i+2,证明G为交换群.证明:对任意a,bGa i+2b i+2=(ab)i+2=(ab) (ab)i+1=(ab) (a i+1b i+1)=a(ba i+1)b i+1,根据消去律可得a i+1b=ba i+1.----------------------(1)同时a i+1b i+1=(ab)i+1=(ab) (ab)i=(ab) (a i b i)=a(ba i)b i+1,根据消去律可得a i b=ba i.---------------------------(2)因此a i+1b=a(a i b)=a(ba i)=(ab)a i----(3)另外ba i+1=(ba)a i----------------------(4)结合(1),(3),(4)有(ab)a i=(ba)a i---------------------(5)由消去律可得到ab=ba.因此G为交换群.16.在群SL2(Q)中,证明元素a=的阶为4,元素b=的阶为3,而ab为无限阶元素.证明:可以直接验证a的阶为4,b的阶为3.因为ab=,对任何正整数n,(ab)n=≠可见ab的阶为无限.[注意] 在一群中,有限阶元素的乘积并不一定也是有限阶的,但两个可交换的有限阶元素的乘积一定是有限阶元素.[问题] 若一群中所有元素的阶数都有限,那么这个群一定是有限群吗?17.如果G为一个交换群,证明G中全体有限阶元素组成一个子群.证明:交换群G中全体有限阶元素组成的集合记为S,任取a,bS,并设a的阶为m,b的阶为n,则(ab)mn=(a m)n(b n)m=e因此ab为有限阶元素,即abS.a-1的阶数与a相同,故此a-1也是有限阶元素,即a-1S.综上可知S为G的一个子群.18.如果G只有有限多个子群,证明G为有限群.证明:采用反证法证明.假设G为无限群,则G中元素只可能有两种情况:(1)G中任意元素的阶数都有限、(2)G中存在一个无限阶元素.(1)首先看第一种情况:G中取a1≠e,并设其阶数为n1,则循环群G1={,…}为G的一个子群;G中取a2G1,并设其阶数为n2,则循环群G2={,…}为G的一个子群;G中取a3G1∪G2,并设其阶数为n3,则循环群G3={,…}为G的一个子群;… … …我们一直这样做下去,可以得到G的互不相同的子群构成的序列G n(n=1,2,…),所以G有无穷多个子群,产生矛盾;(2)再看第二种情况:设a∈G的阶数为无穷,那么序列G1=<>,G2=<>,…,G n=<>,…是G的互不相同的子群,所以G有无穷多个子群,产生矛盾.综上就可知“G是无限群”这个假设不成立,因此G是有限群.19.写出D n的所有正规子群.20.设H,K为群G的子群,HK为G的一子群当且仅当HK=KH.证明:(Ⅰ)设HK=KH,下面证明HK为G的一子群.任取a,b∈HK,可令a=h1k1,b=h2k2这里h i∈H,k i∈K,i=1,2.那么ab=(h1k1)(h2k2)=h1(k1h2)k2 ---------------(1)因HK=KH,故此k1h2= h3k3 ----------------------(2)这里h3∈H,k3∈K.由(1),(2)知ab= h1(h3k3)k2=(h1h3)(k3k2)∈HK. ------------(3)另外,a-1= (h1k1)-1= ∈KH=HK. ----------------- (4)由(3),(4)知HK是G的子群.(Ⅱ) HK为G的一子群,下面证明HK=KH.若a∈HK,易知a-1∈KH. HK是子群,任取a∈HK,有a-1∈HK,因此(a-1)-1=a∈KH,那么有HK KH.若a∈KH,易知a-1∈HK. HK是子群,任取a∈KH,有a-1∈HK,因此(a-1)-1=a∈HK,那么有KH HK.综上知,HK=KH.21.设H,K为有限群G的子群,证明证明:因H∩K为H的子群,那么可设H的左陪集分解式为H=h1(H∩K)∪h2(H∩K)∪…∪h r(H∩K)这里r为H∩K在H中的指数,h i∈H,当i≠j,h i-1h j∉H∩K(事实上等价于h i-1h j∉K),i, j=1,2,…,r.又(H∩K)K=K,所以HK=h1K∪h2K∪…∪h r K.------------(1)注意到h i-1h j∉K,所以当i≠j(i, j=1,2,…,r)时,h i K∩h j K=.----------------(2)由(1),(2)我们得到[总结]左陪集的相关结论设H为G的一子群,那么(1)a∈a H;(2)a∈H⇔aH=H;(3)b∈aH⇔aH=bH;(4)aH=bH⇔a-1b∈H;(5)aH∩bH≠,有aH=bH.22.设M,N是群G的正规子群.证明:(i)MN=NM;(ii)MN是G的一个正规子群;(iii)如果MN={e},那么MN/N与M同构.证明:(i)[方法1]任取a∈MN,可设a=mn(m∈M,n∈N).因为M为G的正规子群,故n-1mn∈M. 所以a=n(n-1mn) ∈NM,故此MN⊆NM.同样的方法可以证明NM⊆MN. 因此MN=NM.[方法2]任取a,b∈MN,可设a=m1n1(m1∈M,n1∈N),b=m2n2(m2∈M,n2∈N).下面只要证明MN为G的一个子群即可(由第20题可知),也就是说只要证明ab-1∈MN即可.因为ab-1=m1n1n2-1m2-1= [m1(n1n2-1m2-1n2n1-1)](n1n2-1),而M为G的正规子群,故n1n2-1m2-1n2n1-1∈M,所以ab-1∈MN.(ii) 由(i)可知MN为G的一个子群.任取a∈MN, 可设a=mn(m∈M,n∈N).因为M和N为G的正规子群,对任意g∈G,有g-1ag= g-1mng= (g-1mg)(g-1ng) ∈MN.所以MN为G的正规子群.(iii) 易知N为MN的正规子群,因此MN/N是一个群. 因为MN={e},对任何m i≠m j∈M, 有m i N≠m j N[注].作一个MN/N到M的映射f[注],f: MN/N→MmNm,那么该映射显然是一一对应,另外f(m i Nm j N)= f(m i m j N)= m i m j,因此f为MN/N到M的同构映射,即MN/N与M同构.[讨论]1. 只要M和N的一个是正规子群,那么MN就是子群,或者说成立MN=NM.这一点我们从(i)的证明方法2可知.2. M和N中有一个不是正规子群时MN一定不是正规子群.[注意]1MN={e},对任何m i≠m j∈M, 有m i N≠m j N.证明:若存在m i≠m j∈M, 有m i N=m j N,那么m i m j-1∈N,而m i m j-1∈M. 因此m i m j-1∈MN,产生矛盾.2. 设f: MN/N→MmNm,则由于对任何m i≠m j∈M, 有m i N≠m j N,故此f为MN/N到M的一个映射.23.设G是一个群,S是G的一非空子集合.令C(S)={x∈G|xa=ax,对一切a∈S}N(S)= {x∈G|x-1Sx=S}.证明:(i) C(S),N(S)都是G的子群;(ii) C(S)是N(S)的正规子群.证明:(i) 首先证明C(S)是G的子群.任取x,y∈C(S),那么对任意a∈S有xa=ax,ya=ay. 那么一方面,(xy)a=x(ya)=x(ay)=(xa)y=(ax)y=a(xy),所以xy∈C(S).另一方面,xa=axa=x-1axax-1=x-1a所以x-1∈C(S).因此,C(S)是G的子群.接着证明N(S)都是G的子群.任取x,y∈N(S),则x-1Sx=S,y-1Sy=S. 那么一方面,(xy)-1S(xy)=x-1(y-1Sy)x=x-1Sx=S所以xy∈N(S).另一方面,x-1Sx=SS=xSx-1所以x-1∈N(S).因此,N(S)是G的子群.(ii) 任取x∈C(S),a∈S,则xa=ax,即a=x-1ax,亦即S= x-1Sx. 因此x∈N(S),即C(S)N(S).任取x∈C(S),y∈N(S),a∈S,则存在a y∈S使得yay-1=a y,因此a=y-1a y y.那么(y-1xy)a(y-1xy)-1=y1[x(yay-1)x-1]y= y1(xa y x-1)y= y-1a y y=a,即(y-1xy)a=a(y-1xy).所以y-1xy∈C(S),因此C(S)是N(S)的正规子群.24.证明任意2阶群都与乘法群{1,-1}同构.证明:略.25.试定出所有互不相同的4阶群.解:我们分类讨论:(1)存在四阶元;(2)不存在四阶元.(1)若存在一个四阶元,并设a为一个四阶元,那么该四阶群为<a>.(2)若不存在四阶元,那么除了单位元e的阶为1,其余元素的阶只能是2,即设四阶群222综上可知,四阶群群在同构意义下只有两种或者是四阶循环群或者是Klein四阶群.26.设p为素数.证明任意两个p阶群必同构.证明:易知当p为素数时,p阶群必存在一个p阶元,即p阶群必是p阶循环群,故两个p 阶群必同构.27.Z为整数环,在集合S=Z×Z上定义(a,b)+(c,d)=(a+c,b+d),(a,b)(c,d)=(ac+bd,ad+bc).证明S在这两个运算下成为幺环.提示:(1,0)为该环的单位元素.证明:略.28.在整数集上重新定义加法“”与乘法“”为ab=ab, ab=a+b试问Z在这两个运算下是否构成一环.答:不构成环.29.设L为交换幺环,在L中定义:ab=a+b-1,ab=a+b-ab.这里e为单位元素,证明在新定义的运算下,L仍称为交换幺环,并且与原来的环同构. 证明:(i)证明L在运算下构成交换群:由的定义,得到(ab)c=(a+b-1)c=a+b-1+c-1=a+b+c-2a(bc)= a(b+c-1)= a+b+c-1-1=a+b+c-2这里2=1+1,所以(ab)c= a(bc).----------------(1)同时由的定义还可以得到a1= 1a=a,------------------------(2)a(2-a)=(2-a)a=1,---------------(3)ab=ba,----------------------------(4)由(1),(2),(3)(4)可知L在运算下构成交换群.(ii)证明L中运算满足结合律和交换律:容易证明这里略过.(iii)证明乘法对加法满足分配律:因为a(bc)= a(b+c-1)=a+(b+c-1)-a(b+c-1)=2a+b+c-ab-ac-1,(ab)(ac)=(a+b-1)(a+c-1)= (a+b-ab)+(a+c-ac)-1=2a+b+c-ab-ac-1,所以a(bc)= (ab)(ac).由于和满足交换律,故此(bc)a= (ba)(ca).因此新定义的乘法对新定义的加法满足分配律(iv) 设0为环(L,+,)的零元,则0a=a0=a由(i),(ii),(iii),(iv)可得到(L,,)为交换幺环.(v) 最后证明(L,+,)与(L,,)同构:设f: L→Lx1-x,容易证明f为(L,+,)到(L,,)的同构映射.30.给出环L与它的一个子环的例子,它们具有下列性质:(i) L具有单位元素,但S无单位元素;(ii) L没有单位元素,但S有单位元素;(iii) L, S都有单位元素,但互不相同;(iv) L不交换,但S交换.解:(i) L=Z,S=2Z;(ii) L={|a,b∈R},S={|a∈R};(iii) L={|a,b∈R},S={|a∈R};(iv) L={|a,b∈R},S={|a∈R};31.环L中元素e L称为一个左单位元,如果对所有的a∈L,e L a= a;元素e R称为右单位元,如果对所有的a∈L,ae R=a.证明:(i)如果L既有左单位元又有右单位元,则L具有单位元素;(ii)如果L有左单位元,L无零因子,则L具有单位元素;(iii)如果L有左单位元,但没有右单位元,则L至少有两个左单位元素.证明:(i) 设e L为一个左单位元,e R为右单位元,则e L e R=e R=e L.记e=e R=e L,则对所有的a∈L,ea=ae=a,因此e为单位元素;(ii) 设e L为一个左单位元,则对所有的a(≠0)∈L,a(e L a)=a2;另一方面,a(e L a)=(ae L)a. 所以a2=(ae L)a.因为L无零因子,所以满足消去律[注],故此a= ae L.另外,若a=0,则a= ae L=e L a.因此左单位元e L正好是单位元.(iii) 设e L为一个左单位元,因为L中无右单位元,故存在x∈L,使得xe L≠x,即xe L-x≠0,则e L+ xe L-x≠e L,但是对所有的a∈L,(e L+ xe L-x)a=a,因此e L+ xe L-x为另一个左单位元,所以L至少有两个左单位元素.[注意] L无零因子,则满足消去律(参考教材46页).32.设F为一域.证明F无非平凡双边理想.证明:设I为F的任意一个理想,且I≠{0},则对任意a(≠0)∈I,则a-1∈F,于是a-1a=1∈I.从而F中任意元素f,有f1=f∈I,故I=F,即F只有平凡双边理想.[讨论] 事实上,一个体(又称除环)无非平凡双边理想. 另一方面,若L是阶数大于1的(交换)幺环,并且除了平凡理想,没有左或右理想,则L是一体(域).33.如果L是交换环,a∈L,(i) 证明La={ra|r∈L}是双边理想;(ii) 举例说明,如果L非交换,则La不一定是双边理想.证明:(i) 容易验证La为L的一个加法群. 任取ra∈La,l∈L,则l(ra)=(lr)a∈La,(ra)l=r(al)=r(la)=(rl)a∈La故La为L的一个双边理想.(ii) 设L=M2(R),那么L显然不是交换环,取h=,下面考察Lh是否为L的理想:取k=,容易验证h∈Lh,hk Lh,因此Lh不是L的一个理想.34.设I是交换环L的一个理想,令rad I={r∈L|r n∈I对某一正整数n},证明rad I也是一个理想.radI叫做理想I的根.35.设L为交换幺环,并且阶数大于1,如果L没有非平凡的理想,则L是一个域.证明:只要证明非零元素均可逆即可.任取a∈L,那么La和aL是L的理想,且La≠{0},aL≠{0},因L无平凡的理想,故此La=aL=L,因此ax=1和ya=1都有解,因而a为可逆元.36.Q是有理数域,M n(Q)为n阶有理系数全体矩阵环.证明无非平凡的理想(这种环称为单环).证明:我们社K为M n(Q)的非零理想,下面证明K=M n(Q).为了证明这一点,只要证明n阶单位矩阵E∈K.记E ij为除了第i行第j列元素为1,其余元素全为0的矩阵.那么E ij E st=而E=E11+E22+…+E nn.我们只要证明E ii∈K(i=1,2,…,n)就有E∈K.设A∈K,且A≠0,又令A=(a ij)n×n,假设a kj≠0,则有E ik AE ji=a kj E ii(i=1,2,…,n).由于a kj≠0,故存在逆元a kj-1.设B= a kj-1E ii,则BE ik AE ji= a kj-1E ii E ik AE ji= a kj-1E ik AE ji=E ik E kj E ji=E ii.因为K为理想,A∈K,所以E ii=BE ik AE ji∈K,证毕.37.设L为一环,a为L中一非零元素.如果有一非零元素b使aba=0,证明a是一个左零因子或一右零因子.证明:若ab=0,则a为左零因子;若ab≠0,则aba=(ab)a=0,故ab为右零因子.38.环中元素x称为一幂零元素,如果有一正整数n使x n=0,设a为幺环中的一幂零元素,证明1-a可逆.证明:设a n=0,那么(1+a+a2+…+a n-1)(1-a)=(1-a) (1+a+a2+…+a n-1)=1-a n=1因此1-a可逆.39.证明:在交换环中,全体幂零元素的集合是一理想.40.设L为有限幺环.证明由xy=1可得yx=1.证明:当L只有一个元素,即L={0},亦即0=1[注],此时显然有xy=1=xy;当L有多于一个元素时(即0≠1时),若xy=1,y不是左零元[注],因此yL=L.又因L为有限环,所以存在z∈L,使得yz=1.注意到(xy)z=z,x(yz)=x,所以x=z,即yx=1.[注意]1.幺环多于一个元素当且仅当0≠1.2.当L有多于一个元素时(即0≠1时),若xy=1,y不是左零元.因为若存在z≠0使得yz=0,则z=(xy)z=x(yz)=0,产生矛盾.41.在幺环中,如果对元素a有b使ab=1但ba≠1,则有无穷多个元素x,适合ax=1. (Kaplansky定理)证明:首先,若ab=1但ba≠1,则a至少有两个右逆元[注].现在假设a只有n(>1)个右逆元,并设这些元素为x i(i=1,2,…,n).那么a(1-x i a+x1)=1(i=1,2,…,n),又当i≠j时,1-x i a+x1≠1-x j a+x1[注],这里i,j=1,2,…,n.于是{x i|i=1,2,…,n}={1-x i a+x1| i=1,2,…,n },故存在x k∈{x i|i=1,2,…,n}使得x1=1-x k a+x1,即x k a=1.因为n>1,我们取x t≠x k∈{x i|i=1,2,…,n},那么(x k a)x t=x t,(x k a)x t =x k(ax t)=x k因此x t=x k,产生矛盾,所以假设不成立,即a有无穷多个右逆元.[注意]1. 若ab=1但ba≠1,则a至少有两个右逆元. 因为易验证1-ba+a就是另一个右逆元.2. 假设当i≠j时,1-x i a+x1=1-x j a+x1,则x i a=x j a,故x i ax1=x j ax1,因此x i=x j,产生矛盾.42.设L是一个至少有两个元素的环. 如果对于每个非零元素a∈L都有唯一的元素b使得aba=a.证明:(i) L无零因子;(ii) bab=b;(iii) L有单位元素;(iv) L是一个体.证明:(i) 先证明L无左零因子,假设a为L的一个左零因子,那么a≠0,且存在c≠0,使得ac=0,于是cac=0. 因a≠0,则存在唯一b使得aba=a.但a(b+c)a=a,b+c≠b产生矛盾,所以L无左零因子.类似可证L无右零因子.(ii) 因aba=a,所以abab=ab. 由(i)的结论知L无零因子,因此满足消去律,而a≠0,故bab=b.(iii) 我们任一选取a(≠0)∈L,再设aba=a(这里b是唯一的),首先证明ab=ba.因为a(a2b-a+b)a=a,所以a2b-a+b=b,即a2b=a=aba,由消去律得到ab=ba.任取c∈L,则ac=abac,故此c=(ba)c=(ab)c;另一方面,ca=caba,故此c=c(ab).综上得到c=(ab)c=c(ab),所以ab就是单位元素,我们记ab=ba=1.(iv) 由(iii)可知任意a(≠0)∈L,ab=ba=1,即任意非零元素都可逆,因此L成为一个体.43.令C[0,1]为全体定义在闭区间[0,1]上的连续函数组成的环.证明:(i) 对于的任一非平凡的理想I,一定有个实数,,使得f()=0对所有的f(x)∈I;(ii) 是一零因子当且仅当点集{x∈[0,1]|f(x)=0} 包含一个开区间.证明:(i) 证明思路:设I为非零的非平凡理想,假设对任意x∈[0,1],存在f(x)∈I使得f(x)≠0,想法构造一个g∈I可逆.(ii) 提示:用连续函数的局部保号性.44.令F=Z/pZ为p个元素的域.求(i) 环M n(F)的元素的个数;(ii) 群GL n(F)的元素的个数.45.设K是一体,a,b∈K,a,b不等于0,且ab≠1.证明华罗庚恒等式:a-(a-1+(b-1-a)-1)-1=aba.证明:因为a-(a-1+(b-1-a)-1)-1=aba⇔1-(a-1+(b-1-a)-1)-1a-1=ab⇔(aa-1+a(b-1-a)-1)-1=1-ab⇔(1+a(b-1-a)-1)-1=1-ab⇔(1+((ab)-1-1)-1)-1=1-ab,为了方便记x=ab,那么1-x,x,x-1-1都可逆,只要证明(1+(x-1-1)-1)-1=1-x即可,或者证明1+(x-1-1)-1=(1-x)-1即可.因为1+(x-1-1)-1=1+(x-1-x-1x)-1=1+(1-x)-1x=(1-x)-1(1-x) +(1-x)-1x=(1-x)-1,所以结论成立,即a-(a-1+(b-1-a)-1)-1=aba.。
高一数学练习册答案:第一章集合与函数概念

2019高一数学练习册答案:第一章集合与函数概念1.1集合1 1 1集合的含义与表示1.D.2.A.3.C.4.{1,-1}.5.{x|x=3n+1,n∈N}.6.{2,0,-2}.7.A={(1,5),(2,4),(3,3),(4,2),(5,1)}.8.1.9.1,2,3,6. 10.列举法表示为{(-1,1),(2,4)},描述法的表示方法不唯一,如可表示为(x,y)|y=x+2,y=x2.11.-1,12,2.1 1 2集合间的基本关系1.D.2.A.3.D.4. ,{-1},{1},{-1,1}.5. .6.①③⑤.7.A=B.8.15,13.9.a≥4.10.A={ ,{1},{2},{1,2}},B∈A.11.a=b=1.1 1 3集合的基本运算(一)1.C.2.A.3.C.4.4.5.{x|-2≤x≤1}.6.4.7.{-3}.8.A∪B={x|x3,或x≥5}.9.A∪B={-8,-7,-4,4,9}.10.1.11.{a|a=3,或-221 1 3集合的基本运算(二)1.A.2.C.3.B.4.{x|x≥2,或x≤1}.5.2或8.6.x|x=n+12,n∈Z.7.{-2}.8.{x|x6,或x≤2}.9.A={2,3,5,7},B={2,4,6,8}.10.A,B的可能情形有:A={1,2,3},B={3,4};A={1,2,4},B={3,4};A={1,2,3,4},B={3 ,4}.11.a=4,b=2.提示:∵A∩ 綂 UB={2},∴2∈A,∴4+2a-12=0 a=4,∴A={x|x2+4x-12=0}={2,-6},∵A∩ 綂 UB={2},∴-6 綂 UB,∴-6∈B,将x=-6代入B,得b2-6b+8=0 b=2,或b=4.①当b=2时,B={x|x2+2x-24=0}={-6,4},∴-6 綂 UB,而2∈ 綂 UB,满足条件A∩ 綂UB={2}.②当b=4时,B={x|x2+4x-12=0}={-6,2}, ∴2 綂 UB,与条件A∩ 綂 UB={2}矛盾.1.2函数及其表示1 2 1函数的概念(一)1.C.2.C.3.D.4.22.5.-2,32∪32,+∞.6.[1,+∞).7.(1)12,34.(2){x|x≠-1,且x≠-3}.8.-34.9.1.10.(1)略.(2)72.11.-12,234.1 2 1函数的概念(二)1.C.2.A.3.D.4.{x∈R|x≠0,且x≠-1}.5.[0,+∞).6.0.7.-15,-13,-12,13.8.(1)y|y≠25.(2)[-2,+∞).9.(0,1].10.A∩B=-2,12;A∪B=[-2,+∞).11.[-1,0).1 2 2函数的表示法(一)1.A.2.B.3.A.4.y=x100.5.y=x2-2x+2.6.1x.7.略.8.x1234y828589889.略.10.1.11.c=-3.1 2 2函数的表示法(二)1.C.2.D.3.B.4.1.5.3.6.6.7.略.8.f(x)=2x(-1≤x0),-2x+2(0≤x≤1).9.f(x)=x2-x+1.提示:设f(x)=ax2+bx+c,由f(0)=1,得c=1,又f(x+1)-f(x)=2x,即a(x+1)2+b(x+1)+c-(ax2+bx+c)=2x,展开得2ax+(a+b)=2x,所以2a=2,a+b=0,解得a=1,b=-1.10.y=1.2(02.4(203.6(404.8(601.3函数的基本性质1 3 1单调性与最大(小)值(一)1.C.2.D.3.C.4.[-2,0),[0,1),[1,2].5.-∞,32.6.k12.7.略.8.单调递减区间为(-∞,1),单调递增区间为[1,+∞).9.略.10.a≥-1.11.设-10,∴(x1x2+1)(x2-x1)(x21-1)(x22-1)0,∴函数y=f(x)在(-1,1)上为减函数.1 3 1单调性与最大(小)值(二)1.D.2.B.3.B.4.-5,5.5.25.6.y=316(a+3x)(a-x)(011.日均利润最大,则总利润就最大.设定价为x元,日均利润为y元.要获利每桶定价必须在12元以上,即x12.且日均销售量应为440-(x-13)·400,即x23,总利润y=(x-12)[440-(x-13)·40]-600(121 3 2奇偶性1.D.2.D.3.C.4.0.5.0.6.答案不唯一,如y=x2.7.(1)奇函数.(2)偶函数.(3)既不是奇函数,又不是偶函数.(4)既是奇函数,又是偶函数.8.f(x)=x(1+3x)(x≥0),x(1-3x)(x0).9.略.10.当a=0时,f(x)是偶函数;当a≠0时,既不是奇函数,又不是偶函数.11.a=1,b=1,c=0.提示:由f(-x)=-f(x),得c=0,∴f(x)=ax2+1bx,∴f(1)=a+1b=2a=2b-1.∴f(x)=(2b-1)x2+1bx.∵f(2)3,∴4(2b-1)+12b32b-32b0 0单元练习1.C.2.D.3.D.4.D.5.D.6.B.7.B.8.C.9.A.10.D.11.{0,1,2}.12.-32.13.a=-1,b=3.14.[1,3)∪(3,5].15.f1217.T(h)=19-6h(0≤h≤11),-47(h11).18.{x|0≤x≤1}.19.f(x)=x只有唯一的实数解,即xax+b=x(*)只有唯一实数解,当ax2+(b-1)x=0有相等的实数根x0,且ax0+b≠0时,解得f(x)=2xx+2,当ax2+(b-1)x=0有不相等的实数根,且其中之一为方程(*)的增根时,解得f(x)=1.20.(1)x∈R,又f(-x)=(-x)2-2|-x|-3=x2-2|x|-3=f(x),所以该函数是偶函数.(2)略.(3)单调递增区间是[-1,0],[1,+∞),单调递减区间是(-∞,-1],[0,1].21.(1)f(4)=4×13=5.2,f(5.5)=5×1.3+0.5×3.9=8.45,f(6.5)=5×1.3+1×3.9+ 0.5×6 5=13.65.(2)f(x)=1.3x(0≤x≤5),3.9x-13(56.5x-28.6(622.(1)值域为[22,+∞).(2)若函数y=f(x)在定义域上是减函数,则任取x1,x2∈(0,1]且x1f(x2)成立,即(x1-x2)2+ax1x20,只要a-2x1x2即可,由于x1,x2∈(0,1],故-2x1x2∈(-2,0),a-2,即a的取值范围是(-∞,-2).(实习编辑:邓杉)。
第1章 随机过程的基本概念习题答案

第一章 随机过程的基本概念1.设随机过程 +∞<<-∞=t t X t X ,cos )(0ω,其中0ω是正常数,而X 是标准正态变量。
试求X (t )的一维概率分布解:∵ 当0cos 0=t ω 即 πω)21(0+=k t 即 πω)21(10+=k t 时 {}10)(==t x p若 0cos 0≠t ω 即 πω)21(10+≠k t 时 {}{}x t X P x x X P t x F ≤=≤=0cos )(),(ω当 0cos 0>t ω时ξπωωξd et x X P t x F t x⎰-=⎭⎬⎫⎩⎨⎧≤=02cos 02021cos ),(此时 ()te xt x F t x f tx 0cos 2cos 121,),(022ωπω⋅=∂∂=-若 0cos 0<t ω时⎭⎬⎫⎩⎨⎧<-=⎭⎬⎫⎩⎨⎧≥=t x x P t x X P t x F 00cos 1cos ),(ωωξπωξd et x⎰--=02cos 02211同理有 tet x f tx 0cos 2cos 121),(022ωπω⋅-=-综上当:0cos 0≠t ω 即 πω)21(10+≠k t 时 tx et x f 022cos 20|t cos |121),(ωωπ-=2.利用投掷一枚硬币的试验,定义随机过程为⎩⎨⎧=,2,cos )(出现反面出现正面t t t X π 假定“出现正面”和“出现反面”的概率各为21。
试确定)(t X 的一维分布函数)21,(x F 和)1,(x F ,以及二维分布函数)1,21;,(21x x F解:(1)先求)21,(x F显然⎩⎨⎧=⎪⎩⎪⎨⎧-=⎪⎭⎫ ⎝⎛出现反面出现正面出现反面出现正面10,212,2cos 21πX随机变量⎪⎭⎫⎝⎛21X 的可能取值只有0,1两种可能,于是21021=⎭⎬⎫⎩⎨⎧=⎪⎭⎫ ⎝⎛X P 21121=⎭⎬⎫⎩⎨⎧=⎪⎭⎫ ⎝⎛X P 所以⎪⎩⎪⎨⎧≥<≤<=⎪⎭⎫ ⎝⎛1110210021,x x x x F再求F (x ,1)显然⎩⎨⎧-=⎩⎨⎧=出现反面出现正面出现反面出现正面 2 1 2cos (1)πX{}{}212)1(-1(1)====X p X p 所以⎪⎪⎩⎪⎪⎨⎧≥<≤<=2121- 21-10,1)(x x x x F(2) 计算)1,21;,(21x x F⎩⎨⎧-=⎩⎨⎧=出现反面出现正面出现反面出现正面21)1(, 1 0)21( X X于是2 ,1 121 ,12 ,10 211 ,00 )1(;211,21;,21212121212121⎪⎪⎪⎩⎪⎪⎪⎨⎧≥><≤->≤<≤-<≥+∞<<∞-<=⎭⎬⎫⎩⎨⎧≤≤⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛x x x x x x x x x x x X x X p x x F x 或或3.设随机过程(){}+∞<<-∞t t X ,共有三条样本曲线t X t X X cos )t,( ,sin )t,( ,1)t,(321===ϖϖϖ且,31)p()p()p(321===ϖϖϖ试求随机过程()t X 数学期望EX(t)和相关函数R x (t 1,t 2)。
(完整版)代数学引论(聂灵沼_丁石孙版)第一章习题答案

第一章代数基本概念1.如果群G中,对任意元素a,b有(ab)2=a2b2,则G为交换群.证明:对任意a,bG,由结合律我们可得到(ab)2=a(ba)b, a2b2=a(ab)b再由已知条件以及消去律得到ba=ab,由此可见群G为交换群.2.如果群G中,每个元素a都适合a2=e, 则G为交换群.证明: [方法1]对任意a,bG,ba=bae=ba(ab)2=ba(ab)(ab)=ba2b(ab)=beb(ab)=b2(ab)=e(ab)=ab因此G为交换群.[方法2]对任意a,bG,a2b2=e=(ab)2,由上一题的结论可知G为交换群.3.设G是一非空的有限集合,其中定义了一个乘法ab,适合条件:(1)a(bc)=(ab)c;(2)由ab=ac推出a=c;(3)由ac=bc推出a=b;证明G在该乘法下成一群.证明:[方法1]设G={a1,a2,…,a n},k是1,2,…,n中某一个数字,由(2)可知若ij(I,j=1,2,…,n),有a k a i a k a j------------<1>a i a k a j a k------------<2>再由乘法的封闭性可知G={a1,a2,…,a n}={a k a1, a k a2,…, a k a n}------------<3>G={a1,a2,…,a n}={a1a k, a2a k,…, a n a k}------------<4>由<1>和<3>知对任意a t G, 存在a m G,使得a k a m=a t.由<2>和<4>知对任意a t G, 存在a s G,使得a s a k=a t.由下一题的结论可知G在该乘法下成一群.下面用另一种方法证明,这种方法看起来有些长但思路比较清楚。
[方法2]为了证明G在给定的乘法运算下成一群,只要证明G内存在幺元(单位元),并且证明G内每一个元素都可逆即可.为了叙述方便可设G={a1,a2,…,a n}.(Ⅰ) 证明G内存在幺元.<1> 存在a t G,使得a1a t=a1.(这一点的证明并不难,这里不给证明);<2> 证明a1a t= a t a1;因为a1(a t a1)a t=(a1a t) (a1a t)=(a1)2a1(a1a t)a t=(a1a1)a t=a1(a1a t)= (a1)2,故此a1(a t a1)a t= a1(a1a t)a t.由条件(1),(2)可得到a1a t= a t a1.<3> 证明a t就是G的幺元;对任意a k G,a1(a t a k) =(a1a t)a k=a1a k由条件(2)可知a t a k=a k.类似可证a k a t=a k.因此a t就是G的幺元.(Ⅱ) 证明G内任意元素都可逆;上面我们已经证明G内存在幺元,可以记幺元为e,为了方便可用a,b,c,…等符号记G 内元素.下面证明任意aG,存在bG,使得ab=ba=e.<1> 对任意aG,存在bG,使得ab=e;(这一点很容易证明这里略过.)<2> 证明ba=ab=e;因为a(ab)b=aeb=ab=ea(ba)b=(ab)(ab)=ee=e再由条件(2),(3)知ba=ab.因此G内任意元素都可逆.由(Ⅰ),(Ⅱ)及条件(1)可知G在该乘法下成一群.4.设G是非空集合并在G内定义一个乘法ab.证明:如果乘法满足结合律,并且对于任一对元素a,bG,下列方程ax=b和ya=b分别在G内恒有解,则G在该乘法下成一群.证明:取一元aG,因xa=a在G内有解, 记一个解为e a ,下面证明e a为G内的左幺元. 对任意bG, ax=b在G内有解, 记一个解为c,那么有ac=b ,所以e a b= e a(ac)= (e a a)c=ac=b,因此e a为G内的左幺元.再者对任意dG, xd=e a在G内有解,即G内任意元素对e a存在左逆元, 又因乘法满足结合律,故此G在该乘法下成一群.[总结]群有几种等价的定义:(1)幺半群的每一个元素都可逆,则称该半群为群.(2)设G是一个非空集合,G内定义一个代数运算,该运算满足结合律, 并且G内包含幺元, G内任意元素都有逆元,则称G为该运算下的群.(3)设G是一个非空集合,G内定义一个代数运算,该运算满足结合律, 并且G内包含左幺元, G内任意元素对左幺元都有左逆元,则称G为该运算下的群.(4)设G是一个非空集合,G内定义一个代数运算,该运算满足结合律, 并且对于任一对元素a,bG,下列方程ax=b和ya=b分别在G内恒有解,则称G为该运算下的群.值得注意的是如果一个有限半群满足左右消去律, 则该半群一定是群.5.在S3中找出两个元素x,y,适合(xy)2x2y2.[思路] 在一个群G中,x,yG, xy=yx (xy)2x2y2(这一点很容易证明).因此只要找到S3中两个不可交换的元素即可. 我们应该在相交的轮换中间考虑找到这样的元素.解: 取x=, y=那么(xy)2= x2y2.[注意]我们可以通过mathematica软件编写S n的群表,输出程序如下:Pr[a_,b_,n_]:=(*两个置换的乘积*)(Table[a[[b[[i]]]],{I,1,n}]);Se[n_]:=(*{1,2,…,n}的所有可能的排列做成一个表格*)(Permutations[Table[i,{I,1,n}]]);Stable[n_]:=(*生成S n群表*)(a=Se[n];Table[pr[a[[i]],a[[j]],n],{I,1,n},{j,1,n}])当n=3时群表如下:[说明]:表示置换, 剩下的类似.为了让更清楚,我们分别用e,a,b,c,d,f表示,,,,那么群表如下:6.对于n>2,作一阶为2n的非交换群.7.设G是一群, a,bG,如果a-1ba=b r,其中r为一正整数,证明a-i ba i=.证明:我们采用数学归纳法证明.当k=1时, a-1ba=b r=, 结论成立;假设当k=n时结论成立, 即a-n ba n=成立, 下面证明当k=n+1时结论也成立.我们注意到a-1b k a== b kr,因此a-(n+1)ba n+1= a-1 (a-n ba n)a=a-1a==,可见k=n+1时结论也成立.由归纳原理可知结论得证.8.证明:群G为一交换群当且仅当映射是一同构映射.证明:(Ⅰ)首先证明当群G为一个交换群时映射是一同构映射.由逆元的唯一性及可知映射为一一对应,又因为,并且群G为一个交换群,可得.因此有.综上可知群G为一个交换群时映射是一同构映射.(Ⅱ)接着证明当映射是一同构映射,则群G为一个交换群.若映射是一同构映射,则对任意有,另一方面,由逆元的性质可知.因此对任意有,即映射是一同构映射,则群G为一个交换群.9.设S为群G的一个非空子集合,在G中定义一个关系a~b当且仅当ab-1S.证明这是一个等价关系的充分必要条件为S是一个子群.证明:首先证明若~是等价关系,则S是G的一个子群.对任意aG,有a~a,故此aa-1=eS;对任意a,bS,由(ab)b-1=aS,可知ab~b,又be-1=bS,故b~e,由传递性可知ab~e,即(ab)e-1=abS.再者因ae-1=aS, 故a~e,由对称性可知e~a,即ea-1=a-1S.可见S是G的一个子群.接着证明当S是G的一个子群,下面证明~是一个等价关系.对任意aG, 有aa-1=eS,故此a~a(自反性);若a~b,则ab-1S,因为S为G的子群,故(ab-1)-1=ba-1S,因此b~a(对称性);若a~b,b~c,那么ab-1S,bc-1S,故ab-1 bc-1=ac-1S,因此a~c(传递性).综上可知~是一个等价关系.10.设n为一个正整数, nZ为正整数加群Z的一个子群,证明nZ与Z同构.证明:我们容易证明为Z到nZ的同构映射,故此nZ与Z同构.11.证明:在S4中,子集合B={e,(1 2)(3 4),(1 3)(2 4),(1 4)(2 3)}是子群,证明B与U4不同构.证明:为其本身),因此B为S4的子群. 这个群(以及与其同构的群)称为Klein(C.L.Klein,1849-1925)四元群.假设B与U4同构,并设f为B到U4的同构映射, 则存在B中一元x使得f(x)=i(i为虚数单位),那么f(x2)= f2(x)=i2=-1另一方面, f(x2)=f(e)=1(注意x2=e),产生矛盾.所以假设不成立, 即B与U4不同构. [讨论] B与U4都是4元交换群,但是后者是循环群, 前者不是, 这是这两个群的本质区别.12.证明:如果在一阶为2n的群中有一n阶子群,它一定是正规子群.证明:[方法1]设H是2n阶群G的n阶子群, 那么对任意aH, 有HaH=,并且aHG,HG,又注意到aH和H中都有n个元素, 故此HaH=G.同理可证对任意aH, 有HHa=, HHa=G,因此对任意aH,有aH=Ha.对任意aH, 显然aHH, HaH又因aH,Ha及H中都有n个元素,故aH=Ha=H.综上可知对任意aG,有aH=Ha,因此H是G的正规子群.[方法2]设H是2n阶群G的n阶子群,那么任取aH, hH, 显然有aha-1H.对给定的xH, 有HxH=, HxH=G.这是因为若假设yHxH, 则存在hH,使得y=xh,即x=yh-1H产生矛盾,因此HxH=;另一方面, xHG,HG, 又注意到xH和H中都有n个元素, 故此HxH=G.那么任取aH,由上面的分析可知axH, 从而可令a=xh1这里h1H.假设存在hH, 使得aha-1H,则必有aha-1xH,从而可令aha-1=xh2这里h2H.那么xh1ha-1=xh2,即a= h2h1hH,产生矛盾.因此,任取aH, hH, 有aha-1H.综上可知对任取aG, hH, 有aha-1H,因此H为G的一个正规子群.13.设群G的阶为一偶数,证明G中必有一元素ae适合a2=e.证明:设bG,且阶数大于2,那么b≠b-1,而b-1的阶数与b的阶数相等.换句话说G中阶数大于2的元素成对出现,幺元e的阶数为1,注意到G的阶数为宜偶数,故此必存在一个2阶元,(切确的说阶数为2的元素有奇数个).[讨论][1] 设G是一2n阶交换群,n为奇数则G中只有一个2阶元.为什么?提示:采用反证法,并注意用Lagrange定理.[2] 群G中,任取aG,有a n=e,那么G一定是有限群吗?如果不是请举出反例,若是有限群,阶数和n有什么关系?14.令A=, B=证明:集合{B,B2,…,B n,AB,AB2,…,AB n}在矩阵的乘法下构成一群, 而这个群与群D n同构. 证明:下面证明G={B,B2,…,B n,AB,AB2,…,AB n}在矩阵的乘法下构成一群.(Ⅰ)首先证明对乘法运算封闭. 下面进行分类讨论:(1)B i B j=B i+j,注意到B n=故此B i B j=B r G这里i+j=kn+r,kZ,0<rn.(2)A B i B j=B r G这里i+j=kn+r,kZ,0<rn.(3)容易证明BAB=A=AB n,BA=B i AB(s+1)n=AB n-t G,这里i=sn+t,kZ,0<tn.那么B i(AB j)=( B i A)B j=(AB n-t)B j G(4)(AB i)(AB j)=A(B i AB j)=A((AB n-t)B j)=A2(B n-t B j)= B n-t B j)G由(1),(2),(3),(4)知G对乘法运算封闭.(Ⅱ)因集合G对矩阵乘法封闭,再由矩阵乘法的性质可知,结合律肯定成立.(Ⅲ)显然B n=A2=E为幺元.(Ⅳ)对B i(i=1,2,…,n),有B i B n-i=E;对AB i(i=1,2,…,n),有(AB i)(B n-i A)=E,因此G内任何一元都可逆.由(Ⅰ),(Ⅱ),(Ⅲ),(Ⅳ)可知G在矩阵乘法下构成一群.最后证明G与D n同构.令f:G→D nf(B i)=T i, f(AB i)=ST i(i=1,2,…,n),可以证明f就是G到D n的同构映射,这里不予证明了.15.设i是一个正整数, 群G中任意元素a,b都适合(ab)k=a k b k, k=I,i+1,i+2,证明G为交换群.证明:对任意a,bGa i+2b i+2=(ab)i+2=(ab) (ab)i+1=(ab) (a i+1b i+1)=a(ba i+1)b i+1,根据消去律可得a i+1b=ba i+1.----------------------(1)同时a i+1b i+1=(ab)i+1=(ab) (ab)i=(ab) (a i b i)=a(ba i)b i+1,根据消去律可得a i b=ba i.---------------------------(2)因此a i+1b=a(a i b)=a(ba i)=(ab)a i----(3)另外ba i+1=(ba)a i----------------------(4)结合(1),(3),(4)有(ab)a i=(ba)a i---------------------(5)由消去律可得到ab=ba.因此G为交换群.16.在群SL2(Q)中,证明元素a=的阶为4,元素b=的阶为3,而ab为无限阶元素.证明:可以直接验证a的阶为4,b的阶为3.因为ab=,对任何正整数n,(ab)n=≠可见ab的阶为无限.[注意] 在一群中,有限阶元素的乘积并不一定也是有限阶的,但两个可交换的有限阶元素的乘积一定是有限阶元素.[问题] 若一群中所有元素的阶数都有限,那么这个群一定是有限群吗?17.如果G为一个交换群,证明G中全体有限阶元素组成一个子群.证明:交换群G中全体有限阶元素组成的集合记为S,任取a,bS,并设a的阶为m,b的阶为n,则(ab)mn=(a m)n(b n)m=e因此ab为有限阶元素,即abS.a-1的阶数与a相同,故此a-1也是有限阶元素,即a-1S.综上可知S为G的一个子群.18.如果G只有有限多个子群,证明G为有限群.证明:采用反证法证明.假设G为无限群,则G中元素只可能有两种情况:(1)G中任意元素的阶数都有限、(2)G中存在一个无限阶元素.(1)首先看第一种情况:G中取a1≠e,并设其阶数为n1,则循环群G1={,…}为G的一个子群;G中取a2G1,并设其阶数为n2,则循环群G2={,…}为G的一个子群;G中取a3G1∪G2,并设其阶数为n3,则循环群G3={,…}为G的一个子群;… … …我们一直这样做下去,可以得到G的互不相同的子群构成的序列G n(n=1,2,…),所以G有无穷多个子群,产生矛盾;(2)再看第二种情况:设a∈G的阶数为无穷,那么序列G1=<>,G2=<>,…,G n=<>,…是G的互不相同的子群,所以G有无穷多个子群,产生矛盾.综上就可知“G是无限群”这个假设不成立,因此G是有限群.19.写出D n的所有正规子群.20.设H,K为群G的子群,HK为G的一子群当且仅当HK=KH.证明:(Ⅰ)设HK=KH,下面证明HK为G的一子群.任取a,b∈HK,可令a=h1k1,b=h2k2这里h i∈H,k i∈K,i=1,2.那么ab=(h1k1)(h2k2)=h1(k1h2)k2 ---------------(1)因HK=KH,故此k1h2= h3k3 ----------------------(2)这里h3∈H,k3∈K.由(1),(2)知ab= h1(h3k3)k2=(h1h3)(k3k2)∈HK. ------------(3)另外,a-1= (h1k1)-1= ∈KH=HK. ----------------- (4)由(3),(4)知HK是G的子群.(Ⅱ) HK为G的一子群,下面证明HK=KH.若a∈HK,易知a-1∈KH. HK是子群,任取a∈HK,有a-1∈HK,因此(a-1)-1=a∈KH,那么有HK KH.若a∈KH,易知a-1∈HK. HK是子群,任取a∈KH,有a-1∈HK,因此(a-1)-1=a∈HK,那么有KH HK.综上知,HK=KH.21.设H,K为有限群G的子群,证明证明:因H∩K为H的子群,那么可设H的左陪集分解式为H=h1(H∩K)∪h2(H∩K)∪…∪h r(H∩K)这里r为H∩K在H中的指数,h i∈H,当i≠j,h i-1h j∉H∩K(事实上等价于h i-1h j∉K),i, j=1,2,…,r.又(H∩K)K=K,所以HK=h1K∪h2K∪…∪h r K.------------(1)注意到h i-1h j∉K,所以当i≠j(i, j=1,2,…,r)时,h i K∩h j K=.----------------(2)由(1),(2)我们得到[总结]左陪集的相关结论设H为G的一子群,那么(1)a∈a H;(2)a∈H⇔aH=H;(3)b∈aH⇔aH=bH;(4)aH=bH⇔a-1b∈H;(5)aH∩bH≠,有aH=bH.22.设M,N是群G的正规子群.证明:(i)MN=NM;(ii)MN是G的一个正规子群;(iii)如果MN={e},那么MN/N与M同构.证明:(i)[方法1]任取a∈MN,可设a=mn(m∈M,n∈N).因为M为G的正规子群,故n-1mn∈M. 所以a=n(n-1mn) ∈NM,故此MN⊆NM.同样的方法可以证明NM⊆MN. 因此MN=NM.[方法2]任取a,b∈MN,可设a=m1n1(m1∈M,n1∈N),b=m2n2(m2∈M,n2∈N).下面只要证明MN为G的一个子群即可(由第20题可知),也就是说只要证明ab-1∈MN即可.因为ab-1=m1n1n2-1m2-1= [m1(n1n2-1m2-1n2n1-1)](n1n2-1),而M为G的正规子群,故n1n2-1m2-1n2n1-1∈M,所以ab-1∈MN.(ii) 由(i)可知MN为G的一个子群.任取a∈MN, 可设a=mn(m∈M,n∈N).因为M和N为G的正规子群,对任意g∈G,有g-1ag= g-1mng= (g-1mg)(g-1ng) ∈MN.所以MN为G的正规子群.(iii) 易知N为MN的正规子群,因此MN/N是一个群. 因为MN={e},对任何m i≠m j∈M, 有m i N≠m j N[注].作一个MN/N到M的映射f[注],f: MN/N→MmNm,那么该映射显然是一一对应,另外f(m i Nm j N)= f(m i m j N)= m i m j,因此f为MN/N到M的同构映射,即MN/N与M同构.[讨论]1. 只要M和N的一个是正规子群,那么MN就是子群,或者说成立MN=NM.这一点我们从(i)的证明方法2可知.2. M和N中有一个不是正规子群时MN一定不是正规子群.[注意]1MN={e},对任何m i≠m j∈M, 有m i N≠m j N.证明:若存在m i≠m j∈M, 有m i N=m j N,那么m i m j-1∈N,而m i m j-1∈M. 因此m i m j-1∈MN,产生矛盾.2. 设f: MN/N→MmNm,则由于对任何m i≠m j∈M, 有m i N≠m j N,故此f为MN/N到M的一个映射.23.设G是一个群,S是G的一非空子集合.令C(S)={x∈G|xa=ax,对一切a∈S}N(S)= {x∈G|x-1Sx=S}.证明:(i) C(S),N(S)都是G的子群;(ii) C(S)是N(S)的正规子群.证明:(i) 首先证明C(S)是G的子群.任取x,y∈C(S),那么对任意a∈S有xa=ax,ya=ay. 那么一方面,(xy)a=x(ya)=x(ay)=(xa)y=(ax)y=a(xy),所以xy∈C(S).另一方面,xa=axa=x-1axax-1=x-1a所以x-1∈C(S).因此,C(S)是G的子群.接着证明N(S)都是G的子群.任取x,y∈N(S),则x-1Sx=S,y-1Sy=S. 那么一方面,(xy)-1S(xy)=x-1(y-1Sy)x=x-1Sx=S所以xy∈N(S).另一方面,x-1Sx=SS=xSx-1所以x-1∈N(S).因此,N(S)是G的子群.(ii) 任取x∈C(S),a∈S,则xa=ax,即a=x-1ax,亦即S= x-1Sx. 因此x∈N(S),即C(S)N(S).任取x∈C(S),y∈N(S),a∈S,则存在a y∈S使得yay-1=a y,因此a=y-1a y y.那么(y-1xy)a(y-1xy)-1=y1[x(yay-1)x-1]y= y1(xa y x-1)y= y-1a y y=a,即(y-1xy)a=a(y-1xy).所以y-1xy∈C(S),因此C(S)是N(S)的正规子群.24.证明任意2阶群都与乘法群{1,-1}同构.证明:略.25.试定出所有互不相同的4阶群.解:我们分类讨论:(1)存在四阶元;(2)不存在四阶元.(1)若存在一个四阶元,并设a为一个四阶元,那么该四阶群为<a>.(2)若不存在四阶元,那么除了单位元e的阶为1,其余元素的阶只能是2,即设四阶群222综上可知,四阶群群在同构意义下只有两种或者是四阶循环群或者是Klein四阶群.26.设p为素数.证明任意两个p阶群必同构.证明:易知当p为素数时,p阶群必存在一个p阶元,即p阶群必是p阶循环群,故两个p 阶群必同构.27.Z为整数环,在集合S=Z×Z上定义(a,b)+(c,d)=(a+c,b+d),(a,b)(c,d)=(ac+bd,ad+bc).证明S在这两个运算下成为幺环.提示:(1,0)为该环的单位元素.证明:略.28.在整数集上重新定义加法“”与乘法“”为ab=ab, ab=a+b试问Z在这两个运算下是否构成一环.答:不构成环.29.设L为交换幺环,在L中定义:ab=a+b-1,ab=a+b-ab.这里e为单位元素,证明在新定义的运算下,L仍称为交换幺环,并且与原来的环同构. 证明:(i)证明L在运算下构成交换群:由的定义,得到(ab)c=(a+b-1)c=a+b-1+c-1=a+b+c-2a(bc)= a(b+c-1)= a+b+c-1-1=a+b+c-2这里2=1+1,所以(ab)c= a(bc).----------------(1)同时由的定义还可以得到a1= 1a=a,------------------------(2)a(2-a)=(2-a)a=1,---------------(3)ab=ba,----------------------------(4)由(1),(2),(3)(4)可知L在运算下构成交换群.(ii)证明L中运算满足结合律和交换律:容易证明这里略过.(iii)证明乘法对加法满足分配律:因为a(bc)= a(b+c-1)=a+(b+c-1)-a(b+c-1)=2a+b+c-ab-ac-1,(ab)(ac)=(a+b-1)(a+c-1)= (a+b-ab)+(a+c-ac)-1=2a+b+c-ab-ac-1,所以a(bc)= (ab)(ac).由于和满足交换律,故此(bc)a= (ba)(ca).因此新定义的乘法对新定义的加法满足分配律(iv) 设0为环(L,+,)的零元,则0a=a0=a由(i),(ii),(iii),(iv)可得到(L,,)为交换幺环.(v) 最后证明(L,+,)与(L,,)同构:设f: L→Lx1-x,容易证明f为(L,+,)到(L,,)的同构映射.30.给出环L与它的一个子环的例子,它们具有下列性质:(i) L具有单位元素,但S无单位元素;(ii) L没有单位元素,但S有单位元素;(iii) L, S都有单位元素,但互不相同;(iv) L不交换,但S交换.解:(i) L=Z,S=2Z;(ii) L={|a,b∈R},S={|a∈R};(iii) L={|a,b∈R},S={|a∈R};(iv) L={|a,b∈R},S={|a∈R};31.环L中元素e L称为一个左单位元,如果对所有的a∈L,e L a= a;元素e R称为右单位元,如果对所有的a∈L,ae R=a.证明:(i)如果L既有左单位元又有右单位元,则L具有单位元素;(ii)如果L有左单位元,L无零因子,则L具有单位元素;(iii)如果L有左单位元,但没有右单位元,则L至少有两个左单位元素.证明:(i) 设e L为一个左单位元,e R为右单位元,则e L e R=e R=e L.记e=e R=e L,则对所有的a∈L,ea=ae=a,因此e为单位元素;(ii) 设e L为一个左单位元,则对所有的a(≠0)∈L,a(e L a)=a2;另一方面,a(e L a)=(ae L)a. 所以a2=(ae L)a.因为L无零因子,所以满足消去律[注],故此a= ae L.另外,若a=0,则a= ae L=e L a.因此左单位元e L正好是单位元.(iii) 设e L为一个左单位元,因为L中无右单位元,故存在x∈L,使得xe L≠x,即xe L-x≠0,则e L+ xe L-x≠e L,但是对所有的a∈L,(e L+ xe L-x)a=a,因此e L+ xe L-x为另一个左单位元,所以L至少有两个左单位元素.[注意] L无零因子,则满足消去律(参考教材46页).32.设F为一域.证明F无非平凡双边理想.证明:设I为F的任意一个理想,且I≠{0},则对任意a(≠0)∈I,则a-1∈F,于是a-1a=1∈I.从而F中任意元素f,有f1=f∈I,故I=F,即F只有平凡双边理想.[讨论] 事实上,一个体(又称除环)无非平凡双边理想. 另一方面,若L是阶数大于1的(交换)幺环,并且除了平凡理想,没有左或右理想,则L是一体(域).33.如果L是交换环,a∈L,(i) 证明La={ra|r∈L}是双边理想;(ii) 举例说明,如果L非交换,则La不一定是双边理想.证明:(i) 容易验证La为L的一个加法群. 任取ra∈La,l∈L,则l(ra)=(lr)a∈La,(ra)l=r(al)=r(la)=(rl)a∈La故La为L的一个双边理想.(ii) 设L=M2(R),那么L显然不是交换环,取h=,下面考察Lh是否为L的理想:取k=,容易验证h∈Lh,hk Lh,因此Lh不是L的一个理想.34.设I是交换环L的一个理想,令rad I={r∈L|r n∈I对某一正整数n},证明rad I也是一个理想.radI叫做理想I的根.35.设L为交换幺环,并且阶数大于1,如果L没有非平凡的理想,则L是一个域.证明:只要证明非零元素均可逆即可.任取a∈L,那么La和aL是L的理想,且La≠{0},aL≠{0},因L无平凡的理想,故此La=aL=L,因此ax=1和ya=1都有解,因而a为可逆元.36.Q是有理数域,M n(Q)为n阶有理系数全体矩阵环.证明无非平凡的理想(这种环称为单环).证明:我们社K为M n(Q)的非零理想,下面证明K=M n(Q).为了证明这一点,只要证明n阶单位矩阵E∈K.记E ij为除了第i行第j列元素为1,其余元素全为0的矩阵.那么E ij E st=而E=E11+E22+…+E nn.我们只要证明E ii∈K(i=1,2,…,n)就有E∈K.设A∈K,且A≠0,又令A=(a ij)n×n,假设a kj≠0,则有E ik AE ji=a kj E ii(i=1,2,…,n).由于a kj≠0,故存在逆元a kj-1.设B= a kj-1E ii,则BE ik AE ji= a kj-1E ii E ik AE ji= a kj-1E ik AE ji=E ik E kj E ji=E ii.因为K为理想,A∈K,所以E ii=BE ik AE ji∈K,证毕.37.设L为一环,a为L中一非零元素.如果有一非零元素b使aba=0,证明a是一个左零因子或一右零因子.证明:若ab=0,则a为左零因子;若ab≠0,则aba=(ab)a=0,故ab为右零因子.38.环中元素x称为一幂零元素,如果有一正整数n使x n=0,设a为幺环中的一幂零元素,证明1-a可逆.证明:设a n=0,那么(1+a+a2+…+a n-1)(1-a)=(1-a) (1+a+a2+…+a n-1)=1-a n=1因此1-a可逆.39.证明:在交换环中,全体幂零元素的集合是一理想.40.设L为有限幺环.证明由xy=1可得yx=1.证明:当L只有一个元素,即L={0},亦即0=1[注],此时显然有xy=1=xy;当L有多于一个元素时(即0≠1时),若xy=1,y不是左零元[注],因此yL=L.又因L为有限环,所以存在z∈L,使得yz=1.注意到(xy)z=z,x(yz)=x,所以x=z,即yx=1.[注意]1.幺环多于一个元素当且仅当0≠1.2.当L有多于一个元素时(即0≠1时),若xy=1,y不是左零元.因为若存在z≠0使得yz=0,则z=(xy)z=x(yz)=0,产生矛盾.41.在幺环中,如果对元素a有b使ab=1但ba≠1,则有无穷多个元素x,适合ax=1. (Kaplansky定理)证明:首先,若ab=1但ba≠1,则a至少有两个右逆元[注].现在假设a只有n(>1)个右逆元,并设这些元素为x i(i=1,2,…,n).那么a(1-x i a+x1)=1(i=1,2,…,n),又当i≠j时,1-x i a+x1≠1-x j a+x1[注],这里i,j=1,2,…,n.于是{x i|i=1,2,…,n}={1-x i a+x1| i=1,2,…,n },故存在x k∈{x i|i=1,2,…,n}使得x1=1-x k a+x1,即x k a=1.因为n>1,我们取x t≠x k∈{x i|i=1,2,…,n},那么(x k a)x t=x t,(x k a)x t =x k(ax t)=x k因此x t=x k,产生矛盾,所以假设不成立,即a有无穷多个右逆元.[注意]1. 若ab=1但ba≠1,则a至少有两个右逆元. 因为易验证1-ba+a就是另一个右逆元.2. 假设当i≠j时,1-x i a+x1=1-x j a+x1,则x i a=x j a,故x i ax1=x j ax1,因此x i=x j,产生矛盾.42.设L是一个至少有两个元素的环. 如果对于每个非零元素a∈L都有唯一的元素b使得aba=a.证明:(i) L无零因子;(ii) bab=b;(iii) L有单位元素;(iv) L是一个体.证明:(i) 先证明L无左零因子,假设a为L的一个左零因子,那么a≠0,且存在c≠0,使得ac=0,于是cac=0. 因a≠0,则存在唯一b使得aba=a.但a(b+c)a=a,b+c≠b产生矛盾,所以L无左零因子.类似可证L无右零因子.(ii) 因aba=a,所以abab=ab. 由(i)的结论知L无零因子,因此满足消去律,而a≠0,故bab=b.(iii) 我们任一选取a(≠0)∈L,再设aba=a(这里b是唯一的),首先证明ab=ba.因为a(a2b-a+b)a=a,所以a2b-a+b=b,即a2b=a=aba,由消去律得到ab=ba.任取c∈L,则ac=abac,故此c=(ba)c=(ab)c;另一方面,ca=caba,故此c=c(ab).综上得到c=(ab)c=c(ab),所以ab就是单位元素,我们记ab=ba=1.(iv) 由(iii)可知任意a(≠0)∈L,ab=ba=1,即任意非零元素都可逆,因此L成为一个体.43.令C[0,1]为全体定义在闭区间[0,1]上的连续函数组成的环.证明:(i) 对于的任一非平凡的理想I,一定有个实数,,使得f()=0对所有的f(x)∈I;(ii) 是一零因子当且仅当点集{x∈[0,1]|f(x)=0} 包含一个开区间.证明:(i) 证明思路:设I为非零的非平凡理想,假设对任意x∈[0,1],存在f(x)∈I使得f(x)≠0,想法构造一个g∈I可逆.(ii) 提示:用连续函数的局部保号性.44.令F=Z/pZ为p个元素的域.求(i) 环M n(F)的元素的个数;(ii) 群GL n(F)的元素的个数.45.设K是一体,a,b∈K,a,b不等于0,且ab≠1.证明华罗庚恒等式:a-(a-1+(b-1-a)-1)-1=aba.证明:因为a-(a-1+(b-1-a)-1)-1=aba⇔1-(a-1+(b-1-a)-1)-1a-1=ab⇔(aa-1+a(b-1-a)-1)-1=1-ab⇔(1+a(b-1-a)-1)-1=1-ab⇔(1+((ab)-1-1)-1)-1=1-ab,为了方便记x=ab,那么1-x,x,x-1-1都可逆,只要证明(1+(x-1-1)-1)-1=1-x即可,或者证明1+(x-1-1)-1=(1-x)-1即可.因为1+(x-1-1)-1=1+(x-1-x-1x)-1=1+(1-x)-1x=(1-x)-1(1-x) +(1-x)-1x=(1-x)-1,所以结论成立,即a-(a-1+(b-1-a)-1)-1=aba.。
第一章:力(力的概念)练习及答案

第一章:力一、力:一、选择题1.下列关于力的说法正确的是[ ]A.一个力可能有两个施力物体B.不存在不受力的物体C.物体受到力的作用,其运动状态未必改变D.物体发生形变时,一定受到力的作用2.关于力的说法,正确的是[ ]A.有力作用在物体上,其运动状态一定改变B.力是使物体产生形变的原因C.力的三要素相同,作用效果一定相同D.一对互相平衡的力一定是相同性质的力二、填空题7.放在桌上的书本,受到支持力的作用,其受力物体是______,施力物体是______;同时,书对桌面的压力,其受力物体是______,施力物体是______。
由此可见,一个物体既是______,又是______。
8.下列各种力:(1)重力(2)拉力(3)支持力(4)弹力(5)浮力(6)摩擦力(7)动力(8)推力。
属于按力的性质分类的是______,属于按作用效果分类的是______(用序号填写)。
二、重力一、选择题3.关于物体的重心,下列说法正确的是[ ]A.物体的重心一定在物体上B.任何物体的重心都在它的几何中心上C.物体的形状发生改变其重心位置一定改变D.物体放置的位置发生改变.重心对物体的位置不会改变4.图1所示的ABC是木匠用的曲尺,它是用粗细不同、质量分布均匀,AB和BC相等的木料做成,D是AC连线的中点,E是AB的中点F和BC的中点G连线的中点,则曲尺的重心在[ ]A.B点B.D点C.E点D.G点5.关于重心的说法,正确的是[ ]A.重心就是物体内最重的一点B.物体的重心位置有可能变化C.把一物抬到高处,其重心在空间的位置也升高了D.背跃式跳高运动员,在跃过横杆时,其重心在身体之外6.关于重力的大小,以下说法正确的是[ ]A.悬挂在竖直绳子上的物体,绳子对它的拉力一定等于其重力B.静止在水平面上的物体对水平面的压力一定等于其重力C.物体所受的重力与它的运动状态无关D.向上运动的物体所受重力可能小于向下运动的物体所受重力二、填空题9.重力是由于______而产生的,它的方向______,重力的作用点可认为作用在物体的______上。
第一章测量基本概念习题及答案

第一章 检测技术的基本概念一、填空题:1、传感器有 、 、 组成2、传感器的灵敏度是指稳态标准条件下,输出 与输入 的比值。
3、从输出曲线看,曲线越陡,灵敏度 。
4、下面公式是计算传感器的 。
9)-(1 %100minmax max L L ⨯-=y y Δγ 5、某位移传感器的输入变化量为5mm ,输出变化量为800mv ,其灵敏度为 。
二、 选择题:1、标准表的指示值100KPa ,甲乙两表的读书各为101.0 KPa 和99.5 KPa 。
它们的绝对误差为 。
A 1.0KPa 和-0.5KPaB 1.0KPa 和0.5KPaC 1.00KPa 和0.5KPa2、下列哪种误差不属于按误差数值表示 。
A 绝对误差B 相对误差C 随机误差D 引用误差3、有一台测量仪表,其标尺范围0—500 KPa ,已知绝对误差最大值 ∆P max=4 KPa ,则该仪表的精度等级 。
A 0.5级B 0.8级C 1级D 1.5级4、选购线性仪表时,必须在同一系列的仪表中选择适当的量程。
应选购的仪表量程为测量值的 倍。
A3倍 B10倍 C 1.5倍 D 0.75倍5、电工实验中,常用平衡电桥测量电阻的阻值,是属于 测量, 而用水银温度计测量水温的微小变化,是属于 测量。
A 偏位式 B 零位式 C 微差式6、因精神不集中写错数据属于 。
系统误差 B 随机误差 C 粗大误差7、有一台精度2.5级,测量范围0—100 KPa ,则仪表的最小分 格。
A45 B40 C30 D 208、重要场合使用的元件或仪表,购入后进行高、低温循环老化试验,目的是为了 。
A 提高精度B 加速其衰老C 测试其各项性能指标D 提高可靠性9、传感器能感知的输入量越小,说明 越高。
A 线性度好B 迟滞小C 重复性好D 分辨率高三、 判断题1、回差在数值上等于不灵敏度 ( )2、灵敏度越大,仪表越灵敏 ( )3、同一台仪表,不同的输入输出段灵敏度不同()4、灵敏度其实就是放大倍数()5、测量值小数点后位数越多,说明数据越准确()6、测量数据中所有的非零数字都是有效数字()7、测量结果中小数点后最末位的零数字为无效数字()四、问答题1、什么是传感器的静态特性,有哪些指标。
近世代数第一章答案

近世代数第一章基本概念答案§ 1 . 集合1.A B ⊂,但B 不是A 的真子集,这个情况什么时候才能出现? 解 由题设以及真子集的定义得,A 的每一个元都属于B ,因此B A ⊂.于是由A B ⊂ B A ⊂得B A =.所以上述情况在A=B 时才能出现.2. 假设B A ⊂,?=⋂B A ?=⋃B A解 (i ) 由于B A ⊂,所以A 的每一个元都属于B ,即A 的每一个元都是A 和B 的共同元,因而由交集的定义得B A A ⋂⊂但显然有A B A ⊂⋂所以A B A =⋂(ii) 由并集的定义,B A ⋃的每一个元素都属于A 和B 之一,但B A ⊂,所以B A ⋃的每一元素都属于B :B B A ⊂⋃另一方面B A B ⋃⊂,所以B B A =⋃.§ 2 . 映射1. A ={1,2,…,100}.找一个A A ⨯到A 的映射.解 用()b a ,表示A A ⨯的任意元素,这里a 和b 都属于A .按照定义做一个满足要求的映射即可,例如 Φ: ()b a ,→a 就是这样的一个,因为Φ替A A ⨯的任何元素()b a ,规定了一个唯一的象a ,而A a ∈.读者应该自己再找几个A A ⨯到A 的映射. 2.在你为习题1所找的映射之下,是不是A 的每一个元都是A A ⨯的一个元的象?解 在上面给出的映射Φ之下,A 的每一个元素都是A A ⨯的一个元的象,因为()b a ,中的a 可以是A 的任一元素.你自己找到的映射的情况如何?有没有出现A 的元素不都是象的情况?假如没有,找一个这样的映射.§ 3 .代数运算1. A ={所有不等于零的偶数}.找一个集合D ,使得普通除法是A A ⨯到D 的代数运算.是不是找得到一个以上的这样的D ?解 一个不等于零的偶数除一个不等于零的偶数所得结果总是一个不等于零的有理数.所以取 D ={所有不等于零的有理数} 普通除法就是一个A A ⨯到D 的代数运算.可以找得到一个以上的满足要求的D .读者可以自己找几个. 2.{}c b a A ,,=.规定A 的两不同的代数运算.解 (i )我们用运算表来给出A 的一个代数运算: a b ca a a ab a a ac a a a按照这个表,通过 ,对于A 的任何两个元素都可以得出一个唯一确定的结果a 来,而a 仍属于A ,所以 是A 的人一个代数运算.这个代数运算也可以用以下方式来加以描述 : ()y x a y x o =→, 对一切A y x ∈, (ii)同理: ()y x x y x o =→, 对一切A y x ∈,也是A 的一个代数运算.读者可用列表的方法来给出这个代数运算.读者应自己给出几个A 的代数运算.§4 .结合律1. A ={所有不等于零的实数}, 是普通的除法:ba b a =o 这个代数运算适合不适合结合律?解 这个代数运算 不适合结合律.例如, 当4=a 2==c b时()122224224)(====o o o o o c b a ()()414224224==⎪⎭⎫ ⎝⎛==o o o o o c b a所以当a ,b 和c 取上述值时()()c b a c b a o o o o ≠2. A ={所有实数},代数运算: (a,b )→a+2b=a b适合不适合结合律?解读者可以用解上一题的方法来证明,所给代数运算不适合结合律.3.A={a,b,c}.由表a b ca ab cb bc ac c a b给出的代数运算适合不适合结合律?解所给代数运算 适合结合律.为了得出这个结论,需要对元素a,b,c的27(=33)种排列(元素允许重复出现)加以验证.但是利用元素a的特性,可以把验证简化.仔细考察运算表,我们发现以下规律:对集合A的任意元素x来说,都有a x=x a=x由此得出,对于有a出现的排列,结合律都成立.这一点读者可以自己验证.还剩下a不出现的排列.这样的排列共有8(=32)种.我们在这里验证4种,其余4种读者可以自己验证.(b b) b=c b=ab (b b)=b c=a所以(b b) b=b (b b)(b b) c=c c=bb (b c)=b a=b所以 (b b) c=b (b c)(b c) b=a b=bb (c b)= b a=b所以 (b c) b=b (c b)(b c) c=a c=cb (c c)=b b=c所以 (b c) c=b (c c)§5.交换律1.A={所有实数}. 是普通减法:a b= a b这个代数运算适合不适合交换律?解容易验证,当a = 1,b = 2时a b b a ≠ 所以这个代数运算不适合交换律. 2. A ={a , b ,c , d},由表 a b c da abcd b b d a c c c a b d d d c a b所给的代数运算适合不适合交换律?解 要回答这个问题,只须考察一下运算表,看一看关于主对角线对称的位置上,有没有不相同的元素.易知此运算表不对称,所以此代数运算不适合交换律。
高一物理必修1第一章、第二章知识点总结及各知识点分析与答案
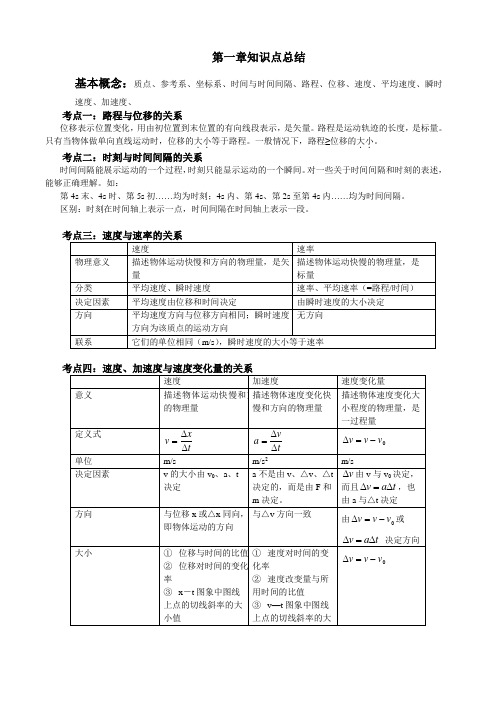
第一章知识点总结基本概念:质点、参考系、坐标系、时间与时间间隔、路程、位移、速度、平均速度、瞬时速度、加速度、考点一:路程与位移的关系位移表示位置变化,用由初位置到末位置的有向线段表示,是矢量。
路程是运动轨迹的长度,是标量。
只有当物体做单向直线运动时,位移的大小..。
..等于路程。
一般情况下,路程≥位移的大小考点二:时刻与时间间隔的关系时间间隔能展示运动的一个过程,时刻只能显示运动的一个瞬间。
对一些关于时间间隔和时刻的表述,能够正确理解。
如:第4s末、4s时、第5s初……均为时刻;4s内、第4s、第2s至第4s内……均为时间间隔。
区别:时刻在时间轴上表示一点,时间间隔在时间轴上表示一段。
考点五:运动图象的理解及应用由于图象能直观地表示出物理过程和各物理量之间的关系,所以在解题的过程中被广泛应用。
在运动学中,经常用到的有x -t 图象和v —t 图象。
1. 理解图象的含义(1) x -t 图象是描述位移随时间的变化规律 (2) v —t 图象是描述速度随时间的变化规律2. 明确图象斜率的含义(1) x -t 图象中,图线的斜率表示速度 (2) v —t 图象中,图线的斜率表示加速度第二章.匀变速直线运动的研究考点一:匀变速直线运动的基本公式和推理1. 基本公式(1) 速度—时间关系式:at v v +=0 (2) 位移—时间关系式:2021at t v x += (3) 位移—速度关系式:ax v v 2202=-三个公式中的物理量只要知道任意三个,就可求出其余两个。
利用公式解题时注意:x 、v 、a 为矢量及正、负号所代表的是方向的不同, 解题时要有正方向的规定。
2. 常用推论(1) 平均速度公式:()v v v +=021(2) 一段时间中间时刻的瞬时速度等于这段时间内的平均速度:()v v v v t +==0221(3) 一段位移的中间位置的瞬时速度:22202v v v x +=(4) 任意两个连续相等的时间间隔(T )内位移之差为常数(逐差相等):()2aT n m x x x n m -=-=∆考点二:对运动图象的理解及应用1. 研究运动图象(1) 从图象识别物体的运动性质(2) 能认识图象的截距(即图象与纵轴或横轴的交点坐标)的意义 (3) 能认识图象的斜率(即图象与横轴夹角的正切值)的意义 (4) 能认识图象与坐标轴所围面积的物理意义 (5) 能说明图象上任一点的物理意义 2. x -t 图象和v —t 图象的比较如图所示是形状一样的图线在x -t 图象和v —t 图象中,1.“追及”、“相遇”的特征“追及”的主要条件是:两个物体在追赶过程中处在同一位置。
工程热力学 课后习题答案 可打印 第三版 第一章

1
第一章 基本概念
p = pe + pb = (1020mmH 2 O × 9.81Pa/mmH 2 O + 900mmHg × 133.3Pa/mmHg) + 755mmHg × 133.3Pa/mmHg = 2.306 × 105 Pa = 0.231MPa
1-6 容器中的真空度为 pv = 600mmHg ,气压计上水银柱高度为
1-12 有一绝对真空的钢瓶, 当阀门的打开时, 在大气压 p0 = 1.013 × 10 Pa 的作用下有体积为
5
0.1m3 的空气被输入钢瓶,求大气对输入钢瓶的空气所作功为多少?
3
第一章 基本概念
解
W = p0V = 1.013 × 105 Pa × 0.1m3 = 1.013 × 104 J = 10.13kJ
p= RgT RgTa = v v
w12 = ∫ pdv = ∫
v1 v5
v2
v2
v1
RgTa v dv = RgTa ln 2 ; v v1
w4−5 = ∫ pdv = ∫
v4
v5
Rg Ta v
v4
dv = RgTa ln
v3 v4
根据已知条件: v1 = v3,v4 = v6,p3 = p2,p6 = p5,T2 = T5 = Ta,T3 = T6 = Tb 得
1-14 据统计资料,上海各发电厂 1983 年平均发 1 千瓦小时的电耗标煤 372 克,若标煤的热值 是 29308kJ/kg ,试求 1983 年上海电厂平均热效率 η t 是多少? 解:ηt =
Wnet 3600kJ = = 33.3% Q1 0.372kg × 29308kJ/kg
第1章电路基本概念与电路定律习题与答案

第1章 习题与解答1-1 2C 的电荷由a 点移到b 点,能量的改变为20J ,若(1)电荷为正且失去能量;(2)电荷为正且获得能量;求ab u 。
解:(1)2C 的电荷由a 点移到b 点,2q C ∆=,这时意味着电流从a 点流到b 点; 电荷为正且失去能量,2W OJ ∆=,ab u 为正且 2102ab W OJu V q C∆===∆ (2)2C 的电荷由a 点移到b 点,2q C ∆=,这时意味着电流从a 点流到b 点; 电荷为正且获得能量,2W OJ ∆=,ab u 为负且 2102ab W OJu V q C∆-===∆ 所以10ab u V =-1-2 在题1-2图中,试问对于A N 与B N ,u i 、的参考方向是否关联?此时下列各组乘积u i ⨯对A N 与B N 分别意味着什么功率?并说明功率是从A N 流向B N 还是相反。
(a )15,20i A u V == (b) 5,100i A u V =-= 题1-2图 (c) 4,50i A u V ==- (d) 16,25i A u V =-=- 解:(a )15,20i A u V == ,此时A N 非关联,3000P ui W ==>,发出功率B N 关联,3000P ui W ==>,吸收功率。
功率从A N 流向B N 。
(b) 5,100i A u V =-= ,此时A N 非关联,5000P ui W ==-<,吸收功率B N 关联,5000P ui W ==-<,发出功率。
功率从B N 流向AN 。
(c) 4,50i A u V ==- ,此时A N 非关联,2000P ui W ==-<,吸收功率B N 关联,2000P ui W ==-<,发出功率。
功率从B N 流向AN 。
(d) 16,25i A u V =-=- ,此时A N 非关联,4000P ui W ==>,发出功率B N 关联,4000P ui W ==>,吸收功率。
第1章 电力系统基本概念(含答案)

1.标出下图中各元件的额定电压。
解: 发电机:10.5kV 变压器 T1:高压侧:242kV 中压侧:121kV 低压侧:10.5kV 变压器 T2:高压侧:110kV 中压侧:38.5kV 低压侧:10.5kV 变压器 T3:高压侧:220kV 低压侧:38.5kV 变压器 T4:高压侧:35kV 低压侧:0.4kV 调相机:10kV
二、选择题 1.以下几个概念中,内涵最广的是(B) A.电力系统 B.动力系统 C.电力网 D.输电网络 2.以下几个概念中,内涵最窄的是(D) A.电力系统 B.动力系统 C.电力网 D.配电网络 3.电气设备都是按照指定的电压来进行设计和制造的,这个指定的电压称为电气设备的
(A) A.额定电压 B.平均额定电压 C.电压降落 D.电压损耗 4.同一电压等级下,电力线路的额定电压比用电设备的额定电压(C) A.高 B.低 C.相等 D.无法确定 5.同一电压等级下,发电机的额定电压与电网的额定电压相比(A)
三、简答题
1.电力系统、动力系统、电力网的概念分别是什么?
答:电力系统是指将生产、输送、分配和消费电能的各种电气设备连接在一起而组成的
统一整体;动力系统是指电力系统中加上各种类型发电厂的动力部分;电力网是指电力系统
中输送和分配电能的部分。
2.电力系统的运行具有哪些特点? 答:(1)电能不能大量存贮;(2)电力系统的暂态过程非常短暂;(3)与国民经济的各
A.高 5% B.低 5% C.高 10% D.低 10% 6.若变压器一次侧直接与发电机相连,则其额定电压与发电机的额定电压相比(B) A.高 5% B.相等 C.低 5% D.低 10% 7.中性点不接地系统发生单相接地时,通过接地点的电流为不接地时每一相对地电容 电流的(C)
(复习指导)第一章第一讲 集合的概念与运算含答案

第一章集合与常用逻辑用语第一讲集合的概念与运算知识梳理·双基自测ZHI SHI SHU LI SHUANG JI ZI CE知识梳理知识点一集合的基本概念一组对象的总体构成一个集合.(1)集合中元素的三大特征:确定性、互异性、无序性.(2)集合中元素与集合的关系:对于元素a与集合A,a∈A或a∉A,二者必居其一.(3)常见集合的符号表示.数集自然数集正整数集整数集有理数集实数集符号N N*Z Q R(4)集合的表示法:列举法、描述法、Venn图法、区间表示法.(5)集合的分类:集合按元素个数的多少分为有限集、无限集,有限集常用列举法表示,无限集常用描述法表示.知识点二集合之间的基本关系关系定义表示相等集合A与集合B中的所有元素都相同A=B子集A中的任意一个元素都是B中的元素A⊆B真子集A是B的子集,且B中至少有一个元素不属于A A B注意:(1)空集用∅表示.(2)若集合A中含有n个元素,则其子集个数为2n,真子集个数为2n-1,非空真子集的个数为2n-2.(3)空集是任何集合的子集,是任何非空集合的真子集.(4)若A⊆B,B⊆C,则A⊆C.知识点三集合的基本运算符号语言交集A∩B 并集A∪B 补集∁U A图形语言意义A∩B={x|x∈A且x∈B}A∪B={x|x∈A或x∈B}∁U A={x|x∈U且x∉A}重要结论1.A∩A=A,A∩∅=∅.2.A∪A=A,A∪∅=A.3.A∩(∁U A)=∅,A∪(∁U A)=U,∁U(∁U A)=A.4.A⊆B⇔A∩B=A⇔A∪B=B⇔∁U A⊇∁U B⇔A∩(∁U B)=∅.双基自测题组一走出误区1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)集合A中含有三个元素0,1,x,且x2∈A,则实数x的值为1或-1或0.(×)(2){x|y=x2}={y|y=x2}={(x,y)|y=x2}.(×)(3)方程x -2 022+(y+2 023)2=0的解集为{2 022,-2 023}.(×)(4)若A∩B=A∩C,则B=C.(×)(5)设U=R,A={x|lg x<1},则∁U A={x|lg x≥1}={x|x≥10}.(×)题组二走进教材2.(必修1P 5B1改编)若集合P={x∈N|x≤ 2 022},a=45,则(D)A.a∈P B.{a}∈PC.{a}⊆P D.a∉P[解析]452=2 025>2 022,∴a∉P,故选D.3.(必修1P7T3(2)改编)若A={x|x=4k-1,k∈Z},B={x=2k-1,k∈Z},则集合A与B 的关系是(B)A.A=B B.A BC.A B D.B⊆A[解析]因为集合B={x|x=2k-1,k∈Z},A={x|x=4k-1,k∈Z}={x|x=2(2k)-1,k∈Z},集合B表示2与整数的积减1的集合,集合A表示2与偶数的积减1的集合,所以A B,故选B.题组三走向高考4.(2020·新高考Ⅱ,1,5分)设集合A={2,3,5,7},B={1,2,3,5,8},则A∩B =(C)A.{1,8} B.{2,5}C.{2,3,5} D.{1,2,3,5,7,8}[解析]∵A={2,3,5,7},B={1,2,3,5,8},∴A∩B={2,3,5},故选C.5.(2020·新高考Ⅰ,1,5分)设集合A ={x |1≤x ≤3},B ={x |2<x <4},则A ∪B =( C ) A .{x |2<x ≤3} B .{x |2≤x ≤3} C .{x |1≤x <4}D .{x |1<x <4}[解析] 已知A ={x |1≤x ≤3},B ={x |2<x <4},在数轴上表示出两个集合,由图易知A ∪B ={x |1≤x <4}.故选C .6.(2020·天津,1,5分)设全集U ={-3,-2,-1,0,1,2,3},集合A ={-1,0,1,2},B ={-3,0,2,3},则A ∩(∁U B )=( C )A .{-3,3}B .{0,2}C .{-1,1}D .{-3,-2,-1,1,3}[解析] 因为U ={-3,-2,-1,0,1,2,3},B ={-3,0,2,3},所以∁U B ={-2,-1,1},又A ={-1,0,1,2},所以A ∩(∁U B )={-1,1},故选C .考点突破·互动探究KAO DIAN TU PO HU DONG TAN JIU 考点一 集合的基本概念——自主练透例1 (1)(多选题)已知集合A ={x |x =3k +1,k ∈Z },则下列表示正确的是( ABD )A .-2∈AB .2 022∉AC .3k 2+1∉AD .-35∈A(2)已知集合A ={0,1,2},则集合B ={(x ,y )|x ≥y ,x ∈A ,y ∈A }中元素的个数是( C ) A .1 B .3 C .6D .9(3)已知集合A ={a +2,(a +1)2,a 2+3a +3},若1∈A ,则2 020a 的值为1;若1∉A ,则a 不可能取得的值为-2,-1,0,-1+52,-1-52.[解析] (1)当-2=3k +1时,k =-1∈Z ,故A 正确;当2 022=3k +1时,k =67323∉Z ,故B 正确;∵k ∈Z ,∴k 2∈Z ,显然3k 2+1∈A ,当-35=3k +1时,k =-12∈Z ,故D 正确.故选A 、B 、D .(2)当x =0时,y =0;当x =1时,y =0或y =1; 当x =2时,y =0,1,2.故集合B ={(0,0),(1,0),(1,1),(2,0),(2,1),(2,2)}, 即集合B 中有6个元素.(3)若a +2=1,则a =-1,A ={1,0,1},不合题意;若(a +1)2=1,则a =0或-2,当a =0时,A ={2,1,3},当a =-2时,A ={0,1,1},不合题意;若a 2+3a +3=1,则a =-1或-2,显然都不合题意;因此a =0,所以2 0200=1.∵1∉A ,∴a +2≠1,∴a ≠-1;(a +1)2≠1,解得a ≠0,-2;a 2+3a +3≠1解得a ≠-1,-2.又∵a +2、(a +1)2、a 2+3a +3互不相等,∴a +2≠(a +1)2得a ≠-1±52;a +2≠a 2+3a+3得a ≠-1;(a +1)2≠a 2+3a +3得a ≠-2;综上a 的值不可以为-2,-1,0,-1+52,-1-52.名师点拨 MING SHI DIAN BO(1)用描述法表示集合,首先要搞清楚集合中代表元素的含义,再看元素的限制条件,明白集合的类型,是数集、点集还是其他类型的集合.(2)集合中元素的互异性常常容易忽略,特别是含有字母的集合,在求出字母的值后,要注意检验集合中元素是否满足互异性.分类讨论的思想方法常用于解决集合问题.考点二 集合之间的基本关系——师生共研例2 (1)(2021·新高考八省联考)已知M ,N 均为R 的子集,且∁R M ⊆N ,则M ∪(∁R N )=( B )A .∅B .MC .ND .R(2)(多选题)已知集合A =⎩⎨⎧⎭⎬⎫-13,12,B ={x |ax +1=0},且B ⊆A ,则实数a 的可能取值为( BCD )A .-3B .-2C .0D .3(3)设集合M =⎩⎨⎧⎭⎬⎫x |x =k 3+16,k ∈Z ,N =⎩⎨⎧⎭⎬⎫x ⎪⎪x =k 6+23,k ∈Z ,则下面正确的是( B ) A .M =N B .MNC .NMD .M ∩N =∅[解析] (1)如图,∁R M ⊆N ,显然(∁R N )⊆M ,∴M ∪(∁R N )=M ,故选B .(2)本题考查集合之间的关系.由题知B ⊆A ,B ={x |ax +1=0},所以B =⎩⎨⎧⎭⎬⎫-13,⎩⎨⎧⎭⎬⎫12,∅.当B =⎩⎨⎧⎭⎬⎫-13时,-13a +1=0,解得a =3;当B =⎩⎨⎧⎭⎬⎫12时,12a +1=0,解得a =-2;当B =∅时,a =0.综上可得实数a 的可能取值为3,0,-2,故选B 、C 、D .(3)解法一:(列举法),由题意知 M =⎩⎨⎧⎭⎬⎫…,-12,-16,16,12,56,76,…N =⎩⎨⎧⎭⎬⎫…,-16,0,16,13,12,23,56,…显然M N ,故选B .解法二:(描述法) M =⎩⎨⎧⎭⎬⎫x |x =2k +16,k ∈Z ,N =⎩⎨⎧⎭⎬⎫x |x =k +46,k ∈Z∵2k +1表示所有奇数,而k +4表示所有整数(k ∈Z ) ∴MN ,故选B .名师点拨 MING SHI DIAN BO 判断集合间关系的3种方法 列举法根据题中限定条件把集合元素表示出来,然后比较集合元素的异同,从而找出集合之间的关系.(如第(3)题解法一)结构法从元素的结构特点入手,结合通分、化简、变形等技巧,从元素结构上找差异进行判断.(如第(3)题解法二)数轴法在同一个数轴上表示出两个集合,比较端点之间的大小关系,从而确定集合与集合之间的关系.(1)集合M =⎩⎨⎧⎭⎬⎫x |x =n 2+1,n ∈Z ,N =⎩⎨⎧⎭⎬⎫y |y =m +12,m ∈Z ,则两集合M ,N 的关系为( D )A .M ∩N =∅B .M =NC .M ⊆ND .N ⊆M(2)(多选题)(2020·湖南长郡中学模拟改编)已知集合M ={y |y =x -|x |,x ∈R },N =⎩⎨⎧⎭⎬⎫y |y =⎝⎛⎭⎫12x ,x ∈R ,则下列结论不正确的是( ABD ) A .M =N B .N ⊆M C .M =∁R ND .(∁R N )∩M =∅(3)已知集合A ={x ∈R |x 2-3x +2=0},B ={x ∈N |0<x <5},则满足条件A ⊆C ⊆B 的集合C 的个数为4.(4)已知集合A ={x |x 2-2 023x +2 022<0},B ={x |x <a },若A ⊆B ,则实数a 的取值范围是[2_022,+∞).[解析] (1)由题意,对于集合M ,当n 为偶数时,设n =2k (k ∈Z ),则x =k +1(k ∈Z ),当n 为奇数时,设n =2k +1(k ∈Z ),则x =k +1+12(k ∈Z ),∴N ⊆M ,故选D .(2)由题意得y =x -|x |=⎩⎪⎨⎪⎧0,x ≥0,2x ,x <0,∴M =(-∞,0],N =(0,+∞),∴M =∁R N .故选A 、B 、D . (3)由题意可得,A ={1,2},B ={1,2,3,4}.又∵A ⊆C ⊆B ,∴C ={1,2}或{1,2,3}或{1,2,4}或{1,2,3,4},∴有4个. (4)由x 2-2 023x +2 022<0,解得1<x <2 022, 故A ={x |1<x <2 022}.又B ={x |x <a },A ⊆B ,如图所示,可得a ≥2 022.考点三 集合的基本运算——多维探究 角度1 集合的运算例3 (1)(2020·课标Ⅱ)已知集合U ={-2,-1,0,1,2,3},A ={-1,0,1},B ={1,2},则∁U (A ∪B )=( A )A .{-2,3}B .{-2,2,3}C .{-2,-1,0,3}D .{-2,-1,0,2,3}(2)(2020·课标Ⅱ)已知集合A ={x ||x |<3,x ∈Z },B ={x ||x |>1,x ∈Z },则A ∩B =( D ) A .∅B .{-3,-2,2,3}C .{-2,0,2}D .{-2,2}(3)(2021·浙江杭州模拟)已知全集U =R ,集合A ={x |x 2-3x +2<0},集合B = {x |log 3(x +1) <1},则A ∪B =(-1,2),( ∁R A )∩B =(-1,1].[解析] (1)∵A ={-1,0,1},B ={1,2},∴A ∪B ={-1,0,1,2},又∵集合U ={-2,-1,0,1,2,3},∴∁U (A ∪B )={-2,3}.故选A .(2)由已知得A ={x |-3<x <3,x ∈Z }={-2,-1,0,1,2},B ={x |x <-1或x >1,x ∈Z },∴A ∩B ={-2,2}.故选D .(3)依题意可知,A ={x |1<x <2},B ={x |0<x +1<3}={x |-1<x <2},所以A ∪B =(-1,2),∁R A ={x |x ≤1或x ≥2},所以(∁R A )∩B =(-1,1].角度2 利用集合的运算求参数例4 (1)已知集合A ={x |x 2-3x <0),B ={1,a },且A ∩B 有4个子集,则实数a的取值范围是( B )A .(0,3)B .(0,1)∪(1,3)C .(0,1)D .(-∞,1)∪(3,+∞)(2)已知集合A ={x |-2≤x ≤5},B ={x |m +1≤x ≤2m -1}≠∅,若A ∩B =B ,则实数m 的取值范围为[2,3].[解析] (1)因为A ∩B 有4个子集,所以A ∩B 中有2个不同的元素,所以a ∈A ,所以a 2-3a <0,解得0<a <3.又a ≠1,所以实数a 的取值范围是(0,1)∪(1,3),故选B .(2)由A ∩B =B 知,B ⊆A .又B ≠∅,则⎩⎪⎨⎪⎧2m -1≥m +1,m +1≥-2,2m -1≤5.解得2≤m ≤3,则实数m 的取值范围为[2,3].[引申1]本例(2)中若B ={x |m +1≤x ≤2m -1}情况又如何? [解析] 应对B =∅和B ≠∅进行分类. ①若B =∅,则2m -1<m +1,此时m <2. ②若B ≠∅,由例得2≤m ≤3.由①②可得,符合题意的实数m 的取值范围为(-∞,3].[引申2]本例(2)中是否存在实数m ,使A ∪B =B ?若存在,求实数m 的取值范围;若不存在,请说明理由.[解析] 由A ∪B =B ,即A ⊆B 得⎩⎪⎨⎪⎧m +1≤-2,2m -1≥5,即⎩⎪⎨⎪⎧m ≤-3,m ≥3,不等式组无解,故不存在实数m ,使A ∪B =B . [引申3]本例(2)中,若B ={x |m +1≤x ≤1-2m },AB ,则m 的取值范围为(-∞,-3].[解析] 由题意可知⎩⎪⎨⎪⎧m +1≤-2,1-2m ≥5,解得m ≤-3.名师点拨 MING SHI DIAN BO集合的基本运算的关注点1.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提. 2.有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决.3.注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和Venn 图. 4.根据集合运算结果求参数,先把符号语言译成文字语言,然后应用数形结合求解. 〔变式训练2〕(1)(角度1)(2020·北京,1,4分)已知集合A ={-1,0,1,2},B ={x |0<x <3},则A ∩B =( D )A .{-1,0,1}B .{0,1}C .{-1,1,2}D .{1,2}(2)(角度1)设全集U =R ,集合A ={x |0≤x ≤2},B ={y |1≤y ≤3},则(∁U A )∪B =( D ) A .(2,3] B .(-∞,1]∪(2,+∞) C .[1,2)D .(-∞,0)∪[1,+∞)(3)(角度2)已知集合A ={x |x <a },B ={x |x 2-3x +2<0},若A ∩B =B ,则实数a 的取值范围是( D )A .a <1B .a ≤1C .a >2D .a ≥2[解析] (1)集合A 与集合B 的公共元素为1,2,由交集的定义知A ∩B ={1,2},故选D . (2)∁U A ={x |x <0或x >2},则(∁U A )∪B ={x |x <0或x ≥1},故选D .(3)集合B ={x |x 2-3x +2<0}={x |1<x <2},由A ∩B =B 可得B ⊆A ,作出数轴如图,可知a ≥2.名师讲坛·素养提升MING SHI JIANG TAN SU YANG TI SHENG集合中的新定义问题例5 定义集合的商集运算为A B =⎩⎨⎧⎭⎬⎫x ⎪⎪x =m n ,m ∈A ,n ∈B ,已知集合A ={2,4,6},B =⎩⎨⎧⎭⎬⎫x ⎪⎪x =k 2-1,k ∈A ,则集合⎝⎛⎭⎫B A ∪B 中的元素个数为( B ) A .6 B .7 C .8D .9[解析] 由题意知,B ={0,1,2},B A =⎩⎨⎧⎭⎬⎫0,16,14,13,12,1,则⎝⎛⎭⎫B A ∪B =⎩⎨⎧⎭⎬⎫0,16,14,13,12,1,2,共有7个元素.名师点拨 MING SHI DIAN BO集合新定义问题的“3定”(1)定元素:确定已知集合中所含的元素,利用列举法写出所有元素.(2)定运算:根据要求及新定义运算,将所求解集合的运算问题转化为集合的交集、并集与补集的基本运算问题,或转化为数的有关运算问题.(3)定结果:根据定义的运算进行求解,利用列举法或描述法写出所求集合中的所有元素. 〔变式训练3〕(2021·江西九江联)设A ,B 是非空集合,定义A ⊗B ={x |x ∈(A ∪B )且x ∉(A ∩B )}.已知M ={y |y =-x 2+2x ,0<x <2},N ={y |y =2x -1,x >0},则M ⊗N =⎝⎛⎦⎤0,12∪(1,+∞) [解析] M ={y |y =-x 2+2x ,0<x <2}=(0,1],N ={y |y =2x -1,x >0}=⎝⎛⎭⎫12,+∞,则M ∪N =(0,+∞),M ∩N =⎝⎛⎦⎤12,1,所以M ⊗N =⎝⎛⎦⎤0,12∪(1,+∞).。
第一章静力学基本概念1、只限物体任何方向移动,不限制物体转动的

第一章:静力学基本概念1、只限物体任何方向移动,不限制物体转动的支座称()支座。
A:固定铰B:可动铰C:固定端D:光滑面【答案】A2、只限物体垂直于支承面方向的移动,不限制物体其它方向运动的支座称()支座。
A:固定铰B:可动铰C:固定端D:光滑面【答案】B3、既限制物体任何方向运动,又限制物体转动的支座称()支座。
A:固定铰B:可动铰C:固定端D:光滑面【答案】C4、平衡是指物体相对地球()的状态。
A、静止B、匀速运动C、匀速运动D、静止或匀速直线运动【答案】D5、如图所示杆ACB ,其正确的受力图为()。
A、图AB、图BC、图CD、图D【答案】A6.加减平衡力系公理适用于()。
A.刚体B.变形体C.任意物体D.由刚体和变形体组成的系统【答案】A7.在下列原理、法则、定理中,只适用于刚体的是()。
A.二力平衡原理 B.力的平行四边形法则C.力的可传性原理 D.作用与反作用定理【答案】C(C )(D)(A )D8.柔索对物体的约束反力,作用在连接点,方向沿柔索()。
A.指向该被约束体,恒为拉力B.背离该被约束体,恒为拉力C.指向该被约束体,恒为压力D.背离该被约束体,恒为压力【答案】B9.图示中力多边形自行不封闭的是()。
A.图(a)B.图(b)C.图(b)D.图(d)【答案】B10.物体在一个力系作用下,此时只能()不会改变原力系对物体的外效应。
A.加上由二个力组成的力系B.去掉由二个力组成的力系C.加上或去掉由二个力组成的力系D.加上或去掉另一平衡力系【答案】D11.物体系中的作用力和反作用力应是()。
A.等值、反向、共线B.等值、反向、共线、同体C.等值、反向、共线、异体D.等值、同向、共线、异体【答案】C12.由F1、F2、F3、F4构成的力多边形如图所示,其中代表合力的是()。
A.F1B.F2C.F4D.F3【答案】C13.物体受五个互不平行的力作用而平衡,其力多边形是()A.三角形B.四边形C.五边形D.六边形【答案】C14.物体受三个互不平行的力作用而平衡,其力多边形是()A.三角形B.四边形C.五边形D.六边形【答案】A15.物体受四个互不平行的力作用而平衡,其力多边形是()A.三角形B.四边形C.五边形D.六边形【答案】B16.物体受六个互不平行的力作用而平衡,其力多边形是()A.三角形B.四边形C.五边形D.六边形【答案】D17.物体受七个互不平行的力作用而平衡,其力多边形是()A.三角形B.七边形C.五边形D.六边形【答案】B18.物体受八个互不平行的力作用而平衡,其力多边形是()A.八角形B.四边形C.五边形D.六边形【答案】A19.加减平衡力系公理适用于()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章概念
1.试述数据、数据库、数据库管理系统、数据库系统的概念。
答:
数据:描述事物的符号记录称为数据。
数据的种类有数字、文字、图形、图像、声音、正文等。
数据与其语义是不可分的。
数据库:数据库是长期储存在计算机内的、有组织的、可共享的数据集合。
数据库中的数据按一定的数据模型组织、描述和储存,具有较小的冗余度、较高的数据独立性和易扩展性,并可为各种用户共享。
数据库管理系统:数据库管理系统是位于用户与操作系统之间的一层数据管理软件,用于科学地组织和存储数据、高效地获取和维护数据。
DBMS的主要功能包括数据定义功能、数据操纵功能、数据库的运行管理功能、数据库的建立和维护功能。
数据库系统:数据库系统是指在计算机系统中引入数据库后的系统构成,一般由数据库、数据库管理系统(及其开发工具)、应用系统、数据库管理员构成。
2.试述文件系统与数据库系统的区别和联系。
答:
文件系统与数据库系统的区别是:
文件系统面向某一应用程序,共享性差,冗余度大,数据独立性差,记录内有结构,整体无结构,由应用程序自己控制。
数据库系统面向现实世界,共享性高,冗余度小,具有较高的物理独立性和一定的逻辑独立型,整体结构化,用数据模型描述,由数据库管理系统提供数据的安全性、完整性、并发控制和恢复能力。
文件系统与数据库系统的联系:
文件系统与数据库系统都是计算机系统中管理数据的软件。
3.试述数据库系统的特点。
答:
(1)数据结构化
(2)数据的共享性高,冗余度低,易扩充
(3)数据独立性高
(4)数据由DBMS统一管理和控制
4.数据库管理系统的主要功能有哪些?
答:
(1)数据库定义功能
(2)数据存取功能
(3)数据库运行管理
(4)数据库建立和维护功能
5.试述数据模型的概念、数据模型的作用和数据模型的三个要素。
答:
数据模型是数据库中用来对现实世界进行抽象的工具,是数据库中用于提供信息表示和操作手段的形式构架。
数据模型是严格定义的概念的集合。
这些概念精确描述了系统的静态特性、动态特性
和完整性约束条件。
因此数据模型通常由数据结构、数据操作和完整性约束三部分组成。
数据结构:是所研究的对象类型的集合,是对系统静态特性的描述。
数据操作:是指对数据库中各种对象(型)的实例(值)允许进行的操作的集合,包括操作及有关的操作规则,是对系统动态特性的描述。
数据的约束条件:是一组完整性规则的集合。
完整性规则是给定的数据模型中数据及其联系所具有的制约合依存规则,用以限定符合数据模型的数据库状态以及变化,以保证数据的正确、有效、相容。
6.试述概念模型的作用。
答:
概念模型实际上是现实世界到机器世界的一个中间层次。
概念模型用于信息世界的建模,是现实世界到信息世界的第一层抽象,是数据库设计人员进行数据库设计的有力工具,也是数据库设计人员和用户之间进行交流的语言。
7.定义并解释概念模型中以下术语。
答:
实体:客观存在并可以相互区分的事物叫实体。
实体型:具有相同属性的实体具有相同的特征和性质,用实体名及其属性名集合来抽象和刻画同类实体,称为实体型。
实体集:同型实体的集合称为实体集。
属性:实体所具有的某一特性,一个实体可由若干个属性来刻画。
码:惟一标识实体的属性集称为码。
实体联系图:提供了表示实体型、属性和联系地方法。
8.试述关系模型的概念,定义并解释以下术语。
答:
关系模型由关系数据结构、关系操作集合和关系完整性约束三部分组成。
在用户的观点下,关系模型中数据的逻辑结构是一张二维表,它由行和列组成。
(1)关系:一个关系对应通常说的一张表。
(2)属性:表中的一列即为一个属性。
(3)域:属性的取值范围。
(4)元组:表中的一行即为一个元组。
(5)主码:表中的某个属性组,它可以惟一确定一个元组。
(6)分量:元组中的一个属性值。
(7)关系模式:对关系的描述,一般表示为:关系名(属性1,属性2,…,属性n)
9.试述关系数据库的特点。
答:
关系数据库具有下列优点:
(1)关系模型与非关系模型不同,它是建立在严格的数学概念的基础上的。
(2)关系模型的概念单一,无论实体还是实体之间的联系都用关系表示,操作的对象和操作的结果都是关系,所以其数据结构简单、清晰,用户易懂易用。
(3)关系模型的存取路径对用户透明,从而具有更高的数据独立性、更好的安全保密性,也简化了程序员的工作和数据库开发建立的工作。
关系数据模型也有缺点,其中最主要的缺点是,由于存取路径对用户透明,查询效率往往不如非关系数据模型。
因此为了提高性能,必须对用户的查询请求进行优化,增加了开发数据库管理系统的难度。
10.试述数据库系统的三级模式结构,这种结构的优点是什么?
答:
数据库系统的三级模式结构由外模式、模式和内模式组成。
数据库系统的三级模式结构是对数据的三个抽象级别,它把数据的具体组织留给DBMS 管理,使用户能逻辑抽象地处理数据,而不必关心数据在计算机中的表示和存储。
为了能够在内部实现这三个抽象层次的联系和转换,数据库系统在这三级模式之间提供了两层映像:外模式/模式映像和模式/内模式映像。
正是这两层映像保证了数据库系统中的数据能够具有较高的而逻辑独立型和物理独立性。
11.定义并解释以下术语。
答:
模式:也称逻辑模式,是数据库中全体数据的逻辑结构和特征的描述,是所有用户的公共数据视图。
模式描述的是数据的全局逻辑结构。
外模式涉及的是数据的局部逻辑结构,通常是模式的子集。
外模式:也称子模式或用户模式,是数据库用户能够看见和使用的局部数据的逻辑结构和特征的描述,是数据库用户的数据视图,是于某一应用有关的数据的逻辑表示。
内模式:也称存储模式,是数据在数据库系统内部的表示,即对数据的物理结构和存储方式的描述。
DDL:数据定义语言,用来定义数据库模式、外模式、内模式的语言。
DML:数据操纵语言,用来对数据库中的数据进行查询、插入、删除和修改的语句。
12.什么叫数据与程序的物理独立性?什么叫数据与程序的逻辑独立性?为什么数据库系统具有数据与程序的独立性?
答:
数据与程序的逻辑独立性:当模式改变时(例如增加新的关系、新的属性、改变属性的数据类型等),由数据库管理员对各个外模式/模式的映像做相应改变,可以使外模式保持不变。
应用程序是依据数据的外模式编写的,从而应用程序不必修改,保证了数据与程序的逻辑独立性,简称数据的逻辑独立型。
数据与程序的物理独立性:当数据库的存储结构改变了,由数据库管理员对模式/内模式映像做相应改变,可以使模式保持不变,从而应用程序也不必改变,保证了数据与程序的物理独立性,简称数据的物理独立性。
数据库管理系统在三级模式之间提供的两层映像保证了数据库系统中数据能够具有较高的逻辑独立性和物理独立性。
13.试述数据库系统的组成。
答:
数据库系统一般有数据库、数据库管理系统(及其开发工具)、应用系统、数据库管理员和用户构成。
14.DBA的职责是什么?
答:
负责全面地管理和控制数据库系统。
具体职责包括:
(1)决定数据库的信息内容和结构;
(2)决定数据库的存储结构和存取策略;
(3)定义数据的安全性要求和完整性约束条件;
(4)监督和控制数据库的使用和运行;
(5)改进和重组数据库系统。
15.系统分析员、数据库设计人员、应用程序员的职责是什么?
答:
系统分析员负责应用系统的需求分析和规范说明,系统分析员要和用户及DBA相结合,确定系统的硬件、软件配置,并参与数据库系统的概要设计。
数据库设计人员负责数据库中数据的确定、数据库各级模式的设计。
数据库设计人员必须参加用户需求调查和系统分析,然后进行数据设计。
在很多情况下,数据库设计人员就由数据库管理员担任。
应用程序员负责设计和编写应用系统的程序模块,并进行调试和安装。
