人教版数学七年级竞赛教程之倍数 约数附答案
倍数与约数之练习题计算倍数和约数

倍数与约数之练习题计算倍数和约数倍数与约数是初中数学中的重要概念,对于提升学生的数学运算能力和逻辑思维能力有着重要意义。
本文将以练习题的形式,帮助读者加深对倍数与约数的理解,并通过解题过程加强对相关知识点的掌握。
一、倍数的计算1. 若正整数a能被正整数b整除,我们就称a是b的倍数,记作a|b或b/a。
2. 倍数的计算可以通过以下练习题进行加强:练习题一:计算下列数的倍数1)11的倍数2)25的倍数3)98的倍数4)72的倍数解答:1)11的倍数:11、22、33、44、55、66、77、88、99、110、121……2)25的倍数:25、50、75、100、125、150、175、200、225、250、275……3)98的倍数:98、196、294、392、490、588、686、784、882、980、1078……4)72的倍数:72、144、216、288、360、432、504、576、648、720、792……二、约数的计算1. 若正整数a能被正整数b整除,我们就称b是a的约数,记作b|a 或a/b。
2. 约数的计算可以通过以下练习题进行加强:练习题二:计算下列数的约数1)12的约数2)37的约数3)60的约数4)92的约数解答:1)12的约数:1、2、3、4、6、122)37的约数:1、373)60的约数:1、2、3、4、5、6、10、12、15、20、30、604)92的约数:1、2、4、23、46、92三、倍数与约数之间的关系1. 若正整数a既是b的倍数,又是c的倍数,那么a是b与c的公倍数。
2. 若正整数a既是b的约数,又是c的约数,那么a是b与c的公约数。
3. 设a、b是两个正整数,且a≠0,b≠0,那么a与b的最小公倍数,记作[a,b],是同时是a的倍数也是b的倍数的最小正整数;a与b的最大公约数,记作(a,b),是同时是a的约数也是b的约数的最大正整数。
练习题三:计算下列数的最小公倍数与最大公约数1)4与6的最小公倍数与最大公约数2)15与20的最小公倍数与最大公约数3)24与32的最小公倍数与最大公约数4)45与60的最小公倍数与最大公约数解答:1)4与6的最小公倍数为12,最大公约数为2。
人教版数学七年级竞赛教程之倍数 约数附答案
倍数约数【知识精读】1两个整数A和B(B≠0),如果B能整除A(记作B|A),那么A叫做B的倍数,B 叫做A的约数。
例如3|15,15是3的倍数,3是15的约数。
2因为0除以非0的任何数都得0,所以0被非0整数整除。
0是任何非0整数的倍数,非0整数都是0的约数。
如0是7的倍数,7是0的约数。
3整数A(A≠0)的倍数有无数多个,并且以互为相反数成对出现,0,±A,±2A,……都是A的倍数,例如5的倍数有±5,±10,……。
4整数A(A≠0)的约数是有限个的,并且也是以互为相反数成对出现的,其中必包括±1和±A。
例如6的约数是±1,±2,±3,±6。
5通常我们在正整数集合里研究公倍数和公约数,几正整数有最小的公倍数和最犬的公约数。
6公约数只有1的两个正整数叫做互质数(例如15与28互质)。
7在有余数的除法中,被除数=除数×商数+余数若用字母表示可记作:A=BQ+R,当A,B,Q,R都是整数且B≠0时,A-R能被B整除例如23=3×7+2则23-2能被3整除。
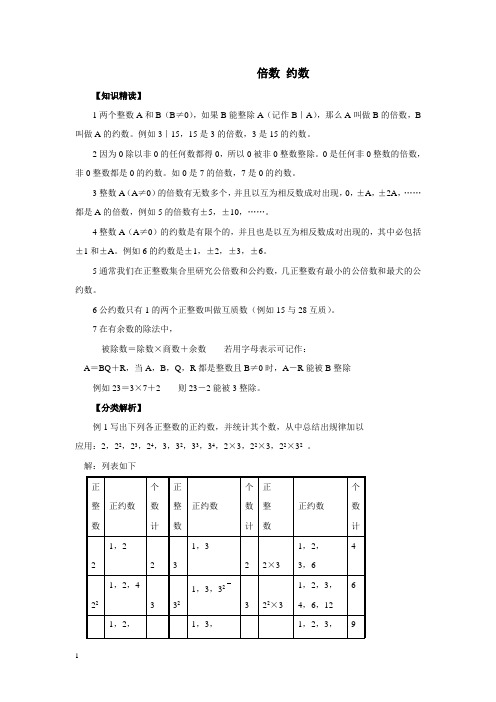
【分类解析】例1写出下列各正整数的正约数,并统计其个数,从中总结出规律加以应用:2,22,23,24,3,32,33,34,2×3,22×3,22×32。
解:列表如下其规律是:设A=a m b n(a,b是质数,m,n是正整数)那么合数A的正约数的个是(m+1)(n+1)例如求360的正约数的个数解:分解质因数:360=23×32×5,360的正约数的个数是(3+1)×(2+1)×(1+1)=24(个)例2用分解质因数的方法求24,90最大公约数和最小公倍数解:∵24=23×3,90=2×32×5∴最大公约数是2×3,记作(24,90)=6最小公倍数是23×32×5=360,记作[24,90]=360例3己知32,44除以正整数N有相同的余数2,求N解:∵32-2,44-2都能被N整除,∴N是30,42的公约数∵(30,42)=6,而6的正约数有1,2,3,6经检验1和2不合题意,∴N=6,3例4一个数被10余9,被9除余8,被8除余7,求适合条件的最小正整数分析:依题意如果所求的数加上1,则能同时被10,9,8整除,所以所求的数是10,9,8的最小公倍数减去1。
人教版初一下数学竞赛试题及答案

人教版初一下数学竞赛试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是最小的正整数?A. 0B. -1C. 1D. 22. 如果a和b是两个连续的整数,且a > b,那么a-b的值是:A. 1B. 0C. -1D. 23. 一个数的平方根是它本身,这个数可以是:A. 1B. -1C. 0D. 44. 一个数的立方等于它本身,这个数有:A. 1个B. 2个C. 3个D. 4个5. 一个圆的半径是r,它的面积是:A. πr²B. 2πrC. πrD. r²6. 一个长方体的长、宽、高分别是a、b、c,它的体积是:A. abcB. 2abcC. a+b+cD. a²b²c²7. 一个等差数列的首项是a,公差是d,第n项是:A. a+(n-1)dB. a+ndC. a-dD. a-d(n-1)8. 如果一个三角形的三边长分别为a、b、c,且a² + b² = c²,那么这个三角形是:A. 直角三角形B. 等边三角形C. 等腰三角形D. 不规则三角形9. 一个分数的分子和分母同时扩大相同的倍数,其值:A. 增大B. 减小C. 不变D. 无法确定10. 一个数的绝对值是它本身,这个数:A. 必须为正数B. 必须为负数C. 可以是正数或零D. 可以是负数或零二、填空题(每题4分,共20分)11. 一个数的平方等于16,这个数是________。
12. 如果一个数的相反数是-5,那么这个数是________。
13. 一个数的绝对值等于5,这个数可以是________。
14. 一个数的立方根是2,那么这个数是________。
15. 一个数的倒数是1/4,这个数是________。
三、解答题(每题10分,共50分)16. 计算下列表达式的值:(3+5)² - 2×(4-1)。
17. 一个长方体的长是10厘米,宽是8厘米,高是6厘米,求它的表面积和体积。
初中数学竞赛-七年级 -整数问题2 - 答案

∴
,
即可.
【解答】解:385 的二位因数有 11,35,55,77, 他们不全相同,
解得,
,
故最大为 77,77,55,和为 209, 最小为 11,11,35,和为 57.
∴100x+y=352=1225, ∴x=12,y=25,
故答案为 209,57.
即:小王现在的年龄是 12 岁,
6.在 100~1999 这一千九百个自然数中,十位与个位数 字相同的共有 190 个.
结论. 【解答】解:∵2m+2006+2m =2m(22006+1) ∵22006 末位是 4, ∴22006+1 末位是 5, 而 2m 是偶数, 所以 2m+2006+2m(m 是正整数)的末位数字是 0.
则 k=0、1 或 2,(0 不合要求,舍去), 因此 A=4001 或 A=8004. 故答案为:4001 或 8004. 15.若 1+2+3+…+k 之和为一完全平方数 N2,并且 N 小 于 100,则 K 的可能值是 1,8 或 49 . 【考点】#9:完全平方数.
与最小公倍数之和等于 ab+1 .
个数仍然为完全平方数,则小王现在的年龄是 12
【考点】#6:约数与倍数. 菁优网版权所有
【分析】由于相邻的两个自然数互为质数,故他们的 最大公约数是 1,最小公倍数是 ab,从而易求答案. 【解答】解:a、b 为两个相邻的自然数,它们的最大
岁. 【考点】#9:完全平方数.
位对应着 1,2,…,19 这 19 种可能即可得出答案.
15,然后左边分解因式,右边分解因数,建立方程组
【解答】解:后两位数字相同,只有 00,11,22,33, 44,55,66,77,88,99 这 10 种可能情形, 而每一种相同的末两位数字相同的数,百位到千位对 应着 1,2,…,19 这 19 种可能,
初一数学专题复习之约数与倍数

初一数学专题复习之约数与倍数
初一数学专题复习之约数与倍数
约数和倍数:若整数a能够被b整除,a叫做b的倍数,b就叫做a的约数。
公约数:几个数公有的约数,叫做这几个数的公约数;其中最大的一个,叫做这几个数的最大公约数。
最大公约数的`性质:
1、几个数都除以它们的最大公约数,所得的几个商是互质数。
2、几个数的最大公约数都是这几个数的约数。
3、几个数的公约数,都是这几个数的最大公约数的约数。
4、几个数都乘以一个自然数m,所得的积的最大公约数等于这几个数的最大公约数乘以m。
例如:12的约数有1、2、3、4、6、12;
18的约数有:1、2、3、6、9、18;
那么12和18的公约数有:1、2、3、6;
那么12和18最大的公约数是:6,记作(12,18)=6;
求最大公约数基本方法:
1、分解质因数法:先分解质因数,然后把相同的因数连乘起来。
2、短除法:先找公有的约数,然后相乘。
3、辗转相除法:每一次都用除数和余数相除,能够整除的那个余数,就是所求的最大公约数。
公倍数:几个数公有的倍数,叫做这几个数的公倍数;其中最小的一个,叫做这几个数的最小公倍数。
12的倍数有:12、24、36、48……;
18的倍数有:18、36、54、72……;
那么12和18的公倍数有:36、72、108……;
那么12和18最小的公倍数是36,记作[12,18]=36;
最小公倍数的性质:
1、两个数的任意公倍数都是它们最小公倍数的倍数。
2、两个数最大公约数与最小公倍数的乘积等于这两个数的乘积。
最小公倍数的求法:1、短除法;2、分解质因数。
数论--约数倍数-第4讲约数和倍数竞赛班学生

第四讲约数和倍数一、基础知识1. 1. 常用的特殊自然数的整除特征1)2系列:被2整除只需看末位能否被2整除被4整除只需看末两位能否被4整除被8整除只需看末三位能否被8整除,依次类推2)5系列:被5整除只需看末位是否为0或5被25整除只需看末两位能否被25整除,即只可能是00,25,50,75我们以被8整除看末三位为例证明以上两个系列的性质假设一个多位数末三位是abc,末三位之前的部分为x那么该数=1000x+abc,由于8|1000,所以8|1000x,因此该数能否被8整除就决定于末三位abc能否被8整除,证毕.3)3系列:被3整除只需看各位数字之和能否被3整除.被9整除只需看各位数字之和能否被9整除.我们以三位数为例来证明被9整除只需看各位数字之和这一性质假设该三位数为abc=100a+10b+c=(99a+9b)+(a+b+c)很明显第一个括号里的数是9的倍数,因此只要a+b+c,即各位数字之和能被9整除,那么这个三位数abc 就能被9整除,反之亦然。
推广到任意位数的自然数,该证明方法仍然成立,请大家自己尝试一下.4)7,11,13系列被7,11,13整除的判别方法:看多位数的末三位和前面部分之差能否被7,11,13整除[思考]:为什么要从末三位把这个数一分为二呢?仔细想一想我们会发现7x11x13=1001,正好比1000大1,由此我们可以得到如下证明和2系列的证明类似,我们仍然设一个多位数的末三位是abc,前面部分是x那么我们要证明的就是这个多位数能否被7,11,13整除决定于abc-x能否被7,11,13整除该数=1000x+abc=1001x+(abc-x)由于1001同时是7,11,13的倍数,所以这个多位数能否被7,11,13整除决定于abc-x能否被7,11,13整除,证毕.特别的,我们还有另外一种判别能否被11整除的性质,就是看奇数位数字之和与偶数为数字之和能否被11整除,若能整除则原数可被11整除,反之亦然.请大家自己想一想这个如何证明?(思考题)2.整除的性质1)已知b|c,a|c,则[a,b]|c,特别地,若(a,b)=1,则有ab|c.2)已知c|ab,(b,c)=1,则c|a.3.最大公约数和最小公倍数两个基本性质一.两个自然数分别除以它们的最大公约数,所得的商互质.即若a=a1*(a,b),b=b1*(a,b),则(a1,b1)=1二.两个数的最大公约和最小公倍的乘积等于这两个数的乘积.[a,b]*(a,b)=ab二、例题部分例1.(★★第16届希望杯第2试)我们用记号“|”表示两个正整数之间的整除关系,如3|12表示3整除12,那么满足x | (y+1)和y | (x+1)的正整数组(x,y)有__________组.例2.(★★第12届希望杯第2试) 两个正整数的和是60,它们的最小公倍数是273,则它们的乘积是__________例3.(★★★★ 1987年北京初二数学竞赛题)x,y,z均为整数,若11|(7x+2y-5z),求证:11|(3x-7y+12z)。
2023年初一数学竞赛教程含例题练习及答案⑸

初一数学竞赛讲座第5讲与年号有关的竞赛题在数学竞赛中,常可以看到某些题目中出现了当年的年号,这类题我们称之为“年号题”。
这类题趣味性强,时间性强,引起了参与竞赛的少年朋友很大的爱好。
“年号题”一般可提成两类,一类是题目的条件中出现了当年的年号,另一类是题目答案中出现了当年的年号。
下面我们分别举例说明这两类问题的解法。
一、题目条件中出现年号的问题1.题目在编制和解答中巧妙地运用了该年年号的数字特性,如年号数值的质因数分解式、是否质数、它的数的整除性等等。
例1 将19到80的两位数顺次排成数A=19202322…7980。
问:这个数A 能否被1980整除?解:由于1980=99×20,因此要考察A能否被1980整除,只需要考察A能否被99和20整除就行了。
能被20整除是显然的。
由于99除100的任何次方所得的余数都是1,所以A=19×10061+20×10060+…+79×100+80除以99的余数与B=19+20+…+79+80=99×31除以99的余数相同。
由于99|B,所以99|A。
于是A能被1980整除。
例2 用S(n)表达自然数n的各位数字之和,又n+S(n)=1999,求自然数n。
11x+2y=89。
注意到x是奇数且x,y都是一位整数,不难求得x=7,y=6,从而n=1976。
例3 在3×3的九宫格中,填上 9个不同的自然数,使得每行三数相乘,每列三数相乘所得的6个乘积都等于P 。
试拟定P 能取1996,1997, 1998,1999,2023,2023这6个数中的哪些值。
解:所填的9个数应为P 的9个不同约数,又P 不能填入九宫格内,故P 的不同约数的个数应不小于10。
1996=22×499,有6个约数; 1997和1999是质数,各有2个约数;1998=2×33×37,有16个约数; 2023=24×53,有20个约数;2023=3×23×29,有8个约数。
数的倍数与约数练习题及答案

数的倍数与约数练习题及答案一、选择题1. 下列哪个数一定是4的倍数?A. 19B. 28C. 35D. 422. 哪个数不是 7 的约数?A. 14B. 21C. 28D. 353. 若一个数同时是2和3的倍数,它最多是多少的倍数?A. 12B. 18C. 24D. 364. 一个数是5的倍数,它一定是10的倍数吗?A. 是B. 否5. 有一个数,在它的乘法表中,找到了数3,4,5,6,8,9,12,16,18,24,27分别是第几行?A. 第1 行B. 第2 行C. 第3 行D. 第4 行6. 某个数能同时被2和5整除,它能被10整除吗?A. 能B.不能7. 分解因式:36 = _____ * _____A. 3, 12B. 2, 18C. 4, 9D. 6, 68. 设 x 是3的倍数, y 是4的倍数,那么 5x + 6y 是____的倍数。
A. 3B. 4C. 5D. 69. 一个整数能同时被2和3整除,它一定是6的倍数吗?A. 是B. 否10. 分解因式:48 = _____ * _____A. 2, 24B. 3, 16C. 4, 12D. 6, 8二、填空题1. 6 的倍数的最小正整数是 ______。
2. 14 是 ______ 的倍数。
3. 有一个数,它是 3 的倍数,也是 2 的倍数,它至少是 ______ 的倍数。
4. 48 是 ______ 的约数。
5. 若一个数同时是 2 和 5 的倍数,它最小是 ______ 的倍数。
6. 20 = 4 * ______。
7. 若一个数同时是 2 和 3 的倍数,那么它一定是 ______ 的倍数。
8. 64 是 ______ 的约数。
三、解答题1. 找出 36 的所有约数。
2. 一个数被 2 除余 1,被 3 除余 2,被 5 除余 4,那么该数最小是多少?3. 分解因式:60 = ______ * ______。
4. 7 的最小倍数是多少?5. 分解因式:72 = ______ * ______。
初一数学竟赛辅导资料(16)(含答案)-.doc

初中数学竞赛辅导资料(16)整数的一种分类甲:内容提要1.余数的定义:在等式A=mB+r中,如果A、B是整数,m是正整数,r为小于m 的非负整数,那么我们称r是A 除以m的余数。
即:在整数集合中:被除数=除数×商+余数 (0≤余数<除数)例如:13,0,-1,-9除以5的余数分别是3,0,4,1(∵-1=5(-1)+4。
-9=5(-2)+1。
)2.显然,整数除以正整数m ,它的余数只有m种。
例如整数除以2,余数只有0和1两种,除以3则余数有0、1、2三种。
3.整数的一种分类:按整数除以正整数m的余数,分为m类,称为按模m分类。
例如:m=2时,分为偶数、奇数两类,记作{2k},{2k-1}(k为整数)m=3时,分为三类,记作{3k},{3k+1},{3k+2}.或{3k},{3k+1},{3k-1}其中{3k-1}表示除以3余2。
m=5时,分为五类,{5k}.{5k+1},{5k+2},{5k+3},{5k+4}或{5k},{5k±1},{5k±2},其中5k-2表示除以5余3。
4.余数的性质:整数按某个模m分类,它的余数有可加,可乘,可乘方的运算规律。
举例如下:①(3k1+1)+(3k2+1)=3(k1+k2)+2 (余数1+1=2)②(4k1+1)(4k2+3)=4(4k1k2+3k1+k2)+3(余数1×3=3)③(5k±2)2=25k2±20k+4=5(5k2±4k)+4(余数22=4)以上等式可叙述为:①两个整数除以3都余1,则它们的和除以3必余2。
②两个整数除以4,分别余1和3,则它们的积除以4必余3。
③如果整数除以5,余数是2或3,那么它的平方数除以5,余数必是4或9。
余数的乘方,包括一切正整数次幂。
如:∵17除以5余2 ∴176除以5的余数是4 (26=64)5.运用整数分类解题时,它的关鍵是正确选用模m。
人大附中华杯赛资料:《约数与倍数(一)》配套练习题

《约数与倍数(一)》配套练习题一、解答题1、2520的约数一共有多少个?2、在30的倍数中,恰有30个约数的共有多少个?3、有一个正偶数,它恰有11个约数(包括1及本身),它最小是多少?4、在840的所有约数中,有多少个是三位数?5、两个自然数不成倍数关系,其最大公约数是18,最小公倍数是216,那么这两个数分别是多少?6、已知两个三位数的最大公约数是29,最小公倍数是4959,则它们的差是多少?7、在1〜600中,恰好有3个约数的数有几个?&求出两个连续的三位数,使得它们的约数个数之和为9、两个自然数的最大公约数为20 ,其中一个有8个约数,另一个有9个约数,这两个自然数分别为多少?10、素数A、B互不相等,已知A的平方的2倍有4个约数,则B的平方的4倍有多少个约数?答案部分1、1一、解答题1、26、3(3 + 1) X (2 + 1) X (1 + 1 ) X (1 + 1 )= 48 (个).2、【正确答案】:30的倍数至少有三个质因数2、3、5 .对于质因数2的个数可能的情况有 1个、2个、4个. 所以符合条件的数共有 3X2X1 = 6 (个).这两个数独有的因数积为 12 = 2X2X3,而且这两个数不成倍数关系, 因此这两个数分别是:18X3 = 54 , 18X4 = 72 .【正确答案】: 48【答案解析】:2520 = 2X2X2X3X3X5X73个2, 2个3, 【答疑编号10256086【正确答案】 1024【答案解析】 有11个约数的数只能有【正确答案】 【答案解析】 由于约数是成对出现的,之对应.而 1〜8都是840的约数,所以【正确答案】 54、72 .【答案解析】 216-18 = 12 【答疑编号102560871个质因数,因此这个数最小是 210 = 1024 .【答疑编号10256088840有一个三位数的约数,就会有一个不超过 840有8个三位数的约数.【答疑编号8的约数与10256089】【答疑编号10256090】【正确答案】:290所以约数一共有:【答案解析】:30 = 2X3X5的商应为互质的整数.两个三位数分别为261和551 ,这9个数的平方数在1〜600之间,共有9个符合要求.9 = 1 + 8 = 2+ 7 = 3 + 6 = 4+5个约数,另一个数 8个约数•不可能,大于 1的数至少有2个约数.个约数,另一个数 7个约数.一个数2个约数这个数一定是奇数(2不可能),另个数和它连续一定是偶数,这个数只能是26 = 64,不正确.的数.所以符合题意的两个三位数是:625、626 .【答疑编号10256094】【答案解析】:20 = 2X2X5另一个质数有1个,这个数只能是 23X5= 40 ;【答案解析】:由两数的最大公约数为 29可知,这两个三位数均能被 29整除,并且它们除以29它们的差是 551 —261 =290 .【答疑编号10256091【正确答案】 【答案解析】有3个约数的数一定是质数的平方.2, 3, 5 , 7,11 , 13, 17 , 19, 238、【正确答案】: 625、626 【答疑编号10256093依次判断:(3) —个数3个约数,另一个数6个约数. 3个约数一定是质数的平方数,依次判断没有符合要求 注意到最小公倍数 4959 = 29X9X19 , 故上述两互质的商的乘积应为9X19 .再结合两数是三位数的限制,商只能取9 和 19 .【答案解析】: (1) 一个数1 (2) 一个数2 (4) 一个数4个约数,另一个数5个约数. 一个数有 5个约数,这个数一定是质数的 4次方.这个数是54时是625 , 626正好有4个因数, 符合题意.【正确答案】:40、 100有8个因数,这个数分解质因数必然是一个质数有3 个,5如果A 不是2,则A 平方的2倍有3X2 = 6个约数,故 A = 2 .所以B 就不能是2,它平方的4倍有3X3 = 9个约数•本题答案为 9.【答疑编号10256096】有9个因数,这个数分解质因数必然是一个质数有 2个,另一个质数也有2个,这个数是 22X52 = 100 .【答疑编号10256095】10、【正确答案】: 【答案解析】:。
初中数学竞赛精品标准教程及练习02倍数约数

初中数学竞赛精品标准教程及练习02倍数约数倍数与约数是初中数学竞赛中经常会涉及到的重要概念,对于解题非常关键。
下面是一个标准的教程及练习题目,帮助学生更好地掌握倍数与约数的相关知识。
教程一、理解倍数的概念倍数是指一些数能被另一个数整除的数,或者说一个数是另一个数的倍数,可以用“整除”来解释。
例如,6是3的倍数,因为6能被3整除,即6÷3=2二、倍数的判断方法判断一个数是否是另一个数的倍数,可以采用两种方法:1.用除法判断:将被判断的数除以给定的数,如果余数为0,则表示它是给定数的倍数,否则不是。
2.用乘法判断:将给定的数乘以一些倍数,如果得到被判断数,即两数相乘等于被判断数,则表示它是给定数的倍数,否则不是。
三、倍数的性质1.一些数的倍数一定是它的约数,例如,6是6的倍数,同时也是6的约数。
2.一个数的倍数有无穷多个,例如,2的倍数有2,4,6,8,10等等。
3.一个数的正负整数倍同样是它的倍数,例如,3的倍数既有3,又有-3,6,-6,9,-9等等。
四、理解约数的概念约数是指能够整除其中一个数的数,或者说一些数可以被其他数整除。
例如,6的约数有1,2,3,6五、约数的判断方法判断一个数是否是另一个数的约数,可以采用两种方法:1.用余数判断:将被判断的数除以给定的数,如果余数为0,则表示它是给定数的约数,否则不是。
2.用除法判断:将给定的数除以一些约数,如果商等于被判断数,即两数相除等于被判断数,则表示它是给定数的约数,否则不是。
六、约数的性质1.一个数的约数个数是有限的,一个数的约数数目与它的大小有关。
2.一个数的约数中,除了1和它自身以外,其他约数都是成对出现的。
练习题1.判断以下哪些数是18的倍数:36、27、45、54、722.一个数是5的倍数,它至少可以被几个数整除?3.一个数是3的倍数,它的4倍是多少?4.求36的所有约数。
5.判断以下哪些数是45的约数:3、5、9、15、30。
初一数学竞赛教程含例题练习及答案⑷

初一数学竞赛教程含例题练习及答案⑷第 4 讲整数的分拆整数的分拆,就是把一个自然数表示成为若干个自然数的和的形式,每一种表示方法,就是自然数的一个分拆。
整数的分拆是古老而又有趣的问题,其中最著名的是哥德巴赫猜想。
在国内外数学竞赛中,整数分拆的问题常常以各种形式出现,如,存在性问题、计数问题、最优化问题等。
例 1 电视台要播放一部30 集电视连续剧,若要求每天安排播出的集数互不相等,则该电视连续剧最多可以播几天?分析与解:由于希望播出的天数尽可能地多,所以,在每天播出的集数互不相等的条件下,每天播放的集数应尽可能地少。
我们知道,1+2+3+4+5+6+7=28。
如果各天播出的集数分别为1,2,3,4,5,6,7时,那么七天共可播出28集,还剩2集未播出。
由于已有过一天播出2 集的情形,因此,这余下的 2 集不能再单独于一天播出,而只好把它们分到以前的日子,通过改动某一天或某二天播出的集数,来解决这个问题。
例如,各天播出的集数安排为1,2,3,4,5,7,8 或1,2,3,4,5,6,9 都可以。
所以最多可以播7 天。
说明:本题实际上是问,把正整数30 分拆成互不相等的正整数之和时,最多能写成几项之和?也可以问,把一个正整数拆成若干个整数之和时,有多少种分拆的办法?例如:5=1+1+1+1+1=1+1+1+,2=1+2+2 =1+1+3=2+3 =1+4,共有6 种分拆法(不计分成的整数相加的顺序)。
例2 有面值为1 分、2 分、5 分的硬币各4 枚,用它们去支付2 角3 分。
问:有多少种不同的支付方法?分析与解:要付2角3分钱,最多只能使用4枚5分币。
因为全部1分和2 分币都用上时,共值12分,所以最少要用3枚5 分币。
当使用3枚5分币时,5X 3=15, 23-15=8,所以使用2分币最多4枚,最少2枚,可有23=15+(2+2+2+2),23=15+(2+2+2+1+1),23=15+(2+2+1+1+1+1),共3种支付方法。
初一数学竞赛教程含例题练习及答案⑴

初一数学竞赛讲座第1讲数论的方法技巧(上)数论是研究整数性质的一个数学分支,它历史悠久,而且有着强大的生命力。
数论问题叙述简明,“很多数论问题可以从经验中归纳出来,并且仅用三言两语就能向一个行外人解释清楚,但要证明它却远非易事”。
因而有人说:“用以发现天才,在初等数学中再也没有比数论更好的课程了。
任何学生,如能把当今任何一本数论教材中的习题做出,就应当受到鼓励,并劝他将来从事数学方面的工作。
”所以在国内外各级各类的数学竞赛中,数论问题总是占有相当大的比重。
数学竞赛中的数论问题,常常涉及整数的整除性、带余除法、奇数与偶数、质数与合数、约数与倍数、整数的分解与分拆。
主要的结论有:1.带余除法:若a,b是两个整数,b>0,则存在两个整数q,r,使得a=bq+r (0≤r<b),且q,r是唯一的。
特别地,如果r=0,那么a=bq。
这时,a被b整除,记作b|a,也称b是a 的约数,a是b的倍数。
2.若a|c,b|c,且a,b互质,则ab|c。
3.唯一分解定理:每一个大于1的自然数n都可以写成质数的连乘积,即其中p1<p2<…<p k为质数,a1,a2,…,a k为自然数,并且这种表示是唯一的。
(1)式称为n的质因数分解或标准分解。
4.约数个数定理:设n的标准分解式为(1),则它的正约数个数为:d(n)=(a1+1)(a2+1)…(a k+1)。
5.整数集的离散性:n与n+1之间不再有其他整数。
因此,不等式x<y与x≤y-1是等价的。
下面,我们将按解数论题的方法技巧来分类讲解。
一、利用整数的各种表示法对于某些研究整数本身的特性的问题,若能合理地选择整数的表示形式,则常常有助于问题的解决。
这些常用的形式有:1.十进制表示形式:n=a n10n+a n-110n-1+…+a0;2.带余形式:a=bq+r;4.2的乘方与奇数之积式:n=2m t,其中t为奇数。
例1 红、黄、白和蓝色卡片各1张,每张上写有1个数字,小明将这4张卡片如下图放置,使它们构成1个四位数,并计算这个四位数与它的各位数字之和的10倍的差。
(人教版数学)七年级竞赛专题讲解:第三十二讲 最大公约数与最小公倍数

第三十二讲 最大公约数与最小公倍数如图,一个圆圈上有n (n <100=个孔.小明像玩跳棋一样,从A 孔出发,逆时针方向将一枚棋子跳动,每步跨过若干个孔,希望跳一圈后回到A 孔.他先每步跳过2个孔,结果只能跳到B 孔;他又试着每步跳过4个孔,结果还是跳到B ;最后他每步跳过6孔,正好回到A 孔.问这个圆圈上一共有多少个孔?思路点拨 依题意,每步跳过2孔,连起点一共要跳过3个孔,故除掉B 孔外,圆圈上的孔数是3的倍数,有3│n —1;每步跳过4个孔,连起点一步要跳过5个孔,故除掉B 孔外,圆圈上的孔数是5的倍数,因此,有5│n —1;又每步跳过6个孔时,可回到A 孔,这表明7│n .因(3,5)=1,故15│n —1.因n<100,故n 只可能是16,31,46,61,76,91,其中仅有91是7的倍数,故n=91,即圆圈上有91个孔.知识要点:1.(1)设a 1,a 2是两个整数,如果d │a 1,,d │a 2,那么d 就称为a 1和a 2的公约数.一般地,设k a a a 、、、 21是k 个整数.如果d │a 1,…d │a k ,那么d 就称为ka a a 、、、 21的公约数.(2)设a 1,a 2是两个不全为零的整数,那么的公约数中最大的称为a 1和a 2的最大公约数,记作(a 1 ,a 2).一般地,设k a a a 、、、 21是k 个不全为零的整数,那么k a a a 、、、 21的公约数中最大的称为k a a a 、、、 21的最大公约数,记作(a 1,a 2,…,a k ).ka a a 、、、 21的公约数一定是最大公约数的约数.2.设a 1,a 2是两个均不等于零的整数,如果a 1│l ,a 2│l ,则称l 是a 1,a 2的公倍数,a 1,a 2的正的公倍数中最小的称为a 1与a 2的最小公倍数.一般地,设k a a a 、、、 21是k 个均不等于零的整数.如果a 1│l ,…,a k │l ,则称l 是k a a a 、、、 21的公倍数,其中正的公倍数中最小的称为k a a a 、、、 21的最小公倍数,其他公倍数一定是最小的公倍数的倍数.3.若将a ,b 进行质因数分解,并将它们表示成m m p p p a ααα 2121=, m m p p p b βββ 2121=. 其中p 1,p 2,…,P m 为质数,α1,α2,,…αm ,β1,β2,…,βm 为非负整数,且设t i 、t s 分别为αi 、βi (I=1,2,…,m)中的较小者与较大者,则(a ,b)= m tm t t p p p 2121,[a ,b]= m s m s s p p p 2121.4.最大公约数与最小公倍数的重要性质(1) r 如果b │a ,则(a ,b)=b ,[a ,b]=a .(2) 对于任意的正整数m ,有(am ,bm)=m(a ,b), [am ,bm]=m[a ,b].(3) 若a=bg+r (a >b ,0≤r <b =,则有(a ,b)=(b ,r).这一性质表示求(a ,b)可转化为求(b ,r).由于b 和r 相对于a 与b 来说要小,求(b ,r)应较求(a ,b)简便.若b 和r 仍比较大,可重复使用这一性质.这种方法称之为辗转相除法.(4) ( a 1,a 2,a 3)=((a l ,a 2),a 3).(5) ab=(a ,b)×[a ,b].5.若(a 1,a 2)=1,则称a 1与a 2互质.若(a 1,…,a k )=1,则称a 1,…,a k 互质.值得注意的是居个数互质,不一定两两互质,如(6,9,10)=1,而(6,9)=3.6.(1)若(a ,b)=1,则 (a ,a ±b)=1,(a ±b ,b)=1,(a ±b ,ab)=1(2)若(a ,b)=1,a │bc ,则a │c .(3)若(a ,b)=1,a │c ,b │c ,则ab │c ;(4)若(a ,b)=1,则(ac ,b)=(c ,b);(5)若(a ,b)=1,c │a ,则(c ,b)=1.【例1】 (黄冈市初中竞赛题)23个不同的正整数的和是4845,试问:这23个数的最大公约数可能达到的最大的值是多少?写出你的结论,并说明理由.思路点拨 设这23个彼此不同的正整数为a 1,a 2…,a 23,并且它们的最大公约数是d ,则a 1=db 1,a 2=db 2,…,,a 23=db 23,依题意,有4845= a 1+a 2+…+a 23=d(b 1+ b 2+…+ b 23).∵ b 1, b 2,…, b 23也是彼此不等的正整数,∴ b 1+ b 2+…+ b 23≥1+2+…+23=276.因此,4845=d(b 1+ b 2+…+ b 23)≥276d ,∴d ≤9251172764845 . 又因为4845=19×17×15,因此d 的最大值可能是17.当a 1=17,a 2=17×2,a 3=17×3,…,a 22=17×22,a 23=17×32时,得a 1+a 2+…+a 23=17(1+2+…+22)十17×32=4845.注 本题的解题思路是:可设这23个不同的正整数为a 1,a 2…,a 23,且a 1=db 1,a 2=db 2,…,,a 23=db 2,则4845=d(b 1+ b 2+…+ b 23).要使d 最大,则b 1+ b 2+…+ b 23应最小.故可求出d 的取值范围,再根据d │14845,求出d 的值.【例2】(希望杯初一数学竞赛试题)古人用天干和地支记次序,其中天干有10个:甲、乙、丙、丁、戊、己、庚、辛、壬、癸,地支有12个:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.将天干的10个汉字和地支的12个汉字分别循环排列成如下两行: 甲乙丙丁戊己庚辛壬癸甲乙丙丁戊己庚辛壬癸…子丑寅卯辰巳午未申酉戌女子丑寅卯辰巳午未申酉戌亥……从左向右数,第1列是甲子,第2列是乙丑,,第3列是丙寅……则当第2次甲和子在同一列时,该列的序号是( )A .31B .6lC .91D . 121思路点拨 “甲”在第一行出现的位置是l0m+1,m=0,1,2,…,“子”在第二行出现的位置是12n+1,n=0,1,2,….∴ “甲”和“子”在同一列时应有l0m 十1=12n 十l :: , —即l0m=12n当m=n=0时是第一次“甲”“子”同列,第二次“甲”“子”同列时应是使得l0m=12n 成立的最小正整数m和n,即m=6,n=5.∴应是第61号位置.故选B.注:“甲”“于”在同一列时,它们的序号相同,这是解题的关键.【例3】 (北京市竞赛试趣)张华、李亮、王民三位同学分别发出新年贺卡x、y、z张.如果已知x,y,z的最小公倍数为60,x和y的最大公约数为4,y和z的最大公约数为3,那么张华发出的新年贺卡是多少张?思路点拨由题意可知,y不仅是3的倍数,而且是4的倍数,即y是12的倍数.同时y是60的约数,故而可求y.∵ (x,y)=4,(y,z)=3,∴y是3与4的倍数,而3与4互质,故y是12的倍数.又∵ [x,y,z]=60,∴ y=12,60.进而可求出x.∵ [x,y,z] =60=3×4×5.当y=12时,x、z中至少有一个含有因数5.若x中有因数5,又x中有因数4,且4与5互质,∴x中有因数20.而[x,y,z]=60,(x,y)=4,故x==20.当x中没有因数5,∵x中有因数4,且x是60的约数,∴x=4,或x=12,而(x,y)=4,故x=4.当y=60时,(x,y)=4,而x中没有因数5,且[x,y,z] =60=3×4×5,故x=4.因此,张华发出的贺年卡为4张或20张.注 (1)本题的切入点是最大公约数和最小公倍数;(2)注意答案的两种可能性.【例4】在一间屋子里有100盏电灯排成一横行,依从左到右的顺序编上号码1,2,3,…,100.每盏电灯上有一根拉线开关,最初所有电灯全是关的,现有100个学生在门外排着队,第一个学生走进屋来,把编号是1的倍数的电灯的开关拉一下;接着第二个学生走进屋来,把凡是编号是2的倍数的电灯开关拉了一下;…;最后第100个学生走进屋来,把编号是100的倍数的电灯的开关拉了一下,这样做过以后,问哪些电灯是亮的?思路点拨由于最初所有电灯是关着的,所以只有那些拉了奇数次开关的电灯才是亮的,而每一盏电灯的拉线开关被拉了多少次取决于这盏灯的编号的数字有多少个不同的正约数,最后亮着的灯的编号只有为完全平方数.所以,只有编号为1,4,9,16,25,36,49,64,81,100的电灯最后是亮着的.注:本题的一个重要条件是最初时灯都是关着的.然后对每个编号分解质因数.【例5】两个正整数的和是60,它们的最小公倍数是273,则它们的乘积是( )A.273 B.819 C.1911 R3549思路点拨设两个正整数为a与b,则a+b=60=22×3 ×5,[a,b]=273=3×7×13.显然,a,b的最大公约数是1或3.如果(a,b)=1,则[a,b]=a×b.a、b只能取21、13,7、39,1、273,3、91,其和均不为60.因此,(a,b)=3,于是a=3 ×7,b=3 ×13,∴ a×b=(3×7)×(3X×3)=819.故选B.注:本题的精妙之处在于由a+b和[a,b]的两个质因式的分解,确定出a和b的最大公为数是1或3.【例6】用整元的人民币购物,若用多于7元的任意元钱去买单价为3元和5元的两种雪糕,一定可以把钱花完,请证明这一结论.思路点拨 用任意元钱n (n >7)去买单价为3元的雪糕,只能余l 元或2元.若余2元时,少买一根3元雪糕,余数就为2+3=5元,恰能买一块5元的雪糕.若余1元时,少买3根3元的雪糕,余数为1+3×3=10元,恰能买2根5元雪糕.若n 能被3整除,就用所有钱去买3元的雪糕,恰合题意.注:由3的同余数入手分类,结合拼凑法使问题得到证明.【例7】已知两数和是60,它们的最大公约数与最小公倍数之和是84,求此二数.思路点拨 设所求二数为x ,y ,且(x ,y)=d ,令x=ad ,y=bd ,则(a ,b)=1.根据题意有⎪⎩⎪⎨⎧=+=+d ab d b a 84160,由于(60,84)=12,所以d=l ,2,3,4,6,12. 而当d :1,2,3,4,6时,方程组无解.当d=12时,方程组变为⎩⎨⎧==+65ab b a ,解之得⎩⎨⎧==32b a 或⎩⎨⎧==23b a 佐::.,故所求的两数为x=24,y=36.【例8】 ( “五羊杯’’竞赛题)设a 与b 是正整数,且a+b=33,最小公倍数[a ,b]=90,则最大公约数(a ,b)=( )A .1B .3C .11D .9思路点拨 令(a ,b)=x ,则x 是a ,b ,a+b 及[a ,b]的公约数,故x 是33和90的公约数,知x=1或x=3.当x=1时,a 与b 互质,而a+b=33,当a 不能被3整除,则b 不能被3整除,而[a ,b]=90,说明a 、b 至少有一个能被3整除.当b 能被3整除,由a+b=33,则b 也能被3整除,故(a ,b)≠1,即x ≠1.当x=3时,即有(a ,b)=3,∴ab=[a ,b],(a ,b)=3×90=32×5×6,而a+b=33,∴a=15,b=18,(a ,b)=3. 故选B .学力训练(A 级)1.( “希望杯”培训题)2001的正约数的个数是( )A .3B .4C .6D .82.( ‘希望杯”竞赛题)下面的四句话中正确的是( )A .正整数a 和b 的最大公约数大于等于aB .正整数a 和b 的最小公倍数大于等于abC 正整数a 和b 的最大公约数小于等于aD .正整数a 和b 的公倍数大于等于ab3.360×473和172×361这两个积的最大公约数是( )A .43B .86C .172D .44.(北京市竞赛题)a ,b 是彼此不相等的非零数字,则ababab 与4017的最大公约数 是 .5.(上海市竞赛题)写出一组4个连续自然数,使它们从小到大顺次是5的倍数、7的倍数、9的倍数、11的倍数,这组自然数依次为.6.甲、乙、丙三人到李老师那里求学,甲每6天去一次,乙每8天去一次,丙每9天去一次,如果8月17日他们三人在李老师处见面,那么下一次在李老师处见面的时间是几月几日呢?(B级)1所有形如abcabc的六位数(a,b,c分别是0~9这十个数之一,可以相同,但a≠0)的最大公约数是( )A.1001 B.101 C. 13 D.112用长为45cm,宽为30cm的一批砖,铺成一块正方形,至少需要( )块.A.6 B.8 C.12 D.163.祖孙两人的年龄都是合数,明年他们的岁数相乘是1610,那么祖孙两人今年的年龄分别是( )A.70岁、23岁 B.69岁、22岁 C.115岁、14岁 D.114岁、13岁4在正整数1,2,3,…,100中,能被2整除但不能被3整除的数的个数是( )A.33 B.34 C.35 D.375(2000年“希望杯”竞赛题)设m和n为大于0的整数,且3m+2n=225.(1)如果m和n的最大公约数为15,则m+n= ;(2)如果m和n的最小公倍数为45,则m+n= .6.个正整数之和为667,其最小公倍数是它们扣最大公约数的120倍,那么满足条件的正整数有组.7.a,b]表示两个正整数a和b的最小公倍数,例如[14,35]=70,则满足[x,y]=-6,[y,z]=15的正整数组(x,y,z)共有组.8.甲地到乙地原来每隔45m要安装一根电线杆,加上两端的两根一共有53根电线杆.现在改成每隔60m安装一根电线杆,除两端两根不需移动外,中途还有多少根不必移动?参考答案。
(含答案)2020-2021学年初中数学竞赛精品讲座及试题02:倍数、约数

A=BQ+R,当A,B,Q,R都是整数且B 0时,A-R能被B整除 例如23=3×7+2 则23-2能被3整除。 二、例题
例1写出下列各正整数的正约数,并统计其个数,从中总结出规律加以 应用:2,22,23,24,3,32,33,34,2×3,22×3,22×32 。 解:列表如下
正 正约数 个 正 正约数
∴最大公约数是2×3, 记作(24,90)=6 最小公倍数是23×32×5=360, 记作[24,90]=360 例3己知32,44除以正整数N有相同的余数2,求N 解:∵32-2,44-2都能被N整除,∴N是30,42的公约数 ∵(30,42)=6,而6的正约数有1,2,3,6 经检验1和2不合题意,∴N=6,3 例4一个数被10余9,被9除余8,被8除余7,求适合条件的最小正整数 分析:依题意如果所求的数加上1,则能同时被10,9,8整除,所以所求的数是10,9,8的 最小公倍数减去1。 解: ∵[10,9,8]=360, ∴所以所求的数是359 三、练习2 1, 12的正约数有_________,16的所有约数是_________________ 2, 分解质因数300=_________,300的正约数的个数是_________ 3, 用分解质因数的方法求20和250的最大公约数与最小公倍数。 4, 一个三位数能被7,9,11整除,这个三位数是_________ 5, 能同时被3,5,11整除的最小四位数是_______最大三位数是________ 6, 己知14和23各除以正整数A有相同的余数2,则A=________ 7, 写出能被2整除,且有约数5,又是3的倍数的所有两位数。答____ 8, 一个长方形的房间长1.35丈,宽1.05丈要用同一规格的正方形瓷砖铺满,问正方形最 大边长可以是几寸?若用整数寸作国边长,有哪几种规格的正方形瓷砖适合? 9, 一条长阶梯,如果每步跨2阶,那么最后剩1阶,如果每步跨3阶,那么最后剩2阶,如 果每步跨4阶,那么最后剩3阶,如果每步跨5阶,那么最后剩4阶,如果每步跨6阶, 那么最后剩5阶,只有每步跨7阶,才能正好走完不剩一阶,这阶梯最少有几阶?
七年级数学上册综合算式专项练习题倍数与约数运算

七年级数学上册综合算式专项练习题倍数与约数运算数学是一门重要的学科,也是我们在学习中最常接触的一门科目。
在七年级上册数学课程中,倍数与约数运算是我们需要掌握和理解的重要概念。
本文将为大家介绍七年级数学上册综合算式专项练习题的倍数与约数运算,希望能够帮助同学们更好地理解和掌握相关知识。
1. 倍数运算倍数是指一个数可以被另一个数整除,即后者是前者的倍数。
在进行倍数运算时,我们需要注意以下几点:(1)对于一个数a,如果b是a的倍数,则任意一个正整数k也是a的倍数。
即ka也是a的倍数。
(2)对于一个数a,所有大于a的数都是a的倍数。
因此,我们通常可以用整除法来判断一个数是否为另一个数的倍数。
如果一个数能够整除另一个数,那么它就是后者的倍数。
举例来说,如果我们要判断15是否是3的倍数,我们可以用整除法进行计算:15÷3=5,得到商为5,没有余数。
因此,15是3的倍数。
2. 约数运算约数是指可以整除一个数的所有数。
在进行约数运算时,我们需要注意以下几点:(1)一个数的所有约数包括1和它本身。
(2)一个数的最小正约数是1,最大约数是它本身。
(3)在进行约数运算时,我们通常可以使用质因数分解的方法。
将一个数分解为质数的乘积,然后再找出所有可能的组合,即可得到所有的约数。
举例来说,如果我们要找出12的所有约数,首先可以将12分解为质数的乘积:12=2×2×3。
然后,我们可以找出所有可能的组合:1,2,3,4,6,12。
因此,12的约数有1,2,3,4,6,12。
综合算式练习题:下面是一些综合算式练习题,包括了倍数与约数运算的考察。
通过解答这些题目,可以帮助同学们更好地掌握和运用倍数与约数的相关知识。
1.判断下列哪些数是12的倍数:(1)20(2)24(3)35(4)482.判断下列哪些数是6的约数:(1)6(2)8(4)123.求下列各数的所有约数:(1)16(2)18(3)20(4)24解答:1. (2)24和(4)48是12的倍数,因为它们可以整除12。
2020-2021学年数学初一培优和竞赛讲练-2-倍数 约数

为一眼而愁肠百转 为一见而不远千里
4
晨起凭栏眺 但见云卷云舒
风月乍起 春寒已淡忘 如今秋凉甚好 几度眼迷离
感谢喧嚣 把你高高卷起 砸向这一处静逸 惊翻了我的万卷 和其中的一字一句 幸遇只因这一次
被你拥抱过,览了 被你默诵过,懂了 被你翻开又合起 被你动了奶酪和心思
【分类解析】
例1写出下列各正整数的正约数,并统计其个数,从中总结出规律加以
应用:2,22,23,24,3,32,33,34,2×3,22×3,22×32 。
解:列表如下
正
个
整 正约数 数
数
计
1,2
2
2
1,2,4
22
3
正 整 正约数 数
1,3 3
1,3,32 32
个正 数整 计数
2 2×3
3 22×3
跨4阶,那么最后剩3阶,如果每步跨5阶,那么最后剩4阶,如果每步跨6阶,那么最后剩5 阶,只有每步跨7阶,才能正好走完不剩一阶,这阶梯最少有几阶?
答案
1. 1,2,3,4,6,12; ±1,±2,±3,±6,±9,±18 2. 22×3×52; 18 3. 2×5; 22×53 4. 693 5. [3,5,11]=165,1155;990 6. A=3 即求14-2与23-2的公约数 7. 30,60,90 8. (135,105)=15,正约数有1,3,5,15 9. 119。∵[2,3,4,5,6]=60,60×2-1=119
5通常我们在正整数集合里研究公倍数和公约数,几正整数有最小的公倍数和最犬的公约数。
6公约数只有1的两个正整数叫做互质数(例如15与28互质)。
7在有余数的除法中,
倍数表达法及练习题答案

倍数表达法及练习题答案
标题:以倍数表达法及练习题答案
倍数表达法是一种数学概念,它可以帮助我们更好地理解和解决数学问题。
在
倍数表达法中,我们使用倍数来描述一个数与另一个数之间的关系,这有助于
我们更直观地理解数学概念。
举个例子,如果我们要找出数字10的倍数,我们可以用倍数表达法来表示为10、20、30、40等等。
这样一来,我们就可以清晰地看到这些数字都是10的
倍数,它们与10之间的关系是倍数关系。
倍数表达法在解决数学问题时也非常有用。
例如,如果我们要找出一个数的所
有因数,我们可以利用倍数表达法来找出这个数的所有倍数,然后再找出它们
的公共因数。
这样一来,我们就可以更快地找到这个数的所有因数。
除此之外,倍数表达法还可以帮助我们更好地理解乘法和除法。
当我们用倍数
表达法来表示一个数的倍数时,我们可以更直观地看到乘法和除法之间的关系,这有助于我们更好地掌握这两种运算。
练习题答案:
1. 找出数字12的所有倍数。
答案:12、24、36、48、60等等。
2. 找出数字15的所有因数。
答案:1、3、5、15。
3. 用倍数表达法表示数字8的倍数。
答案:8、16、24、32、40等等。
4. 用倍数表达法表示数字7的倍数。
答案:7、14、21、28、35等等。
通过以上练习题答案,我们可以更好地理解和掌握倍数表达法,这将有助于我们更好地解决数学问题和提高数学能力。
倍数表达法不仅可以帮助我们更好地理解数学概念,还可以帮助我们更快地解决数学问题,让我们更加喜欢数学学习。
约数与倍数例题

约数与倍数例题1题一个数有8个约数.这个数最小是.正确答案:24详解:24有8个约数:1,2,3,4,6,8,12,24.比24小的数都没有8个约数(12,18,20各有6个约数,其余的数约数个数少于6).例题2题边长1米的正方体2100个,堆成一个实心的长方体.它的高是10米,长、宽都大于高.则长方体长与宽的和是米.正确答案:29提示:由于长方体是用2100个边长为1米的正方体堆成的,就是说,这个长方体的体积应是2100立方米,但长方体的体积=长×宽×高,现在知道高=10米,故长×宽=210米,又,长、宽都大于高,所以本题就是找出210的两个都大于10的约数,使它们的积为210.详解:2100÷10=210, 210=2×3×5×7=(2×7)×(3×5)=14×15.由于14与15都是210的大于10的约数,且其积=210,又只有这一组数据满足题目的要求.∴长方体的长与宽分别为15与14,其和为29.例题3题数360的约数有个.这些约数的和是.正确答案:24;1170详解:360分解质因数:;360的约数可以且只能是,(其中a,b,c均是整数,且a为0~3,b为0~2,c为0~1).因为a、b、c的取值是相互独立的,由计数问题的乘法原理知,约数的个数为(3+1)×(2+1)×(1+1)=24.我们先只改动关于质因数3的约数,可以是1,3,,它们的和为,所以所有360约数的和为;我们再来确定关于质因数2的约数,可以是它们的和为,所以所有360约数的和为;最后确定关于质因数5的约数,可以是1,5,它们的和为(1+5),所以所有360的约数的和为.于是,我们计算出值:13×15×6=1170.所以,360所有约数的和为1170.评注:我们在本题中分析了约数个数、约数和的求法.下面我们给出一般结论:Ⅰ.一个合数的约数的个数是在严格分解质因数之后,将每个质因数的指数(次数)加1后所得的乘积.如:1400严格分解质因数后为,所以它的约数有(3+1)×(2+1)×(1+1)=4×3×2=24个.(包括1和它自身)Ⅱ.约数的和是在严格分解质因数后,将M的每个质因数最高次幂的所有约数的和相乘所得到的积.如:,所以21000所有约数的和为.例题4题从360到630的自然数中有奇数个约数的数有个.正确答案:7详解:一个合数的约数的个数是在严格分解质因数之后,将每个质因数的指数(次数)加1后所得的乘积.如:1400严格分解质因数后为,所以它的约数有(3+1)×(2+1)×(1+1)=4×3×2=24个.(包括1和它自身)如果某个自然数有奇数个约数,那么这个数的所有质因子的个数均为偶数个,这样它们加1后均是奇数,所得的乘积才能是奇数.而所有质因数的个数均是偶数个的数为完全平方数.即完全平方数(除0外)有奇数个约数,反过来,有奇数个约数的数一定是完全平方数.由以上分析知,我们所求的为360~630之间有多少个完全平方数.18×18=324,19×19=361,25×25=625,26×26=676,所以在360~630之间的完全平方数为即360到630的自然数中有奇数个约数的数为361,400,441,484,529,576,625,共7个.例题5题1112111的约数共有个.正确答案:24详解:一般的,一个自然数N可能惟一地表示成一些质因数的乘积:其中是不相同的质数,,那么N的约数的个数公式:∴1112111的约数的个数是:(1+1)×(2+1)×(1+1)×(1+1)=24∴1112111有24个约数例题6题在正好有60个约数的自然数中,1万以内最大的数是.正确答案:9360详解:因为,所以所求数分解质因数后,任何质因数的幂小于14.将60分解为约数小于14的乘积,60=5×12=6×10=2×3×10=2×5×6=3×4×5=2×2×3×5.根据自然数的约数个数的公式,恰有60个约数的小于10000的合数应具有下列形式之一:其中a、b、c、d均为质数.因为都大于10000,所以所求数只能是的形式,所求数是9360 .例题7题有甲、乙、丙3人,甲每分钟行走120米,乙每分钟行走100米,丙每分钟行走70米.如果3个人同时同向,从同地出发,沿周长是300米的圆形跑道行走,那么分钟之后,3人又可以相聚。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
倍数约数
【知识精读】
1两个整数A和B(B≠0),如果B能整除A(记作B|A),那么A叫做B的倍数,B 叫做A的约数。
例如3|15,15是3的倍数,3是15的约数。
2因为0除以非0的任何数都得0,所以0被非0整数整除。
0是任何非0整数的倍数,非0整数都是0的约数。
如0是7的倍数,7是0的约数。
3整数A(A≠0)的倍数有无数多个,并且以互为相反数成对出现,0,±A,±2A,……都是A的倍数,例如5的倍数有±5,±10,……。
4整数A(A≠0)的约数是有限个的,并且也是以互为相反数成对出现的,其中必包括±1和±A。
例如6的约数是±1,±2,±3,±6。
5通常我们在正整数集合里研究公倍数和公约数,几正整数有最小的公倍数和最犬的公约数。
6公约数只有1的两个正整数叫做互质数(例如15与28互质)。
7在有余数的除法中,
被除数=除数×商数+余数若用字母表示可记作:
A=BQ+R,当A,B,Q,R都是整数且B≠0时,A-R能被B整除
例如23=3×7+2则23-2能被3整除。
【分类解析】
例1写出下列各正整数的正约数,并统计其个数,从中总结出规律加以
应用:2,22,23,24,3,32,33,34,2×3,22×3,22×32。
解:列表如下
其规律是:设A=a m b n(a,b是质数,m,n是正整数)
那么合数A的正约数的个是(m+1)(n+1)
例如求360的正约数的个数
解:分解质因数:360=23×32×5,
360的正约数的个数是(3+1)×(2+1)×(1+1)=24(个)
例2用分解质因数的方法求24,90最大公约数和最小公倍数
解:∵24=23×3,90=2×32×5
∴最大公约数是2×3,记作(24,90)=6
最小公倍数是23×32×5=360,记作[24,90]=360
例3己知32,44除以正整数N有相同的余数2,求N
解:∵32-2,44-2都能被N整除,∴N是30,42的公约数
∵(30,42)=6,而6的正约数有1,2,3,6
经检验1和2不合题意,∴N=6,3
例4一个数被10余9,被9除余8,被8除余7,求适合条件的最小正整数
分析:依题意如果所求的数加上1,则能同时被10,9,8整除,所以所求的数是10,9,8的最小公倍数减去1。
解:∵[10,9,8]=360,
∴所以所求的数是359
【实战模拟】
1,12的正约数有_________,16的所有约数是_________________
2,分解质因数300=_________,300的正约数的个数是_________
3,用分解质因数的方法求20和250的最大公约数与最小公倍数。
4,一个三位数能被7,9,11整除,这个三位数是_________
5,能同时被3,5,11整除的最小四位数是_______最大三位数是________
6,己知14和23各除以正整数A有相同的余数2,则A=________
7,写出能被2整除,且有约数5,又是3的倍数的所有两位数。
答____
8,一个长方形的房间长1.35丈,宽1.05丈要用同一规格的正方形瓷砖铺满,问正方形最大边长可以是几寸?若用整数寸作国边长,有哪几种规格的正方形瓷砖适合?
9,一条长阶梯,如果每步跨2阶,那么最后剩1阶,如果每步跨3阶,那么最后剩2阶,如果每步跨4阶,那么最后剩3阶,如果每步跨5阶,那么最后剩4阶,如果每步跨6阶,那么最后剩5阶,只有每步跨7阶,才能正好走完不剩一阶,这阶梯最少有几阶?
答案
1. 1,2,3,4,6,12;±1,±2,±3,±6,±9,±18
2. 22×3×52;18
3. 2×5;22×53
4. 693
5. [3,5,11]=165,1155;990
6. A=3 即求14-2与23-2的公约数
7. 30,60,90
8.(135,105)=15,正约数有1,3,5,15
9.119。
∵[2,3,4,5,6]=60,60×2-1=119。
