《高职数学I》试题库
高职《数学(一)》期末考试试卷及答案

《数学(一)》考试试卷(A )一、填空题(2'×10=20')1、=348 .2、)12(log )(3-=x x f 的定义域为 .3、设⎩⎨⎧-≥--<-=2222)(22x x x x x f ,则=)1(f . 4、用不等号连接下列两数大小(1)4.31.2 5.31.2 (2)4.18.0 4.16.0 5、︒390sin = )30cos(︒-= . 6、函数34+=x y 的反函数为 . 7、若31)180sin(=+︒α,则=αsin . 8、设x y 2sin =,则此函数的最小正周期T= .二、选择题(3'×10=30')1、设}5,3,1{=A ,}5,4,2{=B ,则B A =( )A 、}5,4,3,2,1{B 、}4,2{C 、}3,1{D 、}5{ 2、224)(-b a =( )A 、48-b aB 、44-b aC 、28-b aD 、12-b a 3、=⋅4log 3log 32( )A 、1B 、2C 、3D 、4 4、5|2|<-x 的解集为( )A 、}73|{<<-x xB 、}73|{>-<x x x 或C 、}3|{-<x xD 、}7|{<x x 5、下列函数为偶函数的是( )A 、x y sin =B 、x y tan =C 、x y cos =D 、x y = 6、下列各式中错误的是( )A 、ααπsin )sin(=-B 、ααπcos )cos(=-C 、ααπtan )tan(-=-D 、ααπcot )cot(-=-7、下列函数中在),0(+∞内为单调减的是( )A 、x y 2log =B 、2x y =C 、x y 2=D 、x y )31(=8、设0sin <α且0cot >α,则α为第 象限角 ( ) A 、ⅠB 、ⅡC 、ⅢD 、Ⅳ 9、若a x -=4sin 2,则a 的取值范围为( ) A 、2≤a ≤6B 、a ≤6C 、a ≥2D 、2<a<6 10、设角α的终边过点)3,4(-P ,则=αtan( )A 、53B 、54-C 、43-D 、34-三、解答题(6'×6=36')1、解不等式0652>+-x x .2、51lg 5lg 32lg 4-+.3、判断1)(2+=x x f 在),0(+∞内的单调性.4、解方程813||1=+x5、︒︒300tan 120sin 26、化简:αααcot cos cos 12⋅-四、应用题(14')设x=,求:(+1xf sin)(1)用“五点法”作出)(x2,0[π上的图像.f在](2)根据图像写出)2,0[π上的最大值和最小值.(xf在]《数学(一)》考试试卷(A )参考答案一、填空1、16;2、}21|{>x x ; 3、1; 4、<,>;5、21,23;6、)3(41-=x y ;7、31-; 8、π二、选择1、D2、A3、B4、A5、C6、B7、D8、C9、A 10、C 三、解答1、x<2或x>32、43、单调增4、3±=x5、3-6、αsin四、应用1、如图2、2max =y 0min =y《数学(一)》考试试卷(B )2'×10=20')1、=-234 .2、)1ln()(-=x x f 的定义域为 .3、设⎩⎨⎧-≥--<-=2222)(22x x x x x f ,则=-)3(f . 4、用不等号连接下列两数大小(1)5.31.2 4.31.2 (2)5log 2 6log 2 5、︒390sin = ︒60cos = . 6、函数23+=x y 的反函数为 . 7、设31)180cos(=+︒α,则=αcos . 8、设x y 2cos =,则其最小正周期T=.3'×10=30')1、设}5,3,1{=A ,}5,4,2{=B ,则B A =( ) A 、}5,4,3,2,1{ B 、}4,2{ C 、}3,1{ D 、}5{ 2、223)(--b a =( )A 、46b aB 、46b a -C 、46--b aD 、43b a3、=⋅4log 3log 32 ( )A 、1B 、2C 、3D 、4 4、5|2|>-x 的解集为( )A 、}73|{<<-x xB 、}7|{>x xC 、}73|{>-<x x x 或D 、}3|{-<x x 5、下列函数为奇函数的是( )A 、2x y =B 、x y cos =C 、1+=x yD 、x y sin = 6、下列各式中错误的是( )A 、ααπsin )sin(=-B 、ααπcos )cos(-=-C 、ααπtan )tan(=-D 、ααπcot )cot(-=-7、设0sin <α且0cot >α,则α为第 象限角( )A 、ⅠB 、ⅡC 、ⅢD 、Ⅳ 8、设2tan =α,则=-+ααααcos sin cos sin 2( )A 、2B 、3C 、4D 、5 9、若a x -=4cos 2,则a 的取值范围为( ) A 、2≤a ≤6B 、a ≤6C 、a ≥2D 、2<a<6 10、设角α的终边过点)3,4(-P ,则=αsin( )A 、54B 、53-C 、43D 、34-6'×6=36')1、解不等式0652<+-x x .2、51lg 5lg 32lg 4-+.3、判断1)(2-=x x f 在),0(+∞内的单调性.4、解方程273||1=+x5、︒︒225tan 120cos 26、化简:αααcot cos cos 12⋅-14')设x(+)=,求:1xf sin(1)用“五点法”作出)2,0[π上的图像.f在](x(2)根据图像写出)2,0[π上的最大值和最小值.(xf在]《数学(一)》考试试卷(B )参考答案一、填空1、81; 2、}1|{>x x ; 3、7; 4、>,<;5、21,21;6、)2(31-=x y ;7、31-; 8、π二、选择1、A2、B3、B4、C5、D6、C7、C8、D9、A 10、B 三、解答1、2<x<32、43、单调增4、2±=x5、1-6、αsin四、应用1、如图2、2max =y 0min =y。
高职单独招生考试数学试卷(答案解析) (1)

2022年对口单独招生统一考试数学试卷(满分120分,考试时间120分钟)一、选择题:(本题共20小题,每小题3分,共60分)1.将抛物线24y x =-绕顶点按逆时针方向旋转角π,所得抛物线方程为( ) A. 24y x = B. 24y x =- C. 24x y = D. 24x y =-2.在空间中,下列结论正确的是( ) A.空间三点确定一个平面B.过直线外一点有且仅有一条直线与已知直线垂直C.如果一条直线与平面内的一条直线平行,那么这条直线与此平面平行D.三个平面最多可将空间分成八块3.将抛物线24y x =-绕顶点按逆时针方向旋转角π,所得抛物线方程为( ) A. 24y x = B. 24y x =- C. 24x y = D. 24x y =-6.cos78cos18sin18sin102⋅+⋅=( )A.C.12-D.127.在复平面内,复数z 满足(1)2i z -⋅=,则(z = ) A .2i +B .2i -C .1i -D .1i +6.掷两枚骰子(六面分别标有1至6的点数)一次,掷出点数和小于5的概率为( ) A.16B. 0.25C.19D.5187.已知圆锥底面半径为4,侧面面积为60,则母线长为( ) A. 8B. 16C.152D. 158.函数y = sin2x 的图像如何平移得到函数sin(2)3y x的图像( )A. 向左平移6个单位B. 向右平移6个单位C. 向左平移3个单位D. 向右平移3个单位9.设动点M 到1(13 0)F ,的距离减去它到2(13 0)F ,的距离等于4,则动点M 的轨迹方程为( ) A. 22 1 (2)49x y x ≤ B. 22 1 (2)49x y x ≥ C.22 1 (2)49y x y ≥D.22 1 (x 3)94x y ≥10.已知函数()3sin 3cos f x xx ,则()12f ( ) A.6B.23C.22D.2611.某商场准备了5份不同礼品全部放入4个不同彩蛋中,每个彩蛋至少有一份礼品的放法有( ) A. 280种B. 240种C. 360种D. 144种12.如下图20图在正方体ABCD ‐A ′B ′C ′D ′中,下列结论错误的是( ) A. A ′C ⊥平面DBC ′ B. 平面AB ′D ′//平面BDC ′ C. BC ′⊥AB ′D. 平面AB ′D ′⊥平面A ′AC13. 已知集合A={-1,0,1},集合B={-3,-1,1,3},则A ∩B=( ) A. {-1,1}B. {-1}C. {1,3}D. ∅14. 不等式x2-4x ≤0的解集为( ) A. [0,4]B. (1,4)C. [-4,0)∪(0,4]D. (-∞,0]∪[4,+∞)15. 函数f (x )=ln(x −2)+1x−3的定义域为( )A. (5,+∞)B. [5,+∞)C. (-∞,2]∪[3,+∞)D. (2,3)∪(3,+∞)16. 已知平行四边形ABCD ,则向量AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ =( ) A. BD⃗⃗⃗⃗⃗B. DB⃗⃗⃗⃗⃗C. AC⃗⃗⃗⃗⃗D. CA⃗⃗⃗⃗⃗ 17. 下列函数以π为周期的是( ) A.y =sin (x −π8)B. y =2cos xC. y =sin xD. y =sin 2x18. 本学期学校共开设了20门不同的选修课,学生从中任选2门,则不同选法的总数是( ) A. 180B. 380C. 190D. 12019. 已知直线的倾斜角为60°,则此直线的斜率为( ) A. −√33B.2 C . √3 D.√3320. 若sin α>0且tan α<0,则角α终边所在象限是( ) A. 第一象限B. 第二象限C. 第三象限D.第四象限二、填空题(共10小题,每小题3分;共计30分) 1、执行以下语句后,打印纸上打印出的结果应是:_____.2、角α的顶点在坐标原点,始边与x 轴的非负半轴重合,终边经过点P (1,2),则sin (π﹣α)的值是_____.3、过点)1,2(-p 且与直线0102=+-y x 平行的直线方程是______4、在∆ABC 中,已知∠B=︒30,∠C=︒135,AB=4,则AC=______5、已知函数bx y +-=sin 31的最大值是97,则b=______6、75sin 15sin +的值是______.7、如果∆ABC 的三个内角A ,B ,C 成等差数列,则B 一定等于______. 8、已知2tan -=α,71tan =+)(βα,则βtan 的值为______ .9、三个数2,x ,10成等差数列,则=x ______10、已知b kx x f +=)(,且1)1(=-f ,3)2(=-f ,则=k ______,=b ______ 三、大题:(满分30分) 1、已知函数3()x x b f x x ++=,{}n a 是等差数列,且2(1)a f =,3(2)a f =,4(3)a f =.(1)求{}n a 的前n 项和; (2)求()f x 的极值.2、某学校组织"一带一路”知识竞赛,有A ,B 两类问题・每位参加比赛的同学先在两类问题中选择类并从中随机抽収一个问题冋答,若回答错误则该同学比赛结束;若 回答正确则从另一类问题中再随机抽取一个问題回答,无论回答正确与否,该同学比赛 结束.A 类问题中的每个问题回答正确得20分,否则得0分:B 类问题中的每个问题 回答正确得80分,否则得0分。
2024年高职高考数学试卷

2024年高职高考数学试卷
2024年高职高考数学试卷指的是2024年高职(又称“高职单考”)高考科目的数学试卷。
这种考试主要针对那些打算进入高等职业教育(即高职)的学生,通常在每年的4月份举行。
数学是其中的一门必考科目,测试考生对基础数学知识的掌握和应用能力。
以下是2024年高职高考数学试卷题目:
1. 已知集合A = {x | x² - 3x + 2 = 0},则下列表示正确的是 ( )
A. 0 ∈ A
B. 0 A
C. {0} A
D. A ∈ {0}
2. 函数 y = x + √(x² + 2) 的值域为 ( )
A. [0, +∞)
B. (-∞, -1]
C. [-1,1]
D. [-√2, √2]
3. 下列函数中,周期为π/2 的是 ()
A. y = sin(2x)
B. y = cos(4x)
C. y = tan(x/2)
D. y = sin(4x)
4. 若函数 f(x) = a + log₃x 的定义域和值域都是 [1,3],则实数 a 的值为 _______.
5. 若直线 y = x + b 与曲线 y = √(x) 有且只有一个公共点,则 b 的取值范围是()
A. b ≥ 0
B. b ≥ 1
C. b ≤ 1
D. b ≤ -1。
高职一年级数学期末考试卷

高职一年级数学期末考试卷一、选择题1. 已知直角三角形的斜边长为10,一个锐角的正弦值为0.6,则这个锐角的余切值为()。
A. 0.8B. 1.2C. 1.5D. 2.4答:B. 1.22. 若a是一个正整数,且x+3是一个整数,那么关于x的不等式x + a > 3的解集是()。
A. {x|x>a-3}B. {x|x>3-a}C. {x|x<-a+3}D. {x|x>-a+3}答:D. {x|x>-a+3}3. 若函数y=f(x)关于x的导数f'(x)=3x^2-2x+1,那么f(x)在x=0处的导数为()。
A. 1B. -1C. 2D. 0答:14. 已知a是一个正整数,且x>a+2,则点A(a,2a)在直线y=x+2上的位置在A的下方。
A. 正确B. 错误答:A. 正确二、填空题5. 一个等差数列的前6项分别是-2,1,4,7,10,13,那么这个等差数列的公差为()。
答:36. 若正整数a,b,c满足a^2+b^2=c^2,且a>b>0,则a,b,c可能为()。
答:5, 4, 57. 若函数y=f(x)的一阶导数f'(x)=3x^2-6x+2,那么f(x)的原函数为()。
答:x^3-3x^2+2x+C三、简答题8. 简述直线和平面的交点数量的可能情况。
答:直线与平面相交可能有无穷多个交点、一个交点或者没有交点,取决于直线与平面的相对位置。
9. 简要描述什么是二次函数,以及二次函数的图像特点。
答:二次函数是一个关于未知数的二次方程式,一般表示为y=ax^2+bx+c,其图像为开口朝上或朝下的抛物线。
10. 请列举任意一种直接法解决一元一次方程式。
答:列方程,移项,整理求解。
四、计算题11. 求解下列一元一次方程组:2x + y = 73x - 4y = 2答:x = 3y = 112. 计算下列不等式的解集:2x - 3 > 5x + 4答:x < -7五、综合题13. 请计算下列函数的导数:y = x^3 - 3x^2答:y' = 3x^2 - 6x14. 如果一条直线的斜率为2,并且过点(3, 5),求这条直线的方程。
职高数学统招试题及答案

职高数学统招试题及答案一、选择题(每题4分,共40分)1. 下列哪个数是整数?A. 3.14B. -2C. 0.5D. π2. 函数f(x) = 2x^2 - 3x + 1的顶点坐标是:A. (0,1)B. (3/4, -1/8)C. (1, -1)D. (-1, 2)3. 已知集合A = {1, 2, 3},B = {2, 3, 4},求A∩B的结果是:A. {1}B. {2, 3}C. {4}D. {2, 3, 4}4. 一个圆的半径是5,那么它的周长是:A. 10πB. 20πC. 25πD. 30π5. 已知sinθ = 3/5,且θ为锐角,求cosθ的值:A. 4/5C. 3/5D. -3/56. 一个等差数列的首项是2,公差是3,那么它的第5项是:A. 17B. 14C. 11D. 87. 根据题目所给的统计数据,某班学生的平均身高是165cm,标准差是8cm,那么身高在157cm到173cm之间的学生占该班学生总数的百分比是多少?A. 68%B. 95%C. 99%D. 50%8. 下列哪个是二次方程的解?A. x = 2B. x = -3C. x = 1/2D. x = 09. 一个直角三角形的两条直角边分别是3和4,那么斜边的长度是:A. 5B. 6C. 7D. 810. 已知等比数列的第1项是2,第2项是4,求第3项:B. 16C. 32D. 64二、填空题(每题3分,共15分)11. 计算(3x^2 - 4x + 2) / (x - 1)的结果是______。
12. 如果一个数列的前n项和为S_n,且S_5 = 15,S_10 = 45,那么S_15 = ______。
13. 一个函数的增长速度是指数型的,如果它的初始值是a,增长率是r,那么经过t时间后的值为a * (1 + r)^t,假设初始值为100,增长率为0.05,经过2年后的值为______。
14. 一个长方体的长、宽、高分别是2米、3米和4米,那么它的体积是______立方米。
高职数学I试卷试题库.docx

《高职数学I》试题库一、填空题(每空 2 分)1、函数y lg( 3x )arcsin x 1 的定义域为。
3(知识点:函数的定义域,难度:一般)2、函数 y= lnx +36x 2的定义域是_________。
(知识点:定义域的求法,难度:一般)3、函数y=arccos(x-1)的定义域是。
(知识点:函数的定义域,难度:一般)4、函数y=arccos(x-1)的定义域是。
(知识点:函数的定义域,难度:一般)5、函数f ( x )1的定义域是。
(知识点:函数,难度:较低)x26、函数y ln(x2 -2x1)的定义域是。
(知识点:函数的定义域,难度:一般)7、函数f ( x)arcsin 2 x 1的定义域是。
(知识点:函数定义域,难7度:一般)8、函数f ( x )的定义域是。
(知识点:函数定义域,难度:一般)arcsin ( x - 1)9、函数 y=x 21+ln (4-x2)的定义域为___________。
(知识点:函数定义域,难度:一般)10、函数y 3 - x arc cos x 1 的定义域为。
(知识点:函数定义域,难度:3一般)11、函数y5x 23的复合过程为。
(知识点:复合函数的分解,难度:较低)12、函数 y=arcsin[ln( x+1)] 的复合过程为。
(知识点:复合函数的分解,难度:一般)13、函数y cos x 1 的复合过程为。
(知识点:复合函数的分解,难度:一般)14、函数 y= cos25x的复合过程为。
(知识点:函数,难度:一般)15、函数 y=x31的复合过程为。
(知识点:复合函数分解,难度:较低)16、函数 y=sin2 2x 的复合过程为。
(知识点:复合函数的分解,难度:较高)17、函数 y=arctan( x 3 1 )的复合过程为。
(知识点:复合函数分解,难度:18、函数 y sinx 1 的复合过程为 ________________ 。
(知识点:复合函数分解,难度:一般)19、函数 y=( 3 - x )20 的复合过程为 。
高职专科高等数学练习题

高职专科高等数学练习题一、选择题(每题3分,共30分)1. 函数f(x)=x^2+2x+1的导数是()。
A. 2x+2B. 2x+1C. x^2+2xD. x^2+2x+12. 以下哪个选项是正确的极限表达式?A. \(\lim_{x \to 0} \frac{\sin x}{x} = 1\)B. \(\lim_{x \to 0} \frac{1 - \cos x}{x} = 0\)C. \(\lim_{x \to 0} \frac{e^x - 1}{x} = 0\)D. \(\lim_{x \to 0} \frac{\ln(1+x)}{x} = 1\)3. 函数y=\(\ln(x)\)的定义域是()。
A. \(x > 0\)B. \(x < 0\)C. \(x \geq 0\)D. \(x \leq 0\)4. 以下哪个选项是正确的不定积分?A. \(\int x^2 dx = \frac{x^3}{3} + C\)B. \(\int e^x dx = e^x + C\)C. \(\int \frac{1}{x} dx = \ln|x| + C\)D. \(\int \sin x dx = -\cos x + C\)5. 函数f(x)=\(\cos(x)\)的周期是()。
A. \(2\pi\)B. \(\pi\)C. \(\frac{\pi}{2}\)D. \(\frac{2\pi}{3}\)6. 以下哪个选项是正确的二重积分?A. \(\iint_D x^2 dA = \int_{a}^{b} \int_{c}^{d} x^2 dx dy\)B. \(\iint_D y^2 dA = \int_{a}^{b} \int_{c}^{d} y^2 dy dx\)C. \(\iint_D xy dA = \int_{a}^{b} \int_{c}^{d} xy dx dy\)D. \(\iint_D x+y dA = \int_{a}^{b} \int_{c}^{d} (x+y) dx dy\)7. 以下哪个选项是正确的偏导数?A. \(\frac{\partial}{\partial x}(x^2y) = 2xy\)B. \(\frac{\partial}{\partial y}(x^2y) = x^2\)C. \(\frac{\partial}{\partial x}(xy^2) = y^2\)D. \(\frac{\partial}{\partial y}(xy^2) = 2xy\)8. 以下哪个选项是正确的多元函数的全微分?A. \(dz = \frac{\partial z}{\partial x} dx + \frac{\partial z}{\partial y} dy\)B. \(dz = \frac{\partial z}{\partial y} dx + \frac{\partial z}{\partial x} dy\)C. \(dz = \frac{\partial z}{\partial x} dy + \frac{\partial z}{\partial y} dx\)D. \(dz = \frac{\partial z}{\partial y} dy + \frac{\partial z}{\partial x} dx\)9. 以下哪个选项是正确的级数收敛性判断?A. 级数\(\sum_{n=1}^{\infty} \frac{1}{n^2}\)是收敛的。
高考高职单招数学模拟试题-(1)

点 P 在圆内的概率为 __ *** _ .
(第 17 题图)
18. 在 ABC 中, A 60 , AC 2 3 , BC 3 2 , 则角 B 等于 __
第 2页 共 6页
*** _ .
春季高考高职单招数学模拟试题答题卡
…
…
…
_______
… …
… …
号…
位…
座… …
…
…
______________________
二、 填空题:本大题共 4 个小题, 每小题 5 分,
15.
计算
1 ()
1
log 31 的结果为
***
.
2
共 20 分。请把答案写在答题卡相应的位置上。
16. 复数 (1 i ) i 在复平面内对应的点在第 *** 象限.
17. 如图 , 在边长为 2 的正方形内有一内切圆, 现从正方形内取一点 P, 则
(Ⅰ)证明: AC1∥平面 BDE ; (Ⅱ)证明: AC1 BD .
D1
C1
A1
B1
E
D
C
A
B
(第 21 题图)
22. (本小题满分 10 分)在平面直角坐标系 xOy 中, 角 , (0 合, 始边与 x 轴的正半轴重合, 终边分别与单位圆交于 A, B 两点,
, 22
) 的顶点与原点 O 重
53
15. 2 16. 第 二 象 限
17. 1 4
18. 45 0 或 4
三.解答题 19. (本小题满分 8 分)
解:设等差数列 an 的首项为 a1 , 公差为 d , 因为
a3 7, a5 a 7 26
所以 a1 2d 7 2a1 10d 26
数学试题及答案职高版

数学试题及答案职高版数学试题及答案(职高版)一、选择题(本题共10小题,每小题3分,共30分)1. 下列函数中,为偶函数的是()。
A. y = x^2 + 1B. y = x^3 - 2xC. y = x^2 - 2x + 3D. y = x + 1答案:A2. 已知集合A={1, 2, 3},B={2, 3, 4},则A∩B等于()。
A. {1, 2, 3}B. {2, 3}C. {1, 4}D. {3, 4}答案:B3. 函数f(x) = 2x - 3的反函数为()。
A. f^(-1)(x) = (x + 3) / 2B. f^(-1)(x) = (x - 3) / 2C. f^(-1)(x) = (x + 3) / 4D. f^(-1)(x) = (x - 3) / 4答案:A4. 已知向量a = (3, -2),b = (-1, 2),则向量a与向量b的数量积为()。
A. -7B. 7C. -5D. 5答案:A5. 计算极限lim(x→0) (sin(x) / x)的值为()。
A. 0B. 1C. -1D. ∞答案:B6. 已知双曲线方程为x^2 / a^2 - y^2 / b^2 = 1,其中a > 0,b > 0,若双曲线的渐近线方程为y = ±2x,则a与b的关系为()。
A. a = 2bB. a = b/2C. b = 2aD. b = a/2答案:D7. 计算定积分∫(0 to 1) x^2 dx的值为()。
B. 1/2C. 1D. 2答案:A8. 已知矩阵A = [1 2; 3 4],矩阵B = [5 6; 7 8],则矩阵A与矩阵B的乘积AB为()。
A. [19 22; 43 50]B. [23 30; 53 62]C. [19 22; 43 50]D. [23 30; 53 62]答案:A9. 计算二项式(1 + x)^3的展开式中x^2的系数为()。
2023年济南职业学院高职单招数学考试参考题库含答案详解

2023年济南职业学院高职单招数学考试参考题库含答案详解(图片可自由调整大小)第I卷一.单项选择题(共30题)1.A.1B.-1C.1或-1D.0,1或-1答案:D 本题解析:2.A.x+y+2=0B.x-y+2=0C.x+y-2=0D.x-y-2=0 答案:A本题解析:3.A.见图AB.见图BC.见图CD.见图D 答案:B 本题解析:4.A.见图AB.见图BC.见图CD.见图D 答案:D 本题解析:5.A.sinα>cosα>tanαB.cosα>tanα>sinαC.sinα>tanα>cosαD.tanα>sinα>cosα答案:D本题解析:tanα>1,cosα<sinα<1,tanα>sinα>cosα.6.A.1B.2C.3D.4答案:B本题解析:本题主要考查的知识点为复数的概念.由题意知.7.A.见图AB.见图BC.见图CD.见图D 答案:D本题解析:暂无解析8.A.1-iB.1+iC.-l+iD.-1-i 答案:A 本题解析:9.A.B.2πC.ΠD.4π答案:A本题解析:本题考查了三角函数的周期的知识点.10.A.1B.-1C.252D.-252答案:D本题解析:11.A.见图AB.见图BC.见图CD.见图D 答案:B 本题解析:12.A.见图AB.见图BC.见图CD.见图D 答案:D 本题解析:13.A.5B.10C.20D.30答案:C本题解析:暂无解析14.A.不存在B.有唯一的一个C.有无数个D.只有两个答案:B本题解析:15.A.3-4iB.3+4iC.4-3iD.4+3i答案:C本题解析:16.A.(5,+∞)B.(-∞,5)C.(-∞,5)∪(5,+∞)D.(-∞,+∞)答案:C本题解析:17.A.-26B.-18C.-10D.10答案:A本题解析:18.()A.见图AB.见图BC.见图CD.见图D答案:B本题解析:本题主要考查的知识点为余弦定理.余弦定理是解斜三角形的重要公式,本题利用余弦定理及三角形面积公式19.A.sin19xB.cos19xC.-sin19xD.-cos19x答案:C本题解析:f(cosx)=f[sin(90°-x)]=cos19(90°-x)=cos(270°-19x)=-sin19x.20.A.见图AB.见图BC.见图CD.见图D答案:A本题解析:21.A.1B.2C.3D.4答案:B 本题解析:22.A.-21B.21C.-30D.30答案:B 本题解析:23.A.见图AB.见图BC.见图CD.见图D答案:B本题解析:暂无解析24.A.a≤-4B.a≥-4C.a≥8D.a≤8答案:C 本题解析:25.A.见图AB.见图BC.见图CD.见图D答案:B本题解析:26.A.相交但直线不过圆心B.相交但直线通过圆心C.相切D.相离答案:D本题解析:27.A.-4B.-8/3C.4D.8/3答案:B本题解析:本题主要考查的知识点为直线的斜截式方程.的交点坐标为(4,0),∵l1⊥l2,kl1=-3/2,kl1·kl2=-1,∴kl1=2/3,∴l1:y-0=2/3(χ-4),即y=(2/3)χ-(8/3).28.A.见图AB.见图BC.见图CD.见图D答案:D本题解析:【考情点拨】本题主要考查的知识点为反比例函数的图像【应试指导】本题属于读图题型,在寻求答案时,要着重讨论方程的表达式.∴(1)当χ>0时,∴(2)当χ如图,29.A.见图AB.见图BC.见图CD.见图D答案:C本题解析:30.A.y=-4xB.y=2-xC.y=3x-4D.y=5-x答案:A本题解析:二.问答题(共20题)1.答案:本题解析:12.252.答案:本题解析:3.答案:本题解析:4.答案:本题解析:5.答案:本题解析:【答案】0 【考情点拨】本题主要考查的知识点为复合函数求值.【应试指导】6.答案:本题解析:7.答案:本题解析:8.答案:9.答案:本题解析:本题主要考查的知识点为二次函数的平移.本题解析:11.答案:本题解析:12.答案:本题解析:由于0.20+0.10+(0.1x+0.05)+0.10+(0.1+0.01y)+0.20=1,得10x+y=25,于是两个数据分别为2,5.13.答案:本题解析:14.答案:本题解析:本题考查了三角函数公式的知识点.x为第四象限角,则cosx=15.答案:本题解析:16.答案:本题解析:17.答案:本题解析:【答案】89 【考情点拨】本题主要考查的知识点为随机变量的期望.【应试指导】18.答案:本题解析:19.本题解析:20.答案:本题解析:第II卷一.单项选择题(共30题)1.A.见图AB.见图BC.见图CD.见图D答案:B本题解析:2.A.1341B.669C.1340D.1339答案:A本题解析:列举数列各项为:1,1,0,1,1,0,…,因为2011=3×670+1,所以S2011=2×670+1=1341.3.A.{2,3)B.{0,1,4}C.φD.U答案:C本题解析:4.A.见图AB.见图BC.见图CD.见图D答案:D本题解析:暂无解析5.A.x+y+2=0C.x+y-2=0D.x-y-2=0 答案:A本题解析:6.A.见图AB.见图BC.见图CD.见图D 答案:C 本题解析:7.A.见图AB.见图BC.见图CD.见图D答案:B本题解析:【考情点拨】本题主要考查的知识点为正切函数的两角和公式.【应试指导】由题知8.A.(-3,-2]∪(1,+∞)B.(-3,-2]∪[1,2)C.[-3,-2)∪(1,2]D.(-∞,-3]∪(1,2] 答案:C本题解析:9.A.见图AB.见图BC.见图CD.见图D 答案:A 本题解析:10.A.见图AB.见图BC.见图CD.见图D答案:A本题解析:由题意知,交集为-3≤x≤-1.11.A.(1,+∞)B.(-∞,-1)C.(-1,0)∪(1,+∞)D.(-∞,-1)∪(1,+∞)答案:C本题解析:12.A.见图AB.见图BC.见图CD.见图D 答案:D 本题解析:13.A.见图AB.见图BC.见图CD.见图D答案:B本题解析:14.A.奇函数,且在(0,+∞)单调递增B.偶函数,且在(0,+∞)单调递减C.奇函数,且在(-∞,0)单调递减D.偶函数,且在(-∞,0)单调递增答案:C本题解析:本题主要考查的知识点为函数的奇偶15.A.直线B.圆C.椭圆D.双曲线答案:B本题解析:本题主要考查的知识点为参数方程.得,x2+y2=1,即半径为1的圆,圆心在原点.16.A.见图AB.见图BC.见图CD.见图D 答案:C 本题解析:17.A.见图AB.见图BC.见图CD.见图D答案:B本题解析:有函数定义可知,应选B。
(完整word版)职高数学试题题库

职高数学试题题库(2010—2011 学年上学期适用 )第一章:集合一、填空题(每空分)1、元素 3 与集合 N 之间的关系可以表示为。
2、自然数集 N 与整数集 Z 之间的关系可以表示为 。
3、用列举法表示小于 5的自然数组成的集合:。
4、用列举法表示方程 3x 4 2的解集 。
5、用描述法表示不等式 2x 6 0 的解集。
6、集合 Na,b 子集有 个,真子集有个。
7、已知集合 A 1,2,3,4 ,集合 B 1,3,5,7, ,则A B,B 。
A 8、已知集合 A 1,3,5 ,集合B 2,4,6 ,则 A B, A B 。
9、已知集合 A x 2 x 2 ,集合B x 0 x4,则A B. 10、已知全集 U 1,2,3,4,5,6 ,集合 A 1,2,5 ,则 C U A。
二、选择题(每题分)1、设 M a ,则下列写法正确的是()。
A . a MB.a MC. a MD. a M2、设全集为 R ,集合 A 1,5 ,则 C U A ( )A ., 1B. 5,C.,1 5, D., 15,3、已知 A 1,4 ,集合 B0,5 ,则 A B ( )。
A . 1,5 B. 0,4 C. 0,4D.1,54、已知 A x x 2 ,则下列写法正确的是()。
A .0 AB.0 AC.AD.0 A5、设全集 U 0,1,2,3,4,5,6 ,集合 A 3,4,5,6,则[U A( )。
1A . 0,1,2,6 B.C.3,4,5,D. 0,1,26、已知集合 A 1,2,3 ,集合 B 1,3,5,7 ,则 A B ( )。
A . 1,3,5 B. 1,2,3, C. 1,3D.7、已知集合 A x 0x 2 ,集合 Bx 1 x 3 ,则A B()。
A . A x 0 x 3B. B x 0 x 3C. B x 1 x 2D. B x 0 x 38、已知集合 A 1,2,3 ,集合 B 4,5,6,7 ,则 A B ( )。
高职高专数学试题大一

一.单项选择(每小题2分,5题共10分)
1.函数是(B)函数
偶函数
奇函数
非奇非偶函数
不能判定2.极限(C)
3.曲线在处的切线方程(B)
4.函数
在点处可导是连续的(D)条件.
无关条件
充要条件
必要条件
充分条件5.设,则(C)
二.计算题(每小题5分,17题共85分)
1. 求极限
2.求极限
3.求极限
4..求函数
的间断点并指出类型
5.求函数
的导数 .
6.计算函数
的微分
7.求由方程所确定的隐函数的导数
8.设, 求.9.设,求
9.求函数的单调区间与极值.
10.1.求曲线的凹凸区间和拐点
1.求不定积分
12. 求不定积分
13.求定积分
14.
15.设,求
16. 求曲线的水平和垂直渐近线。
高职数学题库一年级第一学期
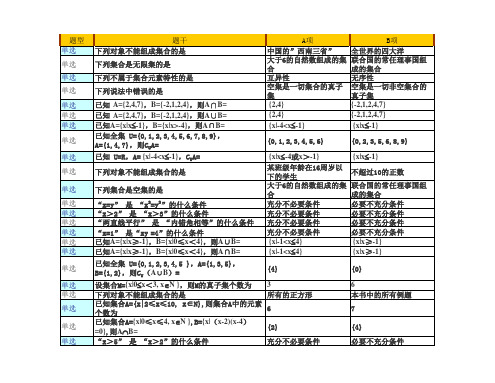
题干 -1∈N 0N+ -2.45∈Z 集合{x|1<x≤5,xZ}可用列举法表示为 {1,2,3,4,5} 小于7的所有实数组成的集合可用描述法表示为 {x|x<7}. {-2,-1,0,1,2,3}{-1,0,1} {-1,2}={x|x - x -2 =0}。 {等腰三角形}{直角三角形}={等腰直角三角形} 已知A={0,1,2},则它的子集个数是8。 18的所有正因数组成的集合是{1,2,3,6,9}。 某烹饪班有学生25人,在某次烹饪大赛中,共设冷拼 和热菜两个比赛项目,已知该班有8人未参加,有 12人参加了冷拼比赛,有11人参加了热菜比赛,问 同时参加了冷拼比赛和热菜比赛的学生有多少人? 已知A={1,2,4,8},B={-2,4,6,7,8},C={3,4,5,6,7,8}, 则(A B)(A C) {1,3,5,15}≠{x|x是15的正约数}。 由小于20的质数组成的集合用列举法表示为 {1,3,5,7,11,13,15,17,19}。 第二象限内的点组成的集合用描述法表示为 {(x,y)|x<0,y>0}。 “c<d”“c-d<0” “四边形是正方形” “四边形四边相等”。 已知A={(x,y)| y=2x+2},B={(x,y)| y=-2x4},则A B=。 已知 A={3,|m-1|,-7},B={-1,1,2},若A B={1}求m 的值。
b>0 【-2,4) |x|>3 { x| x<1} { x| -1<x<1} {x|x<-2或x>4} (-∞,-1) a =2或-2
a+b<0
一元二次方程x -ax+1=0有两个不相等的实 数根,则
若a>|b|,且b<0,则下列各式中成立的是
高职高数考试试卷及答案

一.单项选择题(在每个小题四个备选答案中选出一个正确答案,本大题分10小题, 每小题2分, 共20分)1.下列区间中,函数f (x)= ln (5x+1)为有界的区间是( )A.(-1,51)B.(-51,5)C.(0,51) D.(51,+∞) 2.设函数g (x)在x = a 连续而f (x) = (x-a)g(x),则'f (a) =( ) A.0 B.g '(a) C.f (a)D.g (a)3.设函数f (x)定义在开区间I上,∈0x I ,且点(x 0, f (x 0) )是曲线y= f (x)的拐点,则必有 ( )A.在点(x 0,f (x 0))两侧,曲线y=f (x)均为凹弧或均为凸弧.B.当x<x 0时,曲线y=f (x)是凹弧(或凸弧), 则x>x 0时,曲线y=f (x)是凸弧(或凹弧).C.x<x 0时,f (x)<f(x 0) 而x>x 0时,f(x)>f(x 0).D.x<x 0时,f (x)>f(x 0) 而x>x 0时,f(x)<f(x 0).4.设某商品的需求函数为D(P)=475-10P-P 2,则当P = 5时的需求价格弹性为( ) A.0.25 B.-0.25 C.100 D.-1005.无穷限积分⎰+∞xe -x dx =( )A.-1B.1C.-21D.216.函数f(x)=arcsin(2x-1)的定义域是( )A.(-1,1)B.[-1,1]C.[-1,0]D.[0,1]7.设f(x)=⎩⎨⎧<≥+0x ,x 0x ),x 1ln(, 则=')0(f ( )A.0B.1C.-1D.不存在8.设函数f(x)满足)x (f 0'=0, )x (f 1'不存在, 则( ) A.x=x 0及x=x 1都是极值点 B.只有x=x 0是极值点C.只有x=x 1是极值点D.x=x 0与x=x 1都有可能不是极值点9.设f(x)在[-a,a](a>0)上连续, 则⎰-=aadx )x (f ( )A.0B.2⎰adx )x (fC.⎰-+adx )]x (f )x (f [D.⎰--adx )]x (f )x (f [10.设供给函数S=S(p)(其中p 为商品价格), 则供给价格弹性是( )A.)p (S S p '-B. )p (S S p 'C. )p (S p 'D.)p (S S1'二.计算题(本题50分) 1、(本题5分)求函数6130lg*+-=x xy 的定义域 2、(本题5分)设f(x-1)=x 2-x, 求f(x).3、(本题15分)求下列函数的极限 (1) 20cos 1lim x xx -→(2)xx x In x )sin 1(lim+→(3)设4)(lim =-+∞→xx kx k x ,求k 的值 4.(本题5分)设y=ln(arctan(1-x)),求dxdy 5.(本题20分)求下列函数的导数(1) )21ln(x y -= (2) xxee y +-=11 (3))arccos(2x x y += .(4)xxy cos 1sin +=6.(本题5分)求极限xcos x sec )x 1ln(lim20x -+→三、(本题10分)设函数⎩⎨⎧≤>+=0,0,1)(2x x x x x f ,讨论函数在0=x 处的连续性四、(本题15分)计算下列行列式1.856105342---=D2. 设A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--111111111 , B =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--150421321求:1.2AB - A 2. B A T 高等数学 (参考答案)一.单项选择题(每小题2分, 共20分)1.C2.D3.B4.A5.B6.D7.B8.D9.C 10.B二.计算题(本题55分)2. x2+x3. (1) 1/2 P32 (2) 1 P84 (3) In 24.5 (1)(2)(3)(4)1/2sec2x/26. 1三、(本题10分)在x=0处是间断的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《高职数学I》试题库一、填空题(每空 2 分)1、函数y lg( 3x ) arcsin x 1的定义域为。
3(知识点:函数的定义域,难度:一般)2、函数 y= lnx +36x 2的定义域是_________。
(知识点:定义域的求法,难度:一般)3、函数y=arccos( x-1) 的定义域是。
(知识点:函数的定义域,难度:一般)4、函数y=arccos( x-1) 的定义域是。
(知识点:函数的定义域,难度:一般)1 5、函数f ( x )x的定义域是。
(知识点:函数,难度:较低)26、函数y ln (x2- 2x1)的定义域是。
(知识点:函数的定义域,难度:一般)7、函数f ( x)arcsin 2 x 1的定义域是。
(知识点:函数定义域,难7度:一般)8、函数f ( x )的定义域是。
(知识点:函数定义域,难度:一般)arcsin ( x - 1)9、函数 y=x 21+ln (4-x2)的定义域为___________。
(知识点:函数定义域,难度:一般)10、函数y 3 - x arc cos x 1的定义域为。
(知识点:函数定义域,难度:3一般)11、函数y5x2 3 的复合过程为。
(知识点:复合函数的分解,难度:较低)12、函数y=arcsin[ln(x+1)]的复合过程为。
(知识点:复合函数的分解,难度:一般)13、函数y cos x 1 的复合过程为。
(知识点:复合函数的分解,难度:一般)14、函数 y= cos25x的复合过程为。
(知识点:函数,难度:一般)15、函数 y=x31的复合过程为。
(知识点:复合函数分解,难度:较低)16、函数y=sin22x的复合过程为。
(知识点:复合函数的分解,难度:较高)17、函数 y=arctan ( x 3 1 )的复合过程为。
(知识点:复合函数分解,难度:一般)18、函数y sin x1的复合过程为 ________________ 。
(知识点:复合函数分解,难度:一般)19、函数20的复合过程为。
(知识点:复合函数分解,难度:较低)y=( 3 - x)20、lim(1 1 2 x。
(知识点:两个重要极限,难度:一般))x x 21、lim x sin 1,limx sin1。
(知识点:重要极限,x x x x 无量小乘以有界函数,难度:较高)22、已知f ( x )x1,则 lim f ( x )。
(知识点:极限计算,难度:一x1x1般)x22x k4 ,则k = _ _______。
(知识点:极限,难度:较高)23、若limx3x324、lim sin x=,lim sin x =。
(知识点:第一重要极限,难度:较高)x 0x x xan2bn5则 a=b25、已知lim3n22,。
(知识点:极限计算,难度:n较高)26、假如lim sin mx2,则 m=。
(知识点:两个重要极限,难度:一般)x0x327、lim sin x; lim sin x。
(知识点:极限计算,难度:较高)x x x x228、假如lim 3 sin mx2,则 m=。
(知识点:极限计算,难度:一般)x0 2 x329、假如lim 3 sin mx 2,则 m=。
(知识点:极限计算,难度:一般)x 02 x330、lim 3n322n31=。
n15n(知识点:求数列极限,难度:一般)31、。
(知识点:导数公式,难度:一般)(arcsin x)32、。
(知识点:导数公式,难度:较低)( cot x)33、x)。
(知识点:导数公式,难度:较低)( arccos34、(lg x)35、(arctan x)36、(tan x)37、(csc x)38、(sec x)39、(2x)。
(知识点:导数,难度:较低)____________。
(知识点:导数公式,难度:较低)。
(知识点:导数公式,难度:较低)。
(知识点:导数的基本公式,难度:一般)。
(知识点:导数公式,难度:较低)。
(知识点:导数公式,难度:较低)40、曲线y3x 在点M(1,1)处的切线方程为。
(知识点:导数几何意义,难度:一般)41、曲线y x ln x 在点M(1,0)处的切线方程为。
(知识点:切线的求法,难度:一般)42、曲线y x3 x 1在点M(1,1)处的切线方程为。
(知识点:导数,难度:一般)43、曲线y 1在点 M( 1,1)处的切线方程为。
(知识点:导数几何意义,难x度:一般)44、曲线y x 在点M(1,1)处的切线方程为。
(知识点:导数几何意义,难度:较高)45、曲线y3x22x 在点M(1,1)处的切线方程为。
(知识点:导数几何意义,难度:一般)46、曲线 yx 2 x 1在点 M ( 1, 1)处的切线方程为。
(知识点:导数的几何意义,难度:一般)47、曲线 y x 3 在点 M ( 1, 1)处的切线方程为。
(知识点:导数几何意义,难度:一般)48、曲线 y x21在点 M ( 1, 1)处的切线方程为 。
(知识点:导数的几2 何意义,难度:一般)49、由方程xy e x e y 0 所确立的隐函数在点( 0,0 ) 处的切线方程是。
(知识点:导数几何意义,难度:较高)50、已知 y ln x ,则y。
(知识点:高阶导数,难度:较低) 51、已知 y x e x e x ,则 y。
(知识点:高阶导数,难度:一般) 52、已知 y e x ,则 y。
(知识点:高阶导数,难度:一般) 53、已知 yx1,则 y。
(知识点:高阶导数,难度:一般)x54、已知 y x ,则 y。
(知识点:高阶导数,难度:较低)55、已知 y x ln x ,则 y 。
(知识点:高阶导数,难度:一般)56、已知 y xln x ,则 y。
(知识点:高阶导数,难度:一般)57、已知 y xe x ,则 y。
(知识点:高阶导数,难度:一般)58、已知 y e 2x,则 y _______。
(知识点:高阶导数,难度:一般)59、已知 y x sin x ,则 y。
(知识点:高阶导数,难度:一般)60、已知 ycos 2 x ,则 dy。
(知识点:函数的微分,难度:一般)61、d arcsinx________ (知识点:微分的计算,难度:较难) 62、已知 y ln( 1x)则 dy。
(知识点:求函数的微分,难度:一般)63、已知 yx 2 1 ,则 dy(知识点:微分,难度:较高)64、用适合的函数填入括号,使等式建立:d (______)xdx (知识点:微分公式,难度:一般)d x C(知识点:微分的基本公式,难度:一般)65、 ( 3 )66、 d ( ex 2dx )___________。
(知识点:微分和积分之间的关系,难度:一般)67、 d ___ ___ =2dx(知识点:微分,难度:一般)68、假如 f ( x) 到处可导,则函数y f 2 ( ) 的导数 dy。
(知识点:导数计xdx算,难度:较高)69、 设 f ( x ) 在x a可导,则 limf ( a x) f( a x)。
(知识xx点:导数定义,难度:较高)、设 f ( 3)2 ,则 f ( 3)f ( 3)limh_________。
(知识点: 导数的定义,702hh难度:较高)71、当 x 0 时,无量小量 1 cos2x 等价于无量小量。
(知识点:无量小比较,难度:较高)(知识点:高阶导数的观点,难度:较低)72、函数 y ln( 1x 2 ) 是函数 ysin x 当 x0 时的无量小。
(知识点:无量小的比较,难度:较高)73、不定积分csc 2 xdx =。
(知识点:不定积分公式,难度:一般)1 dx(知识点:积分基本公式,难度:较低)74、x 2175、 (x1)dx(知识点:不定积分计算,难度:一般)76、若在区间上 F ( x ) f( x ) ,则 F( x) 叫做 f( x ) 在该区间上的一个 , f ( x) 的所有原函数叫做f ( x) 在该区间上的 ___ __ 。
(知识点:不定积分的观点,难度:一般)77、由于 d(arcsinx)1x 是 ___ ______的一个原函数。
(知1dx ,因此 arcsinx 2识点:原函数的定义,难度:一般)78、f '( x)dx(知识点:导数和不定积分互为逆运算,难度:一般)79、secx(secx tanx)dx。
(知识点:积分公式,难度:一般)x -x80、 ()(知识点:直接积分,难度:一般)e 3 edx=______________二、选择题(每题) 1、已知等式 关于一确实数都建立,则 是()A. 奇函数B.偶函数C.非奇非偶D.又奇又偶(知识点:函数的奇偶性,难度:较难)2、假如一个函数在闭区间上既有极大值,又有极小值,则( )A. 极大值必定是最大值B. 极小值必定是最小值C.极大值必然大于极小值D.以上说法都不必定建立(知识点:函数的极值最值,难度:一般)3、 , 则 等于( )A. 1B. -1C. 0D.(知识点:导数公式求导数值,难度:一般)、若f ( x)dx sin x , 则 f(x)等于()4A . cosxB.cosx cC.sinx+cD. sinx(知识点:导数和积分的关系,难度:一般)5、( u)( )vA. B. C. D.(知识点:导数运算的除法公式,难度:较低) 6、,则等于()(知识点:函数的导数值求法,难度:一般)7、以下变量在给定的变化过程中为无量小量的是( )A. B.C. D.(知识点:极限的计算,难度:较高)8、设[f(x)dx]sin x,则f ( x )()A.sin xB.sin x CC. cos xD.cos x C(知识点:导数和积分的互逆关系,难度:较高)9、设, 则A. B. C. D.(知识点:极限计算,难度:一般)10、以下函数中,其导数为的是()A. B. C. D.(知识点:导数计算,难度:较高)11、, 则等于()B.-1C.0D.无定义(知识点:导数定义,难度:较低)12 、已知函数yx23xx2在以下哪个自变量变化过程中是无量小量3()A、x3B、x3、x 、xC D(知识点:无量小的观点,难度:较高)13、当时,以下函数中为的高阶无量小的是()A. B. C. D.(知识点:极限,难度:较高)14、,则等于()(知识点:导数,难度:一般)15、是的()A.必需条件 B.充足条件 C.充要条件 D.没关条件(知识点:导数,难度:较低)16、以下说法正确的选项是A.最大值必定不小于最小值C.极大值必定是最大值()B.极大值必定大于极小值D.极小值必定是最小值(知识点:导数的应用,难度:一般)17、已知数列则的表达式是()A. B. C. D.(知识点:函数的定义,难度:一般)18、的反函数是()A. B.C. D.(知识点:反函数的定义,难度:一般)19、, 则等于()(知识点:导数公式,难度:较低)20、若函数f( x)为可微函数,则dy()A.与 x 没关B.为 x 的线性函数.当 x0时为 x的高阶无量小D .与 x 为等价无量小C(知识点:微分定义,难度:较高)231在x21、函数f ( x)3x x 1 处()x2x1A. 左右导数均存在,B.左导数存在,右导数不存在,C. 左导数不存在,右导数存在,D.左右导数均不存在。
