光波在金属表面上的反射和折射
第三节 光在金属表面的反射和折射

第三节光在金属表面的反射和折射
一、金属中的光波
金属(导电媒质)中
导电媒质的波动方程:
对于单色光波
有:(金
属)
(电介质)
定义:复介电常数(复相对介电常数)
类似的:复相速度
复折射率
一般记
其穿透深度为(良导体时,
)
金属的穿透深度一般很小,如铜,,
,得
回到开头
二、金属表面的反射
对于金属界面,电介质表面反射和折射时的菲涅耳公式依然有效只是:
此时:
由菲涅耳公式讨论其反射特性:
1、金属表面有很强的反射能力
正入射时:
当σ=0时,k→0,ρ的表达式与电介质时的相同
σ很大时,k很大,故ρ很大,这样金属表现出高反射比和非透明性。
例:(正入射时,λ=550nm)蒸镀膜比较
铜n=0.756 ρ=0.669
金n=0.331 ρ=0.815
银n=0.055 ρ=0.982
2、反射比与入射波长有关
同一金属在不同波长下有不同ρ
应酌情选取(见图)(银、铝、铜)
3、反射比与入射角有关
与电介质时比较(见图)
相同:=0时,,相合;
=90°时,,→1;有一极小值;
不同:(1)即使=0(正入射),ρ也很大——任何情况下,金属表面有很强的反射
(2)≠0,——金属表面反射时不产生全偏振
4、反射光一般为椭圆偏振光
为复数,→。
13光波在金属表面上的反射和折射

前面讨论了,光在非导电(=0)各向介质 及其界面上的传播规律。
对于金属,它与各向同性介质的主要差别 是电导率()不等于0 ,金属导致光波衰减, 金属对光波几乎不透明;
1.3.1 光波在金属中的传播 1.3.2 光在金属表面的反射和折射 1.3.3 金属表面反射的频率特性
这两个波动方程与(1-13)
式的差别在于以复数值μεα 代替了με。
金属中的单色平面光波, 其光场表示式为
E
E e i(t k~ k0 r ) 0
2/26/2020
复波数 复折射率
复波数 k~ i
复折射率
n~ k~ k~ c
s分量的反射波(波矢k(r)为实数值): 按照反射定律(θr=θi)传播的均匀波(等振幅面与等
相位面一致)。
由于rs为复数值, rs | rs | eirs
在界面上的反射波与入射波也相差一个相位φrs。
2/26/2020
s分量的折射波(波矢k(t)为复数值)
金属中的折射光
是一个沿-z方向
材料的复折射率n,也可求出ε、μ、 σ等物质常数。
- -椭偏法测量金属的折射率
2/26/2020
1.3.3 金属表面反射的频率特性
电子理论的观点,电导率起 因于金属中有密度很大的自 由电子(约1022/cm3)。
当光照射到清洁磨光的金属 表面时,自由电子将在光场 的作用下强迫振动,产生次 波,这些次波构成了很强的 反射波和较弱的透射波,透 射波将很快地被吸收掉。
2/26/2020
p分量的反射、折射波
讨论方法与s分量相同。
由于φrp与φrs不同,金属表面的反射将改变入
精品课件-物理光学与应用光学_第三版(石顺祥)-第1章

第 1 章 光在各向同性介质中的传播特性 5. 光的电磁理论指出, 光电磁场是一种特殊形式的物质, 既然是物质, 就必然有能量, 其电磁场能量密度为
(1.1-20)
而光电磁场又是一种电磁波, 它所具有的能量将以速度v向外 传播。 为了描述光电磁能量的传播, 引入能流密度——坡印 廷(Poynting)矢量S, 它定义为
21
第 1 章 光在各向同性介质中的传播特性
将(1.1-24)式代入, 进行积分,可得
I
S
1 2
n
0c
E02
1 2
0
E02
E02
(1.1-25)
式中, n 是 比/ 例0 系数。由此可见,在同一种介质中, 光强与电场强2度0c振幅的平2 方成正比。 一旦通过测量知道了光强,
便可计算出光波电场的振幅E0。例如,一束105 W的激光,用透镜 聚焦到1×10-10 m2的面积上,则在透镜焦平面上的光强度约为
(1.1-8) (1.1-9) (1.1-10)
10
第 1 章 光在各向同性介质中的传播特性 即D与E、 B与H、 J与E一般不再同向; 当光强度很强时, 光与 介质的相互作用过程会表现出非线性光学特性, 因而描述介质 光学特性的量不再是常数, 而应是与光场强E有关系的量, 例 如介电常数应为ε(E)、 电导率应为σ(E)。对于均匀的各向同 性介质, ε、 μ和σ是与空间位置和方向无关的常数; 在线 性光学范畴内, ε、 σ与光场强无关; 在透明、 无耗介质中, σ=0; 非铁磁性材料的μr可视为1。
(1.1-23)
19
第 1 章 光在各向同性介质中的传播特性
式中, sz 是能流密度方向上的单位矢量。 因为由(1.1-13)
[842]物理光学II 哈工大 航天学院
![[842]物理光学II 哈工大 航天学院](https://img.taocdn.com/s3/m/3a7022d584254b35eefd3487.png)
2012年硕士研究生入学考试大纲
考试科目:物理光学II 考试科目代码:[842]
一、考试要求:
深入理解物理光学的基本概念,了解并熟练掌握物理光学的重要知识,掌握重要的分析问题的方法,具备运用物理光学知识解决有关问题的初步能力。
二、考试内容:
1)光在各向同性介质中的传输特性
麦克斯韦方程;反射定理和折射定理;菲涅尔公式;全反射;光波在金属表面上的反射和折射。
2)光的干涉
双光束干涉;平行平板的多光束干涉;典型干涉仪;光的相干性。
3)光的衍射
衍射的基本理论;夫朗和费衍射;菲涅尔衍射;衍射的应用。
4)光在个向异性介质中的传输特性
晶体的光学各向异性;单色平面光波在晶体中的传播;平面光波在晶体上的反射与折射;晶体光学元件。
5)晶体的感应双折射
电光效应;声光效应;法拉第效应。
6)光的吸收、色散和散射
光的吸收、色散和散射的基本概念。
三、试卷结构:
1)考试时间:180分钟,满分:150分
2)题型结构
a:选择、判断、填空题(30分)
b:简单回答题(50分)
c:应用题、计算题(70分)
四、参考书目:
石顺祥、张海兴、刘劲松编著《物理光学与应用光学》;西安电子科技大学出版社,2000年8月第一版。
光波在晶体界面上的折射和反射

··
i0
激光输出
M1
布儒斯特窗
M2
垂直分量损耗大,不能形成激光,但平行分
量能形成激光。
【思考】如何测量不透明介质的折射率?
有反射光干扰的橱窗
在照相机镜头前加偏振 片消除了反射光的干扰
对布儒斯特定律的定性解释:
折射光波在第二种介质中激起电子做受迫振动,振
动方向沿光矢量方向。振动的原子可看做是电偶极子
x2 + y2 ne2
+ z2 no 2
=1
z平行于C,交迹线方程
x2 + y2 = no2 x2 + y2 = ne2
晶体的旋光现象
¾线偏振波在某些晶体中沿光轴方向传播时, 偏振方向随着光波的传播而旋转,这种现象 称为旋光,能产生旋光的物质称为旋光物质
晶体的旋光现象
¾晶体的旋光性
晶体的旋光现象
线偏振光的产生
• 线偏器的质量指标
– 通光口径
• 透射线偏振光的最大可能光束截面 • 确保元件性能的前提下,允许的入射光束最大孔径角
– 光谱范围:线偏器能适用的光波光谱范围 – 色散:白光透过线偏器后,透射光的传播方向甚
至振动方向都可能因波长而异的现象 – 稳定度:反映元件是否容易因光照、湿度、温度
=
n2 n1
=
n21
若 n1 =1.00 (空气),n2 =1.50(玻璃),
则:空气 → 玻璃
玻璃 → 空气
i0 i0′
= =
tg −1 tg −1
1.50 1.00 1.00 1.50
= =
56 °18 33 °42
⎫ ⎪⎪⎬互余 ⎪ ⎪⎭
例:外腔式激光管加布儒斯特窗减少反射损失
第三节 光在金属表面的反射和折射

第三节光在金属表面的反射和折射
一、金属中的光波
金属(导电媒质)中
导电媒质的波动方程:
对于单色光波
有:(金
属)
(电介质)
定义:复介电常数(复相对介电常数)
类似的:复相速度
复折射率
一般记
其穿透深度为(良导体时,
)
金属的穿透深度一般很小,如铜,,
,得
回到开头
二、金属表面的反射
对于金属界面,电介质表面反射和折射时的菲涅耳公式依然有效只是:
此时:
由菲涅耳公式讨论其反射特性:
1、金属表面有很强的反射能力
正入射时:
当σ=0时,k→0,ρ的表达式与电介质时的相同
σ很大时,k很大,故ρ很大,这样金属表现出高反射比和非透明性。
例:(正入射时,λ=550nm)蒸镀膜比较
铜n=0.756 ρ=0.669
金n=0.331 ρ=0.815
银n=0.055 ρ=0.982
2、反射比与入射波长有关
同一金属在不同波长下有不同ρ
应酌情选取(见图)(银、铝、铜)
3、反射比与入射角有关
与电介质时比较(见图)
相同:=0时,,相合;
=90°时,,→1;有一极小值;
不同:(1)即使=0(正入射),ρ也很大——任何情况下,金属表面有很强的反射
(2)≠0,——金属表面反射时不产生全偏振
4、反射光一般为椭圆偏振光
为复数,→。
1.3光在金属表面的反射和折射ok

穿透深度
z0
1
E( z0 ) E(0) / e
z
对于金属良导体
1
1 1 2 1 [ ( 1 2 2 1)] 2 ( )2 2 2 1 1 2 1 [ ( 1 2 2 1)] 2 ( )2 2 2
金属中的波动方程
由于在金属内部: =0, j E
麦克斯韦方程变为:
E 0 B 0 B E t H E D t
由此,得到波动方程为:
2 E E 2 E 0 2 t t
复传播常数
~2 2 k ( i ) v ~2 k i 2 0
~ k 2
)
金属中的波函数
解方程
有
~2 k i 2 0 ~ k i 1 2 2 2 注:
光波在金属表面的 透射和反射
与前面讨论的均匀透明介质相比,金属最 显著的特点是:一般的它为良导体。 即有 : 电导率σ≠0 ,且 。 1
这里是介电常数,是作用于金属上的外界电 磁场的角频率。上式表明,金属是否为良导体, 不仅与它的σ大小有关,还与外场的频率有关。
光波在金属表面的 透射和反射
E 2 E t 2
2
ˆ 电介质 i Biblioteka =A exp(k r t )
复传播常数怎么得到?
引入复相位速度 和复折射率 n ˆ ˆ
1 ˆ ( i ) 2 ˆ v
ˆ 2 c / v 2 c 2 ( i ˆ n
光学-中国科学院光电技术研究所研究生部

3、掌握驻波概念 4、掌握典型的多光束干涉系统 5、熟练掌握光的相干性基本概念及其应用 6、了解迈克耳孙干涉仪和马赫-曾德尔干涉仪;了解法布里-伯罗干涉仪和光纤干涉仪 7、了解光学薄膜基本原理,掌握单层增透、减反膜的计算结论和实际应用 8、熟练掌握光程差概念以及对条纹的影响及基本的等厚等倾干涉系统,掌握条纹定域 和非定域的概念及条纹可见度概念 (三)光的衍射 1、熟练掌握衍射的基本原理 2、掌握夫琅和费单缝衍射和圆孔衍射 3、了解巴俾涅原理 4、掌握夫琅和费多缝衍射以及典型孔径的衍射计算 5、掌握菲涅耳衍射基本原理及应用,菲涅耳波带片的概念和使用 6、掌握衍射光栅基本原理及应用 7、掌握闪耀光栅的原理和计算 8、掌握衍射极限的概念及在典型光学系统设计中的运用 9、掌握夫琅和费衍射与傅立叶变换的关系 (四)晶体光学基础 1、了解晶体的介电张量 2、掌握单色平面光波在晶体中的传播特性 3、熟练掌握单色平面光波在晶体表面上的反射和折射 4、了解偏振器件及其应用 5、了解琼斯矢量计算和斯托克斯矢量计算 6、了解偏振光的干涉和物质的旋光性 (五)光的吸收、色散和散射 1、了解光与物质相互作用的经典理论 2、掌握光的吸收、光的色散和光的散射基本概念 (六)几何光学基础 1、熟练掌握几何光学基本定律 2、了解费马原理,惠更斯原理 2、掌握单个折射球面的光路计算及近轴区成像 3、掌握球面反射镜成像 4、掌握共轴球面光学系统 5、了解薄透镜成像 6、了解平面折射成像 7、掌握平面镜和棱镜系统 8、熟练掌握基点、焦距、放大率、物像关系、拉赫不变量等概念及相关计算并能熟练 作图,掌握光组组合的计算与作图方法 (七)理想光学系统 1、掌握理想光学系统的基点和基面 2、掌握理想光学系统的物像关系 3、掌握理想光学系统的组合 4、了解厚透镜及其基点与基面 (八)光学系统像差基础
平面电磁波在金属面的反射与折射

编号:XXXXXXXXXXXXXXXXX大学本科毕业论文题目:平面电磁波在金属面的反射与折射学院: ______________________________________专业:____________________________年级: ______________________________________姓名: ______________________________________指导教师:XXX ________________________________完成日期:XXX年XX月XX日目录摘要 (1)Abstract. (2)引言 (1)1 电磁波在金属面反射与折射的基本理论 (1)1.1 电磁波在金属界面上的边值关系 (1)1.1.1 场量的法向分量在介质面上的跃变 (2)1.1.2 场量的切向分量在介质面上的跃变 (3)1.2 电磁波在金属面的反射与折射 (6)1.2.1 电磁波在一般界面上的反射和折射定律 (6)1.2.2 振幅关系Fresnel 公式 (8)2 平面电磁波在良导体面的反射和折射 (10)2.1 良导体面上的折射与良导体内的折射波 (10)2.2 平面电磁波在良导体面的反射 (12)3 结语 (14)参考文献 (15)致谢 (16)个人简历 (17)摘要本文以Maxwell方程组为出发点,用简洁明了的理论推导,给出平面电磁波在两种介质表面上的反射与折射规律,并由此引出了一些重要结论,如趋肤效应,Fresnel公式等。
在对电磁波的传播、电磁波与介质的相互作用等基本规律的认识中,体现电磁学基本规律在信息技术、通信技术中的理论指导意义和其现实意义。
由此得出的结论也为深入理解光的反射与折射奠定了基础。
关键字:平面电磁波,边值关系,麦克斯韦方程,良导体AbstractBased on the Maxwell equati on, it particularly con siders reflect ion and refractio n of the pla nar electromag netic wave on the in terface betwee n two media by a succi net progress of reas oning. With the work above, some con clusi ons will be reached such as the skin effect and Fresnel formula. These basic laws of electromagnetic are fairly sig nifica nt to direct the developme nt of in formati on tech no logy and com muni cati on tech no logy .In additi on, the con clusi on con tributes to un dersta nd the reflecti on and refraction of light better.Key words:Planar electromagnetic wave; Boundary relation; Maxwell equation; Good con ductor .引言平面电磁波在良导体表面上的反射和透射问题,是电动力学研究的重要问题之一,由于它在光学、射电天文学、雷达工程学等方面有着广泛的应用,长1电磁波在金属面反射与折射的基本理论 1.1电磁波在金属界面上的边值关系Mexwell 方程组可以应用于任何连续介质内部.但是在两介质分界面上,由 于一般出现面电荷电流分布,使物理量发生跃变,微分形式的麦克斯韦方程组不 再适用•因此,在介质分界面上,我们要用另一种形式描述界面两侧的场强以及 界面上电荷电流的关系•在电场作用下,介质界面上一般出现面束缚电荷和电流分布•这些电荷电流 的存在又使得界面两侧场量发生跃变•(a)(b)图i 电场在介质面上的跃变Fig.1 Step cha nge of electric field on the object surface例如图1(a)所示的介质与真空分界的情形,在外电场E 0作用下,介质面上期以来受到人们的重视.但因该问题的复杂性 人们仅讨论了某些特定的情况 如在一般文献与教材中,只讨论了正入射的情况 .本文将讨论平面电磁波以任意 角度入射到良导体界面上发生反射和透射的情况 导出反射波、透射波与入射波 的振幅、相移关系式以及反射系数的数学表达式 论.并在此基础上作进一步的讨产生面束缚电荷,这些电荷本身激发的电场在介质内与E0反向,在真空中与E o同向•束缚电荷激发的电场与外电场E o叠加后的总电场如图1(b)所示,由图可以看出两边的电场E l和E2在界面上发生跃变,边值关系就是描述两侧场量与界面上电荷电流的关系.由于场量跃变的原因是面电荷电流激发附加的电磁场,而积分形式的Mexwell方程组可以应用于任意不连续分布的电荷电流所激发的场,因此我们可以用积分形式的Mexwell方程组来研究边值关系1.1.1场量的法向分量在介质面上的跃变Mexwell方程组的积分形式为图2 Mexwell方程在介面上的应用Fig.2 Applicati on of Mexwell equati on on in terface如图2,我们将总电场的Mexwell方程■ = 应用到两介质边界上的一个扁平状柱体•上式左边的面积分遍及柱体的上下底和侧面,Q f和Q p分别为柱体内的总自由电荷和总束缚电荷,它们等于相应的电荷面密度二f和二p乘以底面积:S.当柱体的厚度趋向于零时,对侧面的积分也趋向于零,对于上下底积分得E2n -dL L H^I -I f s D_dS■」dtL S D l_d S = QfLs BdS =0(1)式中I f为通过曲面S的总自由电流,Q f为闭合曲面内的总自由电荷•把这组方程应用到界面上可以得到两侧场量的关系E in.由⑵式得;o E2n - E in - f * P (3)即P2n —■ Pin - - p (4)两式相加,利用D in = ;°E in P in, D2n 二-E2n - P2n ,得D2n ~' D in 二一;「f(5)由式(3)—(5)可以看出,极化矢量法向分量P n的跃变与束缚电荷面密度相关,D n的跃变与自由电荷面密度相关,E n的跃变与总电荷面密度相关•对于磁场B ,把(i)式第四式应用到边界上的扁平状区域上,重复以上推导可以得到B2n = B in(6)上式说明磁感应强度B在边界上没有发生跃变.i.i.2场量的切向分量在介质面上的跃变由于高频电流只分布在导体表面很薄的一层上,所以,根据研究问题性质的不同,对于这种电流分布可以有两种不同的描述方法.一种是对它作比较细致的描述,即把它作为体电流分布J而研究它如何在薄层内变化.另一种描述是对它作整体的描述,即不讨论它如何在薄层内分布,而是把薄层看作几何面,把薄层内流过的体电流看作集中在几何面上的面电流.由以上分析可见,面电流实际上是在靠近表面的相当多分子层内的平均宏观效应.设想薄层的厚度趋近于零,则通过电流的横截面变为横截线.定义电流线密度^,其大小等于垂直通过单位横截线的电流.图3理想薄层内的电流线密度Fig.3 Lin ear curre nt den sity in the图3表示界面的一部分,其上有面电流,其线密度为号,l为横截线.垂直流过厶I段的电流为J .1 (7)由于存在面电流,在界面两侧的磁场强度发生跃变.如图4,在界面两旁取一图4界面两侧的磁场跃变Fig.4 Step cha nge of magn etic field in the two sides of in terface狭长形回路,回路的一长边在介质1中,另一长边在介质2中.长边•许与面电流2正交.把Mexwell方程组⑴ 第二式应用到狭长形回路上.取回路上、下边深入到足够多分子层内部,使面电流完全通过回路内部.从宏观上来说回路短边的长度仍可看作趋向于零,因而有』Hjdf =(H2t-卄)纠(8)其中,et表示沿-l方向的单位矢量.通过回路内的总自由电流为(9) 由于回路所围面积趋向于零,而—为有限量,因而专心总0把这些式子代入(1)第二式中得(10)上式可以用矢量形式表示•设寸为界面上任一线元,瓷为界面的法线方向单位矢量.流过寸的自由电流为I f - e n (11)对狭长形回路用Mexwell方程组⑴第二式得QL H dT= H2 -才=I f = a e n (⑵由于孑为界面上任一矢量,因此(13)式中表示投射到界面上的矢量.上式再用e n矢乘,注意到e n x H2~H1 〃= e n H2-H1,而且e n a = 0,得(14)这就是磁场切向分量的边值关系.同理,由(1)第一式可得电场切向分量的边值关系:e n E2 -岂=0(15)I上式表明界面两侧E的切向分量连续.综上,我们得到的边值关系为e n E2-E1 =0e n H2 —H1 e n D2 D i = ;丁(16)e n B2 - B l = 0上式中的二和•分别代表自由电荷面密度和自由电流线密度是从介质1指向介质2的法向单位矢量.1.2电磁波在金属面的反射与折射1.2.1电磁波在一般界面上的反射和折射定律电磁波入射于介质界面时,发生反射和折射现象•关于反射和折射的规律包括两个方面:(1)入射角、反射角和折射角的关系;(2)入射波、反射波和折射波的振幅比和相对相位•任何波动在两种不同介质的界面上的反射和折射现象都属于边值问题,它是由波动的基本物理量在边界上的行为确定的,对于电磁波来说,是由电和叫的边值关系确定的•所以我们可以用边值关系来研究电磁波的反射和折射规律•前面我们已经推出一般情况下电磁场的边值关系.在一定频率情形下,边值关系(16)不是完全独立的,由第一、二式可以导出其他两式.因此,在研究时谐电磁波时,介质界面上的边值关系只需满足以下二式:e n E2-E1 =0 ;.. (17)e n H2 —H1虽然介质中B是基本物理量,但由于H直接和自由电流相关,而且边界条件也由H表出,因此,在研究电磁波传播问题时,往往用目表示磁场较为方便.设介质1和介质2的分界面为无穷大平面,且平面电磁波从介质1入射于界面上,在该处产生反射波和折射波.设反射波和平面波也是平面波(之后的结果会证明这个假设是正确的).设入射波、反射波和折射波的频率是相同的,电场强度分别为E、E'和旨',波矢量分别为k、k'和;',如图5.他们的平面波表示式分别为E=E0eWZ)E 二Ee ik m (18)E'=Ee ik J易知,介质1中的总场强为入射波与反射波的场强的叠加,而介质2中只有折射波,因此,由(17)得e n E E 二e n E (19)把(18)代入得因此,反射波矢和折射波矢都在同一平面上•以二,J和二''分别代表入射角、反射角和折射角,有k x =ksi nd, k x=k Si n \' k;二k si nJ (23)设V1和V2为电磁波在两介质中的相速,由(14)式有e: E oe”E o e ikx=en E o e ik x(20)此式必须对整个界面成立.选界面为平面z = o和任意x,y成立.所以三个指数因子必须在此平面上完全相等,故有■*. 4 ■*, 4 -4 4k[_x=k_X=k_x z=0因为x和y是任意的,它们的系数应各自相等,有' " I nk x = k x = k x, k y = k y = k y(21)(22)如下图,取入射波矢在xz平面上,有ky=°,由式(22)知k y和k'y也为零.图5界面上的反射波与折射波Fig.5 Reflected wave and refracted wave on thek=k=— k= —V 1V 2再把(23)式和(24)式带入(22)式得V - Jsi nr v i ii --- sinB v2这就是我们熟知的反射和折射定律•对于电磁波来说,v =,因此sin 日 丁卩2名2 (26)------ ' ^ n 2i si nv *;in 2i 为介质2相对于介质1的折射率•由于除铁磁质外,一般介质都有•「…I 。
光波长反射金属

光波长反射金属
光波长反射金属是指金属材料对特定波长的光波展现出良好的反射特性。
根据电磁波理论,当光线照射到金属表面时,部分光波会被金属吸收,转化为热能,并导致金属表面产生反射和折射等现象。
然而,对于某些金属材料来说,它们具有特定的晶体结构和电子能带结构,能够有效地吸收和反射特定波长的光波。
金属材料能够反射光波的原因是由于其电子结构特性。
金属中的自由电子在光波的作用下会发生振动,从而产生电磁波的辐射。
当光波的波长接近或与金属中自由电子的平均自由程相匹配时,金属材料会出现反射现象。
这是因为电磁波与自由电子进行相互作用,电子在反应后将能量传递给周围的电场,并阻止光波的进一步穿透。
光波长反射金属的应用非常广泛。
比如,在光学器件中,金属被用作反射镜和光学镜片的材料,能够有效地反射和聚焦特定波长的光波。
在太阳能电池中,利用金属反射波长来提高光电转化效率。
此外,金属材料在天线设计、激光器、光纤通信等领域也有重要的应用,可以实现对特定波长光波的精确控制和利用。
需要注意的是,金属对光波的反射特性受到金属类型、波长、入射角度等因素的综合影响。
不同的金属材料和波长所具有的反射性能有所区别。
因此,在具体应用中需要根据实际需求选择合适的金属材料和波长来实现预期的反射效果。
物理光学 平面光波在晶体界面上的反射和折射

①式中的 i 、 r、t 都是对波法线方向而言的,尽管
反射光、折射光的波法线均在入射面内,但它们的光 线有可能不在入射面内。
A
B
k i s i n i k r s i n r k t s i n t ( 1 1 0 ) vr vp
A s kB
光在晶体界面上的双反射和双折射
一个半轴长为o,另一个半轴长介于o 和e 之间.
S
B
A
A
R 0
R0 R
e No
1. 惠更斯作图法
将SA 延长与入射光波面相交于R,过 R 作切平面AR,它 就是入射光次波面的包迹—入射光波的波阵面。入射 光的光线方向和波法线方向均为 AR 方向。
S
B
A
A
R 0
R0 R
e No
1. 惠更斯作图法
n no n n o
光轴
ki ke ko
2) 平面光波在主截面内斜入射
平面光波在主截面内斜入射时,在晶体内将分为 o 光 和 e 光, e 光的波法线方向、光线方向一般与o 光不相 同,但都在主截面内。
ki
ko ke
se
光轴
2) 平面光波在主截面内斜入射 当晶体足够厚时,从晶体下表面射出的是两束振动方 向互相垂直的线偏振光,传播方向与入射光相同。
k i s i n i k r s i n r k t s i n t ( 1 1 0 )
或
nisini nrsinr (111) nisini ntsint (112)
(111)式和(112)式就是光在晶体界面上的反射定律和折 射定律。
根据图所示的几何关系,由(108)式和(109)式得到
O
物理光学第3讲-第三节光在金属表面的反射和透射_光的散射

对于稀薄气体介质,设频率为 的光波 E A exp it 入射到气体 介质内,使介质内的束缚电子做受迫振动,由于磁场对电子的 作用远小于电场力,则电子受迫振动方程为
12
第四节 光的吸收、色散和散射
对于固体和液体、压缩气体,周围分子在光场作用下计划所 产生的影响不可以忽略,可以证明这时作用在电子上的电场 E’为 P
E E 3 0
Nq 2 0m Nq 2 3m 0
2 0 2
类似推导得到
n2 1
或者
n2 1 Nq 2 2 2 n 2 3 0 m 0 2
利用光波作用于物质中分子、原子所导致的电偶极子振荡解释散射现象。当光 波射入介质中时,会激发起介质中电子做受迫振动而发出次级电磁波,对于均 匀介质,这些次波叠加使光波沿着反射和折射定律方向传播,不发生散射。当 介质非均匀时,介质内有悬浮微粒而由入射波激发起的次波的振幅和相位不完
全相同,则次波干涉的结果使在非透射方向上不能完全抵消而造成散射光。
~ n1 i 记复折射率为 n
~ ~ k kn kn1 i
0
2、在共振频率附近的选择吸收区,即当入射光频率处于 0
的吸收带附近时,折射率n表示式中的 项不能忽略,此时n是复 数,即 ~ n1 i ~ 2 n2 1 2 i 2n2 2 n n
1 2 s s i s
~ rp
t an t an
2
1
2
~ i p ~ 1 2 r e ~ p 1 2
1.9光波在金属表面的透射和反射1.10光吸收色散和散射课件

此外,由于与周围原子和分子的相互作用,束缚 电子受迫振动的一部分能量将变为其它形式的能 量,例如分子热运动的能量,这部分能量的损耗 就是我们所指的介质对光波的吸收。
§ 1-10光的吸收,色散和散射
(1)一般对可见光来说,各种物质的吸收系 数的差别是很大的。
(2)大多数物质的吸收具有波长选择性。
即,对于不同波长的光,物质的吸收系数 不同。这种特殊性可用吸收系数和波长的关 系曲线来表示。如图1-39
同的悬浮微粒存在。这时,即使不正对着 入射光的方向,也能够清楚的看到光,这 种现象称为光的散射(瑞利散射)。 2、分子散射:是纯净物质的散射现象。 光的散射主要是次波叠加不能完全抵消的 结果。
§ 1-10光的吸收,色散和散射
光的散射现象的规律:
1、瑞利散射定律:
散射光强与入射光波长的四次方成反比,即
2.斜入射时
:
rs
rp
sin( 1 stign((11 t g (1
2 ) 22)) 2)
sin 2
1 nˆ
sin
1
对于金属
由常于所nˆ是理复解数的。折故射角2也的为意复义数。,它不再具有通
§1-9光波在金属表面的
透射和反射
反射率
Rs
rs
2
(n cos1)2 n2k 2 (n1 cos1) n2k 2
研究表明,在 1017HZ的电磁波作用下, 金属内部的自由电子只分布于金属表面。 金属内部电荷体密度=0,并且自由电子在 表层形成表层电流(j= E)。
此电流的存在,将使入射波产生强烈的反射, 并使透入金属内部的波迅速地耗散为电流 的焦耳热。
§1-9光波在金属表面的 透射和反射
故:通常光波只能透入金属表面很薄的一层 内,金属是不透明的。
1.3光在金属表面的反射和折射ok

~ ~ k = kn = kn(1 + iκ )
反射系数 (与电介质区别在于κ)
(n − cosθ1)2 + n2κ 2 Rs = rs = (n1 + cosθ1) + n2κ 2
2
1.垂直入射时反射率 1.垂直入射时反射率
2
1 2 2 2 ) +n κ 2 cosθ1 Rp = rp = 1 (n + ) + n2κ 2 cosθ1 (n −
光波在金属表面的 透射和反射
与前面讨论的均匀透明介质相比,金属最 显著的特点是:一般的它为良导体。 σ 即有 : 电导率σ≠0 ,且 εω >>1 。
这里ε是介电常数,ω是作用于金属上的外界 电磁场的角频率。上式表明,金属是否为良导体, 不仅与它的σ大小有关,还与外场的频率ω有关。
光波在金属表面的 透射和反射
ˆ n −1 n2 (1+ k 2 ) +1− 2n R= r = = 2 ˆ n +1 n (1+ k 2 ) +1+ 2n
2
金属反射曲线的特点
与电介质的反射率曲线相比较有几个特点: 0 R (1) θ1 = 90 时 s = Rp ≈ 1 (2)Rp有一极小值,但 Rp的极小值不等于零。所 以金属没有反射全偏振现象。 (3)相位变化:由于θ2是复数,rs、rp也是复数, 这表示反射光相对于入射光s波和p波都发生了位 相跃变。随着θ1的不同,位相跃变值介于0与π之 间。并且一般地s波和p 波的位相跃变不同。 偏 振态不同(依赖于金属常数) 椭圆偏振法测金 属常数 (4)频率依赖:金属对低频光有较高的反射率。
4.4平面光波在晶体表面上的反射与折射2
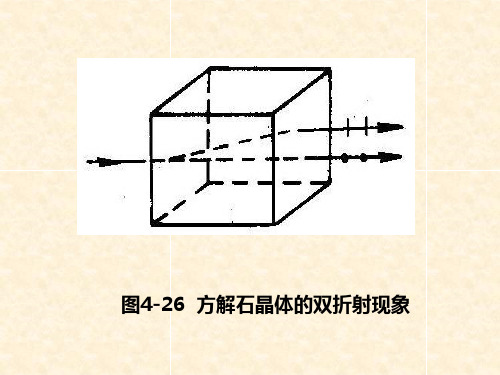
矢面(双壳层曲面)。自A点引一直线平行于入射光波法线方 向,与入射光所在介质的波矢面交于Ni,该ANi即为入射光 波ki。以Ni点作Σ面的垂线交晶体中的波矢面于Nt′和Nt″, ANt′和ANt″就是与入射光ki相应的两个折射光波矢kt′和 kt″。每一个折射光对应着一个光线方向和一个光线速度,
图4-26 方解石晶体的双折射现象
图 4-27 方解石晶体中的双反射现象
4.4.2 光在晶体界面上反射和折射方向
——
1.
惠更斯作图法是利用射线曲面(即波面)确定反射光、折 射光方向的几何作图法。对于各向同性介质,惠更斯原理曾 以次波的包迹是新的波阵面的观点,说明了光波由一种介质 进入另一种介质时为什么会折射,并通过作图法利用次波面 的单层球面特性,确定了次波的包迹——波阵面,从而确定 了折射光的传播方向。
图 4 - 28 惠更斯作图法
图 4 - 29 正入射时晶体中的折射现象(负单轴晶体)
2.
利用折射率曲面也可以确定与入射光相应的反射光、折 射光的传播方向。但为了简明起见,通常是采用波矢曲面进 行。斯涅耳作图法就是利用波矢曲面确定反射光、折射光传
图4-30 给出了以界面Σ上任一点A为原点,在晶体一侧
这就是双折射现象。
对于晶体内部的双反射现象,可以类似处理:以界面上
任一点为原点,在界面Σ两侧画出晶体的波矢面,其中入射
光的波矢面画在晶体外侧,自原点引出与入射光波法线方向
平行的直线,确定出入射波矢ki,过ki末端作Σ的垂线,在
晶体内侧交反射光波矢面于两点,从而可定出两个反射波矢
kr′和kr″
应当指出的是,由这个作图法所确定的两个反射波矢和 两个折射波矢只是允许的或可能的两个波矢,至于实际上两 个波矢是否同时存在,要看入射光是否包含有各反射光或各 折射光的场矢量方向上的分量。
反射和折射的波动理论解释

反射和折射的波动理论解释反射和折射是光在不同介质中传播时遇到的常见现象。
波动理论被广泛应用于解释这些现象。
在波动理论中,光被视为一种波动,具有特定的波长和频率。
通过对波动的性质进行分析,我们可以更深入地理解反射和折射的原理。
首先,让我们来探讨反射现象。
当光线射向一个光滑表面时,如镜子或光洁水面,它会从表面弹回,这就是反射。
波动理论解释这一现象的关键在于考虑到光波的入射角和反射角是相等的。
入射角是光线与垂直于表面的线的夹角,而反射角是光线与法线的夹角。
根据波动理论,光的波长在不同介质中传播速度不同,因此入射角和反射角相等可以解释为光波在不同介质中传播速度改变而导致的。
当光从一种介质传播到另一种介质时,光线会发生折射。
这是因为不同介质中的光速度不同,导致光线的传播方向发生改变。
根据波动理论,折射现象可以通过折射定律进行解释。
折射定律表明,入射角和折射角满足一个简单的数学关系,即n1*sin(theta1) = n2*sin(theta2),其中n1和n2分别表示两种介质的折射率,theta1和theta2分别表示入射角和折射角。
波动理论还可以解释由折射引起的光线弯曲现象。
当光线从一种介质传播到另一种介质时,由于折射定律的存在,光线会弯曲。
这可以解释为波动理论中的相位速度改变。
由于光速在不同介质中的改变,导致光线的相位速度也发生改变,从而导致光线的弯曲。
另一个有趣的现象是全反射现象,它发生在光从一种介质传播到折射率较低的介质时,入射角大于临界角时发生。
对于入射角大于临界角的情况,折射定律无解,因此光线不能穿过界面,而是完全反射回原来的介质。
波动理论可以解释全反射现象,将其视为波在介质边界上的干涉结果。
全反射是光波在垂直于界面的金属或介质中传播的方式之一。
总的来说,反射和折射的波动理论解释涉及到入射角和反射角之间的关系以及入射角和折射角之间的关系。
通过考虑光波的性质,如波长,频率和波速,波动理论提供了对这些现象的深入理解。
反射率和透射率

1>B, rp0,p分量有相位突变
(rs = )
(b).光由光密到光疏(n1 > n2)
1.0
0.5
rs
0.0
-0.5
rp θB
-1.0 0 10 20 30 40 50 60 70 80 90
01<C,rs0,说明
反射光中的s分量与入
射光中的s分量同相位
1<B,rp<0,p分量有相位 突变(rp = ); B<1<C,rp0,p分量同相
则
tan r
cos(1 cos(1
2) 2)
tani
tant cos(1 2 )tani
1.2.6.全内反射现象
1.反射波 2.衰逝波
1. 反射波
光由光密介质射向光疏介质( n1 > n2 )时,产生全反射
sin C
n2 n1
当 1 > C时,有sin 1 > n2/n1,折射定律不再成立。 为了仍然能够运用菲涅耳公式,把 cos 2 表示为虚数:
rs rp
2 arctancos1
sin 2 1 n2 s in 1
5437 5437
菲涅耳菱体
经两次全反射,s 分量和 p 分量的相位差为90
全反射应用 1 ——光纤传输
n0
n2
n1
光纤传光原理
sin M
1 n0
n12 n22
全反射应用 2 ——光纤传感
若n1 < n2,1 ≈ 90°, |rs| = |rp| , rs < 0 , rp < 0 。
因此,在入射点处,入射光矢量Ei与反射光矢量Er方向近似 相反,即掠入射时的反射光在n1 < n2时,将产生半波损失。
倏逝波在金属表面的应用

倏逝波在金属表面的应用
倏逝波在金属表面的应用主要体现在表面等离子体共振(SPR)的实验中。
当光波入射角大于临界角时,射入金属表面的光会在金属表面发生全内反射,并且向介质中射入约一个波长的深度。
这部分折射光被称为界面全反射的倏逝波,它可以引发金属表面的自由电子相对于正电荷密度的起伏振荡,被称为金属的等离子体振荡。
在特定条件下,等离子体振荡与倏逝波的频率和波数相等,二者将发生共振,形成了电子的集体振荡,入射光被吸收,能量转移给表面等离子体,反射光能量急剧下降,在反射光谱上出现共振峰,引起表面等离子共振效应。
为了证明这一原理的存在,可以在A、B介质表面镀上一层金属(如Ag),其厚度要小于100纳米。
当入射光源以相应的波长或相应的角度入射到金
属和介质的中间位置时,表面等离子波就会和倏逝波产生共振。
这种共振现象我们称作表面等离子体共振,相应的入射角称作共振角,相应的波长称作共振波长。
以上信息仅供参考,如需了解更多信息,建议查阅相关文献或咨询专业人士。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
s分量的折射波(波矢k(t)为复数值)
• 金属中的折射光是一 个沿-z方向衰减的非 均匀波。 • z=常数的平面为等振 幅面; • 等相位面为平面,满 足
(k sin θ i ) x − k z( t )' z = 常数
• 在界面上的任意点、任意时刻,折射光与入射光都相差一个相位φts。 在界面上的任意点、任意时刻, • 折射光的透射深度很小(nm级)。入射光只能透入金属表面很薄的一层内。 折射光的透射深度很小(nm (nm级 入射光只能透入金属表面很薄的一层内。 • 在通常情况下,金属是不透明的,只有把它做成很薄的薄膜(比如镀铝的 在通常情况下,金属是不透明的,只有把它做成很薄的薄膜( 半透膜) 才可以变成半透明的。 半透膜)时,才可以变成半透明的。
11.3.3 金属表面反射的频率特性
• 电子理论的观点,电导率起 因于金属中有密度很大的自 由电子(约1022/cm3)。 • 当光照射到清洁磨光的金属 表面时,自由电子将在光场 的作用下强迫振动,产生次 波,这些次波构成了很强的 反射波和较弱的透射波,透 射波将很快地被吸收掉。
• 不同金属自由电子密度越大(电导率越大),反射本领越大。 • 同一种金属,入射光频率(波长)不同, 反射率也不同。频率较低 的红外线主要对金属中的自由电子发生作用,而频率较高的可见光 和紫外光可对金属中的束缚电子发生作用。
p分量的反射、折射波
• 讨论方法与s分量相同。 • 由于φrp与φrs不同,金属表面的反射将改变入 射光的偏振态。
–若入射光为线偏振光,其振动面与入射面间有一定 的夹角,则由于反射光的s分量和p分量之间有一个相 位差Δφ=φrp-φrs,而使反射光变成椭圆偏振光。 –对于椭圆偏振光的参数进行测量,可以确定出金属 材料的复折射率n,也可求出ε、μ、 σ等物质常数。 - -椭偏法测量金属的折射率
− n ' ' ( k 0 ⋅r ) c
• 金属中的单色平面光波场表示式为
E = E0 e
ω
= E0 e
ω
e
−i[ωt − n '( k 0 ⋅r )] c
ω
• 金属中传播的单色平面光波是一个衰减的平面波; • n’是光波在金属中传播时的折射率; • n”是描述光在金属中传播时衰减特性的量,都是 光频率ω的函数。
11.3.2 光在金属表面的反射和折射
• 光在金属表面上的反射和折 射,其讨论方法与电介质界 面的情况相同。 • 分别讨论s分量、p分量的反 射和折射特性。 • 具体讨论不作要求。 • 结论: • s分量的反射波(波矢k(r)为实数值): –按照反射定律(θr=θi)传播的均匀波(等振幅面与 等相位面一致)。 iϕ rs –由于rs为复数值, rs =| rs | e 在界面上的反射波与入射波也相差一个相位φrs。
11.3.1 光波在金属中的传播
• 设金属是一种介电常数为ε、磁导率为μ,电导率为σ的 均匀各向同性介质,则物质方程中的J=σE必须予以考虑。 • 由麦克斯韦方程,可得金属中光波所满足的波动方程为 σ ∂2E • 其中 α = 1 + i ∇ 2 E − µεα =0 εω ∂t 2 这两个波动方程与(11 13)式 (11这两个波动方程与(11-13)式 的差别在于以复数值μεα ∂2H 2 ∇ H − µεα = 0 2 代替了με。 ∂t 金属中的单色平面光波, 金属中的单色平面光波, 其光场表示式为 ~ − i ( ω t − k k 0 ⋅r ) 0
11.3 光波在金属表面上的反射和折射
• 前面讨论了,光在非导电(σ=0)各向同性 均匀介质及其界面上的传播规律。 • 对于金属,它与各向同性介质的主要差别 是电导率(σ)不等于0 ,金属导致光波衰 减,金属对光波几乎不透明。 11.3.1 光波在金属中的传播 11.3.2 光在金属表面的反射和折射 11.3.3 金属表面反射的频率特性
E = E e
复波数 复折射率
• 复波数 • 复折射率
~ σ k = ω µεα = ω µ ε + i ω
~ ~ = c k = c n
ω
• 可写成实部n’、虚部n”
−i[ωt − ( n ' + in n ( k 0 ⋅r )] c
σ µε + i ω ~ n = n '+ in "
