(完整版)QPSK调制原理及matlab程序实现
QPSK调制与解调系统的MATLAB实现

QPSK调制与解调系统的MATLAB实现与性能分析摘要:QPSK是英文QuadraturePhaseShiftKeying的缩略语简称,意为正交相移键控,是一种数字调制方式。
四相相移键控信号简称“QPSK〞。
在现代通信系统中,调制与解调是必不可少的重要手段。
所谓调制,就是把信号转换成适合在信道中传输的形式的一种过程。
解调如此是调制的相反过程,而从已调制信号中恢复出原信号。
本课程设计主要介绍通过进展QPSK调制解调的基带仿真,对实现中影响该系统性能的几个重要问题进展了研究。
针对QPSK的特点,调制前后发生的变化,加上噪声后波形出现的各种变化,通过星座图、眼图、波形图等来观察。
程序设计与仿真均采用MATLAB集成环境下的Simulink仿真平台,最后仿真详单与理论分析一致。
1 引言本课程设计主要是学会运用MATLAB中的Simulink来实现数字基带信号的模拟传输。
在知道其传输原理的情况下,将仿真电路到Simulink之中。
并且对正交振幅调制、解调过程的频谱和波形的分析,同时在无噪声和有噪声的进展分析,参加高斯白噪声,瑞利噪声,莱斯噪声分析调制解调后的频谱、波形,观察其误码率。
通过本课程的学习我们不仅能加深理解和巩固理论课上所学的有关QPSK调制与解调的根本概念、根本理论和根本方法,而且能锻炼我们分析问题和解决问题的能力;同时对我们独立工作的习惯和科学素质进展培养,为今后参加科学工作打下良好的根底。
利用MATLAB集成环境下的Simulink仿真平台,设计一个QPSK调制与解调系统.用示波器观察调制前后的信号波形;用频谱分析模块观察调制前后信号频谱的变化;加上各种噪声源,用误码测试模块测量误码率;最后根据运行结果和波形来分析该系统性能。
1〕熟悉MATLAB环境下的Simulink仿真平台,熟悉QPSK系统的调制解调原理,构建QPSK调制解调电路图.2〕用示波器观察调制前后的信号波形,用频谱分析模块观察调制前后信号的频谱的变化。
BPSK和QPSK调制解调原理及MATLAB程序

2.1 PSK调制方式PSK原理介绍(以2-PSK为例)移相键控(PSK)又称为数字相位调制,二进制移相键控记作2PSK。
绝对相移是利用载波的相位(指初相)直接表示数字信号的相移方式。
二进制相移键控中,通常用相位0 和π来分别表示“0”或“1”。
2PSK 已调信号的时域表达式为s2psk(t)=s(t)cosωct, 2PSK移相键控中的基带信号与频移键控和幅度键控是有区别的,频移键控和幅度键控为单极性非归零矩形脉冲序列,移相键控为为双极性数字基带信号,就模拟调制法而言,与产生2ASK 信号的方法比较,只是对s(t)要求不同,因此2PSK 信号可以看作是双极性基带信号作用下的DSB 调幅信号。
在二进制数字调制中,当正弦载波的相位随二进制数字基带信号离散变化时,则产生二进制移相键控(2PSK)信号。
通常用已调信号载波的 0°和 180°分别表示二进制数字基带信号的 1 和 0。
二进制移相键控信号的时域表达式为e2PSK(t)=[nna g(t-nT s)]cosw c t其中, an与2ASK和2FSK时的不同,在2PSK调制中,an应选择双极性。
1, 发送概率为Pan=-1, 发送概率为1-P若g(t)是脉宽为Ts, 高度为1的矩形脉冲时,则有cosωct, 发送概率为Pe2PSK(t)=-cosωct, 发送概率为1-P由上式(6.2-28)可看出,当发送二进制符号1时,已调信号e2PSK(t)取0°相位,发送二进制符号0时,e2PSK(t)取180°相位。
若用φn表示第n个符号的绝对相位,则有0°, 发送 1 符号φn=180°, 发送 0 符号由于在2PSK信号的载波恢复过程中存在着180°的相位模糊,所以2PSK信号的相干解调存在随机的“倒π”现象,从而使得2PSK 方式在实际中很少采用。
为了解决2PSK 信号解调过程的反向工作问题, 提出了二进制差分相位键控(2DPSK),这里不再详述。
qpsk调制 matlab代码

QPSK(Quadrature Phase Shift Keying)调制是一种常用的数字调制方式,它使用4个相互正交的相位来表示数字信号,从而实现信号的传输和识别。
在无线通信、数字通信和数字电视等领域都有着广泛的应用。
在本文中,我们将使用Matlab编写QPSK调制的代码,以帮助读者更好地理解QPSK调制的原理和实现。
1. QPSK调制简介QPSK调制是一种常用的相位调制方式,它将两路独立的数据流分别调制到正交的载波上,实现了频谱的高效利用和传输速率的提高。
QPSK调制共有4种状态,分别是0°、90°、180°、270°,对应的二进制数据为00、01、10、11。
通过改变相位来表示不同的数字信号,QPSK调制在噪声干扰下具有一定的抗干扰能力,因此在实际应用中得到了广泛的应用。
2. Matlab实现QPSK调制在Matlab中,我们可以利用其强大的信号处理工具箱实现QPSK调制的模拟,并通过仿真结果来验证QPSK调制的正确性。
以下是实现QPSK调制的Matlab代码:```matlab设置参数fc = 1000; 载波频率fs = 0; 采样频率T = 1; 信号持续时间t = 0:1/fs:T-1/fs; 时间序列data = randi([0 1],1,100); 随机生成100个二进制数据数据映射为QPSK调制信号data_I = 2*data(1:2:end)-1; I路数据data_Q = 2*data(2:2:end)-1; Q路数据s = (data_I + 1i*data_Q).*exp(1i*2*pi*fc*t); QPSK调制信号显示QPSK调制信号subplot(211)plot(t,real(s))title('QPSK调制信号-I路')xlabel('时间')ylabel('幅度')subplot(212)plot(t,imag(s))title('QPSK调制信号-Q路')xlabel('时间')ylabel('幅度')```在上述代码中,我们首先设置了载波频率fc、采样频率fs、信号持续时间T和时间序列t,然后随机生成了100个二进制数据,并分别将其映射到I路和Q路数据中。
BPSK和QPSK调制解调原理及MATLAB程序资料

2.1 PSK调制方式PSK原理介绍(以2-PSK为例)移相键控(PSK)又称为数字相位调制,二进制移相键控记作2PSK。
绝对相移是利用载波的相位(指初相)直接表示数字信号的相移方式。
二进制相移键控中,通常用相位0 和π来分别表示“0”或“1”。
2PSK 已调信号的时域表达式为s2psk(t)=s(t)cosωct, 2PSK移相键控中的基带信号与频移键控和幅度键控是有区别的,频移键控和幅度键控为单极性非归零矩形脉冲序列,移相键控为为双极性数字基带信号,就模拟调制法而言,与产生2ASK 信号的方法比较,只是对s(t)要求不同,因此2PSK 信号可以看作是双极性基带信号作用下的DSB 调幅信号。
在二进制数字调制中,当正弦载波的相位随二进制数字基带信号离散变化时,则产生二进制移相键控(2PSK)信号。
通常用已调信号载波的 0°和 180°分别表示二进制数字基带信号的 1 和 0。
二进制移相键控信号的时域表达式为e2PSK(t)=[nna g(t-nT s)]cosw c t其中, an与2ASK和2FSK时的不同,在2PSK调制中,an应选择双极性。
1, 发送概率为Pan=-1, 发送概率为1-P若g(t)是脉宽为Ts, 高度为1的矩形脉冲时,则有cosωct, 发送概率为Pe2PSK(t)=-cosωct, 发送概率为1-P由上式(6.2-28)可看出,当发送二进制符号1时,已调信号e2PSK(t)取0°相位,发送二进制符号0时,e2PSK(t)取180°相位。
若用φn表示第n个符号的绝对相位,则有0°, 发送 1 符号φn=180°, 发送 0 符号由于在2PSK信号的载波恢复过程中存在着180°的相位模糊,所以2PSK信号的相干解调存在随机的“倒π”现象,从而使得2PSK 方式在实际中很少采用。
为了解决2PSK 信号解调过程的反向工作问题, 提出了二进制差分相位键控(2DPSK),这里不再详述。
qpsk 信号 matlab仿真代码

1. 介绍QPSK信号QPSK (Quadrature Phase Shift Keying) 是一种数字调制技术,常用于无线通信和数字通信系统中。
它是通过改变相位来传输数字信息的一种调制方式,相较于单相位调制方式,QPSK可以提高信号传输效率和频谱利用率。
2. QPSK信号的生成原理QPSK信号的产生可以通过正交调制的方式完成,即将数据流分为两个独立的流并分别与正弦和余弦信号相乘,经过合并后即可生成QPSK信号。
具体过程如下:(1) 将二进制数据流分为实部和虚部,分别代表I信号和Q信号;(2) 分别对I信号和Q信号进行调制,得到两路调制信号;(3) 将两路调制信号通过信号合并器得到QPSK信号。
3. QPSK信号的Matlab仿真代码在Matlab中,可以通过编程实现QPSK信号的生成和仿真。
以下是一个简单的QPSK信号Matlab仿真代码示例:```Matlab设置QPSK调制参数M = 4; 调制阶数msg = randi([0 M-1],10000,1); 随机生成10000个0到M-1的整数,模拟二进制信息流txSig = qammod(msg,M); QAM调制绘制星座图scatterplot(txSig) 绘制QPSK星座图添加高斯噪声rxSig = awgn(txSig, 10); 添加信道噪声,信噪比为10dB解调rxMsg = qamdemod(rxSig,M); QPSK解调[numErrors,ber] = biterr(msg,rxMsg); 计算比特错误率disp(['比特错误率为:',num2str(ber)])```4. QPSK信号仿真结果分析通过上述Matlab代码,我们可以得到QPSK信号的仿真结果。
通过绘制星座图可以直观地观察到QPSK信号在复平面上的分布情况。
随后,我们可以添加高斯噪声,模拟信道中的干扰,然后进行解调并计算比特错误率。
5. 结论通过以上QPSK信号的Matlab仿真代码,我们可以成功生成和仿真QPSK信号,并得到比特错误率等性能指标。
(完整word版)BPSK和QPSK调制解调原理及MATLAB程序

2.1 PSK调制方式PSK原理介绍(以2-PSK为例)移相键控(PSK)又称为数字相位调制,二进制移相键控记作2PSK。
绝对相移是利用载波的相位(指初相)直接表示数字信号的相移方式。
二进制相移键控中,通常用相位0 和π来分别表示“0”或“1”。
2PSK 已调信号的时域表达式为s2psk(t)=s(t)cosωct, 2PSK移相键控中的基带信号与频移键控和幅度键控是有区别的,频移键控和幅度键控为单极性非归零矩形脉冲序列,移相键控为为双极性数字基带信号,就模拟调制法而言,与产生2ASK 信号的方法比较,只是对s(t)要求不同,因此2PSK 信号可以看作是双极性基带信号作用下的DSB 调幅信号。
在二进制数字调制中,当正弦载波的相位随二进制数字基带信号离散变化时,则产生二进制移相键控(2PSK)信号。
通常用已调信号载波的 0°和 180°分别表示二进制数字基带信号的 1 和 0。
二进制移相键控信号的时域表达式为e2PSK(t)=[nna g(t-nT s)]cosw c t其中, an与2ASK和2FSK时的不同,在2PSK调制中,an应选择双极性。
1, 发送概率为Pan=-1, 发送概率为1-P若g(t)是脉宽为Ts, 高度为1的矩形脉冲时,则有cosωct, 发送概率为Pe2PSK(t)=-cosωct, 发送概率为1-P由上式(6.2-28)可看出,当发送二进制符号1时,已调信号e2PSK(t)取0°相位,发送二进制符号0时,e2PSK(t)取180°相位。
若用φn表示第n个符号的绝对相位,则有0°, 发送 1 符号φn=180°, 发送 0 符号由于在2PSK信号的载波恢复过程中存在着180°的相位模糊,所以2PSK信号的相干解调存在随机的“倒π”现象,从而使得2PSK 方式在实际中很少采用。
为了解决2PSK 信号解调过程的反向工作问题, 提出了二进制差分相位键控(2DPSK),这里不再详述。
MATLAB_QPSK调制与解调-(4820)
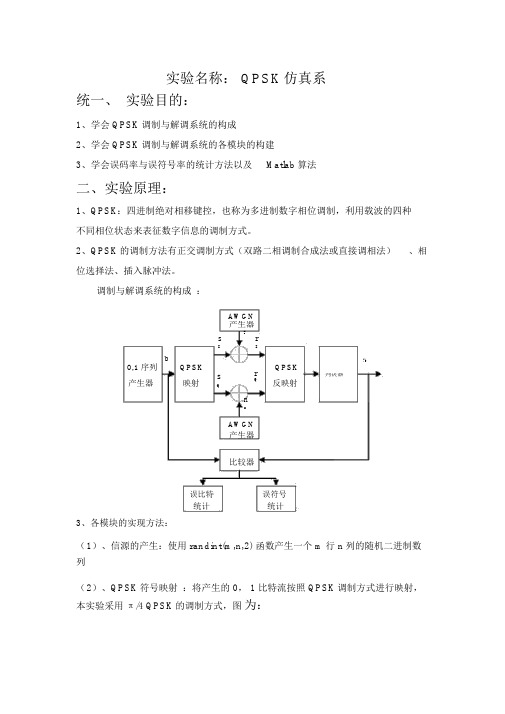
实验名称: QPSK仿真系统一、实验目的:1、学会 QPSK 调制与解调系统的构成2、学会 QPSK 调制与解调系统的各模块的构建3、学会误码率与误符号率的统计方法以及Matlab 算法二、实验原理:1、QPSK:四进制绝对相移键控,也称为多进制数字相位调制,利用载波的四种不同相位状态来表征数字信息的调制方式。
2、QPSK 的调制方法有正交调制方式(双路二相调制合成法或直接调相法)、相位选择法、插入脉冲法。
调制与解调系统的构成:AWGN产生器ncs rI Ib?b0,1序列QPSKr QPSKs判决器产生器映射Q反映射QnsAWGN产生器比较器误比特统计误符号统计3、各模块的实现方法:(1)、信源的产生:使用randint(m,n,2)函数产生一个 m 行 n 列的随机二进制数列(2)、QPSK 符号映射:将产生的 0, 1 比特流按照 QPSK 调制方式进行映射,本实验采用π/4 QPSK 的调制方式,图为:10000111(3)、AWGN 信号产生: AWGN 产生器就是产生满足均值为 0,方差为 1 的高斯白噪声。
实验中使用 randn(m,n)函数产生一个 m 行 n 列的高斯噪声序列。
(4)、信号幅度控制:根据 AWGN 信道模型,接收信号可以分别表示为r Q s Q n Qα 就是当噪声功率归一化为r I s I n I1(0均值,方差为 1)时,根据信噪比关系而计算出来的信号平均幅度SNR 10log v s2vs2SNR v2sqrt v n10 ^10 nv s( 5)、QPSK 反映射及判决:对接收到的信号在 4 种可能的四种信号向量 [(1,0), (0,1), (-1,0), (0,-1)] 上投影 (即进行点积 )。
投影最大的值所对应的信号向量就是所发送信号的符号值,然后恢复出比特流(6)、误码率及误符号率统计:误码率:将检测出来的比特流和发送的原始比特流进行比较,统计出出现错误的比特数误符号率:将检测出来的比特流变成两组,构成符号,和发送端符号映射后的符号流进行比较,只要符号中任错一 bit,就算该符号出错。
QPSK通信系统性能分析与MATLAB仿真

QPSK通信系统性能分析与MATLAB仿真QPSK是一种常见的调制方式,广泛应用于数字通信系统中。
在QPSK通信系统中,传输的数据被分为两个相互正交的子载波进行调制,每个子载波可以携带2位二进制数据。
本文将对QPSK通信系统的性能进行分析,并使用MATLAB进行仿真。
首先,我们需要了解QPSK调制的基本原理。
在QPSK中,发送端的数据被分为两个二进制数据流,分别称为I路和Q路。
通过调制器对I路和Q路进行调制生成正交的载波信号,然后进行并行传输。
接收端接收到信号后,通过对两路信号进行解调,并将解调后的数据进行重新组合,得到原始数据。
为了分析QPSK通信系统的性能,我们需要考虑到噪声的影响。
在传输过程中,信号会受到各种噪声的干扰,如加性高斯白噪声。
这些噪声会使得接收信号误码率增加。
我们可以使用误码率(Bit Error Rate)来评估系统的性能,误码率是指发送的比特和接收到的比特不一致的比率。
为了进行性能分析,我们可以进行理论分析和仿真两个步骤。
在理论分析中,我们可以通过理论计算得到系统的误码率曲线。
而在仿真过程中,我们可以通过编写一段MATLAB代码来模拟整个通信系统,然后进行模拟传输并统计误码率。
在仿真过程中,我们首先需要生成发送端的数据流。
这可以通过随机生成0和1的序列来实现。
然后,我们将数据流分为I路和Q路,并对每一路进行调制生成载波信号。
接下来,我们引入噪声,在信号上添加高斯白噪声。
然后,我们将接收到的信号进行解调,并将解调后的数据重新组合。
最后,我们统计误码率和信噪比(Signal-to-Noise Ratio)之间的关系,并绘制性能曲线。
通过MATLAB进行仿真,我们可以调整信噪比,并观察误码率的变化。
通过仿真实验,我们可以得到系统在不同信噪比下的性能表现。
通过比较理论结果和仿真结果,我们可以验证我们的分析是否准确。
总结起来,QPSK通信系统的性能分析是一个重要的研究课题。
通过理论分析和MATLAB仿真,我们可以得到系统在不同信噪比下的性能表现,并且验证我们的分析是否准确。
MATLAB-QPSK调制与解调

MATLAB仿真QPSK调制与解调2011-06-22 20:16:45| 分类:学习| 标签:qpsk matlab |字号大中小订阅注意B方式的4PSK用的比较多。
I 路信号是用余弦载波,由2进制数据流的奇数序列组成;Q路信号用正弦载波,由2进制数据流的偶数序列组成。
下面的a是Idata,b就是Qdata,它们分布与各自的载波相乘分别输出I 路信号和Q 路信号。
I 路信号加上Q路信号就是QPSK输出信号。
当I 路载波信号是0相位时为1,是180°相位时为0;当Q路载波信号是0相位时为1,是180°相位时为0。
比如下图的‘11’数据cos(theta) + sin(theta) =sqrt(2)*sin(theta + 45°)是相位超前sin(theta) 45°QPSK即四进制移向键控(Quaternary Phase Shift Keying),它利用载波的四种不同相位来表示数字信息,由于每一种载波相位代表两个比特信息,因此每个四进制码元可以用两个二进制码元的组合来表示。
两个二进制码元中的前一个码元用a表示,后一个码元用b表示。
% QPSK调相法基本原理解释clear allclose all% x1是类似[1 1 -1 -1 -1 -1 1 1]的分布,作用是控制相位的180°反转。
%由于仿真中载波的频率是f=1Hz,所以1s的间隔内有一个完整周期的正弦波t=[-1:0.01:7-0.01]; % t共800个数据,-1~7st1 = [0:0.01:8-0.01]; %t1也是800个数据点,0 ~8stt=length(t); % tt=800x1=ones(1,800);for i=1:ttif (t(i)>=-1 & t(i)<=1) | (t(i)>=5& t(i)<=7);x1(i)=1;else x1(i)=-1;endendt2 = 0:0.01:7-0.01; %t2是700个数据点,是QPSK_rc绘图的下标t3 = -1:0.01:7.1-0.01; %t3有810个数据点,是i_rc的时间变量t4 = 0:0.01:8.1-0.01; %t4有810个数据点,是q_rc的时间变量%x2是类似于[1 1 -1 -1 1 1 1 1]的分布,作用是控制相位的180°反转tt1=length(t1);x2=ones(1,800);for i=1:tt1if (t1(i)>=0 & t1(i)<=2) | (t1(i)>=4& t1(i)<=8);x2(i)=1;else x2(i)=-1;endendf=0:0.1:1;xrc=0.5+0.5*cos(pi*f); %xrc是一个低通特性的传输函数y1=conv(x1,xrc)/5.5; %y1和x1 实际上没什么区别,仅仅是上升沿、下降沿有点过渡带y2=conv(x2,xrc)/5.5; % y2和x2 实际上没什么区别,仅仅是上升沿、下降沿有点过渡带n0=randn(size(t2));f1=1;i=x1.*cos(2*pi*f1*t); % x1就是I dataq=x2.*sin(2*pi*f1*t1); %x2就是Q dataI=i(101:800);Q=q(1:700);QPSK=sqrt(1/2).*I+sqrt(1/2).*Q;QPSK_n=(sqrt(1/2).*I+sqrt(1/2).*Q)+n0;n1=randn(size(t2));i_rc=y1.*cos(2*pi*f1*t3); % y1就是I data,i_rc可能是贴近实际的波形,i则是理想波形q_rc=y2.*sin(2*pi*f1*t4); %y2就是Q data,q_rc可能是贴近实际的波形,q则是理想波形I_rc=i_rc(101:800);Q_rc=q_rc(1:700);QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);QPSK_rc_n1=QPSK_rc+n1;figure(1)subplot(4,1,1);plot(t3,i_rc);axis([-1 8 -1 1]);ylabel('a序列');subplot(4,1,2);plot(t4,q_rc);axis([-1 8 -1 1]);ylabel('b序列');subplot(4,1,3);plot(t2,QPSK_rc);axis([-1 8 -1 1]);ylabel('合成序列');subplot(4,1,4);plot(t2,QPSK_rc_n1);axis([-1 8 -1 1]);ylabel('加入噪声');上图解释:合成序列表示的数据:11 01 00 00 01 11 11相对于sin(theta)合成序列相位: Pi/4, 3/4Pi[即sin(theta-45)=sin(theta-45+180)], -3/4Pi[即-sin(theta+45)], -3/4Pi[即-sin(theta+45)] , 3/4Pi, Pi/4, Pi/4。
QPSK调制与解调在MATLAB平台上的实现(word文档良心出品)
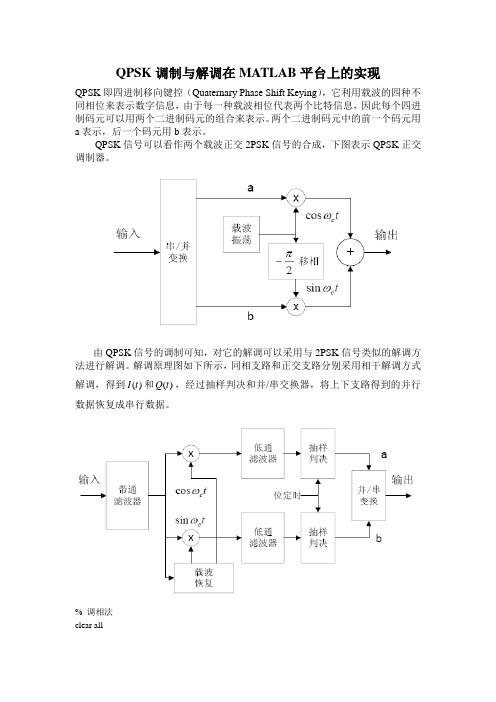
QPSK调制与解调在MATLAB平台上的实现QPSK即四进制移向键控(Quaternary Phase Shift Keying),它利用载波的四种不同相位来表示数字信息,由于每一种载波相位代表两个比特信息,因此每个四进制码元可以用两个二进制码元的组合来表示。
两个二进制码元中的前一个码元用a表示,后一个码元用b表示。
QPSK信号可以看作两个载波正交2PSK信号的合成,下图表示QPSK正交调制器。
由QPSK信号的调制可知,对它的解调可以采用与2PSK信号类似的解调方法进行解调。
解调原理图如下所示,同相支路和正交支路分别采用相干解调方式解调,得到()Q t,经过抽样判决和并/串交换器,将上下支路得到的并行I t和()数据恢复成串行数据。
% 调相法clear allclose allt=[-1:0.01:7-0.01];tt=length(t);x1=ones(1,800);for i=1:ttif (t(i)>=-1 & t(i)<=1) | (t(i)>=5& t(i)<=7);x1(i)=1;else x1(i)=-1;endendt1=[0:0.01:8-0.01];t2=0:0.01:7-0.01;t3=-1:0.01:7.1-0.01;t4=0:0.01:8.1-0.01;tt1=length(t1);x2=ones(1,800);for i=1:tt1if (t1(i)>=0 & t1(i)<=2) | (t1(i)>=4& t1(i)<=8);x2(i)=1;else x2(i)=-1;endendf=0:0.1:1;xrc=0.5+0.5*cos(pi*f);y1=conv(x1,xrc)/5.5;y2=conv(x2,xrc)/5.5;n0=randn(size(t2));f1=1;i=x1.*cos(2*pi*f1*t);q=x2.*sin(2*pi*f1*t1);I=i(101:800);Q=q(1:700);QPSK=sqrt(1/2).*I+sqrt(1/2).*Q;QPSK_n=(sqrt(1/2).*I+sqrt(1/2).*Q)+n0;n1=randn(size(t2));i_rc=y1.*cos(2*pi*f1*t3);q_rc=y2.*sin(2*pi*f1*t4);I_rc=i_rc(101:800);Q_rc=q_rc(1:700);QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);QPSK_rc_n1=QPSK_rc+n1;figure(1)subplot(4,1,1);plot(t3,i_rc);axis([-1 8 -1 1]);ylabel('a序列');subplot(4,1,2);plot(t4,q_rc);axis([-1 8 -1 1]);ylabel('b序列');subplot(4,1,3);plot(t2,QPSK_rc);axis([-1 8 -1 1]);ylabel('合成序列'); subplot(4,1,4);plot(t2,QPSK_rc_n1);axis([-1 8 -1 1]);ylabel('加入噪声');效果图:% 设定T=1,加入高斯噪声clear allclose all% 调制bit_in = randint(1e3, 1, [0 1]);bit_I = bit_in(1:2:1e3);bit_Q = bit_in(2:2:1e3);data_I = -2*bit_I+1;data_Q = -2*bit_Q+1;data_I1=repmat(data_I',20,1);data_Q1=repmat(data_Q',20,1);for i=1:1e4data_I2(i)=data_I1(i);data_Q2(i)=data_Q1(i);end;f=0:0.1:1;xrc=0.5+0.5*cos(pi*f);data_I2_rc=conv(data_I2,xrc)/5.5;data_Q2_rc=conv(data_Q2,xrc)/5.5;f1=1;t1=0:0.1:1e3+0.9;n0=rand(size(t1));I_rc=data_I2_rc.*cos(2*pi*f1*t1);Q_rc=data_Q2_rc.*sin(2*pi*f1*t1); QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc); QPSK_rc_n0=QPSK_rc+n0;% 解调I_demo=QPSK_rc_n0.*cos(2*pi*f1*t1);Q_demo=QPSK_rc_n0.*sin(2*pi*f1*t1);% 低通滤波I_recover=conv(I_demo,xrc);Q_recover=conv(Q_demo,xrc);I=I_recover(11:10010);Q=Q_recover(11:10010);t2=0:0.05:1e3-0.05;t3=0:0.1:1e3-0.1;% 抽样判决data_recover=[];for i=1:20:10000data_recover=[data_recover I(i:1:i+19) Q(i:1:i+19)];end;bit_recover=[];for i=1:20:20000if sum(data_recover(i:i+19))>0data_recover_a(i:i+19)=1;bit_recover=[bit_recover 1];elsedata_recover_a(i:i+19)=-1;bit_recover=[bit_recover -1];endenderror=0;dd = -2*bit_in+1;ddd=[dd'];ddd1=repmat(ddd,20,1);for i=1:2e4ddd2(i)=ddd1(i);endfor i=1:1e3if bit_recover(i)~=ddd(i)error=error+1;endendp=error/1000;figure(1)subplot(2,1,1);plot(t2,ddd2);axis([0 100 -2 2]);title('原序列');subplot(2,1,2);plot(t2,data_recover_a);axis([0 100 -2 2]);title('解调后序列'); 效果图:% 设定T=1, 不加噪声clear allclose all% 调制bit_in = randint(1e3, 1, [0 1]);bit_I = bit_in(1:2:1e3);bit_Q = bit_in(2:2:1e3);data_I = -2*bit_I+1;data_Q = -2*bit_Q+1;data_I1=repmat(data_I',20,1);data_Q1=repmat(data_Q',20,1);for i=1:1e4data_I2(i)=data_I1(i);data_Q2(i)=data_Q1(i);end;t=0:0.1:1e3-0.1;f=0:0.1:1;xrc=0.5+0.5*cos(pi*f);data_I2_rc=conv(data_I2,xrc)/5.5;data_Q2_rc=conv(data_Q2,xrc)/5.5;f1=1;t1=0:0.1:1e3+0.9;I_rc=data_I2_rc.*cos(2*pi*f1*t1);Q_rc=data_Q2_rc.*sin(2*pi*f1*t1); QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);% 解调I_demo=QPSK_rc.*cos(2*pi*f1*t1);Q_demo=QPSK_rc.*sin(2*pi*f1*t1);I_recover=conv(I_demo,xrc);Q_recover=conv(Q_demo,xrc);I=I_recover(11:10010);Q=Q_recover(11:10010);t2=0:0.05:1e3-0.05;t3=0:0.1:1e3-0.1;data_recover=[];for i=1:20:10000data_recover=[data_recover I(i:1:i+19) Q(i:1:i+19)]; end;ddd = -2*bit_in+1;ddd1=repmat(ddd',10,1);for i=1:1e4ddd2(i)=ddd1(i);endfigure(1)subplot(4,1,1);plot(t3,I);axis([0 20 -6 6]);subplot(4,1,2);plot(t3,Q);axis([0 20 -6 6]);subplot(4,1,3);plot(t2,data_recover);axis([0 20 -6 6]); subplot(4,1,4);plot(t,ddd2);axis([0 20 -6 6]);效果图:% QPSK误码率分析SNRindB1=0:2:10;SNRindB2=0:0.1:10;for i=1:length(SNRindB1)[pb,ps]=cm_sm32(SNRindB1(i));smld_bit_err_prb(i)=pb;smld_symbol_err_prb(i)=ps;end;for i=1:length(SNRindB2)SNR=exp(SNRindB2(i)*log(10)/10);theo_err_prb(i)=Qfunct(sqrt(2*SNR)); end;title('QPSK误码率分析');semilogy(SNRindB1,smld_bit_err_prb,'*');axis([0 10 10e-8 1]);hold on;% semilogy(SNRindB1,smld_symbol_err_prb,'o'); semilogy(SNRindB2,theo_err_prb);legend('仿真比特误码率','理论比特误码率'); hold off;function[y]=Qfunct(x)y=(1/2)*erfc(x/sqrt(2));function[pb,ps]=cm_sm32(SNRindB)N=10000;E=1;SNR=10^(SNRindB/10);sgma=sqrt(E/SNR)/2;s00=[1 0];s01=[0 1];s11=[-1 0];s10=[0 -1];for i=1:Ntemp=rand;if (temp<0.25)dsource1(i)=0;dsource2(i)=0;elseif (temp<0.5)dsource1(i)=0;dsource2(i)=1;elseif (temp<0.75)dsource1(i)=1;dsource2(i)=0;elsedsource1(i)=1;dsource2(i)=1;end;end;numofsymbolerror=0;numofbiterror=0;for i=1:Nn=sgma*randn(size(s00));if((dsource1(i)==0)&(dsource2(i)==0))r=s00+n;elseif((dsource1(i)==0)&(dsource2(i)==1)) r=s01+n;elseif((dsource1(i)==1)&(dsource2(i)==0)) r=s10+n;elser=s11+n;end;c00=dot(r,s00);c01=dot(r,s01);c10=dot(r,s10);c11=dot(r,s11);c_max=max([c00 c01 c10 c11]);if (c00==c_max)decis1=0;decis2=0;elseif(c01==c_max)decis1=0;decis2=1;elseif(c10==c_max)decis1=1;decis2=0;elsedecis1=1;decis2=1;end;symbolerror=0;if(decis1~=dsource1(i))numofbiterror=numofbiterror+1;symbolerror=1;end;if(decis2~=dsource2(i))numofbiterror=numofbiterror+1;symbolerror=1;end;if(symbolerror==1)numofsymbolerror=numofsymbolerror+1;end;end;ps=numofsymbolerror/N;pb=numofbiterror/(2*N);效果图:11。
qpsk调制误码率曲线matlab绘制

QPSK(Quadrature Phase Shift Keying)调制是一种常见的数字调制方式,它可以使信号在传输时能够更有效地利用频谱资源。
在数字通信系统中,QPSK调制被广泛应用于各种应用场景中,因其具有高效利用频谱和抗干扰能力强等特点而备受青睐。
在QPSK调制中,误码率是一个非常重要的性能指标,它直接影响到系统的可靠性和稳定性。
对QPSK调制的误码率曲线进行分析和绘制是十分重要的。
1. QPSK调制原理QPSK调制是一种采用正交载波的调制方式,它将两路独立的数字信号分别调制到正交的载波上,然后再将两路调制信号叠加在一起进行传输。
在QPSK调制中,每个符号携带两个比特信息,分别代表实部和虚部,因此可以实现在单位频谱带宽内传输两倍的数据量。
QPSK 调制的信号点图形式如下图所示:(此处插入QPSK调制信号点图)2. QPSK调制误码率QPSK调制的误码率是指在传输过程中由于信道噪声或其他干扰因素引起的信号错误率。
误码率通常用比特错误率(BER)来表示,即单位时间内传输的比特中出现错误的比例。
QPSK调制的误码率曲线是描述在不同信噪比条件下系统性能的重要指标,它反映了系统在不同信噪比条件下的可靠性和稳定性。
通常情况下,我们可以通过理论分析或仿真实验来得到QPSK调制的误码率曲线。
3. Matlab绘制QPSK调制误码率曲线Matlab是一款功能强大的科学计算软件,它提供了丰富的绘图函数和工具,可以方便地进行误码率曲线的绘制。
在Matlab中,我们可以利用通信工具箱中的相关函数和工具来实现QPSK调制误码率曲线的分析和绘制。
下面我们将结合实际代码示例来演示如何使用Matlab 进行QPSK调制误码率曲线的绘制。
```matlab设置信号点数目M = 4;设置信噪比范围EbN0dB = 0:10;EbN0 = 10.^(EbN0dB/10);计算误码率ber = berawgn(EbN0,'qam',M);绘制误码率曲线semilogy(EbN0dB,ber,'linewidth',2);grid on;xlabel('Eb/N0 (dB)');ylabel('Bit Error Rate');title('QPSK Modulation BER Curve');```4. 结论通过Matlab的仿真分析和绘图,我们可以得到QPSK调制的误码率曲线。
(完整版)QPSK调制原理及matlab程序实现

QPSK已调信号生成一、QPSK介绍QPSK是英文Quadrature Phase Shift Keying 的缩写,意为正交相移键控,是一种数字调制方式。
其有抗干扰性强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接入、移动通信及有线电视系统之中。
二、实验平台和实验内容1、实验平台本实验是MATLAB环境中生成基本QPSK已调信号,只需要MATLAB12.0。
2、实验内容1.基带信号为周期127bits伪随机序列,信息比特速率:20kbps,载波频率:20kHz(速率及频率参数现场可调整);2.在MATLAB环境中编写M代码搭建QPSK调制系统模型;3.观测基带时域波形、已调信号时域波形;4.观测基带发射星座图;5.观测已调信号的功率谱(优先)或频谱;三、实现框图及其原理分析1、原理分析及其结构QPSK与二进制PSK一样,传输信号包含的信息都存在于相位中。
载波相位取四个等间隔值之一,如л/4, 3л/4,5л/4,和7л/4。
相应的E为发射信号的每个符号的能量,T为符号持续时间,载波频率f等于nc/T,nc为固定整数。
每一个可能的相位值对应于一个特定的二位组。
例如,可用前述的一组相位值来表示格雷码的一组二位组:10,00,01,11。
Sin(t)=2E/tcos[2]4/+∏i]0<=t<=T)1-ft∏2(其中,i=1,2,3,4。
2、框图四、实验结果与分析图一基带信号为周期为127bits的伪随机序列。
图二:已调信号时域波形带宽为7104 HzB点信号的星座图映射,00、01、10、11组合分别映射成-1-j,-1+j,1-j,1+j。
五、实验源码clc;clear all;Num=127;data=randi([0 1],1,Num);figure(1)plot(data)title('基带时域波形');f=20000; %载波频率20kHzRb=20000; %码元速率20kHzTs=1/f;Ns=8000;sample=1*Ns; %每个码元采点数为8000,采样频率为8000*20kHz N=sample*length(data)/2; %总采样点数data1=2*data-1; %正/负极性变换,产生二进制不归零双极性码元%-------------------------将信息源分成两路,分别对信号进行抽样-------------data_1=zeros(1,N); %定义一个长度为N的空数据data_1for i1=1:Num/2data_1(sample*(i1-1)+1:sample*i1)=data1(2*i1-1); %对奇数码元进行采样enddata_2=zeros(1,N);for i2=1:Num/2data_2(sample*(i2-1)+1:sample*i2)=data1(2*i2); %对偶数码元进行采样enda=zeros(1,N);b=zeros(1,N);for j1=1:Na(j1)=cos(2*pi*f*(j1-1)*Ts/Ns); %对余弦载波抽样每个周期采N个点 b(j1)=-sin(2*pi*f*(j1-1)*Ts/Ns); %对正弦载波抽样每个周期采N个点end%---------------------------调制---------------------------data_a=data_1.*a; %a路用余弦调制data_b=data_2.*b; %b路用正弦调制data_c=data_a+data_b;figure(2)subplot(3,1,1)plot(data_a)title('QPSK已调实部时域信号');subplot(3,1,2)plot(data_b)title('QPSK已调虚部时域信号');subplot(3,1,3)plot(data_c);title('QPSK已调信号时域波形');%---------------------绘制调制后波形的频谱图-------------------data_modul1= data_1(1:502000)+1i*data_2(1:502000);data_modul=data_a+1i*data_b;%调制后总的信号figure(3)plot(data_modul1,'o');axis([-2 2 -2 2]);title('星座图');figure(4)QPSK=10*log10(abs(fftshift(fft(data_modul,2048))).^2); %信号的频率值SFreq=linspace(-Rb*sample/2,Rb*sample/2,length(QPSK)); %信号的频率谱范围plot(SFreq,QPSK);title('QPSK已调信号频谱图');xlabel('Frequency');ylabel('Amplitude');hold on;。
BASK BPSK QPSK MSK调制解调原理以及Matlab代码

目录第一部分仿真的参数设置 (1)第二部分BASK调制与解调 (2)第三部分BPSK调制与解调 (6)第四部分QPSK调制与解调 (10)第五部分MSK调制与解调 (14)第六部分误码率随信噪比变化 (18)参考文献 (20)Matlab代码 (21)BASK (21)BPSK (24)QPSK (27)MSK (31)误码率随着信噪比变化 (35)第一部分仿真的参数设置仿真过程中应用到的参数设置以及相应的解释如表1所示[1]。
表1. 参数设置及其解释第二部分BASK调制与解调BASK调制解调的概要过程如图2.1所示。
图2.1 BASK调制解调原理图首先,信源随机产生1000个二进制(1/0)码并画出其频谱图,如图2.2所示。
图2.2 信源信号的时域波形和频谱图随后,用10Hz的载波频率去调制信源信号完成BASK调制,调制后的时域波形及其频谱如图2.3所示。
可以看到,调制后的频率确搬移到了10Hz处。
图2.3 BASK已调信号的时域波形与频谱图而后,已调信号进入信噪比为20dB的高斯信道。
接收端接收到经过信道信号,其时域波形和频谱如图2.4所示,可以看出分布在整个时间轴上的噪声信号。
图2.4 已调信号经过高斯信道后的时域波形和频谱图接收端接收到信号后,通入BASK解调模块,先乘上载波,获得一个拥有两个频率(10-10;10+10)的信号,其时域波形与频谱图如图2.5所示。
图2.5 BASK解调后的信号时域波形与频谱图而后通入低通滤波器滤除高频载波,时域波形与频谱图如图2.6所示,可以看出此时20Hz处无功率谱密度。
图2.6 通入LPF后的时域波形和频谱图最后将信号进行判决,与信源信号进行对比,如图2.7所示,其误码率为2.14%(如图6.6所示)。
图2.7 信宿恢复信号与信源产生信号波形图对比第三部分BPSK调制与解调BPSK与BASK调制与解调原理基本相同,主要的区别在于信源码是双极性码。
其基本原理如图3.1所示。
(完整版)QPSK调制与解调在MATLAB平台上的实现

QPSK 调制与解调在 MATLAB 平台上的实现李悦QPSK 即四进制移向键控(Quaternary Phase Shift Keyi ng ,它利用载波的四 种不同相位来表示数字信息,由于每一种载波相位代表两个比特信息, 因此每个 四进制码元可以用两个二进制码元的组合来表示。
两个二进制码元中的前一个码 元用a 表示,后一个码元用 b 表示。
QPSK 信号可以看作两个载波正交 2PSK 信号的合成,下图表示QPSK 正交 调制器。
由QPSK 信号的调制可知,对它的解调可以采用与 2PSK 信号类似的解调方 法进行解调。
解调原理图如下所示,同相支路和正交支路分别采用相干解调方式 解调,得到l(t)和Q(t),经过抽样判决和并/串交换器,将上下支路得到的并行 数据恢复成串行数据载波输入磯波 振沏—移相输出输入滤波器抽样 刿决变换低通.抽样判决输出cos g低通 滤液器 位定时b%调相法clear all close all t=[-1:0.01:7-0.01];tt=le ngth(t);x1=o nes(1,800);for i=1:ttif (t(i)>=-1 & t(i)<=1) | (t(i)>=5& t(i)<=7); x1(i)=1;else x1(i)=-1;endend t仁[0:0.01:8-0.01]; t2=0:0.01:7-0.01; t3=-1:0.01:7.1-0.01; t4=0:0.01:8.1-0.01;tt1=le ngth(t1); x2=o nes(1,800); for i=1:tt1if (t1(i)>=0 & t1(i)<=2) | (t1(i)>=4& t1(i)<=8); x2(i)=1;else x2(i)=-1;endend f=0:0.1:1;xrc=0.5+0.5*cos(pi*f);y1=c on v(x1,xrc)/5.5;y2=c on v(x2,xrc)/5.5;n0=randn( size(t2));f1=1;i=x1.*cos(2*pi*f1*t);q=x2.*si n( 2*pi*f1*t1);I=i(101:800);Q=q(1:700);QPSK=sqrt(1/2).*l+sqrt(1/2).*Q;QPSK_n=(sqrt(1/2).*l+sqrt(1/2).*Q)+n0;n 1=ra ndn( size(t2)); i_rc=y1.*cos(2*pi*f1*t3); q_rc=y2.*si n(2*pi*f1*t4);I_rc=i_rc(101:800);Q_rc=q_rc(1:700);QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);QPSK_rc_n1=QPSK_rc+ n1;figure(1)subplot(4,1,1);plot(t3,i_rc);axis([-1 8 -1 1]);ylabel('a 序列'); subplot(4,1,2);plot(t4,q_rc);axis([-1 8 -1 1]);ylabel('b 序列'); subplot(4,1,3);plot(t2,QPSK_rc);axis([-1 8 -1 1]);ylabel('合成序列');subplot(4,1,4);plot(t2,QPSK_rc_n 1);axis([-1 8 -1 1]);ylabel(' 加入噪声'); 效果图:%设定T=1,加入高斯噪声clear allclose all%调制bit_in = randin t(1e3, 1, [0 1]);bit」=bit_i n(1:2:1e3);bit_Q = bit_i n(2:2:1e3);data_I = -2*bit_l+1;data_Q = -2*bit_Q+1;data_I1=repmat(data_I',20,1);data_Q 1=repmat(data_Q',20,1);for i=1:1e4data_I2(i)=data_I1(i);data_Q2(i)=data_Q1(i);en d;f=0:0.1:1;xrc=0.5+0.5*cos(pi*f);data_I2_rc=c on v(data_l2,xrc)/5.5;data_Q2_rc=co nv(data_Q2,xrc)/5.5;f1=1;t1=0:0.1:1e3+0.9;n0=ran d(size(t1));I_rc=data_I2_rc.*cos(2*pi*f1*t1);Q_rc=data_Q2_rc.*si n(2*pi*f1*t1);QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc); QPSK_rc_n0=QPSK_rc+ n0;%解调I_demo=QPSK_rc_ n0.*cos(2*pi*f1*t1);Q_demo=QPSK_rc_n0.*si n(2*pi*f1*t1);%低通滤波I_recover=c on v(I_demo,xrc);Q_recover=c on v(Q_demo,xrc);l=l_recover(11:10010);Q=Q_recover(11:10010);t2=0:0.05:1e3-0.05;t3=0:0.1:1e3-0.1;%抽样判决data_recover=[];for i=1:20:10000data_recover=[data_recover l(i:1:i+19) Q(i:1:i+19)]; en d;bit_recover=[];for i=1:20:20000if sum(data_recover(i:i+19))>0 data_recover_a(i:i+19)=1; bit_recover=[bit_recover 1];elsedata_recover_a(i:i+19)=-1; bit_recover=[bit_recover -1];endenderror=0;dd = -2*bit_i n+1;ddd=[dd'];ddd1=repmat(ddd,20,1);for i=1:2e4ddd2(i)=ddd1(i);endfor i=1:1e3if bit_recover(i)~=ddd(i) error=error+1;endend p=error/1000;figure(1) subplot(2,1,1);plot(t2,ddd2);axis([0 100 -2 2]);title(' 原序列');subplot(2,1,2);plot(t2,data_recover_a);axis([0 100 -2 2]);title('解调后序列’);效果图:%设定T=1,不加噪声clear allclose all%调制bit_in = randin t(1e3, 1, [0 1]);bit」=bit_i n(1:2:1e3);bit_Q = bit_i n(2:2:1e3);data_I = -2*bit_l+1;data_Q = -2*bit_Q+1;data_I1=repmat(data_I',20,1);data_Q 1=repmat(data_Q',20,1);for i=1:1e4data_I2(i)=data_I1(i);data_Q2(i)=data_Q1(i);en d;t=0:0.1:1e3-0.1;f=0:0.1:1;xrc=0.5+0.5*cos(pi*f);data_I2_rc=c on v(data_l2,xrc)/5.5;data_Q2_rc=co nv(data_Q2,xrc)/5.5;f1=1;t1=0:0.1:1e3+0.9;I_rc=data_I2_rc.*cos(2*pi*f1*t1);Q_rc=data_Q2_rc.*si n(2*pi*f1*t1);QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);%解调I_demo=QPSK_rc.*cos(2*pi*f1*t1);Q_demo=QPSK_rc.*si n(2*pi*f1*t1);I_recover=c on v(I_demo,xrc);Q_recover=c on v(Q_demo,xrc);I=I_recover(11:10010);Q=Q_recover(11:10010);t2=0:0.05:1e3-0.05;t3=0:0.1:1e3-0.1;data_recover=[];for i=1:20:10000data_recover=[data_recover l(i:1:i+19) Q(i:1:i+19)];en d;ddd = -2*bit_i n+1;ddd 1= repmat(ddd',10,1);for i=1:1e4ddd2(i)=ddd1(i);endfigure(1)subplot(4,1,1);plot(t3,l);axis([0 20 -6 6]);subplot(4,1,2);plot(t3,Q);axis([0 20 -6 6]);subplot(4,1,3);plot(t2,data_recover);axis([0 20 -6 6]);subplot(4,1,4);plot(t,ddd2);axis([0 20 -6 6]);效果图:20% QPSK误码率分析SNRi ndB仁0:2:10;SNRi ndB2=0:0.1:10;for i=1:le ngth(SNRi ndB1)[pb,ps]=cm_sm32(SNR in dB1(i));smld_bit_err_prb(i)=pb;smld_symbol_err_prb(i)=ps;en d;for i=1:le ngth(SNR in dB2)SNR=exp(SNRi ndB2(i)*log(10)/10);theo_err_prb(i)=Qfu nct(sqrt(2*SNR));en d;title('QPSK误码率分析');semilogy(SNRi ndB1,smld_bit_err_prb,'*');axis([0 10 10e-8 1]);hold on;% semilogy(SNRindB1,smld_symbol_err_prb,'o'); semilogy(SNR in dB2,theo_err_prb);legend('仿真比特误码率','理论比特误码率'); hold off;fun ctio n[y]=Qfu nct(x) y=(1/2)*erfc(x/sqrt(2));fun ctio n[ pb,ps]=cm_sm32(SNRi ndB) N=10000; E=1;SNR=10A(SNRi ndB/10);sgma=sqrt(E/SNR)/2;s00=[1 0];s0仁[0 1];si 仁[-1 0];s10=[0 -1];for i=1:Ntemp=ra nd;if (temp<0.25)dsource1(i)=0;dsource2(i)=0;elseif (temp<0.5) dsource1(i)=0;dsource2(i)=1;elseif (temp<0.75)dsource1(i)=1;dsource2(i)=0;elsedsource1(i)=1;dsource2(i)=1;en d;en d;numo fsymbolerror=0;num ofbiterror=0;for i=1:Nn=sgma*ra ndn( size(s00));if((dsource1(i)==0)&(dsource2(i)==0))r=s00+n;elseif((dsource1(i)==0)&(dsource2(i)==1))r=s01+ n;elseif((dsource1(i)==1)&(dsource2(i)==0))r=s10+n;elser=s11+ n;en d;c00=dot(r,s00);c0仁dot(r,s01);c10=dot(r,s10);c11=dot(r,s11);c_max=max([c00 c01 c10 c11]);if (c00==c_max)decis 1=0 ;decis2=0;elseif(c01==c_max)decis 1=0 ;decis2=1;elseif(c10==c_max)decis 1= 1;decis2=0;elsedecis1=1;decis2=1;en d;symbolerror=0; if(decis1~=dsource1(i)) numofbiterror= num ofbiterror+1; symbolerror=1;en d;if(decis2~=dsource2(i))num ofbiterror= num ofbiterror+1;symbolerror=1;en d;if(symbolerror==1)numo fsymbolerror =numo fsymbolerror+1; en d;en d;ps=numo fsymbolerror/N;pb=num ofbiterror/(2*N);效果图:。
matlab qpsk解调算法

在MATLAB中,QPSK解调算法的实现通常包括以下几个步骤:1. 载波恢复:首先,需要从接收到的信号中恢复出载波。
这通常是通过相乘或相除的方式完成的,即通过将接收到的信号与恢复的载波相乘或相除来去除载波。
2. 符号解调:在恢复载波之后,需要进行符号解调。
这通常是通过比较接收到的信号与参考信号的相位差来实现的。
根据比较结果,可以确定接收到的符号是0还是1。
3. 解调后的信号处理:在解调之后,通常需要对解调后的信号进行一些处理,例如去除直流分量、低通滤波等。
下面是一个简单的MATLAB代码示例,演示了如何实现QPSK解调:生成QPSK信号M = 4; % QPSK的调制阶数data = randi([0 M-1], 1000, 1); % 生成1000个随机数据modData = qammod(data, M); % QPSK调制加入高斯白噪声SNR = 10; % 信噪比noise = sqrt(1/2)*(randn(size(modData)) + 1i*randn(size(modData))); % 生成高斯白噪声receivedSignal = modData + noise; % 加入噪声QPSK解调demodData = qamdemod(receivedSignal, M, 'Peak'); % QPSK解调计算误码率errors = sum(abs(data - demodData)) / length(data); % 计算误码率fprintf('误码率为: %f\n', errors);请注意,这只是一个简单的示例代码,实际应用中可能需要更复杂的处理和优化。
此外,上述代码中使用的`qammod`和`qamdemod`函数是MATLAB中提供的QAM调制和解调函数,对于QPSK来说,它们可以正常工作。
matlab qpsk调制解调代码

一、介绍Matlab是一种专门用于科学计算和数据可视化的强大工具,QPSK调制解调是数字通信领域中常用的调制解调技术。
本文将介绍如何使用Matlab编写QPSK调制解调的代码。
二、QPSK调制原理QPSK是Quadrature Phase Shift Keying的缩写,即正交相移键控。
在QPSK调制中,将输入的数字比特流分成两路,分别用正弦波和余弦波进行调制。
通过将正弦波和余弦波的相位进行调整,可以将数字比特流转换为模拟信号进行传输。
三、QPSK调制过程1.将输入的数字比特流分为两路,分别表示为I路和Q路。
2.将I路比特流进行调制,使用正弦波作为载波信号,调整相位进行调制。
3.将Q路比特流进行调制,使用余弦波作为载波信号,调整相位进行调制。
4.将调制后的信号进行合并,得到QPSK调制信号。
四、QPSK解调过程1.接收到QPSK调制信号后,将信号分为I路和Q路。
2.将I路信号与正弦波进行乘积运算并积分,得到解调后的I路比特流。
3.将Q路信号与余弦波进行乘积运算并积分,得到解调后的Q路比特流。
五、Matlab QPSK调制解调代码实现```matlab生成随机QPSK调制信号data = randi([0, 1], 1, 1000); 生成随机比特流I = data(1:2:end); 取偶数位作为I路数据Q = data(2:2:end); 取奇数位作为Q路数据symbols = 2*I-1 + 1i*(2*Q-1); 将I路和Q路数据映射为QPSK符号显示QPSK调制信号scatterplot(symbols); 显示QPSK调制信号的星座图QPSK解调data_est = zeros(1, length(data));data_est(1:2:end) = real(symbols) > 0; 解调I路数据data_est(2:2:end) = imag(symbols) > 0; 解调Q路数据```六、总结本文介绍了QPSK调制解调的原理和过程,并给出了使用Matlab实现QPSK调制解调的代码。
相干光通信qpsk,qam调制格式等matlab仿真代码

相干光通信qpsk,qam调制格式等matlab仿真代码本文将介绍相干光通信中的两种调制格式——QPSK和QAM,并提供基于MATLAB的仿真代码来说明其工作原理。
我们将逐步解释QPSK和QAM的原理、特点和应用,并展示如何使用MATLAB来模拟这两种调制格式。
1. 引言现代光通信技术已经取得了长足的进展,其中调制格式是实现高速光通信的关键。
QPSK(Quadrature Phase Shift Keying)和QAM(Quadrature Amplitude Modulation)是两种常用的调制格式。
它们具有高效利用频谱资源和抗噪声性能强的优点,在现代光通信系统中得到了广泛的应用。
2. QPSK调制格式QPSK是一种基于相位调制的数字调制方式。
它将两个正交相干的载波用来表示数字比特流的相位信息。
QPSK将比特流分为每两个比特表示一个相位状态的方式,因此可以表示四种不同的相位状态。
这四种相位状态分别是0、90、180和270,对应于比特流“00”、“01”、“10”和“11”。
QPSK的工作原理如下:- 将要传输的比特流拆分成两个比特一组,每组代表一个相位状态。
- 使用正交相干的载波生成这两个相位状态,并将它们进行叠加。
- 叠加后的信号经过输出滤波器,以去除非理想频谱。
下面是基于MATLAB的QPSK调制仿真代码:Matlab定义比特流bit_stream = [0 1 0 1 1 0 0 1];定义相位状态映射表phase_mapping = [0 90 180 270];初始化调制输出modulated_signal = [];QPSK调制for i=1:2:length(bit_stream)phase_index = bit_stream(i)*2 + bit_stream(i+1) + 1; phase = phase_mapping(phase_index);将相位转化为弧度并生成正交载波carrier1 = cosd(phase);carrier2 = sind(phase);将两个载波叠加modulated_signal = [modulated_signal carrier1 carrier2];end显示调制后的信号plot(modulated_signal);3. QAM调制格式QAM是一种基于混合调制的数字调制方式。
qpsk信号matlab仿真程序

qpsk信号matlab仿真程序QPSK信号MATLAB仿真程序—理论与应用导言:随着无线通信技术的迅猛发展,QPSK(Quadrature Phase Shift Keying)信号成为了目前广泛应用于通信领域的一种调制方式。
本文将详细介绍如何使用MATLAB进行QPSK信号的仿真程序设计,并从理论与应用两个方面进行解析,以帮助读者深入理解并灵活应用该仿真程序。
1. 什么是QPSK信号?QPSK信号是一种基于相位调制的数字调制技术,其特点是将数字信号分成4个不同的相位状态进行传输和接收。
其中,每个相位状态代表2个比特的信息,即每个相位状态可以传输2个比特的信息,因此QPSK又被称为4相位调制。
QPSK信号可以通过泰勒展开可以分解成I(In-phase)分量和Q(Quadrature)分量。
2. MATLAB中的QPSK信号仿真程序设计步骤:(1)生成随机比特流。
在MATLAB中,可以使用randi函数生成一串随机的比特流,作为模拟发送端的输入信号。
(2)将比特流转换成QPSK符号。
将生成的比特流进行分组,每两个比特为一组,将每组比特映射到对应的QPSK符号。
一般而言,00表示的是第一象限的点,01表示的是第二象限的点,11表示的是第三象限的点,10表示的是第四象限的点。
(3)通过QPSK符号产生QPSK信号。
通过对每个QPSK符号进行相位调制,可以得到QPSK信号。
(4)添加高斯噪声。
为了模拟仿真实际通信环境,我们需要向信号中添加高斯噪声。
可以使用randn函数生成指定均值和标准差的高斯噪声信号,并将其与QPSK信号相加。
(5)解调QPSK信号。
在接收端,需要进行相位解调操作,从而恢复原始的比特流。
通过解调操作,将接收到的QPSK信号恢复为I和Q两个分量。
(6)计算误码率。
通过比较原始比特流和解调后的比特流,可以统计出误码率,从而评估通信系统的性能。
3. QPSK信号仿真程序的理论分析:对于QPSK信号,可以利用复数域的理论进行分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
QPSK已调信号生成
一、QPSK介绍
QPSK是英文Quadrature Phase Shift Keying 的缩写,意为正交相移键控,是一种数字调制方式。
其有抗干扰性强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接入、移动通信及有线电视系统之中。
二、实验平台和实验内容
1、实验平台
本实验是MATLAB环境中生成基本QPSK已调信号,只需要MATLAB12.0。
2、实验内容
1.基带信号为周期127bits伪随机序列,信息比特速率:20kbps,载波频率:
20kHz(速率及频率参数现场可调整);
2.在MATLAB环境中编写M代码搭建QPSK调制系统模型;
3.观测基带时域波形、已调信号时域波形;
4.观测基带发射星座图;
5.观测已调信号的功率谱(优先)或频谱;
三、实现框图及其原理分析
1、原理分析及其结构
QPSK与二进制PSK一样,传输信号包含的信息都存在于相位中。
载波相位取四个等间隔值之一,如л/4, 3л/4,5л/4,和7л/4。
相应的E为发射信号的每个符号的能量,T为符号持续时间,载波频率f等于nc/T,nc为固定整数。
每一个可能的相位值对应于一个特定的二位组。
例如,可用前述的一组相位值来表示格雷码的一组二位组:10,00,01,11。
Sin(t)=2E/tcos[2]4/
+
∏i]0<=t<=T
)1
-
ft∏
2(
其中,i=1,2,3,4。
2、框图
四、实验结果与分析
图一基带信号为周期为127bits的伪随机序列。
图二:已调信号时域波形
带宽为7104 Hz
B点信号的星座图映射,00、01、10、11组合分别映射成-1-j,-1+j,1-j,1+j。
五、实验源码
clc;
clear all;
Num=127;
data=randi([0 1],1,Num);
figure(1)
plot(data)
title('基带时域波形');
f=20000; %载波频率20kHz
Rb=20000; %码元速率20kHz
Ts=1/f;
Ns=8000;
sample=1*Ns; %每个码元采点数为8000,采样频率为8000*20kHz N=sample*length(data)/2; %总采样点数
data1=2*data-1; %正/负极性变换,产生二进制不归零双极性码元
%-------------------------将信息源分成两路,分别对信号进行抽样-------------
data_1=zeros(1,N); %定义一个长度为N的空数据data_1
for i1=1:Num/2
data_1(sample*(i1-1)+1:sample*i1)=data1(2*i1-1); %对奇数码元进行采样
end
data_2=zeros(1,N);
for i2=1:Num/2
data_2(sample*(i2-1)+1:sample*i2)=data1(2*i2); %对偶数码元进行采样end
a=zeros(1,N);
b=zeros(1,N);
for j1=1:N
a(j1)=cos(2*pi*f*(j1-1)*Ts/Ns); %对余弦载波抽样每个周期采N个点 b(j1)=-sin(2*pi*f*(j1-1)*Ts/Ns); %对正弦载波抽样每个周期采N个点end
%---------------------------调制---------------------------
data_a=data_1.*a; %a路用余弦调制
data_b=data_2.*b; %b路用正弦调制
data_c=data_a+data_b;
figure(2)
subplot(3,1,1)
plot(data_a)
title('QPSK已调实部时域信号');
subplot(3,1,2)
plot(data_b)
title('QPSK已调虚部时域信号');
subplot(3,1,3)
plot(data_c);
title('QPSK已调信号时域波形');
%---------------------绘制调制后波形的频谱图-------------------
data_modul1= data_1(1:502000)+1i*data_2(1:502000);
data_modul=data_a+1i*data_b;%调制后总的信号
figure(3)
plot(data_modul1,'o');
axis([-2 2 -2 2]);
title('星座图');
figure(4)
QPSK=10*log10(abs(fftshift(fft(data_modul,2048))).^2); %信号的频率值SFreq=linspace(-Rb*sample/2,Rb*sample/2,length(QPSK)); %信号的频率谱范围plot(SFreq,QPSK);
title('QPSK已调信号频谱图');
xlabel('Frequency');
ylabel('Amplitude');
hold on;。
