大学物理知识总结习题答案(第八章)振动与波动电子教案
大学物理教案_振动与波动

课时:2课时教学目标:1. 理解简谐运动的概念,掌握简谐运动的特征及描述方法。
2. 掌握波动的基本概念、传播规律和波动方程。
3. 能够运用波动理论解决实际问题。
教学重点:1. 简谐运动的特征及描述方法。
2. 波动的传播规律和波动方程。
教学难点:1. 简谐运动的数学描述。
2. 波动方程的应用。
教学过程:第一课时一、导入1. 提问:什么是振动?什么是波动?2. 引入简谐运动的概念,介绍简谐运动的特征。
二、新课讲解1. 简谐运动的概念及特征- 定义:简谐运动是指质点在某一平衡位置附近,受到与位移成正比、方向相反的力作用而做的周期性运动。
- 特征:周期性、等时性、对称性、振幅、频率、周期、角频率等。
2. 简谐运动的数学描述- 描述方法:位移方程、速度方程、加速度方程等。
- 公式推导:结合牛顿第二定律,推导简谐运动的位移方程、速度方程、加速度方程。
3. 简谐运动的能量分析- 能量守恒:质点在简谐运动过程中,动能和势能相互转化,总能量保持不变。
- 能量表达式:动能、势能、总能量等。
三、课堂练习1. 判断题:简谐运动一定是周期性运动。
()2. 填空题:简谐运动的周期公式为______,角频率公式为______。
四、课堂小结本节课主要介绍了简谐运动的概念、特征、数学描述和能量分析,使学生初步掌握简谐运动的基本知识。
第二课时一、导入1. 回顾上节课所学内容,提问:简谐运动有哪些特征?2. 引入波动的概念,介绍波动的传播规律。
二、新课讲解1. 波动的概念及传播规律- 定义:波动是指质点或物体在空间上传播的振动现象。
- 传播规律:波速、波长、频率、周期、相位等。
2. 波动方程- 建立波动方程:结合波动传播规律,推导波动方程。
- 波动方程的解:驻波、行波、波包等。
3. 波动方程的应用- 举例说明波动方程在物理学中的应用。
三、课堂练习1. 判断题:波速与波长、频率成正比。
()2. 填空题:波动方程为______,其中波速______,波长______,频率______。
大学物理习题解答 第八章

8-1.已知波源在原点(x=0)的平面简谐波的方程为)cos(Cx Bt A y -=式中A,B,C 为正值恒量.试求:(1)波的振幅,波速,频率,周期与波长;(2)写出传播放向上距离波源l 处一点的振动方程;(3)试求任何时刻,在波传播放向上相距为D 的两点的位相差;解:(1) ∵A 、B 、C 为正值恒量,所以该波沿X 轴正方向传播,与平面简谐波的波动方程)(cos cxt A y -=ω比较系数,可得波的振幅为A ,B =ω, π2B f =, B T π2=, C c=ω,C B C c ==ω ,因为f c λ=,所以C B C B CT ππλ22=⋅==. 所以该波的振幅为A,波速为CB,频率为π2B ,周期为B π2,波长为C π2.(2)传播方向上距波源l 处一点的振动方程为:)cos(Cl Bt A y -=.(3)设t 时刻,传播方向上相距为D 的两点分别为x 1,x 2. 那么这两点所对应的波动方程分别为: )cos(11Cx Bt A y -= )cos(22Cx Bt A y -= 所以这两点的相位差Δφ为CD x x C =-=-=∆1221φφφ.8-2. 一列横波沿绳子传播时的波动方程为)410cos(05.0x t y ππ-=,式中x,y 以m 计,t 以s 计.(1)求此波的振幅、波速、频率、和波长;(2)求绳子上各质点振动时的最大速度和最大加速度;(3)求x=0.2m 处的质点在t=1s 时的相位,它是原点处质点在哪一时刻的位相. 这一位相所代表的运动状态在t=1.25s 时刻到达哪一点?在t=1.5s 时刻到达哪一点?(4)分别图示t=1s,1.1s,1.25s,1.5s 各时刻的波形.解:(1)通过与平面简谐波的波动方程比较系数,可得 此波的振幅为:A=0.05m, 波速为:ππ410=c =2.5(m/s). 频率为:ππ210=f =5(HZ). 波长为:f c =λ=0.5(m).答:该波的振幅为0.05m, 波速为2.5m/s, 频率为5HZ,波长为0.5m.(2) ∵平面简谐波的波动方程为:)(cos cxt A y -=ω.∴绳子上各质点的振动速度为: )(sin cxt A t y v --=∂∂=ωω.绳子上各质点的振动加速度为: )(cos 222c xt A ty a --=∂∂=ωω.∴绳子上各质点振动时的最大速度为 ωA v =max =0.5π=1.57(m/s). 绳子上各质点振动时的最大加速度为 2m ax ωA a = =52π=49.35(m/s 2). 答:绳子上各质点振动时的最大速度为1.57m/s ,最大加速度为49.35m/s 2. (3)X=0.2m 处的质点在t=1s 时的位相: φ=9.2π 设该位相是原点处质点在t 时刻的位相,可得 φ=9.2π=10πt t=0.92(s) 这一位相代表的运动状态在t=1.25s 时距离原点的位置为: )(825.0)125.1(2.02.0m c t c x =-+=∆+=同理,在t=1.5s 时,该位相所代表的运动状态,距离原点的位置为: t c x '∆+=2.0=1.45 (m). (4)t=1s 时,x y π4cos 05.0=. t=1.1s 时,x y π4cos 05.0-=. t=1.25s 时,x y π4sin 05.0=. t=1.5s 时,x y π4cos 05.0-=.8-3. 已知平面余弦波波源的振动周期T=21s,所激起的波的波长λ=10m,振幅为0.1m,当t=0时,波源处振动的位移恰为正方向的最大值,取波源处为原点并设波沿+X 方向传播,求: (1)此波的方程;(2)沿波传播方向距离波源为2λ处的振动方程; (3)当4T t =时,波源和距离波源为 4λ,2λ,43λ及λ的各点各自离开平衡位置的位移;(4)当4T t =时,波源和距离波源为 4λ,2λ,43λ及λ的各点自离开平衡位置的位移;并根据(3)(4)计算结果画出波形(y-x)曲线; (5)当4T t =和2T 时,距离波源4λ处质点的振动速度. 解:(1)根据题意可知,该平面余弦波的振幅 A=0.1m, 频率f =2(HZ),波速f c λ==20(m/s),初相位φ0=0. 当取波源为原点并沿该波沿+X 方向传播时,波动方程为 )54cos(1.0x t y ππ-=.(2)沿波传播方向距离波源为λ/2处的振动方程为: )254cos(1.0λππ⋅-=t y =-0.1cos4πt.(3)距离波源分别为4λ,2λ,43λ和λ的各点的振动方程为 t y π4sin 1.0=, t y π4cos 1.0-= t y π4sin 1.0-=, t y π4cos 1.0=当4Tt =时,它们各自离开平衡位置的位移为 44sin 1.01Ty ⋅=π=0.1(m), 2y =0(m),3y =-0.1(m), 4y =0(m)(4)与(3)的方法类似,易求得 4λ=x 时, y=0(m). 2λ=x 时, y=0.1(m).43λ=x 时,y=0(m). λ=x 时,y=-0.1(m).(5)各质点的振动速度,)54sin(4.0x t t y v πππ--=∂∂= 当4Tt =时,距离波源4λ处质点的振动速度为: )4544sin(4.0λπππ⨯-⨯-=T v =0(m/s)同理,当2T t =时,距离波源4λ处质点的振动速度为:v =-0.4π(m/s)答:当4Tt =和2T 时,距离波源4λ处质点的振动速度分别为0m/s 和-0.4πm/s. 8-4. 一波源做简谐振动,周期为1001s,经平衡位置向正方向运动时,作为计时起点.设此振动以c=400m/s 的速度沿直线传播,求: (1)这波沿某一波线的方程;(2)距波源为16m 处和20m 处质点振动方程和初位相; (3)距波源为15m 和16 m 的两质点的位相差是多少?解:(1)根据题意可知,该简谐波的频率为ƒ=100(HZ), 波速c=400m/s, 初相位20πφ-=, 设该平面简谐波的波动方程为 )22cos(0φλπλπ+-=x ct A y 将上面的结果代入可得,)222cos(πλππ--=x t T A y =)22200cos(πππ--x t A(2)距波源为16m 和20m 处质点振动方程为:将x=16m 代入上式,得 )2200()2216200cos(1πππππ-=-⨯-=t Aos t A y同理,)2200cos()2220200cos(2πππππ-=-⨯-=t A t A y 初相位分别为:t=0时,210πφ-=,220πφ-=.(3)距波源为15m 和16m 的两质点的位相差: λπφ2⨯∆=∆x =2π. 8-5. 已知某平面简谐波的波源振动方程为)2sin(06.0πt y =,式中y 以m 计,t 以s计.设波速为2m/s,试求离波源5m 处质点的振动方程.这点的位相所表示的运动状态相当波源在哪一时刻的运动状态?解:离波源5m 处质点的振动方程为:将X=5m 代入波动方程得 )5(2sin06.0c t y -=π=)452sin(06.0ππ-t 设该点的位相所代表的运动状态相当波源在t ′时刻的运动状态,所以 t t '=-2452πππ可得 t ′=(t-2.5)(s).8-6.如图所示,A 和B 是两个同位相的波源,相距d=0.10m,同时以30Hz 的频率发出波动,波速为0.50m/s.P 点位于AB 上方,AP 与AB 夹角为30o ,且PA=4m ,求两波通过P 点位相差.解:依题意可知,PA=4m,AB=0.1m, 利用余弦定理,可得 PB=3.91(m),两波通过P 点相位差: λπφ2)(⨯-=∆PB PA又∵fc=λ ∴Δφ=10.8π. 8-7. S 1和S 2是两个相干波源,相距41波长,S 1比S 2的位相超前2π.设两列波在 S 1,S 2连线方向的强度相同且不随距离变化,问S 1,S 2连线上在S 1外侧各点处的合成波的强度如何?又在S 2外侧各点的强度如何?解:两列相干波在空间任意点P 所形成的振动的振幅为 α∆=cos A 2A +A +A 212221A其中Δα为两列相干波在空间任一点所引起的两个振动的位相差 λπααα2)(1212⨯---=∆r r当P 点在S 1外侧时,根据题中所给的条件,可得 πλλππλπααα-=⨯--=⨯---=∆4222)(1212r r∴0)cos(-2A 2A 2020=+=πA 又∵波的强度与振幅的平方成正比 ∴I=0. 同理,当P 点在S 2外侧时, 02)4(22)(1212=⨯---=⨯---=∆λπλπλπαααr r ⇒A=2A 0 ∴04I I =答:S 1,S 2连线上在S 1外侧各点处的合成波的强度为0,而在S 2外侧合成波的强度为4I 0.8-8.图所示,设平面横波1沿BP 方向传播,它在B 点的振动方程为t y πcos 102.021-⨯=,平面横波2沿AP 方向传播,A 点的振动方程为)2cos(102.022ππ+⨯=-t y ,两式中y 以m计,t以s计,P处与B相距0.40m ,与A 相距0.05m,波速为0.20m/s.求: (1)两波传到P 处的为相差; (2)在P 处合振动的振幅;(3)如果在P 处相遇的两横波,振动方向是互相垂直的,则合振动的振幅又如何?解:(1)两波传到P 处的位相差Δα: λπααα2)(1212⨯---=∆r r由题中给出A,B 两点的振动方程可知,A 比B 的位相超前π ∴ππωππλππα5.22)(22)(-=⨯-⨯-=--=∆CPB PA PB PA (2)在P 处合振动的振幅为:α∆++=cos A 2A A A 2010220210A 21083.2-⨯= (m). (3)由于两列横波振幅相同,频率相同,相位差Δα=25π, 所以,当振动方向相互垂直时,合成的结果是圆周运动. ∴A=A 10=0.2×10-2(m).8-9. 一列正弦式空气波,沿直径为0.14m 的圆柱形管行进,波的平均强度为18*10-3J/s ·m 2,频率为300Hz,波速为300m/s,问: (1)波中的平均能量密度和最大能量密度是多少?(2)每两个相邻的,相位差为2π的同相面(亦即相距1波长的两同相面)之间的波段中有多少能量?解:(1)根据题中所给的条件,由C I ω= 则cI=ω=300/10183-⨯=5106-⨯(J ·m -3). 由)(sin 222c rt A -=ωωρω 可得ωωρω222max ==A =4102.1-⨯(J ·m -3)(2)V W ∆⋅=ωd r 2πω==9.23×710-(J)8-10. 为了保持波源的振动不变,需要消耗4W 的功率,如果波源发出的是球面波,且认为媒质不吸收波的 能量,求距离波源1m 和2m 处的能流密度. 解:因为IS P =,所以距离波源1m 处的能流密度为ππ1442111===r S P I =0.318(w ·m -2)距离波源2m 处的能流密度为222244r S P I π===0.08(w ·m -2). 8-11. 两个波在一根很长的细绳上传播,它们的方程设为 )4(cos 06.01t x y -=π,)4(cos 06.02t x y +=π,式中x,y 以m 计,t 以s 计;(1) 求各波的频率,波长,波速和传播方向;(2) 试求这细绳上是做驻波式振动,求节点的位置和腹点的位置; (3)波腹处的振幅多大?在x=1.2m 处振幅多大?解:(1)与波动方程形式)cos(crt A y -=ω作比较,可得)4(4cos 06.01x t y -=π, )4(4cos 06.02xt y +=ππω41= ⇒πω211=f =2(Hz), s m c /41= 111T c =λ=2(m) 传播方向沿x 轴正方向 πω42=, ƒ2=2(Hz), C 2=-4m/s.222T c =λ =2(m). 传播方向沿x 轴负方向(2)由于两列波同频率,同振幅,同振动方向,并且传播速率相同方向相反,故满足驻波条件,所以做的是驻波式振动t x y y y ππ4cos cos 12.021⋅=+= 节点的位置: 2)12(ππ+=k x (k=0,±1, ±2,………) ⇒2)12(+=k x . 腹点的位置: ππk x = (k=0,±1, ±2, ……) ⇒k x =. (3)波腹处的振幅为0.12m.x=1.2m 处的振幅: )2.1cos(12.0π=0.097(m). 8-12. 设入射波的波动方程为)(2cos 1λπxT t A y +=,在x=0处发生反射,反射点为一自由端.求: (1)反射波的波动方程;(2)合成波(驻波)的方程,并由合成波方程说明哪些点是波腹,哪些点是波节.解:(1)反射波的波动方程为: )(2cos 2λπxT t A y -=(2) )2cos()2cos(221T tx A y y πλπ⋅=+波腹点:πλπk x =2 (k=0,±1, ±2,………) ⇒2λk x =.波节点位置:2)12(2πλπ+=k x (k=0,±1, ±2,………) ⇒4)12(λ+=k x8-13. 在实验室中做驻波试验时,将一根长3米的弦线的一端系于电动音叉的一个臂上,这音叉在 垂直于眩线长度的方向撒谎那个以60Hz 的频率做振动,眩线的质量为60*0.001kg.如果使这根弦线产生有四个波腹的振动,必须给这根弦线施多大的力.解:由8.14题的结论可知 μυTl n n 2=(n=1, 2,3,………) 根据题中所给的已知条件,可得 l =3m,n=44υ=60HZ, μ=60·10-3/3=kg 2102-⨯. 代入上式,解得24)2(nlT υμ==162(N).8-14. 把两端固定的一根弦线波动一下,就有横向振动弦线的两固定端传去,并被反射回来形成驻波图样, 一根长度为l 的弦线,它的驻波图样是一定的,所以它可按呈现一个波腹,二个波腹,三个波腹,……的形式做振动或这种基本振动叠加.试证明:一根长度为l 的弦线只能发出下列一些固有频率.μυTl n n 2=n=1,2,3,….. 式中μ是弦线单位的质量,T 是绳中的张力.证明:假设长度为l 的弦线,它的驻波图样可以产生n 个波腹,则n 2λ=l ① 又因波在弦线中传播的速率为 μTc =其中T 是绳中的张力,μ是弦线单位长度的质量μυυλTc nn == ②联立①②,解得 μυTl n n 2=. 故结论得证. 8-15. (1)有一支频率未知的音叉和一支频率已知为384Hz 的标准音叉一起振动时每秒产生三个拍,当这音叉上涂上少量石蜡时,拍频减少,沃尔玛这支音叉频率是多少?(2)某一波形可以用下式表示:11sin sin 3sin 535Y A x A x A x =+++试分别作出该级数前三项的图形,并作出叠加之后的图形. 解:(1)由拍频的定义,可知 123υυυ-==∴ 312±=υυ 即2υ=387或381(Hz). (2)图如下:11。
大学物理知识点总结:振动及波动

利用超声波的能量作用于人体组织,产生热效应、机械效应等,达到治疗目的,如超声碎石、超声刀 等。
地震监测和预测中振动分析
地震波监测
通过监测地震波在地球内部的传播情况和变化特征,研究地震的发生机制和震源性质。
振动传感器应用
在地震易发区域布置振动传感器,实时监测地面振动情况,为地震预警和应急救援提供 数据支持。
图像
简谐振动的图像是正弦或余弦曲线,表示了物体的位移随时间的变化关系。
能量守恒原理在简谐振动中应用
能量守恒
在简谐振动中,系统的机械能(动能 和势能之和)保持不变。
应用
利用能量守恒原理可以求解简谐振动 的振幅、角频率等物理量。
阻尼振动、受迫振动和共振现象
阻尼振动
当物体受到阻力作用时,其振动会逐渐减弱,直至停止。 这种振动称为阻尼振动。
惠更斯原理在波动传播中应用
01
惠更斯原理指出,波在传播过程中,每一点都可以看作是新的 波源,发出子波。
02
惠更斯原理可以解释波的反射、折射等现象,并推导出斯涅尔
定律等波动传播规律。
在实际应用中,惠更斯原理被为波动现象的研究提供了重要的理论基础。
04
干涉、衍射和偏振现象
误差分析
分析实验过程中可能出现的误差来源,如仪 器误差、操作误差等;对误差进行定量评估 ,了解误差对实验结果的影响程度;提出减 小误差的方法和措施,提高实验精度和可靠
性。
感谢您的观看
THANKS
实例
钟摆的摆动、琴弦的振动、地震波的传播等 。
振动量描述参数
振幅
描述振动大小的物理量,表示物体离开平衡 位置的最大距离。
频率
描述振动快慢的物理量,表示单位时间内振 动的次数。
物理学第3版习题解答_第8章光的波动性

. B
解: (1) 以 A 为原点
x1
B
. A
x
A
图 8-35 习题 8-5 用图
-1
本题需补充一平面简谐波以速度 u = 20 m ⋅ s 沿直线传播
t x y = A cos[ 2 π( − ) + ϕ ] λ = uT = 10 m ,根据 T λ , 有
y = A cos[2π(
t x π − )− ] 0.5 10 2
x1 = 0.04 cos(2t + π 6) x 2 = 0.03 cos(2t − π 6)
试写出合振动的表达式。
解 合振动的振幅为
2 A = A12 + A2 + 2 A1 A2 cos(ϕ 2 − ϕ1 )
⎛ π π⎞ = 0.04 2 + 0.03 2 + 2 × 0.03 × 0.04 × cos⎜ − − ⎟ ⎝ 6 6⎠ = 0.06m
第八章习题解答
8-1 一物体沿 x 轴作简谐振动,振幅为 0.12m,周期为 2s。当 t = 0 时,位移为 0.06m,且 向 x 轴正方向运动。求:(1)初相;(2) t = 0.5s 时,物体的位置;(3)在 x = -0.06m 处, 且向 x 轴负向方向运动。物体从这一状态回到平衡位置的最短时间。 解:
−1
8-8 波长为 589.3nm 的钠光照在一双缝上,在距双缝 200cm 的观察屏幕上测量 10 个条纹的 宽度为 2.2cm,试计算双缝之间的距离。
解:根据 ∆x =
D λ 有 d = 0.536 mm d
8-9 在杨氏干涉实验中,若双缝间距为 0.40mm,在距双缝 100cm 的光屏上出现干涉条纹。 现测得相邻两条明纹中心的间距为 1.5mm,求入射光的波长。
大学物理(第四版)课后习题及答案 波动
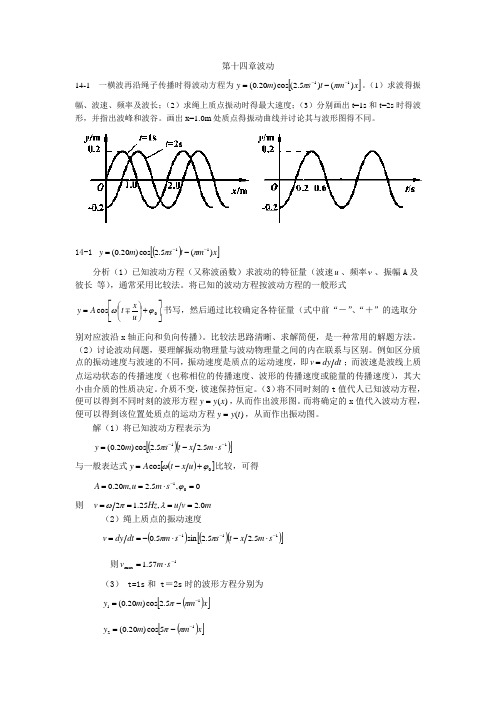
第十四章波动14-1 一横波再沿绳子传播时得波动方程为[]x m t s m y )()5.2(cos )20.0(11---=ππ。
(1)求波得振幅、波速、频率及波长;(2)求绳上质点振动时得最大速度;(3)分别画出t=1s 和t=2s 时得波形,并指出波峰和波谷。
画出x=1.0m 处质点得振动曲线并讨论其与波形图得不同。
14-1 ()[]x m t s m y )(5.2cos )20.0(11---=ππ分析(1)已知波动方程(又称波函数)求波动的特征量(波速u 、频率ν、振幅A 及彼长 等),通常采用比较法。
将已知的波动方程按波动方程的一般形式⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛=0cos ϕωu x t A y 书写,然后通过比较确定各特征量(式中前“-”、“+”的选取分别对应波沿x 轴正向和负向传播)。
比较法思路清晰、求解简便,是一种常用的解题方法。
(2)讨论波动问题,要理解振动物理量与波动物理量之间的内在联系与区别。
例如区分质点的振动速度与波速的不同,振动速度是质点的运动速度,即dt dy v =;而波速是波线上质点运动状态的传播速度(也称相位的传播速度、波形的传播速度或能量的传播速度),其大小由介质的性质决定。
介质不变,彼速保持恒定。
(3)将不同时刻的t 值代人已知波动方程,便可以得到不同时刻的波形方程)(x y y =,从而作出波形图。
而将确定的x 值代入波动方程,便可以得到该位置处质点的运动方程)(t y y =,从而作出振动图。
解(1)将已知波动方程表示为()()[]115.25.2cos )20.0(--⋅-=s m x t s m y π 与一般表达式()[]0cos ϕω+-=u x t A y 比较,可得0,5.2,20.001=⋅==-ϕs m u m A则 m v u Hz v 0.2,25.12====λπω(2)绳上质点的振动速度()()()[]1115.25.2sin 5.0---⋅-⋅-==s m x t s s m dt dy v ππ 则1max 57.1-⋅=s m v(3) t=1s 和 t =2s 时的波形方程分别为()[]x m m y 115.2cos )20.0(--=ππ()[]x m m y 125cos )20.0(--=ππ波形图如图14-1(a )所示。
《大学物理》 第二版 第八章课后习题答案

习题精解8-1 一根无限长直导线有交变电流0sin i I t ω=,它旁边有一与它共面的矩形线圈ABCD ,如图8.3所示,长为l 的AB 和CD 两边与直导向平行,它们到直导线的距离分别为a 和b ,试求矩形线圈所围面积的磁通量,以及线圈中的感应电动势。
解 建立如图8.3所示的坐标系,在矩形平面上取一矩形面元dS ldx =,载流长直导线的磁场穿过该面元的磁通量为02m id B dS ldx xμφπ=⋅= 通过矩形面积CDEF 的总磁通量为 00ln 22bm ai il bldx x aμμφππ==⎰由法拉第电磁感应定律有0ln cos 2m d il bt dt aφμωεωπ=-=- 8-2 有一无限长直螺线管,单位长度上线圈的匝数为n ,在管的中心放置一绕了N 圈,半径为r 的圆形小线圈,其轴线与螺线管的轴线平行,设螺线管内电流变化率为dI dt ,球小线圈中感应的电动势。
解 无限长直螺线管内部的磁场为0B nI μ= 通过N 匝圆形小线圈的磁通量为20m NBS N nI r φμπ== 由法拉第电磁感应定律有20m d dIN n r dt dtφεμπ=-=- 8-3 一面积为S 的小线圈在一单位长度线圈匝数为n ,通过电流为i 的长螺线管内,并与螺线管共轴,若0sin i i t ω=,求小线圈中感生电动势的表达式。
解 通过小线圈的磁通量为0m BS niS φμ==由法拉第电磁感应定律有000cos m d dinS nSi t dt dtφεμμωω=-=-=- 8-4 如图8.4所示,矩形线圈ABCD 放在16.010B T -=⨯的均匀磁场中,磁场方向与线圈平面的法线方向之间的夹角为60α=︒,长为0.20m 的AB 边可左右滑动。
若令AB 边以速率15.0v m s -=∙向右运动,试求线圈中感应电动势的大小及感应电流的方向。
解 利用动生电动势公式0.20()50.6sin(60)0.30()2BAv B dl dl V πε=⨯∙=⨯⨯-︒=⎰⎰感应电流的方向从A B →.8-5 如图8.5所示,两段导体AB 和CD 的长度均为10cm ,它们在B 处相接成角30︒;磁场方向垂直于纸面向里,其大小为22.510B T -=⨯。
振动、波动部分答案(新)

大学物理学——振动和波振 动班级 学号 姓名 成绩内容提要1、简谐振动的三个判据(1);(2);(3)2、描述简谐振动的特征量: A 、T 、γ;T1=γ,πγπω22==T3、简谐振动的描述:(1)公式法 ;(2)图像法;(3)旋转矢量法4、简谐振动的速度和加速度:)2cos()sin(v00πϕωϕωω++=+-==t v t A dt dx m ; a=)()(πϕωϕωω±+=+=0m 0222t a t cos -dtxd A 5、振动的相位随时间变化的关系:6、简谐振动实例弹簧振子:,单摆小角度振动:,复摆:0mgh dt d 22=+θθJ ,T=2mghJπ 7、简谐振动的能量:222m 21k 21A A Eω==系统的动能为:)(ϕωω+==t sin m 21mv 212222A E K ;系统的势能为:)ϕω+==t (cos k 21kx 21222A E P8、两个简谐振动的合成(1)两个同方向同频率的简谐振动的合成合振动方程为:)(ϕω+=t cos x A其中,其中;。
*(2) 两个同方向不同频率简谐振动的合成拍:当频率较大而频率之差很小的两个同方向简谐运动合成时,其合振动的振幅表现为时而加强时而减弱的现象,拍频:12-γγγ=*(3)两个相互垂直简谐振动的合成合振动方程:)(1221221222212-sin )(cos xy 2y x ϕϕϕϕ=--+A A A A ,为椭圆方程。
练习一一、 填空题1.一劲度系数为k 的轻弹簧,下端挂一质量为m 的物体,系统的振动周期为T 1。
若将此弹簧截去一半的长度,下端挂一质量为m/2的物体,则系统的周期T 2等于 。
2.一简谐振动用余弦函数表示,其振动曲线如图所示,则此简谐振动的三个特征量为:A = ;=ω ;=ϕ 。
3.如图,一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上,做成一复摆。
已知细棒绕过其一端的轴的转动惯量J =3/2ml ,此摆作微小振动的周期为 。
大学物理习题及解答(振动与波、波动光学)

1. 有一弹簧,当其下端挂一质量为m 的物体时,伸长量为9.8 ⨯10-2 m 。
假如使物体上下振动,且规定向下为正方向。
〔1〕t =0时,物体在平衡位置上方8.0 ⨯10-2 m处,由静止开始向下运动,求运动方程。
〔2〕t = 0时,物体在平衡位置并以0.60m/s 的速度向上运动,求运动方程。
题1分析:求运动方程,也就是要确定振动的三个特征物理量A 、ω,和ϕ。
其中振动的角频率是由弹簧振子系统的固有性质〔振子质量m 与弹簧劲度系数k 〕决定的,即m k /=ω,k 可根据物体受力平衡时弹簧的伸长来计算;振幅A 和初相ϕ需要根据初始条件确定。
解:物体受力平衡时,弹性力F 与重力P 的大小相等,即F = mg 。
而此时弹簧的伸长量m l 2108.9-⨯=∆。
如此弹簧的劲度系数l mg l F k ∆=∆=//。
系统作简谐运动的角频率为1s 10//-=∆==l g m k ω〔1〕设系统平衡时,物体所在处为坐标原点,向下为x 轴正向。
由初始条件t = 0时,m x 210100.8-⨯=,010=v 可得振幅m 100.8)/(2210102-⨯=+=ωv x A ;应用旋转矢量法可确定初相πϕ=1。
如此运动方程为])s 10cos[()m 100.8(121π+⨯=--t x〔2〕t = 0时,020=x ,120s m 6.0-⋅=v ,同理可得m 100.6)/(22202022-⨯=+=ωv x A ,2/2πϕ=;如此运动方程为]5.0)s 10cos[()m 100.6(122π+⨯=--t x2.某振动质点的x -t 曲线如下列图,试求:〔1〕运动方程;〔2〕点P 对应的相位;〔3〕到达点P 相应位置所需要的时间。
题2分析:由运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题。
此题就是要通过x -t 图线确定振动的三个特征量量A 、ω,和0ϕ,从而写出运动方程。
曲线最大幅值即为振幅A ;而ω、0ϕ通常可通过旋转矢量法或解析法解出,一般采用旋转矢量法比拟方便。
《大学物理》第八章至十一章练习题及资料整理总结

《大学物理》(下)复习提纲第八章静止电荷的电场(1)掌握电场强度的迭加法计算。
掌握库仑定律。
(2)掌握电场强度通量计算方法、高斯定理。
(3)掌握静电场的环路定律,电势能和电势的定义和计算公式。
(4)掌握导体静电平衡时电荷如何分布。
导体静电平衡后的电势计算方法以及平行板电容器的电容公式。
(5)掌握电介质在外电场中极化性质和电介质中的高斯定理。
要会用介质中高斯定理定性分析介质中电场和电势,掌握电场能量计算公式。
1.如图所示,真空中一长为L的均匀带电细直杆,总电荷为q,试求在直杆延长线上距杆的一端距离为d 的P点的电场强度.2.电荷为+q 和-2q 的两个点电荷分别置于x=1 m和x=-1 m处.一试验电荷置于x 轴上何处,它受到的合力等于零?3.若匀强电场的场强为E ,其方向平行于半径为R 的半球面的轴,如图所示.则通过此为半球面的电场强度通量Φe___________________,如果图是B,通量Φ为___________________。
e4.如图所示,一个电荷为q 的点电荷位于立方体的A 角上,则通过侧面abcd 的电场强度通量等于___________________,如果电荷为q 的点电荷位于立方体的中心上,通过侧面abcd 的电场强度通量等于通量e Φ为___________________。
5.根据高斯定理的数学表达式∑⎰=⋅0/εq S d E S可知下述各种说法中,正确的是:(A) 闭合面内的电荷代数和为零时,闭合面上各点场强一定为零.(B) 闭合面内的电荷代数和不为零时,闭合面上各点场强一定处处不为零. (C) 闭合面内的电荷代数和为零时,闭合面上各点场强不一定处处为零. (D) 闭合面上各点场强均为零时,闭合面内一定处处无电荷.6.三个平行的“无限大”均匀带电平面,其电荷面密度都是+σ,如图所示,则A 、B 、C 、D 三个区域的电场强度分别为:E A =_________________,E B =_____________,E C =_______________,E D =_________________ (设方向向右为正).7. 真空中一“无限大”均匀带电平面,其电荷面密度为σ (>0).在平面附近有一质量为m 、电荷为q (>0)的粒子.试求当带电粒子在电场力作用下从静止开始垂直于平面方向运动一段距离l 时的速率.设重力的影响可忽略不计.8. 如图所示,两个“无限长”的、半径分别为R 1和R 2的共轴圆柱面均匀带电,沿轴线方向单位长度上所带电荷分别为λ1和λ2,则在各个区域距离轴线为 r 处的 P 点的电场强度大小E 为 _______________________.9.如图,A 点与B 点间距离为2l ,OCD 是以B 为中心,以l 为半径的半圆路径. A 、B 两处各放有一点电荷,电荷分别为+q 和-q .把另一电荷为Q (Q <0 )的点电荷从D 点沿路径DCO 移到O 点,则电场力所做的功为___________________10. 将电荷均为q 的三个点电荷一个一个地依次从无限远处缓慢搬到x 轴的原点、x = a 和x = 2a 处.求证外界对电荷所作之功为设无限远处电势能为零.11. 如图所示,两同心带电球面,内球面半径为r 1=5 cm ,带电荷q 1=3×10-8C ;外球面半径为r 2=20 cm , 带电荷q 2=-6×10-8C ,设无穷远处电势为零,则空间另一电势为 零的球面半径r = __________________.12. 如图所示,两个同心的均匀带电球面,内球面半径为R1、带电荷Q1,外球面半径为R2、带有电荷Q2.设无穷远处为电势零点,试求下图(A),(B),(C)三图中、距离球心为r 处的P点的电势U为分别为__________________,__________________,__________________。
大学物理习题解答8第八章振动与波动 (2)

第七章 电磁感应本章提要1. 法拉第电磁感应定律· 当穿过闭合导体回路所包围面积的磁通量发生变化时,导体回路中就将产生电流,这种现象称为电磁感应现象,此时产生的电流称为感应电流。
· 法拉第电磁感应定律表述为:通过导体回路所包围面积的磁通量发生变化石,回路中产生地感应电动势i e 与磁通量m Φ变化率的关系为d d t=-F e其中Φ为磁链,负号表示感应电动势的方向。
对螺线管有N 匝线圈,可以有m N Φ=Φ。
2. 楞次定律· 楞次定律可直接判断感应电流方向,其表述为:闭合回路中感应电流的方向总是要用自己激发的磁场来阻碍引起感应电流的磁通量的变化。
3. 动生电动势· 磁感应强度不变,回路或回路的一部分相对于磁场运动,这样产生的电动势称为动生电动势。
动生电动势可以看成是洛仑兹力引起的。
· 由动生电动势的定义可得:()d bab ae 醋ò=v B l· 洛伦兹力不做功,但起能量转换的作用。
4. 感生电动势·当导体回路静止,而通过导体回路磁通量的变化仅由磁场的变化引起时,导体中产生的电动势称为感生电动势。
d dd d d d L S t te F =??蝌Ñ-=-i E r B S 其中E i 为感生电场强度。
5. 自感· 当回路中的电流发生变化,它所激发的磁场产生的通过自身回路的磁通量也会发生变化,此变化将在自身回路中产生感应电动势,这种现象称为自感现象,产生的电动势为自感电动势,其表达式为:d d L iL te =-(L 一定时)负号表明自感电动势阻碍回路中电流的变化,比例系数L 称为电感或自感系数。
· 自感系数表达式为:L iY =· 自感磁能212m W LI =6. 互感· 对于两个临近的载流回路,当其中一回路中的电流变化时,电流所激发的变化磁场在另一回路中产生感应电动势。
大学物理学振动与波动习题答案

大学物理学(上)第四,第五章习题答案第4章振动P174.4.1 一物体沿x轴做简谐振动,振幅A = 0.12m,周期T = 2s.当t = 0时,物体的位移x = 0.06m,且向x轴正向运动.求:(1)此简谐振动的表达式;(2)t = T/4时物体的位置、速度和加速度;(3)物体从x = -0.06m,向x轴负方向运动第一次回到平衡位置所需的时间.[解答](1)设物体的简谐振动方程为x = A cos(ωt + φ),其中A = 0.12m,角频率ω = 2π/T= π.当t = 0时,x = 0.06m,所以cosφ = 0.5,因此φ= ±π/3.物体的速度为v = d x/d t = -ωA sin(ωt + φ).当t = 0时,v = -ωA sinφ,由于v > 0,所以sinφ < 0,因此φ = -π/3.简谐振动的表达式为x= 0.12cos(πt –π/3).(2)当t = T/4时物体的位置为x= 0.12cos(π/2–π/3)= 0.12cosπ/6 = 0.104(m).速度为v = -πA sin(π/2–π/3)= -0.12πsinπ/6 = -0.188(m·s-1).加速度为a = d v/d t = -ω2A cos(ωt + φ)= -π2A cos(πt - π/3)= -0.12π2cosπ/6 = -1.03(m·s-2).(3)方法一:求时间差.当x = -0.06m 时,可得cos(πt1 - π/3) = -0.5,因此πt1 - π/3 = ±2π/3.由于物体向x轴负方向运动,即v< 0,所以sin(πt1 - π/3) > 0,因此πt1 - π/3 = 2π/3,得t1 = 1s.当物体从x= -0.06m处第一次回到平衡位置时,x = 0,v > 0,因此cos(πt2 - π/3) = 0,可得πt2 - π/3 = -π/2或3π/2等.由于t2 > 0,所以πt2 - π/3 = 3π/2,可得t2 = 11/6 = 1.83(s).所需要的时间为Δt = t2 - t1 = 0.83(s).方法二:反向运动.物体从x = -0.06m,向x轴负方向运动第一次回到平衡位置所需的时间就是它从x= 0.06m,即从起点向x 轴正方向运动第一次回到平衡位置所需的时间.在平衡位置时,x = 0,v < 0,因此cos(πt - π/3) = 0,可得πt - π/3 = π/2,解得t = 5/6 = 0.83(s).[注意]根据振动方程x = A cos(ωt + φ),当t = 0时,可得φ = ±arccos(x0/A),(-π < φ≦π),初位相的取值由速度决定.由于v = d x/d t = -ωA sin(ωt + φ),当t = 0时,v = -ωA sinφ,当v > 0时,sinφ < 0,因此φ = -arccos(x0/A);当v < 0时,sinφ > 0,因此φ = arccos(x0/A).可见:当速度大于零时,初位相取负值;当速度小于零时,初位相取正值.如果速度等于零,当初位置x0 = A时,φ = 0;当初位置x0 = -A时,φ= π.4.2 已知一简谐振子的振动曲线如图所示,试由图求:(1)a,b,c,d,e各点的位相,及到达这些状态的时刻t各是多少?已知周期为T;(2)振动表达式;(3)画出旋转矢量图.[解答]方法一:由位相求时间.(1)设曲线方程为x = A cosΦ,其中A表示振幅,Φ = ωt + φ表示相位.由于x a = A,所以cosΦa = 1,因此Φa = 0.由于x b = A/2,所以cosΦb = 0.5,因此Φb = ±π/3;由于位相Φ随时间t增加,b点位相就应该大于a点的位相,因此Φb = π/3.由于x c = 0,所以cosΦc = 0,又由于c点位相大于b位相,因此Φc = π/2.同理可得其他两点位相为Φd = 2π/3,Φe = π.c点和a点的相位之差为π/2,时间之差为T/4,而b点和a点的相位之差为π/3,时间之差应该为T/6.因为b点的位移值与O时刻的位移值相同,所以到达a点的时刻为t a = T/6.到达b点的时刻为t b = 2t a = T/3.到达c点的时刻为t c = t a + T/4 = 5T/12.到达d点的时刻为t d = t c + T/12 = T/2.到达e点的时刻为t e = t a + T/2 = 2T/3.(2)设振动表达式为x = A cos(ωt + φ),当t = 0时,x = A/2时,所以cosφ = 0.5,因此φ =±π/3;由于零时刻的位相小于a点的位相,所以φ = -π/3,因此振动表达式为cos(2)3tx ATπ=π-.另外,在O时刻的曲线上作一切线,由于速度是位置对时间的变化率,所以切线代表速度的方向;由于其斜率大于零,所以速度大于零,因此初位相取负值,从而可得运动方程.(3)如图旋转矢量图所示.方法二:由时间求位相.将曲线反方向延长与t轴相交于f点,由于x f= 0,根据运动方程,可得cos(2)03tTππ-=图6.2所以232f t Tπππ-=±. 显然f 点的速度大于零,所以取负值,解得 t f = -T /12.从f 点到达a 点经过的时间为T /4,所以到达a 点的时刻为t a = T /4 + t f = T /6,其位相为203a a t T Φπ=π-=. 由图可以确定其他点的时刻,同理可得各点的位相.4.3如图所示,质量为10g 的子弹以速度v = 103m·s -1水平射入木块,并陷入木块中,使弹簧压缩而作简谐振动.设弹簧的倔强系数k= 8×103N·m -1,木块的质量为4.99kg ,不计桌面摩擦,试求:(1)振动的振幅; (2)振动方程.[解答](1)子弹射入木块时,由于时间很短,木块还来不及运动,弹簧没有被压缩,它们的动量守恒,即mv = (m + M )v 0.解得子弹射入后的速度为v 0 = mv/(m + M ) = 2(m·s -1),这也是它们振动的初速度.子弹和木块压缩弹簧的过程机械能守恒,可得(m + M ) v 02/2 = kA 2/2,所以振幅为A v =-2(m). (2)振动的圆频率为ω=s -1).取木块静止的位置为原点、向右的方向为位移x 的正方向,振动方程可设为x = A cos(ωt + φ).当t = 0时,x = 0,可得φ = ±π/2;由于速度为正,所以取负的初位相,因此振动方程为x = 5×10-2cos(40t - π/2)(m).4.4 如图所示,在倔强系数为k的弹簧下,挂一质量为M 的托盘.质量为m 的物体由距盘底高h 处自由下落与盘发生完全非弹性碰撞,而使其作简谐振动,设两物体碰后瞬时为t = 0时刻,求振动方程.[解答]物体落下后、碰撞前的速度为v =物体与托盘做完全非弹簧碰撞后,根据动量守恒定律可得它们的共同速度为0m v v m M ==+这也是它们振动的初速度. 设振动方程为x = A cos(ωt + φ),其中圆频率为ω=物体没有落下之前,托盘平衡时弹簧伸长为x 1,则x 1 = Mg/k .物体与托盘碰撞之后,在新的平衡位置,弹簧伸长为x 2,则x 2 = (M + m )g/k .取新的平衡位置为原点,取向下的方向为正,则它们振动的初位移为x 0 = x 1 - x 2 = -mg/k . 因此振幅为图4.3图4.4A===初位相为arctanvxϕω-==4.5重量为P的物体用两根弹簧竖直悬挂,如图所示,各弹簧的倔强系数标明在图上.试求在图示两种情况下,系统沿竖直方向振动的固有频率.[解答](1)可以证明:当两根弹簧串联时,总倔强系数为k=k1k2/(k1+ k2),因此固有频率为2πων===.(2)因为当两根弹簧并联时,总倔强系数等于两个弹簧的倔强系数之和,因此固有频率为2πων===4.6 一匀质细圆环质量为m,半径为R,绕通过环上一点而与环平面垂直的水平光滑轴在铅垂面内作小幅度摆动,求摆动的周期.[解答]方法一:用转动定理.通过质心垂直环面有一个轴,环绕此轴的转动惯量为I c = mR2.根据平行轴定理,环绕过O点的平行轴的转动惯量为I = I c + mR2 = 2mR2.当环偏离平衡位置时,重力的力矩为M = -mgR sinθ,方向与角度θ增加的方向相反.根据转动定理得Iβ = M,即22dsin0dI mgRtθθ+=,由于环做小幅度摆动,所以sinθ≈θ,可得微分方程22ddmgRt Iθθ+=.摆动的圆频率为ω=周期为2πTω=22==方法二:用机械能守恒定律.取环的质心在最底点为重力势能零点,当环心转过角度θ时,重力势能为E p = mg(R - R cosθ),绕O点的转动动能为212kE I=ω,总机械能为21(cos)2E I mg R R=+-ωθ.环在转动时机械能守恒,即E为常量,将上式对时间求导,利用ω= dθ/d t,β=dω/d t,得0 = Iωβ + mgR(sinθ)ω,由于ω ≠ 0,当θ很小有sinθ≈θ,可得振动的微分方程22ddmgRt Iθθ+=,从而可求角频率和周期.[注意]角速度和圆频率使用同一字母(b)图4.5ω,不要将两者混淆.4.7 横截面均匀的光滑的U 型管中有适量液体如图所示,液体的总长度为L ,求液面上下微小起伏的自由振动的频率。
大学物理习题解答8第八章振动及波动(I)

第七章 电磁感应本章提要1. 法拉第电磁感应定律· 当穿过闭合导体回路所包围面积的磁通量发生变化时,导体回路中就将产生电流,这种现象称为电磁感应现象,此时产生的电流称为感应电流。
· 法拉第电磁感应定律表述为:通过导体回路所包围面积的磁通量发生变化石,回路中产生地感应电动势i e 与磁通量m Φ变化率的关系为其中Φ为磁链,负号表示感应电动势的方向。
对螺线管有N 匝线圈,可以有m N Φ=Φ。
2. 楞次定律· 楞次定律可直接判断感应电流方向,其表述为:闭合回路中感应电流的方向总是要用自己激发的磁场来阻碍引起感应电流的磁通量的变化。
3. 动生电动势· 磁感应强度不变,回路或回路的一部分相对于磁场运动,这样产生的电动势称为动生电动势。
动生电动势可以看成是洛仑兹力引起的。
· 由动生电动势的定义可得:· 洛伦兹力不做功,但起能量转换的作用。
4. 感生电动势·当导体回路静止,而通过导体回路磁通量的变化仅由磁场的变化引起时,导体中产生的电动势称为感生电动势。
其中E i 为感生电场强度。
5. 自感· 当回路中的电流发生变化,它所激发的磁场产生的通过自身回路的磁通量也会发生变化,此变化将在自身回路中产生感应电动势,这种现象称为自感现象,产生的电动势为自感电动势,其表达式为:d d L i L te =-(L 一定时) 负号表明自感电动势阻碍回路中电流的变化,比例系数L 称为电感或自感系数。
· 自感系数表达式为:· 自感磁能6. 互感· 对于两个临近的载流回路,当其中一回路中的电流变化时,电流所激发的变化磁场在另一回路中产生感应电动势。
这种现象称为互感现象,对应产生的电动势称为互感电动势,其表达式为:121d d i M te =-(M 一定时) 其中M 为互感系数。
7. 麦克斯韦方程组回顾有关描述静电场和稳恒磁场的基本性质的4个方程:● 静电场高斯定理● 稳恒磁场的高斯定理● 静电场的环路定理● 稳恒磁场的安培环路定理根据上述4个方程,考虑电场或磁场的变化,麦克斯韦对上述方程进行修改,得到如下一组描述任何电场和磁场的方程组。
II2_振动和波+详细解答

振动1. 一倔强系数为k 的轻弹簧,下端挂一质量为m 的物体,系统的振动周期为1T ,若将此弹簧截去一半的长度,下端挂一质量为12m 的物体,则系统振动周期2T 等于 (A )21T (B )1T (C )1T /2 (D )1T /2 (E )1T /4(C )弹簧的弹性系数问题:一根弹簧,弹性系数为k ,把它截短以后,k 不是减小了,而是增大了。
为什么?因为我们知道胡克定律为:f kx =(力的大小),即 f k x=。
下面两根弹簧,本来材料、长度、弹性系数都是完全一样的,但是把其中的一根截短,加上相等的拉力f ,截短以后的弹簧伸长量要小于原来长度的弹簧的伸长量,弹性系数k 增大了。
f12T = 22k k =,下端挂一质量为12m的物体,则系统振动周期2T 为:2T 1112222T π⎛=== ⎝2. 图(下左)中三条曲线分别表示简谐振动中的位移x ,速度v 和加速度a ,下列说法中那一个是正确的?(A )曲线3、1、2分别表示x 、v 、a 曲线。
(B )曲线2、1、3分别表示x 、v 、a 曲线。
(C )曲线1、3、2分别表示x 、v 、a 曲线。
(D )曲线2、3、1分别表示x 、v 、a 曲线。
(E )曲线1、2、3分别表示x 、v 、a 曲线。
(E )位移x 与加速度a 的曲线时刻都是反相的,从图上看曲线1、3反相,曲线2是速度v 曲线;另外,速度比位移的位相超前2π,加速度比速度的位相超前2π,从图上看曲线3比2超前了2π,3是加速度曲线; 曲线2比1超前了2π,1是位移曲线。
3. 在t =0时,周期为T 、振幅为A 的单摆分别处于图(上右)(a)、(b)、(c)三种状态,若选单摆的平衡位置为x 轴的原点,x 轴正向指向右方,则单摆作小角度摆动的振动表达式分别为(1) ; (2) ; (3) 。
关键是写出初位相,用旋转矢量法最方便:0v (a)(b)t(a )φ= -π/2(b )φ= π/2(c )φ= π所以: (1)Y=Acos (t T π2-2π) (2)Y=Acos (t T π2+2π) (3)Y=Acos (t Tπ2+π)4.一系统作谐振动,周期为T ,以余弦函数表达振动时,初位相为零,在0≤t ≤T /2范围内,系统在t = 、 时刻动能和势能相等。
大学物理知识总结习题答案(第八章)振动与波动

第八章 振动与波动本章提要1. 简谐振动· 物体在一定位置附近所作的周期性往复运动称为机械振动。
· 简谐振动运动方程()cos x A t ωϕ=+其中A 为振幅,??为角频率,(?t+?)称为谐振动的相位,t =0时的相位??称为初相位。
· 简谐振动速度方程d ()d sin xv A t tωωϕ==-+ · 简谐振动加速度方程222d ()d cos xa A t tωωϕ==-+· 简谐振动可用旋转矢量法表示。
2. 简谐振动的能量· 若弹簧振子劲度系数为k ,振动物体质量为m ,在某一时刻m 的位移为x ,振动速度为v ,则振动物体m 动能为212k E mv =· 弹簧的势能为212p E kx =· 振子总能量为P22222211()+()221=2sin cos k E E E m A t kA t kA ωωϕωϕ=+=++3. 阻尼振动· 如果一个振动质点,除了受弹性力之外,还受到一个与速度成正比的阻尼作用,那么它将作振幅逐渐衰减的振动,也就是阻尼振动。
· 阻尼振动的动力学方程为222d d 20d d x xx t tβω++= 其中,γ是阻尼系数,2mγβ=。
(1) 当22ωβ>时,振子的运动一个振幅随时间衰减的振动,称阻尼振动。
(2) 当22ωβ=时,不再出现振荡,称临界阻尼。
(3) 当22ωβ<时,不出现振荡,称过阻尼。
4. 受迫振动· 振子在周期性外力作用下发生的振动叫受迫振动,周期性外力称驱动力 · 受迫振动的运动方程为22P 2d d 2d d cos x x F x t t t mβωω++= 其中,2k m ω=,为振动系统的固有频率;2C m β=;F 为驱动力振幅。
· 当驱动力振动的频率p ω等于ω时,振幅出现最大值,称为共振。
(大学物理基础)08第八章振动与波动课后习题

思考题8-13 两列简谐波叠加时,讨论下列各种情况: (1)若两波的振动方向相同,初相位也相同,但频率 不同,能不能发生干涉?(2)若两波的频率相同,初 相位也相同,但振动方向不同,能不能发生干涉?(3) 若两波的频率相同,振动方向也相同,但相位差不能保 持恒定,能不能发生干涉?(4)若两波的频率相同、 振动方向相同、初相位也相同,但振幅不同,能不能发 生干涉?
x 0.02cos4t
(2)振动物体在负方向端点;
t 0 x 0.02m 0.02 0.02cos
x 0.02cos(4t )
(3)振动物体在平衡位置,向负方向运动;
t 0 x 0 0 0.02cos
v 0.08 sin 0
x
0.02
2
cos(4t
)
2
2
x 0.02cos(4t ) v 0.08 sin(4t )
答:振动系统的角频率为
k 40rad s1
m m0
由动量守恒定律得振动的初始速度即子弹和木块的共 同运动初速度为
v0
mv m m0
2.0m / s
初始位移为 x0 0 A
x02
(v0
)2
5.0 102 m
设振动方程为
x Acos(t )
t 0 x0 0
0 Acos
2
v0 A sin 0
能和总能量。
由上题 t 2 s 3
v 0.12 sin t 0.326m / s
2
EK
1 mv2 2
5.31104 J
EP
大学物理下册电子教案

#### 一、课程概述课程名称:大学物理下册适用专业:理工科非物理学类专业教材:《物理学(第七版)》下册,程守洙、江之永编著课程目标:1. 深入理解物理学的基本概念和原理。
2. 掌握物理学的基本分析方法,提高科学思维和解决问题的能力。
3. 了解物理学在科学技术和工程领域的应用。
#### 二、课程内容安排第一周:振动与波动1. 振动的基本概念- 振动的定义- 振动的分类- 振动的特性2. 简谐振动- 简谐振动的定义- 简谐振动的运动方程- 简谐振动的能量3. 波动的基本概念- 波动的定义- 波的类型- 波动方程第二周:光学1. 光的传播- 光的直线传播- 光的折射- 光的全反射2. 光的干涉- 干涉现象- 相干光源- 干涉条纹3. 光的衍射- 衍射现象- 单缝衍射- 双缝衍射第三周:气体动理论1. 理想气体模型- 理想气体的假设- 理想气体的状态方程 - 理想气体的热力学性质2. 分子动理论- 分子的运动- 分子间的相互作用- 分子动理论的应用第四周:热力学基础1. 热力学第一定律- 能量守恒定律- 热力学第一定律的表述- 热力学第一定律的应用2. 热力学第二定律- 热力学第二定律的表述- 熵的概念- 可逆与不可逆过程3. 热力学第三定律- 绝对零度的概念- 热力学第三定律的表述第五周:量子力学基础1. 量子力学的基本原理- 波粒二象性- 玻尔理论- 海森堡不确定性原理2. 量子力学的基本方程- 薛定谔方程- 叠加原理- 波函数的物理意义#### 三、教学方法与考核方式教学方法:1. 讲授法:系统讲解物理学的基本概念、原理和方法。
2. 案例分析法:通过具体实例,帮助学生理解和应用所学知识。
3. 讨论法:鼓励学生积极参与课堂讨论,提高学生的思维能力和表达能力。
考核方式:1. 平时成绩:包括课堂参与、作业完成情况等。
2. 期末考试:闭卷考试,考察学生对课程内容的掌握程度。
#### 四、教学资源1. 教材:《物理学(第七版)》下册,程守洙、江之永编著2. 电子教案:PPT课件、教学视频等3. 参考书:《物理学(第七版)习题分析与解答》《物理学(第七版)思考题分析与解答》《物理学(第七版)学习指导》等通过本课程的学习,学生将能够掌握物理学的基本概念、原理和方法,提高科学思维和解决问题的能力,为今后的学习和工作打下坚实的基础。
大学物理答案第八章 振动

----------专业最好文档,专业为你服务,急你所急,供你所需-------------第八章 振动8-1 解:取固定坐标xOy ,坐标原点O 在水面上(图题所示)设货轮静止不动时,货轮上的A 点恰在水面上,则浮力为S ρga .这时 ga s Mg ρ= 往下沉一点时,合力 )(y a g s Mg F +-=ρ gy s ρ-=. 又 22d d tyMMa F == 故0d d 22=+gy s t y M ρ 022=+y M gs dtdy ρ 故作简谐振动 M gs ρω=2)(35.68.910102101022223334s g s M T =⨯⨯⨯⨯⨯===πρπωπ8-2 解:取物体A 为研究对象,建立坐标Ox 轴沿斜面向下,原点取在平衡位置处,即在初始位置斜下方距离l 0处,此时:)(1.0sin 0m kmg l ==θ(1) (1) A 物体共受三力;重mg, 支持力N, 张力T.不计滑轮质量时,有 T =kx列出A 在任一位置x 处的牛顿方程式220d d )(sin sin txm x l k mg T mg =+-=-θθ将(1)式代入上式,整理后得0d d 22=+x m ktx 习题8-1图----------专业最好文档,专业为你服务,急你所急,供你所需-------------故物体A 的运动是简谐振动,且)rad/s (7==mkω 由初始条件,000⎩⎨⎧=-=v l x 求得,1.00⎩⎨⎧===πϕml A 故物体A 的运动方程为x =0.1cos(7t+π)m(2) 当考虑滑轮质量时,两段绳子中张力数值不等,如图所示,分别为T 1、T 2,则对A 列出任一位置x 处的牛顿方程式为:221d d sin txm T mg =-θ (2)对滑轮列出转动方程为:22221d d 2121t x Mr r a Mr J r T r T =⎪⎭⎫ ⎝⎛==-β (3)式中,T 2=k (l 0+x ) (4)由式(3)、(4)知2201d d 21)(txM x l k T ++=代入(2)式知 22021)(sin dtxd m M x l k mg ⎪⎭⎫ ⎝⎛+=+-θ又由(1)式知0sin kl mg =θ故0d d )21(22=++kx txm M即0)2(d d 22=++x m M ktx m M k +=22ω可见,物体A 仍作简谐振动,此时圆频率为:rad/s)(7.52=+=m M k ω由于初始条件:0,000=-=vl x习题8-2图----------专业最好文档,专业为你服务,急你所急,供你所需-------------可知,A 、ϕ不变,故物体A 的运动方程为:m t x )7.5cos(1.0π+=由以上可知:弹簧在斜面上的运动,仍为简谐振动,但平衡位置发生了变化,滑轮的质量改变了系统的振动频率.8-3 解:简谐振动的振动表达式:)cos(ϕω+=t A x由题图可知,m 1042-⨯=A ,当t=0时,将m 1022-⨯=x 代入简谐振动表达式,得:21cos =ϕ 由)sin(ϕωωυ+-=t A ,当t=0时,ϕωυsin A -= 由图可知,υ>0,即0sin <ϕ,故由21cos =ϕ,取3πϕ-= 又因:t=1s 时,,1022m x -⨯=将其入代简谐振动表达式,得213cos ,3cos 42=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=πωπω由t=1s 时,⎪⎭⎫⎝⎛--=3sin πωωυA <0知,03sin >⎪⎭⎫ ⎝⎛-πω,取33ππω=-, 即 s 32πω=质点作简谐振动的振动表达式为m t x ⎪⎭⎫ ⎝⎛-⨯=-332cos 1042ππ8-4 解:以该球的球心为原点,假设微粒在某一任意时刻位于遂道中的位矢为r,由高斯定理可知304Rr Q E πε=,则微粒在此处受电场力为:r R Qq F304πε-= 式中,负号表明电场F 的方向与r的正方向相反,指向球心.由上式及牛顿定律,得:04d d 04d d 043022302230=+⇒=+=+r mRQq t r r R Qq t r m r RQqF πεπεπε习题8-3图----------专业最好文档,专业为你服务,急你所急,供你所需-------------令 mR Qq3024πεω=则 0d d 222=+r tr ω 故微粒作简谐振动,平衡点在球心处.由ωπ2=T知: QqmR T 3042πεπ=8-5 解:(1)取弹簧原长所在位置为O '点.当弹簧挂上物体A 时,处于静止位置P 点,有:P O k Mg '=将A 与B 粘合后,挂在弹簧下端,静止平衡所在位置O 点,取O 点为原坐标原点如图题8-5所示,则有:g m M O O k )(+='设当B 与A 粘在一起后,在其运动过程的任一位置,弹簧形变量x O O +',则A 、B 系统所受合力为:kx x O O k g m M F -=+'-+=)()(即 0d d )(22=++kx txm M可见A 与B 作简谐和振动. (2) 由上式知,rad/s)(10=+=mM kω以B 与A 相碰点为计时起点,此时A 与B 在P 点,由图题8-5可知kmgk Mg g k m M P O O O OP =-+='-'= 则t=0时,m 02.00-=-=-=kmgOP x (负号表P 点在O 点上方) 又B 与A 为非弹性碰撞,碰撞前B 的速度为:m/s 2220101=-='gh υυ碰撞后,A 、B 的共同速度为:m/s 4.0010=+'=mM m υυ (方向向上)则t=0时,⎩⎨⎧=-=sm mx /4.002.000υ习题8.5图----------专业最好文档,专业为你服务,急你所急,供你所需-------------可求得:)m (0447.022020=+=ωυx Aπωυϕ65.0arctan 00=⎪⎪⎭⎫⎝⎛-=x 可知A 与B 振动系统的振动表达式为:m t x )65.010cos(0447.0π+= (3) 弹簧所受的最大拉力,应是弹簧最大形变时的弹力,最大形变为:m A g kmM A O O x 1447.0=++=+'=∆则最大拉力 N 4.72max ==x k F ∆ 8-6 解:(1) 已知A=0.24m,22ππω==T ,如选x 轴向下为正方向. 已知初始条件0m ,12.000<=υx 即 3,21c o s ,c o s 24.012.0πϕϕϕ±=== 而 ,0sin ,0sin 0><-=ϕϕωυA 取3πϕ=,故:m t x ⎪⎭⎫ ⎝⎛+=32cos 24.0ππ(2) 如图题所示坐标中,在平衡位置上方0.12m, 即x=-0.12m 处,有32322132cos πππππ±=+-=⎪⎭⎫ ⎝⎛+t t因为所求时间为最短时间,故物体从初始位置向上运动,0<υ.故0)32sin(>+ππt则取3232πππ=+t 可得:s t 32min =(3) 物体在平衡位置上方0.12m 处所受合外力2F m x 0.3N =-ω=,指向平衡位置.8-7 解:子弹射入木块为完全非弹性碰撞,设u 为子弹射入木块后二者共同速度,由动量定理可知:m/s)(0.2=+=υmM mu不计摩擦,弹簧压缩过程中系统机械能守恒,即:习题8-6图----------专业最好文档,专业为你服务,急你所急,供你所需-------------2221)(21kx u m M =+ (x 0为弹簧最大形变量) m u kmM x 20100.5-⨯=+=由此简谐振动的振幅 20100.5-⨯==x A系统圆频率rad/s)(40=+=mM kω若取物体静止时的位置O (平衡位置)为坐标原点,Ox 轴水平向右为正,则初始条件为: t =0时,x =0,0m/s 0.20>==u υ由,sin ,cos 00ϕωυϕA A x -==得:2πϕ-=则木块与子弹二者作简谐振动,其振动表达式为:m t x )240cos(100.52π-⨯=-8-8 解:当物体m 1向右移动x 时,左方弹簧伸长x ,右方弹簧缩短x ,但它们物体的作用方向是相同的,均与物体的位移方向相反,即)(21x k x k F +-=令F =-kx ,有:N/m 421=+=k k k 由 kmT π2= 得)kg (1.0442212211≈==ππkT k T m则粘上油泥块后,新的振动系统质量为:kg 20.021=+m m新的周期 )s (4.12212=+=km m T π在平衡位置时,m 2与m 1发生完全非弹性碰撞. 碰撞前,m 1的速度m /s 10.0111πωυ==A 设碰撞后,m 1和m 2共同速度为υ. 根据动量守恒定律,υυ)(2111m m m +=----------专业最好文档,专业为你服务,急你所急,供你所需-------------则 m/s 05.0)(2111πυυ=+=m m m新的振幅 m)(035.0222===πυωυTA 8-9 解:(1)由振动方程)25sin(60.0π-=t x 知,5(rad/s)m,6.0==ωA故振动周期: )s (26.1)s (256.1522≈===πωπT (2) t=0时,由振动方程得:0)25cos(0.3|m60.0000=-==-==πυt dt dx x t (3) 由旋转矢量法知,此时的位相:3πϕ-=速度 m/s)(6.2m/s )23(560.0sin =-⨯⨯-=-=ϕωυA 加速度 )m /s (5.7m /s 21560.0cos 2222-=⨯⨯-=-=ϕωA a 所受力 N)(5.1N )5.7(2.0-=-⨯==ma F(4)设质点在x 处的动能与势能相等,由于简谐振动能量守恒,即:221kA E E E p k ==+ 故有: )21(21212kA E E E p k ===即 22212121kA kx ⨯=可得: m)(42.022±=±=A x 8-10 解:(1)砝码运动到最高点时,加速度最大,方向向下,由牛顿第二定律,有:N mg ma -=maxN 是平板对砝码的支持力.故N)(74.1)4()()(22max =-=-=-=vA g m A g m a g m N πω砝码对板的正压力与N 大小相等,方向相反.砝码运动到最低点时,加速度也是最大,但方向向上,由牛顿第二定律,有:mg N ma -'=max----------专业最好文档,专业为你服务,急你所急,供你所需-------------故 N)(1.8)4()(22max =+=+='A v g m a g m N π砝码对板的正压力与板对砝码的支持力N '大小相等,方向相反. (2)当N=0时,砝码开始脱离平板,故此时的振幅应满足条件:m)(062.040)4(22max max 2===-=v g A vA g m N ππ(3) 由22max 4v g A π=,可知,2m ax v A 与成反比,当v v 2='时,m 0155.041max max=='A A 8-11 解:(1)设振子过平衡位置时的速度为υ,由机械能守恒,有:222121υm kA = A mk=υ 由水平方向动量定理: ⇒='+υm u m m )(υmm mu '+= 此后,系统振幅为A ',由机械能守恒,有:22)(2121u m m A k '+=' 得: A m m mA '+='有: km m T '+='π2 (2)碰撞前后系统总能量变化为:)21()1(2121212222kA m m m m m m kA kA A k E '+'-=-'+=-'=∆式中,负号表示能量损耗,这是泥团与物体的非弹性碰撞所致.(3)当m 达到振幅A 时,m '竖直落在m 上,碰撞前后系统在水平方向的动量均为零,因而系统的振幅仍为A ,周期为k m m '+π2,系统的振动总能量不变,为221kA (非弹性碰撞损耗的能量为源于碰撞前m '的动能). 物体系统过平衡位置时的速度υ'由:22)(2121υ''+=m m kA 得: A m m k'+±='υ----------专业最好文档,专业为你服务,急你所急,供你所需-------------8-12 解:(1)由放置矢量法可知,振子从2A运动到2A -的位置处,角相位的最小变化为:3πϕ∆=则圆频率rad/s 3π∆ϕ∆ω==t 周期 s T 62==ωπ由初始状态,在图示坐标中,初始条件为:m)(1.00m1.000=⇒⎩⎨⎧=-=A x υ则振幅 m 1.022020=+=ωυx A(2)因为E E p 41=又 2221,21kA E kx E p == 故 )21(412122kA kx =得: m)(05.0±=x 根据题意,振子在平衡位置的下方,取x =-0.05m.根据振动系统的能量守恒定律:222212121kA m kx =+υ 故 )s m (091.0122-⋅±=-±=x A ωυ根据题意,取m/s 091.0-=υ 再由 )sin()cos(ϕωωυϕω+-=+=t A t t A x)cos(d d 2ϕωω+-==t A tva x 2ω-= 得: )m /s (055.02=a(3)t=0时,(J)108.681)21(41413222-⨯====mA kA E E p ω (J)102183)21(43433222-⨯====mA kA E E k ω(J)108.273-⨯=+=p k EE E习题8-12图----------专业最好文档,专业为你服务,急你所急,供你所需-------------(4)由简谐振动的振动表达式)cos(ϕω+=t A x 当t=0时,0m /s 091.0m ,05.000<-=-=υx ,可得:πϕ32= 又 3,10.0πω==m A故 m t x )323cos(1.0ππ+= 8-13 解:(1)据题意,两质点振动方程分别为:mt x mt x Q P )3cos(1000.2)3cos(1000.522ππππ-⨯=+⨯=--(2)P 、Q 两质点的速度及加速度表达分别为:)m/s )(3sin(1000.52ππωυ+⨯⨯-==-t dt dx P P )m /s )(3sin(1000.22ππωυ-⨯⨯-==-t dt dx QQ )m/s )(3cos(1000.5222ππωυ+⨯⨯-==-t dt d a P P )m/s )(3cos(1000.2222ππωυ-⨯⨯-==-t dtd a Q Q当t=1s 时,有:)(m/s 1087.9/32cos 1000.2)(m/s 1068.24/34cos 1000.5(m/s)1044.5/32sin 1000.2(m/s)1060.13/34sin 1000.5(m)1000.132cos 1000.2)(m 105.234cos1000.5222222222222222222------------⨯=⨯⨯-=⨯=⨯⨯-=⨯-=⨯⨯-=⨯=⨯⨯-=⨯-=⨯=⨯=⨯=s m a s m a s m s m m x m x Q P Q P Q P ππππππυππυππ(3)由相位差----------专业最好文档,专业为你服务,急你所急,供你所需-------------32)3(3)()(πππϕϕϕωϕωϕ∆=--=-=+-+=Q P Q P t t 可见,P 点的相比Q 点的相位超前32π. 8-14 解:(1)由题意得初始条件:⎪⎩⎪⎨⎧<=02100υA x 可得:3πϕ=(由旋转矢量法可证出)在平衡位置的动能就是质点的总能量)J (1008.3212152222-⨯====⇒=A m kA E m k m kωωω 可求得:s rad m E A /221πω==则振动表达式为:m t x )32cos(1000.52ππ+⨯=-(2) 初始位置势能)32(cos 21212222ππω+==t A m kx E P 当t=0时,3cos 21222πωA m E P =J J 6222221071.73cos )1000.5()2(1000.121---⨯=⨯⨯⨯⨯⨯=ππ 8-15 解:(1)由初始条件:⎩⎨⎧<⨯=-0102.1010υm x 可知,3πϕ=且22ππω==v则振动表达式为:m t x )32cos(24.0ππ+=当t=0.5s 时,----------专业最好文档,专业为你服务,急你所急,供你所需-------------m m x 21000.6)3212cos(24.0-⨯-=+⨯=ππ(2) t=0.5s 时,小球所受力:(N)1048.1)(32-⨯=-==x m ma f ω因t=0.5s 时,小球的位置在m x 21000.6-⨯-=处,即小球在x 轴负方向,而f 的方向是沿x 轴正方向,总是指向平衡位置.(3) 从初始位置m x 10102.1-⨯=到m x 1102.1-⨯-=所需最短时间设为t ,由旋转矢量法知,πϕπϕ32,3,0±=±=处处x x )s (3223=⇒⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧==t t πωπω(4) 因为 )32sin(24.02)sin(πππϕωωυ+⨯-=+-=t t A )32cos(24.04)cos(22πππϕωω+⨯-=+-=t t A a 在s t m x 32102.11=⨯-=-处 )32cos(24.04)3322cos(24.04/1026.3/)3322sin(24.022212ππππππαπππυ+⨯-=+⨯⨯-=⨯-=+⨯⨯-=-t s m s m (5) t=4s 时, 22)]32sin([2121ππωυ+-==t A m m E k (J)1033.5J)342(sin 24.0)2(01.0214222-⨯=+⨯⨯⨯⨯=πππ习题8-15图----------专业最好文档,专业为你服务,急你所急,供你所需-------------)32(cos 21212222ππω+==t A m kx E P (J)1077.1J)342(cos 24.0)2(01.0214222-⨯=+⨯⨯⨯⨯⨯=πππ(J)107.10J 101.77J 1033.5-4-44⨯=⨯+⨯=+=-P k E E E 总8-16 解:设两质点的振动表达式分别为:)cos()cos(2211ϕωϕω+=+=t A x t A x由图题可知,一质点在21Ax =处时对应的相位为: 32/arccos 1πϕω==+A A t同理:另一质点在相遇处时,对应的相位为:352/arccos2πϕω==+A A t 故相位差)()(12ϕωϕωϕ∆+-+=t t πππϕϕ3433512=-=-= 若21υυ与的方向与上述情况相反,故用同样的方法,可得:πππϕϕϕ∆32)3(312=--=-= 8-17 解:由图题8-17(图在课本上P 33)所示曲线可以看出,两个简谐振动的振幅相同,即m 05.021==A A ,周期均匀s 1.0=T ,因而圆频率为:ππω202==T由x -t 曲线可知,简谐振动1在t=0时,,010=x 且010>υ,故可求得振动1的初位相πϕ2310=.同样,简谐振动2在t=0时,πϕυ==-=202020,0,05.0可知m x 故简谐振动1、2的振动表达式分别为:mt x t x )20cos(05.0)2320cos(05.021ππππ+=+=因此,合振动的振幅和初相位分别为:习题8-16图----------专业最好文档,专业为你服务,急你所急,供你所需-------------m A A A A A 210202122211025)cos(2-⨯=-++=ϕϕ2021012021010cos cos sin sin arctanϕϕϕϕϕA A A A ++=ππ4541arctan 或== 但由x-t 曲线知,t=0时,πϕ45,05.021应取因此-=+=x x x . 故合振动的振动表达式:m t x )4520cos(10252ππ+⨯=-8-18 解:(1)它们的合振动幅度初相位分别为:)cos(212212221ϕϕ-++=A A A A Am )535cos(06.005.0206.005.022ππ-⨯⨯⨯++=m 0892.0= 22112211cos cos sin sin arctanϕϕϕϕϕA A A A ++=316819.15.2arctan 5cos06.053cos 05.05sin06.053sin 05.0'︒===++=rad ππππ (2)当πϕϕk 21±=-,即ππϕπϕ53221+±=+±=k k 时,31x x +的振幅最大;当πϕϕ)12(2+±=-k ,即5)12()12(2ππϕϕ++±=++±=k k 时,32x x +的振幅最小.(3)以上两小问的结果可用旋转矢量法表示,如图题8-18所示. 8-19解:根据题意画出振幅矢量合成图,如习题8-19图所示.由习题8-19图及余弦定理可知 cm 233.172023.172030cos 22212122⨯⨯⨯-+=︒-+=AA A A A 0.10m cm 10== 又因为)cos(cos 12ϕϕϕ∆-=0103.172)100300(4002)(2122212=⨯⨯+-=+-=A A A A A习题8-19图----------专业最好文档,专业为你服务,急你所急,供你所需-------------若2πϕ∆=,即第一、第二两个振动的相位差为2π。
大学基础物理学 (习岗 著) 高等教育出版社 第8章 振动和波动课后答案

第八章 振动和波动8-1由T=0.5s, 得ππω42==T, 设简谐振动方程为)4cos(02.0ϕπ+=t x (1)由于物体在正方向端点,由旋转矢量法得 0=ϕ所以振动方程为t x π4cos 02.0=(2)由于物体在负方向端点,由旋转矢量法得πϕ= 所以振动方程为)(ππ+=t x 4cos 02.0 (3)振动物体在平衡位置,向负方向运动,由旋转矢量法得2/πϕ= 所以振动方程为)(24cos 02.0ππ+=t x(4)振动物体在平衡位置,向正方向运动,由旋转矢量法得2/πϕ-= 所以振动方程为)(24cos 02.0ππ-=t x (5)振动物体在x=0.01m 处,向负方向运动,由旋转矢量法得3/πϕ=所以振动方程为)(34cos 02.0ππ+=t x (6)振动物体在x=-0.01m 处,向正方向运动,由旋转矢量法得3/2πϕ= 所以振动方程为)(324cos 02.0ππ+=t x 8-2由振动方程为)38cos(5.0ππ+=t x 得 35.025.028πϕωππω=====m A s T22max max 324πωπω====A a A v(2)t=1s,2s,10s 时的相位分别是:3241349325πππ,, 8-15 (1)波动方程为 )(cos )cos(B Cx t B A Cx Bt A y -=-= 标准波动方程为 )(cos uxt A y -=ω,比较系数得:振幅为A, B =ω, BC u =, ππων22B ==, B T π2=, C B C B uT ππλ22=== (2) ))cos(Cl Bt A y -=(3)dc d==∆λπϕ28-16(1) 设波源振动方程为)cos(ϕω+=t A y ,根据题意得:A = 0.01m, πππω20001.022===T , 由旋转矢量得2/πϕ-=)2/200cos(01.0ππ-=t y(2) 波动方程为)2/)400(200cos(01.0ππ--=xt y(3) 波源8米处振动方程为:)2/)501(200cos(01.0ππ--=t y(4) ππϕ5.049102=-=∆8-17(1) 由题意得 ππλππω5004.0122/2====uT由旋转矢量得2/πϕ=,又 A = 0.03m ,)2/)1(50cos(03.0ππ+-=xt y (2)tt t xt y πππππππ50cos 03.0)250cos(03.0)2/)105.0(50cos(03.0)2/)1(50cos(03.0=+=+-=+-= (3) 02121.0)2/)1045.03(50cos(03.0=+-=ππys m x t v /33.3)2/5050sin(5003.0-=+-⨯-=ππππ8-18由图得:A = 2 cm=0.02m, m 6=λ, s m u /30=, πω102.0==s T 由初始条件:2πϕ-=]2)30(10cos[02.0ππ-+=x t y8-19由于t y π2cos 1.01=,所以传到 P 点的分振动方程为: )42cos(1.0)20(2cos 1.01'1πππ-=-=t r t y由于)2cos(1.02ππ+=t y ,所以传到 P 点的分振动方程为:)42cos(1.0])20[(2cos 1.02'2ππππ-=+-=t r t y m A A A A A A A 2.0cos 221212221=+=∆++=ϕ8-20由题意可设两波源振动方程分别为:)(ϕπ+=t y 200cos 001.01)(2200cos 001.02πϕπ++=t y 则波源的振动传到P 点的振动分别为: )(ϕπ+-=)400(200cos 001.011r t y )(2)500(200cos 001.022πϕπ++-=r t y 所以两振动的相差为:02)50075.34004(200=---=∆ππϕ 所以P 点合振幅为 m A A A 002.021=+=。
振动与波动(习题与答案)

第10章振动与波动一.基本要求1. 掌握简谐振动的基本特征,能建立弹簧振子、单摆作谐振动的微分方程。
2. 掌握振幅、周期、频率、相位等概念的物理意义。
3. 能根据初始条件写出一维谐振动的运动学方程,并能理解其物理意义。
4. 掌握描述谐振动的旋转矢量法,并用以分析和讨论有关的问题。
5. 理解同方向、同频率谐振动的合成规律以及合振幅最大和最小的条件。
6. 理解机械波产生的条件。
7. 掌握描述简谐波的各物理量的物理意义及其相互关系。
8. 了解波的能量传播特征及能流、能流密度等概念。
9. 理解惠更斯原理和波的叠加原理。
掌握波的相干条件。
能用相位差或波程差概念来分析和确定相干波叠加后振幅加强或减弱的条件。
10. 理解驻波形成的条件,了解驻波和行波的区别,了解半波损失。
二. 内容提要1. 简谐振动的动力学特征作谐振动的物体所受到的力为线性回复力,即取系统的平衡位置为坐标原点,则简谐振动的动力学方程(即微分方程)为2. 简谐振动的运动学特征作谐振动的物体的位置坐标x与时间t成余弦(或正弦)函数关系,即由它可导出物体的振动速度)=tAv-ω+ωsin(ϕ物体的振动加速度)=tAa2cos(ϕ-+ωω3. 振幅A 作谐振动的物体的最大位置坐标的绝对值,振幅的大小由初始条件确定,即4. 周期与频率 作谐振动的物体完成一次全振动所需的时间T 称为周期,单位时间内完成的振动次数γ称为频率。
周期与频率互为倒数,即ν=1T 或 T1=ν5. 角频率(也称圆频率)ω 作谐振动的物体在2π秒内完成振动的次数,它与周期、频率的关系为 ωπ=2T 或 πν=ω26. 相位和初相 谐振动方程中(ϕ+ωt )项称为相位,它决定着作谐振动的物体的状态。
t=0时的相位称为初相,它由谐振动的初始条件决定,即应该注意,由此式算得的ϕ在0~2π范围内有两个可能取值,须根据t=0时刻的速度方向进行合理取舍。
7. 旋转矢量法 作逆时针匀速率转动的矢量,其长度等于谐振动的振幅A ,其角速度等于谐振动的角频率ω,且t=0时,它与x 轴的夹角为谐振动的初相ϕ,t=t时刻它与x 轴的夹角为谐振动的相位ϕω+t 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章 振动与波动本章提要1. 简谐振动· 物体在一定位置附近所作的周期性往复运动称为机械振动。
· 简谐振动运动方程()cos x A t ωϕ=+其中A 为振幅,ω 为角频率,(ωt+ϕ)称为谐振动的相位,t =0时的相位ϕ 称为初相位。
· 简谐振动速度方程d ()d sin xv A t tωωϕ==-+ · 简谐振动加速度方程222d ()d cos xa A t tωωϕ==-+· 简谐振动可用旋转矢量法表示。
2. 简谐振动的能量· 若弹簧振子劲度系数为k ,振动物体质量为m ,在某一时刻m 的位移为x ,振动速度为v ,则振动物体m 动能为212k E mv =· 弹簧的势能为212p E kx =· 振子总能量为P22222211()+()221=2sin cos k E E E m A t kA t kA ωωϕωϕ=+=++3. 阻尼振动· 如果一个振动质点,除了受弹性力之外,还受到一个与速度成正比的阻尼作用,那么它将作振幅逐渐衰减的振动,也就是阻尼振动。
· 阻尼振动的动力学方程为222d d 20d d x xx t tβω++= 其中,γ是阻尼系数,2mγβ=。
(1) 当22ωβ>时,振子的运动一个振幅随时间衰减的振动,称阻尼振动。
(2) 当22ωβ=时,不再出现振荡,称临界阻尼。
(3) 当22ωβ<时,不出现振荡,称过阻尼。
4. 受迫振动· 振子在周期性外力作用下发生的振动叫受迫振动,周期性外力称驱动力 · 受迫振动的运动方程为22P 2d d 2d d cos x x F x t t t mβωω++= 其中,2k m ω=,为振动系统的固有频率;2C m β=;F 为驱动力振幅。
· 当驱动力振动的频率p ω等于ω时,振幅出现最大值,称为共振。
5. 简谐振动的合成与分解(1) 一维同频率的简谐振动的合成 若任一时刻t 两个振动的位移分别为111()cos x A t ωϕ=+ 222()cos x A t ωϕ=+合振动方程可表示为()cos x A t ωϕ=+其中,A 和ϕ 分别为合振动的振幅与初相位A =11221122sin sin tan cos cos A A A A ϕϕϕϕϕ+=+(2) 二维同频率的简谐振动的合成若一个质点同时参与两个同频率的简谐振动,且此两个简谐振动分别在x 轴和y 轴上进行,运动方程分别为11()cos x A t ωϕ=+22()cos y A t ωϕ=+其合振动方程为22221212212122()()cos sin x y xy A A A A ϕϕϕϕ+--=- 该为一个椭圆方程,椭圆形状由振幅A 1、A 2及相位差21()ϕϕ-决定。
(3) 二维不同频率的简谐振动的合成如果两个相互垂直的简谐振动的周期成简单的整数比,合运动的轨迹也是稳定的闭合曲线,这样合成振动的轨迹图形称为李萨如图形。
6. 简谐波· 若波源作简谐振动,那么当这种振动在介质中传播时,介质中的各点也作与此频率相同的简谐振动,这样形成的波动称为简谐波。
· 简谐波的波动方程()cos xy A t uω=-或2()cos t x y A T πλ=- 或2()cos xy A t πνλ=-7. 简谐波的能量密度· 单位体积的介质中波的能量称能量密度,用w 表示,其描述了介质中各处能量的分布情况222sin E x w A t V u ρω∆∆⎛⎫==- ⎪⎝⎭· 平均能量密度表示一个周期内能量密度的平均值02220221d 1d 12sin TT w w tT x A t t T u A ρωρω=⎛⎫=- ⎪⎝⎭=⎰⎰ · 波动的能流密度2212I w u u A ρω=⋅=8. 多普勒效应· 当观察者或波源相对于传播的介质运动时,观察者接受到的波的频率与波源的频率不同,这种现象称为多普勒效应。
(1) 波源静止,观察者相对于介质运动 观察者接收到的频率为0011v u v u u vT v ννλ++⎛⎫===+ ⎪⎝⎭ (2) 观察者静止,波源相对于介质运动观察者接收到的频率为11s s svv v vu T vT u T v u ννλλ====---(3) 波源和观察者同时相对于介质运动 观察者接收到的频率为001s sv u v u u T v u ννλ++==--思考题8-1 什么是简谐振动?下列运动哪个是简谐振动?(1)拍皮球时球的运动;(2)人的脉搏运动;(3)一个小球在球形碗底部的微小摆动。
答:简谐振动是物体在回复力(弹性力或准弹性力)作用下的运动。
在运动过程中,平衡位置两侧的回复力方向不同;运动轨迹是正弦曲线 (1) 该现象好象是往复运动,实际上由于在运动过程中重力的方向始终不变,因而不是简谐振动(2) 运动轨迹不是正弦曲线,不是简谐振动。
(3) 一个小球在球形碗底部的微小摆动时,重力的切向分力起着回复力的作用是简谐振动。
8-2 一个弹簧振子振动的振幅增大到两倍时,振动的周期、频率、最大速度、最大加速度和振动能量都将如何变化?答:若弹簧振子振动的振幅增大到原来的两倍时,振动的周期和频率不变,最大速度和最大加速度增加二倍,振动能量增加四倍。
8-3 如果不忽略弹簧的质量,一个弹簧振子的振动周期比忽略弹簧的质量时的振动周期是变大还是变小?答:若不忽略弹簧的质量,弹簧振子的振动周期相对于忽略质量时的周期较大。
8-4 设向右的方向为正方向,试指出在怎样的位置时简谐振动的质点 (1)位移为零;(2)位移最大;(3)速度为零;(4)速度为负最大值;(5)加速度为零;(6)加速度为正最大。
答:(1)考虑简谐振动质点位移表达式()cos x A t ωϕ=+可得2t πωϕ+=时,位移为零。
这时质点在平衡位置。
(2) 同理,当0t ωϕ+=时,位移最大。
这时质点在两侧的端点。
(3) 考虑简谐振动质点速度表达式()sin v A t ωωϕ=-+可得0t ωϕ+=时,速度为零。
这时质点在两侧的端点。
(4) 同理,当2t πωϕ+=时,速度为负最大值。
这时质点从右侧经平衡位置向左运动。
(5) 考虑简谐振动质点加速度表达式2()cos a A t ωωϕ=-+当2t πωϕ+=时,加速度为零。
这时质点在平衡位置。
(6) 同理,当t ωϕπ+=时,加速度为正最大。
这时质点左侧端点(位移最大)位置。
8-5 弹簧振子的简谐振动方程为)cos(ϕω+=t A x ,指出振动物体在下列位置时的位移、速度、加速度和所受弹性力的大小和方向:(1)正方向端点;(2)平衡位置且向负方向运动;(3)平衡位置且向正方向运动;(4)负方向端点。
答:(1)振动物体位于正方向端点的状态如下:位移最大,方向指向正方向,速度为零,加速度最大、方向指向负方向,所受弹性力的大小最大、方向指向平衡位置。
(2)振动物体在平衡位置且向负方向运动的状态如下:位移为零,速度最大、方向指向负方向,加速度为零,所受弹性力的大小为零。
(3)振动物体在平衡位置且向正方向运动的状态如下:位移为零,速度最大、方向指向正方向,加速度为零,所受弹性力的大小为零。
(4)振动物体位于负方向端点的运动状态如下:位移最大、方向指向负方向,速度为零,加速度最大、方向指向正方向,所受弹性力的大小最大、方向指向平衡位置。
8-6 要测定一个未知振动的频率,你有何办法?答:利用李萨如图形方法:用一个已知频率的振动与未知频率进行合成,只要合成的结果是一个闭合稳定的图形,便可以测定未知振动的频率。
8-7 在波的表达式中,坐标原点是否一定要设在波源的位置?在简谐振动的表达式中有几个独立变量?简谐波的表达式中有几个独立变量?比较两个表达式的意义。
答:在波的表达式中,坐标原点不一定要设在波源的位置。
在简谐振动的表达式中有两个独立变量:x和t。
简谐波的表达式中有三个独立变量:x、y和t。
简谐振动的表达式是描写某一个固定点的振动规律,简谐波的表达式是描写在波转播的介质空间中任意点的振动规律及这些振动之间的相互联系。
8-8 当频率为ν,波长为λ的一列波由波速为u的介质进入波速为3/u的介质后,波的频率和波长如何变化?答:当频率为ν,波长为λ的一列波由波速为u的介质进入波速为3/u的介质后,波的频率不变,波长为原波长的三分之一。
8-9 弦乐器上的一根弦的音调是靠什么调节的?演奏时一根弦发出不同的音调又是靠什么调节的?答:弦乐器上的一根弦振动时形成驻波,不同长度,驻波频率不一样,因而发出不同音调。
弦乐器上的一根弦的音调是靠弦的长度来调节,演奏时一根弦发出不同的音调又是靠弦的不同长度来调节。
8-10 在声源运动、接收器不动和声源不动、接收器运动两种情况下,如果使运动速度一样,接收器接收到的声波是否相同?答:在声源运动、接收器不动和声源不动、接收器运动两种情况下,如果使运动速度一样,根据多普勒效应公式可知,接收器相当于观察者,所以接受器所接收到的声波的频率是不相同的。
练习题8-1 如图8-1所示,两个完全相同的弹簧振子,如将一个拉长10cm ,另一个压缩5cm ,然后放手,试问两物体在何处相遇。
解:依题意得两弹簧振子的振动方程11()cos x A t ωϕ=+22()cos x A t ωϕ=+当12x x =时,得Λ,2,1,0,)21(=+=+k k t πϕω,两物体在平衡位置处相遇。
8-2 经验证明,当车辆沿竖直方向振动时,如果振动的加速度不超过1m/s 2,乘客不会有不舒服的感觉。
若车辆竖直振动频率为每分钟90次,为保证乘客没有不舒服的感觉,车辆允许振动的最大振幅为多少?解:由已知可得9023(rad/s)60πωπ⨯== 当()ϕω+=t A x cos 时,加速度方程为()22d cos d 2xa A t tωωϕ==-+根据题意知,车辆允许振动的最大振幅为A m ,且21m A ω≤ ,则22110011(m)9314m A ω≤==⋅⨯⋅ 取等号时是最大振幅。
8-3 放置在水平桌面上的弹簧振子,其简谐振动的振幅A =m 100.22-⨯,周期T = 0.5s ,求起始状态为下列情况的简谐振动方程: (1) 振动物体在正方向端点 (2) 振动物体在负方向端点(3) 振动物体在平衡位置,向负方向运动 (4) 振动物体在平衡位置,向正方向运动(5) 振动物体在m 100.12-⨯=x 处,向负方向运动 (6) 振动物体在m 100.12-⨯-=x 处,向正方向运动解:由于T = 0.5s ,故ππω4/2==T 。
