土力学完整课件土中应力计算
合集下载
第三章 土体中的应力计算(1-3节)

4
3.均质、等向问题 理想弹性体是均质且各向同性的。天然
地基是各向异性的。但当土层性质变化 不大时,这样假定对竖直应力分布引起 的误差通常在容许范围之内。
5
二、地基中的几种应力状态
1.三维应力状态(空间应力状态)
局部荷载作用下,地基中的应力状态属 三维应力状态。每一点的应力可写成矩 阵形式
24
25
在空间将z相同的点连 接成曲面即形成应力泡。
当地基表面作用有几个集中力时,根据弹 性体应力叠加原理求出附加应力的总和
26
(二)水平集中力作用-西罗提解
z
3Ph
2
xz 2 R5
(3- 9)
27
28
二、矩形面积上各种分布荷载作用下的附 加应力计算
(一)矩形面积竖直均布荷载 1.角点下的应力
x
K
s x
p
τ
xz
K
s xz
p
(3- 25) (3- 26)
剪Kx应s和力K分xzs布分系别数为(水表平3向-5应)力,m分布x ,系n 数z和。
BB
55
P
56
57
(三)条形面积竖直三角形分布荷载 条形面积上竖直三角形分布荷载在地基
内引起的应力也可利用应力叠加原理, 通过积分求得。
zM ' (KsI KsII KsIII KsIV ) p
(3 -13a)
37
第二种情况:计算矩形面积外任一点M’ 下深度为z的附加应力(图3-17b)。设法使 M’点为几个小矩形的公共角点,然后将 其应力进行代数迭加。
zM ' (KsI KsII KsIII KsIV ) p
29
3.均质、等向问题 理想弹性体是均质且各向同性的。天然
地基是各向异性的。但当土层性质变化 不大时,这样假定对竖直应力分布引起 的误差通常在容许范围之内。
5
二、地基中的几种应力状态
1.三维应力状态(空间应力状态)
局部荷载作用下,地基中的应力状态属 三维应力状态。每一点的应力可写成矩 阵形式
24
25
在空间将z相同的点连 接成曲面即形成应力泡。
当地基表面作用有几个集中力时,根据弹 性体应力叠加原理求出附加应力的总和
26
(二)水平集中力作用-西罗提解
z
3Ph
2
xz 2 R5
(3- 9)
27
28
二、矩形面积上各种分布荷载作用下的附 加应力计算
(一)矩形面积竖直均布荷载 1.角点下的应力
x
K
s x
p
τ
xz
K
s xz
p
(3- 25) (3- 26)
剪Kx应s和力K分xzs布分系别数为(水表平3向-5应)力,m分布x ,系n 数z和。
BB
55
P
56
57
(三)条形面积竖直三角形分布荷载 条形面积上竖直三角形分布荷载在地基
内引起的应力也可利用应力叠加原理, 通过积分求得。
zM ' (KsI KsII KsIII KsIV ) p
(3 -13a)
37
第二种情况:计算矩形面积外任一点M’ 下深度为z的附加应力(图3-17b)。设法使 M’点为几个小矩形的公共角点,然后将 其应力进行代数迭加。
zM ' (KsI KsII KsIII KsIV ) p
29
土力学:第三章土中应力计算

附加应力的分布规律
平面分布规律
附加应力在平面上的分布呈扩散状,随着深度的 增加而减小。
深度分布规律
在一定深度范围内,附加应力随深度的增加而增 大,达到一定深度后基本保持稳定。
方向分布规律
附加应力在不同方向上的分布不同,与外部荷载 的方向和土体的性质有关。
附加应力的影响因素
01
外部荷载
外部荷载的大小、分布和作用方 式直接影响附加应力的分布和大 小。
在水平方向上,自重应力 表现为均匀分布。
侧向应力
在土体边缘,自重应力表 现为侧向应力,对土体的 稳定性产生影响。
自重应力的影响因素
土的密度
土的密度越大,自重应力越大。
重力加速度
重力加速度越大,自重应力越大。
土体的几何形状和尺寸
土体的几何形状和尺寸对自重应力的分布和大小有显著影响。
04 土中附加应力计算
02
03
土体的性质
边界条件
土体的容重、压缩性、内摩擦角、 粘聚力等性质对附加应力的影响 较大。
土体的边界条件,如固定边界、 自由边界等,对附加应力的分布 和大小也有影响。
05 土中有效应力计算
CHAPTER
有效应力的概念与计算方法
有效应力的概念
有效应力是指土壤颗粒之间的法向应 力,是土壤保持其结构稳定和防止剪 切破坏的主要因素。
土中应力计算的重要性
01
02
03
工程安全
准确的土中应力计算是确 保工程安全的前提,能够 预测可能出现的危险和制 定应对措施。
设计优化
通过土中应力计算,可以 优化设计方案,提高工程 结构的稳定性和经济性。
科学研究
土中应力计算有助于深入 研究土力学性质和规律, 推动土力学学科的发展。
土力学-土中应力计算

(1)地下水位下降情况
水位未降前 scz前=′z
水位下降后
scz后 = z
scz后 scz前
因scz后 scz前 土中有效应力增加
地面沉降
原地下水位 1
变动后地下水位 1′
原自重应力分布曲线
1′
变动后地下水位
1
原地下水位
地下水位变动后的 自重应力分布曲线
2′
2
z
2
2′
z
(2)地下水位上升
地基土和基础的刚度;荷载;基础埋深;地基土性质
基底压力是地基和 基础在上部荷载作 用下相互作用的结 果,受荷载条件、 基础条件和地基条 件的影响
暂不考虑上部结构的影 响,用荷载代替上部结 构,使问题得以简化
•大小
荷载条件: •方向
•分布
基础条件:
• 刚度 • 形状 • 大小 • 埋深
• 土类
地基条件: • 密度
二.水平向自重应力计算
s cx s cy K0s cz
z
K0——侧压力系数
t 0
scz scy
W
scx
F=1
无侧向变形(有侧限)条件下:
scz scx
εx εy 0
σx σy
scy
根据弹性力学中广义虎克定律:
εx
1 E
σx
υ
σy
σz
ch s cx s cy K0s cz
K0
• 土层结构等
1.基础的刚度的影响
柔性基础(EI=0)
Eg.土坝(堤)、路基、油罐等薄板基础、机场跑道。
沉降各处不同, 中央大边缘小
变形地面
反力
基底压力分布与 作用的荷载的分
布完全相同
土力学完整 第3章 土中应力分布及计算ppt课件

CZ r , z 9 .5 8 76 KPa ; b ,点: Z 8 m , 该点位于粘土层中,
CZ r , z rw h w 9 .5 8 10 10 76 100 176 KPa ;
c 点:
Z
12 m , CZ
176 19 .3 4 253 .2 KPa 精选ppt课件2021
地基土通常为成层土。当地基为成层土体时,设各土层
的厚度为hi,重度为ri,则在深度z处土的自重应力计算公式
为:
n
cz i hi i1
n
z hi i1
n—从地面到深度z处的土层数; hi—第i层土的厚度,m。
成层土的自重应力沿深度呈折线分布,转折点位于r值
发生变化的土层界面上。
三.有地下水时土中自重应力计算
◇若IL ≤0,则土处于坚硬(固态)状态,土中自由水受到
土颗粒间结合水膜的阻碍不能传递静水压力,故认为土体不 受水的浮力作用,采用土的饱和重度计算土的自重应力;
◇若0<IL<1,土处于塑性状态,土颗粒是否受到水的浮
力作用就较难肯定,在工程实践中一般均按土体受到 水浮力作用来考虑。
精选ppt课件2021
建筑物荷重基础地基上在地基与基础的接触面上 产生的压力
基底压力分布及其影响因素: ①基础相对刚度、基础大小、形状和埋深; ②地基土的性质; ③作用在基础上的荷载大小、分布和性质。
基础刚度的影响
1.弹性地基上的完全柔性基础(EI=0)
土坝(堤)、路基、油罐等薄板基础、机场跑道。可认 为土坝底部的接触压力 分布与土坝的外形轮廓相同, 其 大小等于各点以上的土柱重量。
1 原地下水位
0-1,-2,线为变动后
,
1
变动后地下水位 自重应力的分布
土力学课件 第3章 土中应力分布及计算.

计算如图所示水下地基土中的自重应力分布
水面 a 8m
粗砂 r=19KN/m3 rsat=19.5KN/m3
黏土r=19.3KN/m3 4m rsat=19.4KN/m3 W=20%,WL=55%,WP=24%
b 76KPa 176KPa c 253.2KPa
解:水下的粗砂层受到 水的浮力作用, 其有效重度: r , rsat rw 19.5 10 9.5 KN / m 3 粘土层因为W WP , 所以I L 0, 故认为土层 不受到水的浮力作用, 土层面上还受到 上面的静水压力作用。 a点:Z 0, CZ 0 KPa; b点:Z 8m, 该点位于粗砂层中,
应力符号规定
法向应力以压为正,剪应力方向的符号规定则与材料力 学相反。材料力学中规定剪应力以顺时针方向为正,土力学 中则规定剪应力以逆时针方向为正。
压为正,拉为负,剪应力以逆时针为正
土中的自重应力计算
土中应力按其起因可分为自重应力和附加应力两种。
自重应力是土受到重力作用产生的应力,自重应力一般是自 土体形成之日起就产生于土中。
二.成层土自重应力计算 地基土通常为成层土。当地基为成层土体时,设各土层 的厚度为hi,重度为ri,则在深度z处土的自重应力计算公 式为:
cz i hi
i 1
n
z hi
i 1
n
n—从地面到深度z处的土层数; hi—第i层土的厚度,m。 成层土的自重应力沿深度呈折线分布,转折点位于r值 发生变化的土层界面上。
◇若0<IL<1,土处于塑性状态,土颗粒是否受到水的 浮力作用就较难肯定,在工程实践中一般均按土体受 到水浮力作用来考虑。
四.存在隔水层时土的自重应力计算
当地基中存在隔水层时,隔水层面以下土的自重应力应 考虑其上的静水压力作用。
第5.0土的有效应力原理ppt课件

24
§5.1 土的有效应力原理
二. 饱和土中孔隙水压力和有效应力的计算 2.附加应力作用情况
(1) 侧限应力状态及一维渗流固结
▪ 实践背景:大面积均布荷载 p
p
饱和压缩层 不透水岩层
σz=p
侧限应力状态
25
§5.1 土的有效应力原理
二. 饱和土中孔隙水压力和有效应力的计算 2.附加应力作用情况
(1) 侧限应力状态及一维渗流固结
1 3
体积V
孔隙流体的体积变化
V1 Cf uA nV
3(1 2) Cs E
土骨架的体积变化 暂时假定土骨架为线弹性体
uA
V2 v V (1 2 3 )V
总应力增量 有效附加应力
应变增量
轴向 1 3 1 3 uA [(1 3 uA ) 2(uA )]/ E
侧向
0
uA
二. 饱和土中孔隙水压力和有效应力的计算 1.自重应力情况
(1) 静水条件 毛细饱和区
总应力 - 孔隙水压力 = 有效应力
H
毛细饱
和区 sat hc
ht
hw
whc -
H whc
H satht
+
whw H satht whw 20
§5.1 土的有效应力原理
二. 饱和土中孔隙水压力和有效应力的计算 1.自重应力情况
u
u w (H h) satH w (H h)
H wh 渗透压力: wh
22
§5.1 土的有效应力原理
二. 饱和土中孔隙水压力和有效应力的计算 1.自重应力情况
取土骨架为隔离体
向上渗流: Δh
向下渗流:
H
粘土层 γsat
H wh
土力学2-土体中的应力计算

应力泡
0.1P 0.05P 0.02P 0.01P
集中荷载的附加应力-基本解
§2.4 附加应力
仁者乐山 智者乐水
矩形面积竖直均布荷载
dP pdxdy
角点下的垂直附加应力:B氏解的应用
p
L B
y
3dP z 3 3p z 3 d z dxdy 5 5 2 R 2 R
x
z K sp
基底压力的影响因素
§2.3
弹性地基,完全柔性基础
基础抗弯刚度EI=0 → M=0
基础变形能完全适应地基表面的变形 基础上下压力分布必须完全相同,若 不同将会产生弯矩
条形基础,竖直均布荷载
弹性地基,绝对刚性基础
抗弯刚度EI=∞ → M≠0
基础只能保持平面下沉不能弯曲 分布: 中间小, 两端无穷大
集中力作用下的 应力分布系数
教材P58页
集中荷载的附加应力-基本解
§2.4 附加应力
仁者乐山 智者乐水
竖直集中力-布辛内斯克课题
z 3 1 P P K 2 [1 (r / z ) 2 ]5 / 2 z 2 Z2
P
σz与α无关,呈轴 对称分布 P作用线上
在某一水平面上 在r﹥0的竖直线上 z等值线-应力泡
§2.3
§2.4
基底压力与基底附加应力
地基中的附加应力
§2.2
zx z +
材料力学
正应力
剪应力
顺时针为正 逆时针为负
zx
土力学
z +
x
xz
-
拉为正 压为负
-
xz
x
压为正 拉为负
土力学课件

若坡高为5m,试确定安全系数为1.2时的稳定坡角。若坡角为60°,试确定安全系数为1.5时的最大坡高
①在稳定坡角时的临界高度:
H cr =KH = 1.2×5=6m
【解答】
稳定因数:9
.80
.1268.17=⨯==c H N cr
s γ由ϕ=15°,N s = 8.9查图得稳定坡角= 57°
②由β=60°,ϕ=15°查图得泰勒稳定数N 为8.6 6.80.128.17=⨯==
库伦理论假定破坏面为一平面,而实际上为曲面。实践证明,计算的主动土压力误差不大,而被动土压力误差较大。
地面荷载作用下的土压力
第八章土坡稳定分析
主要内容
无粘性土土坡稳定分析
粘性土土坡稳定分析
土坡稳定分析中有关问题*
土坡稳定概述天然土坡人工土坡
由于地质作用而
自然形成的土坡
在天然土体中开挖
或填筑而成的土坡坡底坡脚坡角
一、概述
土压力:
挡土结构背后土体的自重或外荷载在结构上产生的侧向作用力。
自重土压力
墙后墙前墙顶
墙底(基底)墙趾
墙跟(踵)
墙
背刚性结构和柔性结构
墙
面
三、Rankine 土压力理论(1857
)
William John Maquorn Rankine
(1820 -1872)
土力学热力学
英国科学家
ττ=
二、地基中的应力计算
地基假设为:
半无限体
弹性
均质
各项同性
地基
如考虑
3. 基底的接触压力
•刚性基础
•柔性基础
•绝对柔性基础
Valentin Joseph Boussinesq(1842-1929)
①在稳定坡角时的临界高度:
H cr =KH = 1.2×5=6m
【解答】
稳定因数:9
.80
.1268.17=⨯==c H N cr
s γ由ϕ=15°,N s = 8.9查图得稳定坡角= 57°
②由β=60°,ϕ=15°查图得泰勒稳定数N 为8.6 6.80.128.17=⨯==
库伦理论假定破坏面为一平面,而实际上为曲面。实践证明,计算的主动土压力误差不大,而被动土压力误差较大。
地面荷载作用下的土压力
第八章土坡稳定分析
主要内容
无粘性土土坡稳定分析
粘性土土坡稳定分析
土坡稳定分析中有关问题*
土坡稳定概述天然土坡人工土坡
由于地质作用而
自然形成的土坡
在天然土体中开挖
或填筑而成的土坡坡底坡脚坡角
一、概述
土压力:
挡土结构背后土体的自重或外荷载在结构上产生的侧向作用力。
自重土压力
墙后墙前墙顶
墙底(基底)墙趾
墙跟(踵)
墙
背刚性结构和柔性结构
墙
面
三、Rankine 土压力理论(1857
)
William John Maquorn Rankine
(1820 -1872)
土力学热力学
英国科学家
ττ=
二、地基中的应力计算
地基假设为:
半无限体
弹性
均质
各项同性
地基
如考虑
3. 基底的接触压力
•刚性基础
•柔性基础
•绝对柔性基础
Valentin Joseph Boussinesq(1842-1929)
土力学清华版第2章 土体中的应力计算
94.0 83.8 57.0 31.6 18.9 12.3
1200 1200 1600 1600 1600
25.6 44.8 60.2 71.7 83.2
88.9 70.4 44.3 25.3 15.6
114.5 115.2 104.5 97.0 98.8
0.970 0.960 0.954 0.948 0.944
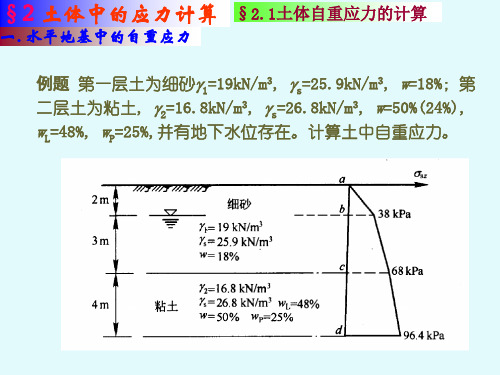
a点:z=0,sz= z=0; b点:z=2m,sz=192=38kPa; c点:z=5m,sz=192+103=68kPa; d点:z=9m,sz=192+103+7.14=96.4kPa 分布如图:
§2 土体中的应力计算
§2.3地基中附加应力的计算
例题 土体表面作用一集中力F=200kN,计算地面深度 z=3m处水平面上的竖向法向应力z分布,以及距F作用点 r=1m处竖直面上的竖向法向应力z分布。
§3.3 地基的最终沉降量计算 四、例题分析 5.计算基础中点下地基中附加应力
7.2
6.确定沉降计算深度zn 根据σz = 0.2σc的确定原则,由计算结果,取zn=7.2m 7.最终沉降计算 根据e-σ曲线,计算各层的沉降量
§3土的压缩性与地基沉降计算
z( m ) 0 1.2 2.4 4.0 5.6 7.2 h σc σz σz+ σc e1 ( kPa ) ( mm ) (kPa) (kPa) (kPa) (kPa)
§2.3地基中附加应力的计算
四. 矩形面积三角形分布荷载作用下的附加应力计算
三角形分布荷载AFD作用在aeOh和ebfO上: z2=z2(aeOh)+
z2(ebfO)=p1(t1+t2)
z2=33.3(0.021+0.045)=2.2kPa
1、土体中的应力计算

σ z α cp
z
M
m=L/B, n=z/B
(推倒公式见课本P18
z
查表1-3
L z c f ( B , L, z ) f ( , ) f ( m , n) B B
矩形面积垂直均布荷载角点下的应力分布系数αc
§1.3 地基附加应力 1.3.2 矩形荷载和圆形荷载作用时的地基附加应力
1.1.1 均质土中自重应力(σcz、σcx)
1.定义:自重应力—由土体自重在土中产生的力。 它是单位土体截面积上的平均应力。 2.计算: 基本假定:地面水平,地基是均质的各向同性的 半无限的直线变形体。
§1.1 土中自重应力
1.1.1 均质土中自重应力
σc z
A Z r rZ A
地面沉降使汛期河水外溢,全镇四周筑堤围堰形成“大包 围”,每年有半年时间靠排水站开泵排水,才能保证镇上 不被淹。 ——苏州东吴市盛泽镇
§1.1 土中自重应力 1.1.4 土质堤坝自身的自重应力
(有限构筑物的自重应力)
计算 面
计算 面
H γH1 H1 γH γH 0
地面
0
计算 面
§1 土中应力
3. 斜向偏心荷载下的基底压力
(参考其他土力学书籍)
将倾斜偏心荷载的合力分解成 竖向分量和水平分量。 竖向分量引起的基底压力按竖 直偏心荷载的计算公式计算 水平分量引起的基底压力按下 式计算 P Pv
Ph
矩形基础:
条形基础:
§1.2 基底压力 1.2.2 基底压力的简化计算
3. 斜向偏心荷载下的基压应力
M′
zm c p ( c1 c 2 )
(2)矩形荷载面边缘内一点的σz
土力学地基中的应力计算

p
arctan
1
2(x / b) 2(z / b)
arctan 1 2(x / b) 2(z / b)
4 z [4( x )2 4( z )2 1]
bb
b
[4( x )2 4( z )2 1]2 16( z )2
b b
b
b
b
13
•带状三角形荷载
b
p
x
z
Mx
(x, z)
z
查表3-3
e 基底压力呈三角形分布
e 基底局部出现拉应力
基底与地基脱开
对于矩形底面,= b
6
37
(1) 矩形底面单轴偏心荷载作用时(e)
由竖向、弯矩平衡方程
P
b 2
(
p1
p2 ) a
M
b 2 ( p1
p2
)
a
(
b 2
b) 3
p1 p2
PM AW
P (1 A
e)
P 1 A
6e b
e a
b
P M Pe
z
p
{x b
(arctan
x z
/ /
b b
arctan
x
/b 1) z/b
z b
(x
/
b
x/b 1)2
1 (z
/
b)2
}
k(x b
,
z b
)
p
•带状梯形荷载
14
5、矩形均布面积荷载作用下附加应力旳计算
1)角点下旳垂直附加应力
dP pdxdy
d z
3dP 2
z3 R5
3p 2
z3 R5
dxdy
土力学第四章 土中应力计算

土体在自身重力、建筑物荷载、交通荷载或其他因素(如地下水渗流、地 震等)作用下,均可产生土中应力。土中应力将引起土体或地基变形,使土 工构筑物(如路堤、土坝等)或建筑物(如房屋、桥梁、涵洞等)产生沉降 、倾斜以及水平位移。土体或地基的变形过大时,往往会影响路堤、房屋和 桥梁等的正常使用。土中应力过大时,又会导致土体的强度破坏,使土工构 筑物发生土坡失稳或使建筑物地基的承载力不足而发生失稳。
建 筑
上部结构 (a)理想柔性基础; (b)路堤下的基底压力
物
设
基础
计
地基
(2)刚性基础。基底压力大小、分布状况与上部荷载的大小、分布状况 不相同。
例如:砂土地基 黏性土地基
— 荷载较小 — 荷载较大
砂性土地基
— 接近弹性解 — 马鞍型 — 抛物线型 — 倒钟型
粘性土地基
三、基底压力的简化计算
1、中心荷载下的基底压力
1H1
sz
2H2
2H3
sy
sx
z
说明:
1.地下水位以上土层采用天然重度,地下水位以下土层采用浮重度 2.非均质土中自重应力沿深度呈折线分布
均质地基
1 (1 2)
2
2
成层地基
例题分析
【例4.1】某地基土层情况及其物理性质指标如下图所示,试计算 a、b、c三个点 处的自重应力,并画出应力分布图。 【解】 首先确定各层土的重度。 粗砂:在水下且透水,采用浮重度,有
2)基础的刚度、平面形状、尺寸大小、埋置深度有关;
3)作用在基础上的荷载性质、大小和分布情况有关;
4)地基土的性质有关。
二、基底压力的分布规律
基础按刚度分为:(1)柔性基础(抗弯曲变形能力为0) (2)刚性基础(抗弯曲变形能力为∞) (3)有限刚性基础(弹性地基上梁板分析方法)
建 筑
上部结构 (a)理想柔性基础; (b)路堤下的基底压力
物
设
基础
计
地基
(2)刚性基础。基底压力大小、分布状况与上部荷载的大小、分布状况 不相同。
例如:砂土地基 黏性土地基
— 荷载较小 — 荷载较大
砂性土地基
— 接近弹性解 — 马鞍型 — 抛物线型 — 倒钟型
粘性土地基
三、基底压力的简化计算
1、中心荷载下的基底压力
1H1
sz
2H2
2H3
sy
sx
z
说明:
1.地下水位以上土层采用天然重度,地下水位以下土层采用浮重度 2.非均质土中自重应力沿深度呈折线分布
均质地基
1 (1 2)
2
2
成层地基
例题分析
【例4.1】某地基土层情况及其物理性质指标如下图所示,试计算 a、b、c三个点 处的自重应力,并画出应力分布图。 【解】 首先确定各层土的重度。 粗砂:在水下且透水,采用浮重度,有
2)基础的刚度、平面形状、尺寸大小、埋置深度有关;
3)作用在基础上的荷载性质、大小和分布情况有关;
4)地基土的性质有关。
二、基底压力的分布规律
基础按刚度分为:(1)柔性基础(抗弯曲变形能力为0) (2)刚性基础(抗弯曲变形能力为∞) (3)有限刚性基础(弹性地基上梁板分析方法)
土力学二章 有效应力课件

土力学二章 有效应力
•
建筑物
•
基础
• 桩端持力层
地基
土力学二章 有效应力
• 基础:建筑物的下部结构,它将整个建筑物 (包括基础)的重量及荷重传递给地基。
• 地基:建筑物修建后,使土体中一定范围内应 力状态发生了变化,这部分由建筑物荷载引起 土体内应力变化的土层叫地基。
• 持力层:直接与基础接触,并承受压力的土层。
土力学二章 有效应力
地基中常见的应力状态
1.一般应力状态——三维问题
z
zx
xy
x
y yz
o x
z y
ij =
x xy xz
yx y yz zx zy z
ij =
土力学二章 有效应力
x xy xz yx y yz
zx zy z
地基中常见的应力状态
轴对称三维问题
ij =
土力学二章 有效应力
x 0xy xz 0yx y 0yz zx 0zy z
3.侧限应力状态
▪应变条件
y x 0;
xyyzzx0
▪应力条件
xyyzzx0; x y;
x E xE yz 0;
xy1zK0z;
▪独立变量 z,z F(z)
K0:侧压力系数
ij =
0 x 0xy 0xz
土力学二章 有效应力
第一节 概述
• 研究地基土中应力的目的 • 1.定量的预测土体变形(如地基沉降)、稳定
性(如地基、边坡、洞室)等。 • 2.选择合理的基础形式、结构形式 • 3.确定建筑物地基勘探的深度和范围
土力学二章 有效应力
几个基本概念
• 地基与基础 • 自重应力与附加应力 • 有效应力
•
建筑物
•
基础
• 桩端持力层
地基
土力学二章 有效应力
• 基础:建筑物的下部结构,它将整个建筑物 (包括基础)的重量及荷重传递给地基。
• 地基:建筑物修建后,使土体中一定范围内应 力状态发生了变化,这部分由建筑物荷载引起 土体内应力变化的土层叫地基。
• 持力层:直接与基础接触,并承受压力的土层。
土力学二章 有效应力
地基中常见的应力状态
1.一般应力状态——三维问题
z
zx
xy
x
y yz
o x
z y
ij =
x xy xz
yx y yz zx zy z
ij =
土力学二章 有效应力
x xy xz yx y yz
zx zy z
地基中常见的应力状态
轴对称三维问题
ij =
土力学二章 有效应力
x 0xy xz 0yx y 0yz zx 0zy z
3.侧限应力状态
▪应变条件
y x 0;
xyyzzx0
▪应力条件
xyyzzx0; x y;
x E xE yz 0;
xy1zK0z;
▪独立变量 z,z F(z)
K0:侧压力系数
ij =
0 x 0xy 0xz
土力学二章 有效应力
第一节 概述
• 研究地基土中应力的目的 • 1.定量的预测土体变形(如地基沉降)、稳定
性(如地基、边坡、洞室)等。 • 2.选择合理的基础形式、结构形式 • 3.确定建筑物地基勘探的深度和范围
土力学二章 有效应力
几个基本概念
• 地基与基础 • 自重应力与附加应力 • 有效应力
土力学课件第二章地基中的应力计算

•矩形基底面的抗弯截面系数
•(二)偏心荷载下的基底压力
•e<r时,基底压力成梯形分布;
•e= r时,基底压力为三角形分布;
•e>r时,基底压力pmin<0
•pmin<0,由于地基与基础之间不能承受拉力,此时基底与地基局部脱离而 使基底压力重新分布。根据基底压力与偏心荷载相平衡的条件,三角形反
力分布如图(c)中的实线所示的形心应在P+G的合力Fv作用线上,由此可 计算基础边缘的最大压力pmax为
的水平面; • (2) 土层为各向同性的弹性介质。
• 因土体中任一垂直截面都为对称面,故任 何垂直截面上的应力均为零,即 txy=txz=tyz=0。所以σx、σy、σz均为主应力 。把上述条件代入应力连续方程得
•二、垂直自重有效压力
•1、不考虑地表荷载
•地下水位以下,用有效重量; 不同土层的重量可以叠加
•地表临空
基本假定
地基土是各向同性、均质、线性变形体 地基土在深度和水平方向都是无限的
•地基:均质各向同性线性变形半空间体 •应用弹性力学关于弹性半空间的理论解答
•一、垂直集中荷载
•位 移 •应 力
•图3-26 集中荷载作用下的应力
•Valentin Joseph Boussinesq (1842-1929)
• 侧向应变为零,即x=y=0,地基在自重作用下的应力状态即属此应力
状态,任何对称面都是对称面,则
三 土力学中应力符号的规定
•表示一点应力状态的最佳工具——摩尔应力圆 •土力学中应力符号的规定:法向应力以压为正,剪应力逆时针为正。 •注意与材料力学规定的不同
•图3.3 关于应力符号的规定
四 应力连续方程
• 一 基底压力的分布规律
• 基底压力的精确数值与分布形式是一个很复杂的问题,涉及上部结
•(二)偏心荷载下的基底压力
•e<r时,基底压力成梯形分布;
•e= r时,基底压力为三角形分布;
•e>r时,基底压力pmin<0
•pmin<0,由于地基与基础之间不能承受拉力,此时基底与地基局部脱离而 使基底压力重新分布。根据基底压力与偏心荷载相平衡的条件,三角形反
力分布如图(c)中的实线所示的形心应在P+G的合力Fv作用线上,由此可 计算基础边缘的最大压力pmax为
的水平面; • (2) 土层为各向同性的弹性介质。
• 因土体中任一垂直截面都为对称面,故任 何垂直截面上的应力均为零,即 txy=txz=tyz=0。所以σx、σy、σz均为主应力 。把上述条件代入应力连续方程得
•二、垂直自重有效压力
•1、不考虑地表荷载
•地下水位以下,用有效重量; 不同土层的重量可以叠加
•地表临空
基本假定
地基土是各向同性、均质、线性变形体 地基土在深度和水平方向都是无限的
•地基:均质各向同性线性变形半空间体 •应用弹性力学关于弹性半空间的理论解答
•一、垂直集中荷载
•位 移 •应 力
•图3-26 集中荷载作用下的应力
•Valentin Joseph Boussinesq (1842-1929)
• 侧向应变为零,即x=y=0,地基在自重作用下的应力状态即属此应力
状态,任何对称面都是对称面,则
三 土力学中应力符号的规定
•表示一点应力状态的最佳工具——摩尔应力圆 •土力学中应力符号的规定:法向应力以压为正,剪应力逆时针为正。 •注意与材料力学规定的不同
•图3.3 关于应力符号的规定
四 应力连续方程
• 一 基底压力的分布规律
• 基底压力的精确数值与分布形式是一个很复杂的问题,涉及上部结
土体中的应力计算—附加应力的计算(土力学课件)

土中任意点所受的附加应力
z 2 p
x
p x
z z
x z
二、条形面积受均布荷载土中附加应力
2.条形面积受三角形荷载作用下的附加应力
土中任意点所受的附加应力
z 3 p
-x 0
z x
p x
z
注意坐标系的建立,以荷载0为坐标原点,向荷 载增大的方向为正方向。
二、条形面积受均布荷载土中附加应力
3.圆形面积均布荷载作用下的竖向附加应力
(1)距离地面越深, 附加应力的分布范围 越广,r/z=2.5范围内。
(2)在距地面为z的平 面上,集中力作用线 下的附加应力最大, 向两侧逐渐减小。
集中力作用下附加应力分布图
一、竖直集中荷载作用下的地基附加应力计算
1、附加应力分布规律
(3)距P作用线为r竖直 线上的附加应力随深 度先增加再减小。
171
332 kPa
134
条形荷载作用下土中附加应力
(1)p1=134kPa
+x
+x
+(x 2)p2=198kPa
-x
z x1 x/b z/b
x2 x/b z/b
00 0 0 1
134 1 0.5 0 0.500 99 233
1 0 0 0.5 0.820 110 1 0.5 0.5 0.410 81 191
条形荷载作用下 土中附加应力
条形荷载作用下土中附加应力
条形荷载作用下土中附加应力
1.条形面积受均布荷载作用下的土中竖向附加应力
土中任意点所受的附加应力 x
z 2 p
2 ——条形均布荷载作用
下的竖向附加应力系数
2 (x / b, z / b)
z 2 p
x
p x
z z
x z
二、条形面积受均布荷载土中附加应力
2.条形面积受三角形荷载作用下的附加应力
土中任意点所受的附加应力
z 3 p
-x 0
z x
p x
z
注意坐标系的建立,以荷载0为坐标原点,向荷 载增大的方向为正方向。
二、条形面积受均布荷载土中附加应力
3.圆形面积均布荷载作用下的竖向附加应力
(1)距离地面越深, 附加应力的分布范围 越广,r/z=2.5范围内。
(2)在距地面为z的平 面上,集中力作用线 下的附加应力最大, 向两侧逐渐减小。
集中力作用下附加应力分布图
一、竖直集中荷载作用下的地基附加应力计算
1、附加应力分布规律
(3)距P作用线为r竖直 线上的附加应力随深 度先增加再减小。
171
332 kPa
134
条形荷载作用下土中附加应力
(1)p1=134kPa
+x
+x
+(x 2)p2=198kPa
-x
z x1 x/b z/b
x2 x/b z/b
00 0 0 1
134 1 0.5 0 0.500 99 233
1 0 0 0.5 0.820 110 1 0.5 0.5 0.410 81 191
条形荷载作用下 土中附加应力
条形荷载作用下土中附加应力
条形荷载作用下土中附加应力
1.条形面积受均布荷载作用下的土中竖向附加应力
土中任意点所受的附加应力 x
z 2 p
2 ——条形均布荷载作用
下的竖向附加应力系数
2 (x / b, z / b)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3dP z 3 3 pxz3 d z 5 dxdy 5 2 R 2bR
积分,得
z t p
Y
t f (m l / b, n z / b)
三角分布矩形荷载角点下的竖向附加应 力系数.可查表. 注意l—荷载不变化边 的长度; b—荷载变化边的长度.
水平均布荷载
q
z
x z
2
2 pz 3
2
2
(二)条形荷载下的附加应力计算 1.均布条形荷载下的附加应力 p O x b/2 b/2 z x M z 2. 三角形荷载的附加应力 pt O x b z x M z
z u p
z x u f u m , n b b
l
pmax pmin
基础底面的抵 抗矩;矩形截 面W=(bl2)/6
讨论:
N 6e pmax 1 bl l min
当e<l/6时,pmax,pmin>0,基底压力呈梯形分布 当e=l/6时,pmax>0,pmin=0,基底压力呈三角形分布 当e>l/6时,pmax>0,pmin<0,基底出现拉应力,基底压力重分布
F=400kN/m 0.1m M=20kN •m/m
3.基底中点下附加压 力计算
1.5m 2m 112.6kPa
0 =18.5kN/m3
292.0kPa
179.4kPa
112.6kPa
分析步骤Ⅳ:
F=400kN/m 0.1m M=20kN •m/m
1.5m
1m 1m 2m 2m 2m
0 =18.5kN/m3
3. r 0 ,随 z 从 0 开始增大, z 先随之增大,后随之减小;
r z 0 4. 2.0 时, 0 ,所以 z
上述规律可用下页的图表示
附加应力分布规律
弹性理论计算的集中力作用下地基表面的沉降S
将z=0, R=r, E=E0 代入Boussinesg的以下公式
P(1 ) z 2 1 wz [ 3 2(1 ) ] 2E R R
2m 202.2kPa 193.7kPa 165.7kPa 111.2kPa 80.9kPa 62.3kPa
地基附加应 力分布曲线
1 竖向平 N p max b l 衡条件 2
2.条形基础 沿长度方向取1m计算, 即取l=1 m 将矩形基础基底压力公式中的N换成N1,取l=1 m, 即得 到条形基础下的基底压力计算公式.
三、基底附加压力(应力)
基底附加压力:建筑物建造后的基底压力应扣除基底标高处原
有的自重应力,才是基底处新增加给地基的附加压力,也称基底 净压力。
3 1 2 5/ 2 2 [1 (r / z ) ]
0.5 0.4
α
0.3 0.2 0.1 0 0.5 1.0 1.5 2.0 2.5 3.0
r/ z
z
的分布规律:
, z ;
1. z=常数,随 r
2.r=0,即 P Q 的作用线上, 0.5 ,所以 z 与 z2 成反比;
S [ wz ] z 0
P(1 2 ) E0 r
E0-地基土的变形模量
叠加原理 由几个外力共同作用时所引起的某一参数(内力、 应力或位移),等于每个外力单独作用时所引起的该 参数值的代数和。
Pa Pb z
两个集中力 作用下σz的 叠加
a
b
z
Pi i 2 z
二、矩形基础地基中的附加应力计算
z s p
z x s f s m , n b b
四. 复杂荷载下的附加应力计算 将复杂荷载分解为两种基本荷载,再按前述方法 计算各自引起的附加应力,然后叠加.
【例题分析】
【例】某条形地基,如下图所示。基础上作用荷载
F=400kN/m,M=20kN•m/m,试求基础中点下的附加 应力,并绘制附加应力分布图
2m A基础引起的附加应力
B 300kPa
3m zB
zA 4 ap A ( a1 a 2 a3 a 4 ) pB
B基础引起的 附加应力
A
1m 2m
200kPa o
2m
1m
1m
三、条形基础地基中的附加应力计算
(一) 均布线荷载下的附加应力
pdy作为集中力,按Boussines 公式计算其在M 点引起的应 力, 再积分可得
分析步骤Ⅱ:
F=400kN/m 0.1m M=20kN •m/m
3 = 18.5kN/m 0 1.5m 1.5m
2m 292.0kPa 112.6kPa
基底标高以上 天然土层的加 权平均重度
基础埋 置深度
2.基底附加压力计算
p0 max pmax 0d p0 min pmin
分析步骤Ⅲ:
一、竖向自重应力
土体中任意深度处的竖向自重应力等于单位面积上土柱 的有效重量 天然地面
cz
zA
A
z
cz
σcz= z
cz
cx
z
cy
1
1
z
二、成层土的自重应力计算
cz 1h1 2 h2 n hn i hi
n
说明:
z1 1q z 2 1q
矩形基础角点下 的竖向附加应力 系数,均为m,n 的函数
【例题分析】 有两相邻基础A和B, 其尺寸、相对位置及 基底附加压力分布见 右图,若考虑相邻荷 载的影响,试求A基础 底面中心点o下2m处的 竖向附加应力
分析
o点的附加应力应该是两个基础共同产生的附加应力之和, 根据叠加原理可以分别进行计算
d
基底附加压力
N
p0 p 0 d
自重应力
基底压力呈梯形分布时, 基底附加压力
p0 max pmax 0d p0 min pmin
一墙下条形基础底宽1.5m,埋深1.5m, 承重墙传来的中心竖向荷载为195kN/m ,地基土天然重度为18.0kN/m3,基础及 回填土平均重度为20kN/m3,试求基底 附加压力。
γ=19.3kN/m3
3 19 .0 57 .0 kPa
188.7kPa
57.0 (20.5 9.81) 2.2 80.5 kPa
104.0 9.81(2.2 2.5) 150.1 kPa
80.5 (19.2 9.81) 2.5 104.0 kPa
第三章
土中应力计算 概述 土的自重应力 基底压力与基底附加应力 地基中附加应力
§3.1 §3.2 §3.3 §3.4
§3.1
土的自重应力
自重应力:由土体本身自重引起的应力
确定土体初始 应力状态
土体在自重作用下,在漫长的地质历史时期,已经 压缩稳定,因此,土的自重应力不再引起土的变形。 但对于新沉积土层或近期人工充填土应考虑自重应力 引起的变形。
150 .1 2 19.3 188 .7 kPa
§3.2
基底压力
基底压力:基础底面传给地基顶面的压力
N
p
一、基底压力分布及其影响因素
1. 基础上荷载大小和分布; 影响因素
2. 基础刚度、形状、尺寸及埋深
3. 基土种类、性质、状态。
(一)柔性基础
基底压力分布与荷载分布相同。
(二)刚性基础 以中心荷载为例,基底压力分布有三种类型:
h1
h2
h3
地下水位以下,砂性土 采用浮重度;黏性 i 1 天然地面 土,IL≥1者为流动态, 粒间存在自由水,可传 递静水压力,用浮重度; 1 IL≤0者为固态,粒间 1 h 1 不存在自由水,不能传 递静水压力,不受浮力 2 作用,计算自重应力时 1 h1 + 2h2 水位面 其上的水重还应考虑, 自身用湿重度;0<IL <1者,土粒是否受浮 3 力作用则难以判定,按 1 h1 + 2h2 + 3h3 不利状态来考虑.
p
面积A
F-基础上的竖向力设计值 G-基础自重设计值及其上回填土的重量
l
2.条形基础(l/b≥10者) N1 p b N1-1m长基础的上部荷载, kN/m
b
(二)偏心荷载作用下的基底压力
1.矩形基础 N e
pmax
min
作用于基础底面 形心上的力矩 M=N∙e
e
b
N M N 6e 1 A W bl l
三、水平向自重应力
天然地面
cz z
cz
cx cy K0 cz
静止侧压 力系数
cx
cy
四、例题分析 【例】一地基由多层土组成,地质剖面如下图所示, 试计算并绘制自重应力σcz沿深度的分布图
黏 土
γ=22kN/m3
黏 土
57.0kPa
80.5kPa 104.0kPa 150.1kPa
硬黏土,埋深和 荷载均较小时
砂土,埋深较大时
砂土,荷载大, 埋深小时
可见刚性基础的基底压力分布比较复杂,准确计算 比较困难。因此通常作简化计算。
二、基底压力的简化计算
试验和计算均表明,刚性基础的基底压力可近似按直线 分布计算,由此对附加应力和变形结果造成的误差不大。 (一)中心荷载作用下的基底压力 N N p A bl 1.矩形基础 式中 N F G N
F
0.1m
M
1.5m 0 =18.5kN/m3 2m
分析步骤I:
F=400kN/m 0.1m M=20kN •m/m
1.5m 2m
0 =18.5kN/m3
1.基底压力计算
319.7kPa
积分,得
z t p
Y
t f (m l / b, n z / b)
三角分布矩形荷载角点下的竖向附加应 力系数.可查表. 注意l—荷载不变化边 的长度; b—荷载变化边的长度.
水平均布荷载
q
z
x z
2
2 pz 3
2
2
(二)条形荷载下的附加应力计算 1.均布条形荷载下的附加应力 p O x b/2 b/2 z x M z 2. 三角形荷载的附加应力 pt O x b z x M z
z u p
z x u f u m , n b b
l
pmax pmin
基础底面的抵 抗矩;矩形截 面W=(bl2)/6
讨论:
N 6e pmax 1 bl l min
当e<l/6时,pmax,pmin>0,基底压力呈梯形分布 当e=l/6时,pmax>0,pmin=0,基底压力呈三角形分布 当e>l/6时,pmax>0,pmin<0,基底出现拉应力,基底压力重分布
F=400kN/m 0.1m M=20kN •m/m
3.基底中点下附加压 力计算
1.5m 2m 112.6kPa
0 =18.5kN/m3
292.0kPa
179.4kPa
112.6kPa
分析步骤Ⅳ:
F=400kN/m 0.1m M=20kN •m/m
1.5m
1m 1m 2m 2m 2m
0 =18.5kN/m3
3. r 0 ,随 z 从 0 开始增大, z 先随之增大,后随之减小;
r z 0 4. 2.0 时, 0 ,所以 z
上述规律可用下页的图表示
附加应力分布规律
弹性理论计算的集中力作用下地基表面的沉降S
将z=0, R=r, E=E0 代入Boussinesg的以下公式
P(1 ) z 2 1 wz [ 3 2(1 ) ] 2E R R
2m 202.2kPa 193.7kPa 165.7kPa 111.2kPa 80.9kPa 62.3kPa
地基附加应 力分布曲线
1 竖向平 N p max b l 衡条件 2
2.条形基础 沿长度方向取1m计算, 即取l=1 m 将矩形基础基底压力公式中的N换成N1,取l=1 m, 即得 到条形基础下的基底压力计算公式.
三、基底附加压力(应力)
基底附加压力:建筑物建造后的基底压力应扣除基底标高处原
有的自重应力,才是基底处新增加给地基的附加压力,也称基底 净压力。
3 1 2 5/ 2 2 [1 (r / z ) ]
0.5 0.4
α
0.3 0.2 0.1 0 0.5 1.0 1.5 2.0 2.5 3.0
r/ z
z
的分布规律:
, z ;
1. z=常数,随 r
2.r=0,即 P Q 的作用线上, 0.5 ,所以 z 与 z2 成反比;
S [ wz ] z 0
P(1 2 ) E0 r
E0-地基土的变形模量
叠加原理 由几个外力共同作用时所引起的某一参数(内力、 应力或位移),等于每个外力单独作用时所引起的该 参数值的代数和。
Pa Pb z
两个集中力 作用下σz的 叠加
a
b
z
Pi i 2 z
二、矩形基础地基中的附加应力计算
z s p
z x s f s m , n b b
四. 复杂荷载下的附加应力计算 将复杂荷载分解为两种基本荷载,再按前述方法 计算各自引起的附加应力,然后叠加.
【例题分析】
【例】某条形地基,如下图所示。基础上作用荷载
F=400kN/m,M=20kN•m/m,试求基础中点下的附加 应力,并绘制附加应力分布图
2m A基础引起的附加应力
B 300kPa
3m zB
zA 4 ap A ( a1 a 2 a3 a 4 ) pB
B基础引起的 附加应力
A
1m 2m
200kPa o
2m
1m
1m
三、条形基础地基中的附加应力计算
(一) 均布线荷载下的附加应力
pdy作为集中力,按Boussines 公式计算其在M 点引起的应 力, 再积分可得
分析步骤Ⅱ:
F=400kN/m 0.1m M=20kN •m/m
3 = 18.5kN/m 0 1.5m 1.5m
2m 292.0kPa 112.6kPa
基底标高以上 天然土层的加 权平均重度
基础埋 置深度
2.基底附加压力计算
p0 max pmax 0d p0 min pmin
分析步骤Ⅲ:
一、竖向自重应力
土体中任意深度处的竖向自重应力等于单位面积上土柱 的有效重量 天然地面
cz
zA
A
z
cz
σcz= z
cz
cx
z
cy
1
1
z
二、成层土的自重应力计算
cz 1h1 2 h2 n hn i hi
n
说明:
z1 1q z 2 1q
矩形基础角点下 的竖向附加应力 系数,均为m,n 的函数
【例题分析】 有两相邻基础A和B, 其尺寸、相对位置及 基底附加压力分布见 右图,若考虑相邻荷 载的影响,试求A基础 底面中心点o下2m处的 竖向附加应力
分析
o点的附加应力应该是两个基础共同产生的附加应力之和, 根据叠加原理可以分别进行计算
d
基底附加压力
N
p0 p 0 d
自重应力
基底压力呈梯形分布时, 基底附加压力
p0 max pmax 0d p0 min pmin
一墙下条形基础底宽1.5m,埋深1.5m, 承重墙传来的中心竖向荷载为195kN/m ,地基土天然重度为18.0kN/m3,基础及 回填土平均重度为20kN/m3,试求基底 附加压力。
γ=19.3kN/m3
3 19 .0 57 .0 kPa
188.7kPa
57.0 (20.5 9.81) 2.2 80.5 kPa
104.0 9.81(2.2 2.5) 150.1 kPa
80.5 (19.2 9.81) 2.5 104.0 kPa
第三章
土中应力计算 概述 土的自重应力 基底压力与基底附加应力 地基中附加应力
§3.1 §3.2 §3.3 §3.4
§3.1
土的自重应力
自重应力:由土体本身自重引起的应力
确定土体初始 应力状态
土体在自重作用下,在漫长的地质历史时期,已经 压缩稳定,因此,土的自重应力不再引起土的变形。 但对于新沉积土层或近期人工充填土应考虑自重应力 引起的变形。
150 .1 2 19.3 188 .7 kPa
§3.2
基底压力
基底压力:基础底面传给地基顶面的压力
N
p
一、基底压力分布及其影响因素
1. 基础上荷载大小和分布; 影响因素
2. 基础刚度、形状、尺寸及埋深
3. 基土种类、性质、状态。
(一)柔性基础
基底压力分布与荷载分布相同。
(二)刚性基础 以中心荷载为例,基底压力分布有三种类型:
h1
h2
h3
地下水位以下,砂性土 采用浮重度;黏性 i 1 天然地面 土,IL≥1者为流动态, 粒间存在自由水,可传 递静水压力,用浮重度; 1 IL≤0者为固态,粒间 1 h 1 不存在自由水,不能传 递静水压力,不受浮力 2 作用,计算自重应力时 1 h1 + 2h2 水位面 其上的水重还应考虑, 自身用湿重度;0<IL <1者,土粒是否受浮 3 力作用则难以判定,按 1 h1 + 2h2 + 3h3 不利状态来考虑.
p
面积A
F-基础上的竖向力设计值 G-基础自重设计值及其上回填土的重量
l
2.条形基础(l/b≥10者) N1 p b N1-1m长基础的上部荷载, kN/m
b
(二)偏心荷载作用下的基底压力
1.矩形基础 N e
pmax
min
作用于基础底面 形心上的力矩 M=N∙e
e
b
N M N 6e 1 A W bl l
三、水平向自重应力
天然地面
cz z
cz
cx cy K0 cz
静止侧压 力系数
cx
cy
四、例题分析 【例】一地基由多层土组成,地质剖面如下图所示, 试计算并绘制自重应力σcz沿深度的分布图
黏 土
γ=22kN/m3
黏 土
57.0kPa
80.5kPa 104.0kPa 150.1kPa
硬黏土,埋深和 荷载均较小时
砂土,埋深较大时
砂土,荷载大, 埋深小时
可见刚性基础的基底压力分布比较复杂,准确计算 比较困难。因此通常作简化计算。
二、基底压力的简化计算
试验和计算均表明,刚性基础的基底压力可近似按直线 分布计算,由此对附加应力和变形结果造成的误差不大。 (一)中心荷载作用下的基底压力 N N p A bl 1.矩形基础 式中 N F G N
F
0.1m
M
1.5m 0 =18.5kN/m3 2m
分析步骤I:
F=400kN/m 0.1m M=20kN •m/m
1.5m 2m
0 =18.5kN/m3
1.基底压力计算
319.7kPa
