格林公式习题课
高等数学教学教案 格林公式及其应用

§11.3 格林公式及其应用授课次序69教 学 基 本 指 标教学课题 §11.3 格林公式及其应用 教学方法 当堂讲授,辅以多媒体教学 教学重点 格林公式及其应用教学难点 各种不同情况下的计算 参考教材 同济大学编《高等数学(第6版)》 自编教材《高等数学习题课教程》作业布置 《高等数学》标准化作业双语教学 微分 :differential calculus ;全微分:total differential ;偏微分:partial differential ;积分:integral ;重积分:multiple integral ;二重积分:double integral ;三重积分:threefold integral课堂教学目标1. 掌握格林公式;2. 会运用平面曲线积分与路径无关的条件; 3. 会求全微分的原函数。
教学过程 1.格林公式(45min );2.平面曲线积分与路径无关的条件(20min ); 3.全微分的原函数(25min )教 学 基 本 内 容§11.3 格林公式及其应用一、格林公式单连通与复连通区域:设D 为平面区域,如果D 内任一闭曲线所围的部分都属于D ,则称D 为平面单连通区域,否则称为复连通区域.对平面区域D 的边界曲线L , 我们规定L 的正向如下: 当观察者沿L 的这个方向行走时,D 内在他近处的那一部分总在他的左边.区域D 的边界曲线L 的方向:定理1设闭区域D 由分段光滑的曲线L 围成,函数P (x ,y )及Q (x ,y )在D 上具有一阶连续偏导数,则有⎰⎰⎰+=∂∂-∂∂L DQdy Pdx dxdy yPx Q )(,其中L 是D 的取正向的边界曲线.简要证明:备注栏仅就D 即是X -型又是Y -型的情形进行证明. 设D ={(x ,y )|ϕ1(x )≤y ≤ϕ2(x ),a ≤x ≤b }.因为yP ∂∂连续,所以由二重积分的计算法有 dx x x P x x P dx dy y y x P dxdy y P b ax x b a D)]}(,[)](,[{}),({12)()(21ϕϕϕϕ-=∂∂=∂∂⎰⎰⎰⎰⎰.另一方面,由对坐标的曲线积分的性质及计算法有⎰⎰⎰⎰⎰+=+=abb aL L Ldx x x P dx x x P Pdx Pdx Pdx )](,[)](,[2121ϕϕdx x x P x x P ba )]}(,[)](,[{21ϕϕ-=⎰.因此⎰⎰⎰=∂∂-L DPdx dxdy yP .设D ={(x ,y )|ψ1(y )≤x ≤ψ2(y ),c ≤y ≤d }.类似地可证⎰⎰⎰=∂∂L DQdx dxdy x Q.由于D 即是X -型的又是Y -型的,所以以上两式同时成立,两式合并即得⎰⎰⎰+=⎪⎭⎫⎝⎛∂∂-∂∂L D Qdy Pdx dxdy y P x Q . 应注意的问题:对复连通区域D ,格林公式右端应包括沿区域D 的全部边界的曲线积分,且边界的方向对区域D 来说都是正向.设区域D 的边界曲线为L , 取P =-y ,Q =x ,则由格林公式得⎰⎰⎰-=L Dydx xdy dxdy 2, 或⎰⎰⎰-==LDydx xdy dxdy A 21.例1.椭圆x =a cos θ,y =b sin θ所围成图形的面积A . 分析:只要1=∂∂-∂∂y P x Q , 就有A dxdy dxdy yP x QDD==∂∂-∂∂⎰⎰⎰⎰)(. 解:设D 是由椭圆x =a cos θ,y =b sin θ所围成的区域. 令y P 21-=,x Q 21=, 则12121=+=∂∂-∂∂y P x Q .于是由格林公式,例2 设L 是任意一条分段光滑的闭曲线,证明⎰=+L dy x xydx 022.证:令P =2xy ,Q =x 2,则022=-=∂∂-∂∂x x yPx Q . 因此,由格林公式有0022=±=+⎰⎰⎰dxdy dy x xydx DL . (为什么二重积分前有“±”号? )3.计算⎰⎰-Dy dxdy e 2,其中D 是以O (0, 0),A (1, 1),B (0, 1)为顶点的三角形闭区域.分析: 要使2y e yP x Q -=∂∂-∂∂,只需P =0,2y xe Q -=.解:令P =0,2y xe Q -=,则2y e yP x Q -=∂∂-∂∂. 因此,由格林公式有⎰⎰⎰++--=BOAB OA y Dy dy xe dxdy e 22)1(2111022----===⎰⎰e dx xe dy xe x OAy . 例4计算⎰+-L y x ydxxdy 22,其中L 为一条无重点、分段光滑且不经过原点的连续闭曲线,L 的方向为逆时针方向.解: 令22y x y P +-=,22y x x Q +=.则当x 2+y 2≠0时,有yP y x x y x Q ∂∂=+-=∂∂22222)(. 记L 所围成的闭区域为D . 当(0, 0)∉D 时,由格林公式得022=+-⎰L y x ydx xdy ;当(0, 0)∈D 时, 在D 内取一圆周l :x 2+y 2=r 2(r >0). 由L 及l 围成了一个复连通区域D 1,应用格林公式得02222=+--+-⎰⎰l L y x ydxxdy y x ydx xdy ,其中l 的方向取逆时针方向.于是⎰⎰+-=+-l L y x ydxxdy y x ydx xdy 2222⎰+=πθθθ2022222sin cos d r r r =2π.二、平面上曲线积分与路径无关的条件曲线积分与路径无关:设G 是一个开区域,P (x ,y )、Q (x ,y )在区域G 内具有一阶连续偏导数.如果对于G 内任意指定的两个点A 、B 以及G 内 从点A 到点B 的任意两条曲线L 1、L 2,等式⎰⎰+=+21L L Qdy Pdx Qdy Pdx恒成立,就说曲线积分⎰+L Qdy Pdx 在G 内与路径无关,否则说与路径有关.设曲线积分⎰+L Qdy Pdx 在G 内与路径无关,L1和L 2是G 内任意两条从点A 到点B 的曲线,则有⎰⎰+=+21L L Qdy Pdx Qdy Pdx ,因为⎰⎰+=+21L L Qdy Pdx Qdy Pdx ⇔021=+-+⎰⎰L L Qdy Pdx Qdy Pdx⇔021=+++⎰⎰-LL Qdy Pdx Qdy Pdx ⇔0)(21=+⎰-+L L Qdy Pdx ,在L 所围成的区域内时, 结论未必成立. 三、二元函数的全微分求积曲线积分在G 内与路径无关, 表明曲线积分的值只与起点从点(x 0,y 0)与终点(x ,y )有关. 如果⎰+LQdy Pdx 与路径无关,则把它记为⎰+),(),(00y x y x Qdy Pdx即⎰⎰+=+),(),(00y x y x L Qdy Pdx Qdy Pdx .若起点(x 0,y 0)为G 内的一定点,终点(x ,y )为G 内的动点,则u (x ,y )⎰+=),(),(0y x y x Qdy Pdx为G 内的的函数.二元函数u (x ,y )的全微分为du (x ,y )=u x (x ,y )dx +u y (x ,y )dy .表达式P (x ,y )dx +Q (x ,y )dy 与函数的全微分有相同的结构,但它未必就是某个函数的全微分.那么在什么条件下表达式P (x ,y )dx +Q (x ,y )dy 是某个二元函数u (x ,y )的全微分呢?当这样的二元函数存在时怎样求出这个二元函数呢?定理 3 设开区域G 是一个单连通域,函数P (x ,y )及Q (x ,y )在G 内具有一阶连续偏导数,则P (x ,y )dx +Q (x ,y )dy 在G 内为某一函数u (x ,y )的全微分的充分必要条件是等式xQ y P ∂∂=∂∂在G 内恒成立.简要证明:必要性:假设存在某一函数u (x ,y ),使得du =P (x ,y )dx +Q (x ,y )dy ,则有y x u x u y y P ∂∂∂=∂∂∂∂=∂∂2)(,xy u y u x x Q ∂∂∂=∂∂∂∂=∂∂2)(.因为y P y x u ∂∂=∂∂∂2、x Q x y u ∂∂=∂∂∂2连续, 所以xy u y x u ∂∂∂=∂∂∂22,即x Q y P ∂∂=∂∂.充分性:因为在G 内xQ y P ∂∂=∂∂, 所以积分⎰+L dy y x Q dx y x P ),(),(在G 内与路径无关.考虑函数u (x ,y )⎰+=),(),(0),(),(y x y x dy y x Q dx y x P .因为 u (x ,y )⎰+=),(),(0),(),(y x y x dy y x Q dx y x P ⎰⎰+=xx y y dx y x P dy y x Q 0),(),(0,所以),(),(),(000y x P dx y x P x dy y x Q x x u x x y y =∂∂+∂∂=∂∂⎰⎰.类似地有),(y x Q yu =∂∂,从而du =P (x ,y )dx +Q (x ,y )dy .即P (x ,y )dx +Q (x ,y )dy 是某一函数的全微分. 求原函数的公式:⎰+=),(),(0),(),(),(y x y x dy y x Q dx y x P y x u ,⎰⎰+=y y xx dy y x Q dx y x P y x u 0),(),(),(0,⎰⎰+=xx y y dx y x P dy y x Q y x u 0),(),(),(0.例6 验证:22yx ydxxdy +-在右半平面(x >0)内是某个函数的全微分,并求出一个这样的函数. 解: 这里22y x y P +-=,22y x x Q +=.。
10-3格林公式及其应用30088

1
0dx
1 ydy 1 .
0
0
2
四、小结
1.连通区域的概念;
2.二重积分与曲线积分的关系
Q P
D
(
x
y
)dxdy
L
Pdx
Qdy
——格林公式;
3. 格林公式的应用.
与路径无关的四个等价命题
条 在单连通开区域D 上P( x, y), Q( x, y)具有 件 连续的一阶偏导数,则以下四个命题成立.
x
例 5 计算 ( x2 2xy)dx ( x2 y4 )dy. 其中 L
L 为由点O(0, 0)到点 B(1, 1)的曲线弧 y sin x .
2
解 P ( x2 2xy) 2x
y y Q ( x2 y4 ) 2x
P Q , y x
G
若区域不止由一条闭曲
线所围成.添加直线段 AB,CE.
则D的边界曲线由 AB,L2,BA, AFC,CE, L3, EC 及 CGA 构成.
D
L2
B
由(2)知
D
(
Q x
P y
)dxdy
L3
E C
F
L1
A
{ } (Pdx Qdy) AB L2 BA AFC CE L3 EC CGA
三、利用曲线积分,求星形线 x a cos3 t , y a sin 3 t 所 围成的图形的面积 .
四、证明曲线积分
(3,4) (6 xy 2 y 3 )dx (6 x 2 y 3 xy 2 )dy 在整个 xoy面 (1,2)
曲线积分习题课

原式
Q P 解 易验证 4 xy e x sin y x y
( , ) 2 ( 0, 0 )
( e x cos y 2 xy 2 )dx ( 2 x 2 y e x sin y)dy
e dx (
2 0 x 0
2
4 4 ( , ) x 2 2 2 2 或:原式 (e cos y x y ) ( 0, 0 ) e 1 4
ydx xdy 1 L x 2 y 2 r 2 1 l ydx xdy r 2
2dxdy 2
D
16
2 2 3 y y 3 x y ( yx e ) dx ( xe xy 8 y ) dy 例5 计算 L: 1 L 2 2 4 9 9x 4 y
(e x sin y my )dx (e x cos y m )dy
8
14
x 2 2 x 例3 证明曲线积分 ( e cos y 2 xy ) dx ( 2 x y e sin y )dy L
与路径无关。若 L为以A( 0,0)到B( 计算积分的值。
2
, )的任意简单曲线,
x2 y2 解: L : 1, 即3x2+4y2=12,所以 4 3 2 2 ( 3 x 4 y )ds 12ds 12a .
L L
又L关于x轴对称,而sin(xy)关于y为奇函数,所以
L
sin( xy )ds 0
于是
I = 12a。
11
(2) 已知L为圆周 : x 2 y 2 a 2 , 求
x 2 y 2 ds
格林公式-习题共36页

8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
格林公式-习题
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的9、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
END
格林公式习题解析

“ u(x, y) (x,y) 2x ydx x2 d y ”. ( x0 , y0 )
图1
又由于积分 u(x, y) (x,y) 2X Y d X X 2 dY 与路径无关, ( x0 , y0 )
也就意味着,我们可以选取使计算简便的路径,通常我们选择 折线路径,如图 1 和图 2 所示.
y
x
y x
符合定理 9.3.2 中的充要条件,因此,积分与路径无关.
再来计算积分值——
本题中并没有指定积分弧段,只取定了起点 (1,1) 和终点 (2,3) . 由于积分与路径无关,
因此,无论沿哪条积分弧段计算曲线积分,积分值都是相同的, 我们可以选择较简便的折线路径(如图 3 所示)进行计算,记
因此,无论沿哪条积分弧段计算曲线积分,积分值都是相同的, 我们可以选择较简便的折线路径(如图 4 所示)进行计算,记
x x
LAB
:
y
2
(x
:1
3)
,
LBC
:
x y
3 y
( y : 2 4) ,则有
图4
(3,4) (6 x y2 y3)dx (6 x2 y 3 x y2 )d y (1,2)
的正向边界;
答案: 1 (e 1) 5
解析: 本题考查课本第 137~138 页知识点——
可简单地理解为曲线上无“尖点”(导数或偏导数不存在的点), 即曲线上处处有切线,且切线随切点的移动而连续转动.
简单地讲,格林公式就是把闭区域内的二重积分和该闭区域边界上的曲线积分联系了起 来,这两种积分可以根据我们的需要相互转化,从而简化计算.
u(x, y) y0 (x2 x02 ) x2 ( y y0) 的全微分,随着 (x0, y0 ) 的不同, u(x, y) 也不同.
格林公式

L
1 ∴ ∫ − y d x + x d y 是 L 所围区域 D 的面积 . 2 L 例1 求椭圆 x = a cos θ , y = b sin θ 所围成图形的面积 A . 1 解 A = ∫ − ydx + xdy 2L 1 2π = ∫ − b sin θ ⋅ d ( a cos θ ) + a cos θ ⋅ d ( b sin θ ) 2 0 2π 1 = ab ∫ dθ = πab. 7 2 0
∂Q ∂P ∵ = ∂x ∂y
y yd x − x d y , 其中 L 为圆 课堂练习 求 ∫ 2 2 L 2( x + y ) P214.3 周 ( x − 1 ) 2 + y 2 = 2 , L 的方向逆时针 . O l D 所围区域为 解 设 L所围区域为 D . y −x P( x, y) = , Q( x, y) = . 2 2 2 2 2( x + y ) 2( x + y ) x2 − y2 ∂P ∂Q ∵ = = 在 D 内不连续 , ( 0,0 )是奇点 . 2 2 2 ∂ y 2( x + y ) ∂x ∴ D 上不能用格林公式 (见 P 202 定理 1条件 ).
在 D 内作小圆周 l : x 2 + y 2 = r 2方向逆时针 (如图 ).
ydx − xdy 用P 205 第 8 −10 ∫ 2( x 2 + y 2 ) ======== 行的方法得 L
L
x
∫
( 小圆 )
l
y d x − x d y 曲线L上的积分可以化成同 上的积分可以化成同 上的积分. 2 ( x 2 + y 2 ) 方向的小圆周 l 上的积分.
《格林公式及其应用》PPT课件

n (cos,cos).
v nds L
(P cos Q cos)ds
L
由格林公式
Pdy Qdx =========
(P Q )d .
L
D y x
(格林公式的另一种形式)
称函数
为平面向量场 v (P(x, y),Q(x, y))
的散度.物理意义:稳定流体通过某一闭曲线的流量,等
于其散度在该闭曲线所的区域上的二重积分之值.
(x y)dx (x y)dy
( L )
x2 y2
0dxdy 0.
D1
首页
上页
返回
下页
结束
铃
这里(L ) 表示多连通区域 D1的正向边界曲线 .这时L按 逆时针方向,而按顺时针方向.因而
(x y)dx (x y)dy
( L )
x2 y2
(x y)dx (x y)dy (x y)dx (x y)dy,
(x y)dx (x y)dy
L
x2 y2
1 r2
2 [r2 (cost sin t)(sin t) r2 (cost sin t)(cost)]dt
0
2
0 1dt 2.
例 4 设函数u(x,y)在有界闭区域D上有连续的二阶
偏导数,L 为D 的边界且逐段光滑.证明:
u
L
u n
ds
y
x
(x2 y)dx (x y2 sin3 y)dy, AO
oA
(x2 y)dx (x y2 sin3 y)dy
AO
0 x2dx 8 .
2
3
首页
上页
返回
下页
结束
铃
当曲线积分 (x2 y)dx (x y2 sin3 y)dy 与路径无 AB
格林公式及其应用

易于计算时,可应用格林公式计算
O
L2 L L1 L3
x
(2)L不封闭时,采取“补线”的方法:
L L l lD ( Q x P y)dx d l y
要求右端的二重积分及曲线l积分易于计算。l 选用直线段、折线、圆、半圆、椭圆、抛物线等。
(3)如在D上P、Q一阶偏导连续,且处处有
(1) 沿D中任意光滑闭曲线 L,有 LPdxQdy0。
(2) 对 D中任一分段光滑曲线 L, 曲线积分
PdxQdy与路径无关, 只与起止点有关.
L
(3)PdxQdy在 D内是某一函数 u(x, y)的全微分, 即 d u ( x ,y ) P d x Q d y
(4) 在 D内每一点都有 P Q 。 y x
注意本题只在不含原点的单连通区域内积分与路径无关内有设pq在单连通域d内具有一阶连续偏导数则有思考与练习且都取正向问下列计算是否正确的半圆计算质点m沿着以ab为直径的半圆从a12运动到故所求功为ab锐角其方向垂直于om且与y轴正向夹角为对质点m所作的功
8.2 格林公式及其应用
8.2.1 格林公式 8.2.2 平面上曲线积分与路径无关的条件
a a xdx1a2
40
6
8.2.2 平面上曲线积分与路径无关的条件
如果在区域G内有
y
PdxQdy L1
PdxQdy L2
B G
L1
A
L2
o
x
则称曲线积分L Pdx Qdy在G 内与路径无关,
否则与路径有关。
平面上曲线积分与路径无关的等价条件 定理8.2.2 设 D是单连通域,函数P (x ,y)Q ,(x ,y)在D内 具有一阶连续偏导数, 则以下四个条件等价:
《高数》第十章习题课-线面积分的计算

12
练习题: P184 题 3(5) ; P185 题6; 10 3(5). 计算
其中L为上半圆周 提示:
沿逆时针方向.
I ex sin y d x (ex cos y 2)dy 2 ydx
L
L
2 ydx
L AB AB
L
L
:
xy
a a
(1 cos sin t
其中L为上半圆周
沿逆时针方向.
P185 6 . 设在右半平面 x > 0 内, 力
构成力场,其中k 为常数,
场力所作的功与所取的路径无关.
证明在此力场中
P185 10. 求力
沿有向闭曲线 所作的
功, 其中 为平面 x + y + z = 1 被三个坐标面所截成三
角形的整个边界, 从 z 轴正向看去沿顺时针方向.
3
16
二、曲面积分的计算法
1. 基本方法
曲面积分
第一类( 第二类(
对面积 对坐标
) )
转化
二重积分
(1) 统一积分变量 — 代入曲面方程
(2)
积分元素投影
第一类: 第二类:
始终非负 有向投影
(3) 确定二重积分域
— 把曲面积分域投影到相关坐标面
17
2. 基本技巧
(1) 利用对称性及重心公式简化计算 重心公式
20
例4. 设 为简单闭曲面, a 为任意固定向量, n 为的 单位外法向向量, 试证
证明: 设 n (cos , cos , cos )
(常向量)
则 cos( n ,a ) d S n a 0 dS
格林公式

= ∫∫ 0dxdy + ∫
D
L1
∫
L1
xdy − ydx
第四章
曲面面积和对曲面的积分
3
第五章
曲线、曲面积分
=
1 r2
∫∫
x2 + y 2 ≤ r 2
2dxdy = 2π .
Green 公式的流体力学解释
例 4: 设平面流场,流速向量
y
C
G ⎛ u ( x, y )⎞ U ( x, y ) = ⎜ ⎜ v ( x, y ) ⎟ ⎟, ⎝ ⎠
π
0
L
π
所以
v ∫
L
− sin y sin x xesin y dy − ye − sin x dx = v ∫ xe dy − ye dx .
(2) 由于 e
sin x
+ e − sin x ≥ 2 ,故由(1)得
π
0
v ∫
C
xesin y dy − ye− sin x dx = π ∫ (esin x + e − sin x ) dx ≥ 2π 2 .
1, (4),(6); 2,(1); 3,(2) ; 4.
v ∫
L
x d l , 其中 L : x 2 + y 2 = r 2 ;
v ∫
例 9. 求 lim
R → +∞
L
x d y , 其中 L : x 2 + y 2 = r 2 的正向.
x2 + y2 =R2
∫
ydx − xdy . ( x + xy + y 2 ) 2
2 2
G
G
G
G
其中 D 是一个有界区域, 域与边界定向的关系:边界 ∂D 是逐段光滑的简单有向闭曲线 (曲线不自相交), 其正向是为使区域 D 总在左侧. z
曲线积分与曲面积分重点总结+例题

第十章曲线积分与曲面积分【教学目标与要求】1.理解两类曲线积分的概念,了解两类曲线积分的性质及两类曲线积分的关系。
2.掌握计算两类曲线积分的方法.3.熟练掌握格林公式并会运用平面曲线积分与路径无关的条件,会求全微分的原函数.4.了解第一类曲面积分的概念、性质,掌握计算第一类曲面积分的方法。
【教学重点】1。
两类曲线积分的计算方法;2。
格林公式及其应用;3。
第一类曲面积分的计算方法;【教学难点】1。
两类曲线积分的关系及第一类曲面积分的关系;2.对坐标的曲线积分与对坐标的曲面积分的计算;3。
应用格林公式计算对坐标的曲线积分;6.两类曲线积分的计算方法;7.格林公式及其应用格林公式计算对坐标的曲线积分;【参考书】[1]同济大学数学系.《高等数学(下)》,第五版.高等教育出版社。
[2]同济大学数学系.《高等数学学习辅导与习题选解》,第六版.高等教育出版社.[3]同济大学数学系。
《高等数学习题全解指南(下)》,第六版.高等教育出版社§11.1 对弧长的曲线积分一、对弧长的曲线积分的概念与性质曲线形构件的质量:设一曲线形构件所占的位置在xOy面内的一段曲线弧L上,已知曲线形构件在点(x,y)处的线密度为μ(x,y)。
求曲线形构件的质量.把曲线分成n小段,∆s1,∆s2,⋅⋅⋅,∆s n(∆s i也表示弧长);任取(ξi,ηi)∈∆s i,得第i小段质量的近似值μ(ξi,ηi)∆s i;整个物质曲线的质量近似为;令λ=max{∆s1,∆s2,⋅⋅⋅,∆s n}→0,则整个物质曲线的质量为.这种和的极限在研究其它问题时也会遇到。
定义设函数f(x,y)定义在可求长度的曲线L上,并且有界。
,将L任意分成n个弧段:∆s1,∆s2,⋅⋅⋅,∆s n,并用∆s i表示第i段的弧长;在每一弧段∆s i上任取一点(ξi,ηi),作和;令λ=max{∆s1,∆s2,⋅⋅⋅,∆s n},如果当λ→0时,这和的极限总存在,则称此极限为函数f(x,y)在曲线弧L上对弧长的曲线积分或第一类曲线积分,记作,即.其中f(x,y)叫做被积函数,L叫做积分弧段。
大一高数课件第十章 10-习题课-1

半圆周 ( x − a ) 2 + y 2 = a 2 , y ≥ 0 ,沿逆时针方向 .
三、证明: 证明:
xdx + ydy 在整个 xoy 平面除去 y 的负半轴及 2 2 x +y
内是某个二元函数的全微分, 原点的开区域 G 内是某个二元函数的全微分,并 求出一个这样的二元函数 .
测验题答案
(2) I2 = ∫ ( x2 − y+ y2)d x + ( y2 − x)d y L
= ∫ ( x2 − y)d x + ( y2 − x)dy + ∫ y2 dx
L L
L: x = acost, y = asint ,
t : 0 →π
= I − ∫ a sin3 t d t = −2a3
0
π 3
非闭
I = ∫ Pdx + Qdy =0
L
闭合
∂P ∂Q ∂P = ≠ ∂y ∂x ∂y ∂x非闭 补充曲线或用公式
∂Q ∂P 闭合 I = ∫∫ ( − )dxdy ∂x ∂y ∂Q D
解
由 I = ∫ ( x2 + 2xy)dx + ( x2 + y4 )dy
1
y
A
∂P ∂ 2 知 = ( x + 2 xy ) = 2 x ∂ y ∂y ∂Q ∂ 2 = ( x + y4 ) = 2 x x ∂x ∂x o 1 ∂P ∂Q 1 2 1 , 即 = 故原式 = ∫ x dx + ∫ (1 + y 4 )dy = 23 . ∂y ∂x 0 0
λ→0 i=1
n
∫ P( x, y)dx+ Q( x, y)dy
5-3格林公式

一、 区域连通性的分类 二、 格林(Green)公式 三、 简单应用 四、 小结 习题课
一、区域连通性的分类
设D为平面区域, 如果D内任一 为平面区域, 如果D 闭曲线所围成的部分都属于D, 闭曲线所围成的部分都属于D, 则称 为平面单连通区域 否则称为复连 单连通区域, D为平面单连通区域, 否则称为复连 通区域. 通区域.
D
闭区域 D 的面积
取 P = 0, Q = x , 得
1 A = ∫L xdy − ydx . 2
A = ∫L xdy
取 P = − y, Q = 0, 得 A = ∫L − ydx
例6 求椭圆
x = a cos t y = b sin t
的面积. (0 ≤ t ≤ 2π ) 的面积
x 2 2 x +y
则当 x + y ≠ 0 时, 有
∂P y −x ∂Q = 2 2 2 = ∂y ∂x ( x + y )
2 2
(1)当 (1)当(0, 0) ∉ D 时,
y L
D
由格林公式知 xdy − ydx ∫L x 2 + y 2 = 0 (2)当 (2) 当 (0,0) ∈ D 时 , 作位于 D 内圆周 2 2 2 l: x + y =r , 所围成, 记 D1由 L 和l 所围成,
o
x
y
L
D1
l
o
r
应用格林公式, 应用格林公式,得
x
xdy − ydx xdy − ydx ∫L x 2 + y 2 − ∫l x 2 + y 2 = 0 xdy − ydx xdy − ydx ∫L x 2 + y 2 = ∫l x 2 + y 2
微积分B(2)第7次习题课参考答案(第二型曲线积分、Green公式、平面向量场)

xy
2
xy
L ( A)
1
1
1
xy
2
xy
xy
2
xy
其中
L + L1
L1
L + L1
∫
e xy y 2 dx + [e xy (1 + xy ) + x]dy
= ∫∫ [( ye xy ( xy + 2) + 1 − y ( xy + 2)e xy ]dxdy
D
= ∫∫ dxdy = A
D
= ∫∫ [(e x cos y − a) − (e x cos y − b)]dxdy
D
= ∫∫ (b − a)dxdy = (b − a)
D
πa 2 2
,
L1
∫ [e
x
sin y − b( x + y )]dx + (e x cos y − a x)dy
= ∫ (−bx)dx = −2a 2 b
2 3 0 L1 2 2 2 1 2 2 2
x = 1 + cos t , 令L : 起点对应 t = π ,终点对应 t = 0 ,则 y = sin t ,
1
∫L 3x
1
2
ydx + ( x3 + x − 2 y )dy
= ∫ 3(1 + cos t ) 2 sin t ⋅ (− sin t ) + (1 + cos t )3 + (1 + cos t ) − 2sin t cos t dt π = ∫ 3sin 2 t − 4cos t + 2sin t cos t − cos 2 t − 9 cos3 t − 4 cos 4 t dt
D21-6格林公式及其应用习题课

ydx y2
arctan
y( 3,3) x (1,0)
π. 3
或
y dy 0 1 y2
arctan x
2
y
y (1, y) (x, y) o (1,0) ( x,0) x
例3 确定常数 ,使在右半平面x 0内的向量值
函数A( x,
y)
2xy( x4
y2 )
i
x2( x4
y2 )
j为某
C(x, y)
u( x,
y)
AB BC
xdy x2
ydx y2
O A(1,0) B( x,0)x
AB
xdy x2
ydx y2
BC
xdy x2
ydx y2
x 1
0 x2
0
dx
y 0
x2
x
y2
dy
arctan
y y x 0
arctan y . x
( 3,3) (1,0)
xdy x2
(x,y) xy2dx x2 ydy
(0,0)
注:起点可以任选, 一般选原点
x
0dx
y x2 ydy x2 y2
0
0
2
原函数可以相差一个常数
u(x, y) x2 y2 C
2
练习
验证
xdy x2
ydx y2
在右半平面(
x
0)内, 是某个函
数的全微分 , 求出一个这样的函数 , 并计算曲线积
全微分式
2. 判别定理
定理3. 设函数P(x,y),Q(x,y)在单连通域D内具有一阶
连续偏导数,则P(x,y)dx+Q(x,y)dy在D内为某一函数
辽宁工业大学高数习题课10-1-2

特殊的有向曲线 L1:x24y22( 0充分小), 规定L1的方向为
逆时针(如图所示)。
y
L
设 L(L1)所围成的区域为D,
L1
则在L(L1)上应用Green 公式,得
0
x
yd x xdyQP
( )dxd 0,y L L 1 x24y2 D x y
所以
ydxxdy
L x24y2
L1
ydxxdy
x24y2 .
而
ydxxdy1 L1 x24y2 2
ydxxdy 1
L1
2
2dxdy
D
故
ydx xdy
L x2 4y2
或利用参数方程计算:令L 1
:xcos,y sin ,
2
从0到2
.
所以 ydxxdy ydxxdy
L x2 4y2 L1 x2 4y2
21 22(s 0
1y}
,
于是
WBO rk3[xdx (1y)d]yk
1d[x2 (1y)2] 2 (0,0) (2,0) [x2 (1y)2]32
1k(2)[x2(1y)2]1 2
(0,0)
k(1
1
).
2
(2,0)
5
感谢您的关注
解: 补直线段 L OA: y 0, x从0变到; 并设曲线LL
所围区域为 D(如图),则由Green公式,得:
ex [1 ( co y )ds x (y siy )n d]y L L
Q
(
D
x
P)dxdy y
yexdxdy
D
y
ysinx
L
dxsinxexydy1 (1 e )
习题二十一格林公式及其应用(续)
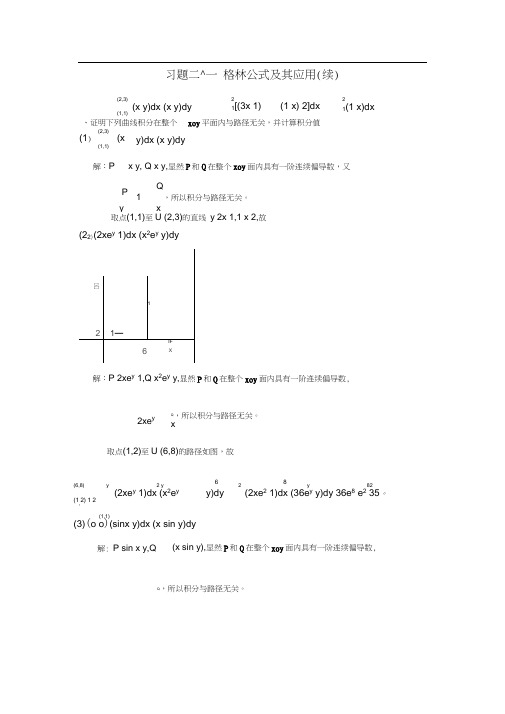
习题二^一 格林公式及其应用(续)、证明下列曲线积分在整个 xoy 平面内与路径无关,并计算积分值 (2,3)(1) (x (1,1) y)dx (x y)dy解:P x y, Q x y,显然P 和Q 在整个xoy 面内具有一阶连续偏导数,又PQ 1 ,所以积分与路径无关。
y x取点(1,1)至U (2,3)的直线 y 2x 1,1 x 2,故(22)(2xe y 1)dx (x 2e y y)dy解:P 2xe y 1,Q x 2e y y,显然P 和Q 在整个xoy 面内具有一阶连续偏导数,取点(1,2)至U (6,8)的路径如图,故(6,8) y2 y 6 2 8y 82 (2xe y 1)dx (x 2e y y)dy (2xe 2 1)dx (36e y y)dy 36e 8 e 2 35。
(1,2) 1 2(1,1) (3)(o o )(sinx y)dx (x sin y)dy(x sin y),显然P 和Q 在整个xoy 面内具有一阶连续偏导数,Q ,所以积分与路径无关。
(2,3) (1,1)(x y)dx (x y)dy 21[(3x 1) (1 x) 2]dx 2 1(1 x)dx 2xe yQ ,所以积分与路径无关。
x 解: P sin x y,Q取点(0,0)至U (1,1)的直线 y x,0 x 1,故(1,1) i(0,0)(sinx y)dx (x siny)dy °[(sinx 2x 上从点(0,0)到点(4,8)。
( )e sin ydx e cos ydy L 1 L 248 4 0 dx e cos ydy 0 04 e sin 8三、设IJe x 2f (x)] ydx f (x)dy 与积分路径L 无关,且f(1) 1 ,求(1,1) I (0,0)[e 2f(x)]ydx f (x)dy 之值。
1x) (x sin x)]dx o 2xdx 1。
高数-格林公式

2(
y),
y]d
y
d c
{Q[
2
(
y),
y]
Q[ 1
(
y),
y]}d
y
D
Q x
dxdy
则有
Q P
(
D
x
y
)dxdy
L
Pdx
Qdy
(1)
证明:(1)设 D 既是 X 型,又是 Y 型区域。
X 型: a x b, 1( x) y 2( x),
L Pdx
D
P y
dxdy
y d
L2 : x 2( y)
D L2
L3
L1
(2)格林公式建立了平面上的曲线积分与二重积分 的关系,它是牛顿莱布尼茨公式在平面上的推广。
主要用途:实现曲线积分与二重积分之间的转换,而 经常用来将复杂的曲线积分转化为二重积分。
D
(
Q x
P y
)dxdy
L
Pdx
Qdy
(1)
(3)便于记忆的形式
若记
Q P x y
x P
y Q
则格林公式可表示为
(
D
x
y
)dxdy
L
Pdx
Qdy
(1)
证明:(1)设 D 既是 X 型,又是 Y 型区域。
X 型: a x b, 1( x) y 2( x),
y L2 : y 2( x)
P
D
y
dxdy
b
a
dx
2 (x) 1 ( x)
P y
dy
ab{
P[
ab
x,2(
2 (x)
P(x, y) | 1 (x)
格林公式例题与习题

L P d x Q d y 在 D 内与路径无关. 对 D 内任意闭曲线 L 有 P d x Q d y 0 L
Q P 在 D 内有 x y 在 D 内有 d u P d x Q d y
P d x Q d y 0 为全微分方程
目录 上页 下页 返回 结束
2 2
y 2 x x 2 上由点(0,0)到点(1,1)的一段弧 .
第四节 目录 上页 下页 返回 结束
y
( x, y )
1 5 x 2x2 y3 y5 C 5
作业 P214 5 (1) , (4) ;
O
( x,0) x
第四节
目录
上页
下页
返回
结束
P 214 / 4. 证明下列曲线积分在整个xOy面内与路径 无关,并计算积分值: (1)
(1,1) ( x y )d x ( x y )d y
定理2目录上页下页返回结束目录上页下页返回结束计算其中l为上半为了使用格林公式添加辅助线段圆周区域为d目录上页下页返回结束验证是某个函数的全微分由定理2可知存在函数u目录上页下页返回结束10由定理2可知存在原函数目录上页下页返回结束11目录上页下页返回结束12设质点在力场作用下沿曲线l移动到求力场所作的功w可见在不含原点的单连通区域内积分与路径无关
y
B(0,1) A(1,1)
D
利用格林公式 , 有
yx
O
D
x
xe xe
y2
dy dy 0 ye
1 y2
y2
OA
dy
1 (1 e 1 ) 2
目录 上页 下页 返回 结束
二、平面上曲线积分与路径无关的等价条件
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题课
1. 格林公式∫+L y Q x P d d
2. 等价条件
在 D 内与路径无关.
y
P x Q ∂∂=∂∂在 D 内有y
Q x P u d d d +=y
x y P x Q D d d ∫∫⎟⎠
⎞
⎜⎝⎛∂∂−∂∂=∫+L
y Q x P d d 对 D 内任意闭曲线 L 有0
d d =+∫L
y Q x P 在 D 内有
设 P , Q 在 D 内具有一阶连续偏导数, 则有
为全微分方程
0d d =+y Q x P
积分与积分与路径无关
路径无关.计算=∂∂∂∂ Q P x y
成立
不成立
添辅助线
曲线L 为闭曲线
曲线L 不是闭曲线
解题步骤:
Green 公式
换路径:一般换成
平行坐标轴的折线
例1 计算
,
d ∫
AB
y x 其中曲线 AB 是半径为 r
的圆在第一象限部分. 解
设 D 是半径为 r 的圆域
A
B
D
O
x
y
在第一象限部分,设其边界为 L , 记 -L 为边界的顺时针方向,∫∫∫−−=−OA BO L
y x y x y x d d d ∫
AB
y x d ∫−=L
y
x d ∫∫−=D
σd 2
41r
π−=应用格林公式有
例 2 计算,
d sin 31d )
e 3(32
y y y x x x y x I L x
⎟⎠
⎞
⎜⎝⎛−++=∫其中 L 是摆线 x = t – sin t , y = 1- cos t ,从点
A (2π, 0) 到点 O (0, 0) 的一段弧.
解 显然,用这段路径来计算是很复杂且困难.
.
,x
Q
y P ∂∂∂∂为此计算.2
x
Q x y P ∂∂==∂∂再选一条路径 L 1:由 A (2π, 0) 沿 x 轴到原点.
x
y
O
L 1
L
A
y y y x x x y x L
x
d )sin 31(d )
e 3(3
2
∫−++,
d )sin 31(d )
e 3(1
32y y y x x x y x L x
∫−++=因为 L 1 上 d y = 0,y = 0 所以上式为y y y x x x y x L x
d )sin 31(d )
e 3(1
32∫−++,
3)π21(e 3d e 3π
20
π2−−==∫x x x
即
()
y y y x x x y x L
x
d sin 31d )
e 3(3
2
∫−++.
3)π21(e 3π
2−−=
解23
.15
=例3由点)0,0(O 到点)1,1(B 的曲线弧sin .2
x y π=其中L 为
x Q
y P ∂∂=∂∂⇒原积分与路径无关。
x y
(1,1)
B •
(1,0)
C •
O
•P y ∂∂x
y x x
x Q 2)(42=+∂∂=∂∂224
(2)().L
x xy dx x y dy +++∫
计算2(2)x xy y ∂=+∂2x =1
2
x dx =∫故原式1
4
0(1)y dy ++∫
例4. 的弧段。
到从上为星形线求 2
0 sin ,cos , 3
3
22πt t a y t a x AB y
x AB ==+∫解1用参数法。
=原式∫+−20
2
3233
333)
sin ()cos ()
cos (sin )sin (cos πt a t a t a td a t a td a dt t t t t ∫+=206633sin cos cos sin 3πt d t t t tan tan 1tan 32
062tan ∫+=π为积分变量
.
2
)arctan(tan 0 2
03tan 3ππ==−t t 为积分变量
解2=原式∫
∈===
20
]
2
,0[,sin ,cos :ππ
θθθθd a y a x L ,y
P
x Q ∂∂=∂∂∵),0,0(),(≠∀y x 上积分与路径无关。
在 0: >+∴y x D ,
),0( )0,( 0)0,( : 2
2
2
的弧段到上从取a B a A y x a y x L ≥≥=+∫+−L y x ydx xdy 22 ∫−=L L ydx xdy a 21 的方程
2
π=
例4. 的弧段。
到从上为星形线求 2
0 sin ,cos , 3
3
22πt t a y t a x AB y
x AB ==+∫
解3改变积分路径。
=原式∫+=a y
a dy a 022, ),( , : a a C CB AC l 其中
取→
+→∫∈=→++],0[,:2
2a y a x AC y a ady 2π=∫∈=→
+−],0[,:22a x a y CB a x adx
∫+−022a a x dx a ∫+=a y a dy a 0222积分?
到顺时针从能否沿 2
2
2
B A a y x =+积分?
到从能否沿 B A OB AO →→+问:例4. 的弧段。
到从上为星形线求 2
0 sin ,cos , 3
3
22πt t a y t a x AB y
x ydx xdy AB ==+−∫
解
2
()P xy y y ∂∂=∂∂()()Q y x x x
ϕ∂∂=∂∂,
),(2
xy y x P =(,)(),
Q x y y x ϕ=例5其中ϕ具有连续的导数,
计算(1,1)
2
(0,0)
().
xy dx y x dy ϕ+∫
因积分与路径无关
.P Q y x
∂∂∴=∂∂即()2y x xy ϕ′=2
(),x x c ϕ⇒=+由0)0(=ϕ知0,c =2
)(x x =⇒ϕ1
0dx =∫.
2
1=故
(1,1)
2
(0,0)
()xy dx y x dy ϕ+∫
2
()L
xy dx y x dy ϕ+∫
与路径无关,
设曲线积分(0)0,ϕ=且2,xy =(),y x ϕ′=x y
(1,1)
B •
(1,0)
C •
O
•1
ydy +∫
例6试用求(2sin )(cos )x y dx x y dy ++的原函数.
解答:2(,)sin u x y x x y =+。
