第三章-组合逻辑电路
第三章 组合逻辑电路

特点
应用举例 8421 BCD 码 → 余 3 码
优点:速度快 缺点:电路比较复杂
集成芯片
CMOS:CC4008 TTL:74283 74LS283
C3 超前进位电路
A3 B3
A2 B2 A1 B1 A0 B0 C0-1 逻辑结构示意图
Σ CI
加法器 比较器 数据选择器和分配器 2. 按开关元件不同:
3. 按集成度不同:
编码器 译码器 只读存储器
CMOS SSI MSI TTL LSI VLSI
3. 1 组合电路的分析方法和设计方法
3. 1. 1 组合电路的基本分析方法
一、分析步骤
逻辑图
逻辑表达式
化简
真值表
说明功能
二、分析举例 [例] 分析图中所示电路的逻辑功能 A 0 0 0 0 1 1 1
4.化简或变换: 根据所用元器件的情况将 函数式进行化简或变换。
5.画逻辑图
3.2 加法器和数值比较器
3.2.1 加法器 一、半加器和全加器
1. 半加器(Half Adder)
两个 1 位二进制数相加(不考虑低位进位)。 Ai+Bi = Si (和) Ci (进位)
真 值 表
Ai 0 0 1 1
比 较 输 入
B = B3B2B1B0
输
A0 B0
真值表
出
A3 B3 A2 B2 A1 B1 L G M
4位数值比较器
A3 B3 A2 B2 A1 B1 A0 B0
A> B A= B A< B
L=1 G=1 M=1
> = = = = < = = =
第3章--组合逻辑电路习题解答

复习思考题3-1 组合逻辑电路的特点? 从电路结构上看,组合电路只由逻辑门组成,不包含记忆元件,输出和输入之间无反馈。
任意时刻的输出仅仅取决于该时刻的输入,而与电路原来的状态无关,即无记忆功能。
3-2 什么是半加?什么是全加?区别是什么?若不考虑有来自低位的进位将两个1位二进制数相加,称为半加。
两个同位的加数和来自低位的进位三者相加,称为全加。
半加是两个1位二进制数相加,全加是三个1位二进制数相加。
3-3 编码器与译码器的工作特点? 编码器的工作特点:将输入的信号编成一个对应的二进制代码,某一时刻只能给一个信号编码。
译码器的工作特点:是编码器的逆操作,将每个输入的二进制代码译成对应的输出电平。
3-4 用中规模组合电路实现组合逻辑函数是应注意什么问题?中规模组合电路的输入与输出信号之间的关系已经被固化在芯片中,不能更改,因此用中规模组合电路实现组合逻辑函数时要对所用的中规模组合电路的产品功能十分熟悉,才能合理地使用。
3-5 什么是竞争-冒险?产生竞争-冒险的原因是什么?如何消除竞争-冒险? 在组合逻辑电路中,当输入信号改变状态时,输出端可能出现虚假信号----过渡干扰脉冲的现象,叫做竞争冒险。
门电路的输入只要有两个信号同时向相反方向变化,这两个信号经过的路径不同,到达输入端的时间有差异,其输出端就可能出现干扰脉冲。
消除竞争-冒险的方法有:接入滤波电容、引入选通脉冲、修改逻辑设计。
习 题3-1试分析图3.55所示各组合逻辑电路的逻辑功能。
解: (a)图 (1) 由逻辑图逐级写出表达式:)()(D C B A Y ⊕⊕⊕=(2) 化简与变换:令DC Y B A Y ⊕=⊕=21则 21Y Y Y ⊕=(3)由表达式列出真值表,见表3.1。
输入 中间变量 中间变量 输出 A B C D Y 1 Y 2 Y 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 10 0 0 0 1 1 1 1 1 1 1 1 0 0 0 00 1 1 0 0 1 1 0 0 1 1 0 0 1 1 00 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0(4)分析逻辑功能:由真值表可知,该电路所能完成的逻辑功能是:判断四个输入端输入1的情况,当输入奇数个1时,输出为1,否则输出为0。
数字电子技术 第三章 组合逻辑电路

2021/6/10
23
3.2.2 二进制编码器
由于每次操作只有一个输入信号,即输入IR、IY、IG 具有互斥性,根据表3.5,将输出变量取值为1对应的输入 变量相加,可得输出Y1、Y0与输入IR、IY、IG之间的逻辑 关系表达式如下。
Y0 = IR + IG Y1 = IY + IG
对Y1、Y0两次取非,得
5. 断开开关S1、S2,观察发光二极管的发光情况,记 录观察到的结果。
2021/6/10
39
3.3.1 任务描述
图3.18所示是开关S1闭合、S2断开时,观察到的现象。
2021/6/10
图3.18 闭合S1、断开S2时观察到的现象
40
3.3.2 二进制译码器
1. 译码器的基本功能 二进制译码真值表如表3.11所示。
2021/6/10
27
3.2.2 二进制编码器
表中的“×”号表示:有优先级高的输入信号输入时, 优先级低的输入信号有输入还是无输入,不影响编码器的 输出。
2021/6/10
28
3.2.2 二进制编码器
3. 集成8线-3线优先编码器 集成8线-3线优先编码器74LS148、74LS348的引脚排 列完全相同,如图3.12(a)所示。
第四步,判断逻辑电路的逻辑功能。其方法是:根据
真值表进行推理判断。在实际应用中,当逻辑电路很复杂
时,一般难以用简明扼要的文字来归纳其逻辑功能,这时
就用真值表来描述其逻辑功能。
2021/6/10
7
3.1.2 组合逻辑电路的分析
2. 分析举例 【例3.1】 试分析图3.1所示电路的逻辑功能。
解:画出图3.1所示电路的逻辑图如图3.4所示。
第三章 组合逻辑电路PPT课件
10
3 、 “与或非” 门
"与或非"门也是一种通用门。
仅当每一个“与项”均为0时,才能使F为1, 否则F为0。
11
4、" 异或 " 门
“ 异或 ” 运算是一种特殊的逻辑运算 , 用符号 表示.
变量A、B取值相同,F为0;变量A、B取值相异,F为1。
24
25
3.3组合逻辑电路的分析
分析的任务:根据给定的组合电路,写出逻辑函数表 达式,并以此来描述它的逻辑功能,确定输入与输出 的关系,必要时对其设计的合理性进行评定。
分析的一般步骤: 第一步: 写出给定组合电路的逻辑函数表达式 第二步: 化简逻辑函数表达式 第三步: 根据化简的结果列出真值表 第四步: 功能评述
“ 同或 ” 运算用符号 表示, 逻辑表达式为:
变量A、B取值相同,F为1;变量A、B取值相异,F为0。
由于同或实际上是异或之非,所以实际应用中通常 用异或门加非门实现同或运算。
12
3.2逻辑函数的实现
函数的表现形式和实际的逻辑电路之间有着对 应的关系,而实际逻辑电路大量使用 “ 与 非 ” 门、 “ 或非 ” 门、 “ 与或非 ” 门 等。
1、“ 与非 ” 门
使用 “ 与非 ” 门可以实现 “ 与 ” 、 “ 或 ” 、 “ 非 ”3 种基本运算 , 并可构 成任何逻辑电路 , 故称为通用逻辑门。
只要变量有一个为0,则函数F为1;仅当变 量全部为1时,函数F为0。
9
2、 “ 或非 ” 门
只要变量中有一个为1,则函数F为0;仅当变 量全部为0时,函数F为1。
闭合 不闭合
闭合 闭合
电子技术 数字电路 第3章 组合逻辑电路

是F,多数赞成时是“1”, 否则是“0”。
0111 1000 1011
2. 根据题意列出真值表。
1101 1111
(3-13)
真值表
ABCF 0000 0010 0100 0111 1000 1011 1101 1111
3. 画出卡诺图,并用卡 诺图化简:
BC A 00
00
BC 01 11 10
010
3.4.1 编码器
所谓编码就是赋予选定的一系列二进制代码以 固定的含义。
一、二进制编码器
二进制编码器的作用:将一系列信号状态编制成 二进制代码。
n个二进制代码(n位二进制数)有2n种 不同的组合,可以表示2n个信号。
(3-17)
例:用与非门组成三位二进制编码器。 ---八线-三线编码器 设八个输入端为I1I8,八种状态,
全加器SN74LS183的管脚图
14 Ucc 2an 2bn2cn-1 2cn
2sn
SN74LS183
1 1an 1bn 1cn-11cn 1sn GND
(3-39)
例:用一片SN74LS183构成两位串行进位全加器。
D2
C
D1
串行进位
sn
cn
全加器
an bn cn-1
sn
cn
全加器
an bn cn-1
1 0 1 1 1 AB
AC
F AB BC CA
(3-14)
4. 根据逻辑表达式画出逻辑图。 (1) 若用与或门实现
F AB BC CA
A
&
B
C
&
1 F
&
(3-15)
(2) 若用与非门实现
第3章-组合逻辑电路

例:3位二进制(3线-8线)译码器框图如下所示:
图3.3.5
3线-8线译码器框图
二进制译码器可采用二极管与门阵列或三极管集 成门电路等构成。
(1)二极管与门阵列译码器电路 0(0V) 1(3V)
表3-3-4
74LS42功能表
74LS42逻辑电路图及各输出表达式如下所示:
Y 0 Y 1 Y 2 Y 3 Y 4 Y5 Y 6 Y 7 Y8 Y9 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0 A 3 A 2 A1 A 0
Y3
Y2
Y1
Y0
§3.3 若干常用的组合逻辑电路
目前,一些常用的逻辑电路已经制成了中、小 规模集成化电路产品。
§3.3.1 编码器(Encoder)
“编码”:即为了区分一系列不同的事物,将其 中的每个事物用一个二值代码表示。 编码器的逻辑功能:把输入的每一个高、低电平 信号变成一个对应的二进制代码。
第三章
Chapter 3
组合逻辑电路
Combinational Logic Circuit
本章主要内容
第一节 第二节 第三节 概述 组合逻辑电路的分析和设计方法 若干常用组合逻辑电路
§3.3.1 编码器(Encoder) §3.3.2 译码器(Decoder) §3.3.3 数据分配器(Demultiplexer)
组合逻辑电路

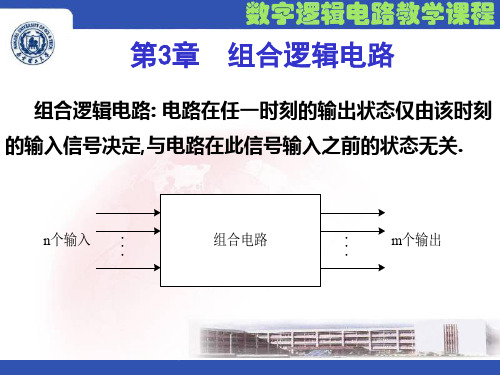
第三章组合逻辑电路基本知识点*组合逻辑电路的特点*组合逻辑电路功能的表示方法及相互转换*组合逻辑电路的分析方法和设计方法*常用集成组合逻辑电路的逻辑功能、使用方法和应用举例*组合逻辑电路中的竞争–冒险现象及消除竞争–冒险现象的常用方法3.1概述在数字电路中根据逻辑功能的不同特点,可将其分为两大类:一类是组合逻辑电路,另一类是时序逻辑电路。
组合逻辑电路在逻辑功能上的共同特点是:任意时刻的输出状态仅取决于该时刻的输入状态,与电路原来的状态无关。
在电路结构上的特点是:它是由各种门电路组成的,而且只有从输入到输出的通路,没有从输出到输入的反馈回路。
由于组合逻辑电路的输出状态与电路的原来状态无关,所以组合逻辑电路是一种无记忆功能的电路。
由此可知第二章中介绍的各种门电路都属于组合逻辑电路。
描述一个组合逻辑电路逻辑功能的方法很多,通常有:逻辑函数表达式、真值表、逻辑图、卡诺图、波形图五种。
它们各有特点,又相互联系,还可以相互转换。
3. 2逻辑功能各种表示方法的特点及其相互转换一、逻辑功能各种表示方法的特点1、逻辑函数表达式逻辑表达式是用与、或、非等基本运算来表示输入变量和输出函数因果关系的逻辑代数式。
其特点是形式简单、书写方便,便于进行运算和转换。
但表达式形式不唯一。
2、真值表真值表是根据给定的逻辑问题,把输入变量的各种取值的组合和对应的输出函数值排列成表格。
其特点是:直观、明了,可直接看出输入变量与输出函数各种取值之间的一一对应关系。
真值表具有唯一性。
3、逻辑图逻辑图是用若干基本逻辑符号连接成的电路图。
其特点是:与实际使用的器件有着对应关系,比较接近于实际的电路,但它只反映电路的逻辑功能而不反映电气参数和性能。
同一种逻辑功能可以用多种逻辑图实现,它不具备唯一性。
4、卡诺图卡诺图是按相邻性原则排列的最小项的方格图。
它实际上是真值表的特定的图示形式。
其特点是在化简逻辑函数时比较直观容易掌握。
卡诺图具有唯一性,但化简后的逻辑表达式不是唯一的。
组合逻辑电路

由上,可作出相应的电路, 如右图所示。
2. 二—十进制优先编码器 若某优先编码器具有的逻辑功能为:将 I1 ~ I9 九个输入信号分别编
1. 依据实际逻辑问题的因果关系,进行逻辑抽象,列出逻辑真值表; 2. 写出相应的逻辑函数式(逻辑表达式); 3. 化间或变换逻辑函数式(逻辑表达式); 4. 画出逻辑电路图 ; 5. 判别和消除冒险现象。
注意:逻辑函数经过化简,最简的逻辑函数表达式可能具有多样 性,根据这些表达式构成的逻辑电路的形式也具有多样性。这是由于在 简化过程中采用不同的合并项得来的。电路的逻辑功能不因为电路的表 达形式不同而不同,这也为逻辑设计的方案选择提供了灵活性。
3.1 概述
一. 组合逻辑电路的特点 逻辑电路的分类: 依据逻辑功能的特点,逻辑电路可分为组合逻辑电路和时序逻辑电路 两大类。 组合逻辑电路: 组合逻辑电路的输出信号仅取决于该时刻的输入信号状态的组合, 而与电路原来所处的状态无关 。
相应地,在电路结构上: (1)输入输出间不必提供反馈延迟通路, (2)电路中不包含记忆元件。
不利用约束条件,依真值表,可写出相应 的逻辑函数式
利用约束条件,即输入 变量取值的组合仅为真值 表中列出的8种状态,则 可得逻辑函数式
依
可作出由三个或门构成的编码 器电路。
二、优先编码器 优先编码器的特点:允许同时输入两个及两个以上编码信号,但对所
有输入信号按优先顺序排队,当几个输入信号同时出现时,只对其中优 先权最高的一个进行编码。
(2)依优先顺序,第一片无编码输入信号时,才对第二片的编码输入信 号进行编码,因此,可用第一片的输出 YS作第二片的选通输入信号 S。 (3)四位码的最高位采用第一片的扩展输出信号 YEX。
《数字电子技术》第3章 组合逻辑电路

Y3 ≥1 I9 I8
Y3
I2I3I6I7
&
Y0 I1 I3 I5 I7 I9
I1I3I5I7I9
I9 I8
逻辑图
Y2
Y1
Y0
≥1
≥1
≥1
I7I6I5I4
I3I2
(a) 由或门构成
Y2
Y1
I1 I0 Y0
&
&
&
I7I6I5I4
I3I2
(b) 由与非门构成
A
消除竞争冒险
B
C
Y AB BC AC
2
& 1
1
3
&
4
&
5
≥1
Y
3.2 编码器
编码
将具有特定含义的信息编 成相应二进制代码的过程。
编码器(即Encoder)
实现编码功能的电路
被编 信号
编 码 器
编码器
二进制编码器 二-十进制编码器
二进制 代码 一般编码器
优先编码器 一般编码器 优先编码器
(1) 二进制编码器
A B F AB AB B
&
&
00
1
01
0
C
&
F &
10 11
0F AABA BC1 AB &
1
AAB BC AB
(4)分析得出逻辑功A能 A B B C AB
A =1
同或逻辑 AB AB B
F
F AB AB A☉B
3.1.3 组合逻辑电路的设计
组合逻辑电路的设计就是根据给出的实际逻 辑问题求出实现这一关系的逻辑电路。
第3章 组合逻辑电路
F
&
&
&
&
A
B
C
本例采用的是“真值表法”,真值表法的优点是规整、清晰; 缺点是不方便,尤其当变量较多时十分麻烦。
例 设计一个组合逻辑电路,用于判别以余3码表示的1 位十进制数是否为合数(一个数,如果除了一和他本身还有 别的因数,这样的数叫做合数,与之相对的是质数)。 解 设输入变量为ABCD,输出函数为 F,当ABCD表示 的十进制数为合数 (4 、 6 、 8、 9) 时,输出 F 为 1,否则 F为 0。
毛刺
使用卡诺图判断一个组合逻辑电路是否存在着 竞争冒险的一般步骤是: • 先画出该电路逻辑函数的卡诺图; • 然后在函数卡诺图上画出与表达式中所有乘积项 相对应的卡诺圈; • 如果图中有相切的卡诺圈,则该逻辑电路存在着 竞争冒险。(“0”冒险是1构成的圈,“1”冒险是 0构成的圈。
所谓卡诺圈相切即两个卡诺圈之间存在不被同一卡 诺圈包含的相邻最小项。
产生冒险的原因
A
1
≥1
F=A+A=1 理想情况
以例说明
A A
F 实际情况
造成冒险的原因是由于A和 A到达或门的时间不同。
再举一例 A C B
1 & BC & AC ≥1
A B F=AC+BC C C AC BC F
(分析中略去与门和或门的延时)
产生冒险的原因 : 电路存在由非门产生的互补信 号,且互补信号的状态发生变化 时有可能出现冒险现
有公用项
经变换后,组成电路时可令其共享同一个异或门,从而 使整体得到进一步简化,其逻辑电路图如下图所示。
多数出组合电路达到最简的关键是在函数化简时找出各输 出函数的公用项,使之在逻辑电路中实现对逻辑门的“共享”, 从而达到电路整体结构最简。
第3章组合逻辑电路

第3章组合逻辑电路3.1 组合逻辑电路的概述按照逻辑功能的不同特点,可以把数字电路分成两大类,一类叫做组合逻辑电路,另一类叫做时序逻辑电路。
什么叫组合逻辑电路呢?在t=a时刻有输入X1、X2、……Zn,那么在t=a时刻就有输出Z1、Z2、……Zm,每个输出都是输入X1、X2、……Zn的函数,Z1=f1(X1、X2、……Xn)Z1=f2(X1、X2、……Xn)Zm=fm(X1、X2、……Xn)从以上概念可以知道组合逻辑电路的特点就是即刻输入,即刻输出。
任何组合逻辑电路可由表达式、真值表、逻辑图和卡诺图等四种方法中的任一种来表示其逻辑功能。
3.2 组合逻辑电路的分析方法和设计方法3.2.1组合逻辑电路的分析方法分析组合逻辑电路的目的,就是要找出电路输入和输出之间的逻辑关系,分析步骤如下:(1)根据已知的逻辑电路,写出逻辑函数表达式(采用逐级写出逻辑函数表达式),最后写出该电路的输出与输入的逻辑表达式。
(2)首先对写出的逻辑函数表达式进行化简,一般系用公式法或卡诺图法。
(3)列出真值表进行逻辑功能的分析。
以上步骤可用框图表示,如图3-2所示。
图3-2 组合逻辑电路分析框图下面举例说明对组合逻辑电路的分析,掌握其基本思路及方法。
【例3-1】 分析图3-3所示电路的逻辑功能图3-3 [例3-1]逻辑电路解:(1)写出输出Z 的逻辑表达式: Z1=B A , Z2=B AZ=21Z Z •=B A B A • (2)化简Z=B A B A •=A B +A B=A ⊕B (3)列出真值表进行逻辑功能说明 列出该函数真值表,如表3.1所示: 表3-1 [例3-1]真值表 A B Z 0 0 0 0 1 1 1 0 1 1 13.2.2组合逻辑电路的设计方法组合逻辑电路的设计步骤与分析步骤相反,设计任务就是根据逻辑功能的要求设计逻辑电路,其步骤如下:(1)首先对命题要求的逻辑功能进行分析,确定哪些是输入变量,哪些为输出函数,以及它们之间的相互逻辑关系,并对它们进行逻辑赋值。
第3章 组合逻辑电路

第3章 组合逻辑电路
3.1 组合逻辑电路的分析方法和设计方法
组合逻辑电路可以有一个或多个输入端,也可以 有一个或多个输出端。其一般框图如图所示。在组合 逻辑电路中,数字信号是单向传递的,即只有从输入 端到输出端的传递,没有反向传递,所以各输出仅与 各输入的即时状态有关。
输 入 I0 I1
„„
组合逻辑电路
1 3 2
F0 = A3 + A1
第3章 组合逻辑电路
一、二进制编码器 1.ASCII码 ASCII码是一种通用的编码,用于大多数计算机 和电子设备中。大多数计算机键盘都以ASCII码为标 准。当输入一个字母、数字、符号或者控制命令时, 相应的ASCII码就会进入计算机中。ASCII码是一种 字母数字混合编码,其中包含字母、数字、标点和其 他一些特殊符号。 ASCII码的标准形式是由7位二进制码表示的128 种字符和符号。
第3章 组合逻辑电路
据二进制译码器的功能,可列出三位二进制译 码器的真值表。
三位二进制译码器的真值表
输入 输出
逻辑表达式:
0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 1
Y0=A2A1A0 Y1=A2A1A0 Y2=A2A1A0 Y3=A2A1A0 Y4=A2A1A0 Y5=A2A1A0 Y6=A2A1A0 Y7=A2A1A0
第3章 组合逻辑电路
其步骤是:
1.根据给定的逻辑电路图,写出各输出端的逻辑表 达式。
2.将得到的逻辑表达式化简。 3.由简化的逻辑表达式列出真值表。 4.根据真值表和逻辑表达式对电路进行分析,判断 该电路所能完成的逻辑功能,作出简要的文字描述, 或进行改进设计。
第3章 组合逻辑电路

例3-5的真值表 C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 F1 F2 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0
图3-9
3.2.2 组合逻辑电路设计举例 例3-3 设计一个三人按少数服从多数的表决电路。并用与 非门实现。 解:(1)由题意可知,三人代表三个输入变量,通过与 否的结果为一个输出变量。三个输入变量用字母A、B、 C表示,输出用F表示。列出真值表,见表3-2,输入变 量“1”表示同意,“0”表示不同意;输出变量“1”表示通 过,“0”表示不通过。 (2)对真值表用卡诺图化简,如图3-4所示,得到化简 函数 F=AB+BC+AC (3)把化简的与或式转换成“与非-与非”表达式`
_ I7 X 1 0 1 1 1 1 1 1 1
表3-6 表3-6 74148的真值表 输 入 输 _ _ _ _ _ _ _ _ _ _ I 6 I5 I4 I3 I2 I 1 I0 Y2 Y 1 Y0 X X X X X X X 1 1 1 1 1 1 1 1 1 1 1 1 1 X X X X X X X 0 0 0 0 X X X X X X 0 0 1 1 0 X X X X X 0 1 0 1 1 0 X X X X 0 1 1 1 1 1 0 X X X 1 0 0 1 1 1 1 0 X X 1 0 1 1 1 1 1 1 0 X 1 1 0 1 1 1 1 1 1 0 1 1 1
S ABC ABC ABC ABC
C′= A B + A C + B C (3)把表达式转化为“与非-与非”表达式
第三章组合逻辑电路 (1)

第三章组合逻辑电路一、概述1、概念逻辑电路分为两大类:组合逻辑电路和时序逻辑电路数字逻辑电路中,当其任意时刻稳定输出仅取决于该时刻的输入变量的取值,而与过去的输出状态无关,则称该电路为组合逻辑电路,简称组合电路2、组合逻辑电路的方框图和特点(1)方框图和输出函数表达式P63输出变量只与当前输入变量有关,无输出端到输入端的信号反馈网络,即组合电路无记忆性,上一次输出不对下一次输出造成影响3、组合逻辑电路逻辑功能表示方法有输出函数表达式、逻辑电路图、真值表、卡诺图4、组合逻辑电路的分类(1)按功能分类常用的有加法器、比较器、编码器、译码器等(2)按门电路类型分类有TTL、CMOS(3)按集成度分类小、中、大、超大规模集成电路二、组合逻辑电路的分析方法 由电路图---电路功能 1、分析步骤(1)分析输入输出变量、写出逻辑表达式 (2)化简逻辑表达式 (3)列出真值表(4)根据真值表说明逻辑电路的功能 例:分析下图逻辑功能第一步:Y=A ⊕B ⊕C ⊕D 第二步: 第三步:A B C D Y 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 0 1 0 0 1 0 1 0 1 0 0 1 1 0 0 0 1 1 1 1 10 0 0 1=1=1=1CDY1 0 0 1 01 0 1 0 01 0 1 1 11 1 0 0 01 1 0 1 11 1 1 0 11 1 1 1 0第四步:即0和1出现的个数不为偶则输出1,奇偶个数的检验器三、组合逻辑电路的设计方法1、概念根据要求,最终画出组合逻辑电路图,称为设计2、步骤(1)确定输入输出变量个数(2)输入输出变量的状态与逻辑0或1对应(3)列真值表(4)根据真值表写出输出变量的逻辑表达式(5)对逻辑表达式化简,写出最简逻辑表达式(6)根据逻辑表达式,画出逻辑电路图例:三部雷达A、B、C, 雷达A、B的功率相等,雷达C是它们的两倍,发电机X最大输出功率等于A的功率,发电机Y输出功率等于A与C的功率之和,设计一个组合逻辑电路,根据雷达启停信号以最省电的方式开关发电机第一步:输入变量3个,输出变量2个第二步:雷达启动为1、发电机发电状态为1第三步:A B C X Y0 0 0 0 00 0 1 0 10 1 0 1 00 1 1 0 11 0 0 1 01 0 1 0 11 1 0 0 11 1 1 1 1第四步:卡诺图化简第五步:写逻辑表达式第六步:画逻辑电路图四、常用中规模标准组合模块电路一些常用的组合逻辑电路,如编码器、译码器、加法器等制成中规模电路,称为中规模标准组合模块电路1、半加器进行两个1位二进制数相加的加法电路称为半加器,如图3-11所示真值表如下:A B S C0 0 0 00 1 1 01 0 1 01 1 0 1根据真值表,写出逻辑表达式如下:S=AB+AB=A⊕BC=AB2、全加器即带低位上产生的进位的加法器真值表如下:A iB iC i-1S i C i0 0 0 0 00 0 1 1 00 1 0 1 00 1 1 0 11 0 0 1 01 0 1 0 11 1 0 0 11 1 1 1 1根据真值表,卡诺图化简后写出逻辑表达式如下:S i=A i⊕B i⊕C i-1C i=A i B i+C i-1(A i⊕B i)(为便于实现)根据逻辑表达式,画出电路图如图3-13所示3、加法器可以实现多位二进制数加法的电路(1)串行进位加法器低位全加器的进位输出端连到高位全加器的进位输入端,如图3-3所示(2)超前进位加法器C i=A i B i+C i-1(A i⊕B i)= A i B i+C i-1(A i B i+ A i B i)= A i B i C i-1+A i B i C i-1 +A i B i C i-1+ A i B i C i-1=A i B i+ B i C i-1+ A i C i-1= A i B i+C i-1(A i+B i)令P i=A i+B i,称P i为第i位的进位传输项,令G i=A i B i,称G i 为第i位的进位产生项,则第0位的进位为C0=G0+P0C-1,第1位的进位为C1=G1+P1 C0, C0带入C1,消去C0,得C1=G1+P1(G0+P0 C-1),同理,得C2= G2+P2(G1+ P1(G0+P0 C-1)),,C3= G3+ P3(G2+ P2(G1+P1(G0+P0 C-1))),即知道相加的二进制数的各位和最低位进位就可以超前确定进位,提高了速度,如图3-4所示4、乘法器完成两个二进制乘法运算的电路(1)乘法器P85(2)并行乘法器P855、数值比较器比较二进制数大小,输入信号是要比较的数,输出为比较结果(1)1位数值比较器A B M G L0 0 0 1 00 1 1 0 01 0 0 0 11 1 0 1 0M=ABG=AB+AB= AB+AB(便于逻辑实现)L=AB逻辑电路图如图3-5所示(2)4位数值比较器多位二进制数比较大小,先看最高位情况,如相等再看次高位情况,以此类推4位比较器为例,8个输入端(A3A2A1A0,B3B2B1B0),三个输出端(L,G,M)A>B,则A3>B3,或A3=B3且A2>B2,或A3=B3,A2=B2,A1>B1,或A3=B3,A2=B2,A1=B1,A0>B0设定AB的第i位比较结果为L i=A i B i,G i=A i B i+A i B i,M i=A i B i,则L=L3+G3L2+G3G2L1+G3G2G1L0同理, A=B 时,G=G3G2G1G0,A<B时,M=M3+G3M2+G3G2M1+G3G2G1M0,因A不大于也不等于B时即小于B,故M=LG=L+G(便于逻辑实现)逻辑电路图如P87图3-18所示(3)集成数值比较器4位数值比较器封装在芯片中,构成4位集成数值比较器,74ls85真值表如图3-6所示考虑到级联,增加了级联输入端(更低位的比较结果),级联时,如构成8位数值比较器,低四位比较结果为高四位数值比较器的级联输入端,而低四位的级联输入端应结为相等的情况(010),74ls85级联如图3-7所示cc14585真值表如图3-8所示,cc14585级联如图3-9所示6、编码器将输入信号用二进制编码形式输出的器件,若有N个输入信号,假设最少输出编码位数为m位,则2m-1<N<2m(1)二进制编码器以2位输出编码为例输入输出I0I1I2I3Y1Y01 0 0 0 0 00 1 0 0 0 10 0 1 0 1 00 0 0 1 1 1故Y1=I2+I3,Y0=I1+I3逻辑电路图如P89图3-22所示但当不止一个输入端有编码要求时该电路不能解决问题(2)二进制优先编码器3位二进制优先编码器为例8个输入端为I0~I7,输出端为Y2~Y1,假设I7的编码优先级最高,则对应真值表为:输入输出I0I1I2I3I4I5I6I7Y2Y1Y0×××××××0 0 0 0 ××××××0 1 0 0 1 ×××××0 110 1 0 ××××0 1110 1 1 ×××0 1111 1 0 0 ××0 11111 1 0 1 ×0 111111 1 1 0 0 1111111 1 1 1 “×”为任意值根据真值表,列出逻辑表达式如P90所示,逻辑图过于麻烦,略以上为低电平有效的情况,高电平有效真值表如图3-10所示,得A2=I4+I5+I6+I7,A1=I2+I3+I6+I7,A0=I1+I3+I5+I7, 逻辑图便于实现(3)8线-3线编码器74ls148编码器图形符号如图3-11所示,真值表如图3-12所示74ls148编码器级联,注意控制信号线的连接,级联图如图3-13所示选通信号有效,当高位芯片输入不全为1时,选通输出端为1,低位芯片不工作且二进制反码输出端为1,与门受高位芯片二进制反码输出端影响,扩展输出端为0,作为A3,根据输入情况不同,得编码0000~0111;选通信号有效,当高位芯片输入全为1时,高位芯片不工作,选通输出信号为0,低位芯片工作,高位芯片扩展输出端为1,作为A3,高位芯片二进制反码输出端全1,与门受低位芯片二进制反码输出端影响,根据输入情况不同,得编码1000~1111,即实现16线-4线编码器功能(4)9线-4线编码器74ls147编码器图形符号、真值表如图3-14所示注意,其输出对应十进制数的8421BCD码的反码(5)码组变换器将输入的一种编码转换为另一种编码的电路参见P92例3-5原理:加0011和加1011的原因7、译码器译码是编码的逆过程,将二进制代码转换成相应十进制数输出的电路(1)3线-8线译码器真值表如图3-15所示逻辑表达式如下:Y0=CBA、Y1=CBA……Y6=CBA、Y7=CBA(2)集成3线-8线译码器74LS138译码器符号如图3-16所示,真值表如图3-17所示注意三个选通信号,在级联时的作用,级联如图3-18所示74LS138译码器典型应用如图3-19所示(3)集成4线-10线译码器74LS42符号如图3-20所示,真值表如图3-21所示逻辑表达式如图3-22所示(4)显示译码器是用来驱动显示器件的译码器(A)LED数码管电能---光能(发光二极管构成)具有共阴极和共阳极两种接法,如图3-23所示,注意非公共端连接高电平或低电平时要串接限流电阻(B)显示译码器74LS47(驱动LED为共阳极接法的电路,驱动共阴极要用74LS48)引脚图如图3-24所示,真值表如图3-25所示要具有一定的带灌电流负载能力才能驱动LED相应段发光,显示效果如P99图3-35所示附加控制端用于扩展电路功能:灯测试输入LT:全亮灭零输入RBI:将不需要的“0”不显示以使得要显示的数据更醒目灭灯输入\灭零输入BI\RBO:作为输入使用,一旦为0则灯灭。
数字电路与逻辑设计第3章组合逻辑电路

(2)根据真值表,用卡诺图(图3-5 a)化简后,
可以得到该电路的逻辑函数表达式:
F AC BC AB
由于题目中没有特别要求以何种逻辑门 输出,所以可用与门和或门输出来实现 该逻辑功能,表达式形式无需转换。
(3)逻辑图 由化简后的表达式和真值 表可以看出,(图 3-5 b)即使该题的逻 辑电路图。
表 3-7 8线—3线编码器的真值表
因为任意时刻 I0 ~ I7 中只有一个值为“1”利 用约束项的知识把上述真值表化简后如表3-8 所示。
表 3-8 化简后的真值表
由真值表写出其对应的逻辑函数表达式:
Y2 I4 I5 I6 I7 I4I5I6I7 Y1 I2 I3 I6 I7 I2I3I6I7 Y0 I1 I3 I5 I7 I1I3I5I7
3) 将表达式转化成用“与非” 逻辑形式实 现的形式:
图3-9 (a)卡诺图 (b)逻辑电路
3.2 编码器
编码就是将特定的逻辑信号变换成 一组二进制的代码,而能够实现这种功 能的逻辑部件就称为编码器。编码器的 功能是将输入信号转换为对应的代码信 号,即是用输出的代码信号来表示相对 应的输入信号,以便于进行对代码进行 存储,传输及运算等处理。
FA A FB AB FC ABC FD ABCD
(3)由上述表达式可得其对应的优先编码逻辑 电路如图3-12所示。
图3-13 16线—4线优先编码器的逻辑电路
(2)根据列写出的逻辑问题的真值表,写出对应 的逻辑函数表达式。
(3)将得到的逻辑函数表达式进行变换和化简。 逻辑函数的化简可以利用我们前面所学习的代 数法或卡诺图法,从而得到逻辑函数的最简表 达式,对于一个逻辑电路,在设计时应尽可能 使用最少数量的逻辑门,逻辑门变量数也应尽 可能少用,还应根据题意变换成适当形式的表 达式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AC
0
0
0
1
0
1
0
1
0
1
0
1
0
1
1
1
L = AB + AC + AD + BCD
4) 画出由与非门组成的逻辑电路。
L = AB + AC + AD + BCD 4) 画出由与非门组成的逻辑电路。
LAB AC AD BCD
3.3 常用组合逻辑电路及中规模集成器件
3.3.1 编码器 3.3.2 译码器 3.3.3 数据选择器 3.3.4 加法器 3.3.5 比较器
A BA BA B
CZ1 AB
00 10
逻辑功能:半加器
10
01
3.2 组合逻辑电路的设计
一. 组合逻辑电路的设计步骤
1.根据实际逻辑问题确定输入、输出变量,并定 义逻辑状态的含义;
2.根据输入、输出的因果关系,列出真值表; 3.由真值表写出逻辑表达式,根据需要简化和变 换逻辑表达式;
4.画出逻辑图。
3.3.1 编码器
编码:赋予二进制代码特定含义的过程称为编码。 如:8421BCD码中用1000表示数字8
编码器:具有编码功能的逻辑电路。 编码器的逻辑功能:能将每一组输入信息变换为相 应二进制的代码输出。
•如4线-2线编码器:将输入的4个状态分别编成 4个2位二进制数码输出; •如8-3编码器:将输入的8个状态分别编成8个 3位二进制数码输出; •如BCD编码器:将10个输入分别编成10个4位 8421BCD码输出。
解:1)由题意进行逻辑抽象。
当特快A=1时,无论直快B,慢车C 为何值,LA=1,LB= LC=0; 当直快B=1,且A= 0 时,无论C为何值,LB=1,LA =LC=0; 当慢车C=1,且A=B=0 时,LC=1,LA= LB=0。
经过逻辑抽象,可列真值表:
2)写出逻辑表达式。
L AA , L BA B , L CA B C
1
AC
10 1 1 1
AB
0
1
3)简化和变换逻辑表达式
1
L = AB+AC+BC
1
3)简化和变换逻辑表达式 L = AB+AC+BC
A B A C B C AA BB CC
4)画出逻辑电路图。
A
&
B
&
&
C
L
&
2. 设计举例
例3 某董事会有一位董事长和三位董事,就某项议题进行表决, 当满足以下条件时决议通过:有三人或三人以上同意;或 者有两人同意,但其中一人必须是董事长。试用两输入与 非门设计满足上述要求的表决电路。
3.3.1 编码器
编码器的分类: 普通编码器 优先编码器
普通编码器:任何时候只允许一个编码输入信号有 效,否则输出就会发生混乱。
优先编码器:允许同时输入两个以上的有效编码信 号。当同时输入几个有效编码信号时,优先编码器 能按预先设定的优先级别,只对其中优先权最高的 一个进行编码。
分析方法:
逻辑电路图
写出逻辑表达式
化简
得出结论(逻辑功能)。
3.2 组合逻辑电路的分析
例1 已知逻辑电路如图所示,
分析该电路的功能。 解:1.根据逻辑图,写出输出逻辑表达式
A =1 Z
B
=1 L
C
LZC (AB)C
ABC 000
ABC
001 010
2. 列写真值表。 3. 确定逻辑功能:
011 100 101
电路具有为奇校验功能。 1 1 0
111
ZAB L(ABC)
0
0
0
1
1
1
1
0
1
1
1
0
0
0
0
1
3.2 组合逻辑电路的分析
例2 一个双输入端、双输出端
的组合逻辑电路如图所示,
分析该电路的功能。
A B
解:SZ2Z3Z2Z3
AABBAB
& Z2
A AB
&
Z1
AB
& S
& Z3
B AB
1 C
A(AB)B(AB)
本章重点与难点:
重点:本章重点有两个:
一是组合逻辑电路的基本分析、设计方 法。
二是常用组合电路的附加功能(如:使 能端、片选端等)。
难点:实际逻辑问题的数学抽象;
各种中规模集成电路器件的真值
表的阅读和理解。
3.1 组合逻辑电路概述
数字电路就结构和工作原理而言,可分为
组合逻辑电路 —无记忆元件 时序逻辑电路 —有记忆元件
3.2 组合逻辑电路的设计
一. 组合逻辑电路的设计步骤
根据题意列真值表
逻辑式化简 卡诺图化简
写最简逻辑式
画逻辑电路图
原则:最简(要求所用器件的种类和数量都尽可能
少,且器件之间的连线也最少)。
二. 设计举例
例1 试用与非门和反相器设计一个优先排队电路。火车有特快、 直快和慢车。它们进出站的优先次序是:特快、直快、 慢 车,同一时刻只能有一列车进出。
解:
+5V
A
要设
B C
计的 逻辑
L
电路
二. 设计举例
例2 设计一个表决电路,该电路输入为A、B、C,输出是L。 当输入有两个或两个以上为1时,输出为1,其他情况输出 为0。用与非门设计该表决电路。
解:1) 根据题意可列出真值表。 0
2) 画出卡诺图。 0
BC A 00 01 11 10
0
BC 00 0 1 0
解 1) 逻辑抽象。
假设:用变量A、B、C、D表示输入,A代表董事长,B、C、D代
表董事,1表示同意,0表示不同意; 用L表示输出,L=1,代表决议通过,L=0,代表不通过。
2) 列出真值表;
3) 画出卡诺图,求输出L的表达式;
4) 画出由与非门组成的逻辑电路。
2) 列出真值表
3) 画出输出L的卡 诺图并化简得
定义:任意时刻的输出状态只决定于该时刻的输入状态, 而与原电路的状态无关。
它们之间的关系是:
X1 X2 X3
组合 逻辑
Z1
Z1= f1(X1, X2, …Xn)
Z2 Z3
Z2= f2(X1, X2, …Xn)
… …
:
电路
:
Xn
Zm
Zm= fm(X1, X2, …Xn)
3.2 组合逻辑电路的分析
1、概 述
3)根据题意,变换成与非形式
设计举例
L AA , L BA B , L CA B C
4)画出逻辑电路图。 LA
A
1
AB
&
1
LB
B
1
&
1
LC
A BC C
二. 设计举例
例2 设计一个表决电路,该电路输入为A、B、C,输出是L。 当输入有两个或两个以上为1时,输出为1,其他情况输出 为0。用与非门设计该表决电路。
根据逻辑图,写出逻辑函数的表达式,然后列 出真值表,经卡诺图化简变换后,得知电路功能。 这个过程就是组合逻辑电路的分析。
分析的目的:是为了确定电路的的逻辑功能。
3.2 组合逻辑电路的分析
2. 组合逻辑电路的分析步骤:
(1) 由逻辑图写出各输出端的逻辑表达式; (2) 化简和变换各逻辑表达式; (3) 列出真值表; (4) 根据真值表和逻辑表达式对逻辑电路进行分析, 最后确定其功能。
