弹性力学—第七章—空间问题的基本理论
弹性力学总结

弹性力学总结第一章绪论一、弹性力学的内容:弹性力学的研究对象、内容和范围。
二、弹性力学的基本量1、外力(1)体力(2)面力2、内力——应力3、应变4、位移以上基本量要求掌握其定义、表达式、分量的符号、正负号规定、量纲。
三、弹性力学中的基本假定1、连续性2、完全弹性3、均匀性4、各向同性以上是对材料性质的假定,凡符合以上四个假定的物体,称为理想弹性体。
5、小变形假定(对物体的变形状态所作的假定)要求掌握各假定的内容和意义(在建立弹性力学基本方程时的作用)。
习题举例:1、弹性力学,是固体力学的一个分支,它的任务是研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的(),从而解决各类工程中所提出的强度、刚度和稳定问题。
A.应力、应变和位移;B.弯矩、扭矩和剪力;C.内力、挠度和变形;D.弯矩、应力和挠度。
2、在弹性力学中,作用于物体的外力分为()。
A.体力和应力;B.应力和面力;C.体力和面力;D.应力和应变。
3、重力和惯性力为(C )。
A .应力;B .面力;C .体力;D .应变。
4、分布在物体体积内的力称为( C )。
A .应力;B .面力;C .体力;D .应变。
5、物体在体内某一点所受体力的集度的表达式及体力分量的量纲为( A )。
A .0lim V F f V∆→∆=∆,-2-2L MT ; B .0lim S F f S ∆→∆=∆,-1-2L MT ; C .0lim A F p A ∆→∆=∆,-1-2L MT ; D .0lim V F f V ∆→∆=∆,-1-2L MT 。
6、弹性力学研究中,在作数学推导时可方便地运用连续和极限的概念,是利用了( )假定。
A .完全弹性;B .连续性;C .均匀性;D .各向同性。
7、( A )四个假设是对物体的材料性质采用的基本假设,凡是符合这四个假设的物体,就称为理想弹性体。
A .完全弹性,连续性,均匀性和各向同性;B .完全弹性,连续性,均匀性和小变形;C .连续性,均匀性,各向同性和小变形;D .完全弹性,连续性,小变形和各向同性。
弹性力学简明教程

弹性简明课程是教育部第十个五年计划的国家计划教科书。
在第二版的基础上,它保留了原有的体系和特征,并根据教学改革的需要和相关的新国家标准进行了修订。
根据从浅到深的原理,本书安排了平面问题的理论和解决方案,空间问题的理论和解决方案以及薄板弯曲的理论。
着重介绍了弹性的数值解,如差分法,变分法和有限元法。
简明课程作为一本介绍性的弹性教科书,着重于基础理论(基础概念,基本方程式和基本解)的阐述和应用,以便学生在掌握基础知识的基础上阅读和应用弹性文献。
理论,并可以初步应用弹性数值解来解决实际工程问题。
主符号表第1章简介1-1弹性的内容1-2弹性的一些基本概念1-3弹性的基本假设第二章平面问题的基本理论2-1平面应力问题和平面应变问题2-2平衡微分方程2-3平面问题中点的应力状态2-4几何方程式刚体位移2-5物理方程式2-6边界条件2-7 Saint Venant原理及其应用2-8通过位移求解平面问题2-9通过应力相容方程求解平面问题2-10在恒力下简化的应力函数练习第三章平面问题的直角坐标解3-1逆解和半逆解多项式解。
3-2矩形梁纯弯曲的计算3-3位移分量3-4均布荷载下的简支梁3-5重力和液压作用下的楔形体第四章平面问题的极坐标解4-1极坐标中的平衡微分方程4-2极坐标中的几何方程和物理方程4-3极坐标中的应力函数和相容性方程4-4应力分量的坐标转换公式4- 5轴对称应力和相应的位移4-6圆环或圆柱体上的压力均匀分布4-7压力通道孔口处的应力集中4-8圆孔4-9边界上的集中力4-10边界上的分布力第5章用差分法和变分法求解平面问题5-1差分公式的推导5-2应力函数的微分分解5-3应力函数的微分分解的例子5-4弹性体的变形势能和外力势能5 -5位移变化方程5-6位移变化方法5-7位移变化方法示例..第6章使用有限元方法解决平面问题。
6-1基本数量和方程的矩阵表示。
6-2有限元方法的概念。
6-3单元的位移模式和解的收敛性。
弹性力学-第7章 空间问题
zx
z
dz
zy
zy
z
dz
z 0
y
y
yx yz
xy
x
yz
yz
y
dy
fz
fy fx
xz
yx
y yx dy
y
y y
dy
zx zy
x
x
x x
dx
z
根椐平衡条件: Fx 0
xz
xzx
x
dx
x
x
x
dx dydz
xdydz
(
yx
yx
x
dy)dxdz
yxdxdz
( zx
zx
z
dz)dxdy
zxdxdy
Xdxdydz
0
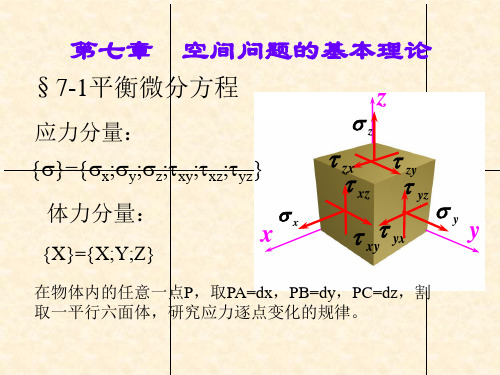
§7-1平衡微分方程
x x
yx y
zx
z
fx
0
xy
y
x
y
zy
z
f y
0
xz yz
x
y
z z fz 0
(7-1)
平面应力问题:
1、平面应力问题z方向应力为零:
0
xz
yz
0
z
2、所有的应力、应变和位移分量均与z无关,仅是x,y的函数。 以上方程可以直接转化为平面应力的平衡方程。
在计算任一平面上的应力时,方向余弦l,m,n可变化,但 均为有限值,故必存在某个平面,其上正应力取得极值。
主平面:正应力取得极值的平面。 主应力:主平面上的正应力。 主方向:主应力的方向,也称应力主向。 在主平面上,正应力取极值、剪应力为零。
二、主应力的确定:
设主平面存在,其外法线为n,
第七章 弹性力学空间问题解答

§7-1 空间问题的基本方程 1. 平衡微分方程方程
2. 几何方程
3. 物理方程
各种弹性常数之间的关系
4. 相容方程
5. 边界条件:
位移边界条件:对于给定的表面Su,其上沿 x,y,z方向给定位移为 ,则
应力边界条件:给定表面上的面力为
• 求解空间问题同样有位移法、应力法和应力函 数法三种方法。
§7-2柱坐标和球坐标系下的基本方程
• 一. 柱坐标系下的基本方程
直角坐标系下,空间一点M的位置由(x,y,z)表示,在柱坐 标系下,空间一点M的位置由(r, q, z)表示。两坐标间的关 系为:
在柱坐标系下的应力分量为
应变分量为 位移分量为
柱坐标表示的基本方程 • 1. 平衡方程
(7-1)
• 2. 几何方程
(7-6)
(2)几何方程:将式(7-5)代入式(7-2),得
(7-7)
(3)物理方程:将式(7-5)代入式(7-4),得
(7-8)
(4)空间轴对称问题位移求解的基本方程
空间轴对称问题共有四个应力分量,两个位移分量。 以位移求解更方便。 将几何方程(7-7)代入物理方程(7-8),得
(7-9)
• 将式(7-9)代入平衡方程(7-6),化简后得
1. 位移法:将几何方程代入物理方程,得到用位移
表示的应力分量,再将应力分量代入平衡方程和应力边 界条件,即得到空间问题的位移法控制方程。
2. 应力法:以应力作为基本未知量。将相容方程用应 力表示——应力控制方程
3. 应力函数法:先引入应力函数,满足微分平衡方
程。 由微分平衡方程得应力函数与应力分量的关系,再将 用应力函数表示的应力分量代入相容方程,得到一组 用应力函数表示的相容方程,即应力函数表示的控制 方程。
《弹性力学》第七章 平面问题的差分解

4 f 1 2 2 4 [4 f 0 2( f1 f 2 f 3 f 4 ) ( f 5 f 6 f 7 f8 )] x y h 0 4 f 4 y 1 4 [6 f 0 4( f 2 f 4 ) ( f10 f12 )] h 0
弹性力学的经典解法存在一定的局限性,当弹性体的边 界条件和受载情况复杂一点,往往无法求得偏微分方程的边 值问题的解析解。因此,各种数值解法便具有重要的实际意 义。差分法就是数值解法的一种。 所谓差分法,是把基本方程和边界条件(一般均为微分 方程)近似地改用差分方程(代数方程)来表示,把求解 微分方程的问题改换成为求解代数方程的问题。
T (T0 Te ) x 0
其中 Te 为边界以外的介质的已知温度。应用差分公式,可得:
T1 T3 (T0 Te ) 2h
解出 T1 ,代入(1)式,即得修正的差分方程:
2h 2h 4 T0 T2 2T3 T4 Te
第七章 平面问题的差分解
§7-1 差分公式的推导 §7-2 稳定温度场的差分解 §7-3 不稳定温度场的差分解 §7-4 应力函数的差分解 §7-5 应力函数差分解的实例 §7-6 温度应力问题的应力函数差分解 §7-7 位移的差分解 §7-8 位移差分解的实例 §7-9 多连体问题的位移差分 解 习题课
2 2 2 T h T 2 T0 TA h 2 x A x A 2 1 T 2 2 T T3 TA (1 )h (1 ) h 2 x x A 2 A
§7-2
稳定温度场的差分解
本节以无热源的、平面的、稳定的温度场为例,说明差分 法的应用。 在无热源的平面稳定场中,t 0, z 微分方程简化为调和方程 2T 0 ,即:
弹性力学课件-弹性力学简明教程电子教案简介与目录

2021/3/18
11
第六章 用有限元法解平面问题 第七章 空间问题的基本理论 第八章 空间问题的解答 第九章 薄板弯曲问题 附录:关于提高课堂教学质量的文章
2021/3/18
12
《弹性力学简明教程》立体化教材体系
—列入高等教育出版社百门精品课程项目
一、《弹性力学简明教程》(第三版,徐芝编) —主教材。
编者
2021/3/18
二零零六年六月16
相信梦想是价值的源泉,相信眼光决定未来的一 切,相信成功的信念比成功本身更重要,相信人 生有挫折没有失败,相信生命的质量来自决不妥
协的信念。
谢谢观看
2021/3/18
17
142021318关于弹性力学简明教程电子教案使用指南本教案是以徐芝纶教授编著的弹性力学简明教程为主教材编写的为便于用户的使用教案分为powerpoint教案弹性力学简明教程电子教案正本和打包后的教案弹性力学简明教程电子教案副本两种形式
20XX年复习资料
大学复习资料
专 业: 班 级: 科目老师: 日 期:
七、《Applied Elasticity》(徐芝纶编),
—供参考和深入学习使用。
八、《弹性力学的问题的有限单元法》(陈国荣
编),—供参考和深入学习使用。
2021/3/18
14
关于《弹性力学简明教程电子教案》使用指南
本教案是以徐芝纶教授编著的《弹性力学简明教程》为主
教材编写的,为便于用户的使用,教案分为powerpoint教案(弹
《弹性力学简明教程》电子教案(光盘), 是《弹性力学简明教程》立体化教材体 系的内容之一,是配合《弹性力学简明教 程》的教学,为教师编写的电子教案。其 中提供了示范的电子板书,及有关教学素 材,以帮助教师备课和形成自己的讲稿。
弹性力学 空间问题基本理论共55页文档

45、自己的饭量自己知道。——苏联来自弹性力学 空间问题基本理论
11、用道德的示范来造就一个人,显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的,对谁都一视同仁。在每件事上,她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由,因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样,法律和法律都是相互依存的。——伯克
41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间,才能认识自 己。——德国
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
弹性力学--CH 7 空间问题的基本理论

CH 7 空间问题的基本理论
7.1 平衡微分方程
M
ab
0
yz zy
同理:
xy yx
zx xz
CH 7 空间问题的基本理论
7.1 平衡微分方程
F F F
x
0 0 0
y
z
x yx zx X 0 x y z y zy xy Y 0 y z x z xz yz Z 0 z x y
解方程得出σ的三个根σ1、σ2、σ3,即为P点的三个主应力。 求解与σ1相应的方向余弦l1、m1、n1。
l1 ( x 1 ) m1 yx n1 zx 0 l1 xy m1 ( y 1 ) n1 zy 0
l1 m1 n1 1
m1 n1 1 可以解出: , 及l1 2 2 l1 l1 1 (m1 / l12 ) 2 (n1 / l12 ) 2
X l x m yx n zx Y m y n zy l xy Z n z l xz m yz
X i l j ji
CH 7 空间问题的基本理论
7.1 平衡微分方程
静力学方面、几何方面和物理学方面建立方程
在物体内的任意 一点P,取一个微小 的平行六面体,它 的六个面垂直于坐 标轴,而棱边的长 度为PA=dx、PB=dy、 PC=dz。一般而论, 应力分量是位置坐 标的函数。
N lX N m YN nZN
7.2 物体内任一点的应力状态
l 2 x m 2 y n 2 z 2m n yz 2nl zx 2lm xy
2 2 2 2 2 2 sN N N XN YN ZN 2 2 2 2 2 N XN YN ZN N
弹塑性力学讲义 第七章弹性力学平面问题的极坐标系解答

d dr
( r
)
dur dr
r
或
d r
dr
r
4. 物理方程(两个)
5
平面应力问题
r
1 E
(
r
) ,
或
r
E 1
2
( r
)
,
平面应变问题时弹性系数替换。
1 E
(
r )
E 1 2
(
r )
5. 按位移法求解
——(b)
考虑位移单值性比较(a)和(b)式:
4Br-F=0 B=F=0
轴对称问题的应力和位移解为:
r
A r2
2C ,
A r2
2C ,
r
0
ur
1 E
(1
)
A r
2Cr (1
)
,
u 0
A、C 由两个力的边界条件确定。
对于无体力圆盘(或圆柱)的轴对称问题,
(rur )
(1 2 ) E
fr
0
相应边界条件:轴对称问题边界 r=r0(常数)
位移边界条件:
ur ur
在 su 上
力的边界条件:
r Fr
在 s 上
平面应力问题的力边界条件用位移表示:
1 2
E
( dur dr
ur r
)
Fr
在 s 上
当 ur 由基本方程和相应边界条件求出后,则相应应变、应力均
但圆环或圆筒为复连域,除了力的边界条件满足外还要考虑位移
弹性力学第七章 主应力

(7-3)
p2
2 n
2 n
px2
p
2 y
pz2
2 n
px2
p
2 y
pz2
2 n
(7-4)
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7-2 物体内一点的应力状态
如果ABC是边界面,px, py , pz 成为面力分量
fx, fy, fz
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7-5 轴对称问题的基本方程
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7-5 轴对称问题的基本方程
轴对称问题: 在空间问题中,如果弹性体的几何形状、约束情况,以及所受的外
力作用,都是对称于某一轴(通过这个轴的任一平面都是对称面),则 所有的应力、变形和位移也就对称于这一轴。轴对称问题的弹性体的形 状一般为是圆柱或半空间。
( x
1)
m1 l1
yx
n1 l1
zx
0
xy
m1 l1
( y
1)
n1 l1
zy
0
可以求得 m1 , n1 的比值,再利用 l 2 m2 n2 1 求出:
l1 l1
l1
1
2
2
1
m1 l1
n1 l1
同样也可以求出其他主应力的方向余弦。
弹性力学简明教程
NORTHEASTERN UNIVERSITY
E
(7-13)
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7-4 几何方程及物理方程
弹性力学及有限元法chapter7精品PPT课件

e
i
j
m
v
j
w j
u
m
i
m
p
vm
wm
j y
u
p
x
vp
w p
第七章 空间问题和空间轴对称问题
7-2-1 位移函数
单元内任一点的位移 {f}假定为座标的线性函数
u
f
v
N
e
w
u 1 2x3y 4z v 5 6x7 y 8z w9 10x 11y 12z
节点i, j, m及 p的坐标分别为(xi,yi,zi),(xj,yj,zj),(xm,ym,zm) 及 (xp,yp,zp),把它们代入上式的第一式,得出各节点在x方 向的位移
第七章 空间问题和空间轴对称问题
ui 1 2 xi 3 yi 4 zi u j 1 2x j 3 y j 4z j um 1 2 xm 3 ym 4 zm up 1 2xp 3 yp 4zp
解方程组,求得 1,2,3,4,代入第一式,整理后得到
u N iu i N ju j N m u m N p u p
其中
Ni 61 Vaibixciydiz
N j 6 1 Vajbjxcjydjz
Nm61 Vambmxcmydmz
Np61 Vapbpxcpydpz
称为形函数,其系数是
第七章 空间问题和空间轴对称问题
xj yj zj ai xm ym zm
xp yp zp
1 xj zj ci 1 xm zm
同样,可以得到
vNivi Njvj NmvmNpvp wNiwi Njwj NmwmNpwp
单元内任一点的位移可以写成如下形式:
f N 0 i N 0 i 0 0
弹性力学讲义-第7,8章空间问题的基本理论

(1 x )(1 y )(1 z ) 1 x y z z x y z x y x y z x y z
u v w
x y z
(7-11)
(7-10)
§7-4 几何方程及物理方程
xzl
yz m
zn
n
( x )l yxm zxn 0 xyl ( y )m zyn 0 xzl yzm ( z )n 0
(c)
方向余弦 l 2 m2 n2 1 (b)
§7-3 主应力 最大与最小的应力
l 2 m2 n2 1 必有非零解
( x xyl
)l ( y
yxm )m
zx zy
n n
0 0
xzl yzm ( z )n 0
(c)
齐次方程组有非 零解的充要条件
x xy xz
yx y
yz
zx zy 0 z
3 1 2 2 3 0
1 x y z
2
x
y
y z
z
x
2 xy
2 yz
2 zx
3
1
0
解答 m 0, n 0 l 1 极值1
n 0, m 1 l 1
2
2
§7-3 主应力 最大与最小的应力
1
3
3
总共得出极值时的六组解答
l 1 0 0
0
m 0 1 0 1 2
n 0 0 1 1 2
2 n
0
0
0 2 3 22
1 2 0
1 2
3 1 22
1
1 2 1 2
n l 2 1 m2 2 n2 3
l2 m2 n2 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何方程及位移边界条件
采用与平面问题的几何方程一致的推导方法, 可以得到:
位移边界条件:
体应变
单位体积的改变称为体应变,用θ表示:
体应变与位移的关系:
物理方程(1)
:体积应力
体积模量
物理方程(2)
用应变表达应力:
空间问题小结
对于空间问题,一共有15个未知函数,它们 是6个形变分量,6个应力分量,3个位移分量。 而我们也有15个基本方程,它们是6个几何方 程,6个物理方程,3个平衡方程。此外,求 出的解还必须满足位移边界条件以及应力边 界条件。
注:该方程的三个解一 定为实数,即总存在三 个互相垂直的主应力。
主应力(4)
1)在受力物体内任意一点,一定存在三个互相垂 直的应力主面以及对应的三个主应力。 2)在受力物体内的任意一点,三个互相垂直的面 上的正应力之和是不变量(不随坐标系变化),并 且等于该点的三个主应力之和。 3)三个主应力中最大的一个就是该点的最大正应 力,最小的一个就是该点的最小正应力。 4)最大与最小的切应力,在数值上等于最大主应 力与最小主应力之差的一半,作用在通过中间主应 力并且“平分最大主应力与最小主应力的夹角”的 平面上。
弹 性 力 学 及 有 限 元
第七章 空间问题的基本理论
胡 衡
武汉大学土木建筑工程学院
二零零八年五月
平衡方程
空 间 问 题
z
P
y
平 面 问 题
x
应力状态(1)
空 间 问 题
z
n’
pz py
P px
y
平 面 问 题
x
应力状态(2)
z
n’
pz py
P px
y x
注:如果已知空间中一点的六个应力分量,就可以得到任 一斜面上的正应力以及切应力,因此可以说六个应力分量 决定了一点的应力状态。
应力边界条件
若图示实线斜面是受有面力 作用的边界面 ,则:
z
n’
P
y x
上式为空间问题的应力边界条件。
主应力(1)
若某一斜面上只有正应力 ,于是该面上的全 应力在坐标上的投影成为:
于是:
因此可求解主应力大小 及方向: 。
又有:
主应力(2)
若有非零解,则:
代入原方程求解 主应力的方向。
主应力的存在(3)
轴对称问题的平衡方程与几何方程
z
Hale Waihona Puke BCPx
A
y
轴对称问题的平衡方程与几何方程
z
B
C
P
x
A
y
其中: 体积应变: 体应力:
轴对称问题的平衡方程与几何方程
z
B
C
P
x
A
y
轴对称问题
在空间问题中,如果弹性体 的几何形状,约束情况以及 所受的外力作用都是对称于 某一轴(通过这个轴的任一 平面都是对称面),则所有 的应力,形变以及位移也就 对称于这一轴。这种问题称 为空间轴对称问题。
z
B C
P
x
A
y
在描述轴对称问题中的应力,形变及位移时,宜采用圆柱 坐标ρ,φ,z。这样可以使得应力分量,应变分量,位移分 量都是ρ,z 的函数,不随 φ 变化。另外,所有物理量必须 对称过 z 轴的任何平面,凡不符合对称性的物理量为零。
