江苏省南京市江宁区2019-2020学年高一第二学期期末调研试卷
2019-2020学年度第二学期期末调研考试高一英语试题【含答案】

2019-2020学年度第⼆学期期末调研考试⾼⼀英语试题【含答案】2019-2020 学年度第⼆学期期末调研考试⾼⼀英语试题选择题部分第⼀部分听⼒(共两节,满分30分)做题时,先将答案标在试卷上。
录⾳内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第⼀节(共5⼩题;每⼩题1.5分,满分7.5分)听下⾯5段对话。
每段对话后有⼀个⼩题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关⼩题和阅读下⼀⼩题。
每段对话仅读⼀遍。
1.What will Peter do at 10:00 tomorrow?A. Go camping.B. Stay at home.C. Have a meeting.2.How much did the woman pay for the skirt?A. $10.B. $20.C.$40.3.What's the weather like now?A. Cloudy.B. Sunny.C. Rainy.4. When does the supermarket open on the weekend?A.At 6:00 am.B. At8:00 am.C.At 9:00 am.5.What will the woman do for her mother's birthday?A. Buy a gift.B.Throw a party.C.Make a cake.第⼆节(共15⼩题;每⼩题1.5分,满分22.5分)听下⾯5段对话或独⽩。
每段对话或独⽩后有⼏个⼩题,从题中所给A、B、C三个选项中选出最佳选项。
听每段对话或独⽩前,你将有时间阅读各个⼩题,每⼩题5秒钟;听完后,各⼩题将给出5秒钟的作答时间。
每段对话或独⽩读两遍。
听第6段材料,回答第6、7题。
6. Where does the woman want to go?A.The nearest bank.B.The nearest hospital.C.The nearest post office.7. How will the woman go there?A. By bus.B. By car.C. On foot.听第7段材料,回答第8、9题。
江苏省南京市江宁中学 2019-2020学年高一数学理下学期期末试题含解析

江苏省南京市江宁中学 2019-2020学年高一数学理下学期期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 三个数a=0.32,之间的大小关系是( )A.b<c<a B.c<b<a C.b<a<c D.a<c<b参考答案:C【考点】根式与分数指数幂的互化及其化简运算.【专题】函数的性质及应用.【分析】利用幂函数、指数函数和对数函数的单调性即可得出.【解答】解:∵0<a=0.32<1,b=log20.3<log31=0,c=20.3>20=1.∴b<a<c.故选:C.【点评】本题考查了幂函数、指数函数和对数函数的单调性,属于基础题.2. 已知等差数列的前项和为,且,则()A.-31 B.20 C. 31 D.40参考答案:D3. 设全集是实数集,,且,则实数的取值范围为()A. B. C. D.参考答案:C7. 若,则等于A. B. C.D.参考答案:A略5. 设等差数列{a n}的前n项和为S n,若,,则S n中最大的是( ).A. B. C. D.参考答案:C分析:利用等差数列的通项公式,化简求得,进而得到,即可作出判定.详解:在等差数列中,,则,整理得,即,所以,又由,所以,所以前项和中最大是,故选C.点睛:本题考查了等差数列的通项公式,及等差数列的前项和的性质,其中解答中根据等差数列的通项公式,化简求得,进而得到是解答的关键,着重考查了学生分析问题和解答问题的能力.6. 下列几何体各自的三视图中,有且仅有两个视图相同的是()A.①②B.①③C.①④D.②④参考答案:D【考点】简单空间图形的三视图.【分析】利用三视图的作图法则,对选项判断,A的三视图相同,圆锥,四棱锥的两个三视图相同,棱台都不相同,推出选项即可.【解答】解:正方体的三视图都相同,而三棱台的三视图各不相同,圆锥和正四棱锥的,正视图和侧视图相同,所以,正确答案为D.故选D【点评】本题是基础题,考查几何体的三视图的识别能力,作图能力,三视图的投影规则是主视、俯视长对正;主视、左视高平齐,左视、俯视宽相等.7. “”是“”成立的()A. 充分非必要条件.B. 必要非充分条件.C. 充要条件.D. 既非充分又非必要条件.参考答案:A【分析】依次分析充分性与必要性是否成立.【详解】时,而时不一定成立,所以“”是“”成立的充分非必要条件,选A.【点睛】本题考查充要关系判定,考查基本分析判断能力,属基础题8. 要得到y=sin的图象,只需将y=cos(﹣)的图象上的所有点()A.向右平移B.向左平移C.向左平移D.向右平移参考答案:A【考点】函数y=Asin(ωx+φ)的图象变换.【分析】利用诱导公式,函数y=Asin(ωx+φ)的图象变换规律,得出结论.【解答】解:将y=cos(﹣)的图象上的所有点向右平移个单位,可得y=cos(﹣)=cos(﹣)=sin的图象,故选:A.【点评】本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.9. 要得到函数的图象,只需将函数y=sin2x的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位参考答案:A【考点】HJ:函数y=Asin(ωx+φ)的图象变换.【分析】先根据诱导公式化简可得y=sin[2(x+)],再根据左加右减的原则进行平移从而可得到答案.【解答】解:∵ =sin(2x+)=sin[2(x+)],∴只需将函数y=sin2x的图象向左平移个单位即可得到函数的图象.故选:A.【点评】本题主要考查两角和与差的公式和三角函数的平移,三角函数平移时一定要遵循左加右减上加下减的原则.10. 已知集合,若,则实数a满足(A)(B)(C) (D)参考答案:D二、填空题:本大题共7小题,每小题4分,共28分11. 设为第二象限角,若,则__________.参考答案:【分析】先求出,再利用二倍角公式求的值.【详解】因为第二象限角,若,所以.所以.故答案:【点睛】本题主要考查同角三角函数的平方关系,考查二倍角的正弦公式,意在考查学生对这些知识的理解掌握水平,属于基础题.12. 化简: .参考答案:。
江苏省南京市2019-2020学年高一下学期两校期末联考数学试卷

2019-2020学年第二学期两校期末联考试高一数学试题2020.07注意事项:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.考生将第Ⅰ卷、第Ⅱ卷答案填涂在答题卡上,答在试卷上无效.一、单项选择题:本题包括8小题,每小题5分,共40分.每小题只有一个选项符合题意.1.若直线l 经过两点(1,3),(3,3)--,则直线l 的斜率为( )A .23B .23-C .32D .32-2.在ABC 中,3,2,sin a b B ===,则角A 等于( ) A .6π B .3π C .23π D .3π或23π 3.把一个棱长为2的正方体木块,切出一个最大体积的圆柱,则该圆柱的体积为( ) A .23π B .π C .2π D .4π 4.若点(1,1)P 为圆2260x y x +-=的弦MN 的中点,则弦MN 所在直线的方程为( )A .210x y --=B .210x y -+=C .230x y +-=D .230x y +-=5.在ABC 中,22tan tan a B b A =,则ABC 的形状为( )A .等腰三角形B .等腰或直角三角形C .等边三角形D .直角三角形6.函数2()3sin cos f x x x x =+的最大值为( )A .2B .C .D .3+7.下列四个正方体图形中,A 、B 为正方体的两个顶点,M 、N 、P 分别为其所在棱的中点,能得出AB ∥平面MNP 的图形的序号是( )A .①③B .①④C .①③④D .②③8.在平面直角坐标系中,记d 为点(cos ,sin )P θθ到直线20x my --=的距离,当θ,m 变化时,d 的最大值为( )A .1B .2C .3D .4二、多项选择题:本题包括4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,部分选对得3分,有选错的得0分.9.下列四个等式其中正确的是( )A .tan 25tan 3525tan 35︒︒︒︒++= B .2tan 22.511tan 22.5︒︒=-C .221cos sin 882ππ-= D .14sin10︒-= 10.平面α,直线m 和n ,从下面的条件中可以推出m n ⊥的是( )A .,//m n αα⊥B .,m a n α⊥⊥C .,m n αα⊥⊂D .//,//m n αα11.下列说法正确的是( )A .截距相等的直线都可以用方程1x y a a+=表示 B .方程20()x my m R +-=∈能表示平行y 轴的一条直线C .经过点(1,1)P ,倾斜角为θ的直线方程为1tan (1)y x θ-=-D .经过两点()()111222,,,P x y P x y 的直线方程()()()()2112110y y x x x x y y -----=12.如图(2,0),(1,1),(1,1),(2,0)A B C D --,CD 是以OD 为直径的圆上一段圆弧,CB 是以BC 为直径的圆上一段圆弧,BA 是以OA 为直径的圆上一段圆弧,三段弧构成曲线W .则下述正确的是( )A .曲线W 与x 轴围成的面积等于2πB .曲线W 有5个整点(横纵坐标均为整数的点)C .CB 所在圆的方程为:22(1)1x y +-=D .CB 与BA 的公切线方程为:1x y +=+三、填空题(本题包括4小题,每小题5分,共20分)13.已知1sin 44x π⎛⎫-= ⎪⎝⎭,则sin2x =_________.14.设R θ∈,则直线sin 10x θ-+=的倾斜角α的取值范围是_________.15.圆锥的母线长为3,底面半径为1,一只蚂蚁从圆锥底面圆周上的一点P 出发,绕着圆锥的侧面爬行一圈,再次回到P 点,则蚂蚁经过的最短路程是__________.16.平面直角坐标系xOy 中,已知点(0,3)A ,圆22:()(24)1C x a y a -+-+=.若圆C 上存在点M ,使2MA MO =,则a 的取值范围是_______________.四、解答题:本题包括6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分10分)已知直线1:230l x y -+=与直线2:2380l x y +-=的交点为M .(1)求过点M 且与直线3:310l x y -+=平行的直线l 的方程;(2)若直线l '过点M ,且点(0,4)P 到l 'l '的方程.18.(本小题满分12分)已知5cos()13αβα+==-,其中α,β均为锐角. (1)求cos()αβ-的值;(2)求tan tan αβ⋅的值.19.(本小题满分12分)已知圆M 上一点(1,1)A -关于直线y x =的对称点仍在圆M 上,直线10x y +-=截得圆M .(1)求圆M 的方程;(2)设P 是直线20x y ++=上的动点,PE 、PF 是圆M 的两条切线,E 、F 为切点,求四边形PEMF 面积的最小值.20.(本小题满分12分)如图,在四棱锥P ABCD -中,底面ABCD 是矩形,PD ⊥平面ABCD .(1)求证:AD PC ⊥;(2)若E 是BC 的中点,F 在PC 上,PA ∥平面DEF ,求PF FC的值. 21.(本小题满分12分)如图,有两条相交成60°角的直路1l ,2l ,交点是O ,警务岗A 、B 分别在12,l l 上,警务岗A 离O 点1千米,警务岗B 离O 点3千米.若警员甲从A 出发沿OA 方向,警员乙从B 出发沿BO 方向,同时以4千米/小时的速度沿途巡逻.(1)当警员甲行至点C 处时,45OBC ︒∠=,求OC 的距离;(2)t 小时后甲乙两人的距离是多少?什么时候两人的距离最短?22.(本小题满分12分)如图,在平面直角坐标系xOy 中,Q 为第一象限内一点,QA 垂直于x 轴,QB 垂直于射线OM ,垂足分别为A ,B ,且10,tan 2QA QB AOB ==∠=-(1)求OQ 的值;(2)已知圆C 通过O ,A ,Q ,B 四点,①求圆C的方程;②设P是圆C上的任意一点,在x轴正半轴及射线OM上是否分别存在定点E,F,使PEPF为定值?若存在,指出定点的位置;若不存在,请说明理由.。
2019-2020学年江苏省南京市物理高一(下)期末达标测试模拟试题含解析

2019-2020学年江苏省南京市物理高一(下)期末达标测试模拟试题一、单项选择题:本题共6小题,每小题5分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的1. (本题9分)下列说法正确的是( )A .电场中两点间电势的差值叫作电势差,也叫电压B .电势差与电势一样,是相对量,与零电势点的选取有关C .AB U 表示B 点与A 点之间的电势差,即AB B A U ϕϕ=-D .A 、B 两点间的电势差是恒定的,不随零电势点的改变而改变,所以AB BA U U =【答案】A【解析】【详解】A.电场中两点间电势的差值叫电势差,也叫电压,选项A 符合题意;B.电势差的大小与零电势点的选取无关,选项B 不符合题意;CD.电势差可以反映出两点电势的高低,AB A B BA U U ϕϕ=-=-,而电压只是电势差的大小,选项C 、D 不符合题意。
2.如图所示,在竖直平面内固定的光滑半圆弧轨道,其两端点M 、N 连线水平,将一轻质小环A 套在轨道上,一细线穿过轻环A ,一端系在M 点,另一端系一质量为m 的小球,小球恰好静止在图示位置,不计所有摩擦,重力加速度大小为g ,下列说法正确的是( )A .轨道对轻环的支持力大小为mgB .细线对M 点的拉力大小为mgC .细线对轻环的作用力大小为mgD .M 点和轻环的连线与竖直方向的夹角为30°【答案】B【解析】【详解】D 、对球分析,受重力和拉力而平衡,故;再对环受力分析,受两个拉力和支持力,如图所示:根据平衡条件,图中∠1=∠2,再根据等腰三角形底角相等,有∠2=∠3,而∠1+∠2+∠3=90°,故∠1=∠2=∠3=30°,M 点和轻环的连线与竖直方向的夹角为∠1+∠2=60°,故D 错误;A、轨道对轻环的支持力大小为:,A错误;B、细线对M点的拉力大小为,B正确;C、细线对轻环的作用力大小为两个拉力的合力,为,故C错误;【点睛】本题主要是考查了共点力的平衡问题,解答此类问题的一般步骤是:确定研究对象、进行受力分析、利用平行四边形法则进行力的合成或者是正交分解法进行力的分解,然后在坐标轴上建立平衡方程进行解答。
江苏省南京市江宁区2020学年高一英语下学期期末调研测试试题(含解析)

江宁区2020学年度第二学期期末调研测试卷高一英语本卷满分为150分,考试时间为120分钟。
考试结束后,请将答题纸交回。
注意事项:答题前,考生务必将自己的学校、姓名、考试号写在答题纸上。
考试结束后,请将答题纸交回。
第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上,录音内容结束后,你将有2分钟的时间将试卷上的答案转涂到答题纸上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话,每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What is the man doing?A. Giving a gift.B. Buying chocolates.C. Making chocolates.【答案】A【解析】【分析】本题考查听力,解析略【详解】M: Would you like these chocolates?W: Oh, I really wasn’t expecting a Valentine’s gift. T his is great! I love chocolates! Thank you so much!2.Where is the woman's father now?A. At home.B. In a hospital.C. At the office. 【答案】B【解析】【分析】本题考查听力,解析略【详解】M: How’s your father now, Karen? I heard he had an operation last month.W: He is much better. Thank you. But he still needs to stay there for two more weeks.3.What is the most probable relationship between the speakers?A. Couple.B. Neighbors.C. Colleagues. 【答案】A【解析】【分析】本题考查听力,解析略【详解】W: Our house is so small. I wish we could buy a bigger one.M: How could we ever manage to buy a bigger house when we’re always just living from salary to salary?W: Oh, be quiet. I wish you would think of ways to make more money, not look for excuses for not buying things.4.Why is the baby crying according to the man?A. He is hungry.B. He is ill.C. He is alone.【答案】C【解析】【分析】本题考查听力,解析略【详解】W: The baby is crying again.M: Leave him alone, and he’ll stop soon enough.W: How can you say that? Perhaps something is wrong with him. Let’s go and see.M: OK. Look, nothing serious. He just wants us to be with him.5.What are the speakers talking about?A. An accident.B. A flight.C. A pilot.【答案】B【解析】【分析】本题考查听力,解析略【详解】W: There was something wrong with the plane last Thursday.M: Which flight?W: Flight 198. Fortunately, there were only a few passengers, and all passengers and crew members were safe when the plane finally landed.M: Oh, that’s good news!第二节(共15小题,每小题1.5分,满分22.5分)听下面5段对话或独白。
新编南京市2019-2020学年度高一第二学期期末学情调研测语文试卷(精校版)

南京市2019-2020学年度第二学期期末高一学情调研测试卷语文注意事项:1.本试卷共8页。
满分160分。
考试时间为150分钟。
2.答题前,考生务必将学校、姓名、班级、学号写在答卷纸的密封线内。
答案写在答卷纸上的指定位置。
考试结束后,交回答卷纸。
一、基础知识和名著阅读(18分)1.下列词语中,加点字注音有误的一项是(▲)(3分)A.濒临(bīn)戛然而止(jiá)卓有成效(zhuó)B.镌刻(jùn )缄口不语(jiān)咬文嚼字(jiáo)C.菲薄( bó)雕阑玉砌(qì)纷繁芜杂(wú)D.恫吓 (dònɡ ) 命途多舛(chuǎn)呼天抢地(qiānɡ)2.下列词语中,书写有误的一项是(▲)(3分)A.社稷甘拜下风慢条斯理B.愧怍和盘托出中石没镞C.部署残羹冷炙钿头云篦D.陷阱良晨美景毁家纾难3.下列句子中,加点成语使用正确的一项是(▲)(3分)A.反腐剧《人民的名义》火爆荧屏,炙手可热,刷新了近年的收视纪录,很多人茶余饭后都在谈论精彩剧情。
B.在“不忘初心·砥砺前行”的演讲比赛中,选手们口蜜腹剑,指点江山,挥斥方遒,赢得观众阵阵掌声。
C.勒索病毒全球大面积爆发,攻击各国政府、学校、医院的网络,说其造成了不可估量的损失绝不是危言耸听。
D.第89届奥斯卡颁奖典礼圆满落下帷幕,巴里·杰金斯执导的《月光男孩》当仁不让地获得了最佳影片奖。
4.下列诗句中,没有使用比喻手法的一项是(▲)(3分)A.回乐峰前沙似雪,受降城外月如霜。
(李益《夜上受降城闻笛》)B.明月不谙离别苦,斜光到晓穿朱户。
(晏殊《蝶恋花》)C.人似秋鸿来有信,事如春梦了无痕。
(苏轼《与潘、郭二生出郊寻春》)D.山河破碎风飘絮,身世浮沉雨打萍。
(文天祥《过零丁洋》)5.下列语段衔接最自然的一组是(▲)(3分)面对今天这种“信息爆炸”、形形色色“异文化”纷至沓来的时代,我们需认真思考怎么办。
2019-2020学年南京市名校新高考高一数学下学期期末监测试题
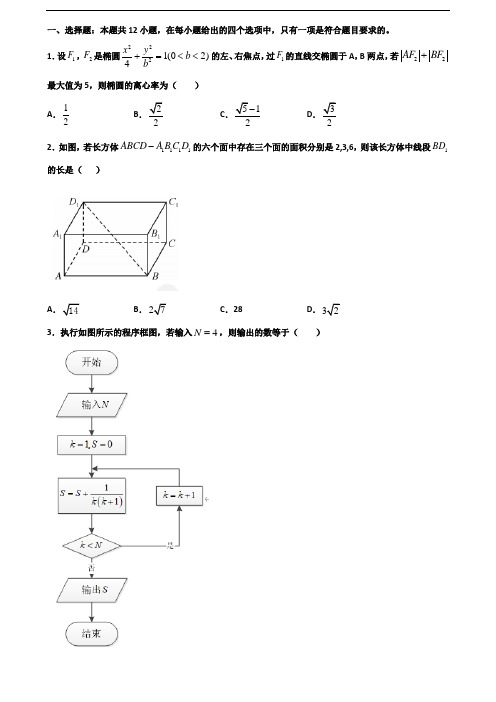
一、选择题:本题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设1F ,2F 是椭圆2221(02)4x yb b+=<<的左、右焦点,过1F 的直线交椭圆于A ,B 两点,若22AF BF +最大值为5,则椭圆的离心率为( ) A .12B .22C .512- D .322.如图,若长方体1111ABCD A B C D -的六个面中存在三个面的面积分别是2,3,6,则该长方体中线段1BD 的长是( )A .14B .27C .28D .323.执行如图所示的程序框图,若输入4N =,则输出的数等于( )A .54B .45C .56D .654.如图,函数tan cos 0,,22y x x x πππ⎛⎫⎡⎫⎛⎤=∈⎪ ⎪⎢⎥⎣⎭⎝⎦⎝⎭的图像是( ) A . B .C .D .5.在ABC ∆中,3AB =,3C π=,O 为ABC ∆的外接圆的圆心,则CO =( )A .3B .23C .3D .66.如图,在正方体ABCD-A 1B 1C 1D 1中,E ,F 分别是C 1D 1,CC 1的中点,则异面直线AE 与BF 所成角的余弦值为( )A .56-B .5-C .6 D .257.已知平面向量(1,2),(2,)a b m ==-,且//a b ,则23a b +=( ) A .(5,10)-- B .()4,8--C .()3,6--D .()2,4-- 8.已知圆,圆,分别为圆和圆上的动点,为直线上的动点,则的最小值为A .B .C .D .9.已知()0,1A -,()0,3B ,则AB =( ) A .2B 10C .4D .1010.已知公式为正数的等比数列{}n a 满足:11a =,22844a a a ⋅=,则前5项和5S =( )A .31B .21C .15D .1111.下列各数中最小的数是( ) A .(9)85B .(6)210C .(4)1000D .(2)11111112.如图,正四棱柱ABCD A B C D ''''-中(底面是正方形,侧棱垂直于底面),3AA AB '=,则异面直线A B '与AD '所成角的余弦值为( )A .910B .45C .710D .35二、填空题:本题共4小题13.在直角坐标系xOy 中,已知任意角θ以坐标原点O 为顶点,以x 轴的非负半轴为始边,若其终边经过点()00,P x y ,且(0)OP r r =>,定义: 00cos y x si rθ-=,称“sicos θ”为“θ的正余弦函数”,若cos 0si θ=,则sin 23πθ⎛⎫-= ⎪⎝⎭_________ . 14.已知α,β为锐角,且(1tan )(1tan )2αβ--=,则αβ+=__________. 15.若角α的终边经过点()2,1P -,则sin 2πα⎛⎫+= ⎪⎝⎭______. 16.(如下图)在正方形ABCD 中,E 为BC 边中点,若AE AB AD λμ=+,则λμ+=__________.三、解答题:解答应写出文字说明、证明过程或演算步骤。
江苏省南京市重点名校2019-2020学年高一下学期期末复习检测物理试题含解析

江苏省南京市重点名校2019-2020学年高一下学期期末复习检测物理试题一、单项选择题:本题共6小题,每小题5分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的1. (本题9分)如图所示,用水平力F 推放在水平粗糙地面上的木箱,关于木箱所受摩擦力下列说法正确的是A .若木箱保持静止,则F 越大,它所受摩擦力越大B .若木箱保持静止,则木箱质量越大,它所受摩擦力越大C .若木箱向前滑动,则F 越大,它所受摩擦力越大D .若木箱向前滑动,则木箱运动越快,它所受摩擦力越大【答案】A【解析】【详解】若木箱保持静止,则静摩擦力与F 大小相等,F 越大,则它所受的摩擦力越大;故A 正确;木箱受到的静摩擦力与质量无关,故B 错误;若木箱滑动,则物体受到的是滑动摩擦力,摩擦力大小与正压力有关,和推力F 无关,故C 错误;滑动摩擦力的大小与运动快慢无关,故D 错误;故选A 。
【点睛】在分析摩擦力时,首先要明确物体受到的是滑动摩擦力还是静摩擦力,再根据摩擦力的性质进行分析解答.滑动摩擦力与正压力成正比、与动摩擦因数成正比,与其他因素无关;静摩擦力根据物体的受力分析进行判断.2. (本题9分)在公路上常会看到凸形和凹形的路面,如图所示.一质量为m 的汽车,通过凸形路面的最高处时对路面的压力为1N ,通过凹形路面最低处时对路面的压力为2N ,则( )A .1N mg >B .2N mg =C .1N mg <D .2N mg <【答案】C【解析】【详解】 AC .汽车过凸形路面的最高点时,设速度为v ,半径为r ,由牛顿第二定律得:mg−N 1=2v m r,解得:N1=mg−2 v mr则N1<mg故A错误,C正确;BD. 汽车过凹形路面的最高低时,设速度为v,半径为r,由牛顿第二定律得:N2−mg=2vmr,解得:N2=mg+2 v mr所以N2>mg故B错误,D错误.故选C.3.(本题9分)关于作用力和反作用力的说法正确的是 ( )A、作用力与反作用力是同种性质的力B、物体间发生相互作用时先有作用力,后有反作用力C 、人加速奔跑时,地对人的作用力大于人对地的作用力D 、作用力和反作用力等值、反向,所以物体一定保持平衡【答案】A【解析】试题分析:根据牛顿第三定律可知,作用力与反作用力大小相等,方向相反,作用在同一条直线上,作用在两个物体上,力的性质相同,它们同时产生,同时变化,同时消失。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南京市江宁区2019—2020学年第二学期高一年级期末考试物理试卷一、单项选择题(本题共有9小题,每小题只有一个选项正确,选对的得3分,共27分)1.下列说法正确的是( )A. 开普勒提出行星运动规律,并发现了万有引力定律B. 牛顿发现了万有引力定律,并通过精确的计算得出万有引力常量C. 万有引力常量是卡文迪许通过扭秤实验测量得出的D. 伽利略发现万有引力定律并测出了万有引力常量2.如图所示,水平转台上放着一枚硬币,当转台匀速转动时,硬币没有滑动。
关于这种情况下硬币的受力情况,下列说法正确的是()A.重力和台面的支持力B.重力、台面的支持力和向心力C.重力、台面的支持力、向心力和静摩擦力D.重力、台面的支持力和静摩擦力3.电场中有一点P,下列说法中正确的是()A.若放在P点的电荷的电荷量减半,则P点的场强减半B.若P点没有试探电荷,则P点场强为零C.P点的场强越大,则同一电荷在P点受到的电场力越大D.P点的场强方向与放在该点的电荷所受电场力的方向相同4.下列图中,能正确描述质点运动到P点时的速度v和加速度a的方向关系的是()5.将质量为100kg的物体从地面提升到10m高处。
在这个过程中,下列说法正确的是()A.重力做正功,重力势能增加1.0×104JB.重力做正功,重力势能减少1.0×104JC.重力做负功,重力势能增加1.0×104JD.重力做负功,重力势能减少1.0×104J6. 如图所示,在光滑绝缘的水平面上,有两个相距较近的带同种电荷的小球,将它们由静止释放,则两球间 ( )A .距离变大,库仑力变大B .距离变大,库仑力变小C .距离变小,库仑力变大D .距离变小,库仑力变小7.如图所示,细绳跨过定滑轮悬挂两物体M 和m ,且M >m ,不计摩擦,在系统由静止开始运动的过程中,下列说法中正确的是 ( )A. M 、m 各自的机械能分别守恒B. M 减少的重力势能等于m 增加的重力势能C. M 增加的动能等于m 增加的动能D. M 减少的机械能等于m 增加的机械能8.如图所示,在粗糙水平面上固定一点电荷Q ,在M 点无初速度释放一带有恒定电荷量的小物块,小物块在Q 的电场中,运动到N 点时静止,则从M 点运动到N 点的过程中 ( )A.小物块所受电场力逐渐变大B.小物块具有的电势能逐渐减小C.M 点的电势一定高于N 点的电势D.小物块电势能变化量的大小一定大于克服摩擦力做的功9.一小球从地面竖直上抛,到最高点后又落回地面,小球运动过程中所受空气阻力大小恒定,取竖直向上为正方向。
下列关于小球运动的速度v 、加速度a 、动能E k 、机械能E 随时间t 或路程x 变化的图象中正确是 ( )二、多项选择题(本题共有5小题,每题4分,漏选得2分、错选得0分,共20分)10.如图所示,绳子的一端固定在O 点,另一端拴一重物在光滑水平面上做匀速圆周运动 ( )A .转速相同时,绳长的容易断B .周期相同时,绳短的容易断C .线速度大小相等时,绳短的容易断D .线速度大小相等时,绳长的容易断t A v O B a O t x C E k O D x E O A11. 如图所示,卫星A 、B 绕地球做匀速圆周运动,用ω、T 、v 、a 分别表示卫星运动的角速度、周期、运行速率、向心加速度.下列关系正确的有 ( )A .ωA =ωB B .v A >v BC .T A >T BD .a A <a B12. 某电场线分布如图所示,P 、Q 为其中的两点,其中P 点处电场线更密集,关于带负电的试探电荷,下列说法正确的是( )A .在P 点所受电场力大于在Q 点所受电场力B .从P 点移动到Q 点,电场力做正功C .在P 点的电势能小于在Q 点的电势能D .从 P 点由静止释放后,此电荷将沿电场线运动到Q 点13.如图所示的电路中,当变阻器R 3的滑动触头P 向a 端移动时( )A .电压表示数变大B .电压表示数变小C .电流表示数变大D .电流表示数变小 14.如图所示,质量为M 的木块静止在光滑的水平面上。
质量为m 的子弹以速度v 0沿水平射中木块,并最终留在木块中,与木块一起以速度v 运动。
已知当子弹相对木块静止时,木块前进距离L ,子弹进入木块的深度为s .若木块对子弹的阻力f 视为恒定,则下列关系式中正确的是 ( )A. f L=Mv 2/2B. f s=mv 2/2C. f s=mv 02/2-(M +m )v 2/2D. f (L +s )=mv 02/2-mv 2/2三、实验题(本大题共有2小题,第15题6分,第16题7分,共13分)15.“验证机械能守恒定律”的实验装置如图所示。
(1)实验中,下面哪些测量工具是必需的________。
A .天平B .直流电源C .刻度尺D .秒表(2)实验中选取一条符合实验要求的纸带如图所示,O 为纸带下落的起始点,A 、B 、C 为纸带上选取的三个连续点。
计算B 点瞬时速度时,甲同学用v B 2=2gx OB ,乙同学用v B=x AC 2T,其中所选方法正确的是________(选填“甲”或“乙”)同学。
(3)实验中,发现重物减少的势能总是大于重物增加的动能,造成这种现象的原因是(回答出其中一条即可)________________________________________________________。
P Q16. 在做测量干电池的电动势和内阻实验中:(1)除待测电池、开关、若干导线外,选用下列哪组仪器,也可以完成实验目的()A.一直流电流表,一电阻箱B.一直流电压表,一电阻箱C.一直流电流表,一滑动变阻器D.一直流电流表,一直流电压表,一滑动变阻器(2)按图示电路进行实验,分别读出电压表和电流表的示数,并画出的U—I图象,如图所示。
则待测电池的电动势为V,内阻r为Ω。
(结果保留两位有效数字)四、计算题(本大题共有3个小题,共40分。
请写出必要的文字说明和重要的演算步骤,只写出答案没有过程,不能得分)17.(12分)如图所示,长为10 cm的轻绳系着一质量为1kg的小球(小球可视为质点),在光滑的水平桌面上以20rad/s的角速度做匀速圆周运动。
已知桌子离地的高度为0.45m,g取10m/s2。
求:(1)小球运动的线速度大小;(2)绳子对小球的拉力大小;(3)若以地面为零势能面,小球在桌面上运动时的机械能.18.(12分)如图所示,A为粒子源,已知极板A和极板B间的电压为U1,水平放置的平行带电板C、D间的电压为U2,平行带电板的长度为L,两板间的距离为d。
现有一个质量为m、电荷量为q的带电粒子从粒子源A射出后(带电粒子的初速度可以忽略不计),被加速电压U1加速,并从两带电板C、D 的中央水平射入,最后从右侧射出。
不计带电粒子的重力,求:(1)带电粒子在射出B板时的速度大小(2)带电粒子从C、D间的电场飞出时,偏离入射方向的距离(3)如果CD间的电压U2可以调节,要使带电粒子不会打在极板D上,其他条件不变,电压U2应满足什么条件?19.(16分)如图所示,水平轨道BC的左端与固定的光滑竖直14圆轨道相切于B点,右端与一倾角为o30的光滑斜面轨道在C点平滑连接(即物体经过C点时速度的大小不变),斜面顶端固定一轻质弹簧。
一质量为2kg的滑块,从圆弧轨道的顶端A点由静止释放,经水平轨道后滑上斜面并压缩弹簧,第一次可将弹簧压缩至D点。
已知光滑圆轨道的半径R=0.45m,水平轨道BC长为1.25m,物体与水平轨道间的动摩擦因数为0.2μ=,斜面轨道上C、D两点间的距离为0.2m,g取10m/s2。
求:(1)滑块经过圆轨道上B点时的速度大小;(2)滑块从B运动到C所用的时间;(3)整个过程中弹簧的最大弹性势能.2019—2020学年第二学期高一年级期末考试物理试卷参考答案一、单项选择题(共有9小题,每小题只有一个..选项正确,选对的得3分,共27分) 1.C 2.D 3.C 4.A 5.C 6.B 7.D 8.B 9.D二、多项选择题(共有5小题,每题4分,漏选得2分、错选和不选得0分,共20分) 10.AC 11.C D 12.AC 13.B C 14.ACD三、填空题(共有2小题,共13分)15.(1). C (2) 乙 (3)纸带与限位孔之间有摩擦或空气阻力(答对一条即可得分) (每空格2分)16.(1)A B D (本题3分,漏选得2分,错选和不选不得分)(2)1.5 1.0 (每空格2分)四、本大题(共3小题,合计40分。
请写出必要的文字说明和重要的演算步骤,只写出答案不能得分)17.(9分) ⑴ 由V=ωr 得,线速度V=2m/s (3分)(2)因物体的向心力F 向等于绳子的拉力F ,故F=mω2r F=40N (3分)(3)物体在桌面上的机械能mgh mv 212o +=E 即E=6.5J (3分) 18.(15分)(1) 由2o 1mv 21q u =(3分) 解得 mq u 2v 1o = (1分) (2)电子在水平金属板间做类平抛运动,有0L t v =(1分) 2at 21y = (1分) 联立解方程可得 122u 4u y L = (3分) (3)要使质子打在带电板D 上,2应满足如下关系:2d at 212≤ (3分) 因0L t v = mq u 2v 1o = md q u a 2= 故电压u2应满足:2212d 2u u L ≤ (3分) 19.(16分)(1)滑块从A 点到B 点,由动能定理可得:2102B mgR m =-v (3分) 解得: 3m/s B v = (2分)(2)滑块从B 到C 做匀减速直线运动 加速度g -a μ= 即2s m -2a = (2分)由 有 t=0.5s (3分) (3)滑块第一次到达D 点时,弹簧具有最大的弹性势能p E .滑块从A 点到D 点,由动能定理可得:o ()(sin 30)0BC CD mgR mgL mgL W μ+-+-+= (3分)p E W =- (2分)解得: E p =2J (1分)20at 21t v x +=。
