2020-2021学年八年级数学同步优化训练:第11章三角形 章末检测【含答案】
第十一章三角形 同步练习 2020-2021学年 人教版八年级数学上册(含答案)
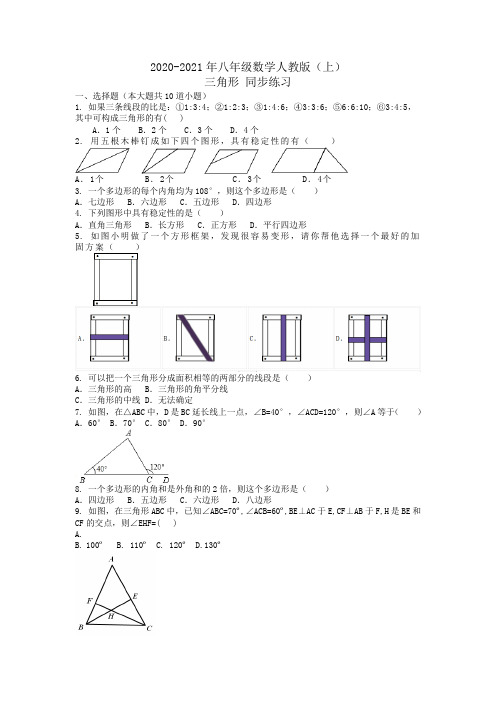
2020-2021年八年级数学人教版(上)三角形同步练习一、选择题(本大题共10道小题)1. 如果三条线段的比是:①1:3:4;②1:2:3;③1:4:6;④3:3:6;⑤6:6:10;⑥3:4:5,其中可构成三角形的有( )A.1个 B.2个 C.3个 D.4个2. 用五根木棒钉成如下四个图形,具有稳定性的有()A.1个B.2个C.3个D.4个3. 一个多边形的每个内角均为108°,则这个多边形是()A.七边形B.六边形C.五边形D.四边形4. 下列图形中具有稳定性的是()A.直角三角形B.长方形C.正方形D.平行四边形5. 如图小明做了一个方形框架,发现很容易变形,请你帮他选择一个最好的加固方案()6. 可以把一个三角形分成面积相等的两部分的线段是()A.三角形的高B.三角形的角平分线C.三角形的中线 D.无法确定7. 如图,在△ABC中,D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A等于()A.60° B.70° C.80° D.90°8. 一个多边形的内角和是外角和的2倍,则这个多边形是()A.四边形B.五边形C.六边形D.八边形9. 如图,在三角形ABC中,已知∠ABC=70º,∠ACB=60º,BE⊥AC于E,CF⊥AB于F,H是BE和CF的交点,则∠EHF=( )A.B.100º B. 110ºC. 120ºD.130º10. 如图:D ,E 分别是△ABC 的边BC 、AC 上的点,若AB=AC ,AD=AE ,则( ) A. 当∠B 为定值时,∠CDE 为定值值 B. 当∠α为定值时,∠CDE 为定值 C. 当∠β为定值时,∠CDE 为定值 D. 当∠γ为定值时,∠CDE 为定值二、填空题(本大题共8道小题)11. 从多边形的一个顶点出发,连接这个点和其他顶点,把多边形分割成16个三角形,则这个多边形的边数是________.12. 如图,已知AB ∥CD ,∠A =55°,∠C =20°,则∠P =___________.13. 在△ABC 中,已知∠A=21∠B=31∠C ,则三角形的形状是 三角形. 14. 如图,BP 、CP 是任意△ABC 中∠B 、∠C 的角平分线,可知∠BPC=90°+21∠A ,把图中的△ABC 变成图中的四边形ABCD ,BP ,CP 仍然是∠B ,∠C 的平分线,猜想∠BPC 与∠A 、∠D 的数量关系是 .15. 在△ABC 中,若∠B -∠A =15°,∠C -∠B =60°,则∠A =______,∠B =______,∠C =______.16. 如图,D 、E 分别是△ABC 边AB 、BC 上的点,AD=2BD,BE=CE,设△ADC 的面积为S1,△ACE 的面积为S2,若S △ABC=6,则S1+S2=_______17. 一个正方形和两个等边三角形的位置如图所示,若∠1+∠2 =100°,则∠3= .18. 如图1所示,圆上均匀分布着11个点A1,A2,A3,…,A11.从A1起每隔k个点顺次连接,当再次与点A1连接时,我们把所形成的图形称为“k+1阶正十一角星”,其中1≤k≤8(k为正整数).例如,图2是“2阶正十一角星”,那么∠A1+∠A2+…+∠A11= ;当∠A1+∠A2+…+∠A11=900°时,k= .三、解答题(本大题共6道小题)19. 一个零件的形状如图,按规定∠A=90º,∠ C=25º,∠B=25º,检验已量得∠BCD=150º,就判断这个零件不合格,运用三角形的有关知识说明零件不合格的理由。
2020-2021学年人教版八年级数学上册第11章《三角形》单元测试含答案

2020-2021学年人教版八年级数学上册第11章《三角形》单元测试含答案第11章《三角形》单元测试时间:100分钟满分:100分班级:_______ 姓名:________得分:_______一.选择题(每题3分,共30分)1.下列长度的每组三根小木棒,能组成三角形的一组是()A.3,3,6 B.4,5,10 C.3,4,5 D.2,5,3 2.在△ABC中,∠A=21°,∠B=34°,则△ABC()A.锐角三角形B.直角三角形C.钝角三角形D.锐角或钝角三角形3.已知三角形两边长为5和8,则第三边长a的取值范围是()A.3<a<13 B.3≤a≤13 C.a>3 D.a<11 4.下列四个图形,具有稳定性的有()A.1个B.2个C.3个D.4个5.若n边形的内角和等于外角和的4倍,则边数n为()A.10 B.8 C.7 D.56.如图,在△ABC中,∠A=35°,∠DCA=100°,则∠B的度数为()A.45°B.55°C.65°D.75°7.下列说法中正确的是()A.三角形的角平分线是一条射线B.三角形的一个外角大于任何一个内角C.任意三角形的外角和都是180°D.内角和是1080°的多边形是八边形8.把一副直角三角板按如图所示的方式摆放在一起,其中∠C=90°,∠F=90°,∠D=30°,∠A=45°,则∠1+∠2等于()A.270°B.210°C.180°D.150°9.如图,△ABC是一把直角三角尺,∠ACB=90°,∠B=30°.把三角尺的直角顶点放在一把直尺的一边上,AC与直尺的另一边交于点D,AB与直尺的两条边分别交于点E,F.若∠AFD=58°,则∠BCE的度数为()A.20°B.28°C.32°D.88°10.如图,平面上有两个全等的正八边形ABCDEFGH、A′B′C′D′E′F′G′H′,若点B与点B′重合,点H与点H′重合,则∠ABA′的度数为()A.15°B.30°C.45°D.60°二.填空题(每题4分,共20分)11.在△ABC中∠A:∠B=2:1,其中∠C的外角等于120°,则∠B=.12.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上根木条.13.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A=.14.三角形一边长为4cm,另一边长为3cm,且第三边长为偶数,则第三边的长为cm.15.如图,在一个三角形的纸片(△ABC)中,∠C=90°,将这个纸片沿直线DE剪去一个角后变成一个四边形ABED,则图中∠1+∠2的度数为°.三.解答题(每题10分,共50分)16.如图,△ABC中,D为BC上一点,∠C=∠BAD,△ABC的角平分线BE交AD 于点F.(1)求证:∠AEF=∠AFE;(2)G为BC上一点,当FE平分∠AFG且∠C=30°时,求∠CGF 的度数.17.如图,已知点D为△ABC的边BC延长线上一点,DF⊥AB于点F,并交AC于点E,其中∠A=∠D=40°.(1)求∠B的度数;(2)求∠ACD的度数.18.(1)把下面的证明补充完整已知:如图,直线AB、CD被直线EF所截,AB∥CD,EG平分∠BEF,FG平分∠DFE,EG、FG交于点G.求证:EG⊥FG.证明:∵AB∥CD(已知)∴∠BEF+∠DFE=180°(),∵EG平分∠BEF,FG平分∠DFE(已知),∴,(),∴∠GEF+∠GFE=(∠BEF+∠DFE)(),∴∠GEF+∠GFE=×180°=90°(),在△EGF中,∠GEF+∠GFE+∠G=180°(),∴∠G=180°﹣90°=90°(等式性质),∴EG⊥FG().(2)请用文字语言写出(1)所证命题:.19.如图,在△ABC中,AD平分∠BAC(1)若P为线段AD上的一个点,过点P作PE⊥AD交线段BC 的延长线于点E①若∠B=34°,∠ACB=86°,则∠E=°;②猜想∠E与∠B、∠A CB之间的数量关系,并给出证明.(2)若P在线段AD的延长线上,过点P作PE⊥AD交直线BC 于点E.请你直接写出∠PED与∠ABC、∠ACB的数量关系.20.解读基础:(1)图1形似燕尾,我们称之为“燕尾形”,请写出∠A、∠B、∠C、∠D之间的关系,并说明理由;(2)图2形似8字,我们称之为“八字形”,请写出∠A、∠B、∠C、∠D之间的关系,并说明理由:应用乐园:直接运用上述两个结论解答下列各题(3)①如图3,在△ABC中,BD、CD分别平分∠ABC和∠ACB,请直接写出∠A和∠D的关系;②如图4,∠A+∠B+∠C+∠D+∠E+∠F=.(4)如图5,∠BAC与∠BDC的角平分线相交于点F,∠GDC与∠CAF的角平分线相交于点E,已知∠B=26°,∠C=54°,求∠F和∠E 的度数.参考答案一.选择1.解:A、3+3=6,不能构成三角形;B、4+5<10,不能构成三角形;C、3+4>5,能够组成三角形;D、2+3=5,不能组成三角形.故选:C.2.解:由题意∠C=180°﹣∠A﹣∠B=180°﹣21°﹣34°=125°,∴△ABC是钝角三角形,故选:C.3.解:∵三角形的第三边大于两边之差小于两边之和,∴三角形的两边长分别是5、8,则第三边长a的取值范围是3<a <13.故选:A.4.解:第一个图形为个三角形,具有稳定性,第二个图形是四边形,不具有稳定性;第三个图形中左侧含有一个四边形,不具有稳定性;第四个图形被分成了三个三角形,具有稳定性,所以具有稳定性的有2个.故选:B.5.解:设这个多边形的边数为n,则依题意可得:(n﹣2)×180°=360°×4,解得n=10.故选:A.6.解:∵∠DCA=∠A+∠B,∠DCA=100°,∠A=35°,∴∠B=100°﹣35°=65°,故选:C.7.解:A、三角形的角平分线是一条线段,故本选项错误;B、三角形的一个外角大于任何一个和它不相邻的内角,故本选项错误;C、任意多边形的外角和都是360°,故本选项错误;D、1080°÷180°+2=8,即内角和是1080°的多边形是八边形,故本选项正确.故选:D.8.解:如图:∵∠1=∠D+∠DOA,∠2=∠F+∠FPB,∵∠DOA=∠COP,∠EPB=∠CPO,∴∠1+∠2=∠D+∠F+∠COP+∠CPO=∠D+∠F+180°﹣∠C=30°+90°+180°﹣90°=210°.故选:B.9.解:∵CE∥DF,∴∠AEC=∠AFD=58°,∵∠AEC=∠B+∠BCE,∴∠BCE=∠AEC﹣∠B=58°﹣30°=28°;故选:B.10.解:∵两个图形为全等的正八边形,∴ABA′H为菱形,∵∠HAB=∠HA′B==135°∴∠ABA′=180°﹣135°=45°.故选:C.二.填空题(共5小题)11.解:设∠A=2x,则∠B=x,∵∠C的外角等于120°,∴∠A+∠B=120°,即2x+x=120°,解得,x=40°,即∠B=40°,故答案为:40°.12.解:根据三角形的稳定性,要使六边形木架不变形,至少再钉上3根木条;故答案为:3.13.解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∴∠ABC=2∠ABP,∠ACM=2∠ACP,又∵∠ABP=20°,∠ACP=50°,∴∠ABC=2×20°=40°,∠ACM=2×50°=100°,∴∠A=∠ACM﹣∠ABC=60°,故答案为60°.14.解:设第三边长为x,则4﹣3<x<4+3,即1<x<7.又x为偶数,因此x=2或4或6.故答案为:2或4或6.15.解:∵∠C=90°,∴∠A+∠B=90°,∵∠1+∠A+∠B+∠2=360°,∴∠1+∠2=360°﹣90°=270°,故答案为:270.三.解答题(共5小题)16.解:(1)证明:∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠ABF+∠BAD=∠CBE+∠C,∵∠AFE=∠ABF+∠BAD,∠AEF=∠CBE+∠C,∴∠AEF=∠AFE;(2)∵FE平分∠AFG,∴∠AFE=∠GFE,∵∠AEF=∠AFE,∴∠AEF=∠GFE,∴FG∥AC,∵∠C=30°,∴∠CGF=180°﹣∠C=150°.17.解:(1)∵DF⊥AB,∴∠BFD=90°,∴∠B+∠D=90°,∵∠D=40°∴∠B=90°﹣∠D=90°﹣40°=50°;(2)∠ACD=∠A+∠B=40°+50°=90°.18.证明:∵AB∥CD(已知)∴∠BEF+∠DFE=180°(两直线平行,同旁内角互补),∵EG平分∠BEF,FG平分∠DFE(已知),∴∠BEG=∠FEG,∠DFG=∠EFG,(角平分线的定义),∴∠GEF+∠GFE=(∠BEF+∠DFE)(等量代换),∴∠GEF+∠GFE=×180°=90°(等式的性质),在△EGF中,∠GEF+∠GFE+∠G=180°(三角形的内角和),∴∠G=180°﹣90°=90°(等式性质),∴EG⊥FG(垂直的定义);(2)请用文字语言写出(1)所证命题:两条平行线被第三条直线所截,同旁内角的平分线互相垂直.故答案为:两直线平行,同旁内角互补,∠BEG=∠FEG,∠DFG =∠EFG,角平分线定义,等量代换,三角形的内角和,垂直的定义,两条平行线被第三条直线所截,同旁内角的平分线互相垂直19.解:(1)①∵∠B=34°,∠ACB=86°,∴∠BAC=180°﹣∠B﹣∠ACB=60°,∵AD平分∠BAC,∴∠BAD=∠BAC=30°,∴∠PDE=∠B+∠BAD=64°,∵PE⊥AD,∴∠E=90°﹣∠PDE=26°;故答案为:26;②数量关系:∠E=(∠ACB﹣∠B);理由如下:设∠B=x,∠ACB=y,∵AD平分∠BAC,∴∠BAD=∠CAD=∠BAC,∵∠B+∠ACB+∠BAC=180°,∴∠CAB=180°﹣x﹣y.∴∠BAD=(180°﹣x﹣y).∴∠PDE=∠B+∠BAD=x+(180°﹣x﹣y)=90°+(x﹣y).∵PE⊥AD,∴∠PDE+∠E=90°,∴∠E=90°﹣[90°+(x﹣y)]=(y﹣x)=(∠ACB﹣∠B).(2)∠PED=(∠ACB﹣∠ABC),理由如下:①当点E在线段BC上时,如图1所示:设∠ABC=n°,∠ACB=m°,∵AD平分∠BAC,∴∠BAD=∠CAD=∠BAC,∵∠B+∠ACB+∠BAC=180°,∴∠CAB=(180﹣n﹣m)°,∴∠BAD=(180﹣n﹣m)°,∴∠PDE=∠ADC=∠ABC+∠BAD=n°+(180﹣n﹣m)°=90°+n°﹣m°,∵PE⊥AD,∴∠DPE=90°,∴∠PED=90°﹣(90°+n°﹣m°)=(m﹣n)°=(∠ACB﹣∠ABC),②当点E在CB的延长线时,如图2所示:同(2)①可得:∠PDE=∠ADC=∠ABC+∠BAD=n°+(180﹣n ﹣m)°=90°+n°﹣m°,∵PE⊥AD,∴∠DPE=90°,∴∠PED=90°﹣(90°+n°﹣m°)=(m﹣n)°=(∠ACB﹣∠ABC),综上所述,∠PED=(∠ACB﹣∠ABC).20.解:(1)∴∠D=∠A+∠B+∠C;理由如下:如图1,∠BDE=∠B+∠BAD,∠CDE=∠C+∠CAD,∴∠BDC=∠B+∠BAD+∠C+∠CAD=∠B+∠BAC+∠C,∴∠D=∠A+∠B+∠C;(2)∠A+∠D=∠B+∠C;理由如下:如图2,在△ADE中,∠AED=180°﹣∠A﹣∠D,在△BCE中,∠BEC=180°﹣∠B﹣∠C,∵∠AED=∠BEC,∴∠A+∠D=∠B+∠C;(3)①∠A=180°﹣∠ABC﹣∠ACB,∠D=180°﹣∠DBC﹣∠DCB,∵BD、CD分别平分∠ABC和∠ACB,∴∠ABC+∠ACB=∠DBC+∠DCB,∴∠D=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90°+∠A,故答案为∠D=90°+∠A,②连结BE,∴∠C+∠D=∠CBE+∠DEB,∴∠A+∠B+∠C+∠D+∠E+∠F=∠A+∠ABE+∠F+∠BEF=360°;故答案为360°;(4)由(1)知,∠BDC=∠B+∠C+∠BAC,∵∠B=26°,∠C=54°,∴∠BDC=80°+∠BAC,∴∠CDF=40°+2∠CAE,∵∠BAC=4∠CAE,∠BDC=2∠CDF,∴∠GDE=90°﹣∠CDF,∠AGD=∠B+∠GDB=26°+180°﹣∠CDF,∠GAE=3∠CAE,∴∠E=360°﹣∠GAE﹣∠AGD﹣∠GDE=64°﹣(2∠CAE﹣∠CDF)=64°+×40°=124°;∠F=180°﹣∠AGF﹣∠GAF=180°﹣(206°﹣∠CDF)﹣2∠CAE =﹣26°+∠CDF﹣2∠CAE=﹣26°+40°=14°;。
人教八年级上册第11章《三角形》同步练习及答案

第 11 章——11.1《与三角形 有关的线段》同步练习及(含答案) 一、选择题Z++ 1.C 2.B 3.A 4.B 5.D 6.B 7.D 8.B 二、填空题 9.4 10.2 11.利用三角形的稳定性使门板不变形. 12..6 13.95°或 35° 14.3 15.12,36 16.AB,CD 17.相等 18.4 三、解答题
人教八年级上册第 11 章《三角形》
22.△ABC 中,AD⊥BC,AE 平分∠BAC 交 BC 于点 E. (1)∠ B= 30°,∠C=70°,求∠EAD 的大小. (2)若∠B<∠C,则 2∠EAD 与∠C-∠B 是否相等?若相等,请说明理由.
23.已知△ABC 中,∠ACB=90°,CD 为 AB 边上的高,BE 平分∠ABC,分别交 CD、AC 于点 第F、E2,2求
第 23
19.证明:∵AD 是△ABC 的角平分线,AF 平分△ABC 的外角, ∴∠1=∠2,∠3=∠4, ∵DF∥BA, ∴∠4=∠ADE,∠1=∠F ∴∠3=∠ADE,∠ 2=∠F ∴DE=EA EF=EA ∴DE=EF
20.在∆ABC中,AB=AC,BD是中线,设AB=x,BC=y.
7 / 28
(第
Z
14
(第 15
(第 16
(第 18
14.如图,在△ABC 中,AC⊥BC,CD⊥AB 于点 D.则图中共有_____个直角三角形.
15.如图,在△ABC 中,BD 是角平分线,BE 是中线,若 AC=24cm,则 AE=
cm,若∠ABC=72°,则∠ABD=_____度.
16.如图所示:
(1)在△ABC 中,BC 边上的高是_____;
二、填空题 9.将一副常规的三角尺按如图方式放置,则图中∠AOB 的度数为____ ____
第11章 三角形 同步练习题 2020-2021学年人教版数学八年级上册(含答案)

2020-2021年八年级数学人教版(上)三角形同步练习题(含答案)一、选择题(本大题共10道小题)1. 五边形的内角和是( )A .180°B .360°C .540°D .600°2. 已知三角形的两边分别为4和9,则此三角形的第三边可能是( )A .4B .5C .9D .133. 下列命题是假命题的是( )A .三角形的三条角平分线相交于一点,并且这一点到三边距离相等B . 等腰三角形底边的中点到两腰的距离相等C . 面积相等的两个三角形全等D . 一个三角形中至少有两个锐角4. 如图,∠BDC=98°,∠C=38°,∠B=23°,∠A 的度数是( )A .61°B .60°C .37°D .39°5. (2021广东汕头)已知三角形两边的长分别是4和10,则此三角形第三边的长可能是【 】A . 5 B.6 C .11 D.166. 下列各组线段能构成三角形的是( )A .2 cm ,2 cm ,4 cmB .2 cm ,3 cm ,4 cmC .2 cm ,2 cm ,5 cmD .2 cm ,3 cm ,6 cm7. 如图,在五边形ABCDE 中,∠A+∠B+∠E=300°,DP 、CP 分别平分∠EDC 、∠BCD ,则∠P 的度数是( )A .60°B .65°C .55°D .50°8. (2021 云南省昆明市) 如图,在ABC △中,6733B C ==∠°,∠°,AD 是ABC △的角平分线,则CAD ∠的度数为( ).(A )40° (B )45° (C )50° (D )55°9. 如图,木工师傅从边长为90cm的正三角形木板上锯出一正六边形木块,那么正六边形木板的边长为()A.34cmB.32cmC.30cmD.28cm10. 已知△ABC,(1)如图1,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+21∠A;(2)如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图3,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-21∠A.上述说法正确的个数是()A.0个 B.1个 C.2个 D.3个二、填空题(本大题共7道小题)11. 为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条这样做的道理是___________________.12. n边形的每个外角都等于45°,则n=______.13. 正多边形的一个外角是°,则这个多边形的内角和的度数是______.14. 若4,5,x是一个三角形的三边,则x的值可能是________ (填写一个即可)15. (2021·烟台)正多边形的一个外角是72°,则这个多边形的内角和的度数是____.16. 如图,小明从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,……照这样走下去,他第一次回到出发地A点时,一共走了米.17. (2021•贵港二模)如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…∠A n﹣1BC的平行线与∠A n﹣1CD的平分线交于点A n,设∠A=θ,则∠A n= .三、解答题(本大题共5道小题)18. 如图,求证:∠A+∠B+∠C+∠D+∠E=180°.19. 【题目】(7分).已知等腰三角形一腰上的中线将三角形的周长分为9cm和15cm两部分,求这个等腰三角形的底边长和腰长.20. 取一张正方形纸片,把它裁成两个等腰直角三角形,取出其中一张如图①,再沿着直角边上的中线AD按图②所示折叠,则AB与DC相交于点G.试问:△AGC和△BGD的面积哪个大?为什么?21. (2021春•苏州期末)观察并探求下列各问题,写出你所观察得到的结论,并说明理由.(1)如图,△ABC中,P为边BC上一点,试观察比较BP+PC与AB+AC的大小,并说明理由.(2)将(1)中点P移至△ABC内,得图②,试观察比较△BPC的周长与△ABC的周长的大小,并说明理由.(3)将(2)中点P变为两个点P1、P2得下图,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由.(4)将(3)中的点P1、P2移至△ABC外,并使点P1、P2与点A在边BC的异侧,且∠P1BC<∠ABC,∠P2CB<∠ACB,得图,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由.(5)若将(3)中的四边形BP1P2C的顶点B、C移至△ABC内,得四边形B1P1P2C1,如图⑤,试观察比较四边形B1P1P2C1的周长与△ABC的周长的大小,并说明理由.22. (12分)平面内的两条直线有相交和平行两种位置关系.(1)如图①,若AB∥CD,点P在AB,CD外部,则有∠B=∠BOD,又因为∠BOD是△POD 的外角,故∠BOD=∠BPD+∠D.得∠BPD=∠B-∠D.将点P移到AB,CD内部,如图②,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论;(2)在如图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?(不需证明);(3)根据(2)的结论求如图④中∠A+∠B+∠C+∠D+∠E的度数.答案一、选择题(本大题共10道小题)1. 【答案】C2. 【答案】C3. 【答案】C4. 【答案】C5. 【答案】C6. 【答案】B7. 【答案】A8. 【答案】A9. 【答案】C ;【解析】图中小三角形也是正三角形,且边长等于正六边形的边长,所以正六边形的周长是正三角形的周长的23,正六边形的周长为90×3×23=180cm,所以正六边形的边长是180÷6=30cm.10. 【答案】C二、填空题(本大题共7道小题)11. 【答案】三角形的稳定性;12. 【答案】813. 【答案】540°14. 【答案】 x满足1<x<9即可15. 【答案】540°16. 【答案】【答案】12017. 【答案】;【解析】解:由三角形的外角性质得,∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,∵∠ABC的平分线与∠ACD的平分线交于点A1,∴∠A1BC=∠ABC,∠A1CD=∠ACD,∴∠A1+∠A1BC=(∠A+∠ABC)=∠A+∠A1BC,∴∠A1=∠A,同理可得∠A2=∠A1==,…,∠A n=.三、解答题(本大题共5道小题)18. 【答案】解:延长BE,交AC于点H,易得∠BFC=∠A+∠B+∠C再由∠EFC=∠D+∠E,上式两边分别相加,得:∠A+∠B+∠C+∠D+∠E=∠BFC+∠EFC=180°.即∠A+∠B+∠C+∠D+∠E=180°19. 【答案】腰长为10cm ,底边长为4cm20. 【答案】解:∵ BD =CD ,∴ ABD ACD S S =△△.∴ ABD ADG ACD ADG S S S S -=-△△△△.∴ ADG BGD S S =△△.21. 【答案】解:(1)BP+PC <AB+AC ,理由:三角形两边之和大于第三边,或两点之间线段最短.(2)△BPC 的周长<△ABC 的周长.理由如下:如图,延长BP 交AC 于M ,在△ABM 中,BP+PM <AB+AM ,在△PMC 中,PC <PM+MC ,两式相加得BP+PC <AB+AC ,于是得:△BPC 的周长<△ABC 的周长.(3)四边形BP 1P 2C 的周长<△ABC 的周长.理由如下:如图,分别延长BP 1、CP 2交于M ,由(2)知,BM+CM <AB+AC ,又P 1P 2<P 1M+P 2M ,可得,BP 1+P 1P 2+P 2C <BM+CM <AB+AC ,可得结论.或:作直线P 1P 2分别交AB 、AC 于M 、N (如图),△BMP 1中,BP 1<BM+MP 1,△AMN 中,MP 1+P 1P 2+P 2M <AM+AN ,△P 2NC 中,P 2C <P 2N+NC ,三式相加得:BP 1+P 1P 2+P 2C <AB+AC ,可得结论.(4)四边形BP 1P 2C 的周长<△ABC 的周长.理由如下:将四边形BP 1P 2C 沿直线BC 翻折,使点P 1、P 2落在△ABC 内,转化为(3)情形,即可.(5)比较四边形B 1P 1P 2C 1的周长<△ABC 的周长.理由如下:如图,分别作如图所示的延长线交△ABC 的边于M 、N 、K 、H ,在△BNM 中,NB 1+B 1P1+P 1M <BM+BN ,又显然有,B 1C 1+C 1K <NB 1+NC+CK ,及C 1P 2+P 2H <C 1K+AK+AH ,及P 1P 2<P 2H+MH+P 1M ,将以上各式相加,得B 1P 1+P 1P 2+P 2C+B 1C 1<AB+BC+AC ,于是得结论.22. 【答案】解:(1)不成立,结论是∠BPD=∠B+∠D.证明:延长BP交CD于点E,∵AB ∥CD,∴∠B=∠BED,又∵∠BPD=∠BED+∠D,∴∠BPD=∠B+∠D(2)∠BPD=∠BQD+∠B+∠D(3)由(2)的结论得:∠AGB=∠A+∠B+∠E且∠AGB=∠CGD,∴∠A+∠B+∠C+∠D +∠E=180°。
2020-2021学年八年级数学人教版上册同步练习11.2与三角形有关的角(含答案解析)

精品“正版”资料系列,由本公司独创。
旨在将“人教版”、”苏教版“、”北师大版“、”华师大版“等涵盖几乎所有版本的教材教案、课件、导学案及同步练习和检测题分享给需要的朋友。
本资源创作于2020年8月,是当前最新版本的教材资源。
包含本课对应内容,是您备课、上课、课后练习以及寒暑假预习的最佳选择。
11.2与三角形有关的角专题一利用三角形的内角和求角度1.如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=50°,则∠D=()A.15°B.20°C.25°D.30°2.如图,已知:在直角△ABC中,∠C=90°,BD平分∠ABC且交AC于D. 若AP平分∠BAC 且交BD于P,求∠BPA的度数.3.已知:如图1,线段AB、CD相交于点O,连接AD、CB,如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:__________;(2)在图2中,若∠D=40°,∠B=30°,试求∠P的度数;(写出解答过程)(3)如果图2中∠D和∠B为任意角,其他条件不变,试写出∠P与∠D、∠B之间的数量关系.(直接写出结论即可)专题二利用三角形外角的性质解决问题4.如图,∠ABD,∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,则∠P的度数为()A.15°B.20°C.25°D.30°5.如图,△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠A=40°,∠B=72°.(1)求∠DCE的度数;(2)试写出∠DCE与∠A、∠B的之间的关系式.(不必证明)6.如图:(1)求证:∠BDC=∠A+∠B+∠C;(2)如果点D与点A分别在线段BC的两侧,猜想∠BDC、∠A、∠ABD、∠ACD这4个角之间有怎样的关系,并证明你的结论.状元笔记【知识要点】1.三角形内角和定理三角形三个内角的和等于180°.2.直角三角形的性质及判定性质:直角三角形的两个锐角互余.判定:有两个角互余的三角形是直角三角形.3.三角形的外角及性质外角:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.性质:三角形的外角等于与它不相邻的两个内角的和.【温馨提示】1.三角形的外角是一边与另一边的延长线组成的角,而不是两边延长线组成的角.2.三角形的外角的性质中的内角一定是与外角不相邻的内角.【方法技巧】1.在直角三角形中已知一个锐角求另一个锐角时,可直接使用“直角三角形的两个锐角互余”.2.由三角形的外角的性质可得出:三角形的外角大于任何一个与它不相邻的内角.1.C 解析:∵∠ABC的平分线与∠ACB的外角平分线相交于点D,∴∠1=12∠ACE,∠2=12∠ABC.又∵∠D=∠1-∠2,∠A=∠ACE-∠ABC,∴∠D=12∠A=25°.故选C.2.解:(法1)因为∠C=90°,所以∠BAC+∠ABC=90°,所以12(∠BAC+∠ABC)=45°.因为BD平分∠ABC,AP平分∠BAC ,∠BAP=12∠BAC,∠ABP=12∠ABC ,即∠BAP+∠ABP=45°,所以∠APB=180°-45°=135°.(法2)因为∠C=90°,所以∠BAC+∠ABC=90°,所以12(∠BAC+∠ABC)=45°,因为BD平分∠ABC,AP平分∠BAC,∠DBC=12∠ABC,∠PAC=12∠BAC ,所以∠DBC+∠PAD=45°.所以∠APB=∠PDA+∠PAD =∠DBC+∠C+∠PAD=∠DBC+∠PAD+∠C =45°+90°=135°.3.解:(1)∠A+∠D=∠B+∠C;(2)由(1)得,∠1+∠D=∠3+∠P,∠2+∠P=∠4+∠B,∴∠1-∠3=∠P-∠D,∠2-∠4=∠B-∠P,又∵AP、CP分别平分∠DAB和∠BCD,∴∠1=∠2,∠3=∠4,∴∠P-∠D=∠B-∠P,即2∠P=∠B+∠D,∴∠P=(40°+30°)÷2=35°.(3)2∠P=∠B+∠D.4.B 解析:延长DC,与AB交于点E.根据三角形的外角等于不相邻的两内角和,可得∠ACD=50°+∠AEC=50°+∠ABD+10°,整理得∠ACD-∠ABD=60°.设AC与BP相交于点O,则∠AOB=∠POC,∴∠P+12∠ACD=∠A+12∠ABD,即∠P=50°-12(∠ACD-∠ABD)=20°.故选B.5.解:(1)∵∠A=40°,∠B=72°,∴∠ACB=68°.∵CD平分∠ACB,∴∠DCB=12∠ACB=34°.∵CE是AB边上的高,∴∠ECB=90°-∠B=90°-72°=18°.∴∠DCE=34°-18°=16°.(2)∠DCE=12(∠B-∠A).6.(1)证明:延长BD交AC于点E,∵∠BEC是△ABE的外角,∴∠BEC=∠A+∠B.∵∠BDC是△CED的外角,∴∠BDC=∠C+∠DEC=∠C+∠A+∠B.(2)猜想:∠BDC+∠ACD+∠A+∠ABD=360°.证明:∠BDC+∠ACD+∠A+∠ABD=∠3+∠2+∠6+∠5+∠4+∠1=(∠3+∠2+∠1)+(∠6+∠5+∠4)=180°+180°=360°.教学反思1 、要主动学习、虚心请教,不得偷懒。
人教版数学八年级上册第11章 三 角形 同步测试题含答案

A.1<x< B.
C.
D.
12.(乐亭县期末)如图,在△BCD 中,BC=4,BD=5, (1)求 CD 的取值范围; (2)若 AE∥BD,∠A=55°,∠BDE=125°,求∠C 的度数.
13.(富顺县校级期末)如图所示,已知 P 是△ABC 内一点,试说明 PA+PB+PC> (AB+BC+AC).
.
故答案为: .
直角三角形.两个锐角互为余角,故一个锐角是 ,则它的另一个锐
角的大小是
.
此题考查的是直角三角形的性质,两锐角互余.
14.【答案】
【解析】解:如图角板的常数以及三角形的一个外角等于与它不相邻的两个内
角的和求出 的度数,再根据直角等于 计算即可得解.
本题考查了三角形的外角性质以及三角形内角和定理,熟知三角板的
如图 ,已知点 P 是 的内角平分线 BP 与 CP 的交点,点 M 是
的 外 角 平 分 线 BM 与 CM 的 交 点 , 则
,
证明规律 1:
、CP 是 的角平分线,
,
,
,
,
.
证明规律 2:
,
,
,
.
请解决以下问题:
写出上述证明过程中步骤 的依据是:______;
如图 ,已知点 Q 是 的内角平分线 BQ 与 的外角
3. 从九边形的一个顶点出发可以引出的对角线的条数为( )
A.3
B.4
C.6
D.9
4. 如图,足球图片正中的黑色正五边形的内角和是
A.180°
B.360°
D.
,
,则 等于
A.
B.
C.
D.
7. 一个三角形三个内角的度数之比是 ,则这个三角形一定是
人教版八年级上册 第11章《三角形》 同步练习及答案(11.3)

第11章《三角形》同步练习(§11.3 多边形及其内角和)班级学号姓名得分1.填空:(1)平面内,由____________________________________________________________叫做多边形.组成多边形的线段叫做______.如果一个多边形有n条边,那么这个多边形叫做______.多边形____________叫做它的内角,多边形的边与它的邻边的______组成的角叫做多边形的外角.连结多边形________________的线段叫做多边形的对角线.(2)画出多边形的任何一条边所在直线,如果整个多边形都在______,那么这个多边形称作凸多边形.(3)各个角______,各条边______的______叫做正多边形.2.(1)n边形的内角和等于____________.这是因为,从n边形的一个顶点出发,可以引______条对角线,它们将此n边形分为______个三角形.而这些三角形的内角和的总和就是此n边形的内角和,所以,此n边形的内角和等于180°×______.(2)请按下面给出的思路,进行推理填空.如图,在n边形A1A2A3…A n-1A n内任取一点O,依次连结______、______、______、……、______、______.则它们将此n边形分为______个三角形,而这些三角形的内角和的总和,减去以O为顶点的一个周角就是此多边形的内角和.所以,n边形的内角和=180°×______-( )=( )×180°.3.任何一个凸多边形的外角和等于______.它与该多边形的______无关.4.正n边形的每一个内角等于______,每一个外角等于______.5.若一个正多边形的内角和2340°,则边数为______.它的外角等于______.6.若一个多边形的每一个外角都等于40°,则它的内角和等于______.7.多边形的每个内角都等于150°,则这个多边形的边数为______,对角线条数为______.8.如果一个角的两边分别垂直于另一个角的两边,其中一个角为65°,则另一个角为______度.9.选择题:(1)如果一个多边形的内角和等于它的外角和的两倍,则这个多边形是( ).(A)四边形(B)五边形(C)六边形(D)七边形(2)一个多边形的边数增加,它的内角和也随着增加,而它的外角和( ).(A)随着增加(B)随着减少(C)保持不变(D)无法确定(3)若一个多边形从一个顶点,只可以引三条对角线,则它是( )边形.(A)五(B)六(C)七(D)八(4)如果一个多边形的边数增加1,那么它的内角和增加( ).(A)0°(B)90°(C)180°(D)360°(5)如果一个四边形四个内角度数之比是2∶2∶3∶5,那么这四个内角中( ).(A)只有一个直角(B)只有一个锐角(C)有两个直角(D)有两个钝角(6)在一个四边形中,如果有两个内角是直角,那么另外两个内角( ).(A)都是钝角(B)都是锐角(C)一个是锐角,一个是直角(D)互为补角10.已知:如图四边形ABCD中,∠ABC的平分线BE交CD于E,∠BCD的平分线CF交AB于F,BE、CF相交于O,∠A=124°,∠D=100°.求∠BOF的度数.11.(1)已知:如图1,求∠1+∠2+∠3+∠4+∠5+∠6___________.图1(2)已知:如图2,求∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8____________.图212.如图,在图(1)中,猜想:∠A+∠B+∠C+∠D+∠E+∠F=______度.请说明你猜想的理由.图1如果把图1成为2环三角形,它的内角和为∠A+∠B+∠C+∠D+∠E+∠F;图2称为2环四边形,它的内角和为∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H;图2则2环四边形的内角和为_____________________________________________度;2环五边形的内角和为________________________________________________度;2环n边形的内角和为________________________________________________度.13.一张长方形的桌面,减去一个角后,求剩下的部分的多边形的内角和.14.一个多边形的内角和与某一个外角的度数总和为1350°,求这个多边形的边数.15.如果一个凸多边形除了一个内角以外,其它内角的和为2570°,求这个没有计算在内的内角的度数.16.小华从点A出发向前走10米,向右转36°,然后继续向前走10米,再向右转36°,他以同样的方法继续走下去,他能回到点A吗?若能,当他走回点A时共走了多少米?若不能,写出理由.参考答案1.略.2.(1)(n -2)×180°,n -3,n -2,n -2.(2)OA 1,OA 2,OA 3……,OA n -1,OA n ,n ,n ,360°,(n -2).3.360°,边数. 4.⋅⨯-n nn oo 360,180)2( 5.十五,24°. 6.1260°. 7.12,54. 8.65°或115°.9.(1)C ,(2)C ,(3)B ,(4)C ,(5)A ,(6)D 10.68°11.(1)360°;(2)360°.12.(1)360°;(2)720°;(3)1080°;(4)2(n -2)×180°.13.180°或360°或540°.14.九.提示:设多边形的边数为n ,某一个外角为α.则(n -2)×180+α =1350. 从而1809071801350)2(αα-+=-=-n . 因为边数n 为正整数,所以α =90,n =9.15.130°.提示:设多边形的边数为n ,没有计算在内的内角为x °.(0<x <180)则(n -2)×180=2570+x . 从而⋅++=-18050142x n 因为边数n 为正整数,所以x =130.16.可以走回到A 点,共走100米.。
人教版2020-2021学年8年级上册同步练习试题及答案:第11章《三角形》-同步练习及答案(11.2)

人教版2020-2021学年8年级上册同步练习试题及答案第11章《三角形》同步练习(§11.2 与三角形有关的角)班级学号姓名得分1.填空:(1)三角形的内角和性质是____________________________________________________.(2)三角形的内角和性质是利用平行线的______与______的定义,通过推理得到的.它的推理过程如下:已知:△ABC,求证:∠BAC+∠ABC+∠ACB=______.证明:过A点作______∥______,则∠EAB=______,∠F AC=______.(___________,___________)∵∠EAF是平角,∴∠EAB+______+______=180°.( )∴∠ABC+∠BAC+∠ACB=∠EAB+∠______+∠______.( )即∠ABC+∠BAC+∠ACB=______.2.填空:(1)三角形的一边与_________________________________________叫做三角形的外角.因此,三角形的任意一个外角与和它相邻的三角形的一个内角互为______.(2)利用“三角形内角和”性质,可以得到三角形的外角性质?如图,∵∠ACD是△ABC的外角,∴∠ACD与∠ACB互为______,即∠ACD=180°-∠ACB.①又∵∠A+∠B+∠ACB=______,∴∠A+∠B=______.②由①、②,得∠ACD=______+______.∴∠ACD>∠A,∠ACD>∠B由上述(2)的说理,可以得到三角形外角的性质如下:三角形的一个外角等于____________________________________________________.三角形的一个外角大于____________________________________________________. 3.(1)已知:如图,∠1、∠2、∠3分别是△ABC的外角,求:∠1+∠2+∠3.(2)结论:三角形的外角和等于______.4.已知:如图,BE与CF相交于A点,试确定∠B+∠C与∠E+∠F之间的大小关系,并说明你的理由.5.已知:如图,CE⊥AB于E,AD⊥BC于D,∠A=30°,求∠C的度数.6.依据题设,写出结论,想一想,为什么?已知:如图,△ABC中,∠ACB=90°,则:(1)∠A+∠B=______.即∠A与∠B互为______;(2)若作CD⊥AB于点D,可得∠BCD=∠______,∠ACD=∠______.7.填空:(1)△ABC中,若∠A+∠C=2∠B,则∠B=______.(2)△ABC中,若∠A∶∠B∶∠C=2∶3∶5,则∠A=______,∠B=______,∠C=______.(3)△ABC中,若∠A∶∠B∶∠C=1∶2∶3,则它们的相应邻补角的比为______.(4)如图,直线a∥b,则∠A=______度.(5)已知:如图,DE⊥AB,∠A=25°,∠D=45°,则∠ACB=______.(6)已知:如图,∠DAC=∠B,∠ADC=115°,则∠BAC=______.(7)已知:如图,△ABC中,∠ABC=∠C=∠BDC,∠A=∠ABD,则∠A=______(8)在△ABC中,若∠B-∠A=15°,∠C-∠B=60°,则∠A=______,∠B=______,∠C=______.8.已知:如图,一轮船在海上往东行驶,在A处测得灯塔C位于北偏东60°,在B处测得灯塔C位于北偏东25°,求∠ACB.9.已知:如图,在△ABC中,AD、AE分别是△ABC的高和角平分线.(1)若∠B=30°,∠C=50°,求∠DAE的度数.(2)试问∠DAE与∠C-∠B有怎样的数量关系?说明理由.10.已知:如图,O是△ABC内一点,且OB、OC分别平分∠ABC、∠ACB.(1)若∠A=46°,求∠BOC;(2)若∠A=n°,求∠BOC;(3)若∠BOC=148°,利用第(2)题的结论求∠A.11.已知:如图,O是△ABC的内角∠ABC和外角∠ACE的平分线的交点.(1)若∠A=46°,求∠BOC;(2)若∠A=n°,用n的代数式表示∠BOC的度数.12.类比第10、11题,若O是△ABC外一点,OB、OC分别平分△ABC的外角∠CBE、∠BCF,若∠A=n°,画出图形并用n的代数表示∠BOC.13.如图,点M是△ABC两个内角平分线的交点,点N是△ABC两个外角平分线的交点,如果∠CMB;∠CNB=3∶2求∠CAB的度数.14.如图,已知线段AD、BC相交于点Q,DM平分∠ADC,BM平分∠ABC,且∠A=27°,∠M=33°,求∠C的度数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020-2021学年八年级数学同步优化训练:第11章三角形章末检测一.选择题(每题4分,共40分)1.下列长度的三根木棒能组成三角形的是()A.3,4,8 B.4,4,8 C.5,6,10 D.6,7,14 2.下列图形中,不是运用三角形的稳定性的是()A.房屋顶支撑架B.自行车三脚架C.拉闸门D.木门上钉一根木条3.正六边形的每个内角度数是()A.60°B.90°C.108°D.120°4.有长为10,7,5,2的四根木条,选其中三根组成三角形的是()A.10,7,5 B.10,7,2 C.10,5,2 D.7,5,2 5.如图:∠A=50°,BP平分∠ABC,DP平分∠ADC,∠P=20°,则∠C=()A.20°B.15°C.5°D.10°6.如图,是一块三角形木板的残余部分,量得∠A=110°,∠B=30°,这块三角形木板缺少的角是()A.30°B.40°C.50°D.60°7.如图,在△ABC中,∠B=60°,AD是△ABC的外角的平分线,DE⊥AC,则∠γ=()A.120°﹣∠βB.90°﹣∠βC.60°﹣∠βD.2∠β﹣60°8.如图,点E、F分别在AB、CD上,∠B=40°,∠C=60°,则∠1+∠2等于()A.70°B.80°C.90°D.100°9.有四根长度分别为3,4,5,x(x为正整数)的木棒,从中任取三根,首尾顺次相接都能组成一个三角形,则组成的三角形的周长()A.最小值是11 B.最小值是12 C.最大值是14 D.最大值是15 10.如图,AE是△ABC的角平分线,AD是△AEC的角平分线,若∠BAC=80°,则∠EAD=()A.30°B.45°C.20°D.60°二.填空题(每题4分,共20分)11.把一副常用的三角尺按如图所示的方式拼在一起,则∠ABC=°.12.如果正n边形的内角是它中心角的两倍,那么边数n的值是.13.如图,已知△OAB中,∠AOB=70°,∠OAB的角平分线与△OBA的外角∠ABN的平分线所在的直线交于点D,则∠ADB的大小为.14.如图,在△ABC中,AD⊥BC于D,那么图中以AD为高的三角形共有个.15.一副直角三角板如上图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,则∠DBC=°.三.解答题(每题10分,共60分)16.如图1:△ABC中,AD是高,AE是∠BAC的平分线,∠ABC=40°,∠ACB=70°.(1)求∠EAD的度数.(2)当∠ABC=α,∠ACB=β,请用α.β表示∠EAD,并写出推导过程(3)当AE是∠BAC的外角∠FAC的平分线,如图2,则此时∠EAD的度数是多少,当∠ABC=α,∠ACB=β,用α,β表示,直接写出结果.17.如图,AD,AE分别是△ABC的角平分线和高线,∠B=45°,∠C=73°.(1)求∠ADB的度数;(2)求∠DAE的度数.18.已知△ABC,P是平面内任意一点(A、B、C、P中任意三点都不在同一直线上).连接PB、PC,设∠PBA=x°,∠PCA=y°,∠BPC=m°,∠BAC=n°.(1)如图,当点P在△ABC内时,①若n=80,x=10,y=20,则m=;②探究x、y、m、n之间的数量关系,并证明你得到的结论.(2)当点P在△ABC外时,直接写出x、y、m、n之间所有可能的数量关系,并画出相应的图形.19.已知:在△ABC中,且∠BAC=70°,AD是△ABC的角平分线,点E是AC边上的一点,点F为直线AB上的一动点,连结EF,直线EF与直线AD交于点P,设∠AEF=α°.(1)如图1,若DE∥AB,则:①∠ADE的度数是.②当∠DPE=∠DEP时,∠AEF=度;当∠PDE=∠PED时,∠AEF=度.(2)如图2,若DE⊥AC,则是否存在这样的α的值,使得△DPE中有两个相等的角?若存在,求出α的值;若不存在,说明理由.20.动手操作:一个三角形的纸片ABC,沿DE折叠,使点A落在点Aˊ处.观察猜想(1)如图1,若∠A=40°,则∠1+∠2=°;若∠A=55°,则∠1+∠2=°;若∠A=n°,则∠1+∠2=°.探索证明:(2)利用图1,探索∠1、∠2与∠A有怎样的关系?请说明理由.拓展应用(3)如图2,把△ABC折叠后,BA′平分∠ABC,CA′平分∠ACB,若∠1+∠2=108°,利用(2)中结论求∠BA′C的度数.21.如图1,点A、B在直线l1上,点C、D在直线l2上,AE平分∠BAC,CE平分∠ACD.且∠EAC+∠ACE=90°(1)判断直线l1与l2的位置关系,并说明理由;(2)如图2,P为线段AC上一定点,Q为直线l2上一动点,当点Q在直线l2上运动时(不与点C合),猜想∠CPQ、∠CQP与∠BAC之间的数量关系,并说明理由.参考答案一.选择题1.解:A、3+4<8,不能构成三角形;B、4+4=8,不能构成三角形;C、5+6>10,能够组成三角形;D、7+6<14,不能组成三角形.故选:C.2.解:伸缩的拉闸门是利用了四边形的不稳定性,A、B、D都是利用了三角形的稳定性,故选:C.3.解:根据多边形的内角和定理可得:正六边形的每个内角的度数=(6﹣2)×180°÷6=120°.故选:D.4.解:A、∵7+5>10,∴5,7,10可以构成三角形,故此选项符合题意;B、∵7+2<10,∴2,7,10无法构成三角形,故此选项不符合题意;C、∵5+2<10,∴2,5,10无法构成三角形,故此选项不符合题意;D、∵5+2=7,∴2,5,7无法构成三角形,故此选项不符合题意;故选:A.5.解:如图,延长PD交BC于M.设∠ADP=∠CDP=x,∠ABP=∠PBC=y.∵∠ADC=∠A+∠ABC+∠C,∴2x=2y+50°+∠C①∵∠PDC=∠DMC+∠C,∠DMC=∠PBC+∠P,∴x=∠C+∠P+y,∴x=∠C+20°+y②,①代入②可得∠C=10°,故选:D.6.解:根据三角形的内角和定理第三个角=180°﹣110°﹣30°=40°,故选:B.7.解:∠FAC=∠B+∠ACB=60°+∠β,∵AD是△ABC的外角的平分线,∴∠DAC=∠FAC=(60°+∠β),∴∠γ=90°﹣(60°+∠β)=60°﹣∠β,故选:C.8.解:∵∠B+∠C+∠CFE+∠BEF=360°,∠1+∠BEF=180°,∠2+∠CFE=180°,∴∠B+∠C+∠CFE+∠BEF=∠1+∠BEF+∠2+∠CFE,∴∠1+∠2=∠B+∠C=100°.故选:D.9.解:由题意知,3,4,x和3,5,x都能组成三角形,∴2<x<7,∵x为正整数,∴x取3或4或5或6,要组成三角形的周长最小,即:x=3时,三边为3,3,4,其最小周长为3+3+4=10;要组成的三角形的周长最大,即:x=6,三边为4,5,6,其周长最大值为4+5+6=15.故选:D.10.解:∵∠BAC=80°,AE是△ABC的角平分线,∴∠EAC=∠BAC=40°,∵AD是△AEC的角平分线,∴∠EAD=∠EAC=20°.故选:C.二.填空题(共5小题)11.解:∵∠BAC=45°,∠C=60°,∴∠ABC=180°﹣45°﹣60°=75°.故答案为:75.12.解:依题意有=×2,解得n=6.故答案为:6.13.解:∠ABN﹣∠OAB=∠AOB=70°,∵AD平分∠OAB,BC平分∠ABN,∴∠ABC=∠ABN,∠BAD=∠OAB,∴∠ADB=∠ABC﹣∠BAD=35°,故答案为:35°.14.解:∵AD⊥BC于D,而图中有一边在直线CB上,且以A为顶点的三角形有6个,∴以AD为高的三角形有6个.故答案为:615.解:∵AB∥CF,∠A=60°,∴∠ACM=∠A=60°,∵∠BCA=30°,∴∠BCD=30°,∵∠EFD=90°,∠E=45°,∴∠EDC=∠E+∠EFD=135°,∴∠DBC=180°﹣30°﹣135°=15°,故答案为:15.三.解答题(共6小题)16.解:(1)∵∠ABC=40°,∠ACB=70°,∴∠BAC=180°﹣40°﹣70°=70°,又∵AE是∠BAC的平分线,∴∠BAE=∠BAC=35°.∵AD⊥BC,∴∠BAD=90°﹣40°=50°,∴∠EAD=∠BAD﹣∠BAE=50°﹣35°=15°.(2)∠DAE=(β﹣α),理由如下:∵∠B=α,∠C=β,∴∠BAC=180°﹣α﹣β.又∵AE是∠BAC的平分线,∴∠BAE=∠BAC=90°﹣α﹣β).∵∠BAD=90°﹣∠B=90°﹣α,∴∠DAE=∠BAD﹣∠BAE=90°﹣α﹣[90°﹣α﹣β)]=(β﹣α).(3)∠EAD=90°+,理由是:∵∠B=α,∠C=β,∴∠FAC=α+β,∵AE平分∠FAC,∴∠CAE=∠CAF=,∵AD⊥BC,∠C=β,∴∠DAC=90°﹣β,∴∠DAE=∠DAC+∠CAE=90°﹣β+=90°+.17.解:(1)因为∠B=45°,∠C=73°,所以∠BAC=180°﹣∠B﹣∠C=180°﹣45°﹣73°=62°.又因为AD是△ABC的角平分线,所以∠BAD=∠CAD=62°×=31°.所以△ABD中,∠ADB=180°﹣∠B﹣∠BAD=104°;(2)因为AE是△ABC的高,所以∠AED=90°,所以△ADE中,∠EAD=∠ADB﹣∠AED=104°﹣90°=14°.18.解:(1)①∵∠A=80°,∴∠ABC+∠ACB=100°,∵∠PBA=10°,∠PCA=20°,∴∠PBC+∠PCB=70°,∴∠BPC=110°,∴m=110,故答案为110.②结论:m=n+x+y.理由:∵∠A+∠ABC+∠ACB=∠A+∠PBA+∠PCA+∠PBC+∠PCB=180°,∠PBC+∠PCB+∠BPC=180°,∴∠A+∠PBA+∠PCA=∠BPC,∴m=n+x+y.(2)x、y、m、n之间所有可能的数量关系:①如图1中,m+x=n+y;②如图2中,n=x+m+y;③如图3中,n+x=m+y;④如图4中,x=m+n+y;⑤如图5中,y=m+n+x;⑥如图6中,x+y+m+n=360°19.解:(1)①∵∠BAC=70°,AD是△ABC的角平分线,∴∠BAD=∠BAC=35°,∵DE∥AB,∴∠ADE=∠BAD=35°,故答案为35°.②在△DPE中,∵∠ADE=35°,∴∠DPE=∠PED=(180°﹣35°)=72.5°,∵∠DPE=∠AEP+∠DAE,∴∠AEF=72.5°﹣35°=37.5°;∵当∠PDE=∠PED时,∠DPE=110°,∴∠AEF=∠DPE﹣∠DAE=75°,故答案为37.5,75;(2)在Rt△ADE中,∠ADE=90°﹣35°=55°.①当DP=DE时,∠DPE=62.5°,∠AEF=∠DPE﹣∠DAC=62.5°﹣35°=27.5°.②当EP=ED时,∠EPD=∠ADE=55°,∠AEF=∠DPE﹣∠DAC=55°﹣35°=20°.③当DP=PE时,∠EPD=180°﹣2×55°=70°,∠AEF=∠DPE﹣∠DAC=70°﹣35°=35°.④如图2中,当点F在BA的延长线上时,只有DE=DP,此时∠AEF=90°﹣27.5°=62.5°.⑤当点F在AB的延长线上时,只有DE=DP,同法可得α=117.5°.20.解:(1)∵点A沿DE折叠落在点A′的位置,∴∠ADE=∠A′DE,∠AED=∠A′ED,∴∠ADE=(180°﹣∠1),∠AED=(180°﹣∠2)在△ADE中,∠A+∠ADE+∠AED=180°,∴40°+(180°﹣∠1)+(180°﹣∠2)=180°,整理得∠1+∠2=80°;同理∠A=55°,则∠1+∠2=110°;∠A=n°,则∠1+∠2=2n°;故答案为:80°;110°;2n°;(2)∠1+∠2=2∠A,理由:∵∠BDE、∠CED是△ADE的两个外角,∴∠BDE=∠A+∠AED,∠CED=∠A+∠ADE,∴∠BDE+∠CED=∠A+∠AED+∠A+∠ADE,∴∠1+∠ADE+∠2+∠AED=2∠A+∠AED+∠ADE,即∠1+∠2=2∠A;(3)由(1)∠1+∠2=2∠A,得2∠A=108°,∴∠A=54°,∵BA'平分∠ABC,CA'平分∠ACB,∴∠A'BC+∠A'CB=(∠ABC+∠ACB)=(180°﹣∠A)=90°﹣∠A.∴∠BA'C=180°﹣(∠A'BC+∠A'CB),=180°﹣(90°﹣∠A)=90°+∠A=90°+×54°=117°.21.解:(1)l1∥l2,理由如下:如图1中,∵AE平分∠BAC,CE平分∠ACD(已知),∴∠BAC=2∠1,∠ACD=2∠2(角平分线的定义),又∵∠1+∠2=90°(已知),∴∠BAC+∠ACD=2∠1+2∠2=2(∠1+∠2)=180°(等量代换),∴l1∥l2(同旁内角互补,两直线平行).(2)①如图2中,当Q在C点左侧时,过点P作PE∥l1,∵l1∥l2(已证),∴PE∥l2(同平行于一条直线的两直线互相平行),∴∠1=∠2,(两直线平行,内错角相等),∠BAC=∠EPC,(两直线平行,同位角相等),又∵∠EPC=∠1+∠CPQ,∴∠BAC=∠CQP+∠CPQ(等量代换).②如图3中,当Q在C点右侧时,过点P作PE∥l1,∵l1∥l2(已证),∴PE∥l2(同平行于一条直线的两直线互相平行),∴∠1=∠2,∠BAC=∠APE,(两直线平行,内错角相等),又∵∠EPC=∠1+∠CPQ,∵∠APE+∠EPC=180°(平角定义),∴∠CPQ+∠CQP+∠BAC=180°.。
