一维非稳态导热的数值计算
一维圆柱非稳态导热方程求解

一维圆柱非稳态导热方程是一个经典的物理问题,通常用于描述一个圆柱体在非均匀温度场中的热量传递过程。
为了求解这个问题,我们可以使用数值方法,如有限差分法、有限元法等。
有限差分法是一种常用的数值计算方法,其基本思想是将连续的时间和空间域离散化为一系列离散的网格点,并将偏微分方程转化为差分方程,从而可以通过计算差分方程来求解偏微分方程。
在一维圆柱非稳态导热方程中,我们可以将圆柱体离散化为一系列环形的网格,并使用有限差分法来求解方程。
具体而言,我们可以将时间域离散化为$N$ 个时刻$t_n$,将空间域离散化为 $M$ 个环形网格,每个网格的宽度为 $\Delta r$,中心为 $r_0$,边界为 $r_M$。
在每个时刻$t_n$,我们可以将非稳态导热方程转化为差分方程,并使用计算机编程语言(如Python、Matlab等)来计算差分方程,从而得到每个时刻每个网格的温度分布。
在计算过程中,我们需要设置初始条件和边界条件。
初始条件通常是指初始时刻每个网格的温度分布,边界条件通常是指圆柱体的表面温度和环境温度。
此外,我们还需要设置时间步长和空间步长,以控制计算的精度和稳定性。
通过使用有限差分法等数值方法,我们可以方便地求解一维圆柱非稳态导热方程,从而得到每个时刻每个网格的温度分布。
这种方法可以用于工程实际中的许多问题,如加热、冷却、热传导等。
课件:非稳态导热问题的数值解法

允许的最大迭代次数
第四章 导热问题的数值解法
24
开始
输入M,N,EPS,K,TTB,TLB,TRB,TBB
ti 1 TBB ti,M 1 TTB ti,j TLB tN 1,j TRB
迭代次数IT=0
TTi,j Tij
Ti ,j
1 4
(Ti
1,j
Ti 1,j
Ti,j 1 Ti,j 1 )
也可以写出其隐式差分格式即
1
t k 1 1 2
t2k 1 x 3
h4(tfk 1
t1k 1)
ec
x
2
tk 1 1
t1k
xt
x
h(t tf)
X
O
x
第四章 导热问题的数值解法
18
整理上式,得
t2k 1
t1k 1
hx
(
t
k f
1
t1k 1
)
ecx2 2
( t1k 1
t1k
)
令 Bi
h x
i-1
(m,i-1)
0 x
m-1, m, m+1 Mx
时间步长:从一个时层到下一个时层的间隔 称为时间步长
i 表示形式
第四章 导热问题的数值解法
3
一维、有内热源、常物性的非稳态导热问题离散方程 的建立过程——热平衡法建立内部节点的离散方程
考察(m,i)点,则扩散项可直接写出:
z
tm(i)1 tm(i) x
tk 1
tk 2
x
h(tfk
tk 1
)
c
x
2
t k 1 1
tk 1
边界的热容项
第四章 导热问题的数值解法
(完整word版)一维非稳态导热的数值计算

int i,j,l;
float cha;
float a,x,y,Fo,Bi;
float t[N][K],b[N][K];
/*打印出题目*/
printf("\t\t\t一维非稳态导热问题\t\t");
printf("\n\t\t\t\t\t\t----何鹏举\n");
printf("\n题目:补充材料练习题三\n");
/*时刻为零时,赋予初场温度*/
for(i=0;i<N;i++)
t[i][0]=1000;
/*循环开始,每次计算一个时刻*/
for(j=0;j<K-1;j++)
{
for(i=0;i<N;i++)
b[i][j]=t[i][j];
/*下面对每一个时刻进行迭代求解对应的温度分布,公式按传热学课本P178页公式*/
y=1;/*y代表Δτ*/
x=0.05/(N-1);
a=34.89/(7800*712);
Fo=(a*y)/(x*x);
Bi=233*x/34.89;
printf("\n显示格式条件:");
printf("\n1、Fo=%3.1f<0.5\t",Fo);
printf("\t2、1-2Fo*Bi-2Fo=%4.2f>0\n\n",1-2*Fo*Bi-2*Fo);
{
printf("\n");
l=0;
}
}ห้องสมุดไป่ตู้
getchar();/*为了是生成的exe文件结果算的后不会立即退出,方便观看*/
传热学-学习课件-4-4 一维非稳态导热问题的数值求解

1
2
a x2
2h cx
2
a x2
t
i
N
1
2h cx
tf
③对称点
t (i)
-1
t (i)
2
传热学 Heat Transfer
2.直接用差分代替微分
①向前差分(forward difference)
i
t
t
i
n
1
t
i
n
n,i
②向后差分(backward difference)
t
t
i
n
t
i
n
1
n,i
i n,i+1
n-1,i n,i n+1,
t
i
n
1
t
n
i
a
t (i1) n 1
2
t
( n
i
1
)
x2
t (i1) n 1
(1,1)
n,i-1 i
n
x
整理成隐式格式:
传热学 Heat Transfer
传热学 Heat Transfer
主讲老师:王舫 适用专业:能源与动力工程专业
传热学 Heat Transfer
§4.4 一维非稳态导热问题的数值求解
在非稳态导热问题中,不但需要对空间区域进 行离散,还需要对时间变量进行离散,接下来以一 个一维非稳态导热问题为例,重点介绍对非稳态项 的离散方法,以及不同离散方法对计算带来的影响 等。
第三章第三节 一维非稳态导热的分析解

θ
( x,τ θ0
)
=
μ1
+
2 sin μ1 sin μ1 cos
μ1
cos(
μ1
e x ) − μ12F0 δ
θ
(0,τ θ0
)
=
θ m (τ θ0
)
=
μ1
+
2 sin μ 1 sin μ1 cos
μ1
e − μ12 F0
第三节一维非稳态导热的分析解
θ
( x,τ θ0
)
=
μ1
+
2 sin μ1 sin μ1 cos
式中常数a ,b ,c ,d 见P75表3-3 a`,b`,c`,d`见P75表3-4
第三节一维非稳态导热的分析解
3 正规热状况的实用计算方法-线算图法
诺谟图
以无限大平板为例,F0>0.2 时,取其级数首项即可
θ (x,τ ) =θ0
μ1
+
2sin μ1 sin μ1 cos
μ1
e−μ12
F0
cos(μ1
第三节一维非稳态导热的分析解
上式化为:
∂θ = a ∂ 2θ
∂τ
∂x 2
θ =θ0
∂θ = 0 ∂x
0 < x < δ ,τ > 0 τ =0 x=0
− λ ∂θ = hθ x = δ ∂x
第三节一维非稳态导热的分析解
用分离变量法可得其分析解为:
θ
( x,τ θ0
)
=
∞
∑
n =1
2 sin( β nδ ) cos( β n x) β nδ + sin( β nδ ) cos( β nδ
4-3非稳态导热的数值计算

t k 1 i 1
)
tik
已知k时层的温度值,求k+1 时层的温度值要联立求解方 程组,即求解复杂,但无条件稳定(、x的取值不受 限制)。
三、边界节点的离散方程
t
1. 第三类边界条件:已知tf、h
tf、h
L
节点的热平衡:
N-1点导入 对流换热传 N节点内
+
=
N点的热量 入N点的热量 能的增量 0 1 N 1 N x
2t ( x2 )i,k
tk i 1
tk i 1
2tik
(x)2
节点 时层
( t
)i,k
t k 1 i
tik
空间用中心差分格式 时间用向前差分格式
将上面两式代入微分方程:
t k 1 i
tik
a
tk i 1
tk i 1
(x)2
2tik
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
tik 1
k N
稳定性条件: 1 2Fo Bi 2Fo 0
或:
Fo 1 2Bi 2
2. 第二类边界条件:已知qw
建立节点0的差分方程(显式格式) t
t k 1 0
2Fo t1k
(1
2Fo)t0k
tf、
L
稳定性条件:
1 2Fo 0
0 1 N 1 N x 绝热
THANKS
非稳态导热 的数值计算
讨论: 一维、无内热源、常物性、非稳态导热
t f (x, )
t
a
2t x 2
一、显式差分格式
1. 内节点
k 1
1) 离散化: t f (x, )
k
一维圆柱非稳态导热方程求解

一维圆柱非稳态导热方程求解引言在工程和科学领域中,导热方程是研究物体内部温度分布变化的重要方程。
本文将介绍一维圆柱非稳态导热方程的求解方法。
问题描述考虑一个半径为 R 的圆柱体,其内部由一个材料填充。
我们想要求解该圆柱体内部的温度分布,其中的热传导过程遵循非稳态导热方程。
在一维情况下,非稳态导热方程可以表示为:equation1equation1其中,T 是温度关于时间和半径的函数,α 是热扩散系数。
数值方法为了求解该方程,我们将应用有限差分法,离散化时间和半径的变量。
首先,我们将时间区域 [0, T] 离散化为 N 个等间距的时间步长,得到:equation2equation2其中,Δt 是时间步长,N 是总的时间步数。
接下来,我们将半径区域 [0, R] 离散化为 M 个等间距的半径步长,得到:equation3equation3其中,Δr 是半径步长,M 是总的半径步数。
将温度T 在时间和半径的离散点上进行近似,我们可以写出离散的导热方程为:equation4equation4其中,上标 n 表示时间步数,下标 i 表示半径步数。
由于我们已经将时间和半径离散化,上述方程可以重写为一个递推关系:equation5equation5数值实验我们将通过一个简单的数值实验来验证我们的数值方法。
设定圆柱体半径 R = 1,热扩散系数α = 1。
令边界条件为半径为 R 处的温度始终为 0,初始条件为半径为 R/2 处的温度为 1,其他位置的温度为 0。
在使用递推关系计算之前,需要选择合适的时间步长Δt 和半径步长Δr。
一般来说,选择小的步长可以提高数值解的准确性,但同时也会增加计算时间。
在这里,我们选择Δt = 0.001,Δr = 0.1。
我们使用一个循环来逐步计算每个时间步骤的温度分布,并在每个时间步骤结束后,使用画图软件绘制温度分布图。
结果与讨论经过数值计算和绘图,我们得到了随时间演化的温度分布图。
一维圆柱非稳态导热方程求解

一维圆柱非稳态导热方程求解摘要:1.问题背景及意义2.一维圆柱非稳态导热方程3.求解方法及步骤4.数值例子与分析5.应用及拓展正文:一、问题背景及意义在工程热传导领域,一维圆柱非稳态导热问题具有广泛的应用背景。
例如在金属加工、半导体制造、建筑节能等许多实际问题中,都需要研究热传导过程。
对于一维圆柱非稳态导热问题,了解其求解方法及过程有助于分析和优化实际工程中的热传导现象。
二、一维圆柱非稳态导热方程考虑一维圆柱非稳态导热问题,我们可以得到以下偏微分方程:$$frac{partial u}{partial t} = kfrac{partial^2 u}{partial r^2}$$其中,$u(r, t)$ 表示圆柱的热量分布,$k$ 为热传导系数,$r$ 为圆柱半径,$t$ 为时间。
三、求解方法及步骤1.边界条件处理:根据实际问题,给出圆柱的边界条件,如温度边界条件、热流密度边界条件等。
2.离散化:将空间坐标和时间坐标进行离散化,得到离散化的偏微分方程。
3.数值求解:采用有限差分法、有限元法等数值方法求解离散化方程。
4.分析结果:根据求解结果,分析圆柱热量分布随时间和空间的变化规律。
四、数值例子与分析以一个简单的一维圆柱非稳态导热问题为例,给出数值求解过程及结果分析。
1.设定参数:热传导系数$k = 10$,圆柱半径$r = 0.1$,时间步长$Delta t = 0.01$,空间步长$Delta r = 0.001$。
2.边界条件:圆柱表面受到均匀热流密度作用,即$q = 100$。
3.数值求解:采用有限差分法求解离散化方程。
4.结果分析:通过观察不同时刻的热量分布图,可以发现热量在圆柱内部传播的速度和规律。
根据分析,可以提出优化热传导过程的方法和措施。
五、应用及拓展一维圆柱非稳态导热方程求解方法不仅适用于金属加工、半导体制造等热传导领域,还可以拓展到其他领域,如地球物理学、生物医学等。
通过改变边界条件和相关参数,可以研究不同条件下一维圆柱非稳态导热现象的特点。
一维非稳态对流换热

一维非稳态对流换热
一维非稳态对流换热是指在一维方向上的流体流动中,由于温度差异而导致的换热过程。
非稳态表示系统的温度分布随时间变化,而对流表示热量通过流体的流动来传递。
一维非稳态对流换热过程可以用非定常对流换热方程描述,该方程可以表示为:
∂T/∂t = α * ∂²T/∂x²
其中,T是温度的分布随时间和空间的函数,t是时间,x是空间位置,∂T/∂t表示温度随时间的变化率,∂²T/∂x²表示温度随空间位置的二阶导数,α是热扩散系数。
该方程描述的是温度随时间和空间位置的变化率,它说明非稳态传热过程中,温度的变化与传热速率有关。
解析解一般比较复杂,可以通过数值方法进行求解,如有限差分法、有限元法等。
在实际应用中,一维非稳态对流换热常见于许多工程和自然过程中,如管道内的流体冷却、物体表面的对流传热等。
研究一维非稳态对流换热过程有助于理解和优化这些过程,从而提高热能利用效率和工程设备的性能。
一维非稳态导热问题的数值解

一维非稳态导热问题的数值解计算传热学程序报告姓名:学号:学院:能源与动力工程学院专业:工程热物理日期:2022年5月25日求解下列热传导问题:2T1T0(0某L)2t某T(某,0)0T(0,t)1,T(L,t)0L1,11.方程离散化对方程进行控制体积分得到:ttt2T1d某dtw某2etttTwtd某dtettt[(TT1)e()w]dt某某ew(TttTt)d某非稳态项:选取T随某阶梯式变化,有ew(TttTt)d某(TpttTpt)某扩散项:选取一阶导数随时间做显示变化,有ttt[(TTTT)e()w]dt[()te()tw]t某某某某进一步取T随某呈分段线性变化,有(TTWTTTPT)eE,()wP某(某)e某(某)w整理可以得到总的离散方程为:t1TEttTPtTEt2TPtTWt某22.计算空间和时间步长取空间步长为:h=L/N网格Fourier数为:F0t某2t(小于0.5时稳定)2某时间步长为:nF03.建立温度矩阵与边界条件T=one(N+1,M+1)T(:,1)=Ti(初始条件温度都为0)T(1,:)=To(边界条件某=0处温度为1)T(N+1,:)=Te(边界条件某=L处温度为0)4.差分法求解温度由离散方程可得到:ttttttTEF0(TE2TPTW)TPh2转化为相应的温度矩阵形式:T(m,k1)F0[T(m1,k)T(m1,k)2T(m,k)]T(m,k)5.输入界面考虑到方程的变量,采用inputdlg函数设置5个输入变量,对这5个变量设置了默认值,如图1所示。
在计算中可以改变不同的数值,得到不同的结果,特别注意稳定条件的临界值是0.5。
根据设置的默认值,得到的计算结果如图2所示。
图1matlab变量输入界面图2默认值的计算结果6.结果分析根据上面的分析,给出了程序的输入界面,以及默认值状态下的数值解。
可以通过改变不同的输入值,得到需要的分析结果,总结出了下面4点结论:(1)取F0=0.48,得到一维非稳态导热结果如下图所示图2F0=0.48时一维非稳态导热从图中可以看出,对于长度L=1的细杆,初始时刻t=0时温度为0,边界条件某=0时,T=1,边界条件某=1时,T=0。
一维非稳态导热CRANK-NICOLSON解法

一维非稳态导热CRANK-NICOLSON解法题目:数值计算一维非稳态导热,长度1米的不锈钢棒原来温度都是0度,一端温度突然变为300度,并保存不变,采用CRANK-NICOLSON 方法数值计算不锈钢内温度分布随时间的变化。
解法:一维导热微分方程边界条件为u(0,t)=0;u(a0,t)=300初值u(x,0)=0;主程序clcclearuX=1; %不锈钢长1米uT=2000; %时长2000秒M=10; %空间轴等分区间数N=1000; %时间轴等分区间数rou=8030; %不锈钢密度cp=502.48; %不锈钢热容kk=16.27; %不锈钢导热率D=kk/rou/cp; %扩散系数phi=inline('0'); %初值psi1=inline('0'); %左边界psi2=inline('300'); %右边界%计算步长dx=uX/M;%x的步长dt=uT/N;%t的步长x=(0:M)*dx;r=D*dt/dx/dx;%步长比Diag=zeros(1,M-1);%矩阵的对角线元素Low=zeros(1,M-2);%矩阵的下对角线元素Up=zeros(1,M-2);%矩阵的上对角线元素for i=1:M-2Diag(i)=1+r;Low(i)=-r/2;Up(i)=-r/2;endDiag(M-1)=1+r;%计算初值和边值U=zeros(M+1,N+1);for i=1:M+1U(i,1)=phi(x(i));endfor j=1:N+1U(1,j)=psi1(t(j));U(M+1,j)=psi2(t(j));endB=zeros(M-1,M-1);for i=1:M-2B(i,i)=1-r;B(i,i+1)=r/2;B(i+1,i)=r/2;endB(M-1,M-1)=1-r;%逐层求解,需要使用追赶法(调用函数EqtsForwardAndBackward)for j=1:Nb1=zeros(M-1,1);b1(1)=r*(U(1,j+1)+U(1,j))/2;b1(M-1)=r*(U(M+1,j+1)+U(M+1,j))/2;b=B*U(2:M,j)+b1;U(2:M,j+1)=zhuiganfa(Low,Diag,Up,b);endU=U';%作出图形xlabel('空间变量x')ylabel('时间变量t')shading interp程序用到了追赶法子程序,代码如下function x=zhuiganfa(L,D,U,b)%追赶法求解三对角线性方程组Ax=b%检查参数的输入是否正确n=length(D);m=length(b);n1=length(L);n2=length(U);if n-n1 ~= 1 || n-n2 ~= 1 || n ~= mdisp('输入参数有误!')x=' ';return;end%追的过程for i=2:nL(i-1)=L(i-1)/D(i-1);D(i)=D(i)-L(i-1)*U(i-1);endx=zeros(n,1);x(1)=b(1);for i=2:nx(i)=b(i)-L(i-1)*x(i-1);end%赶的过程x(n)=x(n)/D(n);for i=n-1:-1:1x(i)=(x(i)-U(i)*x(i+1))/D(i);endreturn;运行主程序,最终得到如图所示结果。
一维非稳态导热方程求解(附Matlab程序)
%%%%%%本文来自互联网%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
初值条件: T ( x, 0) 4 x 4 x ;
2
(0 x 1, 0 t 0.2, a 1)
边值条件:
T (0, t ) 0 ; T (1, t ) 0
使用差分公式
Txx ( xi , t j )
T ( xi h, t j ) 2T ( xi , t j ) T ( xi h, t j ) h2 Tt ( xi , t j ) T ( xi , t j k ) T ( xi , t j ) k
O( h 2 )
Ti 1, j 2T i , j Ti 1, j h2
O( k )
Ti , j 1 Ti , j k
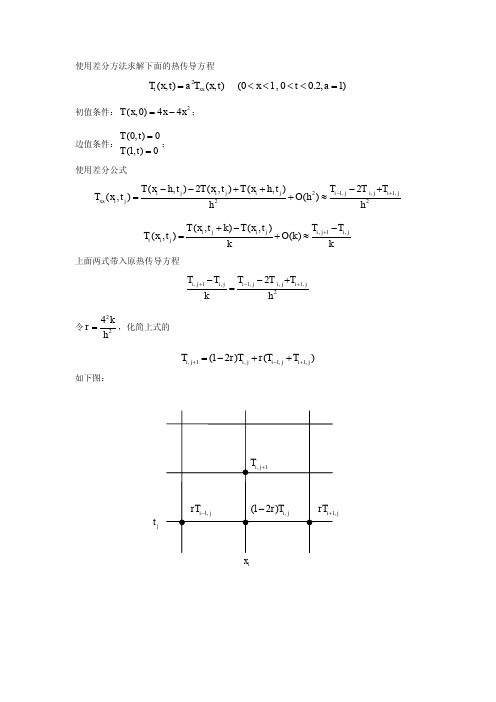
上面两式带入原热传导方程
Ti , j 1 Ti , j k 42 k 令 r 2 ,化简上式的 h
Ti 1, j 2T i , j Ti 1, j h2
% 边值条件: % u(a,t)=g1(t) % u(b,t)=g2(t) % % 参数说明 % c:方程中的系数 % f:初值条件 % g1,g2:边值条件 % xspan=[a,b]: x 的取值范围 % tspan=[ts,tf]:t 的取值范围 % ngrid=[n,m]:网格数量, m 为 x 网格点数量, n 为 t 的网格点数量 % U:方程的数值解 % x,t: x 和 t 的网格点 n=ngrid(1); m=ngrid(2); h=range(xspan)/(m-1); x=linspace(xspan(1),xspan(2),m); k=range(tspan)/(n-1); t=linspace(tspan(1),tspan(2),n); r=c^2*k/h^2; if r>0.5 error('为了保证算法的收敛,请增大步长 h 或减小步长 k!') end s=1-2*r; U=zeros(ngrid); % 边界条件 U(:,1)=g1(t); U(:,m)=g2(t); % 初值条件 U(1,:)=f(x); % 差分计算 for j=2:n for i=2:m-1 U(j,i)=s*U(j-1,i)+r*(U(j-1,i-1)+U(j-1,i+1)); end end
一维圆柱非稳态导热方程求解

一维圆柱非稳态导热方程求解
一维圆柱非稳态导热方程描述了圆柱体内部温度随时间变化的关系。
方程可以写成如下形式:
ρc ∂T/∂t = ∂/∂r (r k ∂T/∂r)
其中,T 是温度随位置和时间的函数,ρ 是圆柱体材料的密度,c 是材料的比热容,k 是材料的导热系数,r 是圆柱体的半径,t 是时间。
为了求解上述方程,需要给定边界条件和初始条件。
常见的边界条件包括固定温度边界条件和热流边界条件。
以下是求解一维圆柱非稳态导热方程的一般步骤:
1. 建立一维圆柱体的坐标系。
选择一个适当的坐标系,例如直角坐标系或极坐标系。
2. 建立方程。
根据给定的物理问题,建立一维圆柱非稳态导热方程。
3. 写出边界条件和初始条件。
根据具体问题的特点,写出适当的边界条件和初始条件。
4. 选择适当的数值方法进行离散化。
根据方程和边界条件,选择合适的数值方法进行离散化,例如差分法或有限元法。
5. 进行数值计算。
根据离散化的方程、边界条件和初始条件,
使用数值方法进行计算。
6. 分析结果。
对计算结果进行分析,例如画出温度随时间变化的曲线或温度分布的图表。
需要注意的是,在实际应用中,可能会遇到更复杂的情况,例如考虑圆柱体的热传导、对流和辐射等效应,或者考虑非线性材料属性。
针对这些情况,需要适当修改方程和边界条件,并选择合适的数值方法进行求解。
一维非稳态导热的数值计算

一维非稳态导热的数值计算一维非稳态导热问题是指材料的温度在时间上发生变化,且只沿一个方向进行传热的问题。
这种问题在实际工程、材料科学和热传导研究中都十分常见。
数值计算是求解这类问题的重要方法之一,接下来我们将介绍一维非稳态导热的数值计算方法。
首先,我们来定义一维非稳态导热的数学模型。
假设我们考虑的材料是一维的杆状物体,其长度为L,温度分布随时间t和空间x而变化,记作T(x,t)。
根据热传导方程,我们可以得到如下的一维非稳态导热方程:∂T/∂t=α*∂^2T/∂x^2其中,α是热扩散系数,反应了材料导热性能的指标。
我们的目标是求解在给定边界条件下的温度分布T(x,t)。
为了使用数值方法求解该方程,我们需要将其离散化。
首先,我们将时间t离散化为一系列的时间步长Δt,将空间x离散化为一系列的空间步长Δx。
然后,我们使用中心差分法来近似替代方程的二阶空间导数项和一阶时间导数项:∂T/∂t≈(T(i,j+1)-T(i,j))/Δt∂^2T/∂x^2≈(T(i+1,j)-2T(i,j)+T(i-1,j))/Δx^2其中,i和j分别表示空间和时间的离散节点索引。
将上述近似代入导热方程中,得到离散的差分方程:(T(i,j+1)-T(i,j))/Δt=α*(T(i+1,j)-2T(i,j)+T(i-1,j))/Δx^2根据上述差分方程,我们可以通过迭代计算来逐步更新温度分布。
首先,我们需要给定初始条件T(x,0)和边界条件T(0,t)和T(L,t)。
然后,我们通过迭代计算来更新温度值,直到达到所需的时间步长和空间步长。
具体来说,我们可以根据以下的更新公式进行迭代计算:T(i,j+1)=T(i,j)+α*Δt*(T(i+1,j)-2T(i,j)+T(i-1,j))/Δx^2其中,T(i,j+1)表示在第j+1个时间步长和第i个空间步长的温度值,T(i,j)表示在第j个时间步长和第i个空间步长的温度值。
总之,一维非稳态导热的数值计算方法可以使用离散化和迭代计算来求解热传导方程。
材料制备传输原理:6.4 一维非稳态导热

m = x =0 =f 6 Fo,Bi 0
(6.36)
6.4 一维非稳态导热
式(6.36)及式(6.35j)就是壁内特定点温度场的解的准则关系式。 图1为中心过余温度的理论解按式(6.36)表示的诺谟图。已知Fo和Bi
准则,从图上可以得到θm/θ0值。
图1 无限大平壁中心温度的诺谟图
(6.39)
6.4 一维非稳态导热
图3为无量纲累计热量Q/Q0与t的诺谟图。为了读图方便, 横坐标取Bi2Fo的组合。
图3 无限大平壁(厚2δ)中累计热量
Q 与时间的诺谟图 Q0
6.4 一维非稳态导热
例 题
例6.6 一块厚200mm的钢板,初始温度为20℃,被送入1000℃高温的热 炉内,两侧受热。已知钢板的λ=34.8QW/(m K),a=0.555 10-5m2/s,加 热过程中的平均表面对流换热系数h=174W/(m2 K).试求: (1)钢板受热表面温度达到500℃所需的时间 (2)此段时间内每平方米截面传入钢板的累计热量 解:(1)在此问题中,钢板半厚δ=100mm,于是在表面上
从图3查得Q/Q0=0.78,再从已知条件得ρc=λ/a=6.27×106,
每平方米截面的累计热量为 Q=0.78Q0=0.78×2×0.1×6.27×106×(20-1000) = -968×108(J) 负号表示热量从炉子传入钢板车。
如何利用线算图 a)对于由时间求温度的步骤为,计算Bi数、Fo数和
采用这些无量纲变量,微分方程式(6.35a)~(6.35c)可转换成为
at 0 2 = 2 X 2
(6.35d)
τ=0时
=1
(6.35e)
τ>0时,X=1处, -
一维非稳态导热问题的数值计算

一维非稳态导热问题的数值计算一、本文概述导热是热量在物质内部由高温部分传向低温部分的过程,它在自然界和工程应用中无处不在,如建筑物的保温隔热、热机的热传递等。
一维非稳态导热问题作为导热理论中的一个重要分支,研究的是热量在一维空间内随时间变化的传递过程。
由于其实用性和理论深度,一维非稳态导热问题一直是热传导研究领域的热点之一。
然而,一维非稳态导热问题的解析解往往难以求得,因此数值计算成为了解决这类问题的主要手段。
数值计算不仅能提供问题的近似解,还能通过改变计算条件和参数,模拟各种实际场景,为工程实践提供有力支持。
本文旨在探讨一维非稳态导热问题的数值计算方法。
我们将首先介绍一维非稳态导热问题的基本理论和数学模型,然后详细阐述几种常用的数值计算方法,如有限差分法、有限元法和谱方法等。
在此基础上,我们将通过具体的算例,分析这些数值方法的计算精度和效率,并讨论其在实际应用中的优缺点。
本文的目标读者主要是对导热理论和数值计算方法感兴趣的学者和工程师。
希望通过本文的介绍,读者能对一维非稳态导热问题的数值计算有更深入的理解,并能将其应用于实际问题的求解中。
二、一维非稳态导热问题的数学模型一维非稳态导热问题是在某一方向上热量随时间变化的热传导过程。
在实际应用中,这类问题常见于金属棒、电缆、管道等物体的热量传递过程。
为了对这一问题进行深入研究,需要建立相应的数学模型。
一维非稳态导热的基本方程是热传导方程,它描述了热量在物体内部随时间和空间的变化。
在一维情况下,该方程可以表示为:\frac{\partial T}{\partial t} = \alpha \frac{\partial^2T}{\partial x^2} ]其中,(T(x, t)) 表示物体在位置 (x) 和时间 (t) 的温度,(\alpha) 是热扩散系数,它决定了热量在物体内部传递的速度。
为了求解这一方程,需要定义初始条件和边界条件。
初始条件指的是物体在初始时刻的温度分布,通常表示为:T(0, t) = T_1(t), \quad T(L, t) = T_2(t) ]其中,(T_1(t)) 和 (T_2(t)) 是边界上的温度分布函数,(L) 是物体的长度。
一维圆柱非稳态导热方程求解

一维圆柱非稳态导热方程求解摘要:一、引言二、一维圆柱非稳态导热方程的建立三、求解方法四、数值计算及结果分析五、结论正文:一、引言在工程热物理领域,非稳态导热问题是一个重要且复杂的研究课题。
近年来,随着我国经济的快速发展,工业生产过程中涉及的温度场问题日益增多。
一维圆柱非稳态导热方程求解是温度场问题中的一个典型例子,对于解决实际工程问题具有重要的理论和实际意义。
本文将针对一维圆柱非稳态导热方程进行求解,并对结果进行分析。
二、一维圆柱非稳态导热方程的建立在一维圆柱坐标系下,我们考虑一个半径为r、高为h 的圆柱体。
假设该圆柱体的热导率是恒定的,为k。
为了简化问题,我们只考虑圆柱体在竖直方向上的非稳态导热过程。
在此基础上,我们可以建立如下非稳态导热方程:T(r,z,t)/t = α(T(r,z,t)/z)其中,T(r,z,t) 表示圆柱体中温度在时间t、半径r 和高度z 处的分布,α表示热扩散系数。
三、求解方法为了求解上述非稳态导热方程,我们可以采用有限差分法进行数值计算。
具体来说,首先将圆柱体离散化为一个网格系统,然后对每个网格点上的温度变化率进行求解。
通过迭代计算,可以得到圆柱体中温度在时间t、半径r 和高度z 处的分布。
四、数值计算及结果分析为了验证所采用方法的有效性,我们选取一个具体的非稳态导热问题进行求解。
假设圆柱体的半径r=0.1m,高度h=0.2m,热导率k=100W/(m·K),热扩散系数α=10 m/s。
此外,我们设置圆柱体的初始温度为T0(r,z)=300 K,并在t=0 时对圆柱体施加热流密度q=1000 W/m。
通过有限差分法求解得到圆柱体中温度在时间t 处的分布。
将计算结果绘制成等温线图,可以发现温度场呈现出明显的径向对称性,且随着时间推移,温度场逐渐趋于稳定。
此外,我们还可以通过计算得到温度场的最大温差和加热时间等参数,为实际工程应用提供参考。
五、结论本文针对一维圆柱非稳态导热方程进行了求解,采用有限差分法进行了数值计算。
一维圆柱非稳态导热方程求解

一维圆柱非稳态导热方程求解 前言:本文将介绍一维圆柱非稳态导热方程的求解方法。
首先,我们将从导热方程的基本原理开始,逐步推导出一维圆柱非稳态导热方程。
然后,我们将介绍求解这个方程的数值方法,并通过实例进行说明和验证。
导热方程描述了物体内部的温度分布随时间的变化关系。
一维圆柱非稳态导热方程特指一个圆柱形物体内部温度分布随时间变化的情况。
为了求解这个方程,我们需要以下几个步骤:建立方程,确定边界条件,选择合适的数值方法,进行数值求解,分析结果。
一、建立方程 假设一维圆柱的半径为r,长度为L,占据的空间为Ω。
假设Ω内部的温度分布为u(r,t),其中r代表半径,t代表时间。
根据热传导定律,我们可以建立一维圆柱非稳态导热方程: ρc∂u/∂t = ∂/∂r(rk∂u/∂r) (1) 其中,ρ为物体的密度,c为物体的比热容,k为物体的导热系数。
二、确定边界条件 为了求解方程(1),我们需要确定边界条件。
边界条件可以分为两种情况:定温边界和定热流边界。
1. 定温边界:在圆柱的表面,我们可以设定特定的温度分布,例如u(0,t) = T0,表示圆柱内部半径为0的地方的温度为T0。
另外,我们还可以设定圆柱外部的温度为T1,即u(L,t) = T1。
2. 定热流边界:除了设定定温边界,我们还可以设定定热流边界。
在这种情况下,我们需要给出表面上的热流密度,例如q(0,t) = q0,表示圆柱内部半径为0的地方的热流密度为q0。
另外,我们也需要给出表面上的平均热流,例如Q(L,t) = Q1,表示圆柱外部的平均热流为Q1。
三、选择数值方法 为了求解方程(1),我们将采用数值方法进行近似求解。
常见的数值方法有有限差分方法、有限元方法和谱方法。
在本文中,我们将采用有限差分方法,因为它是一种简单而又有效的数值方法。
有限差分方法将连续的导热方程离散化为差分方程,然后通过迭代求解差分方程得到近似解。
具体来说,我们将在r和t两个方向上进行离散化,然后使用差分格式逼近方程(1),得到如下的差分方程: ρc(ui,j+1 - ui,j)/Δt = (1/r)(ri+1/2k(ui+1,j - ui,j)/Δr - ri-1/2k(ui,j - ui-1,j)/Δr) (2) 其中,ui,j表示u(r,t)在r=iΔr,t=jΔt处的近似值,Δr为r 方向上的步长,Δt为t方向上的步长。
