一维非稳态导热通用程序(好)

传热学一维稳态和非稳态导热

11.1 通过平壁的一维稳态导热
一、第一类边界条件：表面温度
为常数
单层平壁
a. 几何条件：单层平板；s；
b. 物理条件：、cp、已知；无内热源；
c. 时间条件：稳态导热， ∂T/∂t=0；
d. 边界条件：第一类。
微分方程式可简化：
2T x2
0
直接积分得： TC1xC2
带入边界条件：
CC12
Tw1 (Tw2
流量，并记为qL
qL
Q Tw1 Tw2 L 1 d2 ln 传热学一维稳态和非稳态导热
2 d1
单位长度导热热阻
11.2 通过圆筒壁的一维稳态导热
多层圆筒壁
不同材料构成的多层圆筒壁，其导热热流量可按总温差和总热阻计算
热流量
Q
Tw1 Twn+1 n 1 ln di1
i1 2i L di
单位长度的热流量
2
C1xC2
式中积分常数C1和C2可由边界条件确定，它们分别为：
C2Tw2qv s2; C10
所以，平壁内温度分布为： TTw2qv s2x2
• 可见，该条件下平壁内温度是按抛物线规律分布。令温度分布关系式中的x=0，则得平壁中心温度为：
qv 2 T T s w
2 传热学一维稳态和非稳态导热
• 设在一管道外面包上一层绝热层(如图所示)。
• 此时单位管长的总热阻γΣ为：
d 1 11 2 1 传热1 学ln 一维d d 稳1 2 态和非2 稳态1 导x 热lnd d 2 xd 1 x2
11.2 通过圆筒壁的一维稳态导热
• 式中：α1为管内流体与管内壁之间的给热系数，W/m2℃；α2为绝
qL
1

一维非稳态导热通用程序(好)

!***************************************************************! 一维非稳态导热通用程序(不变部分)! This is a general purpose program to solve 1-D diffusion! problem in the form of:! ρcdt/dz=1/a(x)d/dx(a(x)Γdt/dx)+s!******************2003.7 revised******************************** !...................Define Variables.........................MODULE VARIABLESINTEGER,PARAMETER::L1=130REAL,DIMENSION(L1):: X,XF,XM,XP,R,RF,APREAL,DIMENSION(L1)::AE,AW,CN,T,TAREAL,DIMENSION(L1)::TG,GM,RCINTEGER:: K=1,KM=1,KP=1,OM=1INTEGER:: JB,JE,KE,KI,KF,KN,KR,KT,LS,MD,M1,M2,NFREAL:: AEC,AI,BE,BI,DF,DS,DT,EP,EX,PW,TU,TM,XE,XIREAL:: A1,A2,T2,TC,SC,SP,RO,TE,DN,LMEND!...............................................Main Program...........................................PROGRAM MAINUSE V ARIABLESIMPLICIT NONEINTEGER IOPEN(1,FILE="q.dat")OPEN(2,FILE="temp.dat")NF=1！（求解变量指标）KN=1！（非稳态问题输出局部变量，输出一次加1）TU=0！（当前时间）150 KT=1！（非线性问题迭代次数）CALL Speci !First to specify the problemCALL Grid!Set up grid points200 CALL Difsor!Specify the diff-coeff and source term220 CALL InterOutput!Output intermediate resultsCALL Coeff!Set up coefficients of discretization equationCALL TDMA!Solve the algebraic equation by TDMAIF(LS.EQ.2.OR.LS.EQ.4) THEN ！（对非线性问题）IF(DF.GT.EP) THEN！（如果最大偏差大于允许值）DO I=1,M1TA(I)=TA(I)+OM*(T(I)-TA(I))！（采用亚松弛方式将当前解付给上一次迭代值）END DODF=0！（最大偏差置零）KT=KT+1！（非线性问题迭代次数加1）GOTO 200！（转到DIFSOR模块重新计算扩散系数与源项）END IFEND IFCALL GPRINT !(四类问题均要经过一般输出)IF(LS.EQ.3.OR.LS.EQ.4) THEN！（对非稳态问题）IF(TU.LT.TM) THEN！（时间小于设定的最大值）DO I=1,M1TG(I)=T(I)！（当前计算结果付给上一时层）END DOKT=1IF(LS.EQ.3) THEN！（非稳态线性问题）GOTO 220！（转到中间输出模块）ELSE（非稳态非线性问题）GOTO 200！（转到DIFSOR模块重新计算扩散系数与源项）END IFEND IFEND IF!.............special results print out, if not, just leave it open..........CALL SPRINTIF(NF.NE.KM) THENNF=NF+1GOTO 150END IFCLOSE(2)CLOSE(1)END!...................Subroutine.................SUBROUTINE SETUPUSE V ARIABLESREAL,DIMENSION(L1)::P,QENTRY COEFF!................coefficients of boundary points..........IF(KI.LE.1) THENAP(1)=1AE(1)=0AW(1)=0CN(1)=AIELSEAE(1)=GM(1)/XM(2)AP(1)=AE(1)+BICN(1)=AIEND IFIF(KE.LE.1) THENAP(M1)=1AE(M1)=0AW(M1)=0CN(M1)=AECELSEAW(M1)=GM(M1)/XP(M2)AP(M1)=AW(M1)+BEAE(M1)=0CN(M1)=AECEND IF!...................coefficients of internal points........IF(LS.NE.3.OR.TU.LT.0.5*DT) THENEX=1IF(MD.EQ.3) EX=2AW(2)=GM(2)/XM(2)*RF(2)**EXAE(M2)=GM(M2)/XP(M2)*RF(M1)**EXEND IFDO I=2,M2-1AE(I)=RF(I+1)**EX/(XP(I)/GM(I)+XM(I+1)/GM(I+1))AW(I+1)=AE(I)END DODO I=2,M2AP(I)=AE(I)+AW(I)-AP(I)*(XF(I+1)-XF(I))*R(I)**EXCN(I)=CN(I)*(XF(I+1)-XF(I))*R(I)**EXIF(LS.EQ.3.OR.LS.EQ.4) THENAP(I)=AP(I)+RC(I)*(XF(I+1)-XF(I))*R(I)**EX/DTCN(I)=CN(I)+RC(I)*(XF(I+1)-XF(I))*R(I)**EX/DT*TG(I) END IFEND DORETURNENTRY TDMA !....................elimination.............P(1)=AE(1)/AP(1)Q(1)=CN(1)/AP(1)DO I=2,M1P(I)=AE(I)/(AP(I)-AW(I)*P(I-1))Q(I)=(CN(I)+AW(I)*Q(I-1))/(AP(I)-AW(I)*P(I-1))END DO!..................back substitution..........DO I=M2,1,-1T(I)=P(I)*T(I+1)+Q(I)END DOIF(LS.EQ.2.OR.LS.EQ.4) THENDO I=1,M1DS=ABS(T(I)-TA(I))IF(T(I).GT.1.E-20) DS=DS/T(I)IF(DF.LT.DS) DF=DSEND DOEND IFRETURNENTRY GPRINTIF(LS.EQ.3.OR.LS.EQ.4) THENM=(TU+0.5*DT)/(K*DT)IF(M.NE.KN) THENTU=TU+DTRETURNEND IFEND IF !...................surface flux calculation.......... SELECT CASE(KI)CASE(1)QI=GM(1)*(T(1)-T(2))/XM(2)CASE(2)QI=AICASE(3)QI=AI-BI*T(1)END SELECTSELECT CASE(KE)CASE(1)QE=GM(M1)*(T(M1)-T(M2))/XP(M2) CASE(2)QE=AECCASE(3)QE=AEC-BE*T(M1)END SELECTIF(LS.EQ.1.OR.LS.EQ.2) THENS=0DO I=2,M2QE=QE*RF(M1)**EXAP(I)=AE(I)+AW(I)-AP(I)S=S+CN(I)+AP(I)*T(I)END DOEND IF !................now it is ready to print out.........KN=KN+1IF(KP.NE.2) THENWRITE(*,*) "Dependent Variables Distribution" SELECT CASE(MD)CASE(1)WRITE(*,*) "Cartisian Coordinates"CASE(2)WRITE(*,*) "Cylindrical Coordinates"CASE(3)WRITE(*,*) "Spherical Coordinates"CASE(4)WRITE(*,*) "Nonuniform cross section" END SELECTSELECT CASE(LS)CASE(1)WRITE(*,*) "Linear Steady Problem"CASE(2)WRITE(*,*) "Nonlinear Steady Problem"WRITE(*,*) "Iterative Times=", KTCASE(3)WRITE(*,*) "Linear Unsteady Problem"CASE(4)WRITE(*,*) "Nonlinear Unsteady Problem"WRITE(*,*) "Iterative Times=", KTWRITE(*,*) "At Time=",TEND SELECTJE=0DO WHILE(JE.LT.M1)JB=JE+1JE=JE+4IF(JE.GT.M1) JE=M1WRITE(*,*) "J"DO J=JB,JEWRITE(*,*) JEND DOIF(MD.EQ.2.OR.MD.EQ.3) THENWRITE(*,*) "R"ELSEWRITE(*,*) "X"END IFDO J=JB,JEWRITE(*,*) T(J)END DOEND DOEND IFQI=QI*RF(2)**EXQE=QE*RF(M1)**EXIF(KF.EQ.1) THENWRITE(*,*) "Total Heat Flow At Int.Surface Qi=",QI WRITE(*,*) "Total Heat Flow At Ext.Surface Qe=",QE IF(LS.EQ.1.OR.LS.EQ.2) THENWRITE(*,*) "Total heat Input Form Source Term S=",S WRITE(*,*) "Heat Balance:Qi+Qe+ys=",QI+QE+S END IFEND IFTU=TU+DTRETURNEND。

第三章第三节一维非稳态导热的分析解

θ0 θm θ0
同理，非稳态换热过程所交换的热量也可以利用（3－24）和（3－25）绘制出。
解的应用范围
书中的诺谟图及拟合函数仅适用恒温介质的第三类边界条件或第一类边界条件的加热及冷却过程，并且F0>0.2
3
第三节一维非稳态导热的分析解
上式化为：
∂θ = a ∂ 2θ
∂τ
∂x 2
θ =θ0
∂θ = 0 ∂x
0 < x < δ ,τ > 0 τ =0 x=0
− λ ∂θ = hθ x = δ ∂x
第三节一维非稳态导热的分析解
用分离变量法可得其分析解为：
θ
( x,τ θ0
)
=
∞
∑
n =1
2 sin( β nδ ) cos( β n x) β nδ + sin( β nδ ) cos( β nδ
μ1
cos(
μ1
e x ) −μ12F0 δ
θ
(0,τ θ0
)
=
θ m (τ θ0
)
=
μ1
+
2 sin μ1 sin μ1 cos
μ1
e − μ12 F0
θ (x,τ ) θ m (τ )
=
cos(
μ1
x δ
)
与时间无关
第三节一维非稳态导热的分析解
考察热量的传递 Q 0 = ρ cV ( t 0 − t ∞ ) Q0 ——非稳态导热所能传递的最大热量
及可用一通式表达0aexp?21f0f1y00aexp?21f0bi此处无限大平板yxbihf0az2长圆柱体及球yxrbihrf0azr2此处的ab及函数f1y见p74表322第三节一维非稳态导热的分析解3正规热状况的实用计算方法拟合公式法对上述公式中的ab1j0可用下式拟合2b?11abiaab1?e?cbibacbi1bbij0xabxcx2dx3式中常数abcd见p75表33abcd见p75表34第三节一维非稳态导热的分析解2再根据公式323绘制其线算图xcosxx1fbim3于是平板中任一点的温度为m?0m0同理非稳态换热过程所交换的热量也可以利用324和325绘制出

数值传热学一维非稳态导热

数值传热学一维非稳态导热
数值传热学一维非稳态导热是一个拟表达热量输运多方面考虑下的相关分析技术，例如光斑热传递，带有间断层热传导，恒定物质热传导等等。

本文将重点简要介绍一维非稳态导热模型中的理论方法，为解决该问题提供重要基础。

首先，我们讨论的一维非稳态导热模型是一维的，在这种模型中，温度的变化是由上下相邻的单元格热传导加权平均值决定的，从一个单元格到另一个单元格的变化必须满足偏微分方程的通用表达式。

其次，根据以上的假设，一维非稳态导热的数值解将以定义的步长迭代，用于求解温度在不同单元中的变化。

在数值模拟中，需要对边界条件、热导率和温度输入进行有效描述，以确定最终的解答模式。

同时，本次分析中，利用有限差分和蒙特卡罗方法来求解温度场。

这种有趣且可行的做法，不但实现了所需求解的模式，而且能够精确地给出结果。

此外，在电脑指令中，采取该方法对数值运算很有效，从而提高了计算机解的精度和实现的质量。

最后，一维非稳态导热模型是在一定物理场中进行计算的，通用性很强，其能够很好地模拟简单模型中物理场的变化。

因此，它经常被用于诸如热管道传热、滑动轴热传导、负载温度场仿真等多种领域的研究。

总而言之，一维非稳态导热的数值模拟具有良好的数学基础、使用简单的算法以及电脑指令，从而实现快速求解热传导问题的目的，是今后研究的重要课题。

一维圆柱非稳态导热方程求解

一维圆柱非稳态导热方程求解引言在工程和科学领域中，导热方程是研究物体内部温度分布变化的重要方程。

本文将介绍一维圆柱非稳态导热方程的求解方法。

问题描述考虑一个半径为 R 的圆柱体，其内部由一个材料填充。

我们想要求解该圆柱体内部的温度分布，其中的热传导过程遵循非稳态导热方程。

在一维情况下，非稳态导热方程可以表示为：equation1equation1其中，T 是温度关于时间和半径的函数，α 是热扩散系数。

数值方法为了求解该方程，我们将应用有限差分法，离散化时间和半径的变量。

首先，我们将时间区域 [0, T] 离散化为 N 个等间距的时间步长，得到：equation2equation2其中，Δt 是时间步长，N 是总的时间步数。

接下来，我们将半径区域 [0, R] 离散化为 M 个等间距的半径步长，得到：equation3equation3其中，Δr 是半径步长，M 是总的半径步数。

将温度T 在时间和半径的离散点上进行近似，我们可以写出离散的导热方程为：equation4equation4其中，上标 n 表示时间步数，下标 i 表示半径步数。

由于我们已经将时间和半径离散化，上述方程可以重写为一个递推关系：equation5equation5数值实验我们将通过一个简单的数值实验来验证我们的数值方法。

设定圆柱体半径 R = 1，热扩散系数α = 1。

令边界条件为半径为 R 处的温度始终为 0，初始条件为半径为 R/2 处的温度为 1，其他位置的温度为 0。

在使用递推关系计算之前，需要选择合适的时间步长Δt 和半径步长Δr。

一般来说，选择小的步长可以提高数值解的准确性，但同时也会增加计算时间。

在这里，我们选择Δt = 0.001，Δr = 0.1。

我们使用一个循环来逐步计算每个时间步骤的温度分布，并在每个时间步骤结束后，使用画图软件绘制温度分布图。

结果与讨论经过数值计算和绘图，我们得到了随时间演化的温度分布图。

一维圆柱非稳态导热方程求解

一维圆柱非稳态导热方程求解（最新版）目录一、引言二、一维圆柱非稳态导热方程的建立三、求解方法四、数值计算与结果分析五、结论正文一、引言在工程热物理领域，非稳态导热问题是一个重要研究内容。

在实际应用中，许多热传导过程都是非稳态的，例如，物体在温度场作用下的热膨胀、热应变等过程。

对于这类问题，建立正确的非稳态导热方程并求解，具有重要的理论和实际意义。

本文针对一维圆柱非稳态导热问题，进行了深入研究，以期为解决实际工程问题提供理论依据。

二、一维圆柱非稳态导热方程的建立考虑一个一维圆柱体，其半径为 r，高为 h。

在非稳态热传导过程中，圆柱体内部各点的温度随时间发生变化。

根据热力学第一定律和热传导基本定律，可以建立一维圆柱非稳态导热方程。

假设圆柱体内部材质均匀，热导率恒定，则其非稳态导热方程可表示为：T(r,z,t)/t = α(T(r,z,t)/z)其中，T(r,z,t) 表示圆柱体内部某点的温度，α表示热导率，t 表示时间。

三、求解方法为了求解上述非稳态导热方程，采用有限差分法。

首先将圆柱体内部划分为若干个网格点，每个网格点的坐标为 (r_i, z_j)，其中 i 和 j 为网格点在圆柱体内的位置。

然后，对每个网格点，根据热传导方程，建立有限差分方程。

通过求解有限差分方程，可以得到圆柱体内部各点的温度场随时间的变化。

四、数值计算与结果分析为了验证所建立的非稳态导热方程的正确性，以及有限差分法的有效性，进行了数值计算。

首先，设定圆柱体的半径 r、高度 h、热导率α等参数。

然后，采用不同的时间步长和网格划分，进行数值计算。

计算结果表明，随着时间步长和网格划分的减小，计算结果趋于一致，说明所建立的非稳态导热方程和求解方法的正确性。

通过分析计算结果，可以得到以下结论：在非稳态导热过程中，圆柱体内部温度场呈现出明显的径向和轴向分布特征。

在径向方向，温度分布呈现出从内到外的逐渐降低趋势；在轴向方向，温度分布呈现出从上到下的逐渐降低趋势。

一维圆柱非稳态导热方程求解

一维圆柱非稳态导热方程求解摘要：1.问题背景及意义2.一维圆柱非稳态导热方程3.求解方法及步骤4.数值例子与分析5.应用及拓展正文：一、问题背景及意义在工程热传导领域，一维圆柱非稳态导热问题具有广泛的应用背景。

例如在金属加工、半导体制造、建筑节能等许多实际问题中，都需要研究热传导过程。

对于一维圆柱非稳态导热问题，了解其求解方法及过程有助于分析和优化实际工程中的热传导现象。

二、一维圆柱非稳态导热方程考虑一维圆柱非稳态导热问题，我们可以得到以下偏微分方程：$$frac{partial u}{partial t} = kfrac{partial^2 u}{partial r^2}$$其中，$u(r, t)$ 表示圆柱的热量分布，$k$ 为热传导系数，$r$ 为圆柱半径，$t$ 为时间。

三、求解方法及步骤1.边界条件处理：根据实际问题，给出圆柱的边界条件，如温度边界条件、热流密度边界条件等。

2.离散化：将空间坐标和时间坐标进行离散化，得到离散化的偏微分方程。

3.数值求解：采用有限差分法、有限元法等数值方法求解离散化方程。

4.分析结果：根据求解结果，分析圆柱热量分布随时间和空间的变化规律。

四、数值例子与分析以一个简单的一维圆柱非稳态导热问题为例，给出数值求解过程及结果分析。

1.设定参数：热传导系数$k = 10$，圆柱半径$r = 0.1$，时间步长$Delta t = 0.01$，空间步长$Delta r = 0.001$。

2.边界条件：圆柱表面受到均匀热流密度作用，即$q = 100$。

3.数值求解：采用有限差分法求解离散化方程。

4.结果分析：通过观察不同时刻的热量分布图，可以发现热量在圆柱内部传播的速度和规律。

根据分析，可以提出优化热传导过程的方法和措施。

五、应用及拓展一维圆柱非稳态导热方程求解方法不仅适用于金属加工、半导体制造等热传导领域，还可以拓展到其他领域，如地球物理学、生物医学等。

通过改变边界条件和相关参数，可以研究不同条件下一维圆柱非稳态导热现象的特点。

一维非稳态导热方程求解(附Matlab程序)

%%%%%%本文来自互联网%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
初值条件： T ( x, 0) 4 x 4 x ；
2
(0 x 1, 0 t 0.2, a 1)
边值条件：
T (0, t ) 0 ； T (1, t ) 0
使用差分公式
Txx ( xi , t j )
T ( xi h, t j ) 2T ( xi , t j ) T ( xi h, t j ) h2 Tt ( xi , t j ) T ( xi , t j k ) T ( xi , t j ) k
O( h 2 )
Ti 1, j 2T i , j Ti 1, j h2
O( k )
Ti , j 1 Ti , j k
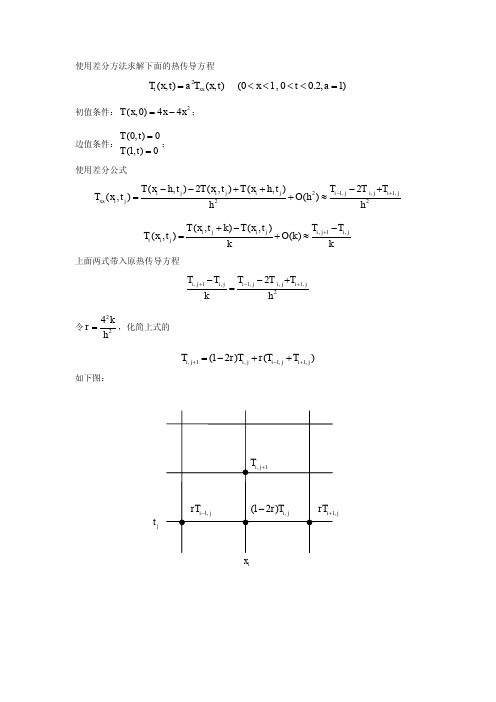
上面两式带入原热传导方程
Ti , j 1 Ti , j k 42 k 令 r 2 ，化简上式的 h

Ti 1, j 2T i , j Ti 1, j h2
% 边值条件： % u(a,t)=g1(t) % u(b,t)=g2(t) % % 参数说明 % c：方程中的系数 % f：初值条件 % g1,g2：边值条件 % xspan=[a,b]： x 的取值范围 % tspan=[ts,tf]：t 的取值范围 % ngrid=[n,m]：网格数量， m 为 x 网格点数量， n 为 t 的网格点数量 % U：方程的数值解 % x,t： x 和 t 的网格点 n=ngrid(1); m=ngrid(2); h=range(xspan)/(m-1); x=linspace(xspan(1),xspan(2),m); k=range(tspan)/(n-1); t=linspace(tspan(1),tspan(2),n); r=c^2*k/h^2; if r>0.5 error('为了保证算法的收敛，请增大步长 h 或减小步长 k!') end s=1-2*r; U=zeros(ngrid); % 边界条件 U(:,1)=g1(t); U(:,m)=g2(t); % 初值条件 U(1,:)=f(x); % 差分计算 for j=2:n for i=2:m-1 U(j,i)=s*U(j-1,i)+r*(U(j-1,i-1)+U(j-1,i+1)); end end

matlab一维非稳态导热 -回复

matlab一维非稳态导热-回复Matlab是一种常用的科学计算软件，广泛应用于工程、物理、数学等领域。

在热传导研究中，非稳态导热问题是一个重要课题。

本文将以Matlab 为工具，介绍一维非稳态导热问题的求解方法。

首先，我们需要了解非稳态导热问题的基本概念。

非稳态导热问题是指热传导过程中温度场随时间的变化，即瞬态问题。

一维非稳态导热问题可以用下面的热传导方程描述：∂T/∂t = α∂²T/∂x²其中，T是温度，t是时间，x是空间坐标，α是热扩散系数。

为了求解上面的偏微分方程，我们需要确定边界条件和初始条件。

假设热导体的两端为x=0和x=L，边界条件可以是温度固定、热流固定或边界绝热（无热量流入或流出）。

初始条件是指在t=0时刻的温度场分布。

首先，我们需要定义问题的参数，包括热扩散系数α、热导体的长度L、时间范围tspan等等。

在Matlab中，可以使用类似下面的语句进行定义：alpha = 0.1; 热扩散系数L = 1; 热导体长度tspan = [0 10]; 时间范围接下来，我们需要定义初始条件和边界条件。

假设在t=0时刻，热导体的温度分布是一个高斯函数，可以使用下面的语句定义初始条件：x = linspace(0, L, 100); 在空间范围内生成100个均匀分布的点T0 = exp(-(x-L/2).^2); 初始温度分布对于边界条件，我们可以选择温度固定的情况，即热导体的两端温度为固定值T1和T2。

可以使用下面的语句定义边界条件：T1 = 1; 左端温度T2 = 0; 右端温度然后，我们可以使用Matlab的pdepe函数来求解一维非稳态导热问题。

pdepe函数是用于求解偏微分方程组的函数，其中包含了默认的边界条件和初始条件设置。

可以使用下面的语句进行求解：sol = pdepe(0,pdefun,icfun,bcfun,x,tspan);在上面的语句中，pdefun是一个用于计算偏微分方程右端项的函数句柄，icfun是一个用于计算初始条件的函数句柄，bcfun是一个用于计算边界条件的函数句柄。

一维圆柱非稳态导热方程求解

一维圆柱非稳态导热方程求解
一维圆柱非稳态导热方程描述了圆柱体内部温度随时间变化的关系。

方程可以写成如下形式：
ρc ∂T/∂t = ∂/∂r (r k ∂T/∂r)
其中，T 是温度随位置和时间的函数，ρ 是圆柱体材料的密度，c 是材料的比热容，k 是材料的导热系数，r 是圆柱体的半径，t 是时间。

为了求解上述方程，需要给定边界条件和初始条件。

常见的边界条件包括固定温度边界条件和热流边界条件。

以下是求解一维圆柱非稳态导热方程的一般步骤：
1. 建立一维圆柱体的坐标系。

选择一个适当的坐标系，例如直角坐标系或极坐标系。

2. 建立方程。

根据给定的物理问题，建立一维圆柱非稳态导热方程。

3. 写出边界条件和初始条件。

根据具体问题的特点，写出适当的边界条件和初始条件。

4. 选择适当的数值方法进行离散化。

根据方程和边界条件，选择合适的数值方法进行离散化，例如差分法或有限元法。

5. 进行数值计算。

根据离散化的方程、边界条件和初始条件，
使用数值方法进行计算。

6. 分析结果。

对计算结果进行分析，例如画出温度随时间变化的曲线或温度分布的图表。

需要注意的是，在实际应用中，可能会遇到更复杂的情况，例如考虑圆柱体的热传导、对流和辐射等效应，或者考虑非线性材料属性。

针对这些情况，需要适当修改方程和边界条件，并选择合适的数值方法进行求解。

一维非稳态导热的数值计算

一维非稳态导热的数值计算一维非稳态导热问题是指材料的温度在时间上发生变化，且只沿一个方向进行传热的问题。

这种问题在实际工程、材料科学和热传导研究中都十分常见。

数值计算是求解这类问题的重要方法之一，接下来我们将介绍一维非稳态导热的数值计算方法。

首先，我们来定义一维非稳态导热的数学模型。

假设我们考虑的材料是一维的杆状物体，其长度为L，温度分布随时间t和空间x而变化，记作T(x,t)。

根据热传导方程，我们可以得到如下的一维非稳态导热方程：∂T/∂t=α*∂^2T/∂x^2其中，α是热扩散系数，反应了材料导热性能的指标。

我们的目标是求解在给定边界条件下的温度分布T(x,t)。

为了使用数值方法求解该方程，我们需要将其离散化。

首先，我们将时间t离散化为一系列的时间步长Δt，将空间x离散化为一系列的空间步长Δx。

然后，我们使用中心差分法来近似替代方程的二阶空间导数项和一阶时间导数项：∂T/∂t≈(T(i,j+1)-T(i,j))/Δt∂^2T/∂x^2≈(T(i+1,j)-2T(i,j)+T(i-1,j))/Δx^2其中，i和j分别表示空间和时间的离散节点索引。

将上述近似代入导热方程中，得到离散的差分方程：(T(i,j+1)-T(i,j))/Δt=α*(T(i+1,j)-2T(i,j)+T(i-1,j))/Δx^2根据上述差分方程，我们可以通过迭代计算来逐步更新温度分布。

首先，我们需要给定初始条件T(x,0)和边界条件T(0,t)和T(L,t)。

然后，我们通过迭代计算来更新温度值，直到达到所需的时间步长和空间步长。

具体来说，我们可以根据以下的更新公式进行迭代计算：T(i,j+1)=T(i,j)+α*Δt*(T(i+1,j)-2T(i,j)+T(i-1,j))/Δx^2其中，T(i,j+1)表示在第j+1个时间步长和第i个空间步长的温度值，T(i,j)表示在第j个时间步长和第i个空间步长的温度值。

总之，一维非稳态导热的数值计算方法可以使用离散化和迭代计算来求解热传导方程。

一维非稳态热传导

一维非稳态热传导简介热传导是一种物质内部热量传递的过程，其中涉及到热传导方程的求解。

在一维非稳态热传导中，我们研究的是沿一个维度上的非稳态热传导问题。

本文档将介绍一维非稳态热传导的基本概念、热传导方程的推导过程以及求解方法。

基本概念在研究非稳态热传导之前，我们先了解一些基本概念。

•温度梯度（Temperature Gradient）：指单位长度内温度的变化率。

在一维情况下，温度梯度表示为dd/dd，其中dd是单位长度内的温度变化，dd是长度单位。

•热流密度（Heat Flux Density）：指单位面积内传导的热量。

在一维情况下，热流密度表示为d=−d(dd/dd)，其中d是物质的热导率。

热传导方程的推导为了描述一维非稳态热传导问题，我们可以利用热传导方程。

推导过程如下：考虑一个以d为坐标的一维物体，在某个时刻d，温度分布为d(d,d)。

我们假设物体是均匀的，且具有恒定的热导率d。

根据温度梯度和热流密度的定义，我们可以得到如下关系：d=−d(dd/dd)根据能量守恒定律，我们可以得到以下方程：$$\\frac{{dq}}{{dt}} = -\\frac{{dE}}{{dt}}$$其中dd是单位时间内通过体积元dd的热量。

根据热流密度和体积元之间的关系，我们可以将上述方程改写为：$$\\frac{{dq}}{{dt}} = -\\frac{{d}}{{dt}}(qA)$$其中d是横截面积。

我们可以使用链式法则推导出：$$\\frac{{dq}}{{dt}} = \\frac{{dq}}{{dx}} \\cdot\\frac{{dx}}{{dt}} = \\frac{{dq}}{{dx}}V$$其中d是体积。

将上述方程带入前面的方程中，我们可以得到热传导方程：$$\\frac{{dq}}{{dx}}V = -\\frac{{d}}{{dt}}(qA)$$进一步简化，我们可以得到：$$\\frac{{dq}}{{dx}} = -\\frac{{d}}{{dt}}(\\frac{{qA}}{{V}})$$由于我们假设物体是均匀的，可以将d/d视为常数，记为d。

一维非稳态导热微分方程求解

一维非稳态导热微分方程求解导热，这个词听起来好像挺高大上的，其实说白了就是热量在物体里怎么传播。

想象一下，你拿着一根热乎乎的香肠，旁边放着一块冰冷的面包，香肠的热量会慢慢地传给面包，最后它俩的温度会平衡。

这个过程，就是导热，听着是不是有点温暖的感觉？但是当我们深入研究这其中的奥妙，就得面对一个不那么简单的家伙——一维非稳态导热微分方程。

嘿，别被这个长长的名字吓到，其实它就像是个神秘的盒子，里面藏着不少有趣的故事。

1. 什么是导热？首先，咱们得搞明白，导热到底是什么。

简单来说，导热就是热能从一个地方传到另一个地方。

比如，冬天你在阳台上晒太阳，阳光照在你身上，热量就会传到你体内，暖和得舒服。

但是，这种热量传递不是一蹴而就的，而是一个渐进的过程。

就像是你上班时，午饭时间到了，香喷喷的饭菜香味慢慢飘过来，让你忍不住口水直流。

这个过程需要时间，也需要一定的规律。

1.1 热量是怎么传的？热量的传递其实有三种方式：传导、对流和辐射。

今天我们重点聊聊传导，因为非稳态导热就是专门研究这种情况的。

传导就像是邻居之间的传话，热量从一个分子传到另一个分子，慢慢地扩散开来。

这就涉及到一个叫做“热导率”的概念，简单来说，就是物质传导热量的能力。

就像有的人说话特别快，有的人说话慢，这就是热导率的差异。

1.2 一维非稳态导热的意义一维非稳态导热的意思就是，咱们只考虑一个方向的热量传递，比如从左到右，或者从上到下。

而“非稳态”就是指热量的分布会随着时间变化，完全不是静态的。

想象一下，你刚把冰淇淋从冰箱拿出来，开始的几分钟它是硬邦邦的，但过了一会儿，它就变得越来越软，这就是非稳态的一个典型例子。

2. 数学模型的建立好吧，听到“数学”这个词，很多小伙伴可能会打退堂鼓，但别着急，我们就简单聊聊。

为了描述这个热量传递的过程，科学家们建立了一个数学模型——一维非稳态导热微分方程。

这个方程就像一把钥匙，能打开导热现象的“黑箱”。

它的基本形式是这样的：frac{partial T{partial t = alpha frac{partial^2 T{partial x^2。

一维圆柱非稳态导热方程求解

一维圆柱非稳态导热方程求解前言：本文将介绍一维圆柱非稳态导热方程的求解方法。

首先，我们将从导热方程的基本原理开始，逐步推导出一维圆柱非稳态导热方程。

然后，我们将介绍求解这个方程的数值方法，并通过实例进行说明和验证。

导热方程描述了物体内部的温度分布随时间的变化关系。

一维圆柱非稳态导热方程特指一个圆柱形物体内部温度分布随时间变化的情况。

为了求解这个方程，我们需要以下几个步骤：建立方程，确定边界条件，选择合适的数值方法，进行数值求解，分析结果。

一、建立方程假设一维圆柱的半径为r，长度为L，占据的空间为Ω。

假设Ω内部的温度分布为u(r,t)，其中r代表半径，t代表时间。

根据热传导定律，我们可以建立一维圆柱非稳态导热方程： ρc∂u/∂t = ∂/∂r(rk∂u/∂r) (1) 其中，ρ为物体的密度，c为物体的比热容，k为物体的导热系数。

二、确定边界条件为了求解方程(1)，我们需要确定边界条件。

边界条件可以分为两种情况：定温边界和定热流边界。

1. 定温边界：在圆柱的表面，我们可以设定特定的温度分布，例如u(0,t) = T0，表示圆柱内部半径为0的地方的温度为T0。

另外，我们还可以设定圆柱外部的温度为T1，即u(L,t) = T1。

2. 定热流边界：除了设定定温边界，我们还可以设定定热流边界。

在这种情况下，我们需要给出表面上的热流密度，例如q(0,t) = q0，表示圆柱内部半径为0的地方的热流密度为q0。

另外，我们也需要给出表面上的平均热流，例如Q(L,t) = Q1，表示圆柱外部的平均热流为Q1。

三、选择数值方法为了求解方程(1)，我们将采用数值方法进行近似求解。

常见的数值方法有有限差分方法、有限元方法和谱方法。

在本文中，我们将采用有限差分方法，因为它是一种简单而又有效的数值方法。

有限差分方法将连续的导热方程离散化为差分方程，然后通过迭代求解差分方程得到近似解。

具体来说，我们将在r和t两个方向上进行离散化，然后使用差分格式逼近方程(1)，得到如下的差分方程： ρc(ui,j+1 - ui,j)/Δt = (1/r)(ri+1/2k(ui+1,j - ui,j)/Δr - ri-1/2k(ui,j - ui-1,j)/Δr) (2) 其中，ui,j表示u(r,t)在r=iΔr，t=jΔt处的近似值，Δr为r 方向上的步长，Δt为t方向上的步长。

matlab一维非稳态导热 -回复

matlab一维非稳态导热-回复Matlab是一款功能强大的数值计算软件，广泛应用于各个领域的工程问题求解。

其中，一维非稳态导热问题是其中的一个经典实例。

在本文中，我们将分步骤回答关于matlab中一维非稳态导热问题的相关问题，并给出相应的代码示例。

一维非稳态导热问题是指在一维空间中，研究物体温度随时间的变化规律。

该问题是一个典型的偏微分方程问题，可以用来模拟物体在热传导过程中的温度分布情况。

首先，我们需要确定问题的边界条件。

在一维导热问题中，通常我们会给定物体的初始温度分布和边界上的温度条件。

假设我们有一个长度为L的物体，在初始时刻t=0，物体的温度分布为T(x,0)，其中x表示空间坐标。

边界条件可以分为两种：第一种是给定物体两端的温度，即T(0,t)和T(L,t)；第二种是给定一段时间内物体的表面温度变化规律，即T(x,0<=t<=T)。

在matlab中求解一维非稳态导热问题，我们可以采用离散化的方法。

具体来说，我们可以将问题的空间和时间坐标都分成若干个离散点，然后用差分来逼近偏微分方程的导数。

这样，我们就得到了一个由代数方程构成的方程组，可以通过求解该方程组得到问题的数值解。

首先，我们需要确定问题的离散化步长。

在matlab中，我们可以用meshgrid函数来生成网格点坐标。

假设我们将空间坐标x划分为N个小段，时间坐标t划分为M个小段，那么我们就可以得到一个(N+1)×(M+1)的网格。

其中，每个网格点的坐标为(xi,tm)，其中i表示空间坐标第i个点，m表示时间坐标第m个点。

我们可以用[X,T]=meshgrid(x,t)来生成网格点坐标。

接下来，我们需要给定初始温度分布。

假设我们的物体的初始温度分布为T(x,0)=sin(2πx/L)，我们可以通过在网格点上计算初始温度值来得到初始温度矩阵T0。

具体来说，我们可以用T0=sin(2πX/L)来计算初始温度矩阵。

然后，我们需要给定边界条件。

一维非稳态导热通用程序(好)

传热学一维稳态和非稳态导热