第二章:正则语言
自动机习题中文解答全
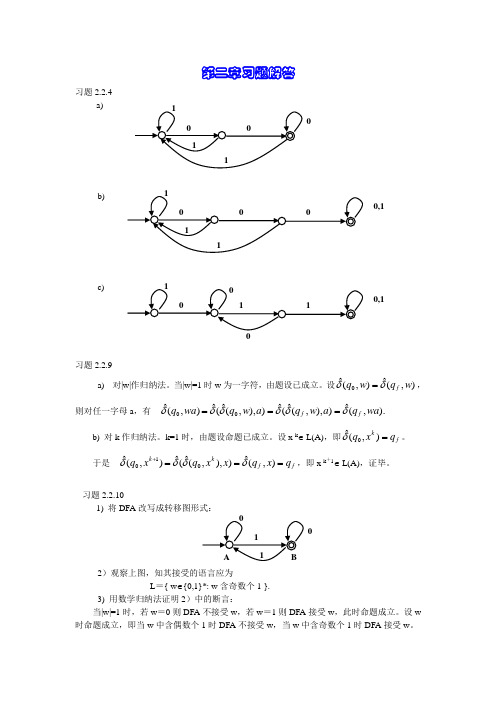
第二章习题解答习题2.2.4a) b) c) 习题2.2.9a) 对|w|作归纳法。
当|w|=1时w 为一字符,由题设已成立。
设),(ˆ),(ˆ0w q w q fδδ=, 则对任一字母a ,有 ).,(ˆ)),,(ˆ(ˆ)),,(ˆ(ˆ ),(ˆ00wa q a w q a w q wa q ff δδδδδδ=== b) 对k 作归纳法。
k=1时,由题设命题已成立。
设x k ∈ L(A),即fkq x q =),(ˆ0δ。
于是 ff k k q x q x x q x q ===+),(ˆ)),,(ˆ(ˆ ),(ˆ010δδδδ,即x k +1∈ L(A),证毕。
习题2.2.101) 将DFA 改写成转移图形式:2)观察上图,知其接受的语言应为L ={ w ∈{0,1}*: w 含奇数个1 }. 3) 用数学归纳法证明2)中的断言:当|w|=1时,若w =0则DFA 不接受w ,若w =1则DFA 接受w ,此时命题成立。
设w 时命题成立,即当w 中含偶数个1时DFA 不接受w ,当w 中含奇数个1时DFA 接受w 。
0,10,1对于任一字符c :若c=0,则当w 中含偶数个1时由于DFA 不接受w ,故A w q =),(ˆ0δ,从而A wc q =),(ˆ0δ;当w 中含奇数个1时由于DFA 接受w ,故B w q =),(ˆ0δ,从而B wc q =),(ˆ0δ。
若c=1,则当w 中含偶数个1时由于DFA 不接受w ,故A w q =),(ˆ0δ,从而B wc q =),(ˆ0δ;当w 中含奇数个1时由于DFA 接受w ,故B w q =),(ˆ0δ,从而A wc q =),(ˆ0δ。
总之,当wc 中含偶数个1时DFA 不接受wc ,当wc 中含奇数个1时DFA 接受wc 。
命题得证。
习题2.2.111) 将DFA 改写成转移图形式:2)观察上图,知其接受的语言应为L ={ w ∈{0,1}*: w 不含子串00 }.3) 用数学归纳法证明2)中的断言,过程与前题类似。
第二章 正则表达式 (2)

另外一种定义 式的集合:
设∑为有限字母表, R表示∑上的所有正则表达
✓是正则表达式,即 R,则有: L( )={ };
✓是正则表达式,即
R ,则有:
L(
)={};
✓a 是正则表达式,即a R,则有: L(a )={a};
(一)正则表达式和正则集的定义
定义1:设∑为有限字母表,∑上的正则表达式和 正则集可递归定义如下:
(1) 和是∑上的正则表达式,它们表示的正 则集分别为{ε}和;
(2) 对任何a∈∑,a 是∑上的正则表达式,它所 表示的正则集为{a};
(3) 若r,s都是正则表达式,它们表示的正则集 分别为R和S, 则(r)、r|s、r•s、(r)*也是正 则表达式,它们分别表示的正则集是:R, R∪S , RS和R*.
Sε
a
ab|ba
12
a
5 b 6ε Z
Sε
a 1
2
(ab|ba )a*b
6ε Z
a(ab|ba )a*b
S
Z
单元总结
两个工具:
有限自动机、正则表达式
四个算法:
NFA到DFA的转换 DFA的化简 正则表达式与FA的相互转换
一个实现:
DFA的实现
练习题:将下述自动机最小化.
a
1
a
0
ba
3
a,b
| 的可结合性
A•B•C =A•(B•C)=(A•B)•C
合性
连接的可结
A•(B|C) =A•B|A•C
连接的可分配性
(A|B)•C =A•C|B•C
形式语言与自动机理论第二章蒋宗礼

2.2 形式定义
• P——为产生式(production)的非空有穷集合。P中的元素均具有 形式αβ,被称为产生式,读作:α定义为β。其中 α∈(V∪T)+,且α中至少有V中元素的一个出现。β∈(V∪T)*。 α称为产生式αβ的左部,β称为产生式αβ的右部。产生 式又叫做定义式或者语法规则。
A1A },A)。
第20页/共106页
2.2 形式定义
⑸ ({S , A , B , C , D},{a , b , c , d,#} , {SABCD , Sabc# , AaaA , ABaabbB , BCbbccC,cCcccC,CDccd# ,CDd#, CD#d},S)。
⑹ ({S},{a , b} , {S00S , S11S , S00 , S11},S)。
第32页/共106页
2.2 形式定义
• 例 2-5 设G=({S,A,B},{0,1},{SA|AB,A0|0A,B1|11},S)
对于n≥1,
A n 0n
首先连续n-1次使用产生式;A0A, 最后使用产生式A0;
A n 0nA
连续n次使用产生式A0A;
B1
使用产生式B1;
B 11
使用产生式B11。
• CFL
• CFG(CNF、GNF)、PDA、CFL的性质。
• TM
• 基本TM、构造技术、TM的修改。
• CSL
• CSG、LBA。
第4页/共106页
教材及主要参考书目
1.蒋宗礼,姜守旭. 形式语言与自动机理论. 北京:清华大学出版 社,2003年
2.John E Hopcroft, Rajeev Motwani, Jeffrey D Ullman. Introduction to Automata Theory, Languages, and Computation (2nd Edition). Addison-Wesley Publishing Company, 2001
第三章(续二)正则语言性质
B
确定有限自动机DFA的化简(极小化)
对DFA M的极小化是找出一个状态数比M少的 DFA M1,使满足 L(M) = L(M1) 1.状态等价和可区分的概念 设DFA M = (Q,T,δ,q0,F) 对不同的状态q1, q2∈Q 和每个ω∈T*, 如果有 (q1,ω)┣* (q,ε) 必有 (q2,ω)┣* (q,ε) 且q∈F , 则称q1与q2状态等价. 记为q1≡q2 否则,称q1, q2可区分.
11
通过合并等价的状态进行 DFA 的优化
举例
a Start 1 a b b 3 b
a a Start [1] a b b [3] b a b [5] [6] b [4] a
a 6 b b 5 b
4 a a
a
– 等价的状态偶对为: (1, 2),(6, 7)
7
a 2 b
– 划分结果: { 1, 2 }, {3}, {4}, {5}, { 6, 7 }
14
针对正则语言的 Pumping 引理
正则语言应满足的一个必要条件
用于判定给定的语言不是正则集。
物理意义:当给定一个正则集和该集合上一个足够长的字符串 时,在该字符串中能找到一个非空的子串,并使子串重复,从
而组成新的字符串。该新串必在同一个正则集内。
定理:
设L是正则集,存在常数k,对所有字符串ω∈L 且|ω|≥k ,则ω可写成ω1ω0ω2,其中|ω1ω0|≤k, |ω0|>0,对 所有的i≥0有ω1ω0iω2∈L。 证明 设 L 是 DFA D = (Q, T, , q0 , F ) 的语言, 取 k = |Q| 即 可. • College of Computer Science & Technology, BUPT
形式语言与自动机理论第二版教学大纲

形式语言与自动机理论第二版教学大纲课程简介该课程主要介绍形式语言、自动机和计算复杂性理论的基本知识。
通过学习这些理论,学生将能够理解计算机语言和计算的本质,以及计算机处理问题时的优劣势和限制。
本课程将重点介绍自动机的概念、使用和应用。
学习目标•理解形式语言和自动机的基本概念和术语,如有限状态自动机、正则语言、上下文无关文法等。
•学习计算复杂性理论的基本知识,理解P、NP等复杂度概念。
•掌握自动机模型的使用和应用,能够构造和证明特定自动机模型的特性和性质。
课程内容第一章:形式语言与自动机•形式语言和自动机的基本概念和术语•正则语言和正则表达式•上下文无关文法和上下文无关语言•上下文有关文法和上下文有关语言第二章:有限状态自动机•有限状态自动机的定义和运作原理•正则语言和有限状态自动机的等价性•正则表达式到有限状态自动机的转换•有限状态自动机的最小化问题第三章:上下文无关文法和语言•上下文无关文法的定义和特点•文法的基本组成部分:终结符、非终结符和产生式•上下文无关语言和上下文无关文法之间的关系•Chomsky范式和柯尔莫戈洛夫复杂度下限第四章:推导树和语法分析器•推导树的概念和用途•自下而上(LR分析器)和自上而下分析器(LL分析器)的概念和区别•LR、LL分析器的构造算法第五章:上下文有关文法和语言•上下文有关文法的定义和特点•上下文有关语言和上下文有关文法之间的关系•推导和语言识别•非概率上下文有关文法和语言第六章:计算复杂性理论•P、NP问题的定义和区别•NP问题的证明方法:证书、多项式可验证和非确定图灵机•NP完全问题和可还原性的概念•NP问题的P约简和相对问题第七章:图灵机及其变体•图灵机的概念和基本结构•图灵机的相对能力•图灵机的变体:可计数和带计数的图灵机•智能计算和互模拟教学方法本课程将采用讲授、课堂互动、案例分析等多种教学方法,以帮助学生更好地理解理论和应用。
在每章节结束时,还将提供一些简单的练习题和课后作业,以帮助掌握相关的理论和算法。
编译原理第二章文法和语言

语言的语法结构
总结词
语言的语法结构是语言形成和发展的核心要素,决定 了语言的表达方式和意义。
详细描述
语言的语法结构是指语言的组织规律和规则,包括词 法、句法、语义等方面的规则。词法规定了词汇的构 成和变化规则,如名词、动词、形容词等词类的划分 ;句法规定了句子结构的规则,如主语、谓语、宾语 等句子的成分及其排列顺序;语义则涉及到词汇和句 子的意义和解释。语言的语法结构是语言理解和生成 的基础,也是语言演变和发展的关键因素。
文法和语言的应用前景
1 2
人工智能领域
文法和语言是人工智能领域的重要基础,可用于 自然语言处理、机器翻译、语音识别等技术的研 究和应用。
计算机科学教育
文法和语言是计算机科学专业的重要课程之一, 对于培养计算机科学人才具有重要意义。
3
软件工程领域
文法和语言可用于软件工程领域中的编译器设计 和开发,提高软件开发的效率和可靠性。
05
文法和语言的未来发展
文法和语言的研究方向
形式语言理论
深入研究形式语言的基本理论, 包括语法、语义和语用等方面, 为自然语言处理和人工智能等领 域提供理论基础。
自然语言处理
结合自然语言处理技术,研究自 然语言的语法、语义和语用规律, 提高自然语言处理的准确性和效 率。
计算语言学
将计算语言学与形式语言理论相 结合,研究语言处理算法和模型, 为机器翻译、语音识别等领域提 供技术支持。
文法和语言的发展趋势
深度学习与文法和语言的结合
01
随着深度学习技术的发展,文法和语言的研究将更加注重与深
度学习的结合,以提高语言处理的性能和效率。
跨媒体语言处理
02
随着多媒体数据的普及,文法和语言的研究将逐渐扩展到跨媒
(11)第二章 第四讲 正则集与正则式及右线性文法

结论:则由右线性文法G产生的语言L(G)=L1L2
。
证明思路:首先证明,当一个语言是正则集时,则该语言 在这里, ε∈L1*,且所有的原L1的 是一个右线性文法G 所产生的语言。 ② 设L1和L2分别是由右线性文法G1和G2产生的右线性语 言,G1=(N1,T,P1,S1),G2=(N2,T,P2,S2)。要证明L1∪L2、L1L2 和L1*都是右线性语言。 3)最后对于L1*,根据G1构造G=(N,T,P,S),其中: N=N1∪{S}, S是不属于N1的一个新的非终结符 生成式P如下: 如果A→αB∈P1,则A→αB∈P 如果A→α∈P1,则A→αS∈P 且A→α∈P S→S1 , S→ε∈P 结论:则由右线性文法G产生的语言L(G)=L1* 。
关系: 字母表上具有某种特殊特征的一些字符串的集合 称为正则集,该集合可以用一种称之为正则式的规范的方 法来表示。 用途: ①搜索命令:许多应用程序(如UNIX中的grep命令 在文件中的搜索模式、文本编辑程序、Web搜索引擎等) 都采用正则式来描述具有某种特征的字符串。 ②词法分析器:利用正则式把源程序分解成一个一 个的“单词”(如标识符、表达式等)。 ③模式识别:如身份识别系统,可用正则式描述人 们的生理特征(虹膜、指纹、人脸等)和行为特征(步态、 声音、笔迹等)的数字化信息,进行自动身份鉴别。
N=N1∪N2∪{S}
P=P1∪P2∪{S→S1,S→S2}, T不变
。
结论:则由右线性文法G产生的语言L(G)=L1∪L2
证明思路:首先证明,当一个语言是正则集时,则该语言 是一个右线性文法G所产生的语言。
② 设L1和L2分别是由右线性文法G1和G2产生的右线性语 言,G1=(N1,T,P1,S1),G2=(N2,T,P2,S2)。要证明L1∪L2、L1L2 和L1*都是右线性语言。 1)首先对于L1∪L2,构造G=(N,T,P,S),其中:
《易语言“正则表达式”教程》

《易语⾔“正则表达式”教程》”与字符串”匹配时,匹配的结果是:成功;匹配到的内容是”整个字符串,表达式中的”将与字符串中最后⼀个《易语⾔“正则表达式”教程》本⽂改编⾃多个⽂档,因此如有雷同,不是巧合。
“正则表达式”的应⽤范围越来越⼴,有了这个强⼤的⼯具,我们可以做很多事情,如搜索⼀句话中某个特定的数据,屏蔽掉⼀些⾮法贴⼦的发⾔,⽹页中匹配特定数据,代码编辑框中字符的⾼亮等等,这都可以⽤正则表达式来完成。
本书分为四个部分。
第⼀部分介绍了易语⾔的正则表达式⽀持库,在这⾥,⼤家可以了解第⼀个正则表达式的易语⾔程序写法,以及⼀个通⽤的⼩⼯具的制作。
第⼆部分介绍了正则表达式的基本语法,⼤家可以⽤上述的⼩⼯具进⾏试验。
第三部分介绍了⽤易语⾔写的正则表达式⼯具的使⽤⽅法。
这些⼯具是由易语⾔⽤户提供的,有的⼯具还带有易语⾔源码。
他们是:monkeycz、零点飞越、寻梦。
第四部分介绍了正则表达式的⾼级技巧。
⽬录《易语⾔“正则表达式”教程》 1⽬录 1第⼀章易语⾔正则表达式⼊门 3⼀.与DOS下的通配符类似 3⼆.初步了解正则表达式的规定 3三.⼀个速查列表 4四.正则表达式⽀持库的命令 54.1第1个正则表达式程序 54.2第2个正则表达式例程 74.3第3个例程 84.4⼀个⼩型的正则⼯具 9第⼆章揭开正则表达式的神秘⾯纱 11引⾔ 12⼀.正则表达式规则 121.1普通字符 121.2简单的转义字符 131.3能够与“多种字符”匹配的表达式 141.4⾃定义能够匹配“多种字符”的表达式 16 1.5修饰匹配次数的特殊符号 171.6其他⼀些代表抽象意义的特殊符号 20⼆.正则表达式中的⼀些⾼级规则 212.1匹配次数中的贪婪与⾮贪婪 212.2反向引⽤\1,\2 (23)2.3预搜索,不匹配;反向预搜索,不匹配 24三.其他通⽤规则 25四.其他提⽰ 27第三章正则表达式⼯具与实例 28⼀.正则表达式⽀持库 291.1“正则表达式”数据类型 291.2“搜索结果”数据类型 30⼆.正则表达式实⽤⼯具 302.1⼀个成品⼯具 302.2易语⾔写的⼯具 33三.应⽤实例 343.1实例1 343.2实例2 363.3实例3 373.4实例4 37第四章正则表达式话题 38引⾔ 38⼀.表达式的递归匹配 381.1匹配未知层次的嵌套 381.2匹配有限层次的嵌套 39⼆.⾮贪婪匹配的效率 402.1效率陷阱的产⽣ 402.2效率陷阱的避免 41附录: 42⼀.17种常⽤正则表达式 42第⼀章易语⾔正则表达式⼊门⼀.与DOS下的通配符类似其实,所谓的“正则表达式”,是⼤家⼀直在使⽤的,记得吗?在搜索⽂件时,会使⽤⼀种威⼒巨⼤的武器——DOS通配符——“?”和“”。
正则语法 且-概述说明以及解释

正则语法且-概述说明以及解释1.引言1.1 概述正则语法是一种用于描述和匹配字符串模式的表达式语言。
它是一种强大且灵活的工具,广泛应用于文本处理、模式识别、数据抽取等领域。
在日常生活中,我们经常需要根据一定的规则来查找、替换或提取特定的文本。
例如,你可能想要查找一个包含特定关键字的文件,或者通过提取邮件地址来建立一个联系人列表。
这些都是正则表达式的典型应用场景。
正则语法由一系列字符和特殊符号组成,通过组合这些元素,可以形成一个用来描述字符串模式的表达式。
正则表达式可以包含普通字符(如字母、数字和标点符号),以及一些特殊字符(如元字符和转义字符),用于表示特定的规则和匹配模式。
正则语法具有很高的灵活性和表达能力。
它可以描述复杂的模式并进行精确匹配,同时还支持各种灵活的匹配规则,如字符集合、重复次数、分组等。
通过结合这些功能,我们可以更加精确地定义我们所需要的字符串模式。
在本文中,我们将深入探讨正则语法的定义与作用,介绍正则表达式的基本语法,以及探讨正则语法在不同领域的应用和优缺点。
通过学习和理解正则语法,我们可以更好地处理和操作文本数据,提高工作效率和准确性。
让我们开始探索正则语法的奥秘吧!1.2 文章结构文章结构的部分应该包括对整篇文章的组织和结构进行介绍。
在这部分,我们可以讨论文章的主要部分、章节和子章节的划分方式,以及每个部分的主要内容和功能。
在本文中,文章结构可以按照以下方式进行描述:文章的主要结构由三个章节构成,分别是引言、正文和结论。
引言部分在文章开始时引入了正则语法的主题,并介绍了本文的目的和概述。
它帮助读者了解正则语法的重要性和应用领域,并为后续的正文部分奠定了基础。
正文部分是整篇文章的核心部分,主要讨论了正则语法的定义与作用以及正则表达式的基本语法。
在2.1小节中,我们将详细介绍正则语法的定义和其在编程和文本处理中的作用。
我们可以阐述正则表达式在字符串匹配、搜索和替换等方面的应用,并给出实际的例子来说明其使用方法和效果。
第二章、正则语言

第2章 正则语言
计算理论导引
第二章 正则语言
计算理论的第一个问题是:什么是计算机? 现实的计算机相当复杂,很难直接对它们建立一个易
于处理的数学理论。于是我们采用称作计算模型的理
想计算机。
从最简单的模型开始.它叫做有穷状态机或有穷自动
机。
计算理论导引
2.1 有穷自动机-1
状态转换表
NEITHER CLOSED OPEN CLOSED CLOSED FRONT OPEN OPEN
计算理论导引
REAR CLOSED OPEN
BOTH CLOSED OPEN
2.1 有穷自动机-3
从数学的角度观察有穷自动机。
图2-4叫做M1的状态图。它有三个状态,记作q1 ,q2 ,q3。 起始状态q1用一个指向它的无出发点的箭头表示。 接受(终结)状态q2带双圈。 从一个状态指向一个状态的箭头叫做转移。
设置起始状态:qeven,因为0是偶数。设置接受状态:
qodd,因为当你看到奇数个1时就打算要接受。
计算理论导引
2.1.4 设计有穷自动机-5
例 2.9
如何设计有穷自动机E2识别含有001作为子串的所有字符串 组成的正则语言。
如果你是E2,你会怎么样识别这个语言?当符号一个接一个 到来时,你开始可能要跳过所有的1。如果你得到一个0,那 么注意到你可能刚刚看见你要寻找的模式001中的第一个符 号。如果接着看见一个1,由于0的个数不够,所以你返回去 跳过1。但是,如果接着看见一个0,你应该记住你已经看见 模式的2个符号。现在你只需要继续扫描直到看见一个1为止。 如果你找到l,那么记住你已经成功地找到模式001,并且继 续读完输入串。
05 正则语言的性质

泵引理的说明
用来证明一个语言不是 RL 不能用泵引理去证明一个语言是 RL。 (1) 由于泵引理给出的是 RL 的必要条件,所以,在用它证明一个语言不 是 RL 时,我们使用反证法。 (2) 泵引理说的是对 RL 都成立的条件,而我们是要用它证明给定语言不 是 RL ,这就是说,相应语言的“仅仅依赖于L的正整数N”实际上是 不存在的。所以,我们一定是无法给出一个具体的数的。因此,人 们往往就用符号N 来表示这个“假定存在”、而实际并不存在的数。 (3) 由于泵引理指出,如果 L 是 RL ,则对任意的 z∈L,只要|z|≥N,一 定会存在u, v, w,使 uviw∈L 对所有的 i 成立。因此,我们在选择 z 时,就需要注意到论证时的简洁和方便。
3
泵引理
4
泵引理
M = ( Q, ∑, δ, q0 , F ) | Q |= N z = a1a2…am , m≥N δ(q0 , a1a2…ah) = qh 状态序列 q0, q1, … ,qN 中,至少有两个状态是相同:qk=qj δ(q0 , a1a2…ak) = qk δ(qk , ak+1…aj) = qj = qk δ(qj , aj+1…am) = qm 因此,可设 z = uvw,其中 u= a1a2…ak,v=ak+1…aj,w = aj+1…am
2
5.1 正则语言的泵引理
qj q1
qk
DFA在处理一个足够长的句子的过程中,必定会重复地经过某一个状态。 换句话说,在 DFA 的状态转移图中,必定存在一条含有回路的从启动状 态到某个终止状态的路。 由于是回路,所以 DFA 可以根据实际需要沿着这个回路循环运行,相当 于这个回路中弧上的标记构成的非空子串可以重复任意多次。
正则语言——精选推荐

第 4 章正则语言的性质本章中我们将会探讨正则语言的性质,在此过程中我们所使用的第一个工具是一个定理,它能够证明某个语言不是正则的。
该定理叫做“泵引理”,我们将在第4.1节中介绍它。
正则语言的一类很重要的性质是“闭包性质”,该性质使得我们能够从一些语言出发,通过一定的运算符,来构造能够识别另一些语言的自动机。
例如,两个正则语言的交仍然是正则语言。
因此,给定能够识别两个不同的正则语言的自动机,我们可以机械地构造一个恰好识别这两个语言的交的自动机。
由于这样构造出来的自动机可能比给定的两个自动机的状态都多,因此这种“闭包性质”可以作为一种构造复杂的自动机的工具。
第2.1节中用很实质的方式使用了这种构造过程。
正则语言的另一类很重要的性质是“判定性质”,通过对这些性质学习使得我们能够给出用来回答关于自动机的很重要的问题的算法。
一个核心的例子是用来判定两个自动机是否定义了同样语言的算法。
我们能够判定该问题的能力使得我们能够把自动机“最小化”,也就是说,找到一个自动机,它等价于某个给定的自动机,并且使它有尽可能少的状态。
这是一个数十年里在开关电路的设计方面的很重要的问题,原因是电路的成本(电路所占有的芯片面积)趋向于随着电路所实现的自动机的状态数减少而减少。
4.1 证明语言的非正则性我们已经确认正则语言类至少有四种不同的描述方法,它们分别是:DFA所接受的语言类、NFA所接受的语言类、ε-NFA所接受的语言类以及正则表达式所定义的语言类。
然而并不是所有的语言都是正则语言。
在本节中,我们将会介绍一个强有力的技术,叫做“泵引理”,它能够证明某个语言不是正则的。
接着我们会给一些非正则语言的例子。
在第4.2节中我们将会看到怎样先后使用泵引理和正则语言的闭包性质来证明另外一些语言不是正则的。
4.1.1正则语言的泵引理我们考虑语言L01 = {0n1n | n≥1}。
该语言包含所有如下形式的串:01, 0011, 000111等等,也就是有一个或多个0后面跟着相同数目的1所构成的串。
Sigil正则表达式入门

实用标准文档Sigil 正则表达式入门 正则表达式,是一种用特殊符号表示文字的方法,主要用在查找和替换方面。
下面的例子可以让你知道正则表达式是干什么用的。
在一个文本中,有这样的一些内容:序章 第一章 ABCDEF 第二章 GHIJKL 第三章 ………… 终章这种内容我们都很熟悉,你有没有想过,用什么办法可以把这些内容一次过 查找出来呢?为了简化,我们先来看这个部分。
第一章 第二章 第三章可以看到,这些内容有着极高的相似性,由“第”,“章”开头和结尾,中 间有着一些数字。
如果我们能用一个什么符号来代表中间的所有字,比如一个圆 点“.”,不就可以用这样的方式来查找出所有这样的内容了吗。
第.章很早之前,就有人发明了一套完整的方案,让我们可以用各种不同的符号来 达到这种目的,那就是我们将要了解的正则表达式。
正则表达式作为一种描述字符的方案,在大量软件、编程语言中都有所运用, 而在这些不同的平台上,正则表达式的使用方式又往往会有或多或少的差异,在 某个平台上管用的表达式,换个地方可能就要改改才能正确运行。
那么在这篇文 章里,我们主要是讲 Sigil 中的正则表达式,至于推广应用,就要靠大家去查找 资料了。
1. 元字符我们前面提到,正则表达式一个重要作用就是用特别的符号来代表一类字符, 而这些符号就叫做“元字符”。
这些元字符在大多数环境下都是通用的。
注意,元字符中所有符号都是半角符号,也就是通常说的英文符号。
文案大全实用标准文档以下是一些常见的元字符,实际上还有更多。
这些元字符都经过测试,在 Sigil 下有效。
符号 意义 说明任意.一个最简单的元字符,匹配任意字符,但不包括换行符“\n”。
字符把元字符改变为普通字符,或者把某些普通字符转变为元\转义 字符。
比如,“\.”就是代表普通的点号,不代表其他字符。
半角空格、制表符等空白字符。
在 Sigil 中还能匹配到换\s空白 字符行符“\n”和空白行,使用要注意。
正则文法的语言描述能力

正则文法的语言描述能力
,介绍正则表达式
正则表达式(Regular Expression,简称 RegEx)是一种精确定义文本结构的模式,可以
匹配文本字符、字符组合等,可以用来执行文本搜索和替换,也可用于校验用户输入的数据。
正则表达式也被称为“正则表示式”或“正则匹配”。
正则表达式通常由两种记号组成:原子和元字符。
原子是由文本字符、特殊字符(如正斜
杠/)和特殊字符序列组成,可以在文本中出现同类字符串。
元字符用于将原子增强以获
得更准确的文本匹配,元字符类型包括重复符、选择符、转义符等。
正则表达式的语法可根据各种情况定义,如通配符语法(如,∗表示任意字符),正则表
达式可以用来查找特定的文本模式,并获取符合模式的字符串。
例如,可以使用正则表达
式编写一个文本搜索程序,用来搜索网页中的关键字,或在文件管理器中查找具有特定格
式的文件。
此外,正则表达式还可以用于数据验证,以确保输入的字符串具有正确的格式,例如验证电子邮件地址是否有效等。
正则表达式经常用于高级程序设计,从简单的文本处理到复杂的语句,它们可以为你带来
很多自由,充分利用它们可以更有效地编写代码甚至缩短编码时间,尤其是在结构化程序中,用正则表达式可以非常容易地找到所需的字符串。
正则表达式已经成为了文本处理能力非常强大的强大武器,具有很多简单而强大的特点,
可以大大简化文本操作,同时也是许多程序语言中的核心组成部分。
无论是文本搜索、代
码开发还是数据验证,使用正则表达式具有很高的通用性。
编译原理讲义(第二章文法与语言)

语言的定义(短语,简单短语)
• 短语:对于文法G[Z],如果Z =>* xUy, U=>+ u。显然,w=xuy是一个句型。我 们称u是句型w中相对于U的短语。 • 简单短语:在上面的定义中,如果U ::= u是G的一个规则,那么,u是句型w中相 对于U的简单短语。 • 例子:P22页例2.13。
语言的定义(短语,句柄)
• 注意:在寻找一个句型的短语(或简单 短语)时,必须要求将这个短语规约为 相应的非终结符号后所得到的符号串仍 然是句型。 • 句柄:一个句型的最左简单短语称为该 句型的句柄。 • 定义句柄的原因:在自底向上识别一个 符号串时,总是规约这个句柄。
语言的定义(文法的语言)
• 文法的语言:一个文法G[Z]的语言,用 L(G[Z])表示,定义如下: L(G[Z]) = {x | Z=>* x 并且 x VT+} • 一个文法的语言就是该文法的所有的句子的 集合。 • 文法的语言是所有终结符号串所组成的集合 的子集,一般是真子集。
• 定理2.7 对于CFG,如果存在句型 x=x1x2…xn且x=>*y,必然存在y1,y2,…,yn 使得: xi=>*yi且y= y1y2…yn。 • 定理2.8 如果:x=>*y,如果x的首符号是 终结符号,则y的首符号也是终结符号; 反之,如果y的首符号是非终结符号,那 么x的首符号也是非终结符号。
形式语言与程序设计语言
• 虽然程序设计语言的语法都使用上下文 无关文法来描述,但是通常语言都是上 下文相关的。 • 使用上下文无关文法描述语言的原因是: 存在高效处理上下文无关文法的技术。
关于CFG的进一步讨论
• Chomsky范式:所有的上下文无关语言 都可以用如下形式的文法产生:所有的 规则都形如:U ::= VW 或者 U::=T,其 中U,V,W为非终结符号,T为终结符号。 • Greibach范式:所有上下文无关语言都能 由这样的文法产生:U::=Tu,这里U为非 终结符号,T为终结符号。
正则语言与正则文法

2
使用正则表达式r表示的语言L(r): ⑴ Φ是∑上的RE,它表示语言Φ; ⑵ ε是∑上的RE,它表示语言{ε}; ⑶ 对于a∈∑,a是∑上的RE,它表示语言{a}; ⑷ 如果r和s分别是∑上表示语言L(r)和L(s)的RE,则: r与s的“和” (r+s)是∑上的RE,(r+s)表达的语言为L(r) ∪ L(s) ; r 与 s 的“乘积” (rs) 是 ∑ 上的 RE , (rs) 表达的语言为 L(r)L(s) ; r的克林闭包(r*)是∑上的RE,(r*)表达的语言为L(r) *。 ⑸ 只有满足⑴、⑵、⑶、⑷的才是∑上的RE。
27
定理2 RL可以用RE表示。
设DFA M=({q1,q2,…,qn},∑,δ ,q1,F) Rkij={x|δ (qi , x)=qj 而 且 对 于 x 的 任 意 前 缀 y(y≠x , y≠ε ) , 如 果 δ (qi , y)=ql , 则 l≤k}。
28
R0ij=
{a|δ (qi,a)=qj} {a|δ (qi,a)=qj}∪{ε }
24
例 3 构造与 (0+1)*0+(00)*等价的FA。
0
25
按照对(0+1)*0+(00)*的“理解” “直接地” 构造出的FA。
,
26
RL可以用RE表示 计算DFA的每个状态对应的集合——字母 表的克林闭包的等价分类,是具有启发 意义的。 这个计算过程难以“机械”地进行。 计算q1到q2的一类串的集合:Rkij 。 图上作业法。
33
例 4 求下图所示的DFA等价的RE 。
34
预处理。
35
去掉状态q3。
36
去掉状态q4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2) ri+1 (ri , wi+1) , i = 0, 1, …, n–1
3) rn F 则 N 接受 w。
30
NFA与DFA的等价性
定理 每一台非确定型有穷自动机都等价于某一台确定型有 1.19 穷自动机。
1 q2
1
q1
度优先好),是用DFA。 直观解释:对应于NFA这样的简单并行,程序中可以串行化。
39
主要内容
可以给出状态和信号之间的计算。
2
3
状态图
变换规则
状态
0 1
1 0
q1
q2
q3
起始状态
0,1
接受状态
4
状态图
0 1
1 0
q1
q2
q3
0,1
010: reject on input “1101”, the machine goes: 11: accept
q1 q2 q2 q3 q2
= “accept”
0
1
1
q1
q2
0
M2 = ( {q1, q2} , {0,1} , , q1, q2 )
L(M2) = { w | w 以 1 结束}
8
有穷自动机举例
例1.3 给定有穷自动机 M3 的状态图。请给出形式化的描述, 并确定其能识别的语言。
0
1
1
q1
q2
0 L(M3) = { w | w 是空串或以 0 结束}
(4) q0Q 是起始状态。 (5) FQ 是接受状态集。
6
有穷自动机举例
例 给定有穷自动机 M1 的状态图。请给出形式化的描述,并 确定其能识别的语言。
0
1
1
0
01
q1
q2
q3
q1 q1 q2
q2 q3 q2
0,1
M1 = ( {q1, q2 , q3} , {0,1} , , q1, q2 )
17
正则运算
例1.11 设字母表 是标准的 26 个字母 {a, b, … , z}。又设
A={good, bad}, B={boy, girl}, 求A∪B , AB 和A*。
18
正则运算
定理 正则语言类在并运算下封闭。 1.12
如果A1和A2是正则语言,则A1∪A2也是正则语言。 设 M1 识别 A1, M2 识别 A2。并设 M1=(Q1, , 1,q1, F1) 和 M2=(Q2, , 2, q2, F2) 构造识别A1∪A2 的 M=(Q, , , q0, F) Q = Q1Q2 = {(r1, r2) | r1Q1 且 r2Q2} ((r1, r2), a ) = (1(r1,a), 2(r2,a) ) q0 = (q1, q2) F = {(r1, r2) | r1F1 或 r2F2}
q1
b
a
a
q2 a, b q3
27
非确定型有穷自动机的形式定义
定义 1.17
非确定型有穷自动机 (NFA) 是一个 5 元组 ( Q, , , q0,
F ),其中
(1) Q 是有穷的状态集。
(2) 是有穷的字母表。
(3) : QεP(Q)是转移函数。
(4) q0Q 是起始状态。 (5) FQ 是接受状态集。
9
有穷自动机举例
例1.4 给定有穷自动机 M4 的状态图。请给出形式化的描述, 并确定其能识别的语言。
s
a
a
b b
q1
r1
a
b
b
a
b q2
r2
a
10
有穷自动机举例
例1.5 给定有穷自动机 M5 的状态图。请给出形式化的描述, 并确定其能识别的语言。
0
2,<RESET>
q1
1
0,<RESET>
1
2
计算理论
1
1.1 有穷自动机
实际示例—自动门控制
前缓冲区
后缓冲区
REAR BOTH NEITHER
FRONT
FRONT REAR BOTH
CLOSED
OPEN
NEITHER
控制器处于CLOSED状态,假设如下输入信号:
FRONT, REAR, NEITHER, FRONT, BOTH, NEITHER, REAR, NEITHER, 考察状态的变化。
定理 正则语言类在连接运算下封闭。 1.23
N1
N2
N
37
NFA与DFA的等价性
定理 正则语言类在星运算下封闭。 1.24
N1
N
38
DFA和NFA能力等价
DFA机器易算,NFA 人易制造, 通常,人造NFA,让机器 把它变成DFA。
当用并行技术去实现时实际上是用NFA。 当对有指数个节点的树搜索和回溯(可能这里广度优先比深
3) rn F 则 M 接受 w。
识别 定义
1.7 如果一个语言被一台有穷自动机
,则称它是
正则语言。
13
计算的形式化定义举例
例1.8 给定有穷自动机 M5 的状态图。令w是字符串 10<RESET>22<RESET>012
给出M5对w计算时进入的状态序列。
0
2,<RESET>
q1
1
0,<RESET>
1
0 q
1
0 q0
0
0,1
1
q00
q001
16
正则运算
定义 1.10
设 A 和 B 是两个语言,定义正则运算并、连接和星号 如下:
(1) 并: A∪B = { x | x∈A 或 x∈B } (2) 连接:AB = { xy | x∈A 且 y∈B } (3) 星号:A* = { x1x2…xk | k ≤ 0 且每一个xi ∈A }
33
NFA与DFA的等价性
推论 一个语言是正则的,当且仅当有一台非确定型有穷自 1.20 动机识别它。
34
NFA 转换成等价的 DFA 举例
例1.21 将图示的 NFA N 转换成等价的 DFA。
1
b
a
2 a, b
a,b
b
{3}
Q ={ , {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3} }
体会形式化描述的优点
12
计算的形式化定义
设 M = (Q, , , q0, F) 是一台有穷自动机, w = w1w2…wn 是
一个字符串,并且 wi 是字母表 的成员。如果存在 Q 中的
状态序列 r0, r1, … , rn,满足下列条件: 1) r0 = q0
2) (ri , wi+1) = ri+1 , i = 0, 1, …, n–1
28
NFA 的形式化描述举例
例1.18 给出图示的 NFA 的形式化描述。
0,1 1
q1
0,
q2
q3
0,1 1
q4
29
NFA 计算的形式化定义
设 N = (Q, , , q0, F) 是一台 NFA, w = w1w2…wn 是一个字
符串,并且 wi 是字母表 的成员。如果存在 Q 中的状态序
19
正则运算
定理 正则语言类在连接运算下封闭。 1.13
证明思路 按照定理1.12证明思路试一下。 输入:M1接受第一段且 M2 接受第二段时,M才接受;
? M不知道在什么地方将它的输入分开 (什么地方第一段结束,第二段开始)
20
举例
Consider the concatenation: 考虑下列连接 {1,01,11,001,011,…} • {0,000,00000,…} (That is: the bit strings that end with a “1”, followed by an odd number of 0’s.) Problem is: given a string w, how does the automaton know where the L1 part stops and the L2 substring starts? 如何知道L1 何处停止? L2 何处开始?切分问题。
1
2
2
q0 1,<RESET>
q2
q0, q1, q1, q0, q2, q1, q0, q0, q1,q0
0
14
设计有穷自动机
例:设计有穷自动机 E1,假设字母表是{0,1},识别的语言由 所有含有奇数个 1 的字符串组成。
0 qeven
0
1
1
qodd
15
设计有穷自动机
例1.9 设计有穷自动机 E2,使其能识别含有 001 作为子串组成 的正则语言。
考虑 N 有 箭头。 对于 M 的任意一个状态 R,定义 E(R) 为从 R 出发只沿着 箭头可以达到的状态集合,包括 R 本身的所有成员在内。 E(R) = { q | 从 R 出发沿着 0 或多个 箭头可以到达 q } 修改 M 的转移函数 (R,a)={ qQ | 存在 rR, 使得 qE((r,a)) } q0=E({q0})
构造识别 A 的 DFA M = (Q, , , q0, F ) (1) Q=P(Q)
(2) 对于 RQ 和 a,令
(R,a)={ qQ | 存在 rR, 使得 q(r,a) }
(3) q0={ q0 }
(4) F = { RQ | R 包含 N 的一个接受状态 }
32
NFA与DFA的等价性
定理 每一台非确定型有穷自动机都等价于某一台确定型有 1.19 穷自动机。
