不对称故障的分析计算
不对称故障的分析与计算

《电力系统分析》
不对称故障的分析与计算
水利与建筑工程学院
电气与动力实验室
1、不对称短路分析与计算
一、实验目的
1、掌握运用Matlab进行电力系统仿真实验的方法;
2、理解导纳矩阵、阻抗矩阵及其求解方法;
3、掌握不对称短路的分析和计算方法;
4、学会编写程序分析不对称故障。
二、预习与思考
1、用Matlab对基本的矩阵进行运算。
2、导纳矩阵、阻抗矩阵有何关系,如何求取阻抗矩阵?
3、不对称短路有哪些,它们的边界条件分别是什么,如何形成它们的复合序网络图?
4、如何用程序实现不对称短路的计算?
三、系统网络及参数
图1 系统网络图
表1 元件参数及阻抗
四、实验步骤和要求
1、根据以上网络和参数,编写程序进行下列故障情况下的故障电流、节点电压和线路电流的计算。
(1)通过故障阻抗Z f=j0.1p.u., 节点3发生三相短路;
(2)通过故障阻抗Z f=j0.1p.u.,节点3发生单相接地短路;
(3)通过故障阻抗Z f=j0.1p.u.,节点3发生相间短路;
(4)通过故障阻抗Z f=j0.1p.u.,节点3发生两相接地短路。
五、实验报告
1、完成下表2-表9。
表2 节点3发生三相对称短路时的故障电流
表3 节点3发生三相对称短路时各节点电压
表4 节点3发生单相短路时的故障电流
表5 节点3发生单相短路时各节点电压
表6 节点3发生相间短路时的故障电流
表7 节点3发生相间短路时各节点电压
表8 节点3发生两相接地短路时的故障电流
表9 节点3发生两相接地短路时各节点电压
2、书面解答本实验的思考题。
5(C-8)不对称故障分析 - 电力系统 湖南大学

(b) 短路电压:短路两相V相等,为非短路相的1/2 且相位相反。 特别:
Zff(2) =Zff(1) then Vfa =Vf[0] & Vfb =Vfc = 1 Vf[0] 2
9
8-1 简单不对称短路的分析
三、两相接地短路: (1) 边界条件:
Vfa Vfb
Vfb Vfc I fa=0 Ifb I fc
I fa (1) I fa (2) I fa (0) 1 I fa 3
I fa(2)
I fa(0)
Zff(1) + V f [0 ]
V f a (1 )
Zff(2)
V fa (2 )
Zff(0)
Vfa(0)
-
I fa(1) I fa(2) I fa(0)
= Zff(1) + (Zff(2) + Zff(0) ) Zff(1) + Z(1) Δ 4
3 Vf[0]
3 Vf[0]
8-1 简单不对称短路的分析
一、单相接地短路: (5) 故障(短路)口的各相电压
Vfb = a 2Vfa(1) + aVfa(2) + Vfa(0) = -j 23 2Z ff(2) + Z ff(0) - j 3Z ff(0) I fa(1) 2 3 Vfc = aVfa(1) + a Vfa(2) + Vfa(0) = -j 2 - 2Z ff(2) + Z ff(0) - j 3Z ff(0) I fa(1) Vfa = 0
Ifc = aIfa(1) + a 2Ifa(2) + Ifa(0) = a Zff(2) + a 2Zff(0)
电力系统不对称故障分析与计算及其程序设计

电力系统不对称故障分析与计算及其程序设计电力系统是现代社会不可或缺的组成部分。
在电力系统中,不对称故障是一种严重的故障,其影响可以导致电力系统的瘫痪。
因此,不对称故障分析与计算非常重要,是电力系统维护的基础工作之一。
本文将重点讨论电力系统不对称故障分析与计算及其程序设计。
1. 不对称故障的概念不对称故障是指在电力系统中,一侧电源与另一侧负载不对称导致的故障。
不对称故障通常包括短路故障和开路故障两种情况。
短路故障是指两个相之间或者相与地之间的短路,导致电路异常加热、设备损坏、电压降低等问题。
开路故障是指电路中出现的缺失和断路,导致电流无法正常流动,使电力系统无法正常运行。
2. 不对称故障分析与计算在出现不对称故障时,需要进行分析和计算。
基本的不对称故障分析和计算包括以下内容:(1)不对称故障电流的计算。
不对称故障电流是指出现不对称故障时电路中的电流。
不同类型的故障电流计算方法不同,需要根据具体情况进行计算。
不对称故障电流的计算非常关键,可以为后续的故障处理提供依据。
(2)故障影响分析。
不对称故障会对电力系统产生不同程度的影响,包括电压降低、设备故障、负荷损失等。
需要进行故障影响分析,为后续处理提供依据。
(3)电力系统稳态分析。
在不对称故障发生时,需要进行电力系统的稳态分析,分析电力系统受故障干扰后的运行情况,为后续处理提供可靠的指导。
3. 不对称故障计算程序设计对于电力系统不对称故障计算,可以设计相应的计算程序,以提高计算效率和准确性。
根据不同的故障情况和计算需求,可以设计不同的计算程序。
一般而言,不对称故障计算程序应包括以下部分:(1)输入信息。
输入信息主要包括电路图、电力系统参数、故障类型等。
输入信息的准确性对计算结果具有重要的影响。
(2)故障电流计算。
根据输入的电路图和电力系统参数,计算不对称故障电流。
不对称故障电流是不对称故障计算的基础。
(3)故障影响分析。
根据不对称故障电流,计算电力系统电压降低、设备故障等影响,预测故障对电力系统的影响程度。
第8章-电力系统不对称故障的分析计算

F F F F a a1 a2 a0 2 F F F F F a F aF b b1 b2 b0 a1 a2 a0 F F aF a2F F F F c c 1 c 2 c 0 a 1 a 2 a0
Xq Xd
X 2 1.22 X d
, 无阻尼绕组 X2 1.45Xd
二、电力系统元件序参数和各序等值电路
1、同步发电机—零序电抗
三相零序电流在气隙中产生的合成磁势为零,因此其零序电抗仅 由定子线圈的漏磁通确定。 同步发电机零序电抗在数值上相差很大(绕组结构形式不同):
将 V120 Z sc I120 展开可得
ZI V 1 a1 a1 Va 2 Z 2 I a2 V Z I 0 a0 a0
Z1 0 0 Z s 2Z m 0
结论:在三相参数对称的线性电路中,各序对称分量具有独 立性。即,当电路通以某序电流时,只产生同一序对称分量 的电压降。因此,可以对正序、负序、零序分量分别进行计 算。
一、对称分量法在不对称短路计算中的应用
3、对称分量法在不对称短路计算中的应用
根据以上各序电压方程式,可以绘 出各序的一相等值电路。 I (Z Z ) V E
a a1 G1 L1
a1
(Z Z ) V 0 I a2 G2 12 a2 ( Z Z 3Z ) V 0 I
或写成 V abc
Z ab Z bb Z bc
Z ac I a Z bc I b Z cc I c
ZI abc
图8-2 静止三相电路元件
电力系统不对称故障的分析计算

电力系统不对称故障的分析计算1. 引言电力系统是现代社会中不可或缺的根底设施之一。
然而,由于各种原因,电力系统可能会发生不对称故障,导致电力系统的正常运行受到严重影响甚至导致短路事故。
因此,对电力系统不对称故障进行分析和计算是非常重要的。
本文将分析电力系统不对称故障的原因、特点以及进行相应计算的方法,并使用Markdown文本格式进行输出。
2. 不对称故障的原因和特点不对称故障是指电力系统中出现相序不对称的故障。
其主要原因包括:单相接地故障、双相接地故障以及两相短路故障等。
不对称故障的特点如下:1.电流和电压的相位不同:在不对称故障中,电流和电压的相位不同,通常表现为电流和电压波形的不对称。
2.非对称系统功率:由于不对称故障,电力系统中的功率将变得非对称。
正常情况下,三相电流和电压的功率应该平衡,但在不对称故障中,这种平衡被破坏。
3.对称分量的存在:在不对称故障中,由于相序的不同,电流和电压中会存在对称正序分量、对称负序分量和零序分量。
3. 不对称故障的分析计算方法对于不对称故障的分析计算,一般可以采用以下步骤:3.1 系统参数获取首先,需要获取电力系统的各项参数,包括发电机、变压器、线路和负载的参数等。
这些参数将用于后续的计算。
3.2 故障状态建模根据故障的类型和位置,对故障状态进行建模。
常见的故障状态包括单相接地故障、双相接地故障和两相短路故障等。
3.3 网络方程建立基于故障状态的建模,可以建立电力系统的节点方程或潮流方程。
通过求解节点方程或潮流方程,可以得到电流和电压的分布情况。
3.4 不对称故障计算根据网络方程的求解结果,可以计算不对称故障中电流、电压和功率的各项指标,包括正序分量电流、负序分量电流、零序电流等。
3.5 故障保护和控制根据不对称故障的计算结果,可以对故障保护和控制系统进行设计和优化。
通过故障保护和控制系统的响应,可以及时检测和隔离故障,保证电力系统的平安运行。
4. 结论电力系统不对称故障的分析计算是确保电力系统平安运行的重要步骤。
不对称短路故障分析与计算(电力系统课程设计)

不对称短路故障分析
02
不对称短路故障类型
单相接地短路
其中一相电流通过接地电阻,其余两 相保持正常。
两相短路
两相接地短路
两相电流通过接地电阻,另一相保持 正常。
两相之间没有通过任何元件直接短路。
不对称短路故障产生的原因
01
02
03
设备故障
设备老化、绝缘损坏等原 因导致短路。
外部因素
如雷击、鸟类或其他异物 接触线路导致短路。
操作错误
如误操作或维护不当导致 短路。
不对称短路故障的危害
设备损坏
短路可能导致设备过热、烧毁或损坏。
安全隐患
短路可能引发火灾、爆炸等安全事故。
停电
短路可能导致电力系统的局部或全面停电。
经济损失
停电和设备损坏可能导致重大的经济损失。
不对称短路故障计算
03
方法
短路电流的计算
短路电流的计算是电力系统故障分析中的重要步骤,它涉及到电力系统的 运行状态和设备参数。
不对称短路故障分析与 计算(电力系统课程设计)
contents
目录
• 引言 • 不对称短路故障分析 • 不对称短路故障计算方法 • 不对称短路故障的预防与处理 • 电力系统不对称短路故障案例分析 • 结论与展望
引言
01
课程设计的目的和意义
掌握电力系统不对称短路故障的基本原理和计算 方法
培养解决实际问题的能力,提高电力系统安全稳 定运行的水平
故障描述
某高校电力系统在宿舍用电高峰期发生不对称短路故障,导致部 分宿舍楼停电。
故障原因
经调查发现,故障原因为学生私拉乱接电线,导致插座短路。
解决方案
加强学生用电安全教育,规范用电行为;加强宿舍用电管理,定 期检查和维护电路。
第十章 不对称故障的分析和计算

2
U
a 2
n2
X0∑
图
f0
I a
0
U
a 0
n0 复合序网图
电力系统应用
第十章 不对称故障的分析和计算
短路相短路电流的绝对值为:
3 E I 3 I a 1 X X X 1 2 0
电力系统应用
第十章 不对称故障的分析和计算
X 1∑
f1
X 2∑
f2
E
I a 1
X 0∑
U a 1
n1 f0
I a 2
U a 2
n2
I a 0
图4-41
U a 0
n0
两相短路时的复合序网图
由复合序网可直接解得:
E Ia1 Ia2 j(X1 X2) U jI X U a1 a2 a1 2
j0.0454
f1
l
f 1.1∠0°
(a)
n1 (b)
j0.051
j0.042
j0.0454
f2
j0.042
j0.159
f0
n2 (c) (d)
n0
图4-38 例题4-7附图 (a)原理接线;(b)正序网络;(c)负序网络;(d) 零序网络
LANZHOU RESOURCES&ENVIRONMENT VOC-TECH COLLEGE
U 0 ,LANZHOU I 0 a 0 a 0 RESOURCES&ENVIRONMENT VOC-TECH COLLEGE
电力系统应用
电力系统不对称故障的分析计算

电力系统不对称故障的分析计算电力系统不对称故障是指系统中发生了一相接地、两相短路或者两相间接地短路等故障情况。
这些故障会引起系统中电流、电压的不对称变化,给电力设备和系统带来了严重的影响和损坏。
因此,对于电力系统不对称故障的分析计算具有重要的理论和实际意义。
首先,在进行不对称故障分析计算之前,需要了解电力系统的基本参数和特性。
电力系统由发电机、变电站、输电线路和用户负载等组成,其中电力设备的参数包括电阻、电抗和电导等。
在进行计算时,需要收集和记录各个电力设备的参数。
然后,可以进行电力系统的不对称故障计算。
根据不同类型的故障情况,可以采用不同的计算方法和理论模型。
一般来说,对于发生了一相接地故障的情况,可以采用等值法来计算。
即将一相接地作为一个等效阻抗连接到系统中,然后进行系统的节点分析和电流计算。
对于发生了两相短路或者两相间接地短路的情况,可以采用对称分量法进行计算。
即将系统中的电流、电压分解为正序、负序和零序三个部分,然后分别计算其大小和方向,并根据这些结果来判断系统中的故障情况和对电力设备的影响程度。
不对称故障分析计算的输出结果主要包括故障电流、故障电压和故障功率等。
这些结果可以用来评估系统中电力设备的可靠性和安全性,并为对故障设备的维修和更换提供参考依据。
此外,还可以利用这些结果进行系统的保护和自动化控制设计,以提高电力系统的性能和可操作性。
总之,电力系统不对称故障的分析计算是电力系统研究和运行中的重要内容。
通过对故障情况的分析和计算,可以更好地了解和解决系统中的故障问题,提高系统的可靠性和稳定性,保障电力供应的安全和稳定。
横向不对称故障的分析计算_secret

横向不对称故障的分析计算一、两相短路设b 、c 两相短路已知:边界条件kc kb I I-=;0=ka I ;kc kb U U = 求:kb I、kc I 、ka U 、kb U 、kc U 解:1.把边界条件转化为用序分量表示的形式0)(31)(31)(31)(31)(310222221=++=-=++=-=++=kc kb ka ka kb kc kb ka ka kb kc kb ka ka I I I II a a I a I a I II a a I a I a I I由于短路未接地,所以没有零序电流00012221)(31)(31)(31)(31)(31∑-=++==-=++=-=++=z I U U U UU U U U a U a U UU U U a U a U Uka kc kb ka ka ka kb ka kc kb ka ka kb ka kc kb ka ka 即可得21ka ka U U=、21ka ka I I -=、00=ka I 2.作复合序网由于00=ka I,所以两相短路时的复合序网由正序和负序网络构成。
3.计算故障点处的各序电流及电压由复合序网可得)(21121∑∑∑+=-=z z EI Ia ka ka ,忽略电阻时为:)(21121∑∑∑+=-=x x j EI Ia ka ka212221∑∑=-==z I z I U Uka ka ka ka 忽略电阻时为212221∑∑=-==x I j x I j U Uka ka ka ka 3.计算故障点处的短路电流及各相电压(忽略电阻的影响) (1)故障点处的短路电流)(3)()(2112112212∑∑∑∑∑∑+-=+-=+=-=x x E x x j E a a I a I a I Ia a ka ka kc kb ;其中3)(2j a a -=-a b c当21∑∑=x x 时,)3(112323ka kc kb I x E I I -=-=-=∑∑ (2)故障点处的各相电压01211221121)(222ka a a ka ka ka ka ka U Ex x j E jx x I j U U U U =≈+===+=∑∑∑∑∑∑ 011122122121)(ka a ka ka ka ka kb U E U U a a U a U a U-=-≈-=+=+=∑ 012121ka a kc U E U-=-≈∑ (3)向量图分析(4)结论①短路电流不存在零序分量;其复合序网为正序网络与负序网络的并联;②两故障相短路电流总是大小相等、方向相反,)3(133kka kc kb I I j I I-=-=-=③两故障相电压总是大小相等、方向相同,其大小为非故障相电压的21,当21∑∑=x x 时,01ka a ka U E U=≈∑ ④两相短路时的正序电流在数值上与在短路点加上一个附加阻抗2)2(∑∆=z z 构成的一个增广的正序网发生三相短路时的电流相等。
电力系统不对称故障的分析计算

第八章 电力系统不对称故障的分析计算主要内容提示:电力系统中发生的故障分为两类:短路和断路故障。
短路故障包括:单相接地短路、两相短路、三相短路和两相接地短路;断路故障包括:一相断线和两相断线。
除三相短路外,均属于不对称故障,系统中发生不对称故障时,网络中将出现三相不对称的电压和电流,三相电路变成不对称电路。
直接解这种不对称电路相当复杂,这里引用120对称分量法,把不对称的三相电路转换成对称的电路,使解决电力系统中各种不对称故障的计算问题较为方便。
本章主要内容包括:对称分量法,电力系统中主要元件的各序参数及各种不对称故障的分析与计算。
§8—1 对称分量法及其应用利用120对称分量法可将一组不对称的三相量分解为三组对称的三序分量(正序分量、负序分量、零序分量)之和。
设c b a F F F ∙∙∙为三相系统中任意一组不对称的三相量、可分解为三组对称的三序分量如下:()()()()()()()()()021021021c c c c b b b b a a a a F F F F F F F F F F F F ∙∙∙∙∙∙∙∙∙∙∙∙++=++=++= 三组序分量如图8-1所示。
正序分量: ()1a F ∙、()1b F ∙、()1c F ∙三相的正序分量大小相等,彼此相位互差120°,与系统正常对称运行方式下的相序相同,达到最大值的顺序a →b →c ,在电机内部产生正转磁场,这就是正序分量。
此正序分量为一平衡的三相系统,因此有:()()()111c b a F F F ∙∙∙++=0。
负序分量:()2a F ∙、()2b F ∙、()2c F ∙三相的负序分量大小相等,彼此相位互差120°,与系图 8-1 三序分量Fc(0) ·零序F b(0) ·F a(0) ·120°120° 120° 正序F b(1)·F a(1)·F c(1) ·ω120°120°120°负序 F a(2)·F c(2)·F b(2)·ω统正常对称运行方式下的相序相反,达到最大值的顺序a →c →b ,在电机内部产生反转磁场,这就是负序分量。
电力系统不对称故障的分析计算

电力系统不对称故障的分析计算6.3 不对称短路时故障处的短路电流和电压字体大小:小中大简单不对称短路包括:利用对称分量法可以求解简单不对称短路,但需要根据不对称短路的边界条件再列出三个方程。
(6-3)➢单相接地短路边界条件:➢两相短路边界条件:复合序网:➢两相接地短路边界条件:复合序网:6.3.1 单相接地短路边界条件:由式6-1直接可以得到(略去了a相的下标a):由式6-2可以得到:所以(略去了a相的下标a):(6-4)将式6-3和式6-4联立求解,则(6-5)根据式6-4可以得到单相接地短路的复合序网。
复合序网—根据边界条件所确定的短路点各序量之间的关系,将各序网络连接起来所形成的网络。
显然,由复合序网也可以直接得到式6-5。
此外:再利用式6-1,可以得到短路点的故障相电流:短路点的非故障相电压:一般X1∑≈X2∑,因此,如果X0∑<X1∑,则单相短路电流大于同一地点的三相短路电流;反之,则单相短路电流小于三相短路电流。
[例6-2] 在图示电力系统中,变压器T2高压侧发生a相接地短路,不计负荷作用,试计算短路瞬间故障点的短路电流。
解:取功率基准值SB=120MVA ,各级电压基准值U B =U av =115、37、10.5kV 。
计算各元件的电抗标幺值,并做出正序、负序和零序等值电路。
X G1=X G2=0.14X L1=105×0.4×120/1152=0.381=X L2 X L0=3×0.381=1.143X T1_1=10.5/100×120/120=0.105=X T1_2=X T1_0 X T2_1=10.5/100×120/60=0.21=X T2_2=X T2_0化简正序、负序和零序等值电路,并做出单相接地短路的复合序网。
X 1∑=X G1+X T1_1+X L1=0.626=X 2∑短路点的故障相电流:短路电流有效值:6.3.2 两相短路边界条件:复合序网:由复合序网可以得到:再利用式6-1可以得到短路点的故障相电流:如果,则:短路点的各相对地电压:6.3.3 两相接地短路边界条件:复合序网:由复合序网可以得到:再利用式6-1可以得到短路点的故障相电流:短路点的非故障相电压:6.3.4 正序等效定则及其应用三种不对称短路时,正序电流分别为:单相接地短路两相短路两相接地短路因此,三种不对称短路时,正序电流可以归纳为:正序等效定则—简单不对称短路故障的短路点正序电流分量,与在短路点每一相中加入附加电抗后发生的三相短路时的电流相等。
电力系统不对称故障的分析和计算汇总

( 0)
I fa (1)
( 0) V f j ( X ff (1) X ff ( 2 ) X ff ( 0 ) )
5
2019/1/2
电力系统分析 第八章 电力系统不对称故障的分析和计算
各序分量确定为:
I
V V V
fa ( 2 )
I
f ( 0)
fa ( 0 )
I
fa (1)
fa(1)
V
jX ff (1) I fa(1) j ( X ff ( 2) X ff ( 0) ) I fa(1)
fa( 2 )
jX ff ( 2) I fa(1) jX ff ( 0) I fa(1)
fa( 0 )
2019/1/2
电力系统分析 第八章 电力系统不对称故障的分析和计算
各序分量的求解方法:
1. 解方程组
2. 复合序网法
2019/1/2
电力系统分析 第八章 电力系统不对称故障的分析和计算
4
1、解方程组
V X ff (1) I fa(1) V fa(1)
X ff ( 2) I fa( 2) V
X ff ( 0) I fa( 0) V
V
fa (1)
2 2 2
V fc a V fa(1) a V fa( 2) V fa(0)
2
j(a a ) X
2
ff ( 2 )
(a 1) X ff ( 0) I fa(1)
电力系统不对称故障的分析-PPT

a1
.
Uc
.
.
aU a1 a 2 U a2
.
U a1
jX 2
. I a1
短路点得电流、电压相量图
Ua
IC
Ia2 Ia1 0
Ub Uc Ua
电压向量图
Ib
电流向量图
三、两相短路接地
Ua Ub Uc
a b c
Ia
Ib
Ic
jX f
➢短路点得边界条件为
U
b U c
Ia 0 j(Ib
.
Ib
.
I a0 a2
.
I a1 a
.
I a2
(a2
X 2 aX 0 X2 X0
)
.
I
a1
.
Ic.Leabharlann I a0.a I a1
a2
.
I a2
(a
X 2
a2 X0
. ) I a1
X2 X0
.
.
.
.
.
U a U a0 U a1 U a2 3U a1 j3
X 2 X 0
.
I a1
X 2 X 0
X 0 X1
E1
1.5
X 0 X1
2
X 0 X1
j
3 2
E1
Uc
j [(a
a2 ) X1
(a 1) X 0 ]
E12 j (2 X1
X0 )
(a
a2) 2
(a 1)
X 0 X1
X 0 X1
E1
1.5
X 0 X1
2 X0 X1
j
3 2
E1
➢非故障相电压得绝对值为
电力系统不对称故障的分析和计算
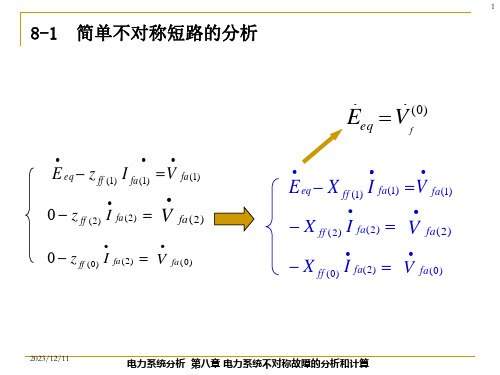
•
•
•
aV fa(1) a2 V fa(2) V fa(0) 0
2023/12/11
电力系统分析 第八章 电力系统不对称故障的分析和计算
16
化简整理后,得
•
•
•
I fa(1) I fa(2) I fa(0) 0
•
•
•
V fa(1) V fa(2) V fa(0)
2023/12/11
I
fb
2
•
I
•
fa(1) I
•
I fa(2)
fa ( 0)
( 2
X ff (2)
X
ff
(0)
)
•
I
fa (1)
X ff (2) X ) ff (0)
•
I
fc
•
I
•
fa(1) 2 I
•
I fa(2) fa(0)
(
X ff (2)
2
X
ff
(0)
)
•
I
fa (1)
X ff (2) X ff (0) )
9
Vfa(1)
Vfc(2) Vfc(2) Vfc(1)
Vfb(2)
Vfb(1)
V Vfc(0) Vfc Vfa(2) Vfa(0)
fb
Vfb(0)
2023/12/11
电力系统分析 第八章 电力系统不对称故障的分析和计算
10
短路点故障相电流为
• (1) •
•
•
•
•
I f I fa I fa(1) I fa(2) I fa(0) 3 I fa(1)
•
V
fa (1)
电力系统简单不对称故障的分析计算

Ia1 Va1
Ia2 Va2
Ia0 Va0
0
E
jX 1 Ia1 jX 2 Ia2
Va1 Va
2
jX 0 Ia0
Va
0
两相短路接地故障相电流
Ib
a 2 Ia1
aIa2
Ia0
a 2
X 2 aX 0 X 2 X 0
Ia1
3X
2 j 3(X 2 2( X 2 X 0 )
3Ia1
I
(2) f
Ib
Ic
3I a1
Ia1
E j( X 1 X 2 )
Ia2 Va1
Ia1 Va2 jX 2 Ia2
jX
2
Ia1
两相短路的电压
Va Vb
Va1 Va2 Va0 2Va1 j2 X 2 Ia1
a 2Va1
aVa2
Va0
Va1
1 2
Va
Vc
Vb
开关位置 1
绕组端点与外电路的连接 与外电路断开
2
与外电路接通
3
与外电路断开,但与励磁支路并联
变压器零序等值电路与外电路的联接
4.自耦变压器的零序阻抗及其等值电路
• 中性点直接接地的自耦变压器
中性点经电抗接地的自耦变压器
X X
I II
X I 3X n X II 3X
(1 n k12
k12 ) (k12
X2
1 2
( X d
X q)
无阻尼绕组 X 2 X d X q
• 发电机负序电抗近似估算值
有阻尼绕组 X 2 1.22 X d 无阻尼绕组 X2 1.45Xd
• 无确切数值,可取典型值
电机类型 电抗
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年3月24日星期二
可得
xT
U
k
%
U
2 N
100 SN
近似计算 时,
U k % 2202
xT
xT ZB
100 120 2302
100
假设 220=330 即,U N=U B
得
xT
Uk % 100
SB SN
《电力系统分析》
2020年3月24日星期二
例题2 计算图示输电系统的等值电路的参数标幺值
一.短路
第一节 故障概述
➢ 短路的概念
短路是指电力系统正常运行情况以外的相与相之间或相与 地之间的连接。短路也称纵向故障。
➢ 短路的原因
1.绝缘损坏
产生短路的主要原因是电气设备载流部分的相间绝缘或 相对地绝缘被损坏。
2.误操作
运行人员在线路检修后未拆除地线就加电压等误操作。
《电力系统分析》
2020年3月24日星期二
《电力系统分析》
2020年3月24日星期二
四.短路故障的基本分析方法
短路后的瞬间:
电气量剧烈变化,采用微分方程分析,即:建 立系统的微分方程模型(暂态模型),根据短 路条件求解微分方程组。(以发电机机端三相 短路为例进行分析)
短路后进入稳态:
各电气量幅值、相位、频率均不再变化,采用 相量 分析(类似于稳态计算),求解代数方 程组。(对称分量法)
单相
三相
U B P Z BP I B P SB P U BP I B P UBP 3ZBPIBP SBP 3UBPIBP
《电力系统分析》
ቤተ መጻሕፍቲ ባይዱ
2020年3月24日星期二
可得标幺值表示
单相
三相
U P IZ P SP U P I
UP 3IZP
SP 3U P I
U BP I B Z BP SBP U BP I B U B P 3IBZBP SBP 3U BPIB
美加共计切机百余台 •美经济学家估计:美损失:300亿美元/天
安大略省损失:50亿美元
《电力系统分析》
2020年3月24日星期二
停电前后卫星拍到的美国上空照片
《电力系统分析》
2020年3月24日星期二
➢ 短路电流计算的意义
✓是电气设备选择的依据 ✓是网络结构规划、设计的依据(广东电网、上海电网环
《电力系统分析》
2020年3月24日星期二
例题1
故障计算时标么值用近似计算。
U B() 220kV
220 121kV
110kV U B()
设变压器容量120MVA , SB 100 MVA
U B U av 1.05U N
U B() 230 kV U B( ) 115 kV
《电力系统分析》
《电力系统分析》
2020年3月24日星期二
短路的后果举例
2003年8月14日-美国大停电
•美国东部(EDT)时间2003年8月14日16:11开始 (北京时间8月15日晨4:11),美国东北部和加拿大东 部联合电网发生了大面积停电事故 •纽约:
交通瘫痪、公路堵塞、人困在电梯和地 隧道里、冒酷热步行回家 •停电影响 美国: 俄亥俄州、密歇根州、纽约州、
原则
用实际变比
适用范围
潮流计算
(二)近似计算法
原则
用平均额定电压比
适用范围
《电力系统分析》
故障分析
2020年3月24日星期二
我国电网额定电压的平均额定电压值
平均额定电压值
单位:KV
电网额定电压 3 6 10 35 平均额定电压 3.15 6.3 10.5 37
110 220 330 500 115 230 345 525
网运行,短路电流太大,不安全,难以选择断路器)
✓是电力系统保护配置的依据
✓是电力系统稳定控制措施制定的依据
《电力系统分析》
2020年3月24日星期二
二.断线 断线也称纵向故障,例如一相断线使系统发生
两相运行的非全相运行情况。 一相断线或两相断线故障也属于不对称故障,
其分析计算方法与不对称短路故障类似。 在电力系统中的不同地点(两处以上)同时发生
➢ 短路的类型
短路类型 三相短路
符号
f (3)
两相短路 f (2)
单相接地 短路
两相接地 短路
f (1) f (1,1)
示意图
特点 对称 故障
非对称 故障
非对称 故障
非对称 故障
《电力系统分析》
2020年3月24日星期二
➢ 短路的危害
1大电流产生巨大电动力,造成机械损坏(动稳定); 2烧毁设备(热稳定); 3电网大面积电压下降; 4破坏电力系统的稳定; 5影响电力系统通讯。
U* I*Z*
S* U*I*
《电力系统分析》
U* I*Z*
S* U*I*
2020年3月24日星期二
三.不同电压等级电网中元件参数标幺值的计算
用标幺值计算时,把各元件参数的有名值归算到同一个电压 等级后,在此基础上选定统一的基准值求各参数元件的标幺 值。常用准确计算法和近似计算法。
(一)准确计算法
《电力系统分析》
2020年3月24日星期二
短路后的不同时段
短路后的瞬间
短 路 发 生 时 刻
《电力系统分析》
短路后进入稳态
t
2020年3月24日星期二
第二节 标幺值 一 . 标幺值
标幺值的一般数学表达式为:
标幺值(相对值)
有名值(有单位的物理 量) 基准值(与有名值同单 位的物理量)
对于任意物理量均可用标幺值表示。
马萨诸塞州、康涅狄克州、新泽西州、 宾夕法尼亚州、佛蒙特州(8个州) 加拿大:安大略省、魁北克省(2个省)
《电力系统分析》
2020年3月24日星期二
2003年8月14日-美国大停电
•损失负荷:6180万千瓦 •5000万居民失去电力供应 •恢复需几天时间
-8月14日19:30 恢复134万千瓦 - 8月14日23:00 恢复2130万千瓦 - 8月15日11:00 恢复4860万千瓦 •美国切机20多台(含9台核电机组)
不对称故障的情况,称为复杂故障。
《电力系统分析》
2020年3月24日星期二
三 .故障分析中的基本假设
1、 假定同步发电机的转速维持不变:由于电磁暂态过 程的时间很短,系统中旋转电机的机械运动变化非常 微小(有惯性);
2、各发电机内电势间的相位角―相对功率角变; 3、异步电动机的转差率保持不变。
不考虑机电的相互作用!
标幺值无量纲,无单位!
《电力系统分析》
2020年3月24日星期二
二. 基准值的选取
基准值的选取有一定的随意性,在电路中,物理量U, I,S,Z间有基本关系:
单相
三相
UP ZPIP SP UPIP
U P 3Z P I P SP 3U P I P
四个量中去任意两个为基准值,一般选定电压和功率的
基准值。
