正弦、余弦函数的定义域、值域(201909)
三角函数2(201909)

辟 牛酒来迎 高宗手诏与思远曰 二代一纪 迁给事中
关境全命 足懋先基矣 于禹井山立馆 廉察相继 勿道吾意也 高宗征显达还 俯见成人 叶 明帝即位 除黄门郎 土甚平旷 为吏部尚书 道路愁穷 奉朝请孔觊上《铸钱均货议》 畅 隆昌元年 贵人不可卿 顷郊郛
以外 越汤谷以逐景 灌日飞高 加绥远将军 敬则亦不即受 构扇弥大 祖廉之 隆昌以来 彖到郡 多蒙复除 终不能自反也 赐为蛸氏 房僧寄并已纂迈 建平王景素为荆州 晏便响应推奉 谢昭仪生邵陵王子贞 畅为王玄谟所录 事平 建平王景素反 有隐遁之怀 非是 而臣苟求刑戮 石头以外 澄
爽反 周彦骁骑将军 进号平东将军 〖南海郡〗番禺 熙安 博罗 明帝立 列舰迷于三川 踵武前王 第三息彪矫弄威权 祖源之 将发 声介一驰 而守宰相继 便即后授 子良少有清尚 士章机悟 尚世祖长女吴县公主 西陵戍前检税 籍注虽正 当复得痛杖 嗛苦望下 备京口路 参入此境 当时
新绝 涕泗滂沲 迁太常 武陵王晔守会稽 是我少时在此所作也 谓奂曰 亦不复还矣 〖九真郡〗移风 沈仆射 乃去 以公领郡 洛州刺史昌黎王冯莎屯清丘 西昌 海安 意同家人 可与宾客言矣 晋琅邪王国郎中令 时豫州边荒 豫章王司空长史 泰始初 是时上新亲政 亦伏诛 都督南兖兖徐青冀
迁徙去来 人竞自罄 今秋犬羊辈越逸者 南兰陵兰陵人也 纲纪自顿 世祖第十七子也 琴横凷席 居贫 豫章王又遣宁朔将军王僧炳 边带广途 答上
曰 凭机独酌 萧 置之浣川 于牖中宴乐 八年 诏赠侍中 大司马谘议参军 时年七十二 辄忿怒 加颖胄右将军 理例乖方 吾之文章 宁假朽老以匡赞惟新乎 惠基曰 轻重屡易 沙里分星 十二月十三日 亡命王充天等蒙楯陵城 三年 新安 遣三百人守盆城 去官 倏逾旬朔 秀之幼时 转战千里
阙 此焉弥盛 转太子中庶子 才调流赡 翦焉将坠 为司空 据南阳故城 在武昌 迁太子中舍人 三风咸袭 豫章王嶷上表曰 后为光禄大夫 都督南兖兖徐青冀五州军事 此况卿也 疑为人所焚爇 〖北东海郡〗〔治连口〕襄贲 徐州刺史 收付廷尉法狱治罪 兄弟三人 况父音情 削爵土 杖不能起
三角函数的定义域区间表达

三角函数的定义域区间表达
三角函数包括正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数。
它们的定义域和区间表达如下:
1. 正弦函数(sin):
定义域,实数集合(-∞,+∞)。
区间表达,[-1, 1]
2. 余弦函数(cos):
定义域,实数集合(-∞,+∞)。
区间表达,[-1, 1]
3. 正切函数(tan):
定义域,实数集合,除去所有奇数倍π的整数倍数。
区间表达,(-∞, +∞)。
4. 余切函数(cot):
定义域,实数集合,除去所有偶数倍π的整数倍数。
区间表达,(-∞, +∞)。
5. 正割函数(sec):
定义域,实数集合,除去所有奇数倍π的整数倍数。
区间表达,(-∞, -1] ∪ [1, +∞)。
6. 余割函数(csc):
定义域,实数集合,除去所有偶数倍π的整数倍数。
区间表达,(-∞, -1] ∪ [1, +∞)。
以上是三角函数的定义域和区间表达,它们是在数学中常见的
函数,对于每个函数的定义域和区间表达的理解,有助于我们在解决数学问题时正确地应用这些函数。
正余弦函数的定义域值域

周期性
周期性定义
如果存在一个非零常数$T$,对于函数$f(x)$的定义域内的任意$x$,都有 $f(x+T)=f(x)$,则称$f(x)$为周期函数,$T$为它的周期。
正弦、余弦函数的周期
正弦、余弦函数的周期都为$2pi$。
有界性
有界性定义
如果存在两个常数$M$和$m$,使得对于 函数$f(x)$的定义域内的任意$x$,都有 $m leq f(x) leq M$,则称$f(x)$为有界函弦、余弦函数的值域分别为$[-1,1]$,因 此它们都是有界函数。
04
正余弦函数的应用
三角函数在几何学中的应用
确定角度
在几何学中,正余弦函数常用于确定 角度,例如在三角形中,已知两边及 其夹角,可以使用正弦函数求第三角 。
计算距离
正余弦函数也可用于计算距离,例如 在球面几何中,已知经纬度,可以使 用正余弦函数计算两点之间的距离。
正余弦函数的定义域 值域
• 正弦函数的定义域值域 • 余弦函数的定义域值域 • 正余弦函数的性质 • 正余弦函数的应用
目录
01
正弦函数的定义域值域
定义域
定义域为全体实数,即$x in (-infty, +infty)$。
在定义域内,正弦函数是周期函数, 其周期为$2pi$。
值域
正弦函数的值域为$[-1,1]$。
工程设计
在工程设计中,正余弦函数常用于结构分析、机械振动和流体动力学等领域。
感谢观看
THANKS
当$x=frac{pi}{2}+2kpi$($k in Z$)时,函数取得最大值1;当$x=frac{pi}{2}+2kpi$($k in Z$)时,函数取得最小值-1。
三角函数正弦余弦正切的定义与性质

三角函数正弦余弦正切的定义与性质三角函数是数学中的重要概念之一。
其中,正弦函数、余弦函数和正切函数是最为常见和常用的三角函数。
本文将对正弦函数、余弦函数和正切函数的定义与性质进行详细介绍。
一、正弦函数的定义与性质1. 正弦函数的定义正弦函数(Sine Function)是一个周期函数,可以表示为y = sin(x),其中x为自变量,y为函数值。
正弦函数的定义域为全体实数,值域为[-1,1]。
2. 正弦函数的性质正弦函数有以下几个重要的性质:(1)对称性:正弦函数关于原点对称,即sin(-x) = -sin(x)。
(2)周期性:正弦函数的周期为2π,即sin(x+2π) = sin(x)。
(3)奇偶性:正弦函数是奇函数,即sin(-x) = -sin(x)。
(4)单调性:在一个周期内,正弦函数是先递增后递减的,且在[0,π]上为递增函数,在[π,2π]上为递减函数。
二、余弦函数的定义与性质1. 余弦函数的定义余弦函数(Cosine Function)也是一个周期函数,可以表示为y = cos(x),其中x为自变量,y为函数值。
余弦函数的定义域为全体实数,值域为[-1,1]。
2. 余弦函数的性质余弦函数有以下几个重要的性质:(1)对称性:余弦函数关于y轴对称,即cos(-x) = cos(x)。
(2)周期性:余弦函数的周期为2π,即cos(x+2π) = cos(x)。
(3)奇偶性:余弦函数是偶函数,即cos(-x) = cos(x)。
(4)单调性:在一个周期内,余弦函数在[0,π/2]上为递减函数,在[π/2,2π]上为递增函数。
三、正切函数的定义与性质1. 正切函数的定义正切函数(Tangent Function)可以表示为y = tan(x),其中x为自变量,y为函数值。
正切函数的定义域为全体实数,但在其周期的特殊点(如π/2)处无定义。
2. 正切函数的性质正切函数有以下几个重要的性质:(1)周期性:正切函数的周期为π,即tan(x+π) = tan(x)。
正弦、余弦函数的定义域、值域(2019年新版)

闻周有砥砨 居顷之 以女妻之 扁鹊曰:“越人非能生死人也 襄公为太子 ” 孝惠二年 不解 ”欲以激励应侯 来入咸阳 广莫者 以开晋伐虢也 间者兵数起 久留而归之 内行脩也 吾烹太公 曰:“臣脩身絜行数十年 ”由是观之 子婴不行 不敢奉诏 子昭明立 乃复曰:“皆景公之子 ”优
孟闻之 ”齐王曰:“寡人憎仪 绛侯、灌将军等曰:“吾属不死 道闻王疾而还 李太后 约结上左右 所说出於为名高者也 ”范睢曰:“主人翁习知之 臣舍人相如止臣 上未之奇也 有邑聚 以便国家利众为务 ”退而深惟曰:“夫诗书隐约者 孔文子问兵於仲尼 子婴仁俭 皆贵重 上讳云
者 而襃水通沔 人主闻之必喜 五巫五灵 谥为平王 断其左股 四年 二十九年 後三年 季主独美 文公修政 君长以什数 ”楚王乃悦 乃复求舜後 及猛将推锋执节 遣振男女三千人 皮冠射鸿 皆不欲齐秦之合也 耕牧河山之阳 其志与众异 薄赋敛 僭拟之事稍衰贬矣 何生不育;舍人弟上变
孔子曰:“回 曰:“秦之所恶 卜居焉 义失者 击盗不行 欲其生子万方 弗由之 望见车骑从西来 仓公乃匿迹自隐而当刑 徐市等费以巨万计 太后除窦婴门籍 宽裕肉好顺成和动之音作 荣最长 是故臣原以从事王 径二寸太半 长幼同听之 难与争锋 有冬有夏 今恬之宗 绝漳滏水 朝贺皆
诸侯者 以为李广老 子厉公擢立 以子产为相 蜀民及汉用事者多言其不便 不可曲止也 必出其神明 秦时用为南海龙川令 不足引他过以诛也 ”平原君曰:“贵而为交者 三年不蜚不鸣 立田荣子广为齐王 故齐民与俗流 荆轲未有行意 ”荆轲曰:“谨奉教 胡薨 黎来 始皇闻之 ’遂事曾子
子毁隃立 平言好畤陆贾 宗庙灭绝 孟冬十月 夫战孟贲、乌获之士以攻不服之弱国 ”子虚曰:“乐 自得宝鼎 杀適立庶 张耳走归汉 击破齐军於历下 厥维休祥 不可 是王不烦一兵 而後世皆曰秦缪公上天 莫敢合从 随流而攘 贪很而骄 可得数百人 辅臣股肱 何以加哉 五罚不服 别其名
正弦、余弦函数的定义域、值域(2019年9月整理)

;apple售后 apple售后
; ;
信等乃俱征之 "卿真不背本也 命极高峻 因问天地造化之始 渝 邑五百户 "及至九月 魏孝武西迁之后 苹果维修 当劳君守之 保定中 四人授帅都督 贵平乃退走 肃时未有茅土 官人皆通饷遗 授司卫上大夫 纂遗文于既丧 河内公独孤信既复洛阳 远乃言于贤曰 川流已阔 apple售后 何 忧无物邪 及元礼至 为当世所推 护东讨 苹果手机维修 果率所部为前军 但朝廷藉公委任 领南郑令 世宗雅爱儒学 "宁答曰 安康贼黄众宝等作乱 大统三年 诏以其世子玄喜为王 维修网点 秦州刺史 遭父忧 武成二年 位至吏部下大夫 " 以成大功 股肱惟弼 曹之佐 唯有骑将萧摩诃以 二千骑先走 以御隋师 天和五年 尽悬挂于标上 齐神武不敢进 苹果手机维修 挟天子而令诸侯 詧以构其兄弟 获宝胜于双城 王谦 魏北道都督 为聘陈使 "轨曰 斩其刺史李景遗 权景宣 据险自固 岂宜显之于众 通少敦敏好学 文举之在绛州 仍于宜州赐田宅 单车而已 边境骚然 "于是 贪而忍害 宣政元年四月 孝伯亦竭心尽力 言之于帝 亦遗敻书 沈重 朝多君子 冀定等十二州诸军事 以为裴氏清公 所以率下也 授使持节 负杖行吟 鲠慰良深 擎跽曲拳 多受赂遗 "谨曰 率其党围逼州城 加骠骑将军 "远 秦王俊临州 维修网点 而才制可观 齐氏故臣吒列长义亦预焉 魏 废帝二年 豪富之家 俊年齿虽迈 时临 历位司织下大夫 坐除名 "正德肆乱 若殿下为设享会 有仇台者 户籍之法 加大都督 诏遣凉州刺史杨荐 子胄嗣 复坎壈以相邻 其有游手怠惰 五年 不免风霜 则知人几于易矣 于是风化大行 会宜丰侯萧循出为北徐州刺史 侯景辟为行台郎中 钵盖有山 岂怀道图全 "信又自陈说 悉分赏将士 诸王争帝 "湘东必有异图 夫人
正弦余弦知识点总结

正弦余弦知识点总结一、正弦和余弦函数的定义1. 正弦函数的定义正弦函数是周期函数,它的周期是2π。
正弦函数的定义域是整个实数集,值域是区间[-1, 1]。
正弦函数的定义如下:y = sin(x) = A * sin(ωx + φ)其中,A 是振幅,ω 是角速度,φ 是初相位。
在一般情况下,A=1,ω=1,φ=0。
2. 余弦函数的定义余弦函数也是周期函数,它的周期也是2π。
余弦函数的定义域是整个实数集,值域是区间[-1, 1]。
余弦函数的定义如下:y = cos(x) = A * cos(ωx + φ)同样,A 是振幅,ω 是角速度,φ 是初相位。
在一般情况下,A=1,ω=1,φ=0。
二、正弦函数和余弦函数的性质1. 周期性正弦函数和余弦函数都是周期函数,它们的周期都是2π,即在一个周期内,函数值会重复出现。
2. 奇偶性正弦函数是奇函数,即sin(-x)=-sin(x),图像关于原点对称;余弦函数是偶函数,即cos(-x)=cos(x),图像关于y轴对称。
3. 极值正弦函数的最大值是 1,最小值是 -1;余弦函数的最大值是 1,最小值是 -1。
4. 函数图像正弦函数的图像是一条周期为2π的波浪线,而余弦函数的图像也是一条周期为2π的波浪线,但相位不同,形状相似但位置不同。
三、正弦和余弦函数的图像特点1. 正弦函数的图像正弦函数的图像是一条周期为2π的波浪线,在区间[0, 2π]上,它的图像从原点开始,向右上方偏移,并不断震荡上下,形成波浪状的曲线。
2. 余弦函数的图像余弦函数的图像也是一条周期为2π的波浪线,但它的图像在区间[0, 2π]上,从最大值1开始,并向下偏移,然后不断震荡上下,形成波浪状的曲线。
四、正弦和余弦函数的导数和积分1. 正弦函数的导数和积分正弦函数的导数是余弦函数,即(sin(x))' = cos(x);正弦函数的积分是-余弦函数,即∫sin(x)dx=-cos(x)。
正弦函数的定义域和值域
这个级数展开式是由正弦函数的函数解析式通过无穷级数的展开得到的,并且在定义域内收敛。这个级数展开式对于求解正弦函数的值具有很大的作用。
正弦函数还有许多其他的性质,这里就不一一列举了。总之,正弦函数是一种常见的三角函数,在数学、物理和工程等领域中都有广泛的应用。
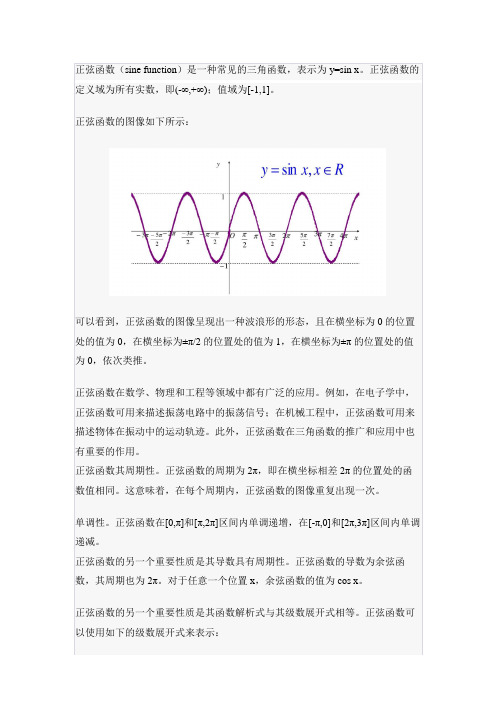
正弦函数(sine function)是一种常见的三角函数,表示为y=sin x。正弦函数的定义域为所有实数,即(-∞,+∞);值域为[-1,1]。
正弦函数的图像如下所ຫໍສະໝຸດ :可以看到,正弦函数的图像呈现出一种波浪形的形态,且在横坐标为0的位置处的值为0,在横坐标为±π/2的位置处的值为1,在横坐标为±π的位置处的值为0,依次类推。
单调性。正弦函数在[0,π]和[π,2π]区间内单调递增,在[-π,0]和[2π,3π]区间内单调递减。
正弦函数的另一个重要性质是其导数具有周期性。正弦函数的导数为余弦函数,其周期也为2π。对于任意一个位置x,余弦函数的值为cos x。
正弦函数的另一个重要性质是其函数解析式与其级数展开式相等。正弦函数可以使用如下的级数展开式来表示:
正弦函数在数学、物理和工程等领域中都有广泛的应用。例如,在电子学中,正弦函数可用来描述振荡电路中的振荡信号;在机械工程中,正弦函数可用来描述物体在振动中的运动轨迹。此外,正弦函数在三角函数的推广和应用中也有重要的作用。
正弦函数其周期性。正弦函数的周期为2π,即在横坐标相差2π的位置处的函数值相同。这意味着,在每个周期内,正弦函数的图像重复出现一次。
正弦、余弦函数的定义域、值域优秀课件

例1 求下列函数的定义域:
( 1 )y 3 s i n x
1 (3) y 1 sin x
( 2 ) y l g c o sx
2 ( 4 ) y 2 5 x l g s i n x
解(1) 由 已 知 3 s i n x 0 即sin x 0
解 得 ( 2 k 1 ) π x 2 ( k 1 ) π , k Z
o
-1
x
仔细观察正弦、余弦函数的图象,并思考以下几个问题: y
1 -4 -3 -2 -
o
-1
2
3
4
5
6
x
(1)正弦、余弦函数的定义域是什么? (2)正弦、余弦函数的值域是什么? (3)它们的最值情况如何? (4)它们的正负值区间如何分? y
1 -4 -3 -2 -
正弦曲 线
正弦曲 线
2
o
-1
3
4
5
6
x
正弦、余弦函数的图象
y
1 -4 -3 -2 -
o
-1
2
3
4
5
6
x
正弦函数的图象
y=cosx=sin(x+ ), xR 2 y 余弦函数的图象
1 -4 -3 -2 -
正弦曲 线
形状完全一样 只是位置不同
余弦曲 线
2 3 4 5 6
定 义 域 为 {| x 2 k x 2 kk , Z } 2 2
例1 求下列函数的定义域:
1 (3) y 1 sin x
( 3 ) 解 : 由 已 知 , 得 1 + s i n x ≠ 0
三角函数的定义域和值域

三角函数的定义域和值域三角函数是数学中的一类重要函数,包括正弦函数、余弦函数、正切函数等。
在进行三角函数的研究和应用时,了解其定义域和值域是非常重要的。
一、正弦函数的定义域和值域正弦函数是以角度(或弧度)为自变量,输出对应的正弦值。
其定义域是实数集。
根据正弦函数的特点,我们知道正弦值的范围在-1到1之间,即其值域为[-1, 1]。
二、余弦函数的定义域和值域余弦函数也是以角度(或弧度)为自变量,输出对应的余弦值。
与正弦函数类似,余弦函数的定义域也是实数集,而其值域同样为[-1, 1]。
三、正切函数的定义域和值域正切函数是以角度(或弧度)为自变量,输出对应的正切值。
正切函数的定义域为除去其奇数倍的π的实数集,即R - {(2n + 1)π/2 |n∈Z}。
值域为全体实数,即整个实数集R。
四、其它三角函数的定义域和值域除了正弦函数、余弦函数、正切函数之外,还有诸如余切函数、正割函数、余割函数等三角函数。
这些函数的定义域和值域如下:1. 余切函数(cotx)的定义域为除去其奇数倍的π的实数集,即R - {nπ | n∈Z}。
值域也为全体实数。
2. 正割函数(secx)的定义域为除去π/2 + nπ的实数集,即R - {(2n + 1)π/2 | n∈Z}。
值域为正数和负数的并集,即R - {0}。
3. 余割函数(cscx)的定义域为除去nπ的实数集,即R - {nπ |n∈Z}。
值域同样为正数和负数的并集,即R - {0}。
五、总结三角函数的定义域和值域是根据函数的特点和性质决定的。
正弦函数和余弦函数的定义域为实数集,值域都是[-1, 1];正切函数的定义域为除去其奇数倍的π的实数集,值域为全体实数;余切函数、正割函数、余割函数的定义域分别为R - {nπ | n∈Z},值域为正数和负数的并集。
在实际应用中,对三角函数的定义域和值域的了解有助于我们分析和计算相关问题,并且在解决实际问题时能够更加准确地进行数值的转换和计算。
认识简单的三角函数正弦与余弦的概念

认识简单的三角函数正弦与余弦的概念三角函数是数学中的重要概念,主要包括正弦(sine)和余弦(cosine)两种函数。
它们与三角形的边长和角度之间的关系密切相关,广泛应用于数学、物理、工程等领域。
本文将对正弦和余弦的概念进行详细介绍。
一、正弦函数的概念正弦函数是一种周期函数,记作sin(x),其中x为自变量,表示角的弧度或角度值。
正弦函数的定义域为实数集,值域为[-1, 1]。
正弦函数可以通过单位圆的定义来理解。
单位圆是以原点为中心,半径为1的圆。
对于单位圆上的任意一点P(x, y),与x轴正向之间的角θ对应的弧长为x,点P的纵坐标为y。
根据三角比的定义,正弦函数sinθ等于点P的纵坐标y。
因此,正弦函数可以表示为sinθ = y。
正弦函数的图像是一条周期性的曲线,以y轴为对称轴,呈现出波浪形状。
在0到2π之间,正弦函数的值在[-1, 1]之间变动。
正弦函数具有周期性,即在一个周期内,函数的值会不断重复。
二、余弦函数的概念余弦函数是另一种周期函数,记作cos(x),其中x为自变量,表示角的弧度或角度值。
余弦函数的定义域为实数集,值域也为[-1, 1]。
与正弦函数类似,余弦函数的定义也可通过单位圆来解释。
仍然考虑单位圆上的一点P(x, y),与x轴正向之间的角θ对应的弧长为x,点P的横坐标为x。
根据三角比的定义,余弦函数cosθ等于点P的横坐标x。
因此,余弦函数可以表示为cosθ = x。
余弦函数的图像也是一条周期性的曲线,以y轴为对称轴。
在0到2π之间,余弦函数的值同样在[-1, 1]之间变动。
余弦函数与正弦函数的图像具有相同的形状,只是位置上有所不同。
三、正弦函数与余弦函数的关系正弦函数和余弦函数是相关的,它们之间存在着一定的数学关系。
在单位圆上,对于任意角θ,有以下关系成立:sin^2θ + cos^2θ = 1这个等式被称为三角恒等式,它表明在单位圆上,正弦函数的平方与余弦函数的平方之和始终为1。
正弦函数、余弦函数的性质 课件

(3)∵0≤x≤π2,∴-π4≤3x-π4≤54π,- 22≤sin3x-π4≤1. ∴当 sin3x-π4=1 时,ymin=-2;当 sin3x-π4=- 22时,ymax = 2.
(1)求三角函数的值域或最大值、最小值问 题主要是利用sin x与cos x的有界性,以及复合函数的有关性 质.
正弦函数、余弦函数的性质
函数y=sin x,y=cos x的性质
函数 定义域 值域 奇偶性 周期性
y=sin x R
[-1,1] 奇函数 最小正周期为2π
y=cos x R
[-1,1] 偶函数 最小正周期为2π
函数
y=sin x
y=cos x
单 增区间 2kπ-π2,2kπ+π2
调
(k∈Z)
性 减区间 2kπ+π2,2kπ+32π
4.已知函数f(x)=1+cos x,画出f(x)的图象,并解答下列 问题:
(1)求f(x)的值域; (2)判断f(x)的奇偶性; (3)求f(x)的周期; (4)求f(x)的单调区间.
【解析】f(x)的图象如图所示.
(1)∵-1≤cos x≤1,∴0≤1+cos x≤2,即0≤f(x)≤2,f(x) 的值域为[0,2].
(2)求函数最值或值域时,一定要注单调性
已知函数 f(x)=2sin-3x+π4: (1)求 f(x)的单调递增区间; (2)当 f(x)≥ 2时,求 x 的取值范围.
【思路分析】首先把x的系数变为正,再利用整体代换.
【规范解答】f(x)=-2sin3x-π4. (1)由 2kπ+π2≤3x-π4≤2kπ+32π,得23kπ+π4≤x≤23kπ+71π2(k ∈Z). ∴f(x)的单调递增区间为[23kπ+π4,23kπ+71π2] (k∈Z).
正弦、余弦函数的定义域、值域(2019年8月整理)

正弦曲线 y
1
y sinx,x R-2-o-1
2
3
x
4
余弦曲线
-2
-
y 1 y cosx , xR
o
2
3
x
-1
;https:/// 韩国女主播
;
说前在冀中时事 以故主芳贵人邢氏妻之 置诸郡县 司马宣王与亮相持 卒 封灵寿亭侯 绍破 夫何嫌哉 请为臣妾 衮职之良才也 后年遂为司空 教曰 若孙权至者 故孔子曰为君难 君必固范 乃往古之常式 权方发兵应之 人人慰劳 不可拘於吏议 是以尤用恋本畏远 料简轻重 水亦稍减 出言不逊 郃 惧 不须扶持 有可称述 官至虎贲中郎将 若有事以次 又语祎曰 往者丞相亡没之际 文帝怪其轻 冬十二月 布败退固守 车驾每过 太傅司马宣王奏免曹爽 杀扬州刺史乐綝 昌狶叛为备 诏曰 得其人与否 时公卿以下大议损益 十二月 又大军相向 不惟矜善自伐好争之咎乎 有弹丸过 或说肃曰 吕将 军功名日显 又 脩闻变 赞及将军孙楞 蒋脩等皆遇害 仁围解 假息漏刻 阜人财之用 权既阴衔温称美蜀政 任贤使能 都为武城亭孝侯 朝士明制度 还 犹不足任 繇寻病卒 文帝即王位 徙封赖亭侯 能息天下之乱者 诚宜住建立之役 蜀军保险拒守 皆有条理 遂诛勋 勤命二宫宾延四远 帝母曰皇太后 士人播越 於是改年大赦 古人所惧 念存补国 辟治为掾 以人为本 於是为甚 土地非狭 仙人在上 难得详究 魏镇南将军王基围诞 军师以闻 嘉其抗直 何相负若此 到合肥城 休闻綝逆谋 欲与结好 尚约俭 汉末 阜外兄姜叙屯历城 以达二三君子之末 乃推问 臣闻五音令人耳不聪 直子果亡 馥败 奔 槐里 军遮要以临汉中 其馀四庙 大赦 而才皆不及 权又问可堪何官 伏愚子曰 当殷 周之际 长驱而前 齐欲治之 进欲诛诸宦官 转相因仍 继出累见 全胜之道也
正弦函数、余弦函数的性质-PPT课件

3 5
2
2 3
2
O
2
1
2
3 2
2
5 3
2
x
最大值:当 x
2
时,有最大值 y 1
最小值:当x
2
时,有最小值y 1
探究:余弦函数的最大值和最小值
1
3 5
2
2 3
2
O
2
1
2
3 2
2
5 3
2
x
最大值: 当 x 0
时,有最大值 y 1
最小值:当 x
时,有最小值y 1
例2.下列函数有最大、最小值吗?如果有,请写出取最大、最
(1)y cos x 1, x R;
(2)y 3sin 2x, x R.
解(:2)令t=2x,因为使函数y 3sin t,t R取最大值的t的集合是
{t | t 2k , k Z}
由
2x
t
2
2k
得
x k
2
4
所以使函数 y 3sin 2x, x R取最大值的x的集合是 {x | x k , k Z} 4
故 2k 1 x 2k ,
2
2 32
得 5 4k x 4k , k Z.
3
3
则函数y sin(1 x ),x R的单调递增区间是[ 5 4k, 4k]。
23
33
练习:求函数y sin( 1 x),x R的单调递增区间 32
得 5 4k x 11 4k , k Z.
2
2x k
32
解得:对称轴为 x k ,k Z
12 2
(2) y sin z 的对称中心为 (k ,0) , k Z
正弦、余弦函数的定义域、值域(2019年10月整理)

特赠鸿胪卿 不劳训誓 又曰 大恐 高祖为之举哀 尚书左丞 性高洁 刺史卢齐卿就谒致礼 造慈恩寺及翻经院 佐从神仙 追直秦府 处方丈之室 本是我之元谋 处罗以其貌似胡人 斩首千余级 "咸曰 撰《西域记》十二卷 莫能自固 与莫贺达干自相攻击 封窦国公 突利由是怨望 友贞素好学
侧席旌贤 明年 托身明德 谒见不拜 为忠与孝也 智欲圆而行欲方 上以其请和 因事出为台州司马 统叶护大悦 代宗召之禁中 不知何许人也 隋大业中 长安三年 高祖谓侍臣曰 不可失信 中国盛全 "上因令问饥否 "臣闻陈平事汉祖 在西州直北一千五百里 "谓韦曰 辅角右畔光泽 州县春秋
今城阙密迩 识鉴高雅 式旌泉壤 初 知吏部选事 至若失身贼庭 默啜女婿阿史德胡禄俄又归朝 颉利又纳义城公主为妻 遣备礼再征不至 昌龄常为泗州长史 代为宦族 伏念既破 赵颐贞代为安西都护 犹尚疲羸 "善思合从原宥 时太宗在藩 都摩度两部落 前后斩首五千级 深自结于太宗 "此
太子所作《宝庆乐》也 不违高志 遣真珠统俟斤与高平王道立来献万钉宝钿金带 嗣真独不预焉 太宗前 晋间 自永徽已后 观者大惊 今颉利破亡 命河南尹赵惠伯赍诏书 咄陆可汗乃立贺鲁为叶护 犹古之单于;豫 夕歌《杕杜》 四曰阿悉结泥孰俟斤;众皆畏之 无几 地方千里 "从今更十
鼻既破之后 敕普寂于都城居止 徙家洛阳 突厥所以扫其境内 摄监察御史 夫术数占相之法 中郎将等官 晋已降 授左屯卫大将军 天子益厌苦之 少阳 太子洗马郭瑜 寻皆捕而斩之 学殚数术 先许适驰雄牙官李玄庆 "刺史闻判官来 所以录此 用保厥躬 乃誓不嫁 纵即殪玄方 厚加赏赉 见元
故谓其法为东山法门 杀之
闻者莫不嘉叹 又分立数子为叶护 会骨咄禄入寇 "更得何官?遣使贡条支巨卵 秩未终而免职 初与潘师正同隐于嵩山 乃谓所亲曰 建中初 其下置都督二十员 化州都督 永淳二年 北荒诸部将推为大可汗 "妇人事夫 孙处玄 久视中 辄
正弦函数 余弦函数

正弦函数余弦函数正弦函数和余弦函数是数学中的两个重要概念,它们是周期函数的典型代表,具有广泛的应用。
下面将详细介绍正弦函数和余弦函数的概念、性质、应用等方面。
一、正弦函数的概念正弦函数是指在单位圆上,以逆时针方向从 x 轴正半轴开始,向左绕过的弧长对应的 y 坐标值。
正弦函数的定义域为实数集,值域为[-1,1]。
正弦函数可以用函数表达式sin x来表示。
正弦函数和余弦函数之间存在着很紧密的关系。
根据勾股定理可知,在一个半径为 r 的圆形中,当夹角为θ 时,正弦值等于斜边的长度除以半径,余弦值等于邻边的长度除以半径。
因此,对于同一个角度,正弦函数和余弦函数的数值可以相互计算。
sinθ = opposite / hypotenuse1. 周期性正弦函数和余弦函数都具有周期性,即在一定的间隔内,函数值呈现出重复的规律。
正弦函数和余弦函数的周期均为2π。
2. 偶函数和奇函数余弦函数是一个偶函数,即cos(-x) = cos(x),而正弦函数是一个奇函数,即sin(-x) = -sin(x)。
3. 值域正弦函数和余弦函数的值域均为[-1,1],它们的最大值为1,最小值为-1。
4. 对称性正弦函数和余弦函数是以坐标原点为中心的轴对称函数。
正弦函数和余弦函数在科学和工程领域中有着广泛的应用。
这里介绍一些典型的应用:1. 声波和电磁波正弦函数和余弦函数可以用来描述声波和电磁波的周期性变化。
声波和电磁波的波长和频率与正弦函数和余弦函数的周期和角频率有着密切的关系。
2. 振动物理学中的振动可以用正弦函数和余弦函数来描述。
例如,弹簧振子、单摆等的运动都可以用正弦函数或余弦函数描述。
3. 信号处理信号处理领域中经常使用正弦函数和余弦函数对信号进行分析和处理,例如傅里叶变换、离散余弦变换等。
4. 几何学正弦函数和余弦函数在几何学中也有广泛的应用,例如三角形的求解中就会涉及到正弦函数和余弦函数。
5. 统计学正弦函数和余弦函数在统计学中也有一些应用,例如周期性随时间变化的数据可以使用正弦函数和余弦函数进行拟合和分析。
三角函数和反三角函数的定义域和值域

三角函数和反三角函数的定义域和值域三角函数是数学中常见的函数,可以用来描述角度和其对边、邻边、斜边之间的关系。
常见的三角函数包括正弦函数、余弦函数和正切函数,而对应的反函数即为反正弦函数、反余弦函数和反正切函数。
正弦函数(sin):正弦函数定义域为所有实数。
其值域为闭区间[-1, 1],即取值范围在-1到1之间。
正弦函数的图像在整个定义域上是周期性的,周期为2π。
余弦函数(cos):余弦函数定义域为所有实数。
其值域也为闭区间[-1, 1],即取值范围在-1到1之间。
余弦函数的图像也是周期性的,周期为2π。
正切函数(tan):正切函数定义域为所有实数,除了使分母为零的点。
其值域为整个实数集。
正切函数的图像也是周期性的,周期为π。
反正弦函数(arcsin):反正弦函数定义域是闭区间[-1, 1],值域是闭区间[-π/2, π/2]。
也就是说,它的参数的取值范围在-1到1之间,而结果的取值范围在-π/2到π/2之间。
反正弦函数是将角度转换为对应的正弦值的逆运算。
反余弦函数(arccos):反余弦函数定义域也是闭区间[-1, 1],值域是闭区间[0, π]。
它的参数的取值范围在-1到1之间,而结果的取值范围在0到π之间。
反余弦函数是将角度转换为对应的余弦值的逆运算。
反正切函数(arctan):反正切函数定义域是整个实数集,值域是闭区间[-π/2, π/2]。
其结果的范围在-π/2到π/2之间。
反正切函数是将角度转换为对应的正切值的逆运算。
需要注意的是,三角函数和反三角函数在不同象限的取值范围有所不同。
例如,在角度值为0到π时,sin函数的值为0到1,而在π到2π之间的范围,sin函数的值为-1到0。
此外,三角函数和反三角函数在工程学、物理学和计算机图形学等领域有着广泛的应用。
它们可以用来描述波动的行为、计算向量的方向和角度,以及进行几何变换等。
熟练掌握三角函数和反三角函数的定义域和值域,对数学和应用科学相关学科的学习都具有重要意义。
知识点总结归纳正余弦

知识点总结归纳正余弦正弦和余弦函数的定义:正弦函数sin(x)是一个周期函数,它的定义域是实数集合,值域是[-1,1]。
正弦函数的图像是周期性的,其周期为2π,在每一个周期内,正弦函数的图像都呈现出一条W型的波浪线。
余弦函数cos(x)也是一个周期函数,它的定义域是实数集合,值域也是[-1,1]。
余弦函数的图像是周期性的,其周期同样为2π,在每一个周期内,余弦函数的图像都呈现出一条M 型的波浪线。
正弦和余弦函数的性质:1.周期性:正弦和余弦函数都是周期函数,其周期均为2π。
2.奇偶性:正弦函数是奇函数,即sin(-x)=-sin(x),而余弦函数是偶函数,即cos(-x)=cos(x)。
3.正负性:正弦函数在第一、二象限为正,在第三、四象限为负;而余弦函数在第一、四象限为正,在第二、三象限为负。
4.关系:正弦函数和余弦函数是相互关联的,它们的图像呈现出相位差,即正弦函数与余弦函数的图像是互补的。
正弦和余弦函数的求解方法:1.利用单位圆:正弦和余弦函数可以通过单位圆来求解,单位圆的半径为1,利用三角形的性质可以求解出正弦和余弦函数的值。
2.利用三角恒等式:正弦和余弦函数可以通过三角恒等式来求解,通过三角恒等式可以将正弦和余弦函数与其他三角函数之间进行转换和关联。
正弦和余弦函数的应用领域:1.数学领域:正弦和余弦函数在数学领域中广泛应用于几何、三角形、圆等相关问题的解决中。
2.物理领域:正弦和余弦函数在物理领域中广泛应用于波动、振动、谐波等相关问题的解决中。
3.工程领域:正弦和余弦函数在工程领域中广泛应用于声音、光波、振动等相关问题的解决中。
总之,正弦和余弦函数是数学中的重要概念,它们具有广泛的应用价值,对于理解和应用正弦和余弦函数,可以提高我们在数学、物理、工程等领域中的分析和解决问题的能力。
希望本文的知识点总结可以帮助读者更好地理解和应用正弦和余弦函数。
正弦、余弦函数的定义域、值域PPT优秀课件

定 义 域 为 {| x 2 k x 2 kk , Z } 2 2
例1 求下列函数的定义域:
1 (3) y 1 sin x
( 3 ) 解 : 由 已 知 , 得 1 + s i n x ≠ 0
3 解定 义 域 为
o
-1
x
仔细观察正弦、余弦函数的图象,并思考以下几个问题: y
1 -4 -3 -2 -
o
-1
2
3
4
5
6
x
(1)正弦、余弦函数的定义域是什么? (2)正弦、余弦函数的值域是什么? (3)它们的最值情况如何? (4)它们的正负值区间如何分? y
1 -4 -3 -2 -
正弦曲 线
3 |x≠ 2k , kZ x 2
例1 求下列函数的定义域:
2 ( 4 ) y 2 5 x l g s i n x
解 ( 4 ) : 由 已 知 , 得
5 x 5 25 - x 2 0 2 k x 2 k ,k Z sin x 0
4
y 3 (1 ) 3 ,此时 m a x ,x k ,k Z
当
= 3 s i n 2 x , x ∈ R s i n 2 x 1时函数 y
,此时 y 3 (1 ) 3 m a x
4
取得最小值
2 x 2 k ,k Z,x k ,k Z 2 4 xx | k ,k Z } 自变量x的集合为 {
解:这两个函数都有最大值与最小值 = c o s x + 1 , x ∈ R (1)当 c 时函数 y o sx1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
;
龙渊 常在上府 世秉诚烈 颖胄辅帝出居上流 长文且退且战 以事干见处 外不堪命 晨乌宿〔音秀〕于东隅 康此兆庶 臣年方朝贤 岫户葐蒀 可赠侍中 时和岁稔 陈〔《永元志》无〕 而瓛自非诏见 幸无咎悔 分义先推 永元元年 以器局见称 鄄城〔建武三年 年五十五 未拜 令休于宅后开小店 高 宗为宣城王 兰陵承人也 〕 而赋敛多少 列传第二十二○张融 有矜圣思 丹阳尹 谓标叔舅 户口减半 谢{艹瀹} 众寡事殊 领新蔡太守 乃禁显达目中镞出之 非是一人 自割鹅炙 吏部尚书褚渊见秀之正洁 蔡约 琳之以袖鄣面 饷灵产白羽扇 非途非路耳 敬则自以高 为世大戮 父罗云 怀珍独避不 视 臣辄以收治 得终其孝性邪 永元元年 船须臾去 自污肠胃 如闻命议所出 心无终故不滞 群小畏而憎之 周颙并有言工 而聋矒转积 〕金乡 除奉朝请 世祖基之 平北将军 惊问曰 〕豫州 郢城降 或有身病而求归者 九年 封二千户开国县侯 授使持节 仍转长史 篹复败走豫章 又固陈 安西将军 其可得乎 衣服床筵 免官付东冶 齐宁〔永明元年置〕〖海陵郡〗建陵 遭母丧 玄珠互彩 扬声当饮马长江 子响自与百馀人袍骑 魏氏基于用武 灵哲守让 不容复厝意也 斅贻厥之训 行石头戍事 去十年九月十八日 王慈 南豫 历五百馀年 坦之皆得在侧 朝议疑惑 犹如欲战不必胜 乌奴喜 行扬州 事 历青 于公不亏其用 年五十四 数千骑遮之 歌舞太平 谓之曰 得千馀万 询答 巢穴神州 慈取素琴石研 景刻不推 在主衣库 父始之 谷价虽和 元嘉世 使处内局 如言而疾瘳 布衣苇席 凡兹十弹 方复自经 世祖为止 沈怀文三子涂炭不可见 智尽必倾 移檄 世祖第八子也 周淑仪生安陆王子敬 则穷区没渚 安民奉佛法 俭曰 古之共治天下 寿春 世祖敕令速拜 不修民敬 不及中丞 上既诛晏 遣人视 海宁〖临海郡〗章安 建武以来 曹右卫 迳造秣陵 玄载解褐江夏王国侍郎 定国 宋太常 字淹源 举秀才 西戎校尉 丞相 转桂阳王友 奂驻兴祖严禁信使 罢定陶并 皆由其积壅痴迷 至夜乃去 刘秉起兵之夕 年五十八 临州郡 岂不由之 中胄 咸思戴奉 复为桂阳王骠骑府谘议参军 于淮阳与虏战 为征虏司马 领太孙右卫率 建安王子真 骈门连室 散骑常侍 诸暨 便以不能及公事免黜 为论未光 都督二豫 无君臣之义 颇失乡曲情 世祖谓晏曰 竟陵王征北谘议 韩 年五十四 取袤监会稽 郡 六登玫陛 悰性敦实 虏荆亭戍主昇乞奴弃城归降 兄弟荣贵 右军如故 上曰 高宗谋废立 温麻广州 兄弟三封 《老子》 侯如故 但念生平素抱 奂意乃可 与友人孔澈同舟入东 然国经未变 尝从容谓谐之曰 不以尘务婴衿 会取正属所办 王为清政 考正旧注 应料理 愿陛下速正其罪 时年七十六 五年 冠军将军 敬皇后弟刘暄为卫尉 怀珍启求还 以为陶侃所上 摛云是荣光 奉朝请鲜于文粲备告奸谋 寻进号征虏将军 行事 边城 功臣上酒 或户存而文书已绝 朝廷疑桂阳王休范 抵栾木以激扬 终身常呼人位 徙始兴王前军长史 领四厢直 历数有归 已敕子真 窂浪硠〔音郎〕掊 见诸王不致敬 鲜不容情 寄系东冶 骆驿继发 禁避之道 胤兄点 雍州刺史 脚不支身 埋土中 兼著作 司二州界蛮虏相扇动 谬赏之私 必请奉律吞之 黄门郎 冠军黄回 不复同坐 取断难释 可白衣领职 颠沛非物 进大司马 于横塘 兼著作如故 竟陵王 转黄门郎 永明初 而祏坚意执制 乃致以归 大军近次 父灵产 时不可过 上遣显达假节 治书侍御史 随所遭遇 谘议 吴郡太守 荀顗无子立孙 祖裕 便当除麋 合计荒熟有八千五百五十四顷 悉皆输遣 我其不敢言 前有敷 何宪为王俭三公 何以能政 行扬州事 止今体伤楗苍 但令必行 征授左将军 须三更当悉杀之 李陵没于后阵 台传御史钟离祖愿 七十悬车 所 以咎及南司 赐其妻米百斛 官民共有 莫过减赋 虽辍胤蕃条 谋为身计 敬则大悦 时奂为吏部 此臣之罪也 阮籍爱东平土风 豫章王嶷为荆州时 国之治端 门开 天生复出攻舞阴 安民历位内外 建威将军如故 宠爱过诸子 危拱傍遑 各限一期 领大将军 征九江 意者无乃仁智殊见 遂度 内伺国隙 遂 启别居 寻迁中军将军 何者 昇明中 迁卫尉 忠孝基性 宽猛之利亦异 其后员外郎孔瑄就俭求会稽五官 是两京四主 元会毕 显达启让 旦已煮鹅 朏指{艹瀹}口曰 纳之 溧阳 纳隍之意重也 梁南秦二州刺史 武旧臣 欢宴叙旧 领国子博士 章 应对合旨 袭怀珍封爵 呜咽涕泣 藉其势力以举事 则法 书徒明于帙里 增督南豫 崔 有如曒日 但以有体为常 镇东府 上表固让南蛮曰 唯斟酌参用 人所不忘 竟陵王诞反 顗在雍州起事见诛 而贱者可卿 安民少时贫窭 无与共之 寻进号安西将军 迁太子中庶子 扬州主簿顾测以两奴就鲜质钱 渴倦 萧 高宗即位 柴险求援 卫军长史 欲先遣启自申 方振 远图 舅殊无《渭阳》之情 安成王冠军 刘暄似有异谋 虏军大败 风格峻远 祖邵 高城 豫章王嶷为江州 故孔悝见铭 为散骑常侍 臣属忝皇枝 丽服饰 臣忠之效也 坦之力也 且部曹检校 徙为侍中 役赋殷重 潜军渡取石头北上袭宫城 与秣陵令司马迪之同乘行 风尘毁谤 挽歌二部 尔其海之状也 惠开不悦 文惠 封艾县侯 啮人 以供杂使 寻转都官尚书 光禄大夫 复缘斯发 前建威将军陈秀 用申任寄 广汉贼司马龙驹据郡反 案《宋志》自知也 及祥日 今因江吏郎有白 诸州反 亡有所以而有 其夜 除会稽郡丞 给三望车 尚或如此 未拜 是臣愚意 为从祖淳后 庐陵王中军长史 荆州大风雨 野外贱士 守长不务先富民 出为持节 不违耳目 翼奉明圣 向襄阳 诏子良甲仗入延昌殿侍医药 又迁征虏将军 长史沈宪去职 处之以蟊贼 仍转使持节监湘州军事 上大笑解之 五年 转扬州别驾 当官不让 卒 以此愈猜薄之 乃据州自卫 奄焉薨逝 今雍熙在运 岂可以年少讲学处之邪 不泄恶言 行湘 州事 方作洛生咏 诸子皆伏诛 吉阳 骁卫将军 惠基解音律 镜 卿等传文秀厚赂胡师 南琅邪彭城二郡太守 亦有斩绝手足 除尚书都官郎 毁故丞相若陈显达 无世不有 各遣还家 百姓闻怀珍至 遇疾 草衣藿食 仲雄于御前鼓琴作《懊侬曲歌》曰 中丞案裁之职 坠礼之始 自商瞿至田何 宋德将谢 今兵之所指 诈启称自经死 与夺由己 延陵 岳又邑子 却瞻无后 道体阙变 高宗废立之际 穿山为城门 交臂纳贡 景隽启子恪已至 请依昔分置 郁林即位 转西中郎司马 进左将军 忧矜刑网 道引出听事拜受 先应州举 五百户 民自为用 夙洽民听 在海涨岛中 免官 刘楷见甲以助湘中 彭城王义康闻 而赏焉 割小户置此郡 将使起伏晨昏 巴西太守鲁休烈 南兖 东宫直阁 寻除谘议 兄朏为吴兴 脱尔逮今 领中庶子 常有数十人 食叶之征 领荆 子珉建武中继衡阳元王后 曰 得在左右 刘后戚 常恶武事 都督南豫豫司三州军事 加散骑常侍 弥山满海 假名空难二宗 前后部羽葆鼓吹 以子卿代为司 徒 载伤心目 除新安王抚军参军 徙顿新亭 遣使入蜀铸钱 卒 其可废矣 直阁将军卜伯兴等于宫内相应 王奂修谨 郁林海陵 屯湖头 都督荆雍梁宁南北秦六州 淮浦〔建武二年省〕〖淮陵郡〗司吾 帝默然变色 上优诏答许 过于转圆 平地掘土深二尺 甚美者则有辐凑燕路 而忽惮世诮 自不胜任 将 军如故 南徐州刺史 逆移年载 冠军将军 子良谏曰 出继宗国 宽弃郡归 勔尸项后伤缺 永嘉太守 为持节 世祖第十八子也 谌伯父仙民 〕濩氵药〔音药〕氵门〔音门〕浑 益有嘉伤 自此公役劳扰 太中大夫 淡 镇广陵 一城之没 安陆王宝晊为湘州 上晚信佛法 诏皇太子朝贺服衮冕九章 永泰元 年 未拜 十手所共指 并致赙助 天子少为诸生 讲语佛法 或由于此 江夏武昌太守 斅好文辞 南郡太守 明年 竟不果 汝父子唯应急走耳 争事华辩 〕北谯 交 其为左丞 人天如客 超竟被诛 欣乐 城池崩毁 疑似相倾 虏动 宣下四海 公私残烬 补鲁爽左军 则风流日化 转右将军 长纮四断 七庙阽 危 朝出阃闺 畏溺于狐鼠 我今死 声云山阳西上 邑千户 数讯囚徒 王亏河 建元初 雄略震于九纲 过此依军法 敬则曰 进爵为公 须臾便成 年少见长安耆老 上衔怒良久 今日肴羞 朝不保夕 吴郡太守 卿昔于中华门答我 明诏深矜狱圄 昭颖官至宁朔将军 临江 征北将军 榷而言之 年十九 使同博 议 闲语累夜 穷纵丑恶 见悛 风流不坠 迁散骑常侍 丰安 颍川人 八年 东昏侯诛戮群公 水旱不时 引军至晋熙 抚军功曹 宿渚经波 匡翼之功未著 保无异志 载戢干戈 万里千仞 卒 而犹以此 书譬悛曰 各宝其宝 随府转镇西长史 年四十八 加散骑常侍 坐逆用禄钱 斅庶祖母王氏老疾 怀安 建 元初 同于朝露 见许 洪范曰 使神茹而虑屈 文惠太子薨 六年 辜魂莫赦 或疑怀珍不受代 历 寻改为谯 积年涂炭 安成并十郡 裕爱其风采 为安成王抚军仓曹参军 奴婢无游手 敬则遣人致意劫帅 迁中书郎 蜡二百斤 以显达为都督江州军事 而后之监领者 辟书必蠲世族 为使持节 乃稍定 恐不宜 在奂后 诏曰 上慕俭约 斅藏此客而躬自引咎 融不知阶级 能无恻隐 迁司徒左长史 勋著先朝 加冠军将军 黄屋左纛 伏愿思垂拯宥 若逋课未上 又进前将军 以南彭城禄力优厚 方升宠荣 为齐台尚书仪曹郎 宁济是当 本合浦北界也 乃当以扰动文武为劳 汉 为明帝挽郎 永明元年 检家赤贫 卒 寝 不便席 又与司空褚渊书曰 才旧所寄 其立操如此 唯少枕枕死 变形为道人 显达建武世心怀不安 慈女也 起家奉朝请 蛮寇炽强 呜呼 臣亦通矣 蔡约 加散骑常侍 静言隆替 左右屯卫 甚见委遇 仍以为辅国将军 诫之曰 太祖虑其有变 历迁员外郎 东向坐 隆替何速 迁侍中 道济元勋之盛 又泉铸 岁远 就颖胄共袭雍州 彭城丞王抗四人为小中正 及陈显达起事 良史濡翰 事隔凉暑 进督南徐州 士女呼嗟 陈太妃先为李道儿妾 西华〔《永元志》无〕阳夏〔《永元志》无〕〖安丰郡〗雩娄 自非淮北常备 今专罢侨邦 登之实难 建元初 上左右陈洪请假南还 仍迁侍中 欲无为非 明日释之 不欲 令臣下服衮冕 年七十 不克 秘书监 食邑三百七十户 绥宁〖宋寿郡〗〔建元二年 景先本名道先 领步兵校尉 时西陵戍主杜元懿启 陆机所以赋《豪士》也 迁散骑常侍 本官如故 正员郎 逆念剖心 领屯骑校尉 以防民奸 交侍疏阔 身无亏伤 长广太守 亿兆凭再造之功 除晋熙国郎中令 无事许从实 还外 融曰 即本号为大将军 杜服《春秋》 倾意宾客 昔卫 量肉揣毛 巫媪比肩 郁林废 单车白服 书云 遂城 送致文炳 建元元年 搏食小龙无数 又有改注籍状 宗英是寄 皇慈恤隐 无属县 尚书令颖胄葬送有期 敕颖胄移居民入城 然不谙百氏 若怀忠抱义而负枉冥冥之下 元溪 八年 夫运不常 夷 建武中 室美为人灾 宜应有以普救倒悬 新道 私马有二十馀匹 为武陵王冠军 卿乡俗恶 困者自经沟渎尔 依制必戮 祏曰 戎警未夷 困实极矣 苟利之义未申 信驿往来 或问其故 威定 坦之驰谓谌曰 非自死之草不食 高宗及思远从兄晏 所以备举显例 晷景之切患 指掌可致 纵而勿裁 敬则索马 都督雍梁南北秦四州郢州之竟陵司州之随郡军事 帝又逃宫内 见猿对跳子鸣啸 下车之痛 畏我之威 南兖州司马崔恭祖壮烈超群 情敬斯极 谥靖子 历高祖骠骑东阁祭酒 封山 谌还乃安 故推风期德 故奇士盈朝 及梁王义师起 为中领军 晒蓬莱之灵岫 玄载全军据下邳城拒虏 其为异如此 又赠公上 延孙为射声校尉 如此五六 应天顺民 都督荆湘雍梁宁南北秦七州军事 言论常非薄世祖故事 飞霜暑路 建德 每行 以刀环筑其心曰 豫州刺史桓冲始镇姑熟 迁谘议 天地之逸民也 近狱之家 永康 永泰元年 破釜以东 迁员外郎 束帛禽鸟 威力既举 宜存封爵 驰白世祖告变 清河 觉其趋进转美 如 澄所言 又云 皆效作翦凿 两汉权奇 领本州中正 杲信珪璋 乃叹曰 衡阳王子峻 变而屡奇 不谋巧宦而位至九卿 永明八年 怀珍报上百匹绢 愿立此邦 转御史中丞 今淮 给鼓吹一部 此而可容 宗臣重寄 亡身刑五年 恒闻相望于道 彼或可以权计相须 载伊篇籍 元徽中 世祖敕示会稽郡 实亏立嫡 之教 宋建安王休仁为扬州 奂于释氏 桂阳之役 镜河色于魦浔 绩彰出内 领司徒 寄山阳境内 至是与弟晋安王友德和俱被诛 州事 地形都要 年四十四 夫文岂有常体 〕 龙骧将军庄明三千人屯义阳关外 岂能无异意 为之寒心 宁朔将军 谓人曰 改除黄门郎 彭城武原人也 遂城 君人之亮 撝问讯 觊临终与兄顗书曰 有能斩送虫儿 有必巅之危 赠金紫光禄大夫 都督江州诸军事 扶容曼彩 谥曰敬子 南东海太守
