博弈论第六章不完全信息静态博弈题库
非完全信息静态博弈习题(含答案)

非完全信息静态博弈习题1、考虑下面的Cournot 双头垄断模型。
市场的反需求函数为Q a Q p -=)(,其中21q q Q +=为市场总产量,两个企业的总成本都为()i i i cq q c =,但需求却不确定:分别以θ的概率为高(H a a =),以θ-1的概率为低(L a a =),此外,信息也是非对称的:企业1知道需求是高还是低,但企业2不知道,所有这些都是共同知识,两企业同时进行决策。
要求:假定H a 、L a 、θ和c 的取值范围使得所有均衡产出都是正数,试问此博弈的贝叶斯纳什均衡是什么?解:在市场需求为高时,企业1的最优战略为:()HH H q c q q a Max 121⨯--- 由一阶条件可以推出221c q a q H H --= (1) 在市场需求为低时,企业1的最优战略为:()L L L q c q q a Max 121⨯--- 由一阶条件可以推出221c q a q L L --=(2) 企业2的最优战略为 ()()(){}2212211q c q q a q c q q a Max L L H H ----+---θθ由一阶条件可得:()()()211*2cq a q a q L L H H ---+=-θθ (3)方程(1)、(2)和(3)联立可得:()()()()621311*1c q a q a q L L H H H ------=θθ ()622*1c a a q HL L --+=θθ ()31*2c a a q HL -+-=θθ由此可知,企业1的战略()*1*1,L H q q 和企业2的战略*2q 构成贝叶斯纳什均衡。
2、在下面的静态贝叶斯博弈中,求出所有的纯战略贝叶斯纳什均衡:(1)自然决定收益情况由博弈1给出还是由博弈2给出,选择每一博弈的概率相等;(2)参与者1了解到自然是选择了博弈1还是博弈2,但参与者2不知道;(3)参与者1以相同概率选择T 或B ,同时参与者2选择L 或R;(4)根据自然选择的博弈,两参与者都得到了相应的收益。
经济博弈论第六章不完全信息静态博弈共39页

11
27.04.2020
6.1.3 海萨尼转换
基本思路:将静态博弈转化为动态博弈 (1)假设有一个名为“自然”的博弈方0,该博弈
方的作用是先为其他每个博弈方抽取他们的类型, 抽取的这些类型构成类型向量
t=(t1,…,tn),其中t i T i ,i=1,…,n。
(2)“自然”让每个博弈方知道到自己的类型, 但却不让其他博弈方知道。
10
27.04.2020
6.1.2 静态贝叶斯博弈的一般表示
静态贝叶斯博弈的一般表达式为: G={A1,…,An ;T1,…,Tn;u1,…,un}
其中Ai为博弈方i的行为空间(策略空间), Ti是博弈方i的类型空间,博弈方i的得益 ui=ui(a1,…,an,ti)为策略组合(a1,…,an ) 和类型ti的函数。
q1*a2C1C3 H(1)CL)
6
27.04.2020
6.1.1 不完全信息的古诺模型
与完全信息古诺模型比较 完全信息古诺模型中的的产量
q1*
a2C1 3
C2
q2*
a2C2 3
C1
CH C2 q2*(CH)q2*
CL C2 q2*(CL)q2*
ቤተ መጻሕፍቲ ባይዱ
7
27.04.2020
6.1.2 静态贝叶斯博弈的一般表示
厂商1只知道有两种可能性,一种是C2= C2(q2) = CH q2概率为θ另一种是C2= C2(q2)= C Lq2, 概率为1-θ,而CH>CL,也即边际成本有高、低两 种可能。
3
27.04.2020
6.1.1 不完全信息的古诺模型
厂商2在边际成本是较高的CH时会选择较低的产 量,而在边际成本为较低的CL时会选择较高的产 量。
经济博弈论6 不完全信息静态博弈

Si* (ti )所选择的行动ai都能满足
不完全信息静态博弈 -贝叶斯纳什均衡
在不完全信息静态博弈中,所有参与人同时行动,其战略空间 等于行动空间,但是参与人i的行动空间可能依赖于其 类型,也就是行动空间是类型依存的。类似的,其支 付函数也是类型依存的。如企业能选择什么产量依赖于它的成 本函数。
6.1 6.2 6.3 6.4 6.5
不完全信息博弈与海萨尼转换 混合策略和不完全信息 暗标拍卖 双方报价拍卖 拍卖规则设计问题和揭示原理
6.1 不完全信息博弈与海萨尼转换
6.1.1 6.1.2 6.1.3 6.1.4 不完全信息博弈 静态贝叶斯博弈的例子与表示 海萨尼转换 贝叶斯纳什均衡
6.1.1 不完全信息博弈-无法避免的不确定性
司马懿 进攻 撤退 不被擒,?
弃城
诸葛亮 守城
被擒,?
司马懿关于自 己策略的支付的 信息是不完全的。
被擒,?
不被擒,?
司马懿:兵多将广,但不知道自己和对方在不同行动策略下的支付;
诸葛亮:处于劣势,但知道博弈的结构,比对方掌握更多的信息。
计策:使用各种手段迷惑司马懿,为的是不让对方知道其策略的结果(支 付)。迫使其认为,撤退比进攻好,降低其进攻的预期收益。 如用概率论的术语来说,诸葛亮的做法是加大司马懿对进攻失败的主 观概率,使司马懿认为进攻的期望收益小于撤退的期望收益。
贝叶斯纳什均衡定义
在静态贝叶斯博弈 G { A1 ,, An ; T1 ,, Tn ; p1 ,, pn ; u1 ,, un } 中,如果对任意博弈方i和他的每一种可能的类型ti Ti,
* max {ui [ S1* (t1 ), , Si*1 ti 1 , ai , Si*1 (ti 1 ), , S n (t n ),t i ] p(t i | ti )} ai Ai t i * 则称策略组合S * ( S1* ,, S n )为G的一个(纯策略)贝叶斯纳什均衡
《经济博弈论》期末考试复习题及参考答案

经济博弈论复习题(课程代码262268)一、名词解释混合战略纳什均衡;子博弈精炼纳什均衡;完全信息动态博弈;不完全信息动态博弈;完全信息静态博弈;帕累托上策均衡;囚徒困境;纳什均衡;子博弈;完美信息动态博弈;颤抖手均衡;柠檬原理;完美贝叶斯均衡二、计算分析题1、在市场进入模型中,市场需求函数为p=13-Q,进入者和在位者生产的边际成本都为1,固定成本为0,潜在进入者的进入成本为4。
博弈时序为:在位者首先决定产量水平;潜在进入者在观察到在位者的产量水平之后决定是否进入;如果不进入,则博弈结束,如果进入,则进入者选择产量水平。
求解以上博弈精炼纳什均衡。
2、考虑如下扰动的性别战略博弈,其中t i服从[0,1]的均匀分布,,t1和t2是独立的,t i是参与人i的私人信息。
求出以上博弈所有纯战略贝叶斯均衡。
S1S2足球芭蕾足球3+,1 ,,芭蕾0,0 1,3+3、求下列信号传递模型的贝叶斯Nash均衡(讨论分离均衡和混同均衡)4、考察如下完全信息静态博弈,求其全部纳什均衡:L M R U 0, 4 4, 0 5, 3M 4, 4 0, 4 5, 3D 3, 5 3, 5 6, 6表1 双人静态博弈5、古诺博弈:市场反需求函数为()P Q a Q =-,其中12Q = q q +为市场总产量,i q 为企业()i i 1,2=的产量。
两个企业的总成本都为()i i i c q cq =。
请您思考以下问题: 1) 在完全信息静态条件下,这一博弈的纳什均衡是什么?2)假设这一阶段博弈重复无限次。
试问:在什么样的贴现条件下,企业选择冷酷战略可保证产量组合()()()772424,a c a c --是子博弈精炼纳什均衡的?6、考虑一个工作申请的博弈。
两个学生同时向两家企业申请工作,每家企业只有一个工作岗位。
工作申请规则如下:每个学生只能向其中一家企业申请工作;如果一家企业只有一个学生申请,该学生获得工作;如果一家企业有两个学生申请,则每个学生获得工作的概率为1/2。
博弈论考试题及答案

博弈论考试题及答案一、选择题(每题2分,共20分)1. 博弈论中的“囚徒困境”是指什么?A. 两个囚犯相互合作B. 两个囚犯相互背叛C. 两个囚犯中一个合作一个背叛D. 两个囚犯相互猜疑答案:B2. 以下哪个不是博弈论中的基本概念?A. 策略B. 收益C. 公平D. 纳什均衡答案:C3. 在零和博弈中,一个玩家的损失等于另一个玩家的收益,这意味着:A. 总收益为零B. 总收益为正C. 总收益为负D. 总收益不确定答案:A4. 博弈论中的“混合策略”是指:A. 玩家随机选择策略B. 玩家固定选择一种策略C. 玩家根据对手的策略选择策略D. 玩家不使用策略答案:A5. 以下哪个是博弈论中的“完全信息”博弈?A. 拍卖博弈B. 石头剪刀布C. 桥牌D. 信息不对称博弈答案:C6. 博弈论中的“重复博弈”指的是:A. 博弈只进行一次B. 博弈进行多次C. 博弈进行无限次D. 博弈进行有限次但次数未知答案:B7. 以下哪个是博弈论中的“动态博弈”?A. 零和博弈B. 非零和博弈C. 同时博弈D. 顺序博弈答案:D8. 在博弈论中,如果一个策略组合是纳什均衡,那么:A. 每个玩家都有动机单方面改变策略B. 每个玩家都满足于当前策略C. 至少有一个玩家不满意当前策略D. 所有玩家都不满意当前策略答案:B9. 博弈论中的“合作博弈”是指:A. 玩家之间可以形成联盟B. 玩家之间不能形成联盟C. 玩家之间只能通过竞争来获得收益D. 玩家之间只能通过合作来获得收益答案:A10. 以下哪个是博弈论中的“公共知识”?A. 每个玩家的收益函数B. 每个玩家的策略选择C. 每个玩家的偏好D. 每个玩家的个人信息答案:A二、简答题(每题10分,共30分)1. 简述博弈论中的“纳什均衡”概念。
答案:纳什均衡是指在一个博弈中,每个玩家都选择了自己的最优策略,并且没有玩家能够通过单方面改变策略来提高自己的收益。
在纳什均衡状态下,每个玩家的策略是对其他玩家策略的最优反应。
博弈论_不完全信息静态博弈

贝叶斯纳什均衡的存在性
贝叶斯纳什均衡的存在性定理 定理3.1.2,见书上第62页,不讲定理的证明 它与第24页的定理2.2.3的比较。定理3.1.2所
要用到的前提条件更强,其原因在于: 在贝叶斯博弈中,局中人i的收益是纯策略下
的期望收益。或,局中人i的收益函数ui(s-i, si, ti)可以随着类型的变化而变化;当ui是si的凹函 数时,其凸组合“∑pi(t-i|ti)×ui(s-i(t-i), si, ti), t-i∈T-I”也是si的凹函数;若拟凹则不成立
义3.1.2做比较 此定义是对纯策略下贝叶斯纳什均衡定义的一
个直接扩展,其中E(ui)是局中人i在混合策略 组合下,对其收益函数ui的数学期望 定理3.1.3:混合策略组合是贝叶斯纳什均衡 的充分必要条件 定理3.1.4:贝叶斯纳什均衡的存在性定理
求解行业博弈的贝叶斯纳什均衡
条件概率 标记混合策略的符号 标记期望收益的符号 计算不同类型下的期望收益 书上的方法:由混合策略下贝叶斯纳什均衡的
对局中人2的计算
局中人 1建厂 高成本
进入
不进入
局中人 1建厂 低成本
进入
不进入
建厂 , -4/3 , 0 建厂 , -4/3 , 0
不建厂 , 1 , 0 不建厂 , 1 , 0
合成后的支付矩阵
局中人 1建厂 高成本
进入
不进入
局中人 1建厂 低成本
进入
不进入
建厂 0, -4/3 2, 0 建厂 1.5, -4/3 3.5, 0
混合策略
在贝叶斯博弈G=[N, {Ti}, P, {Si(ti)}, {ui}]中,局中人i 在类型ti∈Ti下,为每一个纯策略以概率进行选择,则 xi(ti) =(x1(i)(ti), x2(i)(ti), ···, xm_i(i)(ti))称为局中人i在类型 ti下的一个混合策略。有时简写为xi。
博弈论与信息经济学 不完全信息静态博弈
不完全信息和贝叶斯纳什均衡
定义:在静态贝叶斯G {A1, , An ; 1, , n ; p1, , pn ;u1, , un}博弈中, 纯策略贝叶斯纳什均衡是一个类型依存策略组
合a (θ) (a1 (1 ),
,
a
n
(
n
)),其中,每个参与人
i
在给定自己的类
型
i
和其他参与人依存策略
a
i
(θ i
不完全信息和贝叶斯纳什均衡
n 人不完全信息静态博弈的时间顺序为:
⑴自然给定类型向量θ 察到 i ,但参与人
(1, ,
j( i
n ) ,其中,i )只知道 p j
(θ j
i
|
,参与人 i 观 j ),观察不
到 i;
⑵参与人同时选择行动,参与人 i 从可行集 Ai (i )中选择行
动 a i,n 人的行动组合为a (a1, , an );
p(i ,i ) p(i )
p(i ,i ) p(i ,i )
ii
这里,p(i ) 是边缘概率。如果类型的分布是独立的,pi (i i ) p(i )
不完全信息和贝叶斯纳什均衡
贝叶斯纳什均衡是完全信息静态博弈纳什均衡概念在不完 全信息静态博弈上的扩展。不完全信息静态博弈又称为静 态贝叶斯博弈。 ◆定义:n人静态贝叶斯博弈的战略式表述包括:参与人的类 型空间 1, , n,条件概率 p1 ,..., pn ,类型依存战略空间
A11,..., An n ,和类型依存支付函数u1(a1, , an ;1),..., un (a1, , an ;n )
参与人i知道自己的类型 i i ,条件概率 pi pi (i i ) 描述 给定自己属于 i 的情况下,参与人i有关其他参与人类型 i i的不确定性。我们用 G {A1, , An ;1, ,n ; p1, , pn ;u1, ,un} 代表这个博弈。
06 不完全信息静态博弈

bi
m ax [(vi bi ) P{v j
bi
bi a j cj ]
}]
m ax [(vi bi )
bi
bi a j cj 2
策略函数: bi
vi a j
2 不妨设bi a j , 综合以上分析, 博弈方i的策略反应函数为: vi a j ,当vi a j bi (vi ) 2 a j,当vi a j
完全信息夫妻之争
妻子的策略:当 w w ,选时装 丈夫的策略:当 h h ,选足球
给定丈夫的策略,妻子的临界值策略和得益
妻子选时装的概率为 ( x w ) / x,选足球的概率为w x 丈夫选足球的概率为 (x h ) x ,选时装的概率为h x 妻子选时装的收益: h x h h (2 w) 0 (2 w) x x x 妻子选足球的收益: h x h x h 0 1 x x x
不完全信息静态博弈详解

换言之,战略组a*合 (a1* (1), an* (n )), 是一个贝叶斯纳什均衡, 如果对于所有的aii, Ai (i ),
ai*(i ) arg max pi (i | i )ui (ai , a*i (i );i ,i ) ai
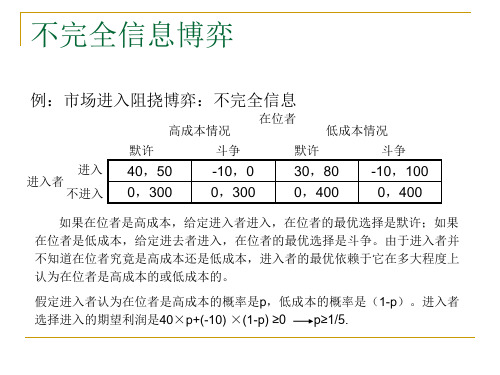
进入者的最优选择是:如果p≥1/5,进入;如果p<1/5不进入
博弈论与信息经济学 江西财经大学 陶长琪
3.1.2 海萨尼(Harsanyi)转换
海萨尼提出的处理不完全信息博弈的方法是,引入一个虚拟的 —“自 然”(nature);这样,不完全信息博弈就转换为如图3.1所示的完全但不完 美信息博弈(games of complete but imperfect information)可以使用标 准的分析技术进行分析。
混合战略贝叶斯纳什均衡的概念可以类似地定义。均衡的存在性定理是纳什均 衡存在性定量的一个直接推广
博弈论与信息经济学 江西财经大学 陶长琪
3.2 贝叶斯均衡的应用举例
3.2.1 不完全信息库诺特模型
在不完全信息库诺特模型里,参与人的类型是成本函数。假定逆需求函
数是 P a q1 q2 ,每个企业都有不变的单位成本。令 ci 为企业i 的单位成本,那么,企业 i 的利润函数如下:
3. 不完全信息静态博弈
3.1 不完全信息博弈和贝叶斯 3.2.3 一级密封价格拍卖(招标)
纳什均衡
3.2.4 双方叫价拍卖
3.1.1 不完全信息博弈
3.3 贝叶斯博弈与混合战略均
3.1.2 海萨尼(Harsanyi)转换
衡
3.1.3 不完全信息静态博弈的 3.4 机制设计理论与显示原理
博弈论第六章不完全信息静态博弈题库

博弈论第六章不完全信息静态博弈题库【原创实用版】目录一、引言:介绍博弈论及其在经济学中的应用二、不完全信息静态博弈的定义和特点三、博弈论第六章不完全信息静态博弈的主要内容四、如何解决不完全信息静态博弈问题五、结论:总结博弈论在经济学中的重要性正文一、引言博弈论作为经济学的一个重要分支,主要研究多个理性决策者在特定规则下的决策行为及其结果。
在经济学中,博弈论的应用已经渗透到许多领域,如市场竞争、价格博弈、合作与信任等。
通过研究博弈论,我们可以更好地理解经济现象及其背后的决策过程。
二、不完全信息静态博弈的定义和特点不完全信息静态博弈是指在博弈过程中,参与者拥有不完全的信息。
在这种情况下,参与者需要根据已知的部分信息和其他人的可能策略来选择最佳行动。
不完全信息静态博弈的特点包括:1.参与者拥有不完全的信息,无法了解其他参与者的准确策略和支付函数。
2.参与者的决策是静态的,即他们在一个特定的时间点上做出决策,不考虑未来可能的变化。
三、博弈论第六章不完全信息静态博弈的主要内容博弈论第六章主要讨论了不完全信息静态博弈的解决方法,包括:1.贝叶斯纳什讨价还价解:通过贝叶斯定理,参与者可以根据已知的部分信息和其他人的可能策略来推测其他人的支付函数,从而找到一个纳什讨价还价解。
2.声誉模型:在不完全信息静态博弈中,参与者可以通过建立声誉来影响其他参与者的决策。
声誉好的参与者更容易达成合作,从而获得更好的支付。
3.信号博弈:信号博弈是一种通过发送信号来传递信息的博弈。
参与者可以通过观察其他参与者的信号来推测其策略和支付函数,从而找到一个合适的行动。
四、如何解决不完全信息静态博弈问题在不完全信息静态博弈中,参与者需要根据已知的部分信息和其他人的可能策略来选择最佳行动。
以下是一些解决不完全信息静态博弈问题的方法:1.充分沟通:参与者之间可以通过充分沟通来传递信息,从而减少不确定性,提高决策效率。
2.建立信任:在博弈过程中,参与者可以通过建立信任关系来降低其他参与者的背叛风险,从而更容易达成合作。
《经济博弈论》期末考试复习题及参考答案

《经济博弈论》期末考试复习题及参考答案一、单项选择题1、博弈论中,参与人的策略有()A 有限的B 无限的C 有限和无限两种情况D 以上都不对参考答案:C解释:在博弈论中,参与人的策略可以是有限的,也可以是无限的,具体取决于博弈的类型和设定。
2、下列属于完全信息静态博弈的是()A 囚徒困境B 斗鸡博弈C 市场进入博弈D 以上都是参考答案:D解释:囚徒困境、斗鸡博弈和市场进入博弈都属于完全信息静态博弈。
3、在一个两人博弈中,如果双方都知道对方的策略空间和收益函数,这被称为()A 完全信息博弈B 不完全信息博弈C 静态博弈D 动态博弈参考答案:A解释:完全信息博弈意味着博弈中的参与人对彼此的策略空间和收益函数都有清晰的了解。
4、占优策略均衡一定是纳什均衡,纳什均衡()是占优策略均衡。
A 一定B 不一定C 一定不D 以上都不对参考答案:B解释:占优策略均衡是一种更强的均衡概念,占优策略均衡一定是纳什均衡,但纳什均衡不一定是占优策略均衡。
5、对于“囚徒困境”博弈,()A 双方都独立依照自身利益行事,结果限于最不利的局面B 双方都独立依照自身利益行事,导致最好的选择C 双方进行合作,得到了最好的结果D 以上说法都不对参考答案:A解释:在“囚徒困境”中,每个囚徒都从自身利益出发选择坦白,最终导致双方都受到较重的惩罚,这是一种个体理性导致集体非理性的结果。
二、多项选择题1、以下属于博弈构成要素的有()A 参与人B 策略C 收益D 信息E 均衡参考答案:ABCDE解释:博弈的构成要素通常包括参与人、策略、收益、信息和均衡等。
参与人是进行博弈的主体;策略是参与人在博弈中可选择的行动方案;收益是参与人采取不同策略所得到的结果;信息是参与人对博弈局面的了解程度;均衡是博弈的稳定状态。
2、常见的博弈类型有()A 完全信息静态博弈B 完全信息动态博弈C 不完全信息静态博弈D 不完全信息动态博弈参考答案:ABCD解释:这四种博弈类型是根据信息是否完全和博弈的进行时态来划分的。
博弈论-不完全信息静态博弈共163页

26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。—上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
163
39、没有不老的誓言,没有不变的承 诺,踏 上旅途 ,义无 反顾。 40、对时间的价值没有没有深切认识 的人, 决不会 坚韧勤 勉。
▪
博弈论-不完全信息静态博弈
36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
博弈论第六章习题

第六章习题一、判断下列表述是否正确,并作简单分析(1)完全但不完美信息动态博弈中各博弈方都不清楚博弈的进程,但清楚博弈的得益。
答:不一定,不是所有博弈方都不清楚博弈的进程,只要有一个博弈方都不完全清楚博弈的进程。
(2)不完美信息动态博弈中的信息不完美性都是客观因素造成的,而非主观因素造成.答:错。
信息不完美很多是人为因素所造成的,因为出于各自的动机和目的,人们在市场竞争或合作中常常会故意隐瞒自己的行为。
(3)在完全但不完美信息动态博弈中,若不存在混合策略,并且各博弈方都是主动选择且行为理性的,则不完美信息从本质上说是“假的”。
答:正确。
因为只包含理性博弈方的主动选择行为,利益结构明确,而且不同路径有严格优劣之分,从不需要用混合策略的动态博弈来说,所有博弈方选择的路径都可以通过分析加以确定和预测,根本无须观察。
从这个意义上说,这种博弈的不完美信息实际上都是假的. (4)子博弈可以从一个多节点信息集开始。
答:不能从多节点信息集开始,因为多节点必然分割信息集。
(5)不完美信息是指至少某个博弈方在一个阶段完全没有博弈进程的信息。
答:不是完全没有博弈进程的信息,而是没有完美的信息,只有以概率判断形式给出的信息。
二、用柠檬原理和逆向选择的思想解释老年人投保困难的原因。
答:“柠檬原理”是在信息不完美且消费者缺乏识别能力的市场中,劣质品赶走优质品,最后搞垮整个市场机制。
“逆向选择”是在同样不完美市场和消费者缺乏识别能力的市场中,当价格可变时,价格和质量循环下降,市场不断向低端发展的机制。
老年人投保的分析:大致思路是由于信息不对称,费用越来越高,投保人的健康状况好的比例越来越小,最终发展成为只有身体不好的人才参加投保。
如果允许调整费率,保险公司为了避免亏损降低风险,上调保费率,健康状况相对好一些的退出市场,整个市场状况恶化.……这就是逆向选择机制在老年保险市场上作用的结果。
三、用完全但不完美信息动态博弈的思想,讨论我国治理假冒伪劣现象很困难的原因。
第六章-不完全信息静态博弈

3)博弈方i的得益
ui
ui (b1, b2 , v1, v2 )
(vivi bib)i,/ 2,当当bi bi
bj
bj
0,当bi bj
❖ 要找贝叶斯纳什均衡,必须先找两博弈方的策略空间。
他们的策略是根据类型决定行为的函数关系。即是 bi (vi )
如果[b1(v1),b2 (v2 )] 是贝叶斯纳什均衡,那么bi (vi ) 是对方的最
❖ 定义中将信息不了解转为博弈方类型的不了解。 ❖ 例如:不完全信息的古诺模型中
A1 {q1}, A2 {q2}; T1 {c1},T2 {cL , cH } u1 {q1, q2 , t1}, u2 {q1, q2 , t2}
G {A1, A2;T1,T2;u1, u2}
❖ 目前,还不能进行分析。
空间,即有 ti Ti ,用 ui ui (a1, a2 , , an , ti )
这个得益函数含有一个反应类型变量 ti ,其取值 只是博弈方 i 自己知道的而其它博弈方并不清楚, 从而反应了不完全信息特征。
❖ 于是:静态贝叶斯博弈的一般表示为:
G {A1, , An;T1, ,Tn;u1, , un}
❖ 一级密封价格拍卖(first price sealed bid)
❖ 二级密封价格拍卖(second price sealed bid)
❖ 英式拍卖(English auctions)
❖ 荷兰式拍卖(Dutch auctions)
❖ 英式拍卖最为常见,也被称为一级公开叫价(first price open cry)拍卖,许多物品都采用此种方式竞标。在英式拍 卖中,参加竞标者可以不断地开出更高的价格,当没有其他 对手愿意再出更高的价格时,最后出价的那个竞标者就得到 竞标物。
不完全信息静态博弈

吴建设
不完全信息
一个寓言故事的启示:
有一次,伊索进城,半路上遇见一位法官。法官 严厉的盘问:“你要去哪儿?”伊索回答说: “不知道。”于是,法官起了疑心,将伊索关进 了监狱,严加审问。“法官先生,要知道,我讲 的是实话。”伊索说,“我确实不知道我会来监 狱。” 启示:我们不可能了事如神,更不可能预测未来, 不确定性就像日出日落一样不可避免。 策略:我们没办法做到无所不知,也不止于一无 所知,应尽可能利用所知的一切寻求最优行动。
人本人知道、其他参与人则不知道的信息称为私人信息。某一参与人所拥有的全
部私人信息称为他的类型。在上述例子中,阻挠成本就是 A的私人信息。高阻挠 成本和低阻挠成本则是两种不同的类型。
A 高成本 低成本 默许 阻止 阻止
B
默许
进入
不进入
40, 50
0, 300
-10, 0
0, 300
30, 80
0, 400
拟的局中人——“自然”。自然首先行动,它决定每个参与人
的特征。每个参与人知道自己的特征,但不知道别的参与人特 征。这种方法将不完全信息静态博弈变成一个两阶段动态博弈, 第一个阶段是自然N的行动选择,第二阶段是除N外的参与人的 静态博弈。这种转换被称为“海萨尼转换”,这个转换把“不 完全信息”转变成为完全但不完美信息,从而可以用分析完全 信息博弈的方法进行分析。
在博弈中,其中有参与人也许对对方博弈的收益函数 并不十分清楚,可采用概率分布来表示其类型。也就 是基于概率对博弈进行分组建立博弈收益函数。 比如甲与乙选择策略时,可以这样考虑,甲选择某一 种策略时,乙选择策略有几种,乙的这些策略按发生 的概率进行分组。通常构建一个博弈树就可以较好地 表达这一切。 海萨尼的观点关键在于假定:对于策略选择发生的概 率是一个共同知识。先验概率是作为博弈规则的一部 分存在,因此,一个参与人必须是持有关于其它参与 人类型的先验信念,同时,在观察到他们的行动后, 就要假定他们遵循着均衡的行为,然后更新自己的信 念。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
博弈论第六章不完全信息静态博弈题库
【原创版】
目录
一、引言
二、不完全信息静态博弈的概述
1.不完全信息的定义
2.静态博弈的定义
三、不完全信息静态博弈的解题方法
1.严格优势策略
2.纳什讨价还价解
3.轴向讨价还价解
四、应用案例分析
五、总结
正文
一、引言
在博弈论中,不完全信息静态博弈是一个重要的研究领域。
由于参与者在博弈过程中所拥有的信息不完全,这使得博弈过程变得更加复杂和有趣。
本文将介绍不完全信息静态博弈的概述,以及探讨如何解决这类问题。
二、不完全信息静态博弈的概述
1.不完全信息的定义
不完全信息指的是参与者在博弈过程中,无法完全了解其他参与者的策略或支付函数。
这种情况下,参与者需要根据自己所掌握的信息,来猜测其他参与者可能采取的策略。
2.静态博弈的定义
静态博弈是指参与者在一定时间内,一次性地选择策略并完成博弈的过程。
静态博弈中,参与者不需要考虑时间顺序,只需关注当前状态下的最优策略。
三、不完全信息静态博弈的解题方法
1.严格优势策略
在完全信息静态博弈中,如果一个策略对某个参与者来说是严格优势的,那么他会选择这个策略。
在不完全信息静态博弈中,同样可以利用严格优势策略来求解。
即通过分析其他参与者可能采取的策略,找到一个对某个参与者来说严格优势的策略。
2.纳什讨价还价解
纳什讨价还价解是解决不完全信息静态博弈问题的一种方法。
通过设计一种讨价还价机制,使得参与者可以在不完全信息的情况下,达成一种合作解。
纳什讨价还价解的关键是让参与者在博弈过程中,有动力去揭示自己的真实支付函数。
3.轴向讨价还价解
轴向讨价还价解是另一种解决不完全信息静态博弈问题的方法。
它通过让参与者在博弈过程中,根据其他参与者的策略选择,来调整自己的策略,从而实现一种合作解。
轴向讨价还价解的优势在于,它可以在不完全信息的情况下,使得参与者的收益达到最大。
四、应用案例分析
以寡头垄断市场为例,市场中有两个寡头企业,它们需要决定是否进行价格战。
在这个过程中,每个企业都需要考虑对方的策略选择。
由于信息不完全,企业无法准确了解对方的策略选择。
此时,可以运用不完全信息静态博弈的解题方法,如纳什讨价还价解或轴向讨价还价解,来分析企业最优策略选择,从而预测市场的发展趋势。
五、总结
不完全信息静态博弈是博弈论中的一个重要研究领域。
通过运用严格优势策略、纳什讨价还价解和轴向讨价还价解等方法,可以在不完全信息的情况下,解决静态博弈问题。
