七年级数学正方体的展开与折叠课件
合集下载
北师大版数学七年级上册1.2.1正方体的展开图课件
数相等.
4. 所有侧棱长都相等.
什么样的图形能折成棱柱?
观察下面的四个图形,想一想哪几个能围成棱柱
(1)、(3)不行
为什么(1)、(3)不行? 在(1)、(3)的基础上进行修改, 使其能围成一个棱柱
展开图能围成棱柱的条件:
1、中间部分是几个长方形,可以围成棱柱的侧面。 2、上、下底面形状大小要相同,
面 侧棱(条) 侧面(个) (个)
三棱柱
6
四棱柱
95 3 3
8 12 6 4 4
五棱柱
10 15 7 5 5
六棱柱
12 18 8 6 6
……
n棱柱
2n 3n n+2 n n
(Ⅱ)动手操作、认识棱柱
侧面
底面
1.棱柱有上下两个底面, 它们的形状相同.
2.侧面的形状都是长方形.
3.侧面数、侧棱数、底面 侧棱 边数和底面多边形的顶点
作业: 位于侧面部分的两 侧
侧面数、侧棱数、底面 边数和底面多边形的顶点数相等.
4.三习棱柱题底面1边.长3为的3cm知, 识技能1、2、3。
五、课堂小结,布置作业
侧面的动形状手都是制长方作形.一个正方体的纸盒及圆柱圆锥
1、课本P12随堂练习 1、棱柱的特征、棱柱的顶点数、棱数、面数的规律 4.三棱柱底面边长为3cm, 2、写出下面图形能折叠成什么多面体。 2、写出下面图形能折叠成什么多面体。
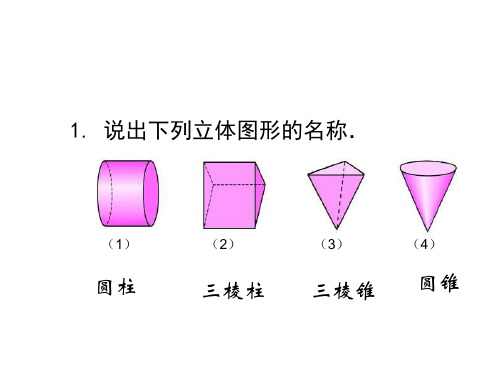
1. 说出下列立体图形的名称.
(1)
圆柱
(2)
三棱柱
(3)
三棱锥
(4)
圆锥
展开
折叠
展开 折叠
展开与折叠(1)
用一个词来形容之前的活动
有些立体图形 展开 平面图形 有些平面图形 折叠 立体图形
4. 所有侧棱长都相等.
什么样的图形能折成棱柱?
观察下面的四个图形,想一想哪几个能围成棱柱
(1)、(3)不行
为什么(1)、(3)不行? 在(1)、(3)的基础上进行修改, 使其能围成一个棱柱
展开图能围成棱柱的条件:
1、中间部分是几个长方形,可以围成棱柱的侧面。 2、上、下底面形状大小要相同,
面 侧棱(条) 侧面(个) (个)
三棱柱
6
四棱柱
95 3 3
8 12 6 4 4
五棱柱
10 15 7 5 5
六棱柱
12 18 8 6 6
……
n棱柱
2n 3n n+2 n n
(Ⅱ)动手操作、认识棱柱
侧面
底面
1.棱柱有上下两个底面, 它们的形状相同.
2.侧面的形状都是长方形.
3.侧面数、侧棱数、底面 侧棱 边数和底面多边形的顶点
作业: 位于侧面部分的两 侧
侧面数、侧棱数、底面 边数和底面多边形的顶点数相等.
4.三习棱柱题底面1边.长3为的3cm知, 识技能1、2、3。
五、课堂小结,布置作业
侧面的动形状手都是制长方作形.一个正方体的纸盒及圆柱圆锥
1、课本P12随堂练习 1、棱柱的特征、棱柱的顶点数、棱数、面数的规律 4.三棱柱底面边长为3cm, 2、写出下面图形能折叠成什么多面体。 2、写出下面图形能折叠成什么多面体。
1. 说出下列立体图形的名称.
(1)
圆柱
(2)
三棱柱
(3)
三棱锥
(4)
圆锥
展开
折叠
展开 折叠
展开与折叠(1)
用一个词来形容之前的活动
有些立体图形 展开 平面图形 有些平面图形 折叠 立体图形
北师大版七年级上册数学 习题课件-1.2.1 正方体的展开与折叠

畜
:
“猪”“牛”“羊”“马”“C鸡”“狗”.将其围成
一个正方体后,与“牛”相对的是( )
A.羊
B.马
C.鸡
D.狗
9.图①是边长为1的六个小正方形组成的图形,它可以 围成图②所示的正方体,则图①中小正方形的顶点A, B在围成的正方体上的距离是( B )
A.0 B.1 C.2 D.3
【点拨】图①中的平面图形围成图②中的正方体后, AB是正方体的一条棱,所以AB=1.故选B.
12.如图,这是一个正方体的展开图,每个面上都标注 了字母,回答下列问题(考虑字母在内表面和外表面):
(1)如果D面是正方体的下底面, 那么哪一面在上面? 解:B面在上面. (2)如果B面在前面,C面在左面,
那么哪一面在上面? A面或E面在上面.
(3)如果E面在右面,F面在后面,那么哪一面在上面?
3.(2018·无锡)下面每个图形都是由6个边长相同的正方 形拼成的,其中能折叠成正方体的是( C )
4.如图,可以折叠成一个无盖正方体盒子的是( D ) A.① B.①② C.②③ D.①③
5.(2018·临安区)马小虎准备制作一个封闭的正方体盒子,
他先用5个大小一样的正方形制成如图所示的拼接图
中小学品教学资源
中小学精品教学资源 中小学精品教学资源
第一章 丰富的图形世界
2 展开与折叠 第1课时 正方体的展开与折叠
1.常见的正方体的展开图有以下几种形状(如图):
2.(2017·长春)下列图形中,可以是正方体表面展开图的 是( D )
A.认 C.复
B.真 D.习
7.(2018·河南)某正方体的每个面上都有一个汉字,下图
是它的一种展开图,那么在原正方体中,与“国”字
北师大版七年级上册数学课件1.2.1正方体的展开图

同学合作,设计并制作一个模型,尽可能使设 计美观、大方。
提示:可以是生活中的常用物品,也可以是正方 体、长方体、圆柱、圆锥、棱柱、棱锥等几何体 或者它们的组合体。
学生合作讨论:
仔细观察,下面各种包装盒分别 下面六个正方形连在一起的图形,经折叠后能围成正方体的图形有哪几个?
开启 智慧
是什么几何体? 将下图中五角星状的图形沿虚线折叠,得到一个几何体,你在生活中见过和这个几何体形状类似的物体吗?
下列图形哪个不是长方体的表面展开图? 仔细观察,下面各种包装盒分别是什么几何体?
下列图形哪个不是长方体的表 面展开图?
B A
C
D
把下面的正三角形沿 虚线折叠后的几何体是 什么?
将下图中五角星状的图形沿虚线 折叠,得到一个几何体,你在生 活中见过和这个几何体形状类似 的物体吗?
下面六个正方形连在一起的图形,经 折叠后能围成正方体的图形有哪几个?
A
B
C
D
E
F
G
4、如图,这是一个正方体的展 开图,如果将它组成原来的正 方体,哪些点与点P重合。
5、有一个正方体,在它的各个面上分别涂了白、红、黄、兰、绿、黑六种颜色。
下面请发挥你的聪明才智,与小组内的其他同学合作,设计并制作一个模型,尽可能使设计美观、大方。
下面请发挥你的聪明才智,与小组内的其他同学合作,设计并制作一个模型,尽可能使设计美观、大方。
6、有一正方体木块,它的六个面分别标上数字1-6,下图是这个正方体木块从不同面所观察到的数字情况。
第三类,中间二连方,两侧各有二个,只有一种.
(1)如果A面在多面体的底部,哪一面会在上面?
第一章 第2节
把圆锥、圆柱的侧面展开,会得到什么图形?
提示:可以是生活中的常用物品,也可以是正方 体、长方体、圆柱、圆锥、棱柱、棱锥等几何体 或者它们的组合体。
学生合作讨论:
仔细观察,下面各种包装盒分别 下面六个正方形连在一起的图形,经折叠后能围成正方体的图形有哪几个?
开启 智慧
是什么几何体? 将下图中五角星状的图形沿虚线折叠,得到一个几何体,你在生活中见过和这个几何体形状类似的物体吗?
下列图形哪个不是长方体的表面展开图? 仔细观察,下面各种包装盒分别是什么几何体?
下列图形哪个不是长方体的表 面展开图?
B A
C
D
把下面的正三角形沿 虚线折叠后的几何体是 什么?
将下图中五角星状的图形沿虚线 折叠,得到一个几何体,你在生 活中见过和这个几何体形状类似 的物体吗?
下面六个正方形连在一起的图形,经 折叠后能围成正方体的图形有哪几个?
A
B
C
D
E
F
G
4、如图,这是一个正方体的展 开图,如果将它组成原来的正 方体,哪些点与点P重合。
5、有一个正方体,在它的各个面上分别涂了白、红、黄、兰、绿、黑六种颜色。
下面请发挥你的聪明才智,与小组内的其他同学合作,设计并制作一个模型,尽可能使设计美观、大方。
下面请发挥你的聪明才智,与小组内的其他同学合作,设计并制作一个模型,尽可能使设计美观、大方。
6、有一正方体木块,它的六个面分别标上数字1-6,下图是这个正方体木块从不同面所观察到的数字情况。
第三类,中间二连方,两侧各有二个,只有一种.
(1)如果A面在多面体的底部,哪一面会在上面?
第一章 第2节
把圆锥、圆柱的侧面展开,会得到什么图形?
七年级数学上册 第一章 丰富的图形世界 2 展开与折叠课件

“凹”“L”型形状.
图1-2-1
2021/12/10
第三页,共四十六页。
例1 (2016四川成都树德实验中学期中)在下面的图形中,是正方体的 展开图的是 ( )
解析(jiě xī) 充分发挥想象力和动手实践能力是解决此类问题的有效途径. 答案(dáàn) C
2021/12/10
第四页,共四十六页。
2021/12/10
第十五页,共四十六页。
6.图1-2-4是一个食品包装盒的表面展开图. (1)请写出这个包装盒的形状的名称; (2)根据图中所标的尺寸,计算此包装盒的表面积和体积.
图1-2-4
解析 (1)包装盒的形状(xíngzhuàn)是四棱柱. (2)表面积为4ab+2b2,体积为ab2.
2021/12/10
方体后,相对面上的两个数之和为6,则x=
,y=
.
答案(dáàn) 5;3 解析 由正方体的展开图知,2所在的面与空白的正方形为相对(xiāngduì)面,1与x
为相对面上的数,3与y为相对面上的数,故x=5,y=3.
2021/12/10
第三十页,共四十六页。
选择题 1.(2017内蒙古包头中考,4,★☆☆)将一个无盖正方体形状盒子的表面 沿某些棱剪开,展开后不能得到的平面图形是 ( )
第十六页,共四十六页。
1.(2017山西农大附中月考)下列展开图不能叠合成无盖正方体的是 ()
答案(dáàn) C 正方体的表面展开图不可能出现“凹”字形,故选C.
2021/12/10
第十七页,共四十六页。
2.如图,四个三角形均为等边三角形,将图形折叠,得到的立体图形是 ()
A.三棱锥 B.圆锥 C.圆柱 D.六面体
初一数学2016年4.1.3正方体的展开与折叠PPT优选课件

2020/10/18
16
知2-讲
导引:将面X固定,将面R、面Y折起来,再适当折
叠面Q,Z,P即可折叠出立体图形,进而可
求得答案.
解:(1)正方体.
(2)相对的面有三对:面P与面X,
面Q与面Y,面R与面Z.
(3)将会重合的边有:边a与边h,
边b与边i,边c与边n,边d与边e,
边f与边g,边j与边k,边m与边l.
知识点 2 特征(图案或文字)正方体的展开与折叠
【例2】如图是一些立体图形的平面展开图,请说出这些 立体图形的名称.
导引:如图所示的图形是常见立体图形的平面展开图,
可以在头脑中进行空间想象,也可以动手用纸
折一折,得到正确答案. 解:①三棱锥;②四棱锥;③五棱锥;
④三棱柱;⑤圆柱;⑥圆锥. (来自《点拨》)
2020/10/18
(来自《典中点》)
19
2 (2015·吉林)如图,有一个正 方体纸巾盒,它的平面展 开图是( )
知2-练
2020/10/18
(来自《典中点》)
20
3 明明用纸(如图)折成了 一个正方体的盒子, 里面装了一瓶墨水, 与其他空盒子混放在一起,只凭观察, 选出墨水在哪个盒子中( )
(来自《典中点》)
12
知1-练
6 如图,将4×3的网格图剪去5个小正方形后,图中
还剩下7个小正方形,为了使余下的部分(小正方形
之间至少要有一条边相连)恰好能折成一个正方体,
需要再剪去一个小正方形,则应剪去的小正方形
的编号是( )
A.7
B.6
C.5
D.4
2020/10/18
(来自《典中点》)
13
知2-讲
或圆锥的展开图.
北师大版数学七年级上册1.2.1展开与折叠课件

2 1 456 3
5 31
24 6
相间、“Z”端是对面
如图是一个正方体,则它的表面展开图可以是( )
1、两底面位于不同侧面。
要把一个长方体的表面剪开展成平面图形,至少
如图所示的图形绕虚线旋转一周,可得到的几何体是( )
A
B
如何找想邻
社
D.
点、线、面之间相互关系:_________________________。
1、如图是长方体的展开图,求长 方体的表面积和体积(单位:cm)
高:(14-10)÷2=2(cm)
表面积:2×6×10+2×6×2+2×10×2=184(cm2)
2
体积:长×宽×高=10×6×2=120(cm3) 答:表面积为184cm2,面积为120cm3.
2、如图是一个圆柱的表面展开图, 这个圆柱的侧面积是多少平方厘米,
图中的两个图形经过折叠能否围成棱柱?
如图所示的图形绕虚线旋转一周,可得到的几何体是( )
谐
C.
把圆锥的侧面展开,会得到什么图形?
点、线、面之间相互关系:_________________________。
和 B.
2、下列平面图形,不能沿虚线折叠成立体图形的是( )
4平方厘米,表面积为244.
明明用纸(如下图左)折成了一个正方体的盒子,
A2
A. 0,1,2. C.1,2,0.
B.2,0,1. D.1,0,2.
01C B
四、重难点的分层应用
23
2. 若要使得图中平面展开图折叠成 正方体后,相对面上的两个数之和为5,
xy
求x+y+z的值. =9
z1
3. 要把一个长方体的表面剪开展成平面图形,至少 需要剪开__7______条棱.
5.3展开与折叠(课件)-七年级数学上册(苏科版)【01】

02 知识精讲 注意:下列平面图形不是正方体的展开图哦~
正方体的展开图
L型
田字型
凹字型
02 知识精讲
探究2:为什么要剪7条棱, 才能得到正方体的展开图呢?
∵正方体共12条棱, 每种展开图内都有5条棱相连, ∴要剪7条棱。
03 典例精析
例1、下列七个图形中是正方体的平面展开图的有( B )
“二二二”型,√
02 知识精讲
同一个正方体展开所得到的平面图形有11种, 在展成平面图形的过程中,一共剪了7条棱。
02 知识精讲 探究1:11种展开图,如何快速记忆呢?
做好分类就行 啦~
“一四一”型
02 知识精讲 “三三”型
“二三一”型 “二二二”型
02 知识精讲
正方体的展开图
“一四一”型:6个 “二三一”型:3个 “三三”型:1个 “二二二”型:1个
× “一四一”型,√
×
×
A. 1个
×
B. 2个
×
C. 3个
D. 4个
03 典例精析
例2、如图是一个正方体,如图哪个选项是它的展开图( B )
A.
B.
C.
D.
03 典例精析 例3、一个正方体的表面展开图如图所示,把它折成正方体后
,与“山”字相对的字是(D )
A.水 B.绿 C.建 D.共
正方体找某一面的对面的口诀: 隔面有面是对面,隔面无面就拐弯。
例3、如图是一个不完整的正方体平面展开图,需再添上一个面, 折叠后才能围成一个正方体.下列添加方式(图中阴影部分)正
确的是( D )
A.
×
B.
×
C.
×
D.
√常见几何体的侧面展开图:来自(1)圆柱:矩形(长方形) (2)圆锥:扇形 (3)正方体:矩形(长方形)
七年级上数学展开图课件

图
“一四一” 型
“二三一” 型
“三三”型
“二二二” 型
判断下列图形能不能折成正方体?
(1)
((7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
原正方体中相对面在展开图中的位置关 关系?
正方体的每对相对面展开后总是 间隔出现,展开后有公共边或有 公共顶点的两个正方形一定是相 邻面.
考考你
1、如果“你”在前面,那么谁在后 面?
了!
太棒
你们
KEY: 棒
2、“坚”在下,“就”在后,胜 利在哪里?
坚
持就是
胜
利
下图是一个正方体的展开图,标注了字 母A的面是正方体的正面,如果正方体的左
面与右面所标注代数式的值相等,求 x 的
值.
-2
3 -4 1
A 3x-2
1、立体图形是由平面图形组成的。 2、能根据展开图判断立体图形。 3、能判断平面图形是否为立体图 形的展开图。
1.请你设计制作一款正方 体形状的产品包装盒。 2.仿照本节课方法探索长 方体的表面展开图。
展开与折叠
圆柱体 展开 长方形
圆锥体 展开 扇形
2.长方形纸
折叠
交流归纳:
有些立体图形 展开 平面图形 有些平面图形 折叠 立体图形
猜一猜
• 将下面四个图形折叠,你能说出这 些多面体的名称吗?
正方体 四棱锥
长方体 三棱柱
正 方 形
将正方体剪开展成一个平面 图形。
的 展 开
注意:剪开时保证每两个正 方形有一条公共边。
【北师大版】七年级数学上册:1.2.1《正方体的展开与折叠》ppt课件

第一章 丰富的图形世界
2 展开与折叠 第1课时 正方体的展开与折叠
课
随
前
堂
热
演
身
练
课前基热础身训练(5分钟)
1. 正 方 体 的 表 面 展 开 图 是 由 ________ 个 ________ 形 构 成 的.
2.如图,立方体的六个面上标着连续的整数,若相对的两 个面上所标两数的和均相等,则这六个数的和为______.
3.下列各图中,不是正方体的展开图的是________(填序 号).
随堂基演础练训(练10分钟)
知识点 1:正方体的展开 1.一个无盖的正方体盒子的平面展开图可以是如图所示图 形中的( )A.只有Fra bibliotek① C.图②,图③
B.图①,图② D.图①,图③
2.下图是一个无盖立方体盒子,请把下列不完整的展开图 补充完整.
课前热身 1.6 正方 2.39 所标数字依次为 4,5,6,7,8,9,其和等于 39. 3.③ 只要有“田”字格的展开图都不是正方体的表面展开图, 所以③不是正方体的展开图.
随堂演练 知识点 1 1.D 考查正方体的展开图. 2.
知识点 2 1.D 考查立体图形的展开图. 2.C 折叠正方体时 6 与 7,2 重合. 3.2 号 4.如图所示(答案不唯一).
4.如图是由 6 个相同的正方形拼成的图形,请你将其中一 个正方形移动到合适的位置,使它与另 5 个正方形能拼成一个 正方体的表面展开图(请在图中将要移动的那个正方形涂黑,并 画出移动后的正方形)
5.如图是一个立方体的展开图,每个面都标上了字母,请 根据要求回答问题:
(1)如果 A 在上面,那么哪一个面在它的下面? (2)如果 F 在上面,从右面看是 E,那么哪一个面在 E 的对 面? (3)如果从左边看是 D,B 在底部,那么哪一个面在上面?
2 展开与折叠 第1课时 正方体的展开与折叠
课
随
前
堂
热
演
身
练
课前基热础身训练(5分钟)
1. 正 方 体 的 表 面 展 开 图 是 由 ________ 个 ________ 形 构 成 的.
2.如图,立方体的六个面上标着连续的整数,若相对的两 个面上所标两数的和均相等,则这六个数的和为______.
3.下列各图中,不是正方体的展开图的是________(填序 号).
随堂基演础练训(练10分钟)
知识点 1:正方体的展开 1.一个无盖的正方体盒子的平面展开图可以是如图所示图 形中的( )A.只有Fra bibliotek① C.图②,图③
B.图①,图② D.图①,图③
2.下图是一个无盖立方体盒子,请把下列不完整的展开图 补充完整.
课前热身 1.6 正方 2.39 所标数字依次为 4,5,6,7,8,9,其和等于 39. 3.③ 只要有“田”字格的展开图都不是正方体的表面展开图, 所以③不是正方体的展开图.
随堂演练 知识点 1 1.D 考查正方体的展开图. 2.
知识点 2 1.D 考查立体图形的展开图. 2.C 折叠正方体时 6 与 7,2 重合. 3.2 号 4.如图所示(答案不唯一).
4.如图是由 6 个相同的正方形拼成的图形,请你将其中一 个正方形移动到合适的位置,使它与另 5 个正方形能拼成一个 正方体的表面展开图(请在图中将要移动的那个正方形涂黑,并 画出移动后的正方形)
5.如图是一个立方体的展开图,每个面都标上了字母,请 根据要求回答问题:
(1)如果 A 在上面,那么哪一个面在它的下面? (2)如果 F 在上面,从右面看是 E,那么哪一个面在 E 的对 面? (3)如果从左边看是 D,B 在底部,那么哪一个面在上面?
北师大版数学七年级上册1.2《展开与折叠》(第2课时)课件

作业
1、 P12习题1.3; 2、资源与学案第1.2节
坚
持就是
胜
利
圆柱体 展开 长方形 侧面
圆锥体 展开 扇形 侧面
棱柱结构特征:
底面
议一议
1.棱柱有上下两个底面, 它们的形状大小相同.
2.侧面的形状都是长方形.
3.侧面的个数和底面图形 侧棱 的边数相等.
4. 所有侧棱长都相等.
侧面
二. 折叠后你能说出这些多面体的名称吗?
想一想、折一折
以下哪些图形经过折叠可以围成一个棱柱?
小结:
(1)正方体的展开图是平面图形; (2)正方体的展开图,因展开方式
的不同而不同,共有11种。
是不是所有的立体图形 展开后,都是平面图形?
球体的展开图是不是平面图形?
考考你
1、如果“你”在前面,那么什么在后面?
了! 太棒 你们
KEY: 棒
2、“坚”在下,“就”在后,“胜”、“利” 在哪里?
长方体 三棱柱
练习:
下列图形中是什么多面体的展开图? (1)
长方体
(2)ห้องสมุดไป่ตู้
五棱锥
(3)
三棱柱
将一个正方体的表面沿某 些棱剪开,展成一个平面 图形.你能得到哪些图形?
想一想:
下列的图形都是正方体的展开图吗?
(1)
(2)
(3)
(√)
(√)
(4)
(5)
(√)
(×)
(√) (6)
(×)
将相对的两个面涂上相同的颜色, 正方体的平面展开图共有以下11种:
同学们 下午好!
田小平
§1.2 展开与折叠 (第二课时)
探索什么样的图形能围成棱柱
1、 P12习题1.3; 2、资源与学案第1.2节
坚
持就是
胜
利
圆柱体 展开 长方形 侧面
圆锥体 展开 扇形 侧面
棱柱结构特征:
底面
议一议
1.棱柱有上下两个底面, 它们的形状大小相同.
2.侧面的形状都是长方形.
3.侧面的个数和底面图形 侧棱 的边数相等.
4. 所有侧棱长都相等.
侧面
二. 折叠后你能说出这些多面体的名称吗?
想一想、折一折
以下哪些图形经过折叠可以围成一个棱柱?
小结:
(1)正方体的展开图是平面图形; (2)正方体的展开图,因展开方式
的不同而不同,共有11种。
是不是所有的立体图形 展开后,都是平面图形?
球体的展开图是不是平面图形?
考考你
1、如果“你”在前面,那么什么在后面?
了! 太棒 你们
KEY: 棒
2、“坚”在下,“就”在后,“胜”、“利” 在哪里?
长方体 三棱柱
练习:
下列图形中是什么多面体的展开图? (1)
长方体
(2)ห้องสมุดไป่ตู้
五棱锥
(3)
三棱柱
将一个正方体的表面沿某 些棱剪开,展成一个平面 图形.你能得到哪些图形?
想一想:
下列的图形都是正方体的展开图吗?
(1)
(2)
(3)
(√)
(√)
(4)
(5)
(√)
(×)
(√) (6)
(×)
将相对的两个面涂上相同的颜色, 正方体的平面展开图共有以下11种:
同学们 下午好!
田小平
§1.2 展开与折叠 (第二课时)
探索什么样的图形能围成棱柱
统编北师大版七年级数学上册优质课件 第1课时 正方体的展开与折叠

D1
C1
A1
B1
D
C
A
B
我们可以知道,不与之 相对 的面均相邻。
随堂练习
3.将正方体的表面分别标上数字1,2,3,4,5,6,使 它的任意两个相对面的数字之和为7,将它沿某 些棱剪开,能展开成下面的平面图形吗 ?
5 6314
2
(1)
1265 3 4
(2)
1 234
65
(3)
5 6314
2
折叠
14
55 正方体的
6 表面展6 开图
1 2 13 2 3 4 54 5
课堂小结
一四一型
①
②
一三二型
⑦
⑧
③④
正方体的
表面展开图
三
三
⑨
型
⑤
⑥
楼梯型
⑩ 二二二⑪型
拓展 如何判断相对面呢?
①
②
⑦
⑧
③
④
⑤
⑥
⑨
⑩
⑪
拓展 如何判断相对面呢?
①
②
⑦
⑧
⑩
③
④
⑤
⑥
你发现了什么规律?
⑨
展开图中 相间 、
“ Z ”端是对面。
课后作业
1.从教材习题中选取, 2.完成练习册本课时的习题.
D1 A1
D A
C1 B1
C B
正方体展开动态视频(2)
点此 播放 视频
正方体要展成一个平面图形,一共要剪Leabharlann 开 7 条棱。D1
C1
?
A1
B1
正方体的展开
D
C
A
B
我们沿着B1-B-A-D-D1-C1-C剪开。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
总 结
长方体的展开图与正方体的展开图类似,区别
在于长方体中相邻面的大小不一定相等.常见的正
方体的展开图有以下几种形状,解答这类题可以根 据几何体的展开图特点,充分发挥空间想象能力直 接判断,或通过动手折叠或展开确定正确结果.
知1-讲
(来自《点拨》)
知1-练
1
(2015· 眉山)下列四个图形中是正方体的平 面展开图的是( )
选出墨水在哪个盒子中(
)
(来自《典中点》)
知2-练
4
(2015· 聊城)图①是一个小正方体的表面展开图,
小正方体从图②所示的位置依次翻到第1格、第2
格、第3格、第4格,这时小正方体朝上一面的字 是( A.梦 ) B.水 C.城 D.美
(来自《典中点》)
知2-练
5 水平放置的正方体六个面分别用“前面、后面、
2
(2015· 辽阳)下列各图不是正方体表面展开 图的是( )
(来自《典中点》)
知1-练
3
将一个无底无盖的正方体沿一条棱剪开得到的平面图形 为( ) B.正方形 D.五边形
A.长方形 C.三角形
4
下列图形可以折叠成一个无盖的正方体盒子的是(
)
A.图① C.图②、图③
B.图①、图② D.图①、图③
(来自《典中点》)
少有一条棱与其它面相连.
知1-讲
1.立体图形的展开图:有些立体图形是由一些平面
图形围成的,将它们的表面适当剪开,可以展开 成平面图形,这样的平面图形称为相应立体图形 的展开图,同时这个平面图形可以折叠成相应的 立体图形. 2.展开和折叠是互逆过程. 3.判断一个平面图形能否折叠成立体图形的方法: 一看面数够不够; 二看各面的位置是否合适,尤其是底面的位置; 三看对应边的长度是否相等.
炼.
(来自《点拨》)
知2-练
1
(2015· 无锡)如图所示的正方体盒子的外表面 上画有3条粗黑线,将这个正方体盒子的表
面展开(外表面《典中点》)
知2-练
2
(2015· 吉林)如图,有一个正 方体纸巾盒,它的平面展 开图是( )
(来自《典中点》)
知2-练
3
明明用纸(如图)折成了 一个正方体的盒子, 里面装了一瓶墨水, 与其他空盒子混放在一起,只凭观察,
(来自《点拨》)
知2-讲
总 结
在解决图形转化问题时,动手操作是一种非常便 捷的方法,“百看不如一折”.另外,要注意积累记 忆常见立体图形的平面展开图.①全部是正方形的展 开图一定是正方体的展开图;②全部是长方形或正方
形的展开图一定是长方体的展开图;③有扇形的展开
图一般是圆锥的展开图;④有圆的展开图一般是圆柱 或圆锥的展开图.
(来自《点拨》)
知1-讲
4.正方体可以得出11种不同的展开图:
知1-讲
分为2类: 第一类,分三排,有三种情形:中间为四个,两侧 各一个,共六种;中间为三个正方形,上为两正方形, 下为一正方形.此时下一正方形可以在任何位置,共
三种;中间为两个正方形,上为两正方形,下为两正方
形,此时只有一种情况; 第二类,分两排,此时只有一种情况.
(来自《点拨》)
知2-讲
【例3】如图,一个立体图形的展开图中,用每个
面内的大写字母表示该面,用小正方形边
上所标注的小写字母表示该边. (1)说出这个立体图形的名称; (2)写出所有相对的面; (3)若把这个展开图折叠成立体图形,
各小正方形的哪些标注有小写字母的边
将会重合?
知2-讲
导引:将面X固定,将面R、面Y折起来,再适当折 叠面Q,Z,P即可折叠出立体图形,进而可
知1-练
5
如图所示,它需再添一个小正方形,折叠后
才能围成一个正方体,图中的灰色小正方形
分别由四位同学补画,其中正确的是( )
(来自《典中点》)
知1-练
6
如图,将4×3的网格图剪去5个小正方形后,图中 还剩下7个小正方形,为了使余下的部分(小正方形 之间至少要有一条边相连)恰好能折成一个正方体, 需要再剪去一个小正方形,则应剪去的小正方形
求得答案.
解:(1)正方体. (2)相对的面有三对:面P与面X,
面Q与面Y,面R与面Z.
(3)将会重合的边有:边a与边h, 边b与边i,边c与边n,边d与边e, 边f与边g,边j与边k,边m与边l.
(来自《点拨》)
知2-讲
总 结
解答本题采用动手操作法.这个问题的解决, 无疑对同学们形成良好的空间观念是一个很好的锻
上面、下面、左面、右面”表示,如图是一个
正方体的表面展开图,若“2”在正方体的前面, 则这个正方体的后面是( A.1 C.快 B.6 D.乐 )
(来自《典中点》)
正方体的表面展开图的形状多种多样,注意
不要遗漏也不要重复,同时注意平面图中有“田” 字形或“凹”字形时,围不成正方体,也就不是 正方体的表面展开图.
知1-讲
【例1】 〈漳州〉如图是一个长方体包装盒,则
它的平面展开图是图中的( A )
导引:利用空间想象或通过动手操作,将展开图还原 成立体图形,看是否构成长方体.根据对面的 判断规则,只有A选项能找到三组对面,因此
只有A选项中的平面展开图折叠起来能形成一
个长方体,故选择A.
(来自《点拨》)
知1-讲
第四章 几何图形初步
4.1
几何图形
第3课时
正方体的展开
与折叠
1 2
课堂讲解 正方体的展开与折叠
特征(图案或文字)正方体的展开与折叠
课时流程
逐点 导讲练 课堂 小结 作业 提升
知1-导
知识点
1 正方体的展开与折叠
请同学们将准备好的小正方体纸盒沿某条棱
任意剪开,看看能得到哪些平面图形?注意:在剪
开正方体棱的过程中,正方体的6个面中每个面至
必做:
1.完成教材P118练习T3,P121习题4.1T7,
T10,T13
2.补充: 请完成《典中点》剩余部分习题
的编号是(
A.7 C.5
)
B.6 D.4
(来自《典中点》)
知2-讲
知识点
2 特征(图案或文字)正方体的展开与折叠
【例2】如图是一些立体图形的平面展开图,请说出这些
立体图形的名称.
导引:如图所示的图形是常见立体图形的平面展开图,
可以在头脑中进行空间想象,也可以动手用纸
折一折,得到正确答案. 解:①三棱锥;②四棱锥;③五棱锥; ④三棱柱;⑤圆柱;⑥圆锥.
