2热力学第二定律
热力学第二定律的两种表述

热力学第二定律的两种表述
一、发生在热力学系统内的任何变化,最终都是使熵增大的:
1. 定义:由巴特斯利于1850年提出的热力学第二定律,又称为“熵定律”,即“在任何物理学或化学变化过程中,温室系统的总熵最终都是
增大的”。
2. 原理:巴特斯利在证明温室熵定理的时候,引入“熵假设”。
即“任何
物理的学变化过程中,都会有热的传递和分布,而在此过程中,伴随
着温度下降而熵增加。
”
3. 熵的变化:热力学第二定律表明,无论发生何种过程,最终的温室
熵都会增加。
例如:把热量从热源降至冷源,则热源的熵降低,冷源
的熵会增加;若热量从内耗到外,则关联表面的熵增加。
4. 影响:这个热力学定律对宏观物理学、分子热力学有着深远的影响。
它印证了大量实验结果,它的实质是发生在热力学系统内的任何变化,最终都是使熵增大的。
二、温室熵增加是热力学第二定律的主要内容:
1. 定义:热力学第二定律也称作“温室熵定理”,主要说明任何热力学
系统最终总是向更复杂的状态发展,使得温室熵发生增加,这个发展
过程是不可逆的。
2. 原理:温室熵定理是建立在熵定理之上的,它向我们提出:无论在
什么样的物理过程中,只要存在伴随着热量流动和物质分离的“变化”,温室熵永远趋于增加,这就是我们所熟悉的第二定律。
3. 熵的变化:热力学第二定律表明,热源的熵减少,冷源的熵增加;
热能运动的过程,熵增加;同时也有可能出现,熵减少并转移到外部
环境的情况。
4. 影响:热力学第二定律为热力学解释宏观世界和分子世界间相互联系,并阐明能量微观结构和宏观方向具有不可逆性,对热力学有深远
影响。
热力学第二定律

热力学第二定律热力学第二定律是热力学中的重要定律之一,它描述了热量在自然界中的传递方向。
热力学第二定律对于理解能量转化和宇宙演化具有重要意义。
在本文中,我们将探讨热力学第二定律的基本原理和应用。
1. 热力学第二定律的基本原理热力学第二定律可以从不同角度进行表述,但最为常见的是开尔文-普朗克表述和卡诺定理。
1.1 开尔文-普朗克表述开尔文-普朗克表述中,热力学第二定律可以简要地概括为“热量不会自发地从低温物体传递到高温物体。
”这意味着热量的传递是不可逆的,自然趋向于热量从高温物体传递到低温物体。
1.2 卡诺定理卡诺定理是另一种常见的表述方式,它描述了理想热机的最高效率。
根据卡诺定理,任何一台工作在两个温度之间的热机的效率都不会超过理论上的最高效率,这个最高效率由热源温度和冷源温度决定。
2. 热力学第二定律的应用热力学第二定律在许多领域都有重要的应用,下面我们将介绍几个常见的应用领域。
2.1 工程领域在工程领域中,热力学第二定律被广泛运用于热能转化系统的设计和优化。
例如,在汽车发动机中,通过合理设计燃烧过程、热能回收和废热利用等手段,可以提高发动机的效率,减少能量的浪费。
2.2 环境科学热力学第二定律的应用也涉及到环境科学领域。
例如,根据热力学第二定律的原理,热力学模型可以用于预测和评估环境中的能量传递和转化过程。
这有助于我们更好地理解和管理环境资源。
2.3 生命科学热力学第二定律在生命科学中也有广泛的应用。
生物体内的能量转化和代谢过程都受到热力学定律的限制。
通过热力学模型的建立和分析,可以深入研究生物体内能量转化的机理与调控。
3. 热力学第二定律的发展与挑战热力学第二定律的发展经历了许多里程碑,但仍然存在一些挑战和未解之谜。
3.1 热力学第二定律与时间箭头热力学第二定律与时间箭头之间的关系是一个待解之谜。
根据热力学第二定律,熵在一个封闭系统中总是增加的,即系统总是趋向于混乱状态。
然而,宇宙的演化似乎表明时间具有一个明确的方向,即宇宙从低熵状态(有序状态)向高熵状态(混乱状态)演化。
热力学第二定律

§10.8热力学第二定律一、热力学第二定律任务自然界中发生的过程总是有方向的。
热力学第二定律正是反映了自然界中热力学过程的方向性问题,是自然界经验的总结。
二、热力学第二定律的两种表述 1、开尔文表述(开氏表述):不可能制成一种循环动作的热机,只从单一热源吸取热量,使它完全变为有用功而不引起其它变化。
说明:1)前提:即工作物质必须循环动作和其它物体不发生任何变化。
2)开尔文说法是从功热转化的角度出发的,它揭示了功热转换是不可逆的,即3)开尔文表述可等价说成“第二类永动机是不可能制造出来的。
” 2、克劳修斯表述(克氏表述):热量不可能自动地从低温物体传到高温物体。
注意:1)条件:“自动地”2)表明热传递的不可逆性 3、两种表述的等效性1)开尔文说法不成立,则克劳修斯说法也不成立;若开氏说法不成立,则热机可从高温热源吸收热量Q 1,全部用来对外作功A= Q 1;这个功A 可用来驱动一台致冷机,从低温热源吸收热量Q 2,同时向高温热源放出热量Q 2+ A= Q 2+ Q 1。
两者总的效果是低温热源的热量传到了高温热源,而没产生其它影响,显然违反了克劳修斯说法。
2)克劳修斯说法不成立,则开尔文说法也不成立;若克劳修斯说法不成立,即热量可自动地从低温热源传到高温热源。
考虑一台工作于高温热源与低温热源的热机。
从高温热源吸收热量Q 1,向低温热源放出热量Q 2,则Q 2能自动地传到高温热源;两者总的效果是热机把从高温热源吸收的热量全部用来对外作功,这显然违反开氏说法。
由此,可以看出热力学第二定律的表述是多种多样的,而且不同的表述是可以相互沟通的。
三、热力学第二定律的本质 1、可逆过程与不可逆过程一个热力学系统经历一个过程P ,从状态A 变到状态B ,若能使系统进行逆向变化,从状态B 又回到状态A ,且外界也同时恢复原状,我们称过程P 为可逆过程;反之,如果用任何方法都不能使系统和外界完全复原,则称为不可逆过程。
热力学第二定律

第三章热力学第二定律3.1 热力学第二定律的克劳修斯说法和开尔文说法热力学第二定律(second law of thermodynamics)有多种说法,各种说法完全等价的,它是人类经验的总结。
下面介绍两种经典说法。
克劳修斯(R. Clausius)说法:热从低温物体传给高温物体而不产生其它变化是不可能的。
开尔文(L. Kelvin)说法:从一个热源吸热,使之完全转化为功而不产生其它变化是不可能的,或第二类永动机是不可能造成的。
注意的是并非热不能从低温物体传给高温物体,而是不产生其它变化,如致冷机需要消耗电能。
另外也不能简单理解开尔文说法为,如理想气体等温膨胀, U = 0 -Q = W,即热全部变为功,但气体体积变大了。
所以是不引起其它变化的条件下,热不能全部转化为功。
所谓第二类永动机乃是一种能够从单一热源吸热,并将所吸收的热全部变为功而无其它影响的机器,那是不可能造成的。
认识热力学第二定律,首先从热、功转化规律开始,所以首先介绍卡诺定理3.2 卡诺定理3.2.1 热机效率如图3.2-1所示,热机从高温热源吸热Q1,对环境作功 -W,同时向低温热源放热Q2,完成一个循环。
图3.2-1 热转化为功热机效率(efficiency of the heat engine)...... (3.2-1)3.2.2 可逆热机效率可逆过程系统做功最大,热机效率也最大。
1. 卡诺循环卡诺(S. Carnot)设想一部理想热机,由理想气体经四个可逆过程来完成一个循环,如图3-2,称卡诺循环。
过程如下:(1)→(2) 恒温可逆膨胀:(2)→(3) 绝热可逆膨胀:即(3)→(4)恒温可逆压缩:(4)→(1) 绝热可逆压缩:即得经一循环 DU = 0,热机所作的净功热机效率......(3.2-2)即结论:卡诺热机(可逆热机)效率的大小与两个热源的温差有关。
不可逆热机效率没有这种关系。
从(3.2-2)式还可以得到 ......(3.2-3)结论:卡诺循环(可逆过程)中热温商(Q/T)之和为零。
热力学第二定律

1、 气、液、固体的定p或定V的变T 过程
定压变温过程:由δQp=dH=nCp,mdT
得:S= 2 Qr T2 nC p,m dT ;
1T
T1 T
视C
为常
p,m
数
S
nC
p ,m n
T2 T1
(2-4-1)
定容变温过程:由δQV=dU=nCV,mdT
同理得:S
nCV ,mn
自发
S孤立 0 或 dS孤立 0平衡
(2-3-4) (2-3-5)
熵增加原理:系统经绝热过程由一状态到达另一状态, 熵值不减少;自发变化的结果,必使孤立系统的熵增加 (孤立系统中可以发生的实际过程都是自发过程)。
方向:孤立系统的熵增加
限度:孤立系统熵值达到最大——平衡态。
二、 熵增原理及平衡的熵判据
mix
S
SA nARn
S 1 yA
BnBnRARnny1VB AVAVnBRBnByRBnnyVBAV(B2V-4B-6)
∵yB < 1,∴ΔmixS > 0
结论:定T定p理气混 合过程系统熵增加
nA, V + nB, V 定温定容 nA+nB, V
AT
BT
BQir BQr S
AT
AT
得:S BQ
AT
或
dS
Q
T
不可逆 可逆
(2-3-3)
——热力学第二定律的数学表达式 依具体情况方向判据的形式
二、 熵增原理及平衡的熵判据
绝热过程,δQ=0,则有
S绝热 0
或
不可逆
dS绝热 0 可逆
物理化学 第二章 热力学第二定律

101.325kPa,变到100℃,253.313 kPa,计
算△S。
S
p S1
S2
T
分析:此题是p、V、T三者都变的过程,若要计 算熵变,需要设计成两个可逆过程再计算。先等 压变温,再等温变压。
S
p S1
S2
T
S
S1
S2
C pm
ln T2 T1
R ln
p1 p2
5 R ln 37315 R ln 101325 114J K 1
-5℃苯(l)→5℃苯(l)
S1
278 Cpm(l) dT 268 T
C pm(l )
ln
T2 T1
126g77 ln 278 268
4 64J K 1
(2) 相变点的相变 5℃苯(l)→5℃苯(s)
S2
H T
9916 08 278
35 66J
K 1
(3) 恒压变温 5℃苯(S)→-5℃苯(S)
4.绝热可逆缩D(p4V4)→A(p1V1)
下面计算每一步的功和热 以1mol理想气体为体系
第一步: U1 0
W1
Q2
RT2
ln V2 V1
第二步:
T1
Q 0 W2 U2 CVmdT
T2
第三步: U3 0 第四步: Q 0
W3
Q1
RT1
ln
V4 V3
T2
W4 U4 CVmdT
T1
解:(1)
S体
nR ln V2 V1
8314 ln10 19 15J
K 1
S环
QR T
nR ln V2 V1
19 15J gK 1
S体 S环 0
热力学第二定律

一、循环过程 物质系统历一系列的变化过程又回到原来的状态, 物质系统历一系列的变化过程又回到原来的状态,这样的周 而复始的变化过程称为循环过程,简称循环。 而复始的变化过程称为循环过程,简称循环。 特征
E = 0
p
曲线所包围的面积 W = ∫ dW =曲线所包围的面积 热力学第一定律 Q = W 净功 总吸热 总放热
p
A
Q1
T1
T1 > T2
B C
高温热源
T1
Q1
卡诺致冷机
W
D
W
Q2 T2
o
卡诺致冷机致冷系数 卡诺致冷机致冷系数 致冷
Q2
V
低温热源 T2
Q2 T2 e= = Q1 Q2 T1 T2
讨 论 图中两卡诺循环
η1 = η2 吗 ?
p
T1
p
T1
W 1
W1 > W2
T3
W 1
W1 = W2
W2
W2
T2
1 个分子回到A N个分子回到A的几率 = N 2
一切实际宏观过程, 一切实际宏观过程 , 由包含微观 态少的宏观态向包含微观态多的宏观 态进行。 态进行。
用热力学第二定律证明:在pV 图上任意两条绝热线不可能相交 用热力学第二定律证明: 用热力学第二定律证明 证 反证法 设两绝热线相交于c 设两绝热线相交于 点,在 绝热线相交于 两绝热线上寻找温度相同 的两点a、 。 的两点 、b。在ab间作一条 间作一条 等温线, 等温线, abca构成一循环过 构成一循环过 在此循环过程 循环过程该中 程。在此循环过程该中
W = Q1 Q2 = Q
Ⅰ
Ⅱ
Q1
热力学第二定律

W Q1 Q2
Q1
Q1
nR(T1
T2
)
ln
V2 V1
nR T1
ln
V2 V1
T1 T2 1 T2
T1
T1
卡诺热机推论:
1 可逆热机的效率与两热源的温度有关,两热源的温差越 大,热机的效率越大,热量的利用越完全;两热源的温差 越小,热机的效率越低。 2 热机必须工作于不同温度两热源之间,把热量从高温热 源传到低温热源而作功。当T1 T2= 0 ,热机效率等于零。 3 当T2 → 0k,可使热机效率→100%,但这是不能实现 的,因热力学第三定律指出绝对零度不可能达到,因此
绝热(Q=0)可逆膨胀,由p2V2T1 到 p3V3T2 (BC)
C(p3V3)
W2 U2
T2 T1
CV dT
nCV ,m (T2
T1)
所作功如BC曲线下的面积所示。
V1
V2
V
卡诺循环第二步
步骤3
等温(T2)可逆压缩,由 p3V3到 p4V4 (CD)
U 3 0
Q2 W3
V4 pdV
1mol理想气体的卡诺循环在pV 图上可以分为四步:
步骤1:等温可逆膨胀,由p1V1到p2V2(AB)
U1 0
Q1 W1
V2 V1
pdV
nRT1
ln
V2 V1
所作功如AB曲线下的面积所示
p A(p1V1) Q1
B(p2V2)
V1
V2 V
卡诺循环第一步
步骤2
p A(p1V1) Q2 B(p2V2)
第二章 热力学第二定律
第一节 自发过程的特征 第二节 热力学第二定律经典表述
第一节 自发过程的共同特征-不可逆性
热力学第二定律

第二节 热力学第二定律
一、热力学第二定律形成的历史背景 二、热力学第二定律的各种表述
1、Clausius的表述: 热不能自动地由低温物体流向高温 物体而不引起其它变化。 2、Kelvin的表述 : 从单一热源取出热使之完全变为功, 而不发生其它变化是不可能的; 第二类永动机是不能 制成的。 3、其它的表述:一定条件下,任何体系都自发地趋向平 衡;孤立体系中自发过程趋向于熵增大; 一切自发过 程是不可逆的。
2. PVT同时变化的过程
例: 态1(T1分为两步: 态1(T1、V1) → 态3(T2、V1)) → ΔvS=∫T1T2 (nCv,m/T)dT, ΔTS=∫12(dU+pdV)/T ΔS=ΔvS+ΔTS 对于理想气体且Cv,m为常数,则 ΔS= nCv,mln(T2/T1)dT+nRln(V2/V1)
态2(T2,V2)
态1(P1、T1) →态3(P1、T2) →态2(P2,T2) ΔS= nCp,mln (T2/T1)dT+nRln(P1/P2) 态1(P1、V1) →态3(P2、V1) →态2(P2,V2) ΔS= nCv,mln (P2/P1)dT+ nCp,mln (V2/V1)
第七节 熵函数的物理意义
(2)相同的物理状态下,复杂的分子比简单的 分子具有更高的熵值。 (3)温度不同时,S高温>S低温。 (4)对于气态物质,压力不同时,S低压>S 高压 。 压力的改变对固态和液态物质的熵值影响不 大。
二、熵与概率 S=klnΩ
第八节 热力学第三定律和规定熵
一、Nernst热定理 (1906年提出) T→0K所发生的过程是一恒熵变过程 W.H.Nernst (德国物理化学家,1864-1941) 二、热力学第三定律(Lewis & Gibson于1920 年提出) 在绝对零度时,任何物质完整晶体的熵等于 零。
热力学第二定律

定理定律
01 定律表述
03 定律质疑
目录
02 定律解释
热力学第二定律(second law of thermodynamics),热力学基本定律之一,克劳修斯表述为:热量不能 自发地从低温物体转移到高温物体。开尔文表述为:不可能从单一热源取热使之完全转换为有用的功而不产生其 他影响。熵增原理:不可逆热力过程中熵的微增量总是大于零。在自然过程中,一个孤立系统的总混乱度(即 “熵”)不会减小。
也就是说,在孤立系统内对可逆过程,系统的熵总保持不变;对不可逆过程,系统的熵总是增加的。这个规 律叫做熵增加原理。这也是热力学第二定律的又一种表述。熵的增加表示系统从几率小的状态向几率大的状态演 变,也就是从比较有规则、有秩序的状态向更无规则,更无秩序的状态演变。熵体现了系统的统计性质。
第二定律在有限的宏观系统中也要保证如下条件: 1.该系统是线性的; 2.该系统全部是各向同性的。 另外有部分推论:比如热辐射:恒温黑体腔内任意位置及任意波长的辐射强度都相同,且在加入任意光学性 质的物体时,腔内任意位置及任意波长的辐射强度都不变。
主词条:热寂论
热寂热寂论是把热力学第二定律推广到整个宇宙的一种理论。宇宙的能量保持不变,宇宙的熵将趋于极大值, 伴随着这一进程,宇宙进一步变化的能力越来越小,一切机械的、物理的、化学的、生命的等多种多样的运动逐 渐全部转化为热运动,最终达到处处温度相等的热平衡状态,这时一切变化都不会发生,宇宙处于死寂的永恒状 态。宇宙热寂说仅仅是一种可能的猜想。
第二定律指出在自然界中任何的过程都不可能自动地复原,要使系统从终态回到初态必需借助外界的作用, 由此可见,热力学系统所进行的不可逆过程的初态和终态之间有着重大的差异,这种差异决定了过程的方向,人 们就用状态函数熵来描述这个差异,从理论上可以进一步证明:
热力学第二定律 概念及公式总结

热力学第二定律一、自发反应-不可逆性(自发反应乃是热力学的不可逆过程)一个自发反应发生之后,不可能使系统和环境都恢复到原来的状态而不留下任何影响,也就是说自发反应是有方向性的,是不可逆的。
二、热力学第二定律1.热力学的两种说法:Clausius:不可能把热从低温物体传到高温物体,而不引起其它变化Kelvin:不可能从单一热源取出热使之完全变为功,而不发生其他的变化2.文字表述:第二类永动机是不可能造成的(单一热源吸热,并将所吸收的热完全转化为功)功热【功完全转化为热,热不完全转化为功】(无条件,无痕迹,不引起环境的改变)可逆性:系统和环境同时复原3.自发过程:(无需依靠消耗环境的作用就能自动进行的过程)特征:(1)自发过程单方面趋于平衡;(2)均不可逆性;(3)对环境做功,可从自发过程获得可用功三、卡诺定理(在相同高温热源和低温热源之间工作的热机)(不可逆热机的效率小于可逆热机)所有工作于同温热源与同温冷源之间的可逆机,其热机效率都相同,且与工作物质无关四、熵的概念1.在卡诺循环中,得到热效应与温度的商值加和等于零:任意可逆过程的热温商的值决定于始终状态,而与可逆途径无关热温商具有状态函数的性质:周而复始数值还原从物理学概念,对任意一个循环过程,若一个物理量的改变值的总和为0,则该物理量为状态函数2. 热温商:热量与温度的商3. 熵:热力学状态函数熵的变化值可用可逆过程的热温商值来衡量:起始的商(数值上相等):终态的熵4. 熵的性质:(1)熵是状态函数,是体系自身的性质是系统的状态函数,是容量性质(2)熵是一个广度性质的函数,总的熵的变化量等于各部分熵的变化量之和(3)只有可逆过程的热温商之和等于熵变(4)可逆过程热温商不是熵,只是过程中熵函数变化值的度量(5)可用克劳修斯不等式来判别过程的可逆性(6)在绝热过程中,若过程是可逆的,则系统的熵不变(7)在任何一个隔离系统中,若进行了不可逆过程,系统的熵就要增大,所以在隔离系统中,一切能自动进行的过程都引起熵的增大。
热力学第二定律

对热力学第二定律的理解一、热力学第二定律的概述1、热力学第二定律建立的历史过程在热力学第一定律之后,人们开始考虑热能转化为功的效率问题。
这时,又有人设计这样一种机械——它可以从一个热源无限地取热从而做功。
这被称为第二类永动机。
19世纪初,巴本、纽可门等发明的蒸汽机经过许多人特别是瓦特的重大改进,已广泛应用于工厂、矿山、交通运输,但当时人们对蒸汽机的理论研究还是非常缺乏的。
热力学第二定律就是在研究如何提高热机效率问题的推动下,逐步被发现的,并用于解决与热现象有关的过程进行方向的问题。
1824年,法国陆军工程师卡诺在他发表的论文“论火的动力”中提出了著名的“卡诺定理”,找到了提高热机效率的根本途径。
但卡诺在当时是采用“热质说”的错误观点来研究问题的。
从1840年到1847年间,在迈尔、焦耳、亥姆霍兹等人的努力下,热力学第一定律以及更普遍的能量守恒定律建立起来了。
“热动说”的正确观点也普遍为人们所接受。
1848年,开尔文爵士(威廉·汤姆生)根据卡诺定理,建立了热力学温标(绝对温标)。
它完全不依赖于任何特殊物质的物理特性,从理论上解决了各种经验温标不相一致的缺点。
这些为热力学第二定律的建立准备了条件。
1850年,克劳修斯从“热动说”出发重新审查了卡诺的工作,考虑到热传导总是自发地将热量从高温物体传给低温物体这一事实,得出了热力学第二定律的初次表述。
后来历经多次简练和修改,逐渐演变为现行物理教科书中公认的“克劳修斯表述”。
与此同时,开尔文也独立地从卡诺的工作中得出了热力学第二定律的另一种表述,后来演变为更精炼的现行物理教科书中公认的“开尔文表述”。
上述对热力学第二定律的两种表述是等价的,由一种表述的正确性完全可以推导出另一种表述的正确性。
他们都是指明了自然界宏观过程的方向性,或不可逆性。
克劳修斯的说法是从热传递方向上说的,即热量只能自发地从高温物体传向低温物体,而不可能从低温物体传向高温物体而不引起其他变化。
热力学第二定律
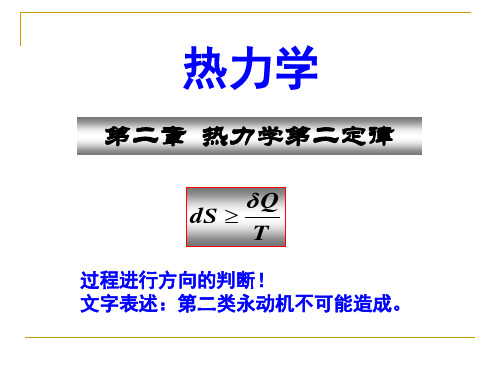
dS 0
不可逆、自发 可 逆、平衡
S 0
S(隔)=S(系统)+S(环境)≥0
四、亥姆霍兹自由能及其判据
Helmholz function and its criteria
1. 亥姆霍兹自由能判据
dS
δQ T( 环 )
不可逆 可逆
T(环)dS δQ
T(环)dS dU δW
自发方向 T1>T2,T1T2 p1>p2,p1p2 h1>h2,h1h2 C1>C2,C1C2 E1>E2,E1E2 ?请思考 ?请思考
推动力 限度
T T0 p p0 h h0 C C0 E E0 ? ?0 ? ?0
二、自发过程的共性 The characteristic of spontaneous processes
Q1
Q1
Q1
-W系统对外作的功(在一个循环过程中) Q1从高温热源吸热 Q2传给低温热源热
二、卡诺循环
卡诺为研究热机效率设计了工作物质为理想 气体的四个可逆步骤组成的循环
1. 恒温可逆膨胀
(p1V1T1)——(p2V2T1) p/[P] p1V1T1 2. 绝热可逆膨胀
(p2V2T1)——(p3V3T2)
nRT2
ln
V2 V1
T1 T2
nRT1ln
V2 V1
T1
Q1 Q2 T1 T2
Q1
T1
Q1 Q2 0 T1 T2
由卡诺循环可知:可逆热机热温商之和等于零
卡诺循环结论:
1、卡诺循环后系统复原,系统从高温热源吸热部 分转化为功,其余的热流向低温热源。热机效 率<1
2、卡诺热机效率只与热源的温度T1 、T2有关,两 热源温差越大,热机效率越高
热力学第二定律公式

热力学第二定律公式
热力学第二定律是一种基本的物理定律,它描述了物质在发生热力学过程时所表现出的一般性规律。
它的公式表达式为ΔS ≥ δQ/T,其中ΔS代表热力学系统的熵增量,δQ代表系统受到的热量,T代表系统的绝对温度。
它的定义如下:当一个物质在发生热力学过程时,物质的熵增量ΔS必须大于系统受到的热量δQ除以系统的绝对温度T,即ΔS ≥ δQ/T。
这一定律表明,当物质发生热力学过程时,物质的熵总是在增加,而不会减少,即熵增量ΔS必须大于等于零,而不能小于零。
当一个物质发生热力学过程时,熵增量ΔS可能会大于δQ/T,这表明物质的熵增量不仅是由外加的热量所决定,还受到系统的温度影响,即熵增量也受到温度的影响,这也是热力学第二定律的一个重要内容。
热力学第二定律是一个重要的物理定律,它描述了物质在发生热力学过程时的一般规律,即物质的熵总是在增加,而不会减少,而且熵增量的大小也受到系统的温度的影响。
鉴于热力学第二定律的重要性,它已经成为热力学研究的基础,它在很多热力学相关问题的研究中都发挥着重要作用。
热力学第二定律公式

热力学第二定律公式
热力学第二定律描述了热能在任何发生物理或化学变化时的按照
规律运动,它是解释物理学中温度变化的关于热能运动的定律。
热力
学第二定律公式简单地表示为热能流动时,它对热源和汇合处的统一性。
其公式为dQ=TdS,其中dQ为热能流动的量,T是温度,dS是热能的熵变。
热力学第二定律是必需有一种热源,即热源处的守恒量需要大于
汇合处的守恒量,以实现传递和传导热能,即利用从热源处至汇合处
之间自然属性的压力。
而TdS,T代表温度,dS代表熵,熵是表示一个热站热量流动的量,它使得熵的变量影响热流的大小。
所以在TdS(T
温度的熵变)的影响下,熵增加量越大,热流量就越大,熵减小量越大,热流越小。
热力学第二定律告诉我们,任何热能运动的原理,其变化只能从
热源处至汇合处,而不是相反。
它也让我们明白,只有熵变才会影响
热流,熵变越大热流也越大,熵变越小热流也越小。
因此,我们可以
从历史和实验中考察物种热量和熵的定义,进而了解它们变化的规律。
热力学第二定律.

S f
2 dQ 1T
系统熵的变化量与熵流之差定义为熵产,用“Sg”表示
Sg S2 S1 S f
(S2 S1) S f Sg
熵流是由于系统与外界的发生热交换而引起的,其取 值可正可负可为零,而熵产是过程不可逆性的度量, 可逆过程熵产为零,不可逆过程熵产大于零,任何过 程的熵产不可能小于零。
• (2)若把此热机当制冷机使用,同样由克劳修斯积分 判断
Q Q1 Q2 2000 800 0.585 kJ / K 0
T T1 T2 973 303
工质经过任意不可逆循环,克劳修斯积分必小于零, 因此循环不能进行。
• 若使制冷循环能从冷源吸热800kJ,假设至少 耗功Wmin,根据孤立系统熵增原理有△Siso=0:
因为工质恢复到原来状态,所以工质熵变
△SE=0
对热源而言,由于热源放热,所以
SH
Q1 T1
2000 973
2.055 kJ / K
• 对冷源而言,冷源吸热
S L
Q2 T2
800 303
2.64 k J
/K
代入得:
Siso (2.055) 2.64 0 0.585 kJ / K 0
2 Q
1T
对于微元过程:
ds
(
dq T
) re v
或 dS
dQ
( T
) re v
mds
由于熵是状态参数,所以不论过程是否可逆,熵 变只由初终状态决定。
可逆与不可逆的情况
S2
S1
2 1
Q
T
02热力学第二定律

Q
Q
四、热力学第二定律数学表达式
Clausius不等式:S 意义:
δQi δQ 或dS Ti T
(1)在热力学可逆过程中, dS δQR
注意: (1) Q是实际过程热,可逆过程与不可逆过程中的Q 不同。 (2)式中的T是环境的温度,可逆过程中, T体系 T环境
T (2)在热力学不可逆过程中, dS > δQIR T (3) dS < δQ 的过程不存在。 T
(3)熵S是广度性质的状态函数,不守恒。
五.熵增加原理
δQi δQ Clausius不等式:S 或dS Ti T 1.绝热过程
δQ 0
S (绝热) 0或dS (绝热) 0 结论:绝热过程中,封闭体系的熵永不减少。 如果过程是可逆的,则熵的数值不变;如果过程 是不可逆的,则熵的数值增加。 思考题:熵变是否与过程有关?
气体流动 溶质扩散
P高P低 c高c低
两处P相等 两处C相等
压力差 浓度差
自发过程的逆过程不能自动发生,但可由环境来完成。
二、热力学第二定律的经典表述
1.开尔文说法:
不可能从单一热源取热使之全部变为功而不产生其它 的变化。
2.克劳修斯说法:
不可能把热从低温物体传到高温物体而不发生其它 变化。
3.Ostwald说法:
T T相
T相
T
例1:1mol金属银在定容下由273.2K加热到303.2K,求 ΔS。 CV ,m 24.48J K -1 mol-1 。 已知在该温度区间银的 解:
T2 303.2 S nCV,m ln 1 24.48 ln T1 273.2 2.531(J K -1 )
绝热可逆过程和绝热不可逆过程所到达的最终状态是不同 的,因而熵也不同,因而不能错误地理解为熵变与过程有关。
热力学第二定律

它变化,即过程结束时,气体的体积增大了。
或: *
第二类永动机 ( 1 )
T Q A
是不可能制造成功的。
第二类永动机实例:
巨轮不断吸收海水,提取 其内能,将其变成冰块, 再抛入海中。就可以持续 航行了。
违反热力学第二定律,是不可能实现的。
注意理解以下四点:
(1) 热力学第一定律和第二定律是互相独立的。 比较: 第一类永动机 第二类永动机
若能使系统 B A
A B
过程
且外界复原 : A B 为可逆过程
若无法使系统
或 B A
B A
A B
为不可逆过程
时外界不能复原
例: 理想气体等温膨胀的可逆性分析 (1) 无摩擦,准静态进行 (2) 有摩擦,准静态进行
(3) 无摩擦,非静态进行
(1)
无摩擦,准静态进行 正向:
V1 V 2
初始状态
几率大
摇动后
几率 很小
气体自由膨胀的不可 逆性可用几率来说明。
A a 隔 b 板
B c
a、b、c 三个分子在A、B两室的分配方式 A室 abc ab bc ca c a b 0
B室
0
c
a
b
ab
bc
1 2
ca
abc
a 分子出现在A室的几率为 a、 b 二分子回到A室的几率为
a 、 、 三分子全部回到A室的几率为 b c
原来生命是一开放系统。其熵变由两部分组成。 开放系统---与外界有物质和能量的交换的系统
S Se Si
Si 系பைடு நூலகம்自身产生的熵,总为正值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
热力学第二定律练习题一、是非题,下列各题的叙述是否正确,对的画√错的画×1、热力学第二定律的克劳修斯说法是:热从低温物体传给高温物体是不可能的 ( )2、组成可变的均相系统的热力学基本方程 d G =-S d T +V d p +∑=1B B μd n B ,既适用于封闭系统也适用于敞开系统。
( )3、热力学第三定律的普朗克说法是:纯物质完美晶体在0 K 时的熵值为零。
( )4、隔离系统的熵是守恒的。
( )5、一定量理想气体的熵只是温度的函数。
( )6、一个系统从始态到终态,只有进行可逆过程才有熵变。
( )7、定温定压且无非体积功条件下,一切吸热且熵减少的反应,均不能自发发生。
( )8、系统由状态1经定温、定压过程变化到状态2,非体积功W ’<0,且有W ’>∆G 和∆G <0,则此状态变化一定能发生。
( )9、绝热不可逆膨胀过程中∆S >0,则其相反的过程即绝热不可逆压缩过程中∆S <0。
( )10、克-克方程适用于纯物质的任何两相平衡。
( )11、如果一个化学反应的∆rH 不随温度变化,则其∆r S 也不随温度变化, ( )12、在多相系统中于一定的T ,p 下物质有从化学势较高的相自发向化学势较低的相转移的趋势。
( )13、在-10℃,101.325 kPa 下过冷的H 2O ( l )凝结为冰是一个不可逆过程,故此过程的熵变大于零。
( )14、理想气体的熵变公式∆S nC V V nC p p p V =⎛⎝ ⎫⎭⎪+⎛⎝ ⎫⎭⎪,,ln ln m m 2121只适用于可逆过程。
( ) 15、系统经绝热不可逆循环过程中∆S = 0,。
( )二、选择题1 、对于只做膨胀功的封闭系统的(∂A /∂T )V 值是:( )(1)大于零 (2) 小于零 (3)等于零 (4)不确定2、 从热力学四个基本过程可导出VU S ∂⎛⎫ ⎪∂⎝⎭=( ) (1) (2) (3) (4) T p S pA H U G V S V T ∂∂∂∂⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭ 3、1mol 理想气体(1)经定温自由膨胀使体积增加1倍;(2)经定温可逆膨胀使体积增加1倍;(3)经绝热自由膨胀使体积增加1倍;(4)经绝热可逆膨胀使体积增加1倍。
在下列结论中何者正确?( )(1)∆S 1= ∆S 2= ∆S 3= ∆S 4 (2)∆S 1= ∆S 2, ∆S 3= ∆S 4=0(3)∆S 1= ∆S 4, ∆S 2= ∆S 3 (4)∆S 1= ∆S 2= ∆S 3, ∆S 4=04、1 mol 理想气体经一等温可逆压缩过程,则:( )。
(1) ∆G > ∆A ; (2) ∆G < ∆A ; (3) ∆G = ∆A ; (4) ∆G 与∆A 无法比较。
5、理想气体从状态I 等温自由膨胀到状态II ,可用哪个状态函数的变量来判断过程的自发性。
( )(1)∆G (2)∆U (3)∆S (4)∆H6、物质的量为n 的理想气体等温压缩,当压力由p 1变到p 2时,其∆G 是:( )。
(1) nRT p p ln 12; (2) n RTp p p p d 12⎰; (3) V p p ()21-; (4) nRT p p ln 21 7、1 mol 理想气体从相同的始态(p 1,V 1,T 1)分别经绝热可逆膨胀到达终态(p 2,V 2,T 2),经绝热不可逆膨胀到达(,,)p V T 222'',则T 2' T 2,V 2' V 2,S 2' S 2。
(选填 >, =, <) 8、若系统经历一个循环过程,则下列各组哪一组所包含的量其改变量均为零:( )(1) U 、Q 、W 、H ; (2) Q 、H 、C 、C V ;(3) U 、H 、S 、G ; (4) △U 、△H 、Q p 、Q V 。
9、 在100℃, 101.325 kPa 下有1 mol 的H 2O( l ),使其与100℃的大热源接触并使其向真空中蒸发,变为100℃,101.325 kPa 的H 2O( g ),对于这一过程可以用哪个量来判断过程的方向?( )(1)∆S (系统) (2)∆S (系统)+∆ S (环境) (3)∆G (4)∆S (环境) )10、液态水在100℃及101.325 kPa 下汽化成水蒸气,则该过程的( )。
(1)∆H = 0; (2)∆S = 0; (3)∆A = 0; (4)∆G = 011、一定条件下,一定量的纯铁与碳钢相比,其熵值是( )(1)S ( 纯铁) > S (碳钢); (2)S ( 纯铁) <S (碳钢); (3)S ( 纯铁)= S (碳钢);12、非理想气体绝热可逆压缩过程的∆S ( )(1)=0; (2)>0; (3)<0;13 、对封闭的单组分均相系统,且W ’=0时,TG p ⎛⎫∂⎪∂⎝⎭的值应是( ) (1)<0 (2)>0 (3)=0 (4)无法判断14、10 mol 某理想气体,由始态300 K ,500 kPa 进行恒温过程的吉布斯函数变∆G =-47.318 kJ 。
则其终态系统的压力为( )。
(1) 125 kPa ; (2) 75.0 kPa ; (3) 7.500 kPa ; (4) 25 kPa )15、 理想气体定温自由膨胀过程为( )(1) △S>0 (2) U<0 (3) Q>0 (4) W<0三、填空题1、等式0T TT U U H V p V ⎛⎫∂∂∂⎛⎫⎛⎫=== ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ 适用于 。
2、 热力学第三定律的普朗克说法的数学表达式为 。
3、 1mol 理想气体由同一始态开始分别经可逆绝热膨胀(Ⅰ)与不可逆绝热膨胀(Ⅱ)至相同终态温度,(选择填>, <, =)则∆U Ⅰ ∆U Ⅱ,∆S Ⅰ ∆S Ⅱ。
4、 1 mol 理想气体从 p 1=0.5 MPa 节流膨胀到 p 2=0.1 MPa 时的熵变为 ∆ S = 。
5、使一过程的∆ S =0,应满足的条件是 。
6、有个学生对理想气体的某个公式记得不太清楚了,他只模糊记得的是 T S nR x p ∂⎛⎫=-⎪∂⎝⎭ 。
你认为,这个公式的正确表达式中,x 应为 。
7、热力学基本方程之一为dH= 。
8、在732 K 时,反应 NH 4Cl(s) == NH 3(g) + HCl(g) 的 ∆r G =-20.8 kJ ·mol -1,∆r H =154 kJ ·mol -1,则该反应的∆r S = 。
9、绝热不可逆膨胀过程系统的∆S 0,绝热不可逆压缩过程系统的∆S 0。
(选填 >,< 或 = )10、 熵增原理表述为 。
11、在热源温度为534 K 及305 K 间工作的可逆热机,每一循环能作功135 J ,求热机在每一循环过程中从高温热源吸取热量为 。
12、在封闭系统中,无论发生何种不可逆绝热过程:(1)决不会出现系统的熵变∆S (系统)的现象;(2)环境的熵变∆S (环)必然是 。
选填> 0 ,≥ 0,< 0, ≤ 0 或 = 0)13、由克拉贝龙方程导出最常用的、最简单的克拉贝龙-克劳修斯方程的积分式时所作的三个近似处理分别是(1) ;(2) ;(3) 。
14、已知某化学反应在25 ℃的标准摩尔熵变为∆r S (298 K),又知该反应的∑νB C p ,m,B ,则温度T 时该反应的标准摩尔熵变∆r S (T ) =⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽。
15、热力学基本方程d H =T d S +V d p +∑μB d n B 的适用条件为组成⎽⎽⎽⎽⎽⎽⎽⎽变的⎽⎽⎽⎽⎽⎽系统和⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽。
四、计算题1、已知0℃冰的饱和蒸气压为0.611 kPa,其升华焓为2820 J·g -1,水汽的C p ,m =30.12 J·K -1·mol -1。
若将0 ℃时的1 g 冰转变为150℃,10.13 kPa 的水汽,系统的熵变为多少?设水汽为理想气体。
已知H 2O 的摩尔质量M =18.02 g·mol -1。
2、固态氨的饱和蒸气压为ln(/)./p T kPa K =-21013754,液态氨的饱和蒸气压为ln(/)./p T kPa K =-17473065。
试求(1)三相点的温度、压力;(2)三相点的蒸发焓、升华焓和熔化焓。
3、 4 mol 某理想气体,其C V ,m = 2.5 R ,由始态531.43 K ,600 kPa ,先等容加热到708.57 K ,在绝热可逆膨胀至500 kPa 的终态。
求终态的温度。
整个过程的∆U 及∆S 各为若干?4、设有2 mol 单原子理想气体,其C p ,m = 2.5 R 。
由298.15 K 及3 MPa 的始态压力突然降到100 kPa 绝热膨胀,作膨胀功2095 J ,试计算系统的熵变∆S 。
5、已知H 2O(l)在298K 时的饱和蒸气压为3168Pa,蒸发焓为44.01 kJ·mol -1,现有2 mol H 2O(l)在298K 、0.1 MPa 下变为同温同压的水蒸气。
计算此过程的∆U , ∆H ,∆S , ∆G 。
设蒸气可视为理想气体。
6、在-59℃时,过冷液态二氧化碳的饱和蒸气压为0.460 MPa ,同温度时固态CO 2的饱和蒸气压为0.434 MPa ,问在上述温度时,将1 mol 过冷液态CO 2转化为固态CO 2时,∆G 为多少?设气体服从理想气体行为。
7、 在70℃时CCl 4的蒸气压为81.613 kPa ,80℃时为112.43 kPa 。
计算:(1)CCl 4的摩尔汽化焓;(2)正常沸点。
8、1 mol 理想气体在300 K 下,等温可逆膨胀体积增加一倍,计算该过程的W ,Q ,∆U ,∆H ,∆G ,∆A 及∆S 。
9、1 mol 水在100℃、101.325 kPa 恒温恒压蒸发为同温同压下的水蒸气,然后将此水蒸气恒温可逆膨胀变为100℃、50 kPa 的水蒸气,求此过程的Q ,W ,∆U ,∆H ,ΔS ,ΔA 和ΔG 。
已知水在100℃、101325 Pa 下的∆vap H m 为40.67 kJ. mol -110、在0 ℃附近,纯水和纯冰成平衡,已知0 ℃时,冰与水的摩尔体积分别为0.01964 ⨯ 10-3 m 3·mol -1和0.01800 ⨯ 10-3 m 3·mol -1,冰的摩尔熔化焓为 ∆fus H m = 6.029 kJ·mol -1,试确定0℃时冰的熔点随压力的变化率d T / d p = ?11、在25℃时1 mol O 2从1000 kPa 自由膨胀到100 kPa ,求此过程的∆U ,∆H ,∆S ,∆A ,∆G (设O 2为理想气体)。
