数字逻辑课后答案 第二章
数字逻辑第二章课后答案

2-1
2-2
均可以作为反相器使用。
与非门:
或非门:
异或门:
2-3 1
Y V
CMOS 与非门的一个输入端通过电阻接地,相当于该输入端输入低电平,输出Y1是高电平。
2Y V
CMOS 或非门的一个输入端通过电阻接高电平与直接接高电平是一样的,输出Y2是低电平。
V 3
Y V 低电平有效的三态门的使能端EN 接高电平,则Y3为高阻态。
4
Y V
与或非门的一个与门输入全为高电平,则输出Y4是低电平。
2-4
E D C B A Y ⋅⋅⋅⋅=1 E D C B A Y ++++=2
))((3F E D C B A Y ++++=
F E D C B A Y ⋅⋅+⋅⋅=4 2-5
当1=EN ,T1`和T2截止,Y=Z (高阻)。
当0=EN ,T1`导通,A A Y ==。
2-7
(1)忽略所有门电路的传输延迟时间,除去开始的一小段时间,与非门的两个输入端总有一个是低电平,输出一直为高电平。
(2)考虑每个门都有传输延迟时间。
假设1级门的传输延迟时间为tpd ,则与非门的两个输入端的输入信号变化实际上并不是同时的。
信号A 经过两级门的传输延迟,比信号B 要晚2tpd 时间到达与非门的输入端。
因此,将出现,在短暂时间里,两个输入端的输入信号都是高电平的情况,输出电压波形出现毛刺。
数字逻辑第四版课后练习题含答案

数字逻辑第四版课后练习题含答案1. 第一章1.1 课后习题1. 将十进制数22转换为二进制数。
答:22 = 101102. 将二进制数1101.11转换为十进制数。
答:1101.11 = 1 x 2^3 + 1 x 2^2 + 0 x 2^1 + 1 x 2^0 + 1 x 2^(-1) + 1 x 2^(-2) = 13.753. 将二进制数1101.01101转换为十进制数。
答:1101.01101 = 1 x 2^3 + 1 x 2^2 + 0 x 2^1 + 1 x 2^0 + 0 x 2^(-1)+ 1 x 2^(-2) + 1 x 2^(-4) + 0 x 2^(-5) + 1 x 2^(-6) = 13.406251.2 实验习题1. 合成与门电路设计一个合成与门电路,使得它的输入A,B和C,只有当A=B=C=1时输出为1,其他情况输出为0。
答:下面是一个合成与门电路的示意图。
合成与门电路示意图其中,S1和S2是两个开关,当它们都被打开时,电路才会输出1。
2. 第二章2.1 课后习题1. 将十进制数168转换为八进制数和二进制数。
答:168 = 2 x 8^3 + 1 x 8^2 + 0 x 8^1 + 0 x 8^0 = 250(八进制)。
168 = 10101000(二进制)。
2. 将八进制数237转换为十进制数和二进制数。
答:237 = 2 x 8^2 + 3 x 8^1 + 7 x 8^0 = 159(十进制)。
237 = 010111111(二进制)。
2.2 实验习题1. 全加器电路设计一个全加器电路,它有三个输入A,B和C_in,两个输出S和C_out。
答:下面是一个全加器电路的示意图。
C_in|/ \\/ \\/ \\/ \\/ \\A|________ \\| | AND Gate______| |B|__| XOR |_| S\\\\ /\\ /\\ /\\ /| | OR Gate| ||_| C_out其中,AND Gate表示与门,XOR Gate表示异或门,OR Gate表示或门。
大学_数字逻辑第四版(欧阳星明著)课后习题答案下载

数字逻辑第四版(欧阳星明著)课后习题答案下载数字逻辑第四版(欧阳星明著)课后答案下载第1章基础概念11.1概述11.2基础知识21.2.1脉冲信号21.2.2半导体的导电特性41.2.3二极管开关特性81.2.4三极管开关特性101.2.5三极管3种连接方法131.3逻辑门电路141.3.1DTL门电路151.3.2TTL门电路161.3.3CML门电路181.4逻辑代数与基本逻辑运算201.4.1析取联结词与正“或”门电路201.4.2合取联结词与正“与”门电路211.4.3否定联结词与“非”门电路221.4.4复合逻辑门电路221.4.5双条件联结词与“同或”电路241.4.6不可兼或联结词与“异或”电路241.5触发器基本概念与分类251.5.1触发器与时钟271.5.2基本RS触发器271.5.3可控RS触发器291.5.4主从式JK触发器311.5.5D型触发器341.5.6T型触发器37习题38第2章数字编码与逻辑代数392.1数字系统中的编码表示392.1.1原码、补码、反码412.1.2原码、反码、补码的运算举例472.1.3基于计算性质的几种常用二-十进制编码48 2.1.4基于传输性质的几种可靠性编码512.2逻辑代数基础与逻辑函数化简572.2.1逻辑代数的基本定理和规则572.2.2逻辑函数及逻辑函数的表示方式592.2.3逻辑函数的标准形式622.2.4利用基本定理简化逻辑函数662.2.5利用卡诺图简化逻辑函数68习题74第3章数字系统基本概念763.1数字系统模型概述763.1.1组合逻辑模型773.1.2时序逻辑模型773.2组合逻辑模型结构的数字系统分析与设计81 3.2.1组合逻辑功能部件分析813.2.2组合逻辑功能部件设计853.3时序逻辑模型下的数字系统分析与设计923.3.1同步与异步933.3.2同步数字系统功能部件分析943.3.3同步数字系统功能部件设计993.3.4异步数字系统分析与设计1143.4基于中规模集成电路(MSI)的数字系统设计1263.4.1中规模集成电路设计方法1263.4.2中规模集成电路设计举例127习题138第4章可编程逻辑器件1424.1可编程逻辑器件(PLD)演变1424.1.1可编程逻辑器件(PLD)1444.1.2可编程只读存储器(PROM)1464.1.3现场可编程逻辑阵列(FPLA)1484.1.4可编程阵列逻辑(PAL)1494.1.5通用阵列逻辑(GAL)1524.2可编程器件设计1604.2.1可编程器件开发工具演变1604.2.2可编程器件设计过程与举例1604.3两种常用的HDPLD可编程逻辑器件164 4.3.1按集成度分类的可编程逻辑器件164 4.3.2CPLD可编程器件1654.3.3FPGA可编程器件169习题173第5章VHDL基础1755.1VHDL简介1755.2VHDL程序结构1765.2.1实体1765.2.2结构体1805.2.3程序包1835.2.4库1845.2.5配置1865.2.6VHDL子程序1875.3VHDL中结构体的描述方式190 5.3.1结构体的行为描述方式190 5.3.2结构体的数据流描述方式192 5.3.3结构体的结构描述方式192 5.4VHDL要素1955.4.1VHDL文字规则1955.4.2VHDL中的数据对象1965.4.3VHDL中的数据类型1975.4.4VHDL的运算操作符2015.4.5VHDL的预定义属性2035.5VHDL的顺序描述语句2055.5.1wait等待语句2055.5.2赋值语句2065.5.3转向控制语句2075.5.4空语句2125.6VHDL的并行描述语句2125.6.1并行信号赋值语句2125.6.2块语句2175.6.3进程语句2175.6.4生成语句2195.6.5元件例化语句2215.6.6时间延迟语句222习题223第6章数字系统功能模块设计2556.1数字系统功能模块2256.1.1功能模块概念2256.1.2功能模块外特性及设计过程2266.2基于组合逻辑模型下的VHDL设计226 6.2.1基本逻辑门电路设计2266.2.2比较器设计2296.2.3代码转换器设计2316.2.4多路选择器与多路分配器设计2326.2.5运算类功能部件设计2336.2.6译码器设计2376.2.7总线隔离器设计2386.3基于时序逻辑模型下的VHDL设计2406.3.1寄存器设计2406.3.2计数器设计2426.3.3并/串转换器设计2456.3.4串/并转换器设计2466.3.5七段数字显示器(LED)原理分析与设计247 6.4复杂数字系统设计举例2506.4.1高速传输通道设计2506.4.2多处理机共享数据保护锁设计257习题265第7章系统集成2667.1系统集成基础知识2667.1.1系统集成概念2667.1.2系统层次结构模式2687.1.3系统集成步骤2697.2系统集成规范2717.2.1基于总线方式的互连结构2717.2.2路由协议2767.2.3系统安全规范与防御2817.2.4时间同步2837.3数字系统的非功能设计2867.3.1数字系统中信号传输竞争与险象2867.3.2故障注入2887.3.3数字系统测试2907.3.4低能耗系统与多时钟技术292习题295数字逻辑第四版(欧阳星明著):内容提要点击此处下载数字逻辑第四版(欧阳星明著)课后答案数字逻辑第四版(欧阳星明著):目录本书从理论基础和实践出发,对数字系统的基础结构和现代设计方法与设计手段进行了深入浅出的论述,并选取作者在实际工程应用中的一些相关实例,来举例解释数字系统的设计方案。
数字逻辑设计习题参考答案 (第2章)

数字逻辑设计习题册班级:学号:姓名:哈尔滨工业大学(威海)计算机科学与技术学院体系结构教研室第2章 逻辑代数基础2—1 填空1.摩根定理表示为:=⋅B A _B A +__;=+B A _B A ⋅__。
2. 函数表达式D C AB Y ++=,则其对偶式为='Y _D C B A ⋅⋅+)(_______。
3.根据反演规则,若C D C B A Y +++=,则=Y C D C B A ⋅++)(。
4.函数式CD BC AB F ++=写成最小项之和的形式结果为()15,14,113,12,11,7,6,3∑m ,写成最大项之积的形式结果为)10,9,8,5,4,2,1,0(∏M。
5. (33.33)10 =(100001.0101 )2 =( 41.2 )8 =( 21.5 )162—2 证明1.证明公式()()A BC A B A C +=++成立。
2.证明此公式B A B A A +=+成立。
3.证明此公式)()()()()(C A B A C B C A B A +⋅+=+⋅+⋅+成立。
左边 (由分配律得)右边BCA BCB C A BC BA AC AA C A B A +=+++=+++=++)1())((BA A AB B B A B A B A AB AB B A B A AB BA B B A +=+++=+++=++=++=)()()(ACBC A B C A AC B C A C B B A ++=+⋅+=+⋅+⋅+=)()()()()(ACBC A B BC A B AC A A ++=+++=4. 证明此公式1))(((=+++⋅++C B D B A C B D C C B A 成立。
左边5.证明此公式D C D C B A D AC D C B D C A ⊕=+++⊕)(成立。
左边2—3 用代数法化简下列各式 1.B A BC A F +=1 2.D C A ABD CD B A F ++=2F 1 F 23.CD D AC ABC C A F +++=3 F 34.)()(4C B A C B A C B A F ++⋅++⋅++=F 41))((0))((=+++=+++⋅=C B D B A C B C B D B A C B D C C B A DC DC BD C D C D C A D C B D C A D AC D C A D C B D C A D AC A B D C D C A D AC B A B D C D C A ⊕=++=⊕++⊕=+++⊕=+++⊕=+++⊕=)()()()()()()(1=++++=B A C B A ADC B C B AD C B C B AD =+=++=)()(CDA CDC B C A CD AC AB C A D A C B C A D D A C BC C A +=+++=+++=+++=+++=)()()()()(CB AC B C B A A C A C B A C A C B A +=++=++=+++=)()(x y x y x =+⋅+)()(5.C DE C BE CD B B A AC F ++++=5F 56.C B A AD C B A CD AB F ++++=6F 67.D BC A BD A BD CD B B A C A F +++++=7F 78. D D C C A B A F +++=8F 8 1=++++=D D C C A B A9. D AC D C A D C B D C D C A F ++++=)(9F 9CE B AC CE D B B AC C E D B AC B AC C E D B C A B AC C E D B D B C B B A AC C E D B D C B B A AC ++=+++=+++=++++=++++=+++++=)()()(DC B A AD B C AB AD D C B C AB AD A A C B D C AB +++=++++=++++=+++++=)()(1)()()()()(=++++=+++++=+++++=+++++=+++++=+++++=A CD B BD A C A A CD B BD B B A C A A CD B B A D A B C A A CD B B A BD D B A C A A BD CD B B A D B C A BD A BD CD B B A D BC C A DC D C D C B D C D C D C D C A D C B D C D C A +=++=++++=)()(10.D B AB C D B AB F +++++=10(y x y x x +=+)2—4用卡诺图化简下列各式1.C B A AB C B F ++=1 2.C B BC B A F ++=2F 1ABC += F 2B A +=3.C B C B C A C A F +++=3F 3C B B A C A ++=4.D C A C B AD C D C A ABD ABC F +++++=4D A F +=4111111111111AB CD0001111000011110D B AB C DB ABCD B AB ++=++⋅⋅=5.D B A AC C B A F ++=5 6.C B A AD C B A D C AB F ++++=6AC D B B A F ++=5 A C B DC F ++=6 7.D BC A BD A CD B B A C A F +F 7=18.D B D B C A C A F +++=8D)⊙(B C)⊙(8⋅=+++=A D C B A ABCD D C B A D C B A F11111111AB CD 00011110000111109.D C B A D AC D C B D C A F +++⊕=)(9D C D C F +=9 10. ))((10C AB B A F ++=C B C A F +=1011. C B AC D C A B A F +++=11AC C B B A F ++=1112.∑=mC B A P )7,6,5,2,1,0(),,(1AC C B B A P ++=2 13.=D C B A P )14,11,10,9,8,7,6,4,3,2,1,0(),,,(2D C C A D A B P +++=2 14.∑=mD C B A P )15,14,13,12,10,9,8,6,4,1,0(),,,(3D A D B C B AB D C P ++++=315. ∑=m D C B A P )15,14,13,11,9,7,6,5,3,1(),,,(4F 15=D+BC2—5 用卡诺图化简下列带有约束条件的逻辑函数 1.∑∑+=d mD C B A P )15,14,13,2,1,0()12,11,9,8,6,3(),,,(1CD A D B C A P ++=1 2.∑∑+=d mD C B A P )15,14,13,10,9,8()12,11,6,5,4,3,2,0(),,,(2C B C BD P ++=23.D C B A D C B A D C A P ++++=3, 约束:0=+AC ABD C B D C A D C A P ++=34.CD B A CD B A P +=4, 约束:A B C D 为互相排斥的一组变量,即在任何情况下它们之中不可能两个同时为1。
数字逻辑课后答案第二章
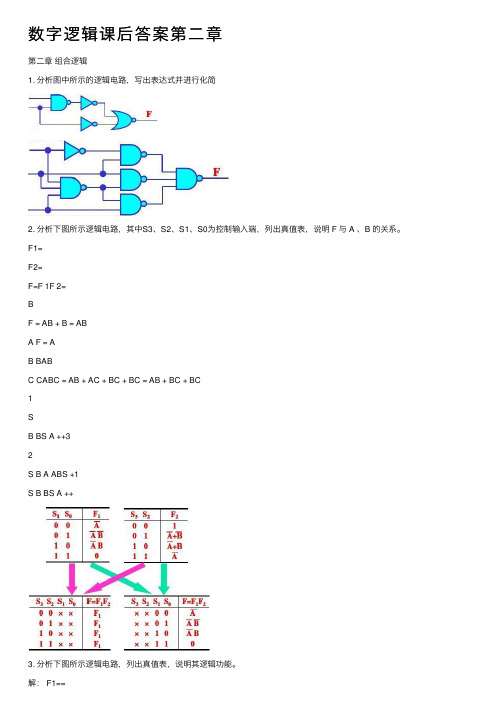
数字逻辑课后答案第⼆章第⼆章组合逻辑1. 分析图中所⽰的逻辑电路,写出表达式并进⾏化简2. 分析下图所⽰逻辑电路,其中S3、S2、S1、S0为控制输⼊端,列出真值表,说明 F 与 A 、B 的关系。
F1=F2=F=F 1F 2=BF = AB + B = ABA F = AB BABC CABC = AB + AC + BC + BC = AB + BC + BC1SB BS A ++32S B A ABS +1S B BS A ++3. 分析下图所⽰逻辑电路,列出真值表,说明其逻辑功能。
解: F1==真值表如下:当B ≠C 时, F1=A 当B=C=1时, F1=A 当B=C=0时, F1=0裁判判决电路,A 为主裁判,在A 同意的前提下,只要有⼀位副裁判(B ,C )同意,成绩就有效。
F2=真值表如下:CB BC A C AB C B A +++ABCC B A ABC C B A C B A +⊕=++)(A B C F 0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 100000111AC BC AB C A C B B A ++=++当A 、B 、C 三个变量中有两个及两个以上同时为“1”时,F2 = 1 。
4.图所⽰为数据总线上的⼀种判零电路,写出F 的逻辑表达式,说明该电路的逻辑功能。
解:F=只有当变量A0~A15全为0时,F = 1;否则,F = 0。
因此,电路的功能是判断变量是否全部为逻辑“0”。
5. 分析下图所⽰逻辑电路,列出真值表,说明其逻辑功能解:因此,这是⼀个四选⼀的选择器。
6. 下图所⽰为两种⼗进制数代码转换器,输⼊为余三码,输出为什么代码?解:A B C F 0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 1000011111514131211109876543210A A A A A A A A A A A A A A A A +++301201101001X A A X A A X A A X A A F +++=这是⼀个余三码⾄8421 BCD 码转换的电路7. 下图是⼀个受 M 控制的4位⼆进制码和格雷码的相互转换电路。
数字逻辑课后习题答案

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制491100016153110101651271111111177635100111101111737.493111.11117.7479.4310011001.0110111231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010101211110161751011100921340.100110.593750.4610111147570110113153.将下列十进制数转换成8421BCD码1997=000110011001011165.312=01100101.0011000100103.1416=0011.00010100000101100.9475=0.10010100011101014.列出真值表,写出X的真值表达式A B C X00000010010001111000101111011111X=A BC+A B C+AB C+ABC5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1)(A⊕B)⊕C=A⊕(B⊕C)A B C(A⊕B)⊕C A⊕(B⊕C)0000000111010110110010011101001100011111所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C00011001000100001111100001011111011111007.证明下列等式(1)A+A B=A+B 证明:左边=A+A B=A(B+B )+A B =AB+A B +A B =AB+A B +AB+A B =A+B =右边(2)ABC+A B C+AB C =AB+AC 证明:左边=ABC+A B C+AB C=ABC+A B C+AB C +ABC =AC(B+B )+AB(C+C )=AB+AC =右边(3)E D C CD A C B A A )(++++=A+CD+E证明:左边=ED C CD A C B A A )(++++=A+CD+A B C +CDE =A+CD+CD E =A+CD+E =右边(4)C B A C B A B A ++=CB C A B A ++证明:左边=CB AC B A B A ++=C B A C AB C B A B A +++)(=C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式(1)F=A+ABC+A C B +CB+C B =A+BC+C B (2)F=(A+B+C )(A+B+C)=(A+B)+C C =A+B (3)F=ABC D +ABD+BC D +ABCD+B C =AB+BC+BD (4)F=C AB C B BC A AC +++=BC(5)F=)()()()(B A B A B A B A ++++=B A 9.将下列函数展开为最小项表达式(1)F(A,B,C)=Σ(1,4,5,6,7)(2)F(A,B,C,D)=Σ(4,5,6,7,9,12,14)10.用卡诺图化简下列各式(1)CAB C B BC A AC F +++=0 ABC00 01 11 1011111化简得F=C(2)CB A D A B A DC AB CD B A F++++=111111AB CD 00 01 11 1000011110化简得F=DA B A +(3)F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)1111111111ABCD 00 01 11 1000011110化简得F=DBC D C A BC A C B D C ++++(4)F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)Φ1ΦΦ1ΦΦ1Φ1AB CD 00 01 11 1000011110化简得F=ACAD B A ++11.利用与非门实现下列函数,并画出逻辑图。
数字逻辑电路__刘常澍主编____第二章习题答案

第2章 习题答案2-1 二极管、三极管用于数字电路中与用于模拟电路有什么不同?答:二极管和三极管在数字电路中主要用作开关,工作于大信号状态,即二极管工作在正向导通和反向截止两个状态,三极管工作在饱和于截止两个状态; 模拟电路中二极管一般工作在小信号状态或反向击穿状态,三极管一般工作在放大状态。
2-2 有两个二极管A 和B ,在相同条件下测得A 管的I F =10mA ,I R =2mA ;B 管的I F=30mA ,I R =0.5μA ;比较而言,哪个性能更好?答:B 管更好,因为其反向漏电流较小而正向允许电流大。
2-3 三极管工作在截止、饱和、放大状态的外部条件各是什么?答:截止时,使发射结反偏即v BE ≤0;饱和时,使基极电流等于或大于基极饱和电流,即i B ≥I BS =V CC /βR C ;放大时,使发射结正偏,而i B <I BS =V CC /βR C 。
2-4 MOS 管工作在截止、恒流、可变电阻区的外部条件各是什么? 答:对于常用的增强型NMOS 管,截止时,使栅源电压小于开启电压V T 即v GS >V GS(th)N ;工作于恒流区时,使v DS >v GS - V GS(th)N ;工作于可变电阻区时,使v DS <v GS - V GS(th)N2-5 二极管电路如图P2-5所示。
v I =5sin ωt (V ),假设二极管是理想二极管,试画出输出 v O 的波形。
若考虑二极管的导通压降V D =0.7V ,画出输出v O 的波形。
解:输出波形如图解P2-5所示。
(a)为输入波形, D 为理想二极管时输出波形为(b), 考虑D 导通压降为0.7伏时输出波形为(c)。
2-6 二极管开关电路如图P2-6所示。
二极管导通电压为0.7V ,试分析输入端A 、B 分别为0V 和5V 时管子的工作状态,输出电压v O =?解:v A =5V ,v B =0V 时,D 2、D 1均导通 v O =–0.7V ; v A =5V ,v B =5V 时, D 2、D 1均导通 v O =4.3V ; v A =0V ,v B =5V 时,D 1 导通、D 2截止 v O =4.3V ; v A =5V, v B =0V 时, D 1截止、D 2导通 v O =4.3V 。
在线网课《数字逻辑(山东联盟-烟台大学)》课后章节测试答案

绪论单元测试1【多选题】(5分)计算机的五大组成部分是()、()、()、输入设备和输出设备。
A.控制器B.运算器C.硬盘D.存储器2【判断题】(5分)数字逻辑课程是计算机专业的一门学习硬件电路的专业基础课。
A.错B.对3【判断题】(5分)计算机的运算器是能够完成算术和逻辑运算的部件,逻辑运算比如与运算。
A.错B.对第一章测试1【单选题】(10分)与二进制数1101011.011对应的十六进制数为()A.53.3B.73.3C.6B.3D.6B.62【单选题】(10分)与二进制数101.011等值的十进制数是()A.5.175B.5.375C.3.625D.5.6753【单选题】(10分)(17)10对应的二进制数是()A.10011B.101111C.10110D.100014【判断题】(10分)数字电路中用“1”和“0”分别表示两种状态,二者通常无大小之分A.错B.对5【判断题】(10分)格雷码具有任何相邻码只有一位码元不同的特性A.对B.错6【多选题】(20分)以下代码中为无权码的为()A.余三码B.格雷码C.5421BCD码D.8421BCD码7【单选题】(10分)十进制数25用8421BCD码表示为()A.00100101B.11010C.11001D.101018【单选题】(10分)BCD码1001对应的余3BCD码是()A.1011B.1100C.1000D.10109【单选题】(10分)8421BCD码001001010100转换成十进制数为()A.252B.1250C.1124D.254第二章测试1【单选题】(5分)在何种输入情况下,“或非”运算的结果是逻辑0A.任一输入为0,其他输入为1B.全部输入是0C.全部输入是1D.任一输入为12【单选题】(5分)一个两输入端的门电路,当输入为1和0时,输出不是1的门是()A.或门B.异或门C.与非门D.或非门3【多选题】(10分)求一个逻辑函数F的对偶式,可将F中的()。
《数字电路与逻辑设计》第二章答案

选 RL=1K 2-6 已知题图 2-6 中各个门电路都是 74H 系列 TTL 电路,试写出各门电路的 输出状态(0,1 或 Z)
Vcc ViH NO_ INPUT
&
Y1
ViL
≥1ViH Y2& NhomakorabeaY3
0
≥1
Vcc ViL EN=1
1
10K
0
ViL
Y4
& Y5
Vcc
1K
=
Y6
100
1
1
0
题图 2-6 2-7 已知 TTL 三态门电路及控制信号 C1 ,C2 的波形如题图 2-7 所示,试分析 此电路能否正常工作。
vI2= vI1 =0.14V
(5)vI1 经 10K 电阻接地 2-3
vI2=1.4V
已知 TTL 门的参数是 VOH=3.5V, VOL=0.1V, VIHmin=2.4V, VILmax =0.3V,IIH=20
μA,IIS=1.0mA, IOH=360μA,IOL=8mA,求题图 2-3 中 R 的取值范围.
A B
100Ω ≥1
A F1 B
& F2
10K
(a) 题图 2-10
(b)
2-11 CMOS 门电路如题图 2-11 所示,试写出各门的输出电平。
题图 2-11 答案:(a)VDD 2-12 (b )0 (c)0
CMOS 与或非门不使用的输入端应如何连接?
答案:当在一起的两个输入端都不使用时,它们同时接地; 当在一起的两个输入端只有一个不使用时,它通过电阻接电源。
cmos的或非门电路可以得到当或非门的个输入端并接到高电平时三个并接的nmos管导通而三个串接的pmos管都截止所以其输入高电平总电流为3iih05167ohihcmos的与非门电路可以得到当与非门的个输入端并接到高电平时三个串接的nmos管都截止所以其输入高电平总电流为3iih05167ohihcmos的或非门电路可以得到当或非门的个输入端并接到低电平时三个并接的nmos管都截止而三个串接的pmos管导通所以其输入低电平总电流为3iil05167ohihcmos的与非门电路可以得到当与非门的个输入端并接到低电平时三个串接的nmos管都截止而三个并接的pmos管导通所以其输入低电平总电流为3iil05167olil总结以上结果对电路a能够驱动167个三输入端或非门对电路b能够驱动167个三输入端与非门
数字逻辑(第二版)毛法尧课后题答案

(27)10 , (00111000)8421BCD ,(135.6)8,(11011001)2 (3AF)16,
9
第二章 逻辑代数基础
2.1 分别指出变量(A,B,C,D)在何种取值时, 下列函数的值为1?
(1)F BD ABC
(0100,0111,1100,1101,1111)
16
(4)F A( A B C)(A C D)(E C D) A( A C D)(E C D) ( AC AD)(E C D) ACE ADE
(5)F AC ABC BC ABC
F AC ABC BC ABC ( AC ABC)(B C)(A B C) C(A B)(B C)(A B C) C(A B)(B C) C(B AC) BC
7
1.10 将下列8421BCD码转换成十进制数和二进制数 (1)011010000011 (2)01000101.1001
解:(1)(011010000011)8421BCD=(683)D=(1010101011)2 (2)(01000101.1001)8421BCD=(45.9)D=(101101.1110)2
21
(2)F ( A, B, C, D) AB ACD AC BC
AB 00
01 11
10
CD
00 1
1
1
0
1
1
01
1
0
11 1
0
10 1
0
1
1
1
1
(2)F ( A, B,C, D) AB AC BC
最简或与表达式: F ABC ABC F F (A B C)(A B C)
20
2.10 用卡诺图化简下列函数 , 并写出最简“与 或”表达式和最简“或 与”表达式
数字逻辑课后习题答案(华中科技大学出版社-欧阳星明主编)ppt课件

精选编辑ppt
7
习题课
1.8 如何判断一个二进制数B=b6b5b4b3b2b1b0能否被(4)整除?
解答: 因 为 B= b6b5b4b3b2b1b0 , 所 以 ( B)2= b6×26+
反函数: FAB C EBD B G E 对偶函数:F 'A B C E B D E B G
精选编辑ppt
17
习题课
2.5 回答下列问题: (1)如果已知X+Y=X+Z,那么Y=Z。正确吗?为什么? (2)如果已知XY=XZ,那么Y=Z。正确吗?为什么? (3)如果已知X+Y=X+Z,且XY=XZ,那么Y=Z。正确吗?
解答:
(1) 反函数:
FAB AB
F A B A B (A B )A ( B ) A B A B
对偶函数: F '(A B )A (B )A B A B
(2) F(A B )A (C )C (D) E E
反函数: F ( A B A C C ( D E )E ) A B E A C E C D E
babaaba?aab?互补率1右边??bbabba???2左边结合率cbaa??cccaba?bbcaccba???bbccaabbccaaccbbaabbaa??????bbccaaccbbaaccbbaa????3左边右边14cacbba??cacbba??cacbabaabc??右边?c?b4右边习题课习题课23用真值表验证下列表达式
习题课
第 一 章 基本知识
1.1 什么是数字信号?什么是模拟信号?试各举一例。
数字逻辑电路第二章部分答案
双向模拟开关 当B=1时Y2=A,且A与Y2间可以双向 时 , 与 间可以双向 传输,还可以传输模拟信号。 传输,还可以传输模拟信号。
B=1 B=0
Y3=A Y3断开
Y4=A 0V 第二种情况:VO 分别等于 和 若负载为一个10K的电阻到地 若负载为一个 的电阻到地 第一种情况: 分别等于9.95V和0V 第一种情况:VO 分别等于 和 第二种情况: 分别等于5V和 第二种情况:VO 分别等于 和0V
三态传输门 当B=0时,允许输出,Y1=A 时 允许输出, 当B=1时,不允许输出,Y1为高阻态 时 不允许输出, 为高阻态 只能单向传输数字信号
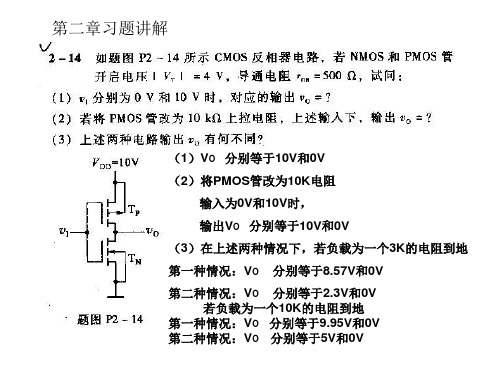
第二章习题讲解
分别等于10V和0V (1)VO 分别等于 ) 和 2) PMOS管改为 管改为10K电阻 (2)将PMOS管改为10K电阻 输入为0V和 输入为 和10V时, 时 输出V 分别等于10V和0V 输出 O 分别等于 和 (3)在上述两种情况下,若负载为一个 的电阻到地 )在上述两种情况下,若负载为一个3K的电阻到地 第一种情况:VO 第一种情况: 分别等于8.57V和0V 分别等于 和
数字逻辑 第二章习题答案
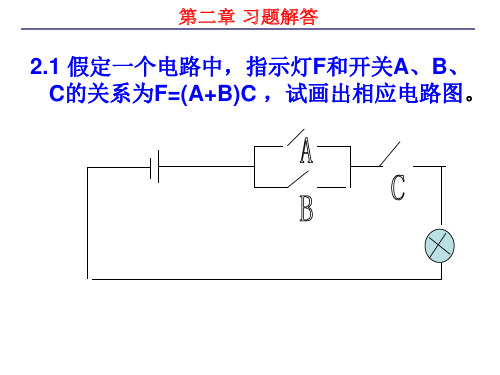
2.6用代数化简法求下列逻辑函数的最简与或表达式。 (1)F=AB+ ABC BC AB ( AB B )C AB ( A B )C AB AC BC AB AC (2) F AB B BCD AB B A B (3) F ( A B C )( A B )( A B C ) ( A B )( A B ) B
(2) AB AB AB AB 1 证明:AB AB AB AB A( B B ) A( B B ) A A 1
(3) AABC ABC ABC ABC 证明:AABC A( A B C ) AB AC AB (C C ) AC ( B B ) ABC ABC ABC ABC ABC ABC ABC
• (2)
• 2.8用卡诺图化简法求出下列逻辑函数的最简“与-或”表达式和最简 “或-与”表达式。
(4) F BC D D( B C )( AC B) BC D ( B C )( AC B) BC D BC ( AC B ) BC D AC B B D AC
• 7. 将下列逻辑函数表示成“最小项之和” 形式及“最大项之积”的简写形式。
(4) ABC ABC AB BC AC 证明: BC AC AB ( A B)( B C )( A C ) ( AB AC BC )( A C ) ABC ABC ABC
2.4求反函数和对偶函数 (2)F=(A+B)( A+C)(C+DE)+ E F [ AB AC C ( D E )]E F ' [ AB AC C ( D E )]E (3) F ( A B )(C D AC ) F AB C ( D A C ) F ' AB C ( D A C )
数字逻辑课后习题答案(科学出版社_第五版)

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 1001111011 11737.493 111.1111 7.7479.43 10011001.0110111 231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010 10 12111101 61 751011100 92 1340.10011 0.59375 0.46101111 47 5701101 13 153.将下列十进制数转换成8421BCD码1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014.列出真值表,写出X的真值表达式A B C X0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1 X=A BC+A B C+AB C+ABC5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1) (A⊕B)⊕C=A⊕(B⊕C)A B C (A⊕B)⊕C A⊕(B⊕C)0 0 0 0 00 0 1 1 10 1 0 1 10 1 1 0 01 0 0 1 11 0 1 0 01 1 0 0 01 1 1 1 1所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C0 0 0 1 10 0 1 0 00 1 0 0 00 1 1 1 11 0 0 0 01 0 1 1 11 1 0 1 11 1 1 0 07.证明下列等式(1)A+A B=A+B证明:左边= A+A B=A(B+B)+A B=AB+A B+A B=AB+A B+AB+A B=A+B=右边(2)ABC+A B C+AB C=AB+AC证明:左边= ABC+A B C+AB C= ABC+A B C+AB C+ABC=AC(B+B)+AB(C+C)=AB+AC=右边(3)EDCCDACBAA)(++++=A+CD+E证明:左边=EDCCDACBAA)(++++=A+CD+A B C+CD E=A+CD+CD E=A+CD+E=右边(4)C B A C B A B A ++=CB C A B A ++证明:左边=CB AC B A B A ++=CB AC AB C B A B A +++)(=C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式(1) F=A+ABC+A C B +CB+C B = A+BC+C B(2) F =(A+B+C )(A+B+C) = (A+B)+C C = A+B(3) F =ABC D +ABD+BC D +ABCD+B C = AB+BC+BD(4) F=C AB C B BC A AC +++= BC(5) F=)()()()(B A B A B A B A ++++=BA 9.将下列函数展开为最小项表达式(1) F(A,B,C) = Σ(1,4,5,6,7)(2) F(A,B,C,D) = Σ(4,5,6,7,9,12,14)10.用卡诺图化简下列各式(1)CAB C B BC A AC F +++=0ABC00 01 11 1011111化简得F=C(2)CB A D A B A DC AB CD B A F++++=111111ABCD 00 01 11 1000011110化简得F=DA B A +(3) F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)1111111111AB CD 00 01 11 1000011110化简得F=DBC D C A BC A C B D C ++++(4) F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)Φ1ΦΦ1ΦΦ1Φ1AB CD 00 01 11 1000011110化简得F=ACAD B A ++11.利用与非门实现下列函数,并画出逻辑图。
数字逻辑第二章作业参考答案1

F AB AC AC AB
• 在只有原变量,没有反变量的输入条件下,采用与 非门设计的函数为:
F ABB ACC A AC A AB
电路图略
第二种方案: • (2) 化简F,得F的与或式:(卡诺图略)
F AC BC AB
• 在只有原变量,没有反变量的输入条件下,采用与 非门设计的函数为:
F ( A C D)(A B)(C B D)
• 在有原变量又有反变量的输入条件下,采用或非门 设计的函数为:
F ( A C D) ( A B) (C B D)
电路图略
P108,5(1)
• 解: 本题有两种设计方案。 • 第一种设计方案 • (1) 化简F,得F的与或式:(卡诺图略)
真值表(略) 由真值表可以看出,若将A、B分别作为一位二进制数,同 时A为被加数,B为加数,C为来自低位的进位,则F1为本 位和,F2为本位向高位的进位,该电路称作“全加器”, 它能实现两个一位二进制数加法运算。
P107,2
F ABS 3 ABS 4 BS1 BS 0 A
从真值表可知,当S0,S1 给定时,函数F的 0 0
S2 0 0 1
S4 0 1 0
F
0
0 0 0 0
0
1 1 1 1
1
0 0 1 1
1
0 1 0 1
A A A A
AB
AB
AB AB AB AB AB AB
0 0 0 0
1
1 1 1 1 1 1 1
0
0 0 0 1 1 1 1
0
0 1 1 0 0 1 1
0
1 0 1 0 1 0 1
数字逻辑电路(王秀敏主编)课后习题答案第二章

第1章 概述检 测 题一、填空题1. 在时间和数值上都是连续变化的信号是_______信号;在时间和数值上是离散和量化的信号是_______信号。
2. 表示逻辑函数常用的方法有4种,它们是_______,________,________,_______。
3. 正逻辑体制高电平用逻辑_____表示,低电平用逻辑_____表示。
4. 任何进位计数制,数值的表示都包含两个基本的要素:_______和_______。
5. 102816(96.75)( )( )( )===二、请完成下列题的进制转换1.210(1011001)( )=810(736.4)( )=1610(34)( )F C =2.112(30)( )=102(16.6875)( )= 3.28(1011101)( )=28(1010010.11010)( )=4.82(127.65)( )=162(9.16)( )A = 5.216(1110101100)( )=216(1111.001)( )=三、选择题1.在下列各数中,最小的数是( )(a) 2(101001) (b) 8(52) (c) 16(2)B (d) 10(96)2. 8421(100110000110)( )BCD 余3BCD(A)100110001001 (B)100110001000 (C)110010000110 (D)101100001100四、简述题1.为什么在数字系统中通常采用二进制/2.何为进位计数制? 何为码制? 何为正、负逻辑?3.算术运算、逻辑运算和关系运算的区别?检测题答案一、填空题1. 答案:模拟,数字2. 答案:真值表,逻辑函数式,逻辑图,卡诺图。
3. 答案:1,0;0,14. 答案:基数,位数5. 答案:1100000.11,140.6,60.0二、请完成下列题的进制转换1. 89; 478.5; 80122. 11110; 10000.10113. 135; 122.624. 1010111.110101; 10011010.000101105. 3AC ; F.2三、选择题1.答案:A2. 答案:A四、简述题答案:略习题[题1.1] 将下列十进制数转换为二进制数。
数字逻辑第二章课后答案

2-1
2-2
均可以作为反相器使用。
与非门:
或非门:
异或门:
2-3 1
Y V
CMOS 与非门的一个输入端通过电阻接地,相当于该输入端输入低电平,输出Y1是高电平。
2Y V
CMOS 或非门的一个输入端通过电阻接高电平与直接接高电平是一样的,输出Y2是低电平。
V 3
Y V 低电平有效的三态门的使能端EN 接高电平,则Y3为高阻态。
4
Y V
与或非门的一个与门输入全为高电平,则输出Y4是低电平。
2-4
E D C B A Y ⋅⋅⋅⋅=1 E D C B A Y ++++=2
))((3F E D C B A Y ++++=
F E D C B A Y ⋅⋅+⋅⋅=4 2-5
当1=EN ,T1`和T2截止,Y=Z (高阻)。
当0=EN ,T1`导通,A A Y ==。
2-7
(1)忽略所有门电路的传输延迟时间,除去开始的一小段时间,与非门的两个输入端总有一个是低电平,输出一直为高电平。
(2)考虑每个门都有传输延迟时间。
假设1级门的传输延迟时间为tpd ,则与非门的两个输入端的输入信号变化实际上并不是同时的。
信号A 经过两级门的传输延迟,比信号B 要晚2tpd 时间到达与非门的输入端。
因此,将出现,在短暂时间里,两个输入端的输入信号都是高电平的情况,输出电压波形出现毛刺。
数字逻辑第2章习题解答

习题二2.1:设A 、B 、C 为逻辑变量,试回答:(1) 若已知A+B=A+C ,则B=C ,对吗?(2) 若已知AB=AC ,则B=C ,对吗?(3) 若已知A+B=A+C 且AB=AC ,则B=C ,对吗?解:(1)不对,当A=1时,B 可以不等于C 。
(2)不对,当A=0时,B 可以不等于C 。
(3)对。
2.2:指出使下列逻辑函数为1的变量取值组合 (1)AB B A B A F +=),( (2) C A AB C B A F +=),,( (3) CD B A D C B A D C B A F )+(+)+(=),,,(解:(1) A 、B=00和11时F=1,否则F=0 (2) C A AB C B A F +=),,(A,B 为11或A,C 为10时F=1,即A,B,C 的取值为100,110,111时F=1,否则F=0。
(3) CD B ACD D C B D A F +++=A,D 为10或B,C,D 为000,或A,C,D 为111,或B,C,D 为011时F=1,即A,B,C,D 的取值为0000, 0011,1000,1010, 1011,1100,1110, 1111时F=1,否则F=0。
2.3、用代数法证明下列等式(1) C A +AB =BCD +C A +AB(2) C +AB =C B +C A +AB(3) D +B A =DC +D A +B +B A D(4) D +B =)+)(+(D +D +BC B DA C B(5) 0=)B +A B)(+A )(B +B)(A +(A(6) A C +C B +B A =+C B +B A A C(7) A D +D C +C +B A =)D C +)(CD C B +BC )(B A +(AB B (8)B A B A ⊕=⊕ (9)D C AB B A D C B A D C B A ++=+++++++(10)C B BD C B BCD D C B CD B A D C B A ACD D C B D C B ++=++++++ 解: (1) C A +AB =BC +C A +AB =BCD +BC +C A +AB =BCD +C A +AB(2) C +AB =C +AB =)C B +A (+AB =C B +C A +AB AB(3) DC +D A ++B +B A =DC +D A +B +B A AD D DD +B A =DC +D +B +B A =D(4) )+)(+(+D +BC =)+)(+(+D +BC B DA B DAD B B DA B DA BC +=++D +BC =)+(+D +BC =(5) 0=A •A =)B +A B)(+A )(B +B)(A +(A(6) BC A C B A A A C C A C ++C B +C B +B A +B A =+C B +B A A C +C B +B A =C B +B A +B A +++C B =A C C C B A BC A A(7) )+)(CD +(ABC =)+)(CD +BC )(+(ABD C B A +ABCD =)+)(+)(+)(+(=A D +D C +C +B A A D D C C B B A BD +B A =AD)++)(+C A +B A (=ABC D C C A D C BC∴ A D +D C +C +B A =)D C +)(CD C B +BC )(B A +(AB B (8)B A B A B A B A B A B A ⊕=+=+=⊕ (9)D C AB B A D C B A D C B A ++=+++++++ (10)C B BD C B BCD D C B CD B A D C B A ACD D C B D C B ++=++++++2.4、用真值表验证下列等式(1) )+)(+(=B A +B A B A B A(2) C B A C B A A ++=)+(+(3) ABC C B A +=A C +C B +B A解:略2.5、用反演规则和对偶规则求下列函数的反函数F 和对偶函数'F 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 组合逻辑
1. 分析图中所示的逻辑电路,写出表达式并进行化简
2. 分析下图所示逻辑电路,其中S3、S2、S1、S0为控制输入端,列出真值表,
说明 F 与 A 、B 的关系。
F1= F2=
F=F 1F 2=
B
F = AB + B = AB
A F = A
B BAB
C CABC = AB + AC + BC + BC = AB + BC + BC
1
S B BS A ++3
2
S B A ABS +1
S B BS A ++
3. 分析下图所示逻辑电路,列出真值表,说明其逻辑功能。
解: F1==
真值表如下:
当B ≠C 时, F1=A 当B=C=1时, F1=A 当B=C=0时, F1=0
裁判判决电路,A 为主裁判,在A 同意的前提下,只要有一位副裁判(B ,C )同意,
成绩就有效。
F2=
真值表如下:
C
B B
C A C AB C B A +++ABC C B A ABC C B A C B A +⊕=++)(A B C F 0 0 00 0 10 1 00 1 11 0 01 0 11 1 0
1 1 1
000001
11AC BC AB C A C B B A ++=++
当A 、B 、C 三个变量中有两个及两个以上同时为“1”时,F2 = 1 。
4.图所示为数据总线上的一种判零电路,写出F 的逻辑表达式,说明该电路的逻辑功能。
解:F=
只有当变量A0~A15全为0时,F = 1;否则,F = 0。
因此,电路的功能是判断变量是否全部为逻辑“0”。
5. 分析下图所示逻辑电路,列出真值表,说明其逻辑功能
解: 真值表如下:
因此,这是一个四选一的选择器。
6. 下图所示为两种十进制数代码转换器,输入为余三码,输出为什么代码?
解:
A B C F 0 0 00 0 10 1 00 1 11 0 01 0 11 1 0
1 1 1
000011
111514131211109876543210A A A A A A A A A A A A A A A A +++301201101001X A A X A A X A A X A A F +++=
这是一个余三码 至8421 BCD 码转换的电路
7. 下图是一个受 M 控制的4位二进制码和格雷码的相互转换电路。
M=1 时,完成自然二进制码至格雷码转换;M=0 时,完成相反转换。
请说明之
解:Y3=X3
当M=1时 Y3=X3
Y2=X2⊕X3 Y1=X1⊕X2 Y0=X0⊕X1 当M=0时 Y3=X3
Y2=X2⊕X3
Y1=X1⊕Y2=X1⊕X2⊕X3 Y0=X0⊕Y1=X0⊕X1⊕X2⊕X3
由真值表可知:M=1 时,完成8421 BCD 码到格雷码的转换;
W= AB+ACD X = BC+BD+BCD Y = CD+CD Z = D
322X X Y ⊕=)22(11Y M MX X Y +⊕=)11(00Y M MX X Y +⊕=
M= 1 的真值表
M=0 时,完成格雷码到8421 BCD 码的转换。
8. 已知输入信号A,B,C,D 的波形如下图所示,选择适当的集成逻辑门电路,设计产生输出 F 波形的组合电路(输入无反变量)
解:
列出真值表如下:
9. 用红、黄、绿三个指示灯表示三台设备的工作情况:绿灯亮表示全部正常;红灯亮表示有一台不正常;黄灯亮表示有两台不正常;红、黄灯全亮表示三台都不正常。
列出控制电路真值表,并选出合适的集成电路来实现。
解:
设:三台设备分别为 A 、B 、C : “1”表示有故障,“0”表示无故障;红、黄、绿灯分别为Y1、Y2、Y3:“1”表示灯亮;“0”表示灯灭。
据题意列出真值表如下:
)(D C A C B A D C B D B B A F 或+++=
于是得:
10. 用两片双四选一数据选择器和与非门实现循环码至8421BCD 码转换。
解:(1)画函数卡诺图;
(2)写逻辑函数表达式:
(1) 画逻辑图:
11. 用一片74LS148和与非门实现8421BCD 优先编码器
C B A C B A Y C B A BC Y C B A Y ++==⊕+=⊕⊕=3)
(21
0Y 123
12. 用适当门电路,设计16位串行加法器,要求进位琏速度最快,计算一次加法时间。
解:全加器真值表如下
要使进位琏速度最快,应使用“与或非”门。
具体连接图如下。
若“与或非”门延迟时间为t1,“非门”延迟时间为t2,则完成一次16位加法运算所需时间为: C AB C B A BC A C B A S +++=11--+=C B C A B A C +1
1--+=BC AC AB C +1
1--+=BC AC AB C +11--+=C B C A B A C +C AB C B A BC A C B A S +++=)
()116(2
11t t t t ++-=
13.用一片4:16线译码器将8421BCD 码转换成余三码,写出表达式 解:
2
B 2
A )8,6,4,2,0(),,,()8,7,4,3,0(),,,()9,4,3,2,1(),,,()9,8,7,6,5(),,,(∑=∑=∑=∑=D C
B A Z D
C B A Y
D C B A X D C B A W
14. 使用一个4位二进制加法器设计8421BCD 码转换成余三码转换器: 解:
B 12A 2B
4:16线译码器
Y 6
Y 8
Y 2Y 4
Y 3
Y 7Y 2Y 6
1O
S 0S 1S 2S 3
8421BCD 码
100
余三码
15. 用74LS283加法器和逻辑门设计实现一位8421 BCD码加法器电路。
解:
进位
+
加6判断修正
和BCD码
16. 设计二进制码/格雷码转换器
解:真值表
得:
17. 设计七段译码器的内部电路,用于驱动共阴极数码管。
解:七段发光二极管为共阴极电路,各段为“1”时亮。
七段译码器真值表如下:
1002
1132233B B G B B G B B G B G ⊕=⊕=⊕==
18. 设计一个血型配比指示器。
解: 用XY 表示供血者代码,MN 表示受血者代码。
代码设定如下:XY = 00 A 型 MN = 00 A 型 01 B 型 01 B 型 10 AB 型 10 AB 型 11 O 型 11 O 型
得:F 1 = Σ(0,2,5,6,10,12,13,14,15)
F1F2=1
2
1
2
1
3
2
1
2
1
3
1
2
1
2
1
2
1
2
1
2
1
1
2
2
2
1
3
A
A A A A A A g A
A A A A A A f A
A A A e A
A A A A A A A A d A
A A c A
A A A A b A
A A A A A a +++=+++=+=+++=++=++=+++=
19. 设计保密锁。
解: 设A,B,C 按键按下为1,F 为开锁信号(F=1为打开),G 为报警信号(G=1为报警)。
F 的卡诺图:
化简得:
G 的卡诺图
化简得:
AB C 00 01 11 10
0 1
1
1
1 AC AB F +=
AB C 00 01 11 10
0 1
1
1
1 C A B A G
+=。
