椭圆中焦点三角形的性质
椭圆的性质二 焦点三角形的性质

||PF|2 |PF|1
a
ex
(a
ex)
2ex
2
4 5
x
,
5
x
0
,
∴0<|F2N|<8,∴0<|OM|<4.
若 P 在椭圆的右半部分时,同样可得出 0<|OM|<4,故选:B.
方法二 极限法,当 P 在左端点时,|OM|=4,在 P 上顶点时,|OM|=0,∴0<|OM|<4.
三 课后练习:
1.(2019·郑州第二次质量预测)已知椭圆 C:ax22+by22=1(a>b>0)的左、右焦点分别为 F1,F2,离心率为23,
x2
令椭圆方程为
a2
y2 b2
1(a b 0)
则由椭圆的定义有 | PF1 | | PF2 | 2a , | F1F2 | 2c ,
∴
| PF1 | | PF2 |
| F1F2 | 2c
sin PF2F1 sin PF1F2 sin F1PF2
又 ∵ PF1F2 5PF2F1 , ∴ PF1F2 750 , PF2F1 150 ,
4.(2019
南昌模拟)P
为椭圆 x2 +y2=1 25 9
上一点,F1,F2
分别是椭圆的左、右焦点,过
P
点作
PH⊥F1F2
于
点 H,若 PF1⊥PF2,则|PH|=( )
A.25
B.8
4
3
C.8
D.9
4
解析:选 D 由椭圆 x2 +y2=1 得 a2=25,b2=9, 25 9
则 c= a2-b2= 25-9=4,∴|F1F2|=2c=8.由椭圆的定义可得|PF1|+|PF2|=2a=10,
A. (0, 3 ] 2
椭圆中的焦点三角形

思路
1:当 F1PF2 最大时,由面积公: SF1PF2
b2tan 2源自可知,焦点三角形的面积也达到最大.
所以焦点三角形的面积最大时,P 在短轴的端点处.
思路 2: S 1 ×底×高. 点 P 的纵坐标的绝对值
2
F1F2 2c
当 P 点在椭圆上运动时,纵坐标的绝对值在短轴的端点处取得最大值,
所以 P 在短轴端点处焦点三角形取得面积的最大值.
证明:在 F1PF2 中,由余弦定理得:
cos
PF12 PF22 F1F22 2PF1 • PF2
(PF1 PF2 )2 2PF1 • PF2 4c2 2PF1 • PF2
4a2 4c2 2PF1 • PF2
1 2a2 2c2 PF1 • PF2
1
2a2 2c2 ( PF1 PF2 )2
1. 建构数学
椭圆的焦点三角形:
(1)定义:椭圆上任意一点(异于长轴端点)与椭 圆的两个焦点所组成的三角形叫椭圆的焦点三 角形.
(2)焦点三角形构成要素之间的关系
以椭圆方程为
x2 a2
y2 b2
1(a
b
0) 为例,两焦点分别为 F1, F2 , 椭圆上
任意一点为 P,设焦点三角形 PF1F2
①焦点三角形的构成: 三边:两条焦半径 PF1, PF2 ,焦距 F1F2 , 三角:设 F1PF2 , PF1F2 , PF2F1 .
1时,点
P
个数为
0
个
② max
90,
2b2 a2
1时,点
P
个数为
2
个
③ max
90,
2b2 a2
1时,点
P
个数为
4
2020高中数学 2.2.4 椭圆中焦点三角形的性质及应用教案 新人教A版选修1-1

高中数学 2.2.4 椭圆中焦点三角形的性质及应用教案 新人教A 版选修1-1,21θ=∠PF F 则2tan221θb S PF F =∆。
θcos 2)2(2122212212PF PF PF PF F F c -+== )cos 1(2)(21221θ+-+=PF PF PF PF θθθcos 12)cos 1(244)cos 1(24)(222222121+=+-=+-+=∴b c a c PF PF PF PF 1222121sin sin tan 21cos 2F PF b S PF PF b θθθθ∆∴===+ 性质二:已知椭圆方程为),0(12222>>=+b a by a x 左右两焦点分别为,,21F F 设焦点三角形21F PF ,若21PF F ∠最大,则点P 为椭圆短轴的端点。
证明:设),(o o y x P ,由焦半径公式可知:o ex a PF +=1,o ex a PF -=1 在21PF F ∆中,2122121212cos PF PF F F PF PF -+=θ21221221242)(PF PF c PF PF PF PF --+=1))((24124422122--+=--=o o ex a ex a b PF PF c a =122222--ox e a b a x a ≤≤-0 22a x o ≤∴性质三:已知椭圆方程为),0(12222>>=+b a b y a x 两焦点分别为,,21F F 设焦点三角形21F PF 中,21θ=∠PF F 则.21cos 2e -≥θ证明:设,,2211r PF r PF ==则在21PF F ∆中,由余弦定理得:1222242)(2cos 212221221221212212221--=--+=-+=r r c a r r c r r r r r r F F r r θ.2112221)2(222222222122e a c a r r c a -=--=-+-≥ 命题得证。
椭圆中焦点三角形的性质及应用

椭圆中焦点三角形的性质及应用
又,故满足:故为直角三角形、说明:考查定义、利用已知、发挥联想,从而解题成功、性质一:已知椭圆方程为两焦点分别为设焦点三角形中则。
性质二:已知椭圆方程为左右两焦点分别为设焦点三角形,若最大,则点P为椭圆短轴的端点。
证明:设,由焦半径公式可知:,在中, = 性质三:过椭圆焦点的所有弦中通径(垂直于焦点的弦)最短,通径为性质四:已知椭圆方程为两焦点分别为设焦点三角形中则证明:设则在中,由余弦定理得:
命题得证。
(2000年高考题)已知椭圆的两焦点分别为若椭圆上存在一点使得求椭圆的离心率的取值范围。
简解:由椭圆焦点三角形性质可知即 ,于是得到的取值范围是性质五:已知椭圆方程为两焦点分别为设焦点三角形,则椭圆的离心率。
由正弦定理得:由等比定理得:而,∴。
已知椭圆的焦点是F1(-1,0)、F2(1,0),P为椭圆上一点,且|F1F2|是|PF1|和|PF2|的等差中项.(1)求椭圆的方程;(2)若点P在第三象限,且∠PF1F2=120,求tanF1PF2.解:(1)由题设2|F1F2|=|PF1|+|PF2|∴2a=4,又2c=2,∴b=∴椭圆的方程为=1.(2)设∠F1PF2=θ,则∠PF2F1=60-θ椭圆的离心率则,整理得:5sinθ=(1+cosθ)∴故,tanF1PF2=tanθ=.
第 1 页共 1 页。
马振保 椭圆焦点三角形的性质

椭圆焦点三角形的性质马振保椭圆是现行高中解析几何学的重要内容之一,且圆锥曲线知识既是高中数学的重点,又是难点.而椭圆焦点三角形相关问题.在求解这类问题时,许多学生常常感到束手无策,部分学生由于计算量大的繁锁,产生厌学数学的情绪.为了解除这种困惑,培养或提高学生学习数学的兴趣,让学生掌握一定的解题方法或数学思想是很必要的.在数学中,我们常常是利用性质去讨论问题,因此,文章首先探讨椭圆焦点三角形的性质,然后再讨论这些性质的应用.椭圆上一点与其两焦点所构成的三角形叫做椭圆的焦点三角形.椭圆焦点三角形的性质以椭圆)0(12222>>=+b a by a x 的两个焦点1F ,2F 及椭圆上任意一点P (除长轴上两个端点外)为顶点的21PF F ∆,叫做椭圆的焦点三角形.设21PF F ∠=θ,21F PF ∠=α,12F PF ∠=β,椭圆的离心率为e ,则有以下性质:图1性质1 θcos 12221+=⋅b PF PF . 证明:在21PF F ∆中,由余弦定理,有2221212221)2(cos 2c F F PF PF PF PF ==⋅⋅-+θa PF PF 221=+221222142a PF PF PF PF =⋅++∴2212124cos 224c PF PF PF PF a =⋅⋅-⋅-∴θ整理,得.cos 12221θ+=⋅b PF PF例1 如图2:1F 、2F 分别为椭圆)0(12222>>=+b a by a x 的左、右焦点,点P 在椭圆上,2POF ∆是面积为1的正三角形,求2b 的值.图2分析:此题按常规思路是从12=∆POF S 入手,即=S 224360sin 21c PO OF =⋅︒,求得.3342=c 所以点P 的坐标分别为2c ,c 23.由于点P 在椭圆上,有⎪⎩⎪⎨⎧=+=+22222221434ac b bc a c 解此方程组就可得到2b 的值.但这涉及到解二元二次方程组,计算量很大,非常麻烦.若用性质1求解可使运算得以简化.解:连接,1PF 则︒=∠9021PF F , 有21221PF F POF S S ∆∆=︒⋅⋅⋅=∴90sin 2121121PF PF.290sin 90cos 1241122=∴⋅+⋅=∴︒︒b b 性质2 .2tan221θ⋅=∆b S PF F证明:由性质1得θsin 212121⋅⋅⋅=∆PF PF S PF F .2tan cos 1sin sin cos 1221222θθθθθ⋅=+⋅=⋅+⋅=b b b 例2 已知1F 、2F 是椭圆1256422=+y x 的两个焦点,P 是椭圆上任一点,且321π=∠PF F ,求21PF F ∆的面积.分析:如果设P 点的坐标为),(y x ,由P 点在已知椭圆上且321π=∠PF F ,利用这两个条件,列出关于x ,y 的两个方程,解出x ,y .再求21PF F ∆的面积,这种方法,运算量大且过程繁杂,须另寻捷径.知道321π=∠PF F ,可以直接利用性质2求解,使运算量简化.解:2tan221θ⋅=∆b S PF F.33256tan2521=⋅=∴∆πPF F S 例3已知点),(00y x P )0(0>y 是椭圆)0(12222>>=+b a by a x 上任一点,且θ=∠21PF F .求证:2tan 20θ⋅=c b y . 证明: 0212221211y c h F F S PF F ⋅⋅=⋅⋅=∆ 2tan221θ⋅=∆b S PF F=⋅⋅∴0221y c 2tan 2θ⋅b00>y.2tan 20θ⋅=∴c b y例4 点P 是椭圆14522=+y x 上一点,以点P 以及焦点1F 、2F 为顶点的三角形的面积等于1,求点P 的坐标.分析:要求点P 的坐标,不妨设P 点坐标为),(00y x ,由P 点在已知椭圆上和21PF F ∆的面积等于1,可列两个方程,解方程可得点P 的坐标.此题也可在例3的基础上进行求解.解:设P 点坐标为),(00y x ,则有cc S c b y PF F 12tan 2120==⋅=∆θ122=-=b a c.1100±=∴=∴y y把10±=y 代入14522=+y x 得.2150±=x .1215121512151215),),(,),(,),(,坐标为(点----∴P 性质3)12arccos(22-≤<ab O θ.证明:由正弦定理,有θαβsin sin sin 2121F F PF PF ==)](180sin[sin sin sin sin sin 2121βαβαθβα+-+=+=+∴F F PF PF2cos2sin 22cos2sin2)sin(sin sin βαβαβαβαβαβα+⋅+⋅-+⋅=++=2sin 12cos 12cos 2cosθβαβαβα=+≤+-=θcos 12-= a PF PF 221=+)(44222221b a c F F -==θθcos 12cos 122222222-≤-∴-≤-∴b a a b a a即2222cos aa b -≥θ. 因为πθ<<0,所以 2222arccos a a b -≤θ.当点P 在长轴上的端点时,0=θ,这时,21PF F ∆不存在,因此,)12arccos(022-≤<ab θ.性质4 离心率 .2cos2cosβαβα-+=e 证明:由正弦定理,有)sin(sin sin sin 212121βαθαβ+===F F F F PF PF2cos2sin 22cos2sin2sin sin )sin(2121βαβαβαβαβαβα-⋅++⋅+=++=+∴PF PF F F .2cos2cosβαβα-+==∴e ac例5(2004年福建高考题)已知1F 、2F 是椭圆的两个焦点,过1F 且与椭圆长轴垂直的直线交椭圆于A 、B 两点,若2ABF ∆是正三角形,求这个椭圆的离心率.分析:由2ABF ∆是正三角形可知122AF AF =,根据椭圆的第一定义可求得a AF 2322⋅=.再由22130cos AF F F =︒可求得离心率e.若用性质4解题,求解更简便.解:根据已知条件有.30,902121︒︒=∠=∠A F F F AF (如图3).3330cos 60cos 23090cos23090cos2cos 2cos ==-+=-+=∴︒︒︒︒︒︒βαβαe图3性质5ee+-=⋅112tan2tanβα. 证明:由正弦定理,有θαβsin sin sin 2121F F PF PF ==βαβαβαθsin sin )sin(sin sin sin 2121++=+=+∴PF PF F F=++==∴βαβαsin sin )sin(a c e 2cos2sin 22cos2sin2βαβαβαβα-+++ 2sin2sin 2cos 2cos 2sin2sin 2cos 2cos 2cos 2cosβαβαβαβαβαβα⋅+⋅⋅-⋅=-+= 2tan2tan12tan 2tan 1βαβα⋅+⋅-= ee+-=⋅∴112tan2tanβα. 例 6 如图4,P 是椭圆12222=+by a x 上一点,1F 、2F 是焦点,已知,2,1221αα=∠=∠F PF F PF 求椭圆的离心率.图4分析:知道,2,1221αα=∠=∠F PF F PF 我们可以直接利用性质5解题. 解:由性质5有e e ee +-=⋅=⋅∴+-=⋅11cos 2cos 2sin cos sin 2cos 2sin1122tan 2tan 22αααααααααee +-=+-∴11cos cos cos 122ααα 化简,得.1cos 2-=αe以上五个椭圆焦点三角形的性质是高考考查的重点也是难点,值得我们去重视这部分内容的教学,而双曲线的焦点三角形性质可以类比椭圆的去学习。
椭圆焦点三角形的性质

椭圆的焦点三角形 基础再现: 已知椭圆22122:1(0)x y C a b a b+=>>的焦点为21,F F ,长轴端点为21,A A ,短轴端点为21,B B ,P 为椭圆上任意一点,O 为坐标原点.1. 焦半径1PF 的范围:[]c a c a +-,.类似的:OP 的范围:[]a b ,.2. 焦点三角形的周长:c a L 22+=.3.[]22221,b c b PF PF -∈⋅,当且仅当P 位于短轴端点时取得22c b -,长轴端点时取得2b . 4. 21PF F ∠在点P 位于短轴端点时取得最大值.类似的:21PA A ∠在点P 位于短轴端点时取得最大值.特别的:过焦点的所有弦中通径通径最短,通径:ab L 22= 5. 焦点三角形的面积: ⅰ.2121sin 21PF F PF PF S ∠⋅⋅=. ⅱ.p y c b b S =⋅=+⋅=2tan cos 1sin 22θθθ,当且仅当点P 位于短轴端点时面积取得最大值bc . 6.22121cos e PF F -≥∠,其中e 为椭圆离心率. 7. PF F F PF PF F e 212121sin sin sin ∠+∠∠=,其中e 为椭圆离心率. 实战演练1.已知椭圆()()221:1,3,0,3,02516x y C A C +=-,B 为椭圆上一点,则在ABC ∆中BC A sin sin sin +的值为 .2.已知21,F F 为椭圆221:12516x y C +=的两个焦点,过1F 的直线交椭圆于B A ,,且1222=+B F A F ,则=AB .3.如图,把椭圆2212516x y +=的长轴AB 分成8分,过每个分点作x 轴的垂线交椭圆的上半部分于1P ,2P ,……7P 七个点,F 是椭圆的一个焦点,则127......PF P F P F +++= .4.已知椭圆()012222>>=+b a b y a x 的左右焦点分别为F ₁(-c ,0)、F ₂(c,0),且椭圆上存在一点P 使得∠F ₁PF ₂ =90°,则椭圆离心率e 的取值范围是: .5.若P 是椭圆16410022=+y x 上的一点,1F 、2F 分别是其左右焦点,且︒=∠6021PF F ,则△21PF F 的面积=S ,点P 的坐标为 .6.已知椭圆1:222=+y ax C (a >1)的左右焦点分别为1F 、2F ,P 为椭圆上一点,且︒=∠6021PF F ,则||||21PF PF ⋅的值为 .7.已知椭圆14:22=+y x C 的左右焦点分别为1F 、2F , P 是椭圆上一点,当△21PF F 的面积为1时,21PF PF ⋅的值为 .8.已知椭圆22194x y +=的左右焦点分别为1F 、2F ,点P 为其上的动点,当12F PF ∠为钝角时,点P 横坐标的取值范围是 .9.已知椭圆221164x y +=的左右焦点分别为1F 、2F ,点M 为其上的动点,当12F MF ∆为直角三角形时,12F MF ∆的面积=S .若将第9题椭圆方程变为2212516x y +=,则12F MF ∆的面积=S . 10.已知椭圆221259x y +=的左右焦点分别为1F 、2F ,点P 为其上的动点,且1260PF F ∠= ,则12F PF ∆的面积=S .11.已知椭圆221259x y +=的左右焦点分别为1F 、2F ,点P 为其上的动点,直线1PF 的斜率为73,则12F PF ∆的面积=S .。
椭圆焦点三角形的性质

一
。
一
1 f P F1
PF 2 l S i n 一
0
0
t an
两个 交 点 ( O , 一6 ) 、 ( 0 , 6 ) 。若 点 P 的 横 坐标 为 0 , 则 点 P在圆 z +Y 一C 上 , 故 /F PF 2为直 角 ; 若 点
P 的横 坐标 ∈( 一a , 0 ) U( 0 , a ) , 则 点 P在圆 z 。 + Y 。 一C 外 , 故 F PF 为锐 角 。 当c >6时 , 椭 导 。
例 2 已知 F 1 、 F z 是椭圆 c: x z T y Z —l ( 口 >6
P F 2 。若 △PF F z的面积 为 9 , 则6 一
四个 交点 。联 立 +西 Y 一 1和 。 +Y 一c , 得 一
,, n 。
。
—
—
解: 由椭 圆焦 点三 角形 的性 质 2 , 知 9 —6 z t d , n
性质 1 : 设以原点为圆心, 以 椭 圆 的 两 个 焦 点 的
由c >b , 知 在 椭 圆 上 存 在 点 P, 使
F P F 是锐角、 直角、 钝角。 设点 P的横 坐标 为 。 由椭 圆焦 点 三 角 形 的 性 质 1及 其 探 究 , 知: 当 F PF 为 直 角 时 , z 一 ± 二 一 ± 3 ;当
2 r l
z ∈ f 一 互 , — - b 2 1 , 则 点P 在 圆 z z + z 一 ≥ 羔 2 ( 字) 一
f 内 , 故 F P F。 为钝 角 。
中学生数理亿. 赢I l 赢三使用
椭 园 焦 点 三 角 开 乡 白 勺J } 生质
一 甘 肃
秒杀题型 焦点三角形(椭圆与双曲线)

2020年高考数学试题调研之秒杀圆锥曲线压轴题之秒杀题型三:椭圆、双曲线焦点三角形椭圆的焦点三角形:椭圆上任意一点P 与两焦点1F 、2F 构成的三角形:12PF F ∆。
秒杀题型一:性质:1.周长为定值:2()a c +。
2.12,F PF θ∠=当点P 靠近短轴端点时θ增大,当点P 靠近长轴端点时θ减小;与短轴端点重合时θ最大。
类比:(注:椭圆中端点三角形(长轴两端点与椭圆上一点构成)当P 在短轴端点时顶角最大。
)。
1.(2017年新课标全国卷I 文12)设A 、B 是椭圆C 1323=+m y x 长轴的两个端点,若C 上存在点M 满足︒=∠120AMB ,则m 的取值范围是()A.(][)+∞,91,0 B.(][)+∞,93,0 C.(][)+∞,41,0 D.(][)+∞,43,0【解析】:当03m <<时,椭圆的焦点在x 轴上,要使C 上存在点M 满足120AMB ∠=,则tan 60ab≥= ,即≥.得01m <≤;当3m >时,椭圆的焦点在y 轴上,要使C 上存在点M 满足120AMB ∠= ,则tan 60ab ≥= ,≥,得9m ≥,故m 的取值范围为(][)+∞,91,0 ,选A.秒杀题型二:3.三角形面积:212tan 22S c y c y b θ=⨯⨯=⨯=,max ,S bc =即P 与短轴端点重合时面积最大。
1.(高考题)已知1F ,2F 是椭圆1:2222=+by a x C )0(>>b a 的两个焦点,P 为椭圆C 上一点,21PF PF ⊥.若21F PF ∆的面积为9,则b =.【解析】:由椭圆焦点三角形面积公式得:94tanb 22==b π,3=∴b 。
〖母题1〗已知12,F F 是椭圆22195x y +=的焦点,点P 在椭圆上且123F PF π∠=,求12F PF ∆的面积.【解析】:由椭圆定义及余弦定理得:533。
椭圆焦点三角形的性质探究与应团

椭圆焦点三角形的性质探究与应团作者:洪汪宝来源:《中学生数理化·高二数学》2019年第01期我们知道,椭圆上任意一点(除去长轴端点)与两焦点所构成的三角形称为椭圆的焦点三角形。
那么该三角形有哪些特殊的性质呢?本文对椭圆的焦点三角形的性质进行探究并举例说明其应用。
一、性质探究为了研究问题的方便,我们以焦点在x轴上的椭圆为例。
有兴趣的读者,可模仿推导焦点在y轴上的椭圆的情况。
性质1:△PF1F2的周长为定值,其值为2a+2c。
性质2:△PFF2的面积为c|y0|,其最大值为bc,当点P位于短轴端点时焦点三角形的面积取到最大值。
性质3:若∠F1PF2=a,则△PF1F2的面积为b2tana/2。
证明:故故性质4:|PF1|=a+ex0,|PF2|=a-ex0。
证明:根据此性质可知椭圆上的点到焦点的最大距离为a+c,最小距离为a-c,此时该点是椭圆长轴的端点。
性质5:∠F1PF2=a,则当点P位于上、下顶点时,a最大。
证明:由余弦定理知:当且仅当|PF1|=|PF2|即当点P位于上、下顶点时cosa取到最小值,又余弦函数在[0,π]上单调递减,此时a最大。
由以上证明过程不难得出cosa≥2b2/a2-1=1-2e2。
性质6:设∠PF1F2=β,∠PF2F1=θ,则椭圆的离心率e=- sin(β+θ)/sin β +sin θ证明:性质7:如图1,作∠F1PF2的补角的平分线PF,过F,2作PF的垂线,垂足为D点,则点D的轨迹是一个圆。
证明:所以点D的轨迹是一个以原点为圆心,半径为a的圆。
性质8:如图2,作圆与线段F、P的延长线、线段F2P、线段F1F2的延长线分别切于点D、E、F,则点F为椭圆的右顶点。
证明:解得xF=a。
所以点F为椭圆的右顶点。
二、性质应用例1Æ已知△PF1F2的面积为_____。
解:根据性质3可知△PF1F2的面积为9tan 45°=9。
例2Æ已知椭圆0)的两个焦点分别为F1,F2,若椭圆C上存在点P使∠F,PFz= 120°,则该椭圆C的离心率的取值范围为_____。
椭圆中三角形面积公式
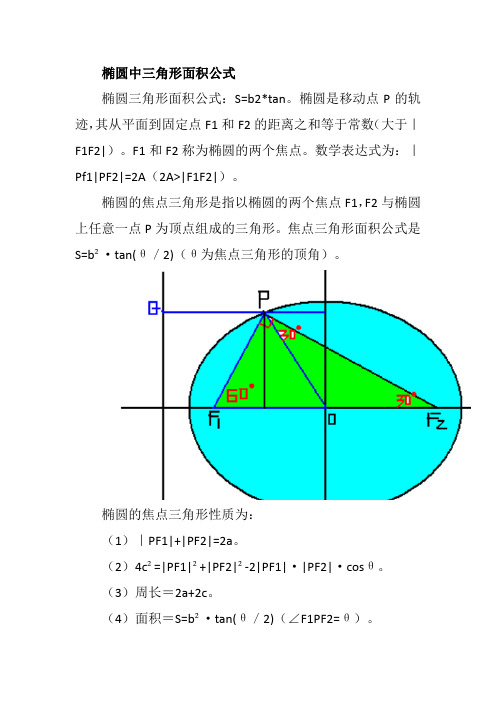
椭圆中三角形面积公式椭圆三角形面积公式:S=b2*tan。
椭圆是移动点P的轨迹,其从平面到固定点F1和F2的距离之和等于常数(大于|F1F2|)。
F1和F2称为椭圆的两个焦点。
数学表达式为:|Pf1|PF2|=2A(2A>|F1F2|)。
椭圆的焦点三角形是指以椭圆的两个焦点F1,F2与椭圆上任意一点P为顶点组成的三角形。
焦点三角形面积公式是S=b²·tan(θ/2)(θ为焦点三角形的顶角)。
椭圆的焦点三角形性质为:(1)|PF1|+|PF2|=2a。
(2)4c²=|PF1|²+|PF2|²-2|PF1|·|PF2|·cosθ。
(3)周长=2a+2c。
(4)面积=S=b²·tan(θ/2)(∠F1PF2=θ)。
椭圆三角形面积公式:S=b^2*tan(θ/2)。
1、离心率由正弦公式推导:F1P/sinα=F2P/sinβ=F1F2/sin θ,sinθ=sin(α+β),F1P+F2P=2a,F1F2=2c,e=c/a。
2、已知tan(θ/2)=sinα/(cosα+1)。
3、焦点三角形面积由余弦公式推导:∠F1PF2=θ,PF1=m,PF2=n。
4、则m+n=2a,在△F1PF2中,由余弦定理:(F1F2)^2=m^2+n^2-2mncosθ。
5、即4c^2=(m+n)^2-2mn-2mncosθ=4a^2-2mn(1+cosθ)。
6、所以mn=2b^2/(1+cosθ)。
7、S=(mnsinθ)/2=b^2*sinθ/(1+cosθ)=b^2*tan(θ/2)。
椭圆三角形表达椭圆是移动点P的轨迹,其从平面到固定点F1和F2的距离之和等于常数(大于|F1F2|)。
F1和F2称为椭圆的两个焦点。
数学表达式为:Pf1|PF2|=2A(2A>|F1F2|)。
焦点三角形面积公式是S=b²·tan(θ/2)(θ为焦点三角形的顶角)。
椭圆焦点三角形性质

椭圆焦点三角形性质是椭圆的一个重要性质,它是椭圆的一种特殊的三角形,它的特点是它的三个顶点都在椭圆的焦点上。
椭圆焦点三角形的性质有以下几点:1、椭圆焦点三角形的三个顶点都在椭圆的焦点上,这是椭圆焦点三角形的最大特点。
2、椭圆焦点三角形的三条边都是椭圆的椭圆轴,也就是说,椭圆焦点三角形的三条边都是椭圆的椭圆轴。
3、椭圆焦点三角形的三个内角都是相等的,也就是说,椭圆焦点三角形的三个内角都是相等的。
4、椭圆焦点三角形的三条边都是等长的,也就是说,椭圆焦点三角形的三条边都是等长的。
5、椭圆焦点三角形的三个外角都是相等的,也就是说,椭圆焦点三角形的三个外角都是相等的。
6、椭圆焦点三角形的三个顶点都在椭圆的焦点上,这意味着椭圆焦点三角形的三个顶点都在椭圆的焦点上,而不是在椭圆的椭圆轴上。
7、椭圆焦点三角形的三条边都是等腰的,也就是说,椭圆焦点三角形的三条边都是等腰的。
8、椭圆焦点三角形的三个外角都是相等的,也就是说,椭圆焦点三角形的三个外角都是相等的。
9、椭圆焦点三角形的三个内角都是相等的,也就是说,椭圆焦点三角形的三个内角都是相等的。
10、椭圆焦点三角形的三条边都是等腰的,也就是说,椭圆焦点三角形的三条边都是等腰的。
椭圆焦点三角形的性质是椭圆的一个重要性质,它是椭圆的一种特殊的三角形,它的特点是它的三个顶点都在椭圆的焦点上,而不是在椭圆的椭圆轴上。
椭圆焦点三角形的三条边都是等长的,三个内角和三个外角都是相等的,这是椭圆焦点三角形的特点。
椭圆焦点三角形的性质在几何学中有着重要的应用,它可以用来求解椭圆的焦点,以及椭圆的椭圆轴的长度等问题。
此外,椭圆焦点三角形的性质也可以用来求解椭圆的面积,以及椭圆的周长等问题。
总之,椭圆焦点三角形的性质是椭圆的一个重要性质,它的特点是它的三个顶点都在椭圆的焦点上,而不是在椭圆的椭圆轴上,它的三条边都是等长的,三个内角和三个外角都是相等的,它在几何学中有着重要的应用。
椭圆焦点三角形的面积

椭圆焦点三角形的面积椭圆焦点三角形的面积是数学中比较复杂的概念,需要一定的几何基础和计算技巧才能理解和运用。
下面将介绍有关椭圆焦点三角形面积的概念、定义、性质及其计算方法。
一、椭圆焦点三角形的定义和性质1. 椭圆焦点三角形是指在椭圆上任取三点,分别作为一个焦点和两个椭圆上的点,连接这两个点与另一个焦点所在的直线的三角形称为椭圆焦点三角形。
2. 椭圆焦点三角形的三条边与椭圆的三条轴互相垂直。
3. 椭圆焦点三角形的三个顶点在椭圆上,其中有一个顶点位于凸部,另外两个顶点位于凹部。
二、椭圆焦点三角形面积的求解方法1. 利用两个焦点和椭圆上的一个点,求出椭圆离心率e的值。
2. 根据椭圆的半长轴a和半短轴b以及离心率e的值,求出椭圆的焦距c和焦点的坐标。
3. 利用椭圆的焦距和焦点的坐标,求出椭圆的方程。
4. 求出椭圆焦点三角形的三角形面积公式:S = 1/2 * a * b * e。
5. 根据已知的椭圆焦点三角形上的两个点和一个焦点的坐标,求出三角形的边长公式。
6. 利用得到的椭圆焦点三角形的边长和三角形面积公式,求出三角形的面积。
三、椭圆焦点三角形面积计算实例1. 已知椭圆的半长轴a = 3,半短轴b = 2,一个焦点坐标为(-2,0),另一个焦点坐标为(2,0),并且椭圆上的一个点坐标为(0,2)。
求椭圆焦点三角形的面积。
解:根据公式,可计算出椭圆的离心率为e = 0.866。
然后,可以求出椭圆的焦距c = 2.449,焦点坐标为(-2.449,0)和(2.449,0),椭圆的方程为(x^2/9) + (y^2/4) = 1。
接着,可以求出椭圆焦点三角形边长:AB = 5.303,AC = 3.606,BC = 4.043。
最后,利用面积公式S = 1/2 * a * b * e = 2.598 ,可得出椭圆焦点三角形的面积为2.598。
12.4.3焦点三角形的性质及椭圆中的最值问题
F1
O
F2
x
x2 (2)已知直线l : x y m 0与椭圆C : y 2 1, 4 交于A, B两点,求|AB | 的最大值.
4 10 5
(2)当F 1PF 2 60 时,求F 1PF 2的面积;
4 3 3
y
F1
o
F2
x
x2 y 2 变式:已知椭圆 2 2 1 (a b 0), 焦点坐标为F1 , F2 , 点P为椭圆上的动点, a b 2 S△ PF1F2 b tan 若F1PF2 时,求F1PF2的面积; 2
2
xp2
yp2
F1
o
P F2
x
PF1 PF2 2 cos F1PF2 0 PF1 PF2 0 ( 5 x p )( 5 x p ) y p 0 | PF1 || PF2 |
4 2 9 3 5 3 5 2 x ( , ) xp 5 y p 0 x p 5 4 x p 0 x p p 9 5 5 5
3. 椭圆上一点到定直线的距离的最值问题
x2 y 2 例1:已知椭圆 1,直线L : 4 x 5 y 40 0, 25 9 椭圆上是否存在一点,它到直线L的距离最小? 最小距离是多少?
解:设直线m平行于l, 则l可写成: 4x 5 y k 0
4 x 5 y k 0 2 2 由方程组 x y 1 25 9 2 2 消去y,得25x 8kx k - 225 0
x2 y 2 2.在椭圆 C: 2 2 1( a b 0 )中, F1 和 F2 是椭圆的两个焦 a b
椭圆专题:椭圆中焦点三角形的6种常见考法高二数学上学期同步讲与练(选择性必修第一册)(原卷版)

椭圆专题:椭圆中焦点三角形的6种常见考法焦点三角形的定义与常用性质1、定义:椭圆上一点与椭圆的两个焦点组成的三角形通常称为“焦点三角形”。
一般利用椭圆的定义、余弦定理和完全平方公式等知识,建立12+AF AF ,2212+AF AF ,12AF AF 之间的关系,采用整体代入的方法解决焦点三角形的面积、周长及角的有关问题(设12∠F AF 为 )2、常用性质性质1:122+=AF AF a ,122+=BF BF a (两个定义)拓展:12∆AF F 的周长为121222++=+AF AF F F a c1∆ABF 的周长为12124+++=AF AF BF BF a性质2:222212121242cos ==+-c F F AF AF AF AF θ(余弦定理)性质3:当A 为短轴的端点时,12∠F AF 最大推导:由性质2得,()222221212121212244c cos 22+--+-==AFAF AF AF c AF AF AF AF AF AF θ()222121212224221--==-a AF AF cb AF AF AF AF .∵212212+=22⎛⎫≤ ⎪⎝⎭AF AF AF AF a ,当且仅当12=AF AF 时,即点A 是短轴端点时取等号,∴2221222cos 11=-≥-b b AF AF aθ.又∵cos =y θ在()0,π上单调递减,∴当A 为短轴的端点时,12∠F AF 最大。
性质4:122121sin tan 22∆===AF F A S AF AF b c y θθ当=A y b ,即A 为短轴的端点时,12∆AF F 的面积最大,最大值为bc推导:由性质3的推导过程得2122cos 1=-b AF AF θ∴21221cos =+b AF AF θ,∴122221222sincos 11222sin sin tan 221cos 22cos 2∆==⋅⋅=⋅=+AF F b S AF AF b b θθθθθθθ题型一椭圆中焦点三角形的周长问题【例1】已知∆ABC 的顶点B ,C 在椭圆2211216x y +=上,顶点A 是椭圆的一个焦点,且椭圆的另一个焦点在BC 边上,则∆ABC的周长是()A.23B.3C.8D.16【变式1-1】已知椭圆()222210x y a b a b+=>>的两个焦点为1F ,2F ,过点1F 的直线交椭圆于A ,B 两点,若2∆ABF 的周长为16,则=a ()A.2B.4C.6D.8【变式1-2】椭圆C :2221(0)x y a a+=>的左、右焦点分别为1F ,2F ,P 为椭圆上异于左右顶点的任意一点,1PF 、2PF 的中点分别为M 、N ,O 为坐标原点,四边形OMPN 的周长为4,则12∆PF F 的周长是_____.【变式1-3】已知椭圆的方程为22194x y +=,过椭圆中心的直线交椭圆于A 、B 两点,2F 是椭圆的右焦点,则2ABF 的周长的最小值为______.题型二椭圆中焦点三角形的面积问题【例2】椭圆C :2214924x y +=的焦点为1F ,2F ,点P 在椭圆上,若18PF =,则12PF F △的面积为()A.48B.40C.28D.24【变式2-1】设12,F F 是椭圆2211224x y +=的两个焦点,P 是椭圆上一点,且1213cos F PF ∠=.则12PF F △的面积为()A.6B.C.8D.【变式2-2】已知1F 、2F 为椭圆22:14x y Γ+=的左、右焦点,M 为Γ上的点,则12MF F △面积的最大值为()B.2C.D.4【变式2-3】已知点P 为椭圆C :22195x y +=上一点,点1F ,2F 分别为椭圆C 的左、右焦点,若122PF PF =,则12PF F △的内切圆半径为()B.155题型三椭圆中焦点三角形的个数问题【例3】已知点1F 、2F 为椭圆22143x y+=的左、右焦点,若点P 为椭圆上一动点,则使得123F PF π∠=的点P 的个数为()A.0B.2C.4D.不能确定【变式3-1】设椭圆22:184x y Γ+=的左、右两焦点分别为1F ,2F ,P 是Γ上的点,则使得12PF F △是直角三角形的点P 的个数为_________.【变式3-2】已知1F 、2F 为椭圆22143x y+=的左、右焦点,若M 为椭圆上一点,且12MF F △的内切圆的周长等于π,则满足条件的点M 的个数为()A.2B.4C.0D.不确定【变式3-3】若1F 、2F 分别是椭圆2212516x y +=的左、右焦点,M 是椭圆上的任意一点,且12MF F △的内切圆的周长为3π,则满足条件的点M 的个数为()A.2B.4C.6D.不确定题型四椭圆中焦点三角形的顶点坐标问题【例4】已知1F 、2F 为双曲线C :221x y -=的左、右焦点,点P 在C 上,21PF F ∠=︒60,则P 到x 轴的距离为()A.2B.2【变式4-1】已知椭圆221169x y +=的左、右焦点分别为1F ,2F ,点P 在椭圆上,若12PF F △为直角三角形,则点P 到x 轴的距离为()或94B.3D.94【变式4-2】椭圆22194x y +=的焦点F 1,F 2,点P 为其上的动点,当∠F 1PF 2为钝角时,点P横坐标的取值范围是()A.B.)C.(﹣5,5)D.(﹣5,5)【变式4-3】椭圆22:14x C y +=的左右焦点分别为12,F F ,点M 为其上的动点,当12F MF ∠为钝角时,点M 的纵坐标的取值范围是____________.题型五椭圆中焦点三角形的中位线问题【例5】设1F ,2F 为椭圆22194x y+=的两个焦点,点P 在椭圆上,若线段1PF 的中点在y 轴上,则21PF PF 的值为()A.513B.45C.27D.49【变式5-1】已知椭圆22195x y +=的左焦点为F ,点P 在椭圆上且在x 轴的上方,若线段PF的中点在以原点O 为圆心,OF 为半径的圆上,则直线PF 的斜率是()B.D.【变式5-2】已知椭圆22:194x y C +=,点M 与C 的焦点不重合,若M 关于C 的焦点的对称点分别为,A B ,线段MN 的中点在椭圆C 上,则AN BN +的值为()A.6B.12C.18D.24【变式5-3】如图,若P 为椭圆C :()222210x y a b a b+=>>上一点,()F -为椭圆的焦点,若以椭圆短轴为直径的圆与PF 相切于中点,则椭圆C 的方程为___________.题型六椭圆中焦点三角形的角平分线问题【例6】已知1F ,2F 是椭圆C :22214x y b+=的左、右焦点,离心率为12,点A 的坐标为3(1,)2,则12F AF ∠的平分线所在直线的斜率为()A.2B.1【变式6-1】已知12F F ,是椭圆221369x y+=的两个焦点,P 是椭圆上任意一点,过1F 引12F PF ∠的外角平分线的垂线,垂足为Q ,则Q 与短轴端点的最近距离为()A.5B.4C.3D.2【变式6-2】已知椭圆()2221024x y b b+=<<,1F ,2F 分别为椭圆的左、右焦点,P 为椭圆上一点,()2,1M ,1MF 平分角12PF F ∠,2MF 是角21PF F ∠的外角平分线,则1MPF 与2MPF 的面积之和为()A.1B.32C.2D.3【变式6-3】已知1F ,2F 是椭圆22221(0)x y a b a b+=>>的两焦点,P 是椭圆上任一点,从2F 引12F PF ∠外角平分线的垂线,垂足为Q ,则点Q 的轨迹为()A.圆B.两个圆C.椭圆D.两个椭圆。
焦点三角形

焦点三角形焦点三角形问题是重要考点,考到的内容有:椭圆或双曲线定义和正余弦定理以及面积公式等。
常与曲线的离心率相结合,注意平面几何知识的应用。
一:椭圆的焦点三角形椭圆的焦点三角形是指以椭圆的两个焦点12,F F 与椭圆上任意一点P 为顶点组成的三角形。
)0(12222>>=+b a by a x性质有:(1)12||||2PF PF a +=(2)2221212124||||2||||cos c PF PF PF PF F PF =+-∠(3)椭圆上的点与两焦点连线的夹角以椭圆短轴顶点与两焦点连线的夹角最大.证明:设P 是椭圆22221x y a b+= (0a b >>,c 为半焦距)上的一点,O 为原点,E 、F 是椭圆的两焦点,PE m =,PF n =则222222244222cos 1122m n c b mn b b EPF mn mn mn a+--∠===-≥-,由余弦函数图象性质知EPF ∠有最大值,当且仅当P 在短轴端点时取到该最大值。
(4)设P 为椭圆上的任意一点,角12F F P α∠=,21F F P β∠=,21F PF θ∠=,则有离心率sin()sin sin e αβαβ+=+,122sin 1cos PF F S b θθ∆=+证明:由正弦定理得:βαβαsin sin )180sin(1221PF PF F F o==--由等比定理得:βαβαsin sin )sin(2121++=+PF PF F F 而)sin(2)sin(21βαβα+=+c F F ,βαβαsin sin 2sin sin 21+=++a PF PF ∴βαβαsin sin )sin(++==a c e 。
例题:1、椭圆22221(,0)x y a b a b+=>的两个焦点12,F F ,点P 在椭圆上,且1212414,||,||33PF PF PF PF ⊥==.求椭圆的方程22194x y +=2、设P 为椭圆12222=+by a x )0(>>b a 上一点,F 1、F 2为焦点,如果 7521=∠F PF ,1512=∠F PF ,则椭圆的离心率为( )A .22 B .23 C .32 D .36 3、1F 、2F 是椭圆17922=+y x 的两个焦点,A 为椭圆上一点,且∠02145=F AF ,则 12AF F ∆的面积为( )A .7B .47 C .27 D .257 4、1F 、2F 是椭圆2212516x y +=的两个焦点,A 为椭圆上一点,且1290,F AF ∠= ,则A 到x 轴的距离为A .163B .165C .161635or D .非上述答案 5、设21F F ,分别是椭圆1162522=+y x 的左、右焦点,P 为椭圆上一点,12,F F P , 是直角三角形的一个顶点,则P 点到x 轴的距离是 A.163 B . 165 C.161653或 D. 非上述答案 6、设21F F ,分别是椭圆221259x y +=的左、右焦点,P 为椭圆上一点,12,F F P , 是是直角三角形的三个顶点,则P 点到x 轴的距离是A.94 B. 95 C . 9954或 D. 非上述答案 7、过椭圆左焦点F ,倾斜角为3π的直线交椭圆于A ,B 两点,若FB FA 2=,则椭圆的离心率为 (构造焦点三角形,两次应用余弦定理,整体处理余弦定理的结果)8、已知Rt ABC ∆,1,AB AC ==点C 为椭圆22221(0)x y a b a b+=>>的右焦点,且AB 为经过椭圆左焦点的弦,求椭圆的离心率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
焦点三角形习题性质一:过椭圆焦点的所有弦中通径(垂直于焦点的弦)最短,通径为ab 22性质二:已知椭圆方程为),0(12222>>=+b a b y a x 两焦点分别为,,21F F 设焦点三角形21F PF 中,21θ=∠PF F 则2tan221θb S PF F =∆.证明:记2211||,||r PF r PF ==,由椭圆的第一定义得.4)(,2222121a r r a r r =+∴=+在△21PF F 中,由余弦定理得:.)2(cos 22212221c r r r r =-+θ配方得:.4cos 22)(22121221c r r r r r r =--+θ 即.4)cos 1(242212c r r a =+-θ.cos 12cos 1)(222221θθ+=+-=∴b c a r r由任意三角形的面积公式得:2tan 2cos 22cos2sin2cos 1sin sin 2122222121θθθθθθθ⋅=⋅=+⋅==∆b b b r r S PF F ..2tan 221θb S PF F =∴∆同理可证,在椭圆12222=+bx a y (a >b >0)中,公式仍然成立.性质三:已知椭圆方程为),0(12222>>=+b a by a x 两焦点分别为,,21F F 设焦点三角形21F PF 中,21θ=∠PF F 则.21cos 2e -≥θ性质三证明:设,,2211r PF r PF ==则在21PF F ∆中,由余弦定理得:1222242)(2cos 212221221221212212221--=--+=-+=r r c a r r c r r r r r r F F r r θ.2112221)2(222222222122e a c a r r c a -=--=-+-≥ 命题得证。
例1. 若P 是椭圆16410022=+y x 上的一点,1F 、2F 是其焦点,且︒=∠6021PF F , 求△21PF F 的面积.例1.解法一:在椭圆16410022=+y x 中,,6,8,10===c b a 而.60︒=θ 记.||,||2211r PF r PF ==Θ点P 在椭圆上,∴由椭圆的第一定义得:.20221==+a r r在△21PF F 中,由余弦定理得:.)2(cos 22212221c r r r r =-+θ配方,得:.1443)(21221=-+r r r r.144340021=-∴r r 从而.325621=r r .336423325621sin 212121=⨯⨯==∆θr r S PF F 解法二:在椭圆16410022=+y x 中,642=b ,而.60︒=θ.336430tan 642tan221=︒==∴∆θb S PF F例2.已知P 是椭圆192522=+y x 上的点,1F 、2F 分别是椭圆的左、右焦点,212121=,则△21PF F 的面积为( ) A. 33 B. 32 C. 3 D.33 解:设θ=∠21PF F ,则21cos 2121==θ,.60︒=∴θ .3330tan 92tan221=︒==∴∆θb S PF F 故选答案A.例3.已知椭圆191622=+y x 的左、右焦点分别是1F 、2F ,点P 在椭圆上. 若P 、1F 、2F 是一个直角三角形的三个顶点,则点P 到x 轴的距离为( ) A.59 B. 779 C. 49 D. 49或779解:若1F 或2F 是直角顶点,则点P 到x 轴的距离为半通径的长492=a b ;若P 是直角顶点,设点P 到x 轴的距离为h ,则945tan 92tan221=︒==∆θb S PF F ,又,7)2(2121h h c S PF F =⋅⋅=∆ 97=∴h ,.779=h 故选D.1. 椭圆1244922=+x y 上一点P 与椭圆两个焦点1F 、2F 的连线互相垂直,则△21PF F 的面积为( )A. 20B. 22C. 28D. 24 解:24,90221=︒==∠b PF F θ,∴2445tan 242tan 221=︒==∆θb S PF F .故选D.2. 椭圆1422=+y x 的左右焦点为1F 、2F , P 是椭圆上一点,当△21PF F 的面积为1时,21PF PF ⋅的值为( )A. 0B. 1C. 3D. 6 解:设θ=∠21PF F ,Θ12tan2tan221===∆θθb S PF F ,∴︒=︒=90,452θθ,021=⋅PF PF .故选A.3. 椭圆1422=+y x 的左右焦点为1F 、2F , P 是椭圆上一点,当△21PF F 的面积最大时,21PF PF ⋅的值为( )A. 0B. 2C. 4D. 2- 解:3,1,2===c b a ,设θ=∠21PF F ,Θ 2tan 2tan 221θθ==∆b S PF F ,∴当△21PF F 的面积最大时,θ为最大,这时点P 为椭圆短轴的端点,︒=120θ, ∴2120cos cos ||||22121-=︒=⋅=⋅a PF PF PF PF θ.故答案选D. 4.已知椭圆1222=+y ax (a >1)的两个焦点为1F 、2F ,P 为椭圆上一点,且︒=∠6021PF F ,则||||21PF PF ⋅的值为( )A .1B .31C .34D .32 解:︒==∠6021θPF F ,1=b ,3330tan 2tan221=︒==∆θb S PF F , 又Θ||||43sin ||||21212121PF PF PF PF S PF F ⋅=⋅=∆θ, ∴33||||4321=⋅PF PF ,从而34||||21=⋅PF PF . 故答案选C.5. 已知椭圆的中心在原点,对称轴为坐标轴,1F 、2F 为焦点,点P 在椭圆上,直线1PF 与2PF 倾斜角的差为︒=∠9021PF F ,△21PF F 的面积是20,且c/a=√5/3, 求椭圆的标准方程.解:设θ=∠21PF F ,则︒=90θ. Θ 2045tan 2tan 22221==︒==∆b b b S PF F θ,又Θ3522=-==a b a ace , ∴95122=-ab ,即952012=-a .解得:452=a .∴所求椭圆的标准方程为1204522=+y x 或1204522=+x y .专题2:离心率求法:1.若椭圆的两个焦点与它的短轴的两个端点是一个 正方形的四个顶点,则椭圆的离心率为( )1.解析:选A.如图所示,四边形B 1F 2B 2F 1为正方形,则△B 2OF 2为等腰直角三角形, ∴c a =22.2.若一个椭圆长轴的长度、短轴的长度和焦距 成等差数列,则该椭圆的离心率是( )2.解析:选B.由题意知2b =a +c ,又b 2=a 2-c 2,∴4(a 2-c 2)=a 2+c 2+2ac .∴3a 2-2ac -5c 2=0.∴5c 2+2ac -3a 2=0.∴5e 2+2e -3=0.∴e =35或e =-1(舍去).3.若椭圆的短轴长为6,焦点到长轴的一个端点的最近距离是1,则椭圆的离心率为________.3.解析:依题意,得b =3,a -c =1.又a 2=b 2+c 2,解得a =5,c =4,∴椭圆的离心率为e =c a =45. 答案:454.已知A 为椭圆x 2a 2+y 2b2=1(a >b >0)上的一个动点,直线AB 、AC 分别过焦点F 1、 F 2,且与椭圆交于B 、C 两点,若当AC 垂直于x 轴时,恰好有|AF 1|∶|AF 2|=3∶1,求该椭圆的离心率.4.解:设|AF 2|=m ,则|AF 1|=3m ,∴2a =|AF 1|+|AF 2|=4m . 又在Rt△AF 1F 2中,|F 1F 2|=|AF 1|2-|AF 2|2=22m .∴e =2c 2a =|F 1F 2|2a =22m 4m =22.5.如图所示,F 1、F 2分别为椭圆的左、右焦点,椭圆上点M 的横坐标等于右焦点的横坐标,其纵坐标等于短半轴长的23,求椭圆的离心率.5. 解:法一:设椭圆的长半轴、短半轴、半焦距长分别为a 、b 、c .则焦点为F 1(-c,0),F 2(c,0),M 点的坐标为(c ,23b ),则△MF 1F 2为直角三角形. 在Rt△MF 1F 2中,|F 1F 2|2+|MF 2|2=|MF 1|2,即4c 2+49b 2=|MF 1|2.而|MF 1|+|MF 2|=4c 2+49b 2+23b =2a ,整理得3c 2=3a 2-2ab .又c 2=a 2-b 2,所以3b =2a .所以b 2a 2=49.∴e 2=c 2a 2=a 2-b 2a 2=1-b 2a 2=59, ∴e =53.法二:设椭圆方程为x 2a 2+y 2b 2=1(a >b >0),则M (c ,23b ).代入椭圆方程,得c 2a 2+4b29b2=1,所以c 2a 2=59,所以c a =53,即e =53.椭圆中焦点三角形的性质及应用(答案)性质二离心率求法:。
