圆曲线正矢计算
python 铁路圆曲线正矢计算

Python程序可以用于计算铁路圆曲线的正矢,这一主题不仅涉及到数学和物理知识,还涉及到工程领域。
接下来,我将详细讨论这一主题,并向您介绍相关的知识和应用。
一、什么是铁路圆曲线正矢计算?铁路圆曲线正矢计算是指通过数学方法,计算铁路轨道在曲线上的几何特征,包括曲线的半径、切线和法线的角度等。
这些几何特征对于铁路设计和施工非常重要,可以保证铁路线路的安全和稳定。
在铁路工程中,正矢是指铁路轨道中心线在曲线上的长度,它是曲线设计和施工的基础参数,也是铁路设计者必须要考虑的参数之一。
通过Python程序计算铁路圆曲线正矢是非常有必要的。
二、Python程序计算铁路圆曲线正矢的基本原理Python程序可以通过数学计算的方法,计算铁路圆曲线的半径、切线和法线的角度,从而得到曲线的正矢。
该程序一般包括了数学计算公式和相关的变量,可以根据用户输入的参数进行计算,并输出结果。
在Python程序中,可能会用到一些数学库,比如math库,来进行数学计算。
通过输入铁路曲线的一些基本参数,比如曲线半径、曲线长度等,可以得到曲线的正矢,从而满足铁路设计和施工的需要。
三、Python程序计算铁路圆曲线正矢的实际应用Python程序计算铁路圆曲线正矢的实际应用非常广泛。
它可以应用于铁路线路的设计和施工,可以帮助工程师们快速、准确地计算曲线参数,从而保证铁路的设计和施工质量。
Python程序计算铁路圆曲线正矢也可以应用于铁路维护和改造工程。
通过对已有铁路线路的曲线参数进行计算,可以及时发现问题并进行改进,保证铁路线路的运营安全和稳定。
四、对这一主题的个人观点和理解铁路圆曲线正矢计算是铁路工程中非常重要的一部分,它关乎到整个铁路线路的安全和稳定。
而Python程序作为计算工具,可以帮助工程师们快速地进行曲线参数的计算,从而提高工作效率和精度。
Python程序计算铁路圆曲线正矢是非常有价值的,它在铁路工程领域具有广泛的应用前景,可以帮助工程师们更好地进行铁路设计、施工和维护工作。
正矢计算公式教学文案
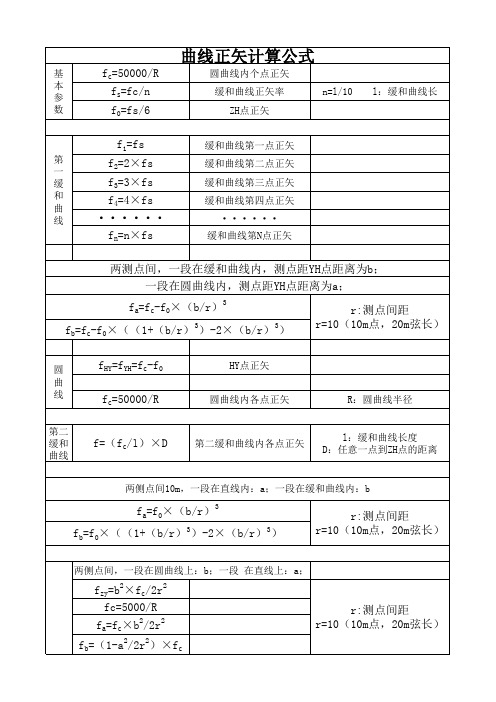
基
fc=50000/R
本 参
fs=fc/n
数
f0=fs/6
圆曲线内个点正矢 缓和曲线正矢率
ZH点正矢
n=l/10 l:缓和曲线长
பைடு நூலகம்
f1=fs
第 一
f2=2×fs
缓
f3=3×fs
和 曲
f4=4×fs
线
······
fn=n×fs
缓和曲线第一点正矢 缓和曲线第二点正矢 缓和曲线第三点正矢 缓和曲线第四点正矢
HY点正矢 圆曲线内各点正矢
R:圆曲线半径
第二
缓和 f=(fc/l)×D
曲线
第二缓和曲线内各点正矢
l:缓和曲线长度 D:任意一点到ZH点的距离
两侧点间10m,一段在直线内:a;一段在缓和曲线内:b
fa=f0×(b/r)3 fb=f0×((1+(b/r)3)-2×(b/r)3)
r:测点间距 r=10(10m点,20m弦长)
两侧点间,一段在圆曲线上:b;一段 在直线上:a;
fzy=b2×fc/2r2 fc=5000/R
fa=fc×b2/2r2 fb=(1-a2/2r2)×fc
r:测点间距 r=10(10m点,20m弦长)
······ 缓和曲线第N点正矢
两测点间,一段在缓和曲线内,测点距YH点距离为b; 一段在圆曲线内,测点距YH点距离为a;
fa=fc-f0×(b/r)3 fb=fc-f0×((1+(b/r)3)-2×(b/r)3)
r:测点间距 r=10(10m点,20m弦长)
圆
fHY=fYH=fc-f0
曲
线
fc=50000/R
圆曲线计划正矢计算公式

在超市购物时的一次奇遇
前几天我去超市买东西,正玩着手机的时候,无意中看到一本关于烘焙的杂志。
里面介绍了一个圆曲线计划,说是能让蛋糕更加美味,想着可以试试看,就买下来了。
回到家里,我开始照着杂志上的步骤准备材料。
首先是面粉、砂糖、鸡蛋和奶油,然后把它们按照一定的比例混合在一起。
接着,我就要开始用计算公式来确定正矢,这个就是决定蛋糕转动方向和速度的重要参数。
我翻开杂志,上面写着圆曲线计划正矢计算公式。
这个公式看起来挺复杂,有各种角度、半径和速度的参数。
我抓起笔和纸,开始认真地算起来。
首先是角度的计算,要考虑到蛋糕在烤箱中的转动角度,然后是半径的确定,这取决于烤盘的大小。
最后就是速度的计算,要让蛋糕在烤箱中均匀受热,这样做出来的蛋糕才会松软美味。
我一遍又一遍地计算着,直到确定了最终的正矢数值。
然后,我把蛋糕放进预热好的烤箱,按照计算好的正矢数值开始转动。
等待的时间总是漫长的,但想到马上可以品尝到美味的蛋糕,心情顿时变得兴奋起来。
终于,定时器响了,我打开烤箱,一个金黄色的蛋糕呈现在我的眼前,散发出阵阵诱人的香味。
我小心地把蛋糕取出来,切下一块,蛋糕松软细腻,入口即化,确实比之前做的更好吃。
圆曲线计划正矢计算公式果然厉害,让我的蛋糕变得更加完美了。
这次的烘焙经历让我更加喜爱厨房的乐趣,也让我明白到科学在日常生活中的应用是如此的神奇。
我决定以后多尝试一些不同的烘焙技巧,让自己的厨艺更上一层楼。
算是这次去超市购物的一次奇遇吧!。
曲线正矢计算

曲线正矢计算曲线半径、弦长、正矢之间的关系:2Lf,8R50000f, 当时, (mm) L,20mR12500 当时, (mm) f,L,10mRf式中—圆曲线正矢(mm)—圆曲线半径(m) R现场正线曲线取弦长为20 m计算正矢值。
现场站线曲线取弦长为10 m计算正矢值。
(一)圆曲线上各测点计划正矢50000f圆曲线计划正矢 (mm) ,cRfcf,圆曲线始终点的计划正矢 (mm) 始,终,2(二)缓和曲线正矢是从直线往圆曲线方向逐渐由小变大的,由直缓点向缓圆点方向变化的大小,叫缓和曲线的正矢递增率。
圆曲线计划正矢f,,c缓和曲线的正矢递增率f, ,,N,,一端缓和曲线分段数N1.缓和曲线始终点计划正矢,,缓和曲线正矢递增率fN,f,,缓和曲线始点正矢始6,,缓和曲线终点正矢,f,,f,缓和曲线始点正矢fc 终始2.缓和曲线中间各测点计划正矢f,Nf iiNfi,1,2?,N,1式中—缓和曲线中间各测点的计划正矢i ( );fN —测点距缓和曲线始点的段数 Ni—缓和曲线的正矢递增率【例题】已知曲线半径R=300m,缓和曲线长为70 m(如图3所示)求缓和曲线上各测点计划正矢值。
【解】5000050000mm f,,,167cR300圆曲线计划正矢f167,,cmm f,,,24N,,一端缓和曲线分段数N7 f24Nmm ,,直缓点ZH正矢,f,,,,4始87654663QZHYYH210ZHHZ mm ,,缓圆点HY正矢,f,,f,f,167,4,163c终始缓和曲线中间各测点的计划正矢为图2缓和曲线f,Nf,1,24,24mm 11Nmm f,Nf,2,24,4822Nmm f,Nf,3,24,7233Nmm f,Nf,4,24,9644Nmm f,Nf,5,24,12055Nmm f,Nf,6,24,14466N。
铁路轨道曲线正矢计算(修正)

第一讲:曲线正矢计算一、曲线的分类:目前我段主要曲线类型有:1、由两端缓和曲线和圆曲线组成的曲线,如正线曲线。
容许行车速度高。
2、由圆曲线构成的曲线。
如道岔导曲线、附带曲线。
二、圆曲线正矢的计算1、曲线头尾正好位于起终点桩上F C=L2/8RL=20M 时,F c=50000/RF ZY=F YZ= F c/22、曲线头尾不在起终点桩上ZY 前点:= (FC/2) * ( S /10) 2ZY 后点:F n =FC-{ (FC/2) * ( T /10) 2}FC:圆曲线正矢S : ZY点到后点的距离T : ZY点到前点的距离三、缓和曲线上整点正矢的计算(起始点正好是测点)(1)缓和曲线头尾的计算:F o=F i/6 (缓和曲线起点) F终二F C-F Q (缓和曲线终点)(2)缓和曲线中间点正矢的计算:F I=F S=F C/N( N=L Q/B :缓和曲线分段数)F2=2 F I F3=3F I F I=IF I (I 为中间任意点)四、半点(5米桩)正矢的计算:a) ZH点后半点正矢的计算:F 后=25/48*F[因为ZH点正矢f o=f1/6,很小一般为1~2MM,其前半点很小(小于1MM ) 因此不作计算。
b) HY (YH)点前半点计划正矢的计算F 前=1/2{[L Q3+ (L o-15) 3]/6R L O+[5L°+25]/2R}- ( L Q-5)3/6R L°c) HY (YH)点后半点计划正矢的计算F 后=1/2{[ ( L Q-5)3 -L Q3]/6R L Q+[5L Q+175]/2R} d) 中间点(5米桩)正矢的计算F 中=(F 前+F 后) /2五、测点不在曲线始终点时缓和曲线计划正矢的计算a)缓和曲线始点(ZH点)处相邻测点的计划正矢F产a u F S(直缓点外点) a u =1/6( S /B)3F n = a n F S (直缓点内点) a n =1/6[(1+ S/B)3-( S /B)3](2) 缓圆点处相邻测点的计划正矢F® =F C- a u F S(缓圆点外点,缓和曲线之外)F e = F C- a n F s (缓圆点内点,缓和曲线之内)(a u、a n查纵距率表《曲线设备与曲线整正》附表二)(3) 缓和曲线中间点各点计划正矢的计算F I=(F C/L°)L I(I为中间任意点)说明:B:半弦长S:缓和曲线内点到ZH、HY (YH)距离L o:缓和曲线长F c:圆曲线正矢第二讲:曲线拨道一、绳正法基本原理1、基本假定:(1)假定拨道前后两端切线方向不变,或起始点位置不变,即曲线终点拨量为零。
曲线计划正矢的计算

曲线计划正矢的计算一、计算方法1、圆曲线计划正矢的计算f c=L2/8R式中:L----弦长,一般为20m,当曲线状态不良为确保曲线圆顺,增加正矢点时,为10m;f c----圆曲线正矢(mm);R----曲线半径(m)。
当L=20m时,f c=L2/8R=20*20/8R=50000/R;当L=10m时,f c=L2/8R=10*10/8R=12500/R;2、缓和曲线计划正矢的计算(1)缓和曲线正矢递增率f s= f c/n式中:f c----圆曲线正矢(mm);n----缓和曲线的分段数,其值为l0/ , 其中l0为缓曲长, 为测点间的距离,一般为10m。
(2)缓和曲线各点的计划正矢缓和曲线始点0点(ZH)点的正矢f0=f s/6缓和曲线第1点的正失f1=f s缓和曲线第2点的正失f2=2f s缓和曲线第3点的正失f3=3f s。
缓和曲线终点(HY)的正矢f hy=f c- f03、测点不在曲线始、终点时计划正矢的计算前述缓和曲线和圆曲线的长度都假定是10m的整数倍,但在实际工作中,缓和曲线的长度一般都设置成10m的整数倍,而圆曲线的长度一般都不是10m的整数倍,因此第二缓和曲线的始、终点就不可能恰好落在测点上。
这样缓和曲线始、终点左右相邻测点的计划正矢,都要作为一种特殊情况另行计算。
(1)第二缓和曲线始点(HZ)左右邻点计划正矢的计算HZ不在测点上,位于缓和曲线上的n点和直线上的n+1点之间,n点距HZ点的距离为b,n+1距HZ点的距离为a,相应的正矢分别为f n和f n+1, 为测点间的距离,等于弦长的一半,a+b= ,则:f n=1/6 f s[(1+b/ )3-2(b/ )3]f n+1=1/6 f s(b/ )3(2)第二缓和曲线终点(YH)左右邻点计划正矢的计算第二缓和曲线终点(YH)不在测点上,位于圆曲线上的n点和缓和曲线上的n+1点之间,n点距YH点的距离为a,n+1点距YH点的距离为b,相应的正矢分别为f n和f ,则:n+1f n = f c-1/6 f s(b/ )3f n+1= f c-1/6 f s[(1+b/ )3-2(b/ )3](3)第二缓和曲线上其他各点计划正矢的计算第二缓和曲线上其他各点计划正矢,可根据各点正矢与其距终点HZ距离成直线比例的关系,按下式求取:f i= f c/ l0*l i式中:f i----缓和曲线上距HZ点为l i的测点正矢;二、算例1、圆曲线长度为10m整数倍的曲线计划正矢的计算已知某曲线半径R=600m,两端缓和曲线长l0=50m,求曲线各测点的计划正矢解:(1)圆曲线计划正矢:f c=L2/8R=20*20/8R=50000/R=50000/600=83.3mm,取84mm(2)缓和曲线正矢递增率:f s= f c/n=84/5=16.8mm(3)直缓(缓直)点正矢:f0=f s/6=16.8/6=2.8mm,取3mm(4)缓和曲线中间各点的正矢:缓和曲线第1点的正失f1=f s=16.8mm,取17mm缓和曲线第2点的正失f2=2f s=2*16.8=33.6mm,取34mm缓和曲线第3点的正失f3=3f s=3*16.8=50.4mm,取50mm缓和曲线第4点的正失f4=4f s=4*16.8=67.2mm,取67mm(5)缓圆(圆缓)点正矢:f hy=f c- f0=84-3=81mm2、圆曲线长度不是10m整数倍的曲线计划正矢的计算已知某曲线半径R=600m,两端缓和曲线l0=50m,圆曲线长304m,求各测点的计划正矢解:(1)第一缓和曲线和圆曲线的计划正矢算法同上;(2)第二缓和曲线各点计划正矢的计算:①第二缓和曲线始(HZ)点相邻测点的计划正矢因为圆曲线长L=304m,故第二缓和曲线始(HZ)点距缓和曲线和直线上相邻点(40点、41点)的距离分别为b≈4m,a≈6m, 为测点间的距离,等于弦长的一半,a+b= 则f40=1/6 f s[(1+b/ )3-2(b/ )3]=1/6*16.8*[(1+4/10)3-2*(4/10)3]=7.32mm,取7mmf41=1/6 f s(b/ )3=1/6*16.8*(4/10)3=0.18mm,取0mm②第二缓和曲线终点(YH)相邻测点的计划正矢第二缓和曲线终点(YH)距圆曲线和缓和曲线上相邻点(35点、36点)的距离分别为a≈4m,b≈6m, 为测点间的距离,等于弦长的一半,a+b=则f35 = f c-1/6 f s(b/ )3=84-1/6*16.8*(6/10)3=84-0.6=83.4mm,取84mmf36= f c-1/6 f s[(1+b/ )3-2(b/ )3]=84-1/6*16.8*[(1+6/10)3-2*(6/10)3]=73.74mm,取74mm③第二缓和曲线上其他各点计划正矢的计算其他各点计划正矢,可根据各点正矢与其距终点(HZ)距离成直线比例的关系,按下式求取:f i=f c/l0*l i则第37点、38点、39点的计划正矢分别为:f37=f c/l0*l37=84/50*34=57.12mm,取57mmf38=f c/l0*l38=84/50*24=40.32mm,取40mmf39=f c/l0*l39=84/50*14=23.52mm,取24mm3、辅助点计划正矢的计算辅助点计划正矢的计算按圆曲线长度不是10m整数倍时缓和曲线的算法计算(1)圆曲线长度为10m整数倍时辅助点计划正矢的计算已知某曲线半径R=600m,两端缓和曲线长l0=50m,求缓和曲线辅助点的计划正矢解:辅助点与测点相距5m,即a=b=5m,①缓和曲线上与始点(ZH、HZ)相邻辅助点计划正矢为:f=1/6 f s[(1+b/ )3-2(b/ )3]=1/6*16.8*[(1+5/10)3-2*(5/10)3]=8.75mm,取9mm②缓和曲线上与终点(YH、HY)相邻辅助点计划正矢为:f= f c-1/6 f s[(1+b/ )3-2(b/ )3]=84-1/6*16.8*[(1+5/10)3-2*(5/10)3]=75.25mm,取75mm③缓和曲线其他各中间辅助点的计划正矢:分别取l i=15、25、35,按f i=f c/l0*l i算得辅助点计划正矢分别为:25mm、42mm、59mm(2)圆曲线长度不是10m整数倍时辅助点计划正矢的计算曲线半径R=600m,缓和曲线长l0=50m,圆曲线长304m,求缓和曲线辅助点的计划正矢解:第一个缓和曲线辅助点的算法同上,第二个缓和曲线上辅助点计划正矢的计算按B=b±5计算,即:①缓和曲线上与始点(ZH、HZ)相邻辅助点计划正矢为(B=4+5=9):f=1/6 f s[(1+B/ )3-2(B/ )3]=1/6*16.8*[(1+9/10)3-2*(9/10)3]=15.12mm,取15mm②缓和曲线上与终点(YH、HY)相邻辅助点计划正矢为(B=6-5=1):f= f c-1/6 f s[(1+B/ )3-2(B/ )3]=84-1/6*16.8*[(1+1/10)3-2*(1/10)3]=80.3mm,取80mm③缓和曲线其他各中间辅助点的计划正矢:分别取l i=19、29、39,按f i=f c/l0*l i算得辅助点计划正矢分别为:32mm、49mm、66mm。
曲线正矢、负矢的计算

曲线正矢、负矢的计算
曲线的正矢和负矢可以用以下方式计算:
1. 首先,确定曲线上某一点的切线方向。
可以通过求导函数得到曲线在该点的斜率,然后求出与曲线切线垂直的斜率。
2. 然后,确定该点的切线方向的正方向和负方向。
可以通过选取曲线上该点两侧的点,然后比较切线的斜率方向来确定。
3. 最后,计算该点的正矢和负矢。
正矢是曲线在该点沿切线方向的长度,而负矢是曲线在该点沿切线相反方向的长度。
可以通过测量切线上该点两侧的弧长来计算。
需要注意的是,以上计算方法仅适用于光学曲线(如球面、抛物线等),对于非光学曲线(如螺旋线、心形曲线等),正矢和负矢的定义可能会有所不同。
曲线正矢计算

第一讲:曲线正矢计算一、曲线得分类:目前我段主要曲线类型有:1、由两端缓与曲线与圆曲线组成得曲线,如正线曲线。
容许行车速度高。
2、由圆曲线构成得曲线。
如道岔导曲线、附带曲线。
二、圆曲线正矢得计算1、曲线头尾正好位于起终点桩上F C=L2/8RL=20M时,FC=50000/RF ZY=FYZ= F C/22、曲线头尾不在起终点桩上ZY前点:Fμ=(FC/2) *(δ/10)2ZY后点:Fη=FC-{(FC/2) *(τ/10)2}FC:圆曲线正矢δ:ZY点到后点得距离τ:ZY点到前点得距离三、缓与曲线上整点正矢得计算(起始点正好就是测点)(1)缓与曲线头尾得计算:F0=F1/6(缓与曲线起点) F终=F C-F0 (缓与曲线终点)(2)缓与曲线中间点正矢得计算:F1=F S= F C/N (N=L0/B:缓与曲线分段数)F2=2F1F3=3F1 FI=IF1(I为中间任意点)四、半点(5米桩)正矢得计算:a)ZH点后半点正矢得计算:F后=25/48*F1因为ZH点正矢f0=f1/6,很小一般为1~2MM,其前半点很小(小于1MM)因此不作计算。
b)HY(YH)点前半点计划正矢得计算F前=1/2{[L03+(L0-15)3]/6R L0+[5L0+25]/2R}-(L0-5)3/6R L0c)HY(YH)点后半点计划正矢得计算F后=1/2{[(L0-5)3-L03]/6R L0+[5L0+175]/2R}d)中间点(5米桩)正矢得计算F中=(F前+F后)/2五、测点不在曲线始终点时缓与曲线计划正矢得计算a)缓与曲线始点(ZH点)处相邻测点得计划正矢Fμ=αυF S(直缓点外点)αυ=1/6(δ/B)3Fη=αηFS(直缓点内点) αη=1/6[(1+δ/B)3-(δ/B)3](2)缓圆点处相邻测点得计划正矢Fφ=FC-αυFS (缓圆点外点,缓与曲线之外)Fθ=FC-αηF S (缓圆点内点,缓与曲线之内)(αυ、αη查纵距率表《曲线设备与曲线整正》附表二)(3)缓与曲线中间点各点计划正矢得计算F I=(F C/L0)L I(I为中间任意点)说明:B:半弦长δ:缓与曲线内点到ZH、HY(YH)距离L0:缓与曲线长F C:圆曲线正矢第二讲:曲线拨道一、绳正法基本原理1、基本假定:(1)假定拨道前后两端切线方向不变,或起始点位置不变,即曲线终点拨量为零。
曲线正矢计算

曲线半径、弦长、正矢之间的关系:当 时, (mm) 当 时, (mm) 式中 —圆曲线正矢(mm)—圆曲线半径(m)现场正线曲线取弦长为20 m 计算正矢值。
现场站线曲线取弦长为10 m 计算正矢值。
(一)圆曲线上各测点计划正矢圆曲线计划正矢 (mm) 圆曲线始终点的计划正矢 (mm) (二)缓与曲线正矢就是从直线往圆曲线方向逐渐由小变大的,由直缓点向缓圆点方向变化的大小,叫缓与曲线的正矢递增率。
1、缓与曲线始终点计划正矢R L f 82=m L 20=Rf 50000=m L 10=Rf 12500=f R Rf c 50000=2c )(f f =终始()()()N f f c N 一端缓和曲线分段数圆曲线计划正矢缓和曲线的正矢递增率=()6N f )(f 缓和曲线正矢递增率缓和曲线始点正矢始=()始终缓和曲线始点正矢缓和曲线终点正矢f f )(f c -=2、缓与曲线中间各测点计划正矢式中 —缓与曲线中间各测点的计划正矢( ); —测点距缓与曲线始点的段数—缓与曲线的正矢递增率【例题】 已知曲线半径R=300m,缓与曲线长为70 m(如图3所示)求缓与曲线上各测点计划正矢值。
【解】mm mm mm mm 0缓与曲线中间各测点的计划正矢为图2缓与曲线mmmmmmmmmmmm Ni i f N f =i f 1,21-=N i,i N N f 1673005000050000≈==R f c ()()247167≈==N f f c N 一端缓和曲线分段数圆曲线计划正矢()46246===N f )(f ZH 始正矢直缓点()1634167=-=-=始终正矢缓圆点f f )(f HY c 2424111=⨯==N f N f 4824222=⨯==N f N f 7224333=⨯==N f N f 9624444=⨯==N f N f 12024555=⨯==N f N f 14424666=⨯==N f N f。
曲线正矢计算

二、算例1、圆曲线长度为10m整数倍的曲线计划正矢的计算已知某曲线半径R=600m,两端缓和曲线长l0=50m,求曲线各测点的计划正矢解:(1)圆曲线计划正矢: fc=L2/8R=20*20/8R=50000/R=50000/600=83.3mm,取84mm(2)缓和曲线正矢递增率: fs= fc/n=84/5=16.8mm(3)直缓(缓直)点正矢: f0=fs/6=16.8/6=2.8mm,取3mm(4)缓和曲线中间各点的正矢:缓和曲线第1点的正失 f1=fs=16.8mm,取17mm缓和曲线第2点的正失 f2=2fs=2*16.8=33.6mm,取34mm 缓和曲线第3点的正失 f3=3fs=3*16.8=50.4mm,取50mm 缓和曲线第4点的正失 f4=4fs=4*16.8=67.2mm,取67mm (5)缓圆(圆缓)点正矢: fhy=fc- f0=84-3=81mm2、圆曲线长度不是10m整数倍的曲线计划正矢的计算已知某曲线半径R=600m,两端缓和曲线l0=50m,圆曲线长304m,求各测点的计划正矢解:(1)第一缓和曲线和圆曲线的计划正矢算法同上;(2)第二缓和曲线各点计划正矢的计算:①第二缓和曲线始(HZ)点相邻测点的计划正矢因为圆曲线长L=304m,故第二缓和曲线始(HZ)点距缓和曲线和直线上相邻点(40点、41点)的距离分别为b≈4m,a≈6m,为测点间的距离,等于弦长的一半,a+b=则f40=1/6 fs[(1+b/)3-2(b/)3]=1/6*16.8*[(1+4/10)3-2*(4/10)3]=7.32mm,取7mm f41=1/6 fs(b/)3=1/6*16.8*(4/10)3=0.18mm,取0mm ②第二缓和曲线终点(YH)相邻测点的计划正矢第二缓和曲线终点(YH)距圆曲线和缓和曲线上相邻点(35点、36点)的距离分别为a≈4m,b≈6m,为测点间的距离,等于弦长的一半,a+b=则f35 = fc-1/6 fs(b/)3=84-1/6*16.8*(6/10)3=84-0.6=83.4mm,取84mm f36= fc-1/6 fs[(1+b/)3-2(b/)3]=84-1/6*16.8*[(1+6/10)3-2*(6/10)3]= 73.74mm,取74mm ③第二缓和曲线上其他各点计划正矢的计算其他各点计划正矢,可根据各点正矢与其距终点(HZ)距离成直线比例的关系,按下式求取:fi=fc/l0*li 则第37点、38点、39点的计划正矢分别为:f37=fc/l0*l37=84/50*34=57.12mm,取57mm f38=fc/l0*l38=84/50*24=40.32mm,取40mm f39=fc/l0*l39=84/50*14=23.52mm,取24mm 3、辅助点计划正矢的计算辅助点计划正矢的计算按圆曲线长度不是10m整数倍时缓和曲线的算法计算(1)圆曲线长度为10m整数倍时辅助点计划正矢的计算已知某曲线半径R=600m,两端缓和曲线长l0=50m,求缓和曲线辅助点的计划正矢解:辅助点与测点相距5m,即a=b=5m,①缓和曲线上与始点(ZH、HZ)相邻辅助点计划正矢为: f=1/6 fs[(1+b/)3-2(b/)3]=1/6*16.8*[(1+5/10)3-2*(5/10)3]=8.75mm,取9mm ②缓和曲线上与终点(YH、HY)相邻辅助点计划正矢为:f= fc-1/6 fs[(1+b/)3-2(b/)3]=84-1/6*16.8*[(1+5/10)3-2*(5/10)3 ]= 75.25mm,取75mm ③缓和曲线其他各中间辅助点的计划正矢:分别取li=15、25、35,按fi=fc/l0*li算得辅助点计划正矢分别为:25mm、42mm、59mm (2)圆曲线长度不是10m整数倍时辅助点计划正矢的计算曲线半径R=600m,缓和曲线长l0=50m,圆曲线长304m,求缓和曲线辅助点的计划正矢解:第一个缓和曲线辅助点的算法同上,第二个缓和曲线上辅助点计划正矢的计算按B=b±5计算,即:①缓和曲线上与始点(ZH、HZ)相邻辅助点计划正矢为(B=4+5=9): f=1/6 fs[(1+B/)3-2(B/)3]=1/6*16.8*[(1+9/10)3-2*(9/10)3]=15.12mm,取15mm ②缓和曲线上与终点(YH、HY)相邻辅助点计划正矢为(B=6-5=1): f= fc -1/6 fs[(1+B/)3-2(B/)3]=84-1/6*16.8*[(1+1/10)3-2*(1/10)3]=80.3mm,取80mm ③缓和曲线其他各中间辅助点的计划正矢:分别取li=19、29、39,按fi=fc/l0*li算得辅助点计划正矢分别为:32mm、49mm、66mm。
曲线正矢计算

第一讲:曲线正矢计算一、曲线的分类:目前我段主要曲线类型有:1、由两端缓和曲线和圆曲线组成的曲线,如正线曲线。
容许行车速度高。
2、由圆曲线构成的曲线。
如道岔导曲线、附带曲线。
二、圆曲线正矢的计算1、曲线头尾正好位于起终点桩上F C=L 2/8RL=20M 时, F C=50000/RF ZY =F YZ = F C/22、曲线头尾不在起终点桩上ZY 前点: Fμ=(FC/2) * (δ /10)2ZY 后点: Fη=FC-{ (FC/2) * (τ /10)2}FC:圆曲线正矢δ: ZY 点到后点的距离τ: ZY 点到前点的距离三、缓和曲线上整点正矢的计算(起始点正好是测点)(1)缓和曲线头尾的计算:终= F C 0 1 (缓和曲线起点)F-F 0 (缓和曲线终点)F=F/6(2)缓和曲线中间点正矢的计算:F1=F S= F C/N(N=L 0/B:缓和曲线分段数)2131I=IF 1( I 为中间任意点)F=2F F =3F F四、半点(5米桩)正矢的计算:a)ZH 点后半点正矢的计算:F 后=25/48*F 1很小一般为,其前半点很小(小于)因为 ZH 点正矢 f 0 11~2MM1MM=f /6,因此不作计算。
b)HY (YH )点前半点计划正矢的计算F 前 =1/2{[L 03+(L 0-15)3]/6R L 0+[5L 0+25]/2R}- (L 0-5)3/6R L0c)HY (YH )点后半点计划正矢的计算F 后=1/2{[(L0-5)3-L03]/6R L0+[5L0+175]/2R}d)中间点( 5 米桩)正矢的计算F 中=(F 前 +F 后)/2五、测点不在曲线始终点时缓和曲线计划正矢的计算a)缓和曲线始点 (ZH 点)处相邻测点的计划正矢Fμ=αυ F S(直缓点外点 )αυ =1/6(δ/B)3Fη=αη F S(直缓点内点 )αη =1/6[(1+ δ/B) 3-(δ/B) 3](2)缓圆点处相邻测点的计划正矢Fφ=F C-αυF S(缓圆点外点,缓和曲线之外 )Fθ= F C-αηF S(缓圆点内点,缓和曲线之内 )(αυ、αη查纵距率表《曲线设备与曲线整正》附表二 )(3)缓和曲线中间点各点计划正矢的计算F I=(F C/L 0)L I(I 为中间任意点)说明: B:半弦长δ:缓和曲线内点到 ZH、HY (YH )距离L 0:缓和曲线长F C:圆曲线正矢第二讲:曲线拨道一、绳正法基本原理1、基本假定:(1)假定拨道前后两端切线方向不变,或起始点位置不变,即曲线终点拨量为零。
曲线正矢、付矢、超高、加宽的计算方法

一、曲线(有缓)正矢、付矢、超高、加宽计算方法(例):例:已知某曲线R=310m,α=26°38′09″,l1=70m,l2=70m,H =125mm,S=5mm,V max=70km / h,求该曲线L全,L外,内距D,外距C,内距B,外距A,F Y及曲线各点F,f,H,S?解:L全=π×α×R/ 180+l1 / 2+l2 / 2 =214.114L外=π×α×R外/ 180+l1 / 2+l2 / 2=214.447内距D=(π×α×R外/ 180+l1 / 2-l2 / 2)-INT((π×α×R外/ 180+l1 / 2-l2 / 2)/10) ×10=4.447 外距C=10-D=5.553内距B=L外-INT(L外/ 10)×10 =4.447外距A=10-B=5.553外距系数a=A/10=0.5553,内距系数b=B/10=0.4447外距系数c=C/10=0.5553,内距系数d=D/10=0.4447F Y=λ2/2 R外=50000/(R+0.7175)=160.918,取161F d1=F Y /(l1/λ)=22.988F d2=F Y /(l2/λ)=22.988因 H d1=H /l1=1.786>H d=1/(9×V max)=1.587H d2=H /l2=1.786>H d=1/(9×V max)=1.587故始端、终端超高顺坡各向直线延伸9m,则 H d1=H /(l1+9)=1.582≤H dH d2=H /(l2+9)=1.582≤H dS d1=S /l1=0.071S d2=S /l2=0.071★始端正矢计算:(整桩)F ZH=F0=F d1/6=3.831,取4因 F n=n d×F d1=(D n / 10)×F d1故 F1=23、F2=46、F3=69、F4=92、F5=115、F6=138F HY=F7=F Y-F d1/6=157.086,取157★始端付矢计算:因 f n=0.75×F n+0.125×F d1故 f1=20、f2=37、f3=55、f4=72、f5=89、f6=106★始端超高、加宽计算:(略)H n=D n ×H d1S n=D n×S d1★终端正矢计算:(破桩)F D=F14=F Y-c3 /6×F d2=160.262,取160=F Y-C3/(12×R外×l2)F C=F15=F Y-(c+d3 /6)×F d2=147.816,取148=F Y-(600C+D3)/(12×R外×l2)因 F n=n d×F d2=(D n / 10)×F d2=(50×D n )/(R外×l2)故 F16=125、F17=102、F18=79、F19=56、F20=33F B=F21=(b+a3 /6)×F d2=10.879,取11=(600B+A3)/(12×R外×l2)F A=F22=b3 /6×F d2=0.337,取0=B2/(12×R外×l2)★终端付矢计算:因 C>5m,故 f YH=f15即 f15=(300×(l2+D)-(D3+2500))/(8×R外×l2)=113因 f n=0.75×F n+0.125×F d2故 f16=97、f17=80、f18=62、f19=45、f20=28f HZ=f21=(2500+600B+30B2-B3)/(24×R外×l2)=11★终端超高、轨距计算:(略)H n=D n ×H d2S n=D n ×S d2二、曲线(无缓)正矢计算方法:曲线全长 L全=π×α×R/ 180曲线外长 L外=π×α×R外/ 180内距 B=L外-INT(L外/ 10)×10外距 A=10-B圆曲线正矢 F Y=λ2/2 R外=50000/(R+0.7175)始端正矢:(整桩) F ZY=1/2×F Y终端正矢:(破桩) F A=1/2×B2/2 R外F B=1/2×(λ+B)2/2 R外-B2/2 R外=F Y-1/2×A 2/2 R外三、曲线(附带)正矢计算方法:曲线全长 L全=π×α×R/ 180(α为辙叉角)曲线外长 L外=π×α×R外/ 180内距 B=L外-INT(L外/ 5)×5外距 A=5-B圆曲线正矢 F Y=λ2/2 R外=12500/(R+0.7175)始端正矢:(整桩) F ZY=1/2×F Y终端正矢:(破桩) F A=1/2×B2/2 R外F B=1/2×(λ+B)2/2 R外-B2/2 R外=F Y-1/2×A 2/2 R外四、曲线(有缓)正矢、付矢、超高、加宽(自动)计算表:五、曲线(无缓)正矢(自动)计算表:六、常用附带曲线正矢(自动计算)表:。
1、曲线养护维修技术管理基础知识
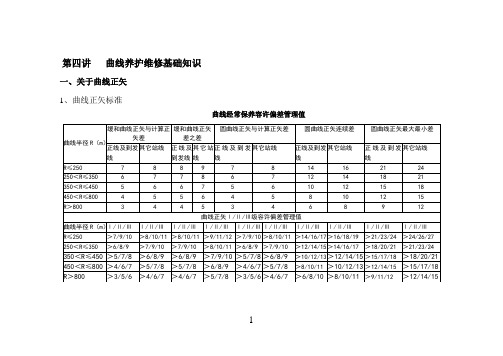
第四讲曲线养护维修基础知识一、关于曲线正矢1、曲线正矢标准曲线经常保养容许偏差管理值12、曲线正矢测点的设置方法合理设置曲线正矢测点是曲线养护维修管理中的一项重要工作,曲线正矢测点的设置方式,一般分“对称型”与“非对称型”。
(1)“对称型”曲线正矢测点设置:根据曲线要素确定曲线的直缓(ZH)、缓圆(HY)、圆缓(YH)、缓直(HZ)点,然后由曲线中点(QZ)向曲线两端均匀设置各个正矢测点(图1—1)。
图1-1(2)“非对称型”曲线正矢测点设置根据曲线要素确定曲线的直缓(ZH)、缓圆(HY)、圆缓(YH)和缓直(HZ)点,然后以曲线直缓(ZH)点(以里程较小的一端为始点),顺里程向曲线另一端均匀设置各个正矢测点(图1—2)。
图1-23、正矢点设置要求曲线正矢测点统一采用非对称设置。
即起端直缓、缓圆点和正矢测点对应,终端圆缓、缓直点不一定和正矢测点对应。
曲线测点按每10m 依次设置,计划正矢按照标准计算和设置。
在曲线单元范围内每测点间增设5m 附点,附点的计划正矢采用公式计算。
为控制曲线头尾位置和曲线头尾反弯或“鹅头”现象的出现,在设置好曲线各正矢点后分别向曲线两头直线段分别延伸3个辅助点。
与曲线正矢同时进行测量,但不纳入曲线拨量的计算。
4、曲线计划正矢计算 圆曲线正矢计算公式:R F 50000=(20m 弦) RF 12500=(10m 弦) 直圆点正矢=圆曲线正矢÷2 圆直点相邻测点的正矢直线一侧F b F z ⋅=22b ——圆曲线一侧测点至圆直点距离÷弦长圆曲线一侧F a F y ⋅-=)21(2a ——直线一侧测点至圆直点距离÷弦长例:单圆曲线全长23.54m ,半径400m ,用10m 弦长丈量。
算出各点计划正矢。
圆曲线正矢:mm)(25.314001250012500===R F 取31mm mm)(1623121≈==F Fmm)(313131432===F mm F mm F mmF a F 2931)2)554.35(1()21(225≈⨯÷--=⋅-=mm F b F 8312)554.3(2226≈⨯÷=⋅=缓和曲线上各正矢计算:缓和曲线正矢递减率=圆曲线正矢÷缓和曲线段数 直缓点正矢=缓和曲线正矢递减率÷6缓和曲线中间各测点的正矢=各点对应的段数×正矢递减率 缓圆点正矢=圆曲线正矢-直缓点正矢例:曲线半径1000m ,曲线全长321.85m ,缓和曲线长100m ,用20m 弦长丈量。
缓和曲线上各测点的计划正矢

缓和曲线上各测点的计划正矢曲线正矢计算教案新乡桥工段教师课堂教学教案一、曲线正矢的计算(1)、圆曲线正矢的计算公式:f=C2/(8R) f—正矢;C—弦长;R—曲线半径。
如果弦长是20m,则:f=202×1000/(8R)=50000/R 如果弦长是10m,则:f=102×1000/(8R)=12500/R圆曲线始终点附近两邻点的正矢=圆曲线正矢×相应的正矢系数;(2)、缓和曲线正矢的计算:fx=nfc/m 式中fx—缓和曲线正矢;n—测点点号;m—缓和曲线分段数;fc —圆曲线正矢。
缓和曲线各测点正矢递增量=圆曲线正矢/缓和曲线分段数缓和曲线始终点正矢的确定:测点在缓和曲线始终点时:缓和曲线始点(直缓、缓直)的正矢=缓和曲线递增量/6;缓和曲线终点(缓圆、圆缓)的正矢=圆曲线正矢-缓和曲线正矢递增量/6新乡桥工段教师课堂教学教案测点不在缓和曲线始终点时:缓和曲线始点(直缓、缓直)的两相邻点的正矢=缓和曲线递增量×正矢系数缓和曲线终点(缓圆、圆缓)的两相邻点的正矢=圆曲线正矢-缓和曲线正矢递增量×正矢系数例如:半径为1000米,圆曲线正矢为50毫米,缓和曲线长为50米,甲为6米,乙为4米,丙为4米,丁为6米,求相邻各测点的正矢? 缓和曲线正矢递增量=50/5=10毫米查正矢系数表:当甲为6米、乙为4米时:测点直正矢系数为0.0107;测点缓正矢系数为0.4360。
当丙为4米、丁为6米时:测点圆正矢系数为0.0360;测点缓正矢系数为0.6107。
根据查得正矢系数计算:起点的测点直正矢=10×0.0107=0.1≈0起点的测点缓正矢=10×0.4360=4.3=4毫米终点的测点缓正矢=50一(10 ×0.6107)新乡桥工段教师课堂教学教案=50—6.1≈44毫米终点的测点圆正矢=50一(10 ×0.0360) =50—0.36≈50毫米在查表时需注意:不要把甲、乙、丙、丁位置搞错。
铁路轨道曲线正矢计算(修正)

第一讲:曲线正矢计算一、曲线的分类:目前我段主要曲线类型有:1、由两端缓和曲线和圆曲线组成的曲线,如正线曲线。
容许行车速度高。
2、由圆曲线构成的曲线。
如道岔导曲线、附带曲线。
二、圆曲线正矢的计算1、曲线头尾正好位于起终点桩上F C=L2/8RL=20M时,F C=50000/RF ZY=F YZ= F C/22、曲线头尾不在起终点桩上ZY前点:Fμ=(FC/2)*(δ/10)2ZY后点:Fη=FC-{(FC/2)*(τ/10)2}FC:圆曲线正矢δ:ZY点到后点的距离τ:ZY点到前点的距离三、缓和曲线上整点正矢的计算(起始点正好是测点)(1)缓和曲线头尾的计算:F0=F1/6(缓和曲线起点)F终= F C-F0(缓和曲线终点)(2)缓和曲线中间点正矢的计算:F1=F S= F C/N (N=L0/B:缓和曲线分段数)F2=2 F1 F3=3F1 F I=IF1(I为中间任意点)四、半点(5米桩)正矢的计算:a)ZH点后半点正矢的计算:F后=25/48*F1因为ZH点正矢f0=f1/6,很小一般为1~2MM,其前半点很小(小于1MM)因此不作计算。
b)H Y(YH)点前半点计划正矢的计算F前=1/2{[L03+(L0-15)3]/6R L0+[5L0+25]/2R}-(L0-5)3/6R L0c)HY(YH)点后半点计划正矢的计算F后=1/2{[ (L0-5)3 -L03]/6R L0+[5L0+175]/2R}d)中间点(5米桩)正矢的计算F中=(F前+F后)/2五、测点不在曲线始终点时缓和曲线计划正矢的计算a)缓和曲线始点(ZH点)处相邻测点的计划正矢Fμ=αυF S(直缓点外点) αυ=1/6(δ/B)3Fη=αηF S(直缓点内点) αη=1/6[(1+δ/B)3-(δ/B)3](2) 缓圆点处相邻测点的计划正矢Fφ=F C-αυF S (缓圆点外点,缓和曲线之外)Fθ= F C-αηF S (缓圆点内点,缓和曲线之内)(αυ、αη查纵距率表《曲线设备与曲线整正》附表二)(3)缓和曲线中间点各点计划正矢的计算F I=(F C/L0)L I(I为中间任意点)说明:B:半弦长δ:缓和曲线内点到ZH、HY(YH)距离L0:缓和曲线长F C:圆曲线正矢第二讲:曲线拨道一、绳正法基本原理1、基本假定:(1)假定拨道前后两端切线方向不变,或起始点位置不变,即曲线终点拨量为零。
曲线正矢计算公式

曲线正矢计算公式
曲线正矢计算公式是在数学和物理学中用于计算曲线的弧长的公式。
在几何学中,曲线的弧长是指曲线上任意两点之间的距离。
曲线正矢是曲线上某一点处的切线方向与曲线的弧长比值,它可以帮助我们计算曲线上某点的速度、加速度等相关物理量。
对于一条曲线上的点P(x, y),其曲线正矢记为S。
根据微积分中的定义,曲线正矢的计算公式为:
S = √(1 + (dy/dx)^2)
其中,dy/dx 是曲线在点P的斜率。
实际上,这个公式是利用了导数的概念来计算曲线正矢。
导数表示曲线在某一点的切线的斜率,而曲线正矢则将这个斜率与曲线的弧长联系起来。
曲线正矢计算公式的应用非常广泛。
在物理学中,它可用于计算质点沿曲线运动的速度和加速度。
在工程中,曲线正矢可用于曲线绘制和路径规划。
在计算机图形学中,曲线正矢可以帮助我们实现曲线的平滑绘制。
总之,曲线正矢计算公式是数学和物理学中一个重要的工具,它能够帮助我们计算曲线上某点处的切线方向与弧长的比值。
通过曲线正矢,我们可以了解曲线上的速度、加速度等重要物理量,并应用于各种实际问题的解决中。
曲线正矢

⑶绳正法拨正曲线的基本要求 l①事先拨正曲线两端直线; l②用钢尺丈量外股钢轨,每l0m设置一个测点; l③拉绳测量测点正矢,取测量三次之平均值; l④按绳正法计算拨道量; l⑤设置拨道桩,按桩拨道。
u某一点的拨后正矢为:该点的现场正矢加上 该点的拨量减去前后两点半拨量之和。
f
曲线半径,用下式求得:
fp
L2 8R
当L=20m时,
fp
5R 0000 R
(mm)
当L=10m时,
fp
125000 R (mm)
曲线半径、弦长、正矢
当实测正矢与计划正矢之间的差值超过下表 所列的数值时,应及时整正
曲线正矢经常保养容许偏差规定值
曲线半径R (m)
R≤250 250<R≤350 350<R≤450 450<R≤800
R>800
缓和曲线的正矢与 计算正矢差(mm)
正线及 到发线
7 6 5 4 3
其他 站线
8 7 6 5 4
圆曲线正矢连续差 (mm)
正线及 到发线
14 12 10 8 6
其他 站线
16 14 12 10 8
圆曲线正矢最大 最小值差(mm)
正线及 到发线
21 18 15 12 9
其他 站线
24 21 18 15 12
en1 2
斜加 平写
9~11列与 4~6列计算 方法相同
第4列=第2 列-第3列
第7列修正 负拨量“先 减后加”
正负相 加为零
点号差调整法
第13列偏 差没有超
出3、6、9
平加 下写
第7列点号差为10 (点号14-点号4)
拨后正 矢=实测 正矢+ 拨量- (前点 拨量+ 后点拨 量)/2
