多元函数积分的计算方法技巧
多元函数积分计算方法

多元函数积分计算方法在数学中,多元函数积分是一种重要的计算方法,能够求解多元函数在给定区域上的面积、体积以及相关的物理量。
本文将介绍一些常见的多元函数积分计算方法,帮助读者更好地理解和应用这一数学工具。
一、重积分的定义重积分是单变量函数积分的推广,用于求解多元函数在给定区域上的面积或体积。
设函数f(x,y)在区域D上有定义,D的边界可以用曲线C表示,则重积分的定义为:∬_D▒〖f(x,y)dA=lim(Δx→0,Δy→0)∑▒f(x_i^*,y_j^*)ΔA〗其中,ΔA为区域D中小面积元素,f(x_i^*,y_j^*)为该小面积元素上一点的函数值。
二、二重积分的计算方法1. 矩形区域上的二重积分计算若D为矩形区域,可以采用迭代积分的方法求解二重积分。
先对x 进行积分,再对y进行积分,即:∬_D▒〖f(x,y)dA=∫_(a_y)^(b_y)▒(∫_(a_x)^(b_x)▒f(x,y)dxdy)〗2. 极坐标下的二重积分计算对于极坐标下的积分区域D,可以将二重积分转化为极坐标形式进行计算。
设D在极坐标下的表示为(r,θ),则二重积分的计算公式为:∬_D▒〖f(x,y)dA=∫_(θ_1)^(θ_2)▒(∫_(r_1(θ))^(r_2(θ))▒f(rcosθ,rsinθ)rdθ)〗三、三重积分的计算方法1. 直角坐标系下的三重积分计算若函数f(x,y,z)在空间区域V上有定义,则三重积分的计算公式为:∭_V▒〖f(x,y,z)dV=∫_(a_z)^(b_z)▒(∫_(a_y)^(b_y)▒(∫_(a_x)^(b_x)▒f(x,y,z)dxdydz )〗2. 柱坐标系或球坐标系下的三重积分计算对于柱坐标或球坐标下的积分区域V,可以将三重积分转化为柱坐标或球坐标形式进行计算。
具体转化公式可以根据坐标系关系进行推导,然后套用相应的公式进行计算。
四、应用举例1. 面积计算对于二维平面上的函数f(x,y),可以通过二重积分来计算给定区域D的面积。
2多元函数积分的计算公式

2多元函数积分的计算公式多元函数积分是微积分中的重要内容,用于计算多元函数在给定区域上的面积、体积以及质量等问题。
在本文中,我将介绍多元函数积分的定义、计算方法以及一些重要性质。
1.多重积分的定义多重积分是对多元函数在给定区域上的进行求和的过程。
对于二重积分来说,可以表示为:\[ \iint_D f(x,y) dA \]其中,f(x,y)是定义在平面区域D上的函数,dA表示面积元素。
对于三重积分来说,可以表示为:\[ \iiint_V f(x,y,z) dV \]其中,f(x,y,z)是定义在空间区域V上的函数,dV表示体积元素。
2.多重积分的计算方法多重积分的计算方法有两种:直接计算和间接计算。
直接计算是通过将积分区域划分成小的子区域,然后在每个子区域上计算函数值,并将所有结果相加。
间接计算是通过将多重积分转化为一重积分进行计算。
对于二重积分,可以使用极坐标转换将其转化为一重积分。
极坐标转换公式为:\[ x = r\cos(\theta) \]\[ y = r\sin(\theta) \]面积元素dA可以表示为:\[ dA = r dr d\theta \]将这个转换应用于二重积分计算中,可以得到:\[ \iint_D f(x,y) dA = \int_\alpha^\beta\int_{r_1(\theta)}^{r_2(\theta)} f(r\cos(\theta), r\sin(\theta)) r dr d\theta \]其中,\(\alpha\)和\(\beta\)是极角的范围,\(r_1(\theta)\)和\(r_2(\theta)\)是每个极角对应的极径范围。
对于三重积分,可以使用柱面坐标或球面坐标进行转换。
柱面坐标转换公式为:\[ x = r\cos(\theta) \]\[ y = r\sin(\theta) \]\[z=z\]体积元素dV可以表示为:\[ dV = r dr d\theta dz \]将这个转换应用于三重积分计算中,可以得到:\[ \iiint_V f(x,y,z) dV = \int_\alpha^\beta\int_{r_1(\theta)}^{r_2(\theta)} \int_{z_1(r, \theta)}^{z_2(r, \theta)} f(r\cos(\theta), r\sin(\theta), z) r dz dr d\theta \]其中,\(\alpha\)和\(\beta\)是极角的范围,\(r_1(\theta)\)和\(r_2(\theta)\)是每个极角对应的极径范围,\(z_1(r, \theta)\)和\(z_2(r, \theta)\)是每个极径和极角对应的高度范围。
多元函数积分的分部积分法

多元函数积分的分部积分法分部积分法是求解多元函数积分时的一种常用方法。
它是根据导数的乘积法则和积分的反运算关系,将被积函数中的一个因子求导,另一个因子求积分,从而将原始的积分问题转化为求解更简单的积分问题。
本文将介绍多元函数积分的分部积分法及其应用。
首先,我们来回顾一下一元函数的分部积分法。
对于一元函数f(x)和g(x),根据乘积的导数公式有:\[\frac{d}{dx}(f(x)g(x))=f'(x)g(x)+f(x)g'(x)\]将该式两边同时进行积分可得:\[\int(f'(x)g(x)+f(x)g'(x))dx=\int\frac{d}{dx}(f(x)g(x))dx\]由积分的反运算关系,右边的积分等于f(x)g(x),即:\[\int(f'(x)g(x)+f(x)g'(x))dx=f(x)g(x)+C\]其中C为积分常数。
这个就是一元函数的分部积分公式。
接下来,我们将分部积分法推广到多元函数。
对于多元函数f(x1,x2,...,xn)和g(x1,x2,...,xn),根据多元函数的导数乘积法则可得:\[\frac{\partial}{\partialx_i}(f(x_1,x_2,...,x_n)g(x_1,x_2,...,x_n))=\frac{\partialf}{\partial x_i}g+f\frac{\partial g}{\partial x_i}\]其中\(\frac{\partial f}{\partial x_i}\)和\(\frac{\partial g}{\partial x_i}\)分别表示对x_i求偏导数。
我们将该式两边同时进行积分可得:\[\int(\frac{\partial f}{\partial x_i}g+f\frac{\partialg}{\partial x_i})dx_i=\int\frac{\partial}{\partialx_i}(f(x_1,x_2,...,x_n)g(x_1,x_2,...,x_n))dx_i\]左边的多元积分可化简为:\[\int(\frac{\partial f}{\partial x_i}g+f\frac{\partialg}{\partial x_i})dx_i=\int[\frac{\partial}{\partialx_i}(fg)]dx_i\]右边的多元积分可化简为:\[\int\frac{\partial}{\partialx_i}(f(x_1,x_2,...,x_n)g(x_1,x_2,...,x_n))dx_i=\int d(fg)\]由于多元积分是对所有变量同时进行积分,因此上述结果可以推广到多个变量上。
高等数学中的多重积分计算技巧

多重积分在高等数学中是一个重要的概念和计算技巧。
它涉及到对多元函数在多个变量上的积分,是对一元函数积分的扩展和推广。
在计算多重积分时,可以运用一些技巧来简化计算和提高效率。
首先,需要了解多重积分的概念和性质。
多重积分可以分为定积分和不定积分。
定积分是指在一定的范围内对给定的函数进行积分。
不定积分是指对给定的函数进行积分,但没有具体的范围和上下限。
对于定积分,可以利用变量代换来简化计算。
变量代换即将积分变量换成其他变量,使得原来的积分变得更容易求解。
常用的变量代换方法有直角坐标系与极坐标系的转换、直角坐标系与球坐标系的转换、直角坐标系与柱坐标系的转换等。
通过适当选择不同的坐标系,可以消去一些变量,从而简化积分的计算。
对于不定积分,可以通过分部积分法、换元积分法等技巧进行计算。
分部积分法适用于需要对一个函数的乘积进行积分的情况,可以将乘积的积分变成两个函数的积分相减。
换元积分法可以通过适当的变量代换将原来的不定积分转化为一个更容易求解的形式。
另外,多重积分中还可以使用对称性等性质来简化计算。
如果被积函数具有对称性,可以将积分区域进行适当的对称分割,从而减少多重积分的计算步骤。
此外,还可以利用积分的可加性性质,将多重积分拆解成多个单重积分的和。
在实际应用中,多重积分经常用于计算物体的体积、质量、重心等物理量。
在计算这些物理量时,可以根据物体的几何形状选择适当的坐标系,并利用多重积分技巧进行求解。
总之,高等数学中的多重积分是一个重要的概念和计算技巧。
在计算多重积分时,可以利用变量代换、分部积分法、换元积分法等技巧进行简化和提高效率。
通过合理选择坐标系和利用对称性等性质,可以进一步简化计算。
多重积分在物理和工程等领域中有广泛的应用,可以用来求解物体的体积、质量、重心等物理量。
多元函数积分的分部积分法

多元函数积分的分部积分法
多元函数积分法是指应用一种数学技术来计算多元函数的定积分,这种技术叫做分部积分法。
分部积分法非常实用,它可以把复杂的多元函数简化成更容易积分的函数,这样可以把整
个积分区域划分成许多分区,每个分区可以用不同的方法来实现复杂函数积分。
分部积分法积分过程可以分为三步来完成:1、将单元函数划分为多个不同的函数,以便
分别积分。
2、对每个函数分别进行积分计算,这里可以使用定积分表、查表法或者是简
单的积分法来计算每一个函数的积分。
3、在进行积分计算之后,对所有函数求和就可以
得出整个积分值。
多元函数积分法,即分部积分法,不仅可以让多元函数的积分变得简单,而且可以把复杂
的多元函数进行分部积分,从而达到分解复杂函数的目的。
这种方法省去了大量的计算量,可以大大简化积分过程,可谓是积分领域中的一大进步。
多元函数的积分

多元函数的积分在数学中,多元函数的积分是一项重要的概念和计算方法。
与一元函数的积分类似,多元函数的积分可以帮助我们求解曲线下的面积、体积等问题,以及解决一些与实际问题相关的计算。
一、二重积分二重积分是多元函数积分中最基础的一种形式。
它的计算方法依赖于重积分的定义以及二重积分的性质。
对于二重积分来说,我们需要将待求的函数转化为极坐标形式、直角坐标形式等,并确定积分区域的范围。
通过分割积分区域成为若干小块,再对每个小块进行积分求和,最后将所有小块的积分结果相加,可以得到二重积分的值。
在实际应用中,二重积分可以用来计算平面图形的面积、求解平面质心等问题。
二、三重积分与二重积分类似,三重积分是多元函数积分中的另一种形式。
三重积分的计算方法也依赖于重积分的定义以及三重积分的性质。
与二重积分不同的是,三重积分需要确定积分区域的范围,并将待求的函数转化为球坐标形式、柱坐标形式等。
同样地,通过分割积分区域成为若干小块,再对每个小块进行积分求和,最后将所有小块的积分结果相加,可以得到三重积分的值。
在实际应用中,三重积分可以用来计算空间图形的体积、质心等问题。
三、重积分的性质重积分具有一些重要的性质,这些性质对于计算积分结果以及简化计算过程都非常有帮助。
其中一些常见的性质包括积分线性性、积分对称性、积分的加法性和积分的估值性等。
积分线性性:对于常数a和b,函数f(x,y)和g(x,y),有∬[D](af(x,y)+bg(x,y))dA = a∬[D]f(x,y)dA + b∬[D]g(x,y)dA。
这个性质使得我们在计算重积分时可以将积分区域分解成若干个子区域进行计算。
积分对称性:如果函数f(x,y)在区域D上关于x轴对称,则有∬[D]f(x,y)dA = 2∬[D1]f(x,y)dA,其中D1是区域D在x轴上方的部分。
类似地,还有关于y轴对称和原点对称的性质。
积分的加法性:对于两个不重叠的区域D1和D2,有∬[D1∪D2]f(x,y)dA = ∬[D1]f(x,y)dA + ∬[D2]f(x,y)dA。
04高数——多元函数积分学知识点速记

多元函数积分学1、不定积分1)原函数定义定义在某区间I 上的函数()f x ,若对I 的一切x ,均有()()F x f x '=,则称()F x 为()f x 在区间I 上的原函数。
若函数()f x 存在原函数,则()f x 就有无穷多个原函数,可表示为()F x C +。
2)不定积分定义函数()f x 的全体原函数称为()f x 的不定积分,记作()d f x x ⎰。
若()F x 是()f x 的一个原函数,则()()d f x x F x C =+⎰(C 为任意常数)3)不定积分计算:①第一类换元积分法:设()f u 具有原函数()F u ,而()u x ϕ=可导,则有()()()()d d f x x x f u u F x C ϕϕϕ'==+⎡⎤⎡⎤⎣⎦⎣⎦⎰⎰②第二类换元积分法:设()x t ϕ=在区间[],αβ上单调可导,且()0t ϕ'≠,又设()()f t t ϕϕ'⎡⎤⎣⎦具有原函数()F t ,则有()()()()()1d d f x x f t t t F t c F x Cϕϕϕ-'⎡⎤==+=+⎡⎤⎣⎦⎣⎦⎰⎰式中,()1x ϕ-为()x t ϕ=的反函数。
高 数多元函数积分学知识点速记③分部积分法:设()u x ,()v x 可微,且()() d v x u x ⎰存在,由公式()d d d uv u v v u =+得到分部积分公式d d u v uv v u=-⎰⎰2、定积分1)两点规定:①当a b =时,()d 0b a f x x =⎰;②当a b >时,()()d d b a a b f x x f x x =-⎰⎰2)积分上限函数及其导数①()d xa f x x ⎰为积分上限函数,记作()()d x ax f x x Φ=⎰,经常写成如下形式()()()d xa f t t a x xb Φ=≤≤⎰②积分上限函数的导数()()()d x a x f t t f x '⎡⎤'Φ==⎢⎥⎣⎦⎰()a xb ≤≤③()()()()()()()d g x h x f t t f g x g x f h x h x '⎡⎤''==⋅-⋅⎡⎤⎡⎤⎣⎦⎣⎦⎢⎥⎣⎦⎰3、定积分的应用旋转体的体积:设由曲线()y f x =,直线x a =,x b =以及x 轴围成的平面图形,绕x 轴旋转一周而生成的旋转体的体积,则()2πd b x aV f x x =⎡⎤⎣⎦⎰平行截面面积为已知的立体的体积:设立体由曲面S ,以及平面x a =、x b =所围成,且对于[],a b 上任一点x 作垂直截面,截得的面积()A A x =为x 的连续函数,则()d bc V A x x =⎰4、二重积分1)二元函数(),f x y 在闭区域D 上的二重积分,记作(),d D f x y σ⎰⎰2)(),d f x y σ⎰⎰表示以曲面(),z f x y =为顶,以区域D 为底,以D 的边D界为准线,母线平行于 Oz 轴的柱面围成的曲顶柱体的体积。
多元函数积分学总结

多元函数积分学总结引言多元函数积分学是微积分的一个重要分支,研究的是多个变量的函数在特定区域上的积分计算和性质。
在实际问题中,我们经常需要求解多元函数的积分,以求得面积、体积、质量等物理量。
本文将对多元函数积分学的基本概念、计算方法和应用进行总结和介绍。
一、多元函数积分的基本概念1. 二重积分二重积分是多元函数积分学中最基本的概念之一。
它表示在二维平面上的一个有界区域上对函数进行积分。
二重积分的计算可以通过投影到坐标轴上的两个一元积分来实现。
根据积分区域的形状和函数性质的不同,二重积分可以分为类型I和类型II两种。
•类型I:积分区域为矩形、正方形或一般的可由直线分割成有限个矩形的区域。
•类型II:积分区域不属于类型I的情况,一般需要进行变量替换或极坐标转化来简化计算。
2. 三重积分三重积分是对三维空间内的函数进行积分。
它可以用于计算体积、质量、重心等与物体形状和密度有关的物理量。
三重积分的计算方法较为复杂,一般需要采用适当的坐标变换或者使用球坐标、柱坐标等不同坐标系下的积分公式来进行计算。
二、多元函数积分的计算方法1. Fubini定理Fubini定理是多元函数积分计算的基础定理之一。
它建立了二重积分和三重积分之间的关系,使得计算复杂多元函数积分时可以拆分为若干个简单的积分。
Fubini定理主要有两种形式:对于矩形区域上的二重积分,可以通过交换积分次序将其转化为两次一元积分。
对于空间区域上的三重积分,也可以利用类似的方法进行计算。
2. 极坐标和球坐标对于具有相关几何特性的问题,使用极坐标和球坐标可以简化多元函数积分的计算过程。
极坐标常用于计算平面上的二重积分,而球坐标常用于计算空间中的三重积分。
通过引入极坐标或球坐标的坐标变换,我们可以将原积分区域变换为一个更简单的形式,从而简化积分计算。
在实际应用中,灵活运用极坐标和球坐标可以大大提高计算效率。
三、多元函数积分的应用多元函数积分在物理学、工程学、经济学等领域有广泛的应用。
10多元函数积分中的三个公式计算及运用

10多元函数积分中的三个公式计算及运用在高等数学中,多元函数积分是一个重要的概念,它在应用数学、物理学等领域中都有着广泛的应用。
为了更好地理解和应用多元函数积分,李正元考研高数基础讲义中介绍了十个多元函数积分的基本公式,其中有三个是重要且常用的公式,它们分别是重积分的线性性、变量代换公式和极坐标系下的积分公式。
首先是重积分的线性性。
重积分的线性性是指如果f(x,y)和g(x,y)是定义在闭区域D上的可积函数,c1和c2是常数,那么c1f(x,y)+c2g(x,y)也是定义在D上的可积函数,并且有以下成立的公式:∫∫D [c1f(x, y) + c2g(x, y)]dxdy = c1∫∫D f(x, y)dxdy +c2∫∫D g(x, y)dxdy这个公式的运用非常广泛,在对多元函数进行积分时经常会用到。
其次是变量代换公式。
在计算多元函数积分时,有时可以通过进行变量代换来简化计算。
设有从平面区域D到平面区域D'的可导函数变换x=x(u,v),y=y(u,v),且这个变换是一一对应,那么就有以下变量代换公式:∫∫D' f(x(u, v), y(u, v)),J(u, v),dudv = ∫∫D f(x,y)dxdy其中J(u,v)是变换的雅可比行列式,即J(u,v)=∂(x,y)/∂(u,v)=∂x/∂u*∂y/∂v-∂x/∂v*∂y/∂u。
这个公式在计算复杂的多元函数积分时非常有用,通过适当的变量代换可以将积分区域转化成更简单的形式,从而简化计算过程。
最后是极坐标系下的积分公式。
当积分区域是一个闭圆盘或圆环时,可以使用极坐标系来进行积分计算。
假设f(r,θ)是定义在圆盘或圆环内的连续函数,那么有以下公式成立:∫∫D f(r, θ)rdrdθ = ∫(θ=a to b) ∫(r=0 to R) f(r,θ)rdrdθ其中D表示积分区域,a和b是角度的取值范围,R是极坐标下的积分区域的半径。
多元函数分部积分法公式

多元函数分部积分法公式多元函数分部积分法公式是一种用于计算多元函数积分的方法。
通常情况下,多元函数分部积分公式应用于数学和物理学等领域,可以帮助数学家和物理学家准确计算一个多元函数的积分值。
本文将介绍多元函数分部积分法公式的定义和公式,以及如何应用多元函数分部积分法公式计算多元函数的积分值。
一、什么是多元函数分部积分法公式多元函数分部积分法公式又被称为分部积分法,它是一种常见的积分计算方法。
它可以帮助我们准确无误地计算多元函数积分的值。
多元函数分部积分公式可以表示为:∫abf(x)dx=∑nk=1aib(f),其中,a是多元函数f(x)的下限,b是多元函数f(x)的上限,n是多元函数f(x)的积分步数,i是多元函数f(x)积分时,分割点的位置,介于a到b之间。
二、如何计算多元函数分部积分法公式?1、选择积分步数n:积分步数n是积分时的重要准备,它指的是将区间[a,b]等分为n个小段,对每一段区间取固定点代入公式进行计算。
n越大积分精度越高,而且计算量越大。
因此,根据需要结合准确度与计算量灵活选择n值,以保证积分的准确性与可行性。
2、计算每一段小区间的积分值:当选择完积分步数n后,就可以计算每一段小区间的积分值了。
此时,先在每一段小区间中选择一个点,分别代入已定义的f(x)函数,计算每一段小区间的积分值。
三种常用的中心点是:左点、中点和右点,其积分值分别为:ai(fL)、ai(fM)和ai(fR)。
3、利用多元函数分部积分法公式计算总积分值:将n段小区间的积分值相加,便可以得到该区间上多元函数的总积分值,即总分值=∑nk=1aib(f)。
三、总结多元函数分部积分法公式是一种计算多元函数积分的方法,它可以帮助我们准确计算一个多元函数的积分值。
多元函数分部积分公式可以表示为:∫abf(x)dx=∑nk=1aib(f)。
为了计算一个多元函数的总积分值,需要根据积分步数n联合计算每一段小区间的积分值,然后把所有的小区间的积分值加起来便可以求出总积分值。
多元函数求积分

多元函数求积分
多元函数求积分是数学中的一个重要概念,它是对多元函数在某个区域内的积分求解。
在实际应用中,多元函数求积分被广泛应用于物理、工程、经济等领域,是解决实际问题的重要工具。
多元函数求积分的基本概念是对多元函数在某个区域内的积分求解。
在多元函数中,每个变量都可以看作是一个独立的自变量,而函数的值则是因变量。
因此,多元函数可以看作是一个自变量为多个变量的函数。
在多元函数中,积分的概念与一元函数中的积分概念类似,只是需要对多个变量进行积分。
在多元函数中,积分的结果是一个数值,表示在某个区域内的函数值的总和。
多元函数求积分的方法有很多种,其中最常用的方法是变量分离法和换元法。
变量分离法是将多元函数中的变量分离出来,然后对每个变量进行积分。
换元法则是将多元函数中的变量进行替换,然后对替换后的函数进行积分。
在实际应用中,多元函数求积分被广泛应用于物理、工程、经济等领域。
例如,在物理学中,多元函数求积分可以用于求解物体的质心、重心、转动惯量等问题;在工程学中,多元函数求积分可以用于求解结构力学、流体力学等问题;在经济学中,多元函数求积分可以用于求解市场需求、供给等问题。
多元函数求积分是数学中的一个重要概念,它在实际应用中具有广泛的应用价值。
通过对多元函数求积分的研究,可以更好地理解和应用数学知识,为解决实际问题提供有力的工具。
多元函数求积分

多元函数求积分多元函数求积分是微积分中的重要内容,它包括二重积分和三重积分两种形式。
在进行多元函数求积分时,我们需要根据具体问题选择合适的积分方法。
下面将介绍二重积分和三重积分的概念及计算方法。
一、二重积分二重积分是对二元函数在一个有界闭区域上的积分求解的方法。
具体而言,若有一个二元函数$f(x,y)$,我们要求解其在闭区域$D$上的积分,即$\iint_D f(x,y)dA$。
其中$dA$表示微元面积,$D$表示平面上的一个有界闭区域。
求解二重积分的方法有两种常见的形式:直角坐标下的二重积分和极坐标下的二重积分。
(1)直角坐标下的二重积分对于直角坐标下的二重积分,我们通常采用分割求和的方法。
将有界闭区域$D$分割成许多小面积的区域,然后对每个小区域内的函数值进行求和,最后取极限即可得到积分的结果。
具体操作时,我们可以选择将$D$划分成矩形形状的小区域,然后分别计算每个小矩形的面积$dA$,并求解$f(x,y)$在每个小矩形上的函数值$f(x_i,y_i)$,其中$(x_i,y_i)$表示小矩形的中心点。
最后的二重积分结果可以表示为$\iint_D f(x,y)dA =\lim_{{\Delta x \to 0} \atop {\Delta y \to 0}} \sum_{i,j} f(x_i,y_j)\Delta A$,其中$\Delta x$和$\Delta y$表示相邻小矩形的边长。
(2)极坐标下的二重积分对于具有旋转对称性的问题,极坐标下的二重积分更加便捷。
我们通过引入极坐标系来简化积分的计算。
首先,我们将直角坐标系转换为极坐标系,即$x =r\cos\theta$和$y = r\sin\theta$。
然后,我们需要计算雅可比行列式$J = \left|\begin{array}{cc}\frac{\partial x}{\partial r} &\frac{\partial y}{\partial r} \\ \frac{\partial x}{\partial \theta} &\frac{\partial y}{\partial \theta}\end{array}\right|$。
多元函数积分的计算方法与技巧

多元函数积分的计算方法与技巧1.多元函数的积分表示:多元函数的积分可以表示为定积分或不定积分。
定积分表示函数在一些区域内的积分值,而不定积分表示函数的原函数。
定积分可以通过区域划分进行求解,而不定积分则可以通过变量替换或部分积分等方法进行求解。
2.变量替换法:变量替换法是求解多元函数积分的常用方法之一、通过适当地选取新的变量,可以将原积分转化为一个更容易求解的形式。
常用的变量替换方法包括极坐标变换、柱面坐标变换、球面坐标变换等。
3.分部积分法:分部积分法是求解多元函数积分的常用方法之一、对于乘积形式的积分,可以将其转化为求解导函数的积分。
通过选择合适的函数进行分解,并利用分部积分公式,可以逐步简化积分的形式。
4.对称性与奇偶性:对称性与奇偶性是求解多元函数积分时常用的技巧。
如果被积函数具有其中一种对称性,可以利用对称性简化积分的计算。
另外,如果被积函数是奇函数或偶函数,则可以利用奇偶性质来简化积分计算。
5.积分次序的变换:对于多元函数的积分,积分次序可以任意交换。
通过变换积分次序,可以选择更合适的积分顺序,从而简化积分的计算。
6.积分区域的选择:对于定积分,选择合适的积分区域也可以简化积分计算。
可以通过变换坐标、利用对称性等方法选择一个更简单的区域进行积分。
除了上述方法与技巧之外,求解多元函数积分还需要熟练运用基本的积分公式和求导公式,灵活运用数学分析的知识。
另外,需要注意积分上下限的选择,确保积分区域与被积函数的定义域一致。
对于难题,可以尝试利用数值积分方法进行近似计算。
综合运用上述方法与技巧,可以更高效地求解多元函数积分,并应用于实际问题的求解。
多元函数的多重积分

多元函数的多重积分多元函数的多重积分是微积分的重要内容之一。
在一元函数的积分中,我们主要关注的是对于一维区间上的函数的积分,而多元函数的多重积分则是涉及到多维空间中的函数积分。
多元函数的多重积分包括二重积分和三重积分,它们在数学理论和实际问题的求解中都扮演着重要的角色。
一、二重积分1. 定义对于定义在有界闭区域D上的连续函数f(x,y),我们可以将D划分为若干小区域,每个小区域选取一点(xi,yi)作为代表点,计算出f(xi,yi)的值,并求和得到的极限,这个极限就是二重积分。
记作∬D f(x,y) dxdy。
2. 计算方法二重积分的计算可以通过对x或y进行分步计算,也可以通过坐标变换来简化计算。
其中,极坐标变换、直角坐标到直角坐标变换、直角坐标到柱坐标变换等是常用的坐标变换方法。
二、三重积分1. 定义对于定义在有界闭区域E上的连续函数f(x,y,z),我们可以将E划分为若干小区域,每个小区域选取一点(xi,yi,zi)作为代表点,计算出f(xi,yi,zi)的值,并求和得到的极限,这个极限就是三重积分。
记作∭E f(x,y,z) dxdydz。
2. 计算方法与二重积分类似,三重积分的计算可以通过分步计算或者坐标变换来进行。
3. 应用多重积分的应用非常广泛,包括物理学、工程学、经济学等各个领域。
例如,在物理学中,我们可以利用三重积分来计算物体的质量、静电荷分布、电场强度等;在经济学中,我们可以利用二重积分来计算收入分配的不平等程度等。
综上所述,多元函数的多重积分是数学中重要的一部分,它的理论和应用价值不可忽视。
通过对多重积分的学习和掌握,我们可以更深入地理解函数在多维空间中的性质和行为,为实际问题的求解提供有效的数学工具。
多元函数求积分

多元函数求积分积分是微积分的重要概念之一,用于求解函数的面积、体积、质量、重心等许多物理和几何问题。
在计算积分时,我们常常会遇到多元函数的积分问题,即在多维空间中对多个变量的函数进行积分。
本文将从基本概念、计算方法和相关参考内容三个方面介绍多元函数的积分。
一、基本概念多元函数的积分是在多维空间中对函数的求和过程,可以用于计算函数在某个区域内的总量。
对于二元函数而言,积分可以表示为∮f(x,y)dA,其中∮表示积分,f(x,y)为要积分的函数,dA表示面积元素。
对于三元函数而言,积分可以表示为∭f(x,y,z)dV,其中∭表示积分,f(x,y,z)为要积分的函数,dV表示体积元素。
多元函数的积分可以从二维空间扩展到任意多维空间。
二、计算方法1.直接计算对于简单的多元函数,可以直接计算积分。
首先需要确定积分的边界,即确定积分的区域。
然后按照积分的定义进行计算,将积分区域划分为许多小的面积元素或体积元素,并对每个元素进行积分。
最后将所有小元素的积分结果相加,即得到整个区域内函数的积分结果。
2.变量替换对于复杂的多元函数,可以通过变量替换的方法简化积分计算。
通过合适的变量替换可以将原函数化简为更简单的形式,从而方便求解积分。
通过变量替换,可以将积分区域变换到更加简单的坐标系中,使得计算变得更加容易。
3.极坐标、球坐标、柱坐标等对于涉及到圆、球、柱等几何形状的函数,可以使用极坐标、球坐标、柱坐标等坐标系进行积分计算。
这些坐标系有助于简化函数表达式和积分区域,从而提高计算效率。
三、相关参考内容1.《高等数学》(同济大学数学系编著):该教材是国内高等院校普遍采用的教材,对多元函数的积分有详细的介绍,并提供了许多例题和习题供读者练习。
2.《数学分析教程》(李修文编著):该教材对多元函数的积分理论和计算方法进行了深入的讲解,包括直接计算、变量替换和不同坐标系下的积分计算方法。
3.《多元函数积分学》(孔祥兴编著):该教材从多元函数积分的基本概念入手,详细介绍了多元函数的积分理论和计算方法,并提供了大量例题和习题供读者练习。
多元函数积分学总结

多元函数积分学总结引言多元函数积分学是微积分的重要分支,研究具有多个变量的函数的积分。
它在物理、工程、经济学等领域都有广泛的应用。
本文旨在总结多元函数积分学的基本概念、技巧和应用。
一、多重积分1.二重积分二重积分即对二元函数在一个有界区域上的积分。
它可以通过将区域分割成小的矩形,并在每个矩形中求函数值乘以该矩形的面积,再将所有矩形的面积相加而得到。
二重积分的计算可以使用极坐标、换元法等方法来简化计算过程。
2.三重积分三重积分即对三元函数在一个有界区域上的积分。
类似于二重积分,三重积分可以通过对区域进行分割,并在每个小的立体元中求函数值乘以立体元的体积,再将所有立体元的体积相加而得到。
三重积分的计算可以使用柱坐标、球坐标等方法来简化计算过程。
3.多重积分的性质–可加性:多重积分具有可加性,即对于函数的积分,可以将区域分割成多个子区域,分别在每个子区域上计算积分,再将这些积分相加。
–定积分的值与路径无关:对于连续函数,在一个闭合曲线上的积分与路径无关,只与路径所围成的区域有关。
二、重要定理1.Fubini定理Fubini定理是二重积分和三重积分的重要定理,它可以将多重积分转换为一重积分的形式,简化积分计算的过程。
2.Green公式和Stokes定理Green公式和Stokes定理是两个重要的向量积分定理。
它们描述了曲线积分和曲面积分与散度、旋度之间的关系。
3.Gauss公式Gauss公式是一个重要的体积积分定理,它表明了三维空间中的散度与体积分之间的关系。
这个定理在电磁学和流体力学中有广泛的应用。
三、应用实例1.质量和质心多重积分在质量和质心的计算中有广泛的应用。
通过将物体划分为无穷小的微元,可以通过多重积分计算物体的总质量和质心的位置。
2.引力和电场的计算在物理学中,多重积分可以用于计算引力和电场的作用。
通过计算物体上的质量或电荷在空间中的分布,可以使用多重积分来求解引力或电场的强度。
3.概率密度函数和统计分析在概率论和统计学中,概率密度函数描述了随机变量的概率分布。
微积分中的多元函数积分法

微积分中的多元函数积分法微积分是数学中一个重要的分支,它包括微分和积分两个方面。
微分主要是研究函数的变化率和导数,积分则是研究函数的面积、体积和曲线长度等。
在微积分中,多元函数积分是一个非常重要的部分,它在计算实际问题中起着重要的作用。
多元函数积分的含义多元函数积分是指对多元函数在一定区间内求积分的操作。
其中,“多元函数”指的是含有多个自变量的函数,如$f(x_1,x_2,\cdots,x_n)$,“积分”则指的是对函数在某个区域内的面积、体积等进行求解。
在实际应用中,多元函数积分经常用来求解各种物理量,如质量、能量、热量等等。
多元函数积分的分类多元函数积分包括两种类型:第一类是二重积分,指对平面上的函数进行积分;第二类是三重积分,指对空间中的函数进行积分。
两种类型的积分都具有不同的求解方法。
多元函数积分的求解方法1. 二重积分的求解方法在二元函数中求积分时,可以采用重积分法进行求解。
重积分法在二元函数中的形式为:$\int\int_Df(x,y)dxdy=\int_{y=y_1}^{y=y_2}\int_{x=x_1}^{x=x_ 2}f(x,y)dxdy$其中,$D$表示积分域,通常是一个矩形或三角形。
在求解二重积分时,需要先将积分域分解为多个小块,然后对每个小块进行单独的积分。
这种方法比较适合于对简单几何形状的二元函数进行积分计算。
2. 三重积分的求解方法在三元函数中进行积分时,可以采用重积分法对积分域进行划分,然后按照各个坐标轴进行积分计算。
在三元函数的情况下,积分域通常是一个立方体或一个球体等。
三重积分的求解方法包括:(1)直接积分法在三个坐标轴上分别进行积分,并根据积分的上下限进行计算。
这种方法比较适合于简单的积分问题。
(2)柱坐标法和球坐标法在柱坐标法和球坐标法中,需要将坐标系从直角坐标系变换为极坐标系或球坐标系。
在这种坐标系下,积分域被转化为球壳体或圆柱体等,可以适用于复杂的积分问题。
多元函数微积分解题技巧二则解读

多元函数微积分解题技巧二则
1. x,y 在函数解析式中具有对称性时求偏导
所谓对称性,即在函数式中把x 换成y,把y 换成x,函数式不变。
如在形成性考核册(以下简称大作业)中,P3,3(2),P4,6,7(2). 现以P4,7(2)为例:e z –xyz=xy 求z x ∂∂, z y ∂∂ 解:方程两边对x 求偏导,得 e z z x ∂∂-y(z+x z x ∂∂)=y ∴z x ∂∂=(1)z y z e xy +-∴ 在此结果中将x,y 交换,即得
z y ∂∂=(1)z x z e xy +- 这样就省去了对y 的求导数。
同样在P3,3(2)中,在求出z x ∂∂=12y x x y -+以后交换x,y 立得z y ∂∂=12x y x y
-+ 2.在计算二重积分时,对坐标系的选择
在选择坐标系时,主要看积分区域,再看被积函数,若积分区域是圆形或圆环形或是它们的一部分时,往往用极坐标方便。
请看大作业P5,8(4) D yd σ⎰⎰ D; 222,,0x y a x y +=≥
本题积分区域是14圆,如右图
采用极坐标 D yd σ⎰⎰=sin D
r rdrd θθ•⎰⎰
=2200sin a
d r dr π
θθ⎰⎰=3
03a r ∣20
cos πθ∣=31103a (-)=313a 如采用直角坐标
D D yd ydxdy σ==⎰⎰⎰⎰22
00a a x ydy -⎰ 显然比用极
坐标麻烦。
x
圆,如右图本题积分区域是1
4。
多元函数积分的计算方法技巧
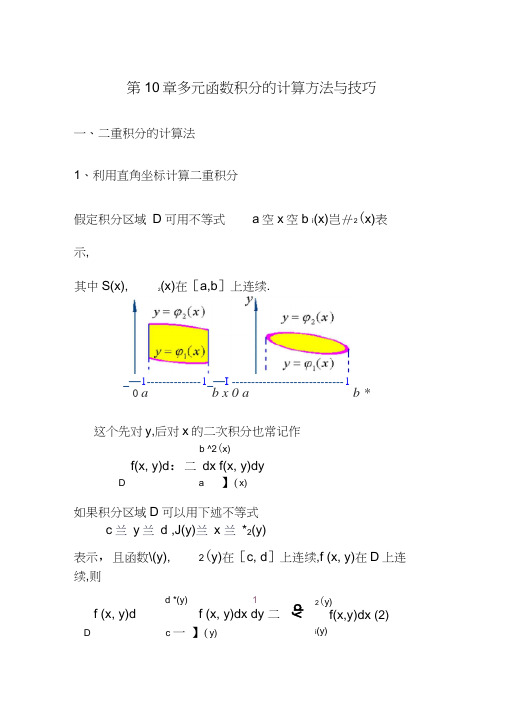
第10章多元函数积分的计算方法与技巧一、二重积分的计算法 1、利用直角坐标计算二重积分假定积分区域 D 可用不等式 a 空x 空b i (x)岂卄 2(x)表示, _—1 -------------- 1_—I ----------------------------- 1 0 a b x 0 a b *这个先对y,后对x 的二次积分也常记作b ^2(x)f(x, y)d :二 dx f(x, y)dy D a 】(x)如果积分区域D 可以用下述不等式c 兰 y 兰d ,J(y)兰 x 兰 *2(y)表示,且函数\(y), 2(y)在[c, d ]上连续,f (x, y)在D 上连续,则d *(y)1f (x, y)df (x, y)dx dy 二Dc 一 】(y)dydi2(y)f(x,y)dx (2)i (y)其中S(x),2(x)在[a,b ]上连续.2显然,(2)式是先对x ,后对y 的二次积分. 积分限的确定几何法.画出积分区域D 的图形(假设的图形如下)在[a, b ]上任取一点x ,过x 作平行于y 轴的直线,该直线穿过区域D ,与区域D 的边界有两个交点(x, i (x ))与(x, 2(x )), 这里的i (x ). 2(x )就是将x ,看作常数而对y 积分时的下限和 上限;又因x 是在区间[a,b ]上任意取的,所以再将x 看作变 量而对x 积分时,积分的下限为a 、上限为b .例1计算D 如,其中D 是由抛物线…及直线…2 所围成的区域. 解:Z)]: 0<x £)2:l<x<4,x-2<y<A/^ 為yda= fj 砂c/b 十fj 秽亦Di\ r>214 V?=\dx \ xydy dx \xycfy 0 — l 工—2V74C A = J- JC -(^-2) 1 2Ld x -勺-Jx4r =0+ f —yx-245dx~~82)2D: _ 1 乞 y 乞 2, y x -2 y 2xyd = dy xydx =D-1 y 21 22 y(y 2)2-2 -i2. 利用极坐标计算二重积分 1、rdrd-就是极坐标中的面积元素2、极坐标系中的二重积分,可以化归为二次积分来计算.:_ 71 _ -£ ) - r - 2⑴其中函数W,二⑴在V / ]上连续.pY)则 f(rcos ,rsin)rdrd 二 d f(rcos,rsin )rdr D:1C)【例5】计算JJt?7 —F 丛创』其中D:x 2 -h y 2 <a 2. D解:加? ms2 2 2\\^~x ~y dxdy = |[e~r -rdrdO D 2 凭 ct 22?z=\ d&\ e~rrdr = J0 0 0 2?r 1 J )朋=兀Q Y0 2注:本题不能利用直角坐标下二重积分计算法来求其精确 值.y 22「1 2 严 d厉X y」2dy-1 yy 5丽458<X ' rcos y rsin dxdy rdrd 匚〉JJ f(rcos,rsin)rdrd0<r<aDT 1尸 ---- e 21住dG 0 < < 2^-3、使用极坐标变换计算二重积分的原则(1)、积分区域的边界曲线易于用极坐标方程表示 (含圆弧, 直线段);⑵、被积函数表示式用极坐标变量表示较简单(含 (x 2 y 2r ,,为实数).解此积分区域为D : 0 乞 x 乞 a , 一 x 乞 y 乞 一 a 一 a 2 一 x 2 该区域在极坐标下的表示形式为D:丁小0 ,°汀」2站32二、三重积分的计算 1、积分区域"可表示成a ^ xb , %(x ) ' y y 2(x ) , ^(x,y )乞 z' Z 2(x, y )by 2(x ) Z 2(x,y ) 贝y !!! f (x, y, z )dv = dx dy f (x, y, z )dzay'x )N (x,y )这就是三重积分的计算公式,它将三重积分化成先对积a -a+\ a 2 _x 2例6计算M dx-xdyx 2 y 2 4a 2 -(x 2 y 2)(a 0)rdrd"D r \ 4a 2 - r 20 -2a si nvd ,dr0 fJIarcsin n -2as in日 r2a2JI2- r 248分变量z ,次对y,最后对x 的三次积分 例1计算…xyzdxdydz ,其中门为球面x^ y^ z^ 1及三坐QJ标面所围成的位于第一卦限的立体 . 解 “在 xoy 面上的投影区域为2 2D xy : x y 「,x 一 0, y — 0确定另一积分变量的变化范围0 岂 z 岂 1 一 X 2 — y 2选择一种次序,化三重积分为三次积分111xyzd xdydzQ1心2c —y 2dx dy xyzdz0 0 01心21dx — xy (10 0 2 12 1 13 13 dx (—xy x y xy )dy0 2 2 2十—1 32 1 4-X y - - xy4 8 06 4 28 6 42x 2 - y 2)dy 0_4xydxI 2 I 3X (1 - X ) X (1 - X ) 11 -0 IL 4n?1 ■J J- _____ 0 I 4 21 sin t cos41 2 1-—x(1 -82 2x) dx-sin t cos 21 - — sin 31 cos 21 -二sin t cos 41 cos tdt 421 dt sin 31 cos 3tdt0 4 2 2 1 4 2兀刁15—sin t cos tdt 082、利用柱面坐标计算三重积分x = r cos 点M的直角坐标与柱面坐标之间有关系式* y = rsinez= z体积为dv 二rdrd ^dz这便是柱面坐标系下的体积元素,并注意到(1)式有I, f (x, y, z)dv 111 f (r cos^ , r sin ^, z)rdrd ^dz3、利用球坐标计算三重积分直角坐标与球面坐标间的关系为x = r sin cos71Iy = r sin sin 二、z = r cos®dv= r2s in ^drd^ d9 这就是球面坐标系下的体积元素。
多元函数的积分

多元函数的积分多元函数的积分是微积分中的一个重要分支,它与单变量函数的积分有很大的不同之处。
在单变量函数的积分中,我们只需要考虑一维空间中的积分问题,而在多元函数的积分中,则必须考虑多维空间的积分问题。
由于空间维度增加,函数的复杂度也随之增加,多元函数的积分也因此变得更加复杂和困难。
多元函数的积分可以分为两类,一类是定积分,即计算函数在一个有限区域内的积分值;另一类是无限积分,即计算函数在无穷区间内的积分值。
无限积分和定积分的计算方法略有不同,有些技巧和方法只适用于其中的一种类型,因此了解两种积分类型的区别和计算方法是必要的。
在多元函数的积分中,常用的计算方法之一是变量代换法。
在单变量的积分中,我们常用变量代换法将积分限制在一段特定的区间内,以此来简化积分的计算。
在多元函数的积分中,变量代换法同样具有重要作用。
通过变量代换,可以将原本复杂的积分转化为更简单的积分。
变量代换的关键在于选择合适的变换方式和变换原理,这需要一定的数学功底和经验。
除了变量代换法外,还有其他很多重要的积分技巧。
例如,积分的分部积分法、换元积分法、极坐标系下的积分等等。
这些方法可以帮助我们计算各种复杂的积分,是多元函数积分中的重要一环。
需要注意的是,多元函数的积分在物理学、工程学、统计学等领域中有很广泛的应用。
例如在热力学中,我们需要计算体积和温度之间的积分以求出物质的热容量;在材料力学中,需要计算弹性应变能密度积分以求解固体材料的力学性能;在概率统计学中,需要计算概率密度函数积分以求出随机变量的期望值等等。
由于多元函数积分在实际应用中有很大的价值,因此学习多元函数积分的相关技巧和方法也是很有意义的。
总之,多元函数积分是一门很重要的学科,与单变量函数积分有很大的不同和区别。
了解多元函数积分的计算方法和技巧对于各种实际应用具有重要意义。
需要注意的是,掌握多元函数积分需要一定的数学功底和经验,需要耐心和勤奋的学习过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第10章 多元函数积分的计算方法与技巧
一、二重积分的计算法
1、利用直角坐标计算二重积分 假
定
积
分
区
域
D 可用不等式
a x
b x y x ≤≤≤≤ϕϕ12()()表示,
其中ϕ1()x , ϕ2()x 在[,]a b 上连续.
这个先对y , 后对x 的二次积分也常记作
f x y d dx f x y dy D
a
b
x x (,)(,)()
()σϕϕ⎰⎰⎰⎰=12
如果积分区域D 可以用下述不等式 c y d y x y ≤≤≤≤,()()φφ12
表示,且函数φ1()y ,φ2()y 在[,]c d 上连续,f x y (,)在D 上连续,则
f x y d f x y dx dy dy f x y dx D y y c d
c d y y (,)(,)(,)()()()()σφφφφ⎰⎰⎰⎰⎰⎰=⎡⎣⎢⎢⎤
⎦
⎥⎥=1212
(2)
显然,(2)式是先对x ,后对y 的二次积分.
积分限的确定
几何法.画出积分区域D 的图形(假设的图形如下 )
在],[b a 上任取一点x ,过x 作平行于y 轴的直线,该直线穿过区域D ,与区域D 的边界有两个交点))(,(1x x ϕ与))(,(2x x ϕ,
这里的)(1x ϕ、
)(2x ϕ就是将x ,看作常数而对y 积分时的下限和上限;又因x 是在区间[,]a b 上任意取的,所以再将x 看作变量而对x 积分时,积分的下限为a 、上限为b .
例1计算xyd D
⎰⎰σ, 其中D 是由抛物线y x 2=及直线
y x =-2所围成的区域.
D y y x y :,-≤≤≤≤+1222
xyd dy xydx x y dy D y y y y σ⎰⎰⎰⎰⎰==⎡⎣⎢⎤
⎦⎥-+-+12
2
212
2
2
212
[]
=+-=-⎰12245
8
2512y y y dy () 2.利用极坐标计算二重积分 1、rdrd θ就是极坐标中的面积元素.
x r →cos θ
y r →sin θdxdy rdrd →θ
f x y dxdy
D
(,)⎰⎰f r r rdrd D
(cos ,sin )θθθ⎰⎰
2、极坐标系中的二重积分, 可以化归为二次积分来计算.
αθβϕθϕθ≤≤≤≤12()()r
其中函数ϕθ1(), ϕθ2()在[,]αβ上连续.
则
f r r rdrd d f r r rdr
D
(cos ,sin )(cos ,sin )()
()
θθθθθθα
β
ϕθϕθ⎰⎰⎰⎰=12
注:本题不能利用直角坐标下二重积分计算法来求其精确值.
3、使用极坐标变换计算二重积分的原则
(1)、积分区域的边界曲线易于用极坐标方程表示( 含圆弧,直线段 );
(2)、被积函数表示式用极坐标变量表示较简单( 含()x y 22+α, α为实数 ).
例
6
计算
I dx
dy
x y a x y a a
x
a a x =+⋅-+>⎰⎰
--+-0
222224022
()
()
解此积分区域为
D x a x y a a x :,022≤≤-≤≤-+- 该区域在极坐标下的表示形式为
D r a :,sin -
≤≤≤≤-π
θθ4002
I rdrd r a r
d dr
a r r a d D
a a =-=-=⎡
⎣⎢⎤⎦⎥⎰⎰
⎰⎰
⎰-
---
θ
θ
θπθθ
π4422
2
4
0220
2024
sin sin arcsin
=-=-=--
⎰()θθθπππd 4
024
2
1232
二、三重积分的计算 1、积分区域Ω可表示成
a x
b y x y y x z x y z z x y ≤≤≤≤≤≤,()(),(,)(,)1212
则 f x y z dv dx dy
f x y z dz a
b
y x y x z x y z x y (,,)(,,)()
()(,)
(,)Ω
⎰⎰⎰⎰⎰⎰=1212
这就是三重积分的计算公式, 它将三重积分化成先对积分变量z , 次对y ,最后对x 的三次积分.
例1计算xyzdxdydz Ω
⎰⎰⎰, 其中Ω为球面x y z 2221++=及
三坐标面所围成的位于第一卦限的立体.
解 Ω在xoy 面上的投影区域为 D x y x y xy :,,22100+≤≥≥
确定另一积分变量的变化范围 0122≤≤--z x y 选择一种次序,化三重积分为三次积分
⎰⎰⎰⎰⎰⎰⎰⎰----Ω--==2
2
22
10
221
010
10
1
0)1(21
x y x x dy
y x xy dx xyzdz
dy dx
xdydz
xyzd
dx
x x x x x x dx xy y x xy dy
xy y x xy dx x x
⎰⎰⎰⎰⎥⎦⎤
⎢⎣⎡-----=⎥⎦⎤⎢⎣⎡--=--=--1
022232101
0423210
3
310)1(81)1(41)1(4
181414
1)212121(2
2
48
12462481246224124241cos sin 8
1cos sin 41cos sin 41cos cos sin 81cos sin 41cos sin 4
12
05203
332
02
04232=⋅⋅⋅⋅
-⋅⋅⋅⋅-⋅⋅=--=⎥⎦⎤
⎢⎣⎡--=⎰⎰⎰⎰π
ππ
π
tdt
t tdt t dt t tdt
t t t t t t 2、利用柱面坐标计算三重积分 点
M 的直角坐标与柱面坐标之间有关系式x r y r z z
===⎧⎨⎪⎪
⎩⎪⎪cos sin θθ
体积为dv rdrd dz =θ
这便是柱面坐标系下的体积元素, 并注意到(1)式有
f x y z dv f r r z rdrd dz (,,)(cos ,sin ,)Ω
Ω
⎰⎰⎰⎰⎰⎰=θθθ
3、利用球坐标计算三重积分
直角坐标与球面坐标间的关系为
x r y r z r ===⎧⎨⎪
⎩⎪sin cos sin sin cos ϕθϕθϕ dv r drd d =2sin ϕϕθ
这就是球面坐标系下的体积元素。
⎰⎰⎰
⎰⎰⎰Ω
Ω
=θϕϕϕθϕθϕd drd r r r r f dv z y x f sin )cos ,sin sin ,cos sin (),,(2。
