第二章 一元回归模型1
一元线性回归模型

几个常用结果以及注释 1. Σei =0
2. Σei
Xi=0
3.样本回归方程过( X , Y )点 样本回归方程过( 4.截距为0的一元线性回归模型参数估 计式 一元线性回归模型参数估计举例( P23页)
四、估计量的统计学性质
1. 线性性:b , b 都是Yi的线性函数。
0 1
∑ x y = ∑ x (Y Y ) = ∑ x Y b = ∑ x ∑ x ∑ x ∑ xY = ∑ x x 令: K = 则: b = ∑ K Y 是 Y ∑ x
4.线性回归模型 的普遍性
在实际经济分析中,由于经济变量之间的关系 在实际经济分析中 由于经济变量之间的关系 往往是非常复杂的,所以直接的精确线性模型是较 往往是非常复杂的 所以直接的精确线性模型是较 所以直接的精确线性模型 少的。 少的。 但是,由于第一,线性模型比较容易研究;第 但是,由于第一,线性模型比较容易研究; 二,现实经济分析中许多非线性问题可以经过简 单的数学处理转化为线性模型;第三, 单的数学处理转化为线性模型;第三,非线性模 型的分析基础是线性模型。 型的分析基础是线性模型。 所以,我们研究的思路是先学习线性回归模型, 所以,我们研究的思路是先学习线性回归模型, 然后学习非线性问题。 然后学习非线性问题。
表示 Xi ,Yi…… 离差形式用小写字母表示 xi ,yi……
三、举例说明
计量经济学模型为什么引入随机扰动项ui ? 例题:需求模型 如前所述需求量Q受到商品价格P、当期 收入Yt 、其它商品价格P1 、前期收入Y t-1 、 经济政策G 、……等因素影响。所以, Q=f(P、 Y t 、P1、Y t-1、G……)
i i i i i 1 2 2 2 i i i i i 2 i i i 2 1 i i i
计量经济学 第二章 一元线性回归模型
第二章 一元线性回归模型2.1 一元线性回归模型的基本假定2.1.1一元线性回归模型有一元线性回归模型(统计模型)如下, y t = β0 + β1 x t + u t上式表示变量y t 和x t 之间的真实关系。
其中y t 称被解释变量(因变量),x t 称解释变量(自变量),u t 称随机误差项,β0称常数项,β1称回归系数(通常未知)。
上模型可以分为两部分。
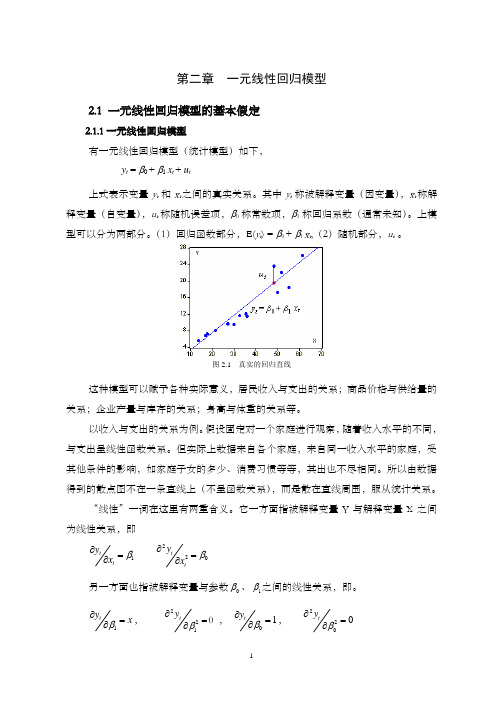
(1)回归函数部分,E(y t ) = β0 + β1 x t ,(2)随机部分,u t 。
图2.1 真实的回归直线这种模型可以赋予各种实际意义,居民收入与支出的关系;商品价格与供给量的关系;企业产量与库存的关系;身高与体重的关系等。
以收入与支出的关系为例。
假设固定对一个家庭进行观察,随着收入水平的不同,与支出呈线性函数关系。
但实际上数据来自各个家庭,来自同一收入水平的家庭,受其他条件的影响,如家庭子女的多少、消费习惯等等,其出也不尽相同。
所以由数据得到的散点图不在一条直线上(不呈函数关系),而是散在直线周围,服从统计关系。
“线性”一词在这里有两重含义。
它一方面指被解释变量Y 与解释变量X 之间为线性关系,即1tty x β∂=∂220tt y x β∂=∂另一方面也指被解释变量与参数0β、1β之间的线性关系,即。
1ty x β∂=∂,221ty β∂=∂0 ,1ty β∂=∂,2200ty β∂=∂2.1.2 随机误差项的性质随机误差项u t 中可能包括家庭人口数不同,消费习惯不同,不同地域的消费指数不同,不同家庭的外来收入不同等因素。
所以在经济问题上“控制其他因素不变”是不可能的。
随机误差项u t 正是计量模型与其它模型的区别所在,也是其优势所在,今后咱们的很多内容,都是围绕随机误差项u t 进行了。
回归模型的随机误差项中一般包括如下几项内容: (1)非重要解释变量的省略, (2)数学模型形式欠妥, (3)测量误差等,(4)随机误差(自然灾害、经济危机、人的偶然行为等)。
计量经济学第二章 一元线性回归模型(1)(肖)

10
2.在经济学中,经济学家要研究个人
消费支出与个人可支配收入的依赖关系。
这种分析有助于估计边际消费倾向,就是
可支配收入每增加一元引起消费支出的平
均变化。
11
3.在企业中,我们很想知道人们对企
业产品的需求与广告费开支的关系。这种
研究有助于估计出相对于广告费支出的需
求弹性,即广告费支出每变化百分之一的
(2.3)
想想:结合表2.1的资料 ,怎样理解式(2.3)
变量Y 的原因, 给定变量X 的值也不能具
体确定变量Y的值, 而只能确定变量Y 的
统计特征,通常称变量X 与Y 之间的这种
关系为统计关系。
16
例如,企业总产出Y 与企业的资本投入
K 、劳动力投入L 之间的关系就是统计关 系。虽然资本K 和劳动力L 是影响产出Y 的两大核心要素,但是给定K 、L 的值并 不能确定产出Y 的值。因为,总产出Y 除 了受资本投入K、劳动力投入L 的影响外
在进入正式的回归理论之前,先斟酌一下变量y与变 量x可以互换的不同名称、术语。 Y 因变量 X 自变量
被解释变量 响应变量
被预测变量
解释变量 控制变量
预测变量
回归子
归回元
22
第二节
一、引例
一元线性回归模型
假定我们要研究一个局部区域的居 民消费问题,该区域共有80户家庭组成 ,将这80户家庭视为一个统计总体。
32
函数f (Xi)采取什么函数形式,是一个
需要解决的重要问题。在实际经济系统
中,我们不会得到总体的全部数据,因
而就无法据已知数据确定总体回归函数 的函数形式。同时,对总体回归函数的 形式只能据经济理论与经验去推断。
第二章 一元线性回归模型(本科生计量经济学)

即:正规方程组揭示的是残差的性质。
26
普通最小二乘估计有关 的其他性质(课后习题)
Y Y
^
e Y e y
i ^ i
^
i
0 0
27
i
2、由普通最小二乘估计系数的性质可证
得普通最小二乘估计与参数的关系如下:
1 1 k i u i
^
0 0 wi ui
( 1) ( 2)
( 1)
0 Y 1 X
^
^
Y
1 n
Y , X X
i 1 i 1 n i 1
n
n
i
18
参数的普通最小二乘估计量
ˆ ˆ X )0 (Yi 0 1 i ˆ ˆ X )X 0 ( Y i 0 1 i i
^
33
三、一元线性回归模型参数的最大似 然法(Maximum Likehood,ML)估计
• 基本原理:似然原理
• 一元线性回归模型ML使用的条件:已知随机扰动 项的分布。
34
Y1 , Y2 ,...,Yn
1 f (Yi ) e 2
1 2
1 2
2
Yi ~ N (0 1 X i , 2 )
w 1
i
22
普通最小二乘估计的例
年份
1991 1992 1993 1994
ED(X)
708 793 958 1278
FI(Y)
3149 3483 4349 5218
ed(x)
-551 -466 -301 19
fi(y)
-2351 -2017 -1151 -282
计量经济学习题集(精炼版) (1)

第一章绪论一、单项选择题1、变量之间的关系可以分为两大类,它们是【】A 函数关系和相关关系B 线性相关关系和非线性相关关系C 正相关关系和负相关关系D 简单相关关系和复杂相关关系2、相关关系是指【】A 变量间的依存关系B 变量间的因果关系C 变量间的函数关系D 变量间表现出来的随机数学关系3、进行相关分析时,假定相关的两个变量【】A 都是随机变量B 都不是随机变量C 一个是随机变量,一个不是随机变量D 随机或非随机都可以4、计量经济研究中的数据主要有两类:一类是时间序列数据,另一类是【】A 总量数据B 横截面数据C平均数据 D 相对数据5、横截面数据是指【】A 同一时点上不同统计单位相同统计指标组成的数据B 同一时点上相同统计单位相同统计指标组成的数据C 同一时点上相同统计单位不同统计指标组成的数据D 同一时点上不同统计单位不同统计指标组成的数据6、下面属于截面数据的是【】A 1991-2003年各年某地区20个乡镇的平均工业产值B 1991-2003年各年某地区20个乡镇的各镇工业产值C 某年某地区20个乡镇工业产值的合计数D 某年某地区20个乡镇各镇工业产值7、同一统计指标按时间顺序记录的数据列称为【】A 横截面数据B 时间序列数据C 修匀数据D原始数据8、经济计量分析的基本步骤是【】A 设定理论模型→收集样本资料→估计模型参数→检验模型B 设定模型→估计参数→检验模型→应用模型C 个体设计→总体设计→估计模型→应用模型D 确定模型导向→确定变量及方程式→估计模型→应用模型9、计量经济模型的基本应用领域有【】A 结构分析、经济预测、政策评价B 弹性分析、乘数分析、政策模拟C 消费需求分析、生产技术分析、市场均衡分析D 季度分析、年度分析、中长期分析10、计量经济模型是指【】A 投入产出模型B 数学规划模型C 包含随机方程的经济数学模型D 模糊数学模型11、设M为货币需求量,Y为收入水平,r为利率,流动性偏好函数为:M=a+bY+cr+u,b’和c’分别为b、c的估计值,根据经济理论,有【】A b’应为正值,c’应为负值B b’应为正值,c’应为正值C b’应为负值,c’应为负值D b’应为负值,c’应为正值12、回归分析中定义【】A 解释变量和被解释变量都是随机变量B 解释变量为非随机变量,被解释变量为随机变量C 解释变量和被解释变量都是非随机变量D 解释变量为随机变量,被解释变量为非随机变量13、线性模型的影响因素【】A 只能是数量因素B 只能是质量因素C 可以是数量因素,也可以是质量因素D 只能是随机因素14、下列选项中,哪一项是统计检验基础上的再检验(亦称二级检验)准则【】A. 计量经济学准则 B 经济理论准则C 统计准则D 统计准则和经济理论准则15、理论设计的工作,不包括下面哪个方面【】A 选择变量B 确定变量之间的数学关系C 收集数据D 拟定模型中待估参数的期望值16、计量经济学模型成功的三要素不包括【】A 理论B 应用C 数据D 方法17、在模型的经济意义检验中,不包括检验下面的哪一项【】A 参数估计量的符号B 参数估计量的大小C 参数估计量的相互关系D 参数估计量的显著性18、计量经济学模型用于政策评价时,不包括下面的那种方法【】A 工具变量法B 工具—目标法C 政策模拟D 最优控制方法19、在经济学的结构分析中,不包括下面那一项【】A 弹性分析B 乘数分析C 比较静力分析D 方差分析二、填空题1、计量经济学是_________的一个分支学科,是以揭示_________中的客观存在的_______ 为内容的分支学科。
计量经济学第2章 一元线性回归模型

ˆ2 ˆ2
) )
ˆ2
0 0
6
Q(ˆ1, ˆ2 ˆ1
Q(ˆ1, ˆ2 ) ˆ2
) [ [
(Yi
ˆ1 ˆ1
ˆ2
X
i
)2
]
2
(Yi
ˆ1 ˆ2
ˆ2
X
i
)2
]
2
Yi ˆ1 ˆ2 X i Yi ˆ1 ˆ2 X i X i
Yi ˆ1 ˆ2 X i 0 Yi ˆ1 ˆ2 X i X i 0
全为零,线性性得证。 i
• ˆ的1 线性性可利用 的ˆ2线性性得到。
ˆ1
Y
ˆ2 X
1 n
i
Yi X
i
biYi
i
(
1 n
Xbi
)Yi
• 可记为
ˆ1 WiYi
i
这表明 同ˆ1 样是Yi的线性组合,其中Wi也不全为零,线性
性也得到证明。
12
• 2.无偏性
• 无偏性指ˆ1和的ˆ2数学期望分别等于总体回归系数的值β1和
5
• 下面用最小二乘法求总体回归系数β1、β2的估计 值 ˆ1和。ˆ2 即令
min Q(ˆ1, ˆ2 ) ei2 (Yi Yˆi )2 [Yi (ˆ1 ˆ2 Xi )]2
i
i
i
• 根据微积分多元函数极值原理,要使上式达到最
小,对ˆ1和ˆ2 的一阶偏导数都等于零,即
Q(ˆ1,
ˆ1 Q(ˆ1,
归模型的基本假定。
4
§2.2 一元线性回归模型的参数估计
• 1.普通最小二乘法(OLS)
• 总体回归模型:
Yi 1 2 X i ui
• 总体回归方程:
E(Yi ) 1 2 X i
第二章 一元线性回归模型 知识点
第二章一元线性回归模型一、知识点列表二、关键词1、回归分析基本概念关键词:回归分析在计量经济学中,回归分析方法是研究某一变量关于另一(些)变量间数量依赖关系的一种方法,即通过后者观测值或预设值来估计或预测前者的(总体)均值。
回归的主要作用是用来描述自变量与因变量之间的数量关系,还能够基于自变量的取值变化对因变量的取值变化进行预测,也能够用来揭示自变量与因变量之间的因果关系关键词:解释变量、被解释变量影响被解释变量的因素或因子记为解释变量,结果变量被称为被解释变量。
2、回归模型的设定关键词:随机误差项(随机干扰项)不包含在模型中的解释变量和其他一些随机因素对被解释变量的总影响称为随机误差项。
产生随机误差项的原因主要有:(1)变量选择上的误差;(2)模型设定上的误差;(3)样本数据误差;(4)其他原因造成的误差。
关键词:残差项(residual )通过样本数据对回归模型中参数估计后,得到样本回归模型。
通过样本回归模型计算得到的样本估计值与样本实际值之差,称为残差项。
也可以认为残差项是随机误差项的估计值。
3、一元线性回归模型中对随机干扰项的假设 关键词:线性回归模型经典假设线性回归模型经典假设有5个,分别为:(1)回归模型的正确设立;(2)解释变量是确定性变量,并能够从样本中重复抽样取得;(3)解释变量的抽取随着样本容量的无限增加,其样本方差趋于非零有限常数;(4)给定被解释变量,随机误差项具有零均值,同方差和无序列相关性。
(5)随机误差项服从零均值、同方差的正态分布。
前四个假设也称为高斯马尔科夫假设。
4、最小二乘估计量的统计性质关键词:普通最小二乘法(Ordinary Least Squares ,OLS )普通最小二乘法是通过构造合适的样本回归函数,从而使得样本回归线上的点与真实的样本观测值点的“总体误差”最小,即:被解释变量的估计值与实际观测值之差的平方和最小。
ββ==---∑∑∑nn n222i i 01ii=111ˆˆmin =min ()=min ()i i i i u y y y x关键词:无偏性由于未知参数的估计量是一个随机变量,对于不同的样本有不同的估计量。
计量经济学第二章一元线性回归模型

回归分析概述 一元线性回归模型的参数估计 一元线性回归模型的检验 一元线性回归模型的预测 实例
§2.1 回归分析概述
一、变量间的关系及回归分析的基本概念 二、总体回归函数(PRF) 三、随机扰动项 四、样本回归函数(SRF)
2020/3/6
LOU YONG
表 2.1.3 家庭消费支出与可支配收入的一个随机样本 Y 800 1100 1400 1700 2000 2300 2600 2900 3200 3500 X 594 638 1122 1155 1408 1595 1969 2078 2585 2530
2020/3/6
LOU YONG
20
• 该样本的散点图(scatter diagram):
分i。
2020/3/6
LOU YONG
17
上式称为总体回归函数(PRF)的随机 设定形式。表明被解释变量除了受解释 变量的系统性影响外,还受其他因素的 随机性影响。
由于方程中引入了随机项,成为计量经 济学模型,因此也称为总体回归模型。
2020/3/6
LOU YONG
18
随机误差项主要包括下列因素 在解释变量中被忽略的因素的影响; 变量观测值的观测误差的影响; 模型关系的设定误差的影响; 其他随机因素的影响。
回归系数(regression coefficients)。
2020/3/6
LOU YONG
15
三、随机扰动项
总体回归函数说明在给定的收入水平Xi下,该社 区家庭平均的消费支出水平。
但对某一个别的家庭,其消费支出可能与该平 均水平有偏差。
称为观察值围绕它的期望值的离差 (deviation),是一个不可观测的随机变量, 又称为随机干扰项(stochastic disturbance)或 随机误差项(stochastic error)。
第2章一元线性回归模型

一元线性回归模型
回归分析是计量经济学的基础内容!
本章介绍一元线性回归模型,最小二乘估计方法及 其性质,参数估计的假设检验、预测等。
浙江财经大学 倪伟才
1
本章主要内容
2 .1 一元线性回归模型
2 .2 参数β0、β1的估计
2 .3 最小二乘估计的性质
2 .4 回归方程的显著性检验 2 .5 残差分析 2 .6 回归系数的区间估计
浙江财经大学 倪伟才 10
回归的术语
y的各种名称: 因变量(dependent variable)或被解释变量 (explained variable)或回归子(regressand)或内 生(endogenous); X的各种名称: 自变量(independent variable)或解释变量 (explanatory variable)或回归元(regressor)或外 生(exogenous) U的各种名称: 随机误差项或随机扰动项(stochastic error term, random disturbance term ): 表示其它因素的影响,是不可观测的随机误差!
浙江财经大学 倪伟才
9
2.1一元线性回归模型
由于两个变量y, x具有明显的线性关系,故考虑直 线方程y=0+1x(函数表达的是确定性关系,有缺 陷!) y=0+1x+u, 其中u表示除x外,影响y的其它一切 因素。 将y与x之间的关系用两部分来描述: a. 一部分0+1x ,由x的变化引起y变化; b.另一部分u ,除x外的其它一切因素引起y变化。 参数(parameters) 0 , 1 ; 0 称为回归常数(截距)(intercept, constant), 1称为回归斜率(slope)
第二章一元线性回归模型1

第二章一元线性回归模型计量经济学在对经济现象建立经济计量模型时,大量地运用了回归分析这一统计技术,本章和下一章将通过一元线性回归模型、多元线性回归模型来介绍回归分析的基本思想。
第一节回归分析的几个基本问题回归分析是经济计量学的主要工具,下面我们将要讨论这一工具的性质。
一、回归分析的性质(一)回归释义回归一词最先由F •加尔顿(Francis Galt on )提出。
加尔顿发现,虽然有一个趋势,父母高,儿女也高:父母矮,儿女也矮,但给定父母的身高,儿女辈的平均身高却趋向于或者“回归” 到全体人口的平均身高。
或者说,尽管父母双亲都异常高或异常矮,而儿女的身高则有走向人口总体平均身高的趋势(普遍回归规律)。
加尔顿的这一结论被他的朋友K •皮尔逊(Karl pearson)证实。
皮尔逊收集了一些家庭出身1000多名成员的身高记录,发现对于一个父亲高的群体,儿辈的平均身高低于他们父辈的身高,而对于一个父亲矮的群体,儿辈的平均身高则高于其父辈的身高。
这样就把高的和矮的儿辈一同“回归”到所有男子的平均身高,用加尔顿的话说,这是“回归到中等” 。
回归分析是用来研究一个变量(被解释变量Explained variable或因变量Dependent variable 与另一个或多个变量(解释变量Explanatory variable或自变量Independent variable之间的关系。
其用意在于通过后者(在重复抽样中)的已知或设定值去估计或预测前者的(总体)均值。
下面通过几个简单的例子,介绍一下回归的基本概念。
例子1.加尔顿的普遍回归规律。
加尔顿的兴趣在于发现为什么人口的身高分布有一种稳定性,我们关心的是,在给定父辈身高的条件下找出儿辈平均身高的变化。
也就是一旦知道了父辈的身高,怎样预测儿辈的平均身高。
为了弄清楚这一点,用图 1.1 表示如下图 1.1 对应于给定父亲身高的儿子身高的假想分布图 1.1 展示了对应于设定的父亲身高, 儿子在一个假想人口总体中的身高分布, 我们不难发现,对应于任一给定的父亲身高, 相对应都有着儿子身高的一个分布范围,同时随着父亲身高的增加,儿子的平均身高也增加,为了清楚起见,在1.1散点图中勾画了一条通过这些散点的直线,以表明儿子的平均身高是怎样随着父亲的身高增加而增加的。
第二章 一元线性回归模型

∂Q ˆ ˆ = −2∑ (Yi − β 0 − β1 X i ) = 0 ∂β ˆ0 ˆ ˆ ∂Q = −2∑ (Y − β − β X )X = 0 i 0 1 i i ˆ ∂β1
化简得: 化简得:
ˆ ˆ ∑ (Yi − β 0 − β1 X i ) = 0 ˆ ˆ ∑ (Yi − β 0 − β1 X i )X i = 0
2.总体回归方程(线)或回归函数 总体回归方程( 总体回归方程 即对( )式两端取数学期望: 即对(2.8)式两端取数学期望:
E y i)= β 0 + β 1 x i (
(2.9)
(2.9)为总体回归方程。由于随机项的影响,所 )为总体回归方程。由于随机项的影响, 有的点( )一般不在一条直线上; 有的点(x,y)一般不在一条直线上;但所有的点 (x,Ey)在一条直线上。总体回归线描述了 与y )在一条直线上。总体回归线描述了x与 之间近似的线性关系。 之间近似的线性关系。
Yi = β X i + ui
需要估计, 这个模型只有一个参数 需要估计,其最 小二乘估计量的表达式为: 小二乘估计量的表达式为:
∑XY ˆ β= ∑X
i i 2 i
例2.2.1:在上述家庭可支配收入-消费支出例中,对 :在上述家庭可支配收入-消费支出例中, 于所抽出的一组样本数据, 于所抽出的一组样本数据,参数估计的计算可通过下面 的表2.2.1进行。 进行。 的表 进行
二、一元线性回归模型 上述模型中, 为线性的, 上述模型中, 若f(Xi)为线性的,这时的模型 为线性的 一元线性回归模型: 即为 一元线性回归模型:
yi = β 0 + β1 xi + ui 其中:yi为被解释变量,xi为解释变量,ui为随机误 差项,β 0、β1为回归系数。
第二章一元线性回归模型

;
(c)比较绝对值 t1 与 tα 2 的大小。若 t1 > tα ,则拒绝原假设,判 定 β1 ≠ 0 ,解释变量 x 解释功效显著;若 t1 < tα ,则接受原假设,
2
判定
, x β1 = 0 不是有效的解释变量。
§2.3 显著性检验
(三)一元线性回归模型示例 例2.1 y=JYL,x=DSCYCZZZL,
ˆ β1 = β1 + ∑
xi − x u 2 i ∑(xi − x)
ˆ Eβ0 = β0
ˆ Eβ1 = β1
OLS估计的统计性质 §2.2 OLS估计的统计性质
在一切线性无偏估计中, ˆ ˆ 3. 在一切线性无偏估计中, β0 , β1独具最小方差
1 x2 ˆ var(β0 ) =σ 2 ( + ) 2 n ∑(xi − x)
0 ≤ R2 ≤ 1
2 R2 = rxy
计算公式
ˆ β12 ∑(xi − x)2 2 R = ∑( yi − y)2
OLS估计的统计性质 §2.2 OLS估计的统计性质
(一)线性回归模型的基本假定:
假定1. 解释变量是确定性变量,不具有随机性 假定2. (零均值假定) 假定3. (同方差假定)
Eui = 0 , i = 1 ,2 ,L, n
y = β0 + β1x + u
yi = β0 + β1xi + ui
{yi , xi }
i =1 ,2 ,L, n
i =1 ,2 ,L, n
§2.1 普通最小平方估计
(一)普通最小平方估计(OLS) 普通最小平方估计 待定回归函数 残差 残差平方和 驻点条件
ˆ ˆ ˆ y = β0 + β1x
第二章 一元线性回归模型

__
__
2
/n
★样本相关系数r是总体相关系数 的一致估计
相关系数有以下特点:
• • • • 相关系数的取值在-1与1之间。 (2)当r=0时,线性无关。 (3)若r>0 ,正相关,若r<0 ,负相关。 (4)当0<|r|<1时,存在一定的线性相关 关系, 越接近于1,相关程度越高。 • (5)当|r|=1时,表明x与y完全线性相关 (线性函数),若r=1,称x与y完全正相关; 若r=-1,称x与y完全负相关。 • 多个变量之间的线性相关程度,可用复相 关系数和偏相关系数去度量。
●假定解释变量X在重复抽样中取固定值。 但与扰动项u是不相关的。(从变量X角度看是外生的)
注意: 解释变量非随机在自然科学的实验研究中相对
Yi 1 2 X i ui
●假定解释变量X是非随机的,或者虽然X是随机的,
容易满足,经济领域中变量的观测是被动不可控的, X非随机的假定并不一定都满足。
E( y xi ) 0 1xi
11
• 可以看出,虽然每个家庭的消费支出存在差 异,但平均来说,家庭消费支出是随家庭可 支配收入的递增而递增的。当x取各种值时, y的条件均值的轨迹接近一条直线,该直线称 为y对x的回归直线。(回归曲线)。 • 把y的条件均值表示为x的某种函数,可写 为:
E( y xi ) 0 1xi
Var ( y xi ) 2
Cov( yi , y j ) 0
y | xi ~ N (0 1xi , )
2
22
第三节 参数估计
• 一、样本回归方程
• 对于
yi 0 1 xi ui
• 在满足古典假定下,两边求条件均值,得到总体 回归函数:
第2章一元线性回归模型

布图上的点接近于一条曲线时,称为非线性相关。简单相关按
符号又可分为 正相关 (见图2.3.4 )、负相关 (见图2.3.8 )和零 相关 (见图2.3.6 )。两个变量趋于在同一个方向变化时,即同
增或同减,称为变量之间存在正相关;当两个变量趋于在相反
方向变化时,即当一个变量增加,另一个变量减少时,称为变 量之间存在负相关;当两个变量的变化相互没有关系时,称为
4、普通最小二乘法
为什么要使用OLS? (1)OLS的应用相对简便; (2)以最小化残差平方和为目标在理论很合理; (3)OLS估计量有很多有用的性质。 1)估计的回归线通过Y和X的均值。下列等式总是
ˆ ˆX 严格成立的:设下,可以证明,OLS是 “最优”的估计方法。
2.2.2 最小二乘估计量的性质
一个用于考察总体的估计量,可从如下几个方面考察其
优劣性: (1)线性。即它是否是另一个随机变量的线性函数;
(2)无偏性。即它的均值或期望是否等于总体的真实值;
(3)有效性。即它是否在所有的线性无偏估计量中具有 最小方差; (4)渐近无偏性。 即样本容量趋于无穷大时,它的均值 序列趋于总体的真值; (5)一致性。即样本容量趋于无穷大时,它是否依概率 收敛于总体的真值;
1.总变差的分解
ˆ b ˆX ˆ b Yt的估计值位于估计的回归线 Y t 0 1 t 上,Y围绕其均值的变异 (Y Y )可被分解为两部分:
ˆ Y ) (1) (Y t
ˆ) (2) (Yt Y t
样本回归函数:
3.相关系数检验
(1)变量相关的定义和分类
相关:指两个或两个以上变量间相互关系的程度或强度。
2 2 ˆ e ( Y Y ) i i OLS 最小化 i i 1 i 1
计量经济学 第二章 一元线性回归模型

计量经济学第二章一元线性回归模型第二章一元线性回归模型第一节一元线性回归模型及其古典假定第二节参数估计第三节最小二乘估计量的统计特性第四节统计显著性检验第五节预测与控制第一节回归模型的一般描述(1)确定性关系或函数关系:变量之间有唯一确定性的函数关系。
其一般表现形式为:一、回归模型的一般形式变量间的关系经济变量之间的关系,大体可分为两类:(2.1)(2)统计关系或相关关系:变量之间为非确定性依赖关系。
其一般表现形式为:(2.2)例如:函数关系:圆面积S =统计依赖关系/统计相关关系:若x和y之间确有因果关系,则称(2.2)为总体回归模型,x(一个或几个)为自变量(或解释变量或外生变量),y为因变量(或被解释变量或内生变量),u为随机项,是没有包含在模型中的自变量和其他一些随机因素对y的总影响。
一般说来,随机项来自以下几个方面:1、变量的省略。
由于人们认识的局限不能穷尽所有的影响因素或由于受时间、费用、数据质量等制约而没有引入模型之中的对被解释变量有一定影响的自变量。
2、统计误差。
数据搜集中由于计量、计算、记录等导致的登记误差;或由样本信息推断总体信息时产生的代表性误差。
3、模型的设定误差。
如在模型构造时,非线性关系用线性模型描述了;复杂关系用简单模型描述了;此非线性关系用彼非线性模型描述了等等。
4、随机误差。
被解释变量还受一些不可控制的众多的、细小的偶然因素的影响。
若相互依赖的变量间没有因果关系,则称其有相关关系。
对变量间统计关系的分析主要是通过相关分析、方差分析或回归分析(regression analysis)来完成的。
他们各有特点、职责和分析范围。
相关分析和方差分析本身虽然可以独立的进行某些方面的数量分析,但在大多数情况下,则是和回归分析结合在一起,进行综合分析,作为回归分析方法的补充。
回归分析(regression analysis)是研究一个变量关于另一个(些)变量的具体依赖关系的计算方法和理论。
一元线性回归模型案例

⼀元线性回归模型案例第⼆章⼀元线性回归模型案例⼀、中国居民⼈均消费模型从总体上考察中国居民收⼊与消费⽀出的关系。
表2.1给出了1990年不变价格测算的中国⼈均国内⽣产总值(GDPP)与以居民消费价格指数(1990年为100)所见的⼈均居民消费⽀出(CONSP)两组数据。
1) 建⽴模型,并分析结果。
输出结果为:对应的模型表达式为:201.1070.3862CONSP GDPP =+(13.51) (53.47) 20.9927,2859.23,0.55R F DW ===从回归估计的结果可以看出,拟合度较好,截距项和斜率项系数均通过了t 检验。
中国⼈均消费增加10000元,GDP 增加3862元。
⼆、线性回归模型估计表2.2给出⿊龙江省伊春林区1999年16个林业局的年⽊材采伐量和相应伐⽊剩余物数据。
利⽤该数据(1)画散点图;(2)进⾏OLS 回归;(3)预测。
表2.2 年剩余物y 和年⽊材采伐量x 数据(1)画散点图先输⼊横轴变量名,再输⼊纵轴变量名得散点图(2)OLS估计弹出⽅程设定对话框得到输出结果如图:由输出结果可以看出,对应的回归表达式为:0.76290.4043t t yx =-+ (-0.625) (12.11)20.9129,146.7166, 1.48R F DW === (3)x=20条件下模型的样本外预测⽅法⾸先修改⼯作⽂件范围将⼯作⽂件范围从1—16改为1—17确定后将⼯作⽂件的范围改为包括17个观测值,然后修改样本范围将样本范围从1—16改为1—17打开x的数据⽂件,利⽤Edit+/-给x的第17个观测值赋值为20将Forecast sample选择区把预测范围从1—17改为17—17,即只预测x=20时的y的值。
由上图可以知道,当x=20时,y的预测值是7.32,yf的分布标准差是2.145。
三、表2.3列出了中国1978—2000年的参政收⼊Y和国内⽣产总值GDP的统计资料。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
回归分析概述
(一)变量间的关系及回归分析的基本概念 1、变量间的关系 经济变量之间的关系,大体可分为两类:
(1)确定性关系或函数关系:研究的是确定现象非随 机变量间的关系。 (2)统计依赖或相关关系:研究的是非确定现象随机 变量间的关系。
例如:函数关系:
圆面积 = f (π , 半径 ) = π ⋅ 半径 2
例2.1中,个别家庭的消费支出为:
yi = E ( y | xi ) + ui = α + β xi + ui
(*)
即,给定收入水平xi ,个别家庭的支出可表示为两部分之和: (1)该收入水平下所有家庭的平均消费支出E(y|xi),称为 系统性(systematic)或确定性(deterministic)部分。 (2)其他随机或非确定性(nonsystematic)部分ui。
• 概念:
在给定解释变量xi条件下被解释变量yi的期望轨迹 称为总体回归线(population regression line),或 更一般地称为总体回归曲线(population regression curve)。 相应的函数:
E ( y | xi ) = f ( xi )
称为总体回归函数(population regression function, PRF)。
ˆx + ε ˆ ˆˆ yi = y + u = α + β i i i i
其中,εi 称为(样本)残差(或剩余)项(residual), 代表其他影响y的随机因素的集合,可看成是ui的估计量. 由于方程中引入了随机项,成为计量经济模型,因此也 称为样本回归模型(sample regression model)。
共计
2420
素的影响,对同一收入水平x, 不同家庭的消费支出不完全相同; (2)但由于调查的完备性,给定收入水平x的消费 支出y的分布是确定的,即以X的给定值为条件的y的 条件分布(Conditional distribution)是已知的, 如: P(y=561|x=800)=1/4。 因此,给定收入x的值xi,可得消费支出y的条件均 值(conditional mean)或条件期望(conditional expectation): E(y|x=xi) 该例中:E(y | x=800)=605
注意: 这里将样本回归线看成总体回归线的近似替代
ˆx ˆ+β ˆ y = α i
= yi E ( yi | xi ) + ui = α + β xi + ui
则
ˆ i为的估计量 y E ( y | xi ) ˆ ˆ,分别为,的估计量 α β α β
样本回归函数的随机形式/样本回归模型:
同样地,样本回归函数也有如下的随机形式:
描出散点图发现:随着收入的增加,消费“平均 地说”也在增加,且y的条件均值均落在一根正 斜率的直线上。这条直线称为总体回归线。
3500 每 月 消 费 支 出 Y (元) 3000 2500 2000 1500 1000 500 0 500 1000 1500 2000 2500 3000 3500 4000 每月可支配收入X(元)
2.1 线性回归模型的基本假设
假设1 ui(i=1,2,…,n)均为服从正态分布的实随机变量; 假设2 ui(i=1,2,…,n)的期望值均为0,即 E(ui)=0 i=1,2, …,n 假设3 ui(i=1,2,…,n)的方差均为同一个常数,即 i=1,2, …,n V (ui)=E(ui 2 )=σu2 =常数 (同方差性) 假设4 不同的随机误差项之间彼此独立,即 i≠j i,j= 1,2, …,n Cov(ui, uj)=0 (非自相关性) 假定5 随机误差项u与解释变量x之间不相关: i=1,2, …,n Cov(xi, ui)=0 在这学期的课程中,都假设xi是非随机的。
▼回归分析的主要目的:根据样本回归函数SRF,估计 总体回归函数PRF。 即,根据 估计
ˆx + ε ˆ+β ˆi + ε i = α yi = y i i yi = E ( y | xi ) + ui = α + β xi + ui
这就要求:
设计一“方法” 构造SRF,以使 SRF尽可能“接 近”PRF,或者 ˆ尽可能 说使 α ˆ, β 接近α,β. 注意:这里PRF可能永 远无法知道。
(*)式称为总体回归函数(方程)PRF的随机设 定形式。表明被解释变量除了受解释变量的系统性影 响外,还受其他因素的随机性影响。 由于方程中引入了随机项,成为计量经济学模型, 因此也称为总体回归模型。
随机误差项主要包括下列因素的影响: 1)在解释变量中被忽略的因素的影响; 2)变量观测值的观测误差的影响; 3)模型关系的设定误差的影响; 4)其它随机因素的影响。
回归分析构成计量经济学的方法论基础,其 主要内容包括: (1)根据样本观察值对经济计量模型参数进行 估计,求得回归方程;
(2)对回归方程、参数估计值进行显著性检验; (3)利用回归方程进行分析、评价及预测。
(二)、总体回归函数
由于变量间关系的随机性,回归分析关心的是根据 解释变量的已知或给定值,考察被解释变量的总体均 值,即当解释变量取某个确定值时,与之统计相关的 被解释变量所有可能出现的对应值的平均值。 例2.1:一个假想的社区有100户家庭组成,要研究 该社区每月家庭消费支出y与每月家庭可支配收入x 的关系。即如果知道了家庭的月收入,能否预测该 社区家庭的平均月消费支出水平。 为达到此目的,将该100户家庭划分为组内收入差不 多的10组,以分析每一收入组的家庭消费支出。
表 2.1.1 某社区家庭每月收入与消费支出统计表 每月家庭可支配收入 X(元) 800 每 月 家 庭 消 费 支 出 Y (元) 561 594 627 638 1100 638 748 814 847 935 968 1400 869 913 924 979 1012 1045 1078 1122 1155 1188 1210 1700 1023 1100 1144 1155 1210 1243 1254 1298 1331 1364 1408 1430 1485 2000 1254 1309 1364 1397 1408 1474 1496 1496 1562 1573 1606 1650 1716 2300 2600 2900 1969 1991 2046 2068 2101 2189 2233 2244 2299 2310 3200 2090 2134 2178 2266 2354 2486 2552 2585 2640 3500 2299 2321 2530 2629 2860 2871 1408 1650 1452 1738 1551 1749 1595 1804 1650 1848 1672 1881 1683 1925 1716 1969 1749 2013 1771 2035 1804 2101 1870 2112 1947 2200 2002 4950 11495 16445 19305 23870 25025
i= 1, 2, , n
y为被解释变量,x为解释变量,α与β为待估参 数, u为随机干扰项
样本回归函数(SRF)
总体的信息往往无法掌握,现实的情况只能是在 一次观测中得到总体的一个样本。 问题:能从一次抽样中获得总体的近似的信息吗? 如果可以,如何从抽样中获得总体的近似信息? 例2.2:在例2.1的总体中有如下一个样本, 问:能否从该样本估计总体回归函数PRF?
以上假设也称为线性回归模型的经典假 设或高斯-马尔可夫(Gauss Markov)假设, 满足该假设的线性回归模型,也称为经典 线性回归模型(Classical Linear Regression Model, CLRM)。
样本散点图近似于一条直线,画一条直线以尽好地拟合该 散点图,由于样本取自总体,可以该线近似地代表总体回归线。 该线称为样本回归线(sample regression lines)。 记样本回归线的函数形式为:
ˆx ˆ+β ˆ= y f ( xi ) = α i i
称为样本回归函数(sample regression function,SRF)。
(三)、随机扰动项
总体回归函数说明在给定的收入水平xi下,该社区 家庭平均的消费支出水平。 但对某一个别的家庭,其消费支出可能与该平均水 平有偏差。
= yi − E ( yi ) i 记 u 称ui为观察值yi围绕它的期望值E(y|xi)的偏差 (deviation),是一个不可观测的随机变量,又称 为随机干扰项(stochastic disturbance)或随机误 差项(stochastic error)。
回归分析的主要目的是要通过样本回归函数(模型) SRF尽可能准确地估计总体回归函数(模型)PRF。 估计方法有多种,其种最广泛使用的是普通最小二 乘法(ordinary least squares, OLS)。 为保证参数估计量具有良好的性质,通常对 模型提出若干基本假设。 注:实际这些假设与所采用的估计方法紧密相关。
▲注意:
①不线性相关并不意味着不相关; ②有相关关系并不意味着一定有因果关系; ③回归分析/相关分析研究一个变量对另一个 (些)变量的统计依赖关系,但它们并不意味着一定 有因果关系。 ④相关分析对称地对待任何(两个)变量,两个 变量都被看作是随机的。回归分析对变量的处理方法 存在不对称性,即区分应变量(被解释变量)和自变 量(解释变量)。
• 含义:
回归函数(PRF)说明被解释变量y的平均状态 (总体条件期望)随解释变量x变化的规律。
• 函数形式:
可以是线性或非线性的。 例2.1中,将居民消费支出看成是其可支配收 入的线性函数时: E ( y | x ) = α +βx
i i
为一线性函数。其中,α,β是未知参数,称为 回归系数(regression coefficients)。 。
