山东建筑大学高等数学试题A卷
2010-2011-1高数A1试题答案

-----5 分
e x x 1 e x C x 1 Ce x ( ) ( )
由y 装订线
x 0ຫໍສະໝຸດ 1 知, C 2
x
所以,所求曲线为 y x 1 2e .
-----6 分
ln 2 1
x 0
.--------6 分
19.
x tan
2
xdx x(sec2 x 1)dx
--------1 分 -------3 分 --------5 分 --------6 分
xd tan x
1 2 x 2
2 x 5x 2 8. (e 1) ;9. ;10. y C1e C 2 e . 2 3
2 2
页第 2 页
-----1 分
1 2 2 y 4 2 y dy
4
4
f (x) 在 [a, b] 上连续,在 (a, b) 内可导,由拉格朗日中值定理知, (a, b)
------6 分 使 -----1 分
1 1 y 2 4 y y 3 18 6 2 2
0
x 1t
1
1
f (t )dt
2x
0
sin t 2 dt x
3
x 0
lim
sin 2 x) 2 ( x 0 3x 2
2
---------3 分
1 1 dt dt t 1 1 e 0 1 t
0 1 et et 1 dt ln | 1 t |0 t ln(1 e t ) 1 ln 2 t 1 1 e
23. 分离变量, 学号
山东建筑大学试卷模版2010-2011-2概率论与数理统计试题A

4、设随机变量X的散布函数为
那么系数A=__________;B=__________.
5、设两个互相独破的随机变量X跟Y的方差分不为4跟2,那么随机变量的方差为__________.
6、设X听从上的平均散布,对X进展三次独破实验,那么至多有两次不雅察值年夜于2的概率为__________.
7、设随机变量X与Y互相独破,且有统一散布列
X
0
1
P
那么随机变量的散布列为____________________.
8、假定一批产物中一、二、三等品各占60%、30%、10%,从中恣意掏出一件,后果不是三等品,那么取到的是一等品的概率为.
9、设跟为两个随机变量,且,,那么.
10、设总体的概率密度为,而是来自总体的复杂随机样本,那么未知参数的矩法估量量为.
18、设,且,那么参数即是〔〕.
〔A〕〔B〕〔C〕〔D〕
19、将一枚硬币反复掷次,以跟分不表现正面向上跟背面向上的次数,那么与的相干联数即是〔〕.
(A);〔B〕;(C);(D).
20、设,,…是来自正态总体的复杂随机样本,是样本均值,记,,,,那么听从自在度为的散布的随机变量是〔〕.
〔A〕;〔B〕;〔C〕;〔D〕.
二、选择题〔每题2分,共20分〕
11、设随机变量A与B互不相容,且,,那么以下关联成破的是〔〕.
〔A〕A与B互相独破;〔B〕A与B不互相独破;
〔C〕A与B互为统一事情;〔D〕A与B不互为统一事情.
12、设X是一个团圆型随机变量,那么〔〕能够成为X的散布列.
〔A〕
1
0
〔p是恣意实数〕
〔B〕
0.1
0.3
0.3
山东建筑大学2019-2020学年第一学期《线性代数》期末试卷A及答案

···········································································································装订线山 东 建 筑 大 学 试 卷 共 4 页 第 1 页2019 至 2020学年第 1 学期 线性代数 (本科)试卷 A 卷 专业: 全校修线性代数的各专业试卷类别:考试 考试形式:闭卷 考试时间 120 分钟 题号 一 二 三 四 五六七总分 分数说明:在本卷中,T A 表示矩阵A 的转置矩阵,*A 表示矩阵A 的伴随矩阵,E 表示单位矩阵,A 表示方阵A 的行列式,()R A 表示矩阵A 的秩。
山东建筑大学复变函数与积分变换A(07-08-01)答案

一、选择题(4分×6=24分)CDACCB二、填空题(4分×4=16分)1.2. 03.__1_ 42π三、计算题(6分×8=48分)1. 计算解: =----------------------------------------------------------------------------------2分22ii keπππ⎛⎫⎛⎫+⎪⎪⎝⎭⎭⎝⎭==-----------------------------------------------------4分cos sin22iππππ⎛⎛⎫=+++⎪⎪ ⎪⎝⎭⎝⎭---------------------------6分2. 利用高阶导数公式计算积分()341zzdzz=-⎰ ,积分曲线取正向.解:()()()213222!1zzz iI dz zzπ====-⎰ --------------------------------------------4分=---------------------------------------------------------------------------------6分3. 利用柯西积分公式计算32sin241zze zdzz z=⎛⎫+⎪++⎝⎭⎰ ,积分曲线取正向.解: 两个奇点-1,-4 其中-4在曲线外边,所以---------------------------------------------2分3322sin22411zz ze zdz dzz z z==⎛⎫⎛⎫+=⎪ ⎪+++⎝⎭⎝⎭⎰⎰-----------------------------------------4分4iπ=----------------------------------------------------------6分4. 已知调和函数22u x xy=-,求()f z u iv=+解: 222u vf i y i xx x∂∂'=+=-+∂∂-------------------------------------------------------2分()2222i x iy iz=++=+---------------------------------------------------------4分所以2222iz dz iz z C+=++⎰,则()22f z iz z C=++-----------------------------6分5. 将函数()()112z z--在环域2z<<+∞内展开为洛朗级数解: 在2z<<+∞环域上, ()()()1111212f zz z z z==---------------------------2分21111111111z z z z z z ⎛⎫=-=-+++ ⎪-⎝⎭- 221111221221z z z z z z ⎛⎫=-=-+++ ⎪-⎝⎭- ----------------------------------------------4分 所以()234137f z z z z=+++ -----------------------------------------------------------6分 6. 留用留数定理计算()220sin 0x x dx a x a +∞>+⎰解: 函数()22z f z z a =+在上半平面有一级极点ai ,故 ()222R e ,ix iz x e dx i s R z e ai x a π+∞-∞⎡⎤=⎣⎦+⎰22aae i i e ππ--==----------------------------------------------------------2分 ()22sin x xf x x a =+为偶函数,所以22220sin 1R e 2ix x x x dx e dx x a x a +∞+∞-∞⎡⎤=⎢⎥++⎣⎦⎰⎰----------4分 而原积分12a I e π-==---------------------------------------------------------------------------6分 7.()() 0 0,0, 0t t f t et ββ-<⎧=>⎨≥⎩求傅氏变换 解:()F ω()j t f t edt ω+∞--∞=⎰ ---------------------------------------------------------------------2分0t j t e e dt βω+∞--=⎰()0j t e dt ωβ+∞-+=⎰()()0j t e j ωβωβ+∞-+⎡⎤=⎢⎥-+⎣⎦--------------------------4分 ()01j ωβ-=-+22j βωβω-=+----------------------------------------------------------6分8.()()sin f t kt k =求正弦函数的拉氏变换为实数解:[sin ]L kt 0sin st kte dt +∞-=⎰------------------------------------------------------------------2分()220sin cos st e s kt k kt s k +∞-=-⋅-⋅+------------------------------------------4分 22ks k =+(Re()0)s >----------------------------------------------------------6分四、证明题(6分×2=12分)1证明拉普拉斯变换得微分性质.()()()0L f t sF s f '=-⎡⎤⎣⎦证明:()()0st L f t f t e dt +∞-''=⎡⎤⎣⎦⎰---------------------------------------------------------------------2分()()00st st f t e s f t e dt +∞+∞--=+⎰-------------------------------------------------------------------------4分()()0(Re())sL f t f s c =->⎡⎤⎣⎦()()0sF s f =-------------------------------------------------6分2、若在1z <内,()f z 解析,并且1()1f z z ≤-, 则()(0)(1)!n f e n <+证: 因 ()1||1!()(0)d 2πi n n n z n n f z f z z +=+=⎰-----------------------------------------------------------------2分故11||1||1!|(0)||d |2π||z (n)n n z n n f z z -+=+≤⎰11111!n 2π2π()n+1n n n nn n +-++≤------------------------------------------------------------------4分1(1)!1e(1)!n n n n ⎛⎫=++<+ ⎪⎝⎭ ----------------6分。
山东建筑大学2007-2008(1)概率论与数理统计试题(A卷)解答

1 3
(B)
2 5
(C)
1 5
( D)
4 15
二.填空题(每小题 3 分,共 15 分) 1. 一个均匀骰子,掷一次,朝上那面点数不小于 2 的概率是___5/6_____. 2. 射击两次,事件 Ai 表示第 i 次命中目标(i=1,2) ,则事件“至多命中一次”可表示为
A1 A2
.
3. 设 P ( A) 0.5, P ( B ) 0.6, P ( A B ) 0.9 , 则 P(B-A)=___0.4_______. 4. 设随机变量 X~N(0,1) ,φ(x)为其分布函数,则φ(x)+φ(-x)=___1____. 5. 设 X 与 Y 相互独立,且 D(X)=3,D(Y)=5,则 D(2X-Y+1)=_17___. 三.解答下列各题(每小题 6 分,共 30 分) 1. 一口袋装有 4 只白球, 5 只红球. 从袋中任取一只球后, 放回去, 再从中任取一只球. 求下列事 件的概率: 1) 取出两只都是红球; 2) 取出的是一只白球, 一只红球. 解:以 A 表示事件“取出两只都是红球” ,以 B 表示“取出的是一只白球, 一只红球” 。 由于是有放回取球,因而样本点总数 n=9×9=81。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。2 分 有利于事件 A 的样本点数 k1=5×5=25 事件 A 发生的概率为 P(A)=k1/n=25/81。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。4 分 有利于事件 B 的样本点数 k2=2×4×5=40 事件 B 发生的概率为 P(B)=k1/n=40/81。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。6 分 2. 有两个口袋,甲袋中盛有 2 个白球,1 个黑球;乙袋中盛有 1 个白球,2 个黑球。由甲袋中任 取一球放入乙袋,再从乙袋任取一球,求从乙袋中取得白球的概率。 解:以 A 表示 “从乙袋中取得白球” ,以 B1、B2 分别表示从甲袋中取得白球、黑球。 由于 B1∪B2=Ω, 可用全概率公式 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。2 分 P(A)=P(B1)×P(A|B1)+P(B2)×P(A|B2) =2/3×2/4+1/3×1/4 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。4 分 =5/12 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。6 分
10-11-2概率论与数理统计A卷(答案)山东建筑大学概率论与数理统计试题A期末考试试题

2010-2011-2 概率与数理统计试卷A 参考答案及评分标准一、填空题(每小题2分,共20分) 1、0.7; 2、)16,1(N ; 3、10; 4、1,1==B A; 5、44; 6、2720;7、 8、32,9、75,10、111-∑=n i i X n 。
二、选择题(每题2分,共20分)11、(B ); 12、(D ); 13、(D ); 14、(B ); 15、(C );16、(B );17、(A );18、(B ); 19、(A ); 20、(B ).三、计算题(共60分)21、(8分) 解 设A 表示事件“从剩下的产品中任取一件是正品”,i B 表示事件“已经出售的2件中有i 件次品”)2,1,0(=i ,则CC B P 210270)(=;85)/(0=B A P ---------------------------------------------------------2分CC C B P 21013171)(=;86)/(1=B A P -------------------------------------------------------4分CC B P 210232)(=;87)/(2=B A P -----------------------------------------------------------6分所以7.0878685)/()()(210232101317210272=⋅+⋅+⋅==∑=C C C C C C C i ii B A P B P A P ------------8分22、(10分)解 (1)X 的可能取值为1-,1,2,----------------------------------------------2分 且3162}1{==-=X P ,2163}1{===X P ,61}2{==X P ,------------------6分所以其概率分布为(2)()1123123≠⎪⎭⎫⎝⎛≠<=⎪⎪⎭⎫ ⎝⎛≠<X P X X P X X P 且-------------------------------------8分 322131==---------------------------------------------------------------------------------10分 23、(12分) 解 (1)由12)()(1=+=+=⎰⎰∞+∞-b adx b ax dx x f ,--------------------------2分 又85283)()(21121 21=+=+==⎭⎬⎫⎩⎨⎧>⎰⎰∞+b a dx b ax dx x f XP ,--------------------------4分所以21,1==b a ------------------------------------5分 (2)327)21()(214121412141=+==⎭⎬⎫⎩⎨⎧≤<⎰⎰dx x dx x f X P -------------------------7分(3)⎰∞-=x dt t f x F )()(当0≤x 时,00)(==⎰∞-xdt x F ;-----------------------------------------------------8分当10≤<x 时,)1(212121)21(0)(200+=+=++=⎰⎰∞-x x x x dt t dt x F x;----------10分当1>x 时,10)21(0)(1010=+++=⎰⎰⎰∞-x dt dt t dt x F ;-----------------------------11分综上, ⎪⎩⎪⎨⎧>≤<+≤=1,110,)1(210,0)(x x x x x x F ---------------------------------12分24、(10分)解 先求X e Y =的分布函数}{}{)(y e P y Y P y F X Y ≤=≤=-------------------------2分当0≤y 时,0)(=y F Y ;--------------------------------------------------------------4分当10<<y 时,00}ln {)(ln ==≤=⎰∞-yY dx y X P y F ;--------------------------------6分当1≥y 时,⎰-=≤=yx Y dx e y X P y F ln 0}ln {)(;--------------------------------------8分所以⎪⎩⎪⎨⎧≥=⋅<='=-1,111,0)()(2ln y y y e y y F y f y Y Y .----------------------------------------10分25、(10分)解),(Y X 的概率分布表为分所以Y X +的分布列为整理得Y X +的分布列为分26、(10分) 解:121122()x xE X edx θθθθθθ--+∞==+⎰---------------------------2分121222211222()2x xE X edx θθθθθθθθ--+∞==++⎰---------------------------4分令 122221122112n ii x x n θθθθθθ=⎧+=⎪⎨++=⎪⎩∑ 解得12,θθ的矩法估计为^2^1n n s x s θθ⎧==⎪⎪⎨⎪=-⎪⎩---------------------------6分似然函数12111221(,)n i i x n nL eθθθθθ=⎡⎤--⎢⎥⎢⎥⎣⎦∑=两边取对数1221121ln (,)ln n i i L n x n θθθθθ=⎡⎤=---⎢⎥⎣⎦∑ 对1θ求偏导,1212ln (,)0L nθθθθ∂=>∂,知L ln 是1θ的递增函数,1θ取到其最大的可能值使L ln 达到最大,故1θ的极大似然估计为^112min{,,}n x x x θ= 。
2010-1011第二学期线性代数试卷A卷

1 0 1 2. (10 分) 设 A 和 B 都是 3 阶方阵 AB E A B , 若 A 0 2 0 , 1 0 1
2
求B 。
山东建筑大学试卷
装订线
2 2 2 (3)求该二次型在 x x1 x2 x3 1 时最小值。
T T T
.
2.若向量组 1 , 2 , 3 与向量组 l1 2 , 2 3 , m 3 1 都线性无关。 则常数 l 与 m 必满足关系式 。
T
x1 x 2 a 2.线性方程组 x 2 x 3 2a 有解的充分必要条件为 a= ( x x 1 1 3
3. 向量组 1 , 2 ,, s s 2 线性无关的充分必要条件是( (A) (B) (C) (D)
2 2 2 5. 已知二次型 f ( x1 , x2 , x3 ) (k 1) x1 正定, 则数 k 的 (k 1) x2 (k 3) x3
取值范围为________。
1 , 2 ,, s 均不为零向量; 1 , 2 ,, s 中任意两个向量不成比例; 1 , 2 ,, s 中任意 s 1 个向量线性无关; 1 , 2 ,, s 中任意一个向量均不能由其余的 s 1 个向量线性表示。
三、综合题(60 分)
1 2 1.(10 分)计算行列式: D 3 4
共 4 页第 3 页
学号 装订线 装订线 姓名
1 x1 x 2 x3 0 4(15 分)设线性方程组 x1 1 x 2 x3 3 ,问 取何值时,此方程组 x x 1 x 2 3 1
《概率论与数理统计 (A)
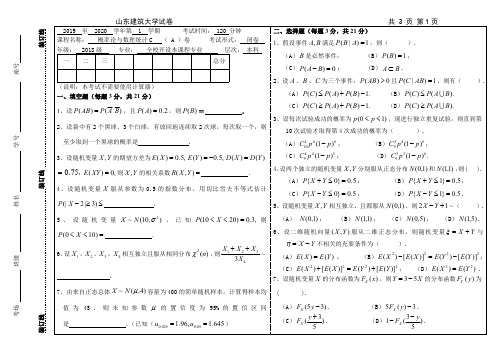
山东建筑大学试卷共3页第1页2019至2020学年第1学期考试时间:120分钟课程名称:概率论与数理统计C (A )卷考试形式:闭卷年级:2018级专业:全校开设本课程专业层次:本科一二三总分(说明:本考试不需要使用计算器)一、填空题(每题3分,共21分)1、设()( )P AB P A B =,且()0.2P A =,则()P B =.2、设袋中有2个黑球、3个白球,有放回地连续取2次球,每次取一个,则至少取到一个黑球的概率是.3、设随机变量Y X ,的期望方差为,5.0)(=X E ,5.0)(-=Y E )()(Y D X D =,75.0=,0)(=XY E 则Y X ,的相关系数=),(Y X R .4、设随机变量X 服从参数为0.5的指数分布,用切比雪夫不等式估计≤≥-)3|2(|X P .5、设随机变量),10(~2σN X ,已知,3.0)2010(=<<X P 则=<<)100(X P .6、设1X ,2X ,3X ,4X 相互独立且服从相同分布2()n χ,则1234~3X X X X ++.7、由来自正态总体)4,(~μN X 容量为400的简单随机样本,计算得样本均值为45,则未知参数μ的置信度为95%的置信区间二、选择题(每题3分,共21分)1、假设事件,A B 满足(|)1P B A =,则().(A)B 是必然事件;(B)()1P B =;(C)()0P A B -=;(D)A B ⊂.2、设A 、B 、C 为三个事件,()0P AB >且(|)1P C AB =,则有().(A)()()() 1.P C P A P B ≤+-(B)()().P C P A B ≤ (C)()()() 1.P C P A P B ≥+-(D)()().P C P A B ≥ 3、设每次试验成功的概率为(01)p p <<,现进行独立重复试验,则直到第10次试验才取得第4次成功的概率为().(A)44610(1)C p p -;(B)3469(1)C p p -;(C)4459(1)C p p -;(D)3369(1).C p p -4、设两个独立的随机变量Y X ,分别服从正态分布)1,0(N 和)1,1(N ,则().(A)5.0}0{=≤+Y X P ;(B)5.0}1{=≤+Y X P ;(C)5.0}0{=≤-Y X P ;(D)5.0}1{=≤-Y X P .5、设随机变量Y X ,相互独立,且都服从)1,0(N ,则~12+-Y X ().(A))1,0(N ;(B))1,1(N ;(C))5,0(N ;(D))5,1(N .6、设二维随机向量),(Y X 服从二维正态分布,则随机变量Y X +=ξ与Y X -=η不相关的充要条件为().(A))()(Y E X E =;(B)2222)]([)()]([)(Y E Y E X E X E -=-;(C)2222)]([)()]([)(Y E Y E X E X E +=+;(D))()(22Y E X E =.7、设随机变量X 的分布函数为()X F x ,则35Y X =-的分布函数()Y F y 为().(A)(53)X F y -.(B)5()3X F y -.(C)3()y F +.(D)31()yF --.考场班级姓名学号座号线装订线装订线山东建筑大学试卷共3页第2页三、计算应用题(共58分)1、(8分)装有10件某产品(其中一等品5件,二等品3件,三等品2件)的箱子中丢失一件产品,但不知是几等品,今从箱中任取2件产品,结果都是一等品,求丢失的也是一等品的概率.2、(12分)设随机变量X 的概率密度为)()(||+∞<<-∞=-x Aex f x ,求:(1)系数A ;(2)X 的分布函数;(3))(X D .3、(8分)设),1,0(~N X 求||X Y =的概率密度.姓名学号线装订线装订线山东建筑大学试卷共3页第3页4、(10分)设二维随机变量),Y X (的联合概率密度为:⎩⎨⎧=0),(2Axy y x f 其他10 ,20<<<<y x 求:(1)参数A ;(2)X 和Y 的边缘概率密度并判断X 和Y 是否独立;(3))5.0,1(≤≥Y X P .5、(12分)设随机变量X 和Y 的联合分布在点(0,1),(1,0)及(1,1)为顶点的三角形区域G 上服从均匀分布,试求),(Y X Cov .6、(8分)设总体X 的概率密度为101,,(;).0,x x f x θθθ-<<⎧=⎨⎩其它(0).θ>12,,,n x x x 是X 的简单样本观测值,试求(1)参数θ的矩估计值;(2)参数θ的极大似然估计值.姓名学号线装订线装订线。
山东建筑大学高等数学2009-2010-A2(A)(新)

2009至2010学年第2学期 课程名称 高等数学A2 (本科)试卷A一、填空题(每小题3分,共15分)1.曲面22y x z +=上与平面042=-+z y x 平行的切平面方程是_______________.2.交换积分次序⎰⎰yydx y x f dy ),(10=_______________________.3.设曲线L 为圆周122=+y x ,则=⎰+L y x ds e22_________.4.设)10()(2≤≤=x x x f ,则函数)(x f 的正弦级数在21-=x 处收敛于_________. 二、选择题(每小题3分,共15分)6. 设函数),y x f z (=的全微分为,ydy xdx dz +=则点(0,0)(A )不是),y x f (的连续点. (B )不是),y x f (的极值点. (C )是),y x f (的极大值点. (D )是),y x f (的极小值点. 7.设区域,1:D 22≤+y x 则=++⎰⎰Ddxdy y x )2(( )0).A ( 2).B ( π).C ( π2D ).(8. 曲线L 的方程为]),1,1[(12-∈-=x x y 起点是,0,1)(- 终点是(1,0), 则dy xxydx L⎰+22=( )0).A ( 1).B ( 2).C ( 1).D (-9.下列级数中,收敛的是( )(A )22111n n n ∞=-+∑ (B )1131n n ∞=+∑ ( C )13(21)!n n n ∞=+∑ (D )11ln(1)n n ∞=+∑三、计算题(每小题7分,共70分)11.求由方程()z y x z y x 3232sin 2-+=-+确定的隐函数)y x z z ,(=的全微分.12. 设(),,xy x f z =其中f 具有二阶连续偏导数,求.2yx z∂∂∂ 13.计算,cos 2⎰⎰Ddxdy y 其中D 由直线121-===x y ,y ,x 所围成的闭区域.14.计算以xOy 面上的圆周ax y x =+22所围成的闭区域为底,以曲面22y x z += 为顶面的曲顶柱体的体积.15.计算⎰-+-=Lx x dy y e dx y y e I )2cos ()2sin (,其中L 为上半圆周),0(,222≥=+y x y x沿逆时针方向.16. 计算曲面积分⎰⎰∑++=dxdy z dzdx y dydz x I 222,∑为锥面222z x y =+与平面2=z 所围成锥体的外侧表面.17. 将函数 231)(2++=x x x f 展开成 )1(-x 的幂级数.18. 求幂级数∑∞=----1121121n n n x n )(的收敛域,并求其和函数.20.已知某曲线经过点(1,1),它的切线在纵轴上的截距等于切点的横坐标,求该曲线方程.2009至2010学年第2学期 课程名称 高等数学A2 (本科)试卷A 答案一、填空题(每小题3分,共15分) 1.0542=--+z y x 2.⎰⎰xxdy y x f dx2),(1. 3.e π2 4.41- 5.xy 1=.二、选择题(每小题3分,共15分)6.D 7.D 8.A 9.C 10.C 三、计算题(每小题7分,共70分)11. ()z y x z y x z y x F 3232sin 2),,(+---+=313)32cos(61)32cos(2=+-+---+-=-=∂∂z y x z y x F F x z z x 323)32cos(62)32cos(4=+-+---+-=-=∂∂z y x z y x F F y z z y 所以 dy dx dy y z dx x z dz 3231+=∂∂+∂∂=12解 令 xy u =,则().,u x f z ='2'1yf f x u u f x f x z +=∂∂⋅∂∂+∂∂=∂∂ ()yf yf y f yf f yx z y y x z ∂∂++∂∂=+∂∂=⎪⎭⎫ ⎝⎛∂∂∂∂=∂∂∂'2'2'1'2'12 x yf f x f yu u f y f y u u f ⋅++⋅=∂∂⋅∂∂++∂∂⋅∂∂="22'2"12'2'2'1⋅++="22'2"12xyf f xf …………………5分 13.解 积分区域D: ⎩⎨⎧<<+<<2011y y x ,4212120222112022sin y sin dy y cos y dx dy y cos dxdy y cos y D====⎰⎰⎰⎰⎰+ 14.解 曲顶柱体在xOy 面上的投影区域为D ={(x , y )|x 2+y 2≤ax }. 在极坐标下}cos 0 ,22|),{(θρπθπθρa D ≤≤≤≤-=, 所以dxdy y x V axy x )(2222+=≤+⎰⎰πθθρρρθππθππ422cos 022442323cos 4a d a d d a ==⋅=⎰⎰⎰-- 15解.添加辅助线x y OA ,0:=从0到2,由格林公式πσ===-+-⎰⎰⎰+DDOAL x xSd dy ye dx y y e22)2cos ()2sin (而00)2cos ()2sin (2==-+-⎰⎰dx dy y e dx y y e OAx x所以,.π=-=⎰⎰+OAOAL I16解 由高斯公式,I dv z y x dv zR y Q x P )222()(++=∂∂+∂∂+∂∂=ΩΩ⎰⎰⎰⎰⎰⎰ππ8222222=⋅===⎰⎰⎰⎰⎰⎰⎰Ωdz z z dxdy zdzzdv zD17.解 )1(31)1(212111231)(2-+--+=+-+=++=x x x x x x x f∑∑∞=∞=-----=-+--+=00 )31()1(31 )21()1(21311131211121n n n n nn x x x x ∑∞=++-⎪⎭⎫ ⎝⎛--=11 )1(3121)1(n n n n n x由1211<-<-x 及1311<-<-x 知,31<<-x . 18.解.nn n u u 1lim +∞→ ,1|1212|lim 21212<=-⋅+=-+∞→x x n n x n n n ,11<<-x 当1-=x 时,级数∑∑∞=∞=----=---11121121)1(121n nn n n n n )()(收敛, 当1=x 时,级数∑∞=---11121n n n )(收敛,所以,收敛域为]1,1[-.设)11(121)(1121≤≤---=∑∞=--x x n x S n n n )(21)1(21122111211111121)(x x x x n x S n n n n n n n n n +=-=-='⎥⎦⎤⎢⎣⎡--='∑∑∑∞=--∞=--∞=--)()()( 两边积分,x dt t dt t SS x S xxarctan 11))0()(020=+='=-⎰⎰(因0)0(=S ,所以,x x S arctan )(=,]1,1[-∈x 20. 解:切线方程为),(x X y y Y -'=-由题意知x Y X ==0代入得,y x y x '-=-即11-=-'y x y 且11==x y ⎪⎪⎭⎫ ⎝⎛+-=⎰⎰⎰-c dx e e y dx x dx x 11⎪⎭⎫ ⎝⎛+-=⎰c dx xx 1()c x x +-=ln由11==x y 得1=c所求曲线方程为:()x x y ln 1-=。
06-07-2线性代数试题及答案 山东建筑大学

2006-2007学年第二学期线性代数试题A 卷一.填空题(本题满分12分,每小题3分)1、设0是矩阵⎪⎪⎪⎭⎫ ⎝⎛=a A 01020101的特征值,则=a _____________2、已知矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=k k k k 111111111111A ,且A 的秩()3=A r ,则=k ___________. 3、设5200210000120011A ⎛⎫ ⎪ ⎪= ⎪- ⎪ ⎪⎝⎭,则1_______A -=. 4、设矩阵2112A ⎛⎫= ⎪-⎝⎭,E 为2阶单位矩阵,矩阵B 满足2BA B E =+,则 =B .二、选择题(本题满分12分,每小题3分,.在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后的括号内)1.设A 是4阶矩阵,且A 的行列式0=A ,则A 中【 】.()A . 必有一列元素全为0;()B . 必有两列元素成比例;()C . 必有一列向量是其余列向量的线性组合;()D . 任意列向量是其余列向量的线性组合.2.设⎪⎪⎪⎭⎫ ⎝⎛=333231232221131211a a a a a a a a a A , ⎪⎪⎪⎭⎫ ⎝⎛+++=133312321131131211232221a a a a a a a a a a a a B ,⎪⎪⎪⎭⎫ ⎝⎛=1000010101P , ⎪⎪⎪⎭⎫ ⎝⎛=1010100012P ,则必有【 】.()A . B P AP =21 ; ()B . B P AP =12 ; ()C . B A P P =21 ; ()D . B A P P =12.3.设12,,,s ααα均为n 维列向量,A 为m n ⨯矩阵,下列选项正确的是【 】(A) 若12,,,s ααα线性相关,则12,,,s A A A ααα线性相关. (B) 若12,,,s ααα线性相关,则12,,,s A A A ααα线性无关. (C) 若12,,,s ααα线性无关,则12,,,s A A A ααα线性相关. (D) 若12,,,s ααα线性无关,则12,,,s A A A ααα线性无关. 4.设21,λλ是矩阵A 的两个不同的特征值,对应的特征向量分别为21,αα,则1α,)(21αα+A 线性无关的充分必要条件是【 】(A) 01≠λ. (B) 02≠λ. (C) 01=λ. (D) 02=λ.三.计算行列式(本题满分6分)11111110000011000011---=n D四.(本题满分12分)设n 阶矩阵A 和B 满足条件:AB B A =+.⑴ 证明:E A -是可逆矩阵,其中E 是n 阶单位.⑵ 已知矩阵⎪⎪⎪⎭⎫ ⎝⎛-=200012031B ,求矩阵A .五.(本题满分14分)当a 、b 为何值时,线性方程组()⎪⎪⎩⎪⎪⎨⎧-=+++=--+-=++=+++12323122043214324324321ax x x x b x x a x x x x x x x x 有唯一解,无解,有无穷多组解,并求出有无穷多组解时的通解.六.(本题满分12分)求矩阵 ⎪⎪⎪⎭⎫ ⎝⎛-=300121103A 的特征值和特征向量,并回答A 是否能对角化?为什么? 七.(本题满分12分)问λ取何值时,二次型32312123222142244x x x x x x x x x f +-+++=λ为正定二次型?八.(本题满分8分)已知三维向量空间的一组基为()0111,,=α,()1012,,=α,()1103,,=α求向量()002,,=β在上述基下的坐标.九.(本题满分12分)设n 维向量组12,,,m ααα线性无关,12,,,,m αααβ线性相关,试用两种..不同的方法证明β可由12,,,m ααα线性表示,且表示法唯一.。
山东建筑大学概率论与数量统计概率论与数理统计A卷答案

^
极大似然估计为 minx1,xn .
………………10’
3
xydy
79 96
………………10’
n
6.解
似然函数
L(
x1
xn
;
)
2 ( xi e i1
)
,
xi
,i 1, 2n ,
………………4’
n
ln L( ) 2 (xi ) , i 1
d ln L 2n 0 , d
所以 L( ) 单调递增,
………………8’
而 xi ,故取 x1, xn 最小者, L( ) 最大,所以
0100 1.
8
8
5. 解(1)当 x 1 时,
………………………10’
fX x
f x, y dy
1 1 xy dy 1 ,
1 4
2
则
fX
x
1 2
,
x 1
0, 其他
……………………………2’
同理
fY
y
1 2
,
y 1
0, 其他
……………………………4’
由于 f x, y f X x fY y,所以 X 和Y 不独立。…………………5’
2015-2016-1《概率论与数理统计》试题(A)参考答案和评分标准
一、1. 2 ; 3
2. 2 ; 5
3.7;
4.0.3;5.20;源自6. 2 (4) ;7.
X
或
1 n
n i 1
Xi
;
8. (19.912, 20.108) .
二、1.(D); 2.(B); 3.(A); 4.(C); 5.(A); 6. (B); 7. (C); 8. (C). 三、
山东建筑大学高等数学试卷(A卷)

2006~2007-2高等数学A2试题A 卷一、填空题(每小题3分,共15分)1.函数),(y x f 在点),(y x 可微分是),(y x f 在该点连续的 条件.2.半径为a 的均匀半圆薄片(面密度为ρ)对其直径边的转动惯量为 . 3.L 为圆周222ay x =+,则()⎰+Lndsy x 22= .4.函数0,0,)(⎩⎨⎧<≤<≤--=ππx x x x x f 的傅里叶级数展开式为()()⎪⎪⎭⎫⎝⎛+++++++-=ΛΛx n n x x x x f 12cos 1215cos 513cos 31cos 42)(222ππ)(ππ≤≤-x ,则级数()ΛΛ++++++22212151311n 的和等于 ..二、选择题(每小题3分,共15分)6.函数()22,y xy x y x f +-=在点)1,1(P 处沿方向⎭⎬⎫⎩⎨⎧=41,41l ρ的方向导数( )。
(A) 最大; (B) 最小; (C) 1; (D) 0. 7.设区域D 是由0,42=-=y x y 围成,则=+=⎰⎰Ddxdy y ax I )(( )。
(A) 0>I ;(B) 0=I ;(C) 0<I ;(D) I 的符号与a 有关. 8.下列各式中正确的是( )(A)022=+-⎰Ly x ydxxdy ,其中1:22=+y x L ,沿逆时针方向; (B)⎰⎰⎰⎰∑∑⎪⎪⎭⎫ ⎝⎛++=++dS R Q P dxdy z y x R dzdx z y x Q dydz z y x P 5325253),,(),,(),,(;其中∑是平面63223=++z y x 在第一卦限的部分的上侧。
(C) ⎰⎰⎰Γ∑⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=++dz y P x Q dy x R z P dx z Q y R Rdxdy Qdzdx Pdydz 其中Γ是∑的边界曲线,且Γ的方向与∑侧符合右手法则;(D) 向量场k z y x R j z y x Q i z y x P z y x A ρρρρ),,(),,(),,(),,(++=的散度ky P x Q j x R z P i z Q y R A div ρϖρϖ⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=. 9.级数∑∞=+-12)1(n nn nb 为( )。
山建大成人教育20级《高等数学》期末考试复习题及参考答案

年级:2020级专业:各专业
一、单项选择
1-6 CCACDB
二、填空题
1.
2.x<0
3.
4.
5.
6.
三、计算题
1.解;
2.解:
3.令
所以 .
4.解
5.解
所以级数收敛
5.设 为上半球面 ,则曲面积分
的值为( )
(A) (B) (C) (D)
6.设 ,则 ( )
(A) ; (B) ;(C) ; (D)
2、填空题(本大题共6小题,每小题5分,共30分。)
1.函数 的反函数是
2.函数 的单调增加区间为_____________.
3.已知曲线 (a,b为常数)那么曲线在 处的法线方程为
1.下列四组函数中 与 表示同一函数的是( ).
A. , B. ,
C. , D. ,
2. 是当 ( )时的无穷小.
A. -B.+C.1D.1
3.下列论断正确的是( )
A、 可导极值点必为驻点 B、 极值点必为驻点
C、 驻点必为可导极值点 D、 驻点必为极值点
4.设有直线 及平面 ,
则 ( )
(A) 平行于 . (B)在 上. (C) 垂直于 . (D) 与 斜交.
___________________
4.向量 在向量 上的投影是 ____________.
5. ,则 =.
6.设 ,则 .
三、计算题(本大题共5小题,每小题8分,共40分。)
1.求极限
2.计算不定积分:
3.设 ,证明 .
4.19-2020学年第2学期类别:函授
2019-2020学年第2学期考试时间:90分钟类别:函授
山东建筑大学线性代数期末试题

06-07-1《线性代数》试题A一、选择题(每小题4分,共20分)1.设四阶矩阵()234,,,A αγγγ=,()234,,,B βγγγ=,其中234,,,,αβγγγ均为4维列向量,且已知行列式4=A ,1=B ,则行列式=+B A ( ) (A ) 5; (B ) 4; (C ) 50; (D ) 40。
2.设A 为3×3矩阵,B 为4×4矩阵,且1=A ,2-=B ,则=A B ( )。
(A ) 2-; (B ) 4-; (C ) 8-; (D ) 1。
3.设A 是n 阶方阵,且n r R <=)(A ,则在A 的n 个行向量中( ). (A )必有r 个行向量线性无关 (B )任意r 个行向量线性无关(C )任意r 个行向量都构成极大线性无关组(D )任意一个行向量都可以由其余1-r 个行向量线性表示4. 若齐次方程组0=AX 有无穷多解,则非齐次方程组B AX = ( )()A 必有无穷多解; ()B 可能有唯一解 ()C 必无解; ()D 有解时必有无穷多组解.5.设三阶方阵A 的三个特征值为λ10=, λ23=, λ36=-,对应于1λ的特征向量为 ()Tx 1011-=,,,对应2λ的特征向量为()Tx 1122,,=,记向量213x x x +=,则( ).()A 3x 是对应于特征值λ10=的特征向量. ()B 3x 是对应于特征值λ23= 的特征向量. ()C 3x 是对应于特征值λ36=-的特征向量. ()D3x 不是A 的特征向量.二、填空题(每小题4分,共20分)11.设n 维向量组)(,,,,n s s s <+121αααα 线性无关, 则向量组s ααα,,, 21 的秩为 .已知矩阵A 与2035B ⎛⎫=⎪-⎝⎭相似,则矩阵A 的特征值为 。
3.行列式dc b a D 000321200503== . 4.设()T9753,,,=α,()T0251,,,-=β,向量γ满足βγα523=-,则=γ .5.设A 为n 阶方阵,且2=A ,则=*AA . 三、(8分) 计算1+n 阶行列式xxx x x a a a a D n n 0000002101--=+四、(8分) 求解下面矩阵方程中的矩阵X⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X 五、(8分)设向量组321ααα,,线性相关,向量组432ααα,,线性无关,证明 (1) 1α能由32αα,线性表示; (2)4α不能由321ααα,,线性表示.2 六、(10分)设⎪⎩⎪⎨⎧-=++-=++-=++223321321321x x x x x x x x x λλλλ,问λ取何值时,此方程组有惟一解,无解或无穷多解?并且有无穷多解时,求通解。
(完整word版)山东建筑大学-.1线性代数试题A卷

线性代数一、单项选择题(每小题3分,共18分)1、设矩阵333223⨯⨯⨯C B A ,,,则下列运算可行的是 【 】.A AC , .B CB , .C ABC .D B A +2、设, A B 为n 阶方阵,E 为n 阶单位矩阵,则下列等式成立的是 【 】.A ()()22B A B A B A -=+- .B ()()E A E A E A -=+-2.C BA AB = .D ()E B A E B A ++=+3、设方阵A 有特征值1、2,a 是与1 对应的特征向量,b 是与2对应的特征向量,下列判断正确的是 【 】.A a 与b 线性无关 .B b a +是A 的特征向量.C a 与b 线性相关 .D a 与b 正交4、设4阶方阵A 的行列式为2,则A 的伴随矩阵*A 的行列式为 【 】(A) 2; (B) 4; (C) 8; (D) 15、112012()2, 1012a A a r A a -⎛⎫ ⎪=-= ⎪ ⎪-⎝⎭若矩阵的秩则的值为 【 】(A)0(B)0 -1(C)-1 (D) 1 1-或 或6、A 与B 为同阶方阵,如果A 与B 具有相同的特征值,则 【 】(A) A 与B 相似;(B) A 与B 合同;(C) A B =; (D) A B =二、填空题(每小题3分,共18分)7、0200003000045000D =,则_______D =. 8、设3阶矩阵A ,且矩阵行列式3=A ,则矩阵行列式=A 2 .9、设矩阵a a a a a a a a A a a a a a a a a ⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭,则A 的非零特征值为____________. 10、若方阵A 有一个特征值是1,则E A -= .11、n 维向量空间的子空间121220(,,,)0n n n x x x W x x x x x ⎧⎫+++=⎧⎪⎪=⎨⎨⎬++=⎩⎪⎪⎩⎭的维数是____ 12、设(,)E i j 表示由n 阶单位矩阵第i 行与第j 行互换得到的初等矩阵,则E 1[(,)]E i j -=_________.三、解答下列各题(每小题6分,共24分)13、计算行列式 7592437102102251-----=D 14、设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=200540321A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=132015001B ,求行列式AB 。
山东建筑大学2013-2014复变函数与积分变换-A卷试卷及答案

2013 至 2014 学年第一学期 试题答案及评分标准课程名称: 复变函数与积分变换 (A )卷 考试形式:( 闭 卷 ) 年级: 2012 专业: 电气自动化等 ; 层次:(本)一、选择题1(C); 2(C); 3(D); 4(D); 5(C); 二、填空题1. 16-i ;2.222215322+=⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭u v ; 3. ln 22,0,1,2,3,3ππ⎛⎫++=±±± ⎪⎝⎭ i k k ; 4. 0; 5. 1--te t .三、综合题 1.解()216,0,1,2,3,4,5.k ie k π+== ……………………………………(2分)1211,122i i i +=+……………..……..(5分)34511,,22i i i =-=-=……………………..(8分)2.解()()112222()ix iy dz x ix d x ix++=++⎰⎰ …………………………(2分)()()1230121i xi x dx ⎡⎤=+--⎣⎦⎰ ………………………………………(4分)1566i =-+ …………………………………………………………………(6分)3.解 当1<r 时,()f z 在z r =只有一个奇点0z =,由高阶导数公式()()!222201121101111z rz rz i z dz dz z z z z z π==='⎛⎫-=== ⎪+--⎝⎭⎰⎰…………………(4分)当1>r 时,()f z 在z r =只有3个奇点0,1,1z z z ===-,以0,1,1z z z ===-为中心,分别作3个小圆周123,,C C C ,使得3个小圆互不相交,互不包含,则由复合闭路定理及高阶导数公式()()()()()()()()11122221111011111111z r C C Cdz z z z z z z z z z z z z ==++=+-+-+-+-⎰⎰⎰⎰………………………(8分)4.解 222222224,4,0vvv vx y x y ∂∂∂∂==-+=∂∂∂∂,所以(),v x y 是调和函数…………(2分) ()()4414v v f z i y i x iz i y x∂∂'=+=-++=+∂∂ ………………………(5分) ()()()242f z f z dz iz i dz iziz C '==+=++⎰⎰ ………………………(7分)代入条件()01f =得,1C =所求函数为()221f z iz iz =++ …………………………………………(8分)5.解 ()22131f z z z =--+ …………………………………………(2分) (1)在13z <<内,11,13z z<<…………………………………………(3分) ()2222121111313113f z z z z z z =-=-⋅-⋅-+-+ ()()2221001011212333nnn nn n n n n n n n z z z z z ∞∞∞∞+====--=-⋅-⋅=-∑∑∑∑………………(6分)(2)在3z <<+∞内,131z z<<…………………………………………(7分)()222212111313111f z z z z z z z =-=⋅-⋅-+-+ ()121111123nn n nn n n n m c zz z∞∞∞--===-=+⋅=∑∑∑()22123,21231,2mnm m n m c n m --⎧⋅=+⎪=⎨⋅+-=⎪⎩ ………………(10分)6.解 函数2222()z a z +在z 平面上有两个二阶极点z ai =±,其中z ai =在上半平面…………………………………(2分)且 2222222221Res ,lim ()()()4z ai z d z ai z ai a z dz a z ai →⎡⎤⎡⎤=-=⎢⎥⎢⎥++⎣⎦⎣⎦……………(4分) 则2222222222220112Res ,()2()2()4x x z dx dx i ai a x a x a z a ππ+∞+∞-∞⎡⎤==⋅=⎢⎥+++⎣⎦⎰⎰ …………………..…(6分)7.解 ()()j t F f t e dt ωω+∞--∞=⎰…………………………………(2分)j tAedt τω-=⎰ …………………………………(4分)()01j t j A Ae e j j τωωτωω--=-=-…………………………………(6分)8.解 ()()0sin 2ststt F s f t e dt e dt +∞+∞--==⋅⎰⎰ ……………………………(2分) 222tj tj st e ee dt j-+∞--=⋅⎰………………………………(4分)22012j j s ts t e e dt j⎛⎫⎛⎫+∞---+ ⎪ ⎪⎝⎭⎝⎭⎛⎫=- ⎪ ⎪⎝⎭⎰ 22111222j j s t s t e e j j j s s +∞⎛⎫⎛⎫---+ ⎪ ⎪⎝⎭⎝⎭⎡⎤⎢⎥⎢⎥=-++⎛⎫⎛⎫⎢⎥-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦………………(6分) 2241s =+ …………………………………………(8分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.设 f x x ln x ,则 f x 在 x 0 处的导数(
A 等于 1 ;
C 等于 0 ;
B 等于 1 ; D 不存在.
1
f x 2 ,以下结论正确的是( 5.已知 lim
x 1
).
A 函数在 x 1 处有定义且 f 1 2 ;
一、填空题(每小题 3 分,共 18 分) 1.设函数 f x
x2 1 ,则 x 1 是 f x 的第 x2 3x 2
2
类间断点.
2.函数 y ln 1 x
,则 y
.
.
3. lim
1 x x x
2x
4.曲线 y
五、(6 分)求曲线 y xe 六、(10 分)设
的拐点及凹凸区间.
f
x dx x e
x
1 C ,求 f x .
2
C
充分必要条件; ) .
B 充分但非必要条件 D
无关条件.
;
2.下列各式正确的是(
A e x dx e x C ;
B ln xdx
1 C ; x
C 1 dx 1 ln1 2 x C ; D 1 dx ln ln x C . 1 2x 2 x ln x
3. 设 f x 在 a , b 上, f x 0 且 f x 0 ,则曲线 y f x 在 a , b 上.
A 沿 x 轴正向上升且为凹的;
C 沿 x 轴正向上升且为凸的;
沿 x 轴正向下降且为凹的; D 沿 x 轴正向下降且为凸的.
sin x
2
,求 y .
x 0 的导数.
x2 1 x 2 dx .
x cos xdx .
1 x
6.方程 y
x 确定函数 y f x ,求 y .
x2
1 y
四、(10 分)已知 e
为 f x 的一个原函数,求
x
x f x dx .
2
B 函数在 x 1 处的某去心邻域内有定义;
C 函数在 x 1 处的左侧某邻域内有定义; D 函数在 x 1 处的右侧某邻域内有定义.
三、计算(每小题 6 分,共 36 分) 1.求极限: lim x sin
x0 2
1 . x
2. 已知 y ln 1 x 3. 求函数 y x 4. 5.
1 1 在点 ,2 处的切线方程为 x 2
3 2
. .
5.函数 y 2 x 3 x 在 1,4 上的最大值 6.
,最小值 .
arctan x dx 1 x2
二、单项选择题(每小题 4 分,共 20 分) 1.数列 x n 有界是它收敛的( ) .
A 必要但非充分条件;
