测量平差课后习题答案

合集下载

测量平差第二章习题与答案

测量平差第二章思考题1 为了鉴定经纬仪的精度，对已知精确测定的水平角'"450000α= 作12次同精度观测，结果为：'"450006'"455955 '"455958 '"450004 '"450003'"450004 '"450000 '"455958 '"455959 '"455959 '"450006 '"450003设a 没有误差，试求观测值的中误差。

2 已知两段距离的长度及中误差分别为300.465m ±4.5cm 及660.894m ±4.5cm ，试说明这两段距离的真误差是否相等？他们的精度是否相等？3 设对某量进行了两组观测，他们的真误差分别为：第一组：3，-3，2，4，-2，-1，0，-4，3，-2第二组：0，-1，-7，2，1，-1，8，0，-3，1试求两组观测值的平均误差1ˆθ、2ˆθ和中误差1ˆσ、2ˆσ，并比较两组观测值的精度。

4 设有观测向量1221[]T X L L =，已知1ˆL σ=2秒，2ˆL σ=3秒，122ˆ2L L σ=-秒，试写出其协方差阵22XX D 。

5 设有观测向量12331[]T X L L L =的协方差阵334202930316XXD -⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦，试写出观测值L 1，L 2，L 3的中误差及其协方差12L L σ、13L L σ和23L L σ。

答案：2.1 ˆ3.62"σ= 2.2 它们的真误差不一定相等，相对精度不相等，后者高于前者2.3 1ˆθ=2.4 2ˆθ=2.4 1ˆσ=2.7 2ˆσ=3.6 两组观测值的平均误差相同，而中误差不同，由于中误差对大的误差反应灵敏，故通常采用中误差做为衡量精度的的指标，本题中1ˆσ<2ˆσ，故第一组观测值精度高 2.4 22242()29XX D -⎛⎫= ⎪-⎝⎭秒 2.51L σ=2, 2L σ=3, 34L σ=,122L L σ=-,130L L σ=,233L L σ=-。

测量平差课后习题答案张书毕

P点坐标的中误差为： x 0.17m, y 0.06m 将各点值代入函数得： X P 2462.66m,Y P 5842.59m p点坐标为x=2462.66 0.17m,y=5842.59 0.06m
10
.解答：
千米 =
AB
1 1 站站 0.0075 3m s 0.08
向量 X 1 Y1 X 1
（1）试求坐标差函数 X X 2 X 1 与 Y Y 2 Y1 的方差—协方差阵；（2）求两点间边长 S X 2 Y 2 与坐标方位角T arctan(Y / X )的方差 —协方差阵。解答：（1）向量 X 1 Y1 X 1 Y 2 T 的协方差阵得
6
d x
.解答：由题意可知:
S AB cos 1 cos TAB 3
S AB sin 1 sin TAB 3
'' sin 2
d 1
S AB sin 1 cos 2 cos TAB 3
'' sin 2 2
d 2
'' sin 2
1 1 f h H A h1 h2 H B 2 2
P
LL
5 8 1 1 协因数阵Q P LL LL 4 1 8 2 32 Q 0 5 Q D LL 0
2
1 8 5 2 1 1 1 2 4 2 4 8 1 2 5 5 8
2
4
.解答：
第 1 页/共 44 页
《测量平差》参考答案 Ch1---Ch4
2 1 0 P LL 1 3 1 0 1 2 Q P LL Q Q

智慧树答案误差理论与测量平差(山东联盟)知到课后答案章节测试2022年

第一章1.误差是不可避免的。

答案:对2.构成观测条件的要素有哪些答案:观测者;测量仪器;外界条件3.对中误差属于那种误差答案:偶然误差第二章1.两随机变量的协方差等于0时，说明这两个随机变量答案:互不相关2.观测量的数学期望就是它的真值答案:错3.衡量系统误差大小的指标为答案:准确度4.精度是指误差分布的密集或离散程度，即离散度的大小。

答案:对5.若两观测值的中误差相同，则它们的答案:精度相同第三章1.设L的权为1，则乘积4L的权P=（）。

答案:1/162.有一角度测20测回，得中误差±0.42秒，如果要使其中误差为±0.28秒，则还需增加的测回数N=（）。

答案:253.在水准测量中，设每站观测高差的中误差均为1cm，今要求从已知点推算待定点的高程中误差不大于5cm，问可以设25站。

答案:对4.已知距离AB=100m，丈量一次的权为2，丈量4次平均值的中误差为2cm，若以同样的精度丈量CD的距离16次，CD=400m，则两距离丈量结果的相对中误差分别为（ 1/5000 ）、（1/20000 ）。

答案:对5.答案:25第四章1.当观测值为正态随机变量时，最小二乘估计可由最大似然估计导出。

答案:对2.多余观测产生的平差数学模型，都不可能直接获得唯一解。

答案:对3.在平差函数模型中，n、t、r、u、s、c等字母各代表什么量？它们之间有何关系？(n观测值的个数 )(t必要观测数 )(r多余观测数,r=n-t )(u所选参数的个数 )(s非独立参数的个数,s=u-t )(c所列方程的个数,c=r+u )答案:对4.答案:对第五章1.关于条件平差中条件方程的说法正确的是：答案:为减少计算工作量，应选用形式简单、易于列立的条件方程。

;这r个条件方程应彼此线性无关;应列出r个条件方程2.在条件平差中，可以根据已列出的法方程计算单位权方差，而不必非得求出改正数V以后才能计算。

答案:对3.测角网条件方程的可能类型有答案:图形条件;圆周条件;极条件;方位角条件;正弦条件4.答案:对5.已知观测值的协因数矩阵为Q,则条件平差法方程的解K的协因数矩阵为（）。

测量平差习题集答案

测量平差习题集答案测量平差习题集答案在测量工作中，平差是一项非常重要的环节。

它通过对测量数据进行处理和分析，消除误差，得到更加准确的测量结果。

为了帮助大家更好地理解和掌握平差的方法和技巧，下面将为大家提供一些测量平差习题集的答案。

1. 题目：某测量队在进行水平控制网的测量时，测得A、B两点的水平角为α1=90°30'20"，α2=269°29'40"，A、B两点的距离为1000米。

已知A点的坐标为(1000, 1000)，求B点的坐标。

解答：根据水平角的定义，可以得到以下关系式：α1 = α2 + 180°即90°30'20" = 269°29'40" + 180°化简得90°30'20" = 449°29'40"由于角度超过360°，需要将其转化为小于360°的形式，可以通过减去360°来实现，即：90°30'20" - 360° = 89°29'40"所以，B点的水平角为89°29'40"。

接下来，根据已知的A点坐标和AB距离，可以利用正弦定理来求解B点的坐标。

设B点的坐标为(x, y)，则有：(x - 1000)^2 + (y - 1000)^2 = 1000^2根据正弦定理，可以得到以下关系式：sin(89°29'40") = (x - 1000) / 1000化简得：(x - 1000) = 1000 * sin(89°29'40")解得：x ≈ 1999.999同理，可得：y ≈ 1000.000所以，B点的坐标为(1999.999, 1000.000)。

误差理论与测量平差基础第6章课后答案

第六章思考题6.1某平差问题有12个同精度观测值，必要观测数t = 6，现选取2个独立的参数参与平差，应列出多少个条件方程？6.2 有水准网如图，A 为已知点，高程为10.000A H m =，同精度观测了5条水准路线，观测值为17.251h m =，20.312h m =，30.097h m =-，4 1.654h m =，50.400h m =，若设AC 间高差平差值ˆˆACh X 为参数，试按附有参数的条件平差法，（1）列出条件方程（2）列出法方程（3）求出待定点C 的最或是高程6.3 下图水准网中，A 为已知点，P1，P2，P3为待定点，观测了高差15~h h ，观测路线长度相等，现选择P3点的高程平差值为参数，求P3点平差后高程的权。

6.4 下图水准网中，A 为已知点，高程为10.000A H m =，P 1~P 4为为待定点，观测高差及路线长度为：h 1=1.270m, S1=2;h 2=-3.380m, S2=2;h 3=2.114m, S3=1;h 4=1.613m, S4=2;h 5=-3.721m, S5=1;h 6=2.931m, S6=2;h 7=0.782m, S7=2;若设P2点高程平差值为参数，求：（1）列出条件方程；（2）列出法方程；（3）求出观测值的改正数及平差值；（4）平差后单位权方差及P2点高程平差值中误差。

6.5 如图测角网中，A 、B 为已知点，C 、D 为待定点，观测了6个角度，观测值为： L1=40。

23’58”， L2=37。

11’36”，L3=53。

49’02”， L4=57。

00’05”L5=31。

59’00”， L4=36。

25’56”若按附有参数的条件平差，（1）需要设哪些量为参数；（2）列出条件方程；（3）求出观测值的改正数及平差值。

思考题参考答案6.2n=5 t=3 r=2 u=1 c=3 6.3n=5 t=3 r=2 u=1 c=3v 1+v 4+v 5+w 1=0v 2+v 3-v 5+w 2=0v 1+v 2-ˆX+w 3=0 ˆˆ11X X Q P ==，6.4（1）v 1+v 2+v 3+4=0v 3+v 4+v 5+6=0v 5+v 6+v 7+8=0v 1+v 7-ˆX=0 （2）123455102041410060015208202410000100K K K K K ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+=-⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦ （3）[]1124044()T v mm =----[]ˆ 1.269 3.381 2.112 1.609 3.721 2.9350.786()T L mm =--（4）22034.7()mm σ=ˆ0.5X Q =，22ˆ17.3()X Q mm =，ˆ 4.2()Xmm σ=6.5 （1）设0ˆ,10310'06"X ADB X =∠=（2）v 1+v 6=0v 2+v 3+v 4+ v 5-17”=0 -0.955 v 1+ 0.220 v 2-0.731 v 3+0.649 v 4-0.396 v 5+ 0.959 v 6+2”=0（3）法方程：123200.00410040.25801700.0040.258 2.9902ˆ10000K K K x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ []0 4.230.3T K =- ˆx =0 []0.3 4.2 4.44 4.30.3(")T V =- ˆ4023'58.3"3711'40.2"5349'06.4"5700'09"3159'04.3"3625'55.7"L ⎡⎤=⎣⎦。

误差理论和测量平差习题5(含答案)

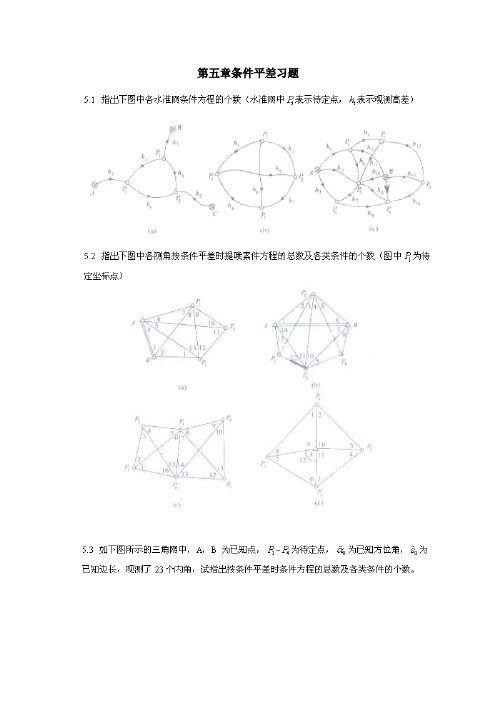
第五章条件平差习题第五章思考题参考答案5.1（a）n=6，t=3，r=3（b）n=6，t=3，r=3（c）n=14，t=5，r=95.2（a）n=13，t=6，r=7共有7个条件方程，其中有5个图形条件，2个极条件。

（b）n=14，t=8，r=6共有6个条件方程，其中有3个图形条件，3个极条件。

（c）n=16，t=8，r=8共有8个条件方程，其中有6个图形条件，2个极条件。

（d）n=12，t=6，r=6共有6个条件方程，其中有4个图形条件，1个圆周条件，1个极条件。

5.3n=23，t=6，r=17共有17个条件方程，其中有9个图形条件，1个圆周条件，1个固定角条件，1个固定边条件，5个极条件。

5.4 （1）n=22，t=9，r=13：7个图形条件，1个圆周条件，2个极条件，2个边长条件，一个基线条件。

（2）12837941314121520111718195610166101119910111213510ˆˆˆ1800ˆˆˆ1800ˆˆˆ1800ˆˆˆ1800ˆˆˆˆ1800ˆˆˆˆ1800ˆˆˆˆ1800ˆˆˆˆˆ1800ˆˆˆsin sin sin L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L ++-=++-=++-=++-=+++-=+++-=+++-=++++-=171961116203614184715192211151217121318124ˆsin 1()ˆˆˆˆsin sin sin sin ˆˆˆˆsin sin sin sin 1()ˆˆˆˆsin sin sin sin ˆˆ()ˆˆˆˆsin sin sin sin ˆˆ(ˆˆˆˆsin sin sin sin FG FG L L L L L L L L L L L L L S S S S L L L L S S L L L L ===→=以大地四边形中心为极以中点四边形D 点为极的边长条件1213611891719ˆˆ)ˆˆˆˆsin sin sin sin ˆˆˆˆsin sin sin sin FG AB S S L L L L S S L L L L →=的边长条件（基线条件）5.5 n=8，t=4，r=4；有多种条件方程的列法，其中之一为：1001000100110000120001001104000011014V ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥-=⎢⎥⎢⎥--⎢⎥⎢⎥---⎣⎦⎣⎦（注意常数项单位为mm ） 5.6 （1）P=3/2，（2）P=15.7 （1）P B =1.6，P C =2.1，P D =2.1，P E =1.6（2）P hCD =1.85.8 []ˆ 2.4998 1.9998 1.3518 1.8515h=2P σ=0.32(mm)5.9 1234561110009100110900101016V V V V V V ⎡⎤⎢⎥⎢⎥-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦ []045452TV mm =---[]ˆ 1.576 2.219 3.7950.867 2.443 1.352T h m =--- 5.10 （1）1ˆ10.3556h m = 2ˆ15.0028h m = 3ˆ20.3556h m = 4ˆ14.5008h m =5ˆ 4.6472h m = 6ˆ 5.8548h m = 7ˆ10.5020h m =（2）±2.2mm。

答案测量平差a

内蒙古工程学校 2011/2012学年第一学期测量平差基础课程考试试卷参考答案（A ）一、名词解释（每小题 5分，共20分）1.系统误差答：在相同的观测条件下作一系列观测。

如果误差在大小、符号上表现出系统性，或者在观测过程中按一定的规律变化，或者为一个常数，那么，这种误差称为系统误差。

2. 偶然误差答：在相同的观测条件作一系列观测，如果误差在大小和符号上都表现出偶然性，即从单个误差看，该列误差的大小和符号没有规律性，但就大量误差的总体而言，具有一定的统计规律，这种误差称为偶然误差。

3. 衡量精度指标答：能够反映误差分布的密集或者离散的程度，即能反映其离散度的大小。

4. 极限误差答：通常以三倍中误差作为偶然误差的极限值，称为极限误差。

二、选择题（每小题 2分，共20分）1. 下面不属于观测误差的产生原因的是（D ）A.测量仪器B.观测者C.外界条件D误差特性2.偶然误差就总体而言有一定统计规律，故又称为（A ）A.随即误差B.规律误差C.系统误差D.统计误差3.为了提高观测成果质量，同时也是为了检查和发现误差存在需要（A ）A.多余观测B.成果检核C.误差平差D.检测4.测量平差的任务是求最可靠值和（B ）A.评定等级B评定成果精度 C.计算误差 D.检查错误5.1794年，高斯提出了（C ），找出观测量最优值。

A.误差理论B.测量学C.最小二乘法.D.概论分布6.一组独立的偶然误差绝对值的数学期望称为（D ）A.平均值B.算数平均误差C.期望误差D.平均误差7.与相对误差对应，真误差、中误差、极限误差都称为（D ）A.相对误差B.真误差C. 计算误差D.绝对误差8.以条件方程为函数的平差方法，称为（A ）A.条件平差法B.方程平差法C.简单平差法D.最优平差法9.对于随即观测量，不相关与独立式等价的，所以把不相关观测值称为（A ）A.独立观测值B.不相关观测值C.等价观测值D.随即观测值10.有时采用（A ）来衡量精度，它是观测值与中误差比值。

测量平差习题参考答案

第一章习题参考答案 1题.略2题.解 (1)222194σσ+（2）2221212219)3(σσL L L +-(3) 222212211212212211211")(cos )sin(sin ")(cos )sin(sin )cos(cos σρσρ⎪⎪⎭⎫ ⎝⎛+++⎪⎪⎭⎫ ⎝⎛++++L L L L L L L L L L L L L 3题. 解TT TLL XY LL YL LL XL B A AD D BAD D AD D ===,,4题.解设路线总长S 公里，按照测量学上的附合路线计算步骤，则路线闭合差B A h H h h H f -++=21由于是路线中点，故()B A h H h h H f v v -++-===21212121 则线路中点高程()()B A B A B A A A H H h h H H h h H h h H h H v h H H ++⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=++-=-++-+=-+=2121212121212121ˆ212121111中点设每公里高差观测中误差为0σ，则021)2/(σσσs h h ==按误差传播定律)(16,10425)52/(41)52/(41)2/(41)2/(414141212100212122220202222ˆ21121km S S s s s s h h h h H ≤≤=⋅⨯+⋅⨯=⨯+⨯=+=⎪⎪⎪⎪⎭⎫⎝⎛-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=σσσσσσσ中点5.解设每个测回的中误差为0σ，需要再增加n 个测回，则)2(2028.0,28.020)1(2042.0,42.0200000+±=±=+±=±=n n σσσσ由上式可解出n.即252023202028.042.020222=-⎪⎭⎫ ⎝⎛⨯=-⨯=n 再增加25个测回6题.解[][][][][][][][][]][][][,100010001...,...)...(2121211212122111⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎣⎡⎥⎦⎤==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎢⎣⎡⎥⎦⎤=+++==p p p p p p p p p P p P p P p Q L L L P p P p P p L p L p L p x n n n p xx n n n n p p pL x][][][][][][p p p p p p p p p p p p p p p nnn⋅⋅++⋅⋅+⋅⋅=1 (1)12221117题。

测量平差第五章条件平差习题参考答案

测量平差第五章条件平差习题参考答案测量平差第五章思考题参考答案5.1 （a ）n=6，t=3，r=3（b ）n=6，t=3，r=3（c ）n=14，t=5，r=95.2 （a ）n=13，t=6，r=7共有7个条件方程，其中有5个图形条件，2个极条件。

（b ）n=14，t=8，r=6共有6个条件方程，其中有3个图形条件，3个极条件。

（c ）n=16，t=8，r=8共有8个条件方程，其中有6个图形条件，2个极条件。

（d ）n=12，t=6，r=6共有6个条件方程，其中有4个图形条件，1个圆周条件，1个极条件。

5.3 n=23，t=6，r=17共有17个条件方程，其中有9个图形条件，1个圆周条件，1个固定角条件，1个固定边条件，5个极条件。

5.4 （1）n=22，t=9，r=13：7个图形条件，1个圆周条件，2个极条件，2个边长条件，一个基线条件。

（2）128379413141215201117181956101661011199101112135101800180018001800?1800?1800?18001800???sin sin sin L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L ++-=++-=++-=++-=+++-=+++-=+++-=++++-= 171961116203614184715192211151217121318124sin 1()sin sin sin sin sin sin sin sin 1()sin sin sin sin ??()sin sin sin sin ??(sin sin sin sin FG FG L L L L L L L L L L L L L S S S S L L L L S S L L L L ===→=以大地四边形中心为极以中点四边形D 点为极的边长条件1213611891719)sin sin sin sin sin sin sin sin FG AB S S L L L L S S L L L L →=的边长条件（基线条件）5.5 n=8，t=4，r=4；有多种条件方程的列法，其中之一为：1001000100110000120001001104000011014V -??? -=-----（注意常数项单位为mm ） 5.6 （1）P=3/2，（2）P=15.7 （1）P B =1.6，P C =2.1，P D =2.1，P E =1.6（2）P hCD =1.85.8 []? 2.4998 1.9998 1.3518 1.8515h=2P σ=0.32(mm) 5.9 1234561110009100110900101016V V V V V V-+=??--????[]045452TV mm =---[]? 1.576 2.219 3.7950.867 2.443 1.352T h m =--- 5.10 （1）1?10.3556h m = 215.0028h m = 3?20.3556h m = 414.5008h m =5? 4.6472h m = 6? 5.8548h m = 7?10.5020h m = （2）±2.2mm。

测量平差练习题及参考答案

计算题1、如图，图中已知A 、B 两点坐标，C 、D 、E 为待定点，观测了所有内角，试用条件平差的方法列出全部条件方程并线性化。

解：观测值个数 n =12，待定点个数t =3，多余观测个数r =n -2t =6① 图形条件4个：)180(0)180(0)180(0)180(0121110121110987987654654321321-++-==-++-++-==-++-++-==-++-++-==-++L L L w w v v v L L L w w v v v L L L w w v v v L L L w w v v v d d c c b b a a② 圆周条件1个：)360(0963963-++-==-++L L L w w v v v e e③ 极条件1个：ρ''--==----++)sin sin sin sin sin sin 1(0cot cot cot cot cot cot 852741774411885522L L L L L L w w v L v L v L v L v L v L f f3、如图所示水准网，A 、B 、C 三点为已知高程点， D 、E 为未知点，各观测高差及路线长度如下表所列。

用间接平差法计算未知点D 、E 的高程平差值及其中误差；ACBDh 1h 2h 3h 4h 5Eh 6高差观测值/m 对应线路长度/km已知点高程/mh 1= -1.348 h 2= 0.691 h 3= 1.265 h 4= -0.662 h 5= -0.088 h 5= 0.763 1 1 1 1 1 1H A =23.000 H B =23.564 C B =23.6633、解：1）本题n=6，t=2，r=n-t=4；选D 、E 平差值高程为未知参数21ˆˆX X 、则平差值方程为：1615142322211ˆˆˆˆˆˆˆˆˆˆˆˆˆX H hH X h H X h H X h H X h X X h AA BAB -=-=-=-=-=-=则改正数方程式为：6165154143232221211ˆˆˆˆˆˆˆl xv l xv l x v l xv l x v l x xv --=-=-=-=-=--=取参数近似值 255.24907.2220221011=+==++=h H X h h H X B B 、令C=1，则观测值的权阵：⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=10111101P ⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=010*********B ⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------------=+-=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=7551000)()()()()()()(016015014023022020110654321X H h H X h H X h H X h H X h X X h d BX h l l l l l l l C A B A B组法方程0ˆ=-W xN ，并解法方程： ⎪⎪⎭⎫ ⎝⎛--==3114PB B N T⎪⎪⎭⎫ ⎝⎛-==107Pl B W T⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛==-311074113111ˆ1W N x求D 、E 平差值：m x X X H m x X X H D C 258.24ˆˆˆ906.22ˆˆˆ20221011=+===+==2）求改正数：⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=-=664734ˆl xB v 则单位权中误差为：mm r pv v T 36.64162ˆ0±=±=±=σ则平差后D 、E 高程的协因数阵为：⎪⎪⎭⎫⎝⎛==-41131111ˆˆNQ X X根据协因数与方差的关系，则平差后D 、E 高程的中误差为：mmmm Q mm mm Q E D 84.311229ˆˆ32.322669ˆˆ220110±=±==±=±==σσσσ4、如图，在三角形ABC 中，同精度观测了三个内角：4000601'''︒=L ，5000702'''︒=L ，7000503''''︒=L ，按间接平差法列出误差方程式。

测量平差基础参考资料[1]

第一章绪论§1-1观测误差测量数据（观测数据）是指用一定的仪器、工具、传感器或其他手段获取的反映地球与其它实体的空间分布有关信息的数据，包含信息和干扰（误差）两部分。

一、误差来源观测值中包含有观测误差，其来源主要有以下三个方面：1. 测量仪器；2. 观测者；3. 外界条件。

二、观测误差分类1. 偶然误差定义，例如估读小数；2. 系统误差定义，例如用具有某一尺长误差的钢尺量距；系统误差与偶然误差在观测过程中总是同时产生的。

3. 粗差定义，例如观测时大数读错。

§1-4 本课程的任务和内容一、测量平差的任务处理带有观测误差的观测值，估计待求量的最佳估值并评定测量成果的精度。

二、测量平差的内容1. 建立观测误差的统计理论，简称误差理论。

研究误差的统计分布，误差的估计与传播；2. 研究衡量观测成果质量的精度指标；3. 建立观测值与待求量之间的函数模型，以及描述观测精度及其相关性的随机模型；4. 研究估计待求量的最优化准则；5. 结合测量实践研究测量平差的各种方法；6. 研究预报和质量控制问题。

第二章误差分布与精度指标§2-1 正态分布概率论中的正态分布是误差理论与测量平差基础中随机变量的基本分布。

一、一维正态分布§2-2偶然误差的规律性2. 直方图由表2-1、表2-2可以得到直方图2-1和图2-2（注意纵、横坐标各表示什么？），直方图形象地表示了误差分布情况。

3. 误差分布曲线（误差的概率分布曲线）在一定的观测条件下得到一组独立的误差，对应着一种确定的误差分布。

当观测值个数的情况下，频率稳定，误差区间间隔无限缩小，图2-1和图2-2中各长方条顶边所形成的折线将分别变成如图2-3所示的两条光滑的曲线，称为误差分布曲线，随着n增大，以正态分布为其极限。

因此，在以后的讨论中，都是以正态分布作为描述偶然误差分布的数学模型。

4. 偶然误差的特性第三章协方差传播律及权在测量实际工作中，往往会遇到某些量的大小并不是直接测定的，而是由观测值通过一定的函数关系间接计算出来的，显然，这些量是观测值的函数。

测量平差课后习题答案

所以 DXY DXX BT ADLL AT BT
习题
1.4：若要在两已知高程点间布设一条附合水准路线（如图所示），已知每千米
观测中误差等于5.0mm，欲使平差后路线中点C点高程中误差不大于10mm，
问该路线长度最多可达几千米？
h1
h2
C
B
解析：设A、B间最大距离为Skm
HC' HA h1 HC" HB h2
x
L
N
1 N
L1
1 N
L2
1 N
L立观测值的算术平均值的中误差=各观测值中误差除以 N
解析：观测值的中误差为：
x
N 0.42''
''
20 0.84 5
' x
N N
''
代入数值后得：0.28'' 0.84 5 20 N
N 25
DXY ADLL (BA)T ADLL AT BT
或
Y BX B
O
X L
X O
A
X L
，
DXY O
A
DXX DLX
DXL DLL
BT O
ADLX
ADLL
BT O
ADLX BT
ADLL AT BT
或 Y BX, X IX
DXY ID XX BT DXX BT
而 DXX ADLL AT
习题
1.2 已知独立观测值L1、L2的中误差分别为m1、m2，求下列函数的中误差：
（1） x 2L1 3L2
（2）x
L12 2
3L1L2 （3） x
sin L1 cos(L1 L2 )

测量平差答案

南京师范大学模拟试卷课程误差理论与测量平差基础一、填空题（20分）1. 某平差问题有以下函数模型(Q=I)（11分） 1L ∧=1x ∧2L ∧=1x ∧-2x ∧3L ∧=-1x ∧+3x ∧4L ∧=-3x ∧+A 5L ∧=-2x ∧-B 1x ∧+3x ∧+C=0试问：（1）以上函数模型为何种平差方法的模型？（3分）答：附有限制条件的间接平差。

（2）本题中，n= ，t= ，c= ，u= ，s= 。

（5分）答：n=5，t=2，c=5，u=3，s=1 （3）将上述方程写成矩阵形式。

（3分）答：5,1L ∧=100110101001010⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎢⎥⎢⎥-⎣⎦3,1x ∧+000A B ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦()1013,1x ∧+C=02. 衡量精度的指标有方差和中误差、平均误差、或然误差、、。

（4分）答：极限误差相对中误差3. 测定A 、B 两点间高差，共布设了16个测站，各测站观测高差是同精度独立观测值，其方差均值为2σ站=1m 2m ，则AB 两点间高差的中误差为ABh σ= 。

（5分）答：ABh σ=4mm 。

二、证明题在间接平差中，参数1n X ∧与1n V 改正数是否相关？试证明之。

（10分）证明：X ∧=0x +x ∧BB N x ∧-TB Pl=0x ∧=1BBN -T B Pl又l=L-oLx ∧=1BBN -T B Pl -1BB N -T B P o L V=B x ∧-l=B 1BBN -TB Pl -B 1BB N -TB P oL -L+oL = (B 1BBN -TB P-E)L- B 1BB N -TB P oL +oL 令 LL Q =Qx vQ ∧=1BB N -TB PQ 1(-E)T T BB BN B P -=1BBN -T B ( P 1BB N -TB P -E) =1BBN -TB P 1BB N -TB P-E 1BB N -TB =1BBN -TB -1BB N -TB =0 ∴1n X ∧与1n V 不相关。

测量平差期末考试题及答案

测量平差期末考试题及答案一、选择题（每题2分，共20分）1. 平差的基本目的是（）。

A. 确定测量数据的准确度B. 确定测量误差的来源C. 消除测量误差D. 优化测量数据的分布答案：C2. 测量误差的来源主要包括（）。

A. 测量仪器的误差B. 测量方法的误差C. 测量环境的误差D. 以上都是答案：D3. 测量平差中，权的概念是指（）。

A. 测量数据的可靠性B. 测量数据的准确性C. 测量数据的重要性D. 测量数据的稳定性答案：A4. 测量平差中，最小二乘法的基本原理是（）。

A. 使得测量误差的绝对值之和最小B. 使得测量误差的平方和最小C. 使得测量误差的平均值最小D. 使得测量误差的方差最小答案：B5. 在测量平差中，观测值的改正数是指（）。

A. 观测值与真值之差B. 观测值与平均值之差C. 观测值与预测值之差D. 观测值与估计值之差答案：A...（此处省略其他选择题）二、填空题（每空2分，共20分）1. 平差的基本任务是_________测量误差，以获得_________的测量结果。

答案：消除或减小；准确可靠2. 测量误差可以分为系统误差和_________误差。

答案：随机3. 权的倒数称为_________。

答案：权的倒数4. 最小二乘法是一种常用的平差方法，其核心思想是使观测值的_________达到最小。

答案：残差平方和5. 测量平差中，观测值的改正数是指观测值与_________之差。

答案：平差值...（此处省略其他填空题）三、简答题（每题10分，共30分）1. 简述最小二乘法在测量平差中的应用。

答案：最小二乘法在测量平差中是一种常用的数据处理方法，它通过最小化观测值的残差平方和来寻找最佳估计值。

在应用时，首先需要建立观测方程，然后通过求解线性方程组来得到未知参数的估计值。

这种方法在处理多个观测数据时，能够合理地分配误差，使得所有观测数据的误差总和最小，从而得到更加准确的测量结果。

2. 解释什么是权，它在测量平差中的作用是什么。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

m22
x
cos2 cos4 (L1
L2 L2 )
m12
sin2 L1 sin2 (L1 L2 ) cos4(L1 L2)
m22
习题
1.3 已知观测值L及其协方差阵DLL ，组成函数 X AL 和Y BX，A、B为常数阵，求协方差阵 DXL 、DYL 和 DXY 。
解：（1） X AL, L IL (I为单位阵)
x
L
N
1 N
L1
1 N
L2
1 N
LN
x
N
N个同精度独立观测值的算术平均值的中误差=各观测值中误差除以 N
解析：观测值的中误差为：
x
N 0.42''
''
20 0.84 5
' x
N N
''
代入数值后得：0.28'' 0.84 5 20 N
N 25
dx (L1 3L2 )dL1 3L1dL2
2 x
(L1
3L2) 2m12
9L12m22
x (L1 3L2 ) 2m12 9L12m22
习题
（3）对此函数式进行全微分或先取对数再求微分，得：
dx
c os L1
cos(L1 L2 ) cos2 (L1
sin L1 L2 )
sin(L1
所以 DXY DXX BT ADLL AT BT
习题
1.4：若要在两已知高程点间布设一条附合水准路线（如图所示），已知每千米
观测中误差等于5.0mm，欲使平差后路线中点C点高程中误差不大于10mm，
问该路线长度最多可达几千米？
h1
h2
C
B
解析：设A、B间最大距离为Skm
HC' HA h1 HC" HB h2
HC
HC'
H
" C
2
H A h1 H B h2 2
h1 h2
S 2
公里
2
2 h1
2 h2
S
2 公里
hC
4
4
10mm S公里 10mm S 16km
hC
2
习题
1.5：有一角度测20测回，得中误差 0.42''，问再增加多少测回其中误差为0.28''?
考点：同精度独立观测值的算术平均值的精度
DXY ADLL (BA)T ADLL AT BT
或
Y BX B
O
X L
X O
A
X L
，
DXY O
A
DXX DLX
DXL DLL
BT O
ADLX
ADLL
BT O
ADLX BT
ADLL AT BT
或 Y BX, X IX
DXY ID XX BT DXX BT
而 DXX ADLL AT
L2
)
dL1
sin L1 sin(L1 cos2 (L1
L2 L2 )
)
dL2
c os L2 cos2 (L1
L2
)
dL1
sin L1 sin(L1 cos2 (L1
L2 L2 )
)
dL2
2 x
cos2 cos4 (L1
L2 L2 )
m12
sin2 L1 sin2 (L1 L2 ) cos4 (L1 L2 )
习题
1.2 已知独立观测值L1、L2的中误差分别为m1、m2，求下列函数的中误差：
（1） x 2L1 3L2
（2）x
L12 2
3L1L2 （3） x
sin L1 cos(L1 L2 )
解：（1）因L1、L2是独立观测值，则
2 x
4m12
9m22
x 4m12 9m22 （2）对此函数式进行全微分，得：
DXL ADLL I T ADLL
（2） Y BX, X AL
Y BAL，又 L IL
DYL BADLL I T BADLL
，
或
Y BX B
O
X L
L IL O
I
X L
DYL B
O
DXX DLX
DXL DLL
O I
BDXX
BDXL
O
BDXL
BADLL
习题
（3） Y BAL, X AL

测量平差课后习题答案

测量平差第二章习题与答案

最新误差理论和测量平差试题+答案

测量平差课后习题答案张书毕

智慧树答案误差理论与测量平差(山东联盟)知到课后答案章节测试2022年

测量平差习题集答案

误差理论与测量平差基础第6章课后答案

误差理论和测量平差习题5(含答案)

答案测量平差a

测量平差习题参考答案

测量平差第五章条件平差习题参考答案

最新误差理论和测量平差试题+答案

测量平差练习题及参考答案

测量平差基础参考资料[1]

测量平差课后习题答案

测量平差答案

测量平差期末考试题及答案

测量平差课后习题答案

测量平差 第二章习题与答案

最新误差理论和测量平差试题+答案

测量平差课后习题答案 张书毕

智慧树答案误差理论与测量平差(山东联盟)知到课后答案章节测试2022年

测量平差习题集答案

误差理论与测量平差基础第6章课后答案

误差理论和测量平差习题5(含答案)

答案 测量平差a

测量平差习题参考答案

测量平差第五章条件平差习题参考答案

最新误差理论和测量平差试题+答案

测量平差练习题及参考答案

测量平差基础参考资料[1]

测量平差课后习题答案

测量平差 答案

测量平差期末考试题及答案

测量平差第二章习题与答案

测量平差课后习题答案张书毕

答案测量平差a

测量平差答案