哈尔滨工业大学理论力学第七版第II篇 第3章 碰撞
理论力学(哈工第七版) 课后练习答案 第三部分
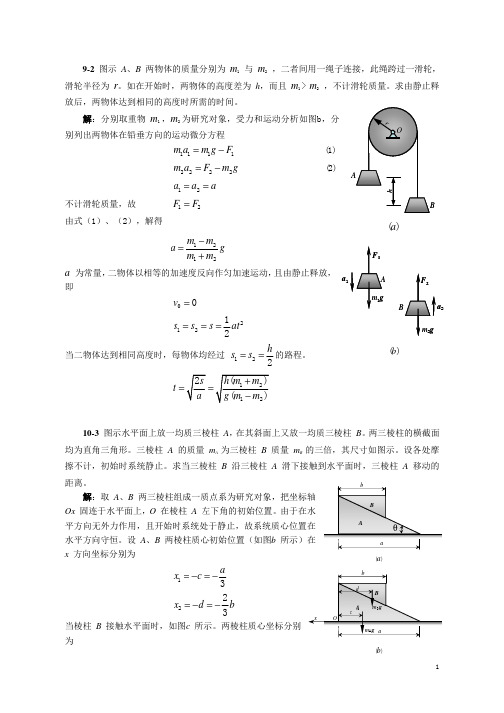
A
ϕ
O
r ϕ
M
W=
2π
∫ 4ϕ dϕ + (m
0
− mB ) g ⋅ 2π r
A B
A mAg
= 8π 2 + (mA − mB ) g ⋅ 2π r = 8π 2 + 1× 9.8 × 2π × 0.5 = 110 (J)
B
mBg
(a)
(b)
7
12-4 图示坦克的履带质量为 m,两个车轮的质量均为 m1。车轮被看成均质圆盘,半径为 R, 两车轮间的距离为 πR。设坦克前进速度为 v,计算此质点系的动能。 解:系统的动能为履带动能和车轮动能之和。将履带分为四部 分,如图b 所示。履带动能:
O
P2 P aB − 1 a A = FN − P 1−P 2 g g
其中, a A = a , aB = 解得
A
a 2 1 (2 P 1−P 2 )a 2g
B
(a)
FN = P 1+P 2 −
v FN
O
v P 1
A
v aA
v aB B
v P2
(b)
11-1 质量为 m 的点在平面 Oxy 内运动,其运动方程为
得
G1
320
B C
SB
S A = 170 mm S B = 90 mm
(b)
2
10-12 图示滑轮中,两重物 A 和 B 的重量分别为 P1 和 P2。如物体 A 以加速度 a 下降, 不计滑轮质量,求支座 O 的约束力。 解:对整体进行分析,两重物的加速度和支座 O 的约束力如图b 所示。由 动量定理知:
整体受力和运动分析如图b因为0xf所以x方向系统守恒有21cos0brbmvmvv??解得121cosbrmmvvm1所以该系统动能为设此时三棱柱a沿三棱柱b下滑的距离为s则其重力作的功为1sinwmgs??系统动能22b211221sin12cosmmtmmvm由系统动能定理tw即1sinwmgs??上式对时间求导并注意到rdsdtv整理后得22112121sinsincosbbrmmmmvamgvm?????得2b2a212b2b2r2122b21122
理论力学第七版答案、高等教育出版社出版

仅供个人学习参考哈工大理论力学(I )第7版部分习题答案1-2两个老师都有布置的题目2-3?2-6?2-14?2-?20?2-30?6-2?6-4?7-9??7-10?7-17?7-21?8-5?8-8?8-16?8-24?10-4?10-6?11-5?11-15?10-3以下题为老师布置必做题目1-1(i,j ),1-2(e,k)2-3,2-6,2-14,2-20,2-306-2,6-47-9,7-10,7-17,7-21,7-268-5,8-8(瞬心后留),8-16,8-2410-3,10-410-611-5,11-1512-10,12-15,综4,15,16,1813-11,13-15,13-166-2图6-2示为把工件送入干燥炉内的机构,叉杆OA=1.5m 在铅垂面内转动,杆AB=0.8m ,A 端为铰链,B 端有放置工件的框架。
在机构运动时,工件的速度恒为0.05m/s ,杆AB 始终铅垂。
设运动开始时,角0=?。
求运动过程中角?与时间的关系,以及点B 的轨迹方程。
10-3如图所示水平面上放1均质三棱柱A ,在其斜面上又放1均质三棱柱B 。
两三棱柱的横截面均为直角三角形。
三棱柱A 的质量为mA 三棱柱B 质量mB 的3倍,其尺寸如图所示。
设各处摩擦不计,初始时系统静止。
求当三棱柱B 沿三棱柱A 滑下接触到水平面时,三棱柱A 移动的距离。
11-4解取A 、B 两三棱柱组成1质点系为研究对象,把坐标轴Ox 固连于水平面上,O 在棱柱A 左下角的初始位置。
由于在水平方向无外力作用,且开始时系统处于静止,故系统 质心位置在水平方向守恒。
设A 、B 两棱柱质心初始位置(如图b 所示)在x 方向坐标分别为当棱柱B 接触水平面时,如图c 所示。
两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4如图所示,均质杆AB ,长l ,直立在光滑的水平面上。
求它从铅直位无初速地倒下时,端点A 相对图b 所示坐标系的轨迹。
理论力学第7版(哈工大)第3章习题

《理论力学》第二章作业习题2-1解:根据题意,取滑轮B 为研究对象,其受力情况如上图所示:物体对其有一铅直向下的拉力P , 沿DB 有一与物体重量相等的拉力P,拉杆AB 的作用力A B F 和支杆CB 的作用力C B F。
建立图示坐标系,列平衡方程0X YF F ⎧=⎪⎨=⎪⎩∑∑co s 30sin 300sin 30co s 300o oA B C B o oC B F F P P F P ⎧++=⎨++=⎩解之得54.64()74.64()A B C B F kN F kN =⎧⎨=-⎩答:拉杆AB 和支杆CB 所受的的力分别为54.64kN (拉)和74.64 kN (压)。
习题2-6解:(1) 取构件BC 为研究对象,其受力情况如上图(a)所示:由于其主动力仅有一个力偶M ,那末B 、C 处所受的约束力BF、CF 必定形成一个阻力偶与之平衡。
列平衡方程()0B M F =∑C M F l -=所以C M F l=(2) 取构件ACD 为研究对象,其受力情况如上图(b)所示:C 处有一约束力C F '与BC 构件所受的约束力C F 互为作用力与反作用力关系,在D 处有一约束力D F,方向向上;在A 处有一约束力A F,其方向可根据三力汇交定理确定,根据构件尺寸,A F与水平方向成45度角。
列平衡方程X F =∑sin 450oA C F F '-=所以222A C C M F F F l'===答:支座A的约束力为2M l,其方向如上图(b)所示。
习题2-9解:主矢RF在各坐标轴上的投影:)(6.4375210121321N F F F F x -=---=∑)(6.1615110321321N F F F F y -=+--=∑力系对O 点的主矩:).(42.21439805120021100)(31mm N F F F F MMOO=-+==∑由于主矢在各坐标轴上的投影均为负值而主矩为正值,合力的作用线应在原点O的左侧且方向向左下方,其大小为()())(5.46622N F F F YXR =+=∑∑其与O 点的距离为:)(96.455.46642.21439mm F M d R O=='=答:力系向O点简化的结果得一方向向左下方的主矢ji F R6.1616.437--='和一沿顺时针方向的力偶,力偶矩为21439.42Nmm; 力系的合力的大小为466.5N ,处于原点O 的左侧且与O 点的距离为45.96mm (如图)。
理论力学经典课件-碰撞

这时,
vA =vB =v AB
于是,有
mA v A mB vB mA mB v AB
v AB
mA vA mB vB mA mB
18 103 0.2 i 0.03 j 0.02 k 0
18 103 6.6 103
0.146 i 0.022 j 0.015 k m/s
AB
vAB A v'A B v'B
由
mA v A mB vB mA vA mB vB
k I2 vB vA I1 vA vB
解得碰撞后两个球的速度分别为
vA
vA
1
k
mA mA mB
vA
vB
vB
vB
1
k mA
mA mB
vA
vB
vA A
B vB
AB
vAB A v'A B v'B
(3)碰撞后阶段
根据平面运动微分方程,有
maC F mgf
JC Fr mgfr
由运动学可知
v vC aCt
C t
C
aC
mg
F FN
由平面运动可知,当 v rC 时,轮开始纯滚
解得: t 1 k 3gl 0.24 s 14gf
突加约束问题
运动的刚体 突然受到其他 物体的阻碍, 发生碰撞,在 接触处发生完 全不可恢复的 变形,亦即产 生完全非弹性 碰撞-突然施 加约束,简称 突加约束。
例题6
质量为m、半径为r的均
质圆柱体,以质心速度vC
§15-1 碰撞现象·碰撞力
碰撞-物体与物体之间,在极短的时间内,发生 有限量的动量传递与能量转换,同时伴随有极大的 撞击力的动力学过程。
理论力学第七版课后习题答案(共9篇)

理论力学第七版课后习题答案(共9篇)理论力学第七版课后习题答案(一): 求理论力学第七版课后习题答案1、很高兴为您回答,但我没有题目内容啊!2、自己亲自做吧.网上(如:百度文库)可能查找到一些答案,一般不全.对搞不懂的题目,可以上传题目内容,以方便为你回答.理论力学第七版课后习题答案(二): 理论力学第六版(哈尔滨工业大学理论力学教研室)高等教育出版社课后习题答案 [email protected]【理论力学第七版课后习题答案】已发送注意查收理论力学第七版课后习题答案(三): 理论力学第七版高等教育出版社PDF 要《理论力学》(I)(第7版),《理论力学》(II)(第7版),《简明理论力学》(第2版)高等教育出版社,理论力学解题指导及习题集(第3版)高等教育出版社,理论力学思考题集高等教育出版社,这些书的PDF 非常谢谢必有重赏在下载了一会上传附件,望等待!!!理论力学第七版课后习题答案(四): 有几道力学题,.理论力学第一题选择题(基本概念和公理)1 理论力学包括()A、静力学、运动力学和动力学.B、运动学和材料力学.C、静动力学和流体力学.D、结构力学和断裂力学.2 静力学是研究()A、物体破坏的规律B、物体平衡的一般规律.C、物体运动的一般规律..D、物体振动的规律..3 关于刚体的说法是()A、很硬的物体.B、刚体内任意两点间的距离可以微小改变..C、刚体内任意两点间的距离保存不变.D、刚体内任意两点间的距离可以改变.4 关于平衡的概念是()A、物体相对于惯性参考系静止.B、物体做加速运动.C、物体相对于惯性参考系运动.D、物体做减速运动5 力是物体间的()A、相互化学作用..B、相互机械作用.C、相互遗传作用.D、相互联接作用.6 力对物体作用的效应取决于力的三要素,三要素是指()A、力的大小、方向和坐标B、力的大小、量纲和作用点.C、力的大小、方向和作用点.D、产生力的原因、方向和作用点.7 在国际单位制中,力的单位是()A、米(m).B、牛顿.米(N.m).C、牛顿.秒(m).D、牛顿(N).8 关于约束的说法是()A、限制物体运动的装置B、物体和物体的链接.C、物体运动的装置.D、使物体破坏的装置.ABCAD CDA理论力学第七版课后习题答案(五): 第七课答案【理论力学第七版课后习题答案】七年级上语文期末复习复习提要 1、语言积累和运用.2、现代文阅读.3、文言文、古诗词阅读.4、作文复习.5、专题训练及总测试.重点 1、注意辨别字形、正字音、释词义,理解语句在具体语境中的含义.2、整体感知课文,理解文章内容和写作特色,领悟作者的思想感情.3、学习文言文,生在朗读、背诵.掌握积累一些文言词语,理解文章大意,学会翻译文言文.4、学会审题,并结合学习生活实际,选取典型的材料进行作文,学会运用学过的词语及写作技巧.难点:1、关键词语的揣摩.2、理解一些重要语句的深刻含义.3、理解诗歌的意境.4、作文的选材立意.课时划分:1、积累与运用(4课时).A、拼音汉字、改正错别字.B、古诗、名句的默写.C、仿写句子、广告标语、综合性学习.D、对对子、名著导读.2、现代文阅读(4课时).A、课内阅读(2课时).B、课外阅读(2课时) 3、文言文阅读(2课时).4、作文(2课时).附:专题练习分工:积累与运用:张桂芬、钟国珍,现代文阅读(课内:王安华、黄卓苗,课外:郑小坚、范远填),文言文阅读:方焕章,作文:王文捷复习教案第一课时复习内容 1、复习本册学过的生字生词,掌握音、形、义.2、熟练运用学过的生字词.一、复习本册学过的生字生词,掌握音、形、义.1、教师指导学生掌握关键词语,让学生读、抄一遍,掌握正确的读音和拼写规则,特别注意平常容易读错的字音和多音多义字的读音.如:A、给下列加点的字注音或根据拼音写汉字.痴()想隐秘()诱惑()xuān( )腾一shùn( )间yùn( )含 B、请你找出并改正词语中的错别字.惊荒失措 _____改为_____ 昂首铤立_____改为_____ 二、进行逐单元进行听写训练.(一般分开在课前进行)三、完成试卷练习.(课后巩固为主)第二课时复习内容 1、复习古诗、名句的默写.2、学会初步赏析一些古诗或《论语》中的名句.一、学生复习要求背诵古诗和名篇.1、学生诵读本册要求背诵的古诗.2、教师指导学生熟记一些名句,会默写.3、掌握重点,理解诗歌的主题思想,体会含义深刻的句子.二、默写练习.(主要针对后进生,以激励为主)如:A、商女不知亡国恨,_______________________.《泊秦淮》 ,浅草才能没马蹄.《钱塘湖春行》B、《观沧海》中展现海岛生机勃勃的诗句是:,.,.《次北固山下》一诗中道出新旧更替的生活哲理的名句是:,.三、课后试卷练习巩固.第三课时复习内容1、仿写句子.2、复习比喻、拟人等修辞方法的辨别和运用.一、明白仿写的意义及方法.1、仿句是按照题目已经给出的语句的形式,再另外写出与之相仿的新句,仿句只是句式仿用,文字内容不能完全一样.只要被模仿的是句子的形式,不管是单句或复句,都列入仿句.2、仿句考查的知识点:(1)、考查同学们对语法、修辞等知识的综合运用,要求同学们根据不同的语境和要求,写出与例句内容和形式相同或相近、意义上有密切关联的句子.例如:生活就是一块五彩斑斓的调色板.希望就是________________________.[解析]这道题目从句式上看是陈述句.在修辞上运用了比喻,同学们要注意比喻运用的得体,比喻的艺术贵在创新,要寻找新鲜、活泼的喻体,保持上下文的协调性.如:希望就是一颗永不陨落的恒星.希望就是一盏永不熄灭的明灯.(2)、考查同学们的语言表达能力,联想、想象能力,创新思维能力.例如:什么样的年龄最理想什么样的心灵最明亮什么样的人生最美好什么样的青春最辉煌鲜花说,我开放的年龄多妩媚;月亮说,____________________________;海燕说,_______________________.太阳说,_________________________________.[解析]该题是问答式的仿写,在回答上运用拟人的修辞,要求天下们针对性进行回答,有一定的开放度,但是在解题时,要注意结合回答对象的特点.如:我纯洁的心灵多明亮;我奋斗的人生极美好;我燃烧的青春极辉煌.(3)、是对同学们思想认识水平的检测,包括道德素质,审美理论力学第七版课后习题答案(六): 理论力学的基本原理和基本假设是什么理论力学是机械运动及物体间相互机械作用的一般规律的学科,也称经典力学.是力学的一部分,也是大部分工程技术科学理论力学的基础.其理论基础是牛顿运动定律,故又称牛顿力学.原理的话就是牛顿三大定理咯.定理都是在基本假设的基础上推出来的,所以想想牛顿三定律是建立在什么假设基础上的我能总结出来的就三点:1.时间是绝对的,其含义是时间流逝的速率与空间位置和物体的速率无关; 2.空间是欧几里德的,也就是说欧几里德几何的假设和定律对空间是成立的;3.经典物理的第三个假设,就是质点的运动可以用位置作为时间的函数来描述.理论力学第七版课后习题答案(七): 大学理论力学的问题(哈工大第七版)有关力矩在平面力对点之炬,这一节中,关于力对点之矩的正负问题中,顺时针和逆时针怎么判断呢以及在力对轴的矩中右手螺旋定则怎么定义的啊利用右手螺旋定则,其实判断力矩正负和以前高中学的判定磁场方向差不多,就是伸出右手,大拇指与其余四个手指垂直,其余四指弯向力的方向,这时候可以有两种判定方法:第一种,如果其余四指弯曲的方向是顺时钟,则力矩为负,反之,则为正;第二种,如果这时大拇指指向为上,那么力矩为正,反之,则为负.总之大体的判断方法就是这样,至于哪种方法更容易,楼主自行体会吧.最后祝你学业进步~理论力学第七版课后习题答案(八): 现代物理学包括哪几部分目前我们学物理是包括了力学,光学,热学,电磁学,原子物理学,理论力学,热力学,统计物理学,电动力学,量子力学,数学物理方法,固体物理学这些学科的理论力学第七版课后习题答案(九): 科学不怕挑战的阅读答案5.本文的中心论点是什么7 (4分)6.第③④段运用了事例来论证,请分别概括这两个事例的内容.(4分)7.第⑤段申两个句子的顺序能否颠倒为什么(4分)8.第⑥段中"科学"一词为什么加上引号(2分)9.说说画线句子在文中的表达作用.(3分)参考答案:5、科学不怕挑战(或“科学不怕挑战,怕挑战的不是科学.”)(2分)6、第③段:量子力学曾受到爱因斯坦理想实验的挑战(1分);第④段:进化论曾受到创世说者的频频发难(1分).7、不能颠倒(1分).这句话有承上启下的作用,前半句总结上文,后半句引出下文(1分).8、为了表示讽刺和否定.(2分)9、运用了比喻论证的方法(1分),将科学不断受到挑战比作了大浪淘沙,证明了科学是不怕挑战的,从而把抽象深奥的道理阐述得生动形象、浅显易懂(1分).。
理论力学(第七版)2

va =
得
va = 2 aω cos 30° aω 1 = 2 aω
ω=
ω1
2
= 1.5 rad/s (逆)
(b)套筒 A 为动点,动系固结于杆 O1 A ;绝对运动为绕 O2 圆周运动,相对运动为沿
va = O2 A ⋅ ω1 = 2aω cos 30° , ve = O1 Aω1 = aω 1 ve aω 1 由图 b1: v a = = cos30° cos30° aω 1 得 2aω cos 30° = cos 30° 2 ω = ω 1 = 2 rad/s (逆) 3 8-8 图 8-8a 所示曲柄滑道机构中,曲柄长 OA = r ,并以等角速度 ω 绕轴 O 转动。 装在水平杆上的滑槽 DE 与水平线成 60° 角。求当曲柄与水平线的交角分别为 ϕ = 0° , 30° , 60° 时,杆 BC 的速度。
y
如图 8-9a 所示,摇杆机构的滑杆 AB 以等速 v 向上运动,初瞬时摇杆 OC 水平。
摇杆长 OC = a ,距离 OD = l 。求当 ϕ =
va ve
C
vr
O
(a) 图 8-9
ϕ
l
(b)
A D
v
x
解 套筒 A 为动点,动系固结于杆 OC;绝对运动为上下直线,相对运动沿 OC 直线, 牵连运动为绕 O 定轴转动。速度分析如图 8-9b 所示,设杆 OC 角速度为 ω ,其转向逆时 针。由题意及几何关系可得 va = v (1)
ve1 − v r1 cos 30° = ve2 b b ω − ω ve1 − ve2 cos30° 1 cos30° 2 4b = = (ω 1 − ω 2 ) v r1 = cos30° cos30° 3 式(3)向 v r2 方向投影,得 1 2b (ω 1 − ω 2 ) = 0.4 m/s v r2 = v r1 = 2 3 0.1 ve2 = × 3 = 0.346 m/s 3 2 ⎧v = v 2 + v 2 = 0.529 m/s e2 r2 ⎪ a 所以 ⎨ ve2 0.346 = ,θ = 40.9° ⎪tan θ = 0 .4 v r2 ⎩
【精编】哈尔滨工业大学理论力学第七版第II篇-第4章-机械振动基础.PPT课件

0
keq m
k1k2 kn m
n个弹簧串联后的等效刚度系数 n个弹簧串联系统的固有频率
keq
1
1
1
1
k1 k2
kn
0
keq m
1
k11
1 k2
1 kn
m
例题3
图示系统中有四根铅直弹簧,它 们的刚度系数分别为 k1 、 k2 、 k3 、 k4 且k1 =2 k2 =3 k3=4 k4 。假设质量为m的物 块被限制在光滑铅直滑道中作平动。
Fe Fd k
c
Fe k x 弹性恢复力
Fd
c
dx dt
粘性阻尼力
物块的运动微分方程为
O
m
m
v
mddt22x
k
xcdx dt
x
阻尼系数
令
02
k, m
d c
2m
dd2t2x2dddxt 02x0
dd2t2x2dddxt 02x0
设其解为 x ert
本征方程 r22dr020
本征根
r1 d d 2 02
本章重点讨论单自由度系统的自由振动和受迫振动。
第四章 机械振动基础
§4-1 单自由度系统的自由振动 §4-2 计算固有频率的能量法 §4-3 单自由度系统的有阻尼自由振动 §4-4 单自由度系统的无阻尼受迫振动 §4-5 单自由度系统的有阻尼受迫振动 §4-6 转子的临界转速 §4-7 隔振 §4-8 两个自由度系统的自由振动 §4-9 两个自由度系统的受迫振动 · 动力减振器
1. 阻 尼
阻尼-振动过程中的阻力。
干摩擦力,润滑表面阻力,液体或气体
等介质的阻力、材料内部的阻力。
理论力学(下册)第3章 碰撞

i 1
i
因为
I (e) i
0
i 1
n
n
n
mivi
mivi
I (e) i
i 1
i 1
i 1
--用于碰撞过程的质点系动量定理 冲量定理
质点系在碰撞开始和结束时动量的变化,等于作用于 质点系的外碰撞冲量的主矢。
n
mvC mvC
I (e) i
i 1
式中 v和C 分vC 别是碰撞开始和结束时质心的速度
2.用于碰撞过程的动量矩定理——冲量矩定理
质点系动量矩定理
d
dt
LO
n i 1
M O (Fi(e) )
n i 1
ri
F (e) i
上式可写成
n
n
dLO ri Fi(e)dt ri dIi(e)
i 1
i 1
dL LO2
n
LO1
O
i 1
t 0
ri
dI
( i
e)
质点系在碰撞开始和结 束时对点O的动量矩的
v2
(1
k
)
m1 m1 m2
(v1
v2
)
(v1
v2
)
(c)
在理想情况下, k=1,有
1
v1
2m2 m1 m2
(v1
v2 ),v2
v2
2m1 m1 m2
(v1
v2 )
如果 m1 m2 则 v1 v2 ,v2 v1
即两物体在碰撞结束时交换了速度
当两物体做塑性碰撞时,即k=0,有
v1
v2
因 LO1 LO2
υ JO m2d 2
m2d
哈尔滨工业大学理论力学课后习题答案
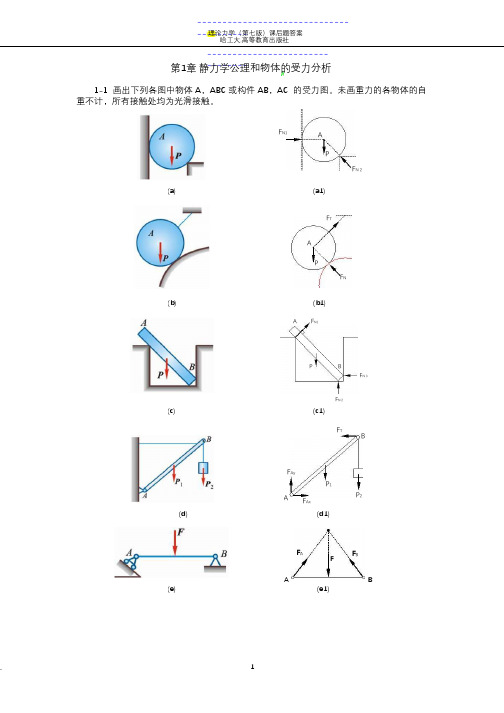
.----------------------------------------理论力学(第七版)课后题答案 哈工大.高等教育出版社 -------------------------------- 第1章 静力学公理和物体的受力分析1-1 画出下列各图中物体 A ,ABC 或构件 AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
F N1A PF N 2(a) (a1)F TA PF N(b)(b1)AF N1P BF N 3F N 2(c) (c1)F TBF AyP 1P 2AF Ax(d) (d1)F AF BFAB(e)(e1)qFF Ay F BF AxA B(f) (f1)FBC F CAF A(g) (g1)F Ay FCCA F Ax BP1 P2(h) (h1)BFCF CF AxDAF Ay(i) (i1)(j) (j1)BF B FCPF AyF AxA(k) (k1)F CAF AB 2 F AC CA2 F ABBF ACF BAA P (l) (l1)(l2)(l3)图 1-11-2 画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所 有接触处均为光滑接触。
F N 2C2 F P 2(a1) F N1N(a)BF N1BC F N 2F NP 2P1P1F AyF Ay F AxF AxAA(a2) (a3)F N1AP1F N3B P 2F N 2(b) (b1)2 F NF N3F N1ABP 2P1F N F N 2(b2)(b3)F AyF AxA C D F N2BP 2P 1F N1(c)(c1)F AyF TAF AxD2 F F N2TBP 1F N1P 2(c2)(c3)F AyF BqBAF AxCDF C(d)(d1)F DyF AyF BqqD2 FDxBAF AxCF Dx D 2 FDyF C(d2) (d3)F Ay2 FBxqBF AyF AxqAB 2F ByF AxF CxC F CyP F BxAB PF Cx (e1)CF ByF Cy(e)(e2)(e3)F 1CF 2F AyF ByABF AxF Bx(f)(f1)F Cx2 FCxCCF 1F CyF 2 F 2F AyCyF ByAF BxF Ax B(f2)(f3)F BF AyCBAF AxP(g)(g1)2 F CyF T2 FCxCF AyF BF TDCF AxBAF Cx P (g2)(g3)DF 1F CyF B2 F 2F BBCF CxBF Ay AF Ax(h)(h1)(h2)A F AxF AyF CyF CxC2 A F EF CyF F OyCDF OxF Cx 2EOB(i)(i1)(i2)A A2 F Ax2 FE2 F AyFEC D F ByF ByF OyF BxF OxF BxOBB (i3)(i4)F AyDE F CxF TA F AxF ByC CHF By F Cy BPF BxF BxB(j)(j1)(j2)F Ay F Dy 22 F Ey2 F CF Cx 2 E F AxT 2 D F T 22FExF ExA D F Dx 2E F DxF T3F T12FCyF DyF Ey(j3)(j4)(j5)EFF BCED2 BF Cx⎝2 2 F DEF Cy(k)(k1)F BF FC BF Cx⎝EC F Cy90︒ ⎝FDED DF AyF AyAAF AxF Ax(k2) (k3)F B2 FBF 1F DBBDCAF AF C(l)(l1)(l2)F 22 DF DF 1F 2DBAC EE F EF AF C F E(l3)(l4)或2 2 F DyF2F 1F F Dy F 2F 1B 2 DF DxF DxBBD D F ExA C E C E F ExF CF EyF AF CF Ey(l2)’(l3)’(l4)’2 F ADAF CyF CxCF 1B(m)(m1)F ADDF ADHEF 2A DF EF HF AD 2(m2)(m3)F N AAF kF N BF OyF OxBO(n) (n1)F N1B Dq2 F BF N 2F N3(n2)FB D FF C F EF AF G GCEA(o)(o1)FBB DFDF BF E F FF C F D2 FEA F AF B 2CD(o2)(o3) (o4) 图 1-2第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心 A ,B 和 C 处受 3个力作用,如图 2-1a 所示。
理论力学 17.碰撞

对于塑性碰撞(k =0):
v1
v2
v
m1v1 m2v2 m1 m2
对于一般情况(0<k <1): v1 v1 , v2 v2
2.正碰撞过程中的动能损失
碰撞开始:
T1
1 2
m1v12
1 2
m2v22
碰撞结束:
T2
1 2
m1v12
1 2
m2v22
则动能损失:
v1 v2
式中v1、v2和v1’、 v2’分别是两物体碰撞前后的速度。
一般0<k<1,各种材料的恢复系数,可查阅书中表。
k=1 理想情况——完全弹性碰撞。
k=0 极限情况——非弹性碰撞或塑性碰撞。
三、碰撞时的动力学基本定理 在理论力学中,我们关心的主要是由于碰撞冲量的作用而
使物体运动速度发生的变化。因此,动量定理和动量矩定理就 成了研究碰撞问题的主要工具。
例1 打桩机。锤:m1,下落高度h;桩:m2,下沉 。两者塑
性碰撞。求碰撞后桩的速度和泥土对桩的平均阻力。 解:碰撞开始时,
锤速 v1 2gh ,
桩速 v2 0
塑性碰撞后, u1 u2 v
m1 2gh m1 m2
根据动能定理,计算下沉 过程中,泥土对桩的平均阻力R。
k I2 v2 v v1 v v2 v1 I1 v v2 v v1 v1 v2
对于两物体正碰撞的情况,恢复系数等于两物体在碰撞结 束与碰撞开始时,质心的相对速度大小的比值。)
联立(1),(2)式,解得:
v1
v1
(1
k)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
害的一面: 鸟祸、机械、仪器及其它物品由于碰撞损坏等。
利的一面:利用碰撞进行工作,如锻打金属,用锤打桩等。 研究碰撞现象,就是为了掌握其规律,以利用其有利的一 面,而避免其危害。
§3-2
用于碰撞过程的基本定理
由于碰撞过程时间短、碰撞力变化规律复杂,因此只分 析碰撞前、后运动的变化。 碰撞过程中有机械能的损失,难以用力的功来计算,因 此一般采用动量定理和动量矩定理的积分形式来确定力 的作用和运动变化的关系。 1. 用于碰撞过程的动量定理—冲量定理
t 对于质点: mv mv Fdt I 0 I 称为碰撞冲量,普通力的冲量忽略不计
§3-3
§3-4
质点对固定面的碰撞 · 恢复因数
碰撞问题举例
§3-5
碰撞冲量对绕定轴转动刚体的作用
· 撞击中心
§3-1
碰撞的分类 · 碰撞问题的简化
1. 碰撞的分类
碰撞时两物体间的相互作用力,称为碰撞力。
(1)两个物体相碰时,按其相处位置,可分为 对心碰撞 ---- 碰撞力的作用线通过两物体的质心。 否则称为偏心碰撞 偏心碰撞 正碰撞 斜碰撞 ---- 碰撞时各自质心的速度均沿着公法线。 否则称为斜碰撞
(i ) Ii 0
n i 1
冲量定理:质点系在碰撞开始和结束时动量的变化,等于作 用于质点系的外碰撞冲量的主矢。
(e ) mvC mvC I i
2. 用于碰撞过程的动量矩定理—冲量矩定理
n n (e) d (e) LO M O ( Fi ) ri Fi dt i 1 i 1 n n (e) (e) dLO ri Fi dt ri dI i i 1 i 1
I 2 v2 v v1 v v2 v1 e I1 v v2 v v1 v1 v2
对于两物体正碰撞的情况,恢复系数等于两物体在碰撞
结束与碰撞开始时,质心的相对速度大小的比值。
联立(1),(2)式,解得:
v1 v1 (1 e)
m2 (v1 v2 ) m1 m2
T T1 T2 0
(恒为正值)
[例] 打桩机。锤:m1,下落高度h;桩:m2,下沉 。两
由于碰撞时碰撞力极大而碰撞时间极短,在研究一般的碰撞
问题时,通常做如下两点简化:
(1)在碰撞过程中,由于碰撞力非常大,重力、弹性力等普
通力远远不能与之相比,因此这些普通力的冲量忽略不计; (2)由于碰撞过程非常短促,碰撞过程中,速度变化为有限
值,物体在碰撞开始和碰撞结束时的位置变化很小,因此在碰 撞过程中,物体的位移忽略不计。
mv2 mv1 I
10 (1.5 6) I ; I 7.65 N s g 碰撞力的变化大致情况如图所示。
平均打击力 F * I / 7650 N,是榔头重的765倍。
可见,即使是很小的物体,当运动速度很高时,瞬时力
可以达到惊人的程度。有关资料介绍,一只重17.8N的飞鸟与
m1 (v1 v2 ) m1 m2 对于完全弹性碰撞(e=1): v2 v2 (1 e)
v1 v1 2m2 2m1 (v1 v2 ) ; v2 v2 (v1 v2 ) m1 m2 m1 m2
若 m1 m2 , 则 v1 v2 , v2 v1 (碰撞后两物体交换速度)
v 2gh1 v 2gh2
v e v
h2 h1
各种材料的恢复因数,可查阅书中表3-1。 一般地,0<e<1 —— 弹性碰撞
e=1 理想情况 ——完全弹性碰撞
e=0 极限情况 ——非弹性碰撞或塑性碰撞
v I 2 e v I1
恢复因数又等于正碰撞的两个阶段中作用于物体的碰撞冲量
(e) LC 2 LC1 M C ( I i )
碰撞前后质点系相对于质心C的动量矩的变化,等于外碰撞冲 量对质心的矩的矢量和(对质心的主矩)
对于平行于其质量对称面运动的平面运动刚体,有
LC J C
(e) J C2 J C1 M C ( I i )
1 T m1 1 1 m2
1) 当m2>> m1时, △T ≈T1,质点系在碰撞开始时的动能几 乎完全损失在碰撞过程中,适用于锻压金属。在工程中采 用比锻锤重很多倍的砧座。 2) 当m2<< m1时, △T ≈0,适用于打桩,碰撞结束时桩获 得较大的动能克服阻力前进,因此在工程中应选取比桩重 得多的锤打桩。又如用锤子钉钉子。 (c) 对于弹性碰撞 (0<e<1 ):
又
v1 v2 e(v1 v2 ) m1m2 T T1 T2 (1 e 2 )(v1 v2 ) 2 2(m1 m2 )
m1m2 T T1 T2 (1 e 2 )(v1 v2 ) 2 2(m1 m2 )
(a) 对于完全弹性碰撞(e =1): T T1 T2 0 系统动能没有损失,可以利用机械能守恒定律求碰撞后的速度。 (b) 对于塑性碰撞 (e =0): T T1 T2
§3-4
碰撞问题举例
例如:两物体对心正碰撞,质量分别为m1和m2,恢复因数为e
v 碰撞前:1 , v2 (v1 v2 ) v 碰撞结束: 1 , v2 (沿质心连线)
(1)分析碰撞结束时两质心的速度。
研究对象:两物体组成的质点系。 由冲量定理,得:
m1v1 m2v2 m1v1 m2v2
(2)正碰撞过程中的动能损失 1 1 2 T1 m1v12 m2 v2 碰撞开始: 2 2 1 1 2 碰撞结束: T2 m1v1 m2 v22 2 2 则动能损失:
1 1 2 2 2 T T1 T2 m1 (v1 v1 ) m2 (v2 v22 ) 2 2 1 1 m1 (v1 v1 )(v1 v1 ) m2 (v2 v2 )(v2 v2 ) 2 2
列出补充方程:
(1)
v2 v1 e v1 v2
(2)
(分别以两物体为研究对象,应用动量定理可得出。具体地 对于第一阶段: m1 (v v1 ) I1 , m2 (v v2 ) I1
对于第二阶段: m1 (v1 v) I 2 , m2 (v2 v) I 2
m1m2 (v1 v2 ) 2 2(m1 m2 )
若第二个物体在塑性碰撞开始时静止,即v2=0,则
m1m2 2 1 m v 2 m2 v1 T 2(m1 m2 ) 2 1 1 m1 m2
1 T m1 1 1 m2
在这种塑性碰撞过程中损失的动能与两物体的质量比有关
m1m2 2 1 m v 2 m2 v T 2(m1 m2 ) 1 2 1 1 m1 m2
vn tan e vn tan
对于实际材料有e < 1, 则有:当碰撞物体表面光滑时,应有
>
在不考虑摩擦的一般情况下,碰撞前后的两个物体都在运 动,此时恢复因数定义为
n vr e n vr
vr n , vrn 分别为碰撞后和碰撞前两物体接触点沿接触面 式中
法线方向的相对速度
由正碰撞结束时两质心的速度公式知: m2 m1 v1 v1 (1 e) (v1 v2 ) ; v2 v2 (1 e) (v1 v2 ) m1 m2 m1 m2 代入上式中,得:
1 m1m2 T (1 e) (v1 v2 )[( v2 v1 ) (v2 v2 )] 2 m1 m2
m1v1m2m2 v2 v ( 2 对于塑性碰撞(e =0): v1 v11 v1 e) (v1 v2 ) m1 m2 1 2
( , 对于一般情况(0<e <1): v v1 1v1 e) v2 m1v2 (v v ) v2 2 1 2 m1 m2
n n n (e) t (e) (e) LO 2 LO1 ri dI i ri I i M O ( I i ) i 1 0 i 1 i 1
冲量矩定理:质点系在碰撞开始和结束时对点O的动量矩的变 化,等于作用于质点系的外碰撞冲量对同一点的主矩。 3. 刚体平面运动的碰撞方程 用于碰撞过程的质点系相对于质心的动量矩定理:
对心正碰撞
对心斜碰撞
(2)两个物体相碰时,按其接触处有无摩擦,可分为
光滑碰撞
非光滑碰撞
(3)两个物体相碰撞时,按物体碰撞后变形的恢复程 度(或能量有无损失),可分为 完全弹性碰撞 弹性碰撞 塑性碰撞
2. 对碰撞问题的两点简化
以榔头打铁为例说明碰撞力的特征: 设榔头重10N,以v1=6m/s的速度撞击铁块,碰撞时间 =1/1000s , 碰撞后榔头以v2=1.5m/s的速度回跳。求榔头打击铁块 的力的平均值。 以榔头为研究对象,根据动量定理
对上式积分
n (e) t LO 2 LO1 ri dI i i 1 0
碰撞过程简化假设(2),作用点矢径是恒量
n n n (e) t (e) (e) LO 2 LO1 ri dI i ri I i M O ( I i ) i 1 0 i 1 i 1
上式不计普通力的冲量矩。
(e) mvC mvC I i
(e) J C2 J C1 M C ( I i )
刚体平面运动的碰撞方程。
§3-3
质点对固定面的碰撞 · 恢复因数
