禁忌搜索算法
车辆调度优化算法最小化运输成本和时间

车辆调度优化算法最小化运输成本和时间车辆调度是物流运输领域中一个重要的问题。
在运输过程中,如何合理安排车辆的调度,以降低运输成本和缩短运输时间,是一个挑战性的任务。
为了解决这个问题,人们提出了各种各样的车辆调度优化算法。
本文将介绍一些常见的车辆调度优化算法,探讨它们的优劣势以及在实际应用中的效果。
1. 贪心算法贪心算法是一种常见的启发式算法,在车辆调度问题中得到广泛应用。
它的核心思想是每次选择局部最优解,通过迭代来逐步得到全局最优解。
在车辆调度问题中,贪心算法可以根据某种规则将任务分配给可用的车辆,并选择最短路径进行运输。
这种算法简单高效,但可能会得到次优解。
2. 遗传算法遗传算法是一种模拟自然界进化过程的优化算法。
它通过模拟遗传、交叉和变异等操作来搜索最优解。
在车辆调度问题中,遗传算法可以将车辆路径表示为染色体,通过不断进化来寻找最佳路径。
遗传算法具有全局搜索能力,但也存在收敛速度慢的问题。
3. 禁忌搜索算法禁忌搜索算法是一种基于局部搜索的优化算法。
它通过记录搜索历史并禁忌一些不良移动,以避免陷入局部最优解。
在车辆调度问题中,禁忌搜索算法可以通过禁忌表来记录不良移动,并选择较优的移动策略。
禁忌搜索算法在寻找局部最优解方面表现出色,但可能无法得到全局最优解。
4. 模拟退火算法模拟退火算法是一种模拟固体退火过程的优化算法。
它通过接受较差解的概率来避免陷入局部最优解,并最终逼近全局最优解。
在车辆调度问题中,模拟退火算法可以通过降温和随机移动来搜索最优解。
模拟退火算法具有全局搜索能力和一定的随机性,但需要合理的参数设置。
5. 蚁群算法蚁群算法是一种模拟蚂蚁觅食行为的优化算法。
它通过模拟蚂蚁在路径选择中的信息素沉积和信息素挥发来搜索最优解。
在车辆调度问题中,蚁群算法可以通过模拟蚂蚁选择路径的过程来寻找最佳路径。
蚁群算法具有全局搜索能力和自适应性,但也存在收敛速度慢的问题。
综上所述,车辆调度优化算法有贪心算法、遗传算法、禁忌搜索算法、模拟退火算法和蚁群算法等多种方法。
车间排程优化问题的禁忌搜索算法研究

车间排程优化问题的禁忌搜索算法研究车间排程优化是制造业中一个重要的问题,通过合理地安排生产任务,可以提高生产效率和资源利用率,减少生产成本和交货期延误。
而禁忌搜索算法作为一种经典的启发式优化算法,可以有效地解决这个问题。
一、问题描述车间排程优化问题是指在给定的工作车间、机器和作业序列的情况下,通过合理的调度工序和机器安排,最大程度地提高生产效率。
该问题涉及到多个因素的综合考虑,如工序之间的先后关系、机器之间的冲突、作业的紧急程度等。
二、禁忌搜索算法原理禁忌搜索算法是一种通过维护一个禁忌列表来避免搜索过程中陷入局部最优解的方法。
它基于贪婪策略,在每一步选择移动方案时,优先考虑能够带来最大改善的邻域解。
同时,它还引入了一个禁忌列表,记录了已经搜索过的解禁忌信息。
在搜索过程中,如果发现一个解与禁忌列表中的解相似度太高,则不会继续搜索该解,以避免重复的计算和陷入局部最优解。
三、禁忌搜索算法在车间排程优化中的应用禁忌搜索算法在车间排程优化中有着广泛的应用。
它可以针对车间排程问题的各种约束条件,自动调整工序的先后次序和机器的分配,以达到最优的排程效果。
1. 邻域解生成禁忌搜索算法中的邻域解一般通过交换相邻工序的位置来产生。
在车间排程中,邻域解的生成可以通过调整工序的先后次序和机器的分配来实现。
通过确定合适的邻域解生成规则,禁忌搜索算法能够快速生成多个可行解,为搜索过程提供了丰富的选择。
2. 目标函数定义在车间排程中,目标函数一般包括生产效率、资源利用率、成本和交货期延误等多个指标。
禁忌搜索算法可以通过合理定义目标函数,将多个指标进行综合考虑,并制定相应的优化策略。
3. 禁忌搜索策略禁忌搜索算法通过维护一个禁忌列表,避免搜索过程中陷入局部最优解。
禁忌列表中的每个元素记录了一个解的局部信息,如交换的工序、机器的分配等。
当在搜索过程中发现一个解与禁忌列表中的解相似度太高时,禁忌搜索算法将终止搜索该解并选择其他的邻域解,以保证搜索的多样性和全局最优解的寻找。
图节点着色问题中的禁忌搜索算法

图节点着色问题中的禁忌搜索算法09-03-25 作者:编辑:校方人员图节点着色问题是组合最优化中典型的非确定多项式(NP)完全问题,也是图论中研究得最久的一类问题。
目前解决该问题的算法很多,如回溯算法、分支界定法、Welsh-Powell算法、神经网络、遗传算法以及模拟退火算法等。
综合比较各种算法,前两种算法是精确算法,但时间复杂性太大;后三种属于近似算法,虽然时间复杂性可接受,能够得到较好的近似解,但算法本身过于复杂,算法效率难以保证。
本文采用禁忌搜索算法,它同时拥有高效性和鲁棒性。
禁忌搜索是一种全局逐步寻优的人工智能算法,它常能有效的应用于一些典型NP问题,如TSP。
但禁忌搜索存在一些参数较难设置,这也是应用于通信系统时研究的热点。
本文提出针对着色问题的禁忌搜索的具体设计方案,较好的设置了参数,并优化了数据结构,通过实验比较得到了较好的效果。
最后提出通过领域简单的变化,禁忌搜索能较好的用于一般算法难以实现的List着色问题。
1图节点着色问题图的着色问题可分为边着色、顶点着色、List着色和全着色,其中最主要的给定一个无向图G=(V,E),其中V是节点集V={1,2,…n},E是边集,其中(i,j)表示有连接(i,j)的一条边。
若,且V i内部的任何两个节点没有E中的边直接相连,则称(V1,V2,…,V n)为V的一个划分。
图的节点着色问题可以描述为:求一个最小的k,使得(V1,V2,…,V n)为V的一个划分。
通常的解决着色问题的算法采用蛮力法、贪婪法、深度优先或广度优先等思想可以得到最优解,但时间复杂性太大,如回溯法,其计算时间复杂性为指数阶的;有的在多项式时间内能得到可行解,但不是最优解,如Welsh-Powell算法和贪婪算法。
Welsh-Powell算法只能保证最多使用(为图中顶点的最大度)种颜色给一个图正常着色,而由Brooks定理,对于既不是完全图又不是奇圈的简单连通图,所需的颜色数。
禁忌搜索算法

3 禁忌搜索的关键参数和操作
3.1 变化因素
目标值的变化
局部搜索主要依赖起点的选取和邻域的结构; 为了得到好的解,可以比较不同的邻域结构和不同 的初始点; 如果初始点的选择足够多,
总可以计算出全局最优解。
2 禁忌搜索
2.1 算法的背景
禁忌搜索算法(Tabu Search)是由美国 科罗拉多州大学的Fred Glover教授在 1986年左右提出来的,是一个用来跳出 局部最优的搜寻方法。在解决最优问题 上,一般区分为两种方式:一种是传统 的方法,另一种方法则是一些启发式搜 索算法。
4.5 T 3.5 T
2 禁忌搜索
2 禁忌搜索示例
四城市非对称TSP问题
第5步
解的形式 A D B C f(x4)=4.5 禁忌对象及长度 B A B 0 C 1 2 C D 候选解
对换 评价值
CD BC BD
7.5 T 8 ☻ 4.5 T
TS算法 框架
(1)是否有其他形式的候选集? (2)禁忌的长度如何确定?如果在算法中记忆下搜索到 的当前最优解,极端的两种情况是:一是将所有的对换 个数作为禁忌长度,此时等价于将候选集中的所有的对 换遍历;另外则取为1,这等价于局部搜索算法。 (3)是否有评价值的其他替代形式?有时计算目标值的 工作量较大,或无法接受计算目标值所花费的时间,于 是需要其他的方法。 (4)被禁的对换能否再一次解禁?有这样的直观现象, 当搜索到一个局部最优解后,它邻域中的其他状态都被 禁,我们是否解禁一些状态以便跳出局部最优?解禁的 功能就是为了获得更大的搜索范围,以免陷入局部最优 。 (5)如何利用更多的信息?在禁忌搜索算法中,还可记 录其他一些信息。如一个被禁对象(交换)被禁的次数 ,评价值变化的大小等。 (6)终止原则,即一个算法停止的条件,怎样给出?
禁忌搜索算法ppt课件

个候选解?
的解替换当前解
用新的解替换 当前解;
否
找出下一个 次好的新解
更新tabulist NI=NI+1
NI=0 Intensification
n=n+1
否 NI=M?
是 Diversification
NI=0 是
n<N
否
25
End
判断是否为tabu, 决定接受与否
接受最好的候选解,并替换当前解
NI=0 是
n<N
否
21
End
求得初始解 BS=初始解
初始解
Sequence The length of the route
132456
28
BS
Sequence The length of the route
132456
28
22
Start
Tabu list 初始化(清空) 设M,N的值
求得初始解 BS=初始解
Sequence The length of the route
当前解 413256
30
Sequence The length of the route
BS
132456
28
Tabu list {41, },NI=1,n=1
26
Start
Tabu list 初始化(清空) 设M,N的值
求得初始解 BS=初始解
The length of the route
30
35
38
40
45
24
Start
Tabu list 初始化(清空) 设M,N的值
求得初始解 BS=初始解
n=0;NI=0
TSP的几种求解方法及其优缺点

TSP的几种求解方法及其优缺点一、什么是TSP问题旅行商问题,简称TSP,即给定n个城市和两两城市之间的距商,要求确定一条经过各城市当且仅当一次的是短路线。
其图论描述为:给定图G= (V, A),其中V为顶点集,A 为各顶点相互连接组成的边集,设(dij)是由顶点i和顶点j之间的距离所组成的距离矩阵,要求确定一条长度最短的Hamihon回路,即遍历所有顶点当且仅当一次的最短距离。
旅行商问题可分为如下两类:1)对称旅行商问题3j=dji, ni, j=l, 2, 3, - , n);2)非对称旅行商问题(dijHdji, Bi, j=1, 2, 3, - , n)o非对称旅行商问题较碓求解,我们一般是探讨对称旅行商问题的求解。
若对于城市V={V H V2, V n - , %}的一个访问顺序为T={l), b, tj, - , tj, - , tj,A其中衣v (i=l, 2, 3,・・・,□),且记t n+l=tl>则旅行商问题的数学模型为:血工Xzr-l TSP是一个典型的组台优化问题,并且是一个NP完全难题,是诸多领域内出现的多种复杂问题的集中槪括和简化形式,并且已成为各种启发式的搜索、优化算法的间接比较标准。
因此,快速、有效地解决TSP有着重要的理论价值和板高的实际应用价值。
二、主要求解方法基于TSP的问题特性,构造型算法成为最先开发的求解算法,如最近邻点、最近台并、最近插入、晨远插入、最近添加、贪婪插入等。
但是,由于构造型算法优化质長较差,迄今为止巳开发了许多性能较好的改迸型搜索算法,主要有:1)模拟退火算法2)禁忌搜索算法3)Hopficld神经网络优化算法4)蚁群算法5)遗传算法6)混合优化策路2.1模拟退火算法方法1)编码选择:采用描述TSP解的臺常用的一种策略——路径编码。
2)SA状态产生函数的设计:对于基于站径编码的SA状态产生函数操作,可将其设计为:①互换操作(SV7AP);②逆序操作(INV);③插入操作仃NS)。
禁忌搜索课件

五.TS举例(8)
迭代5 编码:5-2-1-7-4-6-3
cx= =C20x
结论: 迭代已到5次,得到最优解
5-2-7-1-4-6-3和5-2-1-7-4-6-3
cx = Cx =20
第26页,共46页。
六.TS的中、长期表的使用(1)
引入中长期表的目的 改善TS的广域搜索能力,TS的局域搜索能力很 好,邻域选优快,但广域搜索能力较差。搜索 能力是TS的关键,采用中长期表可改善TS的广 域搜索能力。
数组元加上Tabu-Size;
T表的下半部分,用来记频数,每次(i,j)交换 (i<j),对应的((j,i)+1)来记忆频数。
第30页,共46页。
六.TS的中、长期表的使用(5) 频数表的优点:同一数组作为T表和频数表共同 使用,方便操作又节省了时间。
第31页,共46页。
六.TS的中、长期表的使用(6)
5,4 7,4 3,6 2,3 4,1
cx
6 4 2 0 -1
……
结论:交换4和5
……
T表
1 2 3
第21页,共46页。
五.TS举例(4)
迭代1 编码:2-4-7-3-5-6-1
cx= Cx =16
移动 Sx
3,1 2,3 3,4 7,1 6,1
……
结论:交换1和3
cx
2 1 -1 -2 -4 ……
若
S x T
停止,否则令
k
k
,若
1 k
NG
(其中NG为最大迭代数)停止;
注:邻S域x小 T,T表表长示。非正正常常设终置止为,(T造表成长的度原<邻因域:
大小)。步骤②的作用是设置循环体出口。
禁忌搜索实验报告

一、实验背景禁忌搜索算法(Tabu Search,TS)是一种基于局部搜索的优化算法,最早由Glover和Holland于1989年提出。
该算法通过引入禁忌机制,避免陷入局部最优解,从而提高全局搜索能力。
近年来,禁忌搜索算法在蛋白质结构预测、调度问题、神经网络训练等领域得到了广泛应用。
本次实验旨在验证禁忌搜索算法在求解组合优化问题中的性能,通过改进禁忌搜索算法,提高求解效率,并与其他优化算法进行对比。
二、实验目的1. 研究禁忌搜索算法的基本原理及其在组合优化问题中的应用;2. 改进禁忌搜索算法,提高求解效率;3. 将改进后的禁忌搜索算法与其他优化算法进行对比,验证其性能。
三、实验方法1. 算法实现本次实验采用Python编程语言实现禁忌搜索算法。
首先,初始化禁忌表,存储当前最优解;然后,生成新的候选解,判断是否满足禁忌条件;若满足,则更新禁忌表;否则,保留当前解;最后,重复上述步骤,直到满足终止条件。
2. 实验数据本次实验采用TSP(旅行商问题)和VRP(车辆路径问题)两个组合优化问题作为实验数据。
TSP问题要求在给定的城市集合中找到一条最短的路径,使得每个城市恰好访问一次,并返回起点。
VRP问题要求在满足一定条件下,设计合理的配送路径,以最小化配送成本。
3. 对比算法本次实验将改进后的禁忌搜索算法与遗传算法、蚁群算法进行对比。
四、实验结果与分析1. TSP问题实验结果(1)改进禁忌搜索算法(ITS)实验结果表明,改进后的禁忌搜索算法在TSP问题上取得了较好的效果。
在实验中,设置禁忌长度为20,迭代次数为1000。
改进禁忌搜索算法的求解结果如下:- 最短路径长度:335- 迭代次数:1000- 算法运行时间:0.0015秒(2)遗传算法(GA)实验结果表明,遗传算法在TSP问题上的求解效果一般。
在实验中,设置种群规模为100,交叉概率为0.8,变异概率为0.1。
遗传算法的求解结果如下:- 最短路径长度:345- 迭代次数:1000- 算法运行时间:0.003秒(3)蚁群算法(ACO)实验结果表明,蚁群算法在TSP问题上的求解效果较好。
计算机网络优化算法

计算机网络优化算法计算机网络优化算法(Computer Network Optimization Algorithms)是指通过使用数学、统计学和计算机科学的方法来优化计算机网络系统的性能和效率。
这些算法的设计主要是为了最大化网络资源的利用率、最小化网络延迟和最优化网络吞吐量。
本文将介绍几种常见的计算机网络优化算法,包括贪心算法、动态规划算法、遗传算法和禁忌搜索算法等。
1. 贪心算法贪心算法是一种基于局部最优选择的算法,它每次在作出选择时都只考虑当前状态下的最优解。
在计算机网络中,贪心算法可以用于一些简单的网络优化问题,如最佳路径选择、带宽分配等。
贪心算法的优点是简单易实现,但缺点是可能会导致局部最优解而非全局最优解。
2. 动态规划算法动态规划算法是一种将复杂问题分解为简单子问题并存储中间结果的算法。
在计算机网络中,动态规划算法可以用于一些具有重叠子问题的优化问题,如最短路径问题、最小生成树问题等。
动态规划算法的优点是能够得到全局最优解,但缺点是其计算复杂度较高。
3. 遗传算法遗传算法是一种模拟生物进化过程的优化算法。
在计算机网络中,遗传算法可以用于解决一些复杂的优化问题,如网络布线问题、拓扑优化问题等。
遗传算法的优点是能够找到较好的全局最优解,但缺点是其计算复杂度高且需要大量的计算资源。
4. 禁忌搜索算法禁忌搜索算法是一种通过记录和管理搜索路径来避免陷入局部最优解的优化算法。
在计算机网络中,禁忌搜索算法可以用于解决一些带有约束条件的优化问题,如链路带宽分配问题、网络拓扑优化问题等。
禁忌搜索算法的优点是能够在可行解空间中进行有效搜索,但缺点是其计算复杂度较高且需要适当的启发式规则。
综上所述,计算机网络优化算法是一类用于改善计算机网络系统性能的关键算法。
选择合适的网络优化算法取决于具体的问题和限制条件。
贪心算法适用于简单的问题,动态规划算法适用于具有重叠子问题的问题,遗传算法适用于复杂的问题,禁忌搜索算法适用于带有约束条件的问题。
供应链中使用的优化算法及其应用实践

供应链中使用的优化算法及其应用实践随着全球贸易的快速发展,供应链管理日益成为企业成功的关键因素之一。
在供应链中,如何优化运营,提高效率和降低成本已成为企业追求的目标。
优化算法可以帮助企业实现这些目标。
本文将介绍供应链中常用的优化算法,以及它们在实践中的应用。
1.线性规划算法线性规划是一种优化算法,通过最大化或最小化线性目标函数的方法,在满足一定约束条件下找到最优解。
在供应链中,线性规划可以用于优化资源分配、生产计划和库存管理等方面。
例如,在生产计划中,线性规划可以帮助确定最佳的生产量,以满足需求并最大化利润。
2.整数规划算法整数规划是线性规划的扩展,其中决策变量被限制为整数值。
在供应链中,许多决策变量,如订单数量和仓库位置,通常是离散的。
整数规划算法可以用于优化这些决策变量,以满足需求并最小化成本。
例如,在配送中心位置选择上,整数规划可以帮助确定最佳的仓库位置,以减少运输成本和配送时间。
3.遗传算法遗传算法是一种模拟自然进化过程的优化算法。
它通过对候选解进行交叉、变异和选择操作,逐步优化解空间,找到最优解。
在供应链中,遗传算法可以用于优化生产计划、货车路径规划和仓库布局等方面。
例如,在货车路径规划中,遗传算法可以优化货车的路径,以最小化运输成本和配送时间。
4.模拟退火算法模拟退火算法是一种模拟金属退火过程的优化算法。
它通过接受差解的概率来避免局部最优解,以便在全局解空间中寻找最优解。
在供应链中,模拟退火算法可以用于优化库存管理、订单分配和生产排程等方面。
例如,在库存管理中,模拟退火算法可以帮助确定最佳的库存策略,以满足需求并最小化库存成本。
5.禁忌搜索算法禁忌搜索算法是一种通过禁止某些移动操作,从而避免重复搜索相同解的优化算法。
它通过维护一个禁忌表来避免搜索到已经搜索过的解,并在搜索过程中不断更新禁忌表。
在供应链中,禁忌搜索算法可以用于优化订单分配、仓库布局和供应商选择等方面。
例如,在供应商选择中,禁忌搜索算法可以帮助选择最佳的供应商组合,以满足质量要求并最小化成本。
禁忌搜索算法原理及应用

禁忌搜索算法原理及应用随着计算机技术的不断发展,各种算法也应运而生,其中禁忌搜索算法便是一种比较常用的优化算法。
禁忌搜索算法的一大特点就是能够避免搜索过程中出现循环现象,能够有效地提高搜索效率,因此在许多领域都有广泛的应用。
一、禁忌搜索算法的原理禁忌搜索算法是一种基于局部搜索的优化算法。
其基本思想就是在搜索过程中引入禁忌表,通过记录禁忌元素,避免进入不良搜索状态,从而获得更好的解。
禁忌表的作用是记录已经经过的解的信息,防止搜索陷入局部最优解,增加了搜索的广度和深度。
禁忌搜索算法的核心是寻找最优化解。
具体过程包括:初始化,构造邻域解,选择最优解,更新禁忌表,结束搜索。
当搜索过程中发现某个解是当前状态下的最优解时,将这个最优解加入到禁忌表中,以后在搜索过程中就不再去重复对该最优解的操作。
在禁忌搜索算法中,选择邻域解是非常重要的一环。
邻域解是指与当前解相邻的解,也就是在当前解的基础上进行一定的操作得到的解。
邻域解的选择通常根据问题的不同而定,可以是交换位置、插入、反转等。
而选择最优解的原则则是要在禁忌状态下优先选择不在禁忌表中的最优解,如果所有的最优解都处于禁忌状态,那么就选择设定的禁忌期最短的解。
二、禁忌搜索算法在实际应用中的应用禁忌搜索算法作为一种优化算法,在实际应用中有着广泛的应用。
下面我们就通过几个实际案例来了解禁忌搜索算法的应用。
1. 生产排程问题禁忌搜索算法在制造业的排程问题中有着广泛的应用。
在生产排程问题中,需要考虑的因素非常多,如时间、人员、设备、物料等。
禁忌搜索算法通过构建邻域空间,利用禁忌表避免了进入不良解的状态,从而在生产排程问题中,可以为厂家避免很多因时间不足而导致的决策错误。
2. 组合最优化问题禁忌搜索算法在组合最优化问题中有着很好的应用。
比如在公路路径设计中,需要从成千上万的路径中选择最优解。
禁忌搜索算法不仅可以找到全局最优解,还可以避免局部最优解的产生,使得结果更加准确。
物流系统中的路径优化算法的使用技巧

物流系统中的路径优化算法的使用技巧物流系统中的路径优化算法是一种重要的工具,旨在优化货物的运输路径以提高物流效率。
在现代物流领域中,路径优化的重要性不言而喻。
一个良好设计的路径优化算法可以将运输时间和成本降至最低,同时提高客户的满意度。
本文将介绍物流系统中常用的路径优化算法,并提供一些使用技巧,帮助你在实践中更好地应用这些算法。
1. 最短路径算法最短路径算法是路径优化算法中最常用的一种。
该算法的目标是找到从起点到终点的最短路径,以减少行驶距离和时间。
最短路径算法有多种实现方式,如迪杰斯特拉算法(Dijkstra's algorithm)和弗洛伊德算法(Floyd-Warshall algorithm)。
这些算法在解决不同的问题和场景时具有各自的优势,可以根据具体情况选择合适的算法。
在使用最短路径算法时,需要准备好相关数据,如物流网络的节点、边的距离或成本信息等。
同时,需要考虑实际情况中的一些因素,如道路拥堵、规定时间窗口等。
通过合理地设置权重或约束条件,可以使算法更符合实际情况,提高路径规划的准确性。
2. 遗传算法遗传算法是一种以生物遗传进化过程为模型的启发式优化算法。
它通过模拟自然选择、基因交叉和变异等过程来搜索最优解。
在物流系统中,遗传算法可以用于解决路径规划问题。
通过对路径中的节点进行编码,将路径搜索问题转化为遗传算法的优化问题。
使用遗传算法进行路径优化时,需要确定适当的编码方式和目标函数。
编码方式可以是二进制编码、整数编码等,根据具体场景选择合适的编码方式。
目标函数则是评估路径的指标,如货物运输时间、成本等。
通过不断地迭代、交叉和变异,遗传算法可以快速找到较优的路径解决方案。
3. 蚁群算法蚁群算法受到蚂蚁寻食行为的启发,通过模拟蚂蚁在路径上释放信息素、感知信息素并互相通信的过程来解决优化问题。
在物流系统中,蚁群算法可以用于求解路径规划问题,并具有一定的优势。
在蚁群算法中,需要设置适当的信息素更新规则和启发式函数。
禁忌搜索算法

邻域选优的规则模拟了人类的记忆功能,找过的地方都 记下来,不再找第二次。一定的迭代次数后,早期进入 禁忌表的解被解禁退出。
7.5T 8☻ 4.5T
四城市非对称TSP问题
第 6步
解的形式 A DCB f(x5)=8 禁忌对象及长度 B A C D 候选解
对换 评价值
B
2 C
0 1
CD BC BD
3.5T 4.5T 4☻
谢谢观赏
2、禁忌对象为目标值变化 3、禁忌对象为分量变化 解的简单变化比解的分量变化和目标值变化的受禁范围要小,可 能造成计算时间的增加,但也给予了较大的搜索范围; 解分量的变化和目标值变化的禁忌范围大,减少了计算时间,可 能导致陷在局部最优点。
禁忌长度的选取
禁忌长度过短,一旦陷入局部最优点,出现循环无法跳出; 禁忌长度过长,造成计算时间较大,也可能造成计算无法继续下去。
(2)动态频率信息:从一个解、对换或目标值到另一个解、对换或目标值的变化趋势。
终止规则
(1)确定步数终止,无法保证解的效果,应记录当前最优解; (2)频率控制原则,当某一个解、目标值或元素序列的频率超过 一个给定值时,终止计算; (3)目标控制原则,如果在一个给定步数内,当前最优值没有变 化,可终止计算。
B
C
CD BC BD
4.5☻ 7.5 8
四城市非对称TSP问题
第 2步
解的形式 A B DC f(x1)=4.5 禁忌对象及长度 B A C D 候选解
对换 评价值
第七讲禁忌搜索
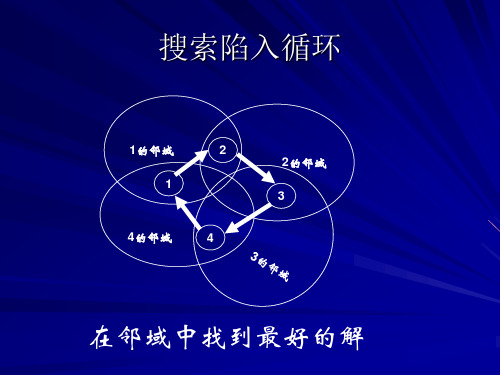
2
一.导言(2)
2. TS的基本思想——避免在搜索过程中的循环
① 只进不退的原则——用Tabu表锁住退路,将近期 历史搜索过程存放在禁忌表中,防止算法重新进 入。
② 不以局部最优作为停止准则,算法接受劣解,只 要不在禁忌表的较好解都可作为下一次迭代的初 始解。
③ 邻域选优的规则模拟了人类的记忆功能——找过
10
(4) 移动与邻域移动
移动是产生新解的途径,从当前解可以进 行的所有的移动构成邻域,因此移动规则 的设计是算法的关键。
移动规则类似于交叉算子,根据具体问题 进行分析设计,如排序问题中采用两两交 换方式的移动规则。
11
(5) 禁忌表(Tabu List)
禁忌表是为了防止搜索过程出现循环而陷入局部 最优的,是禁忌搜索算法的核心。 某些移动经一定迭代次数后被解禁,又可重新访 问,因此禁忌表称为短期表。 禁忌对象:放入禁忌表的元素,主要包括三种, (1)以状态本身或状态变化为禁忌对象,其禁忌 范围适中;(2)以状态分量或状态分量的变化作 为禁忌对象,其禁忌范围较小;(3)以目标值为 禁忌对象,其禁忌范围较大。 禁忌长度:禁忌表的大小。禁忌表越小,计算时 间和存储空间越少,但禁忌表过小,会造成搜索 过程进入循环。禁忌长度分为固定禁忌长度和随 时间变化禁忌长度两类。
16
(7) 渴望水平函数
在有些特定的条件下,不管某个移动是否在禁忌表中, 都接受这个移动并更新当前解和历史最优解。这个特 定的条件即为渴望水平。
渴望水平的设定有如下几种形式:
(1)基于适配值的准则,如果某个候选解的适配值高 于历史最优解,无论是否处于禁忌表中,都选择接受。
(2)基于搜索方向的准则,某禁忌对象进入紧急表时 改善了适配值,而这次这个被禁忌的候选解由改善了 适配值,故破禁。
禁忌搜索算法

破禁策略
• 相关文献亦称藐视准侧、特赦准则、释放准侧等;破禁策 略通常指渴望水平(Aspiration)函数选择,当一个禁忌移动 在随后T次的迭代内再度出现时,如果它能把搜索带到一 个从未搜索过的区域,则应该接受该移动即破禁,不受禁 忌表的限制。 • 衡量标准就是定义一个渴望水平函数,渴望水平函数通常 选取当前迭代之前所获得的最好解的目标值或此移动禁忌 时的目标值作为渴望水平函数。 • 破禁准侧保证了搜索过程在全部候选解被禁或者是有优于 当前最优解的候选解被禁时,能够释放特定的解,从而实 现全局优化搜索。
禁忌搜索算法的关键要素
就这些参数含义一般而言,设计一个禁忌搜索算法需要确 定以下环节: • 初始解 • 邻域和移动 • 候选集 • 禁忌表及其长度 • 选择策略 • 破禁策略 • 停止规则 • 下面对这些环节的一般操作予以讨论。
初始解 • 禁忌搜索对初始解的依赖较大,不同的初始解, 在搜索过程中耗费时间和资源往往不同,同一邻 域结构,不同的初始点会得到不同的计算结果, 好的初始解往往会提高最终的优化效果。一个直 观的结论就是:如果初始点选择的足够好,总可 以计算出全局最优解。 • 初始解的构造可以随机产生,但效果往往不够理 想,常用方法是基于问题的特征信息,借助一下 启发式方法产生,这样可以保证初始解的性能[4] 。
• 四城市非对称TSP问题
第 2步
解的形式 A B DC f(x1)=4.5 禁忌对象及长度 B A B C 3 C D 候选解
对换 评价值
CD BC BD
4.5T 3.5 * 4.5
• 四城市非对称TSP问题
•
• 1997年,Glover与 Laguna合著的第一本禁忌 搜索专著正式出版,标志 着关于禁忌搜索的相关研 究日趋完善,并得到了同 行的认可。 • 目前关于TS的研究主要分 为对TS算法过程和关键步 骤的改进,用TS改进已有 优化算法和应用TS相关算 法求解工程优化问题。
基于禁忌搜索算法参数设置的探讨

[ ] Go e, F 1 lvr .Hert sfritgrpormmiguig sr gt u sc o nee rga n s ur ae ii n o
从表 2可以得 出:①初始解越好 ,T S算 法求 得的最优 解越佳 ;② 2阶 T s法 ( 先利用 求 得初始解 ,再利用
具体实验如下 。
( )迭 代 次 数 :随 机 产 生 2 0个 城 市 坐 标 ,经 历 不 同 1 4
的迭 代 次 数 的实 验 数 据 如 表 l所 示
, 计 数 器 tO = 。设 置 禁 忌 表 为
表 1 迭代次数对 T S算 法 的 影 响
的 目标 函数 值 ,则 = 【 。 f + ”
来 求 解 Q P ( uda cA s n et rbe 问 题 ,L - A Q art si m n olm) i g P a
gn u a& G oe 以小 、 中 、 大 三 种 不 同 变 动 范 围 的禁 忌 表 大 l r v
小 来 求 解 通 信 带 宽 封包 问 题 ( e cmm n ai a d i h T l o u i t nB n wd e c o t
[ ]G o e,F T b a h a J OR A Ju a o o - 3 l r . aus r :pr I[ v ec t ]. S o r l nC r n n
示 , 两 个 城 市 之 间 的 距 离 利 用 两点 问 的 距 离 公 式 来 求 得 。
常 见 的 有 :循 环 迭 代 次 数 、C U 运 行 时 间 、连 续 获 得 没 有 P
改 进 过 解 的次 数 。一 旦 搜 索 达 到 这 些 预设 的 停 止 条 件 .则 停 止 搜 索 ,当 前 的 最 优 解 即 为 最 终 解 。 一 般 情 况 下 选 择 “ 环 迭 代 次 数 ” 作 为停 止 条 件 ,可 以 保 证 在 一 段 迭 代 次 循 数 后 终 止 搜 索 且 不 因使 用 电脑 的 系 统 不 同 而 影 响 解 。 1 法基本步骤如下 : ’ S算 Se :初 始 化 。选 择 一 个 初 始 可 行 解 ( tp0 m.最 大 迭 代 次 数 一, 当 前 解 = 空 以及 禁 忌 表 的大 小 £ 。 Se :停 止 。 如 果 # ,那 么停 止 搜 索 , 当前 解 t 1 p =一 就是最优解 。
基于禁忌搜索算法的路径规划优化研究

基于禁忌搜索算法的路径规划优化研究近年来,随着机器人和自动驾驶汽车等技术的飞速发展,路径规划问题逐渐成为一个备受关注的前沿研究领域。
而基于禁忌搜索算法的路径规划优化研究,也是近年来热点研究方向之一。
一、路径规划问题简介路径规划就是在给定的地图上,寻找一条从起点到终点的最优路径。
在真实世界中,路径规划问题有着广泛的应用。
例如,自动驾驶汽车需要识别周围环境,并规划一条安全高效的行驶路径;机器人需要规划行动路线,避开障碍物、优化运动轨迹等。
因此,路径规划问题的优化问题一直受到学术界和工业界的关注。
二、禁忌搜索算法的原理在路径规划问题中,寻找最优路径是一个NP-hard 问题,也就是说,它的规模越大,计算复杂度呈指数级增长,难以直接用传统的穷举搜索方法来解决。
而禁忌搜索算法正是为了对于这类问题提出的一种通用优化算法。
禁忌搜索算法的基本思想是在候选解空间中搜索最优解。
它类似于爬山算法,每次迭代时,算法会从当前解附近的候选解中选择最优解作为当前解,直到找到满足要求的最优解。
与爬山算法不同的是,禁忌搜索算法在搜索过程中还会维护一个禁忌表,记录已搜索过但不应该再被搜索的解。
这种做法有时会牺牲局部最优解,但可以在更广的解空间中搜索到更优解。
三、禁忌搜索算法在路径规划优化中的应用在路径规划问题中,禁忌搜索算法通常与启发式方法组合使用。
启发式方法是一种基于经验的、高效的搜索算法,能够有效地搜索到候选解中的更优解。
在具体的规划过程中,禁忌搜索算法与启发式方法可以互相补充、协同工作,从而在变化复杂、需要快速响应的环境下找到路径规划问题的较好解。
禁忌搜索算法在路径规划优化中的应用,也得到了众多学者的支持和认可。
一些研究表明,禁忌搜索算法可以有效地较少计算时间,提高路径规划的精度和效率,从而为完成复杂交通任务提供了可靠的帮助。
四、结论基于禁忌搜索算法的路径规划优化研究,是一个前沿、迅速发展的领域。
禁忌搜索算法可以解决大规模、复杂路径规划问题,并将路径规划问题的计算复杂度降至可承受的范围,从而为相关领域的进一步发展绘就基础。
供应链管理中的订单分配优化算法

供应链管理中的订单分配优化算法在现代商业运作中,供应链管理扮演着重要的角色。
供应链管理旨在通过优化供应链中的各个环节,提高整个供应链的效率和效益。
其中,订单分配是供应链管理中的关键环节之一,它涉及到将来自客户的订单分配给不同的供应商或分销商,以满足客户需求并最大化供应链的整体效益。
为了实现有效的订单分配,优化算法被广泛应用。
订单分配的目标是合理分配订单,使得订单可以按照最佳的方式被处理。
优化算法在此过程中发挥重要作用,通过数学模型和计算方法,找到最佳的分配方案。
下面将介绍几种常用的供应链管理中的订单分配优化算法。
1. 贪心算法贪心算法是一种简单而常用的优化算法,它根据当前的情况做出局部最优的选择。
在订单分配中,贪心算法可以根据一定的策略选择最符合条件的供应商或分销商来处理订单。
例如,可以选择距离最近的供应商处理订单,或者选择存货量最充足的供应商。
贪心算法的优势在于计算简单、速度快,但可能无法得到全局最优解。
2. 动态规划算法动态规划算法通过递推的方式,将原问题拆解为多个子问题,并保存已解决的子问题的最优解。
在订单分配中,可以将订单分配问题转化为子问题,通过动态规划算法找到最佳的分配方案。
动态规划算法需要存储大量的中间结果,计算时间较长,但可以得到全局最优解。
3. 遗传算法遗传算法是一种模仿自然界中生物进化过程的优化算法。
在订单分配中,可以将订单分配方案看作是一个个体的染色体,通过模拟自然选择、交叉和变异等操作,逐步优化分配方案。
遗传算法具有全局搜索能力,能够找到相对较优的解,但计算时间较长。
4. 禁忌搜索算法禁忌搜索算法通过维护一个禁忌表,记录已经搜索过但不宜再次选择的解,从而避免陷入局部最优解。
在订单分配中,可以使用禁忌搜索算法来避免重复选择供应商或分销商,以达到更优的分配方案。
禁忌搜索算法具有较好的局部搜索能力,并可以在一定程度上得到全局最优解。
综上所述,供应链管理中的订单分配优化算法有多种选择,包括贪心算法、动态规划算法、遗传算法和禁忌搜索算法等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
tabulist:
0 1 2 3 4 3 4 4
基本禁忌搜索算法:
现代优化计算方法
Northeastern University
禁忌搜索算法的几个关键要素
禁忌搜索算法的几个关键要素 1、解的形式和邻域结构 背包问题: 1 , 0 , 1, 1, 0, 1, 1 , 1 , 1 , 0 ,1 ,1 , ..., 1
禁忌搜索算法的计算机实现
……
现代优化计算方法
Northeastern University
禁忌搜索算法的计算机实现
现代优化计算方法
Northeastern University
The End
现代优化计算方法
3) 目标控制原则:给定步数内目标值没有改进
4) 目标值偏离程度原则:f (x) ZLB
现代优化计算方法
Northeastern University
禁忌搜索算法的应用举例
禁忌搜索算法应用举例
5个城市的TSP
邻域操作:2-opt,交换任意2个城市的位置 禁忌对象:交换城市的位置(i, j)
n个
TSP: 1, 2, 4, 3, 5, 8, 7, 6, 10, 15, 17, 18, ..., n
n个
, 2, 1, 3, 4, 2, 7, (T - 1), (T - 2), 7, 8, ..., (T - 3) 约束机器排序问题: 1
tabulist:
0 1 2 3 4
4
(1,3)
(1,4) (2,3)
ADCBE
AECDB ABDCE
45
60 60
0
0 0
2
3 4
(2,4)
(3,4)
ABEDC
ABCED
59
44
0
0
现代优化计算方法
Northeastern University
禁忌搜索算法的应用举例
3) k = 2 (k maxIter) x cur = (DBCAE), f (x cur) = 43.
SWAP (0,1) (0,2) (0,3) (0,4) (1,2) N (x cur) BECAD CBEAD ABCED DBCAE ECBAD f (x) tenure 58 45 44 43 44 0 0 3 4 0 0 1 x next
t函数
1) 直接评价函数 2) 间接评价函数
现代优化计算方法
Northeastern University
禁忌搜索算法的几个关键要素
禁忌搜索算法的几个关键要素
7、终止规则 1) 确定步数终止:迭代代数超过给定值K,终止计算 2) 频率控制原则:某一解、目标值、元素序列的频率超过给定 标准,终止计算
intelligence. Computer and Operations Research, vol. 13, no. 5, pp. 533-549. 2) Glover (1989a) and (1989b) provide a full description of the method
Glover, F. (1989a) Tabu Search – Part I. INFORMS Journal on Computing, vol. 1,
(1,3)
(1,4) (2,3)
DACBE
DECAB DBACE
43*
58 58
0
0 0
2
3 4
(2,4)
(3,4)
DBEAC
DBCEA
59
44
0
0
现代优化计算方法
Northeastern University
禁忌搜索算法的应用举例
3) k = 3 (k maxIter) x cur = (EBCAD), f (x cur) = 43.
Northeastern University
禁忌搜索算法
三、禁忌搜索算法
现代优化计算方法
Northeastern University
简单的邻域搜索算法(local search)
简单的邻域搜索算法(local search):
到达全局最小点的障碍 初始点 下降方向 局部最小点 全局最小点
现代优化计算方法
禁 忌 表:tabulist
0 1 0 1 2 3 4
2
3 4
现代优化计算方法
Northeastern University
禁忌搜索算法的应用举例
2) k = 1 (k maxIter) x cur = (ABCDE), f (x cur) = 45.
SWAP (0,1) (0,2) (0,3) (0,4) (1,2) N (x cur) BACDE CBADE DBCAE EBCDA ACBDE f (x) tenure 59 44 43* 45 43* 0 0 0 0 0 DBCAE 0 1 x next
现代优化计算方法
Northeastern University
禁忌搜索算法的应用举例
1) 初始化
初 始 解:x cur = (ABCDE), f (x cur) = 45. 禁忌长度:tenure = 4 终止准则:maxIter = 10 特赦准则:接受更好的解或非禁忌的候选解
迭代计数器:k = 0
3、禁忌长度的确定(被禁对象不允许选取的迭代代数,tabu(x) = t )
1) t 为常数,如 t = 10, t = sqrt(n) 2) t [tmin, tmax],如 t [ sqrt(n), sqrt(n)](0 < < ) 3) tmin, tmax的动态选择
现代优化计算方法
n个
现代优化计算方法
Northeastern University
禁忌搜索算法的几个关键要素
禁忌搜索算法的几个关键要素
2、禁忌对象的选取(禁忌表中被禁的那些变化元素) 1) 解的简单变化:ABCDE ACBDE 2) 向量的变化:(1,1,0,1,0,1) (1,0,0,1,0,1) 3) 目标值的变化
1) Glover (1986) introduces tabu search as a “meta-heuristic” superimposed on another heuristic
Glover, F. (1986) Future paths for integer programming and links to artificial
no. 3, pp. 190-206. Glover, F. (1989b) Tabu Search – Part II. INFORMS Journal on Computing, vol. 2,
no. 1, pp. 4-32.
现代优化计算方法
Northeastern University
基本禁忌搜索算法
(1,3)
(1,4) (2,3)
EACBD
EDCAB EBACD
43*
59 59
0
0 0
EACBD
2
3 4
(2,4)
(3,4)
EBDAC
EBCDA
58
45
0
0
现代优化计算方法
Northeastern University
禁忌搜索算法的计算机实现
现代优化计算方法
Northeastern University
Northeastern University
禁忌搜索算法的几个关键要素
禁忌搜索算法的几个关键要素
4、特赦规则(aspiration criteria) 1) 基于评价值的规则:遇到更好的解 ? 2) 基于最小错误的规则:当所有对象都被禁忌时,选择…… 3) 基于影响力的规则:对目标函数的影响大小? 5、候选集合的确定 1) 选择邻域中目标值最佳的若干个邻居 2) 随机选取
By allowing occasional ascent in the search process, we might be able to escape the trap of local minima.
现代优化计算方法
Northeastern University
禁忌搜索算法产生
Tabu search的提出:
Northeastern University
简单的邻域搜索算法(local search)
Solution 1: Randomly select another starting point whenever trapped in a local optima.
Solution 2: Allow search to occasionally go on an ascending direction.
