南邮_数据结构作业答案讲解全解
南京邮电大学考研数据结构(811)00-09年真题和答案
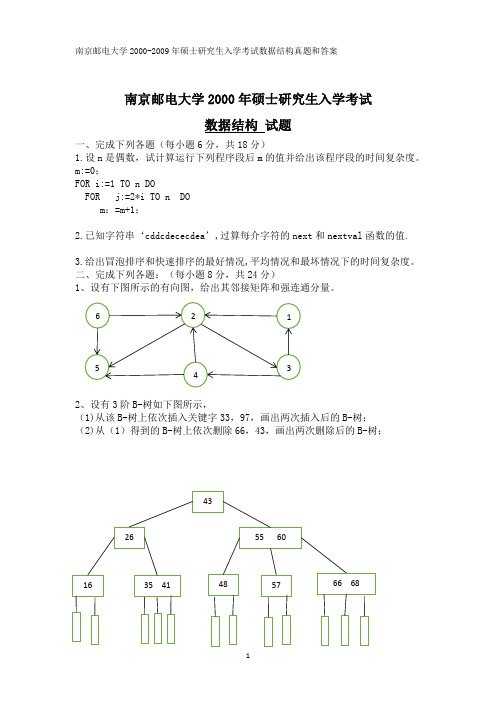
南京邮电大学2000年硕士研究生入学考试数据结构试题一、完成下列各题(每小题6分,共18分)1.设n是偶数,试计算运行下列程序段后m的值并给出该程序段的时间复杂度。
m:=0;FOR i:=1 TO n DOFOR j:=2*i TO n DOm:=m+1;2.已知字符串‘cddcdececd ea’,过算每介字符的next和nextval函数的值.3.给出冒泡排序和快速排序的最好情况,平均情况和最坏情况下的时间复杂度。
二、完成下列各题:(每小题8分,共24分)1、设有下图所示的有向图,给出其邻接矩阵和强连通分量。
2、设有3阶B-树如下图所示,(1)从该B-树上依次插入关键字33,97,画出两次插入后的B-树;(2)从(1)得到的B-树上依次删除66,43,画出两次删除后的B-树;(1)画出据此构造的败选择树(2)画出输出一个记录后的败方树三、阅读下列二叉树算法,每个结点三个域:lchild,element,rchild。
(10分)(1)X(p)对以p为根的二叉树执行什么功能?(2)以下图所示的二叉树调用此算法,则X(p)的执行结果是什么?(3)执行中,栈s中元素个数最多时为多少?给出该时栈中元素的情况。
void X(BinTree *t){struct Stack s;BinTnode *qPush(s,NUL1)While(*p){q=(*p)->lchild(*p)->1child=(*p)->rchild(*p)->rchild=qIf((*p)->lchild)Push(s,(*p)->1child);If((*p)->rchild)Push(s,(*p)->rchild);else(*p)=Pop(s)}}四、阅读下列要求每对顶点之间的最短路径的Floyd算法。
(16分)(1)若对下图所示的有向图执行此算法,写出对k为1到n的各步中,二维数组a和path的值。
数据结构_南京邮电大学中国大学mooc课后章节答案期末考试题库2023年

数据结构_南京邮电大学中国大学mooc课后章节答案期末考试题库2023年1.对线性表进行对半搜索时,要求线性表必须()。
答案:以顺序方式存储,且数据元素有序2.已知循环队列A[80]的队头标识front=45,队尾标识rear=10,此时队列还可以再入队最多______个元素。
答案:343.一棵有538个结点的二叉树具备完全二叉树树型,且为森林转换而来,则森林中树的个数为______。
答案:4.已知5阶B树中具有235个失败结点,该树的高度至少为______。
答案:45.设一个栈输入序列是1、2、3、4、5,则下列序列中不可能是栈的输出序列是()。
答案:145236.二叉树的先序遍历为EFHIGJK,中序遍历序列为HFIEJKG。
该二叉树根结点的左子树的根是()。
答案:7.具有n 个顶点的无向完全图中,边的总数为()条。
答案:n(n-1)/28.一棵非空二叉树的中序遍历序列中,根结点的左边()。
答案:只有左子树上的所有结点9.带表头结点的循环单链表为空的条件是______。
答案:head->next==head10.序列4,6,7,5,3,9是下列______算法两趟排序后的结果答案:直接插入排序11.已知先序遍历和后序遍历序列能唯一确定一棵二叉树。
答案:错误12.序列7,25,89,19,36,17是最小堆。
答案:错误13.一个表示工程的AOE网中的关键路径可以有多条。
答案:正确14.含有20个顶点和10条边的无向图用邻接矩阵存储,矩阵中零元素的数量是390。
答案:错误15.算法的确定性是指算法无论运行多少次,结果都一样。
答案:错误16.高度为6(根的层次为1)的满二叉树有个结点。
答案:6317.设有10阶对称矩阵A,其中矩阵元素用aij表示,i为行下标,i=0,1,...,9,j 为列下标,j=0,1,...,9,将A按照列优先顺序存储下三角元素的方式存储至一维数组B,设每个矩阵元素占4个字节,已知数组B的首地址为50,则,a28的地址是______。
南邮陈慧南版数据结构课后习题答案

template <class T> void LinkedStack<T>::SetNull() { Node<T> *q; while (top) { q=top->link; delete top; top=q; } }
i k(循环次数) 2*i 1 1 21<n 2 2 22<n 2k-1 n 2k<n 2k<n, k<log2n, k=log2n
划线语句的执行次数为 log2n。O(log2n) (3) for(int i=1;i<=n;i++) for(int j=1;j<=i;j++) for (int k=1;k<=j;k++) x++;
习题三(第50页)
3.1 设A、B、C、D、E五个元素依次进栈(进栈后可立即出栈),问 能否得到下列序列。若能得到,则给出相应的push和pop序列;若不 能,则说明理由。 1) A,B,C,D,E 2) A,C,E,B,D 3) C,A,B,D,E 4) E,D,C,B,A 答:2)和3)不能。对2)中的E,B,D而言,E最先出栈则表明,此 时B和D均在栈中,由于,B先于D进栈,所以应有D先出栈。同理3) 也不能。 (1)能。 push,pop,push,pop,push,pop,push,pop,push,pop (4)能。 push,push,push,push,push,pop,pop,pop,pop,pop
template <class T> bool LinkedStack<T>::IsEmpty() const { return !top; }
template <class T> bool LinkedStack<T>::IsFull() const { return false; }
南邮数据结构课后习题课27页PPT

南邮数据结构Βιβλιοθήκη 后习题课26、机遇对于有准备的头脑有特别的 亲和力 。 27、自信是人格的核心。
28、目标的坚定是性格中最必要的力 量泉源 之一, 也是成 功的利 器之一 。没有 它,天 才也会 在矛盾 无定的 迷径中 ,徒劳 无功。- -查士 德斐尔 爵士。 29、困难就是机遇。--温斯顿.丘吉 尔。 30、我奋斗,所以我快乐。--格林斯 潘。
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
南邮_数据结构作业答案讲解 49页PPT文档

1-19.确定下列各程序段的程序步,确定划线语句的执行次 数,计算它们的渐近时间复杂度。 (1) i=1; k=0;
do { k=k+10*i; i++;
} while(i<=n-1) 划线语句的执行次数为 n-1 ,渐近时间复杂度为O(n)
(2)i=1; x=0; do{ x++; i=2*i; } while (i<n);
01.08.2019
7
3-1. 设A,B,C,D,E五个元素依次进栈(进栈 后可立即出栈),问能否得到下列序列。若能得到 ,则给出相应的push和pop序列;若不能,则说 明理由。 (3)C,A,B,D,E
(3)不能得到该序列,在C出栈时,A和B在栈中 ,A比B先进栈,所以B应比A先出栈。
01.08.2019
01.08.2019
9
第四章 习题讲解
4-1. 设线性表采用顺序表示方式,并假定顺序表是 有序的(设表中元素已按非递减次序排列)。编写 函数,实现线性表的如下运算: (1)int Search_Insert(List *lst,T x)
后置条件:在有序的顺序表中搜索元素x。 •若x在表中,则返回x在表中的位置。 •否则,若表未满,则在表中插入新元素x,并且插 入后,线性表仍然是有序的,返回新元素x的位置; •若表已满,无法插入新元素,则返回-1。
② if (IsFull(lst)) //或if(lst->Size==lst->maxList) return -1; //表已满时,无法插入,返回-1
for (j=lst->Size-1; j>=i; j--)
lst->Element[j+1]=lst->Element[j];
南邮数据结构答案

第1 章绪论一、基础题1. A2. C3. C4. A5. C二、扩展题1.数据是计算机加工处理的对象;数据元素是数据的基本单位,在计算机程序中通常作为一个整体进行考虑和处理;数据项是组成数据元素的、不可分割的最小单位。
2.数据结构是按某种逻辑关系组织起来的数据元素的集合,使用计算机语言描述并按一定的存储方式存储在计算机中,并在其上定义了一组运算。
3.集合结构、线性结构、树形结构和图形结构。
集合结构中,元素之间没有关系;线性结构中,元素之间存在一对一的关系;树形结构中,元素之间存在一对多的关系,其中最多只有一个元素没有前驱元素,这个元素就是根;图形结构中,元素之间存在多对多的关系。
4.顺序存储、链式存储、索引存储和散列存储。
5.一个算法是对特定问题的求解步骤的一种描述,是指令的有限序列。
其特征包括:➢输入:算法有零个或多个输入➢输出:算法至少产生一个输出➢确定性:算法的每一条指令都有确切的定义,没有二义性。
➢能行性/可行性:可以通过已经实现的基本运算执行有限次来实现➢有穷性:算法必须总能在执行有限步之后终止6.联系:程序是计算机指令的有序集合,是算法用某种程序设计语言的表述,是算法在计算机上的具体实现。
区别:在语言描述上不同,程序必须是用规定的程序设计语言来写,而算法的描述形式包括自然语言、伪代码、流程图和程序语言等;算法所描述的步骤一定是有限的,而程序可以无限地执行下去,比如一个死循环可以称为程序,但不能称为算法。
7.正确性:算法的执行结果应当满足功能需求,无语法错误,无逻辑错误简明性:思路清晰、层次分明、易读易懂,有利于调试维护健壮性:当输入不合法数据时,应能做适当处理,不至于引起严重后果效率:有效使用存储空间和有高的时间效率最优性:解决同一个问题可能有多种算法,应进行比较,选择最佳算法可使用性:用户友好性8(1)执行次数为n-1(n>=2),n=1时执行1次;时间复杂度为O(n)。
(2)执行次数为⌈log3n⌉;时间复杂度为O(logn)(3) 执行次数为n2;时间复杂度为O(n2)(4)执行次数为⌊√n⌋ + 1;时间复杂度为O(√n)第2 章线性表1.A2.D3.B4.C5.B6.D7.D8.C9.A10.D1.编写程序实现对顺序表逆置。
南京邮电大学数据库系统课后习题答案

R2(CNO, TNAME, TADDR) } F2={CNO→TNAME,TNAME→TADDR}, KEY=(CNO)
ρ中R1、R2的所有属性都是原子的,且没有非
主属性对候选键的部分函数依赖,达到2NF;
2021/4/14
28
(3) 试把R分解成3NF模式集,并说明理由;
2021/4/14
数据库系统
习题课二
8
第四章习题
4.21设有关系模式R(ABC ),其上的FD集为 F={ B→C,C→A }, 那么分解ρ={AB, AC}
相对于F是否是无损分解和保持FD?说明理由
解 (1) ρ中有R1(AB), R2(AC)
R1∩R2=A, R1-R2=B, R2-R1=C 在F中推导不出 A→B或A→C,ρ有损 (2) F1 ={B→A } , F2 = {C→A } (F1∪F2)+ ≠F+,丢失了B→C 分解ρ不保持函数依赖
2021/4/14
数据库系统
习题课二
9
第四章习题
第五章参考答案
• PP.180 5.14
• 某商业集团有三个实体集。一个是“公司”实体集, 属性有公司编号、公司名、地址等。二是“仓库”实 体集,属性有仓库编号、仓库名、地址等。三是“职 工”实体集,属性有职工编号、姓名、性别等。公司 与仓库间存在“隶属”关系,每个公司管辖若干个仓 库,每个仓库只属于一个公司管辖;仓库与间存在 “聘用”联系,每个仓库可聘用多个职工,每个职工 只能在一个仓库工作,仓库聘用职工有聘期和工资。 画出ER图,并在图上注明属性、联系的类型。转换成 关系模式集,并指出每个关系模式的主键和外键。
也可用域约束或断言
①在基表S的定义中,用检查子句
CHECK(AGE BETWEEN 16 AND 25) ②在基表SC的定义中,做以下说明:
南邮数据结构课后习题课

3.2 设计2个栈共享一个数组,画出示意图。 0 n-1
↑ bottom1
↑ ↑ ↑ ⑷写出下列表达式的后缀表达式: bottom2 ① top1 (a+b)/(c+d)top2 ab+cd+/
② b^2-4*a*c b2^4a*c*定义一个足够大的栈空间。该空间的两端分别设为两个栈 的栈底,用bottom1和bottom2指示,让两个栈的栈顶,用 top1和top2指示,都向中间伸展,直到两个栈的栈顶相遇, 才会发生溢出。 栈空,两栈均空:top1=0且 top2=n-1 栈满:top1=top2-1
答: 划线语句的执行次数为 n-1 。O(n)
(2)i=1; x=0; do { x++; i=2*i; } while (i<n);
划线语句的执行次数为 log2n。O(log2n) (3) for(int i=1;i<=n;i++) for(int j=1;j<=i;j++) for (int k=1;k<=j;k++) x++; 划线语句的执行次数为 n(n+1)(n+2)/6 。O(n3)
O(n)
2.5 在类SingleList中增加一个成员函数,将单链表 逆置运算,直接实现该函数并分析其时间复杂度。 template <class T> void SingleList<T>::invert() { Node<T> *p=first,*q; first=NULL; while (p) { q=p->link; p->link=first; first=p; p=q; } }
南邮数据结构课后习题课共27页文档

•
6、黄金时代是在我们的前面,而不在 我们的 后面。
•
7、心急吃不了热汤圆。•8、你可以很有来自性,但某些时候请收 敛。•
9、只为成功找方法,不为失败找借口 (蹩脚 的工人 总是说 工具不 好)。
•
10、只要下定决心克服恐惧,便几乎 能克服 任何恐 惧。因 为,请 记住, 除了在 脑海中 ,恐惧 无处藏 身。-- 戴尔. 卡耐基 。
46、我们若已接受最坏的,就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会,使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首,不会作诗也会吟。——孙洙 50、谁和我一样用功,谁就会和我一样成功。——莫扎特
南邮数据结构习题课

2.2 (2) 在类LinearList 中增加一个成员函数,将顺序 在类LinearList 中增加一个成员函数, 表逆置,实现该函数并分析算法的时间复杂度。 表逆置,实现该函数并分析算法的时间复杂度。不利用类 提供的操作直接实现。 SeqList 提供的操作直接实现。 template <class T> SeqList<T>:: ::Invert() void SeqList<T>::Invert() { T e; i=0 i<length/ for (int i=0;i<length/2;i++) { e=elements[i]; e=elements[i]; elements[i]=elements[length-1-i]; elements[i]=elements[length- i]; elements[length- i]=e; elements[length-1-i]=e; } } O(n)
b^2② b^2-4*a*c b2^4a*c*定义一个足够大的栈空间。该空间的两端分别设为两个栈 定义一个足够大的栈空间。 b2^4a*c*的栈底, bottom1 bottom2 指示, 让两个栈的栈顶, 的栈底 , 用 bottom1 和 bottom2 指示 , 让两个栈的栈顶 , 用 top1 top2指示,都向中间伸展,直到两个栈的栈顶相遇, top1和top2指示,都向中间伸展,直到两个栈的栈顶相遇, 才会发生溢出。 才会发生溢出。 栈空,两栈均空:top1 top2=n栈空,两栈均空:top1=0且 top2=n-1 栈满:top1=top2 栈满:top1=top2-1
template <class T> void Difference(SeqList<T> &LA,SeqList<T> &LB) m=LA.Length(); { int m=LA.Length(); LC(10 10) SeqList<T> LC(10); T x; for (int i=1;i<=m;i++) i=1 i<=m; LA.Find(i,x); { LA.Find(i,x); (LB.Search(x)==0 LC.Insert(LC.Length()+1,x); if (LB.Search(x)==0) LC.Insert(LC.Length()+1,x); } cout<<LC; cout<<LC; } void main() LA(10),LB(10 10),LB(10) { SeqList <int> LA(10),LB(10); i=1 i<=8 LA.Insert(i,i); for (int i=1;i<=8;i++) LA.Insert(i,i); (i=1 i<=3 LB.Insert(i,i+3 for (i=1;i<=3;i++) LB.Insert(i,i+3); InterSection(LA,LB); InterSection(LA,LB); Difference(LA,LB); Difference(LA,LB); }
南邮陈慧南版数据结构课后习题答案

}
65
if (p==root) root=root->lchild;
else q->rchild=p->lchild;
37
e=p->element;
25
delete p;
return true;
14
32
}
7.8 以下列序列为输入,从空树开始构造AVL搜索树。 (1)A,Z,B,Y,C,X (2)A,V,L,T,R,E,I,S,O,K
解:1 调用9.4中的函数InDg计算各个顶点的入度; 2 利用拓扑排序算法依次删去入度为0的顶点发出的边,若最后还
有入度不为0顶点,则该有向图存在有向回路,返回真值。
template <class T>
void LinkedGraph<T>::InDg(ENode<T> *a[],int n,int ind[])
int i,j,top=-1; //top为栈顶元素的下标 ENode<T> *p; for(i=0; i<n; i++)
if(!InDegree[i]) {
时间复杂度。
template <class E,class K>
bool BSTree<E,K>::Delete(E&e)
{ BTNode<E> *p=root,*q=p;
if (!p) return flse;
25
37
91
while (p->rchild)
{ q=p;
14
56
p=p->rchild;
if(!visited[i]) DFS1(i,visited,parent); delete []visited, []parent; }
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3) for(int i=1;i<=n;i++) for(int j=1;j<=i;j++) for (int k=1;k<=j;k++) x++; 划线语句的执行次数为n(n+1)(n+2)/6 ,渐近时间复杂度为O(n3)
(4)x=n;y=0; while(x>=(y+1)*(y+1)) y++; 划线语句的执行次数为 n1/2 ,渐近时间复杂度为O(n1/2)
2018/10/25
7
3-1. 设A,B,C,D,E五个元素依次进栈(进栈 后可立即出栈),问能否得到下列序列。若能得到 ,则给出相应的push和pop序列;若不能,则说 明理由。 (3)C,A,B,D,E (3)不能得到该序列,在C出栈时,A和B在栈中 ,A比B先进栈,所以B应比A先出栈。
2018/10/25
0 3 2 6 2 8 3 10 4 7 4 9
4.7 求对题图4-1的稀疏矩阵执行矩阵转置时数组 num[]和k[]的值。
col num[col] k[col]
2018/10/25
0 1 0
1 0 1
2 2 1
3 1 3
4 2 4
14
第六章 习题讲解
6-2. 对于三个结点A,B和C,可分别组成多少不同 的无序树、有序树和二叉树?
2018/10/25 4
2-12.设计一个算法,将单链表中结点以逆序排列。逆序的 单链表中的结点均为原表中的结点。 Node* pInvert(Node* first) { Node *p=first, *q; first=NULL; while (p) { q=p->Link; p->Link=first; first=p; p=q; } return first; }
8
3-1. 设A,B,C,D,E五个元素依次进栈(进栈 后可立即出栈),问能否得到下列序列。若能得到 ,则给出相应的push和pop序列;若不能,则说 明理由。 (4)E,D,C,B,A (4)能得到该序列。 相应的push和pop序列为:push(A); push(B); push(C); push(D); push(E); pop(); pop(); pop(); pop(); pop();
加权路径长度:WPL=(2+3)×4+5×3+(7+9+12)×2=91
2018/10/25 23
7-4为什么说对半搜索算法只适用于顺序有序表的 情况?为什么说顺序搜索可用于顺序表和链表, 也不受表的有序性限制? 解: 1、对半搜索算法必须针对顺序存储的有序表,要 求满足两个条件: 1)顺序存储,只有顺序存储才可以根据元素下 标(地址)随机存取元素; 2)有序存储,只有有序存储才可以其实现对半 查找。 2、顺序搜索从头到尾逐个查找,所以可用于顺序 表和链表,也不受表的有序性限制。
2018/10/25 21
6-13. 将上图中的树转换成二叉树,并将下图中的二 叉树转换成森林。
2018/10/25
22
6-18. 设S={A,B,C,D,E,F},W={2,3,5,7,9,12}, 对字符集合进行哈夫曼编码,W为各字符的频率 (1)画出哈夫曼树 (2)计算带权路径长度 (3)求各字符的编码 A: B: C: D: E: F: 1010 1011 100 00 01 11
第一章 习题讲解
1-19.确定下列各程序段的程序步,确定划线语句的执行次 数,计算它们的渐近时间复杂度。 (1) i=1; k=0; do { k=k+10*i; i++; } while(i<=n-1) 划线语句的执行次数为 n-1 ,渐近时间复杂度为O(n) (2)i=1; x=0; do{ x++; i=2*i; } while (i<n); 划线语句的执行次数为 log2n ,渐近时间复杂度为O(log2n)
37 25 45 91 76 56
14
建成的二叉树
2018/10/25
65
26
8-1 建立37,45,91,25,14,76,56,65为输入 时的二叉搜索树,再从该树上依次删除76,45,则 树形分别如何?
2018/10/25
20
(4)设计算法,交换一棵二叉树中每个结点的 左、右子树。
void ExchBt(BTree Bt) { Exch(Bt.Root); } void Exch(BTNode *p) { if (p) { BTNode *q=p->LChild; p->LChild=p->RChild; p->RChild=q; Exch(p->LChild); Exch(p->RChild); } }
2018/10/25
6
第三章 习题讲解
3-1. 设A,B,C,D,E五个元素依次进栈(进栈 后可立即出栈),问能否得到下列序列。若能得 到,则给出相应的push和pop序列;若不能,则 说明理由。 (2)A,C,E,B,D (2)不能得到该序列,在E出栈时,B和D在栈 中,B比D先进栈,所以D应比B先出栈。
2018/10/25
2
第二章 习题讲解
2-4.Loc(A[i][j][k])=134+(i*n*p+j*p+k)*2
2018/10/25
3
2-9. 设有长度为n 的一维整型数组A,设计一个算法,将原数 组中的元素以逆序排列 void Invert(T elements[], int length) //length数组长度 //elements[]为需要逆序的数组 { T e; for (int i=1;i<length/2;i++) { e=elements[i-1]; elements[i-1]=elements[length-i]; elements[length-i]=e; } }
2018/10/25
9
第四章 习题讲解
4-1. 设线性表采用顺序表示方式,并假定顺序表是 有序的(设表中元素已按非递减次序排列)。编写 函数,实现线性表的如下运算: (1)int Search_Insert(List *lst,T x) 后置条件:在有序的顺序表中搜索元素x。 •若x在表中,则返回x在表中的位置。 •否则,若表未满,则在表中插入新元素x,并且插 入后,线性表仍然是有序的,返回新元素x的位置; •若表已满,无法插入新元素,则返回-1。
(1)无序树:9棵 (2)有序树:12棵 (3)二叉树:30棵
各6棵 3棵 6棵
6棵
6棵
2018/10/25
15
6-3. 设在度为m的树中,度为1,2,…,m的节点 个数分别为n1,n2,…,nm,求叶子节点的数目。
设度为0的节点个数为n0则: 树的总度数=节点总个数-1 即:1*n1+2*n2+…+m*nm =n0+ n1+n2+n3+….+ nm-1 因此叶子节点数目为:n0=n2+2*n3+….+ (m-1)nm+1
2018/10/25 5
第三章 习题讲解
3-1. 设A,B,C,D,E五个元素依次进栈(进栈 后可立即出栈),问能否得到下列序列。若能得 到,则给出相应的push和pop序列;若不能,则 说明理由。 (1)A,B,C,D,E (1)能得到该序列。 相应的push和pop序列为:push(A); pop(); push(B); pop(); push(C); pop(); push(D); pop(); push(E); pop();
2018/10/25
12
void Search_Delete(List *lst, T x, T y) { if (lst->Size==0) { printf(“The list is empty”); return -1; } int i,j,sum=0; for (i=0;temp[i]<x&&i<n;i++); //找到首个大于等于x的元素位置i if(i>n-1) return; //没有符合条件的元素 for for (j=i;lst[j]<=y&&j<n;j++); (j=i;j<n; ) //找到首个大于 y 的元素位置j if (lst[j]>y) //大于y 的元素前移 sum=j-i; lst[i++]=lst[j++]; while(j<n) //删除 sum个元素 else lst[i++]=lst[j++]; //小于等于 y的元素删除 n=n-sum; { j++; n--; } }
2018/10/25
17
6-6. 设对一棵二叉树进行中序遍历和后序遍历的结果 分别为: (1)中序遍历 (B D C E) A (F H G ) (2)后序遍历 (D E C B)(H G F) A 画出该二叉树。
A B C D E H F G
2018/10/25
18
6-7 写出下图中二叉树的先序、中序和后序遍历结果
先序:DEHFJGCKAB
E
D
A
中序:HEJFGKCDAB 后序:HJKCGFEBAD
H
F5
19
6-8.设二叉树以二叉链表存储,试编写求解下列问 题的递归算法: (3)求一棵二叉树中的叶结点个数;
int SizeL(BTree Bt) { return SizeofLeaf(Bt.Root); } int SizeofLeaf(BTNode *p) { if(!p) return 0; if( (!(p->RChild))&&(!(p->LChild)) ) return 1; return SizeofLeaf(p->LChild)+SizeofLeaf(p->RChild); }
