完美正方形
完美正方形

完美正方形
在数学园地里,开放着许许多多的名花,“图论”是其中名贵的一束,而“完全正方形”在这束鲜花中更是芳香迷人的一朵。
数学中,把一个正方形分成有限个互不重叠的正方形,其中任两个不同,叫做正方形的完全正方化;把用互不相待的正方形组成的正方形叫完全正方形。
1926年,苏联数学家鲁金对“完美正方形”的存在提出了猜想。
所谓“完全正方形”,是指它可以用一些大小各不相同,并且边长为整数的小正方形铺满。
这个问题引起了当时正在英国剑桥大学读书的塔特、斯通等四名学生的兴趣。
到1938年,他们终于找到了一个由63个大小不同的正方形组成的大正方形,人们称它为63阶的完美正方形。
次年有人给出了一个39阶的完美正方形。
1964年,塔特的学生,滑铁卢大学的威尔逊博士找到了一个25阶的完美正方形。
这个图形保持了12年的最佳纪录,这是不是阶数最小的完美正方形呢? 1978年,荷兰特温特技术大学的杜依维斯蒂尤,用大型电子计算机算出了一个21阶的完美正方形。
这是完美正方形的最终目标了。
因为鲁金曾证明,小于21阶的完美正方形是不存在的。
如何出一个完美的正方形

如何出一个完美的正方形正方形,作为几何学中的一种基本形状,具有四条边相等且四个角皆为直角的特点,十分规整美观。
无论是画画、设计、建筑还是手工制作等领域,正方形都是一个常见且重要的要素。
在本文中,我们将探讨如何出一个完美的正方形,并介绍几种常用的方法和技巧。
一、用尺子和直角三角板绘制最常见且简单的方法是使用尺子和直角三角板。
以下是具体步骤:1. 准备工作:选择一张干净的纸或者绘画板,并确保直角三角板的边缘是平整的。
2. 选择边长:根据需要确定正方形的边长,假设边长为a。
3. 绘制边界线:使用尺子绘制一条水平线段,长度为a,作为正方形的一条边界线。
4. 绘制第二条边界线:将直角三角板的一条直边放置在第一条边界线的末端,再用尺子沿着直角三角板的另一条直边绘制一条垂直线段,长度也为a,与第一条边界线相交,形成正方形的两个相邻边。
5. 完成正方形:将直角三角板移至刚刚绘制的垂直线段的末端,并用尺子沿着直角三角板的边绘制直线,长度同样为a,与前两条线段相交,形成正方形的另外两条边。
至此正方形完成。
二、使用绘图软件绘制如今,随着计算机技术的不断进步,绘图软件已成为绘制几何图形的一种常用工具。
以下是使用常见绘图软件绘制正方形的步骤:1. 打开绘图软件:打开你擅长使用的绘图软件,如AutoCAD、Adobe Illustrator等。
2. 创建新文档:选择创建新文档,设置画布大小和单位,并确保画布是方形的。
3. 绘制边界线:使用绘图软件中的直线工具,在画布上绘制一条水平线段,长度为a,作为正方形的一条边界线。
4. 复制并旋转:选择绘制好的水平线段,使用软件中的复制功能复制一份,并旋转90度,使其与水平线段相交,形成正方形的两个相邻边。
5. 连接线段:使用直线工具绘制两条直线,连接旋转后的线段与前两条线段的末端,形成正方形的另外两条边。
至此,在绘图软件上绘制的正方形完成。
三、利用物体或工具辅助绘制除了尺子和绘图软件,我们还可以利用一些常见的物体或工具来辅助绘制正方形。
趣味数学

12345×8 + 5= 98765 123456×8 + 6= 987654 1234567×8 + 7= 9876543 12345678×8 + 8= 98765432 123456789×8 + 9= 987654321
• • • • • • • • • •
9×9 + 7= 88 98×9 + 6= 888 987×9 + 5= 8888 9876×9 + 4= 88888 98765×9 + 3= 888888 987654×9 + 2= 8888888 9876543×9 + 1= 88888888 98765432×9 + 0= 888888888 987654321×9 - 1=8888888888 9876543210×9 - 2=88888888888
1×1=1 11×11=121 111×111=12321 1111×1111=1234321 11111×11111=123454321 111111×111111=12345654321 1111111×1111111=1234567654321 11111111×11111111=123456787654321
• 当乘数超过81时,乘积将至少是十位数,但上述的各种现 象依然存在,真是“吾道一以贯之”。例如: 乘数为9的倍数 12345679×243=2999999997 • 只要把乘积中最左边的一个数2加到最右边的7上,仍呈现 “清一色”。 乘数为3的倍数,但不是9的倍数 12345679×84=1037037036 • 只要把乘积中最左边的一个数1加到最右边的6上,又出现 “三位一体”。 乘数为3K+1或3K+2型 12345679×98=1209876542 • 表面上看来,乘积中出现相同的2,但只要把乘积中最左 边的数1加到最右边的2上去之后,所得数为209876543, 是“缺1”数,仍是轮流“休息”。
华师大版数学八年级下册_知识拓展:完美正方形

完美正方形
我们能不能将一个大正方形分割为一些彼此互不相同的小正方形?或者反过来说,我们能不能用一些大小各不相同的小正方形拼合成一个大正方形?答案是可以的。
这样的一个大正方形,叫做完美正方形(又称完全正方形)。
第一个完美正方形是由英国剑桥大学的四位数学家组成的研究小组于1938年发现的。
这个完美正方形可分为69个小正方形,因此称为69阶完美正方形。
此后,又有许多其他阶的完美正方形被发现。
于是,人们试图寻找一个由个数最少的小正方形拼合而成的(即最低阶的)完美正方形。
利用电子计算机已经证明:不存在20阶或20阶以下的完美正方形。
1978年,荷兰数学家杜伊杰斯廷发现了21阶的完美正
方形,边长为112,如图(图中数字为小正方形边长)。
更加奇妙的是,它还是一个简单完美正方形,即其中的小正方形不构成任何矩形。
杜伊杰斯廷的发现很可能是独一无二的,也就是说,很可能再也没有与此不同的21阶完美正方形了。
第16讲 完美的正方形

第十六讲完美的正方形有一组邻边相等并且有一个角是直角的平行四边形是正方形,换句话说:正方形是各边都相等的矩形,正方形是各角都相等的菱形,正方形既是矩形又是菱形,它具有矩形和菱形的一切性质.矩形、菱形,正方形都是特殊的四边形,它们的概念交错,关系复杂,性质有许多相似之处,一些判定和性质定理又是可逆的,所以在学习中注重概念的理解,着眼于概念间的区别与联系.连正方形的对角线,能得到特殊三角形、全等三角形,由于正方形常常与直角三角形联系在一起,所以在解有关正方形问题时要用到直角三角形性质,具有代数风格,体现数形结合思想.熟悉以下基本图形,基本结论:例题求解【例1】如图,若四边形ABCD是正方形,△CDE是等边三角形,则∠EAB的度数为.(北京市竞赛题)思路点拨图中还有等腰三角形,利用等腰三角形性质计算.注可以证明,在所有用长相等的四边形中,正方形的面积最大.我们熟悉的“七巧板”,那是把一块正方形板切分成三角形、正方形、平行四边形的7块,用它可以拼出许多巧妙的图形,“七巧板”是我国古代人民智慧的结晶.【例2】如图,在正方形ABCD中,O是对角线AC、BD的交点,过O作OC⊥OF,分别交AB、BC 于E、F,若AE=4,CF=3,则EF的长为( )A.7 B.5 C.4 D.3(江苏省泰州市中考题)思路点拨AE、CF、EF不在同一个三角形中,运用全等三角形寻找相等的线段,使分散的条件集中到同一个三角形中.【例3】如图,正方形ABCD中,E、F是AB、BC边上两点,且EF=AC+FC,DG⊥EF于G,求证:DC=DA.(重庆市竞赛题)思路点拨构造AE+FC的线段是解本例的关键.【例4】已知正方形ABCD中,M是AB的中点,E是AB延长线上一点,MN⊥DM且交∠CBZ的平分线于N(如图甲).(1)求证:MD=MN(2)若将上述条件中的“M是AB中点”改为“M是AB上的任意一点”,其余条件不变(如图乙),则结论“MD=MN”还成立吗?如果成立,请证明:如果不成立,请说明理由.(上海市闽行区中考题)思路点拨对于图甲,取AD中点F,通过构造全等三角形证明MD=MN;这种证法能否迁移到图乙情景中去?从而作出正确的判断.注探索是学习的生命线,深入探究、学会探索是时代提出的新要求.数学解题中的探索活动可从以下几个方面进行:(1)在题设条件不变情况下,发现挖掘更多的结论;(2)通过强化或弱化来改变条件,考查结论是否改变或寻求新的结论;(3)构造逆命题.对于例3,请读者思考,在不改变题设条件的前提下,(1)∠EDF等于多少度?(2)怎样证明明逆命题?例4改变点的位置,赋以运动,从特殊到一般,(1)的结果为(2)的猜想提供了借鉴的依据,又为猜想设置了障碍,前面的证明思路是后面的证明模式.【例5】操作:将一把三角尺放在边长为l的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.探究:设A,P两点间的距离为x(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到的结论;(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的关系式,并写出x的取值范围;(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由(图1、图2、图3的形状大小相同,图1供操作、实验用,图2、图3备用).思路点拨本例是探究式的操作型试题,第(1)问需抓住滑动中∠BPQ是直角这一不变量,画出滑动中一般情形的图形,通过观察提出猜想,再给予论证,第(3)问需要在操作中观察出使△PCQ是等腰三角形的两种情形.注数学学习是一个生动活泼的过程,动手实践,自主探索是学习数学的重要形式,它说明了存在的事实是怎样被发现和被发现的现象又是怎样获得证实的,解这类问题,需边操作,边观察、边思考,综合运用相关知识方法探究结论.学力训练1.如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转能与△CBP′重合,若PB=3,则PP′= .河南省中考题)2.如图,正方形ABCD 中,E 为CD 边上一点,F 为BC 延长线上一点,CE=CF ,若∠BEC=60°,则∠EFD 的度数为 . (苏州市中考题)3.如图,∠POQ=90°,边长为2㎝的正方形ABCD 的顶点B 在OP 上,C 在OQ 上,且∠OBC=30°,则A 、D 到OP 的距离分别为 . (南京市中考题)4.如图,正方形ABCD 中,CE ⊥MN ,若∠MCE =35°,则∠ANM 的度数是 .5.如图,E 是边长为l 的正方形ABCD 的对角线BD 上一点,且BE=BC ,P 为CE 上任意一点,PQ ⊥BC 于点Q ,PR ⊥BE 于点R ,则PQ+PR 的值为( ) (河北省中考题)A .22 B .21 C .23 D .326.如图,在四边形ABCD 中,AB=BC ,∠ABC=∠CDA=90°,BE ⊥AD 于E ,8 ABCD S 四边形,则BC 的长为( )A .2B .3C .3D .22 (武汉市选拔赛试题)7.如图,在正方形ABCD 中,C 为CD 上的一点,延长月C 至F ,使CF=CE ,连结DF ,BE 与DF 相交于G ,则下面结论错误的是( )A .BE=DFB .BG ⊥DFC .∠F+∠CEB=90°D .∠FDC+∠ABG =90°(山东省临沂市中考题)8.如图,已知正方形ABCD 的面积为256,点F 在AD 上,点E 在AB 的延长线上,Rt △CEF 的面积为200,则BE 的值是( )A .15B .12C .11D .109.(1)如图甲,若点P 为正方形ABCD 边AB 上一点,以PA 为一边作正方形AEFP ,连BE 、DP ,并延长DP 交BE 于点H ,求证:DH ⊥BF ;(2)如图乙,若点P 为正方形ABCD 内任一点,其余条件不变,(1)的结论是否成立?若成立,请给出证明;若不成立,请说明理由.(泰州市中考题)10.如图,P为正方形ABCD的对角线BD上任一点,PF⊥CD,PE⊥BC,C、F分别为垂足,探索AP与EF的关系.11.如图,正方形ABCD中,AB=3,点E,F分别在BC、CD上,且∠BAE=30°,∠DAF=15°,求△AEF的面积.( “希望杯”邀请赛试题)12.如图,已知E、F分别是正方形ABCD的边BC、CD上的点,AE、AF分别与对角线BD相交于M、N,若∠EAF=50°,则∠CME+∠CNF= .13.如图,在Rt△ABC中,∠C=90°,AC=3,以AB为一边向三角形外作正方形ABEF,正方形的中心为O,OC=24,则BC边的长为.( “希望杯”邀请赛试题)14.如图,A 在线段BG 上,ABCD 和DEFG 都是正方形,面积分别为7㎝2和11㎝2,则△CDE 的面积等于 cm 2.(武汉市选拔赛试题)15.如图,将边长为12cm 的正方形ABCD 折叠,使得A 点落在边CD 上的E 点,然后压平得折痕FG ,若GF 的长为13cm ,则线段CE 的长为 . (北京市竞赛题)16.将一个正方形分割成n 个小正方形(n>1),则n 不可能取( )A .4B .5C .8D .9(江苏省竞赛题)17.如图,正方形ABCD 中,P 、Q 分别是BC 、CD 上的点,若∠PAQ=45°,∠BAP=20°,则∠AQP=( )A .65°B . 60°C .35°D .70°18.如图,ABCD 是边长为1的正方形,EFGH 是内接于ABCD 的正方形,AE=a ,AF=b ,若S EFGH =32,则a b 等于( )A .22B .32C .23D .33 ( “希望杯”邀请赛试题) 19.如图,BF 平行于正方形ADCD 的对角线AC ,点E 在BF 上,且AE=AC ,CF ∥AC ,则∠BCF 等于( )A .150°B .135°C . 105°D .120°20.图甲中,正方形ABDE 、CDFI 、EFGH 的面积分别为17,10,13,图乙中,DPQR 为矩形,对照图乙,计算图甲中六边形ABCIGH 的面积.(江苏省竞赛题)21.如图,在正方形ABCD中,P是CD上一点,且AP=BC+CP,Q为CD中点,求证:∠BAP=2∠QAD.22.如图,有4个动点P、Q、E、F分别从正方形ABCD的4个顶点出发,沿着AB、BC、CD、DA以同样的速度向B、C、D、A各点移动.(1)判定四边形PQEF的形状;(2)PE是否总是经过某一定点,井说明理由;(3)四边形PQEF的顶点位于何处时,其面积最小、最大?各是多少?23.如图a,D为线段AE上任一点,分别以AD、DE为边作正方形ABCD和正方形DEFG,连结BF、AG、CE、BG、BE、BG、BE分别交AD,DC于P、Q两点.(1)①找出图中三对相等的线段(正方形边长相等除外);②找出图中三对相等的钝角;③找出图中一对面积相等的钝角三角形,这两个三角形全等吗?(2)如图b,当正方形ABCD和正方形DEFG都变为菱形,且∠GDE=∠ADC时,(1)中的结论哪些成立,哪些不成立?请对不成立的情况说明理由.(3)如图“当正方形ABCD和正方形DEFG都变为矩形,且DA>DC,DE>DG,△ABD∽△EFD时,(1)中的结论哪些不成立,哪些成立?.如果成立,请证明.(郴州市中考题)24.如图,正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形,P是EF与GH的交点,若矩形PFCH的面积恰是矩形AGPE面积的2倍,试确定∠HAF的大小,并证明你的结论.(北京市竞赛题)。
小学校心理健康教育《完美的正方形》教案

完美的正方形设计意图:《完美的正方形》描写了一个正方形一周七天的经历,生活带给它风雨和伤痛,它却用乐观的心态面对,积极调整自我,让这些阻碍和挫折成就了更好的自己。
佛语中“孔雀食毒而颜色愈加鲜艳,海蚌含沙而珍珠熠熠发光”,你所经历的一切终将成为你生命中的财富,大概就是这个意思。
五年级是小学生思维迅速发展的时期,他们开始能够对事物的本质进行理解与分析,能够联系到自己生活,理解与领悟到绘本故事所表达的内涵。
小学生在生活中也会遇到来自家庭、同伴、学习等方面的困难和挫折,不少孩子缺乏有效的应对方法和策略,实际上,有一些孩子也很难通过告诉他们方法来改变(尤其是那些内在资源和力量较弱的孩子),这时候艺术疗愈的方法能够很好的帮助到孩子们,帮助他们在潜意识开展工作和转化。
发展性艺术治疗以积极心理学为理念,以艺术为手段,通过艺术各种形式,调节、管理不良情绪,有效调节身心平衡,激发个体自身潜能来解决问题,提升生命质量,提高主观幸福感,让生活充满乐观和希望,使个体生命更加充实而有意义。
教学目标:1.通过活动认识到,生活中每个人都会遭遇各种困难与挫折;2.正确看待挫折,尝试用积极的方法来应对和转化挫折,发现生命的多种可能性;3.在创作过程中,整合和疗愈过去的经历,纾解学生的不良情绪。
教学重难点:1.引导学生根据绘本联系到自己现实生活中遇到的问题及困难;2.提供一个温暖而安全的环境,让学生能够走进自己内心。
课时:1课时年级:5年级教学准备:分组4人一组、正方形卡纸、A4纸、三首轻音乐起来看游戏规则(PPT 出示):1.老师给大家30秒钟回忆最近一周发生的事情(可以是任何事情)比如:昨天娇娇老师第一次见到同学们就被大家的热情感动了,我这两天都特别开心! 2.击鼓传花:鼓响时大家开始传,至鼓停止为止;3. 传的人可以下座位,其他人不能下座位(师提醒:只能用传的方式,不能扔、抛);4.此时球在谁手中(或其座位前),谁就来分享;设计意图:在首学环节,通过游戏的方式激发孩子对课堂的兴趣,游戏的内容也跟后面的内容联系紧密,激发学生思考,引出课题。
初三数学完美正方巧妙构造
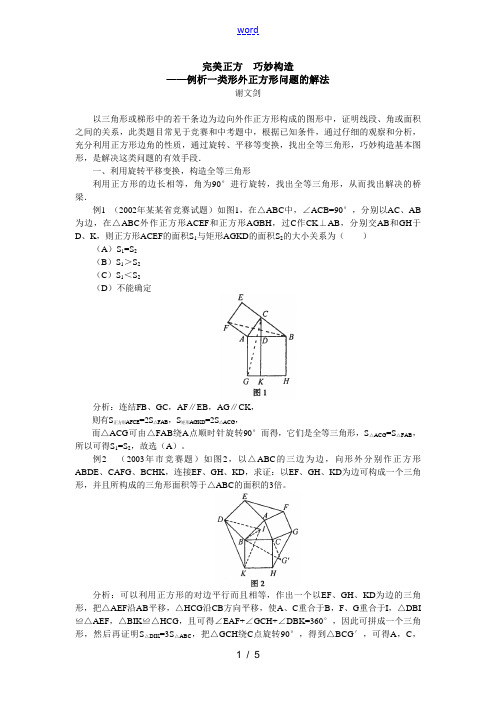
完美正方巧妙构造——例析一类形外正方形问题的解法谢文剑以三角形或梯形中的若干条边为边向外作正方形构成的图形中,证明线段、角或面积之间的关系,此类题目常见于竞赛和中考题中,根据已知条件,通过仔细的观察和分析,充分利用正方形边角的性质,通过旋转、平移等变换,找出全等三角形,巧妙构造基本图形,是解决这类问题的有效手段.一、利用旋转平移变换,构造全等三角形利用正方形的边长相等,角为90°进行旋转,找出全等三角形,从而找出解决的桥梁.例1 (2002年某某省竞赛试题)如图1,在△ABC中,∠ACB=90°,分别以AC、AB 为边,在△ABC外作正方形ACEF和正方形AGBH,过C作CK⊥AB,分别交AB和GH于D、K,则正方形ACEF的面积S1与矩形AGKD的面积S2的大小关系为()(A)S1=S2(B)S1>S2(C)S1<S2(D)不能确定分析:连结FB、GC,AF∥EB,AG∥CK,则有S正方形AFCE=2S△FAB,S矩形AGKD=2S△ACG,而△ACG可由△FAB绕A点顺时针旋转90°而得,它们是全等三角形,S△ACG=S△FAB,所以可得S1=S2,故选(A)。
例2 (2003年市竞赛题)如图2,以△ABC的三边为边,向形外分别作正方形ABDE、CAFG、BCHK,连接EF、GH、KD,求证:以EF、GH、KD为边可构成一个三角形,并且所构成的三角形面积等于△ABC的面积的3倍。
分析:可以利用正方形的对边平行而且相等,作出一个以EF、GH、KD为边的三角形,把△AEF沿AB平移,△HCG沿CB方向平移,使A、C重合于B,F、G重合于I,△DBI ≌△AEF,△BIK≌△HCG,且可得∠EAF+∠GCH+∠DBK=360°,因此可拼成一个三角形,然后再证明S△DIK=3S△ABC,把△GCH绕C点旋转90°,得到△BCG′,可得A,C,G ′在一条直线上,且C 为AG ′的中点。
初中数学竞赛第十六讲完美的正方形(含答案)

第十六讲完美的正方形有一组邻边相等并且有一个角是直角的平行四边形是正方形,换句话说:正方形是各边都相等的矩形,正方形是各角都相等的菱形,正方形既是矩形又是菱形,它具有矩形和菱形的一切性质.矩形、菱形,正方形都是特殊的四边形,它们的概念交错,关系复杂,性质有许多相似之处,一些判定和性质定理又是可逆的,所以在学习中注重概念的理解,着眼于概念间的区别与联系.连正方形的对角线,能得到特殊三角形、全等三角形,由于正方形常常与直角三角形联系在一起,所以在解有关正方形问题时要用到直角三角形性质,具有代数风格,体现数形结合思想.熟悉以下基本图形,基本结论:例题求解【例1】如图,若四边形ABCD是正方形,△CDE是等边三角形,则∠EAB的度数为.(2001年北京市竞赛题)思路点拨图中还有等腰三角形,利用等腰三角形性质计算.注可以证明,在所有用长相等的四边形中,正方形的面积最大.我们熟悉的“七巧板”,那是把一块正方形板切分成三角形、正方形、平行四边形的7块,用它可以拼出许多巧妙的图形,“七巧板”是我国古代人民智慧的结晶.【例2】如图,在正方形ABCD中,O是对角线AC、BD的交点,过O作OC⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的长为( )A.7 B.5 C.4 D.3. (2001年江苏省泰州市中考题)思路点拨AE、CF、EF不在同一个三角形中,运用全等三角形寻找相等的线段,使分散的条件集中到同一个三角形中.【例3】如图,正方形ABCD中,E、F是AB、BC边上两点,且EF=AC+FC,DG⊥EF于G,求证:DC=DA.(重庆市竞赛题)思路点拨构造AE+FC的线段是解本例的关键.【例4】已知正方形ABCD中,M是AB的中点,E是AB延长线上一点,MN⊥DM 且交∠CBZ的平分线于N(如图甲).(1)求证:MD=MN(2)若将上述条件中的“M是AB中点”改为“M是AB上的任意一点”,其余条件不变(如图乙),则结论“MD=MN”还成立吗?如果成立,请证明:如果不成立,请说明理由.(上海市闽行区中考题)思路点拨对于图甲,取AD中点F,通过构造全等三角形证明MD=MN;这种证法能否迁移到图乙情景中去?从而作出正确的判断.注探索是学习的生命线,深入探究、学会探索是时代提出的新要求.数学解题中的探索活动可从以下几个方面进行:(1)在题设条件不变情况下,发现挖掘更多的结论;(2)通过强化或弱化来改变条件,考查结论是否改变或寻求新的结论;(3)构造逆命题.对于例3,请读者思考,在不改变题设条件的前提下,(1)∠EDF等于多少度?(2)怎样证明明逆命题?例4改变点的位置,赋以运动,从特殊到一般,(1)的结果为(2)的猜想提供了借鉴的依据,又为猜想设置了障碍,前面的证明思路是后面的证明模式.【例5】操作:将一把三角尺放在边长为l的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.探究:设A,P两点间的距离为x(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到的结论;(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的关系式,并写出x的取值范围;(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由(图1、图2、图3的形状大小相同,图1供操作、实验用,图2、图3备用).思路点拨 本例是探究式的操作型试题,第(1)问需抓住滑动中∠BPQ 是直角这一不变量,画出滑动中一般情形的图形,通过观察提出猜想,再给予论证,第(3)问需要在操作中观察出使△PCQ 是等腰三角形的两种情形.注 数学学习是一个生动活泼的过程,动手实践,自主探索是学习数学的重要形式,它说明了存在的事实是怎样被发现和被发现的现象又是怎样获得证实的,解这类问题,需边操作,边观察、边思考,综合运用相关知识方法探究结论.学历训练1.如图,P 是正方形ABCD 内一点,将△ABP 绕点B 顺时针方向旋转能与△CBP ′重合,若PB=3,则PP ′= . (2002年河南省中考题)2.如图,正方形ABCD 中,E 为CD 边上一点,F 为BC 延长线上一点,CE=CF ,若∠BEC=60°,则∠EFD 的度数为 . (2000年苏州市中考题)(第1题) (第2题) (第3题) (第4题)3.如图,∠POQ=90°,边长为2㎝的正方形ABCD 的顶点B 在OP 上,C 在OQ 上,且∠OBC=30°,则A 、D 到OP 的距离分别为 . (2003年南京市中考题)4.如图,正方形ABCD 中,CE ⊥MN ,若∠MCE =35°,则∠ANM 的度数是 .(第5题) (第6题) (第7题) (第8题)5.如图,E 是边长为l 的正方形ABCD 的对角线BD 上一点,且BE=BC ,P 为CE 上任意一点,PQ ⊥BC 于点Q ,PR ⊥BE 于点R ,则PQ+PR 的值为( )(2003年河北省中考题)A .22B .21C .23D .32 6.如图,在四边形ABCD 中,AB=BC ,∠ABC=∠CDA=90°,BE ⊥AD 于E ,8 ABCD S 四边形,则BC的长为( )A.2 B.3 C.3D.22(2003年武汉市选拔赛试题)7.如图,在正方形ABCD中,C为CD上的一点,延长月C至F,使CF=CE,连结DF,BE与DF相交于G,则下面结论错误的是( )A.BE=DF B.BG⊥DF C.∠F+∠CEB=90°D.∠FDC+∠ABG=90°(2001年山东省临沂市中考题)8.如图,已知正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF的面积为200,则BE的值是( )A.15 B.12 C .11 D.109.(1)如图甲,若点P为正方形ABCD边AB上一点,以PA为一边作正方形AEFP,连BE、DP,并延长DP交BE于点H,求证:DH⊥BF;(2)如图乙,若点P为正方形ABCD内任一点,其余条件不变,(1)的结论是否成立?若成立,请给出证明;若不成立,请说明理由.(2002年泰州市中考题)10.如图,P为正方形ABCD的对角线BD上任一点,PF⊥CD,PE⊥BC,C、F分别为垂足,探索AP与EF的关系.11.如图,正方形ABCD中,AB=3,点E,F分别在BC、CD上,且∠BAE=30°,∠DAF=15°,求△AEF的面积.(第1l届“希望杯”邀请赛试题)12.如图,已知E、F分别是正方形ABCD的边BC、CD上的点,AE、AF分别与对角线BD相交于M、N,若∠EAF=50°,则∠CME+∠CNF= .(第12题) (第13题) (第14题)13.如图,在Rt △ABC 中,∠C =90°,AC=3,以AB 为一边向三角形外作正方形ABEF ,正方形的中心为O ,OC=24,则BC 边的长为 .(第13 “希望杯”邀请赛试题)14.如图,A 在线段BG 上,ABCD 和DEFG 都是正方形,面积分别为7㎝2和11㎝2,则 △CDE 的面积等于 cm 2.(武汉市选拔赛试题)15.如图,将边长为12cm 的正方形ABCD 折叠,使得A 点落在边CD 上的E 点,然后压平得折痕FG ,若GF 的长为13cm ,则线段CE 的长为 . (2002年北京市竞赛题)(第15题) (第17题) (第18题)16.将一个正方形分割成n 个小正方形(n>1),则n 不可能取( )A .4B .5C .8D .9. (第16届江苏省竞赛题)17.如图,正方形ABCD 中,P 、Q 分别是BC 、CD 上的点,若∠PAQ=45°,∠BAP=20°,则∠AQP=( )A .65°B . 60°C .35°D .70°18.如图,ABCD 是边长为1的正方形,EFGH 是内接于ABCD 的正方形,AE=a ,AF=b ,若S EFGH =32,则a b 等于( ) A .22 B .32 C .23 D .33 (第12届“希望杯”邀请赛试题) 19.如图,BF 平行于正方形ADCD 的对角线AC ,点E 在BF 上,且AE=AC ,CF ∥AC ,则∠BCF 等于( )A .150°B .135°C . 105°D .120°(第19题) (第20题)20.图甲中,正方形ABDE、CDFI、EFGH的面积分别为17,10,13,图乙中,DPQR为矩形,对照图乙,计算图甲中六边形ABCIGH的面积.(第15届江苏省竞赛题)21.如图,在正方形ABCD中,P是CD上一点,且AP=BC+CP,Q为CD中点,求证:∠BAP=2∠QAD.22.如图,有4个动点P、Q、E、F分别从正方形ABCD的4个顶点出发,沿着AB、BC、CD、DA以同样的速度向B、C、D、A各点移动.(1)判定四边形PQEF的形状;(2)PE是否总是经过某一定点,井说明理由;(3)四边形PQEF的顶点位于何处时,其面积最小、最大?各是多少?23.如图a,D为线段AE上任一点,分别以AD、DE为边作正方形ABCD和正方形DEFG,连结BF、AG、CE、BG、BE、BG、BE分别交AD,DC于P、Q两点.(1)①找出图中三对相等的线段(正方形边长相等除外);②找出图中三对相等的钝角;③找出图中一对面积相等的钝角三角形,这两个三角形全等吗?(2)如图b,当正方形ABCD和正方形DEFG都变为菱形,且∠GDE=∠ADC时,(1)中的结论哪些成立,哪些不成立?请对不成立的情况说明理由.(3)如图“当正方形ABCD和正方形DEFG都变为矩形,且DA>DC,DE>DG,△ABD ∽△EFD时,(1)中的结论哪些不成立,哪些成立?.如果成立,请证明.(2003年郴州市中考题)24.如图,正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形,P是EF与GH的交点,若矩形PFCH的面积恰是矩形AGPE面积的2倍,试确定∠HAF的大小,并证明你的结论.(北京市竞赛题)。
完美正方形

完美正方形「完美正方形」是指在一正方形内切割出大小都相异的小正方形.最早由莫伦提出.数学家们一度花了很大精力都无任何结果,以至于1930年苏联著名数学家鲁金猜想,不可能把一个正方形分割成有限个大小不同的正方形.莫伦对此猜想提出了挑战,并提供了一个解决思路:如果同一个矩形有两个不同的正方形剖分,且其中一个剖分的每个正方形都不同于另一个剖分的每个正方形,那么,这两个剖分再添上两个正方形(它异于两个剖分中的任何一个正方形),便可构造出一个完美正方形,而在此之前,完美矩形已经有了比较丰富的成果.1939年,斯普拉格按照莫伦的构想成功地构造出一个55阶的完美正方形,其边长为4205.几个月后,阶数更小(28阶)、边长更短(1015)的完美正方形由剑桥大学三一学院的四位大学生构造出来.1948年,威尔科克斯构造出24阶完美正方形,但其中含有一个完美矩形(此类正方形称为混完美正方形,完全由正方形构造成的正方形称为纯完美正方形),一直到1978年,这个纪录才被打破.1967年,威尔森构造成功25阶、26阶完美正方形.1962年,荷兰特温特技术大学的杜伊维斯廷证明:不存在20阶以下的完美正方形.1978年,杜伊维斯廷借助计算机技术,成功地构造出一个21阶的完美正方形,它是唯一的,且它不仅阶数最低,同时数字也更简单,此外构造上它也有许多优美的特点,比如2的某些次幂恰好位于一条对角线上,等等.杜伊维斯廷同时还证明了:低于21阶的完美正方形不存在.1982年,杜伊维斯廷又证明了:不存在低于24阶的混完美正方形.1992年,布卡姆和杜伊维斯廷给出了21~25阶全部207个纯完美正方形:阶数21 22 23 24 25个数 1 8 12 26 160至此,完美正方形的讨论暂时画上一个句号.但数学家的研究并没有停止,他们又研究了不同大小正方形是否可以填充整个平面的问题,此外他们还将完美剖分的问题推广到莫比乌斯带、圆柱面、环面和克莱茵瓶上,也取得了许多有趣的成果.但是立方体填充被证明是没有的.。
完美正方形与莫比乌斯环的关系

完美正方形与莫比乌斯环的关系英文版The relationship between a perfect square and a Möbius strip is a fascinating concept that explores the interconnectedness of geometry and topology. A perfect square is a shape with four equal sides and four right angles, while a Möbius strip is a surface with only one side and one edge. At first glance, these two shapes may seem unrelated, but upon closer inspection, their relationship becomes clear.To understand the connection between a perfect square and a Möbius strip, we must first examine their properties. A perfect square is a two-dimensional shape that lies flat on a plane, with all four sides meeting at right angles. It has four corners, or vertices, and four sides of equal length. In contrast, a Möbius strip is a three-dimensional shape that twists and turns in a way that creates the illusion of having only one side. It has a single edge that loops around the surface and connects back to itself.The key to understanding the relationship between these two shapes lies in their surfaces. A perfect square has a flat, continuous surface that can be easily visualized and measured. On the other hand, a Möbius strip has a twisted surface that is continuous but non-orientable, meaning it cannot be divided into two distinct sides. This unique property of the Möbius strip allows it to be transformed into a perfect square through a process known as cutting and reattaching.By cutting a Möbius strip along its center line and twisting one of the resulting halves, we can create a perfect square. The twist in the Möbius strip introduces an additional dimension to the shape, transforming it from a two-dimensional surface into a three-dimensional object. This transformation highlights the interconnectedness of geometry and topology, showing how seemingly unrelated shapes can be manipulated and transformed into one another.In conclusion, the relationship between a perfect square and a Möbius strip demonstrates the intricate connections between geometry and topology. By exploring theproperties and transformations of these shapes, we gain a deeper understanding of the fundamental principles that govern the world of mathematics.完美正方形与莫比乌斯环的关系完美正方形和莫比乌斯环之间的关系是一个引人入胜的概念,探讨了几何和拓扑之间的相互关系。
完美正方形与莫比乌斯环的关系

完美正方形与莫比乌斯环的关系完美正方形与莫比乌斯环:一场维度的对话在数学的无尽宇宙中,完美正方形与莫比乌斯环,这两者看似截然不同,却在深层次上揭示了空间、结构和思维的奇妙交织。
它们不仅是几何形状的象征,更是哲学思考的载体,引导我们探索世界的多维面貌。
完美正方形,以其对称性和秩序,代表了二维空间的极致理想。
它的四条边等长,四个角都是直角,这种简洁明了的构造体现了数学的精确性和逻辑性。
它在艺术、建筑和设计中广泛应用,如建筑设计中的对称布局,艺术中的图案设计,甚至是计算机图形学的基础。
正方形的每一个面都独立存在,每个角度都与相邻的角度相等,这是我们在日常生活中直观感知的空间特性。
然而,莫比乌斯环则是一个颠覆我们直观认知的三维结构。
由一条纸带绕自身一周,然后将两端粘合在一起,形成了一个只有一个面、一个边缘和一个孔洞的奇特形状。
这个环体的特性在于,无论你从哪个方向开始走,最后都会回到出发点,而且没有内外之分。
莫比乌斯环的存在挑战了我们关于空间的传统观念,它揭示了连续性和非欧几何的奥秘。
这两个看似不相关的几何元素,其实有着深刻的内在联系。
正方形的每一条边,如果被拉伸并弯曲,可以形成莫比乌斯环的一部分。
这种转换揭示了二维与三维之间的连续性,以及空间的可塑性。
正方形的对称性在莫比乌斯环中得到了扭曲,但并非完全消失,而是以一种全新的方式呈现出来。
从哲学角度看,正方形的完美对称暗示了秩序和平衡,而莫比乌斯环则象征着无限循环和无穷的可能性。
它们都在提示我们,世界并非总是线性的,而是充满了非线性、复杂性和深度。
正方形的局限性与莫比乌斯环的无限性形成对比,启发我们去思考现实世界的多样性和复杂性。
在科学领域,这两个概念也有其应用。
在量子物理中,莫比乌斯环模型被用来研究拓扑量子场论,揭示了物质的奇异性质。
而正方形则在计算机科学中,尤其是在数据结构和算法中扮演着重要角色,它的结构清晰,易于理解和操作。
总的来说,完美正方形与莫比乌斯环,如同两个极端的数学形态,它们在几何、哲学、科学等多个层面展开了一场跨越维度的对话。
完美矩形与完美正方形

若一个矩形可以分割为大小不一的正方形,则称之为完美矩形(perfect rectangle );如果一个正方形可以分割成若干个大小不一的小正方形,则称这个正方形为完美正方形(perfect square ).完美正方形当然是完美矩形.首先考虑一下,为何定义里面要强调“大小不一”?若允许相同,任何正方形都可以分割为若干小正方形,问题就很平凡.例1.十个不同大小的正方形拼成给出了一个完美矩形,最小的一个正方形边长为3,你能求出矩形的边长吗?分析:我们用a 、b 、c 、d 、e 、f 、g 、h 、k 分别表示每个正方形的边长,不难得到以下关系式:a =g +3,h =g -3,b =a +3-d ,e =b -d ,f =d -e ,h =d +f +3,c =b +e ,k =f +h ,e +c =f +k .解出:a =25, b =17, c =23,d =11, e =6, f =5, g =22, h =19, k =24.所以,矩形的长和宽分别是65和47.它可以分割为10个正方形,因此叫做10阶完美矩形.当然,未知数的个数也可以不必这么多,你可以思考一下:设出哪几个正方形的边长就够了?下面是一个9阶完美矩形,其长和宽分别是33和32,组成它的9个正方形边长从小到大依次是:1,4,7,8,9,10,14,15,18.据说这个完美矩形是剑桥大学的学生(布鲁克斯等4人,后来都是著名的组合学家)在1938年发现的.你可以尝试用方程组自己求出它们的边长,培养一点小小的成就感.完美矩形的最小阶数是9,且仅有两种构图,见上图。
我们再欣赏几个10阶完美矩形:完美矩形与完美正方形(65×47) (105×104)(111×98) (115×94)(130×79) (57×55)刚才我们说过,完美矩形的阶数可以很小,边长也不会太大.那么,最小的完美正方形边长多少?是几阶的呢?因为完美正方形不容易找到,所以一开始有人认为完美正方形不存在。
小学心理健康教育《完美的正方形》赛课心得

小学心理健康教育《完美的正方形》赛课心得3月,当教研员发出主题为“生涯、生命、生活”新三生教育时,我是比较懵的,不知从何开始,然后开始查找资料,最后决定用绘本进行教学,这与我校一直开展绘本教育也非常契合,我立即就在网上买了两本绘本《完美的正方形》和《一片叶子落下来》,这两本都是关于生命教育的绘本,经过多次阅读,发现《完美的正方形》更适合小学生,于是我带着忐忑的心情,开启了心理健康教育主题为“生命”的探索旅程。
在锻炼自己的同时,各种思索、醒悟、感受蜂拥而至,充盈在我的头脑中。
一节公开课犹如一面能够透视自我心灵的镜子,照出了我浑身上下,从里到外的不足,看到了自己平时看不到的缺点。
但这个过程,并没有让我感到气馁和失落,而是让我找到了教学梦想的起点,燃起了对教育执着的信念。
静下心来,反思课堂,一节好的心理健康课到底如何上?我想结合自己的这次赛课经历谈一谈自己的理解:一、妙趣横生创设情趣课堂著名教育学家乌申斯基说过:“没有任何兴趣而被迫进行的学习,会扼杀学生掌握知识的意愿。
”兴趣是探究某种活动的倾向,兴趣是求知的起点,是思维的培养和能力提高的内在动力。
一是内容要贴切学生实际生活。
《完美的正方形》讲述的是正方形一周的生活,这跟学生一周七天的生活很相似,每个学生每周七天都会遇到各种各样的问题。
内容很贴近,那如何来导入又是一个问题,找了很多关于正方形的游戏,我在最开始的设计中采用的是“变魔术”的形式,老师一个人在讲台上拿着剪刀和纸在操作,学生虽然很好奇,但是没有参与进来,课堂气氛也不够热烈。
在学校心理健康团队的集体智慧下,又将游戏用变成四人小组创编正方形,学生创意无限,充分发挥了小组成员的智慧,编出了很多不同种类的正方形,但是这也只是为了引出正方形,与后面的内容联系不够,然后继续修改。
然后又想到了一个活动“一周生活”,先让学生安静回忆自己这一周的生活,然后用击鼓传花的形式分享其中的一件事情,这件事可以是高兴、快乐、激动的事情,也可以是伤心、难过、愤怒的事情,既可以是大事也可以是小事,这跟后面的内容联系很紧密,击鼓传花的方式也能够让学生动起来,参与到课堂中来。
完美的正方形 经典讲义

完美的正方形正方形是四边形中最特殊的一种,它是中心对称图形也是轴对称图形,在分析有关条件与结论之间的关系时,可以利用这种性质进行分析,把图形(主要是三角形)进行旋转实现线段与角的位置的转化,在解题过程中综合中心对称、轴对称及等腰三角形、线段的垂直平分线、角的平分线的知识来解决问题。
例1:如图:四边形ABCD 为正方形,以AB 为边向正方形外作等边三角形ABE ,CE 与DB 相交于点F ,则∠AFD= 度.AECDBF例2:如图:将边长为12cm 的正方形ABCD 折叠,使得A 点落在CD 上的E 点,然后压平得折痕FG ,若FG=13cm ,求线段CE 之长.例3:如图:已知E、F分别是正方形ABCD 的边BC 、CD 上的点,AE 、AF 分别与对角线BD 相交于点M 、N .若∠EAF=050,求∠CME +∠CNF 的度数.CMA NDF E例4:如图:正方形ABCD 中,E、F是AB 、BC 边上两点,且EF=AE+FC ,D G ⊥EF 于G . 说明:DG=DA例5:如图,操作:把正方形CGEF 的对角形CE 放在正方形ABCD 的边BC 的延长线上(C G ﹥BC ),取线段AE 的中点M .探索:线段MD 、MF 的关系,并加以说明.FA DB C GEEG上题中,若将正方形CGEF绕点C旋转任意角度(如图),其它条件不变.探究:线段MD、MF的关系,并加以证明.ADBFMCEG课后作业:1.如图,在四边形ABCD 中,AB=BC ,∠ABC =∠CDA=090,BE ⊥AD 于E ,四边形ABCD 的面积为8,则BE 的长为( )A .2 B.3 C.3 D.222.如图,正方形ABCD 的面积为256,点F 在AD 上,点E 在AB 的延长线上,直角三角形CEF 的面积为200,则BE= . 3.如图,A在线段B G上,四边形ABCD 和DEFG 都是正方形,面积分别为7平方厘米和11平方厘米,则△CDE 的面积等于 平方厘米.4.如图,正方形ABCD 的边长为a ,点E 、F 、G 、H 分别在正方形的四条边上,已知E F ∥GH ,EF=GH .(1)若AE=AH=a 31,求四边形EFGH 的周长和面积;(2)求四边形EFGH 的周长的最小值.BCDAEFADBCECD EB AFGADHBEGFC5.如图,已知正方形ABEF 和ACGH 在三角形BAC 的外侧,M 是BC 边的中点。
第3讲 完美的正方形

NM GEF D C B A 图1G E FD CB A 图2H O G E F DC B A 图3E P FD CB A ABCD EFM第三讲 完美的正方形上一讲我们探讨了如何区分各种不同的平行四边形,这一讲我们来研究最特殊的平行四边形——正方形的性质的应用。
之所以称之为完美的正方形,是因为正方形集中了各种平行四边形的所有特征,例如:四边相等、四个内角都是直角、两条对角线相等且互相垂直平分、每条对角线都平分其内角、有四条对称轴、一个对称中心等。
这都将是我们解决实际问题的依据和法宝,我们要会灵活应用。
在实际解题中,我们常对正方形进行割补或折叠,通过平移、旋转、对称等方法把正方形问题转化为特殊的三角形或全等三角形问题来解决。
【例题讲解】1.(1)如图,在正方形ABCD 中,点P ,1P 为正方形内的两点,且PB=PD,BP P CBP AB B P 11,∠=∠=,则P BP 1∠=___________。
(2)如图,P 为正方形ABCD 内一点,若PA ︰PB ︰PC=1︰2︰3,则APB ∠=___________。
(3)如图,正方形ABCD ,E 为BF 上一点,四边形AEFC 恰是一个菱形,AE 交BC 于点M ,则MCE ∠=_________。
(4)如图,在正方形ABCD 中,AB=8,Q 是CD 的中点,设,α=∠DAQ 在CD 上取一点P ,使α2=∠B A P ,则CP=___________。
2. 点F 为正方形ABCD 对角线AC 上任意一点,FE ⊥AB 于E ,FG ⊥AD 于G ,取CF 、BG 的中点M 、N,连结MN.试探求MN 与BG 之间的关系.引申1:若将原题中“点F 在对角线AC 上”改为“点F 在直线AC 上”时,上述结论是否依然成立.引申2:若将原题中的正方形AEFG 绕点A 顺时针旋转任意角度,其它条件不变,则上述结论是否依然成立.3.(1)如图,点F 是正方形ABCD 的边CD 的中点,AF 交BC 延长线于点G ,点E 是CD 延长线上一点,点H 是AE 的中点.∠EAF=45°.求BG DEFH-的值.(2)如图,点E 是正方形ABCD 的边AD 上一点,BE 的中垂线HF 交BC 的延长线于点F ,EF 交CD 于点G ,连接BG .①求∠EBG 的度数;②若正方形ABCD 的边长是3,求△DEG 的周长.【练习】1.如图1,A 在线段BG 上,ABCD 和DEFG 都是正方形,面积分别是27cm 和211cm ,求△CDE 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
完美正方形
完美正方形
「完美正方形」是指在一正方形内切割出大小都相异的小正方形.而我们的研究,则放宽条件,允许同样大小的正方形不超过三个.
我们先估算出正方形中可切割的最大正方形边长范围,再以方格纸手画的方式找出边长1至25的解,在过程中,我们发现可用放大的方式解决边长为合数的正方形.
因此我们将重点放在边长为质数的正方形,我们将正方形分割成两个连续整数边长的正方形,则剩下少一单位的缺角正方形区域.我们探讨缺角正方形区域的解,再讨论分析回原来的正方形.最后解出了边长1至100中全部有解的正方形.
对於更大边长的正方形,我们的方法也可行.所以我们以流程图来表示解决问题的过程,并用电脑试算边长1至1000的完美正方形.
研究动机
在暑假专书研读:名人趣题妙解书中,我们看到了塔尔塔利亚的巧分格纸,觉得很感兴趣,所以我们将完美正方形与巧分格纸两个融合,当作我们科展的题目.
研究目的
「完美正方形」是指,在一正方形内切割成不同大小,边长为整数的正方形,且这些切割出的正方形,均不能全等,这个主题在文献上有不错的研究成果.而我们的研究,则放宽条件,允许每一种同样大小的正方形不超过三个,希望可以探讨边长1~100中哪些正方形有解,哪些正方形无解如果有解如何切割
文献探讨
1926年,苏联数学家鲁金对"完美正方形"的存在提出了猜想.到1938年,他们终于找到了一个由63个大小不同的正方形组成的大正方形,人们称它为63阶的完美正方形.次年有人给出了一个39阶的完美正方形.1964年,塔特的学生,滑铁卢大学的威尔逊博士找到了一个25阶的完美正方形.1948年,威尔科克斯提出了一个24阶的完美正方形,在往后的30年中,人们一度以为24就是完美正方形的最小阶.1978年,荷兰特温特技术大学的杜依维斯蒂尤,用大型电子电脑算出了一个21阶的完美正方形.这是完美正方形的最终目标了.因为鲁金曾证明,小於21阶的完美正方形是不存在的.。
