人教版七年级下知识点试题精选-非负数的性质:算术平方根
人教版七年级下知识点试题精选-关于平方根

七年级下册关于平方根一.选择题(共20小题)1.若m,n是一个正数的平方根,则()A.m=n B.m=﹣n C.m=±n2.若某数的平方等于这个数的本身,则这个数等于()A.0 B.±1 C.﹣1或0 D.1或03.下列语句正确的是()A.﹣的平方根是﹣B.﹣的立方根是C.﹣的平方根是D.的平方根是±4.一个实数的平方根是5a+3和2a﹣3,则这个实数是()A.4 B.9 C.25 D.495.2的平方根是()A.4 B.C.D.6.一个正数a的两个平方根分别是x+2与x﹣3,则x的值为()A.﹣2 B.﹣1 C.1 D.7.9的平方根是()A.3 B.±3 C.D.818.32的平方根是()A.3 B.±3 C.±D.99.(﹣0.5)2的平方根是()A.﹣0.5 B.±0.5 C.0.5 D.0.2510.9的平方根等于()A.﹣3 B.3 C.±3 D.11.2的平方根是()A.B.C.±2 D.212.16的平方根是()A.±4 B.±C.2 D.±213.下列说法正确的是()A.4的平方根是2 B.﹣4的平方根是﹣2C.(﹣2)2没有平方根D.2是4的一个平方根14.已知3m﹣1和m﹣7是数p的平方根,则p的值为()A.100 B.25 C.10或5 D.100或2515.|﹣25|的平方根为()A.5 B.﹣5 C.25 D.5或﹣516.平方根等于它本身的数是()A.正数B.1 C.±1 D.017.(﹣2)2的平方根是()A.2 B.﹣2 C.±2 D.18.5的平方根是()A.B.﹣C.±D.519.(﹣3)2的平方根是()A.﹣3 B.3 C.3或﹣3 D.920.设a是9的平方根,B=()2,则a与B的关系是()A.a=±B B.a=BC.a=﹣B D.以上结论都不对二.填空题(共20小题)21.是的平方根.22.若(x﹣3)2=64,则x=.23.4的负的平方根是.24.10的平方根为.25.一个正数的平方根是2a﹣1和3﹣a,则这个正数是.26.平方根与立方根相等的实数是.27.x2=8,则x分数,整数,有理数.(填“是”或“不是”)28.0和负数没有平方根.29.已知一个自然数的平方根是±a﹙a>0﹚,那么与这个自然数相邻的下一个自然数的平方根是.30.x2=11340中x的值为.31.整数3的平方根是,﹣5的绝对值是.32.如果一个数的平方等于5,那么这个数是.33.0.64的平方根是,=.34.已知正数x的两个不同的平方根为a+2和2a﹣8,则x的值为.35.已知一个数的平方根为a+2与2a﹣11,则这个数是.36.已知2x﹣1的平方根是±6,2x+y﹣1的平方根是±5,2x﹣3y+4的平方根是.37.252﹣242的平方根是,0.04的正负平方根是.38.已知正数x的两个不同的平方根是m+3和2m﹣15,则m=.39.当x满足时,x﹣3有平方根.40.若(x+1)2=9,则x=.三.解答题(共10小题)41.=2.42.16x2﹣25=0.43.已知9x2=16,求x的值.44.如果一个正数的平方根是2a﹣1与3a+6,求这个正数.45.计算下列各式中x得值:(1)x2=25(2)x2﹣81=0(3)25x2=36.46.求下列各式中的x(1)x2=4(2)7x2﹣=0.47.已知5﹣a和2a﹣3是正数m的平方根,求出a和m的值.48.若3a+2与6﹣a是非负数m的平方根,求m的值.49.已知一个正数的平方根为2a﹣1和﹣a+2,求这个正数.50.解方程:2(x﹣1)2﹣8=0.七年级下册关于平方根参考答案与试题解析一.选择题(共20小题)1.若m,n是一个正数的平方根,则()A.m=n B.m=﹣n C.m=±n【分析】根据一个正数有两个平方根,它们互为相反数得出m+n=0,求出即可.【解答】解:∵m,n是一个正数的平方根,∴m+n=0,∴m=﹣n,故选B.【点评】本题考查了对平方根的应用,解此题的关键是能根据题意得出方程m+n=0,注意:一个正数有两个平方根,它们互为相反数.2.若某数的平方等于这个数的本身,则这个数等于()A.0 B.±1 C.﹣1或0 D.1或0【分析】根据平方的定义可知平方后等于这个数的本身的数只有1和0,由此即可确定选择项.【解答】解:平方等于这个数的本身的数只有1和0,故选D.【点评】本题考查了平方的定义.注意:1或0平方等于它的本身.3.下列语句正确的是()A.﹣的平方根是﹣B.﹣的立方根是C.﹣的平方根是D.的平方根是±【分析】分别利用平方根以及立方根的定义分别判断得出即可.【解答】解:A、﹣没有平方根,故此选项错误;B、﹣的立方根是﹣,故此选项错误;C、﹣没有平方根,故此选项错误;D、的平方根是±,此选项正确.故选:D.【点评】此题主要考查了平方根以及立方根的定义,正确把握定义是解题关键.4.一个实数的平方根是5a+3和2a﹣3,则这个实数是()A.4 B.9 C.25 D.49【分析】因为一个非负数的平方根有2个,它们互为相反数,所以5a+3+2a﹣3=0,即a=0,然后可以求出5a+3和2a﹣3的值,最后即可求出这个实数.【解答】解:依题意得5a+3+2a﹣3=0,即a=0,∴5a+3=3,2a﹣3=﹣3,则平方根是±3的数是9.故选B.【点评】本题主要考查了平方根概念的运用.如果x2=a(a≥0),则x是a的平方根.若a>0,则它有两个平方根并且互为相反数,我们把正的平方根叫a的算术平方根.若a=0,则它有一个平方根,即0的平方根是0,0的算术平方根也是0,负数没有平方根.5.2的平方根是()A.4 B.C.D.【分析】如果一个数x2=a(a≥0),那么x就是a的一个平方根.正数有两个平方根,并且互为相反数,利用平方根的定义解答.【解答】解:∵(±)2=2,∴2的平方根是±.故选D.【点评】本题主要考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.6.一个正数a的两个平方根分别是x+2与x﹣3,则x的值为()A.﹣2 B.﹣1 C.1 D.【分析】根据一个正数的两个平方根互为相反数可得出x的值.【解答】解:∵一个正数a的两个平方根分别是x+2与x﹣3,∴x+2+x﹣3=0,解得:x=.故选D.【点评】本题考查了平方根的知识,属于基础题,注意掌握一个正数的两个平方根互为相反数.7.9的平方根是()A.3 B.±3 C.D.81【分析】根据平方与开平方互为逆运算,可得一个正数的平方根.【解答】解:±=±3,故选:B.【点评】本题考查了平方根,根据平方求出平方根,注意一个正数的平方跟有两个.8.32的平方根是()A.3 B.±3 C.±D.9【分析】根据乘方运算,可得幂,根据开方运算,可得平方跟.【解答】解:32=9,=±3,故选:B.【点评】本题考查了平方根,先求出幂,再求平方根,注意一个正数的平方根有两个.9.(﹣0.5)2的平方根是()A.﹣0.5 B.±0.5 C.0.5 D.0.25【分析】根据平方根的定义解答即可.【解答】解:(﹣0.5)2的平方根是±0.5,故选B.【点评】本题考查了平方根的应用,关键是注意:一个正数有两个平方根,它们互为相反数.10.9的平方根等于()A.﹣3 B.3 C.±3 D.【分析】直接根据平方根的定义进行解答即可.【解答】解:∵(±3)2=9,∴9的平方根是±3.故选为:C.【点评】本题考查的是平方根的定义,即如果一个数的平方等于a,这个数就叫做a的平方根,也叫做a的二次方根.11.2的平方根是()A.B.C.±2 D.2【分析】根据平方根的定义解答.【解答】解:∵(±)2=2,∴2的平方根是±.故选B.【点评】本题考查了平方根的定义,注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.12.16的平方根是()A.±4 B.±C.2 D.±2【分析】根据平方根的概念即可求出答案.【解答】解:∵(±4)2=16,∴16的平方根为±4,故选(A)【点评】本题考查平方根的性质,属于基础题型.13.下列说法正确的是()A.4的平方根是2 B.﹣4的平方根是﹣2C.(﹣2)2没有平方根D.2是4的一个平方根【分析】依据平方根的性质即可作出判断.【解答】解:A、4的平方根是±2,故A错误;B、﹣4没有平方根,故B错误;C、(﹣2)2=4,有平方根,故C错误;D、2是4的一个平方根,故D正确.故选:D.【点评】本题主要考查的是平方根的性质,掌握平方根的性质是解题的关键.14.已知3m﹣1和m﹣7是数p的平方根,则p的值为()A.100 B.25 C.10或5 D.100或25【分析】根据一个数的平方根互为相反数或相等,从而可得出m的值,进而可得出p的值.【解答】解:∵3m﹣1和m﹣7是数p的平方根,则3m﹣1=m﹣7或3m﹣1+m﹣7=0,∵当3m﹣1=m﹣7时,解得m=﹣3,∴3m﹣1=﹣10,∴p=100,当3m﹣1+m﹣7=0时,解得m=2,∴3m﹣1=5,∴p=25.故选D.【点评】本题考查了平方根的概念,注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.15.|﹣25|的平方根为()A.5 B.﹣5 C.25 D.5或﹣5【分析】原式利用绝对值的代数意义化简,再利用平方根定义计算即可得到结果.【解答】解:|﹣25|=25,则|﹣25|的平方根为5或﹣5.故选D.【点评】此题考查了平方根,以及绝对值,熟练掌握各自的定义是解本题的关键.16.平方根等于它本身的数是()A.正数B.1 C.±1 D.0【分析】﹣1没有平方根,1的平方根是±1,0的平方根是0,根据以上内容判断即可.【解答】解:只有0的平方根是0,等于它本身.故选:D.【点评】本题考查了对平方根定义的应用,主要考查学生的理解能力和计算能力,注意:负数没有平方根,0的平方根是0,正数有两个平方根,它们互为相反数.17.(﹣2)2的平方根是()A.2 B.﹣2 C.±2 D.【分析】直接利用有理数的乘方化简,进而利用平方根的定义得出答案.【解答】解:∵(﹣2)2=4,∴4的平方根是:±2.故选:C.【点评】此题主要考查了平方根,正确把握平方根的定义是解题关键.18.5的平方根是()A.B.﹣C.±D.5【分析】根据平方根定义求出即可.【解答】解:5的平方根是±,故选C.【点评】本题考查了平方根的应用,能理解平方根定义是解此题的关键,注意:一个正数有两个平方根,它们互为相反数.19.(﹣3)2的平方根是()A.﹣3 B.3 C.3或﹣3 D.9【分析】先求得(﹣3)2的值,然后再依据平方根的定义求解即可.【解答】解:(﹣3)2=9,9的平方根是±3.故选:C.【点评】本题主要考查的是平方根的定义和性质,熟练掌握平方根的定义是解题的关键.20.设a是9的平方根,B=()2,则a与B的关系是()A.a=±B B.a=BC.a=﹣B D.以上结论都不对【分析】由于正数的平方根有两个,且互为相反数,所以在此题中有a两种情况,要考虑全面.【解答】解:∵a是9的平方根,∴a=±3,又B=()2=3,∴a=±b.故选A.【点评】本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.二.填空题(共20小题)21.是5的平方根.【分析】利用平方根的定义求解即可.【解答】解:∵(±)2=5,∴是5的平方根,故答案为5.【点评】本题考查了平方根的知识,一个正实数的平方根有两个,它们互为相反数,但注意说法的逻辑性.22.若(x﹣3)2=64,则x=11或﹣5.【分析】通过直接开平方法解方程,即可求得x的值.【解答】解:∵(x﹣3)2=64,∴x﹣3=±,即x﹣3=±8,∴x=3±8,解得,x=11或﹣5.故答案是:11或﹣5.【点评】本题考查了平方根的概念.注意一个正数有两个平方根,它们互为相反数.23.4的负的平方根是﹣2.【分析】根据平方根的定义即可求解.【解答】解:∵(﹣2)2=4,∴4的负的平方根是:﹣2.故答案是:﹣2.【点评】本题主要考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.24.10的平方根为.【分析】根据开方的意义,可得一个数的平方跟.【解答】解:10的平方根为,故答案为:.【点评】本题考查了平方根,注意一个正数的平方根有两个,它们互为相反数.25.一个正数的平方根是2a﹣1和3﹣a,则这个正数是25.【分析】根据已知得出关于a的方程,求出方程的解即可.【解答】解:∵一个正数的平方根是2a﹣1和3﹣a,∴2a﹣1+3﹣a=0,解得:a=﹣2,2a﹣1=﹣5,即这个正数是25,故答案为:25.【点评】本题考查了平方根的应用,注意:一个正数有两个平方根,它们互为相反数.26.平方根与立方根相等的实数是0.【分析】分别利用立方根和平方根的定义即可求解.【解答】解:∵一个数平方根与立方根相等,设这个数为a,则有=,∴a=0,故答案为0.【点评】此题主要考查立方根的定义、平方根的定义及其它们的应用,比较简单.27.x2=8,则x不是分数,不是整数,不是有理数.(填“是”或“不是”)【分析】先根据平方根的定义求出x的值,再结合分数,整数,有理数的定义求解.【解答】解:∵x2=8,∴x=2,∴x不是分数,不是整数,不是有理数.故答案为:不是,不是,不是.【点评】本题考查了平方根的定义和有理数的分类.平方根定义:如果一个数的平方等于a,这个数就叫做a的平方根,也叫做a的二次方根.一个正数有两个平方根,这两个平方根互为相反数,零的平方根是零,负数没有平方根.28.0和负数没有平方根.错误【分析】根据被开方数为非负数可得出答案.【解答】解:0有平方根,故0和负数没有平方根错误.故填:错误.【点评】本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.29.已知一个自然数的平方根是±a﹙a>0﹚,那么与这个自然数相邻的下一个自然数的平方根是±.【分析】根据题意,利用平方根定义计算即可.【解答】解:根据题意得:这个自然数为a2,下一个自然数为a2+1,则与这个自然数相邻的下一个自然数的平方根是±,故答案为:±【点评】此题考查了平方根,熟练掌握平方根的定义是解本题的关键.30.x2=11340中x的值为±18.【分析】把11340写成324×35,再根据平方根的定义解答.【解答】解:∵11340=324×35,∴x=±18.故答案为:±18.【点评】本题考查了平方根的定义,把11340写成平方数与另一个数相乘的形式是解题的关键.31.整数3的平方根是±,﹣5的绝对值是5.【分析】分别根据平方根的定义以及绝对值的定义即可求解.【解答】解:3的平方根是±,﹣5的绝对值是5.故答案为:±,5.【点评】本题考查了平方根的定义、绝对值的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.32.如果一个数的平方等于5,那么这个数是.【分析】根据平方根的定义即可求解.【解答】解:∵(±)2=5∴这个数是±.故答案是:±【点评】本题主要考查了平方根的定义,一个正数的平方根有两个,这两个互为相反数.33.0.64的平方根是±0.8,=2﹣.【分析】(1)根据平方根的概念和性质求解,并且正数的平方根有两个,且互为相反数;(2)首先判断绝对值内的数的符号,然后根据绝对值的性质化简.【解答】解:(1)0.64的平方根,即±=±0.8;(2)∵<2,∴﹣2<0,∴|﹣2|=﹣(﹣2)=2﹣.故答案为:±0.8,2﹣.【点评】此题考查了平方根的定义及绝对值的性质:一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.绝对值的性质:一个正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是0.34.已知正数x的两个不同的平方根为a+2和2a﹣8,则x的值为16.【分析】根据平方根的性质可得a+2+2a﹣8=0,解方程可得a的值,进而得到这个数的平方根,然后再算出这个数即可.【解答】解:a+2+2a﹣8=0,解得:a=2,则a+2=2+2=4,2a﹣8=﹣4,∵16的平方根是±4,∴这个数是16.故答案为:16.【点评】此题主要考查了平方根,关键是掌握一个正数有两个平方根,这两个平方根互为相反数.35.已知一个数的平方根为a+2与2a﹣11,则这个数是25.【分析】根据正数的两个平方根互为相反数列式求出a的值,然后解答即可.【解答】解:∵一个数的平方根为a+2与2a﹣11,∴a+2+2a﹣11=0,解得a=3,∴a+2=3+2=5,∴这个数是25.故答案为:25.【点评】本题主要考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.36.已知2x﹣1的平方根是±6,2x+y﹣1的平方根是±5,2x﹣3y+4的平方根是±.【分析】根据平方根定义得出2x﹣1=36,2x+y﹣1=25,代入求出2x﹣3y+4的值,根据平方根定义求出即可.【解答】解:∵2x﹣1的平方根是±6,2x+y﹣1的平方根是±5,∴2x﹣1=36,2x+y﹣1=25,∴x=,y=﹣11,∴2x﹣3y+4=74,∴2x﹣3y+4的平方根是±,故答案为:±.【点评】本题考查了平方根定义的应用,能根据平方根定义求出x、y的值是解此题的关键.37.252﹣242的平方根是±7,0.04的正负平方根是±0.2.【分析】原式利用平方根的定义计算即可得到结果.【解答】解:252﹣242=(25﹣24)×(25+24)=49,49的平方根是±7,0.04的正负平方根是±0.2,故答案为:±7;±0.2.【点评】此题考查了平方根,熟练掌握平方根的定义是解本题的关键.38.已知正数x的两个不同的平方根是m+3和2m﹣15,则m=4.【分析】根据正数有两个平方根,它们互为相反数得出方程m+3+2m﹣15=0,求出m.【解答】解:∵正数x的两个平方根是m+3和2m﹣15,∴m+3+2m﹣15=0,∴3m=12,m=4.故答案为:4.【点评】本题考查了平方根和相反数的应用,注意:正数有两个平方根,它们互为相反数.39.当x满足x≥3时,x﹣3有平方根.【分析】根据负数没有平方根,可得答案.【解答】解:根据题意得:x﹣3≥0,解得:x≥3.故答案是:x≥3.【点评】本题主要考查了平方根的定义.关键是掌握一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.40.若(x+1)2=9,则x=2或﹣4.【分析】依据平方根的定义得到x+1的值,然后解关于x的方程即可.【解答】解:∵(x+1)2=9,∴x+1=3或x+1=﹣3,解得:x=2或x=﹣4.故答案为:2或﹣4.【点评】本题主要考查的是平方根的定义,依据平方根的定义列出关于x的一元一次方程是解题的关键.三.解答题(共10小题)41.=2.【分析】首先根据平方根的定义即可求得x﹣的值,即可得到两个一元一次方程,解方程即可求解.【解答】解:根据题意得:x﹣=或x﹣=﹣.则x=+或﹣.【点评】本题考查了平方根的定义,正确利用平方根的定义把原方程转化成一元一次方程是关键.42.16x2﹣25=0.【分析】先求出x2,再根据平方根的定义进行解答.【解答】解:整理得,x2=,x=±.【点评】本题考查了利用平方根的定义求未知数的值,熟记正数的平方根有两个,它们互为相反数;负数没有平方根;0的平方根是0是解题的关键.43.已知9x2=16,求x的值.【分析】将x2的系数化为1,然后开平方即可得出x的值.【解答】解:系数化为1得,x2=,开平方得,x=±.【点评】本题考查了平方根的知识,属于基础题,注意掌握开平方的运算.44.如果一个正数的平方根是2a﹣1与3a+6,求这个正数.【分析】根据一个正数的平方根互为相反数,可得平方根的和为0,根据解一元一次方程,可得a的值,根据乘方运算,可得答案.【解答】解:一个正数的平方根是2a﹣1与3a+6,∴(2a﹣1)+(3a+6)=0解得a=﹣1,2a﹣1=﹣3,(﹣3)2=9,答:这个数是9.【点评】本题考查了平方根,先求出a的值,再平方运算.45.计算下列各式中x得值:(1)x2=25(2)x2﹣81=0(3)25x2=36.【分析】(1)直接利用平方根的定义求出即可;(2)直接利用平方根的定义求出即可;(3)直接利用平方根的定义求出即可.【解答】解:(1)x2=25,则x=±5;(2)x2﹣81=0,则x2=81,故x=±9;(3)25x2=36则x2=,解得;x=±.【点评】此题主要考查了平方根的定义,正确得出x的值是解题关键.46.求下列各式中的x(1)x2=4(2)7x2﹣=0.【分析】(1)(2)两个小题都可以用直接开平方法求出结果.【解答】解:(1)∵(±2)2=4,∴4的平方根是±2,∴x=±2;(2)∵7x2﹣=0,∴7x2=,x2=∵(±)2=,∴的平方根是±.∴x=±.【点评】此题主要考查了平方根的定义,用到的知识点为:一个正数有两个平方根,它们互为相反数.47.已知5﹣a和2a﹣3是正数m的平方根,求出a和m的值.【分析】由于某数的两个平方根应该互为相反数,由此即可列方程解出a,即可求出这个正数.【解答】解:由题意得5﹣a+2a﹣3=0,解得a=﹣2m=(5﹣a)2=72=49.【点评】本题考查了平方根的概念.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.48.若3a+2与6﹣a是非负数m的平方根,求m的值.【分析】利用平方根的意义得出关于a的等式,进而求出m的值.【解答】解:∵3a+2与6﹣a是非负数m的平方根,∴当3a+2+6﹣a=0时,解得:a=﹣4,∴3a+2=﹣10,∴m的值为:100,当3a+2=6﹣a,解得:a=1,故m的值为:25,综上所述:m的值为:25或100.【点评】此题主要考查了平方根的定义,得出关于a的等式是解题关键.49.已知一个正数的平方根为2a﹣1和﹣a+2,求这个正数.【分析】直接利用平方根的定义分析得出答案.【解答】解:∵一个正数的平方根为2a﹣1和﹣a+2,∴2a﹣1﹣a+2=0,解得:a=﹣1,则2a﹣1=﹣3,故这个正数是:(﹣3)2=9.【点评】此题主要考查了平方根,正确得出a的值是解题关键.50.解方程:2(x﹣1)2﹣8=0.【分析】根据平方根的定义可以求得=±a即可解题.【解答】解:2(x﹣1)2﹣8=0整理得:2(x﹣1)2=8,化简得:(x﹣1)2=4,∴x﹣1=2或﹣2,∴x=3或﹣1.【点评】本题考查了平方根的性质,注意=±a是解题的关键.。
第三章 实数 考点3 非负数的性质:算术平方根(原卷版)

第三章实数(原卷板)3、非负数的性质:算术平方根知识点梳理1.非负数的性质:绝对值在实数范围内,任意一个数的绝对值都是非负数,当几个数或式的绝对值相加和为0时,则其中的每一项都必须等于0.根据上述的性质可列出方程求出未知数的值.2.非负数的性质:偶次方偶次方具有非负性.任意一个数的偶次方都是非负数,当几个数或式的偶次方相加和为0时,则其中的每一项都必须等于0.3.非负数的性质:算术平方根(1)非负数的性质:算术平方根具有非负性.(2)利用算术平方根的非负性求值的问题,主要是根据被开方数是非负数,开方的结果也是非负数列出不等式求解.非负数之和等于0时,各项都等于0利用此性质列方程解决求值问题.同步练习一.选择题(共19小题)1.若+|y+3|=0,则的值为()A.B.﹣C.D.﹣2.已知实数x,y,m满足,且y为负数,则m的取值范围是()A.m>6B.m<6C.m>﹣6D.m<﹣63.若+|b+2|=0,那么a﹣b=()A.1B.﹣1C.3D.04.若(m﹣1)2+=0,则m+n的值是()A.﹣1B.0C.1D.25.若|x+2|+,则xy的值为()A.﹣8B.﹣6C.5D.66.已知|x﹣3|+=0,则(x+y)2的值为()A.4B.16C.25D.647.已知实数x,y满足,则y的值是()A.2B.﹣2C.0D.38.已知x,y为实数且|x+1|+=0,则()2012的值为()A.0B.1C.﹣1D.20129.已知,则a+b的值是()A.1B.﹣1C.3D.﹣310.已知|7+b|+=0,则a+b为()A.8B.﹣6C.6D.811.已知△ABC的三边长a、b、c满足+|b﹣1|+(c)2=0,则△ABC一定是()三角形.A.锐角B.钝角C.直角D.一般12.已知,则y的值为()A.1B.﹣2.C.﹣1D.﹣413.若x,y为实数,且,则的值为()A.1B.2011C.﹣1D.﹣201114.若+(y+2)2=0,则(x+y)2020等于()A.﹣1B.1C.32020D.﹣3202015.若|x﹣2|+=0,则xy的值为()A.﹣8B.﹣6C.5D.616.已知实数x,y满足,则x﹣y等于()A.3B.﹣3C.1D.﹣117.如果|x﹣3|+=0,则=()A.2B.C.﹣2D.318.已知+(b+3)2=0,则(a+b)2020的值为()A.0B.1C.﹣1D.202019.已知实数x,y满足+|y+2|=0,则x+y的值为()A.﹣2B.2C.4D.﹣4二.填空题(共17小题)20.已知a、b满足(a﹣1)2+=0,则a+b=.21.当x取时,的值最小,最小值是;当x取时,2﹣的值最大,最大值是.22.已知+|x2﹣3y﹣13|=0,则x+y=.23.如果与(2x﹣4)2互为相反数,那么2x﹣y的平方根是.24.已知+=0,则+=.25.若,则m﹣n的值为.26.如果=0,那么xy的值为.27.当x取时,代数式2﹣取值最大,并求出这个最大值.28.已知+|3x+2y﹣15|=0,则的算术平方根为.29.已知实数x,y满足+(y+1)2=0,则x﹣y等于.30.如果+=0,那么xy的值为.31.已知与(x+y﹣4)2互为相反数,则y﹣x=.32.若+|b2﹣9|=0,则ab=.33.已知,则a b=.34.若=3﹣x,则x的取值范围是.35.若a、b为实数,且(a+)2+=0,则a b的值.36.已知非零实数a,b满足,则a+b等于.三.解答题(共9小题)37.已知|2a+b|与互为相反数.(1)求2a﹣3b的平方根;(2)解关于x的方程ax2+4b﹣2=0.38.已知+|x﹣1|=0.(1)求x与y的值;(2)求x+y的平方根.39.若+(3x+y﹣1)2=0,求的平方根.40.已知a、b、c满足.(1)求a、b、c的值;(2)判断以a、b、c为边的三角形的形状.41.已知+|y3+1|=0,求4x﹣3y的平方根.42.已知x、y满足+|y+1|=0,求x2﹣4y的平方根.43.已知|a+b﹣3|++(a+2)2=0,求(a+c)b的值.44.已知(3x﹣1)2+=0,求18xy的平方根.45.已知实数x,y满足(x﹣4)2+=0,求﹣xy的平方根.。
人教版七年级数学下册第六章第一节平方根复习试题(含答案) (20)

人教版七年级数学下册第六章第一节平方根复习试题(含答案)13的相反数是___________,倒数是________.平方等于16的数是______【答案】13-3 ±4【解析】【分析】根据相反数、倒数和平方根的定义分别进行解答即可.【详解】-1 3的相反数是13,倒数是﹣3;平方得16的数为±4;故答案为13,−3,±4.【点睛】本题考查的知识点是有理数的乘方及相反数和倒数,解题的关键是熟练的掌握有理数的乘方及相反数和倒数.92.若一个正数的两个平方根分别是2a+1和a﹣4,则a的值是________.【答案】1【解析】【分析】由于一个正数的两个平方根互为相反数,得:2a+1+a-4=0,解方程即可求出a.【详解】由题可知:2a+1+a−4=0,解得:a=1.故答案为:1.【点睛】考查平方根,一个正数有两个平方根,它们互为相反数.93.若a﹣3有平方根,则实数a的取值范围是_____.【答案】a≥3.【解析】【分析】根据平方根的定义列出不等式计算即可.【详解】a-≥根据题意,得30.解得: 3.a≥故答案为 3.a≥【点睛】考查平方根的定义,正数有两个平方根,它们互为相反数,0的平方根是0,负数没有平方根.94.如果一个正数m的两个平方根分别是a+3和2a-15,则a=______, m=_____.【答案】4,49【解析】【分析】根据一个正数的两个平方根互为相反数可以求得a的值,进而得出m的值.【详解】∵某正数的两个平方根分别是a+3和2a﹣15,∴a+3+2a﹣15=0,解得:a=4,所以m=(a+3)2=49.故答案为:4,49.【点睛】本题考查了平方根,解答本题的关键是明确它们各自的含义.95的平方根是____________________.【答案】, 3【解析】【分析】根据平方根的定义和算术平方根的定义解答即可.【详解】∵()2=4,;∵92=81,.∵32=9,3.故答案为:,3.【点睛】本题考查了平方根,算术平方根的定义,第二问需要注意先求出进行求解,也是本题容易出错的地方.963x2y150+-=______.【解析】【分析】根据非负数的性质列式求出x、y的值,然后代入代数式进行计算,再根据算术平方根的定义解答.【详解】解:由题意得,x+3=0,3x+2y−15=0,解得x=−3,y=12,3===,.【点睛】本题考查了算术平方根、绝对值等非负数的性质,算术平方根的定义.97.已知3y,则xy的算术平方根是________..【解析】【分析】根据二次根式中的被开方数是非负数列出算式,求出x的值,代入原式求出y的值,根据算术平方根的概念解答即可.【详解】由题意得:x﹣2≥0,2﹣x≥0,解得:x=2,则y=3,∴xy的算术平方根..【点睛】本题考查的是二次根式有意义的条件,掌握二次根式中的被开方数是非负数是解题的关键.982≈________ (精确到百分位).【答案】0.24【解析】2≈2.236﹣2=0.236≈0.24,故答案为:0.24.99.已知2(29-=-9-的平方根是____________; -2 或 2【解析】【分析】根据已知和平方根的定义解答即可.【详解】==±|2=±2).2或2.2或2-【点睛】本题考查了二次根式的性质和完全平方公式的应用,关键是确定出9﹣=(22.100________2的相反数是_________3=_________.【答案】±3 3【解析】【分析】根据开平方运算,可得一个正数的平方根;根据只有符号不同的两个数互为相反数,差的绝对值是大数减小数,可得答案.【详解】解±3; 2的相反数是23=3.故答案为±3, 2-3.【点睛】本题主要考查了算术平方根,相反数和绝对值的概念,熟悉掌握是关键.。
初一数学下册知识点《非负数的性质:算术平方根》150题及解析

初一数学下册知识点《非负数的性质:算术平方根》150题及解析副标题一、选择题(本大题共36小题,共108.0分)1.若与互为相反数,则的值为( )A. 3B. 4C. 6D. 9【答案】A【解析】【分析】本题考查了绝对值的非负性,二次根式的非负性,代数式的值,完全平方公式,相反数.根据相反数的定义得到|x2-4x+4|+=0,再根据非负数的性质得x2-4x+4=0,2x-y-3=0,然后利用完全平方公式变形得到(x-2)2=0,求出x,再求出y,最后计算它们的和即可.【解答】解:根据题意得|x2-4x+4|+=0,∴|x2-4x+4|=0,=0,即(x-2)2=0,2x-y-3=0,∴x=2,y=1,∴x+y=3.故选A.2.若|3x-2y-1|+=0,则x,y的值为()A. B. C. D.【答案】D【解析】解:由题意可知:解得:故选:D.根据二元一次方程组的解法以及非负数的性质即可求出答案.本题考查二元一次方程组的解法,解题的关键是熟练运用二元一次方程组的解法,本题属于基础题型.3.若|3-a|+=0,则a+b的值是()A. 2B. 1C. 0D. -1【答案】B【解析】解:由题意得,3-a=0,2+b=0,解得,a=3,b=-2,a+b=1,故选:B.根据几个非负数的和为0时,这几个非负数都为0列出算式求出a、b的值,计算即可.本题考查的是非负数的性质,掌握几个非负数的和为0时,这几个非负数都为0是解题的关键.4.若+|2a-b+1|=0,则(b-a)2015=( )A. -1B. 1C. 52015D. -52015【答案】A【解析】解:∵+|2a-b+1|=0,∴,解得:,则(b-a)2015=(-3+2)2015=-1.故选:A.利用非负数的性质列出方程组,求出方程组的解得到a与b的值,即可确定出原式的值.此题考查了解二元一次方程组,以及非负数的性质,熟练掌握运算法则是解本题的关键.5.已知等腰三角形的两边长分別为a、b,且a、b满足,则此等腰三角形的周长为( )A. 7或8B. 6或10C. 6或7D. 7或10【答案】A【解析】【分析】本题考查了非负数的性质、等腰三角形的性质以及解二元一次方程组,是基础知识要熟练掌握.先根据非负数的性质求出a,b的值,再分两种情况确定第三边的长,从而得出三角形的周长.【解答】解:∵,∴,解得,当a为底时,三角形的三边长为2,3,3,则周长为8;当b为底时,三角形的三边长为2,2,3,则周长为7;综上所述此等腰三角形的周长为7或8.故选A.6.已知+|b+3|=0,则P(—a,—b)的坐标为()A. (2,3)B. (2,—3)C. (—2,3)D. (—2,—3)【答案】C【解析】【分析】本题考查了点的坐标,非负数的性质,正确求出a,b的值是解题的关键.先由+|b+3|=0,根据非负数的性质求出a=2,b=-3,进而求解即可.【解答】解:∵+|b+3|=0,∴a-2=0,b+3=0,∴a=2,b=-3,∴P(-a,-b)的坐标为(-2,3),故C正确.故选C.7.已知实数x,y满足(x-2)2+=0,则点P(x,y)所在的象限是()A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】D【解析】【分析】本题考查了点的坐标:平面直角坐标系中的点的坐标与实数对一一对应,在第四象限,点的横坐标为正数,纵坐标为负数.也考查了非负数的性质.根据非负数的性质得到x-2=0,y+1=0,则可确定点P(x,y)的坐标为(2,-1),然后根据象限内点的坐标特点即可得到答案.【解答】解:∵(x-2)2+=0,∴x-2=0,y+1=0,∴x=2,y=-1,∴点P(x,y)的坐标为(2,-1),在第四象限.故选D.8.已知x,y为实数,且+(y+2)2=0,则y x的立方根是()A. B. -8 C. -2 D. ±2【答案】C【解析】【分析】此题主要考查了算术平方根的非负性和开立方运算以及偶次方的性质,正确得出x,y 的值是解题关键.直接利用非负数的性质得出x,y的值,再利用立方根的定义求出答案.【解答】解:∵+(y+2)2=0,∴x-3=0,y+2=0,解得:x=3,y=-2,则y x=(-2)3=-8,-8的立方根是:-2.故选C.9.若|3-a|+=0,则a+b的值是()A. -9B. -3C. 3D. 9【答案】B【解析】解:∵|3-a|+=0,∴3=a,b=-6,则a+b=-3.故选B.直接利用绝对值的性质以及二次根式的性质得出a,b的值,进而得出答案.此题主要考查了非负数的性质,正确得出a,b的值是解题关键.10.若+(y+2)2=0,则(x+y)2017=()A. -1B. 1C. 32017D. -32017【答案】A【解析】解:根据题意得x-1=0,y+2=0,解得x=1,y=-2,则原式=(-1)2017=-1.故选:A.根据非负数的性质列出算式,求出x、y的值,计算即可.本题考查的是非负数的性质,掌握当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.11.已知x、y为实数,且+3(y-1)2=0,则x-y的值为()A. 3B. -3C. -1D. 1【答案】D【解析】解:∵且+3(y-1)2=0,∴x=2,y=1.∴x-y=2-1=1.故选:D.先依据非负数的性质求得x、y的值,再代入计算即可.本题主要考查的是非负数的性质、求得x、y的值是解题的关键.12.已知非零实数满足.则等于().A. -1B. 0C. 1D. 2【答案】C【解析】【分析】本题主要考查了算术平方根的性质和根据两个非负数之和等于0,求未知数的值,首先根据算术平方根的被开方数≥0,求出a的范围,进而得出|2a-4|等于原值,代入原式得出+=0.这是两项非负数之和等于0.则可分别求出a和b的值.【解答】解:由题设知a≥3,所以,题设的等式为,于是a=3,b=-2,从而a+b=1.故选C.13.如果+(5-b)2=0,那么点A(a,b)关于原点对称的点A′的坐标为()A. (3,5)B. (3,-5)C. (-3,5)D. (5,-3)【答案】B【解析】【分析】本题考查了关于原点对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数.根据非负数的和等于零,可得a,b的值,根据关于原点对称的点,横坐标与纵坐标都互为相反数,可得答案.【解答】解:由题意,得a+3=0,5-b=0,解得a=-3,b=5,即A(-3,5)关于原点对称的点A′的坐标为(3,-5),故选:B.14.已知a、b满足+|2b+1|=0,则+b的值是()A. B. 1 C. -1 D. 0【答案】D【解析】解:由题意得,a-=0,2b+1=0,解得,a=,b=-,则+b=-=0,故选:D.根据非负数的性质列出算式,求出a、b的值,根据平方根的概念计算即可.本题考查的是非负数的性质,掌握几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.15.已知+(b+)2=0,则a2016b2017的值是()A. 2B. -2C.D. -【答案】D【解析】解:由题意得,a-2=0,b+=0,解得a=2,b=-,所以,a2016b2017=22016(-)2017,=22016(-)2016×(-),=[2×(-)]2016×(-),=-.故选D.根据非负数的性质列方程求出a、b的值,然后代入代数式,再转化为同指数的幂的运算,然后根据积的乘方的性质进行计算即可得解.本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.16.若+|x-3y-17|=0,则x,y的值分别为()A. x=8,y=-3B. x=7,y=7C. x=-8,y=3D. x=-7,y=-7【答案】A【解析】解:由题意得:,解得:,故选:A.根据已知等式,利用非负数的性质列出方程组,求出方程组的解即可得到x与y的值.此题考查了解二元一次方程组,以及非负数的性质,熟练掌握运算法则是解本题的关键.17.已知,则(a+b)2019的值为 ( )A. -1B. 1C. 0D. 2019【答案】A【解析】【分析】本题考查的是非负数的性质,熟知几个非负数的和为0时,每一项必为0是解答此题的关键.先根据非负数的性质求出a、b的值,再代入代数式进行计算即可.【解答】解:∵,∴a-2=0,b+3=0,∴a=2,b=-3,∴(a+b)2019= (2-3)2019 = (-1)2019=-1.故选A.18.已知实数a,b满足+|b-2|=0,那么点P(a,b)的坐标为()A. (-3,2)B. (-3,-2)C. (3,2)D. (3,-2)【答案】A【解析】解:∵+|b-2|=0,∴3+a=0,b-2=0,解得:a=-3,b=2,∴点P(a,b)的坐标为(-3,2),故选:A.根据算术平方根和绝对值具有非负性可得3+a=0,b-2=0,解可得a、b的值,进而可得P的坐标.此题主要考查了算术平方根,关键是掌握算术平方根和绝对值具有非负性.19.下列各式中没有意义的是()A. B. C. D.【答案】A【解析】【分析】本题考查了算术平方根的双重非负性和立方根的知识.根据算术平方根的性质和立方根的性质逐项判断即可.【解答】解:A.的被开方数-7<0,没有意义,故本选项正确;B.的被开方数0.01>0,有意义,故本选项错误;C.的被开方数(-3)2>0,有意义,故本选项错误;D.是开3次方,被开方数-8<0,有意义,故本选项错误;故选A.20.若x,y满足(x+2)2+=0,则的平方根是()A. ±4B. ±2C. 4D. 2【答案】B则=4的平方根是:±2.故选:B.直接利用偶次方的性质以及二次根式的性质得出x,y的值,进而利用平方根的定义得出答案.此题主要考查了算术平方根以及偶次方的性质,正确把握相关定义是解题关键.21.已知△ABC的三边为a,b,c,且a,b,c满足(a-6)2+|10-b|+=0,则△ABC是()A. 直角三角形B. 等腰三角形C. 等边三角形D. 以上都有可能【答案】A【解析】解:∵(a-6)2+|10-b|+=0,∴a-6=0,10-b=0,c-8=0,∴a=6,b=10,c=8,∴a2+c2=b2,∴△ABC是直角三角形,故选:A.根据非负数的性质列出算式,求出a、b、c的值,根据勾股定理的逆定理得出直角三角形即可.本题考查了勾股定理的逆定理,绝对值、偶次方的非负性的应用,能灵活运用勾股定理的逆定理进行推理是解此题的关键.22.已知、为实数,且,则的值为()A. -1B. 1C. -3D. 3【答案】A【解析】【分析】本题考查了代数式求值、偶次幂和二次根式的非负性的知识点,准确确定出x、y的对应关系是解题的关键.根据偶次幂和二次根式的非负性求出x、y,然后代入代数式进行计算即可得解.【解答】解:∵,∴x-1=0,y-2=0,解得:x=1,y=2,把x=1,y=2代入x-y,得:1-2=-1,故选A.23.若+(y+2)2=0,则(y+x)2019等于()A. -1B. 1C. 32018D. -32018【答案】A∴x=1,y=-2,∴(y+x)2019=-1.故选:A.直接利用非负数的性质得出x,y的值,再利用有理数的乘方运算法则计算即可.此题主要考查了非负数的性质,正确得出x,y的值是解题关键.24.已知+|b-2|=0,那么(a+b)2009的值为()A. -1B. 1C. 52009D. -52009【答案】A【解析】【解答】解:根据题意得,3+a=0,b-2=0,解得a=-3,b=2,∴(a+b)2009=(-3+2)2009=-1.故选:A.【分析】根据非负数的性质列式求出a、b的值,再代入代数式进行计算即可求解.本题考查了算术平方根,绝对值非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是求解的关键.25.已知=0,则x+y的值为()A. 10B. -10C. -6D. 不能确定【答案】C【解析】解:∵=0,∴x-2=0,y+8=0,解得x=2,y=-8,∴x+y=2-8=-6.故选:C.先根据非负数的性质求出x、y的值,再求出x+y的值即可.本题考查的是非负数的性质,熟知算术平方根具有非负性是解答此题的关键.26.当的值为最小时,的取值为()A. -1B. 0C.D. 1【答案】C【解析】【分析】本题考查的知识点有:二次根式的非负性,且有最小值,为0;没有最大值.根据二次根式的非负性可知≥0,由此得到4a+1=0为最小值,这样即可得出a的值.【解答】解:取最小值,即4a+1=0.得a=,故选C.27.若,则x,y的值为A. B. C. D.【答案】D【解析】【分析】本题考查二元一次方程组的解法,解题的关键是熟练运用二元一次方程组的解法,本题属于基础题型.根据二元一次方程组的解法以及非负数的性质即可求出答案.【解答】解:由题意可知:解得:故选D.28.如果,那么(xy)2019等于()A. 2019B. -2019C. 1D. -1【答案】D【解析】【分析】本题主要考查了绝对值和偶次方的非负性的运用和二次根式的运算,解答此题根据数的非负性可得关于x,y的方程,然后解之可得x,y的值,最后将x,y的值代入计算即可. 【解答】解:∵,由数的非负性可得:,解得:x=,y=,∴.故选D.29.若x,y为实数,且满足|x-1|+=0,则的算术平方根为( )A.4 B. 4 C. 2 D. 2【答案】C【解析】【分析】本题考查绝对值的非负性,算术平方根的非负性,算术平方根的定义,求代数式的值,关键是先根据绝对值的非负性,算术平方根的非负性求得x,y的值,再代入计算即可解答.【解答】解:因为|x-1|+=0,且|x-1|0,0,所以|x-1|=0,=0,所以x=1,y=15,==4,=2,所以的算术平方根为2.故选C.30.在平面直角坐标系中,点M(a,b)的坐标满足(a-3)2+=0,则点M在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】A【解析】解:∵(a-3)2+=0,∴a=3,b=2,∴点M(3,2),故点M在第一象限.故选:A.直接利用偶次方的性质以及二次根式的性质得出a,b的值,进而确定其所在象限.此题主要考查了非负数的性质,正确得出a,b的值是解题关键.31.若满足,则的平方根是:A. B. C.4 D. 2【答案】B【解析】【分析】此题主要考查了算术平方根以及偶次方的性质,正确把握相关定义是解题关键.直接利用偶次方的性质以及二次根式的性质得出x,y的值,进而利用平方根的定义得出答案.【解答】解:∵,∴x=-2,y=18,则=4的平方根是:±2.故选B.32.若|x﹣2|+=0,则-xy的值为()A. ﹣8B. ﹣6C. 5D. 6【答案】D【解析】【分析】本题考查的是非负数的性质,一元一次方程的解法及代数式的求值.题目注重基础,比较简单.已知任何数的绝对值一定是非负数,二次根式的值一定是一个非负数,由于已知的两个非负数的和是0,根据非负数的性质得到这两个非负数一定都是0,从而得到一个关于x、y的方程组,解方程组就可以得到x、y的值,进而求出-xy的值.【解答】解:∵|x-2|≥0,≥0,而,∴x-2=0且y+3=0,∴x=2,y=-3,∴-xy=-2×(-3)=6.故选D.33.若,则点在第象限.A. 四B. 三C. 二D. 一【答案】D【解析】【分析】本题考查了非负数的性质及平面直角坐标系点的坐标特征,①非负数有最小值是零;②有限个非负数之和仍然是非负数;③有限个非负数的和为零,那么每一个加数也必为零.,初中范围内的非负数有:绝对值,算术平方根和偶次方.先根据非负数的性质求出x和y 的值,再根据平面直角坐标系点的坐标特征判断即可.【解答】解:∵,∴,解之得,∴点在第一象限.故选D.34.若x,y满足|x-3|+=0,则的值是()A. 1B.C.D.【答案】A【解析】解:∵|x-3|+=0,∴x-3=0,x+2y+1=0,解得:∴==1故选:A.根据非负数的性质,非负数之和等于0时,各项都等于0利用此性质列方程解决问题.此题考查了非负数的性质,熟练掌握运算法则是解本题的关键.35.已知+|b+3|=0,则P(-a,-b)的坐标为()A. B. C. D.【答案】C【解析】【分析】本题主要考查了算术平方根和绝对值的非负性的运用,坐标的确定,解答此题可先由数的非负性得到关于a,b的方程,然后解之即可求出a,b的值,从而可得点P的坐标. 【解答】解:∵,∴,解得:,∴点P的坐标为(-2,3),故选C.36.已知,则的值为( )A. 1B. -1C. 2017D. -2017【答案】A【解析】【分析】此题考查了解二元一次方程组,绝对值的非负性及算术平方根的非负性,有理数的乘方,熟练掌握运算法则是解本题的关键.根据非负数的性质列出方程组,求出方程组的解得到a与b的值,即可求出原式的值.【解答】解:∵,∴,解得:,则原式=(1-0)2017=1.故选A.二、填空题(本大题共58小题,共174.0分)37.若实数a、b满足|a+2|,则=______.【答案】1【解析】解:根据题意得:,解得:,则原式==1.故答案是:1.根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.38.若a,b,c为三角形的三边,且a,b满足,第三边c为奇数,则c=________.【答案】9【解析】【分析】本题主要考查了三角形三边关系以及非负数的性质,解题的关键是求出a和b的值,此题难度不大.先根据非负数的性质求出a和b的值,再根据三角形三边关系求出c的取值范围,进而求出c的值.【解答】解:∵a、b满足+(b-2)2=0,∴a-9=0,b-2=0,∴a=9,b=2,∵a、b、c为三角形的三边,∴7<c<11,∵第三边c为奇数,∴c=9.故答案为9.39.已知a、b满足(a-1)2+=0,则a+b=______.【答案】-1【解析】解:∵(a-1)2+=0,∴a=1,b=-2,∴a+b=-1.故答案为:-1.直接利用非负数的性质得出a,b的值,进而得出答案.此题主要考查了非负数的性质,正确得出a,b的值是解题关键.40.已知|2a+1|+=0,则ab= ______ .【答案】1【解析】【分析】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.根据非负数的性质列方程求出a、b的值,然后代入代数式进行计算即可得解.【解答】解:由题意得,2a+1=0,b+2=0,解得a=-,b=-2,所以,ab=(-)×(-2)=1.故答案为1.41.若|x2-16|+=0,则x+y=______.【答案】7或-1【解析】解:∵|x2-16|+=0,∴x2-16=0,y-3=0,解得x=±4,y=3,∴当x=4,y=3时,x+y=4+3=7;或当x=-4,y=3时,x+y=-4+3=-1.故答案为:7或-1.根据非负数的性质和算术平方根的概念求出x、y的值,代入代数式计算即可.本题考查了非负数的性质,掌握当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.42.已知+|3x+2y-15|=0,则的算术平方根为______.【答案】【解析】解:由题意得,x+3=0,3x+2y-15=0,解得x=-3,y=12,所以,==3,所以,的算术平方根为.故答案为:.根据非负数的性质列式求出x、y的值,然后代入代数式进行计算,再根据算术平方根的定义解答.本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.43.若+(b+2)2=0,则点M(a,b)关于y轴的对称点的坐标为______ .【答案】(-3,-2)【解析】解:∵+(b+2)2=0,∴a=3,b=-2;∴点M(a,b)关于y轴的对称点的坐标为(-3,-2).先求出a与b的值,再根据平面直角坐标系中任意一点P(x,y),关于y轴的对称点的坐标是(-x,y),即关于纵轴的对称点,纵坐标不变,横坐标变成相反数;这样就可以求出M的对称点的坐标.本题考查平面直角坐标系中关于坐标轴成轴对称的两点的坐标之间的关系,也考查了非负数的性质.44.如果与(2x﹣4)2互为相反数,那么2x﹣y的平方根是____.【答案】±1【解析】【分析】此题主要考查了平方根以及算术平方根和偶次方的性质,正确得出x,y的值是解题关键.直接利用算术平方根以及偶次方的性质得出2x-y的值,进而得出答案.【解答】解:∵与互为相反数,∴,∴y-3=0,2x-4=0,解得:y=3,x=2,∴2x-y=1,∴2x-y的平方根是:±1.故答案为±1.45.已知,则b a+a c=________.【答案】11【解析】解:根据题意得:a-2=0,b+3=0,c-1=0,解得a=2,b=-3,c=1.则原式=9+2=11.故答案是:11.根据非负数的性质“非负数相加,和为0,这几个非负数的值都为0”求出a、b、c的值,再代入代数式求解.本题主要考查了非负数的性质,初中阶段有三种类型的非负数:(1)绝对值;(2)偶次方;(3)二次根式(算术平方根).当它们的和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.46.若+|b+1|=0,则a-b=______.【答案】3【解析】【分析】本题考查了非负数的性质,掌握几个非负数的和为0,这几个数都为0是解题的关键.根据非负数的性质进行计算即可.【解答】解:∵+|b+1|=0,∴a-2=0,b+1=0,∴a=2,b=-1,∴a-b=2+1=3,故答案为3.47.已知(x-y+1)2+=0,则x+y的值为______.【答案】【解析】解:由题意可知:解得:∴x+y=故答案为:根据非负数的性质以及二元一次方程的解法即可求出答案.本题考查学生的计算能力,解题的关键是正确列出方程组,本题属于基础题型.48.若+|2a-b+1|=0,则(b-a)2016=______.【答案】1【解析】解:∵+|2a-b+1|=0,∴,解得:,则原式=1.故答案为:1.根据题意,利用非负数的性质列出方程组,求出方程组的解得到a与n的值,代入原式计算即可得到结果.此题考查了解二元一次方程组,以及非负数的性质,解方程组利用了消元的思想,消元的方法有:代入消元法与加减消元法.49.已知,则x-20172=_____________。
人教版七年级下知识点试题精选-非负数的性质:算术平方根

非负数的性质:算术平方根一.选择题(共20小题)1.已知非零实数a,b 满足,则a﹣b等于()A.3 B.﹣2 C.1 D.52.已知,那么x﹣y=()A.3 B.﹣3 C.﹣6 D.63.若(x+y)2++|z﹣2y|=0,则x﹣y+z的值()A.0 B.1 C.2 D.44.若与|b+1|互为相反数,则a﹣b的值为()A.B.+1 C.﹣1 D.1﹣5.若|x﹣2|+=0,则x2+y2=()A.10 B.12 C.13 D.不能确定6.,那么(a+b)2012的值为()A.﹣1 B.1 C.﹣52012D.520127.若a,b为实数,且|a+1|+=0,则(ab)2013的值是()A.0 B.1 C.﹣1 D.±18.若实数x、y满足+(y﹣3)2=0,则等于()A.0 B.5 C.4 D.±49.已知+=0,则x﹣y的值为()A.2 B.6 C.2或﹣2 D.6或﹣610.若+(y+2)2=0,则(x+y)2015等于()A.﹣1 B.1 C.32014 D.﹣3201411.若(m﹣3)2+=0,则m+n的平方根是()A.1 B.±1 C.D.±12.若a、b、c为△ABC的三边,且a、b、c满足(a﹣6)2++|c﹣10|=0,则△ABC的周长为()A.48 B.80 C.24 D.4013.+|x﹣3|=0,则x y=()A.81 B.64 C.27 D.6314.若x,y为实数,且|x+1|+=0,则xy的值是()A.1 B.0 C.﹣1 D.﹣215.已知x、y是实数,+(y2﹣6y+9)=0,若axy﹣3x=y,则实数a的值是()A.B.﹣ C.D.﹣16.若(x﹣2)2+=0,则(x+y)2等于()A.2 B.﹣1 C.1 D.2517.若(x+3)2+=0,则(x﹣y)的相反数的值为()A.﹣5 B.﹣1 C.1 D.518.若+(y+3)2=0,则x﹣y的值为()A.1 B.﹣1 C.4 D.﹣719.若,则x2015+y2016的值()A.0 B.1 C.﹣1 D.220.若x,y为实数,且|x+3|+=0,则()2017的值为()A.1 B.2 C.﹣1 D.﹣2二.填空题(共20小题)21.若(a+)2与互为相反数,则a b=.22.已知实数a,b满足,则ab=.23.已知,那么(xy)2005=.24.若+|3﹣y|=0,则2xy=.25.在下列6个等式中,①ab=0;②a+b=0;③;④a2=0;⑤a2+b2=0;⑥中,a一定是零的等式编号是.26.若|x﹣2|和互为相反数,则xy的算术平方根是.27.若实数x,y满足,则xy﹣x2的平方根为.28.已知实数x,y满足+(y+1)2=0,则x﹣y等于.29.已知=0,则b a=.30.已知+|a+b+1|=0,则a b=.31.若(2a+3)2与互为相反数,则a=.b=.32.(a+8)2+|b﹣5|+=0,则a+b+c=.33.|x+1|++(2y﹣4)2=0,则x+y+z=.34.已知|a+2|=0,那么a﹣b=.35.若+=0,则(x﹣1)2+(y+3)2=.36.已知+(y+5)2=0,则(x+y)2012=.37.若(x﹣8)2与互为相反数,则x=y=.38.若a、b为实数,且|a+1|+=0,则的值是.39.当x=时,+5的值最小.40.若x、y为实数,且|x+2|+=0,则(x+y)2016=.三.解答题(共10小题)41.若|m+1|+=0,求m2000﹣n4的值.42.解答下列各题(1)解方程:2(3x﹣1)2=8;(2)已知(x﹣)2+=0,求xy﹣的值.43.已知实数a、b满足,求2a﹣b+1的平方根.44.已知,试求x﹣8y的算术平方根.45.已知|x+3|+=0,求x2﹣6y的值.46.已知x,y满足=0,求x﹣的平方根.47.若二次根式与互为相反数,求2x+3a﹣1的值.48.若+|b2﹣9|=0,求ab的值.49.(1)若(﹣b+1)2与互为相反数,求(a+b)2004的值.(2)已知a的两个平方根为3b﹣1和b+5,求a的值.50.已知实数a,b满足+b2+2b+1=0,求a2+﹣|b|的值.非负数的性质:算术平方根参考答案与试题解析一.选择题(共20小题)1.已知非零实数a,b 满足,则a﹣b等于()A.3 B.﹣2 C.1 D.5【分析】根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.【解答】解:∵(a﹣3)b2≥0,∴a﹣3≥0,∴a≥3,∴2a﹣4>0,∴原式变形为|b+2|+=0,∴b+2=0,(a﹣3)b2=0,∴b=﹣2,a=3,∴a﹣b=3﹣(﹣2)=5.故选D.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.2.已知,那么x﹣y=()A.3 B.﹣3 C.﹣6 D.6【分析】根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.【解答】解:根据题意得:,解得:,则x﹣y=3﹣6=﹣3.故选B.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.3.若(x+y)2++|z﹣2y|=0,则x﹣y+z的值()A.0 B.1 C.2 D.4【分析】根据非负数的性质列出方程,解方程求出x、y、z的值,代入代数式计算即可.【解答】解:由题意得,x+y=0,2x﹣4=0,z﹣2y=0,解得x=2,y=﹣2,z=﹣4,则x﹣y+z=0.故选:A.【点评】本题考查的是非负数的性质,掌握非负数之和等于0时,各项都等于0是解题的关键.4.若与|b+1|互为相反数,则a﹣b的值为()A.B.+1 C.﹣1 D.1﹣【分析】由非负数的性质可知a=﹣,b=﹣1,然后求得a﹣b的值即可.【解答】解:∵与|b+1|互为相反数,∴+|b+1|=0.∴a=﹣,b=﹣1.∴a﹣b=﹣﹣(﹣1)=﹣+1.故选D.【点评】本题主要考查的是非负数的性质,掌握非负数的性质是解题的关键.5.若|x﹣2|+=0,则x2+y2=()A.10 B.12 C.13 D.不能确定【分析】根据非负数的性质列式求解即可得到x、y的值,然后代入代数式进行计算即可.【解答】解:根据题意得,x﹣2=0,y﹣3=0,解得x=2,y=3,∴x2+y2=22+32=4+9=13.故选C.【点评】本题考查了算术平方根非负数,绝对值非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是求解的关键.6.,那么(a+b)2012的值为()A.﹣1 B.1 C.﹣52012D.52012【分析】根据非负数的性质列式求出a、b的值,然后代入代数式进行计算即可得解.【解答】解:根据题意得,3+a=0,b﹣2=0,解得a=﹣3,b=2,所以(a+b)2012=(﹣3+2)2012=1.故选B.【点评】本题考查了绝对值非负数,算术平方根非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是解题的关键.7.若a,b为实数,且|a+1|+=0,则(ab)2013的值是()A.0 B.1 C.﹣1 D.±1【分析】根据非负数的性质列式求出a、b,然后代入代数式进行计算即可得解.【解答】解:根据题意得,a+1=0,b﹣1=0,解得a=﹣1,b=1,所以,(ab)2013=(﹣1×1)2013=﹣1.故选:C.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.8.若实数x、y满足+(y﹣3)2=0,则等于()A.0 B.5 C.4 D.±4【分析】根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.【解答】解:∵+(y﹣3)2=0,∴x﹣2=0,y﹣3=0,解得x=2,y=3,∴==4,故选C.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.9.已知+=0,则x﹣y的值为()A.2 B.6 C.2或﹣2 D.6或﹣6【分析】根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.【解答】解:根据题意得:,解得:x=2,y=﹣4或x=﹣2,y=4.则x﹣y=6或﹣6.故选D.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.10.若+(y+2)2=0,则(x+y)2015等于()A.﹣1 B.1 C.32014 D.﹣32014【分析】根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.【解答】解:∵+(y+2)2=0,∴x=1,y=﹣2,∴(x+y)2015=(1﹣2)2015=﹣1,故选A.【点评】本题考查了非负数的性质:算术平方根和偶次方,几个非负数的和为0时,这几个非负数都为0.11.若(m﹣3)2+=0,则m+n的平方根是()A.1 B.±1 C.D.±【分析】根据非负数的性质列出算式,求出m、n的值,根据平方根的概念解答即可.【解答】解:由题意得,m﹣3=0,n+2=0,解得,m=3,n=﹣2,则m+n=1,则m+n的平方根是±1,故选:B.【点评】本题考查的是非负数的性质,掌握几个非负数的和为0时,这几个非负数都为0是解题的关键.12.若a、b、c为△ABC的三边,且a、b、c满足(a﹣6)2++|c﹣10|=0,则△ABC的周长为()A.48 B.80 C.24 D.40【分析】根据非负数的性质列出算式,求出a、b、c的值,根据三角形的周长公式计算即可.【解答】解:由题意得,a﹣6=0,b﹣8=0,c=10=0,解得,a=6,b=8,c=10,则△ABC的周长=a+b+c=24,故选:C.【点评】本题考查的是非负数的性质,掌握几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.13.+|x﹣3|=0,则x y=()A.81 B.64 C.27 D.63【分析】根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.【解答】解:由题意得,x﹣y+1=0,x﹣3=0,解得x=3,y=4,所以,x y=34=81.故选A.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.14.若x,y为实数,且|x+1|+=0,则xy的值是()A.1 B.0 C.﹣1 D.﹣2【分析】根据非负数的性质列方程求出x、y的值,然后代入代数式进行计算即可得解.【解答】解:由题意得,x+1=0,y﹣1=0,解得x=﹣1,y=1,所以,xy=(﹣1)×1=﹣1.故选C.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.15.已知x、y是实数,+(y2﹣6y+9)=0,若axy﹣3x=y,则实数a的值是()A.B.﹣ C.D.﹣【分析】由于y2﹣6y十9可以写成完全平方式,那么此题就是两个非负数相加为0,意味着每个式子都为0,由此可以求出x和y,然后代入方程计算即可.【解答】解:∵十y2﹣6y十9=0,∴十(y﹣3)2=0∵3x+4=0,y﹣3=0∴x=﹣,y=3,把x,y代入axy﹣3x=y,∴a=.故选A.【点评】主要考查了非负数的性质,解题关键是利用理解两个非负数的和要为0,那只有让这两个非负数为0.16.若(x﹣2)2+=0,则(x+y)2等于()A.2 B.﹣1 C.1 D.25【分析】根据非负数的性质,两个非负数的和是0,则这两非负数同时是0,即可解答.【解答】解:根据题意得:x﹣2=0,y+3=0解得:x=2,y=﹣3;∴(x+y)2=(2﹣3)2=1.故选C.【点评】此题主要考查了非负数的性质,非负数的性质:有限个非负数的和为零,那么每一个加数也必为零,即若a1,a2,…,a n为非负数,且a1+a2+…+a n=0,则必有a1=a2=…=a n=0.17.若(x+3)2+=0,则(x﹣y)的相反数的值为()A.﹣5 B.﹣1 C.1 D.5【分析】根据非负数的性质,可求出x、y的值,进而可求出(x﹣y)的相反数.【解答】解:由题意,得:x+3=0,y﹣2=0,即x=﹣3,y=2,∴x﹣y=﹣3﹣2=﹣5∴﹣(x﹣y)=5.故选D.【点评】此题考查了非负数的性质以及相反数的定义;非负数的性质:非负数的和为0,则每个非负数也必为0;相反数:符号相反,绝对值相等的两个数互为相反数.18.若+(y+3)2=0,则x﹣y的值为()A.1 B.﹣1 C.4 D.﹣7【分析】根据非负数的性质得到关于x、y的方程,解方程求出x、y的值,计算的答案.【解答】解:由题意得,x﹣1=0,y+3=0,解得,x=1,y=﹣3,则x﹣y=1﹣(﹣3)=4,故选:C.【点评】本题考查了非负数的性质,掌握几个非负数的和为0时,这几个非负数都为0是解题的关键.19.若,则x2015+y2016的值()A.0 B.1 C.﹣1 D.2【分析】根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.【解答】解:∵,∴x﹣1=0,x+y=0,∴x=1,y=﹣1,∴x2015+y2016=2,故选D.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.20.若x,y为实数,且|x+3|+=0,则()2017的值为()A.1 B.2 C.﹣1 D.﹣2【分析】根据非负数的性质进行计算即可.【解答】解:∵|x+3|+=0,∴x+3=0,y﹣3=0,∴x=﹣3,y=3,∴()2017=(﹣1)2017=﹣1,故选C.【点评】本题考查了非负数的性质,掌握几个非负数的和为0,这几个数都为0是解题的关键.二.填空题(共20小题)21.若(a+)2与互为相反数,则a b=﹣.【分析】先由一对相反数的和为0,得出(a+)2+=0,再根据非负数的性质求出a与b的值,然后代入所求代数式,计算即可.【解答】解:∵(a+)2与互为相反数,∴(a+)2+=0,∴a+=0,b﹣3=0,∴a=﹣,b=3,∴a b=(﹣)3=﹣.故答案为﹣.【点评】本题考查了相反数、非负数的性质,方程组的解法及代数式求值,关键是根据相反数及非负数的性质求得未知数的解.22.已知实数a,b满足,则ab=﹣4.【分析】根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.【解答】解:根据题意得:,解得:,则ab=﹣4.故答案是:﹣4.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.23.已知,那么(xy)2005=﹣1.【分析】先根据非负数的性质列出关于x、y的方程,求出x、y的值,再把x、y 的值代入所求代数式进行计算即可.【解答】解:∵|2x+1|+=0,∴2x+1=0,解得x=﹣;2﹣y=0,解得y=2.∴(xy)2005=[(﹣)×2]2005=(﹣1)2005=﹣1.故答案为:﹣1.【点评】本题考查的是非负数的性质,几个非负数的和为0时,这几个非负数都为0.24.若+|3﹣y|=0,则2xy=3.【分析】根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.【解答】解:由题意得,4x﹣2=0,3﹣y=0,解得x=,y=3,所以,2xy=2××3=3.故答案为:3.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.25.在下列6个等式中,①ab=0;②a+b=0;③;④a2=0;⑤a2+b2=0;⑥中,a一定是零的等式编号是③④⑤⑥.【分析】①②中,a值可能为0但不是一定为0;③式中,由于分式的分母不为0,因此当分式的值为0时,只有分子为0一种情况,因此a必为0;④⑤⑥可根据非负数的性质求出a值必为0.因此a值一定为0的式子有③④⑤⑥.【解答】解:因为:①ab=0,则a=0或b=0;②a+b=0,则a=﹣b;这两项的a 值不一定为0.③,则a=0且b≠0;④a2=0,则a=0;⑤a2+b2=0,则a=0且b=0;⑥,则a=0且b=0;因此只有③④⑤⑥的a值一定是零.故答案为:③④⑤⑥.【点评】本题考查了非负数的性质.初中阶段有三种类型的非负数:(1)绝对值;(2)偶次方;(3)二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.26.若|x﹣2|和互为相反数,则xy的算术平方根是4.【分析】先列出算式,再由非负数的和为0,即两个0相加,求得x,y的值,再求xy的算术平方根.【解答】解:∵|x﹣2|+=0,∴x﹣2=0,y﹣8=0,解得x=2,y=8,∴xy=2×8=16,∴xy的算术平方根是4.【点评】本题考查了算术平方根的求法和相反数的性质,两个数互为相反数,则和为0.27.若实数x,y满足,则xy﹣x2的平方根为±.【分析】根据非负数的性质列式求出x、y的值,再代入代数式进行计算,再根据平方根的定义进行求解.【解答】解:根据题意得,x﹣2=0,3﹣y=0,解得x=2,y=3,∴xy﹣x2=2×3﹣22=6﹣4=2,∴xy﹣x2的平方根为±.故答案为:±.【点评】本题考查了算术平方根非负数,偶次方非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是解题的关键.28.已知实数x,y满足+(y+1)2=0,则x﹣y等于3.【分析】根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.【解答】解:根据题意得,x﹣2=0,y+1=0,解得x=2,y=﹣1,所以,x﹣y=2﹣(﹣1)=2+1=3.故答案为:3.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.29.已知=0,则b a=﹣.【分析】根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.【解答】解:∵=0,∴a﹣3=0,b+=0,∴a=3,b=﹣,∴b a=(﹣)3=﹣.故答案为﹣.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.30.已知+|a+b+1|=0,则a b=1.【分析】根据非负数的性质列式求出a、b的值,然后代入代数式进行计算即可得解.【解答】解:由题意得,a+1=0,a+b+1=0,解得a=﹣1,b=0,所以,a b=(﹣1)0=1.故答案为:1.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.31.若(2a+3)2与互为相反数,则a=﹣.b=2.【分析】根据互为相反数的两个数的和等于0列出方程,再根据非负数的性质列式求解即可得到a、b的值.【解答】解:∵(2a+3)2与互为相反数,∴(2a+3)2+=0,∴2a+3=0,b﹣2=0,解得a=﹣,b=2.故答案为:﹣,2.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.32.(a+8)2+|b﹣5|+=0,则a+b+c=0.【分析】根据非负数的性质求出a、b、c的值,计算即可.【解答】解:由题意得,a+8=0,b﹣5=0,3﹣c=0,解得,a=﹣8,b=5,c=3,则a+b+c=0,故答案为:0.【点评】本题考查的是非负数的性质,掌握当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.33.|x+1|++(2y﹣4)2=0,则x+y+z=3.【分析】根据非负数的性质列式求出x、y、z的值,然后代入代数式进行计算即可得解.【解答】解:由题意得,x+1=0,z﹣2=0,2y﹣4=0,解得x=﹣1,y=2,z=2,所以,x+y+z=﹣1+2+2=3.故答案为:3.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.34.已知|a+2|=0,那么a﹣b=﹣7.【分析】根据非负数的性质列出算式,分别求出a、b的值,计算即可.【解答】解:由题意得,a+2=0,b﹣5=0,解得,a=﹣2,b=5,则a﹣b=﹣7,故答案为:﹣7.【点评】本题考查的是非负数的性质,掌握非负数之和等于0时,各项都等于0是解题的关键.35.若+=0,则(x﹣1)2+(y+3)2=25.【分析】首先根据非负数的性质可求出x、y的值,再将它们的值代入(x﹣1)2+(y+3)2中求解即可.【解答】解:由题意得x﹣1=0,y﹣2=0;即x=1,y=2;则(x﹣1)2+(y+3)2=(1﹣1)2+(2+3)2=25.故答案为:25.【点评】此题主要考查了非负数的性质,初中阶段有三种类型的非负数:(1)绝对值;(2)偶次方;(3)二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.36.已知+(y+5)2=0,则(x+y)2012=1.【分析】直接利用算术平方根的定义以及偶次方的性质得出x,y的值进而代入求出即可.【解答】解:∵+(y+5)2=0,∴x﹣4=0,y+5=0,解得:x=4,y=﹣5,则(x+y)2012=(4﹣5)2012=1.故答案为:1.【点评】此题主要考查了算术平方根的定义以及偶次方的性质,得出x,y的值是解题关键.37.若(x﹣8)2与互为相反数,则x=8y=2.【分析】利用互为相反数两数之和为0列出关系式,利用非负数的性质求出x与y的值即可.【解答】解:根据题意得:(x﹣8)2+=0,可得x﹣8=0,y﹣2=0,解得:x=8,y=2.故答案为:8;2.【点评】此题考查了非负数的性质:算术平方根及偶次幂,熟练掌握非负数的性质是解本题的关键.38.若a、b为实数,且|a+1|+=0,则的值是.【分析】根据非负数的和为零,可得每个非负数为零,可得a、b的值,根据负数的奇数次幂是负数,可得答案.【解答】解:由|a+1|+=0,得a+1=0,a+b=0,解得a=﹣1,b=1.=(﹣1)2015=﹣1,故答案为:﹣1.【点评】本题考查了非负数的性质,利用非负数的和为零得出a、b的值是解题关键,注意负数的奇数次幂是负数.39.当x=﹣时,+5的值最小.【分析】根据算术平方根具有非负性可得7x+1=0,再解即可.【解答】解:∵≥0,∴当=0时,+5的值最小,由=0得:7x+1=0,解得:x=﹣.故答案为:﹣.【点评】此题主要考查了非负数的性质,关键是掌握算术平方根具有非负性.40.若x、y为实数,且|x+2|+=0,则(x+y)2016=1.【分析】根据绝对值与算术平方根的和为零,可得绝对值与算术平方根同时为零,可得x、y的值,再根据负数的奇数次幂是负数,可得答案.【解答】解:∵|x+2|+=0,∴x+2=0,y﹣3=0,∴x=﹣2,y=3,∴(x+y)2016=1.故答案为:1.【点评】本题考查了非负数的性质,利用绝对值与算术平方根的和为零得出绝对值与算术平方根同时为零是解题关键,注意负数的奇数次幂是负数.三.解答题(共10小题)41.若|m+1|+=0,求m2000﹣n4的值.【分析】根据非负数的性质列式求出m、n,然后代入代数式进行计算即可得解.【解答】解:由题意得,m+1=0,2n﹣1=0,解得m=﹣1,n=,所以,m2000﹣n4=(﹣1)2000﹣()4=1﹣=.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.42.解答下列各题(1)解方程:2(3x﹣1)2=8;(2)已知(x﹣)2+=0,求xy﹣的值.【分析】(1)利用直接开方法求出x的值即可;(2)先根据非负数的性质求出x、y的值,再代入所求代数式进行计算即可.【解答】解:(1)方程两边同时除以2得,(3x﹣1)2=4,直接开方得,3x﹣1=±=±2,解得,x=1或x=﹣;(2)∵(x﹣)2+=0,∴x﹣=0,y+=0,解得x=,y=﹣,∴原式=×(﹣)+=﹣2+=﹣.【点评】本题考查的是非负数的性质及利用直接开方法解一元二次方程,在解答(1)时要注意一个数的平方根有两个,这两个数互为相反数,不要漏解.43.已知实数a、b满足,求2a﹣b+1的平方根.【分析】根据非负数的性质列出二元一次方程组,求出a、b的值,然后代入代数式进行计算,再根据平方根的定义解答.【解答】解:根据题意得,,解得,所以,2a﹣b+1=2×﹣+1=4,∵(±2)2=4,∴2a﹣b+1的平方根是±2.【点评】本题考查了平方数非负数,算术平方根非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是解题的关键.44.已知,试求x﹣8y的算术平方根.【分析】根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.【解答】解:根据题意得:,解得:x=1,y=﹣1.则x﹣8y=1+8=9,则算术平方根是:3.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.45.已知|x+3|+=0,求x2﹣6y的值.【分析】根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.【解答】解:由题知,x+3=0,2﹣3y=0,解得x=﹣3,y=,所以,x2﹣6y=(﹣3)2﹣6×=9﹣4=5.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.46.已知x,y满足=0,求x﹣的平方根.【分析】根据非负数的性质列出算式求出x、y的值,代入代数式计算,根据平方根的概念计算得到答案.【解答】解:由题意得,2x﹣16=0,y﹣1=0,解得,x=8,y=5,则x﹣=4,4的平方根是±2,则x﹣的平方根是±2.【点评】本题考查的是非负数的性质,掌握几个非负数的和为0时,这几个非负数都为0是解题的关键,注意平方根的概念的应用.47.若二次根式与互为相反数,求2x+3a﹣1的值.【分析】直接利用二次根式有意义的条件得出a,x的值,进而代入求出答案.【解答】解:∵二次根式与互为相反数,∴3﹣a=0,x2﹣1=0,解得:a=3,x=±1∴当x=1时,2x+3a﹣1=2+9﹣1=10,当x=﹣1时,2x+3a﹣1=﹣2+9﹣1=6.【点评】此题主要考查了非负数的性质,正确得出a,x的值是解题关键.48.若+|b2﹣9|=0,求ab的值.【分析】首先根据非负数的性质可求出a、b的值,进而可求出a、b的积.【解答】解:∵+|b2﹣9|=0,∴a﹣2=0,b2﹣9=0,解得a=2,b=±3,当a=2,b=3时,ab=6当a=2,b=﹣3时,ab=﹣6.【点评】本题主要考查了非负数的性质,初中阶段有三种类型的非负数:绝对值、偶次方、二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.49.(1)若(﹣b+1)2与互为相反数,求(a+b)2004的值.(2)已知a的两个平方根为3b﹣1和b+5,求a的值.【分析】(1)根据非负数的性质,两个非负数的和等于0,则每个数等于0,据此即可列方程求得a、b的值,进而求解;(2)根据正数的两个平方根互为相反数,据此列方程求得b的值,进而求得a 的值.【解答】解:(1)根据题意得:,解得:,则(a+b)2004=0;(2)根据题意得(3b﹣1)+(b+5)=0,解得:b=﹣1,则a=(3b﹣1)2=(﹣4)2=16.【点评】本题考查了非负数的性质以及算术平方根的性质,理解非负数的性质是关键.50.已知实数a,b满足+b2+2b+1=0,求a2+﹣|b|的值.【分析】首先依据非负数的性质得到a2﹣5a+1=0,b=﹣1,然后再求得a+=5,然后利用完全平方公式求得a2+的值,最后代入求解即可.【解答】解:∵实数a,b满足+b2+2b+1=0,∴a2﹣5a+1=0,b+1=0,∴a+=5,b=﹣1.∴a2+=23.∴原式=23﹣|﹣1|=23﹣1=22.【点评】本题主要考查的是非负数的性质,求得a2+的值是解题的关键.。
平方根(3个知识点+6类热点题型讲练+习题巩固)(原卷版)七年级数学下册
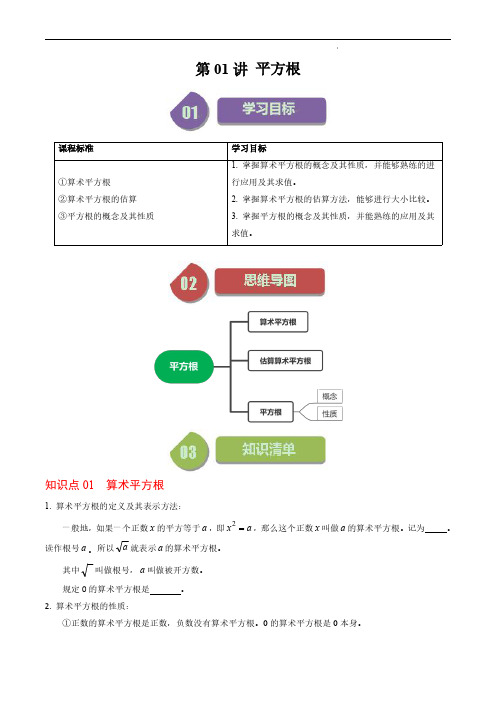
第01讲平方根课程标准学习目标①算术平方根②算术平方根的估算③平方根的概念及其性质1.掌握算术平方根的概念及其性质,并能够熟练的进行应用及其求值。
2.掌握算术平方根的估算方法,能够进行大小比较。
3.掌握平方根的概念及其性质,并能熟练的应用及其求值。
知识点01算术平方根1.算术平方根的定义及其表示方法:一般地,如果一个正数x 的平方等于a ,即a x 2,那么这个正数x 叫做a 的算术平方根。
记为。
读作根号a 。
所以a 就表示a 的算术平方根。
其中叫做根号,a 叫做被开方数。
规定0的算术平方根是。
2.算术平方根的性质:①正数的算术平方根是正数,负数没有算术平方根。
0的算术平方根是0本身。
②算术平方根的双重非负性:只有才有算术平方根,且它的算术平方根也是一个。
所以算术平方根本身,算术平方根的被开方数也。
即a0,a0。
非负性的应用:几个非负数的和等于0,则这几个非负数分别等于0。
即若0...=+++m b a ,则====m b a ...。
③一个正数的算术平方根的平方等于这个数本身。
即()=2a 。
④一个数的平方的算术平方根等于这个数的绝对值。
再根据这个数的正负去绝对值符号。
即=2a 。
【即学即练1】1.求下列各数的算术平方根.(1)196(2)(3)0.04(4)102.【即学即练2】2.(1)=,=,=,=,=,对于任意实数0,猜想=.(2)()2=,()2=,()2=,()2=,对于任意非负数a ,猜想()2=.【即学即练3】3.如果,则=.知识点02估算算术平方根1.估算算术平方根的方法——夹逼法:具体步骤:①估算被开方数在那两个完全平方数之间(若一个数能被写成某个整数的平方,则称这个数为平方数);②确定无理数的整数步骤;③按要求估算。
理论依据:被开方数越大,则对应的算术平方根也越大。
【即学即练1】4.请你估算的大小,大致范围是()A .1<<2B .2<<3C .3<<4D .4<<5知识点03平方根的概念与性质1.平方根的概念:如果一个数的平方等于a ,则这个数就叫做a 的,也叫做a 的二次方根。
部编数学七年级下册专题07算术平方根的非负性(解析版)含答案

专题07 算术平方根的非负性【例题讲解】例1.已知a 、b 、c2+=c a b c ++的平方根为_________.例2.2|1|(1)0b c +++=,求a b c +-的平方根.【综合解答】1.设,A B 均为实数,且A B ==,A B 的大小关系是( )A .A B>B .A B =C .A B <D .A B³【答案】D【解析】【分析】根据算术平方根的定义得出A 是一个非负数,且m-3≥0,推出3-m≤0,得出B≤0,即可得出答案,【详解】解:∵A =∴A 是一个非负数,且m-3≥0,∴m≥3,∵B =,∵3-m≤0,即B≤0,∴A≥B ,故选:D .【点睛】本题考查了算术平方根的定义,平方根和立方根,实数的大小比较等知识点,题目比较好,但有一定的难度.2()240y -=,则22x y +的平方根是______.【答案】【解析】【分析】根据算术平方根以及完全平方式的非负性得出,x y 的值,然后求出22xy +的值,最后求出平方根即可.【详解】解:()240y +-=,∴50,40x y +=-=,∴5,4x y =-=,∴2222(5)4251641x y =-=+=++,∴22x y +的平方根是故答案为:【点睛】本题考查了算术平方根以及完全平方式的非负性、平方根,解题的关键是掌握非负数的性质:有限个非负数的和为零,那么每一个加数也必为零.3.若()230x +=,则()2021x y +=______________.【答案】-1【解析】【分析】由平方与算术平方根的非负性解得x =-3,y =2,再代入计算即可.【详解】解:由题意得,3020,x y +=-=3,2x y \=-=()()20212021-32=-1x y \+=+故答案为:-1.【点睛】本题考查平方与算术平方根的非负性、有理数的乘方等知识,是基础考点,掌握相关知识是解题关键.4.若a __.【答案】2【解析】【分析】利用算术平方根的非负性,计算求值即可;【详解】解:,20a -£,∴a =0,∴=0+2,=2,故答案为:2;【点睛】此题主要考查了算术平方根:如果一个非负数b 的平方等于a ,那么b 叫做a 的算术平方根;非负数a a 叫做被开方数.5.若3y =,则xy =_________.【答案】18【解析】【分析】直接利用二次根式有意义的条件得出x ,y 的值进而得出答案.【详解】解:∴2﹣x ≥0,且x ﹣2≥0,解得:x =2,∴y =-3,∴31=2=8y x -.故答案为:18.【点睛】此题主要考查了二次根式有意义的条件和负指数幂法则,正确得出x 的值是解题关键.6.已知实数a 在数轴上的位置如图,则化简|1﹣_____.【答案】1-2a【解析】【详解】由图可知:10a -<<,∴10a ->,∴11()12a a a -=-+-=-.故答案为12a -.7.当x =______时,式子2018【答案】2017【解析】【分析】0³,然后求解即可.【详解】解:∵2018∴的值最小时,式子20180³,∴20170x -³,∴2017x ³,∴当2017x =时式子2018有最大值.故答案为:2017.【点睛】此题考查了算术平方根的非负性,当被减数为固定值时,要使差最大,则需使减数的值最小,解题的关键是熟练掌握算术平方根的非负性.8.已知a ,b ,c 满足2|(0a c +=.求a 、b 、c 的值【答案】a =5b ,c 【解析】【分析】利用绝对值非负性,算术平方根非负性,平方非负性可求得结果.【详解】解:∵|0a ³0³,2(0c ³且2|(0a c =,∴|=0a ,2(=0c ,即:a ,5=0b -,c ,解得:a =5b ,c 【点睛】本题主要考查的是非负性求值的应用,此类型题较为固定,同时也是常考点,掌握其解题步骤是解题关键.9.已知3y =,求(x +y )2022的值【答案】1【解析】【分析】根据二次根式的性质得到2x =,计算出1x y +=-,从而计算出最终的答案.【详解】∵3y +-∴2020x x -³ìí-³î得22x x ³ìí£î∴2x =∴33y +=-∴202220222022()(23)(1)1x y +=-=-=∴2022()1x y +=.【点睛】本题考查二次根式、幂运算的性质,解题的关键是熟练掌握二次根式、幂运算的相关知识.10.已知实数a 、b 、c |1|a +=(1)求证:b c =;(2)求a b c -++的平方根.【答案】(1)见解析(2)3±【解析】【分析】根据算术平方根的非负性,即可得证;(2)根据(1)的结论,以及非负数之和为0,求得,,a b c 的值,进而求得a b c -++的平方根.(1)证明:0³0,0,0b c c b -³-³,b c \=;(2)解:Q |1|a +=b c =,,1,4a b \=-=,4c b \==,1449a b c \-++=++=,9的平方根是3±.【点睛】本题考查了算术平方根的非负性,非负数之和为0,掌握非负数的性质以及算术平方根的非负性是解题的关键.115的最小值,并求出此时a 的值.【答案】3a =【解析】【分析】根据非负数的性质即可得到结论.【详解】解:0³55³5的最小值是5.此时30a -=,即3a =.【点睛】12.若a ,b 为实数,且b =【答案】-3【解析】【分析】根据二次根式的被开方数为非负数,得到相应的关系式求出a 、b 的值,然后代入求解.【详解】因为a ,b 为实数,且a 2-1≥0,1-a 2≥0,所以a 2-1=1-a 2=0.所以a =±1.又因为a +1≠0,所以a =1.代入原式,得b =12.所以3.【点睛】此题主要考查了二次根式的性质和意义,关键是利用被开方数为非负数的性质求出a 、b 的值.13.已知数a 满足2016a =,求22016a -.【答案】2017.【解析】【详解】试题分析:由二次根式的意义可得20170a -³,即2017a ³,由此可得20162016a a -=-,从而原等式化为:2016a a -=,由此可得220172016a -=,即220162017a -=;试题解析:由二次根式的意义可得20170a -³,即2017a ³,∴20162016a a -=-,∴原等式可化为:2016a a -=,2016=,∴220172016a -=,∴220162017a -=.14.已知a,b (0b -=,求a2005-b2006的值.【答案】-2【解析】【详解】试题分析:根据被开方数大于等于0,求出b 的取值范围,再根据非负数的性质列式求出a 、b 的值,然后代入代数式进行计算即可得解.试题解析:解:由题意得:1﹣b ≥0,∴b ≤1,∴(10b +-=,由非负数的性质得:1+a =0,1﹣b =0,解得a =﹣1,b =1,∴a 2005﹣b 2006=(﹣1)2005﹣12006=﹣1﹣1=﹣2.15.已知实数,b ,c 满足a +=(2a b +的值.【答案】4【解析】【分析】根据二次根式的非负性求得b 的值,然后根据非负数的性质求得,a c 的值,最后代入代数式求解即可.【详解】解:∵a +=∴5050b b -³ìí-³î,5b \=,\a +=0,3,2a c \=-=,\(2a b +()23504=-+-=.【点睛】本题考查了二次根式的非负性,非负数的性质,掌握二次根式的非负性是解题的关键.。
人教版七年级数学下册6.1《平方根(第1课时)算术平方根 》习题含答案

6.1 平方根第1课时算术平方根一、选择题(共10小题)1.9的算术平方根为()A.3 B.C.D.±32.的值等于()A.4 B.﹣4 C.±4 D.±23.如果=5,那么y的值是()A.5 B.﹣5 C.10 D.254.某数的算术平方根等于它本身,那么这个数一定是()A.0 B.1 C.1或0 D.﹣15.一个自然数的算术平方根为a,则下一个自然数的算术平方根是()A.B.C.﹣a+1 D.a2+16.的值等于()A.B.﹣C.±D.7.的算术平方根是()A.±B.C.±D.58.一个矩形的围栏,长是宽的2倍,面积是30m2,则它的宽为()A.m B.2m C.m D.2m 9.若|x|=3,y是4的算术平方根,且|y﹣x|=x﹣y,则x+y的值是()A.5 B.﹣5 C.1 D.﹣110.若a、b为实数,且满足,则b﹣a的值为()A.1 B.0 C.﹣1 D.以上都不对二、填空题(共8小题)11.(﹣9)2算术平方根是.12.的算术平方根是.13.计算:(﹣2)3+=;1﹣=.14.若=2,则x的值为.15.的算术平方根是3,则a=.16.若与互为相反数,则x=,y=.三、解答题(共6小题)17.求下列各式的值:(1);(2);(3);(4);(5).18.求下列各数的算术平方根:121,,1.96,(-10)6.19.已知2a﹣1的算术平方根是3,18﹣b的算术平方根是4,求a+2b的算术平方根.20.小华的书房面积为10.8m2,她数了一下地面所铺的正方形地砖正好是120块,请问每块地砖的边长是多少?21.探究发散:(1)填空:①=;②=;③=;④=;⑤=;⑥=.(2)根据计算结果回答:一定等于a吗?你发现其中的规律了吗?请你用自己的语言描述出来.22.根据如表回答下列问题:x16.2 16.3 16.4 16.5 16.6 16.7 16.8 16.9 17.0 x2262.44 265.69 268.96 272.25 275.56 278.89 282.24 285.61 289 (1)275.56的平方根是;(2)=;(3)在哪两个相邻数之间?为什么?参考答案与试题解析一、选择题(共10小题)1.实数9的算术平方根为()A.3 B.C.D.±3【解答】解:∵32=9,∴9的算术平方根是3.故选:A.2.的值等于()A.4 B.﹣4 C.±4 D.±2【解答】解:=4.故选:A.3.如果=5,那么y的值是()A.5 B.﹣5 C.10 D.25【解答】解:因为=5,所以y=25,故选:D.4.某数的算术平方根等于它本身,那么这个数一定是()A.0 B.1 C.1或0 D.﹣1【解答】解:某数的算术平方根等于它本身,那么这个数一定是1或0.故选:C.5.一个自然数的算术平方根为a,则下一个自然数的算术平方根是()A.B.C.﹣a+1 D.a2+1【解答】解:一个自然数的算术平方根为a,则下一个自然数的算术平方根是,故选:B.6.的值等于()A.B.﹣C.±D.【解答】解:原式==,故选:A.7.的算术平方根是()A.±B.C.±D.5【解答】解:因为=5,所以的算术平方根是,故选:B.8.一个矩形的围栏,长是宽的2倍,面积是30m2,则它的宽为()A.m B.2m C.m D.2m【解答】解:∵一个矩形的围栏,长是宽的2倍,面积是30m2,∴它的宽为:=(m).故选:A.9.若|x|=3,y是4的算术平方根,且|y﹣x|=x﹣y,则x+y的值是()A.5 B.﹣5 C.1 D.﹣1【解答】解:因为|y﹣x|≥0,所以x﹣y≥0,即x≥y.由|x|=3,y是4的算术平方根可知x=3、y=2.则x+y=5,故选:A.10.若a、b为实数,且满足,则b﹣a的值为()A.1 B.0 C.﹣1 D.以上都不对【解答】解:由题意得,a﹣2=0,3﹣b=0,解得,a=2,b=3,则b﹣a=1,故选:A.二、填空题(共8小题)11.(﹣9)2的算术平方根是9 .【解答】解:∵(﹣9)2=81,∴(﹣9)2的算术平方根是9,故答案为:912.的算术平方根是.【解答】解:∵=,∴的算术平方根为,故答案为:.13.计算:(﹣2)3+=﹣5 .计算:1﹣=.【解答】解;原式=﹣8+3=﹣5;原式=1﹣=,故答案为:﹣5,14.若=2,则x的值为 5 .【解答】解:由=2,得到x﹣1=4,解得:x=5.故答案为:5.15.的算术平方根是3,则a=80 .【解答】解:∵的算术平方根是3,∴=9,a+1=81a=80,故答案为80.16.若与互为相反数,则x=8 ,y= 2 .【解答】解:∵与互为相反数,∴+=0,所以,x﹣8=0,y﹣2=0,解得x=8,y=2.故答案为:8,2.三、解答题(共6小题)17.求下列各式的值:(1);(2);(3);(4);(5)【解答】解:(1)=7;(2)=;(3)=0.3;(4)=1.2;(5)=0.1.18.求下列各数的算术平方根:121,,1.96,(-10)6.【解答】解:=11、=、=1.4、()6-=1000.1019.已知2a﹣1的算术平方根是3,18﹣b的算术平方根是4,求a+2b的算术平方根.【解答】解:由题意可知:2a﹣1=9,18﹣b=16.解得:a=5,b=2.∴a+2b=5+2×2=9.∴a+2b的算术平方根是3.20.小华的书房面积为10.8 m2,她数了一下地面所铺的正方形地砖正好是120块,请问每块地砖的边长是多少?【解答】解:设每块地砖的边长是x m,则有120x2=10.8,即x2=0.09.∵x>0,∴x=0.3.答:每块地砖的边长为0.3 m.21.探究发散:(1)填空:①= 3 ;②=0.5 ;③= 6 ;④=0 ;⑤=;⑥=.(2)根据计算结果回答:一定等于a吗?你发现其中的规律了吗?请你用自己的语言描述出来.【解答】解:(1)①==3;=0.5;==6;④=0;⑤=;⑥=故答案为:3;0.5;6;0;;;(2)不一定等于a,当a<0时,=﹣a;当a≥0时,=a;故不一定等于a;从中可以得到规律:正数和零的平方的算术平方根为其本身,负数的平方的算术平方根为其相反数.22.根据如表回答下列问题:x16.2 16.3 16.4 16.5 16.6 16.7 16.8 16.9 17.0 x2262.44 265.69 268.96 272.25 275.56 278.89 282.24 285.61 289 (1)275.56的平方根是±16.6 ;(2)= 1.68 ;(3)在哪两个相邻数之间?为什么?【解答】解:(1)±=±16.6,(2)=1.68,(3)由表得在16.4与16.5之间;故答案为±16.6,1.68.。
七下数学每日一练:非负数的性质:算术平方根练习题及答案_2020年填空题版

七下数学每日一练:非负数的性质:算术平方根练习题及答案_2020年填空题版答案答案答案答案答案答案答案答案答案答案2020年七下数学:数与式_二次根式_非负数的性质:算术平方根练习题~~第1题~~(2019谢家集.七下期中) 若 ,则a =________.考点: 绝对值的非负性;非负数的性质:算术平方根;~~第2题~~(2019乌鲁木齐.七下期中) (2015七下·启东期中) 已知 ,则a+b 为________.考点: 绝对值的非负性;代数式求值;非负数的性质:算术平方根;非负数之和为0;~~第3题~~(2018.七下期中) 化简( )+ =________.考点: 算术平方根;非负数的性质:算术平方根;~~第4题~~(2018越秀.七下期中) 若________.考点: 非负数的性质:算术平方根;非负数之和为0;~~第5题~~(2017北京.七下期中) 若、为实数,且满足,则 的值为________.考点: 非负数的性质:算术平方根;~~第6题~~(2017西城.七下期中) 若 ,则ab=________.考点: 绝对值的非负性;非负数的性质:算术平方根;~~第7题~~(2017磴口.七下期中) 若 +|b ﹣9|=0,则ab=________.考点: 绝对值的非负性;非负数的性质:算术平方根;~~第8题~~(2017长春.七下期中) 已知 +|3x+2y ﹣15|=0,则 的算术平方根为________.考点: 绝对值的非负性;算术平方根;非负数的性质:算术平方根;非负数之和为0;~~第9题~~(2017金山.七下期中) 若,则(a+b )的值为________.考点: 绝对值的非负性;非负数的性质:算术平方根;~~第10题~~(2017济宁.七下期中) 若实数m ,n 满足(m ﹣1)+=0,则(m+n )=________.考点: 偶次幂的非负性;非负数的性质:算术平方根;2020年七下数学:数与式_二次根式_非负数的性质:算术平方根练习题答案b 22m 251.答案:2.答案:3.答案:4.答案:5.答案:6.答案:7.答案:8.答案:9.答案:10.答案:。
(完整)人教版七年级数学下册实数知识点归纳及常见考题。(1),推荐文档

麻益只怕一百嘛十日塞。
实数【知识要点】1•算术平方根:正数a的正的平方根叫做a的算术平方根,记作“ .a”。
2. 如果x2=a,则x叫做a的平方根,记作“ 土. a”(a称为被开方数)。
3. 正数的平方根有两个,它们互为相反数;0的平方根是0;负数没有平方根。
4. 平方根和算术平方根的区别与联系:区别:正数的平方根有两个,而它的算术平方根只有一个。
联系:(1)被开方数必须都为非负数;(2)正数的负平方根是它的算术平方根的相反数,根据它的算术平方根可以立即写出它的负平方根。
(3)0的算术平方根与平方根同为0。
5. 如果x2 3=a,则x叫做a的立方根,记作“诟”(a称为被开方数)。
6. 正数有一个正的立方根;0的立方根是0;负数有一个负的立方根。
7. 求一个数的平方根(立方根)的运算叫开平方(开立方)。
8. 立方根与平方根的区别:一个数只有一个立方根,并且符号与这个数一致;只有正数和0有平方根,负数没有平方根,正数的平方根有2个,并且互为相反数,0的平方根只有一个且为0.9. 一般来说,被开放数扩大(或缩小)n倍,算术平方根扩大(或缩小)n倍,例如25 5,、2500 50.12=62=112 =162=212=22=72=122 =172=222=32=82=132 =182=232=42=92=142 =192=242=52=102=152 =202=252=题型规律总结:1、平方根是其本身的数是0;算术平方根是其本身的数是0和1;立方根是其本身的数是0和土1。
2每一个正数都有两个互为相反数的平方根,其中正的那个是算术平方根;任何一个数都有唯一一个立方根, 这个立方根的符号与原数相同。
3a本身为非负数,有非负性,即卩 a >0;a有意义的条件是a>0。
4、公式:⑴()2=a (a > 0);⑵V a = V a (a取任何数)5、区分(ja )2=a (a 》0),与a = a 6.非负数的重要性质:若几个非负数之和等于【典型例题】 1.下列语句中,正确的是( D )A •一个实数的平方根有两个,它们互为相反数B .负数没有立方根C .一个实数的立方根不是正数就是负数D .立方根是这个数本身的数共有三个 2. 下列说法正确的是( C ) A . -2是(-2) 2的算术平方根 B . 3是-9的算术平方根 C . 16的平方根是土 4 D . 27的立方根是土 33. 已知实数x , y 满足、、x 2+(y+1) 2=0,则x-y 等于 _______________ 解答:根据题意得,x-2=0 , y+仁0,解得 x=2 , y=-1 , 所以,x-y=2-(-1 ) =2+ 仁3.4.求下列各式的值解答:根据题意得,x-2=0 , y+仁0,(1) 81 ; (2) ■■ 16 ;(3).25 ; (4)4)2解答:(1) 因为 92 81 所以土 -81 =± 9. 因为 42 16 所以一 164. (3) 因为,所以259 _3 25 5(4) 因为 424)2,所以.(4)24.5.已知实数x ,y 满足x 2+(y+1) 2=0,则 x-y 等于0,则每一个非负数都为 0 (此性质应用很广,务必掌握)。
新人教版七年级数学下册6.1《平方根》同步练习题及答案

6.1《平方根》同步练习知识点:1.算术平方根:一般地,如果一个正数的平方等于a,那么这个正数叫做a的算术平方根。
A叫做被开方数。
1.平方根:如果一个数的平方等于a,那么这个数叫做a的平方根2.平方根的性质:正数有两个平方根,互为相反数0的平方根是0负数没有平方根同步练习:一、选择题1.如果a是负数,那么a2的平方根是().A.a B.-a C.±a D.±a2.使得-a2有意义的a有().A.0个B.1个C.无数个D.以上都不对3.下列说法中正确的是().A.若a<0,则a2<0B.x是实数,且x2=a,则a>0C.-x有意义时,x≤0D.0.1的平方根是±0.014.若一个数的平方根是±8,则这个数的立方根是().A.2B.±2C.4D.±45.若a2=(-5)2,b3=(-5)3,则a+b的所有可能值为().A.0B.-10C.0或-10D.0或±106.若-1<m<0,且n=3m,则m、n的大小关系是().A.m>n B.m<n C.m=n D.不能确定7.设a=76,则下列关于a的取值范围正确的是().A.8.0<a<8.2B.8.2<a<8.5C.8.5<a<8.8D.8.8<a<9.18.-27的立方根与81的平方根之和是().A.0B.6C.-12或6D.0或-6A .2B . 1C . - 2D . -13. (-4)2 的平方根是, ± 是 的平方根.14.在下列各数中 0, ,a 2 + 1 ,-(- )3,-(-5)2,x 2 + 2 x + 2 ,| a - 1| ,| a | -1 ,17.若 3 x = - ,则 x =,若 3 | x | = 6 ,则 x =.9.若 a , b 满足 | 3 a + 1 | +(b - 2) 2 = 0 ,则 ab 等于().12210.若一个数的一个平方根是 8,则这个数的立方根是().A . ± 2B . ± 4C .2D .411.下列各式中无论 x 为任何数都没有意义的是( ).A . -7 xB . -1999x 3C . -0.1x 2 -1D .3 -6x 2 - 512.下列结论中,正确的是( ).A . 0.0027 的立方根是 0.03B . 0.009 的平方根是 ± 0.3C . 0.09 的平方根是 0.3D .一个数的立方根等于这个数的立方,那么这个数为 1、0、 - 1二、填空题3525 1 4 316 有平方根的个数是个.15.自由落体公式:S = 12g t 2 ( g 是重力加速度,它的值约为9.8m / s 2 ),若物体降落的高度 S = 300m ,用计算器算出降落的时间 T = s (精确到 0.1s ).16.代数式-3 - a +b 的最大值为,这是a, b 的关系是.3518.若 3 (4 - k )3 = k - 4 ,则 k 的值为.19.若 n < 10 < n + 1 ,m < - 8 < m + 1 ,其中 m 、n 为整数,则 m + n =.20.若 m 的平方根是 5a + 1和 a - 19 ,则 m =.三、解答题21.求下列各数的平方根 ⑴ ( 3) 2+ 1⑵ 3 1⑶0 ⑷ -1216⑵ ⑶0 ⑷ - ⑶ ( x - 1)3 + 8 = 0⑷125( x - 2)3 = -343⑶ 3 (-1)2 + 3 -8 - |1 - 3 |⑷ (- )2 - 3 (1- )( - 1) - 1 ÷ 2 - 1.75 ⑹ 3 - - + 3 -343 - 3 2722.求下列各数的立方根:⑴ -210 1 127 64 823.解下列方程:⑴ 64( x - 3)2 - 9 = 0⑵ (4 x - 1)2 = 2251224.计算:⑴ 252 - 72 ⑵ - ( 2 - 3) 2 - 2 | 2 - 3 | - | - 3 |1 5 1 3 9 3⑸ 37 1 5 18 8 2 12525.请你用 2 个边长为 1 的小正方形,裁剪出一个边长为 2 的较大的正方形.如果要裁剪出一个边长为 2 的较大的正方形,要几个边长为 1 的小正方形,如何进行裁剪?26.已知第一个正方形纸盒的棱长是6厘米,第二个正方形纸盒的体积比第一个正方形纸盒的体积大127立方厘米,试求第二个正方形纸盒的棱长.27.已知312x,33y2互为相反数,求代数式12xy的值.28.已知x a b M是M的立方根,y3b6是x的相反数,且M3a7,请你求出x的平方根.29.若y x244x2x2,求2x y的值.30.已知3x4,且(y2x1)2z30,求x y z的值.17. x = -, x = ±216 . 18. k 的值为 4. 19. m + n = 0.20. m =256. 21.⑴±2 ⑵ ± ⑶0 ⑷没有平方根22.⑴ - ⑵ ⑶0 ⑷ -23.⑴ x = 或 x = ⑵ x = 4 或 x = -28.由条件得, ⎨,所以 M = 8 ,,故 x 的平方根是 ± 2 .(b - 6) + (3a - 7) = 0参考答案一、选择题1.C ;2.B ;3.C ;4.C ;5.C ;6.A ;7.C ;8.D ;9.C ; 10.D ;11.C ;12.D二、填空题13.±2, 9 25. 14.7 个.15. 7.8 s . 16. -3 , a, b 的关系是互为相反数.27125三、解答题743 1 14 4 2 27 21 78 8 2⑶ x = 1 - 2 3 2 ⑷ x =24.⑴24 ⑵ 3 2 - 2 3⑶ - 3⑷1⑸ -1⑹ -925.3526.二个正方形纸盒的棱长是 7 厘米.27. 1 + 2 x=3.y⎧a + b = 3⎩29. 2 x + y =4. 30. x + y + z =194.。
2023-2024学年人教版七年级下数学:平方根复习卷附答案解析

17.(2023 秋•西湖区期末)已知一个正方形面积为 5,则其周长为 .
18.(2023 秋•崂山区期末) 25 的值是
.
196
19.(2023 秋•甘州区校级期末) 1 的算术平方根是
.
16
20.(2023•金凤区校级开学)若 3 是 m 的一个平方根,则 m 18 的平方根是
.
三、解答题(共 10 小题)
正数为 ( )
第 1页(共 9页)
A. 1
B.2
C.4
D.9
9.(2023 秋•柯城区校级期中)用符号表示“ 16 的平方根是 4 ”正确的是 (
)
9
3
A. 16 4
93
B. 16 4
93
C. 16 4
93
D. 16 4
93
10.(2023 秋•南关区期末)若 a 4 ,则 a 的值为 ( )
2023-2024 学年人教版七年级下数学 6.1 平方根
考点精练
一、选择题(共 12 小题) 1.(2023 秋•衡阳期末)有理数 4 的平方根是 ( )
A. 2
B. 2
C.2
D. 2
2.(2023 秋•沐川县期末)数 9 的算术平方根是 ( )A.源自3B. 3C. 3
D.3
3.(2023 秋•威宁县期末)2023 的算术平方根是 ( )
二、填空题(共 8 小题)
13.(2023 秋•成都期末)若 x 4 ,则 x .
14.(2023 秋•普陀区校级期末) 1 的平方根是
.
16
15.(2023 秋•德化县期末)若一个正数的平方根为 2a 1 和 2 a ,则 a 的值
是.
16.(2023 秋•拱墅区期末)若 2 a , 2a 都是有理数,则 a .
数学人教版七年级下册平方根习题精选

【巩固练习】一、选择题1. 9的算术平方根是()A.-3 B.3 C.±3 D.81 2.下列计算正确的是()A±2 BC.636=± D.992-=-3.下列说法中正确的是()A.9的平方根是3 B224. 64的平方根是()A.±8 B.±4 C.±2 D5. 4的平方的倒数的算术平方根是()A.4 B.18C.-14D.146.下列结论正确的是()A6)6(2-=--B9)3(2=-C16)16(2±=-D251625162=⎪⎪⎭⎫⎝⎛--7.以下语句及写成式子正确的是()A、7是49的算术平方根,即749±=B、7是2)7(-的平方根,即7)7(2=-C、7±是49的平方根,即749=±D、7±是49的平方根,即749±=8.下列语句中正确的是()A、9-的平方根是3- B、9的平方根是3C、9的算术平方根是3±D、9的算术平方根是39.下列说法:(1)3±是9的平方根;(2)9的平方根是3±;(3)3是9的平方根;(4)9的平方根是3,其中正确的有()A.3个 B.2个C.1个 D.4个10.下列语句中正确的是()A、任意算术平方根是正数B、只有正数才有算术平方根C、∵3的平方是9,∴9的平方根是3D、1-是1的平方根11.下列说法正确的是()A.任何数的平方根都有两个B.只有正数才有平方根C.一个正数的平方根的平方仍是这个数D.2a的平方根是a±12.下列叙述中正确的是()A.(-11)2的算术平方根是±11B.大于零而小于1的数的算术平方根比原数大C.大于零而小于1的数的平方根比原数大D.任何一个非负数的平方根都是非负数13.25的平方根是()A、5B、5- C、5± D、5±14.36的平方根是()A、6B、6±C、6D、6±15.当≥m0时,m表示()A.m的平方根B.一个有理数C.m的算术平方根D.一个正数16.用数学式子表示“169的平方根是43±”应是()A.43169±= B.43169±=±C.43169= D.43169-=-17.算术平方根等于它本身的数是()A、1和0B、0C、1D、1±和018.0196.0的算术平方根是()A、14.0 B、014.0 C、14.0± D、014.0±19.2)6(-的平方根是()A、-6B、36C、±6D、±620.下列各数有平方根的个数是()(1)5;(2)(-4)2;(3)-22;(4)0;(5)-a2;(6)π;(7)-a2-1A.3个 B.4个C.5个 D.6个21.2)5(-的平方根是()A、5± B、5 C、5- D、5±22.下列说法错误的是()A. 1的平方根是1B. –1的立方根是-1C.2是2的平方根 D. –3是2)3(-的平方根23.下列命题正确的是( ) A .49.0的平方根是0.7B .0.7是49.0的平方根C .0.7是49.0的算术平方根D .0.7是49.0的运算结果24.若数a 在数轴上对应的点的位置在原点的左侧,则下列各式中有意义的是( ) A .a B .a - C .2a - D .3a25.3612892=x ,那么x 的值为( )A .1917±=xB .1917=xC .1817=xD .1817±=x 26.下列各式中,正确的是( )A.2)2(2-=- B. 9)3(2=-C. 39±=±D. 393-=-27.下列各式中正确的是( ) A .12)12(2-=- B .6218=⨯ C .12)12(2±=-D .12)12(2=-±28.若a 、b 为实数,且471122++-+-=a a a b ,则b a +的值为( )(A)1± (B) 4 (C) 3或5 (D) 529.若9,422==b a,且0<ab ,则b a -的值为 ( )(A) 2- (B) 5± (C) 5 (D) 5-30.若一个正数的平方根是12-a 和2+-a ,则____=a ,这个正数是 ;31.满足x 是32.已知一个正方形的边长为a ,面积为S ,则( ) A.a S= B.S 的平方根是aC.a 是S 的算术平方根D.S a±=33. 若a 和a -都有意义,则a 的值是( )A.0≥aB.0≤aC.0=aD.0≠a34.22)4(+x 的算术平方根是( )A 、42)4(+x B 、22)4(+xC 、42+x D 、42+x35.2)5(-的平方根是( )A 、5± B 、 5 C 、5- D 、5±36.下列各式中,正确的是( )A. 2)2(2-=-B. 9)3(2=-C. 39±=±D. 393-=-37.下列各式中正确的是( ) A .12)12(2-=- B .6218=⨯C .12)12(2±=-D .12)12(2=-±38.下列各组数中互为相反数的是( ) A 、2)2(2--与 B 、382--与C 、2)2(2-与D 、22与-二、填空题:1.如果x 的平方等于a ,那么x 就是a 的 ,所以的平方根是2.非负数a 的平方根表示为 3.因为没有什么数的平方会等于 ,所以负数没有平方根,因此被开方数一定是4_______;9的平方根是_______.5的平方根是 ,25的平方根记作 ,结果是6.非负的平方根叫 平方根7.2)8(-= , 2)8(= 。
专题04 平方根、立方根、实数期末真题汇编(解析版)-2024学年七年级数学下学期期末(人教版)

专题04平方根、立方根、实数期末真题汇编之十一大题型平方根、算术平方根、立方根概念的理解例题:(23-24七年级上·浙江绍兴·期末)下列说法中正确的是()A .5-是25的一个平方根B .116的平方根是14C .64-的平方根是8-D .64的立方根是4±【变式训练】1.(23-24七年级上·浙江湖州·期末)下列说法正确的是().A4±B .2(3)-的算术平方根是3-C .负数没有立方根D2的算术平方根2.(23-24七年级上·浙江丽水·期末)下列说法正确的是()3A.4的平方根是2B求一个数的算术平方根、平方根、立方根-的立方根是,平方根是.【变式训练】1.(23-24八年级上·山东枣庄·的立方根为.的平方根是.2.(22-23七年级下·湖北随州·的相反数是,4的平方根是,立方根是.利用算术平方根的非负性求解例题:(23-24八年级上·湖南衡阳·80y -=,则xy 的平方根为.【答案】4±【分析】此题主要考查了非负数的性质,算术平方根具有非负性,以及任意一个数的绝对值都是非负数,解答此题的关键是求出x y 、的大小.【变式训练】b+=,则a b等于.1.(23-24八年级上·江苏宿迁·()210x y+-=,则x y-的算术平方根是.2.(23-24八年级上·四川成都·期末)()220x y ∴-的算术平方根是2.故答案为:2.利用平方根、立方根的定义解方程例题:(23-24七年级上·山东滨州·期末)求下列各式中x 的值:(1)2(3)250x --=(2)31(1)322x -=【变式训练】1.(22-23八年级上·江苏淮安·期末)求下列各式中的x 值:(1)25100x -=(2)()334375x -=-.2.(22-23八年级上·江苏盐城·期末)求下列各式中x 的值:(1)2317x +=;(2)32(4)54x -=.【点睛】本题考查了解方程,解题的关键是掌握平方根。
七下数学每日一练:非负数的性质:算术平方根练习题及答案_2020年单选题版

A . ﹣2 B . ﹣1 C . 0 D . 2
考点: 绝对值的非负性;非负数的性质:算术平方根;
答案
~~第4题~~
(2019柳州.七下期中) 若a、b为实数,且满足|a-2|+
=0,则b-a的值为( )
A . 2 B . 0 C . -2 D . 以上都不对
考点: 绝对值的非负性;非负数的性质:算术平方根;
答案
~~第7题~~ (2017抚顺.七下期中) 已知实数x,y满足
,则x﹣y等于( )
A . 3 B . ﹣3 C . 1 D . ﹣1
考点: 偶次幂的非负性;非负数的性质:算术平方根;
答案
~~第8题~~ (2017嘉祥.七下期末) 若
与|2a﹣b+1|互为相反数,则(b﹣a)2017的值为( )
A . ﹣1 B . 1 C . 52015 D . ﹣52015
考点: 绝对值的非负性;非负数的性质:算术平方根;解二元一次方程;
答案
~~第9题~~ (2017蒙阴.七下期末) 已知实数 , 满足
,则
等于( )
A . 3 B . -3 C . 1 D . -1
考点: 偶次幂的非负性;非负数的性质:算术平方根;
答案
~~第10题~~ (2017贵州.七下期末) 已知|a+b﹣1|+
=0,则(a﹣b)2017的值为( )
A . 1 B . ﹣1 C . 2015 D . ﹣2015
考点: 非负数的性质:算术平方根;
答案
2020年 七 下 数 学 : 数 与 式 _二 次 根 式 _非 负 数 的 性 质 : 算 术 平 方 根 练 习 题 答 案
1.答 案 : A 2.答 案 : D 3.答 案 : D 4.答 案 : C 5.答 案 : B 6.答 案 : D 7.答 案 : A 8.答 案 : A 9.答 案 : A 10.答 案 案_2020年单选题
人教版七年级下册6.1平方根知识点复习以及考试题型

平方根知识点复习以及考试题型【知识点梳理】一、算数平方根1.算数平方根定义:如果一个正数x的平方等于a,即x²=a,那么这个正数x叫做a的算数平方根,a的算数平方根记作√a,读作“根号a”,a叫做被开方数。
注:0的算数平方根是02.性质:算数平方根具有双重非负性√a≥0 a≥0二、平方根1.平方根定义:如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根(若x²=a,那么x叫做a的平方根)。
例如,3²=9,3就是9的平方根,而(-3)²=9,-3也是9的平方根,所以可以说9的平方根是±32.性质:正数有两个平方根,而且它们互为相反数;0的平方根是0;负数没有平方根3.开平方:求一个数a的平方根的运算叫做开平方(平方与开平方互为逆运算)三、算术平方根和平方根的区别与联系【考试题型】1.运用算数平方根进行计算(1)√36+√()2−√196(2)√9+√16 (3)√2.25+|√2−1|−(√2)2(4)√25 ×√(15)2−6×1√362.平方根性质的运用(1)一个正数的平方根是3a+2和a+10,求这个正数(2)2a -1的平方根是±3,3a+b -1的平方根是±4,求a+2b 的平方根(3)一个数的算术平方根是a ,则比这个数大8数是__________(4)若|a-2b|+(c+b)2+√c−1=0,求a+b-c的平方根3.用平方根概念解方程(1)(x+1)2-25=0(2)2(x-3)2=32(3)4x2-8=0(4)(x+y)2-4=45,求x+y的值4.比较大小在填“>”、“<”或“=”2 √3√√7√174√38 6 −√18-4 0.8 √0.645.易错点总结(1)求√a的算数平方根(两步运算)例如:求√64的算数平方根(2)根号下a的取值可以是一个数、一个字母、也可以是一个多项式注意的是a的取值是非负数例:√5√a√2a−1(3)(√a)²与√a²的区别(√a)²=a(a≥0)√a²=a(a≥0)√a²=-a(a≤0)。
初一数学下册(人教版)第六章6.1 知识点总结含同步练习及答案

0.72 = 0.49 ,所以 0.49 的算术平方根是 0.7,所以 0.7 的相反数是 −0.7 . )
C.2.7 D.2.8
3. 下列各数与 √7 最接近的是 ( A.2.5
答案: B
B.2.6
− − 4. 已知: √− 20 n 是整数,则满足条件的最小正整数 n 为 (
A.2
答案: D
)
D.5
平方根算术平方根如果一个非负数的平方等于即非负数的算术平方根记作平方根如果一个数的平方等于即非负数的平方根记作方extraction
初一数学下册(人教版)知识点总结含同步练习题及答案
第六章 实数 6.1 平方根
一、学习任务 1. 了解算术平方根的概念,了解开平方和平方为互逆运算,会用根号表示正数的算术平方根, 会利用计算求一个数的算术平方根. 2. 了解算术平方根的非负性,会用平方运算求某些非负数的算术平方根. 3. 理解被开方数扩大(或缩小)与它的算术平方根扩大(或缩小)的规律. 4. 会估计一个无理数的大小. 二、知识清单
平方根
三、知识讲解
1.平方根 描述: 算术平方根 如果一个非负数 x 的平方等于 a ,即 x 2 = a ,那么这个非负数 x 叫做 a 的算术平方根. 2 非负数 a 的算术平方根记作 √a 或 √ a ,读作“根号 a ”, a 叫做被开方数(radicand). 平方根 如果一个数 x 的平方等于 a ,即 x2 = a ,那么这个数 x 叫做 a 的平方根(square root). 非负数 a 的平方根记作 ±√a ,读作“正、负根号 a ”.求一个数的平方根的运算,叫做开平 方(extraction of square root). 算术平方根与平方根的联系与区别 ① 平方根包含算术平方根,算术平方根是平方根的一种; ② 0 的算术平方根和平方根均为 0 ; ③ 一个正数有两个平方根,它们互为相反数,而一个正数的算术平方根只有一个,且为正数; ④ 正数 a 的平方根表示为 ±√a ,正数 a 的算术平方根表示为 √a .
人教版数学七年级下册知识重点与单元测-第六章6.1平方根

第六章实数6.1 平方根(能力提升)【要点梳理】知识点一、平方根和算术平方根的概念1.算术平方根的定义如果一个正数x的平方等于a,即2x a=,那么这个正数x叫做a的算术平方根(规定0的算术平方根还是0);aa的算术平方根”,a叫做被开方数.要点诠释:a0,a≥0.2.平方根的定义如果2x a=,那么x叫做a的平方根.求一个数a的平方根的运算,叫做开平方.平方与开平方互为逆运算.a (a≥0)的平方根的符号表达为0)a≥是a的算术平方根.知识点二、平方根和算术平方根的区别与联系1.区别:(1)定义不同;(2)结果不同:2.联系:(1)平方根包含算术平方根;(2)被开方数都是非负数;(3)0的平方根和算术平方根均为0.要点诠释:(1)正数的平方根有两个,它们互为相反数,其中正的那个叫它的算术平方根;负数没有平方根.(2)正数的两个平方根互为相反数,根据它的算术平方根可以立即写出它的另一个平方根.因此,我们可以利用算术平方根来研究平方根.知识点三、平方根的性质0 ||00a aa aa a>⎧⎪===⎨⎪-<⎩()()20a a a =≥知识点四、平方根小数点位数移动规律被开方数的小数点向右或者向左移动2位,它的算术平方根的小数点就相应地向右或者向左移动1位.例如:62500250=,62525=, 6.25 2.5=,0.06250.25=.【典型例题】类型一、平方根和算术平方根的概念例1、已知2a ﹣1的平方根是±3,3a+b ﹣9的立方根是2,c 是的整数部分,求a+b+c的平方根.【思路点拨】首先根据平方根与立方根的概念可得2a ﹣1与3a+b ﹣9的值,进而可得a 、b 的值;接着估计的大小,可得c 的值;进而可得a+b+c ,根据平方根的求法可得答案. 【答案与解析】解:根据题意,可得2a ﹣1=9,3a+b ﹣9=8;故a=5,b=2;又∵2<<3,∴c=2,∴a+b+c=5+2+2=9,∴9的平方根为±3.【总结升华】此题主要考查了平方根、立方根、算术平方根的定义及无理数的估算能力,还要掌握实数的基本运算技能,灵活应用.举一反三:【变式】已知2a -1与-a +2是m 的两个不同的平方根,求m 的值.【答案】2a -1与-a +2是m 的平方根,所以2a -1与-a +2互为相反数. 解:当2a -1+(-a +2)=0时,a =-1,所以m =()()22221[2(1)1]39a -=⨯--=-= 例2、x 为何值时,下列各式有意义?2x 4x -11x x +-1x -. 【答案与解析】解:(1)因为20x ≥,所以当x(2)由题意可知:40x -≥,所以4x ≥(3)由题意可知:1010x x +≥⎧⎨-≥⎩解得:11x -≤≤.所以11x -≤≤义.(4)由题意可知:1030x x -≥⎧⎨-≠⎩,解得1x ≥且3x ≠.所以当1x ≥且3x ≠时,3x -有意义. 【总结升华】(1)当被开方数不是数字,而是一个含字母的代数式时,一定要讨论,只有当被开方数是非负数时,式子才有意义.(2)当分母中含有字母时,只有当分母不为0时,式子才有意义.举一反三:【变式】已知2b =,求11a b +的算术平方根. 【答案】解:根据题意,得320,230.a a -≥⎧⎨-≥⎩则23a =,所以b =2,∴1131222a b +=+=,∴11a b+= 类型二、平方根的运算例3、求下列各式的值.2234+; 【思路点拨】(1)首先要弄清楚每个符号表示的意义.(2)注意运算顺序. 【答案与解析】解:2234+257535==⨯=;110.63035=⨯-⨯90.26 1.72=--=-.【总结升华】(1)混合运算的运算顺序是先算平方开方,再乘除,后加减,同一级运算按先后顺序进行.(2)初学可以根据平方根、算术平方根的意义和表示方法来解,熟练后直(0)a a =>来解.类型三、利用平方根解方程例4、求下列各式中的x .(1)23610;x -=(2)()21289x +=;(3)()2932640x +-=【答案与解析】解:(1)∵23610x -=∴2361x =∴19x ==±(2)∵()21289x +=∴1x +=∴x +1=±17x =16或x =-18.(3)∵()2932640x +-= ∴()264329x += ∴8323x +=± ∴21499x x ==-或 【总结升华】本题的实质是一元二次方程,开平方法是解一元二次方程的最基本方法.(2)(3)小题中运用了整体思想分散了难度.举一反三:【变式】求下列等式中的x :(1)若2 1.21x =,则x =______; (2)2169x =,则x =______;(3)若29,4x =则x =______; (4)若()222x =-,则x =______. 【答案】(1)±1.1;(2)±13;(3)32±;(4)±2. 类型四、平方根的综合应用例5、已知a 、b 是实数,且|0b =,解关于x 的方程2(2)1a x b a ++=-.【答案与解析】解:∵a 、b |0b =0≥,|0b ≥,∴260a +=,0b -=.∴a =-3,b =把a =-3,b =2(2)1a x b a ++=-,得-x +2=-4,∴x =6.【总结升华】本题是非负数的性质与方程的知识相结合的一道题,应先求出a 、b 的值,再解方程.此类题主要是考查完全平方式、算术平方根、绝对值三者的非负性,只需令每项分别等于零即可.举一反三:0=,求20112012x y +的值. 【答案】0=,得210x -=,10y +=,即1x =±,1y =-.①当x =1,y =-1时,20112012201120121(1)2x y +=+-=.②当x =-1,y =-1时,2011201220112012(1)(1)0x y +=-+-=.例6、小丽想用一块面积为4002cm 的正方形纸片,沿着边的方向裁出一块面积为3002cm 的长方形纸片,使它长宽之比为2:3,请你说明小丽能否用这块纸片裁出符合要求的长方形纸片.【答案与解析】解:设长方形纸片的长为3x (x >0) cm ,则宽为2x cm ,依题意得32300x x ⋅=.26300x=.250x=.∵ x>0,∴ 50x=.∴ 长方形纸片的长为350cm.∵ 50>49,∴507>.∴ 35021>, 即长方形纸片的长大于20cm.由正方形纸片的面积为400 2cm, 可知其边长为20cm,∴ 长方形的纸片长大于正方形纸片的边长.答: 小丽不能用这块纸片裁出符合要求的长方形纸片.【总结升华】本题需根据平方根的定义计算出长方形的长和宽,再判断能否用边长为20cm的正方形纸片裁出长方形纸片.举一反三:【变式】某小区为了促进全民健身活动的开展,决定在一块面积约为1000m2的正方形空地上建一个篮球场,已知篮球场的面积为420m2,其中长是宽的倍,篮球场的四周必须留出1m宽的空地,请你通过计算说明能否按规定在这块空地上建一个篮球场?【答案】解:设篮球场的宽为xm,那么长为2815x m,由题意知,所以x2=225,因为x为正数,所以x==15,又因为=900<1000,所以按规定在这块空地上建一个篮球场.【提升练习】一.选择题1.下列说法中正确的有( ).①只有正数才有平方根. ②2-是4的平方根. ③16的平方根是4±.④2a 的算术平方根是a . ⑤2(6)-的平方根是6-.⑥ 93=±.A .1个B .2个C .3 个D .4个2.若m =40-4,则估计m 的值所在的范围是( )A .1<m <2 B. 2<m <3 C. 3<m <4 D. 4<m <53. 试题下列说法中正确的是( )A.4是8的算术平方根B.16的平方根是4C.6是6的平方根D.-a 没有平方根4. 能使x -3的平方根有意义的x 值是( )A. x >0B. x >3C. x ≥0D. x ≥35.若=a ,则a 的值为( ) A .1 B .﹣1 C .0或1 D .±16. 若x ,y 为实数,且|x +1|1y -=0,则2013x y ⎛⎫ ⎪⎝⎭的值是( )A.0B.1C.-1D.-2011二.填空题7. 10404102= 1.0404__________.8. 如果一个正方形的面积等于两个边长分别是3cm 和5cm 的正方形的面积的和,则这个正方形的边长为 ________.9. 下列各数:81,1625,1.44,12481_______________;算术平方根分别是_______________.10.(1)25的平方根是________;(2)()25-的平方根是________,算术平方根是________;(3)2x 的平方根是________,算术平方根是________;(4)()22x +的平方根是________,算术平方根是________.11.已知,求a ﹣b= . 12. 若,则____________. 三.解答题13.x 为何值时,下列各式有意义? (1)2;x (2);x - (3)2;x (4) 1.x -14.已知:|x ﹣1|+(y ﹣2)2+=0,求x+y+z 值的平方根.15.如图,实数a ,b 对应数轴上的点A 和B ,化简2222()()a b a b a b +---+【答案与解析】一.选择题1. 【答案】A ;【解析】只有②是正确的.2. 【答案】B ;【解析】6407<<,所以2<40-4<3 .3. 【答案】C;【解析】A.∵4是16的算术平方根,故选项A错误;B.∵16的平方根是±4,故选项B 错误;C.∵6是6的一个平方根,故选项C正确;D.当a≤0时,-a也有平方根,故选项D错误.4. 【答案】D;【解析】要使x-3的平方根有意义,∴x-3≥0,即x≥3.5. 【答案】C;【解析】解:∵=a,∴a≥0.当a=0时,=a;当0<a<1时,>a;当a=1时,=a;当a>时,<a;综上可知,若=a,则a的值为0或1.故选C.6. 【答案】C;【解析】x+1=0,y-1=0,解得x=-1;y=1.2013xy⎛⎫⎪⎝⎭=-1.二.填空题7. 【答案】1.02;【解析】被开方数向左移动四位,算术平方根的值向左移动两位.8. 34cm;223534+=9. 【答案】±9;±45;±1.2;±32;±3;9;45;1.2;32;3.10.【答案】(1)±5;(2)±5;5;(3)±x,|x|;(4)±(x+2),| x+2|;2||a a=.11.【答案】-8;【解析】解:根据题意得,a+3=0,b ﹣5=0,解得a=﹣3,b=5,所以,a ﹣b=﹣3﹣5=﹣8.故答案为:﹣8.12.【答案】;【解析】12x +=±,x =. 三.解答题13.【解析】解:(1)2x ≥0,解得x ≥0;(2)-x ≥0,解得x ≤0;(3)20,x ≥解得x 为一切实数;(4)x -1≥0,解得x ≥1.14.【解析】解:∵|x﹣1|+(y ﹣2)2+=0,∴,解得x=1,y=2,z=3,∴x+y+z=1+2+3=6,∴x+y+z 的平方根为.15.2||a a =∵0a b a b <<<且∴原式=-a +b -(b -a )-(a +b ) =-a +b -b +a -a -b =-a -b .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
非负数的性质:算术平方根一.选择题(共20小题)1.已知非零实数a,b 满足,则a﹣b等于()A.3 B.﹣2 C.1 D.52.已知,那么x﹣y=()A.3 B.﹣3 C.﹣6 D.63.若(x+y)2++|z﹣2y|=0,则x﹣y+z的值()A.0 B.1 C.2 D.44.若与|b+1|互为相反数,则a﹣b的值为()A.B.+1 C.﹣1 D.1﹣5.若|x﹣2|+=0,则x2+y2=()A.10 B.12 C.13 D.不能确定6.,那么(a+b)2012的值为()A.﹣1 B.1 C.﹣52012D.520127.若a,b为实数,且|a+1|+=0,则(ab)2013的值是()A.0 B.1 C.﹣1 D.±18.若实数x、y满足+(y﹣3)2=0,则等于()A.0 B.5 C.4 D.±49.已知+=0,则x﹣y的值为()A.2 B.6 C.2或﹣2 D.6或﹣610.若+(y+2)2=0,则(x+y)2015等于()A.﹣1 B.1 C.32014 D.﹣3201411.若(m﹣3)2+=0,则m+n的平方根是()A.1 B.±1 C.D.±12.若a、b、c为△ABC的三边,且a、b、c满足(a﹣6)2++|c﹣10|=0,则△ABC的周长为()A.48 B.80 C.24 D.4013.+|x﹣3|=0,则x y=()A.81 B.64 C.27 D.6314.若x,y为实数,且|x+1|+=0,则xy的值是()A.1 B.0 C.﹣1 D.﹣215.已知x、y是实数,+(y2﹣6y+9)=0,若axy﹣3x=y,则实数a的值是()A.B.﹣ C.D.﹣16.若(x﹣2)2+=0,则(x+y)2等于()A.2 B.﹣1 C.1 D.2517.若(x+3)2+=0,则(x﹣y)的相反数的值为()A.﹣5 B.﹣1 C.1 D.518.若+(y+3)2=0,则x﹣y的值为()A.1 B.﹣1 C.4 D.﹣719.若,则x2015+y2016的值()A.0 B.1 C.﹣1 D.220.若x,y为实数,且|x+3|+=0,则()2017的值为()A.1 B.2 C.﹣1 D.﹣2二.填空题(共20小题)21.若(a+)2与互为相反数,则a b=.22.已知实数a,b满足,则ab=.23.已知,那么(xy)2005=.24.若+|3﹣y|=0,则2xy=.25.在下列6个等式中,①ab=0;②a+b=0;③;④a2=0;⑤a2+b2=0;⑥中,a一定是零的等式编号是.26.若|x﹣2|和互为相反数,则xy的算术平方根是.27.若实数x,y满足,则xy﹣x2的平方根为.28.已知实数x,y满足+(y+1)2=0,则x﹣y等于.29.已知=0,则b a=.30.已知+|a+b+1|=0,则a b=.31.若(2a+3)2与互为相反数,则a=.b=.32.(a+8)2+|b﹣5|+=0,则a+b+c=.33.|x+1|++(2y﹣4)2=0,则x+y+z=.34.已知|a+2|=0,那么a﹣b=.35.若+=0,则(x﹣1)2+(y+3)2=.36.已知+(y+5)2=0,则(x+y)2012=.37.若(x﹣8)2与互为相反数,则x=y=.38.若a、b为实数,且|a+1|+=0,则的值是.39.当x=时,+5的值最小.40.若x、y为实数,且|x+2|+=0,则(x+y)2016=.三.解答题(共10小题)41.若|m+1|+=0,求m2000﹣n4的值.42.解答下列各题(1)解方程:2(3x﹣1)2=8;(2)已知(x﹣)2+=0,求xy﹣的值.43.已知实数a、b满足,求2a﹣b+1的平方根.44.已知,试求x﹣8y的算术平方根.45.已知|x+3|+=0,求x2﹣6y的值.46.已知x,y满足=0,求x﹣的平方根.47.若二次根式与互为相反数,求2x+3a﹣1的值.48.若+|b2﹣9|=0,求ab的值.49.(1)若(﹣b+1)2与互为相反数,求(a+b)2004的值.(2)已知a的两个平方根为3b﹣1和b+5,求a的值.50.已知实数a,b满足+b2+2b+1=0,求a2+﹣|b|的值.非负数的性质:算术平方根参考答案与试题解析一.选择题(共20小题)1.已知非零实数a,b 满足,则a﹣b等于()A.3 B.﹣2 C.1 D.5【分析】根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.【解答】解:∵(a﹣3)b2≥0,∴a﹣3≥0,∴a≥3,∴2a﹣4>0,∴原式变形为|b+2|+=0,∴b+2=0,(a﹣3)b2=0,∴b=﹣2,a=3,∴a﹣b=3﹣(﹣2)=5.故选D.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.2.已知,那么x﹣y=()A.3 B.﹣3 C.﹣6 D.6【分析】根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.【解答】解:根据题意得:,解得:,则x﹣y=3﹣6=﹣3.故选B.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.3.若(x+y)2++|z﹣2y|=0,则x﹣y+z的值()A.0 B.1 C.2 D.4【分析】根据非负数的性质列出方程,解方程求出x、y、z的值,代入代数式计算即可.【解答】解:由题意得,x+y=0,2x﹣4=0,z﹣2y=0,解得x=2,y=﹣2,z=﹣4,则x﹣y+z=0.故选:A.【点评】本题考查的是非负数的性质,掌握非负数之和等于0时,各项都等于0是解题的关键.4.若与|b+1|互为相反数,则a﹣b的值为()A.B.+1 C.﹣1 D.1﹣【分析】由非负数的性质可知a=﹣,b=﹣1,然后求得a﹣b的值即可.【解答】解:∵与|b+1|互为相反数,∴+|b+1|=0.∴a=﹣,b=﹣1.∴a﹣b=﹣﹣(﹣1)=﹣+1.故选D.【点评】本题主要考查的是非负数的性质,掌握非负数的性质是解题的关键.5.若|x﹣2|+=0,则x2+y2=()A.10 B.12 C.13 D.不能确定【分析】根据非负数的性质列式求解即可得到x、y的值,然后代入代数式进行计算即可.【解答】解:根据题意得,x﹣2=0,y﹣3=0,解得x=2,y=3,∴x2+y2=22+32=4+9=13.故选C.【点评】本题考查了算术平方根非负数,绝对值非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是求解的关键.6.,那么(a+b)2012的值为()A.﹣1 B.1 C.﹣52012D.52012【分析】根据非负数的性质列式求出a、b的值,然后代入代数式进行计算即可得解.【解答】解:根据题意得,3+a=0,b﹣2=0,解得a=﹣3,b=2,所以(a+b)2012=(﹣3+2)2012=1.故选B.【点评】本题考查了绝对值非负数,算术平方根非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是解题的关键.7.若a,b为实数,且|a+1|+=0,则(ab)2013的值是()A.0 B.1 C.﹣1 D.±1【分析】根据非负数的性质列式求出a、b,然后代入代数式进行计算即可得解.【解答】解:根据题意得,a+1=0,b﹣1=0,解得a=﹣1,b=1,所以,(ab)2013=(﹣1×1)2013=﹣1.故选:C.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.8.若实数x、y满足+(y﹣3)2=0,则等于()A.0 B.5 C.4 D.±4【分析】根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.【解答】解:∵+(y﹣3)2=0,∴x﹣2=0,y﹣3=0,解得x=2,y=3,∴==4,故选C.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.9.已知+=0,则x﹣y的值为()A.2 B.6 C.2或﹣2 D.6或﹣6【分析】根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.【解答】解:根据题意得:,解得:x=2,y=﹣4或x=﹣2,y=4.则x﹣y=6或﹣6.故选D.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.10.若+(y+2)2=0,则(x+y)2015等于()A.﹣1 B.1 C.32014 D.﹣32014【分析】根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.【解答】解:∵+(y+2)2=0,∴x=1,y=﹣2,∴(x+y)2015=(1﹣2)2015=﹣1,故选A.【点评】本题考查了非负数的性质:算术平方根和偶次方,几个非负数的和为0时,这几个非负数都为0.11.若(m﹣3)2+=0,则m+n的平方根是()A.1 B.±1 C.D.±【分析】根据非负数的性质列出算式,求出m、n的值,根据平方根的概念解答即可.【解答】解:由题意得,m﹣3=0,n+2=0,解得,m=3,n=﹣2,则m+n=1,则m+n的平方根是±1,故选:B.【点评】本题考查的是非负数的性质,掌握几个非负数的和为0时,这几个非负数都为0是解题的关键.12.若a、b、c为△ABC的三边,且a、b、c满足(a﹣6)2++|c﹣10|=0,则△ABC的周长为()A.48 B.80 C.24 D.40【分析】根据非负数的性质列出算式,求出a、b、c的值,根据三角形的周长公式计算即可.【解答】解:由题意得,a﹣6=0,b﹣8=0,c=10=0,解得,a=6,b=8,c=10,则△ABC的周长=a+b+c=24,故选:C.【点评】本题考查的是非负数的性质,掌握几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.13.+|x﹣3|=0,则x y=()A.81 B.64 C.27 D.63【分析】根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.【解答】解:由题意得,x﹣y+1=0,x﹣3=0,解得x=3,y=4,所以,x y=34=81.故选A.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.14.若x,y为实数,且|x+1|+=0,则xy的值是()A.1 B.0 C.﹣1 D.﹣2【分析】根据非负数的性质列方程求出x、y的值,然后代入代数式进行计算即可得解.【解答】解:由题意得,x+1=0,y﹣1=0,解得x=﹣1,y=1,所以,xy=(﹣1)×1=﹣1.故选C.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.15.已知x、y是实数,+(y2﹣6y+9)=0,若axy﹣3x=y,则实数a的值是()A.B.﹣ C.D.﹣【分析】由于y2﹣6y十9可以写成完全平方式,那么此题就是两个非负数相加为0,意味着每个式子都为0,由此可以求出x和y,然后代入方程计算即可.【解答】解:∵十y2﹣6y十9=0,∴十(y﹣3)2=0∵3x+4=0,y﹣3=0∴x=﹣,y=3,把x,y代入axy﹣3x=y,∴a=.故选A.【点评】主要考查了非负数的性质,解题关键是利用理解两个非负数的和要为0,那只有让这两个非负数为0.16.若(x﹣2)2+=0,则(x+y)2等于()A.2 B.﹣1 C.1 D.25【分析】根据非负数的性质,两个非负数的和是0,则这两非负数同时是0,即可解答.【解答】解:根据题意得:x﹣2=0,y+3=0解得:x=2,y=﹣3;∴(x+y)2=(2﹣3)2=1.故选C.【点评】此题主要考查了非负数的性质,非负数的性质:有限个非负数的和为零,那么每一个加数也必为零,即若a1,a2,…,a n为非负数,且a1+a2+…+a n=0,则必有a1=a2=…=a n=0.17.若(x+3)2+=0,则(x﹣y)的相反数的值为()A.﹣5 B.﹣1 C.1 D.5【分析】根据非负数的性质,可求出x、y的值,进而可求出(x﹣y)的相反数.【解答】解:由题意,得:x+3=0,y﹣2=0,即x=﹣3,y=2,∴x﹣y=﹣3﹣2=﹣5∴﹣(x﹣y)=5.故选D.【点评】此题考查了非负数的性质以及相反数的定义;非负数的性质:非负数的和为0,则每个非负数也必为0;相反数:符号相反,绝对值相等的两个数互为相反数.18.若+(y+3)2=0,则x﹣y的值为()A.1 B.﹣1 C.4 D.﹣7【分析】根据非负数的性质得到关于x、y的方程,解方程求出x、y的值,计算的答案.【解答】解:由题意得,x﹣1=0,y+3=0,解得,x=1,y=﹣3,则x﹣y=1﹣(﹣3)=4,故选:C.【点评】本题考查了非负数的性质,掌握几个非负数的和为0时,这几个非负数都为0是解题的关键.19.若,则x2015+y2016的值()A.0 B.1 C.﹣1 D.2【分析】根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.【解答】解:∵,∴x﹣1=0,x+y=0,∴x=1,y=﹣1,∴x2015+y2016=2,故选D.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.20.若x,y为实数,且|x+3|+=0,则()2017的值为()A.1 B.2 C.﹣1 D.﹣2【分析】根据非负数的性质进行计算即可.【解答】解:∵|x+3|+=0,∴x+3=0,y﹣3=0,∴x=﹣3,y=3,∴()2017=(﹣1)2017=﹣1,故选C.【点评】本题考查了非负数的性质,掌握几个非负数的和为0,这几个数都为0是解题的关键.二.填空题(共20小题)21.若(a+)2与互为相反数,则a b=﹣.【分析】先由一对相反数的和为0,得出(a+)2+=0,再根据非负数的性质求出a与b的值,然后代入所求代数式,计算即可.【解答】解:∵(a+)2与互为相反数,∴(a+)2+=0,∴a+=0,b﹣3=0,∴a=﹣,b=3,∴a b=(﹣)3=﹣.故答案为﹣.【点评】本题考查了相反数、非负数的性质,方程组的解法及代数式求值,关键是根据相反数及非负数的性质求得未知数的解.22.已知实数a,b满足,则ab=﹣4.【分析】根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.【解答】解:根据题意得:,解得:,则ab=﹣4.故答案是:﹣4.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.23.已知,那么(xy)2005=﹣1.【分析】先根据非负数的性质列出关于x、y的方程,求出x、y的值,再把x、y 的值代入所求代数式进行计算即可.【解答】解:∵|2x+1|+=0,∴2x+1=0,解得x=﹣;2﹣y=0,解得y=2.∴(xy)2005=[(﹣)×2]2005=(﹣1)2005=﹣1.故答案为:﹣1.【点评】本题考查的是非负数的性质,几个非负数的和为0时,这几个非负数都为0.24.若+|3﹣y|=0,则2xy=3.【分析】根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.【解答】解:由题意得,4x﹣2=0,3﹣y=0,解得x=,y=3,所以,2xy=2××3=3.故答案为:3.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.25.在下列6个等式中,①ab=0;②a+b=0;③;④a2=0;⑤a2+b2=0;⑥中,a一定是零的等式编号是③④⑤⑥.【分析】①②中,a值可能为0但不是一定为0;③式中,由于分式的分母不为0,因此当分式的值为0时,只有分子为0一种情况,因此a必为0;④⑤⑥可根据非负数的性质求出a值必为0.因此a值一定为0的式子有③④⑤⑥.【解答】解:因为:①ab=0,则a=0或b=0;②a+b=0,则a=﹣b;这两项的a 值不一定为0.③,则a=0且b≠0;④a2=0,则a=0;⑤a2+b2=0,则a=0且b=0;⑥,则a=0且b=0;因此只有③④⑤⑥的a值一定是零.故答案为:③④⑤⑥.【点评】本题考查了非负数的性质.初中阶段有三种类型的非负数:(1)绝对值;(2)偶次方;(3)二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.26.若|x﹣2|和互为相反数,则xy的算术平方根是4.【分析】先列出算式,再由非负数的和为0,即两个0相加,求得x,y的值,再求xy的算术平方根.【解答】解:∵|x﹣2|+=0,∴x﹣2=0,y﹣8=0,解得x=2,y=8,∴xy=2×8=16,∴xy的算术平方根是4.【点评】本题考查了算术平方根的求法和相反数的性质,两个数互为相反数,则和为0.27.若实数x,y满足,则xy﹣x2的平方根为±.【分析】根据非负数的性质列式求出x、y的值,再代入代数式进行计算,再根据平方根的定义进行求解.【解答】解:根据题意得,x﹣2=0,3﹣y=0,解得x=2,y=3,∴xy﹣x2=2×3﹣22=6﹣4=2,∴xy﹣x2的平方根为±.故答案为:±.【点评】本题考查了算术平方根非负数,偶次方非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是解题的关键.28.已知实数x,y满足+(y+1)2=0,则x﹣y等于3.【分析】根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.【解答】解:根据题意得,x﹣2=0,y+1=0,解得x=2,y=﹣1,所以,x﹣y=2﹣(﹣1)=2+1=3.故答案为:3.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.29.已知=0,则b a=﹣.【分析】根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.【解答】解:∵=0,∴a﹣3=0,b+=0,∴a=3,b=﹣,∴b a=(﹣)3=﹣.故答案为﹣.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.30.已知+|a+b+1|=0,则a b=1.【分析】根据非负数的性质列式求出a、b的值,然后代入代数式进行计算即可得解.【解答】解:由题意得,a+1=0,a+b+1=0,解得a=﹣1,b=0,所以,a b=(﹣1)0=1.故答案为:1.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.31.若(2a+3)2与互为相反数,则a=﹣.b=2.【分析】根据互为相反数的两个数的和等于0列出方程,再根据非负数的性质列式求解即可得到a、b的值.【解答】解:∵(2a+3)2与互为相反数,∴(2a+3)2+=0,∴2a+3=0,b﹣2=0,解得a=﹣,b=2.故答案为:﹣,2.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.32.(a+8)2+|b﹣5|+=0,则a+b+c=0.【分析】根据非负数的性质求出a、b、c的值,计算即可.【解答】解:由题意得,a+8=0,b﹣5=0,3﹣c=0,解得,a=﹣8,b=5,c=3,则a+b+c=0,故答案为:0.【点评】本题考查的是非负数的性质,掌握当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.33.|x+1|++(2y﹣4)2=0,则x+y+z=3.【分析】根据非负数的性质列式求出x、y、z的值,然后代入代数式进行计算即可得解.【解答】解:由题意得,x+1=0,z﹣2=0,2y﹣4=0,解得x=﹣1,y=2,z=2,所以,x+y+z=﹣1+2+2=3.故答案为:3.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.34.已知|a+2|=0,那么a﹣b=﹣7.【分析】根据非负数的性质列出算式,分别求出a、b的值,计算即可.【解答】解:由题意得,a+2=0,b﹣5=0,解得,a=﹣2,b=5,则a﹣b=﹣7,故答案为:﹣7.【点评】本题考查的是非负数的性质,掌握非负数之和等于0时,各项都等于0是解题的关键.35.若+=0,则(x﹣1)2+(y+3)2=25.【分析】首先根据非负数的性质可求出x、y的值,再将它们的值代入(x﹣1)2+(y+3)2中求解即可.【解答】解:由题意得x﹣1=0,y﹣2=0;即x=1,y=2;则(x﹣1)2+(y+3)2=(1﹣1)2+(2+3)2=25.故答案为:25.【点评】此题主要考查了非负数的性质,初中阶段有三种类型的非负数:(1)绝对值;(2)偶次方;(3)二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.36.已知+(y+5)2=0,则(x+y)2012=1.【分析】直接利用算术平方根的定义以及偶次方的性质得出x,y的值进而代入求出即可.【解答】解:∵+(y+5)2=0,∴x﹣4=0,y+5=0,解得:x=4,y=﹣5,则(x+y)2012=(4﹣5)2012=1.故答案为:1.【点评】此题主要考查了算术平方根的定义以及偶次方的性质,得出x,y的值是解题关键.37.若(x﹣8)2与互为相反数,则x=8y=2.【分析】利用互为相反数两数之和为0列出关系式,利用非负数的性质求出x与y的值即可.【解答】解:根据题意得:(x﹣8)2+=0,可得x﹣8=0,y﹣2=0,解得:x=8,y=2.故答案为:8;2.【点评】此题考查了非负数的性质:算术平方根及偶次幂,熟练掌握非负数的性质是解本题的关键.38.若a、b为实数,且|a+1|+=0,则的值是.【分析】根据非负数的和为零,可得每个非负数为零,可得a、b的值,根据负数的奇数次幂是负数,可得答案.【解答】解:由|a+1|+=0,得a+1=0,a+b=0,解得a=﹣1,b=1.=(﹣1)2015=﹣1,故答案为:﹣1.【点评】本题考查了非负数的性质,利用非负数的和为零得出a、b的值是解题关键,注意负数的奇数次幂是负数.39.当x=﹣时,+5的值最小.【分析】根据算术平方根具有非负性可得7x+1=0,再解即可.【解答】解:∵≥0,∴当=0时,+5的值最小,由=0得:7x+1=0,解得:x=﹣.故答案为:﹣.【点评】此题主要考查了非负数的性质,关键是掌握算术平方根具有非负性.40.若x、y为实数,且|x+2|+=0,则(x+y)2016=1.【分析】根据绝对值与算术平方根的和为零,可得绝对值与算术平方根同时为零,可得x、y的值,再根据负数的奇数次幂是负数,可得答案.【解答】解:∵|x+2|+=0,∴x+2=0,y﹣3=0,∴x=﹣2,y=3,∴(x+y)2016=1.故答案为:1.【点评】本题考查了非负数的性质,利用绝对值与算术平方根的和为零得出绝对值与算术平方根同时为零是解题关键,注意负数的奇数次幂是负数.三.解答题(共10小题)41.若|m+1|+=0,求m2000﹣n4的值.【分析】根据非负数的性质列式求出m、n,然后代入代数式进行计算即可得解.【解答】解:由题意得,m+1=0,2n﹣1=0,解得m=﹣1,n=,所以,m2000﹣n4=(﹣1)2000﹣()4=1﹣=.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.42.解答下列各题(1)解方程:2(3x﹣1)2=8;(2)已知(x﹣)2+=0,求xy﹣的值.【分析】(1)利用直接开方法求出x的值即可;(2)先根据非负数的性质求出x、y的值,再代入所求代数式进行计算即可.【解答】解:(1)方程两边同时除以2得,(3x﹣1)2=4,直接开方得,3x﹣1=±=±2,解得,x=1或x=﹣;(2)∵(x﹣)2+=0,∴x﹣=0,y+=0,解得x=,y=﹣,∴原式=×(﹣)+=﹣2+=﹣.【点评】本题考查的是非负数的性质及利用直接开方法解一元二次方程,在解答(1)时要注意一个数的平方根有两个,这两个数互为相反数,不要漏解.43.已知实数a、b满足,求2a﹣b+1的平方根.【分析】根据非负数的性质列出二元一次方程组,求出a、b的值,然后代入代数式进行计算,再根据平方根的定义解答.【解答】解:根据题意得,,解得,所以,2a﹣b+1=2×﹣+1=4,∵(±2)2=4,∴2a﹣b+1的平方根是±2.【点评】本题考查了平方数非负数,算术平方根非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是解题的关键.44.已知,试求x﹣8y的算术平方根.【分析】根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.【解答】解:根据题意得:,解得:x=1,y=﹣1.则x﹣8y=1+8=9,则算术平方根是:3.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.45.已知|x+3|+=0,求x2﹣6y的值.【分析】根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.【解答】解:由题知,x+3=0,2﹣3y=0,解得x=﹣3,y=,所以,x2﹣6y=(﹣3)2﹣6×=9﹣4=5.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.46.已知x,y满足=0,求x﹣的平方根.【分析】根据非负数的性质列出算式求出x、y的值,代入代数式计算,根据平方根的概念计算得到答案.【解答】解:由题意得,2x﹣16=0,y﹣1=0,解得,x=8,y=5,则x﹣=4,4的平方根是±2,则x﹣的平方根是±2.【点评】本题考查的是非负数的性质,掌握几个非负数的和为0时,这几个非负数都为0是解题的关键,注意平方根的概念的应用.47.若二次根式与互为相反数,求2x+3a﹣1的值.【分析】直接利用二次根式有意义的条件得出a,x的值,进而代入求出答案.【解答】解:∵二次根式与互为相反数,∴3﹣a=0,x2﹣1=0,解得:a=3,x=±1∴当x=1时,2x+3a﹣1=2+9﹣1=10,当x=﹣1时,2x+3a﹣1=﹣2+9﹣1=6.【点评】此题主要考查了非负数的性质,正确得出a,x的值是解题关键.48.若+|b2﹣9|=0,求ab的值.【分析】首先根据非负数的性质可求出a、b的值,进而可求出a、b的积.【解答】解:∵+|b2﹣9|=0,∴a﹣2=0,b2﹣9=0,解得a=2,b=±3,当a=2,b=3时,ab=6当a=2,b=﹣3时,ab=﹣6.【点评】本题主要考查了非负数的性质,初中阶段有三种类型的非负数:绝对值、偶次方、二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.49.(1)若(﹣b+1)2与互为相反数,求(a+b)2004的值.(2)已知a的两个平方根为3b﹣1和b+5,求a的值.【分析】(1)根据非负数的性质,两个非负数的和等于0,则每个数等于0,据此即可列方程求得a、b的值,进而求解;(2)根据正数的两个平方根互为相反数,据此列方程求得b的值,进而求得a 的值.【解答】解:(1)根据题意得:,解得:,则(a+b)2004=0;(2)根据题意得(3b﹣1)+(b+5)=0,解得:b=﹣1,则a=(3b﹣1)2=(﹣4)2=16.【点评】本题考查了非负数的性质以及算术平方根的性质,理解非负数的性质是关键.50.已知实数a,b满足+b2+2b+1=0,求a2+﹣|b|的值.【分析】首先依据非负数的性质得到a2﹣5a+1=0,b=﹣1,然后再求得a+=5,然后利用完全平方公式求得a2+的值,最后代入求解即可.【解答】解:∵实数a,b满足+b2+2b+1=0,∴a2﹣5a+1=0,b+1=0,∴a+=5,b=﹣1.∴a2+=23.∴原式=23﹣|﹣1|=23﹣1=22.【点评】本题主要考查的是非负数的性质,求得a2+的值是解题的关键.。
