信号与系统 王颖民 第十一次作业
信号与系统_洛阳师范学院中国大学mooc课后章节答案期末考试题库2023年

信号与系统_洛阳师范学院中国大学mooc课后章节答案期末考试题库2023年1.复指数信号【图片】的周期为()。
答案:2.求积分【图片】()。
答案:-33.关于【图片】函数描述不正确的是()。
答案:4.信号【图片】的频谱密度函数【图片】()。
答案:5.连续时间周期信号的频谱是()。
答案:离散非周期的6.直流信号【图片】,则【图片】的傅里叶变换【图片】为( )。
答案:7.【图片】的傅里叶变换为()。
答案:8.非周期连续时间信号【图片】满足绝对可积【图片】是其傅里叶变换存在()条件。
答案:充分9.若LTI离散系统的单位样值响应【图片】满足绝对可和,即:【图片】,则系统是稳定性的。
答案:正确10.当离散因果序列z变换的全部极点位于单位圆内或者位于单位圆上【图片】处且为一阶时,该序列终值是存在的。
答案:正确11.双边信号【图片】的傅里叶变换为()。
答案:12.将【图片】信号展开为三角函数形式的傅里叶级数,则该信号的二次谐波分量为()。
答案:13.周期为【图片】的连续时间信号【图片】,若满足【图片】,则其傅里叶级数展开中仅包含()。
答案:正弦分量14.周期【图片】的实连续时间信号【图片】,其三角函数形式的傅里叶级数为:【图片】谐波形式的傅里叶级数为:【图片】指数形式的傅里叶级数为:【图片】则该周期信号的平均功率描述不正确的是()。
答案:15.若系统起始无储能,即【图片】状态为零,则零输入响应为零,但自由响应可以不为零,由激励信号和系统参数共同决定。
答案:正确16.离散时间序列【图片】的周期为()。
答案:3017.线性时不变系统的响应可以分解为零输入响应和零状态响应之和。
其中,零输入响应由【图片】时刻到【图片】时刻不跳变,此时刻若发生跳变仅可能出现在零状态响应分量中。
答案:正确18.零状态响应是指不考虑起始时刻系统储能(起始状态为零),仅由系统外加激励所产生的响应。
答案:正确19.零输入响应是指没有外加激励作用(外加激励为零),仅由系统起始状态(起始时刻系统的储能)所产生的响应。
桂电信号与系统作业参考答案

第一章1.8 系统的数学模型如下,试判断其线性、时不变性和因果性。
其中X (0-)为系统的初始状态。
(2)()()2f t y t e = (5)()()cos2y t f t t = (8)()()2y t f t = 解:(2)()()2f t y t e = ① 线性: 设 ()()()()1122,f t y t f t y t →→,则 ()()()()122212,f t f t y t e y t e ==那么 ()()()()()()()112211222221122a f t a f t a f t a f t a f t a f t y t ee e +⎡⎤⎣⎦+→==,显然,()()()1122y t a y t a y t ≠+,所以是非线性的。
② 时不变性设()()11,f t y t →则 ()()()()10122110,f t t f ty t e y t t e -=-=设()()102,f t t y t -→则()()()102210f t ty t e y t t -==-,所以是时不变的。
③ 因果性因为对任意时刻 t 1,()()121f ty t e =,即输出由当前时刻的输入决定,所以系统是因果的。
(5)()()cos2y t f t t = ① 线性: 设 ()()()()1122,f t y t f t y t →→,则 ()()()()1122cos2,cos2y t f t t y t f t t ==那么()()()()()()()112211221122cos2cos2cos2a f t a f t y t a f t a f t t a f t t a f t t +→=+=+⎡⎤⎣⎦,显然()()()1122y t a y t a y t =+,所以系统是线性的。
② 时不变性设()()11,f t y t →则 ()()()()()1110100cos2,cos2y t f t t y t t f t t t t =-=--设()()102,f t t y t -→则()()()21010cos2y t f t t t y t t =-≠-,所以是时变的。
《信号与系统2010》(A)

八. 分)已知:一反馈因果系统, G(s) (9
s 1 ,使系统稳定,确定 K 的范围, s 4s 4
2
取 k=1,作出幅频特性示意图。
……………………………… 装 ……………………………… 订 ………………………………… 线 ………………………………
课程_______信号与系统_________班级________________________姓名__________________________学号________________________
……………………………… 密……………………………… 封 ………………………………… 线 ………………………………
六. 分) 写出电感 S 域模型的串、并联表达式,并作出其电路模型。 (6
……………………………… 装 ……………………………… 订 ………………………………… 线 ………………………………
课程_____信号与系统_______班级________________________姓名__________________________学号________________________
题号 得分
一 二 三 四 五
徽
六
工
七 八
业
九
大
十
学
十一 十二
试
十三
题
十四
纸(一)
十五 十六 十七 十八 十九 二十 总 分
2009~2010 学年第二学期期末考试《信号与系统》试卷(A)
一. 选择题(15 分)
1.
t 2) ( )dt _______ 2 (a) 0 (b) 2
华侨大学 《信号与系统》证明题(B卷)

X (k )
实部为奇、虚部为偶 虚偶函数 实奇函数
3 . 设 H ( p)
是线性时不变系统的传输算子,且系统起始状态为零,试证明
[ H ( p) (t )]e t H ( p ) (t ) 。
4.设 r (t ) e tu (t ) (t 3k ) ,证明 r (t ) Ae t , 0 t 3 ,并求出 A 值。
即此函数没有波形 cos( nt ) 的分量。
23.完整推导证明窗函数设计难则式 (10 100) 和式 (10 111) 24.试利用另一种方法证明因果系统的 R( ) 与 X ( ) 被希尔伯特变换相互约束。
(1)已知 h(t ) h(t )u (t ), he (t ) 和 h0 (t ) 分别为 h(t ) 的偶分量和奇分量, h(t ) hc (t ) h0 (t ) , 证明: he (t ) h0 (t ) sgn(t ), h0 (t ) he (t ) sgn(t ). ( 2 ) 由 傅 里 叶 变 换 的 奇 偶 虚 实 关 系 , 已 知 H ( j ) R ( ) jX ( ), 其 中
k
1 1 sgn(t )] ; 2 2
(2)利用矩形脉冲取极限 ( ) ;
(3)利用积分定理 [u (t )
t
( )d ]
at a 0
7.证明 f (t ) (t ) f (0) (t ) 2 f (0) (t ) f (0) (t ) 。 8.若 x(n) 为纯虚序列, DFT [ x (n)] X (k ) ,分解为实部与虚部写做: x(k ) X r (k )
20.试证明因果系统的 R( ) 与 X ( ) 被希尔伯特变换相互约束,即若因果系统的
华侨大学《信号与系统》证明题题库(A)答案

华侨大学信息科学与工程学院2010-2011学年二学期课程考试试卷答案(A 卷)课程名称:信号与系统 考试时间:120分钟 年级:xxx 级专业: xxx题目部分,(卷面共有50题,100分,各大题标有题量和总分) 一、证明(50小题,共100分)1.证明(1)设12112()nn i i nic c c c H p p p p p λλλλ==+++=++++∑则1()()()i nti i H p t c eu t λδ-==∑又12112()nnii nic c c c H p p p p p ααλαλαλαλ=+=+++=++++++++∑()11()()()()[()()]i nnk ttittiii i H p t c eu t ec eu t H p t e ααλααδδ----==∴+===∑∑(2)设()122()()rrc c c H p p p p λλλ=++++++则112()()()()r kr H p t c c t c t e u t δ-=+++而1221()12()()()()()()()[()()]rrr tr tc c c H p p p p H p t c c t c t eu t eH p t αλαααλαλαλαδδ----+=++++++++++=++=综合(1)(2)故[()()]()()tH p t e H p a t αδδ-=+得证2.证明[()()]()f t t t dt δϕ∞-∞''⎰{}()()[()]()()()()[()()]()[()()()()]()()[()]()()[()]()()()()[()()]()()()()[(f t t d t f t t t t f t t dtt f t t f t t dt f t t d t f t t d t f t t t t f t t dt f t t t t f ϕδϕδδϕδϕϕϕδϕδϕδδϕϕδδ∞∞∞-∞-∞-∞∞-∞∞∞-∞-∞∞∞-∞-∞''''==-'''=-+''=-+''''=--+-⎰⎰⎰⎰⎰{})()]()[()()()()]()[()()()()]t t dtt f t t f t t dt t f t t f t t dtϕδδϕδϕϕ∞∞-∞-∞∞∞-∞-∞''''''''''=+++⎰⎰⎰⎰()[()()2()()()()](0)(0)2(0)(0)(0)(0)t f t t f t t f t t dtf f f δϕϕϕϕϕϕ∞-∞''''''=++''''''=++⎰[(0)()]()[2(0)()]()[(0)()]()f t t dt f t t dt f t t dt δϕδϕδϕ∞∞∞-∞-∞-∞''''''=+-+⎰⎰⎰()()(0)()2(0)()(0)()f t t f t f t f t δδδδ''''''''∴=-+在这里利用了以下公式: ()()()()(0)()()(0)()()(1)(0)k k k t t dt t t dt t t dt ϕδϕδϕϕδϕϕ∞-∞∞-∞∞-∞⎧=⎪⎪''=-⎨⎪⎪=-⎩⎰⎰⎰ 3.证明2()()t t t dt δϕ∞-∞''⎰222()[()]()()()[()]t t d t t t t t t t dt ϕδϕδδϕ∞∞∞-∞-∞-∞''''==-⎰⎰2()2()()()t t t dt t t t dt δϕδϕ∞∞-∞-∞⎡⎤'''=-+⎢⎥⎣⎦⎰⎰22{2()()()[2()]}{()()()[()]}t t t t t t dt t t t t t t dt ϕδδϕδϕδϕ∞∞∞∞-∞-∞-∞-∞''''=----⎰⎰2()[2()]()2()()2()()()t t dt t t t dt t t t dt t t t dt δϕδϕδϕδϕ∞∞∞∞-∞-∞-∞-∞''''=+++⎰⎰⎰⎰2(0)[2()]()t t dt ϕδϕ∞-∞==⎰2()2()t t t δδ''∴=32()[()][2()]t t t t t t t δδδ''''===0证明()()(1)!()n n n t t n t δδ=-用归纳法()()(1)0!()t t t t δδδ==-()()()[()]()()()[()]t t t dt t t d t t t t t t t dt δϕϕδϕδδϕ∞∞∞∞-∞-∞-∞-∞''==-⎰⎰⎰()()()()()()t t t dt t t dt t t dt ϕδϕδϕδ∞∞∞-∞-∞-∞'=---⎰⎰⎰22()()(1)1!()()2()(1)2!()t t t t t t t t δδδδδδ'∴=-=-''==-⋅又33()()()[()]t t t dt t t d t δδϕδ∞∞-∞-∞'''''=⎰⎰33()()()[()]t t t t t t dt ϕδδϕ∞∞-∞-∞'''''=-⎰2()[3()()]t t t t t dt δϕϕ∞3-∞'''=-+⎰233()()()()t t t dt t t t dt δϕδϕ∞∞-∞-∞'''''=--⎰⎰(3)2()()t t dt δϕ∞-∞=-⋅⎰3()(32)()(1)3!()t t t t δδδ3'''∴=-⨯=-由归纳法可得()()(1)!()nn nt t t δδ=-4.证明:()()(3)tk r t e u t t k δ+∞-=-∞=*-∑其波形如下图所示。
信号系统习题
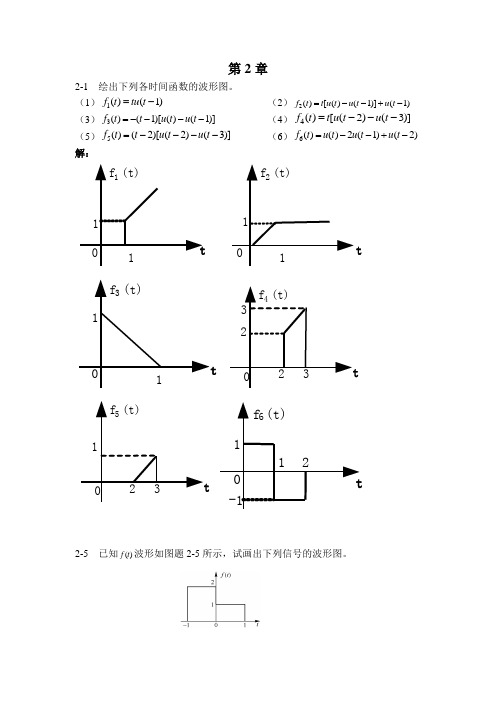
第2章2-1 绘出下列各时间函数的波形图。
(1)1()(1)f t tu t =- (2)2()[()(1)](1)f t t u t u t u t =--+- (3)3()(1)[()(1)]f t t u t u t =---- (4)4()[(2)(3)]f t t u t u t =--- (5)5()(2)[(2)(3)]f t t u t u t =---- (6)6()()2(1)(2)f t u t u t u t =--+-解:2-5 已知()f t 波形如图题2-5所示,试画出下列信号的波形图。
t图 题2-5(3)3()(36)f t f t =+ (5)511()36f t f t ⎛⎫=-- ⎪⎝⎭解:tt2-6 已知()f t 波形如图题2-6所示,试画出下列信号的波形图。
图 题2-6(4)4()(2)(2)f t f t u t =-- (6)6()(1)[()(2)]f t f t u t u t =--- 解:2-7 计算下列各式。
(1)0()()f t t t δ+ (2)00()()d f t t t t t δ∞-∞+-⎰(3)24e (3)d t t t δ-+⎰(4)e sin (1)d t t t t δ∞-+⎰(5)d [e ()]d t t t δ-(6)0()()d f t t t tδ∞-∞-⎰(7)0()()d f t t t tδ∞-∞-⎰(8)00()d 2t t t u t t δ∞-∞⎛⎫--⎪⎝⎭⎰(9)00()(2)d t t u t t t δ∞-∞--⎰(10)(e )(2)d t t t t δ∞-∞++⎰(11)(sin )d 6t t t tδ∞-∞π⎛⎫+- ⎪⎝⎭⎰(12)j 0e [()()]d t t t t t Ωδδ∞--∞--⎰解:(1) 原式0()()f t t δ=(2)原式)2()()(0000t f dt t t t t f =-+=⎰+∞∞-δ(3)原式2334(3)e t dt e δ---=+=⎰(4)原式10sin(1)(1)0((1))e t dt t δδ+∞-=-+=+⎰不在积分区间内(5)原式)()](['0t t e dtd δδ== (6)原式)()()0(00t f dt t t f -=-=⎰+∞∞-δ(7)原式00(0)()()f t t dt f t δ+∞-∞=-=⎰(8)原式⎩⎨⎧><==--=⎰∞+∞-0100)2()2()(000000t t t u dt t t u t t δ(9)原式⎩⎨⎧<>=-=--=⎰∞+∞-0100)()2()(000000t t t u dt t t u t t δ(10)原式22(2)(2)2e t dt e δ+∞---∞=-+=-⎰(11)原式1(sin )()66662t dt ππππδ+∞-∞=+-=+⎰ (12)原式000[()()]1j t j t e t e t t dt e δδ+∞-Ω-Ω-∞=--=-⎰2-8 画出图题2-8所示各信号的偶分量和奇分量的波形。
北京工业大学信号与系统课后习题

信号与系统-作业习题Signals and Systems课程编码:学时数:80学分数:5适用专业:电子信息工程、通信工程专业一.课程教学目标:信号与系统课程是电子学、信息技术、通信、自动化、计算机、信号处理、雷达、测量、系统工程等专业的重要技术基础课。
它继《电路分析基础》之后,集中研究确定信号经线性时不变系统进行传输、处理的基本理论、基本分析方法和工程应用。
本课程目的是为后续众多专业课程,如:模拟电子电路,数字电路,数字信号处理,通信原理,自动控制原理,计算机网络等奠定基础。
二.教学内容基本要求及学时分配本课程在信号分析方面要求学生掌握信号分析的基本理论和方法,包括:连续周期信号的付里叶级数,连续非周期信号的付里叶变换、连续信号的拉普拉斯变换、离散信号(序列)的z变换等。
在性系统分析方面,要求学生掌握系统的各种描述方法,包括:连续系统微分方程的建立、离散系统差分方程的建立,系统的转换算子及转移函数的计算。
在分析方法应用方面,则主要涉及卷积积分、卷积和以及付里叶级数、付里叶变换、拉普拉斯变换、z变换等方法求解线性系统;应用线性系统的稳定性判定条件对连续系统和离散系统进行稳定性分析;用模拟图、信流图概念对系统进行模拟以及状态方程的建立、由输入-输出方程求状态方程;连续系统状态方程的复频域和时域解法;离散系统状态方程的解以及由状态方程作系统的模拟等内容。
本课程的教学重点和难点主要集中在信号在正交函数空间的分解及线性时不变系统的特征函数这两个最基本的概念的展开上。
重点和难点内容包括两个卷积(卷积积分与卷积和)、五个线性变换(傅里叶级数变换,傅里叶积分变换,拉普拉斯变换,Z变换和傅里叶Z 变换)。
学习本课程前应先修《高等数学》,《线性代数》,《积分变换》,《复变函数》,《电路分析基础》等课程。
以本课程为基础的后续课程主要有《模拟电子线路》,《数字电路》,《通信电路》,《数字信号处理》,《通信系统》,《信号检测》,《计算机网络》等等。
北交《信号与系统》在线作业一-0001

D:没有关系
答案:B
信号f(t)=3cos(4t+π/3)的周期是()。
A:2π
B:π
C:π/2
D:π/4
答案:C
系统的h(t)是由其系统函数H(s)的零极点位置决定的。
A:错误
B:正确
答案:A
两个奇信号相加构成的信号一定是偶对称的。
A:错误
B:正确
答案:A
若一个连续LTI系统是因果系统,它一定是一个稳定系统。
A:错误
B:正确
答案:A
非周期的冲激取样信号,其频谱是离散的、周期的。
A:错误
B:正确
答案:A
抽样信号的频率比抽样频率的一半要大。
A:错误
B:正确
答案:A
单位阶跃响应的拉氏变换称为系统函数。
A:错误
B:正确
答案:A
一个系统的零状态响应就等于它的自由响应。
A:错误
B:正确
答案:A
用有限项傅里叶级数表示周期信号,吉布斯现象是不可避免的。
B:时域是周期离散的,则频域也是周期离散的
C:频域不是周期连续的,则时域也不是周期连续的
D:时域是非周期离散的,则频域是周期连续的
答案:A,B,D
下列哪些不是连续周期信号的傅氏变换的特性()。
A:连续的
B:周期性的
C:离散的
D:与单周期的相同
答案:A,B,D
周期信号f(t)=-f(t±T/2 ),(T—周期),下列哪些不是其傅里叶级数展开式的结构特点()。
A:错误
B:正确
答案:B
H(s)的零点与h(t)的形式无关。
A:错误
B:正确
答案:B
已知一系统的H(s)后,可以唯一求出该系统的h(t)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.22已知系统微分方程为
)(2)
()(9)(15)(7)(2
233t f dt
t df t y dt t dy dt t y d dt t y d +=+++,试画出用直接形式模拟系统的方框图和信号流图。
解:3
232239157129157s 2s H(s)-----++++=++++=s
s s s s s s 设中间变量)(s X
)
()(915712)()(H(s)3
232s X s X s s s s s s F s Y ⋅++++==----- 23
23
()(2)()()(17159)()
Y s s s X s F s s s s X s -----⎧=+⎪∴⎨=+++⎪⎩ -1-2-3X(s)(s)-7s X(s)-15s X(s)-9s X(s)F ∴= 方框图:
信号流图:
4.29已知系统传递函数的分母多项式如下,判断系统是否稳定,并说明理由。
65)1(2+-s s
不稳定,有大于零的实根。
(全部系数不同号)
1125)2(23+++s s s
11
01411
125101
23s s s s
罗斯阵列中第一列元素无变号,系统稳定
)2)(1)(5)(3(+-+s s s
不稳定,根1=s
位于s 平面右半平面。
6652)22)(3)(4(23422++++=+++s s s s s s s
4
4620
6265101234s s s s s 辅助方程0622
=+s ,求导得04=s 罗斯阵列第一列元素不变号,所以H(s)在s 平面的右边平面无极点,但由辅助方程解得:j s 3±=,即H(s)的极点中含有一对共轭虚根,所以系统零界
稳定。
s s s 710)5(23++
不稳定,缺0s 相
22)1()6(+s s
不稳定,虚轴上有二阶极点。
4.30已知系统传递函数,试判断系统稳定性,并说明理由。
如果不稳定,指出在
s 平面右半平面根的数目。
8
21
2)()1(2
3++++=s s s s s H 8
068
12101
23-s s s s
系统不稳定,第一列符号改变了两次,即在s 平面的右半平面有两个极点。
322)
1()()2(2
3
42++++-=s s s s s s s H 3
3
23021
3210
1
234ε
ε
-
s
s s s s (ε为正无穷小,则ε
3
2-
为负无穷大)
系统不稳定,第一列符号改变了两次,即在s 平面的右半平面有两个极点。
14222
3)()3(2
345
23++++++++=s s s s s s s s s H 2
12
3
4
51412111
4211
42121ε
εεε
--
-s s s
s s s
(ε为正无穷小,则ε
1
4-为负无穷大,2
14121ε
ε--的极限为21
)
系统不稳定,第一列符号改变了两次,即在s 平面的右半平面有两个极点。
2
2331
3)()4(2
34
53
4+++++++=s s s s s s s s H 0
002312
31345s s s 02324=++⇒s s 064)23(324
=+=++s s s s dt
d 继续完成阵列:
2
322
23640123s s s s
罗斯阵列第一列元素不变号,所以H(s)在s 平面的右边平面无极点,但由辅助方程解得:j s j s
2,±=±=,即H(s)的极点中含有两对共轭虚根,所
以系统零界稳定。
4.32已知系统如图所示,试判断系统在以下情况时是否稳定。
由图得:k
s s s k
+++=+++=86k 4)2)(s s(s k H(s)2
3 12)1(=k
12
8612
H(s)2
3
+++=s s s
120612
68101
23s
s s s
稳定
60)2(=k 2
0260
68101
23--s s s s
不稳定
48)3(=k
12
012486810123s s s s 辅助方程04862
=+s ,求导得012=s
罗斯阵列第一列元素不变号,所以H(s)在s 平面的右边平面无极点,但由辅助方程解得:j s 22±=,即H(s)的极点中含有一对共轭虚根,所以系统零
界稳定。
