七主梁截面承载力与应力验算
钢吊车梁承载力和稳定性验算

SHANXI
山
西
ARCHITECTURE
建
筑
Vol. 39 No. 4 Feb. 2013
· 33·
钢吊车梁承载力和稳定性验算
施其福
( 安徽马钢工程技术有限公司, 安徽 马鞍山 243000 )
重级工作制软钩吊车的吊车梁的欠载系数 α f = 0. 8 。 1 ) 受拉翼缘与腹板连接焊缝附近腹板的主体金属处( 最大弯 矩截面处) , 此处金属属于第 3 类: 珋 y = 3 800 - 1 916. 36 - 36 = 1 847. 64 mm。 α f Δσ = α f M xmax, k 珋 ( hw + tw - y ) = I nx
表1
序号 1 2 吊车 类型 桥式软勾 桥式软勾 吊车 工作制 A6 A6
吊车基本资料
额定起 重量 / t 125 /30 50 /10 吊车 总重 / t 195. 2 63. 9 最大轮压 / kN P1 P2 649. 8 454. 3 649. 8 454. 3
吊车 跨度 / m 27 27
2 76. 87 N / mm2 < [ Δσ] 2 ˑ 10 6 = 118 N / mm 。
M xmax ( y1 - h y ) = 168. 40 N / mm2 。 I xn σ 槡
2 2 + σ2 c - σσ c + 3 τ =
2 ) 横向加劲肋下端点附近腹板的主体金属处, 此处金属属于 第 4 类: α f Δσ = α f M xmax, k 珋 ( hw + tw - y - 50 ) = I nx
混凝土受弯构件正截面承载力计算
r As f y As a1 fcbx x a1 fc
bh0 bh0 f y bh0 f y h0 f y
令
x
h0
则
r
a1 fc
fy
令b为 = r max时的相对受压区高度,即
rmax
b
a1
f
fc
y
= r max时的破坏形态为受压区边缘混凝土达到极限压
c fc e0 e ecu
n
2
1 60
(
fcu,k
50)
2.0
各系数查表4-3
e0 0.002 0.5( fcu,k 50)105 0.002
ecu 0.0033 0.5( fcu,k 50)105 0.0033
4.钢筋应力—应变关系的假定(本构关系)
Ese e e y fy e ey
4.3钢筋混凝土受弯构件正截面试验研究
一、受弯构件正截面破坏过程
受弯构件正截面破坏分为三个阶段 • 第一阶段:裂缝开裂前 • 第二阶段:从开裂到钢筋屈服 • 第三阶段:从钢筋屈服到梁破坏
(1)第I阶段
当荷载比较小时,混凝土基本处 于弹性阶段,截面上应力分布为三 角形,荷载-挠度曲线或弯矩-曲率 曲线基本接近直线。截面抗弯刚度 较大,挠度和截面曲率很小,钢筋 的应力也很小,且都于弯矩近似成 正比。
My
Mu
Failure”,破坏前
可吸收较大的应变
能。
0
f
2.超筋梁(Over reinforced)破坏
钢筋配置过多,将发生这种破坏。 破坏特征:破坏时钢筋没有达到屈服强度,破坏是由 于压区混凝土被压碎引起,没有明显预兆,为脆性破 坏。
七章钢筋混凝土受扭构件承载力计算
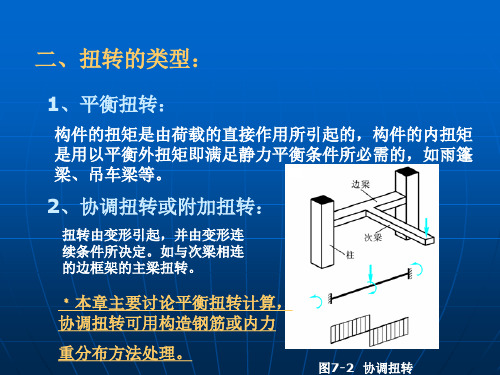
翼缘 —— 纯扭;
腹板—— 剪扭;
全截面——弯剪扭分别配筋再叠加。
(五)箱形截面剪扭构件承载力计算
1、一般剪扭构件 抗扭承载力下式计算:
T 0.35ht ftWt 1.2
f yv
Ast1 Acor s
2、集中力作用下的独立剪扭构件
(7-14)
(六)箱形截面弯剪扭构件承载力计算
(3)按照叠加原则计算剪扭的箍筋用量和纵筋用量。
(二)矩形截面弯扭构件承载力计算
图7-11 弯扭构件的钢筋叠加
(三)矩形截面弯剪扭构件承载力计算
﹡《规范》规定,其纵筋截面面积由受弯承载力和受扭 承载力所需的钢筋截面面积相叠加,箍筋截面面积则由 受剪承载力和受扭承载力所需的箍筋截面面积相叠加, 其具体计算方法如下:
(3)当箍筋或纵筋过多时,为部分超配筋破坏。
(4)当箍筋和纵筋过多时,为完全超配筋破坏。
因此,在实际工程中,尽量把构件设计成(2)、(3), 避免出现(1)、(4)。
(二)抗扭钢筋配筋率对受扭构件受力性能的影响
《规范》采用纵向钢筋与箍筋的配筋强度比值 进行控制, (0.6≤ ≤1.7)
f y Astl s
﹡像矩形、T形和I形截面一样,箱形截面弯剪扭 构件承载力计算中,弯矩按纯弯构件计算剪力和 扭矩按剪扭构件计算。
三、受扭构件计算公式的适用条件及构造要求
(一)截面尺寸限制条件
当 hw b 4
时,
V bh0
T 0.8Wt
0.25c
fc
(7-15)
当
hw
b6
时,
V bh0
T 0.8Wt
0.2c
fc
——混凝土抗拉强度设计值;
采用MIDAS软件分析碳纤维加固钢筋混凝土梁

采用MIDAS软件分析碳纤维加固钢筋混凝土梁?采用MIDAS软件分析碳纤维加固钢筋混凝土梁奉江,肖光辉(四川南充水利电力建筑勘察设计研究院,四川南充637000)【摘要】结合”5?12”兰成渝输油管道龙潭河桥的震后的检测与加固工程,应用桥梁结构有限元分析软件MIDAS,建立有限元分析模型,对该桥进行了粘贴碳纤维布加固设计模拟分析,从而提出了加固设计方案.为今后类似桥梁加固的研究与设计提供了有益经验.【关键词】桥梁加固;碳纤维布;抗弯极限承载力;有限元【中图分类号】TU746.3我国自20世纪80年代起开始,公路建设事业步入了高速发展时期,建设了大量各类桥梁,目前公路桥梁总数已突破57×10座,成为仅次于美国的世界第二桥梁大国.在我国目前的众多桥梁中,因构件老化,实际荷载提高,环境腐蚀及洪水,地震等各种原因,结构构件出现损伤,承载能力降低的旧危桥占相当比例.这些桥梁迫切需要进行桥梁检测,维修加固,才能够适应最新荷载,继续提供通行能力¨J.按旧标准设计建造的桥梁,设计荷载标准偏低,桥面宽度狭窄.随着服役时间推移和交通运输事业的持续蓬勃发展,面临的桥梁养护管理工作任务也日趋艰巨,客观上对桥梁检测,评价,维修加固和养护管理等技术提出了更高的要求.近年来,桥梁加固越来越受到全球的高度重视,被提到刻不容缓的议事日程上来.桥梁建设的重点已经从新桥建设转移到旧桥的加固和改造方面.根据旧危桥的结构体系,病害状况,桥梁环境等综合条件的不同,桥梁的加固方法有多种选择.和配筋加固法,体外预应力加固法,粘贴钢板(筋)按结构和施工方法的不同, 目前国内外主要采用的加固方法有7种:桥面补强层加固法,增大截面加固法,改变结构受力体系加固法,锚喷混凝土加固法,增设构件加固法,增加辅助横梁加固法,粘贴碳纤维布(板)加固法.对于一座旧危桥梁的加固设计应经过系统,反复的设计方案比选来选取在经济,效果,工期,美观等综合指标较高的加固设计.在各加固方法中,碳纤维材料由于其良好的物理,化学性质和工程应用性能,具有巨大的应用前景.1龙潭河桥震害表现龙潭河桥位于甘肃省康县阳坝镇附近,竣工于2000年,是一座3×20m钢筋混凝土简支T梁桥,桥宽8.5m,桥面连续,桥梁全长75m.T梁梁高1.3m,单跨共5片.下部为钢筋混凝土双圆柱式墩,扩大式桥墩基础,重力式U型台.设计荷载为汽一2O,挂一100.桥位处于地震基本烈度Ⅶ度区, 桥头,桥位分别指向广坪,阳坝.桥型图见图1,桥面横向布置图见图2.2008年”5?12”汶川大地震中,龙潭河桥受到严重损【文献标识码】B伤,震后第一时间对其进行了检测与评估.检测工作内容主要包括:超声回弹法综合法探测构件混凝土强度,裂缝检测,桥梁各部位几何测量,构件及联结部位损伤等….检测与评估综合结论:受地震作用影响,桥跨结构梁体出现开裂和裂缝发展,对桥梁承载力产生不利影响;经分析计算,梁体实际极限抗弯承载力为2033kN?m,而在原设计荷载汽一20,挂一100作用下,梁体需达到的极限抗弯承载力为2240kN?m,即该桥已不能满足原设计承载要求.图1龙潭河桥桥型图图2龙潭河桥桥面横向布置图(单位:em)2粘贴碳纤维布加固估算2.1桥梁荷栽标准该桥设计,建造于2000年前,原设计”汽一20,挂一t00”桥梁荷载现已废止,荷载标准可相当于《公路桥涵通用设计规范》(JTGD60—2004)中的公路一Ⅱ级[23,由《公路桥涵通[定稿日期]2011—03—25[作者简介]奉江(1970~),男,工程师,长期从事工业与民用建筑建筑,结构设计工作.四JIl建筑第31卷5期2011.10l8l用设计规范》,本桥对应的荷载标准值为:q=7.875kN/m, Pk:240kN.2.2原桥主梁结构设计计算基本参数T梁梁肋宽度:b=180mm;T梁截面高度:h=1300mm;T梁截面如图3.2.3原设计材料参数受拉钢筋:8根,直径为32him,受拉筋抗拉强度设计值fd=280.00N/mm;受拉钢筋面积A=6432mln;受拉钢筋合力点至截面近边缘的距离n=114mm;受压钢筋面积为0;受压钢筋合力点至截面近边缘的距离.:取为4o.00ITlm.混凝土:强度等级为C30,轴心抗压强度设计值f=13.8N/ram;轴心抗拉强度标准值f【k=2.01N/mm;轴心抗拉强度设计值.:1.39N/ram.圈3龙潭河桥主梁几何尺寸2.4碳纤维材料及粘贴专用胶采用13本东丽碳素纤维制造公司生产的UT70—30型号碳纤维布的力学性能指标作为计算参考.设计厚度0.167 mill;弹性模量Ef≥2.01X10’MPa;极限抗拉强度ff≥3000.00MPa.按T梁腹板底粘贴2层进行试算J.2.5粘贴碳纤维加固面积估算梁底碳纤维片材的截面面积A=60.12mm;考虑二次受力,加固前计算截面上实际作用的初始弯矩M=852 kN?m.该弯矩由加固前桥跨结构本身恒载引起.加固前构件在初始弯矩作用下,截面受拉边缘混凝土的初始应变8:0.0002;考虑二次受力影响,混凝土小于C50,s=0.00033.求解得:8f=0.047,=68mm;≤o=8O Inn,加固后极限抗弯承载力M=2413kN-m,估算满足原设计要求.3龙谭河桥碳纤维抗弯加固的有限元模拟计算分析MIDAS是一种三维空间有限元分析软件,通过三维建模分析,可以不用像二维程序那样计算横向分布系数,建模及后处理更加直观.通过在有限元库中加入各种非线性因素, 结合施工阶段,时间依存性,集合非线性等结构分析理论,能够计算出准确和切合实际的分析结果.MIDAS与其他有限182元分析软件一样,主要包含前处理(PreprocessingMode),求解器(Solver)和后处理(Post—processingMode)三个基本模块.建模过程中的输入工作均在前处理模式完成,而荷载组合,反力,位移,构件内力,应力等分析结果的查看和整理工作则都在后处理模式中进行.后处理模式中对分析结果提供图形和文本两种形式,以便可以对所有结果进行分析和验算.在本文的碳纤维有限元模拟中,采用MIDAS提供的平面应力单元(PlaneStressElement)来模拟,碳纤维的力学特性参数如厚度,宽度,弹性模量,剪切模量,抗拉强度及泊松比等可以在”材料”及”单元建立”选项中自行设置J.本文中选取4节点单元进行模拟.单元的自由度是以单元直角坐标系为依据,每个节点只具有x.y方向的线位移自由度.3.1T梁建模本桥为简支桥梁体系,采用T梁格法建立整桥单跨主梁分析模型.该方法的基本原理:用等效梁格代替桥梁上部结构,将分散在T梁每一区段内的弯曲刚度和抗扭刚度集中于最邻近的等效梁格内,实际结构的纵向刚度集中于纵向梁格构件内,横向刚度集中于横向梁格内.理想的刚度等效原则是:当原型实际结构和对应的等效梁格承受相同的荷载时, 两者的挠曲将是恒等的,并且每一梁格内的弯矩,剪力和扭矩等于该梁格所代表的实际结构部分的内力.由于实际结构和梁格体系在结构特性上的差异,这种等效只是近似的,但对一般的设计,粱格法的计算精度是足够的J.整桥单跨主粱T梁格法模型如图4.因模型在三维空间中建立,不需像二维模型那样计算横向分布系数.图4龙潭河桥单跨主粱MIDAS模型3.2碳纤维的模拟用平面应力单元单元来模拟T梁底粘贴的碳纤维布,通过自定义材料及截面功能输人加固设计所采用的碳纤维布的材料性能参数.通过设置节点间的边界条件来模拟碳纤维布与主梁钢筋混凝土的粘接.选用弹性连接选项中的刚性连接方式,将相应位置的碳纤维布单元节点与T梁节点相连接,来达到协调变形与位移,防止粘接失效与滑移破坏,如图5所示.图5碳纤维布单元节点与主梁节点连接3.3模型计算结果分析四川建筑第31卷5期2011.10结构边界条件,静力荷载与移动荷载,施工阶段定义等相应步骤完成后,即完成软件前处理阶段,可进行求解,进入后处理阶段查看分析结果.主要考察梁体挠度,截面弯矩及正截面抗弯,截面应力及梁体裂缝宽度等方面指标是否符合要求.(1)结构反力:支座最大反力为517.2kN.(2)挠度验算验算得跨中挠度值最大,为0.020m,符合规范中要求,~<//600=0.033m.梁体挠度结果输出如表1.表1截面最大挠度表节点荷载Dx(m)Dz(m)RY([rad])2cLCB2(最大)0.0()ooo0.0oOooO.0o68352cLCB2(最大)一0.00127—0.019800.oo04553cLCB2(最大)一O.oo129—0.01981O.Ooo3754cLCB2(最大)一O.oo130—0.01981O.OO02955cLCB2(最大)一O.o0135—0.01978O.O0o10102cLCB2(最大)一0.oo2610.O0o00一O.0o312最小挠度值出现在端支点截面,为0;最大挠度出现在跨中截面,为1.98em.(3)正截面抗弯验算该桥在公路一Ⅱ级荷载作用下主梁各截面产生的最大及最小弯矩如图6,跨中截面弯矩峰值为2286.3kN?m. Moment,CBCalhcLCB2/Mv4710131619222528,1∞4,%49525558616770737682g58891l∞1m n0de图6荷栽作用下主梁截面弯矩粘贴碳纤维布对龙潭河桥进行加固后,公路一Ⅱ级换算荷载效应下最大弯矩值为2285.8kN?m,而相应截面结构抗力弯矩值为2464.5kN?m,满足设计要求,加固提高幅度为21.2%.(4)截面应力验算荷载作用下主梁各截面最大应力如图7所示,其数值满足各材料容许应力要求.图7荷载作用下主梁各截面最大应力值4整桥加固设计方案在T梁腹板底粘贴2层碳纤维布,并沿腹板两侧向上翻折20em.因梁端至1/4跨径段梁体抗弯能力尚满足要求,故可不予加固,粘贴范围可选取1/5—4/5跨径段.针对此桥抗剪承载能力不足,采用在梁腹板粘贴碳纤维布u型箍方法加固,并在腹板两侧中部,上部水平粘贴压条以达到U型箍锚固效果.碳纤维布U型箍采用单层布,宽度20em,在梁两端至I/4跨径段,剪力效应较大,U型箍净距设置为20em;在1/4跨径至3/4跨径段,u型箍净距设为60 cm.碳纤维布压条宽度10em.用混凝土结构裂缝修补材料处理结构裂缝.其中对于梁体的裂缝处理,须在粘贴碳纤维布加固’前进行.处理措施:对于宽度小于0.15mm的裂缝,采用表面封闭法,用改性环氧胶泥适当加压刮抹以封闭裂缝,防止渗漏和避免钢筋锈蚀;对于宽度大于0.15mm的裂缝,采用自动低压渗注法,以恒定低压持续将裂缝灌注修补胶渗注入裂缝内.对于主梁局部混凝土蜂窝,麻面,凿除病害混凝土;对已锈蚀的钢筋除锈,用喷涂型阻绣剂防护,然后用具微膨胀性的环氧砂浆修补.将桥墩裂缝封闭处理后,在裂缝位置粘贴一层单位克重为1500g/m的碳纤维板;将接头断裂的横隔板凿出适当尺寸的矩形孔洞,侧面植筋后重新浇筑混凝土;拆除下沉,散裂的桥台锥坡,将坡底夯实处理后重新按原设计图施工;更换伸缩缝内变形,隆起的橡胶条.5结论本文在总结已有的粘贴碳纤维复合材料对桥梁进行加固的研究与应用的基础上,以”5?12”汶川地震后兰成渝成品油管线龙潭河桥的检测,评估与加固为工程实例,应用桥梁结构有限元分析软件MIDAS,建立有限元分析模型,对该桥进行了粘贴碳纤维布加固设计模拟分析,从而提出了加固设计方案.通过结合实际震后桥梁的检测与粘贴碳纤维加固工程研究,综合考虑其加固机理,材料特性,计算结果及施工特点等指标,可见在地震造成破坏这种特殊病害环境下, 粘贴碳纤维布对于钢筋混凝土桥梁进行抗弯加固是快速,便捷和行之有效的.这对于震后及时修复桥梁,保障交通”生命线”具有重要意义,为今后类似桥梁加固的研究与设计提供了有益经验.参考文献[1]刘来君,赵小星.桥梁加固设计施工技术[M].北京:人民交通出版社,2004[2]JTG1360—2004公路桥涵设计通用规范[s][3]吕伟荣.粘贴加固受弯构件正截面承载力性能研究[D].湖南大学,20o3[4]MIDAS/CIVILAnalysisforCivilStructures(联机手册)[M].MI—DAS.IT(Beijing)Corporation.2006[5]MIDAS/CIVIL技术资料_T梁梁格分析[M].MIDAS.IT(Bei—jing)Corporation.2007四川建筑第31卷5期2011.1Ol83。
30m预应力混凝土简支箱型梁桥设计
30m预应力混凝土简支箱型梁桥设计1.1上部结构计算设计资料及构造布置1.1.1 设计资料1.桥梁跨径及桥宽标准跨径:30m;主梁全长:29.96m;计算跨径:28.66m;桥面净宽:净—9+2×1.5m。
2.设计荷载车道荷载:公路—I级;人群荷载:3kN/㎡;每侧人行道栏杆的作用力:1.52kN/㎡;每侧人行道重:3.75kN/㎡。
3.桥梁处河道防洪标准为20年一遇设计,50年一遇校核,桥下通过流量1000/s时,落差不超过0.1m。
4.桥下净空取50年一遇洪水位以上0.3m。
5.材料及工艺混凝土:主梁采用C50混凝土;钢绞线:预应力钢束采用Φ15.2钢绞线,每束6根,全梁配5束;钢筋:直径大于等于12mm的采用HRB335钢筋,直径小于12mm的采用R235钢筋。
采用后张法施工工艺制作主梁。
预制时,预留孔道采用内径70mm、外径77mm的预埋金属波纹管成型,钢绞线采用T双作用千斤顶两端同时张拉,锚具采用夹片式群锚。
主梁安装就位后现浇600mm宽的湿接缝,最后施工混凝土桥面铺装层。
6.基本计算数据基本计算数据见表5-1〖注〗本例考虑混凝土强度达到C45时开始张拉预应力钢束。
f'ck和f'tk分别表示钢束张拉时混凝土的抗压、抗拉标准强度,则:f'ck = 29.6MPa,f'tk = 2.51MPa。
1.1.2 方案拟定及桥型选择1.桥型选取的基本原则(1) 在符合线路基本走向的同时,力求接线顺畅、路线短捷、桥梁较短、尽量降低工程造价(2)在满足使用功能的前提下,力求桥型结构安全、适用、经济、美观。
同时要根据桥位区的地形、地貌、气象、水文、地质、地震等条件,结合当地施工条件,选用技术先进可靠、施工工艺成熟、便于后期养护的桥型方案。
(3)尽量降低主桥梁体高度,缩短桥长。
2.桥型方案比选根据桥位的通航要求,结合桥位处的地形地貌、地质等条件,我们对简支梁桥、悬臂梁桥、T型刚构桥三种方案进行比选(1)简支梁桥方案采用预应力混凝土箱形截面形式,此结构为静定结构,结构内力不受地基变形及温度变化等的影响,因此对基础的适应性好。
正截面承载力—受弯、受压、受拉

➢ 我国GBJ10-89规范取0=fcm=1.1fc;
➢ 我国DL/T5057-1996、JTJ267-98、GB50010-2002规范
取0=fc。
美国ACI 318—95、欧洲混凝土委员会模式规范
CEB —FIP 1990以及欧洲共同体委员会规范则以标
准圆柱体(150mm300mm)试件的抗压强度标准值
二、基本公式——对任意截面
1、截面的曲率 :
(a)
2、截面上的混凝土应变: 3、截面上的混凝土应力:
4、截面上的钢筋应力:
2
3
5、微元面积上混凝土压应力的合力:
dNi=ci.dAi=b(y).dy.ci(ci) 即:dNi = b(y).ci(ci).dy 6、平衡方程(b)、(c):
N 0 :
28
2、截面M-关系的计算
(a)
应
力钢理 、筋论 内,上 力的
(b)
的 分 布
混 凝 土 ,
—
弯 矩 曲 率
(c)
截 面 及 其 应
关 系 的 确 定
变 29
由上图,静力平衡条件得 :
(a) (b)
用数值计算时,沿高度把截面划分成若干条带,假 定条带上的应力是个常值,上式可近似写为:
力的影响不明显 ; 对0 大的超筋梁和小偏压柱,基本不变。
因此,有些规范把取为常数。 我国: 0=fc=0.67fcu; 美国ACI:0=/(2)=0.72/(2×0.425)fc=0.85 fc
11
❖1 关于混凝土抗压强度:
我国规范GBJl0—89、GB 50010-2002、水工混凝 土结构设计规范DL/T5057—1996、港工规范JTJ 267-98以及英国混凝土结构设计规范BS8110以标 准立方体试块(150mm×l50mm×l50mm)的抗压强 度标准值作为混凝土强度等级。
对框架主梁截面尺寸为250×650进行计算

C、板模挠度验算:
ωmax=ωq=0.644ql4/100EI=0.644×(3.77/1.2×3664)/(100×40000×1/12×915×183)=0.014mm < [δ]=L/400=366/250=10464
符合要求。
(2)板模横向搁栅验算:
A、板模横向搁栅计算简图:
q=3.77/0.915×0.366=1.51N/mm
=1.38×103×35×18002/24×9000×1/12×70×1503×(3-4×352/18002)+1.38×103×381×18002/24×9000×1/12×70×1503×(3-4×3812/18002)+1.38×103×727×18002/24×9000×1/12×70×1503×(3-4×7272/18002)
a、板底模荷载:
胶合板自重:0.3×0.915×1.2=0.33KN/m
砼自重:24×0.915×0.14×1.2=3.69KN/M
钢筋自重:1.1×0.915×0.14×1.2=0.169KN/m
q1=0.33KN/M+3.69KN/m+0.169KN/M=4.189KN/M=4.189N/mm
乘以折减系数:q=ql×0.9=3.77 N/mm
σ= = =3.6N/mm2<[fm]=13N/mm2满足要求。
3、梁纵向搁栅抗剪强度计算:
V= p= ×5×0.9=2.25KN
τ= =0. 3N/mm2<[fv]=1.4N/mm2满足要求。
4、梁纵向搁栅挠度计算:
W= = =2.62mm
[W]= = =4.5mm则W<[W]满足要求。
五、梁支撑计算:
07 钢筋混凝土受扭构件承载力计算

Astl /3
抗剪箍筋: 抗扭箍筋:
A's + Astl /3
+
As
Astl /3
=
Astl /3
Astl /3
As+ Astl /3
Asv1 s
Ast1 s
Asv1 s
+
=
Asv1 Ast1 + s s
受扭构件承载力公式的适用条件及构造要求
1.截面限制条件
2.构造配筋条件
end
最后得:
四、带翼缘截面纯扭构件的开裂扭矩
7.2 纯扭构件的承载力
配筋形式和构造要求(重要) 受扭箍筋的体积配筋率 ρstv
受扭纵筋的配筋率 ρst
同时承受弯、剪、扭构件的配筋率要求。
配筋强度比ζ
部分超筋构件虽然设计中可以采用,但不经济。 受扭性能和极限承载力不仅与配筋量有关,还与纵筋和箍 筋的配筋强度比ζ 有关。
②最小配筋率
(7-15)
另外,构造配筋条件:
如满足: T
1
d
(0.7 f tWt )
,则只需进行构造配抗扭钢筋。
(7-16)
纯扭构件截面设计的主要步骤(书上没讲):
① 验算截面尺寸; ② 验算构造配筋条件;
③ 令ζ=1.2,根据承载力公式(7-10)计算箍筋截面积Ast1, 并验算最小配筋率;
(7-9)
设计中通常取z =1.2
T
1
d
Tu
1
d
(0.35 f tWt 1.2 z f yv
Tc混凝土骨料 的咬合作用
Ast 1 Acor ) s
(7-10)
Ts钢筋的受 扭承载力
梁截面设计与验算

底层梁左端截面设计=========================================================== 1 已知条件及计算要求:(1)已知条件:矩形梁b=300mm,h=600mm。
砼强度等级 C25,fc=11.90N/mm2,纵筋级别 HRB335,fy=300N/mm2,箍筋级别 HPB235,fy=210N/mm2。
弯矩设计值 M=272.85kN.m,剪力设计值 V=101.10kN,扭矩设计值 T=0.00kN.m。
(2)计算要求:1.正截面受弯承载力计算2.斜截面受剪承载力计算3.受扭承载力计算4.裂缝宽度计算。
----------------------------------------------------------- 2 截面验算:(1)截面验算:V=101.10kN < 0.250βc fcbh=504.26kN 截面满足截面配筋按纯剪计算。
----------------------------------------------------------- 3 正截面受弯承载力计算:(1)按单筋计算:as下=35mm,相对受压区高度ξ=x/h=0.278 < ξb=0.550(2)上部纵筋:按构造配筋As=360mm2,配筋率ρ=0.20%(3)下部纵筋:As=ξa1fcbh/fy=1870mm2ρmin=0.20% < ρ=1.04% < ρmax=2.18%----------------------------------------------------------- 4 斜截面受剪承载力计算:(1)受剪箍筋计算:Asv/s=-334.33mm2/m ρsv =-0.11% < ρsvmin=0.15% 按构造配筋Av/s=435mm2/m----------------------------------------------------------- 5 配置钢筋:(1)上部纵筋:计算As=360mm2,实配2D12+1D14(380mm2ρ=0.21%),配筋满足(2)腰筋:计算构造As=b*hw*0.2%=339mm2,实配4D12(452mm2ρ=0.25%),配筋满足(3)下部纵筋:计算As=1870mm2,实配5D22(1901mm2ρ=1.06%),配筋满足(4)箍筋:计算Av/s=435mm2/m,实配d8@300三肢(503mm2/m ρsv=0.17%),配筋满足-----------------------------------------------------------6 裂缝计算:(1)计算参数:Mk=42.86kN.m,最大裂缝宽度限值0.400mm。
混凝土承载力验算标准

混凝土承载力验算标准一、引言混凝土是一种常用的建筑材料,广泛应用于各种建筑工程中。
在混凝土结构设计中,承载力验算是非常关键的一项工作。
本文将详细介绍混凝土承载力验算标准。
二、混凝土承载力计算基本公式混凝土承载力计算的基本公式为:N = Aσ + βp其中,N为混凝土承载力,A为混凝土截面面积,σ为混凝土的抗拉强度,βp为混凝土的附加应力系数。
三、混凝土的抗拉强度混凝土的抗拉强度是指在拉伸作用下,混凝土所能承受的最大应力值。
混凝土的抗拉强度与其强度等级、水胶比、配合比等因素有关。
根据《混凝土结构设计规范》(GB50010-2010)的规定,混凝土的抗拉强度应符合以下要求:1. 普通混凝土的抗拉强度不应小于0.3fck。
2. 高强混凝土的抗拉强度应符合设计要求。
3. 预应力混凝土的抗拉强度应符合设计要求。
四、混凝土截面面积的计算混凝土截面面积的计算需考虑混凝土梁的几何形状和尺寸。
常见的混凝土截面形状有矩形、T形、L形、梯形等。
根据不同的混凝土截面形状,计算混凝土截面面积的公式也不同。
例如,对于矩形混凝土梁,其截面面积的计算公式为:A = bh其中,b为混凝土梁的宽度,h为混凝土梁的高度。
五、附加应力系数的计算附加应力系数是指混凝土在荷载作用下,由于外部约束而产生的附加应力。
根据《混凝土结构设计规范》(GB50010-2010)的规定,混凝土的附加应力系数应符合以下要求:1. 普通混凝土的附加应力系数为0.6。
2. 预应力混凝土的附加应力系数应符合设计要求。
六、混凝土承载力验算实例下面以矩形混凝土梁为例,介绍混凝土承载力验算的具体步骤。
假设有一根长为5m、宽为0.3m、高为0.5m的矩形混凝土梁,荷载作用为10kN。
已知混凝土的抗拉强度为3.5MPa,附加应力系数为0.6。
则混凝土承载力的计算如下:1. 计算混凝土截面面积:A = bh = 0.3 × 0.5 = 0.15m²2. 计算混凝土的抗拉强度:σ = 0.3fck = 0.3 × 20 = 6MPa3. 计算混凝土的附加应力系数:βp = 0.64. 计算混凝土承载力:N = Aσ + βp = 0.15 × 6 + 0.6 × 10 = 2.4 + 6 = 8.4kN因此,该矩形混凝土梁的承载力为8.4kN,符合设计要求。
钢结构基本原理第三章 构件截面承载力 强度

第三章 构件截面承载力--强度钢结构承载能力分3个层次截面承载力:材料强度、应力性质及其在截面上分布属强度问题。
构件承载力:构件最大截面未到强度极限之前因丧失稳定而失稳,取决于构件整体刚度,指稳定承载力。
结构承载力:与失稳有关。
3.1 轴心受力构件的强度及截面选择3.1.1 轴心受力构件的应用及截面形式主要用于承重钢结构,如平面、空间桁架和网架等。
轴心受力截面形式:1)热轧型钢截面2)冷弯薄壁型钢截面3)型钢和钢板连接而成的组合截面(实腹式、格构式)(P48页)对截面形式要求:1)提供强度所需截面积2)制作简单3)与相邻构件便于连接4)截面开展而壁厚较薄,满足刚度要求(截面积决定了稳定承载力,面积大整体刚度大,构件稳定性好)。
3.1.2 轴心受拉构件强度由εσ-关系可得:承载极限是截面平均应力达到抗拉强度u f ,但缺少安全储备,且y f 后变形过大,不符合继续承载能力,因此以平均应力y f ≤为准则,以孔洞为例。
规范:轴心受力构件强度计算:规定净截面平均应力不应超过钢材强度设计值f A N n ≤=/σN :轴心拉力设计值; An :构件净截面面积;R y f f γ/=: 钢材抗拉强度设计值 R γ:构件抗力分项系数Q235钢078.1=R γ,Q345,Q390,Q420111.1=R γ49页孔洞理解见书例题P493.1.3 轴心受压构件强度原则上与受拉构件没有区别,但一般情况下,轴心受压构件的承载力由稳定性决定,具体见4章。
3.1.4 索的受力性能和强度计算钢索广泛用于悬索结构,张拉结构,桅杆和预应力结构,一般为高强钢丝组成的平行钢丝束,钢绞线,钢丝绳等。
索是一种柔性构件,内力不仅与荷载有关,而且与变形有关,具有很强几何非线性,但我们通常采用下面的假设:1)理想柔性,不能受压,也不能抗弯。
2)材料符合虎克定理。
在此假设下内力与位移按弹性阶段进行计算。
加载初期(0-1)存在少量松弛变形,主要部分(1-2)线性关系,接近强度极限(2-3)明显曲线性质(图见下)实际工程对钢索预拉张,形成虚线应力—应变关系,很大范围是线性的高强度钢丝组成钢索初次拉伸时应力—应变曲线钢索强度计算采用容许应力法:k f A N k k //maxk N :钢索最大拉力标准值 A :钢索有效截面积k f :材料强度标准值 k :安全系数2.5-3.03.2 梁的类型和强度3.2.1 梁类型按制作方法:型钢梁:热轧型钢梁(工字梁、槽钢、H 型钢)。
混凝土梁正截面承载力计算(1)

➢ 由于钢筋混凝土受弯构件由两种材料组成,混凝土 本身为非弹性、非均质的,抗拉强度远低于抗压强 度,因而其受力性能于匀质、弹性材料相比由很大 的不同。
➢ 要建立受弯构件抗弯承载力计算原则,首先要进行 构件的加载试验,以了解钢筋混凝土受弯构件的破 坏过程的特征,研究其截面应力和应变的变化规律。
c
c
Mcr=
MI
My
t<ft
sAs
sAs t=ft(t =tu)
少筋破坏
梁的三种破坏形态
结论一:
•适筋梁具有较好的变形能力,超筋梁和少筋梁的破 坏具有突然性,设计时应予避免;
结论二:
•在适筋和超筋破坏之间存在一种平衡破坏。其破坏 特征是钢筋屈服的同时,混凝土压碎,是区分适筋破 坏和超筋破坏的定量指标;
板的受拉钢筋常用HRB400级和HRB500级钢筋, 常用直径是6mm、8mm、10mm和12mm。为了 防止施工时钢筋被踩下,现浇板的板面钢筋直径不 宜小于8mm。
C、板的砼保护厚度 见前保护层表格
d、板的分布钢筋
分布钢筋宜采用 HRB400级和HRB335 级钢筋,常用直径是 6mm和8mm。
• 若钢筋必须排成两排,上 下两排钢筋应当对齐.
d、混凝土保护层厚度
混凝土规范8.2.1
• 为了保证钢筋不被锈蚀,同时保证钢筋与混凝土的紧密粘结,梁 内钢筋的两侧和近边都应该设有保护层。
• 1、构件中受力钢筋的保护层厚度不应小于钢筋直径;
• 2、设计使用年限50年的结构,最外层钢筋的保护层厚度按下
环境类别
三a类: 受除冰盐影响环境;严寒和寒冷地区水 位变动的环境;海风环境
3.2 正截面承载力计算

3.2 正截面承载力计算钢筋混凝土受弯构件通常承受弯矩和剪力共同作用,其破坏有两种可能:一种是由弯矩引起的,破坏截面与构件的纵轴线垂直,称为沿正截面破坏;另一种是由弯矩和剪力共同作用引起的,破坏截面是倾斜的,称为沿斜截面破坏。
所以,设计受弯构件时,需进行正截面承载力和斜截面承载力计算。
一、单筋矩形截面1.单筋截面受弯构件沿正截面的破坏特征钢筋混凝土受弯构件正截面的破坏形式与钢筋和混凝土的强度以及纵向受拉钢筋配筋率ρ有关。
ρ用纵向受拉钢筋的截面面积与正截面的有效面积的比值来表示,即ρ=As/(bh0),其中A s为受拉钢筋截面面积;b为梁的截面宽度;h0为梁的截面有效高度。
根据梁纵向钢筋配筋率的不同,钢筋混凝土梁可分为适筋梁、超筋梁和少筋梁三种类型,不同类型梁的具有不同破坏特征。
①适筋梁配置适量纵向受力钢筋的梁称为适筋梁。
适筋梁从开始加载到完全破坏,其应力变化经历了三个阶段,如图3.2.1。
第I阶段(弹性工作阶段):荷载很小时,混凝土的压应力及拉应力都很小,应力和应变几乎成直线关系,如图3.2.1a。
当弯矩增大时,受拉区混凝土表现出明显的塑性特征,应力和应变不再呈直线关系,应力分布呈曲线。
当受拉边缘纤维的应变达到混凝土的极限拉应变εtu时,截面处于将裂未裂的极限状态,即第Ⅰ阶段末,用Ⅰa表示,此时截面所能承担的弯矩称抗裂弯矩M cr,如图3.2.1b。
Ⅰa阶段的应力状态是抗裂验算的依据。
第Ⅱ阶段(带裂缝工作阶段):当弯矩继续增加时,受拉区混凝土的拉应变超过其极限拉应变εtu,受拉区出现裂缝,截面即进入第Ⅱ阶段。
裂缝出现后,在裂缝截面处,受拉区混凝土大部分退出工作,拉力几乎全部由受拉钢筋承担。
随着弯矩的不断增加,裂缝逐渐向上扩展,中和轴逐渐上移,受压区混凝土呈现出一定的塑性特征,应力图形呈曲线形,如图3.2.1c。
第Ⅱ阶段的应力状态是裂缝宽度和变形验算的依据。
当弯矩继续增加,钢筋应力达到屈服强度f y,这时截面所能承担的弯矩称为屈服弯矩M y。
MIDAS的PSC设计验算说明

MIDAS的PSC设计验算说明北京迈达斯技术有限公司2007年5月MIDAS/Civil PSC设计验算功能说明一.程序给出的验算结果 (2)二. 程序验算结果说明及与规范中相应条文的对应关系 (3)1、施工阶段正截面法向应力验算:(对应规范7.2.7,7.2.8) (3)2、受拉区钢筋拉应力验算:(对应规范6.1.3~6.1.4,7.1.3~7.1.5) (4)3、使用阶段正截面抗裂验算:(对应规范6.3.1(第1条)和规范6.3.2) (5)4、使用阶段斜截面抗裂验算:(对应规范6.3.1(第2条)和规范6.3.3) (6)5、使用阶段正截面压应力验算:(对应规范6.1.5,6.1.6,7.1.3~7.1.5) (7)6、使用阶段斜截面主压应力验算:(对应规范7.1.3~7.1.6) (8)7、使用阶段裂缝宽度验算:(对应规范6.4.2~6.4.4) (8)8、普通钢筋估算:(对应规范5.2.2~5.2.5) (9)9、预应力钢筋量估算: (10)10、使用阶段正截面抗弯验算:(应规范5.2.2~5.2.5) (11)11、使用阶段斜截面抗剪验算:(对应规范5.2.6~5.2.11) (11)12、使用阶段抗扭验算:(对应规范5.5.1~5.5.6) (12)三、PSC设计验算时错误信息说明 (13)四、PSC设计其它相关说明 (15)MIDAS/Civil PSC设计验算功能说明一.程序给出的验算结果程序一共给出了12项验算结果,如下所列。
根据“PSC设计参数”中“截面设计内力”和“构件类型”选定的内容的不同,给出的具体验算结果是不同的,详见表1。
1)施工阶段正截面法向应力验算2)受拉区钢筋的拉应力验算3)使用阶段正截面抗裂验算*4)使用阶段斜截面抗裂验算*5)使用阶段正截面压应力验算*6)使用阶段斜截面主压应力验算*7)使用阶段裂缝宽度验算8)普通钢筋量估算*9)预应力钢筋量估算*10)使用阶段正截面抗弯验算11)使用阶段斜截面抗剪验算12)使用阶段抗扭验算不同的“PSC设计参数”对应的验算结果应力A类12)项验算项验算项验算部分预应力B类不提供第3)、12)项验算不提供第3)项验算不提供第3)项验算* 以上不提供验算的项目均为规范中不要求验算的内容二. 程序验算结果说明及与规范中相应条文的对应关系1、施工阶段正截面法向应力验算:(对应规范7.2.7,7.2.8)-进行施工阶段正截面法向应力验算时,由预加力和荷载产生的法向应力可分别按照规范第6.1.5条和第7.1.3条进行计算。
一级注册结构专业考试易错点(经典总结)

一级注册结构考试易错点总则:1、在从表格中查取相关数值时,务必了解注解中的相关事项;2、做完试题后,应将解题过程与规程中的注解进行对照一下,确保无遗漏,尤其是注意一些限制条件;3、尽快将一些重要的结论和解题过程复印贴在规范上;一、荷载部分1、荷载计算时应考虑结构的重要性系数,尤其在木结构计算中,但在抗震设计时不需考虑;2、在进行荷载计算时,应注意恒载的计算,不能漏项,并应结合受荷分析图进行计算内力值;同时还应注意恒荷载在有利作用时的分项系数取值。
3、等效均布荷载的计算:等效宽度计算(1、短跨受荷,2、宽度修正(离非支座边较近,两个集中荷载叠加部位)),最大弯矩采用假定设备荷载为集中荷载,设备荷载应考虑动力系数,同时应考虑扣除操作荷载进行计算。
4、活荷载不应与雪荷载同时考虑;当活荷载大于42的工业建筑时,荷载分项系数取1.3;5、动力荷载应考虑动力系数,仅传递至楼板和梁,而不向墙、柱传递,动力系数仅在基本组合和抗裂验算时考虑,而标准组合,准永久组合均不考虑;对于吊车仅为竖向作用考虑动力系数;6、吊车荷载(吊车台数的布置(竖向最多4台,水平向最多2台)及荷载折减,竖向荷载设计值应考虑动力系数,而水平荷载不需考虑动力系数(应力影响线的应用);吊车纵向制动力对于四轮吊车,制动力一侧一般为1只,轻中级工作制吊车梁计算腹板的稳定性时,吊车轮压设计值可乘折减系数0.9;吊车起重量的表示方法20/5t表示主钩为20t,副钩为5t,即该吊车的最大起重量为20t。
求吊车梁最大弯矩:即荷载合力作用点(采用力矩平衡)与某一荷载的中线与梁中线重合即该荷载作用处为梁的最大弯矩处;吊车横向水平荷载的计算,注意对重级工作制吊车,需要考虑小车刹车摆动引起的横向水平荷载()(分摊于四个轮子)和小车摆动引起的横向水平荷载(分摊于一个轮子)两者中的最大值;注意支座处梁的剪力与支座处的压力前者仅考虑一根吊车辆上的荷载,而后者需考虑2根梁上的吊车荷载。
钢筋混凝土受弯构件正截面承载力计算-混凝土结构设计原理

1 /171第四章 钢筋混凝土受弯构件正截面承载力计算本章学习要点:1、掌握单筋矩形截面、双筋矩形截面和T 形截面承载力的计算方法;2、了解配筋率对受弯构件破坏特征的影响和适筋受弯构件在各阶段的受力特点;3、熟悉受弯构件正截面的构造要求。
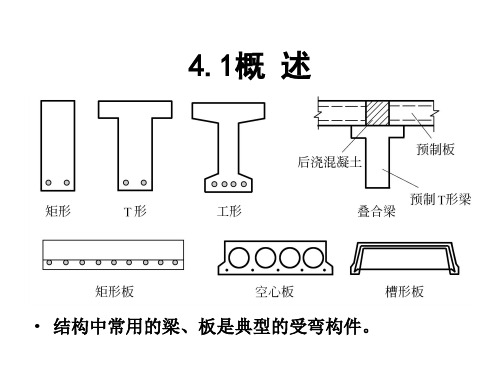
§4-1 概述一、受弯构件的定义同时受到弯矩M 和剪力V 共同作用,而轴力N 可以忽略的构件(图4—1). 梁和板是土木工程中数量最多,使用面最广的受弯构件。
梁和板的区别:梁的截面高度一般大于其宽度,而板的截面高度则远小于其宽度。
受弯构件常用的截面形状如图4-2所示。
图4-1二、受弯构件的破坏特性正截面受弯破坏:沿弯矩最大的截面破坏,破坏截面与构件的轴线垂直。
斜截面破坏:沿剪力最大或弯矩和剪力都较大的截面破坏。
破坏截面与构件轴线斜交。
进行受弯构件设计时,要进行正截面承载力和斜截面承载力计算。
2 /172图4—3 受弯构件的破坏特性§4—2 受弯构件正截面的受力特性一、配筋率对正截面破坏性质的影响配筋率:为纵向受力钢筋截面面积A s 与截面有效面积的百分比.sA bh 式中 s A —-纵向受力钢筋截面面积。
b -—截面宽度,0h —-截面的有效高度(从受压边缘至纵向受力钢筋截面重心的距离)。
构件的破坏特征取决于配筋率、混凝土的强度等级、截面形式等诸多因素,但配筋率的影响最大。
受弯构件依配筋数量的多少通常发生如下三种破坏形式: 1、 少筋破坏当构件的配筋率低于某一定值时,构件不但承载力很低,而且只要其一开裂,裂缝就急速开展,裂缝处的拉力全部由钢筋承担,钢筋由于突然增大的应力而屈服,构件立即发生破坏。
图4—4 受弯构件正截面破坏形态2、适筋破坏当构件的配筋率不是太低也不是太高时,构件的破坏首先是受拉区纵向钢筋屈服,然后压区砼压碎。
钢筋和混凝土的强度都得到充分利用.破坏前有明显的塑性变形和裂缝预兆。
3、超筋破坏当构件的配筋率超过一定值时,构件的破坏是由于混凝土被压碎而引起的。
桥梁结构受弯构件正截面承载力计算

M u
fcd bx(h0
) 2
fsd As (h0
) 2
Mu
•适用条件
fcd x/2
C
fsdAs
x h0
防止超筋 脆性破坏
防止少筋 脆性破坏
x bh0 或
max
b
f cd fsd
As min bh0
◆受弯构件正截面
受弯承载力计算包 括截面设计、截面 复核两类问题。
二、计算内容
•按承载力要求进行新构件设计——截面设计
桥梁结构受弯构件正 截面承载力计算
第一节 钢筋混凝土受弯构件的构造要求
受弯构件:指截面上 通常有弯矩和剪力共同作 用而轴力可以忽略不计的 构件。
pp lll
梁和板是典型的受弯构 M
pl
件。它们是土木工程中数
量最多、使用面最广的一
V
类构件。
p
受弯构件常见的破坏形态
在弯矩作用下发生正截面受弯破坏; 在弯矩和剪力共同作用下发生斜截面受剪或 受弯破坏。
As
f sd (h0
as )
As = As1 + As2
计算步骤:
x bh0
h0 h
As1
M1
As1 fcd bx / fsd , M1 As1 fsd (h0 0.5x)
b
As’
M2 0Md M1,
As2 M 2 /(h0 as' ) fsd
As'
As 2
fsd
/
f
' sd
As2
x
h
h
x
+
h
As b
(a)
As1 b
(b)
As2 b
应力计算

墙身尺寸: 墙身高: 3.5m墙顶宽: 0.6m面坡倾斜坡度: 1:0.3背坡倾斜坡度: 1:0.1采用1个扩展墙址台阶:墙趾台阶b1: 0.5m墙趾台阶h1: 0.6m墙趾台阶与墙面坡坡度相同墙踵台阶b3: 0.5m墙踵台阶h3: 0.6m(一) 滑动稳定性验算基底摩擦系数 = 0.500滑移力= 53.323(kN) 抗滑力= 70.451(kN)滑移验算满足: Kc = 1.321 > 1.300(二) 倾覆稳定性验算相对于墙趾点,墙身重力的力臂 Zw = 1.626 (m)相对于墙趾点,Ey的力臂 Zx = 2.378 (m)相对于墙趾点,Ex的力臂 Zy = 1.224 (m)验算挡土墙绕墙趾的倾覆稳定性倾覆力矩= 65.294(kN-m) 抗倾覆力矩= 246.255(kN-m)倾覆验算满足: K0 = 3.771 > 1.500(三) 地基应力及偏心距验算基础为天然地基,验算墙底偏心距及压应力作用于基础底的总竖向力 = 140.902(kN) 作用于墙趾下点的总弯矩=180.961(kN-m)基础底面宽度 B = 2.940 (m) 偏心距 e = 0.186(m)基础底面合力作用点距离基础趾点的距离 Zn = 1.284(m)基底压应力: 趾部=66.088 踵部=29.764(kPa)最大应力与最小应力之比 = 66.088 / 29.764 = 2.220墙身尺寸: 墙身高: 3.500(m)墙顶宽: 0.600(m)面坡倾斜坡度: 1:0.300背坡倾斜坡度: 1:0.100采用1个扩展墙址台阶:墙趾台阶b1: 0.500(m)墙趾台阶h1: 0.600(m)墙趾台阶面坡坡度为: 1:0.000墙踵台阶b3: 0.500(m)墙踵台阶h3: 0.600(m)(一) 滑动稳定性验算基底摩擦系数 = 0.500滑移力= 30.741(kN) 抗滑力= 64.988(kN)滑移验算满足: Kc = 2.114 > 1.300(二) 倾覆稳定性验算相对于墙趾点,墙身重力的力臂 Zw = 1.462 (m)相对于墙趾点,Ey的力臂 Zx = 2.203 (m)相对于墙趾点,Ex的力臂 Zy = 1.167 (m)验算挡土墙绕墙趾的倾覆稳定性倾覆力矩= 35.865(kN-m) 抗倾覆力矩= 199.763(kN-m)倾覆验算满足: K0 = 5.570 > 1.500(三) 地基应力及偏心距验算基础为天然地基,验算墙底偏心距及压应力作用于基础底的总竖向力 = 129.976(kN) 作用于墙趾下点的总弯矩=163.899(kN-m)基础底面宽度 B = 2.760 (m) 偏心距 e = 0.119(m)基础底面合力作用点距离基础趾点的距离 Zn = 1.261(m)基底压应力: 趾部=59.277 踵部=34.909(kPa)最大应力与最小应力之比 = 59.277 / 34.909 = 1.698作用于基底的合力偏心距验算满足: e=0.119 <= 0.250*2.760 = 0.690(m)墙趾处地基承载力验算满足: 压应力=59.277 <= 600.000(kPa)墙踵处地基承载力验算满足: 压应力=34.909 <= 650.000(kPa)地基平均承载力验算满足: 压应力=47.093 <= 500.000(kPa)(四) 基础强度验算基础为天然地基,不作强度验算(五) 墙底截面强度验算验算截面以上,墙身截面积 = 5.078(m2) 重量 = 116.794 kN相对于验算截面外边缘,墙身重力的力臂 Zw = 1.462 (m)相对于验算截面外边缘,Ey的力臂 Zx = 2.203 (m)相对于验算截面外边缘,Ex的力臂 Zy = 1.167 (m)[容许应力法]:法向应力检算:作用于验算截面的总竖向力 = 129.976(kN) 作用于墙趾下点的总弯矩=163.899(kN-m) 相对于验算截面外边缘,合力作用力臂 Zn = 1.261(m)截面宽度 B = 2.760 (m) 偏心距 e1 = 0.119(m)截面上偏心距验算满足: e1= 0.119 <= 0.300*2.760 = 0.828(m)截面上压应力: 面坡=59.277 背坡=34.909(kPa)压应力验算满足: 计算值= 59.277 <= 2100.000(kPa)切向应力检算:剪应力验算满足: 计算值= -7.699 <= 110.000(kPa)(六) 台顶截面强度验算[土压力计算] 计算高度为 2.900(m)处的库仑主动土压力按实际墙背计算得到:第1破裂角: 28.008(度)Ea=22.963 Ex=21.105 Ey=9.050(kN) 作用点高度 Zy=0.967(m)因为俯斜墙背,需判断第二破裂面是否存在,计算后发现第二破裂面不存在墙身截面积 = 3.704(m2) 重量 = 85.192 kN[强度验算]验算截面以上,墙身截面积 = 3.422(m2) 重量 = 78.706 kN相对于验算截面外边缘,墙身重力的力臂 Zw = 1.001 (m)相对于验算截面外边缘,Ey的力臂 Zx = 1.663 (m)相对于验算截面外边缘,Ex的力臂 Zy = 0.967 (m)[容许应力法]:法向应力检算:作用于验算截面的总竖向力 = 87.756(kN) 作用于墙趾下点的总弯矩=73.456(kN-m) 相对于验算截面外边缘,合力作用力臂 Zn = 0.837(m)截面宽度 B = 1.760 (m) 偏心距 e1 = 0.043(m)截面上偏心距验算满足: e1= 0.043 <= 0.300*1.760 = 0.528(m)截面上压应力: 面坡=57.163 背坡=42.560(kPa)压应力验算满足: 计算值= 57.163 <= 2100.000(kPa)切向应力检算:剪应力验算满足: 计算值= -7.953 <= 110.000(kPa)=================================================各组合最不利结果=================================================(一) 滑移验算安全系数最不利为:组合1(一般情况)抗滑力 = 64.988(kN),滑移力 = 30.741(kN)。
钢筋混凝土轴心受力构件正截面承载力计算

54 第八章 钢筋混凝土构件正常使用极限状态验算本章学习要点:1、了解裂缝出现、分布和开展的过程;2、掌握影响裂缝宽度的主要因素(钢筋直径、配筋率);3、掌握裂缝宽度计算公式的应用;4、掌握挠度计算公式计算挠度的过程;5、掌握最小刚度原则、ψ的含义,减小挠度最有效的措施。
重点:深入理解梁在纯弯区段内的应力重分布全过程,开裂后钢筋和混凝土应变分布规律及其影响因素,ψ等主要参数的物理意义。
难点:裂缝宽度及截面抗弯刚度计算原理。
§8-1 抗裂验算一般要求(1)抗裂就是不允许混凝土开裂。
(2)钢筋混凝土构件正截面抗裂验算应满足下式 tk ct t f ασ≤ (8-1)式中,t σ——由荷载标准组合或准永久组合计算的验算截面的混凝土拉应力值;tk f ——混凝土抗拉强度标准值;ct α——混凝土拉应力限制系数(对水工混凝土结构构件,荷载标准组合时,ct α=0.85;荷载准永久组合时,ct α=0.70)。
§8-2 钢筋混凝土结构裂缝宽度的验算一、裂缝产生的原因:1、荷载引起的裂缝:占20%,t ct f >σ计算[]lim max ωω≤,式中,lim ω −最大裂缝宽度限值。
552、非荷载引起的裂缝:材料收缩、温度变化、混凝土碳化后引起钢筋锈蚀、地基不均匀沉降。
占80%,而为防止温度应力过大引起的开裂,规定了最大伸缩缝之间的间距;为防止由于钢筋周围砼过快的碳化失去对钢筋的保护作用,出现锈胀引起的沿钢筋纵向的裂缝,规定了钢筋的混凝土保护层的最小厚度。
通常,裂缝宽度和挠度一般可分别用控制最大钢筋直径和最大跨高比来控制,只有在构件截面尺寸小,钢筋应力高时进行验算。
二、裂缝宽度的计算方法1、裂缝出现与分布规律图8-2 第一条裂缝至将出现第二条裂缝间混凝土及钢筋应力56 (1)在裂缝未出现前:受拉区钢筋与混凝土共同受力;沿构件长度方向,各截面的受拉钢筋应力及受拉区混凝土拉应力大体上保持均等。
混凝土结构设计原理 第四章 受弯构件正截面承载力的计算

3.2 梁板结构的一般构造
第4章 受弯构件正截面承载力
分布钢筋的作用:
抵抗混凝土收缩和温度变化所引起的内力; 浇捣混凝土时,固定受力钢筋的位置; 将板上作用的局部荷载分散在较大的宽度上,以便 使更多的受力钢筋参与工作; 对四边支撑的单向板,可承受在计算中没有考虑的 长跨方向上实际存在的弯矩。
板中单位长度上的分布钢筋,其截面面积不应小于 单位长度上受力钢筋截面面积的15%,且配筋率不宜小于 0.15%。间距不应大于250mm,直径不宜小于6mm。
4.2 梁板结构的一般构造
第4章 受弯构件正截面承载力
弯起钢筋 架立钢筋
腰筋
箍筋
纵向钢筋
梁的钢筋构造
梁中钢筋由纵向受力钢筋、弯起钢筋、箍筋和架立钢筋组 成,纵向受力钢筋的作用是承受由弯矩在梁内产生的拉力。 常用直径:10~32mm。 当h ≥ 300mm,直径不小于10mm;当h<300mm,直径 不小于8mm。
第4章 受弯构件正截面承载力
梁的配筋率ρ 很小,梁拉区开裂后,钢筋 应力趋近于屈服强度,即开裂弯矩Mcr趋近于拉 区钢筋屈服时的弯矩 My,这意味着第Ⅱ阶段的 缩短,当ρ 减少到当 Mcr=My 时,裂缝一旦出现,
钢筋应力立即达到屈服强度,这时的配筋百分
率ρ 称为最小配筋率ρ
min。
min b max
h0
h
第4章 受弯构件正截面承载力
正截面受弯的三种破坏形态
(1) 适筋破坏形态——破坏始自受拉区 钢筋的屈服
受拉钢筋先屈服,受压区混凝土后 压坏,破坏前有明显预兆——裂缝、变 形急剧发展,为“塑性破坏”。
(2) 超筋破坏形态——破坏始自受压混 凝土的压碎
受压区混凝土先压碎,钢筋不屈服, 破坏前没有明显预兆,为“脆性破坏”。 钢筋的抗拉强度没有被充分利用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10.主梁截面承载力与应力验算预应力混凝土梁从预加力开始到是受荷破坏,需经受预加应力、使用荷载作用,裂缝出现和破坏等四个受力阶段,为保证主梁受力可靠并予以控制。
应对控制截面进行各个阶段的验算。
在以下内容中,先进行持久状态承载能力极限状态承载力验算,再分别验算持久状态抗裂验算和应力验算,最后进行短暂状态构件的截面应力验算。
对于抗裂验算,《公预规》根据公路简支标准设计的经验,对于全预应力梁在使用阶段短期效应组合作用下,只要截面不出现拉应力就可满足。
10.1持久状况承载能力极限状态承载力验算在承载能力极限状态下,预应力混凝土梁沿正截面和斜截面都有可能破坏,下面验算这两类截面的承载力。
10.1.1正截面承载力验算 (1)确定混凝土受压区高度根据《公预规》5.2.3条规定,对于带承托翼缘板的T 形截面; 当''Pd P cd f f f A f b h ≤成立时,中性轴带翼缘板内,否则在腹板内。
左边=Pd P f A =1260×50.4×0.1=6350.4(kN) 右边=''cd f f f b h =22.4×220×15×0.1=7392(kN)''Pd P cd f f f A f b h ≤成立,即中性轴在翼板内。
设中性轴到截面上缘距离为x ,则: x=0'126050.412.89()0.4(200012.85)74.86()22.4220pd p b cd ff A cm h cm f b ξ⨯==<=⨯-=⨯式中:ξb ——预应力受压区高度界限系数,按《公预规》表5.2.1采用,对于C50混凝土和钢绞线,ξb =0.40; h 0——梁的有效高,0p h h a =-, 说明该截面破坏时属于塑性破坏状态。
(2)验算正截面承载力:由《公预规》5.2.5条,正截面承载力按下式计算:'000()2cd f x M f b x h γ≤-式中:γ0——桥梁结构的重要性系数,按《公预规》5.1.5条采用,本设计取1.0。
右边=30.128522.410 2.20.1289(20.1285)11478.732kN m ⨯⨯⨯⨯--=⋅ 08658.42(d M kN m >ϒ=⋅跨中)所以,主梁跨中正截面承载能力满足要求。
(3)验算最小配筋率由《公预规》9.1.12条,预应力混凝土受弯构件最小配筋率应满足下列条件:udcrM 1.0M ≥式中: M ud ——受弯构件正截面抗弯承载力设计植,由以上计算可知M ud =9734.58(kN ·m );Mcr ——受弯构件正截面开裂弯矩值,按下式计算:0()cr PC tk M f W σγ=+02oS W γ=PCp P nnxN M A W σ=+式中:S 0——全截面换算截面重心轴以上(或以下)部分截面对重心轴的面积矩,;W 0——换算截面抗裂边缘的弹性抵抗矩;σpc ——扣除预应力损失预应力筋在构件抗裂边缘产生的混凝土预压应力。
MPa W M A N nx pn ppc 27.21300079594819911.7458727.1081=+=+=σ022297327 1.533387732o S W γ⨯===m N W f M tk pc cr ⋅=⨯⨯⨯+=+=-k 20.982210387732)65.2533.127.21()(30γσudcrM 1.0M <,尚需配置普通钢筋来满足最小配筋率的要求。
①计算受压区高度x)2(00x h x b f M f cd d -'≤γ )28715.12.2(2.2104.2232.119043x x --⨯⨯=求解得0.134()0.7486()b o x m h m ξ=<⨯=②计算普通钢筋s A4222.4 2.20.134126050.4109.04()280cd pd ps sd f bx f A A m f --⨯⨯-⨯⨯===即在梁底部配置6根直径16mm 的HRB335钢筋,s A =12.062cm .以满足最小配筋率的要求。
10.1.2 斜截面承载力验算(1) 斜截面抗剪承载力验算:根据《公预规》5.2.6条,计算受弯构件斜截面抗剪承载力时,其计算位置应按下列规定采用:① 距离支座1/2 h 截面处; ② 受拉区弯起钢筋弯起点处截面;③ 锚于受拉区的纵向钢筋开始不受力处的截面; ④ 箍筋数量或间距改变处的截面; ⑤ 构件腹板宽度变化处的截面。
1) 复核主梁尺寸T 形截面梁当进行斜截面抗剪承载力计算时,其截面尺寸应符合《公预规》5.2.9条规定,即000.5110d V γ-≤⨯式中:d V ——经内力组合后支点截面的最大剪力(kN ),1号梁的d V 为1021.23kN ;b ——支点截面腹板厚度(mm ),即b=550mm ; h 0——支点截面的有效高度(mm),即h 0=h -a p =2000-786.6=11213.4(cm)f cu,k ——混凝土强度等级(MPa ) 上边右式=00.51105501213.42406.701021.23d kN V kN γ-⨯⨯=>=所以本设计主梁的T 形截面尺寸符合要求。
2)截面抗剪承载力验算:验算是否需进行斜截面抗剪承载力计算根据《公预规》5.2.10条规定,若符合下列公式要求时,则不需进行斜截面抗剪承载力计算。
γ0V d ≤0.50×10-3α2 td f bh 0式中:td f —混凝土抗拉强度设计值(MPa )α2—预应力提高系数,对预应力混凝土受压构件,取1.25。
上式右边=0.50×10-3×1.25×1.83×550×1328.5=835.709kN <γ0V d =968.32(kN) 因此该设计需进行斜截面抗剪承载力计算. ①选定斜截面顶端位置距支座h/2处截面的横坐标为x=33900/2-200/2=15950mm,正截面有效高度0h =1328.5mm 。
现取c ’≈ 0h =1328.5mm ,则得到选定的斜截面顶端位置,其横坐标为x=15950-1328.5=14621.5mm 则,,/2d,,/22214.622()157.97(1021.23157.97)902.66533.9d A d l o d l x V V V V L ⨯=+-==+-⨯=KN ②箍筋计算:根据《公预规》9.4.1条,腹板内箍筋直径不小于10mm ,且应采用带肋钢筋,间距不应大于250mm ,本设计选用φ10@200的双肢箍筋,则箍筋的总面积为:A sv =2×78.5=157(mm 2)箍筋间距S V =200mm,箍筋抗拉强度设计值f sv =280MPa,箍筋配筋率ρsv 为:1570.19%200405sv sv v A S b ρ===⨯ 式中:b ——斜截面受压端正截面处T 形截面腹板宽度,此处b=405mm 。
满足《公预规》9.3.13条“箍筋配筋率ρsv ,HRB335钢筋不应小于0.12%”的要求。
同时,根据《公预规》9.4.1条,在距支点一倍梁高范围内,箍筋间距缩小至100mm 。
③抗剪承载力计算根据《公预规》5.2.7条规定,主梁斜截面抗剪承载力应按下式计算:γ0V d ≤V cs +V pb式中:V d ——斜截面受压端正截面内最大剪力组合设计值,为142.67kN;V cs ——斜截面内混凝土与箍筋共同的抗剪承载力 (kN) ,按下式计算:V cs = α1α2α30.45×10-3bh 0sv sv K cu f f P ρ,)6.02(+α1——异号弯矩影响系数,简支梁取1.0;α2——预应力提高系数,对预应力混凝土受弯构件,取1.25; α3——受压翼缘的影响系数,取1.1;b ——斜截面受压端正截面处,T 形截面腹板宽度,此处b=466mm; h 0——斜截面受压端正截面处梁的有效高度, h 0=1574cm ;P ——斜截面内纵向受拉钢筋的陪筋率,P=100ρ,ρ=(A p +A pb )/(bh 0),当P >2.5时,取P=2.5;k cu f ,——混凝土强度等级;sv ρ——斜截面内箍筋配筋率,sv ρ=A sv /(S v b);sv f ——箍筋抗拉设计强度;A sv ——斜截面内配置在同一截面的箍筋各肢总截面面积(mm 2); S v ——斜截面内箍筋间距(mm );pb V ——与斜截面相交的预应力弯起钢束的抗剪承载力(kN),按下式计算:30.7510sin pb pd pb p V f A θ-=⨯∑pb A ——斜截面内在同一弯起平面的预应力弯起钢筋的截面面积(mm 2);pd f ——预应力弯起钢束的抗拉设计强度(MPa ),该设计的—pd f =1260MPa; p θ——预应力弯起钢筋在斜截面受压端正截面处的切线与水平线的夹角,见表如下50.40.0079140.51574p pbA A bh ρ+===⨯1000.791P ρ==0.0019sv sv vAbS ρ==31.0 1.25 1.10.45104661501cs V -=⨯⨯⨯⨯⨯⨯1203.44kN =2sin 840[2(0.03267610.926845)0.1995264+0.2131218]557.23mm pb p A θ=⨯⨯++=∑V pb = 0.75×10-3×1260×557.23=526.58kNV cs +V pb =1203.44+526.58=1730.02kN >γ0V d = 902.665kN说明主梁距支座1/2 h 处斜截面抗剪承载力满足要求,同时也说明上述箍筋的配置是合理的(2)斜截面抗弯承载力验算由《公预规》5.2.12条进行斜截面抗弯强度计算,由于钢束都在梁端锚固,钢束根数沿梁跨几乎没有变化,并且钢束在梁中无截断,锚固长度均满足要求,可不必进行该项承载力验算,通过构造加以保证。
7.2持久状况正常使用极限状态抗裂验算长期以来,桥梁预应力构件的抗裂验算,都是以构件混凝土的拉应力是否超过规定的限值来表示,分为正截面抗裂和斜截面抗裂验算。
10.2.1正截面抗裂验算根据《公预规》6.3.1条,对预制的全预应力混凝土构件,在作用长期菏载效应组合下,应符合下列要求:085.0 -pc st ≤σσ式中:st σ——在作用短期效应组合下构件抗裂验算边缘混凝土的法向拉应力,按下式计算:ox p nx g st W M W M +=1σnxp np pc W M A N +=σ 下表示出了正截面抗裂验算的计算过程和结果,可见其结果符合规范要求。
