2021中考数学专题复习:二次函数综合培优提升训练题1(附答案详解)
【2021中考数学】二次函数培优训练含答案

【二次函数】一.选择题1.抛物线y=x2向左平移1个单位,再向上平移2个单位后,所得抛物线的表达式是()A.y=(x+1)2﹣2B.y=(x﹣1)2+2C.y=(x﹣1)2﹣2D.y=(x+1)2+22.关于二次函数y=﹣2(x+3)2+8的图象,下列说法错误的是()A.开口向下B.对称轴x=﹣3C.最小值是8D.顶点坐标(﹣3,8)3.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(3,0),对称轴为直线x=1.结合图象分析下列结论:①abc>0;②4a+2b+c>0;③一元二次方程ax2+bx+c=0的两根分别为x1=3,x2=﹣1;④2a+c<0.其中正确的结论有()个.A.1B.2C.3D.44.加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率y与加工时间x(单位:min)满足函数表达式y=﹣0.2x2+1.5x﹣2,则最佳加工时间为()A.3min B.3.75min C.5min D.7.5min5.函数y=ax2﹣a与y=ax﹣a(a≠0)在同一坐标系中的图象可能是()A.B.C.D.6.下表是二次函数y=ax2+bx+c的x,y的部分对应值:x…﹣012…y…﹣1﹣m﹣﹣1n…则对于该函数的性质的判断:①该二次函数有最小值;②不等式y>的解集是x<﹣或x>;③方程ax2+bx+c=﹣的实数根分别位于0<x<﹣和<x<2之间;④当x>0时,函数值y随x的增大而增大;其中正确的是()A.①②③B.②③C.①②D.①③④7.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留2m宽的门,已知计划中的建筑材料可建围墙(不包括门)的总长度为50m.设饲养室长为xm,占地面积为ym2,则y关于x的函数表达式是()A.y=﹣x2+50x B.y=﹣x2+24xC.y=﹣x2+25x D.y=﹣x2+26x8.已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合).且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个说法:①△OEF是等腰直角三角形;②△OEF面积的最小值是;③至少存在一个△ECF,使得△ECF的周长是2+;④四边形OECF的面积是1.其中正确的是()A.①②③B.③④C.①②④D.①②③④9.对于二次函数y=3(x﹣2)2+1,下列说法中正确的是()A.图象的开口向上B.函数的最大值为1C.图象的对称轴为直线x=﹣2D.当x<2时y随x的增大而增大10.函数y=ax2+2ax+m(a<0)的图象过点(2,0),则使函数值y>0成立的x的取值范围是()A.x<﹣4或x>2B.﹣4<x<2C.x<0或x>2D.0<x<2二.填空题11.若是二次函数,则k=.12.已知抛物线y=x2,把该抛物线向上或向下平移,如果平移后的抛物线经过点A(2,2),那么平移后的抛物线的表达式是.13.汽车刹车后行驶的距离s(单位:m)关于行驶的时间t(单位:s)的函数解析式是s=12t﹣6t2,汽车刹车后到停下来前进了m.14.已知二次函数y=x2+2x+n,当自变量x的取值在﹣2≤x≤1的范围内时,函数的图象与x轴有且只有一个公共点,则n的取值范围是.15.已知抛物线y1=(x﹣x1)(x﹣x2)与x轴交于A,B两点,直线y2=2x+b经过点(x1,0).若函数w=y1﹣y2的图象与x轴只有一个公共点,则线段AB的长为.三.解答题16.在平面直角坐标系xOy中,抛物线y=ax2+bx﹣5a与y轴交于点A,将点A向左平移4个单位长度,得到点B,点B在抛物线上.(1)求点B的坐标(用含a的式子表示);(2)求抛物线的对称轴;(3)已知点P(﹣1,﹣2a),Q(﹣4,2).若抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.17.某商场经营某种品牌童装,进货时的单价是40元,根据市场调查,当销售单价是60元时,每天销售量是200件,销售单价每降低0.5元,就可多售出10件.(1)当销售单价为58元时,每天销售量是件.(2)求销售该品牌童装获得的利润y(元)与销售单价x(元)之间的函数关系式;(3)若商场规定该品牌童装的销售单价不低于57元且不高于60元,则销售该品牌童装获得的最大利润是多少?18.已知二次函数y=﹣(x﹣h)2+k的部分图象如图所示,A为抛物线顶点.(1)写出二次函数的解析式;(2)若抛物线上两点B(x1,y1),C(x2,y2)的横坐标满足﹣1<x1<x2,则y1y2(用“>”,“<”或“=”填空);(3)观察图象,直接写出当y>0时,x的取值范围.19.已知,二次三项式﹣x2+2x+3.(1)关于x的一元二次方程﹣x2+2x+3=﹣mx2+mx+2(m为整数)的根为有理数,求m的值;(2)在平面直角坐标系中,直线y=﹣2x+n分别交x,y轴于点A,B,若函数y=﹣x2+2|x|+3的图象与线段AB只有一个交点,求n的取值范围.20.二次函数y=ax2+bx+c(a≠0)的自变量x与对应的函数y的值(部分)如表所示:x……﹣3﹣2﹣1012……y……m71﹣117……解答下列问题:(Ⅰ)求这个二次函数的解析式;(Ⅱ)表格中m的值等于;(Ⅲ)在直角坐标系中,画出这个函数的图象;(Ⅳ)将这个函数的图象向右平移2个单位长,向上平移1个单位长,写出平移后的二次函数解析式.参考答案一.选择题1.解:抛物线y=x2向左平移1个单位,再向上平移2个单位得y=(x+1)2+2.故选:D.2.解:∵二次函数y=﹣2(x+3)2+8,∴a=﹣2,则抛物线开口向下,对称轴为x=﹣3,函数有最大值为:8,顶点坐标(﹣3,8)故选项A,B,D正确,不合题意,选项C错误,符合题意.故选:C.3.解:抛物线开口向下,因此a<0,对称轴为x=1>0,因此a、b异号,所以b>0,抛物线与y 轴交点在正半轴,因此c>0,所以abc<0,故①不正确;当x=2时,y=4a+2b+c>0,故②正确;抛物线与x轴交点(3,0),对称轴为x=1.因此另一个交点坐标为(﹣1,0),即方程ax2+bx+c =0的两根为x1=3,x2=﹣1,故③正确;抛物线与x轴交点(﹣1,0),所以a﹣b+c=0,又x=﹣=1,有2a+b=0,所以3a+c=0,而a<0,因此2a+c>0,故④不正确;故选:B.4.解:根据题意:y=﹣0.2x2+1.5x﹣2,当x=﹣=3.75时,y取得最大值,则最佳加工时间为3.75min.故选:B.5.解:①当a>0时,二次函数y=ax2﹣a的图象开口向上、对称轴为y轴、顶点在y轴负半轴,一次函数y=ax﹣a(a≠0)的图象经过第一、三、四象限,且两个函数的图象交于y轴同一点;②当a<0时,二次函数y=ax2﹣a的图象开口向下、对称轴为y轴、顶点在y轴正半轴,一次函数y=ax﹣a(a≠0)的图象经过第一、二、四象限,且两个函数的图象交于y轴同一点.对照四个选项可知D正确.故选:D.6.解:由表格可得,该函数的对称轴是直线x==1,函数图象开口向上,该函数有最小值,故①正确;不等式y>的解集是x<﹣或x>,故②正确;方程ax2+bx+c=﹣的实数根分别位于0<x<﹣和<x<2之间,故③正确;当0<x<1时,y随x的增大而减小,当x>1时,y随x的增大而增大,故④错误;故选:A.7.解:设饲养室长为xm,占地面积为ym2,则y关于x的函数表达式是:y=x•(50+2﹣x)=﹣x2+26x.故选:D.8.解:①∵四边形ABCD是正方形,AC,BD相交于点O,∴OB=OC,∠OBC=∠OCD=45°,在△OBE和△OCF中,∴△OBE≌△OCF(SAS),∴OE=OF,∵∠BOE =∠COF ,∴∠EOF =∠BOC =90°, ∴△OEF 是等腰直角三角形; 故①正确;②∵当OE ⊥BC 时,OE 最小,此时OE =OF =BC =1,∴△OEF 面积的最小值是=,故②正确; ③∵BE =CF ,∴CE +CF =CE +BE =BC =2, 设EC =x ,则BE =CF =2﹣x , ∴EF ==,∵0<x <2, ∴≤EF <2, ∵<<2,∴存在一个△ECF ,使得△ECF 的周长是2+,故③正确;④由①知:△OBE ≌△OCF ,∴S 四边形OECF =S △COE +S △OCF =S △COE +S △OBE =S △OBC =S 正方形ABCD =×2×2=1, 故④正确; 故选:D .9.解:∵二次函数y=3(x﹣2)2+1,a=3,∴该函数图象开口向上,故选项A正确;函数的最小值为1,故选项B错误;函数图象的对称轴为直线x=2,故选项C错误;当x<2时y随x的增大而减小,故选项D错误;故选:A.10.解:∵函数y=ax2+2ax+m(a<0),∴该函数的图象开口向下,对称轴是直线x=﹣=﹣1,又∵函数y=ax2+2ax+m(a<0)的图象过点(2,0),∴该函数图象过点(﹣4,0),∴使函数值y>0成立的x的取值范围是﹣4<x<2,故选:B.二.填空题11.解:∵是二次函数,∴k2+1=2且k﹣1≠0,解得:k=﹣1.故答案为:﹣1.12.解:设所求的函数解析式为y=x2+k,∵点A(2,2)在抛物线上,∴2=22+k解得:k=﹣2,∴平移后的抛物线的表达式是y=x2﹣2.故答案为:y=x2﹣2.13.解:∵s=12t﹣6t2=﹣6(t﹣1)2+6,∴当t=1时,s取得最大值6,即当t=1时,汽车刹车后行驶的距离s取得最大值6m,∴汽车刹车后到停下来前进了6m,故答案为:6.14.解:抛物线的对称轴为直线x=﹣=﹣1,若抛物线与x轴有一个交点,则当x=﹣1,y=0;当x=1,y≥0时,在﹣2≤x≤1的范围内时,抛物线与x轴有且只有一个公共点,即1+2+n≥0且4﹣4+n<0,解得﹣3≤n<0;所以,n的取值范围是n=1或﹣3≤n<0.故答案为n=1或﹣3≤n<0.15.解:∵y1=(x﹣x1)(x﹣x2)与x轴交于A,B两点,而交点为(x1,0)、(x2,0),不妨设A(x1,0)、B(x2,0),∵直线y2=2x+b经过点(x1,0),∴2x1+b=0,∴x1=﹣,A(﹣,0),∵函数w=y1﹣y2的图象与x轴只有一个公共点,∴该公共点就是点A,∴设w==x2+bx+,∴y1=w+y2=x2+bx++2x+b=x2+(b+2)x++b.∴由韦达定理得:x1+x2=﹣(b+6),x1x2=+3b,∴|AB|=|x1﹣x2|===6.故答案为:6.三.解答题16.解:(1)∵抛物线y=ax2+bx﹣5a与y轴交于点A,∴A(0,﹣5a),点A向左平移4个单位长度,得到点B(﹣4,﹣5a);(2)∵A与B关于对称轴x=﹣2对称,∴抛物线对称轴x=﹣2;(3)∵对称轴x=﹣2,∴b=4a,∴y=ax2+4ax﹣5a,①a>0时,点A(0,﹣5a)在y轴负半轴上,此时,点P,Q位于抛物线内部(如图1).所以,抛物线与线段PQ无交点;②当a<0时,点A(0,﹣5a)在y轴正半轴,当Q点在抛物线上时,则2=16a﹣16a﹣5a,解得a=﹣,即当﹣≤a<0时,(如图2),结合图象,抛物线与线段PQ有一个交点;综上,a的取值范围是﹣≤a<0.17.解:(1)200+(60﹣58)×20=240(件),故答案为:240;(2)设该品牌童装获得的利润为y元,根据题意得,y=(x﹣40)(﹣20x+1400)=﹣20x2+2200x﹣56000,∴销售该品牌童装获得的利润y元与销售单价x元之间的函数关系式为:y=﹣20x2+2200x﹣56000;(3)根据题意得57≤x≤60,y=﹣20(x﹣55)2+4500,∵a=﹣20<0∴抛物线开口向下,当57≤x≤60时,y随x的增大而减小,∴当x=57时,y有最大值为4420元,∴商场销售该品牌童装获得的最大利润是4420元.18.解:(1)根据图示知,抛物线顶点坐标是(﹣1,2),则该抛物线的解析式是y=﹣(x+1)2+2;(2)根据图示知,当x<﹣1时,y的值随x的值增大而减小,所以抛物线上两点B(x1,y1),C(x2,y2)的横坐标满足﹣1<x1<x2,则y1>y2;故答案是:>;(3)由抛物线y=﹣(x+1)2+2的对称轴是直线x=﹣1知,抛物线与x轴的另一交点坐标是(1,0),所以当y>0时,x的取值范围是﹣3<x<1.19.解:(1)方程化为(m﹣1)x2+(2﹣m)x+1=0,由已知可得m≠1,△=m2﹣8m+8=(m﹣4)2﹣8,∵m为整数,方程的根为有理数,∴m﹣4=±3,∴m=7或m=1(舍);(2)由已知可得A(,0),B(0,n),∵函数y=﹣x2+2|x|+3的图象与线段AB只有一个交点,当≤﹣3,n<3时,∴n≤﹣6;当>﹣3,n≥3时,∴n≥3;当>3,n≤3时,n不存在;当<3,n≥3时,3≤n<6;当直线与抛物线y=﹣x2+2x+3相切时,也满足条件,可得n=7,综上所述:n≤﹣6或3≤n<6或7.20.解:(Ⅰ)由表格可知,该函数有最小值,当x=0时,y=﹣1,当x=﹣1和x=1时的函数值相等,即该二次函数图象的开口方向向上,对称轴是直线x=0,顶点坐标为(0,﹣1),设二次函数为y=ax2﹣1,把x=1,y=1代入得,1=a﹣1,解得a=2,∴二次函数的解析式为y=2x2﹣1;(Ⅱ)把x=﹣3代入y=2x2﹣1得,y=17;∴m=17,故答案为17;(Ⅲ)在直角坐标系中,画出这个函数的图象如图:(Ⅳ)将这个函数的图象向右平移2个单位长,向上平移1个单位长,则平移后的二次函数解析式为y=2(x﹣2)2.。
2021年中考一轮复习数学九年级二次函数综合题培优提升专题训练(附答案)

2021年九年级数学中考一轮复习二次函数综合题培优提升专题训练(附答案)1.如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:①当x>0时,y1>y2;②当x<0时,x值越大,M值越小;③使得M大于2的x值不存在;④使得M=1的x值是或.其中正确的是()A.①②B.①④C.②③D.③④2.如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C﹣D﹣E上移动,若点C、D、E的坐标分别为(﹣1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为()A.1B.2C.3D.43.如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x﹣m)2+n的顶点在线段AB上运动(抛物线随顶点一起平移),与x轴交于C、D两点(C在D的左侧),点C 的横坐标最小值为﹣3,则点D的横坐标最大值为()A.﹣3B.1C.5D.84.已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点,请你在图中任意画一条抛物线,问所画的抛物线最多能经过81个格点中的多少个()A.6B.7C.8D.95.如图,记抛物线y=﹣x2+1的图象与x正半轴的交点为A,将线段OA分成n等份,设分点分别为P1,P2,…P n﹣1,过每个分点作x轴的垂线,分别与抛物线交于点Q1,Q2,…,Q n﹣1,再记直角三角形OP1Q1,P1P2Q2,…,P n﹣2P n﹣1Q n﹣1的面积分别为S1,S2,…,这样就有S1=,S2=,…;记W=S1+S2+…+S n﹣1,当n越来越大时,你猜想W最接近的常数是()A.B.C.D.6.抛物线y=ax2与直线x=1,x=2,y=1,y=2围成的正方形有公共点,则实数a的取值范围是()A.≤a≤1B.≤a≤2C.≤a≤1D.≤a≤27.如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是()A.16B.15C.24D.138.如图,在平面直角坐标系xOy中,若动点P在抛物线y=ax2上,⊙P恒过点F(0,n),且与直线y=﹣n始终保持相切,则n=(用含a的代数式表示).9.如图,已知一动圆的圆心P在抛物线y=x2﹣3x+3上运动.若⊙P半径为1,点P的坐标为(m,n),当⊙P与x轴相交时,点P的横坐标m的取值范围是.10.如图,已知⊙P的半径为2,圆心P在抛物线y=﹣1上运动,当⊙P与x轴相切时,圆心P的坐标为.11.已知二次函数的图象与x轴分别交于A、B两点(如图所示),与y轴交于点C,点P是其对称轴上一动点,当PB+PC取得最小值时,点P的坐标为.12.如图,抛物线y=ax2+bx+c与x轴的一个交点A在点(﹣2,0)和(﹣1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则:(1)abc0(填“>”或“<”);(2)a的取值范围是.13.如图正方形ABCD的边长为2cm,O是AB的中点,也是抛物线的顶点,OP⊥AB,两半圆的直径分别为OA与OB.抛物线经过C、D两点,且关于OP对称,则图中阴影部分的面积之和为cm2.(π取3.14,结果保留2个有效数字)14.直角坐标系xOy中,O是坐标原点,抛物线y=x2﹣x﹣6与x轴交于A,B两点(点A 在点B左侧),与y轴交于点C.如果点M在y轴右侧的抛物线上,S△AMO=S△COB,那么点M的坐标是.15.已知:如图所示,一次函数有y=﹣2x+3的图象与x轴、y轴分别交于A、C两点,二次函数y=x2+bx+c的图象过点C,且与一次函数在第二象限交于另一点B,若AC:CB =1:2,那么这二次函数的顶点坐标为.16.在平面直角坐标系xOy中,函数F1和F2的图象关于y轴对称,它们与直线x=t(t>0)分别相交于点P,Q.(1)如图,函数F1为y=x+1,当t=2时,PQ的长为;(2)函数F1为y=,当PQ=6时,t的值为;(3)函数F1为y=ax2+bx+c(a≠0),①当t=时,求△OPQ的面积;②若c>0,函数F1和F2的图象与x轴正半轴分别交于点A(5,0),B(1,0),当c≤x≤c+1时,设函数F1的最大值和函数F2的最小值的差为h,求h关于c的函数解析式,并直接写出自变量c的取值范围.17.如图,已知二次函数的图象顶点在原点,且点(2,1)在二次函数的图象上,过点F (0,1)作x轴的平行线交二次函数的图象于M、N两点.(1)求二次函数的表达式;(2)P为平面内一点,当△PMN是等边三角形时,求点P的坐标;(3)在二次函数的图象上是否存在一点E,使得以点E为圆心的圆过点F和点N,且与直线y=﹣1相切.若存在,求出点E的坐标,并求⊙E的半径;若不存在,说明理由.18.如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(4,0),与y轴交于点C,连接BC,点P是线段BC上的动点(与点B,C不重合),连接AP并延长AP交抛物线于点Q,连接CQ,BQ,设点Q的横坐标为m.(1)求抛物线的解析式和点C的坐标;(2)当△BCQ的面积等于2时,求m的值;(3)在点P运动过程中,是否存在最大值?若存在,求出最大值;若不存在,请说明理由.19.在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)经过点A(﹣2,﹣4)和点C(2,0),与y轴交于点D,与x轴的另一交点为点B.(1)求抛物线的解析式;(2)如图1,连接BD,在抛物线上是否存在点P,使得∠PBC=2∠BDO?若存在,请求出点P的坐标;若不存在,请说明理由;(3)如图2,连接AC,交y轴于点E,点M是线段AD上的动点(不与点A,点D重合),将△CME沿ME所在直线翻折,得到△FME,当△FME与△AME重叠部分的面积是△AMC面积的时,请直接写出线段AM的长.20.在平面直角坐标系xOy中(如图),已知抛物线y=x2﹣2x,其顶点为A.(1)写出这条抛物线的开口方向、顶点A的坐标,并说明它的变化情况;(2)我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”.①试求抛物线y=x2﹣2x的“不动点”的坐标;②平移抛物线y=x2﹣2x,使所得新抛物线的顶点B是该抛物线的“不动点”,其对称轴与x轴交于点C,且四边形OABC是梯形,求新抛物线的表达式.21.如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(A在B的左侧),与y轴交于点N,过A点的直线l:y=kx+n与y轴交于点C,与抛物线y=﹣x2+bx+c的另一个交点为D,已知A(﹣1,0),D(5,﹣6),P点为抛物线y=﹣x2+bx+c上一动点(不与A、D重合).(1)求抛物线和直线l的解析式;(2)当点P在直线l上方的抛物线上时,过P点作PE∥x轴交直线l于点E,作PF∥y 轴交直线l于点F,求PE+PF的最大值;(3)设M为直线l上的点,探究是否存在点M,使得以点N、C,M、P为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.22.如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;(2)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标;(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N 从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.23.如图,在平面直角坐标系中,已知点B的坐标为(﹣1,0),且OA=OC=4OB,抛物线y=ax2+bx+c(a≠0)图象经过A,B,C三点.(1)求A,C两点的坐标;(2)求抛物线的解析式;(3)若点P是直线AC下方的抛物线上的一个动点,作PD⊥AC于点D,当PD的值最大时,求此时点P的坐标及PD的最大值.24.如图1,在平面直角坐标系中,一次函数y=﹣x+3的图象与x轴交于点A,与y轴交于B点,抛物线y=﹣x2+bx+c经过A,B两点,在第一象限的抛物线上取一点D,过点D作DC⊥x轴于点C,交直线AB于点E.(1)求抛物线的函数表达式;(2)是否存在点D,使得△BDE和△ACE相似?若存在,请求出点D的坐标,若不存在,请说明理由;(3)如图2,F是第一象限内抛物线上的动点(不与点D重合),点G是线段AB上的动点.连接DF,FG,当四边形DEGF是平行四边形且周长最大时,请直接写出点G的坐标.25.如图,在平面直角坐标系中,直线y=﹣x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B两点且与x轴的负半轴交于点C.(1)求该抛物线的解析式;(2)若点D为直线AB上方抛物线上的一个动点,当∠ABD=2∠BAC时,求点D的坐标;(3)已知E,F分别是直线AB和抛物线上的动点,当以B,O,E,F为顶点的四边形是平行四边形时,直接写出所有符合条件的E点的坐标.参考答案1.解:∵当x>0时,利用函数图象可以得出y2>y1;∴①错误;∵抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;∴当x<0时,根据函数图象可以得出x值越大,M值越大;∴②错误;∵抛物线y1=﹣2x2+2,直线y2=2x+2,与y轴交点坐标为:(0,2),当x=0时,M=2,抛物线y1=﹣2x2+2,最大值为2,故M大于2的x值不存在;∴使得M大于2的x值不存在,∴③正确;∵当﹣1<x<0时,使得M=1时,可能是y1=﹣2x2+2=1,解得:x1=,x2=﹣,当y2=2x+2=1,解得:x=﹣,由图象可得出:当x=>0,此时对应y1=M,∵抛物线y1=﹣2x2+2与x轴交点坐标为:(1,0),(﹣1,0),∴当﹣1<x<0,此时对应y2=M,故M=1时,x1=,x2=﹣,使得M=1的x值是或.∴④正确;故正确的有:③④.故选:D.2.解:由图知:当点B的横坐标为1时,抛物线顶点取C(﹣1,4),设该抛物线的解析式为:y=a(x+1)2+4,代入点B坐标,得:0=a(1+1)2+4,a=﹣1,即:B点横坐标取最小值时,抛物线的解析式为:y=﹣(x+1)2+4.当A点横坐标取最大值时,抛物线顶点应取E(3,1),则此时抛物线的解析式:y=﹣(x﹣3)2+1=﹣x2+6x﹣8=﹣(x﹣2)(x﹣4),即与x轴的交点为(2,0)或(4,0)(舍去),∴点A的横坐标的最大值为2.故选:B.3.解:当点C横坐标为﹣3时,抛物线顶点为A(1,4),对称轴为x=1,此时D点横坐标为5,则CD=8;当抛物线顶点为B(4,4)时,抛物线对称轴为x=4,且CD=8,故C(0,0),D(8,0);由于此时D点横坐标最大,故点D的横坐标最大值为8;故选:D.4.解:由题意,建立如图坐标系,水平为x轴,竖直为y轴,设抛物线解析式为:y=ax2+bx+c,要使得格点最多,抛物线如图所示:取整数点D(0,1),E(1,1),F(2,2)代入抛物线的解析式得,1=a×02+0×b+c,1=a×12+1×b+c,2=a×22+2b+c,解得a=,b=,c=1,故y=x2﹣x+1,∴A(﹣3,7);B(﹣2,4);C(﹣1,2);D(0,1);E(1,1)F(3,4);G(3,4);H(4,7)共8个.建立坐标系的方法:设方格左下角为(0,0),沿着方格的边沿建立直角坐标系.取抛物线为y=(x﹣3)(x﹣4),则它能经过8个格点:(0,6),(1,3),(2,1),(3,0),(4,0),(5,1),(6,3),(7,6).对于任意的二次函数,如果我们依次考察x=0,1,2,…,8时的值,并依次用后一个值减去前一个值,总得到一个等差数列.要使经过的格点尽量多,则这个等差数列的公差要尽量小,且为整数.因此,令公差为1,这相当于取二次项系数为.验证:如果抛物线经过9个格点,那么在抛物线的顶点及一侧至少经过5个格点,由于这5个格点的横坐标都差1,考虑到抛物线的递增或递减趋势,这5点的纵坐标的极差不小于1+2+3+4=10,显然这5个格点不全在8×8网格之内.故选:C.5.解:由图象知S3=,总结出规律:,则w=S1+S2+…+S n﹣1=++…+====﹣﹣+﹣=﹣﹣,当n越来越大时,可知W最接近的常数为.故选:C.6.解:由右图知:A(1,2),B(2,1),再根据抛物线的性质,|a|越大开口越小,把A点代入y=ax2得a=2,把B点代入y=ax2得a=,则a的范围介于这两点之间,故≤a≤2.故选:D.7.解:①如图,开口向下,经过点(0,0),(1,3),(3,3)的抛物线的解析式为y=﹣x2+4x,然后向右平移1个单位,向上平移1个单位一次得到一条抛物线,可平移6次,所以,一共有7条抛物线,同理可得开口向上的抛物线也有7条,所以,满足上述条件且对称轴平行于y轴的抛物线条数是:7+7=14.②当经过点(0,0),(3,3),(6,4)的抛物线的解析式为y=﹣x2+x,将抛物线向上、向右平移一个单位,得到符合条件的新抛物线;可平移4次;∴开口向下共有5条符合条件的抛物线;同理,开口向上的也有5条;∴共有10条.10+14=24(条).故选:C.8.解:如图,连接PF.设⊙P与直线y=﹣n相切于点E,连接PE.则PE⊥AE.∵动点P在抛物线y=ax2上,∴设P(m,am2).∵⊙P恒过点F(0,n),∴PF=PE,即=am2+n.∴n=.故答案为:.9.解:∵圆心P在抛物线y=x2﹣3x+3上运动,点P的坐标为(m,n),∴n=m2﹣3m+3,∵⊙P半径为1,⊙P与x轴相交,∴|n|<1,∴|m2﹣3m+3|<1,∴﹣1<m2﹣3m+3<1,解m2﹣3m+3<1,得:3﹣<m<3+,解m2﹣3m+3>﹣1,得:m<2或m>4,∴点P的横坐标m的取值范围是:3﹣<m<2或4<m<3+.故答案为:3﹣<m<2或4<m<3+.10.解:当⊙P与x轴相切时,P点纵坐标为±2;当y=2时,x2﹣1=2,解得x=±;当y=﹣2时,x2﹣1=﹣2,x无解;故P点坐标为(,2)或(﹣,2).11.解:如图,连接AC交对称轴于P点,连接PB,P点即为所求,由二次函数y=﹣x2﹣x+2,得C(0,2),令y=0,得x1=﹣3,x2=1,故A(﹣3,0),B(1,0),故对称轴为x==﹣1,设直线AC的解析式为y=kx+b,则,解得,直线AC:y=x+2,把x=﹣1代入直线AC的解析式,得y=,∴P的坐标为(﹣1,).故本题答案为:(﹣1,).12.解:(1)观察图形发现,抛物线的开口向下,∴a<0,∵顶点坐标在第一象限,∴﹣>0,∴b>0,而抛物线与y轴的交点在y轴的上方,∴c>0,∴abc<0;(2)顶点C是矩形DEFG上(包括边界和内部)的一个动点,当顶点C与D点重合,顶点坐标为(1,3),则抛物线解析式y=a(x﹣1)2+3,由,解得﹣≤a≤﹣;当顶点C与F点重合,顶点坐标为(3,2),则抛物线解析式y=a(x﹣3)2+2,由,解得﹣≤a≤﹣;∵顶点可以在矩形内部,∴﹣≤a≤﹣.解法二:由题意及图可知:当抛物线经过(﹣2,0),顶点为F(3,2)时,抛物线开口最大,解得a=﹣;当抛物线经过(﹣1,0),顶点为D(1,3)时,抛物线开口最小,解得a=﹣,∵当a<0时,a越小抛物线的开口越小,a越大抛物线的开口越大,∴﹣≤a≤﹣13.解:由题意可得,圆的半径为AB的即0.5cm,根据对称性可知,阴影部分面积为半圆的面积=×π()2≈0.39cm2.14.解:在抛物线y=x2﹣x﹣6中,当y=0时,x=﹣2或3,即A(﹣2,0),B(3,0);当x=0时,y=﹣6,即C(0,﹣6);故S△COB=9,设点M的纵坐标为y,必有×AO•|y|=9,解可得y=±9,将其代入解析式可得x的值为,(舍去),故点M的坐标是(,9).15.解:∵一次函数有y=﹣2x+3的图象与x轴、y轴分别交于A、C两点,∴分别令x=0、y=0,可求出A(,0),C(0,3),因为点B在直线y=﹣2x+3的图象上,所以设B点(x,﹣2x+3),由AC:CB=1:2可知=2,则﹣2x+3=9,解得x=﹣3,把B(﹣3,9)C(0,3)代入二次函数解析式得,解得,故二次函数的解析式为y=x2+x+3,故其顶点坐标为(﹣,).16.解:(1)∵F1:y=x+1,F1和F2关于y轴对称,∴F2:y=﹣x+1,分别令x=2,则2+1=3,﹣2+1=﹣1,∴P(2,3),Q(2,﹣1),∴PQ=3﹣(﹣1)=4,故答案为:4;(2)∵F1:,可得:F2:,∵x=t,可得:P(t,),Q(t,),∴PQ=﹣==6,解得:t=1,经检验:t=1是原方程的解,故答案为:1;(3)①∵F1:y=ax2+bx+c,∴F2:y=ax2﹣bx+c,∵t=,分别代入F1,F2,可得:P(,),Q(,),∴PQ=||=,∴S△OPQ==1;②∵函数F1和F2的图象与x轴正半轴分别交于点A(5,0),B(1,0),而函数F1和F2的图象关于y轴对称,∴函数F1的图象经过A(5,0)和(﹣1,0),∴设F1:y=a(x+1)(x﹣5)=ax2﹣4ax﹣5a,则F2:y=ax2+4ax﹣5a,∴F1的图象的对称轴是直线x=2,且c=﹣5a,∴a=,∵c>0,则a<0,c+1>1,而F2的图象在x>0时,y随x的增大而减小,当0<c<1时,F1的图象y随x的增大而增大,F2的图象y随x的增大而减小,∴当x=c+1时,y=ax2﹣4ax﹣5a的最大值为a(c+1)2﹣4a(c+1)﹣5a,y=ax2+4ax﹣5a的最小值为a(c+1)2+4a(c+1)﹣5a,则h=a(c+1)2﹣4a(c+1)﹣5a﹣[a(c+1)2+4a(c+1)﹣5a]=﹣8ac﹣8a,又∵a=,∴h=;当1≤c≤2时,F1的最大值为=﹣9a,F2的图象y随x的增大而减小,∴F2的最小值为:a(c+1)2+4a(c+1)﹣5a,则h=﹣9a﹣[a(c+1)2+4a(c+1)﹣5a]=﹣a(c+1)2﹣4a(c+1)﹣4a=﹣ac2﹣6ac ﹣9a,又∵a=,∴h=,当c>2时,F1的图象y随x的增大而减小,F2的图象y随x的增大而减小,∴当x=c时,y=ax2﹣4ax﹣5a的最大值为ac2﹣4ac﹣5a,当x=c+1时,y=ax2+4ax﹣5a的最小值为a(c+1)2+4a(c+1)﹣5a,则h=ac2+4ac﹣5a﹣[a(c+1)2+4a(c+1)﹣5a],又∵a=,∴h=2c2+c;综上:h关于x的解析式为:h=.17.解:(1)∵二次函数的图象顶点在原点,故设二次函数表达式为:y=ax2,将(2,1)代入上式并解得:a=,故二次函数表达式为:y=x2;(2)将y=1代入y=x2并解得:x=±2,故点M、N的坐标分别为(﹣2,1)、(2,1),则MN=4,∵△PMN是等边三角形,∴点P在y轴上且PM=4,∴PF=2;∵点F(0,1),∴点P的坐标为(0,1+2)或(0,1﹣2);(3)假设二次函数的图象上存在一点E满足条件,设点Q是FN的中点,则点Q(1,1),故点E在FN的中垂线上.∴点E是FN的中垂线与y=x2图象的交点,∴y=×12=,则点E(1,),EN==,同理EF==,点E到直线y=﹣1的距离为|﹣(﹣1)|=,故存在点E,使得以点E为圆心半径为的圆过点F,N且与直线y=﹣1相切.18.解:(1)∵抛物线经过A(﹣1,0),B(4,0),可得:,解得:,∴抛物线的解析式为:,令x=0,则y=2,∴点C的坐标为(0,2);(2)连接OQ,∵点Q的横坐标为m,∴Q(m,),∴S=S△OCQ+S△OBQ﹣S△OBC=﹣=﹣m2+4m,令S=2,解得:m=或,(3)如图,过点Q作QH⊥BC于H,连接AC,∵AC=,BC=,AB=5,满足AC2+BC2=AB2,∴∠ACB=90°,又∠QHP=90°,∠APC=∠QPH,∴△APC∽△QPH,∴,∵S△BCQ=BC•QH=QH,∴QH=,∴=,∴当m=2时,存在最大值.19.解:(1)∵抛物线y=ax2+bx+2经过点A(﹣2,﹣4)和点C(2,0),则,解得:,∴抛物线的解析式为y=﹣x2+x+2;(2)存在,理由是:在x轴正半轴上取点E,使OB=OE,过点E作EF⊥BD,垂足为F,在y=﹣x2+x+2中,令y=0,解得:x=2或﹣1,∴点B坐标为(﹣1,0),∴点E坐标为(1,0),可知:点B和点E关于y轴对称,∴∠BDO=∠EDO,即∠BDE=2∠BDO,∵D(0,2),∴DE===BD,在△BDE中,×BE×OD=×BD×EF,即2×2=×EF,解得:EF=,∴DF=,∴tan∠BDE=,若∠PBC=2∠BDO,则∠PBC=∠BDE,∵BD=DE=,BE=2,则BD2+DE2>BE2,∴∠BDE为锐角,当点P在第三象限时,∠PBC为钝角,不符合;当点P在x轴上方时,∵∠PBC=∠BDE,设点P坐标为(c,﹣c2+c+2),过点P作x轴的垂线,垂足为G,则BG=c+1,PG=﹣c2+c+2,∴tan∠PBC==,解得:c=,∴﹣c2+c+2=,∴点P的坐标为(,);当点P在第四象限时,同理可得:PG=c2﹣c﹣2,BG=c+1,tan∠PBC=,解得:c=,∴,∴点P的坐标为(,),综上:点P的坐标为(,)或(,);(3)设EF与AD交于点N,∵A(﹣2,﹣4),D(0,2),设直线AD表达式为y=mx+n,则,解得:,∴直线AD表达式为y=3x+2,设点M的坐标为(s,3s+2),∵A(﹣2,﹣4),C(2,0),设直线AC表达式为y=m1x+n1,则,解得:,∴直线AC表达式为y=x﹣2,令x=0,则y=﹣2,∴点E坐标为(0,﹣2),可得:点E是线段AC中点,∴△AME和△CME的面积相等,由于折叠,∴△CME≌△FME,即S△CME=S△FME,由题意可得:当点F在直线AC上方时,∴S△MNE=S△AMC=S△AME=S△FME,即S△MNE=S△ANE=S△MNF,∴MN=AN,FN=NE,∴四边形FMEA为平行四边形,∴CM=FM=AE=AC=,∵M(s,3s+2),∴,解得:s=或0(舍),∴M(,),∴AM=,当点F在直线AC下方时,如图,同理可得:四边形AFEM为平行四边形,∴AM=EF,由于折叠可得:CE=EF,∴AM=EF=CE=,综上:AM的长度为或.20.解:(1)∵a=1>0,故该抛物线开口向上,顶点A的坐标为(1,﹣1),当x>1,y随x的增大而增大,当x<1,y随x增大而减小;(2)①设抛物线“不动点”坐标为(t,t),则t=t2﹣2t,解得:t=0或3,故“不动点”坐标为(0,0)或(3,3);②当OC∥AB时,∵新抛物线顶点B为“不动点”,则设点B(m,m),∴新抛物线的对称轴为:x=m,与x轴的交点C(m,0),∵四边形OABC是梯形,∴直线x=m在y轴左侧,∵BC与OA不平行,∴OC∥AB,又∵点A(1,﹣1),点B(m,m),∴m=﹣1,故新抛物线是由抛物线y=x2﹣2x向左平移2个单位得到的;当OB∥AC时,同理可得:抛物线的表达式为:y=(x﹣2)2+2=x2﹣4x+6,当四边形OABC是梯形,字母顺序不对,故舍去,综上,新抛物线的表达式为:y=(x+1)2﹣1.21.解:(1)将点A、D的坐标代入直线表达式得:,解得:,故直线l的表达式为:y=﹣x﹣1,将点A、D的坐标代入抛物线表达式,同理可得抛物线的表达式为:y=﹣x2+3x+4;(2)直线l的表达式为:y=﹣x﹣1,则直线l与x轴的夹角为45°,即:则PE=PF,设点P坐标为(x,﹣x2+3x+4)、则点F(x,﹣x﹣1),PE+PF=2PF=2(﹣x2+3x+4+x+1)=﹣2(x﹣2)2+18,∵﹣2<0,故PE+PF有最大值,当x=2时,其最大值为18;(3)NC=5,①当NC是平行四边形的一条边时,设点P坐标为(x,﹣x2+3x+4)、则点M(x,﹣x﹣1),由题意得:|y M﹣y P|=5,即:|﹣x2+3x+4+x+1|=5,解得:x=2或0或4(舍去0),则点M坐标为(2+,﹣3﹣)或(2﹣,﹣3+)或(4,﹣5);②当NC是平行四边形的对角线时,则NC的中点坐标为(0,),设点P坐标为(m,﹣m2+3m+4)、则点M(n,﹣n﹣1),N、C,M、P为顶点的四边形为平行四边形,则NC的中点即为PM中点,即:,解得:,故点M(﹣4,3);故点M的坐标为:(2+,﹣3﹣)或(2﹣,﹣3+)或(4,﹣5)或(﹣4,3).22.解:(1)把A(1,0)和C(0,3)代入y=x2+bx+c,解得:b=﹣4,c=3,∴二次函数的表达式为:y=x2﹣4x+3;(2)令y=0,则x2﹣4x+3=0,解得:x=1或x=3,∴B(3,0),∴BC=3,点P在y轴上,当△PBC为等腰三角形时分三种情况进行讨论:如图1,①当CP=CB时,PC=3,∴OP=OC+PC=3+3或OP=PC﹣OC=3﹣3∴P1(0,3+3),P2(0,3﹣3);②当BP=BC时,OP=OC=3,∴P3(0,﹣3);③当PB=PC时,∵OC=OB=3∴此时P与O重合,∴P4(0,0);综上所述,点P的坐标为:(0,3+3)或(0,3﹣3)或(0,﹣3)或(0,0);(3)如图2,设A运动时间为t,由AB=2,得BM=2﹣t,则DN=2t,∴S△MNB=×(2﹣t)×2t=﹣t2+2t=﹣(t﹣1)2+1,即当M(2,0)、N(2,2)或(2,﹣2)时△MNB面积最大,最大面积是1.23.解:(1)OA=OC=4OB=4,故点A、C的坐标分别为(4,0)、(0,﹣4);(2)抛物线的表达式为:y=a(x+1)(x﹣4)=a(x2﹣3x﹣4),即﹣4a=﹣4,解得:a=1,故抛物线的表达式为:y=x2﹣3x﹣4;(3)直线CA过点C,设其函数表达式为:y=kx﹣4,将点A坐标代入上式并解得:k=1,故直线CA的表达式为:y=x﹣4,过点P作y轴的平行线交AC于点H,∵OA=OC=4,∴∠OAC=∠OCA=45°,∵PH∥y轴,∴∠PHD=∠OCA=45°,设点P(x,x2﹣3x﹣4),则点H(x,x﹣4),PD=HP sin∠PHD=(x﹣4﹣x2+3x+4)=﹣x2+2x,∵<0,∴PD有最大值,当x=2时,其最大值为2,此时点P(2,﹣6).24.解:(1)在y=﹣x+3中,令x=0,得y=3,令y=0,得x=4,∴A(4,0),B(0,3),将A(4,0),B(0,3)分别代入抛物线y=﹣x2+bx+c中,得:,解得:,∴抛物线的函数表达式为:y=﹣x2+x+3.(2)存在.如图1,过点B作BH⊥CD于H,设C(t,0),则D(t,),E(t,),H(t,3);∴EC=,AC=4﹣t,BH=t,DH=﹣t2+t,DE=﹣t2+4t∵△BDE和△ACE相似,∠BED=∠AEC∴△BDE∽△ACE或△DBE∽△ACE①当△BDE∽△ACE时,∠BDE=∠ACE=90°,此时BD∥AC,可得D(,3).②当△DBE∽△ACE时,∠BDE=∠CAE∵BH⊥CD∴∠BHD=90°,∴=tan∠BDE=tan∠CAE=,即:BH•AC=CE•DH∴t(4﹣t)=()(﹣t2+t),解得:t1=0(舍),t2=4(舍),t3=,∴D(,);综上所述,点D的坐标为(,3)或(,);(3)如图2,∵四边形DEGF是平行四边形∴DE∥FG,DE=FG设D(m,),E(m,),F(n,),G(n,),则:DE=﹣m2+4m,FG=﹣n2+4n,∴﹣m2+4m=﹣n2+4n,即:(m﹣n)(m+n﹣4)=0,∵m﹣n≠0∴m+n﹣4=0,即:m+n=4过点G作GK⊥CD于K,则GK∥AC∴∠EGK=∠BAO∴=cos∠EGK=cos∠BAO=,即:GK•AB=AO•EG∴5(n﹣m)=4EG,即:EG=(n﹣m)∴DEGF周长=2(DE+EG)=2[(﹣m2+4m)+(n﹣m)]=﹣2+∵﹣2<0,∴当m=时,∴▱DEGF周长最大值=,此时n=4﹣=,则G(,),当E,G互换时,结论也成立,此时G(,),综上所述.G(,)或(,).25.解:(1)在中,令y=0,得x=4,令x=0,得y=2∴A(4,0),B(0,2)把A(4,0),B(0,2),代入,得,解得∴抛物线得解析式为(2)如图,过点B作x轴得平行线交抛物线于点E,过点D作BE的垂线,垂足为F∵BE∥x轴,∴∠BAC=∠ABE∵∠ABD=2∠BAC,∴∠ABD=2∠ABE即∠DBE+∠ABE=2∠ABE∴∠DBE=∠ABE∴∠DBE=∠BAC设D点的坐标为(x,),则BF=x,DF=∵tan∠DBE=,tan∠BAC=∴=,即解得x1=0(舍去),x2=2当x=2时,=3∴点D的坐标为(2,3)(3)当BO为边时,OB∥EF,OB=EF设E(m,),F(m,)EF=|()﹣()|=2解得m 1=2,,当BO为对角线时,OB与EF互相平分过点O作OF∥AB,直线OF交抛物线于点F()和()求得直线EF解析式为或直线EF与AB的交点为E,点E的横坐标为或∴E点的坐标为(2,1)或(,)或()或()或()。
2020-2021中考数学培优专题复习二次函数练习题及答案

2020-2021中考数学培优专题复习二次函数练习题及答案一、二次函数1.如图所示,抛物线2y ax bx c =++的顶点为()2,4M --,与x 轴交于A 、B 两点,且()6,0A -,与y 轴交于点C .()1求抛物线的函数解析式;()2求ABC V 的面积;()3能否在抛物线第三象限的图象上找到一点P ,使APC V 的面积最大?若能,请求出点P 的坐标;若不能,请说明理由.【答案】()1 2134y x x =+-;()212;()27334APC x S =-V 当时,有最大值,点P 的坐标是153,4P ⎛⎫--⎪⎝⎭. 【解析】【分析】 (1)设顶点式并代入已知点()6,0A -即可;(2)令y=0,求出A 、B 和C 点坐标,运用三角形面积公式计算即可;(3)假设存在这样的点,过点P 作PE x ⊥轴于点E ,交AC 于点F ,线段PF 的长度即为两函数值之差,将APC V 的面积计算拆分为APF CPF S S +V V 即可.【详解】()1设此函数的解析式为2()y a x h k =++,∵函数图象顶点为()2,4M --,∴2(2)4y a x =+-,又∵函数图象经过点()6,0A -,∴20(62)4a =-+- 解得14a =, ∴此函数的解析式为21(2)44y x =+-,即2134y x x =+-;()2∵点C 是函数2134y x x =+-的图象与y 轴的交点, ∴点C 的坐标是()0,3-,又当0y =时,有21304y x x =+-=, 解得16x =-,22x =,∴点B 的坐标是()2,0,则11831222ABC S AB OC =⋅=⨯⨯=V ; ()3假设存在这样的点,过点P 作PE x ⊥轴于点E ,交AC 于点F .设(),0E x ,则21,34P x x x ⎛⎫+- ⎪⎝⎭,设直线AC 的解析式为y kx b =+, ∵直线AC 过点()6,0A -,()0,3C -,∴603k b b -+=⎧⎨-=⎩, 解得123k b ⎧=-⎪⎨⎪=-⎩,∴直线AC 的解析式为132y x =--, ∴点F 的坐标为1,32F x x ⎛⎫-- ⎪⎝⎭, 则221113332442PF x x x x x ⎛⎫=---+-=-- ⎪⎝⎭, ∴1122APC APF CPF S S S PF AE PF OE =+=⋅+⋅V V V 2221113393276(3)22424244PF OA x x x x x ⎛⎫=⋅=--⨯=--=-++ ⎪⎝⎭, ∴当3x =-时,APC S V 有最大值274,此时点P 的坐标是153,4P ⎛⎫--⎪⎝⎭. 【点睛】 本题第3问中将所求三角形拆分为两个小三角形进行求解,从而将面积最大的问题转化为PF 最大进行理解.2.童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销该店决定降价销售,经市场调查发现:每降价1元,每星期可多卖10件,已知该款童装每件成本30元,设降价后该款童装每件售价x 元,每星期的销售量为y 件.(1)降价后,当某一星期的销售量是未降价前一星期销售量的3倍时,求这一星期中每件童装降价多少元?(2)当每件售价定为多少元时,一星期的销售利润最大,最大利润是多少?【答案】(1)这一星期中每件童装降价20元;(2)每件售价定为50元时,一星期的销售利润最大,最大利润4000元.【解析】【分析】(1)根据售量与售价x (元/件)之间的关系列方程即可得到结论.(2)设每星期利润为W 元,构建二次函数利用二次函数性质解决问题.【详解】解:(1)根据题意得,(60﹣x )×10+100=3×100,解得:x =40,60﹣40=20元,答:这一星期中每件童装降价20元;(2)设利润为w ,根据题意得,w =(x ﹣30)[(60﹣x )×10+100]=﹣10x 2+1000x ﹣21000=﹣10(x ﹣50)2+4000,答:每件售价定为50元时,一星期的销售利润最大,最大利润4000元.【点睛】本题考查二次函数的应用,一元二次不等式,解题的关键是构建二次函数解决最值问题,利用图象法解一元二次不等式,属于中考常考题型.3.如图,在平面直角坐标系中,二次函数2y ax bx c =++交x 轴于点()4,0A -、()2,0B ,交y 轴于点()0,6C ,在y 轴上有一点()0,2E -,连接AE .(1)求二次函数的表达式;(2)若点D 为抛物线在x 轴负半轴上方的一个动点,求ADE ∆面积的最大值; (3)抛物线对称轴上是否存在点P ,使AEP ∆为等腰三角形,若存在,请直接写出所有P 点的坐标,若不存在请说明理由.【答案】(1)二次函数的解析式为233642y x x =--+;(2)当23x =-时,ADE ∆的面积取得最大值503;(3)P 点的坐标为()1,1-,(1,11-,(1,219--. 【解析】分析:(1)把已知点坐标代入函数解析式,得出方程组求解即可;(2)根据函数解析式设出点D 坐标,过点D 作DG ⊥x 轴,交AE 于点F ,表示△ADE 的面积,运用二次函数分析最值即可;(3)设出点P 坐标,分PA =PE ,PA =AE ,PE =AE 三种情况讨论分析即可.详解:(1)∵二次函数y =ax 2+bx +c 经过点A (﹣4,0)、B (2,0),C (0,6), ∴16404206a b c a b c c -+=⎧⎪++=⎨⎪=⎩, 解得:34326a b c ⎧=-⎪⎪⎪=-⎨⎪=⎪⎪⎩, 所以二次函数的解析式为:y =233642x x --+; (2)由A (﹣4,0),E (0,﹣2),可求AE 所在直线解析式为y =122x --, 过点D 作DN ⊥x 轴,交AE 于点F ,交x 轴于点G ,过点E 作EH ⊥DF ,垂足为H ,如图,设D (m ,233642m m --+),则点F (m ,122m --), ∴DF =233642m m --+﹣(122m --)=2384m m --+, ∴S △ADE =S △ADF +S △EDF =12×DF ×AG +12DF ×EH =12×DF ×AG +12×DF ×EH =12×4×DF =2×(2384m m --+) =23250233m -++(), ∴当m =23-时,△ADE 的面积取得最大值为503. (3)y =233642x x --+的对称轴为x =﹣1,设P (﹣1,n ),又E (0,﹣2),A (﹣4,0),可求PA 29n +PE 212n ++()AE 16425+=,分三种情况讨论: 当PA =PE 29n +212n ++()n =1,此时P (﹣1,1); 当PA =AE 29n +16425+=n =11,此时点P 坐标为(﹣1,11);当PE =AE 212n ++()16425+=n =﹣219P 坐标为:(﹣1,﹣219).综上所述:P 点的坐标为:(﹣1,1),(﹣1,111,﹣219). 点睛:本题主要考查二次函数的综合问题,会求抛物线解析式,会运用二次函数分析三角形面积的最大值,会分类讨论解决等腰三角形的顶点的存在问题时解决此题的关键.4.在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C (0,3).(1)求抛物线的解析式;(2)如图1,P为线段BC上一点,过点P作y轴的平行线,交抛物线于点D,当△CDP为等腰三角形时,求点P的坐标;(3)如图2,抛物线的顶点为E,EF⊥x轴于点F,N是线段EF上一动点,M(m,0)是x 轴一个动点,若∠MNC=90°,请求出m的取值范围.【答案】(1)y=﹣x2+2x+3;(2)点P的坐标为(1,2)或(2,1)或(3﹣2,23)55 4m-≤≤【解析】【分析】(1)利用待定系数法即可求得此抛物线的解析式;(2)由待定系数法即可求得直线BC的解析式,再设P(t,3﹣t),即可得D(t,﹣t2+2t+3),即可求得PD的长,然后分三种情况讨论,求点P的坐标;(3)直角三角形斜边上的中线等于斜边的一半列出关系式m=(n﹣32)2﹣54,然后根据n的取值得到最小值.【详解】解:(1)∵抛物线y=﹣x2+bx+c经过点A、B、C,A(﹣1,0),C(0,3),∴103b cc--+=⎧⎨=⎩,解得b=2,c=3.故该抛物线解析式为:y=﹣x2+2x+3.(2)令﹣x2+2x+3=0,解得x1=﹣1,x2=3,即B(3,0),设直线BC的解析式为y=kx+b′,则330bk b''=⎧⎨+=⎩,解得:k=-1,b’=3故直线BC 的解析式为y =﹣x +3;∴设P (t ,3﹣t ),∴D (t ,﹣t 2+2t +3),∴PD =(﹣t 2+2t +3)﹣(3﹣t )=﹣t 2+3t ,∵OB =OC =3,∴△BOC 是等腰直角三角形,∴∠OCB =45°,当CD =PC 时,则∠CPD =∠CDP ,∵PD ∥y 轴,∴∠CPD =∠OCB =45°,∴∠CDP =45°,∴∠PCD =90°,∴直线CD 的解析式为y =x +3,解2323y x y x x =+⎧⎨=-++⎩得03x y =⎧⎨=⎩或14x y =⎧⎨=⎩∴D (1,4),此时P (1,2);当CD =PD 时,则∠DCP =∠CPD =45°,∴∠CDP =90°,∴CD ∥x 轴,∴D 点的纵坐标为3,代入y =﹣x 2+2x +3得,3=﹣x 2+2x +3,解得x =0或x =2,此时P (2,1);当PC =PD 时,∵PC t , ∴=﹣t 2+3t ,解得t =0或t =3,此时P (3);综上,当△CDP 为等腰三角形时,点P 的坐标为(1,2)或(2,1)或(3) (3)如图2,由(1)y =﹣x 2+2x +3=﹣(x ﹣1)2+4,∴E (1,4),设N (1,n ),则0≤n ≤4,取CM 的中点Q (2m ,32), ∵∠MNC =90°, ∴NQ =12CM , ∴4NQ 2=CM 2,∵NQ 2=(1﹣2m )2+(n ﹣32)2, ∴4[(1﹣2m )2+(n ﹣32)2]=m 2+9, 整理得,m =(n ﹣32)2﹣54, ∵0≤n ≤4,当n =32时,m 最小值=﹣54,n =4时,m =5, 综上,m 的取值范围为:﹣54≤m ≤5.【点睛】此题考查了待定系数法求函数的解析式、平行线的性质、二次函数的最值问题、判别式的应用以及等腰直角三角形的性质等知识.此题综合性很强,难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用.5.如图,菱形ABCD 的边长为20cm ,∠ABC =120°,对角线AC ,BD 相交于点O ,动点P 从点A 出发,以4cm /s 的速度,沿A →B 的路线向点B 运动;过点P 作PQ ∥BD ,与AC 相交于点Q ,设运动时间为t 秒,0<t <5.(1)设四边形PQCB 的面积为S ,求S 与t 的关系式;(2)若点Q 关于O 的对称点为M ,过点P 且垂直于AB 的直线l 交菱形ABCD 的边AD (或CD )于点N ,当t 为何值时,点P 、M 、N 在一直线上?(3)直线PN 与AC 相交于H 点,连接PM ,NM ,是否存在某一时刻t ,使得直线PN 平分四边形APMN 的面积?若存在,求出t 的值;若不存在,请说明理由.【答案】(1) S=﹣231003t +0<t <5); (2)307;(3)见解析. 【解析】【分析】(1)如图1,根据S=S △ABC -S △APQ ,代入可得S 与t 的关系式;(2)设PM=x ,则AM=2x ,可得3,计算x 的值,根据直角三角形30度角的性质可得3AM=AO+OM ,列方程可得t 的值; (3)存在,通过画图可知:N 在CD 上时,直线PN 平分四边形APMN 的面积,根据面积相等可得MG=AP ,由AM=AO+OM ,列式可得t 的值.【详解】解:(1)如图1,∵四边形ABCD 是菱形,∴∠ABD=∠DBC=12∠ABC=60°,AC ⊥BD , ∴∠OAB=30°,∵AB=20,∴OB=10,3由题意得:AP=4t ,∴PQ=2t ,3,∴S=S △ABC ﹣S △APQ , =11··22AC OB PQ AQ -, =111020322322t t ⨯⨯⨯⨯ , =﹣323(0<t <5);(2)如图2,在Rt △APM 中,AP=4t ,∵点Q 关于O 的对称点为M ,∴OM=OQ ,设PM=x ,则AM=2x ,∴AP=3x=4t , ∴x=3, ∴AM=2PM=3, ∵AM=AO+OM ,∴3=103+103﹣23t , t=307; 答:当t 为307秒时,点P 、M 、N 在一直线上; (3)存在,如图3,∵直线PN 平分四边形APMN 的面积, ∴S △APN =S △PMN ,过M 作MG ⊥PN 于G , ∴11··22PN AP PN MG , ∴MG=AP ,易得△APH ≌△MGH , ∴3, ∵AM=AO+OM ,同理可知:3﹣3, 3333t , t=3011. 答:当t 为3011秒时,使得直线PN 平分四边形APMN 的面积.【点睛】考查了全等三角形的判定与性质,对称的性质,三角形和四边形的面积,二次根式的化简等知识点,计算量大,解答本题的关键是熟练掌握动点运动时所构成的三角形各边的关系.6.如图甲,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.(1)求该抛物线的解析式;(2)在该抛物线的对称轴上是否存在点M,使以C,P,M为顶点的三角形为等腰三角形?若存在,请直接写出所符合条件的点M的坐标;若不存在,请说明理由;(3)当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值(图乙、丙供画图探究).【答案】(1)y=x2﹣4x+3;(2)(2,)或(2,7)或(2,﹣1+2)或(2,﹣1﹣2);(3)E点坐标为(,)时,△CBE的面积最大.【解析】试题分析:(1)由直线解析式可求得B、C坐标,利用待定系数法可求得抛物线解析式;(2)由抛物线解析式可求得P点坐标及对称轴,可设出M点坐标,表示出MC、MP和PC 的长,分MC=MP、MC=PC和MP=PC三种情况,可分别得到关于M点坐标的方程,可求得M点的坐标;(3)过E作EF⊥x轴,交直线BC于点F,交x轴于点D,可设出E点坐标,表示出F点的坐标,表示出EF的长,进一步可表示出△CBE的面积,利用二次函数的性质可求得其取得最大值时E点的坐标.试题解析:(1)∵直线y=﹣x+3与x轴、y轴分别交于点B、点C,∴B(3,0),C(0,3),把B、C坐标代入抛物线解析式可得,解得,∴抛物线解析式为y=x2﹣4x+3;(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线对称轴为x=2,P(2,﹣1),设M(2,t),且C(0,3),∴MC=,MP=|t+1|,PC=,∵△CPM为等腰三角形,∴有MC=MP、MC=PC和MP=PC三种情况,①当MC=MP时,则有=|t+1|,解得t=,此时M(2,);②当MC=PC时,则有=2,解得t=﹣1(与P点重合,舍去)或t=7,此时M(2,7);③当MP=PC时,则有|t+1|=2,解得t=﹣1+2或t=﹣1﹣2,此时M(2,﹣1+2)或(2,﹣1﹣2);综上可知存在满足条件的点M,其坐标为(2,)或(2,7)或(2,﹣1+2)或(2,﹣1﹣2);(3)如图,过E作EF⊥x轴,交BC于点F,交x轴于点D,设E(x,x2﹣4x+3),则F(x,﹣x+3),∵0<x<3,∴EF=﹣x+3﹣(x2﹣4x+3)=﹣x2+3x,∴S△CBE=S△EFC+S△EFB=EF•OD+EF•BD=EF•OB=×3(﹣x2+3x)=﹣(x﹣)2+,∴当x=时,△CBE的面积最大,此时E点坐标为(,),即当E点坐标为(,)时,△CBE的面积最大.考点:二次函数综合题.7.如图,已知抛物线的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
2020-2021中考数学 二次函数 培优练习(含答案)附答案解析

2020-2021中考数学 二次函数 培优练习(含答案)附答案解析一、二次函数1.已知,m ,n 是一元二次方程x 2+4x +3=0的两个实数根,且|m |<|n |,抛物线y =x 2+bx +c 的图象经过点A (m ,0),B (0,n ),如图所示. (1)求这个抛物线的解析式;(2)设(1)中的抛物线与x 轴的另一个交点为抛物线的顶点为D ,求出点C ,D 的坐标,并判断△BCD 的形状;(3)点P 是直线BC 上的一个动点(点P 不与点B 和点C 重合),过点P 作x 轴的垂线,交抛物线于点M ,点Q 在直线BC 上,距离点P 为2个单位长度,设点P 的横坐标为t ,△PMQ 的面积为S ,求出S 与t 之间的函数关系式.【答案】(1)223y x x =--;(2)C (3,0),D (1,﹣4),△BCD 是直角三角形;(3)2213(03)2213(03)22t t t S t t t t ⎧-+⎪⎪=⎨⎪-⎪⎩<<<或>【解析】试题分析:(1)先解一元二次方程,然后用待定系数法求出抛物线解析式;(2)先解方程求出抛物线与x 轴的交点,再判断出△BOC 和△BED 都是等腰直角三角形,从而得到结论;(3)先求出QF=1,再分两种情况,当点P 在点M 上方和下方,分别计算即可. 试题解析:解(1)∵2+430x x +=,∴11x =-,23x =-,∵m ,n 是一元二次方程2+430x x +=的两个实数根,且|m|<|n|,∴m=﹣1,n=﹣3,∵抛物线223y x x =--的图象经过点A (m ,0),B (0,n ),∴10{3b c c -+==-,∴2{3b c =-=-,∴抛物线解析式为223y x x =--;(2)令y=0,则2230x x --=,∴11x =-,23x =,∴C (3,0),∵223y x x =--=2(1)4x --,∴顶点坐标D (1,﹣4),过点D 作DE ⊥y 轴,∵OB=OC=3,∴BE=DE=1,∴△BOC 和△BED 都是等腰直角三角形,∴∠OBC=∠DBE=45°,∴∠CBD=90°,∴△BCD 是直角三角形;(3)如图,∵B(0,﹣3),C(3,0),∴直线BC解析式为y=x﹣3,∵点P的横坐标为t,PM⊥x轴,∴点M的横坐标为t,∵点P在直线BC上,点M在抛物线上,∴P(t,t﹣3),M(t,223t t--),过点Q作QF⊥PM,∴△PQF是等腰直角三角形,∵PQ=2,∴QF=1.①当点P在点M上方时,即0<t<3时,PM=t﹣3﹣(223t t--)=23t t-+,∴S=12PM×QF=21(3)2t t-+=21322t t-+,②如图3,当点P在点M下方时,即t<0或t >3时,PM=223t t--﹣(t﹣3)=23t t-,∴S=12PM×QF=12(23t t-)=21322t t-.综上所述,S=2213(03)22{13(03)22t t tt t t t或-+<<-.考点:二次函数综合题;分类讨论.2.如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1, 0)、C(3, 0)、D(3, 4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,以每秒12个单位的速度沿线段AD向点D运动,运动时间为t秒.过点P作PE⊥x轴交抛物线于点M,交AC 于点N.(1)直接写出点A 的坐标,并求出抛物线的解析式; (2)当t 为何值时,△ACM 的面积最大?最大值为多少?(3)点Q 从点C 出发,以每秒1个单位的速度沿线段CD 向点D 运动,当t 为何值时,在线段PE 上存在点H ,使以C 、Q 、N 、H 为顶点的四边形为菱形?【答案】(1)A (1,4);y =-x 2+2x +3;(2)当t =2时,△A MC 面积的最大值为1;(3)2085-或2013. 【解析】(1)由矩形的性质得到点A 的坐标,由抛物线的顶点为A ,设抛物线的解析式为y =a (x -1)2+4,把点C 的坐标代入即可求得a 的值;(2)由点P 的坐标以及抛物线解析式得到点M 的坐标,由A 、C 的坐标得到直线AC 的解析式,进而得到点N 的坐标,即可用关于t 的式子表示MN ,然后根据△ACM 的面积是△AMN 和△CMN 的面积和列出用t 表示的△ACM 的面积,利用二次函数的性质即可得到当t =2时,△A MC 面积的最大值为1;(3)①当点H在N点上方时,由P N=CQ ,PN ∥CQ ,得到四边形PNCQ 为平行四边形,所以当PQ =CQ 时,四边形FECQ 为菱形,据此得到,解得t 值;②当点H在N点下方时,NH=CQ=,NQ =CQ 时,四边形NHCQ 为菱形,NQ 2=CQ 2,得:,解得t 值.解:(1)由矩形的性质可得点A (1,4), ∵抛物线的顶点为A ,设抛物线的解析式为y =a (x -1)2+4, 代入点C (3, 0),可得a =-1. ∴y =-(x -1)2+4=-x 2+2x +3. (2)∵P (112t +,4), 将112x t =+代入抛物线的解析式,y =-(x -1)2+4=2144t -, ∴M (112t +,2144t -), 设直线AC 的解析式为,将A (1,4),C (3,0)代入,得:,将112x t =+代入得,∴N (112t +,),∴MN,∴,∴当t =2时,△A MC 面积的最大值为1. (3)①如图1,当点H在N点上方时, ∵N(112t +,),P (112t +,4), ∴P N=4—()==CQ ,又∵PN ∥CQ ,∴四边形PNCQ 为平行四边形, ∴当PQ =CQ 时,四边形FECQ 为菱形, PQ 2=PD 2+DQ 2 =,∴,整理,得240800t t -+=.解得12085t =-,22085t =+(舍去);②如图2当点H在N点下方时,NH=CQ=,NQ =CQ 时,四边形NHCQ 为菱形, NQ 2=CQ 2,得:.整理,得213728000t t -+=.()()1320400t t --=.所以12013t =,(舍去).“点睛”此题主要考查二次函数的综合问题,会用顶点式求抛物线,会用两点法求直线解析式,会设点并表示三角形的面积,熟悉矩形和菱形的性质是解题的关键.3.对于二次函数 y=ax 2+(b+1)x+(b ﹣1),若存在实数 x 0,使得当 x=x 0,函数 y=x 0,则称x 0 为该函数的“不变值”.(1)当 a=1,b=﹣2 时,求该函数的“不变值”;(2)对任意实数 b ,函数 y 恒有两个相异的“不变值”,求 a 的取值范围;(3)在(2)的条件下,若该图象上 A 、B 两点的横坐标是该函数的“不变值”,且 A 、B 两点关于直线 y=kx-2a+3 对称,求 b 的最小值. 【答案】(1)-1,3;(2)0<a<1;(3)-98【解析】 【分析】(1)先确定二次函数解析式为y=x 2-x-3,根据x o 是函数y 的一个不动点的定义,把(x o ,x o )代入得x 02-x 0-3=x o ,然后解此一元二次方程即可;(2)根据x o 是函数y 的一个不动点的定义得到ax o 2+(b+1)x o +(b-1)=x o ,整理得ax 02+bx o +(b-1)=0,则根据判别式的意义得到△=b 2-4a (b-1)>0,即b 2-4ab+4a>0,把b 2-4ab+4a 看作b 的二次函数,由于对任意实数b ,b 2-4ab+4a>0成立,则(4a )2-4.4a<0,然后解此不等式即可.(3)(利用两点关于直线对称的两个结论,一是中点在已知直线上,二是两点连线和已知直线垂直.找到a ,b 之间的关系式,整理后在利用基本不等式求解可得. 【详解】解:(1)当a=1,b=-2时,二次函数解析式为y=x 2-x-3,把(x o ,x o )代入得x 02-x 0-3=x o ,解得x o =-1或x o =3,所以函数y 的不动点为-1和3;(2)因为y=x o ,所以ax o 2+(b+1)x o +(b-1)=x o ,即ax 02+bx o +(b-1)=0,因为函数y 恒有两个相异的不动点,所以此方程有两个不相等的实数解,所以△=b 2-4a (b-1)>0,即b 2-4ab+4a>0,而对任意实数b ,b 2-4ab+4a>0成立,所以(4a )2-4.4a<0,解得0<a<1.(3)设A (x 1,x 1),B (x 2,x 2),则x 1+x 2b a=- A ,B 的中点的坐标为(1212,22x x x x ++ ),即M (,22b ba a-- ) A 、B 两点关于直线y=kx-2a+3对称, 又∵A ,B 在直线y=x 上,∴k=-1,A ,B 的中点M 在直线y=kx-2a+3上.∴b a -=ba-2a+3 得:b=2a 2-3a 所以当且仅当a=34 时,b 有最小值-98【点睛】本题是在新定义下对函数知识的综合考查,是一道好题.关于两点关于直线对称的问题,有两个结论同时存在,一是中点在已知直线上,二是两点连线和已知直线垂直.4.如图,抛物线y=﹣(x ﹣1)2+c 与x 轴交于A ,B (A ,B 分别在y 轴的左右两侧)两点,与y 轴的正半轴交于点C ,顶点为D ,已知A (﹣1,0).(1)求点B ,C 的坐标;(2)判断△CDB 的形状并说明理由;(3)将△COB 沿x 轴向右平移t 个单位长度(0<t <3)得到△QPE .△QPE 与△CDB 重叠部分(如图中阴影部分)面积为S ,求S 与t 的函数关系式,并写出自变量t 的取值范围. 【答案】(Ⅰ)B(3,0);C(0,3);(Ⅱ)CDB ∆为直角三角形;(Ⅲ)22333(0)221933(3)222t t t S t t t ⎧-+<≤⎪⎪=⎨⎪=-+<<⎪⎩.【解析】 【分析】(1)首先用待定系数法求出抛物线的解析式,然后进一步确定点B ,C 的坐标. (2)分别求出△CDB 三边的长度,利用勾股定理的逆定理判定△CDB 为直角三角形. (3)△COB 沿x 轴向右平移过程中,分两个阶段: ①当0<t≤32时,如答图2所示,此时重叠部分为一个四边形; ②当32<t <3时,如答图3所示,此时重叠部分为一个三角形. 【详解】解:(Ⅰ)∵点()1,0A -在抛物线()21y x c =--+上,∴()2011c =---+,得4c =∴抛物线解析式为:()214y x =--+,令0x =,得3y =,∴()0,3C ; 令0y =,得1x =-或3x =,∴()3,0B . (Ⅱ)CDB ∆为直角三角形.理由如下: 由抛物线解析式,得顶点D 的坐标为()1,4. 如答图1所示,过点D 作DM x ⊥轴于点M , 则1OM =,4DM =,2BM OB OM =-=.过点C 作CN DM ⊥于点N ,则1CN =,1DN DM MN DM OC =-=-=. 在Rt OBC ∆中,由勾股定理得:22223332BC OB OC =+=+=; 在Rt CND ∆中,由勾股定理得:2222112CD CN DN =+=+=; 在Rt BMD ∆中,由勾股定理得:22222425BD BM DM =+=+=.∵222BC CD BD +=, ∴CDB ∆为直角三角形.(Ⅲ)设直线BC 的解析式为y kx b =+, ∵()()3,0,0,3B C ,∴303k b b +=⎧⎨=⎩,解得1,3k b =-=,∴3y x =-+,直线QE 是直线BC 向右平移t 个单位得到,∴直线QE 的解析式为:()33y x t x t =--+=-++; 设直线BD 的解析式为y mx n =+, ∵()()3,0,1,4B D , ∴304m n m n +=⎧⎨+=⎩,解得:2,6m n =-=,∴26y x =-+.连续CQ 并延长,射线CQ 交BD 交于G ,则3,32G ⎛⎫ ⎪⎝⎭. 在COB ∆向右平移的过程中: (1)当302t <≤时,如答图2所示:设PQ 与BC 交于点K ,可得QK CQ t ==,3PB PK t ==-.设QE 与BD 的交点为F ,则:263y x y x t =-+⎧⎨=-++⎩. 解得32x t y t =-⎧⎨=⎩,∴()3,2F t t -.111222QPE PBK FBE F S S S S PE PQ PB PK BE y ∆∆∆=--=⋅-⋅-⋅ ()221113333232222t t t t t =⨯⨯---⋅=-+. (2)当332t <<时,如答图3所示:设PQ 分别与BC BD 、交于点K 、点J . ∵CQ t =,∴KQ t =,3PK PB t ==-.直线BD 解析式为26y x =-+,令x t =,得62y t =-, ∴(),62J t t -.1122PBJ PBK S S S PB PJ PB PK∆∆=-=⋅-⋅ ()()()211362322t t t =---- 219322t t =-+. 综上所述,S 与t 的函数关系式为:2233302219333222t t t S t t t ⎧⎛⎫-+<≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪=-+<< ⎪⎪⎝⎭⎩.5.已知,点M 为二次函数2()41y x b b =--++图象的顶点,直线5y mx =+分别交x 轴正半轴,y 轴于点,A B .(1)如图1,若二次函数图象也经过点,A B ,试求出该二次函数解析式,并求出m 的值. (2)如图2,点A 坐标为(5,0),点M 在AOB ∆内,若点11(,)4C y ,23(,)4D y 都在二次函数图象上,试比较1y 与2y 的大小.【答案】(1)2(2)9y x =--+,1m =-;(2)①当102b <<时,12y y >;②当12b =时,12y y =;③当1425b <<时,12y y < 【解析】 【分析】 (1)根据一次函数表达式求出B 点坐标,然后根据B 点在抛物线上,求出b 值,从而得到二次函数表达式,再根据二次函数表达式求出A 点的坐标,最后代入一次函数求出m 值.(2)根据解方程组,可得顶点M 的纵坐标的范围,根据二次函数的性质,可得答案. 【详解】(1)如图1,∵直线5y mx =+与y 轴交于点为B ,∴点B 坐标为(0,5)又∵(0,5)B 在抛物线上,∴25(0)41b b =--++,解得2b =∴二次函数的表达式为2(2)9y x =--+ ∴当0y =时,得15=x ,21x =- ∴(5,0)A代入5y mx =+得,550m +=,∴1m =-(2)如图2,根据题意,抛物线的顶点M 为(,41)b b +,即M 点始终在直线41y x =+上,∵直线41y x =+与直线AB 交于点E ,与y 轴交于点F ,而直线AB 表达式为5y x =-+解方程组415y x y x =+⎧⎨=-+⎩,得45215x y ⎧=⎪⎪⎨⎪=⎪⎩∴点421(,)55E ,(0,1)F ∵点M 在AOB ∆内,∴405b <<当点,C D 关于抛物线对称轴(直线x b =)对称时,1344b b -=-,∴12b = 且二次函数图象的开口向下,顶点M 在直线41y x =+上 综上:①当102b <<时,12y y >;②当12b =时,12y y =;③当1425b <<时,12y y <.【点睛】本题考查二次函数与一次函数的综合应用,难度系数大同学们需要认真分析即可.6.如图,在平面直角坐标系中,直线483y x =-+与x 轴,y 轴分别交于点A 、B ,抛物线24y ax ax c =-+经过点A 和点B ,与x 轴的另一个交点为C ,动点D 从点A 出发,以每秒1个单位长度的速度向O 点运动,同时动点E 从点B 出发,以每秒2个单位长度的速度向A 点运动,设运动的时间为t 秒,0﹤t ﹤5.(1)求抛物线的解析式;(2)当t 为何值时,以A 、D 、E 为顶点的三角形与△AOB 相似; (3)当△ADE 为等腰三角形时,求t 的值;(4)抛物线上是否存在一点F ,使得以A 、B 、D 、F 为顶点的四边形是平行四边形?若存在,直接写出F 点的坐标;若不存在,说明理由. 【答案】(1)抛物线的解析式为228833y x x =-++; (2)t 的值为3011或5013; (3)t 的值为103或6017或258; (4)符合条件的点F 存在,共有两个1F (4,8),2(227F +,-8). 【解析】(1)由B 、C 两点的坐标,利用待定系数法可求得抛物线的解析式;(2)利用△ADE ∽△AOB 和△AED ∽△AOB 即可求出t 的值;(3)过E 作EH ⊥x 轴于点H ,过D 作DM ⊥AB 于点M 即可求出t 的值;(4)分当AD 为边时,当AD 为对角线时符合条件的点F 的坐标.解:(1)A (6,0),B (0,8),依题意知36240{8a a c c -+==,解得2{38a c =-=, ∴228833y x x =-++. (2)∵ A (6,0),B (0,8),∴OA=6,OB=8,AB=10,∴AD=t ,AE=10-2t , ①当△ADE ∽△AOB 时,AD AE AO AB =,∴102610t t -=,∴3011t =; ②当△AED ∽△AOB 时,AE AD AO AB =,∴102610t t -=,∴5013t =; 综上所述,t 的值为3011或5013. (3) ①当AD=AE 时,t=10-2t ,∴103t =;②当AE=DE 时,过E 作EH ⊥x 轴于点H ,则AD=2AH ,由△AEH ∽△ABO 得,AH=()31025t -,∴()61025t t -=,∴6017t =; ③当AD=DE 时,过D 作DM ⊥AB 于点M ,则AE=2AM ,由△AMD ∽△AOB 得,AM=35t ,∴61025t t -=,∴258t =; 综上所述,t 的值为103或6017或258. (4) ①当AD 为边时,则BF ∥x 轴,∴8F B y y ==,求得x=4,∴F (4,8); ②当AD 为对角线时,则8F B y y =-=-,∴2288833x x -++=-,解得227x =±,∵x ﹥0,∴227x =+,∴()227,8+-.综上所述,符合条件的点F 存在,共有两个1F (4,8),2(227F +,-8).“点睛”本题考查二次函数综合题、相似三角形等知识,解题的关键是学会待定系数法确定函数解析式,学会分类讨论,用方程的思想解决问题,属于中考压轴题.7.如图1,在平面直角坐标系中,直线1y x =-与抛物线2y x bx c =-++交于A B 、两点,其中(),0A m ,()4,B n .该抛物线与y 轴交于点C ,与x 轴交于另一点D .(1)求mn 、的值及该抛物线的解析式; (2)如图2.若点P 为线段AD 上的一动点(不与A D 、重合).分别以AP 、DP 为斜边,在直线AD 的同侧作等腰直角△APM 和等腰直角△DPN ,连接MN ,试确定△MPN 面积最大时P 点的坐标.(3)如图3.连接BD 、CD ,在线段CD 上是否存在点Q ,使得以A D Q 、、为顶点的三角形与△ABD 相似,若存在,请直接写出点Q 的坐标;若不存在,请说明理由.【答案】(1)265y x x =-+-;(2)当2m =,即2AP =时,MPN S ∆最大,此时3OP =,所以()3,0P ;(3)存在点Q 坐标为2-3(,)或78-33⎛⎫ ⎪⎝⎭,. 【解析】分析:(1)把A 与B 坐标代入一次函数解析式求出m 与n 的值,确定出A 与B 坐标,代入二次函数解析式求出b 与c 的值即可;(2)由等腰直角△APM 和等腰直角△DPN ,得到∠MPN 为直角,由两直角边乘积的一半表示出三角形MPN 面积,利用二次函数性质确定出三角形面积最大时P 的坐标即可; (3)存在,分两种情况,根据相似得比例,求出AQ 的长,利用两点间的距离公式求出Q 坐标即可.详解:(1)把A (m ,0),B (4,n )代入y =x ﹣1得:m =1,n =3,∴A (1,0),B (4,3).∵y =﹣x 2+bx +c 经过点A 与点B ,∴101643b c b c -++=⎧⎨-++=⎩,解得:65b c =⎧⎨=-⎩,则二次函数解析式为y =﹣x 2+6x ﹣5;(2)如图2,△APM 与△DPN 都为等腰直角三角形,∴∠APM =∠DPN =45°,∴∠MPN =90°,∴△MPN 为直角三角形,令﹣x 2+6x ﹣5=0,得到x =1或x =5,∴D (5,0),即DP =5﹣1=4,设AP =m ,则有DP =4﹣m ,∴PM =2m ,PN =2(4﹣m ),∴S △MPN =12PM •PN =12×2m ×2(4﹣m )=﹣14m 2﹣m =﹣14(m ﹣2)2+1,∴当m =2,即AP =2时,S △MPN 最大,此时OP =3,即P (3,0);(3)存在,易得直线CD 解析式为y =x ﹣5,设Q (x ,x ﹣5),由题意得:∠BAD =∠ADC =45°,分两种情况讨论:①当△ABD ∽△DAQ 时,AB DA =BD AQ ,即4=4AQ ,解得:AQ =3,由两点间的距离公式得:(x ﹣1)2+(x ﹣5)2=1283,解得:x =73,此时Q (73,﹣83);②当△ABD ∽△DQA 时,BDAQ=1,即AQ ,∴(x ﹣1)2+(x ﹣5)2=10,解得:x =2,此时Q (2,﹣3).综上,点Q 的坐标为(2,﹣3)或(73,﹣83). 点睛:本题属于二次函数综合题,涉及的知识有:待定系数法求函数解析式,二次函数的图象与性质,相似三角形的判定与性质,两点间的距离公式,熟练掌握各自的性质是解答本题的关键.8.如图,某足球运动员站在点O 处练习射门,将足球从离地面0.5m 的A 处正对球门踢出(点A 在y 轴上),足球的飞行高度y(单位:m )与飞行时间t(单位:s )之间满足函数关系y =at 2+5t +c ,已知足球飞行0.8s 时,离地面的高度为3.5m . (1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?(2)若足球飞行的水平距离x(单位:m )与飞行时间t(单位:s )之间具有函数关系x =10t ,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?【答案】(1)足球飞行的时间是85s时,足球离地面最高,最大高度是4.5m;(2)能.【解析】试题分析:(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),于是得到,求得抛物线的解析式为:y=﹣t2+5t+,当t=时,y最大=4.5;(2)把x=28代入x=10t得t=2.8,当t=2.8时,y=﹣×2.82+5×2.8+=2.25<2.44,于是得到他能将球直接射入球门.解:(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),∴,解得:,∴抛物线的解析式为:y=﹣t2+5t+,∴当t=时,y最大=4.5;(2)把x=28代入x=10t得t=2.8,∴当t=2.8时,y=﹣×2.82+5×2.8+=2.25<2.44,∴他能将球直接射入球门.考点:二次函数的应用.9.如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).(1)求点B ,C 的坐标;(2)判断△CDB 的形状并说明理由;(3)将△COB 沿x 轴向右平移t 个单位长度(0<t <3)得到△QPE .△QPE 与△CDB 重叠部分(如图中阴影部分)面积为S ,求S 与t 的函数关系式,并写出自变量t 的取值范围. 【答案】(Ⅰ)B(3,0);C(0,3);(Ⅱ)CDB ∆为直角三角形;(Ⅲ)22333(0)221933(3)222t t t S t t t ⎧-+<≤⎪⎪=⎨⎪=-+<<⎪⎩.【解析】 【分析】(1)首先用待定系数法求出抛物线的解析式,然后进一步确定点B ,C 的坐标. (2)分别求出△CDB 三边的长度,利用勾股定理的逆定理判定△CDB 为直角三角形. (3)△COB 沿x 轴向右平移过程中,分两个阶段: ①当0<t≤32时,如答图2所示,此时重叠部分为一个四边形; ②当32<t <3时,如答图3所示,此时重叠部分为一个三角形. 【详解】解:(Ⅰ)∵点()1,0A -在抛物线()21y x c =--+上,∴()2011c =---+,得4c =∴抛物线解析式为:()214y x =--+,令0x =,得3y =,∴()0,3C ; 令0y =,得1x =-或3x =,∴()3,0B . (Ⅱ)CDB ∆为直角三角形.理由如下: 由抛物线解析式,得顶点D 的坐标为()1,4. 如答图1所示,过点D 作DM x ⊥轴于点M ,则1OM =,4DM =,2BM OB OM =-=.过点C 作CN DM ⊥于点N ,则1CN =,1DN DM MN DM OC =-=-=. 在Rt OBC ∆中,由勾股定理得:22223332BC OB OC =+=+=; 在Rt CND ∆中,由勾股定理得:2222112CD CN DN =+=+=; 在Rt BMD ∆中,由勾股定理得:22222425BD BM DM =+=+=.∵222BC CD BD +=, ∴CDB ∆为直角三角形.(Ⅲ)设直线BC 的解析式为y kx b =+, ∵()()3,0,0,3B C ,∴303k b b +=⎧⎨=⎩,解得1,3k b =-=,∴3y x =-+,直线QE 是直线BC 向右平移t 个单位得到,∴直线QE 的解析式为:()33y x t x t =--+=-++; 设直线BD 的解析式为y mx n =+, ∵()()3,0,1,4B D , ∴304m n m n +=⎧⎨+=⎩,解得:2,6m n =-=,∴26y x =-+.连续CQ 并延长,射线CQ 交BD 交于G ,则3,32G ⎛⎫ ⎪⎝⎭. 在COB ∆向右平移的过程中: (1)当302t <≤时,如答图2所示:设PQ 与BC 交于点K ,可得QK CQ t ==,3PB PK t ==-. 设QE 与BD 的交点为F ,则:263y x y x t=-+⎧⎨=-++⎩.解得32x ty t=-⎧⎨=⎩,∴()3,2F t t -.111222QPE PBK FBE F S S S S PE PQ PB PK BE y ∆∆∆=--=⋅-⋅-⋅ ()221113333232222t t t t t =⨯⨯---⋅=-+. (2)当332t <<时,如答图3所示:设PQ 分别与BC BD 、交于点K 、点J . ∵CQ t =,∴KQ t =,3PK PB t ==-.直线BD 解析式为26y x =-+,令x t =,得62y t =-, ∴(),62J t t -.1122PBJ PBK S S S PB PJPB PK ∆∆=-=⋅-⋅ ()()()211362322t t t =---- 219322t t =-+. 综上所述,S 与t 的函数关系式为:2233302219333222t t t S t t t ⎧⎛⎫-+<≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪=-+<< ⎪⎪⎝⎭⎩.10.如图, 已知抛物线2342y ax x =++的对称轴是直线x=3,且与x 轴相交于A ,B 两点(B 点在A 点右侧)与y 轴交于C 点 .(1)求抛物线的解析式和A 、B 两点的坐标;(2)若点P 是抛物线上B 、C 两点之间的一个动点(不与B 、C 重合),则是否存在一点P ,使△PBC 的面积最大.若存在,请求出△PBC 的最大面积;若不存在,试说明理由; (3)若M 是抛物线上任意一点,过点M 作y 轴的平行线,交直线BC 于点N ,当MN=3时,求M 点的坐标 .【答案】(1)213442y x x =-++,点A 的坐标为(-2,0),点B 的坐标为(8,0);(2)存在点P ,使△PBC 的面积最大,最大面积是16,理由见解析;(3)点M 的坐标为(4-771)、(2,6)、(6,4)或7,71). 【解析】 【分析】(1) 由抛物线的对称轴为直线x=3,利用二次函数的性质即可求出a 值, 进而可得出抛物线的解析式, 再利用二次函数图象上点的坐标特征, 即可求出点A 、B 的坐标; (2) 利用二次函数图象上点的坐标特征可求出点C 的坐标, 由点B 、C 的坐标, 利用待定系数法即可求出直线BC 的解析式, 假设存在, 设点P 的坐标为(x,213-442x x ++),过点P 作PD//y 轴, 交直线BC 于点D ,则点D 的坐标为(x,1-42x +),PD=-14x 2+2x ,利用三角形的面积公式即可得出三角形PBC 的面积关于x 的函数关系式, 再利用二次函数的性质即可解决最值问题;(3) 设点M 的坐标为(m,213-442m m ++),则点N 的坐标为(m,1-42m +),进而可得出MN 2124m m =-+,结合MN=3即可得出关于m 的含绝对值符号的一元二次方程, 解之即可得出结论 . 【详解】(1)Q 抛物线2342y ax x =++的对称轴是直线3x =, 3232a∴-=,解得:14a =-,∴抛物线的解析式为213442y x x =-++.当0y =时,2134042x x -++=,解得:12x =-,28x =,∴点A 的坐标为()2,0-,点B 的坐标为()8,0.(2) 当0x =时,2134442y x x =-++=, ∴点C 的坐标为()0,4.设直线BC 的解析式为()0y kx b k =+≠. 将()8,0B 、()0,4C 代入y kx b =+,804k b b +=⎧⎨=⎩,解得:124k b ⎧=-⎪⎨⎪=⎩, ∴直线BC 的解析式为142y x =-+. 假设存在, 设点P 的坐标为213,442x x x ⎛⎫-++ ⎪⎝⎭,过点P 作//PD y 轴, 交直线BC 于点D ,则点D 的坐标为1,42x x ⎛⎫-+ ⎪⎝⎭,如图所示 .2213114424224PD x x x x x ⎛⎫∴=-++--+=-+ ⎪⎝⎭,()222111·8?28416224PBC S PD OB x x x x x ∆⎛⎫∴==⨯-+=-+=--+ ⎪⎝⎭. 10-<Q ,∴当4x =时,PBC ∆的面积最大, 最大面积是 16 . 08x <<Q ,∴存在点P ,使PBC ∆的面积最大, 最大面积是 16 .(3) 设点M 的坐标为213,442m m m ⎛⎫-++ ⎪⎝⎭,则点N 的坐标为1,42m m ⎛⎫-+ ⎪⎝⎭,2213114424224MN m m m m m ⎛⎫∴=-++--+=-+ ⎪⎝⎭.又3MN =Q ,21234m m ∴-+=.当08m <<时, 有212304m m -+-=, 解得:12m =,26m =,∴点M 的坐标为()2,6或()6,4;当0m <或8m >时, 有212304m m -++=, 解得:3427m =-,4427m =+,∴点M 的坐标为(427-,71)-或(427+,71)--.综上所述:M 点的坐标为(427-,71)-、()2,6、()6,4或(427+,71)--.【点睛】本题考查了二次函数的性质、 二次函数图象上点的坐标特征、 待定系数法求一次函数解析式以及三角形的面积, 解题的关键是: (1) 利用二次函数的性质求出a 的值; (2) 根据三角形的面积公式找出关于x 的函数关系式; (3) 根据MN 的长度, 找出关于m 的含绝对值符号的一元二次方程.11.如图,直线y=﹣x+分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+经过A,B两点.(1)求A、B两点的坐标;(2)求抛物线的解析式;(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC 于点D,求△DMH周长的最大值.【答案】(1)(﹣1,0)(2)y=﹣x2+x+(3)【解析】试题分析:(1)由直线解析式可求得B、C坐标,在Rt△BOC中由三角函数定义可求得∠OCB=60°,则在Rt△AOC中可得∠ACO=30°,利用三角函数的定义可求得OA,则可求得A点坐标;(2)由A、B两点坐标,利用待定系数法可求得抛物线解析式;(3)由平行线的性质可知∠MDH=∠BCO=60°,在Rt△DMH中利用三角函数的定义可得到DH、MH与DM的关系,可设出M点的坐标,则可表示出DM的长,从而可表示出△DMH 的周长,利用二次函数的性质可求得其最大值.试题解析:(1)∵直线y=﹣x+分别与x轴、y轴交于B、C两点,∴B(3,0),C(0,),∴OB=3,OC=,∴tan∠BCO==,∴∠BCO=60°,∵∠ACB=90°,∴∠ACO=30°,∴=tan30°=,即=,解得AO=1,∴A(﹣1,0);(2)∵抛物线y=ax2+bx+经过A,B两点,∴,解得,∴抛物线解析式为y=﹣x2+x+;(3)∵MD∥y轴,MH⊥BC,∴∠MDH=∠BCO=60°,则∠DMH=30°,∴DH=DM,MH=DM,∴△DMH的周长=DM+DH+MH=DM+DM+DM=DM,∴当DM有最大值时,其周长有最大值,∵点M是直线BC上方抛物线上的一点,∴可设M(t,﹣t2+t+),则D(t,﹣t+),∴DM=﹣t2+t+),则D(t,﹣t+),∴DM=﹣t2+t+﹣(﹣t+)=﹣t2+t=﹣(t﹣)2+,∴当t=时,DM有最大值,最大值为,此时DM=×=,即△DMH周长的最大值为.考点:1、二次函数的综合应用,2、待定系数法,3、三角函数的定义,4方程思想12.(本小题满分12分)如图,在平面直角坐标系xOy中,抛物线()与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.(1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示);(2)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为,求a的值;(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.【答案】(1)A(-1,0),;(2);(3)P的坐标为(1,)或(1,-4).【解析】试题分析:(1)在中,令y=0,得到,,得到A(-1,0),B(3,0),由直线l经过点A,得到,故,令,即,由于CD=4AC,故点D的横坐标为4,即有,得到,从而得出直线l的函数表达式;(2)过点E作EF∥y轴,交直线l于点F,设E(,),则F(,),EF==,S△ACE=S△AFE-S△CFE==,故△ACE的面积的最大值为,而△ACE的面积的最大值为,所以,解得;(3)令,即,解得,,得到D (4,5a),因为抛物线的对称轴为,设P(1,m),然后分两种情况讨论:①若AD是矩形的一条边,②若AD是矩形的一条对角线.试题解析:(1)∵=,令y=0,得到,,∴A(-1,0),B(3,0),∵直线l经过点A,∴,,∴,令,即,∵CD=4AC,∴点D的横坐标为4,∴,∴,∴直线l的函数表达式为;(2)过点E作EF∥y轴,交直线l于点F,设E(,),则F(,),EF==,S△ACE=S△AFE-S△CFE===,∴△ACE的面积的最大值为,∵△ACE的面积的最大值为,∴,解得;(3)令,即,解得,,∴D(4,5a),∵,∴抛物线的对称轴为,设P(1,m),①若AD是矩形的一条边,则Q(-4,21a),m=21a+5a=26a,则P(1,26a),∵四边形ADPQ为矩形,∴∠ADP=90°,∴,∴,即,∵,∴,∴P1(1,);②若AD是矩形的一条对角线,则线段AD的中点坐标为(,),Q(2,),m =,则P(1,8a),∵四边形APDQ为矩形,∴∠APD=90°,∴,∴,即,∵,∴,∴P2(1,-4).综上所述,以点A、D、P、Q为顶点的四边形能成为矩形,点P的坐标为(1,)或(1,-4).考点:二次函数综合题.13.已知二次函数y=﹣316x2+bx+c的图象经过A(0,3),B(﹣4,﹣92)两点.(1)求b,c的值.(2)二次函数y=﹣316x2+bx+c的图象与x轴是否有公共点,求公共点的坐标;若没有,请说明情况.【答案】(1)983b c ⎧=⎪⎨⎪=⎩;(2)公共点的坐标是(﹣2,0)或(8,0).【解析】【分析】(1)把点A 、B 的坐标分别代入函数解析式求得b 、c 的值;(2)利用根的判别式进行判断该函数图象是否与x 轴有交点,由题意得到方程﹣239168x x ++3=0,通过解该方程求得x 的值即为抛物线与x 轴交点横坐标. 【详解】(1)把A (0,3),B (﹣4,﹣92)分别代入y=﹣316x 2+bx+c ,得339164162c b c =⎧⎪⎨-⨯-+=-⎪⎩,解得983b c ⎧=⎪⎨⎪=⎩;(2)由(1)可得,该抛物线解析式为:y=﹣316x 2+98x+3, △=(98)2﹣4×(﹣316)×3=22564>0, 所以二次函数y=﹣316x 2+bx+c 的图象与x 轴有公共点, ∵﹣316x 2+98x+3=0的解为:x 1=﹣2,x 2=8, ∴公共点的坐标是(﹣2,0)或(8,0).【点睛】本题考查了抛物线与x 轴的交点,二次函数图象上点的坐标特征.注意抛物线解析式与一元二次方程间的转化关系.14.空地上有一段长为a 米的旧墙MN ,某人利用旧墙和木栏围成一个矩形菜园ABCD ,已知木栏总长为100米.(1)已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图1,求所利用旧墙AD 的长;(2)已知0<α<50,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD 的面积最大,并求面积的最大值.【答案】(1)利用旧墙AD 的长为10米.(2)见解析. 【解析】 【分析】(1)按题意设出AD ,表示AB 构成方程;(2)根据旧墙长度a 和AD 长度表示矩形菜园长和宽,注意分类讨论s 与菜园边长之间的数量关系. 【详解】(1)设AD=x 米,则AB=1002x-米 依题意得,(100)2x x -=450 解得x 1=10,x 2=90 ∵a=20,且x≤a ∴x=90舍去∴利用旧墙AD 的长为10米.(2)设AD=x 米,矩形ABCD 的面积为S 平方米 ①如果按图一方案围成矩形菜园,依题意 得:S=2(100)1(50)125022x x x ---+=,0<x <a ∵0<a <50∴x <a <50时,S 随x 的增大而增大当x=a 时,S 最大=50a-12a 2②如按图2方案围成矩形菜园,依题意得 S=22(1002)[(25)](25)244x a x a a x =+---+++,a≤x <50+2a当a <25+4a <50时,即0<a <1003时, 则x=25+4a 时,S 最大=(25+4a )2=21000020016a a ++,当25+4a ≤a ,即1003≤a <50时,S 随x 的增大而减小 ∴x=a 时,S 最大=(1002)2a a a +-=21502a a -,综合①②,当0<a <1003时,21000020016a a ++-(21502a a -)=2(3100)16a ->021000020016a a ++>21502a a -,此时,按图2方案围成矩形菜园面积最大,最大面积为21000020016a a ++平方米当1003≤a <50时,两种方案围成的矩形菜园面积最大值相等. ∴当0<a <1003时,围成长和宽均为(25+4a )米的矩形菜园面积最大,最大面积为21000020016a a ++平方米;当1003≤a <50时,围成长为a 米,宽为(50-2a)米的矩形菜园面积最大,最大面积为(21502a a -)平方米.【点睛】本题以实际应用为背景,考查了一元二次方程与二次函数最值的讨论,解得时注意分类讨论变量大小关系.15.如图1,抛物线2112y ax x c =-+与x 轴交于点A 和点()1,0B ,与y 轴交于点30,4C ⎛⎫ ⎪⎝⎭,抛物线1y 的顶点为,G GM x ⊥轴于点M .将抛物线1y 平移后得到顶点为B 且对称轴为直l 的抛物线2y .(1)求抛物线2y 的解析式;(2)如图2,在直线l 上是否存在点T ,使TAC ∆是等腰三角形?若存在,请求出所有点T 的坐标:若不存在,请说明理由;(3)点P 为抛物线1y 上一动点,过点P 作y 轴的平行线交抛物线2y 于点Q ,点Q 关于直线l 的对称点为R ,若以,,P Q R 为顶点的三角形与AMC ∆全等,求直线PR 的解析式. 【答案】(1)抛物线2y 的解析式为2111424y x x =-+-;(2)T点的坐标为13(1,4T +,23(1,4T -,377(1,)8T -;(3)PR 的解析式为13y x 24=-+或1124y x =--.【解析】分析:(1)把()1,0B 和30,4C ⎛⎫ ⎪⎝⎭代入2112y ax x c =-+求出a 、c 的值,进而求出y 1,再根据平移得出y 2即可;(2)抛物线2y 的对称轴l 为1x =,设()1,T t ,已知()33,0,0,4A C ⎛⎫- ⎪⎝⎭,过点T 作TE y ⊥轴于E ,分三种情况时行讨论等腰三角形的底和腰,得到关于t 的方程,解方程即可; (3)设2113,424P m m m ⎛⎫--+ ⎪⎝⎭,则2111,424Q m m m ⎛⎫-+- ⎪⎝⎭,根据对称性得21112,424R m m m ⎛⎫--+- ⎪⎝⎭,分点P 在直线的左侧或右侧时,结合以,,P Q R 构成的三角形与AMG ∆全等求解即可. 详解:(1)由题意知,34102c a c ⎧=⎪⎪⎨⎪-+=⎪⎩, 解得14a =-, 所以,抛物线y 的解析式为21113424y x x =--+; 因为抛物线1y 平移后得到抛物线2y ,且顶点为()1,0B , 所以抛物线2y 的解析式为()22114y x =--, 即: 22111424y x x =-+-; (2)抛物线2y 的对称轴l 为1x =,设()1,T t ,已知()33,0,0,4A C ⎛⎫- ⎪⎝⎭,过点T 作TE y ⊥轴于E ,则22221TC TE CE =+=+ 2233254216t t t ⎛⎫-=-+ ⎪⎝⎭,222TA TB AB =+= ()2221316t t ++=+,215316AC =, 当TC AC =时, 即232515321616t t -+=, 解得13137t +=或23137t -=; 当TC AC =时,得21531616t +=,无解; 当TC AC =时,得2232516216t t t -+=+,解得3778t =-; 综上可知,在抛物线2y 的对称轴l 上存在点T 使TAC ∆是等腰三角形,此时T 点的坐标为131371,T ⎛⎫+ ⎪ ⎪⎝⎭,231371,T ⎛⎫- ⎪ ⎪⎝⎭,3771,8T ⎛⎫- ⎪⎝⎭. (3)设2113,424P m m m ⎛⎫--+ ⎪⎝⎭,则2111,424Q m m m ⎛⎫-+- ⎪⎝⎭, 因为,Q R 关于1x =对称,所以21112,424R m m m ⎛⎫--+- ⎪⎝⎭, 情况一:当点P 在直线的左侧时,2113424PQ m m =--+- 21111424m m m ⎛⎫-+-=- ⎪⎝⎭, 22QR m =-,又因为以,,P Q R 构成的三角形与AMG ∆全等,当PQ GM =且QR AM =时,0m =, 可求得30,4P ⎛⎫ ⎪⎝⎭,即点P 与点C 重合 所以12,4R ⎛⎫- ⎪⎝⎭, 设PR 的解析式y kx b =+, 则有3,412.4b k b ⎧=⎪⎪⎨⎪+=-⎪⎩解得12k =-, 即PR 的解析式为1324y x =-+, 当PQ AM =且QR GM =时,无解, 情况二:当点P 在直线l 右侧时,2111424P Q m m '=-+-'- 21131424m m m ⎛⎫--+=- ⎪⎝⎭, 22Q R m ='-', 同理可得512,,0,44P R ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝'⎭' P R ''的解析式为1124y x =--, 综上所述, PR 的解析式为1324y x =-+或1124y x =--. 点睛:本题主要考查了二次函数综合题,此题涉及到待定系数法求函数解析式、等腰三角形的判定与性质、全等三角形的性质等知识,解答(1)问的关键是求出a 、c 的值,解答(2)、(3)问的关键是正确地作出图形,进行分类讨论解答,此题有一定的难度.。
2020-2021中考数学 二次函数 培优练习(含答案)附详细答案

2020-2021中考数学二次函数培优练习(含答案)附详细答案一、二次函数1.(10分)(2015•佛山)如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=x刻画.(1)请用配方法求二次函数图象的最高点P的坐标;(2)小球的落点是A,求点A的坐标;(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.【答案】(1)(2,4);(2)(,);(3);(4)(,).【解析】试题分析:(1)利用配方法抛物线的一般式化为顶点式,即可求出二次函数图象的最高点P的坐标;(2)联立两解析式,可求出交点A的坐标;(3)作PQ⊥x轴于点Q,AB⊥x轴于点B.根据S△POA=S△POQ+S△梯形PQBA﹣S△BOA,代入数值计算即可求解;(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,由于两平行线之间的距离相等,根据同底等高的两个三角形面积相等,可得△MOA的面积等于△POA的面积.设直线PM的解析式为y=x+b,将P(2,4)代入,求出直线PM的解析式为y=x+3.再与抛物线的解析式联立,得到方程组,解方程组即可求出点M的坐标.试题解析:(1)由题意得,y=﹣x2+4x=﹣(x﹣2)2+4,故二次函数图象的最高点P的坐标为(2,4);(2)联立两解析式可得:,解得:,或.故可得点A的坐标为(,);(3)如图,作PQ⊥x轴于点Q,AB⊥x轴于点B.S△POA=S△POQ+S△梯形PQBA﹣S△BOA=×2×4+×(+4)×(﹣2)﹣××=4+﹣=;(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,则△MOA的面积等于△POA的面积.设直线PM的解析式为y=x+b,∵P的坐标为(2,4),∴4=×2+b,解得b=3,∴直线PM的解析式为y=x+3.由,解得,,∴点M的坐标为(,).考点:二次函数的综合题2.已知二次函数的图象以A(﹣1,4)为顶点,且过点B(2,﹣5)(1)求该函数的关系式;(2)求该函数图象与坐标轴的交点坐标;(3)将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△O A′B′的面积.【答案】(1)y=﹣x2﹣2x+3;(2)抛物线与x轴的交点为:(﹣3,0),(1,0)(3)15.【解析】【分析】(1)已知了抛物线的顶点坐标,可用顶点式设该二次函数的解析式,然后将B 点坐标代入,即可求出二次函数的解析式;(2)根据函数解析式,令x=0,可求得抛物线与y轴的交点坐标;令y=0,可求得抛物线与x轴交点坐标;(3)由(2)可知:抛物线与x轴的交点分别在原点两侧,由此可求出当抛物线与x轴负半轴的交点平移到原点时,抛物线平移的单位,由此可求出A′、B′的坐标.由于△OA′B′不规则,可用面积割补法求出△OA′B′的面积.【详解】(1)设抛物线顶点式y=a(x+1)2+4,将B(2,﹣5)代入得:a=﹣1,∴该函数的解析式为:y=﹣(x+1)2+4=﹣x2﹣2x+3;(2)令x=0,得y=3,因此抛物线与y轴的交点为:(0,3),令y=0,﹣x2﹣2x+3=0,解得:x1=﹣3,x2=1,即抛物线与x轴的交点为:(﹣3,0),(1,0);(3)设抛物线与x轴的交点为M、N(M在N的左侧),由(2)知:M(﹣3,0),N(1,0),当函数图象向右平移经过原点时,M与O重合,因此抛物线向右平移了3个单位,故A'(2,4),B'(5,﹣5),∴S△OA′B′=12×(2+5)×9﹣12×2×4﹣12×5×5=15.【点睛】本题考查了用待定系数法求抛物线解析式、函数图象与坐标轴交点、图形面积的求法等知识.熟练掌握待定系数法、函数图象与坐标轴的交点的求解方法、不规则图形的面积的求解方法等是解题的关键.3.如图1,对称轴为直线x=1的抛物线y=12x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.(1)求点B 的坐标和抛物线的表达式;(2)当AE:EP=1:4 时,求点E 的坐标;(3)如图 2,在(2)的条件下,将线段 OC 绕点 O 逆时针旋转得到OC ′,旋转角为α(0°<α<90°),连接C ′D、C′B,求C ′B+ 23C′D 的最小值.【答案】(1)B(3,0);抛物线的表达式为:y=12x2-x-32;(2)E(1,6);(3)C′B+2 3C′D4103【解析】试题分析:(1)由抛物线的对称轴和过点A,即可得到抛物线的解析式,令y=0,解方程可得B的坐标;(2)过点P作PF⊥x轴,垂足为F.由平行线分线段弄成比例定理可得AE AP =AGAF=EGPF=15,从而求出E的坐标;(3)由E(1,6)、A(-1,0)可得AP的函数表达式为y=3x+3,得到D(0,3).如图,取点M(0,43),连接MC′、BM.则可求出OM,BM的长,得到△MOC′∽△C′OD.进而得到MC′=23C′D,由C′B+23C′D=C′B+MC′≥BF可得到结论.试题解析:解:(1)∵抛物线y=12x2+bx+c的对称轴为直线x=1,∴-122b=1,∴b=-1.∵抛物线过点A(-1,0),∴12-b+c=0,解得:c=-32,即:抛物线的表达式为:y=12x2-x-32.令y=0,则12x2-x-32=0,解得:x1=-1,x2=3,即B(3,0);(2)过点P作PF⊥x轴,垂足为F.∵EG∥PF,AE:EP=1:4,∴AEAP =AGAF=EGPF=15.又∵AG=2,∴AF=10,∴F(9,0).当x=9时,y=30,即P(9,30),PF=30,∴EG=6,∴E(1,6).(3)由E(1,6)、A(-1,0)可得AP的函数表达式为y=3x+3,则D(0,3).∵原点O与点C关于该对称轴成轴对称,∴EG=6,∴C(2,0),∴OC′=OC=2.如图,取点M(0,43),连接MC′、BM.则OM=43,BM=2243()3+=97.∵423'23OMOC==,'23OCOD=,且∠DOC′=∠C′OD,∴△MOC′∽△C′OD.∴'2'3MCC D=,∴MC′=23C′D,∴C′B+23C′D=C′B+MC′≥BM=4103,∴C′B+23C′D的最小值为4103.点睛:本题是二次函数的综合题,解答本题主要应用了待定系数法求二次函数的解析式,相似三角形的性质和判定,求得AF的长是解答问题(2)的关键;和差倍分的转化是解答问题(3)的关键.4.如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,抛物线交x轴于A、C两点,与直线y=x﹣1交于A、B两点,直线AB与抛物线的对称轴交于点E.(1)求抛物线的解析式.(2)点P在直线AB上方的抛物线上运动,若△ABP的面积最大,求此时点P的坐标.(3)在平面直角坐标系中,以点B、E、C、D为顶点的四边形是平行四边形,请直接写出符合条件点D的坐标.【答案】(1)y=﹣x2﹣2x+3;(2)点P(32-,154);(3)符合条件的点D的坐标为D1(0,3),D2(﹣6,﹣3),D3(﹣2,﹣7).【解析】【分析】(1)令y=0,求出点A的坐标,根据抛物线的对称轴是x=﹣1,求出点C的坐标,再根据待定系数法求出抛物线的解析式即可;(2)设点P(m,﹣m2﹣2m+3),利用抛物线与直线相交,求出点B的坐标,过点P作PF∥y 轴交直线AB于点F,利用S△ABP=S△PBF+S△PFA,用含m的式子表示出△ABP的面积,利用二次函数的最大值,即可求得点P的坐标;(3)求出点E的坐标,然后求出直线BC、直线BE、直线CE的解析式,再根据以点B、E、C、D为顶点的四边形是平行四边形,得到直线D1D2、直线D1D3、直线D2D3的解析式,即可求出交点坐标.【详解】解:(1)令y=0,可得:x﹣1=0,解得:x=1,∴点A(1,0),∵抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,∴﹣1×2﹣1=﹣3,即点C(﹣3,0),∴309330a ba b++⎧⎨-+⎩==,解得:12ab-⎧⎨-⎩=,=∴抛物线的解析式为:y=﹣x2﹣2x+3;(2)∵点P在直线AB上方的抛物线上运动,∴设点P(m,﹣m2﹣2m+3),∵抛物线与直线y=x﹣1交于A、B两点,∴2231y x xy x⎧--+⎨-⎩==,解得:1145xy-⎧⎨-⎩==,221xy=,=⎧⎨⎩∴点B(﹣4,﹣5),如图,过点P作PF∥y轴交直线AB于点F,则点F(m,m﹣1),∴PF =﹣m 2﹣2m+3﹣m+1=﹣m 2﹣3m+4,∴S △ABP =S △PBF +S △PFA =12(﹣m 2﹣3m+4)(m+4)+12(﹣m 2﹣3m+4)(1﹣m) =-52(m+32 )2+ 1258 , ∴当m =32-时,P 最大, ∴点P(32-,154). (3)当x =﹣1时,y =﹣1﹣1=﹣2,∴点E(﹣1,﹣2),如图,直线BC 的解析式为y =5x+15,直线BE 的解析式为y =x ﹣1,直线CE 的解析式为y =﹣x ﹣3,∵以点B 、C 、E 、D 为顶点的四边形是平行四边形,∴直线D 1D 3的解析式为y =5x+3,直线D 1D 2的解析式为y =x+3,直线D 2D 3的解析式为y =﹣x ﹣9,联立533y x y x +⎧⎨+⎩== 得D 1(0,3), 同理可得D 2(﹣6,﹣3),D 3(﹣2,﹣7),综上所述,符合条件的点D 的坐标为D 1(0,3),D 2(﹣6,﹣3),D 3(﹣2,﹣7).【点睛】本题考查二次函数的综合应用,解决第(2)小题中三角形面积的问题时,找到一条平行或垂直于坐标轴的边是关键;对于第(3)小题,要注意分类讨论、数形结合的运用,不要漏解.5.如图,在平面直角坐标系xOy 中,A 、B 为x 轴上两点,C 、D 为y 轴上的两点,经 过点A 、C 、B 的抛物线的一部分C 1与经过点A 、D 、B 的抛物线的一部分C 2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C 的坐标为(0,),点M 是抛物线C 2:2y mx 2mx 3m =--(m <0)的顶点.(1)求A 、B 两点的坐标;(2)“蛋线”在第四象限上是否存在一点P ,使得△PBC 的面积最大?若存在,求出△PBC 面积的最大值;若不存在,请说明理由;(3)当△BDM 为直角三角形时,求m 的值.【答案】(1)A (,0)、B (3,0).(2)存在.S △PBC 最大值为2716 (3)2m =-或1m =-时,△BDM 为直角三角形. 【解析】【分析】 (1)在2y mx 2mx 3m =--中令y=0,即可得到A 、B 两点的坐标.(2)先用待定系数法得到抛物线C 1的解析式,由S △PBC = S △POC + S △BOP –S △BOC 得到△PBC 面积的表达式,根据二次函数最值原理求出最大值.(3)先表示出DM 2,BD 2,MB 2,再分两种情况:①∠BMD=90°时;②∠BDM=90°时,讨论即可求得m 的值.【详解】解:(1)令y=0,则2mx 2mx 3m 0--=,∵m <0,∴2x 2x 30--=,解得:1x 1=-,2x 3=.∴A (,0)、B (3,0).(2)存在.理由如下:∵设抛物线C 1的表达式为()()y a x 1x 3=+-(a 0≠),把C (0,32-)代入可得,12a =. ∴C1的表达式为:()()1y x 1x 32=+-,即213y x x 22=--. 设P (p ,213p p 22--), ∴ S △PBC = S △POC + S △BOP –S △BOC =23327p 4216--+(). ∵3a 4=-<0,∴当3p 2=时,S △PBC 最大值为2716. (3)由C 2可知: B (3,0),D (0,3m -),M (1,4m -),∴BD 2=29m 9+,BM 2=216m 4+,DM 2=2m 1+.∵∠MBD<90°, ∴讨论∠BMD=90°和∠BDM=90°两种情况:当∠BMD=90°时,BM 2+ DM 2= BD 2,即216m 4++2m 1+=29m 9+,解得:12m 2=-,22m 2=(舍去). 当∠BDM=90°时,BD 2+ DM 2= BM 2,即29m 9++2m 1+=216m 4+,解得:1m 1=-,2m 1=(舍去) .综上所述,2m =-或1m =-时,△BDM 为直角三角形.6.某市实施产业精准扶贫,帮助贫困户承包荒山种植某品种蜜柚.已知该蜜柚的成本价为6元/千克,到了收获季节投入市场销售时,调查市场行情后,发现该蜜柚不会亏本,且每天的销售量y (千克)与销售单价x (元)之间的函数关系如图所示.(1)求y 与x 的函数关系式,并写出x 的取值范围;(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?(3)某村农户今年共采摘蜜柚12000千克,若该品种蜜柚的保质期为50天,按照(2)的销售方式,能否在保质期内全部销售完这批蜜柚?若能,请说明理由;若不能,应定销售价为多少元时,既能销售完又能获得最大利润?【答案】(1)y =﹣20x +500,(x ≥6);(2)当x =15.5时,w 的最大值为1805元;(3)当x =13时,w =1680,此时,既能销售完又能获得最大利润.【解析】【分析】(1)将点(15,200)、(10,300)代入一次函数表达式:y =kx +b 即可求解;(2)由题意得:w =y (x ﹣6)=﹣20(x ﹣25)(x ﹣6),∵﹣20<0,故w 有最大值,即可求解;(3)当x =15.5时,y =190,50×190<12000,故:按照(2)的销售方式,不能在保质期内全部销售完;由50(500﹣20x )≥12000,解得:x ≤13,当x =13时,既能销售完又能获得最大利润.【详解】解:(1)将点(15,200)、(10,300)代入一次函数表达式:y =kx +b 得:2001530010k b k b=+⎧⎨=+⎩, 解得:20500k b =-⎧⎨=⎩, 即:函数的表达式为:y =﹣20x +500,(x ≥6);(2)设:该品种蜜柚定价为x 元时,每天销售获得的利润w 最大,则:w =y (x ﹣6)=﹣20(x ﹣25)(x ﹣6),∵﹣20<0,故w 有最大值,当x =﹣2b a =312=15.5时,w 的最大值为1805元; (3)当x =15.5时,y =190,50×190<12000,故:按照(2)的销售方式,不能在保质期内全部销售完;设:应定销售价为x 元时,既能销售完又能获得最大利润w ,由题意得:50(500﹣20x )≥12000,解得:x ≤13,w =﹣20(x ﹣25)(x ﹣6),当x =13时,w =1680,此时,既能销售完又能获得最大利润.【点睛】本题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值).7.如图,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (1, 0)、C (3, 0)、D (3, 4).以A 为顶点的抛物线y =ax 2+bx +c 过点C .动点P 从点A 出发,以每秒12个单位的速度沿线段AD 向点D 运动,运动时间为t 秒.过点P 作PE ⊥x 轴交抛物线于点M ,交AC 于点N .(1)直接写出点A的坐标,并求出抛物线的解析式;(2)当t为何值时,△ACM的面积最大?最大值为多少?(3)点Q从点C出发,以每秒1个单位的速度沿线段CD向点D运动,当t为何值时,在线段PE上存在点H,使以C、Q、N、H为顶点的四边形为菱形?【答案】(1)A(1,4);y=-x2+2x+3;(2)当t=2时,△AMC面积的最大值为1;(3)2085-或20 13.【解析】(1)由矩形的性质得到点A的坐标,由抛物线的顶点为A,设抛物线的解析式为y=a(x -1)2+4,把点C的坐标代入即可求得a的值;(2)由点P的坐标以及抛物线解析式得到点M的坐标,由A、C的坐标得到直线AC的解析式,进而得到点N的坐标,即可用关于t的式子表示MN,然后根据△ACM的面积是△AMN和△CMN的面积和列出用t表示的△ACM的面积,利用二次函数的性质即可得到当t=2时,△AMC面积的最大值为1;(3)①当点H在N点上方时,由PN=CQ,PN∥CQ,得到四边形PNCQ为平行四边形,所以当PQ=CQ时,四边形FECQ为菱形,据此得到,解得t值;②当点H在N点下方时,NH=CQ=,NQ=CQ时,四边形NHCQ为菱形,NQ2=CQ2,得:,解得t值.解:(1)由矩形的性质可得点A(1,4),∵抛物线的顶点为A,设抛物线的解析式为y=a(x-1)2+4,代入点C(3, 0),可得a=-1.∴y=-(x-1)2+4=-x2+2x+3.(2)∵P(112t+,4),将112x t=+代入抛物线的解析式,y=-(x-1)2+4=2144t-,∴M (112t +,2144t -), 设直线AC 的解析式为,将A (1,4),C (3,0)代入,得:, 将112x t =+代入得, ∴N (112t +,), ∴MN, ∴, ∴当t =2时,△A MC 面积的最大值为1.(3)①如图1,当点H在N点上方时,∵N(112t +,),P (112t +,4), ∴P N=4—()==CQ ,又∵PN ∥CQ , ∴四边形PNCQ 为平行四边形,∴当PQ =CQ 时,四边形FECQ 为菱形,PQ 2=PD 2+DQ 2 =,∴, 整理,得240800t t -+=.解得12085t =-,22085t =+(舍去);②如图2当点H在N点下方时,NH=CQ=,NQ =CQ 时,四边形NHCQ 为菱形,NQ 2=CQ 2,得:.整理,得213728000t t -+=.()()1320400t t --=.所以12013t =,(舍去).“点睛”此题主要考查二次函数的综合问题,会用顶点式求抛物线,会用两点法求直线解析式,会设点并表示三角形的面积,熟悉矩形和菱形的性质是解题的关键.8.如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?【答案】(1)足球飞行的时间是85s时,足球离地面最高,最大高度是4.5m;(2)能.【解析】试题分析:(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),于是得到,求得抛物线的解析式为:y=﹣t2+5t+,当t=时,y最大=4.5;(2)把x=28代入x=10t得t=2.8,当t=2.8时,y=﹣×2.82+5×2.8+=2.25<2.44,于是得到他能将球直接射入球门.解:(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),∴,解得:,∴抛物线的解析式为:y=﹣t2+5t+,∴当t=时,y最大=4.5;(2)把x=28代入x=10t得t=2.8,∴当t=2.8时,y=﹣×2.82+5×2.8+=2.25<2.44,∴他能将球直接射入球门.考点:二次函数的应用.9.如图,抛物线y=ax2+bx(a≠0)过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.(1)求抛物线的表达式;(2)直接写出点C的坐标,并求出△ABC的面积;(3)点P是抛物线上一动点,且位于第四象限,是否存在这样的点P,使得△ABP的面积为△ABC面积的2倍?若存在,求出点P的坐标,若不存在,请说明理由;(4)若点M在直线BH上运动,点N在x轴正半轴上运动,当以点C,M,N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.【答案】(1)y=-x2+4x;(2)C(3,3),面积为3;(3)P的坐标为(5,-5);(4)52或5.【解析】试题分析:(1)利用待定系数法进行求解即可;(2)先求出抛物线的对称轴,利用对称性即可写出点C的坐标,利用三角形面积公式即可求面积;(3)利用三角形的面积以及点P所处象限的特点即可求;(4)分情况进行讨论,确定点M、N,然后三角形的面积公式即可求.试题解析:(1)将A(4,0),B(1,3)代入到y=ax2+bx中,得16403a ba b+=⎧⎨+=⎩,解得14ab=-⎧⎨=⎩,∴抛物线的表达式为y=-x2+4x.(2)∵抛物线的表达式为y=-x2+4x,∴抛物线的对称轴为直线x=2.又C,B关于对称轴对称,∴C(3,3).∴BC=2,∴S△ABC=12×2×3=3.(3)存在点P.作PQ⊥BH于点Q,设P(m,-m2+4m).∵S△ABP=2S△ABC,S△ABC=3,∴S△ABP=6.∵S△ABP+S△BPQ=S△ABH+S梯形AHQP∴6+12×(m-1)×(3+m2-4m)=12×3×3+12×(3+m-1)(m2-4m)整理得m2-5m=0,解得m1=0(舍),m2=5,∴点P的坐标为(5,-5).(4)52或5.提示:①当以M为直角顶点,则S△CMN=52;②当以N为直角顶点,S△CMN=5;③当以C为直角顶点时,此种情况不存在.【点睛】本题是二次函数的综合题,主要考查待定系数法求解析式,三角形面积、直角三角形的判定等,能正确地根据题意确定图形,分情况进行讨论是解题的关键.10.如图,已知点A(0,2),B(2,2),C(-1,-2),抛物线F:y=x2-2mx+m2-2与直线x=-2交于点P.(1)当抛物线F经过点C时,求它的解析式;(2)设点P的纵坐标为y P,求y P的最小值,此时抛物线F上有两点(x1,y1),(x2,y2),且x1<x2≤-2,比较y1与y2的大小.【答案】(1) 221y x x =+-;(2)12y y >.【解析】【分析】 (1)根据抛物线F :y=x 2-2mx+m 2-2过点C (-1,-2),可以求得抛物线F 的表达式; (2)根据题意,可以求得y P 的最小值和此时抛物线的表达式,从而可以比较y 1与y 2的大小.【详解】(1) ∵抛物线F 经过点C (-1,-2),∴22122m m -=++-.∴m 1=m 2=-1.∴抛物线F 的解析式是221y x x =+-.(2)当x=-2时,2442P y m m =++-=()222m +-. ∴当m=-2时,P y 的最小值为-2.此时抛物线F 的表达式是()222y x =+-.∴当2x ≤-时,y 随x 的增大而减小.∵12x x <≤-2,∴1y >2y .【点睛】本题考查二次函数的性质、二次函数图象上点的坐标特征、待定系数法求二次函数解析式,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.11.如果一条抛物线y =ax 2+bx +c (a ≠0)与x 轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a ,b ,c ]称为“抛物线系数”.(1)任意抛物线都有“抛物线三角形”是 (填“真”或“假”)命题;(2)若一条抛物线系数为[1,0,﹣2],则其“抛物线三角形”的面积为 ;(3)若一条抛物线系数为[﹣1,2b ,0],其“抛物线三角形”是个直角三角形,求该抛物线的解析式;(4)在(3)的前提下,该抛物线的顶点为A ,与x 轴交于O ,B 两点,在抛物线上是否存在一点P ,过P 作PQ ⊥x 轴于点Q ,使得△BPQ ∽△OAB ?如果存在,求出P 点坐标;如果不存在,请说明理由.【答案】(1)假;(2)3)y =-x 2+2x 或y =-x 2-2x ;(4)P (1,1)或P (-1,-3)或P (1,-3)或(-1,1).【解析】分析:(1)当△>0时,抛物线与x 轴有两个交点,由此可得出结论;(2)根据“抛物线三角形”定义得到22y x =-,由此可得出结论;(3)根据“抛物线三角形”定义得到y =-x 2+2bx ,它与x 轴交于点(0,0)和(2b ,0);当抛物线三角形是直角三角形时,根据对称性可知它一定是等腰直角三角形,由抛物线顶点为(b ,b 2),以及直角三角形斜边上的中线等于斜边的一半得到2122b b =⨯,解方程即可得到结论; (4)分两种情况讨论:①当抛物线为y =-x 2+2x 时,②当抛物线为y =-x 2-2x 时. 详解:(1)当△>0时,抛物线与x 轴有两个交点,此时抛物线才有“抛物线三角形”,故此命题为假命题;(2)由题意得:22y x =-,令y =0,得:x=,∴ S=122⨯=12x x ; (3)依题意:y =-x 2+2bx ,它与x 轴交于点(0,0)和(2b ,0);当抛物线三角形是直角三角形时,根据对称性可知它一定是等腰直角三角形.∵y =-x 2+2bx =22()x b b --+,∴顶点为(b ,b 2),由直角三角形斜边上的中线等于斜边的一半得到:2122b b =⨯,∴2b b =,解得:b =0(舍去)或b =±1, ∴y =-x 2+2x 或y =-x 2-2x .(4)①当抛物线为y =-x 2+2x 时.∵△AOB 为等腰直角三角形,且△BPQ ∽△OAB ,∴△BPQ 为等腰直角三角形,设P (a ,-a 2+2a ),∴Q ((a ,0), 则|-a 2+2a |=|2-a |,即(2)2a a a -=-.∵a -2≠0,∴1a =,∴a =±1,∴P (1,1)或(-1, -3).②当抛物线为y =-x 2-2x 时.∵△AOB 为等腰直角三角形,且△BPQ ∽△OAB ,∴△BPQ 为等腰直角三角形,设P (a ,-a 2-2a ),∴Q ((a ,0),则|-a 2-2a |=|2+a |,即(2)2a a a +=+.∵a +2≠0,∴1a =,∴a =±1,∴P (1,-3,)或(-1,1).综上所述:P (1,1)或P (-1,-3)或P (1,-3,)或(-1,1).点睛:本题是二次函数综合题.考查了二次函数的性质以及“抛物线三角形”的定义.解题的关键是弄懂“抛物线三角形”的定义以及分类讨论.12. 阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M (1,3)的特征线有:x =1,y =3,y =x +2,y =﹣x +4.问题与探究:如图,在平面直角坐标系中有正方形OABC ,点B 在第一象限,A 、C 分别在x 轴和y 轴上,抛物线21()4y x m n =-+经过B 、C 两点,顶点D 在正方形内部. (1)直接写出点D (m ,n )所有的特征线;(2)若点D 有一条特征线是y =x +1,求此抛物线的解析式; (3)点P 是AB 边上除点A 外的任意一点,连接OP ,将△OAP 沿着OP 折叠,点A 落在点A ′的位置,当点A ′在平行于坐标轴的D 点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP 上?【答案】(1)x =m ,y =n ,y =x +n ﹣m ,y =﹣x +m+n ;(2)21(2)34y x =-+;(3)抛物线向下平移933-或2312距离,其顶点落在OP 上. 【解析】试题分析:(1)根据特征线直接求出点D 的特征线;(2)由点D 的一条特征线和正方形的性质求出点D 的坐标,从而求出抛物线解析式; (2)分平行于x 轴和y 轴两种情况,由折叠的性质计算即可.试题解析:解:(1)∵点D (m ,n ),∴点D (m ,n )的特征线是x =m ,y =n ,y =x +n ﹣m ,y =﹣x +m +n ;(2)点D 有一条特征线是y =x +1,∴n ﹣m =1,∴n =m +1.∵抛物线解析式为21()4y x m n =-+,∴21()14y x m m =-++,∵四边形OABC 是正方形,且D 点为正方形的对称轴,D (m ,n ),∴B (2m ,2m ),∴21(2)24y m m n m =-+=,将n =m +1带入得到m =2,n =3;∴D (2,3),∴抛物线解析式为21(2)34y x =-+.(3)①如图,当点A′在平行于y轴的D点的特征线时:根据题意可得,D(2,3),∴OA′=OA=4,OM=2,∴∠A′OM=60°,∴∠A′OP=∠AOP=30°,∴MN=3=23,∴抛物线需要向下平移的距离=233-=923-.②如图,当点A′在平行于x轴的D点的特征线时,设A′(p,3),则OA′=OA=4,OE=3,EA′=2243-=7,∴A′F=4﹣7,设P(4,c)(c>0),,在Rt△A′FP中,(4﹣7)2+(3﹣c)2=c2,∴c=1647-,∴P(4,1647-),∴直线OP解析式为y=473-x,∴N(2,8273-),∴抛物线需要向下平移的距离=3﹣827 -=127+.综上所述:抛物线向下平移923-或127+距离,其顶点落在OP上.点睛:此题是二次函数综合题,主要考查了折叠的性质,正方形的性质,解答本题的关键是用正方形的性质求出点D的坐标.13.如图,(图1,图2),四边形ABCD是边长为4的正方形,点E在线段BC上,∠AEF=90°,且EF交正方形外角平分线CP于点F,交BC的延长线于点N, FN⊥BC.(1)若点E是BC的中点(如图1),AE与EF相等吗?(2)点E在BC间运动时(如图2),设BE=x,△ECF的面积为y.①求y与x的函数关系式;②当x取何值时,y有最大值,并求出这个最大值.【答案】(1)AE=EF ;(2)①y=-12x 2+2x (0<x <4),②当x=2,y 最大值=2. 【解析】【分析】 (1)在AB 上取一点G ,使AG=EC ,连接GE ,利用ASA ,易证得:△AGE ≌△ECF ,则可证得:AE=EF ;(2)同(1)可证明AE=EF ,利用AAS 证明△ABE ≌△ENF ,根据全等三角形对应边相等可得FN=BE ,再表示出EC ,然后利用三角形的面积公式即可列式表示出△ECF 的面积为y ,然后整理再根据二次函数求解最值问题.【详解】(1)如图,在AB 上取AG=EC ,∵四边形ABCD 是正方形,∴AB=BC ,有∵AG=EC ,∴BG=BE ,又∵∠B=90°,∴∠AGE=135°,又∵∠BCD=90°,CP 平分∠DCN ,∴∠ECF=135°,∵∠BAE +∠AEB=90°,∠AEB +∠FEC=90°,∴∠BAE=∠FEC ,在△AGE 和△ECF 中,AGE ECF AG ECGAE CEF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AGE ≌△ECF ,∴AE=EF ;(2)①∵由(1)证明可知当E 不是中点时同理可证AE=EF ,∵∠BAE=∠NEF ,∠B=∠ENF=90°,∴△ABE ≌△ENF ,∴FN=BE=x ,∴S △ECF =12 (BC-BE)·FN , 即y=12x(4-x ), ∴y=- 12x 2+2x (0<x <4), ②()()222111y x 2x x 4x x 22222=-+=--=--+, 当x=2,y 最大值=2. 【点睛】 本题考查了正方形的性质,全等三角形的判定与性质,二次函数的最值问题,综合性较强,正确添加辅助线、熟练掌握相关知识是解题的关键.14.如图,在平面直角坐标系中,抛物线y =﹣x 2+bx +c 经过点A (﹣1,0)和点C (0,4),交x 轴正半轴于点B ,连接AC ,点E 是线段OB 上一动点(不与点O ,B 重合),以OE 为边在x 轴上方作正方形OEFG ,连接FB ,将线段FB 绕点F 逆时针旋转90°,得到线段FP ,过点P 作PH ∥y 轴,PH 交抛物线于点H ,设点E (a ,0).(1)求抛物线的解析式.(2)若△AOC 与△FEB 相似,求a 的值.(3)当PH =2时,求点P 的坐标.【答案】(1)y =﹣x 2+3x +4;(2)a =165或45;(3)点P 的坐标为(2,4)或(1,4)3+17,4). 【解析】【详解】(1)点C (0,4),则c =4,二次函数表达式为:y =﹣x 2+bx+4,将点A 的坐标代入上式得:0=﹣1﹣b+4,解得:b =3,故抛物线的表达式为:y =﹣x 2+3x+4;(2)tan ∠ACO =AO CO =14, △AOC 与△FEB 相似,则∠FBE =∠ACO 或∠CAO ,即:tan ∠FEB =14或4, ∵四边形OEFG 为正方形,则FE =OE =a ,EB =4﹣a ,则144a a =-或44a a=-, 解得:a =165或45; (3)令y =﹣x 2+3x+4=0,解得:x =4或﹣1,故点B (4,0);分别延长CF 、HP 交于点N ,∵∠PFN+∠BFN =90°,∠FPN+∠PFN =90°,∴∠FPN =∠NFB ,∵GN ∥x 轴,∴∠FPN =∠NFB =∠FBE ,∵∠PNF =∠BEF =90°,FP =FB ,∴△PNF ≌△BEF (AAS ),∴FN =FE =a ,PN =EB =4﹣a ,∴点P (2a ,4),点H (2a ,﹣4a 2+6a+4),∵PH =2,即:﹣4a 2+6a+4﹣4=|2|,解得:a =1或12317+317- 故:点P 的坐标为(2,4)或(1,43+17,4). 【点睛】本题考查的是二次函数综合运用,其中(2)、(3),要注意分类求解,避免遗漏.15.综合与探究如图,抛物线y=211433x x --与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,连接AC ,BC .点P 是第四象限内抛物线上的一个动点,点P 的横坐标为m ,过点P 作PM ⊥x 轴,垂足为点M ,PM 交BC 于点Q ,过点P 作PE ∥AC 交x 轴于点E ,交BC 于点F.(1)求A,B,C三点的坐标;(2)试探究在点P运动的过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请直接写出此时点Q的坐标;若不存在,请说明理由;(3)请用含m的代数式表示线段QF的长,并求出m为何值时QF有最大值.【答案】(1)C(0,﹣4);(2)Q点坐标为(522,522﹣4)或(1,﹣3);(3)当m=2时,QF有最大值.【解析】【分析】(1)解方程13x2−13x-4=0得A(-3,0),B(4,0),计算自变量为0时的二次函数值得C点坐标;(2)利用勾股定理计算出AC=5,利用待定系数法可求得直线BC的解析式为y=x-4,则可设Q(m,m-4)(0<m<4),讨论:当CQ=CA时,则m2+(m-4+4)2=52,当AQ=AC时,(m+3)2+(m-4)2=52;当QA=QC时,(m+3)2+(m-4)2=52,然后分别解方程求出m即可得到对应的Q点坐标;(3)过点F作FG⊥PQ于点G,如图,由△OBC为等腰直角三角形.可判断△FQG为等腰直角三角形,则FG=QG=22FQ,再证明△FGP~△AOC得到34FG PG,则22FQ,所以72FQ,于是得到32,设P(m,13m2-13m-4)(0<m<4),则Q(m,m-4),利用PQ=-13m2+43m得到FQ=327(-13m2+43m),然后利用二次函数的性质解决问题.【详解】(1)当y=0,13x2−13x-4=0,解得x1=-3,x2=4,∴A(-3,0),B(4,0),当x=0,y=13x2−13x-4=-4,∴C (0,-4);(2)AC=2234=5+, 易得直线BC 的解析式为y=x-4,设Q (m ,m-4)(0<m <4),当CQ=CA 时,m 2+(m-4+4)2=52,解得m 1=52,m 2=-52(舍去),此时Q 点坐标为(522,522-4); 当AQ=AC 时,(m+3)2+(m-4)2=52,解得m 1=1,m 2=0(舍去),此时Q 点坐标为(1,-3);当QA=QC 时,(m+3)2+(m-4)2=52,解得m=252(舍去), 综上所述,满足条件的Q 点坐标为(522,522-4)或(1,-3); (3)解:过点F 作FG ⊥PQ 于点G ,如图,则FG ∥x 轴.由B (4,0),C (0,-4)得△OBC 为等腰直角三角形∴∠OBC=∠QFG=45∴△FQG 为等腰直角三角形,∴FG=QG=22FQ , ∵PE ∥AC ,PG ∥CO ,∴∠FPG=∠ACO ,∵∠FGP=∠AOC=90°,∴△FGP ~△AOC .∴FG PG OA CO =,即34FG PG =, ∴PG=43FG=43•22FQ=223FQ , ∴PQ=PG+GQ=23FQ+22FQ=26FQ ,∴PQ,设P(m,13m2-13m-4)(0<m<4),则Q(m,m-4),∴PQ=m-4-(13m2-13m-4)=-13m2+43m,∴(-13m2+43m)(m-2)2∵-7<0,∴QF有最大值.∴当m=2时,QF有最大值.【点睛】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和等腰三角形的性质;会利用待定系数法求函数解析式;理解坐标与图形性质,会利用相似比表示线段之间的关系;会运用分类讨论的思想解决数学问题.。
2020-2021初三数学 二次函数的专项 培优练习题及详细答案

2020-2021初三数学二次函数的专项培优练习题及详细答案一、二次函数1.如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.(1)求抛物线的解析式;(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.【答案】(1)y=38x2﹣34x﹣3(2)运动1秒使△PBQ的面积最大,最大面积是9 10(3)K1(1,﹣278),K2(3,﹣158)【解析】【详解】试题分析:(1)把点A、B的坐标分别代入抛物线解析式,列出关于系数a、b的解析式,通过解方程组求得它们的值;(2)设运动时间为t秒.利用三角形的面积公式列出S△PBQ与t的函数关系式S△PBQ=﹣9 10(t﹣1)2+910.利用二次函数的图象性质进行解答;(3)利用待定系数法求得直线BC的解析式为y=34x﹣3.由二次函数图象上点的坐标特征可设点K的坐标为(m,38m2﹣34m﹣3).如图2,过点K作KE∥y轴,交BC于点E.结合已知条件和(2)中的结果求得S△CBK=94.则根据图形得到:S△CBK=S△CEK+S△BEK=12EK•m+12•EK•(4﹣m),把相关线段的长度代入推知:﹣34m2+3m=94.易求得K1(1,﹣278),K2(3,﹣158).解:(1)把点A(﹣2,0)、B(4,0)分别代入y=ax2+bx﹣3(a≠0),得423016430a ba b--=⎧⎨+-=⎩,解得3834ab⎧=⎪⎪⎨⎪=-⎪⎩,所以该抛物线的解析式为:y=38x2﹣34x﹣3;(2)设运动时间为t秒,则AP=3t,BQ=t.∴PB=6﹣3t.由题意得,点C的坐标为(0,﹣3).在Rt△BOC中,BC=2234+=5.如图1,过点Q作QH⊥AB于点H.∴QH∥CO,∴△BHQ∽△BOC,∴HBOCBGBC=,即Hb35t=,∴HQ=35t.∴S△PBQ=12PB•HQ=12(6﹣3t)•35t=﹣910t2+95t=﹣910(t﹣1)2+910.当△PBQ存在时,0<t<2∴当t=1时,S△PBQ最大=910.答:运动1秒使△PBQ 的面积最大,最大面积是910; (3)设直线BC 的解析式为y=kx+c (k≠0). 把B (4,0),C (0,﹣3)代入,得403k c c +=⎧⎨=-⎩, 解得3k 4c 3⎧=⎪⎨⎪=-⎩,∴直线BC 的解析式为y=34x ﹣3. ∵点K 在抛物线上.∴设点K 的坐标为(m ,38m 2﹣34m ﹣3).如图2,过点K 作KE ∥y 轴,交BC 于点E .则点E 的坐标为(m ,34m ﹣3).∴EK=34m ﹣3﹣(38m 2﹣34m ﹣3)=﹣38m 2+32m .当△PBQ 的面积最大时,∵S △CBK :S △PBQ =5:2,S △PBQ =910. ∴S △CBK =94. S △CBK =S △CEK +S △BEK =12EK•m+12•EK•(4﹣m ) =12×4•EK =2(﹣38m 2+32m ) =﹣34m 2+3m .即:﹣34m 2+3m=94.解得 m 1=1,m 2=3.∴K 1(1,﹣278),K 2(3,﹣158).点评:本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求二次函数解析式和三角形的面积求法.在求有关动点问题时要注意该点的运动范围,即自变量的取值范围.2.如图,抛物线212222y x x =-++与x 轴相交于A B ,两点,(点A 在B 点左侧)与y 轴交于点C.(Ⅰ)求A B ,两点坐标.(Ⅱ)连结AC ,若点P 在第一象限的抛物线上,P 的横坐标为t ,四边形ABPC 的面积为S.试用含t 的式子表示S ,并求t 为何值时,S 最大.(Ⅲ)在(Ⅱ)的基础上,若点,G H 分别为抛物线及其对称轴上的点,点G 的横坐标为m ,点H 的纵坐标为n ,且使得以,,,A G H P 四点构成的四边形为平行四边形,求满足条件的,m n 的值.【答案】(Ⅰ)(2,0),2,0)A B ;(Ⅱ)22(2)42(022)2S t t =--+<<,当2t =时,42S =最大;(Ⅲ)满足条件的点m n 、的值为:234m n ==,或521524m n ==-,或32124m n =-= 【解析】 【分析】(Ⅰ)令y=0,建立方程求解即可得出结论;(Ⅱ)设出点P 的坐标,利用S=S △AOC +S 梯形OCPQ +S △PQB ,即可得出结论;(Ⅲ)分三种情况,利用平行四边形的性质对角线互相平分和中点坐标公式建立方程组即可得出结论. 【详解】解:(Ⅰ)抛物线212222y x x =-++, 令0y =,则212202x x -++=, 解得:2x =-或22x =, ∴()()2,0,22,0A B - (Ⅱ)由抛物线212222y x x =-++,令0x =,∴2y =,∴()0,2C , 如图1,点P 作PQ x ⊥轴于Q , ∵P 的横坐标为t ,∴设(),P t p , ∴2122,22,22p t t PQ p BQ t OQ t =-++==-=, ∴()()11122222222AOC PQB OCPQ S S S S p t t p =++=⨯⨯++⨯+⨯-⨯V V 梯形 11222222t pt p pt p t =+++-=++ 21222222t t t ⎛⎫=-++++ ⎪ ⎪⎭()22242(022)2t t =--+<<,∴当2t =时,42S =最大;(Ⅲ)由(Ⅱ)知,2t =,∴)2,2P,∵抛物线212222y x x =-++的对称轴为22x =, ∴设2122,2,2G m m H n ⎛⎫⎫-++ ⎪⎪ ⎪⎪⎝⎭⎝⎭以,,,A G H P 四点构成的四边形为平行四边形,()A , ①当AP 和HG 为对角线时,∴()211111,2022222222m m m n ⎛⎫⎛⎫=++=-+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,∴324m n =-=, ②当AG 和PH 是对角线时,∴(()211111,2022222222m m m n ⎫⎛⎫=-+++=+⎪ ⎪⎪ ⎪⎭⎝⎭,∴15,24m n ==-, ③AH 和PG 为对角线时,∴(()211111,2202222222m m m n ⎛⎫⎛⎫=+-+++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,∴124m n =-=, 即:满足条件的点m n 、的值为:34m n ==,或154m n ==-,或14m n == 【点睛】此题是二次函数综合题,主要考查了坐标轴上点的特点,三角形的面积公式,梯形的面积公式,平行四边形的性质,中点坐标公式,用方程的思想解决问题是解本题的关键.3.如图,直线y =-12x-3与x 轴,y 轴分别交于点A ,C ,经过点A ,C 的抛物线y =ax 2+bx ﹣3与x 轴的另一个交点为点B(2,0),点D 是抛物线上一点,过点D 作DE ⊥x 轴于点E ,连接AD ,DC .设点D 的横坐标为m . (1)求抛物线的解析式;(2)当点D 在第三象限,设△DAC 的面积为S ,求S 与m 的函数关系式,并求出S 的最大值及此时点D 的坐标;(3)连接BC ,若∠EAD =∠OBC ,请直接写出此时点D 的坐标.【答案】(1)y =14x 2+x ﹣3;(2)S △ADC =﹣34(m+3)2+274;△ADC 的面积最大值为274;此时D(﹣3,﹣154);(3)满足条件的点D 坐标为(﹣4,﹣3)或(8,21). 【解析】 【分析】(1)求出A 坐标,再用待定系数法求解析式;(2)设DE 与AC 的交点为点F.设点D 的坐标为:(m ,14m 2+m ﹣3),则点F 的坐标为:(m ,﹣12m ﹣3),根据S △ADC =S △ADF +S △DFC 求出解析式,再求最值;(3)①当点D 与点C 关于对称轴对称时,D(﹣4,﹣3),根据对称性此时∠EAD =∠ABC .②作点D(﹣4,﹣3)关于x 轴的对称点D′(﹣4,3),直线AD′的解析式为y =32x+9,解方程组求出函数图像交点坐标. 【详解】解:(1)在y =﹣12x ﹣3中,当y =0时,x =﹣6, 即点A 的坐标为:(﹣6,0),将A(﹣6,0),B(2,0)代入y =ax 2+bx ﹣3得:366304230a b a b --=⎧⎨+-=⎩, 解得:141a b ⎧=⎪⎨⎪=⎩,∴抛物线的解析式为:y =14x 2+x ﹣3; (2)设点D 的坐标为:(m ,14m 2+m ﹣3),则点F 的坐标为:(m ,﹣12m ﹣3), 设DE 与AC 的交点为点F. ∴DF =﹣12m ﹣3﹣(14m 2+m ﹣3)=﹣14m 2﹣32m ,∴S △ADC =S △ADF +S △DFC =12DF•AE+12•DF•OE =12DF•OA =12×(﹣14m 2﹣32m)×6 =﹣34m 2﹣92m =﹣34(m+3)2+274,∵a =﹣34<0,∴抛物线开口向下,∴当m =﹣3时,S △ADC 存在最大值274, 又∵当m =﹣3时,14m 2+m ﹣3=﹣154,∴存在点D(﹣3,﹣154),使得△ADC 的面积最大,最大值为274; (3)①当点D 与点C 关于对称轴对称时,D(﹣4,﹣3),根据对称性此时∠EAD =∠ABC . ②作点D(﹣4,﹣3)关于x 轴的对称点D′(﹣4,3), 直线AD′的解析式为y =32x+9, 由2392134y x y x x ⎧=+⎪⎪⎨⎪=+-⎪⎩,解得60x y =-⎧⎨=⎩或821x y =⎧⎨=⎩,此时直线AD′与抛物线交于D(8,21),满足条件, 综上所述,满足条件的点D 坐标为(﹣4,﹣3)或(8,21)【点睛】本题属于二次函数综合题,考查了待定系数法,一次函数的应用,二次函数的性质等知识,解题的关键是学会构建二次函数解决最值问题,学会构建一次函数解决实际问题,属于中考压轴题..4.对于某一函数给出如下定义:若存在实数m,当其自变量的值为m时,其函数值等于﹣m,则称﹣m为这个函数的反向值.在函数存在反向值时,该函数的最大反向值与最小反向值之差n称为这个函数的反向距离.特别地,当函数只有一个反向值时,其反向距离n为零.例如,图中的函数有4,﹣1两个反向值,其反向距离n等于5.(1)分别判断函数y=﹣x+1,y=1x-,y=x2有没有反向值?如果有,直接写出其反向距离;(2)对于函数y=x2﹣b2x,①若其反向距离为零,求b的值;②若﹣1≤b≤3,求其反向距离n的取值范围;(3)若函数y=223()3()x x x mx x x m⎧-≥⎨--<⎩请直接写出这个函数的反向距离的所有可能值,并写出相应m的取值范围.【答案】(1)y=−1x有反向值,反向距离为2;y=x2有反向值,反向距离是1;(2)①b=±1;②0≤n≤8;(3)当m>2或m≤﹣2时,n=2,当﹣2<m≤2时,n=4.【解析】【分析】(1)根据题目中的新定义可以分别计算出各个函数是否有方向值,有反向值的可以求出相应的反向距离;(2)①根据题意可以求得相应的b的值;②根据题意和b的取值范围可以求得相应的n的取值范围;(3)根据题目中的函数解析式和题意可以解答本题.【详解】(1)由题意可得,当﹣m=﹣m+1时,该方程无解,故函数y=﹣x+1没有反向值,当﹣m=1m-时,m=±1,∴n=1﹣(﹣1)=2,故y=1x-有反向值,反向距离为2,当﹣m=m2,得m=0或m=﹣1,∴n=0﹣(﹣1)=1,故y=x2有反向值,反向距离是1;(2)①令﹣m=m2﹣b2m,解得,m=0或m=b2﹣1,∵反向距离为零,∴|b2﹣1﹣0|=0,解得,b=±1;②令﹣m=m2﹣b2m,解得,m=0或m=b2﹣1,∴n=|b2﹣1﹣0|=|b2﹣1|,∵﹣1≤b≤3,∴0≤n≤8;(3)∵y=223()3() x x x mx x x m⎧-≥⎨--<⎩,∴当x≥m时,﹣m=m2﹣3m,得m=0或m=2,∴n=2﹣0=2,∴m>2或m≤﹣2;当x<m时,﹣m=﹣m2﹣3m,解得,m=0或m=﹣4,∴n=0﹣(﹣4)=4,∴﹣2<m≤2,由上可得,当m>2或m≤﹣2时,n=2,当﹣2<m≤2时,n=4.【点睛】本题是一道二次函数综合题,解答本题的关键是明确题目中的新定义,找出所求问题需要的条件,利用新定义解答相关问题.5.如图1,抛物线经过平行四边形的顶点、、,抛物线与轴的另一交点为.经过点的直线将平行四边形分割为面积相等的两部分,与抛物线交于另一点.点为直线上方抛物线上一动点,设点的横坐标为.(1)求抛物线的解析式;(2)当何值时,的面积最大?并求最大值的立方根;(3)是否存在点使为直角三角形?若存在,求出的值;若不存在,说明理由.【答案】(1)抛物线解析式为y=﹣x2+2x+3;(2)当t=时,△PEF的面积最大,其最大值为×,最大值的立方根为=;(3)存在满足条件的点P,t的值为1或【解析】试题分析:(1)由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;(2)由A、C坐标可求得平行四边形的中心的坐标,由抛物线的对称性可求得E点坐标,从而可求得直线EF的解析式,作PH⊥x轴,交直线l于点M,作FN⊥PH,则可用t表示出PM的长,从而可表示出△PEF的面积,再利用二次函数的性质可求得其最大值,再求其最大值的立方根即可;(3)由题意可知有∠PAE=90°或∠APE=90°两种情况,当∠PAE=90°时,作PG⊥y轴,利用等腰直角三角形的性质可得到关于t的方程,可求得t的值;当∠APE=90°时,作PK⊥x 轴,AQ⊥PK,则可证得△PKE∽△AQP,利用相似三角形的性质可得到关于t的方程,可求得t的值.试题解析:(1)由题意可得,解得,∴抛物线解析式为y=﹣x2+2x+3;(2)∵A(0,3),D(2,3),∴BC=AD=2,∵B(﹣1,0),∴C(1,0),∴线段AC的中点为(,),∵直线l将平行四边形ABCD分割为面积相等两部分,∴直线l过平行四边形的对称中心,∵A、D关于对称轴对称,∴抛物线对称轴为x=1,∴E(3,0),设直线l的解析式为y=kx+m,把E点和对称中心坐标代入可得,解得,∴直线l的解析式为y=﹣x+,联立直线l和抛物线解析式可得,解得或,∴F(﹣,),如图1,作PH⊥x轴,交l于点M,作FN⊥PH,∵P点横坐标为t,∴P(t,﹣t2+2t+3),M(t,﹣t+),∴PM=﹣t2+2t+3﹣(﹣t+)=﹣t2+t+,∴S△PEF=S△PFM+S△PEM=PM•FN+PM•EH=PM•(FN+EH)=(﹣t2+t+)(3+)=﹣(t﹣)+×,∴当t=时,△PEF的面积最大,其最大值为×,∴最大值的立方根为=;(3)由图可知∠PEA≠90°,∴只能有∠PAE=90°或∠APE=90°,①当∠PAE=90°时,如图2,作PG⊥y轴,∵OA=OE,∴∠OAE=∠OEA=45°,∴∠PAG=∠APG=45°,∴PG=AG,∴t=﹣t2+2t+3﹣3,即﹣t2+t=0,解得t=1或t=0(舍去),②当∠APE=90°时,如图3,作PK⊥x轴,AQ⊥PK,则PK=﹣t2+2t+3,AQ=t,KE=3﹣t,PQ=﹣t2+2t+3﹣3=﹣t2+2t,∵∠APQ+∠KPE=∠APQ+∠PAQ=90°,∴∠PAQ=∠KPE,且∠PKE=∠PQA,∴△PKE∽△AQP,∴,即,即t2﹣t﹣1=0,解得t=或t=<﹣(舍去),综上可知存在满足条件的点P,t的值为1或.考点:二次函数综合题6.温州茶山杨梅名扬中国,某公司经营茶山杨梅业务,以3万元/吨的价格买入杨梅,包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(2≤x≤10,单位:吨)之间的函数关系如图所示.(1)若杨梅的销售量为6吨时,它的平均销售价格是每吨多少万元?(2)当销售数量为多少时,该经营这批杨梅所获得的毛利润(w)最大?最大毛利润为多少万元?(毛利润=销售总收入﹣进价总成本﹣包装总费用)(3)经过市场调查发现,杨梅深加工后不包装直接销售,平均销售价格为12万元/吨.深加工费用y(单位:万元)与加工数量x(单位:吨)之间的函数关系是y=12x+3(2≤x≤10).①当该公司买入杨梅多少吨时,采用深加工方式与直接包装销售获得毛利润一样?②该公司买入杨梅吨数在范围时,采用深加工方式比直接包装销售获得毛利润大些?【答案】(1)杨梅的销售量为6吨时,它的平均销售价格是每吨10万元;(2)当x=8时,此时W最大值=40万元;(3)①该公司买入杨梅3吨;②3<x≤8.【解析】【分析】(1)设其解析式为y=kx+b,由图象经过点(2,12),(8,9)两点,得方程组,即可得到结论;(2)根据题意得,w=(y﹣4)x=(﹣12x+13﹣4)x=﹣12x2+9x,根据二次函数的性质即可得到结论;(3)①根据题意列方程,即可得到结论;②根据题意即可得到结论.【详解】(1)由图象可知,y是关于x的一次函数.∴设其解析式为y=kx+b,∵图象经过点(2,12),(8,9)两点,∴212 89k bk b+=⎧⎨+=⎩,解得k=﹣12,b=13,∴一次函数的解析式为y=﹣12x+13,当x=6时,y=10,答:若杨梅的销售量为6吨时,它的平均销售价格是每吨10万元;(2)根据题意得,w=(y﹣4)x=(﹣12x+13﹣4)x=﹣12x2+9x,当x =﹣2ba=9时,x =9不在取值范围内, ∴当x =8时,此时W 最大值=﹣12x 2+9x =40万元; (3)①由题意得:﹣12x 2+9x =9x ﹣(12x +3) 解得x =﹣2(舍去),x =3, 答该公司买入杨梅3吨;②当该公司买入杨梅吨数在 3<x ≤8范围时,采用深加工方式比直接包装销售获得毛利润大些.故答案为:3<x ≤8. 【点睛】本题是二次函数、一次函数的综合应用题,难度较大.解题关键是理清售价、成本、利润三者之间的关系.7. 阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M (1,3)的特征线有:x =1,y =3,y =x +2,y =﹣x +4.问题与探究:如图,在平面直角坐标系中有正方形OABC ,点B 在第一象限,A 、C 分别在x 轴和y 轴上,抛物线21()4y x m n =-+经过B 、C 两点,顶点D 在正方形内部. (1)直接写出点D (m ,n )所有的特征线;(2)若点D 有一条特征线是y =x +1,求此抛物线的解析式;(3)点P 是AB 边上除点A 外的任意一点,连接OP ,将△OAP 沿着OP 折叠,点A 落在点A ′的位置,当点A ′在平行于坐标轴的D 点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP 上?【答案】(1)x =m ,y =n ,y =x +n ﹣m ,y =﹣x +m+n ;(2)21(2)34y x =-+;(3)抛物923-2312距离,其顶点落在OP 上. 【解析】试题分析:(1)根据特征线直接求出点D 的特征线;(2)由点D 的一条特征线和正方形的性质求出点D 的坐标,从而求出抛物线解析式; (2)分平行于x 轴和y 轴两种情况,由折叠的性质计算即可.试题解析:解:(1)∵点D (m ,n ),∴点D (m ,n )的特征线是x =m ,y =n ,y =x +n ﹣m ,y =﹣x +m +n ;(2)点D 有一条特征线是y =x +1,∴n ﹣m =1,∴n =m +1.∵抛物线解析式为21()4y x m n =-+,∴21()14y x m m =-++,∵四边形OABC 是正方形,且D 点为正方形的对称轴,D (m ,n ),∴B (2m ,2m ),∴21(2)24y m m n m =-+=,将n =m +1带入得到m =2,n =3;∴D (2,3),∴抛物线解析式为21(2)34y x =-+. (3)①如图,当点A ′在平行于y 轴的D 点的特征线时:根据题意可得,D (2,3),∴OA ′=OA =4,OM =2,∴∠A ′OM =60°,∴∠A ′OP =∠AOP =30°,∴MN 3=33,∴抛物线需要向下平移的距离=333-=9233-.②如图,当点A ′在平行于x 轴的D 点的特征线时,设A ′(p ,3),则OA ′=OA =4,OE =3,EA 2243-7,∴A ′F =47,设P (4,c )(c >0),,在Rt △A ′FP 中,(4﹣7)2+(3﹣c )2=c 2,∴c 1647-∴P (41647-),∴直线OP 解析式为y 47-x ,∴N (2827-∴抛物线需要向下平移的距离=3﹣827-=127+ 综上所述:抛物线向下平移9233-或173+距离,其顶点落在OP 上.点睛:此题是二次函数综合题,主要考查了折叠的性质,正方形的性质,解答本题的关键是用正方形的性质求出点D 的坐标.8.在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”。
2020-2021中考数学培优专题复习二次函数练习题附答案

2020-2021中考数学培优专题复习二次函数练习题附答案一、二次函数1.如图,已知抛物线y =x 2+bx +c 与x 轴交于A 、B 两点(A 点在B 点左侧),与y 轴交于点C (0,-3),对称轴是直线x =1,直线BC 与抛物线的对称轴交于点D .(1)求抛物线的函数表达式;(2)求直线BC 的函数表达式;(3)点E 为y 轴上一动点,CE 的垂直平分线交CE 于点F ,交抛物线于P 、Q 两点,且点P 在第三象限.①当线段PQ =34AB 时,求tan ∠CED 的值; ②当以点C 、D 、E 为顶点的三角形是直角三角形时,请直接写出点P 的坐标.【答案】(1)抛物线的函数表达式为y =x 2-2x -3.(2)直线BC 的函数表达式为y =x -3.(3)①23.①P 1(122),P 2(16,74). 【解析】【分析】已知C 点的坐标,即知道OC 的长,可在直角三角形BOC 中根据∠BCO 的正切值求出OB 的长,即可得出B 点的坐标.已知了△AOC 和△BOC 的面积比,由于两三角形的高相等,因此面积比就是AO 与OB 的比.由此可求出OA 的长,也就求出了A 点的坐标,然后根据A 、B 、C 三点的坐标即可用待定系数法求出抛物线的解析式.【详解】(1)∵抛物线的对称轴为直线x=1, ∴− 221bb a-⨯==1 ∴b=-2 ∵抛物线与y 轴交于点C (0,-3),∴c=-3,∴抛物线的函数表达式为y=x 2-2x-3;(2)∵抛物线与x 轴交于A 、B 两点,当y=0时,x 2-2x-3=0.∴x1=-1,x2=3.∵A点在B点左侧,∴A(-1,0),B(3,0)设过点B(3,0)、C(0,-3)的直线的函数表达式为y=kx+m,则033k mm==+⎧⎨-⎩,∴13 km⎧⎨-⎩==∴直线BC的函数表达式为y=x-3;(3)①∵AB=4,PQ=34 AB,∴PQ=3∵PQ⊥y轴∴PQ∥x轴,则由抛物线的对称性可得PM=32,∵对称轴是直线x=1,∴P到y轴的距离是12,∴点P的横坐标为−12,∴P(−12,−74)∴F(0,−74),∴FC=3-OF=3-74=54∵PQ垂直平分CE于点F,∴CE=2FC=5 2∵点D在直线BC上,∴当x=1时,y=-2,则D(1,-2),过点D作DG⊥CE于点G,∴DG=1,CG=1,∴GE=CE-CG=52-1=32.在Rt△EGD中,tan∠CED=23 GDEG=.②P1(2,-2),P2(6-52).设OE=a,则GE=2-a,当CE为斜边时,则DG2=CG•GE,即1=(OC-OG)•(2-a),∴1=1×(2-a),∴a=1,∴CE=2,∴OF=OE+EF=2∴F、P的纵坐标为-2,把y=-2,代入抛物线的函数表达式为y=x2-2x-3得:2或2∵点P在第三象限.∴P1(2-2),当CD为斜边时,DE⊥CE,∴OE=2,CE=1,∴OF=2.5,∴P和F的纵坐标为:-52,把y=-52,代入抛物线的函数表达式为y=x2-2x-3得:x=1-621+62∵点P在第三象限.∴P2(6-52).综上所述:满足条件为P1(2-2),P2(6-52).【点睛】本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.2.如图,已知A (﹣2,0),B (4,0),抛物线y=ax 2+bx ﹣1过A 、B 两点,并与过A 点的直线y=﹣12x ﹣1交于点C . (1)求抛物线解析式及对称轴;(2)在抛物线的对称轴上是否存在一点P ,使四边形ACPO 的周长最小?若存在,求出点P 的坐标,若不存在,请说明理由;(3)点M 为y 轴右侧抛物线上一点,过点M 作直线AC 的垂线,垂足为N .问:是否存在这样的点N ,使以点M 、N 、C 为顶点的三角形与△AOC 相似,若存在,求出点N 的坐标,若不存在,请说明理由.【答案】(1)抛物线解析式为:y=211184x x --,抛物线对称轴为直线x=1;(2)存在P 点坐标为(1,﹣12);(3)N 点坐标为(4,﹣3)或(2,﹣1) 【解析】 分析:(1)由待定系数法求解即可;(2)将四边形周长最小转化为PC+PO 最小即可; (3)利用相似三角形对应点进行分类讨论,构造图形.设出点N 坐标,表示点M 坐标代入抛物线解析式即可.详解:(1)把A (-2,0),B (4,0)代入抛物线y=ax 2+bx-1,得 042101641a b a b --⎧⎨+-⎩==解得1814a b ⎧⎪⎪⎨⎪-⎪⎩== ∴抛物线解析式为:y=18x 2−14x−1∴抛物线对称轴为直线x=-141 228ba-=-⨯=1(2)存在使四边形ACPO的周长最小,只需PC+PO最小∴取点C(0,-1)关于直线x=1的对称点C′(2,-1),连C′O与直线x=1的交点即为P 点.设过点C′、O直线解析式为:y=kx∴k=-12∴y=-12x则P点坐标为(1,-12)(3)当△AOC∽△MNC时,如图,延长MN交y轴于点D,过点N作NE⊥y轴于点E∵∠ACO=∠NCD,∠AOC=∠CND=90°∴∠CDN=∠CAO由相似,∠CAO=∠CMN∴∠CDN=∠CMN∵MN⊥AC∴M、D关于AN对称,则N为DM中点设点N坐标为(a,-12a-1)由△EDN∽△OAC∴ED=2a∴点D坐标为(0,-52a−1)∵N为DM中点∴点M坐标为(2a,32a−1)把M代入y=18x2−14x−1,解得a=4则N点坐标为(4,-3)当△AOC∽△CNM时,∠CAO=∠NCM∴CM∥AB则点C关于直线x=1的对称点C′即为点N由(2)N(2,-1)∴N点坐标为(4,-3)或(2,-1)点睛:本题为代数几何综合题,考查了待定系数、两点之间线段最短的数学模型构造、三角形相似.解答时,应用了数形结合和分类讨论的数学思想.3.如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.(1)求抛物线的解析式和直线AC的解析式;(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.【答案】(1)抛物线解析式为y=﹣x2+2x+3;直线AC的解析式为y=3x+3;(2)点M的坐标为(0,3);(3)符合条件的点P的坐标为(73,209)或(103,﹣139),【解析】分析:(1)设交点式y=a(x+1)(x-3),展开得到-2a=2,然后求出a即可得到抛物线解析式;再确定C(0,3),然后利用待定系数法求直线AC的解析式;(2)利用二次函数的性质确定D的坐标为(1,4),作B点关于y轴的对称点B′,连接DB′交y轴于M,如图1,则B′(-3,0),利用两点之间线段最短可判断此时MB+MD的值最小,则此时△BDM的周长最小,然后求出直线DB′的解析式即可得到点M的坐标;(3)过点C作AC的垂线交抛物线于另一点P,如图2,利用两直线垂直一次项系数互为负倒数设直线PC的解析式为y=-13x+b,把C点坐标代入求出b得到直线PC的解析式为y=-13x+3,再解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩==得此时P点坐标;当过点A作AC的垂线交抛物线于另一点P时,利用同样的方法可求出此时P点坐标.详解:(1)设抛物线解析式为y=a(x+1)(x﹣3),即y=ax2﹣2ax﹣3a,∴﹣2a=2,解得a=﹣1,∴抛物线解析式为y=﹣x2+2x+3;当x=0时,y=﹣x2+2x+3=3,则C(0,3),设直线AC的解析式为y=px+q,把A(﹣1,0),C(0,3)代入得3p qq-+=⎧⎨=⎩,解得33pq=⎧⎨=⎩,∴直线AC的解析式为y=3x+3;(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D的坐标为(1,4),作B点关于y轴的对称点B′,连接DB′交y轴于M,如图1,则B′(﹣3,0),∵MB=MB′,∴MB+MD=MB′+MD=DB′,此时MB+MD的值最小,而BD的值不变,∴此时△BDM的周长最小,易得直线DB′的解析式为y=x+3,当x=0时,y=x+3=3,∴点M的坐标为(0,3);(3)存在.过点C作AC的垂线交抛物线于另一点P,如图2,∵直线AC 的解析式为y=3x+3,∴直线PC 的解析式可设为y=﹣13x+b , 把C (0,3)代入得b=3,∴直线PC 的解析式为y=﹣13x+3, 解方程组223133y x x y x ⎧-++⎪⎨-+⎪⎩==,解得03x y =⎧⎨=⎩或73209x y ⎧=⎪⎪⎨⎪=⎪⎩,则此时P 点坐标为(73,209); 过点A 作AC 的垂线交抛物线于另一点P ,直线PC 的解析式可设为y=﹣x+b , 把A (﹣1,0)代入得13+b=0,解得b=﹣13, ∴直线PC 的解析式为y=﹣13x ﹣13, 解方程组2231133y x x y x ⎧-++⎪⎨--⎪⎩==,解得10x y =-⎧⎨=⎩或103139x y ⎧=⎪⎪⎨⎪=-⎪⎩,则此时P 点坐标为(103,﹣139). 综上所述,符合条件的点P 的坐标为(73,209)或(103,﹣139). 点睛:本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求函数解析式,理解两直线垂直时一次项系数的关系,通过解方程组求把两函数的交点坐标;理解坐标与图形性质,会运用两点之间线段最短解决最短路径问题;会运用分类讨论的思想解决数学问题.4.一座拱桥的轮廓是抛物线型(如图所示),拱高6m ,跨度20m ,相邻两支柱间的距离均为5m.(1)将抛物线放在所给的直角坐标系中(如图所示),其表达式是2y ax c =+的形式.请根据所给的数据求出a ,c 的值.(2)求支柱MN 的长度.(3)拱桥下地平面是双向行车道(正中间是一条宽2m 的隔离带),其中的一条行车道能否并排行驶宽2m 、高3m 的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.【答案】(1)y=-350x 2+6;(2)5.5米;(3)一条行车道能并排行驶这样的三辆汽车. 【解析】 试题分析:(1)根据题目可知A .B ,C 的坐标,设出抛物线的解析式代入可求解. (2)设N 点的坐标为(5,y N )可求出支柱MN 的长度.(3)设DN 是隔离带的宽,NG 是三辆车的宽度和.做GH 垂直AB 交抛物线于H 则可求解.试题解析: (1) 根据题目条件,A 、B 、C 的坐标分别是(-10,0)、(0,6)、(10,0).将B 、C 的坐标代入2y ax c =+,得 6,0100.c a c =⎧⎨=+⎩解得3,650a c =-=. ∴抛物线的表达式是23650y x =-+. (2) 可设N (5,N y ),于是2356 4.550N y =-⨯+=. 从而支柱MN 的长度是10-4.5=5.5米.(3) 设DE 是隔离带的宽,EG 是三辆车的宽度和,则G 点坐标是(7,0)(7=2÷2+2×3).过G 点作GH 垂直AB 交抛物线于H ,则23176335050H y =-⨯+=+>. 根据抛物线的特点,可知一条行车道能并排行驶这样的三辆汽车.5.如图,抛物线y=ax2+bx(a≠0)过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.(1)求抛物线的表达式;(2)直接写出点C的坐标,并求出△ABC的面积;(3)点P是抛物线上一动点,且位于第四象限,是否存在这样的点P,使得△ABP的面积为△ABC面积的2倍?若存在,求出点P的坐标,若不存在,请说明理由;(4)若点M在直线BH上运动,点N在x轴正半轴上运动,当以点C,M,N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.【答案】(1)y=-x2+4x;(2)C(3,3),面积为3;(3)P的坐标为(5,-5);(4)52或5.【解析】试题分析:(1)利用待定系数法进行求解即可;(2)先求出抛物线的对称轴,利用对称性即可写出点C的坐标,利用三角形面积公式即可求面积;(3)利用三角形的面积以及点P所处象限的特点即可求;(4)分情况进行讨论,确定点M、N,然后三角形的面积公式即可求.试题解析:(1)将A(4,0),B(1,3)代入到y=ax2+bx中,得16403a ba b+=⎧⎨+=⎩,解得14ab=-⎧⎨=⎩,∴抛物线的表达式为y=-x2+4x.(2)∵抛物线的表达式为y=-x2+4x,∴抛物线的对称轴为直线x=2.又C,B关于对称轴对称,∴C(3,3).∴BC=2,∴S△ABC=12×2×3=3.(3)存在点P.作PQ⊥BH于点Q,设P(m,-m2+4m).∵S△ABP=2S△ABC,S△ABC=3,∴S△ABP=6.∵S△ABP+S△BPQ=S△ABH+S梯形AHQP∴6+12×(m -1)×(3+m 2-4m )=12×3×3+12×(3+m -1)(m 2-4m ) 整理得m 2-5m =0,解得m 1=0(舍),m 2=5,∴点P 的坐标为(5,-5). (4)52或5. 提示:①当以M 为直角顶点,则S △CMN =52; ②当以N 为直角顶点,S △CMN =5;③当以C 为直角顶点时,此种情况不存在.【点睛】本题是二次函数的综合题,主要考查待定系数法求解析式,三角形面积、直角三角形的判定等,能正确地根据题意确定图形,分情况进行讨论是解题的关键.6.在平面直角坐标系中,有两点(),A a b 、(),B c d ,若满足:当a b ≥时,c a =,2d b =-;当a b <时,c a <-,d b <,则称点为点的“友好点”.(1)点()4,1的“友好点”的坐标是_______.(2)点(),A a b 是直线2y x =-上的一点,点B 是点A 的“友好点”. ①当B 点与A 点重合时,求点A 的坐标.②当A 点与A 点不重合时,求线段AB 的长度随着a 的增大而减小时,a 的取值范围. 【答案】(1)()41-,;(2)①点A 的坐标是()2,0或()1,1-;②当1a <或322a ≤<时,AB 的长度随着a 的增大而减小; 【解析】 【分析】(1)直接利用“友好点”定义进行解题即可;(2)先利用 “友好点”定义求出B 点坐标,A 点又在直线2y x =-上,得到2b a =-;①当点A 和点B 重合,得2b b =-.解出即可,②当点A 和点B 不重合, 1a ≠且2a ≠.所以对a 分情况讨论,1°、当1a <或2a >时,()222313224AB b b a a a ⎛⎫=--=-+=-- ⎪⎝⎭,所以当a ≤32时,AB 的长度随着a 的增大而减小,即取1a <.2°当12a <<时,()22231+3224AB b b a a a ⎛⎫=--=--=--+⎪⎝⎭,当32a ≥时,AB 的长度随着a 的增大而减小,即取322a ≤<. 综上,当1a <或322a ≤<时,AB 的长度随着a 的增大而减小. 【详解】(1)点()4,1,4>1,根据“友好点”定义,得到点()4,1的“友好点”的坐标是()41-, (2)Q 点(),A a b 是直线2y x =-上的一点,∴2b a =-.Q 2a a >-,根据友好点的定义,点B 的坐标为()2,B a b -,①当点A 和点B 重合,∴2b b =-. 解得0b =或1b =-. 当0b =时,2a =;当1b =-时,1a =,∴点A 的坐标是()2,0或()1,1-.②当点A 和点B 不重合,1a ≠且2a ≠.当1a <或2a >时,()222313224AB b b a a a ⎛⎫=--=-+=-- ⎪⎝⎭. ∴当a ≤32时,AB 的长度随着a 的增大而减小, ∴取1a <.当12a <<时, ()22231+3224AB b b a a a ⎛⎫=--=--=--+ ⎪⎝⎭ .∴当32a ≥时,AB 的长度随着a 的增大而减小, ∴取322a ≤<. 综上,当1a <或322a ≤<时,AB 的长度随着a 的增大而减小. 【点睛】本题属于阅读理解题型,结合二次函数的基本性质进行解题,第二问的第二小问的关键是求出AB 的长用a 进行表示,然后利用二次函数基本性质进行分类讨论7.某商场经营某种品牌的玩具,购进时的单价是3元,经市场预测,销售单价为40元时,可售出600个;销售单价每涨1元,销售量将减少10个设每个销售单价为x 元. (1)写出销售量y (件)和获得利润w (元)与销售单价x (元)之间的函数关系; (2)若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?【答案】(1)y=﹣10x+1000;w=﹣10x2+1300x﹣30000(2)商场销售该品牌玩具获得的最大利润是8640元.【解析】【分析】(1)利用销售单价每涨1元,销售量将减少10个即可表示出y=600﹣10(x﹣40),再利用w= y•(x﹣30)即可表示出w与x之间的关系式;(2)先将w=﹣10x2+1300x﹣30000变成顶点式,找到对称轴,利用函数图像的增减性确定在44≤x≤46范围内当x=46时有最大值,代入求值即可解题.【详解】解:(1)依题意,易得销售量y(件)与销售单价x(元)之间的函数关系:y=600﹣10(x﹣40)=﹣10x+1000获得利润w(元)与销售单价x(元)之间的函数关系为:w=y•(x﹣30)=(1000﹣10x)(x﹣30)=﹣10x2+1300x﹣30000(2)根据题意得,x≥14时且1000﹣10x≥540,解得:44≤x≤46w=﹣10x2+1300x﹣30000=﹣10(x﹣65)2+12250∵a=﹣10<0,对称轴x=65∴当44≤x≤46时,y随x的增大而增大∴当x=46时,w最大值=8640元即商场销售该品牌玩具获得的最大利润是8640元.【点睛】本题考查了二次函数的实际应用,难度较大,求解二次函数与利润之间的关系时,需要用代数式表示销售数量和销售单价,熟悉二次函数顶点式的性质是解题关键.8.如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,3).(1)求抛物线y=x2+bx+c的表达式;(2)点D为抛物线对称轴上一点,当△BCD是以BC为直角边的直角三角形时,求点D的坐标;(3)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值.【答案】(1)y=x2﹣4x+3;(2)(2,﹣1);(3)42【解析】试题分析:(1)利用待定系数法求抛物线解析式;(2)如图1,设D(2,y),利用两点间的距离公式得到BC2=32+32=18,DC2=4+(y﹣3)2,BD2=(3﹣2)2+y2=1+y2,然后讨论:当BD为斜边时得到18+4+(y﹣3)2=1+y2;当CD 为斜边时得到4+(y﹣3)2=1+y2+18,再分别解方程即可得到对应D的坐标;(3)先证明∠CEF=90°得到△ECF为等腰直角三角形,作PH⊥y轴于H,PG∥y轴交BC于G,如图2,△EPG、△PHF都为等腰直角三角形,则PE=22PG,PF=2PH,设P(t,t2﹣4t+3)(1<t<3),则G(t,﹣t+3),接着利用t表示PF、PE,这样PE+EF=2PE+PF=﹣2t2+42t,然后利用二次函数的性质解决问题.试题解析:解:(1)把B(3,0),C(0,3)代入y=x2+bx+c得:9303b cc++=⎧⎨=⎩,解得:43bc=-⎧⎨=⎩,∴抛物线y=x2+bx+c的表达式为y=x2﹣4x+3;(2)如图1,抛物线的对称轴为直线x=﹣42-=2,设D(2,y),B(3,0),C(0,3),∴BC2=32+32=18,DC2=4+(y﹣3)2,BD2=(3﹣2)2+y2=1+y2,当△BCD是以BC为直角边,BD为斜边的直角三角形时,BC2+DC2=BD2,即18+4+(y﹣3)2=1+y2,解得:y=5,此时D点坐标为(2,5);当△BCD是以BC为直角边,CD为斜边的直角三角形时,BC2+DB2=DC2,即4+(y﹣3)2=1+y2+18,解得:y=﹣1,此时D点坐标为(2,﹣1);(3)易得BC的解析式为y=﹣x+3.∵直线y=x+m与直线y=x平行,∴直线y=﹣x+3与直线y=x+m垂直,∴∠CEF=90°,∴△ECF为等腰直角三角形,作PH⊥y轴于H,PG∥y轴交BC于G,如图2,△EPG、△PHF都为等腰直角三角形,PE=22PG,PF=2PH,设P(t,t2﹣4t+3)(1<t<3),则G(t,﹣t+3),∴PF=2PH=2t,PG=﹣t+3﹣(t2﹣4t+3)=﹣t2+3t,∴PE=2PG=﹣2t2+32t,∴PE+EF=PE+PE+PF=2PE+PF=﹣2t2+32t+2t=﹣2t2+42t=﹣2(t﹣2)2+42,当t=2时,PE+EF的最大值为42.点睛:本题考查了二次函数的综合题.熟练掌握等腰直角三角形的性质、二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求二次函数解析式;理解坐标与图形性质,记住两点间的距离公式.9.如图,已知抛物线的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
2021年九年级数学中考一轮复习 二次函数最值的综合应用 培优提升专题训练

2021年九年级数学中考一轮复习二次函数最值的综合应用培优提升专题训练(附答案)1.当m在可取值范围内取不同的值时,代数式的最小值是()A.0B.5C.3D.92.二次函数y=mx2﹣4x+m有最小值﹣3,则m等于()A.1B.﹣4C.1或﹣4D.﹣1或43.若一次函数y=(a+1)x+a的图象过第一、三、四象限,则二次函数y=ax2﹣ax()A.有最大值.B.有最大值﹣.C.有最小值.D.有最小值﹣.4.二次函数y=﹣x2+2x﹣5有()A.最大值﹣5B.最小值﹣5C.最大值﹣4D.最小值﹣45.二次函数y=ax2+bx+c,b2=ac且x=0时y=﹣4,则()A.y最大=﹣4B.y最小=﹣4C.y最大=﹣3D.y最小=﹣36.A(0,3),B(2,3)是抛物线y=﹣x2+bx+c上两点,该二次函数最大值是()A.4B.5C.6D.77.已知二次函数y=a(x+1)2﹣b(a≠0)有最小值,则a、b的大小比较为()A.a>b B.a<b C.a=b D.不能确定8.已知k,n均为非负实数,且2k+n=2,则代数式2k2﹣4n的最小值为()A.﹣40B.﹣16C.﹣8D.09.将4cm长的线段分成两部分,一部分作为正方形的一条边,另一部分作为一个等腰直角三角形的斜边,则这个正方形和等腰直角三角形的面积之和的最小值为()cm2.A.1B.C.16D.10.二次函数y=(x﹣m)2﹣m2﹣1有最小值﹣4,则实数m的值可能是()A.﹣B.﹣3C.D.411.如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B 停止),在运动过程中,四边形P ABQ的面积最小值为()A.19cm2B.16cm2C.15cm2D.12cm212.如图,P为线段AB上一点,以AP为边作一正方形APMN,以BP为底在另一侧作等腰△BPQ,连接MQ,若AB的长为4,则△MPQ的面积的最大值等于.13.函数y=x2﹣4x+5(0≤x≤5)的最小值和最大值分别是,.14.将进货单价为70元的某种商品按零售价100元售出时,每天能卖出20个;若这种商品的零售价在一定范围内每降价2元,其日销售量就增加4个,为了获得最大利润,则售价为元,最大利润为元.15.函数y=x2﹣2(2k﹣1)x+3k2﹣2k+6的最小值为m,则当m达到最大时,x=.16.某电脑商店销售某种品牌的电脑,所获利润y(元)与所销售电脑x(台)之间的函数关系满足y=﹣x2+120x﹣1200,则当天卖出电脑台时,可获得最大利润为元.17.若实数a,b满足a+b2=1,则2a2+7b2的最小值是.18.已知实数x、y满足x2﹣2x+y=5,则x+2y的最大值为.19.如图,抛物线y=x2+2x+c的顶点在双曲线y=上,则y有最小值为.20.如图线段AB=6,点C是AB上一点,点D是AC的中点,分别以AD,DC,CB为边作正方形,则AC=时,三个正方形的面积之和最小.21.如图,在△AOB中,OA=OB=8,∠AOB=90°,矩形CDEF的顶点C、D、F分别在边AO、OB、AB上,若tan CDO=,则矩形CDEF面积的最大值s=.22.如图,正方形ABCD的边长为1,点M、N分别在BC、CD上,且△CMN的周长为2,求△MAN的面积的最小值.23.如图,在△ABC中,∠B=90°,AB=12米,BC=24米,动点P从点A开始沿边AB 向B以2米/秒的速度运动(不与点B重合),动点Q从点B开始沿BC向C以4米/秒的速度运动(不与点C重合).如果P、Q分别从A、B同时出发,设运动时间为x秒,四边形APQC的面积为y平方米.(1)求y与x之间的函数关系式,直接写出自变量x的取值范围;(2)求当x为多少时,y有最小值,最小值是多少?24.某企业为杭州计算机产业基地提供电脑配件.受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x 取整数)之间的函数关系如下表:月份x123456789价格y1(元/件)560580600620640660680700720随着国家调控措施的出台,原材料价格的涨势趋缓,10至12月每件配件的原材料价格y2(元)与月份x(10≤x≤12,且x取整数)之间存在如图所示的变化趋势:(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y1与x之间的函数关系式,根据如图所示的变化趋势,直接写出y2与x之间满足的一次函数关系式;(2)若去年该配件每件的售价为1000元,生产每件配件的人力成本为50元,其它成本30元,该配件在1至9月的销售量p1(万件)与月份x满足关系式p1=0.1x+1.1(1≤x ≤9,且x取整数),10至12月的销售量p2(万件)p2=﹣0.1x+2.9(10≤x≤12,且x 取整数).求去年哪个月销售该配件的利润最大,并求出这个最大利润.25.对称轴为直线x=﹣1的抛物线y=x2+bx+c,与x轴相交于A,B两点,其中点A的坐标为(﹣3,0).(1)求点B的坐标.(2)点C是抛物线与y轴的交点,点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.26.一块三角形废料如图所示,∠A=30°,∠C=90°,BC=6.用这块废料剪出一个平行四边形AGEF,其中,点G,E,F分别在AB,BC,AC上.设CE=x(1)求x=2时,平行四边形AGEF的面积.(2)当x为何值时,平行四边形AGEF的面积最大?最大面积是多少?27.如图,在△ABC中,AB=AC=1,∠A=45°,边长为1的正方形的一个顶点D在边AC上,与△ADC另两边分别交于点E、F,DE∥AB,将正方形平移,使点D保持在AC上(D不与A重合),设AF=x,正方形与△ABC重叠部分的面积为y.(1)求y与x的函数关系式并写出自变量x的取值范围;(2)x为何值时y的值最大?28.如图,四边形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB为⊙O的直径.(1)若AD=2,AB=BC=8,连接OC、OD.①求△COD的面积;②试判断直线CD与⊙O的位置关系,说明理由.(2)若直线CD与⊙O相切于F,AD=x(x>0),AB=8.试用x表示四边形ABCD的面积S,并探索S是否存在最小值,写出探索过程.参考答案1.解:=,当m=1时,取得最小值为5,故选:B.2.解:∵二次函数有最小值,∴m>0且=﹣3,解得m=1.故选:A.3.解:∵一次函数y=(a+1)x+a的图象过第一、三、四象限,∴a+1>0且a<0,∴﹣1<a<0,∴二次函数y=ax2﹣ax有最大值﹣,故选:B.4.解:配方,得y=﹣(x﹣1)2﹣4所以当x=1时,y max=﹣4.故选:C.5.解:把x=0时y=﹣4代入二次函数y=ax2+bx+c,得c=﹣4,代入b2=ac得b2=﹣4a,故a<0,所以二次函数有最大值,把c=﹣4代入最大值公式,则有y最大====﹣3.故选:C.6.解:将A(0,3),B(2,3)代入解析式,得:,解得,则二次函数的解析式为y=﹣x2+2x+3,∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴当x=1时,y取得最大值,最大值为4,故选:A.7.解:∵二次函数y=a(x﹣1)2﹣b有最小值,∴a>0,b=﹣,∴a>b.故选:A.8.解:∵k,n均为非负实数,2k+n=2,∴n=2﹣2k,∴2﹣2k≥0,∴0≤k≤1.∴2k2﹣4n=2k2﹣4(2﹣2k)=2(k+2)2﹣16∴当k=0时,代数式有最小值,∴代数式2k2﹣4n的最小值为﹣8.故选:C.9.解:设等腰直角三角形的斜边为xcm,则正方形的边长为(4﹣x)cm.若等腰直角三角形的面积为S1,正方形面积为S2,则S1=•x•x=x2,S2=(4﹣x)2,面积之和S=x2+(4﹣x)2=x2﹣8x+16.∵>0,∴函数有最小值.即S最小值==(cm2).故选:D.10.解:∵关于x的二次函数y=(x﹣m)2﹣m2﹣1有最小值﹣4,∴m2+1=4,∴m=±,故选:A.11.解:(方法一)在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,∴AC==6cm.设运动时间为t(0≤t≤4),则PC=(6﹣t)cm,CQ=2tcm,∴S四边形P ABQ=S△ABC﹣S△CPQ=AC•BC﹣PC•CQ=×6×8﹣(6﹣t)×2t=t2﹣6t+24=(t﹣3)2+15.∵1>0,∴当t=3时,四边形P ABQ的面积取最小值,最小值为15.(方法二)∵S四边形P ABQ+S△CPQ=S△ABC,∴当△CPQ的面积最大时,四边形P ABQ的面积最小.在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,∴AC==6cm.设运动时间为t(0≤t≤4),则PC=(6﹣t)cm,CQ=2tcm,∴S△CPQ=PC•CQ=×(6﹣t)×2t=﹣t2+6t=﹣(t﹣3)2+9.∵﹣1<0,∴当t=3时,△CPQ的面积取最大值,最大值为9,∴四边形P ABQ的面积最小值为×6×8﹣9=15.故选:C.12.解:设AP=x,则BP=4﹣x,MP=AP=x,Q点到MP的距离等于B点到MP的距离的一半.∵S△MPQ=x=﹣(x﹣2)2+1.∵﹣<0,∴当x=2时,S△MPQ=1为最大值.故答案为:1.13.解:函数y=x2﹣4x+5的顶点坐标为:x=﹣=﹣=2,y===1,即(2,1).x=0时,y=02﹣4×0+5=5,即(0,5);x=5时,y=52﹣4×5+5=10,即(5,10).由函数y=x2﹣4x+5的图象可知,在0≤x≤5范围内,函数最小值和最大值分别是1,10.14.解:设降价x元,利润为y,y=(100﹣70﹣x)(20+2x)=﹣2x2+40x+600=﹣2(x﹣10)2+800,当x=10时,y的最大值为800,即售价为90元时,最大利润为800元.故答案为90,800.15.解:当x=﹣=﹣=2k﹣1时,函数取最小值,最小值m===﹣k2+2k+5=﹣(k﹣1)2+6,当k=1时,m取得最大值,最大值为6,此时,x=2k﹣1=2×1﹣1=1.故答案为:1.16.解:y=﹣x2+120x﹣1200=﹣(x﹣60)2+2400.∵﹣1<0,∴当x=60时,y有最大值,为2400.故答案为60;2400.17.解:∵a+b2=1,∴a=1﹣b2∴2a2+7b2=2(1﹣b2)2+7b2=2b4+3b2+2=2(b2+)2+2﹣=2(b2+)2+,∵b2≥0,∴2(b2+)2+>0,∴当b2=0,即b=0时,2a2+7b2的值最小.∴最小值是2.方法二:∵a+b2=1,∴b2=1﹣a,∴2a2+7b2=2a2+7(1﹣a)=2a2﹣7a+7=2(a﹣)2+,∵b2≥0,∴1﹣a≥0,∴a≤1,∴当a=1,即b=0时,2a2+7b2的值最小.∴最小值是2.18.解:由x2﹣2x+y=5可得:y=5﹣x2+2x,代入x+2y得﹣2x2+5x+10,令z=﹣2x2+5x+10,∵二次函数z=﹣2x2+5x+10中,a=﹣2<0,∴函数有最大值,即z最大===.19.解:抛物线y=x2+2x+c得对称轴为x=﹣=﹣=﹣1,代入双曲线y=,得y==﹣2,即则y有最小值为﹣2.20.解:设AC为x,三个正方形的面积和为y.则BC=6﹣x,AD=CD=,∴y=2×()2+(6﹣x)2=x2﹣12x+36,∴x=﹣=4时,三个正方形的面积之和最小.故答案为4.21.解:设CD=x,CF=y.过F作FH⊥AO于H.在Rt△COD中,∵,∴.∴.∵∠FCH+∠OCD=90°,∴∠FCH=∠CDO.∴.∴.∵△AHF是等腰直角三角形,∴.∴AO=AH+HC+CO.∴.∴.易知,∴当x=5时,矩形CDEF面积的最大值为.故答案为:.22.解:设DN=x,BM=y,∴NC=1﹣x,MC=1﹣y,C△NCM=NC+CM+NM=2,∴NM=x+y.将△DNA绕点A顺时针旋转90°至△ABF,则NM=MF,AM=MA,AN=AF,∴△ANM≌△AFM(SSS).∴∠NAM=45°,∠DNA=∠AFB=∠ANE.过点A作AE⊥NM,垂足为E,∵∠AEN=∠D,∠DNA=∠ANE,AN为公共边,∴△DAN≌△EAN(AAS),∴AE=AD=1,∵在Rt△CNM中,由勾股定理得:CN2+CM2=NM2,∴(1﹣x)2+(1﹣y)2=(x+y)2,∴化简得:xy+x+y﹣1=0,①∴S△ANM=(x+y)②.∵(x﹣y)2≥0,∴(x+y)2≥4xy,∴xy≤,③∴将②③代入①并整理可得S2+2S﹣1≥0,④∴(S+1)2≥2.∵S>0,∴S≥﹣1,∴△MAN的面积的最小值为﹣1.23.解:(1)根据题意知S=S△ABC﹣S△PBQ=×12×24﹣×4x×(12﹣2x)=4x2﹣24x+144,由12﹣2x>0得x<6,∴0<x<6;(2)y=4x2﹣24x+144=4(x﹣3)2+108.∵4>0∴当x=3时,y取得最小值,最小值为108.24.解:(1)利用表格得出函数关系是一次函数关系:设y1=kx+b,解得:,∴y1=20x+540,利用图象得出函数关系是一次函数关系:设y2=ax+c,∴,解得:,∴y2=10x+630.(2)去年1至9月时,销售该配件的利润w=p1(1000﹣50﹣30﹣y1),=(0.1x+1.1)(1000﹣50﹣30﹣20x﹣540)=﹣2x2+16x+418,=﹣2(x﹣4)2+450,(1≤x≤9,且x取整数)∵﹣2<0,1≤x≤9,∴当x=4时,w最大=450(万元);去年10至12月时,销售该配件的利润w=p2(1000﹣50﹣30﹣y2)=(﹣0.1x+2.9)(1000﹣50﹣30﹣10x﹣630),=(x﹣29)2,(10≤x≤12,且x取整数),∵10≤x≤12时,∴当x=10时,w最大=361(万元),∵450>361,∴去年4月销售该配件的利润最大,最大利润为450万元.25.解:(1)∵点A(﹣3,0)与点B关于直线x=﹣1对称,∴点B的坐标为(1,0).(2)∵a=1,∴y=x2+bx+c.∵抛物线过点(﹣3,0),且对称轴为直线x=﹣1,∴∴解得:,∴y=x2+2x﹣3,且点C的坐标为(0,﹣3).设直线AC的解析式为y=mx+n,解得:,∴y=﹣x﹣3如图,设点Q的坐标为(x.y),﹣3≤x≤0.则有QD=﹣x﹣3﹣(x2+2x﹣3)=﹣x2﹣3x=﹣(x+)2+∵﹣3≤﹣≤0,∴当x=﹣时,QD有最大值.∴线段QD长度的最大值为.26.解:设平行四边形AGEF的面积是S.∵四边形AGEF是平行四边形,∴EF∥AG;∵∠A=30°,∠C=90°,CE=x,BC=6,∴∠A=∠CFE=30°,∴CF=x,AC=6,∴AF=6﹣x;∴S=AF•CE=(6﹣x)x=﹣x2+6x,即S=﹣x2+6x;(1)当x=2时,S=﹣4+12=8,即S=8.答:平行四边形AGEF的面积为(平方单位)…4分(2)由S=﹣x2+6x,得,∴,∴当x=3时,平行四边形AGEF的面积最大,最大面积是(平方单位)…9分.27.解:(1)∵AB=AC,∴∠B=∠C,∵DE∥AB,∴∠B=∠CED,∠AFD=∠FDE=90°,∴∠C=∠CED,∴DC=DE.在Rt△ADF中,∵∠A=45°,∴∠ADF=45°=∠A,∴AF=DF=x,∴AD==x,∴DC=DE=1﹣x,∴y=(DE+FB)×DF=(1﹣x+1﹣x)x=﹣(+1)x2+x.∵点D保持在AC上,且D不与A重合,∴0<AD≤1,∴0<x≤1,∴0<x≤.故y=﹣(+1)x2+x,自变量x的取值范围是0<x≤;(2)∵y=﹣(+1)x2+x,∴当x=﹣=﹣1时,y有最大值.28.解:(1)①S△COD=S梯形ABCD﹣S△AOD﹣S△BOC===40﹣4﹣16=20.(或先证明△COD是直角三角形进而求其面积.)②过D作DE⊥BC,E是垂足,从而四边形ABED是矩形.BE=AD=2,CE=6,DE=AB=8.在Rt△CDE中,CD=10.过O作OF⊥CD于F,由S△COD==20,可得OF=4,表明点O到CD的距离等于⊙O的半径,故直线CD与⊙O相切;(2)在四边形ABCD中,∵AD=x>0,设BC=y,则CD=x+y,CE=|y﹣x|,∴在Rt△CDE中,根据勾股定理,得(y﹣x)2+64=(x+y)2,于是,x>0.进而,x>0.∵x>0,,∴当,x=4时,有最小值8,从而S有最小值32.。
2020-2021中考数学 二次函数 培优练习(含答案)附答案

2020-2021中考数学二次函数培优练习(含答案)附答案一、二次函数1.如图,在直角坐标系xOy中,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.(1)求这个二次函数的解析式;(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;(3)对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P 的坐标,并求出△POB的面积;若不存在,请说明理由.【答案】(1)y=x2﹣3x。
(2)点B的坐标为:(4,4)。
(3)存在;理由见解析;【解析】【分析】(1)将原点坐标代入抛物线中即可求出k的值,从而求得抛物线的解析式。
(2)根据(1)得出的抛物线的解析式可得出A点的坐标,也就求出了OA的长,根据△OAB的面积可求出B点纵坐标的绝对值,然后将符合题意的B点纵坐标代入抛物线的解析式中即可求出B点的坐标,然后根据B点在抛物线对称轴的右边来判断得出的B点是否符合要求即可。
(3)根据B点坐标可求出直线OB的解析式,由于OB⊥OP,由此可求出P点的坐标特点,代入二次函数解析式可得出P点的坐标.求△POB的面积时,求出OB,OP的长度即可求出△BOP的面积。
【详解】解:(1)∵函数的图象与x轴相交于O,∴0=k+1,∴k=﹣1。
∴这个二次函数的解析式为y=x2﹣3x。
(2)如图,过点B做BD⊥x轴于点D,令x 2﹣3x=0,解得:x=0或3。
∴AO=3。
∵△AOB 的面积等于6,∴12AO•BD=6。
∴BD=4。
∵点B 在函数y=x 2﹣3x 的图象上,∴4=x 2﹣3x ,解得:x=4或x=﹣1(舍去)。
又∵顶点坐标为:( 1.5,﹣2.25),且2.25<4,∴x 轴下方不存在B 点。
∴点B 的坐标为:(4,4)。
(3)存在。
∵点B 的坐标为:(4,4),∴∠BOD=45°,22BO 442=+=。
若∠POB=90°,则∠POD=45°。
2020-2021中考数学培优专题复习二次函数练习题含答案

2020-2021中考数学培优专题复习二次函数练习题含答案一、二次函数1.如图:在平面直角坐标系中,直线l :y=13x ﹣43与x 轴交于点A ,经过点A 的抛物线y=ax 2﹣3x+c 的对称轴是x=32. (1)求抛物线的解析式;(2)平移直线l 经过原点O ,得到直线m ,点P 是直线m 上任意一点,PB ⊥x 轴于点B ,PC ⊥y 轴于点C ,若点E 在线段OB 上,点F 在线段OC 的延长线上,连接PE ,PF ,且PE=3PF .求证:PE ⊥PF ;(3)若(2)中的点P 坐标为(6,2),点E 是x 轴上的点,点F 是y 轴上的点,当PE ⊥PF 时,抛物线上是否存在点Q ,使四边形PEQF 是矩形?如果存在,请求出点Q 的坐标,如果不存在,请说明理由.【答案】(1)抛物线的解析式为y=x 2﹣3x ﹣4;(2)证明见解析;(3)点Q 的坐标为(﹣2,6)或(2,﹣6). 【解析】 【分析】(1)先求得点A 的坐标,然后依据抛物线过点A ,对称轴是x=32列出关于a 、c 的方程组求解即可;(2)设P (3a ,a ),则PC=3a ,PB=a ,然后再证明∠FPC=∠EPB ,最后通过等量代换进行证明即可;(3)设E (a ,0),然后用含a 的式子表示BE 的长,从而可得到CF 的长,于是可得到点F 的坐标,然后依据中点坐标公式可得到22x x x x Q P F E ++=,22y y y yQ P F E ++=,从而可求得点Q 的坐标(用含a 的式子表示),最后,将点Q 的坐标代入抛物线的解析式求得a 的值即可. 【详解】(1)当y=0时,140 33x-=,解得x=4,即A(4,0),抛物线过点A,对称轴是x=32,得161203322a ca-+=⎧⎪-⎨-=⎪⎩,解得14ac=⎧⎨=-⎩,抛物线的解析式为y=x2﹣3x﹣4;(2)∵平移直线l经过原点O,得到直线m,∴直线m的解析式为y=13x.∵点P是直线1上任意一点,∴设P(3a,a),则PC=3a,PB=a.又∵PE=3PF,∴PC PBPF PE=.∴∠FPC=∠EPB.∵∠CPE+∠EPB=90°,∴∠FPC+∠CPE=90°,∴FP⊥PE.(3)如图所示,点E在点B的左侧时,设E(a,0),则BE=6﹣a.∵CF=3BE=18﹣3a,∴OF=20﹣3a.∴F(0,20﹣3a).∵PEQF为矩形,∴22x x x xQ P F E++=,22y y y yQ P F E++=,∴Q x+6=0+a,Q y+2=20﹣3a+0,∴Q x=a﹣6,Q y=18﹣3a.将点Q的坐标代入抛物线的解析式得:18﹣3a=(a﹣6)2﹣3(a﹣6)﹣4,解得:a=4或a=8(舍去).∴Q(﹣2,6).如下图所示:当点E 在点B 的右侧时,设E (a ,0),则BE=a ﹣6.∵CF=3BE=3a ﹣18, ∴OF=3a ﹣20. ∴F (0,20﹣3a ). ∵PEQF 为矩形,∴22x x x x Q P F E ++=,22y y y yQ P F E ++=, ∴Q x +6=0+a ,Q y +2=20﹣3a+0, ∴Q x =a ﹣6,Q y =18﹣3a .将点Q 的坐标代入抛物线的解析式得:18﹣3a=(a ﹣6)2﹣3(a ﹣6)﹣4,解得:a=8或a=4(舍去). ∴Q (2,﹣6).综上所述,点Q 的坐标为(﹣2,6)或(2,﹣6). 【点睛】本题主要考查的是二次函数的综合应用,解答本题主要应用了矩形的性质、待定系数法求二次函数的解析式、中点坐标公式,用含a 的式子表示点Q 的坐标是解题的关键.2.如图所示,抛物线2y ax bx c =++的顶点为()2,4M --,与x 轴交于A 、B 两点,且()6,0A -,与y 轴交于点C .()1求抛物线的函数解析式; ()2求ABC V 的面积;()3能否在抛物线第三象限的图象上找到一点P ,使APC V 的面积最大?若能,请求出点P 的坐标;若不能,请说明理由.【答案】()1 2134y x x =+-;()212;()27334APC x S =-V 当时,有最大值,点P 的坐标是153,4P ⎛⎫-- ⎪⎝⎭. 【解析】 【分析】(1)设顶点式并代入已知点()6,0A -即可;(2)令y=0,求出A 、B 和C 点坐标,运用三角形面积公式计算即可;(3)假设存在这样的点,过点P 作PE x ⊥轴于点E ,交AC 于点F ,线段PF 的长度即为两函数值之差,将APC V 的面积计算拆分为APF CPF S S +V V 即可. 【详解】()1设此函数的解析式为2()y a x h k =++,∵函数图象顶点为()2,4M --,∴2(2)4y a x =+-, 又∵函数图象经过点()6,0A -, ∴20(62)4a =-+- 解得14a =, ∴此函数的解析式为21(2)44y x =+-,即2134y x x =+-; ()2∵点C 是函数2134y x x =+-的图象与y 轴的交点,∴点C 的坐标是()0,3-, 又当0y =时,有21304y x x =+-=, 解得16x =-,22x =, ∴点B 的坐标是()2,0, 则11831222ABC S AB OC =⋅=⨯⨯=V ;()3假设存在这样的点,过点P 作PE x ⊥轴于点E ,交AC 于点F .设(),0E x ,则21,34P x x x ⎛⎫+- ⎪⎝⎭,设直线AC 的解析式为y kx b =+, ∵直线AC 过点()6,0A -,()0,3C -, ∴603k b b-+=⎧⎨-=⎩,解得123k b ⎧=-⎪⎨⎪=-⎩,∴直线AC 的解析式为132y x =--, ∴点F 的坐标为1,32F x x ⎛⎫-- ⎪⎝⎭, 则221113332442PF x x x x x ⎛⎫=---+-=-- ⎪⎝⎭, ∴1122APC APF CPF S S S PF AE PF OE =+=⋅+⋅V V V 2221113393276(3)22424244PF OA x x x x x ⎛⎫=⋅=--⨯=--=-++ ⎪⎝⎭, ∴当3x =-时,APC S V 有最大值274, 此时点P 的坐标是153,4P ⎛⎫-- ⎪⎝⎭. 【点睛】本题第3问中将所求三角形拆分为两个小三角形进行求解,从而将面积最大的问题转化为PF 最大进行理解.3.函数()2110,>02y x mx x m =-++≥的图象记为1C ,函数()2110,>02y x mx x m =---<的图象记为2C ,其中m 为常数,1C 与2C 合起来的图象记为C .(Ⅰ)若1C 过点()1,1时,求m 的值; (Ⅱ)若2C 的顶点在直线1y =上,求m 的值; (Ⅲ)设C 在42x -≤≤上最高点的纵坐标为0y ,当0392y ≤≤时,求m 的取值范围. 【答案】(Ⅰ)12m =;(Ⅱ)2m =;(Ⅲ)912m ≤≤. 【解析】 【分析】(Ⅰ)将点C 的坐标代入1C 的解析式即可求出m 的值;(Ⅱ)先求出抛物线2C 的顶点坐标,再根据顶点在直线y 1=上得出关于m 的方程,解之即可(Ⅲ)先求出抛物线1C 的顶点坐标,结合(Ⅱ)抛物线2C 的顶点坐标,和x 的取值范围,分三种情形讨论求解即可; 【详解】解:(Ⅰ)将点()1,1代入1C 的解析式,解得1m .2=(Ⅱ)抛物线2C 的顶点坐标为2m m,12⎛⎫-- ⎪⎝⎭, 令2m 112-=,得m 2,=± ∵m>0,∴m 2.=(Ⅲ)∵抛物线1C 的顶点2m P m,12⎛⎫+ ⎪⎝⎭,抛物线2C 的顶点2m Q m,12⎛⎫-- ⎪⎝⎭, 当0m 2<≤时,最高点是抛物线G 1的顶点∴203m y 1922≤=+≤,解得1m 2.≤≤ 当2m 4<≤时,G 1中(2,2m-1)是最高点,0y =2m-1 ∴32≤2m-19≤,解得2m 4.<≤ 当m>4时,G 2中(-4,4m-9)是最高点,0y =4m-9. ∴32≤4m-99≤,解得94m 2<≤. 综上所述,91m 2≤≤即为所求. 【点睛】本题考查二次函数综合题,待定系数法、不等式组等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,利用数形结合的思想解决问题,属于中考压轴题.4.如图所示,已知平面直角坐标系xOy ,抛物线过点A(4,0)、B(1,3)(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;(2)记该抛物线的对称轴为直线l ,设抛物线上的点P(m,n)在第四象限,点P 关于直线l 的对称点为E ,点E 关于y 轴的对称点为F ,若四边形OAPF 的面积为20,求m 、n 的值.【答案】(1)y=-224(2)4y x x x =-+=--+,对称轴为:x=2,顶点坐标为:(2,4)(2)m 、n 的值分别为 5,-5 【解析】(1) 将点A(4,0)、B(1,3) 的坐标分别代入y =-x 2+bx +c ,得: 4b+c-16=0,b+c-1="3" , 解得:b="4" , c=0.所以抛物线的表达式为:24y x x =-+. y=-224(2)4y x x x =-+=--+,所以 抛物线的对称轴为:x=2,顶点坐标为:(2,4). (2) 由题可知,E 、F 点坐标分别为(4-m ,n ),(m-4,n ). 三角形POF 的面积为:1/2×4×|n|= 2|n|, 三角形AOP 的面积为:1/2×4×|n|= 2|n|,四边形OAPF 的面积= 三角形POF 的面积+三角形AOP 的面积=20, 所以 4|n|=20, n=-5.(因为点P(m,n)在第四象限,所以n<0) 又n=-2m +4m ,所以2m -4m-5=0,m=5.(因为点P(m,n)在第四象限,所以m>0) 故所求m 、n 的值分别为 5,-5.5.在平面直角坐标系中,有两点(),A a b 、(),B c d ,若满足:当a b ≥时,c a =,2d b =-;当a b <时,c a <-,d b <,则称点为点的“友好点”.(1)点()4,1的“友好点”的坐标是_______.(2)点(),A a b 是直线2y x =-上的一点,点B 是点A 的“友好点”. ①当B 点与A 点重合时,求点A 的坐标.②当A 点与A 点不重合时,求线段AB 的长度随着a 的增大而减小时,a 的取值范围. 【答案】(1)()41-,;(2)①点A 的坐标是()2,0或()1,1-;②当1a <或322a ≤<时,AB 的长度随着a 的增大而减小; 【解析】 【分析】(1)直接利用“友好点”定义进行解题即可;(2)先利用 “友好点”定义求出B 点坐标,A 点又在直线2y x =-上,得到2b a =-;①当点A 和点B 重合,得2b b =-.解出即可,②当点A 和点B 不重合, 1a ≠且2a ≠.所以对a 分情况讨论,1°、当1a <或2a >时,()222313224AB b b a a a ⎛⎫=--=-+=-- ⎪⎝⎭,所以当a ≤32时,AB 的长度随着a 的增大而减小,即取1a <.2°当12a <<时,()22231+3224AB b b a a a ⎛⎫=--=--=--+⎪⎝⎭,当32a ≥时,AB 的长度随着a 的增大而减小,即取322a ≤<. 综上,当1a <或322a ≤<时,AB 的长度随着a 的增大而减小. 【详解】(1)点()4,1,4>1,根据“友好点”定义,得到点()4,1的“友好点”的坐标是()41-, (2)Q 点(),A a b 是直线2y x =-上的一点,∴2b a =-.Q 2a a >-,根据友好点的定义,点B 的坐标为()2,B a b -,①当点A 和点B 重合,∴2b b =-. 解得0b =或1b =-. 当0b =时,2a =;当1b =-时,1a =,∴点A 的坐标是()2,0或()1,1-.②当点A 和点B 不重合,1a ≠且2a ≠.当1a <或2a >时,()222313224AB b b a a a ⎛⎫=--=-+=-- ⎪⎝⎭. ∴当a ≤32时,AB 的长度随着a 的增大而减小, ∴取1a <.当12a <<时, ()22231+3224AB b b a a a ⎛⎫=--=--=--+ ⎪⎝⎭ .∴当32a ≥时,AB 的长度随着a 的增大而减小,∴取322a ≤<. 综上,当1a <或322a ≤<时,AB 的长度随着a 的增大而减小. 【点睛】本题属于阅读理解题型,结合二次函数的基本性质进行解题,第二问的第二小问的关键是求出AB 的长用a 进行表示,然后利用二次函数基本性质进行分类讨论6.在平面直角坐标系中,抛物线y =﹣x 2+bx +c 经过点A 、B 、C ,已知A (﹣1,0),C (0,3).(1)求抛物线的解析式;(2)如图1,P 为线段BC 上一点,过点P 作y 轴的平行线,交抛物线于点D ,当△CDP 为等腰三角形时,求点P 的坐标;(3)如图2,抛物线的顶点为E ,EF ⊥x 轴于点F ,N 是线段EF 上一动点,M (m ,0)是x 轴一个动点,若∠MNC =90°,请求出m 的取值范围.【答案】(1)y =﹣x 2+2x +3;(2)点P 的坐标为(1,2)或(2,1)或(3﹣2,23)554m -≤≤ 【解析】 【分析】(1)利用待定系数法即可求得此抛物线的解析式;(2)由待定系数法即可求得直线BC 的解析式,再设P (t ,3﹣t ),即可得D (t ,﹣t 2+2t +3),即可求得PD 的长,然后分三种情况讨论,求点P 的坐标; (3)直角三角形斜边上的中线等于斜边的一半列出关系式m =(n ﹣32)2﹣54,然后根据n 的取值得到最小值. 【详解】解:(1)∵抛物线y =﹣x 2+bx +c 经过点A 、B 、C ,A (﹣1,0),C (0,3),∴103b c c --+=⎧⎨=⎩,解得b =2,c =3.故该抛物线解析式为:y =﹣x 2+2x +3.(2)令﹣x 2+2x +3=0, 解得x 1=﹣1,x 2=3, 即B (3,0),设直线BC 的解析式为y =kx +b ′,则330b k b ''=⎧⎨+=⎩,解得:k=-1,b’=3故直线BC 的解析式为y =﹣x +3; ∴设P (t ,3﹣t ), ∴D (t ,﹣t 2+2t +3),∴PD =(﹣t 2+2t +3)﹣(3﹣t )=﹣t 2+3t , ∵OB =OC =3,∴△BOC 是等腰直角三角形, ∴∠OCB =45°,当CD =PC 时,则∠CPD =∠CDP , ∵PD ∥y 轴,∴∠CPD =∠OCB =45°, ∴∠CDP =45°, ∴∠PCD =90°,∴直线CD 的解析式为y =x +3, 解2323y x y x x =+⎧⎨=-++⎩得03x y =⎧⎨=⎩或14x y =⎧⎨=⎩∴D (1,4), 此时P (1,2);当CD =PD 时,则∠DCP =∠CPD =45°, ∴∠CDP =90°, ∴CD ∥x 轴, ∴D 点的纵坐标为3,代入y =﹣x 2+2x +3得,3=﹣x 2+2x +3, 解得x =0或x =2, 此时P (2,1);当PC =PD 时,∵PC t , ∴=﹣t 2+3t ,解得t =0或t =3,此时P (3);综上,当△CDP 为等腰三角形时,点P 的坐标为(1,2)或(2,1)或(3) (3)如图2,由(1)y =﹣x 2+2x +3=﹣(x ﹣1)2+4, ∴E (1,4),设N (1,n ),则0≤n ≤4,取CM 的中点Q (2m ,32), ∵∠MNC =90°, ∴NQ =12CM , ∴4NQ 2=CM 2, ∵NQ 2=(1﹣2m )2+(n ﹣32)2, ∴4[(1﹣2m )2+(n ﹣32)2]=m 2+9, 整理得,m =(n ﹣32)2﹣54, ∵0≤n ≤4,当n =32时,m 最小值=﹣54,n =4时,m =5, 综上,m 的取值范围为:﹣54≤m ≤5.【点睛】此题考查了待定系数法求函数的解析式、平行线的性质、二次函数的最值问题、判别式的应用以及等腰直角三角形的性质等知识.此题综合性很强,难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用.7.如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线对称轴DE交x轴于点E,连接BD.(1)求经过A,B,C三点的抛物线的函数表达式;(2)点P是线段BD上一点,当PE=PC时,求点P的坐标.【答案】(1)y=﹣x2+2x+3;(2)点P的坐标为(2,2).【解析】【分析】(1)利用待定系数法求出过A,B,C三点的抛物线的函数表达式;(2)连接PC、PE,利用公式求出顶点D的坐标,利用待定系数法求出直线BD的解析式,设出点P的坐标为(x,﹣2x+6),利用勾股定理表示出PC2和PE2,根据题意列出方程,解方程求出x的值,计算求出点P的坐标.【详解】解:(1)∵抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,∴10930b cb c--+=⎧⎨-++=⎩,解得23bc=⎧⎨=⎩,∴所求的抛物线的函数表达式为y=﹣x2+2x+3;(2)如图,连接PC,PE.抛物线的对称轴为x=222(1)ba-=-⨯-=1.当x=1时,y=4,∴点D的坐标为(1,4).设直线BD的解析式为y=kx+b,则430 k bk b+=⎧⎨+=⎩,解得26kb=-⎧⎨=⎩.∴直线BD的解析式为:y=2x+6,设点P的坐标为(x,﹣2x+6),又C(0,3),E(1,0),则PC2=x2+(3+2x﹣6)2,PE2=(x﹣1)2+(﹣2x+6)2,∵PC=PE,∴x2+(3+2x﹣6)2=(x﹣1)2+(﹣2x+6)2,解得,x=2,则y=﹣2×2+6=2,∴点P的坐标为(2,2).【点睛】本题考查的是二次函数的图象和性质、待定系数法求函数解析式,掌握二次函数的图象和性质、灵活运用待定系数法是解题的关键.8.如图1,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.(1)求抛物线的解析式;(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.(3)在(1)中抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.(4)如图2,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.【答案】(1)y=﹣x2﹣2x+3;(2)存在符合条件的点P,其坐标为P(﹣110)或P(﹣110P(﹣1,6)或P(﹣1,53);(3)存在,Q(﹣1,2);(4)63 8,315,24E⎛⎫-⎪⎝⎭.【解析】【分析】(1)已知抛物线过A、B两点,可将两点的坐标代入抛物线的解析式中,用待定系数法即可求出二次函数的解析式;(2)可根据(1)的函数解析式得出抛物线的对称轴,也就得出了M点的坐标,由于C是抛物线与y轴的交点,因此C的坐标为(0,3),根据M、C的坐标可求出CM的距离.然后分三种情况进行讨论:①当CP=PM时,P位于CM的垂直平分线上.求P点坐标关键是求P的纵坐标,过P作PQ⊥y轴于Q,如果设PM=CP=x,那么直角三角形CPQ中CP=x,OM的长,可根据M 的坐标得出,CQ=3﹣x,因此可根据勾股定理求出x的值,P点的横坐标与M的横坐标相同,纵坐标为x,由此可得出P的坐标.②当CM=MP时,根据CM的长即可求出P的纵坐标,也就得出了P的坐标(要注意分上下两点).③当CM=C P时,因为C的坐标为(0,3),那么直线y=3必垂直平分PM,因此P的纵坐标是6,由此可得出P的坐标;(3)根据轴对称﹣最短路径问题解答;(4)由于四边形BOCE不是规则的四边形,因此可将四边形BOCE分割成规则的图形进行计算,过E作EF⊥x轴于F,S四边形BOCE=S△BFE+S梯形FOCE.直角梯形FOCE中,FO为E的横坐标的绝对值,EF为E的纵坐标,已知C的纵坐标,就知道了OC的长.在△BFE中,BF=BO﹣OF,因此可用E的横坐标表示出BF的长.如果根据抛物线设出E的坐标,然后代入上面的线段中,即可得出关于四边形BOCE的面积与E的横坐标的函数关系式,根据函数的性质即可求得四边形BOCE的最大值及对应的E的横坐标的值.即可求出此时E的坐标.【详解】(1)∵抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),∴30 9330 a ba b++=⎧⎨-+=⎩,解得:12 ab=-⎧⎨=-⎩.∴所求抛物线解析式为:y=﹣x2﹣2x+3;(2)如答图1,∵抛物线解析式为:y =﹣x 2﹣2x+3,∴其对称轴为x =22-=﹣1, ∴设P 点坐标为(﹣1,a ),当x =0时,y =3,∴C (0,3),M (﹣1,0)∴当CP =PM 时,(﹣1)2+(3﹣a )2=a 2,解得a =53, ∴P 点坐标为:P 1(﹣1,53); ∴当CM =PM 时,(﹣1)2+32=a 2,解得a =±10,∴P 点坐标为:P 2(﹣1,10)或P 3(﹣1,﹣10);∴当CM =CP 时,由勾股定理得:(﹣1)2+32=(﹣1)2+(3﹣a )2,解得a =6, ∴P 点坐标为:P 4(﹣1,6).综上所述存在符合条件的点P ,其坐标为P (﹣1,10)或P (﹣1,﹣10)或P (﹣1,6)或P (﹣1,53); (3)存在,Q (﹣1,2),理由如下:如答图2,点C (0,3)关于对称轴x =﹣1的对称点C′的坐标是(﹣2,3),连接AC′,直线AC′与对称轴的交点即为点Q .设直线AC′函数关系式为:y =kx+t (k≠0).将点A (1,0),C′(﹣2,3)代入,得023k t k t +=⎧⎨-+=⎩, 解得11k t =-⎧⎨=⎩, 所以,直线AC′函数关系式为:y =﹣x+1.将x =﹣1代入,得y =2,即:Q (﹣1,2);(4)过点E 作EF ⊥x 轴于点F ,设E (a ,﹣a 2﹣2a+3)(﹣3<a <0)∴EF =﹣a 2﹣2a+3,BF =a+3,OF =﹣a∴S 四边形BOCE =12BF•EF+12(OC+EF )•OF =12(a+3)•(﹣a 2﹣2a+3)+12(﹣a 2﹣2a+6)•(﹣a ) =﹣32a 2﹣92a+92=﹣32(a+32)2+638, ∴当a =﹣32时,S 四边形BOCE 最大,且最大值为638. 此时,点E 坐标为(﹣32 ,154). 【点睛】本题主要考查了二次函数的综合知识,要注意的是(2)中,不确定等腰三角形哪条边是底边的情况下,要分类进行求解,不要漏解.9.如果一条抛物线y =ax 2+bx +c (a ≠0)与x 轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a ,b ,c ]称为“抛物线系数”.(1)任意抛物线都有“抛物线三角形”是 (填“真”或“假”)命题;(2)若一条抛物线系数为[1,0,﹣2],则其“抛物线三角形”的面积为 ;(3)若一条抛物线系数为[﹣1,2b ,0],其“抛物线三角形”是个直角三角形,求该抛物线的解析式;(4)在(3)的前提下,该抛物线的顶点为A ,与x 轴交于O ,B 两点,在抛物线上是否存在一点P ,过P 作PQ ⊥x 轴于点Q ,使得△BPQ ∽△OAB ?如果存在,求出P 点坐标;如果不存在,请说明理由.【答案】(1)假;(2)223)y =-x 2+2x 或y =-x 2-2x ;(4)P (1,1)或P (-1,-3)或P (1,-3)或(-1,1).【解析】分析:(1)当△>0时,抛物线与x 轴有两个交点,由此可得出结论;(2)根据“抛物线三角形”定义得到22y x =-,由此可得出结论;(3)根据“抛物线三角形”定义得到y =-x 2+2bx ,它与x 轴交于点(0,0)和(2b ,0);当抛物线三角形是直角三角形时,根据对称性可知它一定是等腰直角三角形, 由抛物线顶点为(b ,b 2),以及直角三角形斜边上的中线等于斜边的一半得到2122b b =⨯,解方程即可得到结论; (4)分两种情况讨论:①当抛物线为y =-x 2+2x 时,②当抛物线为y =-x 2-2x 时. 详解:(1)当△>0时,抛物线与x 轴有两个交点,此时抛物线才有“抛物线三角形”,故此命题为假命题;(2)由题意得:22y x =-,令y =0,得:x =2±,∴ S =12222⨯⨯=12x x ; (3)依题意:y =-x 2+2bx ,它与x 轴交于点(0,0)和(2b ,0);当抛物线三角形是直角三角形时,根据对称性可知它一定是等腰直角三角形. ∵y =-x 2+2bx =22()x b b --+,∴顶点为(b ,b 2),由直角三角形斜边上的中线等于斜边的一半得到:2122b b =⨯,∴2b b =,解得:b =0(舍去)或b =±1, ∴y =-x 2+2x 或y =-x 2-2x .(4)①当抛物线为y =-x 2+2x 时.∵△AOB 为等腰直角三角形,且△BPQ ∽△OAB ,∴△BPQ 为等腰直角三角形,设P (a ,-a 2+2a ),∴Q ((a ,0), 则|-a 2+2a |=|2-a |,即(2)2a a a -=-.∵a -2≠0,∴1a =,∴a =±1,∴P (1,1)或(-1, -3).②当抛物线为y =-x 2-2x 时.∵△AOB 为等腰直角三角形,且△BPQ ∽△OAB ,∴△BPQ 为等腰直角三角形,设P (a ,-a 2-2a ),∴Q ((a ,0),则|-a 2-2a |=|2+a |,即(2)2a a a +=+.∵a +2≠0,∴1a =,∴a =±1,∴P (1,-3,)或(-1,1).综上所述:P (1,1)或P (-1,-3)或P (1,-3,)或(-1,1).点睛:本题是二次函数综合题.考查了二次函数的性质以及“抛物线三角形”的定义.解题的关键是弄懂“抛物线三角形”的定义以及分类讨论.10.如图,已知直线y kx 6=-与抛物线2y ax bx c =++相交于A ,B 两点,且点A (1,-4)为抛物线的顶点,点B 在x 轴上。
2021中考数学专题复习:二次函数综合专项训练题1(培优 附答案详解)

(1)求抛物线的解析式;
(2)点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,设△PBC的面积为S,求S关于m的函数表达式(指出自变量m的取值范围)和S的最大值;
(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N使得∠CMN=90°,且△CMN与△OBC相似,如果存在,请求出点M和点N的坐标.(1)求这个抛物 Nhomakorabea的表达式;
(2)已知点D在抛物线上,且横坐标为2,求出△BCD的面积;
(3)点P是直线BC上方的抛物线上一动点,过点P作PQ垂直于x轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
12.如图,抛物线 与 轴交于点 、 ,与 轴交于点 , , 、 两点间的距离为 ,抛物线的对称轴为 .
6.如图,在平面直角坐标系xOy中,直线y=mx+k,与x轴,y轴分别交于点A,B,经过点A的抛物线y=ax2+bx﹣3a与x轴另一个交点为点D,AD=4,将点B向右平移5个单位长度,得到点C.
(1)求点C的坐标(用k表示);
(2)求抛物线的对称轴;
(3)若抛物线的对称轴在y轴右侧,连接BD,BD比BO长1,抛物线与线段BC恰有一个公共点,求直线y=mx+k的解析式和a的取值范围.
(1)求抛物线的解析式;
(2)如图1,对称轴上是否存在点 ,使 ,若存在,求出点 的坐标;若不存在,请说明理由.
(3)如图2,抛物线的顶点为 ,对称轴交 轴于点 ,点 为抛物线上一点,点 不与点 重合.当 时,过点 分别作 轴的垂线和平行线,与 轴交于点 、与对称轴交于点 ,得到矩形 ,求矩形 周长的最大值;
2021中考数学专题复习:二次函数综合培优训练题(精选习题40道 附答案详解)

2021中考数学专题复习:二次函数综合培优训练题(精选习题40道 附答案详解) 1.如图,函数y =-x 2+12x +c (-2020≤x ≤1)的图象记为L 1,最大值为M 1;函数y =-x 2+2cx +1(1≤x ≤2020)的图象记为L 2,最大值为M 2.L 1的右端点为A ,L 2的左端点为B ,L 1,L 2合起来的图形记为L .(1)当c =1时,求M 1,M 2的值;(2)若把横、纵坐标都是整数的点称为“美点”,当点A ,B 重合时,求L 上“美点”的个数;(3)若M 1,M 2的差为4716,直接写出c 的值.2.如图,二次函数21y ax bx =+-的顶点C 的坐标为(11),.(1)求a ,b 的值;(2)已知A 点为抛物线上异于C 的一点,且A 点横、纵坐标相等,B 为x 轴上任意一点,当BA BC +取最小值时,求出B 点坐标和此时ABC ∆的面积.3.如图,二次函数2y ax bx c =++的图象交x 轴于点()2,0A -,点()10B ,,交y 轴于点()0,2C(1)求二次函数的解析式;(2)连接AC ,在直线AC 上方的抛物线上有一点N ,过点N 作y 轴的平行线,交直线AC 于点F ,设点N 的横坐标为n ,线段NF 的长为l ,求l 关于n 的函数关系式; (3)若点M 在x 轴上,是否存在点M ,使以B 、C 、M 为顶点的三角形是等腰三角形,若存在,直接写出点M 的坐标;若不存在,说明理由.4.如图,抛物线1C :212y x bx c =++(b ,c 是常数)经过(4,0)A -、(0,2)B 两点.(1)求b ,c 的值;(2)向右平移抛物线1C ,使它经过点B ,得抛物线2C ,2C 与x 轴的一个交点为C ,且在另一个交点的左侧.①求抛物线2C 的表达式;②D 是点B 关于抛物线2C 对称轴的对称点,E 是线段CD 上一点,EF x ⊥轴,交抛物线2C 于点F ,H 为垂足,设(,0)H t ,线段EF 的长为m ,求t 的值,使m 取得最大值.5.综合与探究已知:p 、q 是方程2650x x -+=的两个实数根,且p q <,抛物线2y x bx c=-++的图像经过点(,0)A p 、(0,)B q .(1)求这个抛物线的解析式;(2)设(1)中抛物线与x 轴的另一交点为C ,抛物线的顶点为D ,试求出点C 、D 的坐标和BCD 的面积;(3)P 是线段OC 上的一点,过点P 作PH x ⊥轴,与抛物线交于H 点,若直线BC 把PCH △分成面积之比为2:3的两部分,请直接写出P 点的坐标 ;(4)若点M 在直线CB 上,点N 在平面上,直线CB 上是否存在点M ,使以点C 、点D 、点M 、点N 为顶点的四边形为菱形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.6.如图,已知抛物线y=ax2+bx+c的图象经过点A(3,3)、B(4,0)和原点O,P为直线OA上方抛物线上的一个动点.(1)求直线OA及抛物线的解析式;(2)过点P作x轴的垂线,垂足为D,并与直线OA交于点C,当△PCO为等腰三角形时,求D的坐标;(3)设P关于对称轴的点为Q,抛物线的顶点为M,探索是否存在一点P,使得△PQM的面积为18,如果存在,求出P的坐标;如果不存在,请说明理由.7.如图1,二次函数y=ax2﹣3ax﹣4a的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,﹣3).(1)求二次函数的表达式及点A、点B的坐标;(2)若点D在二次函数图象上,且45DBC ABCS S△△,求点D的横坐标;(3)将直线BC向下平移,与二次函数图象交于M,N两点(M在N左侧),如图2,过M作ME∥y轴,与直线BC交于点E,过N作NF∥y轴,与直线BC交于点F,当MN+ME的值最大时,求点M的坐标.8.如图,抛物线21y ax x c =-+与x 轴交于点(3,0)A -和点B ,并经过点52,2⎛⎫- ⎪⎝⎭,抛物线1y 的顶点为C .将抛物线1y 平移后得到顶点为B 且对称轴为直线l 的抛物线2y .(1)求抛物线2y 的表达式;(2)在直线l 上是否存在点P ,使PBC ∆为等腰三角形?若存在,请求出所有点P 的坐标;若不存在,请说明理由.9.在平面直角坐标系中,O 为坐标原点,抛物线C :243y x x =++的顶点为M ,与y轴的交点为N .(1)求点M ,N 的坐标;(2)已知点P (4,2),将抛物线C 向上平移得抛物线C ',点N 平移后的对应点为N ',且PN ON ''=,求抛物线C '的解析式;(3)将抛物线C :243y x x =++沿y 轴翻折,得抛物线C '',抛物线C ''与x 轴交于点A ,B (点A 在点B 的左侧),与y 轴交于点D ,平行于x 轴的直线l 与抛物线C ''交于点E (1x ,1y ),F (2x ,2y ),与直线BD 交于点G (3x ,3y ),若1x <2x <3x ,结合函数的图象,求1232x x x ++的取值范围. 10.如图, 已知二次函数2y ax bx c =++(a ,b ,c 为常数)的对称轴为1x =,与y 轴的交点为()0,4C ,y 的最大值为5,顶点为M ,过点()0,1D 且平行于x 轴的直线与抛物线交于点A ,B .(1)求该二次函数的解析式和点A ,B 的坐标.(2)点P 是直线AC 上的动点,若点P ,点C ,点M 所构成的三角形与BCD 相似,求出所有点P 的坐标.11.如图,抛物线L 1:y =-x 2-2x +3交x 轴于A ,B 两点,交y 轴于M 点抛物线L 1向右平移2个单位得到抛物线L 2,L 2交x 轴于C ,D 两点.(1)求抛物线L 2对应的函数表达式;(2)抛物线L 1或L 2在x 轴上方的部分是否存在点N ,使以A ,C ,M ,N 为顶点的四边形是平行四边形?若存在,求出点N 的坐标;若不存在,请说明理由;(3)若点P 是抛物线L 1上的一个动点(P 不与点A ,B 重合),那么点P 关于原点的对称点Q 是否在抛物线L 2上?请说明理由.12.如图,抛物线212y x bx c =-++与x 轴交于A 、B 两点,与y 轴交于点C ,24OB OC ==.(1)求抛物线的解析式;(2)点P 为第一象限抛物线上一点,连接PA 、PC ,设点P 的横坐标为t ,PAC ∆的面积为S ,求S 与t 的函数关系式;(3)在(2)的条件下,点Q 为第四象限抛物线上一点,连接QC ,过点P 作x 轴的垂线交CQ 于点D ,射线BD 交第三象限抛物线于点E ,连接QE ,若32S =,2QEB ABE ∠=∠,求点Q 的坐标.13.在小明的一次投篮中,球出手时离地面高2米,与篮圈中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米.篮球运行的轨迹为抛物线,篮球中心距离地面3米,通过计算说明此球能否投中.探究一:若出手的角度、力度和高度都不变的情况下,求小明朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮筐中?探究二:若出手的角度、力度和高度都发生改变的情况下,但是抛物线的顶点等其他条件不变,求小明出手的高度需要增加多少米才能将篮球投入篮筐中?探究三:若出手的角度、力度都改变,出手高度不变,篮筐的坐标为(6,3.44),球场上方有一组高6米的电线,要想在篮球不触碰电线的情况下,将篮球投入篮筐中,直接写出二次函数解析式中a 的取值范围.14.抛物线213222y x x =--与直线2y x =-交于A 、B 两点,抛物线的顶点记为C .其对称轴与x 轴的交点记为D ;(1)如图1,在线段AB 上有两个动点P 、K ,且2PK =////PE KF y 轴,分别交抛物线于点E 、F ,过点O 作另一条直线//l AB ,当PE FK +取得最大值时,有一动点Q 从E 出发沿某条路径以1个单位每秒的速度先运动到直线l 上的点M 处,再沿垂直于AB 的方向以1个单位每秒的速度从点M 运动到AB 上N 5个单位每秒的速度从点N 回到点A ,运动停止,请求出满足条件的E 点坐标及动点Q 运动总时间的最小值;(2)如图2,连接BD ,将BOD 沿射线DB 平移得B O D '''△,当O '恰好落在∠BDO 的角平分线上时,在x 轴上取一点R ,再将RO B ''△沿RO '翻折得RO B '''△,连接OB ''、B B ''',当DB B '''△为等腰三角形时,求出B ''的坐标.15.如图,抛物线23y ax bx =++与x 轴交于两点()30A -,和()1,0,B 与y 轴交于点,C 动点D 沿ABC 的边AB 以每秒2个单位长度的速度由起点A 向终点B 运动,过点D 作x 轴的垂线,交ABC 的另一边AC 于点,E 将ADE 沿DE 折叠,使点A 落在点F 处,设点D 的运动时间为t 秒.(1)求抛物线的解析式;(2)N 为抛物线上的点(点N 不与点C 重合)且满足NAB ABC SS =直接写出N 点的坐标;(3)是否存在某一时刻t ,使EFC 的面积最大,若存在,求出t 的值和最大面积;若不存在,请说明理由.16.如图,直线y=﹣34x+3与x 轴交于点C ,与y 轴交于点B ,抛物线y=ax 2+34x+c 经过B 、C 两点.(1)求抛物线的解析式;(2)如图,点E 是直线BC 上方抛物线上的一动点,当△BEC 面积最大时,请求出点E 的坐标和△BEC 面积的最大值;(3)在(2)的结论下,过点E 作y 轴的平行线交直线BC 于点M ,连接AM ,点Q 是抛物线对称轴上的动点,在抛物线上是否存在点P ,使得以P 、Q 、A 、M 为顶点的四边形是平行四边形?如果存在,请直接写出点P 的坐标;如果不存在,请说明理由.17.如图.抛物线2y ax bx c =++经过()()()1,04,0 .0.2A B C --、三点. (1)求抛物线的函数关系式;(2)若直线l 是抛物线的对称轴,设点P 是直线l 上的一个动点,当PAC ∆的周长最小时,求点P 的坐标;(3)在线段AB 上是否存在点(),0M m ,使得以线段CM 为直径的圆与边BC 交于Q 点(与点C 不同),且以Q B O 、、点为顶点的三角形是等腰三角形?若存在,求出m 的值;若不存在,请说明理由.18.如图,在平面直角坐标系中,抛物线232y ax x c =-+过点(1,0)A -,(4,0)B ,与y 轴交于点C .点P 是x 轴下方的抛物线上一动点(包含点A ,B ).作直线BC ,若过点P 作x 轴的垂线,交直线BC 于点Q .(1)求抛物线的解析式;(2)在点P 运动的过程中,请求出BCP 面积的最大值及此时点P 的坐标; (3)在点P 运动的过程中,是否存在点P ,使CPQ 是等腰三角形.若存在,请直接写出点P 的横坐标;若不存在,请说明理由.19.如图,已知抛物线y =ax 2+bx +3(a ≠0)经过点A (1,0)和点B (3,0),与y 轴交于点C .(1)求此抛物线的解析式;(2)若点P 是直线BC 下方的抛物线上一动点(不点B ,C 重合),过点P 作y 轴的平行线交直线BC 于点D ,求PD 的长度最大时点P 的坐标.(3)设抛物线的对称轴与BC 交于点E ,点M 是抛物线的对称轴上一点,N 为y 轴上一点,是否存在这样的点M 和点N ,使得以点C 、E 、M 、N 为顶点的四边形是菱形?如果存在,请直接写出点M 的坐标;如果不存在,请说明理由.20.为庆祝新中国成立70周年,国庆期间,北京举办“普天同庆•共筑中国梦”的游园活动,为此,某公园在中央广场处建了一个人工喷泉,如图,人工喷泉有一个竖直的喷水枪AB ,喷水口A 距地面2m ,喷出水流的运动路线是抛物线.如果水流的最高点P 到喷水枪AB 所在直线的距离为1m ,且到地面的距离为3.6m ,求水流的落地点C 到水枪底部B 的距离.21.如图,抛物线22y ax bx =++与x 轴交于两点(1,0)A 和(4,0)B ,与y 轴交于点C ,点D 是抛物线上一个动点,过点D 作x 轴的垂线,与直线BC 相交于点E . (1)求抛物线的解析式;(2)当点D 在直线BC 下方的抛物线上运动时,线段DE 的长度是否存在最大值?存在的话,求出其最大值和此时点D 的坐标;(3)若以O ,C ,D ,E 为顶点的四边形为平行四边形,求点D 的所有坐标.22.如图,二次函数22y ax x c =-+的图像与x 轴交于()()1030A B -,,,两点,与y 轴交于点C ,直线l 是抛物线的对称轴,E 是抛物线的顶点.(1)求抛物线的解析式及顶点E 的坐标;(2)如图,连接BE ,线段OC 上的点F 关于直线l 的对称点F '恰好在线段BE 上,求点F 的坐标.23.已知二次函数243y ax ax b =-++(0a ≠).(1)求出二次函数图象的对称轴;(2)若该二次函数的图象经过点()1,3,且整数a ,b 满足49a b <+<,求二次函数的表达式;(3)对于该二次函数图象上的两点()11,A x y ,()22,B x y ,设11t x t ≤≤+,当25x ≥时,均有12y y ≤,请结合图象,直接写出t 的取值范围.24.如图,已知抛物线2y x bx c =-++与x 轴交于A 、B 两点,4AB =,交y 轴于点C ,对称轴是直线1x =.(1)求抛物线的解析式及点C 的坐标;(2)连接BC ,E 是线段OC 上一点,E 关于直线1x =的对称点F 正好落在BC 上,求点F 的坐标;(3)动点M 从点O 出发,以每秒2个单位长度的速度向点B 运动,过M 作x 轴的垂线交抛物线于点N ,交线段BC 于点Q .设运动时间为t (0t >)秒.若AOC ∆与BMN ∆相似,请求出t 的值.25.如图,在平面直角坐标系xOy 中,直线l 和抛物线W 交于A ,B 两点,其中点A 是抛物线W 的顶点.当点A 在直线l 上运动时,抛物线W 随点A 作平移运动.在抛物线平移的过程中,线段AB 的长度保持不变.应用上面的结论,解决下列问题:在平面直角坐标系xOy 中,已知直线1:2l y x =-.点A 是直线1l 上的一个动点,且点A 的横坐标为t .以A 为顶点的抛物线21:C y x bx c =-++与直线1l 的另一个交点为点B .(1)当0t =时,求抛物线1C 的解析式和AB 的长;(2)当点B 到直线OA 的距离达到最大时,直接写出此时点A 的坐标;(3)过点A 作垂直于y 轴的直线交直线21:2l y x =于点C .以C 为顶点的抛物线22:C y x mx n =++与直线2l 的另一个交点为点D .①当AC ⊥BD 时,求t 的值;②若以A ,B ,C ,D 为顶点构成的图形是凸四边形(各个内角度数都小于180°)时,直接写出满足条件的t 的取值范围.26.已知抛物线224y ax ax a =++-的顶点为点P ,与x 轴分别交于A 、B 两点(A 点在B 点的左侧),与y 轴交于点C .(1)直接写出点P 的坐标为________;(2)如图,若A 、B 两点在原点的两侧,且3OA OB =,四边形MNEF 为正方形,其中顶点E 、F 在x 轴上,M 、N 位于抛物线上,求点E 的坐标;(3)若线段2AB =,点Q 为反比例函数k y x=与抛物线224y ax ax a =++-在第一象限内的交点,设Q 的横坐标为m ,当13m <<时,求k 的取值范围.27.在平面直角坐标系xOy 中,对于图形G ,若存在一个正方形γ,这个正方形的某条边与x 轴垂直,且图形G 上的所有的点都在该正方形的内部或者边上,则称该正方形γ为图形G 的一个正覆盖.很显然,如果图形G 存在一个正覆盖,则它的正覆盖有无数个,我们将图形G 的所有正覆盖中边长最小的一个,称为它的紧覆盖,如图所示,图形G 为三条线段和一个圆弧组成的封闭图形,图中的三个正方形均为图形G 的正覆盖,其中正方形ABCD 就是图形G 的紧覆盖.(1)对于半径为2的O ,它的紧覆盖的边长为____.(2)如图1,点P 为直线23y x =-+上一动点,若线段OP 的紧覆盖的边长为2,求点P 的坐标.(3)如图2,直线33y x =+与x 轴,y 轴分别交于A B ,,①以O 为圆心,r 为半径的O 与线段AB 有公共点,且由O 与线段AB 组成的图形G 的紧覆益的边长小于4,直接写出r 的取值范围;②若在抛物线2220y ax ax a =+-≠() 上存在点C ,使得ABC 的紧覆益的边长为3,直接写出a 的取值范围.28.已知点A(﹣4,8)和点B(2,n)在抛物线y=ax2上.(Ⅰ)求该抛物线的解析式和顶点坐标,并求出n的值;(Ⅱ)求点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求此时点Q的坐标;(Ⅲ)平移抛物线y=ax2,记平移后点A的对应点为A',点B的对应点为B',点C(﹣2,0)是x轴上的定点.①当抛物线向左平移到某个位置时,A'C+CB'最短,求此时抛物线的解析式;②D(﹣4,0)是x轴上的定点,当抛物线向左平移到某个位置时,四边形A'B'CD的周长最短,求此时抛物线的解析式(直接写出结果即可).29.如图,二次函数y=ax2+bx-3的图象与x轴相交于A(-1,0),B(3,0)两点.与y轴相交于点C(1)求这个二次函数的解析式.(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,请问:当点P的坐标为多少时,线段PM的长最大?并求出这个最大值.30.在平面直角坐标系中,直线AB与抛物线y=ax2+bx+c交于A,B(点A在点B的左侧)两点,点C是该抛物线上任意一点,过C点作平行于y轴的直线交AB于D,分别过点A,B作直线CD的垂线,垂足分别为点E,F.特例感悟:(1)已知:a=-2,b=4,c=6.①如图①,当点C 的横坐标为2,直线AB 与x 轴重合时,CD=____,|a|·AE·BF=___. ②如图②,当点C 的横坐标为1,直线AB//x 轴且过抛物线与y 轴的交点时,CD=_____,|a|·AE·BF=_______.③如图③,当点C 的横坐标为2,直线AB 的解析式为y=x-3时,CD=___,|a|·AE·BF=___.猜想论证:(2)由(1)中三种情况的结果,请你猜想在一般情况下CD 与|a|·AE·BF 之间的数量关系,并证明你的猜想.拓展应用.(3)若a=-1,点A ,B 的横坐标分别为-4,2,点C 在直线AB 的上方的抛物线上运动(点C 不与点A ,B 重合),在点C 的运动过程中,利用(2)中的结论求出△ACB 的最大面积.31.已知二次函数212y x bx =-++的图像与y 轴交于点A ,一次函数212y x m =+的图像经过点A ,且与二次函数图像的另一个交点为点B .(1)用含有字母b 代数式表示点B 的坐标.(2)点M 的坐标为(-2,0),过点M 作x 轴的垂线交抛物线于点C .①当x <-2时,y 1<y 2,求b 的取值范围;②若△ABC 是直角三角形,求b 的值.32.如图,抛物线2y x bx c =++经过(1,0),(3,0)A B -两点,与y 轴交于点C .(2)已知点D 为y 轴上一点,点D 关于直线BC 的对称点为'D .①当点'D 刚好落在第四象限的抛物线上时,求出点D 的坐标;②点P 在抛物线上,连接''PD PD DD 、、,是否存在点P ,使'PDD ∆为等腰直角三角形?若存在,请直接写出P 点的坐标;若不存在,请说明理由.33.已知:如图,抛物线2y ax x c =++与x 轴交于点()()1,0,3,0A B -.(1)试确定该抛物线的函数表达式;(2)已知点C 是该抛物线的顶点,求OBC ∆的面积;(3)若点P 是线段BC 上的一动点,求OP 的最小值.34.如图,抛物线2y x 2x 3=-++与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D ,连接BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点(P 不与B ,C 两点重合),过点P 作x 轴的垂线交抛物线于点F ,设点P 的横坐标为()03m m <<(1)当m 为何值时,四边形PEDF 为平行四边形;(2)设BCF 的面积为S ,求S 的最大值.35.某品牌服装公司经过市场调査,得到某种运动服的月销量 y (件)是售价 x (元/件)的一次函数,其售价、月销售量、月销售利润 w (元)的三组对应值如下表:注:月销售利润=月销售量×(售价一进价)(1)求 y 关于 x 的函数解析式(不要求写出自变量的取值范围);(2)当售价是多少时,月销售利润最大?最大利润是多少元?(3)为响应号召,该公司决定每售出 1 件服装,就捐赠 a 元(a > 0),商家规定该服装售价不得超过200 元,月销售量仍满足上关系,若此时月销售最大利润仍可达 9600 元,求 a 的值.36.已知,如图1,抛物线2l y ax bx c =++:过(1,0),(3,0),(0,3)A B C -三点,顶点为点D ,连接,,AC CD DB ,点P 为抛物线对称轴上一点,连接,PC PA ,直线'l y kx n =+:过点,B C 两点.(1)求抛物线l 及直线'l 的函数解析式;(2)求PC PA +的最小值;(3)求证:AOC ∆∽DCB ∆;(4)如图2,若点M 是在抛物线l 上且位于第一象限内的一动点,请直接写出MBC ∆面积的最大值及此时点M 的坐标.37.如图所示,二次函数2(1)2y k x =-+的图象与一次函数2y kx k =-+的图象交于A 、B 两点,点B 在点A 的右侧,直线AB 分别交x 轴、y 轴于C 、D 两点,且k <0. (1)求A ,B 两点横坐标;(2)若△OAB 是以OA 为腰的等腰三角形,求k 的值.38.在平面直角坐标系xOy 中(如图),已知抛物线28(0)3y ax a x c a ⎛⎫=+++≠ ⎪⎝⎭经过点()3,2A --,与y 轴交于点()0,2B -,,抛物线的顶点为点C ,对称轴与x 轴交于点D .(1)求抛物线的表达式及点C 的坐标;(2)点E 是x 轴正半轴上的一点,如果AED BCD ∠=∠,求点E 的坐标;(3)在(2)的条件下,点P 是位于y 轴左侧抛物线上的一点,如果PAE △是以AE 为直角边的直角三角形,求点P 的坐标.39.如图,在平面直角坐标系中,抛物线223y x bx c =-++与y 轴交于点()0,2A 与x 轴交于()3,0B -、C 两点(点B 在点C 的左侧),抛物线的顶点为D .(1)求抛物线的表达式;(2)用配方法求点D 的坐标;(3)点P 是线段OB 上的动点.①过点P 作x 轴的垂线交抛物线于点E ,若PE PC =,求点E 的坐标;线段EF的长;③若点Q是射线OA上的动点,且始终满足OQ OP=,连接AP,DQ,请直接写出AP DQ+的最小值.40.已知点A(t,1)为函数y=ax2+bx+4(a,b为常数,且a≠0)与y=x图象的交点.(1)求t;(2)若函数y=ax2+bx+4的图象与x轴只有一个交点,求a,b;(3)若1≤a≤2,设当12≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.参考答案1.(1)当c =1时,M 1=1716,M 2=2;(2)3030;(3)c =-238或2. 【解析】【分析】(1)当c=1时,把函数的解析式化成顶点式即可求得1M ,2M 的值;(2)由已知可得点A ,B 重合时,122c c -=,12c =-,L 1上有1011个“美点”,L 2上有2020个“美点”.则L 上“美点”的个数是1011+2020-1=3030;(3)当14x =时,1116M c =+,由于L 2的对称轴为x c =,分两种情况求解:当c≥1时,2M =c 2+1;当c <1时,2M =2c ;再由已知列出等式即可求c 的值.【详解】(1)当c =1时,函数y =-x 2+12x +c =-x 2+12x +1=-(x -14)2+1716, 又-2020≤x ≤1,∴M 1=1716, y =-x 2+2cx +1=-x 2+2x +1=-(x -1)2+2,又1≤x ≤2020,∴M 2=2.(2)当x =1时,y =-x 2+12x +c =c -12;y =-x 2+2cx +1=2c . 若点A ,B 重合,则c -12=2c ,c =-12, ∴L 1∶y =-x 2+12x -12 (-2020≤x ≤1); L 2∶y =-x 2-x +1(1≤x ≤2020).在L 1上,x 为奇数的点是“美点”,则L 1上有1011个“美点”;在L 2上,x 为整数的点是“美点”,则L 2上有2020个“美点”.又点A ,B 重合,则L 上“美点”的个数是1011+2020-1=3030;(3)y =-x 2+12x +c (-2020≤x ≤1)上时,当14x =时,1116M c =+,y =-x 2+2cx +1(1≤x ≤2020),对称轴为x c =,当1c ≥时,221M c =+, ∴214711616c c +--=, ∴0c =(舍去)或2c =;当1c <时,22M c =, ∴14721616c c --=, ∴3c =(舍去)或238c =-; 综上,238c =-或2. 【点睛】 本题考查了二次函数的图象及性质;能够根据函数所给的取值范围,通过适当的分类讨论,正确的求函数的最大值是解题的关键.2.(1) 2,4a b =-=; (2) B 点坐标为2,03⎛⎫⎪⎝⎭,16 【解析】【分析】(1)由题意可设2(1)1y a x =-+,将(0,1)-代人即可求出解析式,得到a 与b ;(2)可设A 点坐标为(,)m m ,代入2241y x x =-+-求出m 得到点A 的坐标11,22⎛⎫⎪⎝⎭,,作A 点关于x 轴的对称点'A ,连接A C ',交x 轴于B 点,则此时BA BC A C '+=为最小值,求出直线A C '的解析式,得到直线与x 轴交点B 的坐标,分别作AM ,CN 垂直于x 轴,垂足分别为M ,N ,根据ABCABM NBC AMNC S S S S ∆∆∆=--四边形求出ABC ∆的面积. 【详解】解:(1)由题意可设2(1)1y a x =-+,将(0,1)-代人,得11a +=-,解得2a =-.∴该抛物线的解析式为222(1)1241y x x x =--+=-+-.2,4a b ∴=-=.(2)由题意可设A 点坐标为(,)m m ,代入2241y x x =-+-中,得2241m m m -+-=,解得112m =,21m = (舍去), 故A 点坐标为11,22⎛⎫⎪⎝⎭. 如图,作A 点关于x 轴的对称点'A ,连接A C ',交x 轴于B 点,则此时BA BC A C '+=为最小值.设A C '的解析式为y kx b =+将11,22A '⎛⎫- ⎪⎝⎭和(1,1)C 代入,得 11221k b k b ⎧+=-⎪⎨⎪+=⎩, 解得32k b =⎧⎨=-⎩, 32y x ∴=-,当0y =时,23x =, 故B 点坐标为2,03⎛⎫ ⎪⎝⎭. 分别作AM ,CN 垂直于x 轴,垂足分别为M ,N ,则ABC ABM NBC AMNC S S S S ∆∆∆=--四边形111121112111222232223⎛⎫⎛⎫⎛⎫=⨯⨯+-⨯-⨯-⨯⨯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 16=. 【点睛】此题考查待定系数法求函数解析式,抛物线与几何图形面积问题,轴对称的最短路径问题,图象与坐标轴交点问题.3.(1)y=-x 2-x+2;(2)l=-n 2-2n ;(3)存在,(-1,0)或(0)或(0)或(-32,0). 【解析】【分析】(1)利用交点式求二次函数的解析式;(2)设点N (n ,-n 2-n+2),则点F (n ,n+2),l=-n 2-n+2-(n+2)=-n 2-2n ;(3)分CB=CM 、BC=BM 、BM=CM 三种情况,分别求解即可.【详解】解:(1)∵二次函数y=ax 2+bx+c 的图象交x 轴于A (-2,0),B (1,0),设二次函数的解析式为:y=a (x+2)(x-1),把C (0,2)代入得:2=a (0+2)(0-1),a=-1,∴y=-(x+2)(x-1)=-x 2-x+2,故抛物线的表达式为:y=-x 2-x+2;(2)设直线AC 的解析式为:y=kx+b ,把A (-2,0)、C (0,2)代入得:2=0=2k b b -+⎧⎨⎩, 解得:=1=2k b ⎧⎨⎩, ∴直线AC 的解析式为:y=x+2,设点N (n ,-n 2-n+2),则点F (n ,n+2),l=-n2-n+2-(n+2)=-n2-2n;(3)存在,分三种情况:①如图2,当BC=CM1时,M1(-1,0);②如图2,由勾股定理得:BC=22+=,215以B为圆心,以BC为半径画圆,交x轴于M2、M3,则BC=BM2=BM3=5,此时,M2(1-5,0),M3(1+5,0);③如图3,作BC的中垂线,交x轴于M4,连接CM4,则CM4=BM4,设OM 4=x ,则CM 4=BM 4=x+1,由勾股定理得:22+x 2=(1+x )2,解得:x=32, ∵M 4在x 轴的负半轴上,∴M 4(-32,0), 综上,点M 的坐标为:(-1,0)或(0)或(0)或(-32,0). 【点睛】此题考查二次函数综合题,二次函数的解析式.解题关键在于利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系. 4.(1)52,2;(2)①215222y x x =-+,②3 【解析】【分析】(1)将A 、B 两点坐标代入212y x bx c =++即可求出b ,c 的值. (2)将(1)中求得的抛物线1C 的解析式215222y x x =++化为顶点式,根据2C 和1C 关于y 轴轴对称,即可求得2C 解析式.②先求出(0,2)B 关于直线52x =的对称点(5,2)D ,显然15t <<,求出直线CD 的解析式为1122y x =-,设1,22t E t ⎛⎫- ⎪⎝⎭,215,222F t t t ⎛⎫-+ ⎪⎝⎭,再根据E F EF m y y ==-,得出221513(3)22222m t t t =-+-=--+≤,即可求解. 【详解】(1)∵(4,0)A -,(0,2)B ∴21(4)4022b c c ⎧⨯--+=⎪⎨⎪=⎩解得522 bc⎧=⎪⎨⎪=⎩故答案为:5 2b=,2c=(2)①由(1)得抛物线1C的解析式为2215159222228y x x x⎛⎫=++=+-⎪⎝⎭2C和1C关于y轴轴对称,则2C:2159228y x⎛⎫=--⎪⎝⎭∴215222y x x=-+即为所求.②∵(0,2)B关于直线52x=的对称点为(5,2)D显然15t<<∵(1,0)C,(5,2)D∴直线CD的解析式为1122y x=-∵点E在线段CD上∴1,22tE t⎛⎫-⎪⎝⎭∵点F在抛物线2C上∴215,222F t t t⎛⎫-+⎪⎝⎭令E FEF m y y==-,得221513(3)22222m t t t=-+-=--+≤∴当3t=时,m取得最大值2故答案为:215222y x x =-+;当3t =时,m 取得最大值2 【点睛】 本题是二次函数的综合题目,考查了用待定系数法求二次函数解析式,将二次函数一般式化为顶点式是求抛物线关于y 轴对称图象的函数解析式的方法,以及二次函数最值的求法. 5.(1)y=−x 2−4x+5;(2)15;(3)(−32,0)或(−23,0);(4)存在M 点,M 点坐标为(7,12)或515(,)44- 【解析】【分析】(1)通过解方程即可求出p 、q 的值,那么A 、B 两点的坐标就可求出.然后根据A 、B 两点的坐标即可求出抛物线的解析式.(2)根据(1)得出的抛物线的解析式即可求出C 、D 两点的坐标.由于△BCD 的面积无法直接求出,可用其他图形的面积的“和,差关系”来求出.过D 作DM ⊥x 轴于M ,那么△BCD 的面积=梯形DMOB 的面积+△DCM 的面积-△BOC 的面积.由此可求出△BCD 的面积. (3)由于△PCH 被直线BC 分成的两个小三角形等高,因此面积比就等于底边的比.如果设PH 与BC 的交点为E ,那么EH 就是抛物线与直线BC 的函数值的差,而EP 就是E 点的纵坐标.然后可根据直线BC 的解析式设出E 点的坐标,然后表示出EH ,EP 的长.进而可分两种情况进行讨论:①当EH=32EP 时;②当EH=23EP 时.由此可得出两个不同的关于E 点横坐标的方程即可求出E 点的坐标.也就求出了P 点的坐标.(4)分两种情况讨论,当CD=DM 和当DM CM =时,根据M 点在直线BC 上设出M 点坐标,根据两点间距离公式列出方程即可求解出M 点坐标.【详解】解方程x 2−6x+5=0,(x−1)(x−5)=0,得x 1=5,x 2=1∵p q <,∴p=1,q=5∴点A 、B 的坐标分别为A(1,0),B(0,5).将A(1,0),B(0,5)的坐标分别代入y=−x 2+bx+c .得105b cc-++=⎧⎨=⎩得:45 bc=-⎧⎨=⎩∴抛物线的解析式为y=−x2−4x+5故答案为:y=−x2−4x+5(2)∵y=−x2−4x+5,令y=0,得−x2−4x+5=0,得x1=−5,x2=1,∴C点的坐标为(−5,0)∵4222ba--=-=--,244516944ac ba--⨯-=-=-∴点D(−2,9)过D作x轴的垂线交x轴于M∴S△DMC=12×9×(5−2)=272S梯形MDBO=12×2×(9+5)=14,S△BOC=12×5×5=252∴S△BCD=S梯形MDBO+S△DMC−S△BOC=14+272−252=15故答案为:15(3)设P点的坐标为(a,0)∵B(0,5),C (−5,0)设BC直线的解析式为y=kx+b∴5 50bk b=⎧⎨-+=⎩∴15 kb=⎧⎨=⎩∴BC所在的直线解析式为y=x+5设PH与直线BC的交点坐标为E(a,a+5),PH与抛物线y=−x2−4x+5的交点坐标为H(a,−a2−4a+5)∵①EH=32 EP,即(−a2−4a+5)−(a+5)=32(a+5)∴a=−32或a=−5(舍去)②EH=23 EP,即(−a2−4a+5)−(a+5)=23(a+5)∴a=−23或a=−5(舍去),P点的坐标为(−32,0)或(−23,0)故答案为:(−32,0)或(−23,0)(4)①∵M在直线BC上,设M(m,m+5) 若使四边形CDMN为菱形,则CD=DM ∵C(-5,0),D(-2,9)2222(25)9(2)(4)m m-++=++-解得m=-5或m=7m=-5时,恰好为C点,不符合题意舍去∴m=7 ∴M(7,12) ②∵直线BC 上存在一点'M ,设'(,5)M n n +若使四边形''M DN C 是菱形,则''DM CM =∵C(-5,0),D(-2,9) ∴2222(2)(4)(5)(5)n n n n ++-=+++解得54n =-∴515'(,)44M -综上所述在直线BC 上存在一点M ,且以点C 、点D 、点M 、点N 为顶点的四边形为菱形,此时M 点坐标为(7,12)或515(,)44- 故答案为:存在M 点,M 点坐标为(7,12)或515(,)44-【点睛】本题是二次函数的综合题目,涉及了待定系数法求抛物线方程,利用面积差求图形面积,两点间距离公式求线段长,菱形的判定和性质等知识点.6.(1)直线OA 的解析式为y =x ,二次函数的解析式是y =﹣x 2+4x ;(2)D (32,0-);(3)存在,P (315,24)或(515,24). 【解析】【分析】(1)设直线OA 的解析式为y 1=kx ,把点A 坐标(3,3)代入得:k =1,直线OA 的解析式为y =x ;再设y 2=ax (x−4),把点A 坐标(3,3)代入得:a =−1,即可求解;(2)P 为直线OA 上方抛物线上的一个动点,故0<m <3.此时仅有OC =PC ,CO ODm ,23m m -+=,解得3m =(3)M 到直线PQ 的距离为4−(−n 2+4n )=(n−2)2,要使△PQM 的面积为18,则211(2)28PQ n ⋅⋅-=,即21142(2)28n n ⋅-⋅-=,即可求解. 【详解】解:(1)设直线OA 的解析式为y 1=kx ,把点A 坐标(3,3)代入得:k =1,直线OA 的解析式为y =x ;再设y 2=ax (x ﹣4),把点A 坐标(3,3)代入得:a =﹣1,函数的解析式为y =﹣x 2+4x ,∴直线OA 的解析式为y =x ,二次函数的解析式是y =﹣x 2+4x .(2)设D 的横坐标为m ,则P 的坐标为(m ,﹣m 2+4m ),∵P 为直线OA 上方抛物线上的一个动点,∴0<m <3.此时仅有OC =PC ,CO OD m ,∴23m m -+=,解得3m =∴()3D ;(3)函数的解析式为y =﹣x 2+4x ,∴对称轴为x =2,顶点M (2,4),设P (n ,﹣n 2+4n ),则点P 关于对称轴的对称点Q (4﹣n ,﹣n 2+4n ), M 到直线PQ 的距离为4﹣(﹣n 2+4n )=(n ﹣2)2, 要使△PQM 的面积为18, 则211(2)28PQ n ⋅⋅-=,即21142(2)28n n ⋅-⋅-=, 解得:32n =或52n =, ∴P (315,24)或(515,24).。
2021中考数学 二次函数专项 培优训练(含答案)

2021中考数学二次函数专项培优训练一、选择题(本大题共10道小题)1. 如图,抛物线的函数解析式是()A.y=x2-x+2B.y=x2+x+2C.y=-x2-x+2D.y=-x2+x+22. 已知二次函数y=ax2+bx+c的图象如图,则()A.b>0,c>0B.b>0,c<0C.b<0,c<0D.b<0,c>03. 若二次函数y=ax2-2ax+c的图象经过点(-1,0),则方程ax2-2ax+c=0的解为()A. x1=-3,x2=-1B. x1=1,x2=3C. x1=-1,x2=3D. x1=-3,x2=14. 在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点旋转180°得到抛物线y=x2+5x+6,则原抛物线的解析式是()A. y=-(x-52)2-114 B. y=-(x+52)2-114C. y=-(x-52)2-14 D. y=-(x+52)2+145. 如图,在△ABC中,∠C=90°,AB=10 cm,BC=8 cm,点P从点A沿AC 向点C以1 cm/s的速度运动,同时点Q从点C沿CB向点B以2 cm/s的速度运动(点Q运动到点B时,两点同时停止运动),在运动过程中,四边形P ABQ的面积的最小值为()A.19 cm2B.16 cm2C.15 cm2D.12 cm26. 若二次函数y=x2-6x+c的图象过A(-1,y1),B(2,y2),C(3+2,y3)三点,则y1,y2,y3的大小关系是()A.y1>y2>y3B.y1>y3>y2C.y2>y1>y3D.y3>y1>y27. 将抛物线y=x2-6x+5向上平移2个单位长度,再向右平移1个单位长度后,得到的抛物线的解析式是()A.y=(x-4)2-6 B.y=(x-1)2-3C.y=(x-2)2-2 D.y=(x-4)2-28. 二次函数y=2x2-3的图象是一条抛物线,下列关于该抛物线的说法,正确的是()A. 抛物线开口向下B. 抛物线经过点(2,3)C. 抛物线的对称轴是直线x=1D. 抛物线与x轴有两个交点9. 抛物线y=x2+bx+c(其中b,c是常数)过点A(2,6),且抛物线的对称轴与线段y=0(1≤x≤3)有交点,则c的值不可能是()A. 4B. 6C. 8D. 1010. 2019·丹东如图,二次函数y=ax2+bx+c的图象过点(-2,0),对称轴为直线x=1.有以下结论:①abc>0;②8a+c>0;③若A(x1,m),B(x2,m)是抛物线上的两点,当x=x1+x2时,y=c;④点M,N是抛物线与x轴的两个交点,若在x轴下方的抛物线上存在一点P,使得PM⊥PN,则a的取值范围为a≥1;⑤若方程a(x+2)(4-x)=-2的两根为x1,x2,且x1<x2,则-2≤x1<x2<4.其中结论正确的有()A.2个B.3个C.4个D.5个二、填空题(本大题共8道小题)11. 某抛物线的形状、开口方向与抛物线y=12x2-4x+3相同,顶点坐标为(-2,1),则该抛物线的函数解析式为________________.12. 某商店从厂家以每件21元的价格购进一批商品,该商品可以自行定价,若每件商品的售价为a元,则可卖出(350-10a)件.但物价部门限定每件商品加价不能超过进价的40%,若商店想获得最大利润,则每件商品的价格应定为________元.13. 竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时达到相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t=.14. 已知抛物线y=ax2+4ax+4a+1(a≠0)过点A(m,3),B(n,3)两点,若线段AB的长不大于4,则代数式a2+a+1的最小值是.15. 如图,抛物线y=ax2+c与直线y=mx+n交于A(-1,p),B(3,q)两点,则不等式ax2-mx+c>n的解集是________.16. 已知抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,其部分图象如图所示,下列说法中:①b>0;②a-b+c<0;③b+2c>0;④当-1<x<0时,y>0,正确的是(填写序号).17. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b>0;②a-b +c=0;③一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根;④当x <-1或x>3时,y>0.上述结论中正确的是________.(填上所有正确结论的序号)18. 如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0)和B(3,2),不等式x2+bx+c>x+m的解集为____________.三、解答题(本大题共8道小题)19. 某商店销售一种商品,经市场调查发现,该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如下表: 售价x(元/件) 50 60 80周销售量y(件) 100 80 40周销售利润1000 1600 1600w(元)注:周销售利润=周销售量×(售价-进价)(1)①求y关于x的函数解析式(不要求写出自变量的取值范围);②该商品进价是元/件;当售价是元/件时,周销售利润最大,最大利润是元;(2)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求m的值.20. 旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的运营规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入-管理费)(2)当每辆车的日租金为多少元时,每天的净收入最多?21. 如图,二次函数y=-x2+bx+3的图象与x轴交于点A,B,与y轴交于点C,点A的坐标为(-1,0),点D为OC的中点,点P在抛物线上.(1)b=.(2)若点P在第一象限,过点P作PH⊥x轴,垂足为H,PH与BC,BD分别交于点M,N.是否存在这样的点P,使得PM=MN=NH,若存在,求出点P的坐标;若不存在,请说明理由.22. 如图①,在平面直角坐标系xOy中,已知抛物线y=ax2-2ax-8a与x轴相交于A,B两点(点A在点B的左侧),与y轴交于点C(0,-4).(1)点A的坐标为,点B的坐标为,线段AC的长为,抛物线的解析式为.(2)点P是线段BC下方抛物线上的一个动点.如果在x轴上存在点Q,使得以点B,C,P,Q为顶点的四边形是平行四边形,求点Q的坐标.①23. 如图,抛物线y =13x 2+bx +c 与x 轴交于A (3,0),B (-1,0)两点,过点B 作直线BC ⊥x 轴,交直线y =-2x 于点C. (1)求该抛物线的解析式;(2)求该抛物线的顶点D 的坐标,并判断顶点D 是否在直线y =-2x 上;(3)点P 是抛物线上一动点,是否存在这样的点P (点A 除外),使△PBC 是以BC 为直角边的直角三角形?若存在,求出所有满足条件的点P 的坐标;若不存在,请说明理由.24. 如图,抛物线213922y x x =--与x 轴交于A 、B 两点,与y 轴交于点C ,联结BC 、AC .(1)求AB 和OC 的长;(2)点E 从点A 出发,沿x 轴向点B 运动(点E 与点A 、B 不重合),过点E 作BC 的平行线交AC 于点D .设AE 的长为m ,△ADE 的面积为s ,求s 关于m 的函数关系式,并写出自变量m 的取值范围;(3)在(2)的条件下,联结CE ,求△CDE 面积的最大值;此时,求出以点E 为圆心,与BC 相切的圆的面积(结果保留π).25. 如图,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点D是抛物线的顶点.(1)求直线AC的解析式及B、D两点的坐标;(2)点P是x轴上的一个动点,过P作直线l//AC交抛物线于点Q.试探究:随着点P的运动,在抛物线上是否存在点Q,使以A、P、Q、C为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由;(3)请在直线AC上找一点M,使△BDM的周长最小,求出点M的坐标.26. 如图,在平面直角坐标系xOy中,二次函数y=-x2+2x+8的图象与一次函数y=-x+b的图象交于A、B两点,点A在x轴上,点B的纵坐标为-7.点P 是二次函数图象上A、B两点之间的一个动点(不与点A、B重合),设点P的横坐标为m,过点P作x轴的垂线交AB于点C,作PD⊥AB于点D.(1)求b及sin∠ACP的值;(2)用含m的代数式表示线段PD的长;(3)连接PB,线段PC把△PDB分成两个三角形,是否存在适合的m值,使这两个三角形的面积之比为1∶2?如果存在,直接写出m的值;如果不存在,请说明理由.2021中考数学二次函数专线培优训练-答案一、选择题(本大题共10道小题)1. 【答案】D[解析] 先设出函数解析式,然后把(0,2),(-1,0),(2,0)分别代入函数解析式,列出方程组,求出各系数即可.2. 【答案】B[解析] ∵二次函数y =ax 2+bx +c 的图象开口向下,∴a <0.∵二次函数图象的对称轴x =-b2a >0,∴b >0.∵二次函数图象与y 轴交于负半轴,∴c <0.故选B.3. 【答案】C【解析】∵图象过点(-1,0),∴将点(-1,0)代入方程得a +2a+c =0,即3a +c =0.当x =3时,将(3,0)代入方程也得到3a +c =0成立,当x =-3时,将(-3,0)代入方程也得到15a +c =0(与3a +c =0不相符),∴方程的两个根为x 1=-1,x 2=3.4. 【答案】A 【解析】∵抛物线的解析式为:y =x 2+5x +6,∴绕原点旋转180°变为y =-x 2+5x -6,即y =-(x -52)2+14,∴再向下平移3个单位长度得到的抛物线解析式为y =-(x -52)2+14-3=-(x -52)2-114.5. 【答案】C [解析] 在Rt △ABC 中,∠C =90°,AB =10 cm ,BC =8 cm , ∴AC =AB 2-BC 2=6 cm.设运动时间为t s(0<t≤4),则PC =(6-t)cm ,CQ =2t cm , ∴S四边形PABQ =S △ABC -S △CPQ=12AC·BC -12PC·CQ =12×6×8-12(6-t)×2t =t 2-6t +24=(t -3)2+15,∴当t =3时,四边形PABQ 的面积取得最小值,最小值为15 cm 2. 故选C.6. 【答案】B[解析] 解法一:y =x 2-6x +c =(x -3)2-9+c ,其大致图象如图,对称轴为直线x =3,由图可得y 1>y 3>y 2.解法二:把A ,B ,C 三点的坐标分别代入解析式并化简,得y 1=7+c ,y 2=-8+c ,y 3=-7+c ,所以y 1>y 3>y 2.故选B.7. 【答案】D[解析] y =x 2-6x +5=(x -3)2-4,将其向上平移2个单位长度,再向右平移1个单位长度后,得y =(x -3-1)2-4+2,即y =(x -4)2-2.8. 【答案】D【解析】本题考查了二次函数的性质,由于2>0,所以抛物线的开口向上,所以A 选项错误;由于当x =2时,y =8-3=5,所以B 选项错误;由于y =2x 2-3的对称轴是y 轴,所以C 选项错误;由2x 2-3=0得b 2-4ac =24>0,则该抛物线与x 轴有两个交点,所以D 选项正确.9. 【答案】A 【解析】 由题知,对称轴与线段y =0(1≤x ≤3)有交点,则有1≤-b2≤3,可得到:-6≤b ≤-2,由抛物线经过点A (2,6),代入可得4+2b +c=6,∴b =2-c 2,∴-6≤2-c2≤-2, 解得6≤c ≤14,∴c 的值不可能是4.10. 【答案】A二、填空题(本大题共8道小题)11. 【答案】y =12(x +2)2+1 [解析] 已知抛物线的顶点坐标,可以设顶点式y =a(x -h)2+k.又因为该抛物线的形状、开口方向与抛物线y =12x 2-4x +3相同,所以a =12,所以该抛物线的函数解析式是y =12(x +2)2+1.12. 【答案】28[解析] 设商店所获利润为y 元.根据题意,得y =(a -21)(350-10a)=-10a 2+560a -7350=-10(a -28)2+490, 即当a =28时,可获得最大利润.又21×(1+40%)=21×1.4=29.4,而28<29.4,所以a =28符合要求. 故商店应把每件商品的价格定为28元,此时可获得最大利润.13. 【答案】1.6[解析]设各自抛出后1.1秒时达到相同的最大离地高度h ,则第一个小球的离地高度y=a (t -1.1)2+h (a ≠0), 由题意a (t -1.1)2+h=a (t -1-1.1)2+h , 解得t=1.6.故第一个小球抛出后1.6秒时在空中与第二个小球的离地高度相同.14. 【答案】[解析]∵抛物线y=ax 2+4ax +4a +1(a ≠0)过点A (m ,3),B (n ,3)两点,∴=-=-2.∵线段AB的长不大于4,∴4a+1≥3,∴a≥,∴a2+a+1的最小值为:2++1=.15. 【答案】.x<-1或x>316. 【答案】①③④[解析]根据图象可得:a<0,c>0,对称轴:直线x=-=1,∴b=-2a.∵a<0,∴b>0,故①正确;把x=-1代入y=ax2+bx+c,得y=a-b+ c.由抛物线的对称轴是直线x=1,且过点(3,0),可得当x=-1时,y=0,∴a-b+c=0,故②错误;当x=1时,y=a+b+c>0.∵b=-2a,∴-+b+c>0,即b+2c>0,故③正确;由图象可以直接看出④正确.故答案为:①③④.17. 【答案】②③④[解析] 由图可知,抛物线的对称轴为直线x=1,与x轴的一个交点坐标为(3,0),∴b=-2a,抛物线与x轴的另一个交点坐标为(-1,0).①∵a>0,∴b<0,∴①错误;②当x=-1时,y=0,∴a-b+c=0,∴②正确;③一元二次方程ax2+bx+c+1=0的解是函数y=ax2+bx+c的图象与直线y=-1的交点的横坐标,由图象可知函数y=ax2+bx+c的图象与直线y=-1有两个不同的交点,∴一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根,∴③正确;④由图象可知,y>0时,x<-1或x>3,∴④正确.18. 【答案】x<1或x>3【解析】∵直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0)和B(3,2),∴根据图象可知,不等式x2+bx+c>x+m的解集为x <1或x>3.三、解答题(本大题共8道小题)19. 【答案】解:(1)①设y与x的函数关系式为y=kx+b,依题意,有解得∴y与x的函数关系式是y=-2x+200..②设进价为t元/件,由题意,1000=100×(50-t),解得t=40,∴进价为40元/件; 周销售利润w=(x-40)y=(x-40)(-2x+200)=-2(x-70)2+1800,故当售价是70元/件时,周销售利润最大,最大利润是1800元.故答案为40,70,1800.(2)依题意有,w=(-2x+200)(x-40-m)=-2x2+(2m+280)x-8000-200m=-2x-2+m2-60m+18 00.∵m>0,∴对称轴x=>70,∵-2<0,∴抛物线开口向下,∵x≤65,∴w随x的增大而增大,∴当x=65时,w有最大值(-2×65+200)(65-40-m),∴(-2×65+200)(65-40-m)=1400,∴m=5.20. 【答案】解:(1)由题意知,若观光车能全部租出,则0<x≤100,由50x-1100>0,(2分)解得x>22,(3分)又∵x是5的倍数,∴每辆车的日租金至少应为25元.(5分)(2)设每天的净收入为y元,当0<x≤100时,y1=50x-1100,(6分)∵y1随x的增大而增大,∴当x=100时,y1的最大值为50×100-1100=3900;(8分)当x>100时,y2=(50-x-1005)x-1100=-15x2+70x-1100=-15(x-175)2+5025.(9分)∴当x=175时,y2的最大值是5025,∵5025>3900,∴当每辆车的日租金为175元时,每天的净收入最多是5025元.(10分)21. 【答案】解:(1)2[解析]∵二次函数y=-x2+bx+3的图象过点A(-1,0),∴0=-(-1)2-b+3.∴b=2.故填2.(2)如图①,连接BD,BC,过点P作PH⊥x轴于点H,分别交BC,BD于点M,N.由题意知,抛物线y=-x2+2x+3交x轴于点A(-1,0),B(3,0),交y轴于点C(0,3),且点D为OC的中点,∴D0,.易求直线BC的解析式为y=-x+3,直线BD的解析式为y=-x+.假设存在符合条件的点P(m,-m2+2m+3),则M(m,-m+3),N m,-m+.∵PM=MN=NH,∴-m+=(-m2+2m+3)-(-m+3).整理,得2m2-7m+3=0,解得m 1=,m 2=3(不合题意,舍去). ∴P 使得PM=MN=NH.22. 【答案】[解析](1)令y=0求得点A ,B 坐标,再由点C 坐标求得抛物线的解析式及线段AC 的长;(2)过点C 作x 轴的平行线交抛物线于点P ,通过分类讨论确定点Q 坐标. 解:(1)点A 的坐标为(-2,0),点B 的坐标为(4,0);线段AC 的长为2, 抛物线的解析式为:y=x 2-x -4.(2)过点C 作x 轴的平行线交抛物线于点P .∵点C (0,-4),∴-4=x 2-x -4,解得x 1=2,x 2=0,∴P (2,-4). ∴PC=2,若四边形BCPQ 为平行四边形,则 BQ=CP=2,∴OQ=OB +BQ=6,∴Q (6,0).若四边形BPCQ 为平行四边形,则BQ=CP=2, ∴OQ=OB -BQ=2,∴Q (2,0).故以点B ,C ,P ,Q 为顶点的四边形是平行四边形时,Q 点的坐标为(6,0),(2,0).23. 【答案】(1)∵y =13x 2+bx +c 与x 轴交于A (3,0),B (-1,0)两点,∴⎩⎪⎨⎪⎧13×32+3b +c =013×(-1)2-b +c =0,解得⎩⎪⎨⎪⎧b =-23c =-1, ∴抛物线的解析式为y =13x 2-23x -1;(2)∵a=13,b=-23,c=-1,抛物线的顶点D的坐标为(ab2-,abac442-),∴x D=--232×13=1,y D=4×13×(-1)-(-23)24×13=-43,∴D(1,-43).把x=1代入y=-2x中得y=-2,∵-43≠-2,∴顶点D不在直线y=-2x上;(3)存在.理由如下:如解图,过点C作x轴的平行线,与该抛物线交于点P1,P2,连接BP1,BP2.解图∵直线BC⊥x轴,∴△P1BC、△P2BC都是直角三角形.把x=-1代入y=-2x中得:y=-2×(-1)=2,∴C(-1,2).∴把y=2代入y=13x2-23x-1中得13x2-23x-1=2,解得x1=10+1,x2=-10+1.∴P1(10+1,2),P2(-10+1,2).24. 【答案】(1)由21319(3)(6)222y x x x x=--=+-,得A(-3,0)、B(6,0)、C(0,-9).所以AB=9,OC=9.(2)如图2,因为DE//CB,所以△ADE∽△ACB.所以2()ADEACBS AES AB∆∆=.而18122ACB S AB OC ∆=⋅=,AE =m ,所以222811()()922ADE ACB AE m s S S m AB∆∆==⨯=⨯=.m 的取值范围是0<m <9.图2 图3(3)如图2,因为DE //CB ,所以9CD BE m ADAEm-==.因为△CDE 与△ADE 是同高三角形,所以9CDE ADE S CD m S ADm∆∆-==.所以22291191981()222228CDE m S m m m m m ∆-=⨯=-+=--+.当92m =时,△CDE 的面积最大,最大值为818.此时E 是AB 的中点,92BE =.如图3,作EH ⊥CB ,垂足为H .在Rt △BOC 中,OB =6,OC =9,所以313sin 13B =在Rt △BEH 中,93132713sin 2EH BE B =⋅==.当⊙E 与BC 相切时,r EH =.所以272952S r ππ==.考点伸展在本题中,△CDE 与△BEC 能否相似? 如图2,虽然∠CED =∠BCE ,但是∠B >∠BCA ≥∠ECD ,所以△CDE 与△BEC 不能相似.25. 【答案】(1)由y =-x 2+2x +3=-(x +1)(x -3)=-(x -1)2+4, 得A (-1, 0)、B (3, 0)、C (0, 3)、D (1, 4). 直线AC 的解析式是y =3x +3.(2)Q 1(2, 3),Q 2(17,3+-),Q 3(17,3-).(3)设点B 关于直线AC 的对称点为B ′,联结BB ′交AC 于F . 联结B ′D ,B ′D 与交AC 的交点就是要探求的点M . 作B ′E ⊥x 轴于E ,那么△BB ′E ∽△BAF ∽△CAO .在Rt △BAF 中,1310AF BF AB ==,AB =4,所以1210BF =.在Rt △BB′E 中,''1310B E BE BB ==,24'210BB BF ==,所以12'5B E =,365BE =.所以3621355OE BE OB =-=-=.所以点B ′的坐标为2112(,)55-.因为点M 在直线y =3x +3上,设点M 的坐标为(x , 3x +3).由''''''DD MM B D B M =,得''''yD yB yM yB xD xB xM xB --=--.所以1212433552121155x x -+-=++. 解得935x =.所以点M 的坐标为9132(,)3535.图2 图3考点伸展第(2)题的解题思路是这样的:①如图4,当AP 是平行四边形的边时,CQ //AP ,所以点C 、Q 关于抛物线的对称轴对称,点Q 的坐标为(2, 3).②如图5,当AP 是平行四边形的对角线时,点C 、Q 分居x 轴两侧,C 、Q 到x 轴的距离相等.解方程-x 2+2x +3=-3,得17x =±.所以点Q 的坐标为(17,3+-)或 (17,3--).图4 图526. 【答案】(1)∵当y =0时,-x 2+2x +8=0, 解得∴x 1=-2,x 2=4. ∵点A 在x 轴负半轴上, ∴A (-2,0),OA =2,∵点A 在一次函数y =-x +b 的图象上, ∴2+b =0,∴b =-2,∴一次函数表达式为y =-x -2,如解图,设直线AB 交y 轴于点E ,则E (0,-2),OE =OA =2, ∴△AOE 为等腰直角三角形,∠AEO =45°, ∵PC ⊥x 轴交AB 于点C , ∴PC ∥y 轴,∴∠AEO =∠ACP =45°, ∴sin ∠ACP =sin45;(2)∵点P 在二次函数y =-x 2+2x +8图象上且横坐标为m , ∴P (m ,-m 2+2m +8),∵PC ⊥x 轴且点C 在一次函数y =-x -2的图象上, ∴C (m ,-m -2),∴PC =-m 2+3m +10, ∵PD ⊥AB 于点D ,∴在Rt △CDP 中,sin ∠ACP =PDPC=2,∴PD2+2m+(3)存在,m 的值为-1或2.【解法提示】如解图,分别过点D 、B 作DF ⊥PC ,BG ⊥PC ,垂足分别为F 、G .∵sin ∠ACPcos ∠ACP又∵∠FDP =∠ACP ,∴cos ∠FDP在Rt △PDF 中,DF=-12m 2+32m +5,∵点B 纵坐标为-7,且点B 在直线AB :y =-x -2上, ∴点B (5,-7),∴BG =5-m ,∵P 不与A 、B 两点重合,∴-2<m <5,∴当PCD PBC S S ∆∆=DF BG =12时,解得m 1=-1或m 2=5(舍).当PCD PBC S S ∆∆=DFBG=2时,解得m 1=2或m 2=5(舍), ∴m 的值为-1或2.解图。
中考数学总复习《二次函数综合题》专项提升练习题(附答案)
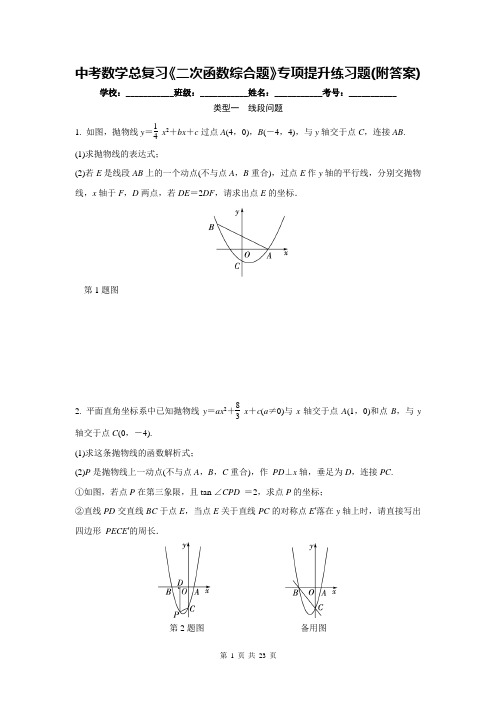
中考数学总复习《二次函数综合题》专项提升练习题(附答案)学校:___________班级:___________姓名:___________考号:___________类型一 线段问题1. 如图,抛物线y =14 x 2+bx +c 过点A (4,0),B (-4,4),与y 轴交于点C ,连接AB .(1)求抛物线的表达式;(2)若E 是线段AB 上的一个动点(不与点A ,B 重合),过点E 作y 轴的平行线,分别交抛物线,x 轴于F ,D 两点,若DE =2DF ,请求出点E 的坐标.第1题图2. 平面直角坐标系中已知抛物线y =ax 2+83 x +c (a ≠0)与x 轴交于点A (1,0)和点B ,与y轴交于点C (0,-4).(1)求这条抛物线的函数解析式;(2)P 是抛物线上一动点(不与点A ,B ,C 重合),作 PD ⊥x 轴,垂足为D ,连接PC . ①如图,若点P 在第三象限,且tan ∠CPD =2,求点P 的坐标;②直线PD 交直线BC 于点E ,当点E 关于直线PC 的对称点E ′落在y 轴上时,请直接写出四边形 PECE ′的周长.第2题图 备用图类型二 面积问题1. 如图,抛物线y =ax 2+bx +5(a ≠0)交x 轴于A (-1,0),B (5,0)两点,交y 轴于点C ,连接AC ,BC ,点G 为线段BC 上方的抛物线上一点,过点G 作GH ∥AC 交BC 于点H . (1)求抛物线的解析式;(2)连接AG ,AH ,BG ,设h =S △AGB -S △AHB ,点G 的横坐标为t ,求h 关于t 的函数解析式,并求出h 的最大值.第1题图2. 在平面直角坐标系中点O 是坐标原点,抛物线y =ax 2+bx (a ≠0)经过点A (3,3),对称轴为直线x =2. (1)求a ,b 的值;(2)已知点B ,C 在抛物线上,点B 的横坐标为t ,点C 的横坐标为t +1.过点B 作x 轴的垂线交直线OA 于点D ,过点C 作x 轴的垂线交直线OA 于点E . (ⅰ)当0<t <2时,求△OBD 与△ACE 的面积之和;(ⅱ)在抛物线对称轴右侧,是否存在点B ,使得以B ,C ,D ,E 为顶点的四边形的面积为32 ?若存在,请求出点B 的横坐标t 的值;若不存在,请说明理由.类型三存在性问题典例精析例如图,在平面直角坐标系xOy中抛物线y=-x2+2x+3与x轴交于点A(-1,0),B(3,0),与y轴交于点C,连接BC,点D为抛物线的顶点.(1)若点M为抛物线对称轴上一点,是否存在点M,使得△BCM为等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由;例题图①【思路点拨】判断等腰三角形存在性问题,一般要进行分类讨论.①BC为腰时:分别以点B,C为圆心,BC长为半径画圆,与直线x=1的交点即为所求作的点;②BC为底时:作线段BC的垂直平分线,与直线x=1的交点即为所求作的点.(2)在抛物线上是否存在一点N,使得△BCN是以BC为直角边的直角三角形?若存在,求出点N的坐标;若不存在,请说明理由;例题图②【思路点拨】判断直角三角形存在性问题,一般要进行分类讨论.①BC 为直角边时:分别过点B ,C 作BC 的垂线,与抛物线的交点即为所求作的N 点; ②BC 为斜边,点N 为直角顶点时:以BC 的中点为圆心,12 BC 的长为半径作圆,所作的圆与抛物线的交点即为所求作的N 点.(3)若点Q 为第一象限内抛物线上一点,过点Q 作QG ⊥x 轴,垂足为G ,连接AC ,OQ .是否存在点Q ,使得△QGO ∽△AOC ?若存在,求出点Q 的坐标;若不存在,请说明理由; 【思路点拨】判断相似三角形存在性问题,通常利用相似三角形的性质,列出线段比例关系,求解即可.例题图③(4)若点E 在抛物线上,点F 在x 轴上,是否存在点E ,使得以D ,C ,E ,F 为顶点的四边形是平行四边形?若存在,求出点E 的坐标;若不存在,请说明理由; 【思路点拨】判断平行四边形存在性问题,一般要进行分类讨论. ①当DE ,FC 是平行四边形对角线时; ②当DF ,EC 是平行四边形对角线时; ③当DC ,EF 是平行四边形对角线时.再利用平行四边形对角线的性质结合中点坐标公式求点坐标即可.例题图④(5)若点H是x轴上一点,点K是平面任意一点,是否存在点H,使得以点A,C,H,K为顶点的四边形是矩形?若存在,求出点H的坐标;若不存在,请说明理由;【思路点拨】判断矩形存在性问题,一般要进行分类讨论.①当AC为矩形的边时,∠ACH=90°;②当AC为矩形的对角线时,∠AHC=90°.再利用勾股定理求解即可.例题图⑤(6)若点S是第一象限抛物线上一点,过点S作ST⊥BC于点T,连接AC,CS,是否存在点S使得△CST中有一个角与∠CAO相等,若存在,求出S点坐标;若不存在,请说明理由.【思路点拨】判断角度存在性问题,一般要进行分类讨论.①若∠SCT=∠CAO;②若∠CST=∠CAO.再构造直角三角形,利用三角函数求解即可.例题图⑥对接中考1. 如图,抛物线y=x2+bx+c过点A(-1,0),点B(5,0),交y轴于点C.(1)求b,c的值;(2)点P(x0,y0)(0<x0<5)是抛物线上的动点.①当x0取何值时,△PBC的面积最大?并求出△PBC面积的最大值;②过点P作PE⊥x轴,交BC于点E,再过点P作PF∥x轴,交抛物线于点F,连接EF,问:是否存在点P,使△PEF为等腰直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.第1题图2. 如图,将一块自制的直角三角板放置在平面直角坐标系中顶点为坐标原点,A(0,-3),B(6,0),将此三角板绕原点O顺时针旋转90°,得到△A′B′O,抛物线L经过点A′,B′,B.(1)求抛物线L的解析式;(2)点Q为平面内一点,在直线AB上是否存在点P,使得以点A,B′,P,Q为顶点的四边形是菱形?若存在,求出点P的坐标;若不存在,请说明理由.第2题图拓展类型二次函数性质综合题1. 在二次函数y=x2-2tx+3(t>0)中(1)若它的图象过点(2,1),则t的值为多少?(2)当0≤x≤3时,y的最小值为-2,求出t的值;(3)如果A(m-2,a),B(4,b),C(m,a)都在这个二次函数的图象上,且a<b<3,求m的取值范围.2. 已知抛物线y=ax2+bx+3(a,b均为常数,且a≠0)的对称轴为直线x=2.(1)求抛物线顶点M的坐标和b的值(用含a的代数式表示);(2)已知点A(x1,y1),B(x2,y2)都在此抛物线上,且x1<2<x2,x1+x2<4,若a>0,试比较y1与y2的大小,并说明理由;(3)若自变量x的值满足-1≤x≤1,与其对应的函数的最大值为18,请直接写出b的值.3. 在平面直角坐标系中抛物线y=ax2-4ax+c(a<0)与x轴交于A(1,0),B两点,与y轴交于点C.(1)若OC=2OB,求抛物线的解析式;(2)若抛物线的最大值为6,求a 的值;(3)若点P (x 0,m ),Q (52,n )在抛物线上,且m <n ,求x 0的取值范围.参考答案类型一 线段问题1. 解:(1)∵抛物线y =14 x 2+bx +c 过点A (4,0),B (-4,4)∴将A (4,0),B (-4,4)分别代入y =14x 2+bx +c 中得⎩⎪⎨⎪⎧4+4b +c =04-4b +c =4 解得⎩⎪⎨⎪⎧b =-12c =-2∴抛物线的表达式为y =14 x 2-12x -2;(2)由点A (4,0),B (-4,4)可得直线AB 的表达式为y =-12 x +2设点E (x ,-12 x +2),其中-4<x <4,则F (x ,14 x 2-12 x -2)∴DE =2-12 x ,DF =|14 x 2-12 x -2|分两种情况讨论:①当点F 在x 轴上方时,即2-12 x =2×(14 x 2-12 x -2)解得x 1=-3,x 2=4(舍去) 将x =-3代入y =-12 x +2中得y =72∴E (-3,72);②当点F 在x 轴下方时,即2-12 x =2×(-14 x 2+12 x +2)解得x 1=-1,x 2=4(舍去)将x =-1代入y =-12 x +2得y =52 ,∴E (-1,52);综上所述,当DE =2DF 时,点E 的坐标为(-3,72 )或(-1,52).2. 解:(1)∵抛物线y =ax 2+83 x +c (a ≠0)与x 轴交于点A (1,0),与y 轴交于点C (0,-4)∴⎩⎪⎨⎪⎧a +83+c =0c =-4 ,解得⎩⎪⎨⎪⎧a =43c =-4∴抛物线的函数解析式为y =43 x 2+83x -4;(2)①如解图①,过点C 作CE ⊥PD 于点E第2题解图①则∠PEC =∠CED =90° ∵C (0,-4) ∴OC =4∵PD ⊥x 轴,垂足为D ∴∠PDO =90°,∠DOC =90° ∴四边形DOCE 是矩形 ∴DE =OC =4 设P (x ,43 x 2+83 x -4)∴CE =-x∴PE =PD -DE =-(43 x 2+83 x -4)-4=-43 x 2-83 x∵tan ∠CPD =CEPE =2∴-x -43x 2-83x =2解得x 1=-138 ,x 2=0(不合题意,舍去)当x =-138 时,43 x 2+83 x -4=-7716∴P (-138 ,-7716);②四边形PECE ′的周长为353 或853.【解法提示】设P (m ,43 m 2+83 m -4),对于y =43 x 2+83 x -4,当y =0时,43 x 2+83 x -4=0,解得x 1=1,x 2=-3,∴B (-3,0),∴OB =3,在Rt △BOC 中由勾股定理得BC =OB 2+OC 2 =5.当点P 在第三象限时,如解图②,过点E 作EF ⊥y 轴于点F第2题解图②则四边形DEFO 是矩形,∴EF =DO =-m ,∵点E 与点E ′关于PC 对称,∴∠ECP =∠E ′CP ,CE =CE ′,PE =PE ′,∵PE ∥y 轴,∴∠EPC =∠PCE ′,∴∠EPC =∠ECP ,∴PE =CE ,∴PE =CE =CE ′=PE ′,∴四边形PECE ′是菱形,∵EF ∥OA ,∴△CEF ∽△CBO ,∴CE CB =EFBO,∴CE 5 =-m 3 ,∴CE =-53m ,设直线BC 的解析式为y =kx +b (k ≠0),把B (-3,0),C (0,-4)代入得,⎩⎪⎨⎪⎧-3k +b =0b =-4 ,解得⎩⎪⎨⎪⎧k =-43b =-4,∴直线BC 的解析式为y =-43 x -4,∴E (m ,-43 m -4),∴PE =-43 m 2-4m ,∵PE =CE ,∴-43 m 2-4m =-53 m ,解得m 1=-74 ,m 2=0(舍去),∴CE =-53 ×(-74 )=3512 ,∴四边形PECE ′的周长为4CE =4×3512 =353;当点P 在第二象限时,如解图③第2题解图③同理可得43 m 2+4m =-53 m ,解得m 1=-174 ,m 2=0(舍去),∴CE =-53 ×(-174 )=8512 ,∴四边形PECE ′的周长为4CE =4×8512 =853 ;综上所述,四边形PECE ′的周长为353 或853.类型二 面积问题1. 解:(1)∵抛物线y =ax 2+bx +5(a ≠0)交x 轴于A (-1,0),B (5,0)两点∴⎩⎪⎨⎪⎧a -b +5=025a +5b +5=0 ,解得⎩⎪⎨⎪⎧a =-1b =4 ∴抛物线的解析式为y =-x 2+4x +5;(2)如解图,过点G 作GD ∥y 轴交BC 于点D ,连接CG ∵当x =0时,y =-x 2+4x +5=5 ∴C (0,5) ∵GH ∥AC ∴S △AGH =S △CGH∴h =S △AGB -S △AHB =S △AGH +S △BGH =S △CGH +S △BGH =S △BGC . 设直线BC 的解析式为y =kx +b 1(k ≠0) 将B (5,0),C (0,5)代入y =kx +b 1中∴⎩⎪⎨⎪⎧5k +b 1=0b 1=5 ,解得⎩⎪⎨⎪⎧k =-1b 1=5 ∴直线BC 的解析式为y =-x +5∵点G 的横坐标为t (0<t <5),∴G (t ,-t 2+4t +5),D (t ,-t +5) ∴GD =-t 2+4t +5-(-t +5)=-t 2+5t ∴h =S △BGC =S △CGD +S △BGD =12 GD ·t +12 GD ·(5-t ) =-52 (t -52 )2+1258∵-52<0,0<t <5∴当t =52 时,h 取最大值,最大值为1258.第1题解图2. 解:(1)由题意得⎩⎪⎨⎪⎧-b 2a =2,9a +3b =3,解得⎩⎪⎨⎪⎧a =-1,b =4;(2)(i)如解图①,延长BD 与x 轴交于点M ,延长CE 与x 轴交于点N ,过点A 作AF ⊥CE 于点F ,连接OB ,AC第2题解图①由(1)知抛物线的解析式为y =-x 2+4x ,易知直线OA 的解析式为y =x ∵点B ,C 在抛物线上,点B 横坐标为t ,点C 的横坐标为t +1 ∴B (t ,-t 2+4t ),C (t +1,-(t +1)2+4(t +1)),D (t ,t ),E (t +1,t +1) ∴OM =t ,BD =-t 2+3t ,CE =-(t +1)2+3(t +1),AF =-t +2 ∵0<t <2 ∴1<t +1<3∴S △OBD +S △ACE =12 OM ·BD +12 CE ·AF =12 t ·(-t 2+3t )+12 [-(t +1)2+3(t +1)]·(-t +2)=2;(ii)存在.如解图②,当点B 在点D 上方,即2<t <3时,过点D 作DQ ⊥EC 于点Q ,连接BE ,CD第2题解图②∵BD ∥EC∴四边形DBEC 为梯形此时,BD =-t 2+3t ,CE =-(t +1)2+3(t +1) ∵DQ =1∴S 四边形DBEC =12 (BD +EC )·DQ =12 [-t 2+3t -(t +1)2+3(t +1)]·1=t -1当S 四边形DBEC =32 时,可得t -1=32 ,解得t =52;当点D 在点B 上方,即t >3时,如解图③,过点D 作DQ ⊥EC 于点Q ,连接BC第2题解图③此时BD =t 2-3t ,CE =(t +1)2-3(t +1)∴S 四边形DBCE =12 (BD +EC )·DQ =12 [t 2-3t +(t +1)2-3(t -1)]·1=t 2-2t -1令t 2-2t -1=32 ,解得t 1=142 +1<3,t 2=-142 +1<3,均舍去;综上所述,t 的值为52.类型三 存在性问题典例精析例 解:(1)存在 设点M (1,m )由题意得BC =32 ,BM =4+m 2 ,CM =1+(m -3)2①当BC 为腰时 a .若BC =BM ,如解图①例题解图①即32=4+m2解得m=±14则M1(1,14),M2(1,-14);b.若BC=CM,如解图②即32=1+(m-3)2,解得m=3±17,则M3(1,3+17),M4(1,3-17);②当BC为底边时,则CM=BM,如解图②,即1+(m-3)2=4+m2解得m=1,则M5(1,1);∴综上所述,满足条件的点M的坐标为(1,14)或(1,-14)或(1,3+17)或(1,3-17)或(1,1);例题解图②(2)存在设点N(x,-x2+2x+3).①当点C为直角顶点时,如解图③,则∠N1CB=90°,过点N1作N1H⊥y轴于点H∵△BOC是等腰直角三角形∴∠BCO=45°∴∠N1CH=180°-90°-45°=45°∴△N1CH是等腰直角三角形∴N1H=HC,即x=-x2+2x+3-3解得x1=0(舍去),x2=1∴N1(1,4);例题解图③②当点B 为直角顶点时,如解图③,则∠CBN 2=90°,过点N 2作N 2G ⊥y 轴,过点B 作BG ⊥x 轴交N 2G 于点G∴同理可得∠BN 2G =45°,△BN 2G 是等腰直角三角形 ∴N 2G =BG ,即3-x =-(-x 2+2x +3) 解得x 1=-2,x 2=3(舍去) ∴N 2(-2,-5).综上所述,满足条件的点N 的坐标为 (1,4)或(-2,-5); (3)存在∵点Q 在第一象限内抛物线上 ∴设Q (m ,-m 2+2m +3),0<m <3 ∵QG ⊥x 轴∴G (m ,0),OG =m ,QG =-m 2+2m +3 ∵△AOC ∽△QGO ∴AO QG =CO OG ,即1-m 2+2m +3 =3m解得m 1=5+1336 或m 2=5-1336 (舍去)此时点Q 的坐标为(5+1336 ,5+13318 );(4)存在设E (m ,-m 2+2m +3),F (n ,0),易得抛物线顶点D 的坐标为(1,4),点C 的坐标为(0,3)①如解图④,当DE ,FC 是平行四边形对角线时 ∵平行四边形对角线互相平分 ∴DE ,FC 的中点重合∴⎩⎪⎨⎪⎧1+m =n +04-m 2+2m +3=0+3 解得m =1+5 或m =1-5∴E 1(1+5 ,-1)或E 2(1-5 ,-1);例题解图④②如解图⑤,当DF ,EC 是平行四边形对角线时,同理DF ,EC 的中点重合∴⎩⎪⎨⎪⎧1+n =m +04+0=-m 2+2m +3+3 解得m =1+3 或m =1-3 ∴E 3(1+3 ,1)或E 4(1-3 ,1);例题解图⑤③当DC ,EF 是平行四边形对角线时,DC ,EF 的中点重合∴⎩⎪⎨⎪⎧1+0=m +n 4+3=-m 2+2m +3+0方程组无实数解.综上所述,满足条件的点E 的坐标为(1+5 ,-1)或(1-5 ,-1)或(1+3 ,1)或(1-3 ,1); (5)存在如解图⑥,由题意知,A (-1,0),C (0,3),设点H 的坐标为(p ,0) ∴AH 2=(p +1)2,CH 2=p 2+32,AC 2=12+32=10 当AC 为矩形的边时,∠ACH =90° ∴AH 2=CH 2+AC 2即(p +1)2=p 2+32+10,解得p =9 ∴点H 的坐标为(9,0);当AC 为矩形的对角线时,∠AHC =90° ∴此时点H 与原点重合,点H 的坐标为(0,0). 综上所述,满足条件的点H 的坐标为(9,0)或(0,0);例题解图⑥(6)存在如解图⑦,过点S 作SZ ⊥x 轴于点Z ,交BC 于点X ∵A (-1,0),B (3,0),C (0,3)∴OA =1,OC =OB =3,易得直线BC 的函数解析式为y =-x +3 ∴∠OBC =∠OCB =45° ∵SZ ⊥x 轴∴∠BXZ =∠SXT =45° ∵ST ⊥BC ∴XT =ST设S (m ,-m 2+2m +3),且0<m <3,则X (m ,-m +3) ∴CX =m 2+(-m +3-3)2 =2 m ,SX =-m 2+3m ∴ST =TX =22 SX =-22 m 2+322m ∴CT =CX -TX =2 m -(-22 m 2+322 m )=22 m 2-22m ①若∠SCT =∠CAO∴tan ∠SCT =tan ∠CAO =OCOA =3∵tan ∠SCT =STCT =3∴ST =3CT ∴-22 m 2+322 m =3×(22 m 2-22m )解得m =32 或m =0(舍去)∴点S 的坐标为(32 ,154 );②若∠CST =∠CAO 则tan ∠CST =tan ∠CAO =3 ∵tan ∠CST =CTST =3∴3ST =CT ∴3×(-22 m 2+322 m )=22 m 2-22m 解得m =52 或m =0(舍去)∴点S 的坐标为(52 ,74);综上所述,存在点S ,使得△CST 中有一个角与∠CAO 相等,点S 的坐标为(32 ,154 )或(52 ,74).例题解图⑦对接中考1. 解:(1)由题意可知,抛物线y =x 2+bx +c 过点A (-1,0),点B (5,0)∴⎩⎪⎨⎪⎧1-b +c =025+5b +c =0 ,解得⎩⎪⎨⎪⎧b =-4c =-5; (2)①如解图,过点P 作y 轴的平行线交BC 于点D ∴S △PBC =S △CPD +S △PDB由(1)可知,c =-5,故点C 的坐标为(0,-5) 易知BC 的表达式为y =x -5∵点P 的坐标为(x 0,y 0)(0<x 0<5),点P 在抛物线上 ∴y 0=x 20 -4x 0-5设点D 的坐标为(x 0,x 0-5)∴|PD |=x 0-5-x 20 +4x 0+5=-x 20 +5x 0∴S △PBC =12 ×|PD |×5=12 ×(-x 20 +5x 0)×5 =-52 (x 0-52 )2+1258∴当x 0=52 时,△PBC 面积最大,最大值为1258;第1题解图②存在.由题意可知,∠EPF =90°,△PEF 为等腰直角三角形 ∴PE =PF∵PE ⊥x 轴,PF ∥x 轴,且点E 在线段BC 上,点F 在抛物线上 由(2)可知PE =-x 20 +5x 0 易知PF =|4-2x 0|∴|PF |=|PE |,即|4-2x 0|=|-x 20 +5x 0|解得x 0=4或x 0=7-332 或x 0=-1(舍去)或x 0=7+332 (舍去)当x 0=4时,解得y =-5当x 0=7-332 时,解得y 0=3-3332∴综上所述,当△PEF 为等腰直角三角形时,点P 的坐标为(4,-5)或(7-332 ,3-332 ).2. 解:(1)由题意得A ′(-3,0),B ′(0,-6),B (6,0)已知抛物线L 经过点A ′,B ′,B ,设抛物线L 的解析式为y =a (x +3)(x -6)(a ≠0) 将点B ′(0,-6)代入抛物线解析式中得-6=a (0+3)(0-6),解得a =13∴抛物线L 的解析式为y =13 (x +3)(x -6)=13 x 2-x -6;(2)存在.∵A (0,-3),B ′(0,-6) ∴AB ′=3设直线AB 的解析式为y =kx +b (k ≠0) 将A (0,-3),B (6,0)代入直线AB 的解析式得⎩⎪⎨⎪⎧b =-36k +b =0 ,解得⎩⎪⎨⎪⎧b =-3k =12∴直线AB 的解析式为y =12 x -3∵点P 在直线AB 上∴设点P (m ,12m -3),分情况讨论:①当以AB ′为边且AP 2=AB ′2时,即m 2+(12 m )2=9解得m 1=655 ,m 2=-655∴点P 的坐标为(655 ,355 -3)或(-655 ,-355 -3);②当以AB ′为边且B ′P 2=AB ′2时,即m 2+(12 m +3)2=9解得m 1=0(舍去),m 2=-125∴P (-125 ,-215 );③当以AB ′为对角线时 ∵AB ′=3∴AB ′的中点坐标为(0,-92 )由菱形的性质可得y P =-92即12 m -3=-92 ,解得m =-3 ∴P (-3,-92);综上所述,点P 的坐标为(655 ,355 -3)或(-655 ,-355 -3)或(-125 ,-215 )或(-3,-92). 拓展类型 二次函数性质综合题1. 解:(1)把点(2,1)代入y =x 2-2tx +3中 得4-4t +3=1解得t =32; (2)∵抛物线对称轴为直线x =t①若0<t ≤3∵a =1>0∴当x =t 时,函数y 取得最小值∵y 的最小值为-2∴t 2-2t 2+3=-2解得t =±5 .∵0<t ≤3∴t =5 ;②若t >3,∵a =1>0∴当0≤x ≤3时,y 随x 的增大而减小∴当x =3时,函数y 取得最小值∵y 的最小值为-2∴9-6t +3=-2解得t =73(不符合题意,舍去). 综上所述,t 的值为5 ;(3)∵A (m -2,a ),C (m ,a )关于对称轴直线x =t 对称∴m -2+m 2=t ,即m -1=t ,且点A 在对称轴左侧,点C 在对称轴右侧. 在y =x 2-2tx +3中令x =0,则y =3∴抛物线与y 轴交点为(0,3)∴此交点关于对称轴直线x =t 的对称点为(2m -2,3).∵a <3,b <3且t >0∴4<2m -2,解得m >3.当点A ,B 都在对称轴左边时∵a <b∴4<m -2,解得m >6∴m >6;当点A ,B 分别在对称轴两侧时∴B 到对称轴的距离大于A 到对称轴的距离∴4-(m -1)>m -1-(m -2),解得m <4∴3<m <4.综上所述,m 的取值范围为3<m <4或m >6.2. 解:(1)由题意得,-b 2a=2 解得b =-4a∴4ac -b 24a =12a -(-4a )24a=3-4a ∴抛物线顶点M 的坐标为(2,3-4a );(2)y 2<y 1,理由如下:由题可知,抛物线的对称轴为直线x =2∴A (x 1,y 1)关于直线x =2的对称点为(4-x 1,y 1)∵x 1<2<x 2,x 1+x 2<4∴2<x 2<4-x 1∵a >0∴抛物线开口向上∴在对称轴右侧y 随x 的增大而增大∴y 2<y 1;(3)b 的值为-12或20.【解法提示】由(1)知,b =-4a ,∴抛物线的解析式为y =ax 2-4ax +3,当a >0时,抛物线开口向上,此时在对称轴左侧,y 随x 的增大而减小,∴当x =-1时,函数值y 最大,最大值为a +4a +3,∴a +4a +3=18,解得a =3,∴b =-4a =-12;当a <0时,抛物线开口向下,此时在对称轴左侧,y 随x 的增大而增大,∴当x =1时,函数值y 最大,最大值为a -4a +3,∴a -4a +3=18,解得a =-5,∴b =-4a =20.综上所述,b 的值为-12或20.3. 解:(1)∵抛物线的对称轴为直线x =--4a 2a=2,抛物线与x 轴的交点为A (1,0),B ∴B (3,0)∴OB =3.∵OC =2OB∴OC =6.∴抛物线开口向下∴C (0,-6).把A (1,0),C (0,-6)代入y =ax 2-4ax +c 中得⎩⎪⎨⎪⎧a -4a +c =0,c =-6, 解得⎩⎪⎨⎪⎧a =-2,c =-6, ∴抛物线的解析式为y =-2x 2+8x -6;(2)由解析式可知抛物线的最大值为4ac -(-4a )24a =4ac -16a 24a=c -4a . ∵抛物线的最大值为6∴c -4a =6.∵抛物线过点A (1,0)∴a -4a +c =0,即c -4a =-a∴-a =6,即a =-6;(3)已知抛物线的对称轴为直线x =2,a <0∴(52 ,n )与(32,n )关于对称轴对称 当点P 在对称轴的左侧(含顶点)时,y 随x 的增大而增大,由m <n ,得x 0<32; 当点P 在对称轴的右侧时,y 随x 的增大而减小,由m <n ,得x 0>52. 综上所述,x 0的取值范围为x 0<32 或x 0>52.。
2021年中考数学 二次函数 培优专题训练(含答案)

2021中考数学二次函数培优专题训练一、选择题1. 抛物线y=-x2+4x-4与坐标轴的交点个数为()A.0B.1C.2D.32. 如果将抛物线y=x2+2向下平移1个单位,那么所得新抛物线的表达式是()A. y=(x-1)2+2B. y=(x+1)2+2C. y=x2+1D. y=x2+33. 在同一直角坐标系中,一次函数y=ax+c和二次函数y=a(x+c)2的图象大致是()4. 已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是()A.b≥-1 B.b≤-1C.b≥1 D.b≤15. 在平面直角坐标系中,已知a≠b,设函数y=(x+a)(x+b)的图象与x轴有M个交点,函数y=(ax+1)(bx+1)的图象与x轴有N个交点,则()A.M=N-1或M=N+1B.M=N-1或M=N+2C.M=N或M=N+1D.M=N或M=N-16. 若抛物线y=x2-2x+3不动,将平面直角坐标系........xOy先沿水平方向向右平移1个单位,再沿铅直方向向上平移3个单位,则原抛物线图象的解析式应变为() A. y=(x-2)2+3 B. y=(x-2)2+5C. y=x2-1D. y=x2+47. 下面的表格列出了函数y=ax2+bx+c(a,b,c是常数,且a≠0)的x与y的部分对应值,那么方程ax2+bx+c=0的一个根x的取值范围是()x … 6.17 6.18 6.19 6.20…y …-0.03-0.010.020.04…A.6<x<6.17 B.6.17<x<6.18C.6.18<x<6.19 D.6.19<x<6.208. 如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x-x2刻画,斜坡可以用一次函数y=x刻画,下列结论错误的是()A.当小球抛出高度达到7.5 m时,小球距O点水平距离为3 mB.小球距O点水平距离超过4 m时呈下降趋势C.小球落地点距O点水平距离为7 mD.斜坡的坡度为1∶29. 2019·丹东如图,二次函数y=ax2+bx+c的图象过点(-2,0),对称轴为直线x=1.有以下结论:①abc>0;②8a+c>0;③若A(x1,m),B(x2,m)是抛物线上的两点,当x=x1+x2时,y=c;④点M,N是抛物线与x轴的两个交点,若在x 轴下方的抛物线上存在一点P,使得PM⊥PN,则a的取值范围为a≥1;⑤若方程a(x+2)(4-x)=-2的两根为x1,x2,且x1<x2,则-2≤x1<x2<4.其中结论正确的有()A.2个B.3个C.4个D.5个10. 若A(2,y1),B(-3,y2),C(-1,y3)三点在抛物线y=x2-4x-m上,则y1,y2,y3的大小关系是()A.y1>y2>y3B.y2>y1>y3C.y2>y3>y1D.y3>y1>y2二、填空题11. 将抛物线y=-(x+2)2向________平移________个单位长度,得到抛物线y =-(x-1)2.12. 已知二次函数y=(x-m)2-1,当x<1时,y随x的增大而减小,则m的取值范围是________.13. 竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时达到相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t=.14. 如图,抛物线y=ax2与直线y=bx+c的两个交点分别为A(-2,4),B(1,1),则方程ax2=bx+c的解是____________.15. 如图,在平面直角坐标系中,抛物线y=ax2(a>0)与y=a(x-2)2交于点B,抛物线y=a(x-2)2交y轴于点E,过点B作x轴的平行线与两条抛物线分别交于D,C两点.若A是x轴上两条抛物线顶点之间的一点,连接AD,AC,EC,ED,则四边形ACED的面积为________.(用含a的代数式表示)16. 已知点(x1,-7)和点(x2,-7)(x1≠x2)均在抛物线y=ax2上,则当x=x1+x2时,y的值是________.17. 2018·湖州如图,在平面直角坐标系xOy中,已知抛物线y=ax2+bx(a>0)的顶点为C,与x轴的正半轴交于点A,它的对称轴与抛物线y=ax2(a>0)交于点B.若四边形ABOC是正方形,则b的值是________.三、解答题 18. 如图,需在一面墙上绘制几个相同的抛物线型图案,按照图中的直角坐标系,最左边的抛物线可以用y =ax 2+bx (a ≠0)表示.已知抛物线上B ,C 两点到地面的距离均为34 m ,到墙边OA 的距离分别为12 m ,32 m.(1)求该抛物线的函数关系式,并求图案最高点到地面的距离;(2)若该墙的长度为10 m ,则最多可以连续绘制几个这样的抛物线型图案?19. 如图,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (1, 0)、C (3, 0)、D (3, 4).以A 为顶点的抛物线y =ax 2+bx +c 过点C .动点P 从点A 出发,沿线段AB 向点B 运动,同时动点Q 从点C 出发,沿线段CD 向点D 运动.点P 、Q 的运动速度均为每秒1个单位,运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E .(1)直接写出点A 的坐标,并求出抛物线的解析式;(2)过点E 作EF ⊥AD 于F ,交抛物线于点G ,当t 为何值时,△ACG 的面积最大?最大值为多少?(3)在动点P 、Q 运动的过程中,当t 为何值时,在矩形ABCD 内(包括边界)存在点H ,使以C 、Q 、E 、H 为顶点的四边形为菱形?请直接写出t 的值.20. 如图,抛物线y =13x 2+bx +c 与x 轴交于A (3,0),B (-1,0)两点,过点B 作直线BC ⊥x 轴,交直线y =-2x 于点C. (1)求该抛物线的解析式;(2)求该抛物线的顶点D 的坐标,并判断顶点D 是否在直线y =-2x 上;(3)点P 是抛物线上一动点,是否存在这样的点P (点A 除外),使△PBC 是以BC 为直角边的直角三角形?若存在,求出所有满足条件的点P 的坐标;若不存在,请说明理由.21. 如图1,已知梯形OABC ,抛物线分别过点O (0,0)、A (2,0)、B (6,3).(1)直接写出抛物线的对称轴、解析式及顶点M 的坐标;(2)将图1中梯形OABC 的上下底边所在的直线OA 、CB 以相同的速度同时向上平移,分别交抛物线于点O 1、A 1、C 1、B 1,得到如图2的梯形O 1A 1B 1C 1.设梯形O 1A 1B 1C 1的面积为S ,A 1、 B 1的坐标分别为 (x 1,y 1)、(x 2,y 2).用含S 的代数式表示x 2-x 1,并求出当S =36时点A 1的坐标;(3)在图1中,设点D 的坐标为(1,3),动点P 从点B 出发,以每秒1个单位长度的速度沿着线段BC 运动,动点Q 从点D 出发,以与点P 相同的速度沿着线段DM 运动.P 、Q 两点同时出发,当点Q 到达点M 时,P 、Q 两点同时停止运动.设P 、Q 两点的运动时间为t ,是否存在某一时刻t ,使得直线PQ 、直线AB 、x 轴围成的三角形与直线PQ 、直线AB 、抛物线的对称轴围成的三角形相似?若存在,请求出t 的值;若不存在,请说明理由.图1 图22021中考数学 二次函数 培优专题训练-答案一、选择题1. 【答案】C [解析]当x=0时,y=-x 2+4x -4=-4,则抛物线与y 轴的交点坐标为(0,-4),当y=0时,-x2+4x-4=0,解得x1=x2=2,抛物线与x轴的交点坐标为(2,0),所以抛物线与坐标轴有2个交点.故选C.2. 【答案】C【解析】根据图象平移变换口诀“左加右减,上加下减”进行解答.把抛物线y=x2+2向下平移1个单位得y=x2+2-1=x2+1.3. 【答案】B4. 【答案】D[解析] 先根据抛物线的性质得到其对称轴为直线x=b,且当x>b 时,y的值随x值的增大而减小.因为当x>1时,y的值随x值的增大而减小,所以b≤1.5. 【答案】C[解析]先把两个函数化成一般形式,若为二次函数,计算当y=0时,关于x的一元二次方程根的判别式,从而确定图象与x轴的交点个数,若为一次函数,则与x轴只有一个交点,据此解答.∵y=(x+a)(x+b)=x2+(a+b)x+ab,∴Δ=(a+b)2-4ab,又∵a≠b,(a+b)2-4ab=(a-b)2>0,∴函数y=(x+a)(x+b)的图象与x 轴有2个交点,∴M=2.∵函数y=(ax+1)(bx+1)=abx2+(a+b)x+1,∴当a≠b,ab≠0时,(a+b)2-4ab=(a-b)2>0,函数y=(ax+1)(bx+1)的图象与x轴有2个交点,即N=2,此时M=N;当ab=0时,不妨令a=0,∵a≠b,∴b≠0,函数y=(ax+1)(bx+1)=bx+1为一次函数,与x轴有一个交点,即N=1,此时M=N+1.综上可知,M=N或M=N+1.故选C.6. 【答案】C【解析】由抛物线y=x2-2x+3得y=(x-1)2+2.保持抛物线不动,将平面直角坐标系先沿水平方向向右平移1个单位,其实质相当于抛物线向左平移1个单位,再将平面直角坐标系向上平移3个单位,则相当于抛物线向下平移3个单位,根据抛物线平移规律:左加右减,上加下减,可得新的抛物线解析式为y=(x-1+1)2+2-3=x2- 1.7. 【答案】C[解析] 由表格中的数据,得在6.17<x<6.20范围内,y随x的增大而增大,当x=6.18时,y=-0.01,当x=6.19时,y=0.02,故方程ax2+bx +c=0的一个根x的取值范围是6.18<x<6.19.8. 【答案】A[解析]根据函数图象可知,当小球抛出的高度为7.5 m时,二次函数y=4x-x2的函数值为7.5,即4x-x2=7.5,解得x1=3,x2=5,故当抛出的高度为7.5 m时,小球距离O点的水平距离为3 m或5 m,A结论错误;由y=4x-x2,得y=-(x-4)2+8,则抛物线的对称轴为直线x=4,当x>4时,y随x值的增大而减小,B结论正确;联立方程y=4x-x2与y=x,解得或则抛物线与直线的交点坐标为(0,0)或7,,C结论正确;由点7,知坡度为∶7=1∶2也可以根据y=x中系数的意义判断坡度为1∶2,D结论正确.故选A.9. 【答案】A10. 【答案】C[解析] ∵二次函数y=x2-4x-m中a=1>0,∴其图象开口向上,对称轴为直线x=-b2a=2.∵点A(2,y1)的横坐标为2,∴y1最小.又∵B(-3,y2),C(-1,y3)都在对称轴的左侧,而在对称轴的左侧,y随x的增大而减小,故y2>y3.∴y2>y3>y1.二、填空题11. 【答案】右 312. 【答案】m≥1[解析] 抛物线的对称轴为直线x=m.∵a=1>0,∴抛物线开口向上,∴当x<m时,y的值随x值的增大而减小,而x<1时,y的值随x值的增大而减小,∴m≥1.13. 【答案】1.6[解析]设各自抛出后1.1秒时达到相同的最大离地高度h,则第一个小球的离地高度y=a(t-1.1)2+h(a≠0),由题意a (t -1.1)2+h=a (t -1-1.1)2+h , 解得t=1.6.故第一个小球抛出后1.6秒时在空中与第二个小球的离地高度相同.14. 【答案】x 1=-2,x 2=1[解析] 方程ax 2=bx +c 的解即抛物线y =ax 2与直线y =bx +c 交点的横坐标.∵交点是A(-2,4),B(1,1),∴方程ax 2=bx +c 的解是x 1=-2,x 2=1.15. 【答案】8a[解析] ∵抛物线y =ax 2(a >0)与y =a(x -2)2交于点B ,∴BD =BC =2, ∴DC =4.∵y =a(x -2)2=ax 2-4ax +4a , ∴E(0,4a),∴S 四边形ACED =S △ACD +S △CDE =12DC·OE =12×4×4a =8a.16. 【答案】0 [解析]依题意可知已知两点关于y 轴对称,∴x 1与x 2互为相反数,即x 1+x 2=0.当x =0时,y =a·02=0.17. 【答案】-2[解析] ∵四边形ABOC 是正方形,∴点B 的坐标为(-b 2a ,-b 2a ). ∵抛物线y =ax 2过点B ,∴-b 2a =a (-b2a )2,解得b 1=0(舍去),b 2=-2.三、解答题18. 【答案】解:(1)由题意知,抛物线y =ax 2+bx(a ≠0)经过点B(12,34),C(32,34), 则⎩⎪⎨⎪⎧14a +12b =3494a +32b =34,解得⎩⎨⎧a =-1b =2,∴抛物线的解析式是y =-x 2+2x.(3分) 根据对称性知,抛物线的对称轴是x =-b2a =1,当x =1时,y =1, ∴顶点坐标是(1,1).答:图案最高点到地面的距离是1 m .(5分) (2)∵抛物线的对称轴是x =1,∴一个图案与地面两交点间的距离是2 m ,10÷2=5. 答:最多可以连续绘制5个这样的抛物线型图案.(8分)19. 【答案】(1)A (1, 4).因为抛物线的顶点为A ,设抛物线的解析式为y =a (x -1)2+4, 代入点C (3, 0),可得a =-1.所以抛物线的解析式为y =-(x -1)2+4=-x 2+2x +3. (2)因为PE //BC ,所以2AP AB PEBC==.因此1122PE AP t ==.所以点E 的横坐标为112t +.将112x t =+代入抛物线的解析式,y =-(x -1)2+4=2144t -.所以点G 的纵坐标为2144t -.于是得到2211(4)(4)44GE t t t t =---=-+. 因此22111()(2)1244ACG AGE CGES S S GE AF DF t t t ∆∆∆=+=+=-+=--+. 所以当t =1时,△ACG 面积的最大值为1. (3)2013t =或2085t =-.第(3)题的解题思路是这样的:因为FE //QC ,FE =QC ,所以四边形FECQ 是平行四边形.再构造点F 关于PE 轴对称的点H ′,那么四边形EH ′CQ 也是平行四边形. 再根据FQ =CQ 列关于t 的方程,检验四边形FECQ 是否为菱形,根据EQ =CQ 列关于t 的方程,检验四边形EH ′CQ 是否为菱形.1(1,4)2E t t +-,1(1,4)2F t +,(3,)Q t ,(3,0)C .如图2,当FQ =CQ 时,FQ 2=CQ 2,因此2221(2)(4)2t t t -+-=.整理,得240800t t -+=.解得12085t =-,22085t =+(舍去). 如图3,当EQ =CQ 时,EQ 2=CQ 2,因此2221(2)(42)2t t t -+-=.整理,得213728000t t -+=.(1320)(40)0t t --=.所以12013t =,240t =(舍去).图2 图320. 【答案】(1)∵y=13x2+bx+c与x轴交于A(3,0),B(-1,0)两点,∴⎩⎪⎨⎪⎧13×32+3b+c=013×(-1)2-b+c=0,解得⎩⎪⎨⎪⎧b=-23c=-1,∴抛物线的解析式为y=13x2-23x-1;(2)∵a=13,b=-23,c=-1,抛物线的顶点D的坐标为(ab2-,abac442-),∴x D=--232×13=1,y D=4×13×(-1)-(-23)24×13=-43,∴D(1,-43).把x=1代入y=-2x中得y=-2,∵-43≠-2,∴顶点D不在直线y=-2x上;(3)存在.理由如下:如解图,过点C作x轴的平行线,与该抛物线交于点P1,P2,连接BP1,BP2.解图∵直线BC⊥x轴,∴△P1BC、△P2BC都是直角三角形.把x=-1代入y=-2x中得:y=-2×(-1)=2,∴C(-1,2).∴把y=2代入y=13x2-23x-1中得13x2-23x-1=2,解得x1=10+1,x2=-10+1.∴P1(10+1,2),P2(-10+1,2).21. 【答案】(1)抛物线的对称轴为直线1x=,解析式为21184y x x=-,顶点为M(1,18-).(2)梯形O1A1B1C1的面积12122(11)3()62x xS x x-+-⨯3==+-,由此得到1223sx x+=+.由于213y y-=,所以22212211111138484y y x x x x-=--+=.整理,得212111()()384x x x x⎡⎤-+-=⎢⎥⎣⎦.因此得到2172x xS-=.当S=36时,212114,2.x xx x+=⎧⎨-=⎩解得126,8.xx=⎧⎨=⎩此时点A1的坐标为(6,3).(3)设直线AB与PQ交于点G,直线AB与抛物线的对称轴交于点E,直线PQ 与x轴交于点F,那么要探求相似的△GAF与△GQE,有一个公共角∠G.在△GEQ中,∠GEQ是直线AB与抛物线对称轴的夹角,为定值.在△GAF中,∠GAF是直线AB与x轴的夹角,也为定值,而且∠GEQ≠∠GAF.因此只存在∠GQE=∠GAF的可能,△GQE∽△GAF.这时∠GAF=∠GQE=∠PQD.由于3tan4GAF∠=,tan5DQ tPQDQP t∠==-,所以345tt=-.解得207t=.图3 图4。
2020-2021中考数学 二次函数 培优练习(含答案)

2020-2021中考数学 二次函数 培优练习(含答案)一、二次函数1.在平面直角坐标系中,我们定义直线y=ax-a 为抛物线y=ax 2+bx+c (a 、b 、c 为常数,a≠0)的“衍生直线”;有一个顶点在抛物线上,另有一个顶点在y 轴上的三角形为其“衍生三角形”.已知抛物线2y x =-+“衍生直线”交于A 、B 两点(点A 在点B 的左侧),与x 轴负半轴交于点C .(1)填空:该抛物线的“衍生直线”的解析式为 ,点A 的坐标为 ,点B 的坐标为 ;(2)如图,点M 为线段CB 上一动点,将△ACM 以AM 所在直线为对称轴翻折,点C 的对称点为N ,若△AMN 为该抛物线的“衍生三角形”,求点N 的坐标;(3)当点E 在抛物线的对称轴上运动时,在该抛物线的“衍生直线”上,是否存在点F ,使得以点A 、C 、E 、F 为顶点的四边形为平行四边形?若存在,请直接写出点E 、F 的坐标;若不存在,请说明理由.【答案】(1)y=;(-2,1,0);(2)N 点的坐标为(0,),(0,);(3)E (-1,F (0)或E (-1,),F (-4,3)【解析】 【分析】(1)由抛物线的“衍生直线”知道二次函数解析式的a 即可;(2)过A 作AD ⊥y 轴于点D ,则可知AN=AC ,结合A 点坐标,则可求出ON 的长,可求出N 点的坐标;(3)分别讨论当AC 为平行四边形的边时,当AC 为平行四边形的对角线时,求出满足条件的E 、F 坐标即可 【详解】(1)∵2y x x =-+a=3-,则抛物线的“衍生直线”的解析式为y=;联立两解析式求交点2y=y x x ⎧=+⎪⎪⎨⎪⎪⎩,解得x=-2⎧⎪⎨⎪⎩x=1y=0⎧⎨⎩,∴A (-2,B (1,0); (2)如图1,过A 作AD ⊥y 轴于点D ,在233y x x =--+y=0可求得x= -3或x=1, ∴C (-3,0),且A (-2,∴由翻折的性质可知∵△AMN 为该抛物线的“衍生三角形”, ∴N 在y 轴上,且AD=2, 在Rt △AND 中,由勾股定理可得, ∵OD=∴ON=或ON=,∴N 点的坐标为(0,),(0,);(3)①当AC 为平行四边形的边时,如图2 ,过F 作对称轴的垂线FH ,过A 作AK ⊥x 轴于点K ,则有AC ∥EF 且AC=EF , ∴∠ ACK=∠ EFH , 在△ ACK 和△ EFH 中ACK=EFHAKC=EHF AC=EF ∠∠⎧⎪∠∠⎨⎪⎩∴△ ACK ≌△ EFH ,∴FH=CK=1,HE=AK= ∵抛物线的对称轴为x=-1, ∴ F 点的横坐标为0或-2, ∵点F 在直线AB 上,∴当F 点的横坐标为0时,则F (0),此时点E 在直线AB 下方,∴E 到y 轴的距离为EH-OF=,即E 的纵坐标为∴ E (-1,-3); 当F 点的横坐标为-2时,则F 与A 重合,不合题意,舍去; ②当AC 为平行四边形的对角线时,∵ C (-3,0),且A (-2,∴线段AC 的中点坐标为(-2.5,), 设E (-1,t ),F (x ,y ),则x-1=2×(-2.5),y+t=∴x= -4,y=,3×(-4)+3,解得t=-3,∴E (-1,),F (-4);综上可知存在满足条件的点F ,此时E (-1,0)或E (-1,),F (-4,3)【点睛】本题是对二次函数的综合知识考查,熟练掌握二次函数,几何图形及辅助线方法是解决本题的关键,属于压轴题2.如图,在平面直角坐标系中有一直角三角形AOB ,O 为坐标原点,OA =1,tan ∠BAO =3,将此三角形绕原点O 逆时针旋转90°,得到△DOC ,抛物线y =ax 2+bx +c 经过点A 、B 、C .(1)求抛物线的解析式;(2)若点P 是第二象限内抛物线上的动点,其横坐标为t ,设抛物线对称轴l 与x 轴交于一点E ,连接PE ,交CD 于F ,求以C 、E 、F 为顶点三角形与△COD 相似时点P 的坐标.【答案】(1)抛物线的解析式为y=﹣x 2﹣2x+3;(2)当△CEF 与△COD 相似时,P 点的坐标为(﹣1,4)或(﹣2,3). 【解析】 【分析】(1)根据正切函数,可得OB ,根据旋转的性质,可得△DOC ≌△AOB ,根据待定系数法,可得函数解析式;(2)分两种情况讨论:①当∠CEF =90°时,△CEF ∽△COD ,此时点P 在对称轴上,即点P 为抛物线的顶点;②当∠CFE =90°时,△CFE ∽△COD ,过点P 作PM ⊥x 轴于M 点,得到△EFC ∽△EMP ,根据相似三角形的性质,可得PM 与ME 的关系,解方程,可得t 的值,根据自变量与函数值的对应关系,可得答案. 【详解】(1)在Rt △AOB 中,OA =1,tan ∠BAO OBOA==3,∴OB =3OA =3. ∵△DOC 是由△AOB 绕点O 逆时针旋转90°而得到的,∴△DOC ≌△AOB ,∴OC =OB =3,OD =OA =1,∴A ,B ,C 的坐标分别为(1,0),(0,3),(﹣3,0),代入解析式为09303a b c a b c c ++=⎧⎪-+=⎨⎪=⎩,解得:123a b c =-⎧⎪=-⎨⎪=⎩,抛物线的解析式为y =﹣x 2﹣2x +3;(2)∵抛物线的解析式为y =﹣x 2﹣2x +3,∴对称轴为l 2ba=-=-1,∴E 点坐标为(﹣1,0),如图,分两种情况讨论:①当∠CEF =90°时,△CEF ∽△COD ,此时点P 在对称轴上,即点P 为抛物线的顶点,P (﹣1,4);②当∠CFE =90°时,△CFE ∽△COD ,过点P 作PM ⊥x 轴于M 点,∵∠CFE=∠PME=90°,∠CEF=∠PEM ,∴△EFC ∽△EMP ,∴13EM EF OD MP CF CO ===,∴MP =3ME . ∵点P 的横坐标为t ,∴P (t ,﹣t 2﹣2t +3).∵P 在第二象限,∴PM =﹣t 2﹣2t +3,ME =﹣1﹣t ,t <0,∴﹣t 2﹣2t +3=3(﹣1﹣t ),解得:t 1=﹣2,t 2=3(与t <0矛盾,舍去).当t =﹣2时,y =﹣(﹣2)2﹣2×(﹣2)+3=3,∴P (﹣2,3).综上所述:当△CEF 与△COD 相似时,P 点的坐标为(﹣1,4)或(﹣2,3). 【点睛】本题是二次函数综合题.解(1)的关键是利用旋转的性质得出OC ,OD 的长,又利用了待定系数法;解(2)的关键是利用相似三角形的性质得出MP =3ME .3.抛物线2y x bx c =-++(b ,c 为常数)与x 轴交于点()1,0x 和()2,0x ,与y 轴交于点A ,点E 为抛物线顶点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021中考数学专题复习:二次函数综合培优提升训练题1(附答案详解)1.如图,抛物线y=ax2+bx+2与x轴交于A,B两点,且OA=2OB,与y轴交于点C,连接BC,抛物线对称轴为直线x=12,D为第一象限内抛物线上一动点,过点D作DE⊥OA于点E,与AC交于点F,设点D的横坐标为m.(1)求抛物线的表达式;(2)当线段DF的长度最大时,求D点的坐标;(3)抛物线上是否存在点D,使得以点O,D,E为顶点的三角形与BOC相似?若存在,求出m的值;若不存在,请说明理由.2.如图,在直角坐标系中,四边形OABC是平行四边形,经过A(﹣2,0),B,C三点的抛物线y=ax2+bx+83(a<0)与x轴的另一个交点为D,其顶点为M,对称轴与x轴交于点E.(1)求这条抛物线对应的函数表达式;(2)已知R是抛物线上的点,使得△ADR的面积是平行四边形OABC的面积的34,求点R的坐标;(3)已知P是抛物线对称轴上的点,满足在直线MD上存在唯一的点Q,使得∠PQE =45°,求点P的坐标.3.如图,抛物线y =ax 2+94x +c 交x 轴于A ,B 两点,交y 轴于点C .直线y =﹣34x +3经过点B ,C . (1)求抛物线的解析式;(2)点P 从点O 出发以每秒2个单位的速度沿OB 向点B 匀速运动,同时点E 从点B 出发以每秒1个单位的速度沿BO 向终点O 匀速运动,当点E 到达终点O 时,点P 停止运动,设点P 运动的时间为t 秒,过点P 作x 轴的垂线交直线BC 于点H ,交抛物线于点Q ,过点E 作EF ⊥BC 于点F .①当PQ =5EF 时,求出t 值;②连接CQ ,当S △CBQ :S △BHQ =5:2时,请直接写出点Q 的坐标.4.已知,在平面直角坐标系中,抛物线22221y x mx m m =-++-的顶点为A ,点B 的坐标为(3,5)(1)求抛物线过点B 时顶点A 的坐标(2)点A 的坐标记为(,)x y ,求y 与x 的函数表达式;(3)已知C 点的坐标为(0,2),当m 取何值时,抛物线22221y x mx m m =-++-与线段BC 只有一个交点5.如图,已知抛物线2113:4L y x =,将抛物线1L 平移后经过点(1,0)A -,(4,0)B 得到抛物线2L ,与y 轴交于点C ;(1)求抛物线2L 的解析式;(2)判断ABC ∆的形状,并说明理由;(3)点P 为抛物线2L 上的动点,过点P 作PD x ⊥轴,与抛物线1L 交于点D ,是否存在点P ,满足2PD OC =?若存在,求出点P 的坐标;若不存在,说明理由.6.如图,抛物线y =x 2+bx +c 经过点(3,12)和(﹣2,﹣3),与两坐标轴的交点分别为A ,B ,C ,它的对称轴为直线l .(1)求该抛物线的表达式;(2)P 是该抛物线上的点,过点P 作l 的垂线,垂足为D ,E 是l 上的点.要使以P 、D 、E 为顶点的三角形与△AOC 全等,求满足条件的点P ,点E 的坐标.7.如图,在平面直角坐标系中,抛物线经过三点(1,0),(3,0),(0,3)A B C -,(0,1)D ,直线AD 与抛物线交于另一点E .(1)求抛物线和直线AD 的解析式;(2)若(),M x y 是直线AD 上方抛物线上的一动点,当x 为何值时AME ∆面积有最大值,最大值是多少;(3)在直线AD 下方抛物线上的一个动点G ,当6AEG S ∆=时,写出点G 的坐标.8.如图,点()2,0A -,点0()1,C 一,点A 、C 关于原点O 的对称点分别为点B 、D .线段AB 沿y 轴向下平移()20m m >个单位长度,得到线段11A B ,抛物线2122y ax bx =++过点1A ,1B .(1)当1m =时,a =__________;(2)求a 与m 之间的关系式;(3)线段CD 沿y 轴向下平移()20n n >个单位长度,得到线段11C D ,抛物线22y ax bx =++过点1C ,1D .①a =__________ ;(用含n 的式子来表示)m 与n 之间的关系式为__________ ;②点(),0P x 在x 轴上,当11PC B △为等腰直角三角形时,直接写出点P 的坐标. 9.如图,已知直线15y x 22=+与x 轴交于点A ,与y 轴交于点C ,过A 、C 两点的抛物线y =ax 2+bx +c 交x 轴于点B (1,0).(1)求A 、C 点的坐标;(2)求抛物线的解析式;(3)在直线AC 上方的抛物线上是否存在点E ,使得∠ECA =2∠CAB ,若存在这样的点E ,求出△ACE 的面积;若不存在,请说明理由.10.如图1,经过原点O 的抛物线y=ax 2+bx (a ≠0)与x 轴交于另一点A (32,0),在第一象限内与直线y=x 交于点B (2,t ).(1)求这条抛物线的表达式; (2)在第四象限内的抛物线上有一点C ,满足以B ,O ,C 为顶点的三角形的面积为2,求点C 的坐标;(3)如图2,若点M 在这条抛物线上,且∠MBO=∠ABO ,在(2)的条件下,是否存在点P ,使得△POC ∽△MOB ?若存在,求出点P 的坐标;若不存在,请说明理由.11.如图,抛物线25y x bx =-++与x 轴交于A ,B 两点.(1)若过点C 的直线2x =是抛物线的对称轴.①求抛物线的解析式;②对称轴上是否存在一点P ,使点B 关于直线OP 的对称点B '恰好落在对称轴上.若存在,请求出点P 的坐标;若不存在,请说明理由.(2)当4b ≥,02x ≤≤时,函数值y 的最大值满足315y ≤≤,求b 的取值范围. 12.已知抛物线22232(0)y ax ax a a =--+≠.(1)求这条抛物线的对称轴;(2)若该抛物线的顶点在x 轴上,求其解析式;(3)设点()1,P m y ,()23,Q y 在抛物线上,若12y y <,求m 的取值范围. 13.已知抛物线C :y =ax 2﹣2ax +3开口向下.(1)当抛物线C 过点(1,4)时,求a 的值和抛物线与y 轴的交点坐标; (2)求二次函数y =ax 2﹣2ax +3的对称轴和最大值(用含a 的式子表示); (3)将抛物线C 向左平移a 个单位得到抛物线C 1,随着a 的变化,抛物线C 1顶点的纵坐标y 与横坐标x 之间存在一个函数关系,求这个函数关系式,并写出自变量x 的取值范围;(4)记(3)所求的函数为D ,抛物线C 与函数D 的图象交于点M ,结合图象,请直接写出点M 的纵坐标的取值范围.14.如图,二次函数()2230y ax x a =++<的图象与x 轴交于点,A B (点A 位于对称轴的左侧),与y 轴交于点C .已知1OA =.()1求该二次函数的对称轴及点B 的坐标.()2点()0,n P 为线段OC 上一点,过点P 作直线//l x 轴交图象于点,D E (点E 在点D 的左侧),将顶点M 作直线l 的对称点1M ,若点1M 在x 轴上方,且到x 轴距离为1,求n 的值.15.如图,在平面直角坐标系xoy 中,已知直线122y x =-与x 轴交于点A ,与y 轴交于点B ,过A 、B 两点的抛物线2y ax bx c =++与x 轴交于另一点(1,0)C -.(1)求抛物线的解析式;(2)在抛物线上是否存在一点P ,使PAB OAB SS =?若存在,请求出点P 的坐标,若不存在,请说明理由;(3)点M 为直线AB 下方抛物线上一点,点N 为y 轴上一点,当MAB △的面积最大时,求12MN ON +的最小值. 16.二次函数y =ax 2﹣2x +c 的图象与x 轴交于A 、C 两点,点C (3,0),与y 轴交于点B (0,﹣3).(1)a = ,c = ;(2)如图1,P 是x 轴上一动点,点D (0,1)在y 轴上,连接PD ,求2PD +PC 的最小值;(3)如图2,点M 在抛物线上,若S △MBC =3,求点M 的坐标.17.如图,已知抛物线经过点A (﹣1,0)、B (3,0)、C (0,3)三点.(1)求抛物线的解析式.(2)点M 是线段BC 上的点(不与B ,C 重合),过M 作MN ∥y 轴交抛物线于N ,若点M 的横坐标为m ,请用m 的代数式表示MN 的长.(3)在(2)的条件下,连接NB 、NC ,是否存在m ,使△BNC 的面积最大?若存在,求m 的值;若不存在,说明理由.18.如图1,抛物线y =ax 2+(a +3)x +3(a ≠0)与x 轴交于点A (4,0),与y 轴交于点B ,在x 轴上有一动点E (m ,0)(0<m <4),过点E 作x 轴的垂线交直线AB 于点N ,交抛物线于点P ,过点P 作PM ⊥AB 于点M .(1)求抛物线的解析式和直线AB 的函数表达式;(2)设△PMN 的周长为C 1,△AEN 的周长为C 2,若12cc =65,求m 的值.19.如图,直线334y x =-+与 x 轴交于点 C ,与 y 轴交于点 B ,抛物线 234y ax x c =++经过 B 、C 两点. (1)求抛物线的解析式;(2)如图,点 E 是抛物线上的一动点(不与 B ,C 两点重合),△BEC 面积记为 S ,当 S 取何值时,对应的点 E 有且只有三个?20.在平面直角坐标系中,Rt ABC ,90ACB ∠=︒, AB x ∥轴,如图1,(1,0)C ,且: OC OA =: 1:2AC BC =.(1)A 点坐标为__________,B 点坐标为__________;(2)求过A 、B 、C 三点的抛物线表达式;(3)如图2,抛物线对称轴与AB 交于点D ,现有一点P 从点A 出发,以每秒1个单位的速度在AB 上向点B 运动,另一点Q 从点D 与点P 同时出发,以每秒5个单位在抛物线对称轴上运动.当点P 到达B 点时,点P 、Q 同时停止运动,问点P 、Q 运动到何处时,PQB △面积最大,试求出最大面积.参考答案1.(1)y =﹣x 2+x+2;(2)D(1,2);(3)存在,m =1或14 【解析】【分析】(1)点A 、B 的坐标分别为(2t ,0)、(﹣t ,0),则x =12=12(2t ﹣t ),即可求解; (2)点D (m ,﹣m 2+m+2),则点F (m ,﹣m+2),则DF =﹣m 2+m+2﹣(﹣m+2)=﹣m 2+2m ,即可求解;(3)以点O ,D ,E 为顶点的三角形与△BOC 相似,则DE OB OE OC =或OC OB ,即DE OE =2或12,即可求解.【详解】解:(1)设OB =t ,则OA =2t ,则点A 、B 的坐标分别为(2t ,0)、(﹣t ,0),则x =12=12(2t ﹣t ),解得:t =1, 故点A 、B 的坐标分别为(2,0)、(﹣1,0),则抛物线的表达式为:y =a (x ﹣2)(x+1)=ax 2+bx+2,解得:a =﹣1,故抛物线的表达式为:y =﹣x 2+x+2;(2)对于y =﹣x 2+x+2,令x =0,则y =2,故点C (0,2),由点A 、C 的坐标得,直线AC 的表达式为:y =﹣x+2,设点D 的横坐标为m ,则点D (m ,﹣m 2+m+2),则点F (m ,﹣m+2),则DF =﹣m 2+m+2﹣(﹣m+2)=﹣m 2+2m ,∵﹣1<0,故DF 有最大值,此时m =1,点D (1,2);(3)存在,理由:点D (m ,﹣m 2+m+2)(m >0),则OD =m ,DE =﹣m 2+m+2,以点O ,D ,E 为顶点的三角形与△BOC 相似, 则DE OB OE OC =或OC OB ,即DE OE =2或12,即22m m m-++=2或12,解得:m =1或﹣2(舍去),故m=1或133.【点睛】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力.会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系是解题的关键.2.(1)y=﹣13x2+23x+83;(2)(1+13,4)或(1﹣13,4)或(1+5,﹣4)或(1﹣5,﹣4);(3)P(1,1202﹣168)【解析】【分析】【详解】解:(1)OA=2=BC,故函数的对称轴为x=1,则x=﹣=1①,将点A的坐标代入抛物线表达式得:0=4a﹣2b+②,联立①②并解得,故抛物线的表达式为:y=﹣x2+x+③;(2)由抛物线的表达式得,点M(1,3)、点D(4,0);∵△ADR的面积是▱OABC的面积的,∴×AD×|y R|=×OA×OB,则×6×|y R|=×2×,解得:y R=±④,联立④③并解得,或故点R的坐标为(1+,4)或(1﹣,4)或(1+,﹣4)或(1﹣,﹣4);(3)作△PEQ 的外接圆R ,∵∠PQE =45°,故∠PRE =90°,则△PRE 为等腰直角三角形,当直线MD 上存在唯一的点Q ,则RQ ⊥MD ,点M 、D 的坐标分别为(1,4)、(4,0),则ME =4,ED =4﹣1=3,则MD =5,过点R 作RH ⊥ME 于点H ,设点P (1,2m ),则PH =HE =HR =m ,则圆R 的半径为m ,则点R (1+m ,m ), S △MED =S △MRD +S △MRE +S △DRE ,即×EM•ED =×MD×RQ+×ED•y R +×ME•RH ,∴×4×3=×5×m+×4×m+×3×m ,解得m =60﹣84,故点P (1,120﹣168). 3.(1)239344y x x ++=﹣;(2)①1174+或5414+;②点Q (125,65)或(285,7425-). 【解析】【分析】 (1)在334y x =-+中,令x=0,则y=3,令y=1,则x=4,故点B 、C 的坐标分别:(4,0)、(0,3),将点B 、C 的坐标代入抛物线函数表达式,即可求解;(2)① 根据已知PQ=5EF ,则2393(2)(2)353445t t t t -++=⨯=,解方程即可; ②分点Q 在BC 上方、BC 下方,两种情况分别求解.【详解】解:(1)y =﹣34x +3,令x =0,则y =3,令y =0,则x =4, 故点B 、C 的坐标分别:(4,0)、(0,3),则BC =5,将点B 、C 的坐标代入抛物线函数表达式得:2390444ca c =⎧⎪∴⎨=⨯+⨯+⎪⎩解得:a =﹣34,c =3, 故抛物线的表达式为239344y x x ++=﹣; (2)①设点P [2t ,﹣34(2t )2+94 (2t )+3],则BE =t , 在Rt BOC 中,设∠OBC=αtan ∠OBC =tanα=34,则sinα=35,cosα=45, 在Rt BEF 中,EF =EB sinα=35t , ∵PQ =5EF ,∴|﹣34(2t )2+94 (2t )+3|=5×35t =3t , 解得:t =117+或541+ (不合题意的值已舍去); ②当点Q 在BC 上方时,∵S △CBQ :S △BHQ =5:2,则BH =25BC =2, 则P B =BH cosα=85,则点P (125,0), 把x=125代入239344y x x ++=﹣得y=65则点Q (125,65); 当点Q 在BC 下方时,∵S△CBQ:S△BHQ=5:2,则BH=25BC=2,则P B=BH cosα=85,则点P(285,0),把x=285代入239344y x x++=﹣得y=-7425则点Q(285,﹣7425);故点Q(125,65)或(285,7425-).【点睛】本题主要考查了待定系数法求二次函数的解析式和与几何图形结合的综合,以及解直角三角形的知识,要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.4.(1)(1,1)或(3,5);(2)y=2x−1;(3)−3≤m≤3且m≠1.【解析】【分析】(1)根据待定系数法求得解析式,然后把解析式化成顶点式即可求得;(2)化成顶点式,求得顶点坐标,即可得出y与x的函数表达式;(3)把C(0,2)代入y=x2−2mx+m2+2m−1,求得m=1或−3,结合(1)根据图象即可求得.【详解】解:(1)∵抛物线y=x2−2mx+m2+2m−1过点B(3,5),∴把B(3,5)代入y=x2−2mx+m2+2m−1,整理得,m2−4m+3=0,解得m1=1,m2=3,当m=1时,y=x2−2x+2=(x−1)2+1,其顶点A的坐标为(1,1);当m =3时,y =x 2−6x +m 2+14=(x−3)2+5,其顶点A 的坐标为(3,5); 综上,顶点A 的坐标为(1,1)或(3,5);(2)∵y =x 2−2mx +m 2+2m−1=(x−m )2+2m−1,∴顶点A 的坐标为(m ,2m−1),∵点A 的坐标记为(x ,y ),∴x =m ,∴y =2x−1;(3)由(2)可知,抛物线的顶点在直线y =2x−1上运动,且形状不变,由(1)知,当m =1或3时,抛物线过B (3,5),把C (0,2)代入y =x 2−2mx +m 2+2m−1,得m 2+2m−1=2,解得m =1或−3,所以当m =1或−3时,抛物线经过点C (0,2),如图所示,当m =−3或3时,抛物线与线段BC 只有一个交点(即线段CB 的端点),当m =1时,抛物线同时过点B 、C ,不合题意,所以m 的取值范围是−3≤m≤3且m≠1.【点睛】本题考查了待定系数法求二次函数的解析式,二次函数的性质,二次函数图象上点的坐标特征,数形结合是解题的关键.5.(1)239344y x x =--;(2)等腰三角形,理由见解析;(3)存在;1414(,)33P -,2(4,18)P - 【解析】【分析】(1)由于二次函数的二次项系数表示的是抛物线的开口大小和开口方向,在平移过程中,抛物线的形状没有发生变化,所以二次项系数仍为34,已知了平移后的抛物线经过x 轴上的A 、B 两点,可由待定系数法求出平移后的抛物线解析式;(2)由坐标轴上点的特征可得C (0,-3),根据两点间的距离公式得到AB ,BC ,AC 的值,再根据等腰三角形的判定即可求解;(3)可设22393,3,,444P a a a D a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,根据PD=2OC ,列出方程即可求解. 【详解】解:(1)设抛物线2L 的解析式为234y x bx c =++, 经过点(1,0)A -、(4,0)B , 根据题意得3041240b c b c ⎧-+=⎪⎨⎪++=⎩, 解得943b c ⎧=-⎪⎨⎪=-⎩所以抛物线2L 的解析式为239344y x x =--. (2)ABC ∆的形状是等腰三角形.理由:根据题意得(0,3)C -,(1,0)A -,(4,0)B .∵4(1)5AB =--=,5BC ==,AC =∴AB BC =,即ABC ∆的形状是等腰三角形.(3)存在,理由: 设22393,3,,444P a a a D a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭, 根据题意,得22393933,34444PD a a a a OC =---=+=. ∵2PD OC = ∴9|3|64a +=,解得124,43a a ==-,∴1414(,)33P -,2(4,18)P -. 【点睛】 此题考查了二次函数综合题,涉及了二次函数图象的平移、待定系数法求函数解析式、等腰三角形的判定以及两点间的距离等知识,综合性较强,难度中等.6.(1)y =x 2+2x ﹣3;(2)点P 的坐标为(2,5)或(﹣4,5);点E 的坐标为(﹣1,2)或(﹣1,8).【解析】【分析】(1)根据待定系数法,将点(3,12)和(﹣2,﹣3)代入抛物线表达式,即可求解; (2)在△AOC 中,OA =OC =3,由题意:以P 、D 、E 为顶点的三角形与△AOC 全等可知PD =DE =3,再分点P 在抛物线对称轴右侧、点P 在抛物线对称轴的左侧两种情况,求解即可.【详解】解:(1)将点(3,12)和(﹣2,﹣3)代入抛物线表达式得1293342b c b c =++⎧⎨-=-+⎩,解得23b c =⎧⎨=-⎩, 故抛物线的表达式为:y =x 2+2x ﹣3;(2)抛物线的对称轴为x =﹣1,令y =0,则x =﹣3或1,令x =0,则y =﹣3, 故点A 、B 的坐标分别为(﹣3,0)、(1,0);点C (0,﹣3),故OA =OC =3,∵∠PDE =∠AOC =90°,∴当PD =DE =3时,以P 、D 、E 为顶点的三角形与△AOC 全等,设点P (m ,n ),当点P 在抛物线对称轴右侧时,m ﹣(﹣1)=3,解得:m =2,故n =22+2×2﹣5=5,故点P (2,5),故点E (﹣1,2)或(﹣1,8);当点P 在抛物线对称轴的左侧时,由抛物线的对称性可得,点P (﹣4,5),此时点E 坐标同上,综上,点P 的坐标为(2,5)或(﹣4,5);点E 的坐标为(﹣1,2)或(﹣1,8).【点睛】本题主要考查了二次函数与几何运用,涉及到三角形全等,掌握数形结合思想是解答关键,其中(2)需要分类求解,避免遗漏.7.(1)抛物线解析式为:2y x 2x 3=-++;直线AD 的解析式为:1y x =+;(2)当12x =时,最大值为278;(3)3,0或()2,5--. 【解析】【分析】 (1)利用待定系数法求抛物线和直线AD 的解析式即可;(2)联立抛物线与直线的解析式,得到点E 的坐标,设点()2,23M x x x -++,过点M 作//MN y 轴,交AE 于N ,则(),1N x x +,利用割补法表示出AME △的面积,得到关于x 的二次函数,利用二次函数求最值即可解决;(3)设()2,23G x x x -++,过点G 作//GP y 轴,交AE 于P ,则(),1P x x +,利用割补法表示出AEG △的面积,得到关于x 的一元二次方程,求解即可.【详解】解:(1)因为抛物线经过()()()1,0,3,0,0,3-,设抛物线的解析式为(1)(3)y a x x =+-,将(0,3)代入得1a =-,所以抛物线的解析式为:()()21323y x x x x =-+-=-++; 设直线解析式为y kx b =+,因为直线经过(-1,0),(0,1)01k b b =-+⎧∴⎨=⎩,解得11k b =⎧⎨=⎩, ∴直线AD 的解析式为:1y x =+;(2)联立抛物线与直线的解析式,可得:2231y x x y x ⎧=-++⎨=+⎩,解得:1xy⎧⎨⎩=-=或23xy=⎧⎨=⎩,∴点E的坐标为:()2,3E,设点()2,23M x x x-++,过点M作//MN y轴,交AE于N,则(),1N x x+,AMN EMNS S S∴=+△△()12E AMN x x=⋅⋅-()132M Ny y=⨯⨯-()2322x x=⨯-++23127228x⎛⎫=--+⎪⎝⎭,∴当12x=时,S有最大值,最大值为278S=;(3)设()2,23G x x x-++,过点G作//GP y轴,交AE于P,则(),1P x x+,AGP EPG S S S ∴=-△△ ()()1122A G E G PG x x PG x x =⋅⋅--⋅⋅- ()12E A PG x x =⋅⋅- ()23262x x =--= 260x x ∴--=解得:3x =或2x =-()3,0G ∴或()2,5G --.【点睛】本题考查待定系数法求解析式、割补法表示面积、二次函数最值等内容,解题的关键是作出辅助线,合理利用割补法表示面积.8.(1)2-;(2)1a m =--;(3)①22a n =--,21m n =+.(或21m n -=);②19,02P ⎛⎫ ⎪⎝⎭,2(4,0)P ,35,03P ⎛⎫ ⎪⎝⎭【解析】【分析】(1)把点代入解析式,列出方程,即可得到结果;(2)由抛物线过点1(2,2)A m --,1(2,2)B m -,代入解析式可得方程组,进而求解即可;(3)①根据已知条件设出()11,2C n --,()11,-2D n ,代入解析式可得到结果;②由题可得()11,2C n -,()12,2B m -,21m n =+,()12,42B n --,根据等腰三角形的性质分类讨论即可得到结果.【详解】(1)当m=1时,图象下移2m ,即2个单位,∵()2,0A -,()2,0B ,∴()12,2A --,()12,2B -,∵1A ,1B 在抛物线上,把1A ,1B 代入, 得2222{2222a b a b -=-+-=++, 解得20a b ⎧=-⎨=⎩,故2a =-;(2)解:抛物线过点1(2,2)A m --,1(2,2)B m -,221(2)2222122222a b m a b m ⎧⨯--+=-⎪⎪∴⎨⎪⨯++=-⎪⎩ 444a m ∴+=-1a m ∴=--(3)①∵CD 下移2n 个单位,∴()11,2C n --,()11,-2D n ,两点都在抛物线上, 可得2222n a b n a b ⎧-=-+⎨-=++⎩,解得22a n =--, 可得112n a =--,1m a =--, 化简得21m n =+②由题可得()11,2C n -,()12,2B m -,∵21m n =+,∴()12,42B n --,当11PC PB =时,过点1B 作1B M x ⊥轴,过点1C 作1C N x ⊥轴,∴122C N PM n x ===-,142-1PN B M n x ==+=,2241n x n x ⎧=-⎨=-⎩, ∴41x x =-, 解得53x =. 故P 点坐标为5,03⎛⎫ ⎪⎝⎭.⑵当111B C B P =,过1B 作l 平行于x 轴,过点1C 作1C M l ⊥,过点P 作l PN ⊥,同理可得:∴11422C M B N n x ==+=-,1423PN B M n ==+=,2+2241n x n ⎧=-⎨=⎩, 解得92x =; 故P 点坐标为9,02⎛⎫ ⎪⎝⎭. ⑶当111PC B C =,过1C 作l 平行于y 轴,过点1B 作1B M l ⊥,过点P 作PN l ⊥,∴1422-1B M PN n n x ==+-=,132B M PN n ===,2+123n x n ⎧=⎨=⎩, 解得4x =;故P 点坐标为()4,0. ∴19,02P ⎛⎫ ⎪⎝⎭,2(4,0)P ,35,03P ⎛⎫ ⎪⎝⎭. 【点睛】本题主要考查了二次函数综合应用,注意平移后点的坐标及计算是解题的关键.9.(1)A (-5,0),C (0,52);(2) 215222y x x =--+ ;(3)存在,152. 【解析】【分析】(1)分别代入x=0,y=0即可求得;(2)待定系数法即可求得抛物线解析式;(3)过点C 作CM ∥AB ,过点E 作EF ⊥CM ,证△CEF ∽△ACO ,得EF FC OC AO =,设点E (m ,215222m m --+),根据比例关系即可求得. 【详解】 解:(1)当y =0时,12x +52=0, 解得:x =-5,则A (-5,0);当x=0时,y=52, ∴C 点坐标为(0,52); (2)设抛物线的解析式为y =ax 2+bx +c ,代入A ,B ,C 三点,2550052a b c a b c c ⎧⎪-+=⎪++=⎨⎪⎪=⎩ ,解得12252a b c ⎧=-⎪⎪=-⎨⎪⎪=⎩, ∴抛物线的解析式为:215222y x x =--+; (3)存在.如图,过点C 作CM ∥AB ,过点E 作EF ⊥CM ,∴∠MCA =∠CAB .∵∠ECA =2∠CAB =∠ECF +∠MCA ,∴∠ECF =∠CAB .∵∠AOC =∠EFC =90°,∴△CEF ∽△ACO , ∴EF FC OC AO=. 设点E (m ,215222m m --+),OC =52, ∴21-22552m m m --=, 解得:m =-3或m =0(不合题意,舍去),∴点E (-3,4)∴S △ACE =12×(3+5)×4-12×32×3-12×5×52=152. 【点睛】本题为二次函数综合题,结合一次函数主要考查用待定系数法求抛物线的解析式、抛物线上点的坐标特征、相似三角形的判定与性质,有一定的综合性,熟练掌握抛物线性质是解题的关键.10.(1)y=2x 2﹣3x ;(2)C (1,﹣1);(3)(4564,316)或(﹣316,4564). 【解析】【分析】(1)由直线解析式可求得B 点坐标,由A 、B 坐标,利用待定系数法可求得抛物线的表达式;(2)过C 作CD ∥y 轴,交x 轴于点E ,交OB 于点D ,过B 作BF ⊥CD 于点F ,可设出C 点坐标,利用C 点坐标可表示出CD 的长,从而可表示出△BOC 的面积,由条件可得到关于C 点坐标的方程,可求得C 点坐标;(3)设MB 交y 轴于点N ,则可证得△ABO ≌△NBO ,可求得N 点坐标,可求得直线BN 的解析式,联立直线BM 与抛物线解析式可求得M 点坐标,过M 作MG ⊥y 轴于点G ,由B 、C 的坐标可求得OB 和OC 的长,由相似三角形的性质可求得OM OP的值,当点P 在第一象限内时,过P 作PH ⊥x 轴于点H ,由条件可证得△MOG ∽△POH ,由OM MG OG OP PH OH ==的值,可求得PH 和OH ,可求得P 点坐标;当P 点在第三象限时,同理可求得P 点坐标.【详解】(1)∵B (2,t )在直线y=x 上,∴t=2,∴B (2,2),把A 、B 两点坐标代入抛物线解析式可得:42293042a b a b +=⎧⎪⎨+=⎪⎩,解得:23a b =⎧⎨=-⎩, ∴抛物线解析式为223y x x =-;(2)如图1,过C 作CD ∥y 轴,交x 轴于点E ,交OB 于点D ,过B 作BF ⊥CD 于点F ,∵点C 是抛物线上第四象限的点,∴可设C (t ,2t 2﹣3t ),则E (t ,0),D (t ,t ),∴OE=t ,BF=2﹣t ,CD=t ﹣(2t 2﹣3t )=﹣2t 2+4t ,∴S △OBC =S △CDO +S △CDB =12CD•OE+12CD•BF=12(﹣2t 2+4t )(t+2﹣t )=﹣2t 2+4t , ∵△OBC 的面积为2,∴﹣2t 2+4t=2,解得t 1=t 2=1,∴C (1,﹣1);(3)存在.设MB交y轴于点N,如图2,∵B(2,2),∴∠AOB=∠NOB=45°,在△AOB和△NOB中,∵∠AOB=∠NOB,OB=OB,∠ABO=∠NBO,∴△AOB≌△NOB(ASA),∴ON=OA=32,∴N(0,32),∴可设直线BN解析式为y=kx+32,把B点坐标代入可得2=2k+32,解得k=14,∴直线BN的解析式为1342y x=+,联立直线BN和抛物线解析式可得:2134223y xy x x⎧=+⎪⎨⎪=-⎩,解得:22xy=⎧⎨=⎩或384532xy⎧=-⎪⎪⎨⎪=⎪⎩,∴M(38-,4532),∵C(1,﹣1),∴∠COA=∠AOB=45°,且B(2,2),∴OB=222,∵△POC∽△MOB,∴2OM OB OP OC ==,∠POC=∠BOM , 当点P 在第一象限时 ,如图3,过M 作MG ⊥y 轴于点G ,过P 作PH ⊥x 轴于点H ,如图3∵∠COA=∠BOG=45°,∴∠MOG=∠POH ,且∠PHO=∠MGO ,∴△MOG ∽△POH ,∴2OM MG OG OP PH OH=== ∵M (38-,4532), ∴MG=38,OG=4532, ∴PH=12MG=316,OH=12OG=4564, ∴P (4564,316); 当点P 在第三象限时,如图4,过M 作MG ⊥y 轴于点G ,过P 作PH ⊥y 轴于点H ,同理可求得PH=12MG=316,OH=12OG=4564, ∴P (﹣316,4564); 综上可知:存在满足条件的点P ,其坐标为(4564,316)或(﹣316,4564).【点睛】本题为二次函数的综合应用,涉及待定系数法、三角形的面积、二次函数的性质、全等三角形的判定和性质、相似三角形的判定和性质、方程思想及分类讨论思想等知识.在(1)中注意待定系数法的应用,在(2)中用C 点坐标表示出△BOC 的面积是解题的关键,在(3)中确定出点P 的位置,构造相似三角形是解题的关键,注意分两种情况.11.(1)①245y x x =-++;②存在,P 或(2,;(2)47b ≤≤. 【解析】【分析】(1)①根据抛物线的对称轴公式即可求出解析式;②如图1,若点P 在x 轴上方,点B 关于OP 对称的点B '在对称轴上,连接OB '、PB ,根据轴对称得到OB OB '=,PB PB '=,求出点B 的坐标,勾股定理得到B ',再根据PB PB '=,列出方程解答,同理得到点P 在x 轴下方时的坐标即可;(2)当4b ≥时,确定对称轴的位置,再结合开口方向,确定当02x ≤≤时,函数的增减性,从而得到当x=2时,函数取最大值,再列出不等式解答即可.【详解】解:(1)①抛物线25y x bx =-++的对称轴为直线2(1)2=-=⨯-b b x , ∴若过点C 的直线2x =是抛物线的对称轴, 则22b =,解得:b=4, ∴245y x x =-++;②存在,如图1,若点P 在x 轴上方,点B 关于OP 对称的点B '在对称轴上,连接OB '、PB , 则OB OB '=,PB PB '=,对于245y x x =-++,令y=0,则2450x x -++=,解得:121,5x x =-=,∴A (-1,0),B (5,0),∴5OB OB '==,∴CB '===,∴B ',设点P (2,m ),由PB PB '=可得:2221(52)m m -=+-,解得:221m =, ∴221(2,)7P , 同理,当点P 在x 轴下方时,221(2,)7P -, 综上所述,点221(2,)7P 或221(2,)7-(2)∵抛物线25y x bx =-++的对称轴为直线2(1)2=-=⨯-b b x , ∴当4b ≥时,22b x =≥, ∵抛物线开口向下,在对称轴左边,y 随x 的增大而增大,∴当02x ≤≤时,取x=2,y 有最大值,即42521y b b =-++=+,∴32115b ≤+≤,解得:17b ≤≤,又∵4b ≥,∴47b ≤≤.【点睛】本题考查了二次函数的综合应用,涉及了二次函数的图象与性质,以及勾股定理的应用,其中第(1)②问要先画出图形再理解,第(2)问运用到了二次函数的增减性,难度不大,解题的关键是熟记二次函数的图象与性质.12.(1)1x =;(2)233322y x x =-+或221y x x =-+-;(3)当233322y x x =-+时,13m -<<;当221y x x =-+-时,1m <-或3m >.【解析】【分析】(1)将二次函数化为顶点式,即可得到对称轴;(2)根据(1)中的顶点式,得到顶点坐标,令顶点纵坐标等于0,解一元二次方程,即可得到a 的值,进而得到其解析式;(3)根据抛物线的对称性求得点Q 关于对称轴的对称点,再结合二次函数的图象与性质,即可得到m 的取值范围.【详解】(1)∵22232y ax ax a =--+,∴22(1)32y a x a a =---+,∴其对称轴为:1x =.(2)由(1)知抛物线的顶点坐标为:2(1,23)a a --, ∵抛物线顶点在x 轴上,∴2230a a --=, 解得:32a =或1a =-, 当32a =时,其解析式为:233322y x x =-+, 当1a =-时,其解析式为:221y x x =-+-, 综上,二次函数解析式为:233322y x x =-+或221y x x =-+-. (3)由(1)知,抛物线的对称轴为1x =,∴()23,Q y 关于1x =的对称点为2(1,)y -, 当函数解析式为233322y x x =-+时,其开口方向向上, ∵()1,P m y 且12y y <,∴13m -<<;当函数解析式为221y x x =-+-时,其开口方向向下,∵()1,P m y 且12y y <,∴1m <-或3m >.【点睛】本题考查了二次函数对称轴,解析式的计算,以及根据二次函数的图象性质求不等式的取值范围,熟知相关计算是解题的关键.13.(1)a =﹣1,(0,3);(2)对称轴为x =1,最大值为﹣a +3;(3)y =x +2(x >1);(4)3<y M <4【解析】【分析】(1)将(1,4)代入解析式求出a 的值,将x =0代入解析式求出y 的值可得其与y 轴的交点坐标;(2)将函数解析式配方成顶点式即可得出答案;(3)由题意得出平移后的抛物线C 1解析式为y =a (x ﹣1+a )2﹣a +3,据此得出抛物线C 1顶点坐标为(1﹣a ,﹣a +3),即x =1﹣a ,y =﹣a +3,求出x ﹣y 即可得出答案;(4)由抛物线C 和函数D 的解析式得出分别过定点(2,4)、(2,3),结合函数图象可得答案.【详解】解:(1)抛物线C :y =ax 2﹣2ax +3过点(1,4),∴a ﹣2a +3=4,解得a =﹣1,当x =0时,y =3,即抛物线与y 轴的交点为(0,3);(2)∵y =ax 2﹣2ax +3=a (x ﹣1)2﹣a +3,抛物线有最高点,∴二次函数y =ax 2﹣2ax +3的对称轴为x =1,最大值为﹣a +3;(3)∵抛物线C :y =a (x ﹣1)2﹣a +3,∴平移后的抛物线C 1:y =a (x ﹣1+a )2﹣a +3,∴抛物线C 1顶点坐标为(1﹣a ,﹣a +3),∴x =1﹣a ,y =﹣a +3,∴x ﹣y =1﹣a +a ﹣3=﹣2,即x﹣y=﹣2,∴y=x+2,∵a<0,a=1﹣x,∴1﹣x<0,∴x>1,∴y与x的函数关系式为y=x+2(x>1);(4)如图,在y=x+2中,当x=2时,y=4,即直线y=x+2横过点(2,4),在y=ax2﹣2ax+3中,当x=2时,y=4a﹣4a+3=3,即抛物线y=ax2﹣2ax+3横过点(2,3),所以由图象知,抛物线C与函数D的图象交点M纵坐标的取值范围为3<y M<4.【点睛】本题是二次函数的综合问题,考查了求二次函数的最值,二次函数的平移,二次函数与一次函数的关系.解题关键是在无图的情况下运用二次函数性质解题,第(4)题结合图象解题体现数形结合的运用.14.()1对称轴直线x=1;B(3,0);()2n=5 2【解析】【分析】(1)根据OA=1,得出A点坐标,根据待定系数法把A点坐标带入二次函数解析式,从而求出a的值,求出二次函数解析式,根据对称轴公式求出对称轴;令y等于0,可求出B点坐标.(2)根据函数解析式求出顶点M的坐标,利用条件M,M1关于直线l对称,且M1到x轴距离为1,求出M 1的坐标,进而可求出n 的值.【详解】()1解:∵OA=1∴A(﹣1,0)把()1,0A -代入223y ax x =++得 230a -+=∴1a =- ∴对称轴2122bx a 令0y =,即2230x x -++=解得1,3A B x x =-=∴()3,0B()22y x 2x 3=-++()214x =--+∴顶点()1,4M1,M M 关于垂线l 对称,且到x 轴距离为1则()11,1M∴1415222M M x x n ++===. 【点睛】本体考查了二次函数的图像与性质,利用待定系数法求函数解析式,求函数对称轴,解题关键在于求出A 点坐标,带入函数解析式求出a 的值,求出函数解析式.15.(1)213222y x x =--;(2)存在点P ,坐标为(2,-3);(3)72 【解析】【分析】(1)分别求出A 、B 坐标,然后将A 、B 、C 三点坐标代入抛物线,即可得出其解析式; (2)首先假设存在点P ,然后根据面积相等构建等式,看是否有解,即可得解;(3)首先设点M 坐标,根据面积最大构建二次函数求最大值得出点M 坐标,然后设点N 坐标,再次构建二次函数求最小值,即可得解.【详解】(1)由题意,令0y =,即1202x -= ∴A 的坐标为(4,0)令0x =,即2y =-∴B 的坐标为(0,-2)将A 、B 、C 三点坐标代入抛物线,得 164020a b c c a b c ++=⎧⎪=-⎨⎪-+=⎩解得12232a c b ⎧=⎪⎪=-⎨⎪⎪=-⎩∴抛物线解析式为:213222y x x =--; (2)假设存在该点P ,设其坐标为(a ,213222a a --) ∵A 的坐标为(4,0),B 的坐标为(0,-2)∴OA=4,OB=2,AB ==∴点P 到直线122y x =-211322a a a ⎛⎫---- ⎪∵142PAB OAB OA O S BS =⋅==∴211322142a a a ⎛⎫---- ⎪⋅=∴2a =∴存在这样的点P ,点P 的坐标为(2,-3)(3)设M 坐标为213,222m m m ⎛⎫-- ⎪⎝⎭2211322142MAB m m m m S m ⎛⎫---- ⎪⋅=-+=△当MAB △的面积最大时,即()22424MAB m m S m =-+=--+△ MAB △的面积最大为4,2m =∴M 坐标为()2,3-设N 的坐标为()0,n111222MN ON n n +=⋅=⋅ 当3n =-时,12MN ON +有最小值, 其值为72. 【点睛】此题主要考查一次函数与二次函数的综合运用,熟练掌握,即可解题.16.(1)a =1,c =﹣3;(2)4;(3)M的坐标为∴M 1),M 2),M 3(1.﹣4),M 4(2,﹣3). 【解析】【分析】(1)利用待定系数法把问题转化为方程组即可求出答案;(2)如图1中,作PH⊥BC 于HDP +PCPD+2PC (PD +PH ),根据垂线段最短可知,当D、P 、HDP +PC DH ′; (3)如图2中,取点E (1,0),作EG ⊥BC于G ,易知EG .由S △EBC =12•BC •EG=12•322⋅=3,推出过点E作BC的平行线交抛物线于M1,M2,则13BCMS=△,23BCMS=△,求出直线M1M2的解析式,利用方程组即可解决问题,同法求出M3,M4的坐标.【详解】(1)把C(3,0),B(0,﹣3)代入y=ax2﹣2x+c得到,3960ca c=-⎧⎨-+=⎩,解得13ac=⎧⎨=-⎩.故答案为1,﹣3.(2)如图1中,作PH⊥BC于H.∵OB=OC=3,∠BOC=90°,∴∠PCH=45°,在Rt△PCH中,PH=22PC.2DP+PC2(PD+22PC2(PD+PH),根据垂线段最短可知,当D、P、H2DP+PC2DH′,在Rt△DH′B中,∵BD=4,∠DBH′=45°,∴DH′=22BD=2,2DP+PC2•2=4.(3)如图2中,取点E (1,0),作EG ⊥BC 于G ,易知EG =2.∵S △EBC =12•BC •EG =12•22⋅3, ∴过点E 作BC 的平行线交抛物线于M 1,M 2,则13BCM S =△,23BCM S=△,∵直线BC 的解析式为y =x ﹣3,∴直线M 1M 2的解析式为y =x ﹣1, 由2123y x y x x =-⎧⎨=--⎩ 解得31721172x y ⎧=⎪⎪⎨⎪=⎪⎩ 或31721172x y ⎧-=⎪⎪⎨-⎪=⎪⎩, ∴M 1317117-- ,M 2317117(++, 根据对称性可知,直线M 1M 2关于直线BC 的对称的直线与抛物线的交点M 3、M 4也满足条件,易知直线M 3M 4的解析式为y =x ﹣5,由2523y x y x x =-⎧⎨=--⎩解得14x y =⎧⎨=-⎩ 或23x y =⎧⎨=-⎩, ∴M 3(1.﹣4),M 4(2,﹣3),综上所述,满足条件的点M 的坐标为∴M 1317-,1172-),M 2(3172,1172),M 3(1.﹣4),M 4(2,﹣3).【点睛】本题属于二次函数综合题,主要考查了待定系数法,线段和最值问题,二次函数与一次函数图像和性质等知识,本题的线段和最值问题属于胡不归问题,把2PC成PH是解题的关键.17.(1)y=﹣x2+2x+3;(2)﹣m2+3m(0<m<3);(3)最大值为27 8【解析】【分析】(1)直接利用待定系数法即可求出抛物线的解析式;(2)先利用待定系数法求出直线BC的解析式,已知点M的横坐标,代入直线BC、抛物线的解析式中,可得到M、N点的坐标,N、M纵坐标的差的绝对值即为MN的长;(3)根据题(1)(2)的结论,列出SΔBNC关于m的表达式,再利用函数的性质求解SΔBNC 的最大值即可.【详解】解:(1)设抛物线的解析式为:y=a(x+1)(x﹣3),则:a(0+1)(0﹣3)=3,a=﹣1;∴抛物线的解析式:y=﹣(x+1)(x﹣3)=﹣x2+2x+3;(2)设直线BC的解析式为:y=kx+b,则有:303k bb+==⎧⎨⎩,解得13kb=-⎧⎨=⎩,故直线BC的解析式:y=﹣x+3.已知点M的横坐标为m,MN∥y,则M(m,﹣m+3)、N(m,﹣m2+2m+3),∴故MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m(0<m<3);(3)如图,∵S △BNC =S △MNC +S △MNB =12MN (OD +DB )=12MN •OB , ∴S △BNC =12(﹣m 2+3m )•3=﹣32(m ﹣32)2+278(0<m <3); ∴当m =32时,△BNC 的面积最大,最大值为278. 【点睛】 本题考查了利用待定系数法求一次函数和二次函数的解析式,以及二次函数图象的性质,较难的是题(3),求出ΔBNC 的面积关于m 的表达式是解题关键.18.(1)239y -x x 344=++ ,3y -x 34=+ (2)m=2 【解析】【分析】(1)令y =0,求出抛物线与x 轴交点,列出方程即可求出a ,即可得出抛物线解析式,根据待定系数法可以确定直线AB 解析式;(2)由△PNM ∽△ANE ,推出65PN AN =,列出方程即可解决问题. 【详解】解:(1)令y =0,则ax 2+(a +3)x +3=0,∴(x +1)(ax +3)=0,∴x =−1或−3a, ∵抛物线y =ax 2+(a +3)x +3(a≠0)与x 轴交于点A (4,0),∴−3a=4, ∴a =−34, ∴抛物线解析式为:239y -x x 344=++; ∵A (4,0),B (0,3),设直线AB 解析式为y =kx +b ,则3{40b k b +==,。
