微电子学物理基础-波函数及薛定谔方程
波函数与薛定谔方程

波函数与薛定谔方程引言:在量子力学中,波函数与薛定谔方程是两个核心概念。
波函数描述了粒子的量子态,而薛定谔方程则给出了波函数的时间演化规律。
本文旨在解释波函数与薛定谔方程的概念,并探讨它们在量子力学中的重要性。
一、波函数的定义与性质:波函数用符号Ψ表示,是随时间和空间变化的数学函数。
对于一个单粒子的量子系统,波函数Ψ(x,t)是描述其位置和时间依赖的函数,其中x表示位置,t表示时间。
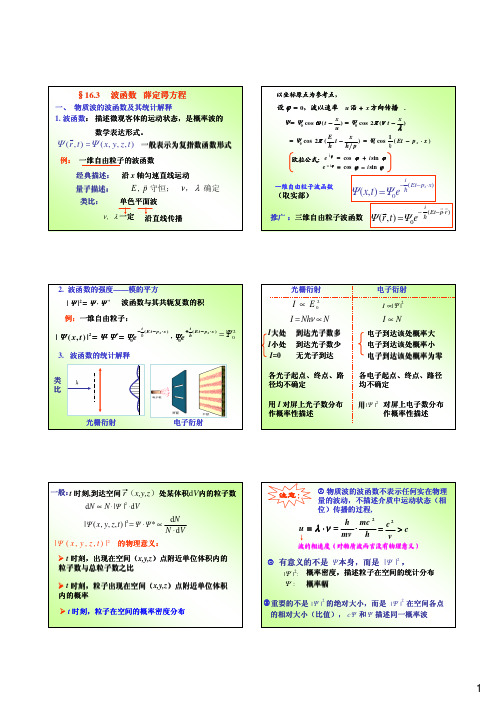
波函数的模的平方|Ψ(x,t)|²(也称为概率密度)给出了在某个位置找到粒子的概率。
波函数的归一化要求概率密度在整个空间积分为1,即∫|Ψ(x,t)|²dx = 1。
另外,波函数是复数形式的,通过它可以得到粒子的相位和幅度信息。
二、薛定谔方程及其意义:薛定谔方程是由奥地利物理学家薛定谔于1925年提出的,用于描述量子系统的演化。
薛定谔方程的一般形式为:ih∂Ψ/∂t = HΨ其中,i是虚数单位,h是普朗克常数,Ψ是波函数,H是哈密顿算符。
薛定谔方程可以看作是一个时间演化方程,它告诉我们波函数如何随时间变化。
三、薛定谔方程的解与量子态的演化:薛定谔方程的解Ψ(x,t)给出了波函数在时间和空间上的演化规律。
解薛定谔方程有多种方法,其中最常见的是分离变量法、微扰法和数值计算法。
通过求解薛定谔方程,我们可以得到粒子在不同时间、不同位置的波函数。
薛定谔方程解的平方Ψ(x,t)²表示了在经典条件下,在某个位置x找到粒子的概率密度分布。
波函数的演化规律是通过薛定谢方程来描述的,因此它反映了量子态的演化过程。
波函数的演化可以告诉我们粒子的位置、动量和能量等重要信息。
四、波函数的物理意义:波函数不仅仅是一个数学概念,它具有重要的物理意义。
首先,波函数的平方给出了在某个位置找到粒子的概率密度分布。
这一点与经典物理中的粒子位置概念是不同的,因为在量子力学中,粒子的位置是模糊的,只能通过概率来描述。
其次,波函数还包含了粒子的相位信息。
波函数和薛定谔方程
px ∂ 2Ψ = − Ψ, ∂x 2 h2
2
py ∂ 2Ψ = − Ψ 2 2 ∂y h pz ∂ 2Ψ = − Ψ ∂z 2 h2
2
2
h p2 2 − ∇ Ψ= Ψ 2m 2m (3)
是同一个量子态的不同表述
Ψ (r,t)是以坐标 r 为自变量的波函数, 坐标空间波函数,坐标表象波函数; C(p, t) 是以动量 p 为自变量的波函数, 动量空间波函数,动量表象波函数; 二者描写同一量子状态。
r r Ψ (r , t ) 与 c( p, t ) 有类似的物理意义 r 2 Ψ (r , t ) 是指在t时刻,粒子在r处出现的概率密度 r 2 c( p, t ) 是指在t时刻,粒子具有动量p的概率密度
与能量为E及动量为p 的粒子相联系的波(物质波) h E 的频率及波长为 λ= ν = p i rr h ( p⋅r − Et ) r 自由粒子平面波函数 ψ (r , t ) = Ae h
2.1 波函数的统计解释
另一种理解: 为防止电子间 发生作用,让 电子一个一个 地入射,发现 时间足够长后 的干涉图样和 大量电子同时 入射时完全相 同。(1989) 粒子是基本的,电子的波动性是大量电子之 间相互作用的结果。
2.3 含时薛定谔方程
2.3.1 经典粒子的动力学方程
r r dr t = t 0时刻,已知初态是: r0 , p0 = m dt
t = t0
2r r d r 粒子满足的方程是牛顿 方程: F = m 2 dt
从牛顿方程,人们可以确定以后任何时刻 t 粒子的状态 r 和 p 。因为初条件知道的是坐标及其对时间的一阶导 数,所以方程是时间的二阶常微分方程。
dτ ∫ ∞
→∞
2.2 态叠加原理
简述薛定谔方程与波函数

简述薛定谔方程与波函数
薛定谔方程是描述量子力学中一个粒子的运动的基本方程之一,其形式为时间-空间偏微分方程。
它是由奥地利物理学家艾尔温·薛定谔于1925年提出的。
薛定谔方程是描述粒子波函数的演化的方程,其中波函数是对一个粒子可能状态的描述。
波函数是一个数学函数,它描述了粒子在给定时刻的位置和动量的所有可能状态。
薛定谔方程将波函数与粒子的能量联系起来。
它描述了波函数在时间和空间上的演化方式,并将粒子的能量表示为波函数的特征值。
薛定谔方程可以用于计算粒子在各种情况下的运动和行为。
这些情况可以是粒子在外场中的运动,或者是两个或多个粒子的相互作用。
波函数是用来描述量子系统的数学对象。
它是一个数学函数,它描述了粒子在空间中的位置和运动状态的可能性。
波函数是一个复数函数,其模的平方表示在给定位置上发现粒子的概率。
波函数的模的平方越大,粒子出现在该位置的概率越高。
波函数在时间和空间上的演化可以由薛定谔方程描述。
波函数会根据薛定谔方程在不同的时间和空间位置上演化。
波函数在时间演化的过程中,其振幅和相位不断地变化。
这些变化可以用波函数的频率和波长来描述。
薛定谔方程和波函数是量子力学的基本概念之一,它们被广泛应用于研究和理解原子、分子和固体等量子系统的行为。
薛定谔方程和波函数的发展使得人们对物质世界的认识有了深刻的改变,也为现代科技的发展做出了重要的贡献。
第二章波函数和薛定谔方程

2
∫ψ
2
dτ = A 2 ∫ dτ = ∞ 这样 C 为零,显然没有意义。
∞
例:假如粒子只在一维空间运动,它的状态可以用波函数
⎧0 ⎪ ψ = ⎨ − i Et π h sin x ⎪ Ae a ⎩
( x ≤ 0, x ≥ a ) (0 ≤ x ≤ x )
在 t=0 时函数曲线如图, 来描述, 式中 E 和 a 分别为确定的常数, 而 A 为任意常数,求 ⑴ 归一化波函数; ⑵ 几率函数(几率密度) w ; ⑶ x, x 的值。 解 ⑴ 在一维空间里
ih
r r ∂ ˆ ψ (r ψ (r , t ) = H , t) ∂t
2.3-1 [*]有量子力学第三原理的说法
若含有状态参量,则方程只能被粒子的部 分状态所满足.而不能被各种可能的状态 所满足.
——波函数随时间变化的规律
ˆ ——为哈密顿算符 式中 H
2.3.1 S-eq 的建立 1. 方程是线性的 2. 这个方程的系数不应包含状态参量(如:动量、能量等) 3. ——在量子力学中微观体系的运动状态是用一个波函数描述,所以,反映微观粒子运动规律的波 函数ψ ( r , t ) 应是对时间的一阶微分方程;
2. 三维情况
∫
∞
−∞ ∞
C ( p )e
i
p x h
dp
(2.2-2)
x
∫
−∞
ψ ( x )e
−i
p
dx
1r r i p⋅ x ⎧ r ∞ r 1 C ( p, t )e h dp x dp y dp z ⎪ψ (r , t ) = (2πh ) 3 / 2 ∫−∞ ⎪ ⎨ i r r − p.r ∞ r r 1 ⎪C ( p h = , t ) ψ ( r , t ) e dxdydz ⎪ (2πh ) 3 / 2 ∫−∞ ⎩
波函数和薛定谔方程

波函数和薛定谔方程波函数和薛定谔方程是量子力学中两个重要的概念。
波函数是用来描述量子系统状态的数学函数,而薛定谔方程则是描述波函数随时间演化的微分方程。
本文将介绍波函数和薛定谔方程的基本原理和应用,并探讨它们对量子力学的重要性。
一、波函数的概念和性质1. 波函数的定义波函数是量子力学中用来描述量子系统的数学函数。
它通常用符号ψ来表示,且是复数函数。
波函数的模的平方表示了找到该系统处于某个状态的概率。
2. 波函数的物理意义波函数的物理意义是描述了量子系统的可能状态和其对应的概率分布。
通过对波函数的求模平方,我们可以得到量子系统在不同状态的概率分布图。
3. 波函数的归一化条件波函数必须满足归一化条件,即在整个空间内积分后等于1。
归一化条件保证了系统一定会处于某个状态,并且概率总和为1。
二、薛定谔方程的基本形式和解析解1. 薛定谔方程的基本形式薛定谔方程是描述量子系统波函数在时间上演化的基本方程。
一维情况下,薛定谔方程可以写为:iħ∂ψ/∂t = -ħ²/2m ∂²ψ/∂x² + V(x)ψ式中符号的含义为ħ为约化普朗克常数,m为粒子的质量,V(x)为势能函数。
2. 薛定谔方程的解析解对于某些特定的势能函数,薛定谔方程存在解析解。
比如自由粒子情况下的薛定谔方程的解为平面波,简谐振子情况下的薛定谔方程的解为倒谐波。
三、波函数和薛定谔方程的应用1. 粒子在势阱中的行为波函数和薛定谔方程被广泛应用于研究粒子在势阱中的行为。
通过对势能函数和初始条件的设定,可以计算出粒子的波函数演化,并分析粒子的行为,比如能量谱和态密度等。
2. 电子在固体中的行为波函数和薛定谔方程在固体物理学中有着重要的应用。
通过求解薛定谔方程,可以得到电子在晶体中的波函数,从而研究电子的能带结构、载流子运动以及材料的电导性等性质。
3. 分子和化学反应波函数和薛定谔方程在化学领域中也有广泛的应用。
通过求解薛定谔方程,可以得到分子的波函数,从而研究化学反应的动力学过程、反应速率以及分子能谱等性质。
波函数及薛定谔方程详解课件

03ቤተ መጻሕፍቲ ባይዱ
CATALOGUE
薛定谔方程在量子力学中的应用
无限深势阱
无限深势阱模型描述粒子被限 制在一定空间范围内运动的情 形,通常用于描述微观粒子在
势能无限高区域的行为。
在无限深势阱中,波函数具有 特定的边界条件,即在势阱边
界处波函数为零。
薛定谔方程在无限深势阱中的 解为分段函数,表示粒子在不 同势阱内的能量状态。
波函数及薛定 谔 方程详解课件
contents
目录
• 波函数简介 • 薛定谔方程概述 • 薛定谔方程在量子力学中的应用 • 波函数与薛定谔方程的关系 • 实验验证与实例分析 • 总结与展望
01
CATALOGUE
波函数简介
波函数的定 义
波函数是一种描述微观粒子状 态的函数,它包含了粒子在空 间中的位置和动量的信息。
06
CATALOGUE
总结与展望
波函数与薛定谔方程的意义
波函数
波函数是描述微观粒子状态的函数, 它包含了粒子在空间中的位置、动量 和自旋等所有信息。通过波函数,我 们可以计算出粒子在给定条件下的行 为和性质。
薛定谔方程
薛定谔方程是描述波函数随时间变化 的偏微分方程,它反映了微观粒子在 运动过程中所遵循的规律。通过求解 薛定谔方程,我们可以预测粒子在不 同条件下的行为和性质。
时间相关形式
在有限域中,薛定谔方程的形式为 ifrac{dpsi}{dt}=Hpsi,其中H为哈密 顿算子。
薛定谔方程的解
分离变量法
对于具有周期性势能的情况,可以将波函数分离为几个独立的函数,分别求解 后再组合得到原方程的解。
微扰法
对于势能存在微小扰动的情况,可以通过微扰法求解薛定谔方程,得到近似解。
波函数和薛定谔方程

一般情况下,如果Ψ1和Ψ2 是体系的可能状态,那么它们的 线性叠加
Ψ= C1Ψ1 + C2Ψ2 (其中C1 和 C2 是复常数) 也是该体系的一个可能状态,这就是量子力学的态叠加原 理。
态叠加原理一般表述:
若Ψ1 ,Ψ2 ,..., Ψn ,...是体系的一系列可能的状态,则这些态的线性 叠加
Ψ= C1Ψ1 + C2Ψ2 + ...+ CnΨn + ... 其中 C1 , C2 ,...,Cn ,...为复常数)。
实验上观测到的电子,总是处于一个小区域内。例如在一个原子 内,其广延不会超过原子大小≈1 Å 。
电子究竟是什么东西呢?是粒子?还是波? “ 电子既不是粒子 也不是波 ”,既不是经典的粒子也不是经典的波, 但是我们也 可以说,“ 电子既是粒子也是波,它是粒子和波动二重性矛盾的 统一。” 这个波不再是经典概念的波,粒子也不是经典概念中的粒子。
p
(
r)
p
(
r'
)dp
(r
r'
)
关系式
由此我们也可以看出把平面波归一化为 函数的目的。
c( p,t) 与 (r ,t) 具有类似的物理含义
dW (r , t) | (r , t) |2 dr t时刻粒子出现在 r点附近
dr 体积元内的几率;
dW ( p, t) | c( p, t) |2 dp t时刻粒子出现在动量p点附近
|Ψ|2 = |C1Ψ1+ C2Ψ2|2 = (C1*Ψ1*+ C2*Ψ2*) (C1Ψ1+ C2Ψ2) = |C1 Ψ1|2+ |C2Ψ2|2 + [C1*C2Ψ1*Ψ2 + C1C2*Ψ1Ψ2*]
lz2波函数和薛定谔方程

2
设
Φ ( x, y, z , t ) 描写粒子的状态.Φ = Φ Φ *
2
dW ( x, y, z , t ) 表示在时刻t,无限小区域内找到粒子的几率.
dW ( x, y, z , t ) = C Φ ( x, y, z , t ) dxdydz
3,态的演化方程 ( s q):i ψ = Hψ t
§2.6
U(x)
一维无限深势阱
U ( x) = 0 U ( x) = ∞
x <a x ≥a
-a
0
a
一维无限深势阱
U(x)只与坐标有关,与t无关.属定态问题,求解定态s-q.
Hψ n = Enψ n
一维:
2 2m 2 2m
d2 ψ = Eψ 2 dx d2 ψ + U 0ψ = Eψ 2 dx
即具有 不与"粒子有确切的轨道"的概念相联系.
波动性(不是经典的波):波的"叠加性",并不与 某种实际的物理量在空间的分布相联系. 几率波(波动性与粒子性的统一):波函数的统计解 释,玻恩(Born)的波函数的统计解释(1926)波函数在空 2 间中某一点的强度( ψ (r , t ) )和在该点找到粒子的几率 成正比. ψ (r , t ) ——几率幅,几率波不是机械波,不代 表什么实在的物理量的波动,只不过刻划粒子在空间的几 率分布而已. 亮纹:几率大 暗纹:几率小
x <a x ≥a
U0 → ∞
边界条件
ψ 根据波函数连续,有限的条件. = 0
证明见附录I, 令
x ≥a
2mE α= 2
d 2ψ ∴由(1) + α 2ψ = 0 dx 2 ψ = A sin αx + B cos αx
波函数和薛定谔方程

波函数和薛定谔方程薛定谔方程是量子力学中最基本的方程之一,描述了微观粒子的运动和性质。
而波函数则是薛定谔方程的解,通过波函数可以得到粒子的位置、动量等信息。
在量子力学中,波函数起着至关重要的作用,它是一种描述微观量子系统的数学工具。
下面将详细介绍波函数和薛定谔方程的基本概念和性质。
在量子力学中,波函数通常用Ψ(psi)来表示,它是一个关于时间和空间的复数函数。
波函数的模的平方|Ψ|² 可以描述粒子存在于某个位置的概率密度,即波函数的绝对值平方代表了粒子在空间中的分布情况。
波函数Ψ满足归一化条件,即积分∫|Ψ|² dV = 1,其中dV表示体积元素。
这意味着波函数描述的是单位概率密度,即粒子存在于空间中的概率为1。
薛定谔方程是描述波函数随时间演化的方程,一般写为:iℏ∂Ψ/∂t = -ℏ²/2m ∇²Ψ + VΨ其中,i表示虚数单位,ℏ是普朗克常数的约化普朗克常数,m是粒子的质量,∇²是拉普拉斯算子,V是势能函数。
薛定谔方程包含了波函数的时间演化和空间演化,可以描述量子粒子在不同势场中的运动和行为。
波函数的物理意义在于可以通过对波函数的操作得到粒子的物理量。
例如,对波函数Ψ做位置算符作用Ψ(x),可以得到粒子的位置期望值;对波函数Ψ做动量算符作用-iℏ∇Ψ(x),可以得到粒子的动量期望值。
波函数还可以描述量子系统的波包运动、干涉效应等现象,展现了量子力学的奇妙之处。
总之,波函数和薛定谔方程是量子力学中的核心概念和基本方程,它们揭示了微观世界的规律性和奇特性。
通过深入理解和研究波函数和薛定谔方程,可以更好地理解量子世界的奥秘,推动量子科学的发展和应用。
希望本文的介绍对读者有所帮助,激发对量子力学的兴趣和研究。
第一章波函数和薛定谔方程108页PPT

, 一定 沿直线传播
以坐标原点为参考点,设 0,以u速 沿 x率 方向.
0c o(t su x) 0co 2 (st x)
0co2s(E hthxp)
1 0cos(E t xpx)
(x,t)0e i(Etpxx) (取实部)
描述自由粒子(三维)可用平面波波函数来描述。
i ( pvrvEt)
而不会出现在 2 小的地方 。 同时 ( 3 ) 又是以波的方式在间传 播 , 于是粒子的运动又表现 出波动性 。 总之 .微粒的运动遵从的是统 计性的规律 , 而不同于经典力学的确 定性规律 。
(3) 波函数的不确定性:
1、常数因子不定性:
( rv)和 C (rv) 描述同一种运动状态。
因为在 t 时刻,空间任意两点 r1 和 r2 处找到粒子的 相对几率之比是:
pv Aeh
如果粒子处于随时间和位置变化的力场中运动, 它的动量和能量不再是常量(或不同时为常量) 粒子的状态就不能用平面波描写,这样的微观 粒子的运动状态也可以用较复杂的波完全描述。
(rv,t)
1.1.2、波粒二象性的解释
1、经典物理学中粒子与波的有关概念
经典概念中粒子意味着: ➢有一定质量、电荷等“颗粒性”的属性; ➢有确定的运动轨道,每一时刻有一定位置和速度。
主要介绍二个基本假设:
A. 微观粒子行为由波函数描述,波函数具有统 计意义。
B. 描述微观粒子行为的波函数由薛定谔方程 解出。
§1.1. 物质波的波函数及其统计解释
1.1.1、波函数的引入
例: 一维自由粒子的波函数
经典描述: 沿 x 轴匀速直线运动
量子描述: E ,p 守恒 , 确 ;定
类比: 单色平面波
1.1.3 Born波函数的统计解释几率波
波函数及薛定谔方程
t 时刻,出现在空间(x,y,z)点附近单位体积内的 粒子数与总粒子数之比
t 时刻,粒子出现在空间(x,y,z)点附近单位体积 内的概率
t 时刻,粒子在空间的概率密度分布
注意:
物质波的波函数不表示任何实在物理 量的波动,不描述介质中运动状态(相 位)传播的过程,
NN
标准条件
Ψ是单值、有限、连续的 。
二、薛定谔方程: 是波函数 Ψ所遵从的方程 — 量子力学的基本方程 , 是量子力学的基本假设之一,其正确性由实验检验。
1. 建立 (简单→复杂, 特殊→一般)
一维自由粒子的振幅方程
Ψ (x,t)
=Ψ e−
i ℏ
(
E
t
−
px
⋅
x
)
0
=
Ψ
0e
+
i ℏ
p
x
⋅x
−i Et
2 x
2m
代入
d2ψ ( x) dx2
=
−
px ℏ2
2
ψ
(
x
)*
得
d 2ψ ( x ) dx2
+
2 mE ℏ2
ψ
(x)
=
0
即 一维自由粒子的振幅方程
p
2 x
=
2mE
一维定态薛定谔方程
粒子在力场中运动,且势能不随时间变化
E
=
Ek
+
Ep
=
p
2 x
2m
+U
px2 = 2m(E −U )
代入
d2ψ ( x) dx2
∴ 建立关于振幅函数 ψ(x)的方程 —— 振幅方程
20 第二十讲 波函数与薜定谔方程、薜定谔方程应用举例

2.粒子在势阱中的概率分布 ◆概率分布不均匀,具有量 子化效应。 ★在两端出现的概率为零。 ★概率密度峰值的个数随n 的增大而增多,峰值间距随 之缩小。 ★ n→∞,峰值个数也为无 穷,峰值间距趋于零,概率 密度几乎各处均等,过渡到 经典理论的结果。
2 2 nπ x ρ = ψ = sin a a
概率密度: ρ ( x, t ) = ψ ( x, t )
2
在区间(-b/2, b/2) 以外找不到粒子。
( x < −b / 2, x > b / 2) ⎧0 ⎪ ρ ( x, t ) = ⎨ 2 2 π x ⎪ b cos ( b ) (−b / 2 ≤ x ≤ b / 2) ⎩
7
§26-3 薛定谔方程
0
E
a
x
ψ ( x ) = A sin( kx + ϕ )
13
ψ ( x ) = A sin( kx + ϕ )
由边界条件和归一化条件来确定待定常数ϕ 和 A:
ψ (0) = A sin ϕ = 0
ka = nπ
ϕ =0
ψ (a) = A sin(ka + ϕ ) = A sin ka = 0
nπ k= , a
29
扫描隧道显微镜
◎扫描隧道显微镜(STM)是20世纪80年代初期出现 的一种新型表面分析工具。其基本原理是基于量子力 学的隧道效应和三维扫描。 ◎它是用一个极细的尖针(针尖头部为单个原子)去 接近样品表面,当针尖和样品表面靠得很近,小于1纳 米时,针尖头部的原子和样品表面原子的电子云发生 重叠。此时若在针尖和样品之间加一个偏压,电子便 会穿过针尖和样品之间的势垒而形成纳安级(10-9A) 的隧道电流。通过控制针尖与样品表面间距的恒定, 并使针尖沿表面进行精确的三维移动,就可将表面形 貌和表面电子态等有关表面信息记录下来。
波函数和薛定谔方程

b a
Ò
S
r r r J (r , t ) dS
得
dJ x ( x, t ) = J x (a, t )- J x (b, t )
J x (a, t )和 J x (b, t ) 分别表示流入和流出Vab
r d 3r r r , t d r=( ) dt 蝌 V
抖 2 y* * y y =y + y 抖 t t t
对于一维的薛定谔方程
抖 ih y ( x, t ) = 抖 t 轾 h2 2 犏 + U ( x, t ) y ( x, t ) 犏 2m x 2 臌
则对于上式,可写为
抖 r ( x, t ) + 抖 t x J x ( x, t ) = 0
有
ì ï 抖 y ih 2y i ï = - Uy ï 2 ï 抖 t 2m x h ï í ï 抖 y* ih 2 y * i * ï = + U y ï 2 ï t 2m x h ï î 抖
不稳定粒子
发生衰变、或湮灭-再生过程的 粒子,则
P (t ) =
ò
¥
么?
守恒性
归一化条件是非相对论性粒子概率意义 的自然要求,也是薛定谔方程的结果。
r d 3r r r , t d r® 0 ( ) ò dt ¥
ò
+
-
y (x, t ) dx = e- t t
2
P (t )是粒子出现在全空间的概率, t 为粒子衰变的寿命。
算符
在位形空间里,描述动量的函数不再 是一般的函数,而是微分算符
ˆx px ? p - ih ¶ ¶x
3第二章 波函数和薛定谔方程

( x, t ) ( x, t ) 0
2
( x b / 2), x b / 2) (b / 2 x b / 2)
( x, t )
2
2 2 x ( x, t ) ( x, t ) cos ( ) b b
2
如图所示,在区间(b/2,b/2) 以外找不到粒子。在x=0处找 到粒子的几率最大。
一、 Born解释(1926年)
电子双 缝衍射 实验
实验结果:
感光时间较短
感光时间足够长
最终
分析及讨论: 底板接收的电 子是一个一个 的完整体 条纹由大量电 子密集与稀疏 有规律交替出 现形成
粒子性表现 衍射波的强度分布对应于 电子数的密度分布 波动性表现
电子聚集密度的分布决定 于单个电子在底板上出现 概率的分布
子是一个一个的完整体粒子性表现条纹由大量电子密集与稀疏有规律交替出现形成波动性表现微观粒子保持完整的颗粒结构在空间以概率波的形式运动的性质波粒二象性waveparticleduality微观粒子的波动性乃是粒子统计运动规律的一种特殊表现电子双缝衍射二波函数的物理意义衍射条纹极大值衍射条纹极小值波动观点粒子观点波的强度最大波函数振幅绝对值的平方即最大感光点的密度最大电子到达的数目多电子出现的概率大波的强度为零波函数振幅绝对值的平方感光点的密度为零到达的电子数目为零电子出现的概率为零感光强度的分布电子出现的概率分布感光强度的分布电子波函数振幅绝对值的平方结论某时刻t在空间某点r处粒子出现的几率正比于该时刻该点处的波函数的模的平方总结
x, t
-b/2
o
b/2
x
第二节
态叠加原理 (State Superposition Principle)
波函数与薛定谔方程

直到1926年波恩提出统计诠释,大多数物理学家接受
在已知给定的条件下,不可能精确地预知结果,只能预言某些 可能结果的概率 粒子的运动遵守概率定律,但概率本身还是受因果规律支配的 但争论仍在继续:
哥本哈根学派:玻尔、海森伯坚持波函数的概率或统计解释 认为它表明了自然界的最终实质 爱因斯坦不喜欢量子力学的“不完备性” 上帝不是跟宇宙玩掷骰子游戏
满足归一化条件 d 3r 1 的波函数
16
例
17
例
18
续
19
例
20
薛定谔方程引言
21
16-2 薛定谔方程
量子力学基本原理之二: 微观粒子体系的波函数ψ满足
薛定谔方程.
起源: 1926年薛定谔对德布罗意的工作了漂亮又简
洁的说明,-----德拜听后说“要真正研究波动,必须
有波动方程.” 几个星期后,薛定谔找到了这个方程.
也是这个体系的一个可能态。
c11 c2 2 cn n cn n
c1, c2, cn为任意常数 n
波函数遵从叠加原理由实验证实: 以双缝实验为例
1、子弹通过双缝的射击实验 (经典)
子弹
宏观粒子 可以跟踪
a P1
b
P2
P
P P1 P2概率叠加
H
i
t
如果知道了 U ,可列出微分方程,解得Ψ,即找到 Ψ 随时 间变化的规律。
27
定态薛定谔方程:如果粒子所处的势场 U( r ) 与时间无关(即
不显含时间), 可用分离变量法求解.
令
H i
r, t
t r
f
t
波函数和薛定谔方程

波函数和薛定谔⽅程波函数和薛定谔⽅程⼀、波函数的统计解释、叠加原理和双缝⼲涉实验微观粒⼦具有波粒⼆象性(德布罗意假设);德布罗意关系(将描述粒⼦和波的物理量联系在⼀起) k n h p h E ====λων物质波(微观粒⼦—实物粒⼦)引⼊波函数(概率波幅)—描述微观粒⼦运动状态对于微观粒⼦来说,如果不考虑“⾃旋”⼀类的“内禀”态,单值波函数是其物理状态的最详尽描述。
⾄少在⽬前量⼦⼒学框架中,我们不能获得⽐波函数更多的物理信息。
微观粒⼦的状态⽤波函数完全描述——量⼦⼒学中的⼀条基本原理该原理包含三⽅⾯内容:粒⼦的状态⽤波函数表⽰、波函数的统计解释和对波函数性质的要求。
要明确“完全”的含义是什么。
按着波函数的统计解释,波函数统计性的描述体系的量⼦态,若已知单粒⼦(不考虑⾃旋)波函数)(r ψ,则不仅可以确定粒⼦的位置概率分布,⽽且如动量等粒⼦的其它⼒学量的概率分布也均可通过波函数⽽完全确定。
由此可见,只要已知体系的波函数,便可获得该体系的⼀切物理信息。
从这个意义上说,有关体系的全部信息已包含在波函数中,所以说微观粒⼦的状态⽤波函数完全描述。
必须强调指出,波函数给出的有关粒⼦的“信息”本质上是统计性质的。
例如,在适当条件下制备动量为p 的粒⼦,然后测量其空间位置,我们根本⽆法预⾔测量的结果,我们只能知道获得各种可能结果的概率。
很⾃然,⼈们会提出这样的疑问:既然量⼦⼒学只能给出统计结果,那就只需引⼊⼀个概率分布函数(象经典统计⼒学那样),何必假定⼀个复值波函数呢?事实上,引⼊复值波函数的物理基础,乃是量⼦⼒学中的⼜⼀条基本原理——叠加原理。
这条原理告诉我们,两种状态的叠加,绝不是概率相加,数学求和)。
正因如此,在双缝⼲涉实验中,我们才能看见屏上的⼲涉花纹。
实物粒⼦双缝⼲涉实验分析我们⾸先只打开⼀条狭缝,根据粒⼦的波动性,可以预⾔屏上将显⽰波长p / =λ(p 为粒⼦动量)的单缝衍射花纹。
但是,根据粒⼦的微粒性,它们将是⼀个⼀个打上去的,怎样将这两种性质的描述调和起来呢?为此,我们想象将⼊射粒⼦束强度降低,直到只⼀个粒⼦通过狭缝,这时屏上会出现很微弱的衍射花纹吗?当然不会!单个粒⼦只能作为⼀个不可分割的整体打到屏上的⼀个点,从⽽出现⼀个⼩斑点。
12-4 波函数 薛定谔方程

在某一时刻,在空间某处,微观粒子出现的概 率正比于该时刻、该地点波函数的平方。 在空间一很小区域(以体积元dV=dx dy dz表征)出 现粒子的概率为:
dV dV
称为概率密度,表示在某一时刻在某点处单
2
2
位体积内粒子出现的概率。 波函数还须满足:
dV 1
2
归一化条件
代入薛定谔方程,采用分离变量,得到:
2 2 f ( t ) 1 1 ( x , y , z ) U ( x , y , z ) ( x , y , z ) i t f ( t ) 2m ( x, y, z )
令等式两端等于同一常数
f (t ) 1 i E t f (t )
得到描写自由粒子的平面波波函数:
( x, t ) 0 e
i
2 ( Et px ) h
物质波的物理意义可以通过与光波的对比来阐明
光波振幅平方大 光强度大 光子在该处出现 的概率大 (微粒观点)
(波动观点)
物质波的 强度大
波函数振幅的平方大 (波动观点) 单个粒子在该处出现 (微粒观点) 的概率大
§12-4 波函数 薛定谔方程
一、波函数及其统计意义
用某种函数表达式来表述与微观粒子相联系 的物质波,该函数表达式称为物质波的波函数。 机械波
y ( x, t ) y0 cos 2 (t x )
y ( x, t ) y0e
i 2 (t x )
或
利用关系
E h, h P
及单值、连续、有限等标准化条件
例1
作一微运动的粒子被束缚在 0<x<a 的范围内。
已知其波函数为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《微电子学物理基础》
Fundamental of Microelectronics Physics
教学大纲
一、课程性质与目的
《微电子物理基础》是微电子学专业的专业选修课。
该课程在普通物理、高等数学、线性代数等基础上,使学生树立起微观粒子运动的基本图像,深刻理解微观粒子运动的表述方式、基本原理及普遍规律,掌握典型微观体系的基本特征。
通过该课程的学习,能够理解波函数的意义,力学量算符的概念,掌握晶体结构,晶格振动和能带理论。
解决一些与专业有关的问题,为今后进一步学习有关专业基础课程奠定必要的理论基础。
二、课程内容及要求:
第一章经典物理学的困难
1、教学基本内容
1.1 经典物理学的困难
2、教学基本要求
了解:十九世纪末二十世纪初经典物理所遇到的困难
第二章波函数及薛定谔方程
1、教学基本内容
2.1波函数
2.2不确定关系
2.3薛定谔方程
2.4粒子流密度和粒子数守恒
2.5定态薛定谔方程
2.6一维无限势阱模型
2.7一维有限势阱模型
2.8一维线性谐振子
2.9势垒贯穿
2、教学基本要求
掌握:微观粒子波函数的Schrödinger方程,定态Schrödinger方程、无限深势阱中粒子的运动、势垒贯穿、线性谐振子等具体问题的求解过程
理解:微观粒子的波、粒二重性及其本质;微观粒子所遵循的态叠加原理
了解:不确定关系原理
第三章量子力学中的力学量
1、教学基本内容
3.1量子力学中的算符
3.2 厄米算符的本征函数的正交性和完全性
3.3 动量算符角动量算符
3.4 电子在库仑场中的运动
3.5 基本的对易关系两力学量同时确定的条件不确定关系
2、教学基本要求
掌握:力学量算符的本征值方程、本征值和本征函数的物理意义;动量、角动量等常见力学量算符的表达式,中心力场问题的求解
理解:力学量与其算符表示之间的对应关系
了解:力学量的不确定度概念,对易关系
第四章微扰理论
1、教学基本内容
4.1 非简并微扰理论
4.2 简并定态微扰
2、教学基本要求
掌握:能够用定态微扰理论求解简单的定态微扰问题
理解:简并和非简并定态微扰理论求解的实质
了解:微扰理论的概念
第五章晶体结构
1、教学基本内容
5.1晶体的共性、密堆积、晶体的周期性
5.2晶列、晶面、倒格子
5.3晶体的对称性
5.4晶格结构的分类
2、教学基本要求
掌握:堆积类型,晶格、原胞、布喇菲格子和复式格子、正格矢、晶体的周期性、倒格矢等物理概念,正格子和倒格子的关系
理解:几种常见晶体的结构类型
了解:晶体的共性,晶体的对称性,晶体结构的分类
第六章晶体的结合
1、教学基本内容
6.1 原子的电负性
6.2晶体结合的类型
6.3 结合力及结合能
2、教学基本要求
掌握:电离能、电负性、电子亲和能等物理概念
理解:掌握原子之间的相互作用势能和相互作用力及其物理性质
了解:晶体的几种结合方式及各自的特点
第七章晶格振动与晶体的热学性质
1、教学基本内容
7.1 一维晶格振动(Ⅰ)
7.2 一维晶格振动(Ⅱ)
7.3 三维晶格的振动
2、教学基本要求
掌握:格波,声子,长光、声学波,晶格振动模式密度,声子的热容量;
理解:一维简单格子和复式格子中格波的求解过程、一维原子链中色散关系了解:三维晶格振动的求解、晶格热容的量子理论。
第八章能带理论基础
1、教学基本内容
8.1 周期场中电子的波函数--- 布洛赫函数
8.2 克龙尼克-潘纳模型
8.3 近自由电子模型
8.4 布里渊区
8.5 紧束缚近似
2、教学基本要求
掌握:布洛赫函数、布洛赫定理、布里渊区等概念,能带理论
理解:克龙尼克-潘纳模型,几种典型格子的布里渊区及对称点的位置;
了解:几种求解晶体能带的方法(近自由电子模型、紧束缚方法)
三、本课程与其他课程的联系与分工
先修课程:《高等数学》、《普通物理》、《线性代数》
后修课程:《半导体物理》,《电子器件》
五、本课程采用的教学方法和教学手段
本课程采用计算机多媒体投影,内容采用Flash-Powerpoint与板书相结合。
六、教材及教学参考资料
教材:刘文楷等,《微电子物理基础》,北京,自编讲义,2004年。
参考书:唐洁影编,《电子工程物理基础》,北京,电子工业出版社,2002年
七、本课程成绩考查方法及评定标准
总成绩以百分制计算,由平时成绩和期末考试成绩两部分组成。
平时成绩占40%,包括考勤、作业和期中考试三部分;期末考试成绩占60%。
八、其它问题的说明
本课程在课外练习方面的要求:课外作业每次课后布置1-3题。
