第四章1球函数及其性质
数学必修一第四章知识点总结

高中数学人教必修第一册第四章知识点讲解对数函数及其性质1.对数函数的概念(1)定义:一般地,我们把函数y =log a x (a >0,且a ≠1)叫做对数函数,其中x 是自变量,函数的定义域是(0,+∞).(2)对数函数的特征:a x 的系数:1a x 的底数:常数,且是不等于1的正实数a x 的真数:仅是自变量x判断一个函数是否为对数函数,只需看此函数是否具备了对数函数的特征.比如函数y =log 7x 是对数函数,而函数y =-3log 4x 和y =log x 2均不是对数函数,其原因是不符合对数函数解析式的特点.【例1-1】函数f (x )=(a 2-a +1)log (a +1)x 是对数函数,则实数a =__________.解析:由a 2-a +1=1,解得a =0,1.又a +1>0,且a +1≠1,∴a =1.答案:1【例1-2】下列函数中是对数函数的为__________.(1)y =log(a >0,且a ≠1);(2)y =log 2x +2;(3)y =8log 2(x +1);(4)y =log x 6(x >0,且x ≠1);(5)y =log 6x .解析:答案:2.对数函数y =log a x (a >0,且a ≠1)的图象与性质(1)图象与性质a >10<a <1图象性质(1)定义域{x |x >0}(2)值域{y |y R }(3)当x =1时,y =0,即过定点(1,0)(4)当x >1时,y >0;当0<x <1时,y <0(4)当x >1时,y <0;当0<x <1时,y >0(5)在(0,+∞)上是增函数(5)在(0,+∞)上是减函数谈重点对对数函数图象与性质的理解对数函数的图象恒在y 轴右侧,其单调性取决于底数.a >1时,函数单调递增;0<a <1时,函数单调递减.理解和掌握对数函数的图象和性质的关键是会画对数函数的图象,在掌握图象的基础上性质就容易理解了.我们要注意数形结合思想的应用.(2)指数函数与对数函数的性质比较解析式y =a x (a >0,且a ≠1)y =log a x (a >0,且a ≠1)性质定义域R (0,+∞)值域(0,+∞)R过定点(0,1)(1,0)单调性单调性一致,同为增函数或减函数奇偶性奇偶性一致,都既不是奇函数也不是偶函数(3)底数a 对对数函数的图象的影响①底数a 与1的大小关系决定了对数函数图象的“升降”:当a>1时,对数函数的图象“上升”;当0<a <1时,对数函数的图象“下降”.②底数的大小决定了图象相对位置的高低:不论是a >1还是0<a <1,在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大.点技巧对数函数图象的记忆口诀两支喇叭花手中拿,(1,0)点处把花扎,若是底数小于1,左上穿点渐右下,若是底数大于1,左下穿点渐右上,绕点旋转底变化,顺时方向底变大,可用直线y =1来切,自左到右a 变大.【例2】如图所示的曲线是对数函数y =log a x 的图象.已知a,43,35,110中取值,则相应曲线C 1,C 2,C 3,C4的a 值依次为()A 43,35,110B 43,110,35C .43,,35,110D .43110,35解析:由底数对对数函数图象的影响这一性质可知,C 4的底数<C 3的底数<C 2的底数<C 1的底数.故相应于曲线C 1,C 2,C 3,C 4,43,35,110.答案:A点技巧根据图象判断对数函数的底数大小的方法(1)方法一:利用底数对对数函数图象影响的规律:在x 轴上方“底大图右”,在x 轴下方“底大图左”;(2)方法二:作直线y =1,它与各曲线的交点的横坐标就是各对数的底数,由此判断各底数的大小.3.反函数(1)对数函数的反函数指数函数y =a x (a >0,且a ≠1)与对数函数y =log a x (a >0,且a ≠1)互为反函数.(2)互为反函数的两个函数之间的关系①原函数的定义域、值域是其反函数的值域、定义域;②互为反函数的两个函数的图象关于直线y =x 对称.(3)求已知函数的反函数,一般步骤如下:①由y =f (x )解出x ,即用y 表示出x ;②把x 替换为y ,y 替换为x ;③根据y =f (x )的值域,写出其反函数的定义域.【例3-1】若函数y =f (x )是函数y =a x (a >0,且a ≠1)的反函数,且f (2)=1,则f (x )=()A .log 2xB .12xC .12log xD .2x-2解析:因为函数y =a x (a >0,且a ≠1)的反函数是f (x )=log a x ,又f (2)=1,即log a 2=1,所以a =2.故f (x )=log 2x .答案:A【例3-2】函数f (x )=3x (0<x ≤2)的反函数的定义域为()A .(0,+∞)B .(1,9]C .(0,1)D .[9,+∞)解析:∵0<x ≤2,∴1<3x ≤9,即函数f (x )的值域为(1,9].故函数f (x )的反函数的定义域为(1,9].答案:B【例3-3】若函数y =f (x )的反函数图象过点(1,5),则函数y =f (x )的图象必过点()A .(5,1)B .(1,5)C .(1,1)D .(5,5)解析:由于原函数与反函数的图象关于直线y =x 对称,而点(1,5)关于直线y =x 的对称点为(5,1),所以函数y =f (x )的图象必经过点(5,1).答案:A 4.利用待定系数法求对数函数的解析式及函数值对数函数的解析式y =log a x (a >0,且a ≠1)中仅含有一个常数a ,则只需要一个条件即可确定对数函数的解析式,这样的条件往往是已知f (m )=n 或图象过点(m ,n )等等.通常利用待定系数法求解,设出对数函数的解析式f (x )=log a x (a >0,且a ≠1),利用已知条件列方程求出常数a 的值.利用待定系数法求对数函数的解析式时,常常遇到解方程,比如log a m =n ,这时先把对数式log a m =n 化为指数式的形式a n =m ,把m 化为以n 为指数的指数幂形式m =k n (k >0,且k ≠1),则解得a =k >0.还可以直接写出1na m =,再利用指数幂的运算性质化简1nm .例如:解方程log a 4=-2,则a -2=4,由于2142-⎛⎫= ⎪⎝⎭,所以12a =±.又a >0,所以12a =.当然,也可以直接写出124a -=,再利用指数幂的运算性质,得11212214(2)22a ---====.【例4-1】已知f (e x )=x ,则f (5)=()A .e 5B .5eC .ln 5D .log 5e解析:(方法一)令t =e x,则x =ln t ,所以f (t )=ln t ,即f (x )=ln x .所以f (5)=ln 5.(方法二)令e x =5,则x =ln 5,所以f (5)=ln 5.答案:C【例4-2】已知对数函数f (x )的图象经过点1,29⎛⎫⎪⎝⎭,试求f (3)的值.分析:设出函数f (x )的解析式,利用待定系数法即可求出.解:设f (x )=log a x (a >0,且a ≠1),∵对数函数f (x )的图象经过点1,29⎛⎫⎪⎝⎭,∴11log 299a f ⎛⎫== ⎪⎝⎭.∴a 2=19.∴a =11222111933⎡⎤⎛⎫⎛⎫==⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦.∴f (x )=13log x .∴f (3)=111331log 3log 3-⎛⎫= ⎪⎝⎭=-1.【例4-3】已知对数函数f (x )的反函数的图象过点(2,9),且f (b )=12,试求b 的值.解:设f (x )=log a x (a >0,且a ≠1),则它的反函数为y =a x (a >0,且a ≠1),由条件知a 2=9=32,从而a =3.于是f (x )=log 3x ,则f (b )=log 3b =12,解得b=123=5.对数型函数的定义域的求解(1)对数函数的定义域为(0,+∞).(2)在求对数型函数的定义域时,要考虑到真数大于0,底数大于0,且不等于1.若底数和真数中都含有变量,或式子中含有分式、根式等,在解答问题时需要保证各个方面都有意义.一般地,判断类似于y =log a f (x )的定义域时,应首先保证f (x )>0.(3)求函数的定义域应满足以下原则:①分式中分母不等于零;②偶次根式中被开方数大于或等于零;③指数为零的幂的底数不等于零;④对数的底数大于零且不等于1;⑤对数的真数大于零,如果在一个函数中数条并存,求交集.【例5】求下列函数的定义域.(1)y =5(2x -1)(5x -4);(3)y =.分析:利用对数函数y =log a x (a >0,且a ≠1)的定义求解.解:(1)要使函数有意义,则1-x >0,解得x <1,所以函数y =log 5(1-x )的定义域是{x |x <1}.(2)要使函数有意义,则54>0,21>0,211,x x x -⎧⎪-⎨⎪-≠⎩解得x >45且x ≠1,所以函数y =log (2x -1)(5x -4)的定义域是4,15⎛⎫⎪⎝⎭(1,+∞).(3)要使函数有意义,则0.5430,log(43)0,x x ->⎧⎨-≥⎩解得34<x ≤1,所以函数y =的定义域是3<14x x ⎧⎫≤⎨⎬⎩⎭.6.对数型函数的值域的求解(1)充分利用函数的单调性和图象是求函数值域的常用方法.(2)对于形如y =log a f (x )(a >0,且a ≠1)的复合函数,其值域的求解步骤如下:①分解成y =log a u ,u =f (x )这两个函数;②求f (x )的定义域;③求u 的取值范围;④利用y =log a u 的单调性求解.(3)对于函数y =f (log a x )(a >0,且a ≠1),可利用换元法,设log a x =t ,则函数f (t )(t ∈R )的值域就是函数f (log a x )(a >0,且a ≠1)的值域.注意:(1)若对数函数的底数是含字母的代数式(或单独一个字母),要考查其单调性,就必须对底数进行分类讨论.(2)求对数函数的值域时,一定要注意定义域对它的影响.当对数函数中含有参数时,有时需讨论参数的取值范围.【例6-1】求下列函数的值域:(1)y =log 2(x 2+4);(2)y =212log (32)x x +-.解:(1)∵x 2+4≥4,∴log 2(x 2+4)≥log 24=2.∴函数y =log 2(x 2+4)的值域为[2,+∞).(2)设u =3+2x -x 2,则u =-(x -1)2+4≤4.∵u >0,∴0<u ≤4.又y =12log u 在(0,+∞)上为减函数,∴12log u ≥-2.∴函数y =212log (32)x x +-的值域为[-2,+∞).【例6-2】已知f (x )=2+log 3x ,x ∈[1,3],求y =[f (x )]2+f (x 2)的最大值及相应的x 的值.分析:先确定y =[f (x )]2+f (x 2)的定义域,然后转化成关于log 3x 的一个一元二次函数,利用一元二次函数求最值.解:∵f (x )=2+log 3x ,x ∈[1,3],∴y =[f (x )]2+f (x 2)=(log 3x )2+6log 3x +6且定义域为[1,3].令t =log 3x (x ∈[1,3]).∵t =log 3x 在区间[1,3]上是增函数,∴0≤t ≤1.从而要求y =[f (x )]2+f (x 2)在区间[1,3]上的最大值,只需求y =t 2+6t +6在区间[0,1]上的最大值即可.∵y =t 2+6t +6在[-3,+∞)上是增函数,∴当t =1,即x =3时,y max =1+6+6=13.综上可知,当x =3时,y =[f (x )]2+f (x 2)的最大值为13.7.对数函数的图象变换及定点问题(1)与对数函数有关的函数图象过定点问题对数函数y =log a x (a >0,且a ≠1)过定点(1,0),即对任意的a >0,且a ≠1都有log a 1=0.这是解决与对数函数有关的函数图象问题的关键.对于函数y =b +k log a f (x )(k ,b 均为常数,且k ≠0),令f (x )=1,解方程得x =m ,则该函数恒过定点(m ,b ).方程f (x )=0的解的个数等于该函数图象恒过定点的个数.(2)对数函数的图象变换的问题①函数y =log a x (a >0,且a ≠1)――----------------→向左(b >0)或向右(b <0)平移|b |个单位长度函数y =log a (x +b )(a >0,且a ≠1)②函数y =log a x (a >0,且a ≠1)――---------------→向上(b >0)或向下(b <0)平移|b |个单位长度函数y =log a x +b (a >0,且a ≠1)③函数y =log a x (a >0,且a ≠1)―----------------―→当x >0时,两函数图象相同当x <0时,将x >0时的图象关于y 轴对称函数y =log a |x |(a >0,且a ≠1)④函数y =log a x (a >0,且a ≠1)――----------------------------------------→保留x 轴上方的图象同时将x 轴下方的图象作关于x 轴的对称变换函数y =|log a x |(a >0,且a ≠1)【例7-1】若函数y =log a (x +b )+c (a >0,且a ≠1)的图象恒过定点(3,2),则实数b ,c 的值分别为__________.解析:∵函数的图象恒过定点(3,2),∴将(3,2)代入y =log a (x +b )+c (a >0,且a ≠1),得2=log a (3+b )+c .又∵当a >0,且a ≠1时,log a 1=0恒成立,∴c =2.∴log a (3+b )=0.∴b =-2.答案:-2,2【例7-2】作出函数y =|log 2(x +1)|+2的图象.解:(第一步)作函数y =log 2x 的图象,如图①;(第二步)将函数y =log 2x 的图象沿x 轴向左平移1个单位长度,得函数y =log 2(x +1)的图象,如图②;(第三步)将函数y =log 2(x +1)在x 轴下方的图象作关于x 轴的对称变换,得函数y =|log 2(x +1)|的图象,如图③;(第四步)将函数y =|log 2(x +1)|的图象,沿y 轴方向向上平移2个单位长度,便得到所求函数的图象,如图④.8.利用对数函数的单调性比较大小两个对数式的大小比较有以下几种情况:(1)底数相同,真数不同.比较同底数(是具体的数值)的对数大小,构造对数函数,利用对数函数的单调性比较大小.要注意:明确所给的两个值是哪个对数函数的两个函数值;明确对数函数的底数与1的大小关系;最后根据对数函数的单调性判断大小.(2)底数不同,真数相同.若对数式的底数不同而真数相同时,可以利用顺时针方向底数增大画出函数的图象,再进行比较,也可以先用换底公式化为同底后,再进行比较.(3)底数不同,真数也不同.对数式的底数不同且指数也不同时,常借助中间量0,1进行比较.(4)对于多个对数式的大小比较,应先根据每个数的结构特征,以及它们与“0”和“1”的大小情况,进行分组,再比较各组内的数值的大小即可.注意:对于含有参数的两个对数值的大小比较,要注意对底数是否大于1进行分类讨论.【例8-1】比较下列各组中两个值的大小.(1)log31.9,log32;(2)log23,log0.32;(3)log aπ,log a3.141.分析:(1)构造函数y=log3x,利用其单调性比较;(2)分别比较与0的大小;(3)分类讨论底数的取值范围.解:(1)因为函数y=log3x在(0,+∞)上是增函数,所以f(1.9)<f(2).所以log31.9<log32.(2)因为log23>log21=0,log0.32<log0.31=0,所以log23>log0.32.(3)当a>1时,函数y=log a x在定义域上是增函数,则有log aπ>log a3.141;当0<a<1时,函数y=log a x在定义域上是减函数,则有log aπ<log a3.141.综上所得,当a>1时,log aπ>log a3.141;当0<a<1时,log aπ<log a3.141.【例8-2】若a2>b>a>1,试比较log a ab,log bba,log b a,log a b的大小.分析:利用对数函数的单调性或图象进行判断.解:∵b>a>1,∴0<ab<1.∴log a ab<0,log a b>log a a=1,log b1<log b a<log b b,即0<log b a<1.由于1<b a <b ,∴0<log b b a <1.由log b a -log b ba=2log b a b ,∵a 2>b >1,∴2ab>1.∴2log b a b >0,即log b a >log b b a.∴log a b >log b a >log b b a >log a ab.9.利用对数函数的单调性解对数不等式(1)根据对数函数的单调性,当a >0,且a ≠1时,有①log a f (x )=log a g (x )⇔f (x )=g (x )(f (x )>0,g (x )>0);②当a >1时,log a f (x )>log a g (x )⇔f (x )>g (x )(f (x )>0,g (x )>0);③当0<a <1时,log a f (x )>log a g (x )⇔f (x )<g (x )(f (x )>0,g (x )>0).(2)常见的对数不等式有三种类型:①形如log a f (x )>log a g (x )的不等式,借助函数y =log a x 的单调性求解,如果a 的取值不确定,需分a >1与0<a <1两种情况讨论.②形如log a f (x )>b 的不等式,应将b 化为以a 为对数的对数式的形式,再借助函数y =log a x 的单调性求解.③形如log a f (x )>log b g (x )的不等式,基本方法是将不等式两边化为同底的两个对数值,利用对数函数的单调性来脱去对数符号,同时应保证真数大于零,取交集作为不等式的解集.④形如f (log a x )>0的不等式,可用换元法(令t =log a x ),先解f (t )>0,得到t 的取值范围.然后再解x 的范围.【例9-1】解下列不等式:(1)1177log log (4)x x >-;(2)log x (2x +1)>log x (3-x ).解:(1)由已知,得>0,4>0,<4,x x x x ⎧⎪-⎨⎪-⎩解得0<x <2.所以原不等式的解集是{x |0<x <2}.(2)当x >1时,有21>3,21>0,3>0,x x x x +-⎧⎪+⎨⎪-⎩解得1<x <3;当0<x <1时,有21<3,21>0,3>0,x x x x +-⎧⎪+⎨⎪-⎩解得0<x <23.所以原不等式的解集是20<<1<<33x x x ⎧⎫⎨⎬⎩⎭或.【例9-2】若22log 3a ⎛⎫ ⎪⎝⎭<1,求a 的取值范围.解:∵22log 3a ⎛⎫ ⎪⎝⎭<1,∴-1<2log 3a <1,即12log log log 3a a a a a <<.(1)∵当a >1时,y =log a x 为增函数,∴123a a <<.∴a >32,结合a >1,可知a >32.(2)∵当0<a <1时,y =log a x 为减函数,∴12>>3a a .∴a <23,结合0<a <1,知0<a <23.∴a 的取值范围是230<<>32a a a ⎧⎫⎨⎬⎩⎭,或.10.对数型函数单调性的讨论(1)解决与对数函数有关的函数的单调性问题的关键:一是看底数是否大于1,当底数未明确给出时,则应对底数a 是否大于1进行讨论;二是运用复合法来判断其单调性;三是注意其定义域.(2)关于形如y =log a f (x )一类函数的单调性,有以下结论:函数y =log a f (x )的单调性与函数u =f (x )(f (x )>0)的单调性,当a >1时相同,当0<a <1时相反.例如:求函数y =log 2(3-2x )的单调区间.分析:首先确定函数的定义域,函数y =log 2(3-2x )是由对数函数y =log 2u 和一次函数u =3-2x 复合而成,求其单调区间或值域时,应从函数u =3-2x 的单调性、值域入手,并结合函数y =log 2u 的单调性考虑.解:由3-2x >0,解得函数y =log 2(3-2x )∞设u =3-2x ,x ∞∵u =3-2x ∞y =log 2u 在(0,+∞)上单调递增,∴函数y =log 2(3-2x )∞∴函数y =log 2(3-2x )∞【例10-1】求函数y =log a (a -a x )解:(1)若a >1,则函数y =log a t 递增,且函数t =a -a x 递减.又∵a -a x >0,即a x <a ,∴x <1.∴函数y =log a (a -a x )在(-∞,1)上递减.(2)若0<a <1,则函数y =log a t 递减,且函数t =a -a x 递增.又∵a -a x >0,即a x <a ,∴x >1.∴函数y =log a (a -a x )在(1,+∞)上递减.综上所述,函数y =log a (a -a x )在其定义域上递减.析规律判断函数y =log a f (x )的单调性的方法函数y =log a f (x )可看成是y =log a u 与u =f (x )两个简单函数复合而成的,由复合函数单调性“同增异减”的规律即可判断.需特别注意的是,在求复合函数的单调性时,首先要考虑函数的定义域,即“定义域优先”.【例10-2】已知f (x )=12log (x 2-ax -a )在1,2⎛⎫-∞-⎪⎝⎭上是增函数,求a 的取值范围.解:1,2⎛⎫-∞-⎪⎝⎭是函数f (x )的递增区间,说明1,2⎛⎫-∞- ⎪⎝⎭是函数u =x 2-ax -a 的递减区间,由于是对数函数,还需保证真数大于0.令u (x )=x 2-ax -a ,∵f (x )=12log ()u x 在1,2⎛⎫-∞-⎪⎝⎭上是增函数,∴u (x )在1,2⎛⎫-∞-⎪⎝⎭上是减函数,且u (x )>0在1,2⎛⎫-∞- ⎪⎝⎭上恒成立.∴1,2210,2a u ⎧≥-⎪⎪⎨⎛⎫⎪-≥ ⎪⎪⎝⎭⎩即1,10.42a aa ≥-⎧⎪⎨+-≥⎪⎩∴-1≤a ≤12.∴满足条件的a 的取值范围是112a a ⎧⎫-≤≤⎨⎬⎩⎭.11.对数型函数的奇偶性问题判断与对数函数有关的函数奇偶性的步骤是:(1)求函数的定义域,当定义域关于原点不对称时,则此函数既不是奇函数也不是偶函数,当定义域关于原点对称时,判断f (-x )与f (x )或-f (x )是否相等;(2)当f (-x )=f (x )时,此函数是偶函数;当f (-x )=-f (x )时,此函数是奇函数;(3)当f (-x )=f (x )且f (-x )=-f (x )时,此函数既是奇函数又是偶函数;(4)当f (-x )≠f (x )且f (-x )例如,判断函数f (x )=log )a x (x ∈R ,a >0,且a ≠1)的奇偶性.解:∵f (-x )+f (x )==log )a x -+log )a x )=log a (x 2+1-x 2)=log a 1=0,∴f (-x )=-f (x ).∴f (x )为奇函数.【例11】已知函数f (x )=1log 1axx+-(a >0,且a ≠1).(1)求函数f (x )的定义域;(2)判断函数f (x )的奇偶性;(3)求使f (x )>0的x 的取值范围.分析:对于第(2)问,依据函数奇偶性的定义证明即可.对于第(3)问,利用函数的单调性去掉对数符号,解出不等式.解:(1)由11xx+->0,得-1<x <1,故函数f (x )的定义域为(-1,1).(2)∵f (-x )=1log 1ax x -+=1log 1a xx+--=-f (x ),又由(1)知函数f (x )的定义域关于原点对称,∴函数f (x )是奇函数.(3)当a >1时,由1log 1a x x +->0=log a 1,得11xx+->1,解得0<x <1;当0<a <1时,由1log 1ax x +->0=log a 1,得0<11xx+-<1,解得-1<x <0.故当a >1时,x 的取值范围是{x |0<x <1};当0<a <1时,x 的取值范围是{x |-1<x <0}.12.对数型函数模型的实际应用地震震级的变化规律、溶液pH 的变化规律、航天问题等,可以用对数函数模型来研究.此类题目,通常给出函数解析式模型,但是解析式中含有其他字母参数.其解决步骤是:(1)审题:弄清题意,分清条件和结论,抓住关键的词和量,理顺数量关系;(2)建模:将文字语言转化成数学语言,利用数学知识,求出函数解析式模型中参数的值;(3)求模:求解函数模型,得到数学结论;(4)还原:将用数学方法得到的结论还原为实际问题的结论.由此看,直接给定参数待定的函数模型时,利用待定系数法的思想,代入已知的数据得到相关的方程而求得待定系数.一般求出函数模型后,还利用模型来研究一些其他问题.代入法、方程思想、对数运算性质,是解答此类问题的方法精髓.【例12】我国用长征二号F 型运载火箭成功发射了“神舟”七号载人飞船,实现了中国历史上第一次的太空漫步,令中国成为世界上第三个有能力把人送上太空并进行太空漫步的国家(其中,翟志刚完全出舱,刘伯明的头部和手部部分出舱).在不考虑空气阻力的条件下,假设火箭的最大速度y (单位:km/s)关于燃料重量x (单位:吨)的函数关系式为y =k ln(m +x )-k )+4ln 2(k ≠0),其中m 是箭体、搭载的飞行器、航天员的重量和.当燃料重量为-1)m 吨时,火箭的最大速度是4km/s .(1)求y =f (x );(2)已知长征二号F 型运载火箭的起飞重量是479.8吨(箭体、搭载的飞行器、航天员、燃料),火箭的最大速度为8km/s ,求装载的燃料重量(e =2.7,精确到0.1).解:(1)由题意得当x =(-1)m 时,y =4,则4=k ln[m +-1)m ]-k ln()+4ln 2,解得k =8.所以y =8ln(m +x )-)+4ln 2,即y =8ln m xm+.(2)由于m +x =479.8,则m =479.8-x ,令479.888ln479.8x=-,解得x ≈302.1.故火箭装载的燃料重量约为302.1吨.。
第四章一次函数的图像与性质

4.3一次函数的图像与性质及确定一次函数解析式知识点1、一次函数的图像与性质图像:在直角坐标系内,所有这些点组成的图形叫做该函数的图像。
画函数图像的一般步骤:(1)(2)(3)例题1、(1)画出正比例函数y=2x的图像。
(2)画出正比例函数y=-2x的图像。
例题2、(1)画出一次函数y=-2x+2的图像;(2)画出一次函数y=-x+1的图像;例题3 (乐山中考)若实数a 、b 、c 满足0a b c ++=,且a b c <<,则函数y ax c =+的图象可能是( )A B C D例题4 如果一次函数y=(2m -3)x+(3-m )的图象经过第一、二、三象限,则m 的取值范围是 。
例题3 若一次函数y kx b =+的函数值y 随x 的增大而减小,且图象与y 轴的负半轴相交,那么k 和b 的符号是____。
随堂练习:1、对于一次函数y =-2x +4,下列结论错误的是( )A .函数值随自变量的增大而减小B .函数图象不经过第三象限C .函数图象向上平移2个单位得到y =-2x 的图象D .函数图象与y 轴的交点坐标是(0,4)2、已知一次函数y =(m +2)x +1,若y 随x 的增大而增大,则m 的取值范围是___________。
知识点2、一次函数(正比例函数)表达式:待定系数法待定系数法:求一次函数y=kx+b 的表达式时,先设出式子中的未知系数,再根据条件求出未知系数,从而求出函数表达式,这种方法叫做待定系数法。
例题1 已知在一次函数b kx y +=(0≠k )中,当x=0时,y =3,当x=2时,y=7。
(1)求y 与x 之间的函数表达式。
(2)计算x =4时,y 的值。
(3)计算y =4时,x 的值。
例题2、若变量 y -3与 x +2 成正比,且当 x =1 时,y =-3, (1)求比例系数k ;(2)y 关于x 的函数解析式为例题3、过点P(8,-2)且与直线y=x+1平行的直线的解析式为例题4、已知直线y=x+b过点A(3,4),(1)求b的值;(2)当x取何值时,y<0 ?随堂练习:1、经过A (-6,5)、B(0,-5) 两点的直线l的解析式为2、如图所示,直线l的解析式为 ( )A.y=3x+3 B.y=3x-3 C.y=-x+3 D.y=-3x+33、如图,把直线l沿x轴正方向向右平移2个单位,得到直线l',则直线l'的解析式为( )A.y=2x+4 B.y=-2x+2 C.y=2x-4 D.y=-2x-2巩固提高部分1、若直线y=kx+b(k≠0)不经过第一象限,则k、b的取值范围是()A.k>0,b<0B.k>0,b≤0C.k<0,b<0D.k<0,b≤02.函数的自变量的取值范围是()A. x≥1B. x=1C. x<1D. x≠13、已知y与x-3成正比例,当x=4时,y=-1,那么当x=-4时,y的值是()A. 1B. 3C. -7D. 74、已知正比例函数y=(3k-1)x,若y随x增大而增大,则k的取值范围是()A. k<0B. k>0C.D.5、直线y=2x-1经过的点是()A. (2,1)B. (0,1)C. (2,0)D.(1,1)6、已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y =x+k的图象大致是图中的()7、直线经过第_____象限,y随x的增大而______。
电子教案-高等数学(工科类)(魏寒柏 骈俊生)ppt-第四章一元函数积分学及其应用-电子课件

计
算
A
1 x2dx
0
1x3 3
1 0
1 3
0
1 3
例 计算下列定积分
41
第 二
(1)
1
dx x
(2) 2 cosxdx 0
节
解:先运用相应的积分公式求出原函数,再
定 积
利用牛顿-莱布尼兹公式计算它在上、下限处
分 的
函数值的差。
计 算
(1)
4 1
1 dx 2 x
x
4 1
4
2
2
(2)
2
2 cosxdx sin x 1 0 1
第
点x1 x2 , , xn1 ,如果记x0 a, xn b,这样就把区
一 节
间[a,b] 任意分成了n 个小区间[xi1, xi ], i 1,2, , n,其长
度对应记为xi xi xi1 ,且将所有小区间长度的最
定 积 分 的 概
大值记为 max{ xi}。在每个小区间[xi1, xi ]上任取一
一 节
“取极限”四个步骤.
定
(1) “分割”
积 分
在区间[0,1]内均匀地插入n 1个分点:
的 概 念
x1
1 n , x2
2 , n
, xn1
n 1 n
得到n个等分小区间,记
小区间对应的小曲边形
面积为si (i 1,2, , n) ,于
是有:A
n
si
i 1
(2) “近似”
第 一 节
以 点每xi 个ni 处小的区函间数的值长度f (xi)x作i 1n高作,底就,可区得间到的n右个端小 矩形,如果把它们的面积分别记作Ai ,(i 1,2, ,n)
第四章一元函数积分知识点梳理

一元函数积分学(1)(第十一周周三)题型•定积分概念(定积分求极限)•定积分性质及其应用(比较定积分大小,估计积分值)•变限定积分函数求导•变限积分函数极限•定积分表示变量的极限•分段求定积分•求解含定积分符号的函数方程•定积分等式与定积分不等式证明3定积分定义求极限其中极限与分点x i 的取法及x i 的取法无关.当函数f (x )在[a , b ]上连续时, 有可用于求某些通项为和式数列的极限,根据积分合式确定被积函数和积分区间→==∑⎰01()d lim ()n b i i a i f x x f x λx ()→∞=--+=∑⎰1lim ()d .n b n a i b a b a f a i f x x n n12lim 1cos 1cos 1cos n n n n n n πππ→+∞++++++11011211cos 1cos 1cos 1cos 1lim 1cos 1cos(n i n n i n i n n nn n n i x dx n nππππππ=→∞=++++++=++=+∑∑⎰()→∞=--+=∑⎰1lim ()d .n b n a i b a b a f a i f x x n n求极限).21(lim 22222nn n n n n n n ++++++∞→ 原式n n 1lim ∞→=∑=+n i ni 12)(11x x d 11102⎰+=4π=()→∞=--+=∑⎰1lim ()d .n b n a i b a b a f a i f x x n n将数列适当放大和缩小,以简化成积分和:11sin k n n k k n π=<<+∑已知11012lim sin sin d ,n n k k x x n n πππ→∞=⋅==∑⎰利用夹逼准则可知2.I π=∑=⋅+n k nn k n n 11sin 1π∑=⋅nk n n k 11sin π11lim =+∞→n n n 求()→∞=--+=∑⎰1lim ()d .n b n a i b a b a f a i f x x n n关于定积分重要性质保号性:()0,f x ≥则有()d 0.ba f x x ≥⎰若f (x )在[a ,b ]上连续, ()0,f x ≥且()0,[,]f x x a b ≡∈/则()d 0.b a f x x >⎰若f (x )在[a , b ]上连续, ≥()0,f x =⎰()d 0,b a f x x 且则()0.f x ≡积分中值定理:若f (x )在[a , b ]上连续, 则至少存在一点(,),a b x ∈使得()d ()().ba f x xb a f x =-⎰第一积分中值定理:若函数f (x ), g (x )在[a , b ]上连续, g (x )在[a , b ]上不变号,则在(a , b )内至少存在一点x , 使=⎰⎰()()d ()()d .b b a af xg x x f g x x x 估值定理:若f (x )在[a , b ]上连续,≤≤(),m f x M -≤≤-⎰()()d ()b am b a f x x M b a令,)(x e x f x-=]0,2[-∈x ,0)(>x f ,0)(02>-∴⎰-dx x e x dx e x ⎰-∴02,02dx x ⎰->于是dx e x ⎰-20.20dx x ⎰-<比较积分值dx e x ⎰-20和dx x ⎰-20的大小.比较定积分大小(积分区间相同,比较函数大小)比较定积分大小(积分区间不同)2222202220cos cos x x x x e dx e dx e xdx e xdx ππππππ---->>⎰⎰⎰⎰22222()2()200cos cos ()cos x u x u x e xdx e u dx e xdx ππππππππ--+-+=-=+=⎰⎰⎰设函数f (x )在[0, 1]上连续, 且单调减少, 试证对任意(0,1),a ∈有≥⎰⎰100()d ()d .a f x x a f x x 证明1:-⎰⎰100()d ()d a f x x a f x x =-⎰⎰00()d ()d a a f x x a f x x -⎰1()d aa f x x=-⎰0(1)()d a a f x x -⎰1()d aa f x x (0,),a α∈(1)()a af α=-(1)()a af β--(,1)a β∈()(1)()()a a f f αβ=--0.≥1100011000()()()01,01()()()()()aa f x dx x at a f at dt a f ax dx a x ax x f ax f x a f x dx a f ax dx f x dx ⇒=⇒=<<<<⇒<⇒≥≤=⎰⎰⎰⎰⎰⎰证明2:12222200sin cos d d .11x x x x x x ππ<++⎰⎰-+⎰220cos sin d 1x x x x π-=+⎰420cos sin d 1x x x x π-++⎰224cos sin d 1x x x x ππ=-+-++⎰⎰42220411(cos sin )d (cos sin )d 11x x x x x x πππx η0=--≥++2211(21)()011x η,sin 31)(3xx f +=],,0[π∈∀x ,1sin 03≤≤x ,31sin 31413≤+≤x ,31sin 31410030dx dx xdx ⎰⎰⎰πππ≤+≤.3sin 31403π≤+≤π∴⎰πdx x 估计积分dx x ⎰π+03sin 31的值. 估计积分值大小证明证:令则令得故变限积分求导2(1)2()sin ,(2)x x x f t dt t f π+==⎰22((1))(23)2(2)cos f x x x x f x xππ++-=15(2)2(2)(2)3x f f f ππ=⇒-=-⇒=-()''()(())(())()(())()g x h x d f t dt f g x g x f h x h x dx =-⎰sin '0()(sin )(),()xF x x t f t dt F x =-⎰求sin 'sin sin 00sin 0()(sin ()())(sin ())()cos ()x x x xd F x xf t tf t dt dx d d x f t tf t dt dx dx x f t dt=-=-=⎰⎰⎰⎰20cos()x d x t dt dx -=⎰2211211x x d x dt dx x t x x -+=++++⎰1x t u+=解:提示:2解:先求定积分,再求导4030sin lim xdt t x x ⎰→求极限00解:此极限为型414sin lim 330==→x x x 原式变限积分函数极限(洛必达,积分中值,等价无穷小)200cos lim x x t dt x →⎰0|sin |limx x t dt x →+∞⎰(1)00|sin ||sin |sin 2,(1)k kt dt t dt tdt x n n x n ππππππ+===∀∃≤<+⎰⎰⎰(1)000(1)0000|sin ||sin |sin |sin |2,sin 2(1)|sin |22(1)(1)|sin |2lim n x n n n x x x t dt t dt tdt t dt n tdt n t dt n n n x n t dt x πππππππ++→+∞≤<==++≤<+=⎰⎰⎰⎰⎰⎰⎰周期性.lim 222dx e x n n x n ⎰+-∞→计算)2(lim lim 22222n n e dx e x n n x n -+=-∞→+-∞→⎰x x x 22lim 2x x x e ∞→=.0=定积分表示变量的极限.01lim 10=+⎰∞→dx x x nn 证明,10n nx xx ≤+≤ dx x dx x x n n ⎰⎰≤+≤∴101010,11+=n ,011lim =+∞→n n 且.01lim 10=+⎰∞→dx x x nn 由夹逼准则可知注意:x x +=+∞→∞→⎰1lim 1lim 10nn n n dx x x (01)x ≤≤.0=错误,可用第一积分中值定理=⎰⎰()()d ()()d .bba a f x g x x f g x x x分段求定积分(含有max,min,取整符号,绝对值,被积函数含参变量)10()|()|F x t t x dt =-⎰101010()()3211()()23x x F x t t x dt x x F x t t x dt ≤⇒=-=-≥⇒=--=-⎰⎰10201()()()11323x x x F x t t x dt t t x dt x x <<⇒=--+-=-+⎰⎰=+⎰21()()1()()设连续,,求f x f x x f x dx f x 求解含定积分符号的函数方程212211()()1()(1)3122()12a f x dx f x ax f x dx ax dx a a a f x x=⇒=+⇒=+⇒=+⇒=-⇒=-⎰⎰⎰令已知函数f (x )满足方程=-⎰120()3()d ,f x x f x x 试求f (x ).解令=⎰120()d ,f x x a 则()f x =-3.x a ⎰120()d f x x a =()=-⎰1203d x a x ()=+-⎰122096d x a ax x =-+233,a a ⇒-+=2430,a a 3a ⇒=或=1,a 故=-()33f x x 或=-()31f x x定积分等式与定积分不等式证明(1) 变上限积分;(2) 积分中值定理;(3) 微分中值定理;(4) 常用不等式(柯西-施瓦茨不等式);(5) 利用Taylor公式;(6) 利用闭区间上连续函数性质.1证明恒等式证:令则因此,)0()(2π<<=x C x f 又4π=故所证等式成立.试证使分析:要证即⎰xaxxg d)(⎰-x a xxf d)(故作辅助函数至少存在一点证明: 令⎰⎰⎰⎰-=ba x ab a x a x x g x x f x x f x x g x F d )(d )(d )(d )()(在上连续,在至少使即0d )()(d )()(=-⎰⎰b a ba x x g f x x f g x x 因在上连续且不为0 ,从而不变号,因此故所证等式成立.故由罗尔定理知,存在一点7设解法1:设且试证:t t f x F x a d )()(⎰=⎰x a t f t )(d 则=')(x F )(2a x --⎰⎢⎣⎡=x a )(t f )(t f t d 2⎥⎦⎤-t t f x f t f x f x a d )()()]()([2⎰-=故F (x ) 单调不减,即②成立.②⎰x a t t f d )(⎰x at f t )(d 2)(a x --8设函数f (x )在[0, 1]上是非负、单调减的连续函数,且0 < a < b < 1, 求证≥⎰⎰0()d ()d .a b a a f x x f x x b ⎰0()d af x x ⎰()d ba f x x 1()f a x =2()()fb a x =-1(0,)a x ∈2(,)ab x ∈(),f a a ≥()()f a b a ≤-(),bf a ≤⎰0()d af x x ()f a a ≥≥⎰()d .ba a f x xb 证明由积分中值定理, 得设f 在[0, π]上连续, 在(0, π)内内可导, 且==⎰⎰00()cos d ()sin d 0,f x x x f x x x ππ证明: 存在(0,),x π∈使得()0.f x '=证明因为在(0, π)内, sin x 0,>又=⎰0()sin d 0,f x x x π故f (x )在(0, π)内必有零点α .若在(0, π)内, f (x )恒正, 则>⎰0()sin d 0;f x x x π若在(0, π)内, f (x )恒负, 则<⎰0()sin d 0;f x x x π零点不唯一:若(0,)απ∈是f (x )的唯一零点, 则,(0,),x x απ≠∈f (x )在x = α的两侧异号. 于是sin()()x f x α-必恒正或恒负,从而-≠⎰0sin()()d 0.x f x x πα39-≠⎰0sin()()d 0.x f x x πα-⎰0sin()()d x f x x πα0()(sin cos f x x πα=⎰-cos sin )d x xα=⎰0cos ()sin d f x x x πα-⎰0sin ()cos d f x x x πα0=与上式矛盾.故f (x )在(0, π)内零点不惟一,Rolle 定理:在(0,),x π∈使得()0.f x '='11,[]()[](){(1)(2)...([])}aa x f x dx a f a f f f a >=-+++⎰证明:1'201[0,1],()()0,()()3x f x f x f x dx f ∈<≤⎰二阶可导,证明:222()[,]()cos ()sin [()]b b b a a a f x a b f x kxdx f x kxdx f x dx ∀+≤⎰⎰⎰在连续且非负,证明:k,满足:[][]sin 2'0()(),()xF x f tx dt F x =⎰222sin 2011()()x x u tx dt du xF x f u du x =⇒==⎰提示:考虑X=0?).2212(lim 12121n n n n n n n n n ++++++∞→()''()(())(())()(())()g x h x d f t dt f g x g x f h x h x dx =-⎰=-⎰()d ()().b af x x b a f x =⎰⎰()()d ()()d .bb aa f x g x x f g x x x 222[()()]()()b b b a a a f x g x dx f x dx g x dx ≤⎰⎰⎰变限积分求导公式:积分中值定理:第一积分中值定理:柯西施瓦茨积分不等式:<<a b x。
第四章一次函数的图象与性质

一次函数的图象与性质教学目标掌握一次函数的图象,了解k 、b 的意义,掌握坐标系内x 、y 的变化规律。
重难点分析重点:1、一次函数的图象;2、一次函数的k 、b 对图象的影响;3、一次函数的图形变化规律。
难点:1、一次函数表达式与图象的关系; 2、一次函数图象的应用。
知识点梳理1、函数的图象:把一个函数的自变量x 与对应的因变量y 的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象。
画函数图象分三步:列表、描点、连线。
注意:函数的图象可以是直线,也可以是曲线,描点时,所描出的点越多,图象就越精确。
有时不能把所有的点都描出,就用平滑的曲线连接描出的点,从而得到函数的近似图象.函数的图象是由函数的表达式决定的,因此函数的表达式与图象之间有一种对应关系。
2、一次函数的图象与性质:对于一次函数b kx y +=(0≠k ) (1)当k >0时,y 随x 的增大而增大; (2)当k <0时,y 随x 的增大而减小。
3、一次函数b kx y +=(0≠k )的图象是一条直线,当k >0时,图象从左向右是上升的,当k <0时,图象从左向右是下降的.k ,b 的符号决定函数图象的位置,具体有六种情况。
(1)0,0>>b k ; (2)0,0<>b k ; (3)0,0><b k ;(4)0,0<<b k ; (5)0,0=>b k ; (6)0,0=<b k 。
知识点1:一次函数(正比例函数)的变化趋势【例1】当自变量x 增大时,下列函数值反而减小的是【 】 A.y=3xB.x y 2=C.y=3x -D.x y 52+-=【例2】函数y =(3m -1)x 是正比例函数,且y 随x 的增大而减小,则m 的取值范围是【 】A .m >13B .m >1C .m <13D .m <1【随堂练习】1、下列函数中,y 随x 的增大而减小的有【 】 ①12+-=x y ②x y -=6③31xy +-= ④x y )21(-=2、直线y =(k 2+3)x 经过第________象限,y 随x 的减小而________。
球bessel函数 -回复

球bessel函数-回复球Bessel函数(spherical Bessel function)是数学中的一种特殊函数,适用于球坐标系的问题。
它们与普通Bessel函数有着相似的性质和应用,只是在计算球对称场问题时更为方便。
在本文中,我们将逐步介绍球Bessel函数的定义、性质和应用。
首先,定义球Bessel函数。
对于非负整数n,球Bessel函数的定义如下:jn(x) = √(π/2x) ∙Jn+1/2(x),其中Jn(x)是普通Bessel函数,√表示开方。
球Bessel函数通常用jn(x)表示,这里的n为球Bessel函数的阶数,x为自变量。
球Bessel函数的定义中,√(π/2x)是为了保证函数的归一化,使得在某些特殊情况下,球Bessel函数满足正交性的定义。
接下来,我们来了解一些球Bessel函数的性质。
首先,球Bessel函数的奇偶性与阶数n有关。
当n为偶数时,jn(x)为偶函数;当n为奇数时,jn(x)为奇函数。
其次,球Bessel函数具有递推关系。
对于球Bessel函数的阶数n,我们可以利用递推公式来求解jn+1(x):jn+1(x) = (2n+1)/x ∙jn(x) - jn-1(x).此外,球Bessel函数还有一个重要的性质是正交性。
两个球Bessel函数的乘积在区间[0, ∞)上的积分为0,即:∫[0,∞) jn(x)jn(x')x^2 dx = δnn' / 2,其中δnn'是Kronecker delta函数。
这一性质在求解球对称问题中非常重要,特别是在电磁学、量子力学和热力学等领域的研究中。
最后,我们来看一些球Bessel函数的应用。
球Bessel函数常常出现在球对称场问题的求解中。
例如,在电磁学中,当我们考虑电场或磁场在球坐标系下的传播和辐射问题时,球Bessel函数可以用于描述场的衰减和增长。
在量子力学中,球Bessel函数常常出现在求解具有球对称势场的薛定谔方程以及求解球对称边界问题时。
高一上数学必修一第四章《4.4幂函数》知识点梳理
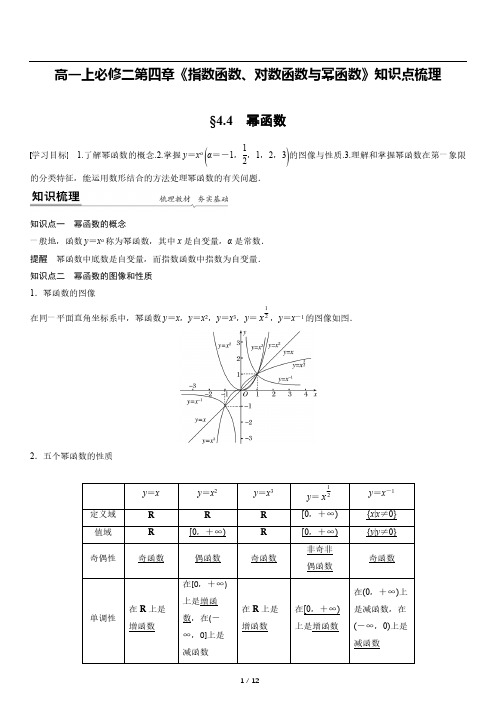
高一上必修二第四章《指数函数、对数函数与幂函数》知识点梳理§4.4 幂函数学习目标 1.了解幂函数的概念.2.掌握y =x α(α=-1,12,1,2,3)的图像与性质.3.理解和掌握幂函数在第一象限的分类特征,能运用数形结合的方法处理幂函数的有关问题.知识点一 幂函数的概念一般地,函数y =x α称为幂函数,其中x 是自变量,α是常数.提醒 幂函数中底数是自变量,而指数函数中指数为自变量.知识点二 幂函数的图像和性质1.幂函数的图像在同一平面直角坐标系中,幂函数y =x ,y =x 2,y =x 3,y =,y =x -1的图像如图.2.五个幂函数的性质y =xy =x 2y =x 3y =y =x -1定义域R R R [0,+∞){x |x ≠0}值域R [0,+∞)R [0,+∞){y |y ≠0}奇偶性奇函数偶函数奇函数非奇非偶函数奇函数单调性在R 上是增函数在[0,+∞)上是增函数,在(-∞,0]上是减函数在R 上是增函数在[0,+∞)上是增函数在(0,+∞)上是减函数,在(-∞,0)上是减函数12x 12x公共点(1,1)1.y =-1x 是幂函数.( × )2.当x ∈(0,1)时,x 2>x 3.( √ )3.y =与y =定义域相同.( × )4.若y =x α在(0,+∞)上为增函数,则α>0.( √ )一、幂函数的概念例1 (1)(多选)下列函数为幂函数的是( )A .y =x 3 B .y =(12)xC .y =4x 2D .y =x答案 AD解析 B 项为指数函数,C 中的函数的系数不为1,AD 为幂函数.(2)已知y =(m 2+2m -2)+2n -3是幂函数,求m ,n 的值.解 由题意得Error!解得Error!或Error!所以m =-3或1,n =32.反思感悟 判断一个函数是否为幂函数的方法判断一个函数是否为幂函数的依据是该函数是否为y =x α(α为常数)的形式,即函数的解析式为一个幂的形式,且需满足:(1)指数为常数;(2)底数为自变量;(3)系数为1.跟踪训练1 已知f (x )=ax 2a +1-b +1是幂函数,则a +b 等于( )A .2 B .1 C.12 D .0答案 A解析 因为f (x )=ax 2a +1-b +1是幂函数,所以a =1,-b +1=0,即a =1,b =1,则a +b =2.32x 64x 22m x二、幂函数的图像例2 如图所示,图中的曲线是幂函数y =x n 在第一象限的图像,已知n 取±2,±12四个值,则对应于c 1,c 2,c 3,c 4的n 依次为( )A .-2,-12,12,2B .2,12,-12,-2C .-12,-2,2,12D .2,12,-2,-12答案 B解析 根据幂函数y =x n 的性质,故c 1的n =2,c 2的n =12,当n <0时,|n |越大,曲线越陡峭,所以曲线c 3的n =-12,曲线c 4的n =-2.反思感悟 解决幂函数图像问题应把握的两个原则(1)依据图像高低判断幂指数大小,相关结论为:在(0,1)上,指数越大,幂函数图像越靠近x 轴(简记为指大图低);在(1,+∞)上,指数越大,幂函数图像越远离x 轴(简记为指大图高).(2)依据图像确定幂指数α与0,1的大小关系,即根据幂函数在第一象限内的图像(类似于y =x -1 或y =或y =x 3)来判断.跟踪训练2 函数f (x )=的大致图像是( )答案 A解析 因为-12<0,所以f (x )在(0,+∞)上单调递减,排除选项B ,C ;又f (x )的定义域为(0,+∞),故排除选项D.三、比较幂值的大小12x 12x例3 比较下列各组数中两个数的大小:(1)(25)0.5与(13)0.5;(2)(-23)-1与(-35)-1;(3)与.解 (1)∵幂函数y =x 0.5在(0,+∞)上是单调递增的,又25>13,∴(25)0.5>(13)0.5.(2)∵幂函数y =x -1在(-∞,0)上是单调递减的,又-23<-35,∴(-23)-1>(-35)-1.(3)∵函数y 1=(23)x为R 上的减函数,又34>23,∴>.又∵函数y 2=在(0,+∞)上是增函数,且34>23,∴>,∴>.反思感悟 比较幂值大小的方法跟踪训练3 比较下列各组值的大小:(1),;(2),,1.42.解 (1)∵y =为R 上的偶函数,∴=.又函数y =为[0,+∞)上的增函数,且0.31<0.35,3423⎛⎫⎪⎝⎭2334⎛⎫⎪⎝⎭2323⎛⎫ ⎪⎝⎭3423⎛⎫ ⎪⎝⎭23x 2334⎛⎫⎪⎝⎭2323⎛⎫ ⎪⎝⎭2334⎛⎫ ⎪⎝⎭3423⎛⎫⎪⎝⎭()650.31-650.35121.2121.465x ()650.31-650.3165x∴<,即<.(2)∵y =在[0,+∞)上是增函数,且1.2<1.4,∴<.又∵y =1.4x 为增函数,且12<2,∴<1.42,∴<<1.42.幂函数性质的应用典例 已知幂函数y =x 3m -9 (m ∈N +)的图像关于y 轴对称且在(0,+∞)上单调递减,求满足的a 的取值范围.解 因为函数y =x 3m -9在(0,+∞)上单调递减,所以3m -9<0,解得m <3.又因为m ∈N +,所以m =1,2.因为函数的图像关于y 轴对称,所以3m -9为偶数,故m =1.则原不等式可化为.因为y =在(-∞,0),(0,+∞)上单调递减,所以a +1>3-2a >0或3-2a <a +1<0或a +1<0<3-2a ,解得23<a <32或a <-1.故a 的取值范围是Error!.[素养提升] (1)幂函数y =x α中只有一个参数α,幂函数的所有性质都与α的取值有关,故可由α确定幂函数的定义域、值域、单调性、奇偶性,也可由这些性质去限制α的取值.(2)通过具体实例抽象出幂函数的概念和性质,并应用单调性求解,体现了数学中数学运算与直观想象的核心素养.650.31650.35()650.31-650.3512x 121.2121.4121.4121.2121.433(1)(32)m m a a --+<-1133(1)(32)a a --+<-13x-1.下列函数是幂函数的是( )A .y =5x B .y =x 5C .y =5x D .y =(x +1)3答案 B解析 函数y =5x 是指数函数,不是幂函数;函数y =5x 是正比例函数,不是幂函数;函数y =(x +1)3的底数不是自变量x ,不是幂函数;函数y =x 5是幂函数.2.幂函数y =x α(α∈R )的图像一定不经过( )A .第四象限 B .第三象限C .第二象限 D .第一象限答案 A解析 由幂函数的图像可知,其图像一定不经过第四象限.3.设α∈{-1,1,12,3},则使函数y =x α的定义域为R 且为奇函数的所有α值为( )A .1,3B .-1,1C .-1,3D .-1,1,3答案 A解析 可知当α=-1,1,3时,y =x α为奇函数,又因为y =x α的定义域为R ,则α=1,3.4.已知幂函数f (x )=kx α(k ∈R ,α∈R )的图像过点(12,2),则k +α等于( )A.12 B .1 C.32 D .2答案 A解析 ∵幂函数f (x )=kx α(k ∈R ,α∈R )的图像过点(12,2),∴k =1,f(12)=(12)α=2,即α=-12,∴k +α=12.5.已知f (x )=,若0<a <b <1,则下列各式中正确的是( )A .f (a )<f (b )<f(1a )<f(1b)B .f (1a )<f(1b )<f (b )<f (a )C .f (a )<f (b )<f (1b )<f(1a )D .f (1a )<f (a )<f(1b )<f (b )12x答案 C解析 因为函数f (x )=在(0,+∞)上是增函数,又0<a <b <1<1b <1a ,故f (a )<f (b )<f(1b )<f(1a).1.知识清单:(1)幂函数的概念.(2)幂函数的图像.(3)幂函数的性质及其应用.2.方法归纳:数形结合.3.常见误区:幂函数与指数函数的区别;幂函数的奇偶性.1.幂函数f (x )=x α的图像经过点(2,4),则f (-12)等于( )A.12B.14 C .-14 D .2答案 B解析 幂函数f (x )=x α的图像经过点(2,4),则2α=4,解得α=2;∴f (x )=x 2,∴f (-12)=(-12)2=14.2.下列函数中,既是偶函数,又在区间(0,+∞)上单调递减的函数是( )A .y =x -2 B .y =x -1C .y =x 2 D .y =答案 A解析 所给选项都是幂函数,其中y =x -2和y =x 2是偶函数,y =x -1和y =不是偶函数,故排除选项B ,D ,又y =x 2在区间(0,+∞)上单调递增,不合题意,y =x -2在区间(0,+∞)上单调递减,符合题意.3.设a =,b =,c =,则a ,b ,c 的大小关系是( )12x 13x13x 2535⎛⎫ ⎪⎝⎭3525⎛⎫⎪⎝⎭2525⎛⎫⎪⎝⎭A .a >c >bB .a >b >cC .c >a >bD .b >c >a答案 A解析 ∵y =(x >0)为增函数,又35>25,∴a >c .∵y =(25)x (x ∈R )为减函数,又25<35,∴c >b .∴a >c >b .4.在同一坐标系内,函数y =x a (a ≠0)和y =ax -1a的图像可能是( )答案 C解析 选项A 中,幂函数的指数a <0,则y =ax -1a 应为减函数,A 错误;选项B 中,幂函数的指数a >1,则y =ax -1a 应为增函数,B 错误;选项D 中,幂函数的指数a <0,则-1a >0,直线y =ax -1a在y 轴上的截距为正,D 错误.5.若幂函数f (x )的图像过点(2,2),则函数g (x )=f (x )-3的零点是( )A.3 B .9 C .(3,0) D .(9,0)答案 B解析 ∵幂函数f (x )=x α的图像过点(2,2),∴f (2)=2α=2,解得α=12,∴f (x )=,∴函数g (x )=f (x )-3=-3,由-3=0,得x =9.∴函数g (x )=f (x )-3的零点是9.6.已知幂函数f (x )=x α的部分对应值如表:x11225x 12x 12x 12xf (x )122则f (x )的单调递增区间是________.答案 [0,+∞)解析 因为f(12)=22,所以(12)α=22,即α=12,所以f (x )=的单调递增区间是[0,+∞).7.已知幂函数f (x )=x α(α∈R )的图像经过点(8,4),则不等式f (6x +3)≤9的解集为________.答案 [-5,4]解析 由题意知8α=4,故α=log 84=23,由于f (x )==x 2为R 上的偶函数且在(0,+∞)上递增,故f (6x +3)≤9即为f (6x +3)≤f (27),所以|6x +3|≤27,解得-5≤x ≤4.8.设a =,b =,c =,则a ,b ,c 从小到大的顺序是________.答案 b <a <c解析 由a =,b =,可利用幂函数的性质,得a >b ,可由指数函数的单调性得c >a ,∴b <a <c .9.已知幂函数f (x )=x α的图像过点P (2,14),试画出f (x )的图像并指出该函数的定义域与单调区间.解 因为f (x )=x α的图像过点P (2,14),所以f (2)=14,即2α=14,得α=-2,即f (x )=x -2,f (x )的图像如图所示,定义域为(-∞,0)∪(0,+∞),单调递减区间为(0,+∞),单调递增区间为(-∞,0).10.已知幂函数f (x )=x 9-3m (m ∈N +)的图像关于原点对称,且在R 上单调递增.(1)求f (x )的解析式;(2)求满足f (a +1)+f (3a -4)<0的a 的取值范围.解 (1)由幂函数f (x )=x 9-3m (m ∈N +)的图像关于原点对称,且在R上单调递增,可得9-3m >0,解得m <3,m ∈N +,可得m =1,2,12x 23x 2312⎛⎫⎪⎝⎭2315⎛⎫ ⎪⎝⎭1312⎛⎫⎪⎝⎭2312⎛⎫ ⎪⎝⎭2315⎛⎫⎪⎝⎭若m =1,则f (x )=x 6的图像不关于原点对称,舍去;若m =2,则f (x )=x 3的图像关于原点对称,且在R 上单调递增,成立.则f (x )=x 3.(2)由(1)可得f (x )是奇函数,且在R 上单调递增,由f (a +1)+f (3a -4)<0,可得f (a +1)<-f (3a -4)=f (4-3a ),即为a +1<4-3a ,解得a <34.11.若函数f (x )=(m +2)x a 是幂函数,且其图像过点(2,4),则函数g (x )= log a (x +m )的单调递增区间为( )A .(-2,+∞) B .(1,+∞)C .(-1,+∞) D .(2,+∞)答案 B解析 由题意得m +2=1,解得m =-1,则f (x )=x a ,将(2,4)代入函数的解析式得,2a =4,解得a =2,故g (x )=log a (x +m )=log 2(x -1),令x -1>0,解得x >1,故g (x )在(1,+∞)上单调递增.12.函数y =-1的图像关于x 轴对称的图像大致是( )答案 B解析 y =的图像位于第一象限且为增函数,所以函数图像是上升的,函数y =-1的图像可看作由y =的图像向下平移一个单位长度得到的(如选项A 中的图所示),将y =-1的图像关于x 轴对称后即为选项B.13.为了保证信息的安全传输,有一种密钥密码系统,其加密、解密原理为:发送方由明文到密文(加密),接收方由密文到明文(解密).现在加密密钥为y =x α(α为常数),如“4”通过加密后得到密文“2”.若接收方接到密文“3”,则解密后得到的明文是________.答案 9解析 由题意可知加密密钥y =x α(α为常数)是一个幂函数,所以要想求得解密后得到的明文,就必须先求出α的值.由题意,得2=4α,解得α=12,则y =.由=3,得x =9,即明文是9.14.已知幂函数f (x )=,若f (a +1)<f (10-2a ),则a 的取值范围是________.12x 12x 12x 12x 12x 12x 12x 12x答案 (3,5)解析 ∵f (x )==1x(x >0),易知f (x )在(0,+∞)上为减函数,又f (a +1)<f (10-2a ),∴Error!解得Error!∴3<a <5.15.幂函数y =x α,当α取不同的正数时,在区间[0,1]上它们的图像是一族美丽的曲线(如图).设点A (1,0),B (0,1),连接AB ,线段AB 恰好被其中的两个幂函数y =x α,y =x β的图像三等分,即有BM =MN =NA ,那么,αβ等于________.答案 1解析 由条件,得M (13,23),N (23,13),可得13=(23)α,23=(13)β,即α=13,β=23.所以αβ=13·23=lg 13lg 23·lg 23lg 13=1.16.已知幂函数g (x )过点(2,12),且f (x )=x 2+ag (x ).(1)求g (x )的解析式;(2)讨论函数f (x )的奇偶性,并说明理由.解 (1)设幂函数的解析式g (x )=x α(α为常数).因为幂函数g (x )过点(2,12),所以2α=12,解得α=-1,所以g (x )=1x.(2)由(1)得f (x )=x 2+a x.①当a =0时,f (x )=x 2.12x 23log 13log 23log 13log由于f(-x)=(-x)2=x2=f(x),可知f(x)为偶函数.②当a≠0时,由于f(-x)=(-x)2+a-x=x2-ax≠x2+ax=f(x),且f(-x)=(-x)2+a-x=x2-ax≠-(x2+a x)=-f(x),所以f(x)是非奇非偶函数.综上,①当a=0时,f(x)为偶函数;②当a≠0时,f(x)为非奇非偶函数.。
高中数学新教材必须第一册第四章《指数函数的图象和性质》教学设计

4.2.2 指数函数的图像和性质一、教材学情分析:本节内容是高中数学新教材人教A版普通必修第一册第四章第4.2.2节《指数函数的图像和性质》。
由于学生已经学习了正反比例函数、一次函数、二次函数,以及函数性质,所以学习这部分内容与先前的函数学习类似。
先画函数图像,然后借助函数图像讨论函数的性质,最后应用的指数函数图象和性质解决问题,体现了研究函数的一般方法,让学生掌握由特殊到一般的思想方法。
培养学生直观想象、数学抽象、数学运算、逻辑推理及数学建模的核心素养。
二、教学目标:1、能画出具体指数函数的图象;2、通过类比,利用具体指数函数图像,归纳出指数函数的一般性质,3、能利用指数函数的图象和性质解决一些简单的应用问题;三、核心素养:1. 运用描点法画指数函数的图象,用图象来研究指数函数的性质,培养学生直观想象和数学抽象的核心素养;2. 从一般到特殊研究问题的方法,培养学生逻辑推理的核心素养;3. 运用指数函数性质解决问题,培养学生数学运算和数学建模核心素养。
四、教学重难点教学重点:指数函数的图象和性质。
教学难点:指数函数的性质的归纳及其应用。
五、教学准备:多媒体课件六、教学过程:(一)创设问题情境你能说说研究函数的一般步骤和方法吗?设计意图:通过回顾研究函数的一般方法,提提供研究思路,进入学习和研究,培养学生的逻辑推理和数学建模的核心素养。
(二)、探索新知1.用描点法作函数y=2x、y=3x、1y()2x=和1y()3x=的图象(如图所示)2.观察这四个图像有何特点?并思考一下几个问题 问题1:图象分别在哪几个象限?问题2:图象的上升、下降与底数a 有联系吗? 问题3:图象有哪些特殊的点? 问题4:图象定义域和值域范围?设计意图:通过对特殊的指数函数图像观察,归纳出指数函数的性质;发展学生数学抽象、数学建模和逻辑推理等核心素养; 3.指数函数的图像与性质图象1a >01a <<定义域 R 值域 (0,)+∞过定点 图象过定点(0,1),即当0x =时,1y =.奇偶性 非奇非偶单调性在R 上是增函数在R 上是减函数例1.说出下列各题中两个值的大小:(1)1.72.5__ 1.73;(2)0.8—1__0.8—2;(3)1.70.5__ 0.82.5解:① ∵函数y=1.7x在R 上是增函数,x a y =xy(0,1)O1y =xa y =xy(0,1)O 1y =又∵ 2.5 < 3 ,∴1.72.5 < 1.73② ∵函数y=0.8x在R 上是减函数,又∵ -1 > -2 ,∴ 0.8—1< 0.8— 2③ ∵ 1.7 0.5> 1.70= 1= 0.80>0.8 2.5, ∴1.70.5> 0.82.5[规律方法] 比较幂的大小的方法1.同底数幂比较大小时构造指数函数,根据其单调性比较2.指数相同底数不同时分别画出以两幂底数为底数的指数函数图象,当x 取相同幂指数时可观察出函数值的大小3.底数、指数都不相同时,取与其中一底数相同与另一指数相同的幂与两数比较,或借助“1”与两数比较4.当底数含参数时,要按底数a>1和0<a<1两种情况分类讨论设计意图:通过典例问题的分析,让学生运用指数函数的性质解决问题。
《高等数学》 第四章 不定积分的概念和性质1—2节 课堂笔记及练习题

高等数学 第四章 不定积分的概念和性质1—2节 课堂笔记及练习题主 题:第四章 不定积分的概念和性质1—2节 学习时间:2015年11月30日—12月6日内 容:这周我们将学习第四章不定积分的概念和性质(1—2节)。
积分运算与微分运算互为逆运算,它们同是高等数学的重点,需要充分重视。
其学习要求及需要掌握的重点内容如下:1、理解原函数与不定积分的概念2、非常熟练地掌握求不定积分的基本方法:基本积分公式、不定积分的性质、换元法。
基本概念:原函数和不定积分的概念知识点:基本积分公式、不定积分的性质、换元法知识结构图一元函数积分学原函数不定积分定义运算法则计算方法直接积分法换元法第一类换元法全体个体第二类换元法第一节、不定积分的概念和性质一、原函数与不定积分的概念(要求理解各概念) 定义1:设)(x f 为某区间I 上的函数,如果存在函数)(x F ,使在该区间上有)()(x f x F ='或,)()(dx x f x dF =则称)(x F 为)(x f 在区间I 上的一个原函数。
原函数存在定理:如果)(x f 在区间I 上连续,则在区间I 上)(x f 的原函数一定存在。
说明:如果)(x F 是)(x f 在区间I 上的一个原函数,显然c c x F ()(+为任意常数)也是)(x f 的原函数,这说明)(x f 如果存在原函数,应有无穷多个,)(x f 的全体原函数是一个函数族。
c x F +)(为)(x f 全体原函数的一般表达式。
定义2:设)(x F 是)(x f 在区间I 的一个原函数,则)(x f 的全体原函数c x F +)(称为)(x f 在区间I 的不定积分,记⎰+=c x F dx x f )()(其中⎰叫积分号,)(x f 叫被积函数,dx x f )(叫被积表达式,x 叫积分变量,c 为任意常数叫积分常数。
范例解析:1、单选题:设)(x f 的一个原函数为x1,则=')(x f ( ) A 、||ln xB 、x1 C 、21x - D 、32x解题思路:因为x 1为)(x f 的原函数,所以21)1()(xx x f -='=,从而32)(xx f ='。
球汉克尔函数

球汉克尔函数球汉克尔函数是数学和物理学中一个非常重要、广泛应用的特殊函数。
它最早由德国物理学家汉克尔(Oskar Edmund Henrik Hörmander)在20世纪初提出,其后又被巴塞尔物理学家利奥·萨瓦西·狄拉克(Dirac)所改进。
球汉克尔函数主要用于解决球形坐标系下的微分方程,是复变函数论中的特殊函数,主要涉及到球面的物理特性。
例如,在纳米技术、量子力学等领域,球汉克尔函数被广泛应用于描述粒子的位置、波函数、势函数等等。
球汉克尔函数与球贝塞尔函数的关系:球汉克尔函数H(n)l(kr)定义为:H(n)l(kr) = i**l * (2/π) * Γ(l + 1/2) * ∫sin(θ) ** (l + 1) *e**(-ikrcos(θ)) * Pn(l)(cos(θ)) * dθ其中,r表示半径,k表示波数,l表示角量子数,n 表示收敛指数,Pn(l)(cos(θ))是勒让德多项式,Γ(l + 1/2)表示阶乘。
特别的,当n=0时,球汉克尔函数变成了球贝塞尔函数,并且有:H(l)l(kr) = (-1)**l * (2l+1)!! * j_(l +1/2)(kr) / (kr)其中,j_(l + 1/2)(kr)是球贝塞尔函数,(2l+1)!!表示(2l+1)*(2l-1)*···*3*1,即奇数的阶乘。
球汉克尔函数的性质:1.对于整数n和非负实数r,球汉克尔函数:H(n)l(kr) 和 H(-n-1)l(kr)具有相同的性质。
2.当r趋近于零时,球汉克尔函数的渐进形式为: H(n)l(kr) ~ (-1)^(n+1) * Γ(l+1/2) (2/kr)^(l+1)3.球汉克尔函数具有正交性质:∫ H(n)l(kr)H(n)l'(kr) r^2dr = delta(ll')/(kr)^2其中, delta(ll')表示克罗内克δ。
高中数学必修一第四章知识点归纳

高中数学必修一第四章知识点归纳全文共5篇示例,供读者参考高中数学必修一第四章知识点归纳篇1指数函数及其性质1、指数函数的概念:一般地,函数叫做指数函数(exponential),其中x是自变量,函数的定义域为r.注意:指数函数的底数的取值范围,底数不能是负数、零和1.2、指数函数的图象和性质【函数的应用】1、函数零点的概念:对于函数,把使成立的实数叫做函数的零点。
2、函数零点的意义:函数的零点就是方程实数根,亦即函数的图象与轴交点的横坐标。
即:方程有实数根函数的图象与轴有交点函数有零点.3、函数零点的求法:求函数的零点:1(代数法)求方程的实数根;2(几何法)对于不能用求根公式的方程,可以将它与函数的图象联系起来,并利用函数的性质找出零点.4、二次函数的零点:二次函数.1)△>0,方程有两不等实根,二次函数的图象与轴有两个交点,二次函数有两个零点.2)△=0,方程有两相等实根(二重根),二次函数的图象与轴有一个交点,二次函数有一个二重零点或二阶零点.3)△<0,方程无实根,二次函数的图象与轴无交点,二次函数无零点.高中数学必修一第四章知识点归纳篇2(1)直线的倾斜角定义:x轴正向与直线向上方向之间所成的角叫直线的倾斜角.特别地,当直线与x轴平行或重合时,我们规定它的倾斜角为0度.因此,倾斜角的取值范围是0°≤α<°(2)直线的斜率①定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率.直线的斜率常用k表示.即.斜率反映直线与轴的倾斜程度.当时,;当时,;当时,不存在.②过两点的直线的斜率公式:注意下面四点:(1)当时,公式右边无意义,直线的斜率不存在,倾斜角为90°;(2)k与p1、p2的顺序无关;(3)以后求斜率可不通过倾斜角而由直线上两点的坐标直接求得;(4)求直线的倾斜角可由直线上两点的坐标先求斜率得到.(3)直线方程①点斜式:直线斜率k,且过点注意:当直线的斜率为0°时,k=0,直线的方程是y=y1.当直线的斜率为90°时,直线的斜率不存在,它的方程不能用点斜式表示.但因l上每一点的横坐标都等于x1,所以它的方程是x=x1.②斜截式:,直线斜率为k,直线在y轴上的截距为b③两点式:直线两点,④截矩式:其中直线与轴交于点,与轴交于点,即与轴、轴的截距分别为.⑤一般式:(a,b不全为0)注意:各式的适用范围特殊的方程如:平行于x轴的直线:(b为常数);平行于y轴的直线:(a为常数);(5)直线系方程:即具有某一共同性质的直线(一)平行直线系平行于已知直线(是不全为0的常数)的直线系:(c为常数) (二)垂直直线系垂直于已知直线(是不全为0的常数)的直线系:(c为常数) (三)过定点的直线系(ⅰ)斜率为k的直线系:,直线过定点;(ⅱ)过两条直线,的交点的直线系方程为(为参数),其中直线不在直线系中.(6)两直线平行与垂直注意:利用斜率判断直线的平行与垂直时,要注意斜率的存在与否.(7)两条直线的交点相交交点坐标即方程组的一组解.方程组无解;方程组有无数解与重合(8)两点间距离公式:设是平面直角坐标系中的两个点(9)点到直线距离公式:一点到直线的距离(10)两平行直线距离公式在任一直线上任取一点,再转化为点到直线的距离进行求解.高中数学必修一第四章知识点归纳篇3对数函数对数函数的一般形式为,它实际上就是指数函数的反函数。
球面谐波函数

球面谐波函数概述球面谐波函数是球坐标系下的一组正交函数,常用于描述球面上的物理问题。
它们在数学物理、电磁学、量子力学等领域有广泛的应用。
本文将详细介绍球面谐波函数的定义、性质和应用。
定义球面谐波函数是指满足拉普拉斯方程在球坐标系下的分离变量解。
球面谐波函数通常用符号Y lm (θ,ϕ)表示,其中l 和m 分别表示角动量量子数和磁量子数。
球面谐波函数可以通过以下公式表示:Y lm (θ,ϕ)=(−1)m √(2l +1)(l −m )!4π(l +m )!P lm (cosθ)e imϕ 其中,P lm (cosθ)是勒让德多项式,θ和ϕ分别表示球坐标系下的极角和方位角。
性质球面谐波函数具有许多重要的性质,下面列举了其中一些常见的性质:1. 正交性:不同的球面谐波函数之间满足正交归一关系,即∫Y lm ∗(θ,ϕ)Y l′m′(θ,ϕ)sinθdθdϕ=δll′δmm′其中,δll′和δmm′分别表示克罗内克δ符号。
2. 归一化:球面谐波函数可以通过归一化系数使其满足归一化条件,即∫|Y lm (θ,ϕ)|2sinθdθdϕ=1这样可以保证球面谐波函数的模长为1。
3. 递推关系:球面谐波函数之间存在递推关系,可以通过递推关系计算不同角动量量子数和磁量子数的球面谐波函数。
4. 旋转性质:球面谐波函数在球坐标系下具有良好的旋转性质,可以通过旋转矩阵与球面谐波函数之间的关系进行描述。
应用球面谐波函数在许多领域有广泛的应用,下面介绍其中几个重要的应用:1.量子力学:球面谐波函数是描述氢原子和其他球对称势场中的粒子的波函数的基础。
它们可以用来计算能级、波函数和选择规则等量子力学性质。
2.电磁学:球面谐波函数可以用于描述电磁场在球面上的分布。
它们在电磁辐射、天线理论和散射等问题中有广泛的应用。
3.地球物理学:球面谐波函数可以用于描述地球重力场和磁场的变化。
地球重力场和磁场的球谐展开可以帮助我们了解地球内部的结构和物理特性。
第四章 ,第一节 可测函数的定义及其简单性质

1可测函数定义
定义:设f(x)是可测集E上的实函数(可取
),
若 a R, E[ f a] 可测,则称f(x)是E上的可测函数。
例 (1) 零集上的任何函数都是可测函数。
注:称外测度为0的集合为零集;零集的子 集,有限并,可数并仍为零集
Th1.可测函数的等价描述
⒈定义:设f(x)是可测集E上的实函数,则f(x)在E上可测 ( 即(1) a R, E[ f a]可测)
(2)E[ f
E[ f a] E[ f
a]
E,
a], a 0 a0
(3)E[ f
E[
f
1 a
]
E[
f
0] E[ f 1 ] a
0] \ E[ f ]
1
a0 a0
E[ f
0] E[ f
] a
a0
(4)E[ f
•
g
a]
E
\
E[
f
{(E[ f 0] • g a] E
若 lim xx0
f (x)
f (x0 )
() ( ) ( )
即 0, 0,当| x x0 | 时,有| f (x) f (x0 ) |
即 0, 0,当x U (x0, )时,有f (x) U ( f (x0 ), )
即 0, 0,使得f (U (x0, )) U ( f (x0 ), )
f(x) 在 x0 [a,b] 处连续(对闭区间端点则用左或右连续)
Th2 可测集E上的连续函数定为可测函数 证明:任取x∈E[f>a], 则f(x)>a,由连续性假设知,
存在x的某邻域U (x,x ) 使得U(x,x ) E E[ f a]
令G
第四章-特殊函数(上)-勒让德多项式和球谐函数

因此,(2 n )!(2 n )!!(2 n 1 )!!
2、勒让德多项式的微分表示
Pl(x)21ll!ddxll (x21)l
(4.1.10)
上式通常又称为勒让德多项式的罗德里格斯(Rodrigues) 表示式.
下面证明表达式 (4.1.10) 和(4.1.7)是相同的.
【证明】 用二项式定理把 (x2 1)l展开
勒让德多项式的图形可通过计算机仿真(如MATLAB仿真) 得到
图 4.1
计算 P l ( 0 ) ,这应当等于多项式 P l ( x ) 的常数项.
如 l 为 2n 1(即为奇数)时, 则 P2n1 ( x)
只含奇 数次幂,不含常数项,所以
P2n1(0)0
(4.1.8)
l 2n (即为偶数)时.,则 P 2 n ( x ) 含有常数项,即 (4.1.7)中 k l 2 n 的那一项,所以
P2n(0)(1)n2(22 nn n!)n !!(1)n(2 (n 2n )1 !)!!! (4.1.9)
式中记号 ( 2 n ) ! ! ( 2 n ) ( 2 n 2 ) ( 2 n 4 ) L 6 4 2
而 ( 2 n 1 ) ! ! ( 2 n 1 ) ( 2 n 3 ) ( 2 n 5 ) L 5 3 1
(4.1.2) 式的解 Y ( , ) 与半径 r 无关,称为球谐函数
பைடு நூலகம்
,或简称为球函数.
球谐函数方程进一步分离变量,令 Y(,) () ()
得到关于 的常微分方程
sin 1 d d sind d l(l 1 )sim n2 2 0 (4.1.3)
称为 l 阶连带勒让德l 方程或缔合勒让德方程
.
令 xcos和 y(x)(x)
人教版高考总复习一轮数学精品课件 第四章 一元函数的导数及其应用-第四节 三次函数的图象与性质

[, ]上恒成立,可得 ≤ + , + ≥ ⋅ = ,当且仅当 = 时取等号,可
得 ≤ .故选D.
2
3
(2)已知函数 = 3 + 2 + + 在 = − 与 = 1处都取得极值.
①求,的值与函数 的单调区间;
解 = 3 + 2 + + ,′ = 3 2 + 2 + ,由
−
−
> ,
−
< ,
即
−
−
−
−
+ > ,
解得 < −.故选B.
−
−
+
+ < ,
(2)(2023扬州校考)设为实数,函数 = − 3 + 3 + .
①求 的极值.
解 ′ = −3 2 + 3,令′ = 0,得 = −1或 = 1.当 ∈ −∞, −1 时,′ < 0;
− ,
3
−
3
和极小值点三等分,类似地,对极小值也有类似结论.
自测诊断
1.已知三次函数 =
1 3
3
− 4 − 1 2 + 152 − 2 − 7 + 2在上是增函数,
则实数的取值范围是() D
A. < 2或 > 4B.−4 < < −2C.2 < < 4D.2 ≤ ≤ 4
为
1 ,2
1 ,2
第四章 指数函数与对数函数(教学课件)——高中数学人教A版(2019)必修一

作业:
1、整理今天的题目 2、周末完成一套综合题目,下周进行讲评
题型二 指数函数的图象与性质
命题点3 解简单的指数不等式 例 3 (1)若 2x2+1≤14x-2,则函数 y=2x 的值域是
A.18,2
√B.18,2
C.-∞,18
D.[2,+∞)
解析 14x-2=(2-2)x-2=2-2x+4, ∴ 2x2+1 ≤2-2x+4,
即x2+1≤-2x+4,即x2+2x-3≤0, ∴-3≤x≤1,此时y=2x的值域为[2-3,21], 即为18,2.
∴t=ax2-4x+3在(-∞,-3)上单调递增,
a<0, 则2a≥-3,
解得 a≤-23.
思维升华
求解与指数函数有关的复合函数问题,要明确复合函数的构成,涉及 值域、单调区间、最值等问题时,都要借助“同增异减”这一性质分 析判断.
题型五 复合函数的应用
例9 已知函数f(x)=loga(8-ax)(a>0,且a≠1),若f(x)>1在区间[1,2]上
第四章 指数函数与对数 函数复习课
课前准备:
1、提前对好答案并改正
2、准备好笔记本做好记录
知识梳理 1.指数函数及其性质 (1)概念:函数y=ax(a>0,且a≠1)叫做指数函数,其中指数x是自变量, 函数的定义域是R,a是底数. (2)指数函数的图象与性质
a>1
数学物理方法球贝塞尔函数

数学物理方法球贝塞尔函数球贝塞尔函数(Spherical Bessel Functions)是一类常见的数学物理方法,它在球坐标系下描述球对称问题中的波动现象。
球贝塞尔函数在数学物理学中具有广泛的应用,尤其在电磁学、量子力学和声学等领域中起着重要的作用。
为了理解球贝塞尔函数的定义和性质,首先需要了解球坐标系。
在球坐标系中,位置可以由径向距离r、极角θ和方位角φ来描述。
球贝塞尔函数正是在此坐标系下描述球对称问题的解。
球贝塞尔函数的定义如下:jₙ(z)=√(π/2z)Jₙ+1/2(z),n=0,1,2,...其中,Jₙ(z)表示的是贝塞尔函数,而jₙ(z)表示的是球贝塞尔函数。
球贝塞尔函数是由归一化的贝塞尔函数通过简单的关系得到的。
球贝塞尔函数具有许多有用的性质。
其中一些重要的性质如下:1. 正交性:球贝塞尔函数具有正交性质,即∫[0,∞]jₙ(z)jₙ(z')z²dz = δ(z-z'),其中δ(z-z')为狄拉克函数。
2. 归一性:球贝塞尔函数具有归一化性质,即∫[0,∞]jₙ²(z)z²dz = 13.递推关系:球贝塞尔函数之间存在递推关系,即jₙ(z)=(2n+1)/zjₙ₋₁(z)-jₙ₋₂(z)。
4. 渐进行为:对于大的z值,球贝塞尔函数有渐近展开式,即jₙ(z) ≈ sin(z-π(n+1/2))/z。
球贝塞尔函数在电磁学中的应用非常广泛。
在电磁波的传播和散射问题中,球贝塞尔函数可以描述球形散射体表面上的电磁波场分布。
球贝塞尔函数还被用于计算有限大小的球形天线和圆柱天线的辐射模式。
在量子力学中,球贝塞尔函数是描述氢原子和其它球对称体系中的径向波函数的解。
在求解薛定谔方程时,需要利用球贝塞尔函数计算波函数的解析解。
球贝塞尔函数在声学中也有重要的应用。
在声学问题中,球贝塞尔函数可以描述球形振膜和声源的辐射特性。
通过求解波动方程,可以利用球贝塞尔函数计算声波的传播和散射过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
将Pn的表达式代入,得
得
经度方向方程的求解
3.4 球函数
在第一节中,我们将球坐标中的拉普拉斯方程的解分解成 了 三个函数的积,并解出: 最后,我们来求解
当趋于零时, 界的调和函数。 外部有界的调和函数。
。 所以, ,
适用于研究内部有 适用于研究
由分离变童法求得的拉普拉斯方程最一般的解为所有可能的 乘积 的线性组合。设坐标原点在某一闭合曲面的内部, 则在该曲面内部拉普拉斯方程分离变量有限解的一般形式为
连带勒让得函数是连带勒让得方程在【-1,1】中有界条件下 的特征函数。还可以写成:
做变量代换,
可以求得:
将前三式代入连带勒让德方程,整理得:
求导并整理得: 得:
可见,连带勒让得方程两个线性无关的解可由勒让得方程 两个线性无关的解确定。
(二)连带勒让得方程的级数解
由上式可以求出连带勒让得方程两个线性无关的解,
拉普拉斯方程
V V V 0 2 2 2 x y z
2 2 2
(一)球坐标中的拉普拉斯算子
球坐标和直角坐标的关系是
利用该关系式直接将直角坐标系中的拉普拉斯算子化算在球 坐标系中,运算比较麻烦,这里我们利用 来推导拉普斯算子在球坐标中的表达式。 如图4-1所示,取一微六面体ABCDEFGH,图 4-1来自 将用于该微六面体,得
其中r为微六面体的体积,i=1,2,…,6表示微六面体 的6个面。 表示 在第i个面上的值,i为第i 个面的面积。 在AEHD上, n与p增加的方向反向,所以有
该面的面积为
,所以
所以有, 在AEFB上,n的方向与增加的方向相反,由于沿增加方 向的线元长度为d,所以, 同理有, 所以有,
(三)级数解的收敛性
当k为偶数时,将上式中的求和指标i换成i+K/2,得
当i足够大时,
考虑到B1(x)中的级数为x2的级数,B2 (x)中的级数为x与一个x2的级数 之积,所以这两上级数均可被当作正项级数处理,由于级数的前面有限项并 不影响级数的收敛性,所以只要 分别无界,B1,B2也无界。
可以证明,当x趋于士1时,y1(x)和y2 (x)分别趋于无穷,也就 是说,y1(x)和y2(x)在x=士1时无界,因而B1 (x)和B2(x)在x =士1时无界。
在ABCD上,n的方向与增加的方向相反,由于沿增加 方向的线元长度为 sin d ,所以
该面的面积为 d d ,所以
得 综合以上几式,得拉普拉斯算子在球坐标中的表达式:
(二)分离变量法
令上式等于零,然后两边同乘以平方 ,得球坐标中的拉普拉 斯方程 分离变量法就是将方程的解分解为依赖于不同自变量的函数 之积。令
我们把上述多项式最高次项的系数规定为 此时该多项式称为n阶勒让得函数,并且 表示。 在上述递推公式中令i=n-2,可以得到:
以此类推,可以得到:
,
….归纳可以得到:
因此,得到勒让德函数的具体表达式:
(四)罗巨格公式
勒让得函数的另一个表达形式是 称为罗巨格公式。
4.3 连带勒让得函数
(一)连带勒让得方程与勒让得方程的关系
(四)连带勒让得函数
为了得到[1,1]中的有界解,我们仍然取a=n(n+1),其中n为大于等 于零的整数,此时 显然,若n为偶数,则B1(x)中的无穷 级数变成多项式,B2(x)中的无穷级数保持为无穷级数;若n为奇数,则 B1(x)中的无穷级数保持为无穷级数,B2 (x)中的无穷级数变成多项式。 这两个多项式都在[一1,1]中有界,因而由它们得到的B1 (x)或B2(x)也有 界。则连带勒让得方程在[-1,1]中的有界解为
得 两边同除以 移项得:
等号两边必然等于同一常数 ,所以
进一步对第二个方程作变量分离,令 有: 移项,并令两边同等于 ,整理得:
令
x cos
将上式进行改化,得连带勒让德方程:
当=0时简化为
称为勒让德方程。
4. 2 勒让得函数
(一)勒让得方程的级数解
勒让得函数是勒让得方程在[一1,1]中有界条件下的特征 函数。勒让得方程还可以写成
令其级数解为
得
将第一项更换指标,
得
显然,要使原级数为勒让得方程的解,上式中x'的系数必须等于零,即
得递推公式 得到两个解
(二)级数解的收敛性
对于上式中的两个级数来说,我们可以将 看成是x平 方的幕级数,将 看成是x与 -x2的幕级数之积。 对于这两个幕级数来说,由于它们具有相同的递推公式, 收敛半径也必然相等,有: 就是说,当x在(-1,1)中时,前面的两个级数解都是收教 的,表明这两个解都有界。当x=士1时,两个级数解均 无界。
(三)勒让得函数
为了解决方程的两个幕级数解在(-1,1)中有界而在x=士1时 均无界的矛盾,令 的值为n(n+1),其中n为大于等于零 的整数,则系数的递推公式变为:
由这个递推公式,使那两个无穷级数中有一个变为多项式。当n为 偶数时, 变为多项式, 仍为无穷级数,当n为奇数时, 仍为无穷级数, 变为多项式。两个多项式都在[一1,1]中有界, 两个无穷级数则都在(一1,1)中有界,在x=士1时无界。因而勒 让得方程在[一1,1]中有界条件下的特征值是n(n十1),对应的特 征函数为相应的多项式。
2( n k )! qnk k ( n k )!
2, k 0 k 1, k 0
习题
1证明:
2 1 x p2 ( x ) p0 ( x ) 3 3
2
2 3 x p3 ( x ) p1( x ) 5 5
3
球函数的几何意义
球函数的几何意义
球函数的几何意义
球函数的规格化
Pnk (cos ) 2( 2n 1 )( n k )! k Pn (cos ) k ( n k )!
A
k n
A
nk
nk
k Bn
k n
Bnk
球函数的规格化
nk qnk ( 2n 1)
4.5球函数的几何意义
(一)勒让得函数的零点
球函数的几何意义
(二)面球函教的几何意义
当k=0时,面球函数退化成P(cos),由于它在0<0<之 间有,n个零点,并且每经过一次零点改变一次正负号,所以, (cos)由纬线将球面分成n十1个正负相间的条带,叫带球函 数,是P3(cos)的示意图,零点为50. 8,90和129. 2
