《物理光学》§1-6电磁场的边值关系解读上课讲义
第五节边值关系

第四节电磁场边值关系
一、介质边界面上的电磁现象
1 导体在静电平衡时的边界行为:
导体静电平衡时,场量的突变发生在界面上。因 为: 内部场强 外部场强
E内 0 E外 0
1)求 Dt 关系:
E2t E1t D2t
2
ห้องสมุดไป่ตู้
D1t
1
2 1
D2t D1t
2)求 En 关系:
D2n D1n E2n 2 E1n1 2 1
E2n E1n
3)求 Bt 关系:
H 2t H1t B2t
2
B1t
1
2 1 B2t B1t
B 向量的法向关系: 将 B dS 0
s
用到小柱体上,可得
n ( B2 B1 ) 0
或 讨论:
B2n B1n 0
1)界面上 f 0 ,Dn 在两侧有突变。 界面上 f 0 ,Dn 在两侧连续。 2)界面两侧 Bn 线总连续。B2n B1n 3)已知 P n (P2 P ) 1
dl1 dl2
n
2 1
1
dl dl
将
L
H dl j f dS D
s s
t
dS
dl1
用到边界的长方形回路上去
L H dl l1 H1 dl1 l2 H 2 dl2 H dl h H1 l1 H2 l2 ( H1 H2 ) l s j f dS 回路面积 j f dS I 当 h 0 I f (l et ) f l (n e ) l (n f ) D dS 0 s t ( H1 H 2 ) l (n f ) l
电磁场数值计算边值问题ppt课件

电磁场数值计算
2
1 0
n
2
0
0
混合边值问题包含了前面三种边值问题。
边值问题就是带有边界条件的偏微分方程
求解问题。
电磁场数值计算
静电场边值问题的三个要素是场源、材料和边 界条件。
静电场求解区域的外边界,一般是导体表面、 对称面或人工边界。
若已知导体电位,则导体表面是第一类边界条 件;
电磁场数值计算
在平行平面静电场中,拉普拉斯算子表示为
2 2 2 x2 y2
平行平面静电场若为开域且正负电荷数量相等, 则在远离源区中心的位置构造圆形人工边界。
在人工边界上将电场看做由相互靠近的两条正 负线电荷产生。
电磁场数值计算
设线电荷密度为 ,正负线电荷距离矢量为 d , 在圆柱坐标系中, d 方向 0 ,则人工边界上电位
电磁场数值计算
其求解区域代表面为 z 轴右侧 r ,z 坐标系的平
面区域。在轴对称静电场中,拉普拉斯算子表示为
2
1 r
r
r
r
2 z 2
在三维坐标系中,如果材料和边界条件沿两个
坐标方向都不变化,则恒定电流场可进一步简化为
一维场。
人工边界和第三类边界条件,参照静电场进行 设置。
电磁场数值计算
2.3 恒定磁场的边值问题
2 n 0
已知求解区域内部的自由电荷分布,给定
求解区域边界 上电位的法向导数与电位之
间的线性关系,计算求解区域中的电位和电场 强度分布,这类问题通常称为第三类边值问 题,又叫做劳平问题。
电磁场数值计算
相应的边界条件称为第三类边界条件。
第三类边值问题表述为
2
n
0 0
静态电磁场边值问题精品PPT课件

场源、边界条件不变
-q
19
待求电位:
点电荷q与-q各自产生电位的叠加:
q q
4r1 4r2
20
待求区域电场强度:
Ex
4qx
1 r13
1 r23
Ey
4qy
1 r13
1 r23
Ez 4qzr13hzr23h
21
导体平面上的感应电荷:
s DnEz
qh
2 x2y2h2 3
qs sdS
n Si gi
i 1,2,, n
gi:边界Si上的位函数外法向偏导数值
10
第三类边值问题
边界条件:求解区域边界分为两部分,一部分边 界上给定位函数值,另一部分边界上 给定位函数沿边界外法向的偏导数值
2
F 0
Si
fi
i 1,2, , k
n Si gi
i k 1, k 2, , n
电磁场与电磁波
静态电磁场边值问题
内容
边值问题 唯一性定理 镜像法 分离变量法
2
作业
1. P137:4.1、4.2、4.3 2. 矩形槽沿直角坐标y方向无限延伸,槽两侧电位为 零,当y→∞时,电位φ→0,底部电位为φ(x, 0) =U0 , 求槽内电位分布。
3
边值问题
概述
静态场问题
分布型问题:已知场源(电荷、电流),直接计 算空间各点的场强或位函数 边值型问题:已知⑴.位函数方程;⑵.空间某一 确定区域内的场源分布;⑶.该区域的边界条件 (边界面上的位函数或位函数的法向导数),求 区域内位函数的分布
分析:待求电位由q与导体平面感应电荷共同产生;
导体平面感应电荷未知,其
电磁场边值关系

电磁场边值关系嘿,朋友们!今天咱来聊聊电磁场边值关系这个有意思的玩意儿。
你说这电磁场边值关系啊,就好像是电磁场世界里的规则制定者。
想象一下,电磁场就像是一个热闹非凡的大舞台,而边值关系呢,就是这个舞台上的各种规矩。
比如说吧,在不同介质的交界处,电磁场的行为就得按照边值关系来。
这就好比你去参加一个聚会,到了门口,就得遵守人家定的规矩,不能想咋样就咋样。
它可重要啦!没有它,电磁场就会变得乱七八糟,没个准头。
就好像没有交通规则的马路,那还不得乱套呀!在实际应用中,边值关系那可是大显身手呢!比如在设计电子设备的时候,工程师们就得好好考虑边值关系,不然设备可能就没法正常工作啦。
你看那些神奇的电子产品,手机啦、电脑啦,它们能这么好用,边值关系可是功不可没呀!再说说我们生活中的电磁波,它们的传播也和边值关系紧密相关呢。
这就像水流,遇到不同的地形会有不同的表现,而边值关系就是决定这些表现的关键因素。
那怎么理解边值关系呢?其实也不难,就把它当成电磁场的“家规”。
不同的介质就像是不同的“家庭”,都有自己的一套规矩。
而且哦,边值关系可不是一成不变的,它会根据具体情况而变化。
这多有趣呀,就像人在不同的场合也会有不同的表现一样。
咱再打个比方,电磁场边值关系就像是一场游戏的规则,只有遵守规则,才能玩得转这场游戏。
总之呢,电磁场边值关系是个很重要但又很有意思的东西。
它让电磁场变得有序,让我们能更好地利用电磁场。
所以啊,可别小瞧了这电磁场边值关系,它可是隐藏在幕后的大功臣呢!咱得好好研究它,利用它,让它为我们的生活带来更多的便利和惊喜呀!原创不易,请尊重原创,谢谢!。
17_电磁场边值关系重点课件

这组方程和麦氏方程积分式一一对应。边值关系表示界面两 侧的场以及界面上电荷电流的制约关系,它们实质上是边界 上的场方程。
15
例: 无穷大平行板电容器内有两层介质(如图),极板 上面电荷密度±σf,求电场和束缚电荷分布。
解: 由对称性可知,电场沿垂直于平板的方向,把边 值关系应用于下板与介质1界面上,因导体内场强 为零,故得 同样,把边值关系应用到上板与介质2界面上得
由此可得: 束缚电荷分布于介质表面上。在两介质界面处, σf= 0,由ε0(E2n−E1n) = σ f + σ p 得:
16
在介质1与下板分界处,由ε0(E2n−E1n) =σf+σp得
在介质2与上板分界处, 容易验证 说明介质整体是电中性的。
17
8
3. 关于磁场强度的边值关系: 面电荷分布使界面两侧电场法向分量发生跃变, 我们可以证明面电流分布使界面两侧磁场切向 分量生跃变。我们先说明表 面电流分布的概念。
☺面电流分布:
面电流实际上是在靠近表 面的相当多分子层内电流 的平均宏观效应。
9
定义电流线密度α,其大小等于垂 直通过单位横截线的电流。 图示为界面的一部分,其上有面 电流,其线密度为α,∆l为横截 线,垂直流过∆l段的电流为:
下面我们分别求出场量的法向分量和切向分量 的跃变。
2
麦氏方程组的积分形式为: (1) (2) (3) (4)
我们先从最简单的开始。在分界面上化简
3
1. 关于磁感强度的边值关系:
将方程
应用到两介质
分界面上的一个扁平状柱体表面。 上式左边的面积分遍及柱体的上 下底和侧面。 当柱体的厚度趋于零时,对侧面 的积分趋于零,对上下底面积分 得(B2n−B1n) ∆S=0 。
电磁场边值关系

S
t (E2 E1) 0
E1//
E2
n21
t
E2 //
2
1
或者
t (E2// E1// ) 0
E1
17
由于 t 是分界面上的任意一个
单位矢量,因此
E2 // E1//
——在界面处电场的切向分 量是连续的;
E1//
上式也可以写成
n21
D2 D1
f
n
由高斯定理可得,交界面上自由 电荷量的面密度为
f D2n D1n
(注:由于此处 n 法向矢量定 义成是从介质1指向介质2的)
2 E2n 1E1n
28
14
2010-9-9
f 2 E2n 1E1n
又根据欧姆定律:
n21
D2
2
1
D1
7
假设:交界面上的有自由电荷面分布
D S
dS
Qf
Qf f S
Q f D2 n21S D1 n21S
D dS S侧
根据 D dS 0 ,得到 S侧
D2
n21
D1
n21
f
——(5.5)
④ 电场法向和磁感应强度的切 向在边界上一般会有跃变。
25
H
Jf
D t
H
L
dl
If
d dt
D dS
S
电磁场边值关系

D E
2 E2n 1E1n f 如果 f 0
2 E2n 1E1n P 0 ( E2n E1n )
P P1n P2n
磁感应强度和磁场强度的边值关系。
SB dS 0
en (B2 B1 ) 0
荷:
DE
en (D2 D1 ) f
f f
E2
2
E1
1
(D2n D1n ) f
下板与介质1: 上板与介质2:
D1 f D2 f
讲时斟酌:考虑面电荷密度 的正负问题
E1
D1
1
f 1
,
E2
D2
2
f 2
由总电场的麦克斯韦方程(5.2)式得:
场线的性质均体现在电磁场的基本规律当中:高斯定理、环路定理,此处 又以边值条件的形式体现出来,殊途同归!
2.切向分量的跃变
沿介质表面流动的电流可以有两种处理方法: 1)有一定厚度的薄层(按体电流处理); 2)没有厚度的几何面(按面电流处理)。
上述1)的情况,厚度趋于零,沿电流方向变 成了横截线(与2相同),故引入电流线密度。
D dS
S
LE
dl
d dt
SB dS
D dS S
Qf
B dl
L
0 I f
0 0
d dt
E dS
S
M dl L
0
J M dS
电磁场的边值关系

dS
d dt
dV n
V
J2 J1
t
机动 目录 上页 下页 返回 结束
边值关系一般表达式
nˆ
(D2
D1 )
nˆ
(B2
B1 )
0
nˆ nˆ
E2 H2
E1 H1
0
理想介质边值关系表达式
nˆ
( D2
D1 )
0
nˆ
(
B2
B1 )
0
nˆ nˆ
E2 E1 0 H2 H1 0
f 0, p 0 总不连续
机动 目录 上页 下页 返回 结束
对均匀各项同性线性介质 D E
2E2n 1E1n f
n
D2 D1
f
f 0
1E1n 2E2n
p 0 E2n E1n
n
E2 E1
f p 0
p P1n P2n
P
n
(P2
P1)
2、B 、H 的法向分量边值关系
2、在不同介质分界面处,由于可能存在电荷电 流分布等情况,使电磁场量产生突变。微分方程 不能适用,但可用积分方程。从积分方程出发, 可以得到在分界面上场量间关系,这称为边值关 系。它是方程积分形式在界面上的具体化。只有 知道了边值关系,才能求解多介质情况下场方程 的解。
机动 目录 上页 下页 返回 结束
sB ds 0
n B2 B1 0, B1n B2n
对于均匀各项同向介质 1H1n 2H2n , 不连续
机动 目录 上页 下页 返回 结束
二、切向分量边值关系
1、H
的 边值关系D
L H dl s(J t ) dS
H2
H1
t
电磁场边值关系

电磁场边值关系
★ 要解决电磁场问题,还需要边界条件;
第五节
电磁场边值关系
★ 要解决电磁场问题,还需要边界条件; ★ 在外场作用下,介质界面会出现面束缚电荷和电流分布;
第五节
电磁场边值关系
★ 要解决电磁场问题,还需要边界条件; ★ 在外场作用下,介质界面会出现面束缚电荷和电流分布; ★ 束缚电荷、电流的存在使得界面两侧场量发生跃变;
问 密
这
§
5.2
法向分量的跃变
D · dS = Qf =
S V
ρf dV
D2 · dS2 + D1 · dS1 + (D1 · δS1 ) + (D2 · δS2 ) = ρf δh ∆S ★ 由于D有限 ,且δS1 ∝ δh → 0故此: 有 (D1 · δS1 ) + (D2 · δS2 ) → 0 (D2 − D1 ) · n ∆S = ρf δh ∆S = σf ∆S ★ 由S选取的任意性可知: n · (D2 − D1 ) = σf
★ 由于dl为平行于边界面的任一二维向量,故此f n,即: n × f = n × [(H2 − H1 ) − αf × n] = 0 n × (H2 − H1 ) = n × (αf × n) = αf − (αf · n) n = αf
★ 由于dl为平行于边界面的任一二维向量,故此f n,即: n × f = n × [(H2 − H1 ) − αf × n] = 0 n × (H2 − H1 ) = n × (αf × n) = αf − (αf · n) n = αf ★ 故此 n × (H2 − H1 ) = αf
§
5.3
切向分量的跃变
d dt
16电磁场的边值关系17光在反射及折射解读

§1-7
光在两个介质面上的 反射和折射
要说明的是:
n A1 exp i(k1 r 1t ) n A1 ' exp i(k1 'r 1 ' t ) n A2 exp i(k2 r 2t )
<1> 上式对任何时刻t都成立, 则 1 1 ' 2 即:入射波,反射波,折射波频率相同。 <2> 上式对界面上的任意位置矢量 r都成立 k1 r k1 'r k 2 r 则
E dl ( AB BC CD DA) E dl B 于是: d 0 t
AB E1 dl CD E2 dl 0或E1 t1l E2 t2l 0
§1-6电磁场的边值关系
§1-6电磁场的边值关系
在光学中,常常要处理光波从一种介质到 另一种介质的传播问题,由于两种介质的物理 性质不同(分别以1、1 和2、2 表征),在 两种介质的分界面上,电磁场将不连续,但他 们之间仍存在一定关系,通常把这种关系称为 电磁场的边值关系。
§1-6电磁场的边值关系
E1 A1 exp i (k1 r 1t ) ' E1 ' A1 ' exp i (k 1 r '1 t ) E2 A2 exp i (k 2 r 2t )
§1-7
光在两个介质面上的 反射和折射
在通过分界时磁场强度的切向分量是连续的。
§1-6电磁场的边值关系
§1-6电磁场的边值关系

§1-6电磁场的边值关系
由于界面两侧的电磁场在介面上并不连续, 因此不能从麦克斯韦方程的微分形式出发来 推导,而应从积分形式出发来讨论: 积分形式的麦克斯韦方程 : ∫∫ D dσ = Q ∫∫ B dσ = 0
B d σ t D H l = I + ∫∫ d d σ ∫ t
∫ E dl = ∫∫
[C (r vt) +C (r + vt)]
1 2
§1-6电磁场的边值关系
三种基本形式的简谐表达: 三种基本形式的简谐表达: π 2 E = Acos (z vt) 平面波简谐表达: λ
E = Aex i(k r ωt) p
[
]
球面波简谐表达: 柱面波简谐表达:
A(r, t) =
A cos[kr ωt + ]
1
r
0
A E = 1 exp i(kr ωt) + r
[
]
0
A A(r, t) = cos[kr ωt +0 ] r
A E= exp i(kr ωt) + r
[
]
0
§1-6电磁场的边值关系
(3)从表达式中可以获得的信息: 介质折射率: 传播速度与方向: 偏振方向: 周期、频率、角频率: 空间周期、空间频率、空间角频率: 平面电磁波的性质:
§1-6电磁场的边值关系
1.前面内容回顾: 1.前面内容回顾: 2.分界面上电磁场法向分量的关系: 2.分界面上电磁场法向分量的关系: 3.分界面上电磁场切向分量的关系: 3.分界面上电磁场切向分量的关系:
§1-6电磁场的边值关系
一、内容回顾: 1.对已讲内容的要求: 1.对已讲内容的要求: (1).了解光的电磁理论、电磁场的波动性; (2).彻底掌握光波在介质中的传播速率、介 质折射率的物理意义及其表达式; (3).深入理解平面、球面、柱面简谐光波场 的时间、空间特性,以及描述平面、球面、 柱面简谐光波的数学表达式中各项参数的物 理意义;
1.5 电磁场边值关系

D dS Q
f
( D2n D1n )S f S
D2n D1n f
规定 n 的方向由介质1指向介质2的法向(本教材)
D2n D1n f
D1n 0 E1n P n 1
D2n 0 E2n P2n
p ( P2n P n ) 1
式中If为通过曲面S的总传导电流,Qf为闭 合曲面内的总自由电荷.
(1)电场的法向分量
模型: 在分界面两侧取一个底面积为 △S的扁 平状柱体。Qf 和Qp 分别为柱体内的总自 由电荷和总束缚电荷,它们等于相应的电 荷面密度 f 和p乘以底面积△S.
把麦氏方程 S 应用到扁平状区域上,当 柱体的厚度趋于零时,对 侧面的积分趋于零,得
1.5 电磁场边值关系
•麦克斯韦方程组可用于任何连续介质内部. •在两介质分界面上,由于一般出现面电荷或面 电流分布,使物理量发生跃变,微分形式的麦 氏方程组不再适用.界面两侧的场强以及界面
上电荷电流的关系?
1. 法向分量的跃变
2. 切向分量的跃变
1. 法向分量的跃变 用积分形式的麦氏方程组研究边值关系
式中
f
为传导电流线密度。当回路
短边的长度趋于零时,回路所围面积 趋于零,而 D t 为有限值,因而
d D dS 0 dt
d D dS 0 dt
由此可得
(H2 H1) l f l
(H2 H1) t f
(H2 H1) t l f l
t n
n (H2 H1 ) f
磁场切向分量的边值关系.
(2)电场场切向分量
7相明(电磁场边值关系--唯一性定理).

5ξ电磁场的边值关系一.引言当介质分布均匀时,出现了界面,→D ,→B 有跃变,界面两侧场值的关系 1.边值关系:描述介质界面两侧的场矢量与界面上电荷,电流的关系 2.麦氏方程组的微分形式要求→E ,→D ,→B ,→H 在介质中连续麦氏方程组的积分形式在场量不连续时不成立。
故不能用微分形式导出边值关系,而用积分形式讨论边值关系。
⎪⎪⎪⎭⎪⎪⎪⎬⎫=∙=∙⎰⎰⎰→→→→s s v S d B dv S d D 0ρ⇒导出法向关系⎪⎪⎪⎭⎪⎪⎪⎬⎫∙∂∂+∙=∙∙∂∂-=∙⎰⎰⎰⎰⎰→→→→→→→→→→s s l l S d t DS d j l d H S d tB l d E ⇒导出切向关系二.边值关系(法向关系证明从略,切向关系讲一例后推论) 1.→D 的法向有跃变⎰⎰=∙→→vsdv S d D ρ⇒σfD D n =-∙→→→)(12 (1)推论:εσσρρε0120)()(1pf v pf sE E n dv S d E +=-∙⇒+=∙→→→→→⎰⎰ (2)dv S d P ps⎰⎰-=∙→→ρ→⇒n )(12→→-∙P P =-σP(3)2.→B 的法向连续0)(0)(0112212=-∙−−−−→−=-∙⇒=∙→→→→→→→→⎰H u H u B B n n S d B s线性各向同性(4) 3.的→E 切向连续→→→→∙-=∙⎰⎰S d B dt d l d E s l 0)(12=-⨯⇒→→→E E n E Et t12= (5)4.的切向跃变→H→→→→→→→→→→=-⨯⇒∙∂∂+∙=∙⎰⎰⎰αf sflH H jn s d t DS d l d H )(12 (6)0)(012=-⨯=→→→→H H n f时,αH Ht t12= (7)线性各向同性:uB uBtt 1122=(8)推论:→→→→→→→→=-⨯⇒∙=∙⎰⎰αm s Ml M M jn S d l d M )(12 (9)5.→jf的法向跃变⎰⎰-=∙→→dv dt dS d sfjρtn f f f jj ∂∂-=-∙⇒→→→σ)(12 (10)0=∂∂t时,0)(12=-∙→→→jj f f n (11)三.说明1.上述关系在介质界面静止时导出,运动时,D ,B 法向关系仍成立,但E ,H 切向改变2.规定:界面法向n 从介质1指向介质2,否则差一负号3.具普遍意义:对任意矢量场,只要场方程与麦式方程组形式相同,其边值关系亦相同。
电磁场的边值关系

电磁场的边值关系
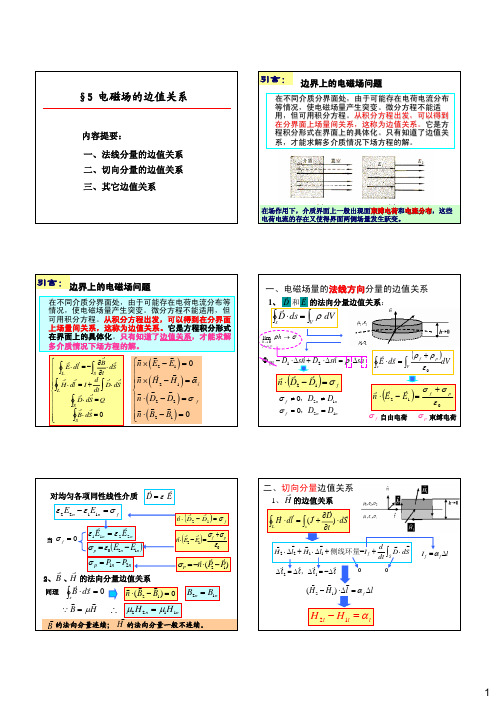
§5 电磁场的边值关系
内容提要: 一、法线分量的边值关系 二、切向分量的边值关系
机动
目录
上页
下页
返回
结束
一、法线方向分量的边值关系
D ds dV
s V
h 0
lim h
侧 D1 sn D2 sn sh
机动
目录
上页
下页
返回
结束
3、无限大平行板电容器内有两层介质,板上面 电荷分为 f ,求电场和束缚电荷分布。
ez f
解: (1)根据对称性,电场沿 n
方向,且为
2
1 f
导体
均匀场,极板为导体,在表面处, f f n D2 D1 E1 ez E2 e z 1 2 (2)两介质分界面上电荷分布
n ( H 2 H1 )
H 2t H1t f
B E t
n E2 E1 0 E2t E1t
电磁场边值关系一般 表达式
n ˆ ( D2 D1 ) ˆ ( B2 B1 ) 0 n ˆ E2 E1 0 n n ˆ H 2 H p f 由n E2 E1 ,在这里 f 0 0
2
2 E2 n f
f f 0 0 p 0 E2 n E1n 0 f 1 2 1 2 1) (2) ( 3) 介质整个是电中性的。 ( p p p 0
n D2 D1 f
2020年山大附中高中物理竞赛提升版课件(光学)04电磁场的边值关系(共12张PPT)

§7 光在两介质分界面上的反射和折射 光在两透明介质分界面上的反射和折射,实质上是光波的电磁 场与物质的相互作用问题,它的精确处理是很复杂的,需要涉 及到次波的产生和相干问题。本节中采用了一种较简单的方法: 用介质的介电系数、磁导率和电导率来表示大量分子的平均作 用,根据麦克斯韦方程组和电磁场的边界条件,研究平面光波 在两介质分界面上的反射和折射问题。 一 反射定律和折射定律 当一个单色平面光波入射到两不同介质的分界面上时,被分为 两个波:折射波和反射波。从电磁场的边值关系可以证明这两 个波的存在,并求出它们的传播方向的关系。
n1
A
B2
n2
A
B d 0
壁
n1、n2分别为柱顶和柱底的外向法线单位矢量。
当柱高h趋于零时,上式的第三项趋于零,且柱顶和柱底趋近 分界面。此时用一个法线方向的单位矢量n来替代n1、n2,方向从
介质2指向介质1,如图1-18所示。
nnB1n1B2n2 0
B1n B2n
这个结果说明:两介质的分界面上B的法向分量是连续的。
一 电磁场法向分量的关系
参见图1-18,假想在两介质的界面上作一个扁平的小圆柱体, 柱高为h,底面积为A,将麦克斯韦方程组的(3)式应用于该 圆柱体,得出
B d 顶 B d 底 B d 壁B d
因为底面积A很小,可认为B是常数。设柱顶和柱底分别是B1
和B2,上面的积分可改写为
B1
E1 t1 l E2 t2 l 0
t1、t2分别为沿AB、CD切线方向的单位矢量, l为AB、CD的长度。
以t表示分界面切线方向的单位矢量,方向由A指向B,则t
t1
t2,
上式可写为
E1 E2 t 0
或
E1t E2t
边值关系
§5 电磁场的边值关系
内容提要: 一、法线分量的边值关系 二、切向分量的边值关系 三、其它边值关系
引言: 边界上的电磁场问题
r M θ
erφ erR
3、无限大平行板电容器内有两层介质,板上面
ev电n 解荷:分(布1为)±根均σ据匀f 对,场称求,性电极,场板电和为场束导沿缚体e电r,n 方荷在向分分,布界且。面为处满足
−σ f ε2
( ) ern ⋅
rr D2 − D1
=σ
r E1
=σf ε1
evn
r E2
=σf ε2
evn
= −σ r M1 =
p
αrM
束缚电荷 面密度
磁化电流 面密度
( ) ∫ ∫ r
sJM
⋅
r dS
=
−
d dt
ρdV ⇒ nr ⋅
V
rr J2 − J1
= − ∂σ ∂t
以后在公式中出现的σ和α, 除特别声明者外,都代表自由电荷面密 度和自由电荷线密度,不再写出角标f。
( ) 切
向
nv ×
矢Ev2量−形Ev式1 = 0
H 2t − H1t = αt
1
H 2t − H1t = αt
上式可以用矢量形式表示。设
Δl为界面上任一线元,t 为Δl 方 向上的单位矢量。 流过了Δl 的 自由电流为
I f = nv × Δlv ⋅αv f = αv f × nv ⋅ Δlv
ar ⋅ (bv ×cr)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§1-6电磁场的边值关系
t1,
t2
分别为沿AB和CD切线方向的单位矢量。
l 为AB 和CD的长度,以t表示分界面的切线方
向单位矢量( 取为 由A向 B)则
t t1t2
(E 1E 2)t0或
E1t E2t
即在通过分界时电场强度的切向分量是连续的。
§1-6电磁场的边值关系
由上式还可看出:
E故1-上E2式垂又直可于写界为面或:者说平n 行 (于E 1界E 面2)法0 线,
同理:在没有电流的情况下由麦克斯韦方
程组也可得到 :
《物理光学》§1-6电磁场的边 值关系解读
§1-6电磁场的边值关系
(4).牢固地掌握光强的概念和计算相对光 强的方法;
2.已讲授的基本结论: (1).光的电磁理论、电磁场的波动性:
光的电磁理论的提出是人们在电磁学方面已有了 深入研究的结果。1864年麦克斯韦把电磁规律总 结为麦克斯韦方程组,建立起完整的经典电磁理 论,同时指出光也是一种电磁波,从而产生了光 的电磁理论。
§1-6电磁场的边值关系
式中 n1,n分2 别为柱顶和柱底的外法线单位矢 量。当高 h0时
上式第三式也趋于零,并且柱顶和柱底趋近 分界面。
以 n表示分界面法线方向的单位矢量(方向 从介质2指向介质1)则有 :
n n 1n 2
§1-6电磁场的边值关系
于是:
n •(B1B2)0或
B1n B2n
球面电磁波:
柱面电磁波:A (r,t)1 rB 1(rv)tB 2(rv)t E A rC 1(rv)tC 2(rv)t
§1-6电磁场的边值关系
三种基本形式的简谐表达:
平面波简谐表达: E E A A ce os2 i ( x k ( zr p v)tt )
球面波简谐表达: A (r,t )A r1co ks rt0
§1-6电磁场的边值关系
两E •种dl 形式的B 麦t•克d 斯韦方程组:EBt
D •d Q
•D
B •d0
•B0
H •dlID t•d
Hj D t
§1-6电磁场的边值关系
电磁场的波动性:
E
B
B
(1) (2)
(3)
B 0
H j
D t
上式表明,在通过分界面时,
磁感应强度B虽然整个的发生跃变,但它 的法向分量却是连续的。
§1-6电磁场的边值关系
在各向同性、均匀、透明介质中,
由于其Q=0则,同样由 D •dQ
可以得到: n•(D1D2)0或
D1n D2n
即:在分界面上没有自由电荷的情况下,电感 强度的法向分量 也是连续的。
B
t E
t
(4)
j E
D E
电导率 介电常数
H
1
B
磁导率
§1-6电磁场的边值关系
无限大、均匀、透明介质中电磁场的波动
方程:
2E 2 B22ttBE 22
2
2 x2
2 y2
2 z2
§1-6电磁场的边值关系
(2)波动方程解的基本形式:
平面电磁波: E f1 ( z v ) t f2 ( z v )t
推导,而应从积分形式出发来讨论:
积分形式的麦克斯韦方程 :
D
d
Q
B
d
0
E dl
H dl I
B t
D t
d d
§1-6电磁场的边值关系
三、分界面上法向分量 n1
:
δS
δh
n
ε1μ1
ε2μ2
n2
设:在分界面上作出一个扁平的小圆柱体的
高为 h
圆面B 积为d s,0由上第2式 :
在光学中,常常要处理光波从一种介质到另一 种介质的传播问题,由于两种介质的物理性质 不同(分别以1、1 和2、2 表征),在两 种介质的分界面上,电磁场将不连续,但他们 之间仍存在一定关系,通常把这种关系称为电 磁场的边值关系。
§1-6电磁场的边值关系
由于界面两侧的电磁场在介面上并不连续, 因此不能从麦克斯韦方程的微分形式出发来
§1-6电磁场的边值关系
四、电磁场切向分量的关系:
把小圆柱换成一个矩形面积ABCD如图1-
19所示:由于
A
ε1μ1 t
δl
t1
B
δh
EdlBtdε2μ2
D
t
2
C
dl取ABC切 D线方向,则
Edl(ABBCCDDA)E•dlBtd
§1-6电磁场的边值关系
若AB和CD长度很短,则在两线段内E 可认 为是常数;在介质1和介质2内分别为E1和E2
E A 1exi(k p rt)
r
0
柱面波简谐表达:
A (r,t)A rco ks rt0
E Aexi(p k rt)
r
0
§1-6电磁场的边值关系
(3)从表达式中可以获得的信息: 介质折射率: 传播速度与方向: 偏振方向: 周期、频率、角频率: 空间周期、空间频率、空间角频率: 平面电磁波的性质:
,此外长方形的高h0,
则沿BC, DA的积分趋于0, 并且,由于面积趋向于零,而 B
t
为有限量,则
Edl (
AB
BC
CD
)E•dl
DA
于是:
B t •d0
A E • d B l C E • d D l 0 或 E 1 t 1 l E 2 t 2 l 0
s 1 SdtA2 1 cos2(krt)dt
0
0
1A2 1 A2
2
2
通常可以写为:
I A2
计算光强时可以用:
~ ~ I A 2EE *
§1-6电磁场的边值关系
二、本节内容的说明:
为了解释一平面波(单色简谐)射向界面时, 其反射波、折射波传播方向的改变规律和振幅 改变规律(前者为反射定律,后者为折射定 律)。
§1-6电磁场的边值关系
应用小圆柱体:则上式左边面积应遍及整个 圆柱体表面:则
B d 顶 B d 壁 B d 底 B d
设圆柱体的面积很小,可以认为B在此范围 内是常数:
则上式变为 :
B 1 n 1 A B 2 n 2 A 壁 B d 0
§1-6电磁场的边值关系
(4)关于光强的概念:
若单位时间内穿过与K相垂直的单位面积的 为能量S (功率密度) ,通常把S在接收器
能分辨的时间间隔内的平均值叫做电磁波 的强度I。
表达式:
1
I
s
sdt
0
考虑到传播方向,可以定义波印廷矢量
S
1
EB
§1-6电磁场的边值关系
平面电磁波的强度:
